). = + U = -U U= mgy (y= H) =0 = mgh. y=0 = U=0
|
|
|
- Ἀλέξανδρος Μαρής
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ). = + U = -U U= mgy (y= H) =0 = mgh. y=0 = U=0 y = mgh mgy, ) ) =mg 2 F=ma F-B=ma Fmg=m.2g F=3mg F=3B B = F/3
2 ) ) W 1 = -mgh W 2 =mgh W = W 1 + W 2 = -mgh + mgh= ) ). 1 = 1 = ½ ( + ) = ½ ((10+20).30 =450 m 2 = 2 = ½. = ½ (30-20) 30 =150 m = 1-2 = = 300 m
3 3768 ) =.t =6.t =6 m/s = ½ t 2 X= 2t 2 ½ = 2 = 4 m/s 2 H = t =4t 4t=6 t= 6/4 =1,5 m/s ) ) F.
4 , W 0 A = W ) ). 1 = 1 = ½ = ½ ((10).20 =100 m 2 = 2 = ½. = ½ (30-20) 5= 25 m = 1-2 = = 75 m
5 ) ) = ½ m 2 = = ½ m (2 2 ) = 4. ½ m 2 =4 = - = 4 - = 3 U= - = F 2 = 0 B 2 -T=0 T=B 2 1 F 1 = 0 T 1 -T-B 1 =0 T 1 = T+B 1 T 1 = B 1 +B
6 ) ). = - t 0 = - t t= t = / d= t ½ t 2 d=. ( / ) ½ ( / ) 2 d= 2 / - 2 /2 d= 2 /2 d 1 = 1 2 /2 d 2 = 2 2 /2 = (2 1 ) 2 /2 = /2 = 4 d ) ) h= ½ gt 2 2 h = ½ gt h = ½ gt 2 h = ½ g(2 t ) 2 h = 4. ½ g t 2 h = 4 h 3774 ) ) F=m.a F 1 - mg= ma
7 F=m.a mg- F 2 = ma mg- F 2 = F 1 - mg F 1 +F 2 = 2 mg 4173 ) ) = F=0 F- T=0 T=F=10N F = 2F F=m.a F - T= m.a 2F-T=m.a 20-10=0,5a 10=o,5a a= 10/0,5 a= 20 m/s ) ) F W= E = ½. = ½ = 20 J
8 J = + U = + U 100= + 80 =20 J = + U 100= 40 + U U =60 J = + U 100= + 10 =90 J ) ) F=m.a B-F=m.a mg F= mg/2 F = mg- mg/2 F= ½ mg F= ½ B
9 ) ) -t > > > t> t > ) ) 1 = ½ m 1 2 = (2 2 ) 2 = = 4 2 ½ m ) 2 2 2
10 ) ) -t ) ) ( ) = ( ) U A + K A =U B +K B 0 + ½ m 2 = mgh +0 = 2.gh = 2.gh = 2.g2h= 2. 2.gh = ) ) F=m.a F=m.a m.a = 2m a a = ½ a
11 ) ) =K + U =0 + mgh E = mgh = K + U = + mgh/2 = + /2 = - /2 = ½ = U 4984 ) ) -t )
12 ). = - t 0 = - t t= t = / d= t ½ t 2 d=. ( / ) ½ ( / ) 2 d= 2 / - 2 /2 d= 2 /2 d 1 = 1 2 /2 d 2 = 2 2 /2 1 > > / > 2 2 / d 1 > d ) ) u 1 = a t 1 U 2 =a t 2 = a.2 t 1 = 2. a t 1 = 2 u ) ) W 1 = -m.gh <0 W 2 = 0 W 1 < W 2
13 ) ) 4989 ) ). 1 : s 1 = E 1 = ½. = ½ 1.t 1 = 1.t 1 2 : s 2 = E 2 = ½. = ½ 1.t 1 s 1 = ½ s
14 ) ) = - = (-40) -0 = -40 m ) A )... -= W = F. x = F. x ½ m u 2 = F. x - = W = F. x = 4F. x ½ m u 2 = 4F. x ½ m u 2 =4. ½ m u 2 u 2 =4 u 2 u =2 u ) A ). = mgh. <mgh
15 ) ). S A = E A = ½. = ½ 1.t 1 S B = E B =. = 1.t 1 =2 S A ) A ) K =.t. - t. - t 1 > 2 1 > 2
16 ) ) 0-t 2 F>0,. t 2 F. t ) ) ( ) = ( ) U A + K A =U B +K B 0 + ½ m 2 = mgh +0 = 2.gh = 2.gh = 2.g2h= 2. 2.gh = 2. = ½ m 2 =½ m 2 = ½ m ( 2 ) 2 = 2. ½ m 2 = 2.K
17 4998 ) ) m A >m B m A /m B >1 K A = ½ m A u 2 = m A >1 K A > K B K B ½ m B u 2 m B ) ) A F>O. 2 >0,. 5043
18 ) ) W 1 = -mgh W 2 =mgh ) ) ( ) = ( ) U A + K A =U B +K B 0 + ½ m 2 = mgh +0 2 = 2.gh 2 = 2.gh (2 ) 2 = 2.gh 4 2 = 2.gh 4. 2.gh =2.gh h =4h 5044
19 ) ) 1 = 1.t 2 = 2.t 2 > 1 2.t > 1.t 2. > ) ) W 1 = -mgh W 2 =mgh W = W 1 + W 2 = -mgh + mgh= ) ) =.t t = / = 1190/340 = 3,5 s
20 5046 ) ). = - t 0 = - t t= t = / d= t ½ t 2 d=. ( / ) ½ ( / ) 2 d= 2 / - 2 /2 d= 2 /2 d 1 = 2 /2 1 d 2 = 2 /2 2 F=m. m 1 1 = m 2 2 m 1 / m 2 = 2 / 1 >1 2 > 1 1/2 2 < 1/2 1 2 /2 2 < 2 /2 1 d 2 < d ) )...
21 -= W ½ m 2 ½ m 2 = W 1 : ½ m 20 2 ½ m 10 2 = W 1 W 1 = 150m I : ½ m 30 2 ½ m 20 2 = W 2 W 2 = 250m W 2 > W ) ) ( ) = ( ) U A + K A =U B +K B 0 + ½ m 2 = mgh +0 2 = 2.gh 2 = 2.gh (2 ) 2 = 2.gh 4 2 = 2.gh 4. 2.gh =2.gh h =4h h/h = ) ) = = ½. = ½ t 1 = < 1 < ½. ½ t 1
22 ) ) F= F 1 2 +F 2 2 = = 25= 5N F= m. a a = F /m = 5/2 =2,5 m/s ) ) s=
23 ) ) 1 : F=m 1.a F-T= m 1.a 2 : F=m 2.a T= m 2.a T= m 1.a F- m 1.a= m 1.a F= 2. m 1.a F= 2.T ) ) F= w=m.g g= w/m h = ½ g t 2 t= 2h/g h g,
24 ) ) = / t= -0 /(4-0) = /4 = / t= -5/(4-0) = -5/4 > ) ) 1 W 1 = U 1 - U 1 = mgh -0=mgh 2 W 2 = U 2 - U 2 = mgh -0=mgh = W ) ) 0<t<t 2 F>0 >0
25 t>t 2 F=0 = ) 100J = + U = + U = =80 J = + U 80= 20 + U U =60 J = + U 80= + 40 =40 J = + U 80= 80 + U U =0 J 5068 ) ) m M >m A F M =F A ( - ) F M =F A m M =m A m M / m A = / >1 >
26 5072 ) ) 1 W 1 = U 1 - U 1 = mgh -0=mgh 2 W 2 = U 2 - U 2 = mgh -0=mgh = W 1 = W... - = W = + W 5072 ) ) 0<t<t 2 F>0 >0 t 2
27 5076 ) ) = ½ m u 2 =1J = K -= ½ m (2u) 2 -½ m u 2 = 4. ½ m u 2 -½ m u 2 =4 - =3 =3.1= 3J 5076 ) ) u=. t t 1 u 1 =. t 1 t 2 u 2 =. t 2 = = 2-1 =. t 2 -. t 1 =. (t 2 -t 1 ) = t t 2 -t 1 t 2 -t 1 t 2 -t 1 F=m.a =
28 5082 ) ) = = ½ ( + ) = ½ (10+8).4 =36m 5082 ) )..., 1 = 2 1 = 2 - = W 0- = -.s K= T.s, s 1 =s 2
29 5090 ) ) = 6t=2t 2 2t 2-6t =0 2t(t-3)=0 t=0 t=3s ) ) = +U = U= mgh = 120J y=h/3, = h h/3 = 2h/3 U=mgH = 2/3 mgh =2/3.120 = 80J = +U 120 = +80 =40 J
30 ) ) x-t 5091 )... =0 - = W =F.x =0 =0 2 2 =2Fx= 2K 4 4 =4Fx= 4K
31 ) ) F=0, F 1 >F 2 F=0 F 1 =F 2 + = F 1 -F 2 = ) ) F>0, W>0... =0 - = W =W>0
32 5102 ) ) x =½ at
33 ) ). = - t 0 = - t t= t = / d= t ½ t 2 d=. ( / ) ½ ( / ) 2 d= 2 / - 2 /2 d= 2 /2 d 1 = 1 2 /2 d 2 = 2 2 /2 = (2 1 ) 2 /2 = /2 = 4 d ) ) 0<t<t 1.
34 5119 ) ) = ½ m A u A 2 = ½ m(2u) 2 = ½ m 4u 2 =2mu 2 B = ½ m B u B 2 = ½ 2m(u) 2 = ½ 2mu 2 =mu 2 = )
35 B) 5125 ) ). = - t 0 = - t t= t = / d= t ½ t 2 d=. ( / ) ½ ( / ) 2 d= 2 / - 2 /2 d= 2 /2 = 10 2 /2.2,5 = 20m 5137 ) ) = / t = (0-20) / (5-0) = -4 m/s2 = = ½. = ½ 5.20 = 50m
36 F=0 F+N=B N= B-F N= 10-F F=0N N= 10-0=10N F=2N N= 10-2=8N F=6N N= 10-6=4N F=10N N= 10-10=0N 5146 ) ) = Z K A +U A =K Z +U Z U A =Kz mgh = ½ m u 2 u 2 =2gh u 2 = u 2 =100 u=10 m/s 5173
37 ) ) =mg B = 10 g =0,5 g B > 5173 ) ) = F=0 F=B=mg P= W/t =mgh/t F =2 =2mg P = W /t =2mgh/t =2 =2.2=4W ) ) 1-3s = =10m/s 1 F=0
38 ) ) F= m.a F-T=2.1=2N F =2F F = m.a F -T=2.3=6N F -T- F+T =6-2 F - F =4 2F-F=4 F=4N 5182 ) A ) >0
39 5182 ) ) Fx=m.a F 1 =m.a Fx= m.a F 1 -F 2 = m.a F 1 -F 1 /3= m.a 2 F 1 /3= m.a 2 m.a/3= m.a a =2 a/ h=180m, U=mgh= =3600J,K=0, E=K+U=3600J 2 h=80m, U=mgh= =1600J,, E=K+U=3600J= K K= 2000J = ½ mu 2 K= ½ 2 u 2 u = K u = 2000 m/s 3 h=0m, U=mgh= =0J,, E=K+U=3600J= K+ 0 K= 3600J, u = K u = 3600 m/s= 60 m/s
40 5184 ) ) s 1 = ½ a t 1 2 S 2 = ½ a t 2 2 = ½ a (2t 1 ) 2 = 4. ½ a t 1 2 = 4 s ) ) =.t =6.t =6 m/s = ½ t 2 X= 2t 2 ½ = 2 = 4 m/s 2 H = t =4t 4t=6 t= 6/4 =1,5 s
41 ) ) U= mgh = E-U K=E- mgh )
42 5200 ) ) A = W 4 - =W W= ) ) F = m.a F 1 -B=m.a F 1 -mg= mg/2 F 1 = mg+mg/2 F 1 =3mg/2 F = m.a -F 2 = m.a mg F 2 =mg/2 F 2 = mg-mg/2 F 2 =mg/2 F 1 =3 F 2
43 5213 ) ) F= m.a F-B=m.a F-mg= mg/3 F=mg+mg/3 F=4mg/3=4B/ ) I ) = = 5/1,2 = 25/6 m/s 2
44 5216 ) ) F= m.a F= 4m 2F= m a 2.4m = (m+3m) a 8m=4m a a = 2m/s ) ) W=E = ½ ( + ) = ½ (5+8).10= 65 J A = W -0 =W =65 J
45 5221 ) ) F= m.a F= m u/ t ) ) F= m.a F=2.2=4 W=F. = 4.4=16J
46 5263 ) ) 1 = 50/1=50 m/s 1 = 200/10=20 m/s 5263 ) ) F= m.a F 1 -B= m.a F 1 -mg=m.a F =10.2 F 1-100=20 F 1 =120N F= m.a -F 2 +B= m.a - F 2 +mg=m.a -F =10.2 -F =20 F 2 =80N F 1 > F 2
47 5276 ) ) S A = ½ ( 3u o +u o ) t 1 = 4u o t 1 /2 S B = u o t 1 /2 S A = 4 S B 5276 ) ) A = W K =W ½ mu 1 2 =F.x 1 = W K =W ½ mu 2 2 =F.x 2 ½ mu 2 2 = 4 F.x 1 ½ mu 2 2 = 4½ mu 1 2 u 2 2 = 4u 1 2 u 2 =2. u 1
48 ) ) ) ) 1 h 1 = ½ gt 2 = ½ g 2 h 2 = ½ gt 2 = ½ g 2 2 = ½ g.4 =4h 1 h 1 2 4
49 y = y y. y =0, ) ) ( ) = ( ) U A + K A =U B +K B 0 + ½ m 2 = mgh +0 2 = 2.gh 2 = 2.gh 2 = 2.gh 2 = 2.g2h 2 =4.gh 2 =2 2 =
50 ) ) -t > > > t> t > ) ) W=0
51 ) ) 2 = / t= 1 /t 1 1 = / t= 2 1 /t 1 = ) ) =0, = t
52 5329 ) ) = 72km/h = /3600= 20 m/s = B ) ) 0-t1,,,
53 ) ) = - t 5330 ) ) F= m.a F-T=m.a F= m.a+t F= m.a 2F-T = m.3.a 2ma +2T= 3ma 2T= ma T=ma/2 T= F/2
54 ) ) =, 1 F=0 F-T=0 F=T=40N O Q/ t =P T =T.u = 40.4=160 J/s 5334 ) ) -t > > > t> t >
55 ) ) A = W -0 =W ½ mu 2 =F.x = W -0 =W ½ mu 2 =F.x ½ m(2u) 2 = F.x 4 ½ mu 2 = F.x 4 F.x= F.x F =4 F ) ) =g.t =
56 ) ) = ½ muo 2 uo 2 = K/2m uo= K/2m u = uo-at 1 0=uo- at 1 at 1 = uo t 1 = uo/a t 1 = K/2m /a 4 4 = ½ muo 2 4 ½ muo 2 = ½ muo 2 uo 2 = 4 uo 2 uo = 2 uo t 2 = 2uo/a t 2 = 2 K/2m /a t 2 = 2 t ) ) W=E = ½ ( + ) = ½ (3 + ) Fo= ½ 4x Fo= 2 x Fo
57 F ) ) = ½ ( + ) t 1
58 = ½ ( + ) t 1 =2 > W A =- F A X A W = F X W A < W 5339 F ) ), g <g < 5340
59 ) )... =0 - = W - =W - =-.s K=T.s s = K/T META... =0 - = W -2 =-W -2 =-.d 2K=T.d d = 2K/T d=2.s 5401 ) ),, ) ) F=m.a F 1 = m.a F =m.a F 1 - F 2 = m. a F 1 - F 1 /3= m. a 2F 1 /3= m. a 2 m.a/3= m. a a =2a/3
60 5510 ) ) 5512 ) b ). = - t 0 = - t t= t = / t 1 = / t 2 =2 / =2t 1
61 5514 ) ) = ½ m B u 2 = ½ 3m u 2 = 3 ½ m u 2 =3K A ) ) F=m.a a 1 = F/m, a 2 = ½ F/m = ½ a 1 X 1 =x 2 ½ a 1 t 1 2 = ½ a 2 t 2 2 a 1 t 1 2 = ½ a 1 t 2 2 t 2 = 2. t 1 u 2 = a 2 t 2 = ½ a 1 2. t 1 = 2 u 1
62 ) ) W> s..., 6154 ) ) =U=mgh =120J h/3 y= h-h/3 =2h/3 U= mgy = 2mgh/3 = 2.120/3 =80 J = +U 120=K+80 K=40J 8996
63 ) ) = = 20- (40)= -20 m 9011 ) ) m, F. -=W 0-K = - Fx - ½ mu 2 =-Fx x=½ mu 2 /F > > 9020 ) ) t 1 : u 1 = at 1 t 1 : u 2 = at 2 = 2 at 1 =2 u 1
64 9020 ) ), F. -=W 0-K = -Fx - =- Fx x= /F 1 = ) ) 2 = / t= 1 /t 1 1 = / t= 2 1 /t 1 = 2 2 F 1 =F 2 m 1 a 1 =m 2 a 2 m 1.2a 2 =m 2.a 2 m 2 =2m 1
65 ) ) = ½ (2 + ) t 1 = 3 t 1 /2 = t 1 = 3 / ) ) F = m 1.a =m 2.a/2 m 1. =m 2 /
66 ) ) to=0 xo=0 t 1 =0,5s x 1 =12,5cm t= t 1 -to=0,5-0=0,5s = 1 - = 12,5-0=12,5 cm = / t = 12,5/0,5= 25 cm/s ) ), = 1 = ) ) F= m.a F=m.a a= F/m a =2F/m = 2a F= m.a F=m.a F= m.a F- =m.a F-F/2=m.a a = F/2m= a/2
67 9096 ) ) 9096 ) ) 2 = / t= 1 /t 1 1 = / t= 2 1 /t 1 = 2 2 F 1 = m 1.a 1 = m 1.2 a 2 = 1 F 1 = F 2 F 2 m 2.a 2 2m 1. a 2
68 9101 ) ) = ½ mu 2 = = ½ m(2u) 2 = 4 ½ mu 2 =4 = = 4 - = ) ),,. 9107
69 ) ) to W=E = ½ ( + ) = ½ [ (2 - )+ 3 ]Fo = ½ 4x.Fo= 2Fo.x ) ) t 1 = 0-1s s 1 = ½ a t 1 2 s 1 = ½ a t 2 = 0-2s s 2 = ½ a t 2 2 s 1 = 2. a s= s 2 -s 1 = 2.a-a/2= 3a/2 = 3s ) ) =.t 1 A = 3.t 1 = 3
70 ) ) =5t = t = 5m/s 9136 ) ) F=m.a F 1 -F 2 =ma 1 F=m.a F 2 =ma 2 F 2 =2 ma 1 F 2 =2(F 1 -F 2 ) F 1 = 2 F 2
71 9150 ) ) g > g g / g >1 h= ½ g t 2 h= ½ g t 2 ½ g t 2 =½ g t 2 t 2 / t 2 = g / g >1 t / t >1 t > t 9153 ) ) g =6,25 g mg =m6,25 g =6,25B F= m.a F= m.a = m.a a = a
72 ) ). 1 = 1 = ½ = ½ ((10).20 =100 m 2 = 2 = ½. = ½ (30-20) 5= 25 m = 1-2 = = 75 m s = 1+ 2 = = 125 m 9158
73 ) ) = g =m.g g >g B DIA > 9158 ) ) = ½ m 2 = = ½ m (2 2 ) = 4. ½ m 2 =4 = - = 4 - = ) B =-= 2 - = 40-(-40)= 80 m
74 9167 ) B ) 0-1 W 1 = ½ Fo.x W 2 = O W 2 =-½ Fo.(3x 1-2x 1 )= -½ Fo.x 1 W=W = W1+W2+W3= ½ Fo.x ½ Fo.x 1 =0 A = W -0 =W K = ) B
75 9330 ) ) 1 = 20m/s 2 u 1 =a 1 t 1 = 20m/s a 2 =0, u 2 =20m/s 3 = -10m/s 2 u 3 =u 1 -a 1 t 3 0= u 1 -a 1 t 3 t 3 = 2s t=4s, t=3s, 9334 ) ) = = ½ ( + ) = ½ ((20-10)+30).30=600m
76 9334 ) ) F= F 9444 ) ) = F=0 F-T=0 F=T F=. F=.mg W= F.S =.mg.s
77 ) ) =5t a= 5m/s 2 = F=m.a = 9447 ) ) F=m.a F 2 +F 2 = m.a 2F 2 = m.a 2. F = m.a a= 2. F / m
78 9451 ) ) F=m.a F 2 +F 2 = m.a 2F 2 = m.a 2. F = m.a a= 2. F / m a= 2. mg / m a= 2. g 9451 ) ) 0-2m W>0 =2 m. =2m
79 9455 ) ) 9455 ) ) = F=0 F-T=0 F=T =F. =
80 9463 ) ) = F=0 F-T=0 F=T 9463 ) ) = F=0 F- =0 F= =Mg P F =F.u= Mg.u
81 9467 =0 F=0 F- =0 F= =Mg= 100.9,5= ) ) = F/m =T/m mg/m = g t=uo/a = uo 2 /2.a
82 9475 ) ) = F-T/m, = F /m 9475 ) ) ( ) = ( ) U A + K A =U B +K B K A = mgh ( ) = ( ) U A + K A =U +K K A = ½ K A + mgh ½ K A = mgh ½ mgh= mgh h= ½ H 9514
83 ) ), 9514 ) ) F x = F. 60 = ½ F, W= ½ F.x 9515 F-T=m.a 5-T=2.m
84 F-T=m.a 15-T=6.m 10=4.m m= 2,5 kg = 5-2.2,5=0 F =m.a = F/m = 10/2,5= 4m/s 2 = 20/2,5=8 m/s ) ) h= ½ gt 2 = ½ = 5m H= ½ G t 2 5 = ½ G 2 2 G= 2,5 m/s ) ) ( ) = ( ) U A + K A =U B +K B mgh= ½ m u 2 u 2 = 2gH = u/2 2 = u 2 /4 = ½ gh ( ) = ( ) E=U z +K z mgh= ½. ½ mgh+ mgh H- ¼ H= h h= ¾ H
85 9572 = t a= u/t=4/1= 4 m/s 2 x= ½ a t 2 = ½ 4.1= 2m = t= 4.2= 8 m/s x= ½ a t 2 = ½ 4.4= 8m = t t=16/4= 4s x= ½ a t 2 x= ½ 4.16=32m 9572 ) ) u= g.t u = g (t-1) u= u-u = g (t-1) - g.t= g =
86 9573 ) ) W 1 = mgh >0 W 2 =0 W 1 > W ) ) =. = mg
87 9574 ) ) = = 10-5/t X= = ½ ( + ) = ½ (5+10). t 9576 ) ) F=m.a B=ma mg=ma a=g u=gt,
88 9576 ) ) S= E= ½. = ½ 40.20=400m =s/t=400/40=10 m/s 9579 ) ) W 1 = F 1. x= 10.2=20J
89 W 2 = ½ F 2. x= ½ 10.2=10J < W 1 W 3 = ½ F 3. x= ½ 10.2=10J= W =ut u= x/t = 20/10 =2 m/s = =ut= 2.5=10m =ut= 2.15=30m 9585 ) ). = + t 3 = + t t=2 t = 2 / d= t + ½ t 2 d=. (2 / ) + ½ (2 / ) 2 d= 2 2 / / d= 4 2 /
90 ) ) = t + ½ t 2 = 5t + 2 t 2 = 5m/s = 4m/s 2 = + t = =25 m/s 9595 ) ) 0-3s u 1 =E=. = 4.2=8 m/s 2-4s u 2 =u 1 =8 m/s 4-6s u 3 = E=. = -2(6-4)=-4 m/s 9598
91 ) ) h = ½ g t 2 h = ½ g t 2 ½ g t 2 = ½ g t 2 g t 2 = 1/6 g t 2 6 t 2 = t 2 t = 6 t t > t 9604 ) ) B =m.g = mg = 6,25 m.g =6,25 B 9607 ) ) 1
92 9607 ) ) = + t+1/2 at 2 =0, =5m/s, =16m/s ) ) h = ½ g t 2 g= 2h/ t 2 =2.2/1= 4 m/s
93 ) ) W 1 = 20.1=20J, W 2 =0, W 3 = -10.1=-10J W o = W 1 +W 2 +W 3 = =10J > ) ) = -=0-0= ) ) F=0 F-T=0 T=F=10N F= m.a 2F-T=m.a 2F-F=m.a F=m.a 10=0,5a a=20m/s ) ) W=E = ½ ( = ½ 20.2 =20J
94 ) ) H F 9627 ) ) F 1 = m.a a =F 1 /m, s= ½ at 2 s= ½ F 1 /m.t 2, W 1 =F 1.s= ½ F 1 2 /m.t 2 F 1 +F 2 = m.a a = F 1 +F 2 /m, s = ½ at 2 s = ½ F 1 +F 2 /m.t 2, W 1 =F 1.s = ½ F 1. F 1 +F 2 /m.t 2 > W 1
95 9633 ) ) F 1 = m.a a =F 1 /m = u/ t = 4/4=1m/s 2 F 2 = m.a a =F 2 /m = 8/4 = 2m/s 2 =u/ t t= u/a = 8/2= 4 m/s ) ) E 1 = W 1 = F 1.x F 1 >F 2 E 1 >E 2 E 2 = W 2 = F 2.x
96 9638 ) ) 0-t 1 t 1 -t 2 F=0 t 2 -t ) ) A = W -0 =W +WF =F.h-B.h =F.hmg.h = =50J
97 ) ) 1 = 2 ½ a 1 t 1 2 = ½ a 2 t 2 2 F 1 /m 1 =F 2 /m 2 F 1 /m 1 =F 2 /2m 1 F 2 =2F ) )... 1 = 2 ½ t 2 =ut ½ at=u at=2u =2u
98 9654 ) ) 9656 ) ) F=0 F-B=0 F=mg=40.10=400N 9656
99 ) ) y= ½ gt 2 = ½ = 20m y= uot+ ½ gt 2 10 = 2uo+20 2uo=-10 uo=-5 m/s ( 9659 ) ) u=gt P 1 =B.u 1 = mggt 1 P 2 =B.u 2 = mggt 2 =2 mggt 1 = 2P ) ) F=m.a F 1 -F 2 =m.a 2F 2 -F 2 =m.a F 2 =m.a a = ½ F 1 /m = F 1 /m= ½ a
100 10079 ) ) W 1 = 10.x, W 2 =-10(2x-x)=- 10x W = W 1 + W 2 = = ) ) u 1 =gt 1, u 2 =gt 2 =2gt 1 =2u 1
101 10080 ) ) F= m.a = m u/ t = m(0-u)/ t= -mu/ t ) ) F=m.a F=10m F = m.a a = F / m= 20m/m = 20 m/s
102 ) W=E = ½. = ½ 20.2=20 J ) ) 1 - =W =F.x 1 1 =F.x =W =F.x 2 2 =4F.x 1 = ) ) = / t= 6/6= 1m/s 2 = F/m = F 1 /m = 2F/m = 2 m/s 2 = / t = 6 / t t =6/2= 3s
103 10084 ) a ), t=15s ) a ) 1 = 10.1 =10km 1 = 20.(3-2) =20km = = 30 km u= / t= 30/3= 10 km/h
104 10085 ) a ) F=0 F- T=0 F=T F=. F= mg F 1 = m 1 g F 2 = m 2 g = 2m 1 g= 2F ) ) 1 = ½ 1 t 2 2 = ½ 2 t 2 2=4 1 ½ 2 t 2 = 4. ½ 1 t 2 = 2 2 =
105 ) ) 1 = ½ (10+20).30= 450 m 2 = ½ (30-20)(-30)= -150 m = = =300m u= a.t, x = ½ at 2 t=2 u=2.2= 4m/s x= ½ =4m t=4 u=2.4=8m/s x= ½ = 16m t=6 u=2.6=12 m/s x= ½ =36m t=8 u=2.8=16 m/s x= ½ =64m h -t 10106
106 ) ) h= ½ gt 2 h= ½ g t 2 ½ gt 2 =½ g t 2 gt 2 = g (3t) 2 g t 2 = g 9t 2 g = g/ ) ) =.t = + t =.t = + t.t - t =. - = /t F/m A F/ m B = /t 1/m A 1/ m B = /t F 1/m A 1/ m B >0 1/m A >1/ m B m A < m B )
107 ) 1 = 20-10/5 =2 m/s 2 a 2 = 0-20/10=-2 m/s 2 =a ) )u =uo + at 3uo= uo + at at =2uo a= 2uo/t ).. -= W K-0 = F.x K = F.x X=0 K=0 2x K=2Fx=2K 3K= Fx 3Fx= Fx x = 3x 4x = F4x=4K
108 10126 ) ) ) )F-T=m.a F= ma+t=
109 10134 ) ) h 1 =h 2 mgh 1 =mgh 2 mgh 1 =2mgh 1 E 1 =2E 1 K 1 =2K 1 =K ) ) =36 km/h = /3600= 10m/s = 1 cm/s = 10-2 m/s = 1/100 m/s / =
110 ) ) 1 F-T = m 1.a T=m 2.a F=(m 1 +m 2 )a 2 F-T = m 2.a T =m 1.a F=(m 1 +m 2 )a = ) )x= xo +ut X= 10+5t u=5m/s ) )... -= W -= -Fx = Fx,
111 10205 ) ) ( ) = ( ) U A + K A =U B +K B U= K A -K B U= K-K B U= K- ½ m (u/2) 2 U= K- ¼ ½ m (u) 2 U= K- K/4 U= 3K/ ) ) ) ) =.t = + t =.t = + t.t - t =. - = /t F /m F / m = /t F F = m /t F F = m /t >0 F > F
112 10211 u=at t=0 u=4.0=4 m/s, t=2 u=4.2=8 m/s t=4 u=4.4=16 m/s t=6 u=4.6=24 m/s, t=6s ) ) = ½ m A u A 2 = ½ m M u M 2 4 m M u A 2 = m M u M 2 4 u A 2 = u M 2 2 u A = u M u A / u M = ½
113 10699 ) ) t ua>ub ua/t>ub/t aa>ab maa>mab Fa>Fb ) ) F 2 = Fx 2 +Fy 2 F 2 = (o,8f) 2 +Fy 2 F 2 = 0,64F 2 +Fy 2 F 2-0,64F 2 =Fy 2 0,36 F 2 =Fy 2 Fy=0,6F
114 10701 ) ) H = + = u 1.t 1 + (-u 1 ) (2t 1 -t 1 ) = u 1.t 1 - u 1.t 1 = ) ) ( ) = ( ) U A + K A =U B +K B K A = U B 2K = U B (Z) = (M) U Z + K Z =U M +K M K Z = U M K = U M 2 U M = U B 2 mgh= mgh h = 2H
115 10702 ) ) ( ) = ( ) U A + K A =U B +K B U A =U B =0 K A = K B = ½ muo ) ) 0-t 1 a 1 =u 1 /t 1 t i -t 2 2 = (0-1 )/ t 3 -t 2 2 = - 1 / 2,5t 1-2t 1 a 2 = -2u 1 /t 1
116 10703 ) ) K = W K 0= W K=W K= F.x K = W K 0= W K =W K = F.x =2 F.x= ) ) F= ma F-B=m.a 3B/2 B =m.a B/2= ma mg/2=ma a= 0,5g
117 10704 ) ) W A = mgh A = h A W B mgh B h B ) ) F= ma F 1 -F 2 -T=m.a =0,5 a 2=0,5a a= 4 m/s 2
118 10712 ) ) P A = W A / t = m A gh/ t = m A >1 P A > P P W / t m gh/ t m ) ) F=0 F-T=0 F=T B/5 =. B/5=. =1/5 =0, )
119 ) P A = W A / t = m A gh/ t = m A = 2 m =2 P A = 2P =2.2=4 k W P W / t m gh/ t m m ) a ) F= m.a F 1 -B=m.a F 1 = mg+ma F= m.a F 2 -B=m.a F 2 = mg+ma= F ) a ) F=0 Fx=T Fx.s=T.s W F =W T F Fx
120 = uot + ½ at 2 4= uo+ ½ a X 2 = uot + ½ at 2 12= uo+ 2 a a= 4m/s 2 uo= 2m/s u 1 = uo+at= 2+4.1= 6m/s u 2 = uo+at= 2+4.2= 10m/s ) ) x= ½ at 2 4= ½ a 2 2 a = 2m/s 2 u=at 2.2= 4m/s
121 10797 ) ) F= m B.a B o - F= m.a m B.a B = m.a m B.a B = 2m.a a B = 2.a ) ) P 1 =F.u 1 =B.u 1 =mgu 1 =mg. gt 1 = P 2 =F.u 2 =B.u 2 =mgu 2 =mg. gt 2 =2 mg. gt 1 =2 P 1
122 10805 ) ) P A = W A / t= 4000/10= 400W P B = W B / t= 1600/4= 400W= P A ) ) u=at u=2t a=2 m/s 2 = F= 10807
123 ) ) F=m.a F-B =mg/3 F=B+mg/3 F= mg+mg/3 F=4mg/3 F=4B/ ) ) x = uot + ½ at 2 x= 10t -2t 2 uo=10m/s a=4 m/s 2, u=uo-at= 10-4t ) ) x 1= ½ at 1 2 x 2= ½ at 2 2 x 2= ½ a(2t 1 ) 2 x 2=4. ½ at 1 2 x 2=4. x 1 x 2=4.10=40m 10820
124 = W K = F. x K= F. x K= F(x-xo) =F.x ) B ) h A = ½ gt A 2 h A = ½ g(2t B ) 2 h A =4. ½ g(t B ) 2 h A =4 h B h B = ½ gt B ) B ) F=0 F=T N=B F N = = = 2
125 10827 ) B ) ( ) = ( ) U A + K A =U B +K B 0 + mgh= K+0 K =mgh 0 + mgh = K +0 K =mgh =2mgh =2K ) ) = ½ u o.t 1
126 10838 ) ) 1 = F=0 F=T = N = mg = F =0 F =T = N = mg = 2 mg= 2F ) ) = F=0 F=T = N = mg = F =0 F =T = N = mg = 2 mg= 2F 10839
127 ) ) ) ) = = ½ F.x = ½ =90 cm t
128 10841 ) ) = / t= 2-1 /t 2 -t 1 =12-4/6-2=8/4=2 m/s ) ) = W K = F. x K= F. x ½ m A u A 2 = F. x 2000 u A 2 = F. x = W K = F. x K= F. x ½ m u 2 = F. x 500 u 2 = F. x 2000 u A 2 =500 u 2 u 2 = 4 u A 2 u = 2 u A
129 10845 ) ), F=0 F 1 -F 2 -T=0 5F-F=T =4F mg=4f =4F/mg ) ) 0-2s a=4m/s 2 u=at= 4.2=8m/s x= ½ at 2 = ½ = 8m 2-4s a=0 x=u.t =8.(4-2)= 16m 4-6s x=uot- ½ at 2 = 8(6-4)- ½ 2 (6-4) 2 = 16-4=12m X = =12m
130 10852 ) ) = W K = F. x K= F. x = W K = F. x K = F. x K = F 60. x= ½ F. x = ½ ) ) =0,
131 10853 ) ) = U= mgh = ½ m u2 u 2 = 2gH u 2 =2gh u 2 /4= 2gh 2g H/4= 2gh H/4= h ) ) = F=0 F-T=0 F=T W B =W N =0, W F = F.Dx W T =-T.DX=-F.DX=-W F 10930
132 ) ) =0 F= 30N, x=5m F=30-10=20N W= E = ½ ( + ) = ½ (30+20).5 = 125J ) ) u= x/t =30/2=15 m/s ) ) = ½ t 2 x= ½ a T / = t 2 = /2
133 10932 ) ) = +U E= 2U+U E=3U U=K/3 mgh= mgh/3 h=h/3 h=9/3 h=3m ) )u= s/ t= 2, m/3h = 2700km/3h=90km/h = ) ) 0-1 s x= ½ at 2 2= ½ a.1 2 a= 4m/s 2 F=m.a m= F/a=64/4=16kg... -=W K-0=W K=W=E = ½ ( + ) = ½ (2+3).64= 160J
ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ. Θετικής - Τεχνολογικής Κατεύθυνσης Φυσική Γ Λυκείου ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ. Επιμέλεια: ΘΕΟΛΟΓΟΣ ΤΣΙΑΡΔΑΚΛΗΣ
ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ Θετικής - Τεχνολογικής Κατεύθυνσης Φυσική Γ Λυκείου Επιμέλεια: ΘΕΟΛΟΓΟΣ ΤΣΙΑΡΔΑΚΛΗΣ e-mail: info@iliaskos.gr www.iliaskos.gr - f= f= f t+ 0 ) max
Leaving Certificate Applied Maths Higher Level Answers
0 Leavin Certificate Applied Maths Hiher Level Answers ) (a) (b) (i) r (ii) d (iii) m ) (a) 0 m s - 9 N of E ) (b) (i) km h - 0 S of E (ii) (iii) 90 km ) (a) (i) 0 6 (ii) h 0h s s ) (a) (i) 8 m N (ii)
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n 1
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n1 x dx = 1 2 b2 1 2 a2 a b b x 2 dx = 1 a 3 b3 1 3 a3 b x n dx = 1 a n +1 bn +1 1 n +1 an +1 d dx d dx f (x) = 0 f (ax) = a f (ax) lim d dx f (ax) = lim 0 =
ΣΥΝΟΨΗ 3 ου Μαθήματος
Ενημέρωση Η διδασκαλία του μαθήματος, πολλά από τα σχήματα και όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή Φυσική» του Hugh Young των Εκδόσεων Παπαζήση, οι οποίες μας επέτρεψαν τη χρήση
γραπτή εξέταση στο μάθημα ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ
η εξεταστική περίοδος από 1/1/14 έως 07/01/15 γραπτή εξέταση στο μάθημα ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ Τάξη: Α Λυκείου Τμήμα: Βαθμός: Ονοματεπώνυμο: Καθηγητές: Θ Ε Μ Α Α Στις παρακάτω ερωτήσεις να επιλέξετε τη σωστή
"BHFC8I7H=CB HC &CH=CB 5B8 &CA9BHIA
ω θ ω = Δθ Δt, θ ω v v = rω ω = v r, r ω α α = Δω Δt, Δω Δt (rad/s)/s rad/s 2 ω α ω α rad/s 2 87.3 rad/s 2 α = Δω Δt Δω Δt α = Δω Δt = 250 rpm 5.00 s. Δω rad/s 2 Δω α Δω = 250 min rev 2π rad rev 60 1 min
Ρ Ο Ν Τ Ι Σ Τ Η Ρ Ι Α ΕΡΥΘΡΑΙΑΣ 1-12134 -ΠΕΡΙΣΤΕΡΙ Τ ΗΛ 210-5757255
ΕΡΥΘΡΑΙΑΣ - -ΠΕΡΙΣΤΕΡΙ Τ ΗΛ 0-77 ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΤΡΙΤΗ 0 ΙΟΥΝΙΟΥ 0 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ
Τετάρτη 5 Νοεμβρίου 2014 ΕΠΙΛΕΓΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ
Τετάρτη 5 Νεμρίυ 014 ΕΠΙΛΕΓΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΘΕΜΑ Β Β1. Ένα κινητό διέρχεται τη χρνική στιγμή to=0 από τη θέση xo=0 ενός πρσανατλισμένυ άξνα Οx, κινύμεν κατά μήκς τυ
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 9 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Γ ΓΥΜΝΑΣΙΟΥ Κυριακή, 8 Απριλίου, 013 Ώρα: 10:00 1:30 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΛΥΣΕΙΣ ΘΕΜΑ 1 (5 μονάδες) (α) Μεταβολή της κινητικής του κατάστασης (μεταβολή της
2. Ένα φορτηγό κινείται ευθύγραμμα με σταθερή ταχύτητα υο = 10 m/s, όταν ο οδηγός του
1. Ένα αυτοκίνητο κινείται κατά μήκος μιας ευθείας χόχ και η εξίσωση της κίνησής του είναι: x = 2t 2 στο S.I. Να υπολογίσετε: Γ1. την επιτάχυνσή του. Γ2. την ταχύτητά του στο τέλος του 5ου δευτερολέπτου
B G [0; 1) S S # S y 1 ; y 3 0 t 20 y 2 ; y 4 0 t 20 y 1 y 2 h n t: r = 10 5 ; a = 10 6 ei n = ỹi n y i t n ); i = 1; 3: r = 10 5 ; a = 10 6 ei n = ỹi n y i t n ); i = 2; 4: r = 10 5 ; a = 10 6 t = 20
Έργο Κινητική Ενέργεια. ΦΥΣ 131 - Διαλ.16 1
Έργο Κινητική Ενέργεια ΦΥΣ 131 - Διαλ.16 1 Είδη δυνάµεων q Δύο είδη δυνάμεων: Ø Συντηρητικές ή διατηρητικές δυνάμεις και μή συντηρητικές ü Μια δύναμη είναι συντηρητική όταν το έργο που παράγει ασκούμενη
Ύλη: Δυναμική, Διατήρηση της Μηχανικής Ενέργειας
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Ον/μο:.. Α Λυκείου Ύλη: Δυναμική, Διατήρηση της Μηχανικής Ενέργειας 23-03-14 Θέμα 1 ο : 1. Μικρό σώμα μάζας m=2κg κινείται ευθύγραμμα και η συνισταμένη δύναμη που δέχεται στον άξονα
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2014. ÄÉÁÍüÇÓÇ
ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ Ηµεροµηνία: Κυριακή 4 Μαΐου 014 ιάρκεια Εξέτασης: ώρες ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις από Α1-Α4 να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και το γράµµα
Α3. Όταν ένα σώμα ισορροπεί, η συνισταμένη των δυνάμεων είναι α) Θετική β) Αρνητική γ) Μηδέν
Α ΛΥΚΕΙΟΥ ΝΕΟ ΕΞΕΤΑΣΤΙΚΟ ΣΥΣΤΗΜΑ ΦΥΣΙΚΗ Τρίτη 0 Μαΐου 014 Επιμέλεια: Φροντιστήρια «ΟΜΟΚΕΝΤΡΟ ΦΛΩΡΟΠΟΥΛΟΥ» ΦΥΣΙΚΗ ΘΕΜΑ Α Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας δίπλα
Θέμα Δ. Λύση. εκτελεί Ε.Ο.Κ, δηλαδή α = 0 κι επομένως εκτελεί Ε.Ο. Επιβραδυνόμενη κίνηση κι επομένως
Θέμα Δ Λύση Δ. ma 5kg A 0m/s σταθερή xo 0 mβ 0kg ο 30m/s αb m/s με φορά αντίθετη της κίνησης Το Το εκτελεί Ε.Ο.Κ, δηλαδή α 0 κι επομένως εκτελεί Ε.Ο. Επιβραδυνόμενη κίνηση κι επομένως Δ. Στην περίπτωση
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ Ονοματεπώνυμο :.. Ημερομηνία: ΘΕΜΑ 1 0 (13 μονάδες) Να επιλέξετε την σωστή απάντηση και οπού χρειάζεται να δικαιολογήσετε την απάντησή σας. 1. H επιτάχυνση ενός κινητού εκφράζει
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 6 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ Κυριακή, 13 Μαΐου, 01 Παρακαλώ διαβάστε πρώτα τα πιο κάτω, πριν απαντήσετε οποιαδήποτε ερώτηση Γενικές Οδηγίες: 1) Είναι πολύ σημαντικό να
Λυμένες ασκήσεις. Έργο σταθερής δύναμης
Λυμένες ασκήσεις Έργο σταθερής δύναμης 1. Στο σώμα που απεικονίζεται δίπλα τα μέτρα των δυνάμεων είναι F = 20 N, F 1 = 20 N, T = 5 N, B = 40 N. Το σώμα μετατοπίζεται οριζόντια κατά S = 10 m. Να βρεθούν
Το άτομο του Υδρογόνου
Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
Φροντιστήρια Δημόκριτος- Κορυφή. α. Ι β. II γ. III. Μονάδες 4. Β. Να δικαιολογήσετε την επιλογή σας.
Φροντιστήρια Δημόκριτος- Κορυφή ΘΕΜΑ Β (3761) Β1. Μικρή σφαίρα αφήνεται να πέσει από αρχικό μικρό ύψος Η, πάνω από το έδαφος και εκτελώντας ελεύθερη πτώση πέφτει στο έδαφος. Α. Να επιλέξετε την σωστή απάντηση.
ΔΙΑΓΏΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ 16-10- 2011. 1) α) Μονάδα μέτρησης ταχύτητας στο Διεθνές Σύστημα μονάδων (S.I.) είναι το 1Km/h.
ΔΙΑΓΏΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ 16- - 2011 ΘΕΜΑ 1 0 Για τις ερωτήσεις 1-5, αρκεί να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και δεξιά από αυτόν, το γράμμα που αντιστοιχεί στη σωστή απάντηση.
Ημερομηνία: Πέμπτη 20 Απριλίου 2017 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
ΤΑΞΗ: ΜΑΘΗΜΑ: Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Ημερομηνία: Πέμπτη 0 Απριλίου 017 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α1 Α4 να γράψετε στο τετράδιό σας τον αριθμό
Γ ΛΥΚΕΙΟΥ (Επαναληπτικός ιαγωνισμός)
4 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Επαναληπτικός ιαγωνισμός) Κυριακή, 5 Απριλίου, 00, Ώρα:.00 4.00 Προτεινόμενες Λύσεις Άσκηση ( 5 μονάδες) Δύο σύγχρονες πηγές, Π και Π, που απέχουν μεταξύ τους
ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ ΦΥΣΙΚΗΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 2016
ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ ΦΥΣΙΚΗΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 016 ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1-β, Α-γ, Α3-β, Α4-δ Α5 Σ,Λ,Σ,Λ,Λ ΘΕΜΑ Β Β1.Η σωστή απάντηση είναι η iii. Η σειρήνα του τρένου είναι η πηγή και ο ακίνητος παρατηρητής
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 19 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ A ΛΥΚΕΙΟΥ Κυριακή, 03 Απριλίου, 2005 Ώρα: 10:00-13:00 Οδηγίες: 1) Το δοκίµιο αποτελείται από έξι (6) θέµατα. 2) Να απαντήσετε τα ερωτήµατα όλων των
Κεφάλαιο 1 ΘΕΣΗ ΜΕΤΑΤΟΠΙΣΗ. Β1: Θέσης. Β2: Σχετική. Β3: Τροχιά. Β4: Ευθύγραµµη, καµπυλόγραµµη. Β5: ιάνυσµα. Β6: Θέση, µετατόπιση.
Κεφάλαιο ΘΕΣΗ ΜΕΤΑΤΟΠΙΣΗ Β: Θέσης Β: Σχετική Β: Τροχιά Β4: Ευθύγραµµη, καµπυλόγραµµη Β5: ιάνυσµα Β6: Θέση, µετατόπιση B7: ιαδροµή B8: Θετική, αρνητική, θετικός B9: Θετική, µικρότερη B: ιανυσµατική, αρνητική
ΛΥΚΕΙΟ ΠΟΛΕΜΙΔΙΩΝ Σχολική Χρονιά ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ Μάθημα: ΦΥΣΙΚΗ Τάξη: A Ενιαίου Λυκείου Βαθμός:...
ΛΥΚΕΙΟ ΠΟΛΕΜΙΔΙΩΝ Σχολική Χρονιά 011-01 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 01 Μάθημα: ΦΥΣΙΚΗ Τάξη: A Ενιαίου Λυκείου Βαθμός:... Ημερομηνία: 3/05/01 Διάρκεια: ώρες Ονοματεπώνυμο:... Τμήμα:... ΟΔΗΓΙΕΣ:
3 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ ΓΙΑ ΕΞΑΣΚΗΣΗ
3 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ ΓΙΑ ΕΞΑΣΚΗΣΗ ΑΠΡΙΛΙΟΣ 004. Η οµογενής ράβδος ΑΒ του σχήµατος έχει µήκος =m, βάρος W=00N και µπορεί να περιστρέφεται γύρω από άξονα, που διέρχεται από σηµείο Ο. Στη ράβδο ασκούνται οι
0,4 2 t (όλα τα μεγέθη στο S.I.). Η σύνθετη ταλάντωση περιγράφεται (στο
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 5: ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ ΘΕΜΑΤΑ ΠΡΟΣ ΕΠΙΛΥΣΗ ΘΕΜΑ Β Ερώτηση. Ένα σώμα εκτελεί κίνηση που προέρχεται από τη σύνθεση δύο απλών αρμονικών ταλαντώσεων, ίδιας
Οδηγοί εξοικονόμησης ενέργειας στη βιομηχανία
Οδηγοί εξοικονόμησης ενέργειας στη βιομηχανία Οδηγοί εξοικονόμησης ενέργειας στη βιομηχανία LBNL, Report 2268E Οδηγοί εξοικονόμησης ενέργειας LBNL, Report 2268E Πλαίσιο και στόχος των διαλέξεων Οι δράσεις
..., ISBN: :.!". # -. $, %, 1983 &"$ $ $. $, %, 1988 $ $. ## -. $, ', 1989 (( ). '. ') "!$!. $, %, 1991 $ 1. * $. $,.. +, 2001 $ 2. $. $,, 1992 # $!
!! " 007 : ISBN: # $! % :!" # - $ % 983 &"$ $ $ $ % 988 $ $ ## - $ ' 989 (( ) ' ') "!$! $ % 99 $ * $ $ + 00 $ $ $ 99!! " 007 -!" % $ 006 ---- $ 87 $ (( %( %(! $!$!" -!" $ $ %( * ( *!$ "!"!* "$!$ (!$! "
Προϋπολογισμός Μελέτης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΕΡΙΦΕΡΕΙΑ ΑΝΑΤΣ ΜΑΚΕΔΟΝΙΑΣ & ΘΡΑΚΗΣ Περιφερειακή Ενότητα Δράμας ΟΤΑ : Δήμος Κάτω Νευροκοπίου ΥΠΟΕΡΓΟ 1: ΤΟΥ ΕΡΓΟΥ: ΠΡΟΥΠΟΛΟΓΙΣΜΟΣ: Ανάπλαση οδών-πεζοδρομίων & ηλεκτροφωτισμού περιμετρικά
Σημειώσεις Ανάλυσης Ι
Σημειώσεις Ανάλυσης Ι 6. Συναρτήσεις Πρωταρχική έννοια στη φυσική είναι η έννοια της συνάρτησης. Π.χ. η θέση ενός σωματιδίου ως συνάρτηση του χρόνου x = f(t) ή x(t). Στη πρώτη περίπτωση προσδιορίζουμε
ΕΞΕΤΑΣΕΙΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ, 8 Μαρτίου 2019 Διδάσκοντες: Βαρσάμης Χρήστος, Φωτόπουλος Παναγιώτης
ΕΞΕΤΑΣΕΙΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 218-219 ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ, 8 Μαρτίου 219 Διδάσκοντες: Βαρσάμης Χρήστος, Φωτόπουλος Παναγιώτης ΘΕΜΑ 1 Διάρκεια εξέτασης 2 ώρες Υλικό σημείο κινείται ευθύγραμμα πάνω στον άξονα
Ασκήσεις υναµικής 1 η ενότητα: Κινηµατική σωµατιδίου
Ασκήσεις υναµικής 1 η ενότητα: Κινηµατική σωµατιδίου 1. Η επιτάχυνση ενός σωµατιδίου καθορίζεται από τη σχέση : α=-4x(1+kx 2 ), όπου το α µετριέται σε m/s 2 και το x σε m. Γνωρίζοντας ότι η ταχύτητα, για
ΠΕΡΙΠΤΩΣΕΙΣ ΜΗΧΑΝΙΚΗΣ ΣΤΑ ΚΟΜΙΚΣ
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ Μάθημα: Ερευνητική Εργασία Β Τετραμήνου Θεματική Ενότητα: Η Φυσική Στα Κόμικς ΠΕΡΙΠΤΩΣΕΙΣ ΜΗΧΑΝΙΚΗΣ ΣΤΑ ΚΟΜΙΚΣ Διερεύνηση της αληθείας ή μη εικόνων
1 2 3 4 5 6 7 8 9 10 2 12,999,976 km 9,136,765 km 1,276,765 km 499,892 km 245,066 km 112,907 km 36,765 km 24,159 km 7899 km 2408 km 76 km 12 14 16 3 6 11 1 12 7 1 2 5 4 3 9 10 8 18 20 21 22 23 24 25 26
2 3 4 5 6 7 8 9 10 12,999,976 km 9,136,765 km 1,276,765 km 499,892 km 245,066 km 112,907 km 36,765 km 24,159 km 7899 km 2408 km 76 km 12 14 16 9 10 1 8 12 7 3 1 6 2 5 4 3 11 18 20 21 22 23 24 26 28 30
!!" #7 $39 %" (07) ..,..,.. $ 39. ) :. :, «(», «%», «%», «%» «%». & ,. ). & :..,. '.. ( () #*. );..,..'. + (# ).
1 00 3 !!" 344#7 $39 %" 6181001 63(07) & : ' ( () #* ); ' + (# ) $ 39 ) : : 00 %" 6181001 63(07)!!" 344#7 «(» «%» «%» «%» «%» & ) 4 )&-%/0 +- «)» * «1» «1» «)» ) «(» «%» «%» + ) 30 «%» «%» )1+ / + : +3
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΛΥΣΕΙΣ
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΕΤΑΡΗ 1 ΙΟΥΝΙΟΥ 019 ΛΥΣΕΙΣ ΘΕΜΑ Α A1. β Α. γ Α3. α Α. γ Α5. α) Λάθος β) Σωστό γ) Λάθος δ) Σωστό ε) Σωστό ΘΕΜΑ Β Β1. Σωστή απάντηση η ii. Μονάδες Εφαρμόζουμε ΑΔΟ για την κρούση των
Γ ΛΥΚΕΙΟΥ (Επαναληπτικός ιαγωνισμός)
4 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Επαναληπτικός ιαγωνισμός) Κυριακή, 5 Απριλίου, 00, Ώρα:.00 4.00 Οδηγίες: ) Το δοκίμιο αποτελείται από έξι (6) θέματα. ) Να απαντήσετε σε όλα τα θέματα. ) Επιτρέπεται
ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ. m γ. Η μονάδα μέτρησης της επιτάχυνσης στο S.I είναι το 1.
ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ Τρίτη 8 Απριλίου 04 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α - Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α. Ποια από τις επόμενες
ΚΕΦΑΛΑΙΟ 2.1 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ
Σχολικό Έτος 016-017 8 ΚΕΦΑΛΑΙΟ.1 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ 1. ΕΡΓΟ Το έργο σαν φυσικό μέγεθος εκφράζει την μεταφορά ενέργειας από ένα σώμα σε ένα άλλο ή την μετατροπή της από μια μορφή σε μια
ΠΑΤΜΑΝΙΔΗΣ PATMANIDIS Δημητρας 15 Ακαδημια Πλάτωνος Αθήνα 10442 Τηλ 2105141807, 2105157906, 2105141132 Φαξ 2105153030.
ΡΟΥΜΠΙΝΕΤΟ AD50 44300-11B00 ΡΟΥΜΠΙΝΕΤΟ AD50 44300-11B00 Κωδικός: 49001001 209000912 ΡΟΥΜΠΙΝΕΤΟ C50 16950-086-000 Κωδικός: 49001002 209000992 ΡΟΥΜΠΙΝΕΤΟ C50 16950-086-000 Κωδικός: 49001003 209000900 ΡΟΥΜΠΙΝΕΤΟ
1951 {0, 1} N = N \ {0} n m M n, m N F x i = (x i 1,..., xi m) x j = (x 1 j,..., xn j ) i j M M i j x i j m n M M M M T f : F m F f(m) f M (f(x 1 1,..., x1 m),..., f(x n 1,..., xn m)) T R F M R M R x
ΔΙΕΥΘΕΤΗΣΗ ΟΡΕΙΝΩΝ ΥΔΑΤΩΝ Ι
Τμήμα Δασολογίας & Διαχείρισης Περιβάλλοντος & Φυσικών Πόρων Εργαστήριο Διευθέτησης Ορεινών Υδάτων και Διαχείρισης Κινδύνου Προπτυχιακό Πρόγραμμα Σπουδών ΔΙΕΥΘΕΤΗΣΗ ΟΡΕΙΝΩΝ ΥΔΑΤΩΝ Ι Κεφάλαιο 1ο Φ. Π. Μάρης
είναι το φυσικό µήκος του ελατηρίου, να βρείτε τις συναρτήσεις F = f ( l)
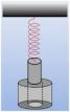ΕΡΓΑΣΙΑ 4 η (Παράδοση: 8/04/005 ) Άσκηση Πάνω σε λείο οριζόντιο δάπεδο βρίσκεται ακίνητη η µάζα m = 4Kg στην οποία είναι δεµένη η µια άκρη του ελατηρίου σταθεράς k = 300N/m. Η µάζα m = Kg κινείται µε ταχύτητα
ΘΕΜΑ Α. Αρχή 1 ης Σελίδας
Αρχή 1 ης Σελίδας ΘΕΜΑ Α Για τις ερωτήσεις 1 έως 4 γράψτε τον αριθμό τις ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Για ένα σώμα που κινείται σε ευθεία γραμμή δίνεται στο διπλανό
1ο ιαγώνισµα Β Τάξης Ενιαίου Λυκείου Κυριακή 9 Νοέµβρη 2014 Φυσική Προσανατολισµού - Μηχανική. Θέµα Α
1ο ιαγώνισµα Β Τάξης Ενιαίου Λυκείου Κυριακή 9 Νοέµβρη 014 Φυσική Προσανατολισµού - Μηχανική Θέµα Α Α.1. Στην άκρη ενός τραπεζιού ϐρίσκονται δύο σφαίρες Σ 1 και Σ. Κάποια χρονική στιγµή η σφαίρα Σ 1 εκτοξεύεται
Αντικείμενο: Κρούσεις Κινήσεις Ελατήριο - Doppler
Αντικείμενο: Κρούσεις Κινήσεις Ελατήριο - Doppler «Όσο μεγαλώνει το νησί της γνώσης τόσο διευρύνεται η ακτή που αντικρίζει τον ωκεανό της άγνοιάς μας» V. Weisskopf Σώμα μάζας m=3 kg είναι δεμένο στην άκρη
1. Η αντίσταση του αέρα λόγω της σταθερής ταχύτητας ανά σταθερή δύναμη και κατά συνέπεια το έργο της είναι: W = ΑΧ = 4υ Χ ή W = J ή W = 6000J
Κεφάλαιο.1 1. Η αντίσταση του αέρα λόγω της σταθερής ταχύτητας ανά σταθερή δύναμη και κατά συνέπεια το έργο της είναι: W = ΑΧ = 4υ Χ ή W = 4-30-50J ή W = 6000J. Α. Η δυναμική ενέργεια του σώματος είναι:
Θέματα.
Θέμα Α Θέματα Στις παρακάτω ερωτήσεις πολλαπλής επιλογής Α-Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α. Ένα σώμα εκτελεί ευθύγραμμη
ΤΖΑΚΙΑ ΕΝΕΡΓΕΙΑΚΑ ΑΕΡΟΘΕΡΜΑ Φ 250 25,6 275 1,700 Φ 250 1,700 Φ 250 1,700 Φ 250 1,700 Φ 250 1,800 Φ 250 1,800 Υ: 1.75 B:0.59 Π: 0.
ΚΑΜΙΝΑΔΑΣ Kw ΒΑΡΟΣ 1 B:0.59 150 25,6 275 1,700 2 3 4 5 ΣΤΡΟΓΓΥΛΟ Τ 90 B:0.73 B:0.76 Υ: 1.72 B:0.62 Π: 0.98 B:0.66 Π:1.06 150 150 24 20 20 20 288 295 305 1,700 1,700 1,700 1,800 ΤΖΑΚΙΑ ΕΝΕΡΓΕΙΑΚΑ ΑΕΡΟΘΕΡΜΑ
ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ. Θετικής - Τεχνολογικής Κατεύθυνσης Μαθηματικά Γ Λυκείου Όρια - Συνέχεια ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ ΣΤΕΦΑΝΟΣ ΗΛΙΑΣΚΟΣ
ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ Θετικής Τεχνολογικής Κατεύθυνσης Μαθηματικά Γ Λυκείου Όρια Συνέχεια ΣΤΕΦΑΝΟΣ ΗΛΙΑΣΚΟΣ mail: info@iliaskosgr wwwiliaskosgr f] g,! R f] g,, f] g
ΛΥΚΕΙΟ ΣΟΛΕΑΣ Σχολική χρονιά 2008-2009
ΛΥΚΕΙΟ ΣΟΛΕΑΣ Σχολική χρονιά 2008-2009 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 2009 ΜΑΘΗΜΑ: Φυσική κατεύθυνσης ΤΑΞΗ: B ΗΜΕΡΟΜΗΝΊΑ: 26/05/2009 ΧΡΟΝΟΣ: 2 ώρες και 30 λεπτά ΒΑΘΜΟΣ: Αριθμητικώς:... Ολογράφως:...
Κεφάλαιο 1 ο : Οι Φυσικοί αριθμοί
2 ΕΡΩΤΗΣΕΙΙΣ ΘΕΩΡΙΙΑΣ ΑΠΟ ΤΗΝ ΥΛΗ ΤΗΣ ΑΡΙΙΘΜΗΤΙΙΚΗΣ -- ΑΛΓΕΒΡΑΣ Κεφάλαιο 1 ο : Οι Φυσικοί αριθμοί Α. 1. 1 1. Ποιοι αριθμοί ονομάζονται φυσικοί και ποια είναι η χαρακτηριστική τους ιδιότητα; Οι αριθμοί
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 2014
1 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 014 ΘΕΜΑ Α.1 Α1. Να χαρακτηρίσετε με (Σ) τις σωστές και με (Λ) τις λανθασμένες προτάσεις Στην ευθύγραμμα ομαλά επιβραδυνόμενη κίνηση: Α. Η ταχύτητα
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα
/&25*+* 24.&6,2(2**02)' 24
!! "#$ % (33 &' ())**,"-.&/(,01.2(*(33*( ( &,.*(33*( ( 2&/((,*(33*( 24 /&25** 24.&6,2(2**02)' 24 " 0 " ( 78,' 4 (33 72"08 " 2/((,02..2(& (902)' 4 #% 7' 2"8(7 39$:80(& 2/((,* (33; (* 3: &
.,, T = N N f = T rad/s. : dφ. ω =. dt
-,.. -. ( ). -.,,.. ( ),. t, t T = N N f = t. s s - /s Hz.,. f = T,, ( ) π ω = = πf T rad/s.... : dφ ω =. dt. 8 -3 ).......,...,. x x = Aηµ ωt (. ).,,. 9 .. -. -... υ = υ συν ωt (.) max a = a ωt (.3) maxηµ
GI_V_FYSP_4_ m/s, ξεκινώντας από το σημείο Κ. Στο σημείο Λ (αντιδιαμετρικό του Κ) βρίσκεται ακίνητο σώμα Σ 2 μάζας m2 1 kg.
Μια ράβδος μήκους R m και αμελητέας μάζας βρίσκεται πάνω σε λείο οριζόντιο επίπεδο και μπορεί να περιστρέφεται γύρω από το σημείο Ο. Στο άλλο άκρο της είναι στερεωμένο σώμα Σ, μάζας m kg το οποίο εκτελεί
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ. (0,5 μόριο) m1υ1 -m2 υ. 0,5 m/s (1 μόριο)
ΑΡΧΗ Η ΕΛΙΔΑ ΛΥΕΙ ΔΙΑΓΩΝΙΜΑΤΟ ΠΕΡΙΟΔΟΥ ΕΠΤΕΜΒΡΙΟΥ Γ ΤΑΞΗ ΗΜΕΡΗΙΟΥ ΚΑΙ Δ ΤΑΞΗ ΕΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ ΕΠΤΕΜΒΡΙΟΥ 8 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΙΚΗ ΠΡΟΑΝΑΤΟΛΙΜΟΥ ΥΝΟΛΟ ΕΛΙΔΩΝ: ΟΚΤΩ (8) Θέμα Α(5 Μονάδες)
Dissertation for the degree philosophiae doctor (PhD) at the University of Bergen
Dissertation for the degree philosophiae doctor (PhD) at the University of Bergen Dissertation date: GF F GF F SLE GF F D Ĉ = C { } Ĉ \ D D D = {z : z < 1} f : D D D D = D D, D = D D f f : D D
Διατήρηση της Ορμής. R=10m. www.ylikonet.gr 1
Διατήρηση της Ορμής. 2.1.Ορµή και ρυθµός µεταβολής της ορµής. Ένα σώµα µάζας m=2kg εκτελεί οµαλή κυκλική κίνηση µε ταχύτητα υ=5m/s σε κύκλο κέντρου Ο και ακτίνας R=10m. i) Υπολογίστε την ορµή του σώµατος
Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ. Παππάς Χρήστος Επίκουρος Καθηγητής
ΗΛΕΚΤΡΟΝΙΚΗ ΟΜΗ ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ Παππάς Χρήστος Επίκουρος Καθηγητής ΤΟ ΜΕΓΕΘΟΣ ΤΩΝ ΑΤΟΜΩΝ Ατομική ακτίνα (r) : ½ της απόστασης μεταξύ δύο ομοιοπυρηνικών ατόμων, ενωμένων με απλό ομοιοπολικό δεσμό.
ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑÏΟΥ- ΙΟΥΝΙΟΥ 2014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΗΜΕΡΟΜΗΝΙΑ: 23/05/2014 ΤΑΞΗ: Α ΛΥΚΕΙΟΥ ΔΙΑΡΚΕΙΑ: 2 ΩΡΕΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:... ΤΜΗΜΑ:...
1 ΛΥΚΕΙΟ ΑΓΙΟΥ ΑΝΤΩΝΙΟΥ ΛΕΜΕΣΟΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 013-014 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑÏΟΥ- ΙΟΥΝΙΟΥ 014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΗΜΕΡΟΜΗΝΙΑ: 3/05/014 ΤΑΞΗ: Α ΛΥΚΕΙΟΥ ΔΙΑΡΚΕΙΑ: ΩΡΕΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:... ΤΜΗΜΑ:... ΒΑΘΜΟΣ:...
1 ο ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ
1 ο ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό της καθεμιάς από τις παρακάτω προτάσεις Α1 έως Α3 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση: Α1. Το μέτρο της
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 3η : ΟΡΜΗ ΦΛΕΒΑΣ ΡΕΥΣΤΟΥ
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 3η : ΟΡΜΗ ΦΛΕΒΑΣ ΡΕΥΣΤΟΥ ΟΡΜΗ ΥΔΑΤΙΝΗΣ ΚΑΤΑΚΟΡΥΦΗΣ ΦΛΕΒΑΣ ΣΕ ΚΥΚΛΙΚΟ ΔΙΣΚΟ ΚΑΙ ΗΜΙΣΦΑΙΡΙΚΟ ΚΥΠΕΛΛΟ Σκοπός της Άσκησης Στην εργαστηριακή άσκηση γίνεται μελέτη της επίδρασης της ορμής
A 1 A 2 A 3 B 1 B 2 B 3
16 0 17 0 17 0 18 0 18 0 19 0 20 A A = A 1 î + A 2 ĵ + A 3ˆk A (x, y, z) r = xî + yĵ + zˆk A B A B B A = A 1 B 1 + A 2 B 2 + A 3 B 3 = A B θ θ A B = ˆn A B θ A B î ĵ ˆk = A 1 A 2 A 3 B 1 B 2 B 3 W = F
P t s st t t t t2 t s st t t rt t t tt s t t ä ör tt r t r 2ö r t ts t t t t t t st t t t s r s s s t är ä t t t 2ö r t ts rt t t 2 r äärä t r s Pr r
r s s s t t P t s st t t t t2 t s st t t rt t t tt s t t ä ör tt r t r 2ö r t ts t t t t t t st t t t s r s s s t är ä t t t 2ö r t ts rt t t 2 r äärä t r s Pr r t t s st ä r t str t st t tt2 t s s t st
Επιτραπέζια μίξερ C LINE 10 C LINE 20
Επιτραπέζια μίξερ C LINE 10 Χωρητικότητα κάδου : 10 lt Ναί Βάρος: 100 Kg Ισχύς: 0,5 Kw C LINE 20 Χωρητικότητα κάδου : 20 lt Βάρος: 105 Kg Ισχύς: 0,7 Kw Ναί Επιδαπέδια μίξερ σειρά C LINE C LINE 10 Χωρητικότητα
ΑΛ/Μ ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ. Τεύχος 6ο: Eπαναληπτικές ασκήσεις
ΑΛ/Μ6 05-06 ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ Τεύχος 6ο: Eπαναληπτικές ασκήσεις ΦΥΣΙΚΗ: Επαναληπτικές ασκήσεις 383 384 ΦΥΣΙΚΗ: Επαναληπτικές ασκήσεις Παράδειγμα Για κινητό που κινείται ευθύγραμμα την χρονική στιγμή
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΔΟΜΟΣΤΑΤΙΚΗΣ. Παραδείγματα για την 9 η παράδοση Συμβολικές πράξεις
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΔΟΜΟΣΤΑΤΙΚΗΣ Μάθημα: Μέθοδοι Επίλυσης με Η/Υ Ακαδ. Έτος: 2014-2015 Παρασκευή, 15/05/2015 Διδάσκοντες: Ν.Δ. Λαγαρός (Επικ. Καθηγητής), Μ. Φραγκιαδάκης
3ο Επαναληπτικό Διαγώνισμα Φυσικής Α τάξης Λυκείου
ο Επαναληπτικό Διαγώνισμα Φυσικής Α τάξης Λυκείου Θέμα Α: (Για τις ερωτήσεις Α. έως και Α.4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη σωστή πρόταση.) Α.
Aριστοβάθμιο Ενδεικτικε ς απαντή σεις στή φυσική Προσανατολισμου Πανελλή νιες
Ενδεικτικε ς απαντή σεις στή φυσική Προσανατολισμου Πανελλή νιες 12-06-2017 Β1) Σωστή απάντηση η (ii). ΘΕΜΑ Α Α1) δ Α2) γ Α3) α Α) δ Α5) α) Λ β) Σ γ) Σ δ) Σ ε) Λ ΘΕΜΑ Β ΘI: F = 0 m g = K Δl o = Δl o =
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2013 ÅÐÉËÏÃÇ
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 03 Ε_3.Φλ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Α ΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ Ηµεροµηνία: Κριακή 8 Απριλίο 03 ιάρκεια Εξέτασης: ώρες Α. δ Α. γ Α3. β Α4. δ Α5. α Σ, β Λ, γ Σ, δ Σ, ε Λ. ΘΕΜΑ Β Β. Α. Σωστή
ΤΙΜΟΚΑΤΑΛΟΓΟΣ ΑΝΤΑΝΑΚΛΑΣΤΙΚΕΣ ΜΕΜΒΡΑΝΕΣ ΔΙΑΣΤΑΣΗ ΠΡΟΙΟΝ ΕΓΓΥΗΣΗ ΚΩΔΙΚΟΣ ΧΡΩΜΑΤΑ ΡΟΛΟΥ. 3290 Λευκό 3271 Κίτρινο. 3279 Καφέ. 3870 Λευκό 3881 Κίτρινο
ΑΝΤΑΝΑΚΛΑΣΤΙΚΕΣ ΜΕΜΒΡΑΝΕΣ ΠΡΟΙΟΝ ΕΓΓΥΗΣΗ ΚΩΔΙΚΟΣ ΧΡΩΜΑΤΑ ΤΥΠΟΥ Ι 3290 Λευκό 3271 Κίτρινο Πλάτος:0,91 ή 1,22 m 7 3272 Κόκκινο 3275 Μπλε ENGINEER 3277 Πράσινο GRADE ΤΜ 3279 Καφέ ΤΥΠΟΥ ΙΙ 3870 Λευκό 3881
γ 1 6 M = 0.05 F M = 0.05 F M = 0.2 F M = 0.2 F M = 0.05 F M = 0.05 F M = 0.05 F M = 0.2 F M = 0.05 F 2 2 λ τ M = 6000 M = 10000 M = 15000 M = 6000 M = 10000 M = 15000 1 6 τ = 36 1 6 τ = 102 1 6 M = 5000
Ο ΗΛΕΚΤΡΙΚΟΣ ΣΙΔΗΡΟΔΡΟΜΟΣ
Τ.Ε.Ι. ΚΑΒΑΛΑΣ ΣΧΟΛΗ Σ.Τ.ΕΦ. ΤΜΗΛ1Λ ΗΛΕΚΤΡΟΛΟΓΊΑΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ Ο ΗΛΕΚΤΡΙΚΟΣ ΣΙΔΗΡΟΔΡΟΜΟΣ ΕΙΣΗΠΙΤΗΣ ΚΑΙ ΕΗΙΒΛΕΗΩΝ: κ. ΜΗΑΝΤΕΚΑΣ ΑΗΜΗΤΡΗΣ ΣΗΟΥΔΑΣΤΕΣ: ΣΤΑ \ ΡΙΔΟΥ ΒΙΟΛΕΤΑ ΚΑΡΑΜΟΥΖΗΣ ΜΑΑΑΜΑΣ ΚΑΒΑΛΑ 2005
ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ
ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ Περίοδοι περιοδικού πίνακα Ο περιοδικός πίνακας αποτελείται από 7 περιόδους. Ο αριθμός των στοιχείων που περιλαμβάνει κάθε περίοδος δεν είναι σταθερός, δηλ. η περιοδικότητα
ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ
ΑΓ.ΚΩΝΣΤΑΝΤΙΝΟΥ 11 -- ΠΕΙΡΑΙΑΣ -- 1853 -- ΤΗΛ. 10-4475, 43687 ΘΕΜΑ 1: Α-δ Β-γ Γ-β Δ-β Ε: α-λ, β-λ, γ-σ, δ-σ, ε-λ ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΘΕΜΑ :. Η σωστή απάντηση είναι το γ. x Αν συγκρίνουμε την δοθείσα
W = 6.34 kn (2) F = u 2 f = u2 i + 2a(x f x i ) a = u2 f u2 i 2x f. F = d U(x) (5)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-2: Φυσική Ι Χειµερινό Εξάµηνο 208 ιδάσκων : Γ. Καφεντζής Λύσεις 3ου Φροντιστηρίων Ασκηση. Επιλέγουµε ως σύστηµα τη σφάιρα. Το σύστηµα είναι µη αποµονωµένο.
ECE 220 / 225 ECE 220XL / 225XL
ECE 220 / 225 ECE 220XL / 225XL Οδηγίες χρήσης 12.06- g 51051918 07.08 Πρόλογος Για την ασφαλή χρήση του µεταφορέα διαδρόµου απαιτούνται γνώσεις που παρέχονται από τις παρούσες ΠΡΩΤΟΤΥΠΕΣ Ο ΗΓΙΕΣ ΧΡΗΣΗΣ.
ΣΥΣΕΥΕΣ ΘΕΡΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ 1η Ενότητα
ΣΥΣΕΥΕΣ ΘΕΡΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ 1η Ενότητα Οκτώβριος 2013 1. Εναλλάκτης σχεδιάζεται ώστε να θερμαίνει 2 kg/s νερού από τους 20 ο C στους 60 ο C. Το θερμό ρευστό είναι επίσης νερό, με θερμοκρασία εισόδου 95
5 η Εβδομάδα Έργο και κινητική ενέργεια. Ομαλή κυκλική κίνηση Έργο δύναμης Κινητική ενέργεια Θεώρημα έργου ενέργειας
5 η Εβδομάδα Έργο και κινητική ενέργεια Ομαλή κυκλική κίνηση Έργο δύναμης Κινητική ενέργεια Θεώρημα έργου ενέργειας Ομαλή κυκλική κίνηση Κίνηση σωματίου σε κύκλο με ταχύτητα σταθερού μέτρου. Επιτάχυνση
2013/2012. m' Z (C) : V= (E): (C) :3,24 m/s. (A) : T= (1-z).g. (D) :4,54 m/s
( ) 03/0 - o l P z o M l =.P S. ( ) m' Z l=m m=kg m =,5Kg g=0/kg : : : : Q. (A) : V= (B) : V= () : V= (D) : V= (): : V :Q. (A) :4m/s (B) :0,4 m/s () :5m/s (D) :0,5m/s (): : M T : Q.3 (A) : T=(-z).g (B)
r t t r t t à ré ér t é r t st é é t r s s2stè s t rs ts t s
r t r r é té tr q tr t q t t q t r t t rrêté stér ût Prés té r ré ér ès r é r r st P t ré r t érô t 2r ré ré s r t r tr q t s s r t t s t r tr q tr t q t t q t r t t r t t r t t à ré ér t é r t st é é
ΘΕΜΑ Α (25 Μονάδες) Α1). Αν p(x) μία πολυωνυμική συνάρτηση, τότε να δείξετε ότι lim
ΔΙΑΡΚΕΙΑΣ 3 ΩΡΩΝ ΝΙΚΟΣ ΤΟΥΝΤΑΣ Ονοματεπώνυμο: ΒΑΘΜΟΣ:. /00 ή. /0 ΘΕΜΑ Α 5 Μονάδες) Α). Αν px) μία πολυωνυμική συνάρτηση, τότε να δείξετε ότι px) pxo). Μονάδες 4) Α). Έστω f μία συνάρτηση. Να αναφέρετε
Κινηματική σε 3 διαστάσεις. r = x x + y y +z z P. Η έννοια της παραγώγου στις 3 διαστάσεις
Κινηματική σε 3 διαστάσεις = + + P παριστάνεται με την επιβατική ακτίνα κάθε σημείο P το χώρο (t τροχιά = Δ Δ (t+ διάνσμα θέσης d v= d μοναδιαία διανύσματα Η έννοια της παραγώγο στις 3 διαστάσεις Μέση
(x y) = (X = x Y = y) = (Y = y) (x y) = f X,Y (x, y) x f X
X, Y f X,Y x, y X x, Y y f X Y x y X x Y y X x, Y y Y y f X,Y x, y f Y y f X Y x y x y X Y f X,Y x, y f X Y x y f X,Y x, y f Y y x y X : Ω R Y : Ω E X < y Y Y y 0 X Y y x R x f X Y x y gy X Y gy gy : Ω
Φυσική Α' Λυκείου. Κεφάλαιο 1.1 Ευθύγραμμη κίνηση. 9η παρουσίαση. Σχολική χρονιά 2013-2014 Φροντιστήριο Μ.Ε. ΤΖΑΝΕΤΟΥ www.frontistiriotzanetou.
Φυσική Α' Λυκείου Κεφάλαιο 1.1 Ευθύγραμμη κίνηση 9η παρουσίαση Σχολική χρονιά 213-214 Φροντιστήριο Μ.Ε. ΤΖΑΝΕΤΟΥ www.frontistiriotzanetou.com 1.1.5 Η έννοια της ταχύτητας στην ευθύγραμμη ομαλή κίνηση Έστω
ΦΥΣΙΚΗ Ι. ΕΙΔΙΚΕΣ ΠΕΡΙΠΤΩΣΕΙΣ ΔΥΝΑΜΕΩΝ Βαρυτική Δύναμη Βάρος Κάθετη Δύναμη σε Επιφάνεια Τάση Νήματος Τριβή Οπισθέλκουσα Δύναμη και Οριακή Ταχύτητα
ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Στυλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟN ΑΘΗΝΩΝ,, 014 01 015 ΝΟΜΟΙ ΤΟΥ ΝΕΥΤΩΝΑ Νόμος της Αδράνειας Αδρανειακό Σύστημα Μάζα και Ορμή Αρχή διατήρησης της Ορμής Δύναμη Δεύτερος Νόμος
ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2019 Β ΦΑΣΗ
ΤΑΞΗ: ΜΑΘΗΜΑ: A ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ Ημερομηνία: Σάββατο 4 Μαΐου 09 Διάρκεια Εξέτασης: ώρες ΘΕΜΑ Α Α. β Α. γ Α3. γ Α4. γ ΑΠΑΝΤΗΣΕΙΣ Α5. α. Σωστό β. Λάθος γ. Λάθος δ. Λάθος ε. Λάθος ΘΕΜΑ Β Β. β. Άπο τη
ΣΥΝΟΨΗ 1 ου Μαθήματος
Ενημέρωση Η διδασκαλία του μαθήματος, πολλά από τα σχήματα και όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή Φυσική» του Hugh Young των Εκδόσεων Παπαζήση, οι οποίες μας επέτρεψαν τη χρήση
ΝΟΜΟΣ ΤΗΣ ΠΕΡΙΟ ΙΚΟΤΗΤΑΣ : Οι ιδιότητες των χηµικών στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.
1. Ο ΠΕΡΙΟ ΙΚΟΣ ΠΙΝΑΚΑΣ Οι άνθρωποι από την φύση τους θέλουν να πετυχαίνουν σπουδαία αποτελέσµατα καταναλώνοντας το λιγότερο δυνατό κόπο και χρόνο. Για το σκοπό αυτό προσπαθούν να οµαδοποιούν τα πράγµατα
!"! #!"!!$ #$! %!"&' & (%!' #!% #" *! *$' *.!! )#/'.0! )#/.*!$,)# * % $ %!!#!!%#'!)$! #,# #!%# ##& )$&# 11!!#2!
# $ #$ % (% # )*%%# )# )$ % # * *$ * #,##%#)#% *-. )#/###%. )#/.0 )#/.* $,)# )#/ * % $ % # %# )$ #,# # %# ## )$# 11 #2 #**##%% $#%34 5 # %## * 6 7(%#)%%%, #, # ## # *% #$# 8# )####, 7 9%%# 0 * #,, :;
m r = F m r = F ( r) m r = F ( v) F = F (x) m dv dt = F (x) vdv = F (x)dx d dt = dx dv dt dx = v dv dx
m r = F m r = F ( r) m r = F ( v) x F = F (x) m dv dt = F (x) d dt = dx dv dt dx = v dv dx vdv = F (x)dx 2 mv2 x 2 mv2 0 = F (x )dx x 0 K = 2 mv2 W x0 x = x x 0 F (x)dx K K 0 = W x0 x x, x 2 x K 2 K =