ΝΟΜΟ ΣΟΤ BOYLE(βαςιςμζνο ςε πείραμα)
|
|
|
- Κυριακή Οικονόμου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 2ο ΠΕΙΡΑΜΑΣΙΚΟ ΛΤΚΕΙΟ ΑΘΗΝΩΝ τθσ Κυπραίου Φωτεινισ 'Eτοσ: ΝΟΜΟ ΣΟΤ BOYLE(βαςιςμζνο ςε πείραμα) O Νόμος του Boyle τθ κερμοδυναμικι ο Νόμοσ του Boyle είναι ζνασ από τουσ τρεισ νόμουσ των αερίων.ωσ Νόμοι των αερίων χαρακτθρίηονται οι φυςικοί νόμοι που περιγράφουν τιν ςυμπεριφορά των αερίων ςφμφωνα με τθν κζρμοκραςια,τθν πίεςθ και τον όγκο.ο Νόμοσ του Μπόιλ, γνωςτόσ και ςαν νόμοσ Μπόιλ-Μαριότ, πιρε το όνομά του αρχικά από τον Ιρλανδό φυςικό φιλόςοφο Ρόμπερτ Μπόιλ (Robert Boyle), ( ), που πρϊτοσ τον διατφπωςε και δθμοςίευςε το Σον ίδιο νόμο διατφπωςε 14 χρόνια αργότερα και ο Γάλλοσ φυςικόσ Ε. Μαριότ (Edme Mariotte) ( ). Εξ ου και θ διπλι ονομαςία. Σφμφωνα με αυτό το νόμο:ο όγκοσ ενόσ αερίου είναι αντιςτρόφωσ ανάλογοσ τθσ πίεςθσ αυτοφ, ςε ςτακερι κερμοκραςία.για τισ μεταβολζσ πίεςθσ και κερμοκραςίασ αν P1 θ αρχικι πίεςθ του αερίου, V1 ο αρχικόσ ειδικόσ όγκοσ του και T θ ςτακερι κερμοκραςία του και προκλθκεί μεταβολι τθσ πίεςθσ και του όγκου του ςε P2 και V2 κατά τρόπο που θ κερμοκραςία μείνει αμετάβλθτθ, τότε μεταξφ των παραπάνω ςτοιχείων του αερίου κα ιςχφει θ μακθματικι ςχζςθ: ι και ακόμθ Η μακθματικι του διατφπωςθ ειναι =ςτακερό για Σ=ςτακερό 'Αρα το γινόμενο είναι ςτακερό και ιςοφται με όπου ο αρικμόσ των γραμμομορίων τοφ αερίου και θ παγκόςμια ςτακερά των ιδανικϊν αερίων που
2 ςτο διεκνζσ ςφςτθμα μονάδων (S.I) ζχει τιμι. Ο νόμοσ των Boyle και Mariotte όπωσ και οι άλλοι νόμοι των αερίων, ιςχφει επακριβϊσ για ιδανικά αζρια. Οι νόμοι όμωσ μποροφν να εφαρμοςτοφν ςαν καλι προςζγγιςθ και ςε πραγματικά αζρια!! ΤΠΟΘΕΗ τθν πειραματικι διαδικαςία που κα καταγράψουμε ςτθν ςυνζχεια και ςφμφωνα με τον νόμο του Boyle,δθλαδι ςτον νόμο με τον οποίο θ πίεςθ οριςμζνθσ ποςότθτασ ιδανικοφ αερίου με κερμοκραςία θ οποία παραμζνει ςτακερι,ειναι αντιςτρόφωσ ανάλογθ με τον όγκο του.συνεπώσ =ςταθερό για Τ=ςταθερό. τθν ακόλουκθ πειραματικι διαδικαςία καταγράφουμε τθν επιβεβαίωςθ του Νομου αυτοφ,αφοφ επικυμοφμε το γινόμενο να παραμείνει ςτακερό αφοφ όλεσ οι μετριςεισ μασ κα ζχουν τθν ίδια κερμοκραςία. ΠΕΙΡΑΜΑΣΙΚΗ ΔΙΑΣΑΞΗ Συναρμολόγηση συσκευής για τη μελέτη του νόμου των αερίων: 1.Tοποκετοφμε ςτο ψθφιακό πολφμετρο το καλϊδιο. Σο ζνα άκρο του καταλιγει ςε δφο μικρά ςιδεράκια διαφορετικοφ πλάτουσ τα οποία τοποκετοφνται ςτο πολφμετρο Σο μεγάλο ςιδεράκι είναι καλό να είναι πιο κοντά ςτθν οκόνθ. Σο άλλο άκρο του καλωδίου τοποκετείται ςτο μεταλλικό κφλινδρο. 2. υνδζουμε το άκρο του ςωλινα του μανομζτρου, με το κυλινδρικό δοχείο και από πάνω ςυνδζουμε τον άλλο ςωλινα που υπάρχει ελεφκεροσ. Σοποκετοφμε το μεταλλικό κφλινδρο μζςα ςτο πλαςτικό κυλινδρικό δοχείο, προςζχοντασ το καλϊδιο να περάςει και αυτό μζςα από τθν εγκοπι του μεταλλικοφ δοχείου και να μθν καταςτραφεί. 3.υνδζουμε ςτο πίςω μζροσ του μεταλλικοφ κυλίνδρου τον χάρακα που είναι θ κλίμακα όγκου. Λειτουργία της συσκευής Αφξηση όγκου: για να αυξιςουμε τον όγκο πιζηουμε προσ τα κάτω τον μοχλό απελευκζρωςθσ που υπάρχει ςτον μεταλλικό κφλινδροκαι τραβάμε προσ τα πάνω το ςτζλεχοσ. Πρϊτα όμωσ γυρίηουμε τισ ςτρόφιγγεσ με τζτοιον τρόπο, ϊςτε να επιτρζπεται θ είςοδοσ αζρα ςτον κάλαμο. Μείωση όγκου: για να μειϊςουμε τον όγκο πιζηουμε τθ χειρολαβι όςεσ φορζσ χρειάηεται για να φτάςουνε ςτον επικυμθτό όγκο. Πρϊτα όμωσ γυρίηουμε τισ ςτρόφιγγεσ με τζτοιον τρόπο, ϊςτε να μθν επιτρζπεται θ είςοδοσ αζρα ςτον
3 κάλαμο. τρόφιγγες: οι ςτρόφιγγεσ ζχουν τρεισ ειςόδουσ. Ανάλογα με τον τρόπο που τισ ζχουμε τοποκετιςει επιτρζπεται ι όχι να μπει αζρασ ςτον κυλινδρικό κάλαμο. ΠΕΙΡΑΜΑΣΙΚΗ ΔΙΑΔΙΚΑΙΑ Η πειραματικι διαδικαςία που ακολουκιςαμε ιταν θ εξισ: Αρχικά ρυκμίςαμε τισ ςτρόφιγγεσ με τζτοιον τρόπο, ϊςτε να επιτρζπεται θ είςοδοσ αζρα ςτον κάλαμο. Πιζςαμε προσ τα κάτω τον μοχλό απελευκζρωςθσ που υπάρχει ςτον μεταλλικό κφλινδρο και τον τραβιξαμε προσ τα πάνω το ςτζλεχοσ. Ανεβάςαμε το ςτζλεχοσ μζχρι τον όγκο 300 ml (το ςτζλεχοσ ζχει μια κόκκινθ χαραγι που μασ δείχνει ςε ςφγκριςθ με τθν κλίμακα από πίςω ςε ποιόν όγκο ζχει φτάςει). Κατόπιν γυρίςαμε τισ ςτρόφιγγεσ ζτςι ϊςτε να μθν ειςζρχεται αζρασ ςτον κάλαμο, αλλά αυτόσ να επικοινωνεί μόνο με το μανόμετρο. Πιζςαμε τθ χειρολαβι και κατεβαίνοντασ κάκε 20 ml ςθμειϊςαμε τθν ζνδειξθ του μανόμετρου. Σθ διαδικαςία τθν ολοκλθρϊνουμε όταν φτάςουμε ςτα 160 ml. ε περίπτωςθ που θ πίεςθ μειϊνεται χωρίσ να μεταβάλλουμε τον όγκο καλό κα είναι να ςτρίβουμε λίγο τθν κάτω ςτρόφιγγα ϊςτε να μθν επικοινωνεί το μανόμετρο με τον κάλαμο και να παραμζνει ςτακερι θ ζνδειξι του. Eπαναφζραμε ςτθν αρχικι κζςθ και πιζηουμε τθ χειρολαβι αλλάηοντασ τον όγκο. Σο ψθφιακό κερμόμετρο καταγράφει τθν κερμοκραςία τθν οποία πρζπει να μετατρζψετε ςε Kelvin και να τθν καταγράψετε ςτθν τρίτθ ςτιλθ του πίνακα ΜΕΣΡΗΕΙ τον ακόλουκο πίνακα εχοφμε τισ μετριςεισ μετά τθν ολοκλιρωςθ του πειράματοσ: Μετριςαμε τθν πίεςθ P, τον όγκοσ V και τθν κερμοκραςία T, υπολογίςαμε το πθλίκο 1/V, το pv/t, το γινόμενο nr και ο αρικμόσ των mole n. (με μετατροπζσ των μονάδων V(από ml ςε m 3 ), P(από bar ςε Pascal), T(από o Cςε K)). 1atm=101254Pa 1 bar =100000Pa R=8,314 j/mol K P(bar) P tot (Pa) V(ml) V(m 3 ) 1/V T( o C) T(K) PV/T nr n 0, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,01184
4 Επεξεργαςία Μετρήςεων- Συμπεράςματα Πειράματοσ το διάγραμμα παριςτάνεται θ πίεςθ P(άξονασ ψ) ςε ςυνάρτθςθ με τον όγκο V(άξονασ χ). Από τθν καταςτατικι εξίςωςθ PV=nRT,ιςχφει P= nrt/v δθλαδι P=a/V. Επομζνωσ όπωσ φαίνεται και ςτο διάγραμμα(1) θ εξίςωςθ είναι τθσ μορφισ ψ=α/χ.το διάγραμμα(2) παριςτάνεται θ ποςότθτα 1/V(άξονασ χ) ςε ςυνάρτθςθ με τθν πίεςθ P (άξονασ ψ). Από τθν καταςτατικι εξίςωςθ PV=nRT ιςχφει 1/V= (1/nRT) P. Η ςχζςθ των μεγεκϊν είναι γραμμικι τθσ μορφισ ψ=αχ και θ κλίςθ τθσ ευκείασ α=1/nrt. Επομζνωσ θ κερμοκραςία Σ είναι ςτακερι και R είναι θ ςτακερά των ιδανικϊν αερίων, μποροφμε από τθν κλίςθ α να υπολογίςουμε τον αρικμό των mole n.από το διάγραμμα P ςε ςυνάρτθςθ του V, που βαςίηεται ςτισ πειραματικζσ μετριςεισ ςυμπεραίνουμε πωσ θ πίεςθ P είναι ανάλογθ τθσ ποςότθτασ 1/V άρα και αντιςτρόφωσ ανάλογθ του όγκου V, άρα ιςχφει ο Νόμοσ του Boyle.Εφόςον θ εξίςωςθ είναι τθσ μορφισ 1/V= (1/nRT)P (ψ=αχ), θ ευκεία κα ζπρεπε να περνάει από τθν αρχι των αξόνων, ενϊ ςτο διάγραμμα παρατθρείται μια μικρι απόκλιςθ. Η απόκλιςθ αυτι οφείλεται ςε ςφάλματα κατά τθ διάρκεια του πειράματοσ όπωσ οι παράγοντεσ του περιβάλλοντοσ που κεωρικθκαν ςτακεροί π.χ κερμοκραςία αλλα κα θ μεταβαλλόμενθ ποςότθτα του αερίου αφοφ το όργανο δεν ιταν ιδανικό. Υπεφθυνοσ Καθηγητήσ:κ.Κατζρθσ Αλζξανδροσ Μακιτρια:Kυπραίου Φωτεινι
5 0, , , ,01157
6
Νόμος του Boyle. Χριστίνα Μαλανδράκη. Ημερομηνία:17/12/2012 Τμήμα : Β3,Β2α. Ο νόμος του Βoyle γενικά.
 2 ο Πρότυπο Πειραματικό Λύκειο Αθηνών Νόμος του Boyle Χριστίνα Μαλανδράκη Ημερομηνία:17/12/2012 Τμήμα : Β3,Β2α Έπειτα από ομαδικό πείραμα που πραγματοποιήθηκε στο εργαστήριο με θέμα τους νόμους των αερίων
2 ο Πρότυπο Πειραματικό Λύκειο Αθηνών Νόμος του Boyle Χριστίνα Μαλανδράκη Ημερομηνία:17/12/2012 Τμήμα : Β3,Β2α Έπειτα από ομαδικό πείραμα που πραγματοποιήθηκε στο εργαστήριο με θέμα τους νόμους των αερίων
Νομός του Boyle (ισόθερμη μεταβολή)
 2 ο Πρότυπο Πειραματικό ΓΕΛ Αθηνών Τμήμα Μάθημα : Β2β θετική : Φυσική Κατεύθυνσης Μαθήτρια : Ελένη Σέρβου Θέμα : Νομός του Boyle (ισόθερμη μεταβολή) 1.Υπόθεση : Η μεταβολή, κατά τη διάρκεια της οποίας
2 ο Πρότυπο Πειραματικό ΓΕΛ Αθηνών Τμήμα Μάθημα : Β2β θετική : Φυσική Κατεύθυνσης Μαθήτρια : Ελένη Σέρβου Θέμα : Νομός του Boyle (ισόθερμη μεταβολή) 1.Υπόθεση : Η μεταβολή, κατά τη διάρκεια της οποίας
2 ο Πειραµατικό Λύκειο Αθηνών Μάθηµα: Φυσική Κατεύθυνσης Η µαθήτρια του τµήµατος Β2α: ΑΘΗΝΑ- ΙΟΝΥΣΙΑ ΓΙΑΝΝΟΠΟΥΛΟΥ
 2 ο Πειραµατικό Λύκειο Αθηνών Μάθηµα: Φυσική Κατεύθυνσης Η µαθήτρια του τµήµατος Β2α: ΑΘΗΝΑ- ΙΟΝΥΣΙΑ ΓΙΑΝΝΟΠΟΥΛΟΥ - 1 - Στη θερµοδυναµική ο Νόµος του Μπόιλ είναι ένας από τους τρεις νόµους των αερίων.
2 ο Πειραµατικό Λύκειο Αθηνών Μάθηµα: Φυσική Κατεύθυνσης Η µαθήτρια του τµήµατος Β2α: ΑΘΗΝΑ- ΙΟΝΥΣΙΑ ΓΙΑΝΝΟΠΟΥΛΟΥ - 1 - Στη θερµοδυναµική ο Νόµος του Μπόιλ είναι ένας από τους τρεις νόµους των αερίων.
Περιεχόµενα 1. Εισαγωγή Νόµος του Boyle Πειραµατική ιάταξη ιαδικασία Πειράµατος Μετρήσεις Συµπεράσµατα...8 2
 2 o Πειραµατικό Γενικό Λύκειο Αθηνών Σχολικό Έτος 2012-2013 Πειραµατική επαλήθευση του νόµου του Boyle Με βάση την 1 η ραστηριότητα του φύλλου εργασίας για τους Νόµους των Αερίων. Κωνσταντίνος Κλοκανάς
2 o Πειραµατικό Γενικό Λύκειο Αθηνών Σχολικό Έτος 2012-2013 Πειραµατική επαλήθευση του νόµου του Boyle Με βάση την 1 η ραστηριότητα του φύλλου εργασίας για τους Νόµους των Αερίων. Κωνσταντίνος Κλοκανάς
Slide 1. Εισαγωγή στη ψυχρομετρία
 Slide 1 Εισαγωγή στη ψυχρομετρία 1 Slide 2 Σφντομη ειςαγωγή ςτη ψυχρομετρία. Διάγραμμα Mollier (πίεςησ-ενθαλπίασ P-H) Σο διάγραμμα Mollier είναι μία γραφικι παράςταςθ ςε ζναν άξονα ςυντεταγμζνων γραμμϊν
Slide 1 Εισαγωγή στη ψυχρομετρία 1 Slide 2 Σφντομη ειςαγωγή ςτη ψυχρομετρία. Διάγραμμα Mollier (πίεςησ-ενθαλπίασ P-H) Σο διάγραμμα Mollier είναι μία γραφικι παράςταςθ ςε ζναν άξονα ςυντεταγμζνων γραμμϊν
Επαλήθευση Νόµων Ιδανικού Αερίου
 Επαλήθευση Νόµων Ιδανικού Αερίου Στοιχεία θεωρίας: για ένα ιδανικό αέριο ισχύει η καταστατική εξίσωση : PV = nrt. Οι νόµοι που θα επαληθευτούν από την πειραµατική διαδικασία προκύπτουν από την καταστατική
Επαλήθευση Νόµων Ιδανικού Αερίου Στοιχεία θεωρίας: για ένα ιδανικό αέριο ισχύει η καταστατική εξίσωση : PV = nrt. Οι νόµοι που θα επαληθευτούν από την πειραµατική διαδικασία προκύπτουν από την καταστατική
2 ο ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΣΧΟΛΙΚΟ ΕΤΟΣ 2011/12 ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΑΘΗΝΩΝ ΠΕΙΡΑΜΑΤΙΚΗ ΕΠΑΛΗΘΕΥΣΗ ΤΟΥ ΝΟΜΟΥ ΤΟΥ BOYLE
 2 ο ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΣΧΟΛΙΚΟ ΕΤΟΣ 2011/12 ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΑΘΗΝΩΝ ΠΕΙΡΑΜΑΤΙΚΗ ΕΠΑΛΗΘΕΥΣΗ ΤΟΥ ΝΟΜΟΥ ΤΟΥ BOYLE ΑΓΓΕΛΙΔΑΚΗ ΔΑΝΑΗ ΔΗΜΗΤΡΑ ΤΜΗΜΑ Β2α ΥΠΕΥΘΥΝΗ ΚΑΘΗΓΗΤΡΙΑ Κα ΑΓΑΛΟΠΟΥΛΟΥ I. ΓΕΝΙΚΑ ΓΙΑ ΤΟΝ ΝΟΜΟ
2 ο ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΣΧΟΛΙΚΟ ΕΤΟΣ 2011/12 ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΑΘΗΝΩΝ ΠΕΙΡΑΜΑΤΙΚΗ ΕΠΑΛΗΘΕΥΣΗ ΤΟΥ ΝΟΜΟΥ ΤΟΥ BOYLE ΑΓΓΕΛΙΔΑΚΗ ΔΑΝΑΗ ΔΗΜΗΤΡΑ ΤΜΗΜΑ Β2α ΥΠΕΥΘΥΝΗ ΚΑΘΗΓΗΤΡΙΑ Κα ΑΓΑΛΟΠΟΥΛΟΥ I. ΓΕΝΙΚΑ ΓΙΑ ΤΟΝ ΝΟΜΟ
Επαναληπτικές Ασκήσεις στα κευ 1 και 2
 Επαναληπτικές Ασκήσεις στα κευ 1 και 2 1. Αζριο με όγκο 0,004 m 3 κερμαίνεται με ςτακερι πίεςθ p =1,2 atm μζχρι ο όγκοσ του να γίνει 0,006 m 3. Τπολογίςτε το ζργο που παράγει το αζριο. Δίνεται 1 atm =
Επαναληπτικές Ασκήσεις στα κευ 1 και 2 1. Αζριο με όγκο 0,004 m 3 κερμαίνεται με ςτακερι πίεςθ p =1,2 atm μζχρι ο όγκοσ του να γίνει 0,006 m 3. Τπολογίςτε το ζργο που παράγει το αζριο. Δίνεται 1 atm =
2. ΠΕΙΡΑΜΑΤΙΚΗ ΔΙΑΤΑΞΗ
 2 Πειραματικό Γενικό Λύκειο Αθηνών Κλεομένης Σαλαπάτας Επιστημονική Αναφορά Για Τον Νόμο του Charles 1. ΥΠΟΘΕΣΗ Η ακόλουθη πειραματική διαδικασία που διεξήχθη βασίζεται σε ένας από τους νόμους των αερίων
2 Πειραματικό Γενικό Λύκειο Αθηνών Κλεομένης Σαλαπάτας Επιστημονική Αναφορά Για Τον Νόμο του Charles 1. ΥΠΟΘΕΣΗ Η ακόλουθη πειραματική διαδικασία που διεξήχθη βασίζεται σε ένας από τους νόμους των αερίων
ΠΕΙΡΑΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΓΙΑ ΤΟ ΝΟΜΟ ΤΟΥ BOYLE
 2ο ΠΕΙΡΑΜΑΤΙΚΟ ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΑΘΗΝΩΝ ΠΕΙΡΑΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΓΙΑ ΤΟ ΝΟΜΟ ΤΟΥ BOYLE Β ΛΥΚΕΙΟΥ Β2α ΦΥΣΙΚΗΚΑΤΕΥΘΥΝΣΗΣ 17/1/2012 ΚΑΤΑΣΤΑΤΙΚΗ ΕΞΙΣΩΣΗ ΑΕΡΙΩΝ Τα δυο πρώτα κεφάλαια,στην υλη της Β λυκείου στη Φυσική
2ο ΠΕΙΡΑΜΑΤΙΚΟ ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΑΘΗΝΩΝ ΠΕΙΡΑΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΓΙΑ ΤΟ ΝΟΜΟ ΤΟΥ BOYLE Β ΛΥΚΕΙΟΥ Β2α ΦΥΣΙΚΗΚΑΤΕΥΘΥΝΣΗΣ 17/1/2012 ΚΑΤΑΣΤΑΤΙΚΗ ΕΞΙΣΩΣΗ ΑΕΡΙΩΝ Τα δυο πρώτα κεφάλαια,στην υλη της Β λυκείου στη Φυσική
Διαγώνισμα Χημείας Γ Λυκείου στα Κεφάλαια 1-4
 Διαγώνισμα Χημείας Γ Λυκείου στα Κεφάλαια 1-4 Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-5 και δίπλα το γράμμα που αντιςτοιχεί ςτθ
Διαγώνισμα Χημείας Γ Λυκείου στα Κεφάλαια 1-4 Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-5 και δίπλα το γράμμα που αντιςτοιχεί ςτθ
Η άςκθςθ αποτελεί τροποποιθμζνθ εκδοχι του κζματοσ φυςικισ, τθσ Ευρωπαϊκισ Ολυμπιάδασ Φυςικών Επιςτθμών 2009_επιμζλεια κζματοσ: Κώςτασ Παπαμιχάλθσ
 ΕΚΦΕ Αχαρνών Η άςκθςθ αποτελεί τροποποιθμζνθ εκδοχι του κζματοσ φυςικισ, τθσ Ευρωπαϊκισ Ολυμπιάδασ Φυςικών Επιςτθμών 9_επιμζλεια κζματοσ: Κώςτασ Παπαμιχάλθσ Εφαρμογζσ τθσ Αρχισ του Αρχιμιδθ & τθσ ςυνκικθσ
ΕΚΦΕ Αχαρνών Η άςκθςθ αποτελεί τροποποιθμζνθ εκδοχι του κζματοσ φυςικισ, τθσ Ευρωπαϊκισ Ολυμπιάδασ Φυςικών Επιςτθμών 9_επιμζλεια κζματοσ: Κώςτασ Παπαμιχάλθσ Εφαρμογζσ τθσ Αρχισ του Αρχιμιδθ & τθσ ςυνκικθσ
ΕΝΟΣΗΣΑ 1: ΓΝΩΡIΖΩ ΣΟΝ ΤΠΟΛΟΓΙΣΗ. ΚΕΦΑΛΑΙΟ 3: Εργονομία
 ΕΝΟΣΗΣΑ 1: ΓΝΩΡIΖΩ ΣΟΝ ΤΠΟΛΟΓΙΣΗ Εργονομία, ωςτι ςτάςθ εργαςίασ, Εικονοςτοιχείο (pixel), Ανάλυςθ οκόνθσ (resolution), Μζγεκοσ οκόνθσ Ποιεσ επιπτϊςεισ μπορεί να ζχει θ πολφωρθ χριςθ του υπολογιςτι ςτθν
ΕΝΟΣΗΣΑ 1: ΓΝΩΡIΖΩ ΣΟΝ ΤΠΟΛΟΓΙΣΗ Εργονομία, ωςτι ςτάςθ εργαςίασ, Εικονοςτοιχείο (pixel), Ανάλυςθ οκόνθσ (resolution), Μζγεκοσ οκόνθσ Ποιεσ επιπτϊςεισ μπορεί να ζχει θ πολφωρθ χριςθ του υπολογιςτι ςτθν
Α ΕΚΦΕ ΑΝ. ΑΤΤΙΚΗΣ Υπ. Κ. Παπαμιχάλθσ. Μζτρηςη του λόγου γ=c P /C V των αερίων με τη μζθοδο Clement Desormes
 Α ΕΚΦΕ ΑΝ. ΑΤΤΙΚΗΣ Υπ. Κ. Παπαμιχάλθσ Μζτρηςη του λόγου γ=c P /C V των αερίων με τη μζθοδο Clement Desormes Στόχοι 1. Ανάλυςθ τθσ λειτουργίασ τθσ πειραματικισ διάταξθσ 2. Εφαρμογι των νόμων τθσ κερμοδυναμικισ
Α ΕΚΦΕ ΑΝ. ΑΤΤΙΚΗΣ Υπ. Κ. Παπαμιχάλθσ Μζτρηςη του λόγου γ=c P /C V των αερίων με τη μζθοδο Clement Desormes Στόχοι 1. Ανάλυςθ τθσ λειτουργίασ τθσ πειραματικισ διάταξθσ 2. Εφαρμογι των νόμων τθσ κερμοδυναμικισ
Electronics μαηί με τα ςυνοδευτικά καλϊδια και το αιςκθτιριο κερμοκραςίασ LM335 που περιζχονται
 Σομζασ: Ηλεκτρονικόσ Εκπαιδευτικόσ: Μπουλταδάκθσ τζλιοσ Μάθημα: υλλογι και μεταφορά δεδομζνων μζςω Η/Τ, Αιςκθτιρεσ-Ενεργοποιθτζσ Αντικείμενο: α) Μζτρθςθ κερμοκραςίασ με το αιςκθτιριο LM335 και μεταφορά
Σομζασ: Ηλεκτρονικόσ Εκπαιδευτικόσ: Μπουλταδάκθσ τζλιοσ Μάθημα: υλλογι και μεταφορά δεδομζνων μζςω Η/Τ, Αιςκθτιρεσ-Ενεργοποιθτζσ Αντικείμενο: α) Μζτρθςθ κερμοκραςίασ με το αιςκθτιριο LM335 και μεταφορά
Θεςιακά ςυςτιματα αρίκμθςθσ
 Θεςιακά ςυςτιματα αρίκμθςθσ Δρ. Χρήστος Ηλιούδης αρικμθτικό ςφςτθμα αρίκμθςθσ (Number System) Αξία (value) παράςταςθ Οι αξίεσ (π.χ. το βάροσ μιασ ποςότθτασ μιλων) μποροφν να παραςτακοφν με πολλοφσ τρόπουσ
Θεςιακά ςυςτιματα αρίκμθςθσ Δρ. Χρήστος Ηλιούδης αρικμθτικό ςφςτθμα αρίκμθςθσ (Number System) Αξία (value) παράςταςθ Οι αξίεσ (π.χ. το βάροσ μιασ ποςότθτασ μιλων) μποροφν να παραςτακοφν με πολλοφσ τρόπουσ
Διάδοση θερμότητας σε μία διάσταση
 Διάδοση θερμότητας σε μία διάσταση Η θεωρητική μελζτη που ακολουθεί πραγματοποιήθηκε με αφορμή την εργαςτηριακή άςκηςη μζτρηςησ του ςυντελεςτή θερμικήσ αγωγιμότητασ του αλουμινίου, ςτην οποία διαγωνίςτηκαν
Διάδοση θερμότητας σε μία διάσταση Η θεωρητική μελζτη που ακολουθεί πραγματοποιήθηκε με αφορμή την εργαςτηριακή άςκηςη μζτρηςησ του ςυντελεςτή θερμικήσ αγωγιμότητασ του αλουμινίου, ςτην οποία διαγωνίςτηκαν
Πανελλαδικε σ Εξετα ςεισ Γ Τα ξησ Ημερη ςιου και Δ Τα ξησ Εςπερινου Γενικου Λυκει ου
 Ζνωςθ Ελλινων Χθμικϊν Πανελλαδικε σ Εξετα ςεισ Γ Τα ξησ Ημερη ςιου και Δ Τα ξησ Εςπερινου Γενικου Λυκει ου Χημεία 03/07/2017 Τμιμα Παιδείασ και Χθμικισ Εκπαίδευςθσ 0 Πανελλαδικε σ Εξετα ςεισ Γ Τα ξησ Ημερη
Ζνωςθ Ελλινων Χθμικϊν Πανελλαδικε σ Εξετα ςεισ Γ Τα ξησ Ημερη ςιου και Δ Τα ξησ Εςπερινου Γενικου Λυκει ου Χημεία 03/07/2017 Τμιμα Παιδείασ και Χθμικισ Εκπαίδευςθσ 0 Πανελλαδικε σ Εξετα ςεισ Γ Τα ξησ Ημερη
ΘΥ101: Ειςαγωγι ςτθν Πλθροφορικι
 Παράςταςη κινητήσ υποδιαςτολήσ ςφμφωνα με το πρότυπο ΙΕΕΕ Δρ. Χρήστος Ηλιούδης το πρότυπο ΙΕΕΕ 754 ζχει χρθςιμοποιθκεί ευρζωσ ςε πραγματικοφσ υπολογιςτζσ. Το πρότυπο αυτό κακορίηει δφο βαςικζσ μορφζσ κινθτισ
Παράςταςη κινητήσ υποδιαςτολήσ ςφμφωνα με το πρότυπο ΙΕΕΕ Δρ. Χρήστος Ηλιούδης το πρότυπο ΙΕΕΕ 754 ζχει χρθςιμοποιθκεί ευρζωσ ςε πραγματικοφσ υπολογιςτζσ. Το πρότυπο αυτό κακορίηει δφο βαςικζσ μορφζσ κινθτισ
ΔΙΑΓΩΝΙΣΜΑ ΧΗΜΕΙΑΣ Γ'ΛΥΚΕΙΟΥ. Ονοματεπϊνυμο:... Ημ/νία:... Τάξθ:...Χρονικι Διάρκεια:...
 ΔΙΑΓΩΝΙΣΜΑ ΧΗΜΕΙΑΣ Γ'ΛΥΚΕΙΟΥ Κεφάλαια 1,2,3,4,5(μέχρι ενότητα 5) Ονοματεπϊνυμο:... Ημ/νία:... Τάξθ:...Χρονικι Διάρκεια:... Βακμόσ: ΘΕΜΑ Α Για τισ προτάςεισ Α1 ζωσ Α5 να γράψετε ςτο τετράδιό ςασ τον αρικμό
ΔΙΑΓΩΝΙΣΜΑ ΧΗΜΕΙΑΣ Γ'ΛΥΚΕΙΟΥ Κεφάλαια 1,2,3,4,5(μέχρι ενότητα 5) Ονοματεπϊνυμο:... Ημ/νία:... Τάξθ:...Χρονικι Διάρκεια:... Βακμόσ: ΘΕΜΑ Α Για τισ προτάςεισ Α1 ζωσ Α5 να γράψετε ςτο τετράδιό ςασ τον αρικμό
Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Ε.Ο.Κ. και Ε.Ο.Μ.Κ.
 Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Ε.Ο.Κ. και Ε.Ο.Μ.Κ. Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα
Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Ε.Ο.Κ. και Ε.Ο.Μ.Κ. Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα
ΧΗΜΕΙΑ Γ ΛΥΚΕΙΟΥ Κεφάλαια: (μέχρι ενότητα 8) Ονοματεπϊνυμο:... Ημ/νία:... Τάξθ:...Χρονικι Διάρκεια:... Βακμόσ:
 ΧΗΜΕΙΑ Γ ΛΥΚΕΙΟΥ Κεφάλαια:1-2-3-4-5(μέχρι ενότητα 8) Ονοματεπϊνυμο:... Ημ/νία:... Τάξθ:...Χρονικι Διάρκεια:... Βακμόσ: ΘΕΜΑ Α Για τισ προτάςεισ Α1 ζωσ Α5 να γράψετε ςτο τετράδιό ςασ τον αρικμό τθσ πρόταςθσ
ΧΗΜΕΙΑ Γ ΛΥΚΕΙΟΥ Κεφάλαια:1-2-3-4-5(μέχρι ενότητα 8) Ονοματεπϊνυμο:... Ημ/νία:... Τάξθ:...Χρονικι Διάρκεια:... Βακμόσ: ΘΕΜΑ Α Για τισ προτάςεισ Α1 ζωσ Α5 να γράψετε ςτο τετράδιό ςασ τον αρικμό τθσ πρόταςθσ
ΔΙΑΓΩΝΙΣΜΑ XHMEIAΣ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΑ:
 ΔΙΑΓΩΝΙΣΜΑ XHMEIAΣ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΑ: 1-2-3-4-5 Ονοματεπϊνυμο:..... Ημ/νία:.. Σάξθ: Χρονικι Διάρκεια:... Βακμόσ: ΘΕΜΑ Α Για τισ προτάςεισ Α1 ζωσ Α5 να γράψετε ςτο τετράδιό ςασ τον αρικμό τθσ πρόταςθσ
ΔΙΑΓΩΝΙΣΜΑ XHMEIAΣ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΑ: 1-2-3-4-5 Ονοματεπϊνυμο:..... Ημ/νία:.. Σάξθ: Χρονικι Διάρκεια:... Βακμόσ: ΘΕΜΑ Α Για τισ προτάςεισ Α1 ζωσ Α5 να γράψετε ςτο τετράδιό ςασ τον αρικμό τθσ πρόταςθσ
ΔΙΑΓΩΝΙΣΜΑ ΧΗΜΕΙΑΣ Γ'ΛΥΚΕΙΟΥ. Κεφάλαια 1,2,3,4,5(μέχρι ενότητα 3) Ονοματεπϊνυμο:... Ημ/νία:... Τάξθ:...Χρονικι Διάρκεια:...
 ΔΙΑΓΩΝΙΣΜΑ ΧΗΜΕΙΑΣ Γ'ΛΥΚΕΙΟΥ Κεφάλαια 1,2,3,4,5(μέχρι ενότητα 3) Ονοματεπϊνυμο:... Ημ/νία:... Τάξθ:...Χρονικι Διάρκεια:... Βακμόσ: ΘΕΜΑ Α Για τισ προτάςεισ Α1 ζωσ Α5 να γράψετε ςτο τετράδιό ςασ τον αρικμό
ΔΙΑΓΩΝΙΣΜΑ ΧΗΜΕΙΑΣ Γ'ΛΥΚΕΙΟΥ Κεφάλαια 1,2,3,4,5(μέχρι ενότητα 3) Ονοματεπϊνυμο:... Ημ/νία:... Τάξθ:...Χρονικι Διάρκεια:... Βακμόσ: ΘΕΜΑ Α Για τισ προτάςεισ Α1 ζωσ Α5 να γράψετε ςτο τετράδιό ςασ τον αρικμό
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 9. ΑΝΩΣΗ Η αρχή του Αρχιμήδη
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 9 ΑΝΩΣΗ Η αρχή του Αρχιμήδη Όργανα Τλικά: Δυναμόμετρο 2 ι 2,5Ν Δοκιμαςτικόσ ςωλινασ Βαρίδι 50g Βάςθ Ράβδοι ςτιριξθσ Δοχείο με νερό κοπόσ τθσ άςκθςθσ: Οι μακθτζσ να κατανοιςουν ότι θ
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 9 ΑΝΩΣΗ Η αρχή του Αρχιμήδη Όργανα Τλικά: Δυναμόμετρο 2 ι 2,5Ν Δοκιμαςτικόσ ςωλινασ Βαρίδι 50g Βάςθ Ράβδοι ςτιριξθσ Δοχείο με νερό κοπόσ τθσ άςκθςθσ: Οι μακθτζσ να κατανοιςουν ότι θ
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα
 Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα Αυτζσ οι οδθγίεσ ζχουν ςτόχο λοιπόν να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο του Άβακα. Παρουςίαςη
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα Αυτζσ οι οδθγίεσ ζχουν ςτόχο λοιπόν να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο του Άβακα. Παρουςίαςη
ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ ΜΕΛΕΣΗ ΣΗ ΚΙΝΗΗ ΩΜΑΣΟ Ε ΠΛΑΓΙΟ ΕΠΙΠΕΔΟ - ΜΕΣΡΗΗ ΣΟΤ ΤΝΣΕΛΕΣΗ ΣΡΙΒΗ ΟΛΙΘΗΗ
 ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ ΜΕΛΕΣΗ ΣΗ ΚΙΝΗΗ ΩΜΑΣΟ Ε ΠΛΑΓΙΟ ΕΠΙΠΕΔΟ - ΜΕΣΡΗΗ ΣΟΤ ΤΝΣΕΛΕΣΗ ΣΡΙΒΗ ΟΛΙΘΗΗ ΕΚΦΕ Α & Β ΑΝΑΣΟΛΙΚΗ ΑΣΣΙΚΗ τόχοι Μετά το πζρασ τθσ εργαςτθριακισ άςκθςθσ, οι μακθτζσ κα πρζπει να είναι ςε κζςθ:
ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ ΜΕΛΕΣΗ ΣΗ ΚΙΝΗΗ ΩΜΑΣΟ Ε ΠΛΑΓΙΟ ΕΠΙΠΕΔΟ - ΜΕΣΡΗΗ ΣΟΤ ΤΝΣΕΛΕΣΗ ΣΡΙΒΗ ΟΛΙΘΗΗ ΕΚΦΕ Α & Β ΑΝΑΣΟΛΙΚΗ ΑΣΣΙΚΗ τόχοι Μετά το πζρασ τθσ εργαςτθριακισ άςκθςθσ, οι μακθτζσ κα πρζπει να είναι ςε κζςθ:
Διαγώνισμα Φυσική ς Κατευ θυνσής Γ Λυκει ου - Ταλαντώσεις
 Διαγώνισμα Φυσική ς Κατευ θυνσής Γ Λυκει ου - Ταλαντώσεις Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί
Διαγώνισμα Φυσική ς Κατευ θυνσής Γ Λυκει ου - Ταλαντώσεις Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί
ΡΑΝΕΛΛΘΝΙΕΣ ΕΞΕΤΑΣΕΙΣ 2014 ΧΗΜΕΙΑ ΘΕΤΙΚΘΣ ΚΑΤΕΥΘΥΝΣΘΣ
 ΡΑΝΕΛΛΘΝΙΕΣ ΕΞΕΤΑΣΕΙΣ 2014 ΧΗΜΕΙΑ ΘΕΤΙΚΘΣ ΚΑΤΕΥΘΥΝΣΘΣ Θζμα Α Α1: γ, Α2: β, Α3: α, Α4: β, A5: β Θζμα Β Β1: Σ ι Λ (ελλιπισ διατφπωςθ), Λ, Σ, Σ, Σ Β2: α) Οι διαφορζσ μεταξφ ς και π δεςμοφ είναι: α. Στον ς
ΡΑΝΕΛΛΘΝΙΕΣ ΕΞΕΤΑΣΕΙΣ 2014 ΧΗΜΕΙΑ ΘΕΤΙΚΘΣ ΚΑΤΕΥΘΥΝΣΘΣ Θζμα Α Α1: γ, Α2: β, Α3: α, Α4: β, A5: β Θζμα Β Β1: Σ ι Λ (ελλιπισ διατφπωςθ), Λ, Σ, Σ, Σ Β2: α) Οι διαφορζσ μεταξφ ς και π δεςμοφ είναι: α. Στον ς
ΑΠΑΝΤΗΣΕΙΣ ΧΗΜΕΙΑΣ Γ ΛΥΚΕΙΟΥ
 ΘΕΜΑ Α A1. i A2. i A. ii A4. i A. iii ΑΠΑΝΤΗΣΕΙΣ ΧΗΜΕΙΑΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Β Β1. -1 0-2 0 4HCl (g) + O 2(g) 2H 2 O (g) + 2Cl 2(g), ΔΘ
ΘΕΜΑ Α A1. i A2. i A. ii A4. i A. iii ΑΠΑΝΤΗΣΕΙΣ ΧΗΜΕΙΑΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Β Β1. -1 0-2 0 4HCl (g) + O 2(g) 2H 2 O (g) + 2Cl 2(g), ΔΘ
3 ο ΓΥΜΝΑΣΙΟ ΤΡΙΚΑΛΩΝ ΕΡΓΑΣΙΑ ΤΕΧΝΟΛΟΓΙΑΣ Γ ΓΥΜΝΑΣΙΟΥ
 3 ο ΓΥΜΝΑΣΙΟ ΤΡΙΚΑΛΩΝ ΕΡΓΑΣΙΑ ΤΕΧΝΟΛΟΓΙΑΣ Γ ΓΥΜΝΑΣΙΟΥ 1) Τίτλοσ τθσ ζρευνασ: «Ποια είναι θ επίδραςθ τθσ κερμοκραςίασ ςτθ διαλυτότθτα των ςτερεϊν ςτο νερό;» 2) Περιγραφι του ςκοποφ τθσ ζρευνασ: Η ζρευνα
3 ο ΓΥΜΝΑΣΙΟ ΤΡΙΚΑΛΩΝ ΕΡΓΑΣΙΑ ΤΕΧΝΟΛΟΓΙΑΣ Γ ΓΥΜΝΑΣΙΟΥ 1) Τίτλοσ τθσ ζρευνασ: «Ποια είναι θ επίδραςθ τθσ κερμοκραςίασ ςτθ διαλυτότθτα των ςτερεϊν ςτο νερό;» 2) Περιγραφι του ςκοποφ τθσ ζρευνασ: Η ζρευνα
ΠΕΙΡΑΜΑΣΙΖΟΜΑΙ ΜΕ ΣΟ ΠΙΣΙ ΜΗΔΕΝΙΚΗ ΕΝΕΡΓΕΙΑΚΗ ΚΑΣΑΝΑΛΩΗ
 ΠΕΙΡΑΜΑΣΙΖΟΜΑΙ ΜΕ ΣΟ ΠΙΣΙ ΜΗΔΕΝΙΚΗ ΕΝΕΡΓΕΙΑΚΗ ΚΑΣΑΝΑΛΩΗ Σο παρϊν ζγγραφο αφοφ το ςυμπλθρϊςετε, το αποκθκεφετε ςτον υπολογιςτι ςασ και το ςτζλνετε ωσ επιςυναπτόμενο (Attachment) ςτθν διεφκυνςθ θλεκτρονικοφ
ΠΕΙΡΑΜΑΣΙΖΟΜΑΙ ΜΕ ΣΟ ΠΙΣΙ ΜΗΔΕΝΙΚΗ ΕΝΕΡΓΕΙΑΚΗ ΚΑΣΑΝΑΛΩΗ Σο παρϊν ζγγραφο αφοφ το ςυμπλθρϊςετε, το αποκθκεφετε ςτον υπολογιςτι ςασ και το ςτζλνετε ωσ επιςυναπτόμενο (Attachment) ςτθν διεφκυνςθ θλεκτρονικοφ
Διαγώνισμα Φυσική ς Α Λυκει ου Έργο και Ενε ργεια
 Διαγώνισμα Φυσική ς Α Λυκει ου Έργο και Ενε ργεια Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί
Διαγώνισμα Φυσική ς Α Λυκει ου Έργο και Ενε ργεια Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί
Παράςταςη ςυμπλήρωμα ωσ προσ 1
 Δρ. Χρήστος Ηλιούδης Θζματα διάλεξησ ΣΤ1 Προςθεςη αφαίρεςη ςτο ΣΤ1 2 ή ΣΤ1 Ονομάηουμε ςυμπλιρωμα ωσ προσ μειωμζνθ βάςθ R ενόσ μθ προςθμαςμζνου αρικμοφ Χ = ( Χ θ-1 Χ θ-2... Χ 0 ) R ζναν άλλον αρικμό Χ'
Δρ. Χρήστος Ηλιούδης Θζματα διάλεξησ ΣΤ1 Προςθεςη αφαίρεςη ςτο ΣΤ1 2 ή ΣΤ1 Ονομάηουμε ςυμπλιρωμα ωσ προσ μειωμζνθ βάςθ R ενόσ μθ προςθμαςμζνου αρικμοφ Χ = ( Χ θ-1 Χ θ-2... Χ 0 ) R ζναν άλλον αρικμό Χ'
Αυτόνομοι Πράκτορες. Αναφορά Εργασίας Εξαμήνου. Το αστέρι του Aibo και τα κόκαλα του
 Αυτόνομοι Πράκτορες Αναφορά Εργασίας Εξαμήνου Το αστέρι του Aibo και τα κόκαλα του Jaohar Osman Η πρόταςθ εργαςίασ που ζκανα είναι το παρακάτω κείμενο : - ξ Aibo αγαπάει πάρα πξλύ ρα κόκαλα και πάμρα ρα
Αυτόνομοι Πράκτορες Αναφορά Εργασίας Εξαμήνου Το αστέρι του Aibo και τα κόκαλα του Jaohar Osman Η πρόταςθ εργαςίασ που ζκανα είναι το παρακάτω κείμενο : - ξ Aibo αγαπάει πάρα πξλύ ρα κόκαλα και πάμρα ρα
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ
 ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Α ΔΙΑΓΩΝΙΣΜΟΣ ΕΠΙΛΟΓΗΣ IMC (Key Stage II) 9 Μαρτίου 2016 ΧΡΟΝΟΣ: 2 ΩΡΕΣ Λύςεισ : Πρόβλημα 1 (α) Να βρείτε τθν τιμι του για να ιςχφει θ πιο κάτω ςχζςθ: (β) Ο Ανδρζασ τελειϊνει
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Α ΔΙΑΓΩΝΙΣΜΟΣ ΕΠΙΛΟΓΗΣ IMC (Key Stage II) 9 Μαρτίου 2016 ΧΡΟΝΟΣ: 2 ΩΡΕΣ Λύςεισ : Πρόβλημα 1 (α) Να βρείτε τθν τιμι του για να ιςχφει θ πιο κάτω ςχζςθ: (β) Ο Ανδρζασ τελειϊνει
Πολυπλέκτες. 0 x 0 F = S x 0 + Sx 1 1 x 1
 Πολυπλέκτες Ο πολυπλζκτθσ (multipleer - ) είναι ζνα ςυνδυαςτικό κφκλωμα που επιλζγει δυαδικι πλθροφορία μιασ από πολλζσ γραμμζσ ειςόδου και τθν κατευκφνει ςε μια και μοναδικι γραμμι εξόδου. Η επιλογι μιασ
Πολυπλέκτες Ο πολυπλζκτθσ (multipleer - ) είναι ζνα ςυνδυαςτικό κφκλωμα που επιλζγει δυαδικι πλθροφορία μιασ από πολλζσ γραμμζσ ειςόδου και τθν κατευκφνει ςε μια και μοναδικι γραμμι εξόδου. Η επιλογι μιασ
Α1. Ροιεσ από τισ δυνάμεισ του ςχιματοσ ζχουν μθδενικι ροπι ωσ προσ τον άξονα (ε) περιςτροφισ του δίςκου;
 ΜΑΘΗΜΑ /ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΡΩΝΥMΟ: ΗΜΕΟΜΗΝΙΑ: 1/3/2015 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: ΚΥΜΑΤΑ ΚΑΙ ΣΤΕΕΟ ΣΩΜΑ ΘΕΜΑ Α Α1. Ροιεσ από τισ δυνάμεισ του ςχιματοσ ζχουν μθδενικι ροπι ωσ προσ τον άξονα (ε)
ΜΑΘΗΜΑ /ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΡΩΝΥMΟ: ΗΜΕΟΜΗΝΙΑ: 1/3/2015 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: ΚΥΜΑΤΑ ΚΑΙ ΣΤΕΕΟ ΣΩΜΑ ΘΕΜΑ Α Α1. Ροιεσ από τισ δυνάμεισ του ςχιματοσ ζχουν μθδενικι ροπι ωσ προσ τον άξονα (ε)
ΑΚΗΕΚ ΚΟΝΣΚΚΗ ΚΟΡΡΟΠΚΑ ΑΚΗΕΚ ME ENAN ΗΛΕΚΣΟΛΤΣΗ
 ΑΚΗΕΚ ΚΟΝΣΚΚΗ ΚΟΡΡΟΠΚΑ ΑΚΗΕΚ ME ENAN ΗΛΕΚΣΟΛΤΣΗ 1 Ποςότθτα αζριασ ΝΗ 3 ίςθ με 2,24 L, μετρθμζνα ςε STP, διαλφεται ςτο νερό οπότε προκφπτει διάλυμα όγκου 2 L ςτο οποίο βρζκθκε ότι *ΟΗ - ]=10-3 Μ a Να υπολογίςετε
ΑΚΗΕΚ ΚΟΝΣΚΚΗ ΚΟΡΡΟΠΚΑ ΑΚΗΕΚ ME ENAN ΗΛΕΚΣΟΛΤΣΗ 1 Ποςότθτα αζριασ ΝΗ 3 ίςθ με 2,24 L, μετρθμζνα ςε STP, διαλφεται ςτο νερό οπότε προκφπτει διάλυμα όγκου 2 L ςτο οποίο βρζκθκε ότι *ΟΗ - ]=10-3 Μ a Να υπολογίςετε
ΔΙΑΘΛΑΗ - ΠΕΙΡΑΜΑΣΙΚΟ ΤΠΟΛΟΓΙΜΟ ΔΕΙΚΣΗ ΔΙΑΘΛΑΗ ΕΛΑΙΟΛΑΔΟΤ
 ΕΚΦΕ ΑΧΑΡΝΩΝ ΔΙΑΘΛΑΗ - ΠΕΙΡΑΜΑΣΙΚΟ ΤΠΟΛΟΓΙΜΟ ΔΕΙΚΣΗ ΔΙΑΘΛΑΗ ΕΛΑΙΟΛΑΔΟΤ Η άςκηςη αποτελεί τροποποιημζνη εκδοχή του θζματοσ τησ Ευρωπαϊκήσ Ολυμπιάδασ Φυςικών Επιςτημών EUSO 2014_Επιμζλεια Παπαμιχάλησ Κ.
ΕΚΦΕ ΑΧΑΡΝΩΝ ΔΙΑΘΛΑΗ - ΠΕΙΡΑΜΑΣΙΚΟ ΤΠΟΛΟΓΙΜΟ ΔΕΙΚΣΗ ΔΙΑΘΛΑΗ ΕΛΑΙΟΛΑΔΟΤ Η άςκηςη αποτελεί τροποποιημζνη εκδοχή του θζματοσ τησ Ευρωπαϊκήσ Ολυμπιάδασ Φυςικών Επιςτημών EUSO 2014_Επιμζλεια Παπαμιχάλησ Κ.
ΑΔΡΑΝΕΙΑ ΜΑΘΗΣΕ: ΜΑΡΙΑΝΝΑ ΠΑΡΑΘΤΡΑ ΑΝΑΣΑΗ ΠΟΤΛΙΟ ΠΑΝΑΓΙΩΣΗ ΠΡΟΔΡΟΜΟΤ ΑΝΑΣΑΙΑ ΠΟΛΤΧΡΟΝΙΑΔΟΤ ΙΩΑΝΝΑ ΠΕΝΓΚΟΤ
 ΑΔΡΑΝΕΙΑ ΜΑΘΗΣΕ: ΜΑΡΙΑΝΝΑ ΠΑΡΑΘΤΡΑ ΑΝΑΣΑΗ ΠΟΤΛΙΟ ΠΑΝΑΓΙΩΣΗ ΠΡΟΔΡΟΜΟΤ ΑΝΑΣΑΙΑ ΠΟΛΤΧΡΟΝΙΑΔΟΤ ΙΩΑΝΝΑ ΠΕΝΓΚΟΤ Οριςμόσ: Με τον όρο αδράνεια ςτθ Φυςικι ονομάηεται θ χαρακτθριςτικι ιδιότθτα των ςωμάτων να αντιςτζκονται
ΑΔΡΑΝΕΙΑ ΜΑΘΗΣΕ: ΜΑΡΙΑΝΝΑ ΠΑΡΑΘΤΡΑ ΑΝΑΣΑΗ ΠΟΤΛΙΟ ΠΑΝΑΓΙΩΣΗ ΠΡΟΔΡΟΜΟΤ ΑΝΑΣΑΙΑ ΠΟΛΤΧΡΟΝΙΑΔΟΤ ΙΩΑΝΝΑ ΠΕΝΓΚΟΤ Οριςμόσ: Με τον όρο αδράνεια ςτθ Φυςικι ονομάηεται θ χαρακτθριςτικι ιδιότθτα των ςωμάτων να αντιςτζκονται
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΑΠΟ ΘΕΜΑΤΑ ΤΕΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ
 Λφκειο Ακρόπολθσ 2015 Επιμζλεια Μάριοσ Πουργουρίδθσ ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΑΠΟ ΘΕΜΑΤΑ ΤΕΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 1. Η πιο κάτω μπάλα αφινεται να πζςει από το ςθμείο Α,κτυπά ςτο ζδαφοσ ςτο ςθμείο Ε και αναπθδά ςε μικρότερο
Λφκειο Ακρόπολθσ 2015 Επιμζλεια Μάριοσ Πουργουρίδθσ ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΑΠΟ ΘΕΜΑΤΑ ΤΕΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 1. Η πιο κάτω μπάλα αφινεται να πζςει από το ςθμείο Α,κτυπά ςτο ζδαφοσ ςτο ςθμείο Ε και αναπθδά ςε μικρότερο
ΦΥΕ 14 ΑΚΑΔ. ΕΤΟΣ Η ΕΡΓΑΣΙΑ. Ημερομηνία παράδοςησ: 12 Νοεμβρίου (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 10 μονάδεσ θ κάκε μία)
 ΦΥΕ ΑΚΑΔ. ΕΤΟΣ 007-008 Η ΕΡΓΑΣΙΑ Ημερομηνία παράδοςησ: Νοεμβρίου 007 (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 0 μονάδεσ θ κάκε μία) Άςκηςη α) Να υπολογιςκεί θ προβολι του πάνω ςτο διάνυςμα όταν: (.
ΦΥΕ ΑΚΑΔ. ΕΤΟΣ 007-008 Η ΕΡΓΑΣΙΑ Ημερομηνία παράδοςησ: Νοεμβρίου 007 (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 0 μονάδεσ θ κάκε μία) Άςκηςη α) Να υπολογιςκεί θ προβολι του πάνω ςτο διάνυςμα όταν: (.
ςυςτιματα γραμμικϊν εξιςϊςεων
 κεφάλαιο 7 Α ςυςτιματα γραμμικϊν εξιςϊςεων αςικζσ ζννοιεσ Γραμμικά, λζγονται τα ςυςτιματα εξιςϊςεων ςτα οποία οι άγνωςτοι εμφανίηονται ςτθν πρϊτθ δφναμθ. Σα γραμμικά ςυςτιματα με δφο εξιςϊςεισ και δφο
κεφάλαιο 7 Α ςυςτιματα γραμμικϊν εξιςϊςεων αςικζσ ζννοιεσ Γραμμικά, λζγονται τα ςυςτιματα εξιςϊςεων ςτα οποία οι άγνωςτοι εμφανίηονται ςτθν πρϊτθ δφναμθ. Σα γραμμικά ςυςτιματα με δφο εξιςϊςεισ και δφο
8 τριγωνομετρία. βαςικζσ ζννοιεσ. γ ςφω. εφω και γ. κεφάλαιο
 κεφάλαιο 8 τριγωνομετρία Α βαςικζσ ζννοιεσ τθν τριγωνομετρία χρθςιμοποιοφμε τουσ τριγωνομετρικοφσ αρικμοφσ, οι οποίοι ορίηονται ωσ εξισ: θμω = απζναντι κάκετθ πλευρά υποτείνουςα Γ ςυνω = εφω = προςκείμενθ
κεφάλαιο 8 τριγωνομετρία Α βαςικζσ ζννοιεσ τθν τριγωνομετρία χρθςιμοποιοφμε τουσ τριγωνομετρικοφσ αρικμοφσ, οι οποίοι ορίηονται ωσ εξισ: θμω = απζναντι κάκετθ πλευρά υποτείνουςα Γ ςυνω = εφω = προςκείμενθ
-Έλεγχοσ μπαταρίασ (χωρίσ φορτίο) Ο ζλεγχοσ αυτόσ μετράει τθν κατάςταςθ φόρτιςθ τθσ μπαταρίασ.
 1 -Έλεγχοσ μπαταρίασ (έλεγχοσ επιφανείασ) Ο ζλεγχοσ αυτόσ γίνεται για τθν περίπτωςθ που υπάρχει χαμθλό ρεφμα εκφόρτιςθσ κατά μικοσ τθσ μπαταρίασ -Έλεγχοσ μπαταρίασ (χωρίσ φορτίο) Ο ζλεγχοσ αυτόσ μετράει
1 -Έλεγχοσ μπαταρίασ (έλεγχοσ επιφανείασ) Ο ζλεγχοσ αυτόσ γίνεται για τθν περίπτωςθ που υπάρχει χαμθλό ρεφμα εκφόρτιςθσ κατά μικοσ τθσ μπαταρίασ -Έλεγχοσ μπαταρίασ (χωρίσ φορτίο) Ο ζλεγχοσ αυτόσ μετράει
Πωσ δθμιουργώ φακζλουσ;
 Πωσ δθμιουργώ φακζλουσ; Για να μπορζςετε να δθμιουργιςετε φακζλουσ ςτο χαρτοφυλάκιό ςασ ςτο Mahara κα πρζπει να μπείτε ςτο ςφςτθμα αφοφ πατιςετε πάνω ςτο ςφνδεςμο Mahara profiles από οποιοδιποτε ςελίδα
Πωσ δθμιουργώ φακζλουσ; Για να μπορζςετε να δθμιουργιςετε φακζλουσ ςτο χαρτοφυλάκιό ςασ ςτο Mahara κα πρζπει να μπείτε ςτο ςφςτθμα αφοφ πατιςετε πάνω ςτο ςφνδεςμο Mahara profiles από οποιοδιποτε ςελίδα
Ένα πρόβλθμα γραμμικοφ προγραμματιςμοφ βρίςκεται ςτθν κανονικι μορφι όταν:
 Μζθοδος Simplex Η πλζον γνωςτι και περιςςότερο χρθςιμοποιουμζνθ μζκοδοσ για τθν επίλυςθ ενόσ γενικοφ προβλιματοσ γραμμικοφ προγραμματιςμοφ, είναι θ μζκοδοσ Simplex θ οποία αναπτφχκθκε από τον George Dantzig.
Μζθοδος Simplex Η πλζον γνωςτι και περιςςότερο χρθςιμοποιουμζνθ μζκοδοσ για τθν επίλυςθ ενόσ γενικοφ προβλιματοσ γραμμικοφ προγραμματιςμοφ, είναι θ μζκοδοσ Simplex θ οποία αναπτφχκθκε από τον George Dantzig.
Κριτθριο αξιολόγηςησ χημείασ προςανατολιςμοφ Γ Λυκείου
 ΘΕΜΑ Α. Στισ παρακάτω ερωτήςεισ πολλαπλήσ επιλογήσ Α1 έωσ και Α4 να επιλέξετε το γράμμα που αντιςτοιχεί ςτη ςωςτή απάντηςη. Α1. Ο αρικμόσ οξείδωςθσ του C ςτθν φορμαλδεΰδθ είναι : α. 0 β. -1 γ. +1 δ. +2
ΘΕΜΑ Α. Στισ παρακάτω ερωτήςεισ πολλαπλήσ επιλογήσ Α1 έωσ και Α4 να επιλέξετε το γράμμα που αντιςτοιχεί ςτη ςωςτή απάντηςη. Α1. Ο αρικμόσ οξείδωςθσ του C ςτθν φορμαλδεΰδθ είναι : α. 0 β. -1 γ. +1 δ. +2
ΔΙΑΓΩΝΙΣΜΑ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΑ: (μέχρι και ενότητα 14) ΧΗΜΕΙΑ. Ονοματεπώνυμο:. Ημ/νία: Τάξθ: Χρονικι Διάρκεια:... Βακμόσ:
 δ. HCl - H 3 O + ΔΙΑΓΩΝΙΣΜΑ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΑ: 1-2-3-4-5(μέχρι και ενότητα 14) ΧΗΜΕΙΑ Ονοματεπώνυμο:. Ημ/νία: Τάξθ: Χρονικι Διάρκεια:... Βακμόσ: ΘΕΜΑ Α Α1. Ποιο από τα παρακάτω ηεφγθ αποτελεί ςυηυγζσ
δ. HCl - H 3 O + ΔΙΑΓΩΝΙΣΜΑ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΑ: 1-2-3-4-5(μέχρι και ενότητα 14) ΧΗΜΕΙΑ Ονοματεπώνυμο:. Ημ/νία: Τάξθ: Χρονικι Διάρκεια:... Βακμόσ: ΘΕΜΑ Α Α1. Ποιο από τα παρακάτω ηεφγθ αποτελεί ςυηυγζσ
ΣΥΣΚΕΥΗ ΝΟΜΟΥ ΤΩΝ ΑΕΡΙΩΝ
 ΣΥΣΚΕΥΗ ΝΟΜΟΥ ΤΩΝ ΑΕΡΙΩΝ Σύριγγα για εισαγωγή αέρα Μανόμετρο για την μέτρηση του Δp Κλίμακα για την μέτρηση του όγκου Έμβολο Μοχλός για την ελευθέρωση του εμβόλου Δύο στρόφιγγες τριών εισόδων Χειροκίνητος
ΣΥΣΚΕΥΗ ΝΟΜΟΥ ΤΩΝ ΑΕΡΙΩΝ Σύριγγα για εισαγωγή αέρα Μανόμετρο για την μέτρηση του Δp Κλίμακα για την μέτρηση του όγκου Έμβολο Μοχλός για την ελευθέρωση του εμβόλου Δύο στρόφιγγες τριών εισόδων Χειροκίνητος
Απάντηση ΘΕΜΑ1 ΘΕΜΑ2. t=t 1 +T/2. t=t 1 +3T/4. t=t 1 +T ΔΙΑΓΩΝΙΣΜΑ ΣΕ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΥΜΑΤΑ 1) (Β), 2. (Γ), 3. (Γ), 4. (Γ), 5. (Δ).
 Απάντηση ΘΕΜΑ1 1) (Β), 2. (Γ), 3. (Γ), 4. (Γ), 5. (Δ). ΘΕΜΑ2 Α)Ανάκλαςθ ςε ακίνθτο άκρο. Το προςπίπτον κφμα ςε χρόνο Τ/2 κα ζχει μετακινθκεί προσ τα δεξιά κατά 2 τετράγωνα όπωσ φαίνεται ςτο ςχιμα. Για
Απάντηση ΘΕΜΑ1 1) (Β), 2. (Γ), 3. (Γ), 4. (Γ), 5. (Δ). ΘΕΜΑ2 Α)Ανάκλαςθ ςε ακίνθτο άκρο. Το προςπίπτον κφμα ςε χρόνο Τ/2 κα ζχει μετακινθκεί προσ τα δεξιά κατά 2 τετράγωνα όπωσ φαίνεται ςτο ςχιμα. Για
Πόςο εκτατό μπορεί να είναι ζνα μη εκτατό νήμα και πόςο φυςικό. μπορεί να είναι ζνα μηχανικό ςτερεό. Συνιςταμζνη δφναμη versus «κατανεμημζνησ» δφναμησ
 Πόςο εκτατό μπορεί να είναι ζνα μη εκτατό νήμα και πόςο φυςικό μπορεί να είναι ζνα μηχανικό ςτερεό. Συνιςταμζνη δφναμη versus «κατανεμημζνησ» δφναμησ Για τθν ανάδειξθ του κζματοσ κα λφνουμε κάποια προβλιματα
Πόςο εκτατό μπορεί να είναι ζνα μη εκτατό νήμα και πόςο φυςικό μπορεί να είναι ζνα μηχανικό ςτερεό. Συνιςταμζνη δφναμη versus «κατανεμημζνησ» δφναμησ Για τθν ανάδειξθ του κζματοσ κα λφνουμε κάποια προβλιματα
ΔΟΜΗ ΑΠΛΗΣ ΕΠΙΛΟΓΗΣ Αςκήςεισ με ψευδογλώςςα/ διάγραμμα ροήσ. Αντώνης Μαϊργιώτης
 ΔΟΜΗ ΑΠΛΗΣ ΕΠΙΛΟΓΗΣ Αςκήςεισ με ψευδογλώςςα/ διάγραμμα ροήσ Αντώνης Μαϊργιώτης Να γραφεί αλγόριθμοσ με τη βοήθεια διαγράμματοσ ροήσ, που να υπολογίζει το εμβαδό Ε ενόσ τετραγώνου με μήκοσ Α. ΑΡΧΗ ΔΙΑΒΑΣΕ
ΔΟΜΗ ΑΠΛΗΣ ΕΠΙΛΟΓΗΣ Αςκήςεισ με ψευδογλώςςα/ διάγραμμα ροήσ Αντώνης Μαϊργιώτης Να γραφεί αλγόριθμοσ με τη βοήθεια διαγράμματοσ ροήσ, που να υπολογίζει το εμβαδό Ε ενόσ τετραγώνου με μήκοσ Α. ΑΡΧΗ ΔΙΑΒΑΣΕ
όπου θ ςτακερά k εξαρτάται από το μζςο και είναι για το κενό
 Φυςικι [1] ΔΤΝΑΜΙΚΟ ΗΛΕΚΣΡΟΣΑΣΙΚΟΤ ΠΕΔΙΟΤ Ειςαγωγή. Γφρω από θλεκτρικά φορτιςμζνα ςώματα δθμιουργείται θλεκτροςτατικό πεδίο. Η μελζτθ του θλεκτρικοφ πεδίου γίνεται με τθ βοικεια των μεγεκών: ζνταςη E (διανυςματικό)
Φυςικι [1] ΔΤΝΑΜΙΚΟ ΗΛΕΚΣΡΟΣΑΣΙΚΟΤ ΠΕΔΙΟΤ Ειςαγωγή. Γφρω από θλεκτρικά φορτιςμζνα ςώματα δθμιουργείται θλεκτροςτατικό πεδίο. Η μελζτθ του θλεκτρικοφ πεδίου γίνεται με τθ βοικεια των μεγεκών: ζνταςη E (διανυςματικό)
Ενδεικτικζσ Λφςεισ Θεμάτων
 c AM (t) x(t) ΤΕΙ Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σειρά Β Ειςηγητήσ: Δρ Απόςτολοσ Γεωργιάδησ ΕΠΙΚΟΙΝΩΝΙΕΣ Ι Ενδεικτικζσ Λφςεισ Θεμάτων Θζμα 1 ο (1 μον.) Ζςτω περιοδικό ςιμα πλθροφορίασ με περίοδο.
c AM (t) x(t) ΤΕΙ Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σειρά Β Ειςηγητήσ: Δρ Απόςτολοσ Γεωργιάδησ ΕΠΙΚΟΙΝΩΝΙΕΣ Ι Ενδεικτικζσ Λφςεισ Θεμάτων Θζμα 1 ο (1 μον.) Ζςτω περιοδικό ςιμα πλθροφορίασ με περίοδο.
Σ ΤΑΤ Ι Σ Τ Ι Κ Η. Statisticum collegium V
 Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium V Στατιςτική Συμπεραςματολογία Ι Σημειακζσ Εκτιμήςεισ Διαςτήματα Εμπιςτοςφνησ Στατιςτική Συμπεραςματολογία (Statistical Inference) Το πεδίο τθσ Στατιςτικισ Συμπεραςματολογία,
Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium V Στατιςτική Συμπεραςματολογία Ι Σημειακζσ Εκτιμήςεισ Διαςτήματα Εμπιςτοςφνησ Στατιςτική Συμπεραςματολογία (Statistical Inference) Το πεδίο τθσ Στατιςτικισ Συμπεραςματολογία,
ΕΓΧΕΙΡΙ ΙΟ Ο ΗΓΙΩΝ ΧΡΗΣΕΩΣ
 ΣΥΣΚΕΥΗ ΝΟΜOY ΤΩΝ ΑΕΡΙΩΝ GLA01 ΕΓΧΕΙΡΙ ΙΟ Ο ΗΓΙΩΝ ΧΡΗΣΕΩΣ ΕΠΙΣΤΗΜΟΝΙΚΕΣ ΕΠΙΧΕΙΡΗΣΕΙΣ Ε.Π.Ε. Αγ.Σαράντα 45, 18346 Μοσχάτο, Τηλ. 2104823421, 2104838270, Fax: 2104820580 ΣΚΟΠΟΣ Η πραγματοποίηση και παρατήρηση
ΣΥΣΚΕΥΗ ΝΟΜOY ΤΩΝ ΑΕΡΙΩΝ GLA01 ΕΓΧΕΙΡΙ ΙΟ Ο ΗΓΙΩΝ ΧΡΗΣΕΩΣ ΕΠΙΣΤΗΜΟΝΙΚΕΣ ΕΠΙΧΕΙΡΗΣΕΙΣ Ε.Π.Ε. Αγ.Σαράντα 45, 18346 Μοσχάτο, Τηλ. 2104823421, 2104838270, Fax: 2104820580 ΣΚΟΠΟΣ Η πραγματοποίηση και παρατήρηση
Δομζσ Αφαιρετικότθτα ςτα Δεδομζνα
 Δομζσ Αφαιρετικότθτα ςτα Δεδομζνα Περιεχόμενα Ζννοια δομισ Οριςμόσ δομισ Διλωςθ μεταβλθτϊν Απόδοςθ Αρχικϊν τιμϊν Αναφορά ςτα μζλθ μιασ δομισ Ζνκεςθ Δομισ Πίνακεσ Δομϊν Η ζννοια τθσ δομισ Χρθςιμοποιιςαμε
Δομζσ Αφαιρετικότθτα ςτα Δεδομζνα Περιεχόμενα Ζννοια δομισ Οριςμόσ δομισ Διλωςθ μεταβλθτϊν Απόδοςθ Αρχικϊν τιμϊν Αναφορά ςτα μζλθ μιασ δομισ Ζνκεςθ Δομισ Πίνακεσ Δομϊν Η ζννοια τθσ δομισ Χρθςιμοποιιςαμε
Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ
 Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί ςτθ
Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί ςτθ
EUROPEAN TRADESMAN PROJECT NOTES ON ELECTRICAL TESTS OF ELECTRICAL INSTALLATIONS
 EUROPEAN TRADESMAN PROJECT NOTES ON ELECTRICAL TESTS OF ELECTRICAL INSTALLATIONS EUROPEAN TRADESMAN PROJECT NOTES ON ELECTRICAL TESTS OF ELECTRICAL INSTALLATIONS Οι μαθηηές να μάθοσν πώς να διενεργήζοσν
EUROPEAN TRADESMAN PROJECT NOTES ON ELECTRICAL TESTS OF ELECTRICAL INSTALLATIONS EUROPEAN TRADESMAN PROJECT NOTES ON ELECTRICAL TESTS OF ELECTRICAL INSTALLATIONS Οι μαθηηές να μάθοσν πώς να διενεργήζοσν
Ερωτιςεισ & απαντιςεισ για τα ξφλινα πνευςτά
 Τα νύλιμα! ΧΟΡΗΓΟΣ Ερωτιςεισ & απαντιςεισ για τα ξφλινα πνευςτά τα ξφλινα! 1. Γιατί τα λζμε ξφλινα πνευςτά; Πνευςτά ονομάηονται τα όργανα ςτα οποία ο ιχοσ παράγεται μζςα ςε ζνα ςωλινα απ όπου περνάει ο
Τα νύλιμα! ΧΟΡΗΓΟΣ Ερωτιςεισ & απαντιςεισ για τα ξφλινα πνευςτά τα ξφλινα! 1. Γιατί τα λζμε ξφλινα πνευςτά; Πνευςτά ονομάηονται τα όργανα ςτα οποία ο ιχοσ παράγεται μζςα ςε ζνα ςωλινα απ όπου περνάει ο
Καζάνης Θεόδωρος ΜΗΧΑΝΟΛΟΓΟΣ ΜΗΧΑΝΙΚΟΣ ΕΜΠ Δ/νηης Πιζηοποίηζης & Εκπαίδεσζης Δικηύοσ
 Καζάνης Θεόδωρος ΜΗΧΑΝΟΛΟΓΟΣ ΜΗΧΑΝΙΚΟΣ ΕΜΠ Δ/νηης Πιζηοποίηζης & Εκπαίδεσζης Δικηύοσ ΚΑΣΑΝΗΣ ΠΙΝΑΚΑ ΔΕΙΓΜΑΣΟΛΗΠΣΙΚΩΝ ΕΛΕΓΧΩΝ ΚΑΙ ΠΑΡΑΛΑΒΩΝ ISO 2859 W Z Z W Προδιαγραφι ΕΣΕΜ 0,6 x 0.7 = 0,42 0.6 L Προδιαγραφι
Καζάνης Θεόδωρος ΜΗΧΑΝΟΛΟΓΟΣ ΜΗΧΑΝΙΚΟΣ ΕΜΠ Δ/νηης Πιζηοποίηζης & Εκπαίδεσζης Δικηύοσ ΚΑΣΑΝΗΣ ΠΙΝΑΚΑ ΔΕΙΓΜΑΣΟΛΗΠΣΙΚΩΝ ΕΛΕΓΧΩΝ ΚΑΙ ΠΑΡΑΛΑΒΩΝ ISO 2859 W Z Z W Προδιαγραφι ΕΣΕΜ 0,6 x 0.7 = 0,42 0.6 L Προδιαγραφι
Εργαστηριακή άσκηση στο μάθημα του Αυτομάτου Ελέγχου (ΜΜ803)
 Εργαστηριακή άσκηση στο μάθημα του Αυτομάτου Ελέγχου (ΜΜ803) Το ςφςτθμα τθσ φωτογραφίασ αποτελείται από ζνα κινθτιρα ςτον άξονα του οποίου ζχουμε προςαρμόςει ζνα φορτίο. Στον κινθτιρα υπάρχει ςυνδεδεμζνοσ
Εργαστηριακή άσκηση στο μάθημα του Αυτομάτου Ελέγχου (ΜΜ803) Το ςφςτθμα τθσ φωτογραφίασ αποτελείται από ζνα κινθτιρα ςτον άξονα του οποίου ζχουμε προςαρμόςει ζνα φορτίο. Στον κινθτιρα υπάρχει ςυνδεδεμζνοσ
ΕΓΚΑΣΑΣΑΕΙ ΚΛΙΜΑΣΙΜΟΤ ΙΙ ΚΟΝΤΟΣ ΟΔΥΣΣΕΑΣ ΠΕ12.04
 ΕΓΚΑΣΑΣΑΕΙ ΚΛΙΜΑΣΙΜΟΤ ΙΙ ΚΟΝΤΟΣ ΟΔΥΣΣΕΑΣ ΠΕ12.04 1 κλιματιςμόσ χώρου ρφκμιςθ χαρακτθριςτικών αζρα: δθμιουργία ςυνκθκών άνεςησ Η ςωςτή ποςότητα του κλιματιςμζνου αζρα που τροφοδοτείται ςτο χώρο από τθν
ΕΓΚΑΣΑΣΑΕΙ ΚΛΙΜΑΣΙΜΟΤ ΙΙ ΚΟΝΤΟΣ ΟΔΥΣΣΕΑΣ ΠΕ12.04 1 κλιματιςμόσ χώρου ρφκμιςθ χαρακτθριςτικών αζρα: δθμιουργία ςυνκθκών άνεςησ Η ςωςτή ποςότητα του κλιματιςμζνου αζρα που τροφοδοτείται ςτο χώρο από τθν
ΘΕΜΟΔΥΝΑΜΙΚΗ IΙ. Ενότθτα 1: Μερικζσ Γραμμομοριακζσ Ιδιότθτεσ. Σογομϊν Μπογοςιάν Ρολυτεχνικι Σχολι Τμιμα Χθμικϊν Μθχανικϊν
 ΘΕΜΟΔΥΝΑΜΙΚΗ IΙ Ενότθτα 1: Μερικζσ Γραμμομοριακζσ Ιδιότθτεσ Σογομϊν Μπογοςιάν Ρολυτεχνικι Σχολι Τμιμα Χθμικϊν Μθχανικϊν Σκοποί ενότθτασ Σκοπόσ τθσ ενότθτασ αυτισ είναι θ ανάπτυξθ μακθματικϊν ςχζςεων μεταξφ
ΘΕΜΟΔΥΝΑΜΙΚΗ IΙ Ενότθτα 1: Μερικζσ Γραμμομοριακζσ Ιδιότθτεσ Σογομϊν Μπογοςιάν Ρολυτεχνικι Σχολι Τμιμα Χθμικϊν Μθχανικϊν Σκοποί ενότθτασ Σκοπόσ τθσ ενότθτασ αυτισ είναι θ ανάπτυξθ μακθματικϊν ςχζςεων μεταξφ
ΕΚΦΕ Μαγνησίας, Θεοδώρα Γουρλά, Σεπτέμβρης /5 ΣΥΣΚΕΥΗ ΝΟΜΟΥ ΤΩΝ ΑΕΡΙΩΝ
 ΕΚΦΕ Μαγνησίας, Θεοδώρα Γουρλά, Σεπτέμβρης 2012 1/5 ΣΥΣΚΕΥΗ ΝΟΜΟΥ ΤΩΝ ΑΕΡΙΩΝ ΕΚΦΕ Μαγνησίας, Θεοδώρα Γουρλά, Σεπτέμβρης 2012 2/5 Επαλήθευση του Νόμου των Ιδανικών Αερίων Α. Νόμος Boyle Ισόθερμη μεταβολή
ΕΚΦΕ Μαγνησίας, Θεοδώρα Γουρλά, Σεπτέμβρης 2012 1/5 ΣΥΣΚΕΥΗ ΝΟΜΟΥ ΤΩΝ ΑΕΡΙΩΝ ΕΚΦΕ Μαγνησίας, Θεοδώρα Γουρλά, Σεπτέμβρης 2012 2/5 Επαλήθευση του Νόμου των Ιδανικών Αερίων Α. Νόμος Boyle Ισόθερμη μεταβολή
1. Εγκατάςταςη κειμενογράφου JCE
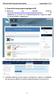 1. Εγκατάςταςη κειμενογράφου JCE 1.1. Πθγαίνουμε ςτθν ακόλουκθ διεφκυνςθ https://www.joomlacontenteditor.net/downloads/editor/joomla-3 και κατεβάηουμε τον JCE Editor 2.5.8. Εναλλακτικά βρίςκουμε το αρχείο
1. Εγκατάςταςη κειμενογράφου JCE 1.1. Πθγαίνουμε ςτθν ακόλουκθ διεφκυνςθ https://www.joomlacontenteditor.net/downloads/editor/joomla-3 και κατεβάηουμε τον JCE Editor 2.5.8. Εναλλακτικά βρίςκουμε το αρχείο
ΑΝΣΙΣΡΟΦΗ ΤΝΑΡΣΗΗ. f y x y f A αντιςτοιχίηεται ςτο μοναδικό x A για το οποίο. Παρατθριςεισ Ιδιότθτεσ τθσ αντίςτροφθσ ςυνάρτθςθσ 1. Η. f A τθσ f.
 .. Αντίςτροφθ ςυνάρτθςθ Ζςτω θ ςυνάρτθςθ : A θ οποία είναι " ". Τότε ορίηεται μια νζα ςυνάρτθςθ, θ μζςω τθσ οποίασ το κάκε ιςχφει y. : A με Η νζα αυτι ςυνάρτθςθ λζγεται αντίςτροφθ τθσ. y y A αντιςτοιχίηεται
.. Αντίςτροφθ ςυνάρτθςθ Ζςτω θ ςυνάρτθςθ : A θ οποία είναι " ". Τότε ορίηεται μια νζα ςυνάρτθςθ, θ μζςω τθσ οποίασ το κάκε ιςχφει y. : A με Η νζα αυτι ςυνάρτθςθ λζγεται αντίςτροφθ τθσ. y y A αντιςτοιχίηεται
Μεθολογία αςκιςεων αραίωςησ και ανάμειξησ διαλυμάτων (με τθν ίδια δ. ουςία).
 Μεθολογία αςκιςεων αραίωςησ και ανάμειξησ διαλυμάτων (με τθν ίδια δ. ουςία). Από τθν τράπεηα κεμάτων Α_ΧΘΜ_0_20651 Διακζτουμε υδατικό διάλυμα (Δ1) KOH 0,1 Μ. α)να υπολογίςετε τθν % w/v περιεκτικότθτα του
Μεθολογία αςκιςεων αραίωςησ και ανάμειξησ διαλυμάτων (με τθν ίδια δ. ουςία). Από τθν τράπεηα κεμάτων Α_ΧΘΜ_0_20651 Διακζτουμε υδατικό διάλυμα (Δ1) KOH 0,1 Μ. α)να υπολογίςετε τθν % w/v περιεκτικότθτα του
Πίεςη. 1. Αν ςε μία επιφάνεια με εμβαδό Α αςκείται κάκετα δφναμθ F Κ,τότε ορίηουμε ωσ πίεςθ Ρ (επιλζξτε μία ςωςτι απάντθςθ):
 9 Πίεςη. 1. Αν ςε μία επιφάνεια με εμβαδό Α αςκείται κάκετα δφναμθ F Κ,τότε ορίηουμε ωσ πίεςθ Ρ (επιλζξτε μία ςωςτι απάντθςθ): A FK α. Ρ=F K S β. P= γ. P= F A 9 K 2.τθ ςυγκεκριμζνθ φράςθ να επιλζξετε μία
9 Πίεςη. 1. Αν ςε μία επιφάνεια με εμβαδό Α αςκείται κάκετα δφναμθ F Κ,τότε ορίηουμε ωσ πίεςθ Ρ (επιλζξτε μία ςωςτι απάντθςθ): A FK α. Ρ=F K S β. P= γ. P= F A 9 K 2.τθ ςυγκεκριμζνθ φράςθ να επιλζξετε μία
Εργαστηριακή άσκηση 1: ΕΠΑΛΗΘΕΥΣΗ ΤΩΝ ΝΟΜΩΝ ΤΩΝ Ι ΑΝΙΚΩΝ ΑΕΡΙΩΝ
 ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Εργαστηριακή άσκηση 1: ΕΠΑΛΗΘΕΥΣΗ ΤΩΝ ΝΟΜΩΝ ΤΩΝ Ι ΑΝΙΚΩΝ ΑΕΡΙΩΝ Τροποποίηση της διαδικασίας η οποία περιγράφεται στον εργαστηριακό οδηγό (Βαγγέλης ηµητριάδης, 4 ο ΓΕΛ Ζωγράφου)
ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Εργαστηριακή άσκηση 1: ΕΠΑΛΗΘΕΥΣΗ ΤΩΝ ΝΟΜΩΝ ΤΩΝ Ι ΑΝΙΚΩΝ ΑΕΡΙΩΝ Τροποποίηση της διαδικασίας η οποία περιγράφεται στον εργαστηριακό οδηγό (Βαγγέλης ηµητριάδης, 4 ο ΓΕΛ Ζωγράφου)
Εργαστηριακό Κέντρο Φυσικών Επιστηµών Αγίων Αναργύρων Υπεύθυνος: Ευάγγελος Κουντούρης, Φυσικός. Εργαστηριακές Ασκήσεις Φυσικής
 Εργαστηριακό Κέντρο Φυσικών Επιστηµών Αγίων Αναργύρων Υπεύθυνος: Ευάγγελος Κουντούρης, Φυσικός Εργαστηριακές Ασκήσεις Φυσικής Β Λυκείου: Πειραµατική επιβεβαίωση των νόµων των ιδανικών αερίων Επιµέλεια-Παρουσίαση:
Εργαστηριακό Κέντρο Φυσικών Επιστηµών Αγίων Αναργύρων Υπεύθυνος: Ευάγγελος Κουντούρης, Φυσικός Εργαστηριακές Ασκήσεις Φυσικής Β Λυκείου: Πειραµατική επιβεβαίωση των νόµων των ιδανικών αερίων Επιµέλεια-Παρουσίαση:
ΟΙ ΝΟΜΟΙ ΤΩΝ ΑΕΡΙΩΝ ( ΕΠΑΛΗΘΕΥΣΗ ΤΗΣ ΚΑΤΑΣΤΑΤΙΚΗΣ ΕΞΙΣΩΣΗΣ )
 1 ο ΕΚΦΕ (Ν. ΣΜΥΡΝΗΣ) Δ Δ/ΝΣΗΣ Δ. Ε. ΑΘΗΝΑΣ 1 ΟΙ ΝΟΜΟΙ ΤΩΝ ΑΕΡΙΩΝ ( ΕΠΑΛΗΘΕΥΣΗ ΤΗΣ ΚΑΤΑΣΤΑΤΙΚΗΣ ΕΞΙΣΩΣΗΣ ) Α. ΣΤΟΧΟΙ Η εξοικείωση με τη χρήση απλών πειραματικών διατάξεων. Η εξοικείωση σε μετρήσεις θερμοκρασίας,
1 ο ΕΚΦΕ (Ν. ΣΜΥΡΝΗΣ) Δ Δ/ΝΣΗΣ Δ. Ε. ΑΘΗΝΑΣ 1 ΟΙ ΝΟΜΟΙ ΤΩΝ ΑΕΡΙΩΝ ( ΕΠΑΛΗΘΕΥΣΗ ΤΗΣ ΚΑΤΑΣΤΑΤΙΚΗΣ ΕΞΙΣΩΣΗΣ ) Α. ΣΤΟΧΟΙ Η εξοικείωση με τη χρήση απλών πειραματικών διατάξεων. Η εξοικείωση σε μετρήσεις θερμοκρασίας,
Τάξη Β. Φυςικθ Γενικθσ Παιδείασ. Τράπεζα ιεμάτων Κεφ.1 ο ΘΕΜΑ Δ. Για όλεσ τισ αςκθςεισ δίνεται η ηλεκτρικθ ςταιερά
 Τάξη Β Φυςικθ Γενικθσ Παιδείασ Τράπεζα ιεμάτων Κεφ.1 ο ΘΕΜΑ Δ Για όλεσ τισ αςκθςεισ δίνεται η ηλεκτρικθ ςταιερά k 2 9 9 10 Nm 2 1. Δφο ακίνθτα ςθμειακά θλεκτρικά φορτία q 1 = - 2 μq και q 2 = + 3 μq, βρίςκονται
Τάξη Β Φυςικθ Γενικθσ Παιδείασ Τράπεζα ιεμάτων Κεφ.1 ο ΘΕΜΑ Δ Για όλεσ τισ αςκθςεισ δίνεται η ηλεκτρικθ ςταιερά k 2 9 9 10 Nm 2 1. Δφο ακίνθτα ςθμειακά θλεκτρικά φορτία q 1 = - 2 μq και q 2 = + 3 μq, βρίςκονται
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο τησ Αριθμογραμμήσ
 Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο τησ Αριθμογραμμήσ Αυτζσ οι οδθγίεσ ζχουν ςτόχο να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο τθσ Αρικμογραμμισ.
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο τησ Αριθμογραμμήσ Αυτζσ οι οδθγίεσ ζχουν ςτόχο να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο τθσ Αρικμογραμμισ.
Σο θλεκτρικό κφκλωμα
 Σο θλεκτρικό κφκλωμα Για να είναι δυνατι θ ροι των ελεφκερων θλεκτρονίων, για να ζχουμε θλεκτρικό ρεφμα, απαραίτθτθ προχπόκεςθ είναι θ φπαρξθ ενόσ κλειςτοφ θλεκτρικοφ κυκλϊματοσ. Είδθ κυκλωμάτων Σα κυκλϊματα
Σο θλεκτρικό κφκλωμα Για να είναι δυνατι θ ροι των ελεφκερων θλεκτρονίων, για να ζχουμε θλεκτρικό ρεφμα, απαραίτθτθ προχπόκεςθ είναι θ φπαρξθ ενόσ κλειςτοφ θλεκτρικοφ κυκλϊματοσ. Είδθ κυκλωμάτων Σα κυκλϊματα
Διαγώνισμα Φυσική ς Α Λυκει ου Δυναμική σε μι α δια στασή και στο επι πεδο
 Διαγώνισμα Φυσική ς Α Λυκει ου Δυναμική σε μι α δια στασή και στο επι πεδο Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα
Διαγώνισμα Φυσική ς Α Λυκει ου Δυναμική σε μι α δια στασή και στο επι πεδο Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα
Αν η ςυνάρτηςη ƒ είναι ςυνεχήσ ςτο να προςδιορίςετε το α.
 1 AΣΚΗΣΕΙΣ 1. Να υπολογιςθοφν τα παρακάτω όρια Ι. ΙΙ. ΙΙΙ. Ιν. ν. νι. νιι. νιιι. 2. Να βρεθοφν τα όρια Ι. ΙΙ. 3. Αν ƒ(χ)= α. Να βρείτε το πεδίο οριςμοφ Β. Να βρείτε τα όρια Ι. ΙΙ. 4. Δίνεται η ςυνάρτηςη
1 AΣΚΗΣΕΙΣ 1. Να υπολογιςθοφν τα παρακάτω όρια Ι. ΙΙ. ΙΙΙ. Ιν. ν. νι. νιι. νιιι. 2. Να βρεθοφν τα όρια Ι. ΙΙ. 3. Αν ƒ(χ)= α. Να βρείτε το πεδίο οριςμοφ Β. Να βρείτε τα όρια Ι. ΙΙ. 4. Δίνεται η ςυνάρτηςη
Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη
 Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη MSc Τραπεζική & Χρηματοοικονομική Τεχνολογικό Εκπαιδευτικό Ίδρυμα Δυτικής Μακεδονίας Western Macedonia University of Applied Sciences Κοίλα Κοζάνης 50100 Kozani GR
Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη MSc Τραπεζική & Χρηματοοικονομική Τεχνολογικό Εκπαιδευτικό Ίδρυμα Δυτικής Μακεδονίας Western Macedonia University of Applied Sciences Κοίλα Κοζάνης 50100 Kozani GR
Γενικά Μαθηματικά ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 5 η : Μερικι Παράγωγοσ Ι Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 5 η : Μερικι Παράγωγοσ Ι Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΣΤΟΙΧΕΙΑ ΜΑΘΗΜΑΤΙΚΗΣ ΛΟΓΙΚΗΣ
 ΣΤΟΙΧΕΙΑ ΜΑΘΗΜΑΤΙΚΗΣ ΛΟΓΙΚΗΣ Λογικι πρόταςθ: Με τον όρο λογικι πρόταςθ (ι απλά πρόταςθ) ςτα μακθματικά, εννοοφμε μια ζκφραςθ με πλιρεσ νόθμα που δζχεται τον χαρακτθριςμό ι μόνο αλθκισ ι μόνο ψευδισ. Παραδείγματα:
ΣΤΟΙΧΕΙΑ ΜΑΘΗΜΑΤΙΚΗΣ ΛΟΓΙΚΗΣ Λογικι πρόταςθ: Με τον όρο λογικι πρόταςθ (ι απλά πρόταςθ) ςτα μακθματικά, εννοοφμε μια ζκφραςθ με πλιρεσ νόθμα που δζχεται τον χαρακτθριςμό ι μόνο αλθκισ ι μόνο ψευδισ. Παραδείγματα:
ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ. 7 θ Διάλεξθ Διαχείριςθ Μνιμθσ Μζροσ Γ
 ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ 7 θ Διάλεξθ Διαχείριςθ Μνιμθσ Μζροσ Γ ελιδοποίθςθ (1/10) Σόςο θ κατάτμθςθ διαμεριςμάτων ςτακεροφ μεγζκουσ όςο και θ κατάτμθςθ διαμεριςμάτων μεταβλθτοφ και άνιςου μεγζκουσ δεν κάνουν
ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ 7 θ Διάλεξθ Διαχείριςθ Μνιμθσ Μζροσ Γ ελιδοποίθςθ (1/10) Σόςο θ κατάτμθςθ διαμεριςμάτων ςτακεροφ μεγζκουσ όςο και θ κατάτμθςθ διαμεριςμάτων μεταβλθτοφ και άνιςου μεγζκουσ δεν κάνουν
Εγχειρίδιο: Honeybee Small
 ΚΟΚΚΙΝΟΣ ΔΗΜΗΤΡΗΣ Τηλ/Fax: 20 993677 Άγιος Δημήτριος, Αττικής 73 42 Ν. Ζέρβα 29 e-mail: Kokkinos@kokkinostoys.gr www.kokkinostoys.gr Εγχειρίδιο: Honeybee Small HEYBEE SMALL CRANE MACHINE DIP SW 2 3 4 5
ΚΟΚΚΙΝΟΣ ΔΗΜΗΤΡΗΣ Τηλ/Fax: 20 993677 Άγιος Δημήτριος, Αττικής 73 42 Ν. Ζέρβα 29 e-mail: Kokkinos@kokkinostoys.gr www.kokkinostoys.gr Εγχειρίδιο: Honeybee Small HEYBEE SMALL CRANE MACHINE DIP SW 2 3 4 5
Δείκτεσ Διαχείριςθ Μνιμθσ. Βαγγζλθσ Οικονόμου Διάλεξθ 8
 Δείκτεσ Διαχείριςθ Μνιμθσ Βαγγζλθσ Οικονόμου Διάλεξθ 8 Δείκτεσ Κάκε μεταβλθτι ςχετίηεται με μία κζςθ ςτθν κφρια μνιμθ του υπολογιςτι. Κάκε κζςθ ςτθ μνιμθ ζχει τθ δικι τθσ ξεχωριςτι διεφκυνςθ. Με άμεςθ
Δείκτεσ Διαχείριςθ Μνιμθσ Βαγγζλθσ Οικονόμου Διάλεξθ 8 Δείκτεσ Κάκε μεταβλθτι ςχετίηεται με μία κζςθ ςτθν κφρια μνιμθ του υπολογιςτι. Κάκε κζςθ ςτθ μνιμθ ζχει τθ δικι τθσ ξεχωριςτι διεφκυνςθ. Με άμεςθ
Λαμβάνοντασ υπόψη ότι κατά την πρόςθεςη δφο δυαδικϊν ψηφίων ιςχφει: Κρατοφμενο
 Αριθμητικά κυκλώματα Ημιαθροιστής (Half Adder) Ο ημιαθροιςτήσ είναι ζνα κφκλωμα το οποίο προςθζτει δφο δυαδικά ψηφία (bits) και δίνει ωσ αποτζλεςμα το άθροιςμά τουσ και το κρατοφμενο. Με βάςη αυτή την
Αριθμητικά κυκλώματα Ημιαθροιστής (Half Adder) Ο ημιαθροιςτήσ είναι ζνα κφκλωμα το οποίο προςθζτει δφο δυαδικά ψηφία (bits) και δίνει ωσ αποτζλεςμα το άθροιςμά τουσ και το κρατοφμενο. Με βάςη αυτή την
Δείκτεσ απόδοςθσ υλικών
 Δείκτεσ απόδοςθσ υλικών Κάκε ςυνδυαςμόσ λειτουργίασ, περιοριςμϊν και ςτόχων, οδθγεί ςε ζνα μζτρο τθσ απόδοςθσ τθσ λειτουργίασ του εξαρτιματοσ και περιζχει μια ομάδα ιδιοτιτων των υλικϊν. Αυτι θ ομάδα των
Δείκτεσ απόδοςθσ υλικών Κάκε ςυνδυαςμόσ λειτουργίασ, περιοριςμϊν και ςτόχων, οδθγεί ςε ζνα μζτρο τθσ απόδοςθσ τθσ λειτουργίασ του εξαρτιματοσ και περιζχει μια ομάδα ιδιοτιτων των υλικϊν. Αυτι θ ομάδα των
ΧΗΥΙΑΚΟ ΔΚΠΑΙΔΔΤΣΙΚΟ ΒΟΗΘΗΜΑ «ΥΤΙΚΗ ΘΔΣΙΚΗ ΚΑΙ ΣΔΦΝΟΛΟΓΙΚΗ ΚΑΣΔΤΘΤΝΗ» ΦΥΣΙΚΗ ΘΔΤΙΚΗΣ ΚΑΙ ΤΔΧΝΟΛΟΓΙΚΗΣ ΚΑΤΔΥΘΥΝΣΗΣ ΘΔΜΑ Α ΘΔΜΑ Β
 4 o ΔΙΓΩΝΙΜ ΠΡΙΛΙΟ 04: ΔΝΔΔΙΚΣΙΚΔ ΠΝΣΗΔΙ ΦΥΣΙΚΗ ΘΔΤΙΚΗΣ ΚΙ ΤΔΧΝΟΛΟΓΙΚΗΣ ΚΤΔΥΘΥΝΣΗΣ 4 ο ΔΙΓΩΝΙΣΜ ΔΝΔΔΙΚΤΙΚΔΣ ΠΝΤΗΣΔΙΣ ΘΔΜ. β. β 3. α 4. γ 5. α.σ β.σ γ.λ δ.σ ε.λ. ΘΔΜ Β Σωςτι είναι θ απάντθςθ γ. Έχουμε ελαςτικι
4 o ΔΙΓΩΝΙΜ ΠΡΙΛΙΟ 04: ΔΝΔΔΙΚΣΙΚΔ ΠΝΣΗΔΙ ΦΥΣΙΚΗ ΘΔΤΙΚΗΣ ΚΙ ΤΔΧΝΟΛΟΓΙΚΗΣ ΚΤΔΥΘΥΝΣΗΣ 4 ο ΔΙΓΩΝΙΣΜ ΔΝΔΔΙΚΤΙΚΔΣ ΠΝΤΗΣΔΙΣ ΘΔΜ. β. β 3. α 4. γ 5. α.σ β.σ γ.λ δ.σ ε.λ. ΘΔΜ Β Σωςτι είναι θ απάντθςθ γ. Έχουμε ελαςτικι
ΣΟΙΧΕΙΟΜΕΣΡΙΚΟΙ ΤΠΟΛΟΓΙΜΟΙ
 ΣΟΙΧΕΙΟΜΕΣΡΙΚΟΙ ΤΠΟΛΟΓΙΜΟΙ Σε κάκε χθμικι αντίδραςθ οι ποςότθτεσ των ουςιϊν που αντιδροφν και παράγονται ζχουν οριςμζνθ ςχζςθ μεταξφ τουσ, θ οποία κακορίηεται από τουσ ςυντελεςτζσ των ουςιϊν ςτθ χθμικι
ΣΟΙΧΕΙΟΜΕΣΡΙΚΟΙ ΤΠΟΛΟΓΙΜΟΙ Σε κάκε χθμικι αντίδραςθ οι ποςότθτεσ των ουςιϊν που αντιδροφν και παράγονται ζχουν οριςμζνθ ςχζςθ μεταξφ τουσ, θ οποία κακορίηεται από τουσ ςυντελεςτζσ των ουςιϊν ςτθ χθμικι
ΕΡΓΑΣΗΡΙΟ ΕΦΑΡΜΟΜΕΝΗ ΠΛΗΡΟΦΟΡΙΚΗ
 Στο εργαςτιριο αυτό κα δοφμε πωσ μποροφμε να προςομοιϊςουμε μια κίνθςθ χωρίσ τθ χριςθ εξειδικευμζνων εργαλείων, παρά μόνο μζςω ενόσ προγράμματοσ λογιςτικϊν φφλλων, όπωσ είναι το Calc και το Excel. Τα δφο
Στο εργαςτιριο αυτό κα δοφμε πωσ μποροφμε να προςομοιϊςουμε μια κίνθςθ χωρίσ τθ χριςθ εξειδικευμζνων εργαλείων, παρά μόνο μζςω ενόσ προγράμματοσ λογιςτικϊν φφλλων, όπωσ είναι το Calc και το Excel. Τα δφο
ΔΙΑΓΩΝΙΜΑ ΧΗΜΕΙΑ Γ ΛΤΚΕΙΟΤ. Ημ/νία: Τάξθ: Χρονικι Διάρκεια:.
 ΔΙΑΓΩΝΙΜΑ ΧΗΜΕΙΑ Γ ΛΤΚΕΙΟΤ ΟΞΕΙΔΟΑΝΑΓΩΓΗ ΘΕΡΜΟΧΗΜΕΙΑ ΧΗΜΙΚΗ ΚΙΝΗΣΙΚΗ ΧΗΜΙΚΗ ΙΟΡΡΟΠΙΑ - ΟΡΓΑΝΙΚΗ Ονοματεπϊνυμο:. Ημ/νία: Τάξθ: Χρονικι Διάρκεια:. Βακμόσ: ΘΕΜΑ Α Να επιλζξετε τθ ςωςτι απάντθςθ ςε κακεμιά
ΔΙΑΓΩΝΙΜΑ ΧΗΜΕΙΑ Γ ΛΤΚΕΙΟΤ ΟΞΕΙΔΟΑΝΑΓΩΓΗ ΘΕΡΜΟΧΗΜΕΙΑ ΧΗΜΙΚΗ ΚΙΝΗΣΙΚΗ ΧΗΜΙΚΗ ΙΟΡΡΟΠΙΑ - ΟΡΓΑΝΙΚΗ Ονοματεπϊνυμο:. Ημ/νία: Τάξθ: Χρονικι Διάρκεια:. Βακμόσ: ΘΕΜΑ Α Να επιλζξετε τθ ςωςτι απάντθςθ ςε κακεμιά
EUROPEAN TRADESMAN PROJECT NOTES ON ELECTRICAL TESTS OF ELECTRICAL INSTALLATIONS
 EUROPEAN TRADESMAN PROJECT NOTES ON ELECTRICAL TESTS OF ELECTRICAL INSTALLATIONS Οι μακθτζσ να μάκουν να χρθςιμοποιοφν ορκά και να διαβάηουν τθν ζνδειξθ των οργάνων για τθν μζτρθςθ: τθσ τάςθσ Σου ρεφματοσ
EUROPEAN TRADESMAN PROJECT NOTES ON ELECTRICAL TESTS OF ELECTRICAL INSTALLATIONS Οι μακθτζσ να μάκουν να χρθςιμοποιοφν ορκά και να διαβάηουν τθν ζνδειξθ των οργάνων για τθν μζτρθςθ: τθσ τάςθσ Σου ρεφματοσ
Ενεργειακά Τηάκια. Πουκεβίλ 2, Ιωάννινα Τθλ. 26510.23822 www.energeiaka-ktiria.gr www.facebook.com/energeiaka.ktiria
 Ενεργειακά Τηάκια Πουκεβίλ 2, Ιωάννινα Τθλ. 26510.23822 www.facebook.com/energeiaka.ktiria Σελ. 2 Η ΕΣΑΙΡΕΙΑ Η εταιρεία Ενεργειακά Κτίρια δραςτθριοποιείται ςτθν παροχι ολοκλθρωμζνων υπθρεςιϊν και ςτθν
Ενεργειακά Τηάκια Πουκεβίλ 2, Ιωάννινα Τθλ. 26510.23822 www.facebook.com/energeiaka.ktiria Σελ. 2 Η ΕΣΑΙΡΕΙΑ Η εταιρεία Ενεργειακά Κτίρια δραςτθριοποιείται ςτθν παροχι ολοκλθρωμζνων υπθρεςιϊν και ςτθν
ΘΕΡΜΟΔΤΝΑΜΙΚΗ Ι. Ενότθτα 3: Μθδενικόσ Νόμοσ - Ζργο. ογομϊν Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικϊν Μθχανικϊν
 ΘΕΡΜΟΔΤΝΑΜΙΚΗ Ι Ενότθτα 3: Μθδενικόσ Νόμοσ - Ζργο ογομϊν Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικϊν Μθχανικϊν κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ είναι θ περιγραφι των οριςμϊν και των κεμελιωδϊν εννοιϊν
ΘΕΡΜΟΔΤΝΑΜΙΚΗ Ι Ενότθτα 3: Μθδενικόσ Νόμοσ - Ζργο ογομϊν Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικϊν Μθχανικϊν κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ είναι θ περιγραφι των οριςμϊν και των κεμελιωδϊν εννοιϊν
1. Κατέβαςμα του VirtueMart
 1. Κατέβαςμα του VirtueMart Αρχικό βήμα (προαιρετικό). Κατζβαςμα και αποςυμπίεςη αρχείων VirtueMart ΠΡΟΟΧΗ. Αυτό το βήμα να παρακαμφθεί ςτο εργαςτήριο. Τα αρχεία θα ςασ δοθοφν από τουσ καθηγητζσ ςασ. Οι
1. Κατέβαςμα του VirtueMart Αρχικό βήμα (προαιρετικό). Κατζβαςμα και αποςυμπίεςη αρχείων VirtueMart ΠΡΟΟΧΗ. Αυτό το βήμα να παρακαμφθεί ςτο εργαςτήριο. Τα αρχεία θα ςασ δοθοφν από τουσ καθηγητζσ ςασ. Οι
Δϋ Δθμοτικοφ 12 θ Κυπριακι Μακθματικι Ολυμπιάδα Απρίλιοσ 2011
 1. Αν τϊρα είναι Απρίλθσ, ποιοσ μινασ κα είναι μετά από 100 μινεσ; Α. Απρίλθσ Β. Αφγουςτοσ. Σεπτζμβρθσ Δ. Μάρτθσ Ε. Ιοφλθσ 2. Ποιο είναι το αποτζλεςμα των πιο κάτω πράξεων; ; Α. 135 Β. 27. 63 Δ. 21 Ε.
1. Αν τϊρα είναι Απρίλθσ, ποιοσ μινασ κα είναι μετά από 100 μινεσ; Α. Απρίλθσ Β. Αφγουςτοσ. Σεπτζμβρθσ Δ. Μάρτθσ Ε. Ιοφλθσ 2. Ποιο είναι το αποτζλεςμα των πιο κάτω πράξεων; ; Α. 135 Β. 27. 63 Δ. 21 Ε.
ΕΘΝΙΚΟ ΜΕΣΟΒΙΟ ΠΟΛΤΣΕΧΝΕΙΟ ΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑTΗΡΙΟ TΕΧΝΟΛΟΓΙΑ ΚΑΤΙΜΩΝ ΚΑΙ ΛΙΠΑΝΣΙΚΩΝ
 ΕΘΝΙΚΟ ΜΕΣΟΒΙΟ ΠΟΛΤΣΕΧΝΕΙΟ ΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑTΗΡΙΟ TΕΧΝΟΛΟΓΙΑ ΚΑΤΙΜΩΝ ΚΑΙ ΛΙΠΑΝΣΙΚΩΝ ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ ΠΡΟΔΙΟΡΙΜΟ ΝΕΡΟΤ Ε ΠΡΟΪΟΝΣΑ ΠΕΣΡΕΛΑΙΟΤ, ΜΕΘΟΔΟ ΑΠΟΣΑΞΗ με βάςη: ASTM D 95 / EN ISO 7 / IP
ΕΘΝΙΚΟ ΜΕΣΟΒΙΟ ΠΟΛΤΣΕΧΝΕΙΟ ΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑTΗΡΙΟ TΕΧΝΟΛΟΓΙΑ ΚΑΤΙΜΩΝ ΚΑΙ ΛΙΠΑΝΣΙΚΩΝ ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ ΠΡΟΔΙΟΡΙΜΟ ΝΕΡΟΤ Ε ΠΡΟΪΟΝΣΑ ΠΕΣΡΕΛΑΙΟΤ, ΜΕΘΟΔΟ ΑΠΟΣΑΞΗ με βάςη: ASTM D 95 / EN ISO 7 / IP
16. Πίνακεσ και Συναρτήςεισ
 Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 16. Πίνακεσ και Συναρτήςεισ Ιωάννθσ Κατάκθσ Σιμερα o Κλιςθ με τιμι o Κλιςθ με αναφορά o Πίνακεσ και ςυναρτιςεισ o Παραδείγματα Ειςαγωγι o Στισ προθγοφμενεσ
Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 16. Πίνακεσ και Συναρτήςεισ Ιωάννθσ Κατάκθσ Σιμερα o Κλιςθ με τιμι o Κλιςθ με αναφορά o Πίνακεσ και ςυναρτιςεισ o Παραδείγματα Ειςαγωγι o Στισ προθγοφμενεσ
ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΥΠΗΡΕΣΙΑ ΑΝΑΠΤΥΞΗΣ ΠΡΟΓΡΑΜΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση Συγγραφή:
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΥΠΗΡΕΣΙΑ ΑΝΑΠΤΥΞΗΣ ΠΡΟΓΡΑΜΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση Συγγραφή:
Ηλιακι Θζρμανςθ οικίασ
 Ηλιακι Θζρμανςθ οικίασ Δυνατότθτα κάλυψθσ κερμαντικϊν αναγκϊν ζωσ και 100% (εξαρτάται από τθν τοποκεςία, τθν ςυλλεκτικι επιφάνεια και τθν μάηα νεροφ αποκθκεφςεωσ) βελτιςτοποιθμζνο ςφςτθμα με εγγυθμζνθ
Ηλιακι Θζρμανςθ οικίασ Δυνατότθτα κάλυψθσ κερμαντικϊν αναγκϊν ζωσ και 100% (εξαρτάται από τθν τοποκεςία, τθν ςυλλεκτικι επιφάνεια και τθν μάηα νεροφ αποκθκεφςεωσ) βελτιςτοποιθμζνο ςφςτθμα με εγγυθμζνθ
