Ζ. Κύκλος αναφοράς και περιστρεφόµενα διανύσµατα
|
|
|
- Ἐφραίμ Χρηστόπουλος
- 10 χρόνια πριν
- Προβολές:
Transcript
1 Ζ. Κύκλος αναφοράς και περιστρεφόµενα διανύσµατα Δυο βήµατα µέχρι τον κύκλο, τρία µέχρι τα περιστρεφόµενα, ένα ακόµη βήµα ασταθές κι ένας πειρασµός.. Ο πειρασµός Τα παραπάνω βάζουν αρκετούς στον πειρασµό να µετατρέψουν τα πλάτη Α 1 και Α των δύο απλών αρµονικών ταλαντώσεων (και όχι µόνο) σε περιστρεφόµενα...διανύσµατα ενός κύκλου αναφοράς και να συνθέτουν απλές αρµονικές ταλαντώσεις απλώς συνθέτοντας (προσθέτοντας) διανύσµατα µε τον κανόνα του παραλληλογράµ- µου. Με δεδοµένο βέβαια ότι ο κανόνας του παραλληλογράµµου δεν είναι τίποτε περισσότερο από το νόµο των συνηµίτονων και των ηµίτονων, οι οποίοι βασικά δεν απαιτούν διανύσµατα, θα µπορούσαµε να συνθέτουµε ευθύγραµµα τµήµατα ΟΜ ή τις επιβατικές ακτίνες του κινητού Μ. υο τρεις λοιπόν τυχερές σχέσεις των µαθηµατικών κάνουν Σχήµα 5.9 τυχερά τα περιστρεφόµενα διανύσµατα, τα οποία, παρόλο ότι είναι ένα τρυκ, µπορούν σε κάποιες περιπτώσεις να δώσουν λύσεις, ακόµη και όταν δεν έχουµε απλές αρµονικές ταλαντώσεις, όπως π.χ. σε προβλήµατα κυκλωµάτων όπου ο διεγέρτης επιβάλλει τη συχνότητά του σε όλα σχεδόν τα µεγέθη του κυκλώµατος. Το πρόβληµα όµως που µπαίνει µετά από όλα αυτά είναι το εξής: Χρειάζονται κύκλοι αναφοράς και περιστρεφόµενα διανύσµατα κατά τη διδασκαλία της Λυκειακής Φυσικής; Κατά τη γνώµη µας όχι µόνο δε χρειάζονται, αλλά δηµιουργούν προβλήµατα! Ας επιχειρη- µατολογήσουµε: 1) Τα περιστρεφόµενα διανύσµατα δεν έχουν καµιά, απολύτως καµιά µαθηµατική δοµή και υποδοµή σαθρή διαθέτουν, αφενός µεν γιατί το επίπεδο στο οποίο περιστρέφονται δεν έχει καµιά σχέση µε το µιγαδικό επίπεδο και αφετέρου γιατί η υποτυπώδης τριγωνοµετρία τους στριµώχνεται στο χώρο και στις γωνίες ενός παραλληλογράµµου. Έτσι λοιπόν, όταν οι αρχικές φάσεις φ 1 και φ των εξισώσεων ταλάντωσης που πρόκειται να συντεθούν διαφέρουν µεταξύ τους περισσότερο από π rad, παραλληλόγραµµο µε γωνία φ 1 φ µεταξύ των πλατών-διανυσµάτων Α 1 και Α δε µπορεί να σχηµατιστεί και συνεπώς πρέπει ή να γίνει εισαγωγή καινούριων κανόνων (αλχηµείες) ώστε να σχηµατιστεί και να αξιοποιηθεί σώνει και καλά το παραλληλόγραµµο ή να καταφύγουµε σε τύπους ουσιαστικά αναπόδεικτους, χωρίς να σχηµατίσουµε παραλληλόγραµµο. Για τους µαθητές πάντως στην περίπτωση αυτή θα υπάρξει µπέρδεµα. ) Τα περιστρεφόµενα διανύσµατα δεν έχουν καµιά, απολύτως καµιά µαθηµατική δοµή και υποδοµή σαθρή διαθέτουν. Έτσι αν σε κάποιο φαινόµενο, αν σε κάποια άσκηση εµφανιστεί γινόµενο ταλαντώσεων π.χ. γινόµενο δύο ρευµάτων i 1 i, γινόµενο δύο αποµακρύνσεων x 1 x, γινόµενο δύο αρµονικών συναρτήσεων γενικά, όλο αυτό το σκηνικό µε τα δια- 1
2 νυσµατοποιηθέντα βαθµωτά µεγέθη, που τόσα µαθήµατα επί µαθηµάτων χρειάστηκε για να στηθεί στα µάτια των µαθητών, θα καταρρεύσει σε δευτερόλεπτα. 3) Μια τυχερή συγκυρία, µια συνωµοσία θα λέγαµε των Μαθηµατικών έκανε να λειτουργήσει αυτό το τρυκ των περιστρεφόµενων διανυσµάτων. Όµως αυτό ξεχνιέται και αλλοιώνεται τελείως η εικόνα και της προέλευσης και των δυνατοτήτων των περιστρεφόµενων διανυσµάτων. Γρήγορα ο εκτροχιασµός είναι πλήρης, αφού ρόλοι αντιστρέφονται και αποδείξεις κακοποιούνται. εν είναι δυνατό να λανσάρεται ως σοβαρή µαθηµατική απόδειξη, η απόδειξη µε περιστρεφόµενα διανύσµατα, σχέσεων τύπου A = A1 + A + A1 Aσυνϕ και Aηµϕ εϕϑ = (5.107) A + A συνϕ Αυτού του είδους οι σχέσεις, που αφορούν τις αρµονικές ταλαντώσεις και που αποδείχθηκαν µε µαθηµατικά ότι είναι έτσι και ότι αφορούν όντως αυτές τις ταλαντώσεις, αυτές ακριβώς οι σχέσεις συνωµότησαν για να υπάρξουν τα περιστρεφόµενα διανύσµατα ως τρυκ και µόνο ως τρυκ. Με άλλα λόγια δηλαδή, δεν αποδεικνύεται µε περιστρεφόµενα διανύσµατα ότι η σύνθεση δύο απλών αρµονικών ταλαντώσεων είναι επίσης απλή αρµονική ταλάντωση, µε πλάτος και αρχική φάση που δίνονται από σχέσεις όπως οι (5.107), αλλά αντίθετα, σχέσεις τύπου (5.107), που αποδεικνύονται µε αυστηρά µαθηµατικά (διαφορικές, τριγωνοµετρία κ.λ.π.) ότι είναι έτσι και ότι όντως αφορούν απλές αρµονικές ή γενικότερα αρµονικές ταλαντώσεις, θυ- µίζουν κανόνα παραλληλογράµµου, µε αποτέλεσµα να στηρίζουν για λίγα µόνο βήµατα την ιδέα των περιστρεφόµενων διανυσµάτων. ίνοντας όµως στα µάτια των παιδιών τέτοιας έκτασης προτεραιότητα σε περιστρεφόµενα διανύσµατα, αλλάζει η σειρά, χαλιούνται συλλογισµοί, κρύβεται η ουσία των πραγµάτων. ε χρειάζονται που δε χρειάζονται τα περιστρεφόµενα, να ανάγονται όµως και σε σοβαρό µαθηµατικό εργαλείο απόλυτης προτεραιότητας, είναι άδικο για τα παιδιά που προσπαθούν να δοµήσουν µια σοβαρή σκέψη. Άδικο όµως και για τα Μαθηµατικά τους που φαντάζουν ανίκανα να λειτουργήσουν και αποστασιοποιηµένα από τις ανάγκες, ακόµη και µιας λυκειακής Φυσικής. Πώς να το πούµε; Όταν δίνουµε τόση σηµασία στα περιστρεφόµενα χαλάει η σειρά των πραγµάτων!!! Αδικούνται τα µαθηµατικά των παιδιών και η Φυσική τους στέκεται µετέωρη και γεµάτη αλχηµείες. 4) Στα µάτια αρκετών από αυτούς που δουλεύουν µε κύκλους αναφοράς και µε περιστρεφόµενα, η ταλάντωση παύει να είναι κίνηση αυτοδύναµη και γίνεται απόλυτα υποβοηθούµενη από την οµαλή κυκλική κίνηση, η οποία στο τέλος παίρνει τη θέση της ταλάντωσης. Αρκετοί νοµίζουν ότι δεν µπορεί να υπάρξει µελέτη µιας ταλάντωσης αν δεν ζωγραφιστούν κύκλοι. Ακούνε ταλάντωση και σκέφτονται κύκλους. Ακούνε γωνιακή συχνότητα και σκέφτονται γωνιακές ταχύτητες. Ακούνε φάση και σκέφτονται γωνίες. Έχουµε και εδώ αναστροφή των προτεραιοτήτων, καθώς, αντί να δοθεί προτεραιότητα στην ταλάντωση, δίνεται στην οµαλή κυκλική κίνηση, που στο κάτω κάτω η εξίσωση κίνησής της µπορεί να θεωρηθεί επαλληλία των εξισώσεων κίνησης δύο αρµονικών ταλαντώσεων οι οποίες εξελίσσονται σε κάθετες διευθύνσεις. Με άλλα λόγια, ενώ οι ταλαντώσεις µπορούν να περιγράψουν την οµαλή κυκλική κίνηση και όχι το αντίθετο, αποκτά κυρίαρχο ρόλο η κυκλική κίνηση. Και κάτι ακόµη πιο οδυνηρό. Η γωνιακή ταχύτητα κορυφαίο διανυσµατικό µέγεθος κυρίαρχο στη µελέτη της κίνησης ενός στερεού, συγκρίνεται, παραλληλίζεται και στο 1
3 τέλος ταυτίζεται µε τη γωνιακή συχνότητα της ταλάντωσης, ένα απλό µονόµετρο µέγεθος. Ας συνοψίσουµε: Η απλή αρµονική ταλάντωση είναι κίνηση ανεξάρτητη, αυτοδύναµη και ευθύγραµ- µη. εν έχει ανάγκη και σχέση ούτε µε κύκλους, ούτε µε ακτίνες, ούτε µε γωνίες και γωνιακές ταχύτητες. Το να εξωθούµε το µαθητή να βλέπει κύκλους και γωνίες σε µια ευθύγραµµη κίνηση είναι επικίνδυνο για τη λογική του. Ό,τι υπάρχει µέσα στον τριγωνοµετρικό αριθµό της εξίσωσης κίνησης µιας α.α.τ. είναι η φάση και δεν είναι γωνία κάποιας κίνησης ή κάποιας περιστροφής. Καλό είναι λοιπόν να τη λέµε µε το όνοµά της, φάση και όχι γωνία. Άλλο φάση και άλλο γωνία!! D Το σύµβολο ω είναι µια συντοµογραφία της ποσότητας που παρουσιάζεται σε m όλες τις σχέσεις της α.α.τ. Το ω επιλέχτηκε θετικό και η αξία του αντλείται από το γεγονός ότι συνδέεται µε την περίοδο της κίνησης. Είναι µια µονόµετρη ποσότητα, ένα απλό όνοµα. εν είναι γωνιακή ταχύτητα και δεν έχει καµιά σχέση µε αυτό το κορυφαίο διανυσµατικό µέγεθος το οποίο πουθενά στην αντιµετώπιση του φαινοµένου δεν υπεισέρχεται. Θα µπορούσαµε αντί του ω να συµβολίζαµε την ποσότητα D µε οποιοδήποτε γράµµα π.χ. γ (βλέπε σελίδες 3 και 413) m εν είναι ανησυχητικό που ελάχιστοι έως κανένας µαθητής δε µας ρώτησε να του σχεδιάσουµε πάνω στην πραγµατική κίνηση, πάνω στη ταλάντωση δηλαδή, την γωνιακή ταχύτητα; εν είναι ανησυχητικό που ελάχιστοι έως κανένας µαθητής δε µας ρώτησε να του σχεδιάσουµε πάνω στην πραγµατική κίνηση τη γωνία που υπάρχει µέσα στο ηµίτονο; Που είναι αυτή η γωνία και που είναι το επίπεδο για να ζωγραφίσει την ω. Γιατί του χαλάµε τη λογική του που πάει µόλις τώρα να φτιάξει µε αυστηρότητα; Με ποιες λογικές άµυνες και ποια συλλογιστικά φίλτρα θα δεχτεί να του ανακατέψουµε µια ευθύγραµµη κίνηση µε κυκλικές κινήσεις φαντασµάτων; Πόσο αλώβητος θα µείνει µετά; 5) Υπάρχουν πολλοί άλλοι τρόποι αυστηρότατοι, πολύ πιο σύντοµοι και πλήρως κατανοητοί από τους µαθητές, που λειτουργώντας θαυµάσια σε όλες τις δυνατές περιπτώσεις σύνθεσης ταλαντώσεων καθιστούν περιττή την καταφυγή στα περιστρεφόµενα.(βλέπε σελίδα 377) 6) Κατά τη διδασκαλία των κύκλων αναφοράς και των περιστρεφόµενων, χρησιµοποιώντας µια τελείως λανθασµένη και µεθοδολογία και ορολογία, µπαίνουν σε αµφισβήτηση ή αποσαθρώνονται έννοιες, ορισµοί και δοµές τόσο της Φυσικής όσο και των Μαθηµατικών. Και είναι ορατός ο κίνδυνος να χαλάσει η σκέψη των µαθητών. Οι ενδείξεις πολλές. Πρώτη ένδειξη: Οι φυσικοί µιλάνε δική τους µαθηµατική διάλεκτο Είναι αδύνατο να κατανοήσει ο µαθηµατικός τι προσπαθεί να κάνει ένας µαθητής του, ό- ταν για να προσθέσει δυο ηµίτονα, τον βλέπει να αφήνει την τριγωνοµετρία που του έµαθε, να µετατρέπει απλούς θετικούς αριθµούς σε διανύσµατα, να τα ζωγραφίζει µαζί µε κύκλους και να τα κάνει να περιστρέφονται. Όσες φορές έδωσα σε µαθηµατικό να διαβάσει κείµενο από εξωσχολικά βοηθήµατα που αναφερόταν σε περιστρεφόµενα διανύσµατα, ο άνθρωπος σταυροκοπιότανε. οκιµάστε το! εύτερη ένδειξη: Χαλιούνται ορισµοί Φυσικής Αρκετές φορές, για να µην πούµε όλες, γράφεται το εξής: Η προβολή Μ στον άξονα y, του άκρου Μ του περιστρεφόµενου διανύσµατος εκτελεί απλή αρµονική ταλάντωση. 3
4 Όµως όλοι ξέρουµε ότι οι σκιές και τα φαντάσµατα δεν κάνουν απλές αρµονικές ταλαντώσεις. Ώρα είναι να γράψουµε για δαύτα και κανένα νόµο του Νεύτωνα. Η συντεταγµένη µιας προβολής µπορεί να δίνεται από κάποια συνάρτηση του χρόνου. Να κάνει όµως απλή αρµονική ταλάντωση είναι κρίµα για τη Φυσική που βλέπει έναν ορισµό της, στηριγµένο σε ειδική κατηγορία δυνάµεων και διαφορικών εξισώσεων, να αποσαθρώνεται. Τρίτη ένδειξη: Χαλιούνται συλλογισµοί και διαλύονται άµυνες Λένε στους µαθητές ότι το πλάτος παριστάνεται µε διάνυσµα, ενώ µόλις χθες τους είχανε πει ότι είναι µονόµετρο θετικό µέγεθος και µετά µια σελίδα του σχολικού βιβλίου, όταν οι συχνότητες των ταλαντώσεων δε θα είναι πια ίδιες, τους ξανάλενε ότι το πλάτος είναι µονό- µετρο µέγεθος και να µη το παριστάνουνε πια ως διάνυσµα, αλλά να χρησιµοποιήσουν τριγωνοµετρία. Ελάχιστοι έως κανένας µαθητής από αυτούς που ακούνε αυτές τις παλινωδίες δεν αντιδρά. Και αυτό είναι πολύ ανησυχητικό! Και το χειρότερο νοµίζουν ότι η Φυσική δεν έχει σχέση µε τα Μαθηµατικά. Μεταφέρω τα λόγια ενός από αυτούς τους µαθητές που ρώτησα γιατί δέχονται τέτοια ρευστά πράµατα. Να τι µου είπε: Το πλάτος ταλάντωσης και µερικά άλλα µεγέθη όπως φορτίο, ένταση ρεύµατος, τάση κ.λ.π. δεν είναι µονόµετρα όπως τα άλλα µονόµετρα µεγέθη π.χ. η µάζα. Έχουν τη δυνατότητα να αντιµετωπίζονται όχι ως διανύσµατα των µαθηµατικών αλλά ως περιστρεφόµενα διανύσµατα. Η Φυσική δεν έχει σχέση µε τα Μαθηµατικά και δεν έχει την αυστηρότητα των Μαθηµατικών. Άλλο τα διανύσµατα των Μαθηµατικών και άλλα τα διανύσµατα της Φυσικής. Στη Φυσική είναι πιο ελαστικά τα πράµατα. Αν κάτι µας βολεύει ως µονόµετρο το ορίζουµε ως µονόµετρο, αν µας βολεύει ως διανυσµατικό το ορίζουµε ως διανυσµατικό. Είναι θέµα ορισµού δηλαδή και κυρίως τι µας βολεύει 7) Κύκλοι αναφοράς και περιστρεφόµενα δεν περιέχονται στο σχολικό βιβλίο Φυσικής Κατεύθυνσης Γ Λυκείου και κατά συνέπεια, µιλώντας κυριολεκτικά, θεωρούνται εκτός ύ- λης. Και είναι ρίσκο η χρήση των περιστρεφοµένων αν δεν υπάρξει οδηγία κατάλληλη από την επιτροπή των εξετάσεων. 8) Η έννοια του περιστρεφόµενου διανύσµατος προσθέτει στους µαθητές πολλές επιπλέον ώρες διδασκαλίας, ατέλειωτες σηµειώσεις και σελίδες εξωσχολικών βοηθηµάτων για διάβασµα, χωρίς να υπάρχει κανένας λόγος. Έτσι πέρα από την οικολογική ζηµιά που γίνεται µε αυτό το ατέλειωτο χαρτοµάνι, οι µαθητές χάνουν ώρες από τη ζωή τους για να διδαχτούν και να αρκετές φορές να πληρώσουν πράγµατα που δε τους χρειάζονται. Είναι τόσο περιορισµένη η εφαρµογή των περιστρεφόµενων και τόσο µεγάλη η απόστασή τους από τη µαθηµατική αυστηρότητα, που δεν αξίζουν ούτε τις ώρες που απαιτεί η διδασκαλία τους, ούτε το χαρτί που σπαταλιέται για δαύτα, ούτε τα χρήµατα που πιθανώς δίνονται. Ουσιαστικά αφορούν µια µόνο σελίδα του σχολικού (σύνθεση απλών αρµονικών ταλαντώσεων ίδιας συχνότητας), αφού στη επόµενη κιόλας σελίδα του σχολικού οι µαθητές θα εξαναγκαστούν να τρέξουν πάλι πίσω στην τριγωνοµετρία τους. Αν όµως ήταν να ξανατρέξουν πίσω στα µαθηµατικά του σχολείου τους, γιατί τα παράτησαν; Άξιζε όλη αυτή η ταλαιπωρία για µια µόνο σελίδα Φυσικής; 9) Με τα περιστρεφόµενα δεν επιλύεται κανένα µα κανένα πρόβληµα Φυσικής που δεν επιλύεται και µε τις σχέσεις που ήδη υπάρχουν στο σχολικό βιβλίο (το δείξαµε στη σελ. 378 κατά την παρουσίαση του 3ου τρόπου σύνθεσης α.α.τ.) ή µε τα µαθηµατικά που ήδη οι µαθητές ξέρουν από το Σχολείο τους. 4
5 10) Από τα παιδιά που θα ακούσουν για περιστρεφόµενα διανύσµατα ελάχιστα έως κανένα δε θα τα χρειαστεί στο πανεπιστήµιο. Πρώτο γιατί οι πιο πολλοί από τους µαθητές που θα ακούσουν για περιστρεφόµενα θα περάσουν σε σχολές που δεν έχουν σχέση µε αυτά. εύτερο γιατί όσοι περάσουν σε σχολή που έχει στο αναλυτικό της πρόγραµµα κυκλώµατα ή συνθέσεις, θα χρησιµοποιήσουν µιγάδες. Και βέβαια αφού έχουν ξεκαθαρίσει στο µυαλό τους και κατανοήσει απόλυτα µε ποιο τρόπο, µε ποιες συµφωνίες και µε ποιες αντιστοιχίες η µελέτη των κυκλωµάτων και των συνθέσεων µπορεί να υποβοηθηθεί από την πανίσχυρη µαθηµατική δοµή των µιγαδικών συναρτήσεων. Έτσι θα ξέρει ο φοιτητής πλέον, ποια είναι τα όρια αυτής της βοήθειας, που αρχίζει και που τελειώνει το τρυκ. Μου φαίνεται απίθανο να υπάρχει σχολή που να αγνοεί την παρουσίαση µε µιγάδες και να χρησιµοποιεί περιστρεφόµενα. Με άλλα λόγια, αν χρειαστεί κάτι σε µια σχολή, δε θα είναι τίποτε από τα περιστρεφόµενα διανύσµατα, αλλά µιγάδες και τριγωνοµετρία. Γιατί λοιπόν να µην ενισχύσουµε το µαθηµατικό τους υπόβαθρο εφαρµόζοντας την τριγωνοµετρία του σχολείου σε παραδείγµατα Φυσικής; 11) Τα παιδιά που παίρνουν ηλεκτρολογία και που αναγκαστικά λόγω... του ανεκδιήγητου και αχαρακτήριστου σχολικού τους βιβλίου θα ακούσουν για περιστρεφόµενα διανύσµατα στα κυκλώµατα εναλλασσόµενων τάσεων. ηλαδή σε εξαναγκασµένες ταλαντώσεις. Όµως Ο αριθµός των παιδιών που επιλέγουν ηλεκτρολογία είναι συντριπτικά µικρότερος από τον αριθµό των παιδιών που δεν επιλέγουν ηλεκτρολογία. ε χρειάζεται τα περιστρεφόµενα να καθιερωθούν στη συνείδηση αυτών των λίγων, έστω, παιδιών και µέσα από τη Φυσική. Πρέπει να τους τονίζονται τα όρια εφαρµογής των περιστρεφόµενων και ο προσδιορισµός τους ως τρυκ. Κατά τη χρησιµοποίηση των περιστρεφόµενων διανυσµάτων στην Ηλεκτρολογία, δε δίνεται ούτε η έκταση, ούτε η σοβαροφάνεια που τους δίνεται στη Φυσική και συνεπώς ο κίνδυνος εκτροχιασµού είναι σαφώς µειωµένος. 1) Παρόλο που δεν νοµίζουµε ότι χρειάζεται, αν θέλαµε να δώσουµε αποδείξεις των σχέσεων που ισχύουν για το πλάτος και την αρχική φάση της συνισταµένης ταλάντωσης, µπορούσαµε να κάνουµε την τριγωνοµετρική απόδειξη της σελ Στο κάτω κάτω είναι µαθηµατικά αυστηρή µε όλους τους απαραίτητους και σωστούς περιορισµούς, είναι απόλυτα κατανοητή από τους µαθητές, καλύπτει όλες τις περιπτώσεις αρχικών φάσεων, είναι πολύ πιο σύντοµη από τις αντίστοιχες αποδείξεις των περιστρεφόµενων διανυσµάτων και το κυριότερο δε χρειάζεται οι µαθητές ούτε να αλλάζουν από µέρα σε µέρα τα µονόµετρα µεγέθη σε διανυσµατικά, ούτε να διδάσκονται καινούρια πράµατα, χωρίς καµιά ουσιαστική αξία. Έτσι κι αλλιώς διδάσκοντας σύνθεση απλών αρµονικών ταλαντώσεων δεν διδάσκουµε κάποιο φυσικό φαινόµενο, αλλά µαθηµατικά παιχνίδια. Προσθέσεις ηµίτονων και συνηµίτονων διδάσκουµε. Ας τις διδάξουµε συνεπώς µε την αίγλη των µαθηµατικών και την αυστηρότητα που αξίζει σε µια άσκηση µαθηµατικών (γιατί άσκηση µαθηµατικών διδάσκουµε κατά βάθος) και όχι µε το τρυκ των περιστρεφόµενων διανυσµάτων (Από το βιβλίο «Θέµατα Φυσικής-Παρανοήσεις και προτάσεις υπέρβασής τους») 5
Προβληματισμοί κατά τη διδασκαλία της σύνθεσης κινήσεων
 Θρασύβουλος Κων. Μαχαίρας Προβληματισμοί κατά τη διδασκαλία της σύνθεσης κινήσεων (α μέρος) 1 Σκοπός αυτής της σειράς διαφανειών είναι να αναδείξει την αξία που έχει η επιλογή της μορφής της εξίσωσης ενός
Θρασύβουλος Κων. Μαχαίρας Προβληματισμοί κατά τη διδασκαλία της σύνθεσης κινήσεων (α μέρος) 1 Σκοπός αυτής της σειράς διαφανειών είναι να αναδείξει την αξία που έχει η επιλογή της μορφής της εξίσωσης ενός
Όταν χαλά η γλώσσα, χαλάει η σκέψη
 Όταν χαλά η γλώσσα, χαλάει η σκέψη (γ µέρος) Πριν από καιρό έγραφα σε κάποιο βιβλίο... «... Η ανησυχία µου, εκτός των άλλων, βρίσκεται και στο γεγονός ότι στο σχολικό βιβλίο και κατά συνέπεια στα εξωσχολικά
Όταν χαλά η γλώσσα, χαλάει η σκέψη (γ µέρος) Πριν από καιρό έγραφα σε κάποιο βιβλίο... «... Η ανησυχία µου, εκτός των άλλων, βρίσκεται και στο γεγονός ότι στο σχολικό βιβλίο και κατά συνέπεια στα εξωσχολικά
Οι θέσεις µου... Ένα υλικό σηµείο κάθε φορά βρίσκεται σε ένα µόνο σε ένα σηµείο του χώρου και άρα κάνει µία µόνο κίνηση.
 Οι θέσεις µου... ) Η παράγραφος.7α του σχολικού βιβλίου Κατεύθυνσης Γ Λυκείου είναι λάθος, γιατί σύνθεση απλών αρµονικών ταλαντώσεων ίδιας συχνότητας ίδιας διεύθυνσης ούτε υπάρχει ούτε υποστηρίζεται θεωρητικά.
Οι θέσεις µου... ) Η παράγραφος.7α του σχολικού βιβλίου Κατεύθυνσης Γ Λυκείου είναι λάθος, γιατί σύνθεση απλών αρµονικών ταλαντώσεων ίδιας συχνότητας ίδιας διεύθυνσης ούτε υπάρχει ούτε υποστηρίζεται θεωρητικά.
Είναι το ηλεκτρικό ρεύµα διανυσµατικό µέγεθος;
 Είναι το ηλεκτρικό ρεύµα διανυσµατικό µέγεθος; Για να εξετάσουµε το κύκλωµα LC µε διδακτική συνέπεια νοµίζω ότι θα πρέπει να τηρήσουµε τους ορισµούς που δώσαµε στα παιδιά στη Β Λυκείου. Ας ξεκινήσουµε
Είναι το ηλεκτρικό ρεύµα διανυσµατικό µέγεθος; Για να εξετάσουµε το κύκλωµα LC µε διδακτική συνέπεια νοµίζω ότι θα πρέπει να τηρήσουµε τους ορισµούς που δώσαµε στα παιδιά στη Β Λυκείου. Ας ξεκινήσουµε
Διαβάζοντας το βιβλίο του Θρασύβουλου εγώ εστιάζω στο εξής:
 Φίλε Λάµπρο σε κάποια θα συµφωνήσω και σε κάποια θα διαφωνήσω. Θα συµφωνήσω ότι στις περιπτώσεις που αναφέρεις και οι τρεις κινήσεις έχουν τα χαρακτηριστικά της ευθύγραµµης οµαλά µεταβαλλόµενης κίνησης
Φίλε Λάµπρο σε κάποια θα συµφωνήσω και σε κάποια θα διαφωνήσω. Θα συµφωνήσω ότι στις περιπτώσεις που αναφέρεις και οι τρεις κινήσεις έχουν τα χαρακτηριστικά της ευθύγραµµης οµαλά µεταβαλλόµενης κίνησης
Ορισµοί και εξισώσεις κίνησης
 Ορισµοί και εξισώσεις κίνησης Σκοπός του κειµένου είναι να υποστηριχθούν οι παρακάτω θέσεις εν έχουν κανένα απολύτως νόηµα φράσεις του τύπου «η φάση της ταλάντωσης είναι» ή «η αρχική φάση της ταλάντωσης
Ορισµοί και εξισώσεις κίνησης Σκοπός του κειµένου είναι να υποστηριχθούν οι παρακάτω θέσεις εν έχουν κανένα απολύτως νόηµα φράσεις του τύπου «η φάση της ταλάντωσης είναι» ή «η αρχική φάση της ταλάντωσης
Περί της «Αρχής ανεξαρτησίας των κινήσεων»
 Περί της «Αρχής ανεξαρτησίας των κινήσεων» Παρακολουθώ στο δίκτυο τις τελευταίες µέρες να γίνεται συζήτηση για την «Αρχή ανεξαρτησίας των κινήσεων» ή την «επαλληλία εξισώσεων κίνησης». Προσπαθώ στο µέτρο
Περί της «Αρχής ανεξαρτησίας των κινήσεων» Παρακολουθώ στο δίκτυο τις τελευταίες µέρες να γίνεται συζήτηση για την «Αρχή ανεξαρτησίας των κινήσεων» ή την «επαλληλία εξισώσεων κίνησης». Προσπαθώ στο µέτρο
Χρονοεξαρτώµενη «Δυναµική Ενέργεια»
 Χρονοεξαρτώµενη «Δυναµική Ενέργεια» Άσκηση Σώµα µάζας m στερεώνεται στο ένα άκρο ιδανικού ελατηρίου του οποίου το άλλο άκρο Ζ εκτελεί αρµονική ταλάντωση της µορφής x1 = Bηµω t. Να βρεθεί η εξίσωση κίνησης
Χρονοεξαρτώµενη «Δυναµική Ενέργεια» Άσκηση Σώµα µάζας m στερεώνεται στο ένα άκρο ιδανικού ελατηρίου του οποίου το άλλο άκρο Ζ εκτελεί αρµονική ταλάντωση της µορφής x1 = Bηµω t. Να βρεθεί η εξίσωση κίνησης
Ελεύθερη αρµονική ταλάντωση χωρίς απόσβεση
 Ελεύθερη αρµονική ταλάντωση χωρίς απόσβεση Παρακολουθώντας τη συζήτηση που έχει αναπτυχθεί, σχετικά µε το «... Αν η αποµάκρυνση x του σώµατος δίνεται από τη σχέση x=αηµ(ωt+φ) η κίνηση του σώµατος ονοµάζεται
Ελεύθερη αρµονική ταλάντωση χωρίς απόσβεση Παρακολουθώντας τη συζήτηση που έχει αναπτυχθεί, σχετικά µε το «... Αν η αποµάκρυνση x του σώµατος δίνεται από τη σχέση x=αηµ(ωt+φ) η κίνηση του σώµατος ονοµάζεται
Για τις παρακάτω 3 ερωτήσεις, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 Επαναληπτικά Θέµατα ΟΕΦΕ 007 Α ΛΥΚΕΙΟΥ Θέµα ο ΦΥΣΙΚΗ Για τις παρακάτω 3 ερωτήσεις, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σε ένα σώµα
Επαναληπτικά Θέµατα ΟΕΦΕ 007 Α ΛΥΚΕΙΟΥ Θέµα ο ΦΥΣΙΚΗ Για τις παρακάτω 3 ερωτήσεις, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σε ένα σώµα
ΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΣΤΙΣ ΜΗΧΑΝΙΚΕΣ ΚΑΙ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
 ΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΣΤΙΣ ΜΗΧΑΝΙΚΕΣ ΚΑΙ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Θέµα Α Στις ερωτήσεις -4 να βρείτε τη σωστή απάντηση. Α. Για κάποιο χρονικό διάστηµα t, η πολικότητα του πυκνωτή και
ΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΣΤΙΣ ΜΗΧΑΝΙΚΕΣ ΚΑΙ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Θέµα Α Στις ερωτήσεις -4 να βρείτε τη σωστή απάντηση. Α. Για κάποιο χρονικό διάστηµα t, η πολικότητα του πυκνωτή και
α. Σύνδεση δύο απλών αρμονικών ταλαντώσεων ίδιας συχνότητας και ίδιας διεύθυνσης, οι οποίες
 ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ α. Σύνδεση δύο απλών αρμονικών ταλαντώσεων ίδιας συχνότητας και ίδιας διεύθυνσης, οι οποίες εξελίσσονται γύρω από την ίδια δέση ισορροπίας Έστω ότι ένα σώμα εκτελεί ταυτόχρονα δύο απλές
ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ α. Σύνδεση δύο απλών αρμονικών ταλαντώσεων ίδιας συχνότητας και ίδιας διεύθυνσης, οι οποίες εξελίσσονται γύρω από την ίδια δέση ισορροπίας Έστω ότι ένα σώμα εκτελεί ταυτόχρονα δύο απλές
Προβληματισμοί κατά τη διδασκαλία της «σύνθεσης κινήσεων».
 Θρασύβουλος Κων. Μαχαίρας Προβληματισμοί κατά τη διδασκαλία της «σύνθεσης κινήσεων». (β μέρος) 1 Στο α μέρος αυτής της σειράς διαφανειών κατέληξα σε ένα πολύ ουσιαστικό συμπέρασμα: 2 Γενικό Συμπέρασμα:
Θρασύβουλος Κων. Μαχαίρας Προβληματισμοί κατά τη διδασκαλία της «σύνθεσης κινήσεων». (β μέρος) 1 Στο α μέρος αυτής της σειράς διαφανειών κατέληξα σε ένα πολύ ουσιαστικό συμπέρασμα: 2 Γενικό Συμπέρασμα:
α) Πως ερµηνεύεται η φράση: «µε γωνιακές συχνότητες που διαφέρουν πολύ λίγο»; γ) Να βρεθούν η γωνιακή συχνότητα ω, η συχνότητα f και η περίοδος Τ των
 Σύνθεση δύο ΑρµονικώνΤαλαντώσεων που εξελίσσονται στην ίδια ευθεία γύρω από την ίδια θέση µε ίδιο πλάτος και γωνιακές συχνότητες που διαφέρουν πολύ λίγο Έστω ότι υλικό σηµείο εκτελεί ταυτόχρονα τις ταλαντώσεις:
Σύνθεση δύο ΑρµονικώνΤαλαντώσεων που εξελίσσονται στην ίδια ευθεία γύρω από την ίδια θέση µε ίδιο πλάτος και γωνιακές συχνότητες που διαφέρουν πολύ λίγο Έστω ότι υλικό σηµείο εκτελεί ταυτόχρονα τις ταλαντώσεις:
Α. Σύνθεση δύο ΑΑΤ της ίδιας συχνότητας, που γίνονται γύρω από το ίδιο σηµείο στην ίδια διεύθυνση
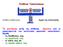 Σύνθεση Ταλαντώσεων Σύνθετη ταλάντωση Αρχή της επαλληλίας Το αποτέλεσµα αυτής της σύνθεσης εξαρτάται από τα χαρακτηριστικά των συνιστωσών αρµονικών ταλαντώσεων, δηλαδή τις διευθύνσεις τους τις συχνότητές
Σύνθεση Ταλαντώσεων Σύνθετη ταλάντωση Αρχή της επαλληλίας Το αποτέλεσµα αυτής της σύνθεσης εξαρτάται από τα χαρακτηριστικά των συνιστωσών αρµονικών ταλαντώσεων, δηλαδή τις διευθύνσεις τους τις συχνότητές
Εναλλασσόμενο και μιγαδικοί
 (olts) Εναλλασσόμενο και μιγαδικοί Γενικά Σε κυκλώματα DC, οι ηλεκτρικές μεγέθη εξαρτώνται αποκλειστικά από τις ωμικές αντιστάσεις, φυσικά μετά την ολοκλήρωση πιθανών μεταβατικών φαινομένων λόγω παρουσίας
(olts) Εναλλασσόμενο και μιγαδικοί Γενικά Σε κυκλώματα DC, οι ηλεκτρικές μεγέθη εξαρτώνται αποκλειστικά από τις ωμικές αντιστάσεις, φυσικά μετά την ολοκλήρωση πιθανών μεταβατικών φαινομένων λόγω παρουσίας
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΤΑΞΗ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 9 ΙΟΥΝΙΟΥ 003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤΑ (7) ΘΕΜΑ 1ο Στις προτάσεις 1.1
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 9 ΙΟΥΝΙΟΥ 003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤΑ (7) ΘΕΜΑ 1ο Στις προτάσεις 1.1
Κάπως έτσι ονειρεύτηκα την Γραμμική Αρμονική Ταλάντωση!!! Μπορεί όμως και να ήταν.
 Ένα όνειρο που ονειρεύεσαι μόνος είναι απλά ένα όνειρο. Ένα όνειρο που ονειρεύεσαι με άλλους μαζί είναι πραγματικότητα. John Lennon Κάπως έτσι ονειρεύτηκα την Γραμμική Αρμονική Ταλάντωση!!! Μπορεί όμως
Ένα όνειρο που ονειρεύεσαι μόνος είναι απλά ένα όνειρο. Ένα όνειρο που ονειρεύεσαι με άλλους μαζί είναι πραγματικότητα. John Lennon Κάπως έτσι ονειρεύτηκα την Γραμμική Αρμονική Ταλάντωση!!! Μπορεί όμως
Εξαρτάται η συχνότητα από τη µάζα στην Απλή Αρµονική Ταλάντωση;
 Εξαρτάται η συχνότητα από τη µάζα στην Απλή Αρµονική Ταλάντωση; Ξεκινώντας θα ήθελα να θυµίσω κάποια στοιχεία που σχετίζονται µε τον ορισµό της συχνότητας σε ένα περιοδικό φαινόµενο, άρα και στην ΑΑΤ.
Εξαρτάται η συχνότητα από τη µάζα στην Απλή Αρµονική Ταλάντωση; Ξεκινώντας θα ήθελα να θυµίσω κάποια στοιχεία που σχετίζονται µε τον ορισµό της συχνότητας σε ένα περιοδικό φαινόµενο, άρα και στην ΑΑΤ.
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
β. Το πλάτος της σύνθετης ταλάντωσης είναι : Α = (Α 1 ² + Α 2 ² + 2 Α 1 Α 2 συν φ) (φ = π rad) Α = (Α 1 ² + Α 2 ² + 2 Α 1 Α 2 συν π) Α = [Α 1 ² + Α 2
 1) Ένα κινητό εκτελεί συγχρόνως δύο απλές αρμονικές ταλαντώσεις που γίνονται στην ίδια διεύθυνση και γύρω από την θέση ισορροπίας με εξισώσεις : x 1 = 3 ημ [(2 π) t] και x 2 = 4 ημ [(2 π) t + φ], (S.I.).
1) Ένα κινητό εκτελεί συγχρόνως δύο απλές αρμονικές ταλαντώσεις που γίνονται στην ίδια διεύθυνση και γύρω από την θέση ισορροπίας με εξισώσεις : x 1 = 3 ημ [(2 π) t] και x 2 = 4 ημ [(2 π) t + φ], (S.I.).
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002 ÈÅÌÅËÉÏ
 ΘΕΜΑ 1ο ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί
ΘΕΜΑ 1ο ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 25 ΑΠΡΙΛΙΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΘΕΜΑ 1ο ΑΡΧΗ 1ΗΣΣΕΛΙ ΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 5 ΑΠΡΙΛΙΟΥ 009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς
ΘΕΜΑ 1ο ΑΡΧΗ 1ΗΣΣΕΛΙ ΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 5 ΑΠΡΙΛΙΟΥ 009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς
Απάντηση 7. Ναι αυτό δήλωσα ιονύση και αυτό το οποίο λες και συ, νοµίζω είναι το σωστό
 Απάντηση 7 1) Γράφεις Διονύση: «...Με ξαφνιάζεις Θρασύβουλε. πρόσεξε τι δήλωσες παραπάνω ότι συµφωνείς: «βλέπω µόνο ένα παράθυρο και θέλω να ξέρω αν οι φάσεις των δύο σηµείων Β και Γ, θα ικανοποιούν την
Απάντηση 7 1) Γράφεις Διονύση: «...Με ξαφνιάζεις Θρασύβουλε. πρόσεξε τι δήλωσες παραπάνω ότι συµφωνείς: «βλέπω µόνο ένα παράθυρο και θέλω να ξέρω αν οι φάσεις των δύο σηµείων Β και Γ, θα ικανοποιούν την
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΣΥΜΒΟΛΗ ΚΥΜΑΤΩΝ. Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός. https://physicscourses.wordpress.
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΣΥΜΒΟΛΗ ΚΥΜΑΤΩΝ Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός Βασικές Έννοιες Στη προηγούμενη παράγραφο μάθαμε πως κάνουμε μελέτη των κυμάτων. Τώρα θα μελετήσουμε τι συμβαίνει
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΣΥΜΒΟΛΗ ΚΥΜΑΤΩΝ Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός Βασικές Έννοιες Στη προηγούμενη παράγραφο μάθαμε πως κάνουμε μελέτη των κυμάτων. Τώρα θα μελετήσουμε τι συμβαίνει
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 29 ΜΑΪOY 2015 ΕΚΦΩΝΗΣΕΙΣ
 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 9 ΜΑΪOY 01 ΕΚΦΩΝΗΣΕΙΣ Θέµα Α Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 9 ΜΑΪOY 01 ΕΚΦΩΝΗΣΕΙΣ Θέµα Α Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΑΠΡΙΛΙΟΣ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΑΠΡΙΛΙΟΣ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Ονοµατεπώνυµο: ΘΕΜΑ 1ο Να γράψετε στο τετράδιο σας
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΑΠΡΙΛΙΟΣ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Ονοµατεπώνυµο: ΘΕΜΑ 1ο Να γράψετε στο τετράδιο σας
1ο ιαγώνισµα - Οριζόντια Βολή - Κυκλική Κίνηση. Θέµα 1ο
 1ο ιαγώνισµα - Οριζόντια Βολή - Κυκλική Κίνηση Ηµεροµηνία : Νοέµβρης 2013 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα 1ο Οµάδα Β Στις ερωτήσεις 1.1 1.4 επιλέξτε την σωστή απάντηση [4 5 = 20 µονάδες]
1ο ιαγώνισµα - Οριζόντια Βολή - Κυκλική Κίνηση Ηµεροµηνία : Νοέµβρης 2013 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα 1ο Οµάδα Β Στις ερωτήσεις 1.1 1.4 επιλέξτε την σωστή απάντηση [4 5 = 20 µονάδες]
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Καμπυλόγραμμες Κινήσεις Επιμέλεια: Αγκανάκης Α. Παναγιώτης, Φυσικός http://phyiccore.wordpre.com/ Βασικές Έννοιες Μέχρι στιγμής έχουμε μάθει να μελετάμε απλές κινήσεις,
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Καμπυλόγραμμες Κινήσεις Επιμέλεια: Αγκανάκης Α. Παναγιώτης, Φυσικός http://phyiccore.wordpre.com/ Βασικές Έννοιες Μέχρι στιγμής έχουμε μάθει να μελετάμε απλές κινήσεις,
ΚΕΦΑΛΑΙΟ 10. Μελέτη ηλεκτρικών δικτύων στην Ηµιτονική Μόνιµη Κατάσταση
 26 ΚΕΦΑΛΑΙΟ 0 Μελέτη ηλεκτρικών δικτύων στην Ηµιτονική Μόνιµη Κατάσταση 0. ) Γενικά για την Ηµιτονική Μόνιµη Κατάσταση ( Η.Μ.Κ.) Η µελέτη ενός ηλεκτρικού δικτύου γίνεται πρώτιστα στο στο πεδίο του χρόνου.
26 ΚΕΦΑΛΑΙΟ 0 Μελέτη ηλεκτρικών δικτύων στην Ηµιτονική Μόνιµη Κατάσταση 0. ) Γενικά για την Ηµιτονική Μόνιµη Κατάσταση ( Η.Μ.Κ.) Η µελέτη ενός ηλεκτρικού δικτύου γίνεται πρώτιστα στο στο πεδίο του χρόνου.
ΜΑΘΗΜΑ - ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ
 ΜΑΘΗΜΑ - ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ ΚΑΘΗΓΗΤΗΣ ΠΑΡΑΡΤΗΜΑ ΙΑΡΚΕΙΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΠΑΝΑΛΗΠΤΙΚΟ ΠΡΟΣΟΜΟΙΩΣΗ ΝΕΟ ΦΡΟΝΤΙΣΤΗΡΙΟ 3 ΩΡΕΣ ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω
ΜΑΘΗΜΑ - ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ ΚΑΘΗΓΗΤΗΣ ΠΑΡΑΡΤΗΜΑ ΙΑΡΚΕΙΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΠΑΝΑΛΗΠΤΙΚΟ ΠΡΟΣΟΜΟΙΩΣΗ ΝΕΟ ΦΡΟΝΤΙΣΤΗΡΙΟ 3 ΩΡΕΣ ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω
ΘΕΜΑ 1 0. Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-5 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 Επαναληπτικό διαγώνισµα Φυσικής Κατεύθυνσης Γ λυκείου 009 ΘΕΜΑ 0 Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -5 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σώµα
Επαναληπτικό διαγώνισµα Φυσικής Κατεύθυνσης Γ λυκείου 009 ΘΕΜΑ 0 Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -5 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σώµα
Προτεινόμενα θέματα για τις εξετάσεις 2011
 Προτεινόμενα θέματα για τις εξετάσεις 011 Τάξη: Γ Γενικού Λυκείου Μάθημα: Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης ΘΕΜΑ Α Α1-A4 Να επιλέξετε τη σωστή από τις απαντήσεις Α1. Ένα σώμα μάζας είναι στερεωμένο
Προτεινόμενα θέματα για τις εξετάσεις 011 Τάξη: Γ Γενικού Λυκείου Μάθημα: Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης ΘΕΜΑ Α Α1-A4 Να επιλέξετε τη σωστή από τις απαντήσεις Α1. Ένα σώμα μάζας είναι στερεωμένο
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε. 2003 ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Θ Ε Μ Α 1 ο Οδηγία: Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε. 2003 ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Θ Ε Μ Α 1 ο Οδηγία: Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα
Σ 1 γράφεται ως. διάνυσµα στο Σ 2 γράφεται ως. Σ 2 y Σ 1
 Στη συνέχεια θεωρούµε ένα τυχαίο διάνυσµα Σ 1 γράφεται ως, το οποίο στο σύστηµα Το ίδιο διάνυσµα µπορεί να γραφεί στο Σ 1 ως ένας άλλος συνδυασµός τριών γραµµικώς ανεξαρτήτων διανυσµάτων (τα οποία αποτελούν
Στη συνέχεια θεωρούµε ένα τυχαίο διάνυσµα Σ 1 γράφεται ως, το οποίο στο σύστηµα Το ίδιο διάνυσµα µπορεί να γραφεί στο Σ 1 ως ένας άλλος συνδυασµός τριών γραµµικώς ανεξαρτήτων διανυσµάτων (τα οποία αποτελούν
x = A ηµ(ω t+φ ο ), υ = A ω συν(ω t+φ ο ) και α = A ω² ηµ(ω t+φ ο )
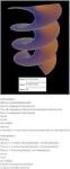 Η ΦΑΣΗ και η ΑΡΧΙΚΗ ΦΑΣΗ 1. ΕΙΣΑΓΩΓΗ Στο προηγούµενο σχόλιο υποστήριξα τη θέση ότι, παρόλο που η Γραµµική Αρµονική Ταλάντωση (ΓΑΤ) ενός κινητού µπορεί να περιγραφεί µαθηµατικά µε διάφορες εναλλακτικές
Η ΦΑΣΗ και η ΑΡΧΙΚΗ ΦΑΣΗ 1. ΕΙΣΑΓΩΓΗ Στο προηγούµενο σχόλιο υποστήριξα τη θέση ότι, παρόλο που η Γραµµική Αρµονική Ταλάντωση (ΓΑΤ) ενός κινητού µπορεί να περιγραφεί µαθηµατικά µε διάφορες εναλλακτικές
Προσδιορισμός ενός επίπεδου απλού αρμονικού κύματος από τις ταλαντώσεις σημείων του
 A A N A B P Y T A ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΠΙΠΕΔΑ ΑΠΛΑ ΑΡΜΟΝΙΚΑ ΚΥΜΑΤΑ 9 5 0 Προσδιορισμός ενός επίπεδου απλού αρμονικού κύματος από τις ταλαντώσεις σημείων του Περιεχόμενα Εισαγωγή και παραδείγματα
A A N A B P Y T A ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΠΙΠΕΔΑ ΑΠΛΑ ΑΡΜΟΝΙΚΑ ΚΥΜΑΤΑ 9 5 0 Προσδιορισμός ενός επίπεδου απλού αρμονικού κύματος από τις ταλαντώσεις σημείων του Περιεχόμενα Εισαγωγή και παραδείγματα
Ο χώρος. 1.Μονοδιάστατη κίνηση
 Ο χώρος Τα χελιδόνια έρχονται και ξανάρχονται. Κάθε χρόνο βρίσκουν μια γωνιά για να χτίσουν τη φωλιά, που θα γίνει το επίκεντρο του χώρου τους. Ο χώρος είναι ένας οργανικός χώρος, όπως εκείνος που αφορά
Ο χώρος Τα χελιδόνια έρχονται και ξανάρχονται. Κάθε χρόνο βρίσκουν μια γωνιά για να χτίσουν τη φωλιά, που θα γίνει το επίκεντρο του χώρου τους. Ο χώρος είναι ένας οργανικός χώρος, όπως εκείνος που αφορά
Σώματα σε επαφή και Απλή Αρμονική Ταλάντωση
 Σώματα σε επαφή και Απλή Αρμονική Ταλάντωση Σε όλες τις περιπτώσεις που θα εξετάσουμε το δάπεδο είναι λείο. Επίσης τα σύμβολα των διανυσματικών μεγεθών αντιπροσωπεύουν τις αλγεβρικές τους τιμές. Α. Η επιφάνεια
Σώματα σε επαφή και Απλή Αρμονική Ταλάντωση Σε όλες τις περιπτώσεις που θα εξετάσουμε το δάπεδο είναι λείο. Επίσης τα σύμβολα των διανυσματικών μεγεθών αντιπροσωπεύουν τις αλγεβρικές τους τιμές. Α. Η επιφάνεια
Αρµονικοί ταλαντωτές
 Αρµονικοί ταλαντωτές ΦΥΣ 131 - Διαλ.30 2 Αρµονικοί ταλαντωτές q Μερικά από τα θέµατα που θα καλύψουµε: q Μάζες σε ελατήρια, εκκρεµή q Διαφορικές εξισώσεις: d 2 x dt 2 + K m x = 0 Ø Mε λύση της µορφής:
Αρµονικοί ταλαντωτές ΦΥΣ 131 - Διαλ.30 2 Αρµονικοί ταλαντωτές q Μερικά από τα θέµατα που θα καλύψουµε: q Μάζες σε ελατήρια, εκκρεµή q Διαφορικές εξισώσεις: d 2 x dt 2 + K m x = 0 Ø Mε λύση της µορφής:
5 Σύνθεση Ταλαντώσεων
 Πρόχειρες Σηµειώσεις 011-01 5 Σύνθεση Ταλαντώσεων Ενα σώµα µπορει να εκτελεί ταυτόχρονα δυο αρµονικές ταλαντώσεις, οι οποίες µπορεί να έχουν οποιαδήποτε διεύθυνση. Το αποτέλεσµα είναι, γενικά, µια πολύπλοκη
Πρόχειρες Σηµειώσεις 011-01 5 Σύνθεση Ταλαντώσεων Ενα σώµα µπορει να εκτελεί ταυτόχρονα δυο αρµονικές ταλαντώσεις, οι οποίες µπορεί να έχουν οποιαδήποτε διεύθυνση. Το αποτέλεσµα είναι, γενικά, µια πολύπλοκη
Θέμα 1 ο (Μονάδες 25) προς τη θετική φορά του άξονα χ. Για τις φάσεις και τις ταχύτητες ταλάντωσης των σημείων Α και Β του μέσου ισχύει:
 ΙΓΩΝΙΣΜ ΦΥΣΙΚΗΣ ΚΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΥ 99 11 -- 1111 Θέμα 1 ο 1. Στο σχήμα φαίνεται το στιγμιότυπο ενός εγκάρσιου αρμονικού κύματος που διαδίδεται προς τη θετική φορά του άξονα χ. Για τις φάσεις και τις ταχύτητες
ΙΓΩΝΙΣΜ ΦΥΣΙΚΗΣ ΚΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΥ 99 11 -- 1111 Θέμα 1 ο 1. Στο σχήμα φαίνεται το στιγμιότυπο ενός εγκάρσιου αρμονικού κύματος που διαδίδεται προς τη θετική φορά του άξονα χ. Για τις φάσεις και τις ταχύτητες
Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ ΕΚΦΩΝΗΣΕΙΣ
 Επαναληπτικά Θέµατα ΟΕΦΕ 009 Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ ΘΕΜΑ ο ΕΚΦΩΝΗΣΕΙΣ Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί
Επαναληπτικά Θέµατα ΟΕΦΕ 009 Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ ΘΕΜΑ ο ΕΚΦΩΝΗΣΕΙΣ Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 9 ΙΟΥΝΙΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΦΥΣΙΚΗ
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 9 ΙΟΥΝΙΟΥ 003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Στις προτάσεις 1.1 έως 1.4 να γράψετε στο τετράδιό σας
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 9 ΙΟΥΝΙΟΥ 003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Στις προτάσεις 1.1 έως 1.4 να γράψετε στο τετράδιό σας
ΙΑΓΩΝΙΣΜΑΤΑ ΠΕΡΙΟ ΟΥ ΝΟΕΜΒΡΙΟΥ- ΕΚΕΜΒΡΙΟΥ 2013 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΤΜΗΜΑΤΑ: ΘΕΡΙΝΗΣ ΠΡΟΕΤΟΙΜΑΣΙΑΣ
 σύγχρονο Φάσµα & Group προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι. µαθητικό φροντιστήριο Γραβιάς 85 ΚΗΠΟΥΠΟΛΗ 50.5.557 50.56.96 5ης Μαρτίου ΠΕΤΡΟΥΠΟΛΗ 50.7.990 50.0.990 5ης Μαρτίου 74 Πλ.ΠΕΤΡΟΥΠΟΛΗΣ 50.50.658 50.60.845
σύγχρονο Φάσµα & Group προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι. µαθητικό φροντιστήριο Γραβιάς 85 ΚΗΠΟΥΠΟΛΗ 50.5.557 50.56.96 5ης Μαρτίου ΠΕΤΡΟΥΠΟΛΗ 50.7.990 50.0.990 5ης Μαρτίου 74 Πλ.ΠΕΤΡΟΥΠΟΛΗΣ 50.50.658 50.60.845
papost/
 Δρ. Παντελής Σ. Αποστολόπουλος http://users.uoa.gr/ papost/ papost@phys.uoa.gr, papost@teiion.gr ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 018-019 Υπάρχουν φυσικά φαινόμενα κατά τα οποία η κίνηση ενός σώματος προκύπτει
Δρ. Παντελής Σ. Αποστολόπουλος http://users.uoa.gr/ papost/ papost@phys.uoa.gr, papost@teiion.gr ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 018-019 Υπάρχουν φυσικά φαινόμενα κατά τα οποία η κίνηση ενός σώματος προκύπτει
Σύνολο Σελίδων: επτά (7) - ιάρκεια Εξέτασης: 3 ώρες Κυριακή 30 Σεπτέµβρη 2018 Βαθµολογία % Ονοµατεπώνυµο:
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Σύνολο Σελίδων: επτά (7) - ιάρκεια Εξέτασης: 3 ώρες Κυριακή 30 Σεπτέµβρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Σύνολο Σελίδων: επτά (7) - ιάρκεια Εξέτασης: 3 ώρες Κυριακή 30 Σεπτέµβρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε
ÁÎÉÁ ÅÊÐÁÉÄÅÕÔÉÊÏÓ ÏÌÉËÏÓ
 Θέµα Α ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ) 3 ΜΑΪOY 016 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει
Θέµα Α ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ) 3 ΜΑΪOY 016 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου 2ο Επαναληπτικό
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου 2ο Επαναληπτικό Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Τρίτη 23 Απρίλη 2019 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου 2ο Επαναληπτικό Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Τρίτη 23 Απρίλη 2019 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε
Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ε π α ν α λ η π τ ι κ ά θ έ µ α τ α 0 0 5 Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 1 ΘΕΜΑ 1 o Για τις ερωτήσεις 1 4, να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και δίπλα το γράµµα που
ε π α ν α λ η π τ ι κ ά θ έ µ α τ α 0 0 5 Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 1 ΘΕΜΑ 1 o Για τις ερωτήσεις 1 4, να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και δίπλα το γράµµα που
1ο ιαγώνισµα - Οριζόντια Βολή - Κυκλική Κίνηση. Θέµα 1ο
 1ο ιαγώνισµα - Οριζόντια Βολή - Κυκλική Κίνηση Ηµεροµηνία : Νοέµβρης 2013 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα 1ο Οµάδα Α Στις ερωτήσεις 1.1 1.4 επιλέξτε την σωστή απάντηση [4 5 = 20 µονάδες]
1ο ιαγώνισµα - Οριζόντια Βολή - Κυκλική Κίνηση Ηµεροµηνία : Νοέµβρης 2013 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα 1ο Οµάδα Α Στις ερωτήσεις 1.1 1.4 επιλέξτε την σωστή απάντηση [4 5 = 20 µονάδες]
43 Χρόνια Φροντιστήρια Μέσης Εκπαίδευσης ΣΑΒΒΑΪ Η ΜΑΝΩΛΑΡΑΚΗ ΠΑΓΚΡΑΤΙ : Χρυσοστόµου Σµύρνης 3 : 210/ /
 43 Χρόνια Φροντιστήρια Μέσης Εκπαίδευσης ΣΑΒΒΑΪ Η ΜΑΝΩΛΑΡΑΚΗ ΠΑΓΚΡΑΤΙ : Χρυσοστόµου Σµύρνης 3 : /76..47 /76..79 ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ (ΚΑΤΕΥΘΥΝΣΗΣ) Γ ΛΥΚΕΙΟΥ Θέµα ο Α. Στις παρακάτω προτάσεις απαντήστε µε Σωστό
43 Χρόνια Φροντιστήρια Μέσης Εκπαίδευσης ΣΑΒΒΑΪ Η ΜΑΝΩΛΑΡΑΚΗ ΠΑΓΚΡΑΤΙ : Χρυσοστόµου Σµύρνης 3 : /76..47 /76..79 ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ (ΚΑΤΕΥΘΥΝΣΗΣ) Γ ΛΥΚΕΙΟΥ Θέµα ο Α. Στις παρακάτω προτάσεις απαντήστε µε Σωστό
ΜΕΘΟΔΟΛΟΓΙΑ ΣΤΗΝ ΟΜΑΛΗ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ ΚΕΝΤΡΟΜΟΛΟΣ ΔΥΝΑΜΗ
 ΜΕΘΟΔΟΛΟΓΙΑ ΣΤΗΝ ΟΜΑΛΗ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ ΚΕΝΤΡΟΜΟΛΟΣ ΔΥΝΑΜΗ 1.Οι περισσότερες ασκήσεις είναι απλή εφαρμογή των τύπων Συνήθως από ένα μέγεθος όπως η συχνότητα f ή η γωνιακή ταχύτητα ω μπορούμε να υπολογίσουμε
ΜΕΘΟΔΟΛΟΓΙΑ ΣΤΗΝ ΟΜΑΛΗ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ ΚΕΝΤΡΟΜΟΛΟΣ ΔΥΝΑΜΗ 1.Οι περισσότερες ασκήσεις είναι απλή εφαρμογή των τύπων Συνήθως από ένα μέγεθος όπως η συχνότητα f ή η γωνιακή ταχύτητα ω μπορούμε να υπολογίσουμε
ΕΚΦΩΝΗΣΕΙΣ. Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 Επαναληπτικά Θέµατα ΟΕΦΕ 008 1 Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΕΚΦΩΝΗΣΕΙΣ ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που
Επαναληπτικά Θέµατα ΟΕΦΕ 008 1 Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΕΚΦΩΝΗΣΕΙΣ ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που
Παρατηρήσεις στη δηµιουργία του στάσιµου*
 Παρατηρήσεις στη δηµιουργία του στάσιµου* Κατά µήκος γραµµικού ελαστικού µέσου το οποίο ταυτίζεται µε τον άξονα χ χ, διαδίδονται κατά αντίθετη φορά, δύο εγκάρσια αρµονικά κύµατα, ίδιου πλάτους και ίδιας
Παρατηρήσεις στη δηµιουργία του στάσιµου* Κατά µήκος γραµµικού ελαστικού µέσου το οποίο ταυτίζεται µε τον άξονα χ χ, διαδίδονται κατά αντίθετη φορά, δύο εγκάρσια αρµονικά κύµατα, ίδιου πλάτους και ίδιας
ΘΕΜΑ 1ο 1.1 Να γράψετε στο τετράδιό σας τα φυσικά µεγέθη από τη Στήλη Ι και, δίπλα σε καθένα, τη µονάδα της Στήλης ΙΙ που αντιστοιχεί σ' αυτό.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 5 ΙΟΥΝΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤΑ (7) ΘΕΜΑ 1ο 1.1 Να γράψετε στο τετράδιό σας τα
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 5 ΙΟΥΝΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤΑ (7) ΘΕΜΑ 1ο 1.1 Να γράψετε στο τετράδιό σας τα
δ. Ο χρόνος ανάμεσα σε δυο διαδοχικούς μηδενισμούς του πλάτους είναι Τ =
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ / Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 01/11/2015 ΘΕΜΑ 1 Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ / Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 01/11/2015 ΘΕΜΑ 1 Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΑΝΕΛΛΗΝΙΕΣ ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΑΝΕΛΛΗΝΙΕΣ 2002 ΘΕΜΑΤΑ ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 6 ΙΟΥΝΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ): ΦΥΣΙΚΗ
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΑΝΕΛΛΗΝΙΕΣ 2002 ΘΕΜΑΤΑ ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 6 ΙΟΥΝΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ): ΦΥΣΙΚΗ
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2012. Ηµεροµηνία: Τετάρτη 18 Απριλίου 2012 ΕΚΦΩΝΗΣΕΙΣ
 ΤΑΞΗ: ΚΑΤΕΥΘΥΝΣΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Ηµεροµηνία: Τετάρτη 18 Απριλίου 2012 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις 1 έως 4 να γράψετε στο τετράδιο σας τον αριθµό
ΤΑΞΗ: ΚΑΤΕΥΘΥΝΣΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Ηµεροµηνία: Τετάρτη 18 Απριλίου 2012 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις 1 έως 4 να γράψετε στο τετράδιο σας τον αριθµό
ΦΥΣΙΚΗ Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2006 ΕΚΦΩΝΗΣΕΙΣ
 ΦΥΣΙΚΗ Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 006 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις - 4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 006 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις - 4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή
Θέµα 1ο. κινητό εκτελεί ταυτόχρονα δύο ή περισσότερες κινήσεις :
 1ο ιαγώνισµα - Οριζόντια Βολή - Κυκλική Κίνηση Ηµεροµηνία : Νοέµβρης 2012 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα 1ο Στις ερωτήσεις 1.1 1.4 επιλέξτε την σωστη απάντηση (4 5 = 20 µονάδες ) 1.1.
1ο ιαγώνισµα - Οριζόντια Βολή - Κυκλική Κίνηση Ηµεροµηνία : Νοέµβρης 2012 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα 1ο Στις ερωτήσεις 1.1 1.4 επιλέξτε την σωστη απάντηση (4 5 = 20 µονάδες ) 1.1.
Φάσμα & Group προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι.
 σύγχρονο Φάσμα & Group προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι. μαθητικό φροντιστήριο 1. 25ης Μαρτίου 111 ΠΕΤΡΟΥΠΟΛΗ 50.27.990 50.20.990 2. 25ης Μαρτίου 74 Πλ. ΠΕΤΡΟΥΠΟΛΗΣ 50.50.658 50.60.845 3. Γραβιάς 85 ΚΗΠΟΥΠΟΛΗ
σύγχρονο Φάσμα & Group προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι. μαθητικό φροντιστήριο 1. 25ης Μαρτίου 111 ΠΕΤΡΟΥΠΟΛΗ 50.27.990 50.20.990 2. 25ης Μαρτίου 74 Πλ. ΠΕΤΡΟΥΠΟΛΗΣ 50.50.658 50.60.845 3. Γραβιάς 85 ΚΗΠΟΥΠΟΛΗ
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 03-01-11 ΘΕΡΙΝΑ ΣΕΙΡΑ Α ΘΕΜΑ 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη
03-01-11 ΘΕΡΙΝΑ ΣΕΙΡΑ Α ΘΕΜΑ 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη
5. Το διάγραμμα του σχήματος παριστάνει την ταχύτητα ενός σώματος που εκτελεί απλή αρμονική ταλάντωση σε συνάρτηση με τον χρόνο.
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 9/0/06 ΘΕΜΑ Α Στις ερωτήσεις 7 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Mια μικρή σφαίρα προσκρούει
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 9/0/06 ΘΕΜΑ Α Στις ερωτήσεις 7 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Mια μικρή σφαίρα προσκρούει
ΣΕΙΡΑ: 3 Κύματα: αρμονικό έως στάσιμο, Στερεό: κινηματική έως διατήρηση στροφορμής
 ΜΑΘΗΜΑ /ΤΑΞΗ: Φυσική Κατεύθυνσης Γ Λυκείου ΟΝΟΜΑΤΕΠΩΝΥMΟ: ΗΜΕΡΟΜΗΝΙΑ: 16/03/014 ΣΕΙΡΑ: 3 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: Κύματα: αρμονικό έως στάσιμο, Στερεό: κινηματική έως διατήρηση στροφορμής ΘΕΜΑ Α Να γράψετε στο τετράδιό
ΜΑΘΗΜΑ /ΤΑΞΗ: Φυσική Κατεύθυνσης Γ Λυκείου ΟΝΟΜΑΤΕΠΩΝΥMΟ: ΗΜΕΡΟΜΗΝΙΑ: 16/03/014 ΣΕΙΡΑ: 3 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: Κύματα: αρμονικό έως στάσιμο, Στερεό: κινηματική έως διατήρηση στροφορμής ΘΕΜΑ Α Να γράψετε στο τετράδιό
ΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΣΤΙΣ ΜΗΧΑΝΙΚΕΣ ΚΑΙ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
 ΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΣΤΙΣ ΜΗΧΑΝΙΚΕΣ ΚΑΙ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Θέµα Α Στις ερωτήσεις 1-4 να βρείτε τη σωστή απάντηση. Α1. Για κάποιο χρονικό διάστηµα t, η πολικότητα του πυκνωτή και
ΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΣΤΙΣ ΜΗΧΑΝΙΚΕΣ ΚΑΙ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Θέµα Α Στις ερωτήσεις 1-4 να βρείτε τη σωστή απάντηση. Α1. Για κάποιο χρονικό διάστηµα t, η πολικότητα του πυκνωτή και
ΦΥΣΙΚΗ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2003
 ΦΥΣΙΚΗ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 003 ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1 4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 003 ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1 4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή
4ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 21 εκέµβρη ο Κεφάλαιο - Κύµατα. Ενδεικτικές Λύσεις. Θέµα Α
 4ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 21 εκέµβρη 2014 Α.1. Τα ηλεκτροµαγνητικά κύµατα : 2ο Κεφάλαιο - Κύµατα Ενδεικτικές Λύσεις Θέµα Α (ϐ) υπακούουν στην αρχή της επαλληλίας. Α.2. υο σύγχρονες πηγές
4ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 21 εκέµβρη 2014 Α.1. Τα ηλεκτροµαγνητικά κύµατα : 2ο Κεφάλαιο - Κύµατα Ενδεικτικές Λύσεις Θέµα Α (ϐ) υπακούουν στην αρχή της επαλληλίας. Α.2. υο σύγχρονες πηγές
ΑΡΧΗ 2ΗΣ ΣΕΛΙ ΑΣ ΤΑΞΗ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΣΠΕΡΙΝΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 5 ΙΟΥΛΙΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Στις
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΣΠΕΡΙΝΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 5 ΙΟΥΛΙΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Στις
3) το παράθυρο Πίνακας τιμών όπου εμφανίζονται οι τιμές που παίρνουν οι παράμετροι
 Ο Δ Η Γ Ι Ε Σ Γ Ι Α Τ Ο M O D E L L U S 0.0 4. 0 5 Για να κατεβάσουμε το πρόγραμμα Επιλέγουμε Download στη διεύθυνση: http://modellus.co/index.php/en/download. Στη συνέχεια εκτελούμε το ModellusX_windows_0_4_05.exe
Ο Δ Η Γ Ι Ε Σ Γ Ι Α Τ Ο M O D E L L U S 0.0 4. 0 5 Για να κατεβάσουμε το πρόγραμμα Επιλέγουμε Download στη διεύθυνση: http://modellus.co/index.php/en/download. Στη συνέχεια εκτελούμε το ModellusX_windows_0_4_05.exe
ΦΥΣΙΚΗ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2003
 ΦΥΣΙΚΗ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 003 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί
ΦΥΣΙΚΗ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 003 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί
ΦΥΣ. 211 ΕΡΓΑΣΙΑ # 8 Επιστροφή την Τετάρτη 30/3/2016 στο τέλος της διάλεξης
 ΦΥΣ. 211 ΕΡΓΑΣΙΑ # 8 Επιστροφή την Τετάρτη 30/3/2016 στο τέλος της διάλεξης 1. Μια µάζα m είναι εξαρτηµένη από το άκρο ενός ελατηρίου µε φυσική συχνότητα ω. Η µάζα αφήνεται να κινηθεί από την κατάσταση
ΦΥΣ. 211 ΕΡΓΑΣΙΑ # 8 Επιστροφή την Τετάρτη 30/3/2016 στο τέλος της διάλεξης 1. Μια µάζα m είναι εξαρτηµένη από το άκρο ενός ελατηρίου µε φυσική συχνότητα ω. Η µάζα αφήνεται να κινηθεί από την κατάσταση
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 11 ΙΟΥΛΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ): ΦΥΣΙΚΗ ΘΕΜΑ 1ο Να γράψετε στο
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 11 ΙΟΥΛΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ): ΦΥΣΙΚΗ ΘΕΜΑ 1ο Να γράψετε στο
Σύστημα σωμάτων vs Στερεό σώμα
 Σύστημα σωμάτων vs Στερεό σώμα Μια σφαίρα μάζας Μ και ακτίνας R είναι συνδεμένη με ράβδο μήκους l και μάζας m μέσω ενός κατακόρυφου άξονα περιστροφής, έτσι ώστε να υπάρχει η δυνατότητα περιστροφής της
Σύστημα σωμάτων vs Στερεό σώμα Μια σφαίρα μάζας Μ και ακτίνας R είναι συνδεμένη με ράβδο μήκους l και μάζας m μέσω ενός κατακόρυφου άξονα περιστροφής, έτσι ώστε να υπάρχει η δυνατότητα περιστροφής της
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Δ ΕΣΠΕΡΙΝΩΝ
 ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ Δ ΕΣΠΕΡΙΝΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 5 ΙΟΥΝΙΟΥ 05 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΠΤΑ
ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ Δ ΕΣΠΕΡΙΝΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 5 ΙΟΥΝΙΟΥ 05 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΠΤΑ
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ 2012
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ 2012 ΘΕΜΑ Α A 1. Α 2. Α 3. Α 4. γ β γ γ Α 5. α. Σ β. Σ γ. Λ δ. Λ ε. Σ ΘΕΜΑ Β Β 1. Σωστή η απάντηση γ Αιτιολόγηση: Για την αρχική
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ 2012 ΘΕΜΑ Α A 1. Α 2. Α 3. Α 4. γ β γ γ Α 5. α. Σ β. Σ γ. Λ δ. Λ ε. Σ ΘΕΜΑ Β Β 1. Σωστή η απάντηση γ Αιτιολόγηση: Για την αρχική
Να γράψετε στο τετράδιό σας τον αριθµό κάθε µιας από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ 1 ο ΓΕΛ ΠΕΤΡΟΥΠΟΛΗΣ ΠΕΜΠΤΗ 18 ΑΠΡΙΛΙΟΥ 2013 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ A Να γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ 1 ο ΓΕΛ ΠΕΤΡΟΥΠΟΛΗΣ ΠΕΜΠΤΗ 18 ΑΠΡΙΛΙΟΥ 2013 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ A Να γράψετε
ΘΕΜΑ 1ο ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΘΕΜΑ 1ο ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 8 ΙΟΥΛΙΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) ΣΥΝΟΛΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΘΕΜΑ 1ο ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 8 ΙΟΥΛΙΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) ΣΥΝΟΛΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. Α.3. Υλικό σημείο μάζας m και ταχύτητας υ κινείται σε περιφέρεια οριζόντιου κύκλου ακτίνας r, όπως στο σχήμα:
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 6 ΙΟΥΛΙΟΥ 200 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Για
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 6 ΙΟΥΛΙΟΥ 200 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Για
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 11: Η ημιτονοειδής διέγερση Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ. ΕΥΔΟΞΟΣ: 50657177
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 11: Η ημιτονοειδής διέγερση Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ. ΕΥΔΟΞΟΣ: 50657177
ΘΕΜΑ 1o. , τότε η ένταση του ρεύµατος στο κύκλωµα γίνεται µέγιστη τη χρονική στιγµή: T t= γ. 4. T 2 Μονάδες 5
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 11 ΙΟΥΛΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ): ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 11 ΙΟΥΛΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ): ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ
Επαναληπτικό ιαγώνισµα Γ Ενιαίου Λυκείου Παρασκευή 23 Γενάρη 2015 Ταλαντώσεις - Κύµατα
 Επαναληπτικό ιαγώνισµα Γ Ενιαίου Λυκείου Παρασκευή 23 Γενάρη 2015 Ταλαντώσεις - Κύµατα Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1
Επαναληπτικό ιαγώνισµα Γ Ενιαίου Λυκείου Παρασκευή 23 Γενάρη 2015 Ταλαντώσεις - Κύµατα Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1
Γ ΛΥΚΕΙΟΥ ΚΥΜΑΤΑ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ. Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός.
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΥΜΑΤΑ Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός / Βασικές Έννοιες Η επιστήμη της Φυσικής συχνά μελετάει διάφορες διαταραχές που προκαλούνται και διαδίδονται στο χώρο.
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΥΜΑΤΑ Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός / Βασικές Έννοιες Η επιστήμη της Φυσικής συχνά μελετάει διάφορες διαταραχές που προκαλούνται και διαδίδονται στο χώρο.
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : OKTΩΒΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : OKTΩΒΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : OKTΩΒΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Αντικείµενο εξέτασης: Όλη η διδακτέα ύλη Χρόνος εξέτασης: 3 ώρες
 ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Αντικείµενο εξέτασης: Όλη η διδακτέα ύλη Χρόνος εξέτασης: 3 ώρες ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε στο φύλλο απαντήσεών σας τον αριθµό
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Αντικείµενο εξέτασης: Όλη η διδακτέα ύλη Χρόνος εξέτασης: 3 ώρες ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε στο φύλλο απαντήσεών σας τον αριθµό
4ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 21 εκέµβρη ο Κεφάλαιο - Κύµατα
 4ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 21 εκέµβρη 2014 2ο Κεφάλαιο - Κύµατα Σύνολο Σελίδων: έξι (6) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
4ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 21 εκέµβρη 2014 2ο Κεφάλαιο - Κύµατα Σύνολο Σελίδων: έξι (6) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ 2012
 ΦΥΙΚΗ ΚΑΤΕΥΘΥΝΗ 0 ΕΚΦΩΝΗΕΙ ΘΕΜΑ Α τις ηµιτελείς προτάσεις Α Α4 να γράψετε στο τετράδιό σας τον αριθµό της πρότασης και δίπλα το γράµµα που αντιστοιχεί στη φράση η οποία τη συµπληρώνει σωστά. Α. Κατά τη
ΦΥΙΚΗ ΚΑΤΕΥΘΥΝΗ 0 ΕΚΦΩΝΗΕΙ ΘΕΜΑ Α τις ηµιτελείς προτάσεις Α Α4 να γράψετε στο τετράδιό σας τον αριθµό της πρότασης και δίπλα το γράµµα που αντιστοιχεί στη φράση η οποία τη συµπληρώνει σωστά. Α. Κατά τη
3ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 27 Σεπτέµβρη 2015 Εξεταζόµενη ύλη: Ταλαντώσεις
 3ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 27 Σεπτέµβρη 2015 Εξεταζόµενη ύλη: Ταλαντώσεις Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις
3ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 27 Σεπτέµβρη 2015 Εξεταζόµενη ύλη: Ταλαντώσεις Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις
1. Τίτλος: Οι κρυµµένοι τριγωνοµετρικοί αριθµοί Συγγραφέας Βλάστος Αιµίλιος. Γνωστική περιοχή των µαθηµατικών: Τριγωνοµετρία
 1. Τίτλος: Οι κρυµµένοι τριγωνοµετρικοί αριθµοί Συγγραφέας Βλάστος Αιµίλιος Γνωστική περιοχή των µαθηµατικών: Τριγωνοµετρία Θέµα- Σκεπτικό της δραστηριότητας. Η ιδέα πάνω στην οποία έχει στηριχτεί ο σχεδιασµός
1. Τίτλος: Οι κρυµµένοι τριγωνοµετρικοί αριθµοί Συγγραφέας Βλάστος Αιµίλιος Γνωστική περιοχή των µαθηµατικών: Τριγωνοµετρία Θέµα- Σκεπτικό της δραστηριότητας. Η ιδέα πάνω στην οποία έχει στηριχτεί ο σχεδιασµός
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
( ) ( ) ( )! r a. Στροφορμή στερεού. ω i. ω j. ω l. ε ijk. ω! e i. ω j ek = I il. ! ω. l = m a. = m a. r i a r j. ra 2 δ ij. I ij. ! l. l i.
 Στροφορμή στερεού q Η στροφορµή του στερεού γράφεται σαν: q Αλλά ο τανυστής αδράνειας έχει οριστεί σαν: q H γωνιακή ταχύτητα δίνεται από: ω = 2 l = m a ra ω ω ra ω e a ΦΥΣ 211 - Διαλ.31 1 r a I j = m a
Στροφορμή στερεού q Η στροφορµή του στερεού γράφεται σαν: q Αλλά ο τανυστής αδράνειας έχει οριστεί σαν: q H γωνιακή ταχύτητα δίνεται από: ω = 2 l = m a ra ω ω ra ω e a ΦΥΣ 211 - Διαλ.31 1 r a I j = m a
ΘΕΜΑ 1ο. Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση 1 Ένα σώμα εκτελεί αρμονική ταλάντωση με ακραίες θέσεις που
ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση 1 Ένα σώμα εκτελεί αρμονική ταλάντωση με ακραίες θέσεις που
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 19/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 19/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 19/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω
Η επιτάχυνση και ο ρόλος της.
 Η επιτάχυνση και ο ρόλος της. Το μέγεθος «επιτάχυνση» το συναντήσαμε κατά τη διδασκαλία στην Α Λυκείου, όπου και ορίσθηκε με βάση την εξίσωση: t Όπου η παραπάνω μαθηματική εξίσωση μας λέει ότι η επιτάχυνση:
Η επιτάχυνση και ο ρόλος της. Το μέγεθος «επιτάχυνση» το συναντήσαμε κατά τη διδασκαλία στην Α Λυκείου, όπου και ορίσθηκε με βάση την εξίσωση: t Όπου η παραπάνω μαθηματική εξίσωση μας λέει ότι η επιτάχυνση:
Φυσικά μεγέθη. Φυσική α λυκείου ΕΙΣΑΓΩΓΗ. Όλα τα φυσικά μεγέθη τα χωρίζουμε σε δύο κατηγορίες : Α. τα μονόμετρα. Β.
 ΕΙΣΑΓΩΓΗ Φυσικά μεγέθη Όλα τα φυσικά μεγέθη τα χωρίζουμε σε δύο κατηγορίες : Α. τα μονόμετρα Β. τα διανυσματικά Μονόμετρα ονομάζουμε τα μεγέθη εκείνα τα οποία για να τα γνωρίζουμε χρειάζεται να ξέρουμε
ΕΙΣΑΓΩΓΗ Φυσικά μεγέθη Όλα τα φυσικά μεγέθη τα χωρίζουμε σε δύο κατηγορίες : Α. τα μονόμετρα Β. τα διανυσματικά Μονόμετρα ονομάζουμε τα μεγέθη εκείνα τα οποία για να τα γνωρίζουμε χρειάζεται να ξέρουμε
Άσκηση µε απλά εκκρεµή και κρούση και άλλα πολλά (για φυσικούς όµως)
 Άσκηση µε απλά εκκρεµή και κρούση και άλλα πολλά (για φυσικούς όµως) Δύο σώµατα µε µάζες m =kg και m =3Kg ηρεµούν στην ίδια οριζόντια ευθεία, κρεµασµένα από δύο σχοινιά ώστε να αποτελούν α- πλά εκκρεµή
Άσκηση µε απλά εκκρεµή και κρούση και άλλα πολλά (για φυσικούς όµως) Δύο σώµατα µε µάζες m =kg και m =3Kg ηρεµούν στην ίδια οριζόντια ευθεία, κρεµασµένα από δύο σχοινιά ώστε να αποτελούν α- πλά εκκρεµή
Ονοματεπώνυμο: Επιμέλεια διαγωνίσματος: Αξιολόγηση :
 Ονοματεπώνυμο: Μάθημα: Υλη: Επιμέλεια διαγωνίσματος: Αξιολόγηση : Φυσική Προσανατολισμου Γ Λυκείου Ταλαντώσεις Σχολικό έτος 2017-2018 Σελίδα 1 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Σύνολο Σελίδων:
Ονοματεπώνυμο: Μάθημα: Υλη: Επιμέλεια διαγωνίσματος: Αξιολόγηση : Φυσική Προσανατολισμου Γ Λυκείου Ταλαντώσεις Σχολικό έτος 2017-2018 Σελίδα 1 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Σύνολο Σελίδων:
ΦάσµαGroup ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΙΑΓΩΝΙΣΜΑΤΑ ΠΕΡΙΟ ΟΥ ΦΕΒΡΟΥΑΡΙΟΥ-ΜΑΡΤΙΟΥ 2015 ΤΜΗΜΑΤΑ: ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ. σύγχρονο. µαθητικό φροντιστήριο
 σύγχρονο ΦάσµαGrop προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι. µαθητικό φροντιστήριο 1. 25ης Μαρτίου 111 ΠΕΤΡΟΥΠΟΛΗ 50.27.990 50.20.990 2. 25ης Μαρτίου 74 ΠΛ. ΠΕΤΡΟΥΠΟΛΗΣ 50.50.658 50.60.845 3. Γραβιάς 85 ΚΗΠΟΥΠΟΛΗ
σύγχρονο ΦάσµαGrop προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι. µαθητικό φροντιστήριο 1. 25ης Μαρτίου 111 ΠΕΤΡΟΥΠΟΛΗ 50.27.990 50.20.990 2. 25ης Μαρτίου 74 ΠΛ. ΠΕΤΡΟΥΠΟΛΗΣ 50.50.658 50.60.845 3. Γραβιάς 85 ΚΗΠΟΥΠΟΛΗ
