ΕΡΓΑΣΤΗΡΙΟ. Άσκηση 2: Βυθοµετρικός χάρτης Βυθοµετρική τοµή

HTML
DOWNLOAD

Μέγεθος: px

Εμφάνιση ξεκινά από τη σελίδα:

Download "ΕΡΓΑΣΤΗΡΙΟ. Άσκηση 2: Βυθοµετρικός χάρτης Βυθοµετρική τοµή"

Νεοπτόλημος Θεοδοσίου
9 χρόνια πριν
Προβολές:

1 ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗ ΤΩΝ ΩΚΕΑΝΩΝ Άσκηση 2: Βυθοµετρικός χάρτης Βυθοµετρική τοµή ιδάσκοντες Καθ. Γ. Φερεντίνος Λέκτορας Μ. Γεραγά Μεταπτυχιακοί φοιτητές: Μαργαρίτα Ιατρού ηµήτρης Χριστοδούλου

2 Βυθοµέτρηση Βυθοµέτρηση (sounding) ονοµάζεται η εξακρίβωση του βάθους (ύψος υδάτινης στήλης) µε χρήση οργάνων σε οποιοδήποτε σηµείο (καλούµενο βυθοµετρικό στίγµα). Σκοπός της βυθοµέτρησης είναι η κατασκευή βυθοµετρικών χαρτών Βυθοµετρικό στίγµα χαρακτηρίζεται ο γεωγραφικός τόπος (σηµείο στην επιφάνεια της θάλασσας, ποταµού ή λίµνης) στο οποίο γίνεται βυθοµέτρηση, κατά την οποία διαπιστώνεται το βάθος και η ποιότητα του βυθού Α x x Β Βάθος 1 οργιά (fathom) = m = 6 πόδια (feet) 1 πόδι (feet) = µέτρα (m) Ισοδιάσταση ανά 100 µέτρα Ύψη σε µέτρα Κλίµακα 1: Μέτρα

βυθοµέτρηση, κατά την οποία διαπιστώνεται το βάθος και η ποιότητα του βυθού Α x 500 590 620 630 600 550 480 470 500 540 590 600 580 550 550 620 680 700 650 580 490 500 550 600 630 650 640 580 580 660

3 Ισοβαθείς καµπύλες Ισοβαθείς καµπύλες ονοµάζονταιοιγραµµές οι οποίες ενώνουν σηµεία µείδιοβάθος Ισοδιάσταση είναι η απόσταση µεταξύ δύο ισοβαθών καµπύλων γραµµών. Όσο πιο µικρή είναι η ισοδιάσταση τόσο καλύτερη απεικόνιση του ανάγλυφου έχουµε Οι ισοβαθείς είναι συνεχείς καµπύλες εν διακόπτονται και δεν διαιρούνται Κάθε ισοβαθής καµπύλη σηµατοδοτεί ένα συγκεκριµένο βάθος Οι ισοβαθείς δεν διασταυρώνονται Όταν οι ισοβαθείς είναι πυκνές αναπαριστούν απότοµη κλίση του πυθµένα Όταν είναι αραιές τότε ο πυθµένας έχει ήπια κλίση

Όσο πιο µικρή είναι η ισοδιάσταση τόσο καλύτερη απεικόνιση του ανάγλυφου έχουµε Οι ισοβαθείς είναι συνεχείς καµπύλες εν

4 Ισοβαθείς καµπύλες Για την αναπαράσταση ενός καναλιού οι ισοβαθείς σχηµατίζουν ένα -V-. H κορυφή του δείχνει πάντα το άνω µέρος του καναλιού Οµόκεντρες ισοβαθείς καµπύλες αναπαριστούν υψώµατα ή βυθίσµατα του πυθµένα. Στα υψώµατα οι τιµές των καµπύλων οποίων αυξάνεται προς το εσωτερικό. Στα βυθίσµατα µικρές γραµµώσεις δείχνουν προς το εσωτερικό του βυθίσµατος

αναπαριστούν υψώµατα ή βυθίσµατα του πυθµένα.

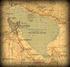
5 Άσκηση 2 Σας δίνεται ο βυθοµετρικόςχάρτηςτουστενούζακύνθου- Κυλλήνης. 1. Χαράξτε τις ισοβαθείς καµπύλες µε ισοδιάσταση 50 µέτρων 2. Κατασκευάστε τις τοµές ΑΒ, Γ και ΕΖ σε ισοµετρική κλίµακα και σε παραµορφωµένη κλίµακα 3. ώστε µια σύντοµη περιγραφή του ανάγλυφου του πυθµένα (εάν είναι οµαλός ή απότοµος και που, προς τα πού βαθαίνει κλπ) κατά την τοµή ΑΒ 4. Να υπολογίσετε την κλίση του πυθµέναστηνπλαγιάτης Ζακύνθου και στην πλαγιά της Κυλλήνης κατά µήκος της τοµής ΑΒ σε ισοµετρική και παραµορφωµένη κλίµακα. ώστε το αποτέλεσµα σεµοίρες και επί τοις 100 (%).

ώστε µια σύντοµη περιγραφή του ανάγλυφου του πυθµένα (εάν είναι οµαλός ή απότοµος και που, προς τα πού βαθαίνει κλπ) κατά την τοµή ΑΒ 4.

7 Χάραξη ισοβαθών καµπύλων Σε περίπτωση που µια ισοβαθής καµπύλη πρέπει να περάσει µεταξύ δύο σηµείων Α και Β, που έχουν αντίστοιχα µεγαλύτερο (α) και µικρότερο βάθος (β) από αυτό που αναφέρεται η ισοβαθής, εφαρµόζεται ο παρακάτω τύπος: I - β Χ = S ( ) α - β Όπου: X, η απόσταση ισοβαθούς από το σηµείο β σε cm S, η απόσταση µεταξύ των σηµείων Α και Β σε cm a, το βάθος στο σηµείο Α σε m β, το βάθος στο σηµείο Β σε m Ι, το βάθος της ισοβαθούς που θα χαράξουµε σεm

τύπος: I - β Χ = S ( ) α - β Όπου: X, η απόσταση ισοβαθούς από το σηµείο β σε cm S, η απόσταση µεταξύ των σηµείων Α

8 a= 700 m β= 600 m Ι= 650 m S = 1.5 cm I - β Χ = S ( ) α - β s x = 1.5 {( )/( )} x = 1.5 x 0.5=0.75 cm Η ισοβαθής των 650 m θα χαραχθεί σε 0,75 cm από την ισοβαθή των 600 m

5 {(650-600)/(700-600)} x = 1.5 x 0.5=0.

9 Κατασκευή βυθοµετρικής τοµής 1. Χαράσσουµε τηντοµή ανάµεσα στα δύο σηµεία Α-Β πάνωστοχάρτη 2. Κατασκευάζουµε σύστηµα αξόνωνx, y. 3. Στον άξονα x τοποθετούµε την απόσταση ΑΒ και στον άξονα y το βάθος του νερού. (Στα 0 m η επιφάνεια της θάλασσας) 4. Όπου οι ισοβαθείς καµπύλες τέµνουν την τοµή Α-Β σηµειώνονται τα σηµεία τοµής πάνω στον άξονα x 5. Για κάθε σηµείο τοµής σηµειώνουµε το αντίστοιχο βάθος της κάθε ισοβαθούς στον άξονα y 6. Ενώνουµε τασηµεία µε (x,y) µε µια καµπύλη γραµµή 1 4 6

10 Ισοµετρική και Παραµορφωµένη Κλίµακα Κλίµακα 1: Ισοµετρική τοµή κατακόρυφη κλίµακα=οριζόντια κλίµακα Παραµορφωµένη τοµή η κατακόρυφη κλίµακα παραµορφώνεται Στο παράδειγµα: 1 cm = 1000 m (x 2,5 φορές)

κλίµακα Παραµορφωµένη τοµή η κατακόρυφη κλίµακα

11 Υπολογισµός κλίσης πυθµένα Η κλίση της πλαγίας σε µια Ισοµετρική τοµή, µπορεί να µετρηθεί απευθείας πάνω στην τοµή (µε µοιρογνωµόνιο) ή µε την εφαπτοµένη: εφθ=μν/κν ΜΝ = 0.4 cm, KN =0.8cm εφθ =ΜΝ/ΚΝ = 0.4 cm/0.8 cm = 0,5 δηλ. θ = 26,5 ο 1 2 3

(µε µοιρογνωµόνιο) ή µε την εφαπτοµένη: εφθ=μν/κν ΜΝ = 0.

12 Κλίση πυθµένα Αυτό δεν είναι δυνατό στην παραµορφωµένη κλίµακα Για να µετρηθεί η κλίση στην παραµορφωµένη τοµή πρέπεινα µετατραπούν οι αποστάσεις µε βάσητηνκλίµακα

13 Υπολογισµός της πραγµατικής κλίσης από την παραµορφωµένη κλίµακα Υπολογίζουµε τηνεφθ, όπου εφ θ = ΜΝ/ΝΚ Μετράµε τις αποστάσεις ΜΝ και ΝΚ σε cm πάνω στην τοµή στους άξονες y και x αντίστοιχα Μετατρέπουµε τις«παραµορφωµένες» αποστάσεις MN και ΝΚ σε πραγµατικές µε βάση την κλίµακα της τοµής ηλ. για το παράδειγµα: ΜΝ = 1 cm στην τοµή = 1000 m στην πραγµατικότητα ΚΝ = 0,8 cm στην τοµή = 2000 m στην πραγµατικότητα Οπότε εφ θ = 1000/2000=0,5 δηλ 26,5 ο

αποστάσεις MN και ΝΚ σε πραγµατικές µε βάση την κλίµακα της τοµής ηλ.

14 Κλίση πυθµένα-παραµορφωµένη Κλίµακα εφθ = MN / KN KN = 0.8 cm = 2000m MN =1 cm=1000m, ΛΑΘΟΣ εφ θ = 1 cm / 0,8 cm = 1.25 δηλ. θ ~ 51 ο ΣΩΣΤΟ εφ θ = 1000 m / 2000 m = 0,5 δηλ. θ ~26,5 ο 1 2 3

15 Κλίση πυθµένα (%) Κλίση (%) = εφ θ x100 Ηκλίσηεπίτοις% εκφράζει τη µεταβολή του υψόµετρου, που αντιστοιχεί σε οριζόντια απόσταση 100 µονάδων µήκους. Κλίση, π.χ., 10% σηµαίνει ότι σε οριζόντια απόσταση 100 µονάδων το υψόµετρο αυξάνεται ή ελαττώνεται κατά 10 αντίστοιχες µονάδες Η κλίση επί τοις εκατό δεν χρησιµοποιείται σε κλίσεις µεγαλύτερες των 45 o ιότι: εφ45 =1 εφ45 (%) = 1 x 100 =100%

ί σε οριζόντια απόσταση 100 µονάδων µήκους. Κλίση, π.χ.

Σχετικά έγγραφα

2o ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑΤΟΣ

2o ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑΤΟΣ Πως αποτυπώνεται το ανάγλυφο από ένα χάρτη Δημιουργία μια τομής χρησιμοποιώντας ένα χάρτη Έννοιες της ισομετρικής κλίμακας και της κατακόρυφης παραμόρφωσης σε μια τομή Κατασκευή