Joint Spectrum Sensing and Resource Allocation for OFDM-based Transmission with a Cognitive Relay
|
|
|
- Μυρίνη Παπαφιλίππου
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Jont Spectrum Sensng and Resource Allocaton for OFDM-based Transmsson wth a Cogntve Relay S. Eman Mahmood 1 K.P. Subbalakshm 1 R. Chandramoul 1 Bahman Abolhassan 1 Department of Electrcal and Computer Engneerng Stevens nsttute of Technology Hoboken NJ USA Department of Electrcal Engneerng ran Unversty of Scence and Technology Tehran ran Abstract n ths paper we nvestgate the ont spectrum sensng and resource allocaton problem to maxmze throughput capacty of an OFDM-based cogntve rado lnk wth a cogntve relay. By applyng a cogntve relay that uses decode and forward (D&F we acheve more relable communcatons generatng less nterference (by needng less transmt power and more dversty gan. n order to account for mperfectons n spectrum sensng the proposed schemes ontly modfy energy detector thresholds and allocates transmt powers to all cogntve rado (CR subcarrers whle smultaneously assgnng subcarrer pars for secondary users (SU and the cogntve relay. Ths problem s cast as a constraned optmzaton problem wth constrants on (1 nterference ntroduced by the SU and the cogntve relay to the PUs; ( mss-detecton and false alarm probabltes and (3 subcarrer parng for transmsson on the SU transmtter and the cogntve relay and (4 mnmum Qualty of Servce (QoS for each CR subcarrer. We propose one optmal and two suboptmal schemes all of whch are compared to other schemes n the lterature. Smulaton results show that the proposed schemes acheve sgnfcantly hgher throughput than other schemes n the lterature for dfferent relay stuatons. Receved on 11 November 013; accepted on 15 March 014; publshed on 11 Aprl 014 Keywords: cogntve rado power allocaton spectrum sensng subcarrer parng cogntve relay OFDM. Copyrght 014 S. Eman Mahmood lcensed to CST. Ths s an open access artcle dstrbuted under the terms of the Creatve Commons Attrbuton lcense ( whch permts unlmted use dstrbuton and reproducton n any medum so long as the orgnal work s properly cted. do: /ws.1.1.e4 between PUs and the CR was calculated for power 1. ntroducton allocaton assumng OFDM for the PU transmsson Cogntve rado networks (CRNs have been envsoned to provde effcent utlzaton of spectra for the secondary (unlcensed users(sus wthout affectng the performance of the prmary users (PUs who as well. Also n [6] a new opportunstc scheme for resourceallocatonwasexpressedbasedonnterference cancellaton.nourprevouswork[7]wedervedthe transmtpowerallocatonswthouttheassumptonsof are the prmary lcensees of the spectrum [1]. perfect knowledge of nterference ntroduced by the Orthogonal Frequency Dvson Multplexng (OFDM s consdered the most approprate modulaton scheme for secondary users [] [3]. Power allocaton for PUs to the SUs. Also several pror works n ths area [4-7] assumed perfect channel sensng whch also s not guaranteed n practce. n [8] by adustng the capacty maxmzaton of an OFDM based CRN sensngthresholdontsensngandresourceallocaton whle keepng the nterference from the cogntve rado (CR to the PUs below a gven threshold was consdered n [4]. n [5] the mutual nterference power s performed. There s a trade-off between achevng maxmum throughput of the CRN and guaranteeng the qualty-of-servce (QoS of the PUs. By accessng more OFDM subchannels the CRN obtans hgher Correspondng author. smahmood@stevens.edu throughput and also ntroduces nterferences caused 1
2 by the mss-detecton. So ont resource allocaton and sensng thresholds selecton s needed to acheve optmum performance. However [8] assumed that both PUs and the CR use OFDM and that the transmt power levels for spectrum sensng at each of the OFDM subchannels are known. n ths paper we allocate transmt power under more practcal consderatons where the sensng mechansms may lead to false alarms and mss probabltes. Decode and Forward (D&F relayng has been shown to acheve more relable transmssons even at lower transmt power levels thereby allowng for less nterference to the PUs [9]. n ths paper we show that by applyng D&F relay we can acheve hgher precson n spectrum sensng and we call such a relay cogntve relay. Here spectrum sensng s performed by the cogntve relay and the sensng thresholds are updated n the frst tme slot transmsson [10]. A cogntve relay network under fadng channels has been proposed [11] where better spectrum opportunty utlzaton has been acheved va hgher dversty gan (and therefore hgher system complexty although under the assumptons of perfect spectrum sensng results. A two pronged approach where mperfect soft sensng and a sensng update has been used to allevate the problem of sensng errors n [1] and [13]. n [1] the SU adapts the transmt power based on the detecton and false alarm probabltes. n our prevous work [13] we maxmzed throughput of the CRN by consderng constrants on nterference and total power for multuser CRN under mperfect sensng condtons characterzed by false alarm probabltes. Management of CR subcarrers s another problem n the cogntve relay transmsson. The cogntve relay can decode and forward data on the same CR subcarrer used by the secondary node [14-16]. However a more effcent soluton s to reconsder throughput capacty maxmzaton of the CRN by CR subcarrer allocaton for the cogntve relay. Ths means that the cogntve relay may not apply the same CR subcarrer as the SU transmtter (TX [17]. Thus two OFDM subcarrers are pared n the frst and second tme slot durng the transmsson by the SU TX and the cogntve relay respectvely. The goal of ths paper s to maxmze the throughput capacty of the CRN by ontly allocatng transmt power levels sensng spectrum (updatng the values of energy detector thresholds and parng CR subcarrers to the SU TX and cogntve relay. Constrants of ths optmzaton problem are: keepng the total nterference ntroduced by the SU and cogntve relay below a gven threshold keepng mss-detecton and false alarm probabltes n each CR subcarrer below a specfed threshold consderng subcarrer parng for subcarrer pars of the SU and cogntve relay and provdng a lower bound on transmt power levels for CR subcarrers. Frst convexty of ths optmzaton problem s verfed. Then usng Lagrange formulaton constrants dualty [18] takng subgradent method [19] and applyng a greedy method ths problem wll be solved. We wll then propose low complexty suboptmal schemes and evaluate them. The rest of ths paper s organzed as follows. Secton descrbes the system model. Secton 3 formulates the optmzaton problem by nterference modelng. Secton 4 proposes the man scheme for ont power allocaton spectrum sensng and subcarrer parng. Secton 5 ntroduces the suboptmal and other schemes comparable to the man proposed scheme. Secton 6 dscusses smulaton results by comparng fve schemes wth each other. Fnally Secton 7 concludes the paper and the expected future works are expressed.. System Model n ths paper we consder a two tme slot D&F relay CRN consstng of a SU transcever and a cogntve relay both of whch coexst wth a number of PUs. n addton to relayng transmtted data streams the cogntve relay also performs wdeband spectrum sensng wth N energy detecton thresholds for the N OFDM subcarrers. Fg. 1 depcts the system model. n the frst tme slot we observe that the SU TX sends data on subcarrer whle the cogntve relay and SU recever (RX receves the data. Then the cogntve relay whch employs D&F transmts decoded data n the second tme slot on subcarrer whle the SU RX receves data. Snce data transmsson of the SU TX and cogntve relay occurs n dfferent tme slots there
3 s no nterference between them. The SU RX apples Maxmum Rato Combnng (MRC to obtan data by explotng spatal dversty. The cogntve relay must decde whch subcarrer to use for data transmsson based on ts channel sensng results. So the cogntve relay may not transmt data n the same subcarrer that the SU TX used. We assume the tme slots are of the same duraton and the coherence tme of channels are much longer than the tme between CS updates hence channel gans (h (ab m n subcarrer m between TX a and RX b n Fg. 1 do not change whle data transmsson perod once t s measured. Also we assume that the sensng perods are smaller than the swtchng tme of the PUs actvtes. n ths paper we mprove the relablty of spectrum sensng results along wth power allocaton and subcarrer parng. To perform wdeband spectrum sensng energy detectors are used for each CR subcarrer. Energy detecton thresholds (λ 1 λ λ N are appled on each of the N CR subcarrers for spectrum sensng [0]. Let the fadng channel gan between the prmary TX and cogntve relay n subcarrer be h (pr. As shown n [0] based on Neyman- Pearson crteron the probabltes of false alarm and detecton n subcarrer are respectvely gven by p f (λ Q( λ Mσn Mσ and p d (λ Q( n λ M(σ n + h (pr Mσ n (σ n + h (pr where M denotes the number of prevous receved samples taken n the cogntve relay for spectrum sensng and σn represents the varance of Addtve Whte Gaussan Nose (AWGN channel. Let the rato of channel gan to nterference power ntroduced by L OFDM subchannels of PUs n subcarrer m from TX a atrxb beγ m (ab. Then γ (sr h (sr σ s + L l1 J (pr(l γ (ss h (ss σ s + L l1 J (ps(l γ (rs h (rs σ s + L l1 J (ps(l where we assume the same AWGN varance σs for all three lnks and L denotes the number of OFDM subchannels occuped by PUs. The nterference power ntroduced by PU s subchannel l to the CR subcarrer s gven by J (ps(l h (ps l Δ l + Δf Φ Δ l Δf PER (wdw [1] where the expected perodogram s Φ PER (w 1 +π πk π φ(l PU (ew ( sn((w νk/ sn((w ν/ dν K s the Fast Fourer Transform (FFT sze of the perodogram w s the normalzed frequency Δ l s the spectral dstance between Secondary transmtter th Prmary transmtter 1 st tme slot nterference to PUs 1 st tme slot (sr Cogntve Relay nd tme slot nterference to PUs Secondary recever th Prmary recever Fgure 1. System Model of the CRN n Two Tme Slot Transmsson. CR subcarrer and PU s subchannel l and φ (l PU s the power spectrum densty (PSD of PU s subchannel l. The achevable weghted rate wth an deal codng scheme for subcarrer par SP( can be expressed as R Δfρ log (1 + γ P where Δf and ρ are the frequency space of OFDM subcarrers and weght factor for subcarrer respectvely [14]. The weght factors are taken nto consderaton to reflect dstnct QoS requrements for each subcarrer n the CRN. Note that ρ s dependent only on CR subcarrer whch s used by the SU TX. γ s the equvalent channel gan of SP( and P s the sum of two powers: the transmt power of SU TX n subcarrer when the cogntve relay s transmttng n subcarrer (P (1 and the transmt power of the cogntve relay n subcarrer when the SU TX s transmttng n subcarrer (P ( P P (1 + P (. The communcatons n our model can ether follow the drect mode or relay mode dependng on whether the channel gans to nose rato (γ s s favorable (relay or not (drect. As n [] the power levels and equvalent channel gan to nose plus nterference rato for SP( n the relay lnk (f γ (sr γ (ss & γ (rs γ (ss are formulated by P (1 P ( γ γ (sr γ (sr γ (sr γ (rs +γ (rs γ (sr γ (ss +γ (rs γ (sr γ (rs +γ (rs P γ (ss γ (ss γ (ss. P (1 3
4 Otherwse for the drect lnk transmsson we have P (1 P P ( 0 γ γ (ss. 3. nterference Modelng and Problem Formulaton We defne an obectve functon for the transmsson lnk on SP( as A B that gves us a sense of both the throughput (A and the capacty (B where A (1 p f (λ (1 p f (λ and B Δf ρ log (1 + γ P. A ncreases as the false alarm decreases ust as we would expect the throughput of the system to do. So n a sense A s related to the throughput. B s a measure of the capacty of the system n transmsson of SP(. Hence the obectve functon for SP( s defned as: C q (1 p f (λ (1 p f (λ Δfρ log (1 + γ P (3 where q s an ndcator functon takng on a value 1 when the SP( s used and zero otherwse. Note that Eqn. (3 has three sets of unknown parameters: the equvalent transmt power levels (P subcarrer parng ndcators (q and energy detector thresholds (λ 1... N. The obectve functon s dscrete because the selecton of subcarrer pars s dscrete. n order to deal wth ths we apply contnuous relaxaton to ths bnary constrant (q by wrtng the obectve functon for SP(as C q (1 p f (λ (1 p f (λ Δfρ ( log (1 + γ P q (4 where the bnary constrant changes to: q N [3]. As llustrated n Fg. 1 the nterference s ntroduced to the PUs by each secondary node transmsson (ether the th subcarrer of the SU TX or the th subcarrer of the cogntve relay. These nterference power levels can be calculated as P (s Ll1 N1 P (1 φ(l s and P(r L N1 l1 P ( φ(l r respectvely. The nterference power spectral denstes ntroduced by CR subcarrer on the prmary subchannel l s gven by φ (l s h(sp l Δl +B T l / s df φ (l r Δ l B l / ( sn(πf T s πf T s h (rp l Δl +B T l / s Δ l B l / ( sn(πf T s πf T df can be calculated assumng deal Nyqust transmtted pulse [1] and OFDM s symbol duraton T s. One of the man constrants n ths optmzaton problem s to keep the nterference power ntroduced by SU and the cogntve relay below the specfed nterference power threshold (P (th. So we consder P (s P (th and P (r P (th whch can be rewrtten as a functon of P by where N1 Ll1 { N 1 P Φ s(l N1 Ll1 { N 1 P Φ r(l Φ s(l Φ r(l γ (sr γ (sr } P (th } P (th. γ (rs +γ (rs γ (ss γ (sr γ (ss +γ (rs γ (ss φ (l s (5 φ (l r. (6 The obectve functon whch s called throughput capacty n ths paper s maxmzed over P q λ: max N1 N1 Δfρ q P qλ (1 p f (λ (1 p f (λ ( P log 1+γ q subect to the connectons n Eqn (5 and: (7 1 p d (λ α 1.. N (8 p f (λ β 1.. N (9 N q N (10 1 N q N (11 1 P ν 1.. N P 0 (1 q N (13 λ N. (14 n Eqn (7 P and q are (N N matrces wth entres (P q 1... N and λ [λ 1 λ...λ N ]. The constrants n Eqns (8 and (9 show that the mssdetecton and false alarm probabltes for each CR subcarrer by the assgned energy detector thresholds 4
5 4.1. The Dual Problem Precse Spectrum Sensng ntal Spectrum Sensng Applyng Channel Condtons for Relayng Subcarrer Parng Fgure. Flowchart of the proposed scheme. Power Allocaton should be kept below gven thresholds to provde both effcent performance of the CRN and convexty of the problem. Also Eqns (10 and (11 respectvely denote that for each of the N number of CR subcarrers allocated to the cogntve relay only one CR subcarrer can be used for the SU TX and for each of CR subcarrers allocated to the SU TX only one CR subcarrer can be used for the cogntve relay. We know that each of P s should be nonnegatve but the constrant n Eqn (1 s used to the convexty of the problem. The proof of the convexty of ths optmzaton problem wth all ts constrants s gven n the Appendx. 4. Jont Subcarrer Parng Power Allocaton and Spectrum Sensng Our obectve s to maxmze throughput capacty (gven by Eqn (7 of the cogntve relay network by ont power allocaton on the qualfed subcarrer parng and spectrum sensng. Fg. llustrates a flowchart of the communcaton procedure from the vew pont of TX to provde an effcent transmsson. Frst the CR obtans an ntal spectrum sensng output from the cogntve relay to know whch OFDM subchannels are dle. Then usng the channel nformaton and applyng Eqns (1 and ( the decson on whether to take a drect lnk or a relay lnk s made. The optmzaton problem s then solved for the optmum transmt power levels energy detector thresholds and subcarrer pars. By applyng Karush-Kahn-Tucker (KKT condtons n the convex optmzaton takng subgradent method n the dual problem and usng an teratve algorthm the optmzaton problem can be solved. We frst obtan Lagrangan formulaton of the obectve functon gven by Eqn (7 and normalzed to the bandwdth as C(P q ληκτ μ δ 1 N1 N1 {ρ q (1 p f (λ (1 p f (λ log (1 + γ q P } + η(p (th + κ(p (th L l1 N1 N1 P Φ s(l L l1 N1 N1 P Φ r(l N 1 τ (1 N 1 q + N 1 μ (β p f (λ + N 1 δ (p d (λ 1+α. (15 where ηκ are Lagrange multplers for the constrant n Eqn (5 and τ μ δ are Lagrange vectors for the constrants n Eqns (10 (9 and (8 respectvely. For convenence we assume the same threshold for mss detecton and fales alarm probabltes n each subcarrer (α α and β β. The constrant n Eqn (11 s studed n the proposed algorthm n Subsecton 4. whch smultaneously consders the satsfacton of ths constrant wth the other constrants. To maxmze the throughput capacty for each SP( gven by Eqn (4 wth respect to transmt power levels we equate C 0: P C P ρ γ (1 p f (λ (1 p f (λ 1+( γ η( L q P l1 Φ s(l κ( L l1 Φ r(l 0. (16 We see that effect of the constrant n Eqn (11 s not consdered n ths formulaton and the obectve functon s maxmzed by optmzng over two Lagrange varables. We solve the dual optmzaton problem wth respect to Eqn (1 and smplfyng Eqn (16 toget P q [ν ρ (1 p f (λ (1 p f (λ η( L l1 Φ s(l +κ( L l1 Φ r(l 1 γ ] + (17 where [x y] + max(x y. Snce the power s dependent on the energy detector thresholds and the subcarrer par selecton we ontly optmze these parameters. Also accordng to Eqn (1 the power may be zero for some subcarrer pars. From Eqn (17 we see that ths occurs when q 0. 5
6 S.E.Mahmoodetal. For spectrum sensng we acheve the values of energy detector thresholds over N CR subcarrers whch are used ether by SU TX or the cogntve relay n transmsson. So the obectve functon gven by Eqn (3 s consdered for one set of N CR subcarrers (for 1... N. Then smplfed formulaton for Eqn (15 s wrtten as C 1 N1 (1 p f (λ log (1 + γ P +η(p(th L N1 N1 l1 P +κ(p (th Φs(l L l1 N1 N1 P Φr(l + N 1 τ (1 N 1 q + N 1 μ (β p f (λ + N 1 δ (p d (λ 1+α. (18 Then to obtan λ wehave C (μ + R e x δ λ 4πMσ + e y n 4πMσn (σn +E( s h (pr (19 where x λ Mσ n Mσ n y λ M(σn +E( s h (pr Mσn (σn +E( s h (pr the normalzed rate of CR subcarrer ; R Δ 1 log (1 + γ [ e 1 1 γ η L l1 Φ s(l +κ L l1 Φ r(l By settng Eqn (19 to zero we have y x and Eqn (1 smplfes to ( λ M(σn +E( s h (pr Mσn (σn +E( s h (pr ln( σ n ξ σ n +E( s h (pr ( λ Mσ n Mσ n and R 1 γ ] +. s (0 ( where the two Lagrange multplers δ and μ are combned and gven by ξ δ.we set μ μ + R 0 n Eqn (3 and by settng a lower bound to satsfy the false alarm constrant gven by Eqn (9 we obtan λ max((q 1 (β M + Mσn λ. (4 We now obtan the optmal subcarrer par ndcators (q s. By substtutng the allocated transmt power levels gven by Eqn (17 nto Eqn (15 we have where C N N1 1 q Ω +((η + κp (th + N 1 τ + N 1 μ (β p f (λ + N 1 δ (p d (λ 1+α (5 Ω ρ log (1 + γ [ν τ η L l1 Φ s(l [ν κ L l1 Φ r(l [ν ρ (1 p f (λ (1 p f (λ η L l1 Φ s(l +κ L l1 Φ r(l ρ (1 p f (λ (1 p f (λ η L l1 Φ s(l +κ L l1 Φ r(l ρ (1 p f (λ (1 p f (λ η L l1 Φ s(l +κ L l1 Φ r(l 1 γ ] + 1 γ ] + 1 γ ] +. (6 As can be seen from Eqn (5 to maxmze throughput capacty of the CRN over subcarrer pars Ω (for 1... N 1... N should be maxmzed. So q s assgned as δ ln( μ + R q ln( 1 arg max Ω 1... N (7 4πMσn (σn +E( s h (pr 4πMσ 0 otherwse 1... N. n (1 However the subcarrer pars obtaned by Eqn (7 do not necessarly satsfy the constrant n Eqn (11 n whch only one CR subcarrer could be allocated for the cogntve relay n each par. Ths problem wll be solved n the followng secton by applyng a greedy method n the proposed algorthm. where ξ δ. By solvng Eqn (14 two values for μ + R λ are obtaned and only one of them s nonnegatve (Constrant (19 and acceptable whch s gven by λ [ Mσ n s h (pr M s h (pr {(σ4 n +σn s h (pr 8σn ln( σnξ σ n + s h(pr Mσ 6 n (σ n + s h (pr ] 1/ + s h (pr } (3 4.. Algorthm Desgn n the prevous subsecton all optmal transmt power levels and subcarrer pars were allocated and energy detector thresholds were obtaned by maxmzng the throughput capacty gven by Eqn (7 subect to constrants expressed n Eqns (6 and (8 to (14 except (11. The constrant n Eqn (11 specfes that each subcarrer should be allocated to one subcarrer par for the cogntve relay transmsson. n order 6
7 to obtan optmal values for transmt power levels and energy detector thresholds as well as optmally par subcarrers and also satsfy Constrant (11 and explot approprate Lagrange multplers we propose an teratve algorthm whch s shown n by Algorthm 1. Algorthm 1 Proposed ont sensng subcarrer parng and power allocaton. 1: ntalze Lagrange multplers (for teraton: k1 : whle all Lagrange multplers have hgher errors than ɛ do 3: compute λ s by Eqn. (4 4: compute Ω s by Eqn. (6 5: compute q s by Eqn. (7 6: codfy q s by Greedy method 7: compute P s by Eqn. (17 8: modfy the values of Lagrange multplers by 9: η (k+1 η (k ε (k N1 Ll1 { N 1 P (k 10: κ (k+1 κ (k ε (k N1 Ll1 { N 1 P (k τ (k ε (k 11: τ (k+1 1: μ (k+1 13: δ (k+1 14: k k +1 15: end whle 1 (P(th Φ s(l } 1 (P(th Φ r(l } (1 N 1 q (k 1... N μ (k ε (k 3 [β p f (λ (k ] δ (k ε (k 4 [p d(λ (k 1+α] Algorthm Greedy method to acheve q by satsfyng constrant (11. 1: t( N 1 q 1... N : for u 1:N do 3: f t(u > 1 then b arg max bu b q bu 1 4: end f 5: whle t(u > 1 do 6: arg mn u τ c arg t(0 7: t(u t(u 1t( t(+1 8: q(c u 0q(c 1 9: end whle 10: end for max b q cu 1 cb Ω c n the proposed algorthm we apply a greedy method smlar to [17 4] for satsfyng Eqn (11 whch s shown by Algorthm. n summary to maxmze Eqn (7 the greedymethodfndsthe columnsofq wth total value of more than one. Then t places ones to the columns wth sum value of zero whle the mnmum devaton to Lagrange multpler τ (for 1.. N s generated. Through ths process we acheve the mnmum decrease n Ω (for 1.. N n the throughput capacty (Eqn (7 of the CRN Complexty Analyss By applyng the above algorthm we ontly optmze the spectrum sensng power allocaton and subcarrer parng n the cogntve relay network. We now compare the complexty of ths algorthm wth that of exhaustve search. Exhaustve search for subcarrer parng has a complexty O(N! and for each fx subcarrer par the complexty of power allocatons accordng to Eqn (17 and energy detector thresholds s O(NlogN. Hence the complexty for exhaustve search s O(N.logN.N! whch could be smplfed to O(N.N!. However by applyng the proposed algorthm the complexty s O(N.logN per teraton. The number of teratons on the algorthm wll depend on the value of ε. Total complexty of ths algorthm wll be O(N.logN (number of teratons. Clearly ths s much smaller than the exhaustve search method. 5. Suboptmal and Classcal Schemes n ths secton we propose a suboptmal scheme (n subsecton 5.1 and ntroduce three classcal schemes (n subsectons and 5.4 for the throughput capacty maxmzaton of the CRN whch s gven by Eqn (7 wth lmted nterference threshold on PUs. All these schemes are compared usng smulatons Alternate Suboptmal Scheme n ths scheme we propose a suboptmal soluton by smplfyng the method of fndng the Lagrange multplers η and κ to calculate energy detector thresholds. To do ths we consder a fxed Lagrange multpler denoted by η and κ and then compute the energy detector thresholds for spectrum sensng. Usng these thresholds transmt power levels and subcarrer pars are calculated. Fnally energy detector thresholds are modfed wth correspondng updated Lagrange multpler for power allocaton (η and κ. Although ths could cause a loss n the throughput capacty the number of smultaneous varables to be calculated 7
8 S.E.Mahmoodetal. decreases and therefore the system complexty reduces. For explotng the normalzed rate we frst consder a unform power dstrbuton and accordng to Eqn (5 we fnd η and κ for subcarrer pars wth nonzero powers. Then by consderng the boundary condtons n Eqn (5 and replacng P wth RHS of Eqn (17 and assumng p f (λ p f (λ 0 we wrte N1 Ll1 { N 1 ( N1 Ll1 { N 1 ( ρ η ( L l1 Φ s(l +κ ( 1 L l1 Φ r(l γ } P (th Φ s(l ρ η ( L l1 Φ s(l +κ ( 1 L l1 Φ r(l γ } P (th Φ r(l (8 and from Eqn (8 η andκ are obtaned. As well ntal energy detector thresholds are calculated by ths η and κ based on Eqn (4. Then resource allocaton s performed by one teraton of step up to step 7 shown n Algorthm 1. Fnally modfed energy detector thresholds are calculated by new updated η and κ obtaned by one teraton of the algorthm. 5.. Fxed Subcarrer Parng (SCP based Scheme Lke [14] we consder a fxed assgnment for subcarrer parng n ths scheme. n ths scheme the assgned subcarrer for the frst tme slot wll be also used n the second tme slot. So we allocate power levels as P P [ν X 1 γ ] + (9 where X s the water level and t s based on the Lagrange multplers η and γ and the false alarm probablty over CR subcarrer. So t s gven by X ρ (1 p f (λ η( L l1 Φ s(l +κ( L l1 Φ r(l. ( Resource Allocaton Based on ntal Spectrum Sensng (SS n ths suboptmal scheme we consder that spectrum sensng s performed by ntal sensng results wthout updatng the energy detector thresholds to obtan false alarm probabltes p f (λ 1...N for each CR subcarrer based on [0]. Then we ontly allocate transmt power levels usng Eqn (17 and manage subcarrer pars usng Eqn ( Classcal Scheme Wthout use of the Cogntve Relay (WCR Eventually we compare the proposed schemes wth a classcal scheme wthout use of the cogntve relay. n ths scheme transmt power s dstrbuted accordng to the waterfllng scheme [5]. Based on Eqn (5and wth regards to the gven nterference power threshold the water levels are obtaned. The power allocated to CR subcarrer s gven by and ϖ s found by solvng L l1 1 P [0 1 ϖ 1 N [0 1 ϖ 1 γ (ss γ (ss ] + (31 ] + φ (l s P(th. (3 So the nterference constrant for the CRN s satsfed. By consderng ths constrant the soluton whch has been obtaned n [4] s acheved. Note that spectrum sensng s performed lke the prevous scheme and false alarm and mss detecton probabltes are obtaned usng [0]. 6. Smulaton Results n ths secton smulaton results are presented and dscussed. The performance of the man proposed scheme ntroduced n Secton 4 s compared wth those of the other four schemes descrbed n Secton 5. We assume that the number of CR subcarrers (N PU occuped channels(l and prevous receved samples taken n the cogntve relay for spectrum sensng (M are and 3 respectvely. n ths system model we consder an OFDM-based CR wth cogntve relayng whch coexsts wth three PUs. Also the CRN uses the ntal soft sensng results as the three PUs occupy 0 1 and 16 subchannels. Note that n each run of the smulaton these three frequency bands of PUs are randomly dstrbuted through OFDM subchannels. For the OFDM based CRN we assume the OFDM frequency spacng (Δf and symbol duraton (T s to be
9 Fgure 3. Throughput capacty of the CRN versus nterference ntroduced to the PUs by several schemes wth E[ γ (sr ]8 E[ γ (ss ]3 and E[ γ (rs ]8. MHz and 7 μs respectvely. AWGN varance n all the channels s assumed to be 10 5 Watts. The PU s transmt power (P PU s consdered to be Watts. n the proposed algorthm ntal values of δ and τ for each CR subcarrer are randomly dstrbuted between 0.01 and wth step sze of 0.05/ k where k s the teraton ndex. The ntal value for η s randomly dstrbuted between 100 and 00 and ε s assumed to be All the communcaton lnks are ndependent of each other n two tme slots and ther channel gans have Raylegh dstrbutons wth gven average channel gans. Except for three channels of h (ss h (rs and h (sr whch have dfferent average channel gans through smulatons the rato of average channel gans to nose plus nterference n other lnks are set to 3. At frst we compare fve schemes n a geographcal stuaton where the cogntve relay s located between the SU TX and RX. So we consder E[ γ (sr ]8 E[ γ (ss ]3 and E[ γ (rs ]8 n Fgs. 3 to 7. Fg. 3 shows the throughput capacty n bts/slot whch s defned n Eqn (7 n terms of nterference power ntroduced to the PUs by the SU TX and the cogntve relay n Watts. n ths fgure α and β are assumed to be 0. and respectvely. As we can see the proposed scheme acheves the hghest throughput for a gven nterference threshold. We also Fgure 4. Maxmum achevable sum rate of the CRN versus nterference ntroduced to the PUs by several. observe that Alternate scheme where the sensng and the ont power allocaton and subcarrer parng are done n two excessve phases performs close to the man proposed scheme. Ths scheme s able to acheve throughout capactes very close to the man proposed scheme but wth more teratons. However decrease of the system complexty n ths scheme s an advantage but should be consdered because t makes the precson of the approach lower. Note that by ncrease of teratons Alternate scheme obtans the throughput close to the man proposed scheme but the system complexty ncreases. The fxed subcarrer parng (SCP based scheme and the scheme based on ntal spectrum sensng (SS acheve less throughput than the proposed scheme and the proposed alternate scheme but acheve more throughput than the scheme wthout use of cogntve relay (WCR. Note that false alarm probablty n SS and WCR based schemes are fxed and assumed to be 0.. We observe that for the nterference equal to 10 3 Watts the man proposed alternate fxed SCP and SS schemes have respectvely 441% 363% 313% and 13% hgher throughput capacty n comparson to WCR. n Fg. 4 we plot the achevable total rate for the CRN versus nterference power ntroduced to the PUs by the SU TX and the cogntve relay. As 9
10 S.E.Mahmoodetal. Fgure 5. Weghted throughput capacty of the CRN versus nterference ntroduced to the PUs by several schemes. Fgure 6. Throughput capacty of the CRN versus probablty of false alarm threshold by several schemes. expected snce qualty of spectrum sensng (false alarm probablty s not consdered for the achevable total rate performance of the man proposed scheme alternate scheme and SS scheme are very close to each other. However as can be understood from Fg. 3 spectrum sensng results are dfferent n these schemes. We also observe that the fxed SCP and WCR acheve smaller rates compared to those of the other schemes. n Fg. 5 we present the weghted throughput capacty gven by Eqn (7 versus nterference power Fgure 7. Average transmt power of the cogntve relay versus nterference ntroduced to the PUs by CRN by several schemes. ntroduced to the PUs by the SU TX and the cogntve relay. So far we consdered ρ (for all 1...N as unty. However n ths fgure we consder weghted rates such that ρ 1+(-1/(N-1. Ths dstrbuton s only an example for the weghted subcarrers n order to satsfy the QoS requrements n each one. n ths condton we observe that our man proposed scheme acheves hgher throughput capacty for weghted CR subcarrers compared wth those of the other schemes. Moreover we observe that all of the schemes have smulaton results smlar to the smulaton results shown n Fg. 3. n Fg. 6 we plot the throughput capacty n terms of probablty of false alarm threshold. Here th and α are assumed to be 10 3 Watts and 0. respectvely. We see that the throughput of the CRN decreases by ncreasng the false alarm probablty. Fg. 7 presents the total transmt power of the cogntve relay for all CR subcarrers versus the nterference ntroduced to PUs by the SU TX and cogntve relay. We see that by subcarrer parng the man proposed alternate and SS schemes allow for hgher transmt power than that of the fxed SCP scheme for a gven nterference threshold. The fxed SCP does not take dynamc subcarrer parng nto account for the system. Therefore ths scheme allocates lower transmt power to the cogntve relay and acheves less total rate for the CRN. 10
11 Fgure 8. Throughput capacty of the CRN versus nterference ntroduced to the PUs by several schemes wth E[ γ (sr ]8 E[ γ (ss ]3 and E[ γ (rs ]8 Fgure 9. Throughput capacty of the CRN versus nterference ntroduced to the PUs by several schemes wth E[ γ (sr ]3 E[ γ (ss ]3 and E[ γ (rs ]8 n Fg. 8 we consder the case where the cogntve relay s located close to the SU TX. So we consder E[ γ (sr ]8 E[ γ (ss ]3 and E[ γ (rs ]3. However n Fg. 9 we assume a stuaton n whch the cogntve relay s close to the SU RX and we have E[ γ (sr ]3 E[ γ (ss ]3 and E[ γ (rs ]8. Both of these fgures show optmalty of the proposed schemes. However comparng Fgs 3 8 and 9 we see that the throughput capacty s lower f the cogntve relay s located close to ether the SU transmtter or recever. 7. Concluson and Future Works n ths paper we optmzed the throughput of a CRN wth cogntve relayng by ont spectrum sensng and resource allocaton under OFDM transmsson. An optmzaton problem was formulated and solved whle meetng constrants such as the nterference power ntroduced by the SU and cogntve relay to the prmary system subcarrer parng the mss-detecton and false alarm probabltes n each CR subcarrer. By solvng the optmzaton problem a new teratve algorthm was proposed to obtan energy detector thresholds subcarrer parng and the transmt power levels of the SU and the cogntve relay. Moreover an alternate low complexty suboptmal scheme was also proposed whch acheves a performance close to the man proposed scheme accordng to the smulatons. Smulaton results llustrate that the proposed schemes acheve sgnfcantly hgher throughput capacty and achevable total rate than those of exstng schemes such as fxed subcarrer parng the scheme based on ntal spectrum sensng results and the classcal scheme wthout use of the cogntve relay as presented quanttatvely n Secton 6. The extenson of ths work can be consdered for multple relays wth consderng relay selecton. Then the work should be on the cogntve mult-relay network envronment whle ont optmzaton of power allocaton subcarrer allocaton subcarrer parng and relay selecton s consdered. Furthermore the purpose s to maxmze the weghted sum rate of the network under mutual nterference constrants. Appendx Verfyng the Convexty of Optmzaton Problem For the obectve functon whch s expressed n (7 f C<0 then C s convex and ts Hessan s not postve sem-defnte. We rewrte the obectve functon as C f 1 (P f (λ λ (33 where f 1 (P log (1 + θ P (34 11
12 S.E.Mahmoodetal. f (λ λ (1 Q( λ Mσ n Mσ n (1 Q( λ Mσ n Mσ n (35 whle θ γ q. As shown n [6] to provde the concavty for f 1 we have γ P > and by followng Eqn (1 ν /γ. Also Hessan determnant of f s Δ H f (λ f (λ f (λ f (λ (f (λ f (λ 1 1 +x π x x e x ( 1 +x x +x π e π x x e x {[1 Q(x ][1 Q(x ] 1 πx x e x +x }. (36 We assume that x and x are postve and so the frst term n RHS of Eqn (36 s postve. Snce n ths scenaro we want to obtan the values of energy levels whch are derved from the same where we assgn x x. Ths means that we ontly restrct the value of energy detector thresholds n the SU TX and cogntve relay whle n the case where both of them apply one CR subcarrer {[1 Q(x ] 1 e x πx } s ncreasng and so we can set the possble least value for x to satsfy postvty of the Hessan whch s obtaned by x So p f (λ β We see that the result of ths s approxmately the same as the one n [6] whch consders a CR wth no relayng. So by the obtaned values for β and ν the concavty of the obectve functon s acheved. Also for Eqn (8 f α 0.5 snce Q(x s convex then ths constrant s convex. We see that both of the obtaned values for α and β ( are reasonable bounds n practce. Acknowledgment Ths work was supported n part by NSF # and # References [1] Haykn S. Cogntve rado: Bran-empowered wreless communcatons. EEE J. Sel. Areas n Commun. 005 Feb; 3(: [] Wess S. and Jondral F. K. Spectrum poolng: an nnovatve strategy for the enhancement of spectrum effcency. EEE Commun. Mag. 004 Mar; 43(3: S8-S14. [3] Setoodeh P. and Haykn S. Robust transmt power control for cogntve rado. Proceedngs of the EEE 009 May; 97(5: [4] Bansal G. and Hossan M. J. and Bhargava V. K. Optmal and suboptmal power allocaton algorthms for OFDM-based cogntve rado systems. EEE Trans. Wreless Commun. 008 Nov; 7(11: [5] Zhao C. and Kwak K. Power/bt loadng n OFDM-based cogntve networks wth comprehensve nterference consderatons: The sngle-su case. EEE Trans. Vehcular Tec. 010 May; 59(4: [6] Maham B. Popovsk R. Zhou X. Houngnes A. Cogntve multple access network wth outage margn n the prmary system. EEE Trans. Wreless Commun. 011 Oct; 10(10: [7] Mahmood S. E. and Abolhassan B. Two new power allocaton schemes for an OFDM cogntve rado wth no knowledge on prmary users nterference. nt. J. Commun. Syst. n Wley 01 Oct; do: /dac.443. [8] Lm H. and Seol D. and m G. Jont sensng adaptaton and resource allocaton for cogntve rado wth mperfect sensng. EEE Trans. Commun. 01 Apr; 60(4: [9] Hossan E. and Km D. and Bhargava V. K. (011 Cooperatve Cellular Wreless Communcatons (Cambrdge Unversty Press 1st ed. [10] Zou Y. and Yao Y. and Zheng B. Cogntve transmssons wth multple relays n cogntve rado networks. EEE Trans. Wreless Commun. 011 Feb; 10(: [11] Letaef K. B. and Zhang W. Cooperatve communcatons for cogntve rado networks. Proc. EEE. 009 May; 97(5: [1] Kang X. B. and Lang Y. and Garg H. K. and Zhang L. Sensng-based spectrum sharng n cogntve rado networks. EEE Trans. Vehcular Tec. 009 Oct; 58(8: [13] Mahmood S. E. and Kordan S. B. and Abolhassan B. A new algorthm for ont sensng and power allocaton n multuser cogntve rado networks. Proc. EEE Wreless Personal Multmeda Commun. (WPMC. 011 Oct; Brest- France [14] Yng W. and Xn-chun Q. and Tong W. and Bao-lng L. Power allocaton and subcarrer parng algorthm for regeneratve OFDM relay system. Proc. EEE Vehcular Tec. Conf. (VTC 007 Apr; Dubln-reland [15] Wang S. and Huang F. and Ge M. and Wang W. Optmal power allocaton for OFDM-based cooperatve relay cogntve rado networks. EEE nternatonal Conf. Commun. (CC 01 Jun; Ottawa-Canada
13 [16] Bharada D. and Bansal G. and Kalgneed P. and Bhargava V. K. Relay and power allocaton schemes for OFDM-based cogntve rado systems. EEE Trans. Wreless Commun. 011 Sep; 10(9: [17] Hsu C. and Su H. and Ln P. Jont subcarrer parng and power allocaton for OFDM transmsson wth decodeand-forward relayng. EEE Trans. Sgnal Proc. 011 Jan; 59(1: [18] Boyd S. and Vandenberghe L. (004 Convex optmzaton. (Cambrdge Unversty Press. [19] Boyd S. and Mutapcc A. (Sprng quarter Subgradent methods. Lecture notes of EE364b. Stanford Unv. Stanford CA. [0] Zh Q. and Shuguang C. and Sayed A. H. and Poor H. V. Optmal multband ont detecton for spectrum sensng n cogntve rado networks. EEE Trans. Sgnal Proc. 009 Mar; 57(3: [1] Wess T. and Hllenbrand J. and Krohn A. and Jondral F. K. Mutual nterference n OFDM-based spectrum poolng systems. Proc. EEE Vehcular Tec. Conf. (VTC 004 May; Mlan-taly [] Vandendorpe L. and Duran R. and Louveaux J. and Zad A. Power allocaton for OFDM transmsson wth DF relayng. Proc. EEE nt. Conf. Commun. (CC 008 May; Duba-U. A. E [3] Yu W. and Coff J. M. FDMA capacty of Gaussan multple-access channels wth S. Trans. Commun. 00 Aug; 50(1: [4] Awad M. K. and Shen X. OFDMA based two hop cooperatve relay network resources allocaton. Proc. EEE nt. Conf. Commun. (CC 008 May; Duba-U. A. E [5] Cover T. M. and Thomas J. A. (1991 Elements of nformaton Theory. (John Wley and Sons nd ed. [6] Bansal G. and Kalgneed P. and Bhargava V. K. Jont sensng and power loadng algorthms for OFDM-based cogntve rado systems. Wreless Commun. and net. Conf. (WCNC 010 Apr; Sdney-Australa
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών. ΗΥ-570: Στατιστική Επεξεργασία Σήµατος. ιδάσκων : Α. Μουχτάρης. εύτερη Σειρά Ασκήσεων.
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
One and two particle density matrices for single determinant HF wavefunctions. (1) = φ 2. )β(1) ( ) ) + β(1)β * β. (1)ρ RHF
 One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
α & β spatial orbitals in
 The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα,
 ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
Vol. 34 ( 2014 ) No. 4. J. of Math. (PRC) : A : (2014) Frank-Wolfe [7],. Frank-Wolfe, ( ).
![Vol. 34 ( 2014 ) No. 4. J. of Math. (PRC) : A : (2014) Frank-Wolfe [7],. Frank-Wolfe, ( ). Vol. 34 ( 2014 ) No. 4. J. of Math. (PRC) : A : (2014) Frank-Wolfe [7],. Frank-Wolfe, ( ).](/thumbs/91/105872052.jpg) Vol. 4 ( 214 ) No. 4 J. of Math. (PRC) 1,2, 1 (1., 472) (2., 714) :.,.,,,..,. : ; ; ; MR(21) : 9B2 : : A : 255-7797(214)4-759-7 1,,,,, [1 ].,, [4 6],, Frank-Wolfe, Frank-Wolfe [7],.,,.,,,., UE,, UE. O-D,,,,,
Vol. 4 ( 214 ) No. 4 J. of Math. (PRC) 1,2, 1 (1., 472) (2., 714) :.,.,,,..,. : ; ; ; MR(21) : 9B2 : : A : 255-7797(214)4-759-7 1,,,,, [1 ].,, [4 6],, Frank-Wolfe, Frank-Wolfe [7],.,,.,,,., UE,, UE. O-D,,,,,
Variance of Trait in an Inbred Population. Variance of Trait in an Inbred Population
 Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Derivation for Input of Factor Graph Representation
 Dervaton for Input of actor Graph Representaton Sum-Product Prmal Based on the orgnal LP formulaton b x θ x + b θ,x, s.t., b, b,, N, x \ b x = b we defne V as the node set allocated to the th core. { V
Dervaton for Input of actor Graph Representaton Sum-Product Prmal Based on the orgnal LP formulaton b x θ x + b θ,x, s.t., b, b,, N, x \ b x = b we defne V as the node set allocated to the th core. { V
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
8.1 The Nature of Heteroskedasticity 8.2 Using the Least Squares Estimator 8.3 The Generalized Least Squares Estimator 8.
 8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
Duals of the QCQP and SDP Sparse SVM. Antoni B. Chan, Nuno Vasconcelos, and Gert R. G. Lanckriet
 Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R. G. Lanckret SVCL-TR 007-0 v Aprl 007 Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R.
Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R. G. Lanckret SVCL-TR 007-0 v Aprl 007 Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R.
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Technical Report: A Unified Framework for Analysis of Path Selection Based Decode-and-Forward (DF) Cooperation in Wireless Systems
 Techncal Report: A Unfed Framework for Analyss of ath Selecton Based Decode-and-Forward DF Cooperaton n Wreless Systems Neeraj Varshney Student ember, IEEE and Adtya K. Jagannatham, ember, IEEE I. VALUES
Techncal Report: A Unfed Framework for Analyss of ath Selecton Based Decode-and-Forward DF Cooperaton n Wreless Systems Neeraj Varshney Student ember, IEEE and Adtya K. Jagannatham, ember, IEEE I. VALUES
Generalized Fibonacci-Like Polynomial and its. Determinantal Identities
 Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
Neutralino contributions to Dark Matter, LHC and future Linear Collider searches
 Neutralno contrbutons to Dark Matter, LHC and future Lnear Collder searches G.J. Gounars Unversty of Thessalonk, Collaboraton wth J. Layssac, P.I. Porfyrads, F.M. Renard and wth Th. Dakonds for the γz
Neutralno contrbutons to Dark Matter, LHC and future Lnear Collder searches G.J. Gounars Unversty of Thessalonk, Collaboraton wth J. Layssac, P.I. Porfyrads, F.M. Renard and wth Th. Dakonds for the γz
LECTURE 4 : ARMA PROCESSES
 LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
8.324 Relativistic Quantum Field Theory II
 Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
1 Complete Set of Grassmann States
 Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Constant Elasticity of Substitution in Applied General Equilibrium
 Constant Elastct of Substtuton n Appled General Equlbru The choce of nput levels that nze the cost of producton for an set of nput prces and a fed level of producton can be epressed as n sty.. f Ltng for
Constant Elastct of Substtuton n Appled General Equlbru The choce of nput levels that nze the cost of producton for an set of nput prces and a fed level of producton can be epressed as n sty.. f Ltng for
A Class of Orthohomological Triangles
 A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
Proposal of Terminal Self Location Estimation Method to Consider Wireless Sensor Network Environment
 1 2 2 GPS (SOM) Proposal of Termnal Self Locaton Estmaton Method to Consder Wreless Sensor Network Envronment Shohe OHNO, 1 Naotosh ADACHI 2 and Yasuhsa TAKIZAWA 2 Recently, large scale wreless sensor
1 2 2 GPS (SOM) Proposal of Termnal Self Locaton Estmaton Method to Consder Wreless Sensor Network Envronment Shohe OHNO, 1 Naotosh ADACHI 2 and Yasuhsa TAKIZAWA 2 Recently, large scale wreless sensor
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα,
 ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Διαδικαστικά Περιεχόμενο και στόχος μαθήματος Έλεγχος δικτύων -
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Διαδικαστικά Περιεχόμενο και στόχος μαθήματος Έλεγχος δικτύων -
8.323 Relativistic Quantum Field Theory I
 MIT OpenCourseWare http://ocwmtedu 8323 Relatvstc Quantum Feld Theory I Sprng 2008 For nformaton about ctng these materals or our Terms of Use, vst: http://ocwmtedu/terms 1 The Lagrangan: 8323 Lecture
MIT OpenCourseWare http://ocwmtedu 8323 Relatvstc Quantum Feld Theory I Sprng 2008 For nformaton about ctng these materals or our Terms of Use, vst: http://ocwmtedu/terms 1 The Lagrangan: 8323 Lecture
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Concomitants of Dual Generalized Order Statistics from Bivariate Burr III Distribution
 Journal of Statstcal Theory and Applcatons, Vol. 4, No. 3 September 5, 4-56 Concomtants of Dual Generalzed Order Statstcs from Bvarate Burr III Dstrbuton Haseeb Athar, Nayabuddn and Zuber Akhter Department
Journal of Statstcal Theory and Applcatons, Vol. 4, No. 3 September 5, 4-56 Concomtants of Dual Generalzed Order Statstcs from Bvarate Burr III Dstrbuton Haseeb Athar, Nayabuddn and Zuber Akhter Department
Phasor Diagram of an RC Circuit V R
 ESE Lecture 3 Phasor Dagram of an rcut VtV m snt V t V o t urrent s a reference n seres crcut KVL: V m V + V V ϕ I m V V m ESE Lecture 3 Phasor Dagram of an L rcut VtV m snt V t V t L V o t KVL: V m V
ESE Lecture 3 Phasor Dagram of an rcut VtV m snt V t V o t urrent s a reference n seres crcut KVL: V m V + V V ϕ I m V V m ESE Lecture 3 Phasor Dagram of an L rcut VtV m snt V t V t L V o t KVL: V m V
Appendix. Appendix I. Details used in M-step of Section 4. and expect ultimately it will close to zero. αi =α (r 1) [δq(α i ; α (r 1)
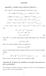 Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Symplecticity of the Störmer-Verlet algorithm for coupling between the shallow water equations and horizontal vehicle motion
 Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
Numerical Analysis FMN011
 Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
Noriyasu MASUMOTO, Waseda University, Okubo, Shinjuku, Tokyo , Japan Hiroshi YAMAKAWA, Waseda University
 A Study on Predctve Control Usng a Short-Term Predcton Method Based on Chaos Theory (Predctve Control of Nonlnear Systems Usng Plural Predcted Dsturbance Values) Noryasu MASUMOTO, Waseda Unversty, 3-4-1
A Study on Predctve Control Usng a Short-Term Predcton Method Based on Chaos Theory (Predctve Control of Nonlnear Systems Usng Plural Predcted Dsturbance Values) Noryasu MASUMOTO, Waseda Unversty, 3-4-1
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
ΜΕΛΕΤΗ ΤΗΣ ΜΑΚΡΟΧΡΟΝΙΑΣ ΠΑΡΑΜΟΡΦΩΣΗΣ ΤΟΥ ΦΡΑΓΜΑΤΟΣ ΚΡΕΜΑΣΤΩΝ ΜΕ ΒΑΣΗ ΑΝΑΛΥΣΗ ΓΕΩΔΑΙΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΜΕΤΑΒΟΛΩΝ ΣΤΑΘΜΗΣ ΤΑΜΙΕΥΤΗΡΑ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΕΛΕΤΗ ΤΗΣ ΜΑΚΡΟΧΡΟΝΙΑΣ ΠΑΡΑΜΟΡΦΩΣΗΣ ΤΟΥ ΦΡΑΓΜΑΤΟΣ ΚΡΕΜΑΣΤΩΝ ΜΕ ΒΑΣΗ ΑΝΑΛΥΣΗ ΓΕΩΔΑΙΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΜΕΤΑΒΟΛΩΝ ΣΤΑΘΜΗΣ ΤΑΜΙΕΥΤΗΡΑ ΔΙΔΑΚΤΟΡΙΚΗ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΕΛΕΤΗ ΤΗΣ ΜΑΚΡΟΧΡΟΝΙΑΣ ΠΑΡΑΜΟΡΦΩΣΗΣ ΤΟΥ ΦΡΑΓΜΑΤΟΣ ΚΡΕΜΑΣΤΩΝ ΜΕ ΒΑΣΗ ΑΝΑΛΥΣΗ ΓΕΩΔΑΙΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΜΕΤΑΒΟΛΩΝ ΣΤΑΘΜΗΣ ΤΑΜΙΕΥΤΗΡΑ ΔΙΔΑΚΤΟΡΙΚΗ
A Method for Determining Service Level of Road Network Based on Improved Capacity Model
 30 4 2013 4 Journal of Hghway and Transportaton Research and Development Vol. 30 No. 4 Apr. 2013 do10. 3969 /j. ssn. 1002-0268. 2013. 04. 018 1 1 2 1. 4000742. 201804 2 U491. 1 + 3 A 1002-0268 201304-0101
30 4 2013 4 Journal of Hghway and Transportaton Research and Development Vol. 30 No. 4 Apr. 2013 do10. 3969 /j. ssn. 1002-0268. 2013. 04. 018 1 1 2 1. 4000742. 201804 2 U491. 1 + 3 A 1002-0268 201304-0101
Congruence Classes of Invertible Matrices of Order 3 over F 2
 International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
Power allocation under per-antenna power constraints in multiuser MIMO systems
 33 0 Vol.33 No. 0 0 0 Journal on Councatons October 0 do:0.3969/.ssn.000-436x.0.0.009 IO 009 IO IO N94 A 000-436X(0)0-007-06 Power allocaton under er-antenna ower constrants n ultuser IO systes HAN Sheng-qan,
33 0 Vol.33 No. 0 0 0 Journal on Councatons October 0 do:0.3969/.ssn.000-436x.0.0.009 IO 009 IO IO N94 A 000-436X(0)0-007-06 Power allocaton under er-antenna ower constrants n ultuser IO systes HAN Sheng-qan,
( ) 2 and compare to M.
 Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
Instruction Execution Times
 1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
Math 6 SL Probability Distributions Practice Test Mark Scheme
 Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
2. THEORY OF EQUATIONS. PREVIOUS EAMCET Bits.
 EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
A Sequential Experimental Design based on Bayesian Statistics for Online Automatic Tuning. Reiji SUDA,
 Bayes, Bayes mult-armed bandt problem Bayes A Sequental Expermental Desgn based on Bayesan Statstcs for Onlne Automatc Tunng Re SUDA, Ths paper proposes to use Bayesan statstcs for software automatc tunng
Bayes, Bayes mult-armed bandt problem Bayes A Sequental Expermental Desgn based on Bayesan Statstcs for Onlne Automatc Tunng Re SUDA, Ths paper proposes to use Bayesan statstcs for software automatc tunng
Notes on the Open Economy
 Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
Second Order RLC Filters
 ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
Example of the Baum-Welch Algorithm
 Example of the Baum-Welch Algorithm Larry Moss Q520, Spring 2008 1 Our corpus c We start with a very simple corpus. We take the set Y of unanalyzed words to be {ABBA, BAB}, and c to be given by c(abba)
Example of the Baum-Welch Algorithm Larry Moss Q520, Spring 2008 1 Our corpus c We start with a very simple corpus. We take the set Y of unanalyzed words to be {ABBA, BAB}, and c to be given by c(abba)
Strain gauge and rosettes
 Strain gauge and rosettes Introduction A strain gauge is a device which is used to measure strain (deformation) on an object subjected to forces. Strain can be measured using various types of devices classified
Strain gauge and rosettes Introduction A strain gauge is a device which is used to measure strain (deformation) on an object subjected to forces. Strain can be measured using various types of devices classified
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Μεταπτυχιακή διατριβή
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Μεταπτυχιακή διατριβή ΣΥΣΧΕΤΙΣΜΟΙ ΠΡΑΓΜΑΤΙΚΗΣ ΠΑΡΑΓΩΓΗΣ ΥΦΙΣΤΑΜΕΝΩΝ ΦΩΤΟΒΟΛΤΑΪΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΝΑΛΟΓΑ ΜΕ ΤΗ ΤΟΠΟΘΕΣΙΑ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Μεταπτυχιακή διατριβή ΣΥΣΧΕΤΙΣΜΟΙ ΠΡΑΓΜΑΤΙΚΗΣ ΠΑΡΑΓΩΓΗΣ ΥΦΙΣΤΑΜΕΝΩΝ ΦΩΤΟΒΟΛΤΑΪΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΝΑΛΟΓΑ ΜΕ ΤΗ ΤΟΠΟΘΕΣΙΑ
10.7 Performance of Second-Order System (Unit Step Response)
 Lecture Notes on Control Systems/D. Ghose/0 57 0.7 Performance of Second-Order System (Unit Step Response) Consider the second order system a ÿ + a ẏ + a 0 y = b 0 r So, Y (s) R(s) = b 0 a s + a s + a
Lecture Notes on Control Systems/D. Ghose/0 57 0.7 Performance of Second-Order System (Unit Step Response) Consider the second order system a ÿ + a ẏ + a 0 y = b 0 r So, Y (s) R(s) = b 0 a s + a s + a
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
5 Haar, R. Haar,. Antonads 994, Dogaru & Carn Kerkyacharan & Pcard 996. : Haar. Haar, y r x f rt xβ r + ε r x β r + mr k β r k ψ kx + ε r x, r,.. x [,
 4 Chnese Journal of Appled Probablty and Statstcs Vol.6 No. Apr. Haar,, 6,, 34 E-,,, 34 Haar.., D-, A- Q-,. :, Haar,. : O.6..,..,.. Herzberg & Traves 994, Oyet & Wens, Oyet Tan & Herzberg 6, 7. Haar Haar.,
4 Chnese Journal of Appled Probablty and Statstcs Vol.6 No. Apr. Haar,, 6,, 34 E-,,, 34 Haar.., D-, A- Q-,. :, Haar,. : O.6..,..,.. Herzberg & Traves 994, Oyet & Wens, Oyet Tan & Herzberg 6, 7. Haar Haar.,
[1] P Q. Fig. 3.1
![[1] P Q. Fig. 3.1 [1] P Q. Fig. 3.1](/thumbs/79/80362156.jpg) 1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
DESIGN OF MACHINERY SOLUTION MANUAL h in h 4 0.
 DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
2002 Journal of Software /2002/13(08) Vol.13, No.8. , )
 000-985/00/3(08)55-06 00 Journal of Software Vol3, No8, (,00084) E-mal: yong98@malstsnghuaeducn http://netlabcstsnghuaeducn :,,, (proportonal farness schedulng, PFS), QoS, : ; ;QoS; : TP393 : A,,,,, (
000-985/00/3(08)55-06 00 Journal of Software Vol3, No8, (,00084) E-mal: yong98@malstsnghuaeducn http://netlabcstsnghuaeducn :,,, (proportonal farness schedulng, PFS), QoS, : ; ;QoS; : TP393 : A,,,,, (
Tridiagonal matrices. Gérard MEURANT. October, 2008
 Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
The Probabilistic Method - Probabilistic Techniques. Lecture 7: The Janson Inequality
 The Probabilistic Method - Probabilistic Techniques Lecture 7: The Janson Inequality Sotiris Nikoletseas Associate Professor Computer Engineering and Informatics Department 2014-2015 Sotiris Nikoletseas,
The Probabilistic Method - Probabilistic Techniques Lecture 7: The Janson Inequality Sotiris Nikoletseas Associate Professor Computer Engineering and Informatics Department 2014-2015 Sotiris Nikoletseas,
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1
 Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
department listing department name αχχουντσ ϕανε βαλικτ δδσϕηασδδη σδηφγ ασκϕηλκ τεχηνιχαλ αλαν ϕουν διξ τεχηνιχαλ ϕοην µαριανι
 She selects the option. Jenny starts with the al listing. This has employees listed within She drills down through the employee. The inferred ER sttricture relates this to the redcords in the databasee
She selects the option. Jenny starts with the al listing. This has employees listed within She drills down through the employee. The inferred ER sttricture relates this to the redcords in the databasee
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
Figure A.2: MPC and MPCP Age Profiles (estimating ρ, ρ = 2, φ = 0.03)..
 Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Lecture 2. Soundness and completeness of propositional logic
 Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
Pricing of Options on two Currencies Libor Rates
 Prcng o Optons on two Currences Lbor Rates Fabo Mercuro Fnancal Models, Banca IMI Abstract In ths document we show how to prce optons on two Lbor rates belongng to two derent currences the ormer s domestc,
Prcng o Optons on two Currences Lbor Rates Fabo Mercuro Fnancal Models, Banca IMI Abstract In ths document we show how to prce optons on two Lbor rates belongng to two derent currences the ormer s domestc,
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΨΥΧΟΛΟΓΙΚΕΣ ΕΠΙΠΤΩΣΕΙΣ ΣΕ ΓΥΝΑΙΚΕΣ ΜΕΤΑ ΑΠΟ ΜΑΣΤΕΚΤΟΜΗ ΓΕΩΡΓΙΑ ΤΡΙΣΟΚΚΑ Λευκωσία 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΨΥΧΟΛΟΓΙΚΕΣ ΕΠΙΠΤΩΣΕΙΣ ΣΕ ΓΥΝΑΙΚΕΣ ΜΕΤΑ ΑΠΟ ΜΑΣΤΕΚΤΟΜΗ ΓΕΩΡΓΙΑ ΤΡΙΣΟΚΚΑ Λευκωσία 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ
the total number of electrons passing through the lamp.
 1. A 12 V 36 W lamp is lit to normal brightness using a 12 V car battery of negligible internal resistance. The lamp is switched on for one hour (3600 s). For the time of 1 hour, calculate (i) the energy
1. A 12 V 36 W lamp is lit to normal brightness using a 12 V car battery of negligible internal resistance. The lamp is switched on for one hour (3600 s). For the time of 1 hour, calculate (i) the energy
Forced Pendulum Numerical approach
 Numerical approach UiO April 8, 2014 Physical problem and equation We have a pendulum of length l, with mass m. The pendulum is subject to gravitation as well as both a forcing and linear resistance force.
Numerical approach UiO April 8, 2014 Physical problem and equation We have a pendulum of length l, with mass m. The pendulum is subject to gravitation as well as both a forcing and linear resistance force.
Supplementary materials for Statistical Estimation and Testing via the Sorted l 1 Norm
 Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
Physical DB Design. B-Trees Index files can become quite large for large main files Indices on index files are possible.
 B-Trees Index files can become quite large for large main files Indices on index files are possible 3 rd -level index 2 nd -level index 1 st -level index Main file 1 The 1 st -level index consists of pairs
B-Trees Index files can become quite large for large main files Indices on index files are possible 3 rd -level index 2 nd -level index 1 st -level index Main file 1 The 1 st -level index consists of pairs
2 Lagrangian and Green functions in d dimensions
 Renormalzaton of φ scalar feld theory December 6 Pdf fle generated on February 7, 8. TODO Examne ε n the two-pont functon cf Sterman. Lagrangan and Green functons n d dmensons In these notes, we ll use
Renormalzaton of φ scalar feld theory December 6 Pdf fle generated on February 7, 8. TODO Examne ε n the two-pont functon cf Sterman. Lagrangan and Green functons n d dmensons In these notes, we ll use
