Μη-Αριθμήσιμα Σύνολα, ιαγωνιοποίηση
|
|
|
- Πρίαμ Οικονόμου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Μη-Αριθμήσιμα Σύνολα, ιαγωνιοποίηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο
2 Αριθμήσιμα Σύνολα Σύνολο πεπερασμένο αν έχει πεπερασμένο πληθικό αριθμό, διαφορετικά άπειρο. Cantor, 1873: Σύγκριση μεγεθών άπειρων συνόλων. Ισάριθμα σύνολα Α και Β: Υπάρχει 1-1 και επί συνάρτηση (αντιστοιχία) f : A B. Υπάρχει τέλειο ταίριασμα μεταξύ στοιχείων Α και στοιχείων Β. Π.χ. {1, 2, 3, 4}, {Α, Β, Γ, }: (1, Α), (2, Β), (3, Γ), (4, ). Πεπερασμένο σύνολο Α: Iσάριθμο του {1,..., n}, για κάποιο φυσικό n 1. Το n είναι ο πληθικός αριθμός του συνόλου Α. Αριθμήσιμο σύνολο Α: πεπερασμένο ή ισάριθμο του Ν. Υπάρχει τέλειο ταίριασμα στοιχείων Α με φυσικούς αριθμούς. Με {1,..., Α } αν Α πεπερασμένο, μεναναάπειρο. ιακριτά Μαθηματικά (Άνοιξη 2016) Μη-Αριθμήσιμα Σύνολα, ιαγωνιοποίηση 2
3 Αριθμήσιμα Σύνολα ιαδικασία (απ)αρίθμησης στοιχείων συνόλου Α: Εξελίσσεται σε διακριτά βήματα: 1, 2, 3,... Κάθε βήμα απαριθμεί διαφορετικό στοιχείο. Κάθε συγκεκριμένο στοιχείο απαριθμείται σε συγκεκριμένο (πεπερασμένο) βήμα. Αριθμήσιμο σύνολο αν επιδέχεται μιας διαδικασίας απαρίθμησης. Παραδείγματα αριθμήσιμων συνόλων: Σύνολο θετικών ζυγών αριθμών: αριθμός i στο βήμα i/2, ή f(i) = i/2. Σύνολο ακεραίων αριθμών: Ένωση πεπερασμένου πλήθους αριθμήσιμων συνόλων. Π.χ. ένωση k άπειρων (ξένων μεταξύ τους) συνόλων: {1,, k} N ιακριτά Μαθηματικά (Άνοιξη 2016) Μη-Αριθμήσιμα Σύνολα, ιαγωνιοποίηση 3
4 Αριθμήσιμα Σύνολα Παραδείγματα αριθμήσιμων συνόλων: Ένωση αριθμήσιμα άπειρου πλήθους αριθμήσιμων συνόλων, π.χ. Ν Ν {4} N {3} N {2} N (2, 0) (2, 1) (2, 2) (2, 3) (2, 4) {1} N (1, 0) (1, 1) (1, 2) (1, 3) (1, 4) {0} N (0, 0) (0, 1) (0, 2) (0, 3) (0, 4) ιακριτά Μαθηματικά (Άνοιξη 2016) 4
5 (Μη-)Αριθμήσιμα Σύνολα Άλλα παραδείγματα αριθμήσιμων συνόλων: Σύνολο ρητών (κλασματικών) αριθμών Q Παρόμοια με το Ν Ν. Σύνολο συμβολοσειρών (πεπερασμένου, αλλά απεριόριστου, μήκους) με γράμματα της Ελληνικής γλώσσας. Λεξικογραφική διάταξη. Υπάρχουν μη-αριθμήσιμα σύνολα; Πραγματικοί αριθμοί R, διαστήματα πραγματικών, π.χ. [0, 1]. υναμοσύνολα (αριθμήσιμα) άπειρων συνόλων, π.χ. 2 Ν. Πως αποδεικνύουμε ότι ένα σύνολο είναι μη-αριθμήσιμο; Cantor: αποδεικτική τεχνική της διαγωνιοποίησης το Σημαντικότατες εφαρμογές, μεταξύ άλλων στη Θεωρία Υπολογισμού και στην Υπολογιστική Πολυπλοκότητα. ιακριτά Μαθηματικά (Άνοιξη 2016) Μη-Αριθμήσιμα Σύνολα, ιαγωνιοποίηση 5
6 Μη-Αριθμήσιμα Σύνολα Το 2 Ν είναι μη-αριθμήσιμο. Έστω ότι 2 Ν αριθμήσιμο, άρα ισάριθμο του Ν. Άρα υπάρχει αντιστοιχία μελών του 2 Ν με φυσικούς στο Ν. Με βάση αυτή, απαριθμούμε S 0, S 1, S 2, S 3,, όλα τα υποσύνολα φυσικών / στοιχεία του 2 Ν. Έστω το σύνολο φυσικών D = { k N : k S k } Σε ποια θέση εμφανίζεται το D στην απαρίθμηση; D S 0 γιατί 0 ανήκει μόνο σε ένα από τα D και S 0. m, D S m γιατί m ανήκει μόνο σε ένα από τα D και S m. Τα D και S m «διαφωνούν» στο στοιχείο m. Άτοπο: το D δεν εμφανίζεται πουθενά στην απαρίθμηση! Άρα το 2 Ν δεν είναι αριθμήσιμο. ιακριτά Μαθηματικά (Άνοιξη 2016) Μη-Αριθμήσιμα Σύνολα, ιαγωνιοποίηση 6
7 ιαγωνιοποίηση Έστω αριθμήσιμο σύνολο Α και (διμελής σχέση) Αριθμήσιμο: θεωρούμε ότι Α = {α 1, α 2, α 3,... } Για κάθε α k A, γραμμή k της R: Συμπλήρωμα διαγωνίου D είναι διαφορετικό από κάθε γραμμή k. ιαφέρει από R(α 1 ) στο α 1, από R(α 2 ) στο α 2, κοκ. a 1 a2 a3 a4 a5 R( a 1) R( a 2) R( a 3) R( a 4) R( a ) ιακριτά Μαθηματικά (Άνοιξη 2016) 7 5
8 Υπόθεση του Συνεχούς Cantor διατύπωσε και προσπάθησε να αποδείξει την Υπόθεση του Συνεχούς (Continuum Hypothesis): εν υπάρχει σύνολο με πληθικό αριθμό ανάμεσα στο Ν και στο R. Gödel (1937) έδειξε ότι υπόθεση είναι συμβατή με τα αξιώματα της συνολοθεωρίας (άρα δεν υπάρχει αντιπαράδειγμα). Cohen (1963) έδειξε ότι άρνηση τηςυπόθεσηςείναισυμβατή με τα αξιώματα της συνολοθεωρίας (άρα δεν υπάρχει απόδειξη). Υπόθεση του Συνεχούς δεν μπορεί ούτε να αποδειχθεί ούτε να καταρριφθεί! ιακριτά Μαθηματικά (Άνοιξη 2016) Μη-Αριθμήσιμα Σύνολα, ιαγωνιοποίηση 8
9 Μη Υπολογισιμότητα Πρόβλημα Τερματισμού (Halting Problem): Μηχανή Turing που με είσοδο μηχανή Turing M και «δεδομένα» w, αποφαίνεται αν M(w) τερματίζει. Α. Turing: Πρόβλημα Τερματισμού δεν είναι επιλύσιμο. Θ.δ.ο. δεν υπάρχει πρόγραμμα Τ που με είσοδο πρόγραμμα Π και δεδομένα, αποφασίζει αν Π( ) τερματίζει. Π( ): εκτέλεση προγράμματος Π με είσοδο αρχείο δεδομένων. ιακριτά Μαθηματικά (Άνοιξη 2016) Μη-Αριθμήσιμα Σύνολα, ιαγωνιοποίηση 9
10 Μη Υπολογισιμότητα Έστω πρόγραμμα Τ: Τ(Π, ) = ΝΑΙ ανν Π( ) τερματίζει. Πρόγραμμα Π και δεδομένα δίνονται στο Τ ως αρχεία Π (αρχείο σε γλώσσα C) και (οποιοδήποτε αρχείο κειμένου). εδομένα μπορεί αρχείο σε γλώσσα C, και αρχείο περιγραφής Π. Τ(Π, Π): ελέγχει αν Π(Π) τερματίζει. Ορίζουμε πρόγραμμα D με είσοδο εκτελέσιμο αρχείο Π, D(Π): if T(Π, Π) = NAI then loop forever else halt D(Π) τερματίζει ανν Π(Π) δεν τερματίζει. Τι παράγει η κλήση D(D); Αν D(D) τερματίζει, Τ(D, D) = NAI, και D(D) δεν τερματίζει! Αν D(D) δεν τερματίζει, Τ(D, D) = ΟΧΙ, και D(D) τερματίζει! Αντίφαση, άρα δεν υπάρχει τέτοιο πρόγραμμα! ιακριτά Μαθηματικά (Άνοιξη 2016) Μη-Αριθμήσιμα Σύνολα, ιαγωνιοποίηση 10
11 ιαγωνιοποίηση Προγράμματα (αρχεία σε C) είναι αριθμήσιμα: Π1, Π2, Π3,... μια απαρίθμησή τους. Έστω ότι υπάρχει πρόγραμμα Τ που για προγράμματα Π i, Π j, Τ(Π i, Π j ) = ΝΑΙ ανν Π i (Π j ) τερματίζει. Πρόγραμμα D που Π i, D(Π i ) τερματίζει ανν Π i (Π i ) δεν τερματίζει. D εμφανίζεται στην απαρίθμηση: (D, Π i ) H ανν (Π i, Π i ) H. Σχέση H: (Π i, Π j ) H ανν Π i (Π j ) τερματίζει. (D, D) ανήκει στην H; ιακριτά Μαθηματικά (Άνοιξη 2016) Π 1 Π 2 Π 3 Π 4 D Π 1 Τ Τ Τ Π 2 Τ Τ Π 3 Τ Τ Π 4 Τ Τ Τ Τ D Τ Τ?
12 Παράδοξο του Russell Σύνολα που ορίζονται με βάση χαρακτηριστική ιδιότητα στοιχείων τους και χωρίς αναφορά σε σύμπαν U. S περιέχει σύνολα που δεν είναι στοιχεία του εαυτού τους. Κατά κανόνα, σύνολα δεν είναι στοιχεία του εαυτού τους, π.χ. Ν δεν είναι ακέραιος, ανθρωπότητα δεν είναι άνθρωπος. Αλλά π.χ. σύνολο ιδεών μπορεί να θεωρηθεί ιδέα. Είναι το S στοιχείο του εαυτού του; ηλ. S S; Αν S S, τότε S S. Αν S S, τότε S S. Αντίφαση! Υπάρχει κουρέας σε χωριό που ξυρίζει οποιονδήποτε δεν ξυρίζεται μόνος του. S(x, y): «x ξυρίζει y». Μη ικανοποιήσιμη δήλωση! (Ποιός ξυρίζει τον κουρέα;) ιακριτά Μαθηματικά (Άνοιξη 2016) Μη-Αριθμήσιμα Σύνολα, ιαγωνιοποίηση 12
13 Παράδοξο του Russel Ανάγκη για αξιωματική θεμελίωση της Θεωρίας Συνόλων και των Μαθηματικών. Σημαντικές ανακαλύψεις και επίδραση στη (μαθηματική) σκέψη. Ορισμός συνόλου με χαρακτηριστική ιδιότητα αναφέρεται σε συγκεκριμένο σύμπαν U. Αν S S, τότε S S. Αν S S, τότε S U ή S S. Άρα S S. ιακριτά Μαθηματικά (Άνοιξη 2016) Μη-Αριθμήσιμα Σύνολα, ιαγωνιοποίηση 13
Θεωρία Υπολογισμού Άρτιοι ΑΜ. Διδάσκων: Σταύρος Κολλιόπουλος. eclass.di.uoa.gr. Περιγραφή μαθήματος
 Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Θεωρία Υπολογισμού Αρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr
 Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Σύνολα ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Ορισμός Συνόλου Σύνολο είναι μια συλλογή
Σύνολα ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Ορισμός Συνόλου Σύνολο είναι μια συλλογή
ιµελής Σχέση ιατεταγµένο ζεύγος (α, β): ύο αντικείµενα (όχι κατ ανάγκη διαφορετικά) σε καθορισµένη σειρά. Γενίκευση: διατεταγµένη τριάδα (α, β, γ), δι
 Σχέσεις ιδάσκοντες: Φ. Αφράτη, Σ. Ζάχος,. Σούλιου Επιµέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιµελής Σχέση ιατεταγµένο ζεύγος (α, β):
Σχέσεις ιδάσκοντες: Φ. Αφράτη, Σ. Ζάχος,. Σούλιου Επιµέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιµελής Σχέση ιατεταγµένο ζεύγος (α, β):
ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Μαθηματική Επαγωγή ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Τεχνικές Απόδειξης Εξαντλητική
Μαθηματική Επαγωγή ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Τεχνικές Απόδειξης Εξαντλητική
ιακριτές Μέθοδοι για την Επιστήμη των Υπολογιστών
 ιακριτές Μέθοδοι για την Επιστήμη των Υπολογιστών ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο
ιακριτές Μέθοδοι για την Επιστήμη των Υπολογιστών ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο
Σχέσεις. ιδάσκοντες:. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Σχέσεις ιδάσκοντες:. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιμελής Σχέση ιατεταγμένο ζεύγος (α, β): ύο αντικείμενα
Σχέσεις ιδάσκοντες:. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιμελής Σχέση ιατεταγμένο ζεύγος (α, β): ύο αντικείμενα
Αρχή Εγκλεισµού-Αποκλεισµού
 Αρχή Εγκλεισµού-Αποκλεισµού ιδάσκοντες:. Φωτάκης,. Σούλιου, Θ. Λιανέας Επιµέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Πληθικός Αριθµός
Αρχή Εγκλεισµού-Αποκλεισµού ιδάσκοντες:. Φωτάκης,. Σούλιου, Θ. Λιανέας Επιµέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Πληθικός Αριθµός
Γνωριµία. ιακριτά Μαθηµατικά. Βιβλία Μαθήµατος. Επικοινωνία. ιδάσκων: Ορέστης Τελέλης. Ωρες γραφείου (502, Γρ.
 Γνωριµία ιακριτά Μαθηµατικά Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς ιδάσκων: Ορέστης Τελέλης e-mail: telelis@unipi.gr Ωρες γραφείου (502, Γρ.Λαµπράκη 26): ευτέρα
Γνωριµία ιακριτά Μαθηµατικά Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς ιδάσκων: Ορέστης Τελέλης e-mail: telelis@unipi.gr Ωρες γραφείου (502, Γρ.Λαµπράκη 26): ευτέρα
ιακριτά Μαθηµατικά Ορέστης Τελέλης Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Σύνολα 1 / 36
 ιακριτά Μαθηµατικά Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Σύνολα 1 / 36 Γνωριµία ιδάσκων: Ορέστης Τελέλης e-mail: telelis@unipi.gr
ιακριτά Μαθηµατικά Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Σύνολα 1 / 36 Γνωριµία ιδάσκων: Ορέστης Τελέλης e-mail: telelis@unipi.gr
Διδάσκοντες: Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Σχέσεις Διδάσκοντες: Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Διμελής Σχέση Διατεταγμένο ζεύγος (α, β):
Σχέσεις Διδάσκοντες: Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Διμελής Σχέση Διατεταγμένο ζεύγος (α, β):
Μια TM µπορεί ένα από τα δύο: να αποφασίζει µια γλώσσα L. να αναγνωρίζει (ηµιαποφασίζει) µια γλώσσα L. 1. Η TM «εκτελεί» τον απαριθµητή, E.
 Οι γλώσσες των Μηχανών Turing Αποφασισιµότητα / Αναγνωρισιµότητα Μια TM µπορεί ένα από τα δύο: να αποφασίζει µια γλώσσα L Αποδέχεται όταν (η είσοδος στην TM) w L. Ορέστης Τελέλης telelis@unipi.gr Τµήµα
Οι γλώσσες των Μηχανών Turing Αποφασισιµότητα / Αναγνωρισιµότητα Μια TM µπορεί ένα από τα δύο: να αποφασίζει µια γλώσσα L Αποδέχεται όταν (η είσοδος στην TM) w L. Ορέστης Τελέλης telelis@unipi.gr Τµήµα
Στοιχεία Προτασιακής Λογικής
 Στοιχεία Προτασιακής Λογικής ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Μαθηματικές Προτάσεις
Στοιχεία Προτασιακής Λογικής ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Μαθηματικές Προτάσεις
Πεπερασμένα Αυτόματα. ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Πεπερασμένα Αυτόματα ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Πεπερασμένα Αυτόματα είναι απλούστερες
Πεπερασμένα Αυτόματα ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Πεπερασμένα Αυτόματα είναι απλούστερες
Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Αρχή του Περιστερώνα Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συναρτήσεις Συνάρτηση:
Αρχή του Περιστερώνα Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συναρτήσεις Συνάρτηση:
Διακριτά Μαθηματικά Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διακριτά Μαθηματικά Ι Θεωρία συνόλων Διδάσκων: Επίκουρος Καθηγητής Σπύρος Κοντογιάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διακριτά Μαθηματικά Ι Θεωρία συνόλων Διδάσκων: Επίκουρος Καθηγητής Σπύρος Κοντογιάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Αριθμήσιμα σύνολα. Μαθηματικά Πληροφορικής 5ο Μάθημα. Παραδείγματα αριθμήσιμων συνόλων. Οι ρητοί αριθμοί
 Αριθμήσιμα σύνολα Μαθηματικά Πληροφορικής 5ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Ορισμός Πόσα στοιχεία έχει το σύνολο {a, b, r, q, x}; Οσα και το σύνολο {,,, 4, 5} που είναι
Αριθμήσιμα σύνολα Μαθηματικά Πληροφορικής 5ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Ορισμός Πόσα στοιχεία έχει το σύνολο {a, b, r, q, x}; Οσα και το σύνολο {,,, 4, 5} που είναι
Συνδυαστική Απαρίθμηση
 Συνδυαστική Απαρίθμηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθμηση Υπολογισμός
Συνδυαστική Απαρίθμηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθμηση Υπολογισμός
Σύνολα. Ορισμός Συνόλου. Υποσύνολα και Κενό Σύνολο. Στοιχεία ενός συνόλου:
 Ορισμός Συνόλου Σύνολα Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Σύνολο είναι μια συλλογή διακεκριμένων
Ορισμός Συνόλου Σύνολα Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Σύνολο είναι μια συλλογή διακεκριμένων
ιδάσκοντες: Φ. Αφράτη, Σ. Ζάχος,. Σούλιου
 Αρχή του Περιστερώνα ιδάσκοντες: Φ. Αφράτη, Σ. Ζάχος,. Σούλιου Επιµέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συναρτήσεις Συνάρτηση: διµελής
Αρχή του Περιστερώνα ιδάσκοντες: Φ. Αφράτη, Σ. Ζάχος,. Σούλιου Επιµέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συναρτήσεις Συνάρτηση: διµελής
Αρχή του Περιστερώνα. ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Αρχή του Περιστερώνα ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συναρτήσεις Συνάρτηση: διμελής σχέση
Αρχή του Περιστερώνα ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συναρτήσεις Συνάρτηση: διμελής σχέση
Συνδυαστική Απαρίθμηση
 Συνδυαστική Απαρίθμηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθμηση
Συνδυαστική Απαρίθμηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθμηση
Συνδυαστική Απαρίθμηση
 Συνδυαστική Απαρίθμηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθμηση Υπολογισμός
Συνδυαστική Απαρίθμηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθμηση Υπολογισμός
Αρχή του Περιστερώνα. ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Αρχή του Περιστερώνα ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συναρτήσεις Συνάρτηση: διμελής σχέση
Αρχή του Περιστερώνα ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συναρτήσεις Συνάρτηση: διμελής σχέση
Κανονικές Γλώσσες. ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Κανονικές Γλώσσες ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κανονικές Γλώσσες Κανονική γλώσσα αν
Κανονικές Γλώσσες ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κανονικές Γλώσσες Κανονική γλώσσα αν
, για κάθε n N. και P είναι αριθμήσιμα.
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΔΙΑΚΡΙΤA ΜΑΘΗΜΑΤΙΚΑ Διδάσκοντες: Δ.Φωτάκης Θ. Σούλιου η Γραπτή Εργασία Ημ/νια παράδοσης 5/4/8 Θέμα (Διαδικασίες Απαρίθμησης.
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΔΙΑΚΡΙΤA ΜΑΘΗΜΑΤΙΚΑ Διδάσκοντες: Δ.Φωτάκης Θ. Σούλιου η Γραπτή Εργασία Ημ/νια παράδοσης 5/4/8 Θέμα (Διαδικασίες Απαρίθμησης.
Συνδυαστική Απαρίθμηση
 Συνδυαστική Απαρίθμηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθμηση Υπολογισμός
Συνδυαστική Απαρίθμηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθμηση Υπολογισμός
Συνδυαστική Απαρίθμηση
 Συνδυαστική Απαρίθμηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθμηση Υπολογισμός
Συνδυαστική Απαρίθμηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθμηση Υπολογισμός
Σχέσεις. Διμελής Σχέση. ΣτοΊδιοΣύνολο. Αναπαράσταση
 Διμελής Σχέση Σχέσεις Διδάσκοντες: Φ. Αφράτη, Δ. Επιμέλεια διαφανειών: Δ. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Διατεταγμένο ζεύγος (α, β): Δύο αντικείμενα
Διμελής Σχέση Σχέσεις Διδάσκοντες: Φ. Αφράτη, Δ. Επιμέλεια διαφανειών: Δ. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Διατεταγμένο ζεύγος (α, β): Δύο αντικείμενα
Διακριτά Μαθηματικά Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διακριτά Μαθηματικά Ι Θεωρία συνόλων Διδάσκων: Επίκουρος Καθηγητής Σπύρος Κοντογιάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διακριτά Μαθηματικά Ι Θεωρία συνόλων Διδάσκων: Επίκουρος Καθηγητής Σπύρος Κοντογιάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Συνδυαστική Απαρίθμηση
 Συνδυαστική Απαρίθμηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθμηση Υπολογισμός
Συνδυαστική Απαρίθμηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθμηση Υπολογισμός
Κανονικές Γλώσσες. Κανονικές Γλώσσες. Κανονικές Γλώσσες και Αυτόματα. Κανονικές Γλώσσες και Αυτόματα
 Κανονικές Γλώσσες Κανονικές Γλώσσες Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Κανονική γλώσσα αν παράγεται από κανονική γραμματική. Παραγωγές P (V Σ) Σ * ((V Σ) ε) Παραγωγές μορφής:
Κανονικές Γλώσσες Κανονικές Γλώσσες Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Κανονική γλώσσα αν παράγεται από κανονική γραμματική. Παραγωγές P (V Σ) Σ * ((V Σ) ε) Παραγωγές μορφής:
Μαθηματική Επαγωγή. Τεχνικές Απόδειξης. Αποδείξεις Ύπαρξης. Μαθηματική Επαγωγή
 Μαθηματική Επαγωγή Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Τεχνικές Απόδειξης Εξαντλητική
Μαθηματική Επαγωγή Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Τεχνικές Απόδειξης Εξαντλητική
Στοιχεία Προτασιακής Λογικής
 Στοιχεία Προτασιακής Λογικής ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Μαθηματικές Προτάσεις (Μαθηματική)
Στοιχεία Προτασιακής Λογικής ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Μαθηματικές Προτάσεις (Μαθηματική)
Μετασχηματισμοί, Αναπαράσταση και Ισομορφισμός Γραφημάτων
 Μετασχηματισμοί, Αναπαράσταση και Ισομορφισμός Γραφημάτων ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο
Μετασχηματισμοί, Αναπαράσταση και Ισομορφισμός Γραφημάτων ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο
Συνδυαστική Απαρίθμηση
 Συνδυαστική Απαρίθμηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθμηση
Συνδυαστική Απαρίθμηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθμηση
Σχέση Μερικής ιάταξης Σχέση Μερικής ιάταξης (ή µερική διάταξη): ανακλαστική, αντισυµµετρική, και µεταβατική. Αριθµοί: α β (αλλά όχι α < β), α β, Σύνολ
 Σχέσεις Μερικής ιάταξης ιδάσκοντες: Φ. Αφράτη, Σ. Ζάχος,. Σούλιου Επιµέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Σχέση Μερικής ιάταξης
Σχέσεις Μερικής ιάταξης ιδάσκοντες: Φ. Αφράτη, Σ. Ζάχος,. Σούλιου Επιµέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Σχέση Μερικής ιάταξης
Πανεπιστήμιο Δυτικής Μακεδονίας. Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών. Διακριτά Μαθηματικά. Ενότητα 4: Εισαγωγή / Σύνολα
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Διακριτά Μαθηματικά Ενότητα 4: Εισαγωγή / Σύνολα Αν. Καθηγητής Κ. Στεργίου e-mail: kstergiou@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Άδειες
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Διακριτά Μαθηματικά Ενότητα 4: Εισαγωγή / Σύνολα Αν. Καθηγητής Κ. Στεργίου e-mail: kstergiou@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Άδειες
Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις.
 Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing: Όλες οι υπολογίσιμες συναρτήσεις
Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing: Όλες οι υπολογίσιμες συναρτήσεις
Σχέσεις Μερικής ιάταξης
 Σχέσεις Μερικής ιάταξης ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Σχέση Μερικής ιάταξης Σχέση Μερικής
Σχέσεις Μερικής ιάταξης ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Σχέση Μερικής ιάταξης Σχέση Μερικής
Εισαγωγικές Έννοιες. ημήτρης Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών. Εθνικό Μετσόβιο Πολυτεχνείο
 Εισαγωγικές Έννοιες ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Εισαγωγικές Έννοιες ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Σχέσεις Μερικής ιάταξης
 Σχέσεις Μερικής ιάταξης ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Σχέση Μερικής ιάταξης Σχέση Μερικής
Σχέσεις Μερικής ιάταξης ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Σχέση Μερικής ιάταξης Σχέση Μερικής
f(t) = (1 t)a + tb. f(n) =
 Παράρτημα Αʹ Αριθμήσιμα και υπεραριθμήσιμα σύνολα Αʹ1 Ισοπληθικά σύνολα Ορισμός Αʹ11 (ισοπληθικότητα) Εστω A, B δύο μη κενά σύνολα Τα A, B λέγονται ισοπληθικά αν υπάρχει μια συνάρτηση f : A B, η οποία
Παράρτημα Αʹ Αριθμήσιμα και υπεραριθμήσιμα σύνολα Αʹ1 Ισοπληθικά σύνολα Ορισμός Αʹ11 (ισοπληθικότητα) Εστω A, B δύο μη κενά σύνολα Τα A, B λέγονται ισοπληθικά αν υπάρχει μια συνάρτηση f : A B, η οποία
HY118-Διακριτά Μαθηματικά
 HY118-Διακριτά Μαθηματικά Παρασκευή, 02/03/2018 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 02-Mar-18
HY118-Διακριτά Μαθηματικά Παρασκευή, 02/03/2018 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 02-Mar-18
Θεωρία Υπολογισμού και Πολυπλοκότητα
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 12. Θεωρία Υπολογισιμότητας 30Μαρτίου, 17 Απριλίου 2007 Δρ. Παπαδοπούλου Βίκη 1 Θέση Church-Turing Τι μπορεί να υπολογιστεί και τι δεν μπορεί να υπολογιστεί?
Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 12. Θεωρία Υπολογισιμότητας 30Μαρτίου, 17 Απριλίου 2007 Δρ. Παπαδοπούλου Βίκη 1 Θέση Church-Turing Τι μπορεί να υπολογιστεί και τι δεν μπορεί να υπολογιστεί?
Συνδυαστική Απαρίθμηση
 Παραδείγματα Συνδυαστική Απαρίθμηση Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο n θρανία στη σειρά
Παραδείγματα Συνδυαστική Απαρίθμηση Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο n θρανία στη σειρά
Σχέσεις Μερικής ιάταξης
 Σχέσεις Μερικής ιάταξης ιδάσκοντες:. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Σχέση Μερικής ιάταξης Σχέση Μερικής
Σχέσεις Μερικής ιάταξης ιδάσκοντες:. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Σχέση Μερικής ιάταξης Σχέση Μερικής
ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 έντρα ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο έντρα έντρο: πρότυπο ιεραρχικής δομής.
έντρα ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο έντρα έντρο: πρότυπο ιεραρχικής δομής.
Συνδυαστική Απαρίθµηση Υπολογισµός (µε συνδυαστικά επιχειρήµατα) του πλήθους των διαφορετικών αποτελεσµάτων ενός «πειράµατος». «Πείραµα»: διαδικασία µ
 Συνδυαστική Απαρίθµηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιµέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθµηση Υπολογισµός
Συνδυαστική Απαρίθµηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιµέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθµηση Υπολογισµός
(Γραμμικές) Αναδρομικές Σχέσεις
 (Γραμμικές) Αναδρομικές Σχέσεις ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις Αναπαράσταση
(Γραμμικές) Αναδρομικές Σχέσεις ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις Αναπαράσταση
Φροντιστήριο 10 Λύσεις
 Άσκηση 1 Φροντιστήριο 10 Λύσεις Να κατασκευάσετε μια μηχανή Turing με δύο ταινίες η οποία να αποδέχεται στην πρώτη της ταινία μια οποιαδήποτε λέξη w {0,1} * και να γράφει τη λέξη w R στη δεύτερη της ταινία.
Άσκηση 1 Φροντιστήριο 10 Λύσεις Να κατασκευάσετε μια μηχανή Turing με δύο ταινίες η οποία να αποδέχεται στην πρώτη της ταινία μια οποιαδήποτε λέξη w {0,1} * και να γράφει τη λέξη w R στη δεύτερη της ταινία.
Γλώσσες Χωρίς Συμφραζόμενα
 Γλώσσα χωρίς Συμφραζόμενα Γλώσσες Χωρίς Συμφραζόμενα Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο
Γλώσσα χωρίς Συμφραζόμενα Γλώσσες Χωρίς Συμφραζόμενα Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο
Στοιχεία Κατηγορηματικής Λογικής
 Στοιχεία Κατηγορηματικής Λογικής ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κατηγορηματική Λογική
Στοιχεία Κατηγορηματικής Λογικής ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κατηγορηματική Λογική
(Γραμμικές) Αναδρομικές Σχέσεις
 (Γραμμικές) Αναδρομικές Σχέσεις ιδάσκοντες:. Φωτάκης. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις Αναπαράσταση
(Γραμμικές) Αναδρομικές Σχέσεις ιδάσκοντες:. Φωτάκης. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις Αναπαράσταση
Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις
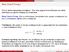 Θέση Church-Turing Κανονική μορφή Kleene Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing:
Θέση Church-Turing Κανονική μορφή Kleene Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing:
Γλώσσες Χωρίς Συμφραζόμενα
 Γλώσσες Χωρίς Συμφραζόμενα Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Γλώσσα χωρίς
Γλώσσες Χωρίς Συμφραζόμενα Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Γλώσσα χωρίς
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας. Διάλεξη 15: Διαγνωσιμότητα (Επιλυσιμότητα) ΙΙ
 ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 15: Διαγνωσιμότητα (Επιλυσιμότητα) ΙΙ Τι θα κάνουμε σήμερα Επιλύσιμα Προβλήματα σχετικά με Ασυμφραστικές Γλώσσες (4.1.2) Το Πρόβλημα του Τερματισμού
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 15: Διαγνωσιμότητα (Επιλυσιμότητα) ΙΙ Τι θα κάνουμε σήμερα Επιλύσιμα Προβλήματα σχετικά με Ασυμφραστικές Γλώσσες (4.1.2) Το Πρόβλημα του Τερματισμού
Στοιχεία Κατηγορηματικής Λογικής
 Στοιχεία Κατηγορηματικής Λογικής Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κατηγορηματική
Στοιχεία Κατηγορηματικής Λογικής Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κατηγορηματική
Συνδυαστική Απαρίθμηση
 Συνδυαστική Απαρίθμηση Διδάσκοντες: Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθμηση Υπολογισμός
Συνδυαστική Απαρίθμηση Διδάσκοντες: Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθμηση Υπολογισμός
10.1 Υπολογίσιμες συναρτήσεις και αναδρομικά σύνολα
 Κεφάλαιο 10 Υπολογισιμότητα Κύρια βιβλιογραφική αναφορά για αυτό το Κεφάλαιο είναι η Hopcroft, Motwani, and Ullman 2007. 10.1 Υπολογίσιμες συναρτήσεις και αναδρομικά σύνολα Μέχρι στιγμής έχουμε δει ουσιαστικά
Κεφάλαιο 10 Υπολογισιμότητα Κύρια βιβλιογραφική αναφορά για αυτό το Κεφάλαιο είναι η Hopcroft, Motwani, and Ullman 2007. 10.1 Υπολογίσιμες συναρτήσεις και αναδρομικά σύνολα Μέχρι στιγμής έχουμε δει ουσιαστικά
Συνδυαστική Απαρίθµηση
 Συνδυαστική Απαρίθµηση ιδάσκοντες:. Φωτάκης,. Σούλιου, Θ. Λιανέας Επιµέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθµηση
Συνδυαστική Απαρίθµηση ιδάσκοντες:. Φωτάκης,. Σούλιου, Θ. Λιανέας Επιµέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Συνδυαστική Απαρίθµηση
Στοιχεία Κατηγορηματικής Λογικής
 Στοιχεία Κατηγορηματικής Λογικής ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κατηγορηματική Λογική
Στοιχεία Κατηγορηματικής Λογικής ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κατηγορηματική Λογική
Κατηγορηµατική Λογική Προτασιακή Λογική: πλαίσιο διατύπωσης και µελέτης επιχειρηµάτων για πεπερασµένο πλήθος «λογικών αντικειµένων». «Λογικό αντικείµε
 Στοιχεία Κατηγορηµατικής Λογικής ιδάσκοντες: Φ. Αφράτη, Σ. Ζάχος,. Σούλιου Επιµέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κατηγορηµατική
Στοιχεία Κατηγορηµατικής Λογικής ιδάσκοντες: Φ. Αφράτη, Σ. Ζάχος,. Σούλιου Επιµέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κατηγορηµατική
Μη γράφετε στο πίσω μέρος της σελίδας
 Μαθηματική Λογική Εξέταση Ιουλίου 2015 Σελ. 1 από 6 Στη σελίδα αυτή γράψτε μόνο τα στοιχεία σας. Γράψτε τις απαντήσεις σας στις επόμενες σελίδες, κάτω από τις αντίστοιχες ερωτήσεις. Στις απαντήσεις σας
Μαθηματική Λογική Εξέταση Ιουλίου 2015 Σελ. 1 από 6 Στη σελίδα αυτή γράψτε μόνο τα στοιχεία σας. Γράψτε τις απαντήσεις σας στις επόμενες σελίδες, κάτω από τις αντίστοιχες ερωτήσεις. Στις απαντήσεις σας
Ασυμπτωτικός Συμβολισμός
 Ασυμπτωτικός Συμβολισμός ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Υπολογιστική Πολυπλοκότητα Υπολογιστική
Ασυμπτωτικός Συμβολισμός ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Υπολογιστική Πολυπλοκότητα Υπολογιστική
Σχέσεις Μερικής Διάταξης
 Σχέση Μερικής Διάταξης Σχέσεις Μερικής Διάταξης Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Σχέση Μερικής Διάταξης (ή μερική
Σχέση Μερικής Διάταξης Σχέσεις Μερικής Διάταξης Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Σχέση Μερικής Διάταξης (ή μερική
Αναδρομικές Σχέσεις «ιαίρει-και-βασίλευε»
 Αναδρομικές Σχέσεις «ιαίρει-και-βασίλευε» ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιαίρει-και-βασίλευε
Αναδρομικές Σχέσεις «ιαίρει-και-βασίλευε» ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιαίρει-και-βασίλευε
2 n N: 0, 1,..., n A n + 1 A
 Θεωρία Υπολογισμού Ενότητα 5: Τεχνικές απόδειξης & Κλειστότητα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Θεωρία Υπολογισμού Ενότητα 5: Τεχνικές απόδειξης & Κλειστότητα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
έντρα ιδάσκοντες:. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο
 έντρα ιδάσκοντες:. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο έντρα έντρο: πρότυπο ιεραρχικής δομής. Αναπαράσταση
έντρα ιδάσκοντες:. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο έντρα έντρο: πρότυπο ιεραρχικής δομής. Αναπαράσταση
Γεννήτριες Συναρτήσεις
 Γεννήτριες Συναρτήσεις ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναπαράσταση Ακολουθιών Ακολουθία:
Γεννήτριες Συναρτήσεις ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναπαράσταση Ακολουθιών Ακολουθία:
Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης. Οταν το πρόβλημα έχει πεπερασμ
 Μαθηματικά Πληροφορικής 4ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
Μαθηματικά Πληροφορικής 4ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
Θεωρία Υπολογισμού και Πολυπλοκότητα
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 1. Μαθηματικό Υπόβαθρο 23, 26 Ιανουαρίου 2007 Δρ. Παπαδοπούλου Βίκη 1 1.1. Σύνολα Ορισμός : Σύνολο μια συλλογή από αντικείμενα Στοιχεία: Μέλη συνόλου Τα στοιχεία
Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 1. Μαθηματικό Υπόβαθρο 23, 26 Ιανουαρίου 2007 Δρ. Παπαδοπούλου Βίκη 1 1.1. Σύνολα Ορισμός : Σύνολο μια συλλογή από αντικείμενα Στοιχεία: Μέλη συνόλου Τα στοιχεία
Εισαγωγικά. 1 η Εβδομάδα. Κάθε Τρίτη (17:00-20:00) και Τετάρτη (13:00 15:00) στην αίθουσα Ι5. 4 ώρες Θεωρία (ΤΡ : 1η-2η ώρα, ΤΕ : 1η-2η ώρα)
 ΜΥΥ204 Διακριτά Μαθηματικά Μθ άι Εισαγωγικά 1 η Εβδομάδα Άνοιξη 2015 Τμήμα Μηχανικών Η/Υ & Πληροφορικής Παν. Ιωαννίνων Μερικά Οργανωτικά Θέματα ιδάσκων: ιαλέξεις: Κάθε Τρίτη (17:00-20:00) και Τετάρτη (13:00
ΜΥΥ204 Διακριτά Μαθηματικά Μθ άι Εισαγωγικά 1 η Εβδομάδα Άνοιξη 2015 Τμήμα Μηχανικών Η/Υ & Πληροφορικής Παν. Ιωαννίνων Μερικά Οργανωτικά Θέματα ιδάσκων: ιαλέξεις: Κάθε Τρίτη (17:00-20:00) και Τετάρτη (13:00
Σειρά Προβλημάτων 1 Λύσεις
 ΕΠΛ: Θεωρία Υπολογισμού και Πολυπλοκότητα Σειρά Προβλημάτων Λύσεις Άσκηση Θεωρείστε τις γλώσσες Α = { n n } και Β = {w η w είναι λέξη επί του αλφαβήτου {,} τ.ώ. w }. (α) Για κάθε μια από τις πιο κάτω γλώσσες
ΕΠΛ: Θεωρία Υπολογισμού και Πολυπλοκότητα Σειρά Προβλημάτων Λύσεις Άσκηση Θεωρείστε τις γλώσσες Α = { n n } και Β = {w η w είναι λέξη επί του αλφαβήτου {,} τ.ώ. w }. (α) Για κάθε μια από τις πιο κάτω γλώσσες
(Γραμμικές) Αναδρομικές Σχέσεις
 (Γραμμικές) Αναδρομικές Σχέσεις Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις
(Γραμμικές) Αναδρομικές Σχέσεις Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Λογική. Ενότητα 1: Εισαγωγή. Δημήτρης Πλεξουσάκης Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Λογική Ενότητα 1: Εισαγωγή Δημήτρης Πλεξουσάκης Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται στην άδεια χρήσης Creative Commons
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Λογική Ενότητα 1: Εισαγωγή Δημήτρης Πλεξουσάκης Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται στην άδεια χρήσης Creative Commons
Σημειώσεις Λογικής I. Εαρινό Εξάμηνο Καθηγητής: Λ. Κυρούσης
 Σημειώσεις Λογικής I Εαρινό Εξάμηνο 2011-2012 Καθηγητής: Λ. Κυρούσης 2 Τελευταία ενημέρωση 28/3/2012, στις 01:37. Περιεχόμενα 1 Εισαγωγή 5 2 Προτασιακή Λογική 7 2.1 Αναδρομικοί Ορισμοί - Επαγωγικές Αποδείξεις...................
Σημειώσεις Λογικής I Εαρινό Εξάμηνο 2011-2012 Καθηγητής: Λ. Κυρούσης 2 Τελευταία ενημέρωση 28/3/2012, στις 01:37. Περιεχόμενα 1 Εισαγωγή 5 2 Προτασιακή Λογική 7 2.1 Αναδρομικοί Ορισμοί - Επαγωγικές Αποδείξεις...................
Άπληστοι Αλγόριθμοι. ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Άπληστοι Αλγόριθμοι ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άπληστοι Αλγόριθμοι... για προβλήματα
Άπληστοι Αλγόριθμοι ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άπληστοι Αλγόριθμοι... για προβλήματα
Άπληστοι Αλγόριθμοι. ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Άπληστοι Αλγόριθμοι ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άπληστοι Αλγόριθμοι... για προβλήματα
Άπληστοι Αλγόριθμοι ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άπληστοι Αλγόριθμοι... για προβλήματα
Γεννήτριες Συναρτήσεις
 Γεννήτριες Συναρτήσεις ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναπαράσταση Ακολουθιών Ακολουθία:
Γεννήτριες Συναρτήσεις ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναπαράσταση Ακολουθιών Ακολουθία:
Σύνολα, Σχέσεις, Συναρτήσεις
 Κεφάλαιο 2 Σύνολα, Σχέσεις, Συναρτήσεις Τα σύνολα, οι σχέσεις και οι συναρτήσεις χρησιμοποιούνται ευρύτατα σε κάθε είδους μαθηματικές αναπαραστάσεις και μοντελοποιήσεις. Στη θεωρία υπολογισμού χρησιμεύουν,
Κεφάλαιο 2 Σύνολα, Σχέσεις, Συναρτήσεις Τα σύνολα, οι σχέσεις και οι συναρτήσεις χρησιμοποιούνται ευρύτατα σε κάθε είδους μαθηματικές αναπαραστάσεις και μοντελοποιήσεις. Στη θεωρία υπολογισμού χρησιμεύουν,
HY118- ιακριτά Μαθηµατικά
 HY118- ιακριτά Μαθηµατικά Πέµπτη, 09/03/2017 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 3/9/2017
HY118- ιακριτά Μαθηµατικά Πέµπτη, 09/03/2017 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 3/9/2017
Μορφές αποδείξεων. Μαθηματικά Πληροφορικής 2ο Μάθημα. Μορφές αποδείξεων (συνέχεια) Εξαντλητική μέθοδος
 Μορφές αποδείξεων Μαθηματικά Πληροφορικής ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
Μορφές αποδείξεων Μαθηματικά Πληροφορικής ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης. Οταν το πρόβλημα έχει πεπερασμ
 Μαθηματικά Πληροφορικής 2ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
Μαθηματικά Πληροφορικής 2ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
ΗΥ Λογική. Διδάσκων: Δημήτρης Πλεξουσάκης Καθηγητής
 ΗΥ 180 - Λογική Διδάσκων: Καθηγητής E-mail: dp@csd.uoc.gr Ώρες διδασκαλίας: Δευτέρα, Τετάρτη 4-6 μμ, Αμφ. Β Ώρες φροντιστηρίου: Πέμπτη 4-6 μμ, Αμφ. Β Ώρες γραφείου: Δευτέρα, Τετάρτη 2-4 μμ, Κ.307 Web site:
ΗΥ 180 - Λογική Διδάσκων: Καθηγητής E-mail: dp@csd.uoc.gr Ώρες διδασκαλίας: Δευτέρα, Τετάρτη 4-6 μμ, Αμφ. Β Ώρες φροντιστηρίου: Πέμπτη 4-6 μμ, Αμφ. Β Ώρες γραφείου: Δευτέρα, Τετάρτη 2-4 μμ, Κ.307 Web site:
Θεωρία Γραφημάτων: Ορολογία και Βασικές Έννοιες
 Θεωρία Γραφημάτων: Ορολογία και Βασικές Έννοιες ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο
Θεωρία Γραφημάτων: Ορολογία και Βασικές Έννοιες ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο
Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity
 και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ.
και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ.
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας. Διάλεξη 1: Μαθηματικό Υπόβαθρο
 ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 1: Μαθηματικό Υπόβαθρο Τι θα κάνουμε σήμερα Εισαγωγικά (0.1) Σύνολα (0.2.1, 0.2.2) Συναρτήσεις & Σχέσεις (;;) (0.2.3) 1 Περιοχές που θα μελετήσουμε
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 1: Μαθηματικό Υπόβαθρο Τι θα κάνουμε σήμερα Εισαγωγικά (0.1) Σύνολα (0.2.1, 0.2.2) Συναρτήσεις & Σχέσεις (;;) (0.2.3) 1 Περιοχές που θα μελετήσουμε
Λογική Πρώτης Τάξης. Γιώργος Κορφιάτης. Νοέµβριος Εθνικό Μετσόβιο Πολυτεχνείο
 Λογική Πρώτης Τάξης Γιώργος Κορφιάτης Εθνικό Μετσόβιο Πολυτεχνείο Νοέµβριος 2008 Σύνταξη Ορισµός (Σύνταξη της λογικής πρώτης τάξης) Λεξιλόγιο Σ = (Φ, Π, r) Συναρτήσεις f Φ Σχέσεις R Π r( ) η πληθικότητα
Λογική Πρώτης Τάξης Γιώργος Κορφιάτης Εθνικό Μετσόβιο Πολυτεχνείο Νοέµβριος 2008 Σύνταξη Ορισµός (Σύνταξη της λογικής πρώτης τάξης) Λεξιλόγιο Σ = (Φ, Π, r) Συναρτήσεις f Φ Σχέσεις R Π r( ) η πληθικότητα
Recursive and Recursively Enumerable sets I
 Recursive and Recursively Enumerable sets I Ορισμός Το σύνολο A είναι αναδρομικό ανν η χαρακτηριστική του συνάρτηση X A είναι αναδρομική. Το σύνολο A είναι αναδρομικά αριθμήσιμο (recursively enumerable)
Recursive and Recursively Enumerable sets I Ορισμός Το σύνολο A είναι αναδρομικό ανν η χαρακτηριστική του συνάρτηση X A είναι αναδρομική. Το σύνολο A είναι αναδρομικά αριθμήσιμο (recursively enumerable)
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας. Διάλεξη 16: Αναγωγές
 ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 16: Αναγωγές Τι θα κάνουμε σήμερα Το Πρόβλημα του Τερματισμού (4.2) Εισαγωγή στις Αναγωγές Ανεπίλυτα Προβλήματα από την Θεωρία των Γλωσσών (5.1) Απεικονιστικές
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 16: Αναγωγές Τι θα κάνουμε σήμερα Το Πρόβλημα του Τερματισμού (4.2) Εισαγωγή στις Αναγωγές Ανεπίλυτα Προβλήματα από την Θεωρία των Γλωσσών (5.1) Απεικονιστικές
Μη γράφετε στο πίσω μέρος της σελίδας
 Μαθηματική Λογική Εξέταση Σεπτεμβρίου 2015 Σελ. 1 από 6 Στη σελίδα αυτή γράψτε μόνο τα στοιχεία σας. Γράψτε τις απαντήσεις σας στις επόμενες σελίδες, κάτω από τις αντίστοιχες ερωτήσεις. Στις απαντήσεις
Μαθηματική Λογική Εξέταση Σεπτεμβρίου 2015 Σελ. 1 από 6 Στη σελίδα αυτή γράψτε μόνο τα στοιχεία σας. Γράψτε τις απαντήσεις σας στις επόμενες σελίδες, κάτω από τις αντίστοιχες ερωτήσεις. Στις απαντήσεις
214 ΚΕΦΑΛΑΙΟ 7. ΕΠΙΛΥΣΙΜΟΤΗΤΑ - ΜΗ ΕΠΙΛΥΣΙΜΟΤΗΤΑ 7.1 Το Πρόβλημα του Τερματισμού Θεώρημα 7.1 (Πρόβλημα του Τερματισμού - ημιαπόφαση) Η γλώσσα του Προβ
 Κεφάλαιο 7 Επιλυσιμότητα - Μη επιλυσιμότητα Σύνοψη Στα προηγούμενα κεφάλαια επικεντρωθήκαμε σε επιλύσιμα προβλήματα και μελετήσαμε υπολογιστικά μοντέλα με δυνατότητες, που συνεχώς διευρύναμε. Το τελευταίο
Κεφάλαιο 7 Επιλυσιμότητα - Μη επιλυσιμότητα Σύνοψη Στα προηγούμενα κεφάλαια επικεντρωθήκαμε σε επιλύσιμα προβλήματα και μελετήσαμε υπολογιστικά μοντέλα με δυνατότητες, που συνεχώς διευρύναμε. Το τελευταίο
Φροντιστήριο 9 Λύσεις
 Άσκηση 1 Φροντιστήριο 9 Λύσεις Να κατασκευάσετε μια μηχανή Turing με δύο ταινίες η οποία να αποδέχεται στην πρώτη της ταινία μια οποιαδήποτε λέξη w {a,b} * και να γράφει τη λέξη w R στη δεύτερη της ταινία.
Άσκηση 1 Φροντιστήριο 9 Λύσεις Να κατασκευάσετε μια μηχανή Turing με δύο ταινίες η οποία να αποδέχεται στην πρώτη της ταινία μια οποιαδήποτε λέξη w {a,b} * και να γράφει τη λέξη w R στη δεύτερη της ταινία.
Στοιχεία Προτασιακής Λογικής
 Μαθηματικές Προτάσεις Στοιχεία Προτασιακής Λογικής Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο
Μαθηματικές Προτάσεις Στοιχεία Προτασιακής Λογικής Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο
Μη γράφετε στο πίσω μέρος της σελίδας
 Μαθηματική Λογική Τελική εξέταση Ιούλιος 2014 α Σελ. 1 από 5 Στη σελίδα αυτή γράψτε μόνο τα στοιχεία σας. Γράψτε τις απαντήσεις σας στις επόμενες σελίδες, κάτω από τις αντίστοιχες ερωτήσεις. Στις απαντήσεις
Μαθηματική Λογική Τελική εξέταση Ιούλιος 2014 α Σελ. 1 από 5 Στη σελίδα αυτή γράψτε μόνο τα στοιχεία σας. Γράψτε τις απαντήσεις σας στις επόμενες σελίδες, κάτω από τις αντίστοιχες ερωτήσεις. Στις απαντήσεις
Μαθηματική Λογική (προπτυχιακό) Εξέταση Ιανουαρίου 2018 Σελ. 1 από 5
 Μαθηματική Λογική (προπτυχιακό) Εξέταση Ιανουαρίου 2018 Σελ. 1 από 5 Στη σελίδα αυτή γράψτε μόνο τα στοιχεία σας. Γράψτε τις απαντήσεις σας στις επόμενες σελίδες, κάτω από τις αντίστοιχες ερωτήσεις. Στις
Μαθηματική Λογική (προπτυχιακό) Εξέταση Ιανουαρίου 2018 Σελ. 1 από 5 Στη σελίδα αυτή γράψτε μόνο τα στοιχεία σας. Γράψτε τις απαντήσεις σας στις επόμενες σελίδες, κάτω από τις αντίστοιχες ερωτήσεις. Στις
Τι είναι σύνολο; Ο ορισμός αυτός είναι σύμφωνος με τη διαισθητική μας κατανόηση για το τι είναι σύνολο
 ΣΥΝΟΛΑ Τι είναι σύνολο; Ένας ορισμός «Μια συλλογή αντικειμένων διακεκριμένων και πλήρως καθορισμένων που λαμβάνονται από τον κόσμο είτε της εμπειρίας μας είτε της σκέψης μας» (Cantor, 19 ος αιώνας) Ο ορισμός
ΣΥΝΟΛΑ Τι είναι σύνολο; Ένας ορισμός «Μια συλλογή αντικειμένων διακεκριμένων και πλήρως καθορισμένων που λαμβάνονται από τον κόσμο είτε της εμπειρίας μας είτε της σκέψης μας» (Cantor, 19 ος αιώνας) Ο ορισμός
Άπληστοι Αλγόριθμοι. Επιμέλεια διαφανειών: Δ. Φωτάκης Τροποποιήσεις: Α. Παγουρτζής. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Άπληστοι Αλγόριθμοι Επιμέλεια διαφανειών: Δ. Φωτάκης Τροποποιήσεις: Α. Παγουρτζής Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άπληστοι Αλγόριθμοι... για προβλήματα
Άπληστοι Αλγόριθμοι Επιμέλεια διαφανειών: Δ. Φωτάκης Τροποποιήσεις: Α. Παγουρτζής Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άπληστοι Αλγόριθμοι... για προβλήματα
Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνο ΣHMΜY
 Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνο ΣHMΜY 2η ενότητα: Βασικές έννοιες θεωρίας υπολογισμού: υπολογιστικά προβλήματα, υπολογισιμότητα, πολυπλοκότητα Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης
Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνο ΣHMΜY 2η ενότητα: Βασικές έννοιες θεωρίας υπολογισμού: υπολογιστικά προβλήματα, υπολογισιμότητα, πολυπλοκότητα Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης
