cjenik za djela grafiëkog oblikovanja
|
|
|
- Άκανθα Μπλέτσας
- 8 χρόνια πριν
- Προβολές:
Transcript
1 KonaËne cijene formiraju se prema konkretnom zadatku i spram træiπne vrijednosti korisnika. Cijene u nastavku minimalne su ili poëetne cijene! Sve netto cijene bez PDV-a sadræe sve poreze i prireze na autorske honorare! I. OSNOVNI GRAFI»KI STANDARDI 1. ZA TITNI ZNAK I/ILI LOGOTIP KAO CJELINA, ILI MASKOTA; Idejno-likovno rjeπenje tj. dizajn tekstualnog i likovnog znaka prepoznavanja tvrtke i izbor karakteristiëne zaπtitne boje, ili izrada maskote, odnosno prepoznatljivog lika u osnovnoj pozi. Znak ili maskota za manje tvrtke: 7.500,00 kn + PDV(1.725,00 kn) = 9.225,00 kn brutto Niæa cijena formira se u iznimnim sluëajevima za vrlo male tvrtke ili obrte i za neprofitabilne djelatnosti. Spram izraæene cijene formira se i cijena preoblikovanja (redizajna) postojeêeg znaka, cijena znaka ili maskote obljetnice, proizvoda i prigodnog znaka. 3. SUSTAV BOJA Kod jednostavnijih identiteta za manje korisnike, sustav boja ne osmiπljava se. Cijena za opseænije identitene iznosi minimalno 5.000,00 kn + PDV (1.150,00 kn) = 6.150,00 kn brutto 4. IZBOR OSNOVNOG PISMA ILI KARAKTERISTI»NE TIPOGRAFIJE i IZBOR SEKUNDARNE TIPOGRAFIJE Osnovno pismo uz zaπtitne boje jest sastavni dio cjelovitog lika. Kao jedan od osnovnih likovnih elemenata, prepoznatljivi je simbol tvrtke. Uz zaπtitni znak koristi se za svaki tekst na sredstvima komuniciranja. Kod jednostavnijih identiteta za manje korisnike, uglavnom se odabire samo osnovno pismo, a minimalna vrijednost djela ukljuëena je u vrijednost oblikovanja primarnih sredstava komunikacije, odnosno u izradu knjige standarda. 5. KNJIGA STANDARDA ILI PRIRU»NIK GRAFI»KIH STANDARDA A- Pri ugovaranju manjeg cjelovitog lika, autor korisniku predaje osnovne grafiëke standarde u obliku jednostavnijeg priruënika, u digitalnom obliku i u tvrdom obliku kao digitalno ispisani uvezani primjerak. Uz ugovoreni znak (I./1.) i ugovorena primarna sredstva komunikacije (II.), priruënik sadræi izbor osnovnog pisma (I./4.) i zaπtitne boje. B-Opπirnija razrada znaka ili maskote, pravilna uporaba istih, razliëite aplikacije istih, dopunski likovni elementi (II./1.), meappleusobni odnosi i veliëine svih ugovorenih elemenata cjelovitog lika, sustav boja (I./3.), pisma ili tipografije (I./4.), konstrukcije, pismena obrazloæenja i opis svih elemenata uobliëuje se u opπiran priruënik. Cijena istog priruënika formira se spram opsegu posla, a minimalno iznosi 8.500,00 kn + PDV(1.955,00 kn) = ,00 kn brutto Iznimno cijena moæe biti niæa kod dopune standarda jednostavnijem priruëniku manjeg cjelovitog lik. II. PRIMARNA SREDSTVA KOMUNIKACIJE 1. - DOPUNSKI ZA TITNI ILI KARAKTERISTI»NI LIKOVNI ELEMENTI PREPOZNAVANJA Dopunski likovni elementi mogu biti razliëite teksture ili podloge (paterni), dopunske boje ili tonovi, vrsta papira, razni likovni elementi poput ilustracija i dr. Ako se ne radi o zahtjevnijim ilustracijama, koje se dopunski naplaêuju, vrijednost dopunskih likovnih elemenata ukljuëena je u oblikovanje primarnih sredstva komunikacije (tiskanice II./2.,3.), odnosno u izradbu knjige standarda (stavka I./5. ovoga cjenika) TISKANICE - listovni papir (memorandum) - osnovna omotnica (u osnovi kuverta american formata) - dvije omotnice izvedene iz osnovne (kuverta za A4 i A5 format) - poslovni peëat - poslovna posjetnica (osnovno rjeπenje vizitke i mutacija do desetak imena pri oblikovanju cjelovitog lika) 3.350,00 kn + PDV (770,50 kn) = 4.120,50 kn brutto
2 3. - POSLOVNA MAPA (FASCIKL ILI FOLDER) - JEDNOSTAVNIJE (TIPOGRAFSKO) RJE ENJE Rjeπenje izvedeno iz osnovnih elemenata cjelovitog lika, jednostavnijeg sadræaja i postojeêeg konstruktivnog rjerπenja (izgleda πtance) ,00 kn + PDV (414,00 kn) = 2.214,00 kn brutto Vrijednost mape dvostruko se moæe uveêati kod opseænijeg i likovno zahtjevnijeg sadræaja, sa eventualno dopunskim slikovnim materijalom (fotografije, ilustracije i dr.) i/ili kod izradbe konstruktivnog rjeπenja (πtance). I./II. CJELOVITI LIK MANJE TVRTKE ILI MALI KORPORATIVNI VIZUALNI IDENTITET - zaπtitni znak i/ili logotip (I./1.) - izbor osnovnog pisma ili karakteristiëne tipografije (I./4.) - primarna sredstva komunikacije (I./1.,2.,3.) - knjiga standarda ili osnovni priruënik grafiëkih standarda (I./5./A) PriruËnik sadræi osnovne standarde, odnose svih elemenata, konstrukcije i obrazloæenja Cijena pri istovremenom ugovaranju navedenih stavki minimalno iznosi ,00 kn + PDV (3.174,00 kn) = ,00 kn brutto III. SEKUNDARNA SREDSTVA KOMUNIKACIJE 1. - APLIKACIJA ELEMENATA KU NOG STILA NA SLUffiBENO VOZILO Rjeπenje izvedeno iz osnovnih elemenata kuênog stila. Osnovna cijena iznosi 2.500,00 kn + PDV (575,00 kn) = 3.075,00 kn brutto 2. - ZASTAVICA 3. - ZASTAVA 4. - FASADNI NATPIS/TOTEM Cijena se formira spram zadatka, tj, ovisi o veliëini, opsegu, odnosno vrsti natpisa ili totema, a prosjeëna cijena moæe iznositi 3.500,00 kn + PDV (805,00 kn) = 4.305,00 kn brutto IV. MEDIJSKA SREDSTVA KOMUNIKACIJE I SREDSTVA DIREKTNE KOMUNIKACIJE 1. - OGLAS PASICA PoËetna cijena iznositi 750,00 kn + PDV (172,50 kn) = 922,50 kn brutto 2. - SADRffiAJNO I ZNA»AJEM JEDNOSTAVNIJI OGLAS 3. - REKLAMNI OGLAS A - koncept za pojedini medij B - koncept za kampanju (tri i viπe medija) 8.000,00 kn + PDV (1.840,00 kn) = 9.840,00 kn brutto C - zahtjevniji oglas 4. - ELEKTRONSKI OGLAS/WEB BANNER Cijena se formira spram zadatka, tj, ovisi o opsegu, o zahtjevnosti eventualne animacije i dr., pa poëetna cijena oblikovanja i programiranja (izvedbe) iznositi 5. - REKLAMNI PANO - OGLEDNI (SHOW) KARTON - PLAKAT SA ZADANIM ELEMENTIMA, ODNOSNO JEDNOSTAVNIJE (TIPOGRAFSKO) RJE ENJE PLAKATA - SLI»NI PROMOTIVNI MATERIJALI 2.000,00 kn + PDV (460,00 kn) = 2.460,00 kn brutto Cijena se moæe uveêati dvostruko i viπe, sukladno likovnoj zahtjevnosti, sadræaju i oglaπivaëkoj vaænosti.
3 6.- BILBOARD (JUMBO PLAKAT) - PLAKAT VRLO SLOffiENOG SADRffiAJA I/ILI POSEBNOG ZNA»AJA I ZAHTJEVA 7.500,00 kn + PDV(1.725,00 kn) = 9.225,00 kn brutto 7. - PISMO NAMJERE (DIRECT MAIL) SLOffiENIJEG SADRffiAJA 3.500,00 kn + PDV (805,00 kn) = 4.305,00 kn brutto 8. - REKLAMNI LETAK (FLYER) 9. - PROSPEKT-LETAK A4 FORMATA (dvije A4 stranice) 1.800,00 kn + PDV (414,00 kn) = 2.214,00 kn brutto PROSPEKT-LETAK A4 FORMATA PRESAVINUT NA 3 DIJELA (6 stranica/american zatvorenog formata) 2.200,00 kn + PDV (506,00 kn) = 2.706,00 kn brutto PROSPEKT-LETAK A3 FORMATA PRESAVINUTOG NA POLA (4 A4 stranice/a4 zatvorenog formata) 2.800,00 kn + PDV (644,00 kn) = 3.444,00 kn brutto PROSPEKT ZAHTJEVNIJEG SADRffiAJA I NEUOBI»AJENOG FORMATA I/ILI PROSPEKT VE EG OBIMA KATALOG ILI BRO URA A - idejno-likovno rje enje-dizajn temeljnog koncepta 2.500,00 kn + PDV (575,00 kn) = 3.075,00 kn brutto B - naslovnica i straænja stranica C - izvedbeno rje enje-razrada, layout po stranici cijena ovisi o zahtjevnosti, obimu, odnosno o broju stranica i prosjeëno iznosi 150,00 kn + PDV (34,50 kn) = 184,50 kn brutto VRE ICE SLOffiENIJEG SADRffiAJA I ZNA»AJA GrafiËko oblikovanje i konstruktivno rjeπenje/idejno-likovno i izvedbeno rjeπenje 3.500,00 kn + PDV (805,00 kn) = 4.305,00 kn brutto VRE ICE JEDNOSTAVNIJEG SADRffiAJA I ZNA»AJA GrafiËko oblikovanje i konstruktivno rjeπenje/idejno-likovno i izvedbeno rjeπenje izvedeno iz osnovnih elemenata cjelovitog lika i/ili jednostavnijeg sadræaja NALJEPNICA 750,00 kn + PDV (172,50 kn) = 922,50 kn brutto OVITAK PROMOTIVNOG CD NOSA»A Jednostavnije rjeπenje izvedeno iz osnovnih elemenata kuênog stila ETIKETA PROMOTIVNOG CD NOSA»A ILI JEDNOSTAVNIJI OVITAK CD NOSA»A Jednostavnije rjeπenje etikete izvedeno iz osnovnih elemenata kuênog stila, ili opsegom jednostavniji ovitak 750,00 kn + PDV (172,50 kn) = 922,50 kn brutto REKLAMNI BLOK ZA ZABILJE KE ILI NEKI PROMOTIVNI PROIZVOD SLI»NOG SADRffiAJA Jednostavnije rjeπenje i/ili rjπenje izvedeno iz osnovnih elemenata kuênog stila POZIVNICA ILI»ESTITKA JEDNOSTAVNIJEG SADRffiAJA 20. -»ESTITKA SLOffiENIJEG SADRffiAJA ILI STOLNI KALENDAR SA»ESTITKOM (American zatvorenog formata) poëetna cijena iznosi
4 21. - DffiEPNI KALENDAR 750,00 kn + PDV (172,50 kn) = 922,50 kn brutto JEDNOSTAVNIJI STOLNI PLANER (jedinstveni list u ponavljanju-npr 48 identiënih listova) TJEDNI STOLNI PLANER (48 razliëitih listova s izraæenim jednim tjednom na svakome listu) ZAGLAVLJE TRODJELNOG KALENDARA ESTEROLISNI KALENDAR (6 + 1 list) 4.000,00 kn + PDV (920,00 kn) = 4.920,00 kn brutto DVANAESTLISNI KALENDAR ( list) 6.000,00 kn + PDV (1.380,00 kn) = 7.380,00 kn brutto DVANAESTLISNI KALENDAR ZAHTJEVNIJEG SADRffiAJA I/ILI ZNA»AJA ( list) ,00 kn + PDV (2.300,00 kn) = ,00 kn brutto STOLNI KALENDAR (npr. spiralno uvezen) A - idejno-likovno rje enje-dizajn temeljnog koncepta 2.000,00 kn + PDV (460,00 kn) = 2.460,00 kn brutto C - izvedbeno rje enje-razrada, layout po stranici (npr. 32 str./16 listova ili 48 str./24 lista) Cijena ovisi o zahtjevnosti, obimu, odnosno o broju stranica i prosjeëno iznosi 35,00 kn + PDV (8,05 kn) = 43,05 kn brutto ROKOVNIK ILI PLANER (npr. spiralno uvezen-) A - idejno-likovno rje enje-dizajn temeljnog koncepta 2.500,00 kn + PDV (575,00 kn) = 3.075,00 kn brutto B - naslovnica i straænja stranica C - izvedbeno rje enje-razrada, layout po stranici (npr. 72 str./36 listova ili 96 str./48 listova) Cijena ovisi o zahtjevnosti, obimu, odnosno o broju stranica i prosjeëno po stranici kalendarija iznosi 35,00 kn + PDV (8,05 kn) = 43,05 kn brutto IV. - PUBLIKACIJE 1. - OVITAK ILI NASLOVNICA KNJIGE 2. - IDEJNO-LIKOVNO RJE ENJE-DIZAJN BIBLIOTEKE Ovisno o opsegu i znaëaju biblioteke, prosjeëna cijena iznosi 2.000,00 kn + PDV (460,00 kn) = 2.460,00 kn brutto 3. - PRIJELOM KNJIGE A - jednostavniji knjiæni blok 10,00 kn + PDV (2,30 kn) = 12,30 kn brutto po stranici B - likovno, tehniëki i/ili opsegom zahtjevniji sadræaj 75,00 kn + PDV (17,25 kn) = 92,25 kn brutto po stranici C - likovno, tehniëki i/ili opsegom vrlo zahtjevan sadræaj-monografija 125,00 kn + PDV (28,75 kn) = 153,75 kn brutto po stranici 4. - GRAFIKON, DIAGRAM, ILI SHEMA ProsjeËna cijena iznosi 400,00 kn + PDV (92,00 kn) = 492,00 kn brutto
5 V. - AMBALAffiA 1. - PRIVJESNICA, PASICA, VRPCA, NALJEPNICA I SL ETIKETA ZA RAZNE PROIZVODE ILI JEDINICA AMBALAffiE ZA PAKIRANJE PROIZVODA Ovisno o vrsti i znaëaju proizvoda, zahtjevnosti i sadræaju ambalaæe poëetna minimalna poëetna cijena iznosi 3.750,00 kn + PDV (862,50 kn) = 4.612,50 kn brutto 3. - AMBALAffiA ZA BOCE ZA PI E Prednja i straænja etiketa, ovratnica i pasica 7.500,00 kn + PDV (1.725,00 kn) = 9.225,00 kn brutto 4. - AMBALAffiA ZA BOCE ZA PI E ZA KORISNIKE S VRLO MALIM PROIZVODNIM KAPACITETOM Prednja i straænja etiketa, ovratnica i pasica 5. - CJELOVITI LIK MANJE KOLEKCIJE PROIZVODA (do 5 jedinica) ,00 kn + PDV (1.725,00 kn) = 9.225,00 kn brutto 6. - CJELOVITI LIK VE E KOLEKCIJE PROIZVODA (viπe od 5 jedinica) ,00 kn + PDV (5.175,00 kn) = ,00 kn brutto 7. - CJELOVITI LIK VE E GRUPE PROIZVODA ,00 kn + PDV (10.350,00 kn) = ,00 kn brutto 8. - TRANSPORTNA AMBALAffiA 3.800,00 kn + PDV (874,00 kn) = 4.674,00 kn brutto 9. - OMOT ZA GLAZBENI ILI FILMSKI CD/DVD ProsjeËna cijena iznosi 7.000,00 kn + PDV (1.610,00 kn) = 8.610,00 kn brutto VI. - WEB STRANICE 1. - IDEJNO-LIKOVNO RJE ENJE/OSNOVNI GRAFI»KI DIZAJN WEB STRANICA sa zadanim elementima cjelovitog lika tvrtke/druπtva Osnovna cijena iznosi 4.800,00 kn + PDV (1.104,00) = 5.904,00 kn brutto 2. - TEMPLATE/IZRADBA PREDLO KA PREMA DIZAJNU STRANICA 2.000,00 kn + PDV (460,00) = 2.460,00 kn brutto 3. - IZRADBA WEB STRANICA/TEHNI»KA IZVEDBA A - do 10 komada PoËetna cijena po stranici iznosi 400,00 kn + PDV (92,00) = 492,00 kn brutto B - preko 10 komada PoËetna cijena po stranici iznosi 200,00 kn + PDV (46,00) = 246,00 kn brutto 5. - PRIJAVA WEB STRANICA NA INTERNET PRETRAffiIVA»E TE NJIHOVE PRILAGODBE Cijena po stranici iznosi 265,00 kn + PDV (60,95) = 325,95 kn brutto 6. - ODRffiAVANJE WEB STRANICA Cijena radnog sata odræavanja iznosi 200,00 kn + PDV (46,00) = 246,00 kn brutto 7. - FLASH ANIMACIJA Idejno-likovno i izvedbeno rjeπenje/layout i programiranje ProsjeËna cijena pojedine animacije iznosi c.c.a ,00 kn + PDV (575,00) = 3.075,00 kn brutto Kao i kod elektronskog oglasa (IV./4.) cijena se formira spram zadatka i ovisi o opsegu i zahtjevnosti animacije. Unaprijed nije moguêe dati toënu cijenu za izradbu kompletnih web stranica, jer cijena ovisi o mnogo Ëimbenika, poput zahtjevnosti i broja stranica, te o dodatnim zahtjevima klijenta, odnosno o interaktivnosti stranica i nadasve o sâmoj strukturi stranica. Ukupna zbirna OKVIRNA MINIMALNA PO»ETNA cijena bez animacije iznos od 5.700,00 do ,00 kn i viπe
6 VII. - IDEJNO-LIKOVNO OSMI LJAVANJE GOTOVIH PROIZVODA 1. - GRAFI»KI DIZAJN/IDEJNO-LIKOVNO RJE ENJE ZA MAJICU, ALICU ILI ZA NEKI SLI»AN PREDMET poëetna cijena iznosi 1.470,00 kn + PDV (338,10 kn) = 1.793,40 kn brutto Kao i kod svih drugih djela, izradba ilustracije dodatno se naplaêuje. U iznimnim sluëajevima kod jednostavnijeg apliciranja zahtjevnije ilustracije, cijena moæe iznositi prosjeënu zbirnu cijenu ilustracije i dizajna majice, odnosno πalice, ili nekog sliënog predmeta. Pri aplikaciji elemenata kuênog stila na reklamne proizvode tvrtke, moæe se primijeniti naëelo vrednovanja djela prema satnici (VIII./1.). VIII. - OSTALE USLUGE 1. - APLIKACIJE DJELA NA GOTOVE PROIZVODE, TEHNI»KE USLUGE I GRAFI»KA PRIPREMA Razni dopunski troπkovi, tehniëki poslovi, izradba grafiëke pripreme (ako ista nije uraëunata u izradbu djela), te djela za koja je iz raznih razloga nemoguêe unaprijed izraziti cijenu, naplaêuju se prema vrijednosti radne satnice. Vrijednost jednog kreativnog radnog sata minimalna je poëetna cijena za jednostavnije tehniëke poslove, odnosno za razne aplikacije elemenata kuênog stila na gotove proizvode. Manje od iste vrijednosti satnice naplaêuje se iznimno obrada fotografija, izrezivanje iz pozadine ( patiranje ), tako da se izraëuna stvarno uloæeno radno vrijema. Vrijednost jednog kreativnog radnog sata iznosi 200,00 kn + PDV (46,00 kn) = 246,00 kn brutto 2. - MINIMALNA PO»ETNA/OSNOVNA CIJENA Za jednostavnije poslove, odnosno za djela vrlo malog znaëaja i/ili za træiπno slabije korisnike, minimalna poëetna cijena pojedinog djela iznosi 750,00 kn + PDV (172,50 kn) = 922,50 kn brutto 3. - POSLOVI ORGANIZACIJE I NADGLED REALIZACIJE Minimalno prema vrijednosti Agencijske provizije, dopunski se naplaêuje organizacija i nadgled tj. supervizija realizacije, odnosno tiska AGENCIJSKA PROVIZIJA I KOMUNIKACIJSKA STRATEGIJA Za usluge vanjskih suradnika ili za pojedine vlastite organizacijske usluge voappleenja promidæbenih odnosno oglaπavaëkih aktivnosti, DESIGN STUDIO BREGAR sa suradnicima naplaêuje Agencijsku proviziju. Pojedine usluge idejnog i organizacijskog voappleenja kompletnih projekata, poput osmiπljavanja Komunikacijske strategije, naplaêuju se pauπalno ili fiksno prema projektu. Agencijska provizija iznosi 15% (petnaest posto) od brutto vrijednosti organiziranih poslova, usluga i djela IZRADBA OP IRNIJE NARU»ENE PONUDE Korisnik i autor sklapaju suradnju i potpisuju autorski ugovor koji se poziva na OpÊe uvjete poslovanja DESIGN STUDIJA BREGAR, na Cijenik usluga DESIGN STUDIJA BREGAR (za dizajn i ilustracije) i na troπkovnike i/ili ponude koje korisniku autor prethodno predoëuje, a korisnik ih odobrava. Na zahtjev korisnika, ili ako priroda posla/zadatka to zahtjeva, autor moæe ponuditi opπirnu, zahtjevnu ciljanu ponudu koja se naplaêuje minimalno 350,00 kn + PDV (80,50 kn) = 430,50 kn brutto 6. - DNEVNICA 350,00 kn + PDV (80,50 kn) = 430,50 kn brutto U Zagrebu, sijeënja god. Tihomir Bregar
ZBIRKA POTPUNO RIJEŠENIH ZADATAKA
**** IVANA SRAGA **** 1992.-2011. ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE POTPUNO RIJEŠENI ZADACI PO ŽUTOJ ZBIRCI INTERNA SKRIPTA CENTRA ZA PODUKU α M.I.M.-Sraga - 1992.-2011.
Uvod. Čestit Božić i sretna Nova godina! Sve cijene u katalogu su izražene bez PDV-a Minimalni iznos narudžbe: 500,00 kn
Uvod Svaka ozbiljnija tvrtka već naveliko razmišlja a o poslovnim darovima kojima će i ove godine obradovati at svoje poslovne ov partnere i još jednom im na simboličan način zahvaliti, na korektnom poslovanju
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
ELEKTROTEHNIČKI ODJEL
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
3.1 Granična vrednost funkcije u tački
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
RIJEŠENI ZADACI I TEORIJA IZ
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Računarska grafika. Rasterizacija linije
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Elementi spektralne teorije matrica
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
radni nerecenzirani materijal za predavanja
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Eliminacijski zadatak iz Matematike 1 za kemičare
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
7 Algebarske jednadžbe
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Linearna algebra 2 prvi kolokvij,
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
TRIGONOMETRIJA TROKUTA
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
Operacije s matricama
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
DUALNOST. Primjer. 4x 1 + x 2 + 3x 3. max x 1 + 4x 2 1 3x 1 x 2 + x 3 3 x 1 0, x 2 0, x 3 0 (P ) 1/9. Back FullScr
DUALNOST Primjer. (P ) 4x 1 + x 2 + 3x 3 max x 1 + 4x 2 1 3x 1 x 2 + x 3 3 x 1 0, x 2 0, x 3 0 1/9 DUALNOST Primjer. (P ) 4x 1 + x 2 + 3x 3 max x 1 + 4x 2 1 3x 1 x 2 + x 3 3 x 1 0, x 2 0, x 3 0 1/9 (D)
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Program za tablično računanje Microsoft Excel
Program za tablično računanje Microsoft Excel Teme Formule i funkcije Zbrajanje Oduzimanje Množenje Dijeljenje Izračun najveće vrijednosti Izračun najmanje vrijednosti 2 Formule i funkcije Naravno da je
Kaskadna kompenzacija SAU
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
Prijedlog sluæbenog cjenika HDD-a za usluge gra Ëkog dizajna
Prijedlog sluæbenog cjenika HDD-a za usluge gra Ëkog dizajna 1 OP I UVJETI NARUDÆBE 1. Vrjednovanje Ovi opêi uvjeti ugovora vrijede za sve ugovore gra Ëkog dizajna izmeappleu gra Ëkog dizajnera (Ëlana
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Riješeni zadaci: Nizovi realnih brojeva
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE
**** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
Računarska grafika. Rasterizacija linije
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
GLAZBENA UMJETNOST. Rezultati državne mature 2010.
GLAZBENA UJETNOST Rezultati državne mature 2010. Deskriptivna statistika ukupnog rezultata PARAETAR VRIJEDNOST N 112 k 61 72,5 St. pogreška mjerenja 5,06 edijan 76,0 od 86 St. devijacija 15,99 Raspon 66
Otpornost R u kolu naizmjenične struje
Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
2742/ 207/ /07.10.1999 «&»
2742/ 207/ /07.10.1999 «&» 1,,,. 2 1. :.,,,..,..,,. 2., :.,....,, ,,..,,..,,,,,..,,,,,..,,,,,,..,,......,,. 3., 1. ' 3 1.., : 1. T,, 2., 3. 2 4. 5. 6. 7. 8. 9..,,,,,,,,, 1 14. 2190/1994 ( 28 ),,..,, 4.,,,,
APROKSIMACIJA FUNKCIJA
APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
POVRŠINA TANGENCIJALNO-TETIVNOG ČETVEROKUTA
POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE)
(Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
Ispitivanje toka i skiciranje grafika funkcija
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ĉetverokut - DOMAĆA ZADAĆA. Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke.
Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
EKSPONENCIJALNE i LOGARITAMSKE FUNKCIJE
**** MLADEN SRAGA **** 0. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE EKSPONENCIJALNE i LOGARITAMSKE FUNKCIJE α LOGARITMI Autor: MLADEN SRAGA Grafički urednik: Mladen Sraga
IZVODI ZADACI (I deo)
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
18. listopada listopada / 13
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
Strukture podataka i algoritmi 1. kolokvij 16. studenog Zadatak 1
Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
Dvanaesti praktikum iz Analize 1
Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Matematička analiza 1 dodatni zadaci
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
T E H N I Č K I N A L A Z I M I Š LJ E NJ E
Mr.sc. Krunoslav ORMUŽ, dipl. inž. str. Stalni sudski vještak za strojarstvo, promet i analizu cestovnih prometnih nezgoda Županijskog suda u Zagrebu Poljana Josipa Brunšmida 2, Zagreb AMITTO d.o.o. U
Zavrxni ispit iz Matematiqke analize 1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
LANCI & ELEMENTI ZA KAČENJE
LANCI & ELEMENTI ZA KAČENJE 0 4 0 1 Lanci za vešanje tereta prema standardu MSZ EN 818-2 Lanci su izuzetno pogodni za obavljanje zahtevnih operacija prenošenja tereta. Opseg radne temperature se kreće
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci iz trigonometrije za seminar
Zadaci iz trigonometrije za seminar FON: 1. Vrednost izraza sin 1 cos 6 jednaka je: ; B) 1 ; V) 1 1 + 1 ; G) ; D). 16. Broj rexea jednaqine sin x cos x + cos x = sin x + sin x na intervalu π ), π je: ;
KONVEKSNI SKUPOVI. Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5. Back FullScr
KONVEKSNI SKUPOVI Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5 KONVEKSNI SKUPOVI Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5 1. Neka su x, y R n,
Teorijske osnove informatike 1
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
TRIGONOMETRIJSKE FUNKCIJE I I.1.
TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
π π ELEKTROTEHNIČKI ODJEL i) f (x) = x 3 x 2 x + 1, a = 1, b = 1;
1. Provjerite da funkcija f definirana na segmentu [a, b] zadovoljava uvjete Rolleova poučka, pa odredite barem jedan c a, b takav da je f '(c) = 0 ako je: a) f () = 1, a = 1, b = 1; b) f () = 4, a =,
numeričkih deskriptivnih mera.
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
KVADRATNA FUNKCIJA. Kvadratna funkcija je oblika: Kriva u ravni koja predstavlja grafik funkcije y = ax + bx + c. je parabola.
KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
1.4 Tangenta i normala
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
Obrada signala
Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
MATEMATIKA 2. Grupa 1 Rexea zadataka. Prvi pismeni kolokvijum, Dragan ori
MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
4. Trigonometrija pravokutnog trokuta
4. Trigonometrij prvokutnog trokut po školskoj ziri od Dkić-Elezović 4. Trigonometrij prvokutnog trokut Formule koje koristimo u rješvnju zdtk: sin os tg tg ktet nsuprot kut hipotenuz ktet uz kut hipotenuz
1. zadatak , 3 Dakle, sva kompleksna re{ewa date jedna~ine su x 1 = x 2 = 1 (dvostruko re{ewe), x 3 = 1 + i
PRIPREMA ZA II PISMENI IZ ANALIZE SA ALGEBROM. zadatak Re{avawe algebarskih jedna~ina tre}eg i ~etvrtog stepena. U skupu kompleksnih brojeva re{iti jedna~inu: a x 6x + 9 = 0; b x + 9x 2 + 8x + 28 = 0;
zastori sunset curtain Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju.
zastori zastori sunset curtain Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju. (mm) (mm) za PROZOR im (mm) tv25 40360 360 400 330x330 tv25 50450 450 500 410x410
INTEGRALNI RAČUN. Teorije, metodike i povijest infinitezimalnih računa. Lucija Mijić 17. veljače 2011.
INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
DIMENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE
TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
Vrijedi relacija: Suma kvadrata cosinusa priklonih kutova sile prema koordinatnim osima jednaka je jedinici.
Za adani sustav prostornih sila i j k () oktant i j k () oktant koje djeluju na materijalnu toku odredite: a) reultantu silu? b) ravnotežnu silu? a) eultanta sila? i j k 8 Vektor reultante: () i 8 j k
ZASTORI SUNSET CURTAIN Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju.
ZSTORI ZSTORI SUNSET URTIN Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju. ŠIRIN (mm) VISIN (mm) Z PROZOR IM. (mm) TV25 40360 360 400 330x330 TV25 50450 450
Dijagrami: Greda i konzola. Prosta greda. II. Dijagrami unutarnjih sila. 2. Popre nih sila TZ 3. Momenata savijanja My. 1. Uzdužnih sila N. 11.
Dijagrami:. Udužnih sia N Greda i konoa. Popre nih sia TZ 3. Momenata savijanja My. dio Prosta greda. Optere ena koncentriranom siom F I. Reaktivne sie:. M A = 0 R B F a = 0. M B = 0 R A F b = 0 3. F =
Dimenzioniranje nosaa. 1. Uvjeti vrstoe
Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
PRILOG. Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C)
PRILOG Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C) Tab 3. Vrednosti sačinilaca α i β za tipične konstrukcije SN-sabirnica Tab 4. Minimalni
( , 2. kolokvij)
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
PRORAČUN GLAVNOG KROVNOG NOSAČA
PRORAČUN GLAVNOG KROVNOG NOSAČA STATIČKI SUSTAV, GEOMETRIJSKE KARAKTERISTIKE I MATERIJAL Statički sustav glavnog krovnog nosača je slobodno oslonjena greda raspona l11,0 m. 45 0 65 ZAŠTITNI SLOJ BETONA
Vesla, teleskopi, nosači za štapove za ribolov
76 Vesla, teleskopi, nosači za štapove za ribolov vesla pala piatta rvena vesla obojana prozirnom poliuretanskom bojom, vrlo čvrsta, sa ravnom lopaticom. Imaju plastično ležište za rašlje Φ43mm. tr13 38180
PROBNI OTISAK IZRADA TISK. FORME IZRADA FILMA MONTAÆA TISAK DIGITALNA GRAFI»KA PRIPREMA DIREKTNO S RA»UNALA NA TIS. FORMU PROBNI OTISAK
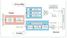IZRADA FILMA MONTAÆA IZRADA TISK. FORME PROBNI OTISAK TISAK A DIGITALNA GRAFI»KA PRIPREMA B computer to plate DIREKTNO S RA»UNALA NA TIS. FORMU PROBNI OTISAK TISAK C computer to print PROBNI OTISAK TISAK
Pismeni dio ispita iz Matematike Riješiti sistem jednačina i diskutovati rješenja u zavisnosti od parametra a:
Zenica, 70006 + y+ z+ 4= 0 y+ z : i ( q) : = = y + z 4 = 0 a) Napisati pavu p u kanonskom, a pavu q u paametaskom obliku b) Naći jednačinu avni koja polazi koz pavu p i okomita je na pavu q ate su pave
Matematika 1 - vježbe. 11. prosinca 2015.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
, Zagreb. Prvi kolokvij iz Analognih sklopova i Elektroničkih sklopova
Grupa A 29..206. agreb Prvi kolokvij Analognih sklopova i lektroničkih sklopova Kolokvij se vrednuje s ukupno 42 boda. rijednost pojedinog zadatka navedena je na kraju svakog zadatka.. a pojačalo na slici
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
STATIČKE KARAKTERISTIKE DIODA I TRANZISTORA
Katedra za elektroniku Elementi elektronike Laboratorijske vežbe Vežba br. 2 STATIČKE KARAKTERISTIKE DIODA I TRANZISTORA Datum: Vreme: Studenti: 1. grupa 2. grupa Dežurni: Ocena: Elementi elektronike -
Sistemi veštačke inteligencije primer 1
Sistemi veštačke inteligencije primer 1 1. Na jeziku predikatskog računa formalizovati rečenice: a) Miloš je slikar. b) Sava nije slikar. c) Svi slikari su umetnici. Uz pomoć metode rezolucije dokazati
41. Jednačine koje se svode na kvadratne
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
ΠΡΟΣΚΛΗΣΗ ΕΚΔΗΛΩΣΗΣ ΕΝΔΙΑΦΕΡΟΝΤΟΣ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΑΓΡΟΤΙΚΗΣ ΑΝΑΠΤΥΞΗΣ ΚΑΙ ΤΡΟΦΙΜΩΝ ΔΙΟΙΚΗΤΙΚΟΣ ΤΟΜΕΑΣ ΚΟΙΝΟΤΙΚΩΝ ΠΟΡΩΝ ΚΑΙ ΥΠΟΔΟΜΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΕΦΑΡΜΟΓΗΣ ΠΑΑ ΑΝΤΑΓΩΝΙΣΤΙΚΟΤΗΤΑ ΕΥΡΩΠΑΪΚΗ ΕΝΩΣΗ ΕΥΡΩΠΑΪΚΟ ΓΕΩΡΓΙΚΟ ΤΑΜΕΙΟ
Moguća i virtuelna pomjeranja
Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +