Σε γαλάζιο φόντο ΔΙΔΑΚΤΕΑ ΥΛΗ ( ) Σε μαύρο φόντο ΘΕΜΑΤΑ ΕΚΤΟΣ ΔΙΔΑΚΤΕΑΣ ΥΛΗΣ ( )

Transcript

1 > Φυσική Β Γυμνασίου >> Αρχική σελίδα ΕΝΕΡΓΕΙΙΑ ΕΕρρωττήήσσεει ιςς ΑΑσσκκήήσσεει ιςς μμ εε ααππααννττήή σσεει ιςς (σελ. 1 ΕΕρρωττήήσσεει ιςς ΑΑσσκκήήσσεει ιςς χχωρρί ίςς ααππααννττήήσσεει ιςς (σελ. 4 ΙΑΒΑΣΕ ΑΥΤΟ, ΠΡΙΝ ΞΕΚΙΝΗΣΕΙΣ ΤΗ ΜΕΛΕΤΗ Οι ερωτήσεις και οι ασκήσεις επανάληψης τής Φυσικής Β Γυμνασίου αποσκοπούν να βοηθήσουν το μαθητή να επαναλάβει τα σημαντικά στοιχεία τής διδακτ έας ύλης. Συμπεριλαμβάνουν μια αφαιρετική επιλογή ερωτήσεων και ασκήσεων τού σχολικού βιβλίου, συμπληρωμένων με επιπλέον ερωτήσεις και ασκήσεις. Η σειρά παρουσίασης τους δεν είναι τυχαία, αλλά προσεγμένη ώστε να αποκαλύπτει το βασικό σκελετό κάθε κεφαλαίου και να υποβοηθά στην κατανόηση τής ύλης. Σε γαλάζιο φόντο ΔΙΔΑΚΤΕΑ ΥΛΗ ( Σε μαύρο φόντο ΘΕΜΑΤΑ ΕΚΤΟΣ ΔΙΔΑΚΤΕΑΣ ΥΛΗΣ ( που μπορεί να συμπληρώσουν τη διδασκαλία ή τη μελέτη Όπου υπάρχει αυτό το εικονίδιο, κάνε κλικ για να δεις σχετική βιντεο-προσομοίωση ενός φαινομένου.

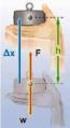
2 ΕΝΕΡΓΕΙΑ 5.1 [Συμπλήρωση λέξεων] Σώματα που μπορούν να αλλάζουν το περιβάλλον τους λέμε ότι κατέχουν ενέργεια και, όταν η δυνατότητά τους αυτή οφείλεται την κίνηση, η ενέργεια χαρακτηρίζεται κινητική. Ένα σώμα αποκτά ή χάνει κινητική ενέργεια, όταν πάνω του δράσει μια δύναμη, στην ίδια ή σε αντίθετη κατεύθυνση με μια μετατόπισή του. Μια τέτοια δύναμη λέμε ότι εκτελεί έργο στο σώμα. Ειδικότερα: Αν η δύναμη δρα προς την κατεύθυνση τής μετατόπισης, τότε το σώμα αυξάνει την κινητική του ενέργεια, γιατί αυξάνεται η ταχύτητά του. Μια τέτοια δύναμη λέμε ότι εκτελεί θετικό έργο στο σώμα. Αν η δύναμη δρα αντίθετα στην κατεύθυνση τής μετατόπισης, τότε το σώμα χάνει κινητική ενέργεια, γιατί μειώνεται η ταχύτητά του. Μια τέτοια δύναμη λέμε ότι εκτελεί αρνητικό έργο στο σώμα. Αν η δύναμη δρα κάθετα στην κατεύθυνση μιας μετατόπισης τού σώματος, δε συμβάλλει στην αλλαγή τής κινητικής του ενέργειας, διότι δεν προκαλεί αλλαγή στο μέτρο τής ταχύτητας. Μια τέτοια δύναμη λέμε ότι εκτελεί μηδενικό έργο στο σώμα. Αν η δύναμη δρα πλάγια στην κατεύθυνση μιας μετατόπισης τού σώματος, τότε αναλύουμε τη δύναμη σε δύο συνιστώσες, μια παράλληλη και μια κάθετη στη μετατόπιση. Έργο στο σώμα εκτελεί μόνο η συνιστώσα τής δύναμης που είναι παράλληλη στη μετατόπιση. Αν η δύναμη δρα σε ένα σώμα που δε μετατοπίζεται, επίσης δεν προκύπτει αλλαγή στην κινητική του ενέργεια. Μια τέτοια δύναμη λέμε ότι εκτελεί μηδενικό έργο στο σώμα. 5. [Συμπλήρωση λέξεων] Η εκτέλεση έργου από μια δύναμη είναι μια από τις διαδικασίες στη φύση, με τις οποίες μεταβιβάζεται ενέργεια. Όταν μια δύναμη είναι σταθερή, το έργο της (συμβολικά W είναι ανάλογο i με την τιμή F τής δύναμης και ii με την τιμή Δx τής μετατόπισης τού σώματος. Αν η δύναμη δρα στην κατεύθυνση τής μετατόπισης, το έργο της είναι W + F Δx Αν η δύναμη δρα αντίθετα στην κατεύθυνση τής μετατόπισης, το έργο της είναι W F Δx Με το φυσικό μέγεθος έργο δύναμης λογαριάζουμε την αυξομείωση τής κινητικής ενέργειας ενός σώματος, η οποία συμβαίνει όταν αλληλεπιδρά (με δυνάμεις με άλλα σώματα. Επειδή το έργο μιας δύναμης εκφράζει ενέργεια που μεταβιβάζεται, η μονάδα μέτρησης τού έργου και της ενέργειας είναι ίδια και, στο διεθνές σύστημα μονάδων (S.I., τη λέμε τζάουλ. 5.3 Το βάρος ενός σώματος έχει τιμή Β 50 N. Να υπολογίσετε το έργο τού βάρους, όταν το σώμα Α ανυψώνεται κατά Δx 10 Καθώς το σώμα ανυψώνεται, η μετατόπισή του είναι αντίθετη στο βάρος του, οπότε το έργο τού βάρους είναι: W Β Δx (50 N J Β κατεβαίνει κατακόρυφα κατά Δx 10 Καθώς το σώμα κατεβαίνει, η μετατόπισή του έχει την κατεύθυνση τού βάρος του, οπότε το έργο τού βάρους είναι: W + Β Δx + (50 N J Γ κινείται οριζόντια κατά Δx 10 Καθώς το σώμα κινείται οριζόντια, η μετατόπισή του είναι κάθετη στο βάρος του, οπότε το έργο τού βάρους είναι: W 0 J Δ δε μετατοπίζεται Αν η μετατόπιση τού σώματος είναι μηδενική, το έργο τού βάρους είναι: W 0 J Τα έργα που υπολογίσατε να εξηγήσετε τι σημαίνουν για την κινητική ενέργεια τού σώματος. Τα παραπάνω έργα σημαίνουν ότι η κινητική ενέργεια τού σώματος: Α μειώθηκε 500 J, Β αυξήθηκε 500 J, ενώ στις δύο τελευταίες περιπτώσεις Γ και Δ δεν άλλαξε. 5.4 Ένα βιβλίο είναι αρχικά ακίνητο πάνω σε οριζόντιο τραπέζι και το σπρώχνουμε με μια οριζόντια δύναμη, οπότε το βιβλίο αρχίζει να ολισθαίνει. Δίνονται τα μέτρα: της οριζόντιας δύναμης F 50 Ν, της τριβής Τ 30 N, του βάρους τού κιβωτίου Β 100 Ν και της δύναμης στήριξης Κ 100 Ν. Α Να σχεδιάσετε τις δυνάμεις που δέχεται το βιβλίο και να υπολογίσετε το έργο καθεμιάς, για μετατόπιση Δx 5. v Έργο οριζόντιας δύναμης (έχει την κατεύθυνση τής μετατόπισης: WF + F Δx + (50 Ν J Έργο τριβής (έχει κατεύθυνση αντίθετη στη μετατόπιση: WΤ Τ Δx (30 N J Έργο βάρους (έχει κατεύθυνση κάθετη στη μετατόπιση: WΒ 0 Κ F T Έργο δύναμης στήριξης (έχει κατεύθυνση κάθετη στη μετατόπιση: WΚ 0 Β Β Να υπολογίσετε το συνολικό τους έργο και να εξηγήσετε τι εκφράζει το έργο αυτό. Ολικό έργο Woλ WF + WΤ + WΒ + WΚ +50 J + ( 150 J + 0 J + 0 J +100 J To έργο αυτό εκφράζει τη συνολική αλλαγή στην κινητική ενέργεια τού βιβλίου, η οποία αυξήθηκε 100 J. 5.5 Να περιγράψετε ποια μορφή ενέργειας χαρακτηρίζουμε κινητική και να εξηγήσετε τον τρόπο υπολογισμού της. Τη μορφή τής ενέργειας ενός σώματος, που σχετίζεται με την κίνηση (τη μεταφορά του στο χώρο, τη λέμε κινητική. Αν ένα σώμα έχει ταχύτητα με μέτρο v, για να λογαριάσουμε την κινητική του ενέργεια: Μπορούμε να υπολογίσουμε τα έργα των δυνάμεων που έδρασαν στο σώμα, από μια στιγμή στο παρελθόν που ήταν ακίνητο μέχρι να αποκτήσει ταχύτητα v. Αν προσθέσουμε (με τα πρόσημά τους τα έργα αυτά, λογαριάζουμε την κινητική ενέργεια τού σώματος που αντιστοιχεί στην ταχύτητα v. Μπορούμε να υπολογίσουμε απευθείας την κινητική ενέργεια τού σώματος, που αντιστοιχεί στην ταχύτητα v, από την εξίσωση: Eκιν v (όπου είναι η μάζα τού σώματος Οι δύο τρόποι δίνουν ακριβώς το ίδιο αποτέλεσμα. 1

3 ΕΝΕΡΓΕΙΑ 5.6 [Άσκηση 5, σελ.11 σχολικού βιβλίου] Ένα αυτοκίνητο έχει μάζα kg. Να βρεθεί η κινητική του ενέργεια, όταν κινείται με ταχύτητα: α 7 k/ και β 144 k/ Γνωρίζοντας την ταχύτητα v και τη μάζα ενός σώματος, η κινητική του ενέργεια υπολογίζεται από την εξίσωση: Eκιν v Για να βρούμε την ενέργεια σε J (τζάουλ, πρέπει η μάζα να εκφράζεται σε kg και η ταχύτητα σε (δηλαδή, όλα τα μεγέθη τής εξίσωσης σε μονάδες τού S.I. k k Μετατροπή τής ταχύτητας σε : 7 7 0, οπότε Η κινητική ενέργεια στα 7 Η κινητική ενέργεια στα 144 (1.000 kg (0 k : Eκιν v (1.000 kg (40 k : Eκιν v J J J J (δηλαδή, στη διπλάσια ταχύτητα αντιστοιχεί τετραπλάσια κινητική ενέργεια 5.7 Εάν ένα σώμα έχει κινητική ενέργεια Εκιν 500 J και μάζα 10 kg, να υπολογίσετε την τιμή τής ταχύτητάς του. Η κινητική ενέργεια ενός σώματος σχετίζεται με τη μάζα και την ταχύτητά του με την εξίσωση: Eκιν v Γνωρίζοντας την κινητική ενέργεια και τη μάζα, μπορούμε να λύσουμε την παραπάνω εξίσωση ως προς την ταχύτητα και να την υπολογίσουμε : Εκιν v Η παραπάνω εξίσωση έχει λύσεις τις v± ή v Eκιν Eκιν, αλλά το μέτρο τής ταχύτητας που ψάχνουμε είναι θετικό, οπότε: v Eκιν 500 J 10 kg [Συμπλήρωση λέξεων] Όποτε ένα σώμα βρίσκεται σε μια ανυψωμένη θέση κοντά στη Γη, μπορούμε να πάρουμε ενέργεια κατά την πτώση του, από το έργο τού βάρους του. Γι αυτό, στην ανυψωμένη θέση του το σώμα κατέχει μια μορφή ενέργειας, που τη λέμε βαρυτική δυναμική. Αν το σώμα έχει βάρος Β και η κατακόρυφη απόσταση τής θέσης του από μια άλλη χαμηλότερη θέση είναι, η δυναμική ενέργεια που κατέχει εκεί είναι όσο και το έργο που εκτελεί το βάρος του κατά την πτώση του, δηλαδή Εδυν Β επί. Την ενέργεια αυτή μπορούμε να θεωρήσουμε ότι το σώμα την απέκτησε με το έργο μιας ανυψωτικής δύναμης, που το έφερε στην ανυψωμένη θέση. Πράγματι, το έργο μιας ανυψωτικής δύναμης F, με μέτρο όσο και το βάρος τού σώματος, η οποία θα ανύψωνε το σώμα, από τη χαμηλότερη θέση στη θέση όπου βρίσκεται δηλαδή σε κατακόρυφη απόσταση ψηλότερα είναι WF F Β, δηλαδή όση και η βαρυτική δυναμική ενέργεια τού σώματος. 5.9 [Παραλλαγή τής άσκησης 1, σελ.113 σχολικού βιβλίου] Ένα παιδί έχει ύψος 1,60 και ανυψώνει ένα βιβλίο, με βάρος 0 Ν, από το πάτωμα σε ένα ράφι, το οποίο βρίσκεται ψηλότερα από το πάτωμα. Να υπολογίσετε τη βαρυτική δυναμική ενέργεια τού βιβλίου Α σε σχέση με το πάτωμα Το ράφι, όπου ακουμπά το βιβλίο, βρίσκεται ψηλότερα από το πάτωμα. Άρα, η βαρυτική δυναμική ενέργεια τού βιβλίου σε σχέση με το πάτωμα είναι: Εδυν Β 0 N 40 J Β σε σχέση με το κεφάλι τού παιδιού Το ράφι βρίσκεται ( 1,6 0,4 ψηλότερα από το κεφάλι τού παιδιού. Άρα, η βαρυτική δυναμική ενέργεια τού βιβλίου σε σχέση με το κεφάλι είναι: Εδυν Β 0 N 0,4 8 J 5.10 [Συμπλήρωση κειμένου] Ένα σώμα κατέχει κινητική ενέργεια όταν κινείται, είτε αλληλεπιδρά βαρυτικά με τη Γη είτε όχι (δηλ. βρίσκεται πολύ μακριά της. Ένα σώμα κατέχει βαρυτική δυναμική ενέργεια, όταν βρίσκεται σε κάποια απόσταση από τη Γη, είτε κινείται είτε όχι. Ένα σώμα κατέχει και τις δύο μορφές ενέργειας, όταν κινείται σε κάποιο ύψος. Το άθροισμα τής κινητικής και της δυναμικής ενέργειας το λέμε μηχανική ενέργεια. Αν σε ένα σώμα εκτελεί έργο μόνο το βάρος του ή δεν εκτελεί έργο καμία δύναμη, τότε η μηχανική του ενέργεια διατηρείται σταθερή. Το παραπάνω συμπέρασμα για τη μηχανική ενέργεια είναι γνωστό ως αρχή διατήρησης τής μηχανικής ενέργειας. Η διατήρηση τής μηχανικής ενέργειας συμβαίνει διότι, με το έργο τού βάρους, η βαρυτική δυναμική ενέργεια μετατρέπεται σε κινητική ενέργεια κατά την πτώση των σωμάτων, ενώ η κινητική ενέργεια μετατρέπεται σε βαρυτική δυναμική ενέργεια κατά την ανύψωση των σωμάτων Μια πέτρα έχει μάζα 0,1 kg και, κοντά στη Γη, βάρος Β 1 N. Πετάμε ψηλά την πέτρα και, όταν βρίσκεται σε ύψος 3, έχει ταχύτητα v 10 /. Nα λογαριάσετε τη μηχανική ενέργεια τής πέτρας. Η μηχανική ενέργεια ενός σώματος είναι το άθροισμα τής κινητικής και της δυναμικής του ενέργειας. Γράφουμε: Εμηχ Εκιν + Εδυν Εκιν v 0,1 kg (10 0, J J 5J Εδυν Β 1 N 3 3 J Άρα, Εμηχ 5 J + 3 J 8 J

4 ΕΝΕΡΓΕΙΑ Μια πέτρα, με μάζα 1 kg έχει, κοντά στη Γη, βάρος 10 Ν. Αν η αντίσταση τού αέρα είναι ασήμαντη, να υπολογίσετε με τι ταχύτητα θα φθάσει στη Γη, αν την αφήσουμε να πέσει από ύψος 3,. Αν κρατάμε την πέτρα σε ύψος 3, πάνω από το έδαφος, στη θέση αυτή η πέτρα κατέχει βαρυτική δυναμική ενέργεια, που σε σχέση με το έδαφος είναι Ε δυν Β 10 N 3, 3 J Η πέτρα, πριν την αφήσουμε, είναι ακίνητη, άρα δεν έχει κινητική ενέργεια. Στην ανυψωμένη θέση της, λοιπόν, η πέτρα έχει μηχανική ενέργεια Ε μηχ Ε κιν + Ε δυν 0 J + 3 J 3 J Aν αφήσουμε την πέτρα να πέσει και θεωρήσουμε ότι η αντίσταση τού αέρα είναι ασήμαντη σε σχέση με το βάρος της, τότε σε όλη τη διαδρομή της μέχρι το έδαφος, η πέτρα δέχεται μόνο τη δύναμη τού βάρους της. Συνεπώς, για την πέτρα ισχύει η αρχή διατήρησης τής μηχανικής ενέργειας, που σημαίνει ότι διατηρεί σταθερή μηχανική ενέργεια σε όλη την πτώση της. Στην αρχική θέση τής διαδρομής η μηχανική ενέργεια είναι μόνο βαρυτική δυναμική ενέργεια, στις ενδιάμεσες θέσεις είναι και βαρυτική δυναμική και κινητική ενέργεια, ενώ στην κατώτερη θέση, η μηχανική ενέργεια έχει γίνει όλη κινητική ενέργεια. Επομένως, φθάνοντας στο έδαφος η πέτρα έχει την ίδια μηχανική ενέργεια με την οποία ξεκίνησε, δηλαδή 50 J, η οποία είναι όλη κινητική ενέργεια. Δηλαδή, στην κατώτερη θέση Ε μηχ Ε κιν 3 J. Μας ζητείται λοιπόν να υπολογίσουμε την ταχύτητα που αντιστοιχεί σ αυτήν την κινητική ενέργεια. Είναι E κιν v και αν λύσουμε ως προς την ταχύτητα: Ε κιν v ή v Eκιν και τελικά v E κιν 3 J 64 1 kg Να διατυπώσετε την αρχή διατήρησης τής ενέργειας και την αρχή διατήρησης τής μηχανικής ενέργειας. Η ενέργεια δε δημιουργείται από το μηδέν ούτε καταστρέφεται. Απλώς μεταφέρεται ή μετατρέπεται σε άλλες μορφές. Κάθε σώμα, λοιπόν, κατέχει διάφορες μορφές ενέργειας, αλλά η συνολική ενέργεια (κάθε μορφής που υπάρχει σε όλο το σύμπαν, διατηρείται σταθερή από τη δημιουργία του. Το συμπέρασμα αυτό είναι γνωστό ως αρχή διατήρησης τής ενέργειας. Το άθροισμα τής βαρυτικής δυναμικής και της κινητικής ενέργειας ενός σώματος το λέμε μηχανική ενέργεια και διατηρείται σταθερό, όταν στο σώμα εκτελεί έργο μόνο το βάρος του ή δεν εκτελεί έργο καμία δύναμη. Το συμπέρασμα αυτό είναι γνωστό ως αρχή διατήρησης τής μηχανικής ενέργειας [Άσκηση 1, σελ.113 σχολικού βιβλίου] Ένα αυτοκίνητο, μάζας 900 kg, κινείται με ταχύτητα 0 /. Ξαφνικά, ο οδηγός πατάει φρένο και το αυτοκίνητο ολισθαίνει. Μεταξύ των τροχών του και του οδοστρώματος αναπτύσσεται δύναμη τριβής, με μέτρο Ν. Α Να υπολογίσετε την κινητική ενέργεια τού αυτοκινήτου πριν το φρενάρισμα. Η κινητική ενέργεια τού αυτοκινήτου πριν το φρενάρισμα είναι: E κιν v (900 kg ( J J Β Να εξηγήσετε σε ποια μορφή ενέργειας μετατρέπεται τελικά η κινητική ενέργεια τού αυτοκινήτου και ποια είναι η δύναμη που, με το έργο της, προκαλεί αυτή την ενεργειακή μετατροπή. Η δύναμη τής τριβής εμποδίζει την ολίσθηση τού αυτοκινήτου και προκαλεί το φρενάρισμά του. Το έργο τής τριβής είναι αρνητικό, διότι δρα αντίθετα στη μετατόπιση και προκαλεί απώλεια στην κινητική ενέργεια τού αυτοκινήτου. Όταν το αυτοκίνητο ακινητοποιείται, η θερμοκρασία των ελαστικών, του οδοστρώματος, ακόμα και του αέρα, έχουν αυξηθεί. Άρα, η κινητική ενέργεια τού αυτοκινήτου, με το αρνητικό έργο τής τριβής, μετασχηματίζεται σε θερμική ενέργεια τού αυτοκινήτου και του περιβάλλοντος. Θερμική ενέργεια ενός σώματος λέμε τη συνολική κινητική ενέργεια που έχουν τα μικροσωματίδιά του (άτομα, μόρια κλπ, εξαιτίας των μικροκινήσεων που κάνουν στο εσωτερικό τού σώματος. Η ενέργεια αυτή σχετίζεται με τη θερμοκρασία κάθε σώματος. Έτσι, όταν η θερμοκρασία ενός σώματος αυξάνεται, σημαίνει ότι έχει αυξηθεί η θερμική του ενέργεια (όπως συμβαίνει κατά το φρενάρισμα. Γ Να υπολογίσετε πόσο θα ολισθήσει το αυτοκίνητο, μέχρι τελικά να σταματήσει. Πριν το φρενάρισμα το αυτοκίνητο έχει κινητική ενέργεια J και, όταν ακινητοποιείται, η ενέργεια αυτή μηδενίζεται (γίνεται θερμική ενέργεια, όπως είπαμε. Kατά το φρενάρισμα, λοιπόν, η μεταβολή τής κινητικής ενέργειας τού αυτοκινήτου είναι Ε κιν (τελική Ε κιν (αρχική 0 J J J (το πλην σημαίνει μείωση Η μεταβολή τής κινητικής ενέργειας οφείλεται στο έργο τής τριβής, δηλαδή W T J Η τριβή έδρασε σε όλο το μήκος Δx τού φρεναρίσματος, οπότε τo έργο της είναι και W T T Δx Επομένως, η μετατόπιση τού αυτοκινήτου, από την έναρξη τού φρεναρίσματος μέχρι την ακινητοποίησή του είναι: Δx WT T J N 0

5 ΕΝΕΡΓΕΙΑ [Συμπλήρωση λέξεων] Τα σώματα, όταν μπορούν να αλλάζουν το περιβάλλον τους, λέμε ότι κατέχουν και, αν η δυνατότητα αυτή οφείλεται στην κίνηση, η ενέργεια χαρακτηρίζεται. Ένα σώμα αποκτά ή χάνει κινητική ενέργεια, όταν πάνω του δράσει μια δύναμη, στην ίδια ή σε αντίθετη κατεύθυνση με τη του. Μια τέτοια δύναμη λέμε ότι στο σώμα. Ειδικότερα: Αν η δύναμη δρα προς την κατεύθυνση τής μετατόπισης, τότε το σώμα αυξάνει την κινητική του ενέργεια, γιατί η ταχύτητά του. Αν η δύναμη δρα αντίθετα στην κατεύθυνση τής μετατόπισης, τότε το σώμα χάνει κινητική ενέργεια, γιατί η ταχύτητά του. Αν η δύναμη δρα στην κατεύθυνση μιας μετατόπισης τού σώματος, δε συμβάλλει στην αλλαγή τής κινητικής του ενέργειας, διότι δεν προκαλεί αλλαγή στο μέτρο τής ταχύτητας. Αν η δύναμη δρα πλάγια στην κατεύθυνση μιας μετατόπισης τού σώματος, τότε αναλύουμε τη δύναμη σε δύο συνιστώσες, μια παράλληλη και μια κάθετη στη. Έργο στο σώμα εκτελεί μόνο η συνιστώσα τής δύναμης που είναι στη μετατόπιση. Αν η δύναμη δρα σε ένα σώμα που δε μετατοπίζεται, επίσης δεν προκύπτει αλλαγή στην κινητική του ενέργεια. 5. [Συμπλήρωση λέξεων] Η εκτέλεση έργου από μια δύναμη είναι μια από τις διαδικασίες στη φύση, με τις οποίες μεταβιβάζεται. Όταν μια δύναμη είναι, το έργο της (συμβολικά W είναι ανάλογο i με το μέτρο F της και ii με το μέτρο Δx της τού σώματος. Αν η δύναμη δρα στην κατεύθυνση τής μετατόπισης, το έργο της είναι W. Αν η δύναμη δρα αντίθετα στην κατεύθυνση τής μετατόπισης, το έργο της είναι W. Με το φυσικό μέγεθος έργο δύναμης λογαριάζουμε την αυξομείωση τής ενέργειας ενός σώματος, η οποία συμβαίνει όταν αλληλεπιδρά (με δυνάμεις με άλλα σώματα. Επειδή το έργο μιας δύναμης εκφράζει ενέργεια που μεταβιβάζεται, η μονάδα μέτρησης τού έργου και της ενέργειας είναι ίδια και, στο διεθνές σύστημα μονάδων (S.I., τη λέμε. 5.3 Το βάρος ενός σώματος έχει μέτρο Β 50 N. Να υπολογίσετε το έργο τού βάρους, όταν το σώμα Α ανυψώνεται κατά Δx 10 Β κατεβαίνει κατακόρυφα κατά Δx 10 Γ κινείται οριζόντια κατά Δx 10 Δ δε μετατοπίζεται Τα έργα που υπολογίσατε να εξηγήσετε τι σημαίνουν για την κινητική ενέργεια τού σώματος. 5.4 Ένα βιβλίο είναι αρχικά ακίνητο πάνω σε οριζόντιο τραπέζι και το σπρώχνουμε με μια οριζόντια δύναμη, οπότε το βιβλίο αρχίζει να ολισθαίνει. Δίνονται τα μέτρα: της οριζόντιας δύναμης F 50 Ν, της τριβής Τ 30 N, του βάρους τού κιβωτίου Β 100 Ν, της δύναμης στήριξης F σ 100 Ν. Α Να σχεδιάσετε τις δυνάμεις που δέχεται το βιβλίο και να υπολογίσετε το έργο καθεμιάς, για μετατόπιση Δx 5. Β Να υπολογίσετε το συνολικό τους έργο και να εξηγήσετε τι εκφράζει το έργο αυτό. 5.5 Να περιγράψετε ποια μορφή ενέργειας χαρακτηρίζεται κινητική και να εξηγήσετε τον τρόπο υπολογισμού της. 5.6 [Άσκηση 5, σελ.11 σχολικού βιβλίου] Ένα αυτοκίνητο έχει μάζα kg. Να βρεθεί η κινητική του ενέργεια, όταν κινείται με ταχύτητα: α 7 k/ και β 144 k/ 5.7 Εάν ένα σώμα έχει κινητική ενέργεια Ε κιν 500 J και μάζα 10 kg, να υπολογίσετε το μέτρο τής ταχύτητάς του. 5.8 [Συμπλήρωση λέξεων] Όποτε ένα σώμα βρίσκεται σε μια ανυψωμένη θέση κοντά στη Γη, μπορούμε να πάρουμε κατά την πτώση του, από το έργο τού του. Γι αυτό, στην ανυψωμένη θέση του το σώμα κατέχει μια μορφή ενέργειας, που τη λέμε. Αν το σώμα έχει βάρος Β και η κατακόρυφη απόσταση τής θέσης του από μια άλλη χαμηλότερη θέση είναι, η δυναμική ενέργεια που κατέχει σε σχέση με τη χαμηλότερη θέση είναι όσο και το έργο τού του κατά την πτώση του, δηλαδή Ε δυν επί. Την ενέργεια αυτή θεωρούμε ότι το σώμα την απέκτησε με το μιας ανυψωτικής δύναμης, που το έφερε στην ανυψωμένη θέση. Πράγματι, το έργο μιας ανυψωτικής δύναμης F με μέτρο όσο και το του σώματος, η οποία θα ανύψωνε το σώμα σε κατακόρυφη απόσταση, μέχρι την ανυψωμένη θέση που βρίσκεται, είναι W F F Β, δηλαδή είναι όση και η ενέργεια τού σώματος. 5.9 Ένα παιδί έχει ύψος 1,60 και ανυψώνει ένα βιβλίο, με βάρος 0 Ν, από το πάτωμα σε ένα ράφι, το οποίο βρίσκεται ψηλότερα από το πάτωμα. Να υπολογίσετε τη βαρυτική δυναμική ενέργεια τού βιβλίου Α σε σχέση με το πάτωμα και Β σε σχέση με το κεφάλι τού παιδιού [Συμπλήρωση κειμένου] Ένα σώμα κατέχει ενέργεια όταν κινείται, είτε αλληλεπιδρά βαρυτικά με τη Γη είτε όχι. Ένα σώμα κατέχει ενέργεια, όταν βρίσκεται σε κάποια απόσταση από τη Γη, είτε είτε όχι. Ένα σώμα κατέχει και τις δύο μορφές ενέργειας, όταν. Το άθροισμα τής κινητικής και της δυναμικής ενέργειας το λέμε. Αν σε ένα σώμα εκτελεί έργο μόνο το βάρος του ή δεν εκτελεί έργο καμία δύναμη, τότε η μηχανική του ενέργεια. Το παραπάνω συμπέρασμα για τη μηχανική ενέργεια είναι γνωστό ως. Η διατήρηση τής μηχανικής ενέργειας συμβαίνει διότι, με το έργο τού βάρους, η ενέργεια μετατρέπεται σε ενέργεια κατά την πτώση των σωμάτων, ενώ η μετατρέπεται σε ενέργεια κατά την ανύψωση των σωμάτων Μια πέτρα έχει μάζα 0,1 kg και, κοντά στη Γη, βάρος Β 1 N. Πετάμε προς τα πάνω την πέτρα και, όταν βρίσκεται σε ύψος 3, έχει ταχύτητα v 10 /. Nα λογαριάσετε τη μηχανική ενέργεια τής πέτρας. 5.1 Μια πέτρα, με μάζα 1 kg έχει, κοντά στη Γη, βάρος 10 Ν. Αν η αντίσταση τού αέρα είναι ασήμαντη, να υπολογίσετε με τι ταχύτητα θα φθάσει στη Γη, αν την αφήσουμε να πέσει από ύψος 3, Να διατυπώσετε την αρχή διατήρησης τής ενέργειας και την αρχή διατήρησης τής μηχανικής ενέργειας [Άσκηση 1, σελ.113 σχολικού βιβλίου] Ένα αυτοκίνητο, μάζας 900 kg, κινείται με ταχύτητα 0 /. Ξαφνικά, ο οδηγός πατάει φρένο και το αυτοκίνητο ολισθαίνει. Μεταξύ των τροχών του και του οδοστρώματος αναπτύσσεται δύναμη τριβής, με μέτρο Ν. Α Να υπολογίσετε την κινητική ενέργεια τού αυτοκινήτου πριν το φρενάρισμα. Β Να εξηγήσετε σε ποια μορφή ενέργειας μετατρέπεται τελικά η κινητική ενέργεια τού αυτοκινήτου και ποια είναι η δύναμη που, με το έργο της, προκαλεί αυτή την ενεργειακή μετατροπή. Γ Να υπολογίσετε πόσο θα ολισθήσει το αυτοκίνητο, μέχρι τελικά να σταματήσει.