ΠΕΡΙΕΧΟΜΕΝΑ ΕΞΙΣΩΣΕΙΣ MAXWELL ΚΥΜΑΤΟΔΗΓΟΣ ΠΑΡΑΛΛΗΛΩΝ ΠΛΑΚΩΝ ΚΥΛΙΝΔΡΙΚΟΣ ΚΥΜΑΤΟΔΗΓΟΣ ΟΜΟΑΞΟΝΙΚΗ ΓΡΑΜΜΗ ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ

Transcript

1 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΔΙΑΤΜΗΜΑΤΙΚΟ ΜΕΤΑΠΤΥΧΙΑΚΟ ΔΙΠΛΩΜΑ ΕΙΔΙΚΕΥΣΗΣ ΡΑΔΙΟΗΛΕΚΤΡΟΛΟΓΙΑΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΗΣ (Ρ/Η) ΘΕΩΡΙΑ ΚΑΙ ΕΦΑΡΜΟΓΕΣ ΜΙΚΡΟΚΥΜΑΤΩΝ ο ΕΞΑΜΗΝΟ Ρ/Η Ιωάννης Γ. Τίγκελης, Αν. Καθηγητής, Τμήμα Φυσικής

2 ΠΕΡΙΕΧΟΜΕΝΑ ΕΞΙΣΩΣΕΙΣ MAXWELL ΚΥΜΑΤΟΔΗΓΟΣ ΠΑΡΑΛΛΗΛΩΝ ΠΛΑΚΩΝ ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ ΚΥΛΙΝΔΡΙΚΟΣ ΚΥΜΑΤΟΔΗΓΟΣ ΟΜΟΑΞΟΝΙΚΗ ΓΡΑΜΜΗ ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ ΠΑΡΑΜΕΤΡΟΙ ΣΚΕΔΑΣΗΣ

3 ΕΞΙΣΩΣΕΙΣ MAXWELL () Εξισώσεις B D E, H J, B, D ρ Maxwell t t Απουσία εξωτερικών πηγών: J, ρ Οριακές Συνθήκες nˆ E ˆ E, nh H Ks nˆ D D σ, nˆ B B K s επιφανειακή πυκνότητα ρεύματος, σ επιφανειακή πυκνότητα φορτίου Η πυκνότητα ισχύος δίνεται από το διάνυσμα Poynting: Sav E H (στο πεδίο του χρόνου) P av Re EH (στο πεδίο της συχνότητας) 3

4 ΕΞΙΣΩΣΕΙΣ MAXWELL () Στην περίπτωση που έχουμε μέσο με πεπερασμένη αγωγιμότητα σ, τότε οι εξισώσεις Maxwell γίνονται: E iωμh E iωμ H H J iωε E H σ iωε E E iωμ σ iωε E Όμως E E E και E Eiωμ σ iωε E Eγ E γ iωμ σ iωε iωμσ ω με ω με i ωε σ 4

5 ΕΞΙΣΩΣΕΙΣ MAXWELL (3) σ γω με i α iβ, ωε όπου β α είναι ο συντελεστής απωλειών σε Neper/m και η σταθερά διάδοσης σε rad/m σ i Οταν σ/( ωε ), τότε γ ω μ ε i i ωμσ α, δ ωε s όπου δs είναι το βάθος διείσδυσης, δηλαδή το μήκος μέσα στον αγωγό, γ, στο οποίο το πλάτος του πεδίου έχει μειωθεί στο /e της τιμής που είχε πάνω στην επιφάνεια του αγωγού. 5

6 ΚΥΜΑΤΟΔΗΓΟΣ ΠΑΡΑΛΛΗΛΩΝ ΠΛΑΚΩΝ () Τέλεια αγώγιμα τοιχώματα Διάδοση στον άξονα z Ανεξαρτησία από τη συντεταγμένη y Ανάλυση στο πεδίο συχνοτήτων για αρμονικά μεταβαλλόμενα πεδία (,, ) Re ( )exp( ) Ε xzt Ex,z iωt, E( x,z) e( x)exp( γz) Η ( xzt,, ) Re H ( x,z)exp( iωt ), H ( x,z ) h ( x )exp( γz ) 6

7 ΚΥΜΑΤΟΔΗΓΟΣ ΠΑΡΑΛΛΗΛΩΝ ΠΛΑΚΩΝ () xˆ yˆ zˆ E iωμh iωμh x e x z γz γz γz e x e e x e e x e x y z Λαμβάνοντας υπόψη ότι προκύπτει: z xˆ yˆ zˆ d e( x) γ iωμh x dx e x e x e x x y z γz 7

8 ΚΥΜΑΤΟΔΗΓΟΣ ΠΑΡΑΛΛΗΛΩΝ ΠΛΑΚΩΝ (3) iωμhxxγeyx.a dez x iωμhy x γex x.b dx dey x iωμhz x.c dx Αντίστοιχα από την εξίσωση H iωε E προκύπτουν: iωε ex x γh x iωε e y x γh x x.b dx dhy x iωε ez x c.c dx y a.a dhz x γ.b 8

9 ΚΥΜΑΤΟΔΗΓΟΣ ΠΑΡΑΛΛΗΛΩΝ ΠΛΑΚΩΝ (4) Οι εξισώσεις (.a), (.c) και (.b) έχουν e z =, μη μηδενικές συνιστώσες τις e y, h x, h z και αντιστοιχούν σε Εγκάρσια Ηλεκτρικά Κύματα (Transverse Electric, TE) Οι εξισώσεις (.b), (.a) και (.c) έχουν h z =, μη μηδενικές συνιστώσες τις h y, e x, e z και αντιστοιχούν σε Εγκάρσια Μαγνητικά Κύματα (Transverse Magnetic,TM) 9

10 ΚΥΜΑΤΟΔΗΓΟΣ ΠΑΡΑΛΛΗΛΩΝ ΠΛΑΚΩΝ (5) Κύματα ΤΕ de iω y γe d y (.a), (.c) και (. b) iωεey γ dx iωμ dx iωμ dey ω ε e γ e e x γ ω μ ε y e x y y y dx e x k e x (.3) y y k γ ω με γ ( ω / c) (.4) Λύση της κυματικής εξίσωσης (.3) isx isx qx qx k s ey x Ae Be Acos sx Bsin sx k q ey x Ae Be ( )

11 ΚΥΜΑΤΟΔΗΓΟΣ ΠΑΡΑΛΛΗΛΩΝ ΠΛΑΚΩΝ (6) Προφανώς στο συγκεκριμένο πρόβλημα θέλουμε περιοδικές λύσεις: y cos sin, ( / ) e x A k x B k x k c y Οριακές Συνθήκες ey x και ey x D ey x A 3, e x D k D mπ, m,,... Η λύση m = απορρίπτεται, γιατί διαφορετικά e y = και h x =. mπ m, δηλαδή ( / ) m k, ω c D D c

12 ΚΥΜΑΤΟΔΗΓΟΣ ΠΑΡΑΛΛΗΛΩΝ ΠΛΑΚΩΝ (7) mπc Ι) γm αποκοπή ωm συχνότητα αποκοπής D ΙΙ) ) γ απόσβεση ωω γ a R m m m m ω ωm ΙΙΙ) γm διάδοση ωωm γm iβmι βm c ω ωm π πf πfm βm c c λ c c λ λ λ π όπου λgm μήκος κύματος μέσα στον κυματοδηγό, β m gm gm m μήκος κύματος ελευθέρου χώρου και μήκος κύματος αποκοπής u φm ω c βm ω / ω c φασι m m κή ταχύτητα ω u / gm c ωm ω c ταχύτητα ομάδας β m

13 ΚΥΜΑΤΟΔΗΓΟΣ ΠΑΡΑΛΛΗΛΩΝ ΠΛΑΚΩΝ (8) mπx β, sin iβ m z m Ey x z A e, Hx x, z Ey x, z D ωμ Ey mπ mπx iβmz Hz x, z A cos e iωμ x iωμ D D Η ισχύς που μεταφέρεται από το ρυθμό είναι: xˆ yˆ zˆ P Re EH Re E Re xe ˆ H ze ˆ H H H av y y z y x x β ˆRe m β ˆ m sin mπ x W z EyEyz A ωμ ωμ D m D βm mπ x βmd W Pολ Pav ds dx A sin A ωμ D 4ωμ m z 3

14 ΚΥΜΑΤΟΔΗΓΟΣ ΠΑΡΑΛΛΗΛΩΝ ΠΛΑΚΩΝ (9) Για τον πρώτο ρυθμό ότε πx iβz E y ( x,z) Asin e D β πx iβz H x ( x,z) Asin e ωμ D π πx H z ( x,z ) A cos e iωμ D D iβ z πx E y ( x,z,t,, ) Asin cos( ωt β z) D β πx H x x,z,t,, Asin cos ωt β z ωμ D π πx π H x,z,t A cos cos ωt z z,, β ωμ D D 4

15 ΚΥΜΑΤΟΔΗΓΟΣ ΠΑΡΑΛΛΗΛΩΝ ΠΛΑΚΩΝ () m m m m c c Οι δύο λύσεις που προκύπτουν για κάθε ω αντιστοιχούν σε διάδοση χ η κατά +z και z, αντίστοιχα y E ωμ Z Κυματική ή χαρακτηριστική αντίσταση του ρυθμού ΤΕ m m y x m Z H β 5

16 ΚΥΜΑΤΟΔΗΓΟΣ ΠΑΡΑΛΛΗΛΩΝ ΠΛΑΚΩΝ () Όταν ο κυματοδηγός έχει τοιχώματα με πεπερασμένη αγωγιμότητα, τότε αυτά εμφανίζουν επιφανειακή αντίσταση, το εφαπτομενικό ηλεκτρικό πεδίο σε αυτά είναι μη μηδενικό και είναι ίσο με Z G Κ s, οπότε έχουμε ωμικές απώλειες στα τοιχώματα: p Re ˆ Re ˆ E H n H n E Re nˆh E Re E nˆh ReZ * GKS KS R G p K S S R G P K dl S S C όπου P ωμ είναι οι ωμικές απώλειες στα τοιχώματα, R G το πραγματικό μέρος της επιφανειακής αντίστασης των τοιχωμάτων και C η επιφάνεια των τοιχωμάτων που έχουν απώλειες. 6

17 ΚΥΜΑΤΟΔΗΓΟΣ ΠΑΡΑΛΛΗΛΩΝ ΠΛΑΚΩΝ () Τότε τα τοιχώματα έχουν αντίσταση: i i i i i Z, E Z K G t G S i σδs π iβz K ) ˆ (, ˆ ˆ (, ˆ S( x xh z) xzh z z) y Α e iω D π iβz ˆ K S ( x ) y Α e iω D π ˆ ˆ ˆ ˆ K S ( x D) x H( D, z) x zhz( D, z) y A cos( ) e iωμ D π iβz ˆ K S x D y Α e iω D Aπ KS x K S x D ωμd iβ z 7

18 ΚΥΜΑΤΟΔΗΓΟΣ ΠΑΡΑΛΛΗΛΩΝ ΠΛΑΚΩΝ (3) i * Ht P Re KS KS KS S S σ S π A π P A S ωμ D S ωμ D Λαμβάνοντας υπόψη και τις απώλειες το ηλεκτρικό πεδίο γίνεται:, e x z e x e e y az m, y iβ z όπου a είναι ο συντελεστής εξασθένισης πεδίου λόγω ωμικών απωλειών. Επομένως η μείωση ισχύος κατά μήκος του κυματοδηγού είναι: ωμ az ΔP P( z ) P z Δz P Δz, Όμως P z e P z αp z P z Δz P z P ωμ P z a Δz P ωμ P z 8

19 ΚΥΜΑΤΟΔΗΓΟΣ ΠΑΡΑΛΛΗΛΩΝ ΠΛΑΚΩΝ (4) Κύματα ΤΜ h x k h x h x Asin k x Bcos k x y y y dhy h iωεe iωεe, h iωεe dx z y x Το εφαπτομενικό ηλεκτρικό πεδίο πρέπει να μηδενίζεται στα τοιχώματα, δηλαδή h x Ak cos k x Bk sin k x = για x και x D y A και k Dmπ,m,,,... iβz H x, z H cos k x e, y Ez xz, Hk sinkxe iωε β Ex x, z H coskxe ωε iβz iβz 9

20 ΚΥΜΑΤΟΔΗΓΟΣ ΠΑΡΑΛΛΗΛΩΝ ΠΛΑΚΩΝ (5) iβz β Για m Hy x, z He και Ex x, z He ωε έχουμε επίπεδο κύμα H,E σε αντίθεσημε ταte. y x iβz

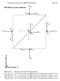
21 ΚΥΜΑΤΟΔΗΓΟΣ ΠΑΡΑΛΛΗΛΩΝ ΠΛΑΚΩΝ (6) Άσκηση. Έστω ότι σε κυματοδηγό παράλληλων πλακών στο επίπεδο z= υπάρχει κατανομή ρεύματος στην κατεύθυνση του θετικού άξονα των y και με συνάρτηση J (x). Να βρείτε το είδος κυμάτων που μπορούν να διαδοθούν στις περιοχές z <και z >. Λύση I nπx Ey( x,z) Ansin exp( γnz), z n D () II nπx Ey ( x,z) Bnsin e( γnz), z n D () xˆ yˆ zˆ E y E iωμ H iωμ H iωμ H x x z z 3 E y

22 ΚΥΜΑΤΟΔΗΓΟΣ ΠΑΡΑΛΛΗΛΩΝ ΠΛΑΚΩΝ (6) I γ n nπx x n n iωμ D n H ( x, z) A sin e γ z, z (4) () (3) () II γ n nπx n H ( ) sin γ z x x,z An e, z (5) n iωμ D II I II I z zˆ Ey Ey Ey x, Ey x, 6 II I II I zˆ H H J H H J x 7 x x () nπx nπx 6 A sin B sin A B () n D n D n n n n (4) n x 7 J x A n nsin D (5) i n D i n x A n J ( x )sin dx nd D

23 exp( ) exp( ) E x y z e x y γz H xyz h xy γz ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ (),,, exp( ),,, exp( ) E x y z e x y γz H xyz h xy γz.4a z x y e iωμ h γe.4b x y z y x y e E iωμ H iωμ h γe.4c y x y x z x e e iωμ h.4d z x y h iωε e γh μ z x y.4e x y z y x γ y h H iωε E iωε e γh.4f y x y x z γ x h h iωε e 3 z x y

24 ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ ().4a 4a hz γ ez.4e iωεe y γey x iωμ y ω ez hz ω γ ey γ iωμ, γ k c y x c e ey x,y γ iωμ h z z.5 k y x ez hz ex x,y γ iωμ.6 k x y Υπέρθεση ΤΕ και ΤΜ κυμάτων ez hz hx x,y iωε γ.7 k y x e h hy x,y iωε γ z z.8 k x y 4

25 ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ (3) (.5),(.6) ) e z k (.7),(.8) x y hz.4c,.4f Μέθοδος χωριζομένων μεταβλητών: Φ xy, X x Y y k Φ x,y x, y S x y Y y X x Y y X x k X x Y y k x, ys x kx X x AxcoskxxBxsin kxx y k cos sin y Y y Ay kyy By kyy y X x Y y X x Y y X X x Y Y x y x y k, k : σταθερές, k k k γ ω/ c 5

26 ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ (4) Κύματα ΤΕ hz h e, h e X z z y x Y y και e x X x Y y x y Οριακές Συνθήκες: z e x x, e y,y και ex x,b ey a,y e x, X( x) Y () xy() B x e x,b Y ( b ) k B sin k b k b nπ, n,,,... x y y y y y e,y X Y y y X B x e a,y X a sin ka kamπ, m,,,... y x x m + n y 6

27 ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ (5) mπ nπ c m n Ι) γmn ωmn c ή f mn α b a b amnz mn mn mn mn ΙΙ) γ ω ω απόσβεση ( e ), a ω ω c ω ω mn ΙΙΙ) γ διάδοση ( iβ z ), mn mn ωωmn e mn, c ω ω c β mn mn c c c Για b a : b f,, a f b f f f f, a δηλ. πρώτος ρυθμός ο TE Αν f f, το κύμα σβήνει εκθετικά κατά μήκος του άξονα διάδοσης και μετά από μερικά cm δεν υπάρχει. 7

28 ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ (6) Κύματα ΤM h, e ( x, y) X( x) Y( y) z z Οριακές συνθήκες: e x, A z e,y A z y x e x,b k b nπ, n,,... z y e a,y k a mπ, m,,... z x m n 8

29 ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ (7) πx iβz H x z H cos e z(, ) a iωμ πx E y ( xz, ) H sin e π a iβa πx H x, z H sin e x( ) π a E E H k β x x z y π, ky a Ρυθμός ΤΕ iβ z iβ z ω π E y ωμ, ZTE c a H β x 9

30 ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ (8) Ισχύς που μεταφέρεται από τον κυματοδηγό: P Re ye ˆ xh ˆ zh ˆ Re ze ˆ H xe ˆ H av y x z y x y z E E y y W ze ˆ y zˆ ZTE ZTE m Re a b 3 sin y TE TE ωμa πx ωμab P ολ H dx dy H π Z a 4πZ Εξασθένιση από την πεπερασμένη αγωγιμότητα των τοιχωμάτων: P S K σ σδ dl s ˆ ˆ π iβ z K ˆ ˆ S x xh x,y,z xzhcos e yhe a iβ z K x a x ˆH x,y,z x ˆzH ˆ cos π e yh ˆ e S iβ z iβ z 3

31 ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ (9) K y y H x, y zh x, xh x, ˆ ˆ ˆ S x z iβ a πx πx K S y z H e xh e π a a K y b yˆh x,b zh ˆ x,b xh ˆ x,b P σ a iβz y ˆ sin ˆ cos S x z iβ a πx πx KS y b z H e xh e π a a α b K S σδ dl dx KS y dy KS x s σδ s iβz ˆ sin ˆ cos 3 a β a W P H b σ σδ s π m β a πzte b a π 3 ωμabσδ s 3 iβ z iβ z 3

32 ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ () Σε κοιλότητα ορθογωνικής διατομής με εγκάρσιες διαστάσεις α και b και διαμήκη L διαδίδεται ο ρυθμός ΤΕ. Να βρείτε τις συχνότητες που μπορούν ναυπάρξουν στην κοιλότητα. πx Ey ( x, z) sin Ae Be a E ( x, z ) AB y iβz iβ z E x z L Ae Be y iββ L iββ L (, ) sin β L β L π,,,..., β ω π ω π π c a c a L ωmn Για τον ΤΕ mn c mπ nπ π a b L 3

33 ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ () Μέτρηση συχνότητας Μεταβάλλοντας το μήκος L της κοιλότητας, παρατηρούμε ότι ηισχύς εξόδου για κάποια τιμή του L μειώνεται. Αυτό σημαίνει ότι έχουμε κατανάλωση ισχύος στην κοιλότητα (δηλ. συντονισμό) και επομένως η συχνότητα λειτουργίας ισούται με τη συχνότητα συντονισμού αυτής: c a L 33

34 ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ () Μέτρηση μήκους κύματος Σε κυματοδηγό τοποθετούμε μια κεραία έτσι ώστε να διαδίδεται μόνο ο ρυθμός ΤΕ και δημιουργούμε ανακλάσεις μέσα στον κυματοδηγό (στάσιμα κύματα). Αν η απόσταση δύο διαδοχικών ελαχίστων είναι Δz, τότε ισχύει: sin βδz βδz π Δz π β λ g π π π λg λ α 34

35 ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ (3) Κατευθυντικός συζεύκτης Για να αλληλοαναιρούνται τα κύματα που φτάνουν στο Σ πρέπει: λ g π βl π L β 4 Προσαρμογή # 4( P ) Q 4 3 Προσαρμογή # 3( P ) Q P P Q P P Q προσπίπτουσα, 3 ανακλώμενη, 4 ρ P Q Q αν, 4 P πρ, P P 35

36 ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ (4) Μαγικό Τ Εισάγοντας δύο κύματα α και α στις θύρες # και #, αντίστοιχα, τότε στην μία έξοδο παίρνουμε το άθροισμα αυτών και στην άλλη τη διαφορά τους. 36

37 ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ (5) Άσκηση η. Σε κυματοδηγό ορθογωνικής διατομής με διαστάσεις α και b, οι περιοχές <x < t και t < x < a περιέχουν υλικά σχετικής διηλεκτρικής σταθερά ε και ε, αντίστοιχα. Να βρεθούν κύματα ΤΕ με ανεξαρτησία από το y, που μπορούν να διαδοθούν στον κυματοδηγό καθώς και ησυχνότητα αποκοπής του ρυθμού ΤΕ. Λύση Oι διαμήκεις κυματαριθμοί των περιοχών Ι και ΙΙ πρέπει να είναι ίδιοι, δηλ. γ γ γ. Για κύματα ΤΕ ισχύει: H x,z f( x)exp( γz), οπότε η κυματική εξίσωση στη γενική μορφή γράφεται: ω μ εε H x,z x z z d ω γ ε i fi x, i, dx c z 37

38 ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ (6) d ω hi fi x, hi γ ει dx c f x A sin hx B cos hx, i, I z i i i i i H x,z A sin hx B cos hx exp( γz) II Hz x,z Asin hx Bcos hx exp( γz) Ez Hz Ez Hz E x,, E y, x y y x I iωμ Ey x,z Acoshx Bsin hx exp( γz) h II iωμ Ey x,z Acoshx Bsin hx exp( γz) h H, H x y 38

39 ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ (7) I Οριακές συνθήκες: Ey ( x ) II Ey ( x a) I II Ey( x t) Ey ( x t) 3 I II Hz ( x t ) Hz ( x t ) 4 A A cos h a B sin h a 4 B cosht A sin h tb cosh t 5 iωμ h iωμ 3 B sin ht A cosh tb sin h t 6 5 h 6 A cos ht Bsin ht tan ht h A sin h t B cos h t h 39

40 ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ (8) tan ht h h B cosha B cos ha ha ht B ht sin cos sin ha ht B ht sin sin cos sin h a t tan ht tan h at h cos h a t h h Για t tan h a sin h a h a mπ Για t α tan ha hamπ Για τη συχνότητα αποκοπής ισχύει: h / c, h / c a a tan tan ( c c / c) ( / c) 4

41 ΚΥΜΑΤΟΔΗΓΟΣ ΟΡΘΟΓΩΝΙΚΗΣ ΔΙΑΤΟΜΗΣ (9) a a Για ε, ε 4, t ( a/) tan tan c c a tan x tan x x c 4 4

42 ΚΥΛΙΝΔΡΙΚΟΣ ΚΥΜΑΤΟΔΗΓΟΣ () E,, z e, e H,, z h, e E ih H i E z z e z e ih.9a h z h i e.9b e e z i h.9c h z h i e.9d e e ihz.9e h h i e.9f z 4

43 ΚΥΛΙΝΔΡΙΚΟΣ ΚΥΜΑΤΟΔΗΓΟΣ ().9b hz ez.9c γ γeρ iωεeρ ρ iωμ ρ iωμ hz ez ez iωμ hz γ eρ γ ω εμeρ keρ γ ρ ρ ρ ρ ez iωμ hz γ ez hz eρ γ, e iωμ k ρ ρ k ρ ρ iω ez hz ez γ hz hρ γ, h k ρ iω k ρ k γ ω c e z ρ, ρ, k h z ρ, 43

44 ΚΥΛΙΝΔΡΙΚΟΣ ΚΥΜΑΤΟΔΗΓΟΣ (3) im k F ρ F ρ R ρ e ρ, k F ρ, F ρ, R ρ e R ρ im R k R ρ ρ ρ ρ R m ρ k R, ρ ρ ρ ρ ρ I) k : R ρ AJ m kρ BY m kρ, λύσεις Bessel και Neumann πρώτου και δευτέρου είδους. AI ξρ BK m mξρ, II) k ξ : R ρ τροποποιημένες Bessel πρώτου και δευτέρου είδους. 44

45 ΚΥΛΙΝΔΡΙΚΟΣ ΚΥΜΑΤΟΔΗΓΟΣ (4) I) ια Y, και για να μην απειρίζεται το πεδίο πρέπει B. m II) ια K, και για να μην απειρίζεται το πεδίο πρέπει B. m III) ια I, και για να μην απειρίζεται το πεδίο πρέπει A. m 45

46 ΚΥΛΙΝΔΡΙΚΟΣ ΚΥΜΑΤΟΔΗΓΟΣ (5) Κύματα ΤΜ cos sin e a, J k a ez ρ, Jm k ρ am m bm m Οριακή συνθήκη: z Πίνακας.: Ρίζες της εξίσωσης J k a m/n m m 46

47 ΚΥΛΙΝΔΡΙΚΟΣ ΚΥΜΑΤΟΔΗΓΟΣ (6) Κύματα ΤΕ cos sin hz ρ, Jm k ρ am m bm m hz Οριακή συνθήκη: ea, e J m k ρ Πίνακας.: Ρίζες της εξίσωσης J k m/n m 47

48 ΚΥΛΙΝΔΡΙΚΟΣ ΚΥΜΑΤΟΔΗΓΟΣ (7) ρ h z J k ρ acos bsin iωμ Ρυθμός ΤΕ sin cos eρ J k ρ a b k ρ e iωμ J k ρ a b cos sin k k a.84 Εκφυλισμός πρώτης τάξης, δηλ. δύο ρυθμοί με κάθετες μεταξύ τους πολώσεις 48

49 ΚΥΛΙΝΔΡΙΚΟΣ ΚΥΜΑΤΟΔΗΓΟΣ (8) Κύματα ΤΕ σε κυματοδηγό κυκλικού τομέα 9 ο cos sin H z ρ,,z AJm k ρ am m bm m e iβz Οριακές Συνθήκες Επιφάνεια ( a): E J k a H z Επιφάνεια ( ) : E E bm H Επιφάνεια 3 ( / ) : E E z m m amsin m bmcosm sin m,,,,... και m,, 4,... m 49

50 ΚΥΛΙΝΔΡΙΚΟΣ ΚΥΜΑΤΟΔΗΓΟΣ (9) Άσκηση 3. Έστω κυλινδρικός κυματοδηγός ακτίνας α στα τοιχώματα του οποίου ικανοποιείται η σχέση E z /H = ζ (σε Ω). Να βρεθεί η συνθήκη για τη διάδοση κυμάτων ΤΜ με ανεξαρτησία από το καθώς και η έκφραση του διανύσματος Poynting. Λύση z, E z AJ k e i z i Ez i H AJ k e k k i z E AJ ka kj ka z I H ( ) i J k a i AJ k a k ˆ ˆ zˆ Re Re P ˆ E E E H ze ˆ H av z z H 5

51 ΚΥΜΑΤΑ ΤΕΜ (E z =, H z = ) xˆ y ˆ zˆ E y Ex E γ iωμ H x y x y E x E E E E E x y E x y y γz, E xyz x, y,z e x, xy e E x, xyz y,z e x, xy e e x x y y Φ Ex Φ e x x y y x ex Φx, y Φ E y Φ y e y y x xy Φ x, y γ z e y x Για να υπάρξει ρυθμός ΤΕΜ πρέπει να υπάρχει εσωτερικός αγωγός 5

52 ΟΜΟΑΞΟΝΙΚΗ ΓΡΑΜΜΗ () Κύματα ΤΕΜ Φ Φ ρ, ρ ρ ρ ρ Φ ρ Aln ρ B A Φ a b a b Φ a Φ Φ Φ Φ Φ Φ b ln ln ln / Φ Φ ln ln ln Φ a B Φ a Φ b ln a/ b ln a/ b V ln ln a/ b Φ ρ ρ B, V Φ Φ V V ˆ ˆ ρ ln a/ b ρ ln a/ b H ρ,,zh ρ, e γ z, h ρ, h ρ ˆ h ρ, γeρ iωμh γ z e ρ, ρ E ρ,,z ρ e 5

53 ˆ ΟΜΟΑΞΟΝΙΚΗ ΓΡΑΜΜΗ () V e ωμ μ γ z ρ H ρ,,z e Z π εμ ρ ln a/ b h β ε Η διαφορά δυναμικού μεταξύ των δύο αγωγών: b V γ z b V z E dρ e ln V e ρ ln a / b a Το φορτίο ανά μονάδα μήκους στον εξωτερικό αγωγό:, Q z πρε E b z ρ Η χωρητικότητα ανά μονάδα μήκους: Q πε C V ln a / b π ε ln a/ b Ve Η ένταση του ρεύματος στον εξωτερικό αγωγό: π Iz Hdl H πb Ve μ ε ln a/ b a γ z γ z γ z 53

54 LC ΟΜΟΑΞΟΝΙΚΗ ΓΡΑΜΜΗ (3) a L ln b i t v z, t Re V z e V cos t z i z t V t z /, cos v Vsin t z V t z z i V sin t z t / ln a/ b sin v / ln a/ b i z v i z t t ω αφού β ω ε μ c L 54

55 ΟΜΟΑΞΟΝΙΚΗ ΓΡΑΜΜΗ (4) v i v z z v z i L L z t z t i vz vzz Lz t i v v Αναλογα: α: c i z i z z C z z t t 55

56 ΟΜΟΑΞΟΝΙΚΗ ΓΡΑΜΜΗ (5) im Κύματα TE : ez, hz ρ, e AJ m kρ BY m k ρ hz Οριακές συνθήκες: e ρ ρa, b AJ ka BY ka και AJ kbby kb m m m m J k a Y k b J k b Y k a m m m m im Κύματα TM: hz, ez ρ, e AJm kρ BYm kρ Οριακές συνθήκες: e z z και e e ρa, b ρa, b AJ k a BY k a και AJ k b BY k b m m m m J k a Y k b J k b Y k a m m m m 56

57 ΟΜΟΑΞΟΝΙΚΗ ΓΡΑΜΜΗ (6) Επιφανειακό ρεύμα σε ομοαξονική γραμμή : K ρˆ H, K ρ ˆ H ρa ρb Ισχύς σε ομοαξονική γραμμή : b π P p ds ρdρ d p ρ, p ρ ρ p ρ ολ av z a b a π iβ z * ρdρ d z Re E ρ, e H ρ, e iβ z 57

58 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ () Για γραμμή μεταφοράς με μήκος l (<< λ, μήκος κύματος ελευθέρου χώρου) γίνεται εφαρμογή των νόμων Kirchhoff, ενώ όταν l λ τότε χρησιμοποιούνται οι εξισώσεις Maxwell. Παρόλα αυτά, και στη δεύτερη περίπτωση αν χωρίσουμε τη γραμμή σε στοιχειώδη μήκη Δz (<<λ ), μπορούμε να εφαρμόσουμε τους νόμους Kirchhoff σε κάθε στοιχειώδες μήκος Δz. 58

59 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ () v i i v Ri L και Gv C z t z t Για αρμονικά μεταβαλλόμενα μ πεδία: Re iωt Re v v z,t V z e, i i z,t I z e dv dv RI LiωI RiωL I dz dz di di GV CiωV GiωCV dz dz dv di R iωl R i dz dz ωlg iωcv dv dv R iωl G iωcv γ V dz dz d I Ανάλογα ισχύει : γ I dz iωt 59

60 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ (3) Οι λύσεις των παραπάνω εξισώσεων είναι: V z V e V e και I z I e I e γz γz γ z γ z dv γ z γ z I z γve γve RiωL dz RiωL G iωc γ z I z Ve Ve R iωl γ z γ z I z V e V e Z γ z R iωl Z είναι η σύνθετη αντίσταση γραμμής μεταφοράς G iωc Γραμμή χωρίς απώλειες L ω Z, γ iω LC iβ, uφ c C β LC εμ 6

61 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ (4) γ z γ z Ve : προσπίπτον κύμα και Ve :ανακλώμενο κύμα γ γ z Vαν Ve V γ z Vπρ Ve V ρ z ρ l e γ z γ z γ z γ z γl V z Ve Ve ρ z Z z ρ z Zz Z Z z Z I z V e V e ρ z Z ρ z Z z ρ z Zw Z z Z z Z ρz Z ρ z Z ρ z Z z Z 6

62 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ (5) Z προσαρμογή Z z Z ρ z Z z ρ z βραχυκύκλωμα Z z ρ z ανοιχτοκύκλωμα Z Z V ρ L ρ l e Z Z V L γl. L Στην είσοδο: Z Z Z Στο φορτίο: Z ζ L Z Z L Z in V V V V V γl γl e Ve Ve Z L V Z Ve Ve Z V V L γl γl είναι η ανηγμένη αντίσταση στο φορτίο V γl γl e 6

63 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ (6) V V V V ζ L e ζl ζl e e ζlζl e V V V V ζ L V γ L γ L γ L γ L γ L V ζ L ζl e ζ L e e e e ζ in γ L V γ L γ L γ L γ L ζl ζl e ζ L e e e e V in γl γl γl γ L L tanh γl ζl cosh γl sinh γl Zin ζ sinh γl cosh γl Z Z L L tanh γl ζ Γραμμη μεταφορας χωρίς απώλειες: Z Z tanh tan γ iβ iω LC I ix i x in, tanh tan, Z Z Z ZL itan Z ZL i tan Z l l 63

64 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ (7) λg l βl π Zin ZL λg π Zin Z l βl ZinZL 4 Z Z Z L 64

65 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ (8) V z V e V e V e e V e e γ z γ z az iβ z az iβ z V az iβ z az iβ z az iβ z az l i zl β V e e e e V e e ρ Le e V az iβ z azl iβ zl iψ L ρl C V z V e e ρ e e Χωρίς απώλειες : V z V e ρ e iβ z i ψ β z l L L cos L sin V z V ρ ψ β zl ρ ψ β zl V ρl ρl cosψβ zl 65

66 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ (9) V V max min ρ L ρ S L ρ L S είναι ο λόγος γςστάσιμου κύματος τάσης VSWR Το πρώτο ελάχιστο τάσης απέχει από το φορτίο απόσταση d l z : cos ψ β z l cos ψβd cos π ψ π ψβd π d β 66

67 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ () Χάρτης Smith Z Z ζ L L iψψ cos sin L L L L L ZL Z ζ L ζ RiX ρ L ρ L L R R ix ix ρ e ρ ψ i ρ ψ u iv R X X X, ψ tan tan R X R R R ix R ix R X R X ρ L R X i X 67

68 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ () u ρ cosψ και v ρ sinψ u,v L L ρ u v L R X X u v R X R X R, R X ρl R R R SWR R R i) R : SWR R ii) R: SWR R L 68

69 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ () ρl uiv ζ RiX ρ uiv R u v R R L u v X X R σταθερό R κύκλος: κέντρο u, v, ακτίνα -X R R X σταθερό κύκλος: κέντρο u, v, ακτίνα R X X 69

70 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ (3) 7

71 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ (4) 7

72 Z Z i ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ (5) i ZL L Z y L Η ανηγμένη αντίσταση ενός σημείου ισούται με την ανηγμένη αγωγιμότητα του αντιδιαμετρικού του σημείου. 7

73 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ (6) Άσκηση 4. Έστω γραμμή μεταφοράς χωρίς απώλειες με χαρακτηριστική αντίσταση 5 Ω, φορτίο Z L =i3 (Ω) και συχνότητα λειτουργίας 5 ΜΗz. Να βρεθεί ο συντελεστής ανάκλασης στο φορτίο, ο λόγος στασίμου κύματος και η θέση του πρώτου ελαχίστου τάσης από το φορτίο αναλυτικά και γραφικά. Λύση Z L ζ L.4 i.6 σημείο M.4,.6 Z.4 i.6.6 i.6.6 o i ρl i e,.4 i.6.4 i.6.3 ρl.557 SWR 3.56 ρ.443 L ο ψ π π πf π ελάχιστο τάσης: d.57 m, β,στο χάρτη Smith κινούμαστε β c 3 68 δξ g δεξιοστρόφα κατά φ 68 τόξο ΜΓ 36 g 73

74 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ (7) Χάρτης Smith για την άσκηση 4 74

75 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ (8) Άσκηση 5. Έστω γραμμή μεταφοράς χωρίς απώλειες με χαρακτηριστική αντίσταση Ωκαιφορτίο65 + i Ω. Κατά μήκος της γραμμής και σε αποστάσεις l =.3λ g συνδέονται τα φορτία φρ Ζ = i87 Ωκαι Ζ = 5 Ω. Αν στην είσοδο της γραμμής τοποθετηθεί πηγή με τάση U S =Vκαι Z S =Ω. Πόση είναι η σύνθετη αντίσταση στην είσοδο της γραμμής καθώς πόση η κατανάλωση ισχύος σε αυτήν; Λύση ζ i σημείο T L yl.45 i.7 σημείο U αντιδιαμετρικό σημείο του T ζ L Ο εξωτερικός κύκλος τέμνεται στο.39λ από την προέκταση της ευθείας OU. Κινούμαστε κατά.3 λ προς την πηγή, δηλ..39λ.3λ.54λ σημείο A y A.3 i.4 g g g L g g 75

76 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ (9) A ζ 5 y. y y y.5 5 i4.4. Νέος κύκλος OOB O,OB. B L Η προέκταση της ακτίνας OB τέμνει τον εξωτερικό κύκλο στο.3. Κινούμαστε προς την πηγή κατά.3, δηλ..3 λ.33 λ.6 λ σημείο C yc. i.75 και y.5 ζ i87.87 i y y y.i.75 i.5.i.4. D C g g g g Ηευθεία OD τέμνει τον εξωτερικό κύκλο στο 3.3. Κινούμαστε ξανά προς την πηγή κατά.3 λ, δηλ..3λ.3λ.47λ σημείο Ε g g g g y. 67 i.. Παίρνουμε το αντιδιαμετρικό σημείο F του Ε, E ζ.4 i. Z 4 i Ω F F g g 76

77 Βήματα επίλυσης. Αντιστοιχίζουμε την ανηγμένη αντίσταση του φορτίου ζ L (=.65+i) στο σημείο Τ. Βρίσκουμε τον κύκλο με R=.65 Βρίσκουμε τον κύκλο με X= Η τομή τους είναι το σημείο Τ Τ. Επειδή οι αντιστάσεις Z και Z συνδέονται με το φορτίο παράλληλα συμφέρει να δουλέψουμε με αγωγιμότητες. Έτσι, αντί για το σημείο Τ, λοιπόν, επιλέγουμε το αντιδιαμετρικό του U, αφού στο χάρτη Smith μπορούν να παρασταθούν τόσο αντιστάσεις όσο και αγωγιμότητες, αρκεί αυτές να είναι ανηγμένες ποσότητες.

78 Βήματα επίλυσης. Αντιστοιχίζουμε την ανηγμένη αντίσταση του φορτίου Z L στο σημείο Τ. Τ. Επειδή οι αντιστάσεις Z και Z συνδέονται με το φορτίο παράλληλα συμφέρει να δουλέψουμε με αγωγιμότητες. Αντί για το σημείο Τ, λοιπόν, επιλέγουμε το αντιδιαμετρικό του U, εφόσον τα σημεία στο χάρτη Smith μπορούν να παριστούν τόσο αντιστάσεις όσο και αγωγιμότητες, αρκεί αυτές να είναι ανηγμένες. U

79 Βήματα επίλυσης 3. Το σημείο U όπως είναι φυσικό αντιστοιχεί στην αγωγιμότητα y L =/(.65+i)=.45-i.7 4. Πράγματι, αυτό μπορεί να επαληθευτεί με το γεγονός ότι το σημείο U στο χάρτη Smith είναι η τομή των κύκλων R=.45 και X=-.7 Τ R=.45 U X=-.7

80 Βήματα επίλυσης 5. Στη συνέχεια μετακινούμαστε σε τόξο μήκους.3λ g, το οποίο αντιστοιχεί σε μετακίνηση η από το φορτίο προς την πηγή, για αυτό και η κίνηση γίνεται δεξιόστροφα. Ερώτηση: Το σημείο Α βρίσκεται μόνο γραφικά; Τ 6. Προσοχή: Είναι λάθος να πέσει το σημείο Α πάνω στον κύκλο R=.45. Α 7. Το σημείο Α απέχει από την αρχή Ο όσο είναι το μέτρο της ακτίνας ΟU. 8. Το σημείο Α έχει ανηγμένη αγωγιμότητα y L =.3 + i.4 και είναι η τομή των κύκλων R=.3 και X=.4..3 λ U

81 Βήματα επίλυσης 9. Στη συνέχεια, προσθέτουμε την ανηγμένη αντίσταση ζ =5, η οποία δεν έχει φανταστικό μρς μέρος.. Προσοχή: ουλεύουμε με ανηγμένες αγωγιμότητες, γι αυτό μετατρέπουμε πρώτα τη ζ σε y =.. Τ. Κινούμαστε πάνω στο τόξο που αντιστοιχεί στο X=.4, αφού το φορτίο Ζ δεν έχει φανταστικό μέρος. Α. Έτσι βρίσκουμε το σημείο Β που αντιστοιχεί σε R=.5 Β U.3λ g

82 Βήματα επίλυσης. Όπως και προηγουμένως υπολογίζουμε την επίδραση του μήκους l της γραμμής μεταφοράς.3λ g μεταξύ των φορτίων Ζ και Ζ, μετακινούμενοι πάλι πάνω σε τόξο.3λ g δεξιόστροφα για τους ίδιους λόγους που αναλύσαμε πριν. X=.75 Τ C R=. 3. Φυσικά το νέο σημείο του κύκλου (Ο, Α ΟΒ) που προκύπτει είναι το σημείο C, το οποίο αντιστοιχεί σε R=. και X=+.75. Β U.3λ g

83 Βήματα επίλυσης 3. Στη συνέχεια, η πρόσθεση της αγωγιμότητας ζ ισοδυναμεί με τη μετακίνηση πάνω στον κύκλο R=. έως το σημείο που τέμνει τον X=-.4. Γιατί; 4. Έτσι βρίσκουμε το σημείο D, το οποίο αντιστοιχεί σε ανηγμένη αγωγιμότητα.-i.4..3λ g X=.75 Α Τ C R=. Β D.3λ g U

84 Βήματα επίλυσης 6. Απομένει να υπολογιστεί η ανηγμένη αγωγιμότητα σε μήκος l=.3λ g από το φορτίο Z καθώς κινούμαστε προς την πηγή..3λ g X=.75 Α Τ C R=. Β Ε D U.3λ g

85 Βήματα επίλυσης 7. Απομένει να υπολογιστεί το σημείο F, το οποίο είναι αντιδιαμετρικό του E, για να πάρουμε τιμές μςγια την ανηγμένη η αντίσταση που ενδιαφέρει. 8. Η ανηγμένη αντίσταση στο σημείο F, είναι: ζ F =.4 + i. Α Β Ε Τ C D F U.3λ g

86 ΓΡΑΜΜΕΣ ΜΕΤΑΦΟΡΑΣ () Άσκηση 6. Σε γραμμή μεταφοράς χωρίς απώλειες με χαρακτηριστική αντίσταση Ωκαιφορτίο5 i75 Ω. Αν το μήκος κύματος στη γραμμή είναι 3cm, να βρεθεί σε ποια θέση πρέπει να τοποθετηθεί παράλληλα μια βραχυκυκλωμένη γραμμή μεταφοράς καθώς και το μήκος αυτής, ώστε να έχουμε προσαρμογή. Λύση 86

87 Βήματα επίλυσης Z = Ω F l N s Σχήμα 6- Z L M τις παράλληλες αντιστάσεις συμφέρει να τις χειριστούμε με αγωγιμότητες. Η ανηγμένη αντίσταση της γραμμής μεταφοράς με χαρακτηριστική αντίσταση Z = Ωπρέπει να είναι ζ = στην είσοδο.. Όμως, η ανηγμένη αντίσταση αυτή είναι ο παράλληλος λ συνδυασμός της ανηγμένης αντίστασης εισόδου της βραχυκυκλωμένης γραμμής μεταφοράς και της αντίστασης εισόδου της γραμμής μεταφοράς με φορτίο Z L. y i,βρ,n y L 3. Η προσαρμογή γίνεται στο σημείο (στη η θέση) N. s Σχήμα 6-4. Η βραχυκυκλωμένη γραμμή μεταφοράς έχει μήκος l και βρίσκεται σε απόσταση s από το φορτίο.

88 5. Η ολική ανηγμένη αγωγιμότητα F y i,βρ,f Z = Ω l N s Σχήμα 6- τις παράλληλες αντιστάσεις όμως μπορούμε να τις χειριστούμε με αγωγιμότητες Z L M του Σχήματος 6- είναι ίση με το άθροισμα της τιμής y i,βρ,ν και y L,Ν 6. Γνωρίζουμε ότι η βραχυκυλωμένη γραμμή μεταφοράς στη θέση (σημείο) F έχει αντίσταση Ω,, δηλαδή ανηγμένη αντίσταση + i. 7. Στη συνέχεια, η y L πρέπει να υπολογιστεί στη θέση N. Για την προσαρμογή πρέπει να ισχύει: y i,βρ,n + y L,N =. y i,βρ,n s Σχήμα 6- y L 8. Τότε R L,N +ix L,N +i Xβρ,N =. Επομένως, R L,N = και X L,N =-X βρ,n, πράγμα που δηλώνει «συζυγή προσαρμογή».

89 9. Η γραμμή μεταφοράς έχει με φορτίο Z L =5-i75 Ω, δηλαδή έχει ανηγμένη αντίσταση ζ L,M =.5 - i.75 στη θέση M, η οποία αντιστοιχεί στο σημείο M Z πάνω στο χάρτη Smith..Κατά τα γνωστά το σημείο αυτό είναι η τομή των κύκλων R=.5 και X=-.75. R=.5 M y.συνεπώς, θα πάρουμε το αντιδιαμετρικό του M y πάνω στον κύκλο της γραμμής μεταφοράς για να βρούμε την ανηγμένη αγωγιμότητα στη θέση Μ. M Z X=-.75

90 .Εφόσον το σημείο Μ y αντιστοιχεί στην αγωγιμότητα του φορτίου Z L στο σημείο Μ, πρέπει αυτή να την βρούμε στη θέση Ν (είσοδο της γραμμής). M y s/λ Ν y i,βρ,n R= y L,N y L N M 3.Άρα, πρέπει να κινηθούμε κατά τόξο μήκους s/λ προς την πηγή. Επειδή το πραγματικό μέρος της ανηγμένης αγωγιμότητας πρέπει είναι, η λύση θα είναι το σημείο τομής της γραμμής μεταφοράς με τον κύκλο R= σημείο Ν. M Z

91 4.Από το χάρτη Smith βρίσκουμε ότι s/λ= Κατά τα γνωστά το σημείο Ν είναι η τομή του κύκλου ύλ με αγωγιμότητα R= και φανταστική αγωγιμότητα γμ X=. M y s/ λ Ν 6.Στην πραγματικότητα, η ολική φανταστική ανηγμένη αγωγιμότητα πρέπει να είναι. Το ρόλο της αντιστάθμισης παίζει η βραχυκυκλωμένη γραμμή μεταφοράς. Αυτή είναι η φυσική σημασία της συζυγούς προσαρμογής, όπου είχαμε βρει ότι πρέπει R= και X L,N = - X βρ,n M Z X=. R=

92 7.Το βραχυχύκλωμα ως ανηγμένη αντίσταση είναι το σημείο F Z. 8.Το βραχυχύκλωμα ως ανηγμένη αγωγιμότητα είναι το σημείο F y. M y s/ λ Ν R= Θυμίζουμε F Z X=. F y l Z L Ν s Μ Σχήμα 6- M Z F

93 9.Εύκολα καταλαβαίνουμε ότι X βρ,ν =-.. Το ζητούμενο μήκος l αντιστοιχεί στο τόξο F y J, όπου το σημείο J αντιστοιχεί σε X βρ,ν =-.. Από το τόξο αυτό βρίσκουμε ότι l/λ=.7. M y s/ λ Ν Θυμίζουμε F X=. F F Z F y R= l Z L Ν s Σχήμα 6- Μ M Z J Χ=-. F

94 .Η τομή του κύκλου της γραμμής μεταφοράς με τον κύκλο R= είναι μόνο το σημείο Ν; s/λ.αν αντί του τόξου Μ y N παίρναμε το τόξο M y K, τότε θα M y είχαμε μεγαλύτερο s. Πώς θα μεταβάλλονταν τότε το μήκος l; Ποιά είναι η βέλτιστη Ν R= περίπτωση; (Αφήνεται ως άσκηση) Θυμίζουμε F Z X=. Κ F y s/λ l Ν s Σχήμα 6- Μ Z L M Z Χ=-. J F

95 ΠΑΡΑΜΕΤΡΟΙ ΣΚΕΔΑΣΗΣ () Κανονικοποιημένες κυματικές τάσεις εισόδου a i εξόδου b i b = S a + S a + S 3 a 3 b = S a + S a + S 3 a 3 b 3 = S 3a + S 3a + S 33a 3 Συντελεστής ανάκλασης στη θύρα # b a a3 ρ SS S3 a a a ρ S α, α 3 Συντελεστής μεταφοράς από τη θύρα στη θύρα S kl b a k k l a il i 95 l

96 ΠΑΡΑΜΕΤΡΟΙ ΣΚΕΔΑΣΗΣ () Ιδιότητες πολύθυρων Χωρίς ρςαπώλειες N N N N P P a b SS I in,i out,i i i i i i i Αμφίδρομα S S, i j S, ij ji j ii Προσαρμοσμένα σε όλες τις θύρες τους, i T 96

97 ΠΑΡΑΜΕΤΡΟΙ ΣΚΕΔΑΣΗΣ (3) Μέτρηση παραμέτρου ανάκλασης S ii Θύρα #4 προσαρμοσμένη ( P4 ) P Q3 Pπρ,K Θύρα #3 προσαρμοσμένη ( P3 ) Q4 P P αν,k P, K S P,K 97

98 ΠΑΡΑΜΕΤΡΟΙ ΣΚΕΔΑΣΗΣ (4) Μέτρηση παραμέτρου μεταφοράς S ij Χωρίς το πολύθυρο Ρυθμίζουμε πλάτος και φάση ώστε A A (η έξοδος του παλμογράφου είναι μηδενική). Ενδείξεις ρυθμιστών: R db, φ Με το πολύθυρο Το πολύθυρο θα προκαλέσει αλλαγή πλάτους και φάσης (η έξοδος του παλμογράφου θα είναι μη μηδενική). Με αλλαγή των ρυθμιστών σε R db, φ (η έξοδος του παλμογράφου θα γίνει πάλι μηδενική). R R S, φ φ φ οι υπόλοιπες 3 θύρες είναι προσαρμοσμένες

99 ΠΑΡΑΜΕΤΡΟΙ ΣΚΕΔΑΣΗΣ (5) I) Για απλό κυματοδηγό S e i e i Με κατάλληλη ρύθμιση του μήκους της γραμμής εισόδου : S II) Για απομονωτή S 99

100 ΠΑΡΑΜΕΤΡΟΙ ΣΚΕΔΑΣΗΣ (6) III) Για εξασθενητή ή3db3 S IV) Για εξασθενητή db S..

101 ΠΑΡΑΜΕΤΡΟΙ ΣΚΕΔΑΣΗΣ (7) Άσκηση 7. Μικροκυματικό τρίθυρο χωρίς απώλειες είναι προσαρμοσμένο σε όλες τις θύρες του, μη αμφίδρομο και με S. Να βρεθεί η μήτρα σκέδασης του τριθύρου. Λύση S S3 S S 3 T S S S 3 S S S3 S3 S3 S3 S3 S S 3 a S3 S3 S3 S3 b SS3 S3S c T SS I S S 3 d SS3 S3S e S3 S 3 f

102 ΠΑΡΑΜΕΤΡΟΙ ΣΚΕΔΑΣΗΣ (8) S, e S 3 iφ f, S S e c, S 3 iφ3 a,3 S3 S3 e 4 b, 4 S 3 5 iφ d,5 S S e 6 iφ3 e iφ S e iφ3 e "Δεξιόστροφος κυκλοφορητής" Για "αριστερόστροφο κυκλοφορητή" θα έπρεπε S

103 ΠΑΡΑΜΕΤΡΟΙ ΣΚΕΔΑΣΗΣ (9) Άσκηση 8. Μικροκυματικό τετράθυρο αμφίδρομο και χωρίς απώλειες είναι προσαρμοσμένο σε όλες τις θύρες του, οι θύρες του και 4 είναι ασύζευκτες, S =k και S 3 =S 4. Να υπολογιστεί η μήτρα σκέδασης του τετράθύρου και να βρεθεί ηισχύς που βγαίνει από κάθε θύρα του, αν η ισχύς εισόδου στη θύρα είναι mw. Λύση b S S3 a b S S3 S3 b3 S3 S3 S34 b4 S3 S34 b b S a b S a k mw b S a b S a k mw b4 3

104 ΠΑΡΑΜΕΤΡΟΙ ΣΚΕΔΑΣΗΣ () S S 3 S S 3 T S S3 S3 S S3 S 3 SS S 3 S3 S 34 S3 S3 S 34 S3 S34 S3 S S S S k S S S S S S S S S S 3 3 S S 3 34 S S S S S S k Ι 4

105 S S ΠΑΡΑΜΕΤΡΟΙ ΣΚΕΔΑΣΗΣ () iφ3 k k e 3 iφ3 S S3 S3 k k e S S3 S iφ iφ 34 k e ke S3 S34 iφφ 3 iφφ 34 k e ke k k e k e ke iφ iφ iφ iφ3 iφ3 i φ3 φ34 i π φ3 φ34 e e e e φ φ3 πφ 3 34 φ φ π φ 3 34 π φ

106 ΒΙΒΛΙΟΓΡΑΦΙΑ Ε. Λεκατσά, Εισαγωγή στη Θεωρία των Μικροκυματικών Στοιχείων, Εκδόσεις Σελλούντος, 979. C. Balanis, Advanced Engineering Electromagnetics, J. Wiley, 989. Ι. Σάχαλου, Μικροκύματα., Εκδόσεις Αϊβαζή-Ζουμπούλη, 99. F. Benson and T. Benson, Fields, Waves and Transmission Lines, Chapman & Hall, 99. R. Collin, Field Theory of Guided Waves, IEEE Press, 99. R. Collin, Foundations for Microwave Engineering, nd Edition, McGraw-Hill, 99. S. Ramo et al., Fields & Waves in Communication Electronics, J. Wiley, 99. Ν. Ουζούνογλου, Εισαγωγή στα Μικροκύματα, Εκδόσεις Παπασωτηρίου

107 ΒΙΒΛΙΟΓΡΑΦΙΑ (συνέχεια) L. C. Chen και J. A. Kong, Εφαρμοσμένος Ηλεκτρομαγνητισμός, Μετάφραση Κ. Λιολιούση, Εκδόσεις Ίων, 995. Σ. Λιβιεράτος και Χ. Βαζούρας, Εργαστήριο Μικροκυμάτων Κεραιών, Σχολή Ναυτικών Δοκίμων, 997. D. Pozar, Μικροκυματική Τεχνολογία, Μετάφραση Κ. Λιολιούση, Εκδόσεις Ίων, 998. Κ. Λιολιούση, Μικροκύματα Ι, Εκδόσεις Ίων. 7