ΑΝΑΛΥΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΦΥΣΙΚΗΣ A ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΚΑΙ Α ΘΕΩΡΗΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΤΕΧΝΙΚΩΝ ΣΧΟΛΩΝ
|
|
|
- ÁἸσαάκ Ρέντης
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ΑΝΑΛΥΤΙΚΟ ΡΟΓΡΑΜΜΑ ΦΥΣΙΚΗΣ A ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΚΑΙ Α ΘΕΩΡΗΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΤΕΧΝΙΚΩΝ ΣΧΟΛΩΝ - 1 -
2 ΕΡΙΕΧΟΜΕΝΑ ΕΝΟΤΗΤΑ ΘΕΜΑ Σελ. ερ. 1 ΕΙΣΑΓΩΓΗ. 1.1 Μονόμετρα και διανυσματικά μεγέθη. 4 0,5 1.2 Το Διεθνές Σύστημα Mονάδων (S.I.). 5 0,5 1.3 Μετατροπές μονάδων μέτρησης και προθέματα μονάδων Δεκαδικά και σημαντικά ψηφία Επιστημονικός συμβολισμός. 7 1 ΣΥΝΟΛΟ ΕΡΙΟΔΩΝ 3 2 ΚΙΝΗΜΑΤΙΚΗ ΥΛΙΚΟΥ ΣΗΜΕΙΟΥ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ. 2.1 Θέση, τροχιά, μετατόπιση και διάστημα Χρονική στιγμή και χρονική διάρκεια. 10 0,5 2.3 Κίνηση. 10 0,5 2.4 Κίνηση με σταθερή ταχύτητα (Ευθύγραμμη ομαλή κίνηση) Ομαλά μεταβαλλόμενη ευθύγραμμη κίνηση (κίνηση με σταθερή επιτάχυνση) ΣΥΝΟΛΟ ΕΡΙΟΔΩΝ 14 3 ΝΟΜΟΙ ΤΟΥ ΝΕΥΤΩΝΑ ΓΙΑ ΤΗΝ ΚΙΝΗΣΗ. 3.1 Δυνάμεις Αδράνεια και πρώτος νόμος Μάζα και δεύτερος νόμος Μάζα και βάρος. 22 0,5 3.5 Τρίτος νόμος. (Νόμος δράσης- αντίδρασης). 22 0,5 ΣΥΝΟΛΟ ΕΡΙΟΔΩΝ 5 4 ΕΦΑΡΜΟΓΕΣ ΤΩΝ ΝΟΜΩΝ ΤΟΥ ΝΕΥΤΩΝΑ. 4.1 Ισορροπία υλικού σημείου Κίνηση σε ευθεία τροχιά υπό την επίδραση σταθερής δύναμης Ελεύθερη πτώση Κίνηση σε κεκλιμένο επίπεδο Εφαρμογές του τρίτου νόμου του Νεύτωνα ΣΥΝΟΛΟ ΕΡΙΟΔΩΝ
3 ΕΡΙΕΧΟΜΕΝΑ ΕΝΟΤΗΤΑ ΘΕΜΑ Σελ. ερ. 5 ΕΡΓΟ ΙΣΧΥΣ ΚΑΙ ΕΝΕΡΓΕΙΑ. 5.1 Έργο σταθερής δύναμης Έργο μεταβλητής δύναμης και σταθερής κατεύθυνσης Ισχύς Βαρυτική δυναμική ενέργεια Ελαστική δυναμική ενέργεια Μηχανική ενέργεια και αρχή διατήρησης της μηχανικής ενέργειας ΣΥΝΟΛΟ ΕΡΙΟΔΩΝ 8 ΓΕΝΙΚΟ ΣΥΝΟΛΟ ΕΡΙΟΔΩΝ ΔΙΔΑΣΚΑΛΙΑΣ 40 ΣΥΝΟΛΟ ΕΡΙΟΔΩΝ ΔΙΑΓΩΝΙΣΜΑΤΩΝ 6 ΣΥΝΟΛΟ ΕΡΙΟΔΩΝ ΓΙΑ ΕΑΝΑΛΗΨΗ 12 ΓΕΝΙΚΟ ΣΥΝΟΛΟ ΕΡΙΟΔΩΝ 58 Σημ. Χρόνος διδασκαλίας και αξιολόγησης = 46 περίοδοι ή 23 εβδομάδες Χρόνος για επανάληψη = 12 περίοδοι ή 6 εβδομάδες - 3 -
4 1. Εισαγωγή. 1.1 Μονόμετρα και διανυσματικά μεγέθη Ορίζουν και διακρίνουν τα μονόμετρα μεγέθη από τα διανυσματικά και δίνουν παραδείγματα Τα μονόμετρα μεγέθη ορίζονται πλήρως με την αριθμητική τιμή και τη μονάδα μέτρησης. (Η αριθμητική τιμή μαζί με τη μονάδα μέτρησης αποτελούν το μέτρο του μεγέθους) Τα διανύσματα για να οριστούν πλήρως απαιτείται, εκτός από το μέτρο (αριθμητική τιμή και μονάδα μέτρησης), η διεύθυνση και η φορά. (Η διεύθυνση μαζί με τη φορά αποτελούν την κατεύθυνση του διανύσματος). 0, Η θερμοκρασία, η μάζα, η πυκνότητα, η πίεση, το μήκος και ο χρόνος είναι παραδείγματα μονόμετρων μεγεθών Η θέση, η μετατόπιση, η δύναμη και η ταχύτητα είναι παραδείγματα διανυσματικών μεγεθών
5 1.2 Το Διεθνές Σύστημα Mονάδων (S.I.) Αναφέρουν τα θεμελιώδη μεγέθη της μηχανικής και τις μονάδες μέτρησής τους στο Διεθνές Σύστημα Μονάδων (S.I) Τα θεμελιώδη μεγέθη της μηχανικής είναι το μήκος, η μάζα και ο χρόνος. Στο Διεθνές Σύστημα Μονάδων (S.I.) οι αντίστοιχες μονάδες μέτρησής τους είναι το 1 μέτρο (1 m), 1 χιλιόγραμμο (1 Kg) και το 1 δευτερόλεπτο (1 s). 0,5-5 -
6 1.3 Μετατροπές μονάδων μέτρησης και προθέματα μονάδων Μετατρέπουν διάφορες μονάδες μέτρησης των θεμελιωδών μεγεθών και βασικών παραγώγων μεγεθών (εμβαδόν, όγκος, πυκνότητα) στις αντίστοιχες μονάδες στο Διεθνές Σύστημα μονάδων (S.I) και αντίστροφα Για το μήκος: 1 mm = 10-3 m, 1 μm = 10-6 m, 1 nm = 10-9 m Για το χρόνο: 1min = 60 s, 1h = 3600 s Για τη μάζα: 1 g = 10-3 Kg, 1 tn = 10 3 Kg Για το εμβαδόν: 1cm 2 = 10-4 m 2, 1 mm 2 = 10-6 m Για τον όγκο: 1 cm 3 = 10-6 m 3, 1 mm 3 = 10-9 m Γνωρίζουν τα βασικά προθέματα των φυσικών μεγεθών Γνώση των προθεμάτων: 1 pico = 1 p = 10-12, 1 nano = 1n = 10-9, 1 micro = 1 μ = 10-6, 1 milli = 1 m = 10-3, 1 kilo = 1 k = 10 3, 1 mega = 1 M = 10 6, 1 giga = 1 G = 10 9, 1 tera = 1 Τ = nanometer = 1 nm = 10-9 m, 1 milligram = 1 mg = 10-3 g = 10-6 Kg, 1 kilojoules = 1 kj = 10 3 J - 6 -
7 1.4 Δεκαδικά και σημαντικά ψηφία Επιστημονικός συμβολισμός Εκφράζουν το αποτέλεσμα της λύσης ενός προβλήματος με ακρίβεια ένα αριθμό δεκαδικών ή σημαντικών ψηφίων, ο οποίος δίνεται στο πρόβλημα Το πρώτο δεκαδικό ψηφίο είναι το πρώτο ψηφίο μετά την υποδιαστολή. Το πρώτο σημαντικό ψηφίο είναι το πρώτο μη μηδενικό ψηφίο. Ο αριθμός 4,39 έχει 2 δεκαδικά ψηφία αλλά 3 σημαντικά ψηφία Οι αριθμοί 34,23, 0,09863, 8,005, 45,00 έχουν όλοι τέσσερα σημαντικά ψηφία Εκφράζουν το αποτέλεσμα σε ένα πρόβλημα χρησιμοποιώντας επιστημονικό συμβολισμό Ένας αριθμός μπορεί να εκφραστεί στη μορφή αx10 n, όπου 1<α<10. Για παράδειγμα: 126,3 = 1,263x10 2, 0,0056 = 5,6x10-3. Ο συμβολισμός αx10 n ονομάζεται επιστημονικός συμβολισμός και χρησιμοποιείται για να δηλώσει τα σημαντικά ψηφία ενός αποτελέσματος
8 2 Κινηματική υλικού σημείου σε μια διάσταση Θέση, τροχιά, μετατόπιση και διάστημα Αναγνωρίζουν ότι η θέση ενός σώματος είναι διανυσματικό μέγεθος και καθορίζεται ως προς ένα σύστημα αξόνων. (σύστημα αναφοράς) Η θέση r (ή x ή y σε μια διάσταση) ενός σώματος μπορεί να καθοριστεί με τις καρτεσιανές συντεταγμένες. Το σύστημα των τριών ορθογώνιων αξόνων αποτελεί ένα σύστημα αναφοράς Ορίζουν και βρίσκουν το διάνυσμα θέσης ενός σώματος σε μια διάσταση με τη βοήθεια μιας κλίμακας αριθμών Η θέση r είναι διάνυσμα και καθορίζεται ως προς την αρχή ενός συστήματος αναφοράς. Το διάνυσμα της θέσης r έχει αρχή την αρχή του συστήματος αναφοράς και τέλος τη θέση του σώματος. Σε μια διάσταση η θέση x μπορεί να καθοριστεί πλήρως με ένα θετικό ή αρνητικό αριθμό ο οποίος λαμβάνεται ως προς ένα σταθερό σημείο, που συνήθως είναι το μηδέν μιας κλίμακας αριθμών. Το θετικό ή αρνητικό πρόσημο του αριθμού, σε αυτή την περίπτωση, καθορίζει την κατεύθυνση της θέσης Ορίζουν την τροχιά ενός σώματος και αναφέρουν παραδείγματα ευθύγραμμης τροχιάς και καμπυλόγραμμης τροχιάς Το σύνολο των διαδοχικών σημείων από τα οποία περνά ένα σώμα ονομάζεται τροχιά Ένας ακροβάτης που περπατά σε τεντωμένο σχοινί κινείται σε ευθεία γραμμή (μια διάσταση). Η τροχιά του είναι ευθύγραμμη. Ένα σώμα που πέφτει ελεύθερα κοντά στην επιφάνεια της γης κινείται επίσης σε ευθύγραμμη τροχιά. Τα οχήματα σε κυκλικό κόμβο, οι πλανήτες και οι δορυφόροι κινούνται σε καμπυλόγραμμες τροχιές
9 2.1.4 Ορίζουν και διακρίνουν τα μεγέθη: μετατόπιση και διάστημα Η μετατόπιση r (ή x ή y σε μια διάσταση) είναι η μεταβολή της θέσης ενός σώματος. Η μετατόπιση είναι διανυσματικό μέγεθος. Το διάνυσμα της μετατόπισης έχει αρχή το αρχικό σημείο που βρίσκεται ένα σώμα και τέλος το τελικό σημείο που βρίσκεται το σώμα. Το διάστημα (x, y σε μια διάσταση ή S σε δύο ή τρεις διαστάσεις) είναι μονόμετρο μέγεθος. Το διάστημα είναι το μήκος της τροχιάς (ευθύγραμμης ή καμπυλόγραμμης) πάνω στην οποία κινήθηκε το σώμα από μια αρχική θέση μέχρι μια τελική θέση Να δοθούν παραδείγματα ποιοτικής διάκρισης των διαφορών μεταξύ των μεγεθών, διάστημα και μετατόπιση, μέσω παράθεσης παραδειγμάτων ευθύγραμμης και καμπύλης τροχιάς Δικαιολογούν και αναγνωρίζουν ότι η θέση και η μετατόπιση είναι διανυσματικά μεγέθη και δίνουν παραδείγματα Υπολογίζουν τη θέση, τη μετατόπιση και το διάστημα σε μια διάσταση Δύο σώματα που διανύουν το ίδιο διάστημα ως προς την αρχή ενός συστήματος αναφοράς δε σημαίνει ότι έχουν και την ίδια θέση. Άρα, επιπλέον από το μέτρο, η διεύθυνση και η φορά για τον καθορισμό της θέσης είναι απαραίτητα. Επομένως η θέση είναι διανυσματικό μέγεθος. Η μετατόπιση από ένα σημείο σε μια συγκεκριμένη απόσταση και μόνο δεν καθορίζει την τελική θέση. Αυτό σημαίνει ότι είναι αναγκαίο να δοθεί και η διεύθυνση και η φορά. Άρα η μετατόπιση είναι διάνυσμα αραδείγματα υπολογισμού θέσης, μετατόπισης και διαστήματος σε ευθύγραμμη τροχιά (ι) χωρίς αλλαγή φοράς και (ιι) με αλλαγή φοράς
10 2. 2 Χρονική στιγμή και χρονική διάρκεια Διακρίνουν τη χρονική στιγμή από τη χρονική διάρκεια Η χρονική στιγμή t είναι οι ενδείξεις του χρονομέτρου και η χρονική διάρκεια Δt είναι η διαφορά δύο χρονικών στιγμών. Η χρονική στιγμή δεν έχει διάρκεια. 0, Ένα γεγονός λαμβάνει χώρα σε ένα τόπο (θέση) και σε μια δεδομένη χρονική στιγμή Αναγνωρίζουν και δικαιολογούν ότι η χρονική διάρκεια είναι πάντα θετική ποσότητα Είναι αδύνατη η πραγματοποίηση ενός ταξιδιού πίσω στο χρόνο. άντα γερνούμε και ποτέ δεν γινόμαστε νεώτεροι Κίνηση Δίνουν ένα ορισμό της κίνησης ενός σώματος και αναγνωρίζουν ότι η κίνηση είναι σχετική έννοια, αναφέροντας παραδείγματα Η κίνηση ενός σώματος είναι η αλλαγή θέσης του ως προς κάποιο σύστημα αναφοράς. Η αλλαγή αυτή της θέσης είναι διαφορετική ως προς ένα διαφορετικό σύστημα αναφοράς και άρα είναι έννοια σχετική Ένας επιβάτης του τρένου κινείται ως προς το έδαφος αλλά είναι ακίνητος ως προς το τρένο ή ένα δεύτερο επιβάτη του τρένου. 0,5-10 -
11 2. 4 Κίνηση με σταθερή ταχύτητα (Ευθύγραμμη ομαλή κίνηση) Αναγνωρίζουν την ανάγκη ορισμού της ταχύτητας ως έννοιας που εκφράζει πόσο γρήγορα αλλάζει θέση ένα κινητό ως προς το χρόνο, σε σχέση με ένα σύστημα αναφοράς Η ταχύτητα είναι ο ρυθμός μεταβολής της θέσης ενός σώματος, και εξαρτάται από το σύστημα αναφοράς Αναγνωρίζουν το διανυσματικό χαρακτήρα της ταχύτητας και ερμηνεύουν το θετικό ή αρνητικό πρόσημό της σε μονοδιάστατη κίνηση Ορίζουν τη μέση ταχύτητα και αναγνωρίζουν ότι αναφέρεται σε μια χρονική διάρκεια Η ταχύτητα είναι διανυσματικό μέγεθος με φορά τη φορά της κίνησης ενός κινητού. Άρα το θετικό ή αρνητικό πρόσημο στην ταχύτητα ταυτίζεται με τη θετική ή την αρνητική φορά κίνησης που ορίσαμε αυθαίρετα (π.χ. δεξιά είναι θετική φορά και αριστερά είναι αρνητική) Η μεταβολή της θέσης σε μια χρονική διάρκεια, δηλαδή η μετατόπιση, δια τη χρονική αυτής διάρκεια, ονομάζεται μέση ταχύτητα. Η μέση ταχύτητα δεν αντιπροσωπεύει κατ ανάγκη την ταχύτητα του κινητού σε κάθε στιγμή της κίνησης Η μέση ταχύτητα είναι διανυσματικό μέγεθος και έχει την ίδια διεύθυνση και φορά με την αντίστοιχη μετατόπιση Υπολογίζουν τη μέση ταχύτητα Ο υπολογισμός της μέσης ταχύτητας περιορίζεται σε ευθύγραμμη κίνηση με βάση: (α) πίνακα τιμών θέσης και των αντίστοιχων χρονικών στιγμών, (β) τη γραφική παράσταση θέσης-χρόνου και (γ) την ευθεία κίνησης με κλίμακα και δεδομένες τις αντίστοιχες χρονικές στιγμές
12 2.4.5 Μετατρέπουν τις μονάδες μέτρησης της ταχύτητας από Km/h σε m/s και αντίστροφα Αναγνωρίζουν πότε μια κίνηση γίνεται με σταθερή ταχύτητα με βάση: (α) τη γραφική παράσταση θέσηςχρόνου, (β) τη χαρτοταινία που λαμβάνεται πειραματικά με τη χρήση του χρονομετρητή (γ) την εξίσωση κίνησης, (δ) παρατηρήσεις πραγματικών καταστάσεων κίνησης Εξάγουν την εξίσωση κίνησης με σταθερή ταχύτητα με βάση τη γραφική παράσταση θέσηςχρόνου Χαράσσουν, από πειραματικές τιμές θέσης και των αντίστοιχων χρονικών στιγμών, την αντίστοιχη γραφική παράσταση και υπολογίζουν από αυτή την σταθερή ταχύτητα του σώματος Μετατρέπουν την ταχύτητα ενός οχήματος από Km/h σε m/s για να μπορούν να χρησιμοποιούν μονάδες στο S.I Μετατρέπουν την ταχύτητα ενός οχήματος από m/s σε km/h για να μπορούν να ερμηνεύουν το αποτέλεσμα ενός προβλήματος, αν κατά πόσο ανταποκρίνεται ή όχι σε πραγματικές καταστάσεις Η κίνηση η οποία γίνεται με σταθερή ταχύτητα ονομάζεται ομαλή ευθύγραμμη κίνηση. Τότε το μέτρο, η διεύθυνση και η φορά της ταχύτητας παραμένουν συνεχώς σταθερά. Δηλαδή ο ρυθμός μεταβολής της θέσης του κινητού είναι συνεχώς σταθερός Η γραφική παράσταση της θέσης με το χρόνο σε μια κίνηση με σταθερή ταχύτητα είναι ευθεία γραμμή. Η θέση x ως συνάρτηση του χρόνου t είναι γραμμική (πρώτου βαθμού) Μελετούν κινήσεις με σταθερή ταχύτητα με τη χρήση του χρονομετρητή ή / και της διασύνδεσης Η κλίση της γραφικής παράστασης θέσης χρόνου, που λαμβάνεται από χαρτοταινία με τη χρήση του χρονομετρητή, ή με τη βοήθεια της διασύνδεσης, είναι η ταχύτητα του σώματος
13 2.4.9 Υπολογίζουν τη θέση και τη μετατόπιση σε δεδομένο χρονικό διάστημα με βάση: (α) τη γραφική παράσταση θέσης χρόνου και (β) την εξίσωση κίνησης Λύουν προβλήματα κίνησης με σταθερή ταχύτητα με βάση τη γραφική παράσταση θέσηςχρόνου ή/ και με βάση τις εξισώσεις κίνησης Σε κάθε στιγμή προσδιορίζεται η θέση x είτε γραφικά είτε από την εξίσωση κίνησης. Η διαφορά της αρχικής από την τελική θέση δίνει τη x. Η απόσταση x σε μια ευθύγραμμη κίνηση ισούται με μετατόπιση το μέτρο της μετατόπισης όταν η φορά κίνησης δεν αλλάζει εριορισμός σε προβλήματα με ένα κινητό ή με δύο κινητά που δεν απαιτούν λύση περίπλοκων συστημάτων εξισώσεων. Να δοθεί έμφαση στην κατανόηση γραφικών παραστάσεων και των εννοιών: θέση, μετατόπιση και ταχύτητα
14 2. 5 Ομαλά μεταβαλλόμενη ευθύγραμμη κίνηση (κίνηση με σταθερή επιτάχυνση) Αναγνωρίζουν ότι η ταχύτητα μπορεί να μεταβάλλεται: (α) σε μέτρο, (β) σε διεύθυνση, (γ) τόσο σε μέτρο όσο και σε διεύθυνση και δίνουν παραδείγματα Ενδεικτικά παραδείγματα μεταβολής της ταχύτητας: (α) αράδειγμα μεταβολής μόνο του μέτρου της ταχύτητας: Ένα λεωφορείο που κινείται σε ευθύγραμμη τροχιά και πλησιάζει την στάση για να παραλάβει επιβάτες. (Ελάττωση του μέτρου της ταχύτητας χωρίς μεταβολή της διεύθυνσης). (β) αράδειγμα μεταβολής μόνο της διεύθυνσης της ταχύτητας: Ένα αυτοκίνητο που κινείται σε κυκλικό κόμβο με σταθερή σε μέτρο ταχύτητα. (Η καμπυλόγραμμη τροχιά του αυτοκινήτου συνεπάγεται και αλλαγή της διεύθυνσης της ταχύτητας). (γ) αράδειγμα μεταβολής τόσο του μέτρου όσο και της διεύθυνσης της ταχύτητας: Ένας αθλητής στο στίβο, σε στροφή, όταν κάνει εκκίνηση. (Αύξηση του μέτρου της ταχύτητας και μεταβολή της διεύθυνσής της) Αναγνωρίζουν τη μεταβαλλόμενη κίνηση ως την κίνηση όπου η ταχύτητα μεταβάλλεται Αναγνώριση μέσα από παραδείγματα της καθημερινής πραγματικότητας Ορίζουν την επιτάχυνση και βρίσκουν τη μονάδα μέτρησής της στο S.I Η επιτάχυνση a είναι ο ρυθμός μεταβολής της ταχύτητας. Η επιτάχυνση είναι διάνυσμα Η μονάδα μέτρησης της επιτάχυνσης στο S.I. είναι m/s 2 (m.s -2 )
15 2.5.4 Ορίζουν τη μέση επιτάχυνση, a, και την υπολογίζουν στην περίπτωση ευθύγραμμης κίνησης Αναγνωρίζουν ότι η επιτάχυνση έχει διεύθυνση και φορά αυτή της μεταβολής της ταχύτητας και όχι εκείνη της ταχύτητας Η μέση επιτάχυνση είναι το πηλίκο της μεταβολής της ταχύτητας δια τη χρονική διάρκεια στην οποία λαμβάνει χώρα Δίνονται παραδείγματα υπολογισμού της μέσης επιτάχυνσης σε ευθύγραμμη κίνηση: (α) με θετική ταχύτητα και το μέτρο της ταχύτητας να αυξάνεται, (β) με αρνητική ταχύτητα και το μέτρο της ταχύτητας να αυξάνεται, (γ) με θετική ταχύτητα και το μέτρο της ταχύτητας να ελαττώνεται και (δ) με αρνητική ταχύτητα και το μέτρο της ταχύτητας να ελαττώνεται. Η θετική ή η αρνητική φορά καθορίζεται αυθαίρετα. Έτσι οι μαθητές αντιλαμβάνονται ότι το πρόσημο της επιτάχυνσης δεν έχει καμιά σχέση ούτε με τη φορά κίνησης του κινητού, η οποία καθορίζεται από το πρόσημο της ταχύτητας, αλλά ούτε και με την αύξηση ή την ελάττωση του μέτρου της ταχύτητας Το πρόσημο της επιτάχυνσης είναι το ίδιο με το πρόσημο της μεταβολής της ταχύτητας και όχι με το πρόσημο της ταχύτητας. Θετική (ή αρνητική) επιτάχυνση σημαίνει θετική (ή αρνητική) μεταβολή της ταχύτητας, δηλαδή αύξηση (ή ελάττωση) της ταχύτητας αντίστοιχα Η θετική ή αρνητική επιτάχυνση δεν έχουν να κάνουν κατ ανάγκη με την αύξηση ή την ελάττωση του μέτρου της ταχύτητας. Κριτήριο για την αύξηση ή την ελάττωση του μέτρου της ταχύτητας δεν είναι δηλαδή το πρόσημο της επιτάχυνσης
16 2.5.6 Εξηγούν με βάση τα διανύσματα της ταχύτητας και της επιτάχυνσης πότε το μέτρο της ταχύτητας ενός κινητού αυξάνεται ή ελαττώνεται Αναγνωρίζουν πότε μια κίνηση σε ευθεία γραμμή γίνεται με σταθερή επιτάχυνση. (ομαλά μεταβαλλόμενη ευθύγραμμη κίνηση) Μέσα από παραδείγματα οι μαθητές να αντιληφθούν ότι η αύξηση ή η ελάττωση του μέτρου της ταχύτητας σε ευθεία γραμμή συνδέεται άμεσα με τη φορά των δύο διανυσμάτων: ταχύτητας και επιτάχυνσης και όχι με το πρόσημο της επιτάχυνσης Το μέτρο της ταχύτητας αυξάνεται ή ελαττώνεται αν τα διανύσματα της ταχύτητας και της επιτάχυνσης έχουν την ίδια φορά (ομόρροπα) ή αντίθετη φορά (αντίρροπα) αντίστοιχα Όταν η διεύθυνση και η φορά της ταχύτητας ενός σώματος είναι σταθερή και το μέτρο της ταχύτητας μεταβάλλεται με σταθερό ρυθμό, η κίνηση του σώματος γίνεται με σταθερή επιτάχυνση, η οποία έχει τη διεύθυνση της ταχύτητας Στην καθημερινή γλώσσα η λέξη επιτάχυνση σημαίνει γενικά αύξηση και η λέξη επιβράδυνση μείωση. Στη γλώσσα της φυσικής η λέξη επιβράδυνση πρέπει να αποφεύγεται εφόσον δεν σημαίνει το ίδιο όπως στην καθομιλουμένη. Το διάνυσμα a, εξάλλου, όπως ορίστηκε πιο πάνω ονομάζεται επιτάχυνση και δεν αλλάζει ονομασία σε επιβράδυνση αν πάρει αρνητική τιμή. Μπορεί, όμως, να χρησιμοποιείται η φράση «το αυτοκίνητο επιταχύνεται» ή το αυτοκίνητο επιβραδύνεται», για να δηλώσουμε αντίστοιχα την αύξηση ή την ελάττωση του μέτρου της ταχύτητας. Δεν χρησιμοποιείται, όμως, για να περιγραφεί κάποια κίνηση, η φράση «ομαλά επιβραδυνόμενη κίνηση». Η κίνηση με επιτάχυνση είναι μόνο επιταχυνόμενη και αν η επιτάχυνση είναι σταθερή είναι ομαλά επιταχυνόμενη
17 2.5.8 Εξάγουν την ομαλά μεταβαλλόμενη διανυσματική εξίσωση κίνησης ενός σώματος με σταθερή επιτάχυνση: 0 t Υπολογίζουν την επιτάχυνση, την ταχύτητα ή τη θέση σε μια ευθύγραμμη κίνηση με σταθερή επιτάχυνση Ερμηνεύουν την κίνηση ενός σώματος σε ευθύγραμμη τροχιά με βάση (α) τη γραφική παράσταση ταχύτητας-χρόνου, (β) στροβοσκοπικές φωτογραφίες της κίνησης του κινητού Μελετούν πειραματικά την ευθύγραμμη κίνηση με σταθερή επιτάχυνση Εξάγεται πρώτα η εξίσωση της ταχύτητας με το χρόνο με βάση τον ορισμό της επιτάχυνσης και στη συνέχεια από τη γραφική παράσταση ταχύτητας-χρόνου εξάγεται η σχέση θέσης-χρόνου, από το εμβαδόν της γραφικής παράστασης. Η εξίσωση θέσης-χρόνου μπορεί επίσης να βρεθεί με βάση τον ορισμό της μέσης ταχύτητας σε μια κίνηση με σταθερή επιτάχυνση Υπολογισμός των μεγεθών επιτάχυνση, θέση και ταχύτητα με βάση (α) τον ορισμό τους ή τις εξισώσεις κίνησης (β) γραφικές παραστάσεις των μεγεθών αυτών σε σχέση με το χρόνο. Στις γραφικές παραστάσεις γίνεται ο περιορισμός: (ι) εύρεση επιτάχυνσης και μετατόπισης από τη γραφική παράσταση ταχύτητας-χρόνου με την κλίση και το εμβαδόν αντίστοιχα, (ιι) εύρεση της θέσης και της ταχύτητας σε μια χρονική στιγμή από τις αντίστοιχες γραφικές παραστάσεις εριορισμός σε κινήσεις με σταθερή επιτάχυνση όπου η φορά της κίνησης μπορεί να αλλάζει Με τη χρήση της διασύνδεσης ή χρονομετρητή γίνεται μελέτη της κίνησης ενός σώματος σε ευθεία γραμμή με σταθερή επιτάχυνση με το μέτρο της ταχύτητας να (ι) αυξάνεται και (ιι) ελαττώνεται. Στη μελέτη υπολογίζεται η επιτάχυνση του κινητού
18 Χαράσσουν τη γραφική παράσταση θέσης-χρόνου από πειραματικά δεδομένα και ερμηνεύουν την κίνηση Διαπιστώνουν πειραματικά ότι η ελεύθερη πτώση κοντά στην επιφάνεια της γης είναι επιταχυνόμενη κίνηση με σταθερή επιτάχυνση και υπολογίζουν την επιτάχυνση αυτή Γράφουν τις εξισώσεις y = f(t) και υ = f(t), για την κατακόρυφη κίνηση υπό την επίδραση μόνο της βαρύτητας, κοντά στην επιφάνεια της γης Λύνουν προβλήματα κίνησης με σταθερή επιτάχυνση, με ένα ή δύο κινητά ταυτόχρονα Με βάση τη χαρτοταινία που λαμβάνεται από το χρονομετρητή ή με τη χρήση της διασύνδεσης, μελετάται ενός σώματος που κινείται σε ευθεία γραμμή με σταθερή επιτάχυνση με το μέτρο της ταχύτητας να (ι) αυξάνεται και (ιι) ελαττώνεται Με βάση πίνακα πειραματικών τιμών θέσης χρόνου ή με βάση στροβοσκοπικές φωτογραφίες της κίνησης Η επιτάχυνση που αποκτούν τα σώματα κοντά στην επιφάνεια της γης, είναι η ίδια για όλα τα σώματα και συμβολίζεται με g Μελέτη της κατακόρυφης κίνησης προς τα πάνω ή πάνω, όπως και της ελεύθερης πτώσης Έμφαση σε προβλήματα κατανόησης των φυσικών φαινομένων και μεγεθών
19 3 Νόμοι του Νεύτωνα για την κίνηση. 3.1 Δυνάμεις Αναλύουν και συνθέτουν δυνάμεις σε κάθετες διευθύνσεις Αναγνωρίζουν δυνάμεις από το περιβάλλον και τις σημειώνουν στο υπό μελέτη σώμα, σε ελεύθερο διάγραμμα δυνάμεων Εξηγούν, με απλό τρόπο, την προέλευση των δυνάμεων: βάρος, κάθετη αντίδραση, δυνάμεις επαφής (όπως από ελατήριο ή νήμα) Ανάλυση δύναμης F σε κάθετες συνιστώσες και εξαγωγή των σχέσεων: F x = Fσυνθ, Fy = Fημθ. Υπολογισμός της συνισταμένης δύο δυνάμεων κάθετων μεταξύ τους. Αναφορά του κανόνα του παραλληλογράμμου για τη γραφική εύρεση της συνισταμένης Σημειώνουν δυνάμεις σε ένα σώμα σε διάφορες περιπτώσεις, όπως: βάρος, κάθετη αντίδραση, τάση νήματος, δύναμη ελατηρίου Το βάρος οφείλεται στη βαρύτητα της γης. Η κάθετη αντίδραση σε ένα σώμα από μια επιφάνεια προέρχεται από την πίεση που δέχεται η επιφάνεια από το σώμα και έχει πάντα κάθετη διεύθυνση στην επιφάνεια. Η τάση του νήματος και η δύναμη από ένα ελατήριο προέρχονται από το βάρος του σώματος που αναρτάται από αυτά και προκαλεί στο νήμα τέντωμα ή στο ελατήριο αλλαγή του φυσικού του μήκους
20 3.2 Αδράνεια και πρώτος νόμος του Νεύτωνα Αναγνωρίζουν ότι αν η συνισταμένη δύναμη σε ένα σώμα είναι μηδέν, τότε το σώμα είτε βρίσκεται σε ηρεμία είτε σε ευθύγραμμη κίνηση με σταθερή ταχύτητα Η επίδραση δύναμης σε ένα σώμα για να διατηρείται η κίνησή του οφείλεται στην ύπαρξη της δύναμης τριβής. Όσο μειώνεται η τριβή τόσο μειώνεται το μέτρο της δύναμης που απαιτείται για να διατηρείται η κίνηση του σώματος. Χωρίς τριβή ένα σώμα σε κίνηση θα συνεχίσει να κινείται με ευθύγραμμη ομαλή κίνηση Ορίζουν την αδράνεια των σωμάτων Η ιδιότητα που έχουν τα σώματα να αντιστέκονται σε οποιαδήποτε μεταβολή της κινητικής τους κατάσταση, ονομάζεται αδράνεια Επιδεικνύουν πειραματικά ή αναφέρουν παραδείγματα εκδήλωσης της αδράνειας στα σώματα Ενδεικτικά παραδείγματα: (α) το νόμισμα πάνω σε ένα χαρτονάκι που τοποθετείται πάνω σε ένα ποτήρι, (β) η ανύψωση μιας βαριάς σφαίρας με τη βοήθεια νήματος, (γ) το απότομο φρενάρισμα ή ξεκίνημα ενός αυτοκινήτου Αναφέρουν και επιδεικνύουν τους παράγοντες από τους οποίους εξαρτάται η εκδήλωση της αδράνειας στα σώματα και αναγνωρίζουν τη μάζα ως το μέτρο της αδράνειας των σωμάτων Όσο πιο μεγάλη είναι η μάζα ενός σώματος ή όσο πιο γρήγορα γίνεται η προσπάθεια μεταβολής της κινητικής κατάστασης ενός σώματος, τόσο πιο έντονα εκδηλώνεται η αδράνεια στα σώματα Διατυπώνουν τον πρώτο νόμο του Νεύτωνα Ένα σώμα βρίσκεται σε κατάσταση ηρεμίας ή ευθύγραμμης ομαλής κίνησης αν η συνισταμένη δύναμη στο σώμα είναι μηδέν
21 3.2.6 Εξηγούν φαινόμενα ή καταστάσεις που οφείλονται στην αδράνεια Ενδεικτικά φαινόμενα: (α) η χρήση της ζώνης ασφαλείας στα οχήματα, (β) η τάση των επιβατών ενός οχήματος να κινηθούν αντίθετα προς τη διεύθυνση που τείνει να αλλάξει η ταχύτητα του οχήματος, όπως σε απότομο φρενάρισμα ή απότομο ξεκίνημα. 3.3 Μάζα και δεύτερος νόμος του Νεύτωνα Αναγνωρίζουν ότι η επίδραση δύναμης σε ένα σώμα προκαλεί μεταβολή της ταχύτητας του σώματος στην ίδια διεύθυνση και φορά με τη δύναμη και αναφέρουν παραδείγματα Ενδεικτικά παραδείγματα: (α) η δύναμη του βάρους αναγκάζει τα σώματα να πέφτουν προς τη γη, (β) η δύναμη αντίστασης του αέρα σε ένα κινούμενο όχημα ή της τριβής των ελαστικών του οχήματος με το δρόμο ελαττώνει το μέτρο της ταχύτητας του οχήματος, (γ) Η δύναμη του συρματόσχοινου σε ένα ανελκυστήρα προκαλεί την ανύψωση του ανελκυστήρα ενάντια στη δύναμη της βαρύτητας Συνάγουν πειραματικά τη σχέση: (α) δύναμης και επιτάχυνσης, (β) επιτάχυνσης και μάζας Με τη χρήση της διασύνδεσης βρίσκουν τη σχέση: (α) δύναμης που επιταχύνει ένα σώμα και της επιτάχυνσης που προκαλεί αυτή η δύναμη και (β) επιτάχυνσης με τη μάζα του σώματος Διατυπώνουν το δεύτερο νόμο του Νεύτωνα Η επιτάχυνση που δέχεται ένα σώμα είναι ανάλογη της δύναμης που την προκαλεί και αντιστρόφως ανάλογη της μάζας του σώματος
22 3.4 Μάζα και βάρος Εξηγούν διαφορές μάζας και βάρους (α) Η μάζα είναι η ποσότητα της ύλης σε ένα σώμα και άρα έχει μονάδες μέτρησης στο S.I. το Kilogram (Kg) ενώ το βάρος είναι δύναμη και άρα έχει μονάδες μέτρησης στο S.I. το newton. (β) Η μάζα ενός σώματος είναι σταθερή ποσότητα, ενώ το βάρος δεν έχει την ίδια τιμή όταν το σώμα αλλάζει θέση στο χώρο. (γ) η μάζα είναι μονόμετρο μέγεθος ενώ το βάρος διάνυσμα. 0,5 3.5 Τρίτος νόμος του Νεύτωνα (Νόμος δράσης-αντίδρασης) Αναγνωρίζουν ότι ένα σώμα δεν μπορεί να δέχεται δύναμη από το πουθενά αλλά από ένα δεύτερο σώμα και αναφέρουν παραδείγματα Το βάρος που δέχεται ένα σώμα οφείλεται στη γη. Η τριβή που δέχονται τα ελαστικά ενός αυτοκινήτου οφείλεται στην επιφάνεια του δρόμου. Η άνωση που δέχεται ένα σώμα βυθισμένο σε ένα υγρό οφείλεται στο ίδιο το υγρό. 0, Διατυπώνουν τον τρίτο νόμο του Νεύτωνα Ένα σώμα που δέχεται μια δύναμη από ένα δεύτερο σώμα, εξασκεί το ίδιο δύναμη ίσου μέτρου αλλά αντίθετης φοράς στο δεύτερο σώμα. Οι δυνάμεις αυτές ονομάζονται ζεύγος δράσης-αντίδρασης Διακρίνουν ζεύγη δυνάμεων δράσης-αντίδρασης Ενδεικτικά συστήματα σωμάτων: (α) μήλο που πέφτει στη γη και η γη. (β) σφαίρα που αιωρείται από νήμα, το νήμα και η γη. (γ) ένα βιβλίο πάνω στο γραφείο, το γραφείο και η γη. (δ) ένας άνθρωπος που κάθεται σε μια καρέκλα, η καρέκλα και η γη. (ε) ένα σώμα που αιωρείται με νήμα από την οροφή ενός ανελκυστήρα ή οχήματος, ο ανελκυστήρας ή το όχημα, και το νήμα
23 4 ΕΦΑΡΜΟΓΕΣ ΤΩΝ ΝΟΜΩΝ ΤΟΥ ΝΕΥΤΩΝΑ. 4.1 Ισορροπία υλικού σημείου Αναγνωρίζουν ότι για την ισορροπία ενός σώματος απαιτείται να ικανοποιείται η συνθήκη F 0, όπου F είναι η συνισταμένη δύναμη σε ένα σώμα Τονίζεται ότι η συνισταμένη δύναμη είναι το διανυσματικό άθροισμα όλων των δυνάμεων που εξασκούνται σε ένα σώμα Χρησιμοποιούν τη συνθήκη ισορροπίας ενός σώματος, F 0, στη λύση προβλημάτων Η εύρεση της συνισταμένης δύναμης απαιτεί μια απλή μεθοδολογία την οποία ο μαθητής θα διδαχθεί. Για παράδειγμα: (α) εύρεση των δυνάμεων που εξασκούνται στο σώμα, σημειώνοντας τις δυνάμεις αυτές σε ελεύθερο διάγραμμα δυνάμεων. (β) ανάλυση των δυνάμεων σε κάθετες διευθύνσεις και υπολογισμός των μέτρων αυτών των δυνάμεων. (γ) εφαρμογή της συνθήκης ισορροπίας στις δύο κάθετες διευθύνσεις. Απάντηση στην ερώτηση του προβλήματος εριορισμός σε προβλήματα ισορροπίας σε σχέση με πραγματικές καθημερινές καταστάσεις και επίδραση στο υπό μελέτη σώμα το πολύ τεσσάρων δυνάμεων. Ενδεικτικά παράδειγμα: (α) Ένας πίνακας που αιωρείται με τη βοήθεια δύο νημάτων που σχηματίζουν γωνία μεταξύ τους. (β) Ισορροπία στερεού σώματος μικρών διαστάσεων σε κεκλιμένο επίπεδο με τη βοήθεια νήματος ή ελατηρίου παράλληλο με το κεκλιμένο επίπεδο
24 4.2 Κίνηση σε ευθύγραμμη τροχιά με την επίδραση σταθερής δύναμης Εφαρμόζουν το δεύτερο νόμο του Νεύτωνα σε προβλήματα κίνησης σε ευθύγραμμη τροχιά Εφαρμογή της σχέσης F m, όπου F είναι η συνισταμένη των δυνάμεων που εξασκούνται στο σώμα, όπως ένα αυτοκίνητο ή ένα αεροπλάνο. Η δύναμη αντίστασης από τον αέρα ή / και η τριβή με το δρόμο μπορεί να δίνεται αριθμητικά στο πρόβλημα Εφαρμογή της σχέσης F m σε συνδυασμό και των σχέσεων: f (t) και x f (t). 4.3 Ελεύθερη πτώση Εφαρμόζουν το δεύτερο νόμο του Νεύτωνα στην ελεύθερη πτώση των σωμάτων Εφαρμογή της σχέσης F mg, όπου F είναι η συνισταμένη των δυνάμεων στο σώμα κατά την ελεύθερη πτώση του προς τη γη Λύση προβλημάτων πτώσης με δύο σώματα στην ίδια κατακόρυφο Κίνηση σε κεκλιμένο επίπεδο Εφαρμόζουν το δεύτερο νόμο του Νεύτωνα για την κίνηση ενός σώματος σε κεκλιμένο επίπεδο Εφαρμόζουν το δεύτερο νόμο του Νεύτωνα για την κίνηση συστήματος σωμάτων σε κεκλιμένο επίπεδο Εφαρμογή της σχέσης F m σε συνδυασμό και των σχέσεων: f (t) και x f (t), όπου F δυνάμεων στο σώμα. είναι η συνισταμένη των Εφαρμογή της σχέσης F σε συνδυασμό και των σχέσεων: m f (t) και x f (t), όπου F είναι η συνισταμένη των δυνάμεων του συστήματος και m ολ είναι η μάζα του συστήματος
25 Να επαληθευτεί η επίλυση των προβλημάτων κίνησης συστήματος σε κεκλιμένο επίπεδο που έγινε με χρήση της F m και με μια μέθοδο η οποία θα συνιστάται από: (α) χωρισμό του συστήματος σε επιμέρους μάζες, (β) εφαρμογή του δεύτερου νόμου του Νεύτωνα σε κάθε μάζα και (γ) συνδυασμός των εξισώσεων που προκύπτουν. 4.5 Εφαρμογές του τρίτου νόμου του Νεύτωνα Εφαρμόζουν τον τρίτο νόμο του Νεύτωνα στη λύση προβλημάτων Ενδεικτικά το πρόβλημα με τους δύο βαρκάρηδες οι οποίοι τραβούν ο ένας τον άλλο με σχοινί
26 5 ΕΡΓΟ ΙΣΧΥΣ ΚΑΙ ΕΝΕΡΓΕΙΑ. 5.1 Έργο σταθερής δύναμης Αναγνωρίζουν ότι όταν μια δύναμη εξασκείται σε ένα σώμα αρχικά ακίνητο, με αποτέλεσμα αυτό να μετατοπίζεται, μεταφέρεται ενέργεια στο σώμα και ονομάζεται αυτή η μεταφερόμενη ενέργεια έργο Δίνεται έμφαση στο γεγονός ότι το έργο είναι μια μορφή μεταφερόμενης ενέργειας στο σώμα που γίνεται με την επίδραση δύναμης. Να γίνει αναφορά στο ότι μια άλλη μορφή μεταφερόμενης ενέργειας είναι η θερμότητα, η οποία μεταφέρεται όταν υπάρχει διαφορά θερμοκρασίας μεταξύ δύο σωμάτων ή συστημάτων Αναγνωρίζουν ότι το έργο μπορεί να είναι θετικό, αρνητικό ή μηδέν και ερμηνεύουν το πρόσημο σε κάθε περίπτωση Θετικό έργο σημαίνει ότι προσφέρεται ενέργεια στο σώμα με την επίδραση δύναμης και άρα αυξάνεται η ενέργειά του. Αρνητικό έργο σημαίνει ότι φεύγει ενέργεια από το σώμα και άρα ελαττώνεται η ενέργειά του. Φυσικά για τη διατήρηση της ενέργειας στο σύστημα, όταν αυξάνεται (ελαττώνεται) η ενέργεια του σώματος, τότε ελαττώνεται (αυξάνεται) στο ίδιο ποσό η ενέργεια του σώματος ή συστήματος που παράγει το έργο Υπολογίζουν το έργο σταθερής δύναμης Με βάση τη σχέση W = Fxσυνθ, όπου F το μέτρο της δύναμης, x το μέτρο της μετατόπισης και θ η γωνία μεταξύ της δύναμης και της μετατόπισης
27 5.2 Έργο μεταβλητής δύναμης με σταθερή διεύθυνση Υπολογίζουν το έργο μεταβλητής δύναμης με σταθερή διεύθυνση Μελετούν πειραματικά τους παράγοντες που επηρεάζουν το μέτρο και τη πολικότητα της ΗΕΔ από επαγωγή που δημιουργείται σε ένα σωληνοειδές Με βάση τη γραφική παράσταση F = f(x), όπου το έργο ισούται με το εμβαδόν της γραφικής παράστασης. (για παράδειγμα ένα ελατήριο) Όταν αλλάζει φορά η δύναμη σε σχέση με τη μετατόπιση το έργο γίνεται αρνητικό και αυτό φαίνεται γραφικά από το γεγονός ότι η δύναμη αλλάζει πρόσημο. Δίνεται έμφαση στην εύρεση του συνολικού έργου και του μέγιστου έργου, δηλαδή στο μέγιστο ποσό ενέργειας που μεταφέρεται στο σώμα Ισχύς Αναγνωρίζουν τη χρησιμότητα του ρυθμού μεταφοράς ή μετατροπής μιας μορφής ενέργειας σε άλλη και δίνουν παραδείγματα που ενισχύουν τη θέση αυτή Ορίζουν τη ισχύ ως το ρυθμό μεταφοράς ή μετατροπής μιας μορφής ενέργειας σε άλλη μορφή Ορίζουν τη μονάδα μέτρησης της ισχύος στο σύστημα S.I Η χρησιμότητα και άρα η αναγκαιότητα του ορισμού της ισχύος μπορεί να φανεί μέσα από παραδείγματα από την καθημερινή ζωή: όπως το έργο που παράγει ένας γερανός σε σύγκριση με αυτό ενός άλλου γερανού και μετά να γίνει σύγκριση του ρυθμού παραγωγής του έργου, ώστε να εξαγάγουμε το συμπέρασμα για το ποιος γερανός είναι περισσότερο αποδοτικός Έμφαση να δίνεται τόσο στον ορισμό με λόγια όσο και στην αντίστοιχη μαθηματική σχέση: P = W/t Watt (W) είναι η ενέργεια σε joules (j) που μεταφέρεται ή μετατρέπεται από μια μορφή σε μια άλλη μορφή ανά δευτερόλεπτο
28 5.4 Βαρυτική δυναμική ενέργεια Αναγνωρίζουν ότι το πεδίο βαρύτητας της γης παράγει έργο στα σώματα που βρίσκονται σ αυτό με την επίδραση της βαρυτικής δύναμης (βάρος) Το βάρος είναι η δύναμη που δέχεται ένα σώμα όταν βρεθεί σε βαρυτικό πεδίο και παράγει έργο όταν προκαλεί μετατόπιση του σώματος Ονομάζουν δυναμική ενέργεια βαρύτητας τη ενέργεια που έχει ένα σώμα λόγω της θέσης του μέσα στο πεδίο βαρύτητας και συνδέουν τη μεταβολή της δυναμικής ενέργειας με το έργο του βάρους Ένα σώμα στο βαρυτικό πεδίο δέχεται τη δύναμη του βάρους. Επομένως για να μετατοπιστεί ενάντια στη δύναμη του βάρους απαιτείται η επίδραση εξωτερικής δύναμης αντίθετης προς το βάρος. Αυτό σημαίνει αύξηση της ενέργειας του σώματος, η οποία αποθηκεύεται στο σώμα ως δυναμική ενέργεια βαρύτητας Υπολογίζουν το έργο του βάρους στην περίπτωση που το μέτρο του βάρους είναι σχεδόν σταθερό Το έργο της δύναμης του βαρυτικού πεδίου για μετατοπίσεις κοντά στην επιφάνεια της γης, όπου η ένταση του πεδίου βαρύτητας είναι σχεδόν σταθερή, ισούται με mgh, όπου h η κατακόρυφη μετατόπιση του σώματος Αναγνωρίζουν ότι η τιμή της δυναμικής ενέργειας σε ένα σημείο του βαρυτικού πεδίου, εξαρτάται από την τιμή της δυναμικής ενέργειας σε ένα δεύτερο σημείο, που λαμβάνεται ως σημείο αναφοράς στο οποίο δίνουμε, αυθαίρετα, την τιμή μηδέν Στην περίπτωση της μετατόπισης ενός σώματος σε σημεία κοντά στην επιφάνεια της γης, λαμβάνουμε ως σημείο αναφοράς για την τιμή μηδέν της βαρυτικής δυναμικής ενέργειας την επιφάνεια της γης. Επομένως μια τιμή της δυναμικής ενέργειας θα αναφέρεται ως προς την επιφάνεια της γης
29 5.4.5 Αναγνωρίζουν και αποδεικνύουν ότι η μεταβολή της βαρυτικής δυναμικής ενέργειας κατά τη μετατόπιση του σώματος από μια θέση σε μια άλλη θέση δεν εξαρτάται από τη διαδρομή που ακολουθεί το σώμα αλλά από την μεταξύ τους κατακόρυφη απόσταση Η απόδειξη γίνεται μέσα από ένα απλό παράδειγμα μετατόπισης του σώματος κατά μήκος ενός κεκλιμένου επιπέδου και της κατακόρυφης μετατόπισης του σώματος στο ίδιο σημείο, όπου υπολογίζεται και συγκρίνεται το έργο του βάρους στις δύο περιπτώσεις. 5.5 Ελαστική δυναμική ενέργεια Ορίζουν την ελαστική δυναμική ενέργεια Η ελαστική δυναμική ενός σώματος είναι το έργο που παράγεται στο σώμα από μια δύναμη της μορφής F = Kx, όπου x είναι η επιμήκυνση ή η συσπείρωση του σώματος (όπως ένα ελατήριο) και Κ είναι μια σταθερά, χαρακτηριστική του σώματος Η ελαστική δυναμική ενέργεια δίνεται από τη σχέση E 1 Kx Μηχανική ενέργεια και αρχή διατήρησης της μηχανικής ενέργειας Ορίζουν το άθροισμα της κινητικής και της συνολικής δυναμικής ενέργειας ενός σώματος ως τη μηχανική ενέργεια του σώματος και εξηγούν τη σημασία αυτού του αθροίσματος Η διατήρηση της μηχανικής ενέργειας υπό ορισμένες προϋποθέσεις λύνει αρκετά προβλήματα στη μηχανική Δίνεται έμφαση στις εφαρμογές της αρχής διατήρησης της μηχανικής ενέργειας, όπως και του θεωρήματος έργου-ενέργειας
ΘΕΜΑ Α Παράδειγμα 1. Α1. Ο ρυθμός μεταβολής της ταχύτητας ονομάζεται και α. μετατόπιση. β. επιτάχυνση. γ. θέση. δ. διάστημα.
 ΘΕΜΑ Α Παράδειγμα 1 Α1. Ο ρυθμός μεταβολής της ταχύτητας ονομάζεται και α. μετατόπιση. β. επιτάχυνση. γ. θέση. δ. διάστημα. Α2. Για τον προσδιορισμό μιας δύναμης που ασκείται σε ένα σώμα απαιτείται να
ΘΕΜΑ Α Παράδειγμα 1 Α1. Ο ρυθμός μεταβολής της ταχύτητας ονομάζεται και α. μετατόπιση. β. επιτάχυνση. γ. θέση. δ. διάστημα. Α2. Για τον προσδιορισμό μιας δύναμης που ασκείται σε ένα σώμα απαιτείται να
Φυσικά μεγέθη. Φυσική α λυκείου ΕΙΣΑΓΩΓΗ. Όλα τα φυσικά μεγέθη τα χωρίζουμε σε δύο κατηγορίες : Α. τα μονόμετρα. Β.
 ΕΙΣΑΓΩΓΗ Φυσικά μεγέθη Όλα τα φυσικά μεγέθη τα χωρίζουμε σε δύο κατηγορίες : Α. τα μονόμετρα Β. τα διανυσματικά Μονόμετρα ονομάζουμε τα μεγέθη εκείνα τα οποία για να τα γνωρίζουμε χρειάζεται να ξέρουμε
ΕΙΣΑΓΩΓΗ Φυσικά μεγέθη Όλα τα φυσικά μεγέθη τα χωρίζουμε σε δύο κατηγορίες : Α. τα μονόμετρα Β. τα διανυσματικά Μονόμετρα ονομάζουμε τα μεγέθη εκείνα τα οποία για να τα γνωρίζουμε χρειάζεται να ξέρουμε
ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΕΠΑΝΑΛΗΨΗ ΘΕΩΡΙΑΣ 2017
 ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΕΠΑΝΑΛΗΨΗ ΘΕΩΡΙΑΣ 2017 ΚΕΦΑΛΑΙΟ 1 ο ΕΙΣΑΓΩΓΗ 1.3 Τα φυσικά μεγέθη και οι μονάδες τους 1. Ποια μεγέθη ονομάζονται θεμελιώδη; Θεμελιώδη ονομάζονται τα μεγέθη τα οποία δεν ορίζονται με
ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΕΠΑΝΑΛΗΨΗ ΘΕΩΡΙΑΣ 2017 ΚΕΦΑΛΑΙΟ 1 ο ΕΙΣΑΓΩΓΗ 1.3 Τα φυσικά μεγέθη και οι μονάδες τους 1. Ποια μεγέθη ονομάζονται θεμελιώδη; Θεμελιώδη ονομάζονται τα μεγέθη τα οποία δεν ορίζονται με
minimath.eu Φυσική A ΛΥΚΕΙΟΥ Περικλής Πέρρος 1/1/2014
 minimath.eu Φυσική A ΛΥΚΕΙΟΥ Περικλής Πέρρος 1/1/014 minimath.eu Περιεχόμενα Κινηση 3 Ευθύγραμμη ομαλή κίνηση 4 Ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 5 Δυναμικη 7 Οι νόμοι του Νεύτωνα 7 Τριβή 8 Ομαλη κυκλικη
minimath.eu Φυσική A ΛΥΚΕΙΟΥ Περικλής Πέρρος 1/1/014 minimath.eu Περιεχόμενα Κινηση 3 Ευθύγραμμη ομαλή κίνηση 4 Ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 5 Δυναμικη 7 Οι νόμοι του Νεύτωνα 7 Τριβή 8 Ομαλη κυκλικη
Φυσική Β Γυμνασίου Συνοπτικές Σημειώσεις Επανάληψης
 Φυσική Β Γυμνασίου Συνοπτικές Σημειώσεις Επανάληψης Επιμέλεια: Αγκανάκης Α. Παναγιώτης Κεφάλαιο 1 Φυσικά Μεγέθη: τα μεγέθη που μελετάει η Φυσική Επιστήμη Κατηγορίες: 1. Θεμελιώδη a. Μάζα (kg) b. Μήκος
Φυσική Β Γυμνασίου Συνοπτικές Σημειώσεις Επανάληψης Επιμέλεια: Αγκανάκης Α. Παναγιώτης Κεφάλαιο 1 Φυσικά Μεγέθη: τα μεγέθη που μελετάει η Φυσική Επιστήμη Κατηγορίες: 1. Θεμελιώδη a. Μάζα (kg) b. Μήκος
Γ. Β Α Λ Α Τ Σ Ο Σ. 4ο ΓΥΜΝΑΣΙΟ ΛΑΜΙΑΣ 1. Γιώργος Βαλατσός Φυσικός Msc
 4ο ΓΥΜΝΑΣΙΟ ΛΑΜΙΑΣ 1 1. Πότε τα σώματα θεωρούνται υλικά σημεία; Αναφέρεται παραδείγματα. Στη φυσική πολλές φορές είναι απαραίτητο να μελετήσουμε τα σώματα χωρίς να λάβουμε υπόψη τις διαστάσεις τους. Αυτό
4ο ΓΥΜΝΑΣΙΟ ΛΑΜΙΑΣ 1 1. Πότε τα σώματα θεωρούνται υλικά σημεία; Αναφέρεται παραδείγματα. Στη φυσική πολλές φορές είναι απαραίτητο να μελετήσουμε τα σώματα χωρίς να λάβουμε υπόψη τις διαστάσεις τους. Αυτό
ΚΙΝΗΜΑΤΙΚΗ ΥΛΙΚΟΥ ΣΗΜΕΙΟΥ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ
 ΚΙΝΗΜΑΤΙΚΗ ΥΛΙΚΟΥ ΣΗΜΕΙΟΥ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ ΘΕΣΗ ΤΡΟΧΙΑ ΜΕΤΑΤΟΠΙΣΗ ΚΑΙ ΔΙΑΣΤΗΜΑ. Παρατηρώντας τις εικόνες προσπαθήστε να ορίσετε τις θέσεις των διαφόρων ηρώων των κινουμένων σχεδίων. Ερώτηση: Πότε ένα σώμα
ΚΙΝΗΜΑΤΙΚΗ ΥΛΙΚΟΥ ΣΗΜΕΙΟΥ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ ΘΕΣΗ ΤΡΟΧΙΑ ΜΕΤΑΤΟΠΙΣΗ ΚΑΙ ΔΙΑΣΤΗΜΑ. Παρατηρώντας τις εικόνες προσπαθήστε να ορίσετε τις θέσεις των διαφόρων ηρώων των κινουμένων σχεδίων. Ερώτηση: Πότε ένα σώμα
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 2014
 1 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 2014 ΘΕΜΑ Α.1 Α1. Να χαρακτηρίσετε με (Σ) τις σωστές και με (Λ) τις λανθασμένες προτάσεις Στην ευθύγραμμα ομαλά επιβραδυνόμενη κίνηση: Α. Η ταχύτητα
1 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 2014 ΘΕΜΑ Α.1 Α1. Να χαρακτηρίσετε με (Σ) τις σωστές και με (Λ) τις λανθασμένες προτάσεις Στην ευθύγραμμα ομαλά επιβραδυνόμενη κίνηση: Α. Η ταχύτητα
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. A.1 Μια διαφορά
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. A.1 Μια διαφορά
1. Ποια μεγέθη ονομάζονται μονόμετρα και ποια διανυσματικά;
 ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Ποια μεγέθη ονομάζονται μονόμετρα και ποια διανυσματικά; Μονόμετρα ονομάζονται τα μεγέθη τα οποία, για να τα προσδιορίσουμε πλήρως, αρκεί να γνωρίζουμε
ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Ποια μεγέθη ονομάζονται μονόμετρα και ποια διανυσματικά; Μονόμετρα ονομάζονται τα μεγέθη τα οποία, για να τα προσδιορίσουμε πλήρως, αρκεί να γνωρίζουμε
1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη;
 ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης. Στην Κινηματική
ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης. Στην Κινηματική
kg(χιλιόγραμμο) s(δευτερόλεπτο) Ένταση ηλεκτρικού πεδίου Α(Αμπέρ) Ένταση φωτεινής πηγής cd (καντέλα) Ποσότητα χημικής ουσίας mole(μόλ)
 ΕΙΣΑΓΩΓΗ- ΦΥΣΙΚΑ ΜΕΓΕΘΗ Στα φυσικά φαινόμενα εμφανίζονται κάποιες ιδιότητες της ύλης. Για να περιγράψουμε αυτές τις ιδιότητες χρησιμοποιούμε τα φυσικά μεγέθη. Τέτοια είναι η μάζα, ο χρόνος, το ηλεκτρικό
ΕΙΣΑΓΩΓΗ- ΦΥΣΙΚΑ ΜΕΓΕΘΗ Στα φυσικά φαινόμενα εμφανίζονται κάποιες ιδιότητες της ύλης. Για να περιγράψουμε αυτές τις ιδιότητες χρησιμοποιούμε τα φυσικά μεγέθη. Τέτοια είναι η μάζα, ο χρόνος, το ηλεκτρικό
Κίνηση ΚΕΦΑΛΑΙΟ 2 Β ΓΥΜΝΑΣΙΟΥ
 Κίνηση ΚΕΦΑΛΑΙΟ 2 Β ΓΥΜΝΑΣΙΟΥ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης.
Κίνηση ΚΕΦΑΛΑΙΟ 2 Β ΓΥΜΝΑΣΙΟΥ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης.
2. Μια μοτοσυκλέτα τρέχει με ταχύτητα 108 km/h. α) Σε πόσο χρόνο διανύει τα 120 m; β) Πόσα μέτρα διανύει σε 5 s;
 1. Αυτοκίνητο κινείται σε ευθύγραμμο δρόμο με σταθερή φορά και το ταχύμετρο του (κοντέρ) δείχνει συνεχώς 36 km/h. α) Τι είδους κίνηση κάνει το αυτοκίνητο; β) Να μετατρέψετε την ταχύτητα του αυτοκινήτου
1. Αυτοκίνητο κινείται σε ευθύγραμμο δρόμο με σταθερή φορά και το ταχύμετρο του (κοντέρ) δείχνει συνεχώς 36 km/h. α) Τι είδους κίνηση κάνει το αυτοκίνητο; β) Να μετατρέψετε την ταχύτητα του αυτοκινήτου
Οδηγός βαθμολόγησης Εξεταστικού Δοκιμίου Α Λυκείου
 ΛΥΚΕΙΟ ΜΑΚΑΡΙΟΥ Γ ΛΑΡΝΑΚΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2014-15 Οδηγός βαθμολόγησης Εξεταστικού Δοκιμίου Α Λυκείου 1) Να γράψετε 3 διανυσματικά μεγέθη και 2 μονόμετρα μεγέθη καθώς και τις μονάδες μέτρησής τους (στο
ΛΥΚΕΙΟ ΜΑΚΑΡΙΟΥ Γ ΛΑΡΝΑΚΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2014-15 Οδηγός βαθμολόγησης Εξεταστικού Δοκιμίου Α Λυκείου 1) Να γράψετε 3 διανυσματικά μεγέθη και 2 μονόμετρα μεγέθη καθώς και τις μονάδες μέτρησής τους (στο
ΚΕΦΑΛΑΙΟ 1.1 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ
 7 ΚΕΦΑΛΑΙΟ 1.1 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ ΘΕΜΑΤΑ Α Α. ΚΙΝΗΣΗ - ΜΕΤΑΤΟΠΙΣΗ ΧΡΟΝΟΣ ΤΑΧΥΤΗΤΑ Στις ακόλουθες προτάσεις να διαλέξετε την σωστή απάντηση: 1. Ένα σημειακό αντικείμενο κινείται σε ευθύγραμμο δρόμο ο οποίος
7 ΚΕΦΑΛΑΙΟ 1.1 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ ΘΕΜΑΤΑ Α Α. ΚΙΝΗΣΗ - ΜΕΤΑΤΟΠΙΣΗ ΧΡΟΝΟΣ ΤΑΧΥΤΗΤΑ Στις ακόλουθες προτάσεις να διαλέξετε την σωστή απάντηση: 1. Ένα σημειακό αντικείμενο κινείται σε ευθύγραμμο δρόμο ο οποίος
ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ ΦΡΟΝΤΙΣΤΗΡΙΟ ΕΠΙΛΟΓΗ
 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Τι ονομάζουμε κίνηση ενός κινητού; 2. Τι ονομάζουμε τροχιά ενός κινητού; 3. Τι ονομάζουμε υλικό σημείο; 4. Ποια μεγέθη ονομάζονται μονόμετρα και ποια διανυσματικά;
ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Τι ονομάζουμε κίνηση ενός κινητού; 2. Τι ονομάζουμε τροχιά ενός κινητού; 3. Τι ονομάζουμε υλικό σημείο; 4. Ποια μεγέθη ονομάζονται μονόμετρα και ποια διανυσματικά;
Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd Email : stvrentzou@gmail.com
 1 1.1 Ευθύγραμμη κίνηση 1. Να αναφέρετε ποια από τα σώματα που φαίνονται στην εικόνα κινούνται. Α. Ως προς τη Γη B. Ως προς το αυτοκίνητο. Α. Ως προς τη Γη κινούνται το αυτοκίνητο, το αεροπλάνο και ο γλάρος.
1 1.1 Ευθύγραμμη κίνηση 1. Να αναφέρετε ποια από τα σώματα που φαίνονται στην εικόνα κινούνται. Α. Ως προς τη Γη B. Ως προς το αυτοκίνητο. Α. Ως προς τη Γη κινούνται το αυτοκίνητο, το αεροπλάνο και ο γλάρος.
Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου
 Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Όταν ένα σώμα ισορροπεί τότε: i. Ο ρυθμός μεταβολής της ταχύτητάς του
Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Όταν ένα σώμα ισορροπεί τότε: i. Ο ρυθμός μεταβολής της ταχύτητάς του
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 2014
 1 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 014 ΘΕΜΑ Α.1 Α1. Να χαρακτηρίσετε με (Σ) τις σωστές και με (Λ) τις λανθασμένες προτάσεις Στην ευθύγραμμα ομαλά επιβραδυνόμενη κίνηση: Α. Η ταχύτητα
1 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 014 ΘΕΜΑ Α.1 Α1. Να χαρακτηρίσετε με (Σ) τις σωστές και με (Λ) τις λανθασμένες προτάσεις Στην ευθύγραμμα ομαλά επιβραδυνόμενη κίνηση: Α. Η ταχύτητα
ΕΝΟΤΗΤΑ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ
 ΕΝΟΤΗΤΑ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ 1. Τι λέμε δύναμη, πως συμβολίζεται και ποια η μονάδα μέτρησής της. Δύναμη είναι η αιτία που προκαλεί τη μεταβολή της κινητικής κατάστασης των σωμάτων ή την παραμόρφωσή
ΕΝΟΤΗΤΑ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ 1. Τι λέμε δύναμη, πως συμβολίζεται και ποια η μονάδα μέτρησής της. Δύναμη είναι η αιτία που προκαλεί τη μεταβολή της κινητικής κατάστασης των σωμάτων ή την παραμόρφωσή
ΛΥΚΕΙΟ ΑΓΙΑΣ ΦΥΛΑΞΕΩΣ ΛΕΜΕΣΟΣ Σχολική Χρονιά: ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ MAIOY - ΙΟΥΝΙΟΥ
 ΛΥΚΕΙΟ ΑΓΙΑΣ ΦΥΛΑΞΕΩΣ ΛΕΜΕΣΟΣ Σχολική Χρονιά: 010-011 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ MAIOY - ΙΟΥΝΙΟΥ Μάθημα: ΦΥΣΙΚΗ Τάξη: Α Ενιαίου Λυκείου Ημερομηνία: 01/06/011 Χρόνος: ΩΡΕΣ Ονοματεπώνυμο:.. Τμήμα: Οδηγίες:
ΛΥΚΕΙΟ ΑΓΙΑΣ ΦΥΛΑΞΕΩΣ ΛΕΜΕΣΟΣ Σχολική Χρονιά: 010-011 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ MAIOY - ΙΟΥΝΙΟΥ Μάθημα: ΦΥΣΙΚΗ Τάξη: Α Ενιαίου Λυκείου Ημερομηνία: 01/06/011 Χρόνος: ΩΡΕΣ Ονοματεπώνυμο:.. Τμήμα: Οδηγίες:
ΦΥΣΙΚΗ ΚΕΦΑΛΑΙΟ 1 Ο. 1) Τα θεµελιώδη µεγέθη: Το µήκος, ο χρόνος και η µάζα
 ΦΥΣΙΚΗ ΚΕΦΑΛΑΙΟ 1 Ο 1) Τα θεµελιώδη µεγέθη: Το µήκος, ο χρόνος και η µάζα Μερικά φυσικά µεγέθη προκύπτουν άµεσα από τη διαίσθησή µας. εν ορίζονται µε τη βοήθεια άλλων µεγεθών. Αυτά τα φυσικά µεγέθη ονοµάζονται
ΦΥΣΙΚΗ ΚΕΦΑΛΑΙΟ 1 Ο 1) Τα θεµελιώδη µεγέθη: Το µήκος, ο χρόνος και η µάζα Μερικά φυσικά µεγέθη προκύπτουν άµεσα από τη διαίσθησή µας. εν ορίζονται µε τη βοήθεια άλλων µεγεθών. Αυτά τα φυσικά µεγέθη ονοµάζονται
ΠΕΡΙΕΧΟΜΕΝΑ 1. ΕΙΣΑΓΩΓΗ
 ΠΕΡΙΕΧΟΜΕΝΑ. ΕΙΣΑΓΩΓΗ.. ΜΟΝΟΜΕΤΡΑ ΚΑΙ ΔΙΑΝΥΣΜΑΤΙΚΑ ΜΕΓΕΘΗ.. ΤΟ ΔΙΕΘΝΕΣ ΣΥΣΤΗΜΑ ΜΟΝΑΔΩΝ SI.3. ΜΟΝΑΔΕΣ ΜΕΤΡΗΣΗΣ ΜΗΚΟΥΣ, ΕΜΒΑΔΟΥ, ΟΓΚΟΥ ΚΑΙ ΠΥΚΝΟΤΗΤΑΣ..4. ΜΕΤΑΒΟΛΗ ΚΑΙ ΡΥΘΜΟΣ ΜΕΤΑΒΟΛΗΣ 3. ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ
ΠΕΡΙΕΧΟΜΕΝΑ. ΕΙΣΑΓΩΓΗ.. ΜΟΝΟΜΕΤΡΑ ΚΑΙ ΔΙΑΝΥΣΜΑΤΙΚΑ ΜΕΓΕΘΗ.. ΤΟ ΔΙΕΘΝΕΣ ΣΥΣΤΗΜΑ ΜΟΝΑΔΩΝ SI.3. ΜΟΝΑΔΕΣ ΜΕΤΡΗΣΗΣ ΜΗΚΟΥΣ, ΕΜΒΑΔΟΥ, ΟΓΚΟΥ ΚΑΙ ΠΥΚΝΟΤΗΤΑΣ..4. ΜΕΤΑΒΟΛΗ ΚΑΙ ΡΥΘΜΟΣ ΜΕΤΑΒΟΛΗΣ 3. ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ
ΕΠΙΣΚΟΠΗΣΗ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ
 ΕΠΙΣΚΟΠΗΣΗ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΕΓΧΕΙΡΙΔΙΟ ΔΙΔΑΚΤΕΑΣ ΥΛΗΣ ΔΗΜΗΤΡΙΟΣ ΘΕΟΔΩΡΙΔΗΣ Κεφάλαιο 1.1 Ευθύγραμμη κίνηση 1. Τι ονομάζουμε κίνηση; Τι ονομάζουμε τροχιά; Ποια είδη τροχιών γνωρίζετε; Κίνηση ενός αντικειμένου
ΕΠΙΣΚΟΠΗΣΗ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΕΓΧΕΙΡΙΔΙΟ ΔΙΔΑΚΤΕΑΣ ΥΛΗΣ ΔΗΜΗΤΡΙΟΣ ΘΕΟΔΩΡΙΔΗΣ Κεφάλαιο 1.1 Ευθύγραμμη κίνηση 1. Τι ονομάζουμε κίνηση; Τι ονομάζουμε τροχιά; Ποια είδη τροχιών γνωρίζετε; Κίνηση ενός αντικειμένου
ΛΥΚΕΙΟ ΠΑΛΟΥΡΙΩΤΙΣΣΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑÏΟΥ- ΙΟΥΝΙΟΥ 2014
 ΛΥΚΕΙΟ ΠΑΛΟΥΡΙΩΤΙΣΣΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2013-2014 ΒΑΘΜΟΣ...... ΟΛΟΓΡΑΦΩΣ... ΥΠΟΓΡΑΦΗ... ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑÏΟΥ- ΙΟΥΝΙΟΥ 2014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΗΜΕΡΟΜΗΝΙΑ: 26/05/2014 ΧΡΟΝΟΣ: 2 ΩΡΕΣ ΩΡΑ: 7.45-9.45
ΛΥΚΕΙΟ ΠΑΛΟΥΡΙΩΤΙΣΣΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2013-2014 ΒΑΘΜΟΣ...... ΟΛΟΓΡΑΦΩΣ... ΥΠΟΓΡΑΦΗ... ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑÏΟΥ- ΙΟΥΝΙΟΥ 2014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΗΜΕΡΟΜΗΝΙΑ: 26/05/2014 ΧΡΟΝΟΣ: 2 ΩΡΕΣ ΩΡΑ: 7.45-9.45
ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ μονόμετρα. διανυσματικά Η μάζα ενός σώματος αποτελεί το μέτρο της αδράνειάς του, πυκνότητα ενός υλικού d = m/v
 ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ Υπάρχουν φυσικά μεγέθη που ορίζονται πλήρως, όταν δοθεί η αριθμητική τιμή τους και λέγονται μονόμετρα.. Μονόμετρα μεγέθη είναι ο χρόνος, η μάζα, η θερμοκρασία, η πυκνότητα, η ενέργεια,
ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ Υπάρχουν φυσικά μεγέθη που ορίζονται πλήρως, όταν δοθεί η αριθμητική τιμή τους και λέγονται μονόμετρα.. Μονόμετρα μεγέθη είναι ο χρόνος, η μάζα, η θερμοκρασία, η πυκνότητα, η ενέργεια,
ΛΥΚΕΙΟ ΠΟΛΕΜΙΔΙΩΝ Σχολική Χρονιά ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ Μάθημα: ΦΥΣΙΚΗ Τάξη: A Ενιαίου Λυκείου Βαθμός:...
 ΛΥΚΕΙΟ ΠΟΛΕΜΙΔΙΩΝ Σχολική Χρονιά 011-01 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 01 Μάθημα: ΦΥΣΙΚΗ Τάξη: A Ενιαίου Λυκείου Βαθμός:... Ημερομηνία: 3/05/01 Διάρκεια: ώρες Ονοματεπώνυμο:... Τμήμα:... ΟΔΗΓΙΕΣ:
ΛΥΚΕΙΟ ΠΟΛΕΜΙΔΙΩΝ Σχολική Χρονιά 011-01 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 01 Μάθημα: ΦΥΣΙΚΗ Τάξη: A Ενιαίου Λυκείου Βαθμός:... Ημερομηνία: 3/05/01 Διάρκεια: ώρες Ονοματεπώνυμο:... Τμήμα:... ΟΔΗΓΙΕΣ:
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα. ΔΙΑΛΕΞΗ 03 Νόμοι κίνησης του Νεύτωνα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 03 Νόμοι κίνησης του Νεύτωνα ΦΥΣ102 1 Δύναμη είναι: Η αιτία που προκαλεί μεταβολή
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 03 Νόμοι κίνησης του Νεύτωνα ΦΥΣ102 1 Δύναμη είναι: Η αιτία που προκαλεί μεταβολή
ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑÏΟΥ- ΙΟΥΝΙΟΥ 2014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΗΜΕΡΟΜΗΝΙΑ: 23/05/2014 ΤΑΞΗ: Α ΛΥΚΕΙΟΥ ΔΙΑΡΚΕΙΑ: 2 ΩΡΕΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:... ΤΜΗΜΑ:...
 1 ΛΥΚΕΙΟ ΑΓΙΟΥ ΑΝΤΩΝΙΟΥ ΛΕΜΕΣΟΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 013-014 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑÏΟΥ- ΙΟΥΝΙΟΥ 014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΗΜΕΡΟΜΗΝΙΑ: 3/05/014 ΤΑΞΗ: Α ΛΥΚΕΙΟΥ ΔΙΑΡΚΕΙΑ: ΩΡΕΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:... ΤΜΗΜΑ:... ΒΑΘΜΟΣ:...
1 ΛΥΚΕΙΟ ΑΓΙΟΥ ΑΝΤΩΝΙΟΥ ΛΕΜΕΣΟΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 013-014 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑÏΟΥ- ΙΟΥΝΙΟΥ 014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΗΜΕΡΟΜΗΝΙΑ: 3/05/014 ΤΑΞΗ: Α ΛΥΚΕΙΟΥ ΔΙΑΡΚΕΙΑ: ΩΡΕΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:... ΤΜΗΜΑ:... ΒΑΘΜΟΣ:...
ΛΥΚΕΙΟ ΕΘΝΟΜΑΡΤΥΡΑ ΚΥΠΡΙΑΝΟΥ(ΣΤΡΟΒΟΛΟΥ) ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ ΤΑΞΗ Α ΛΥΚΕΙΟΥ ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΙΟΥ ΙΟΥΝΙΟΥ 2010
 ΛΥΚΕΙΟ ΕΘΝΟΜΑΡΤΥΡΑ ΚΥΠΡΙΑΝΟΥ(ΣΤΡΟΒΟΛΟΥ) ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2009-10 ΤΑΞΗ Α ΛΥΚΕΙΟΥ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΗΜΕΡΟΜΗΝΙΑ:04/06/2010 Βαθμός.. Ολογράφως. Υπογραφή ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΙΟΥ ΙΟΥΝΙΟΥ 2010 Όνομα μαθητή/τριας...τμήμα...αριθμός...
ΛΥΚΕΙΟ ΕΘΝΟΜΑΡΤΥΡΑ ΚΥΠΡΙΑΝΟΥ(ΣΤΡΟΒΟΛΟΥ) ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2009-10 ΤΑΞΗ Α ΛΥΚΕΙΟΥ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΗΜΕΡΟΜΗΝΙΑ:04/06/2010 Βαθμός.. Ολογράφως. Υπογραφή ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΙΟΥ ΙΟΥΝΙΟΥ 2010 Όνομα μαθητή/τριας...τμήμα...αριθμός...
Ευθύγραμμη ομαλή κίνηση
 Διάγραμμα s - Ευθύγραμμη Κίνηση (m) Μέση αριθμητική ταχύτητα (μονόμετρο) Μέση διανυσματική ταχύτητα Μέση επιτάχυνση 1 4 Διάγραμμα u - (sec) Απόσταση (x) ονομάζουμε την ευθεία που ενώνει την αρχική και
Διάγραμμα s - Ευθύγραμμη Κίνηση (m) Μέση αριθμητική ταχύτητα (μονόμετρο) Μέση διανυσματική ταχύτητα Μέση επιτάχυνση 1 4 Διάγραμμα u - (sec) Απόσταση (x) ονομάζουμε την ευθεία που ενώνει την αρχική και
ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ
 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Το έργο μίας από τις δυνάμεις που ασκούνται σε ένα σώμα. α. είναι μηδέν όταν το σώμα είναι ακίνητο β. έχει πρόσημο το οποίο εξαρτάται από τη γωνία
ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Το έργο μίας από τις δυνάμεις που ασκούνται σε ένα σώμα. α. είναι μηδέν όταν το σώμα είναι ακίνητο β. έχει πρόσημο το οποίο εξαρτάται από τη γωνία
ΕΠΑΝΑΛΗΨΗ Α ΛΥΚΕΙΟΥ στη Φυσική
 Α ΤΑΞΗ ΕΠΑΝΑΛΗΨΗ Α ΛΥΚΕΙΟΥ στη Φυσική ΜΕΡΟΣ 1 : Ευθύγραμμες Κινήσεις 1. Να επαναληφθεί το τυπολόγιο όλων των κινήσεων - σελίδα 2 (ευθύγραμμων και ομαλών, ομαλά μεταβαλλόμενων) 2. Να επαναληφθούν όλες οι
Α ΤΑΞΗ ΕΠΑΝΑΛΗΨΗ Α ΛΥΚΕΙΟΥ στη Φυσική ΜΕΡΟΣ 1 : Ευθύγραμμες Κινήσεις 1. Να επαναληφθεί το τυπολόγιο όλων των κινήσεων - σελίδα 2 (ευθύγραμμων και ομαλών, ομαλά μεταβαλλόμενων) 2. Να επαναληφθούν όλες οι
Τα Θέματα που είναι με σκούρο φόντο φέτος (2014) είναι εκτός ύλης
 Τα Θέματα που είναι με σκούρο φόντο φέτος (2014) είναι εκτός ύλης 2013 ΘΕΜΑ Α Για τις ερωτήσεις 1 έως 4 γράψτε τον αριθμό τις ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Για ένα
Τα Θέματα που είναι με σκούρο φόντο φέτος (2014) είναι εκτός ύλης 2013 ΘΕΜΑ Α Για τις ερωτήσεις 1 έως 4 γράψτε τον αριθμό τις ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Για ένα
ΔΥΝΑΜΕΙΣ ΕΛΕΥΘΕΡΗ ΠΤΩΣΗ
 ΔΥΝΑΜΕΙΣ ΕΛΕΥΘΕΡΗ ΠΤΩΣΗ ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του.
ΔΥΝΑΜΕΙΣ ΕΛΕΥΘΕΡΗ ΠΤΩΣΗ ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του.
ΛΥΚΕΙΟ ΠΟΛΕΜΙΔΙΩΝ Σχολική Χρονιά 2013-2014 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 2014. Μάθημα: ΦΥΣΙΚΗ Τάξη: A Ενιαίου Λυκείου Βαθμός:...
 1 ΛΥΚΕΙΟ ΠΟΛΕΜΙΔΙΩΝ Σχολική Χρονιά 2013-2014 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 2014 Μάθημα: ΦΥΣΙΚΗ Τάξη: A Ενιαίου Λυκείου Βαθμός:... Ημερομηνία: 3/06/2014 Διάρκεια: 2 ώρες Ονοματεπώνυμο:...
1 ΛΥΚΕΙΟ ΠΟΛΕΜΙΔΙΩΝ Σχολική Χρονιά 2013-2014 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 2014 Μάθημα: ΦΥΣΙΚΗ Τάξη: A Ενιαίου Λυκείου Βαθμός:... Ημερομηνία: 3/06/2014 Διάρκεια: 2 ώρες Ονοματεπώνυμο:...
6. Να βρείτε ποια είναι η σωστή απάντηση.
 12ΑΣΚΗΣΕΙΣ ΔΥΝΑΜΙΚΗΣ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ 1. Να βρείτε ποια είναι η σωστή απάντηση. Το όργανο μέτρησης του βάρους ενός σώματος είναι : α) το βαρόμετρο, β) η ζυγαριά, γ) το δυναμόμετρο, δ) ο αδρανειακός ζυγός.
12ΑΣΚΗΣΕΙΣ ΔΥΝΑΜΙΚΗΣ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ 1. Να βρείτε ποια είναι η σωστή απάντηση. Το όργανο μέτρησης του βάρους ενός σώματος είναι : α) το βαρόμετρο, β) η ζυγαριά, γ) το δυναμόμετρο, δ) ο αδρανειακός ζυγός.
ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ
 F ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του. Αν ασκούνται σε αρχικά
F ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του. Αν ασκούνται σε αρχικά
1 ο ΚΕΦΑΛΑΙΟ Α. ΜΟΝΑΔΕΣ Β. ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΓΩΝΙΩΝ ΚΡΕΜΑΣΤΑΣ ΙΩΑΝΝΗΣ
 Α. ΜΟΝΑΔΕΣ Β. ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΓΩΝΙΩΝ 1 ΚΕΦΑΛΑΙΟ 1 Ο ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ- ΘΕΩΡΙΑ Μετατόπιση (Δx): Είναι η διαφορά μεταξύ της αρχικής και της τελικής θέσης ενός σώματος και έχει μονάδες τα μέτρα (m).
Α. ΜΟΝΑΔΕΣ Β. ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΓΩΝΙΩΝ 1 ΚΕΦΑΛΑΙΟ 1 Ο ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ- ΘΕΩΡΙΑ Μετατόπιση (Δx): Είναι η διαφορά μεταξύ της αρχικής και της τελικής θέσης ενός σώματος και έχει μονάδες τα μέτρα (m).
ΚΕΦΑΛΑΙΟ ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ ΘΕΩΡΙΑ
 ΚΕΦΑΛΑΙΟ o ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ ΘΕΩΡΙΑ.) Τ ι γνωρίζετε για την αρχή της ανεξαρτησίας των κινήσεων; Σε πολλές περιπτώσεις ένα σώμα εκτελεί σύνθετη κίνηση, δηλαδή συμμετέχει σε περισσότερες από μία κινήσεις. Για
ΚΕΦΑΛΑΙΟ o ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ ΘΕΩΡΙΑ.) Τ ι γνωρίζετε για την αρχή της ανεξαρτησίας των κινήσεων; Σε πολλές περιπτώσεις ένα σώμα εκτελεί σύνθετη κίνηση, δηλαδή συμμετέχει σε περισσότερες από μία κινήσεις. Για
ΓΥΜΝΑΣΙΟ ΑΓΙΑΣ ΒΑΡΒΑΡΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ ΚΑΤΩ ΠΟΛΕΜΙΔΙΩΝ ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 2016
 ΓΥΜΝΑΣΙΟ ΑΓΙΑΣ ΒΑΡΒΑΡΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2015-2016 ΚΑΤΩ ΠΟΛΕΜΙΔΙΩΝ ΒΑΘΜΟΣ ΦΥΣΙΚΗΣ ΒΑΘΜΟΣ ΦΥΣΙΚΑ Αριθμητικώς:... Ολογρ.:... Υπογραφή:... Αριθμητικώς:... Ολογρ.:... Υπογραφές:... ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ
ΓΥΜΝΑΣΙΟ ΑΓΙΑΣ ΒΑΡΒΑΡΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2015-2016 ΚΑΤΩ ΠΟΛΕΜΙΔΙΩΝ ΒΑΘΜΟΣ ΦΥΣΙΚΗΣ ΒΑΘΜΟΣ ΦΥΣΙΚΑ Αριθμητικώς:... Ολογρ.:... Υπογραφή:... Αριθμητικώς:... Ολογρ.:... Υπογραφές:... ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ
F Στεφάνου Μ. 1 Φυσικός
 F 1 ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του. Αν ασκούνται σε αρχικά
F 1 ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του. Αν ασκούνται σε αρχικά
ΜΕΡΟΣ Α Αποτελείται από 6 ερωτήσεις. Κάθε ορθή απάντηση βαθμολογείται με 5 μονάδες. Να απαντήσετε όλες τις ερωτήσεις.
 ΛΥΚΕΙΟ ΑΓ. ΣΠΥΡΙΔΩΝΑ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2013 2014 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 2014 ΤΑΞΗ: Α ΗΜΕΡ.: 02/06/2014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΟΙΝΟΥ ΚΟΡΜΟΥ Ονοματεπώνυμο: ΔΙΑΡΚΕΙΑ: 2 ώρες Τάξη: ΟΔΗΓΙΕΣ : α) Το εξεταστικό
ΛΥΚΕΙΟ ΑΓ. ΣΠΥΡΙΔΩΝΑ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2013 2014 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 2014 ΤΑΞΗ: Α ΗΜΕΡ.: 02/06/2014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΟΙΝΟΥ ΚΟΡΜΟΥ Ονοματεπώνυμο: ΔΙΑΡΚΕΙΑ: 2 ώρες Τάξη: ΟΔΗΓΙΕΣ : α) Το εξεταστικό
Θεματικές Ενότητες (Διατιθέμενος χρόνος) Διεθνές σύστημα μονάδων Μήκος, μάζα, χρόνος. (4 ώρες)
 Φυσική Α Λυκείου Πρόγραμμα Σπουδών (70 ώρες) Στόχοι ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ Να είναι σε θέση οι μαθητές: Να αναγνωρίζουν την αναγκαιότητα του Διεθνούς Συστήματος Μονάδων και τα θεμελιώδη μεγέθη του Να μετρούν
Φυσική Α Λυκείου Πρόγραμμα Σπουδών (70 ώρες) Στόχοι ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ Να είναι σε θέση οι μαθητές: Να αναγνωρίζουν την αναγκαιότητα του Διεθνούς Συστήματος Μονάδων και τα θεμελιώδη μεγέθη του Να μετρούν
ΛΥΚΕΙΟ ΠΟΛΕΜΙΔΙΩΝ Σχολική Χρονιά 2010-2011 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 2011. Μάθημα: ΦΥΣΙΚΗ Τάξη: A Ενιαίου Λυκείου Βαθμός:...
 ΛΥΚΕΙΟ ΠΟΛΕΜΙΔΙΩΝ Σχολική Χρονιά 010-011 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 011 Μάθημα: ΦΥΣΙΚΗ Τάξη: A Ενιαίου Λυκείου Βαθμός:... Ημερομηνία: 7/05/011 Διάρκεια: ώρες Ονοματεπώνυμο:... Τμήμα:...
ΛΥΚΕΙΟ ΠΟΛΕΜΙΔΙΩΝ Σχολική Χρονιά 010-011 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 011 Μάθημα: ΦΥΣΙΚΗ Τάξη: A Ενιαίου Λυκείου Βαθμός:... Ημερομηνία: 7/05/011 Διάρκεια: ώρες Ονοματεπώνυμο:... Τμήμα:...
1. Κίνηση Υλικού Σημείου
 1. Κίνηση Υλικού Σημείου Εισαγωγή στην Φυσική της Γ λυκείου Τροχιά: Ονομάζεται η γραμμή που συνδέει τις διαδοχικές θέσεις του κινητού. Οι κινήσεις ανάλογα με το είδος της τροχιάς διακρίνονται σε: 1. Ευθύγραμμες
1. Κίνηση Υλικού Σημείου Εισαγωγή στην Φυσική της Γ λυκείου Τροχιά: Ονομάζεται η γραμμή που συνδέει τις διαδοχικές θέσεις του κινητού. Οι κινήσεις ανάλογα με το είδος της τροχιάς διακρίνονται σε: 1. Ευθύγραμμες
ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΚΕΦΑΛΑΙΟ 3 Ο ΔΥΝΑΜΕΙΣ
 ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΚΕΦΑΛΑΙΟ 3 Ο ΔΥΝΑΜΕΙΣ 3.1 Η έννοια της δύναμης ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Στο κεφάλαιο των κινήσεων ασχοληθήκαμε με τη μελέτη της κίνησης χωρίς να μας απασχολούν τα αίτια που προκαλούν την κίνηση
ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΚΕΦΑΛΑΙΟ 3 Ο ΔΥΝΑΜΕΙΣ 3.1 Η έννοια της δύναμης ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Στο κεφάλαιο των κινήσεων ασχοληθήκαμε με τη μελέτη της κίνησης χωρίς να μας απασχολούν τα αίτια που προκαλούν την κίνηση
Δυνάμεις. Οι Δυνάμεις εμφανίζονται μεταξύ 2 σωμάτων. Το ένα ασκεί δύναμη. στο άλλο και αλληλεπιδρούν. Ένα σώμα μόνο του ούτε ασκεί ούτε
 Κεφάλαιο 3 ο Δυνάμεις Δύναμη είναι το αίτιο που μεταβάλλει την ταχύτητα των σωμάτων ή τα παραμορφώνει. Οι Δυνάμεις εμφανίζονται μεταξύ 2 σωμάτων. Το ένα ασκεί δύναμη στο άλλο και αλληλεπιδρούν. Ένα σώμα
Κεφάλαιο 3 ο Δυνάμεις Δύναμη είναι το αίτιο που μεταβάλλει την ταχύτητα των σωμάτων ή τα παραμορφώνει. Οι Δυνάμεις εμφανίζονται μεταξύ 2 σωμάτων. Το ένα ασκεί δύναμη στο άλλο και αλληλεπιδρούν. Ένα σώμα
16. Να γίνει µετατροπή µονάδων και να συµπληρωθούν τα κενά των προτάσεων: α. οι τρεις ώρες είναι... λεπτά β. τα 400cm είναι...
 1. Ο νόµος του Hooke υποστηρίζει ότι οι ελαστικές παραµορφώσεις είναι.των...που τις προκαλούν. 2. Ο τρίτος νόµος του Νεύτωνα υποστηρίζει ότι οι δυνάµεις που αναφέρονται στο νόµο αυτό έχουν... µέτρα,......
1. Ο νόµος του Hooke υποστηρίζει ότι οι ελαστικές παραµορφώσεις είναι.των...που τις προκαλούν. 2. Ο τρίτος νόµος του Νεύτωνα υποστηρίζει ότι οι δυνάµεις που αναφέρονται στο νόµο αυτό έχουν... µέτρα,......
Β Γυμνασίου 22/6/2015. Οι δείκτες Επιτυχίας και δείκτες Επάρκειας Β Γυμνασίου για το μάθημα της Φυσικής
 Β Γυμνασίου /6/05 Οι δείκτες Επιτυχίας και δείκτες Επάρκειας Β Γυμνασίου για το μάθημα της Φυσικής Β Γυμνασίου /6/05 Δείκτες Επιτυχίας (Γνώσεις και υπό έμφαση ικανότητες) Παρεμφερείς Ικανότητες (προϋπάρχουσες
Β Γυμνασίου /6/05 Οι δείκτες Επιτυχίας και δείκτες Επάρκειας Β Γυμνασίου για το μάθημα της Φυσικής Β Γυμνασίου /6/05 Δείκτες Επιτυχίας (Γνώσεις και υπό έμφαση ικανότητες) Παρεμφερείς Ικανότητες (προϋπάρχουσες
Ε Υ Θ Υ Γ Ρ Α Μ Μ Η Κ Ι Ν Η Σ Η - Α Σ Κ Η Σ Ε Ι Σ
 0 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΑΣΚΗΣΕΙΣ Ε Υ Θ Υ Γ Ρ Α Μ Μ Η Κ Ι Ν Η Σ Η - Α Σ Κ Η Σ Ε Ι Σ 0 1 Στρατηγική επίλυσης προβλημάτων Α. Κάνε κατάλληλο σχήμα,τοποθέτησε τα δεδομένα στο σχήμα και ονόμασε
0 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΑΣΚΗΣΕΙΣ Ε Υ Θ Υ Γ Ρ Α Μ Μ Η Κ Ι Ν Η Σ Η - Α Σ Κ Η Σ Ε Ι Σ 0 1 Στρατηγική επίλυσης προβλημάτων Α. Κάνε κατάλληλο σχήμα,τοποθέτησε τα δεδομένα στο σχήμα και ονόμασε
ΛΥΚΕΙΟ ΠΟΛΕΜΙΔΙΩΝ Σχολική Χρονιά ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ Μάθημα: ΦΥΣΙΚΗ Τάξη: A Ενιαίου Λυκείου Βαθμός:...
 ΛΥΚΕΙΟ ΠΟΛΕΜΙΔΙΩΝ Σχολική Χρονιά 01-013 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 013 Μάθημα: ΦΥΣΙΚΗ Τάξη: A Ενιαίου Λυκείου Βαθμός:... Ημερομηνία: 7/05/013 Διάρκεια: ώρες Ονοματεπώνυμο:... Τμήμα:...
ΛΥΚΕΙΟ ΠΟΛΕΜΙΔΙΩΝ Σχολική Χρονιά 01-013 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 013 Μάθημα: ΦΥΣΙΚΗ Τάξη: A Ενιαίου Λυκείου Βαθμός:... Ημερομηνία: 7/05/013 Διάρκεια: ώρες Ονοματεπώνυμο:... Τμήμα:...
ΛΥΚΕΙΟ ΑΓ. ΣΠΥΡΙΔΩΝΑ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΙΟΥ 2012 ΤΑΞΗ: A ΗΜΕΡ.: 28/05/12. Ονοματεπώνυμο: Τμήμα:
 ΛΥΚΕΙΟ ΑΓ. ΣΠΥΡΙΔΩΝΑ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2011-2012 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΙΟΥ 2012 ΤΑΞΗ: A ΗΜΕΡ.: 28/05/12 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΔΙΑΡΚΕΙΑ: 2 ώρες Ονοματεπώνυμο: Τμήμα: Το εξεταστικό δοκίμιο αποτελείται από
ΛΥΚΕΙΟ ΑΓ. ΣΠΥΡΙΔΩΝΑ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2011-2012 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΙΟΥ 2012 ΤΑΞΗ: A ΗΜΕΡ.: 28/05/12 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΔΙΑΡΚΕΙΑ: 2 ώρες Ονοματεπώνυμο: Τμήμα: Το εξεταστικό δοκίμιο αποτελείται από
ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ
 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ Συγγραμμικές δυνάμεις 1 ος -2 ος νόμος του Νεύτωνα 1. Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασμένες; α. Μια δύναμη μπορεί να προκαλέσει αλλαγή στην κινητική
ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ Συγγραμμικές δυνάμεις 1 ος -2 ος νόμος του Νεύτωνα 1. Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασμένες; α. Μια δύναμη μπορεί να προκαλέσει αλλαγή στην κινητική
ΛΑΝΙΤΕΙΟ ΛΥΚΕΙΟ Α ΣΧΟΛΙΚΟ ΕΤΟΣ 2010-2011 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 2011 ΟΝΟΜΑ:... ΤΜΗΜΑ:... ΑΡ.:...
 ΛΑΝΙΤΕΙΟ ΛΥΚΕΙΟ Α ΣΧΟΛΙΚΟ ΕΤΟΣ 2010-2011 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 2011 ΜΑΘΗΜΑ: Φυσική ΤΑΞΗ: Α ΗΜΕΡΟΜΗΝΊΑ: 27 Μαίου 2011 ΧΡΟΝΟΣ: 2 ώρες ΩΡΑ: 11.00 1.00 ΒΑΘΜΟΣ: Αριθμητικά:... Ολογράφως:...
ΛΑΝΙΤΕΙΟ ΛΥΚΕΙΟ Α ΣΧΟΛΙΚΟ ΕΤΟΣ 2010-2011 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 2011 ΜΑΘΗΜΑ: Φυσική ΤΑΞΗ: Α ΗΜΕΡΟΜΗΝΊΑ: 27 Μαίου 2011 ΧΡΟΝΟΣ: 2 ώρες ΩΡΑ: 11.00 1.00 ΒΑΘΜΟΣ: Αριθμητικά:... Ολογράφως:...
1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη;
 ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης. Στην Κινηματική
ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης. Στην Κινηματική
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ / Α ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΑΠΑΝΤΗΣΕΙΣ) ΗΜΕΡΟΜΗΝΙΑ: ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ Μ- ΑΓΙΑΝΝΙΩΤΑΚΗ ΑΝ.-ΠΟΥΛΗ Κ.
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ / Α ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΑΠΑΝΤΗΣΕΙΣ) ΗΜΕΡΟΜΗΝΙΑ: 21-12-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ Μ- ΑΓΙΑΝΝΙΩΤΑΚΗ ΑΝ.-ΠΟΥΛΗ Κ. ΘΕΜΑ A Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ / Α ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΑΠΑΝΤΗΣΕΙΣ) ΗΜΕΡΟΜΗΝΙΑ: 21-12-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ Μ- ΑΓΙΑΝΝΙΩΤΑΚΗ ΑΝ.-ΠΟΥΛΗ Κ. ΘΕΜΑ A Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 2018 ΜΕΣΗΣ ΤΕΧΝΙΚΗΣ ΚΑΙ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ
 ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2017 2018 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 2018 ΜΕΣΗΣ ΤΕΧΝΙΚΗΣ ΚΑΙ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ/ΤΡΙΑΣ:.... ΒΑΘΜΟΣ : /100, /20 ΥΠΟΓΡΑΦΗ:. Μάθημα: ΦΥΣΙΚΗ Τάξη:
ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2017 2018 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 2018 ΜΕΣΗΣ ΤΕΧΝΙΚΗΣ ΚΑΙ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ/ΤΡΙΑΣ:.... ΒΑΘΜΟΣ : /100, /20 ΥΠΟΓΡΑΦΗ:. Μάθημα: ΦΥΣΙΚΗ Τάξη:
Επειδή Μ>m, θα είναι: (1), (2) α 1 <α 2, δηλαδή ο πατέρας έχει μεγαλύτερη μάζα από την κόρη του και θα αποκτήσει μικρότερη επιτάχυνση από αυτήν.
 ΘΕΜΑ 1 ο (10 μονάδες): Λύση α) Ο πατέρας ασκεί δύναμη F στην κόρη του και η κόρη του ασκεί δύναμη F σε αυτόν. Θα ισχύει F=F (3 ος νόμος του Νεύτωνα) β) Σύμφωνα με το ο νόμο του Νεύτωνα θα ισχύει: επιτάχυνση
ΘΕΜΑ 1 ο (10 μονάδες): Λύση α) Ο πατέρας ασκεί δύναμη F στην κόρη του και η κόρη του ασκεί δύναμη F σε αυτόν. Θα ισχύει F=F (3 ος νόμος του Νεύτωνα) β) Σύμφωνα με το ο νόμο του Νεύτωνα θα ισχύει: επιτάχυνση
Φυσικά Μεγέθη Μονάδες Μέτρησης
 ΓΝΩΣΤΙΚΟ ΑΝΤΙΚΕΙΜΕΝΟ: ΦΥΣΙΚΗ A ΛΥΚΕΙΟΥ ΚΟΙΝΟΥ ΚΟΡΜΟΥ ΤΑΞΗ: Α Λυκείου Προσανατολισμού 1,3,4. ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΜΑΘΗΣΙΑΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ Οι μαθητές και οι μαθήτριες να είναι σε θέση να: ΑΝΤΙΣΤΟΙΧΑ
ΓΝΩΣΤΙΚΟ ΑΝΤΙΚΕΙΜΕΝΟ: ΦΥΣΙΚΗ A ΛΥΚΕΙΟΥ ΚΟΙΝΟΥ ΚΟΡΜΟΥ ΤΑΞΗ: Α Λυκείου Προσανατολισμού 1,3,4. ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΜΑΘΗΣΙΑΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ Οι μαθητές και οι μαθήτριες να είναι σε θέση να: ΑΝΤΙΣΤΟΙΧΑ
Θέση-Μετατόπιση -ταχύτητα
 Φυσική έννοια Φυσική έννοια Φαινόμενα ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΙΝΗΣΗΣ ΤΩΝ ΣΩΜΑΤΩΝ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ Θέση-Μετατόπιση -ταχύτητα Ένα τρένο που ταξιδεύει αλλάζει διαρκώς θέση, το ίδιο ένα αυτοκίνητο και ένα πλοίο ή αεροπλάνο
Φυσική έννοια Φυσική έννοια Φαινόμενα ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΙΝΗΣΗΣ ΤΩΝ ΣΩΜΑΤΩΝ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ Θέση-Μετατόπιση -ταχύτητα Ένα τρένο που ταξιδεύει αλλάζει διαρκώς θέση, το ίδιο ένα αυτοκίνητο και ένα πλοίο ή αεροπλάνο
Κ Ι Ν Η Σ Ε Ι Σ ΑΣΚΗΣΕΙΣ
 Κ Ι Ν Η Σ Ε Ι Σ ΑΣΚΗΣΕΙΣ 1. Αυτοκίνητο κινείται σε ευθύγραμμο δρόμο με σταθερή φορά και το ταχύμετρο του (κοντέρ) δείχνει συνεχώς 72km/h. α) Τι είδους κίνηση κάνει το αυτοκίνητο; β) Να μετατρέψετε την
Κ Ι Ν Η Σ Ε Ι Σ ΑΣΚΗΣΕΙΣ 1. Αυτοκίνητο κινείται σε ευθύγραμμο δρόμο με σταθερή φορά και το ταχύμετρο του (κοντέρ) δείχνει συνεχώς 72km/h. α) Τι είδους κίνηση κάνει το αυτοκίνητο; β) Να μετατρέψετε την
ΕΙΣΑΓΩΓΙΚΑ ΣΧΟΛΙΑ Η δύναμη που ασκείται σε ένα σώμα προκαλεί μεταβολή της ταχύτητάς του δηλαδή επιτάχυνση.
 ΕΙΣΑΓΩΓΙΚΑ ΣΧΟΛΙΑ Η δύναμη που ασκείται σε ένα σώμα προκαλεί μεταβολή της ταχύτητάς του δηλαδή επιτάχυνση. Η δύναμη είναι ένα διανυσματικό μέγεθος. Όταν κατά την κίνηση ενός σώματος η δύναμη είναι μηδενική
ΕΙΣΑΓΩΓΙΚΑ ΣΧΟΛΙΑ Η δύναμη που ασκείται σε ένα σώμα προκαλεί μεταβολή της ταχύτητάς του δηλαδή επιτάχυνση. Η δύναμη είναι ένα διανυσματικό μέγεθος. Όταν κατά την κίνηση ενός σώματος η δύναμη είναι μηδενική
GI_V_FYSP_0_3772. ο οδηγός του φρενάρει οπότε το αυτοκίνητο διανύει διάστημα d
 GI_V_FYSP_0_377 Σε αυτοκίνητο που κινείται σε ευθύγραμμο δρόμο με ταχύτητα μέτρου, ο οδηγός του φρενάρει οπότε το αυτοκίνητο διανύει διάστημα d μέχρι να σταματήσει. Αν το αυτοκίνητο κινείται με ταχύτητα
GI_V_FYSP_0_377 Σε αυτοκίνητο που κινείται σε ευθύγραμμο δρόμο με ταχύτητα μέτρου, ο οδηγός του φρενάρει οπότε το αυτοκίνητο διανύει διάστημα d μέχρι να σταματήσει. Αν το αυτοκίνητο κινείται με ταχύτητα
ΚΕΦΑΛΑΙΟ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ
 55 ΚΕΦΑΛΑΙΟ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ Α. ΠΡΟΣΘΕΣΗ ΔΥΝΑΜΕΩΝ ΝΟΜΟΣ ΤΟΥ HOOKE 1. Να σχεδιάσετε δύο αντίρροπες δυνάμεις F 1=5N και F 2=15N με κλίμακα 1cm/2,5N και να βρείτε την συνισταμένη τους. (Απ.: 10
55 ΚΕΦΑΛΑΙΟ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ Α. ΠΡΟΣΘΕΣΗ ΔΥΝΑΜΕΩΝ ΝΟΜΟΣ ΤΟΥ HOOKE 1. Να σχεδιάσετε δύο αντίρροπες δυνάμεις F 1=5N και F 2=15N με κλίμακα 1cm/2,5N και να βρείτε την συνισταμένη τους. (Απ.: 10
Κεφάλαιο 1 ο ΕΙΣΑΓΩΓΗ
 Κεφάλαιο 1 ο ΕΙΣΑΓΩΓΗ Φαινόμενο, ονομάζεται οτιδήποτε συμβαίνει τριγύρω μας. Για παράδειγμα η αύξηση του ύψους του ανθρώπου, η έκρηξη ενός ηφαιστείου κλπ. Τις μεταβολές αυτές, που συμβαίνουν στην φύση
Κεφάλαιο 1 ο ΕΙΣΑΓΩΓΗ Φαινόμενο, ονομάζεται οτιδήποτε συμβαίνει τριγύρω μας. Για παράδειγμα η αύξηση του ύψους του ανθρώπου, η έκρηξη ενός ηφαιστείου κλπ. Τις μεταβολές αυτές, που συμβαίνουν στην φύση
Δ3. Ο χρόνος από τη στιγμή που η απόστασή τους ήταν d μέχρι τη στιγμή που ακουμπά η μία την άλλη. Μονάδες 6
 ΘΕΜΑ Δ 1. Δύο αμαξοστοιχίες κινούνται κατά την ίδια φορά πάνω στην ίδια γραμμή. Η προπορευόμενη έχει ταχύτητα 54km/h και η επόμενη 72km/h. Όταν βρίσκονται σε απόσταση d, οι μηχανοδηγοί αντιλαμβάνονται
ΘΕΜΑ Δ 1. Δύο αμαξοστοιχίες κινούνται κατά την ίδια φορά πάνω στην ίδια γραμμή. Η προπορευόμενη έχει ταχύτητα 54km/h και η επόμενη 72km/h. Όταν βρίσκονται σε απόσταση d, οι μηχανοδηγοί αντιλαμβάνονται
ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ
 ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ 1. Ο άνθρωπος ξεκινά τη στιγμή t=0 από τη θέση x=50 m και όπως φαίνεται στο παρακάτω διάγραμμα κινείται προς τα αριστερά. Στη συνέχεια σε κάθε σημειωμένη θέση στο
ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ 1. Ο άνθρωπος ξεκινά τη στιγμή t=0 από τη θέση x=50 m και όπως φαίνεται στο παρακάτω διάγραμμα κινείται προς τα αριστερά. Στη συνέχεια σε κάθε σημειωμένη θέση στο
ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2013
 ΛΥΚΕΙΟ ΑΓΙΑΣ ΦΥΛΑΞΕΩΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2012-13 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2013 Φυσική Τάξη Α Ημερομηνία: 27 Μαΐου 2013 Βαθμός:. Ώρα: 7 : 30 Ολογράφως:. Χρόνος: 2 ώρες Υπογραφή: Ονοματεπώνυμο
ΛΥΚΕΙΟ ΑΓΙΑΣ ΦΥΛΑΞΕΩΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2012-13 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2013 Φυσική Τάξη Α Ημερομηνία: 27 Μαΐου 2013 Βαθμός:. Ώρα: 7 : 30 Ολογράφως:. Χρόνος: 2 ώρες Υπογραφή: Ονοματεπώνυμο
Κεφάλαιο 1.1 Ευθύγραμμη κίνηση
 Κεφάλαιο 1.1 Ευθύγραμμη κίνηση 1 H θέση ενός κινητού που κινείται σε ένα επίπεδο, προσδιορίζεται κάθε στιγμή αν: Είναι γνωστές οι συντεταγμένες του κινητού (x,y) ως συναρτήσεις του χρόνου Είναι γνωστό
Κεφάλαιο 1.1 Ευθύγραμμη κίνηση 1 H θέση ενός κινητού που κινείται σε ένα επίπεδο, προσδιορίζεται κάθε στιγμή αν: Είναι γνωστές οι συντεταγμένες του κινητού (x,y) ως συναρτήσεις του χρόνου Είναι γνωστό
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ
 16-10-11 ΣΕΙΡΑ Α ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ ΘΕΜΑ 1 ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
16-10-11 ΣΕΙΡΑ Α ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ ΘΕΜΑ 1 ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
Φυσική Α Λυκείου. Σημειώσεις από τη θεωρία του σχολικού βιβλίου (βοήθημα για μια γρήγορη επανάληψη)
 Φυσική Λυκείου Σημειώσεις από τη θερία του σχολικού βιβλίου (βοήθημα για μια γρήγορη επανάληψη) Εισαγγή στις φυσικές επιστήμες Οι φυσικές επιστήμες αποτελούν την προσπάθεια του ανθρώπου να περιγράψει και
Φυσική Λυκείου Σημειώσεις από τη θερία του σχολικού βιβλίου (βοήθημα για μια γρήγορη επανάληψη) Εισαγγή στις φυσικές επιστήμες Οι φυσικές επιστήμες αποτελούν την προσπάθεια του ανθρώπου να περιγράψει και
Μετατόπιση, είναι η αλλαγή (μεταβολή) της θέσης ενός κινητού. Η μετατόπιση εκφράζει την απόσταση των δύο θέσεων μεταξύ των οποίων κινήθηκε το κινητό.
 Μετατόπιση, είναι η αλλαγή (μεταβολή) της θέσης ενός κινητού. Η μετατόπιση εκφράζει την απόσταση των δύο θέσεων μεταξύ των οποίων κινήθηκε το κινητό. Η ταχύτητα (υ), είναι το πηλίκο της μετατόπισης (Δx)
Μετατόπιση, είναι η αλλαγή (μεταβολή) της θέσης ενός κινητού. Η μετατόπιση εκφράζει την απόσταση των δύο θέσεων μεταξύ των οποίων κινήθηκε το κινητό. Η ταχύτητα (υ), είναι το πηλίκο της μετατόπισης (Δx)
ΠΡΟΤΕΙΝΟΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ
 1 ΠΡΟΤΕΙΝΟΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΘΕΜΑ 1 ο 1. Aν ο ρυθμός μεταβολής της ταχύτητας ενός σώματος είναι σταθερός, τότε το σώμα: (i) Ηρεμεί. (ii) Κινείται με σταθερή ταχύτητα. (iii) Κινείται με μεταβαλλόμενη
1 ΠΡΟΤΕΙΝΟΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΘΕΜΑ 1 ο 1. Aν ο ρυθμός μεταβολής της ταχύτητας ενός σώματος είναι σταθερός, τότε το σώμα: (i) Ηρεμεί. (ii) Κινείται με σταθερή ταχύτητα. (iii) Κινείται με μεταβαλλόμενη
 Φίλε μαθητή, Το βιβλίο αυτό, που κρατάς στα χέρια σου προέκυψε τελικά μέσα από την εμπειρία και διδακτική διαδικασία πολλών χρόνων στον Εκπαιδευτικό Όμιλο Άλφα. Είναι το αποτέλεσμα συγγραφής πολλών καθηγητών
Φίλε μαθητή, Το βιβλίο αυτό, που κρατάς στα χέρια σου προέκυψε τελικά μέσα από την εμπειρία και διδακτική διαδικασία πολλών χρόνων στον Εκπαιδευτικό Όμιλο Άλφα. Είναι το αποτέλεσμα συγγραφής πολλών καθηγητών
1.1.3 t. t = t2 - t1 1.1.4 x2 - x1. x = x2 x1 . . 1
 1 1 o Κεφάλαιο: Ευθύγραµµη Κίνηση Πώς θα µπορούσε να περιγραφεί η κίνηση ενός αγωνιστικού αυτοκινήτου; Πόσο γρήγορα κινείται η µπάλα που κλώτσησε ένας ποδοσφαιριστής; Απαντήσεις σε τέτοια ερωτήµατα δίνει
1 1 o Κεφάλαιο: Ευθύγραµµη Κίνηση Πώς θα µπορούσε να περιγραφεί η κίνηση ενός αγωνιστικού αυτοκινήτου; Πόσο γρήγορα κινείται η µπάλα που κλώτσησε ένας ποδοσφαιριστής; Απαντήσεις σε τέτοια ερωτήµατα δίνει
Κ Ε Φ Α Λ Α Ι Ο 1ο Ε Υ Θ Υ Γ Ρ Α Μ Μ Η Κ Ι Ν Η Σ Η
 1 Σκοπός Να αποκτήσουν οι μαθητές τη δυνατότητα να απαντούν σε ερωτήματα που εμφανίζονται στην καθημερινή μας ζωή και έχουν σχέση με την ταχύτητα, την επιτάχυνση, τη θέση ή το χρόνο κίνησης ενός κινητού.
1 Σκοπός Να αποκτήσουν οι μαθητές τη δυνατότητα να απαντούν σε ερωτήματα που εμφανίζονται στην καθημερινή μας ζωή και έχουν σχέση με την ταχύτητα, την επιτάχυνση, τη θέση ή το χρόνο κίνησης ενός κινητού.
ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 2018 ΜΕΣΗΣ ΤΕΧΝΙΚΗΣ ΚΑΙ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ
 ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 017 018 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 018 ΜΕΣΗΣ ΤΕΧΝΙΚΗΣ ΚΑΙ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ/ΤΡΙΑΣ:.... ΒΑΘΜΟΣ : /100, /0 ΥΠΟΓΡΑΦΗ:. Μάθημα: ΦΥΣΙΚΗ Τάξη: Α
ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 017 018 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 018 ΜΕΣΗΣ ΤΕΧΝΙΚΗΣ ΚΑΙ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ/ΤΡΙΑΣ:.... ΒΑΘΜΟΣ : /100, /0 ΥΠΟΓΡΑΦΗ:. Μάθημα: ΦΥΣΙΚΗ Τάξη: Α
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ. Ύλη: Ευθύγραμμη Κίνηση
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Ον/μο:.. A Λυκείου Ύλη: Ευθύγραμμη Κίνηση 13-11-2016 Θέμα 1 ο : 1) Η έκφραση 2m/s 2 όταν αναφέρεται σε κινητό που εκτελεί ευθύγραμμη κίνηση σημαίνει ότι: α) η θέση του κινητού αλλάζει
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Ον/μο:.. A Λυκείου Ύλη: Ευθύγραμμη Κίνηση 13-11-2016 Θέμα 1 ο : 1) Η έκφραση 2m/s 2 όταν αναφέρεται σε κινητό που εκτελεί ευθύγραμμη κίνηση σημαίνει ότι: α) η θέση του κινητού αλλάζει
Κεφάλαιο 1: Κινηματική
 Κεφάλαιο 1: Κινηματική Θέμα Β: 3763 Β 3768 Β1 3770 Β1 377 Β 4980 Β1 498 Β1 4986 Β1 4989 Β 4995 Β1 5044 Β1 5046 Β1 5050 Β1 505 Β1 5090 Β1 515 Β1 518 Β1 513 Β 563 Β1 535 Β1 535 Β 539 Β1 5515 Β1 6154 Β1 8996
Κεφάλαιο 1: Κινηματική Θέμα Β: 3763 Β 3768 Β1 3770 Β1 377 Β 4980 Β1 498 Β1 4986 Β1 4989 Β 4995 Β1 5044 Β1 5046 Β1 5050 Β1 505 Β1 5090 Β1 515 Β1 518 Β1 513 Β 563 Β1 535 Β1 535 Β 539 Β1 5515 Β1 6154 Β1 8996
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Β ΓΥΜΝΑΣΙΟΥ ΣΤΟ ΚΕΦΑΛΑΙΟ ΔΥΝΑΜΕΙΣ
 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Β ΓΥΜΝΑΣΙΟΥ ΣΤΟ ΚΕΦΑΛΑΙΟ ΔΥΝΑΜΕΙΣ 1 η ΕΡΩΤΗΣΗ: Τι ονομάζουμε γήινο βάρος ενός σώματος; 2 η ΕΡΩΤΗΣΗ: Ποιες είναι οι χαρακτηριστικές ιδιότητες του βάρους ενός σώματος; 3 η ΕΡΩΤΗΣΗ:
1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Β ΓΥΜΝΑΣΙΟΥ ΣΤΟ ΚΕΦΑΛΑΙΟ ΔΥΝΑΜΕΙΣ 1 η ΕΡΩΤΗΣΗ: Τι ονομάζουμε γήινο βάρος ενός σώματος; 2 η ΕΡΩΤΗΣΗ: Ποιες είναι οι χαρακτηριστικές ιδιότητες του βάρους ενός σώματος; 3 η ΕΡΩΤΗΣΗ:
Δt 1 x=υo t+ α t 1.2 Εξισώσεις κίνησης
 ΛΥΚΕΙΟ ΛΙΝΟΠΕΤΡΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2013-2014 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2014 ΤΑΞΗ: Α ΛΥΚΕΙΟΥ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΗΜΕΡΟΜΗΝΙΑ: 02/06/2014 ΔΙΑΡΚΕΙΑ: 10.45-12.45 Ονοματεπώνυμο Μαθητή/τριας:.......
ΛΥΚΕΙΟ ΛΙΝΟΠΕΤΡΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2013-2014 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2014 ΤΑΞΗ: Α ΛΥΚΕΙΟΥ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΗΜΕΡΟΜΗΝΙΑ: 02/06/2014 ΔΙΑΡΚΕΙΑ: 10.45-12.45 Ονοματεπώνυμο Μαθητή/τριας:.......
Οι νόμοι των δυνάμεων
 Φυσική Α Λυκείου Οι νόμοι των δυνάμεων 1. Η «αλληλεπίδραση»: Οι δυνάμεις στη φύση εμφανίζονται σε ζευγάρια: «Δράση Αντίδραση». Έτσι, κάθε σώμα που ασκεί σε ένα άλλο μία δύναμη -«δράση», δέχεται από αυτό
Φυσική Α Λυκείου Οι νόμοι των δυνάμεων 1. Η «αλληλεπίδραση»: Οι δυνάμεις στη φύση εμφανίζονται σε ζευγάρια: «Δράση Αντίδραση». Έτσι, κάθε σώμα που ασκεί σε ένα άλλο μία δύναμη -«δράση», δέχεται από αυτό
Η ΚΙΝΗΣΗ ΣΩΜΑΤΙΟ Ή ΥΛΙΚΟ ΣΗΜΕΙΟ Ή ΣΗΜΕΙΑΚΟ ΑΝΤΙΚΕΙΜΕΝΟ
 «Μπορούμε να παρομοιάσουμε τις έννοιες που δεν έχουν καμιά θεμελίωση στη φύση, με τα δάση εκείνα του Βορρά όπου τα δένδρα δεν έχουν καθόλου ρίζες. Αρκεί ένα φύσημα του αγέρα, ένα ασήμαντο γεγονός για να
«Μπορούμε να παρομοιάσουμε τις έννοιες που δεν έχουν καμιά θεμελίωση στη φύση, με τα δάση εκείνα του Βορρά όπου τα δένδρα δεν έχουν καθόλου ρίζες. Αρκεί ένα φύσημα του αγέρα, ένα ασήμαντο γεγονός για να
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
 ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 25 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ A ΛΥΚΕΙΟΥ Κυριακή, 3 Απριλίου, 2011 Ώρα: 10:00-13:00 Οδηγίες: 1) Να απαντήσετε σε όλα τα θέματα. Το δοκίμιο αποτελείται από έξι (6) θέματα. 2) Να
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 25 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ A ΛΥΚΕΙΟΥ Κυριακή, 3 Απριλίου, 2011 Ώρα: 10:00-13:00 Οδηγίες: 1) Να απαντήσετε σε όλα τα θέματα. Το δοκίμιο αποτελείται από έξι (6) θέματα. 2) Να
13 Γενική Μηχανική 2 Δυνάμεις Nόμοι του Newton 15/9/2014
 3 Γενική Μηχανική Δυνάμεις Nόμοι του Newton 5/9/04 Η Φυσική της Α Λυκείου σε 8.00 sec. Η έννοια της Δύναμης Οι νόμοι της κίνησης Η έννοια της δύναμης Όταν ένα αντικείμενο αλλάζει την ταχύτητά του (είτε
3 Γενική Μηχανική Δυνάμεις Nόμοι του Newton 5/9/04 Η Φυσική της Α Λυκείου σε 8.00 sec. Η έννοια της Δύναμης Οι νόμοι της κίνησης Η έννοια της δύναμης Όταν ένα αντικείμενο αλλάζει την ταχύτητά του (είτε
ΒΑΣΙΚΕΣ ΚΑΙ ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΑΠΟ ΤΗΝ Α ΚΑΙ Β ΛΥΚΕΙΟΥ. Από τη Φυσική της Α' Λυκείου
 ΒΑΣΙΚΕΣ ΚΑΙ ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΑΠΟ ΤΗΝ Α ΚΑΙ Β ΛΥΚΕΙΟΥ Από τη Φυσική της Α' Λυκείου Δεύτερος νόμος Νεύτωνα, και Αποδεικνύεται πειραματικά ότι: Η επιτάχυνση ενός σώματος (όταν αυτό θεωρείται
ΒΑΣΙΚΕΣ ΚΑΙ ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΑΠΟ ΤΗΝ Α ΚΑΙ Β ΛΥΚΕΙΟΥ Από τη Φυσική της Α' Λυκείου Δεύτερος νόμος Νεύτωνα, και Αποδεικνύεται πειραματικά ότι: Η επιτάχυνση ενός σώματος (όταν αυτό θεωρείται
13 Γενική Μηχανική 2 Δυνάμεις Nόμοι του Newton 15/9/2014
 13 Γενική Μηχανική Δυνάμεις Nόμοι του Newton 15/9/014 Η Φυσική της Α Λυκείου σε 8.100 sec. Η έννοια της Δύναμης Οι νόμοι της κίνησης Η έννοια της δύναμης Όταν ένα αντικείμενο αλλάζει την ταχύτητά του (είτε
13 Γενική Μηχανική Δυνάμεις Nόμοι του Newton 15/9/014 Η Φυσική της Α Λυκείου σε 8.100 sec. Η έννοια της Δύναμης Οι νόμοι της κίνησης Η έννοια της δύναμης Όταν ένα αντικείμενο αλλάζει την ταχύτητά του (είτε
ENOTHTA 1.1 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ
 ENOTHTA. ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ ΜΕΡΟΣ ο. Πώς προσδιορίζουμε τη θέση των αντικειμένων; A O M B ' y P Ì(,y) Ð Για τον προσδιορισμό της θέσης πάνω σε μία ευθεία πρέπει να έχουμε ένα σημείο της
ENOTHTA. ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ ΜΕΡΟΣ ο. Πώς προσδιορίζουμε τη θέση των αντικειμένων; A O M B ' y P Ì(,y) Ð Για τον προσδιορισμό της θέσης πάνω σε μία ευθεία πρέπει να έχουμε ένα σημείο της
Κίνηση σε μια διάσταση
 Κίνηση σε μια διάσταση Θεωρούμε κίνηση κατά μήκος μιας ευθύγραμμης διαδρομής. Η απόσταση x του κινούμενου σώματος από ένα σημείο του άξονα της κίνησης που παραμένει ακίνητο χρησιμοποιείται ως συντεταγμένη.
Κίνηση σε μια διάσταση Θεωρούμε κίνηση κατά μήκος μιας ευθύγραμμης διαδρομής. Η απόσταση x του κινούμενου σώματος από ένα σημείο του άξονα της κίνησης που παραμένει ακίνητο χρησιμοποιείται ως συντεταγμένη.
γραπτή εξέταση στο μάθημα ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ
 1η εξεταστική περίοδος από 4/10/15 έως 08/11/15 γραπτή εξέταση στο μάθημα ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ Τάξη: Α Λυκείου Τμήμα: Βαθμός: Ονοματεπώνυμο: Καθηγητές: Θ Ε Μ Α Α Στις ερωτήσεις Α1-Α4 να επιλέξετε τη σωστή
1η εξεταστική περίοδος από 4/10/15 έως 08/11/15 γραπτή εξέταση στο μάθημα ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ Τάξη: Α Λυκείου Τμήμα: Βαθμός: Ονοματεπώνυμο: Καθηγητές: Θ Ε Μ Α Α Στις ερωτήσεις Α1-Α4 να επιλέξετε τη σωστή
Όπου m είναι η μάζα του σώματος και υ η ταχύτητά του.
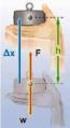 1 ΕΡΓΟ ΕΝΕΡΓΕΙΑ ΙΣΧΥΣ Η ενέργεια είναι από εκείνες τις έννοιες που δύσκολα ορίζονται στη Φυσική. Ένα σώμα μπορεί να έχει, να παίρνει ή να δίνει ενέργεια. Η ίδια η ενέργεια μπορεί να μετατρέπεται από μια
1 ΕΡΓΟ ΕΝΕΡΓΕΙΑ ΙΣΧΥΣ Η ενέργεια είναι από εκείνες τις έννοιες που δύσκολα ορίζονται στη Φυσική. Ένα σώμα μπορεί να έχει, να παίρνει ή να δίνει ενέργεια. Η ίδια η ενέργεια μπορεί να μετατρέπεται από μια
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ Ευθύγραμμη Ομαλή Κίνηση Επιμέλεια: ΑΓΚΑΝΑΚΗΣ.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός https://physicscorses.wordpress.com/ Βασικές Έννοιες Ένα σώμα καθώς κινείται περνάει από διάφορα σημεία.
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ Ευθύγραμμη Ομαλή Κίνηση Επιμέλεια: ΑΓΚΑΝΑΚΗΣ.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός https://physicscorses.wordpress.com/ Βασικές Έννοιες Ένα σώμα καθώς κινείται περνάει από διάφορα σημεία.
ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΙΑΓΩΝΙΣΜΑ
 ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΙΑΓΩΝΙΣΜΑ ΘΕΜΑ 1 Α) Τί είναι µονόµετρο και τί διανυσµατικό µέγεθος; Β) Τί ονοµάζουµε µετατόπιση και τί τροχιά της κίνησης; ΘΕΜΑ 2 Α) Τί ονοµάζουµε ταχύτητα ενός σώµατος και ποιά η µονάδα
ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΙΑΓΩΝΙΣΜΑ ΘΕΜΑ 1 Α) Τί είναι µονόµετρο και τί διανυσµατικό µέγεθος; Β) Τί ονοµάζουµε µετατόπιση και τί τροχιά της κίνησης; ΘΕΜΑ 2 Α) Τί ονοµάζουµε ταχύτητα ενός σώµατος και ποιά η µονάδα
ΒΑΘΜΟΣ ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑÏΟΥ- ΙΟΥΝΙΟΥ 2013 ΧΡΟΝΟΣ: 2 ΩΡΕΣ ΤΑΞΗ: Α ΩΡΑ:
 ΛΥΚΕΙΟ ΠΑΛΟΥΡΙΩΤΙΣΣΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2012-13 ΒΑΘΜΟΣ...... ΟΛΟΓΡΑΦΩΣ... ΥΠΟΓΡΑΦΗ... ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑÏΟΥ- ΙΟΥΝΙΟΥ 2013 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΗΜΕΡΟΜΗΝΙΑ: 31/05/2013 ΧΡΟΝΟΣ: 2 ΩΡΕΣ ΤΑΞΗ: Α ΩΡΑ: 7.45-9.45
ΛΥΚΕΙΟ ΠΑΛΟΥΡΙΩΤΙΣΣΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2012-13 ΒΑΘΜΟΣ...... ΟΛΟΓΡΑΦΩΣ... ΥΠΟΓΡΑΦΗ... ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑÏΟΥ- ΙΟΥΝΙΟΥ 2013 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΗΜΕΡΟΜΗΝΙΑ: 31/05/2013 ΧΡΟΝΟΣ: 2 ΩΡΕΣ ΤΑΞΗ: Α ΩΡΑ: 7.45-9.45
ΟΔΗΓΙΕΣ. Το εξεταστικό δοκίμιο αποτελείται από εννέα (9) σελίδες και χωρίζεται σε δύο μέρη Α και Β στα οποία αντιστοιχούν συνολικά 50 μονάδες.
 ΓΥΜΝΑΣΙΟ ΑΚΡΟΠΟΛΕΩΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2018-2019 ΒΑΘΜΟΣ ΒΑΘΜΟΣ Αριθμητικώς:... / 50 Αριθμητικώς:... / 20 Ολογράφως:... Ολογράφως:... Υπογραφή:... Υπογραφή:.. ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΙΟΥ - ΙΟΥΝΙΟΥ 2019
ΓΥΜΝΑΣΙΟ ΑΚΡΟΠΟΛΕΩΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2018-2019 ΒΑΘΜΟΣ ΒΑΘΜΟΣ Αριθμητικώς:... / 50 Αριθμητικώς:... / 20 Ολογράφως:... Ολογράφως:... Υπογραφή:... Υπογραφή:.. ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΙΟΥ - ΙΟΥΝΙΟΥ 2019
Έργο Δύναμης Έργο σταθερής δύναμης
 Παρατήρηση: Σε όλες τις ασκήσεις του φυλλαδίου τα αντικείμενα θεωρούμε ότι οι δυνάμεις ασκούνται στο κέντρο μάζας των αντικειμένων έτσι ώστε αυτά κινούνται μόνο μεταφορικά, χωρίς να μπορούν να περιστραφούν.
Παρατήρηση: Σε όλες τις ασκήσεις του φυλλαδίου τα αντικείμενα θεωρούμε ότι οι δυνάμεις ασκούνται στο κέντρο μάζας των αντικειμένων έτσι ώστε αυτά κινούνται μόνο μεταφορικά, χωρίς να μπορούν να περιστραφούν.
1.1. Κινηματική Ομάδα Ε
 1.1. Ομάδα Ε 61. Μετά από λίγο αρχίζει να επιταχύνεται. Δυο αυτοκίνητα Α και Β κινούνται σε ευθύγραμμο δρόμο με σταθερές ταχύτητες υ Α=21,8m/s και υ Β=12m/s, προς την ίδια κατεύθυνση. Σε μια στιγμή τα
1.1. Ομάδα Ε 61. Μετά από λίγο αρχίζει να επιταχύνεται. Δυο αυτοκίνητα Α και Β κινούνται σε ευθύγραμμο δρόμο με σταθερές ταχύτητες υ Α=21,8m/s και υ Β=12m/s, προς την ίδια κατεύθυνση. Σε μια στιγμή τα
Τυπολόγιο Κινήσεων 1. Πίνακας 1 - Τυπολόγιο Κινήσεων Τύπος Μας δίνει Παρατηρήσεις Ορισμοί βασικών μεγεθών. Ορισμός Μετατόπισης
 Τυπολόγιο Κινήσεων 1 1 Τυπολόγιο Κινήσεων Πίνακας 1 - Τυπολόγιο Κινήσεων Ορισμοί βασικών μεγεθών = 2 1 Ορισμός Μετατόπισης Αλγεβρικά, κανονικά είναι = 2 1 =, = Ορισμός ταχύτητας Διανυσματικά, αλγεβρικά
Τυπολόγιο Κινήσεων 1 1 Τυπολόγιο Κινήσεων Πίνακας 1 - Τυπολόγιο Κινήσεων Ορισμοί βασικών μεγεθών = 2 1 Ορισμός Μετατόπισης Αλγεβρικά, κανονικά είναι = 2 1 =, = Ορισμός ταχύτητας Διανυσματικά, αλγεβρικά
