Section 8.2 Graphs of Polar Equations
|
|
|
- Κυπριανός Σκλαβούνος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Section 8. Graphs of Polar Equations Graphing Polar Equations The graph of a polar equation r = f(θ), or more generally F(r,θ) = 0, consists of all points P that have at least one polar representation (r, θ) whose coordinates satisfy the equation. EXAMPLE: Sketch the polar curve θ =. Solution: This curve consists of all points (r,θ) such that the polar angle θ is radian. It is the straight line that passes through O and makes an angle of radian with the polar axis. Notice that the points (r,) on the line with r > 0 are in the first quadrant, whereas those with r < 0 are in the third quadrant. EXAMPLE: Sketch the following curves: (a) r =, 0 θ π. (b) r = θ, 0 θ 4π. (c) r = cosθ, 0 θ π.
2 EXAMPLE: Sketch the curve r =, 0 θ π. Solution : Since r =, it follows that r = 4. But r = x +y, therefore x +y = 4 which is a circle of radius with the center at the origin. Solution : We have r, theta Pi 6 r, theta Pi 6 r, theta Pi 6 r, theta 4 Pi 6 r, theta Pi 6 r, theta 6 Pi 6 r, theta 7 Pi 6 r, theta 8 Pi 6 r, theta 9 Pi 6 r, theta 0 Pi 6 r, theta Pi 6 r, theta Pi 6
3 EXAMPLE: Sketch the curve r = θ, 0 θ 4π. r theta, theta Pi r theta, theta Pi r theta, theta Pi r theta, theta 4 Pi r theta, theta Pi r theta, theta 6 Pi r theta, theta 7 Pi r theta, theta 8 Pi r theta, theta 9 Pi r theta, theta 0 Pi r theta, theta Pi r theta, theta Pi
4 EXAMPLE: Sketch the curve r = cosθ, 0 θ π. Solution : Since r = cosθ, it follows that r = rcosθ. But r = x + y and rcosθ = x, therefore x +y = x. This can be rewritten as (x ) +y = which is a circle of radius with the center at (,0). Solution : We have r cos theta, theta Pi r cos theta, theta Pi r cos theta, theta Pi r cos theta, theta 4 Pi r cos theta, theta Pi r cos theta, theta 6 Pi r cos theta, theta 7 Pi r cos theta, theta 8 Pi r cos theta, theta 9 Pi r cos theta, theta 0 Pi r cos theta, theta Pi r cos theta, theta Pi
5 EXAMPLES:
6 EXAMPLE: Sketch the curve r = +sinθ, 0 θ π (cardioid). r sin theta, theta Pi 6.0 r sin theta, theta Pi 6.0 r sin theta, theta Pi r sin theta, theta 4 Pi 6.0 r sin theta, theta Pi 6.0 r sin theta, theta 6 Pi r sin theta, theta 7 Pi 6.0 r sin theta, theta 8 Pi 6.0 r sin theta, theta 9 Pi r sin theta, theta 0 Pi 6.0 r sin theta, theta Pi 6.0 r sin theta, theta Pi
7 EXAMPLE: Sketch the curve r = cosθ, 0 θ π (cardioid). r cos theta, theta Pi 6. r cos theta, theta Pi 6. r cos theta, theta Pi r cos theta, theta 4 Pi 6. r cos theta, theta Pi 6. r cos theta, theta 6 Pi r cos theta, theta 7 Pi 6. r cos theta, theta 8 Pi 6. r cos theta, theta 9 Pi r cos theta, theta 0 Pi 6. r cos theta, theta Pi 6. r cos theta, theta Pi
8 EXAMPLE: Sketch the curve r = +4cosθ, 0 θ π. r 4cos theta, theta Pi 6 r 4cos theta, theta Pi 6 r 4cos theta, theta Pi r 4cos theta, theta 4 Pi 6 r 4cos theta, theta Pi 6 r 4cos theta, theta 6 Pi r 4cos theta, theta 7 Pi 6 r 4cos theta, theta 8 Pi 6 r 4cos theta, theta 9 Pi r 4cos theta, theta 0 Pi 6 r 4cos theta, theta Pi 6 r 4cos theta, theta Pi
9 EXAMPLE: Sketch the curve r = cos(θ), 0 θ π (four-leaved rose). r cos theta, theta Pi 6 r cos theta, theta Pi 6 r cos theta, theta Pi 6 r cos theta, theta 4 Pi 6 r cos theta, theta Pi 6 r cos theta, theta 6 Pi 6 r cos theta, theta 7 Pi 6 r cos theta, theta 8 Pi 6 r cos theta, theta 9 Pi 6 r cos theta, theta 0 Pi 6 r cos theta, theta Pi 6 r cos theta, theta Pi 6 9
10 EXAMPLE: Sketch the curve r = sin(θ), 0 θ π (four-leaved rose). r sin theta, theta Pi 6 r sin theta, theta Pi 6 r sin theta, theta Pi 6 r sin theta, theta 4 Pi 6 r sin theta, theta Pi 6 r sin theta, theta 6 Pi 6 r sin theta, theta 7 Pi 6 r sin theta, theta 8 Pi 6 r sin theta, theta 9 Pi 6 r sin theta, theta 0 Pi 6 r sin theta, theta Pi 6 r sin theta, theta Pi 6 0
11 EXAMPLE: Sketch the curve r = sin(θ), 0 θ π (three-leaved rose). r sin theta, theta Pi r sin theta, theta Pi r sin theta, theta Pi r sin theta, theta 4 Pi r sin theta, theta Pi r sin theta, theta 6 Pi r sin theta, theta 7 Pi r sin theta, theta 8 Pi r sin theta, theta 9 Pi r sin theta, theta 0 Pi r sin theta, theta Pi r sin theta, theta Pi
12 EXAMPLE: Sketch the curve r = sin(4θ), 0 θ π (eight-leaved rose). r sin 4theta, theta Pi 6 r sin 4theta, theta Pi 6 r sin 4theta, theta Pi 6 r sin 4theta, theta 4 Pi 6 r sin 4theta, theta Pi 6 r sin 4theta, theta 6 Pi 6 r sin 4theta, theta 7 Pi 6 r sin 4theta, theta 8 Pi 6 r sin 4theta, theta 9 Pi 6 r sin 4theta, theta 0 Pi 6 r sin 4theta, theta Pi 6 r sin 4theta, theta Pi 6
13 EXAMPLE: Sketch the curve r = sin(θ), 0 θ π (five-leaved rose). r sin theta, theta Pi 6 r sin theta, theta Pi 6 r sin theta, theta Pi 6 r sin theta, theta 4 Pi 6 r sin theta, theta Pi 6 r sin theta, theta 6 Pi 6 r sin theta, theta 7 Pi 6 r sin theta, theta 8 Pi 6 r sin theta, theta 9 Pi 6 r sin theta, theta 0 Pi 6 r sin theta, theta Pi 6 r sin theta, theta Pi 6
14 EXAMPLE: Sketch the curve r = sin(6θ), 0 θ π (twelve-leaved rose). r sin 6theta, theta Pi 6 r sin 6theta, theta Pi 6 r sin 6theta, theta Pi 6 r sin 6theta, theta 4 Pi 6 r sin 6theta, theta Pi 6 r sin 6theta, theta 6 Pi 6 r sin 6theta, theta 7 Pi 6 r sin 6theta, theta 8 Pi 6 r sin 6theta, theta 9 Pi 6 r sin 6theta, theta 0 Pi 6 r sin 6theta, theta Pi 6 r sin 6theta, theta Pi 6 4
15 EXAMPLE: Sketch the curve r = sin(7θ), 0 θ π (seven-leaved rose). r sin 7theta, theta Pi 6 r sin 7theta, theta Pi 6 r sin 7theta, theta Pi 6 r sin 7theta, theta 4 Pi 6 r sin 7theta, theta Pi 6 r sin 7theta, theta 6 Pi 6 r sin 7theta, theta 7 Pi 6 r sin 7theta, theta 8 Pi 6 r sin 7theta, theta 9 Pi 6 r sin 7theta, theta 0 Pi 6 r sin 7theta, theta Pi 6 r sin 7theta, theta Pi 6
16 EXAMPLE: Sketch the curve r = + sin(0θ), 0 θ π. 0 r sin 0theta 0, theta Pi 6 r sin 0theta 0, theta Pi 6 r sin 0theta 0, theta Pi 6 r sin 0theta 0, theta 4 Pi 6 r sin 0theta 0, theta Pi 6 r sin 0theta 0, theta 6 Pi 6 r sin 0theta 0, theta 7 Pi 6 r sin 0theta 0, theta 8 Pi 6 r sin 0theta 0, theta 9 Pi 6 r sin 0theta 0, theta 0 Pi 6 r sin 0theta 0, theta Pi 6 r sin 0theta 0, theta Pi 6 6
17 EXAMPLE: Match the polar equations with the graphs labeled I-VI: (a) r = sin(θ/) (c) r = sinθ+sin (θ/) (e) r = +4cos(θ) (b) r = sin(θ/4) (d) r = θsinθ (f) r = / θ 7
11.4 Graphing in Polar Coordinates Polar Symmetries
.4 Graphing in Polar Coordinates Polar Symmetries x axis symmetry y axis symmetry origin symmetry r, θ = r, θ r, θ = r, θ r, θ = r, + θ .4 Graphing in Polar Coordinates Polar Symmetries x axis symmetry
Areas and Lengths in Polar Coordinates
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Areas and Lengths in Polar Coordinates
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Section 9.2 Polar Equations and Graphs
180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
Practice Exam 2. Conceptual Questions. 1. State a Basic identity and then verify it. (a) Identity: Solution: One identity is csc(θ) = 1
Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Section 8.3 Trigonometric Equations
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
AREAS AND LENGTHS IN POLAR COORDINATES. 25. Find the area inside the larger loop and outside the smaller loop
SECTIN 9. AREAS AND LENGTHS IN PLAR CRDINATES 9. AREAS AND LENGTHS IN PLAR CRDINATES A Click here for answers. S Click here for solutions. 8 Find the area of the region that is bounded by the given curve
CHAPTER 101 FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD
CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Pg The perimeter is P = 3x The area of a triangle is. where b is the base, h is the height. In our case b = x, then the area is
Pg. 9. The perimeter is P = The area of a triangle is A = bh where b is the base, h is the height 0 h= btan 60 = b = b In our case b =, then the area is A = = 0. By Pythagorean theorem a + a = d a a =
Spherical Coordinates
Spherical Coordinates MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Spherical Coordinates Another means of locating points in three-dimensional space is known as the spherical
9.09. # 1. Area inside the oval limaçon r = cos θ. To graph, start with θ = 0 so r = 6. Compute dr
9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
Lecture 26: Circular domains
Introductory lecture notes on Partial Differential Equations - c Anthony Peirce. Not to be copied, used, or revised without eplicit written permission from the copyright owner. 1 Lecture 6: Circular domains
If we restrict the domain of y = sin x to [ π, π ], the restrict function. y = sin x, π 2 x π 2
![If we restrict the domain of y = sin x to [ π, π ], the restrict function. y = sin x, π 2 x π 2](/thumbs/53/31933086.jpg "If we restrict the domain of y = sin x to [ π, π ], the restrict function. y = sin x, π 2 x π 2")
Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
PARTIAL NOTES for 6.1 Trigonometric Identities
PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
Integrals in cylindrical, spherical coordinates (Sect. 15.7)
Integrals in clindrical, spherical coordinates (Sect. 5.7 Integration in spherical coordinates. Review: Clindrical coordinates. Spherical coordinates in space. Triple integral in spherical coordinates.
If we restrict the domain of y = sin x to [ π 2, π 2
Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
Homework 8 Model Solution Section
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
derivation of the Laplacian from rectangular to spherical coordinates
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Trigonometry 1.TRIGONOMETRIC RATIOS
Trigonometry.TRIGONOMETRIC RATIOS. If a ray OP makes an angle with the positive direction of X-axis then y x i) Sin ii) cos r r iii) tan x y (x 0) iv) cot y x (y 0) y P v) sec x r (x 0) vi) cosec y r (y
Reminders: linear functions
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Trigonometric Formula Sheet
Trigonometric Formula Sheet Definition of the Trig Functions Right Triangle Definition Assume that: 0 < θ < or 0 < θ < 90 Unit Circle Definition Assume θ can be any angle. y x, y hypotenuse opposite θ
Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.
Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
CYLINDRICAL & SPHERICAL COORDINATES
CYLINDRICAL & SPHERICAL COORDINATES Here we eamine two of the more popular alternative -dimensional coordinate sstems to the rectangular coordinate sstem. First recall the basis of the Rectangular Coordinate
CRASH COURSE IN PRECALCULUS
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
Section 7.6 Double and Half Angle Formulas
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
Answer sheet: Third Midterm for Math 2339
Answer sheet: Third Midterm for Math 339 November 3, Problem. Calculate the iterated integrals (Simplify as much as possible) (a) e sin(x) dydx y e sin(x) dydx y sin(x) ln y ( cos(x)) ye y dx sin(x)(lne
Second Order Partial Differential Equations
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
DESIGN OF MACHINERY SOLUTION MANUAL h in h 4 0.
DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
ECE Spring Prof. David R. Jackson ECE Dept. Notes 2
ECE 634 Spring 6 Prof. David R. Jackson ECE Dept. Notes Fields in a Source-Free Region Example: Radiation from an aperture y PEC E t x Aperture Assume the following choice of vector potentials: A F = =
Similarly, we may define hyperbolic functions cosh α and sinh α from the unit hyperbola
Universit of Hperbolic Functions The trigonometric functions cos α an cos α are efine using the unit circle + b measuring the istance α in the counter-clockwise irection along the circumference of the
10/3/ revolution = 360 = 2 π radians = = x. 2π = x = 360 = : Measures of Angles and Rotations
//.: Measures of Angles and Rotations I. Vocabulary A A. Angle the union of two rays with a common endpoint B. BA and BC C. B is the vertex. B C D. You can think of BA as the rotation of (clockwise) with
Homework 3 Solutions
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Example Sheet 3 Solutions
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
is like multiplying by the conversion factor of. Dividing by 2π gives you the
Chapter Graphs of Trigonometric Functions Answer Ke. Radian Measure Answers. π. π. π. π. 7π. π 7. 70 8. 9. 0 0. 0. 00. 80. Multipling b π π is like multipling b the conversion factor of. Dividing b 0 gives
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
MathCity.org Merging man and maths
MathCity.org Merging man and maths Exercise 10. (s) Page Textbook of Algebra and Trigonometry for Class XI Available online @, Version:.0 Question # 1 Find the values of sin, and tan when: 1 π (i) (ii)
2 Composition. Invertible Mappings
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
TRIGONOMETRIC FUNCTIONS
Chapter TRIGONOMETRIC FUNCTIONS. Overview.. The word trigonometry is derived from the Greek words trigon and metron which means measuring the sides of a triangle. An angle is the amount of rotation of
Parametrized Surfaces
Parametrized Surfaces Recall from our unit on vector-valued functions at the beginning of the semester that an R 3 -valued function c(t) in one parameter is a mapping of the form c : I R 3 where I is some
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Solutions to Exercise Sheet 5
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Strain gauge and rosettes
Strain gauge and rosettes Introduction A strain gauge is a device which is used to measure strain (deformation) on an object subjected to forces. Strain can be measured using various types of devices classified
2. Μηχανικό Μαύρο Κουτί: κύλινδρος με μια μπάλα μέσα σε αυτόν.
Experiental Copetition: 14 July 011 Proble Page 1 of. Μηχανικό Μαύρο Κουτί: κύλινδρος με μια μπάλα μέσα σε αυτόν. Ένα μικρό σωματίδιο μάζας (μπάλα) βρίσκεται σε σταθερή απόσταση z από το πάνω μέρος ενός
Matrices and Determinants
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Fractional Colorings and Zykov Products of graphs
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
1. (a) (5 points) Find the unit tangent and unit normal vectors T and N to the curve. r(t) = 3cost, 4t, 3sint
1. a) 5 points) Find the unit tangent and unit normal vectors T and N to the curve at the point P, π, rt) cost, t, sint ). b) 5 points) Find curvature of the curve at the point P. Solution: a) r t) sint,,
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
( y) Partial Differential Equations
Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Finite Field Problems: Solutions
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
D Alembert s Solution to the Wave Equation
D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
Problem Set 9 Solutions. θ + 1. θ 2 + cotθ ( ) sinθ e iφ is an eigenfunction of the ˆ L 2 operator. / θ 2. φ 2. sin 2 θ φ 2. ( ) = e iφ. = e iφ cosθ.
Chemistry 362 Dr Jean M Standard Problem Set 9 Solutions The ˆ L 2 operator is defined as Verify that the angular wavefunction Y θ,φ) Also verify that the eigenvalue is given by 2! 2 & L ˆ 2! 2 2 θ 2 +
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Numerical Analysis FMN011
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Mock Exam 7. 1 Hong Kong Educational Publishing Company. Section A 1. Reference: HKDSE Math M Q2 (a) (1 + kx) n 1M + 1A = (1) =
Mock Eam 7 Mock Eam 7 Section A. Reference: HKDSE Math M 0 Q (a) ( + k) n nn ( )( k) + nk ( ) + + nn ( ) k + nk + + + A nk... () nn ( ) k... () From (), k...() n Substituting () into (), nn ( ) n 76n 76n
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 24/3/2007
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
2 2 2 The correct formula for the cosine of the sum of two angles is given by the following theorem.
5 TRIGONOMETRIC FORMULAS FOR SUMS AND DIFFERENCES The fundamental trignmetric identities cnsidered earlier express relatinships amng trignmetric functins f a single variable In this sectin we develp trignmetric
Space Physics (I) [AP-3044] Lecture 1 by Ling-Hsiao Lyu Oct Lecture 1. Dipole Magnetic Field and Equations of Magnetic Field Lines
![Space Physics (I) [AP-3044] Lecture 1 by Ling-Hsiao Lyu Oct Lecture 1. Dipole Magnetic Field and Equations of Magnetic Field Lines](/thumbs/51/28406191.jpg "Space Physics (I) [AP-3044] Lecture 1 by Ling-Hsiao Lyu Oct Lecture 1. Dipole Magnetic Field and Equations of Magnetic Field Lines")
Space Physics (I) [AP-344] Lectue by Ling-Hsiao Lyu Oct. 2 Lectue. Dipole Magnetic Field and Equations of Magnetic Field Lines.. Dipole Magnetic Field Since = we can define = A (.) whee A is called the
Principles of Mathematics 12 Answer Key, Contents 185
Principles of Mathematics Answer Ke, Contents 85 Module : Section Trigonometr Trigonometric Functions Lesson The Trigonometric Values for θ, 0 θ 60 86 Lesson Solving Trigonometric Equations for 0 θ 60
Μονοβάθμια Συστήματα: Εξίσωση Κίνησης, Διατύπωση του Προβλήματος και Μέθοδοι Επίλυσης. Απόστολος Σ. Παπαγεωργίου
Μονοβάθμια Συστήματα: Εξίσωση Κίνησης, Διατύπωση του Προβλήματος και Μέθοδοι Επίλυσης VISCOUSLY DAMPED 1-DOF SYSTEM Μονοβάθμια Συστήματα με Ιξώδη Απόσβεση Equation of Motion (Εξίσωση Κίνησης): Complete
The Simply Typed Lambda Calculus
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
C.S. 430 Assignment 6, Sample Solutions
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
3.4. Click here for solutions. Click here for answers. CURVE SKETCHING. y cos x sin x. x 1 x 2. x 2 x 3 4 y 1 x 2. x 5 2
SECTION. CURVE SKETCHING. CURVE SKETCHING A Click here for answers. S Click here for solutions. 9. Use the guidelines of this section to sketch the curve. cos sin. 5. 6 8 7 0. cot, 0.. 9. cos sin. sin
( ) 2 and compare to M.
Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
ω ω ω ω ω ω+2 ω ω+2 + ω ω ω ω+2 + ω ω+1 ω ω+2 2 ω ω ω ω ω ω ω ω+1 ω ω2 ω ω2 + ω ω ω2 + ω ω ω ω2 + ω ω+1 ω ω2 + ω ω+1 + ω ω ω ω2 + ω
0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
CORDIC Background (2A)
CORDIC Background 2A Copyright c 20-202 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2 or any later
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 6/5/2006
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Equations. BSU Math 275 sec 002,003 Fall 2018 (Ultman) Final Exam Notes 1. du dv. FTLI : f (B) f (A) = f dr. F dr = Green s Theorem : y da
BSU Math 275 sec 002,003 Fall 2018 (Ultman) Final Exam Notes 1 Equations r(t) = x(t) î + y(t) ĵ + z(t) k r = r (t) t s = r = r (t) t r(u, v) = x(u, v) î + y(u, v) ĵ + z(u, v) k S = ( ( ) r r u r v = u
Approximation of distance between locations on earth given by latitude and longitude
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
ω = radians per sec, t = 3 sec
Secion. Linear and Angular Speed 7. From exercise, =. A= r A = ( 00 ) (. ) = 7,00 in 7. Since 7 is in quadran IV, he reference 7 8 7 angle is = =. In quadran IV, he cosine is posiive. Thus, 7 cos = cos
Problem 3.1 Vector A starts at point (1, 1, 3) and ends at point (2, 1,0). Find a unit vector in the direction of A. Solution: A = 1+9 = 3.
Problem 3.1 Vector A starts at point (1, 1, 3) and ends at point (, 1,0). Find a unit vector in the direction of A. Solution: A = ˆx( 1)+ŷ( 1 ( 1))+ẑ(0 ( 3)) = ˆx+ẑ3, A = 1+9 = 3.16, â = A A = ˆx+ẑ3 3.16
4.6 Autoregressive Moving Average Model ARMA(1,1)
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Partial Differential Equations in Biology The boundary element method. March 26, 2013
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Differential equations
Differential equations Differential equations: An equation inoling one dependent ariable and its deriaties w. r. t one or more independent ariables is called a differential equation. Order of differential
Chapter 7 Transformations of Stress and Strain
Chapter 7 Transformations of Stress and Strain INTRODUCTION Transformation of Plane Stress Mohr s Circle for Plane Stress Application of Mohr s Circle to 3D Analsis 90 60 60 0 0 50 90 Introduction 7-1
forms This gives Remark 1. How to remember the above formulas: Substituting these into the equation we obtain with
Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Chapter 1 Complex numbers
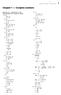Complex numbers MC Qld- Chapter Complex numbers Exercise A Operations on and representations of complex numbers a u ( i) 8i b u + v ( i) + ( + i) + i c u + v ( i) + ( + i) i + + i + 8i d u v ( i) ( + i)
Math 6 SL Probability Distributions Practice Test Mark Scheme
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
ECE 468: Digital Image Processing. Lecture 8
ECE 468: Digital Image Processing Lecture 8 Prof. Sinisa Todorovic sinisa@eecs.oregonstate.edu 1 Image Reconstruction from Projections X-ray computed tomography: X-raying an object from different directions
DiracDelta. Notations. Primary definition. Specific values. General characteristics. Traditional name. Traditional notation
DiracDelta Notations Traditional name Dirac delta function Traditional notation x Mathematica StandardForm notation DiracDeltax Primary definition 4.03.02.000.0 x Π lim ε ; x ε0 x 2 2 ε Specific values
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
2 2 2 The correct formula for the cosine of the sum of two angles is given by the following theorem.
5 TRIGONOMETRIC FORMULAS FOR SUMS AND DIFFERENCES The fundamental trignmetric identities cnsidered earlier express relatinships amng trignmetric functins f a single variable In this sectin we develp trignmetric
COMPLEX NUMBERS. 1. A number of the form.
COMPLEX NUMBERS SYNOPSIS 1. A number of the form. z = x + iy is said to be complex number x,yєr and i= -1 imaginary number. 2. i 4n =1, n is an integer. 3. In z= x +iy, x is called real part and y is called
Derivations of Useful Trigonometric Identities
Derivations of Useful Trigonometric Identities Pythagorean Identity This is a basic and very useful relationship which comes directly from the definition of the trigonometric ratios of sine and cosine
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Forced Pendulum Numerical approach
Numerical approach UiO April 8, 2014 Physical problem and equation We have a pendulum of length l, with mass m. The pendulum is subject to gravitation as well as both a forcing and linear resistance force.
Chapter 6 BLM Answers
Chapter 6 BLM Answers BLM 6 Chapter 6 Prerequisite Skills. a) i) II ii) IV iii) III i) 5 ii) 7 iii) 7. a) 0, c) 88.,.6, 59.6 d). a) 5 + 60 n; 7 + n, c). rad + n rad; 7 9,. a) 5 6 c) 69. d) 0.88 5. a) negative
ST5224: Advanced Statistical Theory II
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
F19MC2 Solutions 9 Complex Analysis
F9MC Solutions 9 Complex Analysis. (i) Let f(z) = eaz +z. Then f is ifferentiable except at z = ±i an so by Cauchy s Resiue Theorem e az z = πi[res(f,i)+res(f, i)]. +z C(,) Since + has zeros of orer at
Every set of first-order formulas is equivalent to an independent set
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Solutions to the Schrodinger equation atomic orbitals. Ψ 1 s Ψ 2 s Ψ 2 px Ψ 2 py Ψ 2 pz
Solutions to the Schrodinger equation atomic orbitals Ψ 1 s Ψ 2 s Ψ 2 px Ψ 2 py Ψ 2 pz ybridization Valence Bond Approach to bonding sp 3 (Ψ 2 s + Ψ 2 px + Ψ 2 py + Ψ 2 pz) sp 2 (Ψ 2 s + Ψ 2 px + Ψ 2 py)
Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων. Εξάμηνο 7 ο
Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων Εξάμηνο 7 ο Procedures and Functions Stored procedures and functions are named blocks of code that enable you to group and organize a series of SQL and PL/SQL