Β ΠΕΡΙΦΕΡΕΙΑ ΠΕΙΡΑΙΩΣ ΠΑΣΟΚ EK. T ΖΑΧΑΡΟΠΟΥΛ ΟΣ ΠΡΟΔΡΟΜΟΣ ΜΥΡΓΙΑΛΗ ΧΡΥΣΟΥΛΑ (ΧΡΥΣΑ) ΜΑΓΙΑΤΗΣ ΙΩΑΝΝΗΣ ΧΑΤΖΗΜΑΝΩΛ ΗΣ ΕΥΑΓΓΕΛΟΣ ΔΙΑΜΑΝΤΙΔΗΣ ΙΩΑΝΝΗΣ

ΣΥΓΚΕΝΤΡΩΤΙΚΗ ΚΑΤΑΣΤΑΣΗ ΙΑΤΡΙΚΩΝ ΕΠΙΣΚΕΨΕΩΝ ΚΑΙ ΠΡΑΞΕΩΝ

ΣΥΓΚΕΝΤΡΩΤΙΚΗ ΚΑΤΑΣΤΑΣΗ ΙΑΤΡΙΚΩΝ ΕΠΙΣΚΕΨΕΩΝ ΚΑΙ ΠΡΑΞΕΩΝ ΤΜΗΜΑ Ο ΠΑΤΡΩΝΥΜΟ. ΑΦΜ. ΕΙΔΙΚΟΤΗΤΑΣ. ΔΙΕΥΘΥΝΣΗ. ΕΠΙΣΚΕΨΕΙΣ ΣΤΟ ΙΑΤΡΕΙΟ ΠΡΩΤΗ ΕΠΙΣΚΕΨΗ (0 ) ΔΕΥΤΕΡΗ ΕΠΙΣΚΕΨΗ (0 ) ΕΠΟΜΕΝΕΣ ΜΕΤΑ ΤΗ ΔΕΥΤΕΡΗ (0 ) ΣΥΝΟΛΟ

ΑΠΟΤΕΛΕΣΜΑΤΑ ΓΡΑΠΤΩΝ ΕΞΕΤΑΣΕΩΝ ΓΙΑ ΤΗΝ ΕΘΝΙΚΗ ΣΧΟΛΗ ΔΙΚΑΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΩΝ ΚΕ ΕΙΣΑΓΩΓΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΔΙΟΙΚΗΤΙΚΗΣ ΔΙΚΑΙΟΣΥΝΗΣ MIS

ΑΠΟΤΕΛΕΣΜΑΤΑ ΓΡΑΠΤΩΝ ΕΞΕΤΑΣΕΩΝ ΓΙΑ ΤΗΝ ΕΘΝΙΚΗ ΣΧΟΛΗ ΔΙΚΑΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΩΝ ΚΕ ΕΙΣΑΓΩΓΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΔΙΟΙΚΗΤΙΚΗΣ ΔΙΚΑΙΟΣΥΝΗΣ MIS 5010725 1 15 4,40 3,50 3,9500 4,50 7,50 6,0000 4,00 4,50 4,2500 5,50 5,00

Ο ΠΕΡΙ ΡΥΘΜΙΣΗΣ ΤΗΣ ΑΓΟΡΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ ΝΟΜΟΣ ΠΑΡΑΡΤΗΜΑ. (Κανονισμός 6) ΤΕΛΗ ΑΔΕΙΩΝ ΠΙΝΑΚΑΣ Α

9 Ο ΠΕΡΙ ΡΥΘΜΙΣΗΣ ΤΗΣ ΑΓΟΡΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ ΝΟΜΟΣ ΠΑΡΑΡΤΗΜΑ (Κανονισμός 6) ΤΕΛΗ ΑΔΕΙΩΝ ΠΙΝΑΚΑΣ Α 1. Άδεια Κατασκευής Εγκαταστάσεων Εισαγωγής/ Αποθήκευσης/ 1.1 Τέλος αίτησης 0.05 σεντ ανά 100 κυβικά μέτρα

Ο ΠΕΡΙ ΧΡΗΜΑΤΙΣΤΗΡΙΟΥ ΑΞΙΩΝ ΚΥΠΡΟΥ ΝΟΜΟΣ ΤΟΥ 2005 ΔΑΣΙΚΕΣ ΒΙΟΜΗΧΑΝΙΕΣ ΚΥΠΡΟΥ ΔΗΜΟΣΙΑ ΛΤΔ Τ Θ 24043, 1700 ΛΕΥΚΩΣΙΑ

Ιδιότητα Παραίτησης ΠΑΥΛΟΣ ΚΑΡΥΔΑΣ (Επαναδιορισμός ΠΑΥΛΟΣ ΚΑΡΥΔΑΣ ΜΗ ΠΟΛΙΤΙΚΟΣ ΜΗΧΑΝΙΚΟΣ ΟΝΟΜΑ ΣΧΕΣΗ Ιδιότητα Παραίτησης ΙΩΣΗΦ ΚΩΝΣΤΑΝΤΙΝΙΔΗΣ (Επαναδιορισμός ΙΩΣΗΦ ΚΩΝΣΤΑΝΤΙΝΙΔΗΣ ΜΗ ΠΟΛΙΤΙΚΟΣ ΜΗΧΑΝΙΚΟΣ

ΣΥΓΚΕΝΤΡΩΤΙΚΗ ΚΑΤΑΣΤΑΣΗ ΙΑΤΡΙΚΩΝ ΕΠΙΣΚΕΨΕΩΝ ΚΑΙ ΠΡΑΞΕΩΝ

ΣΥΓΚΕΝΤΡΩΤΙΚΗ ΚΑΤΑΣΤΑΣΗ ΙΑΤΡΙΚΩΝ ΕΠΙΣΚΕΨΕΩΝ ΚΑΙ ΠΡΑΞΕΩΝ ΤΜΗΜΑ Ο ΠΑΤΡΩΝΥΜΟ. ΑΦΜ. ΕΙΔΙΚΟΤΗΤΑΣ. ΔΙΕΥΘΥΝΣΗ. E-MAIL ΕΠΙΣΚΕΨΕΙΣ ΣΤΟ ΙΑΤΡΕΙΟ ΠΡΩΤΗ ΕΠΙΣΚΕΨΗ (0 ) ΔΕΥΤΕΡΗ ΕΠΙΣΚΕΨΗ (0 ) ΕΠΟΜΕΝΕΣ ΜΕΤΑ ΤΗ ΔΕΥΤΕΡΗ

Κριτήριο παρεµβολής Βοηθητική συνάρτηση. R R τέτοια, ώστε να ισχύει. f(x) x. lim. ii) x 0. lim f (x) = 0. x 0. lim. ( x + x + 4) = 4. x 0.

ΜΑΘΗΜΑ 8.4.5 ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ Κριτήριο παρεµβολής Βοηθητική συνάρτηση R ΑΣΚΗΣΕΙΣ Κριτήριο παρεµβολής. 4 f () Να βρείτε το i) i) ( 4 ) ( 4 ) R R τέτοια, ώστε να ισχύει f () 0 4 0 0 4 για κάθε κοντά στο

ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΓΡΑΠΤΗ ΔΟΚΙΜΑΣΙΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Β ΓΥΜΝΑΣΙΟΥ

μιας οξείας γωνίας; 0,5, 5 2,, 2 5 Σε ορθογώνιο τρίγωνο ΑΒΓ (Α=90 ο ) δίνεται ότι Β=5 ο και 8 τις πλευρές ΑΓ και ΒΓ με προσέγγιση ενός δεκαδικού ψηφίου. (Δίνονται οι τιμές: ημ5 ο =0,57, συν5 ο =0,82, εφ5

Παράρτημα 2. I. Spreadsheet ABC FACTORS. II. Spreadsheet EFG FACTORS. III. Spreadsheet ΛΑΪΚΗ FACTORING. IV. Spreadsheet ΠΕΙΡΑΙΩΣ FACTORING

Παράρτημα 2 I. Spreadsheet ABC FACTORS II. Spreadsheet EFG FACTORS III. Spreadsheet ΛΑΪΚΗ FACTORING IV. Spreadsheet ΠΕΙΡΑΙΩΣ FACTORING I. Spreadsheet ABC FACTORS ABC FACTORS ΧΡΗΣΕΙΣ 31/12/2004 31/12/2005

Ερωτήσεις αντιστοίχισης

Ερωτήσεις αντιστοίχισης. * Σε κάθε γραφική παράσταση C f της στήλης Α του πίνακα Ι να αντιστοιχίσετε τη γραφική παράσταση C f από τη στήλη Β, συµπληρώνοντας τον πίνακα ΙΙ. : C f : C f. - α. 2. β. 2π 3.

ΦΥΛΛΆΔΙΟ ΑΣΚΉΣΕΩΝ 2 ΣΥΝΑΡΤΗΣΕΙΣ

ΦΥΛΛΆΔΙΟ ΑΣΚΉΣΕΩΝ 2 ΣΥΝΑΡΤΗΣΕΙΣ 1. Να βρείτε τα πεδία ορισµού των συναρτήσεων µε τύπο: i) ii) iii) iv) v) 2. Δίνεται η συνάρτηση µε:. Να βρείτε µια περίοδο της. 3. Δίνεται η συνάρτηση µε:. Να αποδείξετε

Γενική Ισορροπία. Παραδείγµατα γενικής ισορροπίας µε ανταλλαγή. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς. 19 Απριλίου 2013

Γενική Ισορροπία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου 2013 1 / 25 Παραδείγµατα γενικής ισορροπίας µε ανταλλαγή. ιαφορετικές προτιµήσεις

lim f ( x) x + f ( x) x a x a x a 2x 1

Ασύµπτωτες γραφικής παραστάσεως συναρτήσεως Ασύµπτωτες της γραφικής παραστάσεως συναρτήσεως y f ( ) ονοµάζονται οι ευθείες που για πολύ µικρές ή µεγάλες τιµές των, y προσεγγίζουν ικανοποιητικά την γραφική

1, με μηδενική ταχύτητα.

Ομάδα Α Ένα ορθογώνιο οικόπεδο έχει πλευρές 100m και 0m. Οι μεγάλες πλευρές είναι τέλεια προσανατολισμένες οικοπέδου. Παίρνοντας ως σημείο αναφοράς την νοτιοανατολική (ΝΑ) πλευρά του οικοπέδου, βρίσκει

2011 ΘΕΜΑΤΑ ΘΕΜΑ Γ 1. Δίνεται η συνάρτηση f: δύο φορές παραγωγίσιμη στο, με f (0) = f(0) = 0, η οποία ικανοποιεί τη σχέση:

ΘΕΜΑΤΑ ΘΕΜΑ Γ. Δίνεται η συνάρτηση f: δύο φορές παραγωγίσιμη στο, με f () f(), η οποία ικανοποιεί τη σχέση: (f () + f () ) f () + f (), για κάθε. Γ. Να αποδείξετε ότι f() ln( ),. Μονάδες 8 Γ. Να μελετήσετε

4.4 ΕΞΙΣΩΣΕΙΣ & ΑΝΙΣΩΣΕΙΣ ΠΟΥ ΑΝΑΓΟΝΤΑΙ

1 4.4 ΕΞΙΣΩΣΕΙΣ & ΑΝΙΣΩΣΕΙΣ ΠΟΥ ΑΝΑΓΟΝΤΑΙ ΣΕ ΠΟΛΥΩΝΥΜΙΚΕΣ Ασκήσεις σχολικού βιβλίου σελίδας 1 14 A Οµάδας 1.i) Να λύσετε την εξίσωση 1 + = 1 Είναι = ( 1) Ε.Κ.Π = ( 1) 0 0 και 1 0 0 και 1 (περιορισµοί)

Κεφάλαιο 3ο: ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ 1o ΜΕΡΟΣ

Κεφάλαιο 3ο: ΙΑΦΟΡΙΚΟ ΟΓΙΜΟ 1o ΜΕΡΟ Ερωτήσεις του τύπου «ωστό - άθος» 1. * Η εφαπτοµένη της γραφικής παράστασης µιας σταθερής συνάρτησης σε οποιοδήποτε σηµείο του πεδίου ορισµού της συµπίπτει µε τη γραφική

Ερωτήσεις αντιστοίχισης

Ερωτήσεις αντιστοίχισης. * Να συµπληρώσετε τον πίνακα ΙΙ, έτσι ώστε σε κάθε γραφική παράσταση συνάρτησης f της στήλης Α του πίνακα Ι να αντιστοιχεί η γραφική παράσταση της παράγουσάς της από τη στήλη Β.

β. Το πλάτος της σύνθετης ταλάντωσης είναι : Α = (Α 1 ² + Α 2 ² + 2 Α 1 Α 2 συν φ) (φ = π rad) Α = (Α 1 ² + Α 2 ² + 2 Α 1 Α 2 συν π) Α = [Α 1 ² + Α 2

1) Ένα κινητό εκτελεί συγχρόνως δύο απλές αρμονικές ταλαντώσεις που γίνονται στην ίδια διεύθυνση και γύρω από την θέση ισορροπίας με εξισώσεις : x 1 = 3 ημ [(2 π) t] και x 2 = 4 ημ [(2 π) t + φ], (S.I.).

Ο ΠΕΡΙ ΧΡΗΜΑΤΙΣΤΗΡΙΟΥ ΑΞΙΩΝ ΚΥΠΡΟΥ ΝΟΜΟΣ ΤΟΥ 2005 ΔΑΣΙΚΕΣ ΒΙΟΜΗΧΑΝΙΕΣ ΚΥΠΡΟΥ ΔΗΜΟΣΙΑ ΛΤΔ Τ Θ 24043, 1700 ΛΕΥΚΩΣΙΑ

Ιδιότητα Παραίτησης ΠΑΥΛΟΣ ΚΑΡΥΔΑΣ (Επαναδιορισμός Καταστατικού) ΠΑΥΛΟΣ ΚΑΡΥΔΑΣ ΜΗ ΑΝΕΞΑΡΤΗΤΟΣ ΠΟΛΙΤΙΚΟΣ ΜΗΧΑΝΙΚΟΣ ΟΝΟΜΑ ΣΧΕΣΗ Ιδιότητα Παραίτησης ΙΩΣΗΦ ΚΩΝΣΤΑΝΤΙΝΙΔΗΣ (Επαναδιορισμός Καταστατικού) ΙΩΣΗΦ

Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ. (ii) f (x) = π. f (x)

I Παράγωγος συνάρτησης σε σηµείο Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ Να βρείτε ( αν υπάρχει ) την παράγωγο της συνάρτησης f στο σηµείο (i) f () = +, = (ii) f () =, = (iii) f () = + 6, = (iv) f () = συν, = Να βρείτε

2018 Φάση 1 ιαγωνίσµατα Προετοιµασίας ΜΑΘΗΜΑΤΙΚΑ. Γ' Γενικού Λυκείου. Θετικών Σπουδών / Σπουδών Οικονοµίας & Πληροφορικής

ΘΕΜΑ Α 2018 Φάση 1 ιαγωνίσµατα Προετοιµασίας ΜΑΘΗΜΑΤΙΚΑ Γ' Γενικού Λυκείου Θετικών Σπουδών / Σπουδών Οικονοµίας & Πληροφορικής Σάββατο 13 Ιανουαρίου 2018 ιάρκεια Εξέτασης: 3 ώρες ΘΕΜΑΤΑ ν Α1. Να αποδειχθεί

ΤΙΜΟΚΑΤΑΛΟΓΟΣ ΥΠΗΡΕΣΙΑΣ - Ο.Κ.ΣΥ.Α./ΣΥ.ΜΕ.Φ.Σ. (ΟΛΟΚΛΗΡΩΜΕΝΗ ΚΕΝΤΡΙΚΗ ΣΥΝ ΕΣΗ ΣΤΟ ΙΚΤΥΟ ADSL- ΣΥΝ ΕΣΗ ΜΕΤΑ ΟΣΗΣ ΣΕ ΦΥΣΙΚΗ ΣΥΝΕΓΚΑΤΑΣΤΑΣΗ)

ΤΙΜΟΚΑΤΑΛΟΓΟΣ ΥΠΗΡΕΣΙΑΣ - Ο.Κ.ΣΥ.Α./ΣΥ.ΜΕ.Φ.Σ. (ΟΛΟΚΛΗΡΩΜΕΝΗ ΚΕΝΤΡΙΚΗ ΣΥΝ ΕΣΗ ΣΤΟ ΙΚΤΥΟ ADSL- ΣΥΝ ΕΣΗ ΜΕΤΑ ΟΣΗΣ ΣΕ ΦΥΣΙΚΗ ΣΥΝΕΓΚΑΤΑΣΤΑΣΗ) Ο.Κ.ΣΥ.Α./ΣΥ.ΜΕ.Φ.Σ. BRAS ΕΘΝΙΚΗ Ο.Κ.ΣΥ.Α OLO-BRAS-ΕΘΝΙΚΗ Gbe Τέλος

1. * Η γραφική παράσταση µιας συνάρτησης f έχει εφαπτοµένη στο x 0 την ευθεία y = αx + β, µε α 0, όταν. είναι + είναι -

Ερωτήσεις πολλαπλής επιλογής. * Η γραφική παράσταση µιας συνάρτησης f έχει εφαπτοµένη στο την ευθεία = α + β, µε α, όταν Α. ( Β. η f είναι συνεχής στο = α R Γ. η f δεν είναι συνεχής στο. το όριο Ε. το

ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2019 A ΦΑΣΗ

ΤΑΞΗ: ΜΑΘΗΜΑ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ / ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Ημερομηνία: Σάββατο Ιανουαρίου 09 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α Α. Σχολικό βιβλίο σελίδα 0 ΑΠΑΝΤΗΣΕΙΣ Α. α. Λάθος β. Λάθος γ. Σωστό δ. Σωστό

2.1. Ασκήσεις σχολικού βιβλίου σελίδας A Oµάδας. 1.i) 1.ii) 1.iii) = 0. f x = x + 1 στο x ο. Να βρείτε την παράγωγο της συνάρτησης ( ) Λύση

. Ασκήσεις σχλικύ βιβλίυ σελίδας 9 A Oµάδας. Να βρείτε την παράγωγ της συνάρτησης ( D R ( ( ( στ. Να βρείτε την παράγωγ της συνάρτησης ( D ( R ( ( ( στ ( ( ( ( ( ( ( (.i Να βρείτε την παράγωγ της συνάρτησης

Διοικητική Λογιστική

Διοικητική Λογιστική Δημήτρης Μπάλιος Κοστολόγηση συνεχούς παραγωγής Πληροφορίες για το κόστος παραγωγής συγκεκριμένης περιόδου Βήμα 1ο : Προσδιορισμός της φυσικής ροής Βήμα 2ο : Προσδιορισμός των ισοδύναμων

Ο ΠΕΡΙ ΧΡΗΜΑΤΙΣΤΗΡΙΟΥ ΑΞΙΩΝ ΚΥΠΡΟΥ ΝΟΜΟΣ ΤΟΥ 2005 ΔΑΣΙΚΕΣ ΒΙΟΜΗΧΑΝΙΕΣ ΚΥΠΡΟΥ ΔΗΜΟΣΙΑ ΛΤΔ Τ Θ 24043, 1700 ΛΕΥΚΩΣΙΑ

εκδότη Ιδιότητα Παραίτησης ΚΛΕΛΙΑ ΒΑΣΙΛΕΙΟΥ ΠΡΟΕΔΡΟΣ Δ. Σ ΜΗ-ΕΚΤΕΛΕΣΤΙΚΟΣ ΠΟΛΙΤΙΚΟΣ ΕΠΙΣΤΗΜΟΝΑΣ ΟΝΟΜΑ ΣΧΕΣΗ εκδότη Ιδιότητα Παραίτησης ΑΛΕΞΗΣ ΑΔΑΜΙΔΗΣ (Επαναδιορισμός σύμφωνα με τις πρόνοιες του Καταστατικού)

i<0. 0<t<T/4. i<0 0- T 4 : i t <0 φόρτιση T/2 T/4 3T/4 T

1 5. ΚΥΚΛΩΜΑ - και πολικότητες. Για q=q συν(ω) και = -I ηµ(ω). 1. < πυκνωτή είναι αρχικά αυτή που φορά της έντασης µόλις κλείσουµε το ιακόπτη είναι επίσης αυτή του σχήµατος µε

ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ

1945 ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΤΕΥΧΟΣ ΠΡΩΤΟ Αρ. Φύλλου 71 30 Μαρτίου 2012 NOMOΣ ΥΠ ΑΡΙΘ. 4063 Κύρωση της Απόφασης του Ευρωπαϊκού Συμβουλίου που τροποποιεί το άρθρο 136 της ΣΛΕΕ,

1.2 Βασικές Τριγωνομετρικές Εξισώσεις

. Βασικές Τριγωνομετρικές Εξισώσεις. Να λύσετε τις εξισώσεις: i) ημ = ημ = i = iv) =. Να λύσετε τις εξισώσεις: i) εφ = εφ = i σφ = iv) σφ =. Να λυθούν οι εξισώσεις: i) ημ = = i εφ = iv) σφ = 4. Να λυθούν

ΜΑΘΗΜΑ ΕΥΤΕΡΟ ΜΑΘΗΜΑΤΙΚΩΝ ΓΙΑ ΟΙΚΟΝΟΜΟΛΟΓΟΥΣ ΑΣΚΗΣΕΙΣ (ΟΡΙΟ ΚΑΙ ΣΥΝΕΧΕΙΑ)

ΜΑΘΗΜΑ ΕΥΤΕΡΟ ΜΑΘΗΜΑΤΙΚΩΝ ΓΙΑ ΟΙΚΟΝΟΜΟΛΟΓΟΥΣ ΑΣΚΗΣΕΙΣ (ΟΡΙΟ ΚΑΙ ΣΥΝΕΧΕΙΑ) A. Εύρεση Πεδίου Τιµών Συναρτήσεων ίνεται η συνάρτηση h, h ( ) = 4+, [ 1,4] Να βρεθεί το πεδίο τιµών της συνάρτησης. Η λογική για

Επαναληπτικές 6ης Απριλίου 1975

ΔΗΜΟΤΙΚΕΣ ΕΚΛΟΓΕΣ 30ης Μαρτίου 1975 και Επαναληπτικές 6ης Απριλίου 1975 Πληθυσμός απογραφής 18.535 Εγγεγραμμένοι εκλογείς 9.981 Ψηφίσαντες 7.951 (Α ΚΥΡΙΑΚΗ) 8.619 (Β ΚΥΡΙΑΚΗ) Εγκυρα 7.862 (Α ΚΥΡΙΑΚΗ) 8.465

ΔΙΑΓΩΝΙΣΜΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ (1 η σειρά)

9 ΘΕΡΙΝΑ ΔΙΑΓΩΝΙΣΜΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ( η σειρά) ΘΕΜΑ ο Α. Έστω η συνάρτηση f με f() ημ. Να αποδείξετε ότι η f είναι παραγωγίσιμη στο και ισχύει f () συν Β. Πότε μια συνάρτηση f λέμε

- ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 5: ΚΡΙΤΗΡΙΟ ΠΑΡΕΜΒΟΛΗΣ - ΤΡΙΓΩΝΟΜΕΤΡΙΚΑ ΟΡΙΑ - ΟΡΙΟ ΣΥΝΘΕΤΗΣ ΣΥΝΑΡΤΗΣΗΣ

ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 5: ΚΡΙΤΗΡΙΟ ΠΑΡΕΜΒΟΛΗΣ - ΤΡΙΓΩΝΟΜΕΤΡΙΚΑ ΟΡΙΑ - ΟΡΙΟ ΣΥΝΘΕΤΗΣ ΣΥΝΑΡΤΗΣΗΣ [Ενότητες Κριτήριο Παρεμβολής - Τριγωνομετρικά Όρια - Όριο Σύνθετης

ΕΡΓΑΣΙΑ 8 ΚΙΝΗΣΗ ΜΕ ΔΥΝΑΜΕΙΣ ΠΟΥ ΔΕΝ ΕΧΟΥΝ ΤΗΝ ΙΔΙΑ ΔΙΕΥΘΥΝΣΗ ΚΑΙ ΤΡΙΒΗ

ΕΡΓΑΣΙΑ 8 ΚΙΝΗΣΗ ΜΕ ΔΥΝΑΜΕΙΣ ΠΟΥ ΔΕΝ ΕΧΟΥΝ ΤΗΝ ΙΔΙΑ ΔΙΕΥΘΥΝΣΗ ΚΑΙ ΤΡΙΒΗ 1. Σώμα μάζας m=2kg είναι ακίνητο πάνω σε οριζόντιο επίπεδο. Στο σώμα ασκείται οριζόντια δύναμη F με φορά προς τα δεξιά. Να βρεθεί

ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ. στο x o = 1. και x o =1. και x o =0.

ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ συνέχεια στο o Nα μελετήσετε ως προς τη συνέχεια στο o τις συναρτήσεις : 4 4 α) f() 4 στο o = 4 5 4 β) f() στο o = γ) ημ f() στο o = Nα μελετήσετε ως προς τη συνέχεια στο o τις συναρτήσεις

ΜΑΘΗΜΑ ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ xο

ΜΑΘΗΜΑ 9.6 ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ ο R Θεωρία Σχόλια - Ασκήσεις ΘΕΩΡΙΑ. Ορισµός f ( ) ο σηµαίνει ότι οι τιµές f ( ) της συνάρτησης f γίνονται µεγαλύτερες από κάθε θετικό αριθµό Μ, καθώς.. Ορισµός f ( )

ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2019 Β ΦΑΣΗ

ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑ: ΑΛΓΕΒΡΑ / ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Ημερομηνία: Σάββατο Μαΐου 09 Διάρκεια Εξέτασης: ώρες ΘΕΜΑ Α A. Σχολικό βιβλίο σελίδα 4. ΑΠΑΝΤΗΣΕΙΣ Α. α. Λάθος, β. Λάθος, γ. Σωστό, δ. Λάθος,

( ) Ίσες συναρτήσεις. = g, Οι συναρτήσεις f, g λέμε ότι είναι ίσες και συμβολίζουμε f. όταν: Έχουν το ίδιο πεδία ορισμού Α

.5.. Ίσες συναρτήσεις ΣΥΝΑΡΤΗΣΕΙΣ 7 Ο ΜΑΘΗΜΑ Οι συναρτήσεις f, g λέμε ότι είναι ίσες και συμβολίζουμε f = g, Έχουν το ίδιο πεδία ορισμού Α Για κάθε x Α ισχύει f ( x) = g( x) Αν για τις συναρτήσεις: f:

Άσκηση 3. Άμεσος Επανεπιμερισμός

Άσκηση 3 Άμεσος Επανεπιμερισμός Α) Σύμφωνα με την μέθοδο του άμεσου επανεπιμερισμού το κόστος κάθε βοηθητικού κέντρου μεταφέρεται σε περισσότερα από ένα κύρια κέντρα κόστους με τη χρησιμοποίηση της αντίστοιχης

ΜΑΘΗΜΑΤΙΚΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ & ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ

9 Ιουνίου ΜΑΘΗΜΑΤΙΚΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ & ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ Απαντήσεις Θεμάτων Επαναληπτικών Πανελλαδικών Εξετάσεων Εσπερινών Γενικών Λυκείων (Νέο & Παλιό Σύστημα)

ΣΥΝ ΕΣΜΟΣ ΣΥΜΒΟΥΛΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ. Ι.Κωλέττη 25Β, Τ.Κ.54627, Θεσσαλονίκη, Τηλ : , Fax : , e mail :

ΣΥΝ ΕΣΜΟΣ ΣΥΜΒΟΥΛΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ Ι.Κωλέττη 25Β, Τ.Κ.54627, Θεσσαλονίκη, Τηλ : 2310 567898, Fax : 2310 567890, e mail : info@sysep.org, www.sysep.org Πίνακας 1 Η εταιρία σας έχει υποβάλλει επενδυτικές προτάσεις

Εφαρμογή Υποβολής Αίτησης Εκδήλωσης Ενδιαφέροντος για την Πιστοποίηση Φορέων Α και Β Βαθμού

Εφαρμογή Υποβολής Αίτησης Εκδήλωσης Ενδιαφέροντος 1 ΠΕΡΙΕΧΟΜΕΝΑ Αίτηση Ενδιαφέροντος... 3 2 Αίτηση Ενδιαφέροντος Εφαρμογή Υποβολής Αίτησης Εκδήλωσης Ενδιαφέροντος Ο χρήστης μεταβαίνει στην ηλεκτρονική

ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ ΕΡΓΑΣΙΑ 7

ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ ΕΡΓΑΣΙΑ 7 3 ος ΝΟΜΟΣ ΝΕΥΤΩΝΑ-ΣΥΝΙΣΤΑΜΕΝΗ-ΑΝΑΛΥΣΗ ΔΥΝΑΜΗΣ ΚΑΙ ΙΣΟΡΡΟΠΙΑ ΣΤΟ ΕΠΙΠΕΔΟ 1. Δύο σώματα με μάζες m 1 =8Kg και m 2 =5Kg που κινούνται σε οριζόντιο επίπεδο με αντίθετες κατευθύνσεις,

ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 16 ΜΑΪΟΥ 2011 ΑΠΑΝΤΗΣΕΙΣ

ΘΕΜΑ Α ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑΛ Β 6 ΜΑΪΟΥ ΑΠΑΝΤΗΣΕΙΣ Α Θεωρία (Θεώρ Frmat) σχολικό βιβλίο σελ 6-6 Α Θεωρία (Ορισµός) σχολικό βιβλίο σελ 8 Α3 ΘΕΜΑ Β α β γ δ ε Σ Σ Λ Λ Σ B Έχουµε από υπόθεση

ΑΣΚΗΣΕΙΣ ΣΤΑ ΟΡΙΑ ΑΣΚΗΣΗ 1. Λύση. α. lim. χ 0 χ. χ χ χ = 2 lim limg(χ) = 2 και. = 2. Θέτω g(χ) = οπότε έχω: χ 1. χ 1. = g(χ)(χ 1). Επομένως.

ΑΣΚΗΣΗ Αν 0 f() 0 f() =, να βρείτε τα όρια f() = f() g() = και f() και f() 0 f( ) =. Θέτω g() = = g()( ). Επομένως = [g()( )] = g() f() οπότε έω: ( ) = ( ) = f( ) = f( ) ( ) ( ) Θέτω = u και έω ότι όταν

- ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 2: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ

ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 2: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ [Κεφ. 1.3: Μονότονες Συναρτήσεις - Αντίστροφη Συνάρτηση σχολικού βιβλίου]. ΣΗΜΕΙΩΣΕΙΣ Μονοτονία

Οριακή Κοστολόγηση. Τιμή Πώλησης 15 Αρχικό απόθεμα 0 Μονάδες παραγωγής Μονάδες πώλησης Τελικό απόθεμα 500

ΑΣΚΗΣΗ 1 Κοστολόγηση Πλήρους Απορρόφησης Πωλήσεις (2.000 x 15 ) 30.000 Μείον κόστος πωληθέντων Αρχικό Απόθεμα 0 Συν Κόστος παραχθέντων προϊόντων 17.600 Προϊόντα διαθέσιμα προς πώληση 17.600 Μείον τελικό

ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΔΙΑΓΩΝΙΣΜΑΤΟΣ ΑΛΓΕΒΡΑΣ Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 7 ΔΕΚΕΜΒΡΙΟΥ 2014

ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΔΙΑΓΩΝΙΣΜΑΤΟΣ ΑΛΓΕΒΡΑΣ Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 7 ΔΕΚΕΜΒΡΙΟΥ 04 ΘΕΜΑ Α Α. Θεωρία από το σχολικό βιβλίο σελίδα 60. Α. α) Θεωρία από το σχολικό βιβλίο σελίδα 3. β) Θεωρία από το σχολικό

ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ Έναρξη μαθημάτων: Τρίτη 28 Φεβρουαρίου 2012

ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2011 2012 ΒΑΣΙΚΕΣ ΗΜΕΡΟΜΗΝΙΕΣ ΓΙΑ ΤΟ ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ Έναρξη μαθημάτων: Τρίτη 28 Φεβρουαρίου 2012 Περίοδος Διδασκαλίας: Έναρξη: Τρίτη 28 Φεβρουαρίου 2012 Λήξη: Παρασκευή

ΣΤΑΘΕΡΗ ΣΥΝΑΡΤΗΣΗ. Το Θεώρημα και το Πόρισμα ισχύουν σε διαστήματα και όχι σε ένωση διαστημάτων.

ΣΤΑΘΕΡΗ ΣΥΝΑΡΤΗΣΗ Θεώρημα Αν μια συνάρτηση f είναι συνεχής σε ένα διάστημα Δ και ισχύει f () = 0 για κάθε εσωτερικό σημείο του Δ, τότε η f είναι σταθερή σ' όλο το διάστημα Δ. Πόρισμα Αν δύο συναρτήσεις

3.1 ΤΡΙΓΩΝΟΜΕΤΡΙΚΗ ΑΡΙΘΜΟΙ ΓΩΝΙΑΣ

ΚΕΦΑΛΑΙΟ Ο : ΤΡΙΓΩΝΟΜΕΤΡΙΑ. ΤΡΙΓΩΝΟΜΕΤΡΙΚΗ ΑΡΙΘΜΟΙ ΓΩΝΙΑΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΟΞΕΙΑΣ ΓΩΝΙΑΣ έ _ ά ί ί _ ά ί έ _ ά ί _ ά ί _ ά έ _ ά ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΤΥΧΑΙΑΣ ΓΩΝΙΑΣ y y y όπου η απόσταση του

2.8. Ασκήσεις σχολικού βιβλίου σελίδας A Οµάδας. 1.i)

1.8 Ασκήσεις σχολικού βιβλίου σελίδας 77 79 A Οµάδας 1.i) Να βρείτε τα διαστήµατα στα οποία η συνάρτηση () 5 5 4 + είναι κυρτή ή κοίλη και να προσδιορίσετε (αν υπάρχουν) τα σηµεία καµπής της γραφικής της

3Νο. ασκήσεις Α Ν Α Λ Υ Σ Η 1Ο Κ Ε Φ Α Λ Α Ι Ο. Θετική Τεχνολογική Κατεύθυνση ( ) ( 0)

Λ Υ Κ Ε Ι Ο Α Ν Α Λ Υ Σ Η 1Ο Κ Ε Φ Α Λ Α Ι Ο ΕΠΙΜΕΛΕΙΑ : Π Δ ΤΡΙΜΗΣ ΜΑΘΗΜΑΤΙΚΟΣ Θετική Τεχνολογική Κατεύθυνση ασκήσεις (ΝΑ ΛΥΘΟΥΝ ΜΕΤΑ ΑΠΟ ΤΙΣ ΑΝΤΙΣΤΟΙΧΕΣ ΤΟΥ ΒΙΒΛΙΟΥ) 3Νο ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ 1 Να μελετήσετε

EL Eνωμένη στην πολυμορφία EL A8-0204/271. Τροπολογία. Kosma Złotowski, Roberts Zīle εξ ονόματος της Ομάδας ECR

22.3.2019 A8-0204/271 271 Άρθρο 1 παράγραφος 1 σημείο 3 στοιχείο β Άρθρο 5 στοιχείο γ γ) να εκτελεί πραγματικά και συνεχώς τις διοικητικές και εμπορικές δραστηριότητές της με τον κατάλληλο διοικητικό εξοπλισμό

ÏÑÏÓÇÌÏ ÇÑÁÊËÅÉÏ ( )( ) ( )( ) Γ' ΤΑΞΗ ΓΕΝ.ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΑ ΑΠΑΝΤΗΣΕΙΣ. ΘΕΜΑ 1 ο. ΘΕΜΑ 2 ο. w w + 1= + 1. α= α.

Γ' ΤΑΞΗ ΓΕΝΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΘΕΜΑ ο Α Σχολικό βιβλίο σελ Β σελ Β σελ Γ α Λ β Σ γ Λ δ Λ ε Σ ΘΕΜΑ ο ΜΑΘΗΜΑΤΙΚΑ ΑΠΑΝΤΗΣΕΙΣ + w z = w z w = + w z zw = + w w w + zw = z w( + z) = z z z

ΥΠΟΒΟΛΗ ΕΠΕΝΔΥΤΙΚΩΝ ΣΧΕΔΙΩΝ ΣΤΟ ΠΛΑΙΣΙΟ ΤΗΣ 1ης ΠΡΟΚΗΡΥΞΗΣ LEADER

Κατερίνη Δευτέρα, 04 Απριλίου 2011 ΔΕΛΤΙΟ ΤΥΠΟΥ ΥΠΟΒΟΛΗ ΕΠΕΝΔΥΤΙΚΩΝ ΣΧΕΔΙΩΝ ΣΤΟ ΠΛΑΙΣΙΟ ΤΗΣ 1ης ΠΡΟΚΗΡΥΞΗΣ LEADER Ολοκληρώθηκε την Πέμπτη 31 Μαρτίου 2011, η υποβολή των επενδυτικών σχεδίων στο πλαίσιο

Διοικητική Λογιστική

Τμήμα Οικονομικών Επιστημών ΕΚΠΑ Νικόλαος Ηρειώτης - Δημήτριος Μπάλιος Διοικητική Λογιστική Νικόλαος Ηρειώτης - Δημήτρης Μπάλιος Κοστολόγηση συνεχούς παραγωγής - Ασκήσεις #4# Πληροφορίες για το κόστος

ΠΑΡΑΡΤΗΜΑ B ΠΙΝΑΚΑΣ 1Α ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ «ΜΕΤΑΠΟΙΗΣΗ» ΧΡΗΜΑΤΟ ΟΤΟΥΜΕΝΕΣ ΚΑΤΗΓΟΡΙΕΣ ΕΝΙΣΧΥΣΕΩΝ (ΕΠΙΛΕΞΙΜΕΣ ΕΝΕΡΓΕΙΕΣ)

ΠΑΡΑΡΤΗΜΑ B ΠΙΝΑΚΑΣ Α ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ «ΜΕΤΑΠΟΙΗΣΗ» ΧΡΗΜΑΤΟ ΟΤΟΥΜΕΝΕΣ ΚΑΤΗΓΟΡΙΕΣ ΕΝΙΣΧΥΣΕΩΝ (ΕΠΙΛΕΞΙΜΕΣ ΕΝΕΡΓΕΙΕΣ) ηµιουργία, επέκταση, αποπεράτωση, : χώρων παραγωγής, αποθήκευσης, διάθεσης, λειτουργίας

ΠΑΡΑΓΩΓΗ ΚΑΙ ΙΣΟΖΥΓΙΟ ΕΙΣΑΓΩΓΩΝ - ΕΞΑΓΩΓΩΝ (MWh) ΖΗΤΗΣΗ ΣΤΟ ΣΥΣΤΗΜΑ ΚΑΙ ΤΟ ΔΙΚΤΥΟ (MWh)

ΜΗΝΙΑΙΟ ΔΕΛΤΙΟ ΙΣΟΖΥΓΙΟΥ ΣΤΟ ΔΙΑΣΥΝΔΕΔΕΜΕΝΟ ΣΥΣΤΗΜΑ & ΔΙΚΤΥΟ Πληροφορίες κ.κ.πετσίνης 210 9466888 ΠΑΡΑΓΩΓΗ ΚΑΙ ΙΣΟΖΥΓΙΟ ΕΙΣΑΓΩΓΩΝ - ΕΞΑΓΩΓΩΝ (MWh) ΙΑΝΟΥΑΡΙΟΣ - ΣΥΝΟΛΟ ΠΑΡΑΓΩΓΗΣ & ΙΣΟΖΥΓΙΟΥ ΕΙΣΑΓΩΓΩΝ -

ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2019 Β ΦΑΣΗ ΣΥΝΕΙΡΜΟΣ

ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ημερομηνία: Σάββατο 4 Μαΐου 09 Διάρκεια Εξέτασης: ώρες ΘΕΜΑ Α Α.. Βιβλίο, 3. παράγραφος Α.. α. Σ β. Λ γ. Λ δ. Σ ε. Λ Α.3. α.

Ενδεικτικά Σχόλια στα πλαίσια της αξιολόγησης:

Ενδεικτικά Σχόλια στα πλαίσια της αξιολόγησης: «Σας είχα ενημερώσει για μία συνέντευξη στην εταιρία... Τελικά με προσέλαβαν! Και μάλιστα στην εταιρεία αυτή χρησιμοποιούν το SAP. Σίγουρα τα σεμινάρια βοήθησαν

ΠΕΡΙΕΧΟΜΕΝΑ. ΜΕΛΕΤΗ ΝΕΟΥ Γ.Π.Σ/(.Σ.Χ.Ο.Ο.Α.Π.) ΠΕΡΙΟΧΗΣ ΔΙΟΙΚΗΤΙΚΩΝ ΟΡΙΩΝ τ. Δ. ΔΥΜΗΣ Ν. ΑΧΑΪΑΣ

ΕΙΣΑΓΩΓΗ Π1 ΔΟΜΙΚΟ ΣΧΕΔΙΟ ΧΩΡΙΚΗΣ ΟΡΓΑΝΩΣΗΣ ΔΗΜΟΤΙΚΗΣ ΕΝΟΤΗΤΑΣ ΔΥΜΗΣ Π1 σελ. 1 1.1. ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΚΑΤΕΥΘΥΝΣΕΙΣ Π1 σελ. 1 1.1.1. ΚΑΤΕΥΘΥΝΣΕΙΣ ΣΤΡΑΤΗΓΙΚΟΥ ΕΠΙΠΕΔΟΥ ΣΧΕΔΙΑΣΜΟΥ Π1 σελ. 2 1.1.2. ΣΤΡΑΤΗΓΙΚΟΙ

2 1, x < 2. f(x) = 3x + 1, x 2. lim. f(x) = lim. x 2. x 1, x < 1. 3x 2 x > 1

ΣΥΝΕΧΕΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Επιμέλεια: Καρράς Ιωάννης Μαθηματικός οὐκ οἴεται θεοὺς εἶναι ὁ ἄθεος, ὁ δὲ δεισιδαίμων οὐ βούλεται, πιστεύει δ ἄκων φοβεῖται γὰρ ἀπιστεῖν. gkarras@gmail.com 2 2 o ΛΥΚΕΙΟ ΓΕΡΑΚΑ - ΚΑΡΡΑΣ

ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 2: ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ - ΚΑΝΟΝΕΣ ΠΑΡΑΓΩΓΙΣΗΣ - ΠΑΡΑΓΩΓΟΣ ΣΥΝΘΕΤΗΣ ΣΥΝΑΡΤΗΣΗΣ

ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ - ΚΑΝΟΝΕΣ ΠΑΡΑΓΩΓΙΣΗΣ - ΠΑΡΑΓΩΓΟΣ ΣΥΝΘΕΤΗΣ ΣΥΝΑΡΤΗΣΗΣ [Κεφ..: Παραγωγίσιμες Συναρτήσεις Παράγωγος Συνάρτηση - Κεφ..: Κανόνες Παραγώγισης του

Επαναληπτικές Ασκήσεις

Επαναληπτικές Ασκήσεις Έστω ότι το υπόλοιπο της διαίρεσης ενός πολυωνύμου ( x ) α Να γράψετε την ταυτότητα της διαίρεσης β Να βρείτε τα 0 και Ρ γ Αν το πολυώνυμο ( x) είναι x να βρείτε: x + x είναι 3x

Ερωτήσεις πολλαπλής επιλογής

Ερωτήσεις πολλαπλής επιλογής. * Το θεώρηµα µέσης τιµής του διαφορικού λογισµού για κάθε α, β R και τη συνάρτηση f () = e εξασφαλίζει την ύπαρξη ενός αριθµού κ R, ώστε να ισχύει Α. e α-β = e κ (α - β) Β.

2.3. Ασκήσεις σχολικού βιβλίου σελίδας A Οµάδας. Να βρείτε την παράγωγο των συναρτήσεων

. Ασκήσεις σχολικού βιβλίου σελίδας 8 4 A Οµάδας. Να βρείτε την παράγωγο των συναρτήσεων 7 i ( 4 6 ii ( ln 4 iii ( 4 iv ( συν i Για κάθε R είναι ( 7 6 4 6 ii Για κάθε (, είναι ( 6 iii Για κάθε R είναι

ΕΠΙΜΕΛΕΙΑ : Π. Δ. ΤΡΙΜΗΣ ΜΑΘΗΜΑΤΙΚΟΣ

Λ Υ Κ Ε Ι Ο Α Ν Α Λ Υ Σ Η 1Ο Κ Ε Φ Α Λ Α Ι Ο ΕΠΙΜΕΛΕΙΑ : Π. Δ. ΤΡΙΜΗΣ ΜΑΘΗΜΑΤΙΚΟΣ Θετική Τεχνολογική Κατεύθυνση ασκήσεις (ΝΑ ΛΥΘΟΥΝ ΜΕΤΑ ΑΠΟ ΤΙΣ ΑΝΤΙΣΤΟΙΧΕΣ ΤΟΥ ΒΙΒΛΙΟΥ) 5Νο ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ 1. Να

2.2. Ασκήσεις σχολικού βιβλίου σελίδας A Οµάδας. e = 2. e, x ο. e f ( ln 2 ) = όταν : 4

. Ασκήσεις σχολικού βιβλίου σελίδας 7 9 A Οµάδας. Να βρείτε την παράγωγο της συνάρτησης στο σηµείο ο όταν : i) ( ), ο ii) ( ), ο 9 iii) ( ) συν, v) ( ) ο 6 π e, ο ln iv) ( ) ln, ο e i) Για κάθε R είναι

ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗ. Εµβαδά., x 1 x f

ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗ Εµβαδά Θέµα 1 ίνεται η συνάρτηση x e e, x< 1 (x) = l nx, x 1 x Να δείξετε ότι η είναι συνεχής και να υπολογίσετε το εµβαδόν του χωρίου που περικλείεται από την C, τον άξονα

Αποθήκη Συντήρηση Κοπή Συναρμολόγηση Προϋπολογιστικά 20.000 15.000 35.000 50.000

Άσκηση 17 Λογ/σμοι Ποσό Βάση κριτήριο Παραγ. Διοίκ. Χρ/κα Διάθεση Μερισμού Αμοιβές προσωπ. 1.200 80%, 20%, 0, 0 960 240 0 0 Εργοδ. Εισφ. 300 80%, 20%, 0,0 240 60 0 0 ΔΕΗ 1.000 0, 70%, 0, 30% 0 700 0 300

Λειτουργία αποτελεσματικών λογαριασμών

Λειτουργία αποτελεσματικών λογαριασμών Περιεχόμενα Λειτουργία ομάδας 2.1 Λειτουργία ομάδας 6.4 Λειτουργία ομάδας 7.7 Προσδιορισμός Κόστους Πωληθέντων...10 Λειτουργία ομάδας 2 Οι λογαριασμοί απογραφών έναρξης

ÈÅÌÅËÉÏ ÅËÅÕÓÉÍÁ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α. Α1. Θεωρία (θεώρηµα Fermat) σχολικό βιβλίο, σελ Α2. Θεωρία (ορισµός) σχολικό βιβλίο, σελ Α3.

ΘΕΜΑ Α ΑΠΑΝΤΗΣΕΙΣ Α Θεωρία (θεώρηµα Frmat) σχολικό βιβλίο, σελ 6-6 Α Θεωρία (ορισµός) σχολικό βιβλίο, σελ 8 Α3 ΘΕΜΑ Β α β γ δ ε Σ Σ Λ Λ Σ B Έχουµε από υπόθεση ότι: z 3i z 3i () Όµως z 3i z 3i z 3 i ()

ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ( ) ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ - Γ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ

ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ (-6-) ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ - Γ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΘΕΜΑ ο : Α. Αν η συνάρτηση είναι παραγωγίσιμη σ ένα σημείο του πεδίου ορισμού της, να γραφεί η εξίσωση της εφαπτομένης της

. lim [2f (x) + 3g (x)] = 13

Ερωτήσεις πολλαπλής επιλογής. * Αν η γραφική παράσταση µιας συνάρτησης f είναι αυτή που φαίνεται στο σχήµα, τότε λάθος είναι Α. f () = 4 B. f () = Γ. f () =. f ( ) = 4 E. f () = 4. * Για τη συνάρτηση f,

1) κατακόρυφη ασύµπτωτη την ευθεία x = x0 =± ( ηλαδή η ευθεία x = x0. είναι κατακόρυφη ασύµπτωτη όταν ένα τουλάχιστον από τα δύο πλευρικά όρια

ΘΕΩΡΙΑ ΑΣΥΜΠΤΩΤΩΝ Η : A έχει: ) κατακόρυφη ασύµπτωτη την ευθεία 0 τ.µ.τ. όταν lim ± ή lim ± ή lim ± ( ηλαδή η ευθεία 0 0 + 0 0 είναι κατακόρυφη ασύµπτωτη όταν ένα τουλάχιστον από τα δύο πλευρικά όρια είναι

ΚΤΗΝΙΑΤΡΙΚΟΣ ΗΛΕΚΤΡΟΚΑΡΔΙΟΓΡΑΦΟΣ CARDISUNY D120 ΚΑΝΑΛΙΩΝ ΜΕ ΔΙΑΓΝΩΣΗ, ΤΟΥ ΟΙΚΟΥ FUKUDA M-E KOGYO ΙΑΠΩΝΙΑΣ

PALMED Γ. ΠΑΠΑΔΑΚΗΣ Ε.ΤΖΟΥΒΑΡΑ Ο.Ε. ΕΙΣΑΓΩΓΕΣ - ΑΝΤΙΠΡΟΣΩΠΕΙΕΣ ΕΜΠΟΡΙΑ ΙΑΤΡΙΚΩΝ ΕΙΔΩΝ ΔΙΟΧΑΡΟΥΣ 12 115 28 ΑΘΗΝΑ ΑΦΜ : 998559399 ΙΖ ΔΟΥ ΑΘΗΝΩΝ ΤΗΛ : 210 9239185 / 210 9229571 FAX : 210 9229571 E_mail :

Εφαρμογή New Extra Μισθοδοσία. Διαχείριση Εργαζομένου Μερικής Απασχόλησης

Εφαρμογή New Extra Μισθοδοσία Διαχείριση Εργαζομένου Μερικής Απασχόλησης Το συγκεκριμένο εγχειρίδιο δημιουργήθηκε για να βοηθήσει την κατανόηση της Διαδικασίας Δημιουργίας Εργαζομένου Μερικής Απασχόλησης.

ÖÑÏÍÔÉÓÔÇÑÉÏ ÏÑÏÓÇÌÏ

ΘΕΜΑ Α ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑΛ Β 6 ΜΑΪΟΥ ΑΠΑΝΤΗΣΕΙΣ Α Θεωρία (θεώρ Frmat) σχολικό βιβλίο, σελ 6-6 Α Θεωρία (ορισµός) σχολικό βιβλίο, σελ 8 Α3 ΘΕΜΑ Β α β γ δ ε Σ Σ Λ Λ Σ B Έχουµε από υπόθεση

ΚΕΦΑΛΑΙΟ 4ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΠΑΡΑΓΟΥΣΑ ΣΥΝΑΡΤΗΣΗ [Αρχική Συνάρτηση του κεφ.3.1 Μέρος Β του σχολικού βιβλίου].

ΚΕΦΑΛΑΙΟ ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΠΑΡΑΓΟΥΣΑ ΣΥΝΑΡΤΗΣΗ [Αρχική Συνάρτηση του κεφ.3. Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα. ΘΕΜΑ Β Να βρείτε την παράγουσα της συνάρτησης f() =,

Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ. Ημερομηνία: Σάββατο 11 Νοεμβρίου 2017 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ

ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Σάββατο Νοεμβρίου 7 Διάρκεια Εξέτασης: ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α Να διατυπώσετε το θεώρημα του Bolzano και να δώσετε τη γεωμετρική

ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2019 A ΦΑΣΗ

ΤΑΞΗ: ΜΑΘΗΜΑ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ / ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Ημερομηνία: Σάββατο 1 Ιανουαρίου 019 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α1. Για κάθε γωνία ω, να αποδείξετε την ταυτότητα ημ ω συν ω

ÖÑÏÍÔÉÓÔÇÑÉÏ ÈÅÌÅËÉÏ ÇÑÁÊËÅÉÏ ÊÑÇÔÇÓ

ΘΕΜΑ Α ΜΑΘΗΜΑΤΙΚΑ (ΑΛΓΕΒΡΑ) ΕΠΑ.Λ. 8 ΙΟΥΝΙΟΥ 07 ΕΚΦΩΝΗΣΕΙΣ Α. Αν οι συναρτήσεις f, g είναι παραγωγίσιµες στο, να αποδείξετε ότι: ( f (x) + g (x)) = f (x) + g(x) Μονάδες 0 Α. Να χαρακτηρίσετε τις προτάσεις

ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΗΣ Γ' ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ

ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΗΣ Γ' ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΟΙ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΑΠΟ ΤΟΝ ΚΑΘΗΓΗΤΗ κύριο ΦΟΥΝΤΟΥΛΑΚΗ ΜΑΝΩΛΗ του ΦΡΟΝΤΙΣΤΗΡΙΟΥ www.orionidf.gr ΘΕΜΑ Α Α. Απόδειξη

ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ

17951 ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΤΕΥΧΟΣ ΔΕΥΤΕΡΟ Αρ. Φύλλου 1257 1 Ιουλίου 2008 ΑΠΟΦΑΣΕΙΣ Αριθμ. 74913/Γ2 Αναλυτικό Πρόγραμμα Σπουδών, των μαθημάτων της ειδι κότητας Σύγχρονης Επιχειρηματικής

KΕΦΑΛΑΙΟ 2o Η ΖΗΤΗΣΗ ΤΩΝ ΑΓΑΘΩΝ

KΕΦΑΛΑΙΟ 2o Η ΖΗΤΗΣΗ ΤΩΝ ΑΓΑΘΩΝ 13. Ελαστικότητα ζήτησης και συνολική δαπάνη των καταναλωτών 6. Άλλοι προσδιοριστικοί παράγοντες της ζήτησης 7. Μεταβολή στη ζητούμενη ποσότητα και μεταβολή στη ζήτηση 15.

ΣΥΜΠΛΗΡΩΜΑΤΙΚΕΣ ΟΔΗΓΙΕΣ ΓΙΑ ΤΗΝ ΠΡΟΣΕΓΓΙΣΤΙΚΗ ΓΕΩΑΝΑΦΟΡΑ ΑΚΙΝΗΤΩΝ ΜΕΣΩ ΔΙΑΔΙΚΤΥΟΥ

ΜΕΣΩ ΔΙΑΔΙΚΤΥΟΥ Για την διευκόλυνση των πολιτών κατά των χωρικό εντοπισμό ακινήτων, εκτός των διευθύνσεων (Οδός και αριθμός), υπάρχουν διαθέσιμα προς αναζήτηση, στοιχεία Διανομών Συνοικισμών ή Αγροκτημάτων

Θεωρία Γραμματίων: Τα γραμμάτια διακρίνονται στους παρακάτω λογαριασμούς:. Ορισμένες φορές για λόγους απλούστευσης ονομάζεται με το όνομα του Πρωτοβάθμιου 31 Γραμμάτια εισπρακτέα. Εκεί καταχωρούνται όλα

ΔΙΑΓΩΝΙΣΜΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 4 ΝΟΕΜΒΡΙΟΥ 2018 ΑΠΑΝΤΗΣΕΙΣ. x 1 x 1 x 1

ΔΙΑΓΩΝΙΣΜΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ ΝΟΕΜΒΡΙΟΥ 08 ΘΕΜΑ A Α. α. Λάθος β. Σωστό γ. Λάθος δ. Σωστό ε. Σωστό στ. Λάθος ΑΠΑΝΤΗΣΕΙΣ Α. Αν η f είναι συνεχής = τότε ισχύει: lim f() = lim

Βοηθήματα Χαμηλής Όρασης (Ε) ΟΠΤΙΚΗΣ ΤΕΙ 1971 ΑΘΗΝΑΣ 1994 7,6 15,36 1,44 ΕΛΛΙΠΗ ΠΡΟΣΟΝΤΑ

Βοηθήματα Χαμηλής Όρασης (Ε) 2 ΓΕΩΡΓΑΝΟΠΟΥΛΟΥ ΓΕΩΡΓΙΑ 1971 ΑΘΗΝΑΣ 1994 7,6 15,36 1,44 ΕΛΛΙΠΗ 4 ΚΑΒΑΛΙΕΡΟΣ ΔΗΜΗΤΡΙΟΣ ΟΠΤΙΚΗΣ & 1984 ΤΕΙ ΑΘΗΝΑΣ 2011 6,1 ΕΛΛΙΠΗ 1 ΣΠΗΛΙΩΤΟΠΟΥΛΟΣ ΧΡΗΣΤΟΣ ΙΑΤΡΙΚΗΣ ΠΑΝ 1964

11.00' 12.00' 13.00' 14.00' 15.00' 16.00' 17.00' 18.00' 19.00 20.00. DESIGN Ι (AutoCad) ΣΙ ΕΡΙ ΟΥ 8.00' ΣΙ ΕΡΙ ΟΥ 9.00' ΣΙ ΕΡΙ ΟΥ 10.

ΤΕΙ ΚΑΒΑΛΑΣ ΣΤΕΓ ΡΑΜΑΣ ΤΜΗΜΑ ΤΟΠΙΟΥ ΩΡΟΛΟΓΙΟ ΠΡΟΓΡΑΜΜΑ ΜΑΘΗΜΑΤΩΝ ΧΕΙΜΕΡΙΝΟΥ ΕΞΑΜΗΝΟΥ 2012-2013 Α ΕΞΑΜΗΝΟΥ ΕΥΤΕΡΑ ΤΡΙΤΗ ΤΕΤΑΡΤΗ ΠΕΜΠΤΗ ΠΑΡΑΣΚΕΥΗ ΣΧΕ ΙΟ (Ε) (Ε) ΤΕΧΝΙΚΟ ΣΧΕ ΙΟ ΠΑΠΑΝΑΣΤΑΣΙΟΥ ΚΑΤΑΣΚΕΥΕΣ ΚΑΤΑΣΚΕΥΕΣ

(2 x) ( x 5) 2(2x 11) 1 x 5

ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟ 1 Ο ΑΝΑΛΥΣΗΣ 1. ίνεται η συνάρτηση ƒ µε τύπο, + 5 6 < + + 7 5 f( ) = < < 5 ( ) ( 5) 006 ( 11) 1 5 Υπολογίστε τα παρακάτω όρια της συνάρτησης, Α) Β) f ( ) f ( ) 1 Γ) f ( ) + και f ( )

0.3 Όρια, Συνέχεια συναρτήσεων

. Όρια, Συνέχεια συναρτήσεων Μπορείτε να «σχεδιάσετε» τις γραφικές παραστάσεις και να τις περιεργαστείτε πληκτρολογώντας στο Matlab το κοµµάτι κώδικα που βρίσκεται µετά τις ασκήσεις. Άσκηση.1 Υπολογίστε

36,9 83,5 2,6 1, Εκλογική Συµπεριφορά ΤΑΣΕΙΣ ΕΚ. 2005, MRB Hellas 1. Συλλογή στοιχείων 24 Νοεµβρίου - 5 εκεµβρίου 2005

4. Αναδροµικός τύπος Είναι ο τύπος που συσχετίζει δύο ή περισσότερους γενικούς όρους µιας ακολουθίας

5. ΑΚΟΛΟΥΘΙΕΣ ΘΕΩΡΙΑ. Ορισµός Ονοµάζουµε ακολουθία πραγµατικών αριθµών κάθε συνάρτηση µε πεδίο ορισµού το το σύνολο N * = {,, 3, 4.} και σύνολο αφίξεως το R Η ακολουθία συµβολίζεται (α ν ) ή (β ν ) κ.λ.π.

ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ. Πιθανότητες. Συνδυαστική Ανάλυση Διδάσκων: Επίκουρος Καθηγητής Κωνσταντίνος Μπλέκας

ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Πιθανότητες Συνδυαστική Ανάλυση Διδάσκων: Επίκουρος Καθηγητής Κωνσταντίνος Μπλέκας Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης

[ α π ο δ ε ί ξ ε ι ς ]

Γ' Λυκείου Κατεύθυνση [ α π ο δ ε ί ξ ε ι ς ] ε ξ ε τ α σ τ έ α ς ύ λ η ς 7-8 Επιμέλεια Κόλλας Αντώνης Όριο πολυωνυμικής στο Αν P( = αν ν + αν ν +... + α + α είναι πολυώνυμο του και, τότε: P( P( P( =...

- ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 7: ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΠΡΑΞΕΙΣ ΜΕ ΣΥΝΕΧΕΙΣ ΣΥΝΑΡΤΗΣΕΙΣ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΣΕ ΔΙΑΣΤΗΜΑΤΑ

ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 7: ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΠΡΑΞΕΙΣ ΜΕ ΣΥΝΕΧΕΙΣ ΣΥΝΑΡΤΗΣΕΙΣ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΣΕ ΔΙΑΣΤΗΜΑΤΑ [Ενότητες Ορισμός της Συνέχειας Πράξεις με Συνεχείς

ικαιούχου ΙΚΤΥΟ ΟΤΕ ΙΚΤΥΟ ΟΤΕ ΟΙΚΕΙΟ Α/Κ ΠΕΛΑΤΗ ΜΓΧή ΙΚΑΙΟΥΧΟΥ ΙΚΑIΟΥΧΟΥ

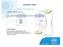ΤΕΡΜΑΤΙΚΟ ΤΜΗΜΑ ΤΕΡΜΑΤΙΚΟ ΤΜΗΜΑ ΣΕ ΟΙΚΕΙΟ ΤΕΡΜΑΤΙΚΟ ΤΜΗΜΑ ΣΕ ΟΙΚΕΙΟ Α/Κ ΠΕΛΑΤΗΣ ΟΙΚΕΙΟ Α/Κ ΠΕΛΑΤΗ Σ.Μ. Τερµατικό Τµήµα : Είναι η συµµετρική σύνδεση αποκλειστικής χωρητικότητας ψηφιακής τεχνολογίας, µεταξύ