PRUŽNOSŤ A PEVNOSŤ PRE ŠPECIÁLNE INŽINIERSTVO
|
|
|
- Φωτεινή Ελευθερίου
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ŽILINSKÁ UNIVERZITA V ŽILINE Fakulta špeciálneho inžinierstva Doc. Ing. Jozef KOVAČIK, CSc. Ing. Martin BENIAČ, PhD. PRUŽNOSŤ A PEVNOSŤ PRE ŠPECIÁLNE INŽINIERSTVO Druhé doplnené a upravené vydanie Určené pre študijné odbory Bezpečnostný manažment, Špeciálny manažment, Doprava v krízových situáciách a Záchranné služby. Vydala Žilinská univerzita 005
2 Recenzenti: prof. Ing. Norbert Szuttor, DrSc. doc. Ing. Josef Reitšpís, PhD. Schválila edičná rada ŽU v Žiline výmerom číslo J.Kovačik, M.Beniač, 004 ISBN h: p a p -dia malp
3 OBSAH PREDSLOV PREHĽAD POUŽITÝCH SYMBOLOV A JEDNOTIEK 1. CIEĽ, ÚLOHY A ZÁKLADNÉ POJMY NÁUKY O PRUŽNOSTI A PEVNOSTI Vonkajšie a vnútorné sily Metóda mysleného (fiktívneho) rezu Druhy namáhania telies Prostý ťah (tlak) Prostý šmyk Prostý krut Prostý ohyb Napätie a druhy napätia Pomerné predĺženie Uhlové pretvorenie Hookov zákon Vplyv zmeny teploty Priečne zúženie. Poissonova konštanta Príklady VÝPOČET A KONTROLA PRÚTOV NAMÁHANÝCH NA ŤAH (TLAK) 33.1 Predpoklady výpočtu Výpočet prúta na prostý ťah (tlak) Pevnostná kontrola a dimenzovanie prútov namáhaných na ťah (tlak) Metóda dovolených napätí Metóda dovolených zaťažení Metóda medzných stavov Príklady... 4
4 3. NAPÄTOSŤ, DEFORMÁCIA A ICH VZÁJOMNÉ SÚVISLOSTI Napätosť a druhy napätosti Priamková napätosť Rovinná napätosť Priestorová napätosť Súvislosť medzi deformáciami a napätosťou v bode telesa Rovnice elasticity Rovnice elasticity pre priamkovú napätosť Rovnice plasticity pre rovinnú napätosť Rovnice plasticity pre priestorovú napätosť Zmena objemu. Hodnota Poissonovej konštanty Príklady PROSTÉ NAMÁHANIE NA ŠMYK (STRIH) Podmienky pevnosti a dovolené namáhanie v šmyku Navrhovanie a posudzovanie na prostý šmyk Výpočet a kontrola nitov a skrutiek Výpočet a kontrola zvarov Tupé zvary Kútové zvary Príklady CHARAKTERSITIKY ROVINNÝCH PRIEREZOV POMOCOU KVADRATICKÝCH MOMENTOV Kvadratický moment (zotrvačnosti) plochy vzhľadom na os Polárny moment zotrvačnosti plochy Deviačný moment plochy Kvadratický moment plochy k rovnobežne posunutým osiam Postup pri výpočte kvadratických momentov plôch Príklady PROSTÉ NAMÁHANIE NA KRUT Výpočet napätia a uhol skrútenia kruhových hriadeľov Výpočet krútenia hriadeľov nekruhového prierezu Príklady
5 7. OHYB PRIAMYCH NOSNÍKOV Pohyblivé bremeno a sústava pohyblivých bremien vplyvové čiary priamych staticky určitých nosníkov Vplyvové čiary na prostom nosníku Vplyvové čiary reakcií Vplyvová čiara priečnych síl Vplyvová čiara ohybových momentov Vplyvové čiary na votknutom nosníku Normálové napätia v ohýbanom nosníku Šmykové napätie v ohýbanom nosníku Nosníky s rovnakou pevnosťou Deformácia nosníkov pri rovinnom ohybe Približná diferenciálna rovnica priehybovej čiary Mohrova metóda výpočtu deformácie nosníka Príklady KOMBINOVANÉ NAMÁHANIE Kombinované namáhanie v tlaku a ohybe Kombinované namáhanie na ohyb a krútenie Príklady STABILITA A NAMÁHANIE NA VZPERNÝ TLAK Výpočet a kontrola stability polohy telies Výpočet a kontrola priamych prútov na vzperný tlak v pružnej oblasti Výpočet kritickej sily v plastickej oblasti Približné metódy Príklady ÚNAVA MATERIÁLU Cyklické (kmitavé) napätie a jeho označovanie Únavový lom Medza únavy Faktory ovplyvňujúce medzu únavy Vplyv veľkosti a druhu namáhania
6 10.4. Vplyv geometrického tvaru súčiastky Vplyv akosti povrchu súčiastky Vplyv povrchovej úpravy súčiastky Miera bezpečnosti so zreteľom na cyklické namáhanie ZÁKLADY EXPERIMENTÁLNEJ PRUŽNOSTI Predmet, ciele a delenie experimentálnej pružnosti Statické experimentálne merania Dynamické experimentálne merania ZÁKLADY TEÓRIE PLASTICITY POUŽITÁ LITERATÚRA
7 PREDSLOV Skriptá Pružnosť a pevnosť sú určené študentom Fakulty špeciálneho inžinierstva ŽU v externej a dennej forme štúdia v odboroch špeciálneho a bezpečnostného manažmentu. Úlohou predmetu pružnosť a pevnosť, spoločne s ďalšími predmetmi tohto zamerania v špeciálnom inžinierstve je, aby analýza príčin a opatrenia prijímané na riešenie krízových situácií boli efektívne a vždy v súlade s ich fyzikálnou podstatou. Obsiahnutá látka z pružnosti a pevnosti je rozdelená do 1 kapitol. Okrem nutnej teórie sú vo väčšine kapitol uvedené na ilustráciu vypočítané príklady a zadania príkladov s výsledkami na získanie potrebnej zručnosti. Štúdium a osvojenie si vedomostí z pružnosti a pevnosti predpokladá znalosti z matematiky a statiky v rozsahu týchto predmetov prednášaných na FŠI ŽU. Pri spracovaní skrípt sme vychádzali z osnovy predmetov v oboch odboroch štúdia a ustálenej metodiky vyučovania pružnosti a pevnosti na technických vysokých školách. Vodidlom nám boli najmä skriptá SVŠT, resp. STU v Bratislave a VŠDS v Žiline. Snažili sme sa o pragmatický prístup - o čo najjednoduchšie a úsporné objasnenie teórie, jej aplikácie v príkladoch, a o využitie vlastných skúseností z praktickej výučby. Ďakujeme prof. Ing. Norbertovi Szuttorovi,DrSc. a doc. Ing. Josefovi Reitšpísovi, PhD. za ich starostlivú recenziu a pripomienky. Autori
8
9 PREHĽAD POUŽITÝCH SYMBOLOV A JEDNOTIEK Symbol Názov Jednotka a dĺžka [m] b šírka [m] d priemer [m] e excentricita [m] g gravitačné zrýchlenie [m.s - ] h výška [m] i polomer momentu zotrvačnosti [m] j jadrová úsečka [m] k stupeň bezpečnosti * [1] l dĺžka [m] m Poissonova konštanta * [1] m,n,m,n roviny rezu - p všeobecné napätie, pohyblivé spojité zaťaženie [Pa], [N.m -1 ] q spojité stále zaťaženie [N.m -1 ] r polomer [m] t hrúbka, teplota [m], [ C] v posunutie, rýchlosť, súčiniteľ veľkosti * [m], [m.s -1 ], [1] x dĺžka [m] x, y, z súradnice - y dĺžka úseku, priehyb [m] A, B reakcie [N] A, B, C, D body - D priemer [m] E modul pružnosti v ťahu (Youngov) [Pa] F plocha [m ] G modul pružnosti v šmyku, hmotnosť [Pa], [kg] I moment zotrvačnosti [m 4 ] M moment [N.m] N vnútorná normálová sila [N]
10 P vnútorná všeobecná sila [N] Q sila tiaže [N] R reakcia, súčiniteľ asymetrie cyklu * [N], [1] S vonkajšia sila [N] T tangenciálna sila, tenzor napätia, ťažisko [N], [Pa], - W modul odporu [m 3 ] Z zemný tlak [Pa] a súčiniteľ teplotnej rozťažnosti, uhol [ C -1 ], [ ] b súčiniteľ vrubového účinku *, uhol [1], [ ] e pomerné predĺženie [m] f uhol [ ] g uhol, uhol pretvorenia (skosenia), merná tiaž [ ],[ ],[Nm -3 ] h poradnica vplyvovej čiary priečnej sily *, momentu [1], [m] ϑ pomerný uhol skrútenia (skosenia) [ ] l štíhlostný pomer * [1] l m medzná štíhlosť * [1] m miera bezpečnosti *, rez roviny, Poissonovo číslo * [1], -, [1] p Ludolfovo číslo (3,14) * [1] r polomer [m] s normálové napätie [Pa] s k medza klzu [Pa] s m medza pevnosti [Pa] s u medza úmernosti [Pa] s dov, t dov dovolené napätia [Pa] t šmykové napätie [Pa] D zmena (dĺžky...) - F rovina rezu *, priemer -, [m] S súčet (suma) - * - bezrozmerné číslo
11 1. CIEĽ, ÚLOHY A ZÁKLADNÉ POJMY NÁUKY O PRUŽNOSTI A PEVNOSTI Pružnosť a pevnosť je všeobecný inžiniersky predmet. Ako súčasť mechaniky (najstaršieho vedného odboru) skúma účinky síl pôsobiacich na telesá. Každé teleso vystavené účinkom vonkajších síl, či zmene teploty sa deformuje mení svoj tvar a rozmery. Teleso deformáciám odporuje a pritom v ňom vzniká napätie. Aby sa teleso neporušilo, nesmú napätia prekročiť určitú hodnotu. Preto všetky konštrukčné prvky (telesá) musia byť navrhnuté, alebo ak už existujú využívané tak, aby spoľahlivo odolávali pôsobeniu vonkajších síl. Popri tejto rozhodujúcej požiadavke - zabezpečenia normálnej funkcie každého prvku - sa očakáva, že konštrukcia ako celok bude čo najlacnejšia. Požiadavky spoľahlivosti a hospodárnosti si ale navzájom odporujú. Prvá vedie spravidla k zväčšeniu rozmerov, množstva materiálu a výdavkov, druhá k subtilnejším prvkom a znižovaniu výloh za ne. Podklady pre správne riešenie tohto rozporu ponúka náuka o pružnosti a pevnosti. Cieľom pružnosti a pevnosti je určiť výpočtové vzťahy na vyjadrenie zákonitostí medzi vonkajším zaťažením a optimálnymi rozmermi konštrukčného prvku, ktoré zaručia dostatočnú bezpečnosť a funkciu konštrukcie počas jej zriadenia a prevádzky, pričom: - Pružnosťou nazývame schopnosť pevných telies nadobudnúť po odstránení vonkajšieho zaťaženia pôvodný tvar. - Pevnosťou nazývame schopnosť prvku (konštrukcie) preniesť zaťaženie bez porušenia. Úlohou pružnosti a pevnosti je skúmať a popísať stav vnútorných síl a pretvorenia telies a ich vzájomné súvislosti v dôsledku pôsobenia vonkajších síl. Presvedčíme sa, že náuka o pružnosti a pevnosti nazývaná často ako mechanika o vnútorných silách je pomenovanie veľmi výstižné. Náuka o pružnosti a pevnosti vznikla a rozvíjala sa tak ako ostatné vedné odbory z bezprostredných a praktických potrieb ľudí. Jej vývoj je preto spojený s vývojom ľudskej spoločnosti. Máme len malé vedomosti o tom, aké fyzikálne znalosti mali najstaršie kultúrne národy. Prvý známy vedecký spis je od Galilea Galileiho (1688), profesora matematiky 11
12 v Padove, ktorý ako prvý skúmal únosnosť votknutých nosníkov. Lineárnu závislosť medzi napätím a predĺžením zistil Robert Hooke (1660), profesor geometrie na Oxfordskej univerzite. Od objavenia Hookovho zákona, ktorý matematicky vyjadril Thomas Young až v roku 1807 sa datuje začiatok pružnosti a pevnosti ako vedy. Na jej vývoji sa odvtedy podieľali mnohí významní objavitelia, napr. Euler, J. a D. Bernoulli, Coulomb, Navier, Couchy, St. Venant, Žuravskij, Timošenko, Maxwel, Hertz, Mohr, Wöhler, Bažant a iní. Zo slovenských vedcov sa najviac o rozvoj pružnosti a pevnosti zaslúžili: Ľudovít Tetmajer (problémy stability) a Aurel Stodola (kmitanie hriadeľov). Náuka o pružnosti a pevnosti je v súčasnosti už vnútorne značne štruktúrovaná. Z viacerých kritérií, podľa ktorých sa rozdeľuje, spomeňme delenie: - podľa rôzneho stupňa presnosti: na matematickú teóriu pružnosti (Pružnosť a pevnosť II.); používa menej zjednodušené predpoklady a technickú (Pružnosť a pevnosť I.), ktorá využíva teoretické výsledky na rýchle riešenie praktických inžinierskych úloh. - podľa rôznych metód riešenia: na analytickú a experimentálnu pružnosť (vtedy, keď výpočet nie je známy, alebo je príliš zložitý, či časovo alebo finančne náročný). 1.1 Vonkajšie a vnútorné sily Na jednotlivé konštrukčné prvky (telesá) pôsobí celý rad síl, ktoré môžeme rozdeliť do dvoch skupín, na: - sily vonkajšie, - sily vnútorné. Vonkajšie sily možno ďalej deliť podľa rôznych kritérií, napr. na: - hmotné a povrchové, - osamelé a spojité zaťaženia, - statické a dynamické, - stále a pohyblivé, atď. Pôsobením síl a ich rovnováhou na dokonale tuhom telese sa zaoberá statika. 1
13 Mernou jednotkou osamelej sily pôsobiacej v bode telesa je newton [1N = 1 kgms - ]. Keď sa sily prenášajú na úzkom páse, vtedy vzťahujeme silu na jednotku dĺžky telesa a meriame ju v [1Nm -1 ]. V technickej praxi sa vzhľadom na veľkosť týchto merných jednotiek často využívajú ich násobky, napr. 1kN = 10 3 N, 1MNm -1 = 10 6 Nm -1, atď. Prvky konštrukcií menia pôsobením vonkajších síl svoje rozmery a tvar. Tejto zmene sa hovorí deformácia, jej veľkosť a druh závisí na štruktúre materiálov. Všetky materiály možno rozdeliť do dvoch skupín, na: - kryštalické, - amorfné. Kryštalické materiály sa skladajú z veľkého počtu malých zŕn. Každé zrno tvorí sústava pravidelne rozložených atómov, ktoré tvoria tzv. kryštalickú mriežku. Naproti tomu amorfné materiály nemajú pravidelne usporiadané atómy. Atómy sa v rovnováhe udržujú navzájom vnútornými silami. Vplyvom vonkajších síl sa vzdialenosti medzi atómami menia (teleso sa deformuje), čo je sprevádzané zmenou síl pôsobiacich medzi atómami. V prvkoch konštrukcie vznikajú teda pôsobením vonkajších síl doplnkové vnútorné sily, ktoré pôsobia proti snahe vonkajších síl porušiť konštrukčný prvok alebo meniť jeho tvar. V ďalšom budeme tieto sily nazývať len vnútornými silami. 1. Metóda mysleného (fiktívneho) rezu Aby sa dal číselne charakterizovať druh a účinok vonkajších síl na deformovaný prvok, treba vedieť odmerať ich odozvu vo vnútri prvku - vypočítať veľkosť vnútorných síl. Na to sa v pružnosti a pevnosti používa tzv. metóda myslených (fiktívnych) rezov. Podľa počtu myslených rezov sa metóda delí na: 13
14 - metódu jedného rezu, ktorým sa teleso fiktívne rozdelí na dve časti o konečnej veľkosti (vedie k rovnici s jednou neznámou), - metódu dvoch veľmi blízko seba situovaných rezov (vedie k riešeniu diferenciálnej rovnice prvého rádu), - metódu troch dvojíc rezov (vedie k riešeniu diferenciálnej rovnice druhého rádu). Podstatu a použitie metódy mysleného rezu si znázorníme príkladom. a) b) Máme určiť výslednicu vnútorných síl v priečnom reze prúta podľa obr Prút je zaťažený vlastnou tiažou a osovou silou S, pôsobiacou na voľnom konci. I Jedným priečnym rezom m. n, vedeným ľubovoľným bodom A, rozdelíme fiktívne prút na dve časti (obr. 1.1b). Pôsobením síl S a Q (vlastná tiaž časti I) by sa časť I prúta začala pohybovať. Vnútorné sily, ktoré pôsobia medzi časticami materiálu v myslenom priereze, bránia vzájomnému pohybu obidvoch častí a udržujú teleso pohromade. Zaťažený prút je v rovnováhe, preto sú v rovnováhe aj časti prúta I a II. I Obr. 1.1 V prípade priameho prizmatického prúta (pravidelného tvaru) ležia sily S, Q 1, P na spoločnej nositeľke. Podľa obr. 1.1b ich rovnováhu vyjadruje rovnica P Q 1 S = 0 14
15 Výslednica vnútorných síl P je ekvivalentná v opačnom zmysle pôsobiacim účinkom oddelenej časti II prúta na časť I. Podľa zákona akcie a reakcie pôsobí časť I prúta na časť II silou P O = P. 1.3 Druhy namáhania telies Uvažujme teleso zaťažené všeobecnou priestorovou sústavou síl S 1, S,..., S n, ktoré sú v rovnováhe (obr. 1.a). Myslime si toto teleso rozdelené ľubovoľnou rovinou Φ na dve časti s konečnou veľkosťou I a II. Obr. 1.a Výslednica vnútorných síl P a vonkajšie sily tvoria rovnovážnu priestorovú sústavu síl. Vo všeobecnom prípade je smer sily P vzhľadom na rovinu rezu ľubovoľný a jej pôsobisko C nemusí byť totožné s ťažiskom T plochy rezu F. Preložme vnútornú silu P do ťažiska T mysleného rezu Φ a rozložme ju do zložiek súradnicových osí x, y, z, z ktorých os x je kolmá na rovinu rezu Φ (obr. 1.b). Tieto zložky výslednej vnútornej sily sú na obrázku vyznačené P x, P y, P z. 15
16 Obr. 1.b Ako vieme zo statiky (lit. 9, kap. ), treba k preloženej sile - aby sa jej účinok na teleso nezmenil, resp. k jej zložkám pripojiť ešte dvojicu síl, ktorej zložky a účinok v súradnicových osiach je M x, M y, M z. V osobitných prípadoch zaťaženia telies sú z uvedených síl a momentov niektoré nulové. Podľa toho, koľko zložiek je nenulových a ktoré z nich to sú, môžu byť telesá namáhané: Jednoduchým (prostým, čistým) druhom (spôsobom) namáhania na: - ťah (tlak), - šmyk, - krut, - ohyb. Spoločným znakom všetkých druhov jednoduchého namáhania v rovine súmernosti telesa je, že v uvažovanom reze Φ pôsobí len jedna zo zložiek P x, (P y, P z ), M x, (M y, M z ). Kombinovaným (zloženým) namáhaním. O kombinovanom namáhaní hovoríme vtedy, keď v ťažisku prierezu v rovine Φ pôsobí súčasne viac síl a momentov, resp. viac druhov jednoduchého namáhania. Podrobnejšie sa kombinovaným namáhaním budeme zaoberať až po zoznámení sa s jednoduchými druhmi namáhania (kap. 8). 16
17 1.3.1 Prostý ťah (tlak) O prostom ťahu alebo tlaku hovoríme vtedy, keď z uvedených síl a momentov pôsobí (je nenulová) len sila P x = N, kolmá na rovinu rezu Φ. Najjednoduchším prípadom namáhania na ťah je tenká priama tyč konštantného prierezu, zaťaženého podľa obr. 1.3a osamelou silou S. Na obr. 1.3b je najjednoduchší prípad namáhania na prostý tlak. a) b) Obr. 1.3 Vieme už, že namáhanie skutočných telies má vždy za následok ich deformáciu (pretvorenie). V prípade ťahu sa teleso predĺži a pri prostom tlaku skráti Prostý šmyk O prostom šmyku hovoríme vtedy, ak zo síl a momentov podľa obr. 1.b pôsobia len sily P y a P z, ktorých nositeľky ležia v reze Φ. Výsledná šmyková sila v reze Φ je daná geometrickým súčtom týchto síl. Najjednoduchší prípad šmykového namáhania je na z obr. 1.4a (z obr. 1.4a je zrejmé, prečo sa prostý prípad šmyku nazýva tiež namáhaním na strih). Na obrázku 1.4b je uvedený iný praktický prípad namáhania šmykom - v drieku nitu v rezoch a, b. 17
18 a) b) Obr. 1.4 Tomuto prípadu namáhania zodpovedá deformácia posunutia (ustrihnutia) rezu v smere výslednice pôsobiacich síl Prostý krut Prostý krut vznikne vtedy, keď v myslenom reze Φ pôsobí len moment M x, ktorého rovina pôsobenia je v reze Φ (obr. 1.5). Takto pôsobiaci moment sa nazýva točivým (M t ) alebo krútiacim momentom (M k ). Obr. 1.5 Prostým krutom sú napr. namáhané rôzne hriadele. Deformácia v tomto prípade je charakteristická pootočením (skrútením) dvoch susedných prierezov, rovnobežných s ľubovoľnou rovinou v zmysle pôsobiaceho momentu. 18
19 1.3.4 Prostý ohyb Prostý ohyb vznikne vtedy, keď v myslenom reze Φ pôsobí len moment M y alebo M z, prípadne obe zložky momentov súčasne - v takom prípade vznikne šikmý ohyb. Geometrický súčet momentov M y a M z sa nazýva ohybový moment a označuje sa spravidla M O. Jednoduchý príklad namáhania prostým ohybom je znázornený na obr Obr. 1.6 Ľubovoľný rez Φ je v tomto telese namáhaný ohybovým momentom a priečnou silou, ktorej účinok však často zanedbávame. Pozn.: Keď tlakom namáhame tyč, malého prierezu, tak tyč niekedy náhle vybočí z osi, prehne sa a nakoniec sa zlomí. Takýto spôsob namáhania tenkých tyčí sa nazýva vzperný tlak (obr. 1.7, bližšie viď. kapitola 9) Obr Napätie a druhy napätia Vo všeobecnom prípade je spojité rozloženie vnútorných síl v rovine rezu telesa nerovnomerné, čo má za následok aj nerovnomerné namáhanie jeho jednotlivých častí. 19
20 Aby sme mohli určiť účinok vnútorných síl zavádzame pomer vnútorných síl na jednotku prierezovej plochy a nazývame ho napätím. Vyberme si veľmi malý element F z plochy Φ na ktorý pôsobí vnútorná sila P (obr. 1.8a) a rozložme túto silu, ktorá môže s normálou roviny zvierať vo všeobecnosti uhol φ, do normálny a tangenty k ploche Φ. Obr. 1.8a Podľa obr. 1.8 platí N = P. cosφ T = P sinφ (1.1) Limita pomeru vnútorných síl P, N, T ku ploche F sa nazýva napätím. Smer a zmysel napätia sa zhoduje so smerom a zmyslom sily (rovnice 1. a 1.3). Základnou mernou jednotkou napätia je 1 Pascal (Pa). Veľkosť a rozmer 1 Pa vyplýva z definície napätia: [1 Pa] = [1Nm - ] Napätia v ďalšom texte budeme označovať písmenami p,, τ. Označenie p budeme používať pre napätie ľubovoľne sklonené k vyšetrovanej ploške, písmenom budeme označovať normálové napätie, ktoré je kolmé k rovine rezu a písmenom τ šmykové napätie, ktoré leží v rovine rezu (obr. 1.8b). Jednotlivé napätia sú definované vzťahmi: p = ΔP lim ΔF ΔF 0 = dp df (1.) Obr. 1.8b = lim Δ F 0 ΔN = ΔF ΔT τ = lim = ΔF 0 ΔF dn df dt df (1.3) 0
21 Normálovému napätiu priraďujeme na rozlíšenie znamienko kladné vtedy, keď zmysel sily N smeruje von z plochy Φ (ako na obr. 1.8a), a nazývame ho ako napätie ťahové. Ak je zmysel sily N opačný, priraďujeme mu znamienko mínus, a takéto napätie nazývame tlakovým. Na zmysle a smere šmykového napätia obvykle nezáleží; záleží iba na jeho veľkosti. Iné napätie, ako ťahové, tlakové alebo šmykové existovať nemôže - je nemysliteľné! Môžu sa však, ako už vieme, vyskytovať samostatne alebo súčasne. Ak do rovnice (1.3) dosadíme (z rovníc 1.1) za N a T dostaneme = p. cosφ (1.4) τ = p. sinφ Umocnením a sčítaním obidvoch rovníc dostaneme p = +τ (1.5) 1.5 Pomerné predĺženie Ak namáhame priamu tyč ťahom (obr. 1.9a), môžeme pozorovať, že sa tyč predlžuje. a) b) Uvažujme nekonečne tenký valček s hrúbkou dy vo vzdialenosti y. Zaťažením silou S sa valček predĺži o dĺžku dy (obr. 1.9b). Obr
22 dy Pomer ε = dy (1.6) sa nazýva pomerným predĺžením. Ak je pomerné predĺženie vo všetkých bodoch prierezu a vo všetkých priečnych rezoch rovnaké, môžeme celkové predĺženie tyče vyjadriť vzťahom: z toho Δl = l l l Δdy = dy = ε dy = ε ε l (1.7) Δl ε = (1.8) l Ako vidieť z rovníc 1.6 a 1.8 je pomerné predĺženie veličinou bezrozmernou. 1.6 Uhlové pretvorenie Uvažujme časticu ABCD s rozmermi dx, dy, dz (obr. 1.10). Častica sa vplyvom šmykových napätí pretvorí. Ak je pretvorenie malé, môžeme zmenu dĺžky dy zanedbať. Posunutie v môžeme potom vyjadriť vzťahom v = tgγ. dy Ak budeme uvažovať dy' dy a vezmeme do úvahy, že uhol γ je veľmi malý, možno uvedený vzťah napísať takto: v = γ.dy. = Obr. 1.10
23 v Uhol γ = (1.9) dy nazývame uhlovým pretvorením (skosením). Tak, ako pomerné predĺženie, je aj uhlové pretvorenie veličina bezrozmerná. 1.7 Hookov zákon Pôsobením vonkajších síl sa teleso deformuje. Deformácia má za následok vznik vnútorných síl a im odpovedajúce napätia. Napätie je preto závislé od deformácie. Na tento vzájomný vzťah majú vplyv mechanické vlastnosti materiálu. Poznatky o mechanických vlastnostiach materiálov sa získavajú pri mechanických skúškach (experimentoch). Jednou z takýchto skúšok je trhacia skúška ťahom. Pri trhacej skúške ťahom sa upnutá tyč normalizovaných rozmerov postupne a plynulo zaťažuje. Počas skúšky sa automaticky zaznamenáva veľkosť zaťaženia a predĺženie skúšobnej tyče. Pri známych rozmeroch tyče (jej ploche F a pôvodnej dĺžke l) možno meraním skutočného predĺženia l vypočítať pomerné predĺženie ε od príslušného napätia. Na obr. 1.11a je diagram napätia a predĺženia mäkkej konštrukčnej ocele. Časť diagramu až po bod U má priamkový priebeh, čiže napätie je priamoúmerné predĺženiu. Napätie prislúchajúce bodu U sa nazýva napätím na medzi úmernosti ( u ). Obr. 1.11a Napätie na medzi pružnosti p je napätie, po ktoré sú predĺženia v podstate pružné (elastické, vratné). 3
24 Napätie K sa nazýva napätím na medzi klzu. Skúšobná tyč s napätosťou väčšou ako K sa začína náhle predlžovať bez zväčšovania napätia. Tento jav sa nazýva klzom (tečením) materiálu. Za tzv. dolnou medzou klzu v bode K pracovný diagram znova stúpa až po bod M Najväčšie napätie v bode M sa nazýva napätím na medzi pevnosti a označujeme ho m. Pri pokračujúcej skúške a napätí m sa tyč roztrhne. Skúšky dokazujú, že pri postupnom znižovaní napätia sa tyč skracuje, pričom toto skracovanie vystihuje priamka rovnobežná s priamkovým priebehom diagramu 01 po napätie na medzi úmernosti u ( 0 U ). Táto priamka pretína os diagramu s hodnotami ε v bode. To dovoľuje definovať celkové pomerné predĺženie tyče pri skúške na ťah, ako ε = ε pl + ε pr, (1.10) v ktorom ε pl značí plastickú, resp. ε pr pružnú časť pomerného predĺženia. Ak sa nedá medza klzu presnejšie zistiť, možno tzv. konvenčnú (dohovorenú) medzu klzu p 0, definovať ako napätie, pri ktorom plastické (trvalé, nevratné) pomerné predĺženie dosahuje max. 0,%. Na obr. 1.11b je diagram ťahovej skúšky liatiny. Liatina patrí medzi látky, ktoré majú veľmi nízku medzu úmernosti a nejasne vyhranenú medzu klzu v ťahu. Obr. 1.11b Ako vidno na obr. 1.11a napätie má až po medzu úmernosti u u mnohých látok (pozor, ale nie všetky látky majú tak zreteľné rozhrania medzí napätia ako konštrukčná mäkká oceľ) priebeh diagramu pri skúške na ťah (tlak) priamkový. 4
25 Platí teda: tg α = = konšt...(e) (1.11) ε Touto konštantou je Youngov modul pružnosti v ťahu... E, čiže (1.1) = ε. E Tento základný zákon pružnosti a pevnosti sa nazýva Hookov zákon. Konštanta E sa nazýva tiež prvou materiálovou konštantou. Pomerné predĺženie závisí (ako vidno z rovnice 1.1) len na druhu materiálu, preto môžeme urobiť dôležitý záver neexistujú dva rôzne materiály, ktoré by mali rovnaký modul pružnosti! Pretože pomerné predĺženie ε je bezrozmerné číslo, má modul pružnosti v ťahu rovnaký rozmer ako napätie, teda E = [N.m - ] alebo [N mm - ] Z rovnice (1.1) tiež vyplýva veľkosť napätia, resp. význam modulu pružnosti. Youngov modul pružnosti je také (myslené) napätie, ktoré by spôsobilo predĺženie skúšobnej tyče o jej celú pôvodnú dĺžku (ε = 1). Hodnota modulu pružnosti E pre oceľ je, MN m - =, N mm -. Ak namáhame nejakú látku prostým šmykom môžeme skúškami určiť tiež vzťah medzi šmykovým napätím τ a pomerným skosením γ (obr. 1.1). Diagram sa podobá diagramu skúšky v ťahu Obr. 1.1 s medzami úmernosti τ u (bod U), resp. klzu τ K v šmyku (bod K). Z diagramu vidieť, že závislosť medzi šmykovým napätím a uhlovým pretvorením (skosením) γ je až do bodu U lineárna. 5
26 Po túto medzu teda platí τ = G.γ alebo (1.13) τ γ = G Kde G je materiálová konštanta a nazýva sa modulom pružnosti v šmyku. Pretože γ je (ods. 1.6) bezrozmerná veličina, má i tento modul (tak ako E) rozmer [N. m - ], resp.[n mm - ]. Na porovnanie uveďme hodnotu tohto modulu pre oceľ G = MN m - = N mm - Zisťujeme, že hodnota modulu pružnosti ocele (E 0 ) je približne,6-krát väčšia ako modul pružnosti v šmyku ocele (G 0 ). Ak je modul pružnosti určitej látky vo všetkých smeroch rovnaký (oceľ, sklo...), hovoríme, že látka je izotropná. Opakom sú látky anizotropné (drevo). Materiály používané v technickej praxi považujeme (až na výnimky) spravidla za izotropné a homogénne (rovnorodé), t. j. také, že majú vo všetkých smeroch rovnaké vlastnosti. Na ilustráciu hodnôt K a m niektorých ocelí tried 11 až 16 podľa príslušných STN a hodnôt modulu pružnosti niektorých materiálov sú tieto hodnoty uvedené v nasledujúcich tabuľkách. 6
27 Hodnoty K, m Tab. 1.1 Označenie ocele podľa STN * Najmenšia medza klzu K [MPa] Medza pevnosti m [MPa] Označenie ocele podľa STN Najmenšia medza klzu K [MPa] Medza pevnosti m [MPa] % m min min * Slovenské technické normy (STN) Hodnoty modulov pružnosti Tab. 1. Materiál 10 5 E [MPa] Materiál 10 5 E [MPa] Materiál 10 5 E [MPa] Nikel,1 Cín 0,43 Pieskovec 0,18 Oceľ,1 Olovo 0,1 Betón 0,15-0,5 Meď 1,15 Sklo 0,7 Drevo 0,1-0,1* Zinok 0,91 Liatina 6,7-1, 0,005-0,01* Zlato 0,78 Bronz 1,1 Bakelit 0,0-0,03 Striebro 0,75 Žula 0,49 Polyetylen,3.0-3 Hliník 0,7 Mramor 0,56 Tehlové, murivo * Drevo ako organický anizotropný materiál má rozdielne mechanické vlastnosti so zreteľom na svoju prirodzenú štruktúru...pozdĺž ( ) a kolmo ( ) na vlákna. Pozn.: Ako bolo spomenuté Hookov zákon neplatí pre všetky technické materiály (napr.: liatina, guma, prírodné kamene, plsť, koža a pod.). V týchto prípadoch sa používa tzv. mocninový zákon. Podľa Bacha je n E 0 ε = (1.14) Kde E 0 je materiálová konštanta a exponent n je u plsti, gumy, kože a pod. menší ako 1 (n < 1), u liatiny, kameňov a pod. je n > 1. 7
28 1.8 Vplyv zmeny teploty Tyč na obr vystavená po celej dĺžke konštantnej zmene teploty o t [ o C] zmení svoju dĺžku o Δl = α t.δt. l (1.15) Kde α t je súčiniteľ teplotnej dĺžkovej rozťažnosti. Rozmerom súčiniteľa α t je Celziov stupeň [ o C -1 ]. Ak je zmena teploty t kladná, ide o ohrev, pri zápornej zmene ide o ochladenie Obr Ak je tyč na oboch koncoch pevne votknutá (staticky neurčitý prípad, obr. 1.14), jej dĺžka sa vplyvom teploty nemôže zmeniť a vznikne v nej napätie t. t = α t. t E (1.16) Obr V tabuľke 1.3 sú uvedené súčinitele α t pre niektoré kovy: Tab. 1.3 Materiál α t [ o C -1 ] Materiál α t [ o C -1 ] Hliník,5 Oceľ 1, Bronz 1,75 Zinok 3,54 Meď 1,65 Liatina 1,04 8
29 1.9 Priečne zúženie. Poissonova konštanta Súčasne s predĺžením tyče v smere osi x objavuje sa skrátenie priečnych rozmerov. Toto skrátenie je, ako skúšky ukázali -ak platí Hookov zákon a u izotropných materiálov - úmerné napätiu a tým i osovému pomernému predĺženiu ε x. Keď vyberieme zo skúšobnej tyče myslený elementárny (veľmi malý) hranolček (obr. 1.15) budú jeho priečne zúženia v smere osí y, z Δdy ε y = dy ε x = m = me μ = E (1.17) Δdz ε z = dz ε x = m = me μ = E Súčiniteľ m sa nazýva Poissonova konštanta. 1 Často je výhodnejšie používať hodnotu μ =, m ktorú nazývame Poissonovym číslom. Pre oceľ má Poissonova konštanta hodnotu 10 m =. 3 Obr Podobne, ako v prípade modulu pružnosti E, ani v prípade Poissonovej konštanty neexistujú dva rôzne materiály, ktoré by mali rovnakú hodnotu m (μ). Preto sa Poissonova konštanta nazýva druhou materiálovou konštantou. 9
30 1.10 Príklady Z akého materiálu je tyč, na ktorú pôsobí osamelá sila S (obr. 1.16), ak je dané: dĺžka tyče l = 1,0m; napätie = 4 MPa a predĺženie tyče Δl = 0,mm. Riešenie: Pôsobením sily S sa tyč dĺžky 1,0m predĺžila o 0,mm a vzniklo v nej napätie o veľkosti 4 MPa. Obr Podľa (1.8) je pomerné predĺženie: Δl 0, mm ε = = = 0,.10 3 l 1.10 mm 3 Po dosadení do (1.1) = ε.e : 3 5 MPa = E E = MPa 4 0,.10.,1.10 Z tabuľky 1. zistíme, že uvedená tyč je z ocele Vypočítajte, o koľko sa predĺži hliníková tyč dĺžky l =,0m (obr. 1.17) pri zmene teploty Δt =10 C. a) b) Obr Riešenie: Súčiniteľ teplotnej dĺžkovej rozťažnosti α t pre hliníkový materiál je: 5 α t =,5.10 C -1 (tab. 1.3) Podľa (1.15) sa tyč predĺži o Δl (obr. 1.17b): Δ l = α Δtl Δ l = C C mm= mm t.., , 45 Tyč sa pri zmene teploty o 10 C predĺži o 0,45mm. 30
31 Pozn.: Vypočítané predĺženie je voči pôvodnej dĺžke tyče veľmi malé. Mohlo by sa zdať, že takáto zmena rozmeru nemá praktický význam. Neskôr si však ukážeme, že i takáto malá zmena dĺžky tyče (vzpery) môže vyvolať veľkú zmenu napätia v ostatných prvkoch konštrukcie, ktorej je súčasťou Vypočítajte pomerné priečne zúženie u oceľovej tyče zaťaženej dvojicou síl S, ktorá vyvolala v tyči napätie = 40 MPa (obr. 1.18). Obr Výsledok: ε y = ε = 5, z Z akého materiálu je tyč dĺžky l = 3,0m (obr. 1.19), ktorá sa pri zmene teploty Δt =10 C predĺži o Δl = 0,36mm? Obr Výsledok: tyč je z ocele. 31
32 3
33 . VÝPOČET A KONTROLA PRÚTOV NAMÁHANÝCH NA ŤAH (TLAK).1 Predpoklady výpočtu Ako vyplýva z definície (ods ) namáhania na prostý ťah (tlak), v myslenom priečnom reze pôsobí len normálová sila P v osi prúta. Takýmto spôsobom sú namáhané prúty v prútových sústavách, centricky tlačené stĺpy, podpery, laná na ťah a pod. Vnútornú osovú silu P možno vo zvolenom priereze určiť metódou mysleného rezu. Zákon rozloženia výslednej vnútornej sily ťahaného prúta po priereze formuloval na základe experimentálneho skúmania deformácie Navier. Podľa ním zdôvodnenej hypotézy (obr..1) zostane os prúta po predĺžení priama, a dva susedné, rovnobežné prierezy kolmé na os, ostanú aj po deformácii rovinné a navzájom rovnobežné. Z hypotézy vyplývajú dva dôležité závery: - v dôsledku zachovania priamosti prúta nie je možné vzájomné priečne posunutie (skosenie) prierezov, t. j. nevznikajú šmykové napätia, - pretože sa všetky vlákna (spojnice bodov rovnako vzdialených od osi prúta) medzi uvažovanými blízkymi prierezmi deformujú rovnako, budú vnútorné sily po celej ploche prierezu rozložené rovnomerne. Obr..1 Podľa toho normálové napätie pri prostom ťahu (tlaku) sa vypočíta z rovnice S = (.1a) F 33
34 Keďže pôsobiaca výslednica vonkajšej ťahovej (tlakovej) sily P vytvára v stave rovnováhy s vnútornou silou N silovú rovnovážnu dvojicu, platí = ± N F (.1b) Kde je... normálne napätie v ťahu (+), resp. v tlaku (-), [Pa] N... vnútorná normálová sila, [N] F... plocha prierezu prúta (b. h), [m ]. Pozn.: Z definície rovnovážnej dvojice síl (axióma statiky!) vyplýva, že rovnováha s vonkajšou silou S vznikne iba vtedy, keď zaťažujúca sila a vnútorná osová sila majú opačný zmysel, rovnakú veľkosť a spoločnú nositeľku.. Výpočet prúta na prostý ťah (tlak) Uvažujme priamy prút konštantného prierezu (obr..a) zaťažený osovou silou S. Na obrázku.b je prút uvoľnený. Odstránenie votknutia na hornom konci je nahradené väzbovou reakciou R. Reakciu vypočítame z rovnováhy vonkajších síl, ktoré na prút pôsobia (vo zvislom smere). - zaťažujúca sila S - vlastná tiaž prúta Q = γ 0. F. l - reakcia R a) b) c) d) e) Obr.. 34
35 V prípade priameho prizmatického prúta z podmienky rovnováhy dostaneme rovnicu R S γ 0 F. l = 0, (.a) v ktorej γ 0 merná špecifická tiaž [Nm -3 ] F plocha priečneho rezu [m ] l dĺžka prúta [m]. Metódou mysleného rezu (obr..d) určíme výslednicu vnútorných síl, ktoré pôsobia v priečnom reze mn prúta. Na dolnú časť prúta pôsobia vonkajšie sily S, Q y = γ 0. F. y a výslednica vnútorných síl N. Podľa podmienky rovnováhy je potrebné, aby nositeľkou sily N bola os prúta y. Podľa obr..d vyjadríme rovnováhu v reze mn rovnicou N S - γ 0. F. y = 0 (.b) z ktorej N = S + γ 0. F. y (.c) Keďže pri namáhaní ťahom pôsobia vnútorné sily rovnomerne v priečnom priereze prúta (Navierova hypotéza), môžeme napätie (podľa rovnice.1b) určiť rovnicou N S = = + γ 0 y (.d) F F Táto lineárna závislosť napätia od y je znázornená na obr..c. Napätie s najväčšou hodnotou pôsobí v priereze, ktorého poloha je určená súradnicou y = l. Jeho hodnotu vypočítame s použitím rovnice.d: S max = + γ 0. l (.e) F Celkové predĺženie elementárnej dĺžky prúta (obr..3) podľa rovnice
36 Δ dy= ε.dy, (.3a) a) b) resp. podľa rovnice (1.8) celkové predĺženie všetkých elementov po celej dĺžke prúta Δl l = 0 ε. dy (.3b) y Obr..3 Použitím Hookovho zákona (rovnica 1.1) môžeme rovnicu.3b napísať γ. y Δ= l + l S 0 ( )dy (.3c) EF. E 0 z ktorej po integrácii bude pomerné predĺženie S. l γ. l Δ l = + 0 (.3d) E. F. E Prvý člen rovnice predstavuje vplyv vonkajšej sily na predĺžení tyče ( Δl S ) a druhý vplyv jej vlastnej tiaže ( Δl q ). Výsledné predĺženie Δl získame sčítaním jednotlivých vplyvov Δ l = Δl S + Δl q (.3e) Postupnému výpočtu jednotlivých vplyvov a nakoniec ich sčítaniu, ako všeobecne zaužívanému postupu, sa pri rešpektovaní určitých predpokladov v pružnosti a pevnosti hovorí zákon superpozície (jednotlivých) vplyvov. Pozn.: Súčin E.F v rovnici.3d sa nazýva tuhosť prúta v ťahu (tlaku). Tuhosť vo význame ako miera odporu prvku (konštrukcie) deformovať sa (meniť v dôsledku vonkajšieho namáhania tvar a rozmery) patrí medzi základné pojmy v pružnosti a pevnosti. 36
37 Pomerná zmena priečneho rezu, zúženie pri namáhaní tyče na ťah sa vypočíta s použitím rovnice 1.17 μ S ε ( 0. y y = + γ ) (.4a) E F V prípade kruhovej prierezovej plochy obr..3b je Δ d = d. ε (.4b) 0 y a po dosadení pravej strany rovnice do rovnice.4a za ε y dostaneme μ. d 0 S Δ d = ( + γ 0. y) (.4c) E F Pri výpočtoch prútov premenného spojitého prierezu (.4a), alebo zloženého prierezu (.4b) sa postupuje podľa rovnakých zásad, ako na prizmatickom prúte. Vlastný výpočet je v týchto prípadoch však o niečo komplikovanejší. Príčinou býva vplyv spojite premennej alebo náhlej zmeny plochy, čo treba vo výpočte zohľadniť. a) b) Pozn.: V prípade spojite premennej zmeny prierezu patrí medzi časté praktické úlohy o. i. tiež výpočet prúta s rovnakou pevnosťou. Obr..4 Staticky neurčitými prípadmi prútov namáhaných na prostý ťah (tlak) viď. zmienka o nich na obr sa zaoberať nebudeme. 37
38 .3 Pevnostná kontrola a dimenzovanie prútov namáhaných na ťah (tlak) Otázka ako určiť rozmery prúta ( nadimenzovať jeho tvar), alebo, ak takýto prút existuje (jeho rozmery sú známe) skontrolovať (posúdiť) či predpokladanej veľkosti sily vyhovie, sú dve stránky tej istej úlohy v pružnosti a pevnosti. Významná a aktuálna úloha ekonomického využitia materiálu musí byť riešená tak, aby konštrukcia, ktorej posudzovaný prút je súčasťou, bola spoľahlivá (bezpečná) i počas dlhodobej prevádzky. V závislosti na úrovni dosiahnutého poznania sa postupne vyvinuli tri metódy riešenia týchto problémov: metóda dovolených napätí metóda dovolených zaťažení metóda medzných stavov.3.1 Metóda dovolených napätí Najstaršia (klasická) metóda dovolených napätí vychádza zo skutočnosti, že rozmery prvku konštrukcie musia byť navrhnuté tak, aby v nich najväčšie napätia vyvolané vonkajším zaťažením (viď. ods..), neprevyšovali hodnotu dovoleného (prípustného) napätia. K dov = alebo μ K m dov = (.5) μ m kde sú: - K, m medze napätia získané trhacími skúškami (ods. 1.7, tab. 1.1), - μ K, μ m miery bezpečnosti. Únosnosť súčiastky pri statickom namáhaní na ťah (tlak) je zabezpečená, keď skutočné maximálne napätie vyhovuje podmienke pevnosti vyjadrenej vzťahom max dov (.6) 38
39 Z uvedeného je zrejmé, že miera bezpečnosti μ K, resp. μ m musí byť väčšia ako 1! Z praktického hľadiska trvalé deformácie nevznikajú, keď napätie je pod medzou úmernosti U. Preto sa hodnota miery bezpečnosti volí tak, aby bola splnená podmienka dov < U. Hodnoty miery bezpečnosti boli záväzne určené v technických normách so zreteľom na druh zaťaženia, materiál a súčiastky v konkrétnej konštrukcii, jej účelu atď. Výhodou tejto metódy v inžinierskej praxi bola jej jednoduchosť. Nevýhody však najmä vzhľadom na univerzálnosť miery bezpečnosti a výhrady voči jej objektívnosti, prevážili. Preto sa už v súčasnosti táto metóda nepoužíva. Orientačné hodnoty dovolených napätí niektorých materiálov sú uvedené v tab..1. Tab..1 dov [MPa] dov [MPa] Materiál ťah tlak Materiál ťah tlak Konštrukčná oceľ Borovica Meď ,5- Hliník Dub Dural ,5 Bakelit Betón 0,1-0, Metóda dovolených zaťažení Na rozdiel od predchádzajúcej metódy sa únosnosť prvku či konštrukcie vyjadruje medznými hodnotami vnútorných síl. Metóda dovolených zaťažení bola u nás zavedená prvýkrát na výpočet betónových a železobetónových konštrukcií - dva rôzne druhy materiálu v posudzovanom priereze - pod názvom metóda posúdenia podľa stupňa bezpečnosti. Podľa tejto metódy sa považuje za vyhovujúci taký konštrukčný prvok, v ktorom pomer výslednice vnútorných síl v priereze na medzi únosnosti prierezu k výslednici vonkajších síl 39
40 je maximálne rovný istému číslu, predpísanému pre jednotlivé typy konštrukčných prvkov a rôzne druhy predpísanej veľkosti namáhania technickými normami. Zmienené pomery (t. j. súčinitele bezpečnosti) sa nazývajú stupňami bezpečnosti K (odtiaľ i názov metódy). Pevnostná podmienka pre limitujúce zaťaženie S max [N] má tvar: S N S max S dov = (.7) K kde: - S dov, S N je dovolené, resp. normové zaťaženie [N], - K stupne bezpečnosti, vždy väčšie ako 1 (k > 1)..3.3 Metóda medzných stavov Jedinou hodnotou miery bezpečnosti, alebo niekoľkými stupňami bezpečnosti (v prípade metódy podľa dovolených zaťažení zvlášť pre betón a nosnú oceľovú výstuž) nie je možné zohľadniť početné faktory, ktoré sa v kombináciách a v rôznych konštrukciách môžu objaviť súčasne. Metóda medzných stavov, podľa ktorej sa v súčasnosti konštrukcie navrhujú a kontrolujú, zachováva podstatu metódy podľa stupňa bezpečnosti (S max S dov ), ale líši sa od nej vo dvoch znakoch: - zavádza posúdenie (kontrolu) konštrukcií vzhľadom na dva medzné stavy, - uvažuje s tromi súčiniteľmi bezpečnosti. Prvý medzný stav medzný stav únosnosti je ten, pri ktorom sa konštrukcia stane nepoužiteľnou vyčerpaním únosnosti - napätia, stability (polohy a tvaru), plasticity a krehkého a únavového lomu. 40
41 Druhý medzný stav medza stavu použiteľnosti konštrukcie. Sem patria nadmerné deformácie (pri splnenom prvom medznom stave zachovania únosnosti i stability!) a príliš veľká dynamická odozva (napr. vibrácie) konštrukcie. Konštrukcia sa podľa metódy medzných stavov považuje za vyhovujúcu, keď sa výpočtom dokáže, že v priebehu jej celej životnosti (počas jej zriadenia a v prevádzke) nenastane ani jeden z medzných stavov. Možnosť vzniku niektorého alebo obidvoch medzných stavov súčasne závisí na niekoľkých činiteľoch, ktoré sa vo výpočte vyjadrujú tromi parciálnymi súčiniteľmi (k, n, m). - kvalita materiálu súčiniteľ rovnorodosti, k < 1, - zaťaženie a ostatné vonkajšie vplyvy súčiniteľ zaťaženia, n 1, - prostredie a podmienky, v ktorých konštrukcia plní svoj účel a podmienky, v ktorých bola vyrobená súčiniteľ podmienok pôsobenia, m 1. Hodnota súčiniteľov k, n, m je v technických normách (STN) určená na základe štatistického vyhodnotenia výsledkov mnohých skúšok a pozorovaní. Treba ešte poznamenať, že každý zo súčiniteľov môže závisieť na viacerých ďalších okolnostiach, t. j. ďalších súčiniteľoch toho istého druhu. To umožňuje lepšie, na úrovni dosiahnutého poznania i skúseností a stále objektívnejšie posudzovanie bezpečnosti a stavu konštrukcií. Bezpečnosť proti dosiahnutiu medzného stavu únosnosti sa posudzuje podľa tohto všeobecného vzťahu: (.8) n.n n Φ(m, kr n, F) kde okrem už vysvetlených symbolov (n, m, k), znamená: - N n... vnútorná sila od normového zaťaženia [N], - R n... najmenšie výpočtové normové namáhanie [N], - F... geometrická charakteristika posudzovaného prierezu, - n. N n skutočné zaťaženie konštrukcie od normového zaťaženia, resp. vypočítaná hodnota vnútornej sily, - kr n vypočítané namáhanie. 41
42 Konštrukčný prvok sa teda považuje za vyhovujúci na únosnosť vtedy, keď vypočítaná hodnota výslednice uvedených síl v posudzovanom priereze neprekročí hodnotu určenú funkciou Φ na pravej strane rovnice. Bezpečnosť konštrukcie proti dosiahnutiu medzného stavu použiteľnosti sa posudzuje podľa vzťahu f (.9) kde je vypočítaná (skutočná) deformácia a f deformácia dovolená. Pri posudzovaní konštrukcií podľa metódy medzných stavov platí: Výpočet (pri dimenzovaní alebo kontrole) konštrukcií podľa prvého medzného stavu je základný musí sa vykonať vždy! Výpočet podľa druhého medzného stavu sa vykonáva len vtedy, keď s ohľadom na možnosť vzniku nadmerných deformácií alebo kmitania to vyžadujú príslušné technické normy (STN). 4
43 .4 Príklady.4.1 Vypočítajte plochu F priečneho rezu prúta (obr..5a), zaťaženého vlastnou tiažou a silou S tak, aby celkové predĺženie prúta bolo nulové. Ďalej vypočítajte a nakreslite priebeh normálového napätia po celej dĺžke prúta. Dané je: sila S = 100 N; modul pružnosti v ťahu E =, MPa; dĺžka prúta l = 1,0 m; hustota materiálu ρ = 7850 kg.m -3 ; gravitačné zrýchlenie g = 9,81 m.s - a) b) c) Obr..5 Riešenie: Podľa (.b) napíšeme rovnicu rovnováhy pre (obr..5b): N + S Q = 0 ; pričom Q = g. ρ. F. y N + S g. ρ. F. y = 0 Pre výpočet normálového napätia platí (.1b): N S = N =. F ; po dosadení = g. ρ. y F F Predĺženie diferenciálneho úseku prúta je (.3a): Δ dy = ε. dy ; a následne po použití (.3b): l l l l g. ρ. yf. S Δ l = Δ dy = ε. dy =. dy =. d y E ; E. F odkiaľ po úprave: Δ l = g l Sl = = S = N. ρ ( ) 0 F 3. E E. F g. ρ. l 9,81( ms. ).7850( kgm. ).1,0( m) Plocha priečneho rezu prúta pri nulovom predĺžení je F = 0,006 m. 43
44 Ďalej vypočítame krajné hodnoty napätia v bodoch A, B: S 100 Ay ( = l) : A = g. ρ. l = 9, ,0 = 38547Pa, l 0, 006 S 100 B( y = 0) : B = g. ρ.0 = = 38461Pa. F 0, 006 Priebeh napätia po celej dĺžke prúta je zobrazený na obr..5c..4. Vypočítajte a nakreslite priebeh vnútorných silových veličín a hodnoty predĺženia v bodoch A, B a C u osovo zaťaženého odstupňovaného prúta (obr..6a), ak je dané: S 1 = 6000 N; S = 9000 N; S 3 = 4000 N; F 1 = 100 mm ; F = 00 mm ; l = 0,5 m; E =.10 5 MPa Riešenie: Podľa (.b) napíšeme rovnice rovnováhy pre každú časť prúta: n prvá časť (obr..6b): S = 0 N + S = 0 N = 6000N, i= 1 n i druhá časť (obr..6c): S = 0 N S + S = 0 N = 3000N, i= 1 n i 1 tretia časť (obr..6d): S = N + S S + S = 0 N 1000 N. i= 1 i = Ďalej vypočítame pomocou (.1b) jednotlivé normálové napätia: = N = 6000( N) 60 MPa 100( ) =, 1 1 F1 mm N 3000 = = = 30 MPa, F1 100 N = = = 5 MPa. F 00 Následne vyjadríme predĺženia (.3d) v daných bodoch A,B a C: Nl. Nl. Nl. Nl. 6000( N).500( mm) Δ A = = + + = ( ).100( ) i i i= 1 Ei Fi EF1 EF1 EF MPa mm Δ A = 0,0875mm 44
45 Nl. N. l Nl i i 3 Δ B = = + = + = 5 5 i= Ei. Fi EF. 1 EF Nl. Nl i i 3 Δ C = = = = 5 i= 3 EF i. i EF , 015mm 0, 065mm Priebeh vnútorných silových veličín a hodnoty predĺženia sú znázornené na obr..6e,f,g. a) D b) c) d) e) f) g) Obr..6 45
46 .4.3 Bremeno o tiaži Q = 100 kn je zavesené pomocou dvoch prútov (obr..7a). Materiál prútov je rovnaký s hodnotou dovoleného napätia dov = 150 MPa. Určite potrebné plochy priečnych prierezov prútov. a) b) Obr..7 Riešenie: Zo statických podmienok rovnováhy pre myslenými rezmi rozdelené prúty (.b) určíme normálové sily (obr..7b): n Six = 0 NAC.sin 30 NAB.sin 45 = 0, i= 1 n Siy = 0 Q+ NAC.cos30 + NAB.cos 45 = 0. i= 1 NAB = 0,518. Q; N = 0, 73. Q AC Napätia v prútoch (.1b) sú: = NAB 0,518. Q AB F = F ; AB AB N AC 0,73. Q AC = = F F AC Potrebné plochy prierezov prútov si vypočítame z pevnostnej podmienky (.6): AB dov ; AC dov potom: F 3 0,518. Q 0, ( N) AB = = 345mm, dov 150( MPa) AC F AC 3 0, 73. Q 0, ( N) = = m. dov 150( MPa) 488m 46
47 .4.4 Vypočítajte plochu priečneho prierezu prúta F, zaťaženého silou S (obr..8) tak, aby celkové predĺženie prúta Δl = mm. Dané je: S = 90kN; l = 0,7m; E =, MPa. Obr..8 Výsledok: F = 150 mm.4.5 Určite priebeh osovej sily, normálového napätia a premiestnenia prierezov 1,,3 tyče premenného prierezu zaťaženej silou S (obr..9a). Vlastnú tiaž zanedbáme. Dané je: S = 100 kn; F = 400 mm ; l = 1,0m; E =, MPa. a) b) c) d) Obr..9 Výsledky: N = 100 kn, priebeh obr..9b; 1, = 50 MPa,,3 = 15 MPa, priebeh obr..9c; Δl -1 = 1,5mm, Δl 3- = 0,65mm, priebeh obr..9d. 47
48 48
49 3. NAPÄTOSŤ, DEFORMÁCIA A ICH VZÁJOMNÉ SÚVISLOSTI 3.1 Napätosť a druhy napätostí Napätosť je vnútorný mechanický stav telesa spôsobený napätím. Napätosťou v určitom bode telesa nazývame súhrn všetkých napätí určených prostredníctvom rovín, ktoré daným bodom možno preložiť. Z praktickej príčiny, ako si ďalej ukážeme, určujeme napätosť v bode v rovinách elementárneho hranola. Napätosť vo všeobecnosti môže byť: - priestorová (trojosá), - rovinná (dvojosá), - priamková (jednoosá). Na určenie druhu napätosti v bode vyberieme z telesa elementárny hranolček s rozmermi dx, dy, dz. Na obr. 3.1a je znázornený všeobecný prípad priestorovej napätosti. Účinok odstraňovaných častí telesa nahradíme vnútornými silami. Vnútorné sily pripadajúce na jednotku Obr. 3.1a plochy, teda napätia p x, p y, p z prechádzajú ťažiskami troch dvojíc rovnobežných plošiek. Indexom pri označovaní napätia je určená plocha na ktorej napätie pôsobí. Napr. x je normála na plochu dy, dz, na ktorej pôsobí napätie p x. 49
50 Dá sa dokázať, že v uvažovanom mieste telesa je vždy možné vybrať elementárny hranolček tak, aby napätia pôsobili len kolmo na jeho steny (obr. 3.1b). Obr. 3.1b Tieto normálové napätia nazývame hlavné napätia a označujeme ich 1,, 3. Keď počiatok súradnicovej sústavy (spoločný bod troch rovín) leží v ťažisku telesa, vtedy sa hlavné napätia (a roviny v ktorých ležia) nazývajú centrálnymi. Ako sme už uviedli na obrázku 3.1a,b je znázornený prípad priestorovej (trojosej) napätosti. Priestorová napätosť vznikne vtedy, keď všetky vyznačené napätia p x, p y, p z sú nenulové. Keď určíme polohu elementárneho hranola tak, že vo dvoch protiľahlých stenách budú napätia (napr. p z ) rovné nule (obr. 3.) a v ostatných sú napätia nenulové, ide o napätosť rovinnú. Ak môžeme dať elementárnemu hranolu v telese takú polohu, keď napr. p y a p z budú nulové (obr. 3.3), potom ide o priamkovú napätosť - p x x (!). Z uvedeného vyplýva, že rovinná a priamková napätosť sú len zvláštne (špeciálne) prípady priestorovej napätosti. To platí tiež pre vzťah medzi rovinnou a priamkovou napätosťou. 50
51 Obr. 3. Pozn.: V indexe napätia τ z je označenie vykonané s ohľadom na skutočnosť, že v danom prípade pôsobia všetky šmykové napätia kolmo na os z. Obr. 3.3 Pre správne ohodnotenie nebezpečia, ohrozujúceho pevnosť (bezpečnosť) súčiastky, treba poznať napätosť nielen v stenách elementárneho hranolčeka, ale aj napätia v ľubovoľne sklonenom reze (obr. 3.4). Obr
52 3.1.1 Priamková napätosť (obr. 3.5). Máme určiť napätosť v ľubovoľnom bode A prúta, zaťaženého osovou silou S Obr. 3.5 Podľa rovnice (.1a ) je S 1 = (3.1) F V ďalšom uvažujme šikmý rez, ktorý prechádza bodom A (obr. 3.6). Normála na plochu rezu zviera s osou prúta uhol φ. Známym spôsobom fiktívneho rezu nahradíme účinok odstránenej časti prúta výslednicou vnútorných síl P. Pre rovnováhu platí P = S. (3.) Obe sily majú spoločnú nositeľku os prúta. a) Zložky N, T sily P = S podľa obr. 3.6a sú N = S. cosφ (3.3) T = S. sinφ (3.4) b) Pri namáhaní na ťah sú napätia v priereze rozložené rovnomerne. Ich veľkosť vypočítame z rovníc (1.3) Obr. 3.6 v tvare N = (3.5) F n T τ =. (3.6) F n Pôsobenie napätí v bode A (a aj v celom priereze) je znázornené na obr. 3.6b. 5
53 Vzájomná závislosť medzi plochami šikmého a priečneho (kolmého) rezu podľa obr. 3.6a je F F n = (3.7) cosϕ Riešením rovnice (3.3, 3.5, 3.7, a 3.1) dostaneme ( x = 1 ) = 1. cos ϕ (3.8) a riešením rovníc (3.1, 3.4, 3.6a 3.7) τ = sinϕ. cosϕ (3.9) 1 Keď podľa známych goniometrických vzorcov dvojnásobného uhla cosφ = cos φ sin φ a sinφ = sinφcosφ a úprave do tvaru 1 cos ϕ sin ϕ cos ϕ = + a sinϕ cosϕ = ich dosadíme do rovníc (3.8 a 3.9) budú napätia určené vzťahmi = cos ϕ + (3.10) 1 τ = 1 sin ϕ (3.11) Keďže v rovniciach 3.10 a 3.11 sa nevyskytuje plocha F a ani žiadna materiálová konštanta, napätie a τ závisí len na napätí 1 a uhle φ. Ďalej z rovníc vidieť, že normálová zložka napätia je najväčšia v rovine kolmej na os prúta (φ = 0 cos0 = 1) a má veľkosť 1, vtedy ale šmykové napätie (sin0 = 0) je τ = 0. 53
54 Naproti tomu šmykové napätie je maximálne v rovine určenej uhlom 45 o (resp. 135 o ) vtedy keď sin. 45 o = sin90 o 1 = 1, a má hodnotu τ = 1. Pritom však normálne napätie ( z rovnice 3.10) aj keď druhý člen rovnice je nulový (cos. 45 o = cos90 o = 0), nulové nie je. Najmenšia hodnota normálového napätia je = 1! Keď upravené rovnice (3.10 a 3.11) 1 1 = cosϕ 1 τ = sin ϕ vyriešime (umocnením a sčítaním), dostaneme ( ) + τ = ( cos ϕ) + ( sin ϕ ) a ďalej po úprave pravej časti rovnice a dosadením za cos ϕ sin ϕ 1 + = (trigonometrická jednotka) ju zjednodušíme na tvar: + = 1 ) (3.1) 1 ( ) τ ( Ak túto rovnicu porovnávame zo všeobecným tvarom rovnice kružnice [(x m) + (y n) = r ] v súradnicovom systéme, τ (obr. 3.7) dostaneme kružnicu napätia. 54
Motivácia Denícia determinantu Výpo et determinantov Determinant sú inu matíc Vyuºitie determinantov. Determinanty. 14. decembra 2010.
 14. decembra 2010 Rie²enie sústav Plocha rovnobeºníka Objem rovnobeºnostena Rie²enie sústav Príklad a 11 x 1 + a 12 x 2 = c 1 a 21 x 1 + a 22 x 2 = c 2 Dostaneme: x 1 = c 1a 22 c 2 a 12 a 11 a 22 a 12
14. decembra 2010 Rie²enie sústav Plocha rovnobeºníka Objem rovnobeºnostena Rie²enie sústav Príklad a 11 x 1 + a 12 x 2 = c 1 a 21 x 1 + a 22 x 2 = c 2 Dostaneme: x 1 = c 1a 22 c 2 a 12 a 11 a 22 a 12
Škola pre mimoriadne nadané deti a Gymnázium
 Škola: Predmet: Skupina: Trieda: Dátum: Škola pre mimoriadne nadané deti a Gymnázium Fyzika Fyzikálne veličiny a ich jednotky Obsah a metódy fyziky, Veličiny a jednotky sústavy SI, Násobky a diely fyzikálnych
Škola: Predmet: Skupina: Trieda: Dátum: Škola pre mimoriadne nadané deti a Gymnázium Fyzika Fyzikálne veličiny a ich jednotky Obsah a metódy fyziky, Veličiny a jednotky sústavy SI, Násobky a diely fyzikálnych
Matematika Funkcia viac premenných, Parciálne derivácie
 Matematika 2-01 Funkcia viac premenných, Parciálne derivácie Euklidovská metrika na množine R n všetkých usporiadaných n-íc reálnych čísel je reálna funkcia ρ: R n R n R definovaná nasledovne: Ak X = x
Matematika 2-01 Funkcia viac premenných, Parciálne derivácie Euklidovská metrika na množine R n všetkých usporiadaných n-íc reálnych čísel je reálna funkcia ρ: R n R n R definovaná nasledovne: Ak X = x
Obvod a obsah štvoruholníka
 Obvod a štvoruholníka D. Štyri body roviny z ktorých žiadne tri nie sú kolineárne (neležia na jednej priamke) tvoria jeden štvoruholník. Tie body (A, B, C, D) sú vrcholy štvoruholníka. strany štvoruholníka
Obvod a štvoruholníka D. Štyri body roviny z ktorých žiadne tri nie sú kolineárne (neležia na jednej priamke) tvoria jeden štvoruholník. Tie body (A, B, C, D) sú vrcholy štvoruholníka. strany štvoruholníka
Kontrolné otázky na kvíz z jednotiek fyzikálnych veličín. Upozornenie: Umiestnenie správnej a nesprávnych odpovedí sa môže v teste meniť.
 Kontrolné otázky na kvíz z jednotiek fyzikálnych veličín Upozornenie: Umiestnenie správnej a nesprávnych odpovedí sa môže v teste meniť. Ktoré fyzikálne jednotky zodpovedajú sústave SI: a) Dĺžka, čas,
Kontrolné otázky na kvíz z jednotiek fyzikálnych veličín Upozornenie: Umiestnenie správnej a nesprávnych odpovedí sa môže v teste meniť. Ktoré fyzikálne jednotky zodpovedajú sústave SI: a) Dĺžka, čas,
Řečtina I průvodce prosincem a začátkem ledna prezenční studium
 Řečtina I průvodce prosincem a začátkem ledna prezenční studium Dobson číst si Dobsona 9. až 12. lekci od 13. lekce už nečíst (minulý čas probírán na stažených slovesech velmi matoucí) Bartoň pořídit si
Řečtina I průvodce prosincem a začátkem ledna prezenční studium Dobson číst si Dobsona 9. až 12. lekci od 13. lekce už nečíst (minulý čas probírán na stažených slovesech velmi matoucí) Bartoň pořídit si
1. Limita, spojitost a diferenciálny počet funkcie jednej premennej
 . Limita, spojitost a diferenciálny počet funkcie jednej premennej Definícia.: Hromadný bod a R množiny A R: v každom jeho okolí leží aspoň jeden bod z množiny A, ktorý je rôzny od bodu a Zadanie množiny
. Limita, spojitost a diferenciálny počet funkcie jednej premennej Definícia.: Hromadný bod a R množiny A R: v každom jeho okolí leží aspoň jeden bod z množiny A, ktorý je rôzny od bodu a Zadanie množiny
Priamkové plochy. Ak každým bodom plochy Φ prechádza aspoň jedna priamka, ktorá (celá) na nej leží potom plocha Φ je priamková. Santiago Calatrava
 Priamkové plochy Priamkové plochy Ak každým bodom plochy Φ prechádza aspoň jedna priamka, ktorá (celá) na nej leží potom plocha Φ je priamková. Santiago Calatrava Priamkové plochy rozdeľujeme na: Rozvinuteľné
Priamkové plochy Priamkové plochy Ak každým bodom plochy Φ prechádza aspoň jedna priamka, ktorá (celá) na nej leží potom plocha Φ je priamková. Santiago Calatrava Priamkové plochy rozdeľujeme na: Rozvinuteľné
ZADANIE 1_ ÚLOHA 3_Všeobecná rovinná silová sústava ZADANIE 1 _ ÚLOHA 3
 ZDNIE _ ÚLOH 3_Všeobecná rovinná silová sústv ZDNIE _ ÚLOH 3 ÚLOH 3.: Vypočítjte veľkosti rekcií vo väzbách nosník zťženého podľ obrázku 3.. Veľkosti známych síl, momentov dĺžkové rozmery sú uvedené v
ZDNIE _ ÚLOH 3_Všeobecná rovinná silová sústv ZDNIE _ ÚLOH 3 ÚLOH 3.: Vypočítjte veľkosti rekcií vo väzbách nosník zťženého podľ obrázku 3.. Veľkosti známych síl, momentov dĺžkové rozmery sú uvedené v
2 η ΑΣΚΗΣΗ Γ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΗ
 2 η ΑΣΚΗΣΗ Γ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΗ Διαθέτουμε τροχό ο οποίος αποτελείται από έναν ομογενή λεπτό δακτύλιο μάζας m = 1 kg και ακτίνας R και τέσσερις λεπτές ομογενείς ράβδους μάζας Μ ρ = ¾m και μήκους l = 2R η
2 η ΑΣΚΗΣΗ Γ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΗ Διαθέτουμε τροχό ο οποίος αποτελείται από έναν ομογενή λεπτό δακτύλιο μάζας m = 1 kg και ακτίνας R και τέσσερις λεπτές ομογενείς ράβδους μάζας Μ ρ = ¾m και μήκους l = 2R η
Pilota600mmrez1. N Rd = N Rd = M Rd = V Ed = N Rd = M y M Rd = M y. M Rd = N 0.
 Bc. Martin Vozár Návrh výstuže do pilót Diplomová práca 8x24.00 kr. 50.0 Pilota600mmrez1 Typ prvku: nosník Prostředí: X0 Beton:C20/25 f ck = 20.0 MPa; f ct = 2.2 MPa; E cm = 30000.0 MPa Ocelpodélná:B500
Bc. Martin Vozár Návrh výstuže do pilót Diplomová práca 8x24.00 kr. 50.0 Pilota600mmrez1 Typ prvku: nosník Prostředí: X0 Beton:C20/25 f ck = 20.0 MPa; f ct = 2.2 MPa; E cm = 30000.0 MPa Ocelpodélná:B500
Το άτομο του Υδρογόνου
 Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
Start. Vstup r. O = 2*π*r S = π*r*r. Vystup O, S. Stop. Start. Vstup P, C V = P*C*1,19. Vystup V. Stop
 1) Vytvorte algoritmus (vývojový diagram) na výpočet obvodu kruhu. O=2xπxr ; S=πxrxr Vstup r O = 2*π*r S = π*r*r Vystup O, S 2) Vytvorte algoritmus (vývojový diagram) na výpočet celkovej ceny výrobku s
1) Vytvorte algoritmus (vývojový diagram) na výpočet obvodu kruhu. O=2xπxr ; S=πxrxr Vstup r O = 2*π*r S = π*r*r Vystup O, S 2) Vytvorte algoritmus (vývojový diagram) na výpočet celkovej ceny výrobku s
ΤΥΠΟΛΟΓΙΟ ΕΔΑΦΟΜΗΧΑΝΙΚΗΣ
 ΤΥΠΟΛΟΓΙΟ ΕΔΑΦΟΜΗΧΑΝΙΚΗΣ (σε αντιστοιχία με το σύγγραμμα «απλά βήματα στην εδαφομηχανική» των ιδίων συγγραφέων) Καθ. Β. Χρηστάρας & Δρ. Μ. Χατζηαγγέλου Εργαστήριο Τεχνικής Γεωλογίας Τμ. Γεωλογίας - ΑΠΘ
ΤΥΠΟΛΟΓΙΟ ΕΔΑΦΟΜΗΧΑΝΙΚΗΣ (σε αντιστοιχία με το σύγγραμμα «απλά βήματα στην εδαφομηχανική» των ιδίων συγγραφέων) Καθ. Β. Χρηστάρας & Δρ. Μ. Χατζηαγγέλου Εργαστήριο Τεχνικής Γεωλογίας Τμ. Γεωλογίας - ΑΠΘ
Pevné ložiská. Voľné ložiská
 SUPPORTS D EXTREMITES DE PRECISION - SUPPORT UNIT FOR BALLSCREWS LOŽISKA PRE GULIČKOVÉ SKRUTKY A TRAPÉZOVÉ SKRUTKY Výber správnej podpory konca uličkovej skrutky či trapézovej skrutky je dôležité pre správnu
SUPPORTS D EXTREMITES DE PRECISION - SUPPORT UNIT FOR BALLSCREWS LOŽISKA PRE GULIČKOVÉ SKRUTKY A TRAPÉZOVÉ SKRUTKY Výber správnej podpory konca uličkovej skrutky či trapézovej skrutky je dôležité pre správnu
3. Striedavé prúdy. Sínusoida
 . Striedavé prúdy VZNIK: Striedavý elektrický prúd prechádza obvodom, ktorý je pripojený na zdroj striedavého napätia. Striedavé napätie vyrába synchrónny generátor, kde na koncoch rotorového vinutia sa
. Striedavé prúdy VZNIK: Striedavý elektrický prúd prechádza obvodom, ktorý je pripojený na zdroj striedavého napätia. Striedavé napätie vyrába synchrónny generátor, kde na koncoch rotorového vinutia sa
5/16/2015. Δρ. Σωτήρης Δέμης. Σημειώσεις Εργαστηριακής Άσκησης Κριτήρια Αστοχίας Διάτμηση Τοιχοποιίας. Πολιτικός Μηχανικός (Πανεπιστημιακός Υπότροφος)
 5/16/015 Σημειώεις Εργατηριακής Άκηης Κριτήρια Ατοχίας Διάτμηη Τοιχοποιίας Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Πανεπιτημιακός Υπότροφος) Έως τώρα Κατατατικός νόμος όλκιμων υλικών (αξονική καταπόνιη
5/16/015 Σημειώεις Εργατηριακής Άκηης Κριτήρια Ατοχίας Διάτμηη Τοιχοποιίας Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Πανεπιτημιακός Υπότροφος) Έως τώρα Κατατατικός νόμος όλκιμων υλικών (αξονική καταπόνιη
ΓΕΝΙΚΗ ΦΥΣΙΚΗ IV: ΚΥΜΑΤΙΚΗ - ΟΠΤΙΚΗ
 Τμήμα Φυσικής Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης ΓΕΝΙΚΗ ΦΥΣΙΚΗ IV: ΚΥΜΑΤΙΚΗ - ΟΠΤΙΚΗ Ι. ΑΡΒΑΝΙΤΙ ΗΣ jarvan@physcs.auth.gr 2310 99 8213 ΘΕΜΑΤΙΚΕΣ ΕΝΟΤΗΤΕΣ ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ ΠΟΛΩΣΗ ΣΥΜΒΟΛΗ ΠΕΡΙΘΛΑΣΗ
Τμήμα Φυσικής Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης ΓΕΝΙΚΗ ΦΥΣΙΚΗ IV: ΚΥΜΑΤΙΚΗ - ΟΠΤΙΚΗ Ι. ΑΡΒΑΝΙΤΙ ΗΣ jarvan@physcs.auth.gr 2310 99 8213 ΘΕΜΑΤΙΚΕΣ ΕΝΟΤΗΤΕΣ ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ ΠΟΛΩΣΗ ΣΥΜΒΟΛΗ ΠΕΡΙΘΛΑΣΗ
r 2 r 1 επιφάνεια. Όταν ο ανιχνευτής μεταλλική επιφάνεια απόσταση
 ΑΠΑΝΤΗΣΕΙΣ ΔΙΑΩΝΙΣΜΑΤΟΣ ΦΥΣΙΚΗΣ ΛΥΚΕΙΟΥ 3/03/04 ΘΕΜΑ Ο δ, γ, 3 γ, 4 δ, 5 α, 6 β, γ, 8 α, 9 α, 0: α Λ, β Λ, γ, δ Λ, ε Λ. ΘΕΜΑ Ο. Α. ωστό το (γ). Β. το χώρο μεταξύ του πομπού και της μεταλλικής επιφάνειας
ΑΠΑΝΤΗΣΕΙΣ ΔΙΑΩΝΙΣΜΑΤΟΣ ΦΥΣΙΚΗΣ ΛΥΚΕΙΟΥ 3/03/04 ΘΕΜΑ Ο δ, γ, 3 γ, 4 δ, 5 α, 6 β, γ, 8 α, 9 α, 0: α Λ, β Λ, γ, δ Λ, ε Λ. ΘΕΜΑ Ο. Α. ωστό το (γ). Β. το χώρο μεταξύ του πομπού και της μεταλλικής επιφάνειας
Άζθεζε 18. Οπηηθό κηθξνζθόπην
 Άζθεζε 18 Οπηηθό κηθξνζθόπην 18.1. θνπόο θνπφο ηεο άζθεζεο είλαη ε εμνηθείσζε ησλ ζπνπδαζηψλ κε ηελ νπηηθή κηθξνζθνπία θαη ε κειέηε κηθξνδνκψλ (κεγέζνπο κηθξνκέηξσλ) κε δηαθνξεηηθέο κεγεζχλζεηο, νη νπνίεο
Άζθεζε 18 Οπηηθό κηθξνζθόπην 18.1. θνπόο θνπφο ηεο άζθεζεο είλαη ε εμνηθείσζε ησλ ζπνπδαζηψλ κε ηελ νπηηθή κηθξνζθνπία θαη ε κειέηε κηθξνδνκψλ (κεγέζνπο κηθξνκέηξσλ) κε δηαθνξεηηθέο κεγεζχλζεηο, νη νπνίεο
Prechod z 2D do 3D. Martin Florek 3. marca 2009
 Počítačová grafika 2 Prechod z 2D do 3D Martin Florek florek@sccg.sk FMFI UK 3. marca 2009 Prechod z 2D do 3D Čo to znamená? Ako zobraziť? Súradnicové systémy Čo to znamená? Ako zobraziť? tretia súradnica
Počítačová grafika 2 Prechod z 2D do 3D Martin Florek florek@sccg.sk FMFI UK 3. marca 2009 Prechod z 2D do 3D Čo to znamená? Ako zobraziť? Súradnicové systémy Čo to znamená? Ako zobraziť? tretia súradnica
Ekvačná a kvantifikačná logika
 a kvantifikačná 3. prednáška (6. 10. 004) Prehľad 1 1 (dokončenie) ekvačných tabliel Formula A je ekvačne dokázateľná z množiny axióm T (T i A) práve vtedy, keď existuje uzavreté tablo pre cieľ A ekvačných
a kvantifikačná 3. prednáška (6. 10. 004) Prehľad 1 1 (dokončenie) ekvačných tabliel Formula A je ekvačne dokázateľná z množiny axióm T (T i A) práve vtedy, keď existuje uzavreté tablo pre cieľ A ekvačných
AerobTec Altis Micro
 AerobTec Altis Micro Záznamový / súťažný výškomer s telemetriou Výrobca: AerobTec, s.r.o. Pionierska 15 831 02 Bratislava www.aerobtec.com info@aerobtec.com Obsah 1.Vlastnosti... 3 2.Úvod... 3 3.Princíp
AerobTec Altis Micro Záznamový / súťažný výškomer s telemetriou Výrobca: AerobTec, s.r.o. Pionierska 15 831 02 Bratislava www.aerobtec.com info@aerobtec.com Obsah 1.Vlastnosti... 3 2.Úvod... 3 3.Princíp
Βασικά Θέµατα στην ενότητα «Συνάρτηση οριζόµενη µε ολοκλήρωµα»
 Κεφάλιο: Ολοκληρώµτ (Ενότητ: Συνάρτηση οριζόµενη µε Ολοκλήρωµ) Βσικά Θέµτ στην ενότητ «Συνάρτηση οριζόµενη µε ολοκλήρωµ» Α Πεδίο ορισµού κι πράωος συνρτήσεων που ορίζοντι µε ολοκλήρωµ κι έχουν τύπους:
Κεφάλιο: Ολοκληρώµτ (Ενότητ: Συνάρτηση οριζόµενη µε Ολοκλήρωµ) Βσικά Θέµτ στην ενότητ «Συνάρτηση οριζόµενη µε ολοκλήρωµ» Α Πεδίο ορισµού κι πράωος συνρτήσεων που ορίζοντι µε ολοκλήρωµ κι έχουν τύπους:
ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ Ο.Κ.Κ - ΟΡΜΗ
 ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ Ο.Κ.Κ - ΟΡΜΗ Ημερομηνία: 21/12/14 Διάρκεια διαγωνίσματος: 120 Υπεύθυνος καθηγητής: Τηλενίκης Ευάγγελος ΖΗΤΗΜΑ 1 Στις ερωτήσεις 1-5 επιλέξτε τη σωστή απάντηση
ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ Ο.Κ.Κ - ΟΡΜΗ Ημερομηνία: 21/12/14 Διάρκεια διαγωνίσματος: 120 Υπεύθυνος καθηγητής: Τηλενίκης Ευάγγελος ΖΗΤΗΜΑ 1 Στις ερωτήσεις 1-5 επιλέξτε τη σωστή απάντηση
Matematika prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad
 Matematika 3-13. prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad Erika Škrabul áková F BERG, TU Košice 15. 12. 2015 Erika Škrabul áková (TUKE) Taylorov
Matematika 3-13. prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad Erika Škrabul áková F BERG, TU Košice 15. 12. 2015 Erika Škrabul áková (TUKE) Taylorov
ΦΥΣΙΚΗ Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2006 ΕΚΦΩΝΗΣΕΙΣ
 ΦΥΣΙΚΗ Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 6 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ ο Ν γράψετε στο τετράδιό σς τον ριθµό κθεµιάς πό τις πρκάτω ερωτήσεις - 4 κι δίπλ το γράµµ πο ντιστοιχεί στη σωστή πάντηση Στο κύκλωµ
ΦΥΣΙΚΗ Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 6 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ ο Ν γράψετε στο τετράδιό σς τον ριθµό κθεµιάς πό τις πρκάτω ερωτήσεις - 4 κι δίπλ το γράµµ πο ντιστοιχεί στη σωστή πάντηση Στο κύκλωµ
M6: Model Hydraulický systém dvoch zásobníkov kvapaliny s interakciou
 M6: Model Hydraulický ytém dvoch záobníkov kvapaliny interakciou Úlohy:. Zotavte matematický popi modelu Hydraulický ytém. Vytvorte imulačný model v jazyku: a. Matlab b. imulink 3. Linearizujte nelineárny
M6: Model Hydraulický ytém dvoch záobníkov kvapaliny interakciou Úlohy:. Zotavte matematický popi modelu Hydraulický ytém. Vytvorte imulačný model v jazyku: a. Matlab b. imulink 3. Linearizujte nelineárny
Αξιολόγηση των Επιδράσεων του Σχεδίου Τοποθέτησης Άνεργων Νέων Αποφοίτων Γυμνασίων, Λυκείων, Τεχνικών Σχολών και Μεταλυκειακής Εκπαίδευσης μέχρι και
 Αξιολόγηση των Επιδράσεων του Σχεδίου Τοποθέτησης Άνεργων Νέων Αποφοίτων Γυμνασίων, Λυκείων, Τεχνικών Σχολών και Μεταλυκειακής Εκπαίδευσης μέχρι και ιετούς ιάρκειας για Απόκτηση Εργασιακής Πείρας σε Επιχειρήσεις/Οργανισμούς
Αξιολόγηση των Επιδράσεων του Σχεδίου Τοποθέτησης Άνεργων Νέων Αποφοίτων Γυμνασίων, Λυκείων, Τεχνικών Σχολών και Μεταλυκειακής Εκπαίδευσης μέχρι και ιετούς ιάρκειας για Απόκτηση Εργασιακής Πείρας σε Επιχειρήσεις/Οργανισμούς
1. písomná práca z matematiky Skupina A
 1. písomná práca z matematiky Skupina A 1. Vypočítajte : a) 84º 56 + 32º 38 = b) 140º 53º 24 = c) 55º 12 : 2 = 2. Vypočítajte zvyšné uhly na obrázku : β γ α = 35 12 δ a b 3. Znázornite na číselnej osi
1. písomná práca z matematiky Skupina A 1. Vypočítajte : a) 84º 56 + 32º 38 = b) 140º 53º 24 = c) 55º 12 : 2 = 2. Vypočítajte zvyšné uhly na obrázku : β γ α = 35 12 δ a b 3. Znázornite na číselnej osi
ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ (1) ημθ n ημθ 1 3 2 3. ημθ2 1 (3) ημθ2. Ο x K. Φροντιστήριο «ΕΠΙΛΟΓΗ»
 ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 5 ΜΑÏΟΥ 0 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ) ΘΕΜΑ Α ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 5 ΜΑÏΟΥ 0 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ) ΘΕΜΑ Α ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ
7. FUNKCIE POJEM FUNKCIE
 7. FUNKCIE POJEM FUNKCIE Funkcia f reálnej premennej je : - každé zobrazenie f v množine všetkých reálnych čísel; - množina f všetkých usporiadaných dvojíc[,y] R R pre ktorú platí: ku každému R eistuje
7. FUNKCIE POJEM FUNKCIE Funkcia f reálnej premennej je : - každé zobrazenie f v množine všetkých reálnych čísel; - množina f všetkých usporiadaných dvojíc[,y] R R pre ktorú platí: ku každému R eistuje
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ» ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α
 3 o ΔΑΓΩΝΣΜΑ ΜΑΡΤOΣ 03: ΕΝΔΕΚΤΚΕΣ ΑΠΑΝΤΗΣΕΣ ΦΥΣΚΗ ΘΕΤΚΗΣ ΚΑ ΤΕΧΝΟΛΟΓΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΑΓΩΝΣΜΑ (ΣΤΕΡΕΟ ΣΩΜΑ) ΕΝΔΕΚΤΚΕΣ ΑΠΑΝΤΗΣΕΣ ΘΕΜΑ Α β δ 3 δ 4 β 5 Λ βσ γλ δσ ελ ΘΕΜΑ Β Σωστή είνι η πάντηση γ Ο ρυθμός
3 o ΔΑΓΩΝΣΜΑ ΜΑΡΤOΣ 03: ΕΝΔΕΚΤΚΕΣ ΑΠΑΝΤΗΣΕΣ ΦΥΣΚΗ ΘΕΤΚΗΣ ΚΑ ΤΕΧΝΟΛΟΓΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΑΓΩΝΣΜΑ (ΣΤΕΡΕΟ ΣΩΜΑ) ΕΝΔΕΚΤΚΕΣ ΑΠΑΝΤΗΣΕΣ ΘΕΜΑ Α β δ 3 δ 4 β 5 Λ βσ γλ δσ ελ ΘΕΜΑ Β Σωστή είνι η πάντηση γ Ο ρυθμός
η = 1,0-(f ck -50)/200 pre 50 < f ck 90 MPa
 1.4.1. Návrh priečneho rezu a pozĺžnej výstuže prierezu ateriálové charakteristiky: - betón: napr. C 0/5 f ck [Pa]; f ctm [Pa]; fck f α [Pa]; γ cc C pričom: α cc 1,00; γ C 1,50; η 1,0 pre f ck 50 Pa η
1.4.1. Návrh priečneho rezu a pozĺžnej výstuže prierezu ateriálové charakteristiky: - betón: napr. C 0/5 f ck [Pa]; f ctm [Pa]; fck f α [Pa]; γ cc C pričom: α cc 1,00; γ C 1,50; η 1,0 pre f ck 50 Pa η
24. Základné spôsoby zobrazovania priestoru do roviny
 24. Základné spôsoby zobrazovania priestoru do roviny Voľné rovnobežné premietanie Presné metódy zobrazenia trojrozmerného priestoru do dvojrozmernej roviny skúma samostatná matematická disciplína, ktorá
24. Základné spôsoby zobrazovania priestoru do roviny Voľné rovnobežné premietanie Presné metódy zobrazenia trojrozmerného priestoru do dvojrozmernej roviny skúma samostatná matematická disciplína, ktorá
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ B ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 Θέμα Α ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ B ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Στις παρακάτω ερωτήσεις πολλαπλής επιλογής Α-Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
Θέμα Α ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ B ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Στις παρακάτω ερωτήσεις πολλαπλής επιλογής Α-Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
Základy automatického riadenia
 Základy automatického riadenia Predná²ka 8 doc. Ing. Anna Jadlovská, PhD., doc. Ing. Ján Jadlovský, CSc. Katedra kybernetiky a umelej inteligencie Fakulta elektrotechniky a informatiky Technická univerzita
Základy automatického riadenia Predná²ka 8 doc. Ing. Anna Jadlovská, PhD., doc. Ing. Ján Jadlovský, CSc. Katedra kybernetiky a umelej inteligencie Fakulta elektrotechniky a informatiky Technická univerzita
γραπτή εξέταση στο μάθημα ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ
 η εξεταστική περίοδος από 1/1/14 έως 07/01/15 γραπτή εξέταση στο μάθημα ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ Τάξη: Α Λυκείου Τμήμα: Βαθμός: Ονοματεπώνυμο: Καθηγητές: Θ Ε Μ Α Α Στις παρακάτω ερωτήσεις να επιλέξετε τη σωστή
η εξεταστική περίοδος από 1/1/14 έως 07/01/15 γραπτή εξέταση στο μάθημα ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ Τάξη: Α Λυκείου Τμήμα: Βαθμός: Ονοματεπώνυμο: Καθηγητές: Θ Ε Μ Α Α Στις παρακάτω ερωτήσεις να επιλέξετε τη σωστή
Einsteinove rovnice. obrázkový úvod do Všeobecnej teórie relativity. Pavol Ševera. Katedra teoretickej fyziky a didaktiky fyziky
 Einsteinove rovnice obrázkový úvod do Všeobecnej teórie relativity Pavol Ševera Katedra teoretickej fyziky a didaktiky fyziky (Pseudo)historický úvod Gravitácia / Elektromagnetizmus (Pseudo)historický
Einsteinove rovnice obrázkový úvod do Všeobecnej teórie relativity Pavol Ševera Katedra teoretickej fyziky a didaktiky fyziky (Pseudo)historický úvod Gravitácia / Elektromagnetizmus (Pseudo)historický
ΑΝΤΙΚΕΙΜΕΝΟ ΘΕΜΑ 1 Ο
 ΑΝΤΙΚΕΙΜΕΝΟ 1 ο κεφάλαιο: «ΤΑΛΑΝΤΩΣΕΙΣ» ΘΕΜΑ 1 Ο 1. Ένα σώµα εκτελεί απλή αρµονική ταλάντωση. Στο διπλανό σχήµα φαίνεται η γραφική παράσταση της ταχύτητας του σώµατος µε το χρόνο. Η αρχική φάση της ταλάντωσης
ΑΝΤΙΚΕΙΜΕΝΟ 1 ο κεφάλαιο: «ΤΑΛΑΝΤΩΣΕΙΣ» ΘΕΜΑ 1 Ο 1. Ένα σώµα εκτελεί απλή αρµονική ταλάντωση. Στο διπλανό σχήµα φαίνεται η γραφική παράσταση της ταχύτητας του σώµατος µε το χρόνο. Η αρχική φάση της ταλάντωσης
KATEDRA DOPRAVNEJ A MANIPULAČNEJ TECHNIKY Strojnícka fakulta, Žilinská Univerzita
 132 1 Absolútna chyba: ) = - skut absolútna ochýlka: ) ' = - spr. relatívna chyba: alebo Chyby (ochýlky): M systematické, M náhoné, M hrubé. Korekcia: k = spr - = - Î' pomerná korekcia: Správna honota:
132 1 Absolútna chyba: ) = - skut absolútna ochýlka: ) ' = - spr. relatívna chyba: alebo Chyby (ochýlky): M systematické, M náhoné, M hrubé. Korekcia: k = spr - = - Î' pomerná korekcia: Správna honota:
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2015
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 5 ΤΕΧΝΟΛΟΓΙΑ (Ι) ΘΕΩΡΗΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Μάθημα: Εφαρμοσμένη Μηχανική Επιστήμη Ημερομηνία
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 5 ΤΕΧΝΟΛΟΓΙΑ (Ι) ΘΕΩΡΗΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Μάθημα: Εφαρμοσμένη Μηχανική Επιστήμη Ημερομηνία
ΕΚΠΑΙΔΕΥΤΙΚΗ ΚΛΙΜΑΚΑ http://edu.klimaka.gr
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 9 ΙΟΥΛΙΟΥ 2010 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) ΣΥΝΟΛΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 9 ΙΟΥΛΙΟΥ 2010 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) ΣΥΝΟΛΟ
Návrh vzduchotesnosti pre detaily napojení
 Výpočet lineárneho stratového súčiniteľa tepelného mosta vzťahujúceho sa k vonkajším rozmerom: Ψ e podľa STN EN ISO 10211 Návrh vzduchotesnosti pre detaily napojení Objednávateľ: Ing. Natália Voltmannová
Výpočet lineárneho stratového súčiniteľa tepelného mosta vzťahujúceho sa k vonkajším rozmerom: Ψ e podľa STN EN ISO 10211 Návrh vzduchotesnosti pre detaily napojení Objednávateľ: Ing. Natália Voltmannová
ΕΠΑΝΑΛΗΠΤΙΚΟ ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2013
 ΕΠΝΛΗΠΤΙΚΟ ΙΓΩΝΙΣΜ ΦΥΣΙΚΗΣ ΚΤΕΥΘΥΝΣΗΣ 0 ΘΕΜ ο Να γράψετε στο φύλλο απαντήσεών σας τον αριµό καεµιάς από τις ακόλοες ηµιτελείς προτάσεις και δίπλα της το γράµµα πο αντιστοιχεί στο σωστό σµπλήρωµά της..
ΕΠΝΛΗΠΤΙΚΟ ΙΓΩΝΙΣΜ ΦΥΣΙΚΗΣ ΚΤΕΥΘΥΝΣΗΣ 0 ΘΕΜ ο Να γράψετε στο φύλλο απαντήσεών σας τον αριµό καεµιάς από τις ακόλοες ηµιτελείς προτάσεις και δίπλα της το γράµµα πο αντιστοιχεί στο σωστό σµπλήρωµά της..
1. Ένα σώμα m=1 kg εκτελεί γ.α.τ. και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο φαίνεται στο σχήμα.
 . Ένα σώμα m= kg εκτελεί γ.α.τ. και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο φαίνεται στο σχήμα. α. Να βρείτε τη σταθερά D και την ολική ενέργεια του ταλαντωτή. β. Να γράψετε τις εξισώσεις
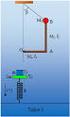
. Ένα σώμα m= kg εκτελεί γ.α.τ. και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο φαίνεται στο σχήμα. α. Να βρείτε τη σταθερά D και την ολική ενέργεια του ταλαντωτή. β. Να γράψετε τις εξισώσεις
1 ο ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 1 ο ΚΕΦΑΛΑΙΟ (ΤΑΛΑΝΤΩΣΕΙΣ)
 δυαδικό ΦΡΟΝΤΙΣΤΗΡΙΑ ο ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο ΚΕΦΑΛΑΙΟ (ΤΑΛΑΝΤΩΣΕΙΣ) ΔΙΑΡΚΕΙΑ: ώρες ΒΑΘΜΟΣ:.. ΗΜΕΡΟΜΗΝΙΑ: /0/009 ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ:
δυαδικό ΦΡΟΝΤΙΣΤΗΡΙΑ ο ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο ΚΕΦΑΛΑΙΟ (ΤΑΛΑΝΤΩΣΕΙΣ) ΔΙΑΡΚΕΙΑ: ώρες ΒΑΘΜΟΣ:.. ΗΜΕΡΟΜΗΝΙΑ: /0/009 ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ:
Matematika 2. časť: Analytická geometria
 Matematika 2 časť: Analytická geometria RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Súradnicové
Matematika 2 časť: Analytická geometria RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Súradnicové
Základy automatického riadenia
 Základy automatického riadenia Predná²ka 6 doc. Ing. Anna Jadlovská, PhD., doc. Ing. Ján Jadlovský, CSc. Katedra kybernetiky a umelej inteligencie Fakulta elektrotechniky a informatiky Technická univerzita
Základy automatického riadenia Predná²ka 6 doc. Ing. Anna Jadlovská, PhD., doc. Ing. Ján Jadlovský, CSc. Katedra kybernetiky a umelej inteligencie Fakulta elektrotechniky a informatiky Technická univerzita
ΠΑΤΡΩΝΥΜΟ / ΟΝΟΜΑ ΣΥΖΥΓΟΥ 1 ΑΓΟΡΑΣΤΟΥ ΜΑΡΙΑ ΤΟΥ ΔΗΜΗΤΡΙΟΥ 2 ΑΘΑΝΑΣΙΑΔΗΣ ΙΩΑΝΝΗΣ ΤΟΥ ΠΑΥΛΟΥ 3 ΑΚΤΣΟΓΛΟΥ ΣΩΚΡΑΤΗΣ ΤΟΥ ΓΕΩΡΓΙΟΥ
 Υποψήφιοι ημοτικοί Σύμβουλοι: ΠΑΤΡΩΝΥΜΟ / ΣΥΖΥΓΟΥ 1 ΑΓΟΡΑΣΤΟΥ ΜΑΡΙΑ ΤΟΥ ΔΗΜΗΤΡΙΟΥ 2 ΑΘΑΝΑΣΙΑΔΗΣ ΙΩΑΝΝΗΣ ΤΟΥ ΠΑΥΛΟΥ 3 ΑΚΤΣΟΓΛΟΥ ΣΩΚΡΑΤΗΣ ΤΟΥ ΓΕΩΡΓΙΟΥ 4 ΑΛΦΑΤΖΗΣ ΙΩΑΝΝΗΣ ΤΟΥ ΓΕΩΡΓΙΟΥ 5 ΑΜΟΡΓΙΑΝΟΣ ΝΙΚΟΛΑΟΣ
Υποψήφιοι ημοτικοί Σύμβουλοι: ΠΑΤΡΩΝΥΜΟ / ΣΥΖΥΓΟΥ 1 ΑΓΟΡΑΣΤΟΥ ΜΑΡΙΑ ΤΟΥ ΔΗΜΗΤΡΙΟΥ 2 ΑΘΑΝΑΣΙΑΔΗΣ ΙΩΑΝΝΗΣ ΤΟΥ ΠΑΥΛΟΥ 3 ΑΚΤΣΟΓΛΟΥ ΣΩΚΡΑΤΗΣ ΤΟΥ ΓΕΩΡΓΙΟΥ 4 ΑΛΦΑΤΖΗΣ ΙΩΑΝΝΗΣ ΤΟΥ ΓΕΩΡΓΙΟΥ 5 ΑΜΟΡΓΙΑΝΟΣ ΝΙΚΟΛΑΟΣ
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΘΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 04/11/12 ΛΥΣΕΙΣ
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 0-03 ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΘΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 04// ΛΥΣΕΙΣ ΘΕΜΑ A Στις ερωτησεις -4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 0-03 ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΘΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 04// ΛΥΣΕΙΣ ΘΕΜΑ A Στις ερωτησεις -4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα
Π Ι Ν Α Κ Α Σ ΔΟΚΙΜΩΝ ΠΥΡΟΣΒΕΣΤΩΝ ΓΕΝΙΚΩΝ ΚΑΘΗΚΟΝΤΩΝ ΠΟΥ ΠΛΗΡΟΥΝ ΤΑ ΠΡΟΣΟΝΤΑ ΚΑΙ ΤΙΣ ΠΡΟΥΠΟΘΕΣΕΙΣ ΓΙΑ ΠΡΟΣΛΗΨΗ Κατηγορία Α7 -Πληροφορικής Α.Τ.Ε.
 1 ΘΕΣΣΑΛΟΝΙΚΗ 697 ΑΗ323276 Α ΑΝΑΓΝΩΣΤΟΥ ΑΝΑΣΤ ΔΗΜΗΤ ΒΑΣΙΛ 30/9/1984 6 ( 61 / 100) Αρ. Ν Ν Ν 1.611 2 ΘΕΣΣΑΛΟΝΙΚΗ 24 ΑΚ435432 Α ΜΕΤΑΞΑΣ ΓΡΗΓΟ ΝΙΚΟΛ ΕΛΕΥΘ 7/6/1985 6 ( 64 / 100) Γ Ν Ν Ν Ν 1.564 3 ΖΑΚΥΝΘΟΣ
1 ΘΕΣΣΑΛΟΝΙΚΗ 697 ΑΗ323276 Α ΑΝΑΓΝΩΣΤΟΥ ΑΝΑΣΤ ΔΗΜΗΤ ΒΑΣΙΛ 30/9/1984 6 ( 61 / 100) Αρ. Ν Ν Ν 1.611 2 ΘΕΣΣΑΛΟΝΙΚΗ 24 ΑΚ435432 Α ΜΕΤΑΞΑΣ ΓΡΗΓΟ ΝΙΚΟΛ ΕΛΕΥΘ 7/6/1985 6 ( 64 / 100) Γ Ν Ν Ν Ν 1.564 3 ΖΑΚΥΝΘΟΣ
Ο13. Μεγεθυντικός φακός. 1. Σκοπός. 2. Θεωρία. θ 1
 13 Μεγεθυντικός φακός 1. Σκοπός ι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
13 Μεγεθυντικός φακός 1. Σκοπός ι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
έχουν απομάκρυνση ίση με το αλγεβρικό άθροισμα των απομακρύνσεων που θα είχαν αν οι δύο παλμοί
 ΕΠΑΛΛΗΛΙΑ (ή ΥΠΕΡΘΕΣΗ) ΚΥΜΑΤΩΝ Πριν τη συνάντηση Κατά τη συνάντηση Μετά τη συνάντηση Θεωρούμε ότι κατά μήκος ενός γραμμικού εαστικού μέσου διαδίδονται ταυτόχρονα δύο κυματικοί παμοί που βρίσκονται στο
ΕΠΑΛΛΗΛΙΑ (ή ΥΠΕΡΘΕΣΗ) ΚΥΜΑΤΩΝ Πριν τη συνάντηση Κατά τη συνάντηση Μετά τη συνάντηση Θεωρούμε ότι κατά μήκος ενός γραμμικού εαστικού μέσου διαδίδονται ταυτόχρονα δύο κυματικοί παμοί που βρίσκονται στο
ΣΧΕΔΙΑΣΜΟΣ ΥΔΡΑΥΛΙΚΩΝ ΑΝΕΛΚΥΣΤΗΡΩΝ Ε Γ ΧΕΙΡΙΔΙΟ Σ ΧΕΔΙΑΣΗΣ
 Ε Γ ΧΕΙΡΙΔΙΟ Σ ΧΕΔΙΑΣΗΣ ΑΝΕΛΚ Υ Σ Τ Η ΡΩΝ ΜΟΝΑΔΑ ΙΣΧΥΟΣ ΣΧΕΔΙΑΣΜΟΣ ΜΗΧΑΝΟΣΤΑΣΙΩΝ ΦΡΕΑΤΙΟ ΥΔΡΑΥΛΙΚΩΝ ΑΝΕΛΚΥΣΤΗΡΩΝ min. 700 Απευθύνεται σε μελετητές: ΑΡΧΙΤΕΚΤΟΝΕΣ ΠΟΛΙΤΙΚΟΥΣ ΜΗΧΑΝΙΚΟΥΣ ΜΗΧΑΝΟΛΟΓΟΥΣ ΜΗΧΑΝΙΚΟΥΣ
Ε Γ ΧΕΙΡΙΔΙΟ Σ ΧΕΔΙΑΣΗΣ ΑΝΕΛΚ Υ Σ Τ Η ΡΩΝ ΜΟΝΑΔΑ ΙΣΧΥΟΣ ΣΧΕΔΙΑΣΜΟΣ ΜΗΧΑΝΟΣΤΑΣΙΩΝ ΦΡΕΑΤΙΟ ΥΔΡΑΥΛΙΚΩΝ ΑΝΕΛΚΥΣΤΗΡΩΝ min. 700 Απευθύνεται σε μελετητές: ΑΡΧΙΤΕΚΤΟΝΕΣ ΠΟΛΙΤΙΚΟΥΣ ΜΗΧΑΝΙΚΟΥΣ ΜΗΧΑΝΟΛΟΓΟΥΣ ΜΗΧΑΝΙΚΟΥΣ
ΜΕΛΕΤΗ ΓΕΩΡΓΙΟΣ ΜΠΑΡΜΠΟΥΤΙ ΗΣ ΠΟΛΙΤΙΚΟΣ ΜΗΧΑΝΙΚΟΣ ΕΡΓΟ: ΚΑΤΑΣΚΕΥΗ ΠΡΟΣΤΑΤΕΥΤΙΚΟΥ ΤΟΙΧΙΟΥ ΝΕΚΡΟΤΑΦΕΙΩΝ ΤΚ ΚΟΡΜΙΣΤΑΣ ΠΡΟΫΠΟΛΟΓΙΣΜΟΣ: 4 0.
 ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΣΕΡΡΩΝ ΗΜΟΣ ΑΜΦΙΠΟΛΗΣ ΤΜΗΜΑ Τ.Υ. ΜΕΛΕΤΗ ΕΡΓΟ: ΚΑΤΑΣΚΕΥΗ ΠΡΟΣΤΑΤΕΥΤΙΚΟΥ ΤΟΙΧΙΟΥ ΝΕΚΡΟΤΑΦΕΙΩΝ ΤΚ ΚΟΡΜΙΣΤΑΣ ΠΡΟΫΠΟΛΟΓΙΣΜΟΣ: 4 0. 0 0 0, 0 0 ΣΑΤΑ 2011, 2013 & ΕΚΤΑΚΤΑ ΑΝΕΙ ΙΚΕΥΤΑ-ΛΟΙΠΑ
ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΣΕΡΡΩΝ ΗΜΟΣ ΑΜΦΙΠΟΛΗΣ ΤΜΗΜΑ Τ.Υ. ΜΕΛΕΤΗ ΕΡΓΟ: ΚΑΤΑΣΚΕΥΗ ΠΡΟΣΤΑΤΕΥΤΙΚΟΥ ΤΟΙΧΙΟΥ ΝΕΚΡΟΤΑΦΕΙΩΝ ΤΚ ΚΟΡΜΙΣΤΑΣ ΠΡΟΫΠΟΛΟΓΙΣΜΟΣ: 4 0. 0 0 0, 0 0 ΣΑΤΑ 2011, 2013 & ΕΚΤΑΚΤΑ ΑΝΕΙ ΙΚΕΥΤΑ-ΛΟΙΠΑ
ΕΞΕΤΑΣΕΙΣ ΣΤΗ ΓΕΝΙΚΗ ΧΗΜΕΙΑ
 ΕΞΕΤΑΣΕΙΣ ΣΤΗ ΓΕΝΙΚΗ ΧΗΜΕΙΑ (Επιλέγετε δέκα από τα δεκατρία θέματα) ΘΕΜΑΤΑ 1. Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λάθος; Γιατί; (α) Από τα στοιχεία Mg, Al, Cl, Xe, C και Ρ, τον μεγαλύτερο
ΕΞΕΤΑΣΕΙΣ ΣΤΗ ΓΕΝΙΚΗ ΧΗΜΕΙΑ (Επιλέγετε δέκα από τα δεκατρία θέματα) ΘΕΜΑΤΑ 1. Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λάθος; Γιατί; (α) Από τα στοιχεία Mg, Al, Cl, Xe, C και Ρ, τον μεγαλύτερο
OBSAH. Svahy Kršlenice nad Plaveckým Mikulášom wettersteinská fácia veterlínskeho príkrovu. Foto: M. Havrila
 OBSAH Príhovor riaditeľa Organizačná schéma Zloženie zamestnancov Organizačná jednotka námestníka riaditeľa pre ekonomiku Rozpočet organizácie Organizačná jednotka námestníka riaditeľa pre vedu a výskum
OBSAH Príhovor riaditeľa Organizačná schéma Zloženie zamestnancov Organizačná jednotka námestníka riaditeľa pre ekonomiku Rozpočet organizácie Organizačná jednotka námestníka riaditeľa pre vedu a výskum
Παράκτια Τεχνικά Έργα
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΔΙΑΘΕΣΗ ΥΓΡΩΝ ΣΤΗ ΘΑΛΑΣΣΑ ΥΠΟΒΡΥΧΙΟΙ ΑΓΩΓΟΙ Ενότητα 4 η : Υπολογισμοί διαχυτήρα & Υποβρυχίων αγωγών Γιάννης Ν. Κρεστενίτης Άδειες Χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΔΙΑΘΕΣΗ ΥΓΡΩΝ ΣΤΗ ΘΑΛΑΣΣΑ ΥΠΟΒΡΥΧΙΟΙ ΑΓΩΓΟΙ Ενότητα 4 η : Υπολογισμοί διαχυτήρα & Υποβρυχίων αγωγών Γιάννης Ν. Κρεστενίτης Άδειες Χρήσης
τα βιβλία των επιτυχιών
 Τα βιβλία των Εκδόσεων Πουκαμισάς συμπυκνώνουν την πολύχρονη διδακτική εμπειρία των συγγραφέων μας και αποτελούν το βασικό εκπαιδευτικό υλικό που χρησιμοποιούν οι μαθητές των φροντιστηρίων μας. Μέσα από
Τα βιβλία των Εκδόσεων Πουκαμισάς συμπυκνώνουν την πολύχρονη διδακτική εμπειρία των συγγραφέων μας και αποτελούν το βασικό εκπαιδευτικό υλικό που χρησιμοποιούν οι μαθητές των φροντιστηρίων μας. Μέσα από
Ι Ο Λ Ο Γ Ι Μ Ο - Α Π Ο Λ Ο Γ Ι Μ Ο Μ Η Ν Ο Γ Δ Κ Δ Μ Β Ρ Ι Ο Υ 2 0 1 5
 Μ Ρ : 0 9 / 0 1 / 2 0 1 6 Ρ. Ρ Ω. : 7 Λ Γ Μ - Λ Γ Μ Μ Η Γ Δ Κ Δ Μ Β Ρ Υ 2 0 1 5 Δ Γ Ρ Ϋ Λ Γ Θ Δ ΚΔ Μ Β Δ Β Ω Θ Δ Δ Ρ Υ Θ Δ 0111 Χ / Γ Δ Θ Μ Θ Δ Ρ Ω Κ - - - 0112 Χ / Γ Λ Ρ Γ Κ Δ 2 3. 2 1 3. 0 0 0, 0 0-2
Μ Ρ : 0 9 / 0 1 / 2 0 1 6 Ρ. Ρ Ω. : 7 Λ Γ Μ - Λ Γ Μ Μ Η Γ Δ Κ Δ Μ Β Ρ Υ 2 0 1 5 Δ Γ Ρ Ϋ Λ Γ Θ Δ ΚΔ Μ Β Δ Β Ω Θ Δ Δ Ρ Υ Θ Δ 0111 Χ / Γ Δ Θ Μ Θ Δ Ρ Ω Κ - - - 0112 Χ / Γ Λ Ρ Γ Κ Δ 2 3. 2 1 3. 0 0 0, 0 0-2
ΤΖΑΚΙΑ ΕΝΕΡΓΕΙΑΚΑ ΑΕΡΟΘΕΡΜΑ Φ 250 25,6 275 1,700 Φ 250 1,700 Φ 250 1,700 Φ 250 1,700 Φ 250 1,800 Φ 250 1,800 Υ: 1.75 B:0.59 Π: 0.
 ΚΑΜΙΝΑΔΑΣ Kw ΒΑΡΟΣ 1 B:0.59 150 25,6 275 1,700 2 3 4 5 ΣΤΡΟΓΓΥΛΟ Τ 90 B:0.73 B:0.76 Υ: 1.72 B:0.62 Π: 0.98 B:0.66 Π:1.06 150 150 24 20 20 20 288 295 305 1,700 1,700 1,700 1,800 ΤΖΑΚΙΑ ΕΝΕΡΓΕΙΑΚΑ ΑΕΡΟΘΕΡΜΑ
ΚΑΜΙΝΑΔΑΣ Kw ΒΑΡΟΣ 1 B:0.59 150 25,6 275 1,700 2 3 4 5 ΣΤΡΟΓΓΥΛΟ Τ 90 B:0.73 B:0.76 Υ: 1.72 B:0.62 Π: 0.98 B:0.66 Π:1.06 150 150 24 20 20 20 288 295 305 1,700 1,700 1,700 1,800 ΤΖΑΚΙΑ ΕΝΕΡΓΕΙΑΚΑ ΑΕΡΟΘΕΡΜΑ
Εισαγωγή Σε Βασικές Έννοιες Της Φυσικής
 Εισαγωγή Σε Βασικές Έννοιες Της Φυσικής Φυσικά Μεγέθη Φυσικά μεγέθη είναι έννοιες που μπορούν να μετρηθούν και χρησιμοποιούνται για την περιγραφή των φαινομένων. Διεθνές σύστημα μονάδων S. I Το διεθνές
Εισαγωγή Σε Βασικές Έννοιες Της Φυσικής Φυσικά Μεγέθη Φυσικά μεγέθη είναι έννοιες που μπορούν να μετρηθούν και χρησιμοποιούνται για την περιγραφή των φαινομένων. Διεθνές σύστημα μονάδων S. I Το διεθνές
 THΛ: THΛ: 270727 222594 919113 949422 #&"'"%$ #"%$!"#$ '"(#"')%$ Α. Για τις παρακάτω προτάσεις 1-4 να γράψετε το γράµµα α, β, γ ή δ, που αντιστοιχεί στην σωστή απάντηση 1. Η υπέρυθρη ακτινοβολία α. είναι
THΛ: THΛ: 270727 222594 919113 949422 #&"'"%$ #"%$!"#$ '"(#"')%$ Α. Για τις παρακάτω προτάσεις 1-4 να γράψετε το γράµµα α, β, γ ή δ, που αντιστοιχεί στην σωστή απάντηση 1. Η υπέρυθρη ακτινοβολία α. είναι
Κεφάλαιο 5 Όριο και συνέχεια συνάρτησης
 Κεφάλαιο 5 Όριο και συνέχεια συνάρτησης 5 Όριο συνάρτησης για єr Θεωρούµε την αραβολή = Θέλουµε να ροσδιορίσουµε την κλίση της εφατοµένης της στο σηµείο (, ) ηλαδή, θέλουµε να βρούµε την εφατοµένη της
Κεφάλαιο 5 Όριο και συνέχεια συνάρτησης 5 Όριο συνάρτησης για єr Θεωρούµε την αραβολή = Θέλουµε να ροσδιορίσουµε την κλίση της εφατοµένης της στο σηµείο (, ) ηλαδή, θέλουµε να βρούµε την εφατοµένη της
Σ Υ Ν Ο Λ Ι Κ Ο Σ Π Ρ Ο Ϋ Π Ο Λ Ο Γ Ι Σ Μ Ο Σ Μ Ε Λ Ε Τ Η Σ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΚΑΒΑΛΑΣ ΔΗΜΟΣ Δ/ΝΣΗ ΤΕΧΝ. ΥΠΗΡΕΣΙΩΝ ΤΜΗΜΑ ΤΕΧΝ. ΥΠΗΡΕΣΙΩΝ ΑΡ. ΜΕΛΕΤΗΣ : 1059/2013 ΕΡΓΟ : ΠΡΟΜΗΘΕΙΑ ΕΙΔΩΝ ΠΑΝΤΟΠΩΛΕΙΟΥ ΔΗΜΟΥ Σ Υ Ν Ο Λ Ι Κ Ο Σ Π Ρ Ο Ϋ Π Ο Λ Ο Γ Ι Σ Μ Ο Σ Μ Ε Λ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΚΑΒΑΛΑΣ ΔΗΜΟΣ Δ/ΝΣΗ ΤΕΧΝ. ΥΠΗΡΕΣΙΩΝ ΤΜΗΜΑ ΤΕΧΝ. ΥΠΗΡΕΣΙΩΝ ΑΡ. ΜΕΛΕΤΗΣ : 1059/2013 ΕΡΓΟ : ΠΡΟΜΗΘΕΙΑ ΕΙΔΩΝ ΠΑΝΤΟΠΩΛΕΙΟΥ ΔΗΜΟΥ Σ Υ Ν Ο Λ Ι Κ Ο Σ Π Ρ Ο Ϋ Π Ο Λ Ο Γ Ι Σ Μ Ο Σ Μ Ε Λ
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy
 Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2012/2013 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2012/2013 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Μονοχρωµατική
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Μονοχρωµατική
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β' ΛΥΚΕΙΟΥ
 05 12 10 ΕΙΡΑ Α ΔΙΑΓΩΝΙΜΑ ΤΗ ΦΥΙΚΗ ΓΕΝΙΚΗ ΠΑΙΔΕΙΑ Β' ΛΥΚΕΙΟΥ ΘΕΜΑ 1 ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
05 12 10 ΕΙΡΑ Α ΔΙΑΓΩΝΙΜΑ ΤΗ ΦΥΙΚΗ ΓΕΝΙΚΗ ΠΑΙΔΕΙΑ Β' ΛΥΚΕΙΟΥ ΘΕΜΑ 1 ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
Η γεωργία στην ΕΕ απαντώντας στην πρόκληση των κλιματικών αλλαγών
 Ευρωπαϊκή Επιτροπή Γε ν ι κ ή Δ ι ε ύ θ υ ν σ η Γε ω ρ γ ί α ς κ α ι Αγ ρ ο τ ι κ ή ς Α ν ά π τ υ ξ η ς Ευρωπαϊκή Επιτροπή Γεωργία και αγροτική ανάπτυξη Για περισσότερες πληροφορίες 200 Rue de la Loi,
Ευρωπαϊκή Επιτροπή Γε ν ι κ ή Δ ι ε ύ θ υ ν σ η Γε ω ρ γ ί α ς κ α ι Αγ ρ ο τ ι κ ή ς Α ν ά π τ υ ξ η ς Ευρωπαϊκή Επιτροπή Γεωργία και αγροτική ανάπτυξη Για περισσότερες πληροφορίες 200 Rue de la Loi,
Μεζνδνινγία επίιπζεο αζθήζεωλ
 Μεζνδνινγία επίιπζεο αζθήζεωλ ακείσησλ κεραληθώλ ηαιαληώζεωλ Α. H ηππηθή άζθεζε Μηα ηππηθή άζθεζε κεραληθώλ ηαιαληώζεσλ (ρσξίο θόιπα), μεθηλάεη κε δεδνκέλo όηη ην είδνο ηεο θίλεζεο είλαη ΓΑΣ θαη κία από
Μεζνδνινγία επίιπζεο αζθήζεωλ ακείσησλ κεραληθώλ ηαιαληώζεωλ Α. H ηππηθή άζθεζε Μηα ηππηθή άζθεζε κεραληθώλ ηαιαληώζεσλ (ρσξίο θόιπα), μεθηλάεη κε δεδνκέλo όηη ην είδνο ηεο θίλεζεο είλαη ΓΑΣ θαη κία από
ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α. Α.1 γ, Α.2 β, Α.3 γ, Α.4 γ. Α.5 Σωστό Σωστό Λάθος Λάθος Σωστό ΘΕΜΑ Β. Β.1 γ. Αιτιολόγηση
 ΠΑΝΕΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΥΚΕΙΟΥ ΚΑΙ ΕΠΑ (ΟΜΑ Α Β ) ΠΑΡΑΣΚΕΥΗ 5 ΜΑÏΟΥ 0 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΩΝ) ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α. γ, Α.
ΠΑΝΕΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΥΚΕΙΟΥ ΚΑΙ ΕΠΑ (ΟΜΑ Α Β ) ΠΑΡΑΣΚΕΥΗ 5 ΜΑÏΟΥ 0 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΩΝ) ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α. γ, Α.
3-2 ΥΓΡΑ ΣΕ ΙΣΟΡΡΟΠΙΑ
 EΞΩΦΥΛΛΟ 89 3- ΕΙΣΑΓΩΓΗ Οι φυσικοί και οι μηχανικοί αποδίδουν το χαρακτηρισμό «ρευστά» στα υγρά και τα αέρια σώματα, τα οποία - αντίθετα με τα στερεά - δεν έχουν δικό τους σχήμα αλλά παίρνουν το σχήμα
EΞΩΦΥΛΛΟ 89 3- ΕΙΣΑΓΩΓΗ Οι φυσικοί και οι μηχανικοί αποδίδουν το χαρακτηρισμό «ρευστά» στα υγρά και τα αέρια σώματα, τα οποία - αντίθετα με τα στερεά - δεν έχουν δικό τους σχήμα αλλά παίρνουν το σχήμα
 Μέτρηση Έργου Εργόμετρα Κοσμάς Χριστούλας Αν. Καθηγητής Τ.Ε.Φ.Α.Α.-Α.Π.Θ. Α.Π.Θ. Η ενέργεια εμφανίζεται με διάφορες μορφές, όπως χ η μ ι κ ή θ ε ρ μ ι κ ή μ η χ α ν ι κ ή η λ ε κ τ ρ ι κ ή η λ ε κ τ ρ
Μέτρηση Έργου Εργόμετρα Κοσμάς Χριστούλας Αν. Καθηγητής Τ.Ε.Φ.Α.Α.-Α.Π.Θ. Α.Π.Θ. Η ενέργεια εμφανίζεται με διάφορες μορφές, όπως χ η μ ι κ ή θ ε ρ μ ι κ ή μ η χ α ν ι κ ή η λ ε κ τ ρ ι κ ή η λ ε κ τ ρ
Αθήνα, 8/1/2014 Αρ. Πρωτ. Φ2-74 ΓΕΝ. ΓΡΑΜΜΑΤΕΙΑ ΕΜΠΟΡΙΟΥ. ΤΜΗΜΑ Δ' Ταχ. Δ/νση: Πλ. Κάνιγγος ΠΡΟΣ : 1. Γεν. Δ/νσεις Ανάπτυξης Ταχ. Κώδ.
 Αθήνα, 8/1/2014 Αρ. Πρωτ. Φ2-74 ΓΕΝ. ΓΡΑΜΜΑΤΕΙΑ ΕΜΠΟΡΙΟΥ Δ/ΝΣΗ ΜΕΤΡΟΛΟΓΙΑΣ ΑΝΑΡΤΗΤΕΑ ΤΜΗΜΑ Δ' Ταχ. Δ/νση: Πλ. Κάνιγγος ΠΡΟΣ : 1. Γεν. Δ/νσεις Ανάπτυξης Ταχ. Κώδ.: 101 81 Αθήνα των Περιφερειών της Πληροφ.:
Αθήνα, 8/1/2014 Αρ. Πρωτ. Φ2-74 ΓΕΝ. ΓΡΑΜΜΑΤΕΙΑ ΕΜΠΟΡΙΟΥ Δ/ΝΣΗ ΜΕΤΡΟΛΟΓΙΑΣ ΑΝΑΡΤΗΤΕΑ ΤΜΗΜΑ Δ' Ταχ. Δ/νση: Πλ. Κάνιγγος ΠΡΟΣ : 1. Γεν. Δ/νσεις Ανάπτυξης Ταχ. Κώδ.: 101 81 Αθήνα των Περιφερειών της Πληροφ.:
ΘΕΩΡΙΑ ΤΩΝ ΗΜΙΑΓΩΓΩΝ ΔΕΥΤΕΡΗ ΕΝΟΤΗΤΑ ΟΜΟΓΕΝΕΙΣ ΗΜΙΑΓΩΓΟΙ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ
 ΘΕΩΡΙΑ ΤΩΝ ΗΜΙΑΓΩΓΩΝ ΔΕΥΤΕΡΗ ΕΝΟΤΗΤΑ ΟΜΟΓΕΝΕΙΣ ΗΜΙΑΓΩΓΟΙ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ 1. Μηχανισμοί σκέδασης των φορέων (ηλεκτρόνια οπές) 2. Ηλεκτρική Αγωγιμότητα 3. Ολίσθηση φορέων (ρεύμα ολίσθησης) 4. Διάχυση
ΘΕΩΡΙΑ ΤΩΝ ΗΜΙΑΓΩΓΩΝ ΔΕΥΤΕΡΗ ΕΝΟΤΗΤΑ ΟΜΟΓΕΝΕΙΣ ΗΜΙΑΓΩΓΟΙ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ 1. Μηχανισμοί σκέδασης των φορέων (ηλεκτρόνια οπές) 2. Ηλεκτρική Αγωγιμότητα 3. Ολίσθηση φορέων (ρεύμα ολίσθησης) 4. Διάχυση
Θ Ε Μ Ε Λ Ι Ω Σ Ε Ι Σ ΚΕΦΑΛΑΙΟ 3
 Τεχνογικό Εκπαιδευτικό Ίδρυµα Σερρών Σχή Τεχνογικών Εφαρµογών Τµήµα Πιτικών οµικών Έργων Θ Ε Μ Ε Λ Ι Ω Σ Ε Ι Σ ΚΕΦΑΛΑΙΟ 3 Επιφανειακές θεµελιώσεις ιδάσκων: Κίρτας Εµµανουήλ Σέρρες, Σεπτέµβριος 010 1 Μάθηµα:
Τεχνογικό Εκπαιδευτικό Ίδρυµα Σερρών Σχή Τεχνογικών Εφαρµογών Τµήµα Πιτικών οµικών Έργων Θ Ε Μ Ε Λ Ι Ω Σ Ε Ι Σ ΚΕΦΑΛΑΙΟ 3 Επιφανειακές θεµελιώσεις ιδάσκων: Κίρτας Εµµανουήλ Σέρρες, Σεπτέµβριος 010 1 Μάθηµα:
ARMA modely čast 2: moving average modely (MA)
 ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2014/2015 ARMA modely časť 2: moving average modely(ma) p.1/24 V. Moving average proces prvého rádu - MA(1) ARMA modely
ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2014/2015 ARMA modely časť 2: moving average modely(ma) p.1/24 V. Moving average proces prvého rádu - MA(1) ARMA modely
EI A ø H TA AEI A O IEK, KO E IA
 Δ 37Ô Ú. Ê ÏÏÔ 10.821 Àƒø 1,30 EYTEPA 22 AY OY TOY 2011 www.enet.gr OI ΔANEIOΛHΠTEΣ TΩN TPAΠEZΩN TΩPA ΔIKAIΩNONTAI Tα δικαστήρια διαγράφουν χρέη νοικοκυριών Δ ƒπ Ó Â ÈÎ ÛÙÈÎ appleôê ÛÂÈ applefi ÈÚËÓÔ ÈÎÂ,
Δ 37Ô Ú. Ê ÏÏÔ 10.821 Àƒø 1,30 EYTEPA 22 AY OY TOY 2011 www.enet.gr OI ΔANEIOΛHΠTEΣ TΩN TPAΠEZΩN TΩPA ΔIKAIΩNONTAI Tα δικαστήρια διαγράφουν χρέη νοικοκυριών Δ ƒπ Ó Â ÈÎ ÛÙÈÎ appleôê ÛÂÈ applefi ÈÚËÓÔ ÈÎÂ,
Odporníky. 1. Príklad1. TESLA TR
 Odporníky Úloha cvičenia: 1.Zistite technické údaje odporníkov pomocou katalógov 2.Zistite menovitú hodnotu odporníkov označených farebným kódom Schématická značka: 1. Príklad1. TESLA TR 163 200 ±1% L
Odporníky Úloha cvičenia: 1.Zistite technické údaje odporníkov pomocou katalógov 2.Zistite menovitú hodnotu odporníkov označených farebným kódom Schématická značka: 1. Príklad1. TESLA TR 163 200 ±1% L
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ» ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 3 o ΔΙΑΓΩΝΙΣΜΑ ΜΑΡΤΙΟΣ 01: ΘΕΜΑΤΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το
3 o ΔΙΑΓΩΝΙΣΜΑ ΜΑΡΤΙΟΣ 01: ΘΕΜΑΤΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το
Príručka pre dimenzovanie drevených tenkostenných nosníkov PALIS. (Stena z OSB/3 Kronoply)
 Palis s.r.o. Kokořov 24, 330 11 Třemošná, Česká republika e- mail: palis@palis.cz Príručka pre dimenzovanie drevených tenkostenných nosníkov PALIS. (Stena z OSB/3 Kronoply) Vypracoval: Ing. Roman Soyka
Palis s.r.o. Kokořov 24, 330 11 Třemošná, Česká republika e- mail: palis@palis.cz Príručka pre dimenzovanie drevených tenkostenných nosníkov PALIS. (Stena z OSB/3 Kronoply) Vypracoval: Ing. Roman Soyka
EL HR. Upute za kori ρtenje CDSM 3416 X PERILICA POSUDJA
 EL HR Β Ε Α Γ Τ Ο Π Γ Φ Upute za kori ρtenje CDSM 3416 X ² «± ± Ά «PERILICA POSUDJA Α Τ Ώ Ο Ε Ρ Ο Η Ώ K Λ Ώ Ρ Γ Κ Η Ώ Γ Ξ Η Ι Ν Α Τ Φ Ο Π Κ ΐ Η ΐ Ώ Π Κ Ν. Ξ Η Ι Μ Ώ Ρ Γ, Ρ Η Θ Ώ Ι Ρ Γ Ο Ν, Γ Ξ Η Ι Μ Ώ
EL HR Β Ε Α Γ Τ Ο Π Γ Φ Upute za kori ρtenje CDSM 3416 X ² «± ± Ά «PERILICA POSUDJA Α Τ Ώ Ο Ε Ρ Ο Η Ώ K Λ Ώ Ρ Γ Κ Η Ώ Γ Ξ Η Ι Ν Α Τ Φ Ο Π Κ ΐ Η ΐ Ώ Π Κ Ν. Ξ Η Ι Μ Ώ Ρ Γ, Ρ Η Θ Ώ Ι Ρ Γ Ο Ν, Γ Ξ Η Ι Μ Ώ
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 o ΔΙΑΓΩΝΙΣΜΑ ΔΕΚΕΜΒΡΙΟΣ 0: ΘΕΜΑΤΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις - 4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα
o ΔΙΑΓΩΝΙΣΜΑ ΔΕΚΕΜΒΡΙΟΣ 0: ΘΕΜΑΤΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις - 4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα
HASLIM112V, HASLIM123V, HASLIM136V HASLIM112Z, HASLIM123Z, HASLIM136Z HASLIM112S, HASLIM123S, HASLIM136S
 PROUKTOVÝ LIST HKL SLIM č. sklad. karty / obj. číslo: HSLIM112V, HSLIM123V, HSLIM136V HSLIM112Z, HSLIM123Z, HSLIM136Z HSLIM112S, HSLIM123S, HSLIM136S fakturačný názov výrobku: HKL SLIMv 1,2kW HKL SLIMv
PROUKTOVÝ LIST HKL SLIM č. sklad. karty / obj. číslo: HSLIM112V, HSLIM123V, HSLIM136V HSLIM112Z, HSLIM123Z, HSLIM136Z HSLIM112S, HSLIM123S, HSLIM136S fakturačný názov výrobku: HKL SLIMv 1,2kW HKL SLIMv
p (kn/m 2 ) 5 A 4 3 B 2 Γ 1 V (m 3 )
 Β.1 Στο πιο κάτω διάγραμμα παριστάνονται τρεις περιπτώσεις Α, Β και Γ αντιστρεπτών μεταβολών τις οποίες μπορεί να υποστεί ποσότητα ιδανικού αερίου. p (kn/m ) 5 A 4 3 B Γ 1 0 0 4 6 8 10 1 V (m 3 ) A) Σε
Β.1 Στο πιο κάτω διάγραμμα παριστάνονται τρεις περιπτώσεις Α, Β και Γ αντιστρεπτών μεταβολών τις οποίες μπορεί να υποστεί ποσότητα ιδανικού αερίου. p (kn/m ) 5 A 4 3 B Γ 1 0 0 4 6 8 10 1 V (m 3 ) A) Σε
ΥΠΟΥΡΓΕΙΟ ΠΑΙ ΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2015 ΟΔΗΓΟΣ ΔΙΟΡΘΩΣΗΣ
 ΥΠΟΥΡΓΕΙΟ ΠΑΙ ΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2015 ΟΔΗΓΟΣ ΔΙΟΡΘΩΣΗΣ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΔΙΑΡΚΕΙΑ ΕΞΕΤΑΣΗΣ : 3 ΩΡΕΣ ΗΜΕΡΟΜΗΝΙΑ: 22 ΜΑΪΟΥ
ΥΠΟΥΡΓΕΙΟ ΠΑΙ ΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2015 ΟΔΗΓΟΣ ΔΙΟΡΘΩΣΗΣ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΔΙΑΡΚΕΙΑ ΕΞΕΤΑΣΗΣ : 3 ΩΡΕΣ ΗΜΕΡΟΜΗΝΙΑ: 22 ΜΑΪΟΥ
Αντισεισμικός Σχεδιασμός Τοίχων Αντιστήριξης & Κρηπιδοτοίχων
 Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΤΕΧΝΙΚΗΣ Αντισεισμικός Σχεδιασμός Τοίχων Αντιστήριξης & Κρηπιδοτοίχων Γ. Δ. Μπουκοβάλας Καθηγητής Ε.Μ.Π. Ημερίδα Συλλόγου Πολιτικών Μηχανικών Ελλάδος
Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΤΕΧΝΙΚΗΣ Αντισεισμικός Σχεδιασμός Τοίχων Αντιστήριξης & Κρηπιδοτοίχων Γ. Δ. Μπουκοβάλας Καθηγητής Ε.Μ.Π. Ημερίδα Συλλόγου Πολιτικών Μηχανικών Ελλάδος
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2012. 7:30-10:30 π.μ.
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2012 Μάθημα: ΦΥΣΙΚΗ Ημερομηνία και ώρα εξέτασης: Τετάρτη, 6 Ιουνίου 2012 7:30-10:30
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2012 Μάθημα: ΦΥΣΙΚΗ Ημερομηνία και ώρα εξέτασης: Τετάρτη, 6 Ιουνίου 2012 7:30-10:30
σημείων της επιφάνειας ενός μουσικού δίσκου που παίζει στο πικ-απ, είναι παραδείγματα κυκλικών
 ΟΜΑΛΗ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ Η κίνηση το ατοκινήτο γύρω από μια κκλική πλατεία, της μπίλιας στη ρολέτα πο περιστρέφεται, των σημείων της επιφάνειας ενός μοσικού δίσκο πο παίζει στο πικ-απ, είναι παραδείγματα κκλικών
ΟΜΑΛΗ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ Η κίνηση το ατοκινήτο γύρω από μια κκλική πλατεία, της μπίλιας στη ρολέτα πο περιστρέφεται, των σημείων της επιφάνειας ενός μοσικού δίσκο πο παίζει στο πικ-απ, είναι παραδείγματα κκλικών
ΑΝΤΙΣΕΙΣΜΙΚΗ ΤΕΧΝΟΛΟΓΙΑ
 ΑΝΤΙΣΕΙΣΜΙΚΗ ΤΕΧΝΟΛΟΓΙΑ Eικ_3 Διερεύνηση της σεισμικής συμπεριφοράς αρχαίων κιόνων με επιστήλια, τα οποία συνδέονται με μεταλλικούς συνδέσμους, 2007. Xρηματοδότης Ε.Ε. Eικ_4 Σεισμική συμπεριφορά φέρουσας
ΑΝΤΙΣΕΙΣΜΙΚΗ ΤΕΧΝΟΛΟΓΙΑ Eικ_3 Διερεύνηση της σεισμικής συμπεριφοράς αρχαίων κιόνων με επιστήλια, τα οποία συνδέονται με μεταλλικούς συνδέσμους, 2007. Xρηματοδότης Ε.Ε. Eικ_4 Σεισμική συμπεριφορά φέρουσας
STATIKA STAVEBNÝCH KONŠTRUKCIÍ I Doc. Ing. Daniela Kuchárová, PhD. Priebeh vnútorných síl na prostom nosníku a na konzole od jednotlivých typov
 Priebeh vnútorných síl na prostom nosníku a na konzole od jednotlivých typov zaťaženia Prostý nosník Konzola 31 Príklad č.14.1 Vypočítajte a vykreslite priebehy vnútorných síl na nosníku s previslými koncami,
Priebeh vnútorných síl na prostom nosníku a na konzole od jednotlivých typov zaťaženia Prostý nosník Konzola 31 Príklad č.14.1 Vypočítajte a vykreslite priebehy vnútorných síl na nosníku s previslými koncami,
ΠΕΡΙΓΡΑΦΙΚΟ ΤΙΜΟΛΟΓΙΟ ΗΛΕΚΤΡΟΜΗΧΑΝΟΛΟΓΙΚΩΝ ΕΡΓΑΣΙΩΝ NET ΗΛΜ - ΕΚΔΟΣΗ 1.0 60 ΟΜΑΔΑ Α: Η/Μ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΕΡΓΩΝ ΟΔΟΠΟΙΙΑΣ
 0-ΓΕΝΙΚΟΙ_ΟΡΟΙ ΠΕΡΙΓΡΑΦΙΚΟ ΤΙΜΟΛΟΓΙΟ ΗΛΕΚΤΡΟΜΗΧΑΝΟΛΟΓΙΚΩΝ ΕΡΓΑΣΙΩΝ NET ΗΛΜ - ΕΚΔΟΣΗ 1.0 60 ΟΜΑΔΑ Α: ΗΜ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΕΡΓΩΝ ΟΔΟΠΟΙΙΑΣ 60.10 ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΦΩΤΙΣΜΟΥ ΟΔΩΝ 60.10.01 Χλύβδινοι ιστοί οδοφωτισμού
0-ΓΕΝΙΚΟΙ_ΟΡΟΙ ΠΕΡΙΓΡΑΦΙΚΟ ΤΙΜΟΛΟΓΙΟ ΗΛΕΚΤΡΟΜΗΧΑΝΟΛΟΓΙΚΩΝ ΕΡΓΑΣΙΩΝ NET ΗΛΜ - ΕΚΔΟΣΗ 1.0 60 ΟΜΑΔΑ Α: ΗΜ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΕΡΓΩΝ ΟΔΟΠΟΙΙΑΣ 60.10 ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΦΩΤΙΣΜΟΥ ΟΔΩΝ 60.10.01 Χλύβδινοι ιστοί οδοφωτισμού
Δ Ι Η Μ Ε Ρ Ι Δ Α Μ Ε Α Φ Ο Ρ Μ Η Τ Η Ν Ε Ο Ρ Τ Η Τ Ω Ν Τ Ρ Ι Ω Ν Ι Ε Ρ Α Ρ Χ Ω Ν
 ΙΕΡΑ ΑΡΧΙΕΠΙΣΚΟΠΗ ΑΘΗΝΩΝ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΙΝΣΤΙΤΟΥΤΟ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ ΙΔΡΥΜΑ ΝΕΟΤΗΤΑΣ ΚΑΙ ΟΙΚΟΓΕΝΕΙΑΣ Δ Ι Η Μ Ε Ρ Ι Δ Α Μ Ε Α Φ Ο Ρ Μ Η Τ Η Ν Ε Ο Ρ Τ Η Τ Ω Ν Τ Ρ Ι Ω
ΙΕΡΑ ΑΡΧΙΕΠΙΣΚΟΠΗ ΑΘΗΝΩΝ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΙΝΣΤΙΤΟΥΤΟ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ ΙΔΡΥΜΑ ΝΕΟΤΗΤΑΣ ΚΑΙ ΟΙΚΟΓΕΝΕΙΑΣ Δ Ι Η Μ Ε Ρ Ι Δ Α Μ Ε Α Φ Ο Ρ Μ Η Τ Η Ν Ε Ο Ρ Τ Η Τ Ω Ν Τ Ρ Ι Ω
ΠΡΟΛΟΓΟΣ. Κλείνει με τις λύσεις όλων των θεμάτων του Μαίου
 ΠΡΟΛΟΓΟΣ Το παρόν τεύχος δημιουργήθηκε για να διευκολύνει τους μαθητές στην ΆΜΕΣΗ κατανόηση των απαιτήσεων των πανελληνίων εξετάσεων δίνοντας τους τα θέματα των 4 χρόνων των κανονικών εξετάσεων του Μαίου
ΠΡΟΛΟΓΟΣ Το παρόν τεύχος δημιουργήθηκε για να διευκολύνει τους μαθητές στην ΆΜΕΣΗ κατανόηση των απαιτήσεων των πανελληνίων εξετάσεων δίνοντας τους τα θέματα των 4 χρόνων των κανονικών εξετάσεων του Μαίου
Goniometrické rovnice a nerovnice. Základné goniometrické rovnice
 Goniometrické rovnice a nerovnice Definícia: Rovnice (nerovnice) obsahujúce neznámu x alebo výrazy s neznámou x ako argumenty jednej alebo niekoľkých goniometrických funkcií nazývame goniometrickými rovnicami
Goniometrické rovnice a nerovnice Definícia: Rovnice (nerovnice) obsahujúce neznámu x alebo výrazy s neznámou x ako argumenty jednej alebo niekoľkých goniometrických funkcií nazývame goniometrickými rovnicami
1.2. Ένα ιδανικό αέριο βρίσκεται στην κατάσταση Α. Το αέριο µπορεί να µεταβεί στην κατάσταση Β µε µια από τις µεταβολές (1), (2) που παριστάνονται στο
 ΡΧΗ 1ΗΣ ΣΕΛΙ Σ ΠΡΟΩΙΚΕΣ ΕΞΕΤΣΕΙΣ ΤΞΗΣ ΕΣΠΕΡΙΝΟΥ ΕΝΙΙΟΥ ΛΥΚΕΙΟΥ ΠΡΣΚΕΥΗ 8 ΜΪΟΥ 004 ΕΞΕΤΖΟΜΕΝΟ ΜΘΗΜ ΘΕΤΙΚΗΣ ΚΙ ΤΕΧΝΟΛΟΙΚΗΣ ΚΤΕΥΘΥΝΣΗΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤ (7) ΘΕΜ 1ο ια κάθε µια από τις προτάσεις
ΡΧΗ 1ΗΣ ΣΕΛΙ Σ ΠΡΟΩΙΚΕΣ ΕΞΕΤΣΕΙΣ ΤΞΗΣ ΕΣΠΕΡΙΝΟΥ ΕΝΙΙΟΥ ΛΥΚΕΙΟΥ ΠΡΣΚΕΥΗ 8 ΜΪΟΥ 004 ΕΞΕΤΖΟΜΕΝΟ ΜΘΗΜ ΘΕΤΙΚΗΣ ΚΙ ΤΕΧΝΟΛΟΙΚΗΣ ΚΤΕΥΘΥΝΣΗΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤ (7) ΘΕΜ 1ο ια κάθε µια από τις προτάσεις
Základné poznatky molekulovej fyziky a termodynamiky
 Základné poznatky molekulovej fyziky a termodynamiky Opakovanie učiva II. ročníka, Téma 1. A. Príprava na maturity z fyziky, 2008 Outline Molekulová fyzika 1 Molekulová fyzika Predmet Molekulovej fyziky
Základné poznatky molekulovej fyziky a termodynamiky Opakovanie učiva II. ročníka, Téma 1. A. Príprava na maturity z fyziky, 2008 Outline Molekulová fyzika 1 Molekulová fyzika Predmet Molekulovej fyziky
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε. 2003
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε. ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο Θέµα Α. α) Έστω η συνάρτηση στο κάθε f δ) R τις τιµές του γ) Αν η συνάρτηση παραγωγίσιµη σε αυτό. Τότε ισχύει
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε. ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο Θέµα Α. α) Έστω η συνάρτηση στο κάθε f δ) R τις τιµές του γ) Αν η συνάρτηση παραγωγίσιµη σε αυτό. Τότε ισχύει
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΕΠΑΝΑΛΗΠΤΙΚΕΣ 009 ΘΕΜΑΤΑ ΘΕΜΑ 1ο ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 11 ΙΟΥΛΙΟΥ 009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΕΠΑΝΑΛΗΠΤΙΚΕΣ 009 ΘΕΜΑΤΑ ΘΕΜΑ 1ο ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 11 ΙΟΥΛΙΟΥ 009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ
