Μάθημα: Ρομποτικός Έλεγχος
|
|
|
- Σκύλλα Αλεβιζόπουλος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Διατμηματικό Πόγαμμα Μεταπτυχιακών Σπουδών «ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ» Ε.Μ.Π., Ακαδημαϊκό Έτος 0 Μάθημα: Ρομποτικός Έλεγχος Αυτόματος Έλεγχος Ρομπότ Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου & Ρομποτικής Σχολή Ηλεκτ. Μηχ/κών & Μηχ/κών Υπολ., Ε.Μ.Π. Τηλ.: (0) (Κτήιο Ηλεκτ., Γαφείο.) Eail: kzaf@c.nua.gr We: hp:// Σχεδιασμός Τοχιάς Ρομποτικών Χειιστών
2 Ιεαχική Δομή Ρομποτικών Συστημάτων Ελέγχου θέσεις στόχου Πόγαμμα Εγασίας c Ευφυής Ελεγκτής μεταβολή θέσεων στόχου Σχεδιασμός Τοχιάς Πειοισμοί p(), i p () i σήματα αναφοάς Αλγόιθμος αντίστοφης κινηματικής q(), i q () i r r Βόχοι Ελέγχου a q(), i q () i Στοιχεία Δάσης Μονάδα Παεμβολής Αισθητήια Στοιχεία 3 Σχεδιασμός Τοχιάς: Βασικές Έννοιες () Δόμος (pah): Καμπύλη που διαγάφει το ομπότ στο χώο, η οποία ώνει δύο (ή πεισσότεες) διάμεσες θέσεις (σημεία διέλευσης) Τοχιά (rajecory): Χονική ακολουθία διάμεσων θέσεων (στο Κατεσιανό χώο) ή διατάξεων (στο χώο των αθώσεων) Τοχιά: ιστοικό θέσεων ή διατάξεων (ήτοι, χονική συνάτηση) Ο αλγόιθμος σχεδιασμού τοχιάς κατασκευάζει συνατήσεις του χόνου για την εξέλιξη των μεταβλητών θέσης (ή διάταξης) του ομπότ, οδηγώντας σε μια συνεχή (ομαλή) καμπύλη μεταξύ των ακαίων σημείων (αχή στόχος), παεμβάλλοντας ουσιαστικά διάμεσες θέσεις (αλγόιθμοι παεμβολής) Οι θέσεις αυτές στέλνονται στον αλγόιθμο αντίστοφης κινηματικής, ο οποίος (σε κάθε δειγματοληπτικό διάστημα Τ ec) δίνει τις τολές κίνησης στουςτοπικούςβόχουςελέγχουτωναθώσεων Εντολή θέσης p(i), Εντολή ταχύτητας p () i τολές κίνησης αθώσεων. Τα p(i) και p () i ικανοποιούν πειοισμούς χωικής ταχύτητας και επιτάχυνσης 4
3 Σχεδιασμός Τοχιάς: Βασικές Έννοιες () Χωικοί Πειοισμοί της Τοχιάς (paial conrain): Εκτέλεση Εγασίας στο Χώο του Τελικού Εγαλείου Δάσης Αποφυγή Εμποδίων, Αποφυγή Ιδιόμοφων Διατάξεων κλπ. Χονικές Ιδιότητες της Τοχιάς (eporal ariue): Χονική Διάκεια απαιτούμη για την εκτέλεση της εγασίας (χονικές στιγμές διέλευσης από διάμεσα σημεία via poin) Πειοισμοί Ταχύτητας και Επιτάχυνσης στις αθώσεις Τοχιά: Χονική Συνάτηση Συνεχής και «Ομαλή» Επιθυμητή Χονική Συνέχεια ως πος την Ταχύτητα και ίσως και ως πος την Επιτάχυνση (για καλύτεο, συνεχεία, έλεγχο του ομποτικού συστήματος) Σχεδιασμός Τοχιάς: (α) στο Χώο Εγασίας, ή (β) στο Χώο Αθώσεων Το (α) πλεονεκτεί τοχιά γική, ανεξάτητη ομποτικού χειιστή, αλλά απαιτεί αντιστοφή κινηματικής για τον έλεγχο του ομπότ 5 Σχεδιασμός Τοχιάς: Βασικές Σχέσεις Αχική θέση φάση επιτάχυνσης (γ) σταθεή ταχύτητα (dp/d) φάση επιβάδυνσης τελικό σημείοστόχος Απαιτούμη μεταβολή θέσης σε κάθε χονική στιγμή i. ή Δ pi () pi () Δ pi Δpi γ (όπου γ επιθυμητή επιτάχυνση κατά μήκος του δόμου) () ( ) ακτίνα καμπυλότητας Αχικό Σημείο Επιτάχυνση (φάση σταθεής ταχύτητας) Εντολή θέσης συσσώευση απαιτούμων μεταβολών θέσης: pi () pi ( ) Δpi () Εντολή ταχύτητας: p () i p ( i ) [ γ ] (αιθμητική ολοκλήωση) Για καμπύλο δόμο: Σημείο διέλευσης Επιβάδυνση Επιτεπόμη επιτάχυνση ελάχιστη ακτίνα καμπυλότητας f(επιτεπόμη φυγόκτη επιτάχυνση σε σχέση με το μέτο της ταχύτητας) Τελικό Σημείο 6
4 Βασικοί αλγόιθμοι παεμβολής Τα διανύσματα p(i) (τέχουσα τολή θέσης) ή Δp(i) (απαιτούμη μεταβολή θέσης), τα οποία υπολογίζονται από τον αλγόιθμο σχεδιασμού τοχιάς, τοφοδοτούν τον αλγόιθμο αντίστοφης κινηματικής Απόλυτοι αλγόιθμοι παεμβολής: p(i) q(i) (αντίστοφο γεωμετικό μοντέλο) Αυξητικοί αλγόιθμοι παεμβολής: p () i q () i (αντίστοφο διαφοικό κινηματικό μοντέλο) q() i q( i ) q () i 7 Απόλυτος αλγόιθμος παεμβολής Σε κάθε βήμα δειγματοληψίας i υπολογίζεται μια νέα διάταξη αναφοάς q(i) (απ ευθείας από το p(i) μέσω αντίστοφου γεωμετικού μοντέλου), η οποία στέλνεται ως τολή στους βόχους ελέγχου Ταχύτητα αναφοάς: Δqi () ( qi () qi ( ) ) qi () Σφάλμα θέσης 0 σε όλα τα διάμεσα σημεία θέση επιθυμητή διάμεσο σημείο σφάλμα θέσης ταχύτητα επιθυμητή αναφοάς Δq αναφοάς (τολή) Δq 8
5 Αυξητικός αλγόιθμος παεμβολής () Σε κάθε βήμα δειγματοληψίας i η ταχύτητα p () i μετασχηματίζεται σε ταχύτητα αναφοάς q () i, η οποία θεωείται σταθεή σε κάθε βήμα Θέση αναφοάς (τολή): i qi () qk ( ) k Συσσωευτικά (αθοιστικά) σφάλματα θέσης (επιθυμητή αναφοάς) (υπολογισμός μέσω ψηφιακής ολοκλήωσης) ταχύτητα επιθυμητή αναφοάς (τολή) θέση επιθυμητή σφάλμα θέσης Δq αναφοάς (τολή) 9 Αυξητικός αλγόιθμος παεμβολής () Σφάλματα παακολούθησης τοχιάς στους αυξητικούς αλγοίθμους παεμβολής Παγματική Τοχιά Δp (χωίς διόθωση) Δp (με διόθωση) Αχή Δp Επιθυμητή Τοχιά Στόχος Σχεδιασμός τοχιάς p(i) p * (i) Δp(i) Αντίστοφη Κινηματική Οθή Κινηματική Βόχος Διόθωσης του συσσωευτικού σφάλματος θέσης πος βόχους ελέγχου q(i) 0
6 Έλεγχος επιλυμένης ταχύτητας q(0) (Reolved oion rae conrol) q(i) Υπολογισμός j A j και A 0 j (j,,n) Υπολογισμός Ιακωβιανής J( q) Βόχος διόθωσης (correcion loop) p p () A :3,4 * i 0 n p(i) p p( i ) p * ( i) d επιθυμητή τοχιά Επίλυση αντίστοφης διαφοικής κινηματικής p J( q) q Εύεση q q( i ) q ( i) q ( i) d d: apling ie i i q( i ), q ( i) πος ελεγκτή θέσης ομπότ ξ() Σχεδιασμός τοχιάς μέσω πολυωνυμικών συνατήσεων παεμβολής (a) Έστω ξ μια μεταβλητή q i (στο χώο των αθώσεων) ή p i (στο χώο του τελικού στοιχείου δάσης) ξ f ξ0 ξ f Αχικές / Τελικές Συνθήκες (oundary condiion) για τοχιά συνεχή, με συνεχή η παάγωγο (ταχύτητα) ξ f ξ(0) ξ 0 ξ( f ) ξ f ξ (0) ξ ( ) 0 ξ ξ f f Πολυωνυμική Συνάτηση Παεμβολής: (3ου βαθμού, 4 παάμετοι) (cuic polynoial) ξ () a a a a a0 ξ0 a ξ 0 a... a 3...
7 Σχεδιασμός τοχιάς μέσω πολυωνυμικών συνατήσεων παεμβολής () Πολυωνυμική Συνάτηση Παεμβολής (3ου βαθμού, 4 παάμετοι) (cuic polynoial) (συνέχεια) ξ () a a a a a0 ξ0, ξ a f a0 a f a f a 3 f, ξ, ξ a a 3a 0 f f 3 f ΕΠΕΚΤΑΣΗ Κυβικές Τοχιές Παεμβολής με Ενδιάμεσα Σημεία (via poin) και Συνεχή Ταχύτητα a0 ξ0, a ξ0, a 3 ( ξ 0) f ξ ξ0 ξf, f f f ξ 0 Α Β Γ ξ f a ( ξ ξ ) ( ξ ξ ) 3 3 f 0 0 f f f 0 A B Γ f 3 ξ() Σχεδιασμός τοχιάς μέσω πολυωνυμικών συνατήσεων παεμβολής () Έστω ξ μια μεταβλητή q i (στο χώο των αθώσεων) ή p i (στο χώο του τελικού στοιχείου δάσης) ξ f ξ 0 ξ0 0 0 f ξ f Αχικές / Τελικές Συνθήκες (oundary condiion) ξ(0) ξ 0 ξ( f ) ξ f ξ (0) ξ 0 ξ ( ) f ξ f ξ (0) ξ ξ ( ) ξ 0 f f 5 Πολυωνυμική Συνάτηση Παεμβολής: ξ () a0 a a a 5 (5ου βαθμού, 6 παάμετοι) Ειδική πείπτωση, όταν ισχύουν οι συνθήκες: a0 ξ0 a a 3... ( ξf ξ ) ( 0 ξ0 ξf ) ξ0 a ξ0 ξf 0, 4... a f ξ0/ a 5... a 5 0 ( πολυώνυμο 4ου βαθμού) 4
8 Σχεδιασμός τοχιάς μέσω πολυωνυμικών συνατήσεων παεμβολής (3) Τοχιές τιών φάσεων (επιτάχυνση, σταθεή ταχύτητα, επιβάδυνση), με πολυώνυμα παεμβολής 4ου βαθμού (και συνέχεια ως πος την επιτάχυνση) Ειδική Πείπτωση: Αχική και Τελική Θέση «στάσει» ξ f ξ f ξ ( ξ ξ0 )/( Δ) f f στην ευθεία που ώνει τα ξ 0 ξ 0 και ξ f ξ f ξ f ξ f ξ f Εαν ( ξ ξ ) ( ξ ξ ) f f 0 0 f 4ου βαθμού ξ 0 ξ 0 ξ 0 ξ 0 Φ Δ Δ Δ Δ Φ Φ3 Πολυώνυμα παεμβολής 4ου βαθμού f Φ: Φ3: ( ξ 0 ξ 0) 0 ξ ( ξ ξ 0 0) ξ Δ Δ Ισχύουν! ( ξf ξ ) f ξ 0 ( ξf ξf) ξ Δ Δ 5 Γαμμικός Έλεγχος Απλής Ρομποτικής Άθωσης 6
9 Συνάτηση μεταφοάς απλής ομποτικής άθωσης () Κινητήας συνεχούς εύματος (DC): υψηλός λόγος οπήςισχύος, γαμμική χαακτηιστική (οπήςταχύτητας) και μικές σταθεές χόνου (οπή αδανείας φοτίου) v R L i e θ J τ * τ L J θ τ L (συντελεστής γαμμικής τιβής) L J L θ L (συντελεστής τιβής φοτίου) λόγος μετάδοσης n Ισοδύναμο Ηλεκτικό Κύκλωμα Οδήγησης Κινητήα DC Μηχανικό Σύστημα Κινητήα DC (μετάδοση κίνησης με οδοντωτούς τοχούς, gear) Ισχύει: rθ rlθ L ή N NLθL όπου r, r L ακτίνες τοχών και N, N L : αιθμοί οδόντων r N Λόγος μετάδοσης: n r N < L L (μειωτήας) θ n θ L L θ n θ θ n θ L () 7 Συνάτηση μεταφοάς απλής ομποτικής άθωσης () Μηχανικό Σύστημα Κινητήα J * () τ() () τl() () άξονας κινητήα τ : οπή που αναπτύσσει ο κινητήας * τ L : οπή από το φοτίο (ανηγμένο στον άξονα του κινητήα) () * * θl Ισχύει (διατήηση έγειας): τl τl θl τl τl n τl (3) θ άξονας φοτίου () (3) τ () J θ () θ () n τ () (4) J θ () τ () θ () L L L L L L (4) (5) ( ) ( ) τ () J θ () θ () L L L L L τ () nj θ () n θ () L L L τ() J n JL () n L () (6) J () (5) () τ () ( J ) μηχανική σταθεά χόνου (Σ) 8
10 Συνάτηση μεταφοάς απλής ομποτικής άθωσης (3) Ηλεκτικό Σύστημα Οδήγησης του DC Κινητήα τ K i όπου Κ Τ : σταθεά οπής κινητήα (N./A) i : ένταση εύματος ότοα και di v R i L e όπου R : ηλεκτική αντίσταση κυκλώματος ότοα d L : αυτεπαγωγή ότοα e : αντιηλεκτεγετική δύναμη του κινητήα e Κ : σταθεά αναλογίας αντιηλεκτικής δύναμης Άα, μετασχηματίζοντας κατά Laplace: v K v ( R L) i K i ( L R) και v K τ K i K ( L R) ηλεκτική σταθεά χόνου (Σ) K θ 9 Συνάτηση μεταφοάς απλής ομποτικής άθωσης (4) Μηχανικό Υποσύστημα τ ( J ) θ μηχανική σταθεά (Σ) χόνου () () ( J ) θ τ Ηλεκτικό Υποσύστημα v e ( L R ) i K K τ θ ηλεκτική σταθεά χόνου (Σ) v K τ K i K ( L R) 0
11 Συνάτηση μεταφοάς απλής ομποτικής άθωσης (5) v ( L R ) i K τ ( J ) θ e K θ v K () K ( J ) ( L R )... v Άα: e G( ) K θ θ όπου: Ισχύει: θ () K v () ( L R )( J ) K K K G( ) ( L R )( J ) θ () G () v () K G() () K G () v () [ ( LJ ) ( RJ L ) ( R KK ) ] Συνάτηση μεταφοάς απλής ομποτικής άθωσης (6) Απλοποίηση μοντέλου: αγνοούμε την επίδαση της αυτεπαγωγής L του ότοα (L 0) Δηλαδή: Θεωούμε την ηλεκτική σταθεά χόνου (Τ e L /R ) του κινητήα πολύ μική σε σχέση με τη μηχανική σταθεά χόνου (Τ e J / ) () K G () v () [ ( R J ) ( R K K )] ή, ισοδύναμα: όπου: () K G () v () [ ] K K ( R K K ) RJ ( R K K ) : Συνάτηση Μεταφοάς (ανοικτού βόχου) απλής άθωσης : σταθεά ίσχυσης του κινητήα : σταθεά χόνου του κινητήα
12 Βασικός βόχος ελέγχου θέσης απλής ομποτικής άθωσης () θl, d e θ K P K D v ( L R ) i K τ ( J ) θ n θ L e K θ Ελεγκτής θέσης PD (proporionalderivaive): v () ( K K ) e () Αντιστάθμιση δύο όων: θέσης και ταχύτητας (δύο όοι : ανάλογος και πααγώγου) Δηλαδή, ελεγκτής θέσης PD: u () v() Ke() K e() P θ D θ όπου: (σήμα ελέγχου, οδήγησης του κινητήα της άθωσης) e θ : σφάλμα θέσης άθωσης e θ θl, d θl (επιθυμητή θέση τέχουσα θέση) θ L, d : επιθυμητή (deired, reference) θέση άθωσης P D θ 3 Βασικός βόχος ελέγχου θέσης απλής ομποτικής άθωσης () θ L, d e θ K P K D GPD n () : συνάτηση μεταφοάς ανοικτού βόχου v θ θ L G( ) n θ L Συνάτηση μεταφοάς ανοικτού βόχου: όπου: ή (L 0): G () ( K K ) G () PD P D () K G () v () [ ( LJ ) ( RJ L ) ( R KK ) ] () K G () v () [ ( R J ) ( R K K )] Συνάτηση μεταφοάς κλειστού βόχου: Όταν L 0: H H PD GPD() () G ( ) K ( K K ) ( RJ ) ( R KK) K K K PD( ) P D [ ] ( ) PD P D 4
13 Βασικός βόχος ελέγχου θέσης απλής ομποτικής άθωσης (3) Συνάτηση μεταφοάς κλειστού βόχου μεμονωμένης ομποτικής άθωσης με αντισταθμιστή θέσης PD H K ( K K ) ( R J ) ( R KK KK) KK PD( ) P D D P ανάδαση ταχύτητας (derivaive er) Επιλογή ισχύσεων ελέγχου θέσης και ταχύτητας Δευτεοβάθμιο Σύστημα: χ.π. ( ζω ) ( ) n ωn ζ: συντελεστής απόσβεσης ω n : ιδιοσυχνότητα ταλαντώσεων (χωίς απόσβεση) εύος ζώνης ανάδαση θέσης (proporional er) ( ) KK P ω n R J ( R KK KKD) ζ ( KK)( RJ ) P 5 Βασικός βόχος ελέγχου θέσης απλής ομποτικής άθωσης (4) Ποδιαγαφές Σχεδίασης Αντισταθμιστή PD Ελέγχου Απλής Ρομποτικής Άθωσης ωr ω n < (ω r : δομική συχνότητα συντονισμού συστήματος) KK ( ) ( ) P ωr ωr ω n < KP ( ) RJ ( R J ) < K Ενίσχυση ανάλογου όου (proporional gain) ζ (κίσιμη ή υπεκίσιμη απόσβεση) ( R KK KK D) ζ ( KK)( RJ ) P K D P ( KK)( RJ ) R KK K 6
Σχεδιασμός Τροχιάς Ρομποτικών Χειριστών
 Σχολή Ηλεκτρολόγων Μηχ/κών και Μηχ/κών Υπολογιστών, Ε.Μ.Π., Ακαδημαϊκό Έτος 00809, 7ο Εξάμηνο Μάθημα: Ρομποτική Ι Αυτόματος Έλεγχος Ρομπότ Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου & Ρομποτικής Σχολή Ηλεκτρ.
Σχολή Ηλεκτρολόγων Μηχ/κών και Μηχ/κών Υπολογιστών, Ε.Μ.Π., Ακαδημαϊκό Έτος 00809, 7ο Εξάμηνο Μάθημα: Ρομποτική Ι Αυτόματος Έλεγχος Ρομπότ Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου & Ρομποτικής Σχολή Ηλεκτρ.
Μάθημα: Ρομποτικός Έλεγχος
 Διατμηματικό Πρόγραμμα Μεταπτυχιακών Σπουδών «ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ» Ε.Μ.Π., Ακαδημαϊκό Έτος 011-1 Μάθημα: Ρομποτικός Έλεγχος Αυτόματος Έλεγχος Ρομπότ (Μη-Γραμμικός Ρομποτικός Έλεγχος Κων/νος Τζαφέστας
Διατμηματικό Πρόγραμμα Μεταπτυχιακών Σπουδών «ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ» Ε.Μ.Π., Ακαδημαϊκό Έτος 011-1 Μάθημα: Ρομποτικός Έλεγχος Αυτόματος Έλεγχος Ρομπότ (Μη-Γραμμικός Ρομποτικός Έλεγχος Κων/νος Τζαφέστας
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΤΥΠΟΛΟΓΙΟ. Επιµέλεια. ΣΕΡΑΦΕΙΜ ΚΑΡΑΜΠΟΓΙΑΣ.
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΤΥΠΟΛΟΓΙΟ Επιµέλεια. ΣΕΡΑΦΕΙΜ ΚΑΡΑΜΠΟΓΙΑΣ. ΑΘΗΝΑ 9 Τιγωνοµετικοί αιθµοί Γωνία π 6 π 4 π 3 π si ϕ 3 3 os ϕ ϕ 3 3 3. Τιγωνοµετικές ταυτότητες. os ± y os os y si si y. si ± y si os y
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΤΥΠΟΛΟΓΙΟ Επιµέλεια. ΣΕΡΑΦΕΙΜ ΚΑΡΑΜΠΟΓΙΑΣ. ΑΘΗΝΑ 9 Τιγωνοµετικοί αιθµοί Γωνία π 6 π 4 π 3 π si ϕ 3 3 os ϕ ϕ 3 3 3. Τιγωνοµετικές ταυτότητες. os ± y os os y si si y. si ± y si os y
Μαθηματι ά ατεύθυνσης
 Β Λυκείου Μαθηματι ά ατεύθυνσης Ο Κύκλος Θεωία Μεθοδολογία -Ασκήσεις Σ υ ν ο π τ ι κ ή Θ ε ω ί α Ονομασία Διατύπωση Σχόλια Σχήμα Α. Κύκλος Οισμός: Ονομάζεται κύκλος με κέντο Ο και ακτίνα το σύνολο των
Β Λυκείου Μαθηματι ά ατεύθυνσης Ο Κύκλος Θεωία Μεθοδολογία -Ασκήσεις Σ υ ν ο π τ ι κ ή Θ ε ω ί α Ονομασία Διατύπωση Σχόλια Σχήμα Α. Κύκλος Οισμός: Ονομάζεται κύκλος με κέντο Ο και ακτίνα το σύνολο των
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧ/ΚΩΝ & ΜΗΧ/ΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧ/ΚΩΝ & ΜΗΧ/ΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ Θέματα Εξετάσεων Ασκήσεις στο Mάθημα: "ΡΟΜΠΟΤΙΚΗ Ι: ΑΝΑΛΥΣΗ, ΕΛΕΓΧΟΣ, ΕΡΓΑΣΤΗΡΙΟ" 1 η Σειρά Θεμάτων Θέμα 1-1 Έστω ρομποτικός
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧ/ΚΩΝ & ΜΗΧ/ΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ Θέματα Εξετάσεων Ασκήσεις στο Mάθημα: "ΡΟΜΠΟΤΙΚΗ Ι: ΑΝΑΛΥΣΗ, ΕΛΕΓΧΟΣ, ΕΡΓΑΣΤΗΡΙΟ" 1 η Σειρά Θεμάτων Θέμα 1-1 Έστω ρομποτικός
ΑΣΚΗΣΗ 14. έκδοση DΥΝI-EXC b
 ΕΡΓΑΣΤΗΡΙΟ ΔΥΝΑΜΙΚΗΣ & ΚΑΤΑΣΚΕΥΩΝ ΤΟΜΕΑΣ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ & ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΑΣΚΗΣΗ 14 έκδοση DΥΝI-EXC14-016b Copyright Ε.Μ.Π. - 016 Σχολή
ΕΡΓΑΣΤΗΡΙΟ ΔΥΝΑΜΙΚΗΣ & ΚΑΤΑΣΚΕΥΩΝ ΤΟΜΕΑΣ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ & ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΑΣΚΗΣΗ 14 έκδοση DΥΝI-EXC14-016b Copyright Ε.Μ.Π. - 016 Σχολή
Σχολή Ηλεκτρολόγων Μηχ/κών και Μηχ/κών Υπολογιστών, Ε.Μ.Π., Ακαδημαϊκό Έτος , 8ο Εξάμηνο. Ρομποτική II. Ευφυή και Επιδέξια Ρομποτικά Συστήματα
 Σχολή Ηλεκτρολόγων Μηχ/κών και Μηχ/κών Υπολογιστών, Ε.Μ.Π., Ακαδημαϊκό Έτος 009-0, 8ο Εξάμηνο Ρομποτική II Ευφυή και Επιδέξια Ρομποτικά Συστήματα Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου & Ρομποτικής
Σχολή Ηλεκτρολόγων Μηχ/κών και Μηχ/κών Υπολογιστών, Ε.Μ.Π., Ακαδημαϊκό Έτος 009-0, 8ο Εξάμηνο Ρομποτική II Ευφυή και Επιδέξια Ρομποτικά Συστήματα Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου & Ρομποτικής
Ρομποτική Ι: Διαφορική Κινηματική Ανάλυση
 Σχολή Ηλεκτρολόγων Μηχ/κών και Μηχ/κών Υπολογιστών, Ε.Μ.Π., Ακαδημαϊκό Έτος 8-9, 7ο Εξάμηνο Ρομποτική Ι: Διαφορική Κινηματική Ανάλυση Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου & Ρομποτικής Σχολή Ηλεκτρ.
Σχολή Ηλεκτρολόγων Μηχ/κών και Μηχ/κών Υπολογιστών, Ε.Μ.Π., Ακαδημαϊκό Έτος 8-9, 7ο Εξάμηνο Ρομποτική Ι: Διαφορική Κινηματική Ανάλυση Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου & Ρομποτικής Σχολή Ηλεκτρ.
ΡΕΥΜΑΤΑ, ΝΟΜΟΣ ΤΟΥ OHM
 Q ΡΥΜΑΤΑ, ΝΟΜΟΣ ΤΟΥ OHM Ισοοπία σε αγωγό μόνον όταν στο εσωτεικό του αγωγού είναι =0 λεύθεο Ηλεκτόνιο Πείσεια ελευθέων ηλεκτονίων ξωτεικό ηλεκτικό πεδίο εσ εξ = εσ = 0 εξ σωτεικό ηλ. πεδίο Ποσθήκη εξωτεικού
Q ΡΥΜΑΤΑ, ΝΟΜΟΣ ΤΟΥ OHM Ισοοπία σε αγωγό μόνον όταν στο εσωτεικό του αγωγού είναι =0 λεύθεο Ηλεκτόνιο Πείσεια ελευθέων ηλεκτονίων ξωτεικό ηλεκτικό πεδίο εσ εξ = εσ = 0 εξ σωτεικό ηλ. πεδίο Ποσθήκη εξωτεικού
ΠΕΙΡΑΜΑ 10. Aεροδυναµική Στερεών Σωµάτων
 ΠΕΙΡΑΜΑ 10 Aεοδυναµική Στεεών Σωµάτων Σκοπός του πειάµατος Σκοπός του πειάµατος αυτού είναι η µελέτη της αντίστασης που αναπτύσσεται κατά τη σχετική κίνηση ενός αντικειµένου µέσα σε ένα αέιο. Οι εξισώσεις
ΠΕΙΡΑΜΑ 10 Aεοδυναµική Στεεών Σωµάτων Σκοπός του πειάµατος Σκοπός του πειάµατος αυτού είναι η µελέτη της αντίστασης που αναπτύσσεται κατά τη σχετική κίνηση ενός αντικειµένου µέσα σε ένα αέιο. Οι εξισώσεις
Συλλογή μεταφορά και έλεγχος Δεδομένων. 1.4 Απλά και σύνθετα συστήματα αυτοματισμού.
 Συλλογή μεταφορά και έλεγχος Δεδομένων 1.4 Απλά και σύνθετα συστήματα αυτοματισμού. Το είδαμε μέχρι τώρα Δομή συστήματος αυτοματισμού Ο ελεγκτής προϋποθέτει την ύπαρξη κάποιων στοιχείων, στα οποία θα επιδράσει
Συλλογή μεταφορά και έλεγχος Δεδομένων 1.4 Απλά και σύνθετα συστήματα αυτοματισμού. Το είδαμε μέχρι τώρα Δομή συστήματος αυτοματισμού Ο ελεγκτής προϋποθέτει την ύπαρξη κάποιων στοιχείων, στα οποία θα επιδράσει
Συστήματα Αυτομάτου Ελέγχου
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τ.Τ Συστήματα Αυτομάτου Ελέγχου Ενότητα #5: Σχεδιασμός ελεγκτών με τη μέθοδο του Τόπου Ριζών 2 Δ. Δημογιαννόπουλος, dimogian@teipir.gr Επ. Καθηγητής
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τ.Τ Συστήματα Αυτομάτου Ελέγχου Ενότητα #5: Σχεδιασμός ελεγκτών με τη μέθοδο του Τόπου Ριζών 2 Δ. Δημογιαννόπουλος, dimogian@teipir.gr Επ. Καθηγητής
Εισαγωγή στην Ρομποτική
 Τμήμα Μηχανολογίας Τ.Ε.Ι. Κρήτης Εισαγωγή στην Ρομποτική 1 Γενική περιγραφή ρομποτικού βραχίονα σύνδεσμοι αρθρώσεις αρπάγη Περιστροφική Πρισματική Βάση ρομποτικού βραχίονα 3 Βασικές ρομποτικές αρθρώσεις
Τμήμα Μηχανολογίας Τ.Ε.Ι. Κρήτης Εισαγωγή στην Ρομποτική 1 Γενική περιγραφή ρομποτικού βραχίονα σύνδεσμοι αρθρώσεις αρπάγη Περιστροφική Πρισματική Βάση ρομποτικού βραχίονα 3 Βασικές ρομποτικές αρθρώσεις
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΡΕΥΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΘΕΡΜΙΚΩΝ ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΡΕΥΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΘΕΡΜΙΚΩΝ ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ ιπλωµατική Εγασία : ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΚΩ ΙΚΑ ΕΠΙΛΥΣΗΣ ΑΞΟΝΟΣΥΜΜΕΤΡΙΚΩΝ ΠΕ ΙΩΝ ΡΟΗΣ ΓΙΑ ΟΜΗΜΕΝΑ ΚΑΙ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΡΕΥΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΘΕΡΜΙΚΩΝ ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ ιπλωµατική Εγασία : ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΚΩ ΙΚΑ ΕΠΙΛΥΣΗΣ ΑΞΟΝΟΣΥΜΜΕΤΡΙΚΩΝ ΠΕ ΙΩΝ ΡΟΗΣ ΓΙΑ ΟΜΗΜΕΝΑ ΚΑΙ
= = σταθ. Ι. που είναι. Η ροπή αδράνειας ενός σώματος μετρά την κατανομή της μάζας γύρω από τον άξονα περιστροφής, έτσι όσο
 Απαντήσεις ΘΕΜΑ Α Α. γ, Α. α, Α3. γ, Α4. α, Α5. Σ, Λ, Λ, Λ, Σ. ΘΕΜΑ Β Β. Σωστή απάντηση είναι η γ. Σε μία τυχαία θέση θα έχουμε: Στ = τf τ w = F g ηµθ θ F Στ = ( c + 0,5g ηµθ) g ηµ θ = c = σταθ. g Άα λοιπό
Απαντήσεις ΘΕΜΑ Α Α. γ, Α. α, Α3. γ, Α4. α, Α5. Σ, Λ, Λ, Λ, Σ. ΘΕΜΑ Β Β. Σωστή απάντηση είναι η γ. Σε μία τυχαία θέση θα έχουμε: Στ = τf τ w = F g ηµθ θ F Στ = ( c + 0,5g ηµθ) g ηµ θ = c = σταθ. g Άα λοιπό
Έλεγχος στροφών κινητήρα DC με ελεγκτή PI, και αντιστάθμιση διαταραχής.
 ΑΕΙ ΠΕΙΡΑΙΑ Τ.Τ Τμήμα Μηχανικών Αυτοματισμού Τ.Ε. Έλεγχος στροφών κινητήρα DC με ελεγκτή PI, και αντιστάθμιση διαταραχής. Α) Σκοπός: Σκοπός της παρούσας άσκησης είναι να επιδειχθεί ο έλεγχος των στροφών
ΑΕΙ ΠΕΙΡΑΙΑ Τ.Τ Τμήμα Μηχανικών Αυτοματισμού Τ.Ε. Έλεγχος στροφών κινητήρα DC με ελεγκτή PI, και αντιστάθμιση διαταραχής. Α) Σκοπός: Σκοπός της παρούσας άσκησης είναι να επιδειχθεί ο έλεγχος των στροφών
ΜΑΘΗΜΑ / ΤΑΞΗ : ΗΛΕΚΤΡΟΤΕΧΝΙΑ / Γ ΕΠΑΛ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 27/01/2013
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΗΛΕΚΤΡΟΤΕΧΝΙΑ / Γ ΕΠΑΛ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 7/0/03 ΘΕΜΑ ο ) Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η
ΜΑΘΗΜΑ / ΤΑΞΗ : ΗΛΕΚΤΡΟΤΕΧΝΙΑ / Γ ΕΠΑΛ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 7/0/03 ΘΕΜΑ ο ) Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η
Ψηφιακός Έλεγχος. 10 η διάλεξη Ασκήσεις. Ψηφιακός Έλεγχος 1
 Ψηφιακός Έλεγχος 10 η διάλεξη Ασκήσεις Ψηφιακός Έλεγχος 1 Άσκηση1 Ασκήσεις Επιθυμούμε να ελέγξουμε την γωνία ανύψωσης μιας κεραίας για να παρακολουθείται η θέση ενός δορυφόρου. Το σύστημα της κεραίας και
Ψηφιακός Έλεγχος 10 η διάλεξη Ασκήσεις Ψηφιακός Έλεγχος 1 Άσκηση1 Ασκήσεις Επιθυμούμε να ελέγξουμε την γωνία ανύψωσης μιας κεραίας για να παρακολουθείται η θέση ενός δορυφόρου. Το σύστημα της κεραίας και
Συστήματα Αυτομάτου Ελέγχου ΙΙ Ασκήσεις Πράξης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΑΤΤΙΚΗΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΗΣ ΣΧΕΔΙΑΣΗΣ & ΠΑΡΑΓΩΓΗΣ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΙΙ ΑΣΚΗΣΕΙΣ ΠΡΑΞΗΣ Αν Καθ: Δ ΔΗΜΟΓΙΑΝΝΟΠΟΥΛΟΣ Επικ Καθ: Σ ΒΑΣΙΛΕΙΑΔΟΥ Συστήματα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΑΤΤΙΚΗΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΗΣ ΣΧΕΔΙΑΣΗΣ & ΠΑΡΑΓΩΓΗΣ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΙΙ ΑΣΚΗΣΕΙΣ ΠΡΑΞΗΣ Αν Καθ: Δ ΔΗΜΟΓΙΑΝΝΟΠΟΥΛΟΣ Επικ Καθ: Σ ΒΑΣΙΛΕΙΑΔΟΥ Συστήματα
ΔΙΑΛΕΞΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ «ΘΕΜΕΛΙΩΣΕΙΣ»
 ΔΙΑΛΕΞΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ «ΘΕΜΕΛΙΩΣΕΙΣ» 7ο Εξ. ΠΟΛ-ΜΗΧ ΜΗΧ. ΕΜΠ - Ακαδ. Ετος 25-6 ΔΙΑΛΕΞΗ 11 Θεμελιώσεις με πασσάλους : Καθιζήσεις πασσάλων 5.1.26 1. Κατηγοίες πασσάλων 2. Αξονική φέουσα ικανότητα μεμονωμένου
ΔΙΑΛΕΞΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ «ΘΕΜΕΛΙΩΣΕΙΣ» 7ο Εξ. ΠΟΛ-ΜΗΧ ΜΗΧ. ΕΜΠ - Ακαδ. Ετος 25-6 ΔΙΑΛΕΞΗ 11 Θεμελιώσεις με πασσάλους : Καθιζήσεις πασσάλων 5.1.26 1. Κατηγοίες πασσάλων 2. Αξονική φέουσα ικανότητα μεμονωμένου
Ρομποτικά Συστήματα Ελέγχου: Διαφορική Κινηματική Ανάλυση
 Διατμηματικό Πρόγραμμα Μεταπτυχιακών Σπουδών «ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ» Ρομποτικά Συστήματα Ελέγχου: Διαφορική Κινηματική Ανάλυση Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου & Ρομποτικής Σχολή Ηλεκτρ. Μηχ/κών
Διατμηματικό Πρόγραμμα Μεταπτυχιακών Σπουδών «ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ» Ρομποτικά Συστήματα Ελέγχου: Διαφορική Κινηματική Ανάλυση Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου & Ρομποτικής Σχολή Ηλεκτρ. Μηχ/κών
1) Ηλεκτρικό πεδίο φορτισμένου φύλλου απείρων διαστάσεων
 1) Ηλεκτικό πεδίο φοτισμένου φύλλου απείων διαστάσεων Σε αυτό το εδάφιο θα υπολογιστεί το ηλεκτικό πεδίο παντού στο χώο ενός φοτισμένου λεπτού φύλλου απείων διαστάσεων και αμελητέου πάχους όπως αυτό που
1) Ηλεκτικό πεδίο φοτισμένου φύλλου απείων διαστάσεων Σε αυτό το εδάφιο θα υπολογιστεί το ηλεκτικό πεδίο παντού στο χώο ενός φοτισμένου λεπτού φύλλου απείων διαστάσεων και αμελητέου πάχους όπως αυτό που
Μάθημα: Θεωρία Δικτύων
 Σχολή Ηλεκτρολόγων Μηχ/κών και Μηχ/κών Υπολογιστών, Ε.Μ.Π., Ακαδημαϊκό Έτος 7-8, 5ο Εξάμηνο Μάθημα: Θεωρία Δικτύων Ανάλυση Ευσταθείας Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου & Ρομποτικής Σχολή Ηλεκτρ.
Σχολή Ηλεκτρολόγων Μηχ/κών και Μηχ/κών Υπολογιστών, Ε.Μ.Π., Ακαδημαϊκό Έτος 7-8, 5ο Εξάμηνο Μάθημα: Θεωρία Δικτύων Ανάλυση Ευσταθείας Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου & Ρομποτικής Σχολή Ηλεκτρ.
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2017 Β ΦΑΣΗ. Ηµεροµηνία: Μ. Τετάρτη 12 Απριλίου 2017
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 07 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΘΕΜΑ A Α. α Α. β Α3. γ Α4. δ Α5. α. Λάθος ΘΕΜΑ Β ΦΥΣΙΚΗ Ηµεοµηνία: Μ. Τετάτη Απιλίου 07 β. Σωστό γ. Λάθος δ. Λάθος
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 07 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΘΕΜΑ A Α. α Α. β Α3. γ Α4. δ Α5. α. Λάθος ΘΕΜΑ Β ΦΥΣΙΚΗ Ηµεοµηνία: Μ. Τετάτη Απιλίου 07 β. Σωστό γ. Λάθος δ. Λάθος
Πα.Δα. Τμήμα Μηχανικών Πληροφορικής και Υπολογιστών ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ
 Πα.Δα. Τμήμα Μηχανικών Πληροφορικής και Υπολογιστών ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ Δημήτριος Νικολόπουλος, Καθηγητής Περιβαλλοντική και Ιατρική Φυσική Εξίσωση και κλίση ευθείας Έστω ότι έχουμε δυο σταθερές α και
Πα.Δα. Τμήμα Μηχανικών Πληροφορικής και Υπολογιστών ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ Δημήτριος Νικολόπουλος, Καθηγητής Περιβαλλοντική και Ιατρική Φυσική Εξίσωση και κλίση ευθείας Έστω ότι έχουμε δυο σταθερές α και
Κεφάλαιο 3: Μοντέλα Θεωρίας Αναμονής
 Κεφάλαιο 3: Μοντέλα Θεωίας Αναμονής Τεχνικές Εκτίμησης Υπολογιστικών Συστημάτων Γιάννης Γαοφαλάκης Αν. Καθηγητής Οισμός συστημάτων αναμονής Συστήματα αναμονής (Queueing Syses): Συστήματα στα οποία οι αφίξεις
Κεφάλαιο 3: Μοντέλα Θεωίας Αναμονής Τεχνικές Εκτίμησης Υπολογιστικών Συστημάτων Γιάννης Γαοφαλάκης Αν. Καθηγητής Οισμός συστημάτων αναμονής Συστήματα αναμονής (Queueing Syses): Συστήματα στα οποία οι αφίξεις
ΜΗΧΑΝΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ. Κινητήρες ΣΡ. Άγγελος Μπουχουράς - Μηχανές Ι
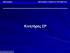 Το ισοδύναμο κύκλωμα ενός κινητήρα ΣΡ: Το κύκλωμα οπλισμού παριστάνεται με μια ιδανική πηγή τάσης ΕΑ και μία αντίσταση RA Στην ουσία πρόκειται για το ισοδύναμο κύκλωμα του δρομέα που περιλαμβάνει: τους
Το ισοδύναμο κύκλωμα ενός κινητήρα ΣΡ: Το κύκλωμα οπλισμού παριστάνεται με μια ιδανική πηγή τάσης ΕΑ και μία αντίσταση RA Στην ουσία πρόκειται για το ισοδύναμο κύκλωμα του δρομέα που περιλαμβάνει: τους
υναµική Μηχανών Ι Ακαδηµαϊκό έτος : Ε. Μ. Π. Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο υναµικής και Κατασκευών ΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι - 14.
 υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 00-0 Ε.Μ.Π. Σχολή Μηχανολόγων Μηχανικών - Εγαστήιο υναµικής και Κατασκευών ΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι - 4. - υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 00-0 Ε.Μ.Π. Σχολή Μηχανολόγων Μηχανικών
υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 00-0 Ε.Μ.Π. Σχολή Μηχανολόγων Μηχανικών - Εγαστήιο υναµικής και Κατασκευών ΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι - 4. - υναµική Μηχανών Ι Ακαδηµαϊκό έτος: 00-0 Ε.Μ.Π. Σχολή Μηχανολόγων Μηχανικών
Δυναμική Μηχανών I. Σύνοψη Εξεταστέας Ύλης
 Δυναμική Μηχανών I 9 1 Σύνοψη Εξεταστέας Ύλης 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com Απαγορεύεται οποιαδήποτε αναπαραγωγή χωρίς άδεια Ύλη Δυναμικής Μηχανών
Δυναμική Μηχανών I 9 1 Σύνοψη Εξεταστέας Ύλης 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com Απαγορεύεται οποιαδήποτε αναπαραγωγή χωρίς άδεια Ύλη Δυναμικής Μηχανών
Ρομποτικός Έλεγχος Δύναμης / Μηχανικής Αντίστασης
 Σχολή Ηλεκτρολόγων Μηχ/κών και Μηχ/κών Υπολογιστών, Ε.Μ.Π., Ακαδημαϊκό Έτος 7-8, 7ο Εξάμηνο Μάθημα: Ρομποτική Ι Αυτόματος Έλεγχος Ρομπότ 3 (Έλεγχος Δύναμης) Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου &
Σχολή Ηλεκτρολόγων Μηχ/κών και Μηχ/κών Υπολογιστών, Ε.Μ.Π., Ακαδημαϊκό Έτος 7-8, 7ο Εξάμηνο Μάθημα: Ρομποτική Ι Αυτόματος Έλεγχος Ρομπότ 3 (Έλεγχος Δύναμης) Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου &
Επανέλεγχος ηλεκτρικής εγκατάστασης
 Επανέλεγχος ηλεκτικής εγκατάστασης Οδηγίες διεξαγωγής μετήσεων και δοκιμών για επανελέγχους ηλεκτικών εγκαταστάσεων με τη χήση σύγχονων ογάνων 1. Εισαγωγή στις απαιτήσεις των επανελέγχων Τα οφέλη του τακτικού
Επανέλεγχος ηλεκτικής εγκατάστασης Οδηγίες διεξαγωγής μετήσεων και δοκιμών για επανελέγχους ηλεκτικών εγκαταστάσεων με τη χήση σύγχονων ογάνων 1. Εισαγωγή στις απαιτήσεις των επανελέγχων Τα οφέλη του τακτικού
ΔΠΜΣ «ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ» «ΕΡΓΑΣΤΗΡΙΟ ΡΟΜΠΟΤΙΚΗΣ» Άσκηση 2. Έλεγχος Pendubot
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρ. Μηχ/κών και Μηχ/κών Υπολογιστών Τομέας Σημάτων, Ελέγχου και Ρομποτικής ΔΠΜΣ «ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ» «ΕΡΓΑΣΤΗΡΙΟ ΡΟΜΠΟΤΙΚΗΣ» Άσκηση 2. Έλεγχος Pendubot Υπεύθυνος
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρ. Μηχ/κών και Μηχ/κών Υπολογιστών Τομέας Σημάτων, Ελέγχου και Ρομποτικής ΔΠΜΣ «ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ» «ΕΡΓΑΣΤΗΡΙΟ ΡΟΜΠΟΤΙΚΗΣ» Άσκηση 2. Έλεγχος Pendubot Υπεύθυνος
H 2 + x 2 cos ϕ. cos ϕ dϕ =
 . Άπειη γαμμική κατανομή ϕοτίου λ Θεωούμε την γαμμική κατανομή ϕοτίου στον άξονα των x και ζητάμε το ηλεκτικό πεδίο στο σημείο A που απέχει από την κατανομή. Το στοιχειώδες τμήμα dx της κατανομής στη θέση
. Άπειη γαμμική κατανομή ϕοτίου λ Θεωούμε την γαμμική κατανομή ϕοτίου στον άξονα των x και ζητάμε το ηλεκτικό πεδίο στο σημείο A που απέχει από την κατανομή. Το στοιχειώδες τμήμα dx της κατανομής στη θέση
Συστήματα Αυτομάτου Ελέγχου ΙΙ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Συστήματα Αυτομάτου Ελέγχου ΙΙ Ενότητα #6: Σχεδιασμός Ελεγκτών με Χρήση Αναλυτικής Μεθόδου Υπολογισμού Παραμέτρων Δημήτριος Δημογιαννόπουλος
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Συστήματα Αυτομάτου Ελέγχου ΙΙ Ενότητα #6: Σχεδιασμός Ελεγκτών με Χρήση Αναλυτικής Μεθόδου Υπολογισμού Παραμέτρων Δημήτριος Δημογιαννόπουλος
Βιομηχανικοί Ελεγκτές
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τ.Τ Βιομηχανικοί Ελεγκτές Ενότητα #13: Ψηφιακός Έλεγχος Κωνσταντίνος Αλαφοδήμος Τμήματος Μηχανικών Αυτοματισμού Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τ.Τ Βιομηχανικοί Ελεγκτές Ενότητα #13: Ψηφιακός Έλεγχος Κωνσταντίνος Αλαφοδήμος Τμήματος Μηχανικών Αυτοματισμού Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό
Συστήματα Αυτομάτου Ελέγχου
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τ.Τ Συστήματα Αυτομάτου Ελέγχου Ενότητα #6: Σχεδιασμός ελεγκτών με χρήση αναλυτικής μεθόδου υπολογισμού παραμέτρων 2 Δ. Δημογιαννόπουλος, dimogian@teipir.gr
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τ.Τ Συστήματα Αυτομάτου Ελέγχου Ενότητα #6: Σχεδιασμός ελεγκτών με χρήση αναλυτικής μεθόδου υπολογισμού παραμέτρων 2 Δ. Δημογιαννόπουλος, dimogian@teipir.gr
1. ΕΙΣΑΓΩΓΗ. 1.1 Ερευνητικό ενδιαφέρον. 1.2 Επισηµάνσεις από τη βιβλιογραφία. 1.3 Προσέγγιση λύσης προβληµάτων:
 . Εευνητικό ενδιαφέον. ΕΙΣΑΓΩΓΗ. Επισηµάνσεις από τη βιβλιογαφία α) Ελλιπείς γνώσεις των πολύπλοκων φυσικών διεγασιών β) Ελάχιστα εφαµόζονται οι νόµοι της Μηχανικής των Ρευστών γ)ελάχιστα βιβλία διεθνώς
. Εευνητικό ενδιαφέον. ΕΙΣΑΓΩΓΗ. Επισηµάνσεις από τη βιβλιογαφία α) Ελλιπείς γνώσεις των πολύπλοκων φυσικών διεγασιών β) Ελάχιστα εφαµόζονται οι νόµοι της Μηχανικής των Ρευστών γ)ελάχιστα βιβλία διεθνώς
Ανάληψη αξονικού φορτίου από πάσσαλο
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΤΕΧΝΙΚΗΣ ΕΠΟΠΤΙΚΟ ΥΛΙΚΟ ΔΙΑΛΕΞΕΩΝ ΤΟΥ ΜΑΘΗΜΑΤΟΣ «Αλληλεπίδαση Εδάφους Κατασκευής» 8 ο Εξ. ΠΟΛ. ΜΗΧ. - Ακαδ. Ετος 6 7 Διδάσκοντες : Γ. Γκαζέτας
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΤΕΧΝΙΚΗΣ ΕΠΟΠΤΙΚΟ ΥΛΙΚΟ ΔΙΑΛΕΞΕΩΝ ΤΟΥ ΜΑΘΗΜΑΤΟΣ «Αλληλεπίδαση Εδάφους Κατασκευής» 8 ο Εξ. ΠΟΛ. ΜΗΧ. - Ακαδ. Ετος 6 7 Διδάσκοντες : Γ. Γκαζέτας
Υπολογισμός γεωστροφικών ρευμάτων με τη χρήση δεδομένων από CTD. Σύγκριση με αποτελέσματα από A.D.C.P. & Drifters.
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΘΑΛΑΣΣΑΣ Υπολογισμός γεωστοφικών ευμάτων με τη χήση δεδομένων από CTD. Σύγκιση με αποτελέσματα από A.D.C.P. & Drifters. ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ (Επιβλέπων:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΘΑΛΑΣΣΑΣ Υπολογισμός γεωστοφικών ευμάτων με τη χήση δεδομένων από CTD. Σύγκιση με αποτελέσματα από A.D.C.P. & Drifters. ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ (Επιβλέπων:
Αυτόματος Έλεγχος. Ενότητα 9 η : Σχεδίαση ελεγκτών με το γεωμετρικό τόπο ριζών. Παναγιώτης Σεφερλής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9 η : Σχεδίαση ελεγκτών με το γεωμετρικό τόπο ριζών Παναγιώτης Σεφερλής Εργαστήριο Δυναμικής Μηχανών Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9 η : Σχεδίαση ελεγκτών με το γεωμετρικό τόπο ριζών Παναγιώτης Σεφερλής Εργαστήριο Δυναμικής Μηχανών Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ:ΗΛΕΚΤΡΙΚΕΣ-ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΘΕΜΑ 1 Ο Στις ερωτήσεις 1-4 να επιλέξετε τη σωστή πρόταση. 1.Σώμα εκτελεί απλή αρμονική ταλάντωση και κάποια
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ:ΗΛΕΚΤΡΙΚΕΣ-ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΘΕΜΑ 1 Ο Στις ερωτήσεις 1-4 να επιλέξετε τη σωστή πρόταση. 1.Σώμα εκτελεί απλή αρμονική ταλάντωση και κάποια
Σερβοκινητήρες πρόωσης σε συστήματα CNC
 Σερβοκινητήρες πρόωσης σε συστήματα CNC τύπος DC μόνιμου μαγνήτη επίδραση ανάδρασης ταχογεννήτρια Γ.Βοσνιάκος-ΕΡΓΑΛΕΙΟΜΗΧΑΝΕΣ Σερβοκινητήρες πρόωσης σε συστήματα CNC Άδεια Χρήσης Το παρόν υλικό υπόκειται
Σερβοκινητήρες πρόωσης σε συστήματα CNC τύπος DC μόνιμου μαγνήτη επίδραση ανάδρασης ταχογεννήτρια Γ.Βοσνιάκος-ΕΡΓΑΛΕΙΟΜΗΧΑΝΕΣ Σερβοκινητήρες πρόωσης σε συστήματα CNC Άδεια Χρήσης Το παρόν υλικό υπόκειται
6 η ΕΡΓΑΣΙΑ. Ημερομηνία Παράδοσης: 1/7/2007
 6 η ΕΡΓΑΣΙΑ Ημομηνία Παάδοσης: /7/7 Τα θέματα ίναι βαθμολογικά ισοδύναμα Άσκηση Θτικό φοτίο Q κατανέμται ομοιόμοφα κατά μήκος του θτικού άξονα y μταξύ των σημίων y και y α. Ένα ανητικό σημιακό φοτίο -
6 η ΕΡΓΑΣΙΑ Ημομηνία Παάδοσης: /7/7 Τα θέματα ίναι βαθμολογικά ισοδύναμα Άσκηση Θτικό φοτίο Q κατανέμται ομοιόμοφα κατά μήκος του θτικού άξονα y μταξύ των σημίων y και y α. Ένα ανητικό σημιακό φοτίο -
Ρομποτική II. Περιεχόμενα Μαθήματος
 Σχολή Ηλεκτρολόγων Μηχ/κών και Μηχ/κών Υπολογιστών, Ε.Μ.Π., Ακαδημαϊκό Έτος 010-11, 8ο Εξάμηνο Ρομποτική II Ευφυή και Επιδέξια Ρομποτικά Συστήματα Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου & Ρομποτικής
Σχολή Ηλεκτρολόγων Μηχ/κών και Μηχ/κών Υπολογιστών, Ε.Μ.Π., Ακαδημαϊκό Έτος 010-11, 8ο Εξάμηνο Ρομποτική II Ευφυή και Επιδέξια Ρομποτικά Συστήματα Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου & Ρομποτικής
Ανάλυση σε Πεπερασμένο Όγκο Αναφοράς. Τρόποι επίλυσης προβλημάτων Μηχανικής Ρευστών. Θεωρητική ανάλυση συστήματος
 Ανάλυση σε Πεπεασμένο Όκο Αναφοάς Τόποι επίλυσης ποβλημάτων Μηχανικής Ρευστών Θεωητική ανάλυση συστήματος Πεπεασμένοόκοαναφοάς Διαφοική ανάλυση σε απειοστό όκο Πειαματική ανάλυση Συστήματα Οι νόμοι της
Ανάλυση σε Πεπεασμένο Όκο Αναφοάς Τόποι επίλυσης ποβλημάτων Μηχανικής Ρευστών Θεωητική ανάλυση συστήματος Πεπεασμένοόκοαναφοάς Διαφοική ανάλυση σε απειοστό όκο Πειαματική ανάλυση Συστήματα Οι νόμοι της
ΔΙΑΛΕΞΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ «ΘΕΜΕΛΙΩΣΕΙΣ»
 ΔΙΑΛΕΞΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ «ΘΕΜΕΛΙΩΣΕΙΣ» 7ο Εξ. ΠΟΛ-ΜΗΧ ΜΗΧ. ΕΜΠ - Ακαδ. Ετος 005-06 ΔΙΑΛΕΞΗ Θεμελιώσεις με πασσάλους : Ομάδες πασσάλων.05.005. Κατηγοίες πασσάλων. Αξονική φέουσα ικανότητα μεμονωμένου πασσάλου.
ΔΙΑΛΕΞΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ «ΘΕΜΕΛΙΩΣΕΙΣ» 7ο Εξ. ΠΟΛ-ΜΗΧ ΜΗΧ. ΕΜΠ - Ακαδ. Ετος 005-06 ΔΙΑΛΕΞΗ Θεμελιώσεις με πασσάλους : Ομάδες πασσάλων.05.005. Κατηγοίες πασσάλων. Αξονική φέουσα ικανότητα μεμονωμένου πασσάλου.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Μηχανική Ι 22 Ιανουαρίου, 2019
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Μηχανική Ι Ιανουαρίου, 9 Καλή σας επιτυχία. Πρόβλημα Α Ένα σωματίδιο μάζας m κινείται υπό την επίδραση του πεδίου δύο σημειακών ελκτικών κέντρων, το ένα εκ των οποίων
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Μηχανική Ι Ιανουαρίου, 9 Καλή σας επιτυχία. Πρόβλημα Α Ένα σωματίδιο μάζας m κινείται υπό την επίδραση του πεδίου δύο σημειακών ελκτικών κέντρων, το ένα εκ των οποίων
Σεµινάριο Αυτοµάτου Ελέγχου
 Σεµινάριο Αυτοµάτου Ελέγχου Μάθηµα 4 Αναλυτική σύνθεση συστηµάτων αυτοµάτου ελέγχου Με συνθήκη µόνιµου σφάλµατος Με συνθήκη επιθυµητών πόλων Με επιθυµητό πρότυπο Καλλιγερόπουλος 4 1 Αναλυτική Σύνθεση συστηµάτων
Σεµινάριο Αυτοµάτου Ελέγχου Μάθηµα 4 Αναλυτική σύνθεση συστηµάτων αυτοµάτου ελέγχου Με συνθήκη µόνιµου σφάλµατος Με συνθήκη επιθυµητών πόλων Με επιθυµητό πρότυπο Καλλιγερόπουλος 4 1 Αναλυτική Σύνθεση συστηµάτων
β. ίδια κατεύθυνση με το μέτρο της γωνιακής ταχύτητας της Α διπλάσιο από το μέτρο της γωνιακής ταχύτητας της Β
 ΜΑΘΗΜΑ /ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ/ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΗΜΕΡΟΜΗΝΙΑ: ΣΕΙΡΑ: ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΜΑΘΗΜΑ /ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ/ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΗΜΕΡΟΜΗΝΙΑ: ΣΕΙΡΑ: ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
Έλεγχος ενός βαθµού ελευθερίας ροµποτικού συστήµατος
 Έλεγχος ενός βαθµού ελευθερίας ροµποτικού συστήµατος Το βασικό σχήµα ελέγχου ενός βαθµού ελευθερίας (µιάς άρθρωσης, ενός τροχού, κλπ) ροµποτικού συστήµατος φαίνεται στο Σχήµα 1. Επιθυµητή θέση Ελεγκτής
Έλεγχος ενός βαθµού ελευθερίας ροµποτικού συστήµατος Το βασικό σχήµα ελέγχου ενός βαθµού ελευθερίας (µιάς άρθρωσης, ενός τροχού, κλπ) ροµποτικού συστήµατος φαίνεται στο Σχήµα 1. Επιθυµητή θέση Ελεγκτής
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α ΗΜΕΡΟΜΗΝΙΑ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-KΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α ΗΜΕΡΟΜΗΝΙΑ: 19-10-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-KΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α ΗΜΕΡΟΜΗΝΙΑ: 19-10-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-KΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4
Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 03-04 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 0/0/03 ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α4 και δίπλα
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 03-04 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 0/0/03 ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α4 και δίπλα
HΛEKTΡOTEXNIA ΙΙ ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ
 HΛEKTΡOTEXNIA ΙΙ 3/0/09 ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ ΘΕΜΑ ο ) Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι σωστή
HΛEKTΡOTEXNIA ΙΙ 3/0/09 ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ ΘΕΜΑ ο ) Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι σωστή
Σχεδίαση τροχιάς. (α) (β) (γ) (δ) Σχήµα 2.5
 Σχεδίαση τροχιάς Η πιο απλή κίνηση ενός βραχίονα είναι από σηµείο σε σηµείο. Με την µέθοδο αυτή το ροµπότ κινείται από µία αρχική θέση σε µία τελική θέση χωρίς να µας ενδιαφέρει η ενδιάµεση διαδροµή που
Σχεδίαση τροχιάς Η πιο απλή κίνηση ενός βραχίονα είναι από σηµείο σε σηµείο. Με την µέθοδο αυτή το ροµπότ κινείται από µία αρχική θέση σε µία τελική θέση χωρίς να µας ενδιαφέρει η ενδιάµεση διαδροµή που
Αριθμητικές μέθοδοι σε ταλαντώσεις μηχανολογικών συστημάτων
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Καθηγητής κ. Σ. Νατσιάβας Αριθμητικές μέθοδοι σε ταλαντώσεις μηχανολογικών συστημάτων Στοιχεία Φοιτητή Ονοματεπώνυμο: Νατσάκης Αναστάσιος Αριθμός Ειδικού Μητρώου:
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Καθηγητής κ. Σ. Νατσιάβας Αριθμητικές μέθοδοι σε ταλαντώσεις μηχανολογικών συστημάτων Στοιχεία Φοιτητή Ονοματεπώνυμο: Νατσάκης Αναστάσιος Αριθμός Ειδικού Μητρώου:
Δυναμική Μηχανών I. Διάλεξη 22. Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ
 Δυναμική Μηχανών I Διάλεξη 22 Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ 1 Ανακοινώσεις Εξέταση Μαθήματος: 1/4/2014, 12.00 Απαιτείται αποδεικτικό ταυτότητας (Α.Τ., Διαβατήριο, Διπλ. Οδ.) Απαγορεύεται
Δυναμική Μηχανών I Διάλεξη 22 Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ 1 Ανακοινώσεις Εξέταση Μαθήματος: 1/4/2014, 12.00 Απαιτείται αποδεικτικό ταυτότητας (Α.Τ., Διαβατήριο, Διπλ. Οδ.) Απαγορεύεται
ΚΕΦΑΛΑΙΟ 5 Ο : ΣΥΝΤΟΝΙΣΜΟΣ ΑΠΛΩΝ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ
 ΚΕΦΑΛΑΙΟ 5 Ο : ΣΥΝΤΟΝΙΣΜΟΣ ΑΠΛΩΝ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ 1 Ο συντονισμός είναι μια κατάσταση κατά την οποία το φανταστικό μέρος της σύνθετης αντίστασης ενός κυκλώματος RCL μηδενίζεται. Αυτό συμβαίνει γιατί
ΚΕΦΑΛΑΙΟ 5 Ο : ΣΥΝΤΟΝΙΣΜΟΣ ΑΠΛΩΝ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ 1 Ο συντονισμός είναι μια κατάσταση κατά την οποία το φανταστικό μέρος της σύνθετης αντίστασης ενός κυκλώματος RCL μηδενίζεται. Αυτό συμβαίνει γιατί
Βιομηχανικοί Ελεγκτές
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τ.Τ Βιομηχανικοί Ελεγκτές Ενότητα #9: Αναλογικά Συστήματα Ελέγχου Κωνσταντίνος Αλαφοδήμος Τμήματος Μηχανικών Αυτοματισμού Τ.Ε. Άδειες Χρήσης Το παρόν
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τ.Τ Βιομηχανικοί Ελεγκτές Ενότητα #9: Αναλογικά Συστήματα Ελέγχου Κωνσταντίνος Αλαφοδήμος Τμήματος Μηχανικών Αυτοματισμού Τ.Ε. Άδειες Χρήσης Το παρόν
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1η (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 21/10/12
 ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1η (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 21/10/12 ΘΕΜΑ 1 ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1η (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 21/10/12 ΘΕΜΑ 1 ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 o ΔΙΑΓΩΝΙΣΜΑ ΔΕΚΕΜΒΡΙΟΣ 20: ΘΕΜΑΤΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις - 4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα
o ΔΙΑΓΩΝΙΣΜΑ ΔΕΚΕΜΒΡΙΟΣ 20: ΘΕΜΑΤΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις - 4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα
α) = β) Α 1 = γ) δ) Μονάδες 5
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 19-10-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-ΚΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4 να γράψετε
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 19-10-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-ΚΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4 να γράψετε
3. Αρμονικά Κύματα Χώρου και Επιφανείας. P, S, Rayleigh και Love
 3. Αμονικά Κύματα Χώου και Επιφανείας P, S, Rayleigh και Lve ΠΕΡΙΕΧΟΜΕΝΑ 3. Κύματα (P & S) σε ομοιογενή χώο 3. Κύματα σε ανομοιογενή μέσα με δι-επιφάνεια 3.3. Επιφανειακά κύματα Πόσθετο ιάβασμα Steven
3. Αμονικά Κύματα Χώου και Επιφανείας P, S, Rayleigh και Lve ΠΕΡΙΕΧΟΜΕΝΑ 3. Κύματα (P & S) σε ομοιογενή χώο 3. Κύματα σε ανομοιογενή μέσα με δι-επιφάνεια 3.3. Επιφανειακά κύματα Πόσθετο ιάβασμα Steven
Ροµποτικός Έλεγχος ύναµης / Μηχανικής Αντίστασης
 Ε.Μ.Π., ΣΗΜΜΥ, Ακαδηµαϊκό Έτος -5, ο Εξάµηνο Μάθηµα: Ροµποτική ΙΙ. ιδάσκων: Κ.Τζαφέστας Ροµποτικός Έλεγχος ύναµης / Μηχανικής Αντίστασης (Παράδειγµα Εφαρµογής Εθνικό Μετσόβιο Πολυτεχνείο, Σχολή ΗΜ&ΜΥ.
Ε.Μ.Π., ΣΗΜΜΥ, Ακαδηµαϊκό Έτος -5, ο Εξάµηνο Μάθηµα: Ροµποτική ΙΙ. ιδάσκων: Κ.Τζαφέστας Ροµποτικός Έλεγχος ύναµης / Μηχανικής Αντίστασης (Παράδειγµα Εφαρµογής Εθνικό Μετσόβιο Πολυτεχνείο, Σχολή ΗΜ&ΜΥ.
Κεφάλαιο 2 Εισαγωγή στα ροϊκά φαινόμενα
 Κεφάλαιο Εισαγωγή στα οϊκά φαινόμενα Σύνοψη Η έννοια του ανοικτού συστήματος (όγκος ελέγχου) Ρυθμός μεταβολής των ιδιοτήτων του συστήματος Νόμος της συνέχειας Νόμος της ομής (δυνάμεις) Γενικευμένη εξίσωση
Κεφάλαιο Εισαγωγή στα οϊκά φαινόμενα Σύνοψη Η έννοια του ανοικτού συστήματος (όγκος ελέγχου) Ρυθμός μεταβολής των ιδιοτήτων του συστήματος Νόμος της συνέχειας Νόμος της ομής (δυνάμεις) Γενικευμένη εξίσωση
Λύσεις θεμάτων Α εξεταστικής περιόδου Χειμερινού εξαμήνου
 Λύσεις θεμάτων Α εξεταστικής περιόδου Χειμερινού εξαμήνου 203 4 ΘΕΜΑ Ο (4,0 μονάδες) Στο παρακάτω σχήμα δίνεται το δομικό (λειτουργικό) διάγραμμα ενός συστήματος ελέγχου κλειστού βρόχου. α. Να προσδιοριστεί
Λύσεις θεμάτων Α εξεταστικής περιόδου Χειμερινού εξαμήνου 203 4 ΘΕΜΑ Ο (4,0 μονάδες) Στο παρακάτω σχήμα δίνεται το δομικό (λειτουργικό) διάγραμμα ενός συστήματος ελέγχου κλειστού βρόχου. α. Να προσδιοριστεί
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 Θέμα 1: ΑΓ.ΚΩΝΣΤΑΝΤΙΝΟΥ 11 -- ΠΕΙΡΑΙΑΣ -- 18532 -- ΤΗΛ. 210-4224752, 4223687 ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΤΑΛΑΝΤΩΣΕΙΣ Α. Στις παρακάτω ερωτήσεις να επιλέξετε την
Θέμα 1: ΑΓ.ΚΩΝΣΤΑΝΤΙΝΟΥ 11 -- ΠΕΙΡΑΙΑΣ -- 18532 -- ΤΗΛ. 210-4224752, 4223687 ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΤΑΛΑΝΤΩΣΕΙΣ Α. Στις παρακάτω ερωτήσεις να επιλέξετε την
Πρέσσες κοχλία. Κινηματική Δυνάμεις Έργο. Πρέσσες κοχλία. Γ.Βοσνιάκος-ΕΡΓΑΛΕΙΟΜΗΧΑΝΕΣ
 Πρέσσες κοχλία Κινηματική Δυνάμεις Έργο Γ.Βοσνιάκος-ΕΡΓΑΛΕΙΟΜΗΧΑΝΕΣ Πρέσσες κοχλία Άδεια Χρήσης Το παρόν υλικό υπόκειται σε άδειες χρήσης Creative Commons και δημιουργήθηκε στο πλαίσιο του Έργου των Ανοικτών
Πρέσσες κοχλία Κινηματική Δυνάμεις Έργο Γ.Βοσνιάκος-ΕΡΓΑΛΕΙΟΜΗΧΑΝΕΣ Πρέσσες κοχλία Άδεια Χρήσης Το παρόν υλικό υπόκειται σε άδειες χρήσης Creative Commons και δημιουργήθηκε στο πλαίσιο του Έργου των Ανοικτών
όπου ε η διηλεκτρική σταθερά του υλικού των σωµατιδίων, η ηλεκτρική διαπερατότητα του 12
 Ασκήσεις Ηλεκτοστατικών φίλτων. Αέιο θεοκασίας 5 o C ειέχει σωατίδια διαέτου, και. Το υλικό των σωατιδίων έχει διηλεκτική σταθεά ε 5. Ποιο το οιακό ηλεκτικό φότισης των σωατιδίων σε ηλεκτικό εδίο εδιακής
Ασκήσεις Ηλεκτοστατικών φίλτων. Αέιο θεοκασίας 5 o C ειέχει σωατίδια διαέτου, και. Το υλικό των σωατιδίων έχει διηλεκτική σταθεά ε 5. Ποιο το οιακό ηλεκτικό φότισης των σωατιδίων σε ηλεκτικό εδίο εδιακής
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. ΘΕΜΑ 1ο α. Τι εννοούμε με τον όρο διαμόρφωση; Ποιο σήμα ονομάζεται φέρον, ποιο διαμορφωτικό και ποιο διαμορφωμένο;
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙ ΙΚΕΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΠΟΦΟΙΤΩΝ Β ΚΥΚΛΟΥ ΤΕΧΝΙΚΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΕΚΠΑΙ ΕΥΤΗΡΙΩΝ ΕΥΤΕΡΑ 18 ΙΟΥΝΙΟΥ 2007 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΕΚΠΟΜΠΗ ΚΑΙ ΛΗΨΗ ΡΑ ΙΟΦΩΝΙΚΟΥ ΣΗΜΑΤΟΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙ ΙΚΕΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΠΟΦΟΙΤΩΝ Β ΚΥΚΛΟΥ ΤΕΧΝΙΚΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΕΚΠΑΙ ΕΥΤΗΡΙΩΝ ΕΥΤΕΡΑ 18 ΙΟΥΝΙΟΥ 2007 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΕΚΠΟΜΠΗ ΚΑΙ ΛΗΨΗ ΡΑ ΙΟΦΩΝΙΚΟΥ ΣΗΜΑΤΟΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
Ακαδημαϊκό Έτος Εξάμηνο Εαρινό Α Εξεταστική Περίοδος Σημειώσεις : ανοικτές/κλειστές Διάρκεια εξέτασης: 2 ώρες. Ημ. εξέτασης:../../.
 A(dB) ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΤΕΙ ΑΘΗΝΑΣ Μάθημα: Αναλογικά Ηλεκτρονικά Εισηγητής: Ηλίας Σταύρακας Θέμα 1 ο (μονάδες 3): Ακαδημαϊκό Έτος 201112 Εξάμηνο Εαρινό Α Εξεταστική Περίοδος Σημειώσεις :
A(dB) ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΤΕΙ ΑΘΗΝΑΣ Μάθημα: Αναλογικά Ηλεκτρονικά Εισηγητής: Ηλίας Σταύρακας Θέμα 1 ο (μονάδες 3): Ακαδημαϊκό Έτος 201112 Εξάμηνο Εαρινό Α Εξεταστική Περίοδος Σημειώσεις :
website:
 Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση και Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 29 Μαρτίου 2017 1 Συναρτήσεις μεταφοράς σε
Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση και Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 29 Μαρτίου 2017 1 Συναρτήσεις μεταφοράς σε
Σύνδεση µε µη αβαρή ράβδο
 Σύνδεση µε µη αβαή άβδο Με τη βοήθεια µιας άβδου µάζας Μ kg και µήκους L συνδέουµε τα κέντα µάζας ενός δίσκου µάζας 4kg και ενός δακτυλίου µάζας m 6kg, όπως αίνεται στο σχήµα. Ο m δίσκος και η άβδος έχουν
Σύνδεση µε µη αβαή άβδο Με τη βοήθεια µιας άβδου µάζας Μ kg και µήκους L συνδέουµε τα κέντα µάζας ενός δίσκου µάζας 4kg και ενός δακτυλίου µάζας m 6kg, όπως αίνεται στο σχήµα. Ο m δίσκος και η άβδος έχουν
Εισαγωγή στη Δυναμική Μηχανών
 Δυναμική Μηχανών Ι Διδάσκων: Αντωνιάδης Ιωάννης Εισαγωγή στη Δυναμική Μηχανών Άδεια Χρήσης Το παρόν υλικό βασίζεται στην παρουσίαση Εισαγωγή στη Δυναμική Μηχανών του καθ. Ιωάννη Αντωνιάδη και υπόκειται
Δυναμική Μηχανών Ι Διδάσκων: Αντωνιάδης Ιωάννης Εισαγωγή στη Δυναμική Μηχανών Άδεια Χρήσης Το παρόν υλικό βασίζεται στην παρουσίαση Εισαγωγή στη Δυναμική Μηχανών του καθ. Ιωάννη Αντωνιάδη και υπόκειται
ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Τ.Ε.
 ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Τ.Ε. ΝΕΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ / σε αντιπαραβολή με το ΠΑΛΑΙΟ που θα ισχύσει από το ακαδημαϊκό έτος 0-04 / Συντομογραφίες ΜΓΥ: Μάθημα Γενικής Υποδομής ΜΕΥ: Μάθημα Ειδικής Υποδομής
ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Τ.Ε. ΝΕΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ / σε αντιπαραβολή με το ΠΑΛΑΙΟ που θα ισχύσει από το ακαδημαϊκό έτος 0-04 / Συντομογραφίες ΜΓΥ: Μάθημα Γενικής Υποδομής ΜΕΥ: Μάθημα Ειδικής Υποδομής
Πολυβάθμια Συστήματα. (συνέχεια)
 Πολυβάθμια Συστήματα (συνέχεια) Ελεύθερη Ταλάντωση Xωρίς Απόσβεση Πολυβάθμια Συστήματα: Δ0- Για ένα πολυβάθμιο σύστημα που ταλαντώνεται ελεύθερα χωρίς απόσβεση, λόγω μόνο επιβαλλόμενων αρχικών μετατοπίσεων
Πολυβάθμια Συστήματα (συνέχεια) Ελεύθερη Ταλάντωση Xωρίς Απόσβεση Πολυβάθμια Συστήματα: Δ0- Για ένα πολυβάθμιο σύστημα που ταλαντώνεται ελεύθερα χωρίς απόσβεση, λόγω μόνο επιβαλλόμενων αρχικών μετατοπίσεων
ΕΞΑΣΘΕΝΗΣΗ ΕΛΑΣΤΙΚΩΝ ΚΥΜΑΤΩΝ
 ΕΞΑΣΘΕΝΗΣΗ ΕΛΑΣΤΙΚΩΝ ΚΥΜΑΤΩΝ Διάδοση κυλινδικού κύματος Καταγαφή σεισμού (Μ5.9) σε διαφοετικό πειβάλλον εξασθένησης ΗΕΞΑΣΘΕΝΗΣΗΤΩΝΕΛΑΣΤΙΚΩΝ ΚΥΜΑΤΩΝ ΣΕ ΣΧΕΣΗ ΜΕ ΤΟ ΜΕΣΟ ΔΙΑΔΟΣΗΣ ΓΕΩΜΕΤΡΙΚΗ ΔΙΑΣΠΟΡΑ ΑΠΟΣΒΕΣΗ
ΕΞΑΣΘΕΝΗΣΗ ΕΛΑΣΤΙΚΩΝ ΚΥΜΑΤΩΝ Διάδοση κυλινδικού κύματος Καταγαφή σεισμού (Μ5.9) σε διαφοετικό πειβάλλον εξασθένησης ΗΕΞΑΣΘΕΝΗΣΗΤΩΝΕΛΑΣΤΙΚΩΝ ΚΥΜΑΤΩΝ ΣΕ ΣΧΕΣΗ ΜΕ ΤΟ ΜΕΣΟ ΔΙΑΔΟΣΗΣ ΓΕΩΜΕΤΡΙΚΗ ΔΙΑΣΠΟΡΑ ΑΠΟΣΒΕΣΗ
Φίλτρα διέλευσης: (α) χαμηλών συχνοτήτων (β) υψηλών συχνοτήτων
 2 1 η ΕΝΟΤΗΤΑ Φίλτρα διέλευσης: (α) χαμηλών συχνοτήτων (β) υψηλών συχνοτήτων 3 ο Εργαστήριο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 3 Άσκηση 3 η. 3.1 Φίλτρο διελεύσεως χαμηλών συχνοτήτων ή Χαμηλοπερατό φίλτρο με μία σταθερά χρόνου.
2 1 η ΕΝΟΤΗΤΑ Φίλτρα διέλευσης: (α) χαμηλών συχνοτήτων (β) υψηλών συχνοτήτων 3 ο Εργαστήριο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 3 Άσκηση 3 η. 3.1 Φίλτρο διελεύσεως χαμηλών συχνοτήτων ή Χαμηλοπερατό φίλτρο με μία σταθερά χρόνου.
ΕΛΕΓΚΤΕΣ PID. Ελεγκτής τριών όρων Η συνάρτηση μεταφοράς του PID ελεγκτή είναι η ακόλουθη:
 ΕΛΕΓΚΤΕΣ PID Εισαγωγή Αυτό το βοήθημα θα σας δείξει τα χαρακτηριστικά καθενός από τους τρεις ελέγχους ενός PID ελεγκτή, του αναλογικού (P), του ολοκληρωτικού (I) και του διαφορικού (D) ελέγχου, καθώς και
ΕΛΕΓΚΤΕΣ PID Εισαγωγή Αυτό το βοήθημα θα σας δείξει τα χαρακτηριστικά καθενός από τους τρεις ελέγχους ενός PID ελεγκτή, του αναλογικού (P), του ολοκληρωτικού (I) και του διαφορικού (D) ελέγχου, καθώς και
Πρόγραμμα Σπουδών Ακαδημαϊκού Έτους
 1 ο Ε ξ ά μ η ν ο ( 6 Μαθήματα) Έ τ ο ς Σ π ο υ δ ώ ν Α 1. Λογισμός μιας Μεταβλητής - Γραμμική Άλγεβρα 5 5 2-2. Τεχνικό Σχέδιο 5 4 2 -. Δομημένος Προγραμματισμός 6 4 2 1 2 Φυσική 5 4 2 1 2 5. Ηλεκτρικές
1 ο Ε ξ ά μ η ν ο ( 6 Μαθήματα) Έ τ ο ς Σ π ο υ δ ώ ν Α 1. Λογισμός μιας Μεταβλητής - Γραμμική Άλγεβρα 5 5 2-2. Τεχνικό Σχέδιο 5 4 2 -. Δομημένος Προγραμματισμός 6 4 2 1 2 Φυσική 5 4 2 1 2 5. Ηλεκτρικές
ΜΕΛΕΤΗ ΣΥΣΤΗΜΑΤΟΣ ΜΑΖΑΣ-ΕΛΑΤΗΡΙΟΥ-ΑΠΟΣΒΕΣΤΗΡΑ
 ΤΕΙ ΚΡΗΤΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΙΙ ΜΕΛΕΤΗ ΣΥΣΤΗΜΑΤΟΣ ΜΑΖΑΣ-ΕΛΑΤΗΡΙΟΥ-ΑΠΟΣΒΕΣΤΗΡΑ Μ. Σφακιωτάκης mfak@taff.teicrete.gr Χειµερινό Οκτώβριος εξάµηνο 2010-11 2017 Σύστηµα Μάζας-Ελατηρίου-Αποσβεστήρα
ΤΕΙ ΚΡΗΤΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΙΙ ΜΕΛΕΤΗ ΣΥΣΤΗΜΑΤΟΣ ΜΑΖΑΣ-ΕΛΑΤΗΡΙΟΥ-ΑΠΟΣΒΕΣΤΗΡΑ Μ. Σφακιωτάκης mfak@taff.teicrete.gr Χειµερινό Οκτώβριος εξάµηνο 2010-11 2017 Σύστηµα Μάζας-Ελατηρίου-Αποσβεστήρα
Εργ.Αεροδυναμικής, ΕΜΠ. Καθ. Γ.Μπεργελές
 ΠΡΟΤΥΠΑ ΡΕΥΣΤΟΜΗΧΑΝΙΚΑ ΠΡΟΒΛΗΜΑΤΑ (Υπολογιστική Ρευστομηχανική-Πεπεασμένες διαφοές) Γ. Μπεγελές Ιανουάιος 6 C 5 4 3 Z 3 3 4 5 6 7 ZC CON:..5..5.3.35.4.45.5.55.6.65.7.75.8.85.9.95 C ΠΕΡΙΕΧΟΜΕΝΑ. Παάδειγμα
ΠΡΟΤΥΠΑ ΡΕΥΣΤΟΜΗΧΑΝΙΚΑ ΠΡΟΒΛΗΜΑΤΑ (Υπολογιστική Ρευστομηχανική-Πεπεασμένες διαφοές) Γ. Μπεγελές Ιανουάιος 6 C 5 4 3 Z 3 3 4 5 6 7 ZC CON:..5..5.3.35.4.45.5.55.6.65.7.75.8.85.9.95 C ΠΕΡΙΕΧΟΜΕΝΑ. Παάδειγμα
Σχεδίαση Ηλεκτρονικών Κυκλωμάτων RF
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ᄃ Σχεδίαση Ηλεκτρονικών Κυκλωμάτων F Ασκήσεις Ενότητας: Φίλτρα και Επαναληπτικές Ασκήσεις Στυλιανός Μυτιληναίος Τμήμα Ηλεκτρονικής,
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ᄃ Σχεδίαση Ηλεκτρονικών Κυκλωμάτων F Ασκήσεις Ενότητας: Φίλτρα και Επαναληπτικές Ασκήσεις Στυλιανός Μυτιληναίος Τμήμα Ηλεκτρονικής,
ΘΕΜΑ 1ο = = 3.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΠΕΜΠΤΗ 6 ΣΕΠΤΕΜΒΡΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ (ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΠΕΜΠΤΗ 6 ΣΕΠΤΕΜΒΡΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ (ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
Ο ελεγκτής PID χοντρικά...
 Ο ελεγκτής PID χοντρικά... Έχετε ένα αμάξι που με τέρμα γκάζι πηγαίνει 200χλμ.. Σας λέει κάποιος λοιπόν ότι θέλει να πάτε με 100 ακριβώς. Λέει κάποιος άλλος..θα πατήσω το γκάζι μέχρι την μέση και άρα θα
Ο ελεγκτής PID χοντρικά... Έχετε ένα αμάξι που με τέρμα γκάζι πηγαίνει 200χλμ.. Σας λέει κάποιος λοιπόν ότι θέλει να πάτε με 100 ακριβώς. Λέει κάποιος άλλος..θα πατήσω το γκάζι μέχρι την μέση και άρα θα
Συστήματα Αυτόματου Ελέγχου
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Συστήματα Αυτόματου Ελέγχου Ενότητα : Ψηφιακός Έλεγχος Συστημάτων Aναστασία Βελώνη Τμήμα Η.Υ.Σ Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Συστήματα Αυτόματου Ελέγχου Ενότητα : Ψηφιακός Έλεγχος Συστημάτων Aναστασία Βελώνη Τμήμα Η.Υ.Σ Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΜΗΧΑΝΙΚΕΣ ΚΑΙ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ 4/11/2012
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΜΗΧΑΝΙΚΕΣ ΚΑΙ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ 4/11/01 ΘΕΜΑ 1 ο Στις ερωτήσεις 1-5 να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΜΗΧΑΝΙΚΕΣ ΚΑΙ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ 4/11/01 ΘΕΜΑ 1 ο Στις ερωτήσεις 1-5 να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και
Βαθµολογία Προβληµάτων ΘΕΜΑ 1 ΘΕΜΑ 2.1 ΘΕΜΑ 2.2 ΘΕΜΑ 2.3 ΘΕΜΑ 3.1 ΘΕΜΑ 3.2 ΘΕΜΑ 4 ΘΕΜΑ 5.1 ΘΕΜΑ 5.2. G(s)
 ΑΠΑΓΟΡΕΥΕΤΑΙ Η ΑΝΑΤΥΠΩΣΗ ΤΩΝ ΘΕΜΑΤΩΝ ΠΡΙΝ ΤΗΝ 3 Σεπτεµβρίου 4 ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΙΙ - Τελική εξέταση Σεπτεµβρίου 4 Να επιστραφεί η εκφώνηση των θεµάτων (υπογεγραµµένη από τον εξεταστή) ΕΠΩΝΥΜΟ
ΑΠΑΓΟΡΕΥΕΤΑΙ Η ΑΝΑΤΥΠΩΣΗ ΤΩΝ ΘΕΜΑΤΩΝ ΠΡΙΝ ΤΗΝ 3 Σεπτεµβρίου 4 ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΙΙ - Τελική εξέταση Σεπτεµβρίου 4 Να επιστραφεί η εκφώνηση των θεµάτων (υπογεγραµµένη από τον εξεταστή) ΕΠΩΝΥΜΟ
1. Ηλεκτρικοί κινητήρες- σερβοκινητήρας 2. Ελεγκτές. ΜΠΔ, 9 Ο Εξάμηνο Σάββας Πιπερίδης
 www.robolab.tuc.gr 1. Ηλεκτρικοί κινητήρες- σερβοκινητήρας 2. Ελεγκτές ΜΠΔ, 9 Ο Εξάμηνο Σάββας Πιπερίδης 1. Ηλεκτρικοί κινητήρες σερβοκινητήρας R/C σέρβο βηματικός κινητήρας 2 1. Ηλεκτρικοί κινητήρες σερβοκινητήρας
www.robolab.tuc.gr 1. Ηλεκτρικοί κινητήρες- σερβοκινητήρας 2. Ελεγκτές ΜΠΔ, 9 Ο Εξάμηνο Σάββας Πιπερίδης 1. Ηλεκτρικοί κινητήρες σερβοκινητήρας R/C σέρβο βηματικός κινητήρας 2 1. Ηλεκτρικοί κινητήρες σερβοκινητήρας
β. Ο συντελεστής ποιότητας Q π δείχνει ότι η τάση U L =U C είναι Q π φορές µεγαλύτερη από την τάση τροφοδοσίας. Σ
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑ Α Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΛ (ΟΜΑ Α Β ) ΣΑΒΒΑΤΟ 6/04/06 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΗΛΕΚΤΡΟΤΕΧΝΙΑ ΙΙ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΕΝ ΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ ο ) Να χαρακτηρίσετε
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑ Α Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΛ (ΟΜΑ Α Β ) ΣΑΒΒΑΤΟ 6/04/06 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΗΛΕΚΤΡΟΤΕΧΝΙΑ ΙΙ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΕΝ ΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ ο ) Να χαρακτηρίσετε
Συστήματα Αυτομάτου Ελέγχου ΙΙ Ασκήσεις Πράξης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΑΤΤΙΚΗΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΗΣ ΣΧΕΔΙΑΣΗΣ & ΠΑΡΑΓΩΓΗΣ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΙΙ ΑΣΚΗΣΕΙΣ ΠΡΑΞΗΣ Αν Καθ: Δ ΔΗΜΟΓΙΑΝΝΟΠΟΥΛΟΣ Καθ Εφαρμ: Σ ΒΑΣΙΛΕΙΑΔΟΥ Συστήματα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΑΤΤΙΚΗΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΗΣ ΣΧΕΔΙΑΣΗΣ & ΠΑΡΑΓΩΓΗΣ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΙΙ ΑΣΚΗΣΕΙΣ ΠΡΑΞΗΣ Αν Καθ: Δ ΔΗΜΟΓΙΑΝΝΟΠΟΥΛΟΣ Καθ Εφαρμ: Σ ΒΑΣΙΛΕΙΑΔΟΥ Συστήματα
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ. γ. υ = χ 0 ωσυνωt δ. υ = -χ 0 ωσυνωt. Μονάδες 5
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 29 ΜΑΪΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ): ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΠΤΑ (7) ΘΕΜΑ 1ο Στις ερωτήσεις
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 29 ΜΑΪΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ): ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΠΤΑ (7) ΘΕΜΑ 1ο Στις ερωτήσεις
Προσομοίωση Monte Carlo
 Κλασσική ατομιστική ποσομοίωση Ποσομοίωση Mot Crlo Δ.Γ. Παπαγεωγίου Λίγη ιστοία 777 Gorgs Lous LClrc, Cot d Buffo: Θεωητική πόβλεψη για το πείαμα τυχαίας ίψης βελόνας. 90 Lzzr: Πειαματική επιβεβαίωση της
Κλασσική ατομιστική ποσομοίωση Ποσομοίωση Mot Crlo Δ.Γ. Παπαγεωγίου Λίγη ιστοία 777 Gorgs Lous LClrc, Cot d Buffo: Θεωητική πόβλεψη για το πείαμα τυχαίας ίψης βελόνας. 90 Lzzr: Πειαματική επιβεβαίωση της
Σύστημα (system) είναι ένα σύνολο φυσικών στοιχείων, πραγμάτων ατόμων, μεγεθών ή εννοιών, που σχηματίζουν μιαν ενότητα και δρα σαν μια ενότητα.
 Σύστημα (system) είναι ένα σύνολο φυσικών στοιχείων, πραγμάτων ατόμων, μεγεθών ή εννοιών, που σχηματίζουν μιαν ενότητα και δρα σαν μια ενότητα. π.χ. Το ηλιακό σύστημα, το σύνολο δηλαδή των πλανητών του
Σύστημα (system) είναι ένα σύνολο φυσικών στοιχείων, πραγμάτων ατόμων, μεγεθών ή εννοιών, που σχηματίζουν μιαν ενότητα και δρα σαν μια ενότητα. π.χ. Το ηλιακό σύστημα, το σύνολο δηλαδή των πλανητών του
ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΙΙ
 ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΙΙ ΕΦΑΡΜΟΣΜΕΝΗ ΘΕΩΡΙΑ ΑΝΑΜΟΝΗΣ ΜΕΡΟΣ Ι Ν. ΔΕΡΒΑΚΟΥ Σημειώσεις Πααδόσεων Αθήνα 23 ΕΦΑΡΜΟΣΜΕΝΗ ΘΕΩΡΙΑ ΑΝΑΜΟΝΗΣ Ι. ΕΙΣΑΓΩΓΗ Βασική Δομή Ποβλημάτων Αναμονής Σύστημα Αναμονής Πηγή ποσέλευσης
ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΙΙ ΕΦΑΡΜΟΣΜΕΝΗ ΘΕΩΡΙΑ ΑΝΑΜΟΝΗΣ ΜΕΡΟΣ Ι Ν. ΔΕΡΒΑΚΟΥ Σημειώσεις Πααδόσεων Αθήνα 23 ΕΦΑΡΜΟΣΜΕΝΗ ΘΕΩΡΙΑ ΑΝΑΜΟΝΗΣ Ι. ΕΙΣΑΓΩΓΗ Βασική Δομή Ποβλημάτων Αναμονής Σύστημα Αναμονής Πηγή ποσέλευσης
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΑΝΕΛΛΗΝΙΕΣ ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΑΝΕΛΛΗΝΙΕΣ 2001 ΘΕΜΑΤΑ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 29 ΜΑΪΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ): ΦΥΣΙΚΗ ΘΕΜΑ 1 ο
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΑΝΕΛΛΗΝΙΕΣ 2001 ΘΕΜΑΤΑ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 29 ΜΑΪΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ): ΦΥΣΙΚΗ ΘΕΜΑ 1 ο
ΤΑΛΑΝΤΩΣΕΙΣ. ενέργεια είναι ίση µε την κινητική ενέργεια. Σε αποµάκρυνση θα ισχύει: 1 της ολικής ενέργειας. t π cm/s.
 Ονοµατεπώνυµο: ιάρκεια: 3 ώρες ΤΑΛΑΝΤΩΣΕΙΣ ΘΕΜΑ 1 Οδηγία: Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Έστω ένα σωµα
Ονοµατεπώνυµο: ιάρκεια: 3 ώρες ΤΑΛΑΝΤΩΣΕΙΣ ΘΕΜΑ 1 Οδηγία: Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Έστω ένα σωµα
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2018 ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2018 ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Α Α1. γ Α2. δ Α3. α Α4. δ Α5. α) Λάθος β) Σωστό γ) Λάθος δ) Σωστό ε) Λάθος ΘΕΜΑ Β Β1. α) Σωστή απάντηση είναι η ( i. ) β)
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2018 ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Α Α1. γ Α2. δ Α3. α Α4. δ Α5. α) Λάθος β) Σωστό γ) Λάθος δ) Σωστό ε) Λάθος ΘΕΜΑ Β Β1. α) Σωστή απάντηση είναι η ( i. ) β)
P l+1 (cosa) P l 1 (cosa) 2δ l,0 1
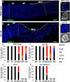 Λεοντσ ίνης Στέφανος Ηλεκτομαγνητισ μός 3 η Σειά Ασ κήσ εων 3 Tο δυναμικό λόγω αζιμουθιακής σ υμμετίας θα έχει τη μοφή φ r, θ [ Al + B l r l+] l cosθ Λόγω l Φ οιακών σ υνθηκών έχω: Φ in r R Φ out r R και
Λεοντσ ίνης Στέφανος Ηλεκτομαγνητισ μός 3 η Σειά Ασ κήσ εων 3 Tο δυναμικό λόγω αζιμουθιακής σ υμμετίας θα έχει τη μοφή φ r, θ [ Al + B l r l+] l cosθ Λόγω l Φ οιακών σ υνθηκών έχω: Φ in r R Φ out r R και
Ταλαντωτές. Ηλεκτρονική Γ Τάξη Β εξάμηνο Μάρτιος 2011 Επ. Καθ. Ε. Καραγιάννη
 Ταλαντωτές Ηλεκτρονική Γ Τάξη Β εξάμηνο Μάρτιος Επ. Καθ. Ε. Καραγιάννη Ταλαντωτές ΑΝΑΔΡΑΣΗ Στοιχεία Ταλάντωσης Ενισχυτής OUT Ταλαντωτής είναι ένα κύκλωμα που παράγει ηλεκτρικό σήμα σταθερής συχνότητας
Ταλαντωτές Ηλεκτρονική Γ Τάξη Β εξάμηνο Μάρτιος Επ. Καθ. Ε. Καραγιάννη Ταλαντωτές ΑΝΑΔΡΑΣΗ Στοιχεία Ταλάντωσης Ενισχυτής OUT Ταλαντωτής είναι ένα κύκλωμα που παράγει ηλεκτρικό σήμα σταθερής συχνότητας
ΚΕΦΑΛΑΙΟ 10 ΤΟ ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΟ ΠΕ ΙΟ
 ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ ΤΟ ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΟ ΠΕ ΙΟ. Εξισώσεις Maxwell Όπως έχουµε, ήδη, αναφέει, ένα ηλεκτοστατικό πεδίο E µποεί να υφίσταται ανεξάτητα από την παουσία ή όχι µαγνητικού πεδίου H, όπως για
ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ ΤΟ ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΟ ΠΕ ΙΟ. Εξισώσεις Maxwell Όπως έχουµε, ήδη, αναφέει, ένα ηλεκτοστατικό πεδίο E µποεί να υφίσταται ανεξάτητα από την παουσία ή όχι µαγνητικού πεδίου H, όπως για
