Kάθε γνήσιο αντίτυπο φέρει την υπογραφή του συγγραφέα. Copyright: Κτενιαδάκης Μιχάλης, Eκδόσεις Zήτη, Ιούνιος 2010, Θεσσαλονίκη

Transcript

1

2 Kάθε γνήσιο αντίτυπο φέρει την υπογραφή του συγγραφέα Με το συγγραφέα επικοινωνείτε: ISBN Copyright: Κτενιαάκης Μιχάης, Eκόσεις Zήτη, Ιούνιος 00, Θεσσαονίκη Tο παρόν έργο πνευματικής ιιοκτησίας προστατεύεται κατά τις ιατάξεις του Eηνικού νόμου (N./993 όπως έχει τροποποιηθεί και ισχύει σήμερα) και τις ιεθνείς συμβάσεις περί πνευματικής ιιοκτησίας. παγορεύεται απούτως η άνευ γραπτής άειας του εκότη και συγγραφέα κατά οποιοήποτε τρόπο ή μέσο αντιγραφή, φωτοανατύπωση και εν γένει αναπαραγωγή, εκμίσθωση ή ανεισμός, μετάφραση, ιασκευή, αναμετάοση στο κοινό σε οποιαήποτε μορφή (ηεκτρονική, μηχανική ή άη) και η εν γένει εκμετάευση του συνόου ή μέρους του έργου. Φωτοστοιχειοθεσία Eκτύπωση Βιβιοεσία Π. ZHTH & Σια OE 8 ο χμ Θεσσαονίκης - Περαίας T.Θ. 47 Περαία Θεσσαονίκης T.K Tη.: Fax: info@ziti.gr BIBΛIOΠΩΛEIO ΘΕΣΣΑΛΟΝΙΚΗΣ - KENTPIKH ΔIΘEΣH: ρμενοπούου Θεσσαονίκη Tη.: Fax sales@ziti.gr BIBΛIOΠΩΛEIO ΘHNΩN - ENΩΣH EKΔOTΩN BIBΛIOY ΘEΣΣΛONIKHΣ: Στοά του Bιβίου (Πεσμαζόγου 5) ΘHN Tη.-Fax: ΠOΘHKH ΘHNΩN - ΠΩΛHΣH XONΔPIKH: σκηπιού 60 - Eξάρχεια 4 7, θήνα Tη.-Fax: athina@ziti.gr ΗΛΕΚΤΡΟΝΙΚΟ ΒΙΒΛΙΟΠΩΛΕΙΟ:

3 Πρόογος Δομή και περιεχόμενο Ο κύριος στόχος αυτού του βιβίου είναι να παρουσιάσει με από, κατανοητό αά και επιστημονικά θεμειωμένο τρόπο, ένα μεγάο μέρος του γνωστικού α- ντικειμένου της «ΜΕΤΑΔΟΣΗΣ ΘΕΡΜΟΤΗΤΑΣ» και συγκεκριμένα αυτό που αποτεεί τον βασικό «κορμό» των σχετικών σπουών στα Πανεπιστήμια και τα ΤΕΙ, ενώ ταυτόχρονα συνέεται περισσότερο με συνήθη τεχνικά προβήματα και εφαρμογές του Μηχανικού. Τα περισσότερα από αυτά τα προβήματα, στα οποία με οποιοήποτε τρόπο εμπέκεται η μεταφορά θερμότητας, μπορούν να αντιμετωπιστούν, με καή προσέγγιση, ως μονοιάστατα και μόνιμα. Σ αυτές τις περιπτώσεις εν απαιτείται η χρήση προχωρημένων μαθηματικών (που, βέβαια, είναι απαραίτητα για την εμβάθυνση σε μεταπτυχιακό επίπεο ή στη μεέτη των χρονικά μεταβαόμενων φαινομένων). Έτσι, για να υπάρχει άμεση πρόσβαση στο απαραίτητο θεωρητικό υπόβαθρο αά και αξιοποίησή του στην επίυση των προβημάτων, επιέχθηκε να καυφθεί η ύη αφενός με μορφή συνοπτικής θεωρίας Τυποογίου και αφετέρου με μια επιογή από αναυτικά υμένες ασκήσεις. Τόσο στη συνοπτική θεωρία Τυποόγιο όσο και στην επεξεργασία των ασκήσεων αποφεύχθηκαν (όσο ήταν επιτρεπτό) τα πούποκα μαθηματικά και οι προαπαιτούμενες εξειικευμένες γνώσεις από άα μαθήματα. Έτσι, αρκετοί φοιτητές εν θα αποθαρρύνονται κατά τη μεέτη τους αά και ποοί επαγγεματίες Μηχανικοί θα μπορούν να προσεγγίσουν ευκοότερα τη ύση καθημερινών τεχνικών προβημάτων. Ωστόσο, και οι μεν και οι ε, ποές φορές βρίσκονται μπροστά στην ανάγκη να έχουν μια άμεση γνώση για: την επίπτωση που έχει στο σχειασμό ή στη ειτουργία ενός συστήματος η μεταβοή μιας παραμέτρου. την επιογή του καταηότερου υικού ή συσκευής προκειμένου να επιτευχθούν ορισμένες απαιτήσεις. την πιθανότητα ανάπτυξης θερμοκρασιών, που θα θέσουν σε κίνυνο την αντοχή κάποιων υικών ή την ομαή εκτέεση κάποιων ιεργασιών κπ.

4 4 Εφαρμογές Μετάοσης Θερμότητας Τα εμφανή αά και τα ενεχομένως μη προφανή αποτεέσματα από μια επέμβαση/ενέργεια σε ένα τεχνικό σύστημα. Για να καυφθεί καύτερα αυτή η ανάγκη, καταβήθηκε προσπάθεια να περιοριστούν στις εντεώς απαραίτητες οι καθαρά θεωρητικές ασκήσεις (που βοηθούν στην αρχική κατανόηση των ιαφόρων φαινομένων) και να περιηφθούν κυρίως ασκήσεις που αναφέρονται σε πρακτικά προβήματα και εφαρμογές που σχετίζονται με τη μετάοση της θερμότητας. Για τον ίιο όγο προτιμήθηκε, αντί να παρουσιαστούν περισσότερες απές ασκήσεις, να περιηφθούν ιγότερες, αά με ιεξοικότερη ανάυση/εξέταση η καθεμία (ιαφορετικά ζητούμενα, ααγή συνθηκών και εομένων, κ.π). Οι ασκήσεις χαρακτηρίζονται, ανάογα με το βαθμό υσκοίας τους, με έως 4 «αστεράκια» ( ), για να μπορεί ο αναγνώστης να προγραμματίσει ή να προσαρμόσει κατάηα τη μεέτη του. Η επεξεργασία των ασκήσεων γίνεται με τρόπο που βοηθά τον αναγνώστη να αξιοποιήσει τις αντίστοιχες γνώσεις από τη θεωρία και να χρησιμοποιήσει μεθοικά τις κατάηες κάθε φορά σχέσεις, ανάογα με τα ιαθέσιμα εομένα και τις ιιαιτερότητες της άσκησης. Μετά το υποογιστικό μέρος, παρατίθεται, στο τέος κάθε άσκησης, ένα σύντομο σχόιο συμπέρασμα τεχνικός κανόνας, ίνοντας έτσι μια «ποιοτική» προσέγγιση, που προκύπτει από την επεξεργασία και τη ύση της. Αυτή η συνοπτική ιατύπωση είναι, συχνά, πού χρήσιμη για τον μηχανικό στην καθημερινή πράξη. Τα σχήματα μπορεί να υποείπονται μιας πιο άρτιας και επεξεργασμένης εμφάνισης, αά σκόπιμα επιέχθηκε να είναι απώς ευπαρουσίαστα, ώστε να πησιάζουν τον τρόπο κατασκευής και σχείασής τους από ένα φοιτητή ή επαγγεματία μηχανικό κατά τη μεέτη ενός προβήματος. Επίσης, για τον γρήγορο εντοπισμό των ασκήσεων που πησιάζουν περισσότερο στο συγκεκριμένο κάθε φορά πρόβημα που έχει να αντιμετωπίσει ο αναγνώστης, έχει συμπεριηφθεί στο βιβίο και ο «Οηγός Αναζήτησης Ασκήσεων». Σ αυτόν ίονται, με μορφή πίνακα: ο αριθμός της άσκησης, μια σύντομη περιγραφή του περιεχομένου της, η επικρατούσα γεωμετρία αυτής καθώς και τυχόν πρόσθετα χαρακτηριστικά στοιχεία. Στο Παράρτημα ίονται οι απαραίτητοι Πίνακες και Διαγράμματα, τα περισσότερα από τα οποία είναι πρωτότυπα, με μορφή που βοηθά στην ευχερή χρήση και ανάγνωσή τους.

5 Πρόογος 5 Ειικές επισημάνσεις Σε όες τις ασκήσεις χρησιμοποιούνται μονάες του συστήματος SI. Οι τυχόν απαιτούμενες μετατροπές μονάων γίνονται εξ αρχής, έτσι ώστε κατά τις αντικαταστάσεις τιμών στις ιάφορες χρησιμοποιούμενες σχέσεις εν αναγράφονται και οι αντίστοιχες μονάες. Μόνο στο τεικό αποτέεσμα γράφεται η μονάα του μεγέθους στο SI. Σε ορισμένες ασκήσεις προτιμήθηκε να ξαναγίνει το σχήμα, συμπηρωμένο με όα τα απαραίτητα για τη ύση, εομένα ή ζητούμενα, μεγέθη (παρά το ότι ίεται στην εκφώνηση). Έτσι ο αναγνώστης θα μπορεί να κατανοήσει πηρέστερα και να εξασκηθεί καύτερα στη ιαικασία αντιμετώπισης του προβήματος. Ακρίβεια 4 σημαντικών ψηφίων είναι αρκετή για προβήματα της καθημερινής πράξης του μηχανικού εκτός πού ίγων εξαιρέσεων. Ποές εξισώσεις ύνονται στις ασκήσεις με τη μέθοο οκιμής σφάματος ή ιαοχικών προσεγγίσεων. Είναι προφανές ότι μπορούν ευκοότερα, γρηγορότερα και ακριβέστερα να υθούν μέσω Η/Υ με τη βοήθεια ογιστικών φύων (π.χ. excel) ή μαθηματικών προγραμμάτων (π.χ. mathcad, matlab κπ). Ευχαριστίες Θεωρώ επιβεβημένο να εκφράσω τις ευχαριστίες μου σε όους τους συναέφους (εκπαιευτικούς και επαγγεματίες), φοιτητές, φίους και συνεργάτες, που με οποιοήποτε τρόπο, άμεσα ή έμμεσα, βοήθησαν στην οοκήρωση και την καύτερη παρουσίαση του βιβίου, με την ενθάρρυνση, τη βοήθεια, τις προτροπές ή τις υποείξεις τους. Ιιαίτερες ευχαριστίες, αά και ευγνωμοσύνη, οφείω στα μέη της οικογένειάς μου, για την ανοχή και υπομονή που έειξαν για όσο καιρό κράτησε η όη προσπάθεια συγγραφής του βιβίου. Αυτονόητο είναι ότι θα θεωρήσω ιιαίτερα ευπρόσεκτο οποιοήποτε εποικοομητικό σχόιο από τους φοιτητές και από κάθε αναγνώστη για άθη ή παραείψεις ή τυχόν υποείξεις για βετίωση του βιβίου (mkten@staff.teicrete.gr). Ηράκειο, Μάιος 00 Μιχ. Ι. Κτενιαάκης

6 Περιεχόμενα Οροογία και Αντιστοιχία Συμβόων Μονάων... 9 Τυποόγιο Κεφάαιο : Αγωγή Μονοιάστατη μετάοση θερμότητας με αγωγή (χωρίς θερμικές πηγές) Μονοιάστατη μετάοση θερμότητας με αγωγή (με θερμικές πηγές)... 8 Κεφάαιο : Συναγωγή (και Αγωγή).... Βασικές έννοιες στη μετάοση θερμότητας με συναγωγή.... Μονοιάστατη μετάοση θερμότητας με συναγωγή και αγωγή....3 Επιφάνειες με πτερύγια Κεφάαιο 3: Θερμική ακτινοβοία επιφανειών Βασικές έννοιες και ορισμοί στην ακτινοβοία Ακτινοβοία μαύρου σώματος Ακτινοβοία γκρίζων σωμάτων Συνααγή θερμότητας με ακτινοβοία Κεφάαιο 4: Σύνθετα φαινόμενα μετάοσης θερμότητας Κεφάαιο 5: Εναάκτες θερμότητας Ασκήσεις Κεφάαιο : Αγωγή Κεφάαιο : Συναγωγή και Αγωγή Κεφάαιο 3: Θερμική Ακτινοβοία Κεφάαιο 4: Σύνθετα Φαινόμενα Κεφάαιο 5: Εναάκτες Θερμότητας

7 8 Εφαρμογές Μετάοσης Θερμότητας Οηγός Αναζήτησης Ασκήσεων Κεφάαιο : Αγωγή Κεφάαιο : Συναγωγή και Αγωγή Κεφάαιο 3: Θερμική Ακτινοβοία Κεφάαιο 4: Σύνθετα Φαινόμενα Κεφάαιο 5: Εναάκτες Θερμότητας Βιβιογραφία Παράρτημα Πίνακες Διαγράμματα και Υποογιστικές Σχέσεις

8 4 Κεφ. : Αγωγή Κεφ. ΑΓΩΓΗ. ΜΟΝΟΔΙΑΣΤΑΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ ΜΕ ΑΓΩΓΗ Νόμος αγωγιμότητας του Fourier Αγωγή ια μέσου απού επίπεου τοιχώματος (πάκας), με σταθ. Τύπος / Σχέση Θερμορροή κατά την κατεύθυνση n, κάθετη σε μια θ ισοθερμοκρασιακή επιφάνεια Α: n Αν η θερμοκρασία μεταβάεται μόνο κατά μία ιεύθυνση x (οπότε dx ): dx dθ (θ θ ) θ (θ θ ) θ ή R: Συντε. θερμικής αντίστασης στρώσης (m K/W) Λ: Συντ. θερμοιαφυγής επίπεης στρώσης (W/m K) R θ : Θερμική αντίσταση επίπεης στρώσης (K/W) Αρ.σχ. {-0} {-0} {-03} {-04} Αγωγή ια μέσου απού επίπεου τοιχώματος (πάκας), με o (+bθ) o b (θ θ ) (θ θ ) + m Επίσης: (θ θ ) όπου m η μέση τιμή του (η. στην θ m θ+ θ ) {-05} {-06} Αγωγή ια μέσου σύνθετου επίπεου τοιχώματος, με n στρώσεις ιαφορετικών υικών, με σταθερούς,, n. Οι θερμοκρασίες ιεπαφής θ, θ 3 κπ. βρίσκονται από σχέσεις της μορφής: θ θ π.χ. π.χ. π.χ. n n θ θ θ 3 θ + 3 θ3 θn n 3 n κ.ο.κ. {-07} {-08} {-09} {-0}

9 Τυποόγιο 5 (ΧΩΡΙΣ ΘΕΡΜΙΚΕΣ ΠΗΓΕΣ) Σχήμα Χρήση / Συνθήκες εφαρμογής / Παρατηρήσεις n dn x dx θ dθ θ θ+dθ Το υικό είναι ομογενές. : Ο συντεεστής θερμικής αγωγιμότητας του υικού (W/mK). Μπορεί να είναι σταθερός ή εξαρτώμενος από τη θερμοκρασία. Ισοθερμοκρασιακές επιφάνειες θ θ Τοίχωμα αρκετά μεγάο, εμβαού Α. Η θερμορροή μεταίεται ομοιόμορφα μόνο κατά την κατεύθυνση x, (κάθετα στο τοίχωμα). θ x Η ιακεκομμένη γραμμή παριστά την μεταβοή της θερμοκρασίας μέσα στο τοίχωμα (γραμμική). : Πυκνότητα θερμορροής (W/m ) θ Τοίχωμα αρκετά μεγάο, εμβαού Α. θ (Αν b>0) Η θερμορροή μεταίεται ομοιόμορφα κατά την κατεύθυνση x, (κάθετα στο τοίχωμα). θ Η ιακεκομμένη γραμμή παριστά την μεταβοή της θερμοκρασίας μέσα στο τοίχωμα (παραβοή). x θ θ θ 3 x θ 3 θ Τοίχωμα αρκετά μεγάο, εμβαού Α. Η θερμορροή μεταίεται ομοιόμορφα κατά την κατεύθυνση x, (κάθετα στο τοίχωμα). Οι στρώσεις βρίσκονται σε πού καή επαφή μεταξύ τους. Διαφορετικά, παρεμβάεται και πρόσθετος συντεεστής θερμικής αντίστασης επαφής, R (m K/W) που προστίθεται στον παρονομαστή. Η ιακεκομμένη γραμμή παριστά την μεταβοή της θερμοκρασίας μέσα στο τοίχωμα (γραμμική, αά με ιαφορετική κίση σε κάθε στρώση). 3

10 6 Κεφ. : Αγωγή Αγωγή ια μέσου απού κυινρικού τοιχώματος (σωήνα), με σταθ. Αγωγή ια μέσου σύνθετου κυινρικού τοιχώματος, με n στρώσεις ιαφορετικών υικών, με σταθερούς,, n. Αγωγή ια μέσου απού σφαιρικού τοιχώματος, με σταθ. Αγωγή ια μέσου σύνθετου σφαιρικού τοιχώματος, με n στρώσεις ιαφορετικών υικών, με σταθερούς,, n. πl (θ θ ) d ln d d ln π d d ln πl d Τύπος / Σχέση θ θ ή l d ln π d R: Συντεεστής θερμικής αντίστασης κυινρικής στρώσης (mk/w) R θ : Θερμική αντίσταση κυινρικής στρώσης (K/W) θ θ l π d π d π d Οι θερμοκρασίες θ θ3 π.χ. ιεπαφής l d ln 3 θ, θ 3 κπ. π d βρίσκονται από σχέσεις π.χ. της μορφής: d ln + d3 ln dn+ ln n n 4π (θ θ ) r r θ θ Επίσης: 4π r r Οι θερμοκρασίες ιεπαφής θ, θ 3 κπ. βρίσκονται από σχέσεις της μορφής: θ θ l π d π d θ θ 34 d3 ln + d4 ln π r r 4nπ rn r n + θ θ π.χ. 4π r r θ θ 3 + 4π r r 4π r r3 Αρ.σχ. {-} {-} {-3} {-4} {-5} {-6} {-7} {-8} {-9}

11 Τυποόγιο 7 Σχήμα Χρήση / Συνθήκες εφαρμογής / Παρατηρήσεις θ Τοίχωμα αρκετά μεγάου μήκους l. Η θερμορροή μεταίεται ομοιόμορφα, μόνο ακτινικά. θ d d θ θ d d d 3 d 4 Τοίχωμα αρκετά μεγάου μήκους l. θ 3 θ Η θερμορροή μεταίεται ομοιόμορφα, μόνο ακτινικά. Οι στρώσεις βρίσκονται σε πού καή επαφή μεταξύ τους. Διαφορετικά, παρεμβάεται και πρόσθετος συντεεστής θερμικής αντίστασης επαφής, R (m K/W). Τότε προστίθεται στον R παρονομαστή ο όρος πd, όπου d R η ιάμετρος στην οποία υπάρχει μη τέεια επαφή των R στρώσεων. θ Η θερμορροή μεταίεται ομοιόμορφα προς όες τις κατευθύνσεις (ακτινικά). r θ r r r r 3 θ θ θ 3 θ Η θερμορροή μεταίεται ομοιόμορφα προς όες τις κατευθύνσεις (ακτινικά). Οι στρώσεις βρίσκονται σε πού καή επαφή μεταξύ τους. r 4

12 8 Κεφ. : Αγωγή. ΜΟΝΟΔΙΑΣΤΑΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ ΜΕ ΑΓΩΓΗ Χαρακτηριστικά θερμικών πηγών Αγωγή σε επίπεο τοίχωμα με πηγές ( σταθ.) Αγωγή σε κυινρικό τοίχωμα με πηγές ( σταθ.) Τύπος / Σχέση Θερμική ισχύς ανά μονάα όγκου ( ειική θερμοϊσχύς: (W/m 3 ) V όπου η θερμική ισχύς που παράγεται μέσα στον όγκο V ενός υικού. ΣΗΜΕΙΩΣΗ: Σε κάθε ισοθερμοκρασιακή επιφάνεια, dθ ισχύει ο νόμος του Fourier: dn Αρ.σχ. {-0} Γενική ύση για την κατανομή της θερμοκρασίας: θ(x) x + Cx + C {-} Οι σταθερές C και C προσιορίζονται από τις οριακές συνθήκες. Επιπέον, σε οποιαήποτε θέση x, θα προκύψει: x C {-} Αν π.χ. είναι γνωστές οι θ και θ, τότε: θ(0) θ και θ() θ Αν υπάρχει μετάοση θερμότητας από μια πευρά, π.χ. στη θέση, του τοιχώματος προς/από ρευστό, θερμοκρασίας θ ο, με αντίστοιχο συντε. μεταφοράς θερμότητας h, τότε: h(θ θ o) {-3} x Γενική ύση για την κατανομή της θερμοκρασίας : θ(r) r + C lnr + C 4 Οι σταθερές C και C προσιορίζονται από τις οριακές συνθήκες. Επιπέον, σε οποιαήποτε θέση r, θα r C προκύψει: r Αν π.χ. είναι γνωστές οι θ και θ, τότε : θ(r ) θ και θ(r ) θ Αν υπάρχει μετάοση θερμότητας από μια επιφάνεια, π.χ. την εξωτερική (r ), του τοιχώματος προς/από ρευστό, θερμοκρασίας θ ο, με συντε. μεταφοράς θερμότητας h, τότε: h(θ θ o) r r {-4} {-5} {-6}

13 Τυποόγιο 9 (ΜΕ ΘΕΡΜΙΚΕΣ ΠΗΓΕΣ) Σχήμα Χρήση / Συνθήκες εφαρμογής/παρατηρήσεις Η θερμική ισχύς που παράγεται (από θερμικές πηγές) είναι θετική. Μπορεί όμως και να απορροφάται (σε θερμικές καταβόθρες) οπότε είναι αρνητική. Οι θερμικές πηγές (ή καταβόθρες) θεωρούνται ομοιόμορφα κατανεμημένες μέσα στη μάζα του υικού. θ θ θ max Τοίχωμα αρκετά μεγάο, εμβαού Α. Η θερμορροή μεταίεται ομοιόμορφα μόνο κατά την κατεύθυνση x, (κάθετα στο τοίχωμα). θ x θ θ θ max Σωήνας αρκετά μεγάου μήκους l. Η θερμορροή μεταίεται ομοιόμορφα, μόνο ακτινικά. d d

14 0 Κεφ. : Αγωγή Συμπαγής κύινρος ακτίνας r c : (ράβος με πηγές ή αγωγός, ιαρρεόμενος από ρεύμα) Αγωγή σε σφαιρικό τοίχωμα με πηγές ( σταθ.) Συμπαγής σφαίρα ακτίνας r s : με πηγές Τύπος / Σχέση Αρ.σχ. Γενική ύση για την κατανομή της θερμοκρασίας: θ(r) r + C {-7} 4 Η σταθερά C ορίζεται από μία οριακή συνθήκη. Αν π.χ. είναι γνωστή η θ, τότε θ(r c ) θ, οπότε προκύπτει: θ(r) θ + (rc r ) {-8} 4 Η μέγιστη θερμοκρασία θ max στο κέντρο της ράβου (r0): θmax θ0 θ + {-9} r c 4 Για ηεκτρικό αγωγό RI, όπου: {-30} Ι Η ένταση του ρεύματος (σε Α) R H ηεκτρική αντίσταση R του αγωγού (σε Ω) (Για την αντίσταση R β. απέναντι ΠΑΡΑΤΗΡΗΣΗ) Γενική ύση για την κατανομή της θερμοκρασίας: C θ(r) r + C {-3} 6 r Οι σταθερές C και C προσιορίζονται από τις οριακές συνθήκες. Αν π.χ. είναι γνωστές οι θ και θ, τότε : θ(r ) θ και θ(r ) θ Αν υπάρχει μετάοση θερμότητας από μια επιφάνεια, π.χ. την εξωτερική (r ), της σφαίρας προς/από ρευστό, θερμοκρασίας θ ο, με συντε. μεταφοράς θερμότητας h, τότε: h(θ θ o) {-3} r r s Γενική ύση για την κατανομή της θερμοκρασίας: θ(r) r + C {-33} 6 Η σταθερά C ορίζεται από μία οριακή συνθήκη. Αν π.χ. είναι γνωστή η θ, τότε θ(r s ) θ, οπότε προκύπτει: θ(r) θ + (rs r ) {-34} 6 Η μέγιστη θερμοκρασία θ max στο κέντρο της σφαίρας (r0): θmax θ0 θ + {-35} r s 6

15 ΑΓΩΓΗ 63 ΑΣΚΗΣΗ - Μια επίπεη μεταική επιφάνεια πρέπει να μονωθεί έτσι ώστε η πυκνότητα θερμορροής να μην ξεπερνά τα 0 W/m. Η θερμοκρασία στην επιφάνεια της πάκας (κάτω από το στρώμα της μόνωσης) είναι 30 C και η θερμοκρασία της εξωτερικής επιφάνειας του μονωτικού στρώματος πρέπει να είναι 40 C. Να προσιορισθεί το απαιτούμενο πάχος της μόνωσης αν: Α. Το μονωτικό έχει σταθερό συντεεστή θερμικής αγωγιμότητας 0,075 W/mK. Β. Το μονωτικό έχει συντεεστή θερμικής αγωγιμότητας που επηρεάζεται από τη θερμοκρασία σύμφωνα με τη σχέση 0,075+0,000. θ, όπου σε W/mK και θ σε C. ΛΥΣΗ Τα εομένα είναι (και για τις ύο περιπτώσεις): θ 30ºC θ 40ºC / 0 W/m Κατευθύνσεις ύσης: Και για τα ύο μονωτικά, με εομένες σταθερές θερμοκρασίες στις ύο πευρές τους και καθορισμένη την πυκνότητα θερμορροής, το απαιτούμενο πάχος () θα προκύψει αμέσως από τις αντίστοιχες σχέσεις αγωγής. Α. Για σταθερό α 0,075 W/mK, έχουμε τη σχέση {-04}: α ( θ θ ) και επομένως Α α (30 40) 0,075 0 α 0, m α 0 α 0 cm 0,075 Β. Σε αυτή την περίπτωση 0,075+0,000. θ. Εφόσον είναι γνωστές οι θερμοκρασίες στις ύο πευρές του μονωτικού, μπορεί να χρησιμοποιηθεί η παραπάνω σχέση, αά παίρνοντας την τιμή m στη μέση θερμοκρασία θ m. (Βέπε και σχέση {-06}) Είναι: θm 80ºC και έτσι m 0,075+0, , W/mK m και έχουμε: ( θ θ ) και επομένως Α β θ θ

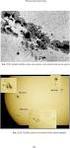
16 64 Κεφάαιο (30 40) 0, 0 β 0,48 m β 4,8 cm 0 β 0, Το απαιτούμενο πάχος μονωτικού υικού για να επιτευχθεί ορισμένη πυκνότητα θερμορροής θα είναι μεγαύτερο στην περίπτωση που ο συντεεστής θερμ. αγωγιμότητας του υικού μεταβάεται αυξητικά με τη θερμοκρασία k k ο (+bτ), σε σύγκριση με το υικό που θα είχε σταθερό k k o. ΑΣΚΗΣΗ - Μια συσκευή για τη μέτρηση του συντεεστή θερμικής αγωγιμότητας (k ή ) ιαφόρων υικών αποτεείται από μια επτή επίπεη ηεκτρική αντίσταση, πάνω στην οποία στερεώνονται (με πού καή επαφή), και από τις ύο πευρές της, ύο επίπεα οκίμια από το υικό, πάχους cm (βέπε σχήμα). Τα οκίμια επικαύπτονται από επτά φύα χακού, ενώ οι υπόοιπες επιφάνειες της όης κατασκευής (πάνω, κάτω, εμπρός και πίσω) στεγανοποιούνται. Το παραπάνω σύνοο βυθίζεται σε οχείο που περιέχει μίγμα πάγου νερού, έτσι ώστε τα φύα χακού να αποκτούν θερμοκρασία 0 C. Η ισχύς που απορροφά η ηεκτρική αντίσταση μπορεί να μεταβάεται, ενώ με σύστημα θερμοστοιχείων, μπορεί να μετρείται η θερμοκρασία πάνω στην ηεκτρική αντίσταση. οκίμιο υικού Ηεκτρική αντίσταση ~ Πάγος νερό Πάγος νερό Λεπτή πάκα χακού cm cm Σε μια μέτρηση όπως παραπάνω, για τον προσιορισμό του ενός μονωτικού υικού, έγιναν μετρήσεις και συμπηρώθηκε ο παρακάτω πίνακας : Μέτρηση (α) Μέτρηση (β) Απορροφούμενη ισχύς στην αντίσταση (W/m ) Θερμοκρασία πάνω στην αντίσταση ( C) 80 48

17 ΑΓΩΓΗ 65 Α. Χρησιμοποιώντας τα στοιχεία της μέτρησης (α), υποογίσετε το (μέσο) συντεεστή θερμικής αγωγιμότητας του υικού. Β. Χρησιμοποιώντας τα στοιχεία της μέτρησης (β), υποογίσετε το (μέσο) συντεεστή θερμικής αγωγιμότητας του υικού. Γ. Δικαιοογήσετε ότι ο του υικού εν είναι ανεξάρτητος της θερμοκρασίας και προσιορίστε τον ως γραμμική συνάρτηση της μορφής: o (+b θ) (σε W/mK όταν θ σε C). ΛΥΣΗ Α. και Β. Κατευθύνσεις ύσης: Σε κάθε μέτρηση, η απορροφούμενη ηεκτρική ισχύς Ρ η στην αντίσταση μεταβιβάζεται με αγωγή μέσα από τις πάκες οκίμια του υικού. Λόγω της καής θερμομόνωσης από τις άες πευρές, μπορούμε να θεωρήσουμε μονοιάστατη αγωγή θερμότητας, κατά το πάχος του κάθε οκιμίου. Λόγω της προφανούς συμμετρίας (ίσα πάχη και 0 C πάνω σε κάθε πευρά) έπεται ότι από κάθε πάκα θα ιέρχεται η μισή ισχύς. Επομένως, χρησιμοποιώντας την απή σχέση της αγωγής, για σταθερή τιμή θα υποογιστούν οι μέσοι συντεεστές θερμικής αγωγιμότητας m, από τις τιμές της κάθε μέτρησης. Τα εομένα, με τα σύμβοα του ιπανού σχήματος (για όα τα ερωτήματα) είναι: cm 0,0 m θ 0 C σταθ. θ α 80 C θ β 48 C Ρ ηα 400 W/m α /Α 00 W/m Ρ ηβ 800 W/m β /Α 400 W/m m Έχουμε, οιπόν, τη σχέση {-06}: (θ θ). Στη μέτρηση (α), έχουμε: mα 00 (80 0) mα 0,05 W/mK 0,0 B. Στη μέτρηση (β), έχουμε: mβ 400 (48 0) 0,0 mβ 0,054 W/mK Γ. Κατευθύνσεις ύσης: Αν ο του υικού ήταν ανεξάρτητος της θερμοκρασίας, οι ύο μετρήσεις θα έιναν τον ίιο m. Αφού αυτό εν ισχύει, σημαίνει ότι ο μεταβάεται με τη θερμοκρασία στην οποία βρίσκεται το υικό. θ θ

18 66 Κεφάαιο Αν ο εξαρτάται γραμμικά από τη θερμοκρασία, θα είναι: o (+b θ). Γνωρίζουμε ότι ο m είναι εκείνος που αντιστοιχεί, κάθε φορά, στη μέση θερμοκρασία: θ m. θ + θ Στην (α) μέτρηση είχαμε θm α 40 C και βρήκαμε mα 0,05 W/mK Επομένως: 0,05 o( + b 40) () Στην (β) μέτρηση είχαμε θm β 74 C και βρήκαμε mβ 0,054 W/mK Επομένως: 0,054 o( + b 74) () Από τη ύση του συστήματος των () και () προκύπτουν οι τιμές των: o 0,0453 και b 0,006 Άρα ο του υικού είναι: 0,0453 ( + 0,006 θ) Για υποογισμούς θερμορροής με αγωγή σε υικά που ο συντεεστής θερμικής αγωγιμότητάς τους μεταβάεται με τη θερμοκρασία, πρέπει να αμβάνεται η τιμή του στη μέση θερμοκρασία ειτουργίας. ΑΣΚΗΣΗ -3 Απαντήστε στα παρακάτω, ικαιοογώντας με σαφήνεια την απάντησή σας:. Σε ποιό από τα ύο τοιχώματα μεταίεται μεγαύτερη πυκνότητα θερμορροής; 0,5 W/mK 0,7 W/mK 0,5 W/mK (0,7+0,0004.θ) W/mK 0 C 4 C 0 C 4 C α β (α) (β) B. Αν, στον τοίχο κατοικίας του παρακάτω σχήματος, το ιάκενο αέρα γεμίσει με συνθετικό μονωτικό υικό, θα αυξηθεί ή θα μειωθεί η πυκνότητα θερμορροής;

19 ΑΓΩΓΗ 67 0 C 4 C 0 C 4 C α β m 5cm 5cm (α) (β) ΛΥΣΗ Α. Κατευθύνσεις ύσης: Με ίιες θερμοκρασίες τοιχωμάτων και ίια πάχη στρώσεων, η θερμορροή καθορίζεται από τους συντε. θερμικής αγωγιμότητας. Έτσι στο (α) τοίχωμα, με σταθερούς και ισχύει η σχέση {-07}: α θ θ α θ θ () + + 0,5 0,7 Ενώ, στο τοίχωμα (β), στη εύτερη στρώση θα πρέπει να χρησιμοποιηθεί κάποια τιμή k m. Οπότε θα είναι: β θ θ β θ θ () + + 0,5 m Εώ, προφανώς, αφού έχουμε θ > 0 C, θα είναι οπωσήποτε k m > 0,7. Άρα από την σύγκριση των () και () προκύπτει ότι: β α > Β. Κατευθύνσεις ύσης: Προφανώς θα ακοουθηθεί όμοια με πριν ιαικασία, αά θα ηφθεί υπόψη η ιιαίτερη θερμική συμπεριφορά του ιακένου αέρα. Σύμφωνα με τον ΠΙΝ. -, έχουμε για κατακόρυφο (κειστό) ιάκενο αέρα, πάχους 5 cm 50 mm, συντεεστή θερμικής αντίστασης / 0,8 m K/W. Έτσι στο (α) τοίχωμα, ισχύει αντίστοιχα η σχέση {-07}: θ θ + + α α α α (3) θ θ + 0,8 + Για το συνθετικό μονωτικό υικό στο τοίχωμα (β), βρίσκουμε από τον ΠΙΝ. -, μ 0,04 W/mK. Οπότε θα έχουμε:

20 68 Κεφάαιο β θ θ μ + + μ β θ θ 0, ,04 θ θ +, + Λόγω της μεγαύτερης θερμικής αντίστασης του μονωτικού, από την σύγκριση των (3) και (4) προκύπτει ότι: β α < Αν γίνει πήρωση ιάκενου ήρεμου αέρα (σε τοίχους ή σε άπεα, οροφές κπ) με σύνηθες θερμομονωτικό υικό (έστω και με κάπως μεγάο συντεεστή θερμ. αγωγιμότητας), τότε βετιώνεται η θερμομονωτική ικανότητα του αντίστοιχου ομικού στοιχείου. (4) ΑΣΚΗΣΗ -4 Στις ύο πευρές μιας χάκινης πάκας, πάχους cm, υπάρχουν ύο στρώσεις εποξειικής κόας ( 0,5 W/mK), πάχους 4 mm η καθεμία. Λόγω μικρών ανωμαιών στην επιφάνεια του χακού, η επαφή χακού κόας εν είναι τέεια, οπότε ημιουργείται μία αντίσταση επαφής, με συντεεστή θερμικής αντίστασης ίσο με 3,6.0 4 m K/W. Οι θερμοκρασίες πάνω στις ύο πευρές της κόας, εξωτερικά, ιατηρούνται σταθερές, έτσι ώστε η θερμοκρασιακή ιαφορά να είναι 00 C. Α. Να υποογιστεί το σφάμα που κάνουμε στον υποογισμό της θερμικής ισχύος ιαμέσου της πάκας, αν αγνοήσουμε την αντίσταση επαφής. Επίσης, να βρεθεί η θερμοκρασιακή πτώση που ημιουργείται όγω της αντίστασης επαφής. Β. Να υποογισθεί πόσο θα γίνει το σφάμα, αν αντί της χάκινης πάκας έχουμε μάρμαρο, ίιου πάχους. Πόση είναι σ αυτή την περίπτωση η θερμοκρασιακή πτώση όγω της αντίστασης επαφής. Σχοιάσετε τα αποτεέσματα. ΛΥΣΗ Α. Έχουμε τα εξής εομένα: 0 mm 0,0 m 4 mm 0,004 m χ 383 W/mK (από ΠΙΝ. - για χακό) μ 3,49 W/mK (από ΠΙΝ. - για μάρμαρο) 0,5 W/mK R 3,6.0-4 m K/W χακός (ή μάρμαρο) ( ) θ κόα ( ) θ Δθ θ θ 00 C ατεής επαφή στρώσεων (συντ.θερμικής αντίστασης R)

21 ΑΓΩΓΗ 69 Κατευθύνσεις ύσης (για Α και Β ερωτήματα): Με γνωστά όα τα θερμοτεχνικά χαρακτηριστικά του τοιχώματος και σταθερές τις θερμοκρασίες στις ύο πευρές του, υποογίζεται από γνωστές σχέσεις η πυκνότητα θερμορροής στις περιπτώσεις: αποποιημένου υποογισμού (/) α, (η. αγνοώντας τις θερμικές αντιστάσεις επαφής) και ακριβούς υποογισμού (/) ε. Στη εύτερη περίπτωση, χρησιμοποιώντας σχέση αγωγής βρίσκουμε τη θερμοκρασιακή πτώση όγω μη καής επαφής. Α. Για την περίπτωση χάκινης πάκας: Εφαρμόζοντας τη σχέση {-07} έχουμε: θ θ + θ θ 0,0 0, ,5 α χ α α 3,5 Δθ Αντίστοιχα, βάζοντας και τις (ύο ίιες) θερμικές αντιστάσεις επαφής: θ θ θ θ ε R ε 0,0306 3,6 0 + χ θ θ 30,538 Δθ ε 0,03746 () ε Οπότε, το σφάμα που κάνουμε είναι: 3,5-30,538 p p 0,05,5% 30,538 Η θερμοκρασιακή πτώση Δθ R όγω της θερμικής αντίστασης επαφής, είναι (βέπε σχέση {-08}): ε Δθ R R Δθ 30, ,6 0 R 4 () Δθ R, C Β. Για την περίπτωση μαρμάρινης πάκας: Εργαζόμενοι παρόμοια, έχουμε: θ θ θ θ 8,68 Δθ (3) 0,0 0,004 α + α + α 3,49 0,5 μ και αντίστοιχα, με τις (ύο ίιες) θερμικές αντιστάσεις επαφής: ε + + μ θ θ R θ θ 0, ,6 0 ε 4

22 70 Κεφάαιο θ θ 8,0 Δθ ε 0, (4) ε Οπότε, το σφάμα που κάνουμε είναι: 8,68-8,0 p p 0,007,07% 8,0 Η θερμοκρασιακή πτώση Δθ R όγω της θερμικής αντίστασης επαφής, είναι: ε Δθ R R Δθ 8,0 00 3,6 0 R 4 Δθ R C ΣΧΟΛΙΑΣΜΟΣ: Το σφάμα που γίνεται, και στις ύο περιπτώσεις (χακού και μαρμάρου), είναι πού μικρό και σχεόν ίιο. Ως προς την προκαούμενη από τις αντιστάσεις θερμοκρασιακή πτώση, παρατηρούμε ότι είναι επίσης πού μικρή και σχεόν ίια για τις ύο περιπτώσεις. Αυτό οφείεται, κυρίως, στο ότι ο συντεεστής θερμικής αντίστασης επαφής είναι μικρός στο παράειγμα αυτό. Αν αυξάνεται ο συντεεστής θερμικής αντίστασης, τότε αυξάνεται αρκετά και το σφάμα και η θερμοκρασιακή πτώση (στην περίπτωση του μαρμάρου είναι μικρότερα). Η θερμική αντίσταση που ημιουργείται όγω μη καής επαφής ύο στρώσεων υικών, πρέπει να αμβάνεται υπόψη σε υποογισμούς μετάοσης θερμότητας με αγωγή. Διαφορετικά, προκύπτει μεγαύτερη θερμορροή και το σφάμα είναι τόσο μεγαύτερο όσο μεγαύτερη είναι αυτή η θερμική αντίσταση επαφής. ΑΣΚΗΣΗ -5 Προκειμένου να θερμομονωθούν τα μεταικά επίπεα τοιχώματα μιας εξαμενής, προσφέρονται με το ίιο κόστος, ύο εναακτικές ύσεις (a) και (b) όπως είχνονται στα αντίστοιχα σχήματα (τομές-οι ιαστάσεις σε cm). Μεταικό τοίχωμα ιάκενο ήρεμου αέρα Μονωτικό ( ιογκωμένο συνθετικό υικό) Μεταικό τοίχωμα Μονωτικό 3 4 Σχ. a Σχ. b

23 ΑΓΩΓΗ 7 Στη ύση (a) οι συντε. θερμικής αγωγιμότητας των υικών μπορούν να θεωρηθούν ανεξάρτητοι της θερμοκρασίας, ενώ στη ύση (b) ο συντε. θερμικής αγωγιμότητας του μονωτικού μεταβάεται με τη θερμοκρασία σύμφωνα με τη σχέση 0, ,0004 θ [σε W/mK όταν θ σε C].. Να εξετασθεί ποιά από τις ύο ύσεις είναι συμφερότερη, αν η θερμοκρασία πάνω στα μεταικά τοιχώματα είναι 50 C, και η θερμοκρασία πάνω στην εξωτερική επιφάνεια του μονωτικού είναι 0 C (και στις ύο περιπτώσεις). B. Ποιά η θερμοκρασία στο κέντρο του μονωτικού της ύσης (a); Γ. Για ποιά θερμοκρασία των μεταικών τοιχωμάτων της εξαμενής οι ύο ύσεις θα ήταν ισούναμες; (Υποτίθεται ότι η θερμοκρασία πάνω στην άη πευρά ιατηρείται στους 0 C). ΛΥΣΗ Α. Κατευθύνσεις ύσης: Συμφερότερη θα είναι η ύση που έχει τις μικρότερες απώειες. Θα υποογιστεί, επομένως η πυκνότητα θερμορροής (/Α) στις ύο περιπτώσεις, εφόσον έχουμε γνωστές θερμοκρασίες, συντεεστές θερμικής αγωγιμότητας και πάχη. Η ιιαιτερότητα στην (a) ύση είναι ότι για το ιάκενο ήρεμου αέρα θα χρησιμοποιήσουμε έτοιμο τον συντ. θερμικής αντίστασης / και στη (b) ύση ότι ο εν είναι σταθερός. Έχουμε τα εομένα: θ 50ºC θ 0 C cm 0,0 m στη ύση (a) 3 cm 0,03 m στη ύση (a) / 0,75 m K/W (με παρεμβοή, από τον ΠΙΝ.-) 0,04 W/mK (από τον ΠΙΝ.-) 3 4 cm 0,04 m στη ύση (b) 0, ,0004 θ στη ύση (b) Μεταικό τοίχωμα ιάκενο ήρεμου αέρα θ 3 θ θ a Μονωτικό ( ιογκωμένο συνθετικό υικό) Μεταικό τοίχωμα Μονωτικό θ θ b 3 Σχ. a Σχ. b

24 7 Κεφάαιο Στη ύση (a) έχουμε (σχέση {-07}): a ,03 0,75 + 0,04 a 44, W/m θ θ + a και αντικαθιστώντας: Στη ύση (b), εφόσον είναι γνωστές οι θερμοκρασίες στις ύο πευρές του μονωτικού, μπορεί να χρησιμοποιηθεί η παραπάνω σχέση, αά παίρνοντας την τιμή m στη μέση θερμοκρασία θ m. (Βέπε και σχέση {-06}) Είναι: θm 30ºC και έτσι m 0,038+0, ,05 W/mK. b m Οπότε: ( θ θ ) και αντικαθιστώντας: Α b 3 0,05 (50 0) b 50W/m Α 0,04 Επομένως, η ύση που συμφέρει είναι η (a), αφού a / < b /. Β. Κατευθύνσεις ύσης: Εφόσον έχει βρεθεί η a /, εύκοα υποογίζεται η ζητούμενη θερμοκρασία στο κέντρο του μονωτικού, έστω θ 3, από απή σχέση αγωγής από θ 3 έως θ, για πάχος 0,5 (Βέπε σχέση {-08}). a θ3 θ θ3 0 και αντικαθιστώντας: 44, θ 3 6,ºC 0,5 0,05 0,04 Γ. Κατευθύνσεις ύσης: Οι υο ύσεις θα είναι ισούναμες όταν a / b /. Έστω θ η θερμοκρασία πάνω στα μεταικά τοιχώματα, για να συμβεί αυτό. Για την a / μπορεί να χρησιμοποιηθεί η προηγούμενη σχέση όπως στο Α. ερώτημα, αά για την b / πρέπει να χρησιμοποιηθεί η αναυτική σχέση {-05}, επειή τώρα εν είναι γνωστές και οι ύο θερμοκρασίες στις επιφάνειες του μονωτικού. Έτσι : Στη ύση (a) έχουμε: a θ θ a θ 0 () 0,03 + 0,75 + 0,04 Στη ύση (b) έχουμε: b o b ( θ θ ) + ( θ 3 θ )

25 ΑΓΩΓΗ 73 Η παραπάνω σχέση ισχύει όταν η μορφή του είναι: o (+bθ), ηαή 0,0004 εώ πρέπει να γραφεί: 0,038 ( + θ) 0,038 ( + 0,0053 θ) 0,038 Οπότε, για την b θα είναι: b 0,038 0,0053 ( θ 0) + ( θ 0 ) 0,04 () Από τις () και () προκύπτει: θ 0 0,038 0,0053 ( θ 0) + ( θ 0 ) 0,03 0,75 + 0,04 0,04 θ 0 0,95 ( θ 0) 0,005 ( 0 + θ ) 0,9067 θ 0 ( θ 0) [0,95 + 0,005 ( θ 0)] 0, ,9067 0,95 + 0,005 ( θ 0) +,09 0,95 + 0,005 θ + 0,05 θ 0,6ºC ΠΑΡΑΤΗΡΗΣΗ: Η θ μπορεί να υποογιστεί έμμεσα, αν υποογιστεί η τιμή m (μέσος συντεεστής θερμικής αγωγιμότητας) του μονωτικού (b), από την ισότητα των, και κατόπιν βρεθεί η θ m θερμοκρασία για την οποία θα ισχύει/προκύπτει πράγματι αυτός ο συγκεκριμένος m και επομένως και η άγνωστη θ. Δηαή: a θ θ b θ θ 3 + και αντικαθιστώντας: 3 + m m 0,03 0,04 0,75 + m 0,044 W/mK 0,04 m Άρα θα πρέπει: 0,044 0, ,0004 θm θ m 5,3ºC και θ + θ θ m θ θm θ θ 5,3 0 θ 0,6ºC Όταν ο συντεεστής θερμ. αγωγιμότητας ενός υικού μεταβάεται με τη θερμοκρασία ο (+bθ), οι ακραίες θερμοκρασίες ειτουργίας του υικού παίζουν καθοριστικό ρόο στη ιαμόρφωση της θερμορροής ια μέσου αυτού με αγωγή.

26 74 Κεφάαιο ΑΣΚΗΣΗ -6 Προκειμένου να κτιστεί ένας τοίχος φούρνου, υπάρχουν ιαθέσιμα ύο είη τούβων, με ίιες ιαστάσεις x 5 x 9 cm. Τα τούβα (α) έχουν συντ. θερμικής αγωγιμότητας α, W/mK και αντέχουν μέχρι θερμοκρασία 000 C, ενώ τα τούβα (β) έχουν συντ. θερμικής αγωγιμότητας β 0,6 W/mK και αντέχουν μέχρι θερμοκρασία 800 C. Τα τούβα έχουν ίιο κόστος/τεμάχιο και μπορούν να κτιστούν με πάχος ή 5 cm. Η πυκνότητα θερμορροής ιαμέσου του τοίχου πρέπει να είναι το πού 600 W/m, όταν η θερμοκρασία πάνω στην εσωτερική πευρά του τοίχου είναι 900 C και στην εξωτερική πευρά (προς το περιβάον) 50 C. Ζητείται να προσιοριστεί η πιο οικονομική επιογή και τοποθέτηση των τούβων (σε μία ή περισσότερες στρώσεις). (Σχετίζεται με την ΑΣΚΗΣΗ 4-8, η οποία είναι συνέχεια αυτής και χρησιμοποιεί τα εομένα της). ΛΥΣΗ Κατευθύνσεις ύσης: Εφόσον τα τούβα έχουν ίιο κόστος/τεμάχιο, η πιο οικονομική επιογή και τοποθέτηση θα είναι εκείνη στην οποία θα ικανοποιούνται οι απαιτήσεις, χρησιμοποιώντας τα ιγότερα τούβα, προφανώς σε ιγότερες κατά το υνατόν στρώσεις. Η κάθε στρώση είναι οικονομικότερο να κτίζεται με πάχος 5 cm (αν, βέβαια, ικανοποιείται η /), αφού έτσι κάθε τούβο θα καύπτει 0, x 0,09 0,098 m, ενώ αν κτίζεται με πάχος cm καύπτει μόνο 0,5 x 0,09 0,035 m. Θα εξεταστούν ιάφορες περιπτώσεις τοποθέτησης και θα υποογίζεται κάθε φορά η πυκνότητα θερμορροής και θα εέγχονται οι θερμοκρασίες των τούβων. Τα εομένα είναι: α, W/mK β 0,6 W/mK α ή 5 cm 0, ή 0,5 m β ή 5 cm 0, ή 0,5 m θ α,max 000 C θ β,max 800 C θ 900 C θ 50 C Η πυκνότητα θερμορροής υποογίζεται από την απή σχέση αγωγής, σε από ή σύνθετο τοίχωμα (σχέση {-04} ή {-07}). Σε όες τις περιπτώσεις το τοίχωμα θα βρίσκεται σε θερμοκρασιακή ιαφορά Δθ θ θ C. Είναι προφανές ότι από την πευρά της θερμοκρασίας των 900 C θα πρέπει να τοποθετηθεί οπωσήποτε τούβο (α), όγω του ότι το τούβο (β) εν αντέχει, αφού θ β,max 800 C.

27 ΑΓΩΓΗ 75 θ θ θ θ θ θ θ α α 5 β 5 α 5 β Περ. Περ. Περ. 3 Περ. : Αρχικά, οιπόν, εξετάζεται τούβο (α), σε μία στρώση των cm α. (Για να επιτυγχάνεται μικρότερη /, σε σχέση με πάχος 5 cm) Δθ 750 α 0,, α 4090,9 W/m > 600 W/m, η. ΑΠΟΚΛΕΙΕΤΑΙ. [Πού περισσότερο αποκείεται και το πάχος α 5 cm] Άρα, πρέπει να τοποθετηθεί και εύτερη στρώση τούβων. Περ. : Εξετάζεται μία στρώση τούβου (α), πάχους α 5 cm και μία στρώση τούβου (β) πάχους επίσης 5 cm β (οικονομικότερη κατασκευή). Δθ 750 α β 0,5 0,5 + +, 0,6 α β 000 W/m > 600 W/m, η. ΑΠΟΚΛΕΙΕΤΑΙ. (Προφανώς αποκείονται ύο στρώσεις τούβου (α) 5 cm, αφού θα προκύψει ακόμη μεγαύτερο /). Περ. 3: Η αμέσως πιο οικονομική ύση είναι η τοποθέτηση μίας στρώσης τούβου (α), πάχους α 5 cm και μία στρώση τούβου (β) πάχους cm β. [Η αντίστροφη τοποθέτηση α cm και β 5 cm,ενώ είναι οικονομικά ισούναμη, οηγεί προφανώς σε μεγαύτερο /].

28 76 Κεφάαιο Δθ 750 α β 0,5 0, + +, 0,6 α β 55 W/m < 600 W/m, η. ΔΕΚΤΗ. Θα πρέπει τώρα να γίνει έεγχος για τα τούβα (β),σε ότι αφορά τη μέγιστη θερμοκρασία τους, που εμφανίζεται στην επιφάνεια ιεπαφής, η. την θ. Θα έχουμε, από αγωγή, στην πρώτη στρώση: θ θ 900 θ 55 α 0,5 α, θ 709,3 C < 800 C, η. ΔΕΚΤΗ. Συνεπώς, αυτή είναι η τεχνικά εκτή και οικονομικότερη ύση. ΠΑΡΑΤΗΡΗΣΗ: Αν τα τούβα (β) άντεχαν σε μικρότερη θερμοκρασία, π.χ. έως 700 C, τότε η πιο πάνω ύση εν θα ήταν εκτή. Θα έπρεπε να εξεταστεί η (ακριβότερη) ύση: α cm και β cm, η οποία θα οηγούσε και σε μικρότερη / 364 W/m και σε χαμηότερη θερμοκρασία θ 650 C. Σε εφαρμογές όπου συναντώνται υψηές (ή χαμηές) θερμοκρασίες, είναι πού πιθανόν ορισμένα υικά να επηρεάζονται (καταστροφή, ομική αοίωση, ααγή των ιιοτήτων τους κπ) και πρέπει να αμβάνονται μέτρα ώστε τα υικά αυτά να μην εκτίθενται σ αυτές τις θερμοκρασίες. ΑΣΚΗΣΗ C Βρείτε τις θερμοκρασίες που είπουν στο κυινρικό τοίχωμα του σχήματος, που έχει σταθερό συντεεστή θερμικής αγωγιμότητας. (Οι ιαστάσεις σε cm). θ 00 C θ ΛΥΣΗ Κατευθύνσεις ύσης: Η κατεύθυνση ροής της θερμότητας είναι από μέσα προς

29 ΑΓΩΓΗ 77 τα έξω. Ο εν είναι γνωστός. Αά, γνωρίζοντας ύο θερμοκρασίες σε ορισμένες θέσεις του κυινρικού τοιχώματος, μπορούν να βρεθούν άες θερμοκρασίες σε άες θέσεις (όπως εώ οι ζητούμενες θ και θ ) με κατάηη χρήση της βασικής σχέσης της αγωγής, για σταθερό. θ 3 Τα εομένα είναι: d 5 cm 0,05 m θ d 6 cm 0,06 m θ d 3 9 cm 0,09 m θ d cm 0, m θ 00 C d d θ 3 50 C Επειή είναι γνωστές οι θ και θ 3 γράφουμε τη σχέση {-} ως εξής: θ θ l d 3 0,09 ln l ln π d π 0,06 Επίσης, για τις θ και θ γράφουμε τη σχέση ως εξής: θ θ θ 00 l d 0,06 ln l ln π d π 0,05 Από τις ισότητες () και () παίρνουμε: θ 00 0,06 ln π 0, ,09 ln π 0, ,83 ( 00) 0, 4055 θ θ 00 0, ,4055 9,5 θ 0, ,55 και θ,5 C Όμοια, για τις θ 3 και θ γράφουμε τη σχέση{-} ως εξής: θ3 θ 50 θ (3) l d4 0, ln l ln π d π 0,09 3 Από τις ισότητες () και (3) παίρνουμε: 50 θ 0,0 ln π 0, ,09 ln π 0,06 50 θ 0, ,4055 d 3 d 4 () ()

30 78 Κεφάαιο 50 0,877 ( 50 θ ) 0, ,38 0,75 0,4055θ θ 4,5 C Όταν σ ένα κυινρικό ή επίπεο ή σφαιρικό τοίχωμα, που έχει σταθερό συντεεστή θερμ. αγωγιμότητας, είναι γνωστές ύο θερμοκρασίες σε συγκεκριμένες θέσεις, τότε μπορεί να υποογιστεί η θερμοκρασία και σε ο- ποιαήποτε άη θέση του τοιχώματος. (εννοείται, για μονοιάστατη μετάοση, χωρίς θερμικές πηγές) ΑΣΚΗΣΗ -8 Μια καμινάα από ενισχυμένο σκυρόεμα (C0/5) έχει εσωτερική ιάμετρο d 700 mm και εξωτερική ιάμετρο d mm. Η καμινάα πρόκειται να επενυθεί εσωτερικά με πυρίμαχη άργιο για να ιατηρείται το σκυρόεμα (για όγους αντοχής του) σε θερμοκρασία οπωσήποτε μικρότερη των 5 C. Δίεται για την πυρίμαχη άργιο: 0,9 W/mK. Ζητείται: Α. Να υποογισθεί το εάχιστο πάχος της επένυσης αυτής, ώστε να ικανοποιείται η παραπάνω απαίτηση, στη (υσμενή) περίπτωση όπου, όγω υψηής θερμοκρασίας περιβάοντος και άπνοιας, η θερμοκρασία πάνω στην εξωτερική επιφάνεια της καπνοόχου μπορεί να φθάσει τους 00 C, ενώ η εσωτερική επιφάνεια της επένυσης αποκτά θερμοκρασία 380 C. Β. Για την καπνοόχο με την παραπάνω επένυση, να βρεθεί η σχέση μεταξύ της θερμοκρασίας που επιτρέπεται να φθάσει το εσωτερικό της επένυσης καθώς θα μεταβάεται η θερμοκρασία πάνω στην εξωτερική επιφάνεια της καπνοόχου. ΛΥΣΗ Το σχήμα της καμινάας μαζί με την επένυση, σε τομή, θα είναι όπως παρακάτω, με τα εομένα: d 700 mm 0,7 m d mm,3 m (πυρίμαχη άργιος, εσωτερική επένυση) 0,9 W/mK (οπ. σκυρόεμα C0/5, από ΠΙΝ. -),03 W/mK θ σκ 5 C θ 380 C θ 00 C Α. Κατευθύνσεις ύσης: Η κατεύθυνση ροής της θερμότητας είναι από μέσα προς τα έξω. Ζητείται η d. Γνωρίζοντας ύο θερμοκρασίες και τον συντεεστή θερμ. αγωγιμότητας για τη μία στρώση (του σκυροέματος), μπορεί να υποογι- θ θ σκ d d d 3 θ

31 ΑΓΩΓΗ 79 στεί η ανά μονάα μήκους θερμορροή και κατόπιν το ζητούμενο πάχος της άης στρώσης (πυρίμαχης αργίου), με χρήση της απής σχέσης αγωγής για σταθερό. Έτσι, για το τοίχωμα της καμινάας, γράφουμε τη σχέση {-}: θσκ θ W/m l d3,3 ln ln l π d π,03 0,7 θ θσκ Και ισχύει και η παρόμοια σχέση για τη στρώση της επένυσης: l d ln και αντικαθιστώντας την ευρεθείσα d l και τα οιπά εομένα: , ,36 ln 55 0,7 ln d π 0,9 π d 0,7 ln 0,3404 d 0,7, 405 d 0,5 m d d d 0,7 0,5 Άρα το πάχος της επένυσης θα είναι: s s 0, m Β. Κατευθύνσεις ύσης: Αν θα αάζει η θερμοκρασία πάνω στην εξωτερική επιφάνεια της καπνοόχου, η. η θ, και η θερμοκρασία στην επένυση, η. η θ, τότε θα αάζει και η θερμορροή /l. Αά πάντα η ίια θερμορροή θα ιαπερνά και τις ύο στρώσεις και, με τον περιορισμό της ορισμένης θερμοκρασίας ιεπαφής, η. θ σκ 5 C, θα προκύψει η σχέση μεταξύ των θερμοκρασιών αυτών θ και θ. Για κάθε μία από τις στρώσεις θα ισχύει η {-}: θ θ θ θ l π d π d σκ σκ d ln d3 ln και αντικαθιστώντας τα εομένα, παίρνουμε: θ 5 5 θ θ 5 5 θ και τεικά: 0,7,3 ln ln 0, ,30495 π 0,9 0,5 π,03 0,7 θ 50,6 θ Δη. η θ μπορεί (επιτρέπεται) να αυξάνεται γραμμικά όσο μειώνεται η εξωτ. επιφανειακή θερμοκρασία θ. Η προσθήκη ενός πυρίμαχου υικού, με κατάηο πάχος, είναι ποές φορές απαραίτητη ενέργεια, προκειμένου να προστατευθεί ένα υικό από την έκθεσή του σε υψηές θερμοκρασίες.