, e + Σε ένα δείγμα ίδιων ραδιενεργών πυρήνων η πιθανότητα διάσπασης για κάποιο συγκεκριμένο πυρήνα είναι τυχαία.
|
|
|
- Φῆλιξ Μανωλάς
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα Πιθανόηα εκπομπής ή διάσπασης ν Σε ένα δείγμα ίδιων ραδιενεργών πυρήνων η πιθανόηα διάσπασης για κάποιο συγκεκριμένο πυρήνα είναι υχαία. Κάθε ραδιενεργός πυρήνας αναποκρίνεαι σε καθορισμένη πιθανόηα εκπομπής ανά μονάδα χρόνου : (6.) Αν σε χρόνο ένας πυρήνας δεν έχει διασπασεί, η πιθανόηα όι θα διασπασεί ο επόμενο χρονικό διάσημα Δ είναι : Δ Δ (6.2) Αν n() ο αριθμός ων ΜΗ διασπασθένων πυρήνων σε χρόνο. Ο αριθμός ων αναμενόμενων πυρήνων να διασπασούν σο διάσημα Δ είναι : Δ Δn n Δ n n Δ (6.3) Για ο όριο Δ, όε η 6.3 γίνεαι : 6_ Pyrhniks_Diaspasis.dc 8
2 dn d n (6.4) Με λύση ης 6.4 ην συνάρηση : () n n (6.5) Πειρμαικά, όμως, ο μερούμενο μέγεθος δεν είναι οι μή διασπασθένες πυρήνες αλλά ο αριμός διασπάσεων ων πυρήνών ανά μονάδα χρόνου. Αν Ι είναι ο ρυθμός διασπάσεων και ο μέσος χρόνος ζωής ου πυρήνα, όε : ( ) dn I I d n I (6.6) Σο σχήμα 4 παρίσααι η σχέση 6.6 όπως βρέθηκε πειραμαικά για ο ισόοπο 94 Ir, ου οποίου ο μέσος χρόνος ζωής.995 x 5 sc. Αυό σημαίνει όι για χρόνο πάνω από sc (.8 ημέρες), που ανισοιχεί σε 9.3 μέσους χρόνους ζωής ή 3.5 χρόνους ημι-ζωής η έναση ων διασπάσεων ελαώνεαι περίπου καά παράγονα. Σχήμα 4 : Πειραμαική μέρηση ου χρόνου ημιζωής ου 94 Ir 6_ Pyrhniks_Diaspasis.dc 82
3 Η πιθανόηα ενόςπυρήνα να διασπάαι σε χρόνο είναι p() και βρίσκεαι : ( ) P( ) () n () p() p P (6.7) n Η πιθανόηα ενός πυρήνα να εκπέμψει σο ελάχισο διάσημα, +Δ, είναι p()δ, Η πιθανόηα ενός πυρήνα να εκπέμψει σο καθορισμένο διάσημα, 2 είναι 2 είναι pd (), και η πιθανόηα ενός πυρήνα να εκπέμψει σε οποιοδήποε διάσημα p() d Ο μέσος χρόνος ζωής ενός πυρήνα ορίζεαι από ( ) p() d d (6.8) Ανικαθισούμε με u /, οπόε η 6.8 γίνεαι : u u du (6.9) Ανίσοιχα ο χρόνος ημι-ζωής είναι :.693 ln 2 2 (6.) ( ) Η πλήρης σχέση λαμβάνονας υπόψη ις σχεικές πιθανόηες είναι : είναι μονάδα 6_ Pyrhniks_Diaspasis.dc 83 p() d, όπου ο παρονομασής p() d
4 Εκπομπή Σωμαιδίων-α Σχήμα 4 : Φωογραφικό γαλάκωμα απεικόνισης ένονων ροχιών σωμαιδίων-α λόγω μεγάλης απώλειας ενέργειας σην ύλη σε σχέση με ην λεπή διακεκομένη ροχιά ηλεκρονίου. Τα σωμαίδια-α είναι πυρήνες Ηλίου και έχουν χρησιμεύσει για ην μελέη ου αόμου από ον Ruhrfrd. Η εκπομπή ων σωμαιδίων-α έχει εξηγηθεί κβανομηχανικά από ον Gamw και ους Cndn και Guny. Σο σχήμα 4 παρουσιάζεαι ένα φωογραφικό γαλάκωμα με ις ροχιές ριών σωμαιδίων-α, αρκεά ένονες λόγω μεγάλης απώλειας ενέργειας ανά μονάδα διαδρομής σην ύλη (σχέση ων Bh-Blch) καθώς και η ευέλικη ροχιά ενός ηλεκρονίου Σύμφωνα με ο σχήμα 2 (κεφάλαιο 3), όπου έχουμε ην ενέργεια σύνδεσης ανά νουκλεόνιο Β/Α ως προς ον μαζικό αριθμό Α, παραηρείαι ένα μέγισο σην περιοχή ου σιδήρου (F, Z26), μέχρι ο οποίο υπάρχει σαθερόηα-β ων πυρήνων και εν συνεχεία θεωρούμε όι α βαρύερα σοιχεία μπορεί να είναι ασαθή και να διασπώναι αυθόρμηα. Η ιμή-q(α, Ζ) (κινηική ενέργεια) που απελευθερώνεαι καά η διάσπαση ου πυρήνα (Α, Ζ) δίδεαι σαν συνάρηση ων ενεγρειών σύνδεσης ου μηρικού και θυγαρικού πυρήνα από η σχέση : (, ) ( 4, 2) 28.3 ( ) Q A Z B A Z + MV B A, Z (6.) Όπου 28.3 MV είναι η πειραμαική ενέργεια σύνδεσης ου σωμαιδίου-α. Έχονας υπόψη όι για πυρήνες που βρίσκοναι πάνω σην καμπύλη β- σαθερόηας, χρησιμοποιώνας ην ημι-εμπειρική σχέση μάζας (3.), μπορούμε να υπολογίσουμε ο Q σαν συνάρηση ου Ζ (ή ου Α). Σο σχήμα 42, παρουσιάζεαι η θεωρηική μεαβολή (σχέση 6.) ου Q(Ζ) για Ζ>5. Αρνηική ιμή ου Q σημαίνει απόλυη σαθερόηα ως προς α-διάσπαση. Τα πειραμαικά σημεία ου σχήμαος 42 προέρχοναι από περιπώσεις όπου ο μηρικός και θυγαρικός πυρήνας είναι β-σαθεροί. Το σημείο γύρω από ον πυρήνα 24 82Pb, έχει πιο σαθερούς πυρήνες λόγω ων διπλά συμπληρωμένων 6_ Pyrhniks_Diaspasis.dc 84
5 φλοιών. Σε μεγαλύερα Ζ, σην περιοχή ου U υπάρχει μια άλλη μικρή περιοχή σχεικής σαθερόηας. Σχήμα 42 : Μεαβολή ου Q(Ζ) για Ζ>5 Οι β-σαθεροί πυρήνες με Ζ>66 είναι ασαθείς ως προς α-διάσπαση. Μέχρι ο Bi(Ζ83) οι χρόνοι ζωής ων β-σαθερών πυρήνων είναι πολλές άξεις μεγέθους μεγαλύερος από ην ηλικία ης γής. Η ΣΥΝΕΧΕΙΑ ΟΠΩΣ ΣΤΟ ΔΙΔΑΚΤΙΚΟ ΒΙΒΛΙΟ ΠΟΥ ΔΙΑΝΕΜΕΤΑΙ 6_ Pyrhniks_Diaspasis.dc 85
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ
 Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
Κεφάλαιο 3 ο. Κυκλώματα με στοιχεία αποθήκευσης ενέργειας
 Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ
 ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ
 Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ
 ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
ΦΥΣΙΚΗ Ι. ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ ΣΩΜΑΤΟΣ Ισορροπία Σωματιδίου Στατική Ισορροπία Στερεού Σώματος
 ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
Εργαστηριακή Άσκηση Το σύστημα αναμονής M/G/1
 Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Κεφάλαιο 5 Πολλαπλοί χημικοί αντιδραστήρες
 Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Η Έννοια της τυχαίας ιαδικασίας
 Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
Γιάννη Σ. Μπούταλη Αναπληρωτή Καθηγητή Δ.Π.Θ. ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθητικές σημειώσεις στο μάθημα ΣΑΕ ΙΙ
 Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
ΦΥΣ 145 Υπολογιστικές Μέθοδοι στη Φυσική. Τελική εξέταση 5 Μάη 2007 Ομάδα 2 η
 ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
Δυναμική συμπεριφορά των λογικών κυκλωμάτων MOS. Διάλεξη 10
 Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Θέματα Περασμένων Εξετάσεων και Απαντήσεις
 Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
ΕΛΕΓΧΟΣ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΚΕΦΑΛΑΙΟ 2 ΚΕΦΑΛΑΙΟ 2. Πλεονεκτήματα ψηφιακού ελέγχου
 ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ. LT και μονάδες στο SI, kgm/s 2 ή N. υνισταμένη. υνισταμένη. d dt. d dt.
 ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
Μεγαλύτερες περιπέτειες
 Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Πως λύνεται ένα πρόβληµα.
 Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
_Σχήµα 2_. Σελίδα 1 από 5. τον οποίο γίνεται η µεταπτωτική κίνηση. Άξονας περιστροφής τροχού. Άξονας γύρω από. τον οποίο γίνεται η µεταπτωτική κίνηση
 ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
Νόμος Αmpere. i r. Β dl = Β(dl ακτ +dl τοξ ) = Β rdθ = 2π. Β dl = μ ο i
 Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
3 Συσχετίσεις σε χρονοσειρές
 3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
Θεματική ενότητα : Βασικά εργαλεία και Μέθοδοι για τον έλεγχο της ποιότητας.
 Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
Εργαστήριο Ηλεκτρικών κυκλωμάτων
 Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ
 ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
13. Συνήθεις διαφορικές εξισώσεις
 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ 90º. 180º ω. Οι απαντήσεις και τα σχετικά σχόλια
 Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
Κεφάλαιο 4 Ιδανικοί χημικοί αντιδραστήρες
 Κεφάλαιο 4 Ιδανικοί χημικοί ανιδρασήρες Με βάση α σοιχεία για ην κινηική και η σοιχειομερία ων ανιδράσεων, μπορούμε ώρα να προχωρήσουμε σην ανάλυση ορισμένων βασικών ύπων χημικών ανιδρασήρων. Η ανάλυση
Κεφάλαιο 4 Ιδανικοί χημικοί ανιδρασήρες Με βάση α σοιχεία για ην κινηική και η σοιχειομερία ων ανιδράσεων, μπορούμε ώρα να προχωρήσουμε σην ανάλυση ορισμένων βασικών ύπων χημικών ανιδρασήρων. Η ανάλυση
ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ. Βιβλίο διδάσκοντα με λύσεις προβλημάτων. Κεφάλαιο 1. ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγητής
 ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Βιβλίο διδάσκονα με λύσεις ροβλημάων Κεφάλαιο ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγηής epapamic@civil.auth.gr ΝΙΚΟΣ ΧΑΡΑΛΑΜΠΑΚΗΣ Καθηγηής charalam@civil.auth.gr Αρισοέλειο Πανισήμιο
ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Βιβλίο διδάσκονα με λύσεις ροβλημάων Κεφάλαιο ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγηής epapamic@civil.auth.gr ΝΙΚΟΣ ΧΑΡΑΛΑΜΠΑΚΗΣ Καθηγηής charalam@civil.auth.gr Αρισοέλειο Πανισήμιο
1η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΘΕΡΜΟΚΡΑΣΙΑ ΑΕΡΑ ΚΑΙ ΜΕΤΑΦΟΡΑ ΑΙΣΘΗΤΗΣ ΘΕΡΜΟΤΗΤΑΣ
 1η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΘΕΡΜΟΚΡΑΣΙΑ ΑΕΡΑ ΚΑΙ ΜΕΤΑΦΟΡΑ ΑΙΣΘΗΤΗΣ ΘΕΡΜΟΤΗΤΑΣ ΜΕΘΟΔΟΙ ΜΕΤΡΗΣΗΣ ΘΕΡΜΟΚΡΑΣΙΑΣ Δισολή (θερμική δισολή σερεών-υγρών-ερίων) Ηλεκρική νίσση (εξάρησή ης πό θερμοκρσί) Θερμοηλεκρικό
1η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΘΕΡΜΟΚΡΑΣΙΑ ΑΕΡΑ ΚΑΙ ΜΕΤΑΦΟΡΑ ΑΙΣΘΗΤΗΣ ΘΕΡΜΟΤΗΤΑΣ ΜΕΘΟΔΟΙ ΜΕΤΡΗΣΗΣ ΘΕΡΜΟΚΡΑΣΙΑΣ Δισολή (θερμική δισολή σερεών-υγρών-ερίων) Ηλεκρική νίσση (εξάρησή ης πό θερμοκρσί) Θερμοηλεκρικό
ΦΥΣΙΚΗ Ι. ΤΜΗΜΑ Α Ε. Στυλιάρης
 (Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
(Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ
 ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ Η ρόοδος ης ανίδρασης μορί να υολογισί: Τιλοδόηση διλών δσμών Μαβολή ου όγκου ου μέσου ης ανίδρασης Μέρηση ης
ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ Η ρόοδος ης ανίδρασης μορί να υολογισί: Τιλοδόηση διλών δσμών Μαβολή ου όγκου ου μέσου ης ανίδρασης Μέρηση ης
Ροπή δύναμης. Τι προκαλεί την επιτάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω του. Τι προκαλεί την γωνιακή επιτάχυνση ενός στερεού σώματος;
 Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ 1 ΣΕΙΡΑΣ FOURIER. Ανάπτυξη σειράς Dirac σε σειρά Fourier (Εκθετική Fourier):
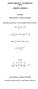 ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ. 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διατμητικής Αντοχής Εδάφους. Διδάσκοντες: Β. Χρηστάρας Καθηγητής Β. Μαρίνος, Αν.
 ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
Μεταλλική συμπεριφορά
 Μεαλλική συμπεριφορά Χαρακηρισικά μεαλλικής συμπεριφοράς Μεγάλη θερμική και ηλεκρονιακή αγωγιμόηα Μεγάλο μέρο ελασικόηας όγκου (Β=10 11 Pa) Μεαλλική λάμψη Ι. Μονέλο Drude (Jelliu) Σύμβαση προσήμου: e:
Μεαλλική συμπεριφορά Χαρακηρισικά μεαλλικής συμπεριφοράς Μεγάλη θερμική και ηλεκρονιακή αγωγιμόηα Μεγάλο μέρο ελασικόηας όγκου (Β=10 11 Pa) Μεαλλική λάμψη Ι. Μονέλο Drude (Jelliu) Σύμβαση προσήμου: e:
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ
 Ελληνικό Σαισικό Ινσιούο Πρακικά 8 ου Πανελληνίου Συνεδρίου Σαισικής (5) σελ.35-34 ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ Παπάνα Αγγελική και Κουγιουμζής Δημήρης
Ελληνικό Σαισικό Ινσιούο Πρακικά 8 ου Πανελληνίου Συνεδρίου Σαισικής (5) σελ.35-34 ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ Παπάνα Αγγελική και Κουγιουμζής Δημήρης
- Ομοιότητα με βάση τις εξισώσεις Νavier-Stokes - 2- διάστατη ασυμπίεστη Ροή
 ΚΕΦΑΛΑΙΟ 8 ΡΟΗ ΠΡΑΓΜΑΤΙΚΟΥ ΡΕΥΣΤΟΥ-ΣΥΝΕΚΤΙΚΗ ΡΟΗ - Ιξώδες - Ομοιόηα με βάση ις εξισώσεις Νaier-Stkes - - διάσαη ασυμπίεση Ροή ΕΞΙΣΩΣΗ ΣΥΝΕΧΕΙΑΣ 0 ΕΞΙΣΩΣΕΙΣ ΟΡΜΗΣ t 1 μ 1 g μ t - Οιακές Συνθήκες B σο -
ΚΕΦΑΛΑΙΟ 8 ΡΟΗ ΠΡΑΓΜΑΤΙΚΟΥ ΡΕΥΣΤΟΥ-ΣΥΝΕΚΤΙΚΗ ΡΟΗ - Ιξώδες - Ομοιόηα με βάση ις εξισώσεις Νaier-Stkes - - διάσαη ασυμπίεση Ροή ΕΞΙΣΩΣΗ ΣΥΝΕΧΕΙΑΣ 0 ΕΞΙΣΩΣΕΙΣ ΟΡΜΗΣ t 1 μ 1 g μ t - Οιακές Συνθήκες B σο -
d k dt k a ky(t) = dt k b kx(t) (3.1)
 Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
Πυρηνικές διασπάσεις. Δήμος Σαμψωνίδης (19-11- 2010) Στοιχεία Πυρηνικής Φυσικής & Φυσικής Στοιχειωδών Σωματιδίων 5 ο Εξάμηνο
 Πυρηνικές διασπάσεις Δήμος Σαμψωνίδης (19-11- 2010) Στοιχεία Πυρηνικής Φυσικής & Φυσικής Στοιχειωδών Σωματιδίων 5 ο Εξάμηνο Ενέργεια σύνδεσης & Κοιλάδα σταθερότητας (επανάληψη) Πυρηνικές διασπάσεις Ραδιενέργεια
Πυρηνικές διασπάσεις Δήμος Σαμψωνίδης (19-11- 2010) Στοιχεία Πυρηνικής Φυσικής & Φυσικής Στοιχειωδών Σωματιδίων 5 ο Εξάμηνο Ενέργεια σύνδεσης & Κοιλάδα σταθερότητας (επανάληψη) Πυρηνικές διασπάσεις Ραδιενέργεια
ιονύσης Μητρόπουλος νόµος του Νεύτωνα έχει για το σωµατίδιο τη µορφή F = (2), (3).
 ιούσης Μηρόπουλος Σερεό ΣΥΣΤΗΜΑ ΣΩΜΑΤΙ ΙΩΝ, ΣΤΕΡΕΟ ΣΩΜΑ ΟΣ ΝΟΜΟΣ ΤΟΥ ΝΕΥΤΩΝΑ Έα σωµαίδιο, Ορµή, Σροφορµή Ο ος όµος ου Νεύωα σε αδραειακό και µη αδραειακό σύσηµα Γωρίζουµε όι η ορµή εός σωµαιδίου µάζας
ιούσης Μηρόπουλος Σερεό ΣΥΣΤΗΜΑ ΣΩΜΑΤΙ ΙΩΝ, ΣΤΕΡΕΟ ΣΩΜΑ ΟΣ ΝΟΜΟΣ ΤΟΥ ΝΕΥΤΩΝΑ Έα σωµαίδιο, Ορµή, Σροφορµή Ο ος όµος ου Νεύωα σε αδραειακό και µη αδραειακό σύσηµα Γωρίζουµε όι η ορµή εός σωµαιδίου µάζας
ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΧΗ ΜΗΝΥΜΑΤΟΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 9 ΙΟΥΛΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο
ΑΡΧΗ ΜΗΝΥΜΑΤΟΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 9 ΙΟΥΛΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο
ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΧΗ ΜΗΝΥΜΑΤΟΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 9 ΙΟΥΛΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό
ΑΡΧΗ ΜΗΝΥΜΑΤΟΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 9 ΙΟΥΛΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό
ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ
 Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
Κεφάλαιο 8: Μαγνητικά Υλικά και Ιδιότητες ΙΙ. Λιαροκάπης Ευθύμιος. Διηλεκτρικές, Οπτικές, Μαγνητικές Ιδιότητες Υλικών
 Σχολή Εφαρμοσμένν Μαθημαικών και Φυσικών Εισημών Εθνικό Μεσόβιο Πολυεχνείο Διηλεκρικές Οικές Μαγνηικές Ιδιόηες Υλικών Κεφάλαιο 8: Μαγνηικά Υλικά και Ιδιόηες ΙΙ Λιαροκάης Ευθύμιος Άδεια Χρήσης Το αρόν εκαιδευικό
Σχολή Εφαρμοσμένν Μαθημαικών και Φυσικών Εισημών Εθνικό Μεσόβιο Πολυεχνείο Διηλεκρικές Οικές Μαγνηικές Ιδιόηες Υλικών Κεφάλαιο 8: Μαγνηικά Υλικά και Ιδιόηες ΙΙ Λιαροκάης Ευθύμιος Άδεια Χρήσης Το αρόν εκαιδευικό
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ
 ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
Σειρά Ασκήσεων στην Αντοχή των Υλικών
 Σιρά Ακήων ην Ανοχή ων Υλικών Άκηη η Σο ημίο Α μιας πίπδης μαλλικής πιφάνιας μ μέρο λαικόηας 00 GP και λόγο Pissn 0.5 μρήθηκαν οι πιμηκύνις ις καυθύνις, και μ η διάαξη ων πιμηκυνιομέρων ου χήμαος, ως 900,
Σιρά Ακήων ην Ανοχή ων Υλικών Άκηη η Σο ημίο Α μιας πίπδης μαλλικής πιφάνιας μ μέρο λαικόηας 00 GP και λόγο Pissn 0.5 μρήθηκαν οι πιμηκύνις ις καυθύνις, και μ η διάαξη ων πιμηκυνιομέρων ου χήμαος, ως 900,
ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 29 ΜΑΪΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 29 ΜΑΪΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης
Α Σ Κ Η Σ Η 1 ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY
 Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
( ) ( 0 ) ( e. ( t) ( ) ( ) λ ( ) λ N λ λ. ln λ / λ. dt = = λ λ. Ιδανική ισορροπία! t, ο λόγος των ενεργοτήτων Β/Α: N b. c b b.
 Αλυσίδες Ραδιενεργών ιασπάσεων A B C ιαδοχικές διασπάσεις: λ λ (σταθερός πυρήνας) dn λnd N 0 η ενεργότητα dn λnd λnd Αρχικές συνθήκες: της πηγης N ( 0) 0 N δεν ειναι λ dn λ N d Nc ( 0) 0 c λ N ( ) N (
Αλυσίδες Ραδιενεργών ιασπάσεων A B C ιαδοχικές διασπάσεις: λ λ (σταθερός πυρήνας) dn λnd N 0 η ενεργότητα dn λnd λnd Αρχικές συνθήκες: της πηγης N ( 0) 0 N δεν ειναι λ dn λ N d Nc ( 0) 0 c λ N ( ) N (
ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 29 ΜΑΪΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 29 ΜΑΪΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό
ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 9 ΜΑΪΟΥ 004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 9 ΜΑΪΟΥ 004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
Εισαγωγή στη Θεωρία Σημάτων και Συστημάτων
 Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
Ανάλυση της µηχανικής συµπεριφοράς της συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα
 Ανάλυση ης µηχανικής συµπεριφοράς ης συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα Β. Καραζαφέρης MΕ, Υποψήφιος διδάκωρ ΕΜΠ Μ. Καής Επίκουρος Καθηγηής ΕΜΠ Λέξεις κλειδιά: FRP, συνάφεια, πεπερασµένα σοιχεία
Ανάλυση ης µηχανικής συµπεριφοράς ης συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα Β. Καραζαφέρης MΕ, Υποψήφιος διδάκωρ ΕΜΠ Μ. Καής Επίκουρος Καθηγηής ΕΜΠ Λέξεις κλειδιά: FRP, συνάφεια, πεπερασµένα σοιχεία
ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ
 1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 24 ΜΑΪΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ : ΦΥΣΙΚΗ
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 24 ΜΑΪΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ : ΦΥΣΙΚΗ ΘΕΜΑ 1ο Στις προτάσεις 1.1-1.4 να γράψετε στο τετράδιό σας τον αριθμό της αρχικής
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 24 ΜΑΪΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ : ΦΥΣΙΚΗ ΘΕΜΑ 1ο Στις προτάσεις 1.1-1.4 να γράψετε στο τετράδιό σας τον αριθμό της αρχικής
ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ
 Ελληνικό Σαισικό Ινσιούο Πρακικά ου Πανελληνίου Συνεδρίου Σαισικής (7), σελ 39-336 ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ Παπάνα Αγγελική, Κουγιουμζής Δημήρης Γενικό Τμήμα
Ελληνικό Σαισικό Ινσιούο Πρακικά ου Πανελληνίου Συνεδρίου Σαισικής (7), σελ 39-336 ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ Παπάνα Αγγελική, Κουγιουμζής Δημήρης Γενικό Τμήμα
Η κοιλάδα σταθερότητας των πυρήνων
 Η κοιλάδα σταθερότητας των πυρήνων Σταθερότητα των πυρήνων Όσο μεγαλύτερη η ενέργεια σύνδεσης ανά νουκλεόνιο δηλαδή όσο χαμηλότερη η μάζα του πυρήνα για δεδομένο Α τόσο πιο σταθερός ο πυρήνας. Ερώτηση:
Η κοιλάδα σταθερότητας των πυρήνων Σταθερότητα των πυρήνων Όσο μεγαλύτερη η ενέργεια σύνδεσης ανά νουκλεόνιο δηλαδή όσο χαμηλότερη η μάζα του πυρήνα για δεδομένο Α τόσο πιο σταθερός ο πυρήνας. Ερώτηση:
Ανάπτυξη και Αξιολόγηση Στρατηγικής Κεντρικού Ελέγχου Ροών σε Αποχετευτικά ίκτυα µε Έµφαση στην Εφαρµογή της στον Ελλαδικό Χώρο
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ: Μηχανικών Παραγωγής & ιοίκησης Ανάπυξη και Αξιολόγηση Σραηγικής Κενρικού Ελέγχου Ροών σε Αποχεευικά ίκυα µε Έµφαση σην Εφαρµογή ης σον Ελλαδικό Χώρο ιαριβή που υπεβλήθη για ην
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ: Μηχανικών Παραγωγής & ιοίκησης Ανάπυξη και Αξιολόγηση Σραηγικής Κενρικού Ελέγχου Ροών σε Αποχεευικά ίκυα µε Έµφαση σην Εφαρµογή ης σον Ελλαδικό Χώρο ιαριβή που υπεβλήθη για ην
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ 29 ΜΑΙΟΥ 2004
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ 29 ΜΑΙΟΥ 2004 ΘΕΜΑ Ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.. Σύμφωνα με την ηλεκτρομαγνητική
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ 29 ΜΑΙΟΥ 2004 ΘΕΜΑ Ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.. Σύμφωνα με την ηλεκτρομαγνητική
Ορισμός: u(t) = 0 (t < 0) και u(t) = 1 (t 0) (4.1) Από τις (4.3) και (4.4), προκύπτει ότι το βηματικό σήμα u(t) είναι σήμα ισχύος.
 4. ΑΝΑΛΥΣΗ ΒΑΣΙΚΩΝ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΗΜΑΤΩΝ 4.. To βημαικό σήμα (step signal) u(t) Ορισμός: u(t) = 0 (t < 0) και u(t) = (t 0) (4.) Μέση ιμή: = (4.) Ενέργεια: Ε = lim [T ] [-, ] u (t).dt (4.3) Μέση
4. ΑΝΑΛΥΣΗ ΒΑΣΙΚΩΝ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΗΜΑΤΩΝ 4.. To βημαικό σήμα (step signal) u(t) Ορισμός: u(t) = 0 (t < 0) και u(t) = (t 0) (4.) Μέση ιμή: = (4.) Ενέργεια: Ε = lim [T ] [-, ] u (t).dt (4.3) Μέση
Εισαγωγή στην Πυρηνική Φυσική και τα Στοιχειώδη Σωμάτια
 Εισαγωγή στην Πυρηνική Φυσική και τα Στοιχειώδη Σωμάτια Κ. Ν. Παπανικόλας, Ε. Στυλιάρης, Πανεπιστήμιο Αθηνών Εαρινό Εξάμηνο 2010-2011 Περιεχόμενα Ενέργεια κατά την α-διάσπαση Θεωρία της α-διάσπασης Χρόνοι
Εισαγωγή στην Πυρηνική Φυσική και τα Στοιχειώδη Σωμάτια Κ. Ν. Παπανικόλας, Ε. Στυλιάρης, Πανεπιστήμιο Αθηνών Εαρινό Εξάμηνο 2010-2011 Περιεχόμενα Ενέργεια κατά την α-διάσπαση Θεωρία της α-διάσπασης Χρόνοι
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Οι ακτίνες Χ α. έχουν φάσµα που είναι µόνο συνεχές.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 24 ΜΑΪΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Στις προτάσεις 1.1-1.4 να γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 24 ΜΑΪΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Στις προτάσεις 1.1-1.4 να γράψετε
y(t) = T [x(t)] (7.1)
![y(t) = T [x(t)] (7.1) y(t) = T [x(t)] (7.1)](/thumbs/93/114087149.jpg) Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
Μάθημα 5 - Πυρηνική 1) Ειδη διασπάσεων και Νόμος ραδιενεργών διασπάσεων 2) αλφα, 3) βητα, 4) γαμμα
 ΦΥΕ 40 Κβαντική Φυσική Μάθημα 5 - Πυρηνική 1) Ειδη διασπάσεων και Νόμος ραδιενεργών διασπάσεων 2) αλφα, 3) βητα, 4) γαμμα Μαθημα 5.1 - διασπάσεις Λέκτορας Κώστας Κορδάς Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης
ΦΥΕ 40 Κβαντική Φυσική Μάθημα 5 - Πυρηνική 1) Ειδη διασπάσεων και Νόμος ραδιενεργών διασπάσεων 2) αλφα, 3) βητα, 4) γαμμα Μαθημα 5.1 - διασπάσεις Λέκτορας Κώστας Κορδάς Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 27 ΜΑΪΟΥ 2005 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6)
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 27 ΜΑΪΟΥ 2005 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ημιτελείς προτάσεις 1.1
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 27 ΜΑΪΟΥ 2005 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ημιτελείς προτάσεις 1.1
Niels Bohr ( ) ΘΕΜΑ Α
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ Niels Bohr (885-962) ΘΕΜΑ Α Στις ερωτήσεις Α -Α να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και, δίπλα το γράμμα που
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ Niels Bohr (885-962) ΘΕΜΑ Α Στις ερωτήσεις Α -Α να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και, δίπλα το γράμμα που
λ Ε Πχ. Ένα σωματίδιο α έχει φορτίο +2 όταν επιταχυνθεί από μια διαφορά Για ακτίνες Χ ή ακτινοβολία γ έχουμε συχνότητα
 Μονάδες Ενέργειας 1 ev = 1,602 10-19 J 1 fj(= 10-15 J) = 6,241 10 3 ev Πχ. Ένα σωματίδιο α έχει φορτίο +2 όταν επιταχυνθεί από μια διαφορά δυναμικού 1000 V αποκτά ενέργεια 2 kev Για ακτίνες Χ ή ακτινοβολία
Μονάδες Ενέργειας 1 ev = 1,602 10-19 J 1 fj(= 10-15 J) = 6,241 10 3 ev Πχ. Ένα σωματίδιο α έχει φορτίο +2 όταν επιταχυνθεί από μια διαφορά δυναμικού 1000 V αποκτά ενέργεια 2 kev Για ακτίνες Χ ή ακτινοβολία
ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα, που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 5 ΜΑΙΟΥ 6 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 5 ΜΑΙΟΥ 6 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό
Σοιχεία Πυρηνικής Φυσικής και Στοιχειωδών Σωματιδίων 5ο εξάμηνο Τμήμα T3: Κ. Κορδάς & Χ. Πετρίδου. Μάθημα 7
 Σοιχεία Πυρηνικής Φυσικής και Στοιχειωδών Σωματιδίων 5ο εξάμηνο 2016-17 Τμήμα T3: Κ. Κορδάς & Χ. Πετρίδου Μάθημα 7 α) Άλφα διάσπαση β) Σχάση και σύντηξη Πετρίδου Χαρά Αριστοτέλειο Πανεπιστήµιο Θεσσαλονίκης
Σοιχεία Πυρηνικής Φυσικής και Στοιχειωδών Σωματιδίων 5ο εξάμηνο 2016-17 Τμήμα T3: Κ. Κορδάς & Χ. Πετρίδου Μάθημα 7 α) Άλφα διάσπαση β) Σχάση και σύντηξη Πετρίδου Χαρά Αριστοτέλειο Πανεπιστήµιο Θεσσαλονίκης
ΖΗΤΗΜΑ 2 ο 220. µετατρέπεται σε βισµούθιο -212 ( Bi) διασπάσεων: 220. Α. Το ραδόνιο 220 ( 1. Να συµπληρώσετε τις παραπάνω εξισώσεις.
 ΦΥΣΙΚΗ- ο ΙΑΓΩΝΙΣΜΑ ΖΗΤΗΜΑ ο Α. Ερώτηση του τύπου Σωστό- Λάθος. Με τον όρο ότι το φως έχει διπλή φύση εννοούµε ότι:. Αποτελείται από θετικά και αρνητικά σωµατίδια.. Συµπεριφέρεται σαν κύµα και σαν σωµατίδιο.
ΦΥΣΙΚΗ- ο ΙΑΓΩΝΙΣΜΑ ΖΗΤΗΜΑ ο Α. Ερώτηση του τύπου Σωστό- Λάθος. Με τον όρο ότι το φως έχει διπλή φύση εννοούµε ότι:. Αποτελείται από θετικά και αρνητικά σωµατίδια.. Συµπεριφέρεται σαν κύµα και σαν σωµατίδιο.
Κεφάλαιο 4. Θεωρήµατα οµής
 Κεφάαιο 4 Θεωρήαα οής Σ' αυό ο εφάαιο θ αποδείξουε α Θεωρήαα οής για πεπερασένα παραγόενα R-πρόυπα, όπου R αέραια περιοχή υρίων ιδεωδών, (απι) 4 Ανάυση σε άθροισα περιοδιού αι εεύθερου, ανάυση σοιχείο
Κεφάαιο 4 Θεωρήαα οής Σ' αυό ο εφάαιο θ αποδείξουε α Θεωρήαα οής για πεπερασένα παραγόενα R-πρόυπα, όπου R αέραια περιοχή υρίων ιδεωδών, (απι) 4 Ανάυση σε άθροισα περιοδιού αι εεύθερου, ανάυση σοιχείο
δ. εξαρτάται µόνο από το υλικό του οπτικού µέσου. Μονάδες 4
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 7 ΙΟΥΛΙΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Στις ερωτήσεις 1-5 να
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 7 ΙΟΥΛΙΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Στις ερωτήσεις 1-5 να
ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα, που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 25 ΜΑΙΟΥ 2006 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 25 ΜΑΙΟΥ 2006 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. 3. Ισότοποι ονοµάζονται οι πυρήνες που ανήκουν στο ίδιο χηµικό στοιχείο και έχουν τον ίδιο: α. µαζικό αριθµό β.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΤΕΛΟΣ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 4 ΙΟΥΝΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΤΕΛΟΣ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 4 ΙΟΥΝΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε
( ) ( 0 ) ( e. ( t) ( ) λ ( ) dn dt. Ιδανική ισορροπία! t, ο λόγος των ενεργοτήτων Β/Α: λ λ. N b. c b b. η ενεργότητα = 0. δεν ειναι λb. tmax.
 Αλυσίδες Ραδιενεργών ιασπάσεων A B C ιαδοχικές διασπάσεις: λ λ (σταθερός πυρήνας dn = λnd N η ενεργότητα dn = λnd λnd Αρχικές συνθήκες: της πηγης N ( = N δεν ειναι λ dn = λ N d Nc ( = c λ N ( = N ( e λ
Αλυσίδες Ραδιενεργών ιασπάσεων A B C ιαδοχικές διασπάσεις: λ λ (σταθερός πυρήνας dn = λnd N η ενεργότητα dn = λnd λnd Αρχικές συνθήκες: της πηγης N ( = N δεν ειναι λ dn = λ N d Nc ( = c λ N ( = N ( e λ
TO MONTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (Reptation Model)
 TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
ΑΓ.ΚΩΝΣΤΑΝΤΙΝΟΥ ΠΕΙΡΑΙΑΣ ΤΗΛ , ΟΔΗΓΙΕΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ. Φως
 ΟΔΗΓΙΕΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Κεφάλαιο 1 ο Φως Ο μαθητής που έχει μελετήσει το κεφάλαιο του φωτός πρέπει: Να γνωρίζει πως εξελίχθηκε ιστορικά η έννοια του φωτός και ποια είναι η σημερινή
ΟΔΗΓΙΕΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Κεφάλαιο 1 ο Φως Ο μαθητής που έχει μελετήσει το κεφάλαιο του φωτός πρέπει: Να γνωρίζει πως εξελίχθηκε ιστορικά η έννοια του φωτός και ποια είναι η σημερινή
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗΣ Προσδιορισμός ης αξίας που δημιουργείαι για ους μεόχους με βάση ο οικονομικό και λογισικό κέρδος σα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗΣ Προσδιορισμός ης αξίας που δημιουργείαι για ους μεόχους με βάση ο οικονομικό και λογισικό κέρδος σα
ΦΥΣΙΚΗ ΙΑΛΕΞΗ 4: Ο ΑΤΟΜΙΚΟΣ ΠΥΡΗΝΑΣ. ιδάσκων Ευθύµιος Τάγαρης Φυσικός, ρ Περιβαλλοντικών Επιστηµών. ρ Ευθύµιος Α. Τάγαρης
 ΦΥΣΙΚΗ ΙΑΛΕΞΗ 4: Ο ΑΤΟΜΙΚΟΣ ΠΥΡΗΝΑΣ ιδάσκων Ευθύµιος Τάγαρης Φυσικός, ρ Περιβαλλοντικών Επιστηµών Σταθερότητα πυρήνων Αριθµός πρωτονίων και νετρονίων Αριθµός νετρονίων (Ν) 20 Σταθεροί πυρήνες Ν=Ζ 20 Αριθµός
ΦΥΣΙΚΗ ΙΑΛΕΞΗ 4: Ο ΑΤΟΜΙΚΟΣ ΠΥΡΗΝΑΣ ιδάσκων Ευθύµιος Τάγαρης Φυσικός, ρ Περιβαλλοντικών Επιστηµών Σταθερότητα πυρήνων Αριθµός πρωτονίων και νετρονίων Αριθµός νετρονίων (Ν) 20 Σταθεροί πυρήνες Ν=Ζ 20 Αριθµός
Διάλεξη 4: Ραδιενέργεια
 Σύγχρονη Φυσική - 216: Πυρηνική Φυσική και Φυσική Στοιχειωδών Σωματιδίων 4/4/16 Διάλεξη 4: Ραδιενέργεια Βασικοί τρόποι αποδιέγερσης Όπως γνωρίζουμε στην φύση υπάρχουν σταθερές πυρηνικές καταστάσεις αλλά
Σύγχρονη Φυσική - 216: Πυρηνική Φυσική και Φυσική Στοιχειωδών Σωματιδίων 4/4/16 Διάλεξη 4: Ραδιενέργεια Βασικοί τρόποι αποδιέγερσης Όπως γνωρίζουμε στην φύση υπάρχουν σταθερές πυρηνικές καταστάσεις αλλά
Ασκήσεις #1 επιστροφή 15/10/2012
 Σοιχεία Πυρηνικής Φυσικής και Στοιχειωδών Σωματιδίων (5ου εξαμήνου, χειμερινό 2012-13) Τμήμα G3: Κ. Κορδάς & Χ. Πετρίδου Ασκήσεις #1 επιστροφή 15/10/2012 Λέκτορας Κώστας Κορδάς Αριστοτέλειο Πανεπιστήμιο
Σοιχεία Πυρηνικής Φυσικής και Στοιχειωδών Σωματιδίων (5ου εξαμήνου, χειμερινό 2012-13) Τμήμα G3: Κ. Κορδάς & Χ. Πετρίδου Ασκήσεις #1 επιστροφή 15/10/2012 Λέκτορας Κώστας Κορδάς Αριστοτέλειο Πανεπιστήμιο
Πανεπιστήµιο Θεσσαλίας
 Πανεπισήιο Θεσσαλίας Τήα Ηλεκρολόγων Μηχανικών & Μηχανικών Υπολογισών Άσκηση : Λυένες Ασκήσεις Έσω ένα σύσηα νήης, σο οποίο έχουε προσθέσει ια κρυφή νήη θυάων 6 θέσεων εαξύ ης κρυφής νήης δεδοένων L και
Πανεπισήιο Θεσσαλίας Τήα Ηλεκρολόγων Μηχανικών & Μηχανικών Υπολογισών Άσκηση : Λυένες Ασκήσεις Έσω ένα σύσηα νήης, σο οποίο έχουε προσθέσει ια κρυφή νήη θυάων 6 θέσεων εαξύ ης κρυφής νήης δεδοένων L και
γ-διάσπαση Διάλεξη 17η Πετρίδου Χαρά Τμήμα G3: Κ. Κορδάς & Χ. Πετρίδου
 γ-διάσπαση Διάλεξη 17η Τμήμα G3: Κ. Κορδάς & Χ. Πετρίδου 1 Τι θα μάθουμε σήμερα 2 Τι είναι η γ-διάσπαση γ-αποδιέγερση ηλεκτρόνια εσωτερικών μετατροπών εσωτερική δημιουργία ζεύγους (e + e - ) Πως προκύπτει?
γ-διάσπαση Διάλεξη 17η Τμήμα G3: Κ. Κορδάς & Χ. Πετρίδου 1 Τι θα μάθουμε σήμερα 2 Τι είναι η γ-διάσπαση γ-αποδιέγερση ηλεκτρόνια εσωτερικών μετατροπών εσωτερική δημιουργία ζεύγους (e + e - ) Πως προκύπτει?
Διάλεξη 7: Αλληλεπιδράσεις νετρονίων & πυρηνική σχάση
 Διάλεξη 7: Αλληλεπιδράσεις νετρονίων & πυρηνική σχάση Αλληλεπιδράσεις νετρονίων Το νετρόνιο ως αφόρτιστο νουκλεόνιο παίζει σημαντικό ρόλο στην πυρηνική φυσική και στην κατανόηση των πυρηνικών αλληλεπιδράσεων.
Διάλεξη 7: Αλληλεπιδράσεις νετρονίων & πυρηνική σχάση Αλληλεπιδράσεις νετρονίων Το νετρόνιο ως αφόρτιστο νουκλεόνιο παίζει σημαντικό ρόλο στην πυρηνική φυσική και στην κατανόηση των πυρηνικών αλληλεπιδράσεων.
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 15 ΜΑΡΤΙΟΥ 2015
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 5 ΜΑΡΤΙΟΥ 05 ΘΕΜΑ Α Στις ερωτήσεις Α-Α4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και, δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 5 ΜΑΡΤΙΟΥ 05 ΘΕΜΑ Α Στις ερωτήσεις Α-Α4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και, δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 4 ΙΟΥΝΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 4 ΙΟΥΝΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 4 ΙΟΥΝΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Βέλισες σραηγικές διακοπής μιας Μαρκοβιανής αλυσίδας ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΒΑΣΙΛΕΙΟΣ ΖΑΧΑΡΙΑΔΗΣ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Βέλισες σραηγικές διακοπής μιας Μαρκοβιανής αλυσίδας ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΒΑΣΙΛΕΙΟΣ ΖΑΧΑΡΙΑΔΗΣ
Μονάδες Η θεωρία των κβάντα:
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 29 ΙΟΥΝΙΟΥ 2007 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤΑ (7) ΘΕΜΑ 1ο Στις ερωτήσεις 1-4
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 29 ΙΟΥΝΙΟΥ 2007 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤΑ (7) ΘΕΜΑ 1ο Στις ερωτήσεις 1-4
Κανονισμός Πυροπροστασίας Κτιρίων (π.δ. 41/2018)
 Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
Εργαστηριακή ή Άσκηση η 3
 Μιχάλης Καλογεράκης 9 ο Εξάμηνο ΣΕΜΦΕ ΑΜ:09101187 Υπεύθυνος Άσκησης: Μ. Κόκκορης Συνεργάτης: Κώστας Καραϊσκος Ημερομηνία Διεξαγωγής: 9/11/005 Εργαστήριο Πυρηνικής Φυσικής και Στοιχειωδών ν Σωματιδίων Εργαστηριακή
Μιχάλης Καλογεράκης 9 ο Εξάμηνο ΣΕΜΦΕ ΑΜ:09101187 Υπεύθυνος Άσκησης: Μ. Κόκκορης Συνεργάτης: Κώστας Καραϊσκος Ημερομηνία Διεξαγωγής: 9/11/005 Εργαστήριο Πυρηνικής Φυσικής και Στοιχειωδών ν Σωματιδίων Εργαστηριακή
Η ραδιοχρονολόγηση µε 14 C - Οδηγίες για τον καθηγητή
 - Τάξη Μάθηµα Γνωστικό αντικείµενο: ιδακτική ενότητα Απαιτούµενος χρόνος Α Λυκείου Χηµεία (Γενικής Παιδείας) Οργανική Χηµεία Αλκοόλες 2 διδακτικές ώρες Ειδικοί διδακτικοί στόχοι Το λογισµικό αυτό θα σας
- Τάξη Μάθηµα Γνωστικό αντικείµενο: ιδακτική ενότητα Απαιτούµενος χρόνος Α Λυκείου Χηµεία (Γενικής Παιδείας) Οργανική Χηµεία Αλκοόλες 2 διδακτικές ώρες Ειδικοί διδακτικοί στόχοι Το λογισµικό αυτό θα σας
ΠΥΡΗΝΙΚΑ ΜΟΝΤΕΛΑ Τάσος Λιόλιος Μάθημα Πυρηνικής Φυσικής
 ΠΥΡΗΝΙΚΑ ΜΟΝΤΕΛΑ Τάσος Λιόλιος Μάθημα Πυρηνικής Φυσικής REF: Σ. Δεδούσης, Μ.Ζαμάνη, Δ.Σαμψωνίδης Σημειώσεις Πυρηνικής Φυσικής Πυρηνικά μοντέλα Βασικός σκοπός της Πυρηνικής Φυσικής είναι η περιγραφή των
ΠΥΡΗΝΙΚΑ ΜΟΝΤΕΛΑ Τάσος Λιόλιος Μάθημα Πυρηνικής Φυσικής REF: Σ. Δεδούσης, Μ.Ζαμάνη, Δ.Σαμψωνίδης Σημειώσεις Πυρηνικής Φυσικής Πυρηνικά μοντέλα Βασικός σκοπός της Πυρηνικής Φυσικής είναι η περιγραφή των
dn λ N dt λ Αρχικές συνθήκες: c b b η ενεργότητα της πηγης b δεν ειναι λb a a a λ λ b b a a b b
 Αυσίδες Ραδιενεργών ιασπάσεων A B C ιαδοχικές διασπάσεις: (σταθερός πυρήνας) dn N dt dn N dt N dt dn N dt c η ενεργότητα της πηγης N δεν ειναι Αρχικές συνθήκες: N 0 N N c 0 0 0 0 t N t N 0e t t N t N 0
Αυσίδες Ραδιενεργών ιασπάσεων A B C ιαδοχικές διασπάσεις: (σταθερός πυρήνας) dn N dt dn N dt N dt dn N dt c η ενεργότητα της πηγης N δεν ειναι Αρχικές συνθήκες: N 0 N N c 0 0 0 0 t N t N 0e t t N t N 0
Απορρόφηση ακτινοβολίας-β από την ύλη
 ΑΣΚΗΣΗ 3 Απορρόφηση ακτινοβολίας-β από την ύλη 1. Εισαγωγή Η β-διάσπαση είναι το συλλογικό όνοµα τριών φαινοµένων, στα οποία εκπέµπονται ηλεκτρόνια και ποζιτρόνια υψηλής ενέργειας ή πραγµατοποιείται σύλληψη
ΑΣΚΗΣΗ 3 Απορρόφηση ακτινοβολίας-β από την ύλη 1. Εισαγωγή Η β-διάσπαση είναι το συλλογικό όνοµα τριών φαινοµένων, στα οποία εκπέµπονται ηλεκτρόνια και ποζιτρόνια υψηλής ενέργειας ή πραγµατοποιείται σύλληψη
Digital Integrated Circuits, 2 nd edition, J. M. Rabaey, A. Chandrakasan, B. Nikolic
 Πρόβληµα 4. gital Itegrated Circuits, d editio, J. M. abaey, A. Chadrakasa, B. Nikolic You are desigig a clock distributio etwork i which it is critical to miimize skew betwee local clocks (CLK, CLK, ad
Πρόβληµα 4. gital Itegrated Circuits, d editio, J. M. abaey, A. Chadrakasa, B. Nikolic You are desigig a clock distributio etwork i which it is critical to miimize skew betwee local clocks (CLK, CLK, ad
? Συμπεριφορά ψαθυρών υλικών 11/6/2018. Δρ. Σωτήρης Δέμης. Σημειώσεις Εργαστηριακής Άσκησης Κριτήρια Αστοχίας Διάτμηση Τοιχοποιίας
 11/6/018 Σημειώεις Εργαηριακής Άκηης Κριήρια Αοχίας Διάμηη Τοιχοποιίας Δρ. Σωήρης Δέμης Πολιικός Μηχανικός (Πανεπιημιακός Υπόροφος) Έως ώρα Καααικός νόμος όλκιμων υλικών (αξονική κααπόνιη ε μία διεύθυνη)
11/6/018 Σημειώεις Εργαηριακής Άκηης Κριήρια Αοχίας Διάμηη Τοιχοποιίας Δρ. Σωήρης Δέμης Πολιικός Μηχανικός (Πανεπιημιακός Υπόροφος) Έως ώρα Καααικός νόμος όλκιμων υλικών (αξονική κααπόνιη ε μία διεύθυνη)
