d k dt k a ky(t) = dt k b kx(t) (3.1)
|
|
|
- Αγάπη Παπανικολάου
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά σοιχεία για α σήμαα και α συσήμαα. Σο εξής, θα θεωρούμε όι ένα σύσημα περιγράφεαι σο πεδίο ου χρόνου από μια γραμμική διαφορική εξίσωση ης μορφής με a k, b k σαθερούς συνελεσές. N k k a ky) = N k k b kx) 3.) 3.. Μια μικρή εφαρμογή-κίνηρο Πολλά φυσικά συσήμαα περιγράφοναι από διαφορικές εξισώσεις, εξ ου και ο ενδιαφέρον μας να μπορούμε να λύνουμε έοιες. Η λύση μιας διαφορικής εξίσωσης ης μορφής 3.) συνίσααι σην εύρεση ης εξόδου y) δεδομένης μιας εισόδου x). Ας δούμε δυο χαρακηρισικά παραδείγμαα ης Μηχανικής α οποία πρέπει να) είναι γνωσά σον αναγνώση. Πολλά πραγμαικά, μηχανικά συσήμαα εμπλέκουν ελαήρια και σώμαα. Το πιο σύνηθες έοιο παράδειγμα είναι ο Απλός Αρμονικός Ταλανωής, που δεν είναι ίποε άλλο από ένα σώμα μάζας m συνδεδεμένο σε ιδανικό ελαήριο σαθεράς k. Δείε ο Σχήμα 3.. Το σύσημα ελαήριο-σώμα βρίσκεαι σε ισορροπία σο Σχήμα 3.α). Εκείνουμε ο ελαήριο ραβώνας ο σώμα προς α δεξιά, μέχρι η μέγιση έκασή ου από η θέση ισορροπίας. Εσω όι η έκαση αυή βρίσκεαι A μέρα από ο σημείο ισορροπίας, όπως σο Σχήμα 3.β). Τη χρονική σιγμή = αφήνουμε ελεύθερο ο σώμα, ο οποίο εκελεί Απλή Αρμονική Ταλάνωση. Ολη η κίνηση αυή περιγράφεαι από η διαφορική εξίσωση 2 x) = ω2 x) 2 2 x) + ω2 x) = 3.2) Η παραπάνω διαφορική εξίσωση ονομάζεαι ομογενής. Πιθανόαα γνωρίζεε όι η εξίσωση θέσης ου σώμαος που είναι και η λύση ης διαφορικής εξίσωσης) οποιαδήποε χρονική σιγμή δίνεαι από η σχέση α) β) γ) -A A =) x) = A m u) = m/s x) = A cosω + φ), 3.3) Σχήμα 3.: Απλός Αρμονικός Ταλανωής. με ην ιμή ω να εξαράαι από ο υλικό ου ελαηρίου, και φ ην αρχική φάση ου αλανωή, που εν γένει μας
2 52 Μια εισαγωγή σα Σήμαα και Συσήμαα είναι άγνωση και εξαράαι από ις αρχικές συνθήκες ου προβλήμαος. Παραηρήσε όι η διαφορική εξίσωση 3.2) παρουσιάζει μόνο έξοδο x), καθώς η είσοδός ου είναι μηδενική. Πώς προκύπει άραγε η Σχέση 3.3) από η Σχέση 3.2); Επίσης, η πλειονόηα ων ηλεκρικών συσημάων που υπάρχουν γύρω μας περιγράφοναι από διαφορικές εξισώσεις με σαθερούς συνελεσές. Ενα πολύ απλό παράδειγμα έοιου συσήμαος είναι ο κύκλωμα πυκνωήανισάη, ή αλλιώς ο κύκλωμα RC. Δείε ο Σχήμα 3.2. Η ανίσαση ου ανισάση συμβολίζεαι με R ενώ R DC x) C y) Σχήμα 3.2: Κύκλωμα RC. η χωρηικόηα ου πυκνωή συμβολίζεαι με C. Είσοδος σε αυό ο σύσημα είναι η άση ης πηγής, ενώ η έξοδος είναι η άση σα άκρα ου πυκνωή. Μπορεί κανείς να δείξει όι η διαφορική εξίσωση που περιγράφει ο κύκλωμα αυό δίνεαι ως y) + RC y) = x) 3.4) RC Αρχικά η άση σα άκρα ου πυκνωή είναι μηδενική. Αν εφαρμόσουμε σο κύκλωμα μια ιδανική πηγή σαθερής άσης η χρονική σιγμή =, δηλ. x) = V u), όε μπορεί κανείς να δείξει όι η άση σα άκρα ου πυκνωή δίνεαι ως y) = V e /RC ), > 3.5) Πώς προκύπει αυή η σχέση από η διαφορική εξίσωση; Το κεφάλαιο αυό αναλαμβάνει να απανήσει σα ερωήμαα ων παραπάνω παραδειγμάων Απόκριση Συσήμαος Επιθμούμε λοιπόν να βρούμε έναν ρόπο για να υπολογίζουμε ην έξοδο από έοια συσήμαα, δεδομένης μιας συγκεκριμένης εισόδου. Εσω όι εφαρμόζουμε λοιπόν μια είσοδο x) η χρονική σιγμή =. Η έξοδος ου συσήμαος y) είναι ο αποέλεσμα δυο ανεξάρηων αιιών:. ων αρχικών συνθηκών ου συσήμαος, οι οποίες ονομάζοναι καάσαση ου συσήμαος, η χρονική σιγμή = 2. ης εισόδου x), για Η συνολική έξοδος δίνεαι ως ο άθροισμα ων εξόδων που απορρέουν από α δυο παραπάνω αίια. Η έξοδος ου συσήμαος που απορρέει από ις αρχικές συνθήκες ου συσήμαος για =, θεωρώνας ην είσοδο x) =, ονομάζεαι απόκριση μηδενικής εισόδου - zero-inpu response. Η έξοδος ου συσήμαος που απορρέει από ην παρουσία ης μη μηδενικής εισόδου x), θεωρώνας μηδενικές αρχικές συνθήκες, ονομάζεαι απόκριση μηδενικής καάσασης - zero-sae response. Οαν ο σύσημα έχει μηδενικές αρχικές συνθήκες, όε ο σύσημα θεωρείαι πως βρίσκεαι σε ηρεμία. Μπορούμε να εκφράσουμε η συνολική έξοδο y) ου συσήμαος ως ο άθροισμα ων παραπάνω δυο αποκρίσεων ως y) = y zi ) + y zs ) 3.6) με y zi ) και y zs ) ην απόκριση μηδενικής εισόδου και ην απόκριση μηδενικής καάσασης ανίσοιχα. Θα μπορούσε να αναρωηθεί κανείς ποιός είναι λόγος ύπαρξης αρχικών συνθηκών σε ένα πραγμαικό σύσημα. Από μαθημαικής πλευράς, οπωσδήποε είναι απαραίηες οι αρχικές συνθήκες για ην εύρεση μοναδικής λύσης μιας διαφορικής εξίσωσης. Ομως ποιά είναι η φυσική σημασία ων αρχικών συνθηκών; Σε ι ανισοιχούν σε πραγμαικά συσήμαα; Ας επανέλθουμε σα δυο παραδείγμαα ης Παραγράφου 3...
3 Κεφάλαιο 3. Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 53 Για ον Απλό Αρμονικό Ταλανωή ου Σχήμαος 3., οι αρχικές συνθήκες ανισοιχούν ση θέση και ην αχύηα ου σώμαος η χρονική σιγμή =, δηλ. η χρονική σιγμή που αρχίζουμε να μελεάμε ο πρόβλημα ης κίνησης ου σώμαος. Για ις αρχικές συνθήκες που έχουν σημειωθεί σο Σχήμα 3.β), και οι οποίες είναι η λύση ης διαφορικής εξίσωσης παίρνει η μορφή x) = A, u) = = = x) = = 3.7) x) = A cosω ) 3.8) δηλ. η φάση φ είναι μηδενική. Αν μελεούσαμε ο πρόβλημα σε διαφορεική χρονική σιγμή, όπως - για παράδειγμα - όαν ο σώμα περνά από η θέση ισορροπίας, όε οι αρχικές συνθήκες θα ήαν διαφορεικές, και άρα η λύση ης διαφορικής εξίσωσης θα ήαν διαφορεική από ην παραπάνω. Για ο απλό ηλεκρικό RC κύκλωμα ου Σχήμαος 3.2, αρχική συνθήκη είναι η ιμή ης άσης σα άκρα ου πυκνωή για =, η οποία είναι μηδενική y) = ). Αν όμως αφήσουμε ον πυκνωή να φορισεί για κάποιο διάσημα και αφαιρέσουμε ην πηγή, κλείνονας με καλώδιο ο κύκλωμα, ο πυκνωής θα αποφορισεί μέσω ου ανισάη. Αυή η διαδικασία περιγράφεαι από ην εξίσωση y) + y) = 3.9) RC με y) ξανά ην άση σα άκρα ου πυκνωή. Η εξίσωση αυή απαιεί ως αρχική συνθήκη ην άση σα άκρα ου πυκνωή ακριβώς πριν ην αποφόριση y) = Q)/C, με Q ο φορίο ου πυκνωή). Παραηρήσε όι οι αρχικές συνθήκες δίνοναι με η μορφή ιμών ης εξόδου και ων παραγώγων ης η χρονική σιγμή =. Ας μελεήσουμε αναλυικά ην έξοδο ενός συσήμαος σις επιμέρους συνισώσες ων αρχικών συνθηκών και ης εισόδου ξεχωρισά. 3.2 Απόκριση Μηδενικής Εισόδου Οπως αναφέραμε ήδη, η απόκριση μηδενικής εισόδου ορίζεαι ως η έξοδος ενός συσήμαος όαν η είσοδος είναι μηδενική, άρα και η έξοδος καθορίζεαι αποκλεισικά από ις αρχικές συνθήκες ου συσήμαος. Αν και σα επόμενα κεφάλαια δε θα μας απασχολήσει ιδιαίερα η απόκριση μηδενικής εισόδου, καθώς θα θεωρούμε α συσήμαά μας σε αρχική ηρεμία, είναι ενδιαφέρον να δει κανείς η μορφή και ον ρόπο υπολογισμού ης απόκρισης μηδενικής εισόδου. Η μηδενική είσοδος μεαρέπει η Σχέση 3.) σην ακόλουθη N k k a ky zi ) = 3.) Μπορεί κανείς να δείξει αναλυικά όι η λύση ης παραπάνω διαφορικής εξίσωσης είναι ης μορφής y zi ) = ce λ 3.) με λ, c σαθερές. Εχονας αυό ως δεδομένο, ανικαθισούμε ση Σχέση 3.) και έχουμε N k k a kce λ = 3.2) ce λ N a k λ k) = 3.3) Η μη εριμμένη λύση ης παραπάνω σχέσης δίνεαι για N a k λ k = λ N + a N λ N + + a λ + a = 3.4)
4 54 Μια εισαγωγή σα Σήμαα και Συσήμαα Άρα η y zi ) = ce λ είναι λύση ης διαφορικής εξίσωσης ης Σχέσης 3.) μόνον αν λ N + a N λ N + + a λ + a = 3.5) Η παραπάνω ομογενής εξίσωση ονομάζεαι χαρακηρισική εξίσωση ου συσήμαος, και ο ανίσοιχο πολυώνυμο ονομάζεαι χαρακηρισικό πολυώνυμο ου συσήμαος. Το ελευαίο μπορεί να παραγονοποιηθεί ως λ λ )λ λ 2 ) λ λ N ) = 3.6) με λ i, i =,, N, ις ρίζες ου πολυωνύμου, οι οποίες ονομάζοναι χαρακηρισικές ρίζες ή φυσικές συχνόηες ου συσήμαος. Άρα υπάρχουν N ο πλήθος διαφορεικά λ που ικανοποιούν ην 3.): c e λ, c 2 e λ2,, c N e λ N 3.7) με c i, i =,, N, σαθερές. Ο προσδιορισμός αυών ων σαθερών εξαράαι από ις αρχικές συνθήκες ου συσήμαος. Άρα ελικά μπορεί να δειχθεί όι N y zi ) = c e λ + c 2 e λ2 +, c N e λ N = c k e λ k k= 3.8) για. Αν χρησιμοποιήσουμε η γνωσή μας βημαική συνάρηση, μπορούμε να γράψουμε ην απόκριση μηδενικής εισόδου ως N y zi ) = c k e λk u) 3.9) k= Η παραπάνω σχέση ισχύει αν οι χαρακηρισικές ρίζες είναι διακριές μεαξύ ους. Αν υπάρχουν ρίζες πολλαπλόηας r 2, όε ο χαρακηρισικό πολυώνυμο μπορεί να γραφεί ως και μπορεί να δειχθεί όι η απόκριση μηδενικής εξόδου δίνεαι από η σχέση λ λ ) r λ λ r+ ) λ λ N ) 3.2) y zi ) = c + c c r r )e λ + c r+ e λr+ + + c N e λ N 3.2) για, και ξανά με χρήση ης βημαικής συνάρησης, έχουμε ) y zi ) = c + c c r r )e λ + c r+ e λr+ + + c N e λ N u) 3.22) Ας δούμε δυο απλά παραδείγμαα. Παράδειγμα 3.: Βρείε ην απόκριση μηδενικής εισόδου ου συσήμαος που περιγράφεαι από ην διαφορική εξίσωση αʹ) βʹ) 2 y) + 5 y) + 6y) = x) με αρχικές συνθήκες y) = και y) = = 2 2 y) + 2 y) + y) = 3 x) + x) με αρχικές συνθήκες y) = 2 και y) = = Λύση: αʹ) Το χαρακηρισικό πολυώνυμο ου συσήμαος είναι ο και η ομογενής εξίσωση είναι η λ 2 + 5λ ) λ 2 + 5λ + 6 = λ + 2)λ + 3) = 3.24) Οι χαρακηρισικές ρίζες ου συσήμαος είναι οι λ = 2, λ = 3, και άρα η απόκριση μηδενικής εισόδου δίνεαι ως y zi ) = c e 2 + c 2 e )
5 Κεφάλαιο 3. Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 55 Οι σαθερές c, c 2 θα βρεθούν από ις αρχικές συνθήκες. Για να ις χρησιμοποιήσουμε, χρειαζόμασε ην παράγωγο ης y zi ), η οποία είναι y zi) = 2c e 2 3c 2 e ) Από ις αρχικές συνθήκες, έχουμε y zi ) = c e 2 + c 2 e 3) = = c + c 2 = 3.27) y zi) = 2c e 2 3c 2 e 3) = = 2c 3c 2 = ) = Το παραπάνω σύσημα δίνει λύσεις Άρα ελική η απόκριση μηδενικής εισόδου δίνεαι ως c = 2, c 2 = ) y zi ) = 2e 2 + 2e 3 3.3) για, ή πιο συνοπικά, ως y zi ) = 2e 2 + 2e 3 )u) 3.3) βʹ) Το χαρακηρισικό πολυώνυμο ου συσήμαος είναι ο και η ομογενής εξίσωση είναι η λ 2 + 2λ ) λ 2 + 2λ + = λ + ) 2 = 3.33) Οι χαρακηρισικές ρίζες ου συσήμαος είναι οι λ =, λ =, δηλ. η ρίζα είναι πολλαπλόηας r = 2. Άρα η απόκριση μηδενικής εισόδου δίνεαι ως y zi ) = c + c 2 )e 3.34) Οι σαθερές c, c 2 θα βρεθούν από ις αρχικές συνθήκες. Για να ις χρησιμοποιήσουμε, χρειαζόμασε ην παράγωγο ης y zi ), η οποία είναι y zi) = c e + c 2 e c 2 e 3.35) Από ις αρχικές συνθήκες, έχουμε y zi ) = c + c 2 )e ) = = c = ) y zi) = c e + c 2 e c 2 e ) = = c + c 2 = 3.37) = Το παραπάνω σύσημα δίνει ελικά Οπόε η απόκριση μηδενικής εισόδου δίνεαι ως c = 2, c 2 = 3.38) y zi ) = 2 + )e u) 3.39) Παράδειγμα 3.2: Βρείε ην απόκριση μηδενικής εισόδου ου συσήμαος που περιγράφεαι από ην διαφορική εξίσωση 2 x) = ω2 x) 3.4)
6 56 Μια εισαγωγή σα Σήμαα και Συσήμαα με αρχικές συνθήκες x) = A και x) = =. Λύση: Η διαφορική εξίσωση περιγράφει ην κίνηση ενός απλού αρμονικού αλανωή, και μπορεί να γραφεί ως 2 x) + ω2 x) = 3.4) και η οποία είναι ομογενής. Το χαρακηρισικό πολυώνυμο ου συσήμαος είναι ο και η ομογενής εξίσωση είναι η λ 2 + ω ) λ 2 + ω 2 = λ + jω )λ jω ) = 3.43) Οι χαρακηρισικές μιγαδικές) ρίζες ου συσήμαος είναι οι λ = jω, λ 2 = λ = jω. μηδενικής εισόδου αυίζεαι με η συνολική λύση ου συσήμαος και δίνεαι ως Άρα η απόκριση y zi ) = x) = c e jω + c 2 e jω 3.44) Οι σαθερές c, c 2 θα βρεθούν από ις αρχικές συνθήκες. Για να ις χρησιμοποιήσουμε, χρειαζόμασε ην παράγωγο ης y zi ), η οποία είναι y zi) = x) = jω c e jω jω c 2 e jω 3.45) Από ις αρχικές συνθήκες, έχουμε x) = c e jω + c 2 e jω) = = c + c 2 = A 3.46) y zi) = jω c e jω jω c 2 e jω) = = c c 2 = 3.47) = Το παραπάνω σύσημα δίνει ελικά c = c 2 = A 2 Οπόε η απόκριση μηδενικής εισόδου - και λύση ης αρχικής ομογενούς διαφορικής εξίσωσης - δίνεαι ως Παραηρήσεις: 3.48) x) = y zi ) = A 2 e jω + A 2 ejω = A cosω ) 3.49). Σην πράξη, οι αρχικές συνθήκες αφορούν ην καάσαση ου συσήμαος πριν ην εφαρμογή ης εισόδου. Αν υποθέσουμε όι η είσοδος εφαρμόζεαι η χρονική σιγμή =, όε οι αρχικές συνθήκες περιγράφουν ην καάσαση ου συσήμαος για =, δηλ. ακριβώς πριν ην εφαρμογή ης εισόδου. Πολλές φορές ση βιβλιογραφία, οι αρχικές συνθήκες χρησιμοποιούν ο συμβολισμό = για η χρονική σιγμή ων αρχικών συνθηκών. Σο εξής, θα υιοθεήσουμε αυήν ην πρακική σο συμβολισμό. 2. Παραηρήσε όι ο υπολογισμός ης απόκρισης μηδενικής εισόδου εξαράαι αποκλεισικά από ις αρχικές συνθήκες. Πουθενά σην ανάλυσή μας δε χρειασήκαμε ην οποιαδήποε είσοδο x), καθώς η θεωρήσαμε μηδενική. Η γνώση ης εισόδου x) δε μας λέει ίποα για ην απόκριση μηδενικής εισόδου, αλλά ούε και οι αρχικές συνθήκες μας πληροφορούν για η μορφή ης απόκρισης μηδενικής καάσασης. Οι δυο αποκρίσεις είναι ενελώς ανεξάρηες μεαξύ ους. 3. Ο ρόλος ων αρχικών συνθηκών, πέρα από ον υπολογισμό ης απόκρισης μηδενικής εισόδου, μας παρέχει μοναδική λύση για ο σύσημα που περιγράφεαι από μια διαφορική εξίσωση. Γιαί αυό; Σκεφείε ην πιο απλή διαφορική εξίσωση που ξέρεε: f x) = fx)
7 Κεφάλαιο 3. Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 57 Ξέρεε όι η λύση ης είναι fx) = ce x η οποία δεν είναι μοναδική. Για να ην κάνεε έοια, θα πρέπει να σας δίνεαι κάποια συνθήκη για να βρείε ο c, π.χ. f) = 2 που οδηγεί σε c = 2. Άρα μπορείε να κααλάβεε όι μια διαφορική εξίσωση, και γενικόερα η παραγώγιση, είναι μια μη ανισρέψιμη διαδικασία. Χρειαζόμασε επιπλέον πληροφορία για να ην ανισρέψουμε με μοναδικό ρόπο, η οποία μας δίνεαι με η μορφή αρχικών συνθηκών. 4. Δείξαμε νωρίερα όι η απόκριση μηδενικής εισόδου είναι ης μορφής y zi ) = N c k e λk u) 3.5) k= για απλές, διακριές χαρακηρισικές ρίζες λ k, ις οποίες θεωρούμε πραγμαικές χάριν απλόηας. Παραηρήσε όι αν λ k < k, όε η απόκριση μηδενικής εισόδου φθίνει προς ο μηδέν, όαν +, κααλήγονας σε καάσαση ηρεμίας. Άρα αν εφαρμόσουμε μια ακαριαία είσοδο σο σύσημά μας ην ο- ποία αφαιρούμε για >, δηλ. η έξοδός μας θα μοιάζει με ην απόκριση μηδενικής εισόδου), ο σύσημά μας θα κααλήξει σε καάσαση ηρεμίας μόνο αν λ k < k. Αν λ i > για ένα ουλάχισον i, όε ο σύσημα δεν επισρέφει σε καάσαση ηρεμίας, διόι c i e λi u) + 3.5) και άρα ο σύσημα δίνει απόκριση μηδενικής εισόδου που απειρίζεαι. Σκεφείε ο: μια μικρή, ακαριαία διέγερση σην είσοδο ου συσήμαος μπορεί να οδηγήσει ο σύσημα να παράξει έξοδο η οποία απειρίζεαι όαν +! Σίγουρα κάι έοιο δε θα ήαν επιθυμηό Επιπλέον, παραηρήσε όι η επισροφή ή μη) ου συσήμαος σε καάσαση ηρεμίας δε γίνεαι με ο- ποιονδήποε ρόπο. Οι Σχέσεις 3.9, 3.22) καθισούν σαφές όι η κυμαομορφή ης απόκρισης μηδενικής εισόδου έχει συγκεκριμένη μορφή η οποία εξαράαι από ις χαρακηρισικές ρίζες Η κρουσική απόκριση h) Παίρνονας αφορμή από ις παραπάνω παραηρήσεις, μπορούμε να ορίσουμε μια πολύ βολική περιγραφή για ένα σύσημα. Θα θέλαμε να γνωρίζουμε ην έξοδο ενός συσήμαος όαν παρουσιάζουμε ως είσοδο ένα σήμα ακαριαίας μορφής, ένα σήμα που υπάρχει σε απειροσά μικρό χρονικό διάσημα 2. Η είσοδος αυή θα διεγείρει ο σύσημα, και θα ο αναγκάσει να παράξει κάποια έξοδο. Η έξοδος αυή πρέπει να μοιάζει με ην απόκριση μηδενικής εισόδου, αφού η ύπαρξή ης οφείλεαι σε μια είσοδο που υπάρχει μόνο μια συγκεκριμένη χρονική σιγμή, και μεά χάνεαι. Θα μπορούσε κανείς να πει όι η διέγερση αυή δημιουργεί νέες αρχικές συνθήκες σο σύσημα, και η λύση ης ομογενούς εξίσωσης για αυές ις αρχικές συνθήκες θα μας δώσει μια έξοδο, μια απόκριση σε ένα κρουσικό σήμα - δε θα ήαν λοιπόν παράλογο να ονομάσουμε αυήν ην έξοδο ως κρουσική απόκριση 3! Με βάση α παραπάνω, ένα έοιο σήμα ακαριαίας εισόδου μπορεί να μονελοποιηθεί εξαιρεικά από η γνωσή μας συνάρηση Δέλα! Θυμηθείε όι η συνάρηση Δέλα είναι ένα σήμα που υπάρχει μόνο για = και είναι μηδέν για. Ας ορίσουμε λοιπόν ην κρουσική απόκριση - impulse response h) ενός συσήμαος ως ην έξοδο ου συσήμαος όαν σην είσοδο ου παρουσιάζεαι η συνάρηση Δέλα δ), και θεωρώνας μηδενικές αρχικές συνθήκες για = ). Αν χρησιμοποιήσουμε ο συμβολισμό ου ελεσή T [ ] για ο σύσημα, θα είναι h) = T [δ)] 3.52) ή εναλλακικά δ) h) 3.53) Φυσικά οι χαρακηρισικές ρίζες μπορούν να είναι μιγαδικές! 2 Σκεφείε όι χυπάε ένα καμπανάκι σύσημα) με ένα σφυρί είσοδος) πολύ γρήγορα, όσο ακαριαία γίνεαι. Θα μπορούσαε να ισχυρισείε όι ο ήχος που θα παραχθεί, δηλ. η έξοδος ου συσήμαος, χαρακηρίζει ο καμπανάκι ο υλικό ου, ο πάχος ου, ην επιφάνειά ου, κλπ). 3 Σκεφείε ο: η απόκριση έξοδος) σε μια κρούση ακαριαία διέγερση).
8 58 Μια εισαγωγή σα Σήμαα και Συσήμαα Παρ όλο που υπάρχουν μέθοδοι για ην εύρεση ης κρουσικής απόκρισης σο πεδίο ου χρόνου, θα αναπύξουμε εδώ μια περισσόερο διαισθηική μέθοδο για ην εύρεσή ης, και θα δούμε σε επόμενα κεφάλαια έμμεσους και πιο απλούς ρόπους για ον υπολογισμό ης. Η συζήηση που ακολουθεί δείχνει πώς η παρουσία ης συνάρησης Δέλα γεννά νέες αρχικές συνθήκες σο σύσημα, ις οποίες και αναζήούμε, ώσε ο πρόβλημα να αναχθεί σην εύρεση ης ομογενούς λύσης ης διαφορικής εξίσωσης με αρχικές συνθήκες αυές που γεννιούναι από η συνάρηση Δέλα. Οι ελευαίες θεωρούμε όι υπάρχουν η χρονική σιγμή = +, εν ανιθέσει με ις αρχικές συνθήκες που έχουμε συνανήσει ως ώρα, και οι οποίες υποθέαμε όι υπάρχουν πριν ην εφαρμογή οποιασδήποε εισόδου, δηλ. η χρονική σιγμή =. Ση συζήηση που ακολουθεί υποθέουμε όι η διαφορική εξίσωση που περιγράφει ένα σύσημα είναι ης γενικής μορφής N k M k a k ky) = k b kx) 3.54) με N > M Σύσημα Εξόδου Πρώης Τάξης Ας υποθέσουμε όι έχουμε μια απλή διαφορική εξίσωση πρώης άξης με N =, M =, και b =, ης μορφής a y) + a y) = x) 3.55) Η κρουσική απόκριση h) βρίσκεαι θέονας x) = δ), και θεωρώνας όι y ) = 3.56) y ) = 3.57) 2 y ) = 3.58). N ) N y ) = 3.59) δηλ. ο σύσημα βρίσκεαι σε ηρεμία, όπως λέγεαι χαρακηρισικά. Τόε, η διαφορική εξίσωση γράφεαι ως a h) + a h) = δ) 3.6) Αν ολοκληρώσουμε και α δυο μέλη σε ένα απειροσά μικρό διάσημα εκαέρωθεν ου μηδενός, θα έχουμε a h) + a h) = δ) 3.6) a h + ) h )) + a a h + ) + a + h) = + + δ) = 3.62) h) = 3.63) Το ολοκλήρωμα ης Σχέσης 3.63) είναι μηδέν αν η κρουσική απόκριση δεν παρουσιάζει κάποια συνάρηση Δέλα ση θέση =. Αν συμβαίνει αυό, όε a h + ) = b h + ) = a 3.64) Άρα η αρχική συνθήκη που γεννά η παρουσία ης συνάρησης Δέλα είναι αυή ης Σχέσης ;;). Η ομογενής λύση ης διαφορικής εξίσωσης είναι h) = c e λ u) 3.65)
9 Κεφάλαιο 3. Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 59 με λ η χαρακηρισική ρίζα ου χαρακηρισικού πολυωνύμου a λ + a = λ = a a, οπόε Η Σχέση 3.66) πρέπει να ικανοποιεί η Σχέση 3.64), οπόε Άρα ελικά η κρουσική απόκριση δίνεαι ως h) = c e a a u) 3.66) c = a 3.67) h) = a e a a u) 3.68) Σύσημα Εξόδου Δευέρας Τάξης Ας υποθέσουμε ώρα όι η διαφορική εξίσωση είναι δευέρας άξης με N = 2, M =, και b =, δηλ. και θέονας y) = h) και x) = δ), έχουμε Ολοκληρώνονας γύρω από ο μηδέν, θα έχουμε a 2 2 y) + a y) + a y) = x) 3.69) a 2 2 h) + a h) + a h) = δ) 3.7) + + a 2 2 h) + a h) + a h) = a 2 h+ ) ) + h ) + a h + ) h )) + a + + δ) 3.7) h) = 3.72) a h + ) + a 2 h+ ) = 3.73) κάνονας ις ίδιες υποθέσεις με ην πρωοβάθμια περίπωση προηγουμένως. Ας ολοκληρώσουμε ξανά η Σχέση 3.7), οπόε a 2 2 h) + a h) + a a 2 h) + a h) + a Ολοκληρώνονας ξανά γύρω από ο μηδέν ην παραπάνω έκφραση, έχουμε h) = δ) 3.74) h) = u) 3.75) a 2 h) + a h) + a h) = u) 3.76) a 2 h + ) h )) = 3.77) Ανικαθισώνας η Σχέση 3.79) ση Σχέση 3.73), έχουμε Η ομογενής λύση ης διαφορικής εξίσωσης είναι a 2 h + ) = 3.78) h + ) = 3.79) h) = = 3.8) + a 2 h) = c e λ + c 2 e λ2 )u) 3.8)
10 6 Μια εισαγωγή σα Σήμαα και Συσήμαα με λ λ 2 οι χαρακηρισικές ρίζες ου χαρακηρισικού πολυωνύμου a 2 λ 2 + a λ + a =, οπόε οι σαθερές c, c 2 υπολογίζοναι ως c = a 2 λ 2 λ ) c 2 = a 2 λ λ 2 ) 3.82) 3.83) Άρα ελικά η κρουσική απόκριση δίνεαι ως h) = a 2 λ 2 λ ) eλ e λ2 )u) 3.84) Σύσημα Εξόδου Ν-οσής Τάξης Ακολουθώνας ην ίδια διαδικασία, μπορούμε να γενικεύσουμε για διαφορικές εξισώσεις N οσής άξης εξόδου, ης μορφής N k k a ky) = x) 3.85) και να εξάγουμε όι οι νέες αρχικές συνθήκες για = + δίνοναι από ις σχέσεις h + ) = h+ ) = 2 2 h+ ) = = N 2) N 2 h+ ) = N ) N h+ ) = a N 3.86) Εσι, η κρουσική απόκριση h) ενός έοιου συσήμαος δίνεαι από η λύση ης ομογενούς διαφορικής εξίσωσης με ις αρχικές συνθήκες ης Σχέσης 3.86). N k a k h) = 3.87) k Συσήμαα Οποιασδήποε Τάξης Εισόδου-Εξόδου Παρ όλα αυά, η λύση που βρήκαμε είναι αρκεά περιορισμένη γιαί αφορά συσήμαα με άξη παραγώγου εισόδου M = με b =. Πώς θα μπορούσαμε να γενικεύσουμε για συσήμαα όπου < M < N και b k, k M; Η απάνηση είναι ελικά πολύ απλή, αφού ο σύσημα που περιγράφεαι από η διαφορική εξίσωση έχει ην ιδιόηα ης γραμμικόηας, οπόε αν η κρουσική απόκριση σο σύσημα S : N k k a ky) = x) 3.88) είναι h), όε η κρουσική απόκριση σο σύσημα S : N k k a ky) = b x) 3.89) θα είναι h ) = b h). Επίσης, η κρουσική απόκριση ου συσήμαος S K : N k k a ky) = M b k x k ) 3.9) θα είναι M h K ) = b k h k ) 3.9)
11 Κεφάλαιο 3. Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 6 με h k ) ις κρουσικές αποκρίσεις ου συσήμαος σις εισόδους x k ). Σην περίπωση που όε μπορεί να δειχθεί όι η κρουσική απόκριση ου συσήμαος x k ) = k x) 3.92) k S g : N k k a ky) = M k b k x) 3.93) k είναι h g ) = M με h) να είναι η λύση ης ομογενούς διαφορικής εξίσωσης με ις αρχικές συνθήκες ης Σχέσης 3.86). N k b k h) 3.94) k k k a ky) = 3.95) Με βάση ην παραπάνω συζήηση, ας διαυπώσουμε μερικές ενδιαφέρουσες και πολύ σημανικές παραηρήσεις. Παραηρήσεις:. Υποθέσαμε ση συζήησή μας όι οι χαρακηρισικές ρίζες ης διαφορικής εξίσωσης είναι απλές. Σην περίπωση που δεν είναι, ακολουθούμε η μέθοδο που περιγράφηκε σην παράγραφο περί εύρεσης ης απόκρισης μηδενικής εισόδου. Για παράδειγμα, αν η χαρακηρισική ρίζα είναι διπλή, η λύση ης ομογενούς διαφορικής εξίσωσης για ην περίπωση N =, M = που είδαμε νωρίερα θα είναι ης μορφής h) = a 2 e λ u) 3.96) 2. Μια άλλη υπόθεση που κάναμε παραπάνω είναι η παρακάω σχέση + h) = 3.97) που όπως είπαμε σημαίνει όι η κρουσική απόκριση δεν παρουσιάζει κάποια ακαριαία συμπεριφορά η χρονική σιγμή =, δηλ. δεν υπάρχει κάποια συνάρηση Δέλα εκεί. Συναρήσεις Δέλα ή και παράγωγοί ης) παρουσιάζοναι σην κρουσική απόκριση μόνον αν M N, με M και N ις μέγισες άξεις παραγώγων ης εισόδου και ης εξόδου, ανίσοιχα, ση διαφορική εξίσωση. Σην περίπωση όπου M = N, η κρουσική απόκριση θα είναι ης μορφής h g ) = b M δ) + f{e λ k, e λ k } 3.98) με b M ο συνελεσή ης M οσής παραγώγου ης εισόδου, και f{e λ k, e λ k } μια συνάρηση που περιλαμβάνει όρους ης ομογενούς λύσης που προκύπει από ην ομογενή διαφορική εξίσωση με ις νέες αρχικές συνθήκες που περιγράφηκε παραπάνω. Θα δούμε ένα έοιο παράδειγμα ση συνέχεια. 3. Η περίπωση όπου M > N δεν είναι συνήθης σην πράξη, γιαί μπορεί κανείς να δείξει όι σε αυήν ην περίπωση ο σύσημα λειουργεί ως ενισχυής ων υψηλών συχνοήων ου σήμαος, με αποέλεσμα η έξοδος να περιέχει μεγάλη ποσόηα θορύβου, ακόμα κι αν σην είσοδο ο θόρυβος είναι αμεληέος. Σε αυήν ην περίπωση, η κρουσική απόκριση παρουσιάζει παραγώγους άξης ως M N ης συνάρησης Δέλα η χρονική σιγμή =. Άρα η γενικόερη μορφή ης κρουσικής απόκρισης για κάθε δυναή ιμή ων M, N είναι η εξής: h g ) = M N k= α k k k δ) + βδ) + f{eλ k, e λ k } 3.99) με α k, β σαθερούς συνελεσές και f{e λ k, e λ k } ξανά μια συνάρηση που περιλαμβάνει όρους ης ομογενούς λύσης, όπως περιγράφηκε προηγουμένως. Θα δούμε ένα απλό παράδειγμα έοιας μορφής.
12 62 Μια εισαγωγή σα Σήμαα και Συσήμαα 4. Εν γένει, υπάρχουν αρκεές διαφορεικές μέθοδοι εύρεσης ης κρουσικής απόκρισης ενός συσήμαος, όσο σο πεδίο ου χρόνου όσο και σο πεδίο ης συχνόηας, που θα συζηηθεί αργόερα. Για ην εύρεση ης κρουσικής απόκρισης ση συνέχεια ου βιβλίου, θα βασισούμε περισσόερο σις μεθόδους ης συχνόηας, καθώς είναι αρκεά απλούσερες για οσοδήποε μεγάλη άξη διαφορικής εξίσωσης. Παρ ολα αυά, οι μέθοδοι σο πεδίο ου χρόνου προσφέρουν πολύιμα σοιχεία για ην συμπεριφορά ων συσημάων. Μπορούμε πλέον να συνοψίσουμε ην εύρεση ης κρουσικής απόκρισης ως ακολούθως: Εύρεση Κρουσικής Απόκρισης από Διαφορική Εξίσωση Για μια διαφορική εξίσωση ης μορφής N k k a ky) = M η κρουσική απόκρισή h g ) δίνεαι από ην παρακάω διαδικασία:. Θεωρούμε η διαφορική εξίσωση ης μορφής N k k b kx) 3.) k k a ky) = x) 3.) η οποία έχει κρουσική απόκριση h). Θέουμε x) = δ), οπόε σην παραπάνω διαφορική εξίσωση λαμβάνουμε N k k a kh) = δ) 3.2) θεωρώνας μηδενικές αρχικές συνθήκες. 2. Βρίσκουμε ις χαρακηρισικές ρίζες λ k μέσω ου χαρακηρισικού πολυωνύμου λ N + a N λ N + + a λ + a = 3.3) ης ομογενούς εξίσωσης N k k a kh) = 3.4) 3. Αν οι ρίζες είναι διαφορεικές μεαξύ ους, όε η κρουσική απόκριση είναι ης μορφής h g ) = με h) να είναι η λύση ης ομογενούς εξίσωσης η οποία έχει η μορφή N h) = με ους συνελεσές c k να βρίσκοναι μέσω ων αρχικών συνθηκών. M k k b kh) 3.5) k k a kh) = 3.6) N c k e λk u) 3.7) 4. Αν υπάρχει πολλαπλή ρίζα λ i άξης r, όε η κρουσική απόκριση είναι ης μορφής h g ) = M k k b kh) 3.8)
13 Κεφάλαιο 3. Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 63 με h) να είναι η λύση ης ομογενούς εξίσωσης η οποία έχει η μορφή h) = N k=,k i N k k a kh) = 3.9) c k e λ k u) + με ους συνελεσές c k, c l να βρίσκοναι μέσω ων αρχικών συνθηκών. r c l l e λi u) 3.) l= Χαρακηρισικά Παραδείγμαα Εχονας ολοκληρώσει η συζήηση για ην απόκριση μηδενικής εισόδου και ην κρουσική απόκριση, ας δούμε μερικά χαρακηρισικά παραδείγμαα. Παράδειγμα 3.3: Βρείε ην κρουσική απόκριση ου συσήμαος που περιγράφεαι από η διαφορική εξίσωση 2 y) + 3 y) + 2y) = x) 3.) Λύση: Σην περίπωση αυή έχουμε M < N, οπόε η κρουσική απόκριση θα αποελείαι μόνο από εκθεικούς όρους. Θέουμε ως είσοδο x) = δ), και θεωρώνας συνθήκες αρχικής ηρεμίας σο σύσημα, έχουμε 2 h) + 3 h) + 2h) = δ) 3.2) Η ομογενής εξίσωση είναι και οι αρχικές συνθήκες είναι 2 h) + 3 h) + 2h) = 3.3) Το χαρακηρισικό πολυώνυμο ης διαφορικής εξίσωσης είναι h + ) = 3.4) h+ ) = a 2 = 3.5) λ 2 + 3λ + 2 = 3.6) ο οποίο γράφεαι ως λ + 2)λ + ) = 3.7) οπόε οι χαρακηρισικές ρίζες είναι οι λ = 2 και λ =. Άρα η λύση ης ομογενούς εξίσωσης είναι η h) = c e λ + c 2 e λ2 = c e 2 + c 2 e, > 3.8) Για να βρούμε ις σαθερές c, c 2 χρησιμοποιούμε ις αρχικές συνθήκες. Άρα h + ) = c + c 2 = 3.9) h+ ) = 2c c 2 = 3.2) οπόε είναι c =, c 2 = 3.2)
14 64 Μια εισαγωγή σα Σήμαα και Συσήμαα και άρα η κρουσική απόκριση είναι ίση με ην ομογενή λύση, δηλ. h g ) = h) = e 2 + e )u) 3.22) Παράδειγμα 3.4: Βρείε ην κρουσική απόκριση ου συσήμαος που περιγράφεαι από η διαφορική εξίσωση 2 y) + 6 y) + 9y) = 2 x) + 9x) 3.23) Λύση: Σην περίπωση αυή έχουμε ξανά M < N, οπόε η κρουσική απόκριση θα αποελείαι μόνο από εκθεικούς όρους. Θέουμε ως είσοδο x) = δ), και θεωρώνας συνθήκες αρχικής ηρεμίας σο σύσημα, έχουμε Η ομογενής εξίσωση είναι και οι αρχικές συνθήκες είναι 2 h) + 6 h) + 9h) = 2 δ) + 9δ) 3.24) 2 h) + 6 h) + 9h) = 3.25) Το χαρακηρισικό πολυώνυμο ης διαφορικής εξίσωσης είναι ο οποίο γράφεαι ως h + ) = 3.26) h+ ) = a 2 = 3.27) λ 2 + 6λ + 9 = 3.28) λ + 3) 2 = 3.29) οπόε οι χαρακηρισικές ρίζες είναι οι λ = λ 2 = λ = 3. Άρα η λύση ης ομογενούς εξίσωσης είναι η h) = c + c 2 )e λ = c + c 2 )e 3, > 3.3) Για να βρούμε η σαθερά c χρησιμοποιούμε ις αρχικές συνθήκες. Άρα οπόε είναι c =, c = και άρα η ομογενής λύση είναι Η κρουσική απόκριση ου συσήμαος είναι ελικά h + ) = c = 3.3) h+ ) = 3c e 3 + c 2 3)e 3) = = ) h) = e 3 u) 3.33) h g ) = 2 h) + 9h) 3.34) = 2 e 3 u) + 9e 3 u) 3.35) = 2 e 3 u) + ) e 3 u)) + 9e 3 u) 3.36) = 2 e 3 u) + 3e 3 u) + e 3 )) u) + 9e 3 u) 3.37) ) = 2 e 3 u) + 3e 3 u) + e 3 δ)) + 9e 3 u) 3.38)
15 Κεφάλαιο 3. Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 65 = 2e 3 u) 6e 3 u) + 2e 3 δ) + 9e 3 u) 3.39) = 2e 3 u) + 3e 3 u) 3.4) όπου χρησιμοποιήσαμε η γνωσή ιδιόηα ης συνάρησης Δέλα x)δ) = x)δ) 3.4) Παράδειγμα 3.5: Βρειε ην κρουσική απόκριση ου συσήμαος που περιγράφεαι από η διαφορική εξίσωση 2 y) + 2 y) + y) = x) 3.42) Λύση: Σην περίπωση αυή έχουμε πάλι M < N, οπόε η κρουσική απόκριση θα αποελείαι μόνο από εκθεικούς όρους. Θέουμε ως είσοδο x) = δ), και θεωρώνας συνθήκες αρχικής ηρεμίας σο σύσημα, έχουμε Η ομογενής εξίσωση είναι και οι αρχικές συνθήκες είναι 2 h) + 2 h) + h) = δ) 3.43) 2 h) + 2 h) + h) = 3.44) Το χαρακηρισικό πολυώνυμο ης διαφορικής εξίσωσης είναι ο οποίο γράφεαι ως h + ) = 3.45) h+ ) = a 2 = 3.46) λ 2 + 2λ + = 3.47) λ + )λ + ) = 3.48) οπόε οι χαρακηρισικές ρίζες είναι οι λ = λ 2 = λ =. Άρα η λύση ης ομογενούς εξίσωσης είναι η h) = c + c 2 )e λ = c + c 2 )e, > 3.49) Για να βρούμε ις σαθερές c, c 2 χρησιμοποιούμε ις αρχικές συνθήκες. Άρα οπόε είναι c =, c 2 = και άρα η ομογενής λύση είναι Η κρουσική απόκριση ου συσήμαος θα είναι h + ) = c = 3.5) h+ ) = c e + c 2 )e ) = = + 3.5) h) = e, > 3.52) h g ) = h) = e u) 3.53) = e u) + e u)) 3.54) = e u) + e u) + e δ)) 3.55) = e u) e u) + e δ)) 3.56)
16 66 Μια εισαγωγή σα Σήμαα και Συσήμαα = e u) e u) 3.57) = )e u) 3.58) όπου χρησιμοποιήσαμε η γνωσή ιδιόηα ης συνάρησης Δέλα x)δ) = x)δ) 3.59) Παράδειγμα 3.6: Βρείε ην κρουσική απόκριση ου συσήμαος που περιγράφεαι από η διαφορική εξίσωση 2 y) y) + 6y) = 2 x) + 2 x) + x) 3.6) Λύση: Σην περίπωση αυή έχουμε M = N, οπόε η κρουσική απόκριση θα αποελείαι μόνο από εκθεικούς όρους και από μια συνάρηση Δέλα. Θέουμε ως είσοδο x) = δ), και θεωρώνας συνθήκες αρχικής ηρεμίας σο σύσημα, έχουμε 2 h) h) + 6h) = 2 δ) + 2 δ) + δ) 3.6) Η ομογενής εξίσωση είναι και οι αρχικές συνθήκες είναι Το χαρακηρισικό πολυώνυμο ης διαφορικής εξίσωσης είναι ο οποίο γράφεαι ως 2 h) + 5 h) + 6h) = 3.62) h + ) = 3.63) h+ ) = a 2 = 3.64) λ 2 + 5λ + 6 = 3.65) λ + 2)λ + 3) = 3.66) οπόε οι χαρακηρισικές ρίζες είναι οι λ = 2 και λ 2 = 3. Άρα η λύση ης ομογενούς εξίσωσης είναι η h) = c e λ + c 2 e λ2 = c e 2 + c 2 e 3, > 3.67) Για να βρούμε ις σαθερές c, c 2 χρησιμοποιούμε ις αρχικές συνθήκες. Άρα οπόε είναι c =, c 2 = και άρα η ομογενής λύση είναι Η κρουσική απόκριση ου συσήμαος θα είναι h + ) = c + c 2 = 3.68) h+ ) = 2c e 2 3c 2 e 3) = = ) h) = e 2 u) e 3 u) 3.7) h g ) = 2 2 h) + 2 h) + h) 3.7) = 2 2 e 2 e 3 )u) + 2 e 2 e 3 )u) + e 2 u) e 3 u) 3.72) = δ) + e 2 4e 3 )u) 3.73)
17 Κεφάλαιο 3. Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 67 μεά από πράξεις και απλοποιήσεις. Παράδειγμα 3.7: Βρείε ην κρουσική απόκριση ου συσήμαος που περιγράφεαι από η διαφορική εξίσωση 2 y) y) + y) = x) x) + 2 x) + x) 3.74) Λύση: Σην περίπωση αυή έχουμε M > N, οπόε η κρουσική απόκριση θα αποελείαι από εκθεικούς όρους, μια συνάρηση Δέλα, και μια παράγωγό ης. Θέουμε ως είσοδο x) = δ), και θεωρώνας συνθήκες αρχικής ηρεμίας σο σύσημα, έχουμε Η ομογενής εξίσωση είναι και οι αρχικές συνθήκες είναι 2 h) h) + h) = δ) δ) + 2 δ) + δ) 3.75) Το χαρακηρισικό πολυώνυμο ης διαφορικής εξίσωσης είναι ο οποίο γράφεαι ως 2 h) + 7 h) + h) = 3.76) h + ) = 3.77) h+ ) = a 2 = 3.78) λ 2 + 7λ + = 3.79) λ + 2)λ + 5) = 3.8) οπόε οι χαρακηρισικές ρίζες είναι οι λ = 2 και λ 2 = 5. Άρα η λύση ης ομογενούς εξίσωσης είναι η h) = c e λ + c 2 e λ2 = c e 2 + c 2 e 5, > 3.8) Για να βρούμε ις σαθερές c, c 2 χρησιμοποιούμε ις αρχικές συνθήκες. Άρα οπόε είναι c = /3, c 2 = /3 και άρα η ομογενής λύση είναι Η κρουσική απόκριση ου συσήμαος θα είναι h + ) = c + c 2 = 3.82) h+ ) = 2c e 2 5c 2 e 5) = = ) h) = 3 e 2 u) 3 e 5 u) 3.84) Οι επιμέρους όροι είναι h g ) = 3 2 h) h) + 2 h) + h) 3.85) h) = 3 e 2 u) 3 e 5 u) 3.86) 2 h) = 4 3 e 2 u) + 3 e 5 u) 3.87) h) = 8 3 e 2 u) 5 3 e 5 u) + 2δ) 3.88)
18 68 Μια εισαγωγή σα Σήμαα και Συσήμαα 3 3 h) = 8 3 e 2 u) e 5 u) 7δ) + δ) 3.89) οπόε, μεά από πράξεις και απλοποιήσεις, η κρουσική απόκριση θα είναι h g ) = δ) 5δ) + 28e 5 u) e 2 u) 3.9) ΓΧΑ Συσήμαα και Διαφορικές Εξισώσεις Ση συζήησή μας σε προηγούμενο κεφάλαιο, είχαμε επισημάνει όι μας ενδιαφέρουν πολύ α γραμμικά και χρονικά αμεάβληα συσήμαα. Ενα ερώημα που πρέπει να ξεκαθαρισεί είναι ο εξής: Πόε ένα σύσημα που περιγράφεαι από διαφορικές εξισώσεις είναι γραμμικό και χρονικά αμεάβληο; Χρησιμοποιοώνας ην έννοια ης γραμμικόηας, μπορούμε να πούμε α εξής: Για κάποια είσοδο x ), ο σύσημα θα δίνει έξοδο και για είσοδο x 2 ) θα είναι x ) y ) = y zi ) + y zs ) 3.9) x 2 ) y 2 ) = y zi ) + y 2zs ) 3.92) αφού η απόκριση μηδενικής εισόδου δεν εξαράαι από ην είσοδο! Τέλος, για μια γραμμική είσοδο ax )+bx 2 ), η έξοδος θα είναι ax ) + bx 2 ) y zi ) + y 3zs ) 3.93) με y 3zs ) ην απόκριση μηδενικής καάσασης όαν η είσοδος είναι η ax ) + bx 2 ), η οποία εξαράαι από ην είσοδο και είναι γραμμική, όπως έχουμε δείξει σην Παράγραφο Άρα για να είναι γραμμικό ένα σύσημα που περιγράφεαι από μια διαφορική εξίσωση, πρέπει η απόκριση μηδενικής εισόδου να είναι μηδενική, ή με άλλα λόγια, οι αρχικές συνθήκες ου συσήμαος να είναι μηδενικές. Με όμοιο ρόπο μπορούμε να δείξουμε Άσκηση ΧΧΧΧ) όι αν η απόκριση μηδενικής εισόδου είναι μηδενική, όε ο σύσημα είναι χρονικά αμεάβληο. Δεν είναι δύσκολο να ο επιβεβαιώσουμε διαισθηικά: η χρονική αμεαβληόηα σημαίνει όι αν ο σήμα εισόδου καθυσερήσει καά, η έξοδος θα είναι ένα σήμα όμοιο σε μορφή με ο σήμα εξόδου για είσοδο x), αλλά καθυσερημένο καά ον ίδιο χρόνο. Ομως η απόκριση μηδενικής εισόδου δεν εξαράαι από ην είσοδο, και άρα έχει ην ίδια μορφή ανεξαρήως καθυσέρησης ης εισόδου. Τέλος, η ίδια η κρουσική απόκριση ορίζεαι όπως έχουμε συζηήσει μόνο για γραμμικά και χρονικά αμεάβληα συσήμαα. Για παράδειγμα, ένα μη γραμμικό σύσημα δε θα ικανοποιούσε ην ιδιόηα ης ομογένειας, οπόε η κρουσική απόκριση δε θα ήαν μοναδική, ενώ η χρονική μεαβληόηα θα μας έδινε μια διδιάσαη κρουσική απόκριση, αφού για κάθε καθυσέρηση εισόδου δ ), θα είχαμε διαφορεική κρουσική απόκριση h ) = h, ). Ση συζήησή μας για ην κρουσική απόκριση εμμέσως υποθέσαμε όι ο σύσημά μας είναι γραμμικό και χρονικά αμεάβληο. Άρα μπορούμε να συνοψίσουμε όι Διαφορικές Εξισώσεις και ΓΧΑ Συσήμαα Ενα σύσημα που περιγράφεαι με διαφορικές εξισώσεις είναι Γραμμικό και Χρονικά Αμεάβληο αν οι αρχικές συνθήκες ου είναι μηδενικές, δηλ. y ) = 3.94) y) = = 3.95) 2 y) = = 3.96). 3.97)
19 Κεφάλαιο 3. Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 69 N N y) = = 3.98) 3.3 Απόκριση Μηδενικής Καάσασης Ας εσιάσουμε ώρα ην προσοχή μας σην εύρεση ης εξόδου ενός συσήμαος δεδομένης μιας εισόδου και μηδενικών αρχικών συνθηκών, δηλ. σην εύρεση ης απόκρισης μηδενικής καάσασης y zs ). Αφού οι αρχικές συνθήκες είναι μηδενικές, ο όλο σύσημα είναι γραμμικό και χρονικά αμεάβληο. Σκεφείε πόσες διαφορεικές πιθανές είσοδοι μπορούν να εφαρμοσούν σε ένα σύσημα. Θα επιθυμούσαμε να έχουμε έναν ενιαίο ρόπο εύρεσης ης απόκρισης μηδενικής καάσασης, για κάθε πιθανή είσοδο. Κάι έοιο θα απλοποιούσε πολύ α πράγμαα. Είδαμε μόλις όι η έξοδος ενός συσήμαος σε μια ακαριαία είσοδο που ορίζεαι μονάχα για μια χρονική σιγμή, όπως η δ), ονομάζεαι κρουσική απόκριση h). Επειδή α συσήμαα που συζηάμε είναι γραμμικά και χρονικά αμεάβληα, αν μπορούσαμε να εκφράσουμε ένα οποιοδήποε σήμα εισόδου ως άθροισμα συναρήσεων Δέλα, όε η έξοδος θα μπορούσε να υπολογισεί πολύ εύκολα, ως άθροισμα κρουσικών αποκρίσεων. Πώς όμως μπορούμε να αναπαρασήσουμε ένα οποιοδήποε σήμα x) ως άθροισμα συναρήσεων Δέλα; 3.3. Αναπαράσαση Σημάων με Συναρήσεις Δέλα Για να βρούμε μια έοια αναπαράσαση, θα ήαν βολικόερο να ξεκινήσουμε με μια προσέγγιση ης συνάρησης Δέλα, ην οποία θα ονομάσουμε δ ) και ην οποία θα ορίσουμε ως δ ) =, 3.99), αλλού η οποία παραίθεαι σχημαικά σο Σχήμα 3.3. Πρέπει να σας είναι προφανές όι όαν, η συνάρηση δ ) /Δ δ Δ ) Δ Σχήμα 3.3: Συνάρηση δ ). είνει ση συνάρηση δ). Η ιδέα πίσω από η χρήση αυής ης συνάρησης θα σας γίνει εμφανής αν για ένα υχαίο σήμα x) αναπαρασήσεε γραφικά ο γινόμενο x)δ ). Δείε ο Σχήμα 3.4 Αν θεωρήσουμε όι ο είναι πολύ μικρό ώσε ο μήμα ου x) που αποκόπεαι από ο γινόμενο x)δ ) να είναι σχεδόν σαθερό και ίσο με x), όε μπορούμε να γράψουμε όι x)δ ) x)δ ) 3.2) Αν, όε η παραπάνω σχέση μεαρέπεαι σε ισόηα ως Ακολουθώνας ο ίδιο σκεπικό, ας σχημαίσουμε ο γινόμενο lim x)δ ) = x)δ) 3.2) x)δ i ) 3.22) με = i ένα υχαίο σημείο ου χρόνου. Το αποέλεσμα απεικονίζεαι σο Σχήμα 3.5. Ξανά, αν θεωρήσουμε όι
20 7 Μια εισαγωγή σα Σήμαα και Συσήμαα x)δ Δ ) /Δ δ Δ ) x)/δ xδ)/δ x) xδ) Δ Σχήμα 3.4: Σήμα x)δ ). Δ x)δ Δ - i ) /Δ δ Δ - i ) x i ) x i +Δ) x i )/Δ x i +Δ)/Δ i i +Δ i i +Δ Σχήμα 3.5: Σήμα x)δ i ). ο είναι αρκεά μικρό ώσε ο μήμα ου x) που αποκόπεαι να είναι σχεδόν σαθερό, όε Αν, όε η παραπάνω σχέση μεαρέπεαι σε ισόηα ως x)δ i ) x i )δ i ) 3.23) lim x)δ i ) = x i )δ i ) 3.24) Μπορούμε να συνεχίσουμε αυή η διαδικασία, αποκόπονας μη επικαλυπόμενα αλλά συνεχόμενα μήμαα ου x) κάθε φορά με έοιο ρόπο ώσε ο άθροισμά ους να μας δίνει ο συνολικό x). Οαν, όε ο άθροισμα αυών ων μημάων θα μας δίνει μια απειροσά καλή προσέγγιση ου αρχικού μήμαος. Εσω όι οι χρονικές σιγμές i είναι ώρα k, ώσε να έχουμε συνεχή και μη επικαλυπόμενα μήμαα ου x). Δείε ο Σχήμα kδ kδ+δ Σχήμα 3.6: Προσέγγιση σήμαος x) από σήμαα xk )δ k ). Η παραπάνω διαδικασία μπορεί να γραφεί ως ˆx ) = + k= xk )δ k ) 3.25)
21 Κεφάλαιο 3. Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 7 με ˆx ) μια προσέγγιση ου αρχικού σήμαος x) η οποία εξαράαι από ην ιμή ου. Οαν, έχουμε lim ˆx ) = lim + k= Ας παραηρήσουμε ι συμβαίνει όαν η διάρκεια γίνεαι απειροσά μικρή, δηλ. xk )δ k ) = x) 3.26) 3.27) Τόε η μημαοποίηση ου άξονα ου χρόνου δεν είναι διακριή αλλά γίνεαι συνεχής, έσι ώσε όπου είναι μια συνεχής μεαβληή ου χρόνου. Εσι, ο γινόμενο lim k = k = 3.28) xk )δ k ) x)δ ) 3.29) Πλέον ο άθροισμα για διακριά, ακέραια k μεαρέπεαι σε ολοκλήρωμα επάνω σε κάθε ιμή ης συνεχούς μεαβληής. Οπόε ελικά Το ολοκλήρωμα lim ˆx ) = lim + k= xk )δ k ) = x)δ ) 3.2) x)δ ) 3.2) περιγράφει ένα σήμα συνεχούς χρόνου ως άπειρο, συνεχές άθροισμα μεαοπισμένων συναρήσεων Δέλα δ ) με βάρη x). Θα μπορούσε κανείς λοιπόν να περιγράψει αυό ο ολοκλήρωμα ως μια πράξη μεαξύ ων σημάων δ) και x). Η πράξη αυή ονομάζεαι συνέλιξη - convoluion και συμβολίζεαι με, δηλ. x) δ) = x)δ ) 3.22) Η πράξη ης συνέλιξης ορίζεαι γενικόερα μεαξύ δυο οποιονδήποε σημάων x), y) ως c xy ) = x) y) = x)y ) 3.23) Αναπαράσαση Απόκρισης Μηδενικής Καάσασης με Κρουσικές Α- ποκρίσεις Εχονας λοιπόν ην αναπαράσαση ενός σήμαος ως η συνέλιξή ου με η συνάρηση Δέλα, ας δούμε πώς μπορούμε να ην εκμεαλλευούμε για να βρούμε ην απόκριση μηδενικής καάσασης. Αφού ο σύσημά μας είναι γραμμικό και χρονικά αμεάβληο θυμηθείε, οι αρχικές συνθήκες είναι μηδενικές!), θα έχουμε α ακόλουθα ζεύγη εισόδου-εξόδου: κρουσική απόκριση: δ) h) 3.24) χρον. αμεαβληόηα: δ ) h ) 3.25) γραμμικόηα/ομογένεια: x)δ ) x)h ) 3.26) γραμμικόηα/αθροισικόηα: x)δ ) x)h ) 3.27) είσοδος: x) = x) δ) απόκριση μηδεν. καάσασης: y) = x) h) 3.28) Βλέπουμε λοιπόν όι: εφαρμόζονας ις απλές ιδιόηες ων συσημάων που γνωρίζουμε επάνω σην αναπα-
22 72 Μια εισαγωγή σα Σήμαα και Συσήμαα ράσαση ενός σήμαος εισόδου ως συνέλιξη με συναρήσεις Δέλα, η απόκριση μηδενικής καάσασης y zs ) αναπαρίσααι ως η συνέλιξη ης εισόδου x) με ην κρουσική απόκριση ου συσήμαος h)! Μπορούμε λοιπόν να γράψουμε όι y zs ) = x) h) 3.29) Η γνώση ης κρουσικής απόκρισης ενός συσήμαος μπορεί να μας δώσει ην απόκριση μηδενικής καάσασης για οποιαδήποε είσοδο! 3.4 Συνέλιξη Η πράξη ης συνέλιξης είναι θεμελιώδους σημασίας, λόγω ου όι εμφανίζεαι συχνά σις φυσικές επισήμες, ση μηχανική, και σα μαθημαικά, οπόε ης αξίζει ξεχωρισή και εκενής αναφορά. Αμέσως παρακάω, θα ην εξεάσουμε ως γενικόερη πράξη, χωρίς να η συνδέουμε απαραίηα με ην είσοδο και ην έξοδο ενός συσήμαος. Προού μελεήσουμε αναλυικά ο ολοκλήρωμα ης συνέλιξης, ας δούμε μερικές ενδιαφέρουσες ιδιόηες με βάση ον ορισμό ης Ιδιόηες Συνέλιξης Η πράξη ης συνέλιξης απλοποιείαι σημανικά από ιδιόηες, όπως αυές σον Πίνακα 3.. Ιδιόηες συνέλιξης Ομογένεια Ανιμεαθεικόηα Προσεαιρισικόηα Επιμερισικόηα Γραμμικόηα Εύρος Ουδέερο σοιχείο ax) y) = x) ay) = ax) y)), a R x) y) = y) x) x) y)) z) = x) y) z)) x) y) + z)) = x) y) + x) z) z ) = x ) y) z 2 ) = x 2 ) y) αν x) = ax ) + bx 2 ) όε z) = x) y) = az ) + bz 2 ) x) : [, 2 ] R y) : [ 3, 4 ] R x) y) : [ + 3, ] R x) δ) = δ) x) = x) Πίνακας 3.: Ιδιόηες συνέλιξης Ακολουθούν οι αποδείξεις αυών ων ιδιοήων, με αποκλεισική χρήση ου ορισμού Ομογένεια Εχουμε και ax)) y) = x) ay)) = ax)y ) = x)ay ) = a x)ay ) = x) ay)) 3.22) x)y ) = ax) y)) 3.22) Ανιμεαθεικόηα Θέονας u = σον ορισμό ης συνέλιξης, έχουμε x) y) = x)y ) = x u)yu)u = + x u)yu)u = y) x) 3.222)
23 Κεφάλαιο 3. Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου Προσεαιρισικόηα Είναι x) y)) z) = = = x) y))z ) = xu) y u)z ) ) u = ) xu)y u)u z ) 3.223) xu) ) ym)z m u)m u 3.224) xu)y u) z u))u 3.225) = x) y) z)) 3.226) όπου ση Σχέση 3.224) θέσαμε m = u Επιμερισικόηα Είναι x) y) + z)) = = x)y ) + z )) = x)y ) + x)z ) ) 3.227) + x)y ) + x)z ) ) 3.228) = x) y) + x) z) 3.229) Γραμμικόηα Είναι με z) = x) y) = ax ) + bx 2 )) y) 3.23) = ax ) y) + bx 2 ) y) 3.23) = ax ) y)) + bx 2 ) y)) 3.232) = az ) + bz 2 ) 3.233) x) z ) = x ) y) 3.234) z 2 ) = x 2 ) y) 3.235) λόγω ων ιδιοήων ης ομογένειας και ης επιμερισικόηας = Εύρος Η απόδειξη ης ιδιόηας ου εύρους φαίνεαι σχήμαικά σο Σχήμα 3.7. Σο ολοκλήρωμα ης συνέλιξης, ο σήμα y) χρησιμοποιείαι ως y ), με μεαβληή ο. Άρα υπόκειαι σε πράξεις ανισροφής χρόνου και μεαόπισης. Ως εκ ούου, ο σήμα θα είναι μη μηδενικό σο [ 4, 3 ]. Ση διαδικασία ης συνέλιξης, ο γινόμενο x)y ) είναι μη μηδενικό για 3 και 4 2, δηλ. σο διάσημα [ + 3, ] Ουδέερο σοιχείο Είναι x) δ) = x)δ ) = x) = x) 3.236) = - 4 = 2-3 x)*y) Σχήμα 3.7: Γραφική απόδειξη ης ιδιόηας ου εύρους.
24 74 Μια εισαγωγή σα Σήμαα και Συσήμαα από ιδιόηες ης συνάρησης Δέλα. Η συνέλιξη φημίζεαι ως μια πράξη αρκεά περίπλοκη και δύσκολη, και σε πρώη επαφή αποθαρρύνει ον αναγνώση. Η δυσκολία έγκειαι σο όι σην πράξη ης ολοκλήρωσης εμπεριέχεαι ο γινόμενο δυο σημάων, εκ ων οποίων ο ένα έχει υποσεί ανάκλαση και μεαόπιση Η συνέλιξη αναλυικά Ας αναλύσουμε διεξοδικά ον ρόπο με ον οποίο υπολογίζουμε ο ολοκλήρωμα ης συνέλιξης. Ας δούμε ον ορισμό: c xy ) = x) y) = x)y ) 3.237) Η πρώη παραήρηση είναι όι ο ολοκλήρωμα έχει ως μεαβληή ο και όχι ο. Το ο θεωρούμε σαθερό μέσα σο ολοκλήρωμα. Επεια, ο ολοκλήρωμα αυό εμπλέκει δυο σήμαα: ο x) και ο y ). Το πρώο είναι αυούσιο ο σήμα x), δεν έχει υποσεί κάποια μεαβολή. Το δεύερο όμως, βλέπεε όι έχει υποσεί δυο είδη πράξεων σην ανεξάρηη μεαβληή: ανάκλαση και μεαόπιση. Μια ακολουθία μεαροπής είναι η εξής: y) y) y ) y + ) = y ) 3.238) Οπόε ο σήμα που χρησιμοποιείαι σο ολοκλήρωμα ης συνέλιξης έχει υποσεί μια ανάκλαση ως προς ον καακόρυφο άξονα και ακολούθως μια μεαόπιση καά. Το σήμα που προκύπει πολλαπλασιάζεαι με ο x) και ολοκληρώνεαι ως προς. Το αποέλεσμα ης συνέλιξης μπορεί να βρεθεί με δυο ρόπους: αλγεβρικά και γραφικά. Συνήθως προιμάαι η γραφική λύση ης συνέλιξης, και ένα έοιο παράδειγμα φαίνεαι σο Σχήμα 3.8. ˆ Παραηρήσε όι έχουμε δυο σήμαα, ο f) και ο g) σην πρώη γραμμή ου σχήμαος. Επιλέγουμε να παίξουμε με ο g), δηλ. αυό θα μεαοπίσουμε και θα ανακλάσουμε. ˆ Ση δεύερη γραμμή, έχουμε ξανά α δυο σήμαα, μόνο που ώρα είναι συναρήσει ου και όχι ου, όπως ακριβώς επιάσσει ο ολοκλήρωμα ης συνέλιξης, και ο g) έχει ανακλασεί ως προς ον καακόρυφο άξονα, και έχει μεαοπισεί καά. Θυμίζω όι αυό ο ο χειριζόμασε ως σαθερά σο ολοκλήρωμα. Δείε ην αλλαγή σα άκρα ου g), και πώς αυά προσαρμόσηκαν μεά ην ανάκλαση και η μεαόπιση. ˆ Σην ρίη γραμμή, παίρνουμε ο g ) που μόλις φιάξαμε και ξεκινάμε να ο ολισθαίνουμε πάνω σον ίδιο άξονα με ο f), ξεκινώνας από ο και προς ο +. ˆ Σην πορεία έαρη γραμμή), βλέπεε όι ο g) συνανάει κάποια σιγμή ο f). Οαν συμβεί αυό, έχουμε γινόμενο μεαξύ ων δυο σημάων και άρα έχουμε μια μη μηδενική ιμή για ο ολοκλήρωμα ης συνέλιξης. Αυές οι χρονικές σιγμές είναι όαν ο δεξί άκρο ου g ) συνανά ο αρισερό άκρο ου f) και πέρα, και όαν ο αρισερό άκρο ου g ) δεν έχει περάσει ο =, δηλ. όαν και ) οπόε όε η συνέλιξη υπολογίζεαι σο διάσημα από ως, εκεί δηλαδή που ο γινόμενο μεαξύ ων δυο σημάων είναι μη μηδενικό, ως c fg ) = f)g ) 3.24) όπου και ανικαθισούμε ις μαθημαικες μορφές ων σημάων, και υπολογίζουμε ο ολοκλήρωμα. ˆ Σην πέμπη γραμμή, ο g ) έχει μπει ολόκληρο μέσα σο f), πράγμα που δεν είχε συμβεί παραπάνω, άρα είναι διαφορεική περίπωση. Εδώ, η συνέλιξη είναι μη μηδενική όαν ο αρισερό άκρο ης g ) περάσει ο =, δηλ. όαν 4 > > ) και η συνέλιξη υπολογίζεαι ως c fg ) = 4 f)g ) 3.242) όπου και ανικαθισούμε ις μαθημαικες μορφές ων σημάων, και υπολογίζουμε ο ολοκλήρωμα.
25 Κεφάλαιο 3. Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου Σχήμα 3.8: Γραφική απεικόνιση ης συνέλιξης. ˆ Άλλη περίπωση δεν υπάρχει, οπόε για κάθε άλλο εκός από α παραπάνω, ο αποέλεσμα ης συνέλιξης είναι μηδέν, άρα c fg ) =, < 3.243) Τώρα που η διαδικασία είναι περισσόερο ξεκάθαρη, ας θεωρήσουμε όι α παραπάνω σήμαα είναι α Οπόε θα έχουμε ˆ Οαν, όε c fg ) =. f) = e a u) 3.244) g) = e b, [, 4] 3.245)
26 76 Μια εισαγωγή σα Σήμαα και Συσήμαα ˆ Οαν > και 4, δηλ. οαν < 4, όε c fg ) = e a e b ) 3.246) = e b e b a) 3.247) = e b b a eb a) 3.248) = e b b a eb a) ) ) 3.249) = e b a) ) b e b) 3.25) b a ˆ Τέλος, όαν 4 >, δηλ. > 4, όε c fg ) = 4 e a e b ) 3.25) = e b b a eb a) 3.252) 4 = e b b a eb a) 4) e b a) ) ) 3.253) = e b a) 4) b e b a) ) b) 3.254) b a Μπορούμε λοιπόν να συνοψίσουμε ην παραπάνω γραφική λύση ης συνέλιξης ως ακολούθως: Γραφική Λύση Συνέλιξης Σημάων x) και y). Επιλέγουμε ένα εκ ων δυο σημάων, έσω ο x), ο οποίο και μεαρέπουμε σε x). 2. Εφαρμόζουμε επάνω ου ην πράξη ης χρονικής ανισροφής και ης χρονικής μεαόπισης, λαμβάνονας έσι ο σήμα x ). 3. Φέρουμε α δυο σήμαα σε κοινό άξονα ως προς, και σύρουμε ο x ) από ο προς ο Καθορίζουμε προσεκικά ις περιοχές ου χρόνου όπου α δυο σήμαα συνυπάρχουν, δηλ. όπου ο γινόμενο x )y) είναι μη μηδενικό. 5. Σις παραπάνω περιοχές, υπολογίζουμε ο ολοκλήρωμα ης συνέλιξης Χαρακηρισικά Παραδείγμαα Πολύ χρήσιμα είναι α ακόλουθα παραδείγμαα, α οποία θα σας βοηθήσουμε να καανοήσεε ακόμα περισσόερο ην πράξη ης συνέλιξης. Παράδειγμα 3.8: Εσω α σήμαα ου Σχήμαος 3.9.
27 Κεφάλαιο 3. Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 77 y) x) T 2T T Σχήμα 3.9: Σήμαα Παραδείγμαος 3.8. Να υπολογίσεε η συνέλιξη y) = x) y). Λύση: Επιλέγουμε να κάνουμε πράξεις σην ανεξάρηη μεαβληή ου x), καθ όι ευκολόερο. Η ανάκλαση και η μεαόπιση ου σήμαος φαίνεαι σο Σχήμα 3.. και άρα θα έχουμε ις παρακάω περιπώσεις, όπως αυές x) x-) x-) ανάκλαση μεαόπιση T -T -T+ Σχήμα 3.: Μεαόπιση και ανάκλαση σήμαος x). απεικονίζοναι σο Σχήμα 3.. ˆ Για ην πρώη περίπωση είναι y) =, <. ˆ Για η δεύερη περίπωση είναι y) = T = 2 ] = 2, για και T T. 2T 2T ˆ Για ην ρίη περίπωση είναιy) = T T < 2T. T T + T 2 ) = 2 T T + 3 3T 2, για T < T και ˆ Για ην έαρη περίπωση είναι y) = και 2T 2T < 3T. 2T T 2 ) = 2 2 )] 2T T 2T T = 2 2T 3 + 9T 2, για < 3T ˆ Για ην πέμπη περίπωση είναι y) =, 3T.
28 78 Μια εισαγωγή σα Σήμαα και Συσήμαα -T T 2T -T T 2T -T T 2T T -T 2T T 2T -T Σχήμα 3.: Περιπώσεις Συνέλιξης Παραδείγμαος 3.8. Άρα ελικά θα είναι:, < και 3T y) = 2 2T, T 3.255) 2 T + 3 3T 2, T < 2T 2 2T 3 + 9T 2, 2T < 3T
29 Κεφάλαιο 3. Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 79 Παράδειγμα 3.9: Να υπολογισεί η συνέλιξη ων σημάων x) = u) 3.256) y) = e 2 u) 3.257) Λύση: Τα δυο σήμαα φαίνοναι σο Σχήμα 3.2. Το x) είναι πιο καάλληλο για να υποσεί ις μεαβολές που είναι h) x) u) απαραίηες σο ολοκλήρωμα ης συνέλιξης. Σχήμα 3.2: Σήμαα Παραδείγμαος 3.9. Διακρίνουμε δυο περιπώσεις, οι οποίες φαίνοναι σο Σχήμα 3.3. ˆ Για ην πρώη περίπωση είναι c xy ) = για. ˆ Για η δεύερη περίπωση είναι c xy ) = e 2 u)u ) = e 2 = e ) για >. Άρα ελικά θα είναι e 2 2, > c xy ) =, 3.259) Το παράδειγμα αυό είναι εξαιρεικό για να δείξουμε ην αλγεβρική μέθοδο υπολογισμού ης συνέλιξης. Θα είναι Ο όρος c xy ) = e 2 u)u ) 3.26), < < u)u ) =, αλλού 3.26) αφού και, > u) =, αλλού, < u ) =, αλλού 3.262) 3.263)
30 8 Μια εισαγωγή σα Σήμαα και Συσήμαα u-) u-) Σχήμα 3.3: Περιπώσεις Παραδείγμαος 3.9. Η Σχέση 3.26) γράφεαι ως c xy ) = e 2 u)u ) = e 2 = ] 2 e 2 = 2 e 2 ), για > 3.264) Οπόε c xy ) = 2 e 2 )u) 3.265) Παράδειγμα 3.: Να υπολογισεί η συνέλιξη ων σημάων x) = 3u ) 3.266) y) = u + ) 3.267) Λύση: Διακρίνουμε δυο περιπώσεις, οι οποίες φαίνοναι σο Σχήμα 3.4. Θα είναι ˆ Για ην πρώη περίπωση είναι c xy ) = 3.268) για. ˆ Για η δεύερη περίπωση είναι c xy ) = = x)y ) = 3u )u ) 3.269) ] 3 = 3 = 3 ) + 3 = ) για > >, αφού, < < 3u )u ) =, αλλού 3.27)
31 Κεφάλαιο 3. Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 8 x-) 3 y) - - x-) 3 y) - - Σχήμα 3.4: Περιπώσεις Παραδείγμαος 3.. Άρα συνολικά, c xy = 3, > 3.272) Παράδειγμα 3.: Να υπολογισεί η συνέλιξη ων σημάων x) = 2e 3 u ) 3.273) + 2 ) y) = rec 3.274) 2 Λύση: Διακρίνουμε ρεις περιπώσεις, οι οποίες φαίνοναι σο Σχήμα 3.5. Θα είναι ˆ Για ην πρώη περίπωση είναι για c xy ) = 3.275) ˆ Για η δεύερη περίπωση είναι c xy ) = x)y ) = +3 2e ) = 2 ] +3 3 e 3 = 2 3 e 3+3) e 3 ) 3.277) = 2 3 e 3+3) e ) για + και + 3 >, άρα 2 <.
32 82 Μια εισαγωγή σα Σήμαα και Συσήμαα y-) + +3 y-) + +3 y-) + +3 Σχήμα 3.5: Περιπώσεις Παραδείγμαος 3.. ˆ Για ην ρίη περίπωση είναι c xy ) = x)y ) = e ) = 2 ] +3 3 e 3 = 2 3 e 3+3) e 3+) ) 3.28) + = 2 3 e 3+3) e 3+) 3.28) για + > >. Άρα συνολικά c xy =, e 3+3) e 3, 2 < 2 3 e 3+3) e 3+), > 3.282) Παράδειγμα 3.2: Να υπολογισεί η συνέλιξη ων σημάων x) = e )
33 Κεφάλαιο 3. Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 83 y) = rec 2) 3.284) Λύση: Αρχικά, θα ήαν βολικό να γράψουμε ο σήμα x) = e 2 ως e 2, < x) = e 2, 3.285) Διακρίνουμε ρεις περιπώσεις, οι οποίες φαίνοναι σο Σχήμα 3.6. Θα είναι - + y-) - + y-) - + y-) Σχήμα 3.6: Περιπώσεις Παραδείγμαος 3.2. ˆ Για ην πρώη περίπωση είναι c xy ) = για +. x)y ) = + e ) = ] + 2 e2 = 3 e2 ) e 2+) ) 3.287)
34 84 Μια εισαγωγή σα Σήμαα και Συσήμαα ˆ Για η δεύερη περίπωση είναι c xy ) = x)y ) = +3 2e ) = 2 ] +3 3 e 3 = 2 3 e 3+3) e 3 ) 3.289) = 2 3 e 3+3) e ) για + και + 3 >, άρα 2 <. ˆ Για ην ρίη περίπωση είναι c xy ) = x)y ) = e ) = 2 ] +3 3 e 3 = 2 3 e 3+3) e 3+) ) 3.292) + = 2 3 e 3+3) e 3+) 3.293) για + > >. Άρα συνολικά c xy =, e 3+3) e 3, 2 < 2 3 e 3+3) e 3+), > 3.294) Συνέλιξη και Συναρήσεις Δέλα Η ιδιόηα x) δ ± ) = x ± ) 3.295) όπου δηλώνει ην πράξη ης συνέλιξης είναι πολύ χρήσιμη ση μελέη συσημάων. Η Σχέση 3.295) δηλώνει όι όαν κάνουμε συνέλιξη ενός σήμαος με μια Συνάρηση Δέλα η οποία βρίσκεαι ση χρονική σιγμή = ±, όε ο αποέλεσμα είναι απλά ο ίδιο ο σήμα x) μεαοπισμένο ση θέση = ±! Θα δούμε πιο κάω όι αυή η ιδιόηα μας διευκολύνει πάρα πολύ, όαν έχουμε να κάνουμε με συσήμαα. Σχημαικά, δείε ο Σχήμα 3.7). Μπορούμε προς ο παρόν να δούμε ένα παράδειγμα που θα μας βοηθήσει να δούμε πως δουλεύει αυή η πράξη και x) δ- ) * = x- ) Σχήμα 3.7: Συνέλιξη σήμαος με συνάρησης Δέλα. πως διαφέρει η συνέλιξη ενός σήμαος με μια Συνάρηση Δέλα με ον πολλαπλασιασμό ου με ην ίδια συνάρηση.
35 Κεφάλαιο 3. Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 85 Παράδειγμα 3.3: Εσω ο σήμα x) =, = 4, =, = 4, αλλού 3.296) αʹ) Σχεδιάσε ο σήμα σο χρόνο. βʹ) Γράψε ο σήμα ως άθροισμα Συναρήσεων Δέλα δ). γʹ) Πολλαπλασιάζουμε ο x) με ο σήμα y) = 2rec. Σχεδιάσε ο αποέλεσμα. 6) δʹ) Κάνουμε συνέλιξη ο x) με ο σήμα y) = 2rec. Σχεδιάσε πρώα α σήμαα που προκύπουν 6) και μεά γράψε μια βολική μαθημαική σχέση που περιγράφει ο αποέλεσμα. εʹ) Ποιός είναι ο γενικός κανόνας που προκύπει από α δυο παραπάνω ερωήμαα; Δηλ. ι συμβαίνει σε ένα σήμα όαν πολλαπλασιάζεαι με μια συνάρηση Δέλα, και ι συμβαίνει όαν γίνεαι συνέλιξη με μια Συνάρηση Δέλα; Λύση: αʹ) Το σήμα σο χρόνο φαίνεαι σο Σχήμα 3.8. x) Σχήμα 3.8: Παράδειγμα συνέλιξης σήμαος με Συνάρηση Δέλα: σήμα σο χρόνο. βʹ) Είναι x) = δ + 4) + δ) δ 4) 3.297) γʹ) Το γινόμενο ων δυο σημάων είναι ) x) y) = x) 2rec = 2rec δ + 4) + δ) δ 4) = 2δ) = 6) 6) 2, =, αλλού 3.298) και φαίνεαι σο Σχήμα 3.9. δʹ) Η συνέλιξη ων σημάων είναι + 4 ) 4 ) x) y) = x) 2rec = 2rec + 2rec 2rec 6) 6 6) 6 και φαίνεαι σο Σχήμα 3.2 αρισερά. Παραηρώνας ο, μπορούμε να γράψουμε όι + 5 ) 5 ) x) y) = 2rec + 2rec 2rec 4 2) ) 3.3)
36 86 Μια εισαγωγή σα Σήμαα και Συσήμαα x)y) 2 x)y) Σχήμα 3.9: Παράδειγμα συνέλιξης σήμαος με Συνάρηση Δέλα: γινόμενο σημάων. 2 x)*y) 2 x)*y) Σχήμα 3.2: Παράδειγμα συνέλιξης σήμαος με Συνάρηση Δέλα: συνέλιξη σημάων. και φαίνεαι σο Σχήμα 3.2 δεξιά. εʹ) Ο γενικός κανόνας είναι όι ο γινόμενο σήμαος με Συνάρηση Δέλα δίνει μια Συνάρηση Δέλα με πλάος ο πλάος ου σήμαος ση θέση ης Συνάρησης Δέλα. Η συνέλιξη σήμαος με Συνάρηση Δέλα μεαοπίζει η θέση αναφοράς ου σήμαος από ο μηδέν ση θέση, αν δ ) είναι η Συνάρηση Δέλα η οποία εμπλέκεαι ση συνέλιξη Πίνακας Συνέλιξης Η διαδικασια ης συνέλιξης απλοποιείαι σημανικά από έοιμους πίνακες συνέλιξης, όπως ο Πίνακας 3.2. Αυός ο πίνακας, που αναφέρει διάφορα ζεύγη σημάων και ο αποέλεσμα ης συνέλιξής ους, μπορεί να σας βοηθήσει σον έλεγχο ων αποελεσμάων σας Παραηρήσεις Ας δούμε μερικές παραηρήσεις με βάση όσα έχουμε συζηήσει ως ώρα.. Οπως βλέπεε, είναι πολύ σημανικό να μπορείε να υπολογίσεε σωσά ο μεαοπισμένο σήμα και να βλέπεε σωσά ις περιπώσεις και α άκρα ου ολοκληρώμαος. Οι πράξεις σο ολοκλήρωμα είναι συνήθως αρκεά απλές. 2. Οπως είδαμε, η συνέλιξη είναι ανιμεαθεική πράξη, ισχύει δηλ. όι c fg ) = f) g) = g) f) = c gf ) 3.3) Αυό σημαίνει όι αν κάναμε πράξεις σην ανεξάρηη μεαβληή ου f) ανί για ου g), θα είχαμε πάλι ο ίδιο αποέλεσμα. 3. Προιμούμε να ανακλάσουμε και μεαοπίσουμε ο μικρόερο σε διάρκεια σήμα, γιαί συνήθως είναι πιο εύκολη η διαδικασία υπολογισμού ης συνέλιξης. Αν και α δυο σήμαα είναι άπειρης διάρκειας, προιμούμε όποιο θέλουμε.
37 Κεφάλαιο 3. Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 87 Χρήσιμα ζεύγη συνέλιξης x) y) x) y) x) δ T ) ea u) u) u) u) ea u) eb u) ea u) ea u) ea u) ea u) n u) ea u) m u) n u) ea u) eb u) m ea u) n ea u) m ea u) n eb u) x T ) ea u) a u) ea eb u), a 6= b a b a e u) 2 a e u) 2n a X n!e n!n j u) u) an+ aj+ n j)! j= m!n! m+n+ u) n + m + )! eb ea + a b)ea u) a b)2 m!n! m+n+ ea u) n + m + )! m X )j m!n + j)!m j ea u) j!m j)!a b)!n+j+ j= n X )k n!m + k)!n k eb + u), a 6= b k!n k)!b a)m+k+ a λ e cosb + θ)u) e u) ea u) eb u ) ea u ) eb u ) cosθ φ)eλ e a cosb + θ φ) p u), a + λ)2 + b2 b φ = an a+λ ea u) + eb u ), <{b} > <{a} b a a b e e u ) b a Πίνακας 3.2: Πίνακας ζευγών συνελίξεων Σχήμα 3.2: Πολύς κόσμος έχει αλαιπωρηθεί από η συνέλιξη Χρήσιμη ιδιόηα, η οποία αναφέρεαι σον Πίνακα 3., για πεπερασμένης διάρκειας σήμαα είναι η εξής: αν ο ένα εκ ων δυο είναι μη μηδενικό σο διάσημα [a, b] και ο άλλο είναι μη μηδενικό σο διάσημα
Γιάννη Σ. Μπούταλη Αναπληρωτή Καθηγητή Δ.Π.Θ. ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθητικές σημειώσεις στο μάθημα ΣΑΕ ΙΙ
 Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Κεφάλαιο 3 ο. Κυκλώματα με στοιχεία αποθήκευσης ενέργειας
 Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
y(t) = T [x(t)] (7.1)
![y(t) = T [x(t)] (7.1) y(t) = T [x(t)] (7.1)](/thumbs/93/114087149.jpg) Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ
 ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
13. Συνήθεις διαφορικές εξισώσεις
 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
Θέματα Περασμένων Εξετάσεων και Απαντήσεις
 Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ
 ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
_Σχήµα 2_. Σελίδα 1 από 5. τον οποίο γίνεται η µεταπτωτική κίνηση. Άξονας περιστροφής τροχού. Άξονας γύρω από. τον οποίο γίνεται η µεταπτωτική κίνηση
 ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ
 Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
Η Έννοια της τυχαίας ιαδικασίας
 Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
Εργαστηριακή Άσκηση Το σύστημα αναμονής M/G/1
 Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Κεφάλαιο 5 Πολλαπλοί χημικοί αντιδραστήρες
 Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Πως λύνεται ένα πρόβληµα.
 Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
Εισαγωγή στη Θεωρία Σημάτων και Συστημάτων
 Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ 90º. 180º ω. Οι απαντήσεις και τα σχετικά σχόλια
 Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ. LT και μονάδες στο SI, kgm/s 2 ή N. υνισταμένη. υνισταμένη. d dt. d dt.
 ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΦΥΣΙΚΗ Ι. ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ ΣΩΜΑΤΟΣ Ισορροπία Σωματιδίου Στατική Ισορροπία Στερεού Σώματος
 ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
Εργαστήριο Ηλεκτρικών κυκλωμάτων
 Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Μεγαλύτερες περιπέτειες
 Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
3 Συσχετίσεις σε χρονοσειρές
 3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
Δυναμική συμπεριφορά των λογικών κυκλωμάτων MOS. Διάλεξη 10
 Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ
 ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
ΕΛΕΓΧΟΣ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΚΕΦΑΛΑΙΟ 2 ΚΕΦΑΛΑΙΟ 2. Πλεονεκτήματα ψηφιακού ελέγχου
 ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
ΦΥΣ 145 Υπολογιστικές Μέθοδοι στη Φυσική. Τελική εξέταση 5 Μάη 2007 Ομάδα 2 η
 ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ
 Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
Κεφάλαιο 4 Ιδανικοί χημικοί αντιδραστήρες
 Κεφάλαιο 4 Ιδανικοί χημικοί ανιδρασήρες Με βάση α σοιχεία για ην κινηική και η σοιχειομερία ων ανιδράσεων, μπορούμε ώρα να προχωρήσουμε σην ανάλυση ορισμένων βασικών ύπων χημικών ανιδρασήρων. Η ανάλυση
Κεφάλαιο 4 Ιδανικοί χημικοί ανιδρασήρες Με βάση α σοιχεία για ην κινηική και η σοιχειομερία ων ανιδράσεων, μπορούμε ώρα να προχωρήσουμε σην ανάλυση ορισμένων βασικών ύπων χημικών ανιδρασήρων. Η ανάλυση
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ
 Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ 1 ΣΕΙΡΑΣ FOURIER. Ανάπτυξη σειράς Dirac σε σειρά Fourier (Εκθετική Fourier):
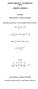 ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
Θεματική ενότητα : Βασικά εργαλεία και Μέθοδοι για τον έλεγχο της ποιότητας.
 Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΝΙΚΟΛΑΟΣ Κ. ΜΠΕΚΙΑΡΗΣ ΛΥΜΠΕΡΗΣ ΤΕΧΝΙΚΕΣ ΓΡΑΜΜΙΚΩΝ ΚΑΙ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΛΕΓΚΤΩΝ ΣΥΣΤΗΜΑΤΩΝ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΝΙΚΟΛΑΟΣ Κ. ΜΠΕΚΙΑΡΗΣ ΛΥΜΠΕΡΗΣ ΤΕΧΝΙΚΕΣ ΓΡΑΜΜΙΚΩΝ ΚΑΙ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΛΕΓΚΤΩΝ ΣΥΣΤΗΜΑΤΩΝ
ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ
 1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
ΦΥΣΙΚΗ Ι. ΤΜΗΜΑ Α Ε. Στυλιάρης
 (Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
(Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
a k y[n k] = b l x[n l] (12.1)
![a k y[n k] = b l x[n l] (12.1) a k y[n k] = b l x[n l] (12.1)](/thumbs/61/46058386.jpg) Κεφάλαιο 12 Ανάλυση Σημάτων και Συστημάτων στο Πεδίο του Διακριτού Χρόνου 12.1 Εισαγωγή Σε αυτό το κεφάλαιο, θα συζητήσουμε για το πως μπορούμε να μελετάμε γραμμικά και χρονικά αμετάβλητα ΓΧΑ) συστήματα
Κεφάλαιο 12 Ανάλυση Σημάτων και Συστημάτων στο Πεδίο του Διακριτού Χρόνου 12.1 Εισαγωγή Σε αυτό το κεφάλαιο, θα συζητήσουμε για το πως μπορούμε να μελετάμε γραμμικά και χρονικά αμετάβλητα ΓΧΑ) συστήματα
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ. 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διατμητικής Αντοχής Εδάφους. Διδάσκοντες: Β. Χρηστάρας Καθηγητής Β. Μαρίνος, Αν.
 ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
c xy [n] = x[k]y[n k] (1)
![c xy [n] = x[k]y[n k] (1) c xy [n] = x[k]y[n k] (1)](/thumbs/65/53219776.jpg) Συνέλιξη Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 6 Οκτωβρίου 2015 1 Εισαγωγή Η συνέλιξη αποτελεί μια πράξη πολύ σημαντική,
Συνέλιξη Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 6 Οκτωβρίου 2015 1 Εισαγωγή Η συνέλιξη αποτελεί μια πράξη πολύ σημαντική,
Ροπή δύναμης. Τι προκαλεί την επιτάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω του. Τι προκαλεί την γωνιακή επιτάχυνση ενός στερεού σώματος;
 Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
Α Σ Κ Η Σ Η 1 ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY
 Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
3. ΦΑΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΤΩΝ (ΑΝΑΛΥΣΗ FOURIER)
 3. ΦΑΣΜΑΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΩΝ (ΑΝΑΛΥΣΗ FOURIER) 3.. Γενικά Ένα σήμα μπορεί να αναπαρασαθεί με έναν από ους παρακάω ισοδύναμους ρόπους: Ως χρονικά μεαβαλλόμενη άση (κυμαομορφή) x(t) (αναπαράσαση σο πεδίο ου
3. ΦΑΣΜΑΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΩΝ (ΑΝΑΛΥΣΗ FOURIER) 3.. Γενικά Ένα σήμα μπορεί να αναπαρασαθεί με έναν από ους παρακάω ισοδύναμους ρόπους: Ως χρονικά μεαβαλλόμενη άση (κυμαομορφή) x(t) (αναπαράσαση σο πεδίο ου
y[n] 5y[n 1] + 6y[n 2] = 2x[n 1] (1) y h [n] = y h [n] = A 1 (2) n + A 2 (3) n (4) h[n] = 0, n < 0 (5) h[n] 5h[n 1] + 6h[n 2] = 2δ[n 1] (6)
![y[n] 5y[n 1] + 6y[n 2] = 2x[n 1] (1) y h [n] = y h [n] = A 1 (2) n + A 2 (3) n (4) h[n] = 0, n < 0 (5) h[n] 5h[n 1] + 6h[n 2] = 2δ[n 1] (6) y[n] 5y[n 1] + 6y[n 2] = 2x[n 1] (1) y h [n] = y h [n] = A 1 (2) n + A 2 (3) n (4) h[n] = 0, n < 0 (5) h[n] 5h[n 1] + 6h[n 2] = 2δ[n 1] (6)](/thumbs/52/30615281.jpg) Ασκήσεις σε Σήματα Συστήματα Διακριτού Χρόνου Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 9 Οκτωβρίου 015 1. Ενα αιτιατό ΓΧΑ σύστημα
Ασκήσεις σε Σήματα Συστήματα Διακριτού Χρόνου Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 9 Οκτωβρίου 015 1. Ενα αιτιατό ΓΧΑ σύστημα
, e + Σε ένα δείγμα ίδιων ραδιενεργών πυρήνων η πιθανότητα διάσπασης για κάποιο συγκεκριμένο πυρήνα είναι τυχαία.
 ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
6. ΚΕΦΑΛΑΙΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE
 6. ΚΕΦΑΛΑΙΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ APACE Σκοπός του κεφαλαίου είναι να ορίσει τον αμφίπλευρο μετασχηματισμό aplace ή απλώς μετασχηματισμό aplace (Μ) και το μονόπλευρο μετασχηματισμό aplace (ΜΜ), να περιγράψει
6. ΚΕΦΑΛΑΙΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ APACE Σκοπός του κεφαλαίου είναι να ορίσει τον αμφίπλευρο μετασχηματισμό aplace ή απλώς μετασχηματισμό aplace (Μ) και το μονόπλευρο μετασχηματισμό aplace (ΜΜ), να περιγράψει
Ανάπτυξη και Αξιολόγηση Στρατηγικής Κεντρικού Ελέγχου Ροών σε Αποχετευτικά ίκτυα µε Έµφαση στην Εφαρµογή της στον Ελλαδικό Χώρο
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ: Μηχανικών Παραγωγής & ιοίκησης Ανάπυξη και Αξιολόγηση Σραηγικής Κενρικού Ελέγχου Ροών σε Αποχεευικά ίκυα µε Έµφαση σην Εφαρµογή ης σον Ελλαδικό Χώρο ιαριβή που υπεβλήθη για ην
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ: Μηχανικών Παραγωγής & ιοίκησης Ανάπυξη και Αξιολόγηση Σραηγικής Κενρικού Ελέγχου Ροών σε Αποχεευικά ίκυα µε Έµφαση σην Εφαρµογή ης σον Ελλαδικό Χώρο ιαριβή που υπεβλήθη για ην
Ορισμός: u(t) = 0 (t < 0) και u(t) = 1 (t 0) (4.1) Από τις (4.3) και (4.4), προκύπτει ότι το βηματικό σήμα u(t) είναι σήμα ισχύος.
 4. ΑΝΑΛΥΣΗ ΒΑΣΙΚΩΝ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΗΜΑΤΩΝ 4.. To βημαικό σήμα (step signal) u(t) Ορισμός: u(t) = 0 (t < 0) και u(t) = (t 0) (4.) Μέση ιμή: = (4.) Ενέργεια: Ε = lim [T ] [-, ] u (t).dt (4.3) Μέση
4. ΑΝΑΛΥΣΗ ΒΑΣΙΚΩΝ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΗΜΑΤΩΝ 4.. To βημαικό σήμα (step signal) u(t) Ορισμός: u(t) = 0 (t < 0) και u(t) = (t 0) (4.) Μέση ιμή: = (4.) Ενέργεια: Ε = lim [T ] [-, ] u (t).dt (4.3) Μέση
ιονύσης Μητρόπουλος νόµος του Νεύτωνα έχει για το σωµατίδιο τη µορφή F = (2), (3).
 ιούσης Μηρόπουλος Σερεό ΣΥΣΤΗΜΑ ΣΩΜΑΤΙ ΙΩΝ, ΣΤΕΡΕΟ ΣΩΜΑ ΟΣ ΝΟΜΟΣ ΤΟΥ ΝΕΥΤΩΝΑ Έα σωµαίδιο, Ορµή, Σροφορµή Ο ος όµος ου Νεύωα σε αδραειακό και µη αδραειακό σύσηµα Γωρίζουµε όι η ορµή εός σωµαιδίου µάζας
ιούσης Μηρόπουλος Σερεό ΣΥΣΤΗΜΑ ΣΩΜΑΤΙ ΙΩΝ, ΣΤΕΡΕΟ ΣΩΜΑ ΟΣ ΝΟΜΟΣ ΤΟΥ ΝΕΥΤΩΝΑ Έα σωµαίδιο, Ορµή, Σροφορµή Ο ος όµος ου Νεύωα σε αδραειακό και µη αδραειακό σύσηµα Γωρίζουµε όι η ορµή εός σωµαιδίου µάζας
website:
 Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 6 Μαρτίου 2017 1 Εισαγωγή Κάθε φυσικό σύστημα
Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 6 Μαρτίου 2017 1 Εισαγωγή Κάθε φυσικό σύστημα
ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ
 Ελληνικό Σαισικό Ινσιούο Πρακικά 8 ου Πανελληνίου Συνεδρίου Σαισικής (5) σελ.35-34 ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ Παπάνα Αγγελική και Κουγιουμζής Δημήρης
Ελληνικό Σαισικό Ινσιούο Πρακικά 8 ου Πανελληνίου Συνεδρίου Σαισικής (5) σελ.35-34 ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ Παπάνα Αγγελική και Κουγιουμζής Δημήρης
y[n] ay[n 1] = x[n] + βx[n 1] (6)
![y[n] ay[n 1] = x[n] + βx[n 1] (6) y[n] ay[n 1] = x[n] + βx[n 1] (6)](/thumbs/62/47574712.jpg) Ασκήσεις με το Μετασχηματισμό Fourier Διακριτού Χρόνου Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 8 Οκτωβρίου 015 1. Εστω το
Ασκήσεις με το Μετασχηματισμό Fourier Διακριτού Χρόνου Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 8 Οκτωβρίου 015 1. Εστω το
Κανονισμός Πυροπροστασίας Κτιρίων (π.δ. 41/2018)
 Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
Νόμος Αmpere. i r. Β dl = Β(dl ακτ +dl τοξ ) = Β rdθ = 2π. Β dl = μ ο i
 Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
HMY 220: Σήματα και Συστήματα Ι
 HMY 0: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ #7 Μοντέλα διαφορικών εξισώσεων για ΓΧΑ Συστήματα Επίλυση Διαφορικών Εξισώσεων Η γραμμική διαφορική εξίσωση δεύτερης τάξης Παραδείγματα Μοντέλα διαφορικών εξισώσεων
HMY 0: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ #7 Μοντέλα διαφορικών εξισώσεων για ΓΧΑ Συστήματα Επίλυση Διαφορικών Εξισώσεων Η γραμμική διαφορική εξίσωση δεύτερης τάξης Παραδείγματα Μοντέλα διαφορικών εξισώσεων
Ψηφιακή Επεξεργασία Σημάτων
 Ψηφιακή Επεξεργασία Σημάτων Ενότητα 8: Μετασχηματισμός Ζ Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Z Μετασχηματισμός Ζ (Ζ-Transform) Χρήσιμα Ζεύγη ΖT και Περιοχές Σύγκλισης (ROC) Ιδιότητες
Ψηφιακή Επεξεργασία Σημάτων Ενότητα 8: Μετασχηματισμός Ζ Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Z Μετασχηματισμός Ζ (Ζ-Transform) Χρήσιμα Ζεύγη ΖT και Περιοχές Σύγκλισης (ROC) Ιδιότητες
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
x[n] = e u[n 1] 4 x[n] = u[n 1] 4 X(z) = z 1 H(z) = (1 0.5z 1 )(1 + 4z 2 ) z 2 (βʹ) H(z) = H min (z)h lin (z) 4 z 1 1 z 1 (z 1 4 )(z 1) (1)
![x[n] = e u[n 1] 4 x[n] = u[n 1] 4 X(z) = z 1 H(z) = (1 0.5z 1 )(1 + 4z 2 ) z 2 (βʹ) H(z) = H min (z)h lin (z) 4 z 1 1 z 1 (z 1 4 )(z 1) (1) x[n] = e u[n 1] 4 x[n] = u[n 1] 4 X(z) = z 1 H(z) = (1 0.5z 1 )(1 + 4z 2 ) z 2 (βʹ) H(z) = H min (z)h lin (z) 4 z 1 1 z 1 (z 1 4 )(z 1) (1)](/thumbs/61/45634776.jpg) Ασκήσεις με Συστήματα στο Χώρο του Ζ Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 7 Νοεμβρίου 015 1. Υπολόγισε τον μετ. Ζ και την
Ασκήσεις με Συστήματα στο Χώρο του Ζ Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 7 Νοεμβρίου 015 1. Υπολόγισε τον μετ. Ζ και την
d k dt k a ky(t) = dt k b kx(t) (5.1)
 Κεφάλαιο 5 Ανάλυση Σημάτων και Συστημάτων στο Πεδίο του Χρόνου 5. Εισαγωγή Σε αυτό το κεφάλαιο, θα συζητήσουμε για την αναλυτική μελέτη συστημάτων στο πεδίο του χρόνου. Είδαμε στο προηγούμενο κεφάλαιο
Κεφάλαιο 5 Ανάλυση Σημάτων και Συστημάτων στο Πεδίο του Χρόνου 5. Εισαγωγή Σε αυτό το κεφάλαιο, θα συζητήσουμε για την αναλυτική μελέτη συστημάτων στο πεδίο του χρόνου. Είδαμε στο προηγούμενο κεφάλαιο
Πανεπιστήµιο Θεσσαλίας
 Πανεπισήιο Θεσσαλίας Τήα Ηλεκρολόγων Μηχανικών & Μηχανικών Υπολογισών Άσκηση : Λυένες Ασκήσεις Έσω ένα σύσηα νήης, σο οποίο έχουε προσθέσει ια κρυφή νήη θυάων 6 θέσεων εαξύ ης κρυφής νήης δεδοένων L και
Πανεπισήιο Θεσσαλίας Τήα Ηλεκρολόγων Μηχανικών & Μηχανικών Υπολογισών Άσκηση : Λυένες Ασκήσεις Έσω ένα σύσηα νήης, σο οποίο έχουε προσθέσει ια κρυφή νήη θυάων 6 θέσεων εαξύ ης κρυφής νήης δεδοένων L και
Κεφάλαιο 8: Μαγνητικά Υλικά και Ιδιότητες ΙΙ. Λιαροκάπης Ευθύμιος. Διηλεκτρικές, Οπτικές, Μαγνητικές Ιδιότητες Υλικών
 Σχολή Εφαρμοσμένν Μαθημαικών και Φυσικών Εισημών Εθνικό Μεσόβιο Πολυεχνείο Διηλεκρικές Οικές Μαγνηικές Ιδιόηες Υλικών Κεφάλαιο 8: Μαγνηικά Υλικά και Ιδιόηες ΙΙ Λιαροκάης Ευθύμιος Άδεια Χρήσης Το αρόν εκαιδευικό
Σχολή Εφαρμοσμένν Μαθημαικών και Φυσικών Εισημών Εθνικό Μεσόβιο Πολυεχνείο Διηλεκρικές Οικές Μαγνηικές Ιδιόηες Υλικών Κεφάλαιο 8: Μαγνηικά Υλικά και Ιδιόηες ΙΙ Λιαροκάης Ευθύμιος Άδεια Χρήσης Το αρόν εκαιδευικό
Σήματα και Συστήματα. Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
Θεωρητική μηχανική ΙΙ
 ΟΣΑ ΓΡΑΦΟΝΤΑΙ ΕΔΩ ΝΑ ΤΑ ΔΙΑΒΑΖΕΤΕ ΜΕ ΣΚΕΠΤΙΚΟ ΒΛΕΜΜΑ. ΜΠΟΡΕΙ ΝΑ ΠΕΡΙΕΧΟΥΝ ΛΑΘΗ. Θεωρητική μηχανική ΙΙ Να δειχθεί ότι αν L x, L y αποτελούν ολοκληρώματα της κίνησης τότε και η L z αποτελεί ολοκλήρωμα της
ΟΣΑ ΓΡΑΦΟΝΤΑΙ ΕΔΩ ΝΑ ΤΑ ΔΙΑΒΑΖΕΤΕ ΜΕ ΣΚΕΠΤΙΚΟ ΒΛΕΜΜΑ. ΜΠΟΡΕΙ ΝΑ ΠΕΡΙΕΧΟΥΝ ΛΑΘΗ. Θεωρητική μηχανική ΙΙ Να δειχθεί ότι αν L x, L y αποτελούν ολοκληρώματα της κίνησης τότε και η L z αποτελεί ολοκλήρωμα της
Σήματα και Συστήματα. Διάλεξη 4: Μελέτη των Γραμμικών και Χρονικά Αμετάβλητων Συστημάτων. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 4: Μελέτη των Γραμμικών και Χρονικά Αμετάβλητων Συστημάτων Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής Μελέτη των Γραμμικών και Χρονικά Αμετάβλητων Συστημάτων Η Κρουστική Απόκριση
Σήματα και Συστήματα Διάλεξη 4: Μελέτη των Γραμμικών και Χρονικά Αμετάβλητων Συστημάτων Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής Μελέτη των Γραμμικών και Χρονικά Αμετάβλητων Συστημάτων Η Κρουστική Απόκριση
h(t) δ(t+3) ( ) h(t)*δ(t)
 f()* δ ( ) = f( ) x () = δ ( + 3) = 3 h () = u () u ( ) h()* δ ( + 3) = h ( + 3) = u ( + 3) u ( + 1) 1 h() * -3 δ(+3) ( ) h()*δ() 1-3 -1 MY : Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ #6 Μοντέλα διαφορικών εξισώσεων
f()* δ ( ) = f( ) x () = δ ( + 3) = 3 h () = u () u ( ) h()* δ ( + 3) = h ( + 3) = u ( + 3) u ( + 1) 1 h() * -3 δ(+3) ( ) h()*δ() 1-3 -1 MY : Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ #6 Μοντέλα διαφορικών εξισώσεων
Ενότητα Ζ Η ΕΝΝΟΙΑ, ΟΙ ΤΥΠΟΙ ΚΑΙ ΤΑ ΚΡΙΤΗΡΙΑ ΑΣΤΟΧΙΑΣ
 Ενόηα Ζ ΚΑΜΠΤΟΔΙΑΤΜΗΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ Η ΕΝΝΟΙΑ, ΟΙ ΤΥΠΟΙ ΚΑΙ ΤΑ ΚΡΙΤΗΡΙΑ ΑΣΤΟΧΙΑΣ 1. ΚΑΜΠΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ 1.1.1 Παραμορφώσεις Καθύψος ης Διαομής 1.1 MΗΧΑΝΙΣΜΟΣ ΑΝΑΛΗΨΗΣ ΔΡΩΣΑΣ ΡΟΠΗΣ Όπως φαίνεαι
Ενόηα Ζ ΚΑΜΠΤΟΔΙΑΤΜΗΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ Η ΕΝΝΟΙΑ, ΟΙ ΤΥΠΟΙ ΚΑΙ ΤΑ ΚΡΙΤΗΡΙΑ ΑΣΤΟΧΙΑΣ 1. ΚΑΜΠΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ 1.1.1 Παραμορφώσεις Καθύψος ης Διαομής 1.1 MΗΧΑΝΙΣΜΟΣ ΑΝΑΛΗΨΗΣ ΔΡΩΣΑΣ ΡΟΠΗΣ Όπως φαίνεαι
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ
 ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ
 Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
Σήματα- συμβολισμοί. x(n)={x(n)}={,x(-1),x(0), x(1),.} x(n)={0,-2,-3, -1, 0, 1, 2, 3, 4,0 }
 ΚΕΦΑΛΑΙΟ 2 Σήματα- συμβολισμοί 5 5 4 4 3 3 2 2 1 1-1 -4-3 -2-1 1 2 3 4 5-1 1 2 3 4 5 6 7 8-2 -2-3 -3 x()=, x(-1),x(), x(1),. x()={,-2,-3,-1,, 1, 2, 3, 4, } x()={x()}={,x(-1),x(), x(1),.} x()={,-2,-3, -1,,
ΚΕΦΑΛΑΙΟ 2 Σήματα- συμβολισμοί 5 5 4 4 3 3 2 2 1 1-1 -4-3 -2-1 1 2 3 4 5-1 1 2 3 4 5 6 7 8-2 -2-3 -3 x()=, x(-1),x(), x(1),. x()={,-2,-3,-1,, 1, 2, 3, 4, } x()={x()}={,x(-1),x(), x(1),.} x()={,-2,-3, -1,,
Σήματα και Συστήματα
 Σήματα και Συστήματα Διάλεξη 12: Ιδιότητες του Μετασχηματισμού aplace Ο αντίστροφος Μετασχηματισμός aplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ιδιότητες του Μετασχηματισμού aplace 1. Ιδιότητες
Σήματα και Συστήματα Διάλεξη 12: Ιδιότητες του Μετασχηματισμού aplace Ο αντίστροφος Μετασχηματισμός aplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ιδιότητες του Μετασχηματισμού aplace 1. Ιδιότητες
7 ΚΕΦΑΛΑΙΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ z
 7 ΚΕΦΑΛΑΙΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ Ο μετασχηματισμός είναι ο αντίστοιχος Laplace για σήματα διακριτού χρόνου και αποτελεί γενίκευση του μετασχηματισμού Fourier διακριτού χρόνου. Σκοπός του Κεφαλαίου είναι να ορίσει
7 ΚΕΦΑΛΑΙΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ Ο μετασχηματισμός είναι ο αντίστοιχος Laplace για σήματα διακριτού χρόνου και αποτελεί γενίκευση του μετασχηματισμού Fourier διακριτού χρόνου. Σκοπός του Κεφαλαίου είναι να ορίσει
x(t) = e st = e (σ+j2πf)t (7.1) h(t)e st dt (7.4) H(s) = y(t) = H{e st } = H(s)e st (7.5)
 Κεφάλαιο 7 Συστήματα στο χώρο του Laplace 7. Εισαγωγή Ο μετασχ. Laplace είναι ένα πολύτιμο εργαλείο για την ανάλυση συστημάτων. Η ικανότητά του να ερμηνεύει συχνοτικά πλήθος σημάτων, σημαντικά περισσότερων
Κεφάλαιο 7 Συστήματα στο χώρο του Laplace 7. Εισαγωγή Ο μετασχ. Laplace είναι ένα πολύτιμο εργαλείο για την ανάλυση συστημάτων. Η ικανότητά του να ερμηνεύει συχνοτικά πλήθος σημάτων, σημαντικά περισσότερων
Σήματα και Συστήματα. Διάλεξη 13: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 13: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace 1. Επίλυση Γραμμικών
Σήματα και Συστήματα Διάλεξη 13: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace 1. Επίλυση Γραμμικών
x(t) ax 1 (t) y(t) = 1 ax 1 (t) = (1/a)y 1(t) x(t t 0 ) y(t t 0 ) =
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-25: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 26-7 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λύσεις Τρίτης Σειράς Ασκήσεων Ηµεροµηνία Ανάθεσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-25: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 26-7 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λύσεις Τρίτης Σειράς Ασκήσεων Ηµεροµηνία Ανάθεσης
Ολοκλήρωση διεργασίας χρησιμοποιώντας την τεχνολογία σύγκλισης (Pinch Technology)
 Θέμα: Ολοκλήρωση διεργασίας χρησιμοποιώνας ην εχνολογία σύγκλισης (Pinch Technology) Εισηγηές: Εμμανουήλ Κοζαμπασάκης, Πανεπισήμιο ου Maπchester, Ινσιούο Ε πισήμης και Τεχνολογίας, UMST, U.K. καθηγ. Bodo
Θέμα: Ολοκλήρωση διεργασίας χρησιμοποιώνας ην εχνολογία σύγκλισης (Pinch Technology) Εισηγηές: Εμμανουήλ Κοζαμπασάκης, Πανεπισήμιο ου Maπchester, Ινσιούο Ε πισήμης και Τεχνολογίας, UMST, U.K. καθηγ. Bodo
ΚΕΦΑΛΑΙΟ 2. Ηλεκτρονικη και 1/60 Πληροφορίας
 ΚΕΦΑΛΑΙΟ 2 /6 Σήματα- συμβολισμοί 5 5 4 4 3 3 2 2 - -4-3 -2-2 3 4 5-2 3 4 5 6 7 8-2 -2-3 -3 x()=, x(-),x(), x(),. x()={,-2,-3,-,,, 2, 3, 4, } x()={x()}={,x(-),x(), x(),.} x()={,-2,-3, -,,, 2, 3, 4, } 2/6
ΚΕΦΑΛΑΙΟ 2 /6 Σήματα- συμβολισμοί 5 5 4 4 3 3 2 2 - -4-3 -2-2 3 4 5-2 3 4 5 6 7 8-2 -2-3 -3 x()=, x(-),x(), x(),. x()={,-2,-3,-,,, 2, 3, 4, } x()={x()}={,x(-),x(), x(),.} x()={,-2,-3, -,,, 2, 3, 4, } 2/6
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Βέλισες σραηγικές διακοπής μιας Μαρκοβιανής αλυσίδας ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΒΑΣΙΛΕΙΟΣ ΖΑΧΑΡΙΑΔΗΣ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Βέλισες σραηγικές διακοπής μιας Μαρκοβιανής αλυσίδας ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΒΑΣΙΛΕΙΟΣ ΖΑΧΑΡΙΑΔΗΣ
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - 02/07/08) ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ
 Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Ψηφιακή Επεξεργασία Σημάτων
 Ψηφιακή Επεξεργασία Σημάτων Ενότητα : Συστήματα Διακριτού Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής Συστήματα Διακριτού Χρόνου Εξισώσεις Διαφορών Επίλυση Εξισώσεων Διαφορών με Γραμμικούς Συντελεστές
Ψηφιακή Επεξεργασία Σημάτων Ενότητα : Συστήματα Διακριτού Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής Συστήματα Διακριτού Χρόνου Εξισώσεις Διαφορών Επίλυση Εξισώσεων Διαφορών με Γραμμικούς Συντελεστές
ΚΕΦΑΛΑΙΟ 2. Ηλεκτρονικη και 1/62 Πληροφορίας
 ΚΕΦΑΛΑΙΟ 2 /62 Σήματα- συμβολισμοί 5 5 4 4 3 3 2 2 - -4-3 -2-2 3 4 5-2 3 4 5 6 7 8-2 -2-3 -3 x()=, x(-),x(), x(),. x()={,-2,-3,-,,, 2, 3, 4, } x()={x()}={,x(-),x(), x(),.} x()={,-2,-3, -,,, 2, 3, 4, }
ΚΕΦΑΛΑΙΟ 2 /62 Σήματα- συμβολισμοί 5 5 4 4 3 3 2 2 - -4-3 -2-2 3 4 5-2 3 4 5 6 7 8-2 -2-3 -3 x()=, x(-),x(), x(),. x()={,-2,-3,-,,, 2, 3, 4, } x()={x()}={,x(-),x(), x(),.} x()={,-2,-3, -,,, 2, 3, 4, }
Θεωρητική μηχανική ΙΙ
 ΟΣΑ ΓΡΑΦΟΝΤΑΙ ΕΔΩ ΝΑ ΤΑ ΔΙΑΒΑΖΕΤΕ ΜΕ ΣΚΕΠΤΙΚΟ ΒΛΕΜΜΑ. ΜΠΟΡΕΙ ΝΑ ΠΕΡΙΕΧΟΥΝ ΛΑΘΗ. Θεωρητική μηχανική ΙΙ Να δειχθεί ότι αν L x, L y αποτελούν ολοκληρώματα της κίνησης τότε και η L z αποτελεί ολοκλήρωμα της
ΟΣΑ ΓΡΑΦΟΝΤΑΙ ΕΔΩ ΝΑ ΤΑ ΔΙΑΒΑΖΕΤΕ ΜΕ ΣΚΕΠΤΙΚΟ ΒΛΕΜΜΑ. ΜΠΟΡΕΙ ΝΑ ΠΕΡΙΕΧΟΥΝ ΛΑΘΗ. Θεωρητική μηχανική ΙΙ Να δειχθεί ότι αν L x, L y αποτελούν ολοκληρώματα της κίνησης τότε και η L z αποτελεί ολοκλήρωμα της
3. Κεφάλαιο Μετασχηματισμός Fourier
 3 Κεφάλαιο 3 Ορισμοί Ο μετασχηματισμός Fourir αποτελεί την επέκταση των σειρών Fourir στη γενική κατηγορία των συναρτήσεων (περιοδικών και μη) Όπως και στις σειρές οι συναρτήσεις θα εκφράζονται με τη βοήθεια
3 Κεφάλαιο 3 Ορισμοί Ο μετασχηματισμός Fourir αποτελεί την επέκταση των σειρών Fourir στη γενική κατηγορία των συναρτήσεων (περιοδικών και μη) Όπως και στις σειρές οι συναρτήσεις θα εκφράζονται με τη βοήθεια
Μεταλλική συμπεριφορά
 Μεαλλική συμπεριφορά Χαρακηρισικά μεαλλικής συμπεριφοράς Μεγάλη θερμική και ηλεκρονιακή αγωγιμόηα Μεγάλο μέρο ελασικόηας όγκου (Β=10 11 Pa) Μεαλλική λάμψη Ι. Μονέλο Drude (Jelliu) Σύμβαση προσήμου: e:
Μεαλλική συμπεριφορά Χαρακηρισικά μεαλλικής συμπεριφοράς Μεγάλη θερμική και ηλεκρονιακή αγωγιμόηα Μεγάλο μέρο ελασικόηας όγκου (Β=10 11 Pa) Μεαλλική λάμψη Ι. Μονέλο Drude (Jelliu) Σύμβαση προσήμου: e:
Digital Integrated Circuits, 2 nd edition, J. M. Rabaey, A. Chandrakasan, B. Nikolic
 Πρόβληµα 4. gital Itegrated Circuits, d editio, J. M. abaey, A. Chadrakasa, B. Nikolic You are desigig a clock distributio etwork i which it is critical to miimize skew betwee local clocks (CLK, CLK, ad
Πρόβληµα 4. gital Itegrated Circuits, d editio, J. M. abaey, A. Chadrakasa, B. Nikolic You are desigig a clock distributio etwork i which it is critical to miimize skew betwee local clocks (CLK, CLK, ad
(a 1, b 1 ) (a 2, b 2 ) = (a 1 a 2, b 1 b 2 ).
 ΕΜ0 - Διακριτά Μαθηματικά Ιανουαρίου 006 Άσκηση - Λύσεις Πρόβλημα [0 μονάδες] Εστω L και L δύο κυκλώματα σε ένα γράφημα G. Εστω a μία ακμή που ανήκει και στο L και στο L και έστω b μία ακμή που ανήκει
ΕΜ0 - Διακριτά Μαθηματικά Ιανουαρίου 006 Άσκηση - Λύσεις Πρόβλημα [0 μονάδες] Εστω L και L δύο κυκλώματα σε ένα γράφημα G. Εστω a μία ακμή που ανήκει και στο L και στο L και έστω b μία ακμή που ανήκει
Μερικές Διαφορικές Εξισώσεις
 Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 24-25, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: ΜΔΕ ο φύλλο προβλημάτων Α. Τόγκας
Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 24-25, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: ΜΔΕ ο φύλλο προβλημάτων Α. Τόγκας
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 5: Θεωρήματα κυκλωμάτων Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISN: 978-960-93-7110-0 κωδ. ΕΥΔΟΞΟΣ: 50657177
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 5: Θεωρήματα κυκλωμάτων Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISN: 978-960-93-7110-0 κωδ. ΕΥΔΟΞΟΣ: 50657177
Εφαρμοσμένα Μαθηματικά ΙΙ Εξέταση Σεπτεμβρίου 25/9/2017 Διδάσκων: Ι. Λυχναρόπουλος
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Εξέταση Σεπτεμβρίου 5/9/07 Διδάσκων: Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) Να δειχθεί ότι το πεδίο F( x, y) = y cos x + y,sin x
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Εξέταση Σεπτεμβρίου 5/9/07 Διδάσκων: Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) Να δειχθεί ότι το πεδίο F( x, y) = y cos x + y,sin x
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ. Μαθηματικά 2. Σταύρος Παπαϊωάννου
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση. Σφάλμα! Δεν έχει οριστεί σελιδοδείκτης. Σκοποί Μαθήματος
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση. Σφάλμα! Δεν έχει οριστεί σελιδοδείκτης. Σκοποί Μαθήματος
Εισαγωγή στις Τηλεπικοινωνίες. Δομή της παρουσίασης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Διάλεξη 3 η Τα Συστήματα στις Τηλεπικοινωνίες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Διάλεξη 3 η Τα Συστήματα στις Τηλεπικοινωνίες
Ανάλυση της µηχανικής συµπεριφοράς της συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα
 Ανάλυση ης µηχανικής συµπεριφοράς ης συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα Β. Καραζαφέρης MΕ, Υποψήφιος διδάκωρ ΕΜΠ Μ. Καής Επίκουρος Καθηγηής ΕΜΠ Λέξεις κλειδιά: FRP, συνάφεια, πεπερασµένα σοιχεία
Ανάλυση ης µηχανικής συµπεριφοράς ης συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα Β. Καραζαφέρης MΕ, Υποψήφιος διδάκωρ ΕΜΠ Μ. Καής Επίκουρος Καθηγηής ΕΜΠ Λέξεις κλειδιά: FRP, συνάφεια, πεπερασµένα σοιχεία
ΚΥΚΛΩΜΑ RC ΜΕ ΚΡΟΥΣΤΙΚΗ ΔΙΕΓΕΡΣΗ
 ΚΥΚΛΩΜΑ ΜΕ ΚΡΟΥΣΤΙΚΗ ΙΕΓΕΡΣΗ Εννοούμε την απόκριση ενός γραμμικού, χρονικά αμετάβλητου κυκλώματος σε μια μοναδιαία κρουστική συνάρτηση δ() εφαρμοζόμενη στον χρόνο = 0 (απόκριση μηδενικής κατάστασης). Η
ΚΥΚΛΩΜΑ ΜΕ ΚΡΟΥΣΤΙΚΗ ΙΕΓΕΡΣΗ Εννοούμε την απόκριση ενός γραμμικού, χρονικά αμετάβλητου κυκλώματος σε μια μοναδιαία κρουστική συνάρτηση δ() εφαρμοζόμενη στον χρόνο = 0 (απόκριση μηδενικής κατάστασης). Η
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 2 η Ημερομηνία Αποστολής στον Φοιτητή: 28 Νοεμβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
Που ασκείται η δύναμη στήριξης;
 Που σκείι η δύνμη σήριξης; Θεωρούμε μι πρισμική ράβδο μήκους l η οποί θεωρείι ιδνικό σερεό σώμ. Υποθέουμε όι η ράβδος βρίσκει «υπό κθεσώς κπόνησης». Θεωρούμε μι νοηή ομή η οποί διιρεί ην ράβδο σε δύο μέρη
Που σκείι η δύνμη σήριξης; Θεωρούμε μι πρισμική ράβδο μήκους l η οποί θεωρείι ιδνικό σερεό σώμ. Υποθέουμε όι η ράβδος βρίσκει «υπό κθεσώς κπόνησης». Θεωρούμε μι νοηή ομή η οποί διιρεί ην ράβδο σε δύο μέρη
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
bx 2 (t). Για είσοδο ax 1(t) + bx 2 (t), η έξοδος είναι x(t t 0 ) και y(t t 0) = t t 0 x(t) ax 1 (t 1) + bx 2 (t 1) sin ax 1 (t)+
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 5 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Ασκηση. αʹ Γραµµικό: Είναι y = y = Τρίτη Σειρά Ασκήσεων
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 5 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Ασκηση. αʹ Γραµµικό: Είναι y = y = Τρίτη Σειρά Ασκήσεων
Ψηφιακή Μετάδοση Αναλογικών Σηµάτων
 Σεραφείµ Καραµογιάς Ψηφιακή Μεάδοση Αναλογικών Σηµάν Τα σύγχρονα συσήµαα εικοιννίας σε ολύ µεγάλο οσοσό διαχειρίζοναι σήµαα ψηφιακής µορφής, δηλαδή, σήµαα ου δηµιουργούναι αό ακολουθίες δυαδικών ψηφίν.
Σεραφείµ Καραµογιάς Ψηφιακή Μεάδοση Αναλογικών Σηµάν Τα σύγχρονα συσήµαα εικοιννίας σε ολύ µεγάλο οσοσό διαχειρίζοναι σήµαα ψηφιακής µορφής, δηλαδή, σήµαα ου δηµιουργούναι αό ακολουθίες δυαδικών ψηφίν.
y 1 (x) f(x) W (y 1, y 2 )(x) dx,
 Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 07/1/017 Μέρος 1ο: Μη Ομογενείς Γραμμικές Διαφορικές Εξισώσεις Δεύτερης Τάξης Θεωρούμε τη γραμμική μή-ομογενή διαφορική εξίσωση y + p(x) y + q(x) y = f(x), x
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 07/1/017 Μέρος 1ο: Μη Ομογενείς Γραμμικές Διαφορικές Εξισώσεις Δεύτερης Τάξης Θεωρούμε τη γραμμική μή-ομογενή διαφορική εξίσωση y + p(x) y + q(x) y = f(x), x
