Νόμος Αmpere. i r. Β dl = Β(dl ακτ +dl τοξ ) = Β rdθ = 2π. Β dl = μ ο i
|
|
|
- Ευρυδίκη Μανωλάς
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα ου επάνω σε υχαία κλεισή διαδροή ισούαι ε ο ρεύα () που διέρχεαι έσα από ην διαδροή επί o Ο νόος ου Ampee βοηθάει σον υπολογισό ου καανοής ρευάων ε κάποια συερία όιπως ο νόος ου Gauss βοηθάει σο υπολογισό ου Ε καανοών ση. φορίοων ε κάποια συερία
2 Να βρεθεί ο λεπού σύραος εγάλου ήκους χρησιοποιώνας ο νόο ου Ampee. dθ dθ Ο κύκλος () κλεισή διαδροή dl = dθ = = ο = Νόος Αmpee Λόγω συερίας δυν. γραές ου δεν είναι: ακινικές σον αγωγό δεν πρέπει να ξεκινούν από κάπου ούε παράλληλες σον αγωγό Το είναι οόκενροι κύκλοι Να βρεθεί ο σο εξωερικό και σο εσωερικό σύραος όπου διέρχεαι ρεύα ε ακίνα διαοής R και εγάλου ήκους χρησιοποιώνας ο νόο ου Amepee. o R Λόγω συερίας o δυν. γραές ου είναι οόκενροι κύκλοι. Ο κύκλος () κλεισή διαδροή dl = dθ = = ο Νόος Αmpee o 2 o = ο Το ρεύα έσα από η διαοή ου R 2 = j = π 2 o = = 0 o R 2 o πr 2 Το ρεύα έσα από η διαοή ου R Γιαί J= σαθερό Για < R Για = 0 Μέγιση ου = o R Για = R
3 Σωληνοειδή o o Ασθενικό αγνηικό πεδίο Ισχυρό οογενές αγνηικό πεδίο Μαγνηικό πεδίο σωληνοειδούς Υπολογίζεαι από ην υπέρθεση ων αγνηικών πεδίων ων κυκλικών δακυλίων που αποελείαι ο σωληνοειδούς
4 Υπολογισός αγνηικού πεδίου σο εσωερικό σωληνοειδούς dl = 0 l Κλεισή διαδροή ένα έρος έσα ένα έξω από ο πηνίο Ρεύα ης κάθε σπείρας dl = Νόος Αmpee l = o ολικό = o Ν l = o Ν = o (Ν / l) = o n O αριθός σπειρών σε ήκος l ανεξάρηο ης εγκάρσιας απόσασης n = Ν / l Υπολογισός αγνηικού πεδίου σο εσωερικό δακυλοειδούς σωληνοειδούς (πηνίο) Ρεύα ης κάθε σπείρας Κλεισή διαδροή dl = = o Ν Νόος Αmpee o N = Παρόοιο ε ο ευθύγραου αγωγού
5 Κίνηση φορίων σε ηλεκρικά και αγνηικού πεδία. v αγν = qv H είναι κάθεη ση v και αλλάζει όνο ην διεύθυνσή ης d dt v 2 = d dt vv = Η είναι η κενροόλος δύναη ης κυκλικής ροχιάς 2v dv dt = 2v /m = 0 άρα α επιροχ =0 α = /m = qv/m = v 2 = mv q = P q ω = v Κύκλορο = q m ν = ω = q m H συχνόηα είναι ανεξάρηη ης v E Έξοδος σωαιδίων Μαγνήης
6 Φορία κινούενα σε διασαυρωένα ηλεκρικά και αγνηικά πεδία. H συνολική δύναη είναι η δύναη Loentz α ηλ v Loentz = qe + qv Με καάλληλη επιλογή ων E, πορεί να συβεί Loentz =0: α = ηλ Ε ή qe = q v ή E = v v 1 v = E / Ε v v 2 Tα σωαίδια ε αυή η αχύηα δέχοναι συνολική δύναη Loentz = 0 όνο αυά διέρχοναι v 3 Αλλάζονας ο λόγο Ε/ επιλέγεαι άλλη ιή για η v που διέρχεαι χωρίς απόκλιση κι έσι βρίσκουε όλες ις καανοές ων αχθήων ων σωαιδίων ιας δέσης Έσι ερήθηκε ο λόγος e/m ου ηλεκρονίου σε καθοδικούς σωλήνες όπου υπήρχαν κάθεα ηλεκρικά και αγνηικά πεδία
7 Φαινόενο Hall Πολύ σηανικό φαινόενο γιαί ε βάση αυό πορούε να προσδιορίσουε ο είδος ων φορέων ου ηλεκρικού ρεύαος (ηλεκρόνια ή οπές) και να υπολογήσουε η συγκέρωσή ους αγωγός διαρρεόενος από ρεύα έσα σε αγνηικό πεδίο d Από ην συσσώρευση ηλεκρονίων ση ια πλευρά δηιουργείαι ηλεκρικό πεδίο, Ε = α ηλ E dq dt α ηλεκρόνια εκρέποναι από η αγνηική δύναη ου αγνηικού πεδίου = +ΔV (Hall) Εκρέποναι επάνω ηλεκρόνια Συγκένρωση ηλεκρονίων enadl dt - v = enav ΔV (Hall) v = ΔV/l = v qe = q v ΔV/d = v Φαινόενο Hall η εφάνιση διαφοράς δυναικού (ΔV) σε αγωγό που διαρρέεαι από ρεύα και ευρίσκεαι έσα σε αγνηικό πεδίο ena ΔV = d ena ηλ = α Μερώνας η διαφορά δυναικού ΔV (Ηall) υπολογίζεαι συγκένρωση (n) και ο είδος ων φορέων (ηλεκρόνια ή οπές) από ο πρόσηο ης ΔV Hall + φορείς ου ρεύαος ηλεκρόνια (+ΔV Hall ) Δηιουργείαι περίσεια ηλεκρονίων και αρνηικού φορίου σην επάνω πλευρά ου ηιαγωγού Σοιχειώδης όγκος v=dl/dt...και έλλεια ηλεκρονίων και εποένως περίσεια θεικού αρνηικού φορίου σην κάνω πλευρά ου ηιαγωγού Εκρέποναι επάνω οπές Από ην συσσώρευση ηλεκρονίων ση ια πλευρά δηιουργείαι διαφορά δυναικού ΔV ή άση Hall V: αχύηα ηλεκρονίων -ΔV (Hall) + - φορείς ου ρεύαος οπές (-ΔV Hall ) Και σις 2 περιπώσεις και όαν ο ρεύα οφείλεαι σε ηλεκρόνια και όαν οφείλεαι σε οπές, και α ηλεκρόνια και οι οπές εκρέποναι προς α επάνω και έσι από ο πρόσηο ης άσης Hall πορούε να προσδιορίσουε ο είδος ων φορέων
8 Μαγνηική δύναη σε ηλεκρικό σύρα θ dl = dq dt = dq dl/v d dq = dl v d = dq v snθ = dl snθ d = dl Λόγω αυής ης δύναης πορούν να καασκευασούν ηλεκρικοί κινηήρες d dl Δυνάεις ανάεσα σε σύραα ' = o d = dl = d/dl = o ' o ' ' dl ο = 4π10-7 Νs 2 /C 2 Ορισός 1 Cb Αν =' και ερούε /l=210-7 Ν/m όε α σύραα διαρρέοναι από ρεύα 1 Ampee όε α σύραα διαρρέει φορίο 1 Coulomb σε 1sec.
9 αθολογία απεροέρου Με η βοήθεια δυναοέρων ερούε η δύναη που έλκοναι οοι αγωγοί =1A =1m o /L = ο = 4π10-7 Νs 2 /C 2 =1A Όαν =1A =1m όε /L = 2 Χ 10-7 Ν/m 1 A 0 A Ρυθίζουε ε η βοήθεια ρυθισικής ανίσασης ο ρεύα ώσε να ερούε σο δυναόερο /l=210-7 Ν/m και όε α σύραα διαρρέοναι από ρεύα 1 Ampee Και καόπιν σηειώνουε ση γραική κλίακα ου αβοθολόγηου απεροέρου ην ένδειξη ου 1Α
10 a b Ροπή περισροφής θ a b Ασκείαι ροπή που περισρέφει ο πλαίσιο αρισερόσροφα = Ροπή σρέψεως σε βρόχο ρεύαος d = dl Περισρφόενο πλαίσιο ε πλευρές a,b που διαρ ρεύα έσα σε αγν πεδίο θ Όαν ο ανίχειρας δείχνει η φορά ης ροπής, όε η φορά ων δακύλων δείχνει η φορά περισροφής ου πλαισίου d = (dq v snθ) = dl snθ= dl 1 = d = dl = L = L Η δύναη ση κάθε πλευρά ου πλαισίουήκους L=a Ο άξονας περισροφής = a = (b/2)snθ + (b/2)snθ = ab snθ Η ροπή σρέψεως σο ζεύγος δυνάεων = snθ Η αγνηική διπολική ροπή ου βρόχου είνει να ευθυγραισεί ε ην περισρέφονας ο πλαίσιο περί η ικρόερη γωνία θ = ab Μαγνηική διπολική ροπή ου βρόχου Δηλ εξωερικό γινόενο ου ε ο = κανόνας δεξιού χεριού Όαν η φορά ων δακύλων δείχνει ο ρεύα όε ο ανίχειρας δείχνει η καθορίζονας η φορά περισροφής U = - Δυναική ενέργεια U : η ενέργεια που κσαναλώνουε για να εαβάλλουε ο προσαναολισό ο πλαισίου H U : ελάχιση όαν, παράλληλα H U : έγιση όαν, ανιπαράλληλα
11 Εύρεση ροπής σρέψεως σε εραγωνικό πλαίσιο: αρχή λειουργίας ηλεκρικού κινηήρα συνεχούς ρεύαος = Τεραγωνικό πλαίσιο διαρρέεαι από ρεύα I έσα σε αγνηικό πεδίο Η φορά περισροφής ου πλαισίου είναι δεξιόσροφη Ο άξονας περισροφής η φορά περισροφής ου πλαισίου ανισρέφεαι και γίνεαι αρισερόσροφη Για να διαηρηθεί η δεξιόσροφη φορά περισροφής ου πλαισίου Πρέπει να ανισραφεί η φορά ου ρεύαος Από πλάγια όψη Η ανισροφή ου ρεύαος πραγαοποιείαι ε η βοήθεια συλλεκών ή εαγωγών όπως σο παρακάω σχήα Με ην ανισροφή ου ρεύαος διαηρείαι η δεξιόσροφη φορά περισροφής ου πλαισίου Συλλέκες ή εαγωγοί Οι ακροδέκες ου πλαισίου αλλάζουν ην επαφή ους ε ους συλλέκες και έσι αλλάζει η φορά ου ρεύαος
12 Συλλέκες ή εαγωγοί + - R Ηλεκρικό οέρ συνεχούς ρεύαος + ψ - R
ΦΥΣΙΚΗ Ι. ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ ΣΩΜΑΤΟΣ Ισορροπία Σωματιδίου Στατική Ισορροπία Στερεού Σώματος
 ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΦΥΣΙΚΗ Ι. ΤΜΗΜΑ Α Ε. Στυλιάρης
 (Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
(Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
_Σχήµα 2_. Σελίδα 1 από 5. τον οποίο γίνεται η µεταπτωτική κίνηση. Άξονας περιστροφής τροχού. Άξονας γύρω από. τον οποίο γίνεται η µεταπτωτική κίνηση
 ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
1. Μαγνητικό Πεδίο Κινούμενου Φορτίου. Το μαγνητικό πεδίο Β σημειακού φορτίου q που κινείται με ταχύτητα v είναι:
 1. Μαγνητικό Πεδίο Κινούενου Φορτίου Το αγνητικό εδίο Β σηειακού φορτίου q ου κινείται ε ταχύτητα v είναι: qv u 4 qvsinφ 4 Το Β είναι ανάλογο του q και του 1/ όως και το Ε. Το Β δεν είναι ακτινικό, είναι
1. Μαγνητικό Πεδίο Κινούενου Φορτίου Το αγνητικό εδίο Β σηειακού φορτίου q ου κινείται ε ταχύτητα v είναι: qv u 4 qvsinφ 4 Το Β είναι ανάλογο του q και του 1/ όως και το Ε. Το Β δεν είναι ακτινικό, είναι
Κεφάλαιο 3 ο. Κυκλώματα με στοιχεία αποθήκευσης ενέργειας
 Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
Μεταλλική συμπεριφορά
 Μεαλλική συμπεριφορά Χαρακηρισικά μεαλλικής συμπεριφοράς Μεγάλη θερμική και ηλεκρονιακή αγωγιμόηα Μεγάλο μέρο ελασικόηας όγκου (Β=10 11 Pa) Μεαλλική λάμψη Ι. Μονέλο Drude (Jelliu) Σύμβαση προσήμου: e:
Μεαλλική συμπεριφορά Χαρακηρισικά μεαλλικής συμπεριφοράς Μεγάλη θερμική και ηλεκρονιακή αγωγιμόηα Μεγάλο μέρο ελασικόηας όγκου (Β=10 11 Pa) Μεαλλική λάμψη Ι. Μονέλο Drude (Jelliu) Σύμβαση προσήμου: e:
ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ 90º. 180º ω. Οι απαντήσεις και τα σχετικά σχόλια
 Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ. LT και μονάδες στο SI, kgm/s 2 ή N. υνισταμένη. υνισταμένη. d dt. d dt.
 ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
Δυναμική συμπεριφορά των λογικών κυκλωμάτων MOS. Διάλεξη 10
 Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Πως λύνεται ένα πρόβληµα.
 Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ = Ο. Μαγνητικό πεδίο ευθύγραµµου ρευµατοφόρου αγωγού. Μαγνητικό πεδίο κυκλικού ρευµατοφόρου αγωγού.
 ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ Μαγνητικό πεδίο είναι ο χώρος που έχει την ιδιότητα να ασκεί αγνητικές δυνάεις σε κατάλληλο υπόθεα (αγνήτες, ρευατοφόροι αγωγοί ) Το αγνητικό πεδίο το ανιχνεύουε ε την βοήθεια ιας αγνητικής
ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ Μαγνητικό πεδίο είναι ο χώρος που έχει την ιδιότητα να ασκεί αγνητικές δυνάεις σε κατάλληλο υπόθεα (αγνήτες, ρευατοφόροι αγωγοί ) Το αγνητικό πεδίο το ανιχνεύουε ε την βοήθεια ιας αγνητικής
Κεφάλαιο 4. Θεωρήµατα οµής
 Κεφάαιο 4 Θεωρήαα οής Σ' αυό ο εφάαιο θ αποδείξουε α Θεωρήαα οής για πεπερασένα παραγόενα R-πρόυπα, όπου R αέραια περιοχή υρίων ιδεωδών, (απι) 4 Ανάυση σε άθροισα περιοδιού αι εεύθερου, ανάυση σοιχείο
Κεφάαιο 4 Θεωρήαα οής Σ' αυό ο εφάαιο θ αποδείξουε α Θεωρήαα οής για πεπερασένα παραγόενα R-πρόυπα, όπου R αέραια περιοχή υρίων ιδεωδών, (απι) 4 Ανάυση σε άθροισα περιοδιού αι εεύθερου, ανάυση σοιχείο
Ροπή δύναμης. Τι προκαλεί την επιτάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω του. Τι προκαλεί την γωνιακή επιτάχυνση ενός στερεού σώματος;
 Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
Εργαστήριο Ηλεκτρικών κυκλωμάτων
 Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ
 Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
ΤΟ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ
 VΙ TO ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ V ΤΟ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ ΒΑΣΙΚΕΣ ΕΝΕΡΓΕΙΑΚΕΣ ΣΧΕΣΕΙΣ ΤΟΥ ΠΕ ΙΟΥ VΙ. Πυκνότητα ενέργειας του ηλεκτρικού πεδίου σε γραικό και ισότροπο έσο we εe VΙ. Πυκνότητα ενέργειας του
VΙ TO ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ V ΤΟ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ ΒΑΣΙΚΕΣ ΕΝΕΡΓΕΙΑΚΕΣ ΣΧΕΣΕΙΣ ΤΟΥ ΠΕ ΙΟΥ VΙ. Πυκνότητα ενέργειας του ηλεκτρικού πεδίου σε γραικό και ισότροπο έσο we εe VΙ. Πυκνότητα ενέργειας του
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ. 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διατμητικής Αντοχής Εδάφους. Διδάσκοντες: Β. Χρηστάρας Καθηγητής Β. Μαρίνος, Αν.
 ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
Μεγαλύτερες περιπέτειες
 Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Γιάννη Σ. Μπούταλη Αναπληρωτή Καθηγητή Δ.Π.Θ. ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθητικές σημειώσεις στο μάθημα ΣΑΕ ΙΙ
 Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Θέματα Περασμένων Εξετάσεων και Απαντήσεις
 Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
13. Συνήθεις διαφορικές εξισώσεις
 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
Κεφάλαιο 5 Πολλαπλοί χημικοί αντιδραστήρες
 Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
ΕΛΕΓΧΟΣ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΚΕΦΑΛΑΙΟ 2 ΚΕΦΑΛΑΙΟ 2. Πλεονεκτήματα ψηφιακού ελέγχου
 ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ
 ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
, e + Σε ένα δείγμα ίδιων ραδιενεργών πυρήνων η πιθανότητα διάσπασης για κάποιο συγκεκριμένο πυρήνα είναι τυχαία.
 ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ
 ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
Η φορά του μαγνητικού πεδίου είναι από το βόρειο (N) στο νότιο πόλο του μαγνήτη (S). Τότε ο δίσκος δημιουργεί μαγνητικό πεδίο + +
 Τι είναι μαγνητικό πεδίο Είναι ο χώρος όπου μπορούν ασκηούν μαγνητικές δυνάμεις. Παράδειγμα μαγνητικού πεπδίου, ο χώρος γύρω από μαγνήτες. Με τη βοήεια ρινισμάτων σιδήρου βρίσκουμε τη διεύυνση του μαγνητικού
Τι είναι μαγνητικό πεδίο Είναι ο χώρος όπου μπορούν ασκηούν μαγνητικές δυνάμεις. Παράδειγμα μαγνητικού πεπδίου, ο χώρος γύρω από μαγνήτες. Με τη βοήεια ρινισμάτων σιδήρου βρίσκουμε τη διεύυνση του μαγνητικού
Κεφάλαιο 9: Ελεύθερα Ηλεκτρόνια σε Μαγνητικό Πεδίο. Λιαροκάπης Ευθύμιος. Διηλεκτρικές, Οπτικές, Μαγνητικές Ιδιότητες Υλικών
 Σχολή Εφαροσένων Μαθηατικών και Φυσικών Επιστηών Εθνικό Μετσόβιο Πολυτεχνείο Διηλεκτρικές, Οπτικές, Μαγνητικές Ιδιότητες Υλικών Κεφάλαιο 9: Ελεύθερα Ηλεκτρόνια σε Μαγνητικό Πεδίο Λιαροκάπης Ευθύιος Άδεια
Σχολή Εφαροσένων Μαθηατικών και Φυσικών Επιστηών Εθνικό Μετσόβιο Πολυτεχνείο Διηλεκτρικές, Οπτικές, Μαγνητικές Ιδιότητες Υλικών Κεφάλαιο 9: Ελεύθερα Ηλεκτρόνια σε Μαγνητικό Πεδίο Λιαροκάπης Ευθύιος Άδεια
Α Σ Κ Η Σ Η 1 ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY
 Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
2. Ποιά από τις παρακάτω γραφικές παραστάσεις αντιστοιχεί στο νόµο του Ohm; (α) (β) (γ) (δ)
 ΘΕΜΑ ο Στις ερωτήσεις - 4 να γράψετε στο τετράδιό σας τον αριθό της ερώτησης και δίπλα το γράα που αντιστοιχεί στη σωστή απάντηση.. Πυκνωτής χωρητικότητας είναι φορτισένος ε φορτίο Q και η τάση στους οπλισούς
ΘΕΜΑ ο Στις ερωτήσεις - 4 να γράψετε στο τετράδιό σας τον αριθό της ερώτησης και δίπλα το γράα που αντιστοιχεί στη σωστή απάντηση.. Πυκνωτής χωρητικότητας είναι φορτισένος ε φορτίο Q και η τάση στους οπλισούς
ΕΡΓΑΣΙΑ 2 (Παράδοση:.) Λύση Ι. Το πεδίο ορισµού Α, θα προκύψει από την απαίτηση ο παρονοµαστής να είναι διάφορος του µηδενός.
 ΕΡΓΑΣΙΑ (Παράδοση:.) Σηείωση: Οι ασκήσεις είναι βαθολογικά ισοδύναες Άσκηση Να προσδιορίσετε τα όρια: sin( ) I. lim, II. lim sin, III. lim ( ln ) sin z Όπου χρειαστεί να θεωρήσετε γνωστό ότι lim z z Ι.
ΕΡΓΑΣΙΑ (Παράδοση:.) Σηείωση: Οι ασκήσεις είναι βαθολογικά ισοδύναες Άσκηση Να προσδιορίσετε τα όρια: sin( ) I. lim, II. lim sin, III. lim ( ln ) sin z Όπου χρειαστεί να θεωρήσετε γνωστό ότι lim z z Ι.
Πανεπιστήµιο Θεσσαλίας
 Πανεπισήιο Θεσσαλίας Τήα Ηλεκρολόγων Μηχανικών & Μηχανικών Υπολογισών Άσκηση : Λυένες Ασκήσεις Έσω ένα σύσηα νήης, σο οποίο έχουε προσθέσει ια κρυφή νήη θυάων 6 θέσεων εαξύ ης κρυφής νήης δεδοένων L και
Πανεπισήιο Θεσσαλίας Τήα Ηλεκρολόγων Μηχανικών & Μηχανικών Υπολογισών Άσκηση : Λυένες Ασκήσεις Έσω ένα σύσηα νήης, σο οποίο έχουε προσθέσει ια κρυφή νήη θυάων 6 θέσεων εαξύ ης κρυφής νήης δεδοένων L και
ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ (ΚΕΦ 27) Μαγνητικές δυνάμεις
 ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ (ΚΕΦ 27) Μαγνητικές δυνάμεις ΠΑΡΑΤΗΡΗΣΕΙΣ εντός 1. Δέσμη φορτισμένων σωματιδίων αποκλίνουν στο πεδίο B ενός μαγνήτη δηλ. Δέχονται μια δύναμη F m κάθετη τόσο στο v όσο και στο B (είτε v
ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ (ΚΕΦ 27) Μαγνητικές δυνάμεις ΠΑΡΑΤΗΡΗΣΕΙΣ εντός 1. Δέσμη φορτισμένων σωματιδίων αποκλίνουν στο πεδίο B ενός μαγνήτη δηλ. Δέχονται μια δύναμη F m κάθετη τόσο στο v όσο και στο B (είτε v
Μάθημα: Ρομποτικός Έλεγχος
 Διαηαικό Πρόγραα Μεαπυχιακών Σπουδών «ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ» Ε.Μ.Π., Ακαδηαϊκό Έος - Μάθηα: Ροποικός Έλεγχος Σαική και Δυναική Ανάλυση Ροποικών Χειρισών Κωνσανίνος Τζαφέσας Τοέας Σηάων, Ελέγχου & Ροποικής
Διαηαικό Πρόγραα Μεαπυχιακών Σπουδών «ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ» Ε.Μ.Π., Ακαδηαϊκό Έος - Μάθηα: Ροποικός Έλεγχος Σαική και Δυναική Ανάλυση Ροποικών Χειρισών Κωνσανίνος Τζαφέσας Τοέας Σηάων, Ελέγχου & Ροποικής
ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ
 Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
ιονύσης Μητρόπουλος νόµος του Νεύτωνα έχει για το σωµατίδιο τη µορφή F = (2), (3).
 ιούσης Μηρόπουλος Σερεό ΣΥΣΤΗΜΑ ΣΩΜΑΤΙ ΙΩΝ, ΣΤΕΡΕΟ ΣΩΜΑ ΟΣ ΝΟΜΟΣ ΤΟΥ ΝΕΥΤΩΝΑ Έα σωµαίδιο, Ορµή, Σροφορµή Ο ος όµος ου Νεύωα σε αδραειακό και µη αδραειακό σύσηµα Γωρίζουµε όι η ορµή εός σωµαιδίου µάζας
ιούσης Μηρόπουλος Σερεό ΣΥΣΤΗΜΑ ΣΩΜΑΤΙ ΙΩΝ, ΣΤΕΡΕΟ ΣΩΜΑ ΟΣ ΝΟΜΟΣ ΤΟΥ ΝΕΥΤΩΝΑ Έα σωµαίδιο, Ορµή, Σροφορµή Ο ος όµος ου Νεύωα σε αδραειακό και µη αδραειακό σύσηµα Γωρίζουµε όι η ορµή εός σωµαιδίου µάζας
ΠΑΡΑΤΗΡΗΣΕΙΣ. Η F m είναι δύναμη εξαρτώμενη από την ταχύτητα
 ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ Μαγνητικές δυνάμεις ΠΑΡΑΤΗΡΗΣΕΙΣ εντός 1. έσμη φορτισμένων σωματιδίων αποκλίνουν στο πεδίο B ενός μαγνήτη δηλ. έχονται μια δύναμη F m κάθετη τόσο στο v όσο και στο B (είτε v B είτε όχι).
ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ Μαγνητικές δυνάμεις ΠΑΡΑΤΗΡΗΣΕΙΣ εντός 1. έσμη φορτισμένων σωματιδίων αποκλίνουν στο πεδίο B ενός μαγνήτη δηλ. έχονται μια δύναμη F m κάθετη τόσο στο v όσο και στο B (είτε v B είτε όχι).
Μαγνητική ροπή. SI: Am 2
 Μαγνητική ροπή Ι Ι Ι I S SI: Μαγνητική ροπή Η αγνητική διπολική ροπή είναι ια βασική ποσότητα για τον αγνητισό (όπως είναι το φορτίο για τον ηλεκτρισό) γιατί καθορίζει: (α) το αγνητοστατικό πεδίο που παράγει
Μαγνητική ροπή Ι Ι Ι I S SI: Μαγνητική ροπή Η αγνητική διπολική ροπή είναι ια βασική ποσότητα για τον αγνητισό (όπως είναι το φορτίο για τον ηλεκτρισό) γιατί καθορίζει: (α) το αγνητοστατικό πεδίο που παράγει
ΦΥΣ 145 Υπολογιστικές Μέθοδοι στη Φυσική. Τελική εξέταση 5 Μάη 2007 Ομάδα 2 η
 ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
TO MONTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (Reptation Model)
 TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
1. Νόμος του Faraday Ορισμός της μαγνητικής ροής στην γενική περίπτωση τυχαίου μαγνητικού πεδίου και επιφάνειας:
 1. Νόμος του Faaday Ορισμός της μαγνητικής ροής στην γενική περίπτωση τυχαίου μαγνητικού πεδίου και επιφάνειας: dφ d A Φ d A Αν το μαγνητικό πεδίο είναι ομογενές και η επιφάνεια επίπεδη: Φ A Ο νόμος του
1. Νόμος του Faaday Ορισμός της μαγνητικής ροής στην γενική περίπτωση τυχαίου μαγνητικού πεδίου και επιφάνειας: dφ d A Φ d A Αν το μαγνητικό πεδίο είναι ομογενές και η επιφάνεια επίπεδη: Φ A Ο νόμος του
8η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 8 ου Κεφαλαίου
 8η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 8 ου Κεφαλαίου 1. Ένα σύρμα μεγάλου μήκους φέρει ρεύμα 30 Α, με φορά προς τα αριστερά κατά μήκος του άξονα x. Ένα άλλο σύρμα μεγάλου μήκους φέρει
8η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 8 ου Κεφαλαίου 1. Ένα σύρμα μεγάλου μήκους φέρει ρεύμα 30 Α, με φορά προς τα αριστερά κατά μήκος του άξονα x. Ένα άλλο σύρμα μεγάλου μήκους φέρει
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ
 ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
Εργαστηριακή Άσκηση Το σύστημα αναμονής M/G/1
 Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ & ΠΕΔΙΑ
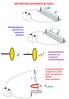 ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ & ΠΕΔΙΑ =0 Αλληλεπιδράσεις μαγνητών με ηλεκτρικά ρεύματα Αλληλεπιδράσεις μαγνητών με κινούμενα ηλεκτρικά φορτία Οι αλληλεπιδράσεις συμβαίνουν μόνον όταν τα ηλεκτρικά φορτία είναι κινούμενα
ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ & ΠΕΔΙΑ =0 Αλληλεπιδράσεις μαγνητών με ηλεκτρικά ρεύματα Αλληλεπιδράσεις μαγνητών με κινούμενα ηλεκτρικά φορτία Οι αλληλεπιδράσεις συμβαίνουν μόνον όταν τα ηλεκτρικά φορτία είναι κινούμενα
ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ
 Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
Ηλεκτρομαγνητισμός. Μαγνητικό πεδίο. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Μαγνητικό πεδίο Νίκος Ν. Αρπατζάνης ύναµη σε ρευµατοφόρους αγωγούς (β) Ο αγωγός δεν διαρρέεται από ρεύμα, οπότε δεν ασκείται δύναμη σε αυτόν. Έτσι παραμένει κατακόρυφος. (γ) Το µαγνητικό
Ηλεκτρομαγνητισμός Μαγνητικό πεδίο Νίκος Ν. Αρπατζάνης ύναµη σε ρευµατοφόρους αγωγούς (β) Ο αγωγός δεν διαρρέεται από ρεύμα, οπότε δεν ασκείται δύναμη σε αυτόν. Έτσι παραμένει κατακόρυφος. (γ) Το µαγνητικό
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ 1 ΣΕΙΡΑΣ FOURIER. Ανάπτυξη σειράς Dirac σε σειρά Fourier (Εκθετική Fourier):
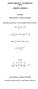 ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
Η Έννοια της τυχαίας ιαδικασίας
 Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ
 Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
Μαγνητικό Πεδίο. Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ
 Μαγνητικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SERWAY, Physics for scientists and engineers YOUNG H.D., University
Μαγνητικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SERWAY, Physics for scientists and engineers YOUNG H.D., University
ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ. Παράδειγµα: Κίνηση φορτισµένου σωµατιδίου µέσα σε µαγνητικό πεδίο. z B. m υ MAΓΝΗTIKΟ ΠΕ ΙΟ
 1 ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ.. Αν δοκιµαστικό φορτίο q βρεθεί κοντά σε αγωγό που διαρρέεται από ρεύµα, υφίσταται δύναµη κάθετη προς την διεύθυνση της ταχύτητάς του και µε µέτρο ανάλογο της ταχύτητάς του, F qυ Β (νόµος
1 ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ.. Αν δοκιµαστικό φορτίο q βρεθεί κοντά σε αγωγό που διαρρέεται από ρεύµα, υφίσταται δύναµη κάθετη προς την διεύθυνση της ταχύτητάς του και µε µέτρο ανάλογο της ταχύτητάς του, F qυ Β (νόµος
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ 1 3.1 ΠΕΙΡΑΜΑΤΑ ΕΠΑΓΩΓΗΣ Το Σχ. 3.1 δείχνει μερικά από τα πειράματα που πραγματοποίησε o Michael Faraday. Στο Σχ. 3.1(α, β, γ) ένα πηνίο συνδέεται με γαλβανόμετρο.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ 1 3.1 ΠΕΙΡΑΜΑΤΑ ΕΠΑΓΩΓΗΣ Το Σχ. 3.1 δείχνει μερικά από τα πειράματα που πραγματοποίησε o Michael Faraday. Στο Σχ. 3.1(α, β, γ) ένα πηνίο συνδέεται με γαλβανόμετρο.
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ
 ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
1η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΘΕΡΜΟΚΡΑΣΙΑ ΑΕΡΑ ΚΑΙ ΜΕΤΑΦΟΡΑ ΑΙΣΘΗΤΗΣ ΘΕΡΜΟΤΗΤΑΣ
 1η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΘΕΡΜΟΚΡΑΣΙΑ ΑΕΡΑ ΚΑΙ ΜΕΤΑΦΟΡΑ ΑΙΣΘΗΤΗΣ ΘΕΡΜΟΤΗΤΑΣ ΜΕΘΟΔΟΙ ΜΕΤΡΗΣΗΣ ΘΕΡΜΟΚΡΑΣΙΑΣ Δισολή (θερμική δισολή σερεών-υγρών-ερίων) Ηλεκρική νίσση (εξάρησή ης πό θερμοκρσί) Θερμοηλεκρικό
1η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΘΕΡΜΟΚΡΑΣΙΑ ΑΕΡΑ ΚΑΙ ΜΕΤΑΦΟΡΑ ΑΙΣΘΗΤΗΣ ΘΕΡΜΟΤΗΤΑΣ ΜΕΘΟΔΟΙ ΜΕΤΡΗΣΗΣ ΘΕΡΜΟΚΡΑΣΙΑΣ Δισολή (θερμική δισολή σερεών-υγρών-ερίων) Ηλεκρική νίσση (εξάρησή ης πό θερμοκρσί) Θερμοηλεκρικό
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ Ηµιαγωγοί και Ηµιαγώγιµες οµές (7 ο Εξάµηνο) Απαντήσεις στην 2 η Σειρά ασκήσεων
 ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ 8-9 Ηιαγωγοί και Ηιαγώγιες οές (7 ο Εξάηνο) Απαντήσεις στην η Σειρά ασκήσεων 1. α) Αν υποθέσουε ότι δύο ηιαγώγια υλικά, όπως τα S και G, έχουν περίπου ίδιες
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ 8-9 Ηιαγωγοί και Ηιαγώγιες οές (7 ο Εξάηνο) Απαντήσεις στην η Σειρά ασκήσεων 1. α) Αν υποθέσουε ότι δύο ηιαγώγια υλικά, όπως τα S και G, έχουν περίπου ίδιες
Που ασκείται η δύναμη στήριξης;
 Που σκείι η δύνμη σήριξης; Θεωρούμε μι πρισμική ράβδο μήκους l η οποί θεωρείι ιδνικό σερεό σώμ. Υποθέουμε όι η ράβδος βρίσκει «υπό κθεσώς κπόνησης». Θεωρούμε μι νοηή ομή η οποί διιρεί ην ράβδο σε δύο μέρη
Που σκείι η δύνμη σήριξης; Θεωρούμε μι πρισμική ράβδο μήκους l η οποί θεωρείι ιδνικό σερεό σώμ. Υποθέουμε όι η ράβδος βρίσκει «υπό κθεσώς κπόνησης». Θεωρούμε μι νοηή ομή η οποί διιρεί ην ράβδο σε δύο μέρη
, δηλαδή το R. είναι µεταβλητό, αλλά κάθε φορά ξέροµε πόσο είναι. Στην πλευρά Α υπάρχει µια γνωστή αντίσταση R
 Εργασία 5, ΦΥΕ 4, 3-4 N Κυλάφης Μια ονάδα ανά άσκηση Σύνολο ονάδων Ηλεκτρονική αοστολή εργασίας αό τους φοιτητές: t 3/4/4 Ηλεκτρονική αοστολή λύσεων αό τον ΣΕΠ: 6/4/4 Άσκηση : Θεωρείστε ένα τετράγωνο λαίσιο
Εργασία 5, ΦΥΕ 4, 3-4 N Κυλάφης Μια ονάδα ανά άσκηση Σύνολο ονάδων Ηλεκτρονική αοστολή εργασίας αό τους φοιτητές: t 3/4/4 Ηλεκτρονική αοστολή λύσεων αό τον ΣΕΠ: 6/4/4 Άσκηση : Θεωρείστε ένα τετράγωνο λαίσιο
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
Θεματική ενότητα : Βασικά εργαλεία και Μέθοδοι για τον έλεγχο της ποιότητας.
 Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
Νόμος Ampere- Διανυσματικό Δυναμικό
 Νόμος Ampere- Διανυσματικό Δυναμικό Δομή Διάλεξης Μαγνητικό πεδίο ευθύγραμμων αγωγών Ο στροβιλισμός και η κλίση μαγνητικού πεδίου: ο νόμος του Ampere Εφαρμογές του Νόμου του Ampere To διανυσματικό δυναμικό
Νόμος Ampere- Διανυσματικό Δυναμικό Δομή Διάλεξης Μαγνητικό πεδίο ευθύγραμμων αγωγών Ο στροβιλισμός και η κλίση μαγνητικού πεδίου: ο νόμος του Ampere Εφαρμογές του Νόμου του Ampere To διανυσματικό δυναμικό
ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ (ΚΕΦ 28)
 ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ (ΚΕΦ 8) B που παράγεται από κινούμενο φορτίο Το Ηλ. Πεδίο στο P (δεν φαίνεται) είναι E = 1 4πε 0 q r rˆ Για το Μαγνητικό Πεδίο στο P προκύπτει πειραματικά ότι: µ 0 qv rˆ B = 4π
ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ (ΚΕΦ 8) B που παράγεται από κινούμενο φορτίο Το Ηλ. Πεδίο στο P (δεν φαίνεται) είναι E = 1 4πε 0 q r rˆ Για το Μαγνητικό Πεδίο στο P προκύπτει πειραματικά ότι: µ 0 qv rˆ B = 4π
(1A) Ε ΟΜΕΝΑ 2Φ10 Σ. Η. ΔΡΙΤΣΟΣ. Yλικά : Άνοιγµα δοκού: l 0-2 = l 2-3 = 4,40 m ΖΗΤΟΥΜΕΝΑ: Σ..Η ΔΡΙΤΣΟΣ
 (A) κός Οπλισένυ Σκυρδέας Ενισχυένη ε Σρώση Οπλισένυ Σκυρδέας- Έλεγχς άρκειας ιφάνειας Ε ΟΜΕΝΑ Άνιγα δκύ: l 0- l -3 4,40 m Φ0 Η. Πλάς δκύ: b 0 mm Πλάς σήριξης: b. ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ σ 0mm 0
(A) κός Οπλισένυ Σκυρδέας Ενισχυένη ε Σρώση Οπλισένυ Σκυρδέας- Έλεγχς άρκειας ιφάνειας Ε ΟΜΕΝΑ Άνιγα δκύ: l 0- l -3 4,40 m Φ0 Η. Πλάς δκύ: b 0 mm Πλάς σήριξης: b. ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ σ 0mm 0
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ και ΕΦΑΡΜΟΓΕΣ
 ΣΧΟΛΗ Ν. ΟΚΙΜΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΤΕΧΝΙΑΣ & Η/Υ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ και ΕΦΑΡΜΟΓΕΣ ρ. Α. ΜΑΓΟΥΛΑΣ Επικ. Καθηγητης Σ.Ν.. 13 I ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ 1 ΣΤΟΙΧΕΙΑ ΑΠΟ ΤΗΝ ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.1 Συστήατα συντεταγένων
ΣΧΟΛΗ Ν. ΟΚΙΜΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΤΕΧΝΙΑΣ & Η/Υ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ και ΕΦΑΡΜΟΓΕΣ ρ. Α. ΜΑΓΟΥΛΑΣ Επικ. Καθηγητης Σ.Ν.. 13 I ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ 1 ΣΤΟΙΧΕΙΑ ΑΠΟ ΤΗΝ ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.1 Συστήατα συντεταγένων
ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23)
 ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23) Υπενθύμιση/Εισαγωγή: Λέμε ότι ένα πεδίο δυνάμεων είναι συντηρητικό (ή διατηρητικό) όταν το έργο που παράγεται από το πεδίο δυνάμεων κατά τη μετατόπιση ενός σώματος από μία
ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23) Υπενθύμιση/Εισαγωγή: Λέμε ότι ένα πεδίο δυνάμεων είναι συντηρητικό (ή διατηρητικό) όταν το έργο που παράγεται από το πεδίο δυνάμεων κατά τη μετατόπιση ενός σώματος από μία
ΚΕΦΑΛΑΙΟ IΙΙ: TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. 1. Τάσεις σε συνεχή μέσα (ε πανάληψη) 2. Τάσεις σε α-συνεχή. μέσα. 3. Ενεργός και Ολική τάση
 ΚΕΦΑΛΑΙΟ IΙΙ: 3. Ενεργός και Ολική άη TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. Τάεις ε υνεχή μέα (ε πανάληψη). Τάεις ε α-υνεχή μέα 4. Γεωαικές άεις (λόγω ιδίου βάρους) 5. Τάεις λόγω εξωερικών φορίων Θεωρία Ελαικόηας Καανομή
ΚΕΦΑΛΑΙΟ IΙΙ: 3. Ενεργός και Ολική άη TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. Τάεις ε υνεχή μέα (ε πανάληψη). Τάεις ε α-υνεχή μέα 4. Γεωαικές άεις (λόγω ιδίου βάρους) 5. Τάεις λόγω εξωερικών φορίων Θεωρία Ελαικόηας Καανομή
ΑΤΟΜΟ Υ ΡΟΓΟΝΟΥ. ΜΟΝΤΕΛΟ BOHR.
 Μάθηα 3 ο, Οκτωβρίο 008 (9:00-:00). ΑΤΟΜΟ Υ ΡΟΓΟΝΟΥ. ΜΟΝΤΕΛΟ BOHR. Φάσα το δρογόνο (93) Γραικό φάσα Boh: εξήγησε την ακτινοβολία το ατόο Η. Ruthfod: πρήνας σγκεντρωένος σε ικρή περιοχή (D~0-5 ) Απόσπαση
Μάθηα 3 ο, Οκτωβρίο 008 (9:00-:00). ΑΤΟΜΟ Υ ΡΟΓΟΝΟΥ. ΜΟΝΤΕΛΟ BOHR. Φάσα το δρογόνο (93) Γραικό φάσα Boh: εξήγησε την ακτινοβολία το ατόο Η. Ruthfod: πρήνας σγκεντρωένος σε ικρή περιοχή (D~0-5 ) Απόσπαση
ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ. Βιβλίο διδάσκοντα με λύσεις προβλημάτων. Κεφάλαιο 1. ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγητής
 ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Βιβλίο διδάσκονα με λύσεις ροβλημάων Κεφάλαιο ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγηής epapamic@civil.auth.gr ΝΙΚΟΣ ΧΑΡΑΛΑΜΠΑΚΗΣ Καθηγηής charalam@civil.auth.gr Αρισοέλειο Πανισήμιο
ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Βιβλίο διδάσκονα με λύσεις ροβλημάων Κεφάλαιο ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγηής epapamic@civil.auth.gr ΝΙΚΟΣ ΧΑΡΑΛΑΜΠΑΚΗΣ Καθηγηής charalam@civil.auth.gr Αρισοέλειο Πανισήμιο
Πα κ έ τ ο Ε ρ γ α σ ί α ς 4 Α ν ά π τ υ ξ η κ α ι π ρ ο σ α ρ µ ο γ ή έ ν τ υ π ο υ κ α ι η λ ε κ τ ρ ο ν ι κ ο ύ ε κ π α ι δ ε υ τ ι κ ο ύ υ λ ι κ ο
 ΠΑΝΕΠΙΣΤΗΜΙΟ Θ ΕΣΣΑΛ ΙΑΣ ΠΟΛ Υ ΤΕΧ ΝΙΚ Η ΣΧ ΟΛ Η ΤΜΗΜΑ ΜΗΧ ΑΝΟΛ ΟΓ Ω Ν ΜΗΧ ΑΝΙΚ Ω Ν Β ΙΟΜΗΧ ΑΝΙΑΣ ΑΝΑΜΟΡΦΩΣΗ Π Π Σ ΣΥ ΝΟΠ Τ Ι Κ Η Ε Κ Θ Ε ΣΗ ΠΕ 4 Α Ν Α ΠΤ Υ Ξ Η Κ Α Ι ΠΡ Ο Σ Α Ρ Μ Ο Γ Η ΕΝ Τ Υ ΠΟ Υ Κ Α
ΠΑΝΕΠΙΣΤΗΜΙΟ Θ ΕΣΣΑΛ ΙΑΣ ΠΟΛ Υ ΤΕΧ ΝΙΚ Η ΣΧ ΟΛ Η ΤΜΗΜΑ ΜΗΧ ΑΝΟΛ ΟΓ Ω Ν ΜΗΧ ΑΝΙΚ Ω Ν Β ΙΟΜΗΧ ΑΝΙΑΣ ΑΝΑΜΟΡΦΩΣΗ Π Π Σ ΣΥ ΝΟΠ Τ Ι Κ Η Ε Κ Θ Ε ΣΗ ΠΕ 4 Α Ν Α ΠΤ Υ Ξ Η Κ Α Ι ΠΡ Ο Σ Α Ρ Μ Ο Γ Η ΕΝ Τ Υ ΠΟ Υ Κ Α
Εισαγωγή στη Θεωρία Σημάτων και Συστημάτων
 Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ ΕΡΩΤΗΜΑΤΟΛΟΓΙΟ
 ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ ΔΙΑΓΩΝΙΣΜΟΣ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΕΤΟΥΣ 5 ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΟΥ Κλάδος-Ειδικότητες: ΠΕ 15 ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ, ΗΛΕΚΤΡΟΝΙΚΩΝ ΜΗΧΑΝΙΚΩΝ, ΦΥΣΙΚΩΝ ΡΑΔΙΟΗΛΕΚΤΡΟΛΟΓΩΝ
ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ ΔΙΑΓΩΝΙΣΜΟΣ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΕΤΟΥΣ 5 ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΟΥ Κλάδος-Ειδικότητες: ΠΕ 15 ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ, ΗΛΕΚΤΡΟΝΙΚΩΝ ΜΗΧΑΝΙΚΩΝ, ΦΥΣΙΚΩΝ ΡΑΔΙΟΗΛΕΚΤΡΟΛΟΓΩΝ
B 2Tk. Παράδειγμα 1.2.1
 Παράδειγμα 1..1 Μία δέσμη πρωτονίων κινείται μέσα σε ομογενές μαγνητικό πεδίο μέτρου,0 Τ, που έχει την κατεύθυνση του άξονα των θετικών z, (Σχ. 1.4). Τα πρωτόνια έχουν ταχύτητα με μέτρο 3,0 10 5 m / s
Παράδειγμα 1..1 Μία δέσμη πρωτονίων κινείται μέσα σε ομογενές μαγνητικό πεδίο μέτρου,0 Τ, που έχει την κατεύθυνση του άξονα των θετικών z, (Σχ. 1.4). Τα πρωτόνια έχουν ταχύτητα με μέτρο 3,0 10 5 m / s
ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ
 1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
Εξίσωση Laplace Θεωρήματα Μοναδικότητας
 Εξίσωση Laplace Θεωρήματα Μοναδικότητας Δομή Διάλεξης Εξίσωση Laplace πλεονεκτήματα μεθόδου επίλυσης της για εύρεση ηλεκτρικού δυναμικού Ιδιότητες λύσεων εξίσωσης Laplace σε 1, 2 και 3 διαστάσεις Θεώρημα
Εξίσωση Laplace Θεωρήματα Μοναδικότητας Δομή Διάλεξης Εξίσωση Laplace πλεονεκτήματα μεθόδου επίλυσης της για εύρεση ηλεκτρικού δυναμικού Ιδιότητες λύσεων εξίσωσης Laplace σε 1, 2 και 3 διαστάσεις Θεώρημα
ΚΕΦΑΛΑΙΟ 6 ΜΑΓΝΗΤΟΣΤΑΤΙΚΟ ΠΕ ΙΟ
 ΚΕΦΑΛΑΙΟ 6 ΚΕΦΑΛΑΙΟ 6 ΜΑΓΝΗΤΟΣΤΑΤΙΚΟ ΠΕ ΙΟ 6. Εισαγωγικά Το αγνητοστατικό πεδίο παράγεται από σταθερά (όνια) ρεύατα ή όνιους αγνήτες, χαρακτηριστικό του δε διάνυσα είναι η αγνητική επαγωγή ή πυκνότητα
ΚΕΦΑΛΑΙΟ 6 ΚΕΦΑΛΑΙΟ 6 ΜΑΓΝΗΤΟΣΤΑΤΙΚΟ ΠΕ ΙΟ 6. Εισαγωγικά Το αγνητοστατικό πεδίο παράγεται από σταθερά (όνια) ρεύατα ή όνιους αγνήτες, χαρακτηριστικό του δε διάνυσα είναι η αγνητική επαγωγή ή πυκνότητα
ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ
 ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ B που παράγεται από κινούμενο φορτίο Το Ηλ. Πεδίο στο P (δεν φαίνεται) είναι E 1 4 0 q r 2 rˆ Για το Μαγνητικό Πεδίο στο P προκύπτει πειραματικά ότι: 0 qv rˆ Έχουμε εισάγει την
ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ B που παράγεται από κινούμενο φορτίο Το Ηλ. Πεδίο στο P (δεν φαίνεται) είναι E 1 4 0 q r 2 rˆ Για το Μαγνητικό Πεδίο στο P προκύπτει πειραματικά ότι: 0 qv rˆ Έχουμε εισάγει την
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
Σχήµα 1. . Μητρόπουλος Στερεό. Άξονας Β. Άξονας Α. ίσκος 2. ίσκος 1. Βάση στήριξης. Σύστηµα στήριξης του δίσκου 1. Κοχλίες σύσφιξης.
 ύο δίσοι µε ιµάν ι πιχνίδι ης σροφορµής () Άξονς Άξονς ίσος ίσος Σχήµ άση σήριξης Η ειονιζόµενη διάξη σο σχήµ είνι έν σύσηµ δύο οριζόνιων δίσων µε µάζες Μ, Μ ι ίνες,, συνεζευγµένων µε ιµάν, που µπορούν
ύο δίσοι µε ιµάν ι πιχνίδι ης σροφορµής () Άξονς Άξονς ίσος ίσος Σχήµ άση σήριξης Η ειονιζόµενη διάξη σο σχήµ είνι έν σύσηµ δύο οριζόνιων δίσων µε µάζες Μ, Μ ι ίνες,, συνεζευγµένων µε ιµάν, που µπορούν
d k dt k a ky(t) = dt k b kx(t) (3.1)
 Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
Φυσική ΙΙ (Ηλεκτρομαγνητισμός Οπτική)
 Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Φυσική ΙΙ (Ηλεκτρομαγνητισμός Οπτική) Διάλεξη 5 η Ιωάννα Ζεργιώτη Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Φυσική ΙΙ (Ηλεκτρομαγνητισμός Οπτική) Διάλεξη 5 η Ιωάννα Ζεργιώτη Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΚΕΦΑΛΑΙΟ 8 ΣΙ ΗΡΟΜΑΓΝΗΤΙΚΑ ΥΛΙΚΑ ΜΑΓΝΗΤΙΚΑ ΚΥΚΛΩΜΑΤΑ
 ΚΕΑΛΑΙΟ 8 ΚΕΑΛΑΙΟ 8 ΣΙ ΗΡΟΜΑΓΝΗΤΙΚΑ ΥΛΙΚΑ ΜΑΓΝΗΤΙΚΑ ΚΥΚΛΩΜΑΤΑ 8. Μαγνήτες, πόλοι, αγνήτιση Στην κλασική ιστορική θεώρηση των αγνητικών φαινοένων ία αγνητισένη ράβδος χαρακτηρίζεται από δύο πόλους, ένα
ΚΕΑΛΑΙΟ 8 ΚΕΑΛΑΙΟ 8 ΣΙ ΗΡΟΜΑΓΝΗΤΙΚΑ ΥΛΙΚΑ ΜΑΓΝΗΤΙΚΑ ΚΥΚΛΩΜΑΤΑ 8. Μαγνήτες, πόλοι, αγνήτιση Στην κλασική ιστορική θεώρηση των αγνητικών φαινοένων ία αγνητισένη ράβδος χαρακτηρίζεται από δύο πόλους, ένα
Κεφάλαιο 6: Διαμαγνητισμός και Παραμαγνητισμός. Λιαροκάπης Ευθύμιος. Διηλεκτρικές, Οπτικές, Μαγνητικές Ιδιότητες Υλικών
 Σχολή Εφαροσένων Μαθηατικών και Φυσικών Επιστηών Εθνικό Μετσόβιο Πολυτεχνείο ιηλεκτρικές, Οπτικές, Μαγνητικές Ιδιότητες Υλικών Κεφάλαιο 6: ιααγνητισός και Παρααγνητισός Λιαροκάπης Ευθύιος Άδεια Χρήσης
Σχολή Εφαροσένων Μαθηατικών και Φυσικών Επιστηών Εθνικό Μετσόβιο Πολυτεχνείο ιηλεκτρικές, Οπτικές, Μαγνητικές Ιδιότητες Υλικών Κεφάλαιο 6: ιααγνητισός και Παρααγνητισός Λιαροκάπης Ευθύιος Άδεια Χρήσης
ΤΥΠΟΛΟΓΙΟ. q e = C Φορτίο Ηλεκτρονίου 1.1. Ηλεκτρικό Πεδίο 2.1. Ηλεκτρικό Πεδίο Σημειακού Φορτίου Q Ηλεκτρικό Πεδίο Σημειακού
 ΤΥΠΟΛΟΓΙΟ q e = 1.6 10 19 C Φορτίο Ηλεκτρονίου 1.1 F = k Q 1 Q 2 r 2 = 9 10 9 Q 1 Q 2 r 2 Νόμος Coulomb 1.2 E = F q E = k Q r 2 E = k Q r 2 e r E = 2kλ ρ E = 2kλ ρ e ρ ε 0 = 1/4πk = 8.85 10 12 S. I. Ε
ΤΥΠΟΛΟΓΙΟ q e = 1.6 10 19 C Φορτίο Ηλεκτρονίου 1.1 F = k Q 1 Q 2 r 2 = 9 10 9 Q 1 Q 2 r 2 Νόμος Coulomb 1.2 E = F q E = k Q r 2 E = k Q r 2 e r E = 2kλ ρ E = 2kλ ρ e ρ ε 0 = 1/4πk = 8.85 10 12 S. I. Ε
Πέντε ερωτήσεις Ηλεκτρομαγνητισμού.
 Πέντε ερωτήσεις Ηλεκτρομαγνητισμού. 1) Μαγνητικό πεδίο ευθύγραμμου αγωγού Στο επίπεδο της σελίδας έχουµε ένα ορθογώνιο τρίγωνο ΚΛΜ. πό τις κορυφές Λ και Μ και κάθετα στο επίπεδο του τριγώνου διέρχονται
Πέντε ερωτήσεις Ηλεκτρομαγνητισμού. 1) Μαγνητικό πεδίο ευθύγραμμου αγωγού Στο επίπεδο της σελίδας έχουµε ένα ορθογώνιο τρίγωνο ΚΛΜ. πό τις κορυφές Λ και Μ και κάθετα στο επίπεδο του τριγώνου διέρχονται
Το πεδίο Η στον σίδηρο εάν η μαγνήτιση είναι ομοιόμορφη είναι. Η μαγνήτιση Μ= m/v, όπου m είναι η μαγνητική ροπή και V ο όγκος του κυλίνδρου
 . Το πεδίο Β μέσα στον σίδηρο δίνεται από τη σχέση Β=μ ο (Η+Μ) Το πεδίο Η στον σίδηρο εάν η μαγνήτιση είναι ομοιόμορφη είναι Η=Η - όπου Η είναι το εξωτερικό πεδίο και Ν ο συντελεστής απομαγνήτισης. Επομένως
. Το πεδίο Β μέσα στον σίδηρο δίνεται από τη σχέση Β=μ ο (Η+Μ) Το πεδίο Η στον σίδηρο εάν η μαγνήτιση είναι ομοιόμορφη είναι Η=Η - όπου Η είναι το εξωτερικό πεδίο και Ν ο συντελεστής απομαγνήτισης. Επομένως
- Ομοιότητα με βάση τις εξισώσεις Νavier-Stokes - 2- διάστατη ασυμπίεστη Ροή
 ΚΕΦΑΛΑΙΟ 8 ΡΟΗ ΠΡΑΓΜΑΤΙΚΟΥ ΡΕΥΣΤΟΥ-ΣΥΝΕΚΤΙΚΗ ΡΟΗ - Ιξώδες - Ομοιόηα με βάση ις εξισώσεις Νaier-Stkes - - διάσαη ασυμπίεση Ροή ΕΞΙΣΩΣΗ ΣΥΝΕΧΕΙΑΣ 0 ΕΞΙΣΩΣΕΙΣ ΟΡΜΗΣ t 1 μ 1 g μ t - Οιακές Συνθήκες B σο -
ΚΕΦΑΛΑΙΟ 8 ΡΟΗ ΠΡΑΓΜΑΤΙΚΟΥ ΡΕΥΣΤΟΥ-ΣΥΝΕΚΤΙΚΗ ΡΟΗ - Ιξώδες - Ομοιόηα με βάση ις εξισώσεις Νaier-Stkes - - διάσαη ασυμπίεση Ροή ΕΞΙΣΩΣΗ ΣΥΝΕΧΕΙΑΣ 0 ΕΞΙΣΩΣΕΙΣ ΟΡΜΗΣ t 1 μ 1 g μ t - Οιακές Συνθήκες B σο -
21/6/2012. Δυνάμεις. Δυναμική Ανάλυση. Δυναμική ΙΔΙΟΤΗΤΕΣ ΤΗΣ ΔΥΝΑΜΗΣ ΔΥΝΑΜΗ
 Δυνάμεις Δυναμική Ανάλυση Δυνάμεις παράγονται από τον άνθρωπο για να ωθήσουν το σώμα ή ένα όργανο Η κατανόηση ενός αθλήματος ή μιας κίνησης απαιτεί την κατανόηση των δυνάμεων που ασκούνται Η αξιολόγηση
Δυνάμεις Δυναμική Ανάλυση Δυνάμεις παράγονται από τον άνθρωπο για να ωθήσουν το σώμα ή ένα όργανο Η κατανόηση ενός αθλήματος ή μιας κίνησης απαιτεί την κατανόηση των δυνάμεων που ασκούνται Η αξιολόγηση
E = E 0 + E = E 0 P ϵ 0. = 1 + χ r. = Q E 0 l
 Πυκνωτής με διηλεκτρικό Πυκνωτής με ορθογώνιους οπλισμούς εμβαδού A και απόσταση μεταξύ των οπλισμών l έχει ϕορτίο Q. Η επιϕανειακή πυκνότητα ϕορτίου σε κάθε οπλισμό θα είνα σ = ±Q/A. Το ηλεκτρικό πεδίο
Πυκνωτής με διηλεκτρικό Πυκνωτής με ορθογώνιους οπλισμούς εμβαδού A και απόσταση μεταξύ των οπλισμών l έχει ϕορτίο Q. Η επιϕανειακή πυκνότητα ϕορτίου σε κάθε οπλισμό θα είνα σ = ±Q/A. Το ηλεκτρικό πεδίο
Α. Ροπή δύναµης ως προς άξονα περιστροφής
 Μηχανική στερεού σώµατος, Ροπή ΡΟΠΗ ΔΥΝΑΜΗΣ Α. Ροπή δύναµης ως προς άξονα περιστροφής Έστω ένα στερεό που δέχεται στο άκρο F Α δύναµη F όπως στο σχήµα. Στο Ο διέρχεται άξονας περιστροφής κάθετος στο στερεό
Μηχανική στερεού σώµατος, Ροπή ΡΟΠΗ ΔΥΝΑΜΗΣ Α. Ροπή δύναµης ως προς άξονα περιστροφής Έστω ένα στερεό που δέχεται στο άκρο F Α δύναµη F όπως στο σχήµα. Στο Ο διέρχεται άξονας περιστροφής κάθετος στο στερεό
Τετραπλή Φωτοηλεκτρική Δέσμη ABH
 Τεραλή Φωλεριή σ ABH Εγχειρίδι Χρήσ 1. εριγραφή εξαράων Εξωερι διασάσει 110mm 103mm Βίδα άθε ρύθισ 440mm Οριζνια ρύθισ Φα Σευρ Tamper Βίδα άθε ρύθισ Οριζνια ρύθισ ια ευθυγράισ Άνιγα ελγχυ άσ Ρύθισ ευαισθσία
Τεραλή Φωλεριή σ ABH Εγχειρίδι Χρήσ 1. εριγραφή εξαράων Εξωερι διασάσει 110mm 103mm Βίδα άθε ρύθισ 440mm Οριζνια ρύθισ Φα Σευρ Tamper Βίδα άθε ρύθισ Οριζνια ρύθισ ια ευθυγράισ Άνιγα ελγχυ άσ Ρύθισ ευαισθσία
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ ΚΑΙ ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ ΚΑΙ ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ 1 1. ΜΑΓΝΗΤΙΣΜΟΣ Μαγνητικά φαινόμενα παρατηρήθηκαν για πρώτη φορά πριν από τουλάχιστον 2500 χρόνια σε κομμάτια μαγνητισμένου σιδηρομεταλλεύματος,
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ ΚΑΙ ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ 1 1. ΜΑΓΝΗΤΙΣΜΟΣ Μαγνητικά φαινόμενα παρατηρήθηκαν για πρώτη φορά πριν από τουλάχιστον 2500 χρόνια σε κομμάτια μαγνητισμένου σιδηρομεταλλεύματος,
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
Ο δεύτερος νόµος του Νεύτωνα για σύστηµα µεταβλητής µάζας
 Ο δεύτερος νόος του Νεύτωνα για σύστηα εταβλητής άζας Όταν εξετάζουε ένα υλικό σύστηα εταβλητής άζας, δηλαδή ένα σύστη α που ανταλλάσσει άζα ε το περιβάλλον του, τότε πρέπει να είαστε πολύ προσεκτικοί
Ο δεύτερος νόος του Νεύτωνα για σύστηα εταβλητής άζας Όταν εξετάζουε ένα υλικό σύστηα εταβλητής άζας, δηλαδή ένα σύστη α που ανταλλάσσει άζα ε το περιβάλλον του, τότε πρέπει να είαστε πολύ προσεκτικοί
Η αρνητική φορά του άξονα z είναι προς τη σελίδα. Για να βρούμε το μέτρο του Β χρησιμοποιούμε την Εξ. (2.3). Στο σημείο Ρ 1 ισχύει
 ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.. Σταθερό ρεύμα 5 Α μέσω χάλκινου σύρματος ρέει προς δεξαμενή ανοδείωσης. Υπολογίστε το μαγνητικό πεδίο που δημιουργείται από το τμήμα του σύρματος μήκους, cm, σε ένα σημείο που
ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.. Σταθερό ρεύμα 5 Α μέσω χάλκινου σύρματος ρέει προς δεξαμενή ανοδείωσης. Υπολογίστε το μαγνητικό πεδίο που δημιουργείται από το τμήμα του σύρματος μήκους, cm, σε ένα σημείο που
Β ΛΥΚΕΙΟΥ Γενικής Παιδείας. ΘΕΜΑ 1 Ο Στις παρακάτω προτάσεις 1 ως και 4 επιλέξτε τη σωστή απάντηση. Μία σε κάθε πρόταση είναι η σωστή απάντηση.
 Β ΛΥΚΕΙΟΥ Γενικής Παιδείας ΘΕΜΑ 1 Ο Στις παρακάτω προτάσεις 1 ως και 4 επιλέξτε τη σωστή απάντηση Μία σε κάθε πρόταση είναι η σωστή απάντηση 1 Με δεδοµένη την ποσότητα 19 e = 1,6 10 του ηλεκτρισµού, από
Β ΛΥΚΕΙΟΥ Γενικής Παιδείας ΘΕΜΑ 1 Ο Στις παρακάτω προτάσεις 1 ως και 4 επιλέξτε τη σωστή απάντηση Μία σε κάθε πρόταση είναι η σωστή απάντηση 1 Με δεδοµένη την ποσότητα 19 e = 1,6 10 του ηλεκτρισµού, από
