Κεφάλαιο 3 ο. Κυκλώματα με στοιχεία αποθήκευσης ενέργειας
|
|
|
- Γιάννη Χριστόπουλος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην εφαρμογή ων κανόνων ου Kirchhoff είναι διαφορικές και όχι αλγεβρικές. Αυό οφείλεαι σην παρουσία σοιχείων αποθήκευσης ενέργειας (, L) σα οποία η σχέση i-υ είναι διαφορική.
2 3.1. Μεαβαική απόκριση. Θα μελεήσουμε αρχικά η συμπεριφορά έοιων κυκλωμάων καά η μεάβασή ους από μία σαθερή καάσαση σε μία άλλη επίσης σαθερή καάσαση Κύκλωμα. Το κύκλωμα ου σχ. 3.1 αποελείαι από μία πηγή άσης, μία ανίσαση και έναν πυκνωή σε σειρά (i c =i =i). i Εφαρμόζονας ον 2 ο κανόνα ου Kirchhoff, έχουμε: υ - υ S () υ () υ () = 0 => υ s ()D υ υ S () i () 1 i d = 0, η οποία γράφεαι ισοδύναμα: 1 dυ s = di c 1 i d d c Σχ Κύκλωμα με ανίσαση dυ ή και πυκνωή σε σειρά. 1 υ d = 1 υ S Λύνουμε η διαφορική εξίσωση με ις παρακάω οριακές συνθήκες: 1 ον για =0 - => υ s (0 - )=0 και ο πυκνωής είναι αφόρισος οπόε και υ c =0 και για 0 => υ s ()=V 0 Οπόε παίρνουμε ην άση και ο ρεύμα ου πυκνωή για >0, υ () = V 0 1 e (3.1) και i = V 0 e / (3.2), όπου V 0 = I 0 η αρχική ιμή ου ρεύμαος για =0. Το γινόμενο αποελεί η σαθερά χρόνου ου κυκλώμαος. Παραηρούμε όι ση μόνιμη καάσαση, όαν δηλ. = => i =0. Με άλλα λόγια σο συνεχές (D) οι πυκνωές συμπεριφέροναι σαν ανοιχοκύκλωμα. υ () i () V 0 V 0 / 0,632V 0 0,328V 0 / (a) (b) Σχ. 3.2 Φόριση πυκνωή μέσω ανίσασης. 2 ον για =0 - => υ s (0 - )=V 0 και ο πυκνωής πλήρως φορισμένος οπόε και υ c =V 0 και για 0 => υ s ()=0 (βραχυκυκλωμένη πηγή άσης). Οπόε παίρνουμε ην άση και ο ρεύμα ου πυκνωή για >0, 32
3 υ () = V 0 e / (3.3) και i = V 0 e / (3.4) υ () i () V 0-0,328V 0 / 0,328V 0 -V 0 / (a) (b) Σχ. 3.3 Εκφόριση πυκνωή μέσω ανίσασης Κύκλωμα L. Το κύκλωμα ου σχ. 3.2 αποελείαι από μία πηγή άσης, μία ανίσαση και ένα πηνίο σε σειρά (i L =i =i). Εφαρμόζονας ον 2 ο i κανόνα ου Kirchhoff, έχουμε: υ s () D υ - Σχ Κύκλωμα με ανίσαση και πηνίο σε σειρά. L υ L υ S () υ () υ L () = 0 => υ s () i L di = 0 d Λύνουμε η διαφορική εξίσωση με ις παρακάω οριακές συνθήκες: 1 ον για =0 - => υ s (0 - )=0 και i=0 και για 0 => υ s ()=V 0. Οπόε παίρνουμε ο ρεύμα και ην άση σα άκρα ου πηνίου για >0: i L () = V 0 1 e L (3.5) και υ L () = V 0 e /L (3.6) Το κλάσμα L/ αποελεί η σαθερά χρόνου ου κυκλώμαος. Παραηρούμε όι ση μόνιμη καάσαση, όαν δηλ. = => υ L =0. Με άλλα λόγια σο συνεχές (D) α πηνία συμπεριφέροναι σαν βραχυκύκλωμα. i L () I 0 υ L () I 0 0,632I 0 0,328I 0 (a) Σχ. 3.5 Αποκαάσαση ου ρεύμαος πηνίου μέσω ανίσασης. 2 ον για =0 - => υ s (0 - )=V 0 και ο ρεύμα έχει αποκαασαθεί πλήρως σην ιμή I 0 = V 0 και για 0 => υ s ()=0 (βραχυκυκλωμένη πηγή άσης). (b) 33
4 Οπόε παίρνουμε ο ρεύμα και ην άση σα άκρα ου πηνίου για >0, i L () = I 0 e /L (3.7) και υ L () = I 0 e /L (3.8) I L () I 0 υ L () -0,328I 0 0,328I 0 -I 0 (a) Σχ. 3.6 Καάργηση ου ρεύμαος πηνίου μέσω ανίσασης. (b) Σημείωση: Από ις εκθεικές εκφράσεις ων άσεων φόρισης και εκφόρισης μπορούμε να υπολογίσουμε ο ποσοσό ους σε σχέση με η μέγιση ιμή σαν συνάρηση ης σαθεράς χρόνου ου κυκλώμαος. Οι σχέσεις αυές εφαρμόζοναι καάλληλα όσο σα κυκλώμαα όσο και σα κυκλώμαα L. Σχ. 3.7 Ποσοσιαία μεαβολή ης άσης σα άκρα ου πυκνωή και ης ανίσασης ανίσοιχα. 34
5 3.2. Απόκριση καά συχνόηα. Η απόκριση καά συχνόηα ενός κυκλώμαος ανάγεαι σον υπολογισμό ης συνάρησης μεαφοράς ου, από ην οποία μπορούμε ση συνέχεια να υπολογίζουμε ην απόκριση (σήμα εξόδου) ου κυκλώμαος σε κάθε διέγερση (σήμα εισόδου). Η συνάρηση μεαφοράς μπορεί να είναι η απολαβή άσης (λόγος ης άσης εξόδου προς ην άση εισόδου), η απολαβή ρεύμαος (λόγος ου ρεύμαος εξόδου προς ο ρεύμα εισόδου) ή και συνδυασμός αυών (άση προς ρεύμα ή ρεύμα προς άση). Η απόκριση σε ημιονικά σήμαα ή απόκριση καά συχνόηα μας παρέχει ένα μέρο για ο πώς αποκρίνεαι ο κύκλωμα σε ένα ημιονικό σήμα υχαίας συχνόηας. Δεδομένου όι η ανάλυση καά Fourier οποιουδήποε σήμαος κααλήγει σε συνδυασμό ημιονικών σημάων, έπεαι όι η απόκριση καά συχνόηα μπορεί να μας δώσει πληροφορία για ην απόκριση ου κυκλώμαος σε οποιοδήποε σήμα Σύνθεη ανίσαση. Η σύνθεη ανίσαση ενός σοιχείου ορίζεαι, κα ανισοιχία με ον νόμο ου Ohm, ως ο λόγος ης ημιονικής άσης που εφαρμόζεαι σο σοιχείο προς ο ρεύμα που ο διαρρέει και είναι συνάρηση ης συχνόηας ου ημιονικού σήμαος. Θεωρούμε δηλαδή όι εφαρμόζουμε σο σοιχείο μία ημιονική άση ης μορφής υ s () = Acosω ή σε μιγαδική μορφή V S (jω) = Αe j00 = A 0. Θα υπολογίσουμε ώρα η σύνθεη ανίσαση καθενός από α βασικά παθηικά σοιχεία ων κυκλωμάων. α) Ωμική ανίσαση Αν εφαρμόσουμε σα άκρα μιας ανίσασης άση ης μορφής: υ s () = Acosω, θα έχουμε από ον νόμο ου Ohm: i () = υ s() = A cosω. Εκφράζουμε αυές ις σχέσεις ση μιγαδική ους μορφή: V (jω) = A 0 και I (jω) = A 0. Από όπου η σύνθεη ανίσαση υπολογίζεαι ως: Ζ = V (jω) = (3.9). I (jω) Βλέπουμε δηλαδή όι η σύνθεη ανίσαση αυίζεαι με ην ωμική. 35
6 β) Πηνίο Αν εφαρμόσουμε σε πηνίο L μία άση ης μορφής: υ s () = Acosω, ο ρεύμα που θα διαρρέει ο πηνίο δίνεαι από η σχέση: i L () = 1 υ L L()d = 1 Acosωd = A sinω = A cos (ω π ) ή σε μιγαδική L ωl ωl 2 μορφή) V L (jω) = A 0 και I L (ω) = A π. Οπόε η σύνθεη ανίσαση ου ωl 2 πηνίου γράφεαι: Ζ L (jω) = V L(jω) = ωl π = jωl (3.10) I L (jω) 2 Βλέπουμε δηλαδή όι σε ένα πηνίο ο μέρο ης ανίσασης είναι ανάλογο ης συχνόηας ου σήμαος, ενώ η άση προηγείαι ου ρεύμαος καά γ) Πυκνωής Για άση διέγερσης υ s () = Acosω, ο ρεύμα σον πυκνωή θα είναι: i () = dυ c() d = dacosω d = (Aωsinω) = ωacos(ω π 2 ) ή σε μιγαδική μορφή V (jω) = A 0 και I (jω) = ωa π 2. Οπόε η σύνθεη ανίσαση ου πυκνωή γράφεαι: Z (jω) = V (jω) = 1 π = j = 1 (3.11) I (jω) ω 2 ω jω Βλέπουμε δηλαδή όι σε έναν πυκνωή ο μέρο ης ανίσασης είναι ανισρόφως ανάλογο ης συχνόηας ου σήμαος, ενώ ο ρεύμα προηγείαι ης άσης καά Κυκλώμαα με ανισάσεις, πυκνωές και πηνία. Είναι φανερό από α παραπάνω όι η ύπαρξη πηνίων ή/και πυκνωών σε ένα κύκλωμα επηρεάζει ην απόκρισή ου καά συχνόηα. Κυκλώμαα με επιλεκική συμπεριφορά ως προς η συχνόηα μπορούν να χρησιμοποιηθούν ως φίλρα συχνοήων επιρέπονας ή εμποδίζονας κάποιες συχνόηες να εμφανισούν σην έξοδό ους. Ση συνέχεια θα αναφερθούμε σε κάποια πολύ απλά κυκλώμαα φίλρων Φίλρα διέλευσης χαμηλών συχνοήων (ΧΣ). α) Φίλρο ΧΣ Το κύκλωμα ου σχ. 3.8 αποελεί ένα απλό φίλρο διέλευσης ΧΣ. 36
7 V i Σχ. 3.8 Φίλρο ΧΣ. Η συνάρηση μεαφοράς (άσης) ου κυκλώμαος υπολογίζεαι από ον διαιρέη άσης που σχημαίζουν οι σύνθεες ανισάσεις ων σοιχείων ου: H(jω) = V O(jω) = Z = 1/jω V i (jω) Z 1 = 1 1jω jω η οποία μπορεί να γραφεί και ως: όπου: Η(jω) = V O H(jω) = H(jω) e j H(jω) (3.12) 1 = 1 και Η(jω) = arcan ω 1(ω) 2 1(ω/ω 0 ) 2 ω 0 με ω 0 = 1. Παραηρούμε όι για ω=0 δηλ. σο D η άση εξόδου ισούαι με ην άση εισόδου. Καθώς η συχνόηα αυξάνει, ο μέρο ης απολαβής Η(jω) μειώνεαι και για ω=ω 0 γίνεαι ίσο με 1/ 2. Η συχνόηα ω 0 ονομάζεαι συχνόηα αποκοπής ου φίλρου. Σο σχ. 3.9 φαίνεαι η μορφή ου μέρου και ης φάσης ης συνάρησης μεαφοράς ου φίλρου ΧΣ συναρήσει ης συχνόηας ου σήμαος. Φάση, deg Πλάος Σχ. 3.9 Χαρακηρισικές μεαφοράς ου φίλρου ΧΣ. β) Φίλρο ΧΣ L Ανίσοιχα μπορούμε να πάρουμε ένα φίλρο ΧΣ χρησιμοποιώνας ο κύκλωμα L ου σχ
8 V i L Σχ Φίλρο ΧΣ L. V O Όπως προηγουμένως, υπολογίζεαι η συνάρηση μεαφοράς ως: H(jω) = 1 1jωL/ (3.13), με συχνόηα αποκοπής ω 0 = L Φίλρα διέλευσης υψηλών συχνοήων (ΥΣ). α) Φίλρο ΥΣ Το κύκλωμα ου σχ αποελεί ένα απλό φίλρο διέλευσης YΣ. Vi Σχ Φίλρο YΣ. η οποία μπορεί να γραφεί και ως: όπου: Η(jω) = VO ω 1(ω) 2 = Η συνάρηση μεαφοράς (άσης) ου κυκλώμαος υπολογίζεαι από ον διαιρέη άσης που σχημαίζουν οι σύνθεες ανισάσεις ων σοιχείων ου: H(jω) = V O(jω) V i (jω) = Z = H(jω) = H(jω) e j H(jω) ω 1 = jω (3.14) 1jω jω 1(ω/ω 0 ) 2 και Η(jω) = 900 arcan ω ω 0 με ω 0 = 1. Παραηρούμε όι για ω=0 δηλ. σο D η άση εξόδου ισούαι με μηδέν. Καθώς η συχνόηα αυξάνει, ο μέρο ης απολαβής Η(jω) είνει ασυμπωικά σο 1, ενώ για ω=ω 0 γίνεαι ίσο με 1/ 2. Η συχνόηα ω 0 ονομάζεαι και πάλι συχνόηα αποκοπής ου φίλρου. Σο σχ φαίνεαι η μορφή ου μέρου και ης φάσης ης συνάρησης μεαφοράς ου φίλρου ΥΣ συναρήσει ης συχνόηας ου σήμαος. 38
9 Πλάος Φάση, deg Σχ Χαρακηρισικές μεαφοράς ου φίλρου YΣ. β) Φίλρο ΥΣ L Ανίσοιχα μπορούμε να πάρουμε ένα φίλρο YΣ χρησιμοποιώνας ο κύκλωμα L ου σχ V i Σχ Φίλρο YΣ L. L V O Όπως προηγουμένως, υπολογίζεαι η συνάρηση μεαφοράς ως: H(jω) = jωl/ 1jωL/ με συχνόηα αποκοπής ω 0 = L. (3.15), Συνονιζόμενα κυκλώμαα. α) L σειράς. Σο σχ φαίνεαι η συνδεσμολογία μιας ανίσασης, ενός πυκνωή και ενός πηνίου σε σειρά. Η σύνθεη ανίσαση ου κυκλώμαος δίνεαι από η σχέση: Z = jωl 1 1 = j(ωl jω ω ) I και ο μέρο ης από ην: V Σχ Συνονιζόμενο κύκλωμα σειράς. L Z = 2 ωl 1 ω 2 (3.16) Η ανίσαση αυή γίνεαι ελάχιση για συχνόηα: ω 0 = 1 (3.17) L Η συχνόηα αυή ονομάζεαι συχνόηα συνονισμού ου κυκλώμαος. 39
10 Ο συνελεσής ποιόηας Q δίνεαι από η σχέση: Q = 1 ω ο = ω οl (3.18) Σχ Καμπύλες απόκρισης συνονιζόμενου κυκλώμαος σειράς. Σο σχ φαίνεαι η μεαβολή ων επί μέρους ανισάσεων ων σοιχείων ου κυκλώμαος καθώς και η σύνθεη ανίσαση και ο ρεύμα, σαν συνάρηση ης συχνόηας ου εφαρμοζόμενου σήμαος. β) L παράλληλης συνδεσμολογίας. Σο σχ φαίνεαι η συνδεσμολογία μιας ανίσασης, ενός πυκνωή και ενός πηνίου σε παράλληλη σύνδεση. Η σύνθεη αγωγιμόηα ου κυκλώμαος δίνεαι από η σχέση: Y = 1 jω 1 jωl = 1 j(ω 1 I ωl ) V L και ο μέρο ης από ην: Σχ Κύκλωμα παράλληλου συνονισμού. Y = 1 2 ω 1 ωl 2 (3.19) Η αγωγιμόηα αυή γίνεαι ελάχιση για συχνόηα: Σχ Κύκλωμα παράλληλου συνονισμού. ω 0 = 1 (3.20) L Η συχνόηα αυή ονομάζεαι συχνόηα συνονισμού ου κυκλώμαος. Ο συνελεσής ποιόηας Q δίνεαι από η σχέση: Q = ω ο = (3.21) ω ο L Σο σχ φαίνεαι η μεαβολή ων επί μέρους αγωγιμοήων ων σοιχείων ου κυκλώμαος καθώς και η σύνθεη αγωγιμόηα, σαν συνάρηση ης συχνόηας ου εφαρμοζόμενου σήμαος. 40
11 Ασκήσεις: 3.1. Ένας θεικός εραγωνικός παλμός U S () με ιμή κορυφής 5V και περίοδο Τ=20msec εφαρμόζεαι σο κύκλωμα ου σχ Αν =1kΩ και =1μF, σχεδιάσε α) ην κυμαομορφή ης άσης σα άκρα ου πυκνωή U και β) ην κυμαομορφή άσης σα άκρα ης ανίσασης U. i υ s ()D υ - υ Σχ Κύκλωμα. Λύση Η σαθερά χρόνου ου κυκλώμαος είναι: ==(1kΩ)(1μF)=1msec. α) Αν αρχικά ο πυκνωής είναι αφόρισος, όαν ην χρονική σιγμή =0 εφαρμοσεί ο εραγωνικός παλμός, ο πυκνωής αρχίζει να φορίζεαι και για =5=5msec η άση σα άκρα ου θα πάρει περίπου ην ελική ης ιμή δηλ. 5V. Ενώ όαν η άση εισόδου γίνει 0 ο πυκνωής εκφορίζεαι μέσω ης ανίσασης. β) Η μορφή ης άσης σα άκρα ης ανίσασης ακολουθεί η μορφή ου ρεύμαος που διαρρέει ο κύκλωμα. Οι κυμαομορφές που προκύπουν φαίνοναι σο σχ V (Vols) U S U 5 U (msec) - 5 Σχ Κυμαομορφές ων άσεων. 3.2.Επαναλάβεε ην ίδια εργασία για =1kΩ και =10μF. 41
Εργαστήριο Κυκλωμάτων και Συστημάτων Ενότητα 3: Κυκλώματα με στοιχεία αποθήκευσης ενέργειας
 Εργαστήριο Κυκλωμάτων και Συστημάτων Ενότητα 3: Κυκλώματα με στοιχεία αποθήκευσης ενέργειας Αραπογιάννη Αγγελική Τμήμα Πληροφορικής και Τηλεπικοινωνιών Περιεχόμενα 1. Σκοποί ενότητας... 3 2. Περιεχόμενα
Εργαστήριο Κυκλωμάτων και Συστημάτων Ενότητα 3: Κυκλώματα με στοιχεία αποθήκευσης ενέργειας Αραπογιάννη Αγγελική Τμήμα Πληροφορικής και Τηλεπικοινωνιών Περιεχόμενα 1. Σκοποί ενότητας... 3 2. Περιεχόμενα
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ
 Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
Γιάννη Σ. Μπούταλη Αναπληρωτή Καθηγητή Δ.Π.Θ. ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθητικές σημειώσεις στο μάθημα ΣΑΕ ΙΙ
 Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Δυναμική συμπεριφορά των λογικών κυκλωμάτων MOS. Διάλεξη 10
 Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Εργαστήριο Ηλεκτρικών κυκλωμάτων
 Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Θέματα Περασμένων Εξετάσεων και Απαντήσεις
 Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ
 ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
d k dt k a ky(t) = dt k b kx(t) (3.1)
 Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
Εισαγωγή στη Θεωρία Σημάτων και Συστημάτων
 Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
13. Συνήθεις διαφορικές εξισώσεις
 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ
 ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
ΕΛΕΓΧΟΣ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΚΕΦΑΛΑΙΟ 2 ΚΕΦΑΛΑΙΟ 2. Πλεονεκτήματα ψηφιακού ελέγχου
 ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
Μεταβατική Ανάλυση - Φάσορες. Κατάστρωση διαφορικών εξισώσεων. Μεταβατική απόκριση. Γενικό μοντέλο. ,, ( ) είναι γνωστές ποσότητες (σταθερές)
 Μεταβατική Ανάλυση - Φάσορες Πρόσθετες διαφάνειες διαλέξεων Αλέξανδρος Πίνο Δεκέμβριος 2017 Γενικό μοντέλο Απόκριση κυκλώματος πρώτης τάξης, δηλαδή με ένα μόνο στοιχείο C ή L 3 Μεταβατική απόκριση Ξαφνική
Μεταβατική Ανάλυση - Φάσορες Πρόσθετες διαφάνειες διαλέξεων Αλέξανδρος Πίνο Δεκέμβριος 2017 Γενικό μοντέλο Απόκριση κυκλώματος πρώτης τάξης, δηλαδή με ένα μόνο στοιχείο C ή L 3 Μεταβατική απόκριση Ξαφνική
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΦΥΣΙΚΗ Ι. ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ ΣΩΜΑΤΟΣ Ισορροπία Σωματιδίου Στατική Ισορροπία Στερεού Σώματος
 ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
Η Έννοια της τυχαίας ιαδικασίας
 Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ
 Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 11: Η ημιτονοειδής διέγερση Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ: 50657177
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 11: Η ημιτονοειδής διέγερση Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ: 50657177
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ 1 ΣΕΙΡΑΣ FOURIER. Ανάπτυξη σειράς Dirac σε σειρά Fourier (Εκθετική Fourier):
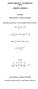 ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
_Σχήµα 2_. Σελίδα 1 από 5. τον οποίο γίνεται η µεταπτωτική κίνηση. Άξονας περιστροφής τροχού. Άξονας γύρω από. τον οποίο γίνεται η µεταπτωτική κίνηση
 ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
Κεφάλαιο 5 Πολλαπλοί χημικοί αντιδραστήρες
 Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
ΦΥΣ 145 Υπολογιστικές Μέθοδοι στη Φυσική. Τελική εξέταση 5 Μάη 2007 Ομάδα 2 η
 ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 16: Απόκριση συχνότητας Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ. ΕΥΔΟΞΟΣ: 50657177
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 16: Απόκριση συχνότητας Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ. ΕΥΔΟΞΟΣ: 50657177
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 6: Παθητικά στοιχεία αποθήκευσης ενέργειας Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ.
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 6: Παθητικά στοιχεία αποθήκευσης ενέργειας Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ.
Α Σ Κ Η Σ Η 1 ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY
 Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
3 Συσχετίσεις σε χρονοσειρές
 3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 5: Θεωρήματα κυκλωμάτων Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISN: 978-960-93-7110-0 κωδ. ΕΥΔΟΞΟΣ: 50657177
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 5: Θεωρήματα κυκλωμάτων Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISN: 978-960-93-7110-0 κωδ. ΕΥΔΟΞΟΣ: 50657177
, e + Σε ένα δείγμα ίδιων ραδιενεργών πυρήνων η πιθανότητα διάσπασης για κάποιο συγκεκριμένο πυρήνα είναι τυχαία.
 ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
Εργαστηριακή Άσκηση Το σύστημα αναμονής M/G/1
 Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ. LT και μονάδες στο SI, kgm/s 2 ή N. υνισταμένη. υνισταμένη. d dt. d dt.
 ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ. 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διατμητικής Αντοχής Εδάφους. Διδάσκοντες: Β. Χρηστάρας Καθηγητής Β. Μαρίνος, Αν.
 ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
Πως λύνεται ένα πρόβληµα.
 Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 8: Βηματική απόκριση κυκλωμάτων RL και R Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ:
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 8: Βηματική απόκριση κυκλωμάτων RL και R Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ:
Νόμος Αmpere. i r. Β dl = Β(dl ακτ +dl τοξ ) = Β rdθ = 2π. Β dl = μ ο i
 Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
Ορισμός: u(t) = 0 (t < 0) και u(t) = 1 (t 0) (4.1) Από τις (4.3) και (4.4), προκύπτει ότι το βηματικό σήμα u(t) είναι σήμα ισχύος.
 4. ΑΝΑΛΥΣΗ ΒΑΣΙΚΩΝ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΗΜΑΤΩΝ 4.. To βημαικό σήμα (step signal) u(t) Ορισμός: u(t) = 0 (t < 0) και u(t) = (t 0) (4.) Μέση ιμή: = (4.) Ενέργεια: Ε = lim [T ] [-, ] u (t).dt (4.3) Μέση
4. ΑΝΑΛΥΣΗ ΒΑΣΙΚΩΝ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΗΜΑΤΩΝ 4.. To βημαικό σήμα (step signal) u(t) Ορισμός: u(t) = 0 (t < 0) και u(t) = (t 0) (4.) Μέση ιμή: = (4.) Ενέργεια: Ε = lim [T ] [-, ] u (t).dt (4.3) Μέση
Θεματική ενότητα : Βασικά εργαλεία και Μέθοδοι για τον έλεγχο της ποιότητας.
 Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 8: Βηματική απόκριση κυκλωμάτων RL και RC Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ:
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 8: Βηματική απόκριση κυκλωμάτων RL και RC Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ:
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 7: Μεταβατική απόκριση κυκλωμάτων RL και RC Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ:
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 7: Μεταβατική απόκριση κυκλωμάτων RL και RC Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ:
Κυκλώματα με ημιτονοειδή διέγερση
 Κυκλώματα με ημιτονοειδή διέγερση Κυκλώματα με ημιτονοειδή διέγερση ονομάζονται εκείνα στα οποία επιβάλλεται τάση της μορφής: = ( ω ϕ ) vt V sin t όπου: V το πλάτος (στιγμιαία μέγιστη τιμή) της τάσης ω
Κυκλώματα με ημιτονοειδή διέγερση Κυκλώματα με ημιτονοειδή διέγερση ονομάζονται εκείνα στα οποία επιβάλλεται τάση της μορφής: = ( ω ϕ ) vt V sin t όπου: V το πλάτος (στιγμιαία μέγιστη τιμή) της τάσης ω
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 3: Συνδυασμός αντιστάσεων και πηγών Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ:
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 3: Συνδυασμός αντιστάσεων και πηγών Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ:
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ
 ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
y(t) = T [x(t)] (7.1)
![y(t) = T [x(t)] (7.1) y(t) = T [x(t)] (7.1)](/thumbs/93/114087149.jpg) Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
Μεγαλύτερες περιπέτειες
 Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 12: Ανάλυση κυκλωμάτων ημιτονοειδούς διέγερσης Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ.
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 12: Ανάλυση κυκλωμάτων ημιτονοειδούς διέγερσης Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ.
Πόλωση των Τρανζίστορ
 Πόλωση των Τρανζίστορ Πόλωση λέμε την κατάλληλη συνεχή τάση που πρέπει να εφαρμόσουμε στο κύκλωμα που περιλαμβάνει κάποιο ηλεκτρονικό στοιχείο (π.χ τρανζίστορ), έτσι ώστε να εξασφαλίσουμε την ομαλή λειτουργία
Πόλωση των Τρανζίστορ Πόλωση λέμε την κατάλληλη συνεχή τάση που πρέπει να εφαρμόσουμε στο κύκλωμα που περιλαμβάνει κάποιο ηλεκτρονικό στοιχείο (π.χ τρανζίστορ), έτσι ώστε να εξασφαλίσουμε την ομαλή λειτουργία
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 3: Συνδυασμός αντιστάσεων και πηγών Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ. ΕΥΔΟΞΟΣ:
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 3: Συνδυασμός αντιστάσεων και πηγών Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ. ΕΥΔΟΞΟΣ:
ΑΝΑΛΥΣΗ ΤΟ ΓΕΝΙΚΟ ΠΛΑΝΟ 2019Κ7-1
 ΑΝΑΛΥΣΗ ΤΟ ΓΕΝΙΚΟ ΠΛΑΝΟ 19Κ7-1 ΤΟ ΜΑΥΡΟ ΚΟΥΤΙ Είσοδος ΜΑΥΡΟ ΚΟΥΤΙ Έξοδος 1. Το περιεχόμενο του μαύρου κουτιού (απλά ηλεκτρικά στοιχεία). Είσοδος: σήματα (κυματομορφές) διέγερσης 3. Έξοδος: απόκριση i.
ΑΝΑΛΥΣΗ ΤΟ ΓΕΝΙΚΟ ΠΛΑΝΟ 19Κ7-1 ΤΟ ΜΑΥΡΟ ΚΟΥΤΙ Είσοδος ΜΑΥΡΟ ΚΟΥΤΙ Έξοδος 1. Το περιεχόμενο του μαύρου κουτιού (απλά ηλεκτρικά στοιχεία). Είσοδος: σήματα (κυματομορφές) διέγερσης 3. Έξοδος: απόκριση i.
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 7: Μεταβατική απόκριση κυκλωμάτων RL και RC Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ:
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 7: Μεταβατική απόκριση κυκλωμάτων RL και RC Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ:
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΠΑΤΡΑΣ 04/02/2011 ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ
 ΘΕΜΑ 1 ο ( μονάδες) Για τον ενισχυτή του παρακάτω σχήματος δίνονται: 1, 0.7, 00 kω, 4 kω, h e. kω και β h 100. (α) Να προσδιορίσετε τις τιμές των αντιστάσεων και ώστε το σημείο λειτουργίας Q (, ) του τρανζίστορ
ΘΕΜΑ 1 ο ( μονάδες) Για τον ενισχυτή του παρακάτω σχήματος δίνονται: 1, 0.7, 00 kω, 4 kω, h e. kω και β h 100. (α) Να προσδιορίσετε τις τιμές των αντιστάσεων και ώστε το σημείο λειτουργίας Q (, ) του τρανζίστορ
R eq = R 1 + R 2 + R 3 = 2Ω + 1Ω + 5Ω = 8Ω. E R eq. I s = = 20V V 1 = IR 1 = (2.5A)(2Ω) = 5V V 3 = IR 3 = (2.5A)(5Ω) = 12.5V
 Πανεπιστήμιο Θεσσαλίας Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Απαντήσεις στο 1 0 Homework στην Ανάλυση Κυκλωμάτων Χειμερινό Εξάμηνο 2014-2015 Πλέσσας Φώτης 1 Πρόβλημα 1 Βρείτε τη συνολική αντίσταση
Πανεπιστήμιο Θεσσαλίας Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Απαντήσεις στο 1 0 Homework στην Ανάλυση Κυκλωμάτων Χειμερινό Εξάμηνο 2014-2015 Πλέσσας Φώτης 1 Πρόβλημα 1 Βρείτε τη συνολική αντίσταση
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
3 V. 0 10v 30 5v v 5000 i0 0 16v 5000 i
 ΗΛΕΚΤΡΙΚ ΚΥΚΛΩΜΤ ΚΙ ΜΕΤΡΗΣΕΙΣ, - ΦΕΡΟΥΡΙΟΣ ΘΕΜ. [%] Στο κύκλωμα στα δεξιά, προσδιορίστε την ενέργεια που αποδίδεται σε ημερήσια βάση (4 ώρες) στον δεξιό κλάδο (εξαρτημένη πηγή και αντίσταση kω). ΠΝΤΗΣΗ
ΗΛΕΚΤΡΙΚ ΚΥΚΛΩΜΤ ΚΙ ΜΕΤΡΗΣΕΙΣ, - ΦΕΡΟΥΡΙΟΣ ΘΕΜ. [%] Στο κύκλωμα στα δεξιά, προσδιορίστε την ενέργεια που αποδίδεται σε ημερήσια βάση (4 ώρες) στον δεξιό κλάδο (εξαρτημένη πηγή και αντίσταση kω). ΠΝΤΗΣΗ
ΦΥΣΙΚΗ Ι. ΤΜΗΜΑ Α Ε. Στυλιάρης
 (Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
(Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΝΙΚΟΛΑΟΣ Κ. ΜΠΕΚΙΑΡΗΣ ΛΥΜΠΕΡΗΣ ΤΕΧΝΙΚΕΣ ΓΡΑΜΜΙΚΩΝ ΚΑΙ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΛΕΓΚΤΩΝ ΣΥΣΤΗΜΑΤΩΝ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΝΙΚΟΛΑΟΣ Κ. ΜΠΕΚΙΑΡΗΣ ΛΥΜΠΕΡΗΣ ΤΕΧΝΙΚΕΣ ΓΡΑΜΜΙΚΩΝ ΚΑΙ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΛΕΓΚΤΩΝ ΣΥΣΤΗΜΑΤΩΝ
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 11: Η ημιτονοειδής διέγερση Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ. ΕΥΔΟΞΟΣ: 50657177
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 11: Η ημιτονοειδής διέγερση Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ. ΕΥΔΟΞΟΣ: 50657177
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 6: Παθητικά στοιχεία αποθήκευσης ενέργειας Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ:
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 6: Παθητικά στοιχεία αποθήκευσης ενέργειας Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ:
Α.3. Στην παρακάτω συνδεσμολογία οι τέσσερις αντιστάσεις R 1, R 2, R 3 και R 4 είναι διαφορετικές μεταξύ τους. Το ρεύμα Ι 3 δίνεται από τη σχέση:
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ' ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 9 ΙΟΥΝΙΟΥ 005 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΗΛΕΚΤΡΟΛΟΓΙΑ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΠΑΡΑΓΩΓΗΣ) ΟΜΑΔΑ Α Για τις παρακάτω προτάσεις,
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ' ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 9 ΙΟΥΝΙΟΥ 005 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΗΛΕΚΤΡΟΛΟΓΙΑ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΥ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΠΑΡΑΓΩΓΗΣ) ΟΜΑΔΑ Α Για τις παρακάτω προτάσεις,
Digital Integrated Circuits, 2 nd edition, J. M. Rabaey, A. Chandrakasan, B. Nikolic
 Πρόβληµα 4. gital Itegrated Circuits, d editio, J. M. abaey, A. Chadrakasa, B. Nikolic You are desigig a clock distributio etwork i which it is critical to miimize skew betwee local clocks (CLK, CLK, ad
Πρόβληµα 4. gital Itegrated Circuits, d editio, J. M. abaey, A. Chadrakasa, B. Nikolic You are desigig a clock distributio etwork i which it is critical to miimize skew betwee local clocks (CLK, CLK, ad
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΤΑΞΗ
 ΟΜΑ Α Α ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΣΠΕΡΙΝΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 26 ΜΑΪΟΥ 2006 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΣ ΤΕΧΝΟΛΟΓΙΑΣ & ΠΑΡΑΓΩΓΗΣ): ΗΛΕΚΤΡΟΛΟΓΙΑ ΣΥΝΟΛΟ ΣΕΛΙ
ΟΜΑ Α Α ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΣΠΕΡΙΝΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 26 ΜΑΪΟΥ 2006 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΣ ΤΕΧΝΟΛΟΓΙΑΣ & ΠΑΡΑΓΩΓΗΣ): ΗΛΕΚΤΡΟΛΟΓΙΑ ΣΥΝΟΛΟ ΣΕΛΙ
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ
 ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
3. ΦΑΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΤΩΝ (ΑΝΑΛΥΣΗ FOURIER)
 3. ΦΑΣΜΑΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΩΝ (ΑΝΑΛΥΣΗ FOURIER) 3.. Γενικά Ένα σήμα μπορεί να αναπαρασαθεί με έναν από ους παρακάω ισοδύναμους ρόπους: Ως χρονικά μεαβαλλόμενη άση (κυμαομορφή) x(t) (αναπαράσαση σο πεδίο ου
3. ΦΑΣΜΑΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΩΝ (ΑΝΑΛΥΣΗ FOURIER) 3.. Γενικά Ένα σήμα μπορεί να αναπαρασαθεί με έναν από ους παρακάω ισοδύναμους ρόπους: Ως χρονικά μεαβαλλόμενη άση (κυμαομορφή) x(t) (αναπαράσαση σο πεδίο ου
Συνδυασμοί αντιστάσεων και πηγών
 ΗΛΕΚΤΡΟΤΕΧΝΙΑ Ι Κεφάλαιο 3 Συνδυασμοί αντιστάσεων και πηγών ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟΥ Σύνδεση σε σειρά. Παράλληλη σύνδεση Ισοδυναμία τριγώνου και αστέρα Διαιρέτης τάσης Διαιρέτης ρεύματος Πραγματικές πηγές.
ΗΛΕΚΤΡΟΤΕΧΝΙΑ Ι Κεφάλαιο 3 Συνδυασμοί αντιστάσεων και πηγών ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟΥ Σύνδεση σε σειρά. Παράλληλη σύνδεση Ισοδυναμία τριγώνου και αστέρα Διαιρέτης τάσης Διαιρέτης ρεύματος Πραγματικές πηγές.
ΚΕΦΑΛΑΙΟ 5 Ο : ΣΥΝΤΟΝΙΣΜΟΣ ΑΠΛΩΝ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ
 ΚΕΦΑΛΑΙΟ 5 Ο : ΣΥΝΤΟΝΙΣΜΟΣ ΑΠΛΩΝ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ 1 Ο συντονισμός είναι μια κατάσταση κατά την οποία το φανταστικό μέρος της σύνθετης αντίστασης ενός κυκλώματος RCL μηδενίζεται. Αυτό συμβαίνει γιατί
ΚΕΦΑΛΑΙΟ 5 Ο : ΣΥΝΤΟΝΙΣΜΟΣ ΑΠΛΩΝ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ 1 Ο συντονισμός είναι μια κατάσταση κατά την οποία το φανταστικό μέρος της σύνθετης αντίστασης ενός κυκλώματος RCL μηδενίζεται. Αυτό συμβαίνει γιατί
1. Χρονικά Εξαρτημένες Πηγές 2. Φάσορες 3. Σύνθετη Αντίσταση 4. Ανάλυση Δικτύων AC
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΚΥΚΛΩΜΑΤΩΝ Πανεπιστήμιο Ιωαννίνων ΑΝΑΛΥΣΗ ΔΙΚΤΥΟΥ 3 ο Κεφάλαιο Γ. Τσιατούχας Τμήμα Μηχανικών Η/Υ και Πληροφορικής ιάρθρωση. Χρονικά Εξαρτημένες Πηγές. Φάσορες 3. Σύνθετη Αντίσταση 4. Ανάλυση
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΚΥΚΛΩΜΑΤΩΝ Πανεπιστήμιο Ιωαννίνων ΑΝΑΛΥΣΗ ΔΙΚΤΥΟΥ 3 ο Κεφάλαιο Γ. Τσιατούχας Τμήμα Μηχανικών Η/Υ και Πληροφορικής ιάρθρωση. Χρονικά Εξαρτημένες Πηγές. Φάσορες 3. Σύνθετη Αντίσταση 4. Ανάλυση
ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ
 Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΕΙΣΑΓΩΓΗ ΣΤΑ ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ
 ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΕΙΣΑΓΩΓΗ ΣΤΑ ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ 1 1. ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ Κύκλωμα είναι ένα σύνολο ηλεκτρικών πηγών και άλλων στοιχείων που είναι συνδεμένα μεταξύ τους και διέρχεται ηλεκτρικό ρεύμα από
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΕΙΣΑΓΩΓΗ ΣΤΑ ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ 1 1. ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ Κύκλωμα είναι ένα σύνολο ηλεκτρικών πηγών και άλλων στοιχείων που είναι συνδεμένα μεταξύ τους και διέρχεται ηλεκτρικό ρεύμα από
Στοιχεία R, L, C στο AC
 Στοιχεία R, L, C στο AC Εμπέδηση (περιγραφή, υπολογισμός για κάθε στοιχείο) Νόμος OHM στο AC Στόχοι μαθήματος Προηγούμενο Εύρεση phasors αρμονικών συναρτήσεων Πράξεις (Πρόσθεση/αφαίρεση κλπ) ημιτονοειδών
Στοιχεία R, L, C στο AC Εμπέδηση (περιγραφή, υπολογισμός για κάθε στοιχείο) Νόμος OHM στο AC Στόχοι μαθήματος Προηγούμενο Εύρεση phasors αρμονικών συναρτήσεων Πράξεις (Πρόσθεση/αφαίρεση κλπ) ημιτονοειδών
1. Χρονικά Εξαρτημένες Πηγές 2. Φάσορες 3. Σύνθετη Αντίσταση 4. Ανάλυση Δικτύων AC
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΚΥΚΛΩΜΑΤΩΝ Πανεπιστήμιο Ιωαννίνων ΑΝΑΛΥΣΗ ΔΙΚΤΥΟΥ 3 ο Κεφάλαιο Γ. Τσιατούχας Τμήμα Μηχανικών Η/Υ και Πληροφορικής ιάρρωση. Χρονικά Εξαρτημένες Πηγές. Φάσορες 3. Σύνετη Αντίσταση 4. Ανάλυση
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΚΥΚΛΩΜΑΤΩΝ Πανεπιστήμιο Ιωαννίνων ΑΝΑΛΥΣΗ ΔΙΚΤΥΟΥ 3 ο Κεφάλαιο Γ. Τσιατούχας Τμήμα Μηχανικών Η/Υ και Πληροφορικής ιάρρωση. Χρονικά Εξαρτημένες Πηγές. Φάσορες 3. Σύνετη Αντίσταση 4. Ανάλυση
ΔΙΔΑΣΚΩΝ: Λ. ΜΠΙΣΔΟΥΝΗΣ ΛΥΣΕΙΣ ΕΞΕΤΑΣΗΣ ΣΤΟ ΜΑΘΗΜΑ «ΤΕΧΝΟΛΟΓΙΑ ΜΕΤΡΗΣΕΩΝ» ΗΜΕΡΟΜΗΝΙΑ: 28/01/2015
 ΛΥΣΕΙΣ ΕΞΕΤΑΣΗΣ ΣΤΟ ΜΑΘΗΜΑ «ΤΕΧΝΟΛΟΓΙΑ ΜΕΤΡΗΣΕΩΝ» ΗΜΕΡΟΜΗΝΙΑ: 8//5 ΘΕΜΑ ο (.5 μονάδες) Η έξοδος του αισθητήρα του παρακάτω σχήματος είναι γραμμικό σήμα τάσης, το οποίο εφαρμόζεται για χρονικό διάστημα
ΛΥΣΕΙΣ ΕΞΕΤΑΣΗΣ ΣΤΟ ΜΑΘΗΜΑ «ΤΕΧΝΟΛΟΓΙΑ ΜΕΤΡΗΣΕΩΝ» ΗΜΕΡΟΜΗΝΙΑ: 8//5 ΘΕΜΑ ο (.5 μονάδες) Η έξοδος του αισθητήρα του παρακάτω σχήματος είναι γραμμικό σήμα τάσης, το οποίο εφαρμόζεται για χρονικό διάστημα
ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ
 1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
Άσκηση 13. Θεωρήματα Δικτύων
 Άσκηση Θεωρήματα Δικτύων. Θεώρημα Βρόχων ΣΚΟΠΟΣ Πειραματική επαλήθευση της μεθόδου των βρογχικών ρευμάτων. ΘΕΩΡΙΑ Με τη μέθοδο των βρογχικών ρευμάτων, η επίλυση ενός κυκλώματος στηρίζεται στον υπολογισμό
Άσκηση Θεωρήματα Δικτύων. Θεώρημα Βρόχων ΣΚΟΠΟΣ Πειραματική επαλήθευση της μεθόδου των βρογχικών ρευμάτων. ΘΕΩΡΙΑ Με τη μέθοδο των βρογχικών ρευμάτων, η επίλυση ενός κυκλώματος στηρίζεται στον υπολογισμό
ΗΛΕΚΤΡΟΤΕΧΝΙΑ Ι Κεφάλαιο 4. Μέθοδοι ανάλυσης κυκλωμάτων
 ΗΛΕΚΤΡΟΤΕΧΝΙΑ Ι Κεφάλαιο 4 Μέθοδοι ανάλυσης κυκλωμάτων ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟΥ Συστήματα εξισώσεων - Ορίζουσες Η μέθοδος των ρευμάτων των κλάδων Η μέθοδος των ρευμάτων βρόχων Η μέθοδος των τάσεων κόμβων
ΗΛΕΚΤΡΟΤΕΧΝΙΑ Ι Κεφάλαιο 4 Μέθοδοι ανάλυσης κυκλωμάτων ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟΥ Συστήματα εξισώσεων - Ορίζουσες Η μέθοδος των ρευμάτων των κλάδων Η μέθοδος των ρευμάτων βρόχων Η μέθοδος των τάσεων κόμβων
0 f(t)e st dt. L[f(t)] = F (s) =
![0 f(t)e st dt. L[f(t)] = F (s) = 0 f(t)e st dt. L[f(t)] = F (s) =](/thumbs/94/118084707.jpg) Α. Δροσόπουλος 3 Ιανουαρίου 29 Περιεχόμενα Μετασχηματισμοί Laplace 2 Αντιστάσεις, πυκνωτές και πηνία 2 3 Διέγερση βαθμίδας σε L κυκλώματα 5 3. Φόρτιση.....................................................
Α. Δροσόπουλος 3 Ιανουαρίου 29 Περιεχόμενα Μετασχηματισμοί Laplace 2 Αντιστάσεις, πυκνωτές και πηνία 2 3 Διέγερση βαθμίδας σε L κυκλώματα 5 3. Φόρτιση.....................................................
2.5 Συνδεσμολογία Αντιστατών
 Κεφάλαιο 2. Ηλεκτρικό Ρεύμα 2.5 Συνδεσμολογία Αντιστατών 1. Τι είναι η ισοδύναμη αντίσταση; Γενικά ονομάζουμε σύστημα (συνδεσμολογία) αντιστατών ένα σύνολο αντιστατών που τους έχουμε συνδέσει με οποιονδήποτε
Κεφάλαιο 2. Ηλεκτρικό Ρεύμα 2.5 Συνδεσμολογία Αντιστατών 1. Τι είναι η ισοδύναμη αντίσταση; Γενικά ονομάζουμε σύστημα (συνδεσμολογία) αντιστατών ένα σύνολο αντιστατών που τους έχουμε συνδέσει με οποιονδήποτε
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 4: Συστηματικές μέθοδοι επίλυσης κυκλωμάτων Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ.
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 4: Συστηματικές μέθοδοι επίλυσης κυκλωμάτων Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ.
ΚΕΦΑΛΑΙΟ 7 Ο : ΘΕΩΡΗΜΑΤΑ ΗΛΕΚΤΡΙΚΩΝ ΔΙΚΤΥΩΝ
 ΚΕΦΑΛΑΙΟ 7 Ο : ΘΕΩΡΗΜΑΤΑ ΗΛΕΚΤΡΙΚΩΝ ΔΙΚΤΥΩΝ Ο βασικός στόχος του θεωρήματος αυτού είναι η μετατροπή της συνδεσμολογίας τύπου αστέρα σε τρίγωνα και το αντίθετο έτσι ώστε τα δίκτυα α και β να είναι ισοδύναμα
ΚΕΦΑΛΑΙΟ 7 Ο : ΘΕΩΡΗΜΑΤΑ ΗΛΕΚΤΡΙΚΩΝ ΔΙΚΤΥΩΝ Ο βασικός στόχος του θεωρήματος αυτού είναι η μετατροπή της συνδεσμολογίας τύπου αστέρα σε τρίγωνα και το αντίθετο έτσι ώστε τα δίκτυα α και β να είναι ισοδύναμα
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 4: Συστηματικές μέθοδοι επίλυσης κυκλωμάτων Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISN: 978-960-93-7110-0 κωδ.
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 4: Συστηματικές μέθοδοι επίλυσης κυκλωμάτων Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISN: 978-960-93-7110-0 κωδ.
3 η ενότητα ΑΠΟΚΡΙΣΗ ΣΥΧΝΟΤΗΤΑΣ ΕΝΙΣΧΥΤΩΝ
 ρ. Λάμπρος Μπισδούνης Καθηγητής 3 η ενότητα ΑΠΟΚΡΙΣΗ ΣΥΧΝΟΤΗΤΑΣ ΕΝΙΣΧΥΤΩΝ T.E.I. ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Περιεχόμενα 3 ης ενότητας Στην τρίτη ενότητα θα μελετήσουμε την απόκριση
ρ. Λάμπρος Μπισδούνης Καθηγητής 3 η ενότητα ΑΠΟΚΡΙΣΗ ΣΥΧΝΟΤΗΤΑΣ ΕΝΙΣΧΥΤΩΝ T.E.I. ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Περιεχόμενα 3 ης ενότητας Στην τρίτη ενότητα θα μελετήσουμε την απόκριση
i C + i R i C + i R = 0 C du dt + u R = 0 du dt + u RC = 0 0 RC dt ln u = t du u = 1 RC dt i C = i R = u R = U 0 t > 0.
 Α. Δροσόπουλος 6 Ιανουαρίου 2010 Περιεχόμενα 1 Κυκλώματα πρώτης τάξης 2 1.1 Εκφόρτιση κυκλωμάτων RC πρώτης τάξης.................................. 2 1.2 Εκφόρτιση κυκλωμάτων RL πρώτης τάξης...................................
Α. Δροσόπουλος 6 Ιανουαρίου 2010 Περιεχόμενα 1 Κυκλώματα πρώτης τάξης 2 1.1 Εκφόρτιση κυκλωμάτων RC πρώτης τάξης.................................. 2 1.2 Εκφόρτιση κυκλωμάτων RL πρώτης τάξης...................................
Να σχεδιαστεί ένας ενισχυτής κοινού εκπομπού (σχ.1) με τα εξής χαρακτηριστικά: R 2.3 k,
 Να σχεδιαστεί ένας ενισχυτής κοινού εκπομπού (σχ) με τα εξής χαρακτηριστικά: 3 k, 50, k, S k και V 5 α) Nα υπολογιστούν οι τιμές των αντιστάσεων β) Να επιλεγούν οι χωρητικότητες C, CC έτσι ώστε ο ενισχυτής
Να σχεδιαστεί ένας ενισχυτής κοινού εκπομπού (σχ) με τα εξής χαρακτηριστικά: 3 k, 50, k, S k και V 5 α) Nα υπολογιστούν οι τιμές των αντιστάσεων β) Να επιλεγούν οι χωρητικότητες C, CC έτσι ώστε ο ενισχυτής
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 13: Ισχύς σε κυκλώματα ημιτονοειδούς διέγερσης Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ.
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 13: Ισχύς σε κυκλώματα ημιτονοειδούς διέγερσης Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ.
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΤΑΞΗ
 ΟΜΑ Α Α ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 21 ΜΑΪΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΣ ΤΕΧΝΟΛΟΓΙΑΣ & ΠΑΡΑΓΩΓΗΣ): ΗΛΕΚΤΡΟΛΟΓΙΑ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
ΟΜΑ Α Α ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 21 ΜΑΪΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΣ ΤΕΧΝΟΛΟΓΙΑΣ & ΠΑΡΑΓΩΓΗΣ): ΗΛΕΚΤΡΟΛΟΓΙΑ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
3. Κεφάλαιο Μετασχηματισμός Fourier
 3 Κεφάλαιο 3 Ορισμοί Ο μετασχηματισμός Fourir αποτελεί την επέκταση των σειρών Fourir στη γενική κατηγορία των συναρτήσεων (περιοδικών και μη) Όπως και στις σειρές οι συναρτήσεις θα εκφράζονται με τη βοήθεια
3 Κεφάλαιο 3 Ορισμοί Ο μετασχηματισμός Fourir αποτελεί την επέκταση των σειρών Fourir στη γενική κατηγορία των συναρτήσεων (περιοδικών και μη) Όπως και στις σειρές οι συναρτήσεις θα εκφράζονται με τη βοήθεια
Ψηφιακή Μετάδοση Αναλογικών Σηµάτων
 Σεραφείµ Καραµογιάς Ψηφιακή Μεάδοση Αναλογικών Σηµάν Τα σύγχρονα συσήµαα εικοιννίας σε ολύ µεγάλο οσοσό διαχειρίζοναι σήµαα ψηφιακής µορφής, δηλαδή, σήµαα ου δηµιουργούναι αό ακολουθίες δυαδικών ψηφίν.
Σεραφείµ Καραµογιάς Ψηφιακή Μεάδοση Αναλογικών Σηµάν Τα σύγχρονα συσήµαα εικοιννίας σε ολύ µεγάλο οσοσό διαχειρίζοναι σήµαα ψηφιακής µορφής, δηλαδή, σήµαα ου δηµιουργούναι αό ακολουθίες δυαδικών ψηφίν.
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ
 Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ 90º. 180º ω. Οι απαντήσεις και τα σχετικά σχόλια
 Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
1. Φάσμα συχνοτήτων 2. Πεδίο μιγαδ
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΚΥΚΛΩΜΑΤΩΝ Πανεπιστήμιο Ιωαννίνων ΑΝΑΛΥΣΗ ΣΥΧΝΟΤΗΤΑΣ 5 ο Κεφάλαιο Γ. Τσιατούχας Τμήμα Μηχανικών Η/Υ και Πληροφορικής Διάρθρωση. Φάσμα συχνοτήτων. Πεδίο μιγαδικής μγ συχνότητας Πόλοι & μηδενικά
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΚΥΚΛΩΜΑΤΩΝ Πανεπιστήμιο Ιωαννίνων ΑΝΑΛΥΣΗ ΣΥΧΝΟΤΗΤΑΣ 5 ο Κεφάλαιο Γ. Τσιατούχας Τμήμα Μηχανικών Η/Υ και Πληροφορικής Διάρθρωση. Φάσμα συχνοτήτων. Πεδίο μιγαδικής μγ συχνότητας Πόλοι & μηδενικά
ΑΠΑΝΤΗΣΗ Εφόσον το κύκλωμα λειτουργεί για πολύ χρόνο, έχει περάσει στη μόνιμη κατάσταση και πρέπει να υπολογίσουμε την κατάστασή του αμέσως πριν το
 13 2019Κ1Φ-2 RC Το κύκλωμα λειτουργεί για πολύ χρόνο Στο t = 0 η πηγή τάσης αντιστρέφει την πολικότητά της και η πηγή ρεύματος πέφτει στα 2 ma Να υπολογιστεί η τάση v o (t) για t 0 2019Κ1Φ-3 RC ΑΠΑΝΤΗΣΗ
13 2019Κ1Φ-2 RC Το κύκλωμα λειτουργεί για πολύ χρόνο Στο t = 0 η πηγή τάσης αντιστρέφει την πολικότητά της και η πηγή ρεύματος πέφτει στα 2 ma Να υπολογιστεί η τάση v o (t) για t 0 2019Κ1Φ-3 RC ΑΠΑΝΤΗΣΗ
Κεφ. 7: Θεωρήματα κυκλωμάτων. Προβλήματα
 Κεφ. 7: Θεωρήματα κυκλωμάτων Προβλήματα 1 Πρόβλημα 1 Χρησιμοποιώντας το θεώρημα της υπέρθεσης, υπολογίστε το ρεύμα μέσω της στο κύκλωμα της παρακάτω εικόνας 1.0kΩ 2 V 1.0kΩ 3 V 2.2kΩ Λύση Απομακρύνουμε
Κεφ. 7: Θεωρήματα κυκλωμάτων Προβλήματα 1 Πρόβλημα 1 Χρησιμοποιώντας το θεώρημα της υπέρθεσης, υπολογίστε το ρεύμα μέσω της στο κύκλωμα της παρακάτω εικόνας 1.0kΩ 2 V 1.0kΩ 3 V 2.2kΩ Λύση Απομακρύνουμε
m e j ω t } ja m sinωt A m cosωt
 ΕΝΟΤΗΤΑ IV ΕΝΑΛΛΑΣΣΟΜΕΝΟ ΡΕΥΜΑ 26 Στρεόµενα διανύσµατα Σε κυκλώµατα όπου η διέγερση είναι περιοδική και ηµιτονοειδής οι τάσεις και τα ρεύµατα αναπαρίστανται µε µιγαδικούς αριθµούς, ή όπως συνήθως λέµε
ΕΝΟΤΗΤΑ IV ΕΝΑΛΛΑΣΣΟΜΕΝΟ ΡΕΥΜΑ 26 Στρεόµενα διανύσµατα Σε κυκλώµατα όπου η διέγερση είναι περιοδική και ηµιτονοειδής οι τάσεις και τα ρεύµατα αναπαρίστανται µε µιγαδικούς αριθµούς, ή όπως συνήθως λέµε
Σχεδίαση Ηλεκτρονικών Κυκλωμάτων RF
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Σχεδίαση Ηλεκτρονικών Κυκλωμάτων F Ενότητα: Φίλτρα και Επαναληπτικές Ασκήσεις Στυλιανός Μυτιληναίος Τμήμα Ηλεκτρονικής, Σχολή
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Σχεδίαση Ηλεκτρονικών Κυκλωμάτων F Ενότητα: Φίλτρα και Επαναληπτικές Ασκήσεις Στυλιανός Μυτιληναίος Τμήμα Ηλεκτρονικής, Σχολή
Ηλεκτρική και Μηχανική ταλάντωση στο ίδιο φαινόμενο
 Ηλεκτρική και Μηχανική ταλάντωση στο ίδιο φαινόμενο Στο σχήμα φαίνεται μια γνώριμη διάταξη δύο παράλληλων αγωγών σε απόσταση, που ορίζουν οριζόντιο επίπεδο, κάθετο σε ομογενές μαγνητικό πεδίο έντασης.
Ηλεκτρική και Μηχανική ταλάντωση στο ίδιο φαινόμενο Στο σχήμα φαίνεται μια γνώριμη διάταξη δύο παράλληλων αγωγών σε απόσταση, που ορίζουν οριζόντιο επίπεδο, κάθετο σε ομογενές μαγνητικό πεδίο έντασης.
ΗΛΕΚΤΡΟΤΕΧΝΙΑ Ι Κεφάλαιο 2. Νόμοι στα ηλεκτρικά κυκλώματα ΠΡΟΒΛΗΜΑΤΑ
 ΗΛΕΚΤΡΟΤΕΧΝΙΑ Ι Κεφάλαιο 2 Νόμοι στα ηλεκτρικά κυκλώματα ΠΡΟΒΛΗΜΑΤΑ Πρόβλημα 2-1 (Άσκηση 2, Κεφ. 2, σελ. 55, Κ. Παπαδόπουλου Ανάλυση ηλεκτρικών κυκλωμάτων ) Να υπολογιστεί η ισχύς που παράγει ή καταναλώνει
ΗΛΕΚΤΡΟΤΕΧΝΙΑ Ι Κεφάλαιο 2 Νόμοι στα ηλεκτρικά κυκλώματα ΠΡΟΒΛΗΜΑΤΑ Πρόβλημα 2-1 (Άσκηση 2, Κεφ. 2, σελ. 55, Κ. Παπαδόπουλου Ανάλυση ηλεκτρικών κυκλωμάτων ) Να υπολογιστεί η ισχύς που παράγει ή καταναλώνει
Ανάλυση της µηχανικής συµπεριφοράς της συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα
 Ανάλυση ης µηχανικής συµπεριφοράς ης συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα Β. Καραζαφέρης MΕ, Υποψήφιος διδάκωρ ΕΜΠ Μ. Καής Επίκουρος Καθηγηής ΕΜΠ Λέξεις κλειδιά: FRP, συνάφεια, πεπερασµένα σοιχεία
Ανάλυση ης µηχανικής συµπεριφοράς ης συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα Β. Καραζαφέρης MΕ, Υποψήφιος διδάκωρ ΕΜΠ Μ. Καής Επίκουρος Καθηγηής ΕΜΠ Λέξεις κλειδιά: FRP, συνάφεια, πεπερασµένα σοιχεία
104Θ Αναλογικά Ηλεκτρονικά 12: Φίλτρα
 4Θ Αναλογικά Ηλεκτρονικά 2: Φίλτρα Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ ΚΑΛΑΜΑΤΑΣ 99 Χειμ Εξάμηνο 24 25 Εισαγωγικά Περιεχόμενα Εισαγωγικά 2 Γενικά
4Θ Αναλογικά Ηλεκτρονικά 2: Φίλτρα Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ ΚΑΛΑΜΑΤΑΣ 99 Χειμ Εξάμηνο 24 25 Εισαγωγικά Περιεχόμενα Εισαγωγικά 2 Γενικά
Κεφάλαιο 2. Ηλεκτρικά Κυκλώματα
 Κεφάλαιο Ηλεκτρικά Κυκλώματα. Μεταβατικά φαινόμενα.. Κύκλωμα C Το κύκλωμα του Σχήματος. είναι το απλούστερο κύκλωμα Α τάξης και αποτελείται από μια πηγή συνεχούς τάσης V, που είναι η διέγερσή του, εν σειρά
Κεφάλαιο Ηλεκτρικά Κυκλώματα. Μεταβατικά φαινόμενα.. Κύκλωμα C Το κύκλωμα του Σχήματος. είναι το απλούστερο κύκλωμα Α τάξης και αποτελείται από μια πηγή συνεχούς τάσης V, που είναι η διέγερσή του, εν σειρά
ΗΛΕΚΤΡΟΝΙΚΗ Ι ΔΙΑΓΡΑΜΜΑΤΑ BODE ΣΥΜΠΛΗΡΩΜΑΤΙΚΟ ΤΕΥΧΟΣ ΣΗΜΕΙΩΣΕΩΝ
 Ε. Μ. Πολυτεχνείο Εργαστήριο Ηλεκτρονικής ΗΛΕΚΤΡΟΝΙΚΗ Ι ΔΙΑΓΡΑΜΜΑΤΑ BODE ΣΥΜΠΛΗΡΩΜΑΤΙΚΟ ΤΕΥΧΟΣ ΣΗΜΕΙΩΣΕΩΝ Γ. ΠΑΠΑΝΑΝΟΣ ΠΑΡΑΡΤΗΜΑ : Συναρτήσεις Δικτύων Βασικοί ορισμοί Ας θεωρήσουμε ένα γραμμικό, χρονικά
Ε. Μ. Πολυτεχνείο Εργαστήριο Ηλεκτρονικής ΗΛΕΚΤΡΟΝΙΚΗ Ι ΔΙΑΓΡΑΜΜΑΤΑ BODE ΣΥΜΠΛΗΡΩΜΑΤΙΚΟ ΤΕΥΧΟΣ ΣΗΜΕΙΩΣΕΩΝ Γ. ΠΑΠΑΝΑΝΟΣ ΠΑΡΑΡΤΗΜΑ : Συναρτήσεις Δικτύων Βασικοί ορισμοί Ας θεωρήσουμε ένα γραμμικό, χρονικά
