ΒΑΣΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ ΙΦ - ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ, 2013
|
|
|
- Μαρδοχαῖος Παπανδρέου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΒΑΣΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ ΙΦ - ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ,
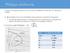
2 Βασικοί Υπολογισμοί Ισορροπίας Φάσεων Ατμών Υγρού Οι βασικοί υπολογισμοί που ενδιαέρουν τον χημικό μηχανικό είναι οι ακόλουθοι : σημείο υσαλίδας σημείο δρόσου εκτόνωση (flash) αποστακτικές στήλες 2
3 Βασικοί Υπολογισμοί Ισορροπίας Φάσεων Ατμών Υγρού Δεδομένα Ζητούμενα Μέθοδος x και T y και Πίεση Σημείου Φυσαλίδας x και y και T Θερμοκρασία Σημείου Φυσαλίδας y και T x και Πίεση Σημείου Δρόσου y και x και T Θερμοκρασία Σημείου Δρόσου T, και F, z L, x και V, y Ισοθερμοκρασιακή εκτόνωση 3
4 Πειραματική διάταξη μέτρησης ΙΦΥΑ (ΣΕΒ, ΣΕΥ, ΕΚΤΟΝΩΣΗ) A B C D E F 4 A : Υπόψυκτο Υγρό Β: Κορεσμένο Υγρό (ΣΕΒ) C,D: Ι.Φ.Υ.Α Ε: Κορεσμένος Ατμός F: Υπέρθερμος Ατμός
5 300 Διάγραμμα -x-y για το σύστημα Μεθανόλη (1)- Νερό (2) στους 90 ο C 5 ressure (ka) Α x1,y1 Β C D E Bubbpe ont Dew ont F Επί της κατακορύου σε σύσταση x10.3 τοποθετήστε τα σημεία Α,Β,C,D,E του προηγούμενου πειράματος
6 Υπολογισμοί Σημείου Φυσαλίδας και Σημείου Δρόσου Στην περίπτωση του σημείου υσαλίδας (ΣΦ), δίνεται υγρό καθορισμένης σύστασης: x 1, x 2,..., και υπολογίζονται: η θερμοκρασία σημείου υσαλίδας σε ορισμένη πίεση, ή η πίεση σημείου υσαλίδας σε ορισμένη θερμοκρασία. Η επαναληπτική διαδικασία σταματά, όταν το άθροισμα των υπολογισμένων y, για όλα y τα συστατικά του μίγματος, είναι ίσο με τη μονάδα: K x 1 6 Στην περίπτωση του σημείου δρόσου (ΣΔ), δίνεται ατμός καθορισμένης σύστασης: y 1, y 2,..., και υπολογίζονται: η θερμοκρασία σημείου δρόσου σε ορισμένη πίεση, ή η πίεση σημείου δρόσου σε ορισμένη θερμοκρασία. Η επαναληπτική διαδικασία σταματά, όταν το άθροισμα των υπολογισμένων y, για όλα y τα συστατικά του μίγματος, είναι ίσο με τη μονάδα: x 1 K
7 7 Ισορροπία Φάσεων Ανάλογα με τη ύση των συστατικών του μίγματος (ή της ολικής πίεσης του συστήματος) οι τάσεις διαυγής υπολογίζονται - ανάλογα και με τη άση - ως: Μη πολικά συστατικά Υψηλές πιέσεις: όπου οι συντελεστές τάσης διαυγής υπολογίζονται με κυβικές καταστατικές εξισώσεις (π.χ. R ή SRK). Antone με Vral με, s s v x f y f L l v v s s l v v e x f y f ) ( γ l v f f x y K Η βασική εξίσωση για όλους τους υπολογισμούς ισορροπίας άσεων ατμούυγρού είτε σε υψηλές είτε σε χαμηλές πιέσεις είναι η ισότητα των τάσεων διαυγής για όλα τα συστατικά του μίγματος: Η ποσοτική περιγραή της ισορροπίας ατμού-υγρού εκράζεται συνήθως με τους λόγους ισορροπίας K : Πολικά συστατικά - Χαμηλές πιέσεις: όπου : UNIFAC Van Laar, Wlson, με ) ( exp ) ( s l RT v e γ v l x y K / / e K v s s γ / ) ( Ιδανικά Διαλύματα Νόμος Raoult K s / 7
8 Υπολογισμός ΣΕΒ (B) Ιδανικό Διάλυμα B calculaton x1 % 30% B lns (mmhg) A-B/(T(K)+C) t (C) Αι Βι C 1s(mmHg) benzene s(mmHg) toluene (mmhg) y y Ιδανικό Διάλυμα x y x s s BT (mmhg) t (C) s(mmHg) s(mmHg) calc y y Intals K C t1 B (K) t2 B (K) mean Tb tral 0 tral 1 tral 2 tral 3 tral 4 tral 5 tral 6 t (n C) T (K) s (mmhg) s (mmhg) (mmhg) Error 9% -20% -7% 1.0% -3% -0.9% 0.0% α
9 Υπολογισμός ΣΕY (D) D calculaton y1 % 30% D lns (mmhg) A-B/(T(K)+C) t (C) 60 Αι Βι C 1s(mmHg) benzene s(mmHg) toluene (mmhg) χ χ Ιδανικό Διάλυμα y 1/ x y s s DT (mmhg) t (C) s(mmHg) s(mmHg) calc χ χ Intals K C t1 B t2 B tral 0 tral 1 tral 2 tral 3 tral 4 tral 5 t (n C) T (K) s (mmhg) s (mmhg) (mmhg) Error 7% -6% 1% -3% -1% 0%
10 Υπολογισμός Καμπύλης ΙΦ hase envelope 420 Ιδανικό Διάλυμα ressure B D oly. (B) oly. (D) x1,y1 B D x1, y1
11 Υπολογισμός ΣΕΒ (B) Πραγματικό Διάλυμα 11 F y x γ s F s (e ) x γ F s Διάγραμμα ροής για τον υπολογισμό της πίεσης σημείου υσαλίδας
12 Υπολογισμός ΣΕY (D) Πραγματικό Διάλυμα 12 y F 1/ γ F s (e ) x y γ F s s Διάγραμμα ροής για τον υπολογισμό της πίεσης σημείου δρόσου
13 13 Διαγράμματα De rester
14 Υπολογισμός ΣΕΒ (B) και ΣΕΥ (D) με κυβικές ΚΕ K y / x L / v f ( x, T, ), L v f ( y, T, ) 14 Αναπτύξτε διάγραμμα ροής για υπολογισμό ΣΕΒ (B) και ΣΕΥ (D) με κυβικές ΚΕ
15 Υπολογισμός Δοχείου Εκτόνωσης Έστω ένα μίγμα, αποτελούμενο από F moles, του οποίου τα γραμμομοριακά κλάσματα των συστατικών είναι ίσα με z 1, z 2,... σε κάποια θερμοκρασία T f και πίεση f. Το μίγμα αυτό εκτονώνεται απότομα διά μέσου μίας βαλβίδας στραγγαλισμού - διεργασία που αναέρεται ως εκτόνωση - και περνά σε ένα δοχείο θερμοκρασίας T και πίεσης (Σχήμα 3.2). 15 Ζητείται, υποθέτοντας ότι έχει επιτευχθεί ισορροπία, να υπολογιστούν: 1. οι ποσότητες του υγρού L και ατμού V, και 2. οι συστάσεις των δύο άσεων. Σχήμα 3.2 Σχηματικό διάγραμμα μίας διεργασίας εκτόνωσης.
16 Υπολογισμός Δοχείου Εκτόνωσης Από το ισοζύγιο μάζας για το συστατικό : F z Lx + V y (Α) Επίσης ισχύει: y K x, και L F - V 16 Εισαγωγή των δύο τελευταίων σχέσεων στην Εξ.(Α) και λύση ως προς x, ορίζοντας α V/F, οδηγεί: z x 1+a( K 1) (Β) K z Ομοίως προκύπτει: y (Γ) 1+a( K 1) Για τον υπολογισμό του α με οποιαδήποτε από τις προηγούμενες εξισώσεις, εαρμόζεται επαναληπτική διαδικασία έως ότου: Q x 1 0 Q y 1 0 x ή: (Δ) Ο υπολογισμός των x και y γίνεται στη συνέχεια απευθείας με τις Εξ. (Β) και (Γ). y
17 Υπολογισμός Δοχείου Εκτόνωσης Σχόλια 1. Ο υπολογισμός του V μπορεί να απλοποιηθεί με τη χρήση αντί των Εξ.(Δ) της διαοράς τους Q (Rachford and Rce, 1952): z ( K 1) Q ( y x) 0 1+ α( K 1) Ο λόγος είναι ότι η παράγωγος (dq/dα ) είναι πάντα αρνητική, γεγονός που οδηγεί σε ταχύτατη σύγκλιση, όταν χρησιμοποιείται η μέθοδος Newton-Raphson, αλλά διευκολύνεται και η πινακοποίηση της λύσης λόγω επαναλαμβανόμενων υπολογισμών. Q' Q ' Q z 2 (ΣΤ) Άλλοι συνηθισμένοι τύποι υπολογισμών εκτόνωσης απαιτούν τον καθορισμό της θερμοκρασίας ή της πίεσης ώστε να ικανοποιείται κάποια προδιαγραή προϊόντος ως προς την ποσότητα ή την ποιότητα. Για την επίλυση τέτοιων προβλημάτων επιλύεται το αρχικό (ευθύ) πρόβλημα πολλές όρες έως ότου ικανοποιηθούν οι προδιαγραές των προϊόντων.
18 Υπολογισμός Δοχείου Εκτόνωσης Κ K1 K2 K3 α13 Q z( K 1) Q 0, Q 1+ α( K 1) α13 Q' Q α ', n+ 1 α n Q ' Q Q Q z n ' n K1 K2 K3 α a0 0.5 a a Component Z K (K-1) z(k-1) Q Q' x y Q Q' x y Q Q' x y 18 A (C1) B (C3) C (n-c5)
19 19 Αποστακτικές στήλες
20 20 ΜΕΡΙΚΟΣ ΣΥΜΠΥΚNΩΤΗΡΑΣ ή ΑΝΑΒΡΑΣΤΗΡΑΣ (Ισοδυναμεί με διαχωριστή ισορροπίας άσεων)
21 21 Ροή ρευστών σε αποστακτική στήλη με δίσκους
22 Σχεδιασμός αποστακτικών στηλών Στόχος: Επεξεργασία συγκεκριμένης τροοδοσίας (ροή και σύσταση) για την παραγωγή προϊόντων επιθυμητών προδιαγραών. Διαδικασία: Ορίζονται ή υπολογίζονται τα ακόλουθα μεγέθη: 22 Πίεση Λειτουργίας Αριθμός Θεωρητικών Βαθμίδων Βαθμός Απόδοσης Δίσκων (ένα από τα δυσκολότερα θέματα με σημαντικά σάλματα) Αριθμός Πραγματικών Δίσκων Κατασκευαστικά στοιχεία των δίσκων με στόχο τη μέγιστη δυνατή επαή Ατμών και Υγρού (βελτίωση απόδοσης), την ελάχιστη δυνατή πτώση πίεσης και τη σταθερότητα της λειτουργίας της στήλης
23 Σχεδιασμός αποστακτικών στηλών Κατασκευαστικά στοιχεία της στήλης: o o o o o o Διάμετρος Απόσταση δίσκων Χώρος υγρού στον πυθμένα της στήλης Χώρος πάνω από τον πρώτο δίσκο της στήλης (κορυή) Διάμετρος εισόδων, εξόδων και αναρροής Διανομέας ατμού κάτω από τον τελευταίο δίσκο 23 Κατασκευαστικά στοιχεία βοηθητικών μηχανημάτων: o o o o o Συμπυκνωτήρας Αναβραστήρας Δοχείο συλλογής προϊόντος κορυής Αντλίες Όργανα μέτρησης/ρύθμισης, μόνωση, εξωτερικές κατασκευές
24 Πίεση λειτουργίας αποστακτικής στήλης Η εκλογή της πίεσης λειτουργίας αποτελεί το πρώτο και καθοριστικό βήμα κατά το σχεδιασμό μιας αποστακτικής στήλης, καθότι επηρεάζει σημαντικά το κόστος του προϊόντος (πάγιο και λειτουργικό κόστος της στήλης) έχοντας άμεση επίδραση στα ακόλουθα: Σχετική πτητικότητα, άρα ευκολία διαχωρισμού Ογκομετρική ροή ατμών, άρα διάμετρο στήλης Πάχος τοιχώματος στήλης Θερμοκρασίες λειτουργίας 24
25 Επιπτώσεις της Πίεσης λειτουργίας της στήλης Αύξηση Πίεσης, K H K L Πυκνότητα ατμών Πάχος τοιχώματος, δ α L,H K L /K H Ογκομετρική Παροχή V Πάγιο Κόστος R N Διάμετρος, D -Κόστος λειτουργίας -Διάμετρος -Μέγεθος εναλλακτών Πάγιο Κόστος Πάγιο Κόστος 25 Θερμοκρασίες λειτουργίας - Επιλογή Ψυκτικού Μέσου πλην νερού - Ενδεχόμενη θερμική διάσπαση προϊόντων - Λειτουργία Αναβραστήρα με ατμό υψηλότερης πίεσης
26 Υπολογισμός Πίεσης λειτουργίας αποστακτικής στήλης Η εκλογή της πίεσης λειτουργίας στηρίζεται στις ακόλουθες παρατηρήσεις: Η ψύξη είναι ακριβότερη από τη θέρμανση (για την ίδια θερμοκρασιακή διαορά). Από το Σχήμα 1 είναι προανές ότι όσο οι συνθήκες λειτουργίας είναι πλησιέστερα στις συνθήκες περιβάλλοντος τόσο το κόστος είναι μικρότερο. Κόστος / Kcal Θερμοκρασία (οc) 26 Το θηνότερο ψυκτικό μέσο είναι το υσικό νερό (θαλασσινό, γεώτρησης, κλπ) Σχήμα 1.
27 Υπολογισμός Πίεσης λειτουργίας αποστακτικής στήλης Στην περίπτωση ολικού συμπυκνωτήρα η ελάχιστη πίεση λειτουργίας εκλέγεται έτσι ώστε η θερμοκρασία έναρξης βρασμού (ΘΕΒ) του προϊόντος κορυής να είναι 8-15 ο C υψηλότερη από τη θερμοκρασία του ψυκτικού μέσου (συνήθως νερού). Ατμός κορυής (ΘΕΥ) Δt 2 Συμπύκνωμα (ΘΕΒt D ) Δt o C Νερό ψύξης (t w ) 27 t D t w +Δt 1 και mn ΕΒ (x D, t D )
28 Υπολογισμός Πίεσης λειτουργίας αποστακτικής στήλης Στην περίπτωση μερικού συμπυκνωτήρα η ελάχιστη πίεση λειτουργίας εκλέγεται έτσι ώστε η θερμοκρασία εξόδου του συμπυκνούμενου μίγματος να είναι τέτοια ώστε να επιτυγχάνεται ο επιθυμητός βαθμός συμπύκνωσης (υπολογισμός flash). H θερμοκρασία αυτή πρέπει να είναι και πάλι να είναι 8-15 ο C υψηλότερη από τη θερμοκρασία του ψυκτικού μέσου (συνήθως νερού). Η πίεση λειτουργίας ορίζεται λίγο μεγαλύτερη από την ελάχιστη ώστε τελικά το συμπύκνωμα να βγαίνει σε υπόψυκτη κατάσταση για να μην δημιουργούνται προβλήματα στις αντλίες που ακολουθούν. 28
29 Υπολογισμός Πίεσης λειτουργίας αποστακτικής στήλης Αν ο υπολογισμός οδηγεί σε πίεση ασύμορα υψηλή τότε χρησιμοποιείται ψυκτικό σύστημα χαμηλής θερμοκρασίας. Αν ο υπολογισμός οδηγεί σε υποατμοσαιρική πίεση συνήθως η πίεση λειτουργίας επιλέγεται ελαρά μεγαλύτερη από την ατμοσαιρική. (γιατί?) Άνω όριο της πίεσης λειτουργίας αποτελεί η πίεση που οδηγεί σε θερμοκρασίες λειτουργίας που προκαλούν διάσπαση συστατικών (επιλογή απόσταξης υπό κενό). 29
30 30
ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ, 2013
 ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ, 2013 1 Ισορροπία Φάσεων Ανάλογα με τη φύση των συστατικών του μίγματος (ή της ολικής πίεσης του συστήματος) οι τάσεις διαφυγής υπολογίζονται - ανάλογα
ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ, 2013 1 Ισορροπία Φάσεων Ανάλογα με τη φύση των συστατικών του μίγματος (ή της ολικής πίεσης του συστήματος) οι τάσεις διαφυγής υπολογίζονται - ανάλογα
Ακρίβεια αποτελεσμάτων σχεδιασμού διεργασιών ΜΑΔ, 2013
 Ακρίβεια αποτελεσμάτων σχεδιασμού διεργασιών ΜΑΔ, 2013 1 ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ ΘΧΜ Σκοπός της θερμοδυναμικής χημικής μηχανικής είναι η παροχή των κατάλληλων θεωρητικών γνώσεων και των απαραίτητων υπολογιστικών-μεθοδολογικών
Ακρίβεια αποτελεσμάτων σχεδιασμού διεργασιών ΜΑΔ, 2013 1 ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ ΘΧΜ Σκοπός της θερμοδυναμικής χημικής μηχανικής είναι η παροχή των κατάλληλων θεωρητικών γνώσεων και των απαραίτητων υπολογιστικών-μεθοδολογικών
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Στόχος: Επεξεργασία συγκεκριμένης τροφοδοσίας (ροή
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Στόχος: Επεξεργασία συγκεκριμένης τροφοδοσίας (ροή
Βασικοί Υπολογισµοί Ισορροπίας Φάσεων Ατµών Υγρού
 Σηµειώσεις Προχωρηµένης Τεχνικής Φυσικών ιεργασιών 33 3 Βασικοί Υπολογισµοί Ισορροπίας Φάσεων Ατµών Υγρού 3.1 Εισαγωγή Οι βασικοί υπολογισµοί ισορροπίας φάσεων ατµών-υγρού που ενδιαφέρουν το χηµικό µηχανικό
Σηµειώσεις Προχωρηµένης Τεχνικής Φυσικών ιεργασιών 33 3 Βασικοί Υπολογισµοί Ισορροπίας Φάσεων Ατµών Υγρού 3.1 Εισαγωγή Οι βασικοί υπολογισµοί ισορροπίας φάσεων ατµών-υγρού που ενδιαφέρουν το χηµικό µηχανικό
Πρόρρηση Ισορροπίας Φάσεων. Υψηλές Πιέσεις
 Πρόρρηση Ισορροπίας Φάσεων Υψηλές Πιέσεις 1 Ισορροπία Φάσεων Η βασική εξίσωση για όλους τους υπολογισμούς ισορροπίας φάσεων ατμού-υγρού είτε σε υψηλές είτε σε χαμηλές πιέσεις είναι η ισότητα των τάσεων
Πρόρρηση Ισορροπίας Φάσεων Υψηλές Πιέσεις 1 Ισορροπία Φάσεων Η βασική εξίσωση για όλους τους υπολογισμούς ισορροπίας φάσεων ατμού-υγρού είτε σε υψηλές είτε σε χαμηλές πιέσεις είναι η ισότητα των τάσεων
ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ 1. ΟΡΙΣΜΟΣ ΣΚΟΠΟΣ ΔΙΕΡΓΑΣΙΑΣ
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ 1. ΟΡΙΣΜΟΣ ΣΚΟΠΟΣ ΔΙΕΡΓΑΣΙΑΣ
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Ι & ΙΙ Εργαστηριακή Άσκηση 4: ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ
 Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Σχεδιασμού, Ανάλυσης & Ανάπτυξης Διεργασιών και Συστημάτων ΕΡΓΑΣΤΗΡΙΟ ΣΧΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διευθυντής: Ι.
Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Σχεδιασμού, Ανάλυσης & Ανάπτυξης Διεργασιών και Συστημάτων ΕΡΓΑΣΤΗΡΙΟ ΣΧΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διευθυντής: Ι.
5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού
 5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού Η αρχική εξίσωση που χρησιμοποιείται για τους υπολογισμούς της ΙΦΥΥ είναι η ικανοποίηση της βασικής θερμοδυναμικής απαίτησης της ισότητας των τάσεων διαφυγής
5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού Η αρχική εξίσωση που χρησιμοποιείται για τους υπολογισμούς της ΙΦΥΥ είναι η ικανοποίηση της βασικής θερμοδυναμικής απαίτησης της ισότητας των τάσεων διαφυγής
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Βασικές αρχές Η διεργασία της απόσταξης στηρίζεται
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Βασικές αρχές Η διεργασία της απόσταξης στηρίζεται
Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης
 Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης Μια αποστακτική στήλη που λειτουργεί σε πίεση 101,3 kpa, διαχωρίζει ένα μίγμα νερούαιθανόλης. Η σύσταση του μίγματος αποτελείται 40 mol% αιθανόλη και η τροφοδοσία
Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης Μια αποστακτική στήλη που λειτουργεί σε πίεση 101,3 kpa, διαχωρίζει ένα μίγμα νερούαιθανόλης. Η σύσταση του μίγματος αποτελείται 40 mol% αιθανόλη και η τροφοδοσία
Αυτόματη ρύθμιση αποστακτικών στηλών
 Αυτόματη ρύθμιση αποστακτικών στηλών Στόχοι-Αναγκαιότητα Παραγωγή προϊόντων επιθυμητών προδιαγραφών και ποσοτήτων Ασφάλεια εγκατάστασης (όρια πίεσης και θερμοκρασίας) Διατήρηση λειτουργικών συνθηκών (αποφυγή
Αυτόματη ρύθμιση αποστακτικών στηλών Στόχοι-Αναγκαιότητα Παραγωγή προϊόντων επιθυμητών προδιαγραφών και ποσοτήτων Ασφάλεια εγκατάστασης (όρια πίεσης και θερμοκρασίας) Διατήρηση λειτουργικών συνθηκών (αποφυγή
Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ. Ερωτήσεις Επανάληψης
 Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ Ερωτήσεις Επανάληψης 1 0.8 0.6 x D = 0.95 y 0.4 x F = 0.45 0.2 0 0 0.2 0.4 0.6 0.8 1 x B = 0.05 Σχήμα 1. Δεδομένα ισορροπίας y-x για δυαδικό μίγμα συστατικών Α και Β και οι
Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ Ερωτήσεις Επανάληψης 1 0.8 0.6 x D = 0.95 y 0.4 x F = 0.45 0.2 0 0 0.2 0.4 0.6 0.8 1 x B = 0.05 Σχήμα 1. Δεδομένα ισορροπίας y-x για δυαδικό μίγμα συστατικών Α και Β και οι
Απρίλιος Λύση: Σύνοψη των δεδομένων: P = 6at, V = 0.6F, L = 0.4F, F = 1 kmol/s. Ζητούμενα: x Fi, x Li
 Φυσικές Διεργασίες Προβλήματα στην απόσταξη που λύθηκαν στην τάξη Πηγή: Δ. Μαρίνος-Κουρής, Ε. Παρλιάρου-Τσάμη, Ασκήσεις Φυσικών Διεργασιών, Παπασωτηρίου, Αθήνα 1994 Απρίλιος 2008 Πρόβλημα 1 Διαχωριστήρας
Φυσικές Διεργασίες Προβλήματα στην απόσταξη που λύθηκαν στην τάξη Πηγή: Δ. Μαρίνος-Κουρής, Ε. Παρλιάρου-Τσάμη, Ασκήσεις Φυσικών Διεργασιών, Παπασωτηρίου, Αθήνα 1994 Απρίλιος 2008 Πρόβλημα 1 Διαχωριστήρας
ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής. Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά)
 ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής (Σηµείωση: Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά) Η απόσταξη στηρίζεται στη διαφορά που υπάρχει στη σύσταση ισορροπίας των
ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής (Σηµείωση: Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά) Η απόσταξη στηρίζεται στη διαφορά που υπάρχει στη σύσταση ισορροπίας των
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διαφορική (batch) Rectifying column Stripping column
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διαφορική (batch) Rectifying column Stripping column
3 Η ΣΕΙΡΑ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΔΙΕΡΓΑΣΙΩΝ - PC-LAB ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ: ΑΣΚΗΣΗ 1 ΠΡΟΣΟΜΟΙΩΣΗ ΜΟΝΑΔΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ
 3 Η ΣΕΙΡΑ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΔΙΕΡΓΑΣΙΩΝ - PC-LAB ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ: 23.12.2015 ΑΣΚΗΣΗ 1 ΠΡΟΣΟΜΟΙΩΣΗ ΜΟΝΑΔΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ Ένα τυπικό φυσικό αέριο έχει την ακόλουθη σύσταση σε % mol: 0.5% Ν 2,
3 Η ΣΕΙΡΑ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΔΙΕΡΓΑΣΙΩΝ - PC-LAB ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ: 23.12.2015 ΑΣΚΗΣΗ 1 ΠΡΟΣΟΜΟΙΩΣΗ ΜΟΝΑΔΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ Ένα τυπικό φυσικό αέριο έχει την ακόλουθη σύσταση σε % mol: 0.5% Ν 2,
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Ορισμός Βασικές έννοιες Απόσταξη (Distillation) είναι
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Ορισμός Βασικές έννοιες Απόσταξη (Distillation) είναι
Κεφάλαιο 4 Κλασματική Απόσταξη
 Κεφάλαιο 4 Κλασματική Απόσταξη Σύνοψη Η κλασματική απόσταξη ή απλά απόσταξη αποτελεί τη διεργασία διαχωρισμού ενός πτητικού συστατικού από ένα λιγότερο πτητικό ή, γενικότερα, ενός μίγματος συστατικών που
Κεφάλαιο 4 Κλασματική Απόσταξη Σύνοψη Η κλασματική απόσταξη ή απλά απόσταξη αποτελεί τη διεργασία διαχωρισμού ενός πτητικού συστατικού από ένα λιγότερο πτητικό ή, γενικότερα, ενός μίγματος συστατικών που
Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί:
 Ψύξη με εκτόνωση Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί: A. Mε ελεύθερη εκτόνωση σε βαλβίδα στραγγαλισμού: ισενθαλπική διεργασία σε χαμηλές θερμοκρασίες,
Ψύξη με εκτόνωση Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί: A. Mε ελεύθερη εκτόνωση σε βαλβίδα στραγγαλισμού: ισενθαλπική διεργασία σε χαμηλές θερμοκρασίες,
ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ ΟΔΗΓΙΕΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΥΓΡΗΣ ΕΚΧΥΛΙΣΗΣ Ελένη Παντελή, Υποψήφια Διδάκτορας Γεωργία Παππά, Δρ. Χημικός Μηχανικός
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ ΟΔΗΓΙΕΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΥΓΡΗΣ ΕΚΧΥΛΙΣΗΣ Ελένη Παντελή, Υποψήφια Διδάκτορας Γεωργία Παππά, Δρ. Χημικός Μηχανικός
Διάλεξη 4β. Συστοιχίες διαχωρισμών
 Διάλεξη 4β Συστοιχίες διαχωρισμών Διαχωρισμός σε απλή στήλη Απλή τροφοδοσία Δύο ρεύματα εξόδου Προσκείμενα κλειδιά διαχωρισμού Στήλη με απλό αναβραστήρα και συμπυκνωτήρα Φθίνουσα πτητικότητα E () Ελαφρύ
Διάλεξη 4β Συστοιχίες διαχωρισμών Διαχωρισμός σε απλή στήλη Απλή τροφοδοσία Δύο ρεύματα εξόδου Προσκείμενα κλειδιά διαχωρισμού Στήλη με απλό αναβραστήρα και συμπυκνωτήρα Φθίνουσα πτητικότητα E () Ελαφρύ
ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ, 2013
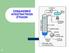 ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ, 2013 1 2 Αποστακτικές στήλες 3 Ροή ρευστών σε αποστακτική στήλη με δίσκους Βασικοί Υπολογισμοί Ισορροπίας Φάσεων Ατμών Υγρού Οι βασικοί υπολογισμοί που ενδιαφέρουν τον
ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ, 2013 1 2 Αποστακτικές στήλες 3 Ροή ρευστών σε αποστακτική στήλη με δίσκους Βασικοί Υπολογισμοί Ισορροπίας Φάσεων Ατμών Υγρού Οι βασικοί υπολογισμοί που ενδιαφέρουν τον
Είδη ΙΦΥΥ δυαδικών μιγμάτων
 Είδη ΙΦΥΥ δυαδικών μιγμάτων T A X 1 X 1 ΙΦΥΥ τριαδικών μιγμάτων Τριγωνικά διαγράμματα C 0.1 0.2 0.3 0.4 0.5 P 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.6 0.7 0.8 0.9 κλάσμα βάρους του B κλάσμα βάρους του C
Είδη ΙΦΥΥ δυαδικών μιγμάτων T A X 1 X 1 ΙΦΥΥ τριαδικών μιγμάτων Τριγωνικά διαγράμματα C 0.1 0.2 0.3 0.4 0.5 P 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.6 0.7 0.8 0.9 κλάσμα βάρους του B κλάσμα βάρους του C
ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΛΑΣΜΑΤΙΚΗΣ ΑΠΟΣΤΑΞΗΣ
 ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΛΑΣΜΑΤΙΚΗΣ ΑΠΟΣΤΑΞΗΣ Παράδειγμα 1 Μια αποστακτική στήλη διαχωρίζει μια τροφοδοσία κορεσμένου ατμού με ρυθμό ροής 100 kmol/h και σύσταση 30 mol% αιθανόλη (E), 25 mol% i- προπανόλη (i-p), 35
ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΛΑΣΜΑΤΙΚΗΣ ΑΠΟΣΤΑΞΗΣ Παράδειγμα 1 Μια αποστακτική στήλη διαχωρίζει μια τροφοδοσία κορεσμένου ατμού με ρυθμό ροής 100 kmol/h και σύσταση 30 mol% αιθανόλη (E), 25 mol% i- προπανόλη (i-p), 35
P. kpa T, C v, m 3 /kg u, kj/kg Περιγραφή κατάστασης και ποιότητα (αν εφαρμόζεται) , ,0 101,
 Ασκήσεις Άσκηση 1 Να συμπληρώσετε τα κενά κελιά στον επόμενο πίνακα των ιδιοτήτων του νερού εάν παρέχονται επαρκή δεδομένα. Στην τελευταία στήλη να περιγράψετε την κατάσταση του νερού ως υπόψυκτο υγρό,
Ασκήσεις Άσκηση 1 Να συμπληρώσετε τα κενά κελιά στον επόμενο πίνακα των ιδιοτήτων του νερού εάν παρέχονται επαρκή δεδομένα. Στην τελευταία στήλη να περιγράψετε την κατάσταση του νερού ως υπόψυκτο υγρό,
Κεφάλαιο 3 Απόσταξη Ισορροπίας
 Κεφάλαιο 3 Απόσταξη Ισορροπίας Σύνοψη Η απόσταξη ισορροπίας ή στιγμιαία απόσταξη αποτελεί μία απλή διεργασία διαχωρισμού, η εφαρμογή της οποίας βασίζεται στην ατμοποίηση μέρους της τροφοδοσίας εντός δοχείου
Κεφάλαιο 3 Απόσταξη Ισορροπίας Σύνοψη Η απόσταξη ισορροπίας ή στιγμιαία απόσταξη αποτελεί μία απλή διεργασία διαχωρισμού, η εφαρμογή της οποίας βασίζεται στην ατμοποίηση μέρους της τροφοδοσίας εντός δοχείου
Energy resources: Technologies & Management
 Πανεπιστήμιο Δυτικής Μακεδονίας Energ resources: echnologies & Management Τεχνολογίες άνθρακα Σχεδιασμός Στηλών Απορρόφησης Αερίων Δρ. Γεώργιος Σκόδρας Αν. Καθηγητής Περιεχόμενα Η διάλεξη που ακολουθεί
Πανεπιστήμιο Δυτικής Μακεδονίας Energ resources: echnologies & Management Τεχνολογίες άνθρακα Σχεδιασμός Στηλών Απορρόφησης Αερίων Δρ. Γεώργιος Σκόδρας Αν. Καθηγητής Περιεχόμενα Η διάλεξη που ακολουθεί
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση α: Συντελεστής Joule Thomson (Τζουλ Τόμσον ) Αθανάσιος Τσεκούρας Τμήμα Χημείας Θεωρία 3 Μετρήσεις 6 3 Επεξεργασία Μετρήσεων 6 Σελίδα Θεωρία Η καταστατική εξίσωση
Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση α: Συντελεστής Joule Thomson (Τζουλ Τόμσον ) Αθανάσιος Τσεκούρας Τμήμα Χημείας Θεωρία 3 Μετρήσεις 6 3 Επεξεργασία Μετρήσεων 6 Σελίδα Θεωρία Η καταστατική εξίσωση
Παρασκευή αιθανόλης-απόσταξη αλκοολούχου διαλύματος. Τεχνική της απόσταξης
 Παρασκευή αιθανόλης-απόσταξη αλκοολούχου διαλύματος Με τον όρο απόσταξη εννοείται η θέρμανση ενός υγρού μέχρι να εξατμισθεί, η συμπύκνωση των ατμών του με ψύξη και η συλλογή τους σε ένα άλλο δοχείο. Με
Παρασκευή αιθανόλης-απόσταξη αλκοολούχου διαλύματος Με τον όρο απόσταξη εννοείται η θέρμανση ενός υγρού μέχρι να εξατμισθεί, η συμπύκνωση των ατμών του με ψύξη και η συλλογή τους σε ένα άλλο δοχείο. Με
Ογκομετρική (PVT) συμπεριφορά καθαρών ρευστών
 Ογκομετρική (PT) συμπεριφορά καθαρών ρευστών Ογκομετρική (PvT) συμπεριφορά Α.Θ Παπαϊωάννου, Θερμοδυναμική: ΤΟΜΟΣ I, Αθήνα, 007 PvT ιάγραμμα για το νερό 3 ιαγράμματα φάσεων καθαρών ουσιών Α.Θ. Παπαϊωάννου,
Ογκομετρική (PT) συμπεριφορά καθαρών ρευστών Ογκομετρική (PvT) συμπεριφορά Α.Θ Παπαϊωάννου, Θερμοδυναμική: ΤΟΜΟΣ I, Αθήνα, 007 PvT ιάγραμμα για το νερό 3 ιαγράμματα φάσεων καθαρών ουσιών Α.Θ. Παπαϊωάννου,
Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ
 Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ Η υγρή εκχύλιση βρίσκει εφαρμογή όταν. Η σχετική πτητικότητα των συστατικών του αρχικού διαλύματος είναι κοντά στη
Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ Η υγρή εκχύλιση βρίσκει εφαρμογή όταν. Η σχετική πτητικότητα των συστατικών του αρχικού διαλύματος είναι κοντά στη
Πρόρρηση. Θερμοδυναμικών Ιδιοτήτων Μιγμάτων
 Πρόρρηση Θερμοδυναμικών Ιδιοτήτων Μιγμάτων 1 Χημικό Δυναμικό μ d = dg U = N V,S,N Για 1 mole καθαρής ουσίας: SdT +Vd j H = N S,,N j A = N V,T,N j G = N ( T, ) ( T,) = T T T,,N j SdT + όπου μ(t',') είναι
Πρόρρηση Θερμοδυναμικών Ιδιοτήτων Μιγμάτων 1 Χημικό Δυναμικό μ d = dg U = N V,S,N Για 1 mole καθαρής ουσίας: SdT +Vd j H = N S,,N j A = N V,T,N j G = N ( T, ) ( T,) = T T T,,N j SdT + όπου μ(t',') είναι
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΛΥΜΕΝΑ ΘΕΜΑΤΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΛΥΜΕΝΑ ΘΕΜΑΤΑ 1 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 Θέμα 1 Επιλέγοντας το κατάλληλο διάγραμμα φάσεων για ένα πραγματικό
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΛΥΜΕΝΑ ΘΕΜΑΤΑ 1 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 Θέμα 1 Επιλέγοντας το κατάλληλο διάγραμμα φάσεων για ένα πραγματικό
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο
 Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 9 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 9 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
ΑΣΚΗΣΕΙΣ ΣΥΣΚΕΥΩΝ ΘΕΡΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ. 1η ενότητα
 1η ενότητα 1. Εναλλάκτης σχεδιάζεται ώστε να θερμαίνει 2kg/s νερού από τους 20 στους 60 C. Το θερμό ρευστό είναι επίσης νερό με θερμοκρασία εισόδου 95 C. Οι συντελεστές συναγωγής στους αυλούς και το κέλυφος
1η ενότητα 1. Εναλλάκτης σχεδιάζεται ώστε να θερμαίνει 2kg/s νερού από τους 20 στους 60 C. Το θερμό ρευστό είναι επίσης νερό με θερμοκρασία εισόδου 95 C. Οι συντελεστές συναγωγής στους αυλούς και το κέλυφος
1 IΔΑΝΙΚΑ ΑΕΡΙΑ 1.1 ΓΕΝΙΚΑ
 1 1 IΔΑΝΙΚΑ ΑΕΡΙΑ 1.1 ΓΕΝΙΚΑ Θα αρχίσουμε τη σειρά των μαθημάτων της Φυσικοχημείας με τη μελέτη της αέριας κατάστασης της ύλης. Η μελέτη της φύσης των αερίων αποτελεί ένα ιδανικό μέσο για την εισαγωγή
1 1 IΔΑΝΙΚΑ ΑΕΡΙΑ 1.1 ΓΕΝΙΚΑ Θα αρχίσουμε τη σειρά των μαθημάτων της Φυσικοχημείας με τη μελέτη της αέριας κατάστασης της ύλης. Η μελέτη της φύσης των αερίων αποτελεί ένα ιδανικό μέσο για την εισαγωγή
(β) Εύρεση του αριθμού των θεωρητικών βαθμίδων με τη μέθοδο McCabe-Thiele
 Κεφάλαιο 2 Απόσταξη 3 (β) Εύρεση του αριθμού των θεωρητικών βαθμίδων με τη μέθοδο McCabe-Thiele Παρακάτω περιγράφουμε τα βήματα που ακολουθούμε με τη μέθοδο McCabe- Thiele για να καθορίσουμε τον αριθμό
Κεφάλαιο 2 Απόσταξη 3 (β) Εύρεση του αριθμού των θεωρητικών βαθμίδων με τη μέθοδο McCabe-Thiele Παρακάτω περιγράφουμε τα βήματα που ακολουθούμε με τη μέθοδο McCabe- Thiele για να καθορίσουμε τον αριθμό
Ειδική Ενθαλπία, Ειδική Θερµότητα και Ειδικός Όγκος Υγρού Αέρα
 θερµοκρασία που αντιπροσωπεύει την θερµοκρασία υγρού βολβού. Το ποσοστό κορεσµού υπολογίζεται από την καµπύλη του σταθερού ποσοστού κορεσµού που διέρχεται από το συγκεκριµένο σηµείο. Η απόλυτη υγρασία
θερµοκρασία που αντιπροσωπεύει την θερµοκρασία υγρού βολβού. Το ποσοστό κορεσµού υπολογίζεται από την καµπύλη του σταθερού ποσοστού κορεσµού που διέρχεται από το συγκεκριµένο σηµείο. Η απόλυτη υγρασία
ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΙΙ ΤΜΗΜΑΤΟΣ ΧΗΜΕΙΑΣ
 ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΙΙ ΤΜΗΜΑΤΟΣ ΧΗΜΕΙΑΣ Ιωάννης Πούλιος ΔΥΑΔΙΚΑ ΣΥΣΤΗΜΑΤΑ ΜΕΛΕΤΗ ΤΩΝ ΔΙΑΓΡΑΜΜΑΤΩΝ ΤΟΥ ΣΗΜΕΙΟΥ ΖΕΣΗΣ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΙΙ ΤΜΗΜΑΤΟΣ ΧΗΜΕΙΑΣ Ιωάννης Πούλιος ΔΥΑΔΙΚΑ ΣΥΣΤΗΜΑΤΑ ΜΕΛΕΤΗ ΤΩΝ ΔΙΑΓΡΑΜΜΑΤΩΝ ΤΟΥ ΣΗΜΕΙΟΥ ΖΕΣΗΣ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
Ισορροπία Υγρού-Υγρού ΠΡΟΧΩΡΗΜΕΝΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ
 Ισορροπία Υγρού-Υγρού ΠΡΟΧΩΡΗΜΕΝΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ Προχωρημένη Θερμοδυναμική Εαρινό εξάμηνο 08-09 Εισαγωγή Σε αντίθεση με τα αέρια τα οποία είναι αναμίξιμα σε όλες τις αναλογίες σε χαμηλές πιέσεις τα υγρά
Ισορροπία Υγρού-Υγρού ΠΡΟΧΩΡΗΜΕΝΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ Προχωρημένη Θερμοδυναμική Εαρινό εξάμηνο 08-09 Εισαγωγή Σε αντίθεση με τα αέρια τα οποία είναι αναμίξιμα σε όλες τις αναλογίες σε χαμηλές πιέσεις τα υγρά
Βασικές Διεργασίες Μηχανικής Τροφίμων
 Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 8: Εκχύλιση, 1ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Τύποι εκχύλισης
Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 8: Εκχύλιση, 1ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Τύποι εκχύλισης
ΥΠΟΔΕΙΓΜΑ ΘΕΩΡΗΤΙΚΩΝ ΕΡΩΤΗΣΕΩΝ ΕΞΕΤΑΣΕΩΝ
 ΥΠΟΔΕΙΓΜΑ ΘΕΩΡΗΤΙΚΩΝ ΕΡΩΤΗΣΕΩΝ ΕΞΕΤΑΣΕΩΝ 1. Πώς ορίζεται η περίσσεια αέρα και η ισχύς μίγματος σε μία καύση; 2. Σε ποιές περιπτώσεις παρατηρείται μή μόνιμη μετάδοση της θερμότητας; 3. Τί είναι η αντλία
ΥΠΟΔΕΙΓΜΑ ΘΕΩΡΗΤΙΚΩΝ ΕΡΩΤΗΣΕΩΝ ΕΞΕΤΑΣΕΩΝ 1. Πώς ορίζεται η περίσσεια αέρα και η ισχύς μίγματος σε μία καύση; 2. Σε ποιές περιπτώσεις παρατηρείται μή μόνιμη μετάδοση της θερμότητας; 3. Τί είναι η αντλία
ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ
 ΜΕΡΟΣ ΙΙ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ 36 ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Πολλές από τις αποφάσεις
ΜΕΡΟΣ ΙΙ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ 36 ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Πολλές από τις αποφάσεις
ΘΕΡΜΟ ΥΝΑΜΙΚΗ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ (ΘΧΜ) 1. ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ 2. ΘΕΜΕΛΙΑ
 ΘΕΡΜΟ ΥΝΑΜΙΚΗ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ (ΘΧΜ) 1. ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ 2. ΘΕΜΕΛΙΑ 1 1. ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ Σκοπός της θερμοδυναμικής χημικής μηχανικής είναι η παροχή των κατάλληλων θεωρητικών γνώσεων και των
ΘΕΡΜΟ ΥΝΑΜΙΚΗ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ (ΘΧΜ) 1. ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ 2. ΘΕΜΕΛΙΑ 1 1. ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ Σκοπός της θερμοδυναμικής χημικής μηχανικής είναι η παροχή των κατάλληλων θεωρητικών γνώσεων και των
Χημική Κινητική Γενικές Υποδείξεις 1. Τάξη Αντίδρασης 2. Ενέργεια Ενεργοποίησης
 Χημική Κινητική Γενικές Υποδείξεις 1. Τάξη Αντίδρασης Γενικά, όταν έχουμε δεδομένα συγκέντρωσης-χρόνου και θέλουμε να βρούμε την τάξη μιας αντίδρασης, προσπαθούμε να προσαρμόσουμε τα δεδομένα σε εξισώσεις
Χημική Κινητική Γενικές Υποδείξεις 1. Τάξη Αντίδρασης Γενικά, όταν έχουμε δεδομένα συγκέντρωσης-χρόνου και θέλουμε να βρούμε την τάξη μιας αντίδρασης, προσπαθούμε να προσαρμόσουμε τα δεδομένα σε εξισώσεις
ΙΣΟΡΡΟΠΙΑ ΦΑΣΕΩΝ ΚΑΙ ΤΑΣΗ ΑΤΜΩΝ
 ΙΣΟΡΡΟΠΙΑ ΦΑΣΕΩΝ ΚΑΙ ΤΑΣΗ ΑΤΜΩΝ 2 Διεργασίες Πολυφασικών συστημάτων Πολλές διεργασίες στη Χημική Μηχανική στηρίζονται στη μεταφορά μάζας μεταξύ διαφορετικών φάσεων (αέρια, υγρή, στερεή) Εξάτμιση-Εξάχνωση
ΙΣΟΡΡΟΠΙΑ ΦΑΣΕΩΝ ΚΑΙ ΤΑΣΗ ΑΤΜΩΝ 2 Διεργασίες Πολυφασικών συστημάτων Πολλές διεργασίες στη Χημική Μηχανική στηρίζονται στη μεταφορά μάζας μεταξύ διαφορετικών φάσεων (αέρια, υγρή, στερεή) Εξάτμιση-Εξάχνωση
Ε. Παυλάτου, 2017 ΔΙΕΡΓΑΣΙΕΣ
 ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ 2 ΔΙΕΡΓΑΣΙΕΣ Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική) Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα (τροφοδοσία) και εξερχόμενα ρεύματα (προϊόντα) Διάγραμμα
ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ 2 ΔΙΕΡΓΑΣΙΕΣ Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική) Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα (τροφοδοσία) και εξερχόμενα ρεύματα (προϊόντα) Διάγραμμα
Οι ιδιότητες των αερίων και καταστατικές εξισώσεις. Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι
 Οι ιδιότητες των αερίων και καταστατικές εξισώσεις Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι Τι είναι αέριο; Λέμε ότι μία ουσία βρίσκεται στην αέρια κατάσταση όταν αυθόρμητα
Οι ιδιότητες των αερίων και καταστατικές εξισώσεις Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι Τι είναι αέριο; Λέμε ότι μία ουσία βρίσκεται στην αέρια κατάσταση όταν αυθόρμητα
Τ.Ε.Ι. ΠΕΙΡΑΙΑ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΜΑΘΗΜΑ: ΕΦΑΡΜΟΣΜΕΝΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ (Ασκήσεις πράξης) ΙΔΑΝΙΚΑ ΑΕΡΙΑ - ΕΡΓΟ
 ΙΔΑΝΙΚΑ ΑΕΡΙΑ - ΕΡΓΟ 1. Να υπολογιστεί η πυκνότητα του αέρα σε πίεση 0,1 MPa και θερμοκρασία 20 ο C. (R air =0,287 kj/kgk) 2. Ποσότητα αέρα 1 kg εκτελεί τις παρακάτω διεργασίες: Διεργασία 1-2: Αδιαβατική
ΙΔΑΝΙΚΑ ΑΕΡΙΑ - ΕΡΓΟ 1. Να υπολογιστεί η πυκνότητα του αέρα σε πίεση 0,1 MPa και θερμοκρασία 20 ο C. (R air =0,287 kj/kgk) 2. Ποσότητα αέρα 1 kg εκτελεί τις παρακάτω διεργασίες: Διεργασία 1-2: Αδιαβατική
Τεχνολογίες Εκμετάλλευσης και Αξιοποίησης Υδρογονανθράκων
 Τεχνολογίες Εκμετάλλευσης και Αξιοποίησης Υδρογονανθράκων Μάθημα 3 ο Εισαγωγή στο διυλιστήριο Τύποι διεργασιών Απόσταξη (ατμοσφαιρική και υπό κενό) Δρ. Στέλλα Μπεζεργιάννη Διύλιση Το αργό πετρέλαιο δεν
Τεχνολογίες Εκμετάλλευσης και Αξιοποίησης Υδρογονανθράκων Μάθημα 3 ο Εισαγωγή στο διυλιστήριο Τύποι διεργασιών Απόσταξη (ατμοσφαιρική και υπό κενό) Δρ. Στέλλα Μπεζεργιάννη Διύλιση Το αργό πετρέλαιο δεν
Εφηρμοσμένη Θερμοδυναμική
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφηρμοσμένη Θερμοδυναμική Ενότητα 8: Θερμοδυναμικά κύκλα Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφηρμοσμένη Θερμοδυναμική Ενότητα 8: Θερμοδυναμικά κύκλα Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ
 . ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 135 ΔΙΑΓΡΑΜΜΑΤΑ ΦΑΣΕΩΝ 1 2 3 4 1 στερεό (solid) 2 υγρό (liquid) 3 ατμός (vapor) 4 αέριο (gas) A 1+2+3
. ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 135 ΔΙΑΓΡΑΜΜΑΤΑ ΦΑΣΕΩΝ 1 2 3 4 1 στερεό (solid) 2 υγρό (liquid) 3 ατμός (vapor) 4 αέριο (gas) A 1+2+3
Φυσικές Διεργασίες Πέμπτη Διάλεξη
 Φυσικές Διεργασίες Πέμπτη Διάλεξη Δευτέρα, 12 Μαΐου 2008 Απορρόφηση αερίων 1. Ορισμός Τι είναι απορρόφηση; Είναι μεταφορά μέσω της διεπιφάνειας αερίου-υγρού ενός συστατικού από αέριο μίγμα σε έναν υγρό
Φυσικές Διεργασίες Πέμπτη Διάλεξη Δευτέρα, 12 Μαΐου 2008 Απορρόφηση αερίων 1. Ορισμός Τι είναι απορρόφηση; Είναι μεταφορά μέσω της διεπιφάνειας αερίου-υγρού ενός συστατικού από αέριο μίγμα σε έναν υγρό
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση 4: Μερικός γραμμομοριακός όγκος Αθανάσιος Τσεκούρας Τμήμα Χημείας . Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 5 4. Τελικά αποτελέσματα... 7 Σελίδα
Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση 4: Μερικός γραμμομοριακός όγκος Αθανάσιος Τσεκούρας Τμήμα Χημείας . Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 5 4. Τελικά αποτελέσματα... 7 Σελίδα
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 Ακαδημαϊκό έτος 34 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Επώνυμο: Όνομα: Προσωπικός Αριθμός: Ημερομηνία: Βαθμολογία θεμάτων 3 4 5 6 7 8 9 Γενικός Βαθμός η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ ΣΤΗ "ΦΥΣΙΚΟΧΗΜΕΙΑ" ΟΔΗΓΙΕΣ ΓΙΑ ΤΗΝ ΕΚΠΟΝΗΣΗ,
Ακαδημαϊκό έτος 34 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Επώνυμο: Όνομα: Προσωπικός Αριθμός: Ημερομηνία: Βαθμολογία θεμάτων 3 4 5 6 7 8 9 Γενικός Βαθμός η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ ΣΤΗ "ΦΥΣΙΚΟΧΗΜΕΙΑ" ΟΔΗΓΙΕΣ ΓΙΑ ΤΗΝ ΕΚΠΟΝΗΣΗ,
Κεφάλαιο 5: Διεργασίες απόσταξης
 92 Κεφάλαιο 5: Διεργασίες απόσταξης Σύνοψη Το κεφάλαιο αυτό συνιστά την πρώτη ολοκληρωμένη ανάλυση μίας διεργασίας. Παρουσιάζονται στην αρχή οι απλές αποστάξεις και στη συνέχεια αναλύεται διεξοδικά η κλασματική
92 Κεφάλαιο 5: Διεργασίες απόσταξης Σύνοψη Το κεφάλαιο αυτό συνιστά την πρώτη ολοκληρωμένη ανάλυση μίας διεργασίας. Παρουσιάζονται στην αρχή οι απλές αποστάξεις και στη συνέχεια αναλύεται διεξοδικά η κλασματική
Πρόρρηση. Φυσικών Ιδιοτήτων Μιγμάτων
 Πρόρρηση Φυσικών Ιδιοτήτων Μιγμάτων Συντελεστής συμπιεστότητας, Ζ Αρχή Αντιστοίχων Καταστάσεων Τριών παραμέτρων Ptzer : z z (0) + ω z (1) Lee-Kesler: z (0), z (1) f(t r,p r ) Εξίσωση Ptzer Κανόνες Ανάμειξης
Πρόρρηση Φυσικών Ιδιοτήτων Μιγμάτων Συντελεστής συμπιεστότητας, Ζ Αρχή Αντιστοίχων Καταστάσεων Τριών παραμέτρων Ptzer : z z (0) + ω z (1) Lee-Kesler: z (0), z (1) f(t r,p r ) Εξίσωση Ptzer Κανόνες Ανάμειξης
Παρασκευαστικό διαχωρισμό πολλών ουσιών με κατανομή μεταξύ των δύο διαλυτών.
 1. ΕΚΧΥΛΙΣΗ Η εκχύλιση είναι μία από τις πιο συνηθισμένες τεχνικές διαχωρισμού και βασίζεται στην ισορροπία κατανομής μιας ουσίας μεταξύ δύο φάσεων, που αναμιγνύονται ελάχιστα μεταξύ τους. Η ευρύτητα στη
1. ΕΚΧΥΛΙΣΗ Η εκχύλιση είναι μία από τις πιο συνηθισμένες τεχνικές διαχωρισμού και βασίζεται στην ισορροπία κατανομής μιας ουσίας μεταξύ δύο φάσεων, που αναμιγνύονται ελάχιστα μεταξύ τους. Η ευρύτητα στη
5 Μετρητές παροχής. 5.1Εισαγωγή
 5 Μετρητές παροχής 5.Εισαγωγή Τρεις βασικές συσκευές, με τις οποίες μπορεί να γίνει η μέτρηση της ογκομετρικής παροχής των ρευστών, είναι ο μετρητής Venturi (ή βεντουρίμετρο), ο μετρητής διαφράγματος (ή
5 Μετρητές παροχής 5.Εισαγωγή Τρεις βασικές συσκευές, με τις οποίες μπορεί να γίνει η μέτρηση της ογκομετρικής παροχής των ρευστών, είναι ο μετρητής Venturi (ή βεντουρίμετρο), ο μετρητής διαφράγματος (ή
Υποθέστε ότι ο ρυθμός ροής από ένα ακροφύσιο είναι γραμμική συνάρτηση της διαφοράς στάθμης στα δύο άκρα του ακροφυσίου.
 ΕΡΩΤΗΜΑ Δίνεται το σύστημα δεξαμενών του διπλανού σχήματος, όπου: q,q : h,h : Α : R : οι παροχές υγρού στις δύο δεξαμενές, τα ύψη του υγρού στις δύο δεξαμενές, η διατομή των δεξαμενών και η αντίσταση ροής
ΕΡΩΤΗΜΑ Δίνεται το σύστημα δεξαμενών του διπλανού σχήματος, όπου: q,q : h,h : Α : R : οι παροχές υγρού στις δύο δεξαμενές, τα ύψη του υγρού στις δύο δεξαμενές, η διατομή των δεξαμενών και η αντίσταση ροής
ΣΤΑΘΜΟΙ ΠΑΡΑΓΩΓΗΣ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΣΤΑΘΜΟΙ ΠΑΡΑΓΩΓΗΣ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ Ενότητα 11: Κύκλα ατμού Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΣΤΑΘΜΟΙ ΠΑΡΑΓΩΓΗΣ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ Ενότητα 11: Κύκλα ατμού Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και
Φυσικοί μετασχηματισμοί καθαρών ουσιών
 Φυσικοί μετασχηματισμοί καθαρών ουσιών Ή εξάτμιση, η τήξη και η μετατροπή του γραφίτη σε διαμάντι αποτελούν συνηθισμένα παραδείγματα αλλαγών φάσης χωρίς μεταβολή της χημικής σύστασης. Ορισμός φάσης: Μια
Φυσικοί μετασχηματισμοί καθαρών ουσιών Ή εξάτμιση, η τήξη και η μετατροπή του γραφίτη σε διαμάντι αποτελούν συνηθισμένα παραδείγματα αλλαγών φάσης χωρίς μεταβολή της χημικής σύστασης. Ορισμός φάσης: Μια
ΥΠΟΔΕΙΓΜΑ ΑΣΚΗΣΕΩΝ ΓΡΑΠΤΩΝ ΕΞΕΤΑΣΕΩΝ
 ΥΠΟΔΕΙΓΜΑ ΑΣΚΗΣΕΩΝ ΓΡΑΠΤΩΝ ΕΞΕΤΑΣΕΩΝ 1. Να υπολογιστεί η μαζική παροχή του ατμού σε (kg/h) που χρησιμοποιείται σε ένα θερμαντήρα χυμού με τα παρακάτω στοιχεία: αρχική θερμοκρασία χυμού 20 C, τελική θερμοκρασία
ΥΠΟΔΕΙΓΜΑ ΑΣΚΗΣΕΩΝ ΓΡΑΠΤΩΝ ΕΞΕΤΑΣΕΩΝ 1. Να υπολογιστεί η μαζική παροχή του ατμού σε (kg/h) που χρησιμοποιείται σε ένα θερμαντήρα χυμού με τα παρακάτω στοιχεία: αρχική θερμοκρασία χυμού 20 C, τελική θερμοκρασία
ΣΥΜΠΥΚΝΩΤΕΣ ΑΝΕΡΧΟΜΕΝΗΣ Ή ΚΑΤΕΡΧΟΜΕΝΗΣ ΣΤΙΒΑ ΑΣ
 Στην προκειµένη περίπτωση, µια φυγοκεντρική αντλία ωθεί το υγρό να περάσει µέσα από τους σωλήνες µε ταχύτητες από 2 µέχρι 6 m/s. Στους σωλήνες υπάρχει επαρκές υδροστατικό ύψος, ώστε να µην συµβεί βρασµός
Στην προκειµένη περίπτωση, µια φυγοκεντρική αντλία ωθεί το υγρό να περάσει µέσα από τους σωλήνες µε ταχύτητες από 2 µέχρι 6 m/s. Στους σωλήνες υπάρχει επαρκές υδροστατικό ύψος, ώστε να µην συµβεί βρασµός
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ. Καθηγητής Δ. Ματαράς
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Καθηγητής Δ. Ματαράς image url 0.Μεταφορά Θερμότητας σε Ρευστά Εναλλάκτης Κελύφους-Αυλών E 2 Β 2 Ατμός F C K Εξαέρωση Β Θερμό Υγρό J E D 2 Α D H Ψυχρό Υγρό Eικόνα
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Καθηγητής Δ. Ματαράς image url 0.Μεταφορά Θερμότητας σε Ρευστά Εναλλάκτης Κελύφους-Αυλών E 2 Β 2 Ατμός F C K Εξαέρωση Β Θερμό Υγρό J E D 2 Α D H Ψυχρό Υγρό Eικόνα
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ ΕΝΤΡΟΠΙΑ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ
 ΕΝΤΡΟΠΙΑ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ 1 ΑΣΚΗΣΗ 1 Το δοχείο του σχήματος είναι απομονωμένο (αδιαβατικά τοιχώματα). Το διάφραγμα χωρίζει το δοχείο σε δύο μέρη. Το αριστερό μέρος έχει όγκο 1 και περιέχει ιδανικό αέριο
ΕΝΤΡΟΠΙΑ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ 1 ΑΣΚΗΣΗ 1 Το δοχείο του σχήματος είναι απομονωμένο (αδιαβατικά τοιχώματα). Το διάφραγμα χωρίζει το δοχείο σε δύο μέρη. Το αριστερό μέρος έχει όγκο 1 και περιέχει ιδανικό αέριο
ΠΑΡΑΡΤΗΜΑ 3 ΥΠΟΛΟΓΙΣΜΟΣ ΔΙΑΓΡΑΜΜΑΤΩΝ ΦΑΣΕΩΝ ΑΠΟ ΘΕΡΜΟΔΥΝΑΜΙΚΑ ΔΕΔΟΜΕΝΑ
 ΠΑΡΑΡΤΗΜΑ 3-ΥΠΟΛΟΓΙΣΜΟΣ ΔΙΑΓΡΑΜΜΑΤΩΝ ΦΑΣΕΩΝ ΠΑΡΑΡΤΗΜΑ 3 ΥΠΟΛΟΓΙΣΜΟΣ ΔΙΑΓΡΑΜΜΑΤΩΝ ΦΑΣΕΩΝ ΑΠΟ ΘΕΡΜΟΔΥΝΑΜΙΚΑ ΔΕΔΟΜΕΝΑ 1 Εισαγωγή Τα διαγράμματα φάσεων δεν είναι εμπειρικά σχήματα αλλά είναι ουσιαστικής σημασίας
ΠΑΡΑΡΤΗΜΑ 3-ΥΠΟΛΟΓΙΣΜΟΣ ΔΙΑΓΡΑΜΜΑΤΩΝ ΦΑΣΕΩΝ ΠΑΡΑΡΤΗΜΑ 3 ΥΠΟΛΟΓΙΣΜΟΣ ΔΙΑΓΡΑΜΜΑΤΩΝ ΦΑΣΕΩΝ ΑΠΟ ΘΕΡΜΟΔΥΝΑΜΙΚΑ ΔΕΔΟΜΕΝΑ 1 Εισαγωγή Τα διαγράμματα φάσεων δεν είναι εμπειρικά σχήματα αλλά είναι ουσιαστικής σημασίας
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις Άσκηση 5: Διαγράμματα σημείων ζέσεως συνθέσεως Αθανάσιος Τσεκούρας Τμήμα Χημείας 1. Θεωρία... 3 2. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 5 Σελίδα 2 1. Θεωρία
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις Άσκηση 5: Διαγράμματα σημείων ζέσεως συνθέσεως Αθανάσιος Τσεκούρας Τμήμα Χημείας 1. Θεωρία... 3 2. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 5 Σελίδα 2 1. Θεωρία
Μηχανική και Ανάπτυξη Διεργασιών
 Μηχανική και Ανάπτυξη Διεργασιών Κωστής Μαγουλάς, Καθηγητής Επαμεινώνδας Βουτσάς, Επ. Καθηγητής 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ . ΟΡΙΣΜΟΣ Οι διαχωρισμοί είναι οι πιο συχνά παρατηρούμενες διεργασίες
Μηχανική και Ανάπτυξη Διεργασιών Κωστής Μαγουλάς, Καθηγητής Επαμεινώνδας Βουτσάς, Επ. Καθηγητής 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ . ΟΡΙΣΜΟΣ Οι διαχωρισμοί είναι οι πιο συχνά παρατηρούμενες διεργασίες
Εφηρμοσμένη Θερμοδυναμική
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφηρμοσμένη Θερμοδυναμική Ενότητα 10: Ψυκτικά κύκλα Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφηρμοσμένη Θερμοδυναμική Ενότητα 10: Ψυκτικά κύκλα Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
Ιωάννης Πούλιος, Καθηγητής Εργ. Φυσικοχημείας Α.Π.Θ. Τηλ
 Φυσικοχημεία II, Διαλύματα Ιωάννης Πούλιος, Καθηγητής Εργ. Φυσικοχημείας Α.Π.Θ. Τηλ. 2310-997785 poulios@chem.auth.gr photocatalysisgroup.web.auth.gr ΚΡΑΜΑΤΑ Χρώμα κραμάτων αποτελούμενα από Χρυσό (Au),
Φυσικοχημεία II, Διαλύματα Ιωάννης Πούλιος, Καθηγητής Εργ. Φυσικοχημείας Α.Π.Θ. Τηλ. 2310-997785 poulios@chem.auth.gr photocatalysisgroup.web.auth.gr ΚΡΑΜΑΤΑ Χρώμα κραμάτων αποτελούμενα από Χρυσό (Au),
Τεχνοοικονομική Μελέτη
 Τμήμα Μηχανολόγων Μηχανικών Τεχνοοικονομική Μελέτη Ενότητα 10: Σχεδιασμός εγκαταστάσεων Σκόδρας Γεώργιος, Αν. Καθηγητής gskodras@uowm.gr Τμήμα Μηχανολόγων Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό
Τμήμα Μηχανολόγων Μηχανικών Τεχνοοικονομική Μελέτη Ενότητα 10: Σχεδιασμός εγκαταστάσεων Σκόδρας Γεώργιος, Αν. Καθηγητής gskodras@uowm.gr Τμήμα Μηχανολόγων Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό
1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17
 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 13 1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17 1.1 Φυσικές Διεργασίες Διαχωρισμού 20 1.1.1 Μια γενική εποπτεία της παραγωγικής Χημικής Βιομηχανίας 21 1.1.2 Σύντομος
ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 13 1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17 1.1 Φυσικές Διεργασίες Διαχωρισμού 20 1.1.1 Μια γενική εποπτεία της παραγωγικής Χημικής Βιομηχανίας 21 1.1.2 Σύντομος
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου (21/6/2017)
 Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο
 Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος 1 ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 7 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος 1 ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 7 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
1. Ο ατμοσφαιρικός αέρας, ως αέριο μίγμα, είναι ομογενές. Άρα, είναι διάλυμα.
 2.8 Διαλύματα Υπόδειξη: Στα αριθμητικά προβλήματα, τα πειραματικά μεγέθη που δίνονται με ένα ή δύο σημαντικά ψηφία θεωρούνται ότι πρακτικά έχουν 3 ή 4 σημαντικά ψηφία. 1. Ο ατμοσφαιρικός αέρας, ως αέριο
2.8 Διαλύματα Υπόδειξη: Στα αριθμητικά προβλήματα, τα πειραματικά μεγέθη που δίνονται με ένα ή δύο σημαντικά ψηφία θεωρούνται ότι πρακτικά έχουν 3 ή 4 σημαντικά ψηφία. 1. Ο ατμοσφαιρικός αέρας, ως αέριο
Enrico Fermi, Thermodynamics, 1937
 I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
Φαινόμενα Μεταφοράς Μάζας θερμότητας
 Φαινόμενα Μεταφοράς Μάζας θερμότητας 2 η Διάλεξη Μηχανισμοί μετάδοσης θερμότητας Εμμανουήλ Σουλιώτης Τμήμα Μηχανικών Περιβάλλοντος Πανεπιστήμιο Δυτικής Μακεδονίας Ακαδημαϊκό Έτος 2018-2019 Μαθησιακοί στόχοι
Φαινόμενα Μεταφοράς Μάζας θερμότητας 2 η Διάλεξη Μηχανισμοί μετάδοσης θερμότητας Εμμανουήλ Σουλιώτης Τμήμα Μηχανικών Περιβάλλοντος Πανεπιστήμιο Δυτικής Μακεδονίας Ακαδημαϊκό Έτος 2018-2019 Μαθησιακοί στόχοι
Κεφάλαιο 20. Θερμότητα
 Κεφάλαιο 20 Θερμότητα Εισαγωγή Για να περιγράψουμε τα θερμικά φαινόμενα, πρέπει να ορίσουμε με προσοχή τις εξής έννοιες: Θερμοκρασία Θερμότητα Θερμοκρασία Συχνά συνδέουμε την έννοια της θερμοκρασίας με
Κεφάλαιο 20 Θερμότητα Εισαγωγή Για να περιγράψουμε τα θερμικά φαινόμενα, πρέπει να ορίσουμε με προσοχή τις εξής έννοιες: Θερμοκρασία Θερμότητα Θερμοκρασία Συχνά συνδέουμε την έννοια της θερμοκρασίας με
Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων
 Φυσικοχημεία II, Διαλύματα Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων o P = N P P = A A A N P o B B B PA + PB = P ολ Τ=const P = Ν ολ P + N P o o A A B B Ν Α + Ν =1 o o o P = P + A N ( ολ
Φυσικοχημεία II, Διαλύματα Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων o P = N P P = A A A N P o B B B PA + PB = P ολ Τ=const P = Ν ολ P + N P o o A A B B Ν Α + Ν =1 o o o P = P + A N ( ολ
ΕΤΚΛ ΕΜΠ. Αργό Πετρέλαιο Χαρακτηριστικά Ιδιότητες. Τεχνολογία Πετρελαίου και. Εργαστήριο Τεχνολογίας Καυσίμων Και Λιπαντικών ΕΜΠ
 Φυσικού Αερίου Σύσταση Αργού Πετρελαίου Σύνθετο Μίγμα Υδρογονανθράκων Περιέχει αέρια διαλελυμένα στα υγρά συστατικά Υδρογονάνθρακες C 1 C 90+ Στοιχειακή Ανάλυση: Αρκετά Ομοιόμορφη Στοιχεία Περιεκτικότητα
Φυσικού Αερίου Σύσταση Αργού Πετρελαίου Σύνθετο Μίγμα Υδρογονανθράκων Περιέχει αέρια διαλελυμένα στα υγρά συστατικά Υδρογονάνθρακες C 1 C 90+ Στοιχειακή Ανάλυση: Αρκετά Ομοιόμορφη Στοιχεία Περιεκτικότητα
ΚΕΦΑΛΑΙΟ 2 ΙΔΙΟΤΗΤΕΣ ΤΩΝ ΚΑΘΑΡΩΝ ΟΥΣΙΩΝ.
 ΚΕΦΑΛΑΙΟ 2 ΙΔΙΟΤΗΤΕΣ ΤΩΝ ΚΑΘΑΡΩΝ ΟΥΣΙΩΝ. 2.1 Η ΕΝΝΟΙΑ ΤΗΣ ΚΑΘΑΡΗΣ ΟΥΣΙΑΣ. Μια ουσία της οποίας η χημική σύσταση παραμένει σταθερή σε όλη της την έκταση ονομάζεται καθαρή ουσία. Δεν είναι υποχρεωτικό να
ΚΕΦΑΛΑΙΟ 2 ΙΔΙΟΤΗΤΕΣ ΤΩΝ ΚΑΘΑΡΩΝ ΟΥΣΙΩΝ. 2.1 Η ΕΝΝΟΙΑ ΤΗΣ ΚΑΘΑΡΗΣ ΟΥΣΙΑΣ. Μια ουσία της οποίας η χημική σύσταση παραμένει σταθερή σε όλη της την έκταση ονομάζεται καθαρή ουσία. Δεν είναι υποχρεωτικό να
ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΘΕΡΜΟ ΥΝΑΜΙΚΗΣ
 ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΘΕΡΜΟ ΥΝΑΜΙΚΗΣ. Μια νοικοκυρά µαγειρεύει σε χύτρα, η οποία είναι: (α) ακάλυπτη, (β) καλυµµένη µε ελαφρύ καπάκι και (γ) καλυµµένη µε βαρύ καπάκι. Σε ποια περίπτωση ο χρόνος µαγειρέµατος θα
ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΘΕΡΜΟ ΥΝΑΜΙΚΗΣ. Μια νοικοκυρά µαγειρεύει σε χύτρα, η οποία είναι: (α) ακάλυπτη, (β) καλυµµένη µε ελαφρύ καπάκι και (γ) καλυµµένη µε βαρύ καπάκι. Σε ποια περίπτωση ο χρόνος µαγειρέµατος θα
Εξοικονόμηση Ενέργειας
 Εξοικονόμηση Ενέργειας Θεωρητικό Υπόβαθρο: Θερμοδυναμική Θερμοδυναμική: Η επιστήμη που ασχολείται με τις μετατροπές ενέργειας από μια μορφή σε μια άλλη «Κάθε παραγωγική διαδικασία βρίσκεται κάτω από τον
Εξοικονόμηση Ενέργειας Θεωρητικό Υπόβαθρο: Θερμοδυναμική Θερμοδυναμική: Η επιστήμη που ασχολείται με τις μετατροπές ενέργειας από μια μορφή σε μια άλλη «Κάθε παραγωγική διαδικασία βρίσκεται κάτω από τον
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΗΧΑΝΟΛΟΓΙΑ (7 Ο ΕΞΑΜΗΝΟ)
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΜΕΤΑΛΛΕΙΩΝ - ΜΕΤΑΛΛΟΥΡΓΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΗΧΑΝΟΛΟΓΙΑ (7 Ο ΕΞΑΜΗΝΟ) Νίκος Μ. Κατσουλάκος Μηχανολόγος Μηχανικός Ε.Μ.Π., PhD, Msc ΜΑΘΗΜΑ 4-1 Ο ΨΥΚΤΙΚΟΣ ΚΥΚΛΟΣ, ΤΟ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΜΕΤΑΛΛΕΙΩΝ - ΜΕΤΑΛΛΟΥΡΓΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΗΧΑΝΟΛΟΓΙΑ (7 Ο ΕΞΑΜΗΝΟ) Νίκος Μ. Κατσουλάκος Μηχανολόγος Μηχανικός Ε.Μ.Π., PhD, Msc ΜΑΘΗΜΑ 4-1 Ο ΨΥΚΤΙΚΟΣ ΚΥΚΛΟΣ, ΤΟ
ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΙΑΧΕΙΡΙΣΗΣ ΕΝΕΡΓΕΙΑΚΩΝ ΠΟΡΩΝ ΘΕΡΜΟ ΥΝΑΜΙΚΗ Ι 1
 ΘΕΡΜΟ ΥΝΑΜΙΚΗ Ι ιδάσκων: Καθ. Α.Γ.Τοµπουλίδης ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΙΑΧΕΙΡΙΣΗΣ ΕΝΕΡΓΕΙΑΚΩΝ ΠΟΡΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΥΤΙΚΗΣ ΜΑΚΕ ΟΝΙΑΣ, ΚΟΖΑΝΗ Εαρινό εξάµηνο 2003-2004 Άσκηση 1: Κυλινδρικό έµβολο περιέχει αέριο το
ΘΕΡΜΟ ΥΝΑΜΙΚΗ Ι ιδάσκων: Καθ. Α.Γ.Τοµπουλίδης ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΙΑΧΕΙΡΙΣΗΣ ΕΝΕΡΓΕΙΑΚΩΝ ΠΟΡΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΥΤΙΚΗΣ ΜΑΚΕ ΟΝΙΑΣ, ΚΟΖΑΝΗ Εαρινό εξάµηνο 2003-2004 Άσκηση 1: Κυλινδρικό έµβολο περιέχει αέριο το
ΦΥΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι
 ΦΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι Ενότητα 6 η - Β ΜΕΡΟΣ ΔΙΑΛΜΑΤΑ Όνομα καθηγητή: ΕΑΓΓΕΛΙΟ ΒΑΣΙΛΙΚΗ Τμήμα: Επιστήμης Τροφίμων και Διατροφής του Ανθρώπου ΣΤΟΧΟΙ ΤΟ ΜΑΘΗΜΑΤΟΣ Στόχος (): Κατανόηση των εννοιών: υγρά διαλύματα,
ΦΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι Ενότητα 6 η - Β ΜΕΡΟΣ ΔΙΑΛΜΑΤΑ Όνομα καθηγητή: ΕΑΓΓΕΛΙΟ ΒΑΣΙΛΙΚΗ Τμήμα: Επιστήμης Τροφίμων και Διατροφής του Ανθρώπου ΣΤΟΧΟΙ ΤΟ ΜΑΘΗΜΑΤΟΣ Στόχος (): Κατανόηση των εννοιών: υγρά διαλύματα,
Εφαρμοσμένη Θερμοδυναμική
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφαρμοσμένη Θερμοδυναμική Ενότητα 5: Πρώτος νόμος της θερμοδυναμικής Εφαρμογή σε ανοικτά συστήματα Χατζηαθανασίου Βασίλειος Καδή Στυλιανή
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφαρμοσμένη Θερμοδυναμική Ενότητα 5: Πρώτος νόμος της θερμοδυναμικής Εφαρμογή σε ανοικτά συστήματα Χατζηαθανασίου Βασίλειος Καδή Στυλιανή
Οδηγίες χρήσης Aspen Plus 7.1
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Εργαστήριο Θερμοδυναμικής & Φαινομένων Μεταφοράς Οδηγίες χρήσης Aspen Plus 7.1 Έναρξη προσομοίωσης (1/2) Έναρξη προσομοίωσης (2/2) Εμφανίζεται το ακόλουθο
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Εργαστήριο Θερμοδυναμικής & Φαινομένων Μεταφοράς Οδηγίες χρήσης Aspen Plus 7.1 Έναρξη προσομοίωσης (1/2) Έναρξη προσομοίωσης (2/2) Εμφανίζεται το ακόλουθο
Εφηρμοσμένη Θερμοδυναμική
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφηρμοσμένη Θερμοδυναμική Ενότητα 11: Μίγματα Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφηρμοσμένη Θερμοδυναμική Ενότητα 11: Μίγματα Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Άδειες
ΝΟΜΟΙ ΑΕΡΙΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ
 ΝΟΜΟΙ ΑΕΡΙΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΑΣΚΗΣΗ 1 Μία θερμική μηχανή λειτουργεί μεταξύ των θερμοκρασιών T h 400 Κ και T c με T c < T h Η μηχανή έχει απόδοση e 0,2 και αποβάλλει στη δεξαμενή χαμηλής θερμοκρασίας θερμότητα
ΝΟΜΟΙ ΑΕΡΙΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΑΣΚΗΣΗ 1 Μία θερμική μηχανή λειτουργεί μεταξύ των θερμοκρασιών T h 400 Κ και T c με T c < T h Η μηχανή έχει απόδοση e 0,2 και αποβάλλει στη δεξαμενή χαμηλής θερμοκρασίας θερμότητα
ΘΕΡΜΑΝΣΗ-ΨΥΞΗ-ΚΛΙΜΑΤΙΣΜΟΣ Ι ΑΣΚΗΣΕΙΣ
 ΘΕΡΜΑΝΣΗ-ΨΥΞΗ-ΚΛΙΜΑΤΙΣΜΟΣ Ι ΑΣΚΗΣΕΙΣ 1. Ψυκτική εγκατάσταση που ακολουθεί στοιχειώδη ψυκτικό κύκλο συμπίεσης ατμών με ψυκτικό μέσο R134a, εργάζεται μεταξύ των ορίων πίεσης 0,12 MΡa και 1 MΡa. Αν η παροχή
ΘΕΡΜΑΝΣΗ-ΨΥΞΗ-ΚΛΙΜΑΤΙΣΜΟΣ Ι ΑΣΚΗΣΕΙΣ 1. Ψυκτική εγκατάσταση που ακολουθεί στοιχειώδη ψυκτικό κύκλο συμπίεσης ατμών με ψυκτικό μέσο R134a, εργάζεται μεταξύ των ορίων πίεσης 0,12 MΡa και 1 MΡa. Αν η παροχή
ΑΕΝ ΜΑΚΕ ΟΝΙΑΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 2013 ΨΥΚΤΙΚΕΣ ΚΑΙ ΚΛΙΜΑΤΙΣΤΙΚΕΣ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΠΛΟΙΩΝ ΣΤ ΕΞΑΜΗΝΟΥ ΑΣΚΗΣΕΙΣ.
 ΑΕΝ ΜΑΚΕ ΟΝΙΑΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 2013 ΨΥΚΤΙΚΕΣ ΚΑΙ ΚΛΙΜΑΤΙΣΤΙΚΕΣ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΠΛΟΙΩΝ ΣΤ ΕΞΑΜΗΝΟΥ ΑΣΚΗΣΕΙΣ. 1. Παροχη αερα 600kg/h περναει από ένα ψυχρο εναλλακτη. Η αρχικη θερμοκρασια
ΑΕΝ ΜΑΚΕ ΟΝΙΑΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 2013 ΨΥΚΤΙΚΕΣ ΚΑΙ ΚΛΙΜΑΤΙΣΤΙΚΕΣ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΠΛΟΙΩΝ ΣΤ ΕΞΑΜΗΝΟΥ ΑΣΚΗΣΕΙΣ. 1. Παροχη αερα 600kg/h περναει από ένα ψυχρο εναλλακτη. Η αρχικη θερμοκρασια
Ιδιότητες Μιγμάτων. Μερικές Μολαρικές Ιδιότητες
 Ιδιότητες Μιγμάτων Μερικές Μολαρικές Ιδιότητες ΙΔΑΝΙΚΟ ΔΙΑΛΥΜΑ = ή διαιρεμένη διά του = x όπου όλα τα προσδιορίζονται στην ίδια T και P. = Όπου ή διαιρεμένη διά του : = x ορίζεται η μερική μολαρική ιδιότητα
Ιδιότητες Μιγμάτων Μερικές Μολαρικές Ιδιότητες ΙΔΑΝΙΚΟ ΔΙΑΛΥΜΑ = ή διαιρεμένη διά του = x όπου όλα τα προσδιορίζονται στην ίδια T και P. = Όπου ή διαιρεμένη διά του : = x ορίζεται η μερική μολαρική ιδιότητα
ΠΡΟΒΛΗΜΑΤΑ Υ/Υ ΕΚΧΥΛΙΣΗΣ Κ. Μάτης
 ΠΡΟΒΛΗΜΑΤΑ Υ/Υ ΕΚΧΥΛΙΣΗΣ Κ. Μάτης Πρόβληµα 36. Μια υγρή τροφοδοσία 3,5 kg/s, που περιέχει µια διαλυτή ουσία Β διαλυµένη σε συστατικό Α, πρόκειται να διεργαστεί µε ένα διαλύτη S σε µια µονάδα επαφής καθ
ΠΡΟΒΛΗΜΑΤΑ Υ/Υ ΕΚΧΥΛΙΣΗΣ Κ. Μάτης Πρόβληµα 36. Μια υγρή τροφοδοσία 3,5 kg/s, που περιέχει µια διαλυτή ουσία Β διαλυµένη σε συστατικό Α, πρόκειται να διεργαστεί µε ένα διαλύτη S σε µια µονάδα επαφής καθ
Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού
 EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Μάθημα Επιλογής 8 ου εξαμήνου Διδάσκων:
EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Μάθημα Επιλογής 8 ου εξαμήνου Διδάσκων:
ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΙΔΑΝΙΚΩΝ ΑΝΤΙΔΡΑΣΤΗΡΩΝ ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΙΔΑΝΙΚΩΝ ΑΝΤΙΔΡΑΣΤΗΡΩΝ
 Εισαγωγή Διαδικασία σχεδιασμού αντιδραστήρα: Καθορισμός του τύπου του αντιδραστήρα και των συνθηκών λειτουργίας. Εκτίμηση των χαρακτηριστικών για την ομαλή λειτουργία του αντιδραστήρα. μέγεθος σύσταση
Εισαγωγή Διαδικασία σχεδιασμού αντιδραστήρα: Καθορισμός του τύπου του αντιδραστήρα και των συνθηκών λειτουργίας. Εκτίμηση των χαρακτηριστικών για την ομαλή λειτουργία του αντιδραστήρα. μέγεθος σύσταση
Βασικές Διεργασίες Μηχανικής Τροφίμων
 Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 8: Εκχύλιση, 1ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Τύποι εκχύλισης
Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 8: Εκχύλιση, 1ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Τύποι εκχύλισης
Σφαιρικές συντεταγμένες (r, θ, φ).
 T T r e r 1 T e r Σφαιρικές συντεταγμένες (r, θ, φ). 1 T e. (2.57) r sin u u e u e u e, (2.58) r r οπότε το εσωτερικό γινόμενο u.t γίνεται: T u T u T u. T ur. (2.59) r r r sin 2.5 Η ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ
T T r e r 1 T e r Σφαιρικές συντεταγμένες (r, θ, φ). 1 T e. (2.57) r sin u u e u e u e, (2.58) r r οπότε το εσωτερικό γινόμενο u.t γίνεται: T u T u T u. T ur. (2.59) r r r sin 2.5 Η ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ
ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ
 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ Κεφάλαιο Πρόλογος i Κατάλογος Σχημάτων και Εικόνων v Ενότητα 1: Εισαγωγή 1-1 1.1 Το μαθηματικό πρότυπο: ισοζύγια και άλλες σχέσεις. 1-1 1.2 Αριστοποίηση 1-2 1.3 Αλλαγή κλίμακας (scale
ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ Κεφάλαιο Πρόλογος i Κατάλογος Σχημάτων και Εικόνων v Ενότητα 1: Εισαγωγή 1-1 1.1 Το μαθηματικό πρότυπο: ισοζύγια και άλλες σχέσεις. 1-1 1.2 Αριστοποίηση 1-2 1.3 Αλλαγή κλίμακας (scale
