ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation
|
|
|
- Κωνσταντίνος Στεφανόπουλος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation
2 ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ 1. ΟΡΙΣΜΟΣ ΣΚΟΠΟΣ ΔΙΕΡΓΑΣΙΑΣ 2. ΕΙΣΑΓΩΓΗ - Ιστορικά στοιχεία -Οπτικό υλικό (φωτός, videos, etc) -Χρήσεις, παραδείγματα -Γενικός εξοπλισμός 3. ΒΑΣΙΚΕΣ ΑΡΧΕΣ -Αρχές ισορροπίας (θερμοδυναμική, Φαινόμενα μεταφοράς, κλπ) -Ειδικά διαγράμματα 4. ΠΕΡΙΓΡΑΦΗ -Διάγραμμα ροής -Ισοζύγια μάζας/ενέργειας -Βασικά μεγέθη/μεταβλητές -Σχεδιαστικό πρόβλημα (δεδομένα, ζητούμενα) 5. ΜΕΘΟΔΟΛΟΓΙΕΣ - Γραφική μέθοδος - Radford rice 6. ΕΞΟΠΛΙΣΜΟΣ-ΣΧΕΔΙΑΣΜΟΣ ΕΞΟΠΛΙΣΜΟΥ 7. ΕΙΔΙΚΕΣ ΠΕΡΙΠΤΩΣΕΙΣ
3 Ορισμός Η απόσταξη ισορροπίας ή στιγμιαία απόσταξη αποτελεί μία απλή διεργασία διαχωρισμού, η εφαρμογή της οποίας βασίζεται στην ατμοποίηση μέρους της τροφοδοσίας εντός δοχείου και την επίτευξη ισορροπίας μεταξύ των δύο φάσεων (υγρής-αέριας) που δημιουργούνται. Η εξάτμιση αποτελεί μια από τις ευκολότερες διεργασίες διαχωρισμού. Ένα υγρό ρεύμα που περιέχει διάφορα συστατικά εξατμίζεται μερικώς σε έναν θάλαμο σε συγκεκριμένη πίεση και θερμοκρασία. Αυτό έχεις ως αποτέλεσμα τη δημιουργία δυο φάσεων: μια ατμώδη φάση, εμπλουτισμένη στα πιο πτητικά συστατικά, και μια υγρή φάση, εμπλουτισμένη στα λιγότερο πτητικά συστατικά.
4 Διάταξη Απόσταξης Ισορροπίας (1) Το υγρό συμπιέζεται και θερμαίνεται και στη συνέχεια διέρχεται μέσω ενός ακροφύσιου μέσα στο θάλαμο. Λόγω της μεγάλης πτώσης πίεσης, ένα μέρος του υγρού ατμοποιείται. Το υγρό ρεύμα συλλέγεται από τον πυθμένα ενώ το αέριο από την κορυφή. Το σύστημα ονομάζεται flash distillation καθώς η εξάτμιση είναι εξαιρετικά γρήγορη από τη στιγμή που εισέρχεται η τροφοδοσία στο θάλαμο. Λόγω της στενής επαφής μεταξύ υγρού και ατμού, το σύστημα στο θάλαμο απόσταξης είναι πολύ κοντά στο στάδιο ισορροπίας.
5 Πότε Χρησιμοποιείται η Απόσταξης Ισορροπίας; Απόσταξη Ισορροπίας= Ένα ενιαίο στάδιο ισορροπίας 1. Όταν απαιτείται πολύ ακατέργαστος διαχωρισμός π.χ. διαχωρισμός ελαίου/ νερού στη διύλιση αργού πετρελαίου 2. Όταν τα πτητικά συστατικά του μίγματος είναι πολύ διαφορετικά π.χ. αφαλάτωση νερού (4000 εργοστάσια παγκοσμίως, παράγουν 13 εκ. lt πόσιμου νερού.
6 Οριζόντια Διάταξη Απόσταξης Ισορροπίας Φίλτρο Ζώνη διαχωρισμού φάσεων Φτερά 1. Είσοδος σε δοχείο εκτόνωσης 2. Ζώνη διαχωρισμού φάσεων / Φτερά: πραγματοποίηση διαχωρισμού 3. Φίλτρο (Deminister): Συγκράτηση σταγονιδίων και επιστροφή τους στην υγρή φάση.
7 Κάθετη Διάταξη Απόσταξης Ισορροπίας
8 Εφαρμογές Απόσταξης Ισορροπίας Παραγωγή φυσικού αερίου Απομάκρυνση CO 2 και H 2 S Αναγέννηση υδρογονανθράκων Απομάκρυνση νερού Απομάκρυνση βαριών υδρογονανθράκων και Κλασματοποίηση (Απόσταξη Ισορροπίας)
9 ΙΣΟΡΡΟΠΙΑ ΦΑΣΕΩΝ y A, y B y A + y B = 1 A. B. p vapor, T vapor p liquid, T liquid A. B. x A, x B x A + x B = 1 Τ liquid = T vapor (στην ισορροπία) p liquid = p vapor (στην ισορροπία) (Χημικό δυναμικό i) liquid = (Χημικό δυναμικό i) vapor Ρυθμός μεταφοράς μάζας = (εμβαδόν) (συντελεστής μεταφοράς μάζας) (δύναμη) Rate Volume = K y a(y A y A ) Rate Volume = K x a(x A x A ) όπου: K y και K x : ολικοί συντελεστές μεταφοράς μάζας αερίου και υγρού y A : γραμμομοριακό κλάσμα αερίου σε ισορροπία με τη συγκέντρωση του υγρού x A xa : γραμμομοριακό κλάσμα υγρού σε ισορροπία με τη συγκέντρωση του αερίου y Aa: εμβαδόν διεπιφάνειας ανά μονάδα όγκου (m2 /m 3 ).
10 Εξίσωση ισορροπίας: Προσδιορισμός K Απόσταξη Ισορροπίας y i = K i x i Μη πολικά συστατικά Υψηλές πιέσεις: K i = y i = f i x i όπου οι συντελεστές τάσης διαφυγής (f i ) υπολογίζονται με κυβικές καταστατικές εξισώσεις (π.χ. PR ή SRK). Τα Κi, όταν αναφέρονται σε ελαφρούς υδρογονάνθρακες, υπολογίζονται από ειδικές σχέσεις ή διαγράμματα (πχ. Εξισώσεις McWilliams ή Διαγράμματα depriester). Πολικά συστατικά - Χαμηλές πιέσεις: K i = γ if i s P i s Pe i f i v P όπου (Pe) i = exp v i l P P RT i s (Pe: Poynting effect) γ i υπολογίζονται με Van Laar, Wilson, UNIFAC f s i, f v i υπολογίζονται με Virial P s i υπολογίζεται με Antoine Ιδανικά διαλύματα/ Νόμος Raoult: K i = P i s P l f i v
11 Προσδιορισμός Κ- Ελαφροί Υδρογονάνθρακες Εξίσωση McWilliams lnk = a T1 T 2 + a T2 T + a T6 + a p1 lnp + a p2 p 2 + a p3 p
12 Διαγράμματα DePriester σε χαμηλές (Αριστερά) και υψηλές (Δεξιά) θερμοκρασίες- Προσδιορισμός Γραφικά
13 Απόσταξη Ισορροπίας Τα προβλήματα απόσταξης ισορροπίας λύνονται με τη χρήση τριών σετ εξισώσεων: Δεδομένα ισορροπίας Ισοζύγια μάζας Ισοζύγια ενέργειας
14 Δεδομένα Ισορροπίας Για Μίγμα Αιθανόλης- Νερού y Eth + y w = 1, x Eth + y w = 1 Τα δεδομένα ισορροπίας δίνονται ως προς το πιο πτητικό συστατικό και μπορούν να παρουσιαστούν γραφικά ως: Διάγραμμα y-x (McCabe- Thiele) Διάγραμμα T- xy Διάγραμμα ενθαλπίας- σύστασης
15 Διάγραμμα y-x (McCabe- Thiele)
16 Διάγραμμα θερμοκρασίας- σύστασης (T- xy) Υπερθερμός ατμός Μίγμα υγρούατμού Υπόψυκτο υγρό Αζεότροπο
17 Θερμοκρασία έναρξης βρασμού- υγροποίησης ΘΕΒ: V = 0 z i = x i z i = y i K i ΘΕY: L = 0 z i = y i z i = K i x i C i=1 C i=1 K i z i = 1 zi K i = 1 Προσδιορισμός κατάστασης ρεύματος διεργασίας Κατάσταση ρεύματος C i=1 K i z i C zi K i i=1 Υπόψυκτο υγρό <1 >1 Κορεσμένο υγρό =1 >1 Μίγμα ατμών- υγρού >1 >1 Κορεσμένος ατμός >1 =1 Υπερθερμός ατμός >1 <1
18 Διάγραμμα ενθαλπίας- σύστασης Σχεδιασμός ισόθερμων ενθαλπίας- σύστασης μέσω χρήσης βοηθητικής γραμμής (Auxiliary line) 1. Φέρετε κάθετη από την καμπύλη κορεσμένου υγρού στη βοηθητική γραμμή. 2. Από τη βοηθητική γραμμή, φέρετε οριζόντια προς την καμπύλη κορεσμένου ατμού. 3. Η γραμμή που συνδέει τα σημεία της καμπύλης κορεσμένου υγρού και ατμού είναι η ισόθερμη.
19 Διάγραμμα ενθαλπίας- σύστασης Σχεδιασμός ισόθερμων ενθαλπίας- σύστασης με βάση το διάγραμμα (Α) θερμοκρασίαςσύστασης και y- x 1. Φέρετε κάθετη από το σημείο Α στο σημείο Α. 2. Σε σταθερή θερμοκρασία, βρίσκεται η σύσταση του ατμού σε ισορροπία (Β ). 3. Φέρετε κάθετη από το σημείο Β στο σημείο Β. 4. Η γραμμή που συνδέει τα σημεία Α και Β είναι η ισόθερμη. Όμοια και με βάση το διάγραμμα x-y
20 Απόσταξη Ισορροπίας- Ισοζύγια Μάζας Παράμετροι Ισοζυγίου Μάζας Σύσταση Τροφοδοσίας: z Σύσταση Ατμώδους Φάσης: y Σύσταση Υγρής Φάσης: x Ρυθμός Ροής Ρεύματος Τροφοδοσίας: F Ρυθμός Ροής Υγρής Φάσης: L Ρυθμός Ροής Ατμώδους Φάσης: V P F T F F X Fi P T P F T F F X Fi P F T F V yi, Hv P F T F FL, xi, h L F z X Fi P T P T P T V yi, Hv V, y, H V V yi, Hv L, xi, h L V yi, Hv L, x, xi, h L X Fi Γενικό Ισοζύγιο Μάζας F = V + L Ισοζύγιο Μάζας Συστατικού ΓΡΑΜΜΗ ΛΕΙΤΟΥΡΓΙΑΣ y = L V x + F V z L, xi, h L F z = V y + L x
21 Εξίσωση Γραμμής Λειτουργίας (1) y = L V x + F z (1) V Γραμμομοριακό κλάσμα της τροφοδοσίας που εξατμίζεται, f = V/F L = F V L V F V = V = 1 V F V F = 1 f f (2) 1, 2 y = 1 f f x + z f Γραμμομοριακό κλάσμα τροφοδοσίας εναπομείναντος υγρού, q = L/F V = F L L V = L F L = L F 1 L F = q 1 q (3) 1, 3 y = q 1 q x q
22 Εξίσωση Γραμμής Λειτουργίας (2) y = L V x + F V z Κλίση y intercept (x=0) slope = L V = 1 f f = q 1 q x intercept (y=0) y intercept x = 0 = F V z = 1 f z = 1 1 q z x intercept y = 0 = F L z = 1 1 f z = 1 q z
23 Γραφική Λύση Απόσταξης Ισορροπίας (1) Η τομή της γραμμής ισορροπίας και της γραμμής λειτουργίας είναι το σημείο στο οποίο το σύστημα βρίσκεται σε ισορροπία x Eth =y Eth =z Eth V/F 1. Φέρετε η γραμμή y=x 2. Φέρετε η γραμμή λειτουργίας με κλίση V/F 3. Το σημείο τομής της γραμμής λειτουργίας με τη γραμμή y=x είναι η σύσταση τροφοδοσίας 4. Οι συστάσεις της υγρής και ατμώδους φάσης προσδιορίζονται από το σημείο τομής της γραμμής λειτουργίας και της καμπύλης ισορροπίας
24 Γραφική Λύση Απόσταξης Ισορροπίας (2) Κλίση Εξίσωσης λειτουργίας: L = 1, V = 0 f = 0 (Μέγιστη σύσταση της ατμώδους φάσης) L = 0, V = 1 f = 1 (Μέγιστη σύσταση της υγρής φάσης) 1 x Fi /f y γραμμή λειτουργίας -(1-f)/f f=0 L=1, V=0 y 0.4 L=0, V=1 0.2 f=1 0 x x Fi x
25 Απόσταξη Ισορροπίας- Ισοζύγια Ενέργειας Παράμετροι Ισοζυγίου Ενέργειας Ενθαλπία: h Θερμότητα θαλάμου απόσταξης: Q flash Θερμοκρασία: Τ Ρυθμός Ροής Ρεύματος Τροφοδοσίας: F Ρυθμός Ροής Υγρής Φάσης: L Ρυθμός Ροής Ατμώδους Φάσης: V P F T F F X Fi P T P F T F F X Fi P F T F V yi, Hv P F F z X Fi P T P T P T V yi, Hv V, y, H V V yi, Hv L, xi, h L V yi, Hv Γενικό Ισοζύγιο Ενέργειας T F FL, xi, h L X Fi L, x, xi, h L Fh F + Q flash = VH v + Lh L, Q flash = 0 (αδιαβατική λειτουργία) L, xi, h L Προσδιορισμός ενθαλπιών τροφοδοσίας, υγρού και αέρια ρεύματος/ Ιδανικά Μίγματα h L T, x = x A C PL,A T T ref Λανθάνουσα θερμότητα Εξάτμισης A (T ref ) h F T F, z = z A C PL,A T F T ref + x B C PL,B T T ref + z B C PL,B T F T ref H v T, y = y A λ A + C pv,a T T ref + y B λ B + C pv,b T T ref
26 Απόσταξη Ισορροπίας - Πολυσυστατικό σύστημα y i = K i x i Fz i = Lx i + Vy i Fz i = Lx i + VK i x i i = 1, C x i = Fz i L + VK i x i = Fz i F V + K i V x i = z i i = 1, C y i = K i z i i = 1, C 1 + K i 1 V F 1 + K i 1 V F C x i = 1, C y i = 1 C x i C y i = 0 C K i z i C z i = 0 i=1 i=1 i=1 i=1 i=1 1 + K i 1 V F i=1 1 + K i 1 V F f V F C = i=1 (K i 1)z i 1 + K i 1 V F = 0 Εξίσωση Rachford-Rice
27 Αλγόριθμος Επίλυσης Απόσταξης- Πολυσυστατικό σύστημα Εξισώσεις: C i=1 C i=1 z i = 1 1 (K i 1)z i 1 + K i 1 V F = 0 (2) x i = z i 1 + K i 1 V F (3) y i = K i x i (4) F = L + V (5) Q = VH v + Lh L Fh F (6)
28 Προσδιορισμός V/F (1) 1 0, ,2 0,4 0,6 0,8 1-0,5-1 c i=1 y i c i=1 x i = 0
29 Διαστασιολόγηση κάθετου εξοπλισμού (1) 1. Προσδιορισμός μέγιστης επιτρεπόμενης ταχύτητας ατμού u perm = K drum ρ L ρ v ρ v, 0.1 K drum Προσδιορισμός εμπειρικής σταθεράς, K drum K drum = Const. exp A + BlnF lv + C(lnF lv ) 2 +D(lnF lv ) 3 +E(lnF lv ) 4 F lv = W L W v ρ v ρ L, Const. = 1.0 ft/s όπου W L, W V : ρυθμός υγρής και ατμώδους φάσης 3. Προσδιορισμός ρυθμού ροής ατμού V lbmol u perm ( ft s )(36000s h = h )A c (ft 2 )ρ v ( lbm ft 3 ) MW vapor ( lbm lbmol ) 4. Εμβαδόν, Διάμετρος και Ύψος θαλάμου κάθετου θαλάμου απόσταξης ισορροπίας A c = V(MW v ) u perm (3600)ρ v D = 4A c π 0.1 h total /D 0.35
30 Διαστασιολόγηση οριζόντιου εξοπλισμού (2) Εμβαδόν και Διάμετρος οριζόντιου θαλάμου απόσταξης ισορροπίας A T = VMW v u perm 3600 ρ v D = VMW v u perm 3600 ρ v C D = VRT, ιδανικά αέρια u perm 3600 C P όπου u perm = K drum ρ L ρ v ρ v, K horizontal = 1.25K vertical
Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης
 Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης Μια αποστακτική στήλη που λειτουργεί σε πίεση 101,3 kpa, διαχωρίζει ένα μίγμα νερούαιθανόλης. Η σύσταση του μίγματος αποτελείται 40 mol% αιθανόλη και η τροφοδοσία
Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης Μια αποστακτική στήλη που λειτουργεί σε πίεση 101,3 kpa, διαχωρίζει ένα μίγμα νερούαιθανόλης. Η σύσταση του μίγματος αποτελείται 40 mol% αιθανόλη και η τροφοδοσία
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Βασικές αρχές Η διεργασία της απόσταξης στηρίζεται
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Βασικές αρχές Η διεργασία της απόσταξης στηρίζεται
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens. ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Περιοχές
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Περιοχές
ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ, 2013
 ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ, 2013 1 Ισορροπία Φάσεων Ανάλογα με τη φύση των συστατικών του μίγματος (ή της ολικής πίεσης του συστήματος) οι τάσεις διαφυγής υπολογίζονται - ανάλογα
ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ, 2013 1 Ισορροπία Φάσεων Ανάλογα με τη φύση των συστατικών του μίγματος (ή της ολικής πίεσης του συστήματος) οι τάσεις διαφυγής υπολογίζονται - ανάλογα
Κεφάλαιο 3 Απόσταξη Ισορροπίας
 Κεφάλαιο 3 Απόσταξη Ισορροπίας Σύνοψη Η απόσταξη ισορροπίας ή στιγμιαία απόσταξη αποτελεί μία απλή διεργασία διαχωρισμού, η εφαρμογή της οποίας βασίζεται στην ατμοποίηση μέρους της τροφοδοσίας εντός δοχείου
Κεφάλαιο 3 Απόσταξη Ισορροπίας Σύνοψη Η απόσταξη ισορροπίας ή στιγμιαία απόσταξη αποτελεί μία απλή διεργασία διαχωρισμού, η εφαρμογή της οποίας βασίζεται στην ατμοποίηση μέρους της τροφοδοσίας εντός δοχείου
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens. ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Gas Absorption
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Gas Absorption Παράγοντες που Επηρεάζουν Διεργασία Απορρόφησης Συνήθως δίνονται: Ρυθμός
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Gas Absorption Παράγοντες που Επηρεάζουν Διεργασία Απορρόφησης Συνήθως δίνονται: Ρυθμός
ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής. Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά)
 ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής (Σηµείωση: Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά) Η απόσταξη στηρίζεται στη διαφορά που υπάρχει στη σύσταση ισορροπίας των
ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής (Σηµείωση: Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά) Η απόσταξη στηρίζεται στη διαφορά που υπάρχει στη σύσταση ισορροπίας των
Ακρίβεια αποτελεσμάτων σχεδιασμού διεργασιών ΜΑΔ, 2013
 Ακρίβεια αποτελεσμάτων σχεδιασμού διεργασιών ΜΑΔ, 2013 1 ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ ΘΧΜ Σκοπός της θερμοδυναμικής χημικής μηχανικής είναι η παροχή των κατάλληλων θεωρητικών γνώσεων και των απαραίτητων υπολογιστικών-μεθοδολογικών
Ακρίβεια αποτελεσμάτων σχεδιασμού διεργασιών ΜΑΔ, 2013 1 ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ ΘΧΜ Σκοπός της θερμοδυναμικής χημικής μηχανικής είναι η παροχή των κατάλληλων θεωρητικών γνώσεων και των απαραίτητων υπολογιστικών-μεθοδολογικών
ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ
 . ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 135 ΔΙΑΓΡΑΜΜΑΤΑ ΦΑΣΕΩΝ 1 2 3 4 1 στερεό (solid) 2 υγρό (liquid) 3 ατμός (vapor) 4 αέριο (gas) A 1+2+3
. ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 135 ΔΙΑΓΡΑΜΜΑΤΑ ΦΑΣΕΩΝ 1 2 3 4 1 στερεό (solid) 2 υγρό (liquid) 3 ατμός (vapor) 4 αέριο (gas) A 1+2+3
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens. ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Τριγωνικές
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Τριγωνικές
ΒΑΣΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ ΙΦ - ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ, 2013
 ΒΑΣΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ ΙΦ - ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ, 2013 1 Βασικοί Υπολογισμοί Ισορροπίας Φάσεων Ατμών Υγρού Οι βασικοί υπολογισμοί που ενδιαέρουν τον χημικό μηχανικό είναι οι ακόλουθοι : σημείο
ΒΑΣΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ ΙΦ - ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ, 2013 1 Βασικοί Υπολογισμοί Ισορροπίας Φάσεων Ατμών Υγρού Οι βασικοί υπολογισμοί που ενδιαέρουν τον χημικό μηχανικό είναι οι ακόλουθοι : σημείο
Πρόρρηση Ισορροπίας Φάσεων. Υψηλές Πιέσεις
 Πρόρρηση Ισορροπίας Φάσεων Υψηλές Πιέσεις 1 Ισορροπία Φάσεων Η βασική εξίσωση για όλους τους υπολογισμούς ισορροπίας φάσεων ατμού-υγρού είτε σε υψηλές είτε σε χαμηλές πιέσεις είναι η ισότητα των τάσεων
Πρόρρηση Ισορροπίας Φάσεων Υψηλές Πιέσεις 1 Ισορροπία Φάσεων Η βασική εξίσωση για όλους τους υπολογισμούς ισορροπίας φάσεων ατμού-υγρού είτε σε υψηλές είτε σε χαμηλές πιέσεις είναι η ισότητα των τάσεων
ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ
 ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Παράδειγμα 1 Σε μονάδα εκχύλισης μιας μόνο βαθμίδας πραγματοποιείται εκχύλιση οξικού οξέος από νερό με χρήση βουτανόλης. Η τροφοδοσία παροχής F= 100 kg/h περιέχει οξικό
ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Παράδειγμα 1 Σε μονάδα εκχύλισης μιας μόνο βαθμίδας πραγματοποιείται εκχύλιση οξικού οξέος από νερό με χρήση βουτανόλης. Η τροφοδοσία παροχής F= 100 kg/h περιέχει οξικό
Φάσεις μιας καθαρής ουσίας
 Αντικείμενο μαθήματος: ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι ΚΑΘΑΡΕΣ ΟΥΣΙΕΣ. Διαδικασίες αλλαγής φάσης. P-v, T-v, και P-T διαγράμματα ιδιοτήτων και επιφάνειες P-v-T Καθαρών ουσιών. Υπολογισμός θερμοδυναμικών ιδιοτήτων από πίνακες
Αντικείμενο μαθήματος: ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι ΚΑΘΑΡΕΣ ΟΥΣΙΕΣ. Διαδικασίες αλλαγής φάσης. P-v, T-v, και P-T διαγράμματα ιδιοτήτων και επιφάνειες P-v-T Καθαρών ουσιών. Υπολογισμός θερμοδυναμικών ιδιοτήτων από πίνακες
3 Η ΣΕΙΡΑ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΔΙΕΡΓΑΣΙΩΝ - PC-LAB ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ: ΑΣΚΗΣΗ 1 ΠΡΟΣΟΜΟΙΩΣΗ ΜΟΝΑΔΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ
 3 Η ΣΕΙΡΑ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΔΙΕΡΓΑΣΙΩΝ - PC-LAB ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ: 23.12.2015 ΑΣΚΗΣΗ 1 ΠΡΟΣΟΜΟΙΩΣΗ ΜΟΝΑΔΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ Ένα τυπικό φυσικό αέριο έχει την ακόλουθη σύσταση σε % mol: 0.5% Ν 2,
3 Η ΣΕΙΡΑ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΔΙΕΡΓΑΣΙΩΝ - PC-LAB ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ: 23.12.2015 ΑΣΚΗΣΗ 1 ΠΡΟΣΟΜΟΙΩΣΗ ΜΟΝΑΔΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ Ένα τυπικό φυσικό αέριο έχει την ακόλουθη σύσταση σε % mol: 0.5% Ν 2,
ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΛΑΣΜΑΤΙΚΗΣ ΑΠΟΣΤΑΞΗΣ
 ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΛΑΣΜΑΤΙΚΗΣ ΑΠΟΣΤΑΞΗΣ Παράδειγμα 1 Μια αποστακτική στήλη διαχωρίζει μια τροφοδοσία κορεσμένου ατμού με ρυθμό ροής 100 kmol/h και σύσταση 30 mol% αιθανόλη (E), 25 mol% i- προπανόλη (i-p), 35
ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΛΑΣΜΑΤΙΚΗΣ ΑΠΟΣΤΑΞΗΣ Παράδειγμα 1 Μια αποστακτική στήλη διαχωρίζει μια τροφοδοσία κορεσμένου ατμού με ρυθμό ροής 100 kmol/h και σύσταση 30 mol% αιθανόλη (E), 25 mol% i- προπανόλη (i-p), 35
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διαφορική (batch) Rectifying column Stripping column
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διαφορική (batch) Rectifying column Stripping column
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Ορισμός Βασικές έννοιες Απόσταξη (Distillation) είναι
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Ορισμός Βασικές έννοιες Απόσταξη (Distillation) είναι
Βασικοί Υπολογισµοί Ισορροπίας Φάσεων Ατµών Υγρού
 Σηµειώσεις Προχωρηµένης Τεχνικής Φυσικών ιεργασιών 33 3 Βασικοί Υπολογισµοί Ισορροπίας Φάσεων Ατµών Υγρού 3.1 Εισαγωγή Οι βασικοί υπολογισµοί ισορροπίας φάσεων ατµών-υγρού που ενδιαφέρουν το χηµικό µηχανικό
Σηµειώσεις Προχωρηµένης Τεχνικής Φυσικών ιεργασιών 33 3 Βασικοί Υπολογισµοί Ισορροπίας Φάσεων Ατµών Υγρού 3.1 Εισαγωγή Οι βασικοί υπολογισµοί ισορροπίας φάσεων ατµών-υγρού που ενδιαφέρουν το χηµικό µηχανικό
5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού
 5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού Η αρχική εξίσωση που χρησιμοποιείται για τους υπολογισμούς της ΙΦΥΥ είναι η ικανοποίηση της βασικής θερμοδυναμικής απαίτησης της ισότητας των τάσεων διαφυγής
5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού Η αρχική εξίσωση που χρησιμοποιείται για τους υπολογισμούς της ΙΦΥΥ είναι η ικανοποίηση της βασικής θερμοδυναμικής απαίτησης της ισότητας των τάσεων διαφυγής
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Στόχος: Επεξεργασία συγκεκριμένης τροφοδοσίας (ροή
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Στόχος: Επεξεργασία συγκεκριμένης τροφοδοσίας (ροή
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Ι & ΙΙ Εργαστηριακή Άσκηση 4: ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ
 Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Σχεδιασμού, Ανάλυσης & Ανάπτυξης Διεργασιών και Συστημάτων ΕΡΓΑΣΤΗΡΙΟ ΣΧΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διευθυντής: Ι.
Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Σχεδιασμού, Ανάλυσης & Ανάπτυξης Διεργασιών και Συστημάτων ΕΡΓΑΣΤΗΡΙΟ ΣΧΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διευθυντής: Ι.
1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17
 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 13 1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17 1.1 Φυσικές Διεργασίες Διαχωρισμού 20 1.1.1 Μια γενική εποπτεία της παραγωγικής Χημικής Βιομηχανίας 21 1.1.2 Σύντομος
ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 13 1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17 1.1 Φυσικές Διεργασίες Διαχωρισμού 20 1.1.1 Μια γενική εποπτεία της παραγωγικής Χημικής Βιομηχανίας 21 1.1.2 Σύντομος
Θερμοδυναμική Ενότητα 4:
 Θερμοδυναμική Ενότητα 4: Ισοζύγια Ενέργειας και Μάζας σε ανοικτά συστήματα - Ασκήσεις Κυρατζής Νικόλαος Τμήμα Μηχανικών Περιβάλλοντος και Μηχανικών Αντιρρύπανσης ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό
Θερμοδυναμική Ενότητα 4: Ισοζύγια Ενέργειας και Μάζας σε ανοικτά συστήματα - Ασκήσεις Κυρατζής Νικόλαος Τμήμα Μηχανικών Περιβάλλοντος και Μηχανικών Αντιρρύπανσης ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΙΣΟΡΡΟΠΙΑ ΦΑΣΕΩΝ ΚΑΙ ΤΑΣΗ ΑΤΜΩΝ
 ΙΣΟΡΡΟΠΙΑ ΦΑΣΕΩΝ ΚΑΙ ΤΑΣΗ ΑΤΜΩΝ 2 Διεργασίες Πολυφασικών συστημάτων Πολλές διεργασίες στη Χημική Μηχανική στηρίζονται στη μεταφορά μάζας μεταξύ διαφορετικών φάσεων (αέρια, υγρή, στερεή) Εξάτμιση-Εξάχνωση
ΙΣΟΡΡΟΠΙΑ ΦΑΣΕΩΝ ΚΑΙ ΤΑΣΗ ΑΤΜΩΝ 2 Διεργασίες Πολυφασικών συστημάτων Πολλές διεργασίες στη Χημική Μηχανική στηρίζονται στη μεταφορά μάζας μεταξύ διαφορετικών φάσεων (αέρια, υγρή, στερεή) Εξάτμιση-Εξάχνωση
ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης
 ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης Πρόβληµα 1. Ένα µίγµα αερίων που περιέχει 65% του Α, 5% Β, 8% C και % D βρίσκεται σε ισορροπία µ' ένα υγρό στους 350 Κ και 300 kn/m. Αν η τάση ατµών των καθαρών συστατικών
ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης Πρόβληµα 1. Ένα µίγµα αερίων που περιέχει 65% του Α, 5% Β, 8% C και % D βρίσκεται σε ισορροπία µ' ένα υγρό στους 350 Κ και 300 kn/m. Αν η τάση ατµών των καθαρών συστατικών
Θερμοδυναμική Ενότητα 4:
 Θερμοδυναμική Ενότητα 4: Ισοζύγια Ενέργειας και Μάζας σε ανοικτά συστήματα Κυρατζής Νικόλαος Τμήμα Μηχανικών Περιβάλλοντος και Μηχανικών Αντιρρύπανσης ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Θερμοδυναμική Ενότητα 4: Ισοζύγια Ενέργειας και Μάζας σε ανοικτά συστήματα Κυρατζής Νικόλαος Τμήμα Μηχανικών Περιβάλλοντος και Μηχανικών Αντιρρύπανσης ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΩΝ Separation Processes. Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens
 ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΩΝ Separation Processes Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens Διεργασίες Διαχωρισμών Ορισμός Φυσικές διεργασίες οι οποίες
ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΩΝ Separation Processes Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens Διεργασίες Διαχωρισμών Ορισμός Φυσικές διεργασίες οι οποίες
διαιρούμε με το εμβαδό Α 2 του εμβόλου (1)
 1)Συνήθως οι πτήσεις των αεροσκαφών γίνονται στο ύψος των 15000 m, όπου η θερμοκρασία του αέρα είναι 210 Κ και η ατμοσφαιρική πίεση 10000 N / m 2. Σε αεροδρόμιο που βρίσκεται στο ίδιο ύψος με την επιφάνεια
1)Συνήθως οι πτήσεις των αεροσκαφών γίνονται στο ύψος των 15000 m, όπου η θερμοκρασία του αέρα είναι 210 Κ και η ατμοσφαιρική πίεση 10000 N / m 2. Σε αεροδρόμιο που βρίσκεται στο ίδιο ύψος με την επιφάνεια
Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί:
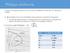 Ψύξη με εκτόνωση Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί: A. Mε ελεύθερη εκτόνωση σε βαλβίδα στραγγαλισμού: ισενθαλπική διεργασία σε χαμηλές θερμοκρασίες,
Ψύξη με εκτόνωση Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί: A. Mε ελεύθερη εκτόνωση σε βαλβίδα στραγγαλισμού: ισενθαλπική διεργασία σε χαμηλές θερμοκρασίες,
Τεχνολογίες Εκμετάλλευσης και Αξιοποίησης Υδρογονανθράκων
 Τεχνολογίες Εκμετάλλευσης και Αξιοποίησης Υδρογονανθράκων Μάθημα 3 ο Εισαγωγή στο διυλιστήριο Τύποι διεργασιών Απόσταξη (ατμοσφαιρική και υπό κενό) Δρ. Στέλλα Μπεζεργιάννη Διύλιση Το αργό πετρέλαιο δεν
Τεχνολογίες Εκμετάλλευσης και Αξιοποίησης Υδρογονανθράκων Μάθημα 3 ο Εισαγωγή στο διυλιστήριο Τύποι διεργασιών Απόσταξη (ατμοσφαιρική και υπό κενό) Δρ. Στέλλα Μπεζεργιάννη Διύλιση Το αργό πετρέλαιο δεν
Energy resources: Technologies & Management
 Πανεπιστήμιο Δυτικής Μακεδονίας Energ resources: echnologies & Management Τεχνολογίες άνθρακα Σχεδιασμός Στηλών Απορρόφησης Αερίων Δρ. Γεώργιος Σκόδρας Αν. Καθηγητής Περιεχόμενα Η διάλεξη που ακολουθεί
Πανεπιστήμιο Δυτικής Μακεδονίας Energ resources: echnologies & Management Τεχνολογίες άνθρακα Σχεδιασμός Στηλών Απορρόφησης Αερίων Δρ. Γεώργιος Σκόδρας Αν. Καθηγητής Περιεχόμενα Η διάλεξη που ακολουθεί
Ογκομετρική (PVT) συμπεριφορά καθαρών ρευστών
 Ογκομετρική (PT) συμπεριφορά καθαρών ρευστών Ογκομετρική (PvT) συμπεριφορά Α.Θ Παπαϊωάννου, Θερμοδυναμική: ΤΟΜΟΣ I, Αθήνα, 007 PvT ιάγραμμα για το νερό 3 ιαγράμματα φάσεων καθαρών ουσιών Α.Θ. Παπαϊωάννου,
Ογκομετρική (PT) συμπεριφορά καθαρών ρευστών Ογκομετρική (PvT) συμπεριφορά Α.Θ Παπαϊωάννου, Θερμοδυναμική: ΤΟΜΟΣ I, Αθήνα, 007 PvT ιάγραμμα για το νερό 3 ιαγράμματα φάσεων καθαρών ουσιών Α.Θ. Παπαϊωάννου,
ΥΛΙΚΑ ΓΙΑ ΕΝΕΡΓΕΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ
 ΥΛΙΚΑ ΓΙΑ ΕΝΕΡΓΕΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ ΑΤΜΟΣΤΡΟΒΙΛΟΙ Σημειώσεις Δ. Κουζούδη Εαρινό Εξάμηνο 2017 ΑΤΜΟ-ΣΤΡΟΒΙΛΟΙ (ΑΤΜΟ-ΤΟΥΡΜΠΙΝΕΣ) Που χρησιμοποιούνται; Για παραγωγή ηλεκτρικής ς σε μεγάλη κλίμακα. Εκτός από τα
ΥΛΙΚΑ ΓΙΑ ΕΝΕΡΓΕΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ ΑΤΜΟΣΤΡΟΒΙΛΟΙ Σημειώσεις Δ. Κουζούδη Εαρινό Εξάμηνο 2017 ΑΤΜΟ-ΣΤΡΟΒΙΛΟΙ (ΑΤΜΟ-ΤΟΥΡΜΠΙΝΕΣ) Που χρησιμοποιούνται; Για παραγωγή ηλεκτρικής ς σε μεγάλη κλίμακα. Εκτός από τα
Απρίλιος Λύση: Σύνοψη των δεδομένων: P = 6at, V = 0.6F, L = 0.4F, F = 1 kmol/s. Ζητούμενα: x Fi, x Li
 Φυσικές Διεργασίες Προβλήματα στην απόσταξη που λύθηκαν στην τάξη Πηγή: Δ. Μαρίνος-Κουρής, Ε. Παρλιάρου-Τσάμη, Ασκήσεις Φυσικών Διεργασιών, Παπασωτηρίου, Αθήνα 1994 Απρίλιος 2008 Πρόβλημα 1 Διαχωριστήρας
Φυσικές Διεργασίες Προβλήματα στην απόσταξη που λύθηκαν στην τάξη Πηγή: Δ. Μαρίνος-Κουρής, Ε. Παρλιάρου-Τσάμη, Ασκήσεις Φυσικών Διεργασιών, Παπασωτηρίου, Αθήνα 1994 Απρίλιος 2008 Πρόβλημα 1 Διαχωριστήρας
2 ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ
 ΙΣΟΖΥΓΙΑ ΕΝΕΡΓΕΙΑΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ 2 ΣΗΜΑΝΤΙΚΟΙ ΟΡΟΙ Αδιαβατικό σύστημα Ισοβαρές σύστημα Ισόχωρο σύστημα Ισοθερμοκρασιακό σύστημα Μεταβλητή διαδρομής (συνάρτηση μετάβασης) Καταστατική μεταβολή (σημειακή
ΙΣΟΖΥΓΙΑ ΕΝΕΡΓΕΙΑΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ 2 ΣΗΜΑΝΤΙΚΟΙ ΟΡΟΙ Αδιαβατικό σύστημα Ισοβαρές σύστημα Ισόχωρο σύστημα Ισοθερμοκρασιακό σύστημα Μεταβλητή διαδρομής (συνάρτηση μετάβασης) Καταστατική μεταβολή (σημειακή
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου (21/6/2017)
 Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
P. kpa T, C v, m 3 /kg u, kj/kg Περιγραφή κατάστασης και ποιότητα (αν εφαρμόζεται) , ,0 101,
 Ασκήσεις Άσκηση 1 Να συμπληρώσετε τα κενά κελιά στον επόμενο πίνακα των ιδιοτήτων του νερού εάν παρέχονται επαρκή δεδομένα. Στην τελευταία στήλη να περιγράψετε την κατάσταση του νερού ως υπόψυκτο υγρό,
Ασκήσεις Άσκηση 1 Να συμπληρώσετε τα κενά κελιά στον επόμενο πίνακα των ιδιοτήτων του νερού εάν παρέχονται επαρκή δεδομένα. Στην τελευταία στήλη να περιγράψετε την κατάσταση του νερού ως υπόψυκτο υγρό,
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο
 Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 9 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 9 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
Εφαρμοσμένη Θερμοδυναμική
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφαρμοσμένη Θερμοδυναμική Ενότητα 2: Ιδιότητες Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφαρμοσμένη Θερμοδυναμική Ενότητα 2: Ιδιότητες Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Άδειες
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 Ακαδημαϊκό έτος 34 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Επώνυμο: Όνομα: Προσωπικός Αριθμός: Ημερομηνία: Βαθμολογία θεμάτων 3 4 5 6 7 8 9 Γενικός Βαθμός η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ ΣΤΗ "ΦΥΣΙΚΟΧΗΜΕΙΑ" ΟΔΗΓΙΕΣ ΓΙΑ ΤΗΝ ΕΚΠΟΝΗΣΗ,
Ακαδημαϊκό έτος 34 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Επώνυμο: Όνομα: Προσωπικός Αριθμός: Ημερομηνία: Βαθμολογία θεμάτων 3 4 5 6 7 8 9 Γενικός Βαθμός η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ ΣΤΗ "ΦΥΣΙΚΟΧΗΜΕΙΑ" ΟΔΗΓΙΕΣ ΓΙΑ ΤΗΝ ΕΚΠΟΝΗΣΗ,
R T ενώ σε ολοκληρωµένη, αν θεωρήσουµε ότι οι ενθαλπίες αλλαγής φάσεως είναι σταθερές στο διάστηµα θερµοκρασιών που εξετάζουµε, είναι
 Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξετάσεις: Περίοδος Σεπτεµβρίου 007-0 (.9.00) Θέµα. Η τάση ατµών του στερεού µονοξειδίου του άνθρακα σε 60 K είναι.6 kpa και σε 65 K είναι. kpa. Η τάση ατµών του υγρού
Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξετάσεις: Περίοδος Σεπτεµβρίου 007-0 (.9.00) Θέµα. Η τάση ατµών του στερεού µονοξειδίου του άνθρακα σε 60 K είναι.6 kpa και σε 65 K είναι. kpa. Η τάση ατµών του υγρού
Πρόρρηση. Φυσικών Ιδιοτήτων Μιγμάτων
 Πρόρρηση Φυσικών Ιδιοτήτων Μιγμάτων Συντελεστής συμπιεστότητας, Ζ Αρχή Αντιστοίχων Καταστάσεων Τριών παραμέτρων Ptzer : z z (0) + ω z (1) Lee-Kesler: z (0), z (1) f(t r,p r ) Εξίσωση Ptzer Κανόνες Ανάμειξης
Πρόρρηση Φυσικών Ιδιοτήτων Μιγμάτων Συντελεστής συμπιεστότητας, Ζ Αρχή Αντιστοίχων Καταστάσεων Τριών παραμέτρων Ptzer : z z (0) + ω z (1) Lee-Kesler: z (0), z (1) f(t r,p r ) Εξίσωση Ptzer Κανόνες Ανάμειξης
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΛΥΜΕΝΑ ΘΕΜΑΤΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΛΥΜΕΝΑ ΘΕΜΑΤΑ 1 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 Θέμα 1 Επιλέγοντας το κατάλληλο διάγραμμα φάσεων για ένα πραγματικό
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΛΥΜΕΝΑ ΘΕΜΑΤΑ 1 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 Θέμα 1 Επιλέγοντας το κατάλληλο διάγραμμα φάσεων για ένα πραγματικό
Είδη ΙΦΥΥ δυαδικών μιγμάτων
 Είδη ΙΦΥΥ δυαδικών μιγμάτων T A X 1 X 1 ΙΦΥΥ τριαδικών μιγμάτων Τριγωνικά διαγράμματα C 0.1 0.2 0.3 0.4 0.5 P 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.6 0.7 0.8 0.9 κλάσμα βάρους του B κλάσμα βάρους του C
Είδη ΙΦΥΥ δυαδικών μιγμάτων T A X 1 X 1 ΙΦΥΥ τριαδικών μιγμάτων Τριγωνικά διαγράμματα C 0.1 0.2 0.3 0.4 0.5 P 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.6 0.7 0.8 0.9 κλάσμα βάρους του B κλάσμα βάρους του C
Κεφάλαιο 5: Διεργασίες απόσταξης
 92 Κεφάλαιο 5: Διεργασίες απόσταξης Σύνοψη Το κεφάλαιο αυτό συνιστά την πρώτη ολοκληρωμένη ανάλυση μίας διεργασίας. Παρουσιάζονται στην αρχή οι απλές αποστάξεις και στη συνέχεια αναλύεται διεξοδικά η κλασματική
92 Κεφάλαιο 5: Διεργασίες απόσταξης Σύνοψη Το κεφάλαιο αυτό συνιστά την πρώτη ολοκληρωμένη ανάλυση μίας διεργασίας. Παρουσιάζονται στην αρχή οι απλές αποστάξεις και στη συνέχεια αναλύεται διεξοδικά η κλασματική
ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ ΟΔΗΓΙΕΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΥΓΡΗΣ ΕΚΧΥΛΙΣΗΣ Ελένη Παντελή, Υποψήφια Διδάκτορας Γεωργία Παππά, Δρ. Χημικός Μηχανικός
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ ΟΔΗΓΙΕΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΥΓΡΗΣ ΕΚΧΥΛΙΣΗΣ Ελένη Παντελή, Υποψήφια Διδάκτορας Γεωργία Παππά, Δρ. Χημικός Μηχανικός
ΦΥΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι
 ΦΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι Ενότητα 6 η - Β ΜΕΡΟΣ ΔΙΑΛΜΑΤΑ Όνομα καθηγητή: ΕΑΓΓΕΛΙΟ ΒΑΣΙΛΙΚΗ Τμήμα: Επιστήμης Τροφίμων και Διατροφής του Ανθρώπου ΣΤΟΧΟΙ ΤΟ ΜΑΘΗΜΑΤΟΣ Στόχος (): Κατανόηση των εννοιών: υγρά διαλύματα,
ΦΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι Ενότητα 6 η - Β ΜΕΡΟΣ ΔΙΑΛΜΑΤΑ Όνομα καθηγητή: ΕΑΓΓΕΛΙΟ ΒΑΣΙΛΙΚΗ Τμήμα: Επιστήμης Τροφίμων και Διατροφής του Ανθρώπου ΣΤΟΧΟΙ ΤΟ ΜΑΘΗΜΑΤΟΣ Στόχος (): Κατανόηση των εννοιών: υγρά διαλύματα,
ΜΟΡΦΕΣ ΕΝΕΡΓΕΙΑΣ. ΕΝΕΡΓΕΙΑ ΔΙΕΡΓΑΣΙΩΝ (Μεταβατικές) ΕΝΕΡΓΕΙΑ ΣΥΣΤΗΜΑΤΟΣ ΕΡΓΟ ΘΕΡΜΟΤΗΤΑ
 Έργο - Θερμότητα ΜΟΡΦΕΣ ΕΝΕΡΓΕΙΑΣ ΕΝΕΡΓΕΙΑ ΔΙΕΡΓΑΣΙΩΝ (Μεταβατικές) ΕΡΓΟ ΘΕΡΜΟΤΗΤΑ ΕΝΕΡΓΕΙΑ ΣΥΣΤΗΜΑΤΟΣ ΕΞΩΤΕΡΙΚΗ (Κινητική, Δυναμική) ΕΣΩΤΕΡΙΚΗ (Εσωτερική [U], Ενθαλπία [Η]) Χαρακτηριστικά και Σύμβαση
Έργο - Θερμότητα ΜΟΡΦΕΣ ΕΝΕΡΓΕΙΑΣ ΕΝΕΡΓΕΙΑ ΔΙΕΡΓΑΣΙΩΝ (Μεταβατικές) ΕΡΓΟ ΘΕΡΜΟΤΗΤΑ ΕΝΕΡΓΕΙΑ ΣΥΣΤΗΜΑΤΟΣ ΕΞΩΤΕΡΙΚΗ (Κινητική, Δυναμική) ΕΣΩΤΕΡΙΚΗ (Εσωτερική [U], Ενθαλπία [Η]) Χαρακτηριστικά και Σύμβαση
ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ
 ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ 2015-2016 2 Ο ΕΞΑΜΗΝΟ Ε. ΠΑΥΛΑΤΟΥ ΑΝ. ΚΑΘΗΓΗΤΡΙΑ ΕΜΠ ΜΟΝΑΔΕΣ ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 3 ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 4 ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 5 Επιφάνεια
ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ 2015-2016 2 Ο ΕΞΑΜΗΝΟ Ε. ΠΑΥΛΑΤΟΥ ΑΝ. ΚΑΘΗΓΗΤΡΙΑ ΕΜΠ ΜΟΝΑΔΕΣ ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 3 ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 4 ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 5 Επιφάνεια
(β) Εύρεση του αριθμού των θεωρητικών βαθμίδων με τη μέθοδο McCabe-Thiele
 Κεφάλαιο 2 Απόσταξη 3 (β) Εύρεση του αριθμού των θεωρητικών βαθμίδων με τη μέθοδο McCabe-Thiele Παρακάτω περιγράφουμε τα βήματα που ακολουθούμε με τη μέθοδο McCabe- Thiele για να καθορίσουμε τον αριθμό
Κεφάλαιο 2 Απόσταξη 3 (β) Εύρεση του αριθμού των θεωρητικών βαθμίδων με τη μέθοδο McCabe-Thiele Παρακάτω περιγράφουμε τα βήματα που ακολουθούμε με τη μέθοδο McCabe- Thiele για να καθορίσουμε τον αριθμό
Ισορροπία Υγρού-Υγρού ΠΡΟΧΩΡΗΜΕΝΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ
 Ισορροπία Υγρού-Υγρού ΠΡΟΧΩΡΗΜΕΝΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ Προχωρημένη Θερμοδυναμική Εαρινό εξάμηνο 08-09 Εισαγωγή Σε αντίθεση με τα αέρια τα οποία είναι αναμίξιμα σε όλες τις αναλογίες σε χαμηλές πιέσεις τα υγρά
Ισορροπία Υγρού-Υγρού ΠΡΟΧΩΡΗΜΕΝΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ Προχωρημένη Θερμοδυναμική Εαρινό εξάμηνο 08-09 Εισαγωγή Σε αντίθεση με τα αέρια τα οποία είναι αναμίξιμα σε όλες τις αναλογίες σε χαμηλές πιέσεις τα υγρά
Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ. Ερωτήσεις Επανάληψης
 Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ Ερωτήσεις Επανάληψης 1 0.8 0.6 x D = 0.95 y 0.4 x F = 0.45 0.2 0 0 0.2 0.4 0.6 0.8 1 x B = 0.05 Σχήμα 1. Δεδομένα ισορροπίας y-x για δυαδικό μίγμα συστατικών Α και Β και οι
Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ Ερωτήσεις Επανάληψης 1 0.8 0.6 x D = 0.95 y 0.4 x F = 0.45 0.2 0 0 0.2 0.4 0.6 0.8 1 x B = 0.05 Σχήμα 1. Δεδομένα ισορροπίας y-x για δυαδικό μίγμα συστατικών Α και Β και οι
ΤΕΧΝΙΚΗ ΧΗΜΙΚΩΝ ΚΑΙ ΒΙΟΧΗΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ
 ΤΕΧΝΙΚΗ ΧΗΜΙΚΩΝ ΚΑΙ ΒΙΟΧΗΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Διδάσκοντες:Ν. Καλογεράκης Π. Παναγιωτοπούλου Γραφείο: K.9 Email: ppanagiotopoulou@isc.tuc.gr Μέρες/Ώρες διδασκαλίας: Δευτέρα (.-3.)-Τρίτη (.-3.) ΤΕΧΝΙΚΗ ΧΗΜΙΚΩΝ
ΤΕΧΝΙΚΗ ΧΗΜΙΚΩΝ ΚΑΙ ΒΙΟΧΗΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Διδάσκοντες:Ν. Καλογεράκης Π. Παναγιωτοπούλου Γραφείο: K.9 Email: ppanagiotopoulou@isc.tuc.gr Μέρες/Ώρες διδασκαλίας: Δευτέρα (.-3.)-Τρίτη (.-3.) ΤΕΧΝΙΚΗ ΧΗΜΙΚΩΝ
Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ
 Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ Η υγρή εκχύλιση βρίσκει εφαρμογή όταν. Η σχετική πτητικότητα των συστατικών του αρχικού διαλύματος είναι κοντά στη
Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ Η υγρή εκχύλιση βρίσκει εφαρμογή όταν. Η σχετική πτητικότητα των συστατικών του αρχικού διαλύματος είναι κοντά στη
ΠΑΡΑΡΤΗΜΑ 3 ΥΠΟΛΟΓΙΣΜΟΣ ΔΙΑΓΡΑΜΜΑΤΩΝ ΦΑΣΕΩΝ ΑΠΟ ΘΕΡΜΟΔΥΝΑΜΙΚΑ ΔΕΔΟΜΕΝΑ
 ΠΑΡΑΡΤΗΜΑ 3-ΥΠΟΛΟΓΙΣΜΟΣ ΔΙΑΓΡΑΜΜΑΤΩΝ ΦΑΣΕΩΝ ΠΑΡΑΡΤΗΜΑ 3 ΥΠΟΛΟΓΙΣΜΟΣ ΔΙΑΓΡΑΜΜΑΤΩΝ ΦΑΣΕΩΝ ΑΠΟ ΘΕΡΜΟΔΥΝΑΜΙΚΑ ΔΕΔΟΜΕΝΑ 1 Εισαγωγή Τα διαγράμματα φάσεων δεν είναι εμπειρικά σχήματα αλλά είναι ουσιαστικής σημασίας
ΠΑΡΑΡΤΗΜΑ 3-ΥΠΟΛΟΓΙΣΜΟΣ ΔΙΑΓΡΑΜΜΑΤΩΝ ΦΑΣΕΩΝ ΠΑΡΑΡΤΗΜΑ 3 ΥΠΟΛΟΓΙΣΜΟΣ ΔΙΑΓΡΑΜΜΑΤΩΝ ΦΑΣΕΩΝ ΑΠΟ ΘΕΡΜΟΔΥΝΑΜΙΚΑ ΔΕΔΟΜΕΝΑ 1 Εισαγωγή Τα διαγράμματα φάσεων δεν είναι εμπειρικά σχήματα αλλά είναι ουσιαστικής σημασίας
ΚΕΦΑΛΑΙΟ 2 ΙΔΙΟΤΗΤΕΣ ΤΩΝ ΚΑΘΑΡΩΝ ΟΥΣΙΩΝ.
 ΚΕΦΑΛΑΙΟ 2 ΙΔΙΟΤΗΤΕΣ ΤΩΝ ΚΑΘΑΡΩΝ ΟΥΣΙΩΝ. 2.1 Η ΕΝΝΟΙΑ ΤΗΣ ΚΑΘΑΡΗΣ ΟΥΣΙΑΣ. Μια ουσία της οποίας η χημική σύσταση παραμένει σταθερή σε όλη της την έκταση ονομάζεται καθαρή ουσία. Δεν είναι υποχρεωτικό να
ΚΕΦΑΛΑΙΟ 2 ΙΔΙΟΤΗΤΕΣ ΤΩΝ ΚΑΘΑΡΩΝ ΟΥΣΙΩΝ. 2.1 Η ΕΝΝΟΙΑ ΤΗΣ ΚΑΘΑΡΗΣ ΟΥΣΙΑΣ. Μια ουσία της οποίας η χημική σύσταση παραμένει σταθερή σε όλη της την έκταση ονομάζεται καθαρή ουσία. Δεν είναι υποχρεωτικό να
Οι ιδιότητες των αερίων και καταστατικές εξισώσεις. Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι
 Οι ιδιότητες των αερίων και καταστατικές εξισώσεις Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι Τι είναι αέριο; Λέμε ότι μία ουσία βρίσκεται στην αέρια κατάσταση όταν αυθόρμητα
Οι ιδιότητες των αερίων και καταστατικές εξισώσεις Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι Τι είναι αέριο; Λέμε ότι μία ουσία βρίσκεται στην αέρια κατάσταση όταν αυθόρμητα
Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων
 Φυσικοχημεία II, Διαλύματα Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων o P = N P P = A A A N P o B B B PA + PB = P ολ Τ=const P = Ν ολ P + N P o o A A B B Ν Α + Ν =1 o o o P = P + A N ( ολ
Φυσικοχημεία II, Διαλύματα Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων o P = N P P = A A A N P o B B B PA + PB = P ολ Τ=const P = Ν ολ P + N P o o A A B B Ν Α + Ν =1 o o o P = P + A N ( ολ
Απορρόφηση Αερίων (2)
 Απορρόφηση Αερίων (2) Λεπτομερής Ανάλυση Θεωρούμε έναν πύργο απορρόφησης που μπορεί να περιέχει δίσκους ή να είναι τύπου πληρωτικού υλικού ή άλλου τύπου. Τελικός σκοπός είναι να βρούμε το μέγεθος του πύργου.
Απορρόφηση Αερίων (2) Λεπτομερής Ανάλυση Θεωρούμε έναν πύργο απορρόφησης που μπορεί να περιέχει δίσκους ή να είναι τύπου πληρωτικού υλικού ή άλλου τύπου. Τελικός σκοπός είναι να βρούμε το μέγεθος του πύργου.
Σύστημα. Ανοικτά Συστήματα. Γενικό Ροϊκό Πεδίο. Περιβάλλον. Θερμότητα. Ροή Μάζας. Ροή Μάζας. Έργο
 ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι ΠΡΩΤΟΣ ΝΟΜΟΣ ΣΕ ΑΝΟΙΚΤΑ ΣΥΣΤΗΜΑΤΑ Όγκος και επιφάνεια ελέγχου Διατήρηση μάζας και ενέργειας Μόνιμες-Μεταβατικές διεργασίες Ισοζύγιο μάζας Έργο Ροής-Ισοζύγιο ενέργειας Διατάξεις μόνιμης
ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι ΠΡΩΤΟΣ ΝΟΜΟΣ ΣΕ ΑΝΟΙΚΤΑ ΣΥΣΤΗΜΑΤΑ Όγκος και επιφάνεια ελέγχου Διατήρηση μάζας και ενέργειας Μόνιμες-Μεταβατικές διεργασίες Ισοζύγιο μάζας Έργο Ροής-Ισοζύγιο ενέργειας Διατάξεις μόνιμης
Παρασκευή αιθανόλης-απόσταξη αλκοολούχου διαλύματος. Τεχνική της απόσταξης
 Παρασκευή αιθανόλης-απόσταξη αλκοολούχου διαλύματος Με τον όρο απόσταξη εννοείται η θέρμανση ενός υγρού μέχρι να εξατμισθεί, η συμπύκνωση των ατμών του με ψύξη και η συλλογή τους σε ένα άλλο δοχείο. Με
Παρασκευή αιθανόλης-απόσταξη αλκοολούχου διαλύματος Με τον όρο απόσταξη εννοείται η θέρμανση ενός υγρού μέχρι να εξατμισθεί, η συμπύκνωση των ατμών του με ψύξη και η συλλογή τους σε ένα άλλο δοχείο. Με
Έκφραση της Ισορροπίας φάσεων ατμών υγρού με τη βοήθεια του Aspen plus
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Εργαστήριο Θερμοδυναμικής & Φαινομένων Μεταφοράς Έκφραση της Ισορροπίας φάσεων ατμών υγρού με τη βοήθεια του Aspen plus Η έννοια της ισορροπίας Εξ ορισμού
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Εργαστήριο Θερμοδυναμικής & Φαινομένων Μεταφοράς Έκφραση της Ισορροπίας φάσεων ατμών υγρού με τη βοήθεια του Aspen plus Η έννοια της ισορροπίας Εξ ορισμού
ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ
 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ Κεφάλαιο Πρόλογος i Κατάλογος Σχημάτων και Εικόνων v Ενότητα 1: Εισαγωγή 1-1 1.1 Το μαθηματικό πρότυπο: ισοζύγια και άλλες σχέσεις. 1-1 1.2 Αριστοποίηση 1-2 1.3 Αλλαγή κλίμακας (scale
ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ Κεφάλαιο Πρόλογος i Κατάλογος Σχημάτων και Εικόνων v Ενότητα 1: Εισαγωγή 1-1 1.1 Το μαθηματικό πρότυπο: ισοζύγια και άλλες σχέσεις. 1-1 1.2 Αριστοποίηση 1-2 1.3 Αλλαγή κλίμακας (scale
Κεφάλαιο 4 Κλασματική Απόσταξη
 Κεφάλαιο 4 Κλασματική Απόσταξη Σύνοψη Η κλασματική απόσταξη ή απλά απόσταξη αποτελεί τη διεργασία διαχωρισμού ενός πτητικού συστατικού από ένα λιγότερο πτητικό ή, γενικότερα, ενός μίγματος συστατικών που
Κεφάλαιο 4 Κλασματική Απόσταξη Σύνοψη Η κλασματική απόσταξη ή απλά απόσταξη αποτελεί τη διεργασία διαχωρισμού ενός πτητικού συστατικού από ένα λιγότερο πτητικό ή, γενικότερα, ενός μίγματος συστατικών που
Φάσεις μιας καθαρής ουσίας. Αλλαγές φάσεων καθαρών ουσιών
 ΘΕΡΜΙΚΕΣ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΚΑΘΑΡΕΣ ΟΥΣΙΕΣ Μια ουσία της οποίας η χημική σύσταση παραμένει σταθερή σε όλη της την έκταση ονομάζεται Καθαρή Ουσία Πχ νερό, άζωτο, ήλιο, διοξείδιο του άνθρακα κλπ. Επίσης θεωρούνται
ΘΕΡΜΙΚΕΣ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΚΑΘΑΡΕΣ ΟΥΣΙΕΣ Μια ουσία της οποίας η χημική σύσταση παραμένει σταθερή σε όλη της την έκταση ονομάζεται Καθαρή Ουσία Πχ νερό, άζωτο, ήλιο, διοξείδιο του άνθρακα κλπ. Επίσης θεωρούνται
Σύστημα. Ανοικτά Συστήματα. Γενικό Ροϊκό Πεδίο. Περιβάλλον. Θερμότητα. Ροή Μάζας. Ροή Μάζας. Έργο
 ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι ΠΡΩΤΟΣ ΝΟΜΟΣ ΣΕ ΑΝΟΙΚΤΑ ΣΥΣΤΗΜΑΤΑ Όγκος και επιφάνεια ελέγχου Διατήρηση μάζας και ενέργειας Μόνιμες-Μεταβατικές διεργασίες Ισοζύγιο μάζας Έργο Ροής-Ισοζύγιο ενέργειας Διατάξεις μόνιμης
ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι ΠΡΩΤΟΣ ΝΟΜΟΣ ΣΕ ΑΝΟΙΚΤΑ ΣΥΣΤΗΜΑΤΑ Όγκος και επιφάνεια ελέγχου Διατήρηση μάζας και ενέργειας Μόνιμες-Μεταβατικές διεργασίες Ισοζύγιο μάζας Έργο Ροής-Ισοζύγιο ενέργειας Διατάξεις μόνιμης
Απορρόφηση Αερίων. 1. Εισαγωγή
 1. Εισαγωγή Απορρόφηση Αερίων Πρόκειται για διαχωρισμό συστατικών από μείγμα αερίου με τη βοήθεια υγρού διαλύτη. Κινητήρια δύναμη είναι η διαφορά διαλυτότητας στο διαλύτη. Στη συνέχεια θα ασχοληθούμε με
1. Εισαγωγή Απορρόφηση Αερίων Πρόκειται για διαχωρισμό συστατικών από μείγμα αερίου με τη βοήθεια υγρού διαλύτη. Κινητήρια δύναμη είναι η διαφορά διαλυτότητας στο διαλύτη. Στη συνέχεια θα ασχοληθούμε με
Σύνοψη ΜΗΧΑΝΙΚΗΣ ΧΗΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Χημική αντίδραση : a 1. + α 2 Α (-a 1 ) A 1. +(-a 2
 ΠΑ- Σύνοψη ΜΗΧΑΝΙΚΗΣ ΧΗΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Χημική αντίδραση : a A + α Α +... ------------>...+a A ή σε μορφή γραμμικής εξίσωσης a A +...+(-a ) A +(-a ) A +... 0 a Στοιχειομετρικοί συντελεστές ως προς Α (
ΠΑ- Σύνοψη ΜΗΧΑΝΙΚΗΣ ΧΗΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Χημική αντίδραση : a A + α Α +... ------------>...+a A ή σε μορφή γραμμικής εξίσωσης a A +...+(-a ) A +(-a ) A +... 0 a Στοιχειομετρικοί συντελεστές ως προς Α (
ΑΕΡΙΑ ΙΔΑΝΙΚΑ ΚΑΙ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ
 ΑΕΡΙΑ ΙΔΑΝΙΚΑ ΚΑΙ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΝΟΜΟΣ ΤΕΛΕΙΩΝ ΑΕΡΙΩΝ O νόμος των τελείων αερίων συνδέει τις ιδιότητες ενός τελείου αερίου σε μια συγκεκριμένη κατάσταση (καταστατική εξίσωση) P V = n R T P: Απόλυτη πίεση
ΑΕΡΙΑ ΙΔΑΝΙΚΑ ΚΑΙ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΝΟΜΟΣ ΤΕΛΕΙΩΝ ΑΕΡΙΩΝ O νόμος των τελείων αερίων συνδέει τις ιδιότητες ενός τελείου αερίου σε μια συγκεκριμένη κατάσταση (καταστατική εξίσωση) P V = n R T P: Απόλυτη πίεση
Ζήτημα 1 0. Επώνυμο... Όνομα... Αγρίνιο 1/3/2015. Επιλέξτε τη σωστή απάντηση
 1 Επώνυμο... Όνομα... Αγρίνιο 1/3/2015 Ζήτημα 1 0 Επιλέξτε τη σωστή απάντηση 1) Η θερμότητα που ανταλλάσει ένα αέριο με το περιβάλλον θεωρείται θετική : α) όταν προσφέρεται από το αέριο στο περιβάλλον,
1 Επώνυμο... Όνομα... Αγρίνιο 1/3/2015 Ζήτημα 1 0 Επιλέξτε τη σωστή απάντηση 1) Η θερμότητα που ανταλλάσει ένα αέριο με το περιβάλλον θεωρείται θετική : α) όταν προσφέρεται από το αέριο στο περιβάλλον,
Ανάπτυξη στατικού προτύπου επίλυσης προβλημάτων αξιολόγησης αποστακτικών στηλών.
 Εθνικό Μετσόβιο Πολυτεχνείο Τμήμα Χημικών Μηχανικών Τομέας ΙΙ : Ανάλυσης, Σχεδιασμού και Ανάπτυξης Διεργασιών και Συστημάτων Ανάπτυξη στατικού προτύπου επίλυσης προβλημάτων αξιολόγησης αποστακτικών στηλών.
Εθνικό Μετσόβιο Πολυτεχνείο Τμήμα Χημικών Μηχανικών Τομέας ΙΙ : Ανάλυσης, Σχεδιασμού και Ανάπτυξης Διεργασιών και Συστημάτων Ανάπτυξη στατικού προτύπου επίλυσης προβλημάτων αξιολόγησης αποστακτικών στηλών.
M V n. nm V. M v. M v T P P S V P = = + = σταθερή σε παραγώγιση, τον ορισµό του συντελεστή διαστολής α = 1, κυκλική εναλλαγή 3
 Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξέταση: Περίοδος εκεµβρίου 04- (//04. ίνονται οι ακόλουθες πληροφορίες για τον διθειάνθρακα (CS. Γραµµοµοριακή µάζα 76.4 g/mol, κανονικό σηµείο ζέσεως 46 C, κανονικό
Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξέταση: Περίοδος εκεµβρίου 04- (//04. ίνονται οι ακόλουθες πληροφορίες για τον διθειάνθρακα (CS. Γραµµοµοριακή µάζα 76.4 g/mol, κανονικό σηµείο ζέσεως 46 C, κανονικό
Φυσικές Διεργασίες Πέμπτη Διάλεξη
 Φυσικές Διεργασίες Πέμπτη Διάλεξη Δευτέρα, 12 Μαΐου 2008 Απορρόφηση αερίων 1. Ορισμός Τι είναι απορρόφηση; Είναι μεταφορά μέσω της διεπιφάνειας αερίου-υγρού ενός συστατικού από αέριο μίγμα σε έναν υγρό
Φυσικές Διεργασίες Πέμπτη Διάλεξη Δευτέρα, 12 Μαΐου 2008 Απορρόφηση αερίων 1. Ορισμός Τι είναι απορρόφηση; Είναι μεταφορά μέσω της διεπιφάνειας αερίου-υγρού ενός συστατικού από αέριο μίγμα σε έναν υγρό
Σύστημα. Ανοικτά Συστήματα. Περιβάλλον. Γενικό Ροϊκό Πεδίο. Όγκος Ελέγχου, Επιφάνεια Ελέγχου. Θερμότητα. Ροή Μάζας. Ροή Μάζας.
 ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι ΠΡΩΤΟΣ ΝΟΜΟΣ ΣΕ ΑΝΟΙΚΤΑ ΣΥΣΤΗΜΑΤΑ Περιβάλλον Ροή Μάζας Έργο Ανοικτά Συστήματα Σύστημα Θερμότητα Ροή Μάζας Κεφάλαιο4, Ενότητα 1, Διαφάνεια 1 Κεφάλαιο4, Ενότητα 1, Διαφάνεια Γενικό Ροϊκό
ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι ΠΡΩΤΟΣ ΝΟΜΟΣ ΣΕ ΑΝΟΙΚΤΑ ΣΥΣΤΗΜΑΤΑ Περιβάλλον Ροή Μάζας Έργο Ανοικτά Συστήματα Σύστημα Θερμότητα Ροή Μάζας Κεφάλαιο4, Ενότητα 1, Διαφάνεια 1 Κεφάλαιο4, Ενότητα 1, Διαφάνεια Γενικό Ροϊκό
Enrico Fermi, Thermodynamics, 1937
 I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ
 ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ 2016-2017 2 Ο ΕΞΑΜΗΝΟ Ε. ΠΑΥΛΑΤΟΥ ΑΝΑΠΛ. ΚΑΘΗΓΗΤΡΙΑ ΕΜΠ 2 ΣΚΟΠΟΣ ΜΑΘΗΜΑΤΟΣ Ε. Παυλάτου, 2017 ΓΝΩΣΤΙΚΟ ΕΠΙΠΕΔΟ Η διδασκαλία και εμπέδωση θεμελιακών εννοιών που σχετίζονται
ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ 2016-2017 2 Ο ΕΞΑΜΗΝΟ Ε. ΠΑΥΛΑΤΟΥ ΑΝΑΠΛ. ΚΑΘΗΓΗΤΡΙΑ ΕΜΠ 2 ΣΚΟΠΟΣ ΜΑΘΗΜΑΤΟΣ Ε. Παυλάτου, 2017 ΓΝΩΣΤΙΚΟ ΕΠΙΠΕΔΟ Η διδασκαλία και εμπέδωση θεμελιακών εννοιών που σχετίζονται
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση : Προσδιορισμός μοριακής μάζας με ζεσεοσκοπία Αθανάσιος Τσεκούρας Τμήμα Χημείας 1. Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 4 Σελίδα 1. Θεωρία
Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση : Προσδιορισμός μοριακής μάζας με ζεσεοσκοπία Αθανάσιος Τσεκούρας Τμήμα Χημείας 1. Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 4 Σελίδα 1. Θεωρία
Τ.Ε.Ι. ΠΕΙΡΑΙΑ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΜΑΘΗΜΑ: ΕΦΑΡΜΟΣΜΕΝΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ (Ασκήσεις πράξης) ΙΔΑΝΙΚΑ ΑΕΡΙΑ - ΕΡΓΟ
 ΙΔΑΝΙΚΑ ΑΕΡΙΑ - ΕΡΓΟ 1. Να υπολογιστεί η πυκνότητα του αέρα σε πίεση 0,1 MPa και θερμοκρασία 20 ο C. (R air =0,287 kj/kgk) 2. Ποσότητα αέρα 1 kg εκτελεί τις παρακάτω διεργασίες: Διεργασία 1-2: Αδιαβατική
ΙΔΑΝΙΚΑ ΑΕΡΙΑ - ΕΡΓΟ 1. Να υπολογιστεί η πυκνότητα του αέρα σε πίεση 0,1 MPa και θερμοκρασία 20 ο C. (R air =0,287 kj/kgk) 2. Ποσότητα αέρα 1 kg εκτελεί τις παρακάτω διεργασίες: Διεργασία 1-2: Αδιαβατική
Κεφάλαιο 6 Απορρόφηση
 Κεφάλαιο 6 Απορρόφηση Σύνοψη Απορρόφηση αεριών ονομάζεται η φυσική διεργασία απομάκρυνσης ενός ή περισσοτέρων συστατικών ενός αερίου ρεύματος προς ένα μη πτητικό υγρό, το οποίο διαλύει αυτό(α) το(α) συστατικό(α).
Κεφάλαιο 6 Απορρόφηση Σύνοψη Απορρόφηση αεριών ονομάζεται η φυσική διεργασία απομάκρυνσης ενός ή περισσοτέρων συστατικών ενός αερίου ρεύματος προς ένα μη πτητικό υγρό, το οποίο διαλύει αυτό(α) το(α) συστατικό(α).
ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι. 1ος Θερμοδυναμικός Νόμος. Σύστημα. Αλληλεπίδραση Συστήματος-Περιβάλλοντος ΕΡΓΟ. f(p k, k =1...N)=0
 ος Θερμοδυναμικός Νόμος ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι ος Θερμοδυναμικός Νόμος Έργο-Έργο ογκομεταβολής Αδιαβατικό Έργο Εσωτερική ενέργεια, U Πρώτος Θερμοδυναμικός Νόμος Θερμότητα Ολική Ενέργεια Ενθαλπία Θερμοχωρητικότητα
ος Θερμοδυναμικός Νόμος ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι ος Θερμοδυναμικός Νόμος Έργο-Έργο ογκομεταβολής Αδιαβατικό Έργο Εσωτερική ενέργεια, U Πρώτος Θερμοδυναμικός Νόμος Θερμότητα Ολική Ενέργεια Ενθαλπία Θερμοχωρητικότητα
ΝΟΜΟΙ ΑΕΡΙΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ
 ΝΟΜΟΙ ΑΕΡΙΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΑΣΚΗΣΗ 1 Μία θερμική μηχανή λειτουργεί μεταξύ των θερμοκρασιών T h 400 Κ και T c με T c < T h Η μηχανή έχει απόδοση e 0,2 και αποβάλλει στη δεξαμενή χαμηλής θερμοκρασίας θερμότητα
ΝΟΜΟΙ ΑΕΡΙΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΑΣΚΗΣΗ 1 Μία θερμική μηχανή λειτουργεί μεταξύ των θερμοκρασιών T h 400 Κ και T c με T c < T h Η μηχανή έχει απόδοση e 0,2 και αποβάλλει στη δεξαμενή χαμηλής θερμοκρασίας θερμότητα
ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι. Ενότητα 8: Θερμοχωρητικότητα Χημικό δυναμικό και ισορροπία. Σογομών Μπογοσιάν Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι Ενότητα 8: Θερμοχωρητικότητα Χημικό δυναμικό και ισορροπία Σογομών Μπογοσιάν Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Σκοπός της ενότητας αυτής είναι η ανάπτυξη μαθηματικών
ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι Ενότητα 8: Θερμοχωρητικότητα Χημικό δυναμικό και ισορροπία Σογομών Μπογοσιάν Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Σκοπός της ενότητας αυτής είναι η ανάπτυξη μαθηματικών
ΕΙΣΑΓΩΓΗ ΣΤΗ ΧΗΜΙΚΗ ΜΗΧΑΝΙΚΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΧΗΜΙΚΗ ΜΗΧΑΝΙΚΗ 2017-2018 1 Ο ΕΞΑΜΗΝΟ Χ. ΚΥΡΑΝΟΥΔΗΣ, ΚΑΘ. ΕΜΠ Ε. ΠΑΥΛΑΤΟΥ, ΑΝ. ΚΑΘ. ΕΜΠ 2 ΣΚΟΠΟΣ ΜΑΘΗΜΑΤΟΣ Ε. Παυλάτου, 2017 ΓΝΩΣΤΙΚΟ ΕΠΙΠΕΔΟ Η διδασκαλία και εμπέδωση θεμελιακών εννοιών που
ΕΙΣΑΓΩΓΗ ΣΤΗ ΧΗΜΙΚΗ ΜΗΧΑΝΙΚΗ 2017-2018 1 Ο ΕΞΑΜΗΝΟ Χ. ΚΥΡΑΝΟΥΔΗΣ, ΚΑΘ. ΕΜΠ Ε. ΠΑΥΛΑΤΟΥ, ΑΝ. ΚΑΘ. ΕΜΠ 2 ΣΚΟΠΟΣ ΜΑΘΗΜΑΤΟΣ Ε. Παυλάτου, 2017 ΓΝΩΣΤΙΚΟ ΕΠΙΠΕΔΟ Η διδασκαλία και εμπέδωση θεμελιακών εννοιών που
Φυσικοί μετασχηματισμοί καθαρών ουσιών
 Φυσικοί μετασχηματισμοί καθαρών ουσιών Ή εξάτμιση, η τήξη και η μετατροπή του γραφίτη σε διαμάντι αποτελούν συνηθισμένα παραδείγματα αλλαγών φάσης χωρίς μεταβολή της χημικής σύστασης. Ορισμός φάσης: Μια
Φυσικοί μετασχηματισμοί καθαρών ουσιών Ή εξάτμιση, η τήξη και η μετατροπή του γραφίτη σε διαμάντι αποτελούν συνηθισμένα παραδείγματα αλλαγών φάσης χωρίς μεταβολή της χημικής σύστασης. Ορισμός φάσης: Μια
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 Θέμα 1 ο ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ 1--015 1. Ορισμένη ποσότητα ιδανικού αερίου υπόκειται σε μεταβολή κατά τη διάρκεια της οποίας η θερμοκρασία του παραμένει σταθερή, ενώ η πίεση του
Θέμα 1 ο ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ 1--015 1. Ορισμένη ποσότητα ιδανικού αερίου υπόκειται σε μεταβολή κατά τη διάρκεια της οποίας η θερμοκρασία του παραμένει σταθερή, ενώ η πίεση του
Πρόρρηση. Θερμοδυναμικών Ιδιοτήτων Μιγμάτων
 Πρόρρηση Θερμοδυναμικών Ιδιοτήτων Μιγμάτων 1 Χημικό Δυναμικό μ d = dg U = N V,S,N Για 1 mole καθαρής ουσίας: SdT +Vd j H = N S,,N j A = N V,T,N j G = N ( T, ) ( T,) = T T T,,N j SdT + όπου μ(t',') είναι
Πρόρρηση Θερμοδυναμικών Ιδιοτήτων Μιγμάτων 1 Χημικό Δυναμικό μ d = dg U = N V,S,N Για 1 mole καθαρής ουσίας: SdT +Vd j H = N S,,N j A = N V,T,N j G = N ( T, ) ( T,) = T T T,,N j SdT + όπου μ(t',') είναι
Σφαιρικές συντεταγμένες (r, θ, φ).
 T T r e r 1 T e r Σφαιρικές συντεταγμένες (r, θ, φ). 1 T e. (2.57) r sin u u e u e u e, (2.58) r r οπότε το εσωτερικό γινόμενο u.t γίνεται: T u T u T u. T ur. (2.59) r r r sin 2.5 Η ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ
T T r e r 1 T e r Σφαιρικές συντεταγμένες (r, θ, φ). 1 T e. (2.57) r sin u u e u e u e, (2.58) r r οπότε το εσωτερικό γινόμενο u.t γίνεται: T u T u T u. T ur. (2.59) r r r sin 2.5 Η ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση α: Συντελεστής Joule Thomson (Τζουλ Τόμσον ) Αθανάσιος Τσεκούρας Τμήμα Χημείας Θεωρία 3 Μετρήσεις 6 3 Επεξεργασία Μετρήσεων 6 Σελίδα Θεωρία Η καταστατική εξίσωση
Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση α: Συντελεστής Joule Thomson (Τζουλ Τόμσον ) Αθανάσιος Τσεκούρας Τμήμα Χημείας Θεωρία 3 Μετρήσεις 6 3 Επεξεργασία Μετρήσεων 6 Σελίδα Θεωρία Η καταστατική εξίσωση
Εφηρμοσμένη Θερμοδυναμική
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφηρμοσμένη Θερμοδυναμική Ενότητα 11: Μίγματα Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφηρμοσμένη Θερμοδυναμική Ενότητα 11: Μίγματα Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Άδειες
Τμήμα Τεχνολογίας Τροφίμων. Ανόργανη Χημεία. Ενότητα 9 η : Διαλύματα & οι ιδιότητές τους. Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής.
 Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 9 η : Διαλύματα & οι ιδιότητές τους Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Διαλύματα 2 Τα ομοιογενή μίγματα μπορούν να ταξινομηθούν
Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 9 η : Διαλύματα & οι ιδιότητές τους Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Διαλύματα 2 Τα ομοιογενή μίγματα μπορούν να ταξινομηθούν
ΘΕΡΜΟΔΥΝΑΜΙΚΗ II Χειμερινό Εξάμηνο Η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΕΡΓ. ΡΕΥΣΤΟΜΗΧΑΝΙΚΗΣΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ II Χειμερινό Εξάμηνο 006-007 3 Η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Άσκηση Ένας κύλινδρος με όγκο 0,4 3 περιέχει μίγμα CH 4 και αέρα (Ο, % - Ν, 79%
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΕΡΓ. ΡΕΥΣΤΟΜΗΧΑΝΙΚΗΣΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ II Χειμερινό Εξάμηνο 006-007 3 Η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Άσκηση Ένας κύλινδρος με όγκο 0,4 3 περιέχει μίγμα CH 4 και αέρα (Ο, % - Ν, 79%
ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ. α. Χρησιμοποιώντας τον πρώτο θερμοδυναμικό νόμο έχουμε : J J J
 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ 1 ος θερμοδυναμικός νόμος 1. α. Αέριο απορροφά θερμότητα 2500 και παράγει έργο 1500. Να υπολογισθεί η μεταβολή της εσωτερικής του ενέργειας. β. Αέριο συμπιέζεται ισόθερμα και αποβάλλει
ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ 1 ος θερμοδυναμικός νόμος 1. α. Αέριο απορροφά θερμότητα 2500 και παράγει έργο 1500. Να υπολογισθεί η μεταβολή της εσωτερικής του ενέργειας. β. Αέριο συμπιέζεται ισόθερμα και αποβάλλει
Εφαρμοσμένη Θερμοδυναμική
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφαρμοσμένη Θερμοδυναμική Ενότητα 5: Πρώτος νόμος της θερμοδυναμικής Εφαρμογή σε ανοικτά συστήματα Χατζηαθανασίου Βασίλειος Καδή Στυλιανή
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφαρμοσμένη Θερμοδυναμική Ενότητα 5: Πρώτος νόμος της θερμοδυναμικής Εφαρμογή σε ανοικτά συστήματα Χατζηαθανασίου Βασίλειος Καδή Στυλιανή
EΡΓΟ-ΘΕΡΜΟΤΗΤΑ-ΕΣΩΤΕΡΙΚΗ ΕΝΕΡΓΕΙΑ
 EΡΓΟ-ΘΕΡΜΟΤΗΤΑ-ΕΣΩΤΕΡΙΚΗ ΕΝΕΡΓΕΙΑ ΠΑΡΑΤΗΡΗΣΕΙΣ 1. Διαδοση θερμοτητας και εργο είναι δυο τροποι με τους οποιους η ενεργεια ενός θερμοδυναμικου συστηματος μπορει να αυξηθει ή να ελαττωθει. Δεν εχει εννοια
EΡΓΟ-ΘΕΡΜΟΤΗΤΑ-ΕΣΩΤΕΡΙΚΗ ΕΝΕΡΓΕΙΑ ΠΑΡΑΤΗΡΗΣΕΙΣ 1. Διαδοση θερμοτητας και εργο είναι δυο τροποι με τους οποιους η ενεργεια ενός θερμοδυναμικου συστηματος μπορει να αυξηθει ή να ελαττωθει. Δεν εχει εννοια
ΑΝΩΤΕΡΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ
 ΑΝΩΤΕΡΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ Διδάσκοντες: Κώστας Περράκης, Δημοσθένης Γεωργίου http://eclass.upatras.gr/ p Βιβλιογραφία Advanced Thermodynamics for Engineers, Kenneth, Jr. Wark Advanced thermodynamics engineering
ΑΝΩΤΕΡΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ Διδάσκοντες: Κώστας Περράκης, Δημοσθένης Γεωργίου http://eclass.upatras.gr/ p Βιβλιογραφία Advanced Thermodynamics for Engineers, Kenneth, Jr. Wark Advanced thermodynamics engineering
ΥΠΟΔΕΙΓΜΑ ΘΕΩΡΗΤΙΚΩΝ ΕΡΩΤΗΣΕΩΝ ΕΞΕΤΑΣΕΩΝ
 ΥΠΟΔΕΙΓΜΑ ΘΕΩΡΗΤΙΚΩΝ ΕΡΩΤΗΣΕΩΝ ΕΞΕΤΑΣΕΩΝ 1. Πώς ορίζεται η περίσσεια αέρα και η ισχύς μίγματος σε μία καύση; 2. Σε ποιές περιπτώσεις παρατηρείται μή μόνιμη μετάδοση της θερμότητας; 3. Τί είναι η αντλία
ΥΠΟΔΕΙΓΜΑ ΘΕΩΡΗΤΙΚΩΝ ΕΡΩΤΗΣΕΩΝ ΕΞΕΤΑΣΕΩΝ 1. Πώς ορίζεται η περίσσεια αέρα και η ισχύς μίγματος σε μία καύση; 2. Σε ποιές περιπτώσεις παρατηρείται μή μόνιμη μετάδοση της θερμότητας; 3. Τί είναι η αντλία
σχηματική αναπαράσταση των βασικών τμημάτων μίας βιομηχανικής εγκατάστασης
 σχηματική αναπαράσταση των βασικών τμημάτων μίας βιομηχανικής εγκατάστασης Αρχές μεταφοράς μάζας Αρχές σχεδιασμού συσκευών μεταφοράς μάζας Διεργασίες μεταφοράς μάζας - Απορρόφηση - Απόσταξη - Εκχύλιση
σχηματική αναπαράσταση των βασικών τμημάτων μίας βιομηχανικής εγκατάστασης Αρχές μεταφοράς μάζας Αρχές σχεδιασμού συσκευών μεταφοράς μάζας Διεργασίες μεταφοράς μάζας - Απορρόφηση - Απόσταξη - Εκχύλιση
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο
 Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος 1 ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 8 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος 1 ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 8 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
Ειδική Ενθαλπία, Ειδική Θερµότητα και Ειδικός Όγκος Υγρού Αέρα
 θερµοκρασία που αντιπροσωπεύει την θερµοκρασία υγρού βολβού. Το ποσοστό κορεσµού υπολογίζεται από την καµπύλη του σταθερού ποσοστού κορεσµού που διέρχεται από το συγκεκριµένο σηµείο. Η απόλυτη υγρασία
θερµοκρασία που αντιπροσωπεύει την θερµοκρασία υγρού βολβού. Το ποσοστό κορεσµού υπολογίζεται από την καµπύλη του σταθερού ποσοστού κορεσµού που διέρχεται από το συγκεκριµένο σηµείο. Η απόλυτη υγρασία
