Energy resources: Technologies & Management
|
|
|
- Οφιούχος Καψής
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Πανεπιστήμιο Δυτικής Μακεδονίας Energ resources: echnologies & Management Τεχνολογίες άνθρακα Σχεδιασμός Στηλών Απορρόφησης Αερίων Δρ. Γεώργιος Σκόδρας Αν. Καθηγητής
2 Περιεχόμενα Η διάλεξη που ακολουθεί βασίζεται στο σύγγραμμα Φυσικές Διεργασίες Εισαγωγή στους Υπολογισμούς τους των κ. Μ. Ασσαέλ και κ. Μ. Μαγγιλιώτου Τεχνολογίες Άνθρακα 2
3 Περιεχόμενα Εισαγωγή Ισορροπία αερίου υγρού Περιγραφή στηλών πληρωτικών υλικών Αραιά μίγματα Ελάχιστος λόγος ροής αερίου / υγρού Σχεδιασμός ισοθερμικής στήλης πληρωτικού υλικού Αναλυτικός υπολογισμός μονάδων μεταφοράς Μέθοδος aker Απόδοση στήλης απορρόφησης Πυκνά μίγματα Σχεδιασμός ισοθερμικής στήλης πληρωτικού υλικού Αναλυτικός υπολογισμός μονάδων μεταφοράς Σχεδιασμός μη ισοθερμοκρασιακής στήλης πληρωτικού υλικού Σχεδιασμός στήλης με δίσκους Τεχνολογίες Άνθρακα 3
4 Περιεχόμενα Διαχωρισμός με απορρόφηση και απογύμνωση Σχεδιασμός για στήλες με δίσκους για αραιά διαλύματα Υπολογισμός βαθμίδων ισορροπίας Βαθμός απόδοσης βαθμίδας και ύψος στήλης Διάμετρος στήλης Σχεδιασμός στήλης με πληρωτικό υλικό για αραιά διαλύματα Σχεδιασμός στήλης με πληρωτικό υλικό για πυκνά διαλύματα Τεχνολογίες Άνθρακα 4
5 Εισαγωγή Απορρόφηση αερίων καλείται ο διαχωρισμός ενός μίγματος αερίων με επαφή τους με ένα υγρό που διαλύει εκλεκτικά ένα ή περισσότερα συστατικά του αερίου μίγματος Η αντίστροφη διεργασία της απορρόφησης καλείται εκρόφηση, οπότε και επιτυγχάνεται η απομάκρυνση ενός ή περισσοτέρων αερίων από ένα διάλυμα με την διαβίβαση αερίου ή ατμού Οι δύο αυτές διεργασίες (απορρόφηση ή εκρόφηση) πραγματοποιούνται σε στήλες παρόμοιες με τις αποστακτικές στήλες με δίσκους ή με πληρωτικά υλικά ή σε άλλες ειδικές στήλες Οι στήλες με δίσκους (διάτρητους) χρησιμοποιούνται κυρίως στις περιπτώσεις έκλυσης μεγάλων ποσών θερμότητας Η διεργασία της απορρόφησης διευκολύνεται με την αύξηση της πίεσης (διαλύεται πιό εύκολα το αέριο στο υγρό) Τεχνολογίες Άνθρακα 5
6 Τεχνική Φυσικών Διεργασιών Ισορροπία αερίου υγρού Τεχνολογίες Άνθρακα 6
7 Ισορροπία αερίου υγρού Η έννοια της ισορροπίας, στις διεργασίες απορρόφησης και εκρόφησης, καθορίζεται από την διαλυτότητα του μεταφερόμενου συστατικού στο αέριο ή στο υγρό Η διαλυτότητα του αερίου εξαρτάται από την μερικήπίεση του αερίου συστατικού στην αέρια φάση και την θερμοκρασία και συνήθως εκφράζεται: είτε ως βάρος αερίου ανά 00 μέρη βάρους διαλύτη σε δεδομένη πίεση και θερμοκρασία είτε μέσω της εξίσωσης Henr (σε θερμοκρασία που ισχύει για το σύστημα αυτό) pi H i όπου: p i = η μερική πίεση του αερίου συστατικού στην αέρια φάση i = το γραμμομοριακό κλάσμα του αερίου συστατικού στην υγρή φάση, και H = η σταθερά του Henr [atm/mol] Τεχνολογίες Άνθρακα 7
8 Ισορροπία αερίου υγρού Στην περίπτωση ιδανικού διαλύματος (έλλειψη αλληλεπιδράσεων μεταξύ όλων των συστατικών) εφαρμόζεται ο νόμος του Raoult: pi i pi όπου: p i μερική πίεση του συστατικού (i) στο μίγμα p 0 i πίεση (τάση ατμών) του καθαρού συστατικού (i) στην θερμοκρασία του διαλύματος Οπότε, στην περίπτωση ιδανικού διαλύματος ισχύει H = p i0, και ο νόμος του Hern μπορεί να γραφεί: Εξίσωση ισορροπίας * i m όπου: Κλίση m m = H / P και P η ολική πίεση του συστήματος Όταν κατά την απορρόφηση ή εκρόφηση εκλύεται ή απορροφάται σημαντική ποσότητα θερμότητας, μεταβάλλεται σημαντικά η θερμοκρασία του διαλύματος και συνεπώς η διαλυτότητα των αερίων, οπότε δεν ισχύει η ευθεία γραμμή 0 Τεχνολογίες Άνθρακα 8
9 Ισορροπία αερίου υγρού Στις περισσότερες διεργασίες μεταφοράς μάζας υπάρχουν δύο φάσεις, πρακτικά μη αναμίξιμες και μια διεπιφάνεια (interface) μεταξύ των δύο φάσεων Έστω συστατικό Α βρίσκεται στην αέρια φάση και διαχέεται προς την υγρή φάση Για να επιτευχθεί μεταφορά μάζας πρέπει να υπάρχει κινούσα δύναμη, ελάττωση της συγκέντρωσης του συστατικού Α κατά μήκος της οδού μεταφοράς Το γραμμομοριακό κλάσμα,, του συστατικού Α στην κύρια μάζα της αέριας φάσης ελαττώνεται στην τιμή i στην διεπιφάνεια των δύο φάσεων Στην υγρή φάση το αντίστοιχο γραμμομοριακό κλάσμα αρχίζει με την τιμή i στην διεπιφάνεια και ελαττώνεται στην τιμή μέσα στην κύρια μάζα της υγρής φάσης A Αέρια Φάση Τεχνολογίες Άνθρακα Η αντίσταση στην μεταφορά μάζας στην διεπιφάνεια, είναι αμελητέα, τα γραμμομοριακά κλάσματα i και i είναι σε ισορροπία και συνδέονται με την σχέση ισορροπίας Υγρή Φάση 9
10 Ισορροπία αερίου υγρού Σε αναλογία με τους συντελεστές μεταφοράς θερμότητας, h, στην μεταφορά μάζας χρησιμοποιούνται οι συντελεστές μεταφοράς μάζας, K (για τα υγρά) και K (για τα αέρια), που ορίζονται από τις σχέσεις: K A A K όπου: Ν Α ο ρυθμός μεταφοράς μάζας του συστατικού Α (kmol.s -.m -2 ) Οι συντελεστές K και K αναφέρονται σε μεταφορά μάζας μέσα σε μία μόνο φάση και γι αυτό ονομάζονται μερικοί συντελεστές μεταφοράς μάζας ως προς την αέρια φάση ή ως προς την υγρή φάση Οι συντελεστές αυτοί περιλαμβάνουν την μοριακή και τυρβώδη διάχυση και προσδιορίζονται πειραματικά Τεχνολογίες Άνθρακα 0
11 Κινούσα δύναμη στην αέρια φάση Ισορροπία αερίου υγρού Γραμμομοριακά κλάσμα στις δύο φάσεις Παραδοχές Αντιστάσεις στη μεταφορά μάζας υπάρχουν μόνο στους δύο υμένες Αμελητέα αντίσταση στη διεπιφάνεια Δεν υπάρχει συσσώρευση μάζας στη διεπιφάνεια Στην διεπιφάνεια υπάρχει θερμοδυναμική ισορροπία φάσεων Γραμμομοριακά κλάσμα στην διεπιφάνεια Κινούσα δύναμη στην υγρή φάση Σύμφωνα με τις ανωτέρω παραδοχές ισχύει: A A K K A K K Μερικοί συντελεστές μεταφοράς μάζας Τεχνολογίες Άνθρακα
12 Τεχνολογίες Άνθρακα Για την αποφυγή των προβλημάτων πειραματικού υπολογισμού των K και K ορίζονται οι ολικοί συντελεστές μεταφοράς μάζας ως: όπου K O ολικός συντελεστής μεταφοράς μάζας στην αέρια φάση K O ολικός συντελεστής μεταφοράς μάζας στην υγρή φάση *, * γραμμομοριακά κλάσματα του συστατικού στην αέρια και υγρή φάση που βρίσκεται σε ισορροπία με υγρό σύστασης ή με αέριο σύστασης Οι ολικοί συντελεστές μεταφοράς μάζας υπολογίζονται ως εξής: Όταν ισχύει ο νόμος του Hern τότε m = m = m 2 τότε: 2 Ισορροπία αερίου υγρού K K O O A * * * * * * O K m K K O K m K K 2 όπου m * 2 * m O K m K K O K m K K
13 Ισορροπία αερίου υγρού Οι προηγούμενες εξισώσεις συνδέουν τους μερικούς συντελεστές μεταφοράς μάζας με τους ολικούς Οι ολικοί συντελεστές μεταφοράς μάζας αναφέρονται σε πραγματικές, πειραματικά μετρήσιμες συγκεντρώσεις ή/και πιέσεις και μπορούν να υπολογιστούν, ενώ από τις προηγούμενες σχέσεις υπολογίζονται και οι μερικοί συντελεστές μεταφοράς μάζας Διακρίνονται δύο ειδικές περιπτώσεις:. Η κύρια αντίσταση στη μεταφορά μάζας βρίσκεται στην αέρια φάση (gas phase controlling) Όταν το m 0, τότε η γραμμή D είναι σχεδόν οριζόντια, δηλαδή, μικρή μεταβολή στην αέρια σύσταση (ή την πίεση του αερίου) έχει αποτέλεσμα μεγάλη μεταβολή στην αντίστοιχη σύσταση ισορροπίας * της υγρής φάσης (δηλαδή το αέριο συστατικό Α είναι πολύ ευδιάλυτο στο υγρό), οπότε ο όρος (m / K ) είναι αμελητέος. Οπότε: K O K K O K και A KO * K * Τεχνολογίες Άνθρακα 3
14 Ισορροπία αερίου υγρού 2. Η κύρια αντίσταση στη μεταφορά μάζας βρίσκεται στην υγρή φάση (liquid phase controlling) Όταν το m 2, τότε η γραμμή C είναι σχεδόν κατακόρυφη, δηλαδή, απαιτείται πολύ μεγάλη μεταβολή στην αέρια σύσταση (ή την πίεση του αερίου) για να συμβεί μικρή μεταβολή στην αντίστοιχη σύσταση ισορροπίας * της υγρής φάσης (δηλαδή το αέριο συστατικό Α είναι σχεδόν αδιάλυτο στο υγρό), οπότε ο όρος [/(m 2.K )] είναι αμελητέος. Οπότε: K KO K O K και K K A O * * * Τεχνολογίες Άνθρακα
15 Ισορροπία αερίου υγρού Στην πράξη, η μεταφορά μάζας διεξάγεται σε όλη την μάζα του ρευστού ή στην επιφάνεια του πληρωτικού υλικού Επειδή είναι δύσκολος ο υπολογισμός της επιφάνειας εναλλαγής, οι συντελεστές μεταφοράς μάζας δίνονται ως ογκομετρικοί Οι ογκομετρικοί συντελεστές είναι οι ίδιοι συντελεστές μεταφοράς μάζας, όπως έχουν οριστεί μέχρι τώρα, πολλαπλασιασμένοι με την ειδική επιφάνεια, a, που ορίζεται από την σχέση: S a V όπου S η επιφάνεια μεταφοράς μάζας V ο όγκος μέσα στον οποίο γίνεται η μεταφορά μάζας Τεχνολογίες Άνθρακα 5
16 Τεχνική Φυσικών Διεργασιών Περιγραφή στηλών πληρωτικών υλικών Τεχνολογίες Άνθρακα 6
17 Περιγραφή στηλών πληρωτικών υλικών Η είσοδος του υγρού γίνεται από την κορυφή μέσω ενός διανομέα Το υγρό περνά μέσα από στρώματα (κλίνες) πληρωτικών υλικών και απομακρύνεται από τον πυθμένα Το αέριο εισέρχεται από τον πυθμένα και εξέρχεται από την κορυφή (στην συνήθη περίπτωση της αντιρροής) Η μεταφορά μάζας του συστατικού είναι ανάλογη της επιφάνειας επαφής των δύο φάσεων, η οποία μπορεί να αυξηθεί με την πλήρωση της στήλης με πληρωτικό υλικό Το υγρό διαβρέχει όλη την επιφάνεια του πληρωτικού υλικού και έτσι αυξάνει πολύ η επιφάνεια επαφής του υγρού με το αέριο Τεχνολογίες Άνθρακα 7
18 Περιγραφή στηλών πληρωτικών υλικών Τεχνολογίες Άνθρακα 8
19 Περιγραφή στηλών πληρωτικών υλικών Τα πληρωτικά υλικά πρέπει να είναι ανθεκτικά στην διάβρωση και την πίεση που επικρατούν στις στήλες και πρέπει να αυξάνουν την επιφάνεια επαφής αερίου υγρού Υπάρχουν πολλά είδη πληρωτικών υλικών και συνήθως είναι τριών τύπων: Δακτύλιοι Rasching Χρησιμοποιήθηκαν από τον Rasching στην ASF το 93 και είναι σήμερα ένα από τα πλέον χρησιμοποιούμενα και αποδοτικά πληρωτικά υλικά. Διαφοροποιήσεις αυτού είναι ο σταυρωτός δακτύλιος Rasching και ο δακτύλιος essing Δακτύλιοι Pall Χρησιμοποιήθηκαν πρώτα το 954 από την ASF, έχουν 20% μικρότερη πίεση και αρκετά υψηλότερη απόδοση από τους δακτυλίους Rasching, αλλά είναι σημαντικά ακριβότεροι Σάγματα Intalo Χρησιμοποιούνται κυρίως λόγω του χαμηλού κόστους, όταν δεν απαιτείται μεγάλη επιφάνεια εναλλαγής Τεχνολογίες Άνθρακα 9
20 Περιγραφή στηλών πληρωτικών υλικών Τα πληρωτικά υλικά είναι συνήθως κατασκευασμένα από χάλυβα ή κεραμικό υλικό, ενώ σε μερικές περιπτώσεις, για αποφυγή διάβρωσης, χρησιμοποιείται χάλυβας Η τοποθέτηση συνήθως γίνεται τυχαία, και μόνο σε πού ειδικές περιπτώσεις, κρίσιμης πτώσης πίεσης, τοποθετούνται με το χέρι (με πολύ μεγάλο κόστος) Χαρακτηριστικά δακτυλίων Rasching τυχαίας τοποθέτησης Μέγεθος (mm) Υλικό Αριθμός (m -3 ) Ειδική επιφάνεια (m - ) Πορώδες κλάσμα, ε Βάρος (kg.m -3 ) Κεραμικό Κεραμικό Κεραμικό Κεραμικό Η ειδική επιφάνεια, a, ορίζεται ως η επιφάνεια του πληρωτικού υλικού ανά μονάδα όγκου κλίνης πληρωτικού υλικού [m 2 /m 3 ] Ως πορώδες, ε, ορίζεται το κλάσμα κενού όγκου της κλίνης, ενώ το βάρος του πληρωτικού υλικού είναι εκφρασμένο σε σχέση με τον όγκο που καταλαμβάνει Τεχνολογίες Άνθρακα 20
21 Περιγραφή στηλών πληρωτικών υλικών Συνήθως οι στήλες απορρόφησης σχεδιάζονται για επιφανειακή ταχύτητα αερίου ~ m / s Εμπειρικά υπάρχει μια σχέση μεταξύ διαμέτρου στήλης D c και διαμέτρου δακτυλίων d p που είναι: Dc 5 d 20 με αυτό τον τρόπο γίνεται μια πρώτη επιλογή διαστάσεων δακτυλίων πληρωτικού υλικού p Την επιλογή κατάλληλου δακτυλίου επηρεάζει και η πλημμύριση, κατάσταση ανάλογη με αυτή των αποστακτικών στηλών 2 U F a 3 g ep 4 w m όπου S η επιφάνεια μεταφοράς μάζας V ο όγκος μέσα στον οποίο γίνεται η μεταφορά μάζας n n 0.2 m 4 8 Τεχνολογίες Άνθρακα 2
22 Η ταχύτητα του αερίου στο σημείο πλημμύρισης καλείται ταχύτητα πλημμύρισης Εμπειρικά δίνεται από την σχέση: όπου Περιγραφή στηλών πληρωτικών υλικών 2 U F a 3 g n n w 0.2 ep 4 ρ, ρ οι πυκνότητες του αερίου και υγρού m, m οι μαζικές ροές υγρού και αερίου η, η w το ιξώδες του υγρού και του νερού a η ειδική επιφάνεια του πληρωτικού υλικού ε το πορώδες της κλίνης g η επιτάχυνση της βαρύτητας Για ένα συγκεκριμένο τύπο πληρωτικού υλικού υπολογίζεται η ταχύτητα πλημμύρισης Οι στήλες σχεδιάζονται ώστε η επιφανειακή ταχύτητα του αερίου να είναι 60 ως 70% της ταχύτητας πλημμύρισης (και συγχρόνως ~ m/s) m m 4 8 Τεχνολογίες Άνθρακα 22
23 Τεχνική Φυσικών Διεργασιών Αραιά μίγματα Τεχνολογίες Άνθρακα 23
24 Αραιά μίγματα Ο σχεδιασμός στήλης απορρόφησης βασίζεται στο ισοζύγιο μάζας για τον προσδιορισμό της γραμμής λειτουργίας και στην εξίσωση ισορροπίας Το ισοζύγιο μάζας είναι χαρακτηριστικό της διεργασίας και, ουσιαστικά, ανεξάρτητο του συγκεκριμένου μίγματος Η σχέση ισορροπίας είναι χαρακτηριστική του μίγματος και, ουσιαστικά, ανεξάρτητη της διεργασίας Εάν η απορρόφηση ή εκρόφηση συνοδεύεται από έκλυση ή απορρόφηση σημαντικής ποσότητας θερμότητας, απαιτείται επιπλέον το ισοζύγιο ενθαλπίας Η παραδοχή των αραιών μιγμάτων απλοποιεί τις εξισώσεις γιατί επιτρέπει να θεωρηθούν σταθερές οι γραμμομοριακές ροές Οι στήλες απορρόφησης ή εκρόφησης μπορούν να λειτουργήσουν κατ αντιρροή ή ομορροή, με την πρώτη να πλεονεκτεί και να χρησιμοποιείται στην πράξη Τεχνολογίες Άνθρακα 24
25 Αραιά μίγματα Στα αραιά μίγματα η ποσότητα του απορροφούμενου /εκροφούμενου είναι πολύ μικρή σε σχέση με την ποσότητα του αδρανούς αερίου και του υγρού διαλύτη Επομένως οι συνολικές γραμμομοριακές ροές του αερίου και του υγρού μπορούν να θεωρηθούν σταθερές, σε όλο το ύψος της στήλης : top (κορυφή) Ρεύματα εισόδου A Ρεύματα εξόδου Τροφοδοσία υγρού [kmol.h -.m -2 διατομής στήλης] = = = = Τροφοδοσία αερίου [kmol.h -.m -2 διατομής στήλης] : bottom (πυθμένας) : bottom (πυθμένας) : top (κορυφή) Τεχνολογίες Άνθρακα 25
26 Αραιά μίγματα Από την παραδοχή των σταθερών γραμμομοριακών ροών ισχύει Στην απορρόφηση η γραμμή λειτουργίας είναι επάνω από την καμπύλη ισορροπίας 0,8 * = f() Τ Το γενικό ισοζύγιο μάζας του απορροφούμενου αερίου εκφράζεται από την σχέση 0,6 0,4 0,2 Β A Στο αέριο ρεύμα η παροχή του απορροφούμενου αερίου μειώνεται από σε, ενώ στο υγρό αυξάνεται από σε Η εξίσωση της γραμμής λειτουργίας για απορρόφηση κατ αντιρροή είναι: 0 0 0,2 0,4 0,6 0,8 γραμμή λειτουργίας Τεχνολογίες Άνθρακα 26
27 Αραιά μίγματα Αντίστοιχα, η εξίσωση της γραμμής λειτουργίας για εκρόφηση κατ αντιρροή επίσης είναι: Στην εκρόφηση η γραμμή 0,8 λειτουργίας είναι κάτω από την καμπύλη ισορροπίας 0,6 0,4 * = f() Τ A Η γραμμή λειτουργίας βρίσκεται πάντοτε κάτω από την καμπύλη ισορροπίας διότι η μεταφορά μάζας γίνεται από την υγρή προς την αέρια φάση Σε τυχαίο ύψος της στήλης, όπου η σύσταση του υγρού είναι, η σύσταση του αερίου είναι < *() ώστε να υπάρχει κινούσα δύναμη για περαιτέρω μεταφορά συστατικού από την υγρή στην αέρια φάση 0, ,2 0,4 0,6 0,8 γραμμή λειτουργίας Β Τεχνολογίες Άνθρακα 27
28 Αραιά μίγματα Αντίστοιχα, στην περίπτωση της ομορροής οι γραμμές λειτουργίας για απορρόφηση και εκρόφηση δίνονται στο σχήμα Τ 0,8 0,6 απορρόφηση * = f() Τ A 0,4 εκρόφηση A Β 0,2 Β 0 0 0,2 0,4 0,6 0,8 απορρόφηση εκρόφηση Τεχνολογίες Άνθρακα 28
29 Αραιά μίγματα Ελάχιστος λόγος ροής αερίου / υγρού Αντίστοιχα με την απόσταξη, στην απορρόφηση ως ελάχιστη ροή υγρού ορίζεται η γραμμομοριακή ροή που αντιστοιχεί σε άπειρο ύψος στήλης ή άπειρο αριθμό θεωρητικών βαθμίδων στήλης απορρόφησης Ζητείται να ελαττωθεί η σύσταση αέριας ροής από σε χρησιμοποιώντας διαθέσιμο διαλύτη σύστασης. Πόσος διαλύτης απαιτείται και ποια η σύσταση του; 0,8 0,6 0,4 0, ,2 0,4 0,6 0,8 * = f() Για να επιτευχθεί ο επιθυμητός διαχωρισμός, η ελάχιστη ροή υγρού θα είναι αυτή κατά την οποία ο εξερχόμενος διαλύτης θα βρίσκεται σε ισορροπία με το εισερχόμενο αέριο min * Τ Β A min * min ή όπου min Τεχνολογίες Άνθρακα 29
30 Αραιά μίγματα Ελάχιστος λόγος ροής αερίου / υγρού Αντίστοιχα για την εκρόφηση το πρόβλημα τίθεται ως εξής: Ζητείται να ελαττωθεί η σύσταση υγρής ροής από σε χρησιμοποιώντας διαθέσιμο αέριο διαλύτη σύστασης. Πόσος αέριος διαλύτης απαιτείται και ποια η σύσταση του; Για να επιτευχθεί ο επιθυμητός διαχωρισμός, η ελάχιστη ροή αερίου θα είναι αυτή κατά την οποία ο εξερχόμενος αέριος διαλύτης θα βρίσκεται σε ισορροπία με το εισερχόμενο υγρό, δηλ. = * = f( ) * 0,8 0,6 0,4 0, ,2 0,4 0,6 0,8 Τεχνολογίες Άνθρακα 30 ma * = f() Η ελάχιστη γραμμομοριακή ροή αερίου χαρακτηρίζει τον μέγιστο λόγο ροής υγρού / αερίου ή τον ελάχιστο λόγο ροής αερίου / υγρού ma ή min όπου min Τ Β A
31 Αραιά μίγματα Σχεδιασμός ισοθερμικής αποστακτικής στήλης πληρωτικού υλικού Η διεργασία απορρόφησης σε στήλες πληρωτικού υλικού γίνεται με διαφορική μεταφορά μάζας και όχι σε συγκεκριμένες βαθμίδες Ο σχεδιασμός της στήλης αναφέρεται στον υπολογισμό του ύψους του πληρωτικού υλικού μέσα στη στήλη Διακρίνονται δύο περιπτώσεις (α) αραιά μίγματα και (β) πυκνά μίγματα Παραδοχές Όταν οι συγκεντρώσεις του μεταφερόμενου συστατικού, σε σχέση με το αδρανές, είναι μικρές, τότε τα μίγματα μπορούν αν θεωρηθούν αραιά, δηλαδή, οι γραμμομοριακές ροές αερίου και υγρού μπορούν αν θεωρηθούν σταθερές σ όλο το ύψος της στήλης Η μέση πίεση του αδρανούς αερίου είναι σταθερή και ίση με την ολική πίεση του συστήματος Οι συντελεστές μεταφοράς μάζας είναι σταθεροί σ όλο το ύψος της στήλης Οι μεταβολές ενθαλπίας μπορούν να θεωρηθούν αμελητέες (ισόθερμη λειτουργία) Τεχνολογίες Άνθρακα 3
32 Αραιά μίγματα Τ Β A Α dz Η στήλη απορρόφησης λειτουργεί κατ αντιρροή (διαφορική μεταφορά μάζας) Το ισοζύγιο του μεταφερόμενου συστατικού είναι: d d d d Αν οριστεί ως A ο ρυθμός μεταφοράς μάζας του μεταφερόμενου συστατικού (kmol.h -.m -2 ) και ds η διαφορική επιφάνεια εναλλαγής μάζας στο τμήμα dz της στήλης, οπότε: Ad Ad A ds Η σχέση αυτή απλοποιείται χρησιμοποιώντας την σχέση του ρυθμού μεταφοράς μάζας A με τους ολικούς συντελεστές μεταφοράς μάζας και αντικαθιστώντας την διαφορική επιφάνεια ds συναρτήσει της ειδικής επιφάνειας a, συγκεκριμένα: A ds K a O * KO * και AdZ ολικό ύψος στήλης Τεχνολογίες Άνθρακα 32
33 Αραιά μίγματα Οπότε: Αέρια φάση d KO a * dz dz K O a d Z * K a * O d Υγρή φάση d KO a * dz dz K O a d Z * K a * O d Αντίστοιχα: όπου: H O Ολικό ύψος μονάδας μεταφοράς Z K O a H O O H O H O d O K a * O H (ή HU) = ύψος μονάδας μεταφοράς (ή U) = αριθμός μανάδων μεταφοράς O d * O Ολικός αριθμός μονάδων μεταφοράς Το ύψος Z του πληρωτικού υλικού υπολογίζεται ως πολλαπλάσιο ενός στοιχειώδους ύψους μιας μονάδας μεταφοράς Τεχνολογίες Άνθρακα 33
34 Αραιά μίγματα Αντίστοιχα για τους μερικούς συντελεστές μεταφοράς Z H H όπου H H K a K a Τεχνολογίες Άνθρακα 34 d d Οι σχέσεις μεταξύ των ολικών και των μερικών υψών μονάδων μεταφοράς είναι (πολλαπλασιάζοντας και διαιρώντας με τον όρο (am/): H H O O H H H H H O H O Αντίστοιχα, για τους αριθμούς μονάδων μεταφοράς είναι: O O O H O όπου λ = m/ = / A f = παράγοντας απορρόφησης m = */
35 Αραιά μίγματα Αναλυτικός υπολογισμός μονάδων μεταφοράς Η αναλυτική ολοκλήρωση του O προτιμάται, για καθαρά μαθηματικούς λόγους, όταν η γραμμή ισορροπίας είναι ευθεία γραμμή, δηλαδή όταν * = m Η εξίσωση λειτουργίας γράφεται: Οπότε: ή * m * * m m m m m c = σταθερό Αντικαθιστώντας στην O d O d * προκύπτει: O * m c m d ln m m c c Τεχνολογίες Άνθρακα 35
36 Τεχνολογίες Άνθρακα 36 Αραιά μίγματα Επίσης: m * * λογαριθμική μέθοδος και O d * Οπότε προκύπτει: m m * * * * m * * Είναι: c m c m m O ln O m * * ln lm O * lm O * () (2) Από τις () και (2) προκύπτει: όπου: lm * * ln * * * αντίστοιχα και για το υγρό
37 Αραιά μίγματα Στην ειδική περίπτωση που ο υγρός διαλύτης εισέρχεται καθαρός δεν περιέχει καθόλου το μεταφερόμενο συστατικό τότε επειδή = 0, η προηγούμενη εξίσωση απλοποιείται και καταλήγει: O ln m m m Τεχνολογίες Άνθρακα 37
38 Αραιά μίγματα Άσκηση Ζητείται να απομακρυνθεί το 95% αερίου Χ από αέριο μίγμα σε στήλη απορρόφησης πληρωτικού υλικού που λειτουργεί κατ αντιρροή. Ο υγρός διαλύτης θα εισέλθει καθαρός στη στήλη και η σχέση ισορροπίας είναι * = m. Αν χρησιμοποιηθεί γραμμομοριακή ροή υγρού ίση με,25 φορές την ελάχιστη και το ολικό ύψος μιας μονάδας μεταφοράς για την αέρια φάση είναι 2 m, να υπολογιστεί το ύψος της στήλης Τ Β A Τεχνολογίες Άνθρακα 38
39 Αραιά μίγματα Άσκηση 2 Στήλη πληρωτικού υλικού κατ αντιρροή χρησιμοποιείται για την απομάκρυνση συστατικού Α από αέρια ροή 00 kmol.h -.m -2 με νερό. Το νερό εισέρχεται καθαρό με ροή 2000 kmol.h -.m -2 και απομακρύνει το 95% του συστατικού Α από το αέριο μίγμα. Οι μερικοί συντελεστές μεταφοράς μάζας για την αέρια και την υγρή φάση είναι 00 και 750 kmol.h -.m -3 αντίστοιχα, ενώ η σταθερά του Hern μπορεί να ληφθεί ίση με 5 bars. Η διεργασία διεξάγεται σε ατμοσφαιρική πίεση και οι ροές μπορούν να θεωρηθούν σταθερές. Να υπολογιστεί το ύψος της στήλης Τ Β A Τεχνολογίες Άνθρακα 39
40 Αραιά μίγματα Μέθοδος aker Από την εξίσωση του ολικού αριθμού μονάδων μεταφοράς ως προς την αέρια φάση προκύπτει: O d * * από την οποία διαπιστώνεται ότι διαχωρισμός ισοδύναμος με μια μονάδα μεταφοράς ( O = ) επιτυγχάνεται όταν η διαφορά Δ είναι ίση με την μέση κινούσα δύναμη ( *) av [εκφρασμένη ως διαφορά γραμμομοριακών κλασμάτων αέριας φάσης], δηλαδή: * av av Τεχνολογίες Άνθρακα 40
41 Αραιά μίγματα Μέθοδος aker Η μέθοδος aker είναι απλούστατη και στηρίζεται στην ανωτέρω έννοια Τα βήματα της μεθόδου είναι: Κατασκευάζεται η γραμμή ισορροπίας Κατασκευάζεται η γραμμή λειτουργίας Κατασκευάζεται η διχοτόμος των κινουσών δυνάμεων, σημειώνοντας τα μέσα των διαδοχικών αποστάσεων ( *) av Από το σημείο φέρεται οριζόντια γραμμή έτσι ώστε C = CE Από το σημείο E φέρεται κάθετη μέχρι το σημείο F Το τρίγωνο EF αποτελεί μια μονάδα μεταφοράς Η διαδικασία συνεχίζεται ομοίως και ο αριθμός των τριγώνων που σχηματίζονται είναι ο ζητούμενος αριθμός των μονάδων μεταφοράς O Η μέθοδος aker βασίζεται στην παραδοχή ότι, προσεγγιστικά, η μέση κινούσα δύναμη ( *) av βρίσκεται στο μέσο της απόστασης E Τεχνολογίες Άνθρακα 4
42 Αραιά μίγματα Άσκηση 3 Ζητείται να ελαττωθεί συγκέντρωση συστατικού Χ, σε αέρια ροή, από 0,095 σε 0,005 γραμμομοριακό κλάσμα. Για την διεργασία αυτή προτείνεται να χρησιμοποιηθεί υπάρχουσα ροή υγρού διαλύτη, που περιέχει ήδη 0,00 γραμμομοριακό κλάσμα συστατικού Χ, σε στήλη πληρωτικού υλικού κατ αντιρροή. Ο λόγος των γραμμομοριακών ροών, αερίου προς υγρού, είναι ίσος με 2, και η σχέση ισορροπίας για το σύστημα αυτό είναι * = 2 2. Εάν το ολικό ύψος μιας μονάδας μεταφοράς για την αέρια φάση είναι ίσο με 2 m, να υπολογιστεί το ύψος της στήλης με (α) αναλυτική ολοκλήρωση και (β) μέθοδο aker Τ Β A Τεχνολογίες Άνθρακα 42
43 Αραιά μίγματα Απόδοση στήλης απορρόφησης Στην περίπτωση των στηλών απορρόφησης συνηθίζεται να χρησιμοποιείται η απόδοση Φ της στήλης με τον εξής ορισμό: και * ό ό ό ή ά ύ Στην περίπτωση καθαρού διαλύτη, = 0, και της ευθείας γραμμής ισορροπίας, * = m, ισχύει: Σε συνδυασμό με τον λόγο των γραμμομοριακών παροχών γίνεται: m * και m Τεχνολογίες Άνθρακα 43
44 Τεχνική Φυσικών Διεργασιών Πυκνά μίγματα Τεχνολογίες Άνθρακα 44
45 Τεχνολογίες Άνθρακα 45 Πυκνά μίγματα Στα πυκνά μίγματα η ποσότητα του μεταφερόμενου συστατικού είναι σημαντική και μεταβάλλονται οι συνολικές γραμμομοριακές ροές του υγρού και του αερίου Στην περίπτωση αυτή οι μόνες σταθερές γραμμομοριακές ροές είναι η ροή του αδρανούς αερίου και του υγρού διαλύτη Οι ροές των αδρανών και συνδέονται με τις συνολικές γρομμομοριακές ροές ως: Και επομένως το ολικό ισοζύγιο μάζας γίνεται: ' και ' ή ' '
46 Πυκνά μίγματα Ορίζονται οι λόγοι μοριακών κλασμάτων: Και αντικαθιστώντας: ' Y Y ' X X X και Y Γενικό ισοζύγιο μάζας Οι γραμμομοριακές ροές είναι οι ροές των αδρανών και αντί των γραμμομοριακών κλασμάτων χρησιμοποιούνται οι λόγοι μοριακών κλασμάτων Τεχνολογίες Άνθρακα 46
47 Πυκνά μίγματα Στην περίπτωση της απορρόφησης σε ομορροή, για τα αραιά μίγματα είναι: Και για τα πυκνά μίγματα: ' Y Y ' X X Τ 0,8 0,6 απορρόφηση * = f() A 0,4 εκρόφηση Β 0, ,2 0,4 0,6 0,8 Τεχνολογίες Άνθρακα 47
48 Πυκνά μίγματα Αναλυτικός υπολογισμός μονάδων μεταφοράς Στα πυκνά μίγματα οι γραμμομοριακές ροές και δεν μπορούν να θεωρηθούν σταθερές σ όλο το μήκος της στήλης Το ισοζύγιο μάζας της στήλης βασίζεται στις ροές των αδρανών, οπότε: και: As ds Ad ' d Ad A ' 2 Στην περίπτωση της διάχυσης του συστατικού σε πυκνά μίγματα, ο ρυθμός μεταφοράς A δίνεται από την σχέση: A A A ds * KO όπου ln ln * * ln Τεχνολογίες Άνθρακα 48
49 Οπότε προκύπτει: και: ' dz d K Πυκνά μίγματα K a 2 O O ' a * Στα πυκνά διαλύματα ο συντελεστής K O a μεταβάλλεται σημαντικά κατά το ύψος της στήλης Όμως το γινόμενο K O a ( ) διατηρείται σταθερό (κατά προσέγγιση), οπότε το πρώτο κλάσμα μπορεί να θεωρηθεί ίσο με το ολικό ύψος μιας μονάδας μεταφοράς H O και συνεπώς: Z H O ln dz ln d * ln d * Τεχνολογίες Άνθρακα 49
50 Πυκνά μίγματα Αν, προσεγγιστικά, η μέση λογαριθμική τιμή θεωρηθεί ίση με την μέση αριθμητική, η ανωτέρω εξίσωση μπορεί να απλοποιηθεί: O * * 2 d και επομένως: αραιά μίγματα O O d * 2 d * d ln 2 διόρθωση Δηλαδή, ο ολικός αριθμός των μονάδων μεταφοράς για τα πυκνά μίγματα αποτελείται από δύο μέρη, το πρώτο είναι το ίδιο με τον αριθμό μονάδων μεταφοράς για αραιά μίγματα, ενώ το δεύτερο μέρος αποτελεί διόρθωση για τα πυκνά μίγματα Τεχνολογίες Άνθρακα 50
51 Τεχνική Φυσικών Διεργασιών Σχεδιασμός μη-ισοθερμικής στήλης πληρωτικού υλικού Τεχνολογίες Άνθρακα 5
52 Σχεδιασμός μη-ισοθερμικής στήλης πληρωτικού υλικού Όταν η θερμότητα απορρόφησης είναι σημαντική, η θερμοκρασία μεταβάλλεται μέσα στη στήλη και επομένως θα υπάρχουν αντίστοιχες καμπύλες διαλυτότητας για κάθε θερμοκρασία Έτσι, σε κάθε ύψος της στήλης ή σε κάθε γραμμομοριακό κλάσμα της στήλης θα αντιστοιχεί μια νέα θερμοκρασία, δηλαδή μια οικογένεια καμπυλών ισορροπίας Αν υπάρχει μια σχέση που συνδέει το γραμμομοριακό κλάσμα με την αντίστοιχη θερμοκρασία, μπορεί να αντικαταστήσει την οικογένεια των καμπυλών Τεχνολογίες Άνθρακα 52
53 Σχεδιασμός μη-ισοθερμικής στήλης πληρωτικού υλικού Έστω c P και c P οι ειδικές θερμότητες του αερίου και του υγρού μίγματος αντίστοιχα, θεωρούμενες σταθερές (kj.kmol -.K - ) και Q η θερμότητα απορρόφησης ή έκλυσης (kw.kmol - ) Θεωρώντας αραιά μίγματα, ένα ισοζύγιο ενέργειας στον στοιχειώδη όγκο είναι: c P d Qd Επειδή η θερμότητα απορρόφησης είναι σημαντική: c d Qd Οπότε: Qd c d, και εισάγοντας το ισοζύγιο μάζας d προκύπτει: d Ολοκληρώνοντας: Q c P d Q c P c Q P c P d Τεχνολογίες Άνθρακα 53 d
54 Σχεδιασμός μη-ισοθερμικής στήλης πληρωτικού υλικού Επομένως, έχοντας γνωστές όλες τις καμπύλες διαλυτότητας και γνωρίζοντας το μοριακό κλάσμα, από την εξίσωση Q c P για κάθε γραμμομοριακό κλάσμα υπολογίζεται η θερμοκρασία Συνεπώς, ορίζονται τα σημεία E i που αποτελούν την νέα καμπύλη ισορροπίας E E 2 E 3 E 4 E 5 που αφορά την συγκεκριμένη διεργασία Στην περίπτωση που είναι γνωστές οι θερμοκρασίες μπορούν να βρεθούν τα αντίστοιχα γραμμομοριακά κλάσματα και να οριστούν τα σημεία E i χρησιμοποιώντας την εξίσωση: c Q P Οι διαφορές στις θερμοκρασίες έχουν συμπεριληφθεί στην νέα καμπύλη και η επίλυση της στήλης γίνεται όπως στην ισοθερμική στήλη Τεχνολογίες Άνθρακα 54
55 Τεχνική Φυσικών Διεργασιών Σχεδιασμός στήλης με δίσκους Τεχνολογίες Άνθρακα 55
56 Σχεδιασμός στήλης με δίσκους Η διεργασία απορρόφησης σε στήλες με δίσκους είναι ανάλογη της απόσταξης σε στήλες με δίσκους και ο υπολογισμός των θεωρητικών βαθμίδων μπορεί να γίνει με την μέθοδο McCabe-hiele Σχεδιάζεται πρώτα η γραμμή λειτουργίας (πάνω από την γραμμή ισορροπίας για απορρόφηση) Με αρχή την κορυφή Τ, (αντίστοιχα με την απόσταξη), κατασκευάζονται οι θεωρητικές βαθμίδες Ο αριθμός των πραγματικών βαθμίδων βρίσκεται χρησιμοποιώντας τον βαθμό απόδοσης Στην περίπτωση πυκνών μιγμάτων χρησιμοποιούνται οι λόγοι των γραμμομοριακών κλασμάτων Τεχνολογίες Άνθρακα 56
57 Τεχνολογίες Άνθρακα 57 Σχεδιασμός στήλης με δίσκους Στην περίπτωση των αραιών μιγμάτων και όταν η γραμμή ισορροπίας μπορεί να θεωρηθεί ευθεία, = m (ισχύει ο νόμος του Henr) και όταν πρόκειται για μεγάλο αριθμό βαθμίδων, χρησιμοποιούνται οι εξισώσεις Kremser Οι εξισώσεις αυτές εξήχθησαν το 930 από τον Kremser και στη συνέχεια το 932 από τους M. Souders και.. rown, και είναι γνωστές ως εξισώσεις Kremser ή εξισώσεις KS Για την περίπτωση της απορρόφησης οι εξισώσεις έχουν την μορφή: όπου ο συντελεστής A f = / (m ) καλείται παράγοντας απορρόφησης Για στήλες εκρόφησης είναι: f f f A A A m ή f f f A A m m A ln ) ln( f f f A A A m ή f f f A A m m A ln ln
58 Τεχνική Φυσικών Διεργασιών Διαχωρισμός με απορρόφηση και απογύμνωση Τεχνολογίες Άνθρακα 58
59 Απορρόφηση απογύμνωση Στην απορρόφηση και την απογύμνωση η μάζα μεταφέρεται μεταξύ μιας αέριας και μιας υγρής φάσης σε κάθε στάδιο, σε όλη την κλίνη Οι συσκευές απορρόφησης συνδυάζονται συχνά με απογυμνωτές για την ανάκτηση του απορροφητικού υλικού Επειδή, η διεργασία της απογύμνωσης δεν είναι τέλεια, το ανακυκλούμενο απορροφητικό υλικό που ανακτάται περιέχει περιέχει και ίχνη της απορροφούμενης ουσίας Κλασσική εφαρμογή απορρόφησης απογύμνωσης είναι η δέσμευση διοξειδίου του άνθρακα από τα απαέρια σταθμών ηλεκτροπαραγωγής με άνθρακα Ένα τυπικό διάγραμμα απορρόφησης-απογύμνωσης παρουσιάζεται στο διάγραμμα που ακολουθεί Τεχνολογίες Άνθρακα 59
60 Απορρόφηση απογύμνωση Τεχνολογίες Άνθρακα 60
61 Σχεδιασμός για στήλες με δίσκους για αραιά διαλύματα Οι γραφικές μέθοδοι για τον υπολογισμό των βαθμίδων ισορροπίας είναι σχετικά χρονοβόρες, με συνέπεια να προτιμώνται αλγεβρικές μέθοδοι Στην απορρόφηση και την απογύμνωση αραιών μιγμάτων εφαρμόζεται η μέθοδος Kremser, όπως τροποποιήθηκε από τον Edmister Το κλάσμα μιας διαλυμένης ουσίας i που απορροφάται, δίνεται από την σχέση: Τεχνολογίες Άνθρακα 6
62 Υπολογισμός βαθμίδων ισορροπίας Οι γραφικές μέθοδοι για τον υπολογισμό των βαθμίδων ισορροπίας είναι σχετικά χρονοβόρες, με συνέπεια να προτιμώνται αλγεβρικές μέθοδοι Στην απορρόφηση και την απογύμνωση αραιών μιγμάτων εφαρμόζεται η μέθοδος Kremser, όπως τροποποιήθηκε από τον Edmister Το κλάσμα μιας διαλυμένης ουσίας i που απορροφάται, δίνεται από την σχέση: Ενώ, το κλάσμα μιας διαλυμένης ουσίας i που απογυμνώνεται, δίνεται από την σχέση: όπου: A i και S i είναι οι συντελεστές απορρόφησης και απογύμνωσης του συστατικού i και Ν ο αριθμός των βαθμίδων Τεχνολογίες Άνθρακα 62
63 Υπολογισμός βαθμίδων ισορροπίας Όταν οι συγκεντρώσεις της διαλυμένης ουσίας είναι χαμηλές, οι συντελεστές απορρόφησης και απογύμνωσης ορίζονται συναρτήσει των και V, που είναι οι ρυθμοί ροής εισόδου του υγρού και του ατμού στη στήλη, αντίστοιχα, και του K i που είναι ο λόγος ισορροπίας ατμού υγρού για τη διαλυμένη ουσία Το K i είναι συνάρτηση της θερμοκρασίας, της πίεσης και της σύστασης της υγρής φάσης Όταν τα μίγματα είναι αραιά και η πίεση πολύ κοντά στην ατμοσφαιρική, το K i υπολογίζεται από σχέσεις, όπως: Ιδανικό διάλυμα και υποκρίσιμη θερμοκρασία Τάση ατμών Διαλυμένη ουσία στην υπερκρίσιμη θερμοκρασία Σταθερά του Hern Μη ιδανικό διάλυμα και υποκρίσιμη θερμοκρασία Συντελεστής ενεργότητας Τεχνολογίες Άνθρακα Μερικώς διαλυτή διαλυμένη ουσία στην υπερκρίσιμη θερμοκρασία Γραμμομοριακό κλάσμα στην ισορροπία 63
64 Υπολογισμός βαθμίδων ισορροπίας Τεχνολογίες Άνθρακα 64
65 Υπολογισμός βαθμίδων ισορροπίας Τεχνολογίες Άνθρακα
66 Υπολογισμός βαθμίδων ισορροπίας Τεχνολογίες Άνθρακα 66
67 Τεχνική Φυσικών Διεργασιών Τεχνολογίες Άνθρακα 67
5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού
 5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού Η αρχική εξίσωση που χρησιμοποιείται για τους υπολογισμούς της ΙΦΥΥ είναι η ικανοποίηση της βασικής θερμοδυναμικής απαίτησης της ισότητας των τάσεων διαφυγής
5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού Η αρχική εξίσωση που χρησιμοποιείται για τους υπολογισμούς της ΙΦΥΥ είναι η ικανοποίηση της βασικής θερμοδυναμικής απαίτησης της ισότητας των τάσεων διαφυγής
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens. ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Gas Absorption
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Gas Absorption Παράγοντες που Επηρεάζουν Διεργασία Απορρόφησης Συνήθως δίνονται: Ρυθμός
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Gas Absorption Παράγοντες που Επηρεάζουν Διεργασία Απορρόφησης Συνήθως δίνονται: Ρυθμός
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens. ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Περιοχές
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Περιοχές
Απορρόφηση Αερίων. 1. Εισαγωγή
 1. Εισαγωγή Απορρόφηση Αερίων Πρόκειται για διαχωρισμό συστατικών από μείγμα αερίου με τη βοήθεια υγρού διαλύτη. Κινητήρια δύναμη είναι η διαφορά διαλυτότητας στο διαλύτη. Στη συνέχεια θα ασχοληθούμε με
1. Εισαγωγή Απορρόφηση Αερίων Πρόκειται για διαχωρισμό συστατικών από μείγμα αερίου με τη βοήθεια υγρού διαλύτη. Κινητήρια δύναμη είναι η διαφορά διαλυτότητας στο διαλύτη. Στη συνέχεια θα ασχοληθούμε με
ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης
 ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης Πρόβληµα 1. Ένα µίγµα αερίων που περιέχει 65% του Α, 5% Β, 8% C και % D βρίσκεται σε ισορροπία µ' ένα υγρό στους 350 Κ και 300 kn/m. Αν η τάση ατµών των καθαρών συστατικών
ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης Πρόβληµα 1. Ένα µίγµα αερίων που περιέχει 65% του Α, 5% Β, 8% C και % D βρίσκεται σε ισορροπία µ' ένα υγρό στους 350 Κ και 300 kn/m. Αν η τάση ατµών των καθαρών συστατικών
Φυσικές Διεργασίες Πέμπτη Διάλεξη
 Φυσικές Διεργασίες Πέμπτη Διάλεξη Δευτέρα, 12 Μαΐου 2008 Απορρόφηση αερίων 1. Ορισμός Τι είναι απορρόφηση; Είναι μεταφορά μέσω της διεπιφάνειας αερίου-υγρού ενός συστατικού από αέριο μίγμα σε έναν υγρό
Φυσικές Διεργασίες Πέμπτη Διάλεξη Δευτέρα, 12 Μαΐου 2008 Απορρόφηση αερίων 1. Ορισμός Τι είναι απορρόφηση; Είναι μεταφορά μέσω της διεπιφάνειας αερίου-υγρού ενός συστατικού από αέριο μίγμα σε έναν υγρό
ΠΡΟΒΛΗΜΑΤΑ Υ/Υ ΕΚΧΥΛΙΣΗΣ Κ. Μάτης
 ΠΡΟΒΛΗΜΑΤΑ Υ/Υ ΕΚΧΥΛΙΣΗΣ Κ. Μάτης Πρόβληµα 36. Μια υγρή τροφοδοσία 3,5 kg/s, που περιέχει µια διαλυτή ουσία Β διαλυµένη σε συστατικό Α, πρόκειται να διεργαστεί µε ένα διαλύτη S σε µια µονάδα επαφής καθ
ΠΡΟΒΛΗΜΑΤΑ Υ/Υ ΕΚΧΥΛΙΣΗΣ Κ. Μάτης Πρόβληµα 36. Μια υγρή τροφοδοσία 3,5 kg/s, που περιέχει µια διαλυτή ουσία Β διαλυµένη σε συστατικό Α, πρόκειται να διεργαστεί µε ένα διαλύτη S σε µια µονάδα επαφής καθ
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens. ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Τριγωνικές
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Τριγωνικές
ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ ΜΕΤΑΦΟΡΑΣ ΜΑΖΑΣ. -Απορρόφηση - Απόσταξη - Εκχύλιση - Κρυστάλλωση - Ξήρανση
 ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ ΜΕΤΑΦΟΡΑΣ ΜΑΖΑΣ -Απορρόφηση - Απόσταξη - Εκχύλιση - Κρυστάλλωση - Ξήρανση Απορρόφηση αερίων φυσική και χημική Παραδείγματα βιομηχανικών εφαρμογών ) Απορρόφηση SΟ 3 κατά την παραγωγή
ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ ΜΕΤΑΦΟΡΑΣ ΜΑΖΑΣ -Απορρόφηση - Απόσταξη - Εκχύλιση - Κρυστάλλωση - Ξήρανση Απορρόφηση αερίων φυσική και χημική Παραδείγματα βιομηχανικών εφαρμογών ) Απορρόφηση SΟ 3 κατά την παραγωγή
ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ
 ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Παράδειγμα 1 Σε μονάδα εκχύλισης μιας μόνο βαθμίδας πραγματοποιείται εκχύλιση οξικού οξέος από νερό με χρήση βουτανόλης. Η τροφοδοσία παροχής F= 100 kg/h περιέχει οξικό
ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Παράδειγμα 1 Σε μονάδα εκχύλισης μιας μόνο βαθμίδας πραγματοποιείται εκχύλιση οξικού οξέος από νερό με χρήση βουτανόλης. Η τροφοδοσία παροχής F= 100 kg/h περιέχει οξικό
Απορρόφηση Αερίων (2)
 Απορρόφηση Αερίων (2) Λεπτομερής Ανάλυση Θεωρούμε έναν πύργο απορρόφησης που μπορεί να περιέχει δίσκους ή να είναι τύπου πληρωτικού υλικού ή άλλου τύπου. Τελικός σκοπός είναι να βρούμε το μέγεθος του πύργου.
Απορρόφηση Αερίων (2) Λεπτομερής Ανάλυση Θεωρούμε έναν πύργο απορρόφησης που μπορεί να περιέχει δίσκους ή να είναι τύπου πληρωτικού υλικού ή άλλου τύπου. Τελικός σκοπός είναι να βρούμε το μέγεθος του πύργου.
ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ ΟΔΗΓΙΕΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΥΓΡΗΣ ΕΚΧΥΛΙΣΗΣ Ελένη Παντελή, Υποψήφια Διδάκτορας Γεωργία Παππά, Δρ. Χημικός Μηχανικός
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ ΟΔΗΓΙΕΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΥΓΡΗΣ ΕΚΧΥΛΙΣΗΣ Ελένη Παντελή, Υποψήφια Διδάκτορας Γεωργία Παππά, Δρ. Χημικός Μηχανικός
Απορρόφηση (Absorption)
 Απορρόφηση (Absorption) Απορρόφηση: η επιλεκτική μεταφορά μιας αέριας ουσίας (απορροφήσιμο μέσο-absorbate) από ένα αέριο ρεύμα σε ένα υγρό (απορροφητικό μέσοabsorbent) με το οποίο βρίσκεται σε επαφή. Βασίζεται
Απορρόφηση (Absorption) Απορρόφηση: η επιλεκτική μεταφορά μιας αέριας ουσίας (απορροφήσιμο μέσο-absorbate) από ένα αέριο ρεύμα σε ένα υγρό (απορροφητικό μέσοabsorbent) με το οποίο βρίσκεται σε επαφή. Βασίζεται
Κεφάλαιο 6 Απορρόφηση
 Κεφάλαιο 6 Απορρόφηση Σύνοψη Απορρόφηση αεριών ονομάζεται η φυσική διεργασία απομάκρυνσης ενός ή περισσοτέρων συστατικών ενός αερίου ρεύματος προς ένα μη πτητικό υγρό, το οποίο διαλύει αυτό(α) το(α) συστατικό(α).
Κεφάλαιο 6 Απορρόφηση Σύνοψη Απορρόφηση αεριών ονομάζεται η φυσική διεργασία απομάκρυνσης ενός ή περισσοτέρων συστατικών ενός αερίου ρεύματος προς ένα μη πτητικό υγρό, το οποίο διαλύει αυτό(α) το(α) συστατικό(α).
ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ. Σχεδιασµός της Στήλης µε Χρήση ενός Προσοµοιωτή. K.A. Μάτης
 ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Σχεδιασµός της Στήλης µε Χρήση ενός Προσοµοιωτή K.A. Μάτης Εισαγωγή Στη διεργασία της απορρόφησης ένα αέριο µίγµα έρχεται σε επαφή µε ένα υγρό (το διαλύτη ή απορροφητικό) ώστε να διαλυθεί
ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Σχεδιασµός της Στήλης µε Χρήση ενός Προσοµοιωτή K.A. Μάτης Εισαγωγή Στη διεργασία της απορρόφησης ένα αέριο µίγµα έρχεται σε επαφή µε ένα υγρό (το διαλύτη ή απορροφητικό) ώστε να διαλυθεί
σχηματική αναπαράσταση των βασικών τμημάτων μίας βιομηχανικής εγκατάστασης
 σχηματική αναπαράσταση των βασικών τμημάτων μίας βιομηχανικής εγκατάστασης Αρχές μεταφοράς μάζας Αρχές σχεδιασμού συσκευών μεταφοράς μάζας Διεργασίες μεταφοράς μάζας - Απορρόφηση - Απόσταξη - Εκχύλιση
σχηματική αναπαράσταση των βασικών τμημάτων μίας βιομηχανικής εγκατάστασης Αρχές μεταφοράς μάζας Αρχές σχεδιασμού συσκευών μεταφοράς μάζας Διεργασίες μεταφοράς μάζας - Απορρόφηση - Απόσταξη - Εκχύλιση
Σφαιρικές συντεταγμένες (r, θ, φ).
 T T r e r 1 T e r Σφαιρικές συντεταγμένες (r, θ, φ). 1 T e. (2.57) r sin u u e u e u e, (2.58) r r οπότε το εσωτερικό γινόμενο u.t γίνεται: T u T u T u. T ur. (2.59) r r r sin 2.5 Η ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ
T T r e r 1 T e r Σφαιρικές συντεταγμένες (r, θ, φ). 1 T e. (2.57) r sin u u e u e u e, (2.58) r r οπότε το εσωτερικό γινόμενο u.t γίνεται: T u T u T u. T ur. (2.59) r r r sin 2.5 Η ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ
ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ. Απορρόφηση 1
 ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ 1. Ισορροπία αερίων- υγρού 2. Ανάλυση διεργασίας Απορρόφησης 3. Απορρόφηση Πολυσύνθετων Μιγμάτων 4. Στήλες Απορρόφησης με πληρωτικά υλικά Απορρόφηση 1 Απορρόφηση Απορρόφηση Αερίων (Gas
ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ 1. Ισορροπία αερίων- υγρού 2. Ανάλυση διεργασίας Απορρόφησης 3. Απορρόφηση Πολυσύνθετων Μιγμάτων 4. Στήλες Απορρόφησης με πληρωτικά υλικά Απορρόφηση 1 Απορρόφηση Απορρόφηση Αερίων (Gas
Βασικές Διεργασίες Μηχανικής Τροφίμων
 Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 8: Εκχύλιση, 1ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Τύποι εκχύλισης
Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 8: Εκχύλιση, 1ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Τύποι εκχύλισης
ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΙΔΑΝΙΚΩΝ ΑΝΤΙΔΡΑΣΤΗΡΩΝ ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΙΔΑΝΙΚΩΝ ΑΝΤΙΔΡΑΣΤΗΡΩΝ
 Εισαγωγή Διαδικασία σχεδιασμού αντιδραστήρα: Καθορισμός του τύπου του αντιδραστήρα και των συνθηκών λειτουργίας. Εκτίμηση των χαρακτηριστικών για την ομαλή λειτουργία του αντιδραστήρα. μέγεθος σύσταση
Εισαγωγή Διαδικασία σχεδιασμού αντιδραστήρα: Καθορισμός του τύπου του αντιδραστήρα και των συνθηκών λειτουργίας. Εκτίμηση των χαρακτηριστικών για την ομαλή λειτουργία του αντιδραστήρα. μέγεθος σύσταση
Είδη ΙΦΥΥ δυαδικών μιγμάτων
 Είδη ΙΦΥΥ δυαδικών μιγμάτων T A X 1 X 1 ΙΦΥΥ τριαδικών μιγμάτων Τριγωνικά διαγράμματα C 0.1 0.2 0.3 0.4 0.5 P 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.6 0.7 0.8 0.9 κλάσμα βάρους του B κλάσμα βάρους του C
Είδη ΙΦΥΥ δυαδικών μιγμάτων T A X 1 X 1 ΙΦΥΥ τριαδικών μιγμάτων Τριγωνικά διαγράμματα C 0.1 0.2 0.3 0.4 0.5 P 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.6 0.7 0.8 0.9 κλάσμα βάρους του B κλάσμα βάρους του C
Χημική Κινητική Γενικές Υποδείξεις 1. Τάξη Αντίδρασης 2. Ενέργεια Ενεργοποίησης
 Χημική Κινητική Γενικές Υποδείξεις 1. Τάξη Αντίδρασης Γενικά, όταν έχουμε δεδομένα συγκέντρωσης-χρόνου και θέλουμε να βρούμε την τάξη μιας αντίδρασης, προσπαθούμε να προσαρμόσουμε τα δεδομένα σε εξισώσεις
Χημική Κινητική Γενικές Υποδείξεις 1. Τάξη Αντίδρασης Γενικά, όταν έχουμε δεδομένα συγκέντρωσης-χρόνου και θέλουμε να βρούμε την τάξη μιας αντίδρασης, προσπαθούμε να προσαρμόσουμε τα δεδομένα σε εξισώσεις
ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής. Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά)
 ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής (Σηµείωση: Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά) Η απόσταξη στηρίζεται στη διαφορά που υπάρχει στη σύσταση ισορροπίας των
ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής (Σηµείωση: Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά) Η απόσταξη στηρίζεται στη διαφορά που υπάρχει στη σύσταση ισορροπίας των
ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ. Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 9 η : Μεταφορά Μάζας
 ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 9 η : Μεταφορά Μάζας Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creatve Coons. Για εκπαιδευτικό
ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 9 η : Μεταφορά Μάζας Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creatve Coons. Για εκπαιδευτικό
ΥΤΙΚΕ ΔΙΕΡΓΑΙΕ ΜΕΣΑΥΟΡΑ ΜΑΖΑ. - Απορρόφηση - Απόσταξη - Εκχύλιση - Κρυστάλλωση - Ξήρανση
 ΥΤΙΚΕ ΔΙΕΡΓΑΙΕ ΜΕΣΑΥΟΡΑ ΜΑΖΑ - Απορρόφηση - Απόσταξη - Εκχύλιση - Κρυστάλλωση - Ξήρανση Εκχύλιση : εκχύλιση υγρών εκχύλιση στερεών διαχωρισμός αναμίξιμων υγρών παραπλήσια σ.ζ. ή α ΑΒ =1 έκπλυση ή διαλυτοποίηση
ΥΤΙΚΕ ΔΙΕΡΓΑΙΕ ΜΕΣΑΥΟΡΑ ΜΑΖΑ - Απορρόφηση - Απόσταξη - Εκχύλιση - Κρυστάλλωση - Ξήρανση Εκχύλιση : εκχύλιση υγρών εκχύλιση στερεών διαχωρισμός αναμίξιμων υγρών παραπλήσια σ.ζ. ή α ΑΒ =1 έκπλυση ή διαλυτοποίηση
Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ. Ερωτήσεις Επανάληψης
 Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ Ερωτήσεις Επανάληψης 1 0.8 0.6 x D = 0.95 y 0.4 x F = 0.45 0.2 0 0 0.2 0.4 0.6 0.8 1 x B = 0.05 Σχήμα 1. Δεδομένα ισορροπίας y-x για δυαδικό μίγμα συστατικών Α και Β και οι
Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ Ερωτήσεις Επανάληψης 1 0.8 0.6 x D = 0.95 y 0.4 x F = 0.45 0.2 0 0 0.2 0.4 0.6 0.8 1 x B = 0.05 Σχήμα 1. Δεδομένα ισορροπίας y-x για δυαδικό μίγμα συστατικών Α και Β και οι
Λύση Παραδείγματος 1. Διάγραμμα ροής διεργασίας. Εκρόφηση χλωριούχου βινυλίου από νερό στους 25 C και 850 mmhg. Είσοδος υγρού.
 Παράδειγμα 1 Μια εγκατάσταση καθαρισμού νερού απομακρύνει χλωριούχο βινύλιο (vinyl cloride) από μολυσμένα υπόγεια ύδατα σε θερμοκρασία 25 C και πίεση 850 mmhg χρησιμοποιώντας στήλη εκρόφησης κατ αντιρροή.
Παράδειγμα 1 Μια εγκατάσταση καθαρισμού νερού απομακρύνει χλωριούχο βινύλιο (vinyl cloride) από μολυσμένα υπόγεια ύδατα σε θερμοκρασία 25 C και πίεση 850 mmhg χρησιμοποιώντας στήλη εκρόφησης κατ αντιρροή.
Ακρίβεια αποτελεσμάτων σχεδιασμού διεργασιών ΜΑΔ, 2013
 Ακρίβεια αποτελεσμάτων σχεδιασμού διεργασιών ΜΑΔ, 2013 1 ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ ΘΧΜ Σκοπός της θερμοδυναμικής χημικής μηχανικής είναι η παροχή των κατάλληλων θεωρητικών γνώσεων και των απαραίτητων υπολογιστικών-μεθοδολογικών
Ακρίβεια αποτελεσμάτων σχεδιασμού διεργασιών ΜΑΔ, 2013 1 ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ ΘΧΜ Σκοπός της θερμοδυναμικής χημικής μηχανικής είναι η παροχή των κατάλληλων θεωρητικών γνώσεων και των απαραίτητων υπολογιστικών-μεθοδολογικών
ΑΠΟΡΡΟΦΗΣΗ (absorption)
 Εισαγωγή ΑΠΟΡΡΟΦΗΣΗ (absorption) Απορρόφηση: η επιλεκτική μεταφορά μιας αέριας ουσίας (απορροφήσιμο μέσοabsorbate ή solute) από ένα αέριο ρεύμα σε ένα υγρό (απορροφητικό μέσο - absorbent), με το οποίο
Εισαγωγή ΑΠΟΡΡΟΦΗΣΗ (absorption) Απορρόφηση: η επιλεκτική μεταφορά μιας αέριας ουσίας (απορροφήσιμο μέσοabsorbate ή solute) από ένα αέριο ρεύμα σε ένα υγρό (απορροφητικό μέσο - absorbent), με το οποίο
Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων
 Φυσικοχημεία II, Διαλύματα Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων o P = N P P = A A A N P o B B B PA + PB = P ολ Τ=const P = Ν ολ P + N P o o A A B B Ν Α + Ν =1 o o o P = P + A N ( ολ
Φυσικοχημεία II, Διαλύματα Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων o P = N P P = A A A N P o B B B PA + PB = P ολ Τ=const P = Ν ολ P + N P o o A A B B Ν Α + Ν =1 o o o P = P + A N ( ολ
μεταβάλλουμε την απόσταση h της μιας τρύπας από την επιφάνεια του υγρού (π.χ. προσθέτουμε ή αφαιρούμε υγρό) έτσι ώστε h 2 =2 Α 2
 ΑΣΚΗΣΕΙΣ ΣΤΑ ΡΕΥΣΤΑ 1 Μια κυλινδρική δεξαμενή ακτίνας 6m και ύψους h=5m είναι γεμάτη με νερό, βρίσκεται στην κορυφή ενός πύργου ύψους 45m και χρησιμοποιείται για το πότισμα ενός χωραφιού α Ποια η παροχή
ΑΣΚΗΣΕΙΣ ΣΤΑ ΡΕΥΣΤΑ 1 Μια κυλινδρική δεξαμενή ακτίνας 6m και ύψους h=5m είναι γεμάτη με νερό, βρίσκεται στην κορυφή ενός πύργου ύψους 45m και χρησιμοποιείται για το πότισμα ενός χωραφιού α Ποια η παροχή
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ Η Επιστήμη της Θερμοδυναμικής ασχολείται με την ποσότητα της θερμότητας που μεταφέρεται σε ένα κλειστό και απομονωμένο σύστημα από μια κατάσταση ισορροπίας σε μια άλλη
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ Η Επιστήμη της Θερμοδυναμικής ασχολείται με την ποσότητα της θερμότητας που μεταφέρεται σε ένα κλειστό και απομονωμένο σύστημα από μια κατάσταση ισορροπίας σε μια άλλη
Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ
 Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ Η υγρή εκχύλιση βρίσκει εφαρμογή όταν. Η σχετική πτητικότητα των συστατικών του αρχικού διαλύματος είναι κοντά στη
Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ Η υγρή εκχύλιση βρίσκει εφαρμογή όταν. Η σχετική πτητικότητα των συστατικών του αρχικού διαλύματος είναι κοντά στη
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διαφορική (batch) Rectifying column Stripping column
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διαφορική (batch) Rectifying column Stripping column
Εναλλαγή θερμότητας. Σχ. 4.1 (α) Διάταξη εναλλάκτη θερμότητας καθ` ομορροή (πάνω) και αντίστοιχο θερμοκρασιακό προφίλ (κάτω)
 Εναλλαγή θερμότητας Σχ. 4.1 (α) Διάταξη εναλλάκτη θερμότητας καθ` ομορροή (πάνω) και αντίστοιχο θερμοκρασιακό προφίλ (κάτω) Σχ. 4.1 (β) Διάταξη εναλλάκτη θερμότητας καντ` αντιρροή (πάνω) και αντίστοιχο
Εναλλαγή θερμότητας Σχ. 4.1 (α) Διάταξη εναλλάκτη θερμότητας καθ` ομορροή (πάνω) και αντίστοιχο θερμοκρασιακό προφίλ (κάτω) Σχ. 4.1 (β) Διάταξη εναλλάκτη θερμότητας καντ` αντιρροή (πάνω) και αντίστοιχο
Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης
 Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης Μια αποστακτική στήλη που λειτουργεί σε πίεση 101,3 kpa, διαχωρίζει ένα μίγμα νερούαιθανόλης. Η σύσταση του μίγματος αποτελείται 40 mol% αιθανόλη και η τροφοδοσία
Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης Μια αποστακτική στήλη που λειτουργεί σε πίεση 101,3 kpa, διαχωρίζει ένα μίγμα νερούαιθανόλης. Η σύσταση του μίγματος αποτελείται 40 mol% αιθανόλη και η τροφοδοσία
Βασικές Διεργασίες Μηχανικής Τροφίμων
 Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 8: Εκχύλιση, 1ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Τύποι εκχύλισης
Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 8: Εκχύλιση, 1ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Τύποι εκχύλισης
Συστήματα Ανάκτησης Θερμότητας
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Εργαστήριο Θερμοδυναμικής & Φαινομένων Μεταφοράς Συστήματα Ανάκτησης Θερμότητας Εισαγωγή Σκοπός των συστημάτων ανάκτησης θερμότητας είναι η αξιοποίηση
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Εργαστήριο Θερμοδυναμικής & Φαινομένων Μεταφοράς Συστήματα Ανάκτησης Θερμότητας Εισαγωγή Σκοπός των συστημάτων ανάκτησης θερμότητας είναι η αξιοποίηση
ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ, 2013
 ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ, 2013 1 Ισορροπία Φάσεων Ανάλογα με τη φύση των συστατικών του μίγματος (ή της ολικής πίεσης του συστήματος) οι τάσεις διαφυγής υπολογίζονται - ανάλογα
ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ, 2013 1 Ισορροπία Φάσεων Ανάλογα με τη φύση των συστατικών του μίγματος (ή της ολικής πίεσης του συστήματος) οι τάσεις διαφυγής υπολογίζονται - ανάλογα
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17
 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 13 1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17 1.1 Φυσικές Διεργασίες Διαχωρισμού 20 1.1.1 Μια γενική εποπτεία της παραγωγικής Χημικής Βιομηχανίας 21 1.1.2 Σύντομος
ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 13 1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17 1.1 Φυσικές Διεργασίες Διαχωρισμού 20 1.1.1 Μια γενική εποπτεία της παραγωγικής Χημικής Βιομηχανίας 21 1.1.2 Σύντομος
M V n. nm V. M v. M v T P P S V P = = + = σταθερή σε παραγώγιση, τον ορισµό του συντελεστή διαστολής α = 1, κυκλική εναλλαγή 3
 Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξέταση: Περίοδος εκεµβρίου 04- (//04. ίνονται οι ακόλουθες πληροφορίες για τον διθειάνθρακα (CS. Γραµµοµοριακή µάζα 76.4 g/mol, κανονικό σηµείο ζέσεως 46 C, κανονικό
Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξέταση: Περίοδος εκεµβρίου 04- (//04. ίνονται οι ακόλουθες πληροφορίες για τον διθειάνθρακα (CS. Γραµµοµοριακή µάζα 76.4 g/mol, κανονικό σηµείο ζέσεως 46 C, κανονικό
διαιρούμε με το εμβαδό Α 2 του εμβόλου (1)
 1)Συνήθως οι πτήσεις των αεροσκαφών γίνονται στο ύψος των 15000 m, όπου η θερμοκρασία του αέρα είναι 210 Κ και η ατμοσφαιρική πίεση 10000 N / m 2. Σε αεροδρόμιο που βρίσκεται στο ίδιο ύψος με την επιφάνεια
1)Συνήθως οι πτήσεις των αεροσκαφών γίνονται στο ύψος των 15000 m, όπου η θερμοκρασία του αέρα είναι 210 Κ και η ατμοσφαιρική πίεση 10000 N / m 2. Σε αεροδρόμιο που βρίσκεται στο ίδιο ύψος με την επιφάνεια
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ. Καθηγητής Δ. Ματαράς
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Καθηγητής Δ. Ματαράς image url 0.Μεταφορά Θερμότητας σε Ρευστά Εναλλάκτης Κελύφους-Αυλών E 2 Β 2 Ατμός F C K Εξαέρωση Β Θερμό Υγρό J E D 2 Α D H Ψυχρό Υγρό Eικόνα
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Καθηγητής Δ. Ματαράς image url 0.Μεταφορά Θερμότητας σε Ρευστά Εναλλάκτης Κελύφους-Αυλών E 2 Β 2 Ατμός F C K Εξαέρωση Β Θερμό Υγρό J E D 2 Α D H Ψυχρό Υγρό Eικόνα
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ. Σωλήνας U
 A A N A B P Y T A 9 5 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Σωλήνας U Γ U= B Θ.Ι. B Κατακόρυφος ισοπαχής σωλήνας σχήματος U περιέχει ιδανικό υγρό, δηλαδή, υγρό που σε κάθε επιφάνεια ασκεί δυνάμεις κάθετες στην
A A N A B P Y T A 9 5 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Σωλήνας U Γ U= B Θ.Ι. B Κατακόρυφος ισοπαχής σωλήνας σχήματος U περιέχει ιδανικό υγρό, δηλαδή, υγρό που σε κάθε επιφάνεια ασκεί δυνάμεις κάθετες στην
Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί:
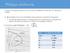 Ψύξη με εκτόνωση Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί: A. Mε ελεύθερη εκτόνωση σε βαλβίδα στραγγαλισμού: ισενθαλπική διεργασία σε χαμηλές θερμοκρασίες,
Ψύξη με εκτόνωση Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί: A. Mε ελεύθερη εκτόνωση σε βαλβίδα στραγγαλισμού: ισενθαλπική διεργασία σε χαμηλές θερμοκρασίες,
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ο ΔΙΑΓΩΝΙΣΜΑ ΡΕΥΣΤΑ - ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ο ΔΙΑΓΩΝΙΣΜΑ ΡΕΥΣΤΑ - ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
ΑΕΡΙΑ ΙΔΑΝΙΚΑ ΚΑΙ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ
 ΑΕΡΙΑ ΙΔΑΝΙΚΑ ΚΑΙ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΝΟΜΟΣ ΤΕΛΕΙΩΝ ΑΕΡΙΩΝ O νόμος των τελείων αερίων συνδέει τις ιδιότητες ενός τελείου αερίου σε μια συγκεκριμένη κατάσταση (καταστατική εξίσωση) P V = n R T P: Απόλυτη πίεση
ΑΕΡΙΑ ΙΔΑΝΙΚΑ ΚΑΙ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΝΟΜΟΣ ΤΕΛΕΙΩΝ ΑΕΡΙΩΝ O νόμος των τελείων αερίων συνδέει τις ιδιότητες ενός τελείου αερίου σε μια συγκεκριμένη κατάσταση (καταστατική εξίσωση) P V = n R T P: Απόλυτη πίεση
MIKΡΕΣ ΟΠΕΣ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 www.pmiras.weebly.cm MIKΡΕΣ ΟΠΕΣ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Περιεχόμενα. Μικρές Οπές. Ασκήσεις ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 www.pmiras.weebly.cm
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 www.pmiras.weebly.cm MIKΡΕΣ ΟΠΕΣ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Περιεχόμενα. Μικρές Οπές. Ασκήσεις ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 www.pmiras.weebly.cm
1 IΔΑΝΙΚΑ ΑΕΡΙΑ 1.1 ΓΕΝΙΚΑ
 1 1 IΔΑΝΙΚΑ ΑΕΡΙΑ 1.1 ΓΕΝΙΚΑ Θα αρχίσουμε τη σειρά των μαθημάτων της Φυσικοχημείας με τη μελέτη της αέριας κατάστασης της ύλης. Η μελέτη της φύσης των αερίων αποτελεί ένα ιδανικό μέσο για την εισαγωγή
1 1 IΔΑΝΙΚΑ ΑΕΡΙΑ 1.1 ΓΕΝΙΚΑ Θα αρχίσουμε τη σειρά των μαθημάτων της Φυσικοχημείας με τη μελέτη της αέριας κατάστασης της ύλης. Η μελέτη της φύσης των αερίων αποτελεί ένα ιδανικό μέσο για την εισαγωγή
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Ι & ΙΙ Εργαστηριακή Άσκηση 4: ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ
 Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Σχεδιασμού, Ανάλυσης & Ανάπτυξης Διεργασιών και Συστημάτων ΕΡΓΑΣΤΗΡΙΟ ΣΧΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διευθυντής: Ι.
Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Σχεδιασμού, Ανάλυσης & Ανάπτυξης Διεργασιών και Συστημάτων ΕΡΓΑΣΤΗΡΙΟ ΣΧΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διευθυντής: Ι.
Απαντήσεις στις ασκήσεις του κεφαλαίου 4 του βιβλίου Χημική Κινητική του ΕΑΠ
 Απαντήσεις στις ασκήσεις του κεφαλαίου 4 του βιβλίου Χημική Κινητική του ΕΑΠ Ασκηση 4.1 Η κινητική εξίσωση της αντίδρασης: βρέθηκε οτι είναι Αντιδράσεις πρώτης τάξης 2A = Προϊόντα r = k[a] Να υπολογίσετε
Απαντήσεις στις ασκήσεις του κεφαλαίου 4 του βιβλίου Χημική Κινητική του ΕΑΠ Ασκηση 4.1 Η κινητική εξίσωση της αντίδρασης: βρέθηκε οτι είναι Αντιδράσεις πρώτης τάξης 2A = Προϊόντα r = k[a] Να υπολογίσετε
3 Η ΣΕΙΡΑ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΔΙΕΡΓΑΣΙΩΝ - PC-LAB ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ: ΑΣΚΗΣΗ 1 ΠΡΟΣΟΜΟΙΩΣΗ ΜΟΝΑΔΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ
 3 Η ΣΕΙΡΑ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΔΙΕΡΓΑΣΙΩΝ - PC-LAB ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ: 23.12.2015 ΑΣΚΗΣΗ 1 ΠΡΟΣΟΜΟΙΩΣΗ ΜΟΝΑΔΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ Ένα τυπικό φυσικό αέριο έχει την ακόλουθη σύσταση σε % mol: 0.5% Ν 2,
3 Η ΣΕΙΡΑ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΔΙΕΡΓΑΣΙΩΝ - PC-LAB ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ: 23.12.2015 ΑΣΚΗΣΗ 1 ΠΡΟΣΟΜΟΙΩΣΗ ΜΟΝΑΔΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ Ένα τυπικό φυσικό αέριο έχει την ακόλουθη σύσταση σε % mol: 0.5% Ν 2,
ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Κ. Α. Μάτης
 3 ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Κ. Α. Μάτης 3. ΕΙΣΑΓΩΓΗ Η γενική θεωρητική επεξεργασία που αναπτύσσεται στα φαινόµενα µεταφοράς συχνά έχει σχέση µε τη µεταφορά µάζας σε µια µοναδική φάση που δεν έχει ασυνέχειες. Αλλά
3 ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Κ. Α. Μάτης 3. ΕΙΣΑΓΩΓΗ Η γενική θεωρητική επεξεργασία που αναπτύσσεται στα φαινόµενα µεταφοράς συχνά έχει σχέση µε τη µεταφορά µάζας σε µια µοναδική φάση που δεν έχει ασυνέχειες. Αλλά
1. Εναλλάκτες θερµότητας (Heat Exchangers)
 1. Εναλλάκτες θερµότητας (Heat Exangers) Οι εναλλάκτες θερµότητας είναι συσκευές µε τις οποίες επιτυγχάνεται η µεταφορά ενέργειας από ένα ρευστό υψηλής θερµοκρασίας σε ένα άλλο ρευστό χαµηλότερης θερµοκρασίας.
1. Εναλλάκτες θερµότητας (Heat Exangers) Οι εναλλάκτες θερµότητας είναι συσκευές µε τις οποίες επιτυγχάνεται η µεταφορά ενέργειας από ένα ρευστό υψηλής θερµοκρασίας σε ένα άλλο ρευστό χαµηλότερης θερµοκρασίας.
Τ.Ε.Ι. ΠΕΙΡΑΙΑ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΜΑΘΗΜΑ: ΕΦΑΡΜΟΣΜΕΝΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ (Ασκήσεις πράξης) ΙΔΑΝΙΚΑ ΑΕΡΙΑ - ΕΡΓΟ
 ΙΔΑΝΙΚΑ ΑΕΡΙΑ - ΕΡΓΟ 1. Να υπολογιστεί η πυκνότητα του αέρα σε πίεση 0,1 MPa και θερμοκρασία 20 ο C. (R air =0,287 kj/kgk) 2. Ποσότητα αέρα 1 kg εκτελεί τις παρακάτω διεργασίες: Διεργασία 1-2: Αδιαβατική
ΙΔΑΝΙΚΑ ΑΕΡΙΑ - ΕΡΓΟ 1. Να υπολογιστεί η πυκνότητα του αέρα σε πίεση 0,1 MPa και θερμοκρασία 20 ο C. (R air =0,287 kj/kgk) 2. Ποσότητα αέρα 1 kg εκτελεί τις παρακάτω διεργασίες: Διεργασία 1-2: Αδιαβατική
Οι ιδιότητες των αερίων και καταστατικές εξισώσεις. Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι
 Οι ιδιότητες των αερίων και καταστατικές εξισώσεις Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι Τι είναι αέριο; Λέμε ότι μία ουσία βρίσκεται στην αέρια κατάσταση όταν αυθόρμητα
Οι ιδιότητες των αερίων και καταστατικές εξισώσεις Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι Τι είναι αέριο; Λέμε ότι μία ουσία βρίσκεται στην αέρια κατάσταση όταν αυθόρμητα
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΛΥΜΕΝΑ ΘΕΜΑΤΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΛΥΜΕΝΑ ΘΕΜΑΤΑ 1 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 Θέμα 1 Επιλέγοντας το κατάλληλο διάγραμμα φάσεων για ένα πραγματικό
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΛΥΜΕΝΑ ΘΕΜΑΤΑ 1 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 Θέμα 1 Επιλέγοντας το κατάλληλο διάγραμμα φάσεων για ένα πραγματικό
Enrico Fermi, Thermodynamics, 1937
 I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
ΣΥΝΔΥΑΣΜΟΣ ΤΗΣ ΑΝΤΙΣΤΑΣΗΣ ΔΙΑΧΥΣΗΣ ΣΤΟΥΣ ΠΟΡΟΥΣ ΜΕ ΚΙΝΗΤΙΚΗ ΕΠΙΦΑΝΕΙΑΚΗΣ ΑΝΤΙΔΡΑΣΗΣ
 ΣΥΝΔΥΑΣΜΟΣ ΤΗΣ ΑΝΤΙΣΤΑΣΗΣ ΔΙΑΧΥΣΗΣ ΣΤΟΥΣ ΠΟΡΟΥΣ ΜΕ ΚΙΝΗΤΙΚΗ ΕΠΙΦΑΝΕΙΑΚΗΣ ΑΝΤΙΔΡΑΣΗΣ Παράγοντας Αποτελεσματικότητας Ειδικά για αντίδραση πρώτης τάξης, ο παράγοντας αποτελεσματικότητας ισούται προς ε = C
ΣΥΝΔΥΑΣΜΟΣ ΤΗΣ ΑΝΤΙΣΤΑΣΗΣ ΔΙΑΧΥΣΗΣ ΣΤΟΥΣ ΠΟΡΟΥΣ ΜΕ ΚΙΝΗΤΙΚΗ ΕΠΙΦΑΝΕΙΑΚΗΣ ΑΝΤΙΔΡΑΣΗΣ Παράγοντας Αποτελεσματικότητας Ειδικά για αντίδραση πρώτης τάξης, ο παράγοντας αποτελεσματικότητας ισούται προς ε = C
ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΓΡΑΜΜΑ ΡΟΗΣ
 ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΓΡΑΜΜΑ ΡΟΗΣ Στη χημική μηχανική έχουμε να κάνουμε με διεργασίες. Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική). Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα
ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΓΡΑΜΜΑ ΡΟΗΣ Στη χημική μηχανική έχουμε να κάνουμε με διεργασίες. Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική). Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα
ΦΑΙΝΟΜΕΝΑ ΠΡΟΣΡΟΦΗΣΕΩΣ ΠΡΟΣΡΟΦΗΣΗ ΟΥΣΙΑΣ ΑΠΟ ΔΙΑΛΥΜΑΤΑ
 ΦΑΙΝΟΜΕΝΑ ΠΡΟΣΡΟΦΗΣΕΩΣ ΠΡΟΣΡΟΦΗΣΗ ΟΥΣΙΑΣ ΑΠΟ ΔΙΑΛΥΜΑΤΑ Έννοιες που πρέπει να γνωρίζετε Ισορροπία φάσεων, εξίσωση Clauiu-Clapeyron Θέμα ασκήσεως Προσρόφηση ουσίας από αραιά διαλύματα. Προσδιορισμός ισόθερμων
ΦΑΙΝΟΜΕΝΑ ΠΡΟΣΡΟΦΗΣΕΩΣ ΠΡΟΣΡΟΦΗΣΗ ΟΥΣΙΑΣ ΑΠΟ ΔΙΑΛΥΜΑΤΑ Έννοιες που πρέπει να γνωρίζετε Ισορροπία φάσεων, εξίσωση Clauiu-Clapeyron Θέμα ασκήσεως Προσρόφηση ουσίας από αραιά διαλύματα. Προσδιορισμός ισόθερμων
ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ
 ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ 2015-2016 2 Ο ΕΞΑΜΗΝΟ Ε. ΠΑΥΛΑΤΟΥ ΑΝ. ΚΑΘΗΓΗΤΡΙΑ ΕΜΠ ΜΟΝΑΔΕΣ ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 3 ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 4 ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 5 Επιφάνεια
ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ 2015-2016 2 Ο ΕΞΑΜΗΝΟ Ε. ΠΑΥΛΑΤΟΥ ΑΝ. ΚΑΘΗΓΗΤΡΙΑ ΕΜΠ ΜΟΝΑΔΕΣ ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 3 ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 4 ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 5 Επιφάνεια
39th International Physics Olympiad - Hanoi - Vietnam Theoretical Problem No. 3. Λύση
 39th International Physics Olymiad - Hanoi - Vietnam - 28 ύση. ια μια στοιχειώδη υψομετρική διαφορά dz, η στοιχειώδης μεταβολή της ατμοσφαιρικής πίεσης είναι: d = ρgdz () όπου g είναι η επιτάχυνση λόγω
39th International Physics Olymiad - Hanoi - Vietnam - 28 ύση. ια μια στοιχειώδη υψομετρική διαφορά dz, η στοιχειώδης μεταβολή της ατμοσφαιρικής πίεσης είναι: d = ρgdz () όπου g είναι η επιτάχυνση λόγω
ΚΕΦΑΛΑΙΟ 4 ΑΠΟΡΡΟΦΗΣΗ- ΕΚΡΟΦΗΣΗ ΑΕΡΙΩΝ
 ΚΕΦΑΛΑΙΟ 4 ΑΠΟΡΡΟΦΗΣΗ- ΕΚΡΟΦΗΣΗ ΑΕΡΙΩΝ Η απορρόφηση αερίων είναι η διεργασία κατά την οποία μία ή περισσότερες συνιστώσες ενός αέριου μείγματος διαλύονται κατά την επαφή με ένα υγρό (Beet & Mers, 96).
ΚΕΦΑΛΑΙΟ 4 ΑΠΟΡΡΟΦΗΣΗ- ΕΚΡΟΦΗΣΗ ΑΕΡΙΩΝ Η απορρόφηση αερίων είναι η διεργασία κατά την οποία μία ή περισσότερες συνιστώσες ενός αέριου μείγματος διαλύονται κατά την επαφή με ένα υγρό (Beet & Mers, 96).
Στο διπλανό σχήμα το έμβολο έχει βάρος Β, διατομή Α και ισορροπεί. Η δύναμη που ασκείται από το υγρό στο έμβολο είναι
 Ερωτήσεις θεωρίας - Θέμα Β Εκφώνηση 1η Στο διπλανό σχήμα το έμβολο έχει βάρος Β, διατομή Α και ισορροπεί. Η δύναμη που ασκείται από το υγρό στο έμβολο είναι α) β) γ) Λύση Εκφώνηση 2η Στο διπλανό υδραυλικό
Ερωτήσεις θεωρίας - Θέμα Β Εκφώνηση 1η Στο διπλανό σχήμα το έμβολο έχει βάρος Β, διατομή Α και ισορροπεί. Η δύναμη που ασκείται από το υγρό στο έμβολο είναι α) β) γ) Λύση Εκφώνηση 2η Στο διπλανό υδραυλικό
Ειδική Ενθαλπία, Ειδική Θερµότητα και Ειδικός Όγκος Υγρού Αέρα
 θερµοκρασία που αντιπροσωπεύει την θερµοκρασία υγρού βολβού. Το ποσοστό κορεσµού υπολογίζεται από την καµπύλη του σταθερού ποσοστού κορεσµού που διέρχεται από το συγκεκριµένο σηµείο. Η απόλυτη υγρασία
θερµοκρασία που αντιπροσωπεύει την θερµοκρασία υγρού βολβού. Το ποσοστό κορεσµού υπολογίζεται από την καµπύλη του σταθερού ποσοστού κορεσµού που διέρχεται από το συγκεκριµένο σηµείο. Η απόλυτη υγρασία
ΑΣΚΗΣΕΙΣ ΣΥΣΚΕΥΩΝ ΘΕΡΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ. 1η ενότητα
 1η ενότητα 1. Εναλλάκτης σχεδιάζεται ώστε να θερμαίνει 2kg/s νερού από τους 20 στους 60 C. Το θερμό ρευστό είναι επίσης νερό με θερμοκρασία εισόδου 95 C. Οι συντελεστές συναγωγής στους αυλούς και το κέλυφος
1η ενότητα 1. Εναλλάκτης σχεδιάζεται ώστε να θερμαίνει 2kg/s νερού από τους 20 στους 60 C. Το θερμό ρευστό είναι επίσης νερό με θερμοκρασία εισόδου 95 C. Οι συντελεστές συναγωγής στους αυλούς και το κέλυφος
ΠΡΟΓΡΑΜΜΑΤΙΣΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΚΥΡΙΑΚΗ 10 ΙΑΝΟΥΑΡΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ - B ΛΥΚΕΙΟΥ
 ΠΡΟΓΡΑΜΜΑΤΙΣΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΚΥΡΙΑΚΗ 10 ΙΑΝΟΥΑΡΙΟΥ 2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ - B ΛΥΚΕΙΟΥ ΘΕΜΑ 1 ο 1. Για να έχουμε επιτάχυνση, τι από τα παρακάτω πρέπει να συμβαίνει: i) Το μέτρο της ταχύτητας να
ΠΡΟΓΡΑΜΜΑΤΙΣΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΚΥΡΙΑΚΗ 10 ΙΑΝΟΥΑΡΙΟΥ 2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ - B ΛΥΚΕΙΟΥ ΘΕΜΑ 1 ο 1. Για να έχουμε επιτάχυνση, τι από τα παρακάτω πρέπει να συμβαίνει: i) Το μέτρο της ταχύτητας να
Τμήμα Τεχνολογίας Τροφίμων. Ανόργανη Χημεία. Ενότητα 7 η : Αέρια Ιδιότητες & συμπεριφορά. Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής.
 Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 7 η : Αέρια Ιδιότητες & συμπεριφορά Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Αέρια & Πίεση Αερίων 2 Ο αέρας είναι ένα τυπικό αέριο
Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 7 η : Αέρια Ιδιότητες & συμπεριφορά Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Αέρια & Πίεση Αερίων 2 Ο αέρας είναι ένα τυπικό αέριο
Κεφάλαιο 4 Κλασματική Απόσταξη
 Κεφάλαιο 4 Κλασματική Απόσταξη Σύνοψη Η κλασματική απόσταξη ή απλά απόσταξη αποτελεί τη διεργασία διαχωρισμού ενός πτητικού συστατικού από ένα λιγότερο πτητικό ή, γενικότερα, ενός μίγματος συστατικών που
Κεφάλαιο 4 Κλασματική Απόσταξη Σύνοψη Η κλασματική απόσταξη ή απλά απόσταξη αποτελεί τη διεργασία διαχωρισμού ενός πτητικού συστατικού από ένα λιγότερο πτητικό ή, γενικότερα, ενός μίγματος συστατικών που
V P P. [3] (α) Να δειχθεί ότι για ένα υδροστατικό σύστημα ισχύει: P V
![V P P. [3] (α) Να δειχθεί ότι για ένα υδροστατικό σύστημα ισχύει: P V V P P. [3] (α) Να δειχθεί ότι για ένα υδροστατικό σύστημα ισχύει: P V](/thumbs/64/51699713.jpg) ΘΕΡΜΟΔΥΝΑΜΙΚΗ (ΦΥΣΙΚΗ I) 1 [1] Θεωρώντας την εσωτερική ενέργεια ενός υδροστατικού συστήματος σα συνάρτηση των Τ και, αποδείξτε τις παρακάτω εξισώσεις: d d dq (1) β () β κ ) ( κ () [] Θεωρώντας την εσωτερική
ΘΕΡΜΟΔΥΝΑΜΙΚΗ (ΦΥΣΙΚΗ I) 1 [1] Θεωρώντας την εσωτερική ενέργεια ενός υδροστατικού συστήματος σα συνάρτηση των Τ και, αποδείξτε τις παρακάτω εξισώσεις: d d dq (1) β () β κ ) ( κ () [] Θεωρώντας την εσωτερική
39th International Physics Olympiad - Hanoi - Vietnam Theoretical Problem No. 3
 ΑΛΛΑΓΗ ΤΗΣ ΘΕΡΜΟΚΡΑΣΙΑΣ ΤΟΥ ΑΕΡΑ ΜΕ ΤΟ ΥΨΟΣ, ΣΤΑΘΕΡΟΤΗΤΑ ΤΗΣ ΑΤΜΟΣΦΑΙΡΑΣ KAI ΡΥΠΑΝΣΗ ΤΟΥ ΑΕΡΑ Στην κατακόρυφη κίνηση του αέρα οφείλονται πολλές ατμοσφαιρικές διαδικασίες, όπως ο σχηματισμός των νεφών και
ΑΛΛΑΓΗ ΤΗΣ ΘΕΡΜΟΚΡΑΣΙΑΣ ΤΟΥ ΑΕΡΑ ΜΕ ΤΟ ΥΨΟΣ, ΣΤΑΘΕΡΟΤΗΤΑ ΤΗΣ ΑΤΜΟΣΦΑΙΡΑΣ KAI ΡΥΠΑΝΣΗ ΤΟΥ ΑΕΡΑ Στην κατακόρυφη κίνηση του αέρα οφείλονται πολλές ατμοσφαιρικές διαδικασίες, όπως ο σχηματισμός των νεφών και
ΥΔΡΑΥΛΙΚΗ ΑΝΟΙΚΤΩΝ ΑΓΩΓΩΝ
 Τμήμα Δασολογίας & Διαχείρισης Περιβάλλοντος & Φυσικών Πόρων Εργαστήριο Διευθέτησης Ορεινών Υδάτων και Διαχείρισης Κινδύνου Προπτυχιακό Πρόγραμμα Σπουδών ΥΔΡΑΥΛΙΚΗ ΑΝΟΙΚΤΩΝ ΑΓΩΓΩΝ Κεφάλαιο 3 ο : Εξίσωση
Τμήμα Δασολογίας & Διαχείρισης Περιβάλλοντος & Φυσικών Πόρων Εργαστήριο Διευθέτησης Ορεινών Υδάτων και Διαχείρισης Κινδύνου Προπτυχιακό Πρόγραμμα Σπουδών ΥΔΡΑΥΛΙΚΗ ΑΝΟΙΚΤΩΝ ΑΓΩΓΩΝ Κεφάλαιο 3 ο : Εξίσωση
ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ 1. ΟΡΙΣΜΟΣ ΣΚΟΠΟΣ ΔΙΕΡΓΑΣΙΑΣ
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ 1. ΟΡΙΣΜΟΣ ΣΚΟΠΟΣ ΔΙΕΡΓΑΣΙΑΣ
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Στόχος: Επεξεργασία συγκεκριμένης τροφοδοσίας (ροή
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Στόχος: Επεξεργασία συγκεκριμένης τροφοδοσίας (ροή
ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ. Τράπεζα θεμάτων. Β Θέμα ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΑΕΡΙΩΝ
 ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Τράπεζα θεμάτων Β Θέμα ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΑΕΡΙΩΝ 16111 Ένα παιδί κρατάει στο χέρι του ένα μπαλόνι γεμάτο ήλιο που καταλαμβάνει όγκο 4 L (σε πίεση
ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Τράπεζα θεμάτων Β Θέμα ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΑΕΡΙΩΝ 16111 Ένα παιδί κρατάει στο χέρι του ένα μπαλόνι γεμάτο ήλιο που καταλαμβάνει όγκο 4 L (σε πίεση
5 Μετρητές παροχής. 5.1Εισαγωγή
 5 Μετρητές παροχής 5.Εισαγωγή Τρεις βασικές συσκευές, με τις οποίες μπορεί να γίνει η μέτρηση της ογκομετρικής παροχής των ρευστών, είναι ο μετρητής Venturi (ή βεντουρίμετρο), ο μετρητής διαφράγματος (ή
5 Μετρητές παροχής 5.Εισαγωγή Τρεις βασικές συσκευές, με τις οποίες μπορεί να γίνει η μέτρηση της ογκομετρικής παροχής των ρευστών, είναι ο μετρητής Venturi (ή βεντουρίμετρο), ο μετρητής διαφράγματος (ή
Παρασκευαστικό διαχωρισμό πολλών ουσιών με κατανομή μεταξύ των δύο διαλυτών.
 1. ΕΚΧΥΛΙΣΗ Η εκχύλιση είναι μία από τις πιο συνηθισμένες τεχνικές διαχωρισμού και βασίζεται στην ισορροπία κατανομής μιας ουσίας μεταξύ δύο φάσεων, που αναμιγνύονται ελάχιστα μεταξύ τους. Η ευρύτητα στη
1. ΕΚΧΥΛΙΣΗ Η εκχύλιση είναι μία από τις πιο συνηθισμένες τεχνικές διαχωρισμού και βασίζεται στην ισορροπία κατανομής μιας ουσίας μεταξύ δύο φάσεων, που αναμιγνύονται ελάχιστα μεταξύ τους. Η ευρύτητα στη
Φυσικοί μετασχηματισμοί καθαρών ουσιών
 Φυσικοί μετασχηματισμοί καθαρών ουσιών Ή εξάτμιση, η τήξη και η μετατροπή του γραφίτη σε διαμάντι αποτελούν συνηθισμένα παραδείγματα αλλαγών φάσης χωρίς μεταβολή της χημικής σύστασης. Ορισμός φάσης: Μια
Φυσικοί μετασχηματισμοί καθαρών ουσιών Ή εξάτμιση, η τήξη και η μετατροπή του γραφίτη σε διαμάντι αποτελούν συνηθισμένα παραδείγματα αλλαγών φάσης χωρίς μεταβολή της χημικής σύστασης. Ορισμός φάσης: Μια
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
Θερμοδυναμική Ενότητα 4:
 Θερμοδυναμική Ενότητα 4: Ισοζύγια Ενέργειας και Μάζας σε ανοικτά συστήματα Κυρατζής Νικόλαος Τμήμα Μηχανικών Περιβάλλοντος και Μηχανικών Αντιρρύπανσης ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Θερμοδυναμική Ενότητα 4: Ισοζύγια Ενέργειας και Μάζας σε ανοικτά συστήματα Κυρατζής Νικόλαος Τμήμα Μηχανικών Περιβάλλοντος και Μηχανικών Αντιρρύπανσης ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΜΑΘΗΜΑ: Τεχνολογία Μετρήσεων ΙΙ
 ΜΑΘΗΜΑ: Τεχνολογία Μετρήσεων ΙΙ ΔΙΔΑΣΚΩΝ: Αν. Καθ. Δρ Μαρία Α. Γούλα ΤΜΗΜΑ: Μηχανικών Περιβάλλοντος & Μηχανικών Αντιρρύπανσης 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΜΑΘΗΜΑ: Τεχνολογία Μετρήσεων ΙΙ ΔΙΔΑΣΚΩΝ: Αν. Καθ. Δρ Μαρία Α. Γούλα ΤΜΗΜΑ: Μηχανικών Περιβάλλοντος & Μηχανικών Αντιρρύπανσης 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Να υπολογίσετε τη μάζα 50 L βενζίνης. Δίνεται η σχετική πυκνότητά της, ως προς το νερό ρ σχ = 0,745.
 1 Παράδειγμα 101 Να υπολογίσετε τη μάζα 10 m 3 πετρελαίου, στους : α) 20 ο C και β) 40 ο C. Δίνονται η πυκνότητά του στους 20 ο C ρ 20 = 845 kg/m 3 και ο συντελεστής κυβικής διαστολής του β = 9 * 10-4
1 Παράδειγμα 101 Να υπολογίσετε τη μάζα 10 m 3 πετρελαίου, στους : α) 20 ο C και β) 40 ο C. Δίνονται η πυκνότητά του στους 20 ο C ρ 20 = 845 kg/m 3 και ο συντελεστής κυβικής διαστολής του β = 9 * 10-4
Κεφάλαιο 5 Εκχύλιση. 5.1 Ισορροπία Υγρού - Υγρού
 Κεφάλαιο 5 Εκχύλιση Σύνοψη Εκχύλιση υγρού/υγρού ονομάζεται η φυσική διεργασία διαχωρισμού ενός ή περισσοτέρων συστατικών ενός υγρού μίγματος με κατεργασία του με κατάλληλο διαλύτη, στον οποίο το(α) συστατικό(α)
Κεφάλαιο 5 Εκχύλιση Σύνοψη Εκχύλιση υγρού/υγρού ονομάζεται η φυσική διεργασία διαχωρισμού ενός ή περισσοτέρων συστατικών ενός υγρού μίγματος με κατεργασία του με κατάλληλο διαλύτη, στον οποίο το(α) συστατικό(α)
Υπολογισµοί του Χρόνου Ξήρανσης
 Η πραγµατική επιφάνεια ξήρανσης είναι διασπαρµένη και ασυνεχής και ο µηχανισµός από τον οποίο ελέγχεται ο ρυθµός ξήρανσης συνίσταται στην διάχυση της θερµότητας και της µάζας µέσα από το πορώδες στερεό.
Η πραγµατική επιφάνεια ξήρανσης είναι διασπαρµένη και ασυνεχής και ο µηχανισµός από τον οποίο ελέγχεται ο ρυθµός ξήρανσης συνίσταται στην διάχυση της θερµότητας και της µάζας µέσα από το πορώδες στερεό.
Συνοπτική Παρουσίαση Σχέσεων για τον Προσδιορισμό του Επιφανειακού Συντελεστή Μεταφοράς της Θερμότητας.
 5 η ΔΙΑΛΕΞΗ Στόχος της διάλεξης αυτής είναι η κατανόηση των διαδικασιών αλλά και των σχέσεων που χρησιμοποιούνται για τον προσδιορισμό του ρυθμού μεταφοράς θερμότητας, Q &, αλλά και του επιφανειακού συντελεστή
5 η ΔΙΑΛΕΞΗ Στόχος της διάλεξης αυτής είναι η κατανόηση των διαδικασιών αλλά και των σχέσεων που χρησιμοποιούνται για τον προσδιορισμό του ρυθμού μεταφοράς θερμότητας, Q &, αλλά και του επιφανειακού συντελεστή
6 Εξαναγκασμένη ροή αέρα
 6 Εξαναγκασμένη ροή αέρα 6.1 Εισαγωγή Όταν θέτουμε σε κίνηση κάποια μόρια ενός ρευστού μέσω μιας αντλίας ή ενός φυσητήρα, η κίνηση μεταδίδεται και στα υπόλοιπα μόρια του ρευστού μέσω των αλληλεπιδράσεων
6 Εξαναγκασμένη ροή αέρα 6.1 Εισαγωγή Όταν θέτουμε σε κίνηση κάποια μόρια ενός ρευστού μέσω μιας αντλίας ή ενός φυσητήρα, η κίνηση μεταδίδεται και στα υπόλοιπα μόρια του ρευστού μέσω των αλληλεπιδράσεων
ΕΞΑΤΜΙΣΗ Θοδωρής Καραπάντσιος
 ΕΞ ΕΞΑΤΜΙΣΗ Θοδωρής Καραπάντσιος ΕΞ.1 Εισαγωγή Αντικείµενο της συµπύκνωσης είναι κατά κύριο λόγο η αποµάκρυνση νερού, µε εξάτµιση, από ένα υδατικό διάλυµα που περιέχει µια ή περισσότερες διαλυµένες ουσίες,
ΕΞ ΕΞΑΤΜΙΣΗ Θοδωρής Καραπάντσιος ΕΞ.1 Εισαγωγή Αντικείµενο της συµπύκνωσης είναι κατά κύριο λόγο η αποµάκρυνση νερού, µε εξάτµιση, από ένα υδατικό διάλυµα που περιέχει µια ή περισσότερες διαλυµένες ουσίες,
Στοιχειομετρικοί Υπολογισμοί στη Χημεία
 Στοιχειομετρικοί Υπολογισμοί στη Χημεία Δομικές μονάδες της ύλης ΑΤΟΜΑ ΜΟΡΙΑ ΣΤΟΙΧΕΙΑ ΕΝΩΣΕΙΣ Αριθμός Avogadro N A = 6,02 10 23 mol -1 Δηλαδή αυτός ο αριθμός παριστάνει την ποσότητα μιας ουσίας που περιέχει
Στοιχειομετρικοί Υπολογισμοί στη Χημεία Δομικές μονάδες της ύλης ΑΤΟΜΑ ΜΟΡΙΑ ΣΤΟΙΧΕΙΑ ΕΝΩΣΕΙΣ Αριθμός Avogadro N A = 6,02 10 23 mol -1 Δηλαδή αυτός ο αριθμός παριστάνει την ποσότητα μιας ουσίας που περιέχει
6.2. ΤΗΞΗ ΚΑΙ ΠΗΞΗ, ΛΑΝΘΑΝΟΥΣΕΣ ΘΕΡΜΟΤΗΤΕΣ
 45 6.1. ΓΕΝΙΚΑ ΠΕΡΙ ΦΑΣΕΩΝ ΜΕΤΑΤΡΟΠΕΣ ΦΑΣΕΩΝ Όλα τα σώµατα,στερεά -ά-αέρια, που υπάρχουν στη φύση βρίσκονται σε µια από τις τρεις φάσεις ή σε δύο ή και τις τρεις. Όλα τα σώµατα µπορεί να αλλάξουν φάση
45 6.1. ΓΕΝΙΚΑ ΠΕΡΙ ΦΑΣΕΩΝ ΜΕΤΑΤΡΟΠΕΣ ΦΑΣΕΩΝ Όλα τα σώµατα,στερεά -ά-αέρια, που υπάρχουν στη φύση βρίσκονται σε µια από τις τρεις φάσεις ή σε δύο ή και τις τρεις. Όλα τα σώµατα µπορεί να αλλάξουν φάση
ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ
 . ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 135 ΔΙΑΓΡΑΜΜΑΤΑ ΦΑΣΕΩΝ 1 2 3 4 1 στερεό (solid) 2 υγρό (liquid) 3 ατμός (vapor) 4 αέριο (gas) A 1+2+3
. ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 135 ΔΙΑΓΡΑΜΜΑΤΑ ΦΑΣΕΩΝ 1 2 3 4 1 στερεό (solid) 2 υγρό (liquid) 3 ατμός (vapor) 4 αέριο (gas) A 1+2+3
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
Εργαστήριο Μετάδοσης Θερμότητας
 ΑΣΚΗΣΗ ΕΝΑΛΛΑΚΤΩΝ ΘΕΡΜΟΤΗΤΑΣ ΣΚΟΠΟΣ Ο υπολογισμός του μεταφερόμενου ποσού θερμότητας σε εναλλάκτη ομόκεντρων σωλήνων, ο συνολικός θερμικός βαθμός απόδοσης, οι θερμοκρασιακές αποδόσεις των δύο ρευμάτων
ΑΣΚΗΣΗ ΕΝΑΛΛΑΚΤΩΝ ΘΕΡΜΟΤΗΤΑΣ ΣΚΟΠΟΣ Ο υπολογισμός του μεταφερόμενου ποσού θερμότητας σε εναλλάκτη ομόκεντρων σωλήνων, ο συνολικός θερμικός βαθμός απόδοσης, οι θερμοκρασιακές αποδόσεις των δύο ρευμάτων
Παραδείγµατα ροής ρευστών (Moody κλπ.)
 Παραδείγµατα ροής ρευστών (Mooy κλπ.) 005-006 Παράδειγµα 1. Να υπολογισθεί η πτώση πίεσης σε ένα σωλήνα από χάλυβα του εµπορίου µήκους 30.8 m, µε εσωτερική διάµετρο 0.056 m και τραχύτητα του σωλήνα ε 0.00005
Παραδείγµατα ροής ρευστών (Mooy κλπ.) 005-006 Παράδειγµα 1. Να υπολογισθεί η πτώση πίεσης σε ένα σωλήνα από χάλυβα του εµπορίου µήκους 30.8 m, µε εσωτερική διάµετρο 0.056 m και τραχύτητα του σωλήνα ε 0.00005
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση 4: Μερικός γραμμομοριακός όγκος Αθανάσιος Τσεκούρας Τμήμα Χημείας . Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 5 4. Τελικά αποτελέσματα... 7 Σελίδα
Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση 4: Μερικός γραμμομοριακός όγκος Αθανάσιος Τσεκούρας Τμήμα Χημείας . Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 5 4. Τελικά αποτελέσματα... 7 Σελίδα
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Πειραιά Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανολογίας
 1 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Πειραιά Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανολογίας Πρόβλημα 1 Μηχανική Ρευστών Κεφάλαιο 1 Λυμένα Προβλήματα Μια αμελητέου πάχους επίπεδη πλάκα διαστάσεων (0 cm)x(0
1 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Πειραιά Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανολογίας Πρόβλημα 1 Μηχανική Ρευστών Κεφάλαιο 1 Λυμένα Προβλήματα Μια αμελητέου πάχους επίπεδη πλάκα διαστάσεων (0 cm)x(0
v = 1 ρ. (2) website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Βασικές έννοιες στη μηχανική των ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 17 Φεβρουαρίου 2019 1 Ιδιότητες των ρευστών 1.1 Πυκνότητα Πυκνότητα
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Βασικές έννοιες στη μηχανική των ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 17 Φεβρουαρίου 2019 1 Ιδιότητες των ρευστών 1.1 Πυκνότητα Πυκνότητα
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου (21/6/2017)
 Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΙΑΧΕΙΡΙΣΗΣ ΕΝΕΡΓΕΙΑΚΩΝ ΠΟΡΩΝ ΘΕΡΜΟ ΥΝΑΜΙΚΗ Ι 1
 ΘΕΡΜΟ ΥΝΑΜΙΚΗ Ι ιδάσκων: Καθ. Α.Γ.Τοµπουλίδης ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΙΑΧΕΙΡΙΣΗΣ ΕΝΕΡΓΕΙΑΚΩΝ ΠΟΡΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΥΤΙΚΗΣ ΜΑΚΕ ΟΝΙΑΣ, ΚΟΖΑΝΗ Εαρινό εξάµηνο 2003-2004 Άσκηση 1: Κυλινδρικό έµβολο περιέχει αέριο το
ΘΕΡΜΟ ΥΝΑΜΙΚΗ Ι ιδάσκων: Καθ. Α.Γ.Τοµπουλίδης ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΙΑΧΕΙΡΙΣΗΣ ΕΝΕΡΓΕΙΑΚΩΝ ΠΟΡΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΥΤΙΚΗΣ ΜΑΚΕ ΟΝΙΑΣ, ΚΟΖΑΝΗ Εαρινό εξάµηνο 2003-2004 Άσκηση 1: Κυλινδρικό έµβολο περιέχει αέριο το
