CAPITOLUL 8. Concentrarea ionilor cu răşini schimbătoare de ioni
|
|
|
- Στράτων Ρόκας
- 8 χρόνια πριν
- Προβολές:
Transcript
1 APITOLUL 8 oncentrarea ionilor cu răşini schimbătoare de ioni 8.1. Noţiuni despre schimbători de ioni Schimbul ionic este definit ca o substituţie a unui ion legat de o matrice inertă cu un alt ion prin desfacerea unei legături ionice şi formarea unei noi legături ionice, fără alte modificări structurale semnificative. [62] In funcţie de natura ionilor schimbaţi, procesul de schimb ionic poate fi de două feluri: schimb de anioni sau schimb de cationi. Procesul de schimbare de anioni (A - cu B - ) poate fi scris:, iar cel de schimbare de cationi (E + cu F + ): R-X + A - + B - R-X + B - + A - R-Y - E + + F + R-Y - F + + E + Schimbătorul de anioni se mai numeşte şi anionit (fiind reprezentat prin R-X + A - ), iar cel de cationi cationit (R-Y - E + ). R- reprezintă scheletul (suportul) inert al răşinii schimbătoare de ioni, pe care se ataşează gruparea funcţională X + sau Y -, la care are loc schimbul de anioni, respectiv cationi. Echilibrul de schimb ionic şi selectivitatea schimbului ionic pot fi discutate pentru fiecare tip de proces în parte. Dacă luăm, spre exmplu, schimbul de anioni scris mai sus, şi considerăm că două specii B sunt implicate în compeţia de schimb anionic, notate cu B 1 - şi B 2 -, atunci vom avea echilibrele de competiţie: R-X + A - + B 1 - R-X + B A - (8.1) R-X + A - + B 2 - R-X + B A - (8.2) j Aceste două echilibre sunt caracterizate de constantele de schimb ionic, notate cu i, în care i şi j sunt ionii care participă la procesul de schimb ionic de mai sus. Pentru echilibrele redate mai sus se pot scrie constantele de schimb ionic redate mai jos, în funcţie de concentraţiile speciilor aflate în schimbătorul de anioni (notate cu indicele r) şi cele din soluţie (notate cu indicele s): B [B1 ] r [A ] s 1 A = [B1 ] s [A ] (8.3) r B [B2 ] r [A ] s 2 A = [B2 ] s [A ] (8.4) r 123
2 Dacă procesul este privit ca o repartiţie a speciilor între cele două faze (schimbătorul de anioni şi soluţie), atunci se pot scrie trei constante de repartiţie, corespunzătoare celor trei specii anionice implicate în procesul de schimb: [A ] r d (A ) = [B1 ] r d (B1 ) = [B2 ] r d (B2 ) = (8.5) [A ] s [B1 ] s [B2 ] s u ajutorul acestor relaţii, constantele de schimb ionic date de ec. (8.3) şi (8.4) pot fi rescrise astfel: 1 B A d (B1 ) = d (A ) B (B ) 2 d 2 = (8.6) A d (A ) Selectivitatea (Δ i,j ) procesului de schimb ionic (măsura în care unul dintre ionii B1 sau B 2 este preferat în procesul de schimb ionic cu A - ) este definit ca raportul constantelor respective de schimb ionic: B A Δi, j = B A 1 2 d (B1 ) = d (B2 ) (8.7) Pe baza datelor experimentale şi din unele consideraţii teoretice, s-au alcătuit următoarele grupe de ioni în ordinea descrescătoare a afinităţilor lor faţă de un schimbător de ioni. Pentru procesul de schimb de cationi ordinea afinităţilor este următoarea: Ba 2+ > Pb 2+ > Sr 2+ > a 2+ > Ni 2+ > d 2+ > u 2+ > o 2+ > Zn 2+ > Mg 2+ > Mn 2+ > Be 2+ > Tl + > Ag + > s + > Rb + > + > N 4 + > Na + > + Pentru procesul de schimb de anioni ordinea afinităţilor este: SO 4 2- > I - > NO 3 - > ro 4 - > Br - > N - > l - > O 3 - > PO 4 - > OO - > 3 OO - > O - apacitatea de schimb ionic a unei răşini schimbătoare de ioni este definită ca numărul de miliechivalenţi-gram de ioni retinuţi per gram de răşină (în stare uscată). Raportarea se poate face şi la volumul de răşină aflată în coloana utilizată la procesul de schimb ionic, cunoscând diametrul acesteia şi înălţimea de coloană umplută cu răşină Reţinerea de cationi pe răşini schimbătoare de anioni Pe o răşină schimbătoare de anioni, notată cu R-X + A -, poate fi reţinută o specie ionică metalică, dacă aceasta este complexată şi devine un anion. Să considerăm o specie cationică Me 2+ introdusă în coloana cu schimbător de anioni, iar eluentul conţine un ligand notat cu L -. In acest caz în soluţie se stabilesc următoarele echilibre de 124
3 complexare în trepte: Me 2+ + L - MeL + MeL + + L - MeL 2 MeL 2 + L - MeL - 3 MeL L - MeL 2-4 omplecşii anionici formaţi vor participa la schimbul anionic şi se vor reţine pe un schimbător de anioni, în timp ce speciile Me 2+ şi MeL + nu se vor reţine, fiind respinse de R-X +. Procesele de schimb anionic care au loc între speciile anionice din soluţia de eluent şi anionit sunt următoarele: R-X + A - + L - R-X + L - + A - R-X + L - + MeL 3 -- R-X + MeL L - R-X + L - + MeL R-X + MeL L - Un exemplu de astfel de posibilitate de utilizare a răşinilor schimbătoare de anioni la separarea unor specii metalice este formarea de cloro-complecşi, prin adăugarea de l în eluent. Mărimea care determină separarea speciilor metalice este constanta echilibrelor de complexare de mai sus şi afinitatea cloro-complecşilor formaţi faţă de răşina schimbătoare de anioni. Din acest punct de vedere, al afinităţii cloro-complecşilor lor faţă de anioniţi, cationii se împart în următoarele grupe: [62] i) ioni metalici nereţinuţi pe anioniţi, deoarece nu formează complecşi stabili în prezenţă de l, cum ar fi: ionii metalelor alcaline sau alcalino-pământoase; ii) ioni metalici slab reţinuţi (cu constantele de formare a cloro-complecşilor mai mici de 10): Ti 3+, V 4+, r 3+, Tl + ; iii) ioni metalici moderat reţinuţi (cu constanta de formare a cloro-complecşilor între 10 şi 100); Ti 4+, Fe 2+, o 2+, u 2+ ; iv) ioni metalici puternic reţinuţi (cu constanta de formare a cloro-complecşilor mai mare de 10 2 ): Fe 3+, u +, Zn 2+, Ga 3+, V 5+, U Tipuri de schimbători de ioni Schimbători anorganici de ioni In general, orice compus ionic greu solubil în apă are proprietatea de schimb ionic. Dintre compuşii anorganici cu utilizări recunoscute în schimbul ionic sunt următorii: a) Aluminosilicaţii naturali sau zeoliţi, care au formula generală: Me 2/x O Al 2 O 3 nsio 2 m O 125
4 Structura lor tridimensională (redată în Fig. 8.1) este caracterizată prin pori uniformi, de o anumită mărime (depinzând de raportul molar Al 2 O 3 /SiO 2 ), în care pot pătrunde specii ionice cu diametrul mai mic decât al porilor şi care participă apoi la schimbul ionic cu Me + sau Me +2 (Na + ; + ; a 2+, Mg 2+, etc). [83] d Fig O imagine tridimensională a structurii zeoliţilor (d diametrul porilor). b) Fosfatul de zirconiu, Zr(PO 4 ) 2 O, sau hidroxiapatita, a 5 (PO 4 ) 3, sunt de asemenea utilizate ca schimbători de ioni. Avantajele schimbătorilor anorganici de ioni sunt date de stabilitatea termică mare, precum şi de o mai bună rezistenţă la acţiunea radiaţiilor. In schimb, stabilitatea la hidroliză este mai slabă decât a celor organici. Schimbători organici de ioni Schimbătorii organici de ioni, numiţi şi răşini schimbătoare de ioni, sunt caracterizaţi prin două componente structurale principale: suportul răşinei, care este de natură organică polimerică, pe care sunt grefate grupările funcţionale care participă la procesul de schimb ionic. Structura polimerică asigură stabilitatea mecanică a schimbătorului de ioni şi stabilitate chimică faţă de mediul solvatant. Grupările funcţionale, cu caracter acid sau bazic, care la rândul lor pot fi cu caracter tare sau slab, asigură interacţiunea electrostatică cu ioni de semn contrar din vecinătate. Ele vor interacţiona atât cu speciile ionice din vecinătatea sa, cât şi cu specii moleculare neutre, cum este apa, prin interacţii ion-ion sau ion-dipol. Principalele tipuri de grupări întâlnite la schimbătorii de ioni sunt redate în tabelul de mai jos. [84] 126
5 Tabel 8.1. Tipuri de grupări funcţionale întâlnite în schimbători organici de ioni. Tip Grupare funcţională în Schimbători de cationi Acid sulfonic -SO Acid carboxilic -OO - + Acid fosforic -(PO 3) - + Acid fosfinic -PO Grupări fenolice -Ar-O - + Acid arsenic -(AsO 3) - + Acid selenoic -SeO Amine cuaternare Schimbători de anioni -N( 3) 3] + - -N( 3) 2()] + - Amine terţiare -N( 3) 2] + - Amine secundare -N( 3)] + - Amine primare -N 3] + - Anioniţii puternici conţin grupări amino cuaternare, în timp ce anioniţii slabi conţin grupări amino mai puţin substituite. Un anionit slab va funcţiona doar atunci când p-ul eluentului este suficient de acid pentru ca să aibă loc protonarea atomilor de azot din grupările funcţionale. Aceasta se poate realiza dacă eluentul conţine l. R-N + l R-N 3 + l - Un schimbător de anioni conţinând gruparea trimetilamino este mult mai puternic decât unul care conţine gruparea dimetil-β-hidroxietilamino. Pe de altă parte, grupările trimetilamino sunt mult mai puţin stabile termic, dar mai rezistente la prezenţa oxidanţilor, decât grupările dimetil-β-hidroxietilamino. 3 + N N 2 3 ationiţii tari pot participa la procesul de schimb ionic pentru un interval larg al p-ului soluţiei, în timp ce cationiţii slabi funcţionează doar la valori bazice ale soluţiei care este trecută prin coloana cu schimbător de cationi. De aceea, soluţia care este trecută peste un cationit slab trebuie să aibă p-ul bazic, ajustat cu Na, astfel încât grupările responsabile de procesul de schimb ionic să fie disociate; astfel, schimbătorii de ioni conţinând gruparea carboxil sunt cationiţi slabi, iar pentru disocierea acestora în soluţia apoasă este adăugat Na, astfel încât să aibă loc disocierea grupărilor carboxil 127
6 la grupări carboxilat: R-O + Na R-OO- Na + + O Exemple de cationiţi puternici sunt cei ce conţin grupări funcţionale de tip sulfonic; ele disociază indiferent de valoarea p-ului soluţiei apoase cu care intră în contact. Suportul polimeric asigură stabilitate mecanică şi chimică faţă de mediul apos. Pe suportul macromolecular se grefează prin diverse procedee chimice grupările funcţionale menţionate anterior. Gradul de reticulare trebuie să permită difuzia ionilor din soluţie în masa răşinii pentru a face posibil schimbul ionic. Schimbătorii de ioni sunt materiale foarte higroscopice şi pot pierde apa reţinută doar după o încălzire îndelungată (până la 60 ) sau prin trecerea unor solvenţi puri (acetonă, alcooli, dimetilformamidă, dimetilsulfoxid). De asemenea, este cunoscut rolul de catalizator al schimbătorilor de ioni în stare uscată în unele procese de sinteză organică. Polimerizarea şi policondensarea reprezintă modalităţi de obţinere a suportului macromolecular de care să se ataşeze grupările funcţionale cu proprietăţi schimbătoare de ioni. De aceea, aceste materiale se mai numesc şi răşini schimbătoare de ioni. In acest scop, stirenul este cel mai important monomer, iar pentru realizarea unei structuri tridimensionale (structură reticulară) se utilizează ca monomer divinilbenzenul. Introducerea grupărilor funcţionale sulfonice se poate face prin modalităţile date mai jos: SO 3 + O-SO 3 (SO 3 l; SO 3 ) SO 3 Suportul polimeric pentru cationiţi slabi se poate obţine prin copolimerizarea divinilbenzenului cu acid acrilic sau metacrilic (exemplificată în reacţia de mai jos), redat în continuare: n 3 + m O O Răşinile obţinute prin policondensare sunt foarte utilizate, având matricea polimerică sintetizată prin reacţia dintre fenol şi formaldehidă. In structura rezultată se găsesc suficiente grupări funcţionale - - care apoi să fie derivatizate la grupări amino. 128
7 n + m =O O SOl 2 + -N( 3 ) 3 -l O N( 3 ) 3 O opolimerizarea dintre divinilbenzen şi clorură de vinil poate fi utilizată la obţinerea anioniţilor, prin modalitatea descrisă în schema următoare: l + N( 3 ) 3 n + m N( 3 ) 3 l apacitatea de schimb ionic depinde în acest caz de raportul de copolimerizare dintre stiren şi clorura de vinil Răşini cu proprietăţi complexante O răşină cu proprietăţi complexante este o matrice polimerică (notată cu Res) în care sunt încorporaţi liganzi (L) prin formarea de legături covalente. Liganzii grefaţi pot forma complecşi prin legături coordinative ( ) cu ioni metalici (Me n+ ), modalitate care diferă de schimbul ionic discutat anterior: Res-L + Me n+ Res-L Me n+ De aceea, răşinile cu proprietăţi complexante diferă de schimbătorii de ioni prin selectivitatea mai înaltă şi prin energia mai mare de interacţie ion metalic ligand. In schimb, viteza de reţinere a ionului metalic este mai mică decât la schimbătorii de ioni. Proprietăţile complexante ale răşinii depind de natura atomilor donori, de factori sterici, 129
8 de structura răşinii şi de condiţiile în care are loc eluţia probei prin coloană. Exemple de grupări complexante, grefate de un suport polimeric, sunt redate în tabelul următor. Tabel 8.2. Exemple de răşini conţinând grupări cu proprietăţi complexante. Tip Gupa ligand Natura polimerului Iminodiacetic acid -N(-O) 2 Polistiren-divinilbenzen (PS-DVB); poliacrilic S N Isotiouree N PS-DVB Acid aminofosfonic N P O Acid ditiocarbamic N S S Acid fosfonic --PO() 2 PS-DVB O N N Acid O etilendiaminotriacetic PS 2 Tiol Amidoxima O -S N N PS; rasini fenolice; poliacrilic. PS-DVB; poliacrilic; rasini fenolice PS-DVB; poliacrilic (DVB); Etilendimetacrilat Poliacrilonitril (DVB) Piridina Tiouree N N S N Polivinil piridină (DVB) Poliacrilonitrile (DVB) 8-idroxichinolina N Etilendimetacrilat 8.5. Aplicaţii analitice De regulă, utilizarea materialelor cu proprietăţi schimbătoare de ioni se face prin plasarea lor într-o coloană de sticlă, cu dimensiuni în funcţie de scopul urmărit. Umplerea unei coloane se face prin simpla introducere mecanică a unei cantităţi măsurate de răşină schimbătoare de ioni uscată, după care se va trece o cantitate de apă deionizată 130
9 pentru umflarea acesteia. Datorită numărului mare de grupări hidrofile din structura schimbătorilor de ioni, aceştia sunt materiale foarte higroscopice. Prin adsorbţia apei la nivelul ionilor reţinuţi şi a grupărilor implicate în schimbul ionic, volumul acestor materiale creşte considerabil, producându-se o umflare a acestora. Gradul de umflare al răşinii depinde de gradul de reticulare şi de flexibilitatea catenelor, astfel că la un grad înalt de reticulare umflarea răşinii este mai mică. De aceea la umplerea unei coloane cu răşină schimbătoare de ioni trebuie ţinut cont de gradul de umflare al acesteia. De asemenea, după cum s-a arătat la ap. 6, răşinile schimbătoare de ioni sunt utilizate ca materiale adsorbante în extracţia în fază solidă, fiind comercializate în format de cartuş sau membrane adsorbante. Schimbătorii de ioni pot reţine doar o cantitate bine definită de ioni, exprimată prin capacitatea de schimb ionic. Regenerarea presupune apoi îndepărtarea ionilor reţinuţi şi înlocuirea lor cu ioni hidroxid (pentru anioniţi) sau protoni (pentru cationiţi). Pentru aceasta se utilizează o soluţie diluată de Na în cazul anioniţilor, respectiv l în cazul cationiţilor. Principalele aplicaţii analitice a schimbătorilor de ioni sunt ca faze staţionare în cromatografia de lichide prin mecanism de schimb ionic (discutată într-un capitol separat). [42,85] In domeniul preparării probelor, schimbătorii de ioni sunt utilizaţi la izolarea şi concentrarea cationilor sau anionilor din probe apoase, în vederea analizei prin tehnica menţionată mai sus, dar şi pentru analize prin alte tehnici, cum ar fi spectrometria de absorbţie sau emisie atomică. Procedura practică de concentrare şi izolare a anumitor ioni dintr-o probă apoasă se desfăşoară asemănător procedurilor SPE, exceptând etapele de uscare a materialului adsorbant, care nu mai au loc. Un exemplu extrem de important este aplicarea procesului de schimb ionic în etapa de preparare a probelor în vederea determinarii ionilor diverşilor izotopi ai actinidelor din probe de mediu (apă, aer sau sol). Datorită efectelor lor extrem de nocive asupra organismelor, limitele maxim admisibile impuse pentru concentraţia acestora din probe de mediu sunt foarte joase (vezi tabelul următor). Analiza acestor elemente din probe din mediu ambiant implică o cantitate mare de probă prelevată, din care aceste specii ionice sunt separate şi concentrate prin metoda schimbătorilor de ioni. Astfel, aceste elemente sunt concentrate în final până la nivelul ppt într-un volum mic de probă, determinabilă prin tehnica IP-MS, care asigură atât selectivitatea determinarilor, cât şi o limită de detecţie joasă, la nivel de ppt. Prin urmare, concentrarea 239 Pu din probe cu conţinut în acest element la limita acceptabilă (0,1 ppq) până la 1 ppt (determinabilă prin această tehnică) presupune un factor de concentrare de ori. Aceasta presupune, de exemplu, trecerea a 100 L probă apoasă printr-o coloană cu cationit, urmată de eluţia ionilor de interes cu 10 ml soluţia acidă. Determinarea conţinutului total de cationi dintr-o probă apoasă se poate efectua prin trecerea unui volum cunoscut din probă printr-o coloană de cationit în forma R-Y - + ; cantitatea globală de cationi din probă se exprimă astfel ca număr de miliechivalenţi-gram de proton schimbaţi şi determinaţi apoi prin titrare cu o soluţie de Na, având titru şi factor cunoscut, în prezenţa unui indicator. In mod similar, se poate stabili conţinutul global de anioni dintr-o probă apoasă, utilizând o coloană cu schimbători de anioni, în forma R-X + -. Un alt exemplu de aplicaţie a schimbătorilor de ioni este dat de eliminarea unor interferenţe în determinarea unor specii ionice. Astfel, în metoda de determinare a ionului oxalat din urină prin generarea de O 2 de către oxalat-oxidază interferă puternic anionii l - şi NO - 3. Indepărtarea acestor interferenţe se poate face foarte uşor prin trecerea 131
10 probei printr-o coloană conţinând o răşină anionit. Un alt exemplu se referă la extracţia unor acizi graşi din ţesuturi biologice, produşi în urma ciclului rebs (acid piruvic, malic, isocitric, citric, lactic, succinic sau fumaric). Pentru extracţia acestor acizi organici se utilizează ca mediu extractant o soluţie de acid percloric, iar după extracţie acesta trebuie îndepărtat din probă dacă analiza se va face prin cromatografie de ioni. Eliminarea sa din probă se face prin trecerea acesteia printr-o coloană umplută cu anionit puternic (de exemplu, SAX). Tabel 8.3. Valori limită impuse pentru izotopi din seria actinidelor în probe de apă şi sol. t Apă Sol Izotop 1/2 (ani) pi/l ppq pi/l ppq 239 Pu 2, ,01 0,163 0,03 0, U 1, ,6 63,6 0,3 31,8 234 U 2, ,6 97,5 0,3 48, U 7, ,6 2, , U 4, ,6 1, , Ra 1, ,5 0,513 0,5 0, Np 2, , ,5 7, Th 7, ,2 0,5 24,1 232 Th 1, , ,5 4, Schimbătorii de ioni sunt utilizaţi la obţinerea apei deionizate, prin trecerea acesteia succesiv printr-o coloană de cationi şi apoi de anioni, eventual procesul fiind repetat pentru ca valoarea conductivitătii apei obţinute să fie foarte scăzută. Există exemple de aplicaţii ale schimbătorilor de ioni în purificarea unor solvenţi. Astfel, urmele de acetaldehidă din etanol pot fi îndepărtate prin trecerea unei probe de etanol peste o răşină anionică în forma bisulfit. Aceasta are capacitatea de a reacţiona cu acetaldehida şi astfel această impuritate din etanol rămâne în coloană. 132
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Capitolul 2 - HIDROCARBURI 2.3.ALCHINE
 Capitolul 2 - HIDROCARBURI 2.3.ALCHINE TEST 2.3.3 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Acetilena poate participa la reacţii de
Capitolul 2 - HIDROCARBURI 2.3.ALCHINE TEST 2.3.3 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Acetilena poate participa la reacţii de
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare.
 Capitolul 3 COMPUŞI ORGANICI MONOFUNCŢIONALI 3.2.ACIZI CARBOXILICI TEST 3.2.3. I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Reacţia dintre
Capitolul 3 COMPUŞI ORGANICI MONOFUNCŢIONALI 3.2.ACIZI CARBOXILICI TEST 3.2.3. I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Reacţia dintre
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
a. 0,1; 0,1; 0,1; b. 1, ; 5, ; 8, ; c. 4,87; 6,15; 8,04; d. 7; 7; 7; e. 9,74; 12,30;1 6,08.
 1. În argentometrie, metoda Mohr: a. foloseşte ca indicator cromatul de potasiu, care formeazǎ la punctul de echivalenţă un precipitat colorat roşu-cărămiziu; b. foloseşte ca indicator fluoresceina, care
1. În argentometrie, metoda Mohr: a. foloseşte ca indicator cromatul de potasiu, care formeazǎ la punctul de echivalenţă un precipitat colorat roşu-cărămiziu; b. foloseşte ca indicator fluoresceina, care
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
REACŢII DE ADIŢIE NUCLEOFILĂ (AN-REACŢII) (ALDEHIDE ŞI CETONE)
 EAŢII DE ADIŢIE NULEFILĂ (AN-EAŢII) (ALDEIDE ŞI ETNE) ompușii organici care conțin grupa carbonil se numesc compuși carbonilici și se clasifică în: Aldehide etone ALDEIDE: Formula generală: 3 Metanal(formaldehida
EAŢII DE ADIŢIE NULEFILĂ (AN-EAŢII) (ALDEIDE ŞI ETNE) ompușii organici care conțin grupa carbonil se numesc compuși carbonilici și se clasifică în: Aldehide etone ALDEIDE: Formula generală: 3 Metanal(formaldehida
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
 4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Capitolul 2 - HIDROCARBURI 2.5.ARENE
 Capitolul 2 - HIDROCARBURI 2.5.ARENE TEST 2.5.2 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Radicalul C 6 H 5 - se numeşte fenil. ( fenil/
Capitolul 2 - HIDROCARBURI 2.5.ARENE TEST 2.5.2 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Radicalul C 6 H 5 - se numeşte fenil. ( fenil/
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].
![Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].](/thumbs/72/67648751.jpg) Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5.1. Noţiuni introductive
 ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
Capitolul 2 - HIDROCARBURI 2.5.ARENE
 Capitolul 2 - HIDROCARBURI 2.5.ARENE TEST 2.5.3 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Sulfonarea benzenului este o reacţie ireversibilă.
Capitolul 2 - HIDROCARBURI 2.5.ARENE TEST 2.5.3 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Sulfonarea benzenului este o reacţie ireversibilă.
Problema a II - a (10 puncte) Diferite circuite electrice
 Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Valori limită privind SO2, NOx şi emisiile de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili
 Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
Criptosisteme cu cheie publică III
 Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
 10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
Tema 5 (S N -REACŢII) REACŢII DE SUBSTITUŢIE NUCLEOFILĂ. ŞI DE ELIMINARE (E - REACŢII) LA ATOMULDE CARBON HIBRIDIZAT sp 3
 Tema 5 REACŢII DE SUBSTITUŢIE NUCLEOFILĂ (S N -REACŢII) ŞI DE ELIMINARE (E - REACŢII) LA ATOMULDE CARBON IBRIDIZAT sp 3 1. Reacții de substituție nucleofilă (SN reacții) Reacţiile de substituţie nucleofilă
Tema 5 REACŢII DE SUBSTITUŢIE NUCLEOFILĂ (S N -REACŢII) ŞI DE ELIMINARE (E - REACŢII) LA ATOMULDE CARBON IBRIDIZAT sp 3 1. Reacții de substituție nucleofilă (SN reacții) Reacţiile de substituţie nucleofilă
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
Componente şi Circuite Electronice Pasive. Laborator 3. Divizorul de tensiune. Divizorul de curent
 Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
ANALIZE FIZICO-CHIMICE MATRICE APA. Tip analiza Tip proba Metoda de analiza/document de referinta/acreditare
 ph Conductivitate Turbiditate Cloruri Determinarea clorului liber si total Indice permanganat Suma Ca+Mg, apa de suprafata, apa, apa grea, apa de suprafata, apa grea, apa de suprafata, apa grea, apa de
ph Conductivitate Turbiditate Cloruri Determinarea clorului liber si total Indice permanganat Suma Ca+Mg, apa de suprafata, apa, apa grea, apa de suprafata, apa grea, apa de suprafata, apa grea, apa de
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Acizi carboxilici heterofuncționali.
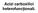 Acizi carboxilici heterofuncționali. 1. Acizi carboxilici halogenați. R R 2 l l R 2 R l Acizi α-halogenați Acizi β-halogenați l R 2 2 l Acizi γ-halogenați Metode de obținere. 1. alogenarea directă a acizilor
Acizi carboxilici heterofuncționali. 1. Acizi carboxilici halogenați. R R 2 l l R 2 R l Acizi α-halogenați Acizi β-halogenați l R 2 2 l Acizi γ-halogenați Metode de obținere. 1. alogenarea directă a acizilor
APA DEIONIZATĂ/DEMINERALIZATĂ
 APA DEIONIZATĂ/DEMINERALIZATĂ Este destul de greu să se dea o definiţie şi să se stabilească norme precise pentru apa distilată, demineralizată sau deionizată. Probabil, cel mai bine pentru a ne familiariza
APA DEIONIZATĂ/DEMINERALIZATĂ Este destul de greu să se dea o definiţie şi să se stabilească norme precise pentru apa distilată, demineralizată sau deionizată. Probabil, cel mai bine pentru a ne familiariza
Reactia de amfoterizare a aluminiului
 Problema 1 Reactia de amfoterizare a aluminiului Se da reactia: Al (s) + AlF 3(g) --> AlF (g), precum si presiunile partiale ale componentelor gazoase in functie de temperatura: a) considerand presiunea
Problema 1 Reactia de amfoterizare a aluminiului Se da reactia: Al (s) + AlF 3(g) --> AlF (g), precum si presiunile partiale ale componentelor gazoase in functie de temperatura: a) considerand presiunea
V O. = v I v stabilizator
 Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
2. Sisteme de forţe concurente...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
Asupra unei inegalităţi date la barajul OBMJ 2006
 Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
1. PROPRIETĂȚILE FLUIDELOR
 1. PROPRIETĂȚILE FLUIDELOR a) Să se exprime densitatea apei ρ = 1000 kg/m 3 în g/cm 3. g/cm 3. b) tiind că densitatea glicerinei la 20 C este 1258 kg/m 3 să se exprime în c) Să se exprime în kg/m 3 densitatea
1. PROPRIETĂȚILE FLUIDELOR a) Să se exprime densitatea apei ρ = 1000 kg/m 3 în g/cm 3. g/cm 3. b) tiind că densitatea glicerinei la 20 C este 1258 kg/m 3 să se exprime în c) Să se exprime în kg/m 3 densitatea
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
ECHILIBRE ACIDO BAZICE - 1
 ECHILIBRE ACIDO-BAZICE 1 DISOCIEREA APEI 2 H 2 O H 3 O + + OH - H 3 O + H + PRODUS IONIC AL APEI: + c P H K = [ H ] [ OH ] = 2 O P H O = 2 = 10 14 M 2 (25 o C ) ÎN APA PURĂ + [ H ] = [ OH ] = PH 2 O =
ECHILIBRE ACIDO-BAZICE 1 DISOCIEREA APEI 2 H 2 O H 3 O + + OH - H 3 O + H + PRODUS IONIC AL APEI: + c P H K = [ H ] [ OH ] = 2 O P H O = 2 = 10 14 M 2 (25 o C ) ÎN APA PURĂ + [ H ] = [ OH ] = PH 2 O =
Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE
 Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE TEST 2.4.1 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. Rezolvare: 1. Alcadienele sunt hidrocarburi
Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE TEST 2.4.1 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. Rezolvare: 1. Alcadienele sunt hidrocarburi
Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE
 Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE Exerciţii şi probleme E.P.2.4. 1. Scrie formulele de structură ale următoarele hidrocarburi şi precizează care dintre ele sunt izomeri: Rezolvare: a) 1,2-butadiena;
Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE Exerciţii şi probleme E.P.2.4. 1. Scrie formulele de structură ale următoarele hidrocarburi şi precizează care dintre ele sunt izomeri: Rezolvare: a) 1,2-butadiena;
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25
 Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
Examen AG. Student:... Grupa:... ianuarie 2011
 Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
Capitolul 14. Asamblari prin pene
 Capitolul 14 Asamblari prin pene T.14.1. Momentul de torsiune este transmis de la arbore la butuc prin intermediul unei pene paralele (figura 14.1). De care din cotele indicate depinde tensiunea superficiala
Capitolul 14 Asamblari prin pene T.14.1. Momentul de torsiune este transmis de la arbore la butuc prin intermediul unei pene paralele (figura 14.1). De care din cotele indicate depinde tensiunea superficiala
2CP Electropompe centrifugale cu turbina dubla
 2CP Electropompe centrifugale cu turbina dubla DOMENIUL DE UTILIZARE Capacitate de până la 450 l/min (27 m³/h) Inaltimea de pompare până la 112 m LIMITELE DE UTILIZARE Inaltimea de aspiratie manometrică
2CP Electropompe centrifugale cu turbina dubla DOMENIUL DE UTILIZARE Capacitate de până la 450 l/min (27 m³/h) Inaltimea de pompare până la 112 m LIMITELE DE UTILIZARE Inaltimea de aspiratie manometrică
Studiu privind soluţii de climatizare eficiente energetic
 Studiu privind soluţii de climatizare eficiente energetic Varianta iniţială O schemă constructivă posibilă, a unei centrale de tratare a aerului, este prezentată în figura alăturată. Baterie încălzire/răcire
Studiu privind soluţii de climatizare eficiente energetic Varianta iniţială O schemă constructivă posibilă, a unei centrale de tratare a aerului, este prezentată în figura alăturată. Baterie încălzire/răcire
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
II. 5. Probleme. 20 c 100 c = 10,52 % Câte grame sodă caustică se găsesc în 300 g soluţie de concentraţie 10%? Rezolvare m g.
 II. 5. Problee. Care ete concentraţia procentuală a unei oluţii obţinute prin izolvarea a: a) 0 g zahăr în 70 g apă; b) 0 g oă cautică în 70 g apă; c) 50 g are e bucătărie în 50 g apă; ) 5 g aci citric
II. 5. Problee. Care ete concentraţia procentuală a unei oluţii obţinute prin izolvarea a: a) 0 g zahăr în 70 g apă; b) 0 g oă cautică în 70 g apă; c) 50 g are e bucătărie în 50 g apă; ) 5 g aci citric
Unitatea atomică de masă (u.a.m.) = a 12-a parte din masa izotopului de carbon
 ursul.3. Mării şi unităţi de ăsură Unitatea atoică de asă (u.a..) = a -a parte din asa izotopului de carbon u. a.., 0 7 kg Masa atoică () = o ărie adiensională (un nuăr) care ne arată de câte ori este
ursul.3. Mării şi unităţi de ăsură Unitatea atoică de asă (u.a..) = a -a parte din asa izotopului de carbon u. a.., 0 7 kg Masa atoică () = o ărie adiensională (un nuăr) care ne arată de câte ori este
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
SERII NUMERICE. Definiţia 3.1. Fie (a n ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0
 SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
Esalonul Redus pe Linii (ERL). Subspatii.
 Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
SEMINAR 14. Funcţii de mai multe variabile (continuare) ( = 1 z(x,y) x = 0. x = f. x + f. y = f. = x. = 1 y. y = x ( y = = 0
 Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
Laborator 11. Mulţimi Julia. Temă
 Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R. 4.1 Proprietăţi topologice ale lui R Puncte de acumulare
 Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Curs 2 Şiruri de numere reale
 Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
Lucrare. Varianta aprilie I 1 Definiţi noţiunile de număr prim şi număr ireductibil. Soluţie. Vezi Curs 6 Definiţiile 1 şi 2. sau p b.
 Lucrare Soluţii 28 aprilie 2015 Varianta 1 I 1 Definiţi noţiunile de număr prim şi număr ireductibil. Soluţie. Vezi Curs 6 Definiţiile 1 şi 2 Definiţie. Numărul întreg p se numeşte număr prim dacă p 0,
Lucrare Soluţii 28 aprilie 2015 Varianta 1 I 1 Definiţi noţiunile de număr prim şi număr ireductibil. Soluţie. Vezi Curs 6 Definiţiile 1 şi 2 Definiţie. Numărul întreg p se numeşte număr prim dacă p 0,
Spatii liniare. Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară. Mulţime infinită liniar independentă
 Noţiunea de spaţiu liniar 1 Noţiunea de spaţiu liniar Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară 2 Mulţime infinită liniar independentă 3 Schimbarea coordonatelor unui vector la o schimbare
Noţiunea de spaţiu liniar 1 Noţiunea de spaţiu liniar Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară 2 Mulţime infinită liniar independentă 3 Schimbarea coordonatelor unui vector la o schimbare
Examen AG. Student:... Grupa: ianuarie 2016
 16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
Proiectarea filtrelor prin metoda pierderilor de inserţie
 FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...4
 SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
Activitatea A5. Introducerea unor module specifice de pregătire a studenţilor în vederea asigurării de şanse egale
 POSDRU/156/1.2/G/138821 Investeşte în oameni! FONDUL SOCIAL EUROPEAN Programul Operaţional Sectorial pentru Dezvoltarea Resurselor Umane 2007 2013 Axa prioritară nr. 1 Educaţiaşiformareaprofesionalăînsprijinulcreşteriieconomiceşidezvoltăriisocietăţiibazatepecunoaştere
POSDRU/156/1.2/G/138821 Investeşte în oameni! FONDUL SOCIAL EUROPEAN Programul Operaţional Sectorial pentru Dezvoltarea Resurselor Umane 2007 2013 Axa prioritară nr. 1 Educaţiaşiformareaprofesionalăînsprijinulcreşteriieconomiceşidezvoltăriisocietăţiibazatepecunoaştere
BARAJ DE JUNIORI,,Euclid Cipru, 28 mai 2012 (barajul 3)
 BARAJ DE JUNIORI,,Euclid Cipru, 8 mi 0 (brjul ) Problem Arătţi că dcă, b, c sunt numere rele cre verifică + b + c =, tunci re loc ineglitte xy + yz + zx Problem Fie şi b numere nturle nenule Dcă numărul
BARAJ DE JUNIORI,,Euclid Cipru, 8 mi 0 (brjul ) Problem Arătţi că dcă, b, c sunt numere rele cre verifică + b + c =, tunci re loc ineglitte xy + yz + zx Problem Fie şi b numere nturle nenule Dcă numărul
Electronegativitatea = capacitatea unui atom legat de a atrage electronii comuni = concept introdus de Pauling.
 Cursul 8 3.5.4. Electronegativitatea Electronegativitatea = capacitatea unui atom legat de a atrage electronii comuni = concept introdus de Pauling. Cantitativ, ea se exprimă prin coeficienţii de electronegativitate
Cursul 8 3.5.4. Electronegativitatea Electronegativitatea = capacitatea unui atom legat de a atrage electronii comuni = concept introdus de Pauling. Cantitativ, ea se exprimă prin coeficienţii de electronegativitate
13. Grinzi cu zăbrele Metoda izolării nodurilor...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...
 SEMINAR GRINZI CU ZĂBRELE METODA IZOLĂRII NODURILOR CUPRINS. Grinzi cu zăbrele Metoda izolării nodurilor... Cuprins... Introducere..... Aspecte teoretice..... Aplicaţii rezolvate.... Grinzi cu zăbrele
SEMINAR GRINZI CU ZĂBRELE METODA IZOLĂRII NODURILOR CUPRINS. Grinzi cu zăbrele Metoda izolării nodurilor... Cuprins... Introducere..... Aspecte teoretice..... Aplicaţii rezolvate.... Grinzi cu zăbrele
4. Măsurarea tensiunilor şi a curenţilor electrici. Voltmetre electronice analogice
 4. Măsurarea tensiunilor şi a curenţilor electrici oltmetre electronice analogice oltmetre de curent continuu Ampl.c.c. x FTJ Protectie Atenuator calibrat Atenuatorul calibrat divizor rezistiv R in const.
4. Măsurarea tensiunilor şi a curenţilor electrici oltmetre electronice analogice oltmetre de curent continuu Ampl.c.c. x FTJ Protectie Atenuator calibrat Atenuatorul calibrat divizor rezistiv R in const.
CONCURSUL DE MATEMATICĂ APLICATĂ ADOLF HAIMOVICI, 2017 ETAPA LOCALĂ, HUNEDOARA Clasa a IX-a profil științe ale naturii, tehnologic, servicii
 Clasa a IX-a 1 x 1 a) Demonstrați inegalitatea 1, x (0, 1) x x b) Demonstrați că, dacă a 1, a,, a n (0, 1) astfel încât a 1 +a + +a n = 1, atunci: a +a 3 + +a n a1 +a 3 + +a n a1 +a + +a n 1 + + + < 1
Clasa a IX-a 1 x 1 a) Demonstrați inegalitatea 1, x (0, 1) x x b) Demonstrați că, dacă a 1, a,, a n (0, 1) astfel încât a 1 +a + +a n = 1, atunci: a +a 3 + +a n a1 +a 3 + +a n a1 +a + +a n 1 + + + < 1
CIRCUITE INTEGRATE MONOLITICE DE MICROUNDE. MMIC Monolithic Microwave Integrated Circuit
 CIRCUITE INTEGRATE MONOLITICE DE MICROUNDE MMIC Monolithic Microwave Integrated Circuit CUPRINS 1. Avantajele si limitarile MMIC 2. Modelarea dispozitivelor active 3. Calculul timpului de viata al MMIC
CIRCUITE INTEGRATE MONOLITICE DE MICROUNDE MMIC Monolithic Microwave Integrated Circuit CUPRINS 1. Avantajele si limitarile MMIC 2. Modelarea dispozitivelor active 3. Calculul timpului de viata al MMIC
3. ECHILIBRE CU TRANSFER DE IONI ŞI MOLECULE 3.1. Echilibre de complexare Aspecte generale
 3. ECHILIBRE CU TRANFER DE IONI ŞI MOLECULE 3.1. Echilibre de complexare 3.1.1. Aspecte generale Dacă într-un echilibru general de forma: Donor Acceptor π particula transferată este ion sau moleculă atunci
3. ECHILIBRE CU TRANFER DE IONI ŞI MOLECULE 3.1. Echilibre de complexare 3.1.1. Aspecte generale Dacă într-un echilibru general de forma: Donor Acceptor π particula transferată este ion sau moleculă atunci
SEMINARUL 3. Cap. II Serii de numere reale. asociat seriei. (3n 5)(3n 2) + 1. (3n 2)(3n+1) (3n 2) (3n + 1) = a
 Capitolul II: Serii de umere reale. Lect. dr. Lucia Maticiuc Facultatea de Hidrotehică, Geodezie şi Igieria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucia MATICIUC SEMINARUL 3. Cap. II Serii
Capitolul II: Serii de umere reale. Lect. dr. Lucia Maticiuc Facultatea de Hidrotehică, Geodezie şi Igieria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucia MATICIUC SEMINARUL 3. Cap. II Serii
Algebra si Geometrie Seminar 9
 Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
Concurs MATE-INFO UBB, 1 aprilie 2017 Proba scrisă la MATEMATICĂ
 UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Concurs MATE-INFO UBB, aprilie 7 Proba scrisă la MATEMATICĂ SUBIECTUL I (3 puncte) ) (5 puncte) Fie matricele A = 3 4 9 8
UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Concurs MATE-INFO UBB, aprilie 7 Proba scrisă la MATEMATICĂ SUBIECTUL I (3 puncte) ) (5 puncte) Fie matricele A = 3 4 9 8
2. Circuite logice 2.4. Decodoare. Multiplexoare. Copyright Paul GASNER
 2. Circuite logice 2.4. Decodoare. Multiplexoare Copyright Paul GASNER Definiţii Un decodor pe n bits are n intrări şi 2 n ieşiri; cele n intrări reprezintă un număr binar care determină în mod unic care
2. Circuite logice 2.4. Decodoare. Multiplexoare Copyright Paul GASNER Definiţii Un decodor pe n bits are n intrări şi 2 n ieşiri; cele n intrări reprezintă un număr binar care determină în mod unic care
Componente şi Circuite Electronice Pasive. Laborator 4. Măsurarea parametrilor mărimilor electrice
 Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
 11.2 CIRCUITE PENTRU FORMAREA IMPULSURILOR Metoda formării impulsurilor se bazează pe obţinerea unei succesiuni periodice de impulsuri, plecând de la semnale periodice de altă formă, de obicei sinusoidale.
11.2 CIRCUITE PENTRU FORMAREA IMPULSURILOR Metoda formării impulsurilor se bazează pe obţinerea unei succesiuni periodice de impulsuri, plecând de la semnale periodice de altă formă, de obicei sinusoidale.
Capitolul 1-INTRODUCERE ÎN STUDIUL CHIMIEI ORGANICE Exerciţii şi probleme
 Capitolul 1- INTRODUCERE ÎN STUDIUL CHIMIEI ORGANICE Exerciţii şi probleme ***************************************************************************** 1.1. Care este prima substanţă organică obţinută
Capitolul 1- INTRODUCERE ÎN STUDIUL CHIMIEI ORGANICE Exerciţii şi probleme ***************************************************************************** 1.1. Care este prima substanţă organică obţinută
ŞTIINŢA ŞI INGINERIA. conf.dr.ing. Liana Balteş curs 7
 ŞTIINŢA ŞI INGINERIA MATERIALELOR conf.dr.ing. Liana Balteş baltes@unitbv.ro curs 7 DIAGRAMA Fe-Fe 3 C Utilizarea oţelului în rândul majorităţii aplicaţiilor a determinat studiul intens al sistemului metalic
ŞTIINŢA ŞI INGINERIA MATERIALELOR conf.dr.ing. Liana Balteş baltes@unitbv.ro curs 7 DIAGRAMA Fe-Fe 3 C Utilizarea oţelului în rândul majorităţii aplicaţiilor a determinat studiul intens al sistemului metalic
VII.2. PROBLEME REZOLVATE
 Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
Conice - Câteva proprietǎţi elementare
 Conice - Câteva proprietǎţi elementare lect.dr. Mihai Chiş Facultatea de Matematicǎ şi Informaticǎ Universitatea de Vest din Timişoara Viitori Olimpici ediţia a 5-a, etapa I, clasa a XII-a 1 Definiţii
Conice - Câteva proprietǎţi elementare lect.dr. Mihai Chiş Facultatea de Matematicǎ şi Informaticǎ Universitatea de Vest din Timişoara Viitori Olimpici ediţia a 5-a, etapa I, clasa a XII-a 1 Definiţii
I X A B e ic rm te e m te is S
 Sisteme termice BAXI Modele: De ce? Deoarece reprezinta o solutie completa care usureaza realizarea instalatiei si ofera garantia utilizarii unor echipamente de top. Adaptabilitate la nevoile clientilor
Sisteme termice BAXI Modele: De ce? Deoarece reprezinta o solutie completa care usureaza realizarea instalatiei si ofera garantia utilizarii unor echipamente de top. Adaptabilitate la nevoile clientilor
Principiul Inductiei Matematice.
 Principiul Inductiei Matematice. Principiul inductiei matematice constituie un mijloc important de demonstratie in matematica a propozitiilor (afirmatiilor) ce depind de argument natural. Metoda inductiei
Principiul Inductiei Matematice. Principiul inductiei matematice constituie un mijloc important de demonstratie in matematica a propozitiilor (afirmatiilor) ce depind de argument natural. Metoda inductiei
CURS XI XII SINTEZĂ. 1 Algebra vectorială a vectorilor liberi
 Lect. dr. Facultatea de Electronică, Telecomunicaţii şi Tehnologia Informaţiei Algebră, Semestrul I, Lector dr. Lucian MATICIUC http://math.etti.tuiasi.ro/maticiuc/ CURS XI XII SINTEZĂ 1 Algebra vectorială
Lect. dr. Facultatea de Electronică, Telecomunicaţii şi Tehnologia Informaţiei Algebră, Semestrul I, Lector dr. Lucian MATICIUC http://math.etti.tuiasi.ro/maticiuc/ CURS XI XII SINTEZĂ 1 Algebra vectorială
Ecuatii exponentiale. Ecuatia ce contine variabila necunoscuta la exponentul puterii se numeste ecuatie exponentiala. a x = b, (1)
 Ecuatii exponentiale Ecuatia ce contine variabila necunoscuta la exponentul puterii se numeste ecuatie exponentiala. Cea mai simpla ecuatie exponentiala este de forma a x = b, () unde a >, a. Afirmatia.
Ecuatii exponentiale Ecuatia ce contine variabila necunoscuta la exponentul puterii se numeste ecuatie exponentiala. Cea mai simpla ecuatie exponentiala este de forma a x = b, () unde a >, a. Afirmatia.
