Θέμα: ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΠΙΘΑΝΟΤΗΤΕΣ (Συνδυασμένη, ολική και δεσμευμένη) ΚΕΦΑΛΑΙΟ 6 KELLER
|
|
|
- Σιληνός Σερπετζόγλου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου, 6 4 ΠΑΤΡΑ Τηλ.: , Φαξ: , mitro@teipat.gr Καθηγητής Ι. Μητρόπουλο ς TECHNOLOGICAL EDUCATIONAL INSTITUTE OF WESTERN GREECE DEPARTMENT: BUSINESS ADMINISTRATION (PATRAS) Address: M. Alexandrou, 6 4 PATRA Greece Tel.:+60 69,Fax: , mitro@teipat.gr Professo r J. Mitropoulos Θέμα: ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΠΙΘΑΝΟΤΗΤΕΣ (Συνδυασμένη, ολική και δεσμευμένη) ΚΕΦΑΛΑΙΟ 6 KELLER Επιμέλεια: ΜΗΤΡΟΠΟΥΛΟΣ Ι. ΒΑΣΙΟΥ Γ. Ημερομηνία: ΜΑΪΟΣ 06
2 ΠΙΘΑΝΟΤΗΤΕΣ Συνδυασμένη, ολική και δεσμευμένη πιθανότητα Τομή ενδεχομένων Τομή δύο ενδεχομένων Α και Β (συμβολίζεται ) είναι το ενδεχόμενο που συμβαίνει όταν τα δύο ενδεχόμενα Α και Β συμβούν ταυτόχρονα. Η πιθανότητα της τομής δύο ενδεχομένων ονομάζεται συνδυασμένη πιθανότητα (join probability). Ένωση ενδεχομένων Ένας άλλος τρόπος συνδυασμού ενδεχομένων είναι η ένωση. Ένωση δύο ενδεχομένων Α ή Β (συμβολίζεται ) είναι το ενδεχόμενο που συμβαίνει όταν συμβεί ένα από τα ενδεχόμενα Α ή Β ή και τα δύο. Ολική πιθανότητα Η ολική πιθανότητα (marginal probability) υπολογίζεται αθροίζοντας μια γραμμή ή μια στήλη του πίνακα ο οποίος περιέχει τις συνδυασμένες πιθανότητες κάποιων ενδεχομένων. (Τέτοιους πίνακες θα δούμε στην επίλυση των ασκήσεων) Δεσμευμένη πιθανότητα Συχνά αυτό που μας ενδιαφέρει είναι πώς σχετίζονται μεταξύ τους δύο ενδεχόμενα και ιδιαίτερα ποιες είναι οι πιθανότητες να συμβεί ένα ενδεχόμενο αν γνωρίζουμε ότι κάποιο άλλο έχει συμβεί. Η πιθανότητα αυτή ονομάζεται δεσμευμένη πιθανότητα (conditional probability) ή αλλιώς πιθανότητα υπό συνθήκη, συμβολίζεται ως P ) και ( διαβάζεται «πιθανότητα του δεδομένου του. Η πιθανότητα ενός ενδεχομένου Α δεδομένου ενός ενδεχομένου Β ) είναι : P ( ). ) Όμοια, η πιθανότητα ενός ενδεχομένου Β δεδομένου του Α είναι : ) P ( ). ) Ανεξάρτητα ενδεχόμενα Ένας από τους στόχους της δεσμευμένης πιθανότητας είναι η εξάρτηση ενός ενδεχομένου από ένα άλλο. Για τον λόγο αυτό εισάγεται η έννοια των ανεξάρτητων ενδεχομένων (independent events). Δύο ενδεχόμενα Α και Β είναι ανεξάρτητα μεταξύ τους αν είναι : P ( ) ) ή P ( ) ) Με απλά λόγια, δύο ενδεχόμενα είναι ανεξάρτητα μεταξύ τους αν η πιθανότητα του ενός δεν επηρεάζεται από την παρουσία του άλλου. Ασκήσεις. Ένα πολυκατάστημα πραγματοποίησε μια έρευνα για τον τρόπο πληρωμής σε σχέση με την τιμή ενός προϊόντος. Για τον λόγο αυτό χρησιμοποίησε ένα δείγμα 00 πελατών και κατέγραψε τα αποτελέσματα στον παρακάτω πίνακα :
3 Πλήθος πελατών Τιμή (σε δολάρια) Μετρητά Πιστωτική κάρτα Χρεωστική κάρτα < > α) Ποιο ποσοστό του συνόλου των αγορών πληρώνεται με χρεωστική κάρτα; β) Να υπολογίσετε την πιθανότητα μια αγορά άνω των 00 δολαρίων να πληρωθεί με πιστωτική κάρτα. γ) Να υπολογίσετε την πιθανότητα μια αγορά να πληρώνεται με πιστωτική ή με χρεωστική κάρτα. α) Από τον πίνακα συμπεραίνουμε ότι το πλήθος των πελατών που πληρώνουν με χρεωστική κάρτα είναι 4+8+4=6. Το αντίστοιχο ποσοστό επί του συνόλου των 00 πελατών είναι 6%. β) Θεωρούμε τα ενδεχόμενα : Α : Η τιμή είναι μικρότερη από 0 δολάρια Α : Η τιμή είναι μεταξύ 0 και 00 δολαρίων Α : Η τιμή είναι μεγαλύτερη από 00 δολάρια Β : Η πληρωμή γίνεται με μετρητά Β : Η πληρωμή γίνεται με πιστωτική κάρτα Β : Η πληρωμή γίνεται με χρεωστική κάρτα Ζητάμε την πιθανότητα του ενδεχομένου δεδομένου του δηλαδή τη δεσμευμένη πιθανότητα P ) η οποία, σύμφωνα με τον αντίστοιχο τύπο, είναι : ( ) P ( ) P ( ) είναι η συνδυασμένη πιθανότητα ) των δύο ενδεχομένων και P ( ) η ολική πιθανότητα του ενδεχομένου. Το πλήθος των πελατών που πλήρωσαν με πιστωτική κάρτα για μια αγορά άνω των 00 δολαρίων είναι και το πλήθος των πελατών που έκαναν αγορές άνω των 00 δολαρίων είναι 9++4=46. Οπότε P ( ) = 46 0, και P ( ) 0, 46. Άρα, τελικά έχουμε : ) 0, P ( ) 0,5 50 % ) 0,46 γ) Οι πελάτες που πλήρωσαν με πιστωτική κάρτα είναι ++=47, ενώ εκείνοι που πλήρωσαν με χρεωστική κάρτα είναι 4+8+4=6. Η πιθανότητα που ζητάμε είναι η ) (πιθανότητα ένωσης ενδεχομένων) όπου τα δύο ενδεχόμενα είναι ανεξάρτητα. Άρα : ) P ( ) ) 0,8 8 % Στον παρακάτω πίνακα φαίνονται οι συνδυασμένες πιθανότητες των άνεργων ανδρών και γυναικών ανά επίπεδο εκπαίδευσης.
4 Επίπεδο εκπαίδευσης Άνδρας Γυναίκα Δεν ολοκλήρωσε τη δευτεροβάθμια 0,08 0,09 Απόφοιτος δευτεροβάθμιας 0,5 0,90 Λίγες σπουδές, χωρίς πτυχίο 0, 0, Πτυχιούχος κολεγίου-πανεπιστημίου 0,09 0,08 α) Αν επιλέξουμε τυχαία έναν άνεργο, ποια είναι η πιθανότητα να μην έχει ολοκληρώσει τη δευτεροβάθμια εκπαίδευση; β) Αν επιλέξουμε τυχαία μια άνεργη γυναίκα, ποια είναι η πιθανότητα να είναι πτυχιούχος; γ) Αν επιλέξουμε τυχαία έναν άνεργο απόφοιτο δευτεροβάθμιας εκπαίδευσης, ποια είναι η πιθανότητα να είναι άνδρας; Θεωρούμε τα ενδεχόμενα : : Ο άνεργος δεν ολοκλήρωσε τη δευτεροβάθμια εκπαίδευση : Ο άνεργος είναι απόφοιτος δευτεροβάθμιας εκπαίδευσης : Ο άνεργος έχει λίγες σπουδές, χωρίς πτυχίο 4 : Ο άνεργος είναι πτυχιούχος κολεγίου-πανεπιστημίου : Ο άνεργος είναι άνδρας : Ο άνεργος είναι γυναίκα α) Η πιθανότητα που ζητάμε είναι η ολική πιθανότητα της ης γραμμής του πίνακα, δηλαδή το άθροισμα των συνδυασμένων πιθανοτήτων της ης γραμμής. P ( ) 0,08 0,09 0,9 9, % β) Η πιθανότητα που ζητάμε είναι η δεσμευμένη πιθανότητα 4) P ( 4 ) 4) είναι η συνδυασμένη πιθανότητα ) των δύο ενδεχομένων η οποία, σύμφωνα με τον παραπάνω πίνακα είναι 0,08 και P ( ) είναι η ολική πιθανότητα του ενδεχομένου η οποία ισούται με το άθροισμα των πιθανοτήτων της ης στήλης δηλαδή 0,09+0,90+0,+0,08=0,54. Άρα : 4) 0,08 P ( 4 ) 0, 0 % ) 0,54 γ) Η πιθανότητα που ζητάμε είναι η δεσμευμένη πιθανότητα ) P ( ) ) είναι η συνδυασμένη πιθανότητα ) των δύο ενδεχομένων η οποία, σύμφωνα με τον παραπάνω πίνακα είναι 0,5 και P ( ) 0,5 0,90 0,4 είναι η ολική πιθανότητα του ενδεχομένου που ι- σούται με το άθροισμα των πιθανοτήτων της ης γραμμής. ) 0,5 Άρα : P ( ) 0,446 44, 6 % ) 0,4. Για το σκοπό μιας ιατρικής έρευνας επιλέχθηκε τυχαία ένα δείγμα 50 ανδρών ηλικίας ετών και καταγράφηκε το πλήθος αυτών που είναι καπνιστές και αυτών 4
5 που δεν είναι καπνιστές καθώς και πόσοι από αυτούς έχουν προσβληθεί από καρκίνο του πνεύμονα και πόσοι όχι. Τα αποτελέσματα φαίνονται στον παρακάτω πίνακα. Καπνιστής Μη καπνιστής Καρκινοπαθής 5 6 Μη καρκινοπαθής 99 Αν επιλέξουμε τυχαία έναν άνδρα, ποιες είναι οι πιθανότητες των παρακάτω ενδεχομένων : α) Να είναι καπνιστής. β) Να μην είναι καρκινοπαθής. γ) Να είναι καρκινοπαθής δεδομένου ότι είναι καπνιστής. δ) Να είναι καρκινοπαθής δεδομένου ότι δεν είναι καπνιστής. Α : Ο άνδρας είναι καρκινοπαθής Α : Ο άνδρας δεν είναι καρκινοπαθής Β : Ο άνδρας είναι καπνιστής Β : Ο άνδρας δεν είναι καπνιστής α) Η πιθανότητα που ζητάμε είναι η ολική πιθανότητα του ενδεχομένου Β. Το πλήθος των καπνιστών είναι 5+=48 οπότε η πιθανότητα ισούται με : 48 P ( ) 0, % 50 β) Η πιθανότητα που ζητάμε είναι η ολική πιθανότητα του ενδεχομένου Α. Το πλήθος των μη καρκινοπαθών είναι +99= οπότε η πιθανότητα ισούται με : P ( ) 0,88 88% 50 ) γ) Ζητάμε τη δεσμευμένη πιθανότητα P ( ) ) 5 ) 0, είναι η συνδυασμένη πιθανότητα των δύο ενδεχομένων 50 και P ( ) 0, είναι η ολική πιθανότητα που βρήκαμε στο (α) σκέλος. Άρα : ) 0, P ( ) 0,5,5 % ) 0, ) δ) Ζητάμε την δεσμευμένη πιθανότητα P ( ) ) 6 ) 0, 04 είναι η συνδυασμένη πιθανότητα των δύο ενδεχομένων και P ( ) 0, 4 είναι η ολική πιθανότητα του ενδεχομένου Α. Άρα : 50 ) 0,04 P ( ) 0,857 8,57 % ) 0,4 4. Μια έρευνα κατέγραψε τον παρακάτω πίνακα συνδυασμένων πιθανοτήτων για τους λόγους και τις ηλικίες απόλυσης εργαζομένων. 5
6 Λόγος απόλυσης Ηλικία Κλείσιμο-μετακίνηση μονάδας 0,05 0,4 0,075 0,07 Μείωση παραγωγής 0,008 0,5 0,07 0,04 Κατάργηση θέσης εργασίας 0,005 0,9 0,054 0,008 α) Ποια είναι η πιθανότητα κάποιος 5-54 ετών να απολυθεί λόγω μείωσης παραγωγής; β) Ποια είναι η πιθανότητα να απολυθεί κάποιος άνω των 65 ετών; γ) Ποια είναι η πιθανότητα να απολυθεί κάποιος άνω των 65 ετών επειδή έκλεισε ή μετακινήθηκε η μονάδα όπου εργαζόταν; Α : Η απόλυση οφείλεται σε κλείσιμο-μετακίνηση μονάδας Α : Η απόλυση οφείλεται σε μείωση παραγωγής Α : Η απόλυση οφείλεται σε κατάργηση θέσης εργασίας Β : Ο απολυμένος έχει ηλικία μεταξύ 0 και 4 ετών Β : Ο απολυμένος έχει ηλικία μεταξύ 5 και 54 ετών Β : Ο απολυμένος έχει ηλικία μεταξύ 55 και 64 ετών Β 4 : Ο απολυμένος έχει ηλικία από 65 ετών και άνω α) Ζητάμε τη δεσμευμένη πιθανότητα P ( ) ) ) ) 0, 5 είναι η συνδυασμένη πιθανότητα των δύο ενδεχομένων όπως φαίνεται στον παραπάνω πίνακα και P ( ) 0,4 0,5 0,9 0,768 είναι η ολική πιθανότητα του ενδεχομένου Β που ισούται με το άθροισμα των συνδυασμένων πιθανοτήτων της ης στήλης του πίνακα. Άρα : ) 0,5 P ( ) 0,9 9, % ) 0,768 β) Ζητάμε την ολική πιθανότητα του ενδεχομένου Β 4 η οποία ισούται με το άθροισμα των συνδυασμένων πιθανοτήτων της 4 ης στήλης του πίνακα, δηλαδή : P ( 4) 0,07 0,04 0,008 0,09,9 % 4 ) γ) Ζητάμε τη δεσμευμένη πιθανότητα P ( 4) ) 4 ) 0, 07 είναι η συνδυασμένη πιθανότητα των δύο ενδεχομένων. Σύμφωνα με τον παραπάνω πίνακα και P ( 4) είναι η ολική πιθανότητα που βρήκαμε στο (β) σκέλος. Άρα : 4 ) 0,07 P ( 4) 0,46 4,6 % ) 0, Μια εταιρία κινητής τηλεφωνίας μελετά τους λογαριασμούς των πελατών της ως προς δύο χαρακτηριστικά. Αν ένας λογαριασμός είναι νέος (λιγότερο από μήνες) 4 6
7 και αν ένας λογαριασμός παρουσιάζει καθυστερήσεις στην εξόφλησή του. Με βάση τα δεδομένα της εταιρίας σχηματίστηκε ο εξής πίνακας συνδυασμένων πιθανοτήτων. Λογαριασμός Παρουσιάζει καθυστερήσεις ΝΑΙ ΟΧΙ Νέος 0,08 0, Παλιός 0,50 0,9 α) Αν ο λογαριασμός παρουσιάζει καθυστέρηση, ποια είναι η πιθανότητα να πρόκειται για νέο λογαριασμό; β) Αν ο λογαριασμός είναι νέος, ποια είναι η πιθανότητα να παρουσιάζει καθυστέρηση; Α : Ο λογαριασμός είναι νέος Α : Ο λογαριασμός είναι παλιός Β : Ο λογαριασμός παρουσιάζει καθυστερήσεις Β : Ο λογαριασμός δεν παρουσιάζει καθυστερήσεις ) α) Ζητάμε τη δεσμευμένη πιθανότητα P ( ) ) ) 0, 08 είναι η συνδυασμένη πιθανότητα των δύο ενδεχομένων, σύμφωνα με τον παραπάνω πίνακα και P ( ) 0,08 0,50 0, 58 είναι η ολική πιθανότητα του ενδεχομένου Β η οποία ισούται με το άθροισμα των συνδυασμένων πιθανοτήτων της ης στήλης του πίνακα. Άρα : ) 0,08 P ( ) 0,79,79 % ) 0,58 ) β) Ζητάμε τη δεσμευμένη πιθανότητα P ( ) ) ) 0, 08 είναι η συνδυασμένη πιθανότητα των δύο ενδεχομένων, σύμφωνα με τον παραπάνω πίνακα και P ( ) 0,08 0, 0, είναι η ολική πιθανότητα του ενδεχομένου Α η οποία ισούται με το άθροισμα των συνδυασμένων πιθανοτήτων της ης γραμμής του πίνακα. Άρα : ) 0,08 P ( ) 0,809 8,09 % ) 0, 6. Το πιστοληπτικό προφίλ είναι μια στατιστική τεχνική που χρησιμοποιούν οι τράπεζες και άλλοι οικονομικοί οργανισμοί για την έγκριση δανείων προς τους πελάτες τους. Από τα στοιχεία που διατηρεί μια τράπεζα για 00 πελάτες προκύπτει ο παρακάτω πίνακας όπου φαίνεται το πλήθος των πελατών που αποπλήρωσαν ή δεν αποπλήρωσαν το δάνειο σε συνδυασμό με το πιστοληπτικό τους προφίλ : 7
8 ΠΙΣΤΟΛΗΠΤΙΚΟ ΔΑΝΕΙΟ ΠΡΟΦΙΛ < ΑΠΟΠΛΗΡΩΘΗΚΕ ΚΑΝΟΝΙΚΑ 9 64 ΔΕΝ ΑΠΟΠΛΗΡΩΘΗΚΕ 4 i) Ποιο είναι το συνολικό ποσοστό των δανείων που αποπληρώθηκε κανονικά; ii) Ποια η πιθανότητα πελάτες με πιστοληπτικό προφίλ μικρότερο του 400 να αποπλήρωσαν κανονικά το δάνειό τους; iii) Ποια η πιθανότητα πελάτες με πιστοληπτικό προφίλ 400 και άνω να αποπλήρωσαν κανονικά το δάνειό τους; iv) Ποια η πιθανότητα ένας πελάτης που δεν αποπλήρωσε το δάνειό του να έχει πιστοληπτικό προφίλ 400 και άνω; Α : Το δάνειο αποπληρώθηκε κανονικά Α : Το δάνειο δεν αποπληρώθηκε Β : Πιστοληπτικό προφίλ <400 Β : Πιστοληπτικό προφίλ 400+ i) Οι πελάτες που αποπλήρωσαν κανονικά το δάνειό τους (ανεξάρτητα από το πιστοληπτικό τους προφίλ) είναι 9+64=8. Οπότε, το αντίστοιχο ποσοστό είναι 8%. ) ii) Ζητάμε τη δεσμευμένη πιθανότητα P ( ) ) 9 ) 0, 9 είναι η συνδυασμένη πιθανότητα των δύο ενδεχομένων, 00 9 σύμφωνα με τον παραπάνω πίνακα και P ( ) 0, είναι η ολική πιθανότητα του ενδεχομένου Β η οποία ισούται με το άθροισμα των συνδυασμένων πιθανοτήτων της ης στήλης του πίνακα. Άρα : ) 0,9 P ( ) 0, ,75 % ) 0, ) iii) Ζητάμε τη δεσμευμένη πιθανότητα P ( ) ) 64 ) 0, 64 είναι η συνδυασμένη πιθανότητα των δύο ενδεχομένων, σύμφωνα με τον παραπάνω πίνακα και P ( ) 0, 68 είναι η ολική πιθανότητα του ενδεχομένου Β η οποία ισούται με το άθροισμα των συνδυασμένων πιθανοτήτων της ης στήλης του πίνακα. Άρα : ) 0,64 P ( ) 0,94 94, % ) 0,68 ) iv) Ζητάμε τη δεσμευμένη πιθανότητα P ( ) ) 8
9 4 ) 0, 04 είναι η συνδυασμένη πιθανότητα των δύο ενδεχομένων, 00 4 σύμφωνα με τον παραπάνω πίνακα και P ( ) 0, 7 είναι η ολική πιθανότητα του ενδεχομένου A η οποία ισούται με το άθροισμα των συνδυασμένων πιθανοτήτων της ης γραμμής του πίνακα. Άρα : ) 0,04 P ( ) 0,5,5 % ) 0,7 7. Ο τρόπος διδασκαλίας της Στατιστικής στα Πανεπιστήμια αλλάζει. Ιστορικά δινόταν έμφαση στους χειρόγραφους υπολογισμούς, αλλά βαθμιαία οι αριθμητικοί υπολογισμοί τείνουν να εκτελούνται από υπολογιστή και κατάλληλο λογισμικό. Μια έρευνα κατέγραψε αν χρησιμοποιείται υπολογιστής και αν οι κύριες σπουδές του εισηγητή είναι στα Μαθηματικά και τη Στατιστική ή σε κάποιον άλλο κλάδο. Τα αποτελέσματα της έρευνας φαίνονται στον παρακάτω πίνακα συνδυασμένων πιθανοτήτων. Μέθοδος υπολογισμών Σπουδές Εισηγητή Χειρόγραφα Υπολογιστής Μαθηματικά/Στατιστική 0, 0,6 Άλλο 0, 0,0 α) Ποια είναι η πιθανότητα ένας εισηγητής να χρησιμοποιεί υπολογιστή; β) Ποια είναι η πιθανότητα ένας εισηγητής με σπουδές στα Μαθηματικά/Στατιστική να προτιμά χειρόγραφους υπολογισμούς; Α : Σπουδές σε Μαθηματικά/Στατιστική Α : Σπουδές σε άλλο αντικείμενο Β : Χειρόγραφοι υπολογισμοί Β : Υπολογισμοί με υπολογιστή α) Ζητάμε την ολική πιθανότητα του ενδεχομένου Β : P ( ) 0,6 0,0 0,66 66% β) Ζητάμε τη δεσμευμένη πιθανότητα ) 0, P ( ) 0,898 9% ) 0, 0,6 9
Θέμα: Ασκήσεις για εύρεση ολικής, συνδυασμένης και δεσμευμένης πιθανότητας. Βιβλίο Keller Κεφάλαιο 6
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου, 6 ΠΑΤΡΑ Τηλ.: 60 6905, Φαξ: 60 968, email: mitro@teipat.gr Καθ η γη τ ής Ι. Μ ητ ρ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου, 6 ΠΑΤΡΑ Τηλ.: 60 6905, Φαξ: 60 968, email: mitro@teipat.gr Καθ η γη τ ής Ι. Μ ητ ρ
Θέμα: Ενδεικτικό Θέμα εξετάσεων: Μέτρα θέσης Παλινδρόμηση
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 263 34 ΠΑΤΡΑ Τηλ.: 2610 369051, Φαξ: 2610 396184, email: mitro@teipat.gr TECHNOLOGICAL
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 263 34 ΠΑΤΡΑ Τηλ.: 2610 369051, Φαξ: 2610 396184, email: mitro@teipat.gr TECHNOLOGICAL
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ TECHNOLOGICAL EDUCATIONAL INSTITUTE OF WESTERN GREECE
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου, 63 34 ΠΑΤΡΑ Τηλ.: 60 36905, Φαξ: 60 39684, email: mitro@teipat.gr Καθηγητής Ι. Μητρόπουλος
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου, 63 34 ΠΑΤΡΑ Τηλ.: 60 36905, Φαξ: 60 39684, email: mitro@teipat.gr Καθηγητής Ι. Μητρόπουλος
Επιµέλεια: Χρυσάνθη Παπαθανασοπούλου
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 263 34 ΠΑΤΡΑ Τηλ.: 2610 369051, Φαξ: 2610 396184, email: mitro@teipat.gr Καθηγητής
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 263 34 ΠΑΤΡΑ Τηλ.: 2610 369051, Φαξ: 2610 396184, email: mitro@teipat.gr Καθηγητής
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ TECHNOLOGICAL EDUCATIONAL INSTITUTE OF WESTERN GREECE
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 263 34 ΠΑΤΡΑ Τηλ.: 2610 369051, Φαξ: 2610 396184, email: mitro@teipat.gr Καθηγητής
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 263 34 ΠΑΤΡΑ Τηλ.: 2610 369051, Φαξ: 2610 396184, email: mitro@teipat.gr Καθηγητής
Θέμα: ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΣΤΗΜΑΤΑ ΕΜΠΙΣΤΟΣΥΝΗΣ ΚΕΦΑΛΑΙΑ 10,12 KELLER
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 63 34 ΠΑΤΡΑ Τηλ.: 610 369051, Φαξ: 610 396184, email: mitro@teipat.gr Καθ η γη τ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 63 34 ΠΑΤΡΑ Τηλ.: 610 369051, Φαξ: 610 396184, email: mitro@teipat.gr Καθ η γη τ
Θέμα: ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΙΣ ΔΙΑΚΡΙΤΕΣ ΚΑΤΑΝΟΜΕΣ ΠΙΘΑΝΟΤΗΤΩΝ ΚΕΦΑΛΑΙΟ 7 ΒΙΒΛΙΟ KELLER
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 263 34 ΠΑΤΡΑ Τηλ.: 2610 369051, Φαξ: 2610 396184, email: mitro@teipat.gr Καθηγητής
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 263 34 ΠΑΤΡΑ Τηλ.: 2610 369051, Φαξ: 2610 396184, email: mitro@teipat.gr Καθηγητής
Θέμα: ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΣΤΗ ΛΗΨΗ ΑΠΟΦΑΣΕΩΝ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 263 34 ΠΑΤΡΑ Τηλ.: 2610 369051, Φαξ: 2610 396184, email: mitro@teipat.gr Καθ η γη
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 263 34 ΠΑΤΡΑ Τηλ.: 2610 369051, Φαξ: 2610 396184, email: mitro@teipat.gr Καθ η γη
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ TECHNOLOGICAL EDUCATIONAL INSTITUTE OF WESTERN GREECE
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου, 263 34 ΠΑΤΡΑ Τηλ.: 260 36905, Φαξ: 260 39684, email: mitro@teipat.gr Καθηγητής Ι. Μητρόπουλος
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου, 263 34 ΠΑΤΡΑ Τηλ.: 260 36905, Φαξ: 260 39684, email: mitro@teipat.gr Καθηγητής Ι. Μητρόπουλος
Θέμα: ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΔΙΑΚΡΙΤΕΣ ΚΑΤΑΝΟΜΕΣ ΠΙΘΑΝΟΤΗΤΩΝ ΚΕΦΑΛΑΙΟ 7 KELLER
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 263 34 ΠΑΤΡΑ Τηλ.: 2610 369051, Φαξ: 2610 396184, email: mitro@teipat.gr TECHNOLOGICAL
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 263 34 ΠΑΤΡΑ Τηλ.: 2610 369051, Φαξ: 2610 396184, email: mitro@teipat.gr TECHNOLOGICAL
Τμήμα Λογιστικής και Χρηματοοικονομικής. Θεωρία Πιθανοτήτων. Δρ. Αγγελίδης Π. Βασίλειος
 Τμήμα Λογιστικής και Χρηματοοικονομικής 1 Θεωρία Πιθανοτήτων Δρ. Αγγελίδης Π. Βασίλειος 2 Περιεχόμενα Έννοια πιθανότητας Ορισμοί πιθανότητας Τρόπος υπολογισμού Πράξεις πιθανοτήτων Χρησιμότητα τους 3 Πείραμα
Τμήμα Λογιστικής και Χρηματοοικονομικής 1 Θεωρία Πιθανοτήτων Δρ. Αγγελίδης Π. Βασίλειος 2 Περιεχόμενα Έννοια πιθανότητας Ορισμοί πιθανότητας Τρόπος υπολογισμού Πράξεις πιθανοτήτων Χρησιμότητα τους 3 Πείραμα
Θέμα: ΛΗΨΗ ΑΠΟΦΑΣΕΩΝ - ΑΣΚΗΣΕΙΣ ΣΤΑ ΠΟΛΥΠΛΟΚΑ ΠΡΟΒΛΗΜΑΤΑ ΑΠΟΦΑΣΕΩΝ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 263 34 ΠΑΤΡΑ Τηλ.: 2610 369051, Φαξ: 2610 396184, TECHNOLOGICAL EDUCATIONAL INSTITUTE
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 263 34 ΠΑΤΡΑ Τηλ.: 2610 369051, Φαξ: 2610 396184, TECHNOLOGICAL EDUCATIONAL INSTITUTE
Θέμα: ΛΗΨΗ ΑΠΟΦΑΣΕΩΝ - ΑΣΚΗΣΕΙΣ ΣΤΑ ΠΟΛΥΠΛΟΚΑ ΠΡΟΒΛΗΜΑΤΑ ΑΠΟΦΑΣΕΩΝ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 263 34 ΠΑΤΡΑ Τηλ.: 2610 369051, Φαξ: 2610 396184, TECHNOLOGICAL EDUCATIONAL INSTITUTE
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 263 34 ΠΑΤΡΑ Τηλ.: 2610 369051, Φαξ: 2610 396184, TECHNOLOGICAL EDUCATIONAL INSTITUTE
Περιπτώσεις που η στατιστική συνάρτηση ελέγχου είναι η Ζ: 1. Η σ είναι γνωστή και ο πληθυσμός κανονικός.
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 263 34 ΠΑΤΡΑ Τηλ.: 2610 369051, Φαξ: 2610 396184, email: mitro@teipat.gr Καθ η γη
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ (Πάτρας) Διεύθυνση: Μεγάλου Αλεξάνδρου 1, 263 34 ΠΑΤΡΑ Τηλ.: 2610 369051, Φαξ: 2610 396184, email: mitro@teipat.gr Καθ η γη
Πιθανότητες. Έννοια πιθανότητας Ορισμοί πιθανότητας Τρόπος υπολογισμού Πράξεις πιθανοτήτων Χρησιμότητα τους
 Πιθανότητες Έννοια πιθανότητας Ορισμοί πιθανότητας Τρόπος υπολογισμού Πράξεις πιθανοτήτων Χρησιμότητα τους «Πείραμα» Tύχης Οτιδήποτε συμβαίνει και δεν γνωρίζουμε από πριν το ακριβές αποτέλεσμά του. Απασχόλησαν
Πιθανότητες Έννοια πιθανότητας Ορισμοί πιθανότητας Τρόπος υπολογισμού Πράξεις πιθανοτήτων Χρησιμότητα τους «Πείραμα» Tύχης Οτιδήποτε συμβαίνει και δεν γνωρίζουμε από πριν το ακριβές αποτέλεσμά του. Απασχόλησαν
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ. Κεφάλαιο 6. Πιθανότητες
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΝΕΣΤΟΡΙΟΥ
 ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΝΕΣΤΟΡΙΟΥ ΕΠΙΜΕΛΕΙΑ : ΓΕΡΓΙΟΣ Ε. ΚΑΡΑΦΕΡΗΣ ΠΕ03 ΜΑΘΗΜΑΤΙΚΟΣ [] ΠΙΘΑΝΟΤΗΤΕΣ ΘΕΡΙΑ: Πείραμα Τύχης Κάθε πείραμα κατά στο οποίο η γνώση των συνθηκών κάτω από τις οποίες εκτελείται καθορίζει πλήρως
ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΝΕΣΤΟΡΙΟΥ ΕΠΙΜΕΛΕΙΑ : ΓΕΡΓΙΟΣ Ε. ΚΑΡΑΦΕΡΗΣ ΠΕ03 ΜΑΘΗΜΑΤΙΚΟΣ [] ΠΙΘΑΝΟΤΗΤΕΣ ΘΕΡΙΑ: Πείραμα Τύχης Κάθε πείραμα κατά στο οποίο η γνώση των συνθηκών κάτω από τις οποίες εκτελείται καθορίζει πλήρως
Δεσμευμένη (ή υπο-συνθήκη) Πιθανότητα (Conditional Probability)
 Δεσμευμένη (ή υπο-συνθήκη) Πιθανότητα (Condtonal robablty) Συχνά μας ενδιαφέρει η συσχέτισή 2 ενδεχομένων Α και Β, δηλ. να δούμε το κατά πόσο η γνώση του ενός από τα δύο (π.χ. Β) επηρεάζει τη πιθανότητα
Δεσμευμένη (ή υπο-συνθήκη) Πιθανότητα (Condtonal robablty) Συχνά μας ενδιαφέρει η συσχέτισή 2 ενδεχομένων Α και Β, δηλ. να δούμε το κατά πόσο η γνώση του ενός από τα δύο (π.χ. Β) επηρεάζει τη πιθανότητα
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ. Κεφάλαιο 5 Συλλογή Δεδομένων & Δειγματοληψία
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
Υ: Νόσος. Χ: Παράγοντας Κινδύνου 1 (Ασθενής) 2 (Υγιής) Σύνολο. 1 (Παρόν) n 11 n 12 n 1. 2 (Απών) n 21 n 22 n 2. Σύνολο n.1 n.2 n..
 Μέτρα Κινδύνου για Δίτιμα Κατηγορικά Δεδομένα Σε αυτή την ενότητα θα ορίσουμε δείκτες μέτρησης του κινδύνου εμφάνισης μίας νόσου όταν έχουμε δίτιμες κατηγορικές μεταβλητές. Στην πιο απλή περίπτωση μας
Μέτρα Κινδύνου για Δίτιμα Κατηγορικά Δεδομένα Σε αυτή την ενότητα θα ορίσουμε δείκτες μέτρησης του κινδύνου εμφάνισης μίας νόσου όταν έχουμε δίτιμες κατηγορικές μεταβλητές. Στην πιο απλή περίπτωση μας
Μέρος IV. Πολυδιάστατες τυχαίες μεταβλητές. Πιθανότητες & Στατιστική 2017 Τμήμα Μηχανικών Η/Υ & Πληροφορικής, Παν. Ιωαννίνων Δ15 ( 1 )
 Μέρος IV Πολυδιάστατες τυχαίες μεταβλητές Πιθανότητες & Στατιστική 07 Τμήμα Μηχανικών Η/Υ & Πληροφορικής Παν. Ιωαννίνων Δ5 ( ) Πολυδιάστατες μεταβλητές Πολλά ποσοτικά χαρακτηριστικά που σχετίζονται με
Μέρος IV Πολυδιάστατες τυχαίες μεταβλητές Πιθανότητες & Στατιστική 07 Τμήμα Μηχανικών Η/Υ & Πληροφορικής Παν. Ιωαννίνων Δ5 ( ) Πολυδιάστατες μεταβλητές Πολλά ποσοτικά χαρακτηριστικά που σχετίζονται με
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
Πινάκες συνάφειας. Βαρύτητα συμπτωμάτων. Φύλο Χαμηλή Υψηλή. Άνδρες. Γυναίκες
 Πινάκες συνάφειας εξερεύνηση σχέσεων μεταξύ τυχαίων μεταβλητών. Είναι λογικό λοιπόν, στην ανάλυση των κατηγορικών δεδομένων να μας ενδιαφέρει η σχέση μεταξύ δύο ή περισσότερων κατηγορικών μεταβλητών. Έστω
Πινάκες συνάφειας εξερεύνηση σχέσεων μεταξύ τυχαίων μεταβλητών. Είναι λογικό λοιπόν, στην ανάλυση των κατηγορικών δεδομένων να μας ενδιαφέρει η σχέση μεταξύ δύο ή περισσότερων κατηγορικών μεταβλητών. Έστω
ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ Ενότητα # 8: Πιθανότητες ΙΙ Εβελίνα Κοσσιέρη Τμήμα Λογιστικής και Χρηματοοικονομικής ΑΔΕΙΕΣ ΧΡΗΣΗΣ Το
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ Ενότητα # 8: Πιθανότητες ΙΙ Εβελίνα Κοσσιέρη Τμήμα Λογιστικής και Χρηματοοικονομικής ΑΔΕΙΕΣ ΧΡΗΣΗΣ Το
Διαστήματα Εμπιστοσύνης
 Διαστήματα Εμπιστοσύνης 00 % Διαστήματα Εμπιστοσύνης για τη μέση τιμή ενός πληθυσμού Κατανομή Διασπορά Μέγεθος δείγματος Διάστημα Εμπιστοσύνης Κανονική Γνωστή Οποιοδήποτε Οποιαδήποτε Γνωστή Μεγάλο 30 Z
Διαστήματα Εμπιστοσύνης 00 % Διαστήματα Εμπιστοσύνης για τη μέση τιμή ενός πληθυσμού Κατανομή Διασπορά Μέγεθος δείγματος Διάστημα Εμπιστοσύνης Κανονική Γνωστή Οποιοδήποτε Οποιαδήποτε Γνωστή Μεγάλο 30 Z
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ. Κεφάλαιο 7. Τυχαίες Μεταβλητές και Διακριτές Κατανομές Πιθανοτήτων
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
ΠΙΘΑΝΟΤΗΤΕΣ Δειγματικός Χώρος. Ενδεχόμενα {,,..., }.
 ΠΙΘΑΝΟΤΗΤΕΣ Δειγματικός Χώρος Το σύνολο των δυνατών αποτελεσμάτων λέγεται δειγματικός χώρος (sample space) και συμβολίζεται συνήθως με το γράμμα Αν δηλαδή ω,,, ω2 ωκ είναι τα δυνατά αποτελέσματα ενός πειράματος
ΠΙΘΑΝΟΤΗΤΕΣ Δειγματικός Χώρος Το σύνολο των δυνατών αποτελεσμάτων λέγεται δειγματικός χώρος (sample space) και συμβολίζεται συνήθως με το γράμμα Αν δηλαδή ω,,, ω2 ωκ είναι τα δυνατά αποτελέσματα ενός πειράματος
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ Ευθύγραμμη Ομαλή Κίνηση Επιμέλεια: ΑΓΚΑΝΑΚΗΣ.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός https://physicscorses.wordpress.com/ Βασικές Έννοιες Ένα σώμα καθώς κινείται περνάει από διάφορα σημεία.
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ Ευθύγραμμη Ομαλή Κίνηση Επιμέλεια: ΑΓΚΑΝΑΚΗΣ.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός https://physicscorses.wordpress.com/ Βασικές Έννοιες Ένα σώμα καθώς κινείται περνάει από διάφορα σημεία.
. Τι πρακτική αξία έχουν αυτές οι πιθανότητες; (5 Μονάδες)
 Εργαστήριο Μαθηματικών & Στατιστικής Α ΣΕΙΡΑ ΘΕΜΑΤΩΝ η Πρόοδος στο Μάθημα Στατιστική //7 ο Θέμα α) Περιγράψτε τη σχέση Θεωρίας Πιθανοτήτων και Στατιστικής. β) Αν Α, Β ενδεχόμενα του δειγματικού χώρου Ω
Εργαστήριο Μαθηματικών & Στατιστικής Α ΣΕΙΡΑ ΘΕΜΑΤΩΝ η Πρόοδος στο Μάθημα Στατιστική //7 ο Θέμα α) Περιγράψτε τη σχέση Θεωρίας Πιθανοτήτων και Στατιστικής. β) Αν Α, Β ενδεχόμενα του δειγματικού χώρου Ω
3.1 ΔΕΙΓΜΑΤΙΚΟΙ ΧΩΡΟΙ ΕΝΔΕΧΟΜΕΝΑ
 ΚΕΦΑΛΑΙΟ : ΠΙΘΑΝΟΤΗΤΕΣ. ΔΕΙΓΜΑΤΙΚΟΙ ΧΩΡΟΙ ΕΝΔΕΧΟΜΕΝΑ Αιτιοκρατικό πείραμα ονομάζουμε κάθε πείραμα για το οποίο, όταν ξέρουμε τις συνθήκες κάτω από τις οποίες πραγματοποιείται, μπορούμε να προβλέψουμε με
ΚΕΦΑΛΑΙΟ : ΠΙΘΑΝΟΤΗΤΕΣ. ΔΕΙΓΜΑΤΙΚΟΙ ΧΩΡΟΙ ΕΝΔΕΧΟΜΕΝΑ Αιτιοκρατικό πείραμα ονομάζουμε κάθε πείραμα για το οποίο, όταν ξέρουμε τις συνθήκες κάτω από τις οποίες πραγματοποιείται, μπορούμε να προβλέψουμε με
Βασικές Έννοιες των Οικονομικών της Εργασίας οικονομικά της εργασίας αγορά αγορά εργασίας μισθός
 Βασικές Έννοιες των Οικονομικών της Εργασίας - Τα οικονομικά της εργασίας μελετούν τον τρόπο με τον οποίο λειτουργεί η αγορά εργασίας. - Ορισμός: Η αγορά ενός αγαθού είναι η διαδικασία (θεσμικό πλαίσιο)
Βασικές Έννοιες των Οικονομικών της Εργασίας - Τα οικονομικά της εργασίας μελετούν τον τρόπο με τον οποίο λειτουργεί η αγορά εργασίας. - Ορισμός: Η αγορά ενός αγαθού είναι η διαδικασία (θεσμικό πλαίσιο)
ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ ΣΤΑΤΙΣΤΙΚΗΣ ΠΑΝΟΣ ΣΑΡΑΚΗΝΟΣ
 ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ ΣΤΑΤΙΣΤΙΚΗΣ ΠΑΝΟΣ ΣΑΡΑΚΗΝΟΣ Άσκηση 1 Οι βαθμοί 5 φοιτητών που πέρασαν το μάθημα της Στατιστικής ήταν: 6 5 7 5 9 5 6 6 8 10 8 5 6 7 5 6 5 7 8 9 5 6 7 5 8 i. Να κάνετε πίνακα κατανομής
ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ ΣΤΑΤΙΣΤΙΚΗΣ ΠΑΝΟΣ ΣΑΡΑΚΗΝΟΣ Άσκηση 1 Οι βαθμοί 5 φοιτητών που πέρασαν το μάθημα της Στατιστικής ήταν: 6 5 7 5 9 5 6 6 8 10 8 5 6 7 5 6 5 7 8 9 5 6 7 5 8 i. Να κάνετε πίνακα κατανομής
Ερευνητική εργασία ( Project) Α Λυκείου. Καταγραφή επαγγελμάτων των γονέων των μαθητών της Α Λυκείου και κατανομή τους στους τρεις τομείς παραγωγής
 1 ο ΓΕΛ ΦΙΛΙΠΠΙΑΔΑΣ Ερευνητική εργασία ( Project) Α Λυκείου Θέμα: Καταγραφή επαγγελμάτων των γονέων των μαθητών της Α Λυκείου και κατανομή τους στους τρεις τομείς παραγωγής Α' Τετράμηνο Σεπτέμβρης 2013
1 ο ΓΕΛ ΦΙΛΙΠΠΙΑΔΑΣ Ερευνητική εργασία ( Project) Α Λυκείου Θέμα: Καταγραφή επαγγελμάτων των γονέων των μαθητών της Α Λυκείου και κατανομή τους στους τρεις τομείς παραγωγής Α' Τετράμηνο Σεπτέμβρης 2013
1.1 ΔΕΙΓΜΑΤΙΚΟΙ ΧΩΡΟΙ ΕΝΔΕΧΟΜΕΝΑ
 ΚΕΦΑΛΑΙΟ : ΠΙΘΑΝΟΤΗΤΕΣ. ΔΕΙΓΜΑΤΙΚΟΙ ΧΩΡΟΙ ΕΝΔΕΧΟΜΕΝΑ Αιτιοκρατικό πείραμα ονομάζουμε κάθε πείραμα για το οποίο, όταν ξέρουμε τις συνθήκες κάτω από τις οποίες πραγματοποιείται, μπορούμε να προβλέψουμε με
ΚΕΦΑΛΑΙΟ : ΠΙΘΑΝΟΤΗΤΕΣ. ΔΕΙΓΜΑΤΙΚΟΙ ΧΩΡΟΙ ΕΝΔΕΧΟΜΕΝΑ Αιτιοκρατικό πείραμα ονομάζουμε κάθε πείραμα για το οποίο, όταν ξέρουμε τις συνθήκες κάτω από τις οποίες πραγματοποιείται, μπορούμε να προβλέψουμε με
ΠΡΟΓΡΑΜΜΑΤΙΣΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΚΥΡΙΑΚΗ 19 ΟΚΤΩΒΡΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ
 ΠΡΟΓΡΑΜΜΑΤΙΣΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΚΥΡΙΑΚΗ 19 ΟΚΤΩΒΡΙΟΥ 2014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ Όνομα/Επίθετο: Ζήτημα 1ο Να γράψετε στη γλώσσα των συνόλων και λεκτικά ποιο ενδεχόμενο παριστάνει κάθε ένα
ΠΡΟΓΡΑΜΜΑΤΙΣΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΚΥΡΙΑΚΗ 19 ΟΚΤΩΒΡΙΟΥ 2014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ Όνομα/Επίθετο: Ζήτημα 1ο Να γράψετε στη γλώσσα των συνόλων και λεκτικά ποιο ενδεχόμενο παριστάνει κάθε ένα
ΑΠΑΝΤΗΣΕΙΣ ΙΟΥΛΙΟΥ Β. α. ΛΑΘΟΣ, β. ΣΩΣΤΟ, γ. ΣΩΣΤΟ, δ. ΛΑΘΟΣ, ε. ΣΩΣΤΟ, στ. ΣΩΣΤΟ. α = 1 δ. im( f (x) x ) = im - 2βx x = - 4β 8 = 4α - 32β =
 ΑΠΑΝΤΗΣΕΙΣ ΙΟΥΛΙΟΥ 005 ΘΕΜΑ ο Α.. Θεωρία s s Α.. CV =, αν > 0, ενώ CV =, αν < 0. - Β. α. ΛΑΘΟΣ, β. ΣΩΣΤΟ, γ. ΣΩΣΤΟ, δ. ΛΑΘΟΣ, ε. ΣΩΣΤΟ, στ. ΣΩΣΤΟ. ΘΕΜΑ ο α. Πρέπει > 0, άρα A f = (0, + ). β. f () = (α
ΑΠΑΝΤΗΣΕΙΣ ΙΟΥΛΙΟΥ 005 ΘΕΜΑ ο Α.. Θεωρία s s Α.. CV =, αν > 0, ενώ CV =, αν < 0. - Β. α. ΛΑΘΟΣ, β. ΣΩΣΤΟ, γ. ΣΩΣΤΟ, δ. ΛΑΘΟΣ, ε. ΣΩΣΤΟ, στ. ΣΩΣΤΟ. ΘΕΜΑ ο α. Πρέπει > 0, άρα A f = (0, + ). β. f () = (α
ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΙΔΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ 9. Κατανομές Δειγματοληψίας
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΙΔΙΚΑ ΘΕΜΑΤΑ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΙΔΙΚΑ ΘΕΜΑΤΑ
Μοντέλα Παλινδρόμησης. Άγγελος Μάρκος, Λέκτορας ΠΤ Ε, ΠΘ
 Μοντέλα Παλινδρόμησης Άγγελος Μάρκος, Λέκτορας ΠΤ Ε, ΠΘ Εισαγωγή (1) Σε αρκετές περιπτώσεις επίλυσης προβλημάτων ενδιαφέρει η ταυτόχρονη μελέτη δύο ή περισσότερων μεταβλητών, για να προσδιορίσουμε με ποιο
Μοντέλα Παλινδρόμησης Άγγελος Μάρκος, Λέκτορας ΠΤ Ε, ΠΘ Εισαγωγή (1) Σε αρκετές περιπτώσεις επίλυσης προβλημάτων ενδιαφέρει η ταυτόχρονη μελέτη δύο ή περισσότερων μεταβλητών, για να προσδιορίσουμε με ποιο
ΣΤΑΤΙΣΤΙΚΗ ΠΙΘΑΝΟΤΗΤΕΣ
 ΤΕΙ ΥΤΙΚΗΣ ΜΑΚΕ ΟΝΙΑΣ ΠΑΡΑΡΤΗΜΑ ΚΑΣΤΟΡΙΑΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ Η/Υ ΣΤΑΤΙΣΤΙΚΗ ΠΙΘΑΝΟΤΗΤΕΣ 6o ΜΑΘΗΜΑ Ι ΑΣΚΩΝ ΒΑΣΙΛΕΙΑ ΗΣ ΓΕΩΡΓΙΟΣ Email: gvasil@math.auth.gr Ιστοσελίδα Μαθήματος: users.auth.gr/gvasil
ΤΕΙ ΥΤΙΚΗΣ ΜΑΚΕ ΟΝΙΑΣ ΠΑΡΑΡΤΗΜΑ ΚΑΣΤΟΡΙΑΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ Η/Υ ΣΤΑΤΙΣΤΙΚΗ ΠΙΘΑΝΟΤΗΤΕΣ 6o ΜΑΘΗΜΑ Ι ΑΣΚΩΝ ΒΑΣΙΛΕΙΑ ΗΣ ΓΕΩΡΓΙΟΣ Email: gvasil@math.auth.gr Ιστοσελίδα Μαθήματος: users.auth.gr/gvasil
ΔΕΙΓΜΑΤΙΚΟΣ ΧΩΡΟΣ ΕΝΔΕΧΟΜΕΝΑ
 κεφ - ΠΙΘΑΝΟΤΗΤΕΣ ΔΕΙΓΜΑΤΙΚΟΣ ΧΩΡΟΣ ΕΝΔΕΧΟΜΕΝΑ Σε ένα συρτάρι υπάρχουν δύο κάρτες, μία άσπρη και μία κόκκινη Παίρνουμε στην τύχη μία κάρτα από το συρτάρι, καταγράφουμε το χρώμα της και την ξαναβάζουμε
κεφ - ΠΙΘΑΝΟΤΗΤΕΣ ΔΕΙΓΜΑΤΙΚΟΣ ΧΩΡΟΣ ΕΝΔΕΧΟΜΕΝΑ Σε ένα συρτάρι υπάρχουν δύο κάρτες, μία άσπρη και μία κόκκινη Παίρνουμε στην τύχη μία κάρτα από το συρτάρι, καταγράφουμε το χρώμα της και την ξαναβάζουμε
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ. Κεφάλαιο 8. Συνεχείς Κατανομές Πιθανοτήτων
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ. Κεφάλαιο 7. Τυχαίες Μεταβλητές και Διακριτές Κατανομές Πιθανοτήτων
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
Ασκήσεις Εξετάσεων. Μεταπτυχιακό Πρόγραμμα Σπουδών στη. Διοίκηση των Επιχειρήσεων
 Ασκήσεις Εξετάσεων Μεταπτυχιακό Πρόγραμμα Σπουδών στη Διοίκηση των Επιχειρήσεων ΑΣΚΗΣΗ 1: Έλεγχος για τη μέση τιμή ενός πληθυσμού Η αντικαπνιστική νομοθεσία υποχρεώνει τους καπνιστές που εργάζονται σε
Ασκήσεις Εξετάσεων Μεταπτυχιακό Πρόγραμμα Σπουδών στη Διοίκηση των Επιχειρήσεων ΑΣΚΗΣΗ 1: Έλεγχος για τη μέση τιμή ενός πληθυσμού Η αντικαπνιστική νομοθεσία υποχρεώνει τους καπνιστές που εργάζονται σε
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ Ευθύγραμμη Ομαλά Μεταβαλλόμενη Κίνηση Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A ΠΑΝΑΓΙΩΤΗΣ, Φυσικός https://physicscourseswordpresscom/ Βασικές έννοιες Ένα σώμα δεν κινείται πάντα με σταθερή
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ Ευθύγραμμη Ομαλά Μεταβαλλόμενη Κίνηση Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A ΠΑΝΑΓΙΩΤΗΣ, Φυσικός https://physicscourseswordpresscom/ Βασικές έννοιες Ένα σώμα δεν κινείται πάντα με σταθερή
Έλεγχος Ανεξαρτησίας x2 του Pearson x2 του Pearson
 Έλεγχος Ανεξαρτησίας x του Parso Έστω ότι λαμβάνουμε δείγμα μεγέθους. Η πιθανότητα π εμφάνισης ενός χαρακτηριστικού να βρεθεί στο κελί (i,j) κάτω από την υπόθεση Η 0 της ανεξαρτησίας δίνεται από την σχέση
Έλεγχος Ανεξαρτησίας x του Parso Έστω ότι λαμβάνουμε δείγμα μεγέθους. Η πιθανότητα π εμφάνισης ενός χαρακτηριστικού να βρεθεί στο κελί (i,j) κάτω από την υπόθεση Η 0 της ανεξαρτησίας δίνεται από την σχέση
Σ ΤΑΤ Ι Σ Τ Ι Κ Η. Statisticum collegium Iii
 Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium Iii Η Κανονική Κατανομή Λέμε ότι μία τυχαία μεταβλητή X, ακολουθεί την Κανονική Κατανομή με παραμέτρους και και συμβολίζουμε X N, αν έχει συνάρτηση πυκνότητας
Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium Iii Η Κανονική Κατανομή Λέμε ότι μία τυχαία μεταβλητή X, ακολουθεί την Κανονική Κατανομή με παραμέτρους και και συμβολίζουμε X N, αν έχει συνάρτηση πυκνότητας
εσµευµένες Πιθανότητες-Λυµένα Παραδείγµατα 3. Επιλέγουµε έναν που δεν είναι άνεργος. Ποια είναι η πιθανότητα να είναι πτυχιούχος; = 0.
 Τµήµα Επιστήµης των Υλικών Μάθηµα: Θεωρία Πιθανοτήτων και Στοχαστικές ιαδικασίες ιδάσκων: Κ. Πετρόπουλος εσµευµένες Πιθανότητες-Λυµένα Παραδείγµατα Παράδειγµα. Το 0% του ενεργού πληθυσµού (εργαζόµενοι
Τµήµα Επιστήµης των Υλικών Μάθηµα: Θεωρία Πιθανοτήτων και Στοχαστικές ιαδικασίες ιδάσκων: Κ. Πετρόπουλος εσµευµένες Πιθανότητες-Λυµένα Παραδείγµατα Παράδειγµα. Το 0% του ενεργού πληθυσµού (εργαζόµενοι
Ερευνητική υπόθεση. Η ερευνητική υπόθεση αναφέρεται σε μια συγκεκριμένη πρόβλεψη σχετικά με τη σχέση ανάμεσα σε δύο ή περισσότερες μεταβλητές.
 Ερευνητική υπόθεση Η ερευνητική υπόθεση αναφέρεται σε μια συγκεκριμένη πρόβλεψη σχετικά με τη σχέση ανάμεσα σε δύο ή περισσότερες μεταβλητές. Στα πειραματικά ερευνητικά σχέδια, η ερευνητική υπόθεση αναφέρεται
Ερευνητική υπόθεση Η ερευνητική υπόθεση αναφέρεται σε μια συγκεκριμένη πρόβλεψη σχετικά με τη σχέση ανάμεσα σε δύο ή περισσότερες μεταβλητές. Στα πειραματικά ερευνητικά σχέδια, η ερευνητική υπόθεση αναφέρεται
1. Πείραμα τύχης. 2. Δειγματικός Χώρος ΣΤΟΙΧΕΙΑ ΑΠΟ ΤΗ ΘΕΩΡΙΑ ΠΙΘΑΝΟΤΗΤΩΝ
 1 ΣΤΟΙΧΕΙ ΠΟ ΤΗ ΘΕΩΡΙ ΠΙΘΝΟΤΗΤΩΝ 1. Πείραμα τύχης Πείραμα τύχης (π.τ.) ονομάζουμε κάθε πείραμα που μπορεί να επαναληφθεί όσες φορές επιθυμούμε υπό τις ίδιες συνθήκες και του οποίου το αποτέλεσμα είναι
1 ΣΤΟΙΧΕΙ ΠΟ ΤΗ ΘΕΩΡΙ ΠΙΘΝΟΤΗΤΩΝ 1. Πείραμα τύχης Πείραμα τύχης (π.τ.) ονομάζουμε κάθε πείραμα που μπορεί να επαναληφθεί όσες φορές επιθυμούμε υπό τις ίδιες συνθήκες και του οποίου το αποτέλεσμα είναι
Δισδιάστατη ανάλυση. Για παράδειγμα, έστω ότι 11 άτομα δήλωσαν ότι είναι άγαμοι (Α), 26 έγγαμοι (Ε), 12 χήροι (Χ) και 9 διαζευγμένοι (Δ).
 Δισδιάστατη ανάλυση Πίνακες διπλής εισόδου Σε πολλές περιπτώσεις μελετάμε περισσότερες από μία μεταβλητές ταυτόχρονα. Π.χ. μία έρευνα που έγινε σε ένα δείγμα 58 ατόμων περιείχε τις ερωτήσεις «ποια είναι
Δισδιάστατη ανάλυση Πίνακες διπλής εισόδου Σε πολλές περιπτώσεις μελετάμε περισσότερες από μία μεταβλητές ταυτόχρονα. Π.χ. μία έρευνα που έγινε σε ένα δείγμα 58 ατόμων περιείχε τις ερωτήσεις «ποια είναι
Στατιστική Επιχειρήσεων Ι
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Τεχνολογικό Εκπαιδευτικό Ίδρυμα Πειραιά Στατιστική Επιχειρήσεων Ι Ενότητα 1: Στοιχεία Πιθανοθεωρίας Μιλτιάδης Χαλικιάς, Επίκουρος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Τεχνολογικό Εκπαιδευτικό Ίδρυμα Πειραιά Στατιστική Επιχειρήσεων Ι Ενότητα 1: Στοιχεία Πιθανοθεωρίας Μιλτιάδης Χαλικιάς, Επίκουρος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης
Υ: Νόσος. Χ: Παράγοντας Κινδύνου 1 (Ασθενής) 2 (Υγιής) Σύνολο. 1 (Παρόν) n 11 n 12 n 1. 2 (Απών) n 21 n 22 n 2. Σύνολο n.1 n.2 n..
 Μέτρα Κινδύνου για Δίτιμα Κατηγορικά Δεδομένα Σε αυτή την ενότητα θα ορίσουμε δείκτες μέτρησης του κινδύνου εμφάνισης μίας νόσου όταν έχουμε δίτιμες κατηγορικές μεταβλητές. Στην πιο απλή περίπτωση μας
Μέτρα Κινδύνου για Δίτιμα Κατηγορικά Δεδομένα Σε αυτή την ενότητα θα ορίσουμε δείκτες μέτρησης του κινδύνου εμφάνισης μίας νόσου όταν έχουμε δίτιμες κατηγορικές μεταβλητές. Στην πιο απλή περίπτωση μας
Κεφάλαιο , 05. Τέλος το ποσό της τελευταίας κατάθεσης (συμπλήρωση του 17 ου έτους) θα τοκισθεί μόνο για 1 έτος
 Κεφάλαιο 5 5. Ράντες 5.. Εισαγωγικές έννοιες και ορισμοί Είναι σύνηθες στις μέρες μας να καταθέτουν οι γονείς κάποιο ποσό για τα παιδιά τους σε μηνιαία, εξαμηνιαία ή ετήσια βάση έτσι ώστε να συσσωρευτεί
Κεφάλαιο 5 5. Ράντες 5.. Εισαγωγικές έννοιες και ορισμοί Είναι σύνηθες στις μέρες μας να καταθέτουν οι γονείς κάποιο ποσό για τα παιδιά τους σε μηνιαία, εξαμηνιαία ή ετήσια βάση έτσι ώστε να συσσωρευτεί
Η αγορά δασκάλων 101
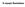 Η αγορά δασκάλων Η αγορά δασκάλων Τα νούμερα των δασκάλων στην Ελλάδα, 2012 Βαθμίδα Σύνολο Άνδρες Γυναίκες Νηπιαγωγείο 14018 162 13856 % [100.0] [1.00] [99.0] Δημοτικό 67314 20565 46749 % [100.0] [31.0]
Η αγορά δασκάλων Η αγορά δασκάλων Τα νούμερα των δασκάλων στην Ελλάδα, 2012 Βαθμίδα Σύνολο Άνδρες Γυναίκες Νηπιαγωγείο 14018 162 13856 % [100.0] [1.00] [99.0] Δημοτικό 67314 20565 46749 % [100.0] [31.0]
Μάθηµα 11. Κεφάλαιο: Στατιστική
 Μάθηµα Κεφάλαιο: Στατιστική Θεµατικές Ενότητες:. Παρουσίαση Στατιστικών εδοµένων (Στατιστικοί Πίνακες). Γενικά για στατιστικούς πίνακες. Τα στατιστικά δεδοµένα καταγράφονται σε στατιστικούς πίνακες (ή
Μάθηµα Κεφάλαιο: Στατιστική Θεµατικές Ενότητες:. Παρουσίαση Στατιστικών εδοµένων (Στατιστικοί Πίνακες). Γενικά για στατιστικούς πίνακες. Τα στατιστικά δεδοµένα καταγράφονται σε στατιστικούς πίνακες (ή
ΣΥΝΔΥΑΣΤΙΚΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΣΥΝΔΥΑΣΤΙΚΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ 1.Έστω ο δειγματικός χώρος Ω = { 1,,, K,10} με ισοπίθανα απλά ενδεχόμενα. Να 4 βρείτε την πιθανότητα ώστε η συνάρτηση f ( x ) = x 4x + λ να
ΣΥΝΔΥΑΣΤΙΚΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ 1.Έστω ο δειγματικός χώρος Ω = { 1,,, K,10} με ισοπίθανα απλά ενδεχόμενα. Να 4 βρείτε την πιθανότητα ώστε η συνάρτηση f ( x ) = x 4x + λ να
2. Στο σχολικό διάλειμμα η Κατερίνα και οι φίλες της παίζουν με ένα ζάρι. Ποια η πιθανότητα να πετύχει η Κατερίνα το νούμερο 3 με την πρώτη φορά;
 Τεστ 1 Κατηγορία: Γυμνάσια (Version 1,2,3) Check questionnaires ΦίλτροΤεστ 1 - Τεστ βασικών γνώσεων Κατηγορία φίλτρου B - Γυμνάσια Εκδοχή 1 Εφαρμογή 1. Oι 200 μαθητές ενός γυμνασίου ερωτήθηκαν σε έρευνα
Τεστ 1 Κατηγορία: Γυμνάσια (Version 1,2,3) Check questionnaires ΦίλτροΤεστ 1 - Τεστ βασικών γνώσεων Κατηγορία φίλτρου B - Γυμνάσια Εκδοχή 1 Εφαρμογή 1. Oι 200 μαθητές ενός γυμνασίου ερωτήθηκαν σε έρευνα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 207-208 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutras@fme.aegea.gr Τηλ: 227035468 ΣΤΑΤΙΣΤΙΚΗ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 207-208 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutras@fme.aegea.gr Τηλ: 227035468 ΣΤΑΤΙΣΤΙΚΗ
ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ Ενότητα # 1: Εισαγωγή στη Στατιστική Εβελίνα Κοσσιέρη Τμήμα Λογιστικής και Χρηματοοικονομικής ΑΔΕΙΕΣ ΧΡΗΣΗΣ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ Ενότητα # 1: Εισαγωγή στη Στατιστική Εβελίνα Κοσσιέρη Τμήμα Λογιστικής και Χρηματοοικονομικής ΑΔΕΙΕΣ ΧΡΗΣΗΣ
Από το Γυμνάσιο στο Λύκειο Δειγματικός χώρος Ενδεχόμενα Εύρεση δειγματικού χώρου... 46
 ΠEΡΙΕΧΟΜΕΝΑ Από το Γυμνάσιο στο Λύκειο................................................ 7 1. Το Λεξιλόγιο της Λογικής.............................................. 11 2. Σύνολα..............................................................
ΠEΡΙΕΧΟΜΕΝΑ Από το Γυμνάσιο στο Λύκειο................................................ 7 1. Το Λεξιλόγιο της Λογικής.............................................. 11 2. Σύνολα..............................................................
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ Τμήμα Βιολογικών Εφαρμογών & Τεχνολογιών Βιοστατιστική, Κεφάλαιο 3: Πιθανότητες Λύσεις ασκήσεων 1 Στο διπλανό πίνακα αναπαράγεται ο αρχικός πίνακας, της ταξινόμησης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ Τμήμα Βιολογικών Εφαρμογών & Τεχνολογιών Βιοστατιστική, Κεφάλαιο 3: Πιθανότητες Λύσεις ασκήσεων 1 Στο διπλανό πίνακα αναπαράγεται ο αρχικός πίνακας, της ταξινόμησης
17/10/2016. Στατιστική Ι. 3 η Διάλεξη
 Στατιστική Ι 3 η Διάλεξη 1 2 Τυχαία μεταβλητή X στο δειγματικό χώρο Ω Μια πραγματική συνάρτηση που αντιστοιχίζει τα στοιχεία του δειγματικού χώρου Ω στο σύνολο των πραγματικών αριθμών τέτοια ώστε για κάθε
Στατιστική Ι 3 η Διάλεξη 1 2 Τυχαία μεταβλητή X στο δειγματικό χώρο Ω Μια πραγματική συνάρτηση που αντιστοιχίζει τα στοιχεία του δειγματικού χώρου Ω στο σύνολο των πραγματικών αριθμών τέτοια ώστε για κάθε
Δειγματοληψία. Πρέπει να γνωρίζουμε πως πήραμε το δείγμα Το πλήθος n ij των παρατηρήσεων σε κάθε κελί είναι τ.μ. με μ ij συμβολίζουμε την μέση τιμή:
 Δειγματοληψία Πρέπει να γνωρίζουμε πως πήραμε το δείγμα Το πλήθος των παρατηρήσεων σε κάθε κελί είναι τ.μ. με μ συμβολίζουμε την μέση τιμή: Επομένως στην δειγματοληψία πινάκων συνάφειας αναφερόμαστε στον
Δειγματοληψία Πρέπει να γνωρίζουμε πως πήραμε το δείγμα Το πλήθος των παρατηρήσεων σε κάθε κελί είναι τ.μ. με μ συμβολίζουμε την μέση τιμή: Επομένως στην δειγματοληψία πινάκων συνάφειας αναφερόμαστε στον
ΜΑΘΗΜΑΤΙΚΑ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΤΩΝ ΑΠΟΦΑΣΕΩΝ
 ΔΙΑΤΜΗΜΑΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑΤΙΚΑ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΤΩΝ ΑΠΟΦΑΣΕΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Ι. Προσωπικές Πληροφορίες Η συμπλήρωση όλων των πεδίων είναι
ΔΙΑΤΜΗΜΑΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑΤΙΚΑ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΤΩΝ ΑΠΟΦΑΣΕΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Ι. Προσωπικές Πληροφορίες Η συμπλήρωση όλων των πεδίων είναι
Οι παραγγελίες ακολουθούν την κατανομή Poisson. Σύμφωνα με τα δεδομένα ο
 ΘΕΜΑ 1 ο (ΜΟΝΑΔΕΣ 10) Μια βιοτεχνία καθαρισμού ρούχων λειτουργεί καθημερινά 8 ώρες. Η βιοτεχνία δέχεται κατά μέσο όρο 4 παραγγελίες την ημέρα για καθαρισμό ενδυμάτων. (ι). Να υπολογισθεί η πιθανότητα να
ΘΕΜΑ 1 ο (ΜΟΝΑΔΕΣ 10) Μια βιοτεχνία καθαρισμού ρούχων λειτουργεί καθημερινά 8 ώρες. Η βιοτεχνία δέχεται κατά μέσο όρο 4 παραγγελίες την ημέρα για καθαρισμό ενδυμάτων. (ι). Να υπολογισθεί η πιθανότητα να
Διμεταβλητές κατανομές πιθανοτήτων
 Διμεταβλητές κατανομές πιθανοτήτων Για να περιγράψουμε την σχέση ανάμεσα σε δύο τυχαίες μεταβλητές χρειαζόμαστε την κοινή κατανομή πιθανοτήτων τους. Η κοινή συνάρτηση πιθανότητ ικανοποιε ί τις συνθ ήκες
Διμεταβλητές κατανομές πιθανοτήτων Για να περιγράψουμε την σχέση ανάμεσα σε δύο τυχαίες μεταβλητές χρειαζόμαστε την κοινή κατανομή πιθανοτήτων τους. Η κοινή συνάρτηση πιθανότητ ικανοποιε ί τις συνθ ήκες
Στατιστική Επιχειρήσεων Ι
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Τεχνολογικό Εκπαιδευτικό Ίδρυμα Πειραιά Στατιστική Επιχειρήσεων Ι Ενότητα 2: Τυχαίες Μεταβλητές Μιλτιάδης Χαλικιάς, Επίκουρος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης Το
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Τεχνολογικό Εκπαιδευτικό Ίδρυμα Πειραιά Στατιστική Επιχειρήσεων Ι Ενότητα 2: Τυχαίες Μεταβλητές Μιλτιάδης Χαλικιάς, Επίκουρος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης Το
Βασικές έννοιες της Στατιστικής: Πληθυσμός - Δείγμα
 Βασικές έννοιες της Στατιστικής: Πληθυσμός - Δείγμα Στατιστική είναι ο κλάδος των μαθηματικών που εμβαθύνει σε μεθόδους συλλογής δεδομένων, οργάνωσης, παρουσίασης των δεδομένων και εξαγωγής συμπερασμάτων
Βασικές έννοιες της Στατιστικής: Πληθυσμός - Δείγμα Στατιστική είναι ο κλάδος των μαθηματικών που εμβαθύνει σε μεθόδους συλλογής δεδομένων, οργάνωσης, παρουσίασης των δεδομένων και εξαγωγής συμπερασμάτων
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ Μ.Ν. Ντυκέν, Πανεπιστήμιο Θεσσαλίας Τ.Μ.Χ.Π.Π.Α. Ε. Αναστασίου, Πανεπιστήμιο Θεσσαλίας Τ.Μ.Χ.Π.Π.Α. ΔΙΑΛΕΞΗ 07 & ΔΙΑΛΕΞΗ 08 ΣΗΜΠΕΡΑΣΜΑΤΙΚΗ ΣΤΑΤΙΣΤΙΚΗ Βόλος, 016-017 ΕΙΣΑΓΩΓΗ ΣΤΗΝ
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ Μ.Ν. Ντυκέν, Πανεπιστήμιο Θεσσαλίας Τ.Μ.Χ.Π.Π.Α. Ε. Αναστασίου, Πανεπιστήμιο Θεσσαλίας Τ.Μ.Χ.Π.Π.Α. ΔΙΑΛΕΞΗ 07 & ΔΙΑΛΕΞΗ 08 ΣΗΜΠΕΡΑΣΜΑΤΙΚΗ ΣΤΑΤΙΣΤΙΚΗ Βόλος, 016-017 ΕΙΣΑΓΩΓΗ ΣΤΗΝ
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ
 Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ Θέμα εξετάσεων 2000 Εξετάσαμε 50 μαθητές ως προς τα βιβλία που έχουν διαβάσει και διαπιστώσαμε ότι: 5 μαθητές δεν έχουν διαβάσει κανένα βιβλίο, 15 μαθητές έχουν
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ Θέμα εξετάσεων 2000 Εξετάσαμε 50 μαθητές ως προς τα βιβλία που έχουν διαβάσει και διαπιστώσαμε ότι: 5 μαθητές δεν έχουν διαβάσει κανένα βιβλίο, 15 μαθητές έχουν
ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ)
 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (7) 25/7/2012 Θέμα Α Α1. Να γράψετε στο τετράδιό
ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (7) 25/7/2012 Θέμα Α Α1. Να γράψετε στο τετράδιό
ΜΑΘΗΜΑΤΙΚΑ Β Γυμνασίου
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΜΑΘΗΜΑΤΙΚΑ Β Γυμνασίου Ενότητα 4: Συναρτήσεις ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΥΠΗΡΕΣΙΑ ΑΝΑΠΤΥΞΗΣ ΠΡΟΓΡΑΜΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΑ Β Γυμνασίου Ενότητα 4: Συναρτήσεις Συγγραφή: Ομάδα Υποστήριξης
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΜΑΘΗΜΑΤΙΚΑ Β Γυμνασίου Ενότητα 4: Συναρτήσεις ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΥΠΗΡΕΣΙΑ ΑΝΑΠΤΥΞΗΣ ΠΡΟΓΡΑΜΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΑ Β Γυμνασίου Ενότητα 4: Συναρτήσεις Συγγραφή: Ομάδα Υποστήριξης
ΕΙΣΑΓΩΓΗ. Βασικές έννοιες
 ΕΙΣΑΓΩΓΗ Βασικές έννοιες Σε ένα ερωτηματολόγιο έχουμε ένα σύνολο ερωτήσεων. Μπορούμε να πούμε ότι σε κάθε ερώτηση αντιστοιχεί μία μεταβλητή. Αν θεωρήσουμε μια ερώτηση, τα άτομα δίνουν κάποιες απαντήσεις
ΕΙΣΑΓΩΓΗ Βασικές έννοιες Σε ένα ερωτηματολόγιο έχουμε ένα σύνολο ερωτήσεων. Μπορούμε να πούμε ότι σε κάθε ερώτηση αντιστοιχεί μία μεταβλητή. Αν θεωρήσουμε μια ερώτηση, τα άτομα δίνουν κάποιες απαντήσεις
ΔΕΣΜΕΥΜΕΝΕΣ Ή ΥΠΟ ΣΥΝΘΗΚΗ ΠΙΘΑΝΟΤΗΤΕΣ
 ΔΕΣΜΕΥΜΕΝΕΣ Ή ΥΠΟ ΣΥΝΘΗΚΗ ΠΙΘΑΝΟΤΗΤΕΣ Έστω ότι επιθυμούμε να μελετήσουμε ένα τυχαίο πείραμα με δειγματικό χώρο Ω και έστω η πιθανότητα να συμβεί ένα ενδεχόμενο Α Ω Υπάρχουν περιπτώσεις όπου ενώ δεν γνωρίζουμε
ΔΕΣΜΕΥΜΕΝΕΣ Ή ΥΠΟ ΣΥΝΘΗΚΗ ΠΙΘΑΝΟΤΗΤΕΣ Έστω ότι επιθυμούμε να μελετήσουμε ένα τυχαίο πείραμα με δειγματικό χώρο Ω και έστω η πιθανότητα να συμβεί ένα ενδεχόμενο Α Ω Υπάρχουν περιπτώσεις όπου ενώ δεν γνωρίζουμε
HY118-Διακριτά Μαθηματικά
 HY118-Διακριτά Μαθηματικά Παρασκευή, 04/05/2018 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr 07-May-18 1 1 Θεωρία πιθανοτήτων 07-May-18 2 2 Τι είδαμε την προηγούμενη φορά Μία τυχαία μεταβλητή Vείναι κάθε
HY118-Διακριτά Μαθηματικά Παρασκευή, 04/05/2018 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr 07-May-18 1 1 Θεωρία πιθανοτήτων 07-May-18 2 2 Τι είδαμε την προηγούμενη φορά Μία τυχαία μεταβλητή Vείναι κάθε
Έρευνα Καταναλωτών Αγοράς 3
 Έρευνα Καταναλωτών Αγοράς 3 Ετοιμάστηκε για το: Γραφείο Επιτρόπου Ρυθμίσεως Ηλεκτρονικών Επικοινωνιών και Ταχυδρομείων Ιούλιος 2015 Ταυτότητα Έρευνας 2 Ταυτότητα έρευνας Έρευνα Καταναλωτών Αγοράς 3 Μέγεθος
Έρευνα Καταναλωτών Αγοράς 3 Ετοιμάστηκε για το: Γραφείο Επιτρόπου Ρυθμίσεως Ηλεκτρονικών Επικοινωνιών και Ταχυδρομείων Ιούλιος 2015 Ταυτότητα Έρευνας 2 Ταυτότητα έρευνας Έρευνα Καταναλωτών Αγοράς 3 Μέγεθος
Από το Γυμνάσιο στο Λύκειο... 7. 3. Δειγματικός χώρος Ενδεχόμενα... 42 Εύρεση δειγματικού χώρου... 46
 ΠEΡΙΕΧΟΜΕΝΑ Από το Γυμνάσιο στο Λύκειο................................................ 7 1. Το Λεξιλόγιο της Λογικής.............................................. 11. Σύνολα..............................................................
ΠEΡΙΕΧΟΜΕΝΑ Από το Γυμνάσιο στο Λύκειο................................................ 7 1. Το Λεξιλόγιο της Λογικής.............................................. 11. Σύνολα..............................................................
ΟΡΟΙ ΧΡΗΣΕΩΣ ΤΗΣ ΥΠΗΡΕΣΙΑΣ ALPHA ALERTS
 ΟΡΟΙ ΧΡΗΣΕΩΣ ΤΗΣ ΥΠΗΡΕΣΙΑΣ ALPHA ALERTS Η Τράπεζα προσφέρει στον πελάτη κάτοχο των καρτών που εκδίδει (εφεξής «Κάτοχος») την «Υπηρεσία Alpha alerts», η οποία αποτελεί υπηρεσία αποστολής γραπτών ενημερωτικών
ΟΡΟΙ ΧΡΗΣΕΩΣ ΤΗΣ ΥΠΗΡΕΣΙΑΣ ALPHA ALERTS Η Τράπεζα προσφέρει στον πελάτη κάτοχο των καρτών που εκδίδει (εφεξής «Κάτοχος») την «Υπηρεσία Alpha alerts», η οποία αποτελεί υπηρεσία αποστολής γραπτών ενημερωτικών
Κεφάλαιο 9. Έλεγχοι υποθέσεων
 Κεφάλαιο 9 Έλεγχοι υποθέσεων 9.1 Εισαγωγή Όταν παίρνουμε ένα ή περισσότερα τυχαία δείγμα από κανονικούς πληθυσμούς έχουμε τη δυνατότητα να υπολογίζουμε στατιστικά, όπως μέσους όρους, δειγματικές διασπορές
Κεφάλαιο 9 Έλεγχοι υποθέσεων 9.1 Εισαγωγή Όταν παίρνουμε ένα ή περισσότερα τυχαία δείγμα από κανονικούς πληθυσμούς έχουμε τη δυνατότητα να υπολογίζουμε στατιστικά, όπως μέσους όρους, δειγματικές διασπορές
Μεθοδολογία προβλημάτων με Δομή Επανάληψης
 Μεθοδολογία προβλημάτων με Δομή Επανάληψης Ενότητες βιβλίου: - Ώρες διδασκαλίας: 3 Μετρητές Σε πολλές ασκήσεις ζητείται να καταμετρηθεί το πλήθος των τιμών που ικανοποιούν μια συνθήκη (π.χ. είναι θετικοί
Μεθοδολογία προβλημάτων με Δομή Επανάληψης Ενότητες βιβλίου: - Ώρες διδασκαλίας: 3 Μετρητές Σε πολλές ασκήσεις ζητείται να καταμετρηθεί το πλήθος των τιμών που ικανοποιούν μια συνθήκη (π.χ. είναι θετικοί
2 ΟΥ και 8 ΟΥ ΚΕΦΑΛΑΙΟΥ
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΙΜΕΛΕΙΑ: ΜΑΡΙΑ Σ. ΖΙΩΓΑ ΚΑΘΗΓΗΤΡΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ 2 ΟΥ και 8 ΟΥ ΚΕΦΑΛΑΙΟΥ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΔΟΜΗ ΕΠΑΝΑΛΗΨΗΣ 1) Πότε χρησιμοποιείται η δομή επανάληψης
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΙΜΕΛΕΙΑ: ΜΑΡΙΑ Σ. ΖΙΩΓΑ ΚΑΘΗΓΗΤΡΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ 2 ΟΥ και 8 ΟΥ ΚΕΦΑΛΑΙΟΥ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΔΟΜΗ ΕΠΑΝΑΛΗΨΗΣ 1) Πότε χρησιμοποιείται η δομή επανάληψης
Η παρουσίαση που ακολουθεί, αφορά την κανονική κατανομή και σκοπό έχει τη διευκόλυνση των φοιτητών του τμήματος Ηλεκτρολόγων Μηχανικών & Μηχανικών
 Η παρουσίαση που ακολουθεί, αφορά την κανονική κατανομή και σκοπό έχει τη διευκόλυνση των φοιτητών του τμήματος Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών να αντιληφθούν τη σημασία της εν λόγω κατανομής
Η παρουσίαση που ακολουθεί, αφορά την κανονική κατανομή και σκοπό έχει τη διευκόλυνση των φοιτητών του τμήματος Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών να αντιληφθούν τη σημασία της εν λόγω κατανομής
ΤΟ ΕΞΕΤΑΣΤΙΚΟ ΔΟΚΙΜΙΟ ΑΠΟΤΕΛΕΙΤΑΙ ΑΠΟ ΟΚΤΩ ( 8 ) ΣΕΛΙΔΕΣ
 ΓΥΜΝΑΣΙΟ ΕΠΙΣΚΟΠΗΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2018-2019 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ- ΙΟΥΝΙΟΥ 2019 ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΤΑΞΗ: A ΗΜΕΡΟΜΗΝΙΑ: 27/5/2019 ΧΡΟΝΟΣ: 2 Ώρες Βαθμός:.. Ολογράφως:.. Υπογραφή:.. ΟΝΟΜΑΤΕΠΩΝΥΜΟ:
ΓΥΜΝΑΣΙΟ ΕΠΙΣΚΟΠΗΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2018-2019 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ- ΙΟΥΝΙΟΥ 2019 ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΤΑΞΗ: A ΗΜΕΡΟΜΗΝΙΑ: 27/5/2019 ΧΡΟΝΟΣ: 2 Ώρες Βαθμός:.. Ολογράφως:.. Υπογραφή:.. ΟΝΟΜΑΤΕΠΩΝΥΜΟ:
Κατανάλωση Ηλεκτρικής Ενέργειας
 Κατανάλωση Ηλεκτρικής Ενέργειας 1.Συνοπτική Παρουσίαση Σεναρίου 1.1 Τίτλος Διδακτικού Σεναρίου Κατανάλωση Ηλεκτρικής Ενέργειας 1.2 Εμπλεκόμενες Γνωστικές Περιοχές Φυσικές Επιστήμες, Μαθηματικά, Πληροφορική
Κατανάλωση Ηλεκτρικής Ενέργειας 1.Συνοπτική Παρουσίαση Σεναρίου 1.1 Τίτλος Διδακτικού Σεναρίου Κατανάλωση Ηλεκτρικής Ενέργειας 1.2 Εμπλεκόμενες Γνωστικές Περιοχές Φυσικές Επιστήμες, Μαθηματικά, Πληροφορική
Τ Ε Ι Ιονίων Νήσων Τμήμα Εφαρμογών Πληροφορικής στη Διοίκηση και την Οικονομία. Υπεύθυνος: Δρ. Κολιός Σταύρος
 Τ Ε Ι Ιονίων Νήσων Τμήμα Εφαρμογών Πληροφορικής στη Διοίκηση και την Οικονομία Υπεύθυνος: Δρ. Κολιός Σταύρος Θεωρία Συνόλων Σύνολο: Το σύνολο εκφράζει μία συλλογή διακριτών μονάδων οποιασδήποτε φύσης.
Τ Ε Ι Ιονίων Νήσων Τμήμα Εφαρμογών Πληροφορικής στη Διοίκηση και την Οικονομία Υπεύθυνος: Δρ. Κολιός Σταύρος Θεωρία Συνόλων Σύνολο: Το σύνολο εκφράζει μία συλλογή διακριτών μονάδων οποιασδήποτε φύσης.
Πρόσθεση, αφαίρεση και πολλαπλασιασμός φυσικών αριθμών
 Πρόσθεση, αφαίρεση και πολλαπλασιασμός φυσικών αριθμών TINΑ ΒΡΕΝΤΖΟΥ www.ma8eno.gr www.ma8eno.gr Σελίδα 1 Πρόσθεση, αφαίρεση και πολλαπλασιασμός φυσικών αριθμών Στους πραγματικούς αριθμούς ορίστηκαν οι
Πρόσθεση, αφαίρεση και πολλαπλασιασμός φυσικών αριθμών TINΑ ΒΡΕΝΤΖΟΥ www.ma8eno.gr www.ma8eno.gr Σελίδα 1 Πρόσθεση, αφαίρεση και πολλαπλασιασμός φυσικών αριθμών Στους πραγματικούς αριθμούς ορίστηκαν οι
ΧΑΡΑΛΑΜΠΟΣ.ΣΠ. ΛΥΚΟΥΔΗΣ - ΠΙΘΑΝΟΤΗΤΕΣ Α ΛΥΚΕΙΟΥ
 Θεωρία Πιθανοτήτων Εάν οι συνθήκες τέλεσης ενός πειράματος καθορίζουν πλήρως το αποτέλεσμα του, τότε το πείραμα λέγεται αιτιοκρατικό. Είναι γνωστό ότι το αποσταγμένο νερό βράζει στους 100 βαθμού κελσίου.
Θεωρία Πιθανοτήτων Εάν οι συνθήκες τέλεσης ενός πειράματος καθορίζουν πλήρως το αποτέλεσμα του, τότε το πείραμα λέγεται αιτιοκρατικό. Είναι γνωστό ότι το αποσταγμένο νερό βράζει στους 100 βαθμού κελσίου.
ΣΗΜΕΙΩΣΕΙΣ ΜΕΛΕΤΗΣ ΙΟΥΝΙΟΥ 2016 (version ) είναι: ( ) f =
 ΣΗΜΕΙΩΣΕΙΣ ΜΕΛΕΤΗΣ ΙΟΥΝΙΟΥ 16 (version 9-6-16) 1. A Να δώσετε τον ορισμό της παραγώγου μιας συνάρτησης σε ένα σημείο x του πεδίο ορισμού της. Απάντηση: Παράγωγος μιας συνάρτησης σε ένα σημείο x του πεδίο
ΣΗΜΕΙΩΣΕΙΣ ΜΕΛΕΤΗΣ ΙΟΥΝΙΟΥ 16 (version 9-6-16) 1. A Να δώσετε τον ορισμό της παραγώγου μιας συνάρτησης σε ένα σημείο x του πεδίο ορισμού της. Απάντηση: Παράγωγος μιας συνάρτησης σε ένα σημείο x του πεδίο
ΚΑΤΑΝΟΜΈΣ. 8.1 Εισαγωγή. 8.2 Κατανομές Συχνοτήτων (Frequency Distributions) ΚΕΦΑΛΑΙΟ
 ΚΑΤΑΝΟΜΈΣ ΚΕΦΑΛΑΙΟ 8 81 Εισαγωγή Οι κατανομές διακρίνονται σε κατανομές συχνοτήτων, κατανομές πιθανοτήτων και σε δειγματοληπτικές κατανομές Στη συνέχεια θα γίνει αναλυτική περιγραφή αυτών 82 Κατανομές
ΚΑΤΑΝΟΜΈΣ ΚΕΦΑΛΑΙΟ 8 81 Εισαγωγή Οι κατανομές διακρίνονται σε κατανομές συχνοτήτων, κατανομές πιθανοτήτων και σε δειγματοληπτικές κατανομές Στη συνέχεια θα γίνει αναλυτική περιγραφή αυτών 82 Κατανομές
Στατιστική Ι. Ενότητα 6: Kατανομή Poisson. Δρ. Γεώργιος Κοντέος Τμήμα Διοίκησης Επιχειρήσεων Γρεβενών
 Στατιστική Ι Ενότητα 6: Kατανομή Poisson Δρ. Γεώργιος Κοντέος Τμήμα Διοίκησης Επιχειρήσεων Γρεβενών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Στατιστική Ι Ενότητα 6: Kατανομή Poisson Δρ. Γεώργιος Κοντέος Τμήμα Διοίκησης Επιχειρήσεων Γρεβενών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ
 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΚΕΦΑΛΑΙΟ 3 ο ΠΙΘΑΝΟΤΗΤΕΣ Συνοπτική Θεωρία Όλες οι αποδείξεις Ερωτήσεις αντικειμενικού τύπου Ασκήσεις από την Τράπεζα Θεμάτων του Υπουργείου και προτεινόμενες Διαγωνίσματα
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΚΕΦΑΛΑΙΟ 3 ο ΠΙΘΑΝΟΤΗΤΕΣ Συνοπτική Θεωρία Όλες οι αποδείξεις Ερωτήσεις αντικειμενικού τύπου Ασκήσεις από την Τράπεζα Θεμάτων του Υπουργείου και προτεινόμενες Διαγωνίσματα
ΠΙΝΑΚΑΣ 1. Αγόρι 390 (51.25%) 360 (43.11%) 750 Κορίτσι 371 (48.75%) 475 (56.89%) (100%) 835 (100%) 1596
 ΙΙ. ΑΝΑΛΥΣΗ ΔΕΔΟΜΕΝΩΝ. Α. Γενικά στοιχεία. Όπως φαίνεται παραπάνω, το 4.55% των ερωτηθέντων μαθητών πηγαίνουν στο Γυμνάσιο ενώ 47.48% αυτών φοιτούν στο Λύκειο ( για το 11.97% των μαθητών του δείγματος
ΙΙ. ΑΝΑΛΥΣΗ ΔΕΔΟΜΕΝΩΝ. Α. Γενικά στοιχεία. Όπως φαίνεται παραπάνω, το 4.55% των ερωτηθέντων μαθητών πηγαίνουν στο Γυμνάσιο ενώ 47.48% αυτών φοιτούν στο Λύκειο ( για το 11.97% των μαθητών του δείγματος
Ενδεικτικές ασκήσεις ΔΙΠ 50
 Ενδεικτικές ασκήσεις ΔΙΠ 50 Άσκηση 1 (άσκηση 1 1 ης εργασίας 2009-10) Σε ένα ράφι μιας βιβλιοθήκης τοποθετούνται με τυχαία σειρά 11 διαφορετικά βιβλία τεσσάρων θεματικών ενοτήτων. Πιο συγκεκριμένα, υπάρχουν
Ενδεικτικές ασκήσεις ΔΙΠ 50 Άσκηση 1 (άσκηση 1 1 ης εργασίας 2009-10) Σε ένα ράφι μιας βιβλιοθήκης τοποθετούνται με τυχαία σειρά 11 διαφορετικά βιβλία τεσσάρων θεματικών ενοτήτων. Πιο συγκεκριμένα, υπάρχουν
1-3 10 1-3 6 3-5 40 3-5 30 5-7 20 5-7 20 7-9 20 7-9 30 9-11 8 9-11 10 11-13 2 11-13 4 Σύνολο 100 Σύνολο 100
 1. (Εξεταστ. Φεβ. 2004) Μια µεγάλη εταιρία θέλει να εξετάσει εάν το εκπαιδευτικό πρόγραµµα που ακολουθήσανε οι 100 πωλητές της ήταν αποτελεσµατικό (δηλαδή εάν αυξήθηκαν οι πωλήσεις). Οι δύο παρακάτω πίνακες
1. (Εξεταστ. Φεβ. 2004) Μια µεγάλη εταιρία θέλει να εξετάσει εάν το εκπαιδευτικό πρόγραµµα που ακολουθήσανε οι 100 πωλητές της ήταν αποτελεσµατικό (δηλαδή εάν αυξήθηκαν οι πωλήσεις). Οι δύο παρακάτω πίνακες
Δυνάμεις Φυσικών Αριθμών
 Δυνάμεις Φυσικών Αριθμών TINΑ ΒΡΕΝΤΖΟΥ www.ma8eno.gr www.ma8eno.gr Σελίδα 1 Δυνάμεις φυσικών αριθμών Δύναμη ονομάζουμε το γινόμενο πολλών ίσων παραγόντων Πχ: 8 8= 64, 4 4 4= 64, 3 3 3 3= 81. Έτσι, το γινόμενο
Δυνάμεις Φυσικών Αριθμών TINΑ ΒΡΕΝΤΖΟΥ www.ma8eno.gr www.ma8eno.gr Σελίδα 1 Δυνάμεις φυσικών αριθμών Δύναμη ονομάζουμε το γινόμενο πολλών ίσων παραγόντων Πχ: 8 8= 64, 4 4 4= 64, 3 3 3 3= 81. Έτσι, το γινόμενο
σ = και σ = 4 αντιστοίχως. Τότε θα ισχύει
 Θέματα ομάδας A 1. Σε κάποιο πείραμα τύχης μία τυχαία μεταβλητή λαμβάνει τις τιμές = 10 και = 10. Τότε η μέση τιμή x της θα είναι α. 10 β. 10 γ.,5 10 δ. 19,5 10 1= 10, = 10,. Δυο τυχαίες μεταβλητές, ακολουθούν
Θέματα ομάδας A 1. Σε κάποιο πείραμα τύχης μία τυχαία μεταβλητή λαμβάνει τις τιμές = 10 και = 10. Τότε η μέση τιμή x της θα είναι α. 10 β. 10 γ.,5 10 δ. 19,5 10 1= 10, = 10,. Δυο τυχαίες μεταβλητές, ακολουθούν
ΓΕΝΙΚΟ ΛΥΚΕΙΟ Λ. ΑΙΔΗΨΟΥ ΣΧΟΛ. ΕΤΟΣ ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΠΕΡΙΟΔΟΥ ΜΑΪΟΥ ΙΟΥΝΙΟΥ ΑΛΓΕΒΡΑ Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ
 ΓΕΝΙΚΟ ΛΥΚΕΙΟ Λ. ΑΙΔΗΨΟΥ ΣΧΟΛ. ΕΤΟΣ 01-013 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΠΕΡΙΟΔΟΥ ΜΑΪΟΥ ΙΟΥΝΙΟΥ ΑΛΓΕΒΡΑ Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Θέμα 1 ο Α. Έστω a ένας πραγματικός αριθμός. Να δώσετε τον ορισμό της απόλυτης
ΓΕΝΙΚΟ ΛΥΚΕΙΟ Λ. ΑΙΔΗΨΟΥ ΣΧΟΛ. ΕΤΟΣ 01-013 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΠΕΡΙΟΔΟΥ ΜΑΪΟΥ ΙΟΥΝΙΟΥ ΑΛΓΕΒΡΑ Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Θέμα 1 ο Α. Έστω a ένας πραγματικός αριθμός. Να δώσετε τον ορισμό της απόλυτης
Στατιστική. Βασικές έννοιες
 Στατιστική Βασικές έννοιες Τι είναι Στατιστική; ή μήπως είναι: Στατιστική είναι ο κλάδος των εφαρμοσμένων επιστημών, η οποία βασίζεται σ ένα σύνολο αρχών και μεθοδολογιών που έχουν σκοπό: Το σχεδιασμό
Στατιστική Βασικές έννοιες Τι είναι Στατιστική; ή μήπως είναι: Στατιστική είναι ο κλάδος των εφαρμοσμένων επιστημών, η οποία βασίζεται σ ένα σύνολο αρχών και μεθοδολογιών που έχουν σκοπό: Το σχεδιασμό
ΠΑΝΕΠΙΣΤΗΜΙΑΚΑ ΦΡΟΝΤΙΣΤΗΡΙΑ ΚΟΛΛΙΝΤΖΑ. Ερωτήσεις πολλαπλής επιλογής. Συντάκτης: Δημήτριος Κρέτσης
 ΠΑΝΕΠΙΣΤΗΜΙΑΚΑ ΦΡΟΝΤΙΣΤΗΡΙΑ ΚΟΛΛΙΝΤΖΑ Ερωτήσεις πολλαπλής επιλογής Συντάκτης: Δημήτριος Κρέτσης 1. Ο κλάδος της περιγραφικής Στατιστικής: α. Ασχολείται με την επεξεργασία των δεδομένων και την ανάλυση
ΠΑΝΕΠΙΣΤΗΜΙΑΚΑ ΦΡΟΝΤΙΣΤΗΡΙΑ ΚΟΛΛΙΝΤΖΑ Ερωτήσεις πολλαπλής επιλογής Συντάκτης: Δημήτριος Κρέτσης 1. Ο κλάδος της περιγραφικής Στατιστικής: α. Ασχολείται με την επεξεργασία των δεδομένων και την ανάλυση
3 ΠΙΘΑΝΟΤΗΤΕΣ. ο δειγματικός χώρος του πειράματος θα είναι το σύνολο: Ω = ω, ω,..., ω }.
 3 ΠΙΘΑΝΟΤΗΤΕΣ 3.1 ΔΕΙΓΜΑΤΙΚΟΣ ΧΡΟΣ - ΕΝΔΕΧΟΜΕΝΑ Πείραμα Τύχης Ένα πείραμα του οποίου δεν μπορούμε εκ των προτέρων να προβλέψουμε το αποτέλεσμα, μολονότι επαναλαμβάνεται φαινομενικά τουλάχιστον κάτω από
3 ΠΙΘΑΝΟΤΗΤΕΣ 3.1 ΔΕΙΓΜΑΤΙΚΟΣ ΧΡΟΣ - ΕΝΔΕΧΟΜΕΝΑ Πείραμα Τύχης Ένα πείραμα του οποίου δεν μπορούμε εκ των προτέρων να προβλέψουμε το αποτέλεσμα, μολονότι επαναλαμβάνεται φαινομενικά τουλάχιστον κάτω από
