3o ΕΡΓΑΣΤΗΡΙΟ. Αλλάζοντας τα πλάτη κάθε φορά και υπολογίζοντας τις διαστάσεις(επιφάνεια,εμβαδό) κάθε τρανζίστορ προκύπτει ότι:
|
|
|
- Μένθη Κοντολέων
- 8 χρόνια πριν
- Προβολές:
Transcript
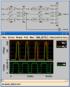
1 ΔΗΜΗΤΡΙΟΣ ΓΡΕΑΣΙΔΗΣ ΑΜ:1624 3o ΕΡΓΑΣΤΗΡΙΟ ΑΣΚΗΣΗ 3.1: Αλλάζοντας τα πλάτη κάθε φορά και υπολογίζοντας τις διαστάσεις(επιφάνεια,εμβαδό) κάθε τρανζίστορ προκύπτει ότι: α) NMOS W=3.2u, L=0.25u, AD= AS = 16p, PD=PS= Wn + 2LD = =13.2u PMOS W=16u, L=0.25u, AD=AS = 80p, PD=PS = Wp + 2LD = *5 = 26u Αλλαγές για το nmos: Wn=3.2u ADn = Wn*LD = 3.2u*5u=16p = ASn, PDn= Wp+2*LD 3.2u+2*5u=13.2u=PSn Αλλαγές για το pmos: Kn/Kp=1 => K n/k p * Wp/Wn=1 => Wp =5*Wn= 16u ADp=Wp*LD =16u*5u=80p =ASp,PDp=16u+2*5u=26u=PSp *Inverter propagation delay (Wn = 3.2) M NMOS W=3.2u L=0.25u AD=16p AS=16p PD=13.2u PS=13.2u M PMOS W=16u L=0.25u AD=80p AS=80p PD=26u PS=26u CLx p
2 3.0V 2.0V 1.0V 0V -1.0V 0s 1ns 2ns 3ns 4ns 5ns 6ns 7ns 8ns 9ns 10ns V(1) V(2) Time β) NMOS W=6u, L=0.25u, AD = AS = 30p, PD =PS= 16u PMOS W=30u, L=0.25u, AD =AS = 150p, PD =PS = Wp + 2 LD = 40u Αλλαγές για το nmos: Wn=6u ADn = Wn*LD = 6u*5u=30p = ASn, PDn= Wp+2*LD 6u+2*5u=16u=PSn Αλλαγές για το pmos: Kn/Kp=1 => K n/k p * Wp/Wn=1 => Wp =5*Wn= 30u
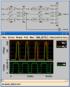
3 ADp=Wp*Lp =30u*5u=150p =ASp, PDp= Wp+2*LD=30u+2*5u=40u=PSp *Inverter propagation delay (Wn = 6) M NMOS W=6u L=0.25u AD=30p AS=30p PD=16u PS=16u M PMOS W=30u L=0.25u AD=150p AS=150p PD=40u PS=40u CLx p 3.0V 2.0V 1.0V 0V -1.0V 0s 1ns 2ns 3ns 4ns 5ns 6ns 7ns 8ns 9ns 10ns V(1) V(2) Time
4 γ) NMOS W=10u, L=0.25u, AD = AS = 50p, PD =PS= 20u PMOS W=50u, L=0.25u, AD =AS = 250p, PD =PS =60u Αλλαγές για το nmos: Wn=10u ADn = Wn*Ln = 10u*5u=50p = ASn, PDn=Wn+2*LD = 10u+2*5u=20u=PSn Αλλαγές για το pmos: Kn/Kp=1 => K n/k p * Wp/Wn=1 => Wp =5*Wn= 50u ADp=Wp*Lp =50u*5u=250p =ASp, PDp=Wp+2*LD= 50u+2*5u=60u=PSp *Inverter propagation delay (Wn = 10) M NMOS W=10u L=0.25u AD=50p AS=50p PD=20u PS=20u M PMOS W=50u L=0.25u AD=250p AS=250p PD=60u PS=60u CLx p Vdd 3 0 DC 3.3 Vin 1 0 PULSE ( n 0.5n 5n 10n)
5 4.0V 2.0V 0V -2.0V 0s 1ns 2ns 3ns 4ns 5ns 6ns 7ns 8ns 9ns 10ns V(1) V(2) Time δ) NMOS W=20u, L=0.25u, AD = AS = 100p, PD =PS= 30u PMOS W=100u, L=0.25u, AD =AS = 500p, PD =PS = 110u Αλλαγές για το nmos: Wn=20u ADn = Wn*Ln=20u*5u=100p=ASn, PDn= Wn+2LD= 20u+2*5u=30u=PSn Αλλαγές για το pmos: Kn/Kp=1 => K n/k p * Wp/Wn=1 => Wp =5*Wn= 100u ADp=Wp*Lp =100u*5u=500p =ASp, PDp=100u+2*5u=110u=PSp *Inverter propagation delay (Wn = 20) M NMOS W=20u L=0.25u AD=100p AS=100p PD=30u PS=30u M PMOS W=100u L=0.25u AD=500p AS=500p PD=110u PS=110u CLx p
6 3.0V 2.0V 1.0V 0V -1.0V 0s 1ns 2ns 3ns 4ns 5ns 6ns 7ns 8ns 9ns 10ns V(1) V(2) V(1) V(2) Time Παρατηρώ ότι όσο αυξάνονται τα πλάτη των τρανζιστορ αυξάνονται και τα tplh και tphl (που είναι ίσα λόγω συμμετρίας)μειώνονται κάθε φορά. Αυτό παρατηρείται πιο εύκολα στο παρακάτω κοινό γραφημα
7 ΚΟΙΝΟ ΓΡΑΦΗΜΑ 4.0V 2.0V 0V -2.0V 0s 1ns 2ns 3ns 4ns 5ns 6ns 7ns 8ns 9ns 10ns V(1) V(2) Time Η μείωση της καθυστέρησης ανόδου και καθόδου επιτυγχάνεται διότι όσο μεγαλύτερα ειναι τα τρανζίστρορ τόσο πιο ισχυρά γίνονται τα τρανζίστορ του συμμετρικού αντιστροφέα και παρατηρείται αύξηση της κατανάλωσης ισχύος αυτού που φορτίζει από τον αντιστροφέα αλλα και αυξηση της ταχύτητας.δηλαδή όταν αυξάνεται το πλάτος του τρανζίστορ, η εσωτερική χωριτηκότητα επικρατεί των Cg (ext) και C wire, με αποτέλεσμα την πτώση του ρυθμού μείωσης της καθυστέρησης. Αυτό συμβαίνει εξαιτίας του φαινομένου της αυτοφόρτωσης.
8 ΑΣΚΗΣΗ 3.2: Στην άσκηση εχουν χρησιμοπιηθεί πλάτη Wn=1Χu,2Χu,3Χu 20Χu. ΚΩΔΙΚΕΣ: *Inverter propagation delay(wn=2x) M NMOS W=4u L=0.25u AD=20p AS=20p PD=14u PS=14u M PMOS W=20u L=0.25u AD=100p AS=100p PD=30u PS=30u *Inverter propagation delay(wn=3x) M NMOS W=6u L=0.25u AD=30p AS=30p PD=16u PS=16u M PMOS W=30u L=0.25u AD=150p AS=150p PD=40u PS=40u
9 *Inverter propagation delay(wn=4x) M NMOS W=8u L=0.25u AD=40p AS=40p PD=18u PS=18u M PMOS W=40u L=0.25u AD=200p AS=200p PD=50u PS=50u
10 *Inverter propagation delay(wn=5x) M NMOS W=10u L=0.25u AD=50p AS=50p PD=20u PS=20u M PMOS W=50u L=0.25u AD=250p AS=250p PD=60u PS=60u *Inverter propagation delay(wn=6x) M NMOS W=12u L=0.25u AD=60p AS=60p PD=22u PS=22u M PMOS W=60u L=0.25u AD=300p AS=300p PD=70u PS=70u.TRAN 0.001n 10
11 *Inverter propagation delay(wn=7x) M NMOS W=14u L=0.25u AD=70p AS=70p PD=24u PS=24u M PMOS W=70u L=0.25u AD=350p AS=350p PD=80u PS=80u *Inverter propagation delay(wn=8x) M NMOS W=16u L=0.25u AD=80p AS=80p PD=26u PS=26u
12 M PMOS W=80u L=0.25u AD=400p AS=400p PD=90u PS=90u *Inverter propagation delay(wn=9x) M NMOS W=18u L=0.25u AD=90p AS=90p PD=28u PS=28u M PMOS W=90u L=0.25u AD=450p AS=450p PD=100u PS=100u
13 *Inverter propagation delay(wn=10x) M NMOS W=20u L=0.25u AD=100p AS=100p PD=30u PS=30u M PMOS W=100u L=0.25u AD=500p AS=500p PD=110u PS=110u *Inverter propagation delay(wn=11x) M NMOS W=22u L=0.25u AD=110p AS=110p PD=32u PS=32u M PMOS W=110u L=0.25u AD=550p AS=550p PD=120u PS=120u
14 *Inverter propagation delay(wn=12x) M NMOS W=24u L=0.25u AD=120p AS=120p PD=34u PS=34u M PMOS W=120u L=0.25u AD=600p AS=600p PD=130u PS=130u *Inverter propagation delay(wn=13x) M NMOS W=26u L=0.25u AD=130p AS=130p PD=36u PS=36u M PMOS W=130u L=0.25u AD=650p AS=650p PD=140u PS=140u
15 *Inverter propagation delay(wn=14x) M NMOS W=28u L=0.25u AD=140p AS=140p PD=38u PS=38u M PMOS W=140u L=0.25u AD=700p AS=700p PD=150u PS=150u *Inverter propagation delay(wn=15x) M NMOS W=30u L=0.25u AD=150p AS=150p PD=40u PS=40u
16 M PMOS W=150u L=0.25u AD=750p AS=750p PD=160u PS=160u *Inverter propagation delay(wn=16x) M NMOS W=32u L=0.25u AD=160p AS=160p PD=42u PS=42u M PMOS W=160u L=0.25u AD=800p AS=800p PD=170u PS=170u
17 *Inverter propagation delay(wn=17x) M NMOS W=34u L=0.25u AD=170p AS=170p PD=44u PS=44u M PMOS W=170u L=0.25u AD=850p AS=850p PD=180u PS=180u *Inverter propagation delay(wn=18x) M NMOS W=36u L=0.25u AD=180p AS=180p PD=46u PS=46u M PMOS W=180u L=0.25u AD=900p AS=900p PD=190u PS=190u
18 *Inverter propagation delay(wn=19x) M NMOS W=38u L=0.25u AD=190p AS=190p PD=48u PS=48u M PMOS W=190u L=0.25u AD=950p AS=950p PD=200u PS=200u *Inverter propagation delay(wn=20x) M NMOS W=40u L=0.25u AD=200p AS=200p PD=50u PS=50u M PMOS W=200u L=0.25u AD=1000p AS=1000p PD=210u PS=210u
19 Επειδή πρόκειται για συμμετρικό αντιστροφέα θα ισχύει ότι tphl =tplh, άρα αρκεί να υπολογίσω μόνο το ένα εκ των δύο: tphl(2 ου αντιστροφέα)=[ CL/ (Kn* (VDD-VTn) ) ]*[ 2*VTn/(VDD-VTn)+ ln( (4* (VDD-VTn)/VDD)-1) ]= ((4,171248*10^ ,81211 * 10^-3) / (20, * 10^-4)) * 1,118 όπου : CL=Cg + CJ+Cwire =4.2 *10^ ,81211 * 10^-3 Cg=(eox/tox)*L*(Wn+Wp)=eox/(50.92)*10^(-9) +0.25*(4+20)= 4.2 *10^-21 = Cg = CLX = εξωτερική για τον 2Χ αντιστροφέα. Ομοίως βγαίνει για τον 3Χ αντιστροφέα, για τον 4Χ αντιστροφέα κ.ο.κ μέχρι και τον 20Χ αντιστροφέα, απλά αλλάζοντας τα αντίστοιχα πλάτη. Cj=Cjar+Cjsw=Cjar(nMos) + Cjsw(nMos) + Cjar(pMos) + Cjsw(pMos)= Cjar *wn*ld + Cjsw *(wn+2*ld) + Cjar *wp*ld + Cjsw *(wp+2*ld) =1,81211 * 10^-3 (χωρητικότητα του 1 ου cmos=1x) Kn= (Kn' * Wn)/L= (2.5*10^-4 * 2*10^-6 ) / 0.25*10^-6= *10^-4 (απο το μοντέλο του tsmc στο nmos στο πεδίο KP)
20 Στην συνέχεια για τον 3Χ αντιστροφέα(wn=6,wp=30), θα διαιρέσω την καθυστέρηση του βασικού αντιστροφέα με 2 και κάθε επόμενη καθυστέρηση θα ισούται με το πηλίκο της καθυστέρησης του βασικού αντιστροφέα/i,όπου i=3,4,5, 19,δηλαδή: Tphl3=tplh3 = tphl2/2 Tphl4=tplh4= Tphl2/3 Tphl5=tplh5= Tphl2/4 Tphl6=tplh6= Tphl2/5 Tphl7=tplh7= Tphl2/6 Tphl8=tplh8= Tphl2/7 Tphl9=tplh9= Tphl2/8 Tphl10=tplh10= Tphl2/9 Tphl11=tplh11= Tphl2/10 Tphl12=tplh12= Tphl2/11 Tphl13=tplh13= Tphl2/12 Tphl14=tplh14= Tphl2/13 Tphl15=tplh15= Tphl2/14 Tphl16=tplh16= Tphl2/15 Tphl17=tplh17= Tphl2/16 Tphl18=tplh18= Tphl2/17 Tphl19=tplh19= Tphl2/18 Tphl20=tplh20= Tphl2/19
21 ΕΝΟΤΗΤΑ 4(Άσκηση 1) Οι τύποι που θα χρησιμοποιήσουμε: l l R Rsq t w w C C pplw 2C ff l Για μια μεμονωμένη (ομοιόμορφη) γραμμή πολυπυριτίου πάνω από υπόστρωμα: l 1000 m w 4 m R sq 30 / sq C pp ff / m 2 C ff = ff/μm R 7. 5 k C 356 ff Για Ν = 2 έχουμε διπλάσιο μήκος, άρα l = 2000μm, το πλάτος παραμένει το ίδιο, w = 4μm. H αντίσταση φύλλου και οι τιμές χωρητικότητας επιφάνειας και περιφέρειας παραμένουν οι ίδιες. Από τους τύπους έχουμε ότι : R = 15 Ω / sq, C = 712 ff Όμοια για Ν=3 : R = 22.5 Ω / sq, C = 1068 ff Ν=4 : R = 30 Ω / sq, C = 1424 ff Ν=5 : R = 37.5 Ω / sq, C = 1780 ff (Χρησιμοποιούμε το επάνω σχήμα με την συνολίκη αντίσταση και χωρητικότητα καθώς μας δίνει το ίδιο αποτέλεσμα και ο κώδικας στο spice είναι μικρότερος.) Οι αντίστοιχοι κώδικες με τις γραφικές παραστάσεις
22 Ν=2 *Interconnection delay analysis R k C p Vin 1 0 PULSE (0 3 20n n 80n).TRAN 0.001n 80n Ν=3 *Interconnection delay analysis R k C p Vin 1 0 PULSE (0 3 20n n 80n).TRAN 0.001n 80n Ν=4
23 *Interconnection delay analysis R k C p Vin 1 0 PULSE (0 3 20n n 80n).TRAN 0.001n 80n Ν=5 *Interconnection delay analysis R k C p Vin 1 0 PULSE (0 3 20n n 80n).TRAN 0.001n 80n
24 Το κοινό διάγραμμα από τα simulations Βλέπουμε πως όσο αυξάνεται το Ν (κατ' επέκταση όσο αυξάνεται το R και το C) η μέγιστη τιμή του V μειώνεται οπώς και η κλίση της σε σχέση με το χρόνο. Για Ν να τίνει στο άπειρο βλέπουμε πως η τιμή συγκλίνει περίπου στα 0.7V. Βλέπουμε πως το βέλτιστο ποιοτικά είναι για Ν=4. ΕΝΟΤΗΤΑ 5(Άσκηση 1) Ν=4 l 5000 m R wire / m C wire =0.1 ff /μm t plh? t phl? *Fanout-of-4 (FO4) inverter delay (for a realistic inverter).subckt rcline 1 2 PARAMS: l=5000 Rw=0.075 Cw=0.1f R1 1 3 {Rw*l/3} R2 3 4 {Rw*l/3} R3 4 2 {Rw*l/3} C1 1 0 {Cw*l/6} C2 3 0 {Cw*l/3} C3 4 0 {Cw*l/3} C4 2 0 {Cw*l/6} S.SUBCKT inv PARAMS: Wn=1u Wp=2u M NMOS W={Wn} L=0.25u AD={Wn*5u} AS={Wn*5u} PD={2*Wn+10u} PS={2*Wn+10u} M PMOS W={Wp} L=0.25u AD={Wp*5u} AS={Wp*5u} PD={2*Wp+10u} PS={2*Wp+10u} S Vdd 99 0 DC 1.8 Vin 1 0 PULSE p 0p 0p 5n 10n X inv PARAMS: Wn=1u Wp=2u X inv PARAMS: Wn=4u Wp=8u X inv PARAMS: Wn=16u Wp=32u X5 4 5 rcline PARAMS: l=5000 Rw=4.8 Cw=6.4f X inv PARAMS: Wn=64u Wp=128u.INC tsmc025.sp.temp 70.TRAN 1p 10n.PROBE V(3) V(5)
25
ADn = Wn*LD = 3.2u*5u=16p = ASn, PDn= Wp+2*LD 3.2u+2*5u=13.2u=PSn
 Ονοματεπώνυμο: Παπαναστασίου Στέφανος Username: stepapan AEM: 1608 Έτος: 2 Άσκηση 3.1 E ισαγωγή στην ηλεκτρονική - LAB3 a)nmos W=3.2u, L=0.25u, AD= AS = 16p, PD=PS= Wn + 2LD = 3.2+10 =13.2u PMOS W=16u,
Ονοματεπώνυμο: Παπαναστασίου Στέφανος Username: stepapan AEM: 1608 Έτος: 2 Άσκηση 3.1 E ισαγωγή στην ηλεκτρονική - LAB3 a)nmos W=3.2u, L=0.25u, AD= AS = 16p, PD=PS= Wn + 2LD = 3.2+10 =13.2u PMOS W=16u,
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΗΛΕΚΤΡΟΝΙΚΗ ΕΡΓΑΣΙΑ 4 ΕΠΙΘΕΤΟ : ΓΡΕΑΣΙΔΗΣ. ΟΝΟΜΑ : ΔΗΜΗΤΡΗΣ ΑΕΜ : 1624 ΕΤΟΣ : 2 ο
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΗΛΕΚΤΡΟΝΙΚΗ ΕΡΓΑΣΙΑ 4 ΕΠΙΘΕΤΟ : ΓΡΕΑΣΙΔΗΣ ΟΝΟΜΑ : ΔΗΜΗΤΡΗΣ ΑΕΜ : 1624 ΕΤΟΣ : 2 ο ΕΝΟΤΗΤΑ 6 ΑΣΚΗΣΗ 1 Οι καθυστερήσεις για κάθε simulation βγαίνουν με τον εξής τρόπο: αρχικά πηγαίνουμε σε ύψος
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΗΛΕΚΤΡΟΝΙΚΗ ΕΡΓΑΣΙΑ 4 ΕΠΙΘΕΤΟ : ΓΡΕΑΣΙΔΗΣ ΟΝΟΜΑ : ΔΗΜΗΤΡΗΣ ΑΕΜ : 1624 ΕΤΟΣ : 2 ο ΕΝΟΤΗΤΑ 6 ΑΣΚΗΣΗ 1 Οι καθυστερήσεις για κάθε simulation βγαίνουν με τον εξής τρόπο: αρχικά πηγαίνουμε σε ύψος
ΔΗΜΗΤΡΗΣ ΓΡΕΑΣΙΔΗΣ ΑΕΜ: 1624
 ΗΛΕΚΤΡΟΝΙΚΗ 1 - ΕΡΓΑΣΙΑ 2 ΔΗΜΗΤΡΗΣ ΓΡΕΑΣΙΔΗΣ ΑΕΜ: 1624 ΕΤΟΣ: 2ο -12- ΑΣΚΗΣΗ 1 Για τεχνολογία TSMC 0.25μm έχω: Υπολογισμός πλάτους ώστε k n /k p = 1 Υπολογισμός πλάτους ώστε k n /k p = 0.25 Υπολογισμός
ΗΛΕΚΤΡΟΝΙΚΗ 1 - ΕΡΓΑΣΙΑ 2 ΔΗΜΗΤΡΗΣ ΓΡΕΑΣΙΔΗΣ ΑΕΜ: 1624 ΕΤΟΣ: 2ο -12- ΑΣΚΗΣΗ 1 Για τεχνολογία TSMC 0.25μm έχω: Υπολογισμός πλάτους ώστε k n /k p = 1 Υπολογισμός πλάτους ώστε k n /k p = 0.25 Υπολογισμός
5 η διάλεξη Ο Αντιστροφέας και οι ιδιότητες του
 5 η διάλεξη Ο Αντιστροφέας και οι ιδιότητες του 1 2 3 Το παραπάνω σχήμα επιδεικνύει το σχηματικό του αντιστροφέα, ο οποίος είναι το πιο θεμελιώδες ηλεκτρονικό, ψηφιακό κύκλωμα. Ο παραπάνω αντιστροφέας
5 η διάλεξη Ο Αντιστροφέας και οι ιδιότητες του 1 2 3 Το παραπάνω σχήμα επιδεικνύει το σχηματικό του αντιστροφέα, ο οποίος είναι το πιο θεμελιώδες ηλεκτρονικό, ψηφιακό κύκλωμα. Ο παραπάνω αντιστροφέας
Επιµέλεια διαφανειών:. Μπακάλης. Πριν την εξοµοίωση Σχεδίαση. Εξοµοίωση CMOS VLSI κυκλωµάτων 2
 Εξοµοίωση CMOS VLSI κυκλωµάτων µε IRSIM και HSPICE Επιµέλεια διαφανειών:. Μπακάλης Πριν την εξοµοίωση Σχεδίαση Εξοµοίωση CMOS VLSI κυκλωµάτων 2 IRSIM Βήµα 1ο: Σχεδίαση layout µε τη βοήθεια του Magic >
Εξοµοίωση CMOS VLSI κυκλωµάτων µε IRSIM και HSPICE Επιµέλεια διαφανειών:. Μπακάλης Πριν την εξοµοίωση Σχεδίαση Εξοµοίωση CMOS VLSI κυκλωµάτων 2 IRSIM Βήµα 1ο: Σχεδίαση layout µε τη βοήθεια του Magic >
Καθυστέρηση στατικών πυλών CMOS
 Καθυστέρηση στατικών πυλών CMOS Πρόχειρες σημειώσεις Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Άνοιξη 2008 Παρόλο που οι εξισώσεις των ρευμάτων των MOS τρανζίστορ μας δίνουν
Καθυστέρηση στατικών πυλών CMOS Πρόχειρες σημειώσεις Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Άνοιξη 2008 Παρόλο που οι εξισώσεις των ρευμάτων των MOS τρανζίστορ μας δίνουν
Μικροηλεκτρονική - VLSI
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 6.1: Συνδυαστική Λογική - Βασικές Πύλες Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 6.1: Συνδυαστική Λογική - Βασικές Πύλες Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
HY330 Ψηφιακά Κυκλώματα - Εισαγωγή στα Συστήματα VLSI.
 HY330 Ψηφιακά Κυκλώματα - Εισαγωγή στα Συστήματα VLSI Διδάσκων: Χ. Σωτηρίου, Βοηθοί: θα ανακοινωθούν http://inf-server.inf.uth.gr/courses/e330 1 Περιεχόμενα Διαισθητική λειτουργία Χαρακτηριστικά Αντιστροφέα
HY330 Ψηφιακά Κυκλώματα - Εισαγωγή στα Συστήματα VLSI Διδάσκων: Χ. Σωτηρίου, Βοηθοί: θα ανακοινωθούν http://inf-server.inf.uth.gr/courses/e330 1 Περιεχόμενα Διαισθητική λειτουργία Χαρακτηριστικά Αντιστροφέα
Μικροηλεκτρονική - VLSI
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 5: Αντιστροφέας CMOS Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 5: Αντιστροφέας CMOS Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες Χρήσης
ΑΣΚΗΣΗ 7. ΘΕΜΑ 1ο MINORITY A B C. C out
 ΑΣΚΗΣΗ 7 ΘΕΜΑ 1ο MINORITY A B C C out S S C out C OUT = MAJ(A,B,C) = Majority(A,B,C) = 1 when at least 2 (majority) of A, B, and C are equal to 1. Opposite Minority MAJ(A,B,C) = AB + BC + AC (PMOS and
ΑΣΚΗΣΗ 7 ΘΕΜΑ 1ο MINORITY A B C C out S S C out C OUT = MAJ(A,B,C) = Majority(A,B,C) = 1 when at least 2 (majority) of A, B, and C are equal to 1. Opposite Minority MAJ(A,B,C) = AB + BC + AC (PMOS and
Εργαστηριακή άσκηση. Θεωρητικός και πρακτικός υπολογισμός καθυστερήσεων σε αναστροφείς CMOS VLSI
 Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Υ52 Σχεδίαση Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων 6: Ταχύτητα Κατανάλωση Ανοχή στον Θόρυβο
 Υ52 Σχεδίαση Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων 6: Ταχύτητα Κατανάλωση Ανοχή στον Θόρυβο Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Εισαγωγή
Υ52 Σχεδίαση Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων 6: Ταχύτητα Κατανάλωση Ανοχή στον Θόρυβο Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Εισαγωγή
Καθυστέρηση αντιστροφέα και λογικών πυλών CMOS. Εισαγωγή στην Ηλεκτρονική
 Καθυστέρηση αντιστροφέα και λογικών πυλών MOS Εισαγωγή στην Ηλεκτρονική Ορισµοί καθυστέρησης λογικών πυλών MOS Καθυστερήσεις διάδοσης (propagaion delays) εισόδουεξόδου: Καθυστέρηση ανόδου ph : η διαφορά
Καθυστέρηση αντιστροφέα και λογικών πυλών MOS Εισαγωγή στην Ηλεκτρονική Ορισµοί καθυστέρησης λογικών πυλών MOS Καθυστερήσεις διάδοσης (propagaion delays) εισόδουεξόδου: Καθυστέρηση ανόδου ph : η διαφορά
Πολυσύνθετες πύλες. Διάλεξη 11
 Πολυσύνθετες πύλες NMOS και CMOS Διάλεξη 11 Δομή της διάλεξης Εισαγωγή ΗσύνθετηλογικήNMOS ΗσύνθετηλογικήCMOS Η πύλη μετάδοσης CMOS Ασκήσεις 2 Πολυσύνθετες πύλες NMOS και CMOS Εισαγωγή 3 Εισαγωγή Στη λογική
Πολυσύνθετες πύλες NMOS και CMOS Διάλεξη 11 Δομή της διάλεξης Εισαγωγή ΗσύνθετηλογικήNMOS ΗσύνθετηλογικήCMOS Η πύλη μετάδοσης CMOS Ασκήσεις 2 Πολυσύνθετες πύλες NMOS και CMOS Εισαγωγή 3 Εισαγωγή Στη λογική
V Vin $N PULSE 1.8V p 0.1p 1n 2n M M1 $N 0002 $N 0001 Vout $N 0002 MpTSMC180 + L=180n + W=720n + AD=0.324p + AS=0.
 Εργασία Μικροηλεκτρονικής 2013-2014 Θέμα: Σχεδίαση και Ανάλυση CMOS Αντιστροφέα και CMOS Λογικών Κυκλωμάτων στο SPICE Ονοματεπώνυμο: Αλέξανδρος Γεώργιος Μουντογιαννάκης Σχολή: Τμήμα Επιστήμης Υπολογιστών
Εργασία Μικροηλεκτρονικής 2013-2014 Θέμα: Σχεδίαση και Ανάλυση CMOS Αντιστροφέα και CMOS Λογικών Κυκλωμάτων στο SPICE Ονοματεπώνυμο: Αλέξανδρος Γεώργιος Μουντογιαννάκης Σχολή: Τμήμα Επιστήμης Υπολογιστών
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 3 η Εργαστηριακή Άσκηση
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 3 η Εργαστηριακή Άσκηση Μελέτη της Κατανάλωσης Ενέργειας και Φυσικός Σχεδιασμός Πυλών CMOS Πολύπλοκης Λογικής Άδειες Χρήσης Το παρόν υλικό διατίθεται με τους
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 3 η Εργαστηριακή Άσκηση Μελέτη της Κατανάλωσης Ενέργειας και Φυσικός Σχεδιασμός Πυλών CMOS Πολύπλοκης Λογικής Άδειες Χρήσης Το παρόν υλικό διατίθεται με τους
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ. Δρ. Δ. Λαμπάκης (10 η σειρά διαφανειών)
 ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (10 η σειρά διαφανειών) Σχεδιασμός και Προσομοίωση Βασικών Κυκλωμάτων Τεχνολογίας CMOS Με βάση το εργαλείο σχεδιασμού Microwind Σκοπός: η
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (10 η σειρά διαφανειών) Σχεδιασμός και Προσομοίωση Βασικών Κυκλωμάτων Τεχνολογίας CMOS Με βάση το εργαλείο σχεδιασμού Microwind Σκοπός: η
ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Διδάσκοντες:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Διδάσκοντες:
Υ52 Σχεδίαση Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων. Δεληγιαννίδης Σταύρος Φυσικός, MsC in Microelectronic Design
 Υ52 Σχεδίαση Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων Δεληγιαννίδης Σταύρος Φυσικός, MsC in Microelectronic Design TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής Τ.Ε.
Υ52 Σχεδίαση Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων Δεληγιαννίδης Σταύρος Φυσικός, MsC in Microelectronic Design TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής Τ.Ε.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ - ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΩΝ ΕΦΑΡΜΟΓΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ - ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΕΧΝΟΛΟΓΙΑ ΠΡΟΗΓΜΕΝΩΝ ΨΗΦΙΑΚΩΝ ΚΥΚΛΩΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ - ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΕΧΝΟΛΟΓΙΑ ΠΡΟΗΓΜΕΝΩΝ ΨΗΦΙΑΚΩΝ ΚΥΚΛΩΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Εργαστήριο Ηλεκτρονικής. Ψηφιακά Ηλεκτρονικά. Οικογένειες Ολοκληρωμένων Κυκλωμάτων Ψηφιακής Λογικής
 Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Οικογένειες Ολοκληρωμένων Κυκλωμάτων Ψηφιακής Λογικής Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Περιεχόμενα Βασικά ηλεκτρικά χαρακτηριστικά
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Οικογένειες Ολοκληρωμένων Κυκλωμάτων Ψηφιακής Λογικής Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Περιεχόμενα Βασικά ηλεκτρικά χαρακτηριστικά
Δυναμική συμπεριφορά των λογικών κυκλωμάτων MOS. Διάλεξη 10
 Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Εργαστήριο Αναλογικών Κυκλωμάτων VLSI Υπεύθυνος καθηγητής Πλέσσας Φώτιος
 Εργαστήριο Αναλογικών Κυκλωμάτων VLSI Υπεύθυνος καθηγητής Πλέσσας Φώτιος Αναφορά αποτελεσμάτων εργαστηριακών μετρήσεων και μετρήσεων προσομοίωσης κυκλωμάτων εργαστηρίου Ονόματα φοιτητών ομάδας Μουστάκα
Εργαστήριο Αναλογικών Κυκλωμάτων VLSI Υπεύθυνος καθηγητής Πλέσσας Φώτιος Αναφορά αποτελεσμάτων εργαστηριακών μετρήσεων και μετρήσεων προσομοίωσης κυκλωμάτων εργαστηρίου Ονόματα φοιτητών ομάδας Μουστάκα
Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άδεια
 Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Cretive Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άδεια χρήσης άλλου τύπου, αυτή πρέπει να αναφέρεται ρητώς. ΠΕΡΙΕΧΟΜΕΝΑ:
Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Cretive Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άδεια χρήσης άλλου τύπου, αυτή πρέπει να αναφέρεται ρητώς. ΠΕΡΙΕΧΟΜΕΝΑ:
Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άδεια
 Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άδεια χρήσης άλλου τύπου, αυτή πρέπει να αναφέρεται ρητώς. 4.1
Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άδεια χρήσης άλλου τύπου, αυτή πρέπει να αναφέρεται ρητώς. 4.1
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ. Δρ. Δ. Λαμπάκης (9 η σειρά διαφανειών)
 ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (9 η σειρά διαφανειών) Διεργασίες Μικροηλεκτρονικής Τεχνολογίας, Οξείδωση, Διάχυση, Φωτολιθογραφία, Επιμετάλλωση, Εμφύτευση, Περιγραφή CMOS
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (9 η σειρά διαφανειών) Διεργασίες Μικροηλεκτρονικής Τεχνολογίας, Οξείδωση, Διάχυση, Φωτολιθογραφία, Επιμετάλλωση, Εμφύτευση, Περιγραφή CMOS
6 η διάλεξη Σχεδίαση και Υλοποίηση Συνδυαστικών Κυκλωμάτων σε επίπεδο Τρανζίστορ
 6 η διάλεξη Σχεδίαση και Υλοποίηση Συνδυαστικών Κυκλωμάτων σε επίπεδο Τρανζίστορ 1 2 Οποιοδήποτε κύκλωμα εμπεριέχει την έννοια της τρέχουσας κατάστασης είναι ακολουθιακό. Έτσι, κυκλώματα όπως ΜΠΚ, καταχωρητές,
6 η διάλεξη Σχεδίαση και Υλοποίηση Συνδυαστικών Κυκλωμάτων σε επίπεδο Τρανζίστορ 1 2 Οποιοδήποτε κύκλωμα εμπεριέχει την έννοια της τρέχουσας κατάστασης είναι ακολουθιακό. Έτσι, κυκλώματα όπως ΜΠΚ, καταχωρητές,
ΗΛΕΚΤΡΟΝΙΚΗ Ι ΔΙΑΓΡΑΜΜΑΤΑ BODE ΣΥΜΠΛΗΡΩΜΑΤΙΚΟ ΤΕΥΧΟΣ ΣΗΜΕΙΩΣΕΩΝ
 Ε. Μ. Πολυτεχνείο Εργαστήριο Ηλεκτρονικής ΗΛΕΚΤΡΟΝΙΚΗ Ι ΔΙΑΓΡΑΜΜΑΤΑ BODE ΣΥΜΠΛΗΡΩΜΑΤΙΚΟ ΤΕΥΧΟΣ ΣΗΜΕΙΩΣΕΩΝ Γ. ΠΑΠΑΝΑΝΟΣ ΠΑΡΑΡΤΗΜΑ : Συναρτήσεις Δικτύων Βασικοί ορισμοί Ας θεωρήσουμε ένα γραμμικό, χρονικά
Ε. Μ. Πολυτεχνείο Εργαστήριο Ηλεκτρονικής ΗΛΕΚΤΡΟΝΙΚΗ Ι ΔΙΑΓΡΑΜΜΑΤΑ BODE ΣΥΜΠΛΗΡΩΜΑΤΙΚΟ ΤΕΥΧΟΣ ΣΗΜΕΙΩΣΕΩΝ Γ. ΠΑΠΑΝΑΝΟΣ ΠΑΡΑΡΤΗΜΑ : Συναρτήσεις Δικτύων Βασικοί ορισμοί Ας θεωρήσουμε ένα γραμμικό, χρονικά
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 2 η Εργαστηριακή Άσκηση Μελέτη των Παρασιτικών Χωρητικοτήτων και της Καθυστέρησης στα Κυκλώματα CMOS Άδειες Χρήσης Το παρόν υλικό διατίθεται με τους όρους της
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 2 η Εργαστηριακή Άσκηση Μελέτη των Παρασιτικών Χωρητικοτήτων και της Καθυστέρησης στα Κυκλώματα CMOS Άδειες Χρήσης Το παρόν υλικό διατίθεται με τους όρους της
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗ - VLSI Ενότητα: Ο Αντιστροφέας CMOS Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. 1 Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗ - VLSI Ενότητα: Ο Αντιστροφέας CMOS Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. 1 Άδειες
Εργαστηριακή άσκηση. Κανόνες σχεδίασης και κατασκευαστικές λεπτομέρειες στη σχεδίασης μασκών (layout) και προσομοίωσης κυκλώματος VLSI
 Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗ - VLSI Ενότητα: Συνδιαστικά κυκλώματα, βασικές στατικές λογικές πύλες, σύνθετες και δυναμικές πύλες Κυριάκης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗ - VLSI Ενότητα: Συνδιαστικά κυκλώματα, βασικές στατικές λογικές πύλες, σύνθετες και δυναμικές πύλες Κυριάκης
Λογικά Κυκλώματα CMOS. Διάλεξη 5
 Λογικά Κυκλώματα CMOS Διάλεξη 5 Δομή της διάλεξης Εισαγωγή Η τεχνολογία αντιστροφέων CMOS Λειτουργία του κυκλώματος Χαρακτηριστική μεταφοράς τάσης Περιθώρια θορύβου Κατανάλωση ισχύος Οι πύλες CMOS NOR
Λογικά Κυκλώματα CMOS Διάλεξη 5 Δομή της διάλεξης Εισαγωγή Η τεχνολογία αντιστροφέων CMOS Λειτουργία του κυκλώματος Χαρακτηριστική μεταφοράς τάσης Περιθώρια θορύβου Κατανάλωση ισχύος Οι πύλες CMOS NOR
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Εργαστήριο Ηλεκτρονικής. Ψηφιακά Ηλεκτρονικά. Δίοδοι, BJT και MOSFET ως Διακόπτες 2
 Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Δίοδοι, BJT και MOSFET ως Διακόπτες Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Ιδανικός διακόπτης ΙΔΑΝΙΚΟΣ ΔΙΑΚΟΠΤΗΣ ΠΡΑΓΜΑΤΙΚΟΣ ΔΙΑΚΟΠΤΗΣ
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Δίοδοι, BJT και MOSFET ως Διακόπτες Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Ιδανικός διακόπτης ΙΔΑΝΙΚΟΣ ΔΙΑΚΟΠΤΗΣ ΠΡΑΓΜΑΤΙΚΟΣ ΔΙΑΚΟΠΤΗΣ
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης
Κεφάλαιο 4 ο. Γ. Τσιατούχας. VLSI Systems and Computer Architecture Lab. Λογικός Φόρτος 2
 ΚΥΚΛΩΜΑΤΑ VLSI Πανεπιστήμιο Ιωαννίνων Λογικός Φόρτος Κεφάλαιο 4 ο Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση. Μοντέλο γραμμικής καθυστέρησης. Λογικός και ηλεκτρικός φόρτος
ΚΥΚΛΩΜΑΤΑ VLSI Πανεπιστήμιο Ιωαννίνων Λογικός Φόρτος Κεφάλαιο 4 ο Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση. Μοντέλο γραμμικής καθυστέρησης. Λογικός και ηλεκτρικός φόρτος
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ - ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΩΝ ΕΦΑΡΜΟΓΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ - ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΕΧΝΟΛΟΓΙΑ ΠΡΟΗΓΜΕΝΩΝ ΨΗΦΙΑΚΩΝ ΚΥΚΛΩΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ - ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΕΧΝΟΛΟΓΙΑ ΠΡΟΗΓΜΕΝΩΝ ΨΗΦΙΑΚΩΝ ΚΥΚΛΩΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ
Ψηφιακή Σχεδίαση με CAD II
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ß -ß ßß Τμήμα Μηχανικών - Η/Υ, Τηλεπικοινωνιών και Δικτύων Ψηφιακή Σχεδίαση με CAD II ONOMA: ΔΙΑΜΑΝΤΑΚΗ ΜΑΡΙΑ ΑΕΜ : 1434 ΕΤΟΣ : 3 ο - ß # nmos - TSMC 0.35μm - 3.3V - 27 o C *nmos
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ß -ß ßß Τμήμα Μηχανικών - Η/Υ, Τηλεπικοινωνιών και Δικτύων Ψηφιακή Σχεδίαση με CAD II ONOMA: ΔΙΑΜΑΝΤΑΚΗ ΜΑΡΙΑ ΑΕΜ : 1434 ΕΤΟΣ : 3 ο - ß # nmos - TSMC 0.35μm - 3.3V - 27 o C *nmos
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα
απόσβεσης, με τη βοήθεια της διάταξης που φαίνεται στο διπλανό σχήμα. Η σταθερά του ελατηρίου είναι ίση με k = 45 N/m και η χρονική εξίσωση της
 1. Ένα σώμα μάζας m =, kg εκτελεί εξαναγκασμένη ταλάντωση μικρής απόσβεσης, με τη βοήθεια της διάταξης που φαίνεται στο διπλανό σχήμα. Η σταθερά του ελατηρίου είναι ίση με k = 45 N/m και η χρονική εξίσωση
1. Ένα σώμα μάζας m =, kg εκτελεί εξαναγκασμένη ταλάντωση μικρής απόσβεσης, με τη βοήθεια της διάταξης που φαίνεται στο διπλανό σχήμα. Η σταθερά του ελατηρίου είναι ίση με k = 45 N/m και η χρονική εξίσωση
ΑΣΚΗΣΗ 3 η Ο ΑΝΤΙΣΤΡΟΦΕΑΣ CMOS
 ΑΣΚΗΣΗ 3 η Ο ΑΝΤΙΣΤΡΟΦΕΑΣ CMOS ΘΕΩΡΙΑ Οι ασκήσεις 3 και 4 αφορούν τον αντιστροφέα CMOS, ο οποίος είναι η απλούστερη αλ α ταυτόχρονα και σημαντικότερη πύλη για την κατανόηση της λειτουργίας των Ολοκληρωμένων
ΑΣΚΗΣΗ 3 η Ο ΑΝΤΙΣΤΡΟΦΕΑΣ CMOS ΘΕΩΡΙΑ Οι ασκήσεις 3 και 4 αφορούν τον αντιστροφέα CMOS, ο οποίος είναι η απλούστερη αλ α ταυτόχρονα και σημαντικότερη πύλη για την κατανόηση της λειτουργίας των Ολοκληρωμένων
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ. Δρ. Δ. Λαμπάκης (2 η σειρά διαφανειών)
 ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (2 η σειρά διαφανειών) Τα ψηφιακά ηλεκτρονικά κυκλώματα χωρίζονται σε κατηγορίες ( λογικές οικογένειες ) ανάλογα με την τεχνολογία κατασκευής
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (2 η σειρά διαφανειών) Τα ψηφιακά ηλεκτρονικά κυκλώματα χωρίζονται σε κατηγορίες ( λογικές οικογένειες ) ανάλογα με την τεχνολογία κατασκευής
Ανάλυση και υλοποίηση ταλαντωτή τύπου Colpitts
 Εργασία στο μάθημα «Εργαστήριο Αναλογικών VLSI» Ανάλυση και υλοποίηση ταλαντωτή τύπου Colpitts Ομάδα Γεωργιάδης Κωνσταντίνος konsgeorg@inf.uth.gr Σκετόπουλος Νικόλαος sketopou@inf.uth.gr ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ
Εργασία στο μάθημα «Εργαστήριο Αναλογικών VLSI» Ανάλυση και υλοποίηση ταλαντωτή τύπου Colpitts Ομάδα Γεωργιάδης Κωνσταντίνος konsgeorg@inf.uth.gr Σκετόπουλος Νικόλαος sketopou@inf.uth.gr ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ
Εισαγωγή στα ψηφιακά κυκλώματα. Διάλεξη 1
 Εισαγωγή στα ψηφιακά κυκλώματα Διάλεξη 1 Δομή της διάλεξης Εισαγωγή στο Μάθημα Βασικές αρχές λογικών κυκλωμάτων Ο BJT ως διακόπτης Μεταβατικά φαινόμενα Παράδειγμα μεταβατικής λειτουργίας Ασκήσεις 2 Εισαγωγή
Εισαγωγή στα ψηφιακά κυκλώματα Διάλεξη 1 Δομή της διάλεξης Εισαγωγή στο Μάθημα Βασικές αρχές λογικών κυκλωμάτων Ο BJT ως διακόπτης Μεταβατικά φαινόμενα Παράδειγμα μεταβατικής λειτουργίας Ασκήσεις 2 Εισαγωγή
 Φόρτιση πυκνωτή μέσω αντίστασης Εάν αρχικά, η τάση στο άκρο του πυκνωτή είναι 0, τότε V DD V(t) για την τάση σε χρόνο t, V(t) θα έχουμε V t ( t ) (1 e ) V DD Αποφόρτιση πυκνωτή Εάν αρχικά, η τάση στο άκρο
Φόρτιση πυκνωτή μέσω αντίστασης Εάν αρχικά, η τάση στο άκρο του πυκνωτή είναι 0, τότε V DD V(t) για την τάση σε χρόνο t, V(t) θα έχουμε V t ( t ) (1 e ) V DD Αποφόρτιση πυκνωτή Εάν αρχικά, η τάση στο άκρο
To θετικό πρόσημο σημαίνει ότι το πεδίο προσφέρει την ενέργεια για τη μετακίνηση αυτή.
 Ασκήσεις 3 ου Κεφαλαίου, Ηλεκτρικό Δυναμικό 23.21.Δύο σημειακά φορτία q 1 =+2,4 nc q 2 =-6,5 nc βρίσκονται σε απόσταση 0,1 m το ένα από το άλλο. Το σημείο Α βρίσκεται στο μέσον της απόστασής τους και το
Ασκήσεις 3 ου Κεφαλαίου, Ηλεκτρικό Δυναμικό 23.21.Δύο σημειακά φορτία q 1 =+2,4 nc q 2 =-6,5 nc βρίσκονται σε απόσταση 0,1 m το ένα από το άλλο. Το σημείο Α βρίσκεται στο μέσον της απόστασής τους και το
HY121 Ηλεκτρικϊ Κυκλώματα
 HY Ηλεκτρικϊ Κυκλώματα Διδϊςκων: Χ. Σωτηρύου, Βοηθού: Ε. Βαςιλϊκησ, Δ. Πούλιοσ http://www.csd.uoc.gr/~hy Περιεχόμενα Στατικζσ Πφλεσ CMOS και Μεγζκθ Τρανηίςτορ Λογικι Λόγου Αντίςταςθσ/Μεγεκών (NMOS) Διαφορικι
HY Ηλεκτρικϊ Κυκλώματα Διδϊςκων: Χ. Σωτηρύου, Βοηθού: Ε. Βαςιλϊκησ, Δ. Πούλιοσ http://www.csd.uoc.gr/~hy Περιεχόμενα Στατικζσ Πφλεσ CMOS και Μεγζκθ Τρανηίςτορ Λογικι Λόγου Αντίςταςθσ/Μεγεκών (NMOS) Διαφορικι
Εργαστηριακή άσκηση. Θεωρητικός και πρακτικός υπολογισμός καθυστερήσεων σε λογικά δίκτυα πολλών σταδίων
 Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Ενότητα 3 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ
 Ενότητα 3 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ Γενικές Γραμμές Οικογένειες Ψηφιακής Λογικής Τάση τροφοδοσίας Λογικά επίπεδα - Περιθώριo θορύβου Χρόνος μετάβασης Καθυστέρηση διάδοσης Κατανάλωση ισχύος Γινόμενο
Ενότητα 3 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ Γενικές Γραμμές Οικογένειες Ψηφιακής Λογικής Τάση τροφοδοσίας Λογικά επίπεδα - Περιθώριo θορύβου Χρόνος μετάβασης Καθυστέρηση διάδοσης Κατανάλωση ισχύος Γινόμενο
1. Ιδανικό κύκλωμα LC εκτελεί ηλεκτρικές ταλαντώσεις και η χρονική εξίσωση του φορτίου του πυκνωτή
 Εισαγωγικές ασκήσεις στις ηλεκτρικές ταλαντώσεις 1. Ιδανικό κύκλωμα L εκτελεί ηλεκτρικές ταλαντώσεις και η χρονική εξίσωση του φορτίου του πυκνωτή δίνεται από τη σχέση q = 10 6 συν(10 ) (S.I.). Ο συντελεστής
Εισαγωγικές ασκήσεις στις ηλεκτρικές ταλαντώσεις 1. Ιδανικό κύκλωμα L εκτελεί ηλεκτρικές ταλαντώσεις και η χρονική εξίσωση του φορτίου του πυκνωτή δίνεται από τη σχέση q = 10 6 συν(10 ) (S.I.). Ο συντελεστής
4.2 Αναπαράσταση δυαδικών τιμών στα ψηφιακά κυκλώματα
 ΚΕΦΑΛΑΙΟ 4 ΤΕΧΝΟΛΟΓΙΕΣ ΥΛΟΠΟΙΗΣΗΣ 4.1 Εισαγωγή Για την υλοποίηση των λογικών πυλών χρησιμοποιήθηκαν αρχικά ηλεκτρονικές λυχνίες κενού και στη συνέχεια κρυσταλλοδίοδοι και διπολικά τρανζίστορ. Τα ολοκληρωμένα
ΚΕΦΑΛΑΙΟ 4 ΤΕΧΝΟΛΟΓΙΕΣ ΥΛΟΠΟΙΗΣΗΣ 4.1 Εισαγωγή Για την υλοποίηση των λογικών πυλών χρησιμοποιήθηκαν αρχικά ηλεκτρονικές λυχνίες κενού και στη συνέχεια κρυσταλλοδίοδοι και διπολικά τρανζίστορ. Τα ολοκληρωμένα
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 1 η Εργαστηριακή Άσκηση Σχεδιασμός και Προσομοίωση Βασικών Κυκλωμάτων Τεχνολογίας CMOS Άδειες Χρήσης Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 1 η Εργαστηριακή Άσκηση Σχεδιασμός και Προσομοίωση Βασικών Κυκλωμάτων Τεχνολογίας CMOS Άδειες Χρήσης Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης
Ενισχυτής κοινής πηγής (common source amplifier)
 Εισαγωγή στην Ηλεκτρονική Βασικά κυκλώµατα ενισχυτών µε transstr MOS Τµήµα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Transstr ως ενισχυτής Ενισχυτής κοινής πηγής (cmmn surce amplfer (κύκλωµα αντιστροφέα
Εισαγωγή στην Ηλεκτρονική Βασικά κυκλώµατα ενισχυτών µε transstr MOS Τµήµα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Transstr ως ενισχυτής Ενισχυτής κοινής πηγής (cmmn surce amplfer (κύκλωµα αντιστροφέα
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα
ΑΣΚΗΣΗ 2 η N-MOS ΚΑΙ P-MOS TRANSISTOR ΩΣ ΔΙΑΚΟΠΤΗΣ
 ΑΣΚΗΣΗ 2 η N-MOS ΚΑΙ P-MOS TRANSISTOR ΩΣ ΔΙΑΚΟΠΤΗΣ ΘΕΩΡΙΑ 1. Εργαλεία εξομοίωσης, SPICE, αρχεία περιγραφής κυκλωμάτων (netlist) (Παρ. 3.4, σελ 152-155) 2. To transistor ως διακόπτης, πύλη διέλευσης. (Παρ
ΑΣΚΗΣΗ 2 η N-MOS ΚΑΙ P-MOS TRANSISTOR ΩΣ ΔΙΑΚΟΠΤΗΣ ΘΕΩΡΙΑ 1. Εργαλεία εξομοίωσης, SPICE, αρχεία περιγραφής κυκλωμάτων (netlist) (Παρ. 3.4, σελ 152-155) 2. To transistor ως διακόπτης, πύλη διέλευσης. (Παρ
ΣΧΕ ΙΑΣΜΟΣ ΟΛΟΚΛΗΡΩΜΕΝΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΣΧΕ ΙΑΣΜΟΣ ΟΛΟΚΛΗΡΩΜΕΝΩΝ ΚΥΚΛΩΜΑΤΩΝ Ι ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ Λάµπρος Μπισδούνης Πάτρα 1996 ΠΕΡΙΕΧΟΜΕΝΑ 1. Σχεδιασµός και εξοµοίωση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΣΧΕ ΙΑΣΜΟΣ ΟΛΟΚΛΗΡΩΜΕΝΩΝ ΚΥΚΛΩΜΑΤΩΝ Ι ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ Λάµπρος Μπισδούνης Πάτρα 1996 ΠΕΡΙΕΧΟΜΕΝΑ 1. Σχεδιασµός και εξοµοίωση
Στατική ηλεκτρική ανάλυση του αντιστροφέα CMOS. Εισαγωγή στην Ηλεκτρονική
 Στατική ηλεκτρική ανάλυση του αντιστροφέα CMO Εισαγωγή στην Ηλεκτρονική Στατική (C) ηλεκτρική ανάλυση του αντιστροφέα CMO Θα εξάγουµε τη χαρακτηριστική τάσης = f( ) (καθώς και τη χαρακτηριστική ρεύµατος
Στατική ηλεκτρική ανάλυση του αντιστροφέα CMO Εισαγωγή στην Ηλεκτρονική Στατική (C) ηλεκτρική ανάλυση του αντιστροφέα CMO Θα εξάγουµε τη χαρακτηριστική τάσης = f( ) (καθώς και τη χαρακτηριστική ρεύµατος
Μνήμες RAM. Διάλεξη 12
 Μνήμες RAM Διάλεξη 12 Δομή της διάλεξης Εισαγωγή Κύτταρα Στατικής Μνήμης Κύτταρα Δυναμικής Μνήμης Αισθητήριοι Ενισχυτές Αποκωδικοποιητές Διευθύνσεων Ασκήσεις 2 Μνήμες RAM Εισαγωγή 3 Μνήμες RAM RAM: μνήμη
Μνήμες RAM Διάλεξη 12 Δομή της διάλεξης Εισαγωγή Κύτταρα Στατικής Μνήμης Κύτταρα Δυναμικής Μνήμης Αισθητήριοι Ενισχυτές Αποκωδικοποιητές Διευθύνσεων Ασκήσεις 2 Μνήμες RAM Εισαγωγή 3 Μνήμες RAM RAM: μνήμη
«Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο
 ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 2 η :
ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 2 η :
Σχεδίαση CMOS Ψηφιακών Ολοκληρωμένων Κυκλωμάτων
 Σχεδίαση MOS Ψηφιακών Ολοκληρωμένων Κυκλωμάτων Ενότητα 5: Γινόμενο R και υπολογισμός καθυστερήσεων σε κύκλωμα Αγγελική Αραπογιάννη Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Απεικόνιση
Σχεδίαση MOS Ψηφιακών Ολοκληρωμένων Κυκλωμάτων Ενότητα 5: Γινόμενο R και υπολογισμός καθυστερήσεων σε κύκλωμα Αγγελική Αραπογιάννη Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Απεικόνιση
Ψηφιακά Ηλεκτρονικά. Μάθηµα 3ο.. Λιούπης
 Ψηφιακά Ηλεκτρονικά Μάθηµα 3ο. Λιούπης Χαρακτηριστική καµπύλη µεταφοράς τάσης TTL V out (volts) εγγυηµένη περιοχή V OH V OH(min) V OL(max) 2.4 Ηκαµπύλη µεταφοράς εξαρτάται από τη θερµοκρασία περιβάλλοντος
Ψηφιακά Ηλεκτρονικά Μάθηµα 3ο. Λιούπης Χαρακτηριστική καµπύλη µεταφοράς τάσης TTL V out (volts) εγγυηµένη περιοχή V OH V OH(min) V OL(max) 2.4 Ηκαµπύλη µεταφοράς εξαρτάται από τη θερµοκρασία περιβάλλοντος
γ) Αν f συνεχής στο[α, β], τότε για κάθε γ Є IR ισχύει f (x)dx f (x)dx f (x)dx
![γ) Αν f συνεχής στο[α, β], τότε για κάθε γ Є IR ισχύει f (x)dx f (x)dx f (x)dx γ) Αν f συνεχής στο[α, β], τότε για κάθε γ Є IR ισχύει f (x)dx f (x)dx f (x)dx](/thumbs/62/46558215.jpg) ΘΕΜΑ A Α. Έστω μια συνάρτηση f ορισμένη σε ένα διάστημα Δ. Αν η f είναι συνεχής στο Δ και f για κάθε εσωτερικό σημείο του Δ, τότε να δείξετε ότι η f είναι σταθερή σε όλο το διάστημα Δ. Μονάδες 5 Α. Να
ΘΕΜΑ A Α. Έστω μια συνάρτηση f ορισμένη σε ένα διάστημα Δ. Αν η f είναι συνεχής στο Δ και f για κάθε εσωτερικό σημείο του Δ, τότε να δείξετε ότι η f είναι σταθερή σε όλο το διάστημα Δ. Μονάδες 5 Α. Να
Φροντιστήριο Ψηφιακών Ηλεκτρονικών
 Φροντιστήριο Ψηφιακών Ηλεκτρονικών Άσκηση 1 Μία TTL πύλη εγγυάται να τραβάει 10 ma χωρίς να ξεπεράσει το δυναμικό εξόδου VOL(max) = 0.4 Volt και να μπορεί να δώσει 5 ma χωρίς να πέσει το δυναμικό εξόδου
Φροντιστήριο Ψηφιακών Ηλεκτρονικών Άσκηση 1 Μία TTL πύλη εγγυάται να τραβάει 10 ma χωρίς να ξεπεράσει το δυναμικό εξόδου VOL(max) = 0.4 Volt και να μπορεί να δώσει 5 ma χωρίς να πέσει το δυναμικό εξόδου
Ένα σύστημα εκτελεί ελεύθερη ταλάντωση όταν διεγερθεί κατάλληλα και αφεθεί στη συνέχεια ελεύθερο να
 ΕΞΑΝΑΓΚΑΣΜΕΝΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Α. Εξαναγκασμένες μηχανικές ταλαντώσεις Ελεύθερη - αμείωτη ταλάντωση και ποια η συχνότητα και η περίοδος της. Ένα σύστημα εκτελεί ελεύθερη ταλάντωση όταν διεγερθεί κατάλληλα
ΕΞΑΝΑΓΚΑΣΜΕΝΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Α. Εξαναγκασμένες μηχανικές ταλαντώσεις Ελεύθερη - αμείωτη ταλάντωση και ποια η συχνότητα και η περίοδος της. Ένα σύστημα εκτελεί ελεύθερη ταλάντωση όταν διεγερθεί κατάλληλα
Επιπλέον, για ευκολία στις πράξεις ορίζουμε τις παρακάτω μεταβλητές
 Αναστροφέας με φορτίο Enhancement OSFE Η απλούστερη υλοποίηση OSFE αναστροφέα με ενεργό φορτίο χρησιμοποιεί δύο N-OSFES. Στην ανάλυση που ακολουθεί θα διαπιστώσουμε ότι η χαρακτηριστική μεταφοράς απέχει
Αναστροφέας με φορτίο Enhancement OSFE Η απλούστερη υλοποίηση OSFE αναστροφέα με ενεργό φορτίο χρησιμοποιεί δύο N-OSFES. Στην ανάλυση που ακολουθεί θα διαπιστώσουμε ότι η χαρακτηριστική μεταφοράς απέχει
Αποκωδικοποιητές Μνημών
 Αποκωδικοποιητές Μνημών Φθινόπωρο 2008 Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Γ. Δημητρακόπουλος ΗΥ422 1 Η χρήση των αποκωδικοποιητών Η δομή της μνήμης (για λόγους πυκνότητας)
Αποκωδικοποιητές Μνημών Φθινόπωρο 2008 Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Γ. Δημητρακόπουλος ΗΥ422 1 Η χρήση των αποκωδικοποιητών Η δομή της μνήμης (για λόγους πυκνότητας)
APEIROSTIKOS LOGISMOS I
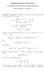 APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 3. Άσκηση : Προσδιορίστε, αν υπάρχουν, τις τιμές τού a για τις οποίες οι παρακάτω συναρτήσεις είναι συνεχείς. + +, αν >
APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 3. Άσκηση : Προσδιορίστε, αν υπάρχουν, τις τιμές τού a για τις οποίες οι παρακάτω συναρτήσεις είναι συνεχείς. + +, αν >
7. ΤΕΛΕΣΤΙΚΟΣ ΕΝΙΣΧΥΤΗΣ
 ΤΕΙ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΣΤΟΧΟΙ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ. Ε. ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΩΝ ΙΙ 7. ΤΕΛΕΣΤΙΚΟΣ ΕΝΙΣΧΥΤΗΣ η κατανόηση της λειτουργίας του τελεστικού ενισχυτή, Ημερομηνία:.... /.... /...... Τμήμα:....
ΤΕΙ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΣΤΟΧΟΙ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ. Ε. ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΩΝ ΙΙ 7. ΤΕΛΕΣΤΙΚΟΣ ΕΝΙΣΧΥΤΗΣ η κατανόηση της λειτουργίας του τελεστικού ενισχυτή, Ημερομηνία:.... /.... /...... Τμήμα:....
Μικροηλεκτρονική - VLSI
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 6.2: Συνδυαστική Λογική - Σύνθετες Πύλες Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 6.2: Συνδυαστική Λογική - Σύνθετες Πύλες Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΜΕΤΑΠΤΥΧΙΑΚΟ ΗΛΕΚΤΡΟΝΙΚΗΣ ΦΥΣΙΚΗΣ ( ΡΑΔΙΟΗΛΕΚΤΡΟΛΟΓΙΑΣ ) ΒΑΡΝΑΒΙΔΟΥ Β. ΧΡΙΣΤΙΝΑ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Ανάλυση λειτουργίας βασικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΜΕΤΑΠΤΥΧΙΑΚΟ ΗΛΕΚΤΡΟΝΙΚΗΣ ΦΥΣΙΚΗΣ ( ΡΑΔΙΟΗΛΕΚΤΡΟΛΟΓΙΑΣ ) ΒΑΡΝΑΒΙΔΟΥ Β. ΧΡΙΣΤΙΝΑ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Ανάλυση λειτουργίας βασικών
Άσκηση 1: Να υπολογιστεί η μέση τραχύτητα R a της κατανομής του σχήματος..
 ΑΣΚΗΣΕΙΣ στο μάθημα Κατεργασίες Αποβολής Υλικού & Ε/Μ CNC (Ε εξαμ.) Άσκηση 1: Να υπολογιστεί η μέση τραχύτητα R a της κατανομής του σχήματος.. Λ Υ Σ Η y α Λόγω ομοιότητας των τριγώνων ισχύει ότι : εφφ
ΑΣΚΗΣΕΙΣ στο μάθημα Κατεργασίες Αποβολής Υλικού & Ε/Μ CNC (Ε εξαμ.) Άσκηση 1: Να υπολογιστεί η μέση τραχύτητα R a της κατανομής του σχήματος.. Λ Υ Σ Η y α Λόγω ομοιότητας των τριγώνων ισχύει ότι : εφφ
Κατανάλωση ισχύος ψηφιακών κυκλωμάτων
 Κατανάλωση ισχύος ψηφιακών κυκλωμάτων Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Γ. Δημητρακόπουλος ΗΥ422 1 Δυναμική κατανάλωση ισχύος Σε κάθε κύκλο μετακινούμε το διακόπτη
Κατανάλωση ισχύος ψηφιακών κυκλωμάτων Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Γ. Δημητρακόπουλος ΗΥ422 1 Δυναμική κατανάλωση ισχύος Σε κάθε κύκλο μετακινούμε το διακόπτη
Κεφάλαιο 2 ο. Γ. Τσιατούχας. VLSI Systems and Computer Architecture Lab
 ΚΥΚΛΩΜΑΤΑ VLSI Πανεπιστήμιο Ιωαννίνων CMOS Αναστροφέας Κεφάλαιο ο Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας VLSI Systems ad Computer Architecture Lab ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση 1. I V χαρακτηριστική
ΚΥΚΛΩΜΑΤΑ VLSI Πανεπιστήμιο Ιωαννίνων CMOS Αναστροφέας Κεφάλαιο ο Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας VLSI Systems ad Computer Architecture Lab ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση 1. I V χαρακτηριστική
1. Πηγή αρμονικών κυμάτων συχνότητας 5 Hz εξαναγκάζει το άκρο Ο ενός γραμμικού ελαστικού μέσου, το
 Η φάση του αρμονικού κύματος 1. Πηγή αρμονικών κυμάτων συχνότητας 5 Hz εξαναγκάζει το άκρο Ο ενός γραμμικού ελαστικού μέσου, το οποίο ταυτίζεται με τον οριζόντιο ημιάξονα O, να εκτελεί απλή αρμονική ταλάντωση
Η φάση του αρμονικού κύματος 1. Πηγή αρμονικών κυμάτων συχνότητας 5 Hz εξαναγκάζει το άκρο Ο ενός γραμμικού ελαστικού μέσου, το οποίο ταυτίζεται με τον οριζόντιο ημιάξονα O, να εκτελεί απλή αρμονική ταλάντωση
Πανεπιστήµιο Αιγαίου Τµήµα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστηµάτων. 3η Άσκηση Logical Effort - Ένα ολοκληρωµένο παράδειγµα σχεδίασης
 Πανεπιστήµιο Αιγαίου Τµήµα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστηµάτων Εισαγωγή σε VLSI 3η Άσκηση Logical Effort - Ένα ολοκληρωµένο παράδειγµα σχεδίασης Μανόλης Καλλίγερος (kalliger@aegean.gr)
Πανεπιστήµιο Αιγαίου Τµήµα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστηµάτων Εισαγωγή σε VLSI 3η Άσκηση Logical Effort - Ένα ολοκληρωµένο παράδειγµα σχεδίασης Μανόλης Καλλίγερος (kalliger@aegean.gr)
ΜΕΛΕΤΗ ΚΑΙ ΧΑΡΑΞΗ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ ΣΥΝΑΡΤΗΣΗΣ
 ΜΕΛΕΤΗ ΚΑΙ ΧΑΡΑΞΗ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ ΣΥΝΑΡΤΗΣΗΣ Για να μελετήσουμε και να χαράξουμε τη γραφική παράταση μιας συνάρτησης ακολουθούμε τα παρακάτω βήματα: 1. Βρίσκουμε το πεδίο ορισμού της.. Εξετάζουμε την
ΜΕΛΕΤΗ ΚΑΙ ΧΑΡΑΞΗ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ ΣΥΝΑΡΤΗΣΗΣ Για να μελετήσουμε και να χαράξουμε τη γραφική παράταση μιας συνάρτησης ακολουθούμε τα παρακάτω βήματα: 1. Βρίσκουμε το πεδίο ορισμού της.. Εξετάζουμε την
ΕΡΓΑΣΤΗΡΙΟ ΠΥΡΗΝΙΚΗΣ 2 ΕΡΓΑΣΙΑ: Χρονική φασματοσκοπία- χρήση συστήματος TAC-μέτρηση μικρών χρόνων ζωής
 ΕΡΓΑΣΤΗΡΙΟ ΠΥΡΗΝΙΚΗΣ 2 ΕΡΓΑΣΙΑ: Χρονική φασματοσκοπία- χρήση συστήματος TAC-μέτρηση μικρών χρόνων ζωής Αλέξανδρος Κετικίδης ΑΕΜ:13299 1/6/14 κ.χαρδάλας Περίληψη Σκοπός αυτής της εργασίας είναι η μέτρηση
ΕΡΓΑΣΤΗΡΙΟ ΠΥΡΗΝΙΚΗΣ 2 ΕΡΓΑΣΙΑ: Χρονική φασματοσκοπία- χρήση συστήματος TAC-μέτρηση μικρών χρόνων ζωής Αλέξανδρος Κετικίδης ΑΕΜ:13299 1/6/14 κ.χαρδάλας Περίληψη Σκοπός αυτής της εργασίας είναι η μέτρηση
ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΠΛΗΡΕΙΣ ΑΠΑΝΤΗΣΕΙΣ. Άρα, για τις αντίστοιχες αλγεβρικές τιμές των ταχυτήτων των δύο σωμάτων πριν από την κρούση τους προκύπτει ότι:
 ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΤΕΤΑΡΤΗ 6 ΣΕΠΤΕΜΒΡΙΟΥ 017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΔΕΚΑ (10) ΘΕΜΑ Α ΠΡΟΤΕΙΝΟΜΕΝΕΣ
ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΤΕΤΑΡΤΗ 6 ΣΕΠΤΕΜΒΡΙΟΥ 017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΔΕΚΑ (10) ΘΕΜΑ Α ΠΡΟΤΕΙΝΟΜΕΝΕΣ
Άλγεβρα Β Λυκείου Επαναληπτικά θέματα ΟΕΦΕ α φάση
 Άλγεβρα Β Λυκείου Επαναληπτικά θέματα ΟΕΦΕ 00-08 α φάση Συναρτήσεις Θεωρούμε τη συνάρτηση Α, 6 wwwaskisopolisgr f κ, με 4,4 και κ η οποία διέρχεται από το σημείο και τμήμα της γραφικής της παράστασης φαίνεται
Άλγεβρα Β Λυκείου Επαναληπτικά θέματα ΟΕΦΕ 00-08 α φάση Συναρτήσεις Θεωρούμε τη συνάρτηση Α, 6 wwwaskisopolisgr f κ, με 4,4 και κ η οποία διέρχεται από το σημείο και τμήμα της γραφικής της παράστασης φαίνεται
m αντίστοιχα, εκτελούν Α.Α.Τ. και έχουν την
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΠΕΡΙΟΔΙΚΟ ΦΑΙΝΟΜΕΝΟ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΚΙΝΗΜΑΤΙΚΗ ΚΑΙ ΔΥΝΑΜΙΚΗ ΠΡΟΣΕΓΓΙΣΗ) Ερώτηση. ΘΕΜΑ Β Δύο σώματα με μάζες m m και m m αντίστοιχα, εκτελούν Α.Α.Τ.
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΠΕΡΙΟΔΙΚΟ ΦΑΙΝΟΜΕΝΟ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΚΙΝΗΜΑΤΙΚΗ ΚΑΙ ΔΥΝΑΜΙΚΗ ΠΡΟΣΕΓΓΙΣΗ) Ερώτηση. ΘΕΜΑ Β Δύο σώματα με μάζες m m και m m αντίστοιχα, εκτελούν Α.Α.Τ.
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 6: Παθητικά στοιχεία αποθήκευσης ενέργειας Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ.
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 6: Παθητικά στοιχεία αποθήκευσης ενέργειας Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ.
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 4 η Εργαστηριακή Άσκηση
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 4 η Εργαστηριακή Άσκηση Σχεδιασμός Πολύπλοκων Κυκλωμάτων CMOS και Μελέτη της Καθυστέρησης Εξόδου (Critical Path Delay) Άδειες Χρήσης Το παρόν υλικό διατίθεται
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 4 η Εργαστηριακή Άσκηση Σχεδιασμός Πολύπλοκων Κυκλωμάτων CMOS και Μελέτη της Καθυστέρησης Εξόδου (Critical Path Delay) Άδειες Χρήσης Το παρόν υλικό διατίθεται
στη θέση 1. Κάποια χρονική στιγμή μεταφέρουμε το διακόπτη από τη θέση 1 στη
 ΠΥΚΝΩΤΗΣ ΣΥΝΔΕΔΕΜΕΝΟΣ ΠΑΡΑΛΛΗΛΑ ΜΕ ΠΗΓΗ. Στο διπλανό κύκλωμα η πηγή έχει ΗΕΔ = V και ο διακόπτης είναι αρχικά στη θέση. Κάποια χρονική στιγμή μεταφέρουμε το διακόπτη από τη θέση στη θέση και αρχίζουν οι
ΠΥΚΝΩΤΗΣ ΣΥΝΔΕΔΕΜΕΝΟΣ ΠΑΡΑΛΛΗΛΑ ΜΕ ΠΗΓΗ. Στο διπλανό κύκλωμα η πηγή έχει ΗΕΔ = V και ο διακόπτης είναι αρχικά στη θέση. Κάποια χρονική στιγμή μεταφέρουμε το διακόπτη από τη θέση στη θέση και αρχίζουν οι
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Οδυσσέας Κουφοπαύλου, Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Οδυσσέας Κουφοπαύλου, Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
4/10/2008. Στατικές πύλες CMOS και πύλες με τρανζίστορ διέλευσης. Πραγματικά τρανζίστορ. Ψηφιακή λειτουργία. Κανόνες ψηφιακής λειτουργίας
 2 η διάλεξη 25 Σεπτεμβρίου Πραγματικά τρανζίστορ Στατικές πύλες CMOS και πύλες με τρανζίστορ διέλευσης Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Η τάση στο gate του τρανζίστορ
2 η διάλεξη 25 Σεπτεμβρίου Πραγματικά τρανζίστορ Στατικές πύλες CMOS και πύλες με τρανζίστορ διέλευσης Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Η τάση στο gate του τρανζίστορ
Μικροηλεκτρονική - VLSI
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 6.3: Συνδυαστική Λογική - Δυναμικές Πύλες Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 6.3: Συνδυαστική Λογική - Δυναμικές Πύλες Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
Ορθή πόλωση της επαφής p n
 Δύο τρόποι πόλωσης της επαφής p n Ορθή πόλωση της επαφής p n Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ορθή πόλωση p n Άνοδος Κάθοδος Ανάστροφη πόλωση p n Άνοδος Κάθοδος
Δύο τρόποι πόλωσης της επαφής p n Ορθή πόλωση της επαφής p n Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ορθή πόλωση p n Άνοδος Κάθοδος Ανάστροφη πόλωση p n Άνοδος Κάθοδος
Ακαδημαϊκό έτος ΘΕΜΑ 1. Η κινητική εξίσωση της αντίδρασης Α + Β = Γ είναι: r = k[a] α [B] β
![Ακαδημαϊκό έτος ΘΕΜΑ 1. Η κινητική εξίσωση της αντίδρασης Α + Β = Γ είναι: r = k[a] α [B] β Ακαδημαϊκό έτος ΘΕΜΑ 1. Η κινητική εξίσωση της αντίδρασης Α + Β = Γ είναι: r = k[a] α [B] β](/thumbs/54/34260399.jpg) Ακαδημαϊκό έτος 4-5 ΘΕΜΑ Η κινητική εξίσωση της αντίδρασης Α + Β = Γ είναι: r = [] α [B] β Χρησιμοποιώντας τη μέθοδο των αρχικών ταχυτήτων βρήκαμε ότι η αντίδραση είναι δεύτερης τάξης ως προς Α και πρώτης
Ακαδημαϊκό έτος 4-5 ΘΕΜΑ Η κινητική εξίσωση της αντίδρασης Α + Β = Γ είναι: r = [] α [B] β Χρησιμοποιώντας τη μέθοδο των αρχικών ταχυτήτων βρήκαμε ότι η αντίδραση είναι δεύτερης τάξης ως προς Α και πρώτης
Ψηφιακά Ηλεκτρονικά. Μάθηµα 6ο.. Λιούπης
 Ψηφιακά Ηλεκτρονικά Μάθηµα 6ο. Λιούπης Κίνδυνοι για ένα ολοκληρωµένο CMOS Ηλεκτροστατική εκκένωση (electrostatic discharge ESD) ανταλλαγή στατικών φορτίων και δηµιουργία σπινθήρα, όταν πλησιάσουν δύο σώµατα
Ψηφιακά Ηλεκτρονικά Μάθηµα 6ο. Λιούπης Κίνδυνοι για ένα ολοκληρωµένο CMOS Ηλεκτροστατική εκκένωση (electrostatic discharge ESD) ανταλλαγή στατικών φορτίων και δηµιουργία σπινθήρα, όταν πλησιάσουν δύο σώµατα
Ψηφιακά Ηλεκτρονικά. Μάθηµα 2ο.. Λιούπης
 Ψηφιακά Ηλεκτρονικά Μάθηµα 2ο. Λιούπης Transistor διπολικής επαφής (BJT) I B B C E I C Στα ψηφιακά κυκλώµατα χρησιµοποιείται κατά κύριο λόγο ως διακόπτης Στο σχήµαφαίνεταιένα τυπικό BJT τύπου NPN I B :
Ψηφιακά Ηλεκτρονικά Μάθηµα 2ο. Λιούπης Transistor διπολικής επαφής (BJT) I B B C E I C Στα ψηφιακά κυκλώµατα χρησιµοποιείται κατά κύριο λόγο ως διακόπτης Στο σχήµαφαίνεταιένα τυπικό BJT τύπου NPN I B :
4.3 Η ΣΥΝΑΡΤΗΣΗ f (x) x
 1 4.3 Η ΣΥΝΑΡΤΗΣΗ f () A Ομάδας Ασκήσεις σχολικού βιβλίου σελίδας 164 167 1. Να βρείτε τη γωνία που σχηματίζει με τον άξονα η ευθεία = + = 3 1 i = + 1 iv) = 3 + εφω = 1 ω = 45 ο εφω = 3 ω = 60 ο i εφω
1 4.3 Η ΣΥΝΑΡΤΗΣΗ f () A Ομάδας Ασκήσεις σχολικού βιβλίου σελίδας 164 167 1. Να βρείτε τη γωνία που σχηματίζει με τον άξονα η ευθεία = + = 3 1 i = + 1 iv) = 3 + εφω = 1 ω = 45 ο εφω = 3 ω = 60 ο i εφω
Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άδεια
 Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης reative ommons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άδεια χρήσης άλλου τύπου, αυτή πρέπει να αναφέρεται ρητώς. Στιλ
Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης reative ommons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άδεια χρήσης άλλου τύπου, αυτή πρέπει να αναφέρεται ρητώς. Στιλ
1)Σε ένα πυκνωτή, η σχέση μεταξύ φορτίου Q και τάσης V μεταξύ των οπλισμών του, απεικονίζεται στο διάγραμμα.
 1)Σε ένα πυκνωτή, η σχέση μεταξύ φορτίου Q και τάσης V μεταξύ των οπλισμών του, απεικονίζεται στο διάγραμμα. Να επιλέξετε τη σωστή απάντηση. Η χωρητικότητα του πυκνωτή είναι: α. 5 F, β. 1 / 5 μf, γ. 5
1)Σε ένα πυκνωτή, η σχέση μεταξύ φορτίου Q και τάσης V μεταξύ των οπλισμών του, απεικονίζεται στο διάγραμμα. Να επιλέξετε τη σωστή απάντηση. Η χωρητικότητα του πυκνωτή είναι: α. 5 F, β. 1 / 5 μf, γ. 5
1. Αν α 3 + β 3 + γ 3 = 3αβγ και α + β + γ 0, δείξτε ότι το πολυώνυµο P (x) = (α - β) x 2 + (β - γ) x + γ - α είναι
 _ ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ 1. Αν α + β + γ = αβγ και α + β + γ 0, δείξτε ότι το πολυώνυµο P () = (α - β) + (β - γ) + γ - α είναι το µηδενικό πολυώνυµο.. Να δειχθεί ότι το πολυώνυµο P () = (κ - ) + (λ + 6) +
_ ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ 1. Αν α + β + γ = αβγ και α + β + γ 0, δείξτε ότι το πολυώνυµο P () = (α - β) + (β - γ) + γ - α είναι το µηδενικό πολυώνυµο.. Να δειχθεί ότι το πολυώνυµο P () = (κ - ) + (λ + 6) +
Τρίτο Σετ Φροντιστηριακών ασκήσεων Ψηφιακών Ηλεκτρονικών. Δρ. Χ. Μιχαήλ
 ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ Η/Υ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ Τρίτο Σετ Φροντιστηριακών ασκήσεων Ψηφιακών Ηλεκτρονικών Δρ. Χ. Μιχαήλ Πάτρα, 2010 ΑΣΚΗΣΗ 1 Ένας μικροεπεξεργαστής πρέπει να οδηγήσει ένα δίαυλο
ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ Η/Υ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ Τρίτο Σετ Φροντιστηριακών ασκήσεων Ψηφιακών Ηλεκτρονικών Δρ. Χ. Μιχαήλ Πάτρα, 2010 ΑΣΚΗΣΗ 1 Ένας μικροεπεξεργαστής πρέπει να οδηγήσει ένα δίαυλο
7 η διάλεξη Ακολουθιακά Κυκλώματα
 7 η διάλεξη Ακολουθιακά Κυκλώματα 1 2 3 4 5 6 7 Παραπάνω βλέπουμε ακολουθιακό κύκλωμα σχεδιασμένο με μανταλωτές διαφορετικής φάσης. Παρατηρούμε ότι συνδυαστική λογική μπορεί να προστεθεί μεταξύ και των
7 η διάλεξη Ακολουθιακά Κυκλώματα 1 2 3 4 5 6 7 Παραπάνω βλέπουμε ακολουθιακό κύκλωμα σχεδιασμένο με μανταλωτές διαφορετικής φάσης. Παρατηρούμε ότι συνδυαστική λογική μπορεί να προστεθεί μεταξύ και των
ΕΝΙΣΧΥΤΗΣ ΙΣΧΥΟΣ PUSH-PULL
 ΕΝΙΣΧΥΤΗΣ ΙΣΧΥΟΣ USH-ULL ΕΠΩΝΥΜΟ ΟΝΟΜΑ Α.Μ. ΤΜΗΜΑ ΗΜΕΡΟΜΗΝΙΑ ΔΙΕΞΑΓΩΓΗΣ:.... /..../ 0.. ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ:.... /..../ 0.. ΤΕΙ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΣΤΟΧΟΙ η κατανόηση της
ΕΝΙΣΧΥΤΗΣ ΙΣΧΥΟΣ USH-ULL ΕΠΩΝΥΜΟ ΟΝΟΜΑ Α.Μ. ΤΜΗΜΑ ΗΜΕΡΟΜΗΝΙΑ ΔΙΕΞΑΓΩΓΗΣ:.... /..../ 0.. ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ:.... /..../ 0.. ΤΕΙ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΣΤΟΧΟΙ η κατανόηση της
1 ο Διαγώνισμα Α Λυκείου Σάββατο 18 Νοεμβρίου 2017
 1 ο Διαγώνισμα Α Λυκείου Σάββατο 18 Νοεμβρίου 017 Διάρκεια Εξέτασης 3 ώρες Ονοματεπώνυμο. ΘΕΜΑ Α: Στις ερωτήσεις Α1 ως και Α4 επιλέξτε την σωστή απάντηση: Α1. Αν υ η ταχύτητα ενός κινητού και α η επιτάχυνσή
1 ο Διαγώνισμα Α Λυκείου Σάββατο 18 Νοεμβρίου 017 Διάρκεια Εξέτασης 3 ώρες Ονοματεπώνυμο. ΘΕΜΑ Α: Στις ερωτήσεις Α1 ως και Α4 επιλέξτε την σωστή απάντηση: Α1. Αν υ η ταχύτητα ενός κινητού και α η επιτάχυνσή
Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης Εφαρμογές
 Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης Εφαρμογές Να βρείτε για καθεμιά από τις παρακάτω γραμμές αν είναι γραφική παράσταση κάποιας συνάρτησης. 4-1 1 () (1) (3) (4) (5) (6) Αν υπάρχει ευθεία
Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης Εφαρμογές Να βρείτε για καθεμιά από τις παρακάτω γραμμές αν είναι γραφική παράσταση κάποιας συνάρτησης. 4-1 1 () (1) (3) (4) (5) (6) Αν υπάρχει ευθεία
(α) Από τα δεδομένα, η επιφάνεια των οπλισμών του πυκνωτή είναι ίση με Α = = m 2
 Πρόβλημα 4.. Ένας φοιτητής κατασκευάζει ένα επίπεδο πυκνωτή χρησιμοποιώντας δυο ορθογώνια μεταλλικά φύλλα διαστάσεων.5 m.5 m τα οποία τα τοποθετεί επάνω σε μια ειδική ευθύγραμμη τροχιά από πλαστικό υλικό
Πρόβλημα 4.. Ένας φοιτητής κατασκευάζει ένα επίπεδο πυκνωτή χρησιμοποιώντας δυο ορθογώνια μεταλλικά φύλλα διαστάσεων.5 m.5 m τα οποία τα τοποθετεί επάνω σε μια ειδική ευθύγραμμη τροχιά από πλαστικό υλικό
