Διαχείριση Ταμιευτήρα
|
|
|
- Αιγιδιος Κεδίκογλου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Διαχείριση Ταμιευτήρα Μονοκριτηριακή βελτιστοποίηση
2 Διαχείριση υδατικών πόρων Ανάγκη σύνθεσης επιστημών Σημερινό μάθημα: έμφαση στη χρήση εννοιών και μεθόδων από την επιχειρησιακή έρευνα Κουτσογιάννης, 2015
3
4 Βελτιστοποίηση χωρίς περιορισμούς (ή με απλό περιορισμό, ως καρτεσιανό γινόμενο) Μηδενισμός μερικών παραγώγων Έλεγχος δεύτερης τάξης παραγώγων Γραμμική παλινδρόμηση: ελαχιστοποίηση του τετραγωνικού αθροίσματος των αποκλίσεων (μέτρηση γραμμικό μοντέλο) Δες βοηθητικές σημειώσεις
5 Γενίκευση. Μία συνεχή συνάρτηση πολλαπλών μεταβλητών παίρνει μία ολική και μία μέγιστη τιμή σε κάθε κλειστή οριοθετημένη περιοχή στην οποία ορίζεται (διάβασε σύνολο εφικτών λύσεων). Τα (υποψήφια σημεία) είναι εσωτερικά σημεία ή τα σύνορα του πεδίου ορισμού. Θα υπάρχει σίγουρα ελάχιστο και μέγιστο η στο εσωτερικό U ή στο όριο U
6 ΠΑΡΑΔΕΙΓΜΑ, ΠΡΟΣΟΧΗ ΣΤΑ ΤΟΠΙΚΑ ΒΕΛΤΙΣΤΑ z 3(1 x ) exp x ( x 1) (0.2 x x x )exp( x x ) 2 x exp ( x 1) 6
7 10 5 multimodal! z x x global max local min saddle x local max local max global lbl min x 1 7
8 Τοπικό μέγιστο παγίδα 8
9
10 Mathematical Description Minimize : f ( x) objective function hx ( ) 0 equality constraints Subject to: gx ( ) 0 inequality constraints where x n, is a vector of n variables ( x1, x2,, x n ) hx ( ) is a vector of equalities of dimension m 1 gx ( ) is a vector of inequalities of dimension m 2 Γενική διατύπωση γενικού προβλήματος βελτιστοποίησης συμβατικού τύπου χωρίς άμεση προσομοίωση 10
11 Χρυσάνθου, 2013
12 Κατανόηση γραμμικού προγραμματισμού Συνάρτηση στόχου: π.χ. επιδιωκόμενο κέρδος (μία συνάρτηση συμμετοχής) Μεταβλητές απόφασης, π.χ. απολήψιμες ποσότητες νερού (μη αρνητικές ποσότητες) Περιορισμοί, περιορισμοί διαθεσιμότητας νερού Υλικοί περιορισμοί Λύση εντός του εφικτού πεδίου (που θα είναι κυρτό).στα σύνορα και μάλιστα στις κορυφές (για γραμμικό προγραμματισμό)
13 Κυρτό πεδίο ορισμού, γραμμικός προγραμματισμός λύση στις κορυφές
14 Πιο γενικά: Ευστρατιαδης, 2013
15 Αλγόριθμος Simplex από κορυφή σε κορυφή Επίσης lingo, Matlab, εξέλ
16 Χρυσάνθου, 2013 x n+k για να γίνουν οι ανισότητες ισότητες (βοηθητικές μεταβλητές)
17 Τονίζεται ότι οι περιορισμοί είναι υπό την μορφή ανισοτήτων αλλά με τις βοηθητικές ζ ρ ρ μ η μ ρφή ή μ ς β η η ς μεταβλητές μετατρέπονται σε ισότητες
18 MATLAB, με πίνακες
19 Σχηματοποίηση Υδατικού Συστήματος Σχηματοποίηση Άλλη προσέγγιση: Υδατικού συστήματος Κόμβοι Κλάδοι Καταναλώσεις: «σημειακές» από κόμβους) Διαθεσιμότητα νερού: από τον αμέσως ανάντη κλάδο (προσέγγιση). Γνώση από προσομοίωση Ανά κλάδο, θεώρηση, ή μη απωλειών η εμπλουτισμού η σταθερή παροχή όπως εδώ The cumulative demand dat the branch 1 2 (d0+d1) are covered with the (MCPWW1) 2 MPWW 1 The demand at branch 0 1 (d0) are covered with the (MCPWW0) node 1 MCPWW 1 MPWW 0 branch 0 node 0 initial sub basin MCPWW 0 = MPWW 0 = MCPWW 0 + MPWW 1 branch ideal representation of the branch in reality Άλλη προσέγγιση διαθεσιμότητα ανάντη κόμβου στον κατάντη κόμβο κατανάλωσης Fig.1: Calculation of the Maximum Cumulative Potential Withdrawal
20 Μερικές διαφορές γραμμικού και μη γραμμικού προγραμματισμού Ακόμη και αν το πεδίο εφικτών λύσεων είναι κυρτό σύνολο (π.χ. λόγω ύπαρξης μόνο γραμμικών περιορισμών) το βέλτιστο δεν είναι απαραίτητα στο σύνορο του πεδίου ορισμού Το πεδίο των εφικτών λύσεων δεν είναι πάντα κυρτό Δυναμική ενσωμάτωση της προσομοίωσης με ευρετικούς αλγορίθμους
21 Μαρκόπουλος και Ευστρατιάδης, uments/week1_introduction_full.pdf
22 Κριτική/ μετάβαση στο επόμενο μάθημα Ύπαρξη πολλαπλών λώ στόχων κριτήρια στη βελτιστοποίηση, συναρτήσεις στόχου. (βλπ πολλαπλά κριτήρια, αποτελεσματικές λύσεις) Δεν μπορούμε να παραμείνουμε σε μία απλή συνθετική συνάρτηση (σύνθεση διαφορετικών ποσοτήτων, βάρη???, ισόρροπες αποφάσεις???) Ενσωμάτωση της αβεβαιότητας β στην απόφαση (βλπασαφή ήλογική) Ανάγκη πρόβλεψης ευκαμψίας, οι οριακές λύσεις (π.χ. μετά από βελτιστοποίηση με αυστηρούς περιορισμούς) σε μία περίπτωση βλάβης οδηγούν σε καθολική αστοχία απόφαση (βλπ δίκτυα διανομής νερού) (βλπ ασαφή λογική και πολλαπλά κριτήρια) Αλληλεπιδραστική διαδικασία Ανάγκη για πιστότερη προσομοίωση του συστήματος (βλπ προσομοίωση+βελτιστοποίηση ή ευρετικοί αλγόριθμοι)
23 Διαχείριση Ταμιευτήρα
24 Προσομοίωση VS Βελτιστοποίηση(?) Προσομοίωση, διάφορα δάφ «τρεξίματα» για την επιλογή της βέλτιστης τιμής, ικανότητα ακριβούς προσομοίωσης. Ενδεχόμενη προσέγγιση βέλτιστης λύσης, καλή λειτουργία Συμβατική βελτιστοποίηση. Η προσομοίωση υπεισέρχεται στο πρόβλημα με απλουστεύσεις. Βέλτιστη λύση αλλά ερώτημα για τις παραδοχές. Ευρετικοί αλγόριθοι. Ρωμαλέα ενσωμάτωση της προσομοίωσης προσέγγιση λύσης κοντά στο βέλτιστο, καλύτερη λύση από την πρώτη περίπτωση, σχετική γνώση, προσοχή στα τοπικά ακρότατα.
25 Βασική εξίσωση στον ταμιευτήρα χωρίς υπερχείλιση Εξίσωση της μάζας: (εισροές (Ι) μείον εκροές (Q) ίσον με μεταβολή στην αποθήκευση (ΔS/Δt): S I Q tt Για διακριτό σταθερό βήμα Δt(π.χ. μήνας) S S I Q i i 1 i i Απλούστευση για βελτιστοποίηση και μία πρώτη εκτίμηση: έστω εκροή ή(ζή (ζήτηση) και εισροή νερού από ανάντη λεκάνη S S I Q Q i i 1 i i i x m i,m
26 Κατά τη διάρκεια του μήνα I i εισροή Δυνατότητα η μη (μόνο θεωρητικά) υπερχείλισης Χρόνος i S i 1 αρχή μήνα κατώφλι Διατήρηση της μάζας SMAX S i τέλος και νέα αρχή μήνα, κατώφλι X i απόληψη
27 Υπερχείλιση Περιορισμός μέγιστης χωρητικότητας. Προφανώς: S S max Αν S<S MAX τότε ο ταμιευτήρας δεν υπερχειλίζει Διαφορετικά, S=S MAX και η περίσσεια θα γίνει υπερχείλιση R Si Ii Qi SMAX
28 Εξάτμιση Στην πραγματικότητα υπάρχει και η εξάτμιση που λαμβάνει χώρα στον ταμιευτήρα (άνω των 1000mm για τα Ελληνικά δεδομένα π.χ. Τήλος 1700mm). Η εξάτμιση εξαρτάται από την επιφάνεια του ταμιευτήρα και αυτή εξαρτάται μη γραμμικά από το ύψος στάθμης του νερού στον ταμιευτήρα. Η θεώρηση της εξάτμισης οδηγεί σε ένα μη γραμμικό πρόβλημα.
29 Παράδειγμα θεώρησης εξάτμισης σε ταμιευτήρα (Ναλμπάντης και τσακίρης, 2008) μη γραμμική σχέση
30 Εφαρμογή βελτιστοποίησης σε ταμιευτήρα γραμμικός προγραμματισμός Δεν επιτρέπουμε υπερχείλιση Δε λαμβάνω υπόψη την εξάτμιση (πρώτη διαστασιολόγηση, μετά τρέχω αναλυτικά το φυσικό ομοίωμα) Ταμιευτήρας «μονής» σκοπιμότητας (μία μόνο χρήση νερού)
31 Χρυσάνθου,, 2013 Δίνεται επίσης, ότι για κάθε μήνα η ελάχιστη παροχή κατάντη του ταμιευτήρα ορίζεται σε 20 10^6m^3 και η μέγιστη σε ^6m^3
32
33
34 Δηλαδή, ο αποθηκευμένος όγκος στον ταμιευτήρα θα είναι μικρότερος από τη μέγιστη χωρητικότητα
35 x 13 Βοηθητική μεταβλητή για μετατροπή της ανισότητας σε ισότητα (για επίλυση χειροκίνητα,, δεν είναι απαραίτητη η θεώρηση της σε υπολογιστικά πακέτα) Περιορισμός θετικών αποθηκεύσεων στον ταμιευτήρα
36 Για n =2 max S S I x S I x I x max S S I I x x Για n = Δηλαδή ο αποθηκευμένος όγκος στον ταμιευτήρα θέλω να είναι μικρότερος από τη μέγιστη χωρητικότητα Χωρίς υπερχείλιση max S S I I I x x x Ομοίως για τους υπόλοιπους μήνες
37
38 Προσομοίωση ταμιευτήρα πολλαπλής χρησιμότητας (πιο ακριβής θεώρηση γενικά, μπορεί να υπάρξει υπερχείλιση, θεώρηση της εξάτμισης) πολλαπλές προσομοιώσεις για διαστασιολόγηση Αξιοπιστία ταμιευτήρα Εκμεταλλεύσιμο μ Επιφανειακό Υδατικό Δυναμικό με ταμίευση
39 Ποιες είναι οι μεταβλητές απόφασης?? (π.χ. χωρητικότητα ταμιευτήρα και/ή προσφορά νερού ανά μήνα σε κάθε χρήστη και/ή κατανομή καλλιεργειών) ) Συνάρτηση στόχου, συνάρτηση των μεταβλητών απόφασης: Γραμμική ή μη Κόστος (ελάχιστο) Χωρητικότητα ταμιευτήρα Απόκλιση από την προσφορά νερού στόχου για κάθε κατανάλωση Ελάχιστες υπερχειλίσεις Μέγιστο κέρδος από την εκμετάλλευση νερού
40 Περιορισμοί που συναρτώνται από τη φυσική προσομοίωση (π.χ. εξίσωση ισοζυγίων μάζας) Τεχνικοί λειτουργικοί. λ ί π.χ. περιορισμός για το ύψος πίεσης Περιορισμοί υλικών πόρων (π.χ. χ διαθέσιμη επένδυση) Περιορισμοί περιβαλλοντικοί (π.χ. οικολογική παροχή), οικονομικοί, κοινωνικοί κλπ Από άλλη σκοπιά, περιορισμοί ως υποκατάστατο των κριτηρίων Λύση εντός του πεδίου των εφικτών λύσεων
4.γ. μερική επανάληψη, εισαγωγή στη βελτιστοποίηση υδατικών συστημάτων. Δρ Μ.Σπηλιώτης
 4.γ. μερική επανάληψη, εισαγωγή στη βελτιστοποίηση υδατικών συστημάτων Δρ Μ.Σπηλιώτης Ολοκληρωμένη διαχείριση υδατικών πόρων (integrated water resources management), έμφαση στην εξέταση όλων των πτυχών
4.γ. μερική επανάληψη, εισαγωγή στη βελτιστοποίηση υδατικών συστημάτων Δρ Μ.Σπηλιώτης Ολοκληρωμένη διαχείριση υδατικών πόρων (integrated water resources management), έμφαση στην εξέταση όλων των πτυχών
ΔΥΠ χρησιμοποιώντας πολύκριτηριακές μεθόδους
 Διαχείριση Ταμιευτήρα ΔΥΠ χρησιμοποιώντας πολύκριτηριακές μεθόδους Διαχείριση Ταμιευτήρα Προσομοίωση VS Βελτιστοποίηση(?) Προσομοίωση, διάφορα δάφ «τρεξίματα» για την επιλογή της βέλτιστης τιμής, ικανότητα
Διαχείριση Ταμιευτήρα ΔΥΠ χρησιμοποιώντας πολύκριτηριακές μεθόδους Διαχείριση Ταμιευτήρα Προσομοίωση VS Βελτιστοποίηση(?) Προσομοίωση, διάφορα δάφ «τρεξίματα» για την επιλογή της βέλτιστης τιμής, ικανότητα
Το µαθηµατικό µοντέλο του Υδρονοµέα
 Ερευνητικό έργο: Εκσυγχρονισµός της εποπτείας και διαχείρισης του συστήµατος των υδατικών πόρων ύδρευσης της Αθήνας Το µαθηµατικό µοντέλο του Υδρονοµέα Ανδρέας Ευστρατιάδης και Γιώργος Καραβοκυρός Τοµέας
Ερευνητικό έργο: Εκσυγχρονισµός της εποπτείας και διαχείρισης του συστήµατος των υδατικών πόρων ύδρευσης της Αθήνας Το µαθηµατικό µοντέλο του Υδρονοµέα Ανδρέας Ευστρατιάδης και Γιώργος Καραβοκυρός Τοµέας
Μοντέλο Υδατικού Ισοζυγίου
 Μοντέλο Υδατικού Ισοζυγίου ΥΔΡΟΚΡΙΤΗΣ Η νοητή γραμμή που συνδέει τα ψηλότερα σημεία των υψωμάτων της επιφάνειας του εδάφους και διαχωρίζει τη ροή των όμβριων υδάτων. ΥΔΡΟΚΡΙΤΗΣ Κουτσογιάννης και Μαμάσης,
Μοντέλο Υδατικού Ισοζυγίου ΥΔΡΟΚΡΙΤΗΣ Η νοητή γραμμή που συνδέει τα ψηλότερα σημεία των υψωμάτων της επιφάνειας του εδάφους και διαχωρίζει τη ροή των όμβριων υδάτων. ΥΔΡΟΚΡΙΤΗΣ Κουτσογιάννης και Μαμάσης,
Α. Επανάληψη και εμπλουτισμός εννοιών Β. Ζήτηση νερού Γ. Επιφανειακό Εκμεταλλεύσιμο Υδατικό Δυναμικό
 Α. Επανάληψη και εμπλουτισμός εννοιών Β. Ζήτηση νερού Γ. Επιφανειακό Εκμεταλλεύσιμο Υδατικό Δυναμικό ΔΥΠ Ορισμός Διαχείριση Υδατικών Πόρων είναι το σύνολο των ενεργειών (μέτρα, έργα, κανονιστικές διατάξεις,
Α. Επανάληψη και εμπλουτισμός εννοιών Β. Ζήτηση νερού Γ. Επιφανειακό Εκμεταλλεύσιμο Υδατικό Δυναμικό ΔΥΠ Ορισμός Διαχείριση Υδατικών Πόρων είναι το σύνολο των ενεργειών (μέτρα, έργα, κανονιστικές διατάξεις,
Μοντέλο Υδατικού Ισοζυγίου
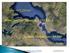 Μοντέλο Υδατικού Ισοζυγίου ΥΔΡΟΚΡΙΤΗΣ Η νοητή γραμμή που συνδέει τα ψηλότερα σημεία των υψωμάτων της επιφάνειας του εδάφους και διαχωρίζει τη ροή των όμβριων υδάτων. ΥΔΡΟΚΡΙΤΗΣ Κουτσογιάννης και Μαμάσης,
Μοντέλο Υδατικού Ισοζυγίου ΥΔΡΟΚΡΙΤΗΣ Η νοητή γραμμή που συνδέει τα ψηλότερα σημεία των υψωμάτων της επιφάνειας του εδάφους και διαχωρίζει τη ροή των όμβριων υδάτων. ΥΔΡΟΚΡΙΤΗΣ Κουτσογιάννης και Μαμάσης,
Το υπολογιστικό σύστηµα Υδρονοµέας και η εφαρµογή του στην µελέτη των έργων εκτροπής του Αχελώου
 Το υπολογιστικό σύστηµα Υδρονοµέας και η εφαρµογή του στην µελέτη των έργων εκτροπής του Αχελώου ηµήτρης Κουτσογιάννης & Ανδρέας Ευστρατιάδης Τοµέας Υδατικών Πόρων Εθνικό Μετσόβιο Πολυτεχνείο Μέρη της
Το υπολογιστικό σύστηµα Υδρονοµέας και η εφαρµογή του στην µελέτη των έργων εκτροπής του Αχελώου ηµήτρης Κουτσογιάννης & Ανδρέας Ευστρατιάδης Τοµέας Υδατικών Πόρων Εθνικό Μετσόβιο Πολυτεχνείο Μέρη της
βλπ και αυτή είναι η διδαχθείσα. Να δώσετε ένα Τι κατανοείται
 Βασικές ερωτήσεις με συνοπτικές απαντήσεις. Για διαφάνειες μαθήματος και σημειώσεις κ. Χρυσάνθου. πλήρη ανάπτυξη βλπ Επίσης, οι ερωτήσεις αυτές είναι οι πλεον βασικές ωστόσο η ύλη είναι ευρύτερη και αυτή
Βασικές ερωτήσεις με συνοπτικές απαντήσεις. Για διαφάνειες μαθήματος και σημειώσεις κ. Χρυσάνθου. πλήρη ανάπτυξη βλπ Επίσης, οι ερωτήσεις αυτές είναι οι πλεον βασικές ωστόσο η ύλη είναι ευρύτερη και αυτή
Διαχείριση Υδατικών Πόρων
 Διαχείριση Υδατικών Πόρων Επαναληπτικό μάθημα (1) Δρ Μ.Σπηλιώτης Λέκτορας ΔΠΘ Λειψυδρία Προσωρινή κατάσταση Φυσικά Αίτια Ξηρασία (drought) Ανθρωπογενή Αίτια Έλλειμμα Νερού (water shortage) Μόνιμη Ξηρότητα
Διαχείριση Υδατικών Πόρων Επαναληπτικό μάθημα (1) Δρ Μ.Σπηλιώτης Λέκτορας ΔΠΘ Λειψυδρία Προσωρινή κατάσταση Φυσικά Αίτια Ξηρασία (drought) Ανθρωπογενή Αίτια Έλλειμμα Νερού (water shortage) Μόνιμη Ξηρότητα
Το υπολογιστικό σύστηµα Υδρονοµέας και η εφαρµογή του στην µελέτη των έργων εκτροπής του Αχελώου
 Το υπολογιστικό σύστηµα Υδρονοµέας και η εφαρµογή του στην µελέτη των έργων εκτροπής του Αχελώου ηµήτρης Κουτσογιάννης & Ανδρέας Ευστρατιάδης Τοµέας Υδατικών Πόρων Εθνικό Μετσόβιο Πολυτεχνείο Μέρη της
Το υπολογιστικό σύστηµα Υδρονοµέας και η εφαρµογή του στην µελέτη των έργων εκτροπής του Αχελώου ηµήτρης Κουτσογιάννης & Ανδρέας Ευστρατιάδης Τοµέας Υδατικών Πόρων Εθνικό Μετσόβιο Πολυτεχνείο Μέρη της
Αστικά υδραυλικά έργα
 Εθνικό Μετσόβιο Πολυτεχνείο Τομέας Υδατικών Πόρων και Περιβάλλοντος Αστικά υδραυλικά έργα Διαστασιολόγηση αγωγών και έλεγχος πιέσεων δικτύων διανομής Δημήτρης Κουτσογιάννης, Καθηγητής ΕΜΠ Σχολή Πολιτικών
Εθνικό Μετσόβιο Πολυτεχνείο Τομέας Υδατικών Πόρων και Περιβάλλοντος Αστικά υδραυλικά έργα Διαστασιολόγηση αγωγών και έλεγχος πιέσεων δικτύων διανομής Δημήτρης Κουτσογιάννης, Καθηγητής ΕΜΠ Σχολή Πολιτικών
Γραµµικός Προγραµµατισµός (ΓΠ)
 Γραµµικός Προγραµµατισµός (ΓΠ) Περίληψη Επίλυση δυσδιάστατων προβληµάτων Η µέθοδος simplex Τυπική µορφή Ακέραιος Προγραµµατισµός Προγραµµατισµός Παραγωγής Προϊόν Προϊόν 2 Παραγωγική Δυνατότητα Μηχ. 4 Μηχ.
Γραµµικός Προγραµµατισµός (ΓΠ) Περίληψη Επίλυση δυσδιάστατων προβληµάτων Η µέθοδος simplex Τυπική µορφή Ακέραιος Προγραµµατισµός Προγραµµατισµός Παραγωγής Προϊόν Προϊόν 2 Παραγωγική Δυνατότητα Μηχ. 4 Μηχ.
Κεφάλαιο 14: Διαστασιολόγηση αγωγών και έλεγχος πιέσεων δικτύων διανομής
 Κεφάλαιο 14: Διαστασιολόγηση αγωγών και έλεγχος πιέσεων δικτύων διανομής Έλεγχος λειτουργίας δικτύων διανομής με χρήση μοντέλων υδραυλικής ανάλυσης Βασικό ζητούμενο της υδραυλικής ανάλυσης είναι ο έλεγχος
Κεφάλαιο 14: Διαστασιολόγηση αγωγών και έλεγχος πιέσεων δικτύων διανομής Έλεγχος λειτουργίας δικτύων διανομής με χρήση μοντέλων υδραυλικής ανάλυσης Βασικό ζητούμενο της υδραυλικής ανάλυσης είναι ο έλεγχος
Επιμέλεια: Δρ Μ. Σπηλιώτης Κείμενα σχήματα Τσακίρης 2008 Και κατά τις παραδόσεις του Κ.Κ.Μπέλλου
 Συλλογικά δίκτυα κλειστών αγωγών υπό πίεση Βελτιστοποίηση Επιμέλεια: Δρ Μ. Σπηλιώτης Κείμενα σχήματα Τσακίρης 2008 Και κατά τις παραδόσεις του Κ.Κ.Μπέλλου Γενικές αρχές Συλλογικό: Μόνιμοι αγωγοί με σκάμμα
Συλλογικά δίκτυα κλειστών αγωγών υπό πίεση Βελτιστοποίηση Επιμέλεια: Δρ Μ. Σπηλιώτης Κείμενα σχήματα Τσακίρης 2008 Και κατά τις παραδόσεις του Κ.Κ.Μπέλλου Γενικές αρχές Συλλογικό: Μόνιμοι αγωγοί με σκάμμα
5 η ΕΝΟΤΗΤΑ ΠΟΛΥΚΡΙΤΗΡΙΑΚΟΣ ΜΗ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΜΠ ΕΙΣΑΓΩΓΗ ΣΤΗN ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΣΥΣΤΗΜΑΤΩΝ 5 η ΕΝΟΤΗΤΑ ΠΟΛΥΚΡΙΤΗΡΙΑΚΟΣ ΜΗ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Μ. Καρλαύτης Ν. Λαγαρός Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΜΠ ΕΙΣΑΓΩΓΗ ΣΤΗN ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΣΥΣΤΗΜΑΤΩΝ 5 η ΕΝΟΤΗΤΑ ΠΟΛΥΚΡΙΤΗΡΙΑΚΟΣ ΜΗ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Μ. Καρλαύτης Ν. Λαγαρός Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Υδροηλεκτρικοί ταμιευτήρες
 Υδροηλεκτρικά Έργα 8ο εξάμηνο Σχολής Πολιτικών Μηχανικών Υδροηλεκτρικοί ταμιευτήρες Ανδρέας Ευστρατιάδης, Νίκος Μαμάσης, & Δημήτρης Κουτσογιάννης Τομέας Υδατικών Πόρων & Περιβάλλοντος, Εθνικό Μετσόβιο
Υδροηλεκτρικά Έργα 8ο εξάμηνο Σχολής Πολιτικών Μηχανικών Υδροηλεκτρικοί ταμιευτήρες Ανδρέας Ευστρατιάδης, Νίκος Μαμάσης, & Δημήτρης Κουτσογιάννης Τομέας Υδατικών Πόρων & Περιβάλλοντος, Εθνικό Μετσόβιο
Η επίδραση της δειγματοληπτικής αβεβαιότητας των εισροών στη στοχαστική προσομοίωση ταμιευτήρα
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ & ΠΕΡΙΒΑΛΛΟΝΤΟΣ Η επίδραση της δειγματοληπτικής αβεβαιότητας των εισροών στη στοχαστική προσομοίωση ταμιευτήρα Ελένη Ζαχαροπούλου
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ & ΠΕΡΙΒΑΛΛΟΝΤΟΣ Η επίδραση της δειγματοληπτικής αβεβαιότητας των εισροών στη στοχαστική προσομοίωση ταμιευτήρα Ελένη Ζαχαροπούλου
ΕΝΟΤΗΤΑ III ΒΑΣΙΚΕΣ ΜΕΘΟ ΟΙ ΑΝΑΛΥΣΗΣ
 ΕΝΟΤΗΤΑ III ΒΑΣΙΚΕΣ ΜΕΘΟ ΟΙ ΑΝΑΛΥΣΗΣ Βασικός τελικός στόχος κάθε επιστηµονικής τεχνολογικής εφαρµογής είναι: H γενική βελτίωση της ποιότητας του περιβάλλοντος Η βελτίωση της ποιότητας ζωής Τα µέσα µε τα
ΕΝΟΤΗΤΑ III ΒΑΣΙΚΕΣ ΜΕΘΟ ΟΙ ΑΝΑΛΥΣΗΣ Βασικός τελικός στόχος κάθε επιστηµονικής τεχνολογικής εφαρµογής είναι: H γενική βελτίωση της ποιότητας του περιβάλλοντος Η βελτίωση της ποιότητας ζωής Τα µέσα µε τα
ΒΑΣΙΚΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΤΗΣ ΜΕΘΟΔΟΥ SIMPLEX
 ΒΑΣΙΚΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΤΗΣ ΜΕΘΟΔΟΥ SIMPLEX Θεμελιώδης αλγόριθμος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού που κάνει χρήση της θεωρίας της Γραμμικής Άλγεβρας Προτάθηκε από το Dantzig (1947) και πλέον
ΒΑΣΙΚΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΤΗΣ ΜΕΘΟΔΟΥ SIMPLEX Θεμελιώδης αλγόριθμος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού που κάνει χρήση της θεωρίας της Γραμμικής Άλγεβρας Προτάθηκε από το Dantzig (1947) και πλέον
ΕΝΝΟΙΕΣ ΚΑΙ ΕΦΑΡΜΟΓΕΣ, διαλ. 4. Ανωτάτη Σχολή Παιδαγωγικής και Τεχνολογικής Εκπαίδευσης 6/5/2017
 ΕΝΝΟΙΕΣ ΚΑΙ ΕΦΑΡΜΟΓΕΣ διαλ. 4 Ανωτάτη Σχολή Παιδαγωγικής και Τεχνολογικής Εκπαίδευσης 6/5/7 Χαρακτηριστικά του προβλήματος Μελέτη αντικειμενικών συναρτήσεων και συναρτήσεων περιορισμών: Απλούστευση προβλήματος
ΕΝΝΟΙΕΣ ΚΑΙ ΕΦΑΡΜΟΓΕΣ διαλ. 4 Ανωτάτη Σχολή Παιδαγωγικής και Τεχνολογικής Εκπαίδευσης 6/5/7 Χαρακτηριστικά του προβλήματος Μελέτη αντικειμενικών συναρτήσεων και συναρτήσεων περιορισμών: Απλούστευση προβλήματος
Υδροηλεκτρικά Έργα. 8ο εξάμηνο Σχολής Πολιτικών Μηχανικών. Ταμιευτήρες. Ανδρέας Ευστρατιάδης, Νίκος Μαμάσης, & Δημήτρης Κουτσογιάννης
 Υδροηλεκτρικά Έργα 8ο εξάμηνο Σχολής Πολιτικών Μηχανικών Ταμιευτήρες Ανδρέας Ευστρατιάδης, Νίκος Μαμάσης, & Δημήτρης Κουτσογιάννης Τομέας Υδατικών Πόρων & Περιβάλλοντος, Εθνικό Μετσόβιο Πολυτεχνείο Ακαδημαϊκό
Υδροηλεκτρικά Έργα 8ο εξάμηνο Σχολής Πολιτικών Μηχανικών Ταμιευτήρες Ανδρέας Ευστρατιάδης, Νίκος Μαμάσης, & Δημήτρης Κουτσογιάννης Τομέας Υδατικών Πόρων & Περιβάλλοντος, Εθνικό Μετσόβιο Πολυτεχνείο Ακαδημαϊκό
Διαχείριση Εφοδιαστικής Αλυσίδας ΙΙ
 Διαχείριση Εφοδιαστικής Αλυσίδας ΙΙ 1 η Διάλεξη: Αναδρομή στον Μαθηματικό Προγραμματισμό 2019, Πολυτεχνική Σχολή Εργαστήριο Συστημάτων Σχεδιασμού, Παραγωγής και Λειτουργιών Περιεχόμενα 1. Γραμμικός Προγραμματισμός
Διαχείριση Εφοδιαστικής Αλυσίδας ΙΙ 1 η Διάλεξη: Αναδρομή στον Μαθηματικό Προγραμματισμό 2019, Πολυτεχνική Σχολή Εργαστήριο Συστημάτων Σχεδιασμού, Παραγωγής και Λειτουργιών Περιεχόμενα 1. Γραμμικός Προγραμματισμός
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος
 Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Υ ΡΟΓΑΙΑ. Λογισµικό ιαχείρισης Υδατικών Πόρων. Υ ΡΟΝΟΜΕΑΣ: : Βέλτιστη διαχείριση υδροσυστηµάτων
 Υ ΡΟΓΑΙΑ Λογισµικό ιαχείρισης Υδατικών Πόρων Υ ΡΟΝΟΜΕΑΣ: : Βέλτιστη διαχείριση υδροσυστηµάτων Υ ΡΟΓΑΙΑ: Υδρονοµέας Hydria Ζυγός Μοντέλο υδρολογικού ισοζυγίου λεκάνης Ρύπος Εκτίµηση ρυπαντικών φορτίων Ηριδανός
Υ ΡΟΓΑΙΑ Λογισµικό ιαχείρισης Υδατικών Πόρων Υ ΡΟΝΟΜΕΑΣ: : Βέλτιστη διαχείριση υδροσυστηµάτων Υ ΡΟΓΑΙΑ: Υδρονοµέας Hydria Ζυγός Μοντέλο υδρολογικού ισοζυγίου λεκάνης Ρύπος Εκτίµηση ρυπαντικών φορτίων Ηριδανός
Ειδικά θέµατα δικτύων διανοµής
 Ειδικά θέµατα δικτύων διανοµής Σηµειώσεις στα πλαίσια του µαθήµατος: Τυπικά υδραυλικά έργα Ακαδηµαϊκό έτος 2005-06 Ανδρέας Ευστρατιάδης & ηµήτρης Κουτσογιάννης Εθνικό Μετσόβιο Πολυτεχνείο Τοµέας Υδατικών
Ειδικά θέµατα δικτύων διανοµής Σηµειώσεις στα πλαίσια του µαθήµατος: Τυπικά υδραυλικά έργα Ακαδηµαϊκό έτος 2005-06 Ανδρέας Ευστρατιάδης & ηµήτρης Κουτσογιάννης Εθνικό Μετσόβιο Πολυτεχνείο Τοµέας Υδατικών
Εισαγωγή στην υδροπληροφορική και βελτιστοποίηση συστημάτων υδατικών πόρων
 Σημειώσεις στα πλαίσια του μαθήματος: Βελτιστοποίηση Συστημάτων Υδατικών Πόρων Υδροπληροφορική Εισαγωγή στην υδροπληροφορική και βελτιστοποίηση συστημάτων υδατικών πόρων Ανδρέας Ευστρατιάδης, Χρήστος Μακρόπουλος
Σημειώσεις στα πλαίσια του μαθήματος: Βελτιστοποίηση Συστημάτων Υδατικών Πόρων Υδροπληροφορική Εισαγωγή στην υδροπληροφορική και βελτιστοποίηση συστημάτων υδατικών πόρων Ανδρέας Ευστρατιάδης, Χρήστος Μακρόπουλος
Μοντελοποίηση προβληµάτων
 Σχεδιασµός Αλγορίθµων Ακέραιος προγραµµατισµός Αποδοτικοί Αλγόριθµοι Μη Αποδοτικοί Αλγόριθµοι Σχεδιασµός Αλγορίθµων Ακέραιος προγραµµατισµός Αποδοτικοί Αλγόριθµοι Μη Αποδοτικοί Αλγόριθµοι Θεωρία γράφων
Σχεδιασµός Αλγορίθµων Ακέραιος προγραµµατισµός Αποδοτικοί Αλγόριθµοι Μη Αποδοτικοί Αλγόριθµοι Σχεδιασµός Αλγορίθµων Ακέραιος προγραµµατισµός Αποδοτικοί Αλγόριθµοι Μη Αποδοτικοί Αλγόριθµοι Θεωρία γράφων
Εισαγωγή στην υδροπληροφορική και βελτιστοποίηση συστημάτων υδατικών πόρων
 Σημειώσεις στα πλαίσια του μαθήματος: Βελτιστοποίηση Συστημάτων Υδατικών Πόρων Υδροπληροφορική Εισαγωγή στην υδροπληροφορική και βελτιστοποίηση συστημάτων υδατικών πόρων Ανδρέας Ευστρατιάδης, Χρήστος Μακρόπουλος
Σημειώσεις στα πλαίσια του μαθήματος: Βελτιστοποίηση Συστημάτων Υδατικών Πόρων Υδροπληροφορική Εισαγωγή στην υδροπληροφορική και βελτιστοποίηση συστημάτων υδατικών πόρων Ανδρέας Ευστρατιάδης, Χρήστος Μακρόπουλος
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΔΠΜΣ ΕΠΙΣΤΗΜΗ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΥΔΡΑΥΛΙΚΩΝ & ΘΑΛΑΣΣΙΩΝ ΕΡΓΩΝ ΜΑΘΗΜΑ: ΔΙΑΧΕΙΡΙΣΗ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΑΣΚΗΣΗ 2 ΚΕΜΕΡΙΔΗΣ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΔΠΜΣ ΕΠΙΣΤΗΜΗ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΥΔΡΑΥΛΙΚΩΝ & ΘΑΛΑΣΣΙΩΝ ΕΡΓΩΝ ΜΑΘΗΜΑ: ΔΙΑΧΕΙΡΙΣΗ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΑΣΚΗΣΗ 2 ΚΕΜΕΡΙΔΗΣ
Διαχείριση Υδατικών Πόρων
 Εθνικό Μετσόβιο Πολυτεχνείο Τομέας Υδατικών Πόρων και Περιβάλλοντος Διαχείριση Υδατικών Πόρων Χρήστος Μακρόπουλος Αναπληρωτής Καθηγητής ΕΜΠ Tα Διαχειριστικά Προβλήματα Μοντέλα που επιβάλουν τους περιορισμούς
Εθνικό Μετσόβιο Πολυτεχνείο Τομέας Υδατικών Πόρων και Περιβάλλοντος Διαχείριση Υδατικών Πόρων Χρήστος Μακρόπουλος Αναπληρωτής Καθηγητής ΕΜΠ Tα Διαχειριστικά Προβλήματα Μοντέλα που επιβάλουν τους περιορισμούς
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Τοµέας Υδατικών Πόρων Μάθηµα: Αστικά Υδραυλικά Έργα Μέρος Α: Υδρευτικά έργα
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Τοµέας Υδατικών Πόρων Μάθηµα: Αστικά Υδραυλικά Έργα Μέρος Α: Υδρευτικά έργα Άσκηση E9: Εκτίµηση παροχών εξόδου κόµβων, υπολογισµός ελάχιστης κατώτατης
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Τοµέας Υδατικών Πόρων Μάθηµα: Αστικά Υδραυλικά Έργα Μέρος Α: Υδρευτικά έργα Άσκηση E9: Εκτίµηση παροχών εξόδου κόµβων, υπολογισµός ελάχιστης κατώτατης
ΠΛΑΙΣΙΟ ΣΤΟΧΑΣΤΙΚΗΣ ΠΡΟΣΟΜΟΙΩΣΗΣ ΓΙΑ ΤΗΝ ΕΚΤΙΜΗΣΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΥΔΡΟΛΟΓΙΚΩΝ & ΕΝΕΡΓΕΙΑΚΩΝ ΜΕΓΕΘΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΔΠΜΣ ΕΠΙΣΤΗΜΗ & ΤΕΧΝΟΛΟΓΙΑ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΠΛΑΙΣΙΟ ΣΤΟΧΑΣΤΙΚΗΣ ΠΡΟΣΟΜΟΙΩΣΗΣ ΓΙΑ ΤΗΝ ΕΚΤΙΜΗΣΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΥΔΡΟΛΟΓΙΚΩΝ & ΕΝΕΡΓΕΙΑΚΩΝ ΜΕΓΕΘΩΝ ΕΚΠΟΝΗΣΗ: ΙΩΑΝΝΑ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΔΠΜΣ ΕΠΙΣΤΗΜΗ & ΤΕΧΝΟΛΟΓΙΑ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΠΛΑΙΣΙΟ ΣΤΟΧΑΣΤΙΚΗΣ ΠΡΟΣΟΜΟΙΩΣΗΣ ΓΙΑ ΤΗΝ ΕΚΤΙΜΗΣΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΥΔΡΟΛΟΓΙΚΩΝ & ΕΝΕΡΓΕΙΑΚΩΝ ΜΕΓΕΘΩΝ ΕΚΠΟΝΗΣΗ: ΙΩΑΝΝΑ
Γραμμικός Προγραμματισμός Μέθοδος Simplex
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Επιχειρησιακή Έρευνα Γραμμικός Προγραμματισμός Μέθοδος Simplex Η παρουσίαση προετοιμάστηκε από τον Ν.Α. Παναγιώτου Περιεχόμενα Παρουσίασης 1. Πρότυπη Μορφή ΓΠ 2. Πινακοποίηση
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Επιχειρησιακή Έρευνα Γραμμικός Προγραμματισμός Μέθοδος Simplex Η παρουσίαση προετοιμάστηκε από τον Ν.Α. Παναγιώτου Περιεχόμενα Παρουσίασης 1. Πρότυπη Μορφή ΓΠ 2. Πινακοποίηση
ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΚΕΦΑΛΑΙΟ 1
 ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΚΕΦΑΛΑΙΟ 1 1 Βελτιστοποίηση Στην προσπάθεια αντιμετώπισης και επίλυσης των προβλημάτων που προκύπτουν στην πράξη, αναπτύσσουμε μαθηματικά μοντέλα,
ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΚΕΦΑΛΑΙΟ 1 1 Βελτιστοποίηση Στην προσπάθεια αντιμετώπισης και επίλυσης των προβλημάτων που προκύπτουν στην πράξη, αναπτύσσουμε μαθηματικά μοντέλα,
Εθνικό Μετσόβιο Πολυτεχνείο Τομέας Υδατικών Πόρων και Περιβάλλοντος. Τεχνολογία Συστημάτων Υδατικών Πόρων
 Εθνικό Μετσόβιο Πολυτεχνείο Τομέας Υδατικών Πόρων και Περιβάλλοντος Τεχνολογία Συστημάτων Υδατικών Πόρων Βελτιστοποίηση Μέρος b: Συμβατικές Μέθοδοι συνέχεια Σύνοψη προηγούμενου μαθήματος Στόχος βελτιστοποίησης:
Εθνικό Μετσόβιο Πολυτεχνείο Τομέας Υδατικών Πόρων και Περιβάλλοντος Τεχνολογία Συστημάτων Υδατικών Πόρων Βελτιστοποίηση Μέρος b: Συμβατικές Μέθοδοι συνέχεια Σύνοψη προηγούμενου μαθήματος Στόχος βελτιστοποίησης:
Συστήματα υποστήριξης αποφάσεων στη διαχείριση υδατικών πόρων: Η περίπτωση του υδροδοτικού συστήματος της Αθήνας
 Ημερίδα της ΕΥΔΑΠ για την Παγκόσμια Ημέρα Νερού Αθήνα, 22 Μαρτίου 2001 Συστήματα υποστήριξης αποφάσεων στη διαχείριση υδατικών πόρων: Η περίπτωση του υδροδοτικού συστήματος της Αθήνας Δημήτρης Κουτσογιάννης
Ημερίδα της ΕΥΔΑΠ για την Παγκόσμια Ημέρα Νερού Αθήνα, 22 Μαρτίου 2001 Συστήματα υποστήριξης αποφάσεων στη διαχείριση υδατικών πόρων: Η περίπτωση του υδροδοτικού συστήματος της Αθήνας Δημήτρης Κουτσογιάννης
Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο
 Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Δ.Π.Μ.Σ.: «ΕΠΙΣΤΗΜΗ & ΤΕΧΝΟΛΟΓΙΑ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ» ΤΟΜΕΑΣ ΔΙΑΧΕΙΡΙΣΗΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ & ΠΕΡΙΒΑΛΛΟΝΤΟΣ Μάθημα: Διαχείριση Υδατικών
Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Δ.Π.Μ.Σ.: «ΕΠΙΣΤΗΜΗ & ΤΕΧΝΟΛΟΓΙΑ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ» ΤΟΜΕΑΣ ΔΙΑΧΕΙΡΙΣΗΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ & ΠΕΡΙΒΑΛΛΟΝΤΟΣ Μάθημα: Διαχείριση Υδατικών
z = c 1 x 1 + c 2 x c n x n
 Τεχνολογικό Εκπαιδευτικό Ιδρυμα Κεντρικής Μακεδονίας - Σέρρες Τμήμα Μηχανικών Πληροφορικής Γραμμικός Προγραμματισμός & Βελτιστοποίηση Δρ. Δημήτρης Βαρσάμης Καθηγητής Εφαρμογών Δρ. Δημήτρης Βαρσάμης Μάρτιος
Τεχνολογικό Εκπαιδευτικό Ιδρυμα Κεντρικής Μακεδονίας - Σέρρες Τμήμα Μηχανικών Πληροφορικής Γραμμικός Προγραμματισμός & Βελτιστοποίηση Δρ. Δημήτρης Βαρσάμης Καθηγητής Εφαρμογών Δρ. Δημήτρης Βαρσάμης Μάρτιος
Διαχείριση Υδατικών Πόρων Εισαγωγή στη βελτιστοποίηση συστημάτων υδατικών πόρων
 Εθνικό Μετσόβιο Πολυτεχνείο Τομέας Υδατικών Πόρων και Περιβάλλοντος Διαχείριση Υδατικών Πόρων Εισαγωγή στη βελτιστοποίηση συστημάτων υδατικών πόρων Δημήτρης Κουτσογιάννης Σχολή Πολιτικών Μηχανικών Άδεια
Εθνικό Μετσόβιο Πολυτεχνείο Τομέας Υδατικών Πόρων και Περιβάλλοντος Διαχείριση Υδατικών Πόρων Εισαγωγή στη βελτιστοποίηση συστημάτων υδατικών πόρων Δημήτρης Κουτσογιάννης Σχολή Πολιτικών Μηχανικών Άδεια
Ένα φειδωλό μοντέλο για την πρόβλεψη των χαμηλών ροών σε μεσογειακά υδατορεύματα
 5 ο ΠΑΝΕΛΛΗΝΙΟ ΣΥΝΕΔΡΙΟ ΑΓΡΟΝΟΜΩΝ & ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ Αθήνα 14 & 15 Οκτωβρίου 2017 Ένα φειδωλό μοντέλο για την πρόβλεψη των χαμηλών ροών σε μεσογειακά υδατορεύματα Κωνσταντίνα Ρίσβα (1), Διονύσιος Νικολόπουλος
5 ο ΠΑΝΕΛΛΗΝΙΟ ΣΥΝΕΔΡΙΟ ΑΓΡΟΝΟΜΩΝ & ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ Αθήνα 14 & 15 Οκτωβρίου 2017 Ένα φειδωλό μοντέλο για την πρόβλεψη των χαμηλών ροών σε μεσογειακά υδατορεύματα Κωνσταντίνα Ρίσβα (1), Διονύσιος Νικολόπουλος
Συστήματα υποστήριξης αποφάσεων στη διαχείριση υδατικών πόρων: Η περίπτωση του υδροδοτικού συστήματος της Αθήνας
 Ημερίδα της ΕΥΔΑΠ για την Παγκόσμια Ημέρα Νερού Αθήνα, 22 Μαρτίου 2001 Συστήματα υποστήριξης αποφάσεων στη διαχείριση υδατικών πόρων: Η περίπτωση του υδροδοτικού συστήματος της Αθήνας Δημήτρης Κουτσογιάννης
Ημερίδα της ΕΥΔΑΠ για την Παγκόσμια Ημέρα Νερού Αθήνα, 22 Μαρτίου 2001 Συστήματα υποστήριξης αποφάσεων στη διαχείριση υδατικών πόρων: Η περίπτωση του υδροδοτικού συστήματος της Αθήνας Δημήτρης Κουτσογιάννης
Βασική Εφικτή Λύση. Βασική Εφικτή Λύση
 Αλγεβρική Μορφή Γενική Μορφή Γραµµικού Προγραµµατισµού n µεταβλητών και m περιορισµών Εστω πραγµατικοί αριθµοί a ij, b j, c i R µε 1 i m, 1 j n Αλγεβρική Μορφή Γενική Μορφή Γραµµικού Προγραµµατισµού n
Αλγεβρική Μορφή Γενική Μορφή Γραµµικού Προγραµµατισµού n µεταβλητών και m περιορισµών Εστω πραγµατικοί αριθµοί a ij, b j, c i R µε 1 i m, 1 j n Αλγεβρική Μορφή Γενική Μορφή Γραµµικού Προγραµµατισµού n
Προβλήματα Μεταφορών (Transportation)
 Προβλήματα Μεταφορών (Transportation) Παραδείγματα Διατύπωση Γραμμικού Προγραμματισμού Δικτυακή Διατύπωση Λύση Γενική Μέθοδος Simplex Μέθοδος Simplex για Προβλήματα Μεταφοράς Παράδειγμα: P&T Co ΗεταιρείαP&T
Προβλήματα Μεταφορών (Transportation) Παραδείγματα Διατύπωση Γραμμικού Προγραμματισμού Δικτυακή Διατύπωση Λύση Γενική Μέθοδος Simplex Μέθοδος Simplex για Προβλήματα Μεταφοράς Παράδειγμα: P&T Co ΗεταιρείαP&T
Fermat, 1638, Newton Euler, Lagrange, 1807
 Εισαγωγή Μαθ Προγρ Κλασικά Προβλ Επεκτάσεις Υπολογιστικές Μέθοδοι στη Θεωρία Αποφάσεων Ενότητα 1 Εισαγωγή Αντώνης Οικονόμου Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Προπτυχιακό πρόγραμμα σπουδών 3 Μαρτίου
Εισαγωγή Μαθ Προγρ Κλασικά Προβλ Επεκτάσεις Υπολογιστικές Μέθοδοι στη Θεωρία Αποφάσεων Ενότητα 1 Εισαγωγή Αντώνης Οικονόμου Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Προπτυχιακό πρόγραμμα σπουδών 3 Μαρτίου
Ιωάννα Ανυφαντή, Μηχανικός Περιβάλλοντος Επιβλέπων: Α. Ευστρατιάδης, ΕΔΙΠ ΕΜΠ. Αθήνα, Ιούλιος 2018
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Δ.Π.Μ.Σ. «ΕΠΙΣΤΗΜΗ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ» ΥΔΡΟΛΟΓΙΑ & ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΔΙΑΧΕΙΡΙΣΗ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΤΟΜΕΑΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Ιωάννα Ανυφαντή, Μηχανικός Περιβάλλοντος
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Δ.Π.Μ.Σ. «ΕΠΙΣΤΗΜΗ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ» ΥΔΡΟΛΟΓΙΑ & ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΔΙΑΧΕΙΡΙΣΗ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΤΟΜΕΑΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Ιωάννα Ανυφαντή, Μηχανικός Περιβάλλοντος
Σχεδιασμός επέκτασης του συστήματος ηλεκτροπαραγωγής με τη χρήση Πολυκριτηριακού Γραμμικού Προγραμματισμού
 3ο Πανελλήνιο Επιστημονικό Συνέδριο Χημικής Μηχανικής Αθήνα,, IούνιοςI 200 Σχεδιασμός επέκτασης του συστήματος ηλεκτροπαραγωγής με τη χρήση Πολυκριτηριακού Γραμμικού Προγραμματισμού Γιώργος Μαυρωτάς Δανάη
3ο Πανελλήνιο Επιστημονικό Συνέδριο Χημικής Μηχανικής Αθήνα,, IούνιοςI 200 Σχεδιασμός επέκτασης του συστήματος ηλεκτροπαραγωγής με τη χρήση Πολυκριτηριακού Γραμμικού Προγραμματισμού Γιώργος Μαυρωτάς Δανάη
Συστήματα Παραγωγής ΠΑΡΑΔΕΙΓΜΑ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ
 Συστήματα Παραγωγής ΠΑΡΑΔΕΙΓΜΑ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Περιεχόμενα 1 Γενικά στοιχεία γραμμικού προγραμματισμού 2 Παράδειγμα γραμμικού προγραμματισμού και γραφικής επίλυσης του 3 Γραμμικός προγραμματισμός
Συστήματα Παραγωγής ΠΑΡΑΔΕΙΓΜΑ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Περιεχόμενα 1 Γενικά στοιχεία γραμμικού προγραμματισμού 2 Παράδειγμα γραμμικού προγραμματισμού και γραφικής επίλυσης του 3 Γραμμικός προγραμματισμός
Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο
 Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Δ.Π.Μ.Σ.: «ΕΠΙΣΤΗΜΗ & ΤΕΧΝΟΛΟΓΙΑ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ» ΤΟΜΕΑΣ ΔΙΑΧΕΙΡΙΣΗΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ & ΠΕΡΙΒΑΛΛΟΝΤΟΣ Μάθημα: Διαχείριση Υδατικών
Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Δ.Π.Μ.Σ.: «ΕΠΙΣΤΗΜΗ & ΤΕΧΝΟΛΟΓΙΑ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ» ΤΟΜΕΑΣ ΔΙΑΧΕΙΡΙΣΗΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ & ΠΕΡΙΒΑΛΛΟΝΤΟΣ Μάθημα: Διαχείριση Υδατικών
Αστικά υδραυλικά έργα
 Εθνικό Μετσόβιο Πολυτεχνείο Τομέας Υδατικών Πόρων και Περιβάλλοντος Αστικά υδραυλικά έργα Υδραυλική ανάλυση δικτύων διανομής Δημήτρης Κουτσογιάννης, Καθηγητής ΕΜΠ Σχολή Πολιτικών Μηχανικών Άδεια Χρήσης
Εθνικό Μετσόβιο Πολυτεχνείο Τομέας Υδατικών Πόρων και Περιβάλλοντος Αστικά υδραυλικά έργα Υδραυλική ανάλυση δικτύων διανομής Δημήτρης Κουτσογιάννης, Καθηγητής ΕΜΠ Σχολή Πολιτικών Μηχανικών Άδεια Χρήσης
Επιχειρησιακή Έρευνα I
 Επιχειρησιακή Έρευνα I Κωστής Μαμάσης Παρασκευή 09:00 12:00 Σημειώσεις των Α. Platis, K. Mamasis Περιεχόμενα 1. Εισαγωγή 2. Γραμμικός Προγραμματισμός 1. Μοντελοποίηση 2. Μέθοδος Simplex 1. Αλγόριθμός Simplex
Επιχειρησιακή Έρευνα I Κωστής Μαμάσης Παρασκευή 09:00 12:00 Σημειώσεις των Α. Platis, K. Mamasis Περιεχόμενα 1. Εισαγωγή 2. Γραμμικός Προγραμματισμός 1. Μοντελοποίηση 2. Μέθοδος Simplex 1. Αλγόριθμός Simplex
Κεφάλαιο 12: Υδραυλική ανάλυση δικτύων διανομής
 Κεφάλαιο 12: Υδραυλική ανάλυση δικτύων διανομής Εννοιολογική αναπαράσταση δίκτυων διανομής Σχηματοποίηση: δικτυακή απεικόνιση των συνιστωσών του φυσικού συστήματος ως συνιστώσες ενός εννοιολογικού μοντέλου
Κεφάλαιο 12: Υδραυλική ανάλυση δικτύων διανομής Εννοιολογική αναπαράσταση δίκτυων διανομής Σχηματοποίηση: δικτυακή απεικόνιση των συνιστωσών του φυσικού συστήματος ως συνιστώσες ενός εννοιολογικού μοντέλου
Διάρθρωση παρουσίασης
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ, ΥΔΡΑΥΛΙΚΩΝ & ΘΑΛΑΣΣΙΩΝ ΕΡΓΩΝ Βέλτιστη Διαχείριση Συστημάτων Ταμιευτήρων Εφαρμογή στο Σύστημα Αχελώου - Θεσσαλίας Διπλωματική
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ, ΥΔΡΑΥΛΙΚΩΝ & ΘΑΛΑΣΣΙΩΝ ΕΡΓΩΝ Βέλτιστη Διαχείριση Συστημάτων Ταμιευτήρων Εφαρμογή στο Σύστημα Αχελώου - Θεσσαλίας Διπλωματική
Υδρολογική διερεύνηση λειτουργίας ταµιευτήρα Πλαστήρα
 ΠΜΣ «Επιστήµη και Τεχνολογία Υδατικών Πόρων» Παρουσίαση στα πλαίσια του µαθήµατος: «Περιβαλλοντικές Επιπτώσεις από Υδραυλικά Έργα» Υδρολογική διερεύνηση λειτουργίας ταµιευτήρα Πλαστήρα Ανδρέας Ευστρατιάδης,
ΠΜΣ «Επιστήµη και Τεχνολογία Υδατικών Πόρων» Παρουσίαση στα πλαίσια του µαθήµατος: «Περιβαλλοντικές Επιπτώσεις από Υδραυλικά Έργα» Υδρολογική διερεύνηση λειτουργίας ταµιευτήρα Πλαστήρα Ανδρέας Ευστρατιάδης,
Β. Βασιλειάδης. Επιχειρησιακή Έρευνα Διάλεξη 5 η -Αλγόριθμος Simplex
 Β. Βασιλειάδης Επιχειρησιακή Έρευνα Διάλεξη 5 η -Αλγόριθμος Simplex Περιεχόμενα Ο αλγόριθμος Simplex Βασικά Βήματα Παραδείγματα Συμπεράσματα 1o Bήμα: εξάλειψη των ανισοτήτων Στη μαθηματική διατύπωση του
Β. Βασιλειάδης Επιχειρησιακή Έρευνα Διάλεξη 5 η -Αλγόριθμος Simplex Περιεχόμενα Ο αλγόριθμος Simplex Βασικά Βήματα Παραδείγματα Συμπεράσματα 1o Bήμα: εξάλειψη των ανισοτήτων Στη μαθηματική διατύπωση του
Προβλήματα Ελάχιστου Κόστους Ροής σε Δίκτυο. Δίκτυα Ροής Ελάχιστου Κόστους (Minimum Cost Flow Networks)
 Προβλήματα Ελάχιστου Κόστους Ροής σε Δίκτυο Ορισμοί Παραδείγματα Δικτυακή Simplex (προβλήματα με και χωρίς φραγμούς). Δίκτυα Ροής Ελάχιστου Κόστους (Minimum ost Flow Networks) Ένα δίκτυο μεταφόρτωσης αποτελείται
Προβλήματα Ελάχιστου Κόστους Ροής σε Δίκτυο Ορισμοί Παραδείγματα Δικτυακή Simplex (προβλήματα με και χωρίς φραγμούς). Δίκτυα Ροής Ελάχιστου Κόστους (Minimum ost Flow Networks) Ένα δίκτυο μεταφόρτωσης αποτελείται
Εθνικό Μετσόβιο Πολυτεχνείο Τομέας Υδατικών Πόρων και Περιβάλλοντος. Διαχείριση Υδατικών Πόρων
 Εθνικό Μετσόβιο Πολυτεχνείο Τομέας Υδατικών Πόρων και Περιβάλλοντος Διαχείριση Υδατικών Πόρων Βελτιστοποίηση Μέρος b: Συμβατικές Μέθοδοι συνέχεια Σύνοψη προηγούμενου μαθήματος Στόχος βελτιστοποίησης: Εύρεση
Εθνικό Μετσόβιο Πολυτεχνείο Τομέας Υδατικών Πόρων και Περιβάλλοντος Διαχείριση Υδατικών Πόρων Βελτιστοποίηση Μέρος b: Συμβατικές Μέθοδοι συνέχεια Σύνοψη προηγούμενου μαθήματος Στόχος βελτιστοποίησης: Εύρεση
Άσκηση 21. Συστήματα Αποφάσεων Εργαστήριο Συστημάτων Αποφάσεων και Διοίκησης
 Εταιρία παράγει σκυρόδεμα με το οποίο προμηθεύει σε καθημερινή βάση διάφορες οικοδομικές επιχειρήσεις. Το σκυρόδεμα παράγεται σε δύο εργοτάξια της εταιρίας, το Α και το Β. Με τα σημερινά δεδομένα, υπάρχει
Εταιρία παράγει σκυρόδεμα με το οποίο προμηθεύει σε καθημερινή βάση διάφορες οικοδομικές επιχειρήσεις. Το σκυρόδεμα παράγεται σε δύο εργοτάξια της εταιρίας, το Α και το Β. Με τα σημερινά δεδομένα, υπάρχει
Συστήματα Ελέγχου με Μικροϋπολογιστές (h9p://courseware.mech.ntua.gr/ml23259/)
 Συστήματα Ελέγχου με Μικροϋπολογιστές (h9p://courseware.mech.ntua.gr/ml23259/) Κων/νος Ι. Κυριακόπουλος Καθηγητής ΕΜΠ (h9p://users.ntua.gr/kkyria/) Kostas J. Kyriakopoulos - Σ.Α.Ε. ΙΙ 1 Δομή της Ύλης του
Συστήματα Ελέγχου με Μικροϋπολογιστές (h9p://courseware.mech.ntua.gr/ml23259/) Κων/νος Ι. Κυριακόπουλος Καθηγητής ΕΜΠ (h9p://users.ntua.gr/kkyria/) Kostas J. Kyriakopoulos - Σ.Α.Ε. ΙΙ 1 Δομή της Ύλης του
Η γραφική μέθοδος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού
 Η γραφική μέθοδος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 τελευταία ενημέρωση: 21/10/2016 1 Γραφική μέθοδος
Η γραφική μέθοδος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 τελευταία ενημέρωση: 21/10/2016 1 Γραφική μέθοδος
ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΠΕΡΣΕΦΟΝΗ ΠΟΛΥΧΡΟΝΙΔΟΥ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΤΕ
 ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΠΕΡΣΕΦΟΝΗ ΠΟΛΥΧΡΟΝΙΔΟΥ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΤΕ 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΠΕΡΣΕΦΟΝΗ ΠΟΛΥΧΡΟΝΙΔΟΥ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΤΕ 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Ανάλυση δικτύων διανομής
 Υδραυλική & Υδραυλικά Έργα 5 ο εξάμηνο Σχολής Πολιτικών Μηχανικών Ανάλυση δικτύων διανομής Χρήστος Μακρόπουλος, Ανδρέας Ευστρατιάδης & Παναγιώτης Κοσσιέρης Τομέας Υδατικών Πόρων & Περιβάλλοντος, Εθνικό
Υδραυλική & Υδραυλικά Έργα 5 ο εξάμηνο Σχολής Πολιτικών Μηχανικών Ανάλυση δικτύων διανομής Χρήστος Μακρόπουλος, Ανδρέας Ευστρατιάδης & Παναγιώτης Κοσσιέρης Τομέας Υδατικών Πόρων & Περιβάλλοντος, Εθνικό
Γραφική Λύση & Πρότυπη Μορφή Μαθηματικού Μοντέλου
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Επιχειρησιακή Έρευνα Γραφική Λύση & Πρότυπη Μορφή Μαθηματικού Μοντέλου Η παρουσίαση προετοιμάστηκε από τον Ν.Α. Παναγιώτου Περιεχόμενα Παρουσίασης 1. Προϋποθέσεις Εφαρμογής
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Επιχειρησιακή Έρευνα Γραφική Λύση & Πρότυπη Μορφή Μαθηματικού Μοντέλου Η παρουσίαση προετοιμάστηκε από τον Ν.Α. Παναγιώτου Περιεχόμενα Παρουσίασης 1. Προϋποθέσεις Εφαρμογής
Γραμμικός Προγραμματισμός
 Γραμμικός Προγραμματισμός Παράδειγμα ΕΠΙΠΛΟΞΥΛ Η βιοτεχνία ΕΠΙΠΛΟΞΥΛ παράγει δύο βασικά προϊόντα: τραπέζια και καρέκλες υψηλής ποιότητας. Η διαδικασία παραγωγής και για τα δύο προϊόντα περιλαμβάνει την
Γραμμικός Προγραμματισμός Παράδειγμα ΕΠΙΠΛΟΞΥΛ Η βιοτεχνία ΕΠΙΠΛΟΞΥΛ παράγει δύο βασικά προϊόντα: τραπέζια και καρέκλες υψηλής ποιότητας. Η διαδικασία παραγωγής και για τα δύο προϊόντα περιλαμβάνει την
1. ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 Η επιχειρησιακή έρευνα επικεντρώνεται στη λήψη αποφάσεων από επιχειρήσεις οργανισμούς, κράτη κτλ. Στα πλαίσια της επιχειρησιακής έρευνας εξετάζονται οι ακόλουθες περιπτώσεις : Γραμμικός προγραμματισμός
Η επιχειρησιακή έρευνα επικεντρώνεται στη λήψη αποφάσεων από επιχειρήσεις οργανισμούς, κράτη κτλ. Στα πλαίσια της επιχειρησιακής έρευνας εξετάζονται οι ακόλουθες περιπτώσεις : Γραμμικός προγραμματισμός
Η γραφική μέθοδος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού
 Η γραφική μέθοδος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού Γεωργία Φουτσιτζή-Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα Τμήμα Μηχανικών Πληροφορικής ΤΕ 2017-2018 τελευταία ενημέρωση: 21/10/2016
Η γραφική μέθοδος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού Γεωργία Φουτσιτζή-Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα Τμήμα Μηχανικών Πληροφορικής ΤΕ 2017-2018 τελευταία ενημέρωση: 21/10/2016
Επιχειρησιακή Έρευνα
 Επιχειρησιακή Έρευνα Ενότητα 7: Επίλυση με τη μέθοδο Simplex (1 ο μέρος) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων (Δ.Ε.Α.Π.Τ.)
Επιχειρησιακή Έρευνα Ενότητα 7: Επίλυση με τη μέθοδο Simplex (1 ο μέρος) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων (Δ.Ε.Α.Π.Τ.)
ΕΙΣΑΓΩΓΗ ΣΤΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΣΥΣΤΗΜΑΤΩΝ
 ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ Α. Ντούνης ΔΙΔΑΣΚΩΝ Χ. Τσιρώνης ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΣΥΣΤΗΜΑΤΩΝ - Αναλυτικές τεχνικές - Ειδικά θέματα θεωρίας - Λύση ασκήσεων πράξης ΑΝΑΛΥΤΙΚΕΣ ΤΕΧΝΙΚΕΣ Τι μάθαμε μέχρι τώρα: Να επιλύουμε
ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ Α. Ντούνης ΔΙΔΑΣΚΩΝ Χ. Τσιρώνης ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΣΥΣΤΗΜΑΤΩΝ - Αναλυτικές τεχνικές - Ειδικά θέματα θεωρίας - Λύση ασκήσεων πράξης ΑΝΑΛΥΤΙΚΕΣ ΤΕΧΝΙΚΕΣ Τι μάθαμε μέχρι τώρα: Να επιλύουμε
είναι πρόβλημα μεγιστοποίησης όλοι οι περιορισμοί είναι εξισώσεις με μη αρνητικούς του σταθερούς όρους όλες οι μεταβλητές είναι μη αρνητικές
 Ένα τυχαίο π.γ.π. maximize/minimize z=c x Αx = b x 0 Τυπική μορφή του π.γ.π. maximize z=c x Αx = b x 0 b 0 είναι πρόβλημα μεγιστοποίησης όλοι οι περιορισμοί είναι εξισώσεις με μη αρνητικούς του σταθερούς
Ένα τυχαίο π.γ.π. maximize/minimize z=c x Αx = b x 0 Τυπική μορφή του π.γ.π. maximize z=c x Αx = b x 0 b 0 είναι πρόβλημα μεγιστοποίησης όλοι οι περιορισμοί είναι εξισώσεις με μη αρνητικούς του σταθερούς
υδρογεωλογικών διεργασιών και λειτουργίας υδροσυστήµατος υτικής Θεσσαλίας
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Τοµέας Υδατικών Πόρων, Υδραυλικών και Θαλάσσιων Έργων Συνδυασµένη προσοµοίωση υδρολογικών-υδρογεωλογικών υδρογεωλογικών διεργασιών και λειτουργίας
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Τοµέας Υδατικών Πόρων, Υδραυλικών και Θαλάσσιων Έργων Συνδυασµένη προσοµοίωση υδρολογικών-υδρογεωλογικών υδρογεωλογικών διεργασιών και λειτουργίας
Τμήμα Μηχανικών Πληροφορικής ΤΕ Δυϊκότητα. Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα. τελευταία ενημέρωση: 1/12/2016
 Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 Δυϊκότητα Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 1/12/2016 1 Το δυϊκό πρόβλημα Για κάθε πρόβλημα Γραμμικού Προγραμματισμού υπάρχει
Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 Δυϊκότητα Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 1/12/2016 1 Το δυϊκό πρόβλημα Για κάθε πρόβλημα Γραμμικού Προγραμματισμού υπάρχει
Αστικά υδραυλικά έργα
 Εθνικό Μετσόβιο Πολυτεχνείο Τομέας Υδατικών Πόρων και Περιβάλλοντος Αστικά υδραυλικά έργα Διαμόρφωση μοντέλου υδραυλικής ανάλυσης δικτύου διανομής Δημήτρης Κουτσογιάννης, Καθηγητής ΕΜΠ Σχολή Πολιτικών
Εθνικό Μετσόβιο Πολυτεχνείο Τομέας Υδατικών Πόρων και Περιβάλλοντος Αστικά υδραυλικά έργα Διαμόρφωση μοντέλου υδραυλικής ανάλυσης δικτύου διανομής Δημήτρης Κουτσογιάννης, Καθηγητής ΕΜΠ Σχολή Πολιτικών
ΒΕΛΤΙΣΤΟΣ ΣΧΕΔΙΑΣΜΟΣ ΤΩΝ ΚΑΤΑΣΚΕΥΩΝ. Δρ. Πολ. Μηχ. Κόκκινος Οδυσσέας
 ΒΕΛΤΙΣΤΟΣ ΣΧΕΔΙΑΣΜΟΣ ΤΩΝ ΚΑΤΑΣΚΕΥΩΝ Δρ. Πολ. Μηχ. Κόκκινος Οδυσσέας Σχεδιασμός αντικειμένων, διεργασιών, δραστηριοτήτων (π.χ. τεχνικά έργα, έπιπλα, σκεύη κτλ) ΠΡΟΚΑΤΑΡΚΤΙΚΗ ΜΕΛΕΤΗ (conceptual design) ΠΡΟΜΕΛΕΤΗ
ΒΕΛΤΙΣΤΟΣ ΣΧΕΔΙΑΣΜΟΣ ΤΩΝ ΚΑΤΑΣΚΕΥΩΝ Δρ. Πολ. Μηχ. Κόκκινος Οδυσσέας Σχεδιασμός αντικειμένων, διεργασιών, δραστηριοτήτων (π.χ. τεχνικά έργα, έπιπλα, σκεύη κτλ) ΠΡΟΚΑΤΑΡΚΤΙΚΗ ΜΕΛΕΤΗ (conceptual design) ΠΡΟΜΕΛΕΤΗ
Επιχειρησιακή έρευνα (ασκήσεις)
 Επιχειρησιακή έρευνα (ασκήσεις) ΤΕΙ Ηπείρου (Τμήμα Λογιστικής και Χρηματοοικονομικής) Γκόγκος Χρήστος (06-01-2015) 1. Γραφική επίλυση προβλημάτων Γραμμικού Προγραμματισμού A) Με τη βοήθεια της γραφικής
Επιχειρησιακή έρευνα (ασκήσεις) ΤΕΙ Ηπείρου (Τμήμα Λογιστικής και Χρηματοοικονομικής) Γκόγκος Χρήστος (06-01-2015) 1. Γραφική επίλυση προβλημάτων Γραμμικού Προγραμματισμού A) Με τη βοήθεια της γραφικής
Γραμμικός Προγραμματισμός
 Γραμμικός Προγραμματισμός Εισαγωγή Το πρόβλημα του Σχεδιασμού στη Χημική Τεχνολογία και Βιομηχανία. Το συνολικό πρόβλημα του Σχεδιασμού, από μαθηματική άποψη ανάγεται σε ένα πρόβλημα επίλυσης συστήματος
Γραμμικός Προγραμματισμός Εισαγωγή Το πρόβλημα του Σχεδιασμού στη Χημική Τεχνολογία και Βιομηχανία. Το συνολικό πρόβλημα του Σχεδιασμού, από μαθηματική άποψη ανάγεται σε ένα πρόβλημα επίλυσης συστήματος
Εισαγωγή στα δίκτυα διανοµής
 Εισαγωγή στα δίκτυα διανοµής Σηµειώσεις στα πλαίσια του µαθήµατος: Τυπικά υδραυλικά έργα Ακαδηµαϊκό έτος 2005-06 Ανδρέας Ευστρατιάδης & ηµήτρης Κουτσογιάννης Εθνικό Μετσόβιο Πολυτεχνείο Τοµέας Υδατικών
Εισαγωγή στα δίκτυα διανοµής Σηµειώσεις στα πλαίσια του µαθήµατος: Τυπικά υδραυλικά έργα Ακαδηµαϊκό έτος 2005-06 Ανδρέας Ευστρατιάδης & ηµήτρης Κουτσογιάννης Εθνικό Μετσόβιο Πολυτεχνείο Τοµέας Υδατικών
Πληροφοριακά Συστήματα Διοίκησης. Επισκόπηση μοντέλων λήψης αποφάσεων Τεχνικές Μαθηματικού Προγραμματισμού
 Πληροφοριακά Συστήματα Διοίκησης Επισκόπηση μοντέλων λήψης αποφάσεων Τεχνικές Μαθηματικού Προγραμματισμού Σημασία μοντέλου Το μοντέλο δημιουργεί μια λογική δομή μέσω της οποίας αποκτούμε μια χρήσιμη άποψη
Πληροφοριακά Συστήματα Διοίκησης Επισκόπηση μοντέλων λήψης αποφάσεων Τεχνικές Μαθηματικού Προγραμματισμού Σημασία μοντέλου Το μοντέλο δημιουργεί μια λογική δομή μέσω της οποίας αποκτούμε μια χρήσιμη άποψη
Ευχαριστίες... 16 Δύο λόγια από την συγγραφέα... 17
 Περιεχόμενα Ευχαριστίες... 16 Δύο λόγια από την συγγραφέα... 17 ΚΕΦΑΛΑΙΟ 1. Το σύνολο των πραγματικών αριθμών... 19 1.1 Σύνολα αριθμών... 19 1.2 Αλγεβρική δομή του R... 20 1.2.1 Ιδιότητες πρόσθεσης...
Περιεχόμενα Ευχαριστίες... 16 Δύο λόγια από την συγγραφέα... 17 ΚΕΦΑΛΑΙΟ 1. Το σύνολο των πραγματικών αριθμών... 19 1.1 Σύνολα αριθμών... 19 1.2 Αλγεβρική δομή του R... 20 1.2.1 Ιδιότητες πρόσθεσης...
Μάθημα Επιλογής 8 ου εξαμήνου
 EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Μάθημα Επιλογής 8 ου εξαμήνου Διδάσκων:
EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Μάθημα Επιλογής 8 ου εξαμήνου Διδάσκων:
Συνδυαστική Βελτιστοποίηση Εισαγωγή στον γραμμικό προγραμματισμό (ΓΠ)
 Εικονικές Παράμετροι Μέχρι στιγμής είδαμε την εφαρμογή της μεθόδου Simplex σε προβλήματα όπου το δεξιό μέλος ήταν θετικό. Δηλαδή όλοι οι περιορισμοί ήταν της μορφής: όπου Η παραδοχή ότι b 0 μας δίδει τη
Εικονικές Παράμετροι Μέχρι στιγμής είδαμε την εφαρμογή της μεθόδου Simplex σε προβλήματα όπου το δεξιό μέλος ήταν θετικό. Δηλαδή όλοι οι περιορισμοί ήταν της μορφής: όπου Η παραδοχή ότι b 0 μας δίδει τη
Επιχειρησιακή Έρευνα. Εισαγωγική Διάλεξη
 Επιχειρησιακή Έρευνα Εισαγωγική Διάλεξη Πληροφορίες Διδάσκων: Αντώνης Δημάκης (dimakis@aueb.gr) Γραφείο: 506, 5 ος όροφος, Τροίας 2 (νέο κτήριο), Ώρες: Πέμπτη 1-3μμ Τηλ: 210-8203-924 Βοηθός: Δέσποινα Μεντζελιώτου
Επιχειρησιακή Έρευνα Εισαγωγική Διάλεξη Πληροφορίες Διδάσκων: Αντώνης Δημάκης (dimakis@aueb.gr) Γραφείο: 506, 5 ος όροφος, Τροίας 2 (νέο κτήριο), Ώρες: Πέμπτη 1-3μμ Τηλ: 210-8203-924 Βοηθός: Δέσποινα Μεντζελιώτου
Κεφάλαιο 13: Διαμόρφωση μοντέλου υδραυλικής ανάλυσης δικτύου διανομής
 Κεφάλαιο 13: Διαμόρφωση μοντέλου υδραυλικής ανάλυσης δικτύου διανομής Κόμβος i Κόμβος j Συνιστώσες μοντέλου υδραυλικής ανάλυσης Κόμβος: Σημείο εισροής ή εκροής νερού ή αλλαγής της γεωμετρίας του δικτύου
Κεφάλαιο 13: Διαμόρφωση μοντέλου υδραυλικής ανάλυσης δικτύου διανομής Κόμβος i Κόμβος j Συνιστώσες μοντέλου υδραυλικής ανάλυσης Κόμβος: Σημείο εισροής ή εκροής νερού ή αλλαγής της γεωμετρίας του δικτύου
υναµικός προγραµµατισµός
 υναµικός προγραµµατισµός Σηµειώσεις στα πλαίσια του µαθήµατος: Βελτιστοποίηση συστηµάτων υδατικών πόρων Ανδρέας Ευστρατιάδης και ηµήτρης Κουτσογιάννης Τοµέας Υδατικών Πόρων και Περιβάλλοντος Εθνικό Μετσόβιο
υναµικός προγραµµατισµός Σηµειώσεις στα πλαίσια του µαθήµατος: Βελτιστοποίηση συστηµάτων υδατικών πόρων Ανδρέας Ευστρατιάδης και ηµήτρης Κουτσογιάννης Τοµέας Υδατικών Πόρων και Περιβάλλοντος Εθνικό Μετσόβιο
Υδρονοµέας Σύστηµα υποστήριξης της διαχείρισης υδατικών πόρων
 Εθνικό Μετσόβιο Πολυτεχνείο Τοµέας Υδατικών Πόρων, Υδραυλικών και Θαλάσσιων Έργων Υδρονοµέας Σύστηµα υποστήριξης της διαχείρισης υδατικών πόρων Γ. Καραβοκυρός Α. Ευστρατιαδης. Κουτσογιάννης Φεβρουάριος
Εθνικό Μετσόβιο Πολυτεχνείο Τοµέας Υδατικών Πόρων, Υδραυλικών και Θαλάσσιων Έργων Υδρονοµέας Σύστηµα υποστήριξης της διαχείρισης υδατικών πόρων Γ. Καραβοκυρός Α. Ευστρατιαδης. Κουτσογιάννης Φεβρουάριος
min f(x) x R n b j - g j (x) = s j - b j = 0 g j (x) + s j = 0 - b j ) min L(x, s, λ) x R n λ, s R m L x i = 1, 2,, n (1) m L(x, s, λ) = f(x) +
 KΕΦΑΛΑΙΟ 4 Κλασσικές Μέθοδοι Βελτιστοποίησης Με Περιορισµούς Ανισότητες 4. ΠΡΟΒΛΗΜΑΤΑ ΜΕ ΠΕΡΙΟΡΙΣΜΟΥΣ ΑΝΙΣΟΤΗΤΕΣ Ζητούνται οι τιµές των µεταβλητών απόφασης που ελαχιστοποιούν την αντικειµενική συνάρτηση
KΕΦΑΛΑΙΟ 4 Κλασσικές Μέθοδοι Βελτιστοποίησης Με Περιορισµούς Ανισότητες 4. ΠΡΟΒΛΗΜΑΤΑ ΜΕ ΠΕΡΙΟΡΙΣΜΟΥΣ ΑΝΙΣΟΤΗΤΕΣ Ζητούνται οι τιµές των µεταβλητών απόφασης που ελαχιστοποιούν την αντικειµενική συνάρτηση
υναµικός προγραµµατισµός
 υναµικός προγραµµατισµός Σηµειώσεις στα πλαίσια του µαθήµατος: Βελτιστοποίηση συστηµάτων υδατικών πόρων Ανδρέας Ευστρατιάδης και ηµήτρης Κουτσογιάννης Τοµέας Υδατικών Πόρων και Περιβάλλοντος Εθνικό Μετσόβιο
υναµικός προγραµµατισµός Σηµειώσεις στα πλαίσια του µαθήµατος: Βελτιστοποίηση συστηµάτων υδατικών πόρων Ανδρέας Ευστρατιάδης και ηµήτρης Κουτσογιάννης Τοµέας Υδατικών Πόρων και Περιβάλλοντος Εθνικό Μετσόβιο
Κεφάλαιο 6: Γενική διάταξη υδρευτικών έργων
 Κεφάλαιο 6: Γενική διάταξη υδρευτικών έργων Γενικές παρατηρήσεις Σκοπός των έργων ύδρευσης είναι η εξασφάλιση του απαιτούμενου νερού, σε επαρκή ποσότητα και κατάλληλη ποιότητα, και η μεταφορά και διανομή
Κεφάλαιο 6: Γενική διάταξη υδρευτικών έργων Γενικές παρατηρήσεις Σκοπός των έργων ύδρευσης είναι η εξασφάλιση του απαιτούμενου νερού, σε επαρκή ποσότητα και κατάλληλη ποιότητα, και η μεταφορά και διανομή
ΕΙΣΑΓΩΓΗ ΣΤΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΣΥΣΤΗΜΑΤΩΝ
 ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ Α. Ντούνης ΔΙΔΑΣΚΩΝ Χ. Τσιρώνης ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΣΥΣΤΗΜΑΤΩΝ ΜΑΘΗΜΑ ΤΕΤΑΡΤΟ - Εφικτός χώρος λύσεων - Συνάρτηση Lagrange - Γενικές συνθήκες ECM ΣΥΝΘΗΚΕΣ CONSTRAINED Ιδιαιτερότητες των προβλημάτων
ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ Α. Ντούνης ΔΙΔΑΣΚΩΝ Χ. Τσιρώνης ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΣΥΣΤΗΜΑΤΩΝ ΜΑΘΗΜΑ ΤΕΤΑΡΤΟ - Εφικτός χώρος λύσεων - Συνάρτηση Lagrange - Γενικές συνθήκες ECM ΣΥΝΘΗΚΕΣ CONSTRAINED Ιδιαιτερότητες των προβλημάτων
Q 12. c 3 Q 23. h 12 + h 23 + h 31 = 0 (6)
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Τοµέας Υδατικών Πόρων Μάθηµα: Τυπικά Υδραυλικά Έργα Μέρος 2: ίκτυα διανοµής Άσκηση E0: Μαθηµατική διατύπωση µοντέλου επίλυσης απλού δικτύου διανοµής
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Τοµέας Υδατικών Πόρων Μάθηµα: Τυπικά Υδραυλικά Έργα Μέρος 2: ίκτυα διανοµής Άσκηση E0: Μαθηµατική διατύπωση µοντέλου επίλυσης απλού δικτύου διανοµής
Φ. Δογάνης I. Bafumba Χ. Σαρίμβεης. Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Χημικών Μηχανικών Μονάδα Αυτόματης Ρύθμισης και Πληροφορικής
 Αριστοποίηση παραγωγής ηλεκτρικής ενέργειας από συντονισμένη αξιοποίηση υδροηλεκτρικών και συμβατικών μονάδων ηλεκτροπαραγωγής με χρήση μικτού ακέραιου τετραγωνικού προγραμματισμού. Φ. Δογάνης I. Bafumba
Αριστοποίηση παραγωγής ηλεκτρικής ενέργειας από συντονισμένη αξιοποίηση υδροηλεκτρικών και συμβατικών μονάδων ηλεκτροπαραγωγής με χρήση μικτού ακέραιου τετραγωνικού προγραμματισμού. Φ. Δογάνης I. Bafumba
ΑΣΚΗΣΗ ΣΤΑΘΜΟΣ ΚΑΤΑΚΡΗΜΝΙΣΕΙΣ ΕΞΑΤΜΙΣΗ. Μ 1 450 mm 150 mm. Μ 2 560 mm 190 mm. Μ 3 480 mm 165 mm. Μ 4 610 mm 173 mm.
 Στην περιοχή που φαίνεται στον χάρτη υπάρχουν πέντε µετεωρολογικοί σταθµοί. Ποίος είναι ο µέσος ισοδύναµος όγκος νερού µε τον οποίο τροφοδοτείται ο υπόγειος υδροφορέας από την κατείσδυση στην περιοχή αυτή
Στην περιοχή που φαίνεται στον χάρτη υπάρχουν πέντε µετεωρολογικοί σταθµοί. Ποίος είναι ο µέσος ισοδύναµος όγκος νερού µε τον οποίο τροφοδοτείται ο υπόγειος υδροφορέας από την κατείσδυση στην περιοχή αυτή
Μάθημα Επιλογής 8 ου εξαμήνου
 EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Μάθημα Επιλογής 8 ου εξαμήνου Διδάσκων:
EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Μάθημα Επιλογής 8 ου εξαμήνου Διδάσκων:
ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΜΑΘΗΜΑΤΙΚΗ ΔΙΑΤΥΠΩΣΗ, Διαλ. 2. Ανωτάτη Σχολή Παιδαγωγικής και Τεχνολογικής Εκπαίδευσης 8/4/2017
 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΜΑΘΗΜΑΤΙΚΗ ΔΙΑΤΥΠΩΣΗ, Διαλ. 2 Ανωτάτη Σχολή Παιδαγωγικής και Τεχνολογικής Εκπαίδευσης 8/4/2017 Αντικειμενικοί στόχοι Η μελέτη των βασικών στοιχείων που συνθέτουν ένα πρόβλημα βελτιστοποίησης
ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΜΑΘΗΜΑΤΙΚΗ ΔΙΑΤΥΠΩΣΗ, Διαλ. 2 Ανωτάτη Σχολή Παιδαγωγικής και Τεχνολογικής Εκπαίδευσης 8/4/2017 Αντικειμενικοί στόχοι Η μελέτη των βασικών στοιχείων που συνθέτουν ένα πρόβλημα βελτιστοποίησης
Η μέθοδος Simplex. Χρήστος Γκόγκος. Χειμερινό Εξάμηνο ΤΕΙ Ηπείρου
 Η μέθοδος Simplex Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 1 / 17 Η μέθοδος Simplex Simplex Είναι μια καθορισμένη σειρά επαναλαμβανόμενων υπολογισμών μέσω των οποίων ξεκινώντας από ένα αρχικό
Η μέθοδος Simplex Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 1 / 17 Η μέθοδος Simplex Simplex Είναι μια καθορισμένη σειρά επαναλαμβανόμενων υπολογισμών μέσω των οποίων ξεκινώντας από ένα αρχικό
3.7 Παραδείγματα Μεθόδου Simplex
 3.7 Παραδείγματα Μεθόδου Simplex Παράδειγμα 1ο (Παράδειγμα 1ο - Κεφάλαιο 2ο - σελ. 10): Το πρόβλημα εκφράζεται από το μαθηματικό μοντέλο: max z = 600x T + 250x K + 750x Γ + 450x B 5x T + x K + 9x Γ + 12x
3.7 Παραδείγματα Μεθόδου Simplex Παράδειγμα 1ο (Παράδειγμα 1ο - Κεφάλαιο 2ο - σελ. 10): Το πρόβλημα εκφράζεται από το μαθηματικό μοντέλο: max z = 600x T + 250x K + 750x Γ + 450x B 5x T + x K + 9x Γ + 12x
Τεχνική Υδρολογία (Ασκήσεις)
 Τμήμα Δασολογίας & Διαχείρισης Περιβάλλοντος & Φυσικών Πόρων Εργαστήριο Διευθέτησης Ορεινών Υδάτων και Διαχείρισης Κινδύνου Προπτυχιακό Πρόγραμμα Σπουδών Τεχνική Υδρολογία (Ασκήσεις) Κεφάλαιο 1 ο : Εισαγωγή
Τμήμα Δασολογίας & Διαχείρισης Περιβάλλοντος & Φυσικών Πόρων Εργαστήριο Διευθέτησης Ορεινών Υδάτων και Διαχείρισης Κινδύνου Προπτυχιακό Πρόγραμμα Σπουδών Τεχνική Υδρολογία (Ασκήσεις) Κεφάλαιο 1 ο : Εισαγωγή
Data Envelopment Analysis
 Data Envelopment Analysis Η μέθοδος των «Βέλτιστων Προτύπων Αποδοτικότητας», γνωστή στην διεθνή βιβλιογραφία ως «Data Envelopment Analysis», εφαρμόζεται για τον υπολογισμό της σχετικής αποδοτικότητας και
Data Envelopment Analysis Η μέθοδος των «Βέλτιστων Προτύπων Αποδοτικότητας», γνωστή στην διεθνή βιβλιογραφία ως «Data Envelopment Analysis», εφαρμόζεται για τον υπολογισμό της σχετικής αποδοτικότητας και
Περιεχόμενα Πρόλογος 5ης αναθεωρημένης έκδοσης ΚΕΦΆΛΆΙΟ 1 Ο ρόλος της επιχειρησιακής έρευνας στη λήψη αποφάσεων ΚΕΦΆΛΆΙΟ 2.
 Περιεχόμενα Πρόλογος 5ης αναθεωρημένης έκδοσης... 11 Λίγα λόγια για βιβλίο... 11 Σε ποιους απευθύνεται... 12 Τι αλλάζει στην 5η αναθεωρημένη έκδοση... 12 Το βιβλίο ως διδακτικό εγχειρίδιο... 14 Ευχαριστίες...
Περιεχόμενα Πρόλογος 5ης αναθεωρημένης έκδοσης... 11 Λίγα λόγια για βιβλίο... 11 Σε ποιους απευθύνεται... 12 Τι αλλάζει στην 5η αναθεωρημένη έκδοση... 12 Το βιβλίο ως διδακτικό εγχειρίδιο... 14 Ευχαριστίες...
ΜΑΘΗΜΑ: ΔΙΑΧΕΙΡΙΣΗ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ
 Τμήμα Δασολογίας & Διαχείρισης Περιβάλλοντος & Φυσικών Πόρων Εργαστήριο Διευθέτησης Ορεινών Υδάτων και Διαχείρισης Κινδύνου Προπτυχιακό Πρόγραμμα Σπουδών ΜΑΘΗΜΑ: ΔΙΑΧΕΙΡΙΣΗ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ Παναγιώτα Γαλιατσάτου
Τμήμα Δασολογίας & Διαχείρισης Περιβάλλοντος & Φυσικών Πόρων Εργαστήριο Διευθέτησης Ορεινών Υδάτων και Διαχείρισης Κινδύνου Προπτυχιακό Πρόγραμμα Σπουδών ΜΑΘΗΜΑ: ΔΙΑΧΕΙΡΙΣΗ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ Παναγιώτα Γαλιατσάτου
3 η ΕΝΟΤΗΤΑ ΜΗ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΕΝΟΣ ΚΡΙΤΗΡΙΟΥ
 ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΜΠ ΕΙΣΑΓΩΓΗ ΣΤΗN ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΣΥΣΤΗΜΑΤΩΝ 3 η ΕΝΟΤΗΤΑ ΜΗ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΕΝΟΣ ΚΡΙΤΗΡΙΟΥ Μ. Καρλαύτης Ν. Λαγαρός Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό
ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΜΠ ΕΙΣΑΓΩΓΗ ΣΤΗN ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΣΥΣΤΗΜΑΤΩΝ 3 η ΕΝΟΤΗΤΑ ΜΗ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΕΝΟΣ ΚΡΙΤΗΡΙΟΥ Μ. Καρλαύτης Ν. Λαγαρός Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό
Πολυκριτηριακός Γραμμικός Προγραμματισμός. Συστήματα Αποφάσεων Εργαστήριο Συστημάτων Αποφάσεων και Διοίκησης
 Πολυκριτηριακός Γραμμικός Προγραμματισμός Πολλαπλά κριτήρια στη λήψη απόφασης Λήψη Αποφάσεων με Πολλαπλά Κριτήρια Διακριτό σύνολο επιλογών Συνεχές σύνολο επιλογών Πολυκριτηριακή Ανάλυση (ELECTRE, Promethee,
Πολυκριτηριακός Γραμμικός Προγραμματισμός Πολλαπλά κριτήρια στη λήψη απόφασης Λήψη Αποφάσεων με Πολλαπλά Κριτήρια Διακριτό σύνολο επιλογών Συνεχές σύνολο επιλογών Πολυκριτηριακή Ανάλυση (ELECTRE, Promethee,
