Χάσιμο επαφής Παρατηρήσεις

HTML
DOWNLOAD

Μέγεθος: px

Εμφάνιση ξεκινά από τη σελίδα:

Download "Χάσιμο επαφής Παρατηρήσεις"

Βακχος Μακρή
8 χρόνια πριν
Προβολές:

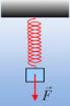
1 Χάσιμο επαφής Α) Έστ σύστημα δύο σμάτν και Σ, με μάζες m και m, που βρίσκονται σε επαφή πάν σε οριζόντιο επίπεδο. Το είναι δεμένο στο άκρο οριζόντιου ελατηρίου (όπς στο σχήμα) σταθεράς ενώ το Σ δεν είναι κολλημένο με το. Μετακινούμε το σύστημα συμπιέζοντας το ελατήριο και το αφήνουμε ελεύθερο, οπότε εκτελεί α.α.τ. Θα μελετήσουμε την κίνηση του Σ, το οποίο F έχει την ίδια γνιακή συχνότητα με το, αλλά σταθερά επαναφοράς, ώστε = (m + m ) m m m. = m ΣF = -. F = -.. H επαφή χάνεται αν F = 0 crit = 0, δηλαδή στη θέση Παρατηρήσεις. Το σύστημα τν σμάτν θα περάσει υποχρετικά από τη ΘΦΜ (αφού είναι η ΘΙ) οπότε η επαφή θα χαθεί οπσδήποτε.. Μπορούμε να προβλέψουμε την απώλεια επαφής στη ΘΦΜ αφού μετά απ αυτήν το μέτρο της ταχύτητας του θα αρχίσει να μειώνεται λόγ της δράσης της δύναμης από το ελατήριο ενώ το Σ δεν δέχεται οριζόντιες δυνάμεις που μπορούν να μειώσουν το μέτρο της ταχύτητάς του και θα συνεχίσει κάνοντας Ευθύγραμμη Ομαλή Κίνηση με ταχύτητα τη μέγιστη ταχύτητα ταλάντσης. 3. Μετά την απώλεια επαφής το σώμα, καθώς παραμένει δεμένο στο ελατήριο, θα κάνει νέα Απλή Αρμονική Ταλάντση η οποία λόγ αλλαγής μάζας θα έχει: την ίδια Θέση Ισορροπίας σταθερά ταλάντσης = διαφορετική γνιακή συχνότητα, αφού = m ίδια μέγιστη ταχύτητα ταλάντσης διαφορετικό πλάτος αφού υ ma, = υ ma,. Α =. Α N Σ Σ B F ελ N F B

2 Β) Έστ σύστημα δύο σμάτν και Σ, με μάζες m και m, που βρίσκονται επαφή. Το είναι δεμένο στο άκρο κατακόρυφου ελατηρίου (όπς στο σχήμα) σταθεράς ενώ το Σ δεν είναι κολλημένο με το. Μετακινούμε το σύστημα συμπιέζοντας το ελατήριο κατά Α και το αφήνουμε ελεύθερο, οπότε εκτελεί α.α.τ. Θα μελετήσουμε την κίνηση του Σ, το οποίο έχει την ίδια γνιακή συχνότητα με το, αλλά σταθερά επαναφοράς, ώστε = (m + m ) = m m m m συστήματος ΣF = 0 F ελ + Β ολ = 0 -.Δl 0 - (m + m )g ( m m )g = 0 Δl 0 = - Σ ΣF = -. F + B = -. F - m g = -. F = m g -., -Α A. Όταν -Α 0 ( κάτ από τη ) F > 0 δεν χάνεται η επαφή. Όταν 0 < Α ( πάν από τη ) η F μπορεί να μηδενιστεί αν F = 0 m g -. crit = 0 crit = mg m g crit = m g crit = Με δεδομένο, το μέγιστο επιτρεπόμενο πλάτος για να μη χαθεί η επαφή είναι g Α = ( m m )g Αν θέσουμε =, βρίσκουμε crit = = Δl 0, δηλαδή η επαφή m m χάνεται στη θέση Παρατηρήσεις. Το σύστημα τν σμάτν δεν περνά υποχρετικά από τη θέση Φ.Μ οπότε δεν είναι βέβαιο ότι η επαφή θα χαθεί. Αυτό εξαρτάται από το πλάτος της ταλάντσης. Η επαφή χάνεται μόνο αν ισχύει Α > Δl 0.. Μπορούμε να προβλέψουμε την απώλεια επαφής στη θέση μια και στη θέση F ελ Δ l 0 Σ F (+) B Σ B F F = - F

3 αυτή το βάρος προσδίδει σε κάθε σώμα επιτάχυνση g, αλλά το σώμα που είναι δεμένο στο ελατήριο θα έχει επιπλέον επιτάχυνση με φορά προς τα κάτ λόγ της δύναμης που δέχεται από το ελατήριο. 3. Μετά την απώλεια επαφής (εφόσον υπάρξει) το σώμα Σ, θα κάνει κατακόρυφη βολή με αρχική ταχύτητα της οποίας το μέτρο (έστ u ) μπορεί να προσδιοριστεί με εφαρμογή της Αρχής Διατήρησης της Ενέργειας της ταλάντσης του συστήματος τν δύο σμάτν: ½ m υ + ½ crit = ½ A 4. Μετά την απώλεια επαφής (εφόσον υπάρξει) το σώμα, καθώς παραμένει δεμένο στο ελατήριο, θα κάνει νέα Απλή Αρμονική Ταλάντση η οποία λόγ αλλαγής μάζας θα έχει: διαφορετική Θέση Ισορροπίας σταθερά ταλάντσης = διαφορετική γνιακή συχνότητα, αφού = m πλάτος ταλάντσης Α που υπολογίζεται με εφαρμογή της Αρχής Διατήρησης της Ενέργειας της ταλάντσης, για την νέα ταλάντση του. Εννοείται πς πρέπει να απομακρυνθεί με κάποιον τρόπο το σώμα Σ ώστε να μην έχουμε κρούση τν δύο σμάτν κατά την κάθοδό του. Γ) Έστ σύστημα δύο σμάτν και Σ, με μάζες m και m, που βρίσκονται επαφή πάν σε κεκλιμένο επίπεδο γνίας κλίσης φ. Το είναι δεμένο στο άκρο ελατηρίου σταθεράς (όπς στο σχήμα), ενώ το Σ δεν είναι κολλημένο με το. Μετακινούμε το σύστημα συμπιέζοντας το ελατήριο κατά Α και το αφήνουμε ελεύθερο, οπότε εκτελεί α.α.τ. Θα μελετήσουμε την κίνηση του Σ, το οποίο έχει την ίδια γνιακή συχνότητα με το, αλλά σταθερά επαναφοράς, ώστε = (m + m ) = m m m m. Δ l 0 F ελ N B ψ Σ B F F B ψ F = - F (+) φ Σ N B συστήματος ΣF = 0 F ελ + Β ολ, = 0 -.Δl 0 - (m + m )gημφ = 0

4 m Δl 0 = - ( m )gημφ Σ ΣF = -. F + B, = -. F - m gημφ = -. F = m gημφ -., -Α A Όταν -Α 0 ( κάτ από τη ) F > 0 δεν χάνεται η επαφή. Όταν 0 < Α ( πάν από τη ) η F μπορεί να μηδενιστεί αν mgημφ mgημφ F = 0 m gημφ - crit = 0 crit = crit = m gημφ crit = Με δεδομένο, το μέγιστο επιτρεπόμενο πλάτος για να μη χαθεί η επαφή είναι gημφ Α = ( m m)gημφ Αν θέσουμε =, βρίσκουμε crit = = Δl 0, δηλαδή η m m επαφή χάνεται στη θέση Παρατηρήσεις. Το σύστημα τν σμάτν δεν περνά υποχρετικά από τη θέση οπότε δεν είναι βέβαιο ότι η επαφή θα χαθεί. Αυτό εξαρτάται από το πλάτος της ταλάντσης. Η επαφή χάνεται μόνο αν ισχύει Α> Δl 0.. Μπορούμε να προβλέψουμε την απώλεια επαφής στη θέση μια και στη θέση αυτή η συνιστώσα Β του βάρους προσδίδει σε κάθε σώμα επιτάχυνση gημφ, αλλά το σώμα που είναι δεμένο στο ελατήριο θα έχει επιπλέον επιτάχυνση με φορά προς τα κάτ λόγ της δύναμης που δέχεται από το ελατήριο. 3. Μετά την απώλεια επαφής (εφόσον υπάρξει) το σώμα Σ, θα κάνει ομαλά επιβραδυνόμενη κίνηση με αρχική ταχύτητα της οποίας το μέτρο (έστ u ) μπορεί να προσδιοριστεί με εφαρμογή της Αρχής Διατήρησης της Ενέργειας της ταλάντσης του συστήματος τν δύο σμάτν: ½ m υ + ½ crit = ½ A 4. Μετά την απώλεια επαφής (εφόσον υπάρξει) το σώμα, καθώς παραμένει δεμένο στο ελατήριο, θα κάνει νέα Απλή Αρμονική Ταλάντση η οποία θα έχει: διαφορετική Θέση Ισορροπίας σταθερά ταλάντσης = διαφορετική γνιακή συχνότητα, αφού = m πλάτος ταλάντσης Α που υπολογίζεται με εφαρμογή της Αρχής Διατήρησης της Ενέργειας της ταλάντσης, για την νέα ταλάντση του. Εννοείται πς πρέπει να απομακρυνθεί με κάποιον τρόπο το σώμα Σ ώστε να μην έχουμε κρούση τν δύο σμάτν κατά την κάθοδό του.

5 Δ) Έστ σύστημα δύο σμάτν και Σ, με μάζες m και m, που βρίσκονται σε επαφή πάν σε οριζόντιο επίπεδο. Το είναι δεμένο στο άκρο οριζόντιου ελατηρίου (όπς στο σχήμα) σταθεράς ενώ το Σ βρίσκεται πάν στο, είναι κολλημένο με το και παρουσιάζει συντελεστή στατικής τριβής μ σ. Μετακινούμε το σύστημα συμπιέζοντας το ελατήριο και το αφήνουμε ελεύθερο, οπότε εκτελεί α.α.τ. Θα μελετήσουμε την κίνηση του Σ, το οποίο έχει την ίδια γνιακή συχνότητα με το, αλλά σταθερά επαναφοράς, ώστε = (m + m ) = m m m m Σ ΣF = -. Τ σ = -., -Α A Δ) Με δεδομένο πλάτος Α. Στις ακραίες θέσεις απαιτείται το μεγαλύτερο μέτρο της στατικής τριβής, που είναι Τ σ,ma =.A A Για να μη χάνεται η επαφή Τ σ,ma Τ ορ.a μ σ m g μ σ μ σ,min = m g m Α μ σ,min = m g Α g T σ N B Σ N F N ελ T σ = - Τ σ B Σ T σ Δ) Με δεδομένο συντελεστή στατικής τριβής μ σ μσg μσg Τ σ,ma Τ ορ.a μ σ m g A A ma = E) Έστ σύστημα δύο σμάτν και Σ, με μάζες m και m, που βρίσκονται σε επαφή πάν σε κεκλιμένο επίπεδο γνίας κλίσης φ. Το είναι δεμένο στο άκρο οριζόντιου ελατηρίου (όπς στο σχήμα) σταθεράς ενώ το Σ βρίσκεται πάν στο, είναι κολλημένο με το και παρουσιάζει συντελεστή στατικής τριβής μ σ. Το σύστημα αρχικά ισορροπεί. Μετακινούμε το σύστημα συμπιέζοντας το ελατήριο και το αφήνουμε ελεύθερο, οπότε εκτελεί α.α.τ.

6 Θα μελετήσουμε την κίνηση του Σ, το οποίο έχει την ίδια γνιακή συχνότητα με το, αλλά Δ l 0 (+) σταθερά επαναφοράς, ώστε = (m + m ) = m m m m. Σ φ συστήματος ΣF = 0 F ελ + Β ολ, = 0 -.Δl 0 - (m + m )gημφ = 0 ( m m)gημφ Δl 0 = - Σ ΣF = -. T σ + B, = -. T σ - m gημφ = -. T σ = m gημφ -. Ε) Με δεδομένο πλάτος Α Στην κάτ ακραία θέση = -A απαιτείται το μεγαλύτερο μέτρο της στατικής τριβής, που είναι Τ σ,ma = m gημφ +.A F ελ N N Για να μη χάνεται η επαφή Τ σ,ma Τ ορ m gημφ +.A μ σ m gσυνφ T σ B N ψ B T σ μ σ mgnμφ A m gσυνφ μ σ,min = mgnμφ m Α m gσυνφ μ σ,min = gnμφ Α gσυνφ Ε) Με δεδομένο συντελεστή στατικής τριβής μ σ mg.(μ σσυνφ ημφ) Τ σ,ma Τ ορ m gημφ +.A μ σ m gσυνφ Α m g.(μ σσυνφ ημφ) Α ma = Ανδρέας Ριζόπουλος

Σχετικά έγγραφα

Σώματα σε επαφή και Απλή Αρμονική Ταλάντωση

Σώματα σε επαφή και Απλή Αρμονική Ταλάντωση Σε όλες τις περιπτώσεις που θα εξετάσουμε το δάπεδο είναι λείο. Επίσης τα σύμβολα των διανυσματικών μεγεθών αντιπροσωπεύουν τις αλγεβρικές τους τιμές. Α. Η επιφάνεια