ΕΙΔΙΚΑ ΘΕΜΑΤΑ ΔΙΔΑΚΤΙΚΗΣ ΕΙΔΙΚΑ
|
|
|
- Μαγδαληνή Πρωτονοτάριος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΕΙΔΙΚΑ ΘΕΜΑΤΑ ΔΙΔΑΚΤΙΚΗΣ ΕΙΔΙΚΑ ΘΕΜΑΤΑ ΔΙΔΑΚΤΙΚΗΣ ΜΑΘΗΜΑΤΙΚΩΝ Μαρία Καλδρυμίδου, Μαριάννα Τζεκάκη, Χαράλαμπος Λεμονίδης Ζωή Δεληφωτάκη 0695 Βασιλική Μίχου 0704 Ελένη Σπάχου 0718 The Development of Fifth-Grade Children's Problem-Posing Abilities Author(s): Lyn D. English Source: Educational Studies in Mathematics, Vol. 34, No. 3 (Dec., 1997), pp Published by: Springer Stable URL: Accessed: :20 UTC 1
2 κατασκευή προβλημάτων Η κατασκευή προβλημάτων είναι σημαντικό μέρος του σχεδίου προγράμματος των μαθηματικών και θεωρείται ότι βρίσκεται στην καρδιά της Μαθηματικής δραστηριότητας (Brown Walter, 1983, 1993; Kilpatrick, 1987; Moses, Bjork, & Goldenberg, National Council of Teachers of Mathematics [NCTM] 1989, 1991; Silver, 1990, 1994). κατασκευή προβλημάτων προγενέστερες μελέτες συνέδεσαν την δεξιότητα της κατασκευής προβλήματος με την δημιουργικότητα και την πρωτοτυπία Όμως η φύση αυτής της σχέσης παραμένει θολή (Silver, 1994, Haylock, 1987) Και φαίνεται να υπάρχει μια πιο καθαρή σχέση μεταξύ της δεξιότητας στα μαθηματικά και της κατασκευής προβλημάτων (Ellerton, 1986; Leung, 1993) 2
3 κατασκευή προβλημάτων Η έλλειψη έρευνας στα ΑΠΣ που είναι σχεδιασμένα να βοηθήσουν την κατασκευή προβλήματος από τα παιδιά αναδεικνύει τα λίγα πλαίσια που υπάρχουν για να καθοδηγήσουν την εξέλιξη προγράμματος (Silver, 1994) κάποιες ιδέες μπορούμε να βρούμε από τις δραστηριότητες που δίνουν οι Brown and Walter (1993), και από το 'Realistic Mathematics Education' curriculum (Ολλανδία) δίνει σημαντική έμφαση στην κατασκευή προβλημάτων από τους μαθητές σε όλες τις μαθηματικές δραστηριότητες, με δημιουργίες και ελεύθερες παραγωγές στην διαδικασία διδασκαλίας και μάθησης (Freudenthal, 1991; Streefland, 1993; Treffers, 1993; Van den Heuvel- Panhuizen et al., 1995 ) κατασκευή προβλημάτων Η κατασκευή προβλήματος δεν είναι ενσωματωμένη μαθησιακή διαδικασία σε ένα ολοκληρωμένο πρόγραμμα σπουδών για τα μαθηματικά. Προϋποθέτει πρώτα την δημιουργία ενός πλαισίου το οποίο θα οδηγούσε την διαμόρφωση κατάλληλων δραστηριοτήτων μάθησης (English, 1997) 3
4 Πλαίσιο κατασκευής προβλημάτων η ανάπτυξη αυτού του Πλαισίου και πρόγραμμα των δραστηριοτήτων πρέπει να βασίζονται σε κάποια στοιχεία ερευνών και επιστημονικών απόψεων όπως του Freudenthal (1991) 'thought experiment, δηλ. να δει κανείς εκ των προτέρων πως θα εξελιχθεί η διαδικασία διδασκαλίας μάθησης πριν εφαρμόσει δραστηριότητες στην τάξη. μετά την εφαρμογή του πλαισίου, προσπάθεια εύρεσης αποδείξεων που δείχνουν αν πραγματοποιήθηκαν τα αναμενόμενα η ανατροφοδότηση της πρακτικής εμπειρίας σε νέα πειράματα σκέψης παράγει έναν κύκλο εξέλιξης προγράμματος σπουδών και έρευνας (English, 1997). Πλαίσιο κατασκευής προβλημάτων Η κατάρτιση του Πλαισίου πρέπει να βασίζεται στα ευρήματα και στις οδηγίες που υπάρχουν σε έρευνες για την επίλυση και την κατασκευή προβλημάτων Να λαμβάνεται υπόψη το μαθηματικό υπόβαθρο των μαθητών που συμμετείχαν Και οπωσδήποτε να περιλαμβάνει.. 1. την αντίληψη και τη χρήση δομών προβλημάτων 2. τις αντιλήψεις και τις προτιμήσεις διαφόρων τύπων προβλημάτων και 3.την ανάπτυξη Μαθηματικής σκέψης με διάφορους τρόπους 4
5 αντίληψη και χρήση δομών προβλημάτων αντίληψη του προβλήματος σαν ένα βασικό συστατικό του Πλαισίου αφορά στην ικανότητα των μαθητών να αναγνωρίζουν την δομή που βρίσκεται στο πρόβλημα και να εντοπίζουν αντίστοιχες δομές σε σχετικά προβλήματα η δομή μπορεί να οριστεί σαν μία φόρμα αφηρημένη από την προφορική της έκφραση (Freudenthal, 1991, p. 20). αντίληψη και χρήση δομών προβλημάτων Ωστόσο αν τα παιδιά πρόκειται να χρησιμοποιήσουν υπάρχοντα προβλήματα για να παράγουν νέα παραδείγματα και ερωτήματα, τότε πρέπει.. να είναι σε θέση να αναγνωρίζουν τις μαθηματικές δομές αυτών των προβλημάτων να μπορούν να θέσουν χαρακτηριστικά στο υπόβαθρο και να δώσουν σημασία στα δομικά συστατικά τα παιδιά να δημιουργήσουν νοερά μοντέλα με σημασία ή αναπαραστάσεις,οι οποίες αναγνωρίζουν τις σημαντικές μαθηματικές ιδέες και πως αυτές σχετίζονται μεταξύ τους (e.g., English, in press c; English & Halford, 1995; Holyoak and Koh, 1987; Nesher, 1988; Novick, 1988; Silver, 1981) 5
6 αντίληψη και χρήση δομών προβλημάτων Μελέτες δείχνουν την τάση των μαθητών να εστιάζουν στα επιφανειακά χαρακτηριστικά των προβλημάτων, παρά στα υποκείμενα δομικά στοιχεία κάτι που.. περιορίζει σοβαρά τις ικανότητες των μαθητών στην επίλυση προβλημάτων (Novick, 1988, 1992; Silver, 1981; Stavy and Tirosh, 1993) αντιλήψεις και τις προτιμήσεις διαφόρων τύπων προβλημάτων το δεύτερο συστατικό του Πλαισίου σχετίζεται με την εστίαση στις αντιλήψεις των παιδιών για διαφορετικά προβλήματα συμπεριλαμβάνοντας ποιά προβλήματα προτιμούν και ποια δεν προτιμούν σε συνήθεις και μη καταστάσεις (Borasi, 1993; Brown and Walter, 1993; English, 1996; McLeod, 1992). Αν πρόκειται να διδάξουμε μαθηματικά με τέτοιο τρόπο που σέβεται τις ιδέες των μαθητών είναι βασικό να γνωρίζουμε πώς οι μαθητές αντιλαμβάνονται τα προβλήματα ( Van den Heuvel- Panhuizen et al., 1995) 6
7 αντιλήψεις και τις προτιμήσεις διαφόρων τύπων προβλημάτων Η ενθάρρυνση να εκφράσουν οι μαθητές τις αντιλήψεις τους για τα προβλήματα, δημιουργεί απόψεις που οδηγούν σε μελλοντική διδασκαλία λίγες μελέτες που να σχετίζονται με τις αντιλήψεις των μαθητών η μελέτη του Van den Heuvel-Panhuizen et al.'s (1995) έδωσε ενδιαφέρουσες απόψεις στην δημιουργία προβλημάτων ποσοστών από τους μαθητές και τις αντιλήψεις που αποκόμισαν από τα προβλήματα που είχαν δημιουργήσει αντιλήψεις και τις προτιμήσεις διαφόρων τύπων προβλημάτων δραστηριότητες στις οποίες οι μαθητές εκφράζουν τις αντιλήψεις τους για διαφορετικά προβλήματα και τις συγκρίνουν με τις διάφορες γνώμες των συμμαθητών τους μπορεί να γίνουν ένας πολύ ισχυρός τρόπος που να προάγει την μαθηματική κατανόηση (Van den Heuvel-Panhuizen et al., 1995) τέτοιες δραστηριότητες μπορούν επίσης να αυξήσουν την γνώση των μαθητών σε σχέση με τις διαφορετικές προσεγγίσεις στην παραγωγή και λύση προβλημάτων και να ενδυναμώσουν την εμπιστοσύνη στην προσπάθεια επίλυσης μιας μεγαλύτερης έκτασης τύπων προβλημάτων (Brown and Walter, 1993; De Lange, 1993; Moses, Bjork, and Goldenberg, 1993). έτσι οι μαθητές έχουν μία πιο πλούσια βάση για να δημιουργήσουν νέα προβλήματα και ερωτήματα 7
8 ανάπτυξη Μαθηματικής σκέψης με διάφορους τρόπους το τρίτο συστατικό του πλαισίου είναι οι ικανότητες των μαθητών να αντιληφθούν μαθηματικές καταστάσεις με διαφορετικούς τρόπους αυτό δεν είναι μόνο πολύ σημαντικό στην εξέλιξη της κατασκευής προβλημάτων για τους μαθητές αλλά επίσης και στην γενικότερη μαθηματική τους βελτίωση (English and Halford, 1995; NCTM, 1989; Resnick, 1987; Smith and Silver, 1995). ανάπτυξη Μαθηματικής σκέψης με διάφορους τρόπους Η ικανότητα να προσεγγίσει κανείς μία μαθηματική έκφραση με περισσότερους από ένα τρόπους είναι ιδιαίτερα σημαντική στην αντίληψη των μαθητών σχετικά με καταστάσεις πράξεων και με την ικανότητά τους να παράγουν νέα προβλήματα πράξεων Αν και υπάρχει σημαντική βιβλιογραφία για τις ικανότητες των παιδιών να λύνουν προβλήματα πράξεων (e.g., Bergeron and Herscovics, 1990; Carpenter and Moser, 1984; Carpenter et al., 1993; Fus- on, 1992; Greer, 1992; Kouba, 1989; Riley, Greeno, and Heller, 1983),. υπάρχουν λίγες πληροφορίες σχετικά με τις ικανότητες των μαθητών να κατασκευάσουν τέτοια προβλήματα 8
9 Μονοετής μελέτη Τέσσερεις φάσεις Μεθοδολογία o Αρχική επιλογή συμμετεχόντων o Προκαταρκτικές συνεντεύξεις o Εφαρμογή προγράμματος o Μετά τις συνεντεύξεις Αρχική επιλογή συμμετεχόντων Τάξη 5, Ηλικία 10ετών, Ν=150 Εκτιμήθηκαν ως προς την αίσθηση του αριθμού (NCTM, Sowder,1988 & 1992) o Κατανόηση φυσικού αριθμού σχετικά μεγέθη αριθμού αναπαράσταση σχέσεων αριθμού με χειρισμούς αναγνώριση μη λογικών αποτελεσμάτων για υπολογισμούς αναγνώριση ποικιλίας καταστάσεων και δομών προβλημάτων Την επίλυση νέων προβλημάτων o Η ικανότητα επίλυσης νέων μη υπολογιστικών προβλημάτων, χωρίς άμεσα διαθέσιμες μεθόδους επίλυσης (Baroody, 1993; Charles and Lester, 1982) o Παραπλανητικά-επαγωγικά-χωρικά προβλήματα λογικήςσυνδυαστικά παραδείγματα-παραδείγματα σημαντικών στοιχείων του ΑΠΣ (Baroody, 1993; English and Halford, 1995; NCTM, 1989) 9
10 Ομάδες Αρχική επιλογή συμμετεχόντων Ισχυρή αίσθηση αριθμού αδυναμία στην επίλυση νέων προβλημάτων Αδυναμία στην αίσθηση του αριθμού ισχυρή δυνατότητα επίλυσης νέων προβλημάτων Ισχυρή δυνατότητα και στα δύο 10 εβδομάδες Τοποθέτηση προβλήματος 2 συνεδρίες 35 /εβδομάδα Τρόπος διεξαγωγής Ομαδική συζήτηση Μικρή ομαδική εργασία Ανταλλαγή ιδεών ολόκληρης ομάδας Δόθηκε έμφαση στις αλληλεπιδράσεις των παιδιών με τους συμμαθητές και το δάσκαλό τους ( Η συνεργασία ενσωματώνει την εκμάθηση)(vygostky,1978) Δάσκαλος : Οδηγός και διευκολυντής 10
11 Εξελίξεις που παρατηρήθηκαν στις ικανότητες των παιδιών να κατασκευάζουν προβλήματα Δόθηκε έμφαση στις αντιλήψεις και τις προτιμήσεις των παιδιών στην αναγνώριση δομών προβλημάτων κατασκευή προβλημάτων από δεδομένα συστατικά. προβλήματα που παρήχθησαν από συμβολικές εκφράσεις μοντελοποίηση νέων προβλημάτων βάσει υπαρχόντων δομικών προβλημάτων. Τα προβλήματα περιλάμβαναν Ένα υπολογιστικό πρόβλημα με πολλά βήματα που είχε να κάνει με χρήματα Ένα πρόβλημα λογικής επεξεργασίας Ένα πρόβλημα αφαίρεσης που περιλαμβάνει μία σύγκριση Ένα πρόβλημα συνδυαστικό 11
12 οι αντιλήψεις και οι προτιμήσεις των παιδιών σε διαφορετικούς τύπους προβλημάτων Προβλήματα για τα οποία οι μαθητές έδειξαν ενδιαφέρον : Προβλήματα λογικής «είναι δύσκολα και σε κάνουν να σκεφτείς Και αυτό μου αρέσει» Προβλήματα αφαίρεσης «είναι εύκολο να το λύσεις» «είναι απλά ένα πρόβλημα αφαίρεσης» οι αντιλήψεις και οι προτιμήσεις των παιδιών σε διαφορετικούς τύπους προβλημάτων Προβλήματα για τα οποία οι μαθητές δεν έδειξαν ενδιαφέρον : Συνδυαστικά προβλήματα «Είναι μπέρδεμα» «είναι πολύ δύσκολο» «Είναι πολλά πράγματα που πρέπει να γίνουν» προβλήματα πολλών βημάτων με τα χρήματα. Τα ασυνήθιστα προβλήματα σε κάποιους μαθητές άρεσαν περισσότερο και σε κάποιους λιγότερο. 12
13 Η αναγνώριση των δομών στα προβλήματα Παρουσιάστηκαν: συνηθισμένα και ασυνήθιστα προβλήματα Προβλήματα με παρόμοια δομή σε διαφορετικές θεματικές ιστορίες προβλήματα με διαφορετικές δομές στην ίδια θεματική ιστορία έγινε ομαδοποίηση των προβλημάτων σύμφωνα με ομοιότητες στην διαδικασία λύσης Προβλήματα με παρόμοια δομή. (1) 1α) Carla έχει ένα μπλε t-shirt,ένα κόκκινο t-shirt, και ένα πράσινο t-shirt. Επίσης έχει μία μαύρη φούστα, μία καφέ φούστα, και μία γκρι φούστα. Πόσα διαφορετικά ντυσίματα μπορεί να κάνει; 1β)Η Sally, η Mary, ο Bill, και η Jane αγόρασαν ένα καινούργιο της t-shirt o καθένας. Ένα t-shirt ήταν μπλε,ένα ήταν κόκκινο, ένα ήταν πράσινο και ένα ήταν μαύρο. Η Sally αγόρασε το κόκκινο t-shirt, ο Bill δεν αγόρασε το μπλε t-shirt. Στη Jane δεν αρέσουν ούτε τα πράσινα ούτε τα μπλε t-shirts. Ποια t-shirts αγόρασαν η Sally, η Mary, ο Bill, και η Jane ; 13
14 Προβλήματα με παρόμοια δομή. (2) 2α) Η Sally και η Joan αποταμίευσαν η καθεμία για να αγοράσουν ένα τηλεκατευθυνόμενο αυτοκίνητο. Η Sally έχει αποταμιεύσει 32 δολάρια. Αν αποταμιεύσει ακόμη 25 δολάρια τότε θα έχει τόσα όσα έχει αποταμιεύσει η Joan. Πόσα χρήματα έχει αποταμιεύσει η Joan ; 2β) Η Kelly και ο Jim έχουν ο καθένας αποταμιεύσει για να αγοράσουν ένα τηλεκατευθυνόμενο αυτοκίνητο. Η Kelly έχει αποταμιεύσει 25 δολάρια και ο Jim έχει αποταμιεύσει 42 δολάρια. Πόσα ακόμα δολάρια πρέπει να αποταμιεύσει η Kelly για να έχει τόσα όσα και ο Jim ; εξηγήσεις από τους μαθητές για την ομαδοποίηση των προβλημάτων Βασική εξήγηση Εντοπισμός της κοινής πράξης ή αναγνώριση της ομοιότητας στον στόχο του προβλήματος Περιεκτική εξήγηση Ξεκάθαρη αντιστοίχιση των δομών των δύο προβλημάτων. Το πρόγραμμα είχε επιτυχία στην ανάπτυξη της κατανόησης της δομής ενός προβλήματος όπως και στην ικανότητα των παιδιών για την αναγνώριση των αντίστοιχων δομών. 14
15 μοντελοποίηση νέων προβλημάτων σε υπάρχουσες δομές ανάλογα με το είδος και το τύπο του προβλήματος η αίσθηση αριθμού και οι ικανότητες να λύσουν καινούργια προβλήματα παίζουν σημαντικό ρόλο στην δημιουργία νέων προβλημάτων πάνω σε υπάρχουσες δομές. βελτίωση των ικανοτήτων μοντελοποίησης σε ένα νέο πρόβλημα από μία υπάρχουσα δομή Οι μαθητές γίνονται ικανοί: να διαφοροποιήσουν το θέμα της ιστορίας του προβλήματος. να αντιληφθούν ότι τη η δομή του προβλήματος είναι ανεξάρτητη από ένα συγκεκριμένο θέμα να δώσουν μεγαλύτερη ευελιξία στην δημιουργία των προβλημάτων. να δημιουργήσουν θέματα που τα ίδια βρίσκουν ενδιαφέροντα και με νόημα σε αντίθεση με αυτά τα οποία εμείς κατασκευάζουμε για αυτά 15
16 δημιουργία προβλημάτων από δεδομένα συστατικά προβλήματος (συμβολικές εκφράσεις ) Tα προβλήματα που δημιούργησαν οι μαθητές σε σχέση με την μαθηματική δομή του προβλήματος χαρακτηρίστηκαν ως: Βασικά Όταν τα προβλήματα δημιουργούνταν με στοιχειώδεις αλλαγές κατάστασης Σύνθετα Όταν τα προβλήματα είχαν μεγαλύτερη ποικιλία στον τρόπο σκέψης και περιλάμβαναν πιο δύσκολες περιπτώσεις όπως o σύγκριση και εξίσωση καταστάσεων για πρόσθεση και αφαίρεση o προβλήματα σύγκρισης με πολλαπλασιασμό. o συνδυαστικά προβλήματα Δημιουργία νέων προβλημάτων σε υφιστάμενες δομές Συνδυαστικό πρόβλημα Η επιχείρηση «Lazy Days Icecream Parlour» έχει παγωτό φράουλα παγωτό σοκολάτα και μάνγκο παγωτό. Έχει πράσινους κώνους και μοβ κώνους. Έχει, επίσης, σιρόπι κεράσι, μπανάνα και βατόμουρου. Πόσους διαφορετικούς συνδυασμούς παγωτών θα μπορούσατε να αγοράσετε, αν κάθε παγωτό έχει μια γεύση, έναν κώνο και ένα είδος σιροπιού; (Δοσμένο πρόβλημα) Η επιχείρηση «Greg Chapple Cricket» έχει τριών ειδών ρόπαλα κρίκετ: kookaburra, Mark Waugh και Alan Border. Κάθε ρόπαλο χρειάζεται μια λαβή και οι λαβές είναι πολύχρωμες, μπλε και καρό. Εάν κάθε ρόπαλο του κρίκετ είχε διαφορετική λαβή, πόσα διαφορετικά είδη ροπάλων μπορούν να υπάρχουν; (πρόβλημα μαθητή,) 16
17 Πρόβλημα που ακολουθεί ένα μοτίβο o Ο Sam μοιράζει φυλλάδια για να κερδίσει το χαρτζιλίκι του. Την πρώτη ημέρα παρέδωσε 150 φυλλάδια. Τη δεύτερη ημέρα παρέδωσε 165 φυλλάδια και την Τρίτη ημέρα 180 φυλλάδια. Αν συνεχίζει να μοιράζει φυλλάδια σε αυτό το μοτίβο, πόσες μέρες θα του πάρει, για να παραδώσει 210 φυλλάδια; (Δοσμένο πρόβλημα) o Η Τζένη μετακομίζει και έχει πολλά πράγματα να συσκευάσει σε κουτιά. Την πρώτη ημέρα έβαλε 20 πράγματα σε ένα κουτί. Τη δεύτερη ημέρα έβαλε 25 πράγματα σε ένα κουτί και την τρίτη ημέρα έβαλε 30. Αν συνεχίζει να συσκευάσει κουτιά σε αυτό το μοτίβο, πόσες μέρες θα της πάρει, για να συσκευάσει 50 πράγματα; (πρόβλημα μαθήτριας) Πρόβλημα επαγωγικού συλλογισμού o Τέσσερις διάσημοι άνθρωποι των σπορ εισήλθαν σε ένα τηλεοπτικό στούντιο. Ένας ήταν ένας παίκτης του τένις, ένας ήταν κολυμβητής, ένας ήταν παίχτης του γκολφ και ένας ήταν παίκτης σκακιού. Χρησιμοποιήστε τις ενδείξεις για να μάθετε ποιος έπαιξε ποιο άθλημα. Ενδείξεις: 1. Ο κ. Bowler δεν είναι καλός στο σκάκι. 2. Τόσο το άθλημα του κ.big όσο και της κα.ace περιλαμβάνει μια μπάλα. 3. Η κα. Fish δεν μπορεί να κολυμπήσει. 4. Ούτε η κα.ace ούτε η κα.fish παίζουν τένις. (Δοσμένο πρόβλημα) o Ο Adam, ο Chris, Amy, και η Kate αγόρασαν κάποια παιχνίδια. Υπήρχε ένα φορτηγό, ένα αυτοκίνητο, μια μπάλα και ένα πόνι. Η Amy δεν αγόρασε το φορτηγό, ούτε το αυτοκίνητο. Ο Adam δεν αγόρασε την μπάλα ούτε το πόνι. Η Kate αγόρασε το αυτοκίνητο. Ο Chris δεν αγόρασε το φορτηγό ή το πόνι. Ποιο παιχνίδι αγόρασε ο Adam, η Amy και ο Chris; (πρόβλημα μαθητή) 17
18 Δημιουργία προβλημάτων από δεδομένα στοιχεία (συμβολικές εκφράσεις) Παραδείγματα μαθητών o Για το στοιχείο 12: 3 Ο Adam έχει 12 καρότα. Φύτεψε 3 σειρές. Πόσα καρότα θα είναι σε κάθε σειρά; o Για το στοιχείο 3: 4 Είχα 3 κέικ. Αν μπορούσαν να τα μοιραστούν 4 φίλοι μου χωρίζοντάς τα σε τέταρτα, πόσα κομμάτια του κάθε κέικ θα έπαιρνε καθένας; Ο Adam έχει 3 κέικ. Θα πρέπει να μοιραστούν ίσα σε 4 φίλους μου. Πόσες φέτες θα πάρει το καθένα; Δημιουργία νέων προβλημάτων σε υφιστάμενες δομές Παραδείγματα μαθητών Για το στοιχείο Ο Bill έχει 132 Lego κομμάτια. Έχει 29 λιγότερα από τον Adam. Πόσα Lego κομμάτια έχει Adam; Η Jane έχει 132 μπίλιες και ο Aaron έχει 29 λιγότερες από την Jane. Πόσες έχει ο Aaron; Για το στοιχείο 4x3 Ο Tony φύτεψε καρότα. Έκανε 4 σειρές και σε κάθε σειρά είχε 3 καρότα. Πόσα καρότα φύτεψε ο Τόνι; Η Kelly έχει 4 παντελόνια και 3 πουκάμισα. Πόσα διαφορετικά ντυσίματα μπορεί να κάνει; 18
19 Τελικά Θα πρέπει οι εκπαιδευτικοί να αφιερώνουν περισσότερο χρόνο στην κριτική εκτίμηση των μαθητών για τις δικές τους κατασκευές προβλημάτων καθώς και στην εκτίμηση των προβλημάτων που δημιουργούν οι φίλοι τους Η κατασκευή προβλημάτων από μαθητές θα έπρεπε να γίνει σημαντική μαθησιακή διαδικασία μέσα στο συνολικό πρόγραμμα σπουδών και όχι απλά μέσα σε κάποιες δραστηριότητες. Ευχαριστούμε! 19
Ειδικά Θέµατα Διδακτικής Μαθηµατικών Θέµα: Κατασκευή προβλήµατος, σηµασία και εφαρµογές
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΔΙΑΤΜΗΜΑΤΙΚΟ - ΔΙΑΠΑΝΕΠΙΣΤΗΜΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΔΙΔΑΚΤΙΚΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ» Ειδικά Θέµατα
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΔΙΑΤΜΗΜΑΤΙΚΟ - ΔΙΑΠΑΝΕΠΙΣΤΗΜΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΔΙΔΑΚΤΙΚΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ» Ειδικά Θέµατα
Γράφοντας ένα σχολικό βιβλίο για τα Μαθηματικά. Μαριάννα Τζεκάκη Αν. Καθηγήτρια Α.Π.Θ. Μ. Καλδρυμίδου Αν. Καθηγήτρια Πανεπιστημίου Ιωαννίνων
 Γράφοντας ένα σχολικό βιβλίο για τα Μαθηματικά Μαριάννα Τζεκάκη Αν. Καθηγήτρια Α.Π.Θ. Μ. Καλδρυμίδου Αν. Καθηγήτρια Πανεπιστημίου Ιωαννίνων Εισαγωγή Η χώρα μας απέκτησε Νέα Προγράμματα Σπουδών και Νέα
Γράφοντας ένα σχολικό βιβλίο για τα Μαθηματικά Μαριάννα Τζεκάκη Αν. Καθηγήτρια Α.Π.Θ. Μ. Καλδρυμίδου Αν. Καθηγήτρια Πανεπιστημίου Ιωαννίνων Εισαγωγή Η χώρα μας απέκτησε Νέα Προγράμματα Σπουδών και Νέα
Θέμα: Κατασκευή προβλήματος, σημασία και εφαρμογές
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΔΙΑΤΜΗΜΑΤΙΚΟ ΔΙΑΠΑΝΕΠΙΣΤΗΜΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΔΙΔΑΚΤΙΚΗ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΔΙΑΤΜΗΜΑΤΙΚΟ ΔΙΑΠΑΝΕΠΙΣΤΗΜΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΔΙΔΑΚΤΙΚΗ
Ο πρώτος ηλικιακός κύκλος αφορά μαθητές του νηπιαγωγείου (5-6 χρονών), της Α Δημοτικού (6-7 χρονών) και της Β Δημοτικού (7-8 χρονών).
 Μάθημα 5ο Ο πρώτος ηλικιακός κύκλος αφορά μαθητές του νηπιαγωγείου (5-6 χρονών), της Α Δημοτικού (6-7 χρονών) και της Β Δημοτικού (7-8 χρονών). Ο δεύτερος ηλικιακός κύκλος περιλαμβάνει την ηλικιακή περίοδο
Μάθημα 5ο Ο πρώτος ηλικιακός κύκλος αφορά μαθητές του νηπιαγωγείου (5-6 χρονών), της Α Δημοτικού (6-7 χρονών) και της Β Δημοτικού (7-8 χρονών). Ο δεύτερος ηλικιακός κύκλος περιλαμβάνει την ηλικιακή περίοδο
Θεωρείτε και σε τι βαθμό, έγκαιρη την ενημέρωσή σας για την ημερίδα στην οποία και συμμετείχατε;
 Θεωρείτε και σε τι βαθμό, έγκαιρη την ενημέρωσή σας για την ημερίδα στην οποία και συμμετείχατε; 4% 56% ΚΑΘΟΛΟΥ 4% 36% Θεωρείτε και σε τι βαθμό ικανοποιητικό τον συντονισμό, την οργάνωση και τη διεξαγωγή
Θεωρείτε και σε τι βαθμό, έγκαιρη την ενημέρωσή σας για την ημερίδα στην οποία και συμμετείχατε; 4% 56% ΚΑΘΟΛΟΥ 4% 36% Θεωρείτε και σε τι βαθμό ικανοποιητικό τον συντονισμό, την οργάνωση και τη διεξαγωγή
BELIEFS ABOUT THE NATURE OF MATHEMATICS, MATHEMATICS TEACHING AND LEARNING AMONG TRAINEE TEACHERS
 BELIEFS ABOUT THE NATURE OF MATHEMATICS, MATHEMATICS TEACHING AND LEARNING AMONG TRAINEE TEACHERS Effandi Zakaria and Norulpaziana Musiran The Social Sciences, 2010, Vol. 5, Issue 4: 346-351 Στόχος της
BELIEFS ABOUT THE NATURE OF MATHEMATICS, MATHEMATICS TEACHING AND LEARNING AMONG TRAINEE TEACHERS Effandi Zakaria and Norulpaziana Musiran The Social Sciences, 2010, Vol. 5, Issue 4: 346-351 Στόχος της
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ-Β ΦΑΣΗ ΘΕΜΑ ΔΙΔΑΣΚΑΛΙΑΣ: ΣΤΡΑΤΗΓΙΚΕΣ ΔΙΑΧΕΙΡΙΣΗΣ ΑΡΙΘΜΩΝ-19 ο ΚΕΦΑΛΑΙΟ ΣΧΟΛΕΙΟ: 2 ο ΠΕΙΡΑΜΑΤΙΚΟ ΦΛΩΡΙΝΑΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ-Β ΦΑΣΗ ΘΕΜΑ ΔΙΔΑΣΚΑΛΙΑΣ: ΣΤΡΑΤΗΓΙΚΕΣ ΔΙΑΧΕΙΡΙΣΗΣ ΑΡΙΘΜΩΝ-19 ο ΚΕΦΑΛΑΙΟ ΣΧΟΛΕΙΟ: 2 ο ΠΕΙΡΑΜΑΤΙΚΟ ΦΛΩΡΙΝΑΣ
Μαθηµατική. Μοντελοποίηση
 Μαθηµατική Μοντελοποίηση Μοντελοποίηση Απαιτητική οικονοµία και αγορά εργασίας Σύνθετες και περίπλοκες προβληµατικές καταστάσεις Μαθηµατικές και τεχνολογικές δεξιότητες Επίλυση σύνθετων προβληµάτων Μαθηµατικοποίηση
Μαθηµατική Μοντελοποίηση Μοντελοποίηση Απαιτητική οικονοµία και αγορά εργασίας Σύνθετες και περίπλοκες προβληµατικές καταστάσεις Μαθηµατικές και τεχνολογικές δεξιότητες Επίλυση σύνθετων προβληµάτων Μαθηµατικοποίηση
Σχεδιάζοντας τη διδασκαλία των Μαθηματικών: Βασικές αρχές
 Σχεδιάζοντας τη διδασκαλία των Μαθηματικών: Βασικές αρχές Φοιτητής: Σκαρπέντζος Γεώργιος Καθηγήτρια: Κολέζα Ευγενία ΠΕΡΙΕΧΟΜΕΝΑ Βασικές θεωρίες σχεδιασμού της διδασκαλίας Δραστηριότητες και κατανόηση εννοιών
Σχεδιάζοντας τη διδασκαλία των Μαθηματικών: Βασικές αρχές Φοιτητής: Σκαρπέντζος Γεώργιος Καθηγήτρια: Κολέζα Ευγενία ΠΕΡΙΕΧΟΜΕΝΑ Βασικές θεωρίες σχεδιασμού της διδασκαλίας Δραστηριότητες και κατανόηση εννοιών
Inquiry based learning (ΙΒL)
 Inquiry based learning (ΙΒL) ΟόροςIBL αναφέρεται σε μαθητοκεντρικούς τρόπους διδασκαλίας: Διατυπώνουν δικά τους επιστημονικά προσανατολισμένα ερωτήματα Δίνουν προτεραιότητα σε ενδείξεις/αποδεικτικά στοιχεία
Inquiry based learning (ΙΒL) ΟόροςIBL αναφέρεται σε μαθητοκεντρικούς τρόπους διδασκαλίας: Διατυπώνουν δικά τους επιστημονικά προσανατολισμένα ερωτήματα Δίνουν προτεραιότητα σε ενδείξεις/αποδεικτικά στοιχεία
Εφαρμογές (apps) για εξάσκηση με τα κλάσματα σε επίπεδο Γ Δημοτικού
 Εφαρμογές (apps) για εξάσκηση με τα κλάσματα σε επίπεδο Γ Δημοτικού Fractions & Smart Pirates (δωρεάν) Ένα διαδραστικό παιχνίδι όπου οι μαθητές πρέπει να φέρουν εις πέρας δοκιμασίες που τους ανατίθενται.
Εφαρμογές (apps) για εξάσκηση με τα κλάσματα σε επίπεδο Γ Δημοτικού Fractions & Smart Pirates (δωρεάν) Ένα διαδραστικό παιχνίδι όπου οι μαθητές πρέπει να φέρουν εις πέρας δοκιμασίες που τους ανατίθενται.
Δημήτρης Ρώσσης, Φάνη Στυλιανίδου Ελληνογερμανική Αγωγή. http://www.creative-little-scientists.eu
 Τι έχουμε μάθει για την προώθηση της Δημιουργικότητας μέσα από τις Φυσικές Επιστήμες και τα Μαθηματικά στην Ελληνική Προσχολική και Πρώτη Σχολική Ηλικία; Ευρήματα για την εκπαίδευση στην Ελλάδα από το
Τι έχουμε μάθει για την προώθηση της Δημιουργικότητας μέσα από τις Φυσικές Επιστήμες και τα Μαθηματικά στην Ελληνική Προσχολική και Πρώτη Σχολική Ηλικία; Ευρήματα για την εκπαίδευση στην Ελλάδα από το
Αξιολόγηση της διαδικασίας επίλυσης προβλημάτων
 Αξιολόγηση της διαδικασίας επίλυσης προβλημάτων Δ.Δ.Π.Μ.Σ. «ΔΙΔΑΚΤΙΚΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩ Ν» ΜΑΘΗΜΑ: ΕΙΔΙΚΑ ΘΕΜΑΤΑ ΔΙΔΑΚΤΙΚΗΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚ ΩΝ ΚΑΘΗΓΗΤΡΙΑ : ΤΖΕΚΑΚΗ Μ. Assessing Problem-Solving Thought Annette
Αξιολόγηση της διαδικασίας επίλυσης προβλημάτων Δ.Δ.Π.Μ.Σ. «ΔΙΔΑΚΤΙΚΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩ Ν» ΜΑΘΗΜΑ: ΕΙΔΙΚΑ ΘΕΜΑΤΑ ΔΙΔΑΚΤΙΚΗΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚ ΩΝ ΚΑΘΗΓΗΤΡΙΑ : ΤΖΕΚΑΚΗ Μ. Assessing Problem-Solving Thought Annette
Ανάπτυξη Χωρικής Αντίληψης και Σκέψης
 Ανάπτυξη Χωρικής Αντίληψης και Σκέψης Clements & Sarama, 2009; Sarama & Clements, 2009 Χωρική αντίληψη και σκέψη Προσανατολισμός στο χώρο Οπτικοποίηση (visualization) Νοερή εικονική αναπαράσταση Νοερή
Ανάπτυξη Χωρικής Αντίληψης και Σκέψης Clements & Sarama, 2009; Sarama & Clements, 2009 Χωρική αντίληψη και σκέψη Προσανατολισμός στο χώρο Οπτικοποίηση (visualization) Νοερή εικονική αναπαράσταση Νοερή
5.4. ΑΠΟΤΕΛΕΣΜΑΤΑ ΕΡΕΥΝΩΝ ΜΕ ΡΗΤΟΥΣ ΑΡΙΘΜΟΥΣ ΤΗΣ ΣΧΟΛΗΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΤΗΣ ΦΥΣΗΣ ΚΑΙ ΤΗΣ ΖΩΗΣ
 5.4. ΑΠΟΤΕΛΕΣΜΑΤΑ ΕΡΕΥΝΩΝ ΜΕ ΡΗΤΟΥΣ ΑΡΙΘΜΟΥΣ ΤΗΣ ΣΧΟΛΗΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΤΗΣ ΦΥΣΗΣ ΚΑΙ ΤΗΣ ΖΩΗΣ 5.4.1. Αποτελέσματα από το πρόγραμμα εξ αποστάσεως επιμόρφωσης δασκάλων και πειραματικής εφαρμογής των νοερών
5.4. ΑΠΟΤΕΛΕΣΜΑΤΑ ΕΡΕΥΝΩΝ ΜΕ ΡΗΤΟΥΣ ΑΡΙΘΜΟΥΣ ΤΗΣ ΣΧΟΛΗΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΤΗΣ ΦΥΣΗΣ ΚΑΙ ΤΗΣ ΖΩΗΣ 5.4.1. Αποτελέσματα από το πρόγραμμα εξ αποστάσεως επιμόρφωσης δασκάλων και πειραματικής εφαρμογής των νοερών
Κοινωνικογνωστικές θεωρίες μάθησης. Διδάσκουσα Φ. Αντωνίου
 Κοινωνικογνωστικές θεωρίες μάθησης Διδάσκουσα Φ. Αντωνίου Περίγραμμα Νοοκατασκευαστική θεώρηση της μάθησης Ιστορικό υπόβαθρο Top-down * bottom up Ομαδοσυνεργατική μάθηση Νοοκατασκευαστικές μέθοδοι στην
Κοινωνικογνωστικές θεωρίες μάθησης Διδάσκουσα Φ. Αντωνίου Περίγραμμα Νοοκατασκευαστική θεώρηση της μάθησης Ιστορικό υπόβαθρο Top-down * bottom up Ομαδοσυνεργατική μάθηση Νοοκατασκευαστικές μέθοδοι στην
ΕΠΙΜΟΡΦΩΤΙΚΗ ΗΜΕΡΙΔΑ «Η ΑΞΙΟΛΟΓΗΣΗ ΤΟΥ ΜΑΘΗΤΗ ΣΥΜΦΩΝΑ ΜΕ ΤΑ ΝΕΑ ΠΡΟΓΡΑΜΜΑΤΑ ΣΠΟΥΔΩΝ»
 ΕΠΙΜΟΡΦΩΤΙΚΗ ΗΜΕΡΙΔΑ «Η ΑΞΙΟΛΟΓΗΣΗ ΤΟΥ ΜΑΘΗΤΗ ΣΥΜΦΩΝΑ ΜΕ ΤΑ ΝΕΑ ΠΡΟΓΡΑΜΜΑΤΑ ΣΠΟΥΔΩΝ» ΕΙΣΗΓΗΣΗ: «Πρακτικές αξιολόγησης κατά τη διδασκαλία των Μαθηματικών» Γιάννης Χριστάκης Σχολικός Σύμβουλος 3ης Περιφέρειας
ΕΠΙΜΟΡΦΩΤΙΚΗ ΗΜΕΡΙΔΑ «Η ΑΞΙΟΛΟΓΗΣΗ ΤΟΥ ΜΑΘΗΤΗ ΣΥΜΦΩΝΑ ΜΕ ΤΑ ΝΕΑ ΠΡΟΓΡΑΜΜΑΤΑ ΣΠΟΥΔΩΝ» ΕΙΣΗΓΗΣΗ: «Πρακτικές αξιολόγησης κατά τη διδασκαλία των Μαθηματικών» Γιάννης Χριστάκης Σχολικός Σύμβουλος 3ης Περιφέρειας
Εκπαίδευση Ενηλίκων: Εμπειρίες και Δράσεις ΑΘΗΝΑ, Δευτέρα 12 Οκτωβρίου 2015
 Εκπαίδευση Ενηλίκων: Εμπειρίες και Δράσεις ΑΘΗΝΑ, Δευτέρα 12 Οκτωβρίου 2015 Μάθηση και γνώση: μια συνεχής και καθοριστική αλληλοεπίδραση Αντώνης Λιοναράκης Στην παρουσίαση που θα ακολουθήσει θα μιλήσουμε
Εκπαίδευση Ενηλίκων: Εμπειρίες και Δράσεις ΑΘΗΝΑ, Δευτέρα 12 Οκτωβρίου 2015 Μάθηση και γνώση: μια συνεχής και καθοριστική αλληλοεπίδραση Αντώνης Λιοναράκης Στην παρουσίαση που θα ακολουθήσει θα μιλήσουμε
Μάθηση & διδασκαλία στην προσχολική εκπαίδευση: βασικές αρχές
 Μάθηση & διδασκαλία στην προσχολική εκπαίδευση: βασικές αρχές Σκοποί ενότητας Να συζητηθούν βασικές παιδαγωγικές αρχές της προσχολικής εκπαίδευσης Να προβληματιστούμε για τους τρόπους με τους οποίους μπορεί
Μάθηση & διδασκαλία στην προσχολική εκπαίδευση: βασικές αρχές Σκοποί ενότητας Να συζητηθούν βασικές παιδαγωγικές αρχές της προσχολικής εκπαίδευσης Να προβληματιστούμε για τους τρόπους με τους οποίους μπορεί
ΑΛΛΑΓΗ ΣΤΗ ΔΙΔΑΣΚΑΛΙΑ ΤΩΝ ΜΑΘΗΜΑΤΙΚΏΝ:
 ΑΛΛΑΓΗ ΣΤΗ ΔΙΔΑΣΚΑΛΙΑ ΤΩΝ ΜΑΘΗΜΑΤΙΚΏΝ: σύγχρονες αναγνώσεις Καβάλα 14/11/2015 ΜΑΡΙΑΝΝΑ ΤΖΕΚΑΚΗ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ 2 Γιατί αλλαγές; 1 3 Για ουσιαστική μαθηματική ανάπτυξη, Σύγχρονο πρόγραμμα
ΑΛΛΑΓΗ ΣΤΗ ΔΙΔΑΣΚΑΛΙΑ ΤΩΝ ΜΑΘΗΜΑΤΙΚΏΝ: σύγχρονες αναγνώσεις Καβάλα 14/11/2015 ΜΑΡΙΑΝΝΑ ΤΖΕΚΑΚΗ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ 2 Γιατί αλλαγές; 1 3 Για ουσιαστική μαθηματική ανάπτυξη, Σύγχρονο πρόγραμμα
Δραστηριότητες & Υλικό για τα Μαθηματικά του Δημοτικού
 Δραστηριότητες & Υλικό για τα Μαθηματικά του Δημοτικού Πέτρος Κλιάπης kliapis@sch.gr 1 Ο Ρόλος του εκπαιδευτικού Αξιολογεί την αρχική μαθηματική κατάσταση κάθε παιδιού, ομαδοποιεί τα παιδιά σύμφωνα με
Δραστηριότητες & Υλικό για τα Μαθηματικά του Δημοτικού Πέτρος Κλιάπης kliapis@sch.gr 1 Ο Ρόλος του εκπαιδευτικού Αξιολογεί την αρχική μαθηματική κατάσταση κάθε παιδιού, ομαδοποιεί τα παιδιά σύμφωνα με
Διερευνητική μάθηση We are researchers, let us do research! (Elbers and Streefland, 2000)
 Διερευνητική μάθηση We are researchers, let us do research! (Elbers and Streefland, 2000) Πρόκειται για την έρευνα που διεξάγουν οι επιστήμονες. Είναι μια πολύπλοκη δραστηριότητα που απαιτεί ειδικό ακριβό
Διερευνητική μάθηση We are researchers, let us do research! (Elbers and Streefland, 2000) Πρόκειται για την έρευνα που διεξάγουν οι επιστήμονες. Είναι μια πολύπλοκη δραστηριότητα που απαιτεί ειδικό ακριβό
ΕΠΕΚΤΑΣΗ Παρουσίαση των εργασιών της οµάδας στο άλλο τµήµα της τάξης. ηµοσίευση στην ιστοσελίδα του σχολείου µας. ΑΞΙΟΛΟΓΗΣΗ Η εµπέδωση των εννοιών
 ΕΚΦΩΝΗΣΗ ΕΛΕΥΘΕΡΟΥ ΘΕΜΑΤΟΣ (µικρές τάξεις ηµοτικού) Σχεδιασµός σεναρίου µε θέµα «Ισότητα και διαµοιρασµός» µε τη χρήση λογισµικών γενικής χρήσης, οπτικοποίησης, διαδικτύου και λογισµικών εννοιολογικής
ΕΚΦΩΝΗΣΗ ΕΛΕΥΘΕΡΟΥ ΘΕΜΑΤΟΣ (µικρές τάξεις ηµοτικού) Σχεδιασµός σεναρίου µε θέµα «Ισότητα και διαµοιρασµός» µε τη χρήση λογισµικών γενικής χρήσης, οπτικοποίησης, διαδικτύου και λογισµικών εννοιολογικής
Τομέας Εκπαιδευτικής Τεχνολογίας Παιδαγωγικό Ινστιτούτο Κύπρου ATS2020 ΤΟΜΕΙΣ ΙΚΑΝΟΤΗΤΩΝ ΚΑΙ ΔΕΞΙΟΤΗΤΩΝ ΜΕ ΣΤΟΧΟΥΣ ΕΠΙΤΕΥΞΗΣ
 ATS2020 ΤΟΜΕΙΣ ΙΚΑΝΟΤΗΤΩΝ ΚΑΙ ΔΕΞΙΟΤΗΤΩΝ ΜΕ ΣΤΟΧΟΥΣ ΕΠΙΤΕΥΞΗΣ ΤΟΜΕΑΣ ΠΛΗΡΟΦΟΡΙΑΚΟΥ ΓΡΑΜΜΑΤΙΣΜΟΥ 1. Σχεδιασμός στρατηγικών για διερεύνηση 1.1. Εντοπίζουν σημαντικές ανάγκες/ προβλήματα/ ερωτήματα για διερεύνηση
ATS2020 ΤΟΜΕΙΣ ΙΚΑΝΟΤΗΤΩΝ ΚΑΙ ΔΕΞΙΟΤΗΤΩΝ ΜΕ ΣΤΟΧΟΥΣ ΕΠΙΤΕΥΞΗΣ ΤΟΜΕΑΣ ΠΛΗΡΟΦΟΡΙΑΚΟΥ ΓΡΑΜΜΑΤΙΣΜΟΥ 1. Σχεδιασμός στρατηγικών για διερεύνηση 1.1. Εντοπίζουν σημαντικές ανάγκες/ προβλήματα/ ερωτήματα για διερεύνηση
Προτιμήσεις εκπαιδευτικών στην επίλυση προβλημάτων με συμμετρία. Στόχος έρευνας
 Προτιμήσεις εκπαιδευτικών στην επίλυση προβλημάτων με συμμετρία Πουλιτσίδου Νιόβη- Χριστίνα Τζιρτζιγάνης Βασίλειος Φωκάς Δημήτριος Στόχος έρευνας Να διερευνηθούν οι παράγοντες, που επηρεάζουν την επιλογή
Προτιμήσεις εκπαιδευτικών στην επίλυση προβλημάτων με συμμετρία Πουλιτσίδου Νιόβη- Χριστίνα Τζιρτζιγάνης Βασίλειος Φωκάς Δημήτριος Στόχος έρευνας Να διερευνηθούν οι παράγοντες, που επηρεάζουν την επιλογή
Μαθηματικά A Δημοτικού. Πέτρος Κλιάπης Σεπτέμβρης 2007
 Μαθηματικά A Δημοτικού Πέτρος Κλιάπης Σεπτέμβρης 2007 Το σύγχρονο μαθησιακό περιβάλλον των Μαθηματικών Ενεργή συμμετοχή των παιδιών Μάθηση μέσα από δραστηριότητες Κατανόηση ΌΧΙ απομνημόνευση Αξιοποίηση
Μαθηματικά A Δημοτικού Πέτρος Κλιάπης Σεπτέμβρης 2007 Το σύγχρονο μαθησιακό περιβάλλον των Μαθηματικών Ενεργή συμμετοχή των παιδιών Μάθηση μέσα από δραστηριότητες Κατανόηση ΌΧΙ απομνημόνευση Αξιοποίηση
Διήμερο εκπαιδευτικού επιμόρφωση Μέθοδος project στο νηπιαγωγείο. Έλενα Τζιαμπάζη Νίκη Χ γαβριήλ-σιέκκερη
 Διήμερο εκπαιδευτικού επιμόρφωση Μέθοδος project στο νηπιαγωγείο Έλενα Τζιαμπάζη Νίκη Χ γαβριήλ-σιέκκερη Δομή επιμόρφωσης 1 η Μέρα Γνωριμία ομάδας Παρουσίαση θεωρητικού υποβάθρου Προσομοίωση : α) Επιλογή
Διήμερο εκπαιδευτικού επιμόρφωση Μέθοδος project στο νηπιαγωγείο Έλενα Τζιαμπάζη Νίκη Χ γαβριήλ-σιέκκερη Δομή επιμόρφωσης 1 η Μέρα Γνωριμία ομάδας Παρουσίαση θεωρητικού υποβάθρου Προσομοίωση : α) Επιλογή
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΓΙΑ ΤΗ ΜΑΘΗΣΗ ΚΑΙ ΤΗ ΔΙΔΑΣΚΑΛΙΑ ΣΤΗΝ ΠΡΟΣΧΟΛΙΚΗ ΕΚΠΑΙΔΕΥΣΗ
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΓΙΑ ΤΗ ΜΑΘΗΣΗ ΚΑΙ ΤΗ ΔΙΔΑΣΚΑΛΙΑ ΣΤΗΝ ΠΡΟΣΧΟΛΙΚΗ ΕΚΠΑΙΔΕΥΣΗ ΑΝΑΓΝΩΡΙΖΟΝΤΑΣ ΤΗ ΔΙΑΦΟΡΕΤΙΚΟΤΗΤΑ & ΑΝΑΠΤΥΣΣΟΝΤΑΣ ΔΙΑΦΟΡΟΠΟΙΗΜΕΝΕΣ ΠΡΟΣΕΓΓΙΣΕΙΣ Διαστάσεις της διαφορετικότητας Τα παιδιά προέρχονται
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΓΙΑ ΤΗ ΜΑΘΗΣΗ ΚΑΙ ΤΗ ΔΙΔΑΣΚΑΛΙΑ ΣΤΗΝ ΠΡΟΣΧΟΛΙΚΗ ΕΚΠΑΙΔΕΥΣΗ ΑΝΑΓΝΩΡΙΖΟΝΤΑΣ ΤΗ ΔΙΑΦΟΡΕΤΙΚΟΤΗΤΑ & ΑΝΑΠΤΥΣΣΟΝΤΑΣ ΔΙΑΦΟΡΟΠΟΙΗΜΕΝΕΣ ΠΡΟΣΕΓΓΙΣΕΙΣ Διαστάσεις της διαφορετικότητας Τα παιδιά προέρχονται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΑΓΩΓΗΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΕΡΓΑΣΙΑ ΓΙΑ ΤΟ ΜΑΘΗΜΑ: ΘΕΜΑ: «Αριθμοί στην καθημερινή ζωή»
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΑΓΩΓΗΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΕΡΓΑΣΙΑ ΓΙΑ ΤΟ ΜΑΘΗΜΑ: ΔΙΔΑΚΤΙΚΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΙΙ ΘΕΜΑ: «Αριθμοί στην καθημερινή ζωή» Βόκα Δέσποινα & Δούρου
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΑΓΩΓΗΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΕΡΓΑΣΙΑ ΓΙΑ ΤΟ ΜΑΘΗΜΑ: ΔΙΔΑΚΤΙΚΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΙΙ ΘΕΜΑ: «Αριθμοί στην καθημερινή ζωή» Βόκα Δέσποινα & Δούρου
9l')lI21)l ftqft11(jl P.J-FΣ jl)l OfTCP)l ΦΙΆ 'Σ 'ΣTJ{W rι'ά ΞΚ 21 '2 rι'ory 13 V ijjf:μdrrι1(οry'σχοjlρ.ιοrycpο210ry
 ΣΧΟΛΗ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ feqx[')ltσi)i: 9l'CPQrι'01(Ojljl 021121)l 'Σ1(jljf1QW 'Σq)l 9l')lI21)l ftqft11(jl P.J-FΣ jl)l OfTCP)l ΦΙΆ 'Σ 'ΣTJ{W rι'ά ΞΚ 21 '2 rι'ory
ΣΧΟΛΗ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ feqx[')ltσi)i: 9l'CPQrι'01(Ojljl 021121)l 'Σ1(jljf1QW 'Σq)l 9l')lI21)l ftqft11(jl P.J-FΣ jl)l OfTCP)l ΦΙΆ 'Σ 'ΣTJ{W rι'ά ΞΚ 21 '2 rι'ory
ΕΝΟΤΗΤΑ 10 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΚΑΙ ΔΙΑΙΡΕΣΗ
 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΚΑΙ ΔΙΑΙΡΕΣΗ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΑΡΙΘΜΟΙ Υπολογισμοί και εκτίμηση Αρ1.15 Αναπτύσσουν την έννοια του πολλαπλασιασμού ως αθροιστικής επανάληψης ίσων προσθετέων και διαισθητικά την έννοια της
ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΚΑΙ ΔΙΑΙΡΕΣΗ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΑΡΙΘΜΟΙ Υπολογισμοί και εκτίμηση Αρ1.15 Αναπτύσσουν την έννοια του πολλαπλασιασμού ως αθροιστικής επανάληψης ίσων προσθετέων και διαισθητικά την έννοια της
Διδακτική της Πληροφορικής
 Διδακτική της Πληροφορικής ΟΜΑΔΑ ΕΡΓΑΣΙΑΣ Ανδρέας Σ. Ανδρέου (Αναπλ. Καθηγητής ΤΕΠΑΚ - Συντονιστής) Μάριος Μιλτιάδου, Μιχάλης Τορτούρης (ΕΜΕ Πληροφορικής) Νίκος Ζάγκουλος, Σωκράτης Μυλωνάς (Σύμβουλοι Πληροφορικής)
Διδακτική της Πληροφορικής ΟΜΑΔΑ ΕΡΓΑΣΙΑΣ Ανδρέας Σ. Ανδρέου (Αναπλ. Καθηγητής ΤΕΠΑΚ - Συντονιστής) Μάριος Μιλτιάδου, Μιχάλης Τορτούρης (ΕΜΕ Πληροφορικής) Νίκος Ζάγκουλος, Σωκράτης Μυλωνάς (Σύμβουλοι Πληροφορικής)
ΡΟΜΠΟΤΙΚΗ ΚΑΙ ΕΚΠΑΙΔΕΥΣΗ
 ΡΟΜΠΟΤΙΚΗ ΚΑΙ ΕΚΠΑΙΔΕΥΣΗ Γιατί η Ρομποτική στην Εκπαίδευση; A) Τα παιδιά όταν σχεδιάζουν, κατασκευάζουν και προγραμματίζουν ρομπότ έχουν την ευκαιρία να μάθουν παίζοντας και να αναπτύξουν δεξιότητες Η
ΡΟΜΠΟΤΙΚΗ ΚΑΙ ΕΚΠΑΙΔΕΥΣΗ Γιατί η Ρομποτική στην Εκπαίδευση; A) Τα παιδιά όταν σχεδιάζουν, κατασκευάζουν και προγραμματίζουν ρομπότ έχουν την ευκαιρία να μάθουν παίζοντας και να αναπτύξουν δεξιότητες Η
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Υπεύθυνος καθηγητής Χαράλαμπος Λεμονίδης Μέντορας Γεώργιος Γεωργιόπουλος ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗΣ Θέμα Διδασκαλίας Πρόσθεση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Υπεύθυνος καθηγητής Χαράλαμπος Λεμονίδης Μέντορας Γεώργιος Γεωργιόπουλος ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗΣ Θέμα Διδασκαλίας Πρόσθεση
ΔΕΞΙΟΤΗΤΕΣ ΜΙΑ ΣΥΖΗΤΗΣΗ ΣΗΜΕΡΑ ΓΙΑ ΤΟ ΑΥΡΙΟ ΤΩΝ ΜΑΘΗΤΩΝ
 ΔΕΞΙΟΤΗΤΕΣ ΜΙΑ ΣΥΖΗΤΗΣΗ ΣΗΜΕΡΑ ΓΙΑ ΤΟ ΑΥΡΙΟ ΤΩΝ ΜΑΘΗΤΩΝ Η αφορμή ( 1 ) Ήρθε η ώρα να παρουσιάσουν τις εργασίες τους. Η μια δεν ήξερε να βάλει το στικάκι στη θύρα, ενώ ο άλλος παιδευόταν να ανοίξει την
ΔΕΞΙΟΤΗΤΕΣ ΜΙΑ ΣΥΖΗΤΗΣΗ ΣΗΜΕΡΑ ΓΙΑ ΤΟ ΑΥΡΙΟ ΤΩΝ ΜΑΘΗΤΩΝ Η αφορμή ( 1 ) Ήρθε η ώρα να παρουσιάσουν τις εργασίες τους. Η μια δεν ήξερε να βάλει το στικάκι στη θύρα, ενώ ο άλλος παιδευόταν να ανοίξει την
ΕΝΟΤΗΤΑ 5 ΜΟΤΙΒΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΥ, ΚΛΑΣΜΑΤΑ ΕΜΒΑΔΟΝ ΚΑΙ ΠΕΡΙΜΕΤΡΟΣ ΟΡΘΟΓΩΝΙΟΥ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ
 ΜΟΤΙΒΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΥ, ΚΛΑΣΜΑΤΑ ΕΜΒΑΔΟΝ ΚΑΙ ΠΕΡΙΜΕΤΡΟΣ ΟΡΘΟΓΩΝΙΟΥ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΑΡΙΘΜΟΙ Διερεύνηση αριθμών Αρ2.5 Αναπαριστούν, συγκρίνουν και σειροθετούν ομώνυμα κλάσματα και δεκαδικούς αριθμούς,
ΜΟΤΙΒΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΥ, ΚΛΑΣΜΑΤΑ ΕΜΒΑΔΟΝ ΚΑΙ ΠΕΡΙΜΕΤΡΟΣ ΟΡΘΟΓΩΝΙΟΥ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΑΡΙΘΜΟΙ Διερεύνηση αριθμών Αρ2.5 Αναπαριστούν, συγκρίνουν και σειροθετούν ομώνυμα κλάσματα και δεκαδικούς αριθμούς,
ΘΕΩΡΊΕς ΜΆΘΗΣΗς ΚΑΙ ΜΑΘΗΜΑΤΙΚΆ
 ΘΕΩΡΊΕς ΜΆΘΗΣΗς ΚΑΙ ΜΑΘΗΜΑΤΙΚΆ ΔΟΜΕΣ Δομή Ομάδας Σύνολο Α και μια πράξη η πράξη είναι κλειστή ισχύει η προσεταιριστική ιδότητα υπάρχει ουδέτερο στοιχείο υπάρχει αντίστροφο στοιχείο ισχύει η αντιμεταθετική
ΘΕΩΡΊΕς ΜΆΘΗΣΗς ΚΑΙ ΜΑΘΗΜΑΤΙΚΆ ΔΟΜΕΣ Δομή Ομάδας Σύνολο Α και μια πράξη η πράξη είναι κλειστή ισχύει η προσεταιριστική ιδότητα υπάρχει ουδέτερο στοιχείο υπάρχει αντίστροφο στοιχείο ισχύει η αντιμεταθετική
H Συμβολή της Υπολογιστικής Σκέψης στην Προετοιμασία του Αυριανού Πολίτη
 H Συμβολή της Υπολογιστικής Σκέψης στην Προετοιμασία του Αυριανού Πολίτη Κοτίνη Ι., Τζελέπη Σ. Σχ. Σύμβουλοι Κ. Μακεδονίας στην οικονομία, στη τέχνη, στην επιστήμη, στις ανθρωπιστικές και κοινωνικές επιστήμες.
H Συμβολή της Υπολογιστικής Σκέψης στην Προετοιμασία του Αυριανού Πολίτη Κοτίνη Ι., Τζελέπη Σ. Σχ. Σύμβουλοι Κ. Μακεδονίας στην οικονομία, στη τέχνη, στην επιστήμη, στις ανθρωπιστικές και κοινωνικές επιστήμες.
Δημιουργικό Παιχνίδι ΕΝΣΩΜΑΤΩΣΗ ΤΩΝ ΠΑΙΧΝΙΔΙΩΝ ΣΤΟ ΜΑΘΗΜΑ ΤΗΣ Φ.Α. Διάλεξη 3η
 Δημιουργικό Παιχνίδι ΕΝΣΩΜΑΤΩΣΗ ΤΩΝ ΠΑΙΧΝΙΔΙΩΝ ΣΤΟ ΜΑΘΗΜΑ ΤΗΣ Φ.Α. Διάλεξη 3η Σκοποί της παρουσίασης Εξέταση των προϋποθέσεων καταλληλότητας των παιχνιδιών σε σχέση με τα προγράμματα Φ.Α. Εισαγωγή στα
Δημιουργικό Παιχνίδι ΕΝΣΩΜΑΤΩΣΗ ΤΩΝ ΠΑΙΧΝΙΔΙΩΝ ΣΤΟ ΜΑΘΗΜΑ ΤΗΣ Φ.Α. Διάλεξη 3η Σκοποί της παρουσίασης Εξέταση των προϋποθέσεων καταλληλότητας των παιχνιδιών σε σχέση με τα προγράμματα Φ.Α. Εισαγωγή στα
Μεταγνωστικές διαδικασίες και κοινωνική αλληλεπίδραση μεταξύ των μαθητών στα μαθηματικά: ο ρόλος των σχολικών εγχειριδίων
 Μεταγνωστικές διαδικασίες και κοινωνική αλληλεπίδραση μεταξύ των μαθητών στα μαθηματικά: ο ρόλος των σχολικών εγχειριδίων Πέτρος Χαβιάρης & Σόνια Καφούση chaviaris@rhodes.aegean.gr; kafoussi@rhodes.aegean.gr
Μεταγνωστικές διαδικασίες και κοινωνική αλληλεπίδραση μεταξύ των μαθητών στα μαθηματικά: ο ρόλος των σχολικών εγχειριδίων Πέτρος Χαβιάρης & Σόνια Καφούση chaviaris@rhodes.aegean.gr; kafoussi@rhodes.aegean.gr
 ΜΕΡΟΣ ΠΕΜΠΤΟ Εισαγωγή στην έννοια του αριθμού Το παιδί πρέπει να αντιληφθεί τον αριθμό με την έννοια του πλήθους συγκεκριμένων αντικειμένων που αποτελούν ένα σύνολο (πληθικός αριθμός συνόλου = φυσικός
ΜΕΡΟΣ ΠΕΜΠΤΟ Εισαγωγή στην έννοια του αριθμού Το παιδί πρέπει να αντιληφθεί τον αριθμό με την έννοια του πλήθους συγκεκριμένων αντικειμένων που αποτελούν ένα σύνολο (πληθικός αριθμός συνόλου = φυσικός
ΔΙΔΑΣΚΑΛΙΑ ΓΝΩΣΤΙΚΗΣ ΣΤΡΑΤΗΓΙΚΗΣ ΓΙΑ ΤΗΝ ΚΑΤΑΝΟΗΣΗ Δρ. Ζαφειριάδης Κυριάκος Οι ικανοί αναγνώστες χρησιμοποιούν πολλές στρατηγικές (συνδυάζουν την
 1 ΔΙΔΑΣΚΑΛΙΑ ΓΝΩΣΤΙΚΗΣ ΣΤΡΑΤΗΓΙΚΗΣ ΓΙΑ ΤΗΝ ΚΑΤΑΝΟΗΣΗ Δρ. Ζαφειριάδης Κυριάκος Οι ικανοί αναγνώστες χρησιμοποιούν πολλές στρατηγικές (συνδυάζουν την παλαιότερη γνώση τους, σημειώνουν λεπτομέρειες, παρακολουθούν
1 ΔΙΔΑΣΚΑΛΙΑ ΓΝΩΣΤΙΚΗΣ ΣΤΡΑΤΗΓΙΚΗΣ ΓΙΑ ΤΗΝ ΚΑΤΑΝΟΗΣΗ Δρ. Ζαφειριάδης Κυριάκος Οι ικανοί αναγνώστες χρησιμοποιούν πολλές στρατηγικές (συνδυάζουν την παλαιότερη γνώση τους, σημειώνουν λεπτομέρειες, παρακολουθούν
Ελένη Μοσχοβάκη Σχολική Σύμβουλος 47ης Περιφέρειας Π.Α.
 Ελένη Μοσχοβάκη Σχολική Σύμβουλος 47ης Περιφέρειας Π.Α. Τι θα Δούμε. Γιατί αλλάζει το Αναλυτικό Πρόγραμμα Σπουδών. Παιδαγωγικό πλαίσιο του νέου Α.Π.Σ. Αρχές του νέου Α.Π.Σ. Μαθησιακές περιοχές του νέου
Ελένη Μοσχοβάκη Σχολική Σύμβουλος 47ης Περιφέρειας Π.Α. Τι θα Δούμε. Γιατί αλλάζει το Αναλυτικό Πρόγραμμα Σπουδών. Παιδαγωγικό πλαίσιο του νέου Α.Π.Σ. Αρχές του νέου Α.Π.Σ. Μαθησιακές περιοχές του νέου
Η διάρκεια πραγματοποίησης της ανοιχτής εκπαιδευτικής πρακτικής ήταν 2 διδακτικές ώρες
 ΣΧΟΛΕΙΟ Η εκπαιδευτική πρακτική αφορούσε τη διδασκαλία των μεταβλητών στον προγραμματισμό και εφαρμόστηκε σε μαθητές της τελευταίας τάξης ΕΠΑΛ του τομέα Πληροφορικής στα πλαίσια του μαθήματος του Δομημένου
ΣΧΟΛΕΙΟ Η εκπαιδευτική πρακτική αφορούσε τη διδασκαλία των μεταβλητών στον προγραμματισμό και εφαρμόστηκε σε μαθητές της τελευταίας τάξης ΕΠΑΛ του τομέα Πληροφορικής στα πλαίσια του μαθήματος του Δομημένου
A ΤΑΞΗ ΑΝΑΛΥΤΙΚΗ ΠΑΡΟΥΣΙΑΣΗ ΠΕΡΙΕΧΟΜΕΝΟΥ ΑΝΑ ΕΝΟΤΗΤΑ
 1 A ΤΑΞΗ ΑΝΑΛΥΤΙΚΗ ΠΑΡΟΥΣΙΑΣΗ ΠΕΡΙΕΧΟΜΕΝΟΥ ΑΝΑ ΕΝΟΤΗΤΑ 2 ΕΝΟΤΗΤΑ 1 ΚΑΝΩ ΟΜΑΔΕΣ, ΜΟΤΙΒΑ, ΑΝΤΙΣΤΟΙΧΙΣΗ ΠΕΡΙΕΧΟΜΕΝΟ ΕΝΟΤΗΤΑΣ -Ομαδοποίηση αντικειμένων με διαφορετικούς τρόπους. -Εντοπισμός ομοιοτήτων και
1 A ΤΑΞΗ ΑΝΑΛΥΤΙΚΗ ΠΑΡΟΥΣΙΑΣΗ ΠΕΡΙΕΧΟΜΕΝΟΥ ΑΝΑ ΕΝΟΤΗΤΑ 2 ΕΝΟΤΗΤΑ 1 ΚΑΝΩ ΟΜΑΔΕΣ, ΜΟΤΙΒΑ, ΑΝΤΙΣΤΟΙΧΙΣΗ ΠΕΡΙΕΧΟΜΕΝΟ ΕΝΟΤΗΤΑΣ -Ομαδοποίηση αντικειμένων με διαφορετικούς τρόπους. -Εντοπισμός ομοιοτήτων και
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΔΙΔΑΚΤΙΚΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ»
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΔΙΔΑΚΤΙΚΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ» ΕΙΔΙΚΑ ΘΕΜΑΤΑ ΔΙΔΑΚΤΙΚΗΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ Μαριάννα Τζεκάκη Παρουσίαση των άρθρων:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΔΙΔΑΚΤΙΚΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ» ΕΙΔΙΚΑ ΘΕΜΑΤΑ ΔΙΔΑΚΤΙΚΗΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ Μαριάννα Τζεκάκη Παρουσίαση των άρθρων:
Θεωρητικές και μεθοδολογικές προσεγγίσεις στη μελέτη της περιοδικότητας: Μια συστημική προσέγγιση. Δέσποινα Πόταρη, Τμήμα Μαθηματικών, ΕΚΠΑ
 Θεωρητικές και μεθοδολογικές προσεγγίσεις στη μελέτη της περιοδικότητας: Μια συστημική προσέγγιση Δέσποινα Πόταρη, Τμήμα Μαθηματικών, ΕΚΠΑ Δομή της παρουσίασης Δυσκολίες μαθητών γύρω από την έννοια της
Θεωρητικές και μεθοδολογικές προσεγγίσεις στη μελέτη της περιοδικότητας: Μια συστημική προσέγγιση Δέσποινα Πόταρη, Τμήμα Μαθηματικών, ΕΚΠΑ Δομή της παρουσίασης Δυσκολίες μαθητών γύρω από την έννοια της
Τα Διδακτικά Σενάρια και οι Προδιαγραφές τους. του Σταύρου Κοκκαλίδη. Μαθηματικού
 Τα Διδακτικά Σενάρια και οι Προδιαγραφές τους του Σταύρου Κοκκαλίδη Μαθηματικού Διευθυντή του Γυμνασίου Αρχαγγέλου Ρόδου-Εκπαιδευτή Στα προγράμματα Β Επιπέδου στις ΤΠΕ Ορισμός της έννοιας του σεναρίου.
Τα Διδακτικά Σενάρια και οι Προδιαγραφές τους του Σταύρου Κοκκαλίδη Μαθηματικού Διευθυντή του Γυμνασίου Αρχαγγέλου Ρόδου-Εκπαιδευτή Στα προγράμματα Β Επιπέδου στις ΤΠΕ Ορισμός της έννοιας του σεναρίου.
ΣΧΕ ΙΟ ΕΡΓΑΣΙΑΣ ή PROJECT
 ΣΧΕ ΙΟ ΕΡΓΑΣΙΑΣ ή PROJECT Η διεξαγωγή σχεδίων εργασίας στο σύγχρονο σχολείο, προβάλλει ως αναγκαιότητα, για την ανάπτυξη της κριτικής και δηµιουργικής σκέψης των µαθητών, καθώς και όλων εκείνων των ιδιοτήτων
ΣΧΕ ΙΟ ΕΡΓΑΣΙΑΣ ή PROJECT Η διεξαγωγή σχεδίων εργασίας στο σύγχρονο σχολείο, προβάλλει ως αναγκαιότητα, για την ανάπτυξη της κριτικής και δηµιουργικής σκέψης των µαθητών, καθώς και όλων εκείνων των ιδιοτήτων
Ο ΑΞΟΝΑΣ της ΔΙΑΘΕΜΑΤΙΚΟΤΗΤΑΣ στο ψηφιακό μουσικό ανθολόγιο ΕΥΤΕΡΠΗ ΜΑΙΗ ΚΟΚΚΙΔΟΥ
 Ο ΑΞΟΝΑΣ της ΔΙΑΘΕΜΑΤΙΚΟΤΗΤΑΣ στο ψηφιακό μουσικό ανθολόγιο ΕΥΤΕΡΠΗ ΜΑΙΗ ΚΟΚΚΙΔΟΥ Διαθεματικότητα -Ιδανικό της ολιστικής γνώσης -Διασυνδέσεις με νόημα μεταξύ γνωστικών περιοχών -Μελέτη σύνθετων ερωτημάτων
Ο ΑΞΟΝΑΣ της ΔΙΑΘΕΜΑΤΙΚΟΤΗΤΑΣ στο ψηφιακό μουσικό ανθολόγιο ΕΥΤΕΡΠΗ ΜΑΙΗ ΚΟΚΚΙΔΟΥ Διαθεματικότητα -Ιδανικό της ολιστικής γνώσης -Διασυνδέσεις με νόημα μεταξύ γνωστικών περιοχών -Μελέτη σύνθετων ερωτημάτων
Η ΙΚΑΝΟΤΗΤΑ ΚΑΤΑΣΚΕΥΗΣ ΜΑΘΗΜΑΤΙΚΟΥ ΠΡΟΒΛΗΜΑΤΟΣ ΚΑΙ Η ΣΧΕΣΗ ΤΗΣ ΜΕ ΤΗΝ ΕΠΙ ΟΣΗ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ. Περίληψη
 Η ΙΚΑΝΟΤΗΤΑ ΚΑΤΑΣΚΕΥΗΣ ΜΑΘΗΜΑΤΙΚΟΥ ΠΡΟΒΛΗΜΑΤΟΣ ΚΑΙ Η ΣΧΕΣΗ ΤΗΣ ΜΕ ΤΗΝ ΕΠΙ ΟΣΗ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Ριάνα Θεοδούλου Τµήµα Επιστηµών της Αγωγής, Πανεπιστήµιο Κύπρου, e-mail: rianath@hotmail.com Γεώργιος Φιλίππου
Η ΙΚΑΝΟΤΗΤΑ ΚΑΤΑΣΚΕΥΗΣ ΜΑΘΗΜΑΤΙΚΟΥ ΠΡΟΒΛΗΜΑΤΟΣ ΚΑΙ Η ΣΧΕΣΗ ΤΗΣ ΜΕ ΤΗΝ ΕΠΙ ΟΣΗ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Ριάνα Θεοδούλου Τµήµα Επιστηµών της Αγωγής, Πανεπιστήµιο Κύπρου, e-mail: rianath@hotmail.com Γεώργιος Φιλίππου
τα βιβλία των επιτυχιών
 Τα βιβλία των Εκδόσεων Πουκαμισάς συμπυκνώνουν την πολύχρονη διδακτική εμπειρία των συγγραφέων μας και αποτελούν το βασικό εκπαιδευτικό υλικό που χρησιμοποιούν οι μαθητές των φροντιστηρίων μας. Μέσα από
Τα βιβλία των Εκδόσεων Πουκαμισάς συμπυκνώνουν την πολύχρονη διδακτική εμπειρία των συγγραφέων μας και αποτελούν το βασικό εκπαιδευτικό υλικό που χρησιμοποιούν οι μαθητές των φροντιστηρίων μας. Μέσα από
Μελέτη περίπτωσης ψηφιακά μέσα, εικονικοί κόσμοι, εκπαιδευτικά παιχνίδια, βίντεο ανοιχτού περιεχομένου για μαθηματικά
 Σελίδα 1 Μελέτη περίπτωσης ψηφιακά μέσα, εικονικοί κόσμοι, εκπαιδευτικά παιχνίδια, βίντεο ανοιχτού περιεχομένου για μαθηματικά μελέτη περίπτωσης πληροφορίες 1. Γενικές Πληροφορίες Επίπεδο (ηλικία των μαθητών)
Σελίδα 1 Μελέτη περίπτωσης ψηφιακά μέσα, εικονικοί κόσμοι, εκπαιδευτικά παιχνίδια, βίντεο ανοιχτού περιεχομένου για μαθηματικά μελέτη περίπτωσης πληροφορίες 1. Γενικές Πληροφορίες Επίπεδο (ηλικία των μαθητών)
Διδακτικές προσεγγίσεις στην Πληροφορική. Η εποικοδομιστική προσέγγιση για τη γνώση. ως ενεργητική και όχι παθητική διαδικασία
 Διδακτικές προσεγγίσεις στην Πληροφορική Η εποικοδομιστική προσέγγιση για τη γνώση ως ενεργητική και όχι παθητική διαδικασία ως κατασκευή και όχι ως μετάδοση ως αποτέλεσμα εμπειρίας και όχι ως μεταφορά
Διδακτικές προσεγγίσεις στην Πληροφορική Η εποικοδομιστική προσέγγιση για τη γνώση ως ενεργητική και όχι παθητική διαδικασία ως κατασκευή και όχι ως μετάδοση ως αποτέλεσμα εμπειρίας και όχι ως μεταφορά
Διαφοροποιημένη Διδασκαλία. Ε. Κολέζα
 Διαφοροποιημένη Διδασκαλία Ε. Κολέζα Τι είναι η διαφοροποιημένη διδασκαλία; Είναι μια θεώρηση της διδασκαλίας που βασίζεται στην προϋπόθεση ότι οι δάσκαλοι πρέπει να προσαρμόσουν τη διδασκαλία τους στη
Διαφοροποιημένη Διδασκαλία Ε. Κολέζα Τι είναι η διαφοροποιημένη διδασκαλία; Είναι μια θεώρηση της διδασκαλίας που βασίζεται στην προϋπόθεση ότι οι δάσκαλοι πρέπει να προσαρμόσουν τη διδασκαλία τους στη
Οι συζητήσεις Δρ Δημήτριος Γκότζος
 Οι συζητήσεις Δρ Δημήτριος Γκότζος Οι διαφάνειες αποτελούν προϊόν μελέτης και αποδελτίωσης του Ι.Ε.Π. (2017). Οδηγός Εκπαιδευτικού για την Περιγραφική Αξιολόγηση στο Δημοτικό http://iep.edu.gr/images/iep/epistimoniki_ypiresia/epist_monades/a_kyklos/evaluation/2017/2a_perigrafiki_d
Οι συζητήσεις Δρ Δημήτριος Γκότζος Οι διαφάνειες αποτελούν προϊόν μελέτης και αποδελτίωσης του Ι.Ε.Π. (2017). Οδηγός Εκπαιδευτικού για την Περιγραφική Αξιολόγηση στο Δημοτικό http://iep.edu.gr/images/iep/epistimoniki_ypiresia/epist_monades/a_kyklos/evaluation/2017/2a_perigrafiki_d
Πίνακας Μαθησιακών Αποτελεσμάτων
 Πίνακας Μαθησιακών Αποτελεσμάτων Τα Μαθησιακά Αποτελέσματα στον παρακάτω πίνακα έχουν σχηματιστεί με βάση τα συμπεράσματα στη Διεθνική Αναφορά Έρευνας Ο1 που περιέχει τα ευρήματα της έρευνας που διεξήχθη
Πίνακας Μαθησιακών Αποτελεσμάτων Τα Μαθησιακά Αποτελέσματα στον παρακάτω πίνακα έχουν σχηματιστεί με βάση τα συμπεράσματα στη Διεθνική Αναφορά Έρευνας Ο1 που περιέχει τα ευρήματα της έρευνας που διεξήχθη
Διδακτικές Τεχνικές (Στρατηγικές)
 Διδακτικές Τεχνικές (Στρατηγικές) Ενδεικτικές τεχνικές διδασκαλίας: 1. Εισήγηση ή διάλεξη ή Μονολογική Παρουσίαση 2. Συζήτηση ή διάλογος 3. Ερωταποκρίσεις 4. Χιονοστιβάδα 5. Καταιγισμός Ιδεών 6. Επίδειξη
Διδακτικές Τεχνικές (Στρατηγικές) Ενδεικτικές τεχνικές διδασκαλίας: 1. Εισήγηση ή διάλεξη ή Μονολογική Παρουσίαση 2. Συζήτηση ή διάλογος 3. Ερωταποκρίσεις 4. Χιονοστιβάδα 5. Καταιγισμός Ιδεών 6. Επίδειξη
Μάθηση & Εξερεύνηση στο περιβάλλον του Μουσείου
 Βασίλειος Κωτούλας vaskotoulas@sch.gr h=p://dipe.kar.sch.gr/grss Αρχαιολογικό Μουσείο Καρδίτσας Μάθηση & Εξερεύνηση στο περιβάλλον του Μουσείου Η Δομή της εισήγησης 1 2 3 Δυο λόγια για Στόχοι των Ερευνητική
Βασίλειος Κωτούλας vaskotoulas@sch.gr h=p://dipe.kar.sch.gr/grss Αρχαιολογικό Μουσείο Καρδίτσας Μάθηση & Εξερεύνηση στο περιβάλλον του Μουσείου Η Δομή της εισήγησης 1 2 3 Δυο λόγια για Στόχοι των Ερευνητική
Αναζητήσεις στο Διαδίκτυο
 Αναζητήσεις στο Διαδίκτυο Πλεονεκτήματα από τη χρήση του Διαδικτύου για την αναζήτηση πληροφοριών Υπάρχει πληθώρα πληροφοριών (που περιλαμβάνουν μεγάλο εύρος από media). Οι μαθητές καθίστανται «ερευνητές
Αναζητήσεις στο Διαδίκτυο Πλεονεκτήματα από τη χρήση του Διαδικτύου για την αναζήτηση πληροφοριών Υπάρχει πληθώρα πληροφοριών (που περιλαμβάνουν μεγάλο εύρος από media). Οι μαθητές καθίστανται «ερευνητές
Ι ΑΚΤΙΚΟ ΣΕΝΑΡΙΟ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ
 1. Τίτλος Ι ΑΚΤΙΚΟ ΣΕΝΑΡΙΟ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ «Ισοδύναµα κλάσµατα» 2. Εµπλεκόµενες γνωστικές περιοχές Το σενάριο µπορεί να αξιοποιηθεί από τους µαθητές της Γ δηµοτικού και εντάσσεται στις γνωστικές περιοχές
1. Τίτλος Ι ΑΚΤΙΚΟ ΣΕΝΑΡΙΟ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ «Ισοδύναµα κλάσµατα» 2. Εµπλεκόµενες γνωστικές περιοχές Το σενάριο µπορεί να αξιοποιηθεί από τους µαθητές της Γ δηµοτικού και εντάσσεται στις γνωστικές περιοχές
ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ 2 ΗΣ ΤΗΛΕΔΙΑΣΚΕΨΗΣ
 ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ 2 ΗΣ ΤΗΛΕΔΙΑΣΚΕΨΗΣ ΟΔΥΣΣΕΑΣ 2008 Ερευνητικό Εκπαιδευτικό Πρόγραμμα Εξ Αποστάσεως Εκπαίδευσης σε Δημοτικά Σχολεία της Ελλάδος 70 Ο Δημοτικό Σχολείο Αθήνας Δημοτικό Σχολείο Μαγούλας ( Νομού
ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ 2 ΗΣ ΤΗΛΕΔΙΑΣΚΕΨΗΣ ΟΔΥΣΣΕΑΣ 2008 Ερευνητικό Εκπαιδευτικό Πρόγραμμα Εξ Αποστάσεως Εκπαίδευσης σε Δημοτικά Σχολεία της Ελλάδος 70 Ο Δημοτικό Σχολείο Αθήνας Δημοτικό Σχολείο Μαγούλας ( Νομού
Η λογική και η διδακτική προσέγγιση του βιβλίου
 Το νέο σχολικό βιβλίο «Μαθηματικά Στ` ημοτικού» Η λογική και η διδακτική προσέγγιση του βιβλίου Πέτρος Κλιάπης Το παραδοσιακό μαθησιακό περιβάλλον των Μαθηματικών «Ισχυρή αντίληψη» για τα μαθηματικά: μια
Το νέο σχολικό βιβλίο «Μαθηματικά Στ` ημοτικού» Η λογική και η διδακτική προσέγγιση του βιβλίου Πέτρος Κλιάπης Το παραδοσιακό μαθησιακό περιβάλλον των Μαθηματικών «Ισχυρή αντίληψη» για τα μαθηματικά: μια
Μαθηματικά και Πληροφορική. Διδακτική Αξιοποίηση του Διαδικτύου για τη Μελέτη και την Αυτο-αξιολόγηση των Μαθητών.
 Μαθηματικά και Πληροφορική. Διδακτική Αξιοποίηση του Διαδικτύου για τη Μελέτη και την Αυτο-αξιολόγηση των Μαθητών. Α. Πέρδος 1, I. Σαράφης, Χ. Τίκβα 3 1 Ελληνογαλλική Σχολή Καλαμαρί perdos@kalamari.gr
Μαθηματικά και Πληροφορική. Διδακτική Αξιοποίηση του Διαδικτύου για τη Μελέτη και την Αυτο-αξιολόγηση των Μαθητών. Α. Πέρδος 1, I. Σαράφης, Χ. Τίκβα 3 1 Ελληνογαλλική Σχολή Καλαμαρί perdos@kalamari.gr
ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΧΗΜΕΙΑΣ
 ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΧΗΜΕΙΑΣ Κατερίνα Σάλτα ΔιΧηΝΕΤ 2017-2018 Θέματα Διδακτικής Φυσικών Επιστήμων 1. ΟΙ ΙΔΕΕΣ ΤΩΝ ΜΑΘΗΤΩΝ 2. ΤΑ ΜΟΝΤΕΛΑ ΚΑΙ Η ΜΟΝΤΕΛΟΠΟΙΗΣΗ 3. ΤΟ ΕΡΓΑΣΤΗΡΙΟ & ΤΟ ΠΕΙΡΑΜΑ 4. ΔΙΔΑΚΤΙΚΕΣ ΠΡΟΣΕΓΓΙΣΕΙΣ
ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΧΗΜΕΙΑΣ Κατερίνα Σάλτα ΔιΧηΝΕΤ 2017-2018 Θέματα Διδακτικής Φυσικών Επιστήμων 1. ΟΙ ΙΔΕΕΣ ΤΩΝ ΜΑΘΗΤΩΝ 2. ΤΑ ΜΟΝΤΕΛΑ ΚΑΙ Η ΜΟΝΤΕΛΟΠΟΙΗΣΗ 3. ΤΟ ΕΡΓΑΣΤΗΡΙΟ & ΤΟ ΠΕΙΡΑΜΑ 4. ΔΙΔΑΚΤΙΚΕΣ ΠΡΟΣΕΓΓΙΣΕΙΣ
ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΤΕΑΠΗ ΜΑΘΗΜΑ: Μαθηματικά στην προσχολική εκπαίδευση ΕΞΑΜΗΝΟ: Ε (2015 2016) ΟΔΗΓΟΣ ΜΑΘΗΜΑΤΟΣ
 ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΤΕΑΠΗ ΜΑΘΗΜΑ: Μαθηματικά στην προσχολική εκπαίδευση ΕΞΑΜΗΝΟ: Ε (2015 2016) ΟΔΗΓΟΣ ΜΑΘΗΜΑΤΟΣ 1. ΠΕΡΙΕΧΟΜΕΝΟ ΤΟΥ ΜΑΘΗΜΑΤΟΣ 1 ος κύκλος (Μαθήματα 1-3): Περιεχόμενο και βασικός
ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΤΕΑΠΗ ΜΑΘΗΜΑ: Μαθηματικά στην προσχολική εκπαίδευση ΕΞΑΜΗΝΟ: Ε (2015 2016) ΟΔΗΓΟΣ ΜΑΘΗΜΑΤΟΣ 1. ΠΕΡΙΕΧΟΜΕΝΟ ΤΟΥ ΜΑΘΗΜΑΤΟΣ 1 ος κύκλος (Μαθήματα 1-3): Περιεχόμενο και βασικός
των σχολικών μαθηματικών
 Μια σύγχρονη διδακτική θεώρηση των σχολικών μαθηματικών «Οι περισσότερες σημαντικές έννοιες και διαδικασίες των μαθηματικών διδάσκονται καλύτερα μέσω της επίλυσης προβλημάτων (ΕΠ)» Παραδοσιακή προσέγγιση:
Μια σύγχρονη διδακτική θεώρηση των σχολικών μαθηματικών «Οι περισσότερες σημαντικές έννοιες και διαδικασίες των μαθηματικών διδάσκονται καλύτερα μέσω της επίλυσης προβλημάτων (ΕΠ)» Παραδοσιακή προσέγγιση:
ΑΝΑΠΑΡΑΣΤΑΣΗ ΔΕΔΟΜΕΝΩΝ. Η αγαπημένη γεύση παγωτού των παιδιών
 ΑΝΑΠΑΡΑΣΤΑΣΗ ΔΕΔΟΜΕΝΩΝ 1. Η αγαπημένη γεύση παγωτού των παιδιών Γεύση παγωτού Βανίλια Αριθμός παιδιών Σοκολάτα Φράουλα Λεμόνι Κάθε αντιστοιχεί σε 4 παιδιά Πόσα παιδιά προτιμούν το παγωτό βανίλιας; Απάντηση:
ΑΝΑΠΑΡΑΣΤΑΣΗ ΔΕΔΟΜΕΝΩΝ 1. Η αγαπημένη γεύση παγωτού των παιδιών Γεύση παγωτού Βανίλια Αριθμός παιδιών Σοκολάτα Φράουλα Λεμόνι Κάθε αντιστοιχεί σε 4 παιδιά Πόσα παιδιά προτιμούν το παγωτό βανίλιας; Απάντηση:
Στοιχείαδιδακτικής. Στόχοι μαθήματος φύλλα εργασίας ΒΙΟΛΟΓΙΑ. Γεωργάτου Μάνια ΣχολικήΣύμβουλοςΠΕ04
 Στοιχείαδιδακτικής Στόχοι μαθήματος φύλλα εργασίας ΒΙΟΛΟΓΙΑ Γεωργάτου Μάνια ΣχολικήΣύμβουλοςΠΕ04 Βασικά χαρακτηριστικά ενός μαθήματος: Να έχει συγκεκριμένους και ξεκάθαρους στόχους. Ερώτηση: Τιδιδάσκω;
Στοιχείαδιδακτικής Στόχοι μαθήματος φύλλα εργασίας ΒΙΟΛΟΓΙΑ Γεωργάτου Μάνια ΣχολικήΣύμβουλοςΠΕ04 Βασικά χαρακτηριστικά ενός μαθήματος: Να έχει συγκεκριμένους και ξεκάθαρους στόχους. Ερώτηση: Τιδιδάσκω;
ΑΝΑΣΤΟΧΑΣΜΟΣ 1ης ΔΙΔΑΚΤΙΚΗΣ ΠΑΡΕΜΒΑΣΗΣ
 Αναστοχασμός ΑΝΑΣΤΟΧΑΣΜΟΣ 1ης ΔΙΔΑΚΤΙΚΗΣ ΠΑΡΕΜΒΑΣΗΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ(A) : Αθηνά Ανδριανοπούλου ΠΕ19 ΤΙΤΛΟΣ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ: Προγραμματισμός σε Ψευδογλώσσα - Δομές Επανάληψης. Το πρόβλημα ελαστικής/ανελαστικής
Αναστοχασμός ΑΝΑΣΤΟΧΑΣΜΟΣ 1ης ΔΙΔΑΚΤΙΚΗΣ ΠΑΡΕΜΒΑΣΗΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ(A) : Αθηνά Ανδριανοπούλου ΠΕ19 ΤΙΤΛΟΣ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ: Προγραμματισμός σε Ψευδογλώσσα - Δομές Επανάληψης. Το πρόβλημα ελαστικής/ανελαστικής
Αναλυτικό Πρόγραμμα Μαθηματικών
 Αναλυτικό Πρόγραμμα Μαθηματικών Σχεδιασμός... αντιμετωπίζει ενιαία το πλαίσιο σπουδών (Προδημοτική, Δημοτικό, Γυμνάσιο και Λύκειο), είναι συνέχεια υπό διαμόρφωση και αλλαγή, για να αντιμετωπίζει την εξέλιξη,
Αναλυτικό Πρόγραμμα Μαθηματικών Σχεδιασμός... αντιμετωπίζει ενιαία το πλαίσιο σπουδών (Προδημοτική, Δημοτικό, Γυμνάσιο και Λύκειο), είναι συνέχεια υπό διαμόρφωση και αλλαγή, για να αντιμετωπίζει την εξέλιξη,
Έννοιες Φυσικών Επιστημών Ι
 Τμήμα Εκπαίδευσης και Αγωγής στην Προσχολική Ηλικία Έννοιες Φυσικών Επιστημών Ι Ενότητα 4: Σύνοψη Σπύρος Κόλλας (Βασισμένο στις σημειώσεις του Βασίλη Τσελφέ) 1 Περιεχόμενο Γιατί διδάσκουμε Φ.Ε. στη Γ.Ε.;
Τμήμα Εκπαίδευσης και Αγωγής στην Προσχολική Ηλικία Έννοιες Φυσικών Επιστημών Ι Ενότητα 4: Σύνοψη Σπύρος Κόλλας (Βασισμένο στις σημειώσεις του Βασίλη Τσελφέ) 1 Περιεχόμενο Γιατί διδάσκουμε Φ.Ε. στη Γ.Ε.;
ΕΝΟΤΗΤΑ 10 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΚΑΙ ΔΙΑΙΡΕΣΗ
 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΚΑΙ ΔΙΑΙΡΕΣΗ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΑΡΙΘΜΟΙ Υπολογισμοί και εκτίμηση Αρ1.15 Αναπτύσσουν την έννοια του πολλαπλασιασμού ως αθροιστικής επανάληψης ίσων προσθετέων και διαισθητικά την έννοια της
ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΚΑΙ ΔΙΑΙΡΕΣΗ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΑΡΙΘΜΟΙ Υπολογισμοί και εκτίμηση Αρ1.15 Αναπτύσσουν την έννοια του πολλαπλασιασμού ως αθροιστικής επανάληψης ίσων προσθετέων και διαισθητικά την έννοια της
ΑΠΟΤΕΛΕΣΜΑΤΑ ΥΛΟΠΟΙΗΣΗΣ ΠΑΡΕΜΒΑΣΗΣ 1 MASCIL
 Αναστοχασμός ΑΠΟΤΕΛΕΣΜΑΤΑ ΥΛΟΠΟΙΗΣΗΣ ΠΑΡΕΜΒΑΣΗΣ 1 MASCIL Αρχικά συζητήσαμε με τα παιδιά την ανάγκη σύνδεσης του τομέα Πληροφορικής με την καθημερινή πραγματικότητα και την αγορά εργασίας. Τους ρωτήσαμε
Αναστοχασμός ΑΠΟΤΕΛΕΣΜΑΤΑ ΥΛΟΠΟΙΗΣΗΣ ΠΑΡΕΜΒΑΣΗΣ 1 MASCIL Αρχικά συζητήσαμε με τα παιδιά την ανάγκη σύνδεσης του τομέα Πληροφορικής με την καθημερινή πραγματικότητα και την αγορά εργασίας. Τους ρωτήσαμε
Νέες τάσεις στη διδακτική των Μαθηματικών
 Νέες τάσεις στη διδακτική των Μαθηματικών Μέχρι πριν λίγα χρόνια ηαντίληψη που επικρατούσε ήταν ότι ημαθηματική γνώση είναι ένα αγαθό που έχει παραχθεί και καλούνται οι μαθητές να το καταναλώσουν αποστηθίζοντάς
Νέες τάσεις στη διδακτική των Μαθηματικών Μέχρι πριν λίγα χρόνια ηαντίληψη που επικρατούσε ήταν ότι ημαθηματική γνώση είναι ένα αγαθό που έχει παραχθεί και καλούνται οι μαθητές να το καταναλώσουν αποστηθίζοντάς
Επιμόρφωση Εκπαιδευτικών Α Τάξης Δημοτικού. Νοέμβρης 2012 1/11/2012. Φιλοσοφία διδασκαλίας. What you learn reflects how you learned it.
 Επιμόρφωση Εκπαιδευτικών Α Τάξης Δημοτικού Νοέμβρης 2012 Χρύσω Αθανασίου (Σύμβουλος Μαθηματικών ) Ελένη Δεληγιάννη (Συγγραφική Ομάδα) Άντρη Μάρκου (Σύμβουλος Μαθηματικών) Ελένη Μιχαηλίδου (Σύμβουλος Μαθηματικών)
Επιμόρφωση Εκπαιδευτικών Α Τάξης Δημοτικού Νοέμβρης 2012 Χρύσω Αθανασίου (Σύμβουλος Μαθηματικών ) Ελένη Δεληγιάννη (Συγγραφική Ομάδα) Άντρη Μάρκου (Σύμβουλος Μαθηματικών) Ελένη Μιχαηλίδου (Σύμβουλος Μαθηματικών)
ΒΙΒΛΙΟΓΡΑΦΙΚΕΣ ΠΑΡΑΠΟΜΠΕΣ ΚΑΙ ΑΝΑΦΟΡΕΣ
 ΒΙΒΛΙΟΓΡΑΦΙΚΕΣ ΠΑΡΑΠΟΜΠΕΣ ΚΑΙ ΑΝΑΦΟΡΕΣ Κάθε αναφορά απόψεις που προέρχεται από εξωτερικές πηγές -βιβλία, περιοδικά, ηλεκτρονικά αρχεία, πρέπει να επισημαίνεται, τόσο μέσα στο κείμενο όσο και στη βιβλιογραφία,
ΒΙΒΛΙΟΓΡΑΦΙΚΕΣ ΠΑΡΑΠΟΜΠΕΣ ΚΑΙ ΑΝΑΦΟΡΕΣ Κάθε αναφορά απόψεις που προέρχεται από εξωτερικές πηγές -βιβλία, περιοδικά, ηλεκτρονικά αρχεία, πρέπει να επισημαίνεται, τόσο μέσα στο κείμενο όσο και στη βιβλιογραφία,
ΜΑΘΗΜΑΤΙΚΑ Γ ΤΑΞΗΣ. ΕΠΑΝΑΛΗΨΗ 3 ης. Όνομα: Ημ/νία: 1. Βρίσκω το γινόμενο στους πιο κάτω πολλαπλασιασμούς: 3 Χ 9 = 8 Χ 8 = 10 Χ 8 = 9 Χ 9 =
 ΜΑΘΗΜΑΤΙΚΑ Γ ΤΑΞΗΣ ΕΠΑΝΑΛΗΨΗ 3 ης ΕΝΟΤΗΤΑΣ Όνομα: Ημ/νία: 1. Βρίσκω το γινόμενο στους πιο κάτω πολλαπλασιασμούς: 3 Χ 9 = 8 Χ 8 = 10 Χ 8 = 9 Χ 9 = 3 Χ 5 = 6 Χ 7 = 11 Χ 9 = 8 Χ 5 = 6 Χ 5 = 7 Χ 8 = 6 Χ 11
ΜΑΘΗΜΑΤΙΚΑ Γ ΤΑΞΗΣ ΕΠΑΝΑΛΗΨΗ 3 ης ΕΝΟΤΗΤΑΣ Όνομα: Ημ/νία: 1. Βρίσκω το γινόμενο στους πιο κάτω πολλαπλασιασμούς: 3 Χ 9 = 8 Χ 8 = 10 Χ 8 = 9 Χ 9 = 3 Χ 5 = 6 Χ 7 = 11 Χ 9 = 8 Χ 5 = 6 Χ 5 = 7 Χ 8 = 6 Χ 11
Ενότητα στις Εικαστικές Τέχνες
 Ενότητα στις Εικαστικές Τέχνες Τίτλος: Ιστορίες δωματίων Βαθμίδα: 2 Τάξη: Ε Διάρκεια: 6 Χ 80 Περιγραφή Ενότητας Οι μαθητές και οι μαθήτριες μέσα από διάφορες δραστηριότητες που αφορούν στο δωμάτιό τους
Ενότητα στις Εικαστικές Τέχνες Τίτλος: Ιστορίες δωματίων Βαθμίδα: 2 Τάξη: Ε Διάρκεια: 6 Χ 80 Περιγραφή Ενότητας Οι μαθητές και οι μαθήτριες μέσα από διάφορες δραστηριότητες που αφορούν στο δωμάτιό τους
ATS2020 Μαθησιακός Σχεδιασμός
 ATS2020 Μαθησιακός Σχεδιασμός CC BY-NC-SA Συγγραφέας: Άντρη Αρμεύτη Σχολείο: Γυμνάσιο Λύκειο Λευκάρων Υποστηρίκτρια: Μαρία Κωνσταντίνου (Παιδαγωγικό Ινστιτούτο) Χώρα: Κύπρος Γλώσσα: Ελληνικά Γενική περιγραφή
ATS2020 Μαθησιακός Σχεδιασμός CC BY-NC-SA Συγγραφέας: Άντρη Αρμεύτη Σχολείο: Γυμνάσιο Λύκειο Λευκάρων Υποστηρίκτρια: Μαρία Κωνσταντίνου (Παιδαγωγικό Ινστιτούτο) Χώρα: Κύπρος Γλώσσα: Ελληνικά Γενική περιγραφή
ΕΝΟΤΗΤΑ 6 ΜΟΤΙΒΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΥ, ΚΛΑΣΜΑΤΑ ΕΜΒΑΔΟΝ ΚΑΙ ΠΕΡΙΜΕΤΡΟΣ ΟΡΘΟΓΩΝΙΟΥ
 ΜΟΤΙΒΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΥ, ΚΛΑΣΜΑΤΑ ΕΜΒΑΔΟΝ ΚΑΙ ΠΕΡΙΜΕΤΡΟΣ ΟΡΘΟΓΩΝΙΟΥ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΑΡΙΘΜΟΙ Διερεύνηση αριθμών Αρ2.5 Αναπαριστούν, συγκρίνουν και σειροθετούν ομώνυμα κλάσματα και δεκαδικούς αριθμούς,
ΜΟΤΙΒΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΥ, ΚΛΑΣΜΑΤΑ ΕΜΒΑΔΟΝ ΚΑΙ ΠΕΡΙΜΕΤΡΟΣ ΟΡΘΟΓΩΝΙΟΥ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΑΡΙΘΜΟΙ Διερεύνηση αριθμών Αρ2.5 Αναπαριστούν, συγκρίνουν και σειροθετούν ομώνυμα κλάσματα και δεκαδικούς αριθμούς,
Δάσκαλοι και μαθητές Παίζουμε και μαθαίνουμε!
 Δάσκαλοι και μαθητές Παίζουμε και μαθαίνουμε! Συντελεστές: Γιάννης Π. Κρόκος - Μαθηματικός Βασίλης Τσιλιβής Μαθηματικός Φιλίππια Γαλιατσάτου - Δασκάλα Πολιτικός Μηχανικός «Η επίλυση των προβλημάτων & των
Δάσκαλοι και μαθητές Παίζουμε και μαθαίνουμε! Συντελεστές: Γιάννης Π. Κρόκος - Μαθηματικός Βασίλης Τσιλιβής Μαθηματικός Φιλίππια Γαλιατσάτου - Δασκάλα Πολιτικός Μηχανικός «Η επίλυση των προβλημάτων & των
Ενότητα εκπαίδευσης και κατάρτισης για τις δεξιότητες ηγεσίας
 3 Ενότητα εκπαίδευσης και κατάρτισης για τις δεξιότητες ηγεσίας Παρακινώντας τους άλλους Οι ενότητες κατάρτισης για τις δεξιότητες ηγεσίας έχουν αναπτυχθεί για να σας βοηθήσουν να προετοιμαστείτε για το
3 Ενότητα εκπαίδευσης και κατάρτισης για τις δεξιότητες ηγεσίας Παρακινώντας τους άλλους Οι ενότητες κατάρτισης για τις δεξιότητες ηγεσίας έχουν αναπτυχθεί για να σας βοηθήσουν να προετοιμαστείτε για το
Math. Mathematics Μαθηματικά. Φυσικές Επιστήμες. Εφαρμοσμένη Μηχανική
 Math Science, Technology, Engineering Φυσικές Επιστήμες Τεχνολογία Εφαρμοσμένη Μηχανική Mathematics Μαθηματικά STEM EDUCATION Κατεχάκη 52, 115 25 Αθήνα Τηλ. 210 6777285 e-mail: info@stem.edu.gr www.stem.edu.gr
Math Science, Technology, Engineering Φυσικές Επιστήμες Τεχνολογία Εφαρμοσμένη Μηχανική Mathematics Μαθηματικά STEM EDUCATION Κατεχάκη 52, 115 25 Αθήνα Τηλ. 210 6777285 e-mail: info@stem.edu.gr www.stem.edu.gr
O μετασχηματισμός μιας «διαθεματικής» δραστηριότητας σε μαθηματική. Δέσποινα Πόταρη Πανεπιστήμιο Πατρών
 O μετασχηματισμός μιας «διαθεματικής» δραστηριότητας σε μαθηματική Δέσποινα Πόταρη Πανεπιστήμιο Πατρών Η έννοια της δραστηριότητας Δραστηριότητα είναι κάθε ανθρώπινη δράση που έχει ένα κίνητρο και ένα
O μετασχηματισμός μιας «διαθεματικής» δραστηριότητας σε μαθηματική Δέσποινα Πόταρη Πανεπιστήμιο Πατρών Η έννοια της δραστηριότητας Δραστηριότητα είναι κάθε ανθρώπινη δράση που έχει ένα κίνητρο και ένα
ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΤΟ ΑΠ ΤΟΥ ΔΗΜΟΤΙΚΟΥ ΣΧΟΛΕΙΟΥ
 ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΤΟ ΑΠ ΤΟΥ ΔΗΜΟΤΙΚΟΥ ΣΧΟΛΕΙΟΥ Τι είναι Μαθηματικά; Ποια είναι η αξία τους καθημερινή ζωή ανάπτυξη λογικής σκέψης αισθητική αξία και διανοητική απόλαυση ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΤΟ ΑΠ ΤΟΥ ΔΗΜΟΤΙΚΟΥ
ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΤΟ ΑΠ ΤΟΥ ΔΗΜΟΤΙΚΟΥ ΣΧΟΛΕΙΟΥ Τι είναι Μαθηματικά; Ποια είναι η αξία τους καθημερινή ζωή ανάπτυξη λογικής σκέψης αισθητική αξία και διανοητική απόλαυση ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΤΟ ΑΠ ΤΟΥ ΔΗΜΟΤΙΚΟΥ
Εκπαιδευτική Διαδικασία και Μάθηση στο Νηπιαγωγείο Ενότητα 2: Μάθηση & διδασκαλία στην προσχολική εκπαίδευση: βασικές αρχές
 Εκπαιδευτική Διαδικασία και Μάθηση στο Νηπιαγωγείο Ενότητα 2: Μάθηση & διδασκαλία στην προσχολική εκπαίδευση: βασικές αρχές Διδάσκουσα: Μαρία Καμπεζά Τμήμα Επιστημών της Εκπαίδευσης και της Αγωγής στην
Εκπαιδευτική Διαδικασία και Μάθηση στο Νηπιαγωγείο Ενότητα 2: Μάθηση & διδασκαλία στην προσχολική εκπαίδευση: βασικές αρχές Διδάσκουσα: Μαρία Καμπεζά Τμήμα Επιστημών της Εκπαίδευσης και της Αγωγής στην
ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΧΗΜΕΙΑΣ
 ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΧΗΜΕΙΑΣ Κατερίνα Σάλτα ΔιΧηΝΕΤ 2017-2018 ΘΕΜΑΤΑ ΕΡΕΥΝΑΣ ΔΙΔΑΚΤΙΚΗΣ ΤΗΣ ΧΗΜΕΙΑΣ Διεπιστημονικότητα Ιστορία & Φιλοσοφία της Χημείας Γλωσσολογία Χημεία Διδακτική της Χημείας Παιδαγωγική Ψυχολογία
ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΧΗΜΕΙΑΣ Κατερίνα Σάλτα ΔιΧηΝΕΤ 2017-2018 ΘΕΜΑΤΑ ΕΡΕΥΝΑΣ ΔΙΔΑΚΤΙΚΗΣ ΤΗΣ ΧΗΜΕΙΑΣ Διεπιστημονικότητα Ιστορία & Φιλοσοφία της Χημείας Γλωσσολογία Χημεία Διδακτική της Χημείας Παιδαγωγική Ψυχολογία
Αξιολόγηση του Εκπαιδευτικού Προγράμματος. Εκπαίδευση μέσα από την Τέχνη. [Αξιολόγηση των 5 πιλοτικών τμημάτων]
![Αξιολόγηση του Εκπαιδευτικού Προγράμματος. Εκπαίδευση μέσα από την Τέχνη. [Αξιολόγηση των 5 πιλοτικών τμημάτων] Αξιολόγηση του Εκπαιδευτικού Προγράμματος. Εκπαίδευση μέσα από την Τέχνη. [Αξιολόγηση των 5 πιλοτικών τμημάτων]](/thumbs/25/6784763.jpg) Αξιολόγηση του Εκπαιδευτικού Προγράμματος Εκπαίδευση μέσα από την Τέχνη [Αξιολόγηση των 5 πιλοτικών τμημάτων] 1. Είστε ικανοποιημένος/η από το Πρόγραμμα; Μ. Ο. απαντήσεων: 4,7 Ικανοποιήθηκαν σε απόλυτο
Αξιολόγηση του Εκπαιδευτικού Προγράμματος Εκπαίδευση μέσα από την Τέχνη [Αξιολόγηση των 5 πιλοτικών τμημάτων] 1. Είστε ικανοποιημένος/η από το Πρόγραμμα; Μ. Ο. απαντήσεων: 4,7 Ικανοποιήθηκαν σε απόλυτο
ΤΙΤΛΟΣ ΑΝΟΙΧΤΗΣ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΡΑΚΤΙΚΗΣ
 ΤΙΤΛΟΣ ΑΝΟΙΧΤΗΣ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΡΑΚΤΙΚΗΣ ΔΗΜΟΤΙΚΟ ΣΧΟΛΕΙΟ ΣΚΥΔΡΑΣ Ομάδα ανάπτυξης Μαρία Τσικαλοπούλου, Μαθηματικός Σ Κ Υ Δ Ρ Α / 2 0 1 5 Το αντικείμενο με το οποίο θα ασχοληθούμε είναι τα μαθηματικά της
ΤΙΤΛΟΣ ΑΝΟΙΧΤΗΣ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΡΑΚΤΙΚΗΣ ΔΗΜΟΤΙΚΟ ΣΧΟΛΕΙΟ ΣΚΥΔΡΑΣ Ομάδα ανάπτυξης Μαρία Τσικαλοπούλου, Μαθηματικός Σ Κ Υ Δ Ρ Α / 2 0 1 5 Το αντικείμενο με το οποίο θα ασχοληθούμε είναι τα μαθηματικά της
ΕΠΕΑΕΚ: ΑΝΑΜΟΡΦΩΣΗ ΤΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΣΠΟΥΔΩΝ ΤΟΥ ΤΕΦΑΑ ΠΘ - ΑΥΤΕΠΙΣΤΑΣΙΑ ΠΕΤΟΣΦΑΙΡΙΣΗ ΚΜ: : 305 ΠΑΤΣΙΑΟΥΡΑΣ ΑΣΤΕΡΙΟΣ
 ΕΠΕΑΕΚ: ΑΝΑΜΟΡΦΩΣΗ ΤΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΣΠΟΥΔΩΝ ΤΟΥ ΤΕΦΑΑ ΠΘ - ΑΥΤΕΠΙΣΤΑΣΙΑ ΠΕΤΟΣΦΑΙΡΙΣΗ ΚΜ: : 305 ΠΑΤΣΙΑΟΥΡΑΣ ΑΣΤΕΡΙΟΣ ΔΙΑΔΙΚΑΣΙΑ ΜΑΘΗΣΗΣ ΔΕΞΙΟΤΗΤΩΝ ΣΤΟ ΒΟΛΕΪ Η μάθηση μιας κίνησης είναι το σύνολο των εσωτερικών
ΕΠΕΑΕΚ: ΑΝΑΜΟΡΦΩΣΗ ΤΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΣΠΟΥΔΩΝ ΤΟΥ ΤΕΦΑΑ ΠΘ - ΑΥΤΕΠΙΣΤΑΣΙΑ ΠΕΤΟΣΦΑΙΡΙΣΗ ΚΜ: : 305 ΠΑΤΣΙΑΟΥΡΑΣ ΑΣΤΕΡΙΟΣ ΔΙΑΔΙΚΑΣΙΑ ΜΑΘΗΣΗΣ ΔΕΞΙΟΤΗΤΩΝ ΣΤΟ ΒΟΛΕΪ Η μάθηση μιας κίνησης είναι το σύνολο των εσωτερικών
ΟΔΗΓΙΕΣ ΓΙΑ ΤΗ ΔΙΔΑΚΤΙΚΗ ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΚΑΙ ΕΡΓΑΣΤΗΡΙΑΚΩΝ ΜΑΘΗΜΑΤΩΝ. Σύνδεση της εμπειρίας των μαθητών με το διδακτικό αντικείμενο
 1 ΠΕΚ ΠΑΤΡΩΝ Α' ΦΑΣΗ ΕΙΣΑΓΩΓΙΚΗΣ ΕΠΙΜΟΡΦΩΣΗΣ 2010-2011 ΕΚΠ/ΚΩΝ Β/ΘΜΙΑΣ ΕΚΠ/ΣΗΣ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΔΙΔΑΚΤΙΚΗ ΜΑΘΗΜΑΤΩΝ ΕΠΙΜΟΡΦΩΤΗΣ: ΑΡΙΣΤΟΤΕΛΗΣ ΠΑΠΑΣΑΒΒΑΣ ΔΙΠΛ. ΗΛΕΚΤΡΟΛΟΓΟΣ ΜΗΧΑΝΙΚΟΣ Ε.Μ.Π., Msc Υ/ΝΤΗΣ
1 ΠΕΚ ΠΑΤΡΩΝ Α' ΦΑΣΗ ΕΙΣΑΓΩΓΙΚΗΣ ΕΠΙΜΟΡΦΩΣΗΣ 2010-2011 ΕΚΠ/ΚΩΝ Β/ΘΜΙΑΣ ΕΚΠ/ΣΗΣ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΔΙΔΑΚΤΙΚΗ ΜΑΘΗΜΑΤΩΝ ΕΠΙΜΟΡΦΩΤΗΣ: ΑΡΙΣΤΟΤΕΛΗΣ ΠΑΠΑΣΑΒΒΑΣ ΔΙΠΛ. ΗΛΕΚΤΡΟΛΟΓΟΣ ΜΗΧΑΝΙΚΟΣ Ε.Μ.Π., Msc Υ/ΝΤΗΣ
Η Εκπαίδευση στην εποχή των ΤΠΕ
 Η Εκπαίδευση στην εποχή των ΤΠΕ «Ενσωμάτωση και αξιοποίηση των εννοιολογικών χαρτών στην εκπαιδευτική διαδικασία μέσα από μία δραστηριότητα εποικοδομητικού τύπου» Δέγγλερη Σοφία Μουδατσάκη Ελένη Λιόβας
Η Εκπαίδευση στην εποχή των ΤΠΕ «Ενσωμάτωση και αξιοποίηση των εννοιολογικών χαρτών στην εκπαιδευτική διαδικασία μέσα από μία δραστηριότητα εποικοδομητικού τύπου» Δέγγλερη Σοφία Μουδατσάκη Ελένη Λιόβας
Ελληνικό Παιδικό Μουσείο Κυδαθηναίων 14, 105 58 Αθήνα Τηλ.: 2103312995, Fax: 2103241919 E-Mail: info@hcm.gr, www.hcm.gr
 Ελληνικό Παιδικό Μουσείο Κυδαθηναίων 14, 105 58 Αθήνα Τηλ.: 2103312995, Fax: 2103241919 E-Mail: info@hcm.gr, www.hcm.gr Το έργο υλοποιείται με δωρεά από το Σύντομη περιγραφή Το Ελληνικό Παιδικό Μουσείο
Ελληνικό Παιδικό Μουσείο Κυδαθηναίων 14, 105 58 Αθήνα Τηλ.: 2103312995, Fax: 2103241919 E-Mail: info@hcm.gr, www.hcm.gr Το έργο υλοποιείται με δωρεά από το Σύντομη περιγραφή Το Ελληνικό Παιδικό Μουσείο
TEACHING GAMES FOR UNDERSTANDING (TGFU)*
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΕΠΙΣΤΗΜΗΣ ΦΥΣΙΚΗΣ ΑΓΩΓΗΣ ΚΑΙ ΑΘΛΗΤΙΣΜΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΦΥΣΙΚΗΣ ΑΓΩΓΗΣ ΚΑΙ ΑΘΛΗΤΙΣΜΟΥ Εργαστήριο Αθλητικής Παιδαγωγικής και Διδακτικής TEACHING GAMES
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΕΠΙΣΤΗΜΗΣ ΦΥΣΙΚΗΣ ΑΓΩΓΗΣ ΚΑΙ ΑΘΛΗΤΙΣΜΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΦΥΣΙΚΗΣ ΑΓΩΓΗΣ ΚΑΙ ΑΘΛΗΤΙΣΜΟΥ Εργαστήριο Αθλητικής Παιδαγωγικής και Διδακτικής TEACHING GAMES
ΑΠΑΝΤΗΣΗ ΕΛΕΥΘΕΡΟΥ ΘΕΜΑΤΟΣ 1. Τίτλος ΟΙ ΣΥΓΚΟΙΝΩΝΙΕΣ 2. Εµπλεκόµενες γνωστικές περιοχές Γεωγραφία, Γλώσσα 3. Γνώσεις και πρότερες ιδέες ή αντιλήψεις τ
 ΕΚΦΩΝΗΣΗ ΕΛΕΥΘΕΡΟΥ ΘΕΜΑΤΟΣ (µεγάλες τάξεις ηµοτικού) Σχεδιασµός σεναρίου µε θέµα «Οι συγκοινωνίες» µε τη χρήση λογισµικών γενικής χρήσης, οπτικοποίησης, διαδικτύου και λογισµικών εννοιολογικής χαρτογράφησης.
ΕΚΦΩΝΗΣΗ ΕΛΕΥΘΕΡΟΥ ΘΕΜΑΤΟΣ (µεγάλες τάξεις ηµοτικού) Σχεδιασµός σεναρίου µε θέµα «Οι συγκοινωνίες» µε τη χρήση λογισµικών γενικής χρήσης, οπτικοποίησης, διαδικτύου και λογισµικών εννοιολογικής χαρτογράφησης.
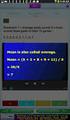
Χειρισμός προβλημάτων με ποσοστά
 Χειρισμός προβλημάτων με ποσοστά Στα προβλήματα με ποσοστά υπάρχει πάντα μία αρχική τιμή, μία μεταβολή της αρχικής τιμής (αύξηση ή μείωση), το ποσοστό της μεταβολής (αύξησης ή μείωσης) της αρχικής τιμής
Χειρισμός προβλημάτων με ποσοστά Στα προβλήματα με ποσοστά υπάρχει πάντα μία αρχική τιμή, μία μεταβολή της αρχικής τιμής (αύξηση ή μείωση), το ποσοστό της μεταβολής (αύξησης ή μείωσης) της αρχικής τιμής
ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΔΙΑΧΕΙΡΙΣΗΣ ΠΟΛΙΤΙΣΜΙΚΟΥ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΚΑΙ ΝΕΩΝ ΤΕΧΝΟΛΟΓΙΩΝ ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΙΜΕΛΕΙΑ: ΘΕΟΔΩΡΟΥ ΕΛΕΝΗ ΑΜ:453 ΕΞ.: Ζ ΕΙΣΗΓΗΤΗΣ: ΔΡ. ΔΗΜΗΤΡΗΣ ΤΣΩΛΗΣ ΚΟΛΟΜΒΟΥ ΑΦΡΟΔΙΤΗ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΔΙΑΧΕΙΡΙΣΗΣ ΠΟΛΙΤΙΣΜΙΚΟΥ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΚΑΙ ΝΕΩΝ ΤΕΧΝΟΛΟΓΙΩΝ ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΙΜΕΛΕΙΑ: ΘΕΟΔΩΡΟΥ ΕΛΕΝΗ ΑΜ:453 ΕΞ.: Ζ ΕΙΣΗΓΗΤΗΣ: ΔΡ. ΔΗΜΗΤΡΗΣ ΤΣΩΛΗΣ ΚΟΛΟΜΒΟΥ ΑΦΡΟΔΙΤΗ
ΑΡΗΣ ΑΣΛΑΝΙΔΗΣ Φυσικός, M.Ed. Εκπαιδευτικός-Συγγραφέας
 ΑΡΗΣ ΑΣΛΑΝΙΔΗΣ Φυσικός, M.Ed. Εκπαιδευτικός-Συγγραφέας Ομιλία με θέμα: ΕΡΕΥΝΗΤΙΚΕΣ ΕΡΓΑΣΙΕΣ & ΦΥΣΙΚΕΣ ΕΠΙΣΤΗΜΕΣ ΕΝΩΣΗ ΕΛΛΗΝΩΝ ΦΥΣΙΚΩΝ Εκδήλωση αριστούχων μαθητών: Οι μαθητές συναντούν τη Φυσική και η Φυσική
ΑΡΗΣ ΑΣΛΑΝΙΔΗΣ Φυσικός, M.Ed. Εκπαιδευτικός-Συγγραφέας Ομιλία με θέμα: ΕΡΕΥΝΗΤΙΚΕΣ ΕΡΓΑΣΙΕΣ & ΦΥΣΙΚΕΣ ΕΠΙΣΤΗΜΕΣ ΕΝΩΣΗ ΕΛΛΗΝΩΝ ΦΥΣΙΚΩΝ Εκδήλωση αριστούχων μαθητών: Οι μαθητές συναντούν τη Φυσική και η Φυσική
Η ανάλυση της κριτικής διδασκαλίας. Περιεχόμενο ή διαδικασία? Βασικό δίλημμα κάθε εκπαιδευτικού. Περιεχόμενο - η γνώση ως μετάδοση πληροφορίας
 Η ανάλυση της κριτικής διδασκαλίας Περιεχόμενο ή διαδικασία? Βασικό δίλημμα κάθε εκπαιδευτικού Περιεχόμενο - η γνώση ως μετάδοση πληροφορίας Διαδικασία η γνώση ως ανάπτυξη υψηλών νοητικών λειτουργιών (
Η ανάλυση της κριτικής διδασκαλίας Περιεχόμενο ή διαδικασία? Βασικό δίλημμα κάθε εκπαιδευτικού Περιεχόμενο - η γνώση ως μετάδοση πληροφορίας Διαδικασία η γνώση ως ανάπτυξη υψηλών νοητικών λειτουργιών (
