1.Σύνολα. 2. Υποσύνολα
|
|
|
- Μυρίνα Μπουκουβαλαίοι
- 8 χρόνια πριν
- Προβολές:
Transcript
1 1.Σύνολα Σύνολο είναι μια ολότητα από σαφώς καθορισμένα και διακεκριμένα αντικείμενα. Τα φωνήεντα του ελληνικού αλφαβήτου θεωρούμενα ως μια ολότητα αποτελούν ένα σύνολο, το σύνολο των φωνηέντων του ελληνικού αλφαβήτου. Οποιαδήποτε ευθεία μπορεί να θεωρηθεί ως το σύνολο των σημείων πού την αποτελούν. Τα αντικείμενα πού απαρτίζουν ένα σύνολο ονομάζονται μέλη ή στοιχεία του συνόλου. Ή παράσταση ενός συνόλου γίνεται με δύο άγκιστρα {}, ανάμεσα στα όποια αναγράφουμε τα στοιχεία του συνόλου, π.χ. {1,2,3,4,5,6,7,8,9}. Γ Η παράσταση ενός συνόλου μπορεί να γίνει και με άλλο τρόπο. Έτσι το προηγούμενο σύνολο μπορεί να παρασταθεί: {Χ : χ φυσικός αριθμός μικρότερος από το 10} και διαβάζεται «το σύνολο των στοιχείων χ, όπου χ φυσικός αριθμός μικρότερος από το 10». Ό παραπάνω συμβολισμός μερικές φορές γράφεται {χ χ φυσικός αριθμός μικρότερος από το 10}. Το σύμβολο : ή το σύμβολο διαβάζεται «όπου» και στις δύο περιπτώσεις, αλλά μόνο όταν βρίσκεται ανάμεσα, σε δύο μεταβλητές. 2. Υποσύνολα Κάθε σύνολο έχει υποσύνολα. Υποσύνολο ενός συνόλου είναι ένα σύνολο πού αποτελείται από κανένα, από μερικά ή από όλα τα στοιχεία του συνόλου. Στα υποσύνολα ενός συνόλου Χ περιλαμβάνεται αυτό το ίδιο το σύνολο Χ και το κενό σύνολο. "Ας υποθέσουμε ότι θεωρούμε το σύνολο Χ = {Νίκος, Σάββας, Μαρία, Ελένη}. Παραδείγματα υποσυνόλων του Χ είναι {Νίκος, Μαρία}, {Σάββας, Μαρία, Ελένη} και, βέβαια, { Νίκος, Σάββας, Μαρία, Ελένη }. Χρησιμοποιούμε ένα κεφαλαίο γράμμα για να παριστάνουμε ένα σύνολο και χρησιμοποιούμε το σύμβολο πού σημαίνει «είναι στοιχείο (μέλος) του» ή «ανήκει». Στο παραπάνω σύνολο, Ελένη Χ καί διαβάζεται «ή Ελένη είναι μέλος του συνόλου Χ». Κενό σύνολο είναι ένα σύνολο χωρίς στοιχεία και παριστάνεται με το σύμβολο 0.
2 Τα υποσύνολα του {1,2,3} είναι 0,{1}, {2}, {3}, {1,2}, {1,3}, {2, 3}, {1,2, 3}, δηλ. 8 τον αριθμό. Το 8 είναι 2 3 και μπορεί να δημιουργηθεί ή απορία αν υπάρχει καμιά σημασία στο γεγονός ότι αυτό το αποτέλεσμα είναι μια δύναμη του 2. Το ότι αυτό συμβαίνει πάντοτε μπορεί να δειχτεί εύκολα. Άς υποθέσουμε ότι έχουμε ένα σύνολο με ν στοιχεία. Τότε σε ένα υποσύνολο μπορούμε να δεχτούμε ή να απορρίψουμε οποιοδήποτε στοιχείο του συνόλου. Ό ολικός αριθμός των τρόπων με τούς όποιους μπορούμε να το κάνουμε αυτό είναι 2x2x2x...x2(ν φορές), δηλ. 2 ν. Επομένως υπάρχουν 2 ν υποσύνολα για ένα σύνολο πού έχει ν μέλη. Το Ν είναι το σύνολο όλων των θετικών ακεραίων. Γράψτε με σύμβολα αν οι ακόλουθοι αριθμοί είναι (ή δεν είναι) στοιχεία του Ν. (α) 5, (β) -4, (γ) 1-1 (δ) VX (ε) 9. ['Υπόδειξη. 5 Ν.] Γράψτε όλα τα υποσύνολα του {1,3,5,7}. Πόσα υποσύνολα υπάρχουν; Γράψτε το σύνολο πού σχηματίζεται από τούς αρχικούς 7 πρώτους αριθμούς (περιλαμβάνοντας και τον 1). Πόσα υποσύνολα έχει το σύνολο αυτό; Βρείτε ποιοί από τούς αριθμούς 47,57,257,289 είναι στοιχεία του συνόλου των πρώτων αριθμών.
3 3. Συμβολισμός Το σύμβολο σημαίνει «είναι υποσύνολο του», π.χ. Χ διαβάζεται «το Χ είναι υποσύνολο του Υ». Ή προηγούμενη σχέση ισχύει όταν, και μόνον όταν, κάθε στοιχείο του Χ είναι και στοιχείο του Υ. Ομοίως το σύμβολο σημαίνει «περιέχει ως υποσύνολο». Π.χ. Y X διαβάζεται «το Υ περιέχει το Χ ως υποσύνολο». Οι δύο σχέσεις Χ Υ καί Υ Χ είναι ίδιες καί μπορούμε νά γράψουμε: X Y<=>Y X. Αν, όμως, X Y και Y X, τότε Χ = Υ, επειδή κάθε στοιχείο του Χ είναι στοιχείο του Υ και, αντίστροφα, κάθε στοιχείο του Υ είναι στοιχείο του Χ και συνεπώς το Χ και το Υ είναι το ίδιο σύνολο. Π.x Αν Χ = {1, 3, 4, 6, 7} και Α = {1, 3, 5}, Β ={1, 3, 6}, Γ ={1, 3, 7), ποιό από τα σύνολα Α, Β, Γ είναι υποσύνολο τον Χ; Προφανώς B X και Γ Χ, γιατί κάθε στοιχείο του Β καί του Γ είναι στοιχείο του Χ, ενώ το Α δεν είναι υποσύνολο του Χ, γιατί ένα στοιχείο του Α (το 5) δεν είναι στοιχείο του Χ. 4. Διαγράμματα του Venn Συχνά μας διευκολύνει να γράφουμε ένα ορθογώνιο γύρω από όλα τα στοιχεία πού θεωρούμε και να το ονομάζουμε βασικό ή γενικό σύνολο Ε. Ας υποθέσουμε, π.χ., ότι θέλουμε να δείξουμε ότι το σύνολο των μαθητών του τμήματος Α 2 είναι ένα υποσύνολο των παιδιών της Α' τάξης σε ένα σχολείο, και ότι αυτό με τη σειρά του είναι ένα υποσύνολο του συνόλου όλων των μαθητών του σχολείου. "Ας θέσουμε Α = { χ χ μαθητής του τμήματος Α 2 } Β = { χ χ μαθητής της Α' τάξης } Γ = { χ χ μαθητής του σχολείου }. Τότε και στο διάγραμμα του Venn το Γ είναι το βασικό σύνολο. Γ Α Β
4 5. Ισότητα συνόλων Δύο σύνολα Α και Β είναι ίσα, όταν έχουν ακριβώς τα ίδια στοιχεία, ανεξάρτητα από τη σειρά πού εμφανίζονται, οπότε γράφουμε: Α = Β. Παραδείγματα : 1. Τα σύνολα Α = {α, β, γ, δ} καί Β = {β, δ, γ, α} είναι ίσα. 2. Τα σύνολα Χ= {x x γράμμα της λέξης «ρίζα»} καί Υ = {y y γράμμα της λέξης «ζάρι»} είναι ίσα, γιατί έχουν τα ίδια στοιχεία ρ, ι, ζ, α. 3. Τα σύνολα Α= {x x ψηφίο του αριθμού 1979} και Β = {1,7,9} είναι ίσα, γιατί αποτελούνται από τα ίδια στοιχεία. Ιδιότητες 1. Κάθε σύνολο Α είναι ίσο με τον εαυτό του, δηλαδή : Α = Α ανακλαστική ιδιότητα 2.Αν για τα σύνολα Α, Β ισχύει Α = Β, τότε και Β = Α, δηλαδή : Α = Β => Β = Α συμμετρική ιδιότητα 3.Αν για τα σύνολα Α, Β, Γ ισχύουν Α = Β καί Β = Γ, τότε καί Α = Γ, δηλαδή : Α = Β και Β = Γ => Α = Γ μεταβατική ιδιότητα 6. Ιδιότητες της σχέσης εγκλεισμού Το σύμβολο «C» ονομάζεται σύμβολο εγκλεισμού. Από τον ορισμό του κενού συνόλου προκύπτει αμέσως ότι: 1.Το κενό σύνολο 0 είναι υποσύνολο κάθε συνόλου Α, επομένως και τού εαυτού του, δηλαδή : 0 C Α και 0 C 0.
5 Για τη σχέση εγκλεισμού ισχύουν οι έξης ιδιότητες : 2.Για κάθε σύνολο Α ισχύει: A C Α ανακλαστική ιδιότητα 3.Αν για τα σύνολα Α, Β, Γ ισχύουν A C Β και Β C Γ, τότε A C Γ, δηλαδή : A C Β και Β C Γ => A C Γ μεταβατική ιδιότητα 4.Άν για τα σύνολα Α, Β ισχύουν A C Β και Β C Α, τότε Α = Β, δηλαδή : A C Β και Β C Α =» Α = Β αντισυμμετρική ιδιότητα.
6 7. Τομή συνόλων Στο σαλόνι ενός σπιτιού βρίσκονται ή Μητέρα, ό Πατέρας, ό Αντρέας, ό Νίκος, ή γάτα και το καναρίνι. Το γενικό σύνολο των έμψυχων πού βρίσκονται στο σαλόνι είναι: Ε = { Μητέρα, Πατέρας, Αντρέας, Νίκος, γάτα, καναρίνι }. Το υποσύνολο αυτού των θηλαστικών Θ, είναι: Θ = { Μητέρα, Πατέρας, Αντρέας, Νίκος, γάτα }, και το υποσύνολο των ζώων, Ζ, είναι: Ζ = { γάτα, καναρίνι}.έτσι έχουμε γάτα Θ καί γάτα Ζ αλλά Ζ Θ και Θ Ζ, οπότε, αν και το Θ και το Ζ έχουν ένα μη κενό υποσύνολο κοινό, δηλαδή το σύνολο {γάτα }, κανένα από τα σύνολα Ζ, Θ δεν είναι υποσύνολο του άλλου συνόλου. μ π Α Ν Ε γ κ Τα σύνολα Ζ και Θ λέμε ότι τέμνονται και το σύμβολο πού χρησιμοποιείται είναι τό. "Ετσι έχουμε Θ Ζ = { γάτα }. Αυτό διαβάζεται: Ή τομή του Θ και του Ζ είναι το σύνολο πού έχει ένα στοιχείο, τη γάτα. Προφανώς το σύνολο {γάτα } είναι υποσύνολο του Θ και του Ζ. "Αν δύο υποσύνολα του Ε δεν έχουν κοινό στοιχείο, έχουμε A B = 0 (κενό σύνολο). Σε μια τέτοια περίπτωση τα σύνολα Α και Β ονομάζονται ξένα μεταξύ τους. 8. Ένωση συνόλου Άς υποθέσουμε ότι έχουμε τα σύνολα {1,2} και {1,3}. Καθένα τα σύνολα αυτά έχει δύο στοιχεία, αλλά στα δύο αυτά σύνολα εμφανίζονται μόνο τρία στοιχεία, οι αριθμοί 1, 2, 3. Το σύνολο {1, 2, 3} είναι ή εν των δύο προηγούμενων συνόλων.
7 Αν αντιστρέψουμε το σύμβολο της τομής, έχουμε το σύμβολο το όποιο χρησιμοποιείται για την ένωση δύο συνόλων. "Έτσι το διαβάζεται «ή ένωση του Α και του Β» Αν πάρουμε τα σύνολα Α = {1, 3, 5, 7} και Β = {1, 2, 3, 4}, τότε A B = { 1, 2, 3,4, 5, 7 } ε Αξίζει να παρατηρήσουμε ότι τα στοιχεία των συνόλων Α και Β εμφανίζονται μόνο μία φορά στην ένωση, ακόμη και αν υπάρχουν και στα δύο σύνολα. Ορισμός. Ένωση δύο συνόλων είναι τό σύνολο όλων των στοιχείων πού παρουσιάζονται ή στο ένα σύνολο ή στο άλλο (δεν αποκλείεται κάποιο στοιχείο να ανήκει και στα δύο) και κάθε στοιχείο γράφεται μόνο μία φορά.
8 Παράδειγμα Α = {1, 3, 5, 8}, Β = {2, 4, 6, 8}, Γ = {5, 6, 7, 8}. Βρείτε (α) Α (Β Γ), (β) (Α Β) Γ, (γ) (Α Γ) (Β Γ), (δ) (Α Γ)(Β Γ). (α) Πρώτα βρίσκουμε τό σύνολο (Β Γ). "Έχουμε Β Γ = {2,4, 6, 8} {5, 6, 7,8} = {6, 8}. Επομένως Α (Β Γ) Α ={1,3, 5, 8} {6, 8} = {1, 3, 5,6, 8}. (β) Προχωρώντας με τον ίδιο τρόπο όπως παραπάνω στο (α), βρίσκουμε το σύνολο πού είναι μέσα στην παρένθεση. Έτσι A B = {1,3, 5, 8} {2,4,6, 8} = {1,2, 3,4, 5,6, 8} οπότε (Α Β) Γ ={1,2, 3,4, 5, 6, 8} {5, 6, 7, 8}= {5,6,8}. Τα αποτελέσματα στις περιπτώσεις (α) και (β) δεν είναι ακριβώς τα ίδια, παρόλο πού οι θέσεις των συμβόλων Α, Β, Γ και των συμβόλων της τομής και της ένωσης είναι ίδιες. Αυτό σημαίνει ότι ή σειρά των πράξεων, δηλ. ή τοποθέτηση των παρενθέσεων είναι θεμελιώδους σημασίας. (γ) "Έχουμε Α Γ = {1, 3, 5, 8} {5, 6, 7, 8}= {5,8} Και Β Γ = {2,4, 6, 8} {5, 6, 7,8}= {6,8}. Επομένως (Α Γ)(Β Γ) = {5, 8}{6, 8}= {5, 6, 8} (δ) Επίσης (Α Γ) (Β Γ) = {5, 8} {6, 8}= {8}. Παράδειγμα Ένας σύλλογος έχει 24 μέλη, από τα οποία 16 παίζουν τένις, 14 παίζουν μπάσκετ και 9 παίζουν και τα δύο παιχνίδια. Πόσοι δεν παίζουν κανένα παιχνίδι; Ο απλούστερος τρόπος είναι να φτιάξουμε ένα διάγραμμα του Venn. Επίσης εισάγουμε έναν απλό ορισμό, δηλ. ότι η(α) είναι ό αριθμός των στοιχείων στο Α.
9 Ε Βάζουμε 9 στην τομή [δηλ. n(t B) = 9], οπότε ο αριθμός των μελών του Τ πού δεν υπάρχουν στο Τ Β είναι 7 και ο αριθμός των μελών του Β πού δεν υπάρχουν στο Τ Β είναι 5. Επομένως n(t B) = = 21 (αυτός είναι ό αριθμός των μελών στην ένωση του Τ και του Β). Αλλά η Ε = 24,άρα n(ε)-n(t B) = = 3. Αυτός είναι ό αριθμός εκείνων πού δεν παίζουν κανένα παιχνίδι.
10
11
Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd Email : stvrentzou@gmail.com
 Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd Email : stvrentzou@gmail.com 1 1.Σύνολα Σύνολο είναι μια ολότητα από σαφώς καθορισμένα και διακεκριμένα αντικείμενα. Τα φωνήεντα
Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd Email : stvrentzou@gmail.com 1 1.Σύνολα Σύνολο είναι μια ολότητα από σαφώς καθορισμένα και διακεκριμένα αντικείμενα. Τα φωνήεντα
ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ. Η συνεπαγωγή. Η Ισοδυναμία ή διπλή συνεπαγωγή. Ο σύνδεσμος «ή» Ο σύνδεσμος «και»
 Η συνεπαγωγή ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ Αν P και Q είναι δύο ισχυρισμοί, τέτοιοι ώστε, όταν αληθεύει ο P να αληθεύει και ο Q, τότε λέμε ότι: «ο P συνεπάγεται τον Q» και γράφουμε P Q. Παράδειγμα: x=3 x 2 =9. Ο
Η συνεπαγωγή ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ Αν P και Q είναι δύο ισχυρισμοί, τέτοιοι ώστε, όταν αληθεύει ο P να αληθεύει και ο Q, τότε λέμε ότι: «ο P συνεπάγεται τον Q» και γράφουμε P Q. Παράδειγμα: x=3 x 2 =9. Ο
Εισαγωγικά Παραδείγματα: Παρατηρήσεις:
 1 Εισαγωγικά Η έννοια του συνόλου είναι πρωταρχική στα Μαθηματικά, δεν μπορεί δηλ. να οριστεί από άλλες έννοιες. Γενικά, μπορούμε να πούμε ότι σύνολο είναι μια συλλογή αντικειμένων. υτά λέμε ότι περιέχονται
1 Εισαγωγικά Η έννοια του συνόλου είναι πρωταρχική στα Μαθηματικά, δεν μπορεί δηλ. να οριστεί από άλλες έννοιες. Γενικά, μπορούμε να πούμε ότι σύνολο είναι μια συλλογή αντικειμένων. υτά λέμε ότι περιέχονται
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ. 118 ερωτήσεις θεωρίας με απάντηση 324 416 ασκήσεις για λύση. 20 συνδυαστικά θέματα εξετάσεων
 ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ 118 ερωτήσεις θεωρίας με απάντηση 34 416 ασκήσεις για λύση ερωτήσεις κατανόησης λυμένα παραδείγματα 0 συνδυαστικά θέματα εξετάσεων Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Εισαγωγική ενότητα Το λεξιλόγιο
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ 118 ερωτήσεις θεωρίας με απάντηση 34 416 ασκήσεις για λύση ερωτήσεις κατανόησης λυμένα παραδείγματα 0 συνδυαστικά θέματα εξετάσεων Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Εισαγωγική ενότητα Το λεξιλόγιο
Η έννοια του συνόλου. Εισαγωγικό κεφάλαιο 27
 Εισαγωγικό κεφάλαιο 27 Η έννοια του συνόλου Σύνολο είναι κάθε συλλογή αντικειμένων, που προέρχονται από την εμπειρία μας ή τη διανόησή μας, είναι καλά ορισμένα και διακρίνονται το ένα από το άλλο. Αυτός
Εισαγωγικό κεφάλαιο 27 Η έννοια του συνόλου Σύνολο είναι κάθε συλλογή αντικειμένων, που προέρχονται από την εμπειρία μας ή τη διανόησή μας, είναι καλά ορισμένα και διακρίνονται το ένα από το άλλο. Αυτός
ΜΑΘΗΜΑΤΙΚΑ Β Γυμνασίου
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΜΑΘΗΜΑΤΙΚΑ Β Γυμνασίου Ενότητα 1: Σύνολα ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΥΠΗΡΕΣΙΑ ΑΝΑΠΤΥΞΗΣ ΠΡΟΓΡΑΜΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΑ Β Γυμνασίου Ενότητα 1: Σύνολα Συγγραφή: Ομάδα Υποστήριξης Μαθηματικών
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΜΑΘΗΜΑΤΙΚΑ Β Γυμνασίου Ενότητα 1: Σύνολα ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΥΠΗΡΕΣΙΑ ΑΝΑΠΤΥΞΗΣ ΠΡΟΓΡΑΜΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΑ Β Γυμνασίου Ενότητα 1: Σύνολα Συγγραφή: Ομάδα Υποστήριξης Μαθηματικών
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΣΥΝΟΛΑ. 6ο ΓΕΛ ΛΑΜΙΑΣ ΧΡΙΣΤΟΣ ΤΡΙΑΝΤΑΦΥΛΛΟΥ ΜΑΘΗΜΑΤΙΚΟΣ
 ΣΥΝΟΛ 6ο ΓΕΛ ΛΜΙΣ ΧΡΙΣΤΟΣ ΤΡΙΝΤΦΥΛΛΟΥ ΜΘΗΜΤΙΚΟΣ ΣΥΝΟΛ Στοιχεία θεωρίας Σύνολο είναι μια συλλογή από αντικείμενα. Το σύνολο όλων των ελληνικών ποδοσφαιρικών ομάδων. Το σύνολο όλων των χωρών της Ευρώπης.
ΣΥΝΟΛ 6ο ΓΕΛ ΛΜΙΣ ΧΡΙΣΤΟΣ ΤΡΙΝΤΦΥΛΛΟΥ ΜΘΗΜΤΙΚΟΣ ΣΥΝΟΛ Στοιχεία θεωρίας Σύνολο είναι μια συλλογή από αντικείμενα. Το σύνολο όλων των ελληνικών ποδοσφαιρικών ομάδων. Το σύνολο όλων των χωρών της Ευρώπης.
Τι είναι σύνολο; Ο ορισμός αυτός είναι σύμφωνος με τη διαισθητική μας κατανόηση για το τι είναι σύνολο
 ΣΥΝΟΛΑ Τι είναι σύνολο; Ένας ορισμός «Μια συλλογή αντικειμένων διακεκριμένων και πλήρως καθορισμένων που λαμβάνονται από τον κόσμο είτε της εμπειρίας μας είτε της σκέψης μας» (Cantor, 19 ος αιώνας) Ο ορισμός
ΣΥΝΟΛΑ Τι είναι σύνολο; Ένας ορισμός «Μια συλλογή αντικειμένων διακεκριμένων και πλήρως καθορισμένων που λαμβάνονται από τον κόσμο είτε της εμπειρίας μας είτε της σκέψης μας» (Cantor, 19 ος αιώνας) Ο ορισμός
ΘΕΩΡΙΑ ΣΥΝΟΛΩΝ. x Σ και. x Σ και διαβάζουµε «το x δεν ανήκει στο Σ». ΕΙΣΑΓΩΓΗ :
 ΕΙΣΑΓΩΓΗ : ΘΕΩΡΙΑ ΣΥΝΟΛΩΝ Η έννοια του συνόλου στα µαθηµατικά είναι έννοια πρωταρχική και έτσι δεν ορίζεται αυστηρά µαθηµατικά. Μπορούµε όµως επεξηγηµατικά αντί ορισµού να πούµε: Σύνολο, είναι µια συλλογή
ΕΙΣΑΓΩΓΗ : ΘΕΩΡΙΑ ΣΥΝΟΛΩΝ Η έννοια του συνόλου στα µαθηµατικά είναι έννοια πρωταρχική και έτσι δεν ορίζεται αυστηρά µαθηµατικά. Μπορούµε όµως επεξηγηµατικά αντί ορισµού να πούµε: Σύνολο, είναι µια συλλογή
Σ αυτή την παράγραφο θα γνωρίσουμε τέσσερις βασικές έννοιες της λογικής, οι οποίες θα μας φανούν χρήσιμες στα επόμενα κεφάλαια του βιβλίου.
 Σ αυτή την παράγραφο θα γνωρίσουμε τέσσερις βασικές έννοιες της λογικής, οι οποίες θα μας φανούν χρήσιμες στα επόμενα κεφάλαια του βιβλίου. Η προσέγγιση των εννοιών αυτών θα γίνει με τη βοήθεια απλών παραδειγμάτων,
Σ αυτή την παράγραφο θα γνωρίσουμε τέσσερις βασικές έννοιες της λογικής, οι οποίες θα μας φανούν χρήσιμες στα επόμενα κεφάλαια του βιβλίου. Η προσέγγιση των εννοιών αυτών θα γίνει με τη βοήθεια απλών παραδειγμάτων,
Άλγεβρα 1 ο Κεφάλαιο ... ν παράγοντες
 1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Τι ονομάζεται δύναμη α ν με βάση τον πραγματικό αριθμό α και εκθέτη το φυσικό αριθμό >1; H δύναμη με βάση έναν πραγματικό αριθμό α και εκθέτη ένα φυσικό αριθμό ν, συμβολίζεται
1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Τι ονομάζεται δύναμη α ν με βάση τον πραγματικό αριθμό α και εκθέτη το φυσικό αριθμό >1; H δύναμη με βάση έναν πραγματικό αριθμό α και εκθέτη ένα φυσικό αριθμό ν, συμβολίζεται
5.1 ΣΥΝΟΛΑ. 2. Παράσταση συνόλου. 3. Εποπτική παράσταση συνόλου : Γίνεται µε το διάγραµµα Venn, δηλαδή µε
 1 5.1 ΣΥΝΟΛΑ ΘΕΩΡΙΑ 1. Ορισµός του συνόλου Σύνολο λέγεται κάθε συλλογή πραγµατικών ή φανταστικών αντικειµένων, που είναι καλά ορισµένα και διακρίνονται το ένα από το άλλο. Τα παραπάνω αντικείµενα λέγονται
1 5.1 ΣΥΝΟΛΑ ΘΕΩΡΙΑ 1. Ορισµός του συνόλου Σύνολο λέγεται κάθε συλλογή πραγµατικών ή φανταστικών αντικειµένων, που είναι καλά ορισµένα και διακρίνονται το ένα από το άλλο. Τα παραπάνω αντικείµενα λέγονται
ΕΙΣΑΓΩΓΙΚΟ ΚΕΦΑΛΑΙΟ. a β a β.
 ΕΙΣΑΓΩΓΙΚΟ ΚΕΦΑΛΑΙΟ Ε.1 ΤΟ ΛΕΞΙΛΟΓΙΟ ΤΗΣ ΛΟΓΙΚΗΣ Στη παράγραφο αυτή θα γνωρίσουμε μερικές βασικές έννοιες της Λογικής, τις οποίες θα χρησιμοποιήσουμε στη συνέχεια, όπου αυτό κρίνεται αναγκαίο, για τη σαφέστερη
ΕΙΣΑΓΩΓΙΚΟ ΚΕΦΑΛΑΙΟ Ε.1 ΤΟ ΛΕΞΙΛΟΓΙΟ ΤΗΣ ΛΟΓΙΚΗΣ Στη παράγραφο αυτή θα γνωρίσουμε μερικές βασικές έννοιες της Λογικής, τις οποίες θα χρησιμοποιήσουμε στη συνέχεια, όπου αυτό κρίνεται αναγκαίο, για τη σαφέστερη
K15 Ψηφιακή Λογική Σχεδίαση 3: Προτασιακή Λογική / Θεωρία Συνόλων
 K15 Ψηφιακή Λογική Σχεδίαση 3: Προτασιακή Λογική / Θεωρία Συνόλων Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Στοιχεία προτασιακής λογικής Περιεχόμενα
K15 Ψηφιακή Λογική Σχεδίαση 3: Προτασιακή Λογική / Θεωρία Συνόλων Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Στοιχεία προτασιακής λογικής Περιεχόμενα
ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΕΙΣΑΓΩΓΗ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ. ΤΙ ΕΙΝΑΙ ΤΑ ΜΑΘΗΜΑΤΙΚΑ; Η επιστήμη των αριθμών Βασανιστήριο για τους μαθητές και φοιτητές Τέχνη για τους μαθηματικούς ΜΑΘΗΜΑΤΙΚΑ Α Εξάμηνο ΙΩΑΝΝΗΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΕΙΣΑΓΩΓΗ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ. ΤΙ ΕΙΝΑΙ ΤΑ ΜΑΘΗΜΑΤΙΚΑ; Η επιστήμη των αριθμών Βασανιστήριο για τους μαθητές και φοιτητές Τέχνη για τους μαθηματικούς ΜΑΘΗΜΑΤΙΚΑ Α Εξάμηνο ΙΩΑΝΝΗΣ
Το σύνολο Z των Ακεραίων : Z = {... 2, 1, 0, 1, 2, 3,... } Να σηµειώσουµε ότι οι φυσικοί αριθµοί είναι και ακέραιοι.
 1 E. ΣΥΝΟΛΑ ΘΕΩΡΙΑ 1. Ορισµός του συνόλου Σύνολο λέγεται κάθε συλλογή πραγµατικών ή φανταστικών αντικειµένων, που είναι καλά ορισµένα και διακρίνονται το ένα από το άλλο. Τα παραπάνω αντικείµενα λέγονται
1 E. ΣΥΝΟΛΑ ΘΕΩΡΙΑ 1. Ορισµός του συνόλου Σύνολο λέγεται κάθε συλλογή πραγµατικών ή φανταστικών αντικειµένων, που είναι καλά ορισµένα και διακρίνονται το ένα από το άλλο. Τα παραπάνω αντικείµενα λέγονται
Ας θεωρήσουμε δύο πραγματικούς αριθμούς. Είναι γνωστό ότι:,. Αυτό σημαίνει ότι: «=», «
 .1 Στη παράγραφο αυτή θα γνωρίσουμε μερικές βασικές έννοιες της Λογικής, τις οποίες θα χρησιμοποιήσουμε στη συνέχεια, όπου αυτό κρίνεται αναγκαίο, για τη σαφέστερη διατύπωση μαθηματικών εννοιών, προτάσεων
.1 Στη παράγραφο αυτή θα γνωρίσουμε μερικές βασικές έννοιες της Λογικής, τις οποίες θα χρησιμοποιήσουμε στη συνέχεια, όπου αυτό κρίνεται αναγκαίο, για τη σαφέστερη διατύπωση μαθηματικών εννοιών, προτάσεων
Σύνολα, Σχέσεις, Συναρτήσεις
 Κεφάλαιο 2 Σύνολα, Σχέσεις, Συναρτήσεις Τα σύνολα, οι σχέσεις και οι συναρτήσεις χρησιμοποιούνται ευρύτατα σε κάθε είδους μαθηματικές αναπαραστάσεις και μοντελοποιήσεις. Στη θεωρία υπολογισμού χρησιμεύουν,
Κεφάλαιο 2 Σύνολα, Σχέσεις, Συναρτήσεις Τα σύνολα, οι σχέσεις και οι συναρτήσεις χρησιμοποιούνται ευρύτατα σε κάθε είδους μαθηματικές αναπαραστάσεις και μοντελοποιήσεις. Στη θεωρία υπολογισμού χρησιμεύουν,
5. 1 ΣΥΝΟΛΑ. Η έννοια του συνόλου
 ΜΕΡΟΣ Α 5.1 ΣΥΝΟΛΑ 359 5. 1 ΣΥΝΟΛΑ Η έννοια του συνόλου Ονομάζουμε σύνολο στα Μαθηματικά κάθε ομάδα αντικειμένων τα οποία διακρίνονται μεταξύ τους με απόλυτη σαφήνεια Κάθε αντικείμενο που περιέχεται σε
ΜΕΡΟΣ Α 5.1 ΣΥΝΟΛΑ 359 5. 1 ΣΥΝΟΛΑ Η έννοια του συνόλου Ονομάζουμε σύνολο στα Μαθηματικά κάθε ομάδα αντικειμένων τα οποία διακρίνονται μεταξύ τους με απόλυτη σαφήνεια Κάθε αντικείμενο που περιέχεται σε
LÔseic Ask sewn sta Jemèlia twn Majhmatik n I
 LÔseic Ask sewn sta Jemèlia twn Majhmatik n I Rwmanìc-Diogènhc Maliki shc Tetˆrth, 6 OktwbrÐou 2010 Άσκηση 1. Για τυχόντα σύνολα A, B, C, D, να δειχθεί ότι (α ) A (B \ C) = ((A B) \ C) (A C). (β ) (A \
LÔseic Ask sewn sta Jemèlia twn Majhmatik n I Rwmanìc-Diogènhc Maliki shc Tetˆrth, 6 OktwbrÐou 2010 Άσκηση 1. Για τυχόντα σύνολα A, B, C, D, να δειχθεί ότι (α ) A (B \ C) = ((A B) \ C) (A C). (β ) (A \
Σημεία Προσοχής στην Παράγραφο Ε2.
 Σημεία Προσοχής στην Παράγραφο Ε2. 1. Ίσα Σύνολα Δεν αρκεί δύο σύνολα να έχουν τον ίδιο αριθμό στοιχέιων για να είναι ίσα. Πρέπει να έχουν ακριβώς τα ίδια στοιχεία. ΠΑΡΑΔΕΙΓΜΑ Έχουμε τα σύνολα Α={1,α,5}
Σημεία Προσοχής στην Παράγραφο Ε2. 1. Ίσα Σύνολα Δεν αρκεί δύο σύνολα να έχουν τον ίδιο αριθμό στοιχέιων για να είναι ίσα. Πρέπει να έχουν ακριβώς τα ίδια στοιχεία. ΠΑΡΑΔΕΙΓΜΑ Έχουμε τα σύνολα Α={1,α,5}
lnx ln x ln l x 1. = (0,1) (1,7].
![lnx ln x ln l x 1. = (0,1) (1,7]. lnx ln x ln l x 1. = (0,1) (1,7].](/thumbs/56/38550944.jpg) ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 1: ΕΝΝΟΙΑ ΠΡΑΓΜΑΤΙΚΗΣ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ. IΣΟΤΗΤΑ ΣΥΝΑΡΤΗΣΕΩΝ - ΠΡΑΞΕΙΣ ΜΕ ΣΥΝΑΡΤΗΣΕΙΣ - ΣΥΝΘΕΣΗ ΣΥΝΑΡΤΗΣΕΩΝ [Ενότητα
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 1: ΕΝΝΟΙΑ ΠΡΑΓΜΑΤΙΚΗΣ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ. IΣΟΤΗΤΑ ΣΥΝΑΡΤΗΣΕΩΝ - ΠΡΑΞΕΙΣ ΜΕ ΣΥΝΑΡΤΗΣΕΙΣ - ΣΥΝΘΕΣΗ ΣΥΝΑΡΤΗΣΕΩΝ [Ενότητα
ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ
 ΚΕΦΑΛΑΙΟ 2 Ο : ΚΛΑΣΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Όταν ένα μέγεθος ή ένα σύνολο χωριστεί σε ν ίσα μέρη, το κάθε ένα από αυτά ονομάζεται.. και συμβολίζεται : 2. Κάθε τμήμα του μεγέθους ή του συνόλου αντικειμένων,
ΚΕΦΑΛΑΙΟ 2 Ο : ΚΛΑΣΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Όταν ένα μέγεθος ή ένα σύνολο χωριστεί σε ν ίσα μέρη, το κάθε ένα από αυτά ονομάζεται.. και συμβολίζεται : 2. Κάθε τμήμα του μεγέθους ή του συνόλου αντικειμένων,
Κεφάλαιο 1 ο. Αλγεβρικές παραστάσεις.
 Μαθηματικά Γ Γυμνασίου Κεφάλαιο 1 ο. Αλγεβρικές παραστάσεις. Μέρος Α Θεωρία. 1. Πως προσθέτουμε δύο πραγματικούς αριθμούς; 2. Πως πολλαπλασιάζουμε δύο πραγματικούς αριθμούς; 3. Ποιες είναι οι ιδιότητες
Μαθηματικά Γ Γυμνασίου Κεφάλαιο 1 ο. Αλγεβρικές παραστάσεις. Μέρος Α Θεωρία. 1. Πως προσθέτουμε δύο πραγματικούς αριθμούς; 2. Πως πολλαπλασιάζουμε δύο πραγματικούς αριθμούς; 3. Ποιες είναι οι ιδιότητες
τα βιβλία των επιτυχιών
 Τα βιβλία των Εκδόσεων Πουκαμισάς συμπυκνώνουν την πολύχρονη διδακτική εμπειρία των συγγραφέων μας και αποτελούν το βασικό εκπαιδευτικό υλικό που χρησιμοποιούν οι μαθητές των φροντιστηρίων μας. Μέσα από
Τα βιβλία των Εκδόσεων Πουκαμισάς συμπυκνώνουν την πολύχρονη διδακτική εμπειρία των συγγραφέων μας και αποτελούν το βασικό εκπαιδευτικό υλικό που χρησιμοποιούν οι μαθητές των φροντιστηρίων μας. Μέσα από
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 8: Σχέσεις - Πράξεις Δομές Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 8: Σχέσεις - Πράξεις Δομές Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Αριθμητής = Παρονομαστής
 Η ΕΝΝΟΙΑ ΤΟΥ ΚΛΑΣΜΑΤΟΣ To κλάσμα κ εκφράζει τα κ μέρη από τα ν ίσα μέρη στα οποία έχει χωριστεί μία ποσότητα ν Αριθμητής = Παρονομαστής Το ν α = 0 = α κ ν = κ ν ονομάζεται κλασματική μονάδα 8 = α α = Άρα
Η ΕΝΝΟΙΑ ΤΟΥ ΚΛΑΣΜΑΤΟΣ To κλάσμα κ εκφράζει τα κ μέρη από τα ν ίσα μέρη στα οποία έχει χωριστεί μία ποσότητα ν Αριθμητής = Παρονομαστής Το ν α = 0 = α κ ν = κ ν ονομάζεται κλασματική μονάδα 8 = α α = Άρα
Τμήμα Τεχνολόγων Γεωπόνων-Κατεύθυνση Αγροτικής Οικονομίας Μαθηματικά για Οικονομολόγους 2 ο Μάθημα: Σύνολα αριθμών-συναρτήσεις Διδάσκουσα:
 Τμήμα Τεχνολόγων Γεωπόνων-Κατεύθυνση Αγροτικής Οικονομίας Μαθηματικά για Οικονομολόγους 2 ο Μάθημα: Σύνολα αριθμών-συναρτήσεις Διδάσκουσα: Κοντογιάννη Αριστούλα Σύνολα Σύνολο: Μία συλλογή διακριτών αντικειμένων
Τμήμα Τεχνολόγων Γεωπόνων-Κατεύθυνση Αγροτικής Οικονομίας Μαθηματικά για Οικονομολόγους 2 ο Μάθημα: Σύνολα αριθμών-συναρτήσεις Διδάσκουσα: Κοντογιάννη Αριστούλα Σύνολα Σύνολο: Μία συλλογή διακριτών αντικειμένων
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις
 Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις Ορισμός: Έστω Α, Β R. Πραγματική συνάρτηση πραγματικής μεταβλητής από το σύνολο Α στο σύνολο Β ονομάζουμε την διαδικασία κατά την οποία κάθε στοιχείο του συνόλου
Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις Ορισμός: Έστω Α, Β R. Πραγματική συνάρτηση πραγματικής μεταβλητής από το σύνολο Α στο σύνολο Β ονομάζουμε την διαδικασία κατά την οποία κάθε στοιχείο του συνόλου
ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟΔΕΙΞΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ
 ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟΔΕΙΞΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ Κεφάλαιο ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ο ΜΕΡΟΣ Απαντήσεις στις ερωτήσεις του τύπου Σωστό-Λάθος. Σ 6. Λ 8. Λ. Σ 7. Σ 9. Λ 3. Λ 8. Λ 3. Σ 4. Σ 9. Σ 3. α Σ 5. Σ. Σ β Σ 6. Λ.
ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟΔΕΙΞΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ Κεφάλαιο ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ο ΜΕΡΟΣ Απαντήσεις στις ερωτήσεις του τύπου Σωστό-Λάθος. Σ 6. Λ 8. Λ. Σ 7. Σ 9. Λ 3. Λ 8. Λ 3. Σ 4. Σ 9. Σ 3. α Σ 5. Σ. Σ β Σ 6. Λ.
Μαθηματικά Γ Γυμνασίου
 Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
ΗΥ118: Διακριτά Μαθηματικά Εαρινό εξάμηνο 2019 Λύσεις ασκήσεων προόδου
 ΗΥ118: Διακριτά Μαθηματικά Εαρινό εξάμηνο 2019 Λύσεις ασκήσεων προόδου Θέμα 1: a. Δείξτε κατά πόσον η πρόταση ((p q) r) ((p q) (q r)) αποτελεί ή όχι ταυτολογία. Κάποιος ιδιόρρυθμος δικαστής ρωτήθηκε κατά
ΗΥ118: Διακριτά Μαθηματικά Εαρινό εξάμηνο 2019 Λύσεις ασκήσεων προόδου Θέμα 1: a. Δείξτε κατά πόσον η πρόταση ((p q) r) ((p q) (q r)) αποτελεί ή όχι ταυτολογία. Κάποιος ιδιόρρυθμος δικαστής ρωτήθηκε κατά
ΠΙΘΑΝΟΤΗΤΕΣ Δειγματικός Χώρος. Ενδεχόμενα {,,..., }.
 ΠΙΘΑΝΟΤΗΤΕΣ Δειγματικός Χώρος Το σύνολο των δυνατών αποτελεσμάτων λέγεται δειγματικός χώρος (sample space) και συμβολίζεται συνήθως με το γράμμα Αν δηλαδή ω,,, ω2 ωκ είναι τα δυνατά αποτελέσματα ενός πειράματος
ΠΙΘΑΝΟΤΗΤΕΣ Δειγματικός Χώρος Το σύνολο των δυνατών αποτελεσμάτων λέγεται δειγματικός χώρος (sample space) και συμβολίζεται συνήθως με το γράμμα Αν δηλαδή ω,,, ω2 ωκ είναι τα δυνατά αποτελέσματα ενός πειράματος
Παράδειγμα δομικής επαγωγής Ορισμός δομικής επαγωγής Συμβολοσειρές Γλώσσες Δυαδικά δένδρα Μαθηματικά Πληροφορικής 3ο Μάθημα Αρχικός συγγραφέας: Ηλίας
 Μαθηματικά Πληροφορικής 3ο Μάθημα Αρχικός συγγραφέας: Ηλίας Κουτσουπιάς Τροποποιήσεις: Σταύρος Κολλιόπουλος Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Δομική επαγωγή Η ιδέα της μαθηματικής
Μαθηματικά Πληροφορικής 3ο Μάθημα Αρχικός συγγραφέας: Ηλίας Κουτσουπιάς Τροποποιήσεις: Σταύρος Κολλιόπουλος Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Δομική επαγωγή Η ιδέα της μαθηματικής
6.1 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ
 ΟΡΙΣΜΟΣ 6. ΣΥΝΑΡΤΗΣΕΙΣ 6.1 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ Ονομάζουμε συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β μια διαδικασία (κανόνα) f, με την οποία κάθε στοιχείο του συνόλου Α αντιστοιχίζεται σε ένα ακριβώς
ΟΡΙΣΜΟΣ 6. ΣΥΝΑΡΤΗΣΕΙΣ 6.1 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ Ονομάζουμε συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β μια διαδικασία (κανόνα) f, με την οποία κάθε στοιχείο του συνόλου Α αντιστοιχίζεται σε ένα ακριβώς
ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΕΝΟΤΗΤΑ Α.1.2. ΠΡΑΞΕΙΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ ΚΑΙ ΙΔΙΟΤΗΤΕΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΕΝΟΤΗΤΑ Α.1.2. ΠΡΑΞΕΙΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ ΚΑΙ ΙΔΙΟΤΗΤΕΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΗΜΕΡΟΜΗΝΙΑ / / ΠΡΟΣΘΕΣΗ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ 12+ 7 = 19 Οι αριθμοί 12 και 7 ονομάζονται ενώ το 19 ονομάζεται.. 3+5 =, 5+3 =...
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΕΝΟΤΗΤΑ Α.1.2. ΠΡΑΞΕΙΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ ΚΑΙ ΙΔΙΟΤΗΤΕΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΗΜΕΡΟΜΗΝΙΑ / / ΠΡΟΣΘΕΣΗ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ 12+ 7 = 19 Οι αριθμοί 12 και 7 ονομάζονται ενώ το 19 ονομάζεται.. 3+5 =, 5+3 =...
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ Σχολική Χρονιά: Α ΓΥΜΝΑΣΙΟΥ
 Ενότητα 1: Σύνολα 1. Με τη βοήθεια του πιο κάτω διαγράμματος να γράψετε με αναγραφή τα σύνολα: Ω A 5. 1. B Ω =. 6. 4. 3. 7. 8.. Από το διπλανό διάγραμμα, να γράψετε με αναγραφή τα σύνολα: 3. Δίνεται το
Ενότητα 1: Σύνολα 1. Με τη βοήθεια του πιο κάτω διαγράμματος να γράψετε με αναγραφή τα σύνολα: Ω A 5. 1. B Ω =. 6. 4. 3. 7. 8.. Από το διπλανό διάγραμμα, να γράψετε με αναγραφή τα σύνολα: 3. Δίνεται το
ΧΑΡΑΛΑΜΠΟΣ.ΣΠ. ΛΥΚΟΥΔΗΣ - ΠΙΘΑΝΟΤΗΤΕΣ Α ΛΥΚΕΙΟΥ
 Θεωρία Πιθανοτήτων Εάν οι συνθήκες τέλεσης ενός πειράματος καθορίζουν πλήρως το αποτέλεσμα του, τότε το πείραμα λέγεται αιτιοκρατικό. Είναι γνωστό ότι το αποσταγμένο νερό βράζει στους 100 βαθμού κελσίου.
Θεωρία Πιθανοτήτων Εάν οι συνθήκες τέλεσης ενός πειράματος καθορίζουν πλήρως το αποτέλεσμα του, τότε το πείραμα λέγεται αιτιοκρατικό. Είναι γνωστό ότι το αποσταγμένο νερό βράζει στους 100 βαθμού κελσίου.
5. 3 ΕΝΝΟΙΑ ΤΗΣ ΠΙΘΑΝΟΤΗΤΑΣ
 ΜΕΡΟΣ Α. ΕΟΙΑ ΤΗΣ ΠΙΘΑΟΤΗΤΑΣ 77. ΕΟΙΑ ΤΗΣ ΠΙΘΑΟΤΗΤΑΣ Κλασικός ορισμός πιθανότητας Αν ένα στοιχείο του συνόλου του δειγματικού χώρου επιλέγεται στην τύχη και δεν έχει κανένα πλεονέκτημα έναντι των άλλων,
ΜΕΡΟΣ Α. ΕΟΙΑ ΤΗΣ ΠΙΘΑΟΤΗΤΑΣ 77. ΕΟΙΑ ΤΗΣ ΠΙΘΑΟΤΗΤΑΣ Κλασικός ορισμός πιθανότητας Αν ένα στοιχείο του συνόλου του δειγματικού χώρου επιλέγεται στην τύχη και δεν έχει κανένα πλεονέκτημα έναντι των άλλων,
ΑΣΚΗΣΕΙΣ ΣΤΑ ΣΥΝΟΛΑ. 1. Να εκφράσετε ως πράξεις μεταξύ των Α και Β, τα σύνολα που αντιστοιχούν στα χρωματισμένα μέρη των παρακάτω διαγραμμάτων Venn.
 ΑΣΚΗΣΕΙΣ ΣΤΑ ΣΥΝΟΛΑ 1 Να εκφράσετε ως πράξεις μεταξύ των Α και Β, τα σύνολα που αντιστοιχούν στα χρωματισμένα μέρη των παρακάτω διαγραμμάτων Venn 2 Δίνεται το παρακάτω διάγραμμα Venn Να παραστήσετε με
ΑΣΚΗΣΕΙΣ ΣΤΑ ΣΥΝΟΛΑ 1 Να εκφράσετε ως πράξεις μεταξύ των Α και Β, τα σύνολα που αντιστοιχούν στα χρωματισμένα μέρη των παρακάτω διαγραμμάτων Venn 2 Δίνεται το παρακάτω διάγραμμα Venn Να παραστήσετε με
of Mathematics των I.Stewart και D.Tall, Oxford University Press.
 Σημειώσεις του Μαθήματος ΜΕΜ 103 Θεμέλια των Μαθηματικών Βασισμένες στο βιβλίο των I.Stewart και D.Tall Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2018 Εισαγωγή Αρχίζοντας τη μελέτη των
Σημειώσεις του Μαθήματος ΜΕΜ 103 Θεμέλια των Μαθηματικών Βασισμένες στο βιβλίο των I.Stewart και D.Tall Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2018 Εισαγωγή Αρχίζοντας τη μελέτη των
Περιεχόμενα. Πρόλογος 3
 Πρόλογος Τα πρώτα μαθήματα, σχεδόν σε όλους τους κλάδους των μαθηματικών, περιέχουν, ή θεωρούν γνωστές, εισαγωγικές έννοιες που αφορούν σύνολα, συναρτήσεις, σχέσεις ισοδυναμίας, αλγεβρικές δομές, κλπ.
Πρόλογος Τα πρώτα μαθήματα, σχεδόν σε όλους τους κλάδους των μαθηματικών, περιέχουν, ή θεωρούν γνωστές, εισαγωγικές έννοιες που αφορούν σύνολα, συναρτήσεις, σχέσεις ισοδυναμίας, αλγεβρικές δομές, κλπ.
Χρησιμοποιείται για να αποφασίσει το πρόγραμμα αν θα κάνει κάτι σε ένα σημείο της εκτέλεσής του, εξετάζοντας αν ισχύει ή όχι μια συνθήκη.
 Εργαστήριο 4: 4.1 Η Δομή Ελέγχου if Χρησιμοποιείται για να αποφασίσει το πρόγραμμα αν θα κάνει κάτι σε ένα σημείο της εκτέλεσής του, εξετάζοντας αν ισχύει ή όχι μια συνθήκη. Γενική Μορφή: Παρατηρήσεις:
Εργαστήριο 4: 4.1 Η Δομή Ελέγχου if Χρησιμοποιείται για να αποφασίσει το πρόγραμμα αν θα κάνει κάτι σε ένα σημείο της εκτέλεσής του, εξετάζοντας αν ισχύει ή όχι μια συνθήκη. Γενική Μορφή: Παρατηρήσεις:
Ορισμός παραγώγου Εξίσωση εφαπτομένης
 9 Ορισμός παραγώγου Εξίσωση εφαπτομένης Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ι Ορισμός παράγωγου αριθμού Ορισμός 1 Μια συνάρτηση f λέμε ότι είναι παραγωγίσιμη σ ένα σημείο του πεδίου ορισμού της, αν f( f( υπάρχει
9 Ορισμός παραγώγου Εξίσωση εφαπτομένης Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ι Ορισμός παράγωγου αριθμού Ορισμός 1 Μια συνάρτηση f λέμε ότι είναι παραγωγίσιμη σ ένα σημείο του πεδίου ορισμού της, αν f( f( υπάρχει
11. Ποιες είναι οι άμεσες συνέπειες της διαίρεσης;
 10. Τι ονομάζουμε Ευκλείδεια διαίρεση και τέλεια διαίρεση; Όταν δοθούν δύο φυσικοί αριθμοί Δ και δ, τότε υπάρχουν δύο άλλοι φυσικοί αριθμοί π και υ, έτσι ώστε να ισχύει: Δ = δ π + υ. Ο αριθμός Δ λέγεται
10. Τι ονομάζουμε Ευκλείδεια διαίρεση και τέλεια διαίρεση; Όταν δοθούν δύο φυσικοί αριθμοί Δ και δ, τότε υπάρχουν δύο άλλοι φυσικοί αριθμοί π και υ, έτσι ώστε να ισχύει: Δ = δ π + υ. Ο αριθμός Δ λέγεται
of Mathematics των I.Stewart και D.Tall, Oxford University Press.
 Σημειώσεις του Μαθήματος Μ1124 Θεμέλια των Μαθηματικών Βασισμένες στο βιβλίο των I.Stewart και D.Tall Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2012 Εισαγωγή Αρχίζοντας τη μελέτη των μαθηματικών
Σημειώσεις του Μαθήματος Μ1124 Θεμέλια των Μαθηματικών Βασισμένες στο βιβλίο των I.Stewart και D.Tall Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2012 Εισαγωγή Αρχίζοντας τη μελέτη των μαθηματικών
ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟ ΕΙΞΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ
 ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟ ΕΙΞΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ 3 Κεφάλαιο ο: ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ο ΜΕΡΟΣ Απαντήσεις στις ερωτήσεις του τύπου Σωστό-Λάθος. Σ 6. Λ 8. Λ. Σ 7. Σ 9. Λ 3. Λ 8. Λ 3. Σ 4. Σ 9. Σ 3. α) Σ 5. Σ. Σ β) Σ 6.
ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟ ΕΙΞΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ 3 Κεφάλαιο ο: ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ο ΜΕΡΟΣ Απαντήσεις στις ερωτήσεις του τύπου Σωστό-Λάθος. Σ 6. Λ 8. Λ. Σ 7. Σ 9. Λ 3. Λ 8. Λ 3. Σ 4. Σ 9. Σ 3. α) Σ 5. Σ. Σ β) Σ 6.
ΛΟΓΙΚΗ - ΣΥΝΟΛΑ ΤΟ ΛΕΞΙΛΟΓΙΟ ΤΗΣ ΛΟΓΙΚΗΣ
 ΛΟΓΙΚΗ - ΣΥΝΟΛ ΤΟ ΛΕΞΙΛΟΓΙΟ ΤΗΣ ΛΟΓΙΚΗΣ Η συνεπαγωγή ν P και Q είναι δύο ισχυρισμοί τέτοιοι ώστε όταν αληθεύει ο P να αληθεύει και ο Q τότε λέμε ότι το P συνεπάγεται το Q και γράφουμε P Q Π.χ, όταν α=β
ΛΟΓΙΚΗ - ΣΥΝΟΛ ΤΟ ΛΕΞΙΛΟΓΙΟ ΤΗΣ ΛΟΓΙΚΗΣ Η συνεπαγωγή ν P και Q είναι δύο ισχυρισμοί τέτοιοι ώστε όταν αληθεύει ο P να αληθεύει και ο Q τότε λέμε ότι το P συνεπάγεται το Q και γράφουμε P Q Π.χ, όταν α=β
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει:
 Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει: Να αναγνωρίζει πότε μια αλγεβρική παράσταση της πραγματικής μεταβλητής x, είναι πολυώνυμο και να διακρίνει τα στοιχεία του: όροι, συντελεστές, σταθερός
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει: Να αναγνωρίζει πότε μια αλγεβρική παράσταση της πραγματικής μεταβλητής x, είναι πολυώνυμο και να διακρίνει τα στοιχεία του: όροι, συντελεστές, σταθερός
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - 2 ο ΘΕΜΑ
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ ο : ΠΙΘΑΝΟΤΗΤΕΣ. Ένα τηλεοπτικό παιχνίδι παίζεται με ζεύγη αντιπάλων των δυο φύλων. Στο παιχνίδι συμμετέχουν άντρες: ο Δημήτρης (Δ), ο Κώστας (Κ), ο Μιχάλης (Μ) και γυναίκες:
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ ο : ΠΙΘΑΝΟΤΗΤΕΣ. Ένα τηλεοπτικό παιχνίδι παίζεται με ζεύγη αντιπάλων των δυο φύλων. Στο παιχνίδι συμμετέχουν άντρες: ο Δημήτρης (Δ), ο Κώστας (Κ), ο Μιχάλης (Μ) και γυναίκες:
Α Γυμνασίου, Μέρο Α : Αριθμητική Άλγεβρα, Κεφάλαιο 2 - Κλάσματα
 Α Γυμνασίου, Μέρο Α : Αριθμητική Άλγεβρα, Κεφάλαιο 2 - Κλάσματα Μαθηματικά Α Γυμνασίου Μέρο Α - Κεφάλαιο 2 Α. 2.1. Όταν ένα μέγεθο ή ένα σύνολο ομοειδών αντικειμένων χωρισθεί σε ν ίσα μέρη, το κάθε ένα
Α Γυμνασίου, Μέρο Α : Αριθμητική Άλγεβρα, Κεφάλαιο 2 - Κλάσματα Μαθηματικά Α Γυμνασίου Μέρο Α - Κεφάλαιο 2 Α. 2.1. Όταν ένα μέγεθο ή ένα σύνολο ομοειδών αντικειμένων χωρισθεί σε ν ίσα μέρη, το κάθε ένα
4.2 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ
 14 4 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ Ας υποθέσουμε ότι θέλουμε να βρούμε το πηλίκο και το υπόλοιπο της διαίρεσης του με τον Σύμφωνα με το γνωστό αλγόριθμο της διαίρεσης, το πηλίκο θα είναι ένας ακέραιος κ, τέτοιος,
14 4 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ Ας υποθέσουμε ότι θέλουμε να βρούμε το πηλίκο και το υπόλοιπο της διαίρεσης του με τον Σύμφωνα με το γνωστό αλγόριθμο της διαίρεσης, το πηλίκο θα είναι ένας ακέραιος κ, τέτοιος,
Διάλεξη 1 - Σημειώσεις 1
 Διάλεξη 1 - Σημειώσεις 1 Σύνολα Πως διαβάζουμε κάποιους συμβολισμούς: ανήκει και η άρνηση, δηλαδή δεν ανήκει υπάρχει για κάθε : τέτοιο ώστε. Επίσης το σύμβολο έχει την ερμηνεία «τέτοιο ώστε» και ή υπονοεί
Διάλεξη 1 - Σημειώσεις 1 Σύνολα Πως διαβάζουμε κάποιους συμβολισμούς: ανήκει και η άρνηση, δηλαδή δεν ανήκει υπάρχει για κάθε : τέτοιο ώστε. Επίσης το σύμβολο έχει την ερμηνεία «τέτοιο ώστε» και ή υπονοεί
i) Για να δείξουμε την επιθυμητή ισότητα, δείχνουμε πως A B {A x : x B} και πως {A x : x B} A B. Για τον πρώτο εγκλεισμό, έστω a A B, δηλάδη a A και a
 Θεωρία Συνόλων Χειμερινό Εξάμηνο 2016 2017 Λύσεις 1. Άσκηση 1.9 (σελ. 17), από τις σημειώσεις του Σκανδάλη. Εστω A, B δεδομένα σύνολα. Θα χρησιμοποιήσουμε τα αξιώματα αλλά αναφερόμενοι, αποκλειστικά, είτε
Θεωρία Συνόλων Χειμερινό Εξάμηνο 2016 2017 Λύσεις 1. Άσκηση 1.9 (σελ. 17), από τις σημειώσεις του Σκανδάλη. Εστω A, B δεδομένα σύνολα. Θα χρησιμοποιήσουμε τα αξιώματα αλλά αναφερόμενοι, αποκλειστικά, είτε
ΕΠΑΝΑΛΗΨΗ Β ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ
 ΕΠΑΝΑΛΗΨΗ Β ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό σας. ΚΕΦΑΛΑΙΟ 1 1. Να συμπληρώσετε
ΕΠΑΝΑΛΗΨΗ Β ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό σας. ΚΕΦΑΛΑΙΟ 1 1. Να συμπληρώσετε
Πέμπτη 8 εκεμβρίου 2016 Θεόδωρος Τζουραμάνης Επίκουρος Καθηγητής. ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ Τμήμα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστημάτων
 ιακριτά Μαθηματικά Ι https://www.icsd.aegean.gr/t.tzouramanis/courses/dm1 ttzouram@aegean.gr Πέμπτη 8 εκεμβρίου 2016 Θεόδωρος Τζουραμάνης Επίκουρος Καθηγητής ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ Τμήμα Μηχανικών Πληροφοριακών
ιακριτά Μαθηματικά Ι https://www.icsd.aegean.gr/t.tzouramanis/courses/dm1 ttzouram@aegean.gr Πέμπτη 8 εκεμβρίου 2016 Θεόδωρος Τζουραμάνης Επίκουρος Καθηγητής ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ Τμήμα Μηχανικών Πληροφοριακών
ΣΥΝΑΡΤΗΣΕΙΣ I. ΣΥΝΟΛΑ
 ΣΥΝΑΡΤΗΣΕΙΣ I. ΣΥΝΟΛΑ 1.Τι ονοµάζεται σύνολο; Σύνολο ονοµάζεται κάθε συλλογή αντικειµένων, που προέρχονται από την εµπειρία µας ή την διανόηση µας, είναι καλά ορισµένα και διακρίνονται το ένα από το άλλο.
ΣΥΝΑΡΤΗΣΕΙΣ I. ΣΥΝΟΛΑ 1.Τι ονοµάζεται σύνολο; Σύνολο ονοµάζεται κάθε συλλογή αντικειµένων, που προέρχονται από την εµπειρία µας ή την διανόηση µας, είναι καλά ορισµένα και διακρίνονται το ένα από το άλλο.
ΘΕΜΑ 2. βρείτε. (Μονάδες 15) με διαφορά ω.
 ΘΕΜΑ ΘΕΜΑ Έστω α, β πραγµατικοί αριθµοί για τους οποίους ισχύουν: α β = 4 και αβ + αβ = 0 α) Να αποδείξετε ότι: α + β = 5. (Μονάδες 0) β) Να κατασκευάσετε εξίσωση ου βαθµού µε ρίζες τους αριθµούς α, β
ΘΕΜΑ ΘΕΜΑ Έστω α, β πραγµατικοί αριθµοί για τους οποίους ισχύουν: α β = 4 και αβ + αβ = 0 α) Να αποδείξετε ότι: α + β = 5. (Μονάδες 0) β) Να κατασκευάσετε εξίσωση ου βαθµού µε ρίζες τους αριθµούς α, β
ΠΙΘΑΝΟΤΗΤΕΣ Α ΛΥΚΕΙΟΥ Ανδρεσάκης Δ. ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΠΙΘΑΝΟΤΗΤΕΣ
 ΛΓΕΡ ΛΥΚΕΙΟΥ ΠΙΘΝΟΤΗΤΕΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙ 1 Tα πειράματα των οποίων δεν μπορούμε εκ των προτέρων να προβλέψουμε το αποτέλεσμα, μολονότι επαναλαμβάνονται (φαινομενικά τουλάχιστον) κάτω από τις ίδιες συνθήκες
ΛΓΕΡ ΛΥΚΕΙΟΥ ΠΙΘΝΟΤΗΤΕΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙ 1 Tα πειράματα των οποίων δεν μπορούμε εκ των προτέρων να προβλέψουμε το αποτέλεσμα, μολονότι επαναλαμβάνονται (φαινομενικά τουλάχιστον) κάτω από τις ίδιες συνθήκες
Ας δούμε λίγο την θεωρία με την οποία ασχοληθήκαμε μέχρι τώρα.
 Ας δούμε λίγο την θεωρία με την οποία ασχοληθήκαμε μέχρι τώρα. Είδαμε τι είναι πρόβλημα, τι είναι αλγόριθμος και τέλος τι είναι πρόγραμμα. Πρέπει να μπορείτε να ξεχωρίζετε αυτές τις έννοιες και να αντιλαμβάνεστε
Ας δούμε λίγο την θεωρία με την οποία ασχοληθήκαμε μέχρι τώρα. Είδαμε τι είναι πρόβλημα, τι είναι αλγόριθμος και τέλος τι είναι πρόγραμμα. Πρέπει να μπορείτε να ξεχωρίζετε αυτές τις έννοιες και να αντιλαμβάνεστε
Παράδειγμα δομικής επαγωγής Ορισμός δομικής επαγωγής Συμβολοσειρές Γλώσσες Δυαδικά δένδρα Μαθηματικά Πληροφορικής 3ο Μάθημα Τμήμα Πληροφορικής και Τηλ
 Μαθηματικά Πληροφορικής 3ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Δομική επαγωγή Η ιδέα της μαθηματικής επαγωγής μπορεί να επεκταθεί και σε άλλες δομές εκτός από το σύνολο N
Μαθηματικά Πληροφορικής 3ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Δομική επαγωγή Η ιδέα της μαθηματικής επαγωγής μπορεί να επεκταθεί και σε άλλες δομές εκτός από το σύνολο N
"ΕΙΣΑΓΩΓΗ στις ΒΑΣΕΙΣ και στις ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ των ΜΑΘΗΜΑΤΙΚΩΝ Ι"
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΑΙ ΑΓΩΓΙΚΟ ΤΜΗΜΑ ΗΜΟΤΙΚΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΑΚΑ ΗΜΑΪΚΟ ΕΤΟΣ 2013-2014 Εαρινό Εξάµηνο Ρόδος, Μάιος 2014 ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑΤΙΚΩΝ, Ι ΑΚΤΙΚΗΣ και ΠΟΛΥΜΕΣΩΝ Μάθηµα: ΥΓ00003 "ΕΙΣΑΓΩΓΗ στις ΒΑΣΕΙΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΑΙ ΑΓΩΓΙΚΟ ΤΜΗΜΑ ΗΜΟΤΙΚΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΑΚΑ ΗΜΑΪΚΟ ΕΤΟΣ 2013-2014 Εαρινό Εξάµηνο Ρόδος, Μάιος 2014 ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑΤΙΚΩΝ, Ι ΑΚΤΙΚΗΣ και ΠΟΛΥΜΕΣΩΝ Μάθηµα: ΥΓ00003 "ΕΙΣΑΓΩΓΗ στις ΒΑΣΕΙΣ
ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 2015
 ΓΥΜΝΑΣΙΟ ΑΡΧ. ΜΑΚΑΡΙΟΥ Γ - ΠΛΑΤΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 014-015 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 015 ΒΑΘΜΟΣ : ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Αριθμητικά.. ΗΜΕΡΟΜΗΝΙΑ: 1/6/015 ΒΑΘΜΟΣ:... ΤΑΞΗ: Α Ολογράφως:... ΧΡΟΝΟΣ: ώρες
ΓΥΜΝΑΣΙΟ ΑΡΧ. ΜΑΚΑΡΙΟΥ Γ - ΠΛΑΤΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 014-015 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 015 ΒΑΘΜΟΣ : ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Αριθμητικά.. ΗΜΕΡΟΜΗΝΙΑ: 1/6/015 ΒΑΘΜΟΣ:... ΤΑΞΗ: Α Ολογράφως:... ΧΡΟΝΟΣ: ώρες
ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ 1 ο : Όριο Συνέχεια Συνάρτησης
 ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ ο : Όριο Συνέχεια Συνάρτησης Φυλλάδιο Φυλλάδι555 4 ο ο.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ ο : Όριο Συνέχεια Συνάρτησης Φυλλάδιο Φυλλάδι555 4 ο ο.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
Συνάρτηση f, λέγεται η διαδικασία µε βάση την. Παρατηρήσεις - Σχόλια f
 Συνάρτηση f, λέγεται η διαδικασία µε βάση την οποία σε κάθε στοιχείο χ ενός συνόλου Α αντιστοιχούµε ακριβώς ένα στοιχείο ενός άλλου συνόλου Β. Το σύνολο Α λέγεται πεδίο ορισµού ( ή σύνολο ορισµού ) της
Συνάρτηση f, λέγεται η διαδικασία µε βάση την οποία σε κάθε στοιχείο χ ενός συνόλου Α αντιστοιχούµε ακριβώς ένα στοιχείο ενός άλλου συνόλου Β. Το σύνολο Α λέγεται πεδίο ορισµού ( ή σύνολο ορισµού ) της
HY118-Διακριτά Μαθηματικά
 HY118-Διακριτά Μαθηματικά Παρασκευή, 02/03/2018 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 02-Mar-18
HY118-Διακριτά Μαθηματικά Παρασκευή, 02/03/2018 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 02-Mar-18
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου
 Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει να είναι σε θέση:
 Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει να είναι σε θέση: Να γνωρίζει: α. την έννοια του μιγαδικού αριθμού και β. πότε δύο μιγαδικοί αριθμοί είναι ίσοι. Να μπορεί να βρίσκει: α. το άθροισμα,
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει να είναι σε θέση: Να γνωρίζει: α. την έννοια του μιγαδικού αριθμού και β. πότε δύο μιγαδικοί αριθμοί είναι ίσοι. Να μπορεί να βρίσκει: α. το άθροισμα,
ΣΗΜΕΙΩΣΕΙΣ. Από προηγούμενες τάξεις γνωρίζουμε ότι το τετράγωνο οποιουδήποτε πραγματικού αριθμού
 ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i ΙΔΙΟΤΗΤΕΣ
ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i ΙΔΙΟΤΗΤΕΣ
N(F I G) = = N N(F ) N(I ) N(G)+N(FI ) + N(FG)+N(IG) N(FIG) = = = 200
 Διακριτά Μαθηματικά Ι Φροντιστήριο Αρχή Εγκλεισμού-Αποκλεισμού 1 / 9 Σε ένα σχολείο υπάρχουν 1000 μαθητές. Απ αυτούς οι 400 μιλάνε Γαλλικά, οι 300 Ιταλικά και 200 μιλάνε Γερμανικά. Εάν υπάρχουν 200 μαθητές,που
Διακριτά Μαθηματικά Ι Φροντιστήριο Αρχή Εγκλεισμού-Αποκλεισμού 1 / 9 Σε ένα σχολείο υπάρχουν 1000 μαθητές. Απ αυτούς οι 400 μιλάνε Γαλλικά, οι 300 Ιταλικά και 200 μιλάνε Γερμανικά. Εάν υπάρχουν 200 μαθητές,που
Θεωρία Υπολογισμού και Πολυπλοκότητα Μαθηματικό Υπόβαθρο
 Θεωρία Υπολογισμού και Πολυπλοκότητα Μαθηματικό Υπόβαθρο Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Σύνολα Συναρτήσεις και Σχέσεις Γραφήματα Λέξεις και Γλώσσες Αποδείξεις ΕΠΛ 211 Θεωρία
Θεωρία Υπολογισμού και Πολυπλοκότητα Μαθηματικό Υπόβαθρο Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Σύνολα Συναρτήσεις και Σχέσεις Γραφήματα Λέξεις και Γλώσσες Αποδείξεις ΕΠΛ 211 Θεωρία
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ. Το 1ο Θέμα στις πανελλαδικές εξετάσεις
 Επιμέλεια Καραγιάννης Β. Ιωάννης Σχολικός Σύμβουλος Μαθηματικών ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ Το ο Θέμα στις πανελλαδικές εξετάσεις Ερωτήσεις+Απαντήσεις
Επιμέλεια Καραγιάννης Β. Ιωάννης Σχολικός Σύμβουλος Μαθηματικών ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ Το ο Θέμα στις πανελλαδικές εξετάσεις Ερωτήσεις+Απαντήσεις
ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ. 3 2 x. β)
 ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ. Να λυθούν οι εξισώσεις και οι ανισώσεις : α) γ) x x 3x 7x 9 4 5 0 x x x 3 6 3 4 β) δ) 3x x 3 x 4 3 5 x x. 4 4 3 5 x. Να λυθούν οι εξισώσεις: α) 3x x 3 3 5x x β) 4 3 x x x 0
ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ. Να λυθούν οι εξισώσεις και οι ανισώσεις : α) γ) x x 3x 7x 9 4 5 0 x x x 3 6 3 4 β) δ) 3x x 3 x 4 3 5 x x. 4 4 3 5 x. Να λυθούν οι εξισώσεις: α) 3x x 3 3 5x x β) 4 3 x x x 0
Μαθηματικά: Αριθμητική και Άλγεβρα. Μάθημα 11 ο, Τμήμα Α. Γεωμετρία
 Μαθηματικά: ριθμητική και Άλγεβρα Μάθημα 11 ο, Τμήμα Γεωμετρία Η γεωμετρία σε σχέση με την άλγεβρα ή την αριθμητική έχει την εξής ιδιαιτερότητα: πρέπει να είμαστε πολύ ακριβείς στην περιγραφή μας (σκέψη
Μαθηματικά: ριθμητική και Άλγεβρα Μάθημα 11 ο, Τμήμα Γεωμετρία Η γεωμετρία σε σχέση με την άλγεβρα ή την αριθμητική έχει την εξής ιδιαιτερότητα: πρέπει να είμαστε πολύ ακριβείς στην περιγραφή μας (σκέψη
ΣΗΜΕΙΩΣΕΙΣ. Η έννοια του μιγαδικού Το σύνολο των μιγαδικών. Από προηγούμενες τάξεις γνωρίζουμε ότι το τετράγωνο οποιουδήποτε πραγματικού αριθμού
 ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i ΙΔΙΟΤΗΤΕΣ
ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i ΙΔΙΟΤΗΤΕΣ
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 14: Γραμματικές Χωρίς Συμφραζόμενα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Θεωρία Υπολογισμού Ενότητα 14: Γραμματικές Χωρίς Συμφραζόμενα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
αριθμούς Βασικές ασκήσεις Βασική θεωρία iii) φυσικοί; ii) ακέραιοι; iii) ρητοί;
 Πράξεις με πραγματικούς αριθμούς Βασικές ασκήσεις Βασική θεωρία Ρητοί και άρρητοι αριθμοί. α) Ποιοι αριθμοί ονομάζονται: iii) φυσικοί; ii) ακέραιοι; iii) ρητοί; iv) άρρητοι; v) πραγματικοί; β) Να βρείτε
Πράξεις με πραγματικούς αριθμούς Βασικές ασκήσεις Βασική θεωρία Ρητοί και άρρητοι αριθμοί. α) Ποιοι αριθμοί ονομάζονται: iii) φυσικοί; ii) ακέραιοι; iii) ρητοί; iv) άρρητοι; v) πραγματικοί; β) Να βρείτε
Να επιλύουμε και να διερευνούμε γραμμικά συστήματα. Να ορίζουμε την έννοια του συμβιβαστού και ομογενούς συστήματος.
 Ενότητα 2 Γραμμικά Συστήματα Στην ενότητα αυτή θα μάθουμε: Να επιλύουμε και να διερευνούμε γραμμικά συστήματα. Να ορίζουμε την έννοια του συμβιβαστού και ομογενούς συστήματος. Να ερμηνεύουμε γραφικά τη
Ενότητα 2 Γραμμικά Συστήματα Στην ενότητα αυτή θα μάθουμε: Να επιλύουμε και να διερευνούμε γραμμικά συστήματα. Να ορίζουμε την έννοια του συμβιβαστού και ομογενούς συστήματος. Να ερμηνεύουμε γραφικά τη
2. Να γράψετε έναν αριθμό που είναι μεγαλύτερος από το 3,456 και μικρότερος από το 3,457.
 1. Ένα κεφάλαιο ενός βιβλίου ξεκινάει από τη σελίδα 32 και τελειώνει στη σελίδα 75. Από πόσες σελίδες αποτελείται το κεφάλαιο; Αν το κεφάλαιο ξεκινάει από τη σελίδα κ και τελειώνει στη σελίδα λ, από πόσες
1. Ένα κεφάλαιο ενός βιβλίου ξεκινάει από τη σελίδα 32 και τελειώνει στη σελίδα 75. Από πόσες σελίδες αποτελείται το κεφάλαιο; Αν το κεφάλαιο ξεκινάει από τη σελίδα κ και τελειώνει στη σελίδα λ, από πόσες
α Α και α Β, β Α και β Β, γ Α και γ Β, δ Α και δ Β, ε Α και ε Β, ζ Β και ζ Β, η Α και η Β, θ Α και θ Β.
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2017-2018 Χειμερινό Εξάμηνο Ρόδος, Νοέμβριος 2017 ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑΤΙΚΩΝ, ΔΙΔΑΚΤΙΚΗΣ και ΠΟΛΥΜΕΣΩΝ Μάθημα: ΥΓ00003 "ΕΙΣΑΓΩΓΗ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2017-2018 Χειμερινό Εξάμηνο Ρόδος, Νοέμβριος 2017 ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑΤΙΚΩΝ, ΔΙΔΑΚΤΙΚΗΣ και ΠΟΛΥΜΕΣΩΝ Μάθημα: ΥΓ00003 "ΕΙΣΑΓΩΓΗ
y x y x+2y=
 ΜΕΡΟΣ Α 3.1 Η ΕΝΝΟΙΑ ΤΗΣ ΓΡΑΜΜΙΚΗΣ ΕΞΙΣΩΣΗΣ 59 3. 1 Η ΕΝΝΟΙΑ ΤΗΣ ΓΡΑΜΜΙΚΗΣ ΕΞΙΣΩΣΗΣ Η εξίσωση α+β=γ Λύση μιας εξίσωσης α + β = γ ονομάζεται κάθε ζεύγος αριθμών (, ) που την επαληθεύει. Για παράδειγμα η
ΜΕΡΟΣ Α 3.1 Η ΕΝΝΟΙΑ ΤΗΣ ΓΡΑΜΜΙΚΗΣ ΕΞΙΣΩΣΗΣ 59 3. 1 Η ΕΝΝΟΙΑ ΤΗΣ ΓΡΑΜΜΙΚΗΣ ΕΞΙΣΩΣΗΣ Η εξίσωση α+β=γ Λύση μιας εξίσωσης α + β = γ ονομάζεται κάθε ζεύγος αριθμών (, ) που την επαληθεύει. Για παράδειγμα η
Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ. (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα.
 Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα. (2) Ποιοι είναι οι άρτιοι και ποιοι οι περιττοί αριθμοί; Γράψε από τρία παραδείγματα.
Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα. (2) Ποιοι είναι οι άρτιοι και ποιοι οι περιττοί αριθμοί; Γράψε από τρία παραδείγματα.
Μαθηματικά Α Γυμνασίου
 Μαθηματικά Α Γυμνασίου Επαναληπτικές ασκήσεις Στέλιος Μιχαήλογλου Ασκήσεις. Δίνεται η παράσταση 7 : α) Να αποδείξετε ότι Α=8. β) Ο αριθμός Α είναι πρώτος ή σύνθετος; γ) Να αναλύσετε τον αριθμό Α σε γινόμενο
Μαθηματικά Α Γυμνασίου Επαναληπτικές ασκήσεις Στέλιος Μιχαήλογλου Ασκήσεις. Δίνεται η παράσταση 7 : α) Να αποδείξετε ότι Α=8. β) Ο αριθμός Α είναι πρώτος ή σύνθετος; γ) Να αναλύσετε τον αριθμό Α σε γινόμενο
Ερωτήσεις-Απαντήσεις Θεωρίας
 1 ΓΙΑΝΝΗΣ ΚΑΡΑΓΙΑΝΝΗΣ Σχολικός Σύμβουλος Μαθηματικών ΕΡΩΤΗΣΕΙΣ-ΑΠΑΝΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΕΡΟΣ Β 2 ΕΡΩΤΗΣΕΙΣ-ΑΠΑΝΤΗΣΕΙΣ
1 ΓΙΑΝΝΗΣ ΚΑΡΑΓΙΑΝΝΗΣ Σχολικός Σύμβουλος Μαθηματικών ΕΡΩΤΗΣΕΙΣ-ΑΠΑΝΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΕΡΟΣ Β 2 ΕΡΩΤΗΣΕΙΣ-ΑΠΑΝΤΗΣΕΙΣ
Επιμέλεια: Σπυρίδων Τζινιέρης-ΘΕΩΡΙΑ ΚΛΑΣΜΑΤΩΝ ΓΙΑ ΤΗΝ Α ΓΥΜΝΑΣΙΟΥ ΘΕΩΡΙΑ ΚΛΑΣΜΑΤΩΝ Α ΓΥΜΝΑΣΙΟΥ
 Τι είναι κλάσμα; Κλάσμα είναι ένα μέρος μιας ποσότητας. ΘΕΩΡΙΑ ΚΛΑΣΜΑΤΩΝ Α ΓΥΜΝΑΣΙΟΥ Κλάσμα είναι ένας λόγος δύο αριθμών(fraction is a ratio of two whole numbers) Πως εκφράζετε συμβολικά ένα κλάσμα; Εκφράζετε
Τι είναι κλάσμα; Κλάσμα είναι ένα μέρος μιας ποσότητας. ΘΕΩΡΙΑ ΚΛΑΣΜΑΤΩΝ Α ΓΥΜΝΑΣΙΟΥ Κλάσμα είναι ένας λόγος δύο αριθμών(fraction is a ratio of two whole numbers) Πως εκφράζετε συμβολικά ένα κλάσμα; Εκφράζετε
ΣΤ ΕΝΟΤΗΤΑ. Βασικές έννοιες των συναρτήσεων. ΣΤ.1 (6.1 παρ/φος σχολικού βιβλίου) ΣΤ.2 (6.2 παρ/φος σχολικού βιβλίου)
 ΣΤ ΕΝΟΤΗΤΑ Βασικές έννοιες των συναρτήσεων ΣΤ. (6. παρ/φος σχολικού βιβλίου) Η έννοια της συνάρτησης ΣΤ. (6. παρ/φος σχολικού βιβλίου) Γραφική παράσταση συνάρτησης ΣΤ.3 (6.3 παρ/φος σχολικού βιβλίου) Η
ΣΤ ΕΝΟΤΗΤΑ Βασικές έννοιες των συναρτήσεων ΣΤ. (6. παρ/φος σχολικού βιβλίου) Η έννοια της συνάρτησης ΣΤ. (6. παρ/φος σχολικού βιβλίου) Γραφική παράσταση συνάρτησης ΣΤ.3 (6.3 παρ/φος σχολικού βιβλίου) Η
1 ΘΕΩΡΙΑΣ...με απάντηση
 1 ΘΕΩΡΙΑΣ.....με απάντηση ΑΛΓΕΒΡΑ Κεφάλαιο 1 0 Εξισώσεις Ανισώσεις 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση που περιέχει πράξεις μεταξύ αριθμών.
1 ΘΕΩΡΙΑΣ.....με απάντηση ΑΛΓΕΒΡΑ Κεφάλαιο 1 0 Εξισώσεις Ανισώσεις 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση που περιέχει πράξεις μεταξύ αριθμών.
( ) ( ) Τοα R σημαίνει ότι οι συντελεστές δεν περιέχουν την μεταβλητή x. αντικ σταση στο που = α. [ ο αριθµ ός πουτο µηδεν ίζει
 μέρος πρώτο v v 1 v 1 Γενική μορφή πολυωνύμου: ( ) 1 1 Όροι του ( ) v v v P = a v + av 1 + av +... + a + a 1 + a, ν Ν, α ν R Τοα R σημαίνει ότι οι συντελεστές δεν περιέχουν την μεταβλητή. P : a, a, a,...,
μέρος πρώτο v v 1 v 1 Γενική μορφή πολυωνύμου: ( ) 1 1 Όροι του ( ) v v v P = a v + av 1 + av +... + a + a 1 + a, ν Ν, α ν R Τοα R σημαίνει ότι οι συντελεστές δεν περιέχουν την μεταβλητή. P : a, a, a,...,
Μαθηματικα Γ Γυμνασιου
 Μαθηματικα Γ Γυμνασιου Θεωρια και παραδειγματα livemath.eu σελ. απο 9 Περιεχομενα Α ΜΕΡΟΣ: ΑΛΓΕΒΡΑ ΚΑΙ ΠΙΘΑΝΟΤΗΤΕΣ 4 ΣΥΣΤΗΜΑΤΑ Χ 4 ΜΟΝΩΝΥΜΑ & ΠΟΛΥΩΝΥΜΑ 5 ΜΟΝΩΝΥΜΑ 5 ΠΟΛΥΩΝΥΜΑ 5 ΡΙΖΑ ΠΟΛΥΩΝΥΜΟΥ 5 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ
Μαθηματικα Γ Γυμνασιου Θεωρια και παραδειγματα livemath.eu σελ. απο 9 Περιεχομενα Α ΜΕΡΟΣ: ΑΛΓΕΒΡΑ ΚΑΙ ΠΙΘΑΝΟΤΗΤΕΣ 4 ΣΥΣΤΗΜΑΤΑ Χ 4 ΜΟΝΩΝΥΜΑ & ΠΟΛΥΩΝΥΜΑ 5 ΜΟΝΩΝΥΜΑ 5 ΠΟΛΥΩΝΥΜΑ 5 ΡΙΖΑ ΠΟΛΥΩΝΥΜΟΥ 5 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ. 8. Πότε το γινόμενο δύο ή περισσοτέρων αριθμών παραγόντων είναι ίσο με το μηδέν ;
 ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ( ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ) ΠΑΡΑΤΗΡΗΣΗ : Το κεφάλαιο αυτό περιέχει πολλά θέματα που είναι επανάληψη εννοιών που διδάχθηκαν στο Γυμνάσιο γι αυτό σ αυτές δεν θα επεκταθώ αναλυτικά
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ( ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ) ΠΑΡΑΤΗΡΗΣΗ : Το κεφάλαιο αυτό περιέχει πολλά θέματα που είναι επανάληψη εννοιών που διδάχθηκαν στο Γυμνάσιο γι αυτό σ αυτές δεν θα επεκταθώ αναλυτικά
Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ
 Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ (Α ΜΕΡΟΣ: ΣΥΝΑΡΤΗΣΕΙΣ) Μαθηματικά Προσανατολισμού Γ Λυκείου- Μαθηματικός Περιηγητής ΕΝΟΤΗΤΑ
Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ (Α ΜΕΡΟΣ: ΣΥΝΑΡΤΗΣΕΙΣ) Μαθηματικά Προσανατολισμού Γ Λυκείου- Μαθηματικός Περιηγητής ΕΝΟΤΗΤΑ
ΤΑΞΗ Β ΜΑΘΗΜΑΤΙΚΑ ΚΕΦΑΛΑΙΟ 0 ΟΔΗΓΟΣ ΕΠΑΝΑΛΗΨΗΣ α α (ii)
 ΤΑΞΗ Β ΜΑΘΗΜΑΤΙΚΑ ΚΕΦΑΛΑΙΟ ΟΔΗΓΟΣ ΕΠΑΝΑΛΗΨΗΣ 1-13 1 Ποιοι αριθμοί ονομάζονται ομόσημοι και ποιοι ετερόσημοι; 1 Δίνονται οι αριθμοί: 1,,.1,,, 9, + 3, 3 3.1 Ποιοι από αυτούς είναι θετικοί και ποιοι αρνητικοί;.
ΤΑΞΗ Β ΜΑΘΗΜΑΤΙΚΑ ΚΕΦΑΛΑΙΟ ΟΔΗΓΟΣ ΕΠΑΝΑΛΗΨΗΣ 1-13 1 Ποιοι αριθμοί ονομάζονται ομόσημοι και ποιοι ετερόσημοι; 1 Δίνονται οι αριθμοί: 1,,.1,,, 9, + 3, 3 3.1 Ποιοι από αυτούς είναι θετικοί και ποιοι αρνητικοί;.
6.1 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ
 6. Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ ΘΕΩΡΙΑ. Ορισµός της συνάρτησης Συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β λέγεται µια διαδικασία (κανόνας τρόπος ), µε την οποία κάθε στοιχείο του συνόλου Α αντιστοιχίζεται σε
6. Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ ΘΕΩΡΙΑ. Ορισµός της συνάρτησης Συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β λέγεται µια διαδικασία (κανόνας τρόπος ), µε την οποία κάθε στοιχείο του συνόλου Α αντιστοιχίζεται σε
ΠΑΡΑΓΡΑΦΟΣ 1. 2 ΠΡΟΣΘΕΣΗ ΑΦΑΙΡΕΣΗ ΚΑΙ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ
 ΠΑΡΑΓΡΑΦΟΣ 1. 2 ΠΡΟΣΘΕΣΗ ΑΦΑΙΡΕΣΗ ΚΑΙ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ ΑΣΚΗΣΕΙΣ ΜΕ ΑΘΡΟΙΣΜΑΤΑ ΚΑΙ ΑΦΑΙΡΕΣΕΙΣ ( 1 ) Να υπολογίσετε τις παραστάσεις Α = 3 + 23 + 19 Β = 8 +13 +45-7 Γ = 3 + 0 Α = 3+23 +19 =
ΠΑΡΑΓΡΑΦΟΣ 1. 2 ΠΡΟΣΘΕΣΗ ΑΦΑΙΡΕΣΗ ΚΑΙ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ ΑΣΚΗΣΕΙΣ ΜΕ ΑΘΡΟΙΣΜΑΤΑ ΚΑΙ ΑΦΑΙΡΕΣΕΙΣ ( 1 ) Να υπολογίσετε τις παραστάσεις Α = 3 + 23 + 19 Β = 8 +13 +45-7 Γ = 3 + 0 Α = 3+23 +19 =
a. a + b = 3. b. a διαιρεί τ ο b. c. a - b = 0. d. ΜΚΔ(a, b) = 1. e. ΕΚΠ(a, b) = 6.
 ΗΥ118 Διακριτά Μαθηματικά Εαρινό Εξάμηνο 2016 4 η Σειρά Ασκήσεων - Λύσεις Άσκηση 4.1 [1 μονάδα] Βρείτε όλα τα διατεταγμένα ζεύγη στη σχέση R από το Α={0,1,2,3} στο Β={0,1,2,3,4} όπου (a,b) R αν και μόνο
ΗΥ118 Διακριτά Μαθηματικά Εαρινό Εξάμηνο 2016 4 η Σειρά Ασκήσεων - Λύσεις Άσκηση 4.1 [1 μονάδα] Βρείτε όλα τα διατεταγμένα ζεύγη στη σχέση R από το Α={0,1,2,3} στο Β={0,1,2,3,4} όπου (a,b) R αν και μόνο
ΣΥΝΑΡΤΗΣΕΙΣ. H Εννοια του διανυσματος. Σ υ ν ο λ α - Ο ρ ι σ μ ο ι
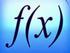 ΣΥΝΑΡΤΗΣΕΙΣ Σ υ ν ο λ α - Ο ρ ι σ μ ο ι Συνολο λεγεται καθε συλλογη 3. Να δειχτει αντικειμενων, οτι α + 0 που προερχονται 0α. Ποτε ισχυει απ την το εμπειρια ισον; μας η τη διανοηση 3 3. μας, Aν α, ειναι
ΣΥΝΑΡΤΗΣΕΙΣ Σ υ ν ο λ α - Ο ρ ι σ μ ο ι Συνολο λεγεται καθε συλλογη 3. Να δειχτει αντικειμενων, οτι α + 0 που προερχονται 0α. Ποτε ισχυει απ την το εμπειρια ισον; μας η τη διανοηση 3 3. μας, Aν α, ειναι
Α) Να γράψετε με τη βοήθεια των πράξεων των συνόλων το ενδεχόμενο που παριστάνει το σκιασμένο εμβαδόν σε καθένα από τα παρακάτω διαγράμματα Venn.
 Άσκηση 1 Α) Να γράψετε με τη βοήθεια των πράξεων των συνόλων το ενδεχόμενο που παριστάνει το σκιασμένο εμβαδόν σε καθένα από τα παρακάτω διαγράμματα Venn. B) Αν ( ), ( ), ( ), να εκφράσετε τις πιθανότητες
Άσκηση 1 Α) Να γράψετε με τη βοήθεια των πράξεων των συνόλων το ενδεχόμενο που παριστάνει το σκιασμένο εμβαδόν σε καθένα από τα παρακάτω διαγράμματα Venn. B) Αν ( ), ( ), ( ), να εκφράσετε τις πιθανότητες
ΕΠΑΝΑΛΗΨΗ. Μαθηματικών Α Γυμνασίου. Μαριλένα Νικολαΐδου-Μουσουλίδου
 ΕΠΑΝΑΛΗΨΗ Μαθηματικών Α Γυμνασίου ΑΡΙΘΜΟΙ Σύνολο είναι μια καλώς ορισμένη συλλογή διαφορετικών μεταξύ τους αντικειμένων. Τα αντικείμενα που αποτελούν ένα σύνολο λέγονται στοιχεία ή μέλη του συνόλου. Για
ΕΠΑΝΑΛΗΨΗ Μαθηματικών Α Γυμνασίου ΑΡΙΘΜΟΙ Σύνολο είναι μια καλώς ορισμένη συλλογή διαφορετικών μεταξύ τους αντικειμένων. Τα αντικείμενα που αποτελούν ένα σύνολο λέγονται στοιχεία ή μέλη του συνόλου. Για
