Respuesta temporal de sistemas. Prof. Mª Jesús de la Fuente ISA-UVA
|
|
|
- Χαρικλώ Γούναρης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Repuea empoal de iema Pof. Mª Jeú de la Fuee ISA-UVA
2 Cocepo Repuea empoal de iema de pime ode Repuea empoal de iema de egudo ode Ioducció a la ideificació de iema Repuea de iema de ode upeio Nocioe de eabilidad ISA-UVA
3 Baado e modelo Aálii Dieño Cool La caaceíica de la epuea del iema e deduce del modelo El poceo o el coolado e dieña uado el modelo y la epecificacioe El modelo e ua explíciamee e el coolado paa el cálculo de la eñal de cool ISA-UVA 3
4 Repuea empoal Señale omalizada 1 Tiempo Tafomada e iempo 3 Deduci la caaceíica de la epuea e iempo del iema diecamee de la fució de afeecia G() Ideificació: ifei el modelo (G()) a pai de dao expeimeale (dao de eada u() y alida y()). ISA-UVA 4
5 Siema de pime ode τ dy() d u0 q F y() 0 h Ku() u()u dh τ h d A h0 τ k Kq K h k ISA-UVA 5 Fució de afeecia: U() K τ 1 Repuea a ua eada alo e u() dede el equilibio 0 Y()
6 Repuea a u alo e u τ dy() d y() Ku() U() K τ 1 Y() Y() paa paa 1 τ Y() y() ( τ 1) ( 1 τ) 0 K u Ku 1 1 Ku( ); 1 τ Ku(1 e τ ) τ K Ku τ α τ τ; u β α β 1 τ y() τ; α L 1 Ku Compobació: β Ku [ Y() ] α( 1 τ) ( 1 τ) Ku L β ( 1 τ) 1 L 1 1 ISA-UVA 6 1 e τ Ku τ τ 1 Ku(1 e τ τ ) Ku
7 Repuea a u alo e u τ dy() d y() Ku() U() K τ 1 Y() y() Ku(1 e τ τ > 0 coae de iempo Repuea eable, i eado i cambio de cocavidad y obeamoiguada Gaacia K Ku/u ) y() u Ku ISA-UVA 7
8 Iepeació e y() Ku(1 e τ ) U() K τ 1 Y() Plao x τ 10 polo -1/τ polo e la pae eal izquieda del plao y() Ku Si τ > 0 Repuea eable, i cambio de cocavidad y obeamoiguada ISA-UVA 8
9 Eabilidad Eada-Salida BIBO eable U() G() Y() ieable U iema e eable eada-alida cuado a ua eada acoada le coepode ua alida acoada ISA-UVA 9
10 Iepeació e (τ<0) y() Ku(1 e τ ) U() K τ 1 Y() Plao τ 10 polo -1/τ poiivo y() x polo e la pae eal deecha del plao Si τ < 0 Repuea ieable ISA-UVA 10
11 Oo ipo de eada Ejemplo: Impulo U() K τ 1 Y() Y() y() L ( τ 1) ( 1 τ) 1 K Ku y() e τ [ Y() ] τ u K τ Ku L τ 1 u 1 1 τ La eabilidad viee deemiada po la poició del polo, o po el ipo de eada ISA-UVA 11
12 Tiempo de aeamieo Plao x -1/τ 1-1/τ x U() K τ 1 Y() y() 0.95Ku y( τ y() Ku(1 e τ ) 95 τ ) 0.95Ku Ku(1 e ) 95 τ 1 < τ ISA-UVA 1
13 Coae de iempo y() y( τ) Ku(1 Ku(1 e e τ 1 Deivada e el oige d y() d d y() d 0 Ku (e τ Ku τ τ ) ) ) 0.63Ku 0.63Ku y() U() τ Ku τ K τ 1 SyQuake Y() ep Ku ISA-UVA 13
14 Ideificació El modelo e obiee a pai de dao expeimeale de eada-alida del poceo U U Poceo Y Y Modelo ISA-UVA 14
15 Ideificació u() u Si la epuea dede el equilibio a u alo u e u() e como la figua iema de pime ode Eimació de paámeo: K y/ u τ do méodo 0.63 y y() y() y τ ISA-UVA 15
16 Siema de egudo ode d x d d x d y 1 a a x x 1 [ c c ] 1 C Ai () F() a a 1 14 x x 1 b b b b u U() Reaco ioémico C B () Kω δω ω A B C A C Ai C B A Y() F ISA-UVA 16
17 Siema de egudo ode d δω ωy() Kω y() d dy() d u() A B C Ai U() Kω δω ω Y() C B u()u u0 0 Repuea a ua eada alo e u() K gaacia δ amoiguamieo ω fecuecia popia o amoiguada ISA-UVA 17
18 Siema de egudo ode U() Kω δω ω Y() Polo: i δω δω ω > 0 ω ± 4δ 0 ω 4ω i δ 1 aice eale egaiva i δ < 1 aice compleja cojugada δω δω ± jω ISA-UVA 18 ± ω 1 δ δ 1
19 Repuea a u alo e u, δ >1 a δω b δω ω ω δ δ 1 1 U() Kab ( a)( b) Y() Y() paa paa paa ( a)( b) 0 a -b Kab u α Kabu αab a α( a)( b) β( b) γ( a) ( a)( b) ( a)( b) ( a)( b) β α Kabu β( a)( a b) Kabu γ(-b)(-b a) γ b Ku β Kub /(a b) γ Kua/(a - b) δ δ 1 Ku δ 1 δ δ 1 Ku δ 1 ISA-UVA 19
20 Repuea a u alo e u, δ >1 a δω b δω ω ω δ δ 1 1 U() Kab ( a)( b) Y() K 1 1 ( 1)( 1) a b Y() y() y(0) α ( L 0 1 [ Y() ] y() α βe β a γ ); a b 1 α L L γe y( ) b 1 β L a 1 γ b δ δ 1 a Ku(1 e δ 1 Ku fució moóoa coae de iempo 1/a, 1/b δ δ 1 e δ 1 ceciee b ) ISA-UVA 0
21 Repuea a u alo e u, δ >1 a δω b δω ω ω δ δ 1 1 U() Kab ( a)( b) Y() K 1 1 ( 1)( 1) a b y() α βe a γe b Ku(1 δ δ 1 e δ 1 a δ δ 1 e δ 1 b ) Repuea eable, i eado co cambio de cocavidad y obeamoiguada Gaacia K Ku/u y() Ku u ISA-UVA 1
22 Plao -b x polo e la pae eal izquieda del plao Iepeació e U() El polo ma a la deecha domia e la deapaició del aioio -a x Kab ( a)( b) y() Y() y() α βe u a γe b epx P. Domiae cocavidad SyQuake Ku ISA-UVA
23 Ideificació u() u Si la epuea dede el equilibio a u alo u e u() e como la figua iema de egudo ode co aice eale y() Eimació de paámeo: K y/ u coae de iempo difícile de eima y() y ISA-UVA 3
24 Apoximació y() Kab ( a)( b) Ke d τ 1 d La epuea del iema de egudo ode puede apoximae po la de uo de pime ode ma u eado ISA-UVA 4
25 Ideificació co u alo e u g de máxima pediee y valo eacioaio y Κ y/u d τ u u d Ke τ 1 ISA-UVA 5
26 Ideificació de FOPD Ke d τ 1 y() Ku(1 e d τ ) y() Evaluado la epuea paa iae de iempo 1 dτ y dτ/3 : d 1 y() y() Ku(1 Ku(1 e e 1 1/ 3 ) 0.63Ku ) 0.83Ku Tomado medida de 1 dτ y dτ/3 puede calculae d y τ ISA-UVA 6
27 Ideificació co u alo e u y 0.63y 0.83y y τ 1.5 ( - 1 ) d - τ Κ y/u 1 u u d Ke τ 1 Poblema03 ISA-UVA 7
28 Cambiado de calo Te e lazo abieo ISA-UVA 8
29 Cambiado de calo K ( )/ d 0.75 τ 1.4 ISA-UVA 9
30 Repuea a u alo e u, δ 1 U() Ka ( a) Y() a δω Y() Ka u α β ( a) a ( a) γ α( a) ( a) β( a) ( a) γ ( a) paa 0 Ka u αa α Ku paa paa a a Ka Ka u u γ( a) Ku4a βa γ Kua Kua Kuδω β -Ku ISA-UVA 30
31 Repuea a u alo e u, δ 1 Y() y() y() y(0) α ( L L [ Y() ] α βe β a α L a Ku(1 e γe a 1 y( ) γ ( a) a δω β Ku L a e ); a ) 1 U() γ ( a) y() Ka ( a) Y() a δω Ku Fució moóoa ceciee u ISA-UVA 31
32 Repuea a u alo e u, δ <1 Y() y() -1 L Kω δω ω [ Y() ] u Ku δ e U() δω e( ω Kω δω ω 1 δ φ) Y() φ acg 1 δ δ y() Si δω >0 Repuea eable, i eado y ubamoiguada ISA-UVA 3
33 w ISA-UVA 33
34 Repuea a u alo e u, δ <1 U() Kω δω ω Y() 1 δω y() Ku 1 e e( ω 1 δ φ) 1 δ y(0) 0; y( ) Ku; Gaacia : Ku/u K φ acg 1 δ δ Fecuecia de ocilació : y() ω d ω 1 δ Ku ISA-UVA 34
35 y() d y() d d y() d Ku 1 p 0 Ku 1 δ 1 1 δ e [ ] δω δω δω e e( ω 1 δ φ) e co( ω 1 δ φ) ω 1 δ δω Tiempo de pico e( ω 1 δ φ) ; φ acg 1 δ δ p Tiempo que acue haa el pime máximo y() p Ku ISA-UVA 35
36 Tiempo de pico d y() d d y() d δω g( ω ω e p δω 1 δ p Ku 1 δ ω p 1 δ e( ω p 0 p ± π π [ δω ω δ φ ω δ φ ω δ ] δω δω e e( 1 ) e co( 1 ) 1 1 δ φ) 1 δ π ω d p 1 δ δ φ) e δω g( φ) y() p co( ω 1 δ p p φ) ω 1 δ ISA-UVA 36 Ku g e( π φ) eφ co( π φ) coφ
37 Sobepico y() M M p p 1 δω Ku 1 e e( ω 1 δ 1 δ y( p ) Ku 100 e % p Ku ω π δω 100 ω 1 δ e e( π φ) 1 δ δ e πδ 1 δ 1 δ y() φ) π 1 δ δ e πδ 1 δ φ acg e( φ) 1 δ δ M p 100e πδ 1 δ e % p Ku ISA-UVA 37
38 Tiempo de aeamieo y() Ku Ku Ku 1 max al que 1 1 δ 1 1 δ 1 e 1 δ δω e e e( ω δω δω e( ω e( ω 1 δ φ) 1 δ 1 δ φ acg φ) φ) δ δ Ecuació implícia Apoximadamee: y() ± 5% 3 5 L δω δω Ku ISA-UVA 38
39 Iepeació e Plao x ω 1 δ U() Polo: Kω δω ω δω Y() ± jω 1 δ δω x y() polo complejo cojugado co la pae eal e el emiplao izquiedo ISA-UVA 39
40 Iepeació e Polo: δω ± jω 1 δ Plao x δω x β ω 1 δ y() 3 5 L δω δω g( β) δ 1 δ M ω p p d ω 1 δ ω 100e π 1 δ πδ 1 δ π ω d e % polo complejo cojugado co la pae eal e el emiplao izquiedo ep ISA-UVA 40
41 Iepeació e ω 1 δ x y() i Ku 1 δω < 0 1 δω e e( ω 1 δ iema ieable 1 δ φ) Plao δω x y() U() Kω δω ω Y() ISA-UVA 41
42 Ideificació u() u Si la epuea dede el equilibio a u alo u e u() e como la figua iema de egudo ode co aice compleja cojugada y() p y Kω δω ω Poblema56 Eimació de paámeo: K y/ u M ISA-UVA 4 p p 100e ω π πδ 1 δ 1 δ e % π ω d
43 Repuea a u alo e u, δ 0 Kω Y() ω y() L -1 u π [ Y() ] Ku 1 e( ω ) U() Kω ω Y() Como δ 0 la epuea o e amoigua uca. Repuea e el límie de la eabilidad y() ISA-UVA 43 Ku
44 Iepeació e jω x Plao Kω ω y() polo: ω -1 π L ) 0 ± jω [ Y() ] Ku 1 e( ω jω x y() Polo obe el eje imagiaio: límie de eabilidad ep SyQuake Ku ISA-UVA 44
45 Polo e el oige: Iegadoe U() Ka ( a) Y() Y() paa paa paa Ku ( a) 0 a a Ka u α β Kau βa Kau γa Kau αa αa Ku Ku α( a) β( a) ( a) ( a) a γ ( a) Ku βa γa γ β γ Ku / a α -Ku / a Repuea a u alo u e la eada ISA-UVA 45
46 ISA-UVA 46 Polo e el oige: Iegadoe ( ) a a e a 1 a 1 Ku e y() a L L L [Y()] L y() a u a Ka Y() γ β α γ β α γ β α a) ( Ka U() Y() y() Plao x SyQuake epx
47 Polo e el oige: Iegadoe Eada: Impulo u U() Ka ( a) Y() Y() y() L ( a) 1 Ka u [Y()] Ku 1 a [ e ] y() x Plao Ku Límie de eabilidad: depede de la eada ISA-UVA 47
48 Siema de ode upeio U() G() Y() epx Y() y() y() α ( L L 1 1 [ Y() ] α βe β a α L a 1 γe γ b b β υ ( b) L a υe 1 b... γ... e L b δω σ δω 1 υ ( b) ω...);... L e( ω 1 δ φ)... 1 σ δω ω... La eabilidad y ipo de epuea la deemia lo polo. Lo ceo modifica la foma de la epuea peo o la eabilidad ISA-UVA 48
49 Efeco de ceo obe la epuea 1 G ()( 1) G() c 1 c G() La epuea a la mima eada del iema co u ceo e -c, e obiee umado a la epuea del iema i ceo u deivada muliplicada po u faco 1/c ISA-UVA 49
50 Efeco de ceo obe la epuea u y() d y() d 1/c Co c > 0, e adelaa la epuea. No poduce ocilacioe i la epuea i ceo o la iee, peo puede poduci obepico -c -b x -a x Plao ceo e la pae eal izquieda del plao ISA-UVA 50
51 Efeco de ceo obe la epuea u y() Co c < 0, e poduce ua epuea ivea iicialmee (fae o-míima) d y() d 1/c Plao -b -a -c x x ceo e la pae eal deecha del plao ISA-UVA 51
52 Iepeació de lo ceo U() 1 (ak 1) - Y() epceo K (b 1) K1 K () U() (a 1) (b 1) K 1(b 1) K(a 1) U() (a 1)(b 1) (K1b Ka) (K1 K (a 1)(b 1) Y ) U() Se geea u ceo como eulado de do efeco difeee de la mima caua. Si lo efeco o de eido coaio puede apaece u ceo ieable ISA-UVA 5
53 Cambiado de calo ISA-UVA 53
54 Reaco Ioemo d c d d c d A B c 0.33 c A B F 0 c Ai C Ai A A B F C A C B C Ai () F() i i C B () ISA-UVA 54
55 Malab ISA-UVA 55
56 Caio ISA-UVA 56
57 Do depoio h1 q u Puo de opeació: q17.8 l/m u 70 % F l/m h0 4 m A10. dm A10. dm F() h LT U() 0.16 (1.01 1)(1.14 1) % m H () F ISA-UVA 57
58 Ideificació El modelo e obiee a pai de dao expeimeale de eada-alida del poceo U U Poceo Y Y Modelo ISA-UVA 58
59 Meodología de la ideificació Coocimieo pevio y dieño de expeimeo Toma de dao expeimeale Aálii y aamieo de dao Selecció del ipo de modelo Eimació de paámeo Validació del modelo ISA-UVA 59
60 Ideificació po epuea alo u Do expeimeo: Cambio e u co F ce. Cambio e F co u ce. Ajue co fucioe de pime ode h F LT H H d 0.71 K qe 0.17e () U() U() τq K f 0.5 () F() F() τ f ISA-UVA 60
61 Míimo cuadado Cieio de eimació: Dado u cojuo de dao expeimeale u(), y(), buca lo paámeo del modelo, θ, que miimiza la fució de coe V : N N 1 1 V e () ( () m (, ) N N u 1 1 Poceo [ y y θ ] v y e() Modelo ISA-UVA 61 y m
62 Caio ISA-UVA 6
63 Cambiado de calo (LS) ISA-UVA 63
64 Cambiado de calo (LS) ISA-UVA 64
65 Reaco Químico Eudio implificado: Se coidea ce. la vaiable elacioada co el poduco: F, Ti, Cai Solo e eudia la empeaua e el eaco TT T i F Refigeae Reaco T T MV: caudal de efigeae CV: Tempeaua del eaco DV: empeaua de eada del efigeae ISA-UVA 65
66 Reaco Químico - Tempeaua ISA-UVA 66
67 Modelo educido, co coveió x Coveió x x c B /c Ai c A c Ai (1- x ) V d c d A Fc Fc Vke c Ai A E RT A Vc d T E ρ e FcT ρ e i FcT ρ e Vke RT c A H UAT ( T ) d V c d T ρ e Fρce Ti FρceT UA( T T ) d ISA-UVA 67
68 ISA-UVA 68 Modelo educido, liealizació x) (1 ke x V F d x d RT E T ) UA(T H x) (1 c Vke T c F T c F d dt c V Ai RT E e i e e ρ ρ ρ T ) x (1 e RT ke x ) ke V F ( d x d 0 RT E 0 RT E T a x a d x d 1 11 e e e 0 Ai 0 RT E 0 e Ai RT E T ) c V UA ( T ) c V UA c H ) x (1 c RT kee V F ( x ) c H c ke ( d T d 0 0 ρ ρ ρ ρ 3 1 T a T a x a d T d
69 ISA-UVA 69 Modelo educido, liealizació T ) UA(T T c F T c F d dt c V e i e e ρ ρ ρ i 0 0 i0 0 e e T ) V F ( F ) V T T ( T ) V F c V UA ( T ) c V UA ( d T d ρ ρ i T b F b T a T a d T d ( ) ( ) i i T F 0 0 T T x T T F b b T T x a a 0 a a a 0 a a T T x & & &
70 Eimació de paámeo u F T i TT Reaco T T, x Paa calcula lo paámeo del modelo (U, F 0, E,.) eceiamo hace medida del poceo. Uaemo dao omado de Caio e alguo puo eacioaio, y lo uiuiemo e el modelo paa calcula lo paámeo decoocido, peo ee pocedimieo o pemie calcula odo lo paámeo. ISA-UVA 70
71 Puo de opeació u F T i TT Reaco T, x T T 9 ºC x 0.90 T 75.6 ºC F 47.8 l/m T i 50 ºC u 4 % Oo: Oo: T 88.6 ºC x T 71.8 ºC F 30. l/m T i 30 ºC u. % T 33.6 ºC x 0.10 T 3. ºC F 47.8 l/m T i 30 ºC u 4 % ISA-UVA 71
72 Eimació de paámeo E RT 0 Fx Vke (1 x) E RT Vke (1 x)caih UA 0 F(Ti T) (T T ) ρc ρc UA 0 F (Ti T ) (T T ) ρ c e e e T 9 ºC x 0.90 T 75.6 ºC F 47.8 l/m T i 50 ºC u 4 % F Vke 0 F(T i E R(9 73.) Vke 9) E R(9 73.) UA ( ) ρ c (1 0.90) e (1 0.90)c ρc e (9 75.6) l 0.90 l Ai F Vk E l(1 0.90) R(9 73.) H UA (9 75.6) ρce UA ρ c 74.5 ISA-UVA 7 e
73 T 9 ºC x 0.90 T 75.6 ºC F 47.8 l/m T i 50 ºC u 4 % Eimació de paámeo T 4.5 ºC x T 1.9 ºC F 100 l/m T i 0 ºC u 100 % T 88.8 ºC x 0.88 T 7 ºC F 56.8 l/m T i 50 ºC u 5 % F E E l 0.90 l l(1 0.90) Vk R(9 73.) R F E F l 0.88 l l(1 0.88) 6.46e - 01 Vk R( ) Vk E caih R(9 73.) Vke (1 0.90)c AiH UA F(Ti 9) (9 75.6) ρce ρce ρce UA E 1.460e R( ) Vke (1 0.88)c AiH UA ρcevk 0 F(Ti 88.8) (88.8 7) ρce ρce Ti 5.54 Ma oa e el ece puo ISA-UVA 73
74 Eimació de paámeo caih ρc UA ρc Vk T i e e u 5.54 F T i e TT Reaco T, x E R F 6.46e Vk UA ρ c e 74.5 T - 01 Supoiedo: V V l F l/mi ρc e 4180 j/k l ρ c e 4000 j/k l Reula: k e010 c Ai H UA Reaco Malab ISA-UVA 74
75 Modelo liealizado u dx d T d dt d F T i ke ( UA ( V ρ c E RT ρc e TT F ( ke V c e Ai Reaco E RT T, x UA ) T ( V ρ c e F V 0 T ke E 0 RT ) x e (1 x 0 ) T RT 0 0 E RT H F0 kee ) x ( V RT 0 0 d 0 0 ) T c Ai (1 x ρc T ( i0 E el puo de opeació: e 0 T 9 ºC x 0.90 T 75.6 ºC F 47.8 l/m T i 50 ºC u 4 % ) H UA UA ) T ( ) T Vρc Vρc T V 0 ) F Suiuyedo e: ISA-UVA 75 e F ( V 0 ) T i e
76 ISA-UVA 76 Maiz de afeecia ( ) ( ) i i T F 0 0 T T x T T F T T x T T x & & & [ ] B A C I G() T i () F () T()? u
77 Modelo e Reaco T i () F () T() oo(deomiado) i i Ceo Gaacia -5.1 (T i ) (F ) Puo de opeació eable ISA-UVA 77
78 Repuea alo F 1 oo(d) i i T Polo domiae ISA-UVA 78
79 Oo puo de opeació u F T i T i () F () TT Reaco 3 3 T, x T E el puo de opeació: T 74.9 ºC x T 58.9 ºC F 47.8 l/m T i 34 ºC u 4 % T() ISA-UVA 79
80 Ampliude F 1 Oo puo de opeació T i () F () T() Sep Repoe T Polo: i i Time (ec) ISA-UVA 80
81 U puo de opeació ieable u F T i T i () F () TT Reaco 3 3 T, x T E el puo de opeació: T 68.1 ºC x T 54.6 ºC F 47.8 l/m T i 3.7 ºC u 4 % T() ISA-UVA 81
82 U puo de opeació ieable T i () T 68.1 ºC x T 54.6 ºC F 47.8 l/m T i 3.7 ºC u 4 % F () T() Polo: ISA-UVA 8
83 Bloque e eie U() G 1 () X() G () Y() Y() G ()X() G ()G 1 ()U() G()U() U() G() Y() G() G ()G 1 () ISA-UVA 83
84 Siema ealimeado W() - E() R() U() G() Y() Y() G()U() Y() [ 1 G()R() ] G()R() Y() W() 1 G()R() G()R()E() G()R() G()R()W() [ W() Y() ] ISA-UVA 84
85 Siema ealimeado W() - E() R() U() G() Y() H() Y() Y() G()U() [ 1 G()R()H() ] G()R()E() G()R() Y() W() 1 G()R()H() G()R() G()R()W() [ W() H()Y() ] ISA-UVA 85
86 ISA-UVA 86 G() R U() - Y() W() Peubacioe E() [ ] [ ] V() G()R()H() 1 D() W() G()R()H() 1 G()R() Y() D()V() G()R()W() G()R()H() 1 Y() D()V() Y()H() W() G()R() D()V() G()R()E() D()V() G()U() Y() D() V() H()
87 Tamio-Regulado V() D() W() - E() R() U() % G() Y() ºC ma ºC ma ºC ma Si el egulado ua la calibació del amio, y la diámica del amio e ápida fee a la del poceo, puede depeciae la fució de afeecia e la ealimeació. ISA-UVA 87
88 Lazo ceado V() D() W() - E() R() U() G() Y() Y() G()R() 1 G()R() D() W() V() 1 G()R() Expeió fudameal paa aaliza o dieña ISA-UVA 88
89 Lazo ceado- Señal de cool V() D() W() - E() R() U() G() Y() U() R()E() R()[W() Y()] R()[W() G()U() D()V()] U()[1 R()G()] R()[W() D()V()] R() R()D() U() W() V() 1 G()R() 1 G()R() ISA-UVA 89
90 Repuea e lazo ceado V() D() W() - E() R() U() G() Y() La epuea empoal ae cambio e w() ó v() puede calculae co la F.T. e lazo ceado: Y() G()R() 1 G()R() D() W() V() 1 G()R() ISA-UVA 90
91 ISA-UVA 91 K p U() - Y() W() Ejemplo E() V() 1) )( KK 1 ( 1) ( K W() KK 1 KK V() K 1 K 1 1 K W() K 1 K 1 K 1 K V() G()K 1 D() W() G()K 1 G()K Y() d p d p p p d d p p p p p τ τ τ τ τ τ τ τ V() 1 K τ 1 K d d τ
92 Ecuació caaceíica Y() G()R() 1 G()R() D() W() V() 1 G()R() El ipo de epuea y la eabilidad e lazo ceado viee deemiada po lo polo de la fució de afeecia e lazo ceado, que o la aíce de la ecuació caaceíica: 1G()R() 0 Cambiado el egulado R() podemo modifica la foma de la epuea ISA-UVA 9
93 Ceo e lazo ceado Y() G()R() 1 G()R() D() W() V() 1 G()R() G()R() Num() De() Num() G()R() De() 1 G()R() Num() 1 De() D() 1 G()R() 1 Lo ceo e lazo abieo apaece Num() ambié como De() Num() ceo e lazo ceado D() Num() De() De()D() De() Num() ISA-UVA 93
94 Ceo ieable G()R() Num() De() Num() G()R() De() 1 G()R() Num() 1 De() D() D() 1 G()R() Num() 1 De() Num() De() Num() De()D() De() Num() y() y c () Si la epuea e lazo abieo peea fae o miima, ambie la peeaa e lazo ceado idepedieemee de R() ISA-UVA 94
95 Reaco Químico ISA-UVA 95
96 Reaco Químico ISA-UVA 96
97 Reaco Químico Paa K p -4 lo polo e lazo ceado o: i i El ceo e: -5.1 La epuea e alo ae u cambio de gado e el SP ISA-UVA 97
A 1 A 2 A 3 B 1 B 2 B 3
16 0 17 0 17 0 18 0 18 0 19 0 20 A A = A 1 î + A 2 ĵ + A 3ˆk A (x, y, z) r = xî + yĵ + zˆk A B A B B A = A 1 B 1 + A 2 B 2 + A 3 B 3 = A B θ θ A B = ˆn A B θ A B î ĵ ˆk = A 1 A 2 A 3 B 1 B 2 B 3 W = F
Α Ρ Ι Θ Μ Ο Σ : 6.913
Α Ρ Ι Θ Μ Ο Σ : 6.913 ΠΡΑΞΗ ΚΑΤΑΘΕΣΗΣ ΟΡΩΝ ΔΙΑΓΩΝΙΣΜΟΥ Σ τ η ν Π ά τ ρ α σ ή μ ε ρ α σ τ ι ς δ ε κ α τ έ σ σ ε ρ ι ς ( 1 4 ) τ ο υ μ ή ν α Ο κ τ ω β ρ ί ο υ, η μ έ ρ α Τ ε τ ά ρ τ η, τ ο υ έ τ ο υ ς δ
Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α
Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ
3/5/016 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΣΥΡΜΑΤΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Παραδείγματα Κεραιών Αθανάσιος Κανάτας Καθηγητής Παν/μίου Πειραιώς Δίπολο Hetz L d
m r = F m r = F ( r) m r = F ( v) F = F (x) m dv dt = F (x) vdv = F (x)dx d dt = dx dv dt dx = v dv dx
m r = F m r = F ( r) m r = F ( v) x F = F (x) m dv dt = F (x) d dt = dx dv dt dx = v dv dx vdv = F (x)dx 2 mv2 x 2 mv2 0 = F (x )dx x 0 K = 2 mv2 W x0 x = x x 0 F (x)dx K K 0 = W x0 x x, x 2 x K 2 K =
www.absolualarme.com met la disposition du public, via www.docalarme.com, de la documentation technique dont les rιfιrences, marques et logos, sont
w. ww lua so ab me lar m.co t me la sit po dis ion du c, bli pu via lar ca do w. ww me.co m, de la ion nta t do cu me on t ed hn iqu tec les en ce s, rι fιr ma rq ue se t lo go s, so nt la pr op riι tι
Problemas resueltos del teorema de Bolzano
Problemas resueltos del teorema de Bolzano 1 S e a la fun ción: S e puede af irm a r que f (x) está acotada en el interva lo [1, 4 ]? P or no se r c ont i nua f (x ) e n x = 1, la f unció n no e s c ont
1. Functions and Operators (1.1) (1.2) (1.3) (1.4) (1.5) (1.6) 2. Trigonometric Identities (2.1) (2.2) (2.3) (2.4) (2.5) (2.6) (2.7) (2.8) (2.
ECE 3 Mh le Sprig, 997. Fucio d Operor, (. ic( i( π (. ( β,, π (.3 Im, Re (.4 δ(, ; δ( d, < (.5 u( 5., (.6 rec u( + 5. u( 5., > rc( β /, π + rc( β /,
Molekulare Ebene (biochemische Messungen) Zelluläre Ebene (Elektrophysiologie, Imaging-Verfahren) Netzwerk Ebene (Multielektrodensysteme) Areale (MRT, EEG...) Gene Neuronen Synaptische Kopplung kleine
ESCUELA TÉCNICA SUPERIOR DE INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIÓN
ESCUELA TÉCNICA SUPERIOR DE INENIEROS INDUSTRIALES Y DE TELECOMUNICACIÓN UNIVERSIDAD DE CANTABRIA CARACTERÍSTICAS DE LA RESPUESTA FRECUENCIAL DE LAS FUNCIONES BICUADRÁTICAS Joé M. Drake CTR Computadore
!!" #7 $39 %" (07) ..,..,.. $ 39. ) :. :, «(», «%», «%», «%» «%». & ,. ). & :..,. '.. ( () #*. );..,..'. + (# ).
1 00 3 !!" 344#7 $39 %" 6181001 63(07) & : ' ( () #* ); ' + (# ) $ 39 ) : : 00 %" 6181001 63(07)!!" 344#7 «(» «%» «%» «%» «%» & ) 4 )&-%/0 +- «)» * «1» «1» «)» ) «(» «%» «%» + ) 30 «%» «%» )1+ / + : +3
Note: Please use the actual date you accessed this material in your citation.
MIT OpeCueWae hp://cw.m.eu 6.13/ESD.13J Elecmagec a pplca, Fall 5 Pleae ue he llwg ca ma: Maku Zah, Ech Ippe, a Dav Sael, 6.13/ESD.13J Elecmagec a pplca, Fall 5. (Maachue Iue Techlgy: MIT OpeCueWae). hp://cw.m.eu
( ) ΘΕ ΑΝ4 / 2 0. α) β) f(x) f ( x) cos x
Η ΑΝΕΠ Η Η Ν Ω Ν Ω ΑΘΗ Α ΑΝIV Ε ε ά ει Ν επ ε β ί 5 (3-9-5) Επώ : Ό α: ΑΝ Ν: ΘΕ ΑΝ Τα π α Chebyshev T ( ) α π ω μ ( ) y y y (,,, ) π [,] Η ω α α α π α μ / d d T ( ) Tm ( ) [ T ( )] Α απ f ( ) 3, [,], α
Finite Integrals Pertaining To a Product of Special Functions By V.B.L. Chaurasia, Yudhveer Singh University of Rajasthan, Jaipur
Global Joal of Scece oe eeac Vole Ie 4 Veo Jl Te: Doble Bld Pee eewed Ieaoal eeac Joal Pble: Global Joal Ic SA ISSN: 975-5896 e Iegal Peag To a Podc of Secal co B VBL Caaa Ydee Sg e of aaa Ja Abac - A
! "# $ % $&'& () *+ (,-. / 0 1(,21(,*) (3 4 5 "$ 6, ::: ;"<$& = = 7 + > + 5 $?"# 46(A *( / A 6 ( 1,*1 B"',CD77E *+ *),*,*) F? $G'& 0/ (,.
! " #$%&'()' *('+$,&'-. /0 1$23(/%/4. 1$)('%%'($( )/,)$5)/6%6 7$85,-9$(- /0 :/986-$, ;2'$(2$ 1'$-/-$)('')5( /&5&-/ 5(< =(4'($$,'(4 1$%$2/996('25-'/(& ;/0->5,$ 1'$-/%'')$(($/3?$%9'&-/?$( 5(< @6%-'9$
Ventiladores helicoidales murales o tubulares, versión PL equipados con hélice de plástico y versión AL equipados con hélice de aluminio.
HCH HCT HCH HCT Ventiladores helicoidales murales o tubulares, de gran robustez Ventiladores helicoidales murales o tubulares, versión PL equipados con hélice de plástico y versión AL equipados con hélice
tel , version 1-7 Feb 2013
!"## $ %&' (") *+ '#),! )%)%' *, -#)&,-'" &. % /%%"&.0. )%# "#",1 2" "'' % /%%"&30 "'' "#", /%%%" 4"," % /%%5" 4"," "#",%" 67 Y% !"!"# $ %& & # &$ ' '#( ''# ))'%&##& *'#$ ##''' "#$ %% +, %'# %+)% $
ο ο 3 α. 3"* > ω > d καΐ 'Ενορία όλις ή Χώρί ^ 3 < KN < ^ < 13 > ο_ Μ ^~~ > > > > > Ο to X Η > ο_ ο Ο,2 Σχέδι Γλεγμα Ο Σ Ο Ζ < o w *< Χ χ Χ Χ < < < Ο
18 ρ * -sf. NO 1 D... 1: - ( ΰ ΐ - ι- *- 2 - UN _ ί=. r t ' \0 y «. _,2. "* co Ι». =; F S " 5 D 0 g H ', ( co* 5. «ΰ ' δ". o θ * * "ΰ 2 Ι o * "- 1 W co o -o1= to»g ι. *ΰ * Ε fc ΰ Ι.. L j to. Ι Q_ " 'T
2. Α ν ά λ υ σ η Π ε ρ ι ο χ ή ς. 3. Α π α ι τ ή σ ε ι ς Ε ρ γ ο δ ό τ η. 4. Τ υ π ο λ ο γ ί α κ τ ι ρ ί ω ν. 5. Π ρ ό τ α σ η. 6.
Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α 1. Ε ι σ α γ ω γ ή 2. Α ν ά λ υ σ η Π ε ρ ι ο χ ή ς 3. Α π α ι τ ή σ ε ι ς Ε ρ γ ο δ ό τ η 4. Τ υ π ο λ ο γ ί α κ τ ι ρ ί ω ν 5. Π ρ ό τ α σ η 6. Τ ο γ ρ α φ ε ί ο 1. Ε ι σ α γ ω
FORMULARIO DE ELASTICIDAD
U. D. Resistencia de Mateiales, Elasticidad Plasticidad Depatamento de Mecánica de Medios Continuos Teoía de Estuctuas E.T.S. Ingenieos de Caminos, Canales Puetos Univesidad Politécnica de Madid FORMULARIO
Radio détection des rayons cosmiques d ultra-haute énergie : mise en oeuvre et analyse des données d un réseau de stations autonomes.
Radio détection des rayons cosmiques d ultra-haute énergie : mise en oeuvre et analyse des données d un réseau de stations autonomes. Diego Torres Machado To cite this version: Diego Torres Machado. Radio
T : g r i l l b a r t a s o s Α Γ Ί Α Σ Σ Ο Φ Ί Α Σ 3, Δ Ρ Α Μ Α. Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 0 1 : 0 0 π μ
Α Γ Ί Α Σ Σ Ο Φ Ί Α Σ 3, Δ Ρ Α Μ Α g r i l l b a r t a s o s Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 1 : 0 π μ Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 0 1 : 0 0 π μ T ortiyas Σ ο υ
m i N 1 F i = j i F ij + F x
N m i i = 1,..., N m i Fi x N 1 F ij, j = 1, 2,... i 1, i + 1,..., N m i F i = j i F ij + F x i mi Fi j Fj i mj O P i = F i = j i F ij + F x i, i = 1,..., N P = i F i = N F ij + i j i N i F x i, i = 1,...,
5 Ι ^ο 3 X X X. go > 'α. ο. o f Ο > = S 3. > 3 w»a. *= < ^> ^ o,2 l g f ^ 2-3 ο. χ χ. > ω. m > ο ο ο - * * ^r 2 =>^ 3^ =5 b Ο? UJ. > ο ο.
728!. -θ-cr " -;. '. UW -,2 =*- Os Os rsi Tf co co Os r4 Ι. C Ι m. Ι? U Ι. Ι os ν ) ϋ. Q- o,2 l g f 2-2 CT= ν**? 1? «δ - * * 5 Ι -ΐ j s a* " 'g cn" w *" " 1 cog 'S=o " 1= 2 5 ν s/ O / 0Q Ε!θ Ρ h o."o.
C M. V n: n =, (D): V 0,M : V M P = ρ ρ V V. = ρ
»»...» -300-0 () -300-03 () -3300 3.. 008 4 54. 4. 5 :.. ;.. «....... :. : 008. 37.. :....... 008.. :. :.... 54. 4. 5 5 6 ... : : 3 V mnu V mn AU 3 m () ; N (); N A 6030 3 ; ( ); V 3. : () 0 () 0 3 ()
Vers un assistant à la preuve en langue naturelle
Vers un assistant à la preuve en langue naturelle Thévenon Patrick To cite this version: Thévenon Patrick. Vers un assistant à la preuve en langue naturelle. Autre [cs.oh]. Université de Savoie, 2006.
Points de torsion des courbes elliptiques et équations diophantiennes
Points de torsion des courbes elliptiques et équations diophantiennes Nicolas Billerey To cite this version: Nicolas Billerey. Points de torsion des courbes elliptiques et équations diophantiennes. Mathématiques
! "# " #!$ &'( )'&* $ ##!$2 $ $$ 829 #-#-$&2 %( $8&2(9 #."/-0"$23#(&&#
! "# " #!$ %""! &'( )'&* $!"#$% &$'#( )*+#'(,#* /$##+(#0 &1$( #& 23 #(&&# +, -. % ($4 ($4 ##!$2 $567 56 $$ 829 #-#-$&2 %( $8&2(9 #."/-0"$23#(&&# 6 < 6 6 6 66 6< <
Formulario Básico ( ) ( ) ( ) ( ) ( 1) ( 1) ( 2) ( 2) λ = 1 + t t. θ = t ε t. Mecánica de Medios Continuos. Grado en Ingeniería Civil.
Mecánica e Meios Continos. Gao en Ingenieía Ciil. Fomlaio Básico Tema. Descipción el moimiento χ (,) t χ (,) t (,) t χ (,) t t t Tema. Defomación s S X E X e i ij j i ij j F X X U F J T T T U U i j Uk
F (x) = kx. F (x )dx. F = kx. U(x) = U(0) kx2
F (x) = kx x k F = F (x) U(0) U(x) = x F = kx 0 F (x )dx U(x) = U(0) + 1 2 kx2 x U(0) = 0 U(x) = 1 2 kx2 U(x) x 0 = 0 x 1 U(x) U(0) + U (0) x + 1 2 U (0) x 2 U (0) = 0 U(x) U(0) + 1 2 U (0) x 2 U(0) =
() min. xt δεν έχει μετασχηματισμό LAPLACE () () () Αν Λ= το σήμα ( ) Αν Λ, έστω σ. Το σύνολο μιγαδικών αριθμών. s Q το ολοκλήρωμα (1) υπάρχει.
Έστω xt : Ο (αμφίπλευρος) μετασχηματισμός LAPLACE ορίζεται : X: L { xt} : X xt e dt = = μιγαδική συνάρτηση της μιγαδικής μεταβλητής = σ+ j Ο (μονόπλευρος) μετασχηματισμός LAPLACE ορίζεται : L { xt } :
Το άτομο του Υδρογόνου
Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
! " #$% & '()()*+.,/0.
! " #$% & '()()*+,),--+.,/0. 1!!" "!! 21 # " $%!%!! &'($ ) "! % " % *! 3 %,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,0 %%4,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,5
!"!# ""$ %%"" %$" &" %" "!'! " #$!
" "" %%"" %" &" %" " " " % ((((( ((( ((((( " %%%% & ) * ((( "* ( + ) (((( (, (() (((((* ( - )((((( )((((((& + )(((((((((( +. ) ) /(((( +( ),(, ((((((( +, 0 )/ (((((+ ++, ((((() & "( %%%%%%%%%%%%%%%%%%%(
9.BbF`2iBbB2`mM; A,.Bz2`2Mx2Mp2`7?`2M 7Ƀ` T `ib2hh2.bz2`2mib H;H2B+?mM;2M 8.BbF`2iBbB2`mM; AA, 6BMBi2 1H2K2Mi2 o2`7?`2m
R R R K h ( ) L 2 (Ω) H k (Ω) H0 k (Ω) R u h R 2 Φ i Φ i L 2 A : R n R n n N + x x Ax x x 2 A x 2 x 3 x 3 a a n A := a n a nn A x = ( 2 5 9 A = )( x ( ) 2 5 9 x 2 ) ( ) 2x +5x = 2. x +9x 2 Ax = b 2x +5x
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΡΟΥΣΕΙΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΕΜΠΤΗ 10 ΣΕΠΤΕΜΒΡΙΟΥ 2015
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΡΟΥΣΕΙΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΕΜΠΤΗ 0 ΣΕΠΤΕΜΒΡΙΟΥ 05 ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α γ Α β Α δ Α4 β Α5. α Λάθος β Σωστό γ Λάθος δ Σωστό ε Λάθος ΘΕΜΑ Β Β. Σωστό το β Αό
1. Τριγωνοµετρικές ταυτότητες.
. Τριγωνοµετρικές ταυτότητες. co( y co( co( y i( i( y i( y i( co( y co( i( y ± m (. ± ± (. π m (. 3 co ± i( i ± π ± co( (. co( co ( i ( (. 5 i( i( co( (. 6 j j co( + (. 7 j j j i ( (. 8 ( ( y ( y + ( +
Ax = b. 7x = 21. x = 21 7 = 3.
3 s st 3 r 3 t r 3 3 t s st t 3t s 3 3 r 3 3 st t t r 3 s t t r r r t st t rr 3t r t 3 3 rt3 3 t 3 3 r st 3 t 3 tr 3 r t3 t 3 s st t Ax = b. s t 3 t 3 3 r r t n r A tr 3 rr t 3 t n ts b 3 t t r r t x 3
Parts Manual. Trio Mobile Surgery Platform. Model 1033
Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
! " # $ $ % # & ' (% & $ &) % & $ $ # *! &+, - &+
! " # $ $ % # & ' (% & $ &) % & $ $ # *! &+, - &+ &) + ) &) $, - &+ $ " % +$ ". # " " (% +/ ". 0 + 0 1 +! 1 $ 2 1 &3 # 2 45 &.6#4 2 7$ 2 2 2! $/, # 8 ! "#" $% & '( %! %! # '%! % " "#" $% % )% * #!!% '
W τ R W j N H = 2 F obj b q N F aug F obj b q Ψ F aug Ψ ( ) ϱ t + + p = 0 = 0 Ω f = Γ Γ b ϱ = (, t) = (, t) Ω f Γ b ( ) ϱ t + + p = V max 4 3 2 1 0-1 -2-3 -4-4 -3-2 -1 0 1 2 3 4 x 4 x 1 V mn V max
Q π (/) ^ ^ ^ Η φ. <f) c>o. ^ ο. ö ê ω Q. Ο. o 'c. _o _) o U 03. ,,, ω ^ ^ -g'^ ο 0) f ο. Ε. ιη ο Φ. ο 0) κ. ο 03.,Ο. g 2< οο"" ο φ.
II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
μ μ μ s t j2 fct T () = a() t e π s t ka t e e j2π fct j2π fcτ0 R() = ( τ0) xt () = α 0 dl () pt ( lt) + wt () l wt () N 2 (0, σ ) Time-Delay Estimation Bias / T c 0.4 0.3 0.2 0.1 0-0.1-0.2-0.3 In-phase
COMPLICITY COLLECTION autumn / winter
COMP LI C I TY COLLE C TI ON a ut umn / winte r 2 0 1 7 1 8 «T o ρ ο ύ χ ο ε ί ν α ι τ ο σ π ί τ ι τ ο υ σ ώ μ ατ ο ς». Τ ο σ ώ μ α ν τ ύ ν ε τα ι μ ε φ υ σ ι κ ά ν ή μ ατα κ α ι υφά σ μ ατα α π ό τ η
ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης 02/06/2017 1
ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης /6/7 Διάρκεια ώρες. Θέμα. Θεωρηστε ενα συστημα δυο σωματων ισων μαζων (μαζας Μ το καθενα) και δυο ελατηριων (χωρις μαζα) με σταθερες ελατηριων
ITU-R P (2012/02) &' (
ITU-R P.530-4 (0/0) $ % " "#! &' ( P ITU-R P. 530-4 ii.. (IPR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.itu.int/itu-r/go/patents/en. ITU-T/ITU-R/ISO/IEC (http://www.itu.int/publ/r-rec/en ) () ( ) BO BR BS
). = + U = -U U= mgy (y= H) =0 = mgh. y=0 = U=0
3761 5226 9585 ). = + U = -U U= mgy (y= H) =0 = mgh. y=0 = U=0 y = mgh mgy, 3761 5226 ) ) =mg 2 F=ma F-B=ma Fmg=m.2g F=3mg F=3B B = F/3 3763 5208 ) ) W 1 = -mgh W 2 =mgh W = W 1 + W 2 = -mgh + mgh=0 3763
Alterazioni del sistema cardiovascolare nel volo spaziale
POLITECNICO DI TORINO Corso di Laurea in Ingegneria Aerospaziale Alterazioni del sistema cardiovascolare nel volo spaziale Relatore Ing. Stefania Scarsoglio Studente Marco Enea Anno accademico 2015 2016
Lifting Entry (continued)
ifting Entry (continued) Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion Planar state equations MARYAN 1 01 avid. Akin - All rights reserved http://spacecraft.ssl.umd.edu
Α Ρ Η Θ Μ Ο : ΠΡΑΞΗ ΣΡΟΠΟΠΟΙΗΗ ΠΡΑΞΗ ΚΑΣΑΘΕΗ ΟΡΩΝ
Α Ρ Η Θ Μ Ο : 6.984 ΠΡΑΞΗ ΣΡΟΠΟΠΟΙΗΗ ΠΡΑΞΗ ΚΑΣΑΘΕΗ ΟΡΩΝ ΔΙΑΓΩΝΙΜΟΤ η ε λ Π ά η ξ α ζ ή κ ε ξ α ζ η η ο ε ί θ ν ζ η κ ί α ( 2 1 ) η ν π κ ή λ α Μ α ξ η ί ν π, ε κ έ ξ α Γ ε π η έ ξ α, η ν π έ η ν π ο δ
... 5 A.. RS-232C ( ) RS-232C ( ) RS-232C-LK & RS-232C-MK RS-232C-JK & RS-232C-KK
RS-3C WIWM050 014.1.9 P1 :8... 1... 014.0.1 1 A... 014.0. 1... RS-3C()...01.08.03 A.. RS-3C()...01.08.03 3... RS-3C()... 003.11.5 4... RS-3C ()... 00.10.01 5... RS-3C().008.07.16 5 A.. RS-3C().0 1.08.
!"#!"!"# $ "# '()!* '+!*, -"*!" $ "#. /01 023 43 56789:3 4 ;8< = 7 >/? 44= 7 @ 90A 98BB8: ;4B0C BD :0 E D:84F3 B8: ;4BG H ;8
Ε Π Ι Μ Ε Λ Η Τ Η Ρ Ι Ο Κ Υ Κ Λ Α Δ Ω Ν
Ε ρ μ ο ύ π ο λ η, 0 9 Μ α ρ τ ί ο υ 2 0 1 2 Π ρ ο ς : Π ε ρ ιφ ε ρ ε ι ά ρ χ η Ν ο τ ίο υ Α ιγ α ί ο υ Α ρ ι θ. Π ρ ω τ. 3 4 2 2 κ. Ι ω ά ν ν η Μ α χ α ι ρ ί δ η F a x : 2 1 0 4 1 0 4 4 4 3 2, 2 2 8 1
CENTRIFUGAL AIR COOLED CONDENSERS CONDENSADORES DE AIRE CENTRÍFUGOS. GPC, GMC and GSC Series. Series GPC, GMC y GSC
CENTRIFUGAL AIR COOLED CONDENSERS GPC, GMC and GSC Series CONDENSADORES DE AIRE CENTRÍFUGOS Series GPC, GMC y GSC Key Example / Ejemplo de nomenclatura de modelos GP Direct Drive 900/100 rpm / Transmisión
ƒˆˆ-ˆœ œ Ÿ ˆ ˆ Š ˆˆ ƒ ˆ ˆˆ
Ó³ Ÿ. 2018.. 15, º 6218).. 467Ä475 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ. ˆŸ ƒˆˆ-ˆœ œ Ÿ ˆ ˆ Š ˆˆ ƒ ˆ ˆˆ.. Ê 1 Œμ ±μ ± μ Ê É Ò Ê É É ³. Œ.. μ³μ μ μ, Œμ ± μ± μ, ÎÉμ ³μ Ë ± Í Ö ³³ É Î ±μ, μ ² μ μ ƒ ²Ó ÉÊ μ² μ ²μÉ μ É É μ Ô -
Ο αντίστροφος μετασχηματισμός Laplace ορίζεται από το μιγαδικό ολοκλήρωμα : + +
Μετασχηματισμός aplace ορίζεται ως εξής : t X() [x( t)] xte () dt = = Ο αντίστροφος μετασχηματισμός aplace ορίζεται από το μιγαδικό ολοκλήρωμα : t x(t) = [ X()] = X() e dt π j c C είναι μία καμπύλη που
ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μανόλης Παπαδρακάκης Καθηγητής ΕΜΠ Εργαστήριο Στατικής & Αντισεισμικών Ερευνών 2007 2008 1 1 Ειδικά κεφάλαια μητρωικής ανάλυσης ραβδωτών φορέων Συνοριακές
!"#$ % &# &%#'()(! $ * +
,!"#$ % &# &%#'()(! $ * + ,!"#$ % &# &%#'()(! $ * + 6 7 57 : - - / :!", # $ % & :'!(), 5 ( -, * + :! ",, # $ %, ) #, '(#,!# $$,',#-, 4 "- /,#-," -$ '# &",,#- "-&)'#45)')6 5! 6 5 4 "- /,#-7 ",',8##! -#9,!"))
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n 1
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n1 x dx = 1 2 b2 1 2 a2 a b b x 2 dx = 1 a 3 b3 1 3 a3 b x n dx = 1 a n +1 bn +1 1 n +1 an +1 d dx d dx f (x) = 0 f (ax) = a f (ax) lim d dx f (ax) = lim 0 =
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
o ΔΙΑΓΩΝΙΣΜΑ ΔΕΚΕΜΒΡΙΟΣ 0: ΘΕΜΑΤΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις - 4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα
TRIGONOMETRIA. hipotenusa L 2. hipotenusa
TRIGONOMETRIA. Calcular las razones trigonométricas de 0º, º y 60º. Para calcular las razones trigonométricas de º, nos ayudamos de un triángulo rectángulo isósceles como el de la figura. cateto opuesto
κ α ι θ έ λ ω ν α μ ά θ ω...
{ ( a -r ν ρ ι -Μ Π ώτ 1 Γ '- fj T O O J CL κ α ι θ έ λ ω ν α μ ά θ ω < US η ixj* ί -CL* λ ^ t A u t\ * < τ : ; Γ ν c\ ) *) «*! «>» Μ I Λ 1,ν t f «****! ( y \ \, 0 0 # Περικλή_ Χαντζόπουλο κ α ι θ έ λ
Sarò signor io sol. α α. œ œ. œ œ œ œ µ œ œ. > Bass 2. Domenico Micheli. Canzon, ottava stanza. Soprano 1. Soprano 2. Alto 1
Sarò signor io sol Canzon, ottava stanza Domenico Micheli Soprano Soprano 2 Alto Alto 2 Α Α Sa rò si gnor io sol del mio pen sie io sol Sa rò si gnor io sol del mio pen sie io µ Tenor Α Tenor 2 Α Sa rò
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Φυσική Σημασία του Μετασχηματισμού Fourier Ο μετασχηματισμός Fourier
Κβαντομηχανική Ι Λύσεις προόδου. Άσκηση 1
Κβαντομηχανική Ι Λύσεις προόδου Άσκηση 1 ψ(x) = A Sin (k x), < x < α) Sin (k x) = eikx e ikx i Mε πιθανές τιμές ορμής p = ± ħk, από τον τύπο του De Broglie. Kαθεμιά έχει πιθανότητα 50%. b) p = ψ p ψ =
Φυσική για Μηχανικούς
Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
ΜΕΡΙΚΕΣ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ
ΜΑΣ 3: Συνήθεις Διαφορικές Εξισώσεις, Εαρινό Εξάμηνο 4 ΜΕΡΙΚΕΣ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ Να ταξινομηθούν οι πιο κάτω ΣΔΕ με βάση τα εξής: τάξη, γραμμική ή μή Να δοθούν επίσης οι ανεξάρτητες και εξαρτημένες μεταβλητές
Assessment of otoacoustic emission probe fit at the workfloor
Assessment of otoacoustic emission probe fit at the workfloor t s st tt r st s s r r t rs t2 t P t rs str t t r 1 t s ér r tr st tr r2 t r r t s t t t r t s r ss r rr t 2 s r r 1 s r r t s s s r t s t
ΓΗ ΚΑΙ ΣΥΜΠΑΝ. Εικόνα 1. Φωτογραφία του γαλαξία μας (από αρχείο της NASA)
ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
Japanese Fuzzy String Matching in Cooking Recipes
1 Japanese Fuzzy String Matching in Cooking Recipes Michiko Yasukawa 1 In this paper, we propose Japanese fuzzy string matching in cooking recipes. Cooking recipes contain spelling variants for recipe
1 La teoría de Jeans. t + (n v) = 0 (1) b) Navier-Stokes (conservación del impulso) c) Poisson
1 La teoría de Jeans El caso ás siple de evolución de fluctuaciones es el de un fluído no relativista. las ecuaciones básicas son: a conservación del núero de partículas n t + (n v = 0 (1 b Navier-Stokes
1. Ένα σώμα m=1 kg εκτελεί γ.α.τ. και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο φαίνεται στο σχήμα.
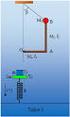. Ένα σώμα m= kg εκτελεί γ.α.τ. και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο φαίνεται στο σχήμα. α. Να βρείτε τη σταθερά D και την ολική ενέργεια του ταλαντωτή. β. Να γράψετε τις εξισώσεις
Πρακτικές μέθοδοι αποδιαμόρφωσης FM. Ανίχνευση μηδενισμών Διευκρίνιση ολίσθησης φάσης Μετατροπή FM σε ΑΜ Ανάδραση συχνότητας
Αποδιαμόρφωση FM Πρακτικές μέθοδοι αποδιαμόρφωσης FM Ανίχνευση μηδενισμών Διευκρίνιση ολίσθησης φάσης Μετατροπή FM σε ΑΜ Ανάδραση συχνότητας Ανίχνευση μηδενισμών Η έξοδος είναι ανάλογη του ρυθμού των μηδενισμών,
ME 365: SYSTEMS, MEASUREMENTS, AND CONTROL (SMAC) I
ME 365: SYSTEMS, MEASUREMENTS, AND CONTROL SMAC) I Dynamicresponseof 2 nd ordersystem Prof.SongZhangMEG088) Solutions to ODEs Forann@thorderLTIsystem a n yn) + a n 1 y n 1) ++ a 1 "y + a 0 y = b m u m)
P P Ó P. r r t r r r s 1. r r ó t t ó rr r rr r rí st s t s. Pr s t P r s rr. r t r s s s é 3 ñ
P P Ó P r r t r r r s 1 r r ó t t ó rr r rr r rí st s t s Pr s t P r s rr r t r s s s é 3 ñ í sé 3 ñ 3 é1 r P P Ó P str r r r t é t r r r s 1 t r P r s rr 1 1 s t r r ó s r s st rr t s r t s rr s r q s
ΕΞΕΤΑΣΕΙΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ Διδάσκοντες: Βαρσάμης Χρήστος, Φωτόπουλος Παναγιώτης
ΕΞΕΤΑΣΕΙΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 218-219 ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ Διδάσκοντες: Βαρσάμης Χρήστος, Φωτόπουλος Παναγιώτης ΘΕΜΑ 1 Διάρκεια εξέτασης 2 ώρες Υλικό σημείο κινείται ευθύγραμμα πάνω στον άξονα x με ταχύτητα,
Modèles de représentation multi-résolution pour le rendu photo-réaliste de matériaux complexes
Modèles de représentation multi-résolution pour le rendu photo-réaliste de matériaux complexes Jérôme Baril To cite this version: Jérôme Baril. Modèles de représentation multi-résolution pour le rendu
ibemo Kazakhstan Republic of Kazakhstan, West Kazakhstan Oblast, Aksai, Pramzone, BKKS office complex Phone: ; Fax:
γ 1 6 M = 0.05 F M = 0.05 F M = 0.2 F M = 0.2 F M = 0.05 F M = 0.05 F M = 0.05 F M = 0.2 F M = 0.05 F 2 2 λ τ M = 6000 M = 10000 M = 15000 M = 6000 M = 10000 M = 15000 1 6 τ = 36 1 6 τ = 102 1 6 M = 5000
1487 Ν. 151/86. Αριθμός 151 του 1986 ΝΟΜΟΣ ΤΡΟΠΟΠΟΙΩΝ ΤΟΥΣ ΠΕΡΙ ΤΕΛΩΝΕΙΑΚΩΝ ΔΑΣΜΩΝ ΚΑΙ ΦΟΡΩΝ ΚΑΤΑΝΑΛΩΣΕΩΣ ΝΟΜΟΥΣ ΤΟΥ 1978 ΕΩΣ 1985
E.E., Παρ. I, Αρ. 214, 24.10.6 147 Ν. 151/6 περί Τελνειακών Δασμών και Φόρν Καταναλώσες (Τρππιητικός) Νόμς τυ 196 εκδίδεται με δημσίευση στην επίσημη εφημερίδα της Κυπριακής Δημκρατίας σύμφνα με τ Άρθρ
-! " #!$ %& ' %( #! )! ' 2003
-! "#!$ %&' %(#!)!' ! 7 #!$# 9 " # 6 $!% 6!!! 6! 6! 6 7 7 &! % 7 ' (&$ 8 9! 9!- "!!- ) % -! " 6 %!( 6 6 / 6 6 7 6!! 7 6! # 8 6!! 66! #! $ - (( 6 6 $ % 7 7 $ 9!" $& & " $! / % " 6!$ 6!!$#/ 6 #!!$! 9 /!
6. ΙΑΦΟΡΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΡΟΗΣ
6.1 ΚΙΝΗΜΑΤΙΚΗ ΡΟΪΚΟΥ ΣΤΟΙΧΕΙΟΥ 6. ΙΑΦΟΡΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΡΟΗΣ -Λεπτοµέρειες της ροής Απειροστός όγκος ελέγχου - ιαφορική Ανάλυση Περιγραφή πεδίων ταχύτητας και επιτάχυνσης Euleian, Lagangian U U(x,y,,t)
TeSys contactors a.c. coils for 3-pole contactors LC1-D
References a.c. coils for 3-pole contactors LC1-D Control circuit voltage Average resistance Inductance of Reference (1) Weight Uc at 0 C ± 10 % closed circuit For 3-pole " contactors LC1-D09...D38 and
ΠΕΡΙΟΔΙΚΟ ΣΥΣΤΗΜΑ ΤΩΝ ΣΤΟΙΧΕΙΩΝ (1) Ηλία Σκαλτσά ΠΕ ο Γυμνάσιο Αγ. Παρασκευής
ΠΕΡΙΟΔΙΚΟ ΣΥΣΤΗΜΑ ΤΩΝ ΣΤΟΙΧΕΙΩΝ (1) Ηλία Σκαλτσά ΠΕ04.01 5 ο Γυμνάσιο Αγ. Παρασκευής Όπως συμβαίνει στη φύση έτσι και ο άνθρωπος θέλει να πετυχαίνει σπουδαία αποτελέσματα καταναλώνοντας το λιγότερο δυνατό
4. Zapiši Eulerjeve dinamične enačbe za prosto osnosimetrično vrtavko. ω 2
Mehanikateoretičnavprašanjainodgovori 1/12 Newtonovamehanika 1. Določiravninogibanjatočkevpoljucentralnesile. Ravninagibanjagreskozicentersileinimanormalovsmerivrtilne količine 2. Zapišiperiodogibanjapremočrtnegagibanjapodvplivompotenciala
Ε.Ε. Παρ. I(II) Αρ. 3887,
.. Π. I() Α. 887, 2.7.2004 402 Ν. 25(ΙΙ)/2004 εί Συμλμτικύ Πϋλγισμύ Νόμς (Α. ) τυ 2004 εκδίδετι με δμσίευσ στν ίσμ φμείδ τς Κυικής Δμκτίς σύμφν με τ Αθ 52 τυ Συντάγμτς. Πίμι. 75() τν 200. Συντικός τίτλς.
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ» 1 o ΔΙΑΓΩΝΙΣΜΑ ΙΑΝΟΥΑΡΙΟΣ 2014: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α. β.. α. 3. δ. 4. α. 5. α-λ, β-σ, γ-λ, δ-λ, ε-σ. ΘΕΜΑ B. Η σωστή απάντηση είναι το γ. Το μέγιστο ρεύμα σε μια ηλεκτρική
ΣΤΟΙΧΕΙΑ ΔΙΑΝΥΣΜΑΤΙΚΟΥ ΛΟΓΙΣΜΟΥ
ΣΤΟΙΧΕΙΑ ΔΙΑΝΥΣΜΑΤΙΚΟΥ ΛΟΓΙΣΜΟΥ A u B Μέτρο Διεύθυνση Κατεύθυνση (φορά) Σημείο Εφαρμογής Διανυσματικά Μεγέθη : μετάθεση, ταχύτητα, επιτάχυνση, δύναμη Μονόμετρα Μεγέθη : χρόνος, μάζα, όγκος, θερμοκρασία,
V S C V C -10. V t C dv c dt
ÕÛÎÛ Το παρακάτω ηλεκτρικό κύκλωµα, διεγείρεται από παλµοσειρά περιόδου Τ s. Οι παράµετροι του κυκλώµατος είναι R = 0 ΚΩ και = 00 µf. Το κύκλωµα αρχικά (τη χρονική στιγµή 0) δεν έχει αποθηκευµένη ενέργεια.
! "#" "" $ "%& ' %$(%& % &'(!!")!*!&+ ,! %$( - .$'!"
! "#" "" $ "%& ' %$(%&!"#$ % &'(!!")!*!&+,! %$( -.$'!" /01&$23& &4+ $$ /$ & & / ( #(&4&4!"#$ %40 &'(!"!!&+ 5,! %$( - &$ $$$".$'!" 4(02&$ 4 067 4 $$*&(089 - (0:;
(m m m...)r m R MR. m 1 υ 1 +m 2 υ 2 = m 1 υ 1 +m 2 υ 2 και επειδή m 1 = m 2 : υ 1 +υ 2 = υ 1 +υ 2 υ 1 - υ 1 = υ 2 - υ 2 (1) g (4) 2 T R T R MR(2) (5)
ΛΥΣΕΙΣ α Χωρίζουμε το δακτύλιο σε άπειρες σημειακές μάζες (m, m, m, Η ροπή αδράνειας ολόκληρου του δακτυλίου είναι ίση με το άθροισμα των ροπών αδράνειας κάθε σημειακής μάζας ή I I I I m R m R m R Σωστή
σ (t) = (sin t + t cos t) 2 + (cos t t sin t) = t )) 5 = log 1 + r (t) = 2 + e 2t + e 2t = e t + e t
ΛΥΣΕΙΣ. Οι ακήεις από το βιβλίο των Mrsden - Tromb.. 3.)e) Είναι t) sin t + t os t, os t t sin t, 3) οπότε t) sin t + t os t) + os t t sin t) + 3 t + 4 και το μήκος είναι ίο με t t) dt t + 4 dt t + 4 +
Κλασσική Θεωρία Ελέγχου
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Ο μετασχηματισμός Laplace Νίκος Καραμπετάκης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
E.E. Παρ. Ill (I) 883 Κ.Δ.Π. 304/88 Αρ. 2370, Αριθμός 304 Ο ΠΕΡΙ ΠΟΛΕΟΔΟΜΙΑΣ ΚΑΙ ΧΩΡΟΤΑΞΙΑΣ ΝΟΜΟΣ (ΝΟΜΟΙ 90 ΤΟΥ 1972 ΚΑΙ 56 ΤΟΥ 1982)
E.E. Παρ. Ill (I) 88 Κ.Δ.Π. 04/88 Αρ. 270, 9.12.88 Αριθμός 04 ΠΕΡΙ ΠΛΕΔΜΙΑΣ ΚΑΙ ΧΩΡΤΑΞΙΑΣ ΝΜΣ (ΝΜΙ 90 ΤΥ 1972 ΚΑΙ 56 ΤΥ 1982) Διάταγμα Διατήρησης σύμφωνα με τ άρθρ 8(1) Ασκώντας τις εξσίες π χρηγύνται
6.4 Superposition of Linear Plane Progressive Waves
.0 - Marine Hydrodynamics, Spring 005 Lecture.0 - Marine Hydrodynamics Lecture 6.4 Superposition of Linear Plane Progressive Waves. Oblique Plane Waves z v k k k z v k = ( k, k z ) θ (Looking up the y-ais
Déformation et quantification par groupoïde des variétés toriques
Défomation et uantification pa goupoïde de vaiété toiue Fédéic Cadet To cite thi veion: Fédéic Cadet. Défomation et uantification pa goupoïde de vaiété toiue. Mathématiue [math]. Univeité d Oléan, 200.
Microscopie photothermique et endommagement laser
Microscopie photothermique et endommagement laser Annelise During To cite this version: Annelise During. Microscopie photothermique et endommagement laser. Physique Atomique [physics.atom-ph]. Université
Veliine u mehanici. Rad, snaga i energija. Dinamika. Meunarodni sustav mjere (SI) 1. Skalari. 2. Vektori - poetak. 12. dio. 1. Skalari. 2.
Vele u ehc Rd, g eegj D. do. Sl. Veo 3. Tezo II. ed 4. Tezo IV. ed. Sl: 3 0 pod je jedc (ezo ulog ed). Veo: 3 3 pod je jedc (ezo pog ed) 3. Tezo dugog ed 3 9 pod je jedc 4. Tezoeog ed 3 4 8 pod je jedc
Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté
Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté Alexis Nuttin To cite this version: Alexis Nuttin. Physique des réacteurs
HONDA. Έτος κατασκευής
Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V