ΑΙΟΛΙΚΑ ΣΥΣΤΗΜΑΤΑ: ΑΕΡΟΔΥΝΑΜΙΚΗ
|
|
|
- Βαραββᾶς Κουβέλης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΑΙΟΛΙΚΑ ΣΥΣΤΗΜΑΤΑ: Δρ. Κονταξάκης Κώστας Επικ. καθηγητής ΤΕΙ Κρήτης 1
2 2
3 Ροϊκός σωλήνας δρομέα ανεμοκινητήρα 3
4 Για τη μελέτη του αεροδυναμικού πεδίου γύρω από το δίσκο θα εφαρμοστούν οι γνωστοί νόμοι της Μηχανικής των Ρευστών και πιο συγκεκριμένα: Η εξίσωση διατήρησης της μάζας Η εξίσωση διατήρησης της ορμής Ενεργειακός ισολογισμός Σε πρώτη προσέγγιση επίλυσης του προβλήματος γίνονται οι ακόλουθες παραδοχές: Η εναλλαγή ενέργειας μεταξύ ρευστού και δίσκου γίνεται χωρίς απώλειες. Ομοιόμορφη κατανομή της ταχύτητας στο δίσκο Η φόρτιση (διαφορά πίεσης πριν και μετά) πάνω σε ολόκληρο το δίσκο είναι σταθερή. Ο δίσκος δεν περιστρέφει τη φλέβα της ροής. Η παραδοχή αυτή πρακτικά μπορεί να επιτευχθεί με την ύπαρξη δύο αντίθετα στρεφόμενων δρομέων ενώ οι παραδοχές 2 & 3 απαιτούν άπειρο αριθμό και πτερύγια κατάλληλης σχεδίασης. 4
5 ΔΙΑΤΗΡΗςΗ ΤΗΣ ΜΑΖΑς ΑΙΟΛΙΚΑ ΣΥΣΤΗΜΑΤΑ Η μάζα του ρέει μέσα στο ροϊκό σωλήνα, διατηρείται σταθερή και ίση με: m = ρ Α δ V = ρ π R 2 s V s Τότε: U A = Vs Αδ = V A + 5
6 ΔΙΑΤΗΡΗςΗ ΤΗΣ ΟΡΜΗΣ Η ώση ισούται με την εν θέσει μεταβολή της ροής της ορμής: ΑΙΟΛΙΚΑ ΣΥΣΤΗΜΑΤΑ 2 T ρ U A ρ Α Vs V Q U = δ Η παροχή Q διαμέσου της παράπλευρης επιφάνειας του κυλινδρικού όγκου ισολογισμού είναι: Q = ρ A U ρ Αδ V s 6
7 ΔΙΑΤΗΡΗςΗ ΤΗΣ ΟΡΜΗΣ ΑΙΟΛΙΚΑ ΣΥΣΤΗΜΑΤΑ ( ) Συνεπάγεται: T Α V U V s = ρ δ 7
8 8 ΕΝΕΡΓΕΙΑΚΟΣ ΙςΟΛΟΓΙςΜΟΣ V s p U p ρ ρ + = V s p V p ρ ρ + = + + ( ) V U p p = + ρ + = = p p p A T δ
9 ΕΝΕΡΓΕΙΑΚΟΣ ΙςΟΛΟΓΙςΜΟΣ T Aδ + = p = p p ( U V ) T ρ A Vs = δ T A δ = ρ V s ( U V ) 1 V s =. + 2 ( U V ) 9
10 Εισαγωγή του συντελεστή αξονικής επαγωγής ή αλληλεπίδρασης (axial interference factor), της ταχύτητας του ανέμου: α Τότε: V s V a = = U = U ( U V ) U s ( 1 a) ( 1 2α ) 10
11 P = T V s P T ρ ( 1 ) 2 3 = 2.. Aδ. U. a a 2 = 2. ρ. A. U. a 1 δ ( a) P C p = 1 3 ρ U. A δ 2 Υποδηλώνει το ποσοστό της ενέργειας που έχει ο άνεμος που πλησιάζει το δίσκο (λίγο πριν από το δίσκο) και που μετατρέπεται σε ισχύ πάνω στο δρομέα ( είναι η ισχύς που έχει ο άνεμος ταχύτητας που περνάει από επιφάνεια ) T C T = 1 3 ρ U. A δ 2 Εκφράζει το συντελεστή αντίστασης που παρουσιάζει ο δρομέας στη ροή 11
12 Αντικαθιστώντας: C p = ( 1 ) 2 4a a ΑΙΟΛΙΚΑ ΣΥΣΤΗΜΑΤΑ C T = 4a 1 ( a) Ακρότατα συνάρτησης: dc p dα α = =
13 Όριο του Betz: C p max = % Και άρα για βέλτιστο δρομέα: V s V = = ( 2 / 3) U ( 1/ 3) U 13
14 14
15 Στοιχεία αεροδυναμικής 15
16 Στοιχεία αεροδυναμικής 16
17 T = ρ S V ( V 2) 1 V και 1 V =. + 2 ( V 1 V 2) Αντικαθιστώντας την V : Τ = ρs (V 1 2 V 22 ) /2 H ισχύς μεγιστοποιείται όταν V 2 = V 1 / 3 (θεωρία του Betz) Τότε : Τ = (4/9) ρ S V 1 2 και V = (2/3) V 1 επομένως : Τ = ρ S V 2 Αν κάθε στοιχείο της επιφάνειας σάρωσης συμβάλλει αναλογικά με το εμβαδόν του στην ώση, η συμβολή του στοιχείου που βρίσκεται μεταξύ r και r+dr είναι : df = ρ V 2 ds = 2 π ρ V 2 r dr (σχέση 1.) 17
18 Απλουστευμένος υπολογισμός πτερύγωσης Το αεροδυναμικό φορτίο, dr, αναλύεται σε 2 συνιστώσες: την άνωση (lift), dr z, και την αντίσταση (drag), dr x. dr z = (1/2) ρ C z W 2 l dr και dr x = (1/2) ρ C x W 2 l dr H συνισταμένη δύναμη: dr = dr z / cos ε όπου (ε) είναι η γωνία μεταξύ του dr και dr z και (l) η χορδή του προφίλ στην απόσταση r. 18
19 Απλουστευμένος υπολογισμός πτερύγωσης Επίσης : W = V/sinI και dr= (½) ρ C z (W 2 l/cos ε) dr dr= (½) ρ C z (V 2 /sin 2 I) (l/cos ε) dr Αν προβάλουμε τη συνισταμένη dr σε επίπεδο κατά τη διεύθυνση του ανέμου θα έχουμε την ώση, Τ, του στοιχείου που βρίσκεται μεταξύ των ακτίνων r και r + dr και αν p ο αριθμός των πτερύγων: dt = (½) ρ C z p (V 2 /sin 2 I) (l/cos ε) (cos(i-ε)) l dr και αν το εξισώσουμε με τη σχέση 1.: C z p 1 = 4 π r sin 2 I cos ε/cos(i-ε) δηλαδή: C z p 1 = 4 π r (tan 2 I cosi)/(1+tan ε tani) (σχέση 2.) 19
20 Απλουστευμένος υπολογισμός πτερύγωσης Η γωνία Ι συνδέεται με την ταχύτητα του ανέμου V 1 από την παρακάτω σχέση : cotanι = ωr/v = (2/3) ωr/v 1 = (3/2) λ και η (2) γίνεται: Υπό κανονικές συνθήκες, η τιμή του tan ε είναι πολύ χαμηλή. H βέλτιστη τιμή του tan ε, για μια συνηθισμένη αεροτομή είναι της τάξεως του 0,05, οπότε η παρένθεση είναι περίπου ίση με τη μονάδα και η προηγούμενη σχέση μπορεί να γραφτεί ως εξής : 20
21 Απλουστευμένος υπολογισμός πτερύγωσης και λ=λ0 (r/r) 21
22 Απλουστευμένος υπολογισμός πτερύγωσης Βήματα υπολογισμού κατασκευαστικών παραμέτρων πτέρυγας: μήκους πτέρυγας (r), γωνίας σφήνωσης (α) και μήκους χορδής (l ή c). Υπολογισμός μήκους πτέρυγας διάμετρος πτερύγωσης, D, από τη σχέση P=z*D 2 *V 3 όπου z ϵ{ }. Επιλογή ή υπολογισμός λ 0 λ r υπολογισμός Ι. Επιλογή αεροτομής Cz =f(i) και Cx=f(i) Επιλογή γωνιών προσβολής, i. Υπολογισμός γωνίας σφήνωσης α=i-i. Υπολογισμός γινομένου Cz*p*l = f(λ) και υπολογισμός χορδής, l. 22
23 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST 23
24 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST 24
25 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST 25
26 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST Πίσω από κάθε πτέρυγα ενός ρότορα δημιουργείται μια στιβάδα δινών που αποτελείται κυρίως από δύο στροβίλους που γεννιούνται ο ένας κοντά στον άξονα του δρομέα και ο άλλος στο ακροπτερύγιο κάθε πτέρυγας. Οι περιφερειακοί στρόβιλοι, που γεννιούνται στο ακροπτερύγιο κάθε πτέρυγας, σχηματίζουν έλικες που αποσπώνται, κατάντη της πτερύγωσης, από τα ακροπτερύγια. Οι στρόβιλοι που γεννιούνται κοντά στον άξονα του δρομέα περιστρέφονται και αυτοί σχηματίζοντας ένα σπιράλ γύρω από τον άξονα του δρομέα. Τα πτερύγια μπορούν να υποκατασταθούν από στροβίλους που έχουν σαν άξονα την κάθε πτέρυγα. Η συνισταμένη ταχύτητα του αέρα έχει σαν συνιστώσες τη φυσική ταχύτητα του ανέμου και την ταχύτητα που επάγεται από το σύστημα στροβίλων. Το πεδίο ταχυτήτων που επάγονται από το σύστημα των στροβίλων μπορεί να θεωρηθεί σαν το αποτέλεσμα της υπέρθεσης των τριών παρακάτω συστημάτων στροβίλων: ένα κεντρικός στρόβιλος με κυκλοφορία pγ = Γ 0 ( Γ : η κυκλοφορία του στροβίλου μιας πτέρυγας, p : ο αριθμός των πτερύγων), μια στιβάδα περιφερειακών στροβίλων αποτελούνται κυρίως από τις δίνες που στρέφονται σχηματίζοντας μια έλικα γύρω από τον άξονα του δρομέα, τους στρόβιλους που αναπτύσσονται στις πτέρυγες. 26
27 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST Με βάση το νόμο των Biot και Savart ή το θεώρημα του Ampere, υπολογίζονται τα μαγνητικά πεδία που δημιουργούνται από ρεύματα που ρέουν σε κυκλώματα με που έχουν την ίδια μορφή με το σύστημα των στροβίλων. Το ηλεκτρικό σύστημα που φαίνεται παραπάνω αποτελείται από: Έναν κεντρικό αγωγό που διαρρέεται από ρεύμα p Ι = Ι 0, Ένα σύνολο αγωγών που περιστρέφονται σε έλικα γύρω από τον άξονα του δρομέα, παρέχοντας καθένας ένα ρεύμα Ι στους αγωγούς που αντιπροσωπεύουν τις πτέρυγες. Ένα σύνολο p αγωγών μήκους R τοποθετημένα σε «αστέρα», το καθένα να διαρρέεται από ρεύμα I, έχοντας σα κοινό σημείο τον προηγούμενο αγωγό με ρεύμα Ι 0. 27
28 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST Ανάντη του δίσκου το πεδίο που οφείλεται στα ρεύματα που περνάνε από το δίσκο (είναι ίσο αλλά σε αντίθετη διεύθυνση με τα πεδία που δημιουργούνται από τον κεντρικό και τους μεσημβρινούς αγωγούς. Αυτό το πεδίο που ασκείται σ ένα σημείο Μ ανάντη του δίσκου είναι ίσο και αντίθετο με το πεδίο που ασκείται σ ένα σημείο Μ που βρίσκεται σε απόσταση r από τον άξονα απέναντι από το σημείο Μ αλλά ανάντη του δίσκου και οφείλεται και αυτό επίσης στα ρεύματα που διαρρέουν το δίσκο. Άρα: Κατάντη του δίσκου, τα μαγνητικά πεδία, και προστίθενται. Το συνιστάμενο πεδίο Η, σε μια απόσταση r από τον άξονα είναι: 28
29 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST Πάνω στο δίσκο το μαγνητικό πεδίο που οφείλεται στα ρεύματα που διαρρέουν το δίσκο είναι μηδενικό αφού το πεδίο που δημιουργείται από κάθε κυκλικό τομέα αναιρείται από το αντίθετό του πάνω στο δίσκο. Σαν αποτέλεσμα το πεδίο πάνω στο δίσκο σε απόσταση r από τον άξονα περιστροφής είναι: Ας προσδιορίσουμε τώρα το μαγνητικό πεδίο που δημιουργείται από τις κυκλικές σπείρες που σχηματίζουν ένα πηνίο. Έστω n 1 ο αριθμός των σπειρών ανά μονάδα μήκους. Στο κέντρο του πηνίου το αξονικό μαγνητικό πεδίο είναι: H S = n 1 I και στο άκρο του πηνίου είναι: H S / 2 = n 1 I / 2 29
30 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST 30
31 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST 31
32 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST Τρίγωνο ταχυτήτων 32
33 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST Υπολογισμός των αξονικών και εφαπτομενικών δυνάμεων. Υπολογισμός ροπής. Έχουμε: dr z = (1/2) ρ C z W 2 l dr και dr x = (1/2) ρ C x W 2 l dr Με προβολή στον άξονα του δρομέα έχουμε την αξονική συνιστώσα df V = dr z cos Ι + dr x sin I = (1/2) ρ W 2 l dr ( C z cos I + C x sin I ) και με προβολή στο επίπεδο περιστροφής (ταχύτητα U), έχουμε την εφαπτομενική συνιστώσα df u = dr z sin Ι dr x cos I = (1/2) ρ W 2 l dr ( C z sin I C x cos I ) Οι εκφράσεις αυτές μπορούν να γραφούν, θέτοντας tan ε = drx/drz = Cx/Cz, df V = (1/2) ρ l W 2 C z (cos(i-ε) / cosε) dr και df u = (1/2) ρ l W 2 C z (sin(i-ε) / cosε) dr Η συνεισφορά των στοιχείων των p πτερυγίων του δρομέα που βρίσκονται μεταξύ των αποστάσεων r και r + dr στην ώση καθώς και στη ροπή είναι αντίστοιχα : df = p df V = (1/2) ρ p l W 2 C z (cos(i-ε) / cosε) dr dm = r p d F u = (1/2) ρ p l r W 2 C z (sin(i-ε) / cosε) dr 33
34 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST Σύμφωνα με το θεώρημα του Euler για μια δακτυλιοειδή φλέβα του ρευστού που διέρχεται από το δρομέα μεταξύ της ακτίνας r και r + dr, η στοιχειώδης αξονική ώση είναι: df = ρ π r dr V 2 ( 1 k 2 ) και η στοιχειώδης ροπή: dm = ρ π r 3 dr V 1 ( 1+ k ) Ω = ρ π r 3 dr ω V 1 ( 1 + k ) ( h 1 ) Εξισώνοντας τα αποτελέσματα από τους δύο τρόπους υπολογισμού των αεροδυναμικών φορτίων και αν αντικαταστήσουμε την W = f(v 1) έχουμε: Κάνοντας το ίδιο για τη ροπή έχουμε: 34
35 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST Από αυτές τις ισότητες, μπορούμε να εξάγουμε τις παραμέτρους G kai E: Και διαιρώντας κατά μέλη: 35
36 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST Τοπικός συντελεστής ισχύος Η ισχύς που μπορεί να εξαχθεί από τη στοιχειώδη φλέβα του ρευστού που περνά μέσα από το δρομέα μεταξύ r και r + dr δίνεται από την έκφραση: dp u = ω dm = ρ π r 3 dr ω 2 V 1 ( 1 + k ) ( h 1 ) Αυτή η τιμή αντιστοιχεί στον τοπικό συντελεστή ισχύος : όπου : λ = ω r / V 1 36
37 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST Μέγιστος τοπικός συντελεστής ισχύος ενός ιδανικού δρομέα Εστω ότι οι αεροτομές των πτερύγων έχουν συντελεστή αντίστασης C x = 0 και επομένως tan ε = C x / C z = 0. Τότε το G/E γράφεται: Λύνοντας ως προς h: Ο συντελεστής ισχύος Cp γίνεται: 37
38 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST Μέγιστος τοπικός συντελεστής ισχύος ενός ιδανικού δρομέα Για μια δεδομένη τιμή του λ, ο συντελεστής ισχύος διέρχεται από ένα μέγιστο ως συνάρτηση του k για : dcp/dk =0 Υπολογίζοντας αυτήν την παράγωγο προκύπτει το μέγιστο Cp το οποίο επιτυγχάνεται για μια τιμή του k τέτοια ώστε: δηλαδή: 4 k 3 3k ( λ ) + λ = 0 Έστω: k = (λ 2 +1) cosθ Αντικαθιστώντας το k στην προηγούμενη σχέση και διαιρώντας με το ( λ ) 3/2 προκύπτει : 38
39 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST Μέγιστος τοπικός συντελεστής ισχύος ενός ιδανικού δρομέα αλλά : 4 cos 3 θ 3 cos θ = cos 3θ ή διαφορετικά: Οπότε: Για κάθε τιμή του λ, μπορούμε να υπολογίσουμε την αντίστοιχη γωνία θ,το k και ως εκ τούτου, τη μέγιστη δυνατή τιμή του συντελεστή ισχύος Cp. 39
40 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST Βέλτιστες τιμές της γωνίας κλίσης Ι και του Cz p l Η γωνία Ι και το γινόμενο C z p l είναι: Για τον υπολογισμό του C z p l, θεωρούμε μια ιδανική πτερύγωση, στο οποίο το ε ισούται με μηδέν κατά τα προηγούμενα. Έτσι η τιμή για το C z p l / r είναι: λαμβάνοντας υπόψη τη σχέση cotan I = λ e Οι σχέσεις αυτές χρησιμοποιούνται για τον υπολογισμό των τιμών του C z p l / r και Ι. Η γνώση αυτών των τιμών είναι απαραίτητη ώστε να οριστεί σε κάθε σημείο της πτερύγωσης η χορδή l του προφίλ και της γωνίας σφήνωσης, α. 40
41 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST Πίνακας υπολογισμού Ι και Cz p l για κάθε αεροτομή της πτέρυγας 41
42 Άβακας υπολογισμού Ι και Cz p l για κάθε αεροτομή της πτέρυγας 42
43 Μέθοδος δινορευμάτων του Glauert βελτιωμένη από ερευνητές του AMHERST Από τον άβακα: Η εφαρμογή των κανόνων εργασίας οδηγεί στα ακόλουθα αποτελέσματα : I = 9º C z p l / r =0,3 Για αυτήν την ενότητα με συγκεκριμένη ταχύτητα λ θεωρείται ίση με 4,2 ( λ = λ 0 r / R ). Για αυτή τη τιμή του λ, ο πίνακας δείχνει : I = 8º,93 και C z p l / r =0,305 Με την επανάληψη της λειτουργίας για άλλες τιμές του r λαμβάνεται η γωνία κλίσης Ι και η ποσότητα C z p l / r σε όλο το μήκος της πτέρυγας. Εν συνεχεία, μπορούμε να καθορίσουμε τις χορδές των διαφόρων προφίλ και τις γωνίες σφήνωσης. Το ίδιο ισχύει και για την γωνία σφήνωσης α όπου συνδέεται με τη γωνία προσβολής με τη σχέση α = Ι i. Για την επίλυση του προβλήματος, πρέπει να έχει επιλεχθεί η κατανομή της γωνίας προσβολής. 43
Σ.Τ.Εφ. - Τμήμα Μηχανολογίας Τ.Ε.Ι. ΚΡΗΤΗΣ. Μάθημα: ΑΙΟΛΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΙΑΣ ΠΤΕΡΥΓΩΣΕΩΝ
 Σ.Τ.Εφ. - Τμήμα Μηχανολογίας Τ.Ε.Ι. ΚΡΗΤΗΣ Μάθημα: ΑΙΟΛΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΙΑΣ ΠΤΕΡΥΓΩΣΕΩΝ Κώστας Κονταξάκης Σελίδα 1 από 39 ΠΕΡΙΕΧΟΜΕΝΑ ΕΙΣΑΓΩΓΗ ΣΤΗ ΘΕΩΡΙΑ ΠΤΕΡΥΓΩΣΕΩΝ... 3 ΘΕΩΡΙΑ ΤΟΥ ΔΙΣΚΟΥ
Σ.Τ.Εφ. - Τμήμα Μηχανολογίας Τ.Ε.Ι. ΚΡΗΤΗΣ Μάθημα: ΑΙΟΛΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΙΑΣ ΠΤΕΡΥΓΩΣΕΩΝ Κώστας Κονταξάκης Σελίδα 1 από 39 ΠΕΡΙΕΧΟΜΕΝΑ ΕΙΣΑΓΩΓΗ ΣΤΗ ΘΕΩΡΙΑ ΠΤΕΡΥΓΩΣΕΩΝ... 3 ΘΕΩΡΙΑ ΤΟΥ ΔΙΣΚΟΥ
Πτυχιακή εργασία. Μελέτη και σχεδιασμός πτερύγωσης ανεμογεννήτριας. Νουχάι Εσμεράλντ (AM: 5245) E-mail: themis_89@hotmail.gr.
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Κρήτης Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανολογίας Πτυχιακή εργασία Μελέτη και σχεδιασμός πτερύγωσης ανεμογεννήτριας Νουχάι Εσμεράλντ (AM: 5245) E-mail: themis_89@hotmail.gr
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Κρήτης Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανολογίας Πτυχιακή εργασία Μελέτη και σχεδιασμός πτερύγωσης ανεμογεννήτριας Νουχάι Εσμεράλντ (AM: 5245) E-mail: themis_89@hotmail.gr
Σ.Τ.Εφ. - Τμήμα Μηχανολογίας Τ.Ε.Ι. ΚΡΗΤΗΣ. Μάθημα: ΑΙΟΛΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΙΑΣ ΠΤΕΡΥΓΩΣΕΩΝ
 Σ.Τ.Εφ. - Τμήμα Μηχανολογίας Τ.Ε.Ι. ΚΡΗΤΗΣ Μάθημα: ΑΙΟΛΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΙΑΣ ΠΤΕΡΥΓΩΣΕΩΝ ΗΡΑΚΛΕΙΟ 0 Κώστας Κονταξάκης Επίκουρος καθηγητής ΤΕΙ Κρήτης ΠΕΡΙΕΧΟΜΕΝΑ I. ΕΙΣΑΓΩΓΗ ΣΤΗ ΘΕΩΡΙΑ ΠΤΕΡΥΓΩΣΕΩΝ...
Σ.Τ.Εφ. - Τμήμα Μηχανολογίας Τ.Ε.Ι. ΚΡΗΤΗΣ Μάθημα: ΑΙΟΛΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΙΑΣ ΠΤΕΡΥΓΩΣΕΩΝ ΗΡΑΚΛΕΙΟ 0 Κώστας Κονταξάκης Επίκουρος καθηγητής ΤΕΙ Κρήτης ΠΕΡΙΕΧΟΜΕΝΑ I. ΕΙΣΑΓΩΓΗ ΣΤΗ ΘΕΩΡΙΑ ΠΤΕΡΥΓΩΣΕΩΝ...
Αιολική Ενέργεια & Ενέργεια του Νερού
 Αιολική Ενέργεια & Ενέργεια του Νερού Ενότητα 5: Σχεδίαση Πτερυγίων 1 Γεώργιος Λευθεριώτης, Επίκουρος Καθηγητής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Στοιχείο πτέρυγας ανάλυση ασκούμενων
Αιολική Ενέργεια & Ενέργεια του Νερού Ενότητα 5: Σχεδίαση Πτερυγίων 1 Γεώργιος Λευθεριώτης, Επίκουρος Καθηγητής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Στοιχείο πτέρυγας ανάλυση ασκούμενων
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Κρήτης Διατμηματικό Πρόγραμμα Μεταπτυχιακών Σπουδών «Ενεργειακά Συστήματα»
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Κρήτης Διατμηματικό Πρόγραμμα Μεταπτυχιακών Σπουδών «Ενεργειακά Συστήματα» ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΠΑΡΑΜΕΤΡΙΚΟΣ ΣΧΕΔΙΑΣΜΟΣ ΠΤΕΡΥΓΩΣΗΣ ΚΑΜΠΥΛΗΣ ΓΕΩΜΕΤΡΙΑΣ» Του Μεταπτυχιακού
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Κρήτης Διατμηματικό Πρόγραμμα Μεταπτυχιακών Σπουδών «Ενεργειακά Συστήματα» ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΠΑΡΑΜΕΤΡΙΚΟΣ ΣΧΕΔΙΑΣΜΟΣ ΠΤΕΡΥΓΩΣΗΣ ΚΑΜΠΥΛΗΣ ΓΕΩΜΕΤΡΙΑΣ» Του Μεταπτυχιακού
ΑΕΡΟΔΥΝΑΜΙΚΗ Διδάσκων: Δρ. Ριζιώτης Βασίλης Θεωρία δίσκου ορμής στοιχεία πτερύγωσης
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΒΙΟΜΗΧΑΝΙΚΗΣ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΑΕΡΟΔΥΝΑΜΙΚΗ Διδάσκων: Δρ. Ριζιώτης Βασίλης Θεωρία δίσκου ορμής στοιχεία πτερύγωσης Άδεια
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΒΙΟΜΗΧΑΝΙΚΗΣ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΑΕΡΟΔΥΝΑΜΙΚΗ Διδάσκων: Δρ. Ριζιώτης Βασίλης Θεωρία δίσκου ορμής στοιχεία πτερύγωσης Άδεια
Αιολική Ενέργεια & Ενέργεια του Νερού
 Αιολική Ενέργεια & Ενέργεια του Νερού Ενότητα 8: Θεωρία ορμής - Σχεδίαση ρότορα αιολικής μηχανής οριζόντιου άξονα Γεώργιος Λευθεριώτης, Επίκουρος Καθηγητής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί
Αιολική Ενέργεια & Ενέργεια του Νερού Ενότητα 8: Θεωρία ορμής - Σχεδίαση ρότορα αιολικής μηχανής οριζόντιου άξονα Γεώργιος Λευθεριώτης, Επίκουρος Καθηγητής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί
Μαγνητικά Πεδία σε Σύγχρονες Μηχανές. 3.1 Μαγνητικά πεδία σε μηχανές με ομοιόμορφο διάκενο.
 Χ. Δημουλιά, Σύγχρονες Ηλεκτρικές Μηχανές Κεφάλαιο 3 1 Κεφάλαιο 3 Μαγνητικά Πεδία σε Σύγχρονες Μηχανές 3.1 Μαγνητικά πεδία σε μηχανές με ομοιόμορφο διάκενο. Θα εξετάσουμε εδώ το μαγνητικό πεδίο στο διάκενο
Χ. Δημουλιά, Σύγχρονες Ηλεκτρικές Μηχανές Κεφάλαιο 3 1 Κεφάλαιο 3 Μαγνητικά Πεδία σε Σύγχρονες Μηχανές 3.1 Μαγνητικά πεδία σε μηχανές με ομοιόμορφο διάκενο. Θα εξετάσουμε εδώ το μαγνητικό πεδίο στο διάκενο
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
8. ΜΑΓΝΗΤΙΣΜΟΣ. Φυσική ΙΙ Δ. Κουζούδης. Πρόβλημα 8.6.
 1 8. ΜΑΓΝΗΤΙΣΜΟΣ Πρόβλημα 8.6. Το σύρμα του παρακάτω σχήματος έχει άπειρο μήκος και διαρρέεται από ρεύμα I. Υπολογίστε με τη βοήθεια του νόμου του Biot-Savart με ολοκλήρωση το μέτρο και την κατεύθυνση
1 8. ΜΑΓΝΗΤΙΣΜΟΣ Πρόβλημα 8.6. Το σύρμα του παρακάτω σχήματος έχει άπειρο μήκος και διαρρέεται από ρεύμα I. Υπολογίστε με τη βοήθεια του νόμου του Biot-Savart με ολοκλήρωση το μέτρο και την κατεύθυνση
Ασκήσεις 6 ου Κεφαλαίου
 Ασκήσεις 6 ου Κεφαλαίου 1. Μία ράβδος ΟΑ έχει μήκος l και περιστρέφεται γύρω από τον κατακόρυφο άξονα Οz, που είναι κάθετος στο άκρο της Ο με σταθερή γωνιακή ταχύτητα ω. Να βρεθεί r η επαγώμενη ΗΕΔ στη
Ασκήσεις 6 ου Κεφαλαίου 1. Μία ράβδος ΟΑ έχει μήκος l και περιστρέφεται γύρω από τον κατακόρυφο άξονα Οz, που είναι κάθετος στο άκρο της Ο με σταθερή γωνιακή ταχύτητα ω. Να βρεθεί r η επαγώμενη ΗΕΔ στη
Αρχή λειτουργίας στοιχειώδους γεννήτριας εναλλασσόμενου ρεύματος
 Αρχή λειτουργίας στοιχειώδους γεννήτριας εναλλασσόμενου ρεύματος ΣΤΟΧΟΣ : Ο μαθητής να μπορεί να, εξηγεί την αρχή λειτουργίας στοιχειώδους γεννήτριας εναλλασσόμενου ρεύματος, κατανοεί τον τρόπο παραγωγής
Αρχή λειτουργίας στοιχειώδους γεννήτριας εναλλασσόμενου ρεύματος ΣΤΟΧΟΣ : Ο μαθητής να μπορεί να, εξηγεί την αρχή λειτουργίας στοιχειώδους γεννήτριας εναλλασσόμενου ρεύματος, κατανοεί τον τρόπο παραγωγής
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΡΗΤΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΡΗΤΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΑΞΙΟΛΟΓΗΣΗ ΠΡΩΤΟΤΥΠΩΝ ΠΤΕΡΥΓΩΣΕΩΝ ΑΝΕΜΟΓΕΝΝΗΤΡΙΩΝ Σπουδαστής: Σάκα Χρηστάκη ΑΜ:5454 Εισηγητής:
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΡΗΤΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΑΞΙΟΛΟΓΗΣΗ ΠΡΩΤΟΤΥΠΩΝ ΠΤΕΡΥΓΩΣΕΩΝ ΑΝΕΜΟΓΕΝΝΗΤΡΙΩΝ Σπουδαστής: Σάκα Χρηστάκη ΑΜ:5454 Εισηγητής:
ΑΣΚΗΣΗ 4 η ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΗΧΑΝΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΑΣΚΗΣΗ 4 η ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΗΧΑΝΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της αρχής λειτουργίας των μηχανών συνεχούς ρεύματος, β) η ανάλυση της κατασκευαστικών
ΑΣΚΗΣΗ 4 η ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΗΧΑΝΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της αρχής λειτουργίας των μηχανών συνεχούς ρεύματος, β) η ανάλυση της κατασκευαστικών
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΑΠΕ. Βισκαδούρος Γ. Ι. Φραγκιαδάκης Φ. Μαυροματάκης
 ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΑΠΕ Βισκαδούρος Γ. Ι. Φραγκιαδάκης Φ. Μαυροματάκης Ισχύς κινητικής ενέργειας φλέβας ανέμου P αν de dt, 1 2 ρdvυ dt P όπου, S, το εμβαδόν του κύκλου της φτερωτής και ρ, η πυκνότητα του αέρα.
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΑΠΕ Βισκαδούρος Γ. Ι. Φραγκιαδάκης Φ. Μαυροματάκης Ισχύς κινητικής ενέργειας φλέβας ανέμου P αν de dt, 1 2 ρdvυ dt P όπου, S, το εμβαδόν του κύκλου της φτερωτής και ρ, η πυκνότητα του αέρα.
πάχος 0 πλάτος 2a μήκος
 B1) Δεδομένου του τύπου E = 2kλ/ρ που έχει αποδειχθεί στο μάθημα και περιγράφει το ηλεκτρικό πεδίο Ε μιας άπειρης γραμμής φορτίου με γραμμική πυκνότητα φορτίου λ σε σημείο Α που βρίσκεται σε απόσταση ρ
B1) Δεδομένου του τύπου E = 2kλ/ρ που έχει αποδειχθεί στο μάθημα και περιγράφει το ηλεκτρικό πεδίο Ε μιας άπειρης γραμμής φορτίου με γραμμική πυκνότητα φορτίου λ σε σημείο Α που βρίσκεται σε απόσταση ρ
Η αρνητική φορά του άξονα z είναι προς τη σελίδα. Για να βρούμε το μέτρο του Β χρησιμοποιούμε την Εξ. (2.3). Στο σημείο Ρ 1 ισχύει
 ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.. Σταθερό ρεύμα 5 Α μέσω χάλκινου σύρματος ρέει προς δεξαμενή ανοδείωσης. Υπολογίστε το μαγνητικό πεδίο που δημιουργείται από το τμήμα του σύρματος μήκους, cm, σε ένα σημείο που
ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.. Σταθερό ρεύμα 5 Α μέσω χάλκινου σύρματος ρέει προς δεξαμενή ανοδείωσης. Υπολογίστε το μαγνητικό πεδίο που δημιουργείται από το τμήμα του σύρματος μήκους, cm, σε ένα σημείο που
Αεροδυναμική του δρομέα
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΒΙΟΜΗΧΑΝΙΚΗΣ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΑΙΟΛΙΚΗ ΕΝΕΡΓΕΙΑ Διδάσκων: Δρ. Ριζιώτης Βασίλης Αεροδυναμική του δρομέα Άδεια Χρήσης Το
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΒΙΟΜΗΧΑΝΙΚΗΣ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΑΙΟΛΙΚΗ ΕΝΕΡΓΕΙΑ Διδάσκων: Δρ. Ριζιώτης Βασίλης Αεροδυναμική του δρομέα Άδεια Χρήσης Το
Ορμή και Δυνάμεις. Θεώρημα Ώθησης Ορμής
 501 Ορμή και Δυνάμεις Θεώρημα Ώθησης Ορμής «Η μεταβολή της ορμής ενός σώματος είναι ίση με την ώθηση της δύναμης που ασκήθηκε στο σώμα» = ή Το θεώρημα αυτό εφαρμόζεται διανυσματικά. 502 Θεώρημα Ώθησης
501 Ορμή και Δυνάμεις Θεώρημα Ώθησης Ορμής «Η μεταβολή της ορμής ενός σώματος είναι ίση με την ώθηση της δύναμης που ασκήθηκε στο σώμα» = ή Το θεώρημα αυτό εφαρμόζεται διανυσματικά. 502 Θεώρημα Ώθησης
website:
 Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση και Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 29 Μαρτίου 2017 1 Συναρτήσεις μεταφοράς σε
Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση και Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 29 Μαρτίου 2017 1 Συναρτήσεις μεταφοράς σε
Ανύψωση τάσης στην έξοδο της γεννήτριας παραγωγής. Υποβιβασμός σε επίπεδα χρησιμοποίησης. Μετατροπή υψηλής τάσης σε χαμηλή με ρεύματα χαμηλής τιμής
 Είδη μετασχηματιστών Μετασχηματιστές Ισχύος Μετασχηματιστές Μονάδος Ανύψωση τάσης στην έξοδο της γεννήτριας παραγωγής Μετασχηματιστές Υποσταθμού Υποβιβασμός σε επίπεδα διανομής Μετασχηματιστές Διανομής
Είδη μετασχηματιστών Μετασχηματιστές Ισχύος Μετασχηματιστές Μονάδος Ανύψωση τάσης στην έξοδο της γεννήτριας παραγωγής Μετασχηματιστές Υποσταθμού Υποβιβασμός σε επίπεδα διανομής Μετασχηματιστές Διανομής
1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 120 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει:
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΩΝ ΕΠΙΛΟΓΩΝ Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο 1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 10 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει: (α)
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΩΝ ΕΠΙΛΟΓΩΝ Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο 1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 10 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει: (α)
ΥδροδυναµικέςΜηχανές
 ΥδροδυναµικέςΜηχανές Τρίγωνα ταχυτήτων στροβιλοµηχανών Εργαστήριο Αιολικής Ενέργειας Τ.Ε.Ι. Κρήτης ηµήτρης Αλ. Κατσαπρακάκης Κυλινδρικέςσυντεταγµένες Στα σχήµατα παριστάνονται αξονικές τοµές και όψεις
ΥδροδυναµικέςΜηχανές Τρίγωνα ταχυτήτων στροβιλοµηχανών Εργαστήριο Αιολικής Ενέργειας Τ.Ε.Ι. Κρήτης ηµήτρης Αλ. Κατσαπρακάκης Κυλινδρικέςσυντεταγµένες Στα σχήµατα παριστάνονται αξονικές τοµές και όψεις
Ηλεκτρικές Μηχανές ΙΙ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 1: Βασικές Αρχές Ηλεκτρικών Μηχανών Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων Μηχανικών ΤΕ Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 1: Βασικές Αρχές Ηλεκτρικών Μηχανών Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων Μηχανικών ΤΕ Άδειες Χρήσης
Τμήμα Ηλεκτρολόγων Μηχανικών ΧΑΡΑΚΤΗΡΙΣΤΙΚΕΣ ΡΟΠΗΣ ΤΑΧΥΤΗΤΑΣ ΕΠΑΓΩΓΙΚΩΝ ΚΙΝΗΤΗΡΩΝ
 Αν είναι γνωστή η συμπεριφορά των μαγνητικών πεδίων στη μηχανή, είναι δυνατός ο προσεγγιστικός προσδιορισμός της χαρακτηριστικής ροπής-ταχύτητας του επαγωγικού κινητήρα Όπως είναι γνωστό η επαγόμενη ροπή
Αν είναι γνωστή η συμπεριφορά των μαγνητικών πεδίων στη μηχανή, είναι δυνατός ο προσεγγιστικός προσδιορισμός της χαρακτηριστικής ροπής-ταχύτητας του επαγωγικού κινητήρα Όπως είναι γνωστό η επαγόμενη ροπή
ΟΝΟΜ/ΝΥΜΟ: ΜΠΑΛΑΜΠΑΝΗ ΓΕΩΡΓΙΑ ΑΜ:6105 ΜΑΘΗΜΑ: ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ ΕΡΓΑΣΙΑ ΤΙΤΛΟΣ: ΤΡΟΠΟΣ ΛΕΙΤΟΥΡΓΙΑΣ ΜΙΑΣ ΣΥΓΧΡΟΝΗΣ ΓΕΝΗΤΡΙΑΣ
 ΟΝΟΜ/ΝΥΜΟ: ΜΠΑΛΑΜΠΑΝΗ ΓΕΩΡΓΙΑ ΑΜ:6105 ΜΑΘΗΜΑ: ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ ΕΡΓΑΣΙΑ ΤΙΤΛΟΣ: ΤΡΟΠΟΣ ΛΕΙΤΟΥΡΓΙΑΣ ΜΙΑΣ ΣΥΓΧΡΟΝΗΣ ΓΕΝΗΤΡΙΑΣ 1 Η γεννήτρια ή ηλεκτρογεννήτρια είναι μηχανή που βασίζεται στους νόμους της
ΟΝΟΜ/ΝΥΜΟ: ΜΠΑΛΑΜΠΑΝΗ ΓΕΩΡΓΙΑ ΑΜ:6105 ΜΑΘΗΜΑ: ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ ΕΡΓΑΣΙΑ ΤΙΤΛΟΣ: ΤΡΟΠΟΣ ΛΕΙΤΟΥΡΓΙΑΣ ΜΙΑΣ ΣΥΓΧΡΟΝΗΣ ΓΕΝΗΤΡΙΑΣ 1 Η γεννήτρια ή ηλεκτρογεννήτρια είναι μηχανή που βασίζεται στους νόμους της
ΑΣΚΗΣΗ 4 η ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ ΣΥΓΧΡΟΝΟΥ ΤΡΙΦΑΣΙΚΟΥ ΚΙΝΗΤΗΡΑ
 ΑΣΚΗΣΗ 4 η ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ ΣΥΓΧΡΟΝΟΥ ΤΡΙΦΑΣΙΚΟΥ ΚΙΝΗΤΗΡΑ Σκοπός της άσκησης: Σκοπός της άσκησης είναι: 1. Να εξοικειωθεί ο σπουδαστής με την διαδικασία εκκίνησης ενός σύγχρονου τριφασικού
ΑΣΚΗΣΗ 4 η ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ ΣΥΓΧΡΟΝΟΥ ΤΡΙΦΑΣΙΚΟΥ ΚΙΝΗΤΗΡΑ Σκοπός της άσκησης: Σκοπός της άσκησης είναι: 1. Να εξοικειωθεί ο σπουδαστής με την διαδικασία εκκίνησης ενός σύγχρονου τριφασικού
ΑΡΧΕΣ ΛΕΙΤΟΥΡΓΙΑΣ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΕΝΑΛΛΑΣΣΟΜΕΝΟΥ ΡΕΥΜΑΤΟΣ
 ΑΡΧΕΣ ΛΕΙΤΟΥΡΓΙΑΣ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΕΝΑΛΛΑΣΣΟΜΕΝΟΥ ΡΕΥΜΑΤΟΣ Οι ηλεκτρικές μηχανές εναλλασσομένου ρεύματος (ΕΡ) χωρίζονται σε δύο κατηγορίες: στις σύγχρονες (που χρησιμοποιούνται συνήθως ως γεννήτριες)
ΑΡΧΕΣ ΛΕΙΤΟΥΡΓΙΑΣ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΕΝΑΛΛΑΣΣΟΜΕΝΟΥ ΡΕΥΜΑΤΟΣ Οι ηλεκτρικές μηχανές εναλλασσομένου ρεύματος (ΕΡ) χωρίζονται σε δύο κατηγορίες: στις σύγχρονες (που χρησιμοποιούνται συνήθως ως γεννήτριες)
d E dt Σχήμα 3.4. (α) Σχηματικό διάγραμμα απλού εναλλάκτη, όπου ένας αγώγιμος βρόχος περιστρέφεται μέσα
 Παράδειγμα 3.1. O περιστρεφόμενος βρόχος με σταθερή γωνιακή ταχύτητα ω μέσα σε σταθερό ομογενές μαγνητικό πεδίο είναι το πρότυπο μοντέλο ενός τύπου γεννήτριας εναλλασσόμενου ρεύματος, του εναλλάκτη. Αναπτύσσει
Παράδειγμα 3.1. O περιστρεφόμενος βρόχος με σταθερή γωνιακή ταχύτητα ω μέσα σε σταθερό ομογενές μαγνητικό πεδίο είναι το πρότυπο μοντέλο ενός τύπου γεννήτριας εναλλασσόμενου ρεύματος, του εναλλάκτη. Αναπτύσσει
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 12 ΣΤΡΟΒΙΛΟΚΙΝΗΤΗΡΩΝ
 ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΘΕΡΜΟΚΙΝΗΤΗΡΩΝ ΚΑΙ ΘΕΡΜΙΚΩΝ ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ ΔΙΔΑΚΤΙΚΗ ΠΕΡΙΟΧΗ: ΕΡΓΑΣΤΗΡΙΟ ΣΤΡΟΒΙΛΟΚΙΝΗΤΗΡΩΝ Υπεύθυνος: Επικ. Καθηγητής Δρ. Α. ΦΑΤΣΗΣ ΕΡΓΑΣΤΗΡΙΑΚΗ
ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΘΕΡΜΟΚΙΝΗΤΗΡΩΝ ΚΑΙ ΘΕΡΜΙΚΩΝ ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ ΔΙΔΑΚΤΙΚΗ ΠΕΡΙΟΧΗ: ΕΡΓΑΣΤΗΡΙΟ ΣΤΡΟΒΙΛΟΚΙΝΗΤΗΡΩΝ Υπεύθυνος: Επικ. Καθηγητής Δρ. Α. ΦΑΤΣΗΣ ΕΡΓΑΣΤΗΡΙΑΚΗ
ΑΣΚΗΣΗ 5 η ΑΣΥΓΧΡΟΝΟΣ ΤΡΙΦΑΣΙΚΟΣ ΚΙΝΗΤΗΡΑΣ. 1. Η μελέτη της δομής και της αρχής λειτουργίας ενός ασύγχρονου τριφασικού κινητήρα.
 Σκοπός της άσκησης: ΑΣΚΗΣΗ 5 η ΑΣΥΓΧΡΟΝΟΣ ΤΡΙΦΑΣΙΚΟΣ ΚΙΝΗΤΗΡΑΣ Σκοπός της εργαστηριακής άσκησης είναι: 1. Η μελέτη της δομής και της αρχής λειτουργίας ενός ασύγχρονου τριφασικού κινητήρα. 1. Γενικά Οι
Σκοπός της άσκησης: ΑΣΚΗΣΗ 5 η ΑΣΥΓΧΡΟΝΟΣ ΤΡΙΦΑΣΙΚΟΣ ΚΙΝΗΤΗΡΑΣ Σκοπός της εργαστηριακής άσκησης είναι: 1. Η μελέτη της δομής και της αρχής λειτουργίας ενός ασύγχρονου τριφασικού κινητήρα. 1. Γενικά Οι
ΣΤΟΙΧΕΙΑ ΠΡΑΓΜΑΤΙΚΩΝ ΜΗΧΑΝΩΝ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΣΤΟΙΧΕΙΑ ΠΡΑΓΜΑΤΙΚΩΝ ΜΗΧΑΝΩΝ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΒΑΣΙΚΑ ΤΜΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΜΗΧΑΝΗΣ ΣΡ Αναλύοντας τη δομή μιας πραγματικής μηχανής ΣΡ, αναφέρουμε τα ακόλουθα βασικά μέρη: Στάτης: αποτελεί το ακίνητο τμήμα
ΣΤΟΙΧΕΙΑ ΠΡΑΓΜΑΤΙΚΩΝ ΜΗΧΑΝΩΝ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΒΑΣΙΚΑ ΤΜΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΜΗΧΑΝΗΣ ΣΡ Αναλύοντας τη δομή μιας πραγματικής μηχανής ΣΡ, αναφέρουμε τα ακόλουθα βασικά μέρη: Στάτης: αποτελεί το ακίνητο τμήμα
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 11 ΣΤΡΟΒΙΛΟΚΙΝΗΤΗΡΩΝ
 ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΘΕΡΜΟΚΙΝΗΤΗΡΩΝ ΚΑΙ ΘΕΡΜΙΚΩΝ ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ ΔΙΔΑΚΤΙΚΗ ΠΕΡΙΟΧΗ: ΕΡΓΑΣΤΗΡΙΟ ΣΤΡΟΒΙΛΟΚΙΝΗΤΗΡΩΝ Υπεύθυνος: Επικ. Καθηγητής Δρ. Α. ΦΑΤΣΗΣ ΕΡΓΑΣΤΗΡΙΑΚΗ
ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΘΕΡΜΟΚΙΝΗΤΗΡΩΝ ΚΑΙ ΘΕΡΜΙΚΩΝ ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ ΔΙΔΑΚΤΙΚΗ ΠΕΡΙΟΧΗ: ΕΡΓΑΣΤΗΡΙΟ ΣΤΡΟΒΙΛΟΚΙΝΗΤΗΡΩΝ Υπεύθυνος: Επικ. Καθηγητής Δρ. Α. ΦΑΤΣΗΣ ΕΡΓΑΣΤΗΡΙΑΚΗ
Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 03-04 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 0/0/03 ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α4 και δίπλα
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 03-04 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 0/0/03 ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α4 και δίπλα
Ασκήσεις ενότητας: «Αιολική Ενέργεια»
 Ασκήσεις ενότητας: «Αιολική Ενέργεια» «Εισαγωγή στην Αεροδυναμική» 1. Αν S 2 =2 S 1 πόσο αλλάζουν οι V και P; P 2 P 1 S 1 V 1 S 2 V 2 L 1 = V 1 t L 2 = V 2 t 2. Αν Re critical = 680.000, V=10m/s, ποιό
Ασκήσεις ενότητας: «Αιολική Ενέργεια» «Εισαγωγή στην Αεροδυναμική» 1. Αν S 2 =2 S 1 πόσο αλλάζουν οι V και P; P 2 P 1 S 1 V 1 S 2 V 2 L 1 = V 1 t L 2 = V 2 t 2. Αν Re critical = 680.000, V=10m/s, ποιό
Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας.
 ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Ο πυκνωτής Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας. Η απλούστερη μορφή πυκνωτή είναι ο επίπεδος πυκνωτής, ο οποίος
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Ο πυκνωτής Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας. Η απλούστερη μορφή πυκνωτή είναι ο επίπεδος πυκνωτής, ο οποίος
Τμήμα Ηλεκτρολόγων Μηχανικών ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΠΑΡΑΜΕΤΡΩΝ ΣΤΟ ΙΣΟΔΥΝΑΜΟ ΚΥΚΛΩΜΑ
 Το ισοδύναμο κύκλωμα ενός επαγωγικού κινητήρα αποτελεί ένα πολύ σημαντικό εργαλείο για τον προσδιορισμό της απόκρισης του κινητήρα στις αλλαγές του φορτίου του Για να χρησιμοποιηθεί αυτό το ισοδύναμο θα
Το ισοδύναμο κύκλωμα ενός επαγωγικού κινητήρα αποτελεί ένα πολύ σημαντικό εργαλείο για τον προσδιορισμό της απόκρισης του κινητήρα στις αλλαγές του φορτίου του Για να χρησιμοποιηθεί αυτό το ισοδύναμο θα
Έλικες Θεωρία γραμμής άνωσης
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΒΙΟΜΗΧΑΝΙΚΗΣ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΑΕΡΟΔΥΝΑΜΙΚΗ Διδάσκων: Δρ. Ριζιώτης Βασίλης Έλικες Θεωρία γραμμής άνωσης Άδεια Χρήσης Το
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΒΙΟΜΗΧΑΝΙΚΗΣ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΑΕΡΟΔΥΝΑΜΙΚΗ Διδάσκων: Δρ. Ριζιώτης Βασίλης Έλικες Θεωρία γραμμής άνωσης Άδεια Χρήσης Το
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ 1 3.1 ΠΕΙΡΑΜΑΤΑ ΕΠΑΓΩΓΗΣ Το Σχ. 3.1 δείχνει μερικά από τα πειράματα που πραγματοποίησε o Michael Faraday. Στο Σχ. 3.1(α, β, γ) ένα πηνίο συνδέεται με γαλβανόμετρο.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ 1 3.1 ΠΕΙΡΑΜΑΤΑ ΕΠΑΓΩΓΗΣ Το Σχ. 3.1 δείχνει μερικά από τα πειράματα που πραγματοποίησε o Michael Faraday. Στο Σχ. 3.1(α, β, γ) ένα πηνίο συνδέεται με γαλβανόμετρο.
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ
 ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
7. Στρέψη. Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών. 7. Στρέψη/ Μηχανική Υλικών
 7. Στρέψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 7. Στρέψη/ Μηχανική Υλικών 2015 1 Εισαγωγή Σε προηγούμενα κεφάλαια μελετήσαμε πώς να υπολογίζουμε τις ροπές και τις τάσεις σε δομικά μέλη τα
7. Στρέψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 7. Στρέψη/ Μηχανική Υλικών 2015 1 Εισαγωγή Σε προηγούμενα κεφάλαια μελετήσαμε πώς να υπολογίζουμε τις ροπές και τις τάσεις σε δομικά μέλη τα
Πηγές μαγνητικού πεδίου Νόμος Ampere. Ιωάννης Γκιάλας 21 Μαίου 2014
 Πηγές μαγνητικού πεδίου Νόμος Ampere Ιωάννης Γκιάλας 21 Μαίου 214 Στόχοι διάλεξης Να κατανοηθεί πως προκαλείται το μαγνητικό πεδίο Νόμος Biot-Savart Μαγνητικό πεδίο ευθύγραμμου ρευματοφόρου αγωγού Μαγνητική
Πηγές μαγνητικού πεδίου Νόμος Ampere Ιωάννης Γκιάλας 21 Μαίου 214 Στόχοι διάλεξης Να κατανοηθεί πως προκαλείται το μαγνητικό πεδίο Νόμος Biot-Savart Μαγνητικό πεδίο ευθύγραμμου ρευματοφόρου αγωγού Μαγνητική
Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 03-0 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΛΥΣΕΙΣ) ΗΜΕΡΟΜΗΝΙΑ: 0/0/03 ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 03-0 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΛΥΣΕΙΣ) ΗΜΕΡΟΜΗΝΙΑ: 0/0/03 ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α
Μαγνητικό Πεδίο. Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ
 Μαγνητικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SERWAY, Physics fo scientists and enginees YOUNG H.D., Univesity
Μαγνητικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SERWAY, Physics fo scientists and enginees YOUNG H.D., Univesity
Κινηματική ρευστών. Ροή ρευστού = η κίνηση του ρευστού, μέσα στο περιβάλλον του
 301 Κινηματική ρευστών Ροή ρευστού = η κίνηση του ρευστού, μέσα στο περιβάλλον του Είδη ροής α) Σταθερή ή μόνιμη = όταν σε κάθε σημείο του χώρου οι συνθήκες ροής, ταχύτητα, θερμοκρασία, πίεση και πυκνότητα,
301 Κινηματική ρευστών Ροή ρευστού = η κίνηση του ρευστού, μέσα στο περιβάλλον του Είδη ροής α) Σταθερή ή μόνιμη = όταν σε κάθε σημείο του χώρου οι συνθήκες ροής, ταχύτητα, θερμοκρασία, πίεση και πυκνότητα,
ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Γ
 ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Γ ΜΑΘΗΜΑ 1 Δομή Σύγχρονης Ηλεκτρικής Μηχανής Μαγνητικά Πεδία σε ΣΗΜ Επαγόμενες Τάσεις και αλληλεπίδραση μαγνητικών Πεδίων Ουρεϊλίδης Κωνσταντίνος, Υποψ. Διδακτωρ Πρόβλημα 1. Έστω ότι
ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Γ ΜΑΘΗΜΑ 1 Δομή Σύγχρονης Ηλεκτρικής Μηχανής Μαγνητικά Πεδία σε ΣΗΜ Επαγόμενες Τάσεις και αλληλεπίδραση μαγνητικών Πεδίων Ουρεϊλίδης Κωνσταντίνος, Υποψ. Διδακτωρ Πρόβλημα 1. Έστω ότι
ΚΕΦΑΛΑΙΟ 3 Ο : ΙΣΧΥΣ ΚΥΚΛΩΜΑΤΩΝ ΣΤΟ ΕΝΑΛΛΑΣΣΟΜΕΝΟ ΡΕΥΜΑ
 ΚΕΦΑΛΑΙΟ 3 Ο : ΙΣΧΥΣ ΚΥΚΛΩΜΑΤΩΝ ΣΤΟ ΕΝΑΛΛΑΣΣΟΜΕΝΟ ΡΕΥΜΑ 1 Ως ισχύς ορίζεται ο ρυθμός παροχής ή κατανάλωσης ενέργειας. Η ηλεκτρική ισχύς ορίζεται ως το γινόμενο της τάσης επί το ρεύμα: p u i Ιδανικό πηνίο
ΚΕΦΑΛΑΙΟ 3 Ο : ΙΣΧΥΣ ΚΥΚΛΩΜΑΤΩΝ ΣΤΟ ΕΝΑΛΛΑΣΣΟΜΕΝΟ ΡΕΥΜΑ 1 Ως ισχύς ορίζεται ο ρυθμός παροχής ή κατανάλωσης ενέργειας. Η ηλεκτρική ισχύς ορίζεται ως το γινόμενο της τάσης επί το ρεύμα: p u i Ιδανικό πηνίο
Λύση: Η δύναμη σε ρευματοφόρο αγωγό δίνεται από την
 1) Στο παρακάτω σχήμα το τμήμα της καμπύλης ΚΛ μεταξύ x = 1 και x = 3.5 αντιστοιχεί σε ένα αγωγό που διαρρέεται από ρεύμα Ι = 1.5 Α με τη φορά που δείχνεται. Η καμπύλη είναι δευτεροβάθμια ως προς x με
1) Στο παρακάτω σχήμα το τμήμα της καμπύλης ΚΛ μεταξύ x = 1 και x = 3.5 αντιστοιχεί σε ένα αγωγό που διαρρέεται από ρεύμα Ι = 1.5 Α με τη φορά που δείχνεται. Η καμπύλη είναι δευτεροβάθμια ως προς x με
( ) Στοιχεία που αποθηκεύουν ενέργεια Ψ = N Φ. διαφορικές εξισώσεις. Πηνίο. μαγνητικό πεδίο. του πηνίου (κάθε. ένα πηνίο Ν σπειρών:
 Στοιχεία που αποθηκεύουν ενέργεια Λέγονται επίσης και δυναμικά στοιχεία Οι v- χαρακτηριστικές τους δεν είναι αλγεβρικές, αλλά ολοκληρο- διαφορικές εξισώσεις. Πηνίο: Ουσιαστικά πρόκειται για έναν περιεστραμμένο
Στοιχεία που αποθηκεύουν ενέργεια Λέγονται επίσης και δυναμικά στοιχεία Οι v- χαρακτηριστικές τους δεν είναι αλγεβρικές, αλλά ολοκληρο- διαφορικές εξισώσεις. Πηνίο: Ουσιαστικά πρόκειται για έναν περιεστραμμένο
Αιολική Ενέργεια & Ενέργεια του Νερού
 Αιολική Ενέργεια & Ενέργεια του Νερού Ενότητα 4: Αιολικές Μηχανές Γεώργιος Λευθεριώτης, Επίκουρος Καθηγητής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Κατηγοριοποίηση αιολικών μηχανών Κινητήρια
Αιολική Ενέργεια & Ενέργεια του Νερού Ενότητα 4: Αιολικές Μηχανές Γεώργιος Λευθεριώτης, Επίκουρος Καθηγητής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Κατηγοριοποίηση αιολικών μηχανών Κινητήρια
Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων
 Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων Ενότητα 6: Δυναμική μηχανής συνεχούς ρεύματος Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών
Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων Ενότητα 6: Δυναμική μηχανής συνεχούς ρεύματος Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών
ΠΕΡΙΕΧΟΜΕΝΑ ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1
 ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1 1 ΟΙ ΒΑΣΙΚΟΙ ΝΟΜΟΙ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟΥ ΠΕΔΙΟΥ 7 1.1 Μονάδες και σύμβολα φυσικών μεγεθών..................... 7 1.2 Προθέματα φυσικών μεγεθών.............................. 13 1.3 Αγωγοί,
ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1 1 ΟΙ ΒΑΣΙΚΟΙ ΝΟΜΟΙ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟΥ ΠΕΔΙΟΥ 7 1.1 Μονάδες και σύμβολα φυσικών μεγεθών..................... 7 1.2 Προθέματα φυσικών μεγεθών.............................. 13 1.3 Αγωγοί,
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Χωρητικότητα Εικόνα: Όλες οι παραπάνω συσκευές είναι πυκνωτές, οι οποίοι αποθηκεύουν ηλεκτρικό φορτίο και ενέργεια. Ο πυκνωτής είναι ένα είδος κυκλώματος που μπορούμε να συνδυάσουμε
Φυσική για Μηχανικούς Χωρητικότητα Εικόνα: Όλες οι παραπάνω συσκευές είναι πυκνωτές, οι οποίοι αποθηκεύουν ηλεκτρικό φορτίο και ενέργεια. Ο πυκνωτής είναι ένα είδος κυκλώματος που μπορούμε να συνδυάσουμε
Κινητήρας παράλληλης διέγερσης
 Κινητήρας παράλληλης διέγερσης Ισοδύναμο κύκλωμα V = E + I T V = I I T = I F L R F I F R Η διέγερση τοποθετείται παράλληλα με το κύκλωμα οπλισμού Χαρακτηριστική φορτίου Έλεγχος ταχύτητας Μεταβολή τάσης
Κινητήρας παράλληλης διέγερσης Ισοδύναμο κύκλωμα V = E + I T V = I I T = I F L R F I F R Η διέγερση τοποθετείται παράλληλα με το κύκλωμα οπλισμού Χαρακτηριστική φορτίου Έλεγχος ταχύτητας Μεταβολή τάσης
ΥΔΡΑΥΛΙΚΗ ΑΝΟΙΚΤΩΝ ΑΓΩΓΩΝ
 Τμήμα Δασολογίας & Διαχείρισης Περιβάλλοντος & Φυσικών Πόρων Εργαστήριο Διευθέτησης Ορεινών Υδάτων και Διαχείρισης Κινδύνου Προπτυχιακό Πρόγραμμα Σπουδών ΥΔΡΑΥΛΙΚΗ ΑΝΟΙΚΤΩΝ ΑΓΩΓΩΝ Κεφάλαιο 3 ο : Εξίσωση
Τμήμα Δασολογίας & Διαχείρισης Περιβάλλοντος & Φυσικών Πόρων Εργαστήριο Διευθέτησης Ορεινών Υδάτων και Διαχείρισης Κινδύνου Προπτυχιακό Πρόγραμμα Σπουδών ΥΔΡΑΥΛΙΚΗ ΑΝΟΙΚΤΩΝ ΑΓΩΓΩΝ Κεφάλαιο 3 ο : Εξίσωση
ΣΤΟΧΟΙ : Ο μαθητής να μπορεί να :
 ΠΗΝΙΟ ΣΤΟΧΟΙ : Ο μαθητής να μπορεί να : Αναφέρει τι είναι το πηνίο Αναφέρει από τι αποτελείται το πηνίο Αναφέρει τις ιδιότητες του πηνίου Αναφέρει το βασικό χαρακτηριστικό του πηνίου Αναφέρει τη σχέση
ΠΗΝΙΟ ΣΤΟΧΟΙ : Ο μαθητής να μπορεί να : Αναφέρει τι είναι το πηνίο Αναφέρει από τι αποτελείται το πηνίο Αναφέρει τις ιδιότητες του πηνίου Αναφέρει το βασικό χαρακτηριστικό του πηνίου Αναφέρει τη σχέση
ΟΝΟΜ/ΩΝΥΜΟ:ΣΤΕΦΑΝΟΣ ΓΚΟΥΝΤΟΥΣΟΥΔΗΣ Α.Μ:6750 ΕΡΓΑΣΙΑ ΕΞΑΜΗΝΟΥ:ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ (ΕΡΓΑΣΤΗΡΙΟ)
 ΟΝΟΜ/ΩΝΥΜΟ:ΣΤΕΦΑΝΟΣ ΓΚΟΥΝΤΟΥΣΟΥΔΗΣ Α.Μ:6750 ΕΡΓΑΣΙΑ ΕΞΑΜΗΝΟΥ:ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ (ΕΡΓΑΣΤΗΡΙΟ) Περιγραφή Λειτουργίας Σύγχρονου Κινητήρα Σκοπός: Η παρούσα εργασία έχει σκοπό να περιγράψει τη λειτουργία ενός
ΟΝΟΜ/ΩΝΥΜΟ:ΣΤΕΦΑΝΟΣ ΓΚΟΥΝΤΟΥΣΟΥΔΗΣ Α.Μ:6750 ΕΡΓΑΣΙΑ ΕΞΑΜΗΝΟΥ:ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ (ΕΡΓΑΣΤΗΡΙΟ) Περιγραφή Λειτουργίας Σύγχρονου Κινητήρα Σκοπός: Η παρούσα εργασία έχει σκοπό να περιγράψει τη λειτουργία ενός
Γεννήτριες ΣΡ Κινητήρες ΣΡ
 Γεννήτριες ΣΡ Κινητήρες ΣΡ - Στοιχειώδεις Ηλεκτρικές Μηχανές Επαγωγή λέγεται το φαινόμενο κατά το οποίο αναπτύσσεται ΗΕΔ: a. Στα άκρα αγωγού όταν αυτός κινείται με ταχύτητα υ μέσα σε μαγνητικό πεδίο επαγωγής
Γεννήτριες ΣΡ Κινητήρες ΣΡ - Στοιχειώδεις Ηλεκτρικές Μηχανές Επαγωγή λέγεται το φαινόμενο κατά το οποίο αναπτύσσεται ΗΕΔ: a. Στα άκρα αγωγού όταν αυτός κινείται με ταχύτητα υ μέσα σε μαγνητικό πεδίο επαγωγής
ΕΡΓΑΣΙΑ 6. Ημερομηνία Παράδοσης: 29/6/09
 ΕΡΓΑΣΙΑ 6 Ημερομηνία Παράδοσης: 9/6/9 1. Ένας ομογενώς φορτισμένος μονωτικός κυκλικός δίσκος ακτίνας με συνολικό φορτίο τοποθετείται στο επίπεδο xy. Να βρείτε το ηλεκτρικό πεδίο σε σημείο P που βρίσκεται
ΕΡΓΑΣΙΑ 6 Ημερομηνία Παράδοσης: 9/6/9 1. Ένας ομογενώς φορτισμένος μονωτικός κυκλικός δίσκος ακτίνας με συνολικό φορτίο τοποθετείται στο επίπεδο xy. Να βρείτε το ηλεκτρικό πεδίο σε σημείο P που βρίσκεται
ΔΙΑΓΩΝΙΣΜΑ Β. Θέµα 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 ΔΙΑΓΩΝΙΣΜΑ Β Θέµα ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση Ένα πρωτόνιο και ένας πυρήνας ηλίου εισέρχονται σε οµογενές
ΔΙΑΓΩΝΙΣΜΑ Β Θέµα ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση Ένα πρωτόνιο και ένας πυρήνας ηλίου εισέρχονται σε οµογενές
1. Ιδανικό κύκλωμα LC εκτελεί ηλεκτρικές ταλαντώσεις και η χρονική εξίσωση του φορτίου του πυκνωτή
 Εισαγωγικές ασκήσεις στις ηλεκτρικές ταλαντώσεις 1. Ιδανικό κύκλωμα L εκτελεί ηλεκτρικές ταλαντώσεις και η χρονική εξίσωση του φορτίου του πυκνωτή δίνεται από τη σχέση q = 10 6 συν(10 ) (S.I.). Ο συντελεστής
Εισαγωγικές ασκήσεις στις ηλεκτρικές ταλαντώσεις 1. Ιδανικό κύκλωμα L εκτελεί ηλεκτρικές ταλαντώσεις και η χρονική εξίσωση του φορτίου του πυκνωτή δίνεται από τη σχέση q = 10 6 συν(10 ) (S.I.). Ο συντελεστής
ΤΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ
 ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ 3.3 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΤΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ Οι μαγνητικοί πόλοι υπάρχουν πάντοτε σε ζευγάρια. ΔΕΝ ΥΠΑΡΧΟΥΝ ΜΑΓΝΗΤΙΚΑ ΜΟΝΟΠΟΛΑ. Οι ομώνυμοι πόλοι απωθούνται, ενώ οι
ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ 3.3 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΤΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ Οι μαγνητικοί πόλοι υπάρχουν πάντοτε σε ζευγάρια. ΔΕΝ ΥΠΑΡΧΟΥΝ ΜΑΓΝΗΤΙΚΑ ΜΟΝΟΠΟΛΑ. Οι ομώνυμοι πόλοι απωθούνται, ενώ οι
Πρόβλημα 7.1. την πρώτη, ένα R όταν συγκλίνει στην δεύτερη). Επομένως
 Πρόβλημα 7.1 (a) Αν Q είναι το φορτίο του εσωτερικού κελύφους, τότε στο χώρο ανάμεσα στα δύο κελύφη, και (c) Για πολύ μεγάλο b (b>>a), ο δεύτερος όρος είναι αμελητέος, και Ουσιαστικά όλη η αντίσταση είναι
Πρόβλημα 7.1 (a) Αν Q είναι το φορτίο του εσωτερικού κελύφους, τότε στο χώρο ανάμεσα στα δύο κελύφη, και (c) Για πολύ μεγάλο b (b>>a), ο δεύτερος όρος είναι αμελητέος, και Ουσιαστικά όλη η αντίσταση είναι
ΜΗΧΑΝΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ. Κινητήρες ΣΡ. Άγγελος Μπουχουράς - Μηχανές Ι
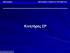 Το ισοδύναμο κύκλωμα ενός κινητήρα ΣΡ: Το κύκλωμα οπλισμού παριστάνεται με μια ιδανική πηγή τάσης ΕΑ και μία αντίσταση RA Στην ουσία πρόκειται για το ισοδύναμο κύκλωμα του δρομέα που περιλαμβάνει: τους
Το ισοδύναμο κύκλωμα ενός κινητήρα ΣΡ: Το κύκλωμα οπλισμού παριστάνεται με μια ιδανική πηγή τάσης ΕΑ και μία αντίσταση RA Στην ουσία πρόκειται για το ισοδύναμο κύκλωμα του δρομέα που περιλαμβάνει: τους
( ) = ( ) Ηλεκτρική Ισχύς. p t V I t t. cos cos 1 cos cos 2. p t V I t. το στιγμιαίο ρεύμα: όμως: Άρα θα είναι: Επειδή όμως: θα είναι τελικά:
 Η στιγμιαία ηλεκτρική ισχύς σε οποιοδήποτε σημείο ενός κυκλώματος υπολογίζεται ως το γινόμενο της στιγμιαίας τάσης επί το στιγμιαίο ρεύμα: Σε ένα εναλλασσόμενο σύστημα τάσεων και ρευμάτων θα έχουμε όμως:
Η στιγμιαία ηλεκτρική ισχύς σε οποιοδήποτε σημείο ενός κυκλώματος υπολογίζεται ως το γινόμενο της στιγμιαίας τάσης επί το στιγμιαίο ρεύμα: Σε ένα εναλλασσόμενο σύστημα τάσεων και ρευμάτων θα έχουμε όμως:
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ και ΕΦΑΡΜΟΓΕΣ ΕΡΩΤΗΜΑΤΟΛΟΓΙΟ ΜΑΘΗΜΑΤΟΣ
 1 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ και ΕΦΑΡΜΟΓΕΣ ΕΡΩΤΗΜΑΤΟΛΟΓΙΟ ΜΑΘΗΜΑΤΟΣ 1) Να αναφέρετε τις 4 παραδοχές που ισχύουν για το ηλεκτρικό φορτίο 2) Εξηγήστε πόσα είδη κατανοµών ηλεκτρικού φορτίου υπάρχουν. ιατυπώστε τους
1 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ και ΕΦΑΡΜΟΓΕΣ ΕΡΩΤΗΜΑΤΟΛΟΓΙΟ ΜΑΘΗΜΑΤΟΣ 1) Να αναφέρετε τις 4 παραδοχές που ισχύουν για το ηλεκτρικό φορτίο 2) Εξηγήστε πόσα είδη κατανοµών ηλεκτρικού φορτίου υπάρχουν. ιατυπώστε τους
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ. Ένα μεταβαλλόμενο μαγνητικό πεδίο γεννά ηλεκτρικό ρεύμα
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ Ένα μεταβαλλόμενο μαγνητικό πεδίο γεννά ηλεκτρικό ρεύμα ΠΕΙΡΑΜΑΤΑ ΕΠΑΓΩΓΗΣ Όταν κλείνουμε το διακόπτη εμφανίζεται στιγμιαία ρεύμα στο δεξιό πηνίο Michael Faraday 1791-1867 Joseph
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ Ένα μεταβαλλόμενο μαγνητικό πεδίο γεννά ηλεκτρικό ρεύμα ΠΕΙΡΑΜΑΤΑ ΕΠΑΓΩΓΗΣ Όταν κλείνουμε το διακόπτη εμφανίζεται στιγμιαία ρεύμα στο δεξιό πηνίο Michael Faraday 1791-1867 Joseph
Μαγνητικό Πεδίο. Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ
 Μαγνητικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SERWAY, Physics for scientists and engineers YOUNG H.D., University
Μαγνητικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SERWAY, Physics for scientists and engineers YOUNG H.D., University
Δυναμική Ηλεκτρικών Μηχανών
 Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΣΧΕΔΙΑΣΜΟΣ ΠΤΕΡΥΓΩΣΗΣ ΚΑΙ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΑΝΕΜΟΚΙΝΗΤΗΡΟΣ ΟΡΙΖΟΝΤΙΟΥ ΑΞΟΝΑ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΕΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΝΕΡΓΕΙΑΚΟΣ ΤΟΜΕΑΣ ΣΧΕΔΙΑΣΜΟΣ ΠΤΕΡΥΓΩΣΗΣ ΚΑΙ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΑΝΕΜΟΚΙΝΗΤΗΡΟΣ ΟΡΙΖΟΝΤΙΟΥ ΑΞΟΝΑ ΣΠΟΥΔΑΣΤΗΣ: ΕΙΣΗΓΗΤΗΣ:
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΕΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΝΕΡΓΕΙΑΚΟΣ ΤΟΜΕΑΣ ΣΧΕΔΙΑΣΜΟΣ ΠΤΕΡΥΓΩΣΗΣ ΚΑΙ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΑΝΕΜΟΚΙΝΗΤΗΡΟΣ ΟΡΙΖΟΝΤΙΟΥ ΑΞΟΝΑ ΣΠΟΥΔΑΣΤΗΣ: ΕΙΣΗΓΗΤΗΣ:
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 5 ΣΤΡΟΒΙΛΟΚΙΝΗΤΗΡΩΝ
 ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΘΕΡΜΟΚΙΝΗΤΗΡΩΝ ΚΑΙ ΘΕΡΜΙΚΩΝ ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ ΔΙΔΑΚΤΙΚΗ ΠΕΡΙΟΧΗ: ΕΡΓΑΣΤΗΡΙΟ ΣΤΡΟΒΙΛΟΚΙΝΗΤΗΡΩΝ Υπεύθυνος: Επικ. Καθηγητής Δρ. Α. ΦΑΤΣΗΣ ΕΡΓΑΣΤΗΡΙΑΚΗ
ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΘΕΡΜΟΚΙΝΗΤΗΡΩΝ ΚΑΙ ΘΕΡΜΙΚΩΝ ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ ΔΙΔΑΚΤΙΚΗ ΠΕΡΙΟΧΗ: ΕΡΓΑΣΤΗΡΙΟ ΣΤΡΟΒΙΛΟΚΙΝΗΤΗΡΩΝ Υπεύθυνος: Επικ. Καθηγητής Δρ. Α. ΦΑΤΣΗΣ ΕΡΓΑΣΤΗΡΙΑΚΗ
Προηγμένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών
 Προηγμένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών Το εκπαιδευτικό υλικό που ακολουθεί αναπτύχθηκε στα πλαίσια του έργου «Προηγμένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών», του Μέτρου «Εισαγωγή
Προηγμένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών Το εκπαιδευτικό υλικό που ακολουθεί αναπτύχθηκε στα πλαίσια του έργου «Προηγμένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών», του Μέτρου «Εισαγωγή
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α ΗΜΕΡΟΜΗΝΙΑ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-KΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α ΗΜΕΡΟΜΗΝΙΑ: 19-10-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-KΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α ΗΜΕΡΟΜΗΝΙΑ: 19-10-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-KΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4
Υδραυλικές Μηχανές και Ενέργεια
 Υδραυλικές Μηχανές και Ενέργεια Διάλεξη 8. - Υδροστρόβιλοι αντιδράσεως - Ολοκλήρωση θεωρίας για υδροστρόβιλους δράσεως Σκουληκάρης Χαράλαμπος Ηλεκτρολόγος Μηχανικός & Μηχ. Η/Υ, MSc, PhD hskoulik@civil.auth.gr
Υδραυλικές Μηχανές και Ενέργεια Διάλεξη 8. - Υδροστρόβιλοι αντιδράσεως - Ολοκλήρωση θεωρίας για υδροστρόβιλους δράσεως Σκουληκάρης Χαράλαμπος Ηλεκτρολόγος Μηχανικός & Μηχ. Η/Υ, MSc, PhD hskoulik@civil.auth.gr
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
ΑΣΚΗΣΗ 8 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ
 ΑΣΚΗΣΗ 8 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της λειτουργίας του κινητήρα συνεχούς
ΑΣΚΗΣΗ 8 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της λειτουργίας του κινητήρα συνεχούς
ΑΣΚΗΣΗ 5 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΧΑΡΑΚΤΗΡΙΣΤΙΚΕΣ ΚΑΜΠΥΛΕΣ
 ΑΣΚΗΣΗ 5 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΧΑΡΑΚΤΗΡΙΣΤΙΚΕΣ ΚΑΜΠΥΛΕΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της λειτουργίας της γεννήτριας συνεχούς ρεύματος
ΑΣΚΗΣΗ 5 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΧΑΡΑΚΤΗΡΙΣΤΙΚΕΣ ΚΑΜΠΥΛΕΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της λειτουργίας της γεννήτριας συνεχούς ρεύματος
10 - ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ
 10 - ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Ηλεκτρική μηχανή ονομάζεται κάθε διάταξη η οποία μετατρέπει τη μηχανική ενεργεια σε ηλεκτρική ή αντίστροφα ή μετατρεπει τα χαρακτηριστικά του ηλεκτρικού ρεύματος. Οι ηλεκτρικες
10 - ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Ηλεκτρική μηχανή ονομάζεται κάθε διάταξη η οποία μετατρέπει τη μηχανική ενεργεια σε ηλεκτρική ή αντίστροφα ή μετατρεπει τα χαρακτηριστικά του ηλεκτρικού ρεύματος. Οι ηλεκτρικες
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ. Μια παράσταση που περιέχει πράξεις με μεταβλητές (γράμματα) και αριθμούς καλείται αλγεβρική, όπως για παράδειγμα η : 2x+3y-8
 ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 3: Συνδυασμός αντιστάσεων και πηγών Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ. ΕΥΔΟΞΟΣ:
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 3: Συνδυασμός αντιστάσεων και πηγών Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ. ΕΥΔΟΞΟΣ:
Ο τελευταίος όρος είναι πάνω από την επιφάνεια στο άπειρο όπου J = 0,έτσι είναι μηδέν. Επομένως
 Πρόβλημα 9.1 Αλλά και αφού είναι: Αλλά Και Έτσι Όμοια Επί πλέον (οι άλλοι δύο όροι αναιρούνται αφού Επομένως: Ο τελευταίος όρος είναι πάνω από την επιφάνεια στο άπειρο όπου J = 0,έτσι είναι μηδέν. Επομένως
Πρόβλημα 9.1 Αλλά και αφού είναι: Αλλά Και Έτσι Όμοια Επί πλέον (οι άλλοι δύο όροι αναιρούνται αφού Επομένως: Ο τελευταίος όρος είναι πάνω από την επιφάνεια στο άπειρο όπου J = 0,έτσι είναι μηδέν. Επομένως
ΕΝΟΤΗΤΑ ΙΙΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ
 ΕΝΟΤΗΤΑ ΙΙΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ 19 Μαγνητικό πεδίο Μαγνητικό πεδίο ονοµάζεται ο χώρος στον οποίο ασκούνται δυνάµεις σε οποιοδήποτε κινούµενο φορτίο εισάγεται σε αυτόν. Επειδή το ηλεκτρικό ρεύµα είναι διατεταγµένη
ΕΝΟΤΗΤΑ ΙΙΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ 19 Μαγνητικό πεδίο Μαγνητικό πεδίο ονοµάζεται ο χώρος στον οποίο ασκούνται δυνάµεις σε οποιοδήποτε κινούµενο φορτίο εισάγεται σε αυτόν. Επειδή το ηλεκτρικό ρεύµα είναι διατεταγµένη
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
Φυσική ΙΙ (Ηλεκτρομαγνητισμός Οπτική)
 Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Φυσική ΙΙ (Ηλεκτρομαγνητισμός Οπτική) Διάλεξη 5 η Ιωάννα Ζεργιώτη Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Φυσική ΙΙ (Ηλεκτρομαγνητισμός Οπτική) Διάλεξη 5 η Ιωάννα Ζεργιώτη Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
B 2Tk. Παράδειγμα 1.2.1
 Παράδειγμα 1..1 Μία δέσμη πρωτονίων κινείται μέσα σε ομογενές μαγνητικό πεδίο μέτρου,0 Τ, που έχει την κατεύθυνση του άξονα των θετικών z, (Σχ. 1.4). Τα πρωτόνια έχουν ταχύτητα με μέτρο 3,0 10 5 m / s
Παράδειγμα 1..1 Μία δέσμη πρωτονίων κινείται μέσα σε ομογενές μαγνητικό πεδίο μέτρου,0 Τ, που έχει την κατεύθυνση του άξονα των θετικών z, (Σχ. 1.4). Τα πρωτόνια έχουν ταχύτητα με μέτρο 3,0 10 5 m / s
ΑΣΚΗΣΗ 1 η ΜΕΤΑΣΧΗΜΑΤΙΣΤΕΣ ΙΣΧΥΟΣ ΕΙΣΑΓΩΓΗ. Στόχοι της εργαστηριακής άσκησης είναι η εξοικείωση των σπουδαστών με την:
 Σκοπός της Άσκησης: ΑΣΚΗΣΗ η ΜΕΤΑΣΧΗΜΑΤΙΣΤΕΣ ΙΣΧΥΟΣ ΕΙΣΑΓΩΓΗ Στόχοι της εργαστηριακής άσκησης είναι η εξοικείωση των σπουδαστών με την: α. Κατασκευή μετασχηματιστών. β. Αρχή λειτουργίας μετασχηματιστών.
Σκοπός της Άσκησης: ΑΣΚΗΣΗ η ΜΕΤΑΣΧΗΜΑΤΙΣΤΕΣ ΙΣΧΥΟΣ ΕΙΣΑΓΩΓΗ Στόχοι της εργαστηριακής άσκησης είναι η εξοικείωση των σπουδαστών με την: α. Κατασκευή μετασχηματιστών. β. Αρχή λειτουργίας μετασχηματιστών.
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ
 ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ ΕΙΣΑΓΩΓΙΚΑ Η ηλεκτρική μηχανή είναι μια διάταξη μετατροπής μηχανικής ενέργειας σε ηλεκτρική και αντίστροφα. απώλειες Μηχανική ενέργεια Γεννήτρια Κινητήρας Ηλεκτρική ενέργεια
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ ΕΙΣΑΓΩΓΙΚΑ Η ηλεκτρική μηχανή είναι μια διάταξη μετατροπής μηχανικής ενέργειας σε ηλεκτρική και αντίστροφα. απώλειες Μηχανική ενέργεια Γεννήτρια Κινητήρας Ηλεκτρική ενέργεια
ηλεκτρικό ρεύμα ampere
 Ηλεκτρικό ρεύμα Το ηλεκτρικό ρεύμα είναι ο ρυθμός με τον οποίο διέρχεται ηλεκτρικό φορτίο από μια περιοχή του χώρου. Η μονάδα μέτρησης του ηλεκτρικού ρεύματος στο σύστημα SI είναι το ampere (A). 1 A =
Ηλεκτρικό ρεύμα Το ηλεκτρικό ρεύμα είναι ο ρυθμός με τον οποίο διέρχεται ηλεκτρικό φορτίο από μια περιοχή του χώρου. Η μονάδα μέτρησης του ηλεκτρικού ρεύματος στο σύστημα SI είναι το ampere (A). 1 A =
(α) 1. (β) Το σύστημα βρίσκεται υπό διαφορά δυναμικού 12 V: U ολ = 1 2 C ολ(δv) 2 = J.
 4 η Ομάδα Ασκήσεων Δύο πυκνωτές C=5 μf και C=40 μf συνδέονται παράλληλα στους ακροδέκτες πηγών τάσης VS=50 V και VS=75 V αντίστοιχα και φορτίζονται Στην συνέχεια αποσυνδέονται και συνδέονται μεταξύ τους,
4 η Ομάδα Ασκήσεων Δύο πυκνωτές C=5 μf και C=40 μf συνδέονται παράλληλα στους ακροδέκτες πηγών τάσης VS=50 V και VS=75 V αντίστοιχα και φορτίζονται Στην συνέχεια αποσυνδέονται και συνδέονται μεταξύ τους,
ΘΕΜΑ 1 2 Ι =Ι. ομοιόμορφα στη διατομή του αγωγού θα ισχύει: = 2. Επομένως Β = μbοb r / 2παP P, για r α. I π r r
 I (,5 I = I Εισαγωγή στις Φυσικές Επιστήμες (9-7-006) ΘΕΜΑ 1 Α. Κυλινδρικός αγωγός ακτίνας α =,5 cm διαρρέεται κατά μήκος του από ρεύμα I =,5 A. Το ρεύμα είναι ομοιόμορφα κατανεμημένο καθ όλη τη διατομή
I (,5 I = I Εισαγωγή στις Φυσικές Επιστήμες (9-7-006) ΘΕΜΑ 1 Α. Κυλινδρικός αγωγός ακτίνας α =,5 cm διαρρέεται κατά μήκος του από ρεύμα I =,5 A. Το ρεύμα είναι ομοιόμορφα κατανεμημένο καθ όλη τη διατομή
ΘΕΜΑ A Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 0-04 ΜΑΘΗΜΑ /ΤΑΞΗ: ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΗΜΕΡΟΜΗΝΙΑ: ΣΕΙΡΑ: ΘΕΜΑ A Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α4 και δίπλα το γράμμα που αντιστοιχεί στη
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 0-04 ΜΑΘΗΜΑ /ΤΑΞΗ: ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΗΜΕΡΟΜΗΝΙΑ: ΣΕΙΡΑ: ΘΕΜΑ A Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α4 και δίπλα το γράμμα που αντιστοιχεί στη
ΒΑΣΙΚΕΣ ΚΑΙ ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΑΠΟ ΤΗΝ Α ΚΑΙ Β ΛΥΚΕΙΟΥ. Από τη Φυσική της Α' Λυκείου
 ΒΑΣΙΚΕΣ ΚΑΙ ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΑΠΟ ΤΗΝ Α ΚΑΙ Β ΛΥΚΕΙΟΥ Από τη Φυσική της Α' Λυκείου Δεύτερος νόμος Νεύτωνα, και Αποδεικνύεται πειραματικά ότι: Η επιτάχυνση ενός σώματος (όταν αυτό θεωρείται
ΒΑΣΙΚΕΣ ΚΑΙ ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΑΠΟ ΤΗΝ Α ΚΑΙ Β ΛΥΚΕΙΟΥ Από τη Φυσική της Α' Λυκείου Δεύτερος νόμος Νεύτωνα, και Αποδεικνύεται πειραματικά ότι: Η επιτάχυνση ενός σώματος (όταν αυτό θεωρείται
Εργ.Αεροδυναμικής,ΕΜΠ. Καθ. Γ.Μπεργελές
 Η Τεχνολογία των Ελικοπτέρων Τι είναι τα ελικόπτερα Κατηγορίες Ελικοπτέρων Τυπικό ελικόπτερο Υβριδικό αεροσκάφος Tilt-rotor Πως λειτουργεί μιά έλικα Ι U = ταχύτητα πτήσης η σχετική ταχύτητα του αέρα ως
Η Τεχνολογία των Ελικοπτέρων Τι είναι τα ελικόπτερα Κατηγορίες Ελικοπτέρων Τυπικό ελικόπτερο Υβριδικό αεροσκάφος Tilt-rotor Πως λειτουργεί μιά έλικα Ι U = ταχύτητα πτήσης η σχετική ταχύτητα του αέρα ως
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ ΚΑΙ ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ ΚΑΙ ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ 1 1. ΜΑΓΝΗΤΙΣΜΟΣ Μαγνητικά φαινόμενα παρατηρήθηκαν για πρώτη φορά πριν από τουλάχιστον 2500 χρόνια σε κομμάτια μαγνητισμένου σιδηρομεταλλεύματος,
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ ΚΑΙ ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ 1 1. ΜΑΓΝΗΤΙΣΜΟΣ Μαγνητικά φαινόμενα παρατηρήθηκαν για πρώτη φορά πριν από τουλάχιστον 2500 χρόνια σε κομμάτια μαγνητισμένου σιδηρομεταλλεύματος,
α) = β) Α 1 = γ) δ) Μονάδες 5
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 19-10-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-ΚΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4 να γράψετε
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 19-10-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-ΚΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4 να γράψετε
Φυσική των Ανεμογεννητριών
 Φυσική των Ανεμογεννητριών Από την καθημερινή μας εμπειρία γνωρίζουμε ότι ο άνεμος σε ακραίες περιπτώσεις μπορεί να προκαλέσει σημαντικές υλικές φθορές ή να μετακινήσει τεράστιες αέριες ή θαλάσσιες μάζες
Φυσική των Ανεμογεννητριών Από την καθημερινή μας εμπειρία γνωρίζουμε ότι ο άνεμος σε ακραίες περιπτώσεις μπορεί να προκαλέσει σημαντικές υλικές φθορές ή να μετακινήσει τεράστιες αέριες ή θαλάσσιες μάζες
ΥδροδυναµικέςΜηχανές
 ΥδροδυναµικέςΜηχανές Χαρακτηριστικές καµπύλες υδροστροβίλων Εργαστήριο Αιολικής Ενέργειας Τ.Ε.Ι. Κρήτης ηµήτρης Αλ. Κατσαπρακάκης Θεωρητικήχαρακτηριστική υδροστροβίλου Θεωρητική χαρακτηριστική υδροστροβίλου
ΥδροδυναµικέςΜηχανές Χαρακτηριστικές καµπύλες υδροστροβίλων Εργαστήριο Αιολικής Ενέργειας Τ.Ε.Ι. Κρήτης ηµήτρης Αλ. Κατσαπρακάκης Θεωρητικήχαρακτηριστική υδροστροβίλου Θεωρητική χαρακτηριστική υδροστροβίλου
ΑΣΚΗΣΗ 10 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΔΙΕΓΕΡΣΗΣ ΣΕΙΡΑΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ
 ΑΣΚΗΣΗ 10 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΔΙΕΓΕΡΣΗΣ ΣΕΙΡΑΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση των τρόπων ελέγχου της ταχύτητας ενός
ΑΣΚΗΣΗ 10 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΔΙΕΓΕΡΣΗΣ ΣΕΙΡΑΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση των τρόπων ελέγχου της ταχύτητας ενός
2 Η ΠΡΟΟΔΟΣ. Ενδεικτικές λύσεις κάποιων προβλημάτων. Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση
 2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
ΑΣΚΗΣΗ 1 η ΜΕΛΕΤΗ ΛΕΙΤΟΥΡΓΙΑΣ ΤΡΙΦΑΣΙΚΗΣ ΣΥΓΧΡΟΝΗΣ ΓΕΝΝΗΤΡΙΑΣ (ΕΝΑΛΛΑΚΤΗΡΑ) ΓΙΑ ΤΟΝ ΠΡΟΣΔΙΟΡΙΣΜΟ ΤΟΥ ΙΣΟΔΥΝΑΜΟΥ ΚΥΚΛΩΜΑΤΟΣ
 ΑΣΚΗΣΗ 1 η ΜΕΛΕΤΗ ΛΕΙΤΟΥΡΓΙΑΣ ΤΡΙΦΑΣΙΚΗΣ ΣΥΓΧΡΟΝΗΣ ΓΕΝΝΗΤΡΙΑΣ (ΕΝΑΛΛΑΚΤΗΡΑ) ΓΙΑ ΤΟΝ ΠΡΟΣΔΙΟΡΙΣΜΟ ΤΟΥ ΙΣΟΔΥΝΑΜΟΥ ΚΥΚΛΩΜΑΤΟΣ Σκοπός της άσκησης: 1. Ο πειραματικός προσδιορισμός της χαρακτηριστικής λειτουργίας
ΑΣΚΗΣΗ 1 η ΜΕΛΕΤΗ ΛΕΙΤΟΥΡΓΙΑΣ ΤΡΙΦΑΣΙΚΗΣ ΣΥΓΧΡΟΝΗΣ ΓΕΝΝΗΤΡΙΑΣ (ΕΝΑΛΛΑΚΤΗΡΑ) ΓΙΑ ΤΟΝ ΠΡΟΣΔΙΟΡΙΣΜΟ ΤΟΥ ΙΣΟΔΥΝΑΜΟΥ ΚΥΚΛΩΜΑΤΟΣ Σκοπός της άσκησης: 1. Ο πειραματικός προσδιορισμός της χαρακτηριστικής λειτουργίας
