ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ
|
|
|
- Ἄδραστος Πανταζής
- 9 χρόνια πριν
- Προβολές:
Transcript
1 4 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ 4. Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ Εισαγωγή Σε πολλά καθημερινά φαινόμενα εμφανίζονται δύο μεγέθη, τα οποία μεταβάλλονται έτσι, ώστε η τιμή του ενός να καθορίζει την τιμή του άλλου. Η διαδικασία με την οποία κάθε τιμή του ενός μεγέθους αντιστοιχίζεται σε μια ακριβώς τιμή του άλλου μεγέθους, πολλές φορές περιγράφεται από ένα μαθηματικό τύπο, όπως φαίνεται στα παρακάτω παραδείγματα.. Ο τόκος Τ σε ευρώ που αποδίδει κεφάλαιο 5000 ευρώ σε ένα έτος με ε ετήσιο επιτόκιο ε%, δίνεται κατά τα γνωστά από τον τύπο Τ Ο τύπος αυτός περιγράφει μια διαδικασία, με την οποία κάθε τιμή του ε αντιστοιχίζεται σε μια ακριβώς τιμή του Τ. Για παράδειγμα, αν ε 3, τότε Τ 50, ενώ αν ε 5, τότε Τ 50 κτλ.. Το διάστημα S σε km που διανύθηκε από ποδηλάτη σε χρονικό διάστημα h, με μέση ταχύτητα υ σε km/h, δίνεται από τον τύπο S υ. Ο τύπος αυτός περιγράφει μια διαδικασία, με την οποία κάθε τιμή του υ α- ντιστοιχίζεται σε μια ακριβώς τιμή του S. Για παράδειγμα, αν υ 60, τότε S 0, ενώ αν υ 70, τότε S 40, κτλ. 3. Το εμβαδό Ε ενός κύκλου ακτίνας ρ δίνεται από τον τύπο Ε πρ. Ο- μοίως και ο τύπος αυτός περιγράφει μια διαδικασία, με την οποία κάθε τιμή του ρ αντιστοιχίζεται σε μια ακριβώς τιμή του Ε. Για παράδειγμα αν ρ, τότε Ε π, ενώ αν ρ, τότε Ε 4π κτλ. Υπάρχουν όμως και περιπτώσεις όπου η διαδικασία αντιστοίχισης ανάμεσα στις τιμές δύο μεγεθών δεν περιγράφεται ή έστω δεν γνωρίζουμε αν περιγράφεται από κάποιο τύπο. Για παράδειγμα: Οι ώρες της ημέρας και οι αντίστοιχες θερμοκρασίες τους.
2 98 4. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Οι μέρες του έτους και οι τιμές ενός ξένου νομίσματος (π.χ. του δολαρίου). Παρατηρούμε ότι σε όλα τα παραπάνω παραδείγματα υπάρχει κάποια διαδικασία, με την οποία κάθε στοιχείο ενός συνόλου Α αντιστοιχίζεται σε ένα ακριβώς στοιχείο κάποιου άλλου συνόλου Β. Μια τέτοια διαδικασία λέγεται συνάρτηση από το Α στο Β. Δηλαδή: ΟΡΙΣΜΟΣ Συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β λέγεται μια διαδικασία (κανόνας) με την οποία κάθε στοιχείο του συνόλου Α αντιστοιχίζεται σε ένα ακριβώς στοιχείο του συνόλου Β. Το σύνολο Α λέγεται πεδίο ορισμού ή σύνολο ορισμού της. Οι συναρτήσεις παριστάνονται συνήθως με τα μικρά γράμματα, g, h κτλ. του Λατινικού αλφαβήτου. Αν με μια συνάρτηση από το Α στο Β, το x Α αντιστοιχίζεται στο y Β, τότε γράφουμε: y x και διαβάζουμε «y ίσον του x». Το x λέγεται τότε τιμή της στο x. Τo γράμμα x, που παριστάνει οποιοδήποτε στοιχείο του πεδίου ορισμού της, ονομάζεται ανεξάρτητη μεταβλητή, ενώ το y, που παριστάνει την τιμή της συνάρτησης στο x, ονομάζεται εξαρτημένη μεταβλητή. Το σύνολο, που έχει για στοιχεία του τις τιμές ( x ) για όλα τα x Α, λέγεται σύνολο τιμών της και το συμβολίζουμε με Α. Η παραπάνω συνάρτηση συμβολίζεται ως εξής: : Α Β x ( x) Έτσι π.χ. η συνάρτηση, με την οποία κάθε μη αρνητικός αριθμός αντιστοιχίζεται στην τετραγωνική του ρίζα, συμβολίζεται ως εξής: :0, x x Για καλύτερη κατανόηση του παραπάνω ορισμού ας δούμε τα παραδείγματα που ακολουθούν: ο ΠΑΡΑΔΕΙΓΜΑ Έστω η συνάρτηση με την οποία κάθε ημέρα μιας ορισμένης εβδομάδας ενός μήνα αντιστοιχίζεται στην υψηλότερη θερμοκρασία της.
3 4. Η έννοια της συνάρτησης 99 Για τη συνάρτηση αυτή, το πεδίο ορισμού είναι το σύνολο Α,,3,4,5,6,7}, ενώ το σύνολο τιμών το σύνολο (Α) 9,,, 3, 5 Β Με αφορμή το παράδειγμα αυτό τονίζουμε τα ακόλουθα χαρακτηριστικά μιας συνάρτησης :Α Β. Κάθε στοιχείο του Α αντιστοιχίζεται σε ένα ακριβώς στοιχείο του Β. Μερικά στοιχεία του Β μπορεί να μην αποτελούν τιμές της (π.χ. 8 0 ). Δύο ή περισσότερα στοιχεία του Α μπορεί να αντιστοιχίζονται στο ίδιο στοιχείο του Β (π.χ. τα 3 και 7 αντιστοιχίζονται στο 3 ). ο ΠΑΡΑΔΕΙΓΜΑ Θεωρούμε τα σύνολα Α={α, β, γ} και Β={,, 3, 4, 5}, καθώς επίσης και τα παρακάτω σχήματα (βελοδιαγράμματα). Παρατηρούμε ότι: Το σχήμα (α) παριστάνει συνάρτηση, αφού κάθε στοιχείο του Α αντιστοιχίζεται σε ένα ακριβώς στοιχείο του Β. Το σχήμα (β) δεν παριστάνει συνάρτηση, αφού το σε δύο στοιχεία του Β. Το σχήμα (γ) δεν παριστάνει συνάρτηση, αφού το γ Α δεν αντιστοιχίζεται σε κανένα στοιχείο του Β. Το σχήμα (δ) δεν παριστάνει συνάρτηση. Πρώτον διότι το α Α αντιστοιχίζεται αντιστοιχίζεται σε κανένα στοιχείο του Β και δεύτερον διότι το αντιστοιχίζεται σε δύο στοιχεία του Β. γ Α δεν α Α
4 00 4. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Σχήμα α Σχήμα β Σχήμα γ Σχήμα δ Συντομογραφία συνάρτησης Είδαμε παραπάνω ότι, για να οριστεί μια συνάρτηση, πρέπει να δοθούν τρία στοιχεία: Το πεδίο ορισμού της Α Το σύνολο Β και Το xγια κάθε x Α Οι συναρτήσεις, με τις οποίες θα ασχοληθούμε στο βιβλίο αυτό, είναι της μορφής :Α Β, όπου Α και Β, είναι δηλαδή, όπως λέμε, πραγματικές συναρτήσεις μιας πραγματικής μεταβλητής. Πολλές φορές αναφερόμαστε σε μια συνάρτηση δίνοντας μόνον τον τύπο με τον οποίο εκφράζεται το x. Λέμε π.χ. δίνεται «η συνάρτηση, με x 4x» ή, πιο σύντομα, «η συνάρτηση 4 «η συνάρτηση y 4x». Σε μια τέτοια περίπτωση θα θεωρούμε συμβατικά ότι: x x» ή, ακόμα, Το πεδίο ορισμού Α της είναι το «ευρύτερο» από τα υποσύνολα του στα οποία το x έχει νόημα. Το σύνολο Β είναι ολόκληρο το σύνολο των πραγματικών αριθμών. Έτσι για τη συνάρτηση x 4x το πεδίο ορισμού είναι το σύνολο Α, 4, αφού πρέπει 4 0 x, ενώ το σύνολο Β είναι όλο το.
5 4. Η έννοια της συνάρτησης 0 ΣΗΜΕΙΩΣΗ Πολλές φορές μια συνάρτηση περιγράφεται με έναν τύπο που έχει κλάδους, όπως για παράδειγμα η συνάρτηση: x x, αν 0 x. x, αν x 0 Για να υπολογίσουμε τις τιμές της στα σημεία, 0 και εργαζόμαστε ως εξής: Για 0 Για 0 x, από τον κλάδο x x, έχουμε:. x, από τον κλάδο x x 0 0. Τέλος, για 0, έχουμε: x, από τον κλάδο x x 0., έχουμε: ΣΧΟΛΙΟ Αν και, γενικά, χρησιμοποιούμε το γράμμα για τα συμβολισμό μιας συνάρτησης και το γράμμα x για το συμβολισμό του τυχαίου στοιχείου του πεδίου ορισμού της, ωστόσο μπορούμε να χρησιμοποιήσουμε και άλλα γράμματα. Έτσι για παράδειγμα οι x x 4x7, gt t 4t7 και hs s 4s 7 ορίζουν την ίδια συνάρτηση. Επομένως το x στον τύπο μιας συνάρτησης θα παίζει το ρόλο μιας «άδειας θέσης». Με αυτό το σκεπτικό, η παραπάνω συνάρτηση θα μπορούσε να έχει τη μορφή 4 7, όπου οι παρενθέσεις έχουν πάρει τη θέση ενός γράμματος. Έτσι για να υπολογίσουμε το απλά τοποθετούμε το στις θέσεις, που ορίζουν οι παρενθέσεις: Ομοίως, έχουμε x 3x 4 3x 7 9x x7 Υπάρχει όμως και μια παραπέρα απλοποίηση των εκφράσεών µας που σχετίζονται µε συναρτήσεις. Πολλές φορές αντί να λέμε «η συνάρτηση
6 0 4. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ s t gt», θα λέµε «η συνάρτηση s gt», δηλαδή γράφουμε s υπονοώντας το s(t). Αυτή η απλοποίηση γίνεται συχνότατα σε διάφορες επιστή- μες, που χρησιμοποιούν τη μαθηματική γλώσσα και τα μαθηματικά εργαλεία, όπως η φυσική, η χημεία κτλ. Συνήθως στις περιπτώσεις αυτές υπάρχει κάποιο πείραμα, όπου το t είναι η τιμή ενός μεγέθους, που υπεισέρχεται στο πείραμα, και το s(t) η αντίστοιχη τιμή κάποιου άλλου μεγέθους. ΕΦΑΡΜΟΓΗ Να βρεθεί το πεδίο ορισμού της συνάρτησης x x x ΛΥΣΗ Η συνάρτηση ορίζεται για εκείνα μόνο τα x για τα οποία ισχύει ή, ισοδύναμα, για x 0 και x 0 x και x Άρα το πεδίο ορισμού της είναι το σύνολο Α,, (Σχήμα) ΑΣΚΗΣΕΙΣ Α ΟΜΑΔΑΣ. Να βρείτε το πεδίο ορισμού των παρακάτω συναρτήσεων: i) x 4 5 x ii) x x 6 x 4x iii) x x iv) x x x
7 4. Η έννοια της συνάρτησης 03. Ομοίως των συναρτήσεων: i) x x x ii) x x iii) x x 4x 3 iv) x 4 x 3. Δίνεται η συνάρτηση x x 3, αν x 0 x 3, αν x 0 Να βρείτε τις τιμές 5, 0 και Μια συνάρτηση ορίζεται ως εξής: Σκέψου έναν φυσικό αριθμό, πρόσθεσε σ αυτόν το, πολλαπλασίασε το άθροισμα με 4 και στο γινόμενο πρόσθεσε το τετράγωνο του αριθμού. i) Να βρείτε τον τύπο της και στη συνέχεια τις τιμές της για x = 0, x, x και x 3. Τι παρατηρείτε; ii) Να βρείτε τους φυσικούς αριθμούς x για τους οποίους ισχύει ( x) 36, ( x) 49, ( x) 00 και ( x) Δίνονται οι συναρτήσεις: i) x 4 5 x, ii) gx x 6 x 4x Να βρείτε τις τιμές του x για τις οποίες ισχύει: i) ( x) 7 ii) gx ( ) και iii) και iii) hx x. hx ( ). 5
8 4. ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ Καρτεσιανές συντεταγμένες Η παράσταση ενός σημείου του επιπέδου με ένα διατεταγμένο ζεύγος πραγματικών αριθμών, βοήθησε στην επίλυση γεωμετρικών προβλημάτων με αλγεβρικές μεθόδους. Η παράσταση αυτή, όπως μάθαμε σε προηγούμενες τάξεις, γίνεται ως εξής: Πάνω σε ένα επίπεδο σχεδιάζουμε δύο κάθετους άξονες x' x και yy ' με κοινή αρχή ένα σημείο Ο. Από αυτούς ο οριζόντιος x' x λέγεται άξονας των τετμημένων ή άξονας των x, ενώ ο κατακόρυφος yy ' άξονας των τεταγμένων ή άξονας των y. Όπως είναι γνωστό, σε κάθε σημείο Μ του επιπέδου των αξόνων μπορούμε να αντιστοιχίσουμε ένα διατεταγμένο ζεύγος ( αβ, ) πραγματικών αριθμών και αντιστρόφως, σε κάθε διατεταγμένο ζεύγος ( αβ, ) πραγματικών αριθμών, μπορούμε να αντιστοιχίσουμε ένα μοναδικό σημείο Μ του επιπέδου, όπως φαίνεται στο σχήμα: Οι αριθμοί α, β λέγονται συντεταγμένες του Μ. Ειδικότερα ο α λέγεται τετμημένη και ο β τεταγμένη του σημείου Μ. Το σημείο Μ που έχει συντεταγμένες α και β συμβολίζεται με Μαβ (, ) ή, απλά, με ( αβ., ) Επειδή η ιδέα της χρησιμοποίησης ζευγών για την παράσταση σημείων του επιπέδου ανήκει στον Καρτέσιο, το παραπάνω ζεύγος των αξόνων το λέμε καρτεσιανό σύστημα συντεταγμένων στο επίπεδο και το συμβολίζουμε Οxy, ενώ το επίπεδο στο οποίο ορίστηκε το σύστημα αυτό το λέμε καρτεσιανό επίπεδο. Αν επιπλέον οι μονάδες των αξόνων έχουν το ίδιο μήκος, το σύστημα Οxy λέγεται ορθοκανονικό. ΣΗΜΕΙΩΣΗ: Στα επόμενα, εκτός αν αναφέρεται διαφορετικά, όταν λέμε καρτεσιανό σύ-
9 4. Γραφική παράσταση συνάρτησης 05 στημα συντεταγμένων, θα εννοούμε ορθοκανονικό καρτεσιανό σύστημα συντεταγμένων. Ας θεωρήσουμε τώρα ένα σύστημα Oxy συντεταγμένων στο επίπεδο. Τότε: Τα σημεία του άξονα x' x και μόνο αυτά έχουν τεταγμένη ίση με το μηδέν, ενώ τα σημεία του άξονα yy ' και μόνο αυτά έχουν τετμημένη ίση με το μηδέν Οι άξονες χωρίζουν το επίπεδο σε τέσσερα τεταρτημόρια, που είναι τα εσωτερικά των γωνιών xoy, yox ', x' Oy ' και yox ' και ο- νομάζεται ο, ο, 3 ο και 4 ο, τεταρτημόριο, α- ντιστοίχως. Τα πρόσημα των συντεταγμένων των σημείων τους φαίνονται στο διπλανό σχήμα. Αν Ααβ, είναι ένα σημείο του καρτεσιανού επιπέδου, με τη βοήθεια της συμμετρίας ως προς άξονα και ως προς κέντρο, διαπιστώνουμε ότι: x x είναι το σημείο Δα, β Το συμμετρικό του ως προς τον άξονα ' που έχει ίδια τετμημένη και αντίθετη τεταγμένη (Σχ. α ). Το συμμετρικό του ως προς τον άξονα ' που έχει ίδια τεταγμένη και αντίθετη τετμημένη (Σχ. α )., yy είναι το σημείο B αβ,, Το συμμετρικό του ως προς την αρχή των αξόνων είναι το σημείο Γ α, β, που έχει αντίθετες συντεταγμένες (Σχ. α ). Το συμμετρικό του ως προς τη διχοτόμο της ης και 3 ης γωνίας των αξόνων είναι το σημείο Α' β, α που έχει τετμημένη την τεταγμένη του Α και τεταγμένη την τετμημένη του Α (Σχ. β ). Σχήμα α Σχήμα β
10 06 4. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Απόσταση σημείων Έστω Oxy ένα σύστημα συντεταγμένων στο επίπεδο και, Α x y και Β x, y δύο σημεία αυτού. Θα δείξουμε ότι οι απόστασή τους δίνεται από τον τύπο: ΑΒ x x y y ΑΠΟΔΕΙΞΗ: Από το ορθογώνιο τρίγωνο ΚΑΒ του διπλανού σχήματος έχουμε: ( ΑΒ) ( ΚΑ) ( ΚΒ) οπότε: x x y y x x y y ΑΒ x x y y. Ο παραπάνω τύπος ισχύει και στην περίπτωση που η ΑΒ είναι παράλληλη με τον άξονα x' x (Σχήμα γ ) ή παράλληλη με τον άξονα yy ' (Σχήμα δ ). Σχήμα γ Σχήμα δ Για παράδειγμα, αν Α (3,), Β (3,5) και Γ (-,) είναι οι κορυφές ενός τριγώνου ΑΒΓ, τότε θα είναι: ( ΑΒ) (3-3) (5) 4 4 ( ΑΓ) (--3) ( ) 4 4 ( ΒΓ) (--3) (5) Αφού, λοιπόν, είναι ( ΑΒ) ( ΑΓ ), το τρίγωνο ΑΒΓ είναι ισοσκελές και επειδή επιπλέον ισχύει ( ΑΒ) ( ΑΓ) 3 ( ΒΓ), το τρίγωνο ΑΒΓ είναι και ορ- θογώνιο.
11 4. Γραφική παράσταση συνάρτησης 07 ΕΦΑΡΜΟΓΗ Έστω C o κύκλος με κέντρο την αρχή O των αξόνων και ακτίνα ρ. Να αποδειχτεί ότι ένα σημείο Μ x, y ανήκει στον κύκλο C, αν και μόνο αν ισχύει x y ρ ΑΠΟΔΕΙΞΗ Είναι προφανές ότι ένα σημείο Μ xy, ανήκει στον κύκλο C, αν και μόνο αν ισχύει ΟΜ ρ. Όμως ΟΜ x y, οπότε έχουμε: ΟΜ ρ x y ρ x y ρ Επομένως το σημείο Μ xy, ανήκει στο κύκλο C Ο, ρ, αν και μόνο αν οι συντεταγμένες του ικανοποιούν την εξίσωση x y ρ () Η εξίσωση (), που ικανοποιείται από τις συντεταγμένες των σημείων του κύκλου C Ο, ρ και μόνο από αυτές, λέγεται εξίσωση του κύκλου με κέντρο Ο και ακτίνα ρ. Για παράδειγμα, η εξίσωση του κύκλου με κέντρο Ο και ακτίνα ρ είναι η x y. Ο κύκλος αυτός λέγεται και μοναδιαίος κύκλος. Γραφική παράσταση συνάρτησης Έστω μια συνάρτηση με πεδίο ορισμού Α και Oxy ένα σύστημα συντεταγμένων στο επίπεδο. Το σύνολο των σημείων M ( xy, ) για τα οποία ισχύει y ( x), δηλαδή το σύνολο των σημείων M ( x, ( x )), x A, λέγεται γραφική παράσταση της και συμβολίζεται συνήθως με C. Η εξίσωση, λοιπόν, y ( x) επαληθεύεται από τα σημεία της C και μόνο από αυτά. Επομένως, η y ( x) είναι η εξίσωση της γραφικής παράστασης της. Για το λόγο αυτό, τη γραφική παράσταση C της τη συμβολίζουμε, πολλές φορές, απλά με την εξίσωσή της, δηλαδή με y ( x). Επειδή κάθε x A αντιστοιχίζεται σε ένα μόνο y, δεν υπάρχουν σημεία της γραφικής παράστασης της με την ίδια τετμημένη. Αυτό σημαίνει ότι κάθε κατακόρυφη ευθεία έχει με τη γραφική παράσταση της το πολύ ένα κοινό σημείο (Σχ. α ). Έτσι, ο κύκλος δεν αποτελεί γραφική παράσταση συνάρτησης (Σχ. β ).
12 08 4. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Σχήμα α Σχήμα β Όταν δίνεται η γραφική παράσταση μιας συνάρτησης μπορούμε, επίσης, να σχεδιάσουμε και τη γραφική παράσταση της συνάρτησης, παίρνοντας τη συμμετρική της γραφικής παράστασης της ως προς τον άξονα x x και τούτο διότι η γραφική παράστασης της αποτελείται από τα σημεία M ( x, ( x)) που είναι συμμετρικά των σημείων M ( x, ( x )) της γραφικής παράστασης της ως προς τον άξονα x x. ΕΦΑΡΜΟΓΗ Στο διπλανό σχήμα δίνονται οι γραφικές παραστάσεις δύο συναρτήσεων και g, που είναι ορισμένες σε όλο το. i) Να βρείτε τις τιμές της στα σημεία: 3,,, 0, και ii) Να λύσετε τις εξισώσεις: ( x) 0, ( x) & ( x) g( x). iii) Να λύσετε τις ανισώσεις: ( x) 0 και ( x) g( x). ΛΥΣΗ i) Είναι: 3, 0,, 0, 0 και. ii) Οι ρίζες της εξίσωσης x 0 είναι οι τετμημένες των κοινών σημείων της γραφικής παράστασης της και του άξονα και x. x ' x, δηλαδή οι αριθμοί x
13 4. Γραφική παράσταση συνάρτησης 09 Οι ρίζες της εξίσωσης x είναι οι τετμημένες των σημείων της γραφικής παράστασης της που έχουν τεταγμένη, δηλαδή οι αριθμοί x 3 και x. Οι ρίζες της εξίσωσης x g( x) είναι οι τετμημένες των κοινών σημείων των γραφικών παραστάσεων των συναρτήσεων και g, δηλαδή οι αριθμοί x, x 0 και x3. iii) Οι λύσεις της ανίσωσης x 0 είναι οι τετμημένες των σημείων της γραφικής παράστασης της που βρίσκονται πάνω από τον άξονα τα x (, ) (,. ) x ' x, δηλαδή όλα Οι λύσεις της ανίσωσης x g( x) είναι οι τετμημένες των σημείων της γραφικής παράστασης της που βρίσκονται πάνω από τη γραφική παράσταση της g, δηλαδή όλα τα x (, ) (0,). ΑΣΚΗΣΕΙΣ Α ΟΜΑΔΑΣ. Να σημειώσετε σε ένα καρτεσιανό επίπεδο τα σημεία: Α,, 3, 4 0,0 Γ 3, 0, 0, 5 Β, Ο,. Ένα σημείο Μ xy, κινείται μέσα στο ορθογώνιο ΑΒΓΔ του διπλανού σχήματος. Ποιοι περιορισμοί ισχύουν για τα x, y ; 3. Να βρείτε το συμμετρικό του σημείου Α, 3, i) ως προς τον άξονα x ' x ii) ως προς τον άξονα y ' y iii) ως προς τη διχοτόμο της γωνίας iv) ως προς την αρχή O των αξόνων. xο y Δ και, 3 Ε. 4. Να βρείτε τις αποστάσεις των σημείων: 4, i) 0,0 Ο και Α, ii) Α, και 3, 4 Β, iii) Α3, και Β,, iv) Α, και, 4 Β.
14 0 4. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ 5. Να αποδείξετε ότι: i) Τα σημεία Α,, Β 4,- και 3,5 τριγώνου. ii) Τα σημεία Α,, Β, και 4, τριγώνου. Γ είναι κορυφές ισοσκελούς Γ είναι κορυφές ορθογωνίου 6. Να σχεδιάσετε το πολύγωνο με κορυφές τα σημεία:,5 5,, 3 Δ, Α, Β, Γ, και στη συνέχεια να αποδείξετε ότι αυτό είναι ρόμβος. 7. Σε καθεμιά από τις παρακάτω περιπτώσεις να βρείτε την τιμή του k για την οποία το σημείο Μ ανήκει στη γραφική παράσταση της συνάρτησης. i) x x k, Μ,6 ii) 3 g x kx, Μ,8 iii) hx k x, 3,8 Μ. 8. Σε καθεμιά από τις παρακάτω περιπτώσεις, να βρείτε τις συντεταγμένες των κοινών σημείων της γραφικής παράστασης της συνάρτησης με τους άξονες. i) x x 4 ii) g x x x 3 iii) hx( x ) iv) q x x x v) φx x x vi) ψ x x x Δίνεται η συνάρτηση x x. Να βρείτε: i) Τα σημεία τομής της C με τους άξονες. ii) Τις τετμημένες των σημείων της ξονα x ' x. C που βρίσκονται πάνω από τον ά- 0. Δίνεται οι συναρτήσεις x x 5x 4 και g x x 6 i) Τα κοινά σημεία των C και C g. ii) Τις τετμημένες των σημείων της. Να βρείτε: C που βρίσκονται κάτω από την C g.
15 4.3 Η ΣΥΝΑΡΤΗΣΗ: ( x) αx β Συντελεστής διεύθυνσης ευθείας Έστω Oxy ένα σύστημα συντεταγμένων στο επίπεδο και ε μια ευθεία που τέμνει τον άξονα x x στο σημείο Α. Τη γωνία ω που διαγράφει η ημιευθεία Αx, όταν στραφεί γύρω από το Α κατά τη θετική φορά () μέχρι να πέσει πάνω στην ευθεία ε, τη λέμε γωνία που σχηματίζει η ε με τον άξονα x x. Αν η ευθεία ε είναι παράλληλη προς τον άξονα xx ή συμπίπτει με αυτόν, τότε λέμε ότι η ευθεία ε σχηματίζει με τον άξονα xx γωνία ω 0. Σε κάθε περίπτωση για τη γωνία ω ισχύει 0 ω 80. Ως συντελεστή διεύθυνσης ή ως κλίση μιας ευθείας ε ορίζουμε την εφαπτομένη της γωνίας ω που σχηματίζει η ε με τον άξονα x x. Ο συντελεστής διεύθυνσης μιας ευθείας ε συμβολίζεται συνήθως με λε ή απλά με λ. Είναι φανερό ότι ο συντελεστής διεύθυνσης της ευθείας ε είναι θετικός, αν η γωνία ω είναι οξεία, αρνητικός, αν η γωνία ω είναι αμβλεία και μηδέν, αν η γωνία ω είναι μηδέν. Στην περίπτωση που η γωνία ω είναι ίση με 90, δηλαδή όταν η ευθεία ε είναι κάθετη στον άξονα x x, δεν ορίζουμε συντελεστή διεύθυνσης για την ε. Γραφική παράσταση της συνάρτησης ( x) αx β Ας θεωρήσουμε τη συνάρτηση ( x) 0,5x. Όπως πρακτικά διαπιστώσαμε στο Γυμνάσιο, η γραφική παράσταση της είναι ευθεία γραμμή με εξίσωση y 0,5x (Σχήμα). () Ως θετική φορά περιστροφής εννοούμε τη φορά κατά την οποία πρέπει να περιστραφεί ο ημιάξονας Οx για να συμπέσει με τον ημιάξονα Οy, αφού προηγουμένως διαγράψει γωνία 90 0.
16 4. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Η ευθεία αυτή: Τέμνει τον άξονα x' x στο σημείο Α(-,0), αφού για y 0 βρίσκουμε x, και τον άξονα yy ' στο σημείο Β(0,), αφού για x 0 βρίσκουμε y και Έχει κλίση: (ΟΒ) λεφω 0,5 (ΟΑ) Παρατηρούμε, δηλαδή, ότι η κλίση λ της ευθείας y 0,5x είναι ίση με το συντελεστή του x. Γενικά, όπως θα αποδείξουμε στην Β Λυκείου, η γραφική παράσταση της συνάρτησης ( x) αx β είναι μία ευθεία, με εξίσωση y αx β, η οποία τέμνει τον άξονα των y στο σημείο Β(0,β) και έχει κλίση λ α. Είναι φανερό ότι: αν α 0, τότε 0 ω 90 αν α 0, τότε 90 ω 80 αν α 0, τότε ω 0. Στην περίπτωση που είναι α 0, η συνάρτηση παίρνει την μορφή ( x) β και λέγεται σταθερή συνάρτηση, διότι η τιμή της είναι η ίδια για κάθε x. Ας θεωρήσουμε τώρα δύο τυχαία σημεία Α( x, y ) και Β( x, y ) της ευθείας y αx β.
17 4.3 Η συνάρτηση (x)=αx+β 3 Τότε θα ισχύει: y αx β και y αx β, οπότε θα έχουμε: y y ( αx β) ( αx β) α( x x). Επομένως θα είναι: y y α x x Για παράδειγμα, η ευθεία που διέρχεται από τα σημεία A(,3) και B (3,6) 6 3 έχει κλίση α 0,75. Επομένως, η ευθεία αυτή σχηματίζει με τον 3 ( ) άξονα xx γωνία ω με εφω 0,75, οπότε θα είναι ω 36,87. Η συνάρτηση ( x) αx Αν β 0, τότε η παίρνει τη μορφή ( x) αx, οπότε η γραφική της παράσταση είναι η ευθεία y αx και περνάει από την αρχή των αξόνων. Ειδικότερα: Για α έχουμε την ευθεία y= x. Για τη γωνία ω, που σχηματίζει η ευθεία αυτή με τον άξονα x x, ισχύει εφω α, δηλαδή ω 45 ο. Επομένως η ευθεία y x είναι η διχοτόμος των γωνιών xoy ˆ και x Oy ˆ των αξόνων. Για α έχουμε την ευθεία y x. Για τη γωνία ω, που σχηματίζει η ευθεία αυτή με τον άξονα x x, ισχύει εφω α, δηλαδή ω 35 ο. Επομένως η ευθεία y x είναι η διχοτόμος των γωνιών yox ˆ και yox ˆ των αξόνων. Σχετικές θέσεις δύο ευθειών Ας θεωρήσουμε δύο ευθείες ε και ε με εξισώσεις y αx β και y αx β αντιστοίχως και ας υποθέσουμε ότι οι ευθείες αυτές σχηματίζουν με τον άξονα x x γωνίες ω και ω αντιστοίχως. Αν α α, τότε εφω εφω, οπότε ω ω και άρα οι ευθείες ε και ε είναι παράλληλες ή συμπίπτουν. Ειδικότερα :
18 4 4. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Αν α ακαι β β, τότε οι ευθείες είναι παράλληλες (Σχ. α ), ενώ Αν α α και β β, τότε οι ευθείες ταυτίζονται. Αν α α, τότε εφω εφω, οπότε ω ω και άρα οι ευθείες ε και ε τέμνονται. (Σχ. β ) Σχήμα α Σύμφωνα με τα παραπάνω συμπεράσματα: Οι ευθείες της μορφής y αx, με α, όπως είναι για παράδειγμα οι ευθείες: y x, y x, yx κτλ., διέρχονται όλες από το ίδιο σημείο, το σημείο του άξονα yy ' Γενικά, οι ευθείες της μορφής y αx β, όπου β σταθερό και α μεταβλητό διέρχονται όλες από το Σχήμα β σημείο β του άξονα yy. ' Οι ευθείες της μορφής y x β, β, όπως είναι για παράδειγμα οι ευθείες: y x, y x, y x 3 κτλ., είναι παράλληλες μεταξύ τους, αφού έχουν όλες κλίση α= Γενικά, οι ευθείες της μορφής y αx β, όπου α σταθερό και β μεταβλητό, είναι όλες παράλληλες μεταξύ τους.
19 4.3 Η συνάρτηση (x)=αx+β 5 Η συνάρτηση x x Σύμφωνα με τον ορισμό της απόλυτης τιμής έχουμε: x, αν x0 x x x, αν x 0 Επομένως η γραφική παράσταση της συνάρτησης x x αποτελείται από τις δύο ημιευθείες: y x, με x 0 και y x, με x 0 που διχοτομούν τις γωνίες x' Oy ˆ και xoy ˆ αντιστοίχως. ΕΦΑΡΜΟΓΗ Στο διπλανό σχήμα δίνεται η γραφική παράσταση μιας συνάρτησης που είναι ορισμένη σε όλο το. i) Να βρείτε την εξίσωση της ευθείας που διέρχεται από τα σημεία Α και Β και στη συνέχεια να δείξετε ότι η ευθεία αυτή διέρχεται και από το σημείο Γ. ii) Να λύσετε γραφικά την ανίσωση ( x) 0,5 x. ΛΥΣΗ i) Η ευθεία ΑΒ έχει εξίσωση της μορφής y αx β και επειδή διέρχεται από τα σημεία Α,0 και Β 0, θα ισχύει: 0α β και α0 β, οπότε θα έχουμε: α 0,5 και β Άρα η εξίσωση της ΑΒ είναι: y 0,5x. Για να δείξουμε τώρα ότι το σημείο Γ
20 6 4. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ανήκει στην ευθεία ΑΒ, αρκεί να δείξουμε ότι το ζεύγος, των συντεταγμένων του επαληθεύει την εξίσωση αυτής, δηλαδή αρκεί να δείξουμε ότι 0,5, που ισχύει. ii) Οι λύσεις της ανίσωσης x 0,5x είναι οι τετμημένες των σημείων της γραφικής παράστασης της που βρίσκονται πάνω από την ευθεία με εξίσωση y 0,5x, δηλαδή πάνω από την ευθεία ΑΒ. Επομένως, η ανίσωση αυτή αληθεύει για x,0,. ΑΣΚΗΣΕΙΣ Α ΟΜΑΔΑΣ. Να βρείτε τη γωνία που σχηματίζει με τον άξονα x ' x η ευθεία: i) y x ii) y 3x iii) y x iv) y 3x.. Να βρείτε την κλίση της ευθείας που διέρχεται από τα σημεία: i) A (, ) και B (,3) ii) A (, ) και B (,) iii) A (,) και B(,) iv) A (, 3) και B (,). 3. Να βρείτε την εξίσωση της ευθείας η οποία: i) Έχει κλίση α και τέμνει τον άξονα y ' y στο σημείο B(0, ). ii) Σχηματίζει με τον άξονα y ' y στο σημείο B (0,). x ' x γωνία ω 45 και τέμνει τον άξονα iii) Είναι παράλληλη με την ευθεία y x 3 και διέρχεται από το σημείο A (,).
21 4.3 Η συνάρτηση (x)=αx+β 7 4. Να βρείτε την εξίσωση της ευθείας που διέρχεται από τα σημεία: i) A (, ) και B (,3) ii) A (, ) και B (,) iii) A (,) και B(,) iv) A (, 3) και B (,). 5. Να αποδείξετε ότι η εξίσωση της ευθείας που παριστάνει τη σχέση μεταξύ της θερμοκρασίας C σε βαθμούς Celsius και της θερμοκρασίας F σε βαθμούς Fahrenheit είναι η 5 C = ( F- 3) 9 Γνωρίζουμε ότι το νερό παγώνει σε 0 o C ή 3 ο F και βράζει σε 00 o C ή ο F. Υπάρχει θερμοκρασία που να εκφράζεται και στις δύο κλίμακες με τον ίδιο αριθμό; 6. Να παραστήσετε γραφικά τη συνάρτηση: ì- x+, αν x< 0 ( x) = ï í, αν 0 x< ï ïî x+, αν x 7. Στο διπλανό σχήμα δίνονται η γραφική παράσταση μιας συνάρτησης που είναι ορισμένη σε όλο το και η ευθεία y= x. Να λύσετε γραφικά: i) Τις εξισώσεις: ( x) και ( x) x. ii) Τις ανισώσεις: ( x) και ( x) x. 8. i) Στο ίδιο σύστημα συντεταγμένων να χαράξετε τις γραφικές παραστάσεις των συναρτήσεων ( x) x και gx= ( ) και με τη βοήθεια αυτών να λύσετε τις ανισώσεις: x και x. ii) Να επιβεβαιώσετε αλγεβρικά τις απαντήσεις σας στο προηγούμενο ερώτημα.
22 8 4. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Β ΟΜΑΔΑΣ. Η πολυγωνική γραμμή ΑΒΓΔΕ του παρακάτω σχήματος είναι η γραφική παράσταση μιας συνάρτησης που είναι ορισμένη στο διάστημα 6,5. i) Να βρείτε την τιμή της συνάρτησης σε κάθε ακέραιο x [ 6,5]. ii) Να λύσετε τις εξισώσεις: ( x) 0, ( x) και ( x) iii) Να βρείτε την εξίσωση της ευθείας ΒΔ και στη συνέχεια να λύσετε γραφικά την ανίσωση ( x) 0,5 x.. Μια φωτεινή ακτίνα κινείται κατά μήκος της ευθείας y x και ανακλάται στον άξονα x ' x. Να γράψετε την εξίσωση της ευθείας κατά μήκος της οποίας κινείται η ανακλώμενη ακτίνα. 3. Σε μια δεξαμενή υπάρχουν 600 λίτρα βενζίνης. Ένα βυτιοφόρο που περιέχει 000 λίτρα βενζίνης αρχίζει να γεμίζει τη δεξαμενή. Αν η παροχή του βυτιοφόρου είναι 00 λίτρα το λεπτό και η δεξαμενή χωράει όλη τη βενζίνη του βυτιοφόρου: i) Να βρείτε τις συναρτήσεις που εκφράζουν, συναρτήσει του χρόνου t, την ποσότητα της βενζίνης: α) στο βυτιοφόρο και β) στη δεξαμενή. ii) Να παραστήσετε γραφικά τις παραπάνω συναρτήσεις και να βρείτε τη χρονική στιγμή κατά την οποία το βυτιοφόρο και η δεξαμενή έχουν την ίδια ποσότητα βενζίνης. 4. Στο διπλανό σχήμα το σημείο Μ διαγράφει το ευθύγραμμο τμήμα ΑΒ από το Α προς το Β. Συμβολίζουμε με x το μήκος της διαδρομής ΑΜ του σημείου Μ και με ( x ) το εμβαδόν του τριγώνου Μ ΓΔ. Να βρείτε το πεδίο ορισμού και τον τύπο της συνάρτησης E= ( x ) και στη συνέχεια να την παραστήσετε γραφικά.
23 4.3 Η συνάρτηση (x)=αx+β 9 5. Δύο κεριά Κ και Κ, ύψους 0cm το καθένα, άρχισαν να καίγονται την ίδια χρονική στιγμή και το πρώτο κερί κάηκε σε 3 ώρες, ενώ το δεύτερο κάηκε σε 4 ώρες. Τα ύψη των κεριών Κ και Κ, συναρτήσει του χρόνου t, κατά το χρονικό διάστημα που καθένα από αυτά καιγόταν, παριστάνονται με τα ευθύγραμμα τμήματα k και k του παρακάτω σχήματος. i) Να βρείτε τις συναρτήσεις h h () t και h () h t που εκφράζουν, συναρτήσει του χρόνου t, τα ύψη των κεριών Κ και Κ αντιστοίχως. ii) Να βρείτε πότε το κερί Κ είχε διπλάσιο ύψος από το κερί Κ. iii) Να λύσετε το ίδιο πρόβλημα και στη γενική περίπτωση που το αρχικό ύψος των κεριών ήταν ίσο με υ. Τι παρατηρείτε;
24 4.4 ΚΑΤΑΚΟΡΥΦΗ ΟΡΙΖΟΝΤΙΑ ΜΕΤΑΤΟΠΙΣΗ ΚΑΜΠΥΛΗΣ Κατακόρυφη μετατόπιση καμπύλης α) Ας θεωρήσουμε τη συνάρτηση x x. Επειδή x, αν x0 x, x, αν x 0 η γραφική παράσταση της συνάρτησης x x, θα α- ποτελείται από τις ημιευθείες y x, με x 0 και y x, με x 0, που έχουν αρχή το σημείο του άξονα yy ' και είναι παράλληλες με τις διχοτόμους των γωνιών x' Oy ˆ και xoy ˆ από τις οποίες, όπως είναι γνωστό, αποτελείται η γραφική παράσταση της φx x (Σχήμα). φ x Επομένως, αν μετατοπίσουμε τη γραφική παράσταση της x κατακόρυφα () και προς τα πάνω κατά μονάδα, τότε αυτή θα συμπέσει με τη γραφική παράσταση της x x. Αυτό, άλλωστε, ήταν αναμενόμενο, αφού ισχύει : που σημαίνει ότι για κάθε x το του φx. Γενικά: x φ x, για κάθε x, Η γραφική παράσταση της συνάρτησης, με: x φ x c, όπου c 0, x είναι κατά μονάδα μεγαλύτερο προκύπτει από μια κατακόρυφη μετατόπιση της γραφικής παράστασης της φ κατά c μονάδες προς τα πάνω (Σχήμα α ) () Δηλαδή παράλληλα με τον άξονα y ' y.
25 4.4 Κατακόρυφη Οριζόντια μετατόπιση καμπύλης Σχήμα α β) Ας θεωρήσουμε τη συνάρτηση x x x η γραφική παράσταση της x x, θα αποτελείται από τις ημιευθείες y x, με x 0 και. Επειδή x, αν x0, x, αν x 0 y x, με x 0, που έχουν αρχή το σημείο - του άξονα yy ' και είναι παράλληλες με τις διχοτόμους των γωνιών x' Oy ˆ και xoy ˆ από τις οποίες αποτελείται η γραφική παράσταση της φ x x (Σχήμα). φ x Επομένως, αν μετατοπίσουμε τη γραφική παράσταση της x κατακόρυφα και προς τα κάτω κατά μονάδα, τότε αυτή θα συμπέσει με τη γραφική παράσταση της x x ισχύει : που σημαίνει ότι για κάθε x το φx. του Γενικά:. Αυτό, άλλωστε, ήταν αναμενόμενο, αφού x φ x, για κάθε x, Η γραφική παράσταση της συνάρτησης, με: x φ x c, όπου c 0, x είναι κατά μονάδα μικρότερο προκύπτει από μια κατακόρυφη μετατόπιση της γραφικής παράστασης της φ κατά c μονάδες προς τα κάτω (Σχήμα β )
26 4. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Σχήμα β Οριζόντια μετατόπιση καμπύλης α) Ας θεωρήσουμε τη συνάρτηση x x. Επειδή x η γραφική παράσταση της x x, θα αποτελείται από τις ημιευθείες y x, με x και x, αν x, x, αν x y x, με x, που έχουν αρχή το σημείο του άξονα x' x και είναι παράλληλες με τις διχοτόμους των γωνιών x' Oy ˆ και xoy ˆ από τις οποίες αποτελείται η γραφική παράσταση της φ x x (Σχήμα). φ x Επομένως, αν μετατοπίσουμε τη γραφική παράσταση της x οριζόντια () και προς τα δεξιά κατά μονάδα, τότε αυτή θα συμπέσει με τη γραφική παράσταση της x x. Αυτό, άλλωστε, ήταν αναμενόμενο, αφού ισχύει xφ x, για κάθε x, που σημαίνει ότι η τιμή της x x στη θέση x είναι ίδια με την τιμή της φx Γενικά: x στη θέση x. () Δηλαδή παράλληλα με τον άξονα x ' x.
27 4.4 Κατακόρυφη Οριζόντια μετατόπιση καμπύλης 3 Η γραφική παράσταση της συνάρτησης με: x φ xc, όπου c 0, προκύπτει από μια οριζόντια μετατόπιση της γραφικής παράστασης της φ κατά c μονάδες προς τα δεξιά (Σχήμα γ ). Πράγματι επειδή xφ x c, η τιμή της στη θέση x είναι ίδια με την τιμή της φ στη θέση x c, που βρίσκεται c μονάδες αριστερότερα της θέσης x. Άρα, η γραφική παράσταση της θα βρίσκεται c μονάδες δεξιότερα της γραφικής παράστασης της φ (Σχήμα γ ). Σχήμα γ β) Ας θεωρήσουμε τη συνάρτηση x x. Επειδή x, αν x x, x, αν x η γραφική παράσταση της x x, θα αποτελείται από τις ημιευθείες y x, με x και y x, με x, που έχουν αρχή το σημείο - του άξονα x' x και είναι παράλληλες με τις διχοτόμους των γωνιών x' Oy ˆ και xoy ˆ από τις οποίες αποτελείται η γραφική παράσταση της φ x x (Σχήμα). φ x Επομένως, αν μετατοπίσουμε τη γραφική παράσταση της x οριζόντια και προς τα αριστερά κατά μονάδα, τότε αυτή θα συμπέσει με τη γρα-
28 4 4. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ φική παράσταση της x x. Αυτό, άλλωστε, ήταν αναμενόμενο, αφού ισχύει x φ x, για κάθε x, που σημαίνει ότι η τιμή της x x στη θέση x είναι ίδια με την τιμή της φx x στη θέση x. Γενικά: Η γραφική παράσταση της συνάρτησης, με: x φ xc, όπου c 0, προκύπτει από μια οριζόντια μετατόπιση της γραφικής παράστασης της φ κατά c μονάδες προς τα αριστερά (Σχήμα δ ). Πράγματι επειδή xφ x c, η τιμή της στη θέση x είναι ίδια με την τιμή της φ στη θέση x c, που βρίσκεται c μονάδες δεξιότερα της θέσης x. Άρα, η γραφική παράσταση της θα βρίσκεται c μονάδες αριστερότερα της γραφικής παράστασης της φ (Σχήμα δ ). Σχήμα δ ΕΦΑΡΜΟΓΗ Να παρασταθεί γραφικά η συνάρτηση ( x) x3. ΛΥΣΗ Αρχικά χαράσσουμε την y x 3, που όπως είδαμε προκύπτει από μια οριζόντια μετατόπιση της y x κατά 3 μονάδες προς τα αριστερά. Στη συνέχεια χαράσσουμε την y x3,που όπως είδαμε προκύπτει από μια κα-
29 4.4 Κατακόρυφη Οριζόντια μετατόπιση καμπύλης 5 τακόρυφη μετατόπιση της γραφικής παράστασης της y x 3 κατά μονάδες προς τα πάνω. Επομένως, η γραφική παράσταση της ( x) x3 προκύπτει από δύο διαδοχικές μετατοπίσεις της συνάρτησης y x, μιας οριζόντιας κατά 3 μονάδες προς τα αριστερά και μιας κατακόρυφης κατά μονάδες προς τα πάνω (Σχήμα). ΣΗΜΕΙΩΣΗ: Με ανάλογο τρόπο, δουλεύουμε για να παραστήσουμε γραφικά τις συναρτήσεις της μορφής: ( x) φ( xc) d, με cd, 0 Δηλαδή, αξιοποιούμε τόσο την οριζόντια όσο και την κατακόρυφη μετατόπιση καμπύλης. ΑΣΚΗΣΕΙΣ A ΟΜΑΔΑΣ. Στο ίδιο σύστημα συντεταγμένων να παραστήσετε γραφικά τις συναρτήσεις: φx. Ομοίως για τις συναρτήσεις: φx x x x g x x., και x, h x x 3. Ομοίως για τις συναρτήσεις: φ x x F x x και q x x. G x x., και
30 6 4. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ 4. Στο παρακάτω σχήμα δίνεται η γραφική παράσταση μιας συνάρτησης φ που αποτελείται από την διχοτόμο της δεύτερης γωνίας των αξόνων και από το ημικύκλιο που ανήκει στο ο τεταρτημόριο και έχει διάμετρο που ορίζουν τα σημεία O (0,0) και A (,0). Στο ίδιο σύστημα συντεταγμένων να παραστήσετε γραφικά τις συναρτήσεις: i) ( x) = φ( x) + και gx ( ) = φ( x) - ii) hx ( ) = φ( x + 3) και qx ( ) = φ( x - 3) iii) F( x) = φ( x + 3) + και Gx ( ) = φ( x -3)-. 5. Δίνεται η συνάρτηση φ x ( ) x. Να βρείτε τον τύπο της συνάρτησης της οποίας η γραφική παράσταση προκύπτει από δύο διαδοχικές μετατοπίσεις της γραφικής παράστασης της φ: i) κατά μονάδες προς τα δεξιά και κατά μονάδα προς τα πάνω. ii) κατά 3 μονάδες προς τα δεξιά και κατά μονάδες προς τα κάτω. iii) κατά μονάδες προς τα αριστερά και κατά μονάδες προς τα πάνω. iv) κατά 3 μονάδες προς τα αριστερά και κατά μονάδες προς τα κάτω.
31 4.5 ΜΟΝΟΤΟΝΙΑ-ΑΚΡΟΤΑΤΑ-ΣΥΜΜΕΤΡΙΕΣ ΣΥΝΑΡΤΗΣΗΣ Μονοτονία συνάρτησης Στο παρακάτω σχήμα δίνεται η γραφική παράσταση της συνάρτησης T t που εκφράζει τη θερμοκρασία Τ ενός τόπου συναρτήσει του χρόνου t κατά το χρονικό διάστημα από τα μεσάνυχτα μιας ημέρας t 0 μέχρι τα μεσάνυχτα της επόμενης μέρας t 4. α) Παρατηρούμε ότι στο διάστημα 4,6 η γραφική παράσταση της θερμοκρασίας ανέρχεται.
32 8 4. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Αυτό σημαίνει ότι στο διάστημα αυτό, με την πάροδο του χρόνου, η θερμοκρασία αυξάνεται, δηλαδή για οποιαδήποτε t, t 4,6 με t t ισχύει: t t Για το λόγο αυτό λέμε ότι η συνάρτηση T t είναι γνησίως αύξουσα στο διάστημα 4,6. Γενικά: ΟΡΙΣΜΟΣ Μια συνάρτηση λέγεται γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της, όταν για οποιαδήποτε x, x Δ με x x ισχύει: x x Για να δηλώσουμε ότι η συνάρτηση είναι γνησίως αύξουσα στο διάστημα Δ γράφουμε Δ. Για παράδειγμα, η συνάρτηση x x 3 είναι γνησίως αύξουσα στο. Πράγματι έστω x, x,με x x. Τότε έχουμε: x x x x x 3x 3 x x Γενικά: Η συνάρτηση xαx β, με α 0 είναι γνησίως αύξουσα στο. β) Στο ίδιο σχήμα, παρατηρούμε επιπλέον ότι στο διάστημα 6,4 η γραφική παράσταση της θερμοκρασίας κατέρχεται.
33 4.5 Μονοτονία Ακρότατα Συμμετρίες συνάρτησης 9 Αυτό σημαίνει ότι στο διάστημα αυτό, με την πάροδο του χρόνου, η θερμοκρασία μειώνεται, δηλαδή για οποιαδήποτε t, t 6,4 με t t ισχύει: t t Για το λόγο αυτό λέμε ότι η συνάρτηση T t είναι γνησίως φθίνουσα στο διάστημα 6,4. Γενικά: ΟΡΙΣΜΟΣ Μια συνάρτηση λέγεται γνησίως φθίνουσα σε ένα διάστημα Δ του πεδίου ορισμού της, όταν για οποιαδήποτε x, x Δ με x xισχύει: x x Για να δηλώσουμε ότι η συνάρτηση είναι γνησίως φθίνουσα στο διάστημα Δ γράφουμε Δ Για παράδειγμα, η συνάρτηση x x 5 είναι γνησίως φθίνουσα στο. Πράγματι έστω x, x, με x x. Τότε έχουμε: x x x x x5x 5 x x Γενικά: Η συνάρτηση xαx β, με α 0 είναι γνησίως φθίνουσα στο. Μια συνάρτηση που είναι είτε γνησίως αύξουσα είτε γνησίως φθίνουσα σε ένα διάστημα Δ λέγεται γνησίως μονότονη στο Δ. Ελάχιστο και μέγιστο συνάρτησης Ας θεωρήσουμε και πάλι τη γραφική παράσταση της συνάρτησης T t.
34 30 4. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Παρατηρούμε ότι: α) Τη χρονική στιγμή t 4 η θερμοκρασία του τόπου παίρνει την ελάχιστη τιμή της, που είναι η 4 3 βαθμοί Κελσίου. Δηλαδή ισχύει: t 4 3, για κάθε t 0,4 T t 4 3. Γενικά: Για το λόγο αυτό λέμε ότι η συνάρτηση λάχιστο, το ΟΡΙΣΜΟΣ παρουσιάζει στο t 4 ε- Μια συνάρτηση, με πεδίο ορισμού ένα σύνολο Α, λέμε ότι παρουσιάζει στο x0 Α (ολικό) ελάχιστο όταν: x x 0, για κάθε x Α Το x0 Α λέγεται θέση ελαχίστου, ενώ το 0 ελάχιστο της συνάρτησης και το συμβολίζουμε με min x. 4 Για παράδειγμα, ας θεωρήσουμε τη συνάρτηση x x 4 x 0, για κάθε x, θα είναι 4 3x 0, για κάθε x, οπότε θα έχουμε 4 3x, για κάθε x. Επομένως: x 0, για κάθε x Άρα, η παρουσιάζει ελάχιστο στο x, το x ολικό ελάχιστο ή απλώς 3. Επειδή β) Τη χρονική στιγμή t 6 η θερμοκρασία του τόπου παίρνει τη μέγιστη τιμή της, που είναι η T 6 βαθμοί Κελσίου. Δηλαδή ισχύει: t 6, για κάθε t 0,4 Για το λόγο αυτό λέμε ότι η συνάρτηση T t μέγιστο, το 6. Γενικά: ΟΡΙΣΜΟΣ παρουσιάζει στο t 6 Μια συνάρτηση, με πεδίο ορισμού ένα σύνολο Α, λέμε ότι παρουσιάζει στο x0 Α (ολικό) μέγιστο όταν x x 0, για κάθε x Α
35 4.5 Μονοτονία Ακρότατα Συμμετρίες συνάρτησης 3 Το x0 Α λέγεται θέση μεγίστου, ενώ το x 0 ολικό μέγιστο ή απλώς μέγιστο της και το συμβολίζουμε με max x. 4 Για παράδειγμα, ας θεωρήσουμε τη συνάρτηση x x θα είναι οπότε θα έχουμε 4 x 0, για κάθε x, 4 3x 0, για κάθε x, 4 3x, για κάθε x. Επομένως: ( x) 0, για κάθε x Άρα, η παρουσιάζει μέγιστο στο x, το 3. Επειδή Το (ολικό) μέγιστο και το (ολικό) ελάχιστο μιας συνάρτησης λέγονται ολικά ακρότατα αυτής. ΣΧΟΛΙΟ: Μια συνάρτηση ενδέχεται να έχει και μέγιστο και ελάχιστο (Σχ. α) ή μόνο ελάχιστο (Σχ. β ) ή μόνο μέγιστο (Σχ. γ ) ή να μην έχει ούτε μέγιστο ούτε ελάχιστο (Σχ. δ ). Σχήμα α Σχήμα β Σχήμα γ Σχήμα δ
36 3 4. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Άρτια συνάρτηση α) Στο διπλανό σχήμα δίνεται η γραφική παράσταση C μιας συνάρτησης που έχει πεδίο ορισμού όλο το. Παρατηρούμε ότι η C έχει άξονα συμμετρίας τον άξονα y' y, αφού το συμμετρικό κάθε σημείου της C ως προς τον άξονα y' y ανήκει στην C. Επειδή, όμως, το συμμετρικό του τυχαίου σημείου M ( xy, ) της C ως προς τον άξονα y' y είναι το σημείο M '( xy, ) και επειδή τα σημεία M ( xy, ) και M '( xy, ) ανήκουν στην C, θα ισχύει y x και y x, οπότε θα έχουμε: x x Η συνάρτηση με την παραπάνω ιδιότητα λέμε λέγεται άρτια. Γενικά: ΟΡΙΣΜΟΣ: Μια συνάρτηση, με πεδίο ορισμού ένα σύνολο Α, θα λέγεται άρτια, όταν για κάθε x Α ισχύει: x Α x x και Η γραφική παράσταση μιας άρτιας συνάρτησης έχει άξονα συμμετρίας τον άξονα y y 4 Για παράδειγμα, η συνάρτηση x x x είναι άρτια συνάρτηση, αφού έχει πεδίο ορισμού όλο το και για κάθε x ισχύει: 4 4 x x x x x x Συνεπώς, η γραφική της παράσταση έχει άξονα συμμετρίας τον άξονα yy. ' Περιττή συνάρτηση β) Στο διπλανό σχήμα δίνεται η γραφική παράσταση C μιας συνάρτησης που έχει πεδίο ορισμού όλο το. Παρατηρούμε ότι η C έχει κέντρο συμμετρίας την αρχή των αξόνων, αφού το συμμετρικό κάθε σημείου της C ως προς την αρχή των αξόνων ανήκει στην C.
37 4.5 Μονοτονία Ακρότατα Συμμετρίες συνάρτησης 33 Επειδή, όμως, το συμμετρικό του τυχαίου σημείου M ( xy, ) της C ως προς την αρχή των αξόνων είναι το σημείο M '( x, y) και επειδή τα σημεία M ( xy, ) και M '( x, y) ανήκουν στην C, θα ισχύει y x, οπότε θα έχουμε: x x Η συνάρτηση με την παραπάνω ιδιότητα λέγεται περιττή. Γενικά: y x και ΟΡΙΣΜΟΣ: Μια συνάρτηση, με πεδίο ορισμού ένα σύνολο Α, θα λέγεται περιττή, όταν για κάθε x Α ισχύει: x Α και x x Η γραφική παράσταση μιας περιττής συνάρτησης έχει κέντρο συμμετρίας την αρχή των αξόνων. 3 Για παράδειγμα, η συνάρτηση x x x είναι περιττή συνάρτηση, διότι έχει πεδίο ορισμού όλο το και για κάθε x ισχύει: 3 3 x x x x x x Συνεπώς, η γραφική της παράσταση έχει κέντρο συμμετρίας την αρχή των αξόνων. ΣΗΜΕΙΩΣΗ: Ο όρος άρτια προέκυψε αρχικά από το γεγονός ότι οι συναρτήσεις y x, 4 6 y x, y x κτλ., που έχουν άρτιο εκθέτη, έχουν άξονα συμμετρίας τον άξονα yy, ' είναι δηλαδή άρτιες συναρτήσεις, ενώ ο όρος περιττή προέρχεται από το γεγονός ότι οι συναρτήσεις y x, y x, y x κτλ., που έ- 3 5 χουν περιττό εκθέτη, έχουν κέντρο συμμετρίας την αρχή των αξόνων, είναι δηλαδή περιττές συναρτήσεις. ΕΦΑΡΜΟΓΗ Στο παρακάτω σχήμα δίνονται ορισμένα τμήματα της γραφικής παράστασης μιας άρτιας συνάρτησης που έχει πεδίο ορισμού το διάστημα [ 6,6]. Να χαραχθούν και τα υπόλοιπα τμήματα της γραφικής παράστασης της συνάρτησης και με τη βοήθεια αυτής:
38 34 4. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ α) Να βρεθούν τα διαστήματα στα οποία η συνάρτηση : i) είναι γνησίως αύξουσα, ii) είναι γνησίως φθίνουσα iii) είναι σταθερή. β) Να βρεθεί η μέγιστη και η ελάχιστη τιμή της, καθώς επίσης οι θέσεις των ακροτάτων αυτών. ΛΥΣΗ Επειδή η συνάρτηση είναι άρτια, η γραφική της παράσταση θα έχει άξονα συμμετρίας τον άξονα yy. ' Επομένως, αν πάρουμε τα συμμετρικά ως προς τον άξονα yy ' των δοθέντων τμημάτων της γραφικής παράστασης της, θα έχουμε ολόκληρη τη γραφική παράσταση της, που είναι η πολυγωνική γραμμή Α Β Γ ΟΓΒΑ (Σχήμα). Από την παραπάνω γραφική παράσταση προκύπτει ότι: α) Η συνάρτηση : i) είναι γνησίως αύξουσα σε καθένα από τα διαστήματα [0,] και [5,6], ii) είναι γνησίως φθίνουσα σε καθένα από τα διαστήματα [-,0] και [-6,- 5], τα οποία είναι συμμετρικά ως προς το Ο των διαστημάτων [0,] και [5,6] αντιστοίχως στα οποία η είναι γνησίως αύξουσα. iii) είναι σταθερή σε καθένα από τα διαστήματα [-5,- ] και [,5] τα οποία είναι συμμετρικά μεταξύ τους ως προς το Ο.
39 4.5 Μονοτονία Ακρότατα Συμμετρίες συνάρτησης 35 β) Η μέγιστη τιμή της είναι ίση με 4 και παρουσιάζεται όταν το x πάρει τις τιμές - 6 και 6. Δηλαδή ισχύει: max ( x) ( 6) (6) 4 Η ελάχιστη τιμή της είναι ίση με 0 και παρουσιάζεται όταν το x πάρει την τιμή 0. Δηλαδή ισχύει: min ( x) (0) 0. ΑΣΚΗΣΕΙΣ Α ΟΜΑΔΑΣ ) Να βρείτε τα διαστήματα στα οποία καθεμιά από τις παρακάτω συναρτήσεις είναι: α) γνησίως αύξουσα και β) γνησίως φθίνουσα. ) Να προσδιορίσετε τα ολικά ακρότατα των συναρτήσεων της προηγούμενης άσκησης, καθώς και τις θέσεις των ακροτάτων αυτών. 3) Να δείξετε ότι: i) Η συνάρτηση x ii) Η συνάρτηση gx ( ) x ( x) x 6x 0 παρουσιάζει ελάχιστο για x 3. παρουσιάζει μέγιστο για x. 4) Να βρείτε ποιες από τις παρακάτω συναρτήσεις είναι άρτιες και ποιες είναι περιττές: 4 i) x3x 5x ii) x 3 x iii) 3 x x 3 5 x x iv) 4 x x 3x v) 5 x vi) 6 x x x.
40 36 4. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ 5) Ομοίως για τις συναρτήσεις: i) x x iv) x ii) x x iii) x x x 4 v) 5 x x vi) 3 x x x ( x) x 6 = -. 6) Να βρείτε ποιες από τις παρακάτω γραμμές είναι γραφικές παραστάσεις άρτιας και ποιες περιττής συνάρτησης. 7) Ομοίως για τις παρακάτω γραμμές 8) Να συμπληρώσετε τις παρακάτω γραμμές ώστε να παριστάνουν γραφικές παραστάσεις α) Άρτιας συνάρτησης και β) Περιττής συνάρτησης.
41 4.5 Μονοτονία Ακρότατα Συμμετρίες συνάρτησης 37 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ 4 ου ΚΕΦΑΛΑΙΟΥ I) Σε καθεμιά από τις παρακάτω περιπτώσεις να κυκλώσετε το γράμμα Α, αν ο ισχυρισμός είναι αληθής και το γράμμα Ψ, αν ο ισχυρισμός είναι ψευδής.. Υπάρχει συνάρτηση της οποίας η γραφική παράσταση, Β, 3. διέρχεται από τα σημεία Α και. Οι ευθείες y α x και y x τέμνονται. Α Ψ 3. Αν μία συνάρτηση είναι γνησίως αύξουσα, τότε η είναι γνησίως φθίνουσα. 4. Μία γνησίως μονότονη συνάρτηση έχει το πολύ μία ρίζα. Α Ψ 5. Υπάρχει γνησίως μονότονη συνάρτηση που διέρχεται από,, Γ 3,3. τα σημεία Α, Β και 6. Αν μια συνάρτηση είναι γνησίως φθίνουσα και έχει ρίζα τον αριθμό, τότε θα ισχύει (0) Αν μια συνάρτηση είναι γνησίως μονότονη και η γραφική της παράσταση διέρχεται από τα σημεία Α, και Β,5, τότε η είναι γνησίως αύξουσα. 8. Αν η μέγιστη τιμή μιας συνάρτησης είναι ίση με, τότε η εξίσωση ( x) είναι αδύνατη. 9. Η συνάρτηση :-, με x 3x Α Α Α Α Α Α Ψ Ψ Ψ Ψ Ψ Ψ είναι άρτια. Α Ψ 0. Αν μια συνάρτηση είναι άρτια ή περιττή και έχει ρίζα τον αριθμό ρ, τότε θα έχει ρίζα και τον αριθμό ρ.. Αν μία συνάρτηση είναι άρτια, τότε η δεν είναι γνησίως μονότονη. Α Ψ. Αν μία συνάρτηση είναι άρτια, τότε η είναι περιττή. Α Ψ II) Να επιλέξετε τη σωστή απάντηση για την παρακάτω συνάρτηση. Η συνάρτηση, της οποίας η γραφική παράσταση προκύπτει από δύο διαδοχικές μετατοπίσεις της γραφικής παράστασης της συνάρτησης φx 3x 4, μιας οριζόντιας κατά μονάδα προς τα αριστερά και μιας κατακόρυφης κατά μονάδες προς τα πάνω, έχει τύπο: 4 4 Α) x 3( x) Β) x x 3( ), 4 4 Γ) x 3( x) Δ) x x 3( ) Α Ψ
42 38 4. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΙΣΤΟΡΙΚΟ ΣΗΜΕΙΩΜΑ Η ιδέα της χρησιμοποίησης διατεταγμένων ζευγών για τα σημεία ενός επιπέδου και της περιγραφής καμπύλων με εξισώσεις, ανήκει στον Rene Descartes ( ) και στον Pierre de Fermat (60-665). Ο Descartes (Καρτέσιος) γεννήθηκε στη La Haye (σημερινή Ντερκατ) της Touraine και πέθανε στη Στοκχόλμη. Σε ηλικία 0 χρόνων εγγράφηκε στο Βασιλικό Κολλέγιο της La Fleche, όπου δίδασκαν Ιησουίτες. Από εκείνη τη στιγμή αρχίζει και το ενδιαφέρον του για τα μαθηματικά. Στη ζωή του υπήρξε φιλόσοφος, αλλά ένα μεγάλο μέρος του χρόνου του το διέθετε για τα μαθηματικά. Τα αποτελέσματα και οι μέθοδοί του, που δημοσίευσε το 637 στο βιβλίο του Le Geometrie, δημιούργησαν ένα νέο κλάδο των μαθηματικών που αργότερα ονομάστηκε Αναλυτική Γεωμετρία. Ο Καρτέσιος διείδε τη δύναμη της Άλγεβρας για τη λύση γεωμετρικών προβλημάτων και η σκέψη του αντιπροσώπευε μια ριζική απόκλιση από την μέχρι τότε επικρατούσα άποψη για τη Γεωμετρία. Ο όρος «Καρτεσιανές συντεταγμένες», οφείλεται στο όνομά του. Ο Fermat, που έζησε στην Toulouse της νότιας Γαλλίας, αν και ήταν νομικός στο επάγγελμα, υπήρξε ένας από τους μεγαλύτερους μαθηματικούς του 7ου αιώνα. Τις ιδέες του για συντεταγμένες στη Γεωμετρία, τυποποίησε στις αρχές του 69 και τις κυκλοφόρησε με αλληλογραφία, αλλά δεν δημοσιεύτηκαν πριν από το 679. Ο Fermat συνέδεσε το όνομά του με τον ισχυρισμό: «Για κάθε ν είναι αδύνατο να βρούμε θετικούς ακέραιους α, β, γ που ν ν ν να ικανοποιούν την σχέση a β γ» που είναι γνωστός ως το «τελευταίο θεώρημα του Fermat». Τον ισχυρισμό του αυτόν έγραψε ο Fermat στο περιθώριο ενός βιβλίου του προσθέτοντας και τα εξής: «Έχω βρει μια πραγματικά θαυμάσια απόδειξη την οποία το περιθώριο αυτό είναι πολύ στενό για να χωρέσει». Ο ισχυρισμός αυτός του Fermat αποδείχτηκε αληθής το 994 από τον Άγγλο μαθηματικό Α. Wiles, αφού υπήρξε για 350 χρόνια ένα από τα διασημότερα άλυτα προβλήματα της Θεωρίας Αριθμών.
Κεφάλαιο 2 ο ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ
 Κεφάλαιο ο ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ Σε προηγούμενες τάξεις γνωρίσαμε την έννοια της συνάρτησης και μελετήσαμε ορισμένες βασικές συναρτήσεις. Στο κεφάλαιο αυτό θα μελετήσουμε στη γενική τους μορφή ιδιότητες
Κεφάλαιο ο ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ Σε προηγούμενες τάξεις γνωρίσαμε την έννοια της συνάρτησης και μελετήσαμε ορισμένες βασικές συναρτήσεις. Στο κεφάλαιο αυτό θα μελετήσουμε στη γενική τους μορφή ιδιότητες
ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ
 5 ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Εισαγωγή Στο κεφάλαιο αυτό θα δούμε πώς, με τη βοήθεια των πληροφοριών που α- ποκτήσαμε μέχρι τώρα, μπορούμε να χαράξουμε με όσο το δυνατόν μεγαλύτερη ακρίβεια τη γραφική παράσταση
5 ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Εισαγωγή Στο κεφάλαιο αυτό θα δούμε πώς, με τη βοήθεια των πληροφοριών που α- ποκτήσαμε μέχρι τώρα, μπορούμε να χαράξουμε με όσο το δυνατόν μεγαλύτερη ακρίβεια τη γραφική παράσταση
Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης
 Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης Ορθοκανονικό σύστημα αξόνων ονομάζεται ένα σύστημα από δύο κάθετους άξονες με κοινή αρχή στους οποίους οι μονάδες έχουν το ίδιο μήκος. Υπάρχουν περιπτώσεις
Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης Ορθοκανονικό σύστημα αξόνων ονομάζεται ένα σύστημα από δύο κάθετους άξονες με κοινή αρχή στους οποίους οι μονάδες έχουν το ίδιο μήκος. Υπάρχουν περιπτώσεις
4.3 Η ΣΥΝΑΡΤΗΣΗ f (x) x
 1 4.3 Η ΣΥΝΑΡΤΗΣΗ f () A Ομάδας Ασκήσεις σχολικού βιβλίου σελίδας 164 167 1. Να βρείτε τη γωνία που σχηματίζει με τον άξονα η ευθεία = + = 3 1 i = + 1 iv) = 3 + εφω = 1 ω = 45 ο εφω = 3 ω = 60 ο i εφω
1 4.3 Η ΣΥΝΑΡΤΗΣΗ f () A Ομάδας Ασκήσεις σχολικού βιβλίου σελίδας 164 167 1. Να βρείτε τη γωνία που σχηματίζει με τον άξονα η ευθεία = + = 3 1 i = + 1 iv) = 3 + εφω = 1 ω = 45 ο εφω = 3 ω = 60 ο i εφω
ΣΥΝΑΡΤΗΣΕΩΝ. f3 x = και
 7 ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Στο κεφάλαιο αυτό θα δούμε πώς, με τη βοήθεια των πληροφοριών που α- ποκτήσαμε μέχρι τώρα, μπορούμε να χαράξουμε με όσο το δυνατόν μεγαλύτερη ακρίβεια τη γραφική παράσταση
7 ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Στο κεφάλαιο αυτό θα δούμε πώς, με τη βοήθεια των πληροφοριών που α- ποκτήσαμε μέχρι τώρα, μπορούμε να χαράξουμε με όσο το δυνατόν μεγαλύτερη ακρίβεια τη γραφική παράσταση
δίου ορισμού, μέσου του τύπου εξαρτημένης μεταβλητής του πεδίου τιμών που λέγεται εικόνα της f για x α f α.
 3.1 Η έννοια της συνάρτησης Ορισμοί Συνάρτηση f από ένα συνόλου Α σε ένα σύνολο Β είναι μια αντιστοιχία των στοιχείων του Α στα στοιχεία του Β, κατά την οποία κάθε στοιχείο του Α αντιστοιχεί σε ένα μόνο
3.1 Η έννοια της συνάρτησης Ορισμοί Συνάρτηση f από ένα συνόλου Α σε ένα σύνολο Β είναι μια αντιστοιχία των στοιχείων του Α στα στοιχεία του Β, κατά την οποία κάθε στοιχείο του Α αντιστοιχεί σε ένα μόνο
6.1 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ
 ΟΡΙΣΜΟΣ 6. ΣΥΝΑΡΤΗΣΕΙΣ 6.1 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ Ονομάζουμε συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β μια διαδικασία (κανόνα) f, με την οποία κάθε στοιχείο του συνόλου Α αντιστοιχίζεται σε ένα ακριβώς
ΟΡΙΣΜΟΣ 6. ΣΥΝΑΡΤΗΣΕΙΣ 6.1 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ Ονομάζουμε συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β μια διαδικασία (κανόνα) f, με την οποία κάθε στοιχείο του συνόλου Α αντιστοιχίζεται σε ένα ακριβώς
1 ΘΕΩΡΙΑΣ...με απάντηση
 1 ΘΕΩΡΙΑΣ.....με απάντηση ΑΛΓΕΒΡΑ Κεφάλαιο 1 0 Εξισώσεις Ανισώσεις 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση που περιέχει πράξεις μεταξύ αριθμών.
1 ΘΕΩΡΙΑΣ.....με απάντηση ΑΛΓΕΒΡΑ Κεφάλαιο 1 0 Εξισώσεις Ανισώσεις 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση που περιέχει πράξεις μεταξύ αριθμών.
α) γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της (Σχ.α), όταν β) γνησίως φθίνουσα σε ένα διάστημα Δ του πεδίου ορισμού της (Σχ.
 ΜΟΝΟΤΟΝΙΑ. ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ. ΜΟΝΟΤΟΝΙΑ - ΑΚΡΟΤΑΤΑ - ΣΥΜΜΕΤΡΙΕΣ Μια συνάρτηση f λέγεται: α) γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της (Σχ.α), όταν για οποιαδήποτε χ,χ Δ με χ
ΜΟΝΟΤΟΝΙΑ. ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ. ΜΟΝΟΤΟΝΙΑ - ΑΚΡΟΤΑΤΑ - ΣΥΜΜΕΤΡΙΕΣ Μια συνάρτηση f λέγεται: α) γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της (Σχ.α), όταν για οποιαδήποτε χ,χ Δ με χ
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
1ο τεταρτημόριο x>0,y>0 Ν Β
 ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ( 6.2 ) Καρτεσιανό σύστημα συντεταγμένων ονομάζεται ένα επίπεδο εφοδιασμένο με δύο κάθετους άξονες οι οποίοι έχουν κοινή αρχή Ο και είναι αριθμημένοι με τις ίδιες μονάδες μήκους.
ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ( 6.2 ) Καρτεσιανό σύστημα συντεταγμένων ονομάζεται ένα επίπεδο εφοδιασμένο με δύο κάθετους άξονες οι οποίοι έχουν κοινή αρχή Ο και είναι αριθμημένοι με τις ίδιες μονάδες μήκους.
Ας υποθέσουμε ότι καταθέτουμε στην τράπεζα ένα κεφάλαιο ευρώ με ανατοκισμό
 5. Ακολουθίες ΠΡΟΟΔΟΙ Κεφάλαιο 5ο Η έννοια της ακολουθίας Ας υποθέσουμε ότι καταθέτουμε στην τράπεζα ένα κεφάλαιο 0000 ευρώ με ανατοκισμό ανά έτος και με επιτόκιο %. Αυτό σημαίνει ότι σε ένα χρόνο οι τόκοι
5. Ακολουθίες ΠΡΟΟΔΟΙ Κεφάλαιο 5ο Η έννοια της ακολουθίας Ας υποθέσουμε ότι καταθέτουμε στην τράπεζα ένα κεφάλαιο 0000 ευρώ με ανατοκισμό ανά έτος και με επιτόκιο %. Αυτό σημαίνει ότι σε ένα χρόνο οι τόκοι
6.1 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ
 6.1 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΣΜΟΣ ΣΥΝΑΡΤΗΣΗΣ Συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β λέγεται μια διαδικασία (κανόνας), με την οποία κάθε στοιχείο του συνόλου Α αντιστοιχίζεται σε ακριβώς ένα στοιχείο
6.1 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΣΜΟΣ ΣΥΝΑΡΤΗΣΗΣ Συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β λέγεται μια διαδικασία (κανόνας), με την οποία κάθε στοιχείο του συνόλου Α αντιστοιχίζεται σε ακριβώς ένα στοιχείο
ΔΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ. ΘΕΜΑ 2ο
 Β ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΔΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ ΘΕΜΑ ο ΘΕΜΑ 8603 Δίνεται τρίγωνο και σημεία και του επιπέδου τέτοια, ώστε 5 και 5. α) Να γράψετε το διάνυσμα ως γραμμικό
Β ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΔΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ ΘΕΜΑ ο ΘΕΜΑ 8603 Δίνεται τρίγωνο και σημεία και του επιπέδου τέτοια, ώστε 5 και 5. α) Να γράψετε το διάνυσμα ως γραμμικό
Ρητοί αριθμοί λέγονται οι αριθμοί που έχουν ή μπορούν να πάρουν τη μορφή
 ΣΥΝΑΡΤΗΣΕΙΣ (ΕΙΣΑΓΩΓΗ)-ΘΕΩΡΕΙΑ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ Το σύνολο των πραγματικών αριθμών Υπενθυμίζουμε ότι το σύνολο των πραγματικών αριθμώv αποτελείται από τους ρητούς και τους άρρητους αριθμούς και παριστάνεται
ΣΥΝΑΡΤΗΣΕΙΣ (ΕΙΣΑΓΩΓΗ)-ΘΕΩΡΕΙΑ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ Το σύνολο των πραγματικών αριθμών Υπενθυμίζουμε ότι το σύνολο των πραγματικών αριθμώv αποτελείται από τους ρητούς και τους άρρητους αριθμούς και παριστάνεται
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ, ΠΟΛΙΤΙΣΜΟΥ ΚΑΙ ΑΘΛΗΤΙΣΜΟΥ
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ, ΠΟΛΙΤΙΣΜΟΥ ΚΑΙ ΑΘΛΗΤΙΣΜΟΥ ΙΝΣΤΙΤΟΥΤΟ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΕΚΔΟΣΕΩΝ «ΔΙΟΦΑΝΤΟΣ» y y=x 2 y=(x-2) 2 y=(x-2) 2-1 0 1 2 3 x -1 Τόμος 4ος Άλγεβρα και Στοιχεία Πιθανοτήτων
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ, ΠΟΛΙΤΙΣΜΟΥ ΚΑΙ ΑΘΛΗΤΙΣΜΟΥ ΙΝΣΤΙΤΟΥΤΟ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΕΚΔΟΣΕΩΝ «ΔΙΟΦΑΝΤΟΣ» y y=x 2 y=(x-2) 2 y=(x-2) 2-1 0 1 2 3 x -1 Τόμος 4ος Άλγεβρα και Στοιχεία Πιθανοτήτων
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΑΠΟΣΤΟΛΟΥ ΓΙΩΡΓΟΣ ΜΑΘΗΜΑΤΙΚΟΣ
 6ο κεφάλαιο: Συναρτήσεις ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΑΠΟΣΤΟΛΟΥ ΓΙΩΡΓΟΣ ΜΑΘΗΜΑΤΙΚΟΣ ) Copyright 2014 Αποστόλου Γιώργος Αποστόλου Γεώργιος apgeorge2004@yahoo.com άδεια χρήσης 3η Εκδοση, Αύγουστος 2014 Περιεχόµενα
6ο κεφάλαιο: Συναρτήσεις ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΑΠΟΣΤΟΛΟΥ ΓΙΩΡΓΟΣ ΜΑΘΗΜΑΤΙΚΟΣ ) Copyright 2014 Αποστόλου Γιώργος Αποστόλου Γεώργιος apgeorge2004@yahoo.com άδεια χρήσης 3η Εκδοση, Αύγουστος 2014 Περιεχόµενα
ΑΛΓΕΒΡΑ B ΛΥΚΕΙΟΥ. Γενικής Παιδείας ΑΠΑΝΤΗΣΕΙΣ ΛΥΣΕΙΣ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ
 ΑΛΓΕΒΡΑ B ΛΥΚΕΙΥ Γενικής Παιδείας ΑΠΑΝΤΗΣΕΙΣ ΛΥΣΕΙΣ ΣΧΛΙΚΥ ΒΙΒΛΙΥ Σχολικό βιβλίο: Απαντήσεις Λύσεις Κεφάλαιο ο: Συστήματα Γραμμικά συστήματα Α ΜΑΔΑΣ Έχουμε: = 4 i = 6 = + = + = = Άρα, η λύση του συστήματος
ΑΛΓΕΒΡΑ B ΛΥΚΕΙΥ Γενικής Παιδείας ΑΠΑΝΤΗΣΕΙΣ ΛΥΣΕΙΣ ΣΧΛΙΚΥ ΒΙΒΛΙΥ Σχολικό βιβλίο: Απαντήσεις Λύσεις Κεφάλαιο ο: Συστήματα Γραμμικά συστήματα Α ΜΑΔΑΣ Έχουμε: = 4 i = 6 = + = + = = Άρα, η λύση του συστήματος
) = Απόσταση σημείου από ευθεία. Υπολογισμός Εμβαδού Τριγώνου. και A
 [Επιλογή Ιαν.. Εμβαδόν Τριγώνου ΣΤΟΧΟΙ: Ο µαθητής ϖρέϖει: να είναι ικανός να υϖολογίζει την αϖόσταση σηµείου αϖό ευθεία να είναι ικανός να υϖολογίζει το εµβαδό ενός τριγώνου αϖό τις συντεταγµένες των κορυφών
[Επιλογή Ιαν.. Εμβαδόν Τριγώνου ΣΤΟΧΟΙ: Ο µαθητής ϖρέϖει: να είναι ικανός να υϖολογίζει την αϖόσταση σηµείου αϖό ευθεία να είναι ικανός να υϖολογίζει το εµβαδό ενός τριγώνου αϖό τις συντεταγµένες των κορυφών
Ιωάννης Σ. Μιχέλης Μαθηματικός
 1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Τι ονομάζεται αριθμητική και τι αλγεβρική παράσταση; Μία παράσταση, που περιέχει πράξεις με αριθμούς ονομάζεται αριθμητική παράσταση. Μία παράσταση, που περιέχει πράξεις
1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Τι ονομάζεται αριθμητική και τι αλγεβρική παράσταση; Μία παράσταση, που περιέχει πράξεις με αριθμούς ονομάζεται αριθμητική παράσταση. Μία παράσταση, που περιέχει πράξεις
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ. ΜΕΡΟΣ 1ο ΑΛΓΕΒΡΑ
 1. Τι καλείται μεταβλητή; ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΑ Β ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 1ο ΑΛΓΕΒΡΑ Μεταβλητή είναι ένα γράμμα (π.χ., y, t, ) που το χρησιμοποιούμε για να παραστήσουμε ένα οποιοδήποτε στοιχείο ενός συνόλου..
1. Τι καλείται μεταβλητή; ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΑ Β ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 1ο ΑΛΓΕΒΡΑ Μεταβλητή είναι ένα γράμμα (π.χ., y, t, ) που το χρησιμοποιούμε για να παραστήσουμε ένα οποιοδήποτε στοιχείο ενός συνόλου..
2 Ο ΚΕΦΑΛΑΙΟ Ενότητα 5.
 Ευθεία Ο ΚΕΦΑΛΑΙΟ Ενότητα 5. Εξίσωση γραμμής Συντελεστής διεύθυνσης ευθείας Συνθήκες καθετότητας και παραλληλίας ευθειών Εξίσωση ευθείας ειδικές περιπτώσεις Σχόλιο Το σημείο είναι ο θεμελιώδης λίθος της
Ευθεία Ο ΚΕΦΑΛΑΙΟ Ενότητα 5. Εξίσωση γραμμής Συντελεστής διεύθυνσης ευθείας Συνθήκες καθετότητας και παραλληλίας ευθειών Εξίσωση ευθείας ειδικές περιπτώσεις Σχόλιο Το σημείο είναι ο θεμελιώδης λίθος της
Άλγεβρα Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ. Τόμος 1ος 1η ΕΚΔΟΣΗ
 Άλγεβρα Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Τόμος 1ος 1η ΕΚΔΟΣΗ Συγγραφική ομάδα: Ανδρεαδάκης Στυλιανός Καθηγητής Πανεπιστημίου Αθηνών Κατσαργύρης Βασίλειος Καθηγητής μαθηματικών Βαρβακείου Πειραμ. Λυκείου Παπασταυρίδης
Άλγεβρα Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Τόμος 1ος 1η ΕΚΔΟΣΗ Συγγραφική ομάδα: Ανδρεαδάκης Στυλιανός Καθηγητής Πανεπιστημίου Αθηνών Κατσαργύρης Βασίλειος Καθηγητής μαθηματικών Βαρβακείου Πειραμ. Λυκείου Παπασταυρίδης
Κεφάλαιο 2 ο ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ
 Κεφάλαιο ο ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ Σε προηγούμενες τάξεις γνωρίσαμε την έννοια της συνάρτησης και μελετήσαμε ορισμένες βασικές συναρτήσεις. Στο κεφάλαιο αυτό θα μελετήσουμε στη γενική τους μορφή ιδιότητες
Κεφάλαιο ο ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ Σε προηγούμενες τάξεις γνωρίσαμε την έννοια της συνάρτησης και μελετήσαμε ορισμένες βασικές συναρτήσεις. Στο κεφάλαιο αυτό θα μελετήσουμε στη γενική τους μορφή ιδιότητες
Άλγεβρα Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ. Τόμος 1ος
 Άλγεβρα Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Τόμος 1ος Συγγραφική ομάδα: Ανδρεαδάκης Στυλιανός Καθηγητής Πανεπιστημίου Αθηνών Κατσαργύρης Βασίλειος Καθηγητής μαθηματικών Βαρβακείου Πειραμ. Λυκείου Παπασταυρίδης Στάυρος
Άλγεβρα Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Τόμος 1ος Συγγραφική ομάδα: Ανδρεαδάκης Στυλιανός Καθηγητής Πανεπιστημίου Αθηνών Κατσαργύρης Βασίλειος Καθηγητής μαθηματικών Βαρβακείου Πειραμ. Λυκείου Παπασταυρίδης Στάυρος
Η συνάρτηση y = αχ 2. Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd
 Η συνάρτηση y = αχ Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 1 Η συνάρτηση y = αχ με α 0 Μια συνάρτηση της μορφής y = α + β + γ με α 0 ονομάζεται τετραγωνική συνάρτηση.
Η συνάρτηση y = αχ Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 1 Η συνάρτηση y = αχ με α 0 Μια συνάρτηση της μορφής y = α + β + γ με α 0 ονομάζεται τετραγωνική συνάρτηση.
ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Α
 ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση θεωρίας 1 ΘΕΜΑ Α Τι ονομάζουμε πραγματική συνάρτηση
ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση θεωρίας 1 ΘΕΜΑ Α Τι ονομάζουμε πραγματική συνάρτηση
Κεφάλαιο 1 o Εξισώσεις - Ανισώσεις
 2 ΕΡΩΤΗΣΕΙΙΣ ΘΕΩΡΙΙΑΣ ΑΠΟ ΤΗΝ ΥΛΗ ΤΗΣ Β ΤΑΞΗΣ ΜΕΡΟΣ Α -- ΑΛΓΕΒΡΑ Κεφάλαιο 1 o Εξισώσεις - Ανισώσεις Α. 1 1 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση
2 ΕΡΩΤΗΣΕΙΙΣ ΘΕΩΡΙΙΑΣ ΑΠΟ ΤΗΝ ΥΛΗ ΤΗΣ Β ΤΑΞΗΣ ΜΕΡΟΣ Α -- ΑΛΓΕΒΡΑ Κεφάλαιο 1 o Εξισώσεις - Ανισώσεις Α. 1 1 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση
ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ 1 ο : Όριο Συνέχεια Συνάρτησης
 ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ ο : Όριο Συνέχεια Συνάρτησης Φυλλάδιο Φυλλάδι555 4 ο ο.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ ο : Όριο Συνέχεια Συνάρτησης Φυλλάδιο Φυλλάδι555 4 ο ο.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου
 Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου Αριθμοί 1. ΑΡΙΘΜΟΙ Σύνολο Φυσικών αριθμών: Σύνολο Ακέραιων αριθμών: Σύνολο Ρητών αριθμών: ακέραιοι με Άρρητοι αριθμοί: είναι οι μη ρητοί π.χ. Το σύνολο Πραγματικών
Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου Αριθμοί 1. ΑΡΙΘΜΟΙ Σύνολο Φυσικών αριθμών: Σύνολο Ακέραιων αριθμών: Σύνολο Ρητών αριθμών: ακέραιοι με Άρρητοι αριθμοί: είναι οι μη ρητοί π.χ. Το σύνολο Πραγματικών
Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις
 Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις Ορισμός: Έστω Α, Β R. Πραγματική συνάρτηση πραγματικής μεταβλητής από το σύνολο Α στο σύνολο Β ονομάζουμε την διαδικασία κατά την οποία κάθε στοιχείο του συνόλου
Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις Ορισμός: Έστω Α, Β R. Πραγματική συνάρτηση πραγματικής μεταβλητής από το σύνολο Α στο σύνολο Β ονομάζουμε την διαδικασία κατά την οποία κάθε στοιχείο του συνόλου
Μαθηματικά προσανατολισμού Β Λυκείου
 Μαθηματικά προσανατολισμού Β Λυκείου Συντεταγμένες Διανύσματος wwwaskisopolisgr wwwaskisopolisgr Συντεταγμένες στο επίπεδο Άξονας Πάνω σε μια ευθεία επιλέγουμε δύο σημεία Ο και Ι, έτσι το διάνυσμα i OI
Μαθηματικά προσανατολισμού Β Λυκείου Συντεταγμένες Διανύσματος wwwaskisopolisgr wwwaskisopolisgr Συντεταγμένες στο επίπεδο Άξονας Πάνω σε μια ευθεία επιλέγουμε δύο σημεία Ο και Ι, έτσι το διάνυσμα i OI
Κεφάλαιο 7 ο : Θετικοί και Αρνητικοί αριθμοί
 ΕΡΩΤΗΣΕΙΙΣ ΘΕΩΡΙΙΑΣ ΕΠΑΝΑΛΗΨΗ ΒΑΣΙΙΚΩΝ ΕΝΝΟΙΙΩΝ ΑΠΟ ΤΗΝ ΥΛΗ ΤΗΣ Α ΤΑΞΗΣ Κεφάλαιο 7 ο : Θετικοί και Αρνητικοί αριθμοί Α. 7. 1 1. Τι είναι τα πρόσημα και πως χαρακτηρίζονται οι αριθμοί από αυτά; Τα σύμβολα
ΕΡΩΤΗΣΕΙΙΣ ΘΕΩΡΙΙΑΣ ΕΠΑΝΑΛΗΨΗ ΒΑΣΙΙΚΩΝ ΕΝΝΟΙΙΩΝ ΑΠΟ ΤΗΝ ΥΛΗ ΤΗΣ Α ΤΑΞΗΣ Κεφάλαιο 7 ο : Θετικοί και Αρνητικοί αριθμοί Α. 7. 1 1. Τι είναι τα πρόσημα και πως χαρακτηρίζονται οι αριθμοί από αυτά; Τα σύμβολα
Ορισμός Τετραγωνική ονομάζεται κάθε συνάρτηση της μορφής y = αx 2 + βx + γ με α 0.
 ΜΕΡΟΣ Α. Η ΣΥΝΑΡΤΗΣΗ =α +β+γ,α 0 337. Η ΣΥΝΑΡΤΗΣΗ =α +β+γ ME α 0 Ορισμός Τετραγωνική ονομάζεται κάθε συνάρτηση της μορφής = α + β + γ με α 0. Η συνάρτηση = α +β+γ με α > 0 Η γραφική παράσταση της συνάρτησης
ΜΕΡΟΣ Α. Η ΣΥΝΑΡΤΗΣΗ =α +β+γ,α 0 337. Η ΣΥΝΑΡΤΗΣΗ =α +β+γ ME α 0 Ορισμός Τετραγωνική ονομάζεται κάθε συνάρτηση της μορφής = α + β + γ με α 0. Η συνάρτηση = α +β+γ με α > 0 Η γραφική παράσταση της συνάρτησης
Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ. (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα.
 Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα. (2) Ποιοι είναι οι άρτιοι και ποιοι οι περιττοί αριθμοί; Γράψε από τρία παραδείγματα.
Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα. (2) Ποιοι είναι οι άρτιοι και ποιοι οι περιττοί αριθμοί; Γράψε από τρία παραδείγματα.
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΕΥΡΙΠΙΔΟΥ 80 ΝΙΚΑΙΑ ΝΕΑΠΟΛΗ ΤΗΛΕΦΩΝΟ 0965897 ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ ΒΡΟΥΤΣΗ ΕΥΑΓΓΕΛΙΑ ΜΠΟΥΡΝΟΥΤΣΟΥ ΚΩΝ/ΝΑ ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Η έννοια του μιγαδικού
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΕΥΡΙΠΙΔΟΥ 80 ΝΙΚΑΙΑ ΝΕΑΠΟΛΗ ΤΗΛΕΦΩΝΟ 0965897 ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ ΒΡΟΥΤΣΗ ΕΥΑΓΓΕΛΙΑ ΜΠΟΥΡΝΟΥΤΣΟΥ ΚΩΝ/ΝΑ ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Η έννοια του μιγαδικού
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΗΣ Β ΛΥΚΕΙΟΥ
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΗΣ Β ΛΥΚΕΙΟΥ Διανύσματα Πολλαπλασιασμός αριθμού με διάνυσμα ο Θέμα _8603 Δίνεται τρίγωνο ΑΒΓ και σημεία Δ και Ε του επιπέδου τέτοια, ώστε 5 και
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΗΣ Β ΛΥΚΕΙΟΥ Διανύσματα Πολλαπλασιασμός αριθμού με διάνυσμα ο Θέμα _8603 Δίνεται τρίγωνο ΑΒΓ και σημεία Δ και Ε του επιπέδου τέτοια, ώστε 5 και
OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β, 8B, 9 Έστω Α ένα υποσύνολο του Ονομάζουμε
OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β, 8B, 9 Έστω Α ένα υποσύνολο του Ονομάζουμε
Συναρτήσεις. Αν λοιπόν έχουμε μια συνάρτηση f από ένα σύνολο Α σε ένα σύνολο Β γράφουμε f Α Β και χ f (χ)
 Συναρτήσεις Ορισμός Συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β λέγεται μια διαδικασία με την οποία σε κάθε στοιχείο χ του συνόλου Α αντιστοιχίζεται ένα και μόνο στοιχείο ψ του συνόλου Β. Η μεταβλητή χ
Συναρτήσεις Ορισμός Συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β λέγεται μια διαδικασία με την οποία σε κάθε στοιχείο χ του συνόλου Α αντιστοιχίζεται ένα και μόνο στοιχείο ψ του συνόλου Β. Η μεταβλητή χ
OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 Ο ΚΕΦΑΛΑΙΟ : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β Έστω
Ο ΚΕΦΑΛΑΙΟ : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β Έστω
i) Αν (,, ) είναι μια πυθαγόρεια τριάδα και είναι ένας θετικός ακέραιος, να αποδείξετε ότι και η τριάδα (,,
 1. i) Να αποδείξετε την ταυτότητα 1 ( ) ( ) ( ) + + = + +. ii) Να αποδείξετε ότι για όλους τους,, ισχύει Πότε ισχύει ισότητα; + + + +.. Λέμε ότι μια τριάδα θετικών ακεραίων (,, ) είναι όταν είναι πλευρές
1. i) Να αποδείξετε την ταυτότητα 1 ( ) ( ) ( ) + + = + +. ii) Να αποδείξετε ότι για όλους τους,, ισχύει Πότε ισχύει ισότητα; + + + +.. Λέμε ότι μια τριάδα θετικών ακεραίων (,, ) είναι όταν είναι πλευρές
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ Ε.1 I. 1. α 2 = 9 α = 3 ψ p: α 2 = 9, q: α = 3 Σύνολο αλήθειας της p: Α = {-3,3}, Σύνολο αλήθειας της q: B = {3} A B 2. α 2 = α α = 1 ψ p: α 2 = α, q: α = 1 Σύνολο
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ Ε.1 I. 1. α 2 = 9 α = 3 ψ p: α 2 = 9, q: α = 3 Σύνολο αλήθειας της p: Α = {-3,3}, Σύνολο αλήθειας της q: B = {3} A B 2. α 2 = α α = 1 ψ p: α 2 = α, q: α = 1 Σύνολο
Σύνολα. 1) Με αναγραφή των στοιχείων π.χ. 2) Με περιγραφή των στοιχείων π.χ.
 Σύνολα Ορισµός συνόλου (κατά Cantor): Σύνολο είναι κάθε συλλογή αντικειµένων, που προέρχεται από το µυαλό µας ή την εµπειρία µας, είναι καλά ορισµένο και τα αντικείµενα ξεχωρίζουν το ένα από το άλλο, δηλαδή
Σύνολα Ορισµός συνόλου (κατά Cantor): Σύνολο είναι κάθε συλλογή αντικειµένων, που προέρχεται από το µυαλό µας ή την εµπειρία µας, είναι καλά ορισµένο και τα αντικείµενα ξεχωρίζουν το ένα από το άλλο, δηλαδή
ΑΣΚΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ Ασκήσεις σχολικού βιβλίου σελίδας
 ΑΣΚΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ Ασκήσεις σχολικού βιβλίου σελίδας 07 3. Να αποδείξετε την ταυτότητα + + αβ βγ γα = Να αποδείξετε ότι για όλους τους α, β, γ ισχύει + + αβ + βγ + γα Πότε ισχύει ισότητα; = = + + =
ΑΣΚΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ Ασκήσεις σχολικού βιβλίου σελίδας 07 3. Να αποδείξετε την ταυτότητα + + αβ βγ γα = Να αποδείξετε ότι για όλους τους α, β, γ ισχύει + + αβ + βγ + γα Πότε ισχύει ισότητα; = = + + =
Τράπεζα Θεμάτων Διαβαθμισμένης Δυσκολίας- Άλγεβρα Β ΓΕ.Λ.-Σχολικό έτος 2014-2015 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΔΙΑΒΑΘΜΙΣΜΕΝΗΣ ΔΥΣΚΟΛΙΑΣ. Σχολικό έτος: 2014-2015
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΔΙΑΒΑΘΜΙΣΜΕΝΗΣ ΔΥΣΚΟΛΙΑΣ Α Λ Γ Ε Β Ρ Α Β Λ Υ Κ Ε Ι Ο Υ Σχολικό έτος: 014-015 Τα θέματα εμπλουτίζονται με την δημοσιοποίηση και των νέων θεμάτων από το Ι.Ε.Π. Γ ε ν ι κ ή Ε π ι μ έ λ ε ι
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΔΙΑΒΑΘΜΙΣΜΕΝΗΣ ΔΥΣΚΟΛΙΑΣ Α Λ Γ Ε Β Ρ Α Β Λ Υ Κ Ε Ι Ο Υ Σχολικό έτος: 014-015 Τα θέματα εμπλουτίζονται με την δημοσιοποίηση και των νέων θεμάτων από το Ι.Ε.Π. Γ ε ν ι κ ή Ε π ι μ έ λ ε ι
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να
ΑΣΚΗΣΕΙΣ ΚΑΤΑ Ι ΑΚΤΙΚΗ ΕΝΟΤΗΤΑ
 Ο ΚΕΦΑΛΑΙΟ ΑΣΚΗΣΕΙΣ ΚΑΤΑ Ι ΑΚΤΙΚΗ ΕΝΟΤΗΤΑ ΣΥΝΟΛΑ ΕΡΩΤΗΣΕΙΣ ΤΥΠΟΥ «ΣΩΣΤΟ ΛΑΘΟΣ». {,3,5,7,... } { / = ν +, ν Ν} =. = {} 0 3. Αν Α Β τότε Α Β = Α 4. 5 {,3,5,7 } 5. Αν Α= {, 3,7} και Β= {,3} 7, τότε Α=Β 6.
Ο ΚΕΦΑΛΑΙΟ ΑΣΚΗΣΕΙΣ ΚΑΤΑ Ι ΑΚΤΙΚΗ ΕΝΟΤΗΤΑ ΣΥΝΟΛΑ ΕΡΩΤΗΣΕΙΣ ΤΥΠΟΥ «ΣΩΣΤΟ ΛΑΘΟΣ». {,3,5,7,... } { / = ν +, ν Ν} =. = {} 0 3. Αν Α Β τότε Α Β = Α 4. 5 {,3,5,7 } 5. Αν Α= {, 3,7} και Β= {,3} 7, τότε Α=Β 6.
Τράπεζα συναρτήσει των διανυσμάτων α,β,γ. Μονάδες 13 β) να αποδείξετε ότι τα σημεία Α, Β, Γ είναι συνευθειακά. Μονάδες 12
 Τράπεζα 0- Πολλαπλασιασμός αριθμού με διάνυσμα.58 Θεωρούμε τα διανύσματα α,β,γ και τυχαίο σημείο Ο. Αν α β 5γ, α 3β 4γ και 3α β 6γ, τότε: α) να εκφράσετε τα διανύσματα, συναρτήσει των διανυσμάτων α,β,γ.
Τράπεζα 0- Πολλαπλασιασμός αριθμού με διάνυσμα.58 Θεωρούμε τα διανύσματα α,β,γ και τυχαίο σημείο Ο. Αν α β 5γ, α 3β 4γ και 3α β 6γ, τότε: α) να εκφράσετε τα διανύσματα, συναρτήσει των διανυσμάτων α,β,γ.
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ Β ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 1ο «ΑΛΓΕΒΡΑ»
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ Β ΓΥΜΝΑΣΙΥ ΜΕΡΣ ο «ΑΛΓΕΒΡΑ». Να υπολογίσετε την τιμή της παράστασης: Α = ( + ) 4( ) 8, όταν = 0,45. Απλοποιούμε πρώτα την παράσταση : Α = ( + ) 4( ) 8 = = + 6 4 + 4 8
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ Β ΓΥΜΝΑΣΙΥ ΜΕΡΣ ο «ΑΛΓΕΒΡΑ». Να υπολογίσετε την τιμή της παράστασης: Α = ( + ) 4( ) 8, όταν = 0,45. Απλοποιούμε πρώτα την παράσταση : Α = ( + ) 4( ) 8 = = + 6 4 + 4 8
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ. Μια παράσταση που περιέχει πράξεις με μεταβλητές (γράμματα) και αριθμούς καλείται αλγεβρική, όπως για παράδειγμα η : 2x+3y-8
 ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
12. Το εμβαδόν ενός τριγώνου ΑΒΓ είναι ίσο με
 ΓΕΝΙΚΟ ΥΚΕΙΟ ΚΑΤΡΙΤΙΟΥ ΕΠΙΜΕΕΙΑ: Kωνσταντόπουλος Κων/νος Μαθηματικός ΜSc Η ΕΥΘΕΙΑ ΤΟ ΕΠΙΠΕΔΟ. ε κάθε μια από τις παρακάτω περιπτώσεις να κυκλώσετε το γράμμα, αν ο ισχυρισμός είναι αληθής διαφορετικά να
ΓΕΝΙΚΟ ΥΚΕΙΟ ΚΑΤΡΙΤΙΟΥ ΕΠΙΜΕΕΙΑ: Kωνσταντόπουλος Κων/νος Μαθηματικός ΜSc Η ΕΥΘΕΙΑ ΤΟ ΕΠΙΠΕΔΟ. ε κάθε μια από τις παρακάτω περιπτώσεις να κυκλώσετε το γράμμα, αν ο ισχυρισμός είναι αληθής διαφορετικά να
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΘΕΜΑ Α Ερώτηση θεωρίας Αν η συνάρτηση f είναι παραγωγίσιμη στο R και c είναι μια πραγματική σταθερά, να δείξετε ότι: ( c f( )) = c f ( ),. Έστω F( )
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΘΕΜΑ Α Ερώτηση θεωρίας Αν η συνάρτηση f είναι παραγωγίσιμη στο R και c είναι μια πραγματική σταθερά, να δείξετε ότι: ( c f( )) = c f ( ),. Έστω F( )
ΣΥΣΤΗΜΑΤΑ. 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις)
 6 ΣΥΣΤΗΜΑΤΑ 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις) Η εξίσωση αx βy γ Στο Γυμνάσιο διαπιστώσαμε με την βοήθεια παραδειγμάτων ότι η εξίσωση αx βy γ, με α 0 ή β 0, που λέγεται γραμμική εξίσωση,
6 ΣΥΣΤΗΜΑΤΑ 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις) Η εξίσωση αx βy γ Στο Γυμνάσιο διαπιστώσαμε με την βοήθεια παραδειγμάτων ότι η εξίσωση αx βy γ, με α 0 ή β 0, που λέγεται γραμμική εξίσωση,
ΑΣΚΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ
 ΑΣΚΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ i) Να αποδείξετε την ταυτότητα α β γ αββγγα α β βγ γα ii) Να αποδείξετε ότι για όλους τους αβγ,, ισχύει Πότε ισχύει ισότητα; α β γ αβ βγ γα Λέμε ότι μια τριάδα θετικών ακεραίων β,
ΑΣΚΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ i) Να αποδείξετε την ταυτότητα α β γ αββγγα α β βγ γα ii) Να αποδείξετε ότι για όλους τους αβγ,, ισχύει Πότε ισχύει ισότητα; α β γ αβ βγ γα Λέμε ότι μια τριάδα θετικών ακεραίων β,
Μαθηματικά Προσανατολισμού Β Λυκείου Στάμου Γιάννης
 Μαθηματικά Προσανατολισμού Β Λυκείου Στάμου Γιάννης Αναλυτική θεωρία Λυμένα παραδείγματα Ερωτήσεις κατανόησης Ασκήσεις Επαναληπτικά διαγωνίσματα ΠΕΡΙΕΧΟΜΕΝΑ Κεφάλαιο ο : Διανύσματα Ενότητα I: Η έννοια
Μαθηματικά Προσανατολισμού Β Λυκείου Στάμου Γιάννης Αναλυτική θεωρία Λυμένα παραδείγματα Ερωτήσεις κατανόησης Ασκήσεις Επαναληπτικά διαγωνίσματα ΠΕΡΙΕΧΟΜΕΝΑ Κεφάλαιο ο : Διανύσματα Ενότητα I: Η έννοια
ΘΕΜΑ ίνονται τα διανύσµαταα, β. α) Να υπολογίσετε τη γωνία. β) Να αποδείξετε ότι 2α+β= β) το συνηµίτονο της γωνίας των διανυσµάτων
 ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΣΕ ΟΛΗ ΤΗΝ ΥΛΗ! ΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΙΑΝΥΣΜΑ ΘΕΜΑ 005 Θεωρούµε τα σηµεία Ρ, Λ, Κ και Μ του επιπέδου για τα οποία ισχύει η σχέση 5ΡΛ
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΣΕ ΟΛΗ ΤΗΝ ΥΛΗ! ΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΙΑΝΥΣΜΑ ΘΕΜΑ 005 Θεωρούµε τα σηµεία Ρ, Λ, Κ και Μ του επιπέδου για τα οποία ισχύει η σχέση 5ΡΛ
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΘΕΜΑ Α Ερώτηση θεωρίας Αν η συνάρτηση f είναι παραγωγίσιμη στο R και c είναι μια πραγματική σταθερά, να δείξετε ότι: ( c f) = c f, Έστω F = c f Έχουμε
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΘΕΜΑ Α Ερώτηση θεωρίας Αν η συνάρτηση f είναι παραγωγίσιμη στο R και c είναι μια πραγματική σταθερά, να δείξετε ότι: ( c f) = c f, Έστω F = c f Έχουμε
Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ
 Ε π ι μ έ λ ε ι α Κ Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ Πραγματική Συνάρτηση ρισμός Έστω Α ένα υποσύνολο του R. νομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α μια διαδικασία (κανόνα) f, με την οποία κάθε στοιχείο
Ε π ι μ έ λ ε ι α Κ Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ Πραγματική Συνάρτηση ρισμός Έστω Α ένα υποσύνολο του R. νομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α μια διαδικασία (κανόνα) f, με την οποία κάθε στοιχείο
y x y x+2y=
 ΜΕΡΟΣ Α 3.1 Η ΕΝΝΟΙΑ ΤΗΣ ΓΡΑΜΜΙΚΗΣ ΕΞΙΣΩΣΗΣ 59 3. 1 Η ΕΝΝΟΙΑ ΤΗΣ ΓΡΑΜΜΙΚΗΣ ΕΞΙΣΩΣΗΣ Η εξίσωση α+β=γ Λύση μιας εξίσωσης α + β = γ ονομάζεται κάθε ζεύγος αριθμών (, ) που την επαληθεύει. Για παράδειγμα η
ΜΕΡΟΣ Α 3.1 Η ΕΝΝΟΙΑ ΤΗΣ ΓΡΑΜΜΙΚΗΣ ΕΞΙΣΩΣΗΣ 59 3. 1 Η ΕΝΝΟΙΑ ΤΗΣ ΓΡΑΜΜΙΚΗΣ ΕΞΙΣΩΣΗΣ Η εξίσωση α+β=γ Λύση μιας εξίσωσης α + β = γ ονομάζεται κάθε ζεύγος αριθμών (, ) που την επαληθεύει. Για παράδειγμα η
ΑΣΚΗΣΕΙΣ ΘΕΜΑ Β. 0και 4 x 3 0.
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 1: ΕΝΝΟΙΑ ΠΡΑΓΜΑΤΙΚΗΣ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ. IΣΟΤΗΤΑ ΣΥΝΑΡΤΗΣΕΩΝ - ΠΡΑΞΕΙΣ ΜΕ ΣΥΝΑΡΤΗΣΕΙΣ - ΣΥΝΘΕΣΗ ΣΥΝΑΡΤΗΣΕΩΝ [Ενότητα
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 1: ΕΝΝΟΙΑ ΠΡΑΓΜΑΤΙΚΗΣ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ. IΣΟΤΗΤΑ ΣΥΝΑΡΤΗΣΕΩΝ - ΠΡΑΞΕΙΣ ΜΕ ΣΥΝΑΡΤΗΣΕΙΣ - ΣΥΝΘΕΣΗ ΣΥΝΑΡΤΗΣΕΩΝ [Ενότητα
2 Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕΔΟ. Εισαγωγή
 Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕΔΟ Εισαγωγή Η ιδέα της χρησιμοποίησης ενός συστήματος συντεταγμένων για τον προσδιορισμό της θέσης ενός σημείου πάνω σε μια επιφάνεια προέρχεται από την Γεωγραφία και ήταν γνωστή στους
Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕΔΟ Εισαγωγή Η ιδέα της χρησιμοποίησης ενός συστήματος συντεταγμένων για τον προσδιορισμό της θέσης ενός σημείου πάνω σε μια επιφάνεια προέρχεται από την Γεωγραφία και ήταν γνωστή στους
3 ΚΩΝΙΚΕΣ ΤΟΜΕΣ ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ
 ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ. Νρεθεί η εξίσωση του κύκλου σε καθεμιά από τις παρακάτω περιπτώσεις: α) έχει κέντρο την αρχή των αξόνων και ακτίνα β) έχει κέντρο το σημείο (3, - ) και ακτίνα 5 γ) έχει κέντρο το σημείο
ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ. Νρεθεί η εξίσωση του κύκλου σε καθεμιά από τις παρακάτω περιπτώσεις: α) έχει κέντρο την αρχή των αξόνων και ακτίνα β) έχει κέντρο το σημείο (3, - ) και ακτίνα 5 γ) έχει κέντρο το σημείο
= π 3 και a = 2, β =2 2. a, β
 1 of 68 Δίνονται τα διανύσματα a και β με a, β = π 3 και a =, β =. α) Να βρείτε το εσωτερικό γινόμενο a β. (Μονάδες 8) β) Αν τα διανύσματα a + β και κ a + β είναι κάθετα να βρείτε την τιμή του κ. γ) Να
1 of 68 Δίνονται τα διανύσματα a και β με a, β = π 3 και a =, β =. α) Να βρείτε το εσωτερικό γινόμενο a β. (Μονάδες 8) β) Αν τα διανύσματα a + β και κ a + β είναι κάθετα να βρείτε την τιμή του κ. γ) Να
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ - ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1. Δίνεται παραλληλόγραμμο ΑΒΓΔ με τρεις κορυφές τα σημεία Α (1,1), Γ (4,3) και Δ (,3). α) Να υπολογίσετε τα μήκη
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ - ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1. Δίνεται παραλληλόγραμμο ΑΒΓΔ με τρεις κορυφές τα σημεία Α (1,1), Γ (4,3) και Δ (,3). α) Να υπολογίσετε τα μήκη
ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ ΚΑΤΑΚΟΡΥΦΗ-ΟΡΙΖΟΝΤΙΑ ΜΕΤΑΤΟΠΙΣΗ ΚΑΜΠΥΛΗΣ Να σχεδιάσετε στο ίδιο σύστημα αξόνων τις γραφικές παραστάσεις των συναρτήσεων: f ()=, g()= +3,h()= -3 Να σχεδιάσετε στο ίδιο σύστημα
ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ ΚΑΤΑΚΟΡΥΦΗ-ΟΡΙΖΟΝΤΙΑ ΜΕΤΑΤΟΠΙΣΗ ΚΑΜΠΥΛΗΣ Να σχεδιάσετε στο ίδιο σύστημα αξόνων τις γραφικές παραστάσεις των συναρτήσεων: f ()=, g()= +3,h()= -3 Να σχεδιάσετε στο ίδιο σύστημα
Παραδείγµατα συναρτήσεων: f:[0,+ ) IR, f(x)=2+ x f:ir IR: f(x)=
 ΣΥΝΑΡΤΗΣΕΙΣ - 9 - ΚΕΦΑΛΑΙ ΚΕΦΑΛΑΙ ο - ΣΥΝΑΡΤΗΣΕΙΣ.. ρισµός Συνάρτηση από ένα σύνολο Α σ ένα σύνολο Β είναι ένας κανόνας µε τον οποίο κάθε στοιχείο του Α απεικονίζεται σε ένα ακριβώς στοιχείο του Β. Το
ΣΥΝΑΡΤΗΣΕΙΣ - 9 - ΚΕΦΑΛΑΙ ΚΕΦΑΛΑΙ ο - ΣΥΝΑΡΤΗΣΕΙΣ.. ρισµός Συνάρτηση από ένα σύνολο Α σ ένα σύνολο Β είναι ένας κανόνας µε τον οποίο κάθε στοιχείο του Α απεικονίζεται σε ένα ακριβώς στοιχείο του Β. Το
1.4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕΔΟ
 34 4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕΔΟ Άξονας Πάνω σε μια ευθεία επιλέγουμε δύο σημεία Ο και Ι, έτσι ώστε το διάνυσμα OI να έχει μέτρο και να βρίσκεται στην ημιευθεία O Λέμε τότε ότι έχουμε έναν άξονα με αρχή
34 4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕΔΟ Άξονας Πάνω σε μια ευθεία επιλέγουμε δύο σημεία Ο και Ι, έτσι ώστε το διάνυσμα OI να έχει μέτρο και να βρίσκεται στην ημιευθεία O Λέμε τότε ότι έχουμε έναν άξονα με αρχή
ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
 ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του
ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του
ΚΩΝΙΚΕΣ ΤΟΜΕΣ. Κεφάλαιο 4ο: Ερωτήσεις του τύπου «Σωστό - Λάθος» k R
 Κεφάλαιο 4ο: ΚΩΝΙΚΕΣ ΤΟΜΕΣ Α. ΚΥΚΛΟΣ Ερωτήσεις του τύπου «Σωστό - Λάθος» 1. * Η εξίσωση ( x x ) + ( y y ) = k, k R είναι πάντοτε εξίσωση κύκλου. o o. * Η εξίσωση x + y + Ax + By + Γ = 0 παριστάνει κύκλο
Κεφάλαιο 4ο: ΚΩΝΙΚΕΣ ΤΟΜΕΣ Α. ΚΥΚΛΟΣ Ερωτήσεις του τύπου «Σωστό - Λάθος» 1. * Η εξίσωση ( x x ) + ( y y ) = k, k R είναι πάντοτε εξίσωση κύκλου. o o. * Η εξίσωση x + y + Ax + By + Γ = 0 παριστάνει κύκλο
ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ. ΘΕΜΑ 2ο
 ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να είναι αδύνατο. β) Να παραστήσετε γραφικά
ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να είναι αδύνατο. β) Να παραστήσετε γραφικά
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 2 ο : ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ
 Άλγεβρα Β Λυκείου, ο Κεφάλαιο ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ ΟΡΙΣΜΟΣ 1 Μια συνάρτηση ƒ λέγεται γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της, όταν για οποιαδήποτε
Άλγεβρα Β Λυκείου, ο Κεφάλαιο ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ ΟΡΙΣΜΟΣ 1 Μια συνάρτηση ƒ λέγεται γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της, όταν για οποιαδήποτε
Άλγεβρα Β Λυκείου. Στέλιος Μιχαήλογλου.
 Άλγεβρα Β Λυκείου Στέλιος Μιχαήλογλου wwwaskisopolisgr Το φυλλάδιο αυτό δημιουργήθηκε για να χρησιμοποιηθεί ως επέκταση του σχολικού βιβλίου και όχι αυτόνομα δ έκδοση 0--06 Συστήματα Γραμμικές Εξισώσεις
Άλγεβρα Β Λυκείου Στέλιος Μιχαήλογλου wwwaskisopolisgr Το φυλλάδιο αυτό δημιουργήθηκε για να χρησιμοποιηθεί ως επέκταση του σχολικού βιβλίου και όχι αυτόνομα δ έκδοση 0--06 Συστήματα Γραμμικές Εξισώσεις
Η συνάρτηση y = αχ 2 + βχ + γ
 Η συνάρτηση y αχ + βχ + γ Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 1 Η συνάρτηση y αx + βx + γ με α 0 Μια συνάρτηση της μορφής y αx + βx + γ με α 0 ονομάζεται τετραγωνική
Η συνάρτηση y αχ + βχ + γ Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 1 Η συνάρτηση y αx + βx + γ με α 0 Μια συνάρτηση της μορφής y αx + βx + γ με α 0 ονομάζεται τετραγωνική
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ, ΠΟΛΙΤΙΣΜΟΥ ΚΑΙ ΑΘΛΗΤΙΣΜΟΥ
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ, ΠΟΛΙΤΙΣΜΟΥ ΚΑΙ ΑΘΛΗΤΙΣΜΟΥ ΙΝΣΤΙΤΟΥΤΟ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΕΚΔΟΣΕΩΝ «ΔΙΟΦΑΝΤΟΣ» y y=x 2 y=(x-2) 2 y=(x-2) 2-1 0 1 2 3 x -1 Τόμος 5ος Άλγεβρα και Στοιχεία Πιθανοτήτων
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ, ΠΟΛΙΤΙΣΜΟΥ ΚΑΙ ΑΘΛΗΤΙΣΜΟΥ ΙΝΣΤΙΤΟΥΤΟ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΕΚΔΟΣΕΩΝ «ΔΙΟΦΑΝΤΟΣ» y y=x 2 y=(x-2) 2 y=(x-2) 2-1 0 1 2 3 x -1 Τόμος 5ος Άλγεβρα και Στοιχεία Πιθανοτήτων
7.1 ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ
 7.1 ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ f ( ) 1. Μορφή της συνάρτησης f ( ) Ιδιότητες Έχει πεδίο ορισµού ολο το R Είναι άρτια, άρα συµµετρική ως προς τον άξονα y y Είναι γνησίως φθίνουσα στο διάστηµα (,0] Είναι γνησίως
7.1 ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ f ( ) 1. Μορφή της συνάρτησης f ( ) Ιδιότητες Έχει πεδίο ορισµού ολο το R Είναι άρτια, άρα συµµετρική ως προς τον άξονα y y Είναι γνησίως φθίνουσα στο διάστηµα (,0] Είναι γνησίως
ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ
 1 ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Πότε µια συνάρτηση f σε ένα διάστηµα του πεδίου ορισµού της λέγεται γνησίως αύξουσα και πότε γνησίως φθίνουσα; 2. Να αποδείξετε ότι η παράγωγος
1 ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Πότε µια συνάρτηση f σε ένα διάστηµα του πεδίου ορισµού της λέγεται γνησίως αύξουσα και πότε γνησίως φθίνουσα; 2. Να αποδείξετε ότι η παράγωγος
Μελέτη της συνάρτησης ψ = α χ 2
 Μελέτη της συνάρτησης ψ = α χ Η γραφική της παράσταση είναι μια καμπύλη που λέγεται παραβολή. Ανάλογα με το πρόσημο του α έχω και τα αντίστοιχα συμπεράσματα. αν α > 0 1) Η γραφική της παράσταση είναι πάνω
Μελέτη της συνάρτησης ψ = α χ Η γραφική της παράσταση είναι μια καμπύλη που λέγεται παραβολή. Ανάλογα με το πρόσημο του α έχω και τα αντίστοιχα συμπεράσματα. αν α > 0 1) Η γραφική της παράσταση είναι πάνω
1 x και y = - λx είναι κάθετες
 Κεφάλαιο ο: ΕΥΘΕΙΑ Ερωτήσεις του τύπου «Σωστό-Λάθος» 1. * Συντελεστής διεύθυνσης μιας ευθείας (ε) είναι η εφαπτομένη της γωνίας που σχηματίζει η ευθεία (ε) με τον άξονα. Σ Λ. * Ο συντελεστής διεύθυνσης
Κεφάλαιο ο: ΕΥΘΕΙΑ Ερωτήσεις του τύπου «Σωστό-Λάθος» 1. * Συντελεστής διεύθυνσης μιας ευθείας (ε) είναι η εφαπτομένη της γωνίας που σχηματίζει η ευθεία (ε) με τον άξονα. Σ Λ. * Ο συντελεστής διεύθυνσης
και 2, 2 2 είναι κάθετα να βρείτε την τιμή του κ. γ) Αν στο τρίγωνο ΑΒΓ επιπλέον ισχύει Α(3,1), να βρείτε τις συντεταγμένες των κορυφών του Β και Γ.
 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ (ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ) 8556 ΘΕΜΑ Δίνονται τα διανύσματα και με, και, 3 α) Να βρείτε το εσωτερικό γινόμενο β) Αν τα διανύσματα γ) Να βρείτε το μέτρο του διανύσματος 8558 ΘΕΜΑ
Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ (ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ) 8556 ΘΕΜΑ Δίνονται τα διανύσματα και με, και, 3 α) Να βρείτε το εσωτερικό γινόμενο β) Αν τα διανύσματα γ) Να βρείτε το μέτρο του διανύσματος 8558 ΘΕΜΑ
Κεφάλαιο 2: Διανυσματικός λογισμός συστήματα αναφοράς
 Κεφάλαιο 2: Διανυσματικός λογισμός συστήματα αναφοράς 2.1 Η έννοια του διανύσματος Ο τρόπος που παριστάνομε τα διανυσματικά μεγέθη είναι με τη μαθηματική έννοια του διανύσματος. Διάνυσμα δεν είναι τίποτε
Κεφάλαιο 2: Διανυσματικός λογισμός συστήματα αναφοράς 2.1 Η έννοια του διανύσματος Ο τρόπος που παριστάνομε τα διανυσματικά μεγέθη είναι με τη μαθηματική έννοια του διανύσματος. Διάνυσμα δεν είναι τίποτε
ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 2014 Θ ΕΩΡΙA 15
 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΛΓΕΒΡΑΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 04 Θ ΕΩΡΙA 5 ΘΕΜΑ A Α Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στην κόλλα σας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση τη
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΛΓΕΒΡΑΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 04 Θ ΕΩΡΙA 5 ΘΕΜΑ A Α Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στην κόλλα σας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση τη
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Β ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ
 1 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Β ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ ΘΕΜΑ ο GI_V_ALG 16950 1.1 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να είναι αδύνατο. β)
1 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Β ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ ΘΕΜΑ ο GI_V_ALG 16950 1.1 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να είναι αδύνατο. β)
ΤΟΠΙΚΑ ΑΚΡΟΤΑΤΑ ΠΡΟΒΛΗΜΑΤΑ ΑΚΡΟΤΑΤΩΝ
 Ενότητα 1 ΤΟΠΙΚΑ ΑΚΡΟΤΑΤΑ ΠΡΟΒΛΗΜΑΤΑ ΑΚΡΟΤΑΤΩΝ Ασκήσεις για λύση 3 3, < 1). Δίνεται η συνάρτηση f ( ). 6, Να βρείτε : i ) την παράγωγο της f, ii) τα κρίσιμα σημεία της f. ). Να μελετήσετε ως προς τη μονοτονία
Ενότητα 1 ΤΟΠΙΚΑ ΑΚΡΟΤΑΤΑ ΠΡΟΒΛΗΜΑΤΑ ΑΚΡΟΤΑΤΩΝ Ασκήσεις για λύση 3 3, < 1). Δίνεται η συνάρτηση f ( ). 6, Να βρείτε : i ) την παράγωγο της f, ii) τα κρίσιμα σημεία της f. ). Να μελετήσετε ως προς τη μονοτονία
Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης
 Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης Ορθοκανονικό σύστημα αξόνων ονομάζεται ένα σύστημα από δύο κάθετους άξονες με κοινή αρχή στους οποίους οι μονάδες έχουν το ίδιο μήκος. Υπάρχουν περιπτώσεις
Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης Ορθοκανονικό σύστημα αξόνων ονομάζεται ένα σύστημα από δύο κάθετους άξονες με κοινή αρχή στους οποίους οι μονάδες έχουν το ίδιο μήκος. Υπάρχουν περιπτώσεις
ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΔΙΑΝΥΣΜΑΤΑ Επιμέλεια: Άλκης Τζελέπης ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΕΝΝΟΙΑ - ΠΡΑΞΕΙΣ. Αν τα διανύσματα,, σχηματίζουν τρίγωνο, να αποδείξετε ότι το ίδιο συμβαίνει
ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΔΙΑΝΥΣΜΑΤΑ Επιμέλεια: Άλκης Τζελέπης ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΕΝΝΟΙΑ - ΠΡΑΞΕΙΣ. Αν τα διανύσματα,, σχηματίζουν τρίγωνο, να αποδείξετε ότι το ίδιο συμβαίνει
Άλγεβρα 1 ο Κεφάλαιο ... ν παράγοντες
 1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Τι ονομάζεται δύναμη α ν με βάση τον πραγματικό αριθμό α και εκθέτη το φυσικό αριθμό >1; H δύναμη με βάση έναν πραγματικό αριθμό α και εκθέτη ένα φυσικό αριθμό ν, συμβολίζεται
1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Τι ονομάζεται δύναμη α ν με βάση τον πραγματικό αριθμό α και εκθέτη το φυσικό αριθμό >1; H δύναμη με βάση έναν πραγματικό αριθμό α και εκθέτη ένα φυσικό αριθμό ν, συμβολίζεται
ΚΥΚΛΟΣ. Μ(x,y) Ο C ΘΕΩΡΙΑ ΕΠΙΜΕΛΕΙΑ: ΣΩΣΤΟ-ΛΑΘΟΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΧΡΑΣ ΓΙΑΝΝΗΣ ΑΣΚΗΣΕΙΣ. 3ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΚΕΝΤΡΙΚΟ Ν. ΣΜΥΡΝΗΣ
 Φ3 ΚΥΚΛΟΣ y Μ(x,y) A(x,y) ε Ο C x ΕΠΙΜΕΛΕΙΑ: ΧΡΑΣ ΓΙΑΝΝΗΣ ΘΕΩΡΙΑ ΣΩΣΤΟ-ΛΑΘΟΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΑΣΚΗΣΕΙΣ ΚΕΝΤΡΙΚΟ 3ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ Ν. ΣΜΥΡΝΗΣ 0-0 ΘΕΩΡΙΑ. Τι ονομάζεται κύκλος με κέντρο το σημείο K( x0,
Φ3 ΚΥΚΛΟΣ y Μ(x,y) A(x,y) ε Ο C x ΕΠΙΜΕΛΕΙΑ: ΧΡΑΣ ΓΙΑΝΝΗΣ ΘΕΩΡΙΑ ΣΩΣΤΟ-ΛΑΘΟΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΑΣΚΗΣΕΙΣ ΚΕΝΤΡΙΚΟ 3ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ Ν. ΣΜΥΡΝΗΣ 0-0 ΘΕΩΡΙΑ. Τι ονομάζεται κύκλος με κέντρο το σημείο K( x0,
ΣΥΝΑΡΤΗΣΕΙΣ. H Εννοια του διανυσματος. Σ υ ν ο λ α - Ο ρ ι σ μ ο ι
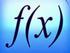 ΣΥΝΑΡΤΗΣΕΙΣ Σ υ ν ο λ α - Ο ρ ι σ μ ο ι Συνολο λεγεται καθε συλλογη 3. Να δειχτει αντικειμενων, οτι α + 0 που προερχονται 0α. Ποτε ισχυει απ την το εμπειρια ισον; μας η τη διανοηση 3 3. μας, Aν α, ειναι
ΣΥΝΑΡΤΗΣΕΙΣ Σ υ ν ο λ α - Ο ρ ι σ μ ο ι Συνολο λεγεται καθε συλλογη 3. Να δειχτει αντικειμενων, οτι α + 0 που προερχονται 0α. Ποτε ισχυει απ την το εμπειρια ισον; μας η τη διανοηση 3 3. μας, Aν α, ειναι
3.5 Η ΣΥΝΑΡΤΗΣΗ y=α/x-η ΥΠΕΡΒΟΛΗ Ποσά αντιστρόφως ανάλογα- Η υπερβολή
 ΣΥΝΑΡΤΗΣΗ y=α/ Η ΥΠΕΡΒΟΛΗ.5 Η ΣΥΝΑΡΤΗΣΗ y=α/-η ΥΠΕΡΒΟΛΗ Ποσά αντιστρόφως ανάλογα- Η υπερβολή Δύο ποσά λέγονται αντιστρόφως ανάλογα, όταν η τιμή του ενός πολλαπλασιαστεί επί έναν αριθµό, τότε η τιµή του
ΣΥΝΑΡΤΗΣΗ y=α/ Η ΥΠΕΡΒΟΛΗ.5 Η ΣΥΝΑΡΤΗΣΗ y=α/-η ΥΠΕΡΒΟΛΗ Ποσά αντιστρόφως ανάλογα- Η υπερβολή Δύο ποσά λέγονται αντιστρόφως ανάλογα, όταν η τιμή του ενός πολλαπλασιαστεί επί έναν αριθµό, τότε η τιµή του
II. Συναρτήσεις. math-gr
 II Συναρτήσεις Παντελής Μπουμπούλης, MSc, PhD σελ blogspotcom, bouboulismyschgr ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ Α Βασικές Έννοιες Ορισμός: Έστω Α ένα υποσύνολο του συνόλου των πραγματικών αριθμών R Ονομάζουμε πραγματική
II Συναρτήσεις Παντελής Μπουμπούλης, MSc, PhD σελ blogspotcom, bouboulismyschgr ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ Α Βασικές Έννοιες Ορισμός: Έστω Α ένα υποσύνολο του συνόλου των πραγματικών αριθμών R Ονομάζουμε πραγματική
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΟΜΑΔΕΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ : ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΡΟΛΟΓΟΣ Σε κάθε ενότητα αυτού του βιβλίου θα βρείτε : Βασική θεωρία με τη μορφή ερωτήσεων Μεθοδολογίες και σχόλια
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΟΜΑΔΕΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ : ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΡΟΛΟΓΟΣ Σε κάθε ενότητα αυτού του βιβλίου θα βρείτε : Βασική θεωρία με τη μορφή ερωτήσεων Μεθοδολογίες και σχόλια
ΘΕΩΡΙΑ ( ΚΑΡΤΕΣΙΑΝΕΣ ΣΥΝΤΕΤΑΓΜΕΝΕΣ )
 ΘΕΩΡΙΑ ( ΚΑΡΤΕΣΙΑΝΕΣ ΣΥΝΤΕΤΑΓΜΕΝΕΣ ) Έχουμε δύο κάθετους άξονες x x και y y με κοινή αρχή 0. Από ένα σημείο Μ του επιπέδου φέρνουμε τις κάθετες στους δύο άξονες x x και y y. Ονομάζουμε τετμημένη του σημείου
ΘΕΩΡΙΑ ( ΚΑΡΤΕΣΙΑΝΕΣ ΣΥΝΤΕΤΑΓΜΕΝΕΣ ) Έχουμε δύο κάθετους άξονες x x και y y με κοινή αρχή 0. Από ένα σημείο Μ του επιπέδου φέρνουμε τις κάθετες στους δύο άξονες x x και y y. Ονομάζουμε τετμημένη του σημείου
Διαφορικός Λογισμός. Κεφάλαιο Συναρτήσεις. Κατανόηση εννοιών - Θεωρία. 1. Τι ονομάζουμε συνάρτηση;
 Κεφάλαιο 1 Διαφορικός Λογισμός 1.1 Συναρτήσεις Κατανόηση εννοιών - Θεωρία 1. Τι ονομάζουμε συνάρτηση; 2. Πως ορίζονται οι πράξεις της πρόσθεσης, της διαφοράς, του γινομένου και του πηλίκου μεταξύ δύο συναρτήσεων;
Κεφάλαιο 1 Διαφορικός Λογισμός 1.1 Συναρτήσεις Κατανόηση εννοιών - Θεωρία 1. Τι ονομάζουμε συνάρτηση; 2. Πως ορίζονται οι πράξεις της πρόσθεσης, της διαφοράς, του γινομένου και του πηλίκου μεταξύ δύο συναρτήσεων;
2.1 ΜΟΝΟΤΟΝΙΑ ΑΚΡΟΤΑΤΑ ΣΥΜΜΕΤΡΙΕΣ ΣΥΝΑΡΤΗΣΗ
 ΚΕΦΑΛΑΙΟ Ο : ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ. ΜΟΝΟΤΟΝΙΑ ΑΚΡΟΤΑΤΑ ΣΥΜΜΕΤΡΙΕΣ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΣΜΟΣ ΣΥΝΑΡΤΗΣΗΣ Συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β λέγεται μια διαδικασία (κανόνας), με την οποία κάθε στοιχείο του
ΚΕΦΑΛΑΙΟ Ο : ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ. ΜΟΝΟΤΟΝΙΑ ΑΚΡΟΤΑΤΑ ΣΥΜΜΕΤΡΙΕΣ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΣΜΟΣ ΣΥΝΑΡΤΗΣΗΣ Συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β λέγεται μια διαδικασία (κανόνας), με την οποία κάθε στοιχείο του
Άλγεβρα Β Λυκείου. Στέλιος Μιχαήλογλου.
 Άλγεβρα Β Λυκείου Στέλιος Μιχαήλογλου wwwaskisopolisgr Το φυλλάδιο αυτό δημιουργήθηκε για να χρησιμοποιηθεί ως επέκταση του σχολικού βιβλίου και όχι αυτόνομα δ έκδοση 0--06 Συστήματα Γραμμικές Εξισώσεις
Άλγεβρα Β Λυκείου Στέλιος Μιχαήλογλου wwwaskisopolisgr Το φυλλάδιο αυτό δημιουργήθηκε για να χρησιμοποιηθεί ως επέκταση του σχολικού βιβλίου και όχι αυτόνομα δ έκδοση 0--06 Συστήματα Γραμμικές Εξισώσεις
Μαθηματικά προσανατολισμού Β Λυκείου. ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΟΕΦΕ α φάση. Διανύσματα
 Μαθηματικά προσανατολισμού Β Λυκείου wwwaskisopolisgr ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΟΕΦΕ 00-018α φάση Διανύσματα 1 Σε σύστημα συντεταγμένων Oxy θεωρούμε τρία σημεία Α, Β, Γ του μοναδιαίου κύκλου, για τα οποία υπάρχει
Μαθηματικά προσανατολισμού Β Λυκείου wwwaskisopolisgr ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΟΕΦΕ 00-018α φάση Διανύσματα 1 Σε σύστημα συντεταγμένων Oxy θεωρούμε τρία σημεία Α, Β, Γ του μοναδιαίου κύκλου, για τα οποία υπάρχει
ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ ΜΙΑ ΠΡΟΕΤΟΙΜΑΣΙΑ ΓΙΑ ΤΙΣ ΕΞΕΤΑΣΕΙΣ
 2 ΓΥΜΝΑΣΙΟ ΥΜΗΤΤΟΥ ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ ΜΙΑ ΠΡΟΕΤΟΙΜΑΣΙΑ ΓΙΑ ΤΙΣ ΕΞΕΤΑΣΕΙΣ - Σελίδα 1 από 6 - 1. Η ΔΟΜΗ ΤΩΝ ΘΕΜΑΤΩΝ ΤΩΝ ΕΞΕΤΑΣΕΩΝ Στις εξετάσεις του Μαίου-Ιουνίου µας δίνονται δύο θέµατα θεωρίας και
2 ΓΥΜΝΑΣΙΟ ΥΜΗΤΤΟΥ ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ ΜΙΑ ΠΡΟΕΤΟΙΜΑΣΙΑ ΓΙΑ ΤΙΣ ΕΞΕΤΑΣΕΙΣ - Σελίδα 1 από 6 - 1. Η ΔΟΜΗ ΤΩΝ ΘΕΜΑΤΩΝ ΤΩΝ ΕΞΕΤΑΣΕΩΝ Στις εξετάσεις του Μαίου-Ιουνίου µας δίνονται δύο θέµατα θεωρίας και
Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ
 Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ (Α ΜΕΡΟΣ: ΣΥΝΑΡΤΗΣΕΙΣ) Μαθηματικά Προσανατολισμού Γ Λυκείου- Μαθηματικός Περιηγητής ΕΝΟΤΗΤΑ
Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ (Α ΜΕΡΟΣ: ΣΥΝΑΡΤΗΣΕΙΣ) Μαθηματικά Προσανατολισμού Γ Λυκείου- Μαθηματικός Περιηγητής ΕΝΟΤΗΤΑ
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΣΑΝΑΤΛΙΣΜΥ Β ΛΥΚΕΙΥ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΥ Να δώσετε τους ορισμούς: διάνυσμα, μηδενικό διάνυσμα, μέτρο διανύσματος, μοναδιαίο διάνυσμα Διάνυσμα AB ονομάζεται ένα ευθύγραμμο
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΣΑΝΑΤΛΙΣΜΥ Β ΛΥΚΕΙΥ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΥ Να δώσετε τους ορισμούς: διάνυσμα, μηδενικό διάνυσμα, μέτρο διανύσματος, μοναδιαίο διάνυσμα Διάνυσμα AB ονομάζεται ένα ευθύγραμμο
