Διάλεξη 6. Fourier Ανάλυση Σημάτων. (Επανάληψη Κεφ Κεφ. 10.3, ) Ανάλυση σημάτων. Τι πρέπει να προσέξουμε
|
|
|
- Ἑλένη Γεωργίου
- 9 χρόνια πριν
- Προβολές:
Transcript
1 University of Cyprus Biomedical Imaging & Applied Optics Διάλεξη (Επανάληψη Κεφ Κεφ. 10.3, ) Ανάλυση σημάτων Τι πρέπει να προσέξουμε Επαρκής ψηφιοποίηση στο χρόνο (Nyquist) Αναδίπλωση (aliasing) λόγω ψηφιοποίησης Επαρκής ψηφιοποίηση στη συχνότητα (μέγεθος FFT) Επαρκές μέγεθος FFT ώστε να αποφεύγουμε κυκλική συνέλιξη Ευκρίνεια του μετασχηματισμού λόγω παράθυρου (window) στο χρόνο 1
2 Επαρκής συχνότητα ψηφιοποίησης Nyquist: Ω max Για πιο ακριβείς μετρήσεις χρησιμοποιήστε -8 Ω max (αν το σύστημα σας το επιτρέπει) f s Αναδίπλωση (aliasing) λόγω ψηφιοποίησης Αν το σήμα δεν έχει πεπερασμένο (finite) φάσμα Φίλτρο Η(jΩ) αποκόπτει τις συχνότητες πάνω από f s / 3 Επαρκής ψηφιοποίηση στη συχνότητα (μέγεθος FFT) Ψηφιοποίηση πρέπει να είναι επαρκής ώστε να μπορούμε να βλέπουμε μικρές συχνότητες Nyquist στη συχνότητα dω το μισό της μικρότερης συχνότητας που μπορούμε να δούμε π dω k = NT π k Ω k = NT Επαρκές μέγεθος FFT ώστε να αποφεύγουμε κυκλική συνέλιξη Μόνο αν θα ακολουθήσει συνέλιξη Ν FFT = Ν 1 + Ν -1 Το μέγεθος του FFT καθορίζεται και από τους δύο πιο πάνω παράγοντες
3 Παράδειγμα Σήμα Φάσμα Χ c (jω)=0 για Ω π(500) Θέλω τα δείγματα του φάσματος να μην απέχουν περισσότερο από π(10) rad/s Προσοχή! Αυτό δεν είναι το ίδιο με την ευκρίνεια! Συχνότητα δειγματοληψίας: Αριθμός στοιχείων FFT: Σημείο του FFT που αντιστοιχεί σε συχνότητα 1000 Hz: Αν το σύστημα δειγματοληψίας μας επιτρέπει μόνο μέχρι 000 samples/s; 5 Ευκρίνεια του μετασχηματισμού λόγω παράθυρου (window) στο χρόνο Πραγματικά σήματα μεγάλος χρόνος σε σχέση με FFT Χρησιμοποιούμε μόνο μέρος του σήματος Πολλαπλασιασμός με παράθυρο Συνέλιξη του φάσματος με φάσμα του παραθύρου Μειώνεται η ευκρίνεια στο χώρο της συχνότητας 3
4 Ευκρίνεια του μετασχηματισμού λόγω παράθυρου (window) στο χρόνο Παράδειγμα Δύο συνημίτονα Ω 0 και Ω 1 Τετραγωνικό παράθυρο w[n] 7 Ευκρίνεια του μετασχηματισμού λόγω παράθυρου (window) στο χρόνο Παράδειγμα Δύο συνημίτονα Ω 0 και Ω 1 Τετραγωνικό παράθυρο w[n] 8
5 Ευκρίνεια του μετασχηματισμού λόγω παράθυρου (window) στο χρόνο Κυριότερα προβλήματα με το φάσμα του παραθύρου Πλάτος του κυρίως λοβού (main lobe) Δ ml Σχετικό ύψος πλευρικού λοβού / κυρίως λοβού (relative side-main lobe level) Α sl Μείωση των πλευρικών λοβών ανά δεκάδα (side-lobe roll off per decade) Α ro w[n] 9 Ευκρίνεια του μετασχηματισμού λόγω παράθυρου (window) στο χρόνο Window type -3 db Main-lobe width Max sidelobe level [db] Sidelobe roll-off [db/decade] Rectangular π/t Hamming 8π/t Hanning 8π/t Blackman 1π/t
6 Παράδειγμα Φωνητικό σήμα (π.χ. ομιλία) Φάσμα 1-0 khz Διάρκεια 3 ώρες Ζητούμενα Να διακρίνονται διαφορές συχνότητας 100 Hz Να διακρίνονται συχνότητες με διαφορά στο πλάτος -5 db (ονομάζεται και δυναμικό εύρος ή dynamic range) Θα ακολουθήσει επεξεργασία με FFT και με συνέλιξη μεταξύ δύο τέτοιων σημάτων Χαρακτηριστικά Παράθυρο: fs: Ν: Ν fft : 11 Σήματα των οποίων η συχνότητα μεταβάλλεται με το χρόνο (π.χ. chirp) Ένας FFT δεν είναι αρκετός Μετασχηματισμός Fourier Εξαρτώμενος από το χρόνο (Time Dependent Fourier Transform) n διακριτό και λ συνεχές Σανναβλέπουμετοσήμαμέσααπό ένα παράθυρο Θέλουμε παράθυρο με χαμηλούς πλευρικούς λοβούς και όσο το μεγαλύτερο γίνεται (γιατί;) Υπάρχει και ο αντίστροφος ΜΦ 1
7 Διακριτός χρόνος και συχνότητα Παράθυρο μήκους L N συχνότητες, ομοιόμορφα κατανεμημένες, λ k =πk/ν Αν Ν L τότε μπορούμε να ανακτήσουμε το σήμα από n μέχρι n+l-1 13 Διακριτός χρόνος και συχνότητα Μπορούμε να ανακτήσουμε το σήμα μεταξύ από το μεταξύ από το κλπ Άρα Για N L R Και όχι για L>N, R>L Γιατί; 1 7
8 Διακριτόςχρόνοςκαισυχνότητα Συνέλιξη στη συχνότητα Σειρά από φίλτρα (Filter bank) Μπορούμε να ανακτήσουμε το σήμα αν ισχύουν όσα είδαμε πιο πριν 15 Παράδειγμα Ανάλυση σημάτων από φωνή Wideband fs = 1kHz.7 ms Hamming window (L=108) R=1 (1 ms) Narrowband fs = 1kHz 5 ms Hamming window (L=70) R=1 (1 ms) 1 8
9 ΔΜΦ Φάσμα σήματος Ικανοποιητικά αποτελέσματα Περιοδικά σήματα Ψηλός SNR Θόρυβος ; Περιοδικότητα κρυμμένη στο θόρυβο Σήματα που μοιάζουν με θόρυβο Προβλήματα στη εκτίμηση του φάσματος Φάσμα Ισχύος (Power Spectrum) Χρήσιμο στην ανάλυση τυχαίων σημάτων Μπορεί να υπολογιστεί με διάφορους τρόπου Μη-Παραμετρικές Μέθοδοι Παραμετρικές Μέθοδοι 17 Υπολογισμός με DFT - Περιοδόγραμμα (Periodogram) P xx προσέγγιση P ss Περιοδόγραμμα (Periodogram) Τετραγωνικό Παράθυρο Τροποποιημένο Περιδόγραμμα (Modified Periodogram) Άλλο παράθυρο Υπολογισμός με ΔΜΦ σε συγκεκριμένες συχνότητες Το U αφαιρεί πόλωση (bias) λόγω του παραθύρου Τετραγωνικό Παράθυρο: U=1 Άλλα Παράθυρα: 0 < U <
10 Ιδιότητες του Περιοδογράμματος Ασυμπτοτικά μη πολωμένο (Asymptotically unbiased) Τείνει προς τη πραγματική μέση τιμή (expected value) δηλ. πόλωση 0 με L Μη-Συμβιβαστό (Non- Consistent) Η εκτίμηση δεν γίνεται καλύτερη με μεγαλύτερο L Σχέση με συσχέτιση (correlation) Όπου c vv είναι η μη-περιοδική συσχέτιση (aperiodic correlation) του v[n] Var[I(ω)] > 0 με L 19 Παράδειγμα x[n] σειρά από τυχαίους αριθμούς με ομοιόμορφη κατανομή (uniform distribution) Θεωρητικά ΔΜΦ (Ν=10) για L=1,, 5, 10 Τετραγωνικό Παράθυρο (U=1) 0 10
11 Προβλήματα με το περιοδόγραμμα Πόλωση (bias) του σήματος Κορυφή στη συχνότητα 0 Μπορεί να είναι τόσο μεγάλη που να επισκιάσει άλλα κοντινά σήματα Αφαιρούμε εκτίμηση του μέσου όρου πριν το ΔΜΦ Random (uniform) sequence x[n] with mean=0 Random (uniform) sequence x[n] with mean= PSD of x[n] with mean=0 1 PSD of x[n] with mean= Προβλήματα με το περιοδόγραμμα Διακυμάνσεις σε όλες τις συχνότητες Μεταβολές στις τιμές τις συσχέτισης όταν δεν υπάρχει μεγάλη επικάλυψη Δεν βελτιώνεται με μεγαλύτερο L 10 PSD (N=10) of x[n] with L= PSD (N=10) of x[n] with L= PSD (N=10) of x[n] with L= ( 19 30)
12 Μέσος Όρος Περιοδογράμματος (Periodogram averaging) Σήμα μήκους Q R τμήματα μήκους L Μέθοδος Bartlett Μέσος όρος με τετράγωνο παράθυρο R>Q/L τα τμήματα επικαλύπτονται R=Q/L τα τμήματα είναι συνεχή Μειώνεται η διασπορά (variance) Υπολογισμός με ΔΜΦ Για Κ Αυξάνεται το εύρος (width) του κεντρικού λοβού Μειώνεται το πλάτος (amplitude) του κεντρικού λοβού Για σταθερό Q Όσο αυξάνεται το L μειώνεται το Κ Γιακαλύτερααποτελέσματαπρέπει να αυξηθεί το Q 3 Μέσος Όρος Περιοδογράμματος (Periodogram averaging) Α=0.5, ω0=π/1 0 θ< π τυχαία - 3 e[n] < 3, ομοιόμορφη κατανομή σ e = 1 Τετραγωνικό παράθυρο fs = 1 Hz Q = 10 L = 10, 5,, 1 Κ = 1, 7, 31,17 (επικάλυψη L/ γιατατρία τελευταία) Ν fft = 10 1
13 Μέσος Όρος Περιοδογράμματος (Periodogram averaging) Q = 10 L = 10, 5,, 1 Κ = 1, 7, 31,17 (επικάλυψη L/ γιατατρία τελευταία) Ν fft = 10 5 Φάσμα Ισχύος από αυτοσυσχέτιση (autocorrelation) Ακόμα ένας τρόπος να αποφευχθούν τα προβλήματα του περιοδογράμματος Όχι κατ ανάγκη καλύτερος τρόπος Βολικός όταν χρειάζεται και η αυτοσυσχέτιση για άλλους λόγους Το Φάσμα Ισχύος πρέπει να είναι θετικό για όλα τα k Ισχύει μόνο για τριγωνικό παράθυρο (Bartlett window) Ευκρίνεια και διασπορά Εξαρτώνται από το μήκος του παράθυρου όπως και πριν Q για καλύτερα αποτελέσματα Μπορούμε να επιλέξουμε Μ-1τμήμα του φ Αποφεύγουμε τις διακυμάνσεις στη συχνότητα Εξομάλυνση του φάσματος λόγω συνέλιξης με παράθυρο 13
14 Φάσμα Ισχύος από αυτοσυσχέτιση (autocorrelation) Υπολογισμός με ΔΜΦ 1. (Μ-1) μηδενικά στο τέλος του x[n] (για να αποφύγετε την αναδίπλωση). ΔΜΦ 3. X(k). Αντίστροφος ΔΜΦ 5. Δια Q. Πολλαπλασιασμός με παράθυρο 7. ΔΜΦ 7 Παραμετρικές Μέθοδοι Μοντέλο Αυτοπαλλινδρόμισης (Autoregressive Model) Εκτίμηση (estimation) με αυτοπαλλινδρόμιση Σήμα που μοιάζει με θόρυβο Εκτίμηση με βάση k προηγούμενες τιμές και μια τυχαία σειρά e[m] Συντελεστές α k Ο αριθμός εξαρτάται από το σήμα Αρκετοί ώστε το φάσμα να ανταποκρίνεται στο πραγματικό Όχιυπερβολικοίγιατίμετάέχουμε θόρυβο Διάφορες μέθοδοι υπολογισμού Π.χ. Μέθοδος Burg Ελαχιστοποίηση (ελάχιστα τετράγωνο) του σφάλματος Εκτίμηση του Φάσματος Ισχύος Από τους συντελεστές α k Ποιο κοντά στο πραγματικό για σήματα μικρής διάρκειας xm [ ] = em [ ] + axm [ k] k = 1 k = 1 ym [ ] = xm [ ] + nm [ ] p p ym [ ] = axm [ k] + em [ ] + nm [ ] P AR xx = k k ˆ σ x p jπ fk 1 ae ˆk k= 1 8 1
FFT. Θα επικεντρωθούμε στο ΔΜΦ αλλά όλα ισχύουν και για τον
 University of Cyprus Biomedical Imaging & Applied Optics Διάλεξη 5 και Ανάλυση με (Κεφ. 9.0-9.5, 10.0-10.2) ΟΔΜΦ Ο αντίστροφος ΔΜΦ Θα επικεντρωθούμε στο ΔΜΦ αλλά όλα ισχύουν και για τον αντίστροφο ΔΜΦ
University of Cyprus Biomedical Imaging & Applied Optics Διάλεξη 5 και Ανάλυση με (Κεφ. 9.0-9.5, 10.0-10.2) ΟΔΜΦ Ο αντίστροφος ΔΜΦ Θα επικεντρωθούμε στο ΔΜΦ αλλά όλα ισχύουν και για τον αντίστροφο ΔΜΦ
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων. Διάλεξη 22: Γρήγορος Μετασχηματισμός Fourier Ανάλυση σημάτων/συστημάτων με το ΔΜΦ
 HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 22: Γρήγορος Μετασχηματισμός Fourier Ανάλυση σημάτων/συστημάτων με το ΔΜΦ Γρήγορος Μετασχηματισμός Fourier Το ζεύγος εξισώσεων που ορίζουν το
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 22: Γρήγορος Μετασχηματισμός Fourier Ανάλυση σημάτων/συστημάτων με το ΔΜΦ Γρήγορος Μετασχηματισμός Fourier Το ζεύγος εξισώσεων που ορίζουν το
Διάλεξη 3. Δειγματοληψία και Ανακατασκευή Σημάτων. Δειγματοληψία και Ανακατασκευή Σημάτων. (Κεφ & 4.6,4.8)
 University of Cyprus Biomedical Imaging & Applied Optics Διάλεξη 3 Δειγματοληψία και Ανακατασκευή (Κεφ. 4.0-4.3 & 4.6,4.8) Περιοδική δειγματοληψία (periodic sampling) Περίοδος (sampling period) T Συχνότητα
University of Cyprus Biomedical Imaging & Applied Optics Διάλεξη 3 Δειγματοληψία και Ανακατασκευή (Κεφ. 4.0-4.3 & 4.6,4.8) Περιοδική δειγματοληψία (periodic sampling) Περίοδος (sampling period) T Συχνότητα
Διάλεξη 10. Σχεδιασμός Φίλτρων. Κεφ. 7.0-7.2. Φίλτρο Διαφοροποιεί το φάσμα ενός σήματος Π.χ. αφήνει να περάσουν ή σταματά κάποιες συχνότητες
 University of Cyprus Biomedical Imaging & Applied Optics Διάλεξη 10 Κεφ. 7.0-7.2 Φίλτρο Διαφοροποιεί το φάσμα ενός σήματος Π.χ. αφήνει να περάσουν ή σταματά κάποιες συχνότητες Σχεδιασμός Φίλτρου Καθορίζονται
University of Cyprus Biomedical Imaging & Applied Optics Διάλεξη 10 Κεφ. 7.0-7.2 Φίλτρο Διαφοροποιεί το φάσμα ενός σήματος Π.χ. αφήνει να περάσουν ή σταματά κάποιες συχνότητες Σχεδιασμός Φίλτρου Καθορίζονται
HMY 799 1: Αναγνώριση Συστημάτων
 HMY 799 : Αναγνώριση Συστημάτων Διάλεξη 5 Εκτίμηση φάσματος ισχύος Συνάφεια Παραδείγματα Στοχαστικά Διανύσματα Autoregressive model with exogenous inputs (ARX y( t + a y( t +... + a y( t n = bu( t +...
HMY 799 : Αναγνώριση Συστημάτων Διάλεξη 5 Εκτίμηση φάσματος ισχύος Συνάφεια Παραδείγματα Στοχαστικά Διανύσματα Autoregressive model with exogenous inputs (ARX y( t + a y( t +... + a y( t n = bu( t +...
Στοχαστικά Σήµατα και Εφαρµογές
 Στοχαστικά Σήµατα & Εφαρµογές Εκτίµηση Φάσµατος ιδάσκων: Ν. Παπανδρέου (Π.. 47/8) Πανεπιστήµιο Πατρών ΤµήµαΜηχανικώνΗ/Υ και Πληροφορικής CEID 7-8 Μη παραµετρικές µέθοδοι: Περιοδόγραµµα Φάσµα ισχύοςµιας
Στοχαστικά Σήµατα & Εφαρµογές Εκτίµηση Φάσµατος ιδάσκων: Ν. Παπανδρέου (Π.. 47/8) Πανεπιστήµιο Πατρών ΤµήµαΜηχανικώνΗ/Υ και Πληροφορικής CEID 7-8 Μη παραµετρικές µέθοδοι: Περιοδόγραµµα Φάσµα ισχύοςµιας
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων. Διάλεξη 20: Διακριτός Μετασχηματισμός Fourier (Discrete Fourier Transform DFT)
 HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 20: Διακριτός Μετασχηματισμός Fourier (Discrete Fourier Transform DFT) Εισαγωγή Μέχρι στιγμής έχουμε δει το Μετασχηματισμό Fourier Διακριτού
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 20: Διακριτός Μετασχηματισμός Fourier (Discrete Fourier Transform DFT) Εισαγωγή Μέχρι στιγμής έχουμε δει το Μετασχηματισμό Fourier Διακριτού
3-Μαρτ-2009 ΗΜΥ Γρήγορος Μετασχηματισμός Fourier Εφαρμογές
 ΗΜΥ 429 9. Γρήγορος Μετασχηματισμός Fourier Εφαρμογές 1 Ζεύγη σημάτων Συνάρτηση δέλτα: ΔΜΦ δ[ n] u[ n] u[ n 0.5] (συχνότητα 0-0.5) Figure από Scientist s and engineer s guide to DSP. 2 Figure από Scientist
ΗΜΥ 429 9. Γρήγορος Μετασχηματισμός Fourier Εφαρμογές 1 Ζεύγη σημάτων Συνάρτηση δέλτα: ΔΜΦ δ[ n] u[ n] u[ n 0.5] (συχνότητα 0-0.5) Figure από Scientist s and engineer s guide to DSP. 2 Figure από Scientist
Ψηφιακή Επεξεργασία Σημάτων
 Ψηφιακή Επεξεργασία Σημάτων Ενότητα 7: Μετατροπή Σήματος από Αναλογική Μορφή σε Ψηφιακή Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετατροπή Αναλογικού Σήματος σε Ψηφιακό Είδη Δειγματοληψίας: Ιδανική
Ψηφιακή Επεξεργασία Σημάτων Ενότητα 7: Μετατροπή Σήματος από Αναλογική Μορφή σε Ψηφιακή Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετατροπή Αναλογικού Σήματος σε Ψηφιακό Είδη Δειγματοληψίας: Ιδανική
ΑΝΑΛΥΣΗ ΣΗΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΜΕ ΤΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟ FOURIER
 ΑΝΑΛΥΣΗ ΣΗΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΜΕ ΤΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟ FOURIER Ανάλυση σημάτων και συστημάτων Ο μετασχηματισμός Fourier (DTFT και DFT) είναι σημαντικότατος για την ανάλυση σημάτων και συστημάτων Εντοπίζει
ΑΝΑΛΥΣΗ ΣΗΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΜΕ ΤΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟ FOURIER Ανάλυση σημάτων και συστημάτων Ο μετασχηματισμός Fourier (DTFT και DFT) είναι σημαντικότατος για την ανάλυση σημάτων και συστημάτων Εντοπίζει
Ο μετασχηματισμός Fourier
 Ο μετασχηματισμός Fourier είναι από τα διαδεδομένα εργαλεία μετατροπής δεδομένων και συναρτήσεων (μιας ή περισσοτέρων διαστάσεων) από αυτό που ονομάζεται περιοχή χρόνου (time domain) στην περιοχή συχνότητας
Ο μετασχηματισμός Fourier είναι από τα διαδεδομένα εργαλεία μετατροπής δεδομένων και συναρτήσεων (μιας ή περισσοτέρων διαστάσεων) από αυτό που ονομάζεται περιοχή χρόνου (time domain) στην περιοχή συχνότητας
Ψηφιακή Επεξεργασία Σημάτων
 Ψηφιακή Επεξεργασία Σημάτων Ενότητα 11: Εφαρμογές DFT Ταχύς Μετασχηματισμός Fourier (FFT) Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Διακριτός Μετασχηματισμός Fourier Υπολογισμός Γραμμικής Συνέλιξης
Ψηφιακή Επεξεργασία Σημάτων Ενότητα 11: Εφαρμογές DFT Ταχύς Μετασχηματισμός Fourier (FFT) Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Διακριτός Μετασχηματισμός Fourier Υπολογισμός Γραμμικής Συνέλιξης
Εφαρμογή στις ψηφιακές επικοινωνίες
 Δειγματοληψία Εφαρμογή στις ψηφιακές επικοινωνίες Γεννήτρια σήματος RF, (up converter Ενισχυτής) Προενισχυτής down-converter Ψηφιοποιητής σήματος RF Μονάδα ψηφ. επεξεργασίας Μονάδα ψηφ. επεξεργασίας 100
Δειγματοληψία Εφαρμογή στις ψηφιακές επικοινωνίες Γεννήτρια σήματος RF, (up converter Ενισχυτής) Προενισχυτής down-converter Ψηφιοποιητής σήματος RF Μονάδα ψηφ. επεξεργασίας Μονάδα ψηφ. επεξεργασίας 100
Εξεταστική Ιανουαρίου 2007 Μάθηµα: «Σήµατα και Συστήµατα»
 Εξεταστική Ιανουαρίου 27 Μάθηµα: «Σήµατα και Συστήµατα» Θέµα 1 ο (3%) Έστω δύο διακριτά σήµατα: x(n) = {1,,, -1} και h(n) = {1,, 1} µε το πρώτο δείγµα να αντιστοιχεί σε n= και για τα δύο. Υπολογίστε τα
Εξεταστική Ιανουαρίου 27 Μάθηµα: «Σήµατα και Συστήµατα» Θέµα 1 ο (3%) Έστω δύο διακριτά σήµατα: x(n) = {1,,, -1} και h(n) = {1,, 1} µε το πρώτο δείγµα να αντιστοιχεί σε n= και για τα δύο. Υπολογίστε τα
ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΥΣΗ FOURIER ΔΙΑΚΡΙΤΩΝ ΣΗΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ. DTFT και Περιοδική/Κυκλική Συνέλιξη
 ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΥΣΗ FOURIER ΔΙΑΚΡΙΤΩΝ ΣΗΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ DTFT και Περιοδική/Κυκλική Συνέλιξη Διακριτός μετασχηματισμός συνημιτόνου DCT discrete cosine transform Η σχέση αποτελεί «πυρήνα»
ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΥΣΗ FOURIER ΔΙΑΚΡΙΤΩΝ ΣΗΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ DTFT και Περιοδική/Κυκλική Συνέλιξη Διακριτός μετασχηματισμός συνημιτόνου DCT discrete cosine transform Η σχέση αποτελεί «πυρήνα»
Θεώρημα δειγματοληψίας
 Δειγματοληψία Θεώρημα δειγματοληψίας Ένα βαθυπερατό σήμα πεπερασμένης ενέργειας που δεν περιέχει συχνότητες μεγαλύτερες των W Hertz μπορεί να περιγραφθεί πλήρως από τις τιμές του σε χρονικές στιγμές ισαπέχουσες
Δειγματοληψία Θεώρημα δειγματοληψίας Ένα βαθυπερατό σήμα πεπερασμένης ενέργειας που δεν περιέχει συχνότητες μεγαλύτερες των W Hertz μπορεί να περιγραφθεί πλήρως από τις τιμές του σε χρονικές στιγμές ισαπέχουσες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 5 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst215
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 5 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst215
27-Ιαν-2009 ΗΜΥ (ι) Βασική στατιστική (ιι) Μετατροπές: αναλογικό-σεψηφιακό και ψηφιακό-σε-αναλογικό
 ΗΜΥ 429 2. (ι) Βασική στατιστική (ιι) Μετατροπές: αναλογικό-σεψηφιακό και ψηφιακό-σε-αναλογικό 1 (ιι) Μετατροπές: αναλογικό-σεψηφιακό και ψηφιακό-σε-αναλογικό 2 Βασικά μέρη συστήματος ΨΕΣ Φίλτρο αντι-αναδίπλωσης
ΗΜΥ 429 2. (ι) Βασική στατιστική (ιι) Μετατροπές: αναλογικό-σεψηφιακό και ψηφιακό-σε-αναλογικό 1 (ιι) Μετατροπές: αναλογικό-σεψηφιακό και ψηφιακό-σε-αναλογικό 2 Βασικά μέρη συστήματος ΨΕΣ Φίλτρο αντι-αναδίπλωσης
20-Φεβ-2009 ΗΜΥ Διακριτός Μετασχηματισμός Fourier
 ΗΜΥ 429 8. Διακριτός Μετασχηματισμός Fourier 1 Μετασχηματισμός Fourier 4 κατηγορίες: Μετασχηματισμός Fourier: σήματα απεριοδικά και συνεχούς χρόνου Σειρά Fourier: σήματα περιοδικά και συνεχούς χρόνου Μετασχηματισμός
ΗΜΥ 429 8. Διακριτός Μετασχηματισμός Fourier 1 Μετασχηματισμός Fourier 4 κατηγορίες: Μετασχηματισμός Fourier: σήματα απεριοδικά και συνεχούς χρόνου Σειρά Fourier: σήματα περιοδικά και συνεχούς χρόνου Μετασχηματισμός
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών
 HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 12: Δειγματοληψία και ανακατασκευή (IV) Παρεμβολή (Interpolation) Γενικά υπάρχουν πολλοί τρόποι παρεμβολής, π.χ. κυβική παρεμβολή (cubic spline
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 12: Δειγματοληψία και ανακατασκευή (IV) Παρεμβολή (Interpolation) Γενικά υπάρχουν πολλοί τρόποι παρεμβολής, π.χ. κυβική παρεμβολή (cubic spline
Σήματα και Συστήματα. Διάλεξη 7: Μετασχηματισμός Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 7: Μετασχηματισμός Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Fourier 1. Ορισμός του Μετασχηματισμού Fourier 2. Φυσική Σημασία του Μετασχηματισμού
Σήματα και Συστήματα Διάλεξη 7: Μετασχηματισμός Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Fourier 1. Ορισμός του Μετασχηματισμού Fourier 2. Φυσική Σημασία του Μετασχηματισμού
Σχήµα 1: Χρήση ψηφιακών φίλτρων για επεξεργασία σηµάτων συνεχούς χρόνου
 ΜΑΘΗΜΑ 6: ΣΧΕ ΙΑΣΗ ΦΙΛΤΡΩΝ 6. Εισαγωγή Τα φίλτρα είναι µια ειδική κατηγορία ΓΧΑ συστηµάτων τα οποία τροποποιούν συγκεκριµένες συχνότητες του σήµατος εισόδου σε σχέση µε κάποιες άλλες. Η σχεδίαση ψηφιακών
ΜΑΘΗΜΑ 6: ΣΧΕ ΙΑΣΗ ΦΙΛΤΡΩΝ 6. Εισαγωγή Τα φίλτρα είναι µια ειδική κατηγορία ΓΧΑ συστηµάτων τα οποία τροποποιούν συγκεκριµένες συχνότητες του σήµατος εισόδου σε σχέση µε κάποιες άλλες. Η σχεδίαση ψηφιακών
Ψηφιακή Επεξεργασία Σημάτων
 Ψηφιακή Επεξεργασία Σημάτων Ενότητα 10: Διακριτός Μετασχηματισμός Fourier (DFT) Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Fourier Διακριτού Χρόνου Διακριτός Μετασχηματισμός Fourier (DFT)
Ψηφιακή Επεξεργασία Σημάτων Ενότητα 10: Διακριτός Μετασχηματισμός Fourier (DFT) Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Fourier Διακριτού Χρόνου Διακριτός Μετασχηματισμός Fourier (DFT)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙςΤΗΜΗς & ΤΕΧΝΟΛΟΓΙΑς ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 2 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst233
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙςΤΗΜΗς & ΤΕΧΝΟΛΟΓΙΑς ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 2 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst233
Στοχαστικές Μέθοδοι στους Υδατικούς Πόρους Φασματική ανάλυση χρονοσειρών
 Στοχαστικές Μέθοδοι στους Υδατικούς Πόρους Φασματική ανάλυση χρονοσειρών Δημήτρης Κουτσογιάννης Τομέας Υδατικών Πόρων και Περιβάλλοντος, Σχολή Πολιτικών Μηχανικών, Εθνικό Μετσόβιο Πολυτεχνείο Αθήνα Επανέκδοση
Στοχαστικές Μέθοδοι στους Υδατικούς Πόρους Φασματική ανάλυση χρονοσειρών Δημήτρης Κουτσογιάννης Τομέας Υδατικών Πόρων και Περιβάλλοντος, Σχολή Πολιτικών Μηχανικών, Εθνικό Μετσόβιο Πολυτεχνείο Αθήνα Επανέκδοση
Α. Αιτιολογήστε αν είναι γραμμικά ή όχι και χρονικά αμετάβλητα ή όχι.
 ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΟΣ ΕΞ. ΠΕΡΙΟΔΟΣ Β ΧΕΙΜ. 00 - ΩΡΕΣ ΘΕΜΑ Για τα παρακάτω συστήματα εισόδου εξόδου α. y ( 3x( x( n ) β. y ( x( n ) / γ. y ( x( x( n ) δ. y( x( n ) Α. Αιτιολογήστε αν είναι γραμμικά
ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΟΣ ΕΞ. ΠΕΡΙΟΔΟΣ Β ΧΕΙΜ. 00 - ΩΡΕΣ ΘΕΜΑ Για τα παρακάτω συστήματα εισόδου εξόδου α. y ( 3x( x( n ) β. y ( x( n ) / γ. y ( x( x( n ) δ. y( x( n ) Α. Αιτιολογήστε αν είναι γραμμικά
Ανάλυση ΓΧΑ Συστημάτων
 University of Cyprus Biomedical Imaging & Applied Optics Διάλεξη 9 με Μετασχηματισμούς Κεφ. 5 (εκτός 5.7.4 και 5.3 μόνο από διάλεξη) Ένα ΓΧΑ σύστημα καθορίζεται πλήρως από Κρουστική απόκριση (impulse response)
University of Cyprus Biomedical Imaging & Applied Optics Διάλεξη 9 με Μετασχηματισμούς Κεφ. 5 (εκτός 5.7.4 και 5.3 μόνο από διάλεξη) Ένα ΓΧΑ σύστημα καθορίζεται πλήρως από Κρουστική απόκριση (impulse response)
Διάλεξη 2. Συστήματα Εξισώσεων Διαφορών ΔιακριτάΣήματαστοΧώροτης Συχνότητας
 University of Cyprus Biomedical Imaging & Applied Optics Διάλεξη 2 Συστήματα Εξισώσεων Διαφορών Συστήματα Εξισώσεων Διαφορών Γραμμικές Εξισώσεις Διαφορών με Σταθερούς Συντελεστές (Linear Constant- Coefficient
University of Cyprus Biomedical Imaging & Applied Optics Διάλεξη 2 Συστήματα Εξισώσεων Διαφορών Συστήματα Εξισώσεων Διαφορών Γραμμικές Εξισώσεις Διαφορών με Σταθερούς Συντελεστές (Linear Constant- Coefficient
Kεφάλαιο 5 DFT- FFT ΔΙΑΚΡΙΤΟΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER DISCRETE FOURIER TRANSFORM 1/ 80. ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΟΣ DFT-FFT Σ.
 Kεφάλαιο 5 DFT- FFT ΔΙΑΚΡΙΤΟΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER DISCRETE FOURIER TRASFORM / x X x X x X x 3 x DFT X 3 X x 5 X 5 x 6 X 6 x 7 X 7 / DFT - Ορισμοί αναφέρεται σε μία πεπερασμένου μήκους ακολουθία σημείων
Kεφάλαιο 5 DFT- FFT ΔΙΑΚΡΙΤΟΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER DISCRETE FOURIER TRASFORM / x X x X x X x 3 x DFT X 3 X x 5 X 5 x 6 X 6 x 7 X 7 / DFT - Ορισμοί αναφέρεται σε μία πεπερασμένου μήκους ακολουθία σημείων
Σήματα και Συστήματα. Διάλεξη 6: Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 6: Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier 1. Ανάπτυγμα σήματος σε Σειρά Fourier
Σήματα και Συστήματα Διάλεξη 6: Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier 1. Ανάπτυγμα σήματος σε Σειρά Fourier
Διάλεξη 7. Μετασχηματισμός Hilbert. Κεφ. 11 (εκτός 11.0 και ) Για κάθε συνάρτηση ισχύει. Αν η συνάρτηση είναι αιτιατή (causal)
 University of Cyprus Biomedical Imaging & Applied Optics Διάλεξη 7 Κεφ. 11 (εκτός 11.0 και 11.4.1) Για κάθε συνάρτηση ισχύει Αν η συνάρτηση είναι αιτιατή (causal) Ησυνάρτισηx[n] καθορίζεται από x e [n]
University of Cyprus Biomedical Imaging & Applied Optics Διάλεξη 7 Κεφ. 11 (εκτός 11.0 και 11.4.1) Για κάθε συνάρτηση ισχύει Αν η συνάρτηση είναι αιτιατή (causal) Ησυνάρτισηx[n] καθορίζεται από x e [n]
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών
 HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 19: Φίλτρα (IV) Σχεδιασμός φίλτρων FIR Είδαμε ότι για φίλτρα IIR συνήθως σχεδιάζουμε ένα φίλτρο ΣΧ και μετασχηματίζουμε Για φίλτρα FIR θα δούμε
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 19: Φίλτρα (IV) Σχεδιασμός φίλτρων FIR Είδαμε ότι για φίλτρα IIR συνήθως σχεδιάζουμε ένα φίλτρο ΣΧ και μετασχηματίζουμε Για φίλτρα FIR θα δούμε
Ημιτονοειδή σήματα Σ.Χ.
 Ημιτονοειδή σήματα Σ.Χ. Αρμονική ταλάντωση και επειδή Ω=2πF Περιοδικό με βασική περίοδο Τ p =1/F Ημιτονοειδή σήματα Σ.Χ. 1 Ημιτονοειδή σήματα Σ.Χ. Σύμφωνα με την ταυτότητα του Euler Το ημιτονοειδές σήμα
Ημιτονοειδή σήματα Σ.Χ. Αρμονική ταλάντωση και επειδή Ω=2πF Περιοδικό με βασική περίοδο Τ p =1/F Ημιτονοειδή σήματα Σ.Χ. 1 Ημιτονοειδή σήματα Σ.Χ. Σύμφωνα με την ταυτότητα του Euler Το ημιτονοειδές σήμα
Ενδεικτικές Ασκήσεις για το μάθημα: «Μετρήσεις Φυσικών Μεγεθών»
 Ενδεικτικές Ασκήσεις για το μάθημα: «Μετρήσεις Φυσικών Μεγεθών» Άσκηση 1 Τα φίλτρα Butterworth χαρακτηρίζονται από την ιδιότητα, η συνάρτηση απόκρισής τους να είναι ιδιαίτερα επίπεδη στην περιοχή διέλευσης.
Ενδεικτικές Ασκήσεις για το μάθημα: «Μετρήσεις Φυσικών Μεγεθών» Άσκηση 1 Τα φίλτρα Butterworth χαρακτηρίζονται από την ιδιότητα, η συνάρτηση απόκρισής τους να είναι ιδιαίτερα επίπεδη στην περιοχή διέλευσης.
H ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΟΣ. στις τηλεπικοινωνίες
 H ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΟΣ στις τηλεπικοινωνίες Διάταξη συστήματος ψηφιακής επικοινωνίας Γεννήτρια σήματος RF, (up-coverter Ενισχυτής Προενισχυτής- dow-coverter- Ψηφιοποιητής σήματος RF Μονάδα ψηφ.
H ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΟΣ στις τηλεπικοινωνίες Διάταξη συστήματος ψηφιακής επικοινωνίας Γεννήτρια σήματος RF, (up-coverter Ενισχυτής Προενισχυτής- dow-coverter- Ψηφιοποιητής σήματος RF Μονάδα ψηφ.
x[n] = e u[n 1] 4 x[n] = u[n 1] 4 X(z) = z 1 H(z) = (1 0.5z 1 )(1 + 4z 2 ) z 2 (βʹ) H(z) = H min (z)h lin (z) 4 z 1 1 z 1 (z 1 4 )(z 1) (1)
![x[n] = e u[n 1] 4 x[n] = u[n 1] 4 X(z) = z 1 H(z) = (1 0.5z 1 )(1 + 4z 2 ) z 2 (βʹ) H(z) = H min (z)h lin (z) 4 z 1 1 z 1 (z 1 4 )(z 1) (1) x[n] = e u[n 1] 4 x[n] = u[n 1] 4 X(z) = z 1 H(z) = (1 0.5z 1 )(1 + 4z 2 ) z 2 (βʹ) H(z) = H min (z)h lin (z) 4 z 1 1 z 1 (z 1 4 )(z 1) (1)](/thumbs/61/45634776.jpg) Ασκήσεις με Συστήματα στο Χώρο του Ζ Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 7 Νοεμβρίου 015 1. Υπολόγισε τον μετ. Ζ και την
Ασκήσεις με Συστήματα στο Χώρο του Ζ Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 7 Νοεμβρίου 015 1. Υπολόγισε τον μετ. Ζ και την
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΗΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΗΣ ΦΑΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ ΗΧΗΤΙΚΩΝ ΣΗΜΑΤΩΝ ΜΕ ΤΟ ΜΑTLAΒ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ Σπουδαστές: Θεοδωρίδης Σταύρος, Τσιόρλας Νικόλαος.
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΗΣ ΦΑΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ ΗΧΗΤΙΚΩΝ ΣΗΜΑΤΩΝ ΜΕ ΤΟ ΜΑTLAΒ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ Σπουδαστές: Θεοδωρίδης Σταύρος, Τσιόρλας Νικόλαος.
ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΟΣ ΑΣΚΗΣΗ 5
 ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΟΣ ΑΣΚΗΣΗ 5 Α. Σχεδίαση Ψηφιακών Φίλτρων Β. Φίλτρα FIR Σχετικές εντολές του Matlab: fir, sinc, freqz, boxcar, triang, hanning, hamming, blackman, impz, zplane, kaiser. Α. ΣΧΕΔΙΑΣΗ
ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΟΣ ΑΣΚΗΣΗ 5 Α. Σχεδίαση Ψηφιακών Φίλτρων Β. Φίλτρα FIR Σχετικές εντολές του Matlab: fir, sinc, freqz, boxcar, triang, hanning, hamming, blackman, impz, zplane, kaiser. Α. ΣΧΕΔΙΑΣΗ
17-Φεβ-2009 ΗΜΥ Ιδιότητες Συνέλιξης Συσχέτιση
 ΗΜΥ 429 7. Ιδιότητες Συνέλιξης Συσχέτιση 1 Μαθηματικές ιδιότητες Αντιμεταθετική: a [ * b[ = b[ * a[ παρόλο που μαθηματικά ισχύει, δεν έχει φυσικό νόημα. Προσεταιριστική: ( a [ * b[ )* c[ = a[ *( b[ * c[
ΗΜΥ 429 7. Ιδιότητες Συνέλιξης Συσχέτιση 1 Μαθηματικές ιδιότητες Αντιμεταθετική: a [ * b[ = b[ * a[ παρόλο που μαθηματικά ισχύει, δεν έχει φυσικό νόημα. Προσεταιριστική: ( a [ * b[ )* c[ = a[ *( b[ * c[
Ήχος. Τεχνολογία Πολυμέσων και Πολυμεσικές Επικοινωνίες 04-1
 Ήχος Χαρακτηριστικά του ήχου Ψηφιοποίηση με μετασχηματισμό Ψηφιοποίηση με δειγματοληψία Κβαντοποίηση δειγμάτων Παλμοκωδική διαμόρφωση Συμβολική αναπαράσταση μουσικής Τεχνολογία Πολυμέσων και Πολυμεσικές
Ήχος Χαρακτηριστικά του ήχου Ψηφιοποίηση με μετασχηματισμό Ψηφιοποίηση με δειγματοληψία Κβαντοποίηση δειγμάτων Παλμοκωδική διαμόρφωση Συμβολική αναπαράσταση μουσικής Τεχνολογία Πολυμέσων και Πολυμεσικές
HMY 220: Σήματα και Συστήματα Ι
 Σύγκλιση Σειρών Fourier Ιδιότητες Σειρών Fourier Παραδείγματα HMY 0: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ #10 Σειρές Fourier: Προσέγγιση Οι Σειρές Fourier μπορούν να αναπαραστήσουν μια πολύ μεγάλη κλάση περιοδικών
Σύγκλιση Σειρών Fourier Ιδιότητες Σειρών Fourier Παραδείγματα HMY 0: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ #10 Σειρές Fourier: Προσέγγιση Οι Σειρές Fourier μπορούν να αναπαραστήσουν μια πολύ μεγάλη κλάση περιοδικών
HMY 799 1: Αναγνώριση Συστημάτων
 HMY 799 : Αναγνώριση Συστημάτων Διαλέξεις 3 4 Στοχαστικά/τυχαία / χ διανύσματα Ντετερμινιστικά και στοχαστικά σήματα στο πεδίο της συχνότητας Στοχαστικά σήματα και γραμμικά συστήματα Deterministic and
HMY 799 : Αναγνώριση Συστημάτων Διαλέξεις 3 4 Στοχαστικά/τυχαία / χ διανύσματα Ντετερμινιστικά και στοχαστικά σήματα στο πεδίο της συχνότητας Στοχαστικά σήματα και γραμμικά συστήματα Deterministic and
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ. Ενότητα : ΤΑΧΥΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Ενότητα : ΤΑΧΥΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Aναστασία Βελώνη Τμήμα Η.Υ.Σ 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Ενότητα : ΤΑΧΥΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Aναστασία Βελώνη Τμήμα Η.Υ.Σ 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό
Τεχνολογία Πολυμέσων. Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το
Τεχνολογία Πολυμέσων Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το
Μετασχημ/μός Fourier Διακριτών Σημάτων - Διακριτός Μετασχημ/μός Fourier. Στην απόκριση συχνότητας ενός ΓΧΑ συστήματος ο μετασχηματισμός :
 Μετασχημ/μός Fourir Διακριτών Σημάτων - Διακριτός Μετασχημ/μός Fourir Στην απόκριση συχνότητας ενός ΓΧΑ συστήματος ο μετασχηματισμός : j h(i) H( Ω ) ορίζεται ως μετασχηματισμός Fourir της ακολουθίας h(i)
Μετασχημ/μός Fourir Διακριτών Σημάτων - Διακριτός Μετασχημ/μός Fourir Στην απόκριση συχνότητας ενός ΓΧΑ συστήματος ο μετασχηματισμός : j h(i) H( Ω ) ορίζεται ως μετασχηματισμός Fourir της ακολουθίας h(i)
2 Ανάλυση Χρονοσειρών στο Πεδίο των Συχνοτήτων
 Ανάλυση Χρονοσειρών στο Πεδίο των Συχνοτήτων Η ανάλυση χρονοσειρών στο πεδίο των συχνοτήτων είναι συμπληρωματική της ανάλυσης στο πεδίο του χρόνου, αλλά μπορεί να διερευνήσει χαρακτηριστικά που δεν εντοπίζονται
Ανάλυση Χρονοσειρών στο Πεδίο των Συχνοτήτων Η ανάλυση χρονοσειρών στο πεδίο των συχνοτήτων είναι συμπληρωματική της ανάλυσης στο πεδίο του χρόνου, αλλά μπορεί να διερευνήσει χαρακτηριστικά που δεν εντοπίζονται
10-Μαρτ-2009 ΗΜΥ Παραθύρωση Ψηφιακά φίλτρα
 -Μαρτ-9 ΗΜΥ 49. Παραθύρωση Ψηφιακά φίλτρα . Παραθύρωση / Ψηφιακά Φίλτρα -Μαρτ-9 Είδη παραθύρων Bartlett τριγωνικό: n, n Blacman: πn 4πn.4.5cos +.8cos, n < . Παραθύρωση / Ψηφιακά Φίλτρα -Μαρτ-9 3 Hamming:
-Μαρτ-9 ΗΜΥ 49. Παραθύρωση Ψηφιακά φίλτρα . Παραθύρωση / Ψηφιακά Φίλτρα -Μαρτ-9 Είδη παραθύρων Bartlett τριγωνικό: n, n Blacman: πn 4πn.4.5cos +.8cos, n < . Παραθύρωση / Ψηφιακά Φίλτρα -Μαρτ-9 3 Hamming:
HMY 220: Σήματα και Συστήματα Ι
 Σύγκλιση Σειρών Fourier Ιδιότητες Σειρών Fourier Παραδείγματα HMY 220: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ #10 Τρεις ισοδύναμες μορφές: () = = = = Σειρές Fourier j( 2π ) t Τ.. x () t FS a jω0t xt () = ae =
Σύγκλιση Σειρών Fourier Ιδιότητες Σειρών Fourier Παραδείγματα HMY 220: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ #10 Τρεις ισοδύναμες μορφές: () = = = = Σειρές Fourier j( 2π ) t Τ.. x () t FS a jω0t xt () = ae =
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας. Ακαδημαϊκό Έτος Παρουσίαση Νο. 2. Δισδιάστατα Σήματα και Συστήματα #1
 Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ακαδημαϊκό Έτος 06-7 Παρουσίαση Νο. Δισδιάστατα Σήματα και Συστήματα # Βασικοί ορισμοί () Κάθε εικόνα είναι ένα δισδιάστατο (-D) σήμα. Αναλογική εικόνα: x t, t,
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ακαδημαϊκό Έτος 06-7 Παρουσίαση Νο. Δισδιάστατα Σήματα και Συστήματα # Βασικοί ορισμοί () Κάθε εικόνα είναι ένα δισδιάστατο (-D) σήμα. Αναλογική εικόνα: x t, t,
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Στοιχεία Επεξεργασίας Σήματος Δρ. Ν. Π. Σγούρος 2 Εργοδικές Διαδικασίες Η μέση τιμή διαφόρων στιγμιότυπων της διαδικασίας (στατιστική μέση τιμή) ταυτίζεται με τη χρονική μέση
Συμπίεση Δεδομένων 2014-2015 Στοιχεία Επεξεργασίας Σήματος Δρ. Ν. Π. Σγούρος 2 Εργοδικές Διαδικασίες Η μέση τιμή διαφόρων στιγμιότυπων της διαδικασίας (στατιστική μέση τιμή) ταυτίζεται με τη χρονική μέση
Ενότητα 4: Δειγματοληψία - Αναδίπλωση
 Ενότητα 4: Δειγματοληψία - Αναδίπλωση Σήματα και Συστήματα Τα συστήματα επεξεργάζονται ένα ή περισσότερα σήματα: Το παραπάνω σύστημα μετατρέπει το σήμα x(t) σε y(t). π.χ. Σε ένα σήμα ήχου μπορεί να ενισχύσει
Ενότητα 4: Δειγματοληψία - Αναδίπλωση Σήματα και Συστήματα Τα συστήματα επεξεργάζονται ένα ή περισσότερα σήματα: Το παραπάνω σύστημα μετατρέπει το σήμα x(t) σε y(t). π.χ. Σε ένα σήμα ήχου μπορεί να ενισχύσει
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας. Ακαδημαϊκό Έτος Παρουσίαση Νο. 2. Δισδιάστατα Σήματα και Συστήματα #1
 Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ακαδημαϊκό Έτος 009-0 Παρουσίαση Νο. Δισδιάστατα Σήματα και Συστήματα # Βασικοί ορισμοί () Κάθε εικόνα είναι ένα δισδιάστατο (-D) σήμα. Αναλογική εικόνα: x α Ψηφιακή
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ακαδημαϊκό Έτος 009-0 Παρουσίαση Νο. Δισδιάστατα Σήματα και Συστήματα # Βασικοί ορισμοί () Κάθε εικόνα είναι ένα δισδιάστατο (-D) σήμα. Αναλογική εικόνα: x α Ψηφιακή
27/4/2009. Για την υλοποίηση τέτοιων αλγορίθμων επεξεργασίας απαιτείται η χρήση μνήμης. T η περίοδος δειγματοληψίας. Επίκ. Καθηγητής.
 Μάθημα: «Ψηφιακή Επεξεργασία Ήχου» Διάλεξη 6 η : «Επεξεργαστές με Μνήμη (Mέρος ΙI)» Φλώρος Ανδρέας Επίκ. Καθηγητής Από προηγούμενο μάθημα... Αναπαράσταση καθυστέρησης ενός δείγματος η περίοδος δειγματοληψίας
Μάθημα: «Ψηφιακή Επεξεργασία Ήχου» Διάλεξη 6 η : «Επεξεργαστές με Μνήμη (Mέρος ΙI)» Φλώρος Ανδρέας Επίκ. Καθηγητής Από προηγούμενο μάθημα... Αναπαράσταση καθυστέρησης ενός δείγματος η περίοδος δειγματοληψίας
Εισαγωγή στην Επεξεργασία Σήματος. Νόκας Γιώργος
 Εισαγωγή στην Επεξεργασία Σήματος Νόκας Γιώργος Βιβλιογραφία στον εύδοξο 1. Γ. Β. Μουστακίδης, Βασικές Τεχνικές Ψηφιακής Επεξεργασίας Σημάτων και Συστημάτων, εκδόσεις Α. Τζιόλα & Υιοί Ο.Ε., Θεσσαλονίκη,
Εισαγωγή στην Επεξεργασία Σήματος Νόκας Γιώργος Βιβλιογραφία στον εύδοξο 1. Γ. Β. Μουστακίδης, Βασικές Τεχνικές Ψηφιακής Επεξεργασίας Σημάτων και Συστημάτων, εκδόσεις Α. Τζιόλα & Υιοί Ο.Ε., Θεσσαλονίκη,
Στοιχεία επεξεργασίας σημάτων
 Στοιχεία επεξεργασίας σημάτων ΕΜΠ - ΣΧΟΛΗ ΑΤΜ Ακ. Έτος 2004-2005 Β.Βεσκούκης, Δ.Παραδείσης, Δ.Αργιαλάς, Δ.Δεληκαράογλου, Β.Καραθανάση, Β.Μασσίνας Γενικά στοιχεία για το μάθημα Εισάγεται στα πλαίσια της
Στοιχεία επεξεργασίας σημάτων ΕΜΠ - ΣΧΟΛΗ ΑΤΜ Ακ. Έτος 2004-2005 Β.Βεσκούκης, Δ.Παραδείσης, Δ.Αργιαλάς, Δ.Δεληκαράογλου, Β.Καραθανάση, Β.Μασσίνας Γενικά στοιχεία για το μάθημα Εισάγεται στα πλαίσια της
Σήματα και Συστήματα. Διάλεξη 10: Γραμμικά Φίλτρα. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 10: Γραμμικά Φίλτρα Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Γραμμικά Φίλτρα 1. Ιδανικά Γραμμικά Φίλτρα Ιδανικό Κατωδιαβατό Φίλτρο Ιδανικό Ανωδιαβατό Φίλτρο Ιδανικό Ζωνοδιαβατό
Σήματα και Συστήματα Διάλεξη 10: Γραμμικά Φίλτρα Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Γραμμικά Φίλτρα 1. Ιδανικά Γραμμικά Φίλτρα Ιδανικό Κατωδιαβατό Φίλτρο Ιδανικό Ανωδιαβατό Φίλτρο Ιδανικό Ζωνοδιαβατό
Σήματα και Συστήματα. Διάλεξη 8: Ιδιότητες του Μετασχηματισμού Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 8: Ιδιότητες του Μετασχηματισμού ourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ιδιότητες του Μετασχηματισμού ourier 1. Ιδιότητες του Μετασχηματισμού ourier 2. Θεώρημα
Σήματα και Συστήματα Διάλεξη 8: Ιδιότητες του Μετασχηματισμού ourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ιδιότητες του Μετασχηματισμού ourier 1. Ιδιότητες του Μετασχηματισμού ourier 2. Θεώρημα
ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΟΣ ΑΣΚΗΣΗ 3
 ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΟΣ ΑΣΚΗΣΗ 3 Διακριτός Μετασχηματισμός Fourier (DFT) Ο διακριτός μετασχηματισμός Fourier (DFT) αποτελεί το βασικό εργαλείο της Σχετικές εντολές του Matlab: fft, abs, rand, randn,
ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΟΣ ΑΣΚΗΣΗ 3 Διακριτός Μετασχηματισμός Fourier (DFT) Ο διακριτός μετασχηματισμός Fourier (DFT) αποτελεί το βασικό εργαλείο της Σχετικές εντολές του Matlab: fft, abs, rand, randn,
δ[n kp ], k Z (1) 1 cos πn, N 1 n N 1 + N 2 2N
![δ[n kp ], k Z (1) 1 cos πn, N 1 n N 1 + N 2 2N δ[n kp ], k Z (1) 1 cos πn, N 1 n N 1 + N 2 2N](/thumbs/66/55089135.jpg) ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 2015 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Τέταρτο Εργαστήριο - Ηµεροµηνία : 27/11/2015 Σηµείωση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 2015 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Τέταρτο Εργαστήριο - Ηµεροµηνία : 27/11/2015 Σηµείωση
Ψηφιακή Επεξεργασία Σημάτων
 Ψηφιακή Επεξεργασία Σημάτων Ενότητα 6: Απόκριση Συχνότητας Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Fourier Διακριτού Χρόνου Η έννοια της Απόκρισης Συχνότητας Ιδιότητες της Απόκρισης
Ψηφιακή Επεξεργασία Σημάτων Ενότητα 6: Απόκριση Συχνότητας Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Fourier Διακριτού Χρόνου Η έννοια της Απόκρισης Συχνότητας Ιδιότητες της Απόκρισης
1) Να σχεδιαστούν στο matlab οι γραφικές παραστάσεις των παρακάτω ακολουθιών στο διάστημα, χρησιμοποιώντας τις συναρτήσεις delta και step.
 1) Να σχεδιαστούν στο matlab οι γραφικές παραστάσεις των παρακάτω ακολουθιών στο διάστημα, χρησιμοποιώντας τις συναρτήσεις delta και step. Α) Β) Ε) F) G) H) Ι) 2) Αν το διακριτό σήμα x(n) είναι όπως στην
1) Να σχεδιαστούν στο matlab οι γραφικές παραστάσεις των παρακάτω ακολουθιών στο διάστημα, χρησιμοποιώντας τις συναρτήσεις delta και step. Α) Β) Ε) F) G) H) Ι) 2) Αν το διακριτό σήμα x(n) είναι όπως στην
Μετάδοση πληροφορίας - Διαμόρφωση
 Μετάδοση πληροφορίας - Διαμόρφωση MYE006: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Διάρθρωση μαθήματος Μετάδοση Βασικές έννοιες Διαμόρφωση ορισμός είδη
Μετάδοση πληροφορίας - Διαμόρφωση MYE006: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Διάρθρωση μαθήματος Μετάδοση Βασικές έννοιες Διαμόρφωση ορισμός είδη
Δειγματοληψία και ανακατασκευή αναλογικών σημάτων
 Δειγματοληψία και ανακατασκευή αναλογικών σημάτων, ή το φάσμα ενός ανα- Ο συνεχούς χρόνου μετασχηματισμός Fourier (CTFT), λογικού σήματος είναι X ( ω ) x (t) jω t X ω = x t e dt x ( ) ( ) = 1 j ω t e d
Δειγματοληψία και ανακατασκευή αναλογικών σημάτων, ή το φάσμα ενός ανα- Ο συνεχούς χρόνου μετασχηματισμός Fourier (CTFT), λογικού σήματος είναι X ( ω ) x (t) jω t X ω = x t e dt x ( ) ( ) = 1 j ω t e d
1/3/2009. Τα ψηφιακά ηχητικά συστήματα πρέπει να επικοινωνήσουν με τον «αναλογικό» ανθρώπινο κόσμο. Φλώρος Ανδρέας Επίκ. Καθηγητής.
 Από το προηγούμενο μάθημα... Μάθημα: «Ψηφιακή Επεξεργασία Ήχου» Δάλ Διάλεξη 2 η : «Βασικές Β έ αρχές ψηφιακού ήχου» Φλώρος Ανδρέας Επίκ. Καθηγητής Τα ψηφιακά ηχητικά συστήματα πρέπει να επικοινωνήσουν
Από το προηγούμενο μάθημα... Μάθημα: «Ψηφιακή Επεξεργασία Ήχου» Δάλ Διάλεξη 2 η : «Βασικές Β έ αρχές ψηφιακού ήχου» Φλώρος Ανδρέας Επίκ. Καθηγητής Τα ψηφιακά ηχητικά συστήματα πρέπει να επικοινωνήσουν
20-Μαρ-2009 ΗΜΥ Φίλτρα απόκρισης πεπερασμένου παλμού (FIR)
 ΗΜΥ 429 14. Φίλτρα απόκρισης πεπερασμένου παλμού (FIR) 1 Γενικά βήματα για σχεδιασμό φίλτρων (1) Προσδιορισμός χαρακτηριστικών του φίλτρου: Χαρακτηριστικά σήματος (π.χ. μέγιστη συχνότητα) Χαρακτηριστικά
ΗΜΥ 429 14. Φίλτρα απόκρισης πεπερασμένου παλμού (FIR) 1 Γενικά βήματα για σχεδιασμό φίλτρων (1) Προσδιορισμός χαρακτηριστικών του φίλτρου: Χαρακτηριστικά σήματος (π.χ. μέγιστη συχνότητα) Χαρακτηριστικά
Μετάδοση πληροφορίας - Διαμόρφωση
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Μετάδοση πληροφορίας - Διαμόρφωση MYE006-ΠΛΕ065: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου Διάρθρωση μαθήματος Βασικές έννοιες μετάδοσης Διαμόρφωση ορισμός
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Μετάδοση πληροφορίας - Διαμόρφωση MYE006-ΠΛΕ065: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου Διάρθρωση μαθήματος Βασικές έννοιες μετάδοσης Διαμόρφωση ορισμός
Εισαγωγή στις Τηλεπικοινωνίες
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στις Τηλεπικοινωνίες Ενότητα 3: Δειγματοληψία και Ανακατασκευή Σημάτων Όνομα Καθηγητή: Δρ. Ηρακλής Σίμος Τμήμα: Ηλεκτρονικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στις Τηλεπικοινωνίες Ενότητα 3: Δειγματοληψία και Ανακατασκευή Σημάτων Όνομα Καθηγητή: Δρ. Ηρακλής Σίμος Τμήμα: Ηλεκτρονικών
Ψηφιακή Επεξεργασία Σημάτων
 Ψηφιακή Επεξεργασία Σημάτων Ενότητα 8: Μετασχηματισμός Ζ Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Z Μετασχηματισμός Ζ (Ζ-Transform) Χρήσιμα Ζεύγη ΖT και Περιοχές Σύγκλισης (ROC) Ιδιότητες
Ψηφιακή Επεξεργασία Σημάτων Ενότητα 8: Μετασχηματισμός Ζ Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Z Μετασχηματισμός Ζ (Ζ-Transform) Χρήσιμα Ζεύγη ΖT και Περιοχές Σύγκλισης (ROC) Ιδιότητες
Διακριτός Μετασχηματισμός Fourier
 Διακριτός Μετασχηματισμός Fourier 1 Διακριτός Μετασχηματισμός Fourier Ο μετασχηματισμός Fourier αποτελεί τον ακρογωνιαίο λίθο της επεξεργασίας σήματος αλλά και συχνή αιτία πονοκεφάλου για όσους πρωτοασχολούνται
Διακριτός Μετασχηματισμός Fourier 1 Διακριτός Μετασχηματισμός Fourier Ο μετασχηματισμός Fourier αποτελεί τον ακρογωνιαίο λίθο της επεξεργασίας σήματος αλλά και συχνή αιτία πονοκεφάλου για όσους πρωτοασχολούνται
ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΥΣΗ FOURIER ΔΙΑΚΡΙΤΩΝ ΣΗΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ. Διακριτός Μετασχηματισμός Fourier DFT
 ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΥΣΗ FOURIER ΔΙΑΚΡΙΤΩΝ ΣΗΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ Διακριτός Μετασχηματισμός Fourier DFT Διακριτός μετασχηματισμός συνημιτόνου DCT discrete cosine transform Η σχέση αποτελεί «πυρήνα»
ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΥΣΗ FOURIER ΔΙΑΚΡΙΤΩΝ ΣΗΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ Διακριτός Μετασχηματισμός Fourier DFT Διακριτός μετασχηματισμός συνημιτόνου DCT discrete cosine transform Η σχέση αποτελεί «πυρήνα»
Σήματα και Συστήματα. Διάλεξη 1: Σήματα Συνεχούς Χρόνου. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
Σήματα και Συστήματα ΙΙ
 Σήματα και Συστήματα ΙΙ Ενότητα 3: Διακριτός και Ταχύς Μετασχηματισμός Fourier (DTF & FFT) Α. Ν. Σκόδρας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Επιμέλεια: Αθανάσιος Ν. Σκόδρας, Καθηγητής
Σήματα και Συστήματα ΙΙ Ενότητα 3: Διακριτός και Ταχύς Μετασχηματισμός Fourier (DTF & FFT) Α. Ν. Σκόδρας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Επιμέλεια: Αθανάσιος Ν. Σκόδρας, Καθηγητής
Επαναληπτικές Ασκήσεις για το µάθηµα Ψηφιακή Επεξεργασία Σηµάτων
 Άσκηση η α) Πώς θα µετρήσετε πρακτικά πόσο κοντά είναι ένα σήµα σε λευκό θόρυβο; Αναφέρατε 3 διαφορετικές µεθόδους (κριτήρια) για την απόφαση: "Ναι, πρόκειται για σήµα που είναι πολύ κοντά σε λευκό θόρυβο"
Άσκηση η α) Πώς θα µετρήσετε πρακτικά πόσο κοντά είναι ένα σήµα σε λευκό θόρυβο; Αναφέρατε 3 διαφορετικές µεθόδους (κριτήρια) για την απόφαση: "Ναι, πρόκειται για σήµα που είναι πολύ κοντά σε λευκό θόρυβο"
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ. Ενότητα : ΔΙΑΚΡΙΤΟΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Ενότητα : ΔΙΑΚΡΙΤΟΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Aναστασία Βελώνη Τμήμα Η.Υ.Σ 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Ενότητα : ΔΙΑΚΡΙΤΟΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Aναστασία Βελώνη Τμήμα Η.Υ.Σ 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό
x[n] x(nt s ) y c x c Discrete Time System D /C Conversion C/D Conversion Conv. From continous to discrete and from discrete to continous x trne
![x[n] x(nt s ) y c x c Discrete Time System D /C Conversion C/D Conversion Conv. From continous to discrete and from discrete to continous x trne x[n] x(nt s ) y c x c Discrete Time System D /C Conversion C/D Conversion Conv. From continous to discrete and from discrete to continous x trne](/thumbs/68/58299929.jpg) Πανεπιστημιο Κυπρου Τμημα Ηλεκτρολογων Μηχανικων και Μηχανικων Υπολογιστων ΗΜΥ 1: Σηματα και Συστηματα για Μηχανικους Υπολογιστων Κεφάλαιο 8: Δειγματοληψία Η γέφυρα από τα συνεχή στα διακριτά!"#!"#! "#$%
Πανεπιστημιο Κυπρου Τμημα Ηλεκτρολογων Μηχανικων και Μηχανικων Υπολογιστων ΗΜΥ 1: Σηματα και Συστηματα για Μηχανικους Υπολογιστων Κεφάλαιο 8: Δειγματοληψία Η γέφυρα από τα συνεχή στα διακριτά!"#!"#! "#$%
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 9 ο : Δειγματοληψία και Ανασύσταση
Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 9 ο : Δειγματοληψία και Ανασύσταση
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών. Χρόνου (Ι)
 HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 5: Στοχαστικά/Τυχαία Σήματα Διακριτού Διάλεξη 5: Στοχαστικά/Τυχαία Σήματα Διακριτού Χρόνου (Ι) Στοχαστικά σήματα Στα προηγούμενα: Ντετερμινιστικά
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 5: Στοχαστικά/Τυχαία Σήματα Διακριτού Διάλεξη 5: Στοχαστικά/Τυχαία Σήματα Διακριτού Χρόνου (Ι) Στοχαστικά σήματα Στα προηγούμενα: Ντετερμινιστικά
ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ
 ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Α. ΣΚΟΔΡΑΣ ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΙΙ (22Y603) ΕΝΟΤΗΤΑ 3 ΔΙΑΛΕΞΗ 1 ΔΙΑΦΑΝΕΙΑ 1 Διαφορετικοί Τύποι Μετασχηµατισµού Fourier Α. ΣΚΟΔΡΑΣ ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΙΙ (22Y603)
ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Α. ΣΚΟΔΡΑΣ ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΙΙ (22Y603) ΕΝΟΤΗΤΑ 3 ΔΙΑΛΕΞΗ 1 ΔΙΑΦΑΝΕΙΑ 1 Διαφορετικοί Τύποι Μετασχηµατισµού Fourier Α. ΣΚΟΔΡΑΣ ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΙΙ (22Y603)
1. Εισαγωγή στη Φασµατική εκτίµηση
 1. Εισαγωγή στη Φασµατική εκτίµηση Γνωρίζουµε ότι η ανάλυση Fourier είναι ένα χρήσιµο εργαλείο για την περιγραφή και ανάλυση διακριτού χρόνου αιτιοκρατικών σηµάτων. Η ανάλυση Fourier παίζει σηµαντικό ρόλο
1. Εισαγωγή στη Φασµατική εκτίµηση Γνωρίζουµε ότι η ανάλυση Fourier είναι ένα χρήσιµο εργαλείο για την περιγραφή και ανάλυση διακριτού χρόνου αιτιοκρατικών σηµάτων. Η ανάλυση Fourier παίζει σηµαντικό ρόλο
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας. Εισηγητής Αναστάσιος Κεσίδης
 Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Επεξεργασία στο πεδίο της συχνότητας Φασματικές τεχνικές Γενικά Τεχνικές αναπαράστασης και ανάλυσης
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Επεξεργασία στο πεδίο της συχνότητας Φασματικές τεχνικές Γενικά Τεχνικές αναπαράστασης και ανάλυσης
HMY 799 1: Αναγνώριση Συστημάτων
 HMY 799 : Αναγνώριση Συστημάτων Διάλεξη Στοχαστικές Τυχαίες Μεταβλητές/ Στοχαστικά Σήματα Πειραματικά δεδομένα >Επιλογή τύπου μοντέλου >Επιλογή κριτηρίου >Υπολογισμός >Επικύρωση Προσαρμογή καμπύλης (Curve
HMY 799 : Αναγνώριση Συστημάτων Διάλεξη Στοχαστικές Τυχαίες Μεταβλητές/ Στοχαστικά Σήματα Πειραματικά δεδομένα >Επιλογή τύπου μοντέλου >Επιλογή κριτηρίου >Υπολογισμός >Επικύρωση Προσαρμογή καμπύλης (Curve
Kεφάλαιο 5 DFT- FFT ΔΙΑΚΡΙΤΟΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER DISCRETE FOURIER TRANSFORM ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΟΣ DFT-FFT. Σ.
 Kεφάλαιο 5 DFT- FFT ΔΙΑΚΡΙΤΟΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER DISCRETE FOURIER TRASFORM x x x IDFT X X X x 3 x 4 DFT X 3 X 4 x 5 X 5 x 6 X 6 x 7 X 7 DFT - Ορισμοί αναφέρεται σε μία πεπερασμένου μήκους ακολουθία
Kεφάλαιο 5 DFT- FFT ΔΙΑΚΡΙΤΟΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER DISCRETE FOURIER TRASFORM x x x IDFT X X X x 3 x 4 DFT X 3 X 4 x 5 X 5 x 6 X 6 x 7 X 7 DFT - Ορισμοί αναφέρεται σε μία πεπερασμένου μήκους ακολουθία
Ραδιοτηλεοπτικά Συστήματα Ενότητα 5: Ψηφιοποίηση και συμπίεση σημάτων ήχου
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ραδιοτηλεοπτικά Συστήματα Ενότητα 5: Ψηφιοποίηση και συμπίεση σημάτων ήχου Δρ. Νικόλαος- Αλέξανδρος Τάτλας Τμήμα Ηλεκτρονικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ραδιοτηλεοπτικά Συστήματα Ενότητα 5: Ψηφιοποίηση και συμπίεση σημάτων ήχου Δρ. Νικόλαος- Αλέξανδρος Τάτλας Τμήμα Ηλεκτρονικών
Ιατρικά Ηλεκτρονικά. Χρήσιμοι Σύνδεσμοι. ΙΑΤΡΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ - ΔΙΑΛΕΞΗ 5α. Σημειώσεις μαθήματος: E mail:
 Ιατρικά Ηλεκτρονικά Δρ. Π. Ασβεστάς Τμήμα Μηχανικών Βιοϊατρικής Τεχνολογίας Τ.Ε Χρήσιμοι Σύνδεσμοι Σημειώσεις μαθήματος: http://medisp.bme.teiath.gr/eclass/courses/tio127/ E mail: pasv@teiath.gr 2 1 Περιοδικά
Ιατρικά Ηλεκτρονικά Δρ. Π. Ασβεστάς Τμήμα Μηχανικών Βιοϊατρικής Τεχνολογίας Τ.Ε Χρήσιμοι Σύνδεσμοι Σημειώσεις μαθήματος: http://medisp.bme.teiath.gr/eclass/courses/tio127/ E mail: pasv@teiath.gr 2 1 Περιοδικά
Σεισμολογικά Όργανα Κεφάλαιο 8. Chang Heng 132 π.χ.
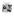 Σεισμολογικά Όργανα Κεφάλαιο 8 Chang Heng 132 π.χ. Οι πρώτες προσπάθειες Chang Heng Guatemala Earthquake 1976 Σεισμολογικά Όργανα Σεισμοσκόπια (δεν υπάρχει χρονική κλίμακα αναφοράς) Forbes' seismometer
Σεισμολογικά Όργανα Κεφάλαιο 8 Chang Heng 132 π.χ. Οι πρώτες προσπάθειες Chang Heng Guatemala Earthquake 1976 Σεισμολογικά Όργανα Σεισμοσκόπια (δεν υπάρχει χρονική κλίμακα αναφοράς) Forbes' seismometer
Ραδιοτηλεοπτικά Συστήματα Ενότητα 3: Θεωρία Ψηφιοποίησης
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ραδιοτηλεοπτικά Συστήματα Ενότητα 3: Θεωρία Ψηφιοποίησης Δρ. Νικόλαος- Αλέξανδρος Τάτλας Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε Κάντε
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ραδιοτηλεοπτικά Συστήματα Ενότητα 3: Θεωρία Ψηφιοποίησης Δρ. Νικόλαος- Αλέξανδρος Τάτλας Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε Κάντε
Κεφάλαιο 6 Σχεδιασμός FIR φίλτρων
 Κεφάλαιο 6 Σχεδιασμός FIR φίλτρων Φίλτρα πεπερασμένης κρουστικής απόκρισης Finite Impulse Response (FIR) filters y(n) = M k= bk x(n k) / 68 παράδειγμα (εισαγωγικό) y(n) = 9 x(n k ) k= 2/ 68 Βασικές κατηγορίες
Κεφάλαιο 6 Σχεδιασμός FIR φίλτρων Φίλτρα πεπερασμένης κρουστικής απόκρισης Finite Impulse Response (FIR) filters y(n) = M k= bk x(n k) / 68 παράδειγμα (εισαγωγικό) y(n) = 9 x(n k ) k= 2/ 68 Βασικές κατηγορίες
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών. στο χώρο της συχνότητας
 HMY 49: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 3: Σήματα και Συστήματα διακριτού χρόνου Διάλεξη 3: Σήματα και Συστήματα διακριτού χρόνου στο χώρο της συχνότητας Μιγαδικά εκθετικά σήματα και
HMY 49: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 3: Σήματα και Συστήματα διακριτού χρόνου Διάλεξη 3: Σήματα και Συστήματα διακριτού χρόνου στο χώρο της συχνότητας Μιγαδικά εκθετικά σήματα και
Παράμετροι σχεδίασης παλμών (Μορφοποίηση παλμών)
 Παράμετροι σχεδίασης παλμών (Μορφοποίηση παλμών) Κύριοι παράμετροι στη σχεδίαση παλμών είναι (στο πεδίο συχνοτήτων): Η Συχνότητα του 1ου μηδενισμού (θέλουμε μικρό BW). H ελάχιστη απόσβεση των πλαγίων λοβών
Παράμετροι σχεδίασης παλμών (Μορφοποίηση παλμών) Κύριοι παράμετροι στη σχεδίαση παλμών είναι (στο πεδίο συχνοτήτων): Η Συχνότητα του 1ου μηδενισμού (θέλουμε μικρό BW). H ελάχιστη απόσβεση των πλαγίων λοβών
ΣΕΙΡΕΣ ΚΑΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ FOURIER. e ω. Το βασικό πρόβλημα στις σειρές Fourier είναι ο υπολογισμός των συντελεστών c
 ΣΕΙΡΕΣ ΚΑΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ FOURIER x(t+kτ) = x(t) = π/ω f = / x(t) = = 8 c j t e ω c = (a-jb ) Το βασικό πρόβλημα στις σειρές Fourier είναι ο υπολογισμός των συντελεστών c. Αυτός γίνεται κατορθωτός αν
ΣΕΙΡΕΣ ΚΑΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ FOURIER x(t+kτ) = x(t) = π/ω f = / x(t) = = 8 c j t e ω c = (a-jb ) Το βασικό πρόβλημα στις σειρές Fourier είναι ο υπολογισμός των συντελεστών c. Αυτός γίνεται κατορθωτός αν
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Οικονομίας Διοίκησης και Πληροφορικής Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Αρχές Τηλ/ων Συστημάτων Εργαστήριο 7 ο : Δειγματοληψία και Ανασύσταση Βασική
Σχολή Οικονομίας Διοίκησης και Πληροφορικής Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Αρχές Τηλ/ων Συστημάτων Εργαστήριο 7 ο : Δειγματοληψία και Ανασύσταση Βασική
Σήματα και Συστήματα. Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
Πιθανότητες & Τυχαία Σήματα. Διγαλάκης Βασίλης
 Πιθανότητες & Τυχαία Σήματα Διγαλάκης Βασίλης Γραμμικά Συστήματα Σύστημα: x(t) T y(t) Κατηγορίες: Συνεχή/Διακριτά Γραμμικά/Μη Γραμμικά Αν Τότε Γραμμικά Συστήματα Σύστημα: x(t) T y(t) Κατηγορίες: Χρονικά
Πιθανότητες & Τυχαία Σήματα Διγαλάκης Βασίλης Γραμμικά Συστήματα Σύστημα: x(t) T y(t) Κατηγορίες: Συνεχή/Διακριτά Γραμμικά/Μη Γραμμικά Αν Τότε Γραμμικά Συστήματα Σύστημα: x(t) T y(t) Κατηγορίες: Χρονικά
Κεφάλαιο 3 Προεπεξεργασία Σήµατος Οµιλίας
 Κεφάλαιο 3 Προεπεξεργασία Σήµατος Οµιλίας σελ.83 Κεφάλαιο 3 Προεπεξεργασία Σήµατος Οµιλίας 3.1 Eισαγωγή Τα στάδια που προηγούνται της βασικής διαδικασίας αναγνώρισης, αναφέρονται σαν στάδια προεπεξεργασίας
Κεφάλαιο 3 Προεπεξεργασία Σήµατος Οµιλίας σελ.83 Κεφάλαιο 3 Προεπεξεργασία Σήµατος Οµιλίας 3.1 Eισαγωγή Τα στάδια που προηγούνται της βασικής διαδικασίας αναγνώρισης, αναφέρονται σαν στάδια προεπεξεργασίας
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Ενότητα : ΑΝΑΛΥΣΗ FOURIER (H ΣΕΙΡΑ FOURIER ΚΑΙ Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER) Aναστασία Βελώνη Τμήμα Η.Υ.Σ 1 Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Ενότητα : ΑΝΑΛΥΣΗ FOURIER (H ΣΕΙΡΑ FOURIER ΚΑΙ Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER) Aναστασία Βελώνη Τμήμα Η.Υ.Σ 1 Άδειες
ΗΜΥ Διακριτός Μετασχηματισμός Fourier
 1 ΗΜΥ 480 5. Διακριτός Μετασχηματισμός Fourier ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Μετασχηματισμός Fourier MF: μιγαδικός αριθμός που δείχνει πώς: 1 συγκεκριμένες συχνότητες συμβάλλουν στο σήμα πραγματικό μέρος πώς
1 ΗΜΥ 480 5. Διακριτός Μετασχηματισμός Fourier ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Μετασχηματισμός Fourier MF: μιγαδικός αριθμός που δείχνει πώς: 1 συγκεκριμένες συχνότητες συμβάλλουν στο σήμα πραγματικό μέρος πώς
Επομένως το εύρος ζώνης του διαμορφωμένου σήματος είναι 2.
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΠΛΗ ΓΙΑ ΤΙΣ ΕΞΕΤΑΣΕΙΣ ΘΕΜΑ Το φέρον σε ένα σύστημα DSB διαμόρφωσης είναι c t A t μηνύματος είναι το m( t) sin c( t) sin c ( t) ( ) cos 4 c και το σήμα. Το διαμορφωμένο σήμα διέρχεται
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΠΛΗ ΓΙΑ ΤΙΣ ΕΞΕΤΑΣΕΙΣ ΘΕΜΑ Το φέρον σε ένα σύστημα DSB διαμόρφωσης είναι c t A t μηνύματος είναι το m( t) sin c( t) sin c ( t) ( ) cos 4 c και το σήμα. Το διαμορφωμένο σήμα διέρχεται
f s > 2B, (9.1) T s < 1 2B (9.2) f s > 2B (9.3) x(t) X(f) X(0)
 Κεφάλαιο 9 Δειγματοληψία 9.1 Εισαγωγή Οι περισσότερες μετρήσιμες φυσικές διαδικασίες που συμβαίνουν στον κόσμο μας είναι συνεχούς χρόνου, και συνήθως αναλογικές. Από την ηλιακή ακτινοβολία, την ανθρώπινη
Κεφάλαιο 9 Δειγματοληψία 9.1 Εισαγωγή Οι περισσότερες μετρήσιμες φυσικές διαδικασίες που συμβαίνουν στον κόσμο μας είναι συνεχούς χρόνου, και συνήθως αναλογικές. Από την ηλιακή ακτινοβολία, την ανθρώπινη
ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΩΝ Κυκλική Συνέλιξη. Εµµανουήλ Ζ. Ψαράκης Πολυτεχνική Σχολή Τµήµα Μηχανικών Η/Υ & Πληροφορικής
 ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΩΝ Κυκλική Συνέλιξη Εµµανουήλ Ζ. Ψαράκης Πολυτεχνική Σχολή Τµήµα Μηχανικών Η/Υ & Πληροφορικής Διακριτού Χρόνου Σειρές Fourier Περιοδική Επέκταση Σήµατος Πεπερασµένης Χρονικής Διάρκειας.
ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΩΝ Κυκλική Συνέλιξη Εµµανουήλ Ζ. Ψαράκης Πολυτεχνική Σχολή Τµήµα Μηχανικών Η/Υ & Πληροφορικής Διακριτού Χρόνου Σειρές Fourier Περιοδική Επέκταση Σήµατος Πεπερασµένης Χρονικής Διάρκειας.
y[n] ay[n 1] = x[n] + βx[n 1] (6)
![y[n] ay[n 1] = x[n] + βx[n 1] (6) y[n] ay[n 1] = x[n] + βx[n 1] (6)](/thumbs/62/47574712.jpg) Ασκήσεις με το Μετασχηματισμό Fourier Διακριτού Χρόνου Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 8 Οκτωβρίου 015 1. Εστω το
Ασκήσεις με το Μετασχηματισμό Fourier Διακριτού Χρόνου Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 8 Οκτωβρίου 015 1. Εστω το
