ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ
|
|
|
- Κλειώ Αργυριάδης
- 4 χρόνια πριν
- Προβολές:
Transcript
1 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ R ΑΒ Μέσα στον καταλύτη ΑΒ πόροι στερεό Διδακτικές Σημειώσεις στο Μάθημα «Φαινόμενα Μεταφοράς» Ν. Ανδρίτσος και Β. Μποντόζογλου Βόλος, Απρίλιος 019 Πανεπιστημιακές Εκδόσεις Θεσσαλίας
2 1. ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΜΕΤΑΦΟΡΑΣ ΜΑΖΑΣ 1.1. Εισαγωγή Όταν ένα σύστημα περιέχει δύο ή περισσότερα συστατικά των οποίων οι συγκεντρώσεις διαφέρουν από σημείο σε σημείο, τότε διαμορφώνεται η φυσική τάση να μεταφερθεί μάζα ώστε να ελαχιστοποιηθούν οι διαφορές της συγκέντρωσης μέσα στο σύστημα. Μεταφορά μάζας (mass transfer) είναι η μεταφορά ενός συστατικού από μία περιοχή στην οποία υπάρχει υψηλή συγκέντρωση του συστατικού σε μια περιοχή με χαμηλή συγκέντρωση. Υπάρχουν και άλλες φυσικές διεργασίες που μπορεί να οδηγήσουν σε μεταφορά μάζας, όπως είναι η ύπαρξη κλίσης θερμοκρασίας (φαινόμενο Soret), κλίσης πίεσης (pressure diffusion) και διαφορών που δημιουργούνται από εξωτερικές δυνάμεις (βαρύτητα, μαγνητικά πεδία κ.α.). H μεταφορά μάζας αποτελεί τη βάση για πολλές χημικές και βιολογικές διεργασίες, αλλά και για πολλές καθημερινές μας συνήθειες, όπως είναι η διαλυτοποίηση της ζάχαρης στον πρωινό καφέ και η διάχυση ενός αρώματος. Παραδείγματα διεργασιών στις οποίες η μεταφορά μάζας παίζει κυρίαρχο ρόλο είναι, μεταξύ άλλων, η απόσταξη, η προσρόφηση, η ξήρανση, οι διεργασίες μεμβρανών, η διάβρωση, η κατάλυση, η χημική εναπόθεση ατμού, ο τεχνητός νεφρός (αιμοκάθαρση), η οξυγόνωση του αίματος και η μεταφορά αμινοξέων μέσα στα κύτταρα. Σε πολλές από τις διεργασίες μεταφοράς μάζας έχουμε και ταυτόχρονη μεταφορά θερμότητας ή/και ορμής. Η μεταφορά μάζας επιτυγχάνεται συνήθως με συνδυασμό των μηχανισμών της διάχυσης (μοριακός μηχανισμός, που περιγράφηκε αρχικά από τον Parrot το 1815) και της συναγωγής. Η διάχυση στα υγρά είναι μία ιδιαίτερα αργή διαδικασία. Στο διπλανό παράδειγμα παρουσιάζεται η υπέρθεση δύο υδατικών διαλυμάτων αλατιού διαφορετικής συγκέντρωσης. Αν η τοποθέτηση των διαλυμάτων γίνει ιδεατά έτσι ώστε να αποφευχθεί Νερό Αλατόνερο οποιαδήποτε ανακίνηση, η εξομάλυνση των διαφορών συγκέντρωσης σε αλάτι θα γίνει αποκλειστικά με τον μηχανισμό της διάχυσης. Στην περίπτωση αυτή, η επιφανειακή συγκέντρωση θα φτάσει το 87% της μέσης συγκέντρωσης ύστερα από 10 χρόνια, και το 99% της μέσης συγκέντρωσης ύστερα από 5 χρόνια! Βεβαίως, αν υπάρχει μία τυπική ανάδευση (π.χ. 0 rpm) επιτυγχάνεται σχεδόν πλήρης ανάμειξη μέσα σε 60 se. Η ανάμειξη λοιπόν, όπως τη γνωρίζουμε στην καθημερινή μας ζωή, είναι προϊόν συναγωγής, αν και η μοριακή διάχυση εξακολουθεί να παίζει κεντρικό ρόλο σε μικροσκοπικό και μοριακό επίπεδο. Στα βιολογικά συστήματα η διάχυση είναι ο κύριος τρόπος μεταφοράς των θρεπτικών συστατικών, π.χ. των αμινοξέων μέσα στο κύτταρο. s Σημειώσεις Μεταφοράς Μάζας 1
3 1.. Μηχανισμός Ανάμειξης Η διάχυση προχωρεί με ικανοποιητική ταχύτητα στα αέρια, αλλά είναι ιδιαίτερα αργή στα υγρά (χαρακτηριστικές τιμές μοριακής διαχυτότητας 10 1 m /s και 10 5 m /s, αντίστοιχα). Ο μηχανισμός με τον οποίο η μακροσκοπική κίνηση επιταχύνει την ανάμειξη (συναγωγή) φαίνεται στο παρακάτω σχήμα. Ειδικότερα, κατά την ανάμειξη συμβαίνει εκτεταμένη επιμήκυνση και αναδίπλωση των «σωματιδίων» του υγρού (strething and folding). Έτσι, σχηματίζεται μεγάλη διεπιφάνεια μεταξύ περιοχών με διαφορετική σύσταση, η οποία επιτρέπει να επιτευχθεί με τη διάχυση η ουσιαστική εξομάλυνση της σύστασης. Τελικά Αρχικά Ο συνδυασμός διάχυσης και συναγωγής αναφέρεται συχνά με τον όρο διασπορά (dispersion). Η διάχυση και η διασπορά περιγράφονται σχεδόν με παρόμοιες μαθηματικές εκφράσεις Ορισμοί Συγκέντρωσης, Ταχύτητας, Διάχυσης και Συναγωγής Ορισμοί Συγκέντρωσης σε πολυσυστατικά μείγματα Σε ένα πολυσυστατικό μείγμα η συγκέντρωση ενός χημικού συστατικού μπορεί να εκφραστεί με δύο διαφορετικούς τρόπους. (α) Μαζική συγκέντρωση (mass onentration) ή πυκνότητα, ρ i. Η μάζα του συστατικού i ανά μονάδα όγκου του μείγματος σε kg/m 3. Η συνολική μαζική συγκέντρωση είναι το άθροισμα των συγκεντρώσεων όλων των n συστατικών του μείγματος, δηλ. ρ= ρi, όπου n είναι o αριθμός των συστατικών στο μείγμα. i1 Ως μαζικό κλάσμα (ή κλάσμα μάζας mass fration) του συστατικού i ορίζεται: ω=ρ / ισχύει: ω= i 1. n i1 Σημειώσεις Μεταφοράς Μάζας n i i i i1 ρi ρ. Προφανώς ρ (β) Γραμμομοριακή συγκέντρωση (molar onentration), i. Ορίζεται ως ο αριθμός των γραμμομορίων του συστατικού i ανά μονάδα όγκου του μείγματος σε kmol/m 3. Εξ ορισμού 1 kmol αντιστοιχεί σε M i (μοριακό βάρος του i) kg, δηλ.: 3 i i Mi kg/kmol 3 m ρ kg / m kmol = [ ] ni pi Όταν αναφερόμαστε σε (ιδανικά) αέρια ισχύει: = i, όπου p i είναι η μερική πίεση του i, Τ η απόλυτη V RT θερμοκρασία και R η σταθερά των αερίων. Η συνολική γραμμομοριακή συγκέντρωση είναι το άθροισμα των συγκεντρώσεων όλων των συστατικών του μείγματος, δηλ. =. Από τον νόμο των ιδανικών αερίων έχουμε p, δηλ. η συγκέντρωση είναι σταθερή σε συγκεκριμένη θερμοκρασία και πίεση. RT n i1 i
4 Ως γραμμομοριακό κλάσμα (molar fration) του συστατικού i ορίζεται ο λόγος της i ως προς τη συνολική i i συγκέντρωση. Για υγρά και στερεά συμβολίζεται συνήθως με x=, ενώ για αέρια με y=. Εξ ορισμού i i n n xi 1 και yi 1, ενώ για τα ιδανικά αέρια ισχύει pi i i1 i1 πίεση του συστατικού i στο αέριο μείγμα). y= p (όπου p είναι η συνολική πίεση και p i η μερική Ταχύτητες Σε ένα πολυσυστατικό μείγμα τα διάφορα συστατικά μπορεί να κινούνται με διαφορετική ταχύτητα. Συνήθως ορίζονται τρεις μέσες ταχύτητες. (α) Μέση μαζική ταχύτητα (mass average veloity / bulk veloity). Η ταχύτητα του μείγματος με όρους των μαζικών συγκεντρώσεων (ή μαζικών κλασμάτων) και της ταχύτητας κάθε συστατικού n ρu ρu u n i i i i n i1 i1 n ρ i1 ρi i1 ωu i i όπου u i είναι η απόλυτη ταχύτητα του συστατικού i αναφορικά με σταθερό σύστημα συντεταγμένων. [Η κάτω παύλα στο σύμβολο ενός μεγέθους δείχνει ότι το μέγεθος αυτό είναι διανυσματικό.] Να σημειωθεί ότι η ποσότητα ρu είναι ο τοπικός ρυθμός με τον οποίο η μάζα διέρχεται μέσω μοναδιαίας επιφάνειας, κάθετης στην ταχύτητα u. Αυτή είναι η ταχύτητα που μετρείται με το Pitot tube, με ταχυμετρία Laser Doppler, με σύστημα απεικόνισης ταχυτήτων σωματιδίων (PIV) κτλ. Ακόμη, αυτή η ταχύτητα χρησιμοποιείται στις εξισώσεις Navier Stokes και στο ισοζύγιο ενέργειας. (β) Μέση γραμμομοριακή ταχύτητα (molar average veloity). Η ταχύτητα του μείγματος με όρους των γραμμομοριακών συγκεντρώσεων και της ταχύτητας κάθε συστατικού n u u u x u n i i i i n i1 i1 n i1 i i1 (γ) Μέση ταχύτητα όγκου, η οποία ορίζεται ως v n n Vi i i i i i M i1 i i1 u ρ u Vu i i Σημειώσεις Μεταφοράς Μάζας 3 (1.1) (1.) (1.3) όπου V i είναι ο μερικός γραμμομοριακός όγκος του συστατικού i. Η ταχύτητα αυτή είναι η ταχύτητα των συστατικών που δεν διαχέονται. v Αν δεν υπάρχει διάχυση τότε ισχύει u u u, όπως συμβαίνει σε σύστημα ενός συστατικού. Η ταχύτητα ενός συστατικού σε σχέση με μια μέση ταχύτητα ορίζεται ως ταχύτητα διάχυσης (diffusion veloity) του i. Έτσι, μπορούμε να ορίσουμε τρεις διαφορετικές ταχύτητες διάχυσης: (α) ui u: η ταχύτητα του i σε σχέση με τη μέση μαζική ταχύτητα και (β) ui u : η ταχύτητα του i σε σχέση με τη μέση γραμμομοριακή ταχύτητα. v (γ) u : η ταχύτητα του i σε σχέση με τη μέση ταχύτητα όγκου. ui
5 Διάχυση και Συναγωγή Μία ιδιαιτερότητα της διάχυσης είναι ότι μπορεί από μόνη της να προκαλέσει συναγωγή, η οποία υπερτίθεται στην υπόλοιπη μακροσκοπική κίνηση. Ήδη το 1860 ο Maxwell είχε αναφέρει ότι «η μεταφορά μάζας οφείλεται μερικώς στην κίνηση της περιστροφής και μερικώς στην κίνηση ανάδευσης». Το γεγονός αυτό οφείλεται στο ότι με τη μεταφορά μάζας με τον μοριακό μηχανισμό (διάχυση) έχουμε ουσιαστικά ροή μάζας, δηλαδή ανάπτυξη ταχύτητας, ενώ η μεταφορά θερμότητας με μοριακό μηχανισμό (αγωγή) δεν προκαλεί ροή μάζας. Όπως θα διαπιστώσουμε στη συνέχεια, η συναγωγή που δημιουργείται από τη διάχυση είναι αμελητέα στα αραιά διαλύματα, διαφοροποιεί όμως αισθητά τα αποτελέσματα σε ειδικές περιπτώσεις πυκνών διαλυμάτων. Μικρή ειδική ροή Ποιοτικό Παράδειγμα: Μεγάλο δοχείο που περιέχει βενζόλιο (πτητικό υγρό) συνδέεται με τον περιβάλλοντα αέρα μέσω ενός τριχοειδούς σωλήνα. Το βενζόλιο εξατμίζεται και ρέει μέσα στο σωλήνα προς το περιβάλλον. Μπορούμε να διακρίνουμε τρεις περιπτώσεις μεταφοράς μάζας μέσω του σωλήνα, ανάλογα με τη θερμοκρασία του ρευστού: (α) Στους 6 C, σε χαμηλή δηλ. θερμοκρασία, η συγκέντρωση των ατμών του βενζολίου είναι μικρή (η τάση ατμών είναι μικρή) και οι ατμοί διαχέονται μέσω προς κίνησης Brown στον αέρα που περιέχεται στον σωλήνα. Η μεταφορά επιτελείται με απλή διάχυση. (β) Προς 80,1 C, το βενζόλιο βρίσκεται στο σημείο ζέσεως και οι ατμοί του ρέουν με μεγάλη ταχύτητα μέσα στο σωλήνα. Η ροή αυτή σχετίζεται κυρίως με τη διαφορά πίεσης (συναγωγή) και λίγη σχέση έχει με τη διάχυση. (γ) Προς 60 C, τόσο η απλή διάχυση όσο και η συναγωγή είναι σημαντικοί μηχανισμοί. (Οι μηχανισμοί αυτοί αναλύονται διεξοδικότερα παρακάτω.) Υψηλή ειδική ροή Μέση ειδική ροή 1.4. Βασικές Σχέσεις Μεταφοράς Μάζας Παρά τη φαινομενικά ανάλογη συμπεριφορά με τη μεταφορά θερμότητας, η μεταφορά μάζας είναι περισσότερο πολύπλοκη. Στη μεταφορά μάζας συνυπάρχουν πάντα μοριακή διάχυση και συναγωγή, ενώ η ροή μπορεί να θεωρηθεί είτε σε σχέση με σταθερές συντεταγμένες ή σε σχέση με μία μέση ταχύτητα. Η πολυπλοκότητα της μεταφοράς μάζας ενισχύεται και από προς διαφορετικές μονάδες που χρησιμοποιούνται, μαζικές ή γραμμομοριακές. Τέλος, σύγχυση προσθέτει και ο διαφορετικός συμβολισμός των διαφόρων μεγεθών στα σχετικά συγγράμματα (δες ΠΑΡΑΡΤΗΜΑ ΙΙ). Η ωθούσα δύναμη (driving fore) για τη μοριακή διάχυση είναι η κλίση της συγκέντρωσης. Όπως ήδη έχει αναφερθεί, μεταφορά μάζας μπορεί να προκληθεί και από άλλες ωθούσες δυνάμεις, από την κλίση της πίεσης ή της θερμοκρασίας ή από κάποια εξωτερική δύναμη (π.χ. καθίζηση λόγω βαρύτητας). Οι ειδικές ροές συστατικών στη μεταφορά μάζας ορίζονται ως προς σταθερές ή ως προς κινούμενες συντεταγμένες και γράφονται είτε σε μαζικές ή σε γραμμομοριακές μονάδες. Οι ειδικές ροές που θα χρησιμοποιήσουμε ορίζονται παρακάτω. Εδώ να θυμηθούμε ότι ειδική ροή (flux) είναι η ποσότητα ενός μεγέθους (εδώ της μάζας σε kg ή σε kmol) που διέρχεται ανά μονάδα χρόνου και μονάδα επιφανείας κάθετης στη διεύθυνση της μεταφοράς. Ως προς σταθερό σύστημα συντεταγμένων, η ειδική ροή (flux relative to fixed axis) μπορεί να οριστεί: Σημειώσεις Μεταφοράς Μάζας 4
6 (i) Μαζική ειδική ροή (mass flux) του συστατικού i: n ρ u (σε kg/m s) (1.4) i i i όπου u είναι η μέση ταχύτητα των «σωματιδίων» (π.χ. μορίων) του συστατικού i σε κάθε σημείο του i μείγματος. Από τη σχέση αυτή και την Εξ. 1.1 συνεπάγεται ότι: n i ρu i i ρu u n /ρ (1.5) i (ii) Γραμμομοριακή ειδική ροή (molar flux) του i: N u (σε kmol/m s) (1.6) i i i από την οποία, σε συνδυασμό με την Εξ. 1. προκύπτει ότι: N u u u N / i i i i (1.7) Προσοχή: Εδώ να σημειώσουμε τη διαφοροποίηση των συμβόλων που χρησιμοποιούνται για τις ειδικές ροές σε σχέση με τα σύμβολα που χρησιμοποιούνται στο βιβλίο των Brodkey & Hersey. Στο βιβλίο αυτό τα ίδια σύμβολα χρησιμοποιούνται για να εκφράσουν ροές (μαζικές ή γραμμομοριακές). Οι ειδικές ροές συμβολίζονται στις σημειώσεις αυτές ως n i, N κτλ., ενώ στο βιβλίο ως ( n / ), ( N /) κτλ. i i i Ως προς κινούμενο σύστημα συντεταγμένων, η ειδική ροή μπορεί να οριστεί αντίστοιχα ως: (i) Μαζική ειδική ροή του i σε σχέση με τη μέση μαζική ταχύτητα (mass flux relative to the mass average veloity) σε kg/(m s): ji ρ(u i i u) (1.8) [Επίσης ή μαζική ειδική ροή μπορεί να γραφεί και σε σχέση με τη μέση γραμμομοριακή ταχύτητα, v v j ρ(u u ), ή τη μέση ταχύτητα όγκου, j ρ(u u )] i i i i i i (ii) Γραμμομοριακή ειδική ροή του i σε σχέση με τη μέση γραμμομοριακή ταχύτητα (molar flux relative to the molar average veloity) σε kmol/(m s): J (u u ) (1.9) i i i [Αντίστοιχα, μπορεί να γραφεί σε σχέση με τη μέση μαζική ταχύτητα, Ji (u i i u), ή τη μέση ταχύτητα όγκου, v i i i v J (u u )] Έτσι, από τις (1.4) και (1.7) προκύπτει: ni ρu i i ρ(u i iu) ρu i ji ρu i (1.10) Από τις (1.5) και (1.8) προκύπτει: N u (u u ) u J u (1.11) i i i i i i i i Ο νόμος του Fik, που ισχύει αυστηρά για δυαδικό μείγμα Α και Β (binary mixture), μπορεί να γραφεί σε σχέση με σύστημα συντεταγμένων σταθερό στο χώρο ή σε σχέση με σύστημα συντεταγμένων που κινείται με τη μέση μαζική ή τη μέση γραμμομοριακή ταχύτητα. (1) Η ειδική μαζική ροή του συστατικού Α σε σχέση με τη μέση μαζική ταχύτητα του δυαδικού μείγματος γράφεται ως j ρd ω (1.1) B Για τη διεύθυνση z η παραπάνω σχέση παίρνει τη μορφή: dω j,z ρdb (1.13) dz Σημειώσεις Μεταφοράς Μάζας 5
7 και όταν η ολική μαζική συγκέντρωση είναι σταθερή (ρ=σταθ.): dρ dz,z DB (ή γενικότερα B j j D ρ ). () Η ειδική γραμμομοριακή ροή σε σχέση με τη μέση γραμμομοριακή ταχύτητα του δυαδικού μείγματος (που δεν περιορίζεται σε ισοβαρείς και ισοθερμοκρασιακές συνθήκες) ορίζεται ως: B J D y (1.14) Όταν η συνολική συγκέντρωση παραμένει παντού σταθερή (όπως ισχύει για τα ιδανικά αέρια σε ισοβαρείς και ισοθερμοκρασιακές συνθήκες) τότε J D B (1.15) Αν η διάχυση γίνεται μόνο στη διεύθυνση z: d Jz DB (1.16) dz [Στο ΠΑΡΑΡΤΗΜΑ Ι παρουσιάζεται ο νόμος του Fik (Εξ. 1.14) για τα τρία συστήματα συντεταγμένων.] Για ένα δυαδικό σύστημα εύκολα μπορεί να προκύψουν οι εξής σχέσεις για την ειδική ροή του Α στη διεύθυνση z, οι οποίες συχνά αποτελούν το σημείο εκκίνησης για την επίλυση αρκετών προβλημάτων μεταφοράς μάζας: και dω dρ nz ρd B ω(nz n Bz) ή αν ρ=σταθ. ρ nz D B (nz n Bz) (1.17) dz dz ρ dy d Nz D B y (Nz N Bz) ή αν =σταθ. N z DB (Nz N Bz) (1.18) dz dz Συνολική μεταφορά Διάχυση: η κίνηση του συστατικού σε σχέση με τη μέση γραμμομοριακή ταχύτητα λόγω διαφοράς στη συγκέντρωση N u (u u ) u J u D B d dz u Εξ ορισμού Συναγωγή: συνεισφορά λόγω της συνολικής μετακίνησης Από τις παραπάνω σχέσεις προκύπτει εύκολα ότι για δυαδικό σύστημα ισχύει D B =D B. Για σύστημα με πολλά συστατικά η Εξ γράφεται ως n dy N,z DM y Ni,z (1.19) dz i1 όπου D είναι η διαχυτότητα του Α σε σχέση με το μείγμα των n συστατικών (και προφανώς D M B D B ). Επίσης για τα ιδανικά αέρια ισχύει ότι y p /p και y p /p, όπου p B B και p B είναι οι μερικές πιέσεις των Α και Β και p η ολική πίεση του συστήματος. Επειδή 1 dp p Nz DB Nz NBz RT dz p p, η Εξ μπορεί να γραφεί και ως: RT (1.18β) Σημειώσεις Μεταφοράς Μάζας 6
8 Πριν γίνει προσπάθεια να λυθούν οι παραπάνω εξισώσεις θα πρέπει συνήθως να απαλείψουμε το Αυτό μπορεί να γίνει αν γνωρίζουμε κάτι για τον λόγο N /N B, ο οποίος συνήθως καθορίζεται από τις συνοριακές συνθήκες που διέπονται από το φυσικό πρόβλημα και εξαρτάται από τις ιδιαιτερότητες του κάθε προβλήματος (χάριν απλότητας δεν βάζουμε το δείκτη z). Τρεις βασικές υποπεριπτώσεις που θα εξετάσουμε στη συνέχεια είναι η ισογραμμομοριακή αντιδιάχυση ( N N ), η διάχυση σε στάσιμο αέριο ( N 0 B B ) και η διάχυση με αντίδραση σε καταλυτική επιφάνεια. Ποια όμως μέση ταχύτητα θα πρέπει να χρησιμοποιήσουμε στις ειδικές ροές; Ή, καλύτερα, ποια εξίσωση θα χρησιμοποιήσουμε; Μας ενδιαφέρει η μέση ταχύτητα (u ή u ) να είναι κοντά 0, έτσι ώστε ο όρος της συναγωγής να απαλειφθεί. α) Στα ιδανικά αέρια συχνά ισχύει u 0 (αν και u 0), όπως φαίνεται στο διπλανό σχήμα, επειδή η μοριακή Ν Η συγκέντρωση παραμένει σταθερή παντού και, επομένως, βολεύει η χρήση της μέσης μοριακής ταχύτητας. Η ίδια N N n B nb u 0 u 0 ταχύτητα επίσης χρησιμοποιείται όταν υπάρχουν χημικές αντιδράσεις. β) Στα υγρά, όπου η πυκνότητα είναι σχεδόν πάντα σταθερή (π.χ. για μικρές συγκεντρώσεις της διαλυμένης ουσίας), η μαζική ταχύτητα είναι σχεδόν μηδέν γλυκερίνης νερού. N B. (u 0, αλλά u 0) ). Παράδειγμα, αραιό διάλυμα 1.5. Ισοζύγιο Μάζας και Βήματα Επίλυσης Προβλημάτων Από το γενικό ισοζύγιο μεγέθους σε καρτεσιανές συντεταγμένες [Εξ. (6.16) στις σημειώσεις του Καθ. Β. Μποντόζογλου ή Εξ. (3.48) στο βιβλίο των Brodkey & Hersey], αντικαθιστώντας, N και G C,G παίρνουμε την εξίσωση συνεχείας του συστατικού Α σε γραμμομοριακές μονάδες (ή εξίσωση ισοζυγίου μάζας του Α): όπου t N C 0 ή,g N N x y N z C,G0 (1.0α) t x y z C,G αντιπροσωπεύει τον καθαρό ρυθμό σχηματισμού (net rate of formation) του Α με ομοιογενή χημική αντίδραση ανά μονάδα όγκου (kmol/m 3 s). Η σύμβαση για το πρόσημο του C,G είναι ότι ο ρυθμός είναι θετικός εάν υπάρχει σχηματισμός του συστατικού Α και αρνητικός στην περίπτωση καθαρής κατανάλωσης. Στο ΠΑΡΑΡΤΗΜΑ Ι δίνονται οι σχέσεις του ισοζυγίου μάζας στα τρία συστήματα συντεταγμένων. Από την παραπάνω σχέση για μόνιμη κατάσταση, απουσία χημικής αντίδρασης και διάχυση μόνο στη διεύθυνση z, προκύπτει ότι: dnz 0 Nz = σταθερή (για όλο το μήκος της διάχυσης) (1.0β) dz Για κυλινδρικές και σφαιρικές συντεταγμένες και για ροή στη διεύθυνση r προκύπτει rn r σταθ., αντίστοιχα. rnr σταθ. και Σημειώσεις Μεταφοράς Μάζας 7
9 Με αντίστοιχο τρόπο [, n και G,G] μπορεί να εξαχθεί η εξίσωση συνεχείας του συστατικού Α σε μαζικές μονάδες: n,g n n x y n z 0 ή,g 0 (1.0γ) t t x y z Για δυαδικό μείγμα ισχύει για τα συστατικά Α και Β: n,g B 0 και nb B,G 0 (1.0δ) t t Αν προσθέσουμε τις δύο παραπάνω εξισώσεις και λάβουμε υπόψη ότι,g B,G 0, τότε παίρνουμε τη γνωστή μας εξίσωση συνεχείας για το μείγμα: (n n B) 0 και από την Εξ. 1.5 ( u) 0. t t [Αντίστοιχη εξίσωση μπορούμε να πάρουμε και σε γραμμομοριακές μονάδες, αλλά μόνο στην περίπτωση που C,G C B,G 0, δηλ. όταν το Α ουσιαστικά συμπίπτει με το Β.] Αν αντικαταστήσουμε την (1.17) σε διανυσματική μορφή στην (1.0γ) προκύπτει για σταθερή συνολική μαζική συγκέντρωση ρ (δηλ. μπορούμε να το εφαρμόσουμε σε υγρά διαλύματα, όχι όμως σε αέρια όπου η συνολική συγκέντρωση = + B είναι σταθερή, εκτός αν πρόκειται για αραιά διαλύματα), σταθερή D B και ασυμπίεστη ροή: ρ uρdb ρ,g (1.0ε) t Διαιρώντας την παραπάνω σχέση με το μοριακό βάρος του Α, M, έχουμε udb C,G (1.0στ) t Προσοχή, η Εξ. (1.0στ) ισχύει μόνο για δυαδικά συστήματα και για ρ=σταθερό! Στο ΠΑΡΑΡΤΗΜΑ Ι παρουσιάζεται η Εξ. 1.0στ στα τρία συστήματα συντεταγμένων. Κανονικά για την επίλυση προβλημάτων θα ξεκινούσαμε από την Εξ. 1στ, αλλά η σχέση αυτή παρουσιάζει προβλήματα (ιδιαίτερα για αέρια συστήματα), γιατί προϋποθέτει ότι η συνολική μαζική συγκέντρωση είναι σταθερή. Τέλος, για u 0,,G 0 και διάχυση μόνο στην κατεύθυνση z, προκύπτει ο ος νόμος της διάχυσης του Fik, για τον οποίο θα συζητήσουμε σε επόμενο κεφάλαιο: t D z B (1.0ζ) Η υπόθεση της απουσίας ροής περιορίζει την εφαρμογή της παραπάνω εξίσωσης σε στερεά ή σε ακίνητα υγρά. Επίσης σε δυαδικά αέρια συστήματα όπου ισχύει N NB. Πριν αναλύσουμε κάποιες περιπτώσεις διάχυσης θα ήταν καλό για τον/τη φοιτητή/τρια να ανατρέξει στις κυριότερες συνοριακές συνθήκες που συναντάμε στη μεταφορά μάζας, οι οποίες παρουσιάστηκαν στις σημειώσεις της «Μονοδιάστατης Μεταφοράς». Τα βήματα για την επίλυση προβλημάτων με μοριακή διάχυση σε δυαδικά συστήματα είναι τα εξής: 1) Αν μπορούμε, κάνουμε ένα σκαρίφημα του φυσικού προβλήματος και ορίζουμε τις συνοριακές συνθήκες. Σκεφτόμαστε αν υπάρχει ή όχι παραγωγή ή κατανάλωση του συστατικού. Σημειώσεις Μεταφοράς Μάζας 8
10 ) Γράφουμε τις παραδοχές που κάνουμε για την επίλυση του προβλήματος (π.χ. μόνιμη κατάσταση, μεταφορά μόνο στη διεύθυνση r κτλ.). 3) Επιλέγουμε το σύστημα συντεταγμένων που θα δουλέψουμε ανάλογα με το φυσικό πρόβλημα (π.χ. κυλινδρικές). Από εδώ και πέρα προχωράμε με μία από τις δύο προσεγγίσεις που παρουσιάστηκαν στις σημειώσεις «Μονοδιάστατη Μεταφορά». Στην πρώτη προσέγγιση ξεκινάμε από την εξίσωση συνεχείας στο κατάλληλο σύστημα συντεταγμένων για ένα συστατικό (π.χ. Α) σε όρους ειδικής γραμμομοριακής ροής σε σχέση με σταθερούς άξονες (Πίνακας ΙΙ του Παραρτήματος) ή από την εξίσωση διατήρησης του συστατικού Α σε όρους συγκέντρωσης για δυαδικό ή ψευδο δυαδικό μείγμα σε καρτεσιανές, κυλινδρικές και σφαιρικές συντεταγμένες (Πίνακας ΙΙΙ του Παραρτήματος). Επειδή η τελευταία εξίσωση προϋποθέτει σταθερό ρ, η εφαρμογή της περιορίζεται μόνο σε ορισμένα υγρά διαλύματα και σε πολύ αραιά αέρια μείγματα. Ακολούθως απαλείφουμε τους μηδενικούς όρους των παραπάνω διαφορικών εξισώσεων. Για παράδειγμα για την εξίσωση συνεχείας του Α: (i) Εάν η διεργασία γίνεται σε μόνιμη κατάσταση, τότε / t 0. (ii) Εάν δεν συμβαίνει αντίδραση μέσα στη μάζα του ρευστού τότε C,G =0. (iii) Εάν η μοριακή μεταφορά μάζας γίνεται σε κυλινδρικές συντεταγμένες στις διευθύνσεις r και z, τότε 1 z N rnr N r r z Στη δεύτερη προσέγγιση κάνουμε ένα ισοζύγιο του υλικού σε μία κατάλληλη «φέτα» ή σε ένα «κέλυφος» και καταλήγουμε στην ίδια διαφορική εξίσωση. Εν συνεχεία, αντικαθιστούμε το γενικευμένο νόμο του Fik (Εξ ή 1.8) και προσπαθούμε να βρούμε τη συσχέτιση μεταξύ N και N B (ή n και n B ). 4) Αναγνωρίζουμε και εξειδικεύουμε τις συνοριακές και τις αρχικές συνθήκες του προβλήματος. 5) Λύνουμε τις διαφορικές εξισώσεις όπως στις σημειώσεις ή, αν αυτό είναι δύσκολο, κάνουμε και άλλες παραδοχές. Προσοχή! Θα δουλέψουμε με σταθερή μαζική συγκέντρωση ρ ή με σταθερή γραμμομοριακή συγκέντρωση ; 1.6. Ειδικές Περιπτώσεις Διάχυσης Ιδανικών Αερίων Ισογραμμομοριακή αντιδιάχυση Θεωρούμε ένα δυαδικό, ισόθερμο μείγμα ιδανικών αερίων με ομοιόμορφη πίεση παντού, pp pb, όπως παρουσιάζεται στο Σχήμα 1, όπου οι συγκεντρώσεις των συστατικών στα δύο δοχεία (1 και ) παραμένουν πάντα σταθερές. Επίσης ισχύει ότι y,0 >y,l. Θέλουμε να εξαγάγουμε τη σχέση για την ειδική ροή του συστατικού Α και την κατανομή της συγκέντρωσής του στον αγωγό διάχυσης μήκους L. Πως σκεφτόμαστε να προσεγγίσουμε αυτό το πρόβλημα; Μπορούμε να χρησιμοποιήσουμε την εξίσωση διατήρησης του συστατικού Α (Εξ. Ι.10) που ισχύει για καρτεσιανές συντεταγμένες; Προφανώς όχι γιατί οι εξισώσεις αυτές ισχύουν για σταθερό ρ, κάτι που δεν ισχύει γενικά σε αέρια συστήματα. Επομένως, είτε προχωράμε με ένα ισοζύγιο σε μια «φέτα» Δz, είτε προσφεύγουμε στην Εξ. Ι.6. Επειδή δεν έχουμε συσσώρευση και παραγωγή και η διάχυση γίνεται σε μία διάσταση (την z) από την Εξ. Ι.6 προκύπτει: Σημειώσεις Μεταφοράς Μάζας 9
11 dn z 0 dz Δηλαδή, το N z είναι σταθερό σε όλο το μήκος διάχυσης. Προφανώς, στο ίδιο συμπέρασμα θα φτάσουμε και με το ισοζύγιο του Α σε μία διαφορική «φέτα». Το Nz τώρα είναι και συνάρτηση και του N Bz [από τη σχέση dy του νόμου του Fik σε δυαδικό σύστημα: Nz D B y (Nz N Bz) ]. Άρα χρειαζόμαστε κάποια σχέση που dz να συσχετίζει τα N z και N Bz. Σε αυτό το πρόβλημα είναι κατανοητό ότι το συστατικό Α θα διαχέεται μέσω του αγωγού από το δοχείο 1 στο και το B από το στο 1 με τον ίδιο (γραμμομοριακό) ρυθμό. Συνεπώς, η συνολική ειδική γραμμομοριακή ροή σε σχέση με σταθερές συντεταγμένες, π.χ. στη διεύθυνση z, παραμένει μηδενική (ως αποτέλεσμα της σταθερής πίεσης και θερμοκρασίας του συστήματος), δηλαδή δεν υπάρχει καθαρή ροή συστατικού. Η διεργασία αυτή καλείται ισογραμμομοριακή αντιδιάχυση. Επομένως, 1 Nz NBz 0 Nz NBz και uz Nz NBz 0 1 p /p y,0,0 p /p yb,0 B,0 z N,z L N B,z y,l yb,l p /p,l p /p B,L z=0 z=l Σχήμα 1. Κατανομή μερικής πίεσης ή συγκέντρωσης σε ισογραμμομοριακή αντιδιάχυση. Άρα : dy Nz Jz DB dz dyb NBz JBz D B dz dy dyb dz dz dp dpb dz dz Οι κλίσεις των γραμμομοριακών κλασμάτων και των μερικών πιέσεων είναι αντίθετες Σημειώσεις Μεταφοράς Μάζας 10
12 Στη γενική περίπτωση, επειδή η γραμμομοριακή ροή W N είναι σταθερή, ολοκληρώνοντας από 0 μέχρι L (ή από το z 1 μέχρι το z ), λαμβάνουμε την παρακάτω σχέση στην περίπτωση που η επιφάνεια Α δεν είναι σταθερή και εξαρτάται από το z: L dz yl (Nz) DB dy 0 (z) y0 (1.1) Για σταθερή επιφάνεια Α: y0 yl 0 L Nz DB DB L L (1.α) ή D p B,0 p,l Nz RT L (1.β) Από την παραπάνω σχέση συνάγεται ότι η συγκέντρωση (ή η μερική πίεση) του συστατικού Α μεταβάλλεται γραμμικά κατά μήκος της διαδρομής διάχυσης (0, L), όπως απεικονίζεται και στο Σχήμα 1. Αντίστοιχες σχέσεις παίρνουμε και για το συστατικό Β. εύκολα ότι Πως όμως υπολογίζουμε την κατανομή συγκέντρωσης στο μήκος L; Από τη σχέση d dz dnz dz 0 προκύπτει 0, από την οποία με διπλή ολοκλήρωση παίρνουμε: C1z C. Λαμβάνοντας υπόψη τις συνοριακές συνθήκες, δηλ. (i) στο z0, 0 και (ii) στο zl, L, η κατανομή της συγκέντρωσης του Α παίρνει τη μορφή: 0 z (1.3) L L Μονογραμμομοριακή διάχυση ή διάχυση σε στάσιμο αέριο Η περίπτωση αυτή αναφέρεται στη διάχυση του συστατικού Α μέσω ενός στάσιμου αερίου Β (unimoleular diffusion / diffusion of one gas through a seond stagnant gas), όπως παρουσιάζεται σχηματικά στο Σχήμα. Το σύστημα συχνά αναφέρεται και ως «κελί rnold». Παραδείγματα αυτού του τύπου διάχυσης αποτελούν η εξάτμιση ενός συστατικού Α σε μία στήλη, η εκλεκτική προσρόφηση ενός συστατικού από ένα μείγμα (π.χ. μείγμα N και CO διέρχεται από μία επιφάνεια διαλύματος ΝαΟΗ, στο οποίο διάλυμα το δεύτερο συστατικό είναι πολύ περισσότερο διαλυτό και απορροφάται αμέσως, ενώ το πρώτο αέριο είναι «στάσιμο» διαχωρισμός σε πλυντρίδες), η συμπύκνωση κ.ά. Μείγμα Α+Β z=l, y L, y BL L N z Υγρό Α z=0, y o, y Bo Σχήμα. Κατανομή μερικής πίεσης ή συγκέντρωσης σε διάχυση σε στάσιμο αέριο. Σημειώσεις Μεταφοράς Μάζας 11
13 Όπως συζητήσαμε προηγουμένως, η ειδική γραμμομοριακή ροή κάθε συστατικού (στην κατεύθυνση z) είναι σταθερή σε όλη τη διαδρομή διάχυσης (δηλ. dn z /dz=0, αλλά και dn Bz /dz =0). Ειδικά για τις περιπτώσεις της μονομοριακής διάχυσης, η ειδική ροή για το «αδρανές» συστατικό Β είναι μηδέν, δηλαδή N 0. Το γεγονός αυτό μπορεί να τεκμηριωθεί αν εξετάσουμε τι συμβαίνει στη διεπιφάνεια των δύο φάσεων. Bz Για παράδειγμα, στην περίπτωση της εξάτμισης ο αέρας ούτε εκροφάται από το νερό, ούτε διαλύεται σε αυτό. Άρα, η ειδική ροή του στη διεπιφάνεια είναι ίση με μηδέν. Επειδή όμως η ειδική ροή είναι σταθερή παντού, αν σε κάποιο σημείο της διαδρομής διάχυσης έχει την τιμή μηδέν, τότε η τιμή της είναι παντού μηδέν. Στη διεπιφάνεια (π.χ. για εξάτμιση) έχουμε συνήθως y o =y s (ή αντίστοιχα 0 = s ), όπου y s είναι το γραμμομοριακό κλάσμα κορεσμού του Α (y s =p s /p, όπου p s είναι η τάση ατμών του Α στις συνθήκες του πειράματος και p η συνολική πίεση). Εάν y o >y L (όπως συμβαίνει συχνά και, μάλιστα, στις περισσότερες περιπτώσεις έχουμε y L =0), το υγρό Α εξατμίζεται και μεταφέρεται προς τα πάνω με διάχυση. Ισχύει προφανώς: Nz 0 και NBz 0 (1.4α) Ακόμη, η ειδική ροή του Α θα είναι σταθερή σε κάθε z (ή από την 1.0β): dn z 0 dz Nz σταθερή (1.4β) Η γενική σχέση της ειδικής ροής του συστατικού Α (νόμος του Fik) γράφεται: Nz D dy B yn Λόγω της κίνησης του Α z dz ή 1 dy N z D B 1 y dz (1.5) Είναι προφανές ότι η ειδική ροή του Α αυξάνει κατά 1/(1 y ) λόγω της συναγωγής (της μέσης κίνησης δηλ. της κύριας μάζας του μείγματος). Ολοκληρώνοντας την παραπάνω εξίσωση από 0 μέχρι L έχουμε yl L 1 DB 1 yl Nz dzd 0 B dy Nz ln y 1y 0 L 1 y 0 Υπενθυμίζεται εδώ ότι τα παραπάνω ισχύουν για σταθερή διατομή της διαδρομής διάχυσης. Εάν το (1.6) εμβαδόν της διατομής μεταβάλλεται και είναι συνάρτηση της απόστασης z, Α(z), τότε η σταθερή, αλλά ο όρος Nz(z) είναι σταθερός και η εξ. (1.6) γράφεται ως yl L 1 1 z B 0 (z) 1 y y N (z) dz D dy 0 N z δεν είναι (1.6α) Συχνά χρειαζόμαστε και την κατανομή της συγκέντρωσης. Για σταθερή πίεση, θερμοκρασία, ολική συγκέντρωση και διαχυτότητα από την Εξ. (1.5), και επειδή dn / dz 0, προκύπτει: d 1 dy 0 dz 1 y dz Ολοκληρώνοντας δύο φορές την παραπάνω διαφορική εξίσωση έχουμε: ln(1 y ) C1z C Οι σταθερές C 1 και C υπολογίζονται με τη χρήση των συνοριακών συνθηκών: Σ.Σ. 1: στο z=0, y =y o z (1.7) Σημειώσεις Μεταφοράς Μάζας 1
14 Σ.Σ. : στο z=l, y =y L Οπότε η κατανομή του γραμμομοριακού κλάσματος (ή της συγκέντρωσης) του Α για σταθερή διατομή της στήλης γίνεται: 1y 1yL 1yo 1yo Επειδή y B =1 y μπορούμε να γράψουμε επίσης: z/l z/l (1.8) y B y BL (1.9) ybo ybo Από την κατανομή της συγκέντρωσης μπορεί να υπολογιστεί (για σταθερή πάντα διατομή της στήλης) η ειδική γραμμομοριακή ροή του Α στο z=0: DB 1 yl Nz Nz ln z 0 (1.6) L 1 yo Η παραπάνω σχέση συμπίπτει προφανώς με την εξ. (1.6). Η μέση λογαριθμική συγκέντρωση του Β (ουσιαστικά η μέση τιμή της y Β κατά μήκος της διαδρομής διάχυσης) ορίζεται ως: ybl ybo y oyl yb,lm ybl 1 yl ln ln ybo 1 yo και επομένως (αναφερόμαστε πάντα σε σταθερή επιφάνεια): N z DB 1 (y 0 y L) L y Η ποσότητα που περικλείεται από την B,lm κόκκινη γραμμή είναι η ειδική ροή του Α (1.30) σε αραιά διαλύματα. Ο όρος (1/y B,lm ) δίνει την επίδραση της συναγωγής. Επειδή n/v p/rt και y p /p, η παραπάνω σχέση μπορεί να γραφεί και με τη μορφή: N D p p p B o L z (1.31α) L RT pb,lm Η ίδια εξίσωση μπορεί να εφαρμοστεί και για διάχυση σε μία στάσιμη, υποθετική «στιβάδα» (υμένα film) πάχους δ (βλ. Σχήμα 3), η οποία θεωρείται ότι αντιπροσωπεύει τη συνολική αντίσταση της μεταφοράς μάζας (που οφείλεται στο συνδυασμό μοριακής διάχυσης και διάχυσης λόγω ανάμειξης από το ρευστό που κινείται): DB p ps p Nz. (1.31β) RT pb,lm Εφαρμογές: απορρόφηση, αφύγρανση, εξάτμιση κτλ. Αέρας δ z=l, y δ =0 z=0, y o =y s Υγρό Α Σχήμα 3. Το μοντέλο του λεπτού υμένα για μεταφορά μάζας του συστατικού Α σε ένα κινούμενο αέριο ρεύμα. Σημειώσεις Μεταφοράς Μάζας 13
15 Τέλος, η παραπάνω εξίσωση χρησιμοποιήθηκε για τη περιγραφή του συντελεστή μεταφοράς μάζας με συναγωγή με την λεγόμενη θεωρία υμένα (film theory, film onept). Βασίζεται στο γεγονός ότι η συνολική αντίσταση στη διάχυση από την υγρή επιφάνεια προς την κύρια μάζα του αέρα μπορεί να υποτεθεί ότι συμβαίνει σε έναν στάσιμο υμένα σταθερού πάχους δ. Με άλλα λόγια, το δ είναι ένα φανταστικό πάχος το οποίο αντιπροσωπεύει την ίδια αντίσταση στη μοριακή διάχυση για τη συνδυασμένη διεργασία. Πρόβλημα 1. Εξάτμιση από ανοικτή δεξαμενή. Ανοικτή κυκλική δεξαμενή διαμέτρου 6 m περιέχει βενζόλιο θερμοκρασίας C. Η κύρια αντίσταση στην εξάτμιση του βενζολίου στο περιβάλλον οφείλεται στη διάχυση διαμέσου του αέρα. Η αντίσταση αυτή μπορεί να παρασταθεί από ένα υποθετικό στρώμα στάσιμου αέρα πάχους 5 mm, και η συγκέντρωση βενζολίου στον αέρα έξω από το στάσιμο στρώμα είναι αμελητέα. Η τάση ατμών του βενζολίου στους C είναι 100 mm Hg και η διαχυτότητα στους 0 C είναι 0, m /s. Πόση είναι η ημερήσια απώλεια βενζολίου από τη δεξαμενή; Λύση: Είναι προφανές ότι έχουμε να κάνουμε με διάχυση μέσα σε στάσιμο αέριο Β. Αρχικά θα πρέπει να διορθώσουμε το συντελεστή διάχυσης: ~1,75 1,75 Po T 95 D Do 0,7710 0,8810 m /s P To 73 Οι μερικές πιέσεις είναι: p 0,0 atm, s,1 benzol p p 100 / 760 0,1315 atm p pp 1 atm B,, p p p 0,8685 atm B,1,1 Από τη σχέση (1.31β) m 0,8810 1,0atm DBp pb, s 1 5 kmol N z ln ln 1, RT pb,1 m atm 0,8685 ms 0, K 0, 005 m Kkmo l ΜΒ (benz.)=6 1, ,00797=78,11 kg/kmol, και 5 N w M 78,11 3 1, 0310, kg/s =185 kg/day z z Πρόβλημα. Ψευδο μόνιμες συνθήκες Μέτρηση διαχυτότητας. Σε πολλές διεργασίες η διεπιφάνεια υγρούαερίου μετατοπίζεται με σχετικά αργό ρυθμό. Σε αυτές τις περιπτώσεις μπορούμε να υποθέσουμε τις λεγόμενες «ψευδο μόνιμες» συνθήκες (pseudo steady state onditions), δηλ. ότι η ειδική ροή του συστατικού παραμένει σταθερή για κάποιο μικρό χρονικό διάστημα. Με την υπόθεση αυτή μπορούμε να μετρήσουμε τη διαχυτότητα ενός αερίου και των ατμών ενός υγρού με το λεγόμενο «κελί rnold». Να υπολογιστεί ο συντελεστής διάχυσης του τολουολίου στον αέρα από την εξής μέτρηση: κατακόρυφος λεπτός γυάλινος σωλήνας γεμίζεται με τολουόλιο μέχρι σημείου που απέχει z 0 =1,9 m από το ανοικτό άκρο της κορυφής. Ύστερα από 75 ώρες η επιφάνεια του υγρού έχει κατέβει στα z F =7,9 m από την κορυφή. Η διάμετρος του σωλήνα είναι 0,3 m, η θερμοκρασία του πειράματος παραμένει σταθερή στους 39,4 C, η πυκνότητα του τολουολίου είναι 0,85 g/m 3, το μοριακό βάρος 9.1 και η τάση ατμών του στις προαναφερθείσες συνθήκες είναι 57,3 mmhg. Σημειώσεις Μεταφοράς Μάζας 14
16 Λύση: Σε κάθε z θεωρούμε ότι ισχύει η Εξ. (1.30). Σε μία διαφορική φέτα Δz στην επιφάνεια του υγρού, υποθέτοντας ότι η ειδική γραμμομοριακή ροή αέρας είναι N, σε χρόνο dt εξατμίζονται Nz d dt kmol του Α ( είναι το d εμβαδόν της διατομής του λεπτού σωλήνα). Αυτά τα γραμμομόρια προέρχονται από την εξάτμιση της υγρής «φέτας» dz, δηλ. (ddz) ρ,l / M, όπου ρ,l είναι η πυκνότητα του υγρού τολουολίου και Μ Α το μοριακό του βάρος, δηλ. ρ,l dz N z M dt (i) Από την Εξ. (1.6) και την (i) προκύπτει εύκολα ότι: z F z z o y y 1 DB dtβz dz (ii) Σχήμα 4. Το κελί rnold. ρ,l 1 όπου ο όρος β= M 1 y ln 1 y1 είναι μία σταθερά. Ολοκληρώνοντας την Εξ. (ii) από t=0 μέχρι t και από z o μέχρι z F έχουμε: zf z0 DB tβ (iii) 3 Τα δεδομένα του προβλήματος είναι: y 0, y 57,3 / 760, p / RT 0,039 kmol / m, από τα οποία 1 προκύπτει: D B m /s Διάχυση με ετερογενή κατάλυση (Diffusion with heterogeneous hemial reation) Αρχικά να διευκρινίσουμε: ομοιογενής αντίδραση (homogeneous reation) είναι η αντίδραση που συμβαίνει ομοιόμορφα σε όλη τη μάζα της φάσης (δηλαδή είναι αντίστοιχη διεργασία με την παραγωγή θερμότητας). Από την άλλη μεριά, η ετερογενής αντίδραση συμβαίνει στη διεπιφάνεια μιας φάσης, δηλαδή αποτελεί ένα διεπιφανειακό φαινόμενο και μπορούμε να το χειριστούμε ως συνοριακή συνθήκη. Η παρουσία του καταλύτη επιταχύνει σημαντικά τον ρυθμό της αντίδρασης, χωρίς όμως ο καταλύτης να συμμετέχει σε αυτήν. Θεωρούμε ένα σχετικά μεγάλο επίπεδο σωματίδιο καταλύτη, το οποίο περιβάλλεται από έναν στάσιμο αέριο υμένα πάχους δ, μέσα από τον οποίο το αντιδρών Α θα πρέπει να διαχυθεί προς την επιφάνεια του καταλύτη, όπως απεικονίζεται στο Σχήμα 5. Υποθέτουμε ότι η αντίδραση διάσπασης B συμβαίνει στην επιφάνεια του καταλύτη, και η αντίδραση αυτή είναι ακαριαία, δηλαδή πάνω στην επιφάνεια η συγκέντρωση του Α είναι μηδέν. Το προϊόν Β θα πρέπει να διαχυθεί μέσα στον υμένα πάχους δ και να εξέλθει στο τυρβώδες πεδίο, μακριά από τη στερεή επιφάνεια. Στην πραγματικότητα αυτός ο υμένας δεν υπάρχει, αλλά είναι χρήσιμος στην ανάλυση πραγματικών προβλημάτων. Επειδή τώρα από ένα μόριο Α προκύπτουν δυο μόρια Β και το Α και το Β ρέουν σε αντίθετη κατεύθυνση ισχύει: N Bz N z [Στη συσχέτιση μεταξύ των N z και N Bz θα πρέπει να δοθεί ιδιαίτερη προσοχή από τους φοιτητές, αφού συχνά γράφουν την αντίστροφη σχέση!] Σημειώσεις Μεταφοράς Μάζας 15
17 z=0 y Bο y ο Υποθετική στιβάδα του αερίου z z=δ B y Βδ B Β δ Σχήμα 5. Διάχυση με ετερογενή αντίδραση. Αντικαθιστώντας την παραπάνω σχέση στη γενική εξίσωση της ειδικής γραμμομοριακής ροής του συστατικού Α (γενικευμένος νόμος του Fik για δυαδικό μείγμα) προκύπτει : N 1 dy z D B (1.3) 1 y dz Όπως και στις δύο προηγούμενες περιπτώσεις διάχυσης σε δυαδικό σύστημα ανάμεσα σε δύο παράλληλα επίπεδα, η ειδική γραμμομοριακή ροή είναι σταθερή σε όλο το πάχος του υμένα δ, δηλαδή : dn z 0 dz ή N z =σταθ. (1.4β) Ολοκληρώνοντας την Εξ. (1.3) από z=0 και y =y 0 στο z=δ και y =0 παίρνουμε: DB 1 DB Nz ln ln1y0 (1.33) 1y0 Για να βρούμε την κατανομή τη συγκέντρωσης, εργαζόμαστε όπως στα προηγούμενα παραδείγματα. dnz Εισάγουμε στη διαφορική εξίσωση 0 dz το N z από την Εξ. (1.3) και ολοκληρώνουμε δυο φορές, οπότε παίρνουμε (για σταθερή και σταθερή D ): B dy 0 ln1 y C1z C d 1 dz 1 y dz Οι σταθερές C και C υπολογίζονται από τις συνοριακές συνθήκες : 1 Σ.Σ. 1: στο z=0, y y0 Σ.Σ. : στο z=δ, y 0 Το τελικό αποτέλεσμα για την κατανομή της συγκέντρωσης είναι: 1 y 1 y z 1 0 Μικρότερη ροή από ότι στην ισογραμμομοριακή αντιδιάχυση, (1.34) Επίσης, αφού η ειδική γραμμομοριακή ροή του συστατικού Α μέσω του υμένα είναι σταθερή σε όλο το δ, αυτή μπορεί να υπολογιστεί στη θέση z=0 και να πάρουμε από άλλη προσέγγιση την Εξ. (1.33): D 1 D N N ln ln1y B B z z 0 z0 1y0 (1.33) Σημειώσεις Μεταφοράς Μάζας 16
18 Εδώ θα πρέπει να διευκρινίσουμε ότι, αν και η μετατροπή του Α σε Β γίνεται ακαριαία στην καταλυτική επιφάνεια, η συνολική διεργασία δεν είναι τόσο γρήγορη λόγω του συγκεκριμένου ρυθμού διάχυσης που συμβαίνει «σε σειρά» με την αντίδραση. Σε μια τέτοια διεργασία λέμε ότι η διάσπαση (αντίδραση) του Α σε Β ελέγχεται από τη διεργασία της διάχυσης (diffusion ontrolled proess). Είναι αρκετά εύκολο τώρα να γενικεύσουμε την αντίδραση μετατροπής: βb (1.35) όπου β κάποιος θετικός αριθμός, ακέραιος (δηλώνει διάσπαση του μορίου Α σε β μόρια του Β) ή αντίστροφος ακέραιου αριθμού (δηλώνει πολυμερισμό). Η σχέση (1.3) γίνεται : N 1 dy z D B (1.36) 1 y 1 β dz Χρησιμοποιώντας τις ίδιες οριακές συνθήκες προκύπτει για την κατανομή της συγκέντρωσης : z βy 1 1 βy 0, (1.37) ενώ η ειδική γραμμομοριακή ροή δίνεται από τη σχέση: 1 1 Nz DB ln δ1 β 11βy 0 Έτσι αν β= προκύπτει η σχέση (1.33), ενώ για β 1 / (δηλ. γίνεται πολυμερισμός) έχουμε: N D ln 1 z B δ 1 y 0 / (1.38) (1.39) Διάχυση με αργή ετερογενή αντίδραση (Diffusion with slow heterogeneous reation) Ας θεωρήσουμε τώρα ότι η αντίδραση B δεν είναι ακαριαία στην καταλυτική επιφάνεια (z=δ) και ότι ο ρυθμός με τον οποίο μετατρέπεται το Α είναι ανάλογος της συγκέντρωσης του Α στην επιφάνεια : N k ky (1.40) z 1 1 όπου k 1 είναι η σταθερά της (ψεύδο πρώτης τάξης) αντίδρασης (σε m/s). Μπορούμε να προχωρήσουμε όπως στο προηγούμενο παράδειγμα με την αντικατάσταση της δεύτερης Σ.Σ. ως εξής: Nz Σ.Σ. : στο z=δ, y (1.40α) k 1 όπου το N z είναι βεβαίως σταθερό σε όλο τον υμένα. Προφανώς ισχύει η Εξ. (1.3), από την οποία με ολοκλήρωση μπορούμε να πάρουμε τη σχέση για την ειδική γραμμομοριακή ροή : N /k z 1 1 N dzd dy z B 1 y 0 y 0 N D 1N /k B z 1 z ln 1y0 Σημειώσεις Μεταφοράς Μάζας 17 (1.41) Για την εύρεση της κατανομής της συγκέντρωσης δουλεύουμε πάλι όπως και στην περίπτωση της ενότητας 1.6.3, με τον υπολογισμό των σταθερών της ολοκλήρωσης με τη Σ.Σ. (Εξ. 1.40α) και την Σ.Σ. 1, δηλ. στο δ=0, y =y 0. Η σχέση για την κατανομή του γραμμομοριακού κλάσματος είναι: z z 1y 1 1y N k 1 z 1 0 (1.4)
19 Βεβαίως και από την Εξ. (1.41) μπορούμε να υπολογίσουμε το N z (Εξ. 1.41), αλλά με περισσότερη άλγεβρα. H Εξ. (1.41) είναι δύσκολο να λυθεί αναλυτικά. Όμως, αν το k 1 είναι αρκετά μεγάλο [δηλαδή, N z /k1 1], ο όρος ln 1 N z / k1 μπορεί να γραφεί ως ανάπτυγμα Taylor (για ε πολύ μικρό ln(1 ) 3 / / 3... ). Κρατώντας μόνο τον πρώτο όρο παίρνουμε τη σχέση: DB ln 1 y0 Nz (1.43) 1D B /k1 Η Εξ. (1.43) εκφράζει τον ρυθμό της διεργασίας που συνδυάζει διάχυση και αντίδραση. Ο αδιάστατος αριθμός DB περιγράφει την επίδραση του ρυθμού της επιφανειακής καταλυτικής αντίδρασης στη συνολική διεργασία kδ 1 διάχυσης αντίδρασης. Ο αντίστροφος του αδιάστατου αυτού αριθμού ονομάζεται αριθμός Damköhler ΙΙ (προς τιμήν του Gerhard Damköhler, ), II k 1 /DB χρόνος διάχυσης Da [ ] (1.44) D B /k1 χρόνος αντίδρασης II Προφανώς, καθώς ο αριθμός Da τείνει στο άπειρο προκύπτει η εξ. (1.39) Λάθη που απορρέουν από την Παράλειψη της Συναγωγής Όταν δεν λαμβάνεται υπόψη η επίδραση της συναγωγής (π.χ. όταν μελετάμε αραιά διαλύματα) ισχύει η εξ. (1.α): DB N z (ys y L ), (1.α) L ενώ, αν λάβουμε υπόψη τη συναγωγή στη μεταφορά μάζας ισχύει η εξ. (1.6): N D 1 y ln B L z L 1 ys (1.6) Το λάθος από τυχόν παράλειψη της συναγωγής σε κάποιο φυσικό πρόβλημα μπορεί να δειχθεί με το παράδειγμα του Σχήματος 6. Αέρας διέρχεται πάνω από σωλήνα που συνδέει δεξαμενή βενζολίου με αποτέλεσμα την εξάτμισή του. αέρας L, y L, p L =0 αέρας L, y L, p L =0 L s, y s, p s L s, y s, p s Βενζόλιο, 6 C Τάση ατμών βενζολίου Βενζόλιο, 60 C Τάση ατμών βενζολίου Σχήμα 6. Διάχυση σε στάσιμο αέριο για δύο διαφορετικές θερμοκρασίες. 1) Στους 6 C η τάση ατμών του βενζολίου είναι 37 mmhg. Άρα το γραμμομοριακό κλάσμα στη διεπιφάνεια είναι: Σημειώσεις Μεταφοράς Μάζας 18
20 p 37 p 760 s s ys 0,049 DB DB Nz Jz 0, ,049 L L Από την (1.) DB 1 0 DB Από την (1.30) Nz ln 0,050 L 1 0,049 L % Μικρό λάθος 395 ) Στους 60 C, έχουμε ps 395 mmhg ys 0, Από την (1.) D L B Nz 0,5 DB 1 0 DB Από την (1.30) Nz ln 0,73 L 1 0,5 L 40% Σημαντικό λάθος 1.8. Μεταβατική Μεταφορά Μάζας: Διάχυση σε Ημιάπειρη Πλάκα Μέχρι τώρα πραγματευτήκαμε προβλήματα σε μία διάσταση τα οποία μπορεί να προσομοιωθούν από διαφορικές εξισώσεις που λύνονται αναλυτικά σχετικά εύκολα. Σε αυτή την ενότητα θα συζητήσουμε ένα πρόβλημα διάχυσης ως προς δύο μεταβλητές, τον χρόνο και το μήκος, δηλ. το πρόβλημα που παριστάνεται από τον δεύτερο νόμο του Fik: t D z B (1.0ζ) Η διαφορική αυτή εξίσωση μπορεί να λυθεί αναλυτικά με διάφορους τρόπους, ανάλογα με τις συνοριακές και αρχικές συνθήκες: (α) με τη μέθοδο της υπέρθεσης (superposition method), (β) τη μέθοδο διαχωρισμού των μεταβλητών (separation of variables), (γ) με μετασχηματισμό Laplae και (δ) τη μέθοδο ομοιότητας. Εδώ θα συζητήσουμε μόνο την τελευταία μέθοδο. Η διάχυση σε ημιάπειρη πλάκα (unsteady diffusion in a semi infinite slab) βρίσκει εφαρμογή (σε μονοδιάστατη γεωμετρία) σε αέρια σε περίπτωση ισογραμμοριακής αντιδιάχυσης, σε στάσιμα υγρά και σε στερεά, σε περιπτώσεις δηλαδή όπου η ταχύτητα είναι μηδέν και δεν υπάρχει παραγωγή ή κατανάλωση συστατικού. Εφαρμογές που έχουμε διάχυση σε ημιάπειρο μέσο είναι η ξήρανση στερεών και οι διάφορες θερμικές και επιφανειακές κατεργασίες (π.χ. ενανθράκωση και εναζώτωση). Αναλυτική προσέγγιση για τη διάχυση σε στερεά γίνεται στο 5 ο Κεφάλαιο του βιβλίου «Φυσική Μεταλλουργία» του κ. Χαϊδεμενόπουλου. Θεωρούμε μια ημιάπειρη «πλάκα», η οποία αρχίζει από z=0 και εκτείνεται στο άπειρο, όπως παρουσιάζεται στο Σχήμα 7. Μπορεί να είναι στερεά, υγρή ή και αέρια «πλάκα». Παντού η συγκέντρωση του Α είναι,i. Σε χρόνο t 0 η πλευρά στο z=o εκτίθεται συνεχώς σε συγκέντρωση s. Θέλουμε να βρούμε την κατανομή της συγκέντρωσης ως προς το χρόνο και την απόσταση από την επιφάνεια. Αν και εκ πρώτης όψεως το φυσικό αυτό πρόβλημα φαίνεται να σπανίζει, σε μικρούς χρόνους ακόμη και μία μεμβράνη μπορεί να θεωρηθεί ημιάπειρο μέσο. Σε μεγάλους χρόνους βέβαια η μεμβράνη μπορεί να θεωρηθεί λεπτή, με την κατανομή της συγκέντρωσης να γίνεται γραμμική μέσα στη μεμβράνη. Η εύρεση της εξίσωσης που περιγράφει το παραπάνω πρόβλημα μπορεί να γίνει: (α) με ένα ισοζύγιο μάζας σε μια λεπτή φέτα όγκου ΑΔz: Σημειώσεις Μεταφοράς Μάζας 19
21 Συσσώρευση του Α Ρυθμός διάχυσης του Α Ρυθμός διάχυσης του Α στον όγκο ΑΔz προς στη στιβάδα στο z από το z+δz ή z Jz Jz t z zz (0,t) Δz Χρόνος z=0,i z Σχήμα 7. Κατανομή συγκέντρωσης σε μεταβατική διάχυση σε ημιάπειρο μέσο. Διαιρώντας με ΑΔz και για z0λαμβάνουμε J z t z Συνδυάζοντας την παραπάνω εξίσωση με τον νόμο του Fik (για αραιά διαλύματα/μείγματα) παίρνουμε τελικά B D (1.45α) t z Η εξίσωση αυτή, όπως έχει λεχθεί και προηγουμένως, συχνά ονομάζεται δεύτερος νόμος του Fik. Αντίστοιχα, σε μονάδες μάζας η εξ. (1.45α) γράφεται ως: ρ t D ρ B z (1.45β) (β) Η ίδια εξίσωση προκύπτει θεωρώντας την εξίσωση του ισοζυγίου μεταφοράς μάζας (Εξ. I.10, ΠΑΡΑΡΤΗΜΑ Ι, ή Εξ. 5.8Α, Πίνακας 5.4, βιβλίο του Brodkey) και διαγράφοντας τους μηδενικούς όρους. Η σχέση (1.45α) υπόκειται στις παρακάτω συνθήκες: Για t=0 και σε κάθε z:,i Για t>0 και για z=0:,s Για z,i (δηλ. το διαχεόμενο συστατικό διεισδύει μόνο σε μικρή απόσταση) Σημείωση: οι συγκεντρώσεις,i και,s παραμένουν πάντα σταθερές. Όπως έχει συζητηθεί προηγουμένως, αυτού του είδους η διαφορική εξίσωση με τις συγκεκριμένες συνθήκες λύνεται με τον ορισμό της μεταβλητής ομοιότητας ζ (η λύση δόθηκε από τον Boltzmann το 1894), Σημειώσεις Μεταφοράς Μάζας 0
22 z (1.46) 4Dt Η λύση της εξ. (1.45α) είναι :,i,s,s erf ή όπου,s erf exp s ds είναι η συνάρτηση σφάλματος της ζ. 0 Η συνάρτηση σφάλματος μπορεί να προσεγγιστεί από τις σχέσεις: 3 5 erf...) για 0, erf 1 (1...) για 1 4 4,i,i 1erferf (1.47) Σε πολλά πρακτικά προβλήματα, ο υπολογισμός της ειδικής ροής του συστατικού Α στην πλάκα έχει μεγαλύτερη σημασία από την κατανομή της συγκέντρωσης. Η ειδική ροή βρίσκεται από την Εξ. (1.46) και τον νόμο του Fik z D 4Dt,s,i J D e (1.48) z t Στο z=0: D J z0,s,i t (1.49) Αυτή η ειδική γραμμομοριακή ροή αντιστοιχεί στη χρονική στιγμή t. Η μέση τιμή της, από t=0 μέχρι τη χρονική στιγμή Τ, υπολογίζεται ολοκληρώνοντας την παραπάνω σχέση ως προς t και διαιρώντας δια Τ: D J z0,s,i T (1.49α) Πολλαπλασιάζοντας την J z0 επί τον ολικό χρόνο Τ (σε μονάδες SI) παίρνουμε τα kmol/m που έχουν διαχυθεί σε χρόνο Τ. Πόσο «άπειρη» όμως μπορεί να είναι η πλάκα για να ισχύουν οι προϋποθέσεις αυτής της λύσης; Ας εκτιμήσουμε το μήκος (από z=0), στο οποίο σε χρόνο t η διαφορά συγκέντρωσης έχει την αυθαίρετη τιμή 99,5% της (,i,s ):,s 0,995 erf 4 Dt,i,s 4Dt 4Dt Άρα για δεδομένο χρόνο t το απαιτούμενο μήκος είναι 4 Dt, ενώ για πλάκα μήκους θα ισχύει η υπόθεση της ημιάπειρης πλάκας μόνο για χρόνους μικρότερους από /16D. Μία άλλη ενδιαφέρουσα εφαρμογή του ου Νόμου του Fik είναι η λεγόμενη «διάχυση ή απόσβεση παλμού» (deay of a pulse). Για παράδειγμα, συγκεκριμένη ποσότητα άνθρακα, Μ/Α (άτομα/m, kmol/m, kg/m ) τοποθετείται με η μορφή επίστρωσης σε άκρο επιμήκους ράβδου από σίδηρο. Στη συνέχεια, μία παρόμοια ράβδος συγκολλάται στο επικαλυμμένο άκρο (Σχήμα 8). Ακολούθως το σύστημα υφίσταται Σημειώσεις Μεταφοράς Μάζας 1
23 ανόπτηση σε υψηλή θερμοκρασία, με αποτέλεσμα η διαχυτότητα του άνθρακα στον σίδηρο να αυξηθεί τάξεις μεγέθους. Επιθυμούμε να υπολογίσουμε την κατανομή συγκέντρωσης του άνθρακα (z,t) στις δύο ράβδους. Συμμετρική κατανομή της συγκέντρωσης γύρω από το z=0 z 0 z Σχήμα 8. Κατανομή συγκέντρωσης στην «απόσβεση» παλμού. Και σε αυτή την περίπτωση ισχύει ο δεύτερος νόμος του Fik: DB (1.45α) t z με τις ακόλουθες συνοριακές συνθήκες και την αρχική συνθήκη: Για t>0 και για z ±, 0 Για t>0 και για z=0, 0 z M Για t=0, δ(z) (οι μονάδες του δ(z) είναι οι αντίστροφες των μονάδων του z, δηλ. 1/m ή 1/m) Εδώ δ(z) είναι η συνάρτηση Dira, η οποία είναι παντού 0 εκτός από το z=0, όπου η τιμή της απειρίζεται. Ισχύει: δ(z)dz 1 Το πρόβλημα αυτό με τις παραπάνω συνθήκες μπορεί να λυθεί εύκολα με μετασχηματισμό Laplae και να πάρουμε τη λεγόμενη «λύση λεπτής στιβάδας» (thin film solution): z M/ 4Dt e 4Dt Αν η διάχυση γίνεται μόνο σε μία διεύθυνση, τότε προφανώς η είναι διπλάσια. Συχνά αυτή η λύση εφαρμόζεται στη διασπορά ρύπων. M/ (z,t) z Για z=0, τότε, όποτε μπορούμε να πάρουμε: exp. 4Dt (0,t) 4Dt Πάλι τίθεται το ερώτημα. Πόσο «ημιάπειρη» μπορεί να είναι η πλάκα; Αν υποθέσουμε ότι μέσα στην πλάκα θα υπάρχει το 99% της αρχικής μάζας, τότε 4 Dt. Σημειώσεις Μεταφοράς Μάζας
24 1.9. Μοριακές Διαχυτότητες Η διαχυτότητα είναι μέτρο της «αντίστασης» που συναντά ένα μόριο καθώς μετακινείται σε ένα μέσο κάτω από τη επίδραση της «ωθούσας δύναμης», δηλαδή της κλίσης της συγκέντρωσης. Είναι σημαντικό να έχουμε πάντα στο μυαλό μας την τάξη μεγέθους της διαχυτότητας στα πιο συνηθισμένα συστήματα. Τυπικές τιμές διαχυτότητας Για αέρια 10 1 m /s [0,1 1 m /s σε 1 atm, π.χ. για το σύστημα αέρας νερό στους 0 C, D B =0,178 m /s] Για υγρά 10 5 m /s [για οργανικά υγρά, υδράργυρο, τηγμένο σίδηρο εξαίρεση διαλυμένες ουσίες μεγάλου μοριακού βάρους όπως η αιμοσφαιρίνη, το πολυστυρένιο, η αλμπουμίνη κτλ.]. Αυτή η τάξη μεγέθους ισχύει και για τα αέρια στα υγρά (π.χ. στους 5 C, για Ο σε νερό, D B =, m /s ) Για πολυμερή 10 8 m /s [μεγάλη εξάρτηση από τη θερμοκρασία] Για στερεά m /s [πολύ αργή διάχυση, ισχυρή εξάρτηση από τη θερμοκρασία] Αέρια σε στερεά m /s Υπολογισμός Διαχυτότητας Αερίων Οι διαχυτότητες των αερίων μπορούν να υπολογιστούν με τη βοήθεια της κινητικής θεωρίας των αερίων από τη σχέση 3/ 3 1/ T κbn o 3/ P M D (1.50) όπου Τ είναι η απόλυτη θερμοκρασία, P η πίεση του συστήματος, κ Β η σταθερά Boltzmann, Ν ο ο αριθμός vogadro (6,0 013 μόρια/mol), M το μοριακό βάρος του Α και σ Α η διάμετρος του σφαιρικού μορίου κατά Lennard Jones. Από αυτή τα σχέση έχουμε: 1 DB P 3/ και T DB Για μη πολικά και μη αντιδρώντα μεταξύ τους μόρια (διάχυση του Α στο Β ή και αντίστροφα) προτείνεται η σχέση των Chapman Enskog 3/ 0, T 1 1 DB (1.51) ΩP B B D M M όπου σ ΑΒ είναι η «διάμετρος σύγκρουσης» [σ ΑΒ =(σ Α +σ Β )/ σε Å, μία παράμετρος Lennard Jones] και Ω D είναι το «ολοκλήρωμα σύγκρουσης» για τη διάχυση, το οποίο υπολογίζεται από πίνακες ως συνάρτηση της αδιάστατης θερμοκρασίας BT/ B ( B B, ε ΑΒ η μέγιστη ενέργεια έλξης μεταξύ δύο μονοατομικών μορίων, η δεύτερη παράμετρος Lennard Jones). Η θερμοκρασία είναι σε Κ και η υπολογιζόμενη διαχυτότητα σε m /s. Σημειώνεται ότι στα αέρια η διαχυτότητα δεν εξαρτάται από τη συγκέντρωση του συστατικού. H σχέση αυτή δίνει καλά αποτελέσματα για τα περισσότερα συστήματα αερίων. Έχουν επίσης προταθεί και πολλές εμπειρικές ή ημι εμπειρικές συσχετίσεις. Μία από αυτές είναι η σχέση των Fuller, Shetter & Giddings (1966), η οποία χρησιμοποιείται όταν δεν υπάρχουν δεδομένα για τις παραμέτρους Lennard Jones: Σημειώσεις Μεταφοράς Μάζας 3
25 1,75 1/ 3 T (1/M 1/M B) B B 1/3 1/3 D D 10 P B (1.5) όπου Τ σε Κ, P σε atm, D B σε m /s, ενώ είναι ο ατομικός όγκος διάχυσης (βρίσκεται από πίνακες προσθέτοντας του όγκους διάχυσης ατόμων ή δομικών μονάδων). Οι προηγούμενες σχέσεις χρησιμοποιούνται για χαμηλές πιέσεις (αραιά αέρια). Για αέρια σε υψηλή πίεση μπορεί να χρησιμοποιηθεί (με προσοχή όμως) η σχέση: DD / (1.53) o o όπου ο δείκτης 0 δηλώνει ιδιότητες σε χαμηλή πίεση αλλά στην ίδια θερμοκρασία. Υπολογισμός της διαχυτότητας στα υγρά Στα υγρά η κινητική θεωρία δεν έχει αναπτυχθεί σε ικανοποιητικό επίπεδο ώστε να προβλέπει τις διαχυτότητες. Η κυρίαρχη θεωρία βασίζεται σε ένα υδροδυναμικό μοντέλο, αλλά οι προβλέψεις της δεν είναι πάντα ικανοποιητικές. Μία σχετικά απλή σχέση από την υδροδυναμική θεωρία είναι η συσχέτιση Stokes Einstein: DBμB 1 (1.54) κt B 6πR όπου μ Β είναι το ιξώδες του διαλύτη και R η ακτίνα του διαλυμένου «σωματιδίου». Η σχέση ισχύει για μεγάλα μόρια σε διαλύτες μικρού μοριακού βάρους (>1000) ή για αιωρούμενα κολλοειδή σφαιρικά σωματίδια. Αντίστοιχες σχέσεις μπορούν να γραφούν και για μη σφαιρικά σωματίδια. Παρατηρούνται μεγάλες αποκλίσεις σε ιξώδη υγρά. Στη βιβλιογραφία έχουν προταθεί πολλές εμπειρικές ή ημιεμπειρικές σχέσεις. Μία από αυτές είναι η συσχέτιση των Wilke Chang, που ισχύει για αραιά διαλύματα μη ηλεκτρολυτών: D 8 1/ B B 0.6 BV 7,4 10 ( M ) T (σε m /s) (1.55) όπου μ Β το ιξώδες του διαλύτη σε p, Τ η απόλυτη θερμοκρασία (σε Κ), είναι η αδιάστατη συνδετική παράμετρος (solvent assoiation fator) για τον διαλύτη Β (=,6 για το νερό, 1,9 για τη μεθανόλη, 1,5 για την αιθανόλη και 1,0 για το βενζόλιο), Μ Β το μοριακό βάρος του διαλύτη και V ο γραμμομοριακός όγκος της διαλυμένης ουσίας στο σημείο ζέσεως, που δίνεται από πίνακες (σε m 3 /mol ή m 3 /kmol). H Εξ. (1.55) δίνεται και μονάδες SI. Ο συντελεστής διάχυσης στα υγρά επηρεάζεται από τη συγκέντρωση της διαλυμένης ουσίας και έχουν προταθεί αρκετές προσεγγίσεις για τη διόρθωσή του. Υπολογισμός της διαχυτότητας στα στερεά Η εκτίμηση της διαχυτότητας στα στερεά δεν μπορεί να είναι ακριβής και οι τιμές της διαχυτότητας βασίζονται μόνο σε πειραματικές μετρήσεις. Στα στερεά οι διαχυτότητες μπορούν να διαφέρουν περισσότερο από 10 10, σε αντίθεση με τα αέρια όπου η μέγιστη διαφορά είναι της τάξης του 10. Επιπλέον, η εξάρτηση της διαχυτότητας από τη θερμοκρασία είναι ιδιαίτερα μεγάλη και μη γραμμική. Για παράδειγμα, η διαχυτότητα του υδρογόνου στο σίδηρο είναι 1, m /s στους 10 C, 11, m /s στους 50 C και m /s στους 100 C. Συχνά, η επίδραση της θερμοκρασίας μπορεί να παρασταθεί από μία εξίσωση τύπου rrhenius D B D exp[ E/RT] (1.56) o Σημειώσεις Μεταφοράς Μάζας 4
26 όπου D B είναι η διαχυτότητα του συστατικού Α στο στερεό Β, D o ένας προεκθετικός παράγοντας, E η ενέργεια ενεργοποίησης (J/mol), R η σταθερά των αερίων και Τ η απόλυτη θερμοκρασία σε Κ Διάχυση σε στερεά Στα στερεά η διάχυση αποτελεί το μηχανισμό με τον οποίο συμβαίνουν πολλές σημαντικές διεργασίες, όπως για παράδειγμα η σκλήρυνση του χάλυβα, η «νόθευση» (doping εισαγωγή προσμίξεων) καθαρών ημιαγωγών, η οξείδωση των μετάλλων, η κατάλυση, η γυψοποίηση του μαρμάρου και η ξήρανση στερεών. Μερικά άλλα παραδείγματα διάχυσης σε στερεά μέσα: Θερμική επεξεργασία μετάλλων κραμάτων Διάχυση και καταλυτική αντίδραση σε πορώδη υλικά. Ιδιαίτερα σημαντική στις διεργασίες κατάλυσης. Διεργασίες απορρόφησης (π.χ. χρωματογραφία) Δευτερογενής ανάκτηση πετρελαίου Επεξεργασία στερεών σε μεγάλη θερμοκρασία Διεργασίες ξήρανσης ξυλείας, τροφίμων κτλ. Η διεργασία ξήρανσης τροφίμων ή φαρμάκων «freeze drying» (λυοφιλίωση) εξαρτάται από τη μεταφορά του νερού ατμού από την πορώδη μάζα του αποξηραμένου υλικού. Διεργασίες με μεμβράνη (UF, NF, RO): μπορεί να θεωρηθεί ροή σε πορώδη μέσα Μικροπορώδεις δομές σε ζώντες οργανισμούς (π.χ. οστά). Η πρόβλεψη της μεταφοράς αερίων ή υγρών σε πορώδη μέσα είναι δύσκολη, αλλά και προκλητική συνάμα. Η μάζα μεταφέρεται σε πορώδη μέσα με διάφορους μηχανισμούς: (i) Κανονική διάχυση (εξισώσεις Maxwell Stefan) (ii) Διάχυση Knudsen (iii) Ιξώδης ροή σύμφωνα με την εξίσωση Hagen Poiseuille (iv) Επιφανειακή διάχυση (π.χ. μέσω της επιφάνειας των κρυσταλλικών κόκκων και όχι μέσα από τη κρυσταλλική δομή) (v) Θερμική διάχυση. Τέλος, μία ακόμη δυσκολία της διάχυσης σε πορώδη μέσα προέρχεται από το γεγονός της αλλαγής της δομής των πορωδών μέσων κατά την προσθήκη ή την απομάκρυνση ουσιών από αυτά. Για παράδειγμα, με τη ξήρανση πολλά από αυτά τα μέσα συρρικνώνονται. Διάχυση Knudsen Όταν οι πόροι σε ένα πορώδες υλικό είναι μικροί, τα μόρια ενός ιδανικού μονοατομικού αερίου θα συγκρούονται συχνότερα με τα τοιχώματα, ενώ δεν θα συγκρούονται τόσο έντονα μεταξύ τους. Η κίνηση αυτή είναι σημαντική όταν η μέση ελεύθερη διαδρομή των μορίων, λ C, είναι αρκετά μεγαλύτερη από τη διάμετρο του πόρου d, δηλ. λ C >>d, το οποίο μπορεί να συμβεί για μικρή πυκνότητα του αερίου. Ο αριθμός Knudsen ορίζεται ως εξής: Kn=λ C /d. Για Kn>100 η διάχυση Knudsen είναι σημαντική. Για τα υγρά, των οποίων η μέση ελεύθερη διαδρομή των μορίων είναι της τάξης των μερικών Å, ο αριθμός Kn είναι μικρός και η διάχυση Knudsen ασήμαντη. Αντίθετα, σε πολλά αέρια (σε χαμηλές πιέσεις) η διάχυση Knudsen Σημειώσεις Μεταφοράς Μάζας 5
27 είναι σημαντική. Για παράδειγμα, η μέση ελεύθερη διαδρομή των μορίων του υδρογόνου στους 300 C και στη 1 atm είναι μεγαλύτερη από 000 Å και η λ C των μορίων του αζώτου στους 0 C και στη 1 atm περίπου 600 Å. Υπάρχουν πολλές περιπτώσεις πορωδών μέσων (π.χ. στην κατάλυση), των οποίων η διάμετρος των πόρων είναι πολύ μικρότερη από τις παραπάνω τιμές της λ C. Η διάχυση Knudsen μπορεί να περιγραφεί από τη σχέση: d Nz DKn (1.57) dz όπου D Κn είναι η διαχυτότητα Knudsen, η οποία όμως δεν αποτελεί καταστατική ιδιότητα όπως η διαχυτότητα. Η παραπάνω σχέση δεν περιλαμβάνει συναγωγή. Για αραιά διαλύματα η διαχυτότητα Knudsen είναι ανεξάρτητη της πίεσης και δίνεται σε m /s από τη σχέση: D 4,850d T/M (1.58) Kn όπου d είναι η διάμετρος των πόρων σε m, T η θερμοκρασία σε Κ και M το μοριακό βάρος του αερίου σε g/mol. Αν δύο αέρια διαχέονται σε ροή Knudsen, τότε ο λόγος των ροών τους είναι αντιστρόφως ανάλογος με την τετραγωνική ρίζα των μοριακών τους βαρών (Νόμος του Graham): N N B MB M 1/. (1.59) Επιφανειακή Διάχυση Ο τύπος αυτός της διάχυσης είναι σημαντικός στην κατάλυση αν και η διασάφηση των φαινομένων είναι προβληματική. Με την επιφανειακή διάχυση γίνεται προσπάθεια να εξηγηθεί γιατί παρατηρούνται μεγαλύτεροι ρυθμοί διάχυσης από ότι σε κανονική ροή. Έτσι, η πραγματική διάχυση σε ένα πόρο μπορεί να γραφεί ως:,surfae,kn J J J (1.60) όπου ο όρος J,surfae εκφράζει την ταχεία, επιφανειακή διάχυση στα τοιχώματα του αγωγού. Διάχυση σε Πορώδη μέσα Πορώδες μέσο: ετερογενές υλικό που αποτελείται από το στερεό σκελετό (πορώδες σύστημα) και τους συνδεδεμένους πόρους. Οι πόροι γεμίζονται με : Αέρα μη διαβρέχον ρευστό Νερό διαβρέχον ρευστό Πετρέλαιο Ορισμός του πορώδους (Porosity / void fration), ε: όγκος πόρων στον στοιχειώδη όγκο ε στοιχειώδης όγκος Η μοριακή διάχυση μέσω της δαιδαλώδους διαδρομής μέσα στους πόρους (και όχι διαμέσου του στερεού υλικού) μπορεί να περιγραφεί μέσω μιας ενεργού διαχυτότητας D eff (effetive diffusivity): o L o, το μήκος διάχυσης >>L o Σημειώσεις Μεταφοράς Μάζας 6
28 d dz Η ενεργός διαχυτότητα D eff δίνεται είτε από τη σχέση: N Deff (1.61) Deff D (1.6) όπου D η διαχυτότητα μέσα στους πόρους, είτε από τη σχέση: όπου L o Deff D D (1.63) είναι ο συντελεστής στρεβλότητας (tortuosity). Ο συντελεστής αυτός παίρνει υπόψη το πραγματικό μήκος των πόρων ανά μονάδα μήκους στη διεύθυνση της διάχυσης, αποτελεί εμπειρική παράμετρο και παίρνει συνήθως τιμές από το μέχρι το 6, με μέση τιμή το 3. Αντίθετα, το πορώδες μετριέται πειραματικά με προσρόφηση αζώτου ή υδραργύρου. Διάχυση σε Πορώδη Στερεά Στην περίπτωση περιοδικά παρατεταγμένων σφαιρών η διάχυση γίνεται από ανοίγματα, αλλά και μέσα από το στερεό. Η ενεργός διαχυτότητα για αραιά, «ιδανικα» αιωρήματα μπορεί να υπολογιστεί επακριβώς: s D D eff s D Ds D (1.64) D s Ds D Ds D όπου D είναι η διαχυτότητα ανάμεσα στα ανοίγματα, D s η διαχυτότητα διαμέσου των σφαιρών και s το κλάσμα όγκου των σφαιρών. Η D eff εξαρτάται από το s αλλά όχι από τη διάμετρο των σφαιρών. Μπορούμε να διακρίνουμε δύο οριακές περιπτώσεις: 1) Στις περισσότερες περιπτώσεις το D s μικρό ή μηδέν: D 1 eff s (1.65) D s 1 Deff Για παράδειγμα : s, δηλαδή 40% μικρότερο D 5 ) Για Ds (πολύ γρήγορη διάχυση μέσα στις σφαίρες): Deff 1s 1 Deff και για s 4. D 1 s D Οι παραπάνω θεωρητικές σχέσεις έχουν περιορισμένες εφαρμογές στην πράξη. Σημειώσεις Μεταφοράς Μάζας 7
29 1.11. Άλλες Περιπτώσεις Διάχυσης Διάχυση και χημική αντίδραση στο εσωτερικό πορώδους καταλύτη Μέχρι τώρα πραγματευτήκαμε απλές γεωμετρίες. Πως όμως μπορούμε να περιγράψουμε τη διάχυση και τη χημική αντίδραση ενός αερίου προς ένα άλλο που συμβαίνει συχνά στο εσωτερικό ενός (π.χ. σφαιρικού) καταλύτη, όπως απεικονίζεται στο Σχήμα 9; Αρχικά μπορούμε να θεωρήσουμε μία «ψευδο ομοιογενή» αντίδραση πρώτης τάξης, που συμβαίνει σε όλη τη μάζα του καταλύτη. Έτσι, η γραμμομοριακή κατανάλωση (αρνητική παραγωγή) του συστατικού Α, C R kα, όπου,g 1 1 C,G, δίνεται από την κινητική της αντίδρασης πρώτης τάξης k είναι η σταθερά της αντίδρασης και α η ενεργός επιφάνεια ανά μονάδα όγκου. (Σημειώνεται ότι η κινητική της αντίδρασης μηδενικής τάξης είναι C k. ) Πως πραγματευόμαστε τη,g o διάχυση στους πόρους; Θεωρούμε πάλι ένα «ψευδο ομοιογενές» σύστημα με «ενεργό διαχυτότητα» D eff (effetive diffusivity) του συστατικού Α στο πορώδες μέσο. Ο περίπλοκος μηχανισμός διάχυσης στους πόρους (διάχυση Fik, διάχυση Knudsen κ.α.) λαμβάνεται υπόψη μέσω της D eff. Η D eff προσδιορίζεται πειραματικά και εξαρτάται από την πίεση, τη θερμοκρασία και το πορώδες του καταλύτη. Στο συγκεκριμένο πρόβλημα θεωρούμε ότι η συγκέντρωση του Α στην επιφάνεια του καταλύτη είναι R και ότι το συστατικό αυτό διαχέεται μέσα από τις δαιδαλώδεις διόδους στον καταλύτη όπου μετατρέπεται σε Β. R ΑΒ Μέσα στον καταλύτη ΑΒ πόροι R στερεό Σχήμα 9. Σχηματική απεικόνιση διάχυσης και χημικής αντίδρασης στο εσωτερικού καταλυτικού σωματιδίου. Είτε από ένα ισοζύγιο μάζας σε κατάλληλο διαφορικό κέλυφος ή από τις σχέσεις μεταφοράς μάζας για σταθερή μαζική συγκέντρωση (αφού πρακτικά δεν αλλάζει η πυκνότητα του καταλύτη με τη διάχυση του αερίου), η διαφορική εξίσωση της μεταφοράς μάζας στο παραπάνω σύστημα (με την αντικατάσταση του D B από την ενεργό διαχυτότητα D eff ) είναι: 1 d d D r C k r dr dr eff,g 1 d με Nr Deff dr Οι συνοριακές συνθήκες που ισχύουν για τη συγκεκριμένη γεωμετρία είναι: Σ.Σ 1: για rr, R d Σ.Σ. : για r0, 0 ή η έχει συγκεκριμένη τιμή. dr Η λύση της παραπάνω εξίσωσης μπορεί να γίνει με τη γνωστή τεχνική της αλλαγής της μεταβλητής Σημειώσεις Μεταφοράς Μάζας 8
30 Άρα k k r D D 1 df 1 df 1 f(r) f ή f, όπου R dr eff dr eff k k fe e osh r sinh Με εφαρμογή των Σ.Σ. προκύπτει: R r r R r Deff r Deff R sinhr r sinhr (1.66) Στη μελέτη αυτού του προβλήματος μάς ενδιαφέρει συνήθως η συνολική ροή του συστατικού Α στο r=r: d W 4R N 4R D 4RD 1Roth R (1.67),R R eff eff R dr rr Το αποτέλεσμα αυτό δίνει τον ρυθμό μετατροπής του Α στο Β στην επιφάνεια σφαιρικού καταλύτη, r=r. Αν σε όλη την καταλυτική επιφάνεια ίσχυε = R, τότε ο ρυθμός μετατροπής του Α θα ήταν : 4 W διαθέσιμη επιφάνεια k R k R 1 R (1.68) Μπορούμε να συγκρίνουμε τους ρυθμούς στις δύο περιπτώσεις υπολογίζοντας τον λόγο η W R /W, ο οποίος καλείται συντελεστής αποτελεσματικότητας (effetiveness fator): 3 η oth1 (1.69) όπου k1 R R. Η ποσότητα αυτή καλείται μέτρο Thiele (Thiele modulus). Ισχύει: Deff Για 1 n 1 Για 1 n~ Διάχυση σε αραιό υγρό διάλυμα με αργή ετερογενή αντίδραση Έστω ότι το πρόβλημα της διάχυσης με αργή ετερογενή = 0 z=0 αντίδραση πάνω σε μία επίπεδη καταλυτική επιφάνεια δεν γίνεται στην αέρια φάση (Ενότητα 1.6.4), αλλά σε z ένα αραιό υγρό διάλυμα. Σε αυτή την περίπτωση z=δ θεωρούμε ένα ψεύδο δυαδικό σύστημα στο οποίο η διαχυτότητα του Α στο διάλυμα, D, είναι προφανώς διαφορετική από τη διαχυτότητα του Β στο διάλυμα, D Β. Ακόμη, από το γεγονός ότι το διάλυμα είναι αραιό, η συνολική μαζική συγκέντρωση ρ είναι σταθερή και μπορούμε να χρησιμοποιήσουμε την Εξ. (Ι.10), η οποία μετά τις απαλοιφές για την περίπτωση αυτή είναι: d dz 0 C z C (1.70) 1 Οι σταθερές C 1 και C βρίσκονται από τις συνοριακές συνθήκες: Σ.Σ. 1: στο z=0, 0 Υποθετική στιβάδα υγρού B B δ Σ.Σ. : στο z=δ, N k z 1 Σημειώσεις Μεταφοράς Μάζας 9
31 Οι σταθερές της ολοκλήρωσης είναι: C (N /k )/ και C 1 z Η κατανομή της συγκέντρωσης έχει τη μορφή: N z z 0 0 k1 με την ειδική γραμμομοριακή ροή να υπολογίζεται ως εξής d N z 1 Nz Nz D D 0 z0 dz z0 k1 Αναδιατάσσοντας την παραπάνω σχέση προκύπτει: N z D0 1 1 (D /k ) 1 (1.71) (1.7) Διάχυση σε στρωτή πίπτουσα στιβάδα Συχνά, η μεταφορά μάζας συμβαίνει συγχρόνως με μία συναγωγική ροή, με αποτέλεσμα η μεταφορά μάζας να επηρεάζεται σημαντικά από το πεδίο ροής, όπως έχουμε συζητήσει ήδη στην περίπτωση του οριακού στρώματος μάζας. Όταν η ροή είναι τυρβώδης δεν είναι δυνατή κάποια αναλυτική λύση. Όμως και στην περίπτωση της στρωτής ροής, αν και απλούστερη στη μοντελοποίησή της, ο συνδυασμός της με μεταφορά μάζας δημιουργεί πολλές πολυπλοκότητες που δυσκολεύουν την επίτευξη αναλυτικής λύσης. Βέβαια, ύστερα από κάποιες παραδοχές είναι πολλές φορές εφικτό να επιτυγχάνεται αναλυτική λύση. Ένα παράδειγμα που επιδέχεται αναλυτική λύση, ύστερα από κάποιες παραδοχές, είναι η διάχυση σε στρωτή πίπτουσα στιβάδα υγρού (diffusion into a falling film). Η μεταφορά μάζας σε αυτή τη γεωμετρία βρίσκει αρκετές εφαρμογές, όπως στην απορρόφηση ενός ελάχιστα διαλυτού αερίου (π.χ. του οξυγόνου) στο νερό και η εξάτμιση ενός πτητικού συστατικού από ένα υγρό διάλυμα. Ας θεωρήσουμε την περίπτωση του ελάχιστα διαλυτού αερίου Α στο υγρό Β σε μόνιμη κατάσταση. Θεωρούμε τη ροή του υγρού Β πάνω σε μία κατακόρυφη πλάκα με τη μορφή λεπτής στρωτής στιβάδας με σταθερό πάχος h χωρίς κυματισμούς. Σε αυτή την περίπτωση η κατανομή της ταχύτητας έχει δειχθεί ότι δίνεται από τη σχέση: gh y u(y) x 1 h Η Eξ. (1.73) γράφεται και με τη μορφή y u(y) x umax 1 h Διάχυση του Α (1.73) (1.73α) όπου u max είναι η μέγιστη ταχύτητα της στιβάδας στην ελεύθερη επιφάνεια. Επειδή η μαζική συγκέντρωση (ή η πυκνότητα) της υγρής φάσης μένει σταθερή μπορούμε να ξεκινήσουμε από την Εξ. (Ι.10) με το να ορίζεται ως η συγκέντρωση του διαλυμένου αερίου μέσα στην υγρή στιβάδα: ux uy uz C,G DB DB DB (Ι.10) t x y z x x y y z z u x (y) u max y=0 x h y Σημειώσεις Μεταφοράς Μάζας 30
32 Στην περίπτωση που πραγματευόμαστε δεν υπάρχει ταχύτητα στην y και στην z διεύθυνση, θεωρούμε μόνιμη κατάσταση και σταθερή διαχυτότητα και δεν έχουμε παραγωγή μάζας, οπότε οι μόνοι όροι που μένουν είναι: ux DB (1.74) x x y Εδώ μπορούμε να κάνουμε ακόμη μία υπόθεση, ότι μεταφορά στη διεύθυνση x γίνεται κυρίως με συναγωγή και όχι με μοριακή διάχυση, ενώ στη διεύθυνση y γίνεται μόνο με διάχυση. Μπορεί να δειχθεί ότι αυτό ισχύει όταν o αριθμός Pelet είναι αρκετά μεγαλύτερος της μονάδας (Pe u h / D 1). Με αυτό τον τρόπο η Εξ. max B (1.74) απλοποιείται περαιτέρω και εισάγοντας την Εξ. (1.73) για την u x παίρνουμε: y umax 1 DB (1.75) h x y Βέβαια στην ίδια εξίσωση μπορούμε να καταλήξουμε κάνοντας ένα ισοζύγιο μάζας σε έναν διαφορικό όγκο ΔxΔyb (όπου b το πλάτος της πλάκας). Οι τρεις συνοριακές συνθήκες του προβλήματος είναι: Σ.Σ. 1: Στο x0, i (αν και συνήθως 0) Σ.Σ. : Στο y0, 0, δηλ. η συγκέντρωση κορεσμού του Α στο υγρό Β (νόμος του Henry). Υπονοείται ότι το Α είναι καλά αναμεμειγμένο στην αέρια φάση. Σ.Σ. 3: Στο yh, N 0 ή / y 0, δηλ. το τοίχωμα είναι αδιαπέραστο στο Α. Η αναλυτική λύση του σύνθετου αυτού προβλήματος είναι (Johnstone and Pigford, 194):,L 0 5,113 39,318 0,7857 e 0,1001e... (1.76) i 0 όπου,l είναι η μέση συγκέντρωση του Α στην έξοδο της ροής (μήκος στιβάδας L) και το αδιάστατο μέγεθος DB L η ορίζεται ως. umax h Εδώ θα πραγματευθούμε την περίπτωση του «μικρού χρόνου έκθεσης» της στιβάδας στο Α ή, με άλλα λόγια, όταν το (ελάχιστα διαλυτό) αέριο Α διεισδύει μόνο σε κάποιο μικρό βάθος μέσα στη στιβάδα. Το εξωτερικό αυτό τμήμα της στιβάδας ρέει προφανώς προς τα κάτω με (σχεδόν) τη μέγιστη ταχύτητα u max. Επίσης, το αέριο δεν θα προσεγγίσει ποτέ το τοίχωμα (y=h) και δεν θα ικανοποιείται η Σ.Σ. 3. Η συνθήκη αυτή τροποποιείται ως εξής: Σ.Σ. 3 : Στο y, i [Εάν υποθέσουμε ότι το Α διεισδύει σε βάθος στο οποίο η ταχύτητα u x είναι 0,9 u max, τότε το βάθος διείσδυσης είναι: y 0,316h. ] Επομένως έχουμε να λύσουμε την διαφορική εξίσωση: umax DB (1.77) x y με συνοριακές συνθήκες τις Σ.Σ. 1, Σ.Σ. και Σ.Σ. 3. Το πρόβλημα αυτό είναι αντίστοιχο με το πρόβλημα της μη μόνιμης ροής από τη μετακίνηση μίας πλάκας σε ένα ημιάπειρο ρευστό ή με το πρόβλημα της μεταφοράς μάζας σε μία διεύθυνση σε ένα ημιάπειρο στερεό: ux ux και D B, αντίστοιχα. Εδώ, η ποσότητα x/u t max αντικαταστάθηκε από το χρόνο t. y t y Μπορούμε εύκολα να αδιαστατοποιήσουμε τη συγκέντρωση ως: i 0 i οπότε η Εξ. (1.78) και οι συνοριακές συνθήκες γράφονται Σημειώσεις Μεταφοράς Μάζας 31
33 B D (x / u ) max y Σ.Σ. 1: Στο x0, 0 Σ.Σ. : Στο y0, 1 Σ.Σ. 3 : Στο y, 0 (1.78) Το πρόβλημα αυτό δεν περιλαμβάνει κάποιο χαρακτηριστικό μήκος, δεν υπάρχει δηλαδή κάποια συνοριακή συνθήκη στο x=l, και μπορεί να λυθεί με τη λεγόμενη μέθοδο ομοιότητας. Με την τεχνική αυτή μειώνεται ο αριθμός των ανεξάρτητων μεταβλητών σε μία μερική διαφορική εξίσωση με την εισαγωγή μιας μεταβλητής ομοιότητας. Στην περίπτωση αυτή μπορούμε να ορίσουμε τη μεταβλητή ομοιότητας ως y η= 4D B (x /u max ) Για λόγους απλούστευσης ορίζουμε D=D B και t=x/u max (καλείται και χρόνος έκθεσης exposure time). Οι παράγωγοι στην Εξ. (1.78) μπορούν να εκφραστούν με όρους της η : t y η y y 1η d d d d dη t t 4Dt dη t 4Dt dη t dη d η 1 d dη y 4Dt dη d / y η d 1 d 1 1 d y y y dη t dη 4Dt dη 4Dt 4Dt dη Επομένως, η Εξ. (1.78) μετασχηματίζεται στην κανονική διαφορική εξίσωση d d η 0 dη dη (1.79) με συνοριακές συνθήκες: Σ.Σ. 1 : Στο η, 0 (από τις Σ.Σ. 1 και 3, δηλαδή είτε x 0 ή y ) Σ.Σ. : Στο η0, 1 (από τη Σ.Σ. ) Θέτουμε d φ dη, όποτε παίρνουμε τη διαφορική εξίσωση πρώτης τάξης: dφ 1 ηφ 0 dφ ηdη (1.80) dη φ με λύση lnφ η C 1 και αντικαθιστώντας το φ η ' ' d C exp( η ) C exp( )dc dη όπου είναι μία εικονική μεταβλητή (dummy variable). To 0 στο ολοκλήρωμα είναι αυθαίρετο, μπορεί να θέσουμε οποιαδήποτε άλλη τιμή, κάτι που θα οδηγούσε σε διαφορετική εκτίμηση της C. Οι σταθερές υπολογίζονται με τη βοήθεια των Σ.Σ. και παίρνουμε: η exp( )d η exp( )d1erfη=erfη exp( )d 0 (1.81) Σημειώσεις Μεταφοράς Μάζας 3
34 όπου erfη είναι η συνάρτηση σφάλματος (error funtion) της η (Σχήμα 1.10), η οποία υπολογίζεται μέσω πινάκων ή με τη βοήθεια λογισμικών, και erfη είναι η συμπληρωματική συνάρτηση σφάλματος (omplementary error funtion) της η. Αντικαθιστώντας το i y 1erf 0 i 4DB x / u max και το η παίρνουμε: (1.8) erf(0)=0 erf(3) 1 d erf(η) e dη η Σχήμα 10. Η συνάρτηση σφάλματος. Τις περισσότερες φορές δεν μας ενδιαφέρει η κατανομή της συγκέντρωσης, αλλά η ειδική γραμμομοριακή ροή στο y=0. Η τοπική ειδική ροή μάζας στη διεπιφάνεια είναι: d N (x) J (x) D ( ) B max y 0 B 0 i y0 dy x y0 και η συνολική γραμμομοριακή ροή για μήκος L και πλάτος b της στιβάδας υπολογίζεται ως D u (1.83) b L 4DB umax y 0 0 i (1.84) L 0 0 W N (x) dxdz bl( ) H σχέση αυτή δείχνει ότι η συνολική γραμμομοριακή ροή είναι αντιστρόφως ανάλογη του χρόνου έκθεσης στο υγρό, L/u max. Σε ποιες όμως περιπτώσεις επιτρέπεται να χρησιμοποιήσουμε τη λύση ομοιότητας; Όπως έχει λεχθεί έχουμε υποθέσει ότι το Α διεισδύει σε βάθος στο οποίο η ταχύτητα u x είναι 0,9 u max και το βάθος διείσδυσης είναι: y 0,316 h. Κάνουμε και μία άλλη παραδοχή. Η αδιάστατη συγκέντρωση στο μέγιστο βάθος διείσδυσης να μην είναι μεγαλύτερη του 10%, δηλ. =0,1. Επομένως, με αυτές τις παραδοχές η μεταβλητή ομοιότητας στο μέγιστο βάθος διείσδυσης έχει την τιμή 1,15 [αφού erf(1,15)=0,10], δηλ.: y 1,15= 4D B (x /u max ) Θέτοντας y 0,316h προκύπτει εύκολα ότι το μήκος της στιβάδας στο οποίο μπορεί να εφαρμοστεί η λύση που συζητήθηκε είναι: L humax 0,019 (1.85) h D B Σημειώσεις Μεταφοράς Μάζας 33
35 . ΜΕΤΑΦΟΡΑ ΜΑΖΑΣ ΜΕ ΣΥΝΑΓΩΓΗ (Convetive mass transfer).1 Διάχυση και Συναγωγή Πριν προχωρήσουμε σε κάποια πρακτικά θέματα ας προσπαθήσουμε να κάνουμε τη διαφοροποίηση μεταξύ διάχυσης και συναγωγής σε ένα απλουστευμένο δυαδικό μείγμα. Μοριακή Διάχυση (moleular diffusion) του συστατικού Α στο συστατικό Β (δυαδικό σύστημα) είναι η διεργασία με την οποία μόρια ή ιόντα κινούνται από μία περιοχή με σχετικά υψηλή συγκέντρωση σε μία περιοχή που υπάρχει μικρότερη συγκέντρωση. Η ειδική γραμμομοριακή ροή του συστατικού Α (flux) στη διεύθυνση z (σε σχέση με τη μέση γραμμομοριακή ταχύτητα του μείγματος) είναι ανάλογη της κλίσης του γραμμομοριακού κλάσματος του Α και δίνεται από τον εμπειρικό νόμο του Fik dy J D B (kmol/m s) dz όπου D B είναι η δυαδική διαχυτότητα (ή συντελεστής διάχυσης binary diffusion oeffiient) του συστατικού Α που διαχέεται μέσω του συστατικού Β και dy / dz είναι η κλίση του γραμμομοριακού κλάσματος του Α στην διεύθυνση z. Ο γενικός νόμος του Fik για ισοβαρή και ισοθερμοκρασιακά δυαδικά συστήματα στις τρεις διευθύνσεις (διάνυσμα) γράφεται ως: B J D y ή αν η συγκέντρωση είναι σταθερή και ως J D. B Επιφάνεια Α Υψηλή συγκέντρωση «flux» Χαμηλή συγκέντρωση Η Μεταφορά μάζας με συναγωγή (onvetive mass transfer) περιλαμβάνει τη μεταφορά μάζας μεταξύ ενός στερεού συνόρου και ενός κινούμενου ρευστού ή μεταξύ δύο μη αναμείξιμων ρευστών που κινούνται και διαχωρίζονται από μία κινούμενη διεπιφάνεια. Η ειδική γραμμομοριακή ροή του συστατικού Α (από μία επιφάνεια, στερεή ή υγρή, παράλληλη προς τη διεύθυνση της ροής) σε σταθερές συντεταγμένες δίνεται από την εμπειρική σχέση: N k (kmol/m s) Διεύθυνση ροής «flux» Επιφάνεια Α Σημειώσεις Μεταφοράς Μάζας 34
36 όπου k είναι ο συντελεστής μεταφοράς μάζας και είναι η διαφορά συγκέντρωσης του Α μεταξύ της συγκέντρωσης στην επιφάνεια του στερεού ή στη διεπιφάνεια μεταξύ των δύο ρευστών και της συγκέντρωσης στην κύρια μάζα του ρευστού (bulk onentration). Όπως έχουμε ήδη αναφέρει, οι ροές ορμής, θερμότητας και μάζας αυξάνονται σημαντικά όταν μέσα στα ρευστά υπάρχει μακροσκοπική κίνηση, λόγω του μηχανισμού της συναγωγής. Μακροσκοπική κίνηση προκαλείται από δυνάμεις που επιβάλλονται εξωτερικά (εξαναγκασμένη συναγωγή), ή από χωρικές διαφοροποιήσεις της πυκνότητας που οδηγούν σε ανωστικά ρεύματα (ελεύθερη συναγωγή)... Ορισμός συντελεστή μεταφοράς μάζας Η μεταφορά μάζας με συναγωγή δεν αποτελεί στην πραγματικότητα ανεξάρτητο μηχανισμό, αλλά αποτελεί συνδυασμό του μοριακού μηχανισμού μεταφοράς με τις διαφοροποιήσεις στο πεδίο συγκεντρώσεων που προκαλεί η μακροσκοπική κίνηση. Στις περισσότερες περιπτώσεις το πρόβλημα είναι εξαιρετικά πολύπλοκο και η ολοκληρωμένη επίλυσή του αδύνατη. Για τον λόγο αυτό η ποσοτική περιγραφή των ρυθμών μεταφοράς γίνεται με τρόπο συνοπτικό και βασίζεται σε συσχετίσεις με ημιεμπειρικό χαρακτήρα. Τα βασικά χαρακτηριστικά της μεταφοράς μάζας με συναγωγή μπορούν να παρουσιαστούν με αναφορά στο παράδειγμα του στρωτού οριακού στρώματος. Συγκεκριμένα, θεωρούμε την επίπεδη πλάκα του παρακάτω σχήματος, παράλληλα με την οποία κινείται ένα ρεύμα αέρα. Αν η πλάκα αποτελείται από ένα υλικό Α που εξαχνώνεται (π.χ. ναφθαλίνιο), τότε πραγματοποιείται μεταφορά μάζας από την επιφάνεια του τοιχώματος προς την κύρια μάζα του αέρα. (Αντίστοιχη περίπτωση έχουμε για ροή νερού παράλληλα σε πλάκα από υλικό που διαλύεται ελάχιστα στο νερό, όπως το βενζοϊκό οξύ.) Η συνολική ωθούσα δύναμη για τη μεταφορά μάζας προκύπτει από δύο χαρακτηριστικές συγκεντρώσεις των ατμών ναφθαλινίου στον αέρα: (1) Τη συγκέντρωση ισορροπίας, Αs, που επικρατεί στον π.χ. αέρας ή νερό Α αέρα, πολύ κοντά στο στερεό τοίχωμα. (Ως γνωστόν, στη διεπιφάνεια δύο διαφορετικών φάσεων ισχύουν οι συνθήκες ισορροπίας όπως προβλέπονται από τη θερμοδυναμική των μιγμάτων). y x Αs u, Α () Τη συγκέντρωση των ατμών ναφθαλινίου,, στην L κύρια μάζα του αέρα, προτού το αέριο ρεύμα προσεγγίσει το τοίχωμα ή πολύ μακριά από αυτό. π.χ. ναφθαλίνιο ή βενζοϊκό οξύ Επειδή η υψηλή συγκέντρωση είναι κοντά στο τοίχωμα και η χαμηλή μακριά από αυτό, η μεταφορά μάζας γίνεται προς τη διεύθυνση y, κάθετα προς την κύρια διεύθυνση ροής. Ο προσανατολισμός αυτός ισχύει γενικότερα, δηλαδή η ροή συστατικού γίνεται κάθετα προς τη διεπιφάνεια που χωρίζει δύο φάσεις, ενώ η μακροσκοπική κίνηση του ρευστού είναι συνήθως παράλληλη προς τη διεπιφάνεια. Από το ισοζύγιο μάζας του ναφθαλινίου στη διεπιφάνεια στερεού αερίου υπολογίζουμε αμέσως ότι ο ρυθμός εξάχνωσης στο τοίχωμα ισούται με τη ροή του συστατικού κάθετα προς τη διεπιφάνεια από την πλευρά του αέρα. Έχει σημασία να τονιστεί ότι η ειδική ροή του συστατικού Α εξακολουθεί να δίνεται από τη γνωστή σχέση του νόμου του Fik, δηλαδή: y DB y y 0 J (.1) Σημειώσεις Μεταφοράς Μάζας 35
37 Η δυσκολία ανάλυσης της συναγωγής σε σχέση με την απλή διάχυση οφείλεται στο ότι η κίνηση του ρευστού επηρεάζει έντονα την κατανομή συγκέντρωσης (x,y), με τρόπο που είναι συνήθως αδύνατον να προβλεφθεί θεωρητικά. Ποιοτικά μπορεί να γίνει κατανοητό ότι η μακροσκοπική κίνηση αυξάνει τη μεταφορά μάζας, με τον εξής συλλογισμό: θεωρούμε διαφορικό όγκο αέρα που προσεγγίζει την πλάκα και θα κινηθεί σε μικρή απόσταση από αυτή. Όσο μεγαλύτερη είναι η ταχύτητα του όγκου του αέρα τόσο λιγότερο θα έχει προλάβει να κορεστεί σε ατμούς ναφθαλινίου προτού φτάσει σε μία ορισμένη θέση y επάνω από την πλάκα. Σύμφωνα όμως με την παραπάνω σχέση του νόμου του Fik, μικρή συγκέντρωση κοντά στη διεπιφάνεια, σε συνδυασμό με τη μεγάλη συγκέντρωση κορεσμού πάνω στη διεπιφάνεια, συνεπάγεται υψηλή κλίση συγκέντρωσης και, συνεπώς, αυξημένο ρυθμό μεταφοράς μάζας. Εξαιτίας της δυσκολίας για αναλυτική επίλυση του προβλήματος συναγωγής επιλέγουμε μία συνοπτική προσέγγιση και εκφράζουμε την ειδική γραμμομοριακή ροή του συστατικού Α από το τοίχωμα προς τον αέρα (σε σχέση με σταθερές συντεταγμένες), που συνήθως οφείλεται στο συνδυασμό συναγωγής και διάχυσης, ως γραμμική συνάρτηση της συνολικής ωθούσας δύναμης, σύμφωνα με τη σχέση N k (s ) (.) όπου s είναι η συγκέντρωση του Α στην στερεή επιφάνεια (ή στη διεπιφάνεια υγρού αερίου ή υγρού υγρού) και η συγκέντρωση του Α στην κύρια μάζα του ρευστού. Στην περίπτωση του οριακού στρώματος. (Ποια θα ήταν η κατάλληλη συγκέντρωση της κύριας μάζας σε ροή σε σωλήνα;) Η «σταθερά αναλογίας» k είναι ο συντελεστής μεταφοράς μάζας με συναγωγή (ή συντελεστής συναγωγής onvetive mass transfer oeffiient) και η παραπάνω σχέση μπορεί να θεωρηθεί ως ο ορισμός του. Στην πραγματικότητα, ο συντελεστής συναγωγής κρύβει όλη την άγνοιά μας για τις λεπτομέρειες των πεδίων ταχύτητας και συγκέντρωσης. Συνεπώς, δεν αποτελεί θερμοφυσική ιδιότητα του ρευστού, αλλά εξαρτάται σημαντικά και από τις συνθήκες ροής, τις ιδιότητες του ρευστού και τη γεωμετρία του συστήματος. Όπως θα δούμε παρακάτω, η τιμή του συντελεστή συναγωγής υπολογίζεται από ημιεμπειρικές συσχετίσεις με κατάλληλους αδιάστατους αριθμούς. Οι συσχετίσεις αυτές είναι αποτέλεσμα συνδυασμού διαστατικής ανάλυσης και πειραματικών μετρήσεων. Η παραπάνω μεθοδολογία ανάλυσης προβλημάτων μεταφοράς μάζας με συναγωγή έχει πολλές αναλογίες με την ανάλυση αντίστοιχων προβλημάτων μεταφοράς θερμότητας. Έτσι, το τοίχωμα του παραπάνω σχήματος θα μπορούσε να θεωρηθεί ότι διατηρείται σε διαφορετική θερμοκρασία, T s, από τη θερμοκρασία, T, με την οποία προσεγγίζει ο αέρας την πλάκα. Στην περίπτωση αυτή, η ειδική θερμορροή περιγράφεται συναρτήσει του συντελεστή μεταφοράς θερμότητας με συναγωγή, h, σύμφωνα με τη σχέση qh(ts T ) (.3) Οι δύο συντελεστές συναγωγής h και k συνδέονται μεταξύ τους μέσω των αναλογιών μεταφοράς θερμότητας/μάζας που θα αναπτύξουμε στη συνέχεια. Για παράδειγμα, ο τοπικός συντελεστής μεταφοράς μάζας στην περίπτωση του οριακού στρώματος έχουμε βρει ότι υπολογίζεται από τη σχέση kx 0,5 0,33 Shx 0,33 Rex S (.4) DB Η σχέση αυτή είναι απόλυτα ανάλογη της αντίστοιχης συσχέτισης για τη μεταφορά θερμότητα, αν ο αδιάστατος αριθμός S (S / D B) αντικατασταθεί από τον αριθμό Pr και ο Sh από τον Nu. Γενικότερα, τα φαινόμενα μεταφοράς θερμότητας και μάζας με συναγωγή συσχετίζονται στενά στις περιπτώσεις που υπάρχει πλήρης αναλογία, όπως για παράδειγμα στο οριακό στρώμα. Μία διαφοροποίηση μεταξύ τους έχει να κάνει με τις εφαρμογές: μεταφορά θερμότητας πραγματοποιείται συνήθως διαμέσου Σημειώσεις Μεταφοράς Μάζας 36
38 τοιχωμάτων και συνεπώς ενδιαφέρει σχεδόν αποκλειστικά η συναγωγή μεταξύ ρευστού και στερεού συνόρου. Αντίθετα, οι εφαρμογές μεταφοράς μάζας συχνά αφορούν στην εναλλαγή ενός συστατικού μεταξύ δύο διαφορετικών ρευστών φάσεων (συνήθως μίας υγρής και μίας αέριας). Στις περιπτώσεις αυτές ενδιαφέρει η συναγωγή μεταξύ της κύριας μάζας του ρευστού και της διεπιφάνειας συνόρου. Επειδή το αντίστοιχο πεδίο ροής της δεύτερης περίπτωσης είναι αισθητά διαφορετικό από το πεδίο ροής της πρώτης, παρουσιάζονται θεμελιώδεις διαφορές στους αντίστοιχους συντελεστές συναγωγής. Στη συνέχεια παρουσιάζεται ένα παράδειγμα μεταφοράς μάζας με συναγωγή σε συνθήκες τυρβώδους ροής. Ειδικότερα, περιγράφεται η επίδραση των χαρακτηριστικών της τυρβώδους ροής στη μεταφορά και παρέχεται περαιτέρω αιτιολόγηση για τη μορφή της βασικής σχέσης που ορίζει τον συντελεστή μεταφοράς μάζας. Στο παράδειγμα αυτό ένα ρευστό ρέει μέσα σε έναν αγωγό, του οποίου τα εσωτερικά τοιχώματα είναι επενδυμένα από ένα ελάχιστα διαλυτό στερεό, όπως το βενζοϊκό οξύ. Αυτό διαλύεται και μεταφέρεται κάθετα στη ροή από το τοίχωμα. Όταν ένα συστατικό Α διαλύεται από μια στερεή επιφάνεια, υπάρχει υψηλή συγκέντρωση του συστατικού αυτού κοντά στο τοίχωμα, ενώ η συγκέντρωση του μειώνεται (σε γενικές γραμμές) με την απόσταση από το τοίχωμα. Λόγω ύπαρξης δινών στη ροή γειτονικά στοιχεία του ρευστού δεν έχουν απαραίτητα την ίδια συγκέντρωση του συστατικού Α. Τρεις περιοχές μεταφοράς μάζας μπορούν να διακριθούν. Η πρώτη είναι ένα λεπτό ιξώδες υπόστρωμα (visous sublayer film). Η μεταφορά μάζας σε αυτή την περιοχή επιτελείται μόνο με μοριακά μέσα, επειδή ελάχιστες δίνες καταφέρνουν να φτάσουν μέχρι εκεί. Αναμένεται να υπάρχει σημαντική μείωση της συγκέντρωσης του Α μέσα σε αυτή τη λεπτή στιβάδα. Ακολουθεί η μεταβατική περιοχή (transition or buffer region), στην οποία η μεταφορά μάζας συντελείται τόσο με μοριακά μέσα όσο και μέσω των δινών. Η τυρβώδης περιοχή είναι η τρίτη περιοχή, όπου η μεταφορά μάζας γίνεται σχεδόν μόνο με συναγωγή (τυρβώδης διάχυση) και όπου η συγκέντρωση είναι σχεδόν ίδια παντού, μια που οι δίνες ομοιογενοποιούν την περιοχή. Συγκέντρωση s Μέση τιμή z 1 Απόσταση από το τοίχωμα z z Επειδή όπως έχει λεχθεί και προηγουμένως οι γνώσεις μας για τη μεταφορά μάζας με τυρβώδη ροή είναι περιορισμένες, προσπαθούμε να γράψουμε τις εξισώσεις της τυρβώδους διάχυσης με τρόπο αντίστοιχο με τη μοριακή διάχυση δηλαδή: d N (D B M) (.5) dz όπου ε Μ είναι η δινοδιαχυτότητα (σε m /s). Η τιμή της ε Μ προφανώς μεταβάλλεται στις τρεις περιοχές (είναι σχεδόν 0 στο ιξώδες υπόστρωμα) και μπορούμε να υποθέσουμε μια μέση τιμή M. Τότε ολοκληρώνοντας την παραπάνω σχέση ανάμεσα σε δύο θέσεις έχουμε: Σημειώσεις Μεταφοράς Μάζας 37
39 D N B M s z1 z (.6) Η ειδική ροή N ορίζεται σε σχέση με την επιφάνεια Α 1, μια που η διατομή μεταφοράς μάζας μπορεί να μην είναι σταθερή. Επίσης στις περισσότερες περιπτώσεις η απόσταση (z z 1 ) δεν είναι γνωστή. Έτσι μπορούμε να περιγράψουμε το φαινόμενο με την εξ. (.): s N k k (.) όπου k ο συντελεστής μεταφοράς μάζας με συναγωγή. Περιμένουμε ότι η ροή της μεταφερόμενης μάζας είναι ανάλογη της επιφάνειας μεταφοράς και της διαφοράς συγκέντρωσης του συστατικού: ροή μάζας εμβαδόν διαφορά k που μεταφέρεται επιφανείας μεταφοράς συγκέντρωσης.3. Εκφράσεις του συντελεστή μεταφοράς μάζας Για αέρια και για ισογραμμομοριακή αντιδιάχυση ή για αραιά διαλύματα η ειδική γραμμομοριακή ροή μάζας μπορεί να γραφεί ως : N k (1 ) k p(p1 p ) k y(y1 y ) (.7) όπου p είναι η μερική πίεση και y το γραμμομοριακό κλάσμα. Οι τρεις συντελεστές k, k p, k y συσχετίζονται μεταξύ τους ως εξής: P k k kp p ky (.8) RT όπου P είναι η συνολική πίεση, R η σταθερά των αερίων και T η απόλυτη θερμοκρασία. Συσχέτιση των συντελεστών μπορεί να γίνει και σε άλλες περιπτώσεις, π.χ. για διάχυση μέσω στάσιμου Β (π.χ. N k (1 )/yb,lm). Οι διαφορετικοί τύποι συντελεστών μεταφοράς μάζας χρησιμοποιούνται: N k 1 N kp p N k ky y m m k, σε παλαιότερη βιβλιογραφία και συχνά λόγω s s της φυσικής σημασίας kmol kmol k, p m spa m satm y στην απορρόφηση αερίων και σε βιολογικά συστήματα kmol προτιμάται σε θεωρητικούς υπολογισμούς, ms ιδιαίτερα με αέρια Στην όλη προσέγγιση του συντελεστή μεταφοράς μάζας προκύπτουν κάποια εύλογα ερωτηματικά: 1) Η ειδική ροή είναι ανάλογη πάντοτε του Δ; (Ναι, αλλά για σχετικά αραιά διαλύματα.) ) Ποια επιφάνεια μπαίνει στους υπολογισμούς της ροής; 3) Πως χειριζόμαστε τις μεταβολές της συγκέντρωσης; Για τα υγρά μπορούμε να γράψουμε αντίστοιχα: N k k k x x (.9) 1 L 1 x 1 όπου x είναι το γραμμομοριακό κλάσμα του Α. Σημειώσεις Μεταφοράς Μάζας 38
40 .4. Συσχετίσεις των συντελεστών μεταφοράς μάζας και θερμότητας Συχνά δεν είναι εφικτό σε μια γεωμετρία και σε ένα σύστημα να γίνουν πρώτα πειραματικές μετρήσεις ώστε να προσδιορίσουμε τους συντελεστές μεταφοράς μάζας και θερμότητας και γι αυτό καταφεύγουμε σε συσχετίσεις για τις ίδιες ή παρόμοιες συνθήκες που υπάρχουν στη βιβλιογραφία. Οι συσχετίσεις αυτές δίνονται συνήθως με τη μορφή αδιάστατων αριθμών. Είναι σημαντικό να κατανοήσουμε πως ορίζονται μερικές μεταβλητές στο φυσικό σύστημα που μελετούμε. Για παράδειγμα ως χαρακτηριστικό μήκος,, στον αριθμό Sherwood, k /D, λαμβάνεται το πάχος της μεμβράνης σε μια διεργασία μεμβρανών, ενώ σε μια σφαίρα που διαλυτοποιείται λαμβάνεται η διάμετρος της σφαίρας. Με άλλα λόγια, μια τιμή του Sh= έχει διαφορετική σημασία στις μεμβράνες και διαφορετική σε άλλες γεωμετρίες. Ορισμοί Αδιάστατων Αριθμών Αριθμός Reynolds u u u u u u x δυνάμεις αδρανείας Re u u δυνάμεις ιξώδους x όπου Αριθμός Prandtl ρ = πυκνότητα ρευστού u = ταχύτητα = χαρακτηριστικό μήκος μ = δυναμικό ιξώδες ν = κινηματικό ιξώδες Pr k p a = θερμοδιαχυτότητα k = θερμική αγωγιμότητα p = θερμοχωρητικότητα διαχυτότητα ορμής θερμική διαχυτότητα Αριθμός Shmidt διαχυτότητα ορμής S D D διαχυτότητα μάζας D = διαχυτότητα Αριθμός Sherwood k k συνολική μεταφορά μάζας Sh D D μεταφορά με διάχυση k = συντελεστής μεταφοράς μάζας αναφέρεται σε ισογραμμοριακή αντιδιάχυση ή σε μικρή τιμή του y Αριθμός Nusselt h ht συνολική μεταφορά θερμότητας Nu k k T μεταφορά θερμότητας με αγωγή h= συντελεστής μεταφοράς θερμότητας (.10) (.11) (.1) (.13) (.14) Σημειώσεις Μεταφοράς Μάζας 39
41 Αριθμός Lewis θερμική διαχυτότητα Le D διαχυτότητα μάζας Χρησιμοποιείται κατά την ταυτόχρονη μεταφορά μάζας και θερμότητας με συναγωγή. (.15) Οι αριθμοί S, Pr και Le αποτελούν συνδυασμό ιδιοτήτων των ρευστών. Έτσι, κάθε αριθμός μπορεί να θεωρηθεί ως ιδιότητα του υλικού που μεταφέρεται..5. Παραδείγματα Συσχετίσεων Οι συσχετίσεις μεταφοράς μάζας διακρίνονται σε συσχετίσεις για διεπιφάνειες ρευστού ρευστού και για διεπιφάνειες ρευστού στερεού. Οι πρώτες είναι σημαντικότερες, όπως για την προσρόφηση αερίου, εκχύλιση υγρού υγρού κτλ. Επίσης, δεν είναι γνωστό να υπάρχουν παρόμοιες συσχετίσεις στη μεταφορά θερμότητας, όπου βέβαια οι διεπιφάνειες ρευστού ρευστού είναι σπανιότατες. Γενικά γράφουμε: b Sh are S d (.16) όπου a, b, και d είναι σταθερές. Διεπιφάνειες ρευστού ρευστού Υγρό σε στήλη με πληρωτικό υλικό: 0,45 0,5 Sh 5 Re S (.17) όπου d είναι το ονομαστικό μέγεθος πληρωτικού υλικού Κλασική σχέση, όχι και τόσο επιτυχής Αέριο σε στήλη με πληρωτικό υλικό: 0,36 0,64 1/3 Sh 1, 1 Re S (.18) Ρέουσα στιβάδα (falling film): όπου ε είναι κλάσμα κενού της κλίνης Κλασική σχέση. 0,5 Sh 0,69 Re (.19) Για χαρακτηριστικό μήκος: z, θέση κατά μήκος της στιβάδας Για την ταχύτητα u m, μέση ταχύτητα στιβάδας Διεπιφάνειες ρευστού στερεού Στρωτή ροή σε κυλινδρικό αγωγό: Τυρβώδης ροή σε κυλινδρικό αγωγό: για Re<1000 0,8 Sh 1,86 Re (.0) για Re>000 0,83 1/3 Sh 0,03 Re S (.1) D: διάμετρος αγωγού Γενικά, οι παραπάνω σχέσεις έχουν ακρίβεια ±30%. Για συστήματα με παρόμοια γεωμετρία, οι αντίστοιχες σχέσεις για μεταφορά θερμότητας γράφονται με αντικατάσταση του αριθμού Sh από τον Nu και του S από τον αριθμό Pr. Ροή γύρω από μια σφαίρα: 0,5 1/3 du p av Sh 0,6 Re S Re (.) Για στάσιμο ρευστό: Sh= (.3) 0,5 1/3 Για Re>>1: Sh 0,6 Re S (.4) 1 Προσοχή στον τοπικό και στον μέσο συντελεστή μεταφοράς, ο οποίος ως γνωστόν είναι: k k s ds s. Σημειώσεις Μεταφοράς Μάζας 40
42 .6. Θεωρίες για τον συντελεστή μεταφοράς μάζας Ενδιαφερόμαστε να συσχετίσουμε τους εμπειρικούς συντελεστές μεταφοράς μάζας με τη διαχυτότητα και τον τύπο της ροής του ρευστού. Αρχικά απαιτείται να οριστεί ο τύπος της ροής. Υποτίθεται ότι η ροή διέπεται από άλλους μηχανισμούς, όπως η κλίση της πίεσης του ρευστού, και όχι από τη διάχυση. Από τις εμπειρικές συσχετίσεις για το συντελεστή μεταφορά μάζας (.17.1) προκύπτει ότι : 0,5 /3 k D ή D καθώς και k u 0,7 Θα θέλαμε να υπάρχουν θεωρητικές προσπάθειες (και φυσικά μοντέλα) που να μπορούν να προβλέψουν αυτή τη συμπεριφορά όσο είναι δυνατόν καλύτερα. Εδώ και περισσότερο από 100 χρόνια έχουν γίνει σημαντικές προσπάθειες για την ανάπτυξη θεωριών για την ερμηνεία του μηχανισμού ή των μηχανισμ μεταφοράς μάζας σε εξαναγκασμένη ροή (τυρβώδη ροή). Συνοψίζονται οι σπουδαιότερες προσπάθειες. 1) Η θεωρία λεπτού υμένα (film theory) [στο βιβλίο των Brodkey Hersey, σελ. 70] 1 Όριο στρωτής ροής Πραγματική καμπύλη Η θεωρία λεπτού υμένα αποτελεί το απλούστερο και παλαιότερο μοντέλο που αναπτύχθηκε από τους Nernst (1904) και Lewis (1918). Όταν ένα ρευστό ρέει δίπλα σε ένα τοίχωμα, το μοντέλο υποθέτει ότι υπάρχει ένα στρωτό λεπτό στρώμα υμένας κοντά στην επιφάνεια. Ο λεπτός αυτός υμένας βέβαια δε βρίσκεται πειραματικά και είναι υποθετικός. Με άλλα λόγια υποτίθεται ότι η z F πάχος ενεργού υμένα συνολική αντίσταση στη μεταφορά μάζας βρίσκεται μόνο z στο λεπτό υποθετικό υμένα μέσα στον οποίο η μεταφορά δ z F Απόσταση από το τοίχωμα ελέγχεται από τη μοριακή διάχυση. Η θεωρία του λεπτού υμένα «φαντάζεται» ότι η συγκέντρωση ακολουθεί την διακεκομμένη γραμμή μέχρι το z F (ή δ, πάχος του «ενεργού» υμένα ) και ότι η μεταφορά από το 1 στο γίνεται με μοριακά μέσα D k B N 1 1 zf D k k Sh 1 δηλ. k ~D B B DB Προσδιορίζεται πειραματικά, αλλά δεν μπορεί προφανώς να μετρηθεί άμεσα 0,8 0,9 Στην πράξη βέβαια k D B και βεβαίως το k εξαρτάται και από πολλούς άλλους παράγοντες. Παρόλα τα σημαντικά μειονεκτήματα αυτής της θεωρίας, ακόμη και σήμερα μιλάμε για «film oeffiients». ) Θεωρία διεισδύσεως (penetration theory) [στο βιβλίο των Brodkey Hersey, σελ. 7] Από το βιβλίο του R. E. Treybal, Mass Transfer Operations, M Graw Hill Η θεωρία αυτή προσφέρει πειστικότερη φυσική ερμηνεία στο φαινόμενο μεταφοράς μάζας στην υγρή φάση κατά την προσρόφηση αερίων και προτάθηκε από τον Higbie το Ο Higbie εκτίμησε ότι σε πολλές περιπτώσεις ο χρόνος έκθεσης του ρευστού στη μεταφορά μάζας είναι μικρός, έτσι ώστε η κλίση της συγκέντρωσης στη θεωρία υμένα δεν θα είχε τον κατάλληλο χρόνο να δημιουργηθεί. Σημειώσεις Μεταφοράς Μάζας 41
43 i, στο υγρό αέριο z b Τυρβώδης ροή b Χρόνος θ L b υγρό L/u o =θ, χρόνος έκθεσης (exposure time) ο Ας υποθέσουμε στο παραπάνω σχήμα ότι μια δίνη b ανέρχεται από την κύρια μάζα του υγρού και παραμένει εκτεθειμένη στον αέρα (ή στην αέρια φάση) για χρόνο θ, πριν περάσει ξανά ολοκληρωτικά στην υγρή μάζα. Στη θεωρία αυτή ο χρόνος έκθεσης θ όλων των δινών ή των σωματιδίων θεωρείται ο ίδιος. Αρχικά η συγκέντρωση του διαλυμένου αερίου στη δίνη είναι ομοιόμορφη, o, και εσωτερικά η δίνη θεωρείται στάσιμη. Κατά τη διάρκεια της έκθεσης της δίνης στην αέρια φάση, η συγκέντρωση στη διεπιφάνεια γίνεται i, η οποία μπορεί να θεωρηθεί ως η διαλυτότητα ισορροπίας του αερίου στο υγρό. Κατά τη διάρκεια του χρονικού διαστήματος θ, το «υγρό σωματίδιο» υπόκειται σε μεταβατική διάχυση ή διείσδυση (penetration) της διαλυμένης ουσίας στην z κατεύθυνση, η οποία μπορεί να περιγραφεί προσεγγιστικά ως : t D B z (.5) Για μικρούς χρόνους και για αργούς ρυθμούς διάχυσης, τα μόρια του αερίου δεν μπορούν να φτάσουν σε βάθος z b (πάχος της δίνης), το οποίο φαίνεται για αυτά ότι βρίσκεται στο άπειρο. Έτσι : ο για t=0, σε όλα τα z i για t>0 και z=0 για t>0 και z ο Η λύση του προβλήματος, δηλαδή η κατανομή της συγκέντρωσης, δίνεται από τη σχέση: z/td 0,5 B n o i o1 e dn (.6) 0 Στη διεπιφάνεια και εάν ο ρυθμός απορρόφησης είναι αμελητέος στο χρόνο t (δηλαδή N N 0 ) τότε B N,z0 B i 0 z Z0 DB kli 0 t D (.7) και N t D B 0 t D i 0 kl, i 0 t0 t i 0 B,average ave (.8) οπότε k D B L,ave t ή k ~D L,ave 0,5 B Αυτή η σχέση ισχύει πράγματι για μικρούς χρόνους έκθεσης όπως έχει λεχθεί και προηγουμένως, στην πράξη όμως o εκθέτης παίρνει τιμές από 0 μέχρι και 0,8 0,9. Σημειώσεις Μεταφοράς Μάζας 4
44 3) Θεωρία επιφανειακής ανανέωσης (surfae renewal model) [Dankwerts, 1951] Η θεωρία διείσδυσης έχει σχετικά καλή σύμφωνα με πολλά πειραματικά δεδομένα για μικρούς χρόνους έκθεσης, παρά την i, ύπαρξη πολλών περιορισμών. Ο Dankwerts παρουσίασε ένα Καλά αναμεμιγμένη περισσότερο ρεαλιστικό μοντέλο στο οποίο οι δίνες εκτίθενται 1 περιοχή, στο αέριο σε διαφορετικούς χρόνους. 1 Η θεωρία αναγνωρίζει δυο περιοχές ρευστών: στην επιφάνεια και στην κύρια μάζα του υγρού. Στην επιφάνεια η μεταφορά μάζας γίνεται με την θεωρία διείσδυσης με τις δίνες αέριο να έχουν διαφορετικό χρόνο έκθεσης. Οι μικροί όγκοι του υγρού από την επιφανειακή περιοχή δεν είναι στατικοί, αλλά υγρό εναλλάσσονται με την περιοχή της κύριας μάζας του ρευστού. Αυτή η θεωρία της «ανανέωσης» καθιστά τη θεωρία διείσδυσης ως μέρος της θεωρίας της επιφανειακής ανανέωσης. Ύστερα από τον ορισμό της κατανομής του χρόνου παραμονής, Ε(t) E(t) όπου τ είναι ο μέσος χρόνος παραμονής ενός στοιχείου στην επιφάνεια, προκύπτει: t/ e / (.9) DB N z 0 i 0 t Η μέση ειδική ροή του συστατικού δίνεται : DB E(t) και L,ave 0 N N dt,ave z 0 i 0 (.30) k D B (.31) Η θεωρία αυτή είναι επιτυχής στην ερμηνεία φαινόμενων μεταφοράς μάζας με συναγωγή, ιδιαίτερα όταν συνοδεύονται από χημικές αντιδράσεις στην υγρή φάση. 4) Άλλες Θεωρίες Συνδυασμός θεωριών υμένα διείσδυσης ανανέωσης Θεωρία οριακού στρώματος που έχει ήδη αναπτυχθεί. Σημειώσεις Μεταφοράς Μάζας 43
45 .7. Προβλήματα που λύνονται με τη χρήση συντελεστών μεταφοράς μάζας Πολλά προβλήματα μεταφοράς μάζας μπορούν να λυθούν με την εφαρμογή του κατάλληλου ισοζυγίου μάζας σε συνδυασμό με τις κατάλληλες συνοριακές ή/και αρχικές συνθήκες. Με άλλα λόγια, η ειδική ροή συσχετίζεται με το ισοζύγιο του υλικού σε κάποιο κατάλληλο όγκο. Τα βήματα για να μοντελοποιήσουμε κάποιες, απλές σχετικά, διεργασίες μεταφοράς μάζας με συναγωγή είναι: ΒΗΜΑ 1: Εξετάζουμε προσεκτικά το φυσικό πρόβλημα και βλέπουμε τι γίνεται στη διεπιφάνεια. Έχουμε προσθήκη ή απομάκρυνση υλικού; Αν είναι δυνατόν σχεδιάζουμε το σύστημα που θέλουμε να μοντελοποιήσουμε. ΒΗΜΑ : Καταγράφουμε τις παραδοχές που κάνουμε ανάλογα με το πρόβλημα. Βέβαια, αν χρειαστεί, περαιτέρω υποθέσεις μπορούμε να κάνουμε και αργότερα. ΒΗΜΑ3: Γράφουμε το ισοζύγιο μάζας του υλικού που μεταφέρεται και ακολούθως ενσωματώνουμε σε αυτό την κατάλληλη ( ες) συσχέτιση ( εις). Οι διεργασίες στις οποίες το ελέγχον στάδιο είναι η συναγωγή μπορούν να διακριθούν σε δύο κατηγορίες: (α) Όγκος ελέγχου καλά αναμεμειγμένος με ομοιόμορφη παντού συγκέντρωση, π.χ. ένα αναδευόμενο δοχείο, και ψάχνουμε τη μεταβολή της συγκέντρωσης με τον χρόνο. (β) Διαφορικός όγκος ελέγχου με μεταβολή της συγκέντρωσης του Α σε μία διεύθυνση, π.χ. ροή σε σωλήνα. Εδώ συνήθως ζητείται η μεταβολή της συγκέντρωσης του Α με το μήκος του αγωγού σε μόνιμη κατάσταση. Ορίζουμε το Δ και επιλέγουμε (αν με μας δίνεται) η κατάλληλη σχέση για τον υπολογισμό του k. ΒΗΜΑ 4: Σκεφτόμαστε και αναγνωρίζουμε τις συνοριακές ή αρχικές συνθήκες του προβλήματος. ΒΗΜΑ 5: Λύνουμε την αλγεβρική ή διαφορικά εξίσωση (ή εξισώσεις) από το ισοζύγιο μάζας για να βρούμε την κατανομή της συγκέντρωσης με το μήκος ή τον χρόνο κτλ. Παράδειγμα: Εφύγρανση. Νερό εξατμίζεται σε αρχικά ξηρό αέρα μέσα σε κλειστό δοχείο, όπως φαίνεται στο παρακείμενο σχήμα. Το δοχείο βρίσκεται σε θερμοκρασία 5 C, οπότε η τάση ατμών του νερού είναι 3,8 mmhg. Το δοχείο περιέχει 0,8 L νερού με ελεύθερη επιφάνεια 150 m σε συνολικό όγκο 19, L. Ύστερα από 3 min ο αέρας είναι κορεσμένος στο 0,05%. Ποια είναι η τιμή του συντελεστή μεταφοράς μάζας; Σε πόσο χρόνο ο αέρας θα είναι κατά 90% κορεσμένος; Αέρας, V, (t) s s =συγκ. κορεσμού Λύση: Σε ποια φάση έχουμε μεταβολή της συγκέντρωσης; Προφανώς στην αέρια φάση. Η υγρή μεταβάλλεται ελάχιστα. Θεωρούμε ότι ο όγκος της αέριας φάσης V είναι σταθερός και έχουμε πολύ καλή ανάμειξη για τον ατμό. Άρα κάνουμε ένα ισοζύγιο μάζας στην αέρια φάση: [ΕΙΣ.] + [ΠΑΡ.]=[ΕΚΡ.] + [ΣΥΣ] δηλ. d(v ) d N V dt dt (i) όπου το Ν Α είναι σε mol/s και Α είναι το εμβαδόν της διεπιφάνειας. Η ειδική ροή δίνεται από τη σχέση: Nk (s ) (ii) όπου s είναι η συγκέντρωση κορεσμού του νερού στη διεπιφάνεια και η συγκέντρωση του ατμού στην κύρια μάζα της αέριας φάσης, συνάρτηση προφανώς του χρόνου. Πώς όμως υπολογίζουμε τον k; Θα υποθέσουμε ότι είναι σταθερός. Τι δεδομένα έχουμε; Ότι ύστερα από 3 min ο αέρας είναι 0,05% κορεσμένος, δηλ. πρακτικά το είναι πολύ μικρότερο από το s και το Ν Α είναι σταθερό σε αυτό το διάστημα. Το Ν Α σε αυτό το διάστημα μπορεί να υπολογιστεί αν διαιρέσουμε τον συνολικό αριθμό γραμμομορίων που υπάρχουν στην αέρια φάση με την επιφάνεια εξάτμισης και το χρόνο εξάτμισης, δηλαδή: Σημειώσεις Μεταφοράς Μάζας 44
46 (Συγκ. ατμού) (Όγκος αέρα) N (iii) (Υγρή επιφάνεια) (Χρόνος) Η συγκέντρωση κορεσμού στη διεπιφάνεια, s, βρίσκεται από τη σχέση: p 3,8 / 760atm s 3 1,810 s mol/l (iv) RT 0,806Latm/Kmol 98K Η συγκέντρωση του ατμού στην αέρια φάση ύστερα από 3 λεπτά έκθεσης είναι (0,05 % κορεσμένος): 7 0,0510 6,40 10,3min s mol/l Αντικαθιστώντας την παραπάνω τιμή στην (iii), η ειδική ροή εξάτμισης υπολογίζεται ως: 7 6,40 10 mol/l(19, 0,8) L 10 mol N 4, m 180 s m s Συγχρόνως όμως ισχύει η Εξ. (ii), όπου όπως είπαμε είναι η συγκέντρωση του ατμού στην κύρια μάζα του αέρα, η οποία όμως σε μικρούς χρόνους είναι πρακτικά μηδέν. Έτσι: 10 mol 4,410 N m s 4 m k 3, s 1,8 10 mol/l 0, 001L/m s Ο χρόνος που απαιτείται για τον κορεσμό του αέρα με νερό κατά 90% υπολογίζεται από ένα ισοζύγιο μάζας σε ψευδομόνιμες συνθήκες (Eξ. i), υποθέτοντας ότι ο συντελεστής μεταφοράς παραμένει σταθερός: Συσσώρευση Ρυθμός = d (V ) N k s στην αέρια φάση εξάτμισης dt Ο αέρας αρχικά είναι ξηρός. Έτσι για t=0, =0. Επομένως, η λύση της εξ. (ΙΙΙ) είναι: (t) k 1exp t V (v) s Λύνοντας ως προς t, βρίσκουμε το χρόνο που απαιτείται για να κορεστεί ο αέρας κατά 90%: V 3 3 m m/s m 18,3 10 s hr 5 t ln1 ln(1 0,9) 8, k s 3, Να σημειωθεί ότι το k σε m/s βρίσκεται προφανώς και από την παραπάνω σχέση για t=180 s, V=18, m 3, =150 m και / s =0, Εισαγωγή στη Διάχυση σε Μεμβράνη Σε μία μεμβράνη έχουμε διάχυση αρχικά του συστατικού στον υμένα (film) της πλευράς 1, ακολούθως μέσα στη μεμβράνη και, τέλος, στον υμένα της πλευράς. Ο συντελεστής κατανομής (partition oeffiient) Κ ορίζεται ως ' s 1is is K (.3) L 1i i Στο παράπλευρο σχήμα προφανώς Κ <1. Οι ειδικές ροές μέσω κάθε φάσης πρέπει να είναι ίδιες και επομένως: DB N k1 1 1i 1is is k i (.33) L όπου k 1 και k είναι οι συντελεστές μεταφοράς μάζας σε m/s στους υμένες των πλευρών 1 και αντίστοιχα. Συνδυάζοντας τις (.3) και (.33) παίρνουμε: ' DBK 1i i m 1i i 1 1i 1is N P (.34) L L i is Σημειώσεις Μεταφοράς Μάζας 45
47 όπου η ποσότητα P Επίσης μπορούμε να γράψουμε: 1 1i 1i i i Για ιδανικά αέρια: m ' DBK ορίζεται ως η διαπερατότητα (permeability) της μεμβράνης στο συστατικό Α. L N k 1 N P m N k y y p p, p RT t t 1i t N k P k 1 m Γενικά, η υψηλή πίεση επηρεάζει ευνοϊκά τη θερμοδυναμική ισορροπία στη διεπιφάνεια. (.35) Παράδειγμα: Αιματοδιαπίδυση (haemodialysis) αιμοκάθαρση: η απομάκρυνση της ουρίας από το αίμα. Να υπολογιστεί η ειδική ροή και η ροή απομάκρυνσης της ουρίας σε μόνιμες συνθήκες σε g/h από το αίμα σε μεμβράνη σελοφάν στους 37ºC. Η μεμβράνη έχει πάχος 0,05 mm και επιφάνεια m. Ο συντελεστής 5 μεταφοράς μάζας στη μεριά του αίματος εκτιμάται σε k 1,5 10 m/s και στην υδατική φάση 5 6 k 3,33 10 m/s. Η διαπερατότητα της μεμβράνης είναι 8,73 10 m / s. Η συγκέντρωση της ουρίας στο αίμα είναι 0,0 g / 100 ml και στο υγρό διαπίδυσης υποτίθεται 0. 1 Λύση: 0,0 4 3 x 10 g / ml 00 g / m, ροή αίματος 10 0 =0 Καλά αναμεμιγμένο διάλυμα άλατος μεμβράνη σελοφάνης αίμα δ/μα Αντικαθιστώντας στην (1.73): 1 n 8,91 x 10 g / sm k P k 1 m 4 Για 1 h και για m : 4 w 8,9110 ( g / sm ) 3600( s) ( m ) 0,4 g ουρίας/ hr Η διαδικασία αιμοκάθαρσης είναι ιδιαίτερα χρονοβόρα, περίπου 15 0 ώρες την εβδομάδα. Αν αυξηθεί η μεταφορά μάζας, θα μειωθεί και ο χρόνος παραμονής. Πως όμως μπορεί να γίνει αυτό; (α) Με καλύτερη ανάμειξη του αλμυρού διαλύματος και (β) Χρησιμοποιώντας λεπτότερη μεμβράνη (αν και μάλλον πρακτικά φθάσαμε στα όρια). Σημειώσεις Μεταφοράς Μάζας 46
48 .9. Διεργασίες Μεμβρανών Ο διαχωρισμός με μεμβράνες γίνεται όλο και πιο σημαντικός σε ποικίλες βιομηχανικές περιβαλλοντικές και φυσιολογικές εφαρμογές. Μείγματα αερίων μπορούν να διαχωριστούν αποτελεσματικά με διάφορες διεργασίες μεμβρανών: 1) Διάχυση αερίων μέσω πορώδους υλικού (π.χ. από πυριτία, ζεόλιθους κτλ.) N =f(μέγεθος πόρων, μοριακό βάρος) [έγινε συζήτηση στη διάχυση Knudsen] ) Διαπεράτοτητα αερίου από μια μεμβράνη Η μεμβράνη συνήθως πολυμερική (ελαστική, πολυαμίδιο, όχι πορώδες υλικό) Το αέριο αρχικά «διαλύεται» στη μεμβράνη, μετά διαχέεται στο στερεό μέχρι να περάσει από την άλλη μεριά Παραδείγματα: διαχωρισμός He/φυσικού αερίου μέσω φθοριούχων πολυμερικών μεμβρανών και η διάχυση Η μέσω ελαστικού. Οι κυριότερες διεργασίες μεμβρανών για υγρά είναι: 1) Διαπίδυση (dialysis): μικρά μόρια διαπερνούν τη μεμβράνη προς μια άλλη υγρή φάση λόγω διαφοράς συγκέντρωσης, π.χ. διαχωρισμός H SO 4 από NiSO 4 /CuSO 4, τεχνητός νεφρός κτλ. ) Ηλεκτροδιαπίδυση (eletrodialysis): ηλεκτροχημική διεργασία απομάκρυνσης ιόντων ή άλλων ουσιών από το νερό με τη χρήση ηλεκτρικά αγώγιμων μεμβρανών και ένα ηλεκτρικό δυναμικό για την κίνηση των ιόντων. 3) Αντίστροφη ώσμωση (revesre osmosis, RO): διεργασία διαχωρισμού των διαλυτών συστατικών του νερού (αφαλάτωση). Η κινητήρια δύναμη του διαχωρισμού είναι η πίεση ( kpa), η οποία υπερβαίνει την ωσμωτική πίεση του προς επεξεργασία διαλύματος και εξαναγκάζει τη διέλευση καθαρού νερού διαμέσου της ημιπερατής μεμβράνης. Έτσι από τη διεργασία παράγεται ένα ρεύμα προϊόντος και ένα, συνήθως μικρότερο, ρεύμα με υψηλή συγκέντρωση αλάτων. 4) Νανοδιήθηση (nanofiltration, NF): κυρίως για αποσκλήρυνση νερού 5) Υπερδιήθηση (ultrafiltration, UF): η μεμβράνη συγκρατεί μικρά ή μεγάλα σωματίδια 0,005 μm λόγω διαφοράς πίεσης( kpa). Χρησιμοποιείται για διαχωρισμό πρωτεϊνών, κολλοειδών, ιών, ενδοτοξινών κτλ. Δεν σχετίζεται με την ωσμωτική πίεση. 6) Μικροδιήθηση (mirofiltration, MF): απομακρύνονται σωματίδια 0,05 μm (π.χ. αιωρούμενα στερεά, βακτήρια) επιβάλλοντας σχετικά μικρή πίεση. Σημειώσεις Μεταφοράς Μάζας 47
49 Σημειώσεις Μεταφοράς Μάζας 48
ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ
 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ R ΑΒ Μέσα στον καταλύτη ΑΒ πόροι στερεό Διδακτικές Σημειώσεις στο Μάθημα «Φαινόμενα Μεταφοράς» Ν. Ανδρίτσος και Β. Μποντόζογλου Βόλος, Απρίλιος 018 Πανεπιστημιακές
ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ R ΑΒ Μέσα στον καταλύτη ΑΒ πόροι στερεό Διδακτικές Σημειώσεις στο Μάθημα «Φαινόμενα Μεταφοράς» Ν. Ανδρίτσος και Β. Μποντόζογλου Βόλος, Απρίλιος 018 Πανεπιστημιακές
Διδακτικές Σημειώσεις στο Μάθημα «Φαινόμενα Μεταφοράς»
 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΜΑΖΑΣ C R ΑΒ Μέσα στον καταλύτη ΑΒ πόροι στερεό Διδακτικές Σημειώσεις στο Μάθημα «Φαινόμενα Μεταφοράς» Ν. Ανδρίτσος και Β. Μποντόζογλου
ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΜΑΖΑΣ C R ΑΒ Μέσα στον καταλύτη ΑΒ πόροι στερεό Διδακτικές Σημειώσεις στο Μάθημα «Φαινόμενα Μεταφοράς» Ν. Ανδρίτσος και Β. Μποντόζογλου
Σφαιρικές συντεταγμένες (r, θ, φ).
 T T r e r 1 T e r Σφαιρικές συντεταγμένες (r, θ, φ). 1 T e. (2.57) r sin u u e u e u e, (2.58) r r οπότε το εσωτερικό γινόμενο u.t γίνεται: T u T u T u. T ur. (2.59) r r r sin 2.5 Η ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ
T T r e r 1 T e r Σφαιρικές συντεταγμένες (r, θ, φ). 1 T e. (2.57) r sin u u e u e u e, (2.58) r r οπότε το εσωτερικό γινόμενο u.t γίνεται: T u T u T u. T ur. (2.59) r r r sin 2.5 Η ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ
ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ. Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 9 η : Μεταφορά Μάζας
 ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 9 η : Μεταφορά Μάζας Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creatve Coons. Για εκπαιδευτικό
ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 9 η : Μεταφορά Μάζας Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creatve Coons. Για εκπαιδευτικό
ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ. Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 9 η : Μεταφορά Μάζας. Διάχυση Νόμος Fick
 ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 9 η : Μεταφορά Μάζας. Διάχυση Νόμος Fck Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creatve
ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 9 η : Μεταφορά Μάζας. Διάχυση Νόμος Fck Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creatve
ΣΥΝΔΥΑΣΜΟΣ ΤΗΣ ΑΝΤΙΣΤΑΣΗΣ ΔΙΑΧΥΣΗΣ ΣΤΟΥΣ ΠΟΡΟΥΣ ΜΕ ΚΙΝΗΤΙΚΗ ΕΠΙΦΑΝΕΙΑΚΗΣ ΑΝΤΙΔΡΑΣΗΣ
 ΣΥΝΔΥΑΣΜΟΣ ΤΗΣ ΑΝΤΙΣΤΑΣΗΣ ΔΙΑΧΥΣΗΣ ΣΤΟΥΣ ΠΟΡΟΥΣ ΜΕ ΚΙΝΗΤΙΚΗ ΕΠΙΦΑΝΕΙΑΚΗΣ ΑΝΤΙΔΡΑΣΗΣ Παράγοντας Αποτελεσματικότητας Ειδικά για αντίδραση πρώτης τάξης, ο παράγοντας αποτελεσματικότητας ισούται προς ε = C
ΣΥΝΔΥΑΣΜΟΣ ΤΗΣ ΑΝΤΙΣΤΑΣΗΣ ΔΙΑΧΥΣΗΣ ΣΤΟΥΣ ΠΟΡΟΥΣ ΜΕ ΚΙΝΗΤΙΚΗ ΕΠΙΦΑΝΕΙΑΚΗΣ ΑΝΤΙΔΡΑΣΗΣ Παράγοντας Αποτελεσματικότητας Ειδικά για αντίδραση πρώτης τάξης, ο παράγοντας αποτελεσματικότητας ισούται προς ε = C
v = 1 ρ. (2) website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Βασικές έννοιες στη μηχανική των ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 17 Φεβρουαρίου 2019 1 Ιδιότητες των ρευστών 1.1 Πυκνότητα Πυκνότητα
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Βασικές έννοιες στη μηχανική των ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 17 Φεβρουαρίου 2019 1 Ιδιότητες των ρευστών 1.1 Πυκνότητα Πυκνότητα
Διδακτικές Σημειώσεις στο Μάθημα «Φαινόμενα Μεταφοράς»
 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΜΑΖΑΣ C R ΑΒ Μέσα στον καταλύτη ΑΒ πόροι στερεό Διδακτικές Σημειώσεις στο Μάθημα «Φαινόμενα Μεταφοράς» Ν. Ανδρίτσος και Β. Μποντόζογλου
ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΜΑΖΑΣ C R ΑΒ Μέσα στον καταλύτη ΑΒ πόροι στερεό Διδακτικές Σημειώσεις στο Μάθημα «Φαινόμενα Μεταφοράς» Ν. Ανδρίτσος και Β. Μποντόζογλου
1. Στοιχεία Μεταφοράς Μάζας και Εξισώσεις Διατήρησης
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Μηχανολόγων Μηχανικών Ετερογενή Μείγματα & Συστήματα Καύσης 1. Στοιχεία Μεταφοράς Μάζας και Εξισώσεις Διατήρησης Δ. Κολαΐτης Μ. Φούντη Δ.Π.Μ.Σ. «Υπολογιστική Μηχανική»
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Μηχανολόγων Μηχανικών Ετερογενή Μείγματα & Συστήματα Καύσης 1. Στοιχεία Μεταφοράς Μάζας και Εξισώσεις Διατήρησης Δ. Κολαΐτης Μ. Φούντη Δ.Π.Μ.Σ. «Υπολογιστική Μηχανική»
σχηματική αναπαράσταση των βασικών τμημάτων μίας βιομηχανικής εγκατάστασης
 σχηματική αναπαράσταση των βασικών τμημάτων μίας βιομηχανικής εγκατάστασης Αρχές μεταφοράς μάζας Αρχές σχεδιασμού συσκευών μεταφοράς μάζας Διεργασίες μεταφοράς μάζας - Απορρόφηση - Απόσταξη - Εκχύλιση
σχηματική αναπαράσταση των βασικών τμημάτων μίας βιομηχανικής εγκατάστασης Αρχές μεταφοράς μάζας Αρχές σχεδιασμού συσκευών μεταφοράς μάζας Διεργασίες μεταφοράς μάζας - Απορρόφηση - Απόσταξη - Εκχύλιση
ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ. Σημειώσεις. Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ
 ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ Σημειώσεις Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ Αθήνα, Απρίλιος 13 1. Η Έννοια του Οριακού Στρώματος Το οριακό στρώμα επινοήθηκε για
ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ Σημειώσεις Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ Αθήνα, Απρίλιος 13 1. Η Έννοια του Οριακού Στρώματος Το οριακό στρώμα επινοήθηκε για
Οι ιδιότητες των αερίων και καταστατικές εξισώσεις. Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι
 Οι ιδιότητες των αερίων και καταστατικές εξισώσεις Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι Τι είναι αέριο; Λέμε ότι μία ουσία βρίσκεται στην αέρια κατάσταση όταν αυθόρμητα
Οι ιδιότητες των αερίων και καταστατικές εξισώσεις Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι Τι είναι αέριο; Λέμε ότι μία ουσία βρίσκεται στην αέρια κατάσταση όταν αυθόρμητα
Αγωγιμότητα στα μέταλλα
 Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
Υπολογισµοί του Χρόνου Ξήρανσης
 Η πραγµατική επιφάνεια ξήρανσης είναι διασπαρµένη και ασυνεχής και ο µηχανισµός από τον οποίο ελέγχεται ο ρυθµός ξήρανσης συνίσταται στην διάχυση της θερµότητας και της µάζας µέσα από το πορώδες στερεό.
Η πραγµατική επιφάνεια ξήρανσης είναι διασπαρµένη και ασυνεχής και ο µηχανισµός από τον οποίο ελέγχεται ο ρυθµός ξήρανσης συνίσταται στην διάχυση της θερµότητας και της µάζας µέσα από το πορώδες στερεό.
Αγωγιμότητα στα μέταλλα
 Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
Ταχύτητα χημικών αντιδράσεων
 Ταχύτητα χημικών αντιδράσεων Η στιγμιαία ταχύτητα μιας αντίδρασης είναι η κλίση της εφαπτομένης στη γραφική παράσταση της συγκέντρωσης ως προς το χρόνο. Για αρνητικές κλίσεις, το πρόσημο αλλάζει, έτσι
Ταχύτητα χημικών αντιδράσεων Η στιγμιαία ταχύτητα μιας αντίδρασης είναι η κλίση της εφαπτομένης στη γραφική παράσταση της συγκέντρωσης ως προς το χρόνο. Για αρνητικές κλίσεις, το πρόσημο αλλάζει, έτσι
ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Περιεχόμενα. Φαινόμενα μεταφοράς Ορισμοί. Ενεργός διατομή 3. Ενεργός διατομή στο μοντέλο των σκληρών σφαιρών
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Περιεχόμενα. Φαινόμενα μεταφοράς Ορισμοί. Ενεργός διατομή 3. Ενεργός διατομή στο μοντέλο των σκληρών σφαιρών
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ. ΘΕΜΑ 1 ο
 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ 1 ο 1.1. Φορτισμένο σωματίδιο αφήνεται ελεύθερο μέσα σε ομογενές ηλεκτρικό πεδίο χωρίς την επίδραση της βαρύτητας. Το σωματίδιο: α. παραμένει ακίνητο. β. εκτελεί ομαλή κυκλική κίνηση.
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ 1 ο 1.1. Φορτισμένο σωματίδιο αφήνεται ελεύθερο μέσα σε ομογενές ηλεκτρικό πεδίο χωρίς την επίδραση της βαρύτητας. Το σωματίδιο: α. παραμένει ακίνητο. β. εκτελεί ομαλή κυκλική κίνηση.
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ Η Επιστήμη της Θερμοδυναμικής ασχολείται με την ποσότητα της θερμότητας που μεταφέρεται σε ένα κλειστό και απομονωμένο σύστημα από μια κατάσταση ισορροπίας σε μια άλλη
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ Η Επιστήμη της Θερμοδυναμικής ασχολείται με την ποσότητα της θερμότητας που μεταφέρεται σε ένα κλειστό και απομονωμένο σύστημα από μια κατάσταση ισορροπίας σε μια άλλη
(1) ταχύτητα, v δεδομένη την πιο πάνω κατανομή θερμοκρασίας; 6. Γιατί είναι σωστή η προσέγγιση του ερωτήματος [2]; Ποια είναι η
![(1) ταχύτητα, v δεδομένη την πιο πάνω κατανομή θερμοκρασίας; 6. Γιατί είναι σωστή η προσέγγιση του ερωτήματος [2]; Ποια είναι η (1) ταχύτητα, v δεδομένη την πιο πάνω κατανομή θερμοκρασίας; 6. Γιατί είναι σωστή η προσέγγιση του ερωτήματος [2]; Ποια είναι η](/thumbs/62/47887680.jpg) ΜΕΤΑΦΟΡΑ ΘΕΡΜΟΤΗΤΑΣ Σειρά Ασκήσεων σε Συναγωγή Θερμότητας Οι λύσεις θα παρουσιαστούν στις παραδόσεις του μαθήματος μετά την επόμενη εβδομάδα. Για να σας φανούν χρήσιμες στην κατανόηση της ύλης του μαθήματος,
ΜΕΤΑΦΟΡΑ ΘΕΡΜΟΤΗΤΑΣ Σειρά Ασκήσεων σε Συναγωγή Θερμότητας Οι λύσεις θα παρουσιαστούν στις παραδόσεις του μαθήματος μετά την επόμενη εβδομάδα. Για να σας φανούν χρήσιμες στην κατανόηση της ύλης του μαθήματος,
ΚΕΦΑΛΑΙΟ ΕΚΤΟ ΤΕΧΝΟΛΟΓΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ ΣΤΕΡΕΑΣ ΚΑΤΑΣΤΑΣΗΣ. Περιληπτική θεωρητική εισαγωγή
 ΚΕΦΑΛΑΙΟ ΕΚΤΟ ΤΕΧΝΟΛΟΓΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ ΣΤΕΡΕΑΣ ΚΑΤΑΣΤΑΣΗΣ Περιληπτική θεωρητική εισαγωγή α) Τεχνική zchralski Η πιο συχνά χρησιμοποιούμενη τεχνική ανάπτυξης μονοκρυστάλλων πυριτίου (i), αρίστης ποιότητας,
ΚΕΦΑΛΑΙΟ ΕΚΤΟ ΤΕΧΝΟΛΟΓΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ ΣΤΕΡΕΑΣ ΚΑΤΑΣΤΑΣΗΣ Περιληπτική θεωρητική εισαγωγή α) Τεχνική zchralski Η πιο συχνά χρησιμοποιούμενη τεχνική ανάπτυξης μονοκρυστάλλων πυριτίου (i), αρίστης ποιότητας,
ηλεκτρικό ρεύμα ampere
 Ηλεκτρικό ρεύμα Το ηλεκτρικό ρεύμα είναι ο ρυθμός με τον οποίο διέρχεται ηλεκτρικό φορτίο από μια περιοχή του χώρου. Η μονάδα μέτρησης του ηλεκτρικού ρεύματος στο σύστημα SI είναι το ampere (A). 1 A =
Ηλεκτρικό ρεύμα Το ηλεκτρικό ρεύμα είναι ο ρυθμός με τον οποίο διέρχεται ηλεκτρικό φορτίο από μια περιοχή του χώρου. Η μονάδα μέτρησης του ηλεκτρικού ρεύματος στο σύστημα SI είναι το ampere (A). 1 A =
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Πειραιά Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανολογίας
 1 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Πειραιά Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανολογίας Πρόβλημα 1 Μηχανική Ρευστών Κεφάλαιο 1 Λυμένα Προβλήματα Μια αμελητέου πάχους επίπεδη πλάκα διαστάσεων (0 cm)x(0
1 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Πειραιά Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανολογίας Πρόβλημα 1 Μηχανική Ρευστών Κεφάλαιο 1 Λυμένα Προβλήματα Μια αμελητέου πάχους επίπεδη πλάκα διαστάσεων (0 cm)x(0
ΦΥΣΙΚΟΧΗΜΕΙΑ ΙΙΙ. Διάχυση Συναγωγή. Δημήτριος Τσιπλακίδης e mail: dtsiplak@chem.auth.gr url: users.auth.gr/~dtsiplak
 1 ΦΥΣΙΚΟΧΗΜΕΙΑ ΙΙΙ Διάχυση Συναγωγή Δημήτριος Τσιπλακίδης e mail: dtsiplak@chem.auth.gr url: users.auth.gr/~dtsiplak Μεταφορά μάζας Κινητήρια δύναμη: Διαφορά συγκέντρωσης, ΔC Μηχανισμός: Διάχυση (diffusion)
1 ΦΥΣΙΚΟΧΗΜΕΙΑ ΙΙΙ Διάχυση Συναγωγή Δημήτριος Τσιπλακίδης e mail: dtsiplak@chem.auth.gr url: users.auth.gr/~dtsiplak Μεταφορά μάζας Κινητήρια δύναμη: Διαφορά συγκέντρωσης, ΔC Μηχανισμός: Διάχυση (diffusion)
ΚΙΝΗΜΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ
 ΚΙΝΗΜΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ ΕΙΣΑΓΩΓΗ Σκοπός της κινηματικής είναι η περιγραφή της κίνησης του ρευστού Τα αίτια που δημιούργησαν την κίνηση και η αναζήτηση των δυνάμεων που την διατηρούν είναι αντικείμενο της
ΚΙΝΗΜΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ ΕΙΣΑΓΩΓΗ Σκοπός της κινηματικής είναι η περιγραφή της κίνησης του ρευστού Τα αίτια που δημιούργησαν την κίνηση και η αναζήτηση των δυνάμεων που την διατηρούν είναι αντικείμενο της
Μακροσκοπική ανάλυση ροής
 Μακροσκοπική ανάλυση ροής Α. Παϊπέτης 6 ο Εξάμηνο Μηχανικών Επιστήμης Υλικών Εισαγωγή Μακροσκοπική ανάλυση Όγκος ελέγχου και νόμοι της ρευστομηχανικής Θεώρημα μεταφοράς Εξίσωση συνέχειας Εξίσωση ορμής
Μακροσκοπική ανάλυση ροής Α. Παϊπέτης 6 ο Εξάμηνο Μηχανικών Επιστήμης Υλικών Εισαγωγή Μακροσκοπική ανάλυση Όγκος ελέγχου και νόμοι της ρευστομηχανικής Θεώρημα μεταφοράς Εξίσωση συνέχειας Εξίσωση ορμής
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΜΕΤΑΦΟΡΑ ΟΡΜΗΣ ΡΕΟΛΟΓΙΑ. (συνέχεια) Περιστροφικά ιξωδόμετρα μεγάλου διάκενου.
 ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΜΕΤΑΦΟΡΑ ΟΡΜΗΣ ΡΕΟΛΟΓΙΑ (συνέχεια) Περιστροφικά ιξωδόμετρα μεγάλου διάκενου. Στα ιξωδόμετρα αυτά ένας μικρός σε διάμετρο κύλινδρος περιστρέφεται μέσα σε μια μεγάλη μάζα του ρευστού. Για
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΜΕΤΑΦΟΡΑ ΟΡΜΗΣ ΡΕΟΛΟΓΙΑ (συνέχεια) Περιστροφικά ιξωδόμετρα μεγάλου διάκενου. Στα ιξωδόμετρα αυτά ένας μικρός σε διάμετρο κύλινδρος περιστρέφεται μέσα σε μια μεγάλη μάζα του ρευστού. Για
3. Τριβή στα ρευστά. Ερωτήσεις Θεωρίας
 3. Τριβή στα ρευστά Ερωτήσεις Θεωρίας Θ3.1 Να συμπληρωθούν τα κενά στις προτάσεις που ακολουθούν: α. Η εσωτερική τριβή σε ένα ρευστό ονομάζεται. β. Η λίπανση των τμημάτων μιας μηχανής οφείλεται στις δυνάμεις
3. Τριβή στα ρευστά Ερωτήσεις Θεωρίας Θ3.1 Να συμπληρωθούν τα κενά στις προτάσεις που ακολουθούν: α. Η εσωτερική τριβή σε ένα ρευστό ονομάζεται. β. Η λίπανση των τμημάτων μιας μηχανής οφείλεται στις δυνάμεις
Φαινόμενα Μεταφοράς Μάζας θερμότητας
 Φαινόμενα Μεταφοράς Μάζας θερμότητας 2 η Διάλεξη Μηχανισμοί μετάδοσης θερμότητας Εμμανουήλ Σουλιώτης Τμήμα Μηχανικών Περιβάλλοντος Πανεπιστήμιο Δυτικής Μακεδονίας Ακαδημαϊκό Έτος 2018-2019 Μαθησιακοί στόχοι
Φαινόμενα Μεταφοράς Μάζας θερμότητας 2 η Διάλεξη Μηχανισμοί μετάδοσης θερμότητας Εμμανουήλ Σουλιώτης Τμήμα Μηχανικών Περιβάλλοντος Πανεπιστήμιο Δυτικής Μακεδονίας Ακαδημαϊκό Έτος 2018-2019 Μαθησιακοί στόχοι
1 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΕΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ
 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΕΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού Οριακού
η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΕΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού Οριακού
Χημικές Διεργασίες: Εισαγωγή
 : Εισαγωγή Ορολογία Μοναδιαίες Διεργασίες ( Unit Processes ) - Οξείδωση - Υδρογόνωση - Αφυδρογόνωση - Πυρόλυση - Ενυδάτωση κλπ Ορολογία Μοναδιαίες Διεργασίες ( Unit Processes ) - Οξείδωση - Υδρογόνωση
: Εισαγωγή Ορολογία Μοναδιαίες Διεργασίες ( Unit Processes ) - Οξείδωση - Υδρογόνωση - Αφυδρογόνωση - Πυρόλυση - Ενυδάτωση κλπ Ορολογία Μοναδιαίες Διεργασίες ( Unit Processes ) - Οξείδωση - Υδρογόνωση
Απαντήσεις στις ασκήσεις του κεφαλαίου 4 του βιβλίου Χημική Κινητική του ΕΑΠ
 Απαντήσεις στις ασκήσεις του κεφαλαίου 4 του βιβλίου Χημική Κινητική του ΕΑΠ Ασκηση 4.1 Η κινητική εξίσωση της αντίδρασης: βρέθηκε οτι είναι Αντιδράσεις πρώτης τάξης 2A = Προϊόντα r = k[a] Να υπολογίσετε
Απαντήσεις στις ασκήσεις του κεφαλαίου 4 του βιβλίου Χημική Κινητική του ΕΑΠ Ασκηση 4.1 Η κινητική εξίσωση της αντίδρασης: βρέθηκε οτι είναι Αντιδράσεις πρώτης τάξης 2A = Προϊόντα r = k[a] Να υπολογίσετε
ΦΑΙΝΟΜΕΝΑ ΠΡΟΣΡΟΦΗΣΕΩΣ ΠΡΟΣΡΟΦΗΣΗ ΟΥΣΙΑΣ ΑΠΟ ΔΙΑΛΥΜΑΤΑ
 ΦΑΙΝΟΜΕΝΑ ΠΡΟΣΡΟΦΗΣΕΩΣ ΠΡΟΣΡΟΦΗΣΗ ΟΥΣΙΑΣ ΑΠΟ ΔΙΑΛΥΜΑΤΑ Έννοιες που πρέπει να γνωρίζετε Ισορροπία φάσεων, εξίσωση Clauiu-Clapeyron Θέμα ασκήσεως Προσρόφηση ουσίας από αραιά διαλύματα. Προσδιορισμός ισόθερμων
ΦΑΙΝΟΜΕΝΑ ΠΡΟΣΡΟΦΗΣΕΩΣ ΠΡΟΣΡΟΦΗΣΗ ΟΥΣΙΑΣ ΑΠΟ ΔΙΑΛΥΜΑΤΑ Έννοιες που πρέπει να γνωρίζετε Ισορροπία φάσεων, εξίσωση Clauiu-Clapeyron Θέμα ασκήσεως Προσρόφηση ουσίας από αραιά διαλύματα. Προσδιορισμός ισόθερμων
Το σύστημα των μη αλληλεπιδραστικών ροών και η σημασία του στην ερμηνεία των ιδιοτήτων των ιδανικών αερίων.
 Το σύστημα των μη αλληλεπιδραστικών ροών και η σημασία του στην ερμηνεία των ιδιοτήτων των ιδανικών αερίων. Θεωρώντας τα αέρια σαν ουσίες αποτελούμενες από έναν καταπληκτικά μεγάλο αριθμό μικροσκοπικών
Το σύστημα των μη αλληλεπιδραστικών ροών και η σημασία του στην ερμηνεία των ιδιοτήτων των ιδανικών αερίων. Θεωρώντας τα αέρια σαν ουσίες αποτελούμενες από έναν καταπληκτικά μεγάλο αριθμό μικροσκοπικών
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού
ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΙΔΑΝΙΚΩΝ ΑΝΤΙΔΡΑΣΤΗΡΩΝ ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΙΔΑΝΙΚΩΝ ΑΝΤΙΔΡΑΣΤΗΡΩΝ
 Εισαγωγή Διαδικασία σχεδιασμού αντιδραστήρα: Καθορισμός του τύπου του αντιδραστήρα και των συνθηκών λειτουργίας. Εκτίμηση των χαρακτηριστικών για την ομαλή λειτουργία του αντιδραστήρα. μέγεθος σύσταση
Εισαγωγή Διαδικασία σχεδιασμού αντιδραστήρα: Καθορισμός του τύπου του αντιδραστήρα και των συνθηκών λειτουργίας. Εκτίμηση των χαρακτηριστικών για την ομαλή λειτουργία του αντιδραστήρα. μέγεθος σύσταση
ΔΥΝΑΜΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ- ΕΞΙΣΩΣΕΙΣ NAVIER STOKES
 ΔΥΝΑΜΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ- ΕΞΙΣΩΣΕΙΣ NAVIER STOKES ΙΣΟΡΡΟΠΙΑ ΔΥΝΑΜΕΩΝ ΣΕ ΕΝΑΝ ΑΠΕΙΡΟΣΤΟ ΟΓΚΟ ΡΕΥΣΤΟΥ Στο κεφάλαιο αυτό θα εξετάσουμε την ισορροπία των δυνάμεων οι οποίες ασκούνται σε ένα τυχόν σωματίδιο ρευστού.
ΔΥΝΑΜΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ- ΕΞΙΣΩΣΕΙΣ NAVIER STOKES ΙΣΟΡΡΟΠΙΑ ΔΥΝΑΜΕΩΝ ΣΕ ΕΝΑΝ ΑΠΕΙΡΟΣΤΟ ΟΓΚΟ ΡΕΥΣΤΟΥ Στο κεφάλαιο αυτό θα εξετάσουμε την ισορροπία των δυνάμεων οι οποίες ασκούνται σε ένα τυχόν σωματίδιο ρευστού.
ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ. Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 10 η : Μεταβατική Διάχυση και Συναγωγή Μάζας
 ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 10 η : Μεταβατική Διάχυση και Συναγωγή Μάζας Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 10 η : Μεταβατική Διάχυση και Συναγωγή Μάζας Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Σύνοψη ΜΗΧΑΝΙΚΗΣ ΧΗΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Χημική αντίδραση : a 1. + α 2 Α (-a 1 ) A 1. +(-a 2
 ΠΑ- Σύνοψη ΜΗΧΑΝΙΚΗΣ ΧΗΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Χημική αντίδραση : a A + α Α +... ------------>...+a A ή σε μορφή γραμμικής εξίσωσης a A +...+(-a ) A +(-a ) A +... 0 a Στοιχειομετρικοί συντελεστές ως προς Α (
ΠΑ- Σύνοψη ΜΗΧΑΝΙΚΗΣ ΧΗΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Χημική αντίδραση : a A + α Α +... ------------>...+a A ή σε μορφή γραμμικής εξίσωσης a A +...+(-a ) A +(-a ) A +... 0 a Στοιχειομετρικοί συντελεστές ως προς Α (
Τμήμα Τεχνολογίας Τροφίμων. Ανόργανη Χημεία. Ενότητα 10 η : Χημική κινητική. Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής.
 Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 10 η : Χημική κινητική Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Ταχύτητες Αντίδρασης 2 Ως ταχύτητα αντίδρασης ορίζεται είτε η αύξηση
Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 10 η : Χημική κινητική Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Ταχύτητες Αντίδρασης 2 Ως ταχύτητα αντίδρασης ορίζεται είτε η αύξηση
Τ, Κ Η 2 Ο(g) CΟ(g) CO 2 (g) Λύση Για τη συγκεκριμένη αντίδραση στους 1300 Κ έχουμε:
 ΘΕΜΑΤΑ ΤΕΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΗ ΦΥΣΙΚΟΧΗΜΕΙΑ - ΑΣΚΗΣΕΙΣ 5-6 (Α. Χημική Θερμοδυναμική) η Άσκηση Η αντίδραση CO(g) + H O(g) CO (g) + H (g) γίνεται σε θερμοκρασία 3 Κ. Να υπολογιστεί το κλάσμα των ατμών του
ΘΕΜΑΤΑ ΤΕΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΗ ΦΥΣΙΚΟΧΗΜΕΙΑ - ΑΣΚΗΣΕΙΣ 5-6 (Α. Χημική Θερμοδυναμική) η Άσκηση Η αντίδραση CO(g) + H O(g) CO (g) + H (g) γίνεται σε θερμοκρασία 3 Κ. Να υπολογιστεί το κλάσμα των ατμών του
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου (21/6/2017)
 Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
P 1 V 1 = σταθ. P 2 V 2 = σταθ.
 ΝΟΜΟΙ ΤΩΝ ΑΕΡΙΩΝ 83 Την κατάσταση ενός αερίου μέσα σε ένα δοχείο μπορούμε να την κατανοήσουμε, άρα και να την περιγράψουμε πλήρως, αν γνωρίζουμε τις τιμές των παραμέτρων εκείνων που επηρεάζουν την συμπεριφορά
ΝΟΜΟΙ ΤΩΝ ΑΕΡΙΩΝ 83 Την κατάσταση ενός αερίου μέσα σε ένα δοχείο μπορούμε να την κατανοήσουμε, άρα και να την περιγράψουμε πλήρως, αν γνωρίζουμε τις τιμές των παραμέτρων εκείνων που επηρεάζουν την συμπεριφορά
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα. Μετάδοση Θερμότητας. Ενότητα 3: Βασικές Αρχές Θερμικής Συναγωγιμότητας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μετάδοση Θερμότητας Ενότητα 3: Βασικές Αρχές Θερμικής Συναγωγιμότητας Κωνσταντίνος - Στέφανος Νίκας Τμήμα Μηχανολόγων Μηχανικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μετάδοση Θερμότητας Ενότητα 3: Βασικές Αρχές Θερμικής Συναγωγιμότητας Κωνσταντίνος - Στέφανος Νίκας Τμήμα Μηχανολόγων Μηχανικών
Σχεδιασμός Χημικών Διεργασιών και Βιομηχανιών Διάλεξη 6
 Σχεδιασμός Χημικών Διεργασιών και Βιομηχανιών Διάλεξη 6 Δευτέρα, 14 Απριλίου 008 Οικονομική Ανάλυση Βιομηχανιών και Διεργασιών 1 Εισαγωγή Αριστοποίηση: ενός κριτηρίου (αντικειμενικής συνάρτησης) πολυκριτηριακή
Σχεδιασμός Χημικών Διεργασιών και Βιομηχανιών Διάλεξη 6 Δευτέρα, 14 Απριλίου 008 Οικονομική Ανάλυση Βιομηχανιών και Διεργασιών 1 Εισαγωγή Αριστοποίηση: ενός κριτηρίου (αντικειμενικής συνάρτησης) πολυκριτηριακή
ΑΡΧΕΣ ΜΕΤΑΦΟΡΑΣ ΘΕΡΜΟΤΗΤΑΣ
 1 ΑΡΧΕΣ ΜΕΤΑΦΟΡΑΣ ΘΕΡΜΟΤΗΤΑΣ Προβλήματα μεταφοράς θερμότητας παρουσιάζονται σε κάθε βήμα του μηχανικού της χημικής βιομηχανίας. Ο υπολογισμός των θερμικών απωλειών, η εξοικονόμηση ενέργειας και ο σχεδιασμός
1 ΑΡΧΕΣ ΜΕΤΑΦΟΡΑΣ ΘΕΡΜΟΤΗΤΑΣ Προβλήματα μεταφοράς θερμότητας παρουσιάζονται σε κάθε βήμα του μηχανικού της χημικής βιομηχανίας. Ο υπολογισμός των θερμικών απωλειών, η εξοικονόμηση ενέργειας και ο σχεδιασμός
Enrico Fermi, Thermodynamics, 1937
 I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
Φυσικοί μετασχηματισμοί καθαρών ουσιών
 Φυσικοί μετασχηματισμοί καθαρών ουσιών Ή εξάτμιση, η τήξη και η μετατροπή του γραφίτη σε διαμάντι αποτελούν συνηθισμένα παραδείγματα αλλαγών φάσης χωρίς μεταβολή της χημικής σύστασης. Ορισμός φάσης: Μια
Φυσικοί μετασχηματισμοί καθαρών ουσιών Ή εξάτμιση, η τήξη και η μετατροπή του γραφίτη σε διαμάντι αποτελούν συνηθισμένα παραδείγματα αλλαγών φάσης χωρίς μεταβολή της χημικής σύστασης. Ορισμός φάσης: Μια
Κινηματική ρευστών. Ροή ρευστού = η κίνηση του ρευστού, μέσα στο περιβάλλον του
 301 Κινηματική ρευστών Ροή ρευστού = η κίνηση του ρευστού, μέσα στο περιβάλλον του Είδη ροής α) Σταθερή ή μόνιμη = όταν σε κάθε σημείο του χώρου οι συνθήκες ροής, ταχύτητα, θερμοκρασία, πίεση και πυκνότητα,
301 Κινηματική ρευστών Ροή ρευστού = η κίνηση του ρευστού, μέσα στο περιβάλλον του Είδη ροής α) Σταθερή ή μόνιμη = όταν σε κάθε σημείο του χώρου οι συνθήκες ροής, ταχύτητα, θερμοκρασία, πίεση και πυκνότητα,
ηλεκτρικό ρεύµα ampere
 Ηλεκτρικό ρεύµα Το ηλεκτρικό ρεύµα είναι ο ρυθµός µε τον οποίο διέρχεται ηλεκτρικό φορτίο από µια περιοχή του χώρου. Η µονάδα µέτρησης του ηλεκτρικού ρεύµατος στο σύστηµα SI είναι το ampere (A). 1 A =
Ηλεκτρικό ρεύµα Το ηλεκτρικό ρεύµα είναι ο ρυθµός µε τον οποίο διέρχεται ηλεκτρικό φορτίο από µια περιοχή του χώρου. Η µονάδα µέτρησης του ηλεκτρικού ρεύµατος στο σύστηµα SI είναι το ampere (A). 1 A =
ΚΕΦΑΛΑΙΟ 3 Ο ΡΕΥΣΤΑ ΣΕ ΚΙΝΗΣΗ
 166 Α. ΕΡΩΤΗΣΕΙΣ ΑΝΟΙΚΤΟΥ ΤΥΠΟΥ: ΚΕΦΑΛΑΙΟ 3 Ο ΡΕΥΣΤΑ ΣΕ ΚΙΝΗΣΗ 1. Να αναφέρεται παραδείγματα φαινομένων που μπορούν να ερμηνευτούν με την μελέτη των ρευστών σε ισορροπία. 2. Ποια σώματα ονομάζονται ρευστά;
166 Α. ΕΡΩΤΗΣΕΙΣ ΑΝΟΙΚΤΟΥ ΤΥΠΟΥ: ΚΕΦΑΛΑΙΟ 3 Ο ΡΕΥΣΤΑ ΣΕ ΚΙΝΗΣΗ 1. Να αναφέρεται παραδείγματα φαινομένων που μπορούν να ερμηνευτούν με την μελέτη των ρευστών σε ισορροπία. 2. Ποια σώματα ονομάζονται ρευστά;
Κεφάλαιο 7. Θερμοκρασία
 Κεφάλαιο 7 Θερμοκρασία Θερμοδυναμική Η θερμοδυναμική περιλαμβάνει περιπτώσεις όπου η θερμοκρασία ή η κατάσταση ενός συστήματος μεταβάλλονται λόγω μεταφοράς ενέργειας. Η θερμοδυναμική ερμηνεύει με επιτυχία
Κεφάλαιο 7 Θερμοκρασία Θερμοδυναμική Η θερμοδυναμική περιλαμβάνει περιπτώσεις όπου η θερμοκρασία ή η κατάσταση ενός συστήματος μεταβάλλονται λόγω μεταφοράς ενέργειας. Η θερμοδυναμική ερμηνεύει με επιτυχία
Θεωρητική Εξέταση. Τρίτη, 15 Ιουλίου /3
 Θεωρητική Εξέταση. Τρίτη, 15 Ιουλίου 2014 1/3 Πρόβλημα 2. Καταστατική Εξίσωση Van der Waals (11 ) Σε ένα πολύ γνωστό μοντέλο του ιδανικού αερίου, του οποίου η καταστατική εξίσωση περιγράφεται από το νόμο
Θεωρητική Εξέταση. Τρίτη, 15 Ιουλίου 2014 1/3 Πρόβλημα 2. Καταστατική Εξίσωση Van der Waals (11 ) Σε ένα πολύ γνωστό μοντέλο του ιδανικού αερίου, του οποίου η καταστατική εξίσωση περιγράφεται από το νόμο
Διαλύματα - Περιεκτικότητες διαλυμάτων Γενικά για διαλύματα
 Διαλύματα - Περιεκτικότητες διαλυμάτων Γενικά για διαλύματα Μάθημα 6 6.1. SOS: Τι ονομάζεται διάλυμα, Διάλυμα είναι ένα ομογενές μίγμα δύο ή περισσοτέρων καθαρών ουσιών. Παράδειγμα: Ο ατμοσφαιρικός αέρας
Διαλύματα - Περιεκτικότητες διαλυμάτων Γενικά για διαλύματα Μάθημα 6 6.1. SOS: Τι ονομάζεται διάλυμα, Διάλυμα είναι ένα ομογενές μίγμα δύο ή περισσοτέρων καθαρών ουσιών. Παράδειγμα: Ο ατμοσφαιρικός αέρας
ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΚΑΙ ΣΤΟΙΧΕΙΟΜΕΤΡΙΑ
 ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΚΑΙ ΣΤΟΙΧΕΙΟΜΕΤΡΙΑ Τυπική Βιοδιεργασία Μαθηματικό μοντέλο Μαθηματικό μοντέλο ή προσομοίωμα ενός συστήματος ονομάζουμε ένα σύνολο σχέσεων μεταξύ των μεταβλητών του συστήματος που ενδιαφέρουν.
ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΚΑΙ ΣΤΟΙΧΕΙΟΜΕΤΡΙΑ Τυπική Βιοδιεργασία Μαθηματικό μοντέλο Μαθηματικό μοντέλο ή προσομοίωμα ενός συστήματος ονομάζουμε ένα σύνολο σχέσεων μεταξύ των μεταβλητών του συστήματος που ενδιαφέρουν.
Θέµα 1 ο. iv) πραγµατοποιεί αντιστρεπτές µεταβολές.
 ΜΑΘΗΜΑ ΟΝΟΜΑΤΕΠΩΝΥΜΟ Θέµα 1 ο α) Ορισµένη ποσότητα ιδανικού αερίου πραγµατοποιεί µεταβολή AB από την κατάσταση A (p, V, T ) στην κατάσταση B (p, V 1, T ). i) Ισχύει V 1 = V. ii) Η µεταβολή παριστάνεται
ΜΑΘΗΜΑ ΟΝΟΜΑΤΕΠΩΝΥΜΟ Θέµα 1 ο α) Ορισµένη ποσότητα ιδανικού αερίου πραγµατοποιεί µεταβολή AB από την κατάσταση A (p, V, T ) στην κατάσταση B (p, V 1, T ). i) Ισχύει V 1 = V. ii) Η µεταβολή παριστάνεται
1.1. Διαφορική Εξίσωση και λύση αυτής
 Εισαγωγή στις συνήθεις διαφορικές εξισώσεις 9 Διαφορική Εξίσωση και λύση αυτής Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση μιας πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα
Εισαγωγή στις συνήθεις διαφορικές εξισώσεις 9 Διαφορική Εξίσωση και λύση αυτής Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση μιας πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα
Βασικές Διεργασίες Μηχανικής Τροφίμων
 Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 8: Εκχύλιση, 1ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Τύποι εκχύλισης
Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 8: Εκχύλιση, 1ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Τύποι εκχύλισης
ΥΔΡΑΥΛΙΚΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ
 ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΞΑΝΘΗ ΥΔΡΑΥΛΙΚΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Αγγελίδης Π., Αναπλ. καθηγητής ΚΕΦΑΛΑΙΟ ΙΑΧΥΣΗ Α ΡΑΝΩΝ ΡΥΠΩΝ ΙΑΧΥΣΗ Α ΡΑΝΩΝ ΡΥΠΩΝ Στην αρχική περιοχή
ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΞΑΝΘΗ ΥΔΡΑΥΛΙΚΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Αγγελίδης Π., Αναπλ. καθηγητής ΚΕΦΑΛΑΙΟ ΙΑΧΥΣΗ Α ΡΑΝΩΝ ΡΥΠΩΝ ΙΑΧΥΣΗ Α ΡΑΝΩΝ ΡΥΠΩΝ Στην αρχική περιοχή
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ο ΔΙΑΓΩΝΙΣΜΑ ΡΕΥΣΤΑ - ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ο ΔΙΑΓΩΝΙΣΜΑ ΡΕΥΣΤΑ - ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ
 ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
ΜΑΘΗΜΑ: Τεχνολογία Μετρήσεων ΙΙ
 ΜΑΘΗΜΑ: Τεχνολογία Μετρήσεων ΙΙ ΔΙΔΑΣΚΩΝ: Αν. Καθ. Δρ Μαρία Α. Γούλα ΤΜΗΜΑ: Μηχανικών Περιβάλλοντος & Μηχανικών Αντιρρύπανσης 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΜΑΘΗΜΑ: Τεχνολογία Μετρήσεων ΙΙ ΔΙΔΑΣΚΩΝ: Αν. Καθ. Δρ Μαρία Α. Γούλα ΤΜΗΜΑ: Μηχανικών Περιβάλλοντος & Μηχανικών Αντιρρύπανσης 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Η κίνηση του νερού εντός των φυτών (Soil-Plant-Atmosphere Continuum) Δημήτρης Κύρκας
 Η κίνηση του νερού εντός των φυτών (Soil-Plant-Atmosphere Continuum) Δημήτρης Κύρκας Η Σεκόγια (Sequoia) «Redwood» είναι το ψηλότερο δέντρο στο κόσμο και βρίσκεται στην Καλιφόρνια των ΗΠΑ 130 μέτρα ύψος
Η κίνηση του νερού εντός των φυτών (Soil-Plant-Atmosphere Continuum) Δημήτρης Κύρκας Η Σεκόγια (Sequoia) «Redwood» είναι το ψηλότερο δέντρο στο κόσμο και βρίσκεται στην Καλιφόρνια των ΗΠΑ 130 μέτρα ύψος
1 IΔΑΝΙΚΑ ΑΕΡΙΑ 1.1 ΓΕΝΙΚΑ
 1 1 IΔΑΝΙΚΑ ΑΕΡΙΑ 1.1 ΓΕΝΙΚΑ Θα αρχίσουμε τη σειρά των μαθημάτων της Φυσικοχημείας με τη μελέτη της αέριας κατάστασης της ύλης. Η μελέτη της φύσης των αερίων αποτελεί ένα ιδανικό μέσο για την εισαγωγή
1 1 IΔΑΝΙΚΑ ΑΕΡΙΑ 1.1 ΓΕΝΙΚΑ Θα αρχίσουμε τη σειρά των μαθημάτων της Φυσικοχημείας με τη μελέτη της αέριας κατάστασης της ύλης. Η μελέτη της φύσης των αερίων αποτελεί ένα ιδανικό μέσο για την εισαγωγή
ΧΗΜΙΚΗ ΚΙΝΗΤΙΚΗ. Εισαγωγή. 3.1 Γενικά για τη χημική κινητική και τη χημική αντίδραση - Ταχύτητα αντίδρασης
 3 ΧΗΜΙΚΗ ΚΙΝΗΤΙΚΗ 3 ΧΗΜΙΚΗ ΚΙΝΗΤΙΚΗ Εισαγωγή Στην μέχρι τώρα γνωριμία μας με τη χημεία υπάρχει μια «σημαντική απουσία»: ο χρόνος... Είναι λοιπόν «καιρός» να μπει και ο χρόνος ως παράμετρος στη μελέτη ενός
3 ΧΗΜΙΚΗ ΚΙΝΗΤΙΚΗ 3 ΧΗΜΙΚΗ ΚΙΝΗΤΙΚΗ Εισαγωγή Στην μέχρι τώρα γνωριμία μας με τη χημεία υπάρχει μια «σημαντική απουσία»: ο χρόνος... Είναι λοιπόν «καιρός» να μπει και ο χρόνος ως παράμετρος στη μελέτη ενός
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ. Καθηγητής Δ. Ματαράς
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Καθηγητής Δ. Ματαράς 9.Μεταφορά Θερμότητας, Αγωγή Αγωγή Αν σε συνεχές μέσο υπάρχει βάθμωση θερμοκρασίας τότε υπάρχει ροή θερμότητας χωρίς ορατή κίνηση της ύλης.
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Καθηγητής Δ. Ματαράς 9.Μεταφορά Θερμότητας, Αγωγή Αγωγή Αν σε συνεχές μέσο υπάρχει βάθμωση θερμοκρασίας τότε υπάρχει ροή θερμότητας χωρίς ορατή κίνηση της ύλης.
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ ΚΑΤΑΝΟΜΕΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ
 ΚΑΤΑΝΟΜΕΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ 1 Θέμα 1 α) Προσδιορίστε τον όγκο V ιδανικού αερίου, στον οποίο η σχετική διακύμανση είναι α = 10-6 και η συγκέντρωση των σωματιδίων είναι n =,7 10 19 cm -3. β) Προσδιορίστε
ΚΑΤΑΝΟΜΕΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ 1 Θέμα 1 α) Προσδιορίστε τον όγκο V ιδανικού αερίου, στον οποίο η σχετική διακύμανση είναι α = 10-6 και η συγκέντρωση των σωματιδίων είναι n =,7 10 19 cm -3. β) Προσδιορίστε
ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ
 . ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 135 ΔΙΑΓΡΑΜΜΑΤΑ ΦΑΣΕΩΝ 1 2 3 4 1 στερεό (solid) 2 υγρό (liquid) 3 ατμός (vapor) 4 αέριο (gas) A 1+2+3
. ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 135 ΔΙΑΓΡΑΜΜΑΤΑ ΦΑΣΕΩΝ 1 2 3 4 1 στερεό (solid) 2 υγρό (liquid) 3 ατμός (vapor) 4 αέριο (gas) A 1+2+3
Να υπολογίσετε τη μάζα 50 L βενζίνης. Δίνεται η σχετική πυκνότητά της, ως προς το νερό ρ σχ = 0,745.
 1 Παράδειγμα 101 Να υπολογίσετε τη μάζα 10 m 3 πετρελαίου, στους : α) 20 ο C και β) 40 ο C. Δίνονται η πυκνότητά του στους 20 ο C ρ 20 = 845 kg/m 3 και ο συντελεστής κυβικής διαστολής του β = 9 * 10-4
1 Παράδειγμα 101 Να υπολογίσετε τη μάζα 10 m 3 πετρελαίου, στους : α) 20 ο C και β) 40 ο C. Δίνονται η πυκνότητά του στους 20 ο C ρ 20 = 845 kg/m 3 και ο συντελεστής κυβικής διαστολής του β = 9 * 10-4
Εισαγωγή στις Ετερογενείς Χημικές Αντιδράσεις
 Στα ετερογενή συστήματα υπάρχουν δύο παράγοντες, οι οποίοι περιπλέκουν την ανάλυση και την περιγραφή τους, και οι οποίοι πρέπει να ληφθούν υπόψη επιπλέον αυτών που εξετάζονται στα ομογενή συστήματα. Καταρχήν
Στα ετερογενή συστήματα υπάρχουν δύο παράγοντες, οι οποίοι περιπλέκουν την ανάλυση και την περιγραφή τους, και οι οποίοι πρέπει να ληφθούν υπόψη επιπλέον αυτών που εξετάζονται στα ομογενή συστήματα. Καταρχήν
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών
 Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
Φυσική ΜΕΤΑΛΛΟΥΡΓΙΑ. Ενότητα 6: Διάχυση. Γρηγόρης Ν. Χαϊδεμενόπουλος Πολυτεχνική Σχολή Μηχανολόγων Μηχανικών
 Φυσική ΜΕΤΑΛΛΟΥΡΓΙΑ Ενότητα 6: Διάχυση Γρηγόρης Ν. Χαϊδεμενόπουλος Πολυτεχνική Σχολή Μηχανολόγων Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Φυσική ΜΕΤΑΛΛΟΥΡΓΙΑ Ενότητα 6: Διάχυση Γρηγόρης Ν. Χαϊδεμενόπουλος Πολυτεχνική Σχολή Μηχανολόγων Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Energy resources: Technologies & Management
 Πανεπιστήμιο Δυτικής Μακεδονίας Energ resources: echnologies & Management Τεχνολογίες άνθρακα Σχεδιασμός Στηλών Απορρόφησης Αερίων Δρ. Γεώργιος Σκόδρας Αν. Καθηγητής Περιεχόμενα Η διάλεξη που ακολουθεί
Πανεπιστήμιο Δυτικής Μακεδονίας Energ resources: echnologies & Management Τεχνολογίες άνθρακα Σχεδιασμός Στηλών Απορρόφησης Αερίων Δρ. Γεώργιος Σκόδρας Αν. Καθηγητής Περιεχόμενα Η διάλεξη που ακολουθεί
ΕΣΩΤΕΡΙΚΗ ΕΝΕΡΓΕΙΑ Μηχανική ενέργεια Εσωτερική ενέργεια:
 ΕΣΩΤΕΡΙΚΗ ΕΝΕΡΓΕΙΑ Μηχανική ενέργεια (όπως ορίζεται στη μελέτη της μηχανικής τέτοιων σωμάτων): Η ενέργεια που οφείλεται σε αλληλεπιδράσεις και κινήσεις ολόκληρου του μακροσκοπικού σώματος, όπως η μετατόπιση
ΕΣΩΤΕΡΙΚΗ ΕΝΕΡΓΕΙΑ Μηχανική ενέργεια (όπως ορίζεται στη μελέτη της μηχανικής τέτοιων σωμάτων): Η ενέργεια που οφείλεται σε αλληλεπιδράσεις και κινήσεις ολόκληρου του μακροσκοπικού σώματος, όπως η μετατόπιση
Διατύπωση μαθηματικών εκφράσεων για τη περιγραφή του εγγενούς ρυθμού των χημικών αντιδράσεων.
 25/9/27 Εισαγωγή Διατύπωση μαθηματικών εκφράσεων για τη περιγραφή του εγγενούς ρυθμού των χημικών αντιδράσεων. Οι ρυθμοί δεν μπορούν να μετρηθούν απευθείας => συγκεντρώσεις των αντιδρώντων και των προϊόντων
25/9/27 Εισαγωγή Διατύπωση μαθηματικών εκφράσεων για τη περιγραφή του εγγενούς ρυθμού των χημικών αντιδράσεων. Οι ρυθμοί δεν μπορούν να μετρηθούν απευθείας => συγκεντρώσεις των αντιδρώντων και των προϊόντων
website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 6 Ιουνίου 18 1 Οριακό στρώμα και χαρακτηριστικά μεγέθη Στις αρχές του ου αιώνα ο Prandtl θεμελίωσε τη θεωρία
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 6 Ιουνίου 18 1 Οριακό στρώμα και χαρακτηριστικά μεγέθη Στις αρχές του ου αιώνα ο Prandtl θεμελίωσε τη θεωρία
Διαφορική ανάλυση ροής
 Διαφορική ανάλυση ροής Α. Παϊπέτης 6 ο Εξάμηνο Μηχανικών Επιστήμης Υλικών ΜΕ και ΔΕ ροής: Διαφορές Οριακές και αρχικές συνθήκες Οριακές συνθήκες: Φυσική σημασία αλληλεπίδραση του όγκου ελέγχου με το περιβάλλον
Διαφορική ανάλυση ροής Α. Παϊπέτης 6 ο Εξάμηνο Μηχανικών Επιστήμης Υλικών ΜΕ και ΔΕ ροής: Διαφορές Οριακές και αρχικές συνθήκες Οριακές συνθήκες: Φυσική σημασία αλληλεπίδραση του όγκου ελέγχου με το περιβάλλον
ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΘΕΩΡΙΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΘΕΩΡΙΑ Περιεχόμενα 1. Όρια καταστατικής εξίσωσης ιδανικού αερίου 2. Αποκλίσεις των Ιδιοτήτων των πραγματικών αερίων από τους Νόμους
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΘΕΩΡΙΑ Περιεχόμενα 1. Όρια καταστατικής εξίσωσης ιδανικού αερίου 2. Αποκλίσεις των Ιδιοτήτων των πραγματικών αερίων από τους Νόμους
Physics by Chris Simopoulos
 ΘΕΜΑ 1 ο 1 ΘΕΜΑ 1 ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΘΕΜΑ 1 ο 1 ΘΕΜΑ 1 ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
Χημικές αντιδράσεις καταλυμένες από στερεούς καταλύτες
 Χημικές αντιδράσεις καταλυμένες από στερεούς καταλύτες Σε πολλές χημικές αντιδράσεις, οι ταχύτητές τους επηρεάζονται από κάποια συστατικά τα οποία δεν είναι ούτε αντιδρώντα ούτε προϊόντα. Αυτά τα υλικά
Χημικές αντιδράσεις καταλυμένες από στερεούς καταλύτες Σε πολλές χημικές αντιδράσεις, οι ταχύτητές τους επηρεάζονται από κάποια συστατικά τα οποία δεν είναι ούτε αντιδρώντα ούτε προϊόντα. Αυτά τα υλικά
Ισορροπία (γενικά) Ισορροπίες σε διαλύματα. Εισαγωγική Χημεία
 Ισορροπία (γενικά) Ισορροπίες σε διαλύματα Εισαγωγική Χημεία 2013-14 1 Χημική Ισορροπία Εισαγωγική Χημεία 2013-14 2 Ισορροπία: Βαθμός συμπλήρωσης αντίδρασης Ν 2 (g) + 3H 2(g) 2NH 3 (g) Όταν αναφερόμαστε
Ισορροπία (γενικά) Ισορροπίες σε διαλύματα Εισαγωγική Χημεία 2013-14 1 Χημική Ισορροπία Εισαγωγική Χημεία 2013-14 2 Ισορροπία: Βαθμός συμπλήρωσης αντίδρασης Ν 2 (g) + 3H 2(g) 2NH 3 (g) Όταν αναφερόμαστε
ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΞΑΝΘΗ ΡΕΥΣΤΟΜΗΧΑΝΙΚΗ
 ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΞΑΝΘΗ ΡΕΥΣΤΟΜΗΧΑΝΙΚΗ Αγγελίδης Π., Αναπλ. Καθηγητής ΚΕΦΑΛΑΙΟ 5 ΣΤΡΩΤΗ ΡΟΗ ΓΥΡΩ ΑΠΟ ΣΤΕΡΕΗ ΣΦΑΙΡΑ ΓΙΑ ΜΙΚΡΟΥΣ ΑΡΙΘΜΟΥΣ REYNOLDS
ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΞΑΝΘΗ ΡΕΥΣΤΟΜΗΧΑΝΙΚΗ Αγγελίδης Π., Αναπλ. Καθηγητής ΚΕΦΑΛΑΙΟ 5 ΣΤΡΩΤΗ ΡΟΗ ΓΥΡΩ ΑΠΟ ΣΤΕΡΕΗ ΣΦΑΙΡΑ ΓΙΑ ΜΙΚΡΟΥΣ ΑΡΙΘΜΟΥΣ REYNOLDS
Basic definitions. c c c molar density of solution (Kg-moles/m 3 ) / M όπου M. Additional relations
 ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΕΤΟΣ: Α.Μ: as deftos ddtoal relatos mass desty of soluto (Kg/m 3 ) mass oetrato of (Kg of /m 3 of soluto) mass frato of molar desty of soluto (Kg-moles/m 3 ) molar oetrato of (Kg-moles of
ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΕΤΟΣ: Α.Μ: as deftos ddtoal relatos mass desty of soluto (Kg/m 3 ) mass oetrato of (Kg of /m 3 of soluto) mass frato of molar desty of soluto (Kg-moles/m 3 ) molar oetrato of (Kg-moles of
Υποστηρικτικό υλικό για την εργασία «Πειραματική διάταξη για τη μελέτη της ροής ρευστού σε σωλήνα» του Σπύρου Χόρτη.
 Υποστηρικτικό υλικό για την εργασία «Πειραματική διάταξη για τη μελέτη της ροής ρευστού σε σωλήνα» του Σπύρου Χόρτη. Η εργασία δημοσιεύτηκε στο 9ο τεύχος του περιοδικού Φυσικές Επιστήμες στην Εκπαίδευση,
Υποστηρικτικό υλικό για την εργασία «Πειραματική διάταξη για τη μελέτη της ροής ρευστού σε σωλήνα» του Σπύρου Χόρτη. Η εργασία δημοσιεύτηκε στο 9ο τεύχος του περιοδικού Φυσικές Επιστήμες στην Εκπαίδευση,
ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ. Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 2 η : Αγωγή Μονοδιάστατη αγωγή
 ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα η : Αγωγή Μονοδιάστατη αγωγή Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Ceative Cmmns.
ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα η : Αγωγή Μονοδιάστατη αγωγή Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Ceative Cmmns.
διαιρούμε με το εμβαδό Α 2 του εμβόλου (1)
 1)Συνήθως οι πτήσεις των αεροσκαφών γίνονται στο ύψος των 15000 m, όπου η θερμοκρασία του αέρα είναι 210 Κ και η ατμοσφαιρική πίεση 10000 N / m 2. Σε αεροδρόμιο που βρίσκεται στο ίδιο ύψος με την επιφάνεια
1)Συνήθως οι πτήσεις των αεροσκαφών γίνονται στο ύψος των 15000 m, όπου η θερμοκρασία του αέρα είναι 210 Κ και η ατμοσφαιρική πίεση 10000 N / m 2. Σε αεροδρόμιο που βρίσκεται στο ίδιο ύψος με την επιφάνεια
Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων
 Φυσικοχημεία II, Διαλύματα Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων o P = N P P = A A A N P o B B B PA + PB = P ολ Τ=const P = Ν ολ P + N P o o A A B B Ν Α + Ν =1 o o o P = P + A N ( ολ
Φυσικοχημεία II, Διαλύματα Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων o P = N P P = A A A N P o B B B PA + PB = P ολ Τ=const P = Ν ολ P + N P o o A A B B Ν Α + Ν =1 o o o P = P + A N ( ολ
Για την επίλυση αυτής της άσκησης, αλλά και όλων των παρόμοιων χρησιμοποιούμε ιδιότητες των αναλογιών (χιαστί)
 ΜΕΘΟΔΟΛΟΓΙΑ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΠΟΥ ΑΦΟΡΟΥΝ ΔΙΑΛΥΜΑΤΑ Οι ασκήσεις διαλυμάτων που αφορούν τις περιεκτικότητες % w/w, % w/v και % v/v χωρίζονται σε 3 κατηγορίες: α) Ασκήσεις όπου πρέπει να βρούμε ή
ΜΕΘΟΔΟΛΟΓΙΑ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΠΟΥ ΑΦΟΡΟΥΝ ΔΙΑΛΥΜΑΤΑ Οι ασκήσεις διαλυμάτων που αφορούν τις περιεκτικότητες % w/w, % w/v και % v/v χωρίζονται σε 3 κατηγορίες: α) Ασκήσεις όπου πρέπει να βρούμε ή
Χημική Κινητική Γενικές Υποδείξεις 1. Τάξη Αντίδρασης 2. Ενέργεια Ενεργοποίησης
 Χημική Κινητική Γενικές Υποδείξεις 1. Τάξη Αντίδρασης Γενικά, όταν έχουμε δεδομένα συγκέντρωσης-χρόνου και θέλουμε να βρούμε την τάξη μιας αντίδρασης, προσπαθούμε να προσαρμόσουμε τα δεδομένα σε εξισώσεις
Χημική Κινητική Γενικές Υποδείξεις 1. Τάξη Αντίδρασης Γενικά, όταν έχουμε δεδομένα συγκέντρωσης-χρόνου και θέλουμε να βρούμε την τάξη μιας αντίδρασης, προσπαθούμε να προσαρμόσουμε τα δεδομένα σε εξισώσεις
ΕΣΩΤΕΡΙΚΗ ΕΝΕΡΓΕΙΑ. κινητική + + δυναμική
 ΕΣΩΤΕΡΙΚΗ ΕΝΕΡΓΕΙΑ Εσωτερική ενέργεια: Το άθροισμα της κινητικής (εσωτερική κινητική ενέργεια ή θερμική ενέργεια τυχαία, μη συλλογική κίνηση) και δυναμικής ενέργειας (δεσμών κλπ) όλων των σωματιδίων (ατόμων
ΕΣΩΤΕΡΙΚΗ ΕΝΕΡΓΕΙΑ Εσωτερική ενέργεια: Το άθροισμα της κινητικής (εσωτερική κινητική ενέργεια ή θερμική ενέργεια τυχαία, μη συλλογική κίνηση) και δυναμικής ενέργειας (δεσμών κλπ) όλων των σωματιδίων (ατόμων
ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης
 ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης Πρόβληµα 1. Ένα µίγµα αερίων που περιέχει 65% του Α, 5% Β, 8% C και % D βρίσκεται σε ισορροπία µ' ένα υγρό στους 350 Κ και 300 kn/m. Αν η τάση ατµών των καθαρών συστατικών
ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης Πρόβληµα 1. Ένα µίγµα αερίων που περιέχει 65% του Α, 5% Β, 8% C και % D βρίσκεται σε ισορροπία µ' ένα υγρό στους 350 Κ και 300 kn/m. Αν η τάση ατµών των καθαρών συστατικών
Η Φυσική των ζωντανών Οργανισμών (10 μονάδες)
 Η Φυσική των ζωντανών Οργανισμών (10 μονάδες) Δεδομένα: Κανονική Ατμοσφαιρική Πίεση, P 0 = 1.013 10 5 Pa = 760 mmhg Μέρος A. Η φυσική του κυκλοφορικού συστήματος. (4.5 μονάδες) Q3-1 Στο Μέρος αυτό θα μελετήσετε
Η Φυσική των ζωντανών Οργανισμών (10 μονάδες) Δεδομένα: Κανονική Ατμοσφαιρική Πίεση, P 0 = 1.013 10 5 Pa = 760 mmhg Μέρος A. Η φυσική του κυκλοφορικού συστήματος. (4.5 μονάδες) Q3-1 Στο Μέρος αυτό θα μελετήσετε
Τμήμα Τεχνολογίας Τροφίμων. Ανόργανη Χημεία. Ενότητα 7 η : Αέρια Ιδιότητες & συμπεριφορά. Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής.
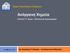 Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 7 η : Αέρια Ιδιότητες & συμπεριφορά Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Αέρια & Πίεση Αερίων 2 Ο αέρας είναι ένα τυπικό αέριο
Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 7 η : Αέρια Ιδιότητες & συμπεριφορά Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Αέρια & Πίεση Αερίων 2 Ο αέρας είναι ένα τυπικό αέριο
Διαδικασίες Υψηλών Θερμοκρασιών
 Διαδικασίες Υψηλών Θερμοκρασιών Θεματική Ενότητα 4: Διαδικασίες σε υψηλές θερμοκρασίες Τίτλος: Διάχυση Ονόματα Καθηγητών: Κακάλη Γλυκερία, Ρηγοπούλου Βασιλεία Σχολή Χημικών Μηχανικών Άδειες Χρήσης Το παρόν
Διαδικασίες Υψηλών Θερμοκρασιών Θεματική Ενότητα 4: Διαδικασίες σε υψηλές θερμοκρασίες Τίτλος: Διάχυση Ονόματα Καθηγητών: Κακάλη Γλυκερία, Ρηγοπούλου Βασιλεία Σχολή Χημικών Μηχανικών Άδειες Χρήσης Το παρόν
ΝΟΜΟΙ ΑΕΡΙΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ
 ΝΟΜΟΙ ΑΕΡΙΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΑΣΚΗΣΗ 1 Μία θερμική μηχανή λειτουργεί μεταξύ των θερμοκρασιών T h 400 Κ και T c με T c < T h Η μηχανή έχει απόδοση e 0,2 και αποβάλλει στη δεξαμενή χαμηλής θερμοκρασίας θερμότητα
ΝΟΜΟΙ ΑΕΡΙΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΑΣΚΗΣΗ 1 Μία θερμική μηχανή λειτουργεί μεταξύ των θερμοκρασιών T h 400 Κ και T c με T c < T h Η μηχανή έχει απόδοση e 0,2 και αποβάλλει στη δεξαμενή χαμηλής θερμοκρασίας θερμότητα
2. Κατά την ανελαστική κρούση δύο σωμάτων διατηρείται:
 Στις ερωτήσεις 1-4 να επιλέξετε μια σωστή απάντηση. 1. Ένα πραγματικό ρευστό ρέει σε οριζόντιο σωλήνα σταθερής διατομής με σταθερή ταχύτητα. Η πίεση κατά μήκος του σωλήνα στην κατεύθυνση της ροής μπορεί
Στις ερωτήσεις 1-4 να επιλέξετε μια σωστή απάντηση. 1. Ένα πραγματικό ρευστό ρέει σε οριζόντιο σωλήνα σταθερής διατομής με σταθερή ταχύτητα. Η πίεση κατά μήκος του σωλήνα στην κατεύθυνση της ροής μπορεί
Υπολογισμός & Πρόρρηση. Θερμοδυναμικών Ιδιοτήτων
 Υπολογισμός & Πρόρρηση Θερμοδυναμικών Ιδιοτήτων d du d Θερμοδυναμικές Ιδιότητες d dh d d d du d d dh U A H G d d da d d dg d du dq dq d / d du dq Θεμελιώδεις Συναρτήσεις περιέχουν όλες τις πληροφορίες
Υπολογισμός & Πρόρρηση Θερμοδυναμικών Ιδιοτήτων d du d Θερμοδυναμικές Ιδιότητες d dh d d d du d d dh U A H G d d da d d dg d du dq dq d / d du dq Θεμελιώδεις Συναρτήσεις περιέχουν όλες τις πληροφορίες
ΚΕΦΑΛΑΙΟ 3 Ο ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΤΩΝ ΙΔΑΝΙΚΩΝ ΑΕΡΙΩΝ
 Σχολικό Έτος 016-017 67 ΚΕΦΑΛΑΙΟ Ο ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΤΩΝ ΙΔΑΝΙΚΩΝ ΑΕΡΙΩΝ Α. ΕΙΣΑΓΩΓΗ ΣΤΑ ΑΕΡΙΑ 1. Σχετικές Ατομικές και Μοριακές Μάζες Σχετική Ατομική Μάζα (Α r) του ατόμου ενός στοιχείου, ονομάζεται ο αριθμός
Σχολικό Έτος 016-017 67 ΚΕΦΑΛΑΙΟ Ο ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΤΩΝ ΙΔΑΝΙΚΩΝ ΑΕΡΙΩΝ Α. ΕΙΣΑΓΩΓΗ ΣΤΑ ΑΕΡΙΑ 1. Σχετικές Ατομικές και Μοριακές Μάζες Σχετική Ατομική Μάζα (Α r) του ατόμου ενός στοιχείου, ονομάζεται ο αριθμός
ΙΑΧΥΣΗ. Σχήµα 1: Είδη διάχυσης
 ΙΑΧΥΣΗ ΟΡΙΣΜΟΣ - ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ιάχυση (diffusin) είναι ο µηχανισµός µεταφοράς ατόµων (όµοιων ή διαφορετικών µεταξύ τους) µέσα στη µάζα ενός υλικού, λόγω θερµικής διέγερσής τους. Αποτέλεσµα της διάχυσης
ΙΑΧΥΣΗ ΟΡΙΣΜΟΣ - ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ιάχυση (diffusin) είναι ο µηχανισµός µεταφοράς ατόµων (όµοιων ή διαφορετικών µεταξύ τους) µέσα στη µάζα ενός υλικού, λόγω θερµικής διέγερσής τους. Αποτέλεσµα της διάχυσης
