Ταξινομητές Νευρωνικών ικτύων
|
|
|
- Ιολανθη Δημητρακόπουλος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Αναγνώριση Προτύπων Ταξινομητές Νευρωνικών ικτύων Χριστόδουλος Χαμζάς 011 Τμήμα του περιεχομένου των παρουσιάσεων προέρχονται από τις παρουσιάσεις του αντίστοιχου διδακτέου μαθήματος του καθ. Σέργιο Θεοδωρίδη,, Τμ. Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήμιο Αθηνών
2 Γιατί μη γραμμικοί ταξινομητές; Πρόβλημα κατηγοριών: Αν ο αριθμός των προτύπων είναι μικρότερος από τον αριθμό των συνιστωσών κάθε προτύπου, τότε υπάρχει πάντα υπερεπίπεδο που τα διαχωρίζει. Επομένως οι γραμμικοί ταξινομητέςείναι χρήσιμοι: σε προβλήματα πολύ μεγάλης διαστατικότητας Σε προβλήματα μέτριας διαστατικότητας, όπου υπάρχει ένας σχετικά μικρός αριθμός προτύπων εκπαίδευσης Επιπλέον ο αριθμός των συνιστωσών ενός προτύπου μπορεί να αυξηθεί αυθαίρετα με την προσθήκη νέων συνιστωσών που είναι μη γραμμικές συναρτήσεις των αρχικών συνιστωσών (π.χ. πολυώνυμα) Υπάρχουν πολλά προβλήματα που δεν μπορούν να επιλυθούν με γραμμικούς ταξινομητές Στις προηγούμενες μεθόδους, η κύρια δυσκολία είναι η εύρεση της μη γραμμικής συνάρτησης ρη ης Μια κατηγορία μη γραμμικών ταξινομητών είναι και τα πολυστρωματικά νευρωνικά δίκτυα Σε αυτά η μορφή της μη γραμμικής συνάρτησης διαχωρισμού μαθαίνεται από τα δεδομένα εκμάθησης
3 Το απλό perceptron (γραμμικός ταξινομητής) Αρχιτεκτονική: Μονοστρωματικό δίκτυο με N εισόδους και Μ νευρώνες διατεταγμένους σε ένα στρώμα νευρώνων. Συναπτικές συνδέσεις συνδέουν όλους τους νευρώνες με όλες τις εισόδους. Νευρώνες: Τύπου McCulloch-Ptts με hard lmter και προσαρμοζόμενο κατώφλι ενεργοποίησης y sgn( wx w ) j j 0 j Δεδομένου ότι οι έξοδοι είναι ανεξάρτητες μεταξύ τους, μπορούμε να τις μελετήσουμε και ανεξάρτητα, α θεωρώντας κάθε νευρώνα του perceptron χωριστά: x 1 w w 1 x y sgn( w x w ) w n x n w 0-1 y Σ f=sgn +1 j sgn( wxw ) j j 0 3 0
4 Το πρόβλημα: Δίνεται ένα σύνολο P προτύπων { x, 1,,..., P} n διαμερισμένο σε κατηγορίες C { x, 1,,..., K} C { x, K 1, K,..., P} 1 που είναι γραμμικά διαχωρίσιμες, δηλαδή υπάρχει ένα διάνυσμα wx ˆ 0 x C, wx ˆ 0 x C 1 ŵ ώστε Το ζητούμενο είναι να βρεθεί ένα τέτοιο διάνυσμα που να διαχωρίζει γραμμικά τις κατηγορίες με επαναληπτικό τρόπο. 4
5 Η γεωμετρία του προβλήματος g ( x) w T x w0 x w 0 /w w x D w 0 /w 1 x 1 5
6 Motvaton Natural Systems perform very complex nformaton processng tass wth completely dfferent "hardware" than conventonal (von Neumann) computers The 100-step program constrant [Jerry Feldman} Neurons operate n 1ms Humans do sophstcated processng n 0.1s Only 100 seral steps massve parallelsm 6
7 7
8 Artfcal Neural Networ (ANN) 8
9 Defnton: An Artfcal Neural Networ (ANN) s an nformaton processng devce consstng of a large number of hghly nterconnected processng elements. Each processng element (unt) performs only very smple computatons. Remars: Each unt computes a sngle actvaton-value Envronmental nteracton through a subset of unts Behavor depends on nterconnecton structure Structure may adapt by learnng 9
10 The XOR problem ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ Non Lnear Classfers x 1 x XOR Class B A A B 10
11 There s no sngle lne (hyperplane) that separates class A from class B. On the contrary, AND and OR operatons are lnearly separable problems 11
12 The Two-Layer Perceptron For the XOR problem, draw two, nstead, of one lnes 1
13 Then class B s located outsde the shaded area and class A nsde. Ths s a two-phase desgn. Phase 1: Draw two lnes (hyperplanes) g1( x) g( x) 0 Each of them s realzed by a perceptron. outputs of the perceptrons wll be y 0 f ( g ( x )) 1, 1 dependng on the poston of x. The Phase : Fnd the poston of x w.r.t. both lnes, based on the values of y 1, y. 13
14 1 st phase nd x 1 x y 1 y phase 0 0 0(-) 0(-) B(0) 0 1 1(+) 0(-) A(1) 1 0 1(+) 0(-) A(1) 1 1 1(+) 1(+) B(0) Equvalently: The computatons of the frst phase T perform a mappng x y y, y ] [ 1 14
15 The decson s now performed on the transformed data. y g( y) 0 Ths can be performed va a second lne, whch can also be realzed by a perceptron. 15
16 Computatons of the frst phase perform a mappng that transforms the nonlnearly separable problem to a lnearly separable one. The archtecture 16
17 Ths s nown as the two layer (*) perceptron wth one hdden and one output layer. The actvaton functons are 0 0 f (.) 1 The neurons (nodes) of the fgure realze the followng lnes (hyperplanes) g g g 1 ( x ) x 1 x 0 3 ( x) x1 x 0 1 y) y1 y 0 1 ( (*) NOTE: Duba, Hart and Stor, n ther boo they call t a three layer perceptron. In general n ther notaton, what we call N-layer they call t (N+1)-Layer 17
18 Classfcaton capabltes of the two-layer perceptron The mappng performed by the frst layer neurons s onto the vertces of the unt sde square, e.g., (0, 0), (0, 1), (1, 0), (1, 1). The more general case, x R x l y 0, 1 1, p [ y1,... y p ], y,... T 18
19 performs a mappng of a vector onto the vertces of the unt sde H p hypercube The mappng s acheved wth p neurons each realzng a hyperplane. The output of each of these neurons s 0 or 1 dependng on the relatve poston of x w.r.t. the hyperplane. 19
20 Intersectons of these hyperplanes form regons n the l-dmensonal space. Each regon corresponds to a vertex of the H p unt hypercube. 0
21 For example, the 001 vertex corresponds to the regon whch s located to the (-) sde of g 1 (x)=0 to the (-) sde of g (x)=0 to the (+) sde of g 3 (x)=0 1
22 The output neuron realzes a hyperplane n the transformed y space, that separates some of the vertces from the others. Thus, the two layer perceptron has the capablty to classfy vectors nto classes that consst of unons of polyhedral regons. But NOT ANY unon. It depends on the relatve poston of the correspondng vertces.
23 Three layer-perceptrons The archtecture w j y j = f(net j ) Ths s capable to classfy vectors nto classes consstng of ANY unon of polyhedral regons. The dea s smlar to the XOR problem. It realzes p more than one planes n the space. y R 3
24 Three layer-perceptrons wth C classes The archtecture for more than classes w j y j = f(net j ) 4
25 A sngle bas unt s connected to each unt other than the nput unts d d t 0 xw j w j. x, 1 0 Net actvaton: net j xw j w j where the subscrpt ndexes unts n the nput layer, j n the hdden; w j denotes the nput-to-hdden layer weghts at the hdden unt j. (In neurobology, such weghts or connectons are aecalled aed synapses ) apses) Each hdden unt emts an output that s a nonlnear functon of ts actvaton, that s: y j =f(net) j 5
26 The reasonng For each vertex, correspondng to class, say A, construct a hyperplane whch leaves THIS vertex on one sde (+) and ALL the others to the other sde (-). The output neuron realzes an OR gate Overall: The frst layer of the networ forms the hyperplanes, the second layer forms the regons and the output neuron forms the classes. Desgnng Multlayer Perceptrons One drecton s to adopt the above ratonale and develop a structure that classfes correctly all the tranng patterns. The other drecton s to choose a structure and compute the synaptc weghts to optmze a cost functon. 6
27 Expressve Power of mult-layer Networs Queston: Can every decson be mplemented by a three-layer networ descrbed by equaton (1)? Answer: Yes (due to A. Kolmogorov) Any contnuous functon from nput to output can be mplemented n a three-layer net, gven suffcent number of hdden unts n H, proper nonlneartes, and weghts. g( x ) n 1 j j1 n ( x ) x I ( I [0,1];n ) j for properly chosen functons j and j 7
28 Each of the n+1 hdden unts j taes as nput a sum of d nonlnear functons, one for each nput feature x Each hdden unt emts a nonlnear functon j of ts total nput The output unt emts the sum of the contrbutons of the hdden unts Unfortunately: Kolmogorov s theorem tells us very lttle about how to fnd the nonlnear functons based on data; ths s the central problem n networ-based pattern recognton 8
29 Bacpropagaton Algorthm Any functon from nput to output t can be mplemented as a three-layer neural networ These results are of greater theoretcal nterest than practcal, snce the constructon of such a networ requres the nonlnear functons and the weght values whch are unnown! 9
30 (*) (*) (*) Στο σχήμα αυτό, αντικατέστησε two layer με one layer και three layer με two layer 30
31 Our goal now s to set the nterconnexon weghts based on the tranng patterns and the desred outputs In a three-layer networ, t s a straghtforward matter to understand how the output, and thus the error, depend on the hdden-to-output layer weghts The power of bacpropagaton s that t enables us to compute an effectve error for each hdden unt, and thus derve a learnng rule for the nput-to- hdden weghts, ths s nown as: 31
32 The Bacpropagaton Algorthm Ths s an algorthmc procedure that computes the synaptc weghts teratvely, so that an adopted cost functon s mnmzed (optmzed) In a large number of optmzng procedures, computaton of dervatves are nvolved. Hence, dscontnuous actvaton functons pose a problem,.e., 1 x 0 f ( x ) 0 x 0 There s always an escape path!!! The logstc functon 1 f ( x) 1 exp( ax) s an example. Other functons are also possble and n some cases more desrable. 3
33 33
34 The steps: Adopt an optmzng cost functon, e.g., Least Squares Error Relatve Entropy between desred responses and actual responses of the networ for the avalable tranng patterns. That s, from now on we have to lve wth errors. We only try to mnmze them, usng certan crtera. Adopt an algorthmc procedure for the optmzaton of the cost functon wth respect to the synaptc weghts e.g., Gradent descent Newton s algorthm Conjugate gradent 34
35 The tas s a nonlnear optmzaton one. For the gradent descent method r r r w 1 (new) w 1 (old) w 1 w r 1 J ww 1 r 1 η s the learnng rate 35
36 The Procedure: Intalze unnown weghts randomly wth small values. Compute the gradent terms bacwards, startng wth the weghts of the last (3 rd ) layer and then movng towards the frst Update the weghts Repeat the procedure untl a termnaton procedure s met Two major phlosophes: Batch mode: The gradents of the last layer are computed once ALL tranng data have appeared to the algorthm,.e., by summng up all error terms. Pattern mode: The gradents are computed every tme a new tranng data par appears. Thus gradents are based on successve ndvdual errors. 36
37 37
38 A major problem: The algorthm may converge to a local l mnmum 38
39 The Cost functon choce Examples: The Least Squares J N 1 E ( ) E( ) e ˆ m( ) ( ym( ) y m ( )) 1,,..., N m1 m1 Desred response of the m th output neuron (1 or 0) for x( y m () ) yˆ m () Actual response of the m th output neuron, n the nterval [0, 1], for nput x() 39
40 The cross-entropy N 1 J E ( ) E( ) ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ m1 y m ( ) ln yˆ m ( ) (1 y m ( )) ln(1 yˆ m ( )) Ths presupposes an nterpretaton of y and ŷ as probabltes Classfcaton error rate. Ths s also nown as dscrmnatve learnng. Most of these technques use a smoothed verson of the classfcaton error. 40
41 Remar 1: A common feature of all the above s the danger of local mnmum convergence. Well formed cost functons guarantee convergence to a good soluton, that s one that classfes correctly ALL tranng patterns, provded such a soluton exsts. The cross-entropy cost functon s awellformedone. The Least Squares s not. 41
42 Remar : Both, the Least Squares and the cross entropy lead to output values yˆ m ( ) that approxmate optmally class a-posteror probabltes!!! yˆ m ( ) P( m x( )) x() That s, the probablty of class m gven. Ths s a very nterestng result. It does not depend on the underlyng dstrbutons. It s a characterstc of certan cost functons. How good or bad s the approxmaton, depends on the underlyng model. Furthermore, t s only vald at the global mnmum. 4
43 net ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ Networ Learnng d d t xw w 0 xw w. x, 1 0 Let t be the -th target (or desred) output and z be the - th computed output wth = 1,, c and w represents all the weghts of the networ The tranng error:( Least Square) c 1 J( w ) ( t z 1 ) 1 t z The bacpropagaton learnng rule s based on gradent descent The weghts are ntalzed wth pseudo-random values and are changed n a drecton that wll reduce the error: w J w 43
44 where s the learnng rate whch ndcates the relatve sze of the change n weghts w(m +1) = w(m) + w(m) where m s the m-th pattern presented Error on the hdden to-output weghts J w j J net net. w j net w where the senstvty of unt s defned as: j J net and descrbes how the overall error changes wth the actvaton of the unt s net J J z. ( t z ) f' ( net ) net z net 44
45 Snce net =w t t.y therefore: net w j y j Concluson: the weght update (or learnng rule) for the hdden-to-output output weghts s: w j = y j = (t z )f (net )y j Error on the nput-to-hdden unts J w j J y y j. net net. w j j j j 45
46 ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ However, c c c j c j j net z y z z t z t y y J 1 1 ) ( ) ( 1 Smlarly as n the precedng case, we defne the j j w net f z t y net net z z t 1 1 ) ( ' ) (. ) ( y p g, senstvty for a hdden unt: c j j j w net f 1 ) ( ' whch means that: The senstvty at a hdden unt s smply the sum of the ndvdual senstvtes at the output 1 smply the sum of the ndvdual senstvtes at the output unts weghted by the hdden-to-output weghts w j ; all multpled by f (net j ) Concluson: The learnng rule for the nput-to-hdden weghts s: 46 j j j j x net f w x w j ) ( '
47 STOCHASTIC BACKPROPAGATION Startng wth a pseudo-random weght confguraton, the stochastc bacpropagaton p algorthm can be wrtten as: Begn ntalze n H ; w, crteron,, m 0 do m m + 1 x m randomly chosen pattern w j w j + j x ; w j w j + y j untl J(w) < return w End 47
48 BATCH BACKPROPAGATION Startng wth a pseudo-random weght confguraton, the batch bacpropagaton algorthm can be wrtten as: Begn ntalze n H ; w, crteron,, r 0 do r r + 1 (epoch) m 0; Δw j 0; Δw j 0 do m m + 1 x m select pattern Δw j Δw j + j x ; Δw j Δw j + y j untl m=n w j w j + j x ; w j w j + y j untl J(w) < return w End 48
49 Stoppng crteron ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ The algorthm termnates when the change n the crteron functon J(w) s smaller than some preset value There are other stoppng crtera that lead to better performance than ths one So far, we have consdered the error on a sngle pattern, but we want to consder an error defned over the entrety of patterns n the tranng set The total tranng error s the sum over the errors of n ndvdual patterns n J p1 J p (1) 49
50 Stoppng crteron (cont.) A weght update may reduce the error on the sngle pattern beng presented but can ncrease the error on the full tranng set However, gven a large number of such ndvdual updates, the total error of equaton (1) decreases 50
51 Tranng set: Defntons A set of examples used for learnng, that s to ft the parameters [.e., weghts] of the classfer. Valdaton set: A set of examples used to tune the parameters [.e., archtecture, not weghts] of a classfer, for example to choose the number of hdden unts n a neural networ. Test set: A set of examples used only to assess the performance [generalzaton] of a fully-specfed classfer.
52 HOLD OUT METHOD Snce our goal s to fnd the networ havng the best performance on new data, the smplest approach to the comparson of dfferent networs s to evaluate the error functon usng data whch s ndependent of that used for tranng. Varous networs are traned by mnmzaton of an approprate error functon defned wth respect to a tranng data set. The performance of the networs s then compared by evaluatng the error functon usng an ndependent valdaton set, and the networ havng the smallest error wth respect to the valdaton set s selected. Ths approach s called the hold out method. Snce ths procedure can tself lead to some overfttng to the valdaton set, the performance of the selected networ should be confrmed by measurng ts performance on a thrd ndependent set of data called a test set. The crucal pont s that t a test t set s never used to choose among two or more networs, so that the error on the test set provdes an unbased estmate of the generalzaton error. Any data set that s used to choose the best of two or more networs s, by defnton, a valdaton set, and the error of the chosen networ on the valdaton set s optmstcally based. Read more:
53 Learnng Curves Before tranng starts, the error on the tranng set s hgh; through the learnng process, the error becomes smaller The error per pattern depends on the amount of tranng data and the expressve power (such as the number of weghts) n the networ The average error on an ndependent test set s always hgher than on the tranng set, and t can decrease as well as ncrease A valdaton set s used n order to decde when to stop tranng ; we do not want to overft the networ and decrease the power of the classfer generalzaton we stop tranng at a mnmum of the error on the valdaton set 53
54 54
55 REGULARIZATION Choce of the networ sze. How bg a networ can be. How many layers and how many neurons per layer?? There are two major drectons 55
56 Prunng Technques These technques start from a large networ and then weghts and/or neurons are removed teratvely, accordng to a crteron. 56
57 ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ Methods based on parameter senstvty j j j w w h w h w g J hgher order terms where j j w w J h, w J g Near a mnmum and assumng that j 1 h w J 57
58 Prunng s now acheved n the followng procedure: Tran the networ usng Bacpropagaton for a number of steps Compute the salences s hw Remove weghts wth small s. Repeat the process Methods based on functon regularzaton J N 1 E( ) ae p ( w) 58
59 The second term favours small values for the weghts, e.g., E p ( ) h( w ) h( w ) w w 0 w w 0 1 where After some tranng steps, weghts wth small values are removed. 59
60 Constructve technques They start wth a small networ and eep ncreasng t, accordng to a predetermned d procedure and crteron. 60
61 Remar: Why not start wth a large networ and leave the algorthm to decde whch weghts are small?? Ths approach s just naïve. It overloos that classfers must have good generalzaton propertes. A large networ can result n small errors for the tranng set, snce t can learn the partcular detals of the tranng set. On the other hand, t wll not be able to perform well when presented wth data unnown to t. The sze of the networ must be: Large enough to learn what maes data of the same class smlar and data from dfferent classes dssmlar Small enough not to be able to learn underlyng dfferences between data of the same class. Ths leads to the so called overfttng. 61
62 Example: 6
63 Overtranng s another sde of the same con,.e., the networ adapts to the peculartes of the tranng set. 63
64 Generalzed Lnear Classfers Remember the XOR problem. The mappng f (.) x f ( g1 ( x)) y f ( g( x)) The actvaton functon transforms the nonlnear tas nto a lnear one. In the more general case: l Let and a nonlnear classfcaton tas. x R f (.), 1,,..., 64
65 Are there any functons and an approprate, so that the mappng x y f ( x 1 )... f ( x) transforms the tas nto a lnear one, n the space? If ths s true, then there exsts a hyperplane so that y R w R If w w T 0 w y 0, x T 0 w y 0, x 1 65
66 In such a case ths s equvalent wth approxmatng the nonlnear dscrmnant functon g(x), n terms of (x),.e., f g ( x ) w0 w f ( x ) ( ) 0 1 Gven f ( x), the tas of computng the weghts s a lnear one. 0 How sensble s ths?? From the numercal analyss pont of vew, ths s justfed f f (x) are nterpolaton functons. From the Pattern Recognton pont of vew, ths s justfed by Cover s theorem 66
67 Capacty of the l-dmensonall space n Lnear Dchotomes l Assume N ponts n R assumed to be n general poston, thatt s: Not 1 of these le on a 1 dmensonal space 67
68 Cover s theorem states: The number of groupngs that can be formed by (l-1)-dmensonal hyperplanes to separate N ponts n two classes s O( N, l) N 1, l N N 1 ( N 1)! ( N 1 )!! 0 Example: N=4, l=, O(4,)=14 Notce: The total number of possble groupngs s 4 =16 68
69 Probablty of groupng N ponts n two lnearly separable classes s O( N, l) l P N N N r( l 1) 69
70 Thus, the probablty of havng N ponts n lnearly separableable classes tends to 1, for large l, po provded N<( +1) l Hence, by mappng to a hgher dmensonal space, we ncrease the probablty of lnear separablty, provded the space s not too densely populated. 70
71 Radal Bass Functon Networs (RBF) Choose 71
72 f ( x ) exp x c Equvalent to a sngle layer networ, wth RBF actvatons and lnear output node. 7
73 ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ Example: The XOR problem Defne: , c, c ) exp( ) exp( 1 c x c x y , ,
74 g( y) y1 y 1 0 g( x) exp( x c1 ) exp( x c )
75 Tranng of the RBF networs Fxed centers: Choose centers randomly among the data ponts. Also fx σ s. Then g ( x ) w 0 w T y s a typcal lnear classfer desgn. Tranng of the centers: Ths s a nonlnear optmzaton tas Combne supervsed and unsupervsed learnng procedures. The unsupervsed up part reveals clusterng tendences of the data and assgns the centers at the cluster representatves. 75
76 Unversal Approxmators It has been shown that any nonlnear contnuous functon can be approxmated arbtrarly close, both, by a two layer perceptron, wth sgmod actvatons, and an RBF networ, provded a large enough number of nodes s used. Multlayer Perceptrons vs. RBF networs MLP s nvolve actvatons of global nature. All ponts on a plane w T x c gve the same response. RBF networs have actvatons of a local nature, due to the exponental decrease as one moves away from the centers. MLP s learn slower but have better generalzaton propertes 76
77 Support Vector Machnes: The non-lnear case Recall that the probablty of havng lnearly separable classes ncreases as the dmensonalty of the feature vectors ncreases. Assume the mappng: x R l y R, l Then use SVM n R Recall that n ths case the dual problem formulaton wll be maxmze ( where y 1 N T j y y j y y ) j 1, j R 77
78 Also, the classfer wll be g T ( y) w y w0 where x N s y 1 y R y y Thus, nner products n a hgh dmensonal space are nvolved, hence Hgh complexty 78
79 Somethng clever: Compute the nner products n the hgh dmensonal space as functons of nner products performed n the low dmensonal space!!! Is ths POSSIBLE?? Yes. Here s an example Let Let x x x 1 y, x T R x x 1 x x 1 R Then, t s easy to show that y T y j T ( x x j ) 3 79
80 Mercer s Theorem ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ Let x ( x) H Then, the nner product n H r r ( x ) ( y ) K ( x, y ) r where Κ ( x, y ) g ( x ) g ( y ) d xd y 0 for any g(x), x: g ( x) d x K(x,y) symmetrc functon nown as ernel. 80
81 The opposte s also true. Any ernel, wth the above propertes, corresponds to an nner product n SOME space!!! Examples of ernels Radal bass Functons: Polynomal: K ( x, z ) exp x z Hyperbolc Tangent: T q K( x, z) ( x z 1), q K( x, z) tanh( x z ) for approprate values of β, γ. T 0 81
82 SVM Formulaton ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ Step 1: Choose approprate ernel. Ths mplctely assumes a mappng to a hgher dmensonal (yet, not nown) space. Step : 1 max ( j y subject to : 0, j C, y 0 y j K ( x, x j 1,,..., N )) Ths results to an mplct combnaton w N s y 1 ( x ) 8
83 Step 3: Assgn x to N s 1( ) f g( x) y Κ( x, x) w0 ( ) 0 1 The SVM Archtecture 83
84 84
85 Decson Trees ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ Ths sa famly of non-lnear classfers. They are multstage t decson systems, n whch classes are sequentally rejected, untl a fnally accepted class s reached. To ths end: The feature space s splt nto unque regons n a sequental manner. Upon the arrval of a feature vector, sequental decsons, assgnng features to specfc regons, are performed along a path of nodes of an approprately p constructed tree. The sequence of decsons s appled to ndvdual features, and the queres performed n each node are of the type: s feature x a where α s a pre-chosen (durng tranng) threshold. 85
86 The fgures below are such examples. Ths type of trees s nown as Ordnary Bnary Classfcaton Trees (OBCT). The decson hyperplanes, splttng the space nto regons, are parallel to the axs of the spaces. Other types of partton are also possble, yet less popular. 86
87 Desgn Elements that defne a decson tree. Eachnode,t, s assocated wth a subset Χ t X, where X s the tranng set. At each node, X t s splt nto two (bnary splts) dsjont descendant subsets X t,y and X t,n, where X t,y X t,n = Ø X t,y X t,n = X t X t,y s the subset of X t for whch the answer to the query at node t s YES. X tn t,n s the subset correspondng to NO. The splt s decded accordng to an adopted queston (query). 87
88 Asplttng crteron must be adopted for the best splt of X t nto X t,y and X t,n. A stop-splttng splttng crteron must be adopted that controls the growth of the tree and a node s declared as termnal (leaf). A rule s requred that assgns each (termnal) leaf to a class. 88
89 Set of Questons: In OBCT trees the set of questons s of the type x a s? The choce of the specfc x andthevalueofthethresholdα, for each node t, are the results of searchng, durng tranng, among the features and a set of possble threshold values. The fnal combnaton s the one that results to the best value of a crteron. 89
90 Splttng Crteron: The man dea behnd splttng at each node s the resultng descendant subsets X t,y and X t,n to be more class homogeneous compared to X t. Thus the crteron must be n harmony wth such a goal. A commonly used crteron s the node mpurty: M 1 tlog P t I( t) P and P t N t where s the number of data ponts n X t that belong to class. The decrease n node mpurty s defned as: Nt, Nt, N I( t) I( t) I( t ) I( tn ) N N t N N t t t t 90
91 The goal s to choose the parameters n each node (feature and threshold) that result n a splt wth the hghesth decrease n mpurty. Why hghest decrease? Observe that the hghest value of I(t) s acheved f all classes are equprobable,.e., X t s the least homogenous. Stop - splttng rule. Adopt a threshold T andstopsplttnga node (.e., assgn t as a leaf),fthempurtydecreasesless than T. That s, node t s pure enough. Class Assgnment Rule: Assgn a leaf to a class j, where: j arg max P( t) 91
92 Summary of an OBCT algorthmc scheme: 9
93 Remars: ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ A crtcal factor n the desgn s the sze of the tree. Usually one grows a tree to a large sze and then apples varous prunng technques. Decson trees belong to the class of unstable classfers. Ths can be overcome by a number of averagng technques. Baggng s a popular technque. Usng bootstrap technques n X, varous trees are constructed, T, =1,,, B. The decson s taen accordng to a majorty votng rule. 93
94 Combnng Classfers The basc phlosophy behnd the combnaton of dfferent classferss les n the fact that eenthe even best classfer fals n some patterns that other classfers may classfy correctly. Combnng classfers ams at explotng ths complementary nformaton resdng n the varous classfers. Thus, one desgns dfferent optmal classfers and then combnes the results wth a specfc rule. Assume that each of the, say, L desgned classfers provdes at ts output the posteror probabltes: P( x), 1,,..., M 94
95 Product Rule: Assgn x to the class : P where j th classfer. j L arg max P x x j1 SumRule:Assgn x to the class : j s the respectve posteror probablty of the arg max P j x L j1 j 95
96 Majorty Votng Rule: Assgn x to the class for whch there s a consensus or when at least c of the classfers agree on the class label of x where: L 1, L even c L 1, L odd otherwse the decson s rejecton, that s no decson s taen. Thus, correct decson s made f the majorty of the classfers agree on the correct label, and wrong decson f the majorty agrees n the wrong label. 96
97 Dependent or not Dependent classfers? Although there are not general theoretcal results, expermental evdence has shown that the more ndependent n ther decson the classfers are, the hgher the expectaton should be for obtanng mproved results after combnaton. However, there s no guarantee that combnng classfers results n better performance compared to the best one among the classfers. Towards Independence: A number of Scenaros. Tran the ndvdual classfers usng dfferent tranng data ponts. To ths end, choose among a number of possbltes: Bootstrappng: Ths s a popular technque to combne unstable classfers such as decson trees (Baggng belongs to ths category of combnaton). 97
98 Stacng:Tran the combner wth data ponts that have been excluded from the set used to tran the ndvdual classfers. Use dfferent subspaces to tran ndvdual classfers: Accordng to the method, each ndvdual classfer operates n a dfferent feature subspace. That s, use dfferent features for each classfer. Remars: The majorty votng and the summaton schemes ran among the most popular combnaton schemes. Tranng ndvdual classfers n dfferent subspaces seems to lead to substantally better mprovements compared to classfers operatng n the same subspace. Besdes the above three rules, other alternatves are also possble, such as to use the medan value of the outputs of ndvdual classfers. 98
99 The Boostng Approach The orgns: Is t possble a wea learnng algorthm (one that performs slghtly better than a random guessng) to be boosted nto a strong algorthm? (Vllant 1984). The procedure to acheve t: Adopt a wea classfer nown as the base classfer. Employng the base classfer, desgn a seres of classfers, n a herarchcal fashon, each tme employng a dfferent weghtng g of the tranng samples. Emphass n the weghtng s gven on the hardest samples,.e., the ones that eep falng. Combne the herarchcally desgned d classfers by a weghted average procedure. 99
100 The AdaBoost Algorthm. Construct an optmally desgned classfer of the form: where: where x; bnary class label: s a parameter vector. f ( x) sgn F( x) K F ( x ) a x ; 1 denotes the base classfer that returns a ; 1,1 x 100
101 The essence of the method. Desgn the seres of classfers: x, x;,..., x; The parameter vectors ; 1, 1,,..., K are optmally computed so as: To mnmze the error rate on the tranng set. Each tme, the tranng samples are re-weghted so that the weght of each sample depends on ts hstory. Hard samples that nsst on falng to be predcted correctly, by the prevously desgned classfers, are more heavly weghted. 101
102 Updatng the weghts for each sample w m ( m 1) w exp y a Z m x ; x, 1,,..., N Z m s a normalzng factor common for all samples. a m 1 1 P ln P m m m where P m <0.5 (by assumpton) s the error rate of the optmal classfer x; m at stage m. Thus α m >0. The term: ep exp y a m x ; taes a large value f x m (wrong classfcaton) and a small value n the case of correct classfcaton m y ; 0} { y x m m ; 0 The update equaton s of a multplcatve nature. That s, successve large values of weghts (hard samples) result n larger weght for the next teraton 10
103 The algorthm 103
104 Remars: ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ Tranng error rate tends to zero after a few teratons. The test error levels to some value. AdaBoost s greedy n reducng the margn that samples leave from the decson surface. 104
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών. ΗΥ-570: Στατιστική Επεξεργασία Σήµατος. ιδάσκων : Α. Μουχτάρης. εύτερη Σειρά Ασκήσεων.
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
α & β spatial orbitals in
 The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
8.1 The Nature of Heteroskedasticity 8.2 Using the Least Squares Estimator 8.3 The Generalized Least Squares Estimator 8.
 8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
One and two particle density matrices for single determinant HF wavefunctions. (1) = φ 2. )β(1) ( ) ) + β(1)β * β. (1)ρ RHF
 One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
1 Complete Set of Grassmann States
 Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας. Version 2
 Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας Verson ΧΑΡΤΟΓΡΑΦΗΣΗ ΤΟΥ ΧΩΡΟΥ ΤΩΝ ΤΑΞΙΝΟΜΗΤΩΝ Ταξινομητές Ταξινομητές συναρτ. διάκρισης Ταξινομητές επιφανειών απόφ. Παραμετρικοί ταξινομητές Μη παραμετρικοί
Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας Verson ΧΑΡΤΟΓΡΑΦΗΣΗ ΤΟΥ ΧΩΡΟΥ ΤΩΝ ΤΑΞΙΝΟΜΗΤΩΝ Ταξινομητές Ταξινομητές συναρτ. διάκρισης Ταξινομητές επιφανειών απόφ. Παραμετρικοί ταξινομητές Μη παραμετρικοί
8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ. ICA: συναρτήσεις κόστους & εφαρμογές
 8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ ICA: συναρτήσεις κόστους & εφαρμογές ΚΎΡΤΩΣΗ (KUROSIS) Αθροιστικό (cumulant) 4 ης τάξεως μίας τ.μ. x με μέσο όρο 0: kurt 4 [ x] = E[ x ] 3( E[ y ]) Υποθέτουμε διασπορά=: kurt[ x]
8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ ICA: συναρτήσεις κόστους & εφαρμογές ΚΎΡΤΩΣΗ (KUROSIS) Αθροιστικό (cumulant) 4 ης τάξεως μίας τ.μ. x με μέσο όρο 0: kurt 4 [ x] = E[ x ] 3( E[ y ]) Υποθέτουμε διασπορά=: kurt[ x]
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας. Version 2
 Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας Verson ΜΗ ΓΡΑΜΜΙΚΟΙ ΤΑΞΙΝΟΜΗΤΕΣ ΝΕΥΡΩΝΙΚΑ ΔΙΚΤΥΑ Η παραπάνω ανάλυση ήταν χρήσιμη προκειμένου να κατανοήσουμε τη λογική των δικτύων perceptrons πολλών επιπέδων
Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας Verson ΜΗ ΓΡΑΜΜΙΚΟΙ ΤΑΞΙΝΟΜΗΤΕΣ ΝΕΥΡΩΝΙΚΑ ΔΙΚΤΥΑ Η παραπάνω ανάλυση ήταν χρήσιμη προκειμένου να κατανοήσουμε τη λογική των δικτύων perceptrons πολλών επιπέδων
8.324 Relativistic Quantum Field Theory II
 Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Lecture 2. Soundness and completeness of propositional logic
 Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Variance of Trait in an Inbred Population. Variance of Trait in an Inbred Population
 Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 6/5/2006
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα,
 ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας. Version 2
 Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας Verson ΧΑΡΤΟΓΡΑΦΗΣΗ ΤΟΥ ΧΩΡΟΥ ΤΩΝ ΤΑΞΙΝΟΜΗΤΩΝ Ταξινομητές Ταξινομητές συναρτ. διάκρισης Ταξινομητές επιφανειών απόφ. Παραμετρικοί ταξινομητές Μη παραμετρικοί
Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας Verson ΧΑΡΤΟΓΡΑΦΗΣΗ ΤΟΥ ΧΩΡΟΥ ΤΩΝ ΤΑΞΙΝΟΜΗΤΩΝ Ταξινομητές Ταξινομητές συναρτ. διάκρισης Ταξινομητές επιφανειών απόφ. Παραμετρικοί ταξινομητές Μη παραμετρικοί
Derivation for Input of Factor Graph Representation
 Dervaton for Input of actor Graph Representaton Sum-Product Prmal Based on the orgnal LP formulaton b x θ x + b θ,x, s.t., b, b,, N, x \ b x = b we defne V as the node set allocated to the th core. { V
Dervaton for Input of actor Graph Representaton Sum-Product Prmal Based on the orgnal LP formulaton b x θ x + b θ,x, s.t., b, b,, N, x \ b x = b we defne V as the node set allocated to the th core. { V
LECTURE 4 : ARMA PROCESSES
 LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Ο ρώξνο ησλ ραξαθηεξηζηηθώλ ηεκαρίδεηαη ζε κνλαδηθέο πεξηνρέο κε έλαλ αθνινπζηαθό ηξόπν.
 Δέλδξα Απόθαζεο Πξόθεηηαη γηα κηα νηθνγέλεηα κε γξακκηθώλ ηαμηλνκεηώλ. Είλαη ζπζηήκαηα απόθαζεο πνιιώλ ζηαδίσλ (multstage), όπνπ νη θιάζεηο απνξξίπηνληαη δηαδνρηθά (sequentally), έσο όηνπ θηάζνπκε ζε κηα
Δέλδξα Απόθαζεο Πξόθεηηαη γηα κηα νηθνγέλεηα κε γξακκηθώλ ηαμηλνκεηώλ. Είλαη ζπζηήκαηα απόθαζεο πνιιώλ ζηαδίσλ (multstage), όπνπ νη θιάζεηο απνξξίπηνληαη δηαδνρηθά (sequentally), έσο όηνπ θηάζνπκε ζε κηα
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Symplecticity of the Störmer-Verlet algorithm for coupling between the shallow water equations and horizontal vehicle motion
 Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
The challenges of non-stable predicates
 The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
Physical DB Design. B-Trees Index files can become quite large for large main files Indices on index files are possible.
 B-Trees Index files can become quite large for large main files Indices on index files are possible 3 rd -level index 2 nd -level index 1 st -level index Main file 1 The 1 st -level index consists of pairs
B-Trees Index files can become quite large for large main files Indices on index files are possible 3 rd -level index 2 nd -level index 1 st -level index Main file 1 The 1 st -level index consists of pairs
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
Phasor Diagram of an RC Circuit V R
 ESE Lecture 3 Phasor Dagram of an rcut VtV m snt V t V o t urrent s a reference n seres crcut KVL: V m V + V V ϕ I m V V m ESE Lecture 3 Phasor Dagram of an L rcut VtV m snt V t V t L V o t KVL: V m V
ESE Lecture 3 Phasor Dagram of an rcut VtV m snt V t V o t urrent s a reference n seres crcut KVL: V m V + V V ϕ I m V V m ESE Lecture 3 Phasor Dagram of an L rcut VtV m snt V t V t L V o t KVL: V m V
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Vol. 34 ( 2014 ) No. 4. J. of Math. (PRC) : A : (2014) Frank-Wolfe [7],. Frank-Wolfe, ( ).
![Vol. 34 ( 2014 ) No. 4. J. of Math. (PRC) : A : (2014) Frank-Wolfe [7],. Frank-Wolfe, ( ). Vol. 34 ( 2014 ) No. 4. J. of Math. (PRC) : A : (2014) Frank-Wolfe [7],. Frank-Wolfe, ( ).](/thumbs/91/105872052.jpg) Vol. 4 ( 214 ) No. 4 J. of Math. (PRC) 1,2, 1 (1., 472) (2., 714) :.,.,,,..,. : ; ; ; MR(21) : 9B2 : : A : 255-7797(214)4-759-7 1,,,,, [1 ].,, [4 6],, Frank-Wolfe, Frank-Wolfe [7],.,,.,,,., UE,, UE. O-D,,,,,
Vol. 4 ( 214 ) No. 4 J. of Math. (PRC) 1,2, 1 (1., 472) (2., 714) :.,.,,,..,. : ; ; ; MR(21) : 9B2 : : A : 255-7797(214)4-759-7 1,,,,, [1 ].,, [4 6],, Frank-Wolfe, Frank-Wolfe [7],.,,.,,,., UE,, UE. O-D,,,,,
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in
 Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Μηχανική Μάθηση. Ενότητα 10: Support Vector Machines. Ιωάννης Τσαμαρδίνος Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Ενότητα 10: Support Vector Machnes Ιωάννης Τσαμαρδίνος Τμήμα Επιστήμης Υπολογιστών Support Vector Machnes Decson surface s a hyperplane (lne n 2D)
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Ενότητα 10: Support Vector Machnes Ιωάννης Τσαμαρδίνος Τμήμα Επιστήμης Υπολογιστών Support Vector Machnes Decson surface s a hyperplane (lne n 2D)
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
Lecture Notes for Chapter 8
 Data Mnng Cluster Analyss Lecture otes for Chapter 8 Clusterng Target: Dvde data nto a set of groups (clusters) based on smlarty Smlar samples are grouped together, whle dssmlar samples are placed n dfferent
Data Mnng Cluster Analyss Lecture otes for Chapter 8 Clusterng Target: Dvde data nto a set of groups (clusters) based on smlarty Smlar samples are grouped together, whle dssmlar samples are placed n dfferent
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
Block Ciphers Modes. Ramki Thurimella
 Block Ciphers Modes Ramki Thurimella Only Encryption I.e. messages could be modified Should not assume that nonsensical messages do no harm Always must be combined with authentication 2 Padding Must be
Block Ciphers Modes Ramki Thurimella Only Encryption I.e. messages could be modified Should not assume that nonsensical messages do no harm Always must be combined with authentication 2 Padding Must be
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
PARTIAL NOTES for 6.1 Trigonometric Identities
 PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Appendix. Appendix I. Details used in M-step of Section 4. and expect ultimately it will close to zero. αi =α (r 1) [δq(α i ; α (r 1)
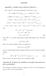 Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Math 6 SL Probability Distributions Practice Test Mark Scheme
 Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Generalized Fibonacci-Like Polynomial and its. Determinantal Identities
 Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Numerical Analysis FMN011
 Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Section 9.2 Polar Equations and Graphs
 180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΨΥΧΟΛΟΓΙΚΕΣ ΕΠΙΠΤΩΣΕΙΣ ΣΕ ΓΥΝΑΙΚΕΣ ΜΕΤΑ ΑΠΟ ΜΑΣΤΕΚΤΟΜΗ ΓΕΩΡΓΙΑ ΤΡΙΣΟΚΚΑ Λευκωσία 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΨΥΧΟΛΟΓΙΚΕΣ ΕΠΙΠΤΩΣΕΙΣ ΣΕ ΓΥΝΑΙΚΕΣ ΜΕΤΑ ΑΠΟ ΜΑΣΤΕΚΤΟΜΗ ΓΕΩΡΓΙΑ ΤΡΙΣΟΚΚΑ Λευκωσία 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Reminders: linear functions
 Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Overview. Transition Semantics. Configurations and the transition relation. Executions and computation
 Overview Transition Semantics Configurations and the transition relation Executions and computation Inference rules for small-step structural operational semantics for the simple imperative language Transition
Overview Transition Semantics Configurations and the transition relation Executions and computation Inference rules for small-step structural operational semantics for the simple imperative language Transition
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Proposal of Terminal Self Location Estimation Method to Consider Wireless Sensor Network Environment
 1 2 2 GPS (SOM) Proposal of Termnal Self Locaton Estmaton Method to Consder Wreless Sensor Network Envronment Shohe OHNO, 1 Naotosh ADACHI 2 and Yasuhsa TAKIZAWA 2 Recently, large scale wreless sensor
1 2 2 GPS (SOM) Proposal of Termnal Self Locaton Estmaton Method to Consder Wreless Sensor Network Envronment Shohe OHNO, 1 Naotosh ADACHI 2 and Yasuhsa TAKIZAWA 2 Recently, large scale wreless sensor
Parametrized Surfaces
 Parametrized Surfaces Recall from our unit on vector-valued functions at the beginning of the semester that an R 3 -valued function c(t) in one parameter is a mapping of the form c : I R 3 where I is some
Parametrized Surfaces Recall from our unit on vector-valued functions at the beginning of the semester that an R 3 -valued function c(t) in one parameter is a mapping of the form c : I R 3 where I is some
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
Neutralino contributions to Dark Matter, LHC and future Linear Collider searches
 Neutralno contrbutons to Dark Matter, LHC and future Lnear Collder searches G.J. Gounars Unversty of Thessalonk, Collaboraton wth J. Layssac, P.I. Porfyrads, F.M. Renard and wth Th. Dakonds for the γz
Neutralno contrbutons to Dark Matter, LHC and future Lnear Collder searches G.J. Gounars Unversty of Thessalonk, Collaboraton wth J. Layssac, P.I. Porfyrads, F.M. Renard and wth Th. Dakonds for the γz
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
Generalized Linear Model [GLM]
![Generalized Linear Model [GLM] Generalized Linear Model [GLM]](/thumbs/93/113885699.jpg) Generalzed Lnear Model [GLM]. ก. ก Emal: nkom@kku.ac.th A Lttle Hstory Multple lnear regresson normal dstrbuton & dentty lnk (Legendre, Guass: early 19th century). ANOVA normal dstrbuton & dentty lnk (Fsher:
Generalzed Lnear Model [GLM]. ก. ก Emal: nkom@kku.ac.th A Lttle Hstory Multple lnear regresson normal dstrbuton & dentty lnk (Legendre, Guass: early 19th century). ANOVA normal dstrbuton & dentty lnk (Fsher:
the total number of electrons passing through the lamp.
 1. A 12 V 36 W lamp is lit to normal brightness using a 12 V car battery of negligible internal resistance. The lamp is switched on for one hour (3600 s). For the time of 1 hour, calculate (i) the energy
1. A 12 V 36 W lamp is lit to normal brightness using a 12 V car battery of negligible internal resistance. The lamp is switched on for one hour (3600 s). For the time of 1 hour, calculate (i) the energy
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
forms This gives Remark 1. How to remember the above formulas: Substituting these into the equation we obtain with
 Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων. Εξάμηνο 7 ο
 Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων Εξάμηνο 7 ο Procedures and Functions Stored procedures and functions are named blocks of code that enable you to group and organize a series of SQL and PL/SQL
Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων Εξάμηνο 7 ο Procedures and Functions Stored procedures and functions are named blocks of code that enable you to group and organize a series of SQL and PL/SQL
A Class of Orthohomological Triangles
 A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
Αλγόριθμοι και πολυπλοκότητα NP-Completeness (2)
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα NP-Completeness (2) Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών NP-Completeness (2) x 1 x 1 x 2 x 2 x 3 x 3 x 4 x 4 12 22 32 11 13 21
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα NP-Completeness (2) Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών NP-Completeness (2) x 1 x 1 x 2 x 2 x 3 x 3 x 4 x 4 12 22 32 11 13 21
2. THEORY OF EQUATIONS. PREVIOUS EAMCET Bits.
 EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
ΜΕΛΕΤΗ ΤΗΣ ΜΑΚΡΟΧΡΟΝΙΑΣ ΠΑΡΑΜΟΡΦΩΣΗΣ ΤΟΥ ΦΡΑΓΜΑΤΟΣ ΚΡΕΜΑΣΤΩΝ ΜΕ ΒΑΣΗ ΑΝΑΛΥΣΗ ΓΕΩΔΑΙΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΜΕΤΑΒΟΛΩΝ ΣΤΑΘΜΗΣ ΤΑΜΙΕΥΤΗΡΑ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΕΛΕΤΗ ΤΗΣ ΜΑΚΡΟΧΡΟΝΙΑΣ ΠΑΡΑΜΟΡΦΩΣΗΣ ΤΟΥ ΦΡΑΓΜΑΤΟΣ ΚΡΕΜΑΣΤΩΝ ΜΕ ΒΑΣΗ ΑΝΑΛΥΣΗ ΓΕΩΔΑΙΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΜΕΤΑΒΟΛΩΝ ΣΤΑΘΜΗΣ ΤΑΜΙΕΥΤΗΡΑ ΔΙΔΑΚΤΟΡΙΚΗ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΕΛΕΤΗ ΤΗΣ ΜΑΚΡΟΧΡΟΝΙΑΣ ΠΑΡΑΜΟΡΦΩΣΗΣ ΤΟΥ ΦΡΑΓΜΑΤΟΣ ΚΡΕΜΑΣΤΩΝ ΜΕ ΒΑΣΗ ΑΝΑΛΥΣΗ ΓΕΩΔΑΙΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΜΕΤΑΒΟΛΩΝ ΣΤΑΘΜΗΣ ΤΑΜΙΕΥΤΗΡΑ ΔΙΔΑΚΤΟΡΙΚΗ
Instruction Execution Times
 1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
EPL 603 TOPICS IN SOFTWARE ENGINEERING. Lab 5: Component Adaptation Environment (COPE)
 EPL 603 TOPICS IN SOFTWARE ENGINEERING Lab 5: Component Adaptation Environment (COPE) Performing Static Analysis 1 Class Name: The fully qualified name of the specific class Type: The type of the class
EPL 603 TOPICS IN SOFTWARE ENGINEERING Lab 5: Component Adaptation Environment (COPE) Performing Static Analysis 1 Class Name: The fully qualified name of the specific class Type: The type of the class
Chapter 3: Ordinal Numbers
 Chapter 3: Ordinal Numbers There are two kinds of number.. Ordinal numbers (0th), st, 2nd, 3rd, 4th, 5th,..., ω, ω +,... ω2, ω2+,... ω 2... answers to the question What position is... in a sequence? What
Chapter 3: Ordinal Numbers There are two kinds of number.. Ordinal numbers (0th), st, 2nd, 3rd, 4th, 5th,..., ω, ω +,... ω2, ω2+,... ω 2... answers to the question What position is... in a sequence? What
Constant Elasticity of Substitution in Applied General Equilibrium
 Constant Elastct of Substtuton n Appled General Equlbru The choce of nput levels that nze the cost of producton for an set of nput prces and a fed level of producton can be epressed as n sty.. f Ltng for
Constant Elastct of Substtuton n Appled General Equlbru The choce of nput levels that nze the cost of producton for an set of nput prces and a fed level of producton can be epressed as n sty.. f Ltng for
Bayesian statistics. DS GA 1002 Probability and Statistics for Data Science.
 Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
