Προβλήματα φακών/κατόπτρων
|
|
|
- Ναβαδίας Παπάγος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Προβλήματα φακών/κατόπτρων 1. Χρησιμοποιείστε την τεχνική των ακτινών και σχηματισμών ειδώλου για να βρείτε το είδωλο, που δημιουργείται από ένα κοίλο σφαιρικό κάτοπτρο, ενός αντικειμένου που τοποθετείται (α) μεταξύ του C και F, (C κέντρο καμπυλότητας, F εστία) (β) στο C και (γ) μεταξύ του F και του κατόπτρου. Σε κάθε περίπτωση, χαρακτηρίστε την εικόνα, αν είναι δυνατόν. C F Το είδωλο είναι πραγματικό, ανεστραμμένο, περίπου δύο φορές μεγαλύτερο, πέρα από C. Το είδωλο είναι πραγματικο, ανεστραμμένο, ίδιο μέγεθος, στο C. Το είδωλο είναι εικονικό, όρθιο, περίπου 30% μεγαλύτερο, πίσω από το κάτοπτρο.
2 2. Ένα αντικείμενο τοποθετείται 25 cm μπροστά από ένα κοίλο κάτοπτρο εστιακού μήκους 30 cm. Υπολογίστε την απόσταση του ειδώλου και τη μεγέθυνση. Χαρακτηρίστε το είδωλο. Κάνουμε χρήση του υποκεφαλαίου 2.4 Κοίλο κάτοπτρο, f = +30. Αφού το αντικείμενο είναι μπροστά στο κάτοπτρο, o = +25. Σχέση φακών 1/o + 1/i = 1/f => 1/i = 1/f - 1/o = (o-f) / fo => i = fo / (o-f) = (30)(25)/(25-30) = -150 cm. Αφού i < 0, το είδωλο είναι πίσω από το κάτοπτρο, και φανταστικό. Η μεγέθυνση δίνεται από τη σχέση M = -i/o = -f / (o-f) = -30 / (25-30) = +6. Το είδωλο είναι μεγαλύτερο 6 φορές σε σχέση με το αντικείμενο Το είδωλο είναι όρθιο αφού η μεγέθυνση είναι θετική.
3 3. Ένα αντικείμενο τοποθετείται 25 cm μπροστά από ένα κυρτό κάτοπτρο εστιακού μήκους 30 cm. Υπολογίστε την απόσταση του ειδώλου και τη μεγέθυνση. Χαρακτηρίστε το είδωλο. Κυρτό κάτοπτρο, f = -30 εκ. Αφού το αντικείμενο είναι μπροστά στο κάτοπτρο, o = +25 εκ. Σχέση φακών 1/o + 1/i = 1/f =>1/i = 1/f - 1/o = (o-f) / fo => i = fo / (o-f) = (-30)(25)/[25 - (-30)] = -150/11 cm = cm. Αφού i < 0, το είδωλο είναι πίσω από το κάτοπτρο, φανταστικό Η μεγέθυνση δίνεται από τη σχέση M = -i/o = -f / (o-f) = -(-30) / [25 - (-30)] = +30/55 = +6/11 = Το είδωλο είναι μεγαλύτερο 55% σε σχέση με το αντικείμενο. Το είδωλο είναι όρθιο αφού η μεγέθυνση είναι θετική.
4 4. Ένας συγκλίνων φακός έχει εστιακό μήκος 20 cm. Σε ποια απόσταση πρέπει να κρατάτε αυτόν το φακό μπροστά από ένα γραμματόσημο, αν το είδωλο της σφραγίδας του γραμματόσημου θέλουμε να είναι διπλάσιο σε σχέση με το αντικείμενο και θέλουμε (α) η εικόνα αναστρέφεται, ή (β) η εικόνα είναι όρθια; Ένας συγκλίνων φακός, f = +20 cm. (a) Όταν θέλουμε το είδωλο να είναι αντεστραμμένο και διπλάσιο σε μέγεθος τότε θέλουμε Μ= -2. M = -i/o, οπότε i = 2o [1] Σχέση φακών 1/o + 1/i = 1/f. Κάνουμε χρήση του [1] i = 2o 1/o + 1/2o = 1/f, o = 3f/2 = 3(20 cm)/2 = 30 cm. Οπότε i = 2(30 cm) = 60 cm. (b) Όταν θέλουμε το είδωλο να είναι όρθιο και διπλάσιο σε μέγεθος τότε θέλουμε M = +2. Οπότε i = -2o [2] Σχέση φακών+[2] 1/o + 1/i = 1/f => 1/o - 1/2o = 1/f => o = ½f = ½(20 cm) = 10 cm. Οπότε i = -2(10 cm) = -20 cm.
5 5. Δύο συγκλίνοντες φακοί έχουν εστιακά μήκη f 1 = 30 cm και f 2 = 20 cm. Αυτά είναι τοποθετημένα 60 cm μεταξύ τους κατά μήκος του ίδιου άξονα και ένα αντικείμενο τοποθετείται 50 εκατοστά από φακό # 1 στην απέναντι πλευρά του φακού # 2. Εντοπίστε το τελική είδωλο και να υπολογίσετε τη συνολική μεγέθυνση του. Να αναφέρετε τα τελικά χαρακτηριστικά του ειδώλου σε σχέση με το αρχικό αντικείμενο. Σχεδιάστε το διάγραμμα ακτινών. ΠΡΩΤΟΣ ΦΑΚΟΣ Δεδομένα o 1 = 50 cm και f 1 = 30 cm. Σχέση φακών 1/o 1 + 1/i 1 = 1/f 1 => i 1 = f 1 o 1 / (o 1 - f 1 ) = (30)(50)/(50-30) = 75 cm. Το είδωλο που δημιουργείται από τον πρώτο φακό είναι το αντικείμενο για το δεύτερο φακό ΔΕΥΤΕΡΟΣ ΦΑΚΟΣ Αφού οι φακοί είναι σε 60 cm απόσταση το «αντικείμενο» του φακου2 είναι από αυτόν 15 cm από την πλευρά της διαπερατότητας του φωτός. Το «αντικείμενο» αυτό είναι φανταστικό, o 2 = -15 cm. Δίνεται f 2 = 20 cm. Σχέση φακών 1/o 2 + 1/i 2 = 1/f 2 => i 2 = f 2 o 2 / (o 2 - f 2 ) = (20)(-15)/(-15-20) = cm. Το τελικό είδωλο είναι στη πλευρά της διαπερατότητας του φωτός από τον δεύτερο φακό και είναι πραγματικό Ολική μεγέθυνση: M = M 1 M 2 = (-i 1 /o 1 ) (-i 1 /o 1 ) = -(+75)/(+50) -(-15)/(+8.57) = Το τελικό είδωλο είναι αντεστραμμένο και 86% του αρχικού.
6 6. Για το οπτικό σύστημα που δείχνεται παρακάτω, καθορίστε την τελική θέση του ειδώλου, όπως φαίνεται από τον παρατηρητή του αντικειμένου στη θέση Ο, λόγω των φακών και του επίπεδο κάτοπτρου. Πρώτος φακός Δεδομένα o 1 = 15 cm και f 1 = 10 cm. Σχέση φακών 1/o 1 + 1/i 1 = 1/f 1 => i 1 = f 1 o 1 / (o 1 - f 1 ) = (10)(15)/(15-10) = 30 cm. Το είδωλο που δημιουργείται από τον πρώτο φακό είναι το αντικείμενο για το δεύτερο φακό ΔΕΥΤΕΡΟΣ ΦΑΚΟΣ Αφού οι φακοί είναι σε 40 cm απόσταση το «αντικείμενο» του φακού 2 είναι από αυτόν 10 cm από την πλευρά της διαπερατότητας του φωτός. Το «αντικείμενο» αυτό είναι πραγματικό, o 2 = +10 cm. Μας δίνεται f 2 = 5 cm. Σχέση φακών 1/o 2 + 1/i 2 = 1/f 2 => i 2 = f 2 o 2 / (o 2 - f 2 ) = (5)(10)/(10-5) = +10 cm. Το τελικό είδωλο είναι στη πλευρά της διαπερατότητας του φωτός από τον δεύτερο φακό και είναι «αντικείμενο» για το επίπεδο κάτοπτρο. Το «αντικείμενο» είναι 30 εκ μακριά από το κάτοπτρο, οπότε ένας παρατηρητής βλέποντας τον καθρέπτη θα δει ένα ανακλώμενο είδωλο 30 εκ μακριά από το κάτοπτρο. Το τελικό είδωλο είναι πίσω από το κάτοπτρο και γιατί είναι φανταστικό. Ολική μεγέθυνση: M = M 1 M 2 M mirror = (-i 1 /o 1 ) (-i 1 /o 1 ) 1 = -(+30)/(+15) -(+10)/(+10) 1 = +2 Το τελικό είδωλο είναι ορθό και διπλάσιο του αρχικού. Είναι σημαντικό που είναι ο παρατηρητής? Τι θα πρέπει να κάνουμε εάν ο παρατηρητής ήταν στην ίδια πλευρά του φακού # 1 με το αντικείμενο και αναζητούσε το είδωλο μέσα από το φακό;
7 Προβλήματα διάθλασης/πόλωσης 7. Μια ακτίνα του ήλιου συναντά μια πλάκα από οπτικό γυαλί χαμηλής διασποράς και χαμηλό δείκτη διάθλασης (crown glass) με γωνία 45. Εάν ο δείκτης διάθλασης για το κόκκινο φως σε γυαλί είναι n κοκ = και για το υπεριώδες φως n υπερ = 1.538, βρείτε τη γωνία μεταξύ της ιώδους ακτίνας και της κόκκινης ακτίνας στο γυαλί. Η γωνία διάθλασης βρίσκεται από τον νόμου του Snell, n 1 sin(θ 1 ) = n 2 sin(θ 2 ). Αν θεωρήσουμε ότι n 1 και θ 1 αφορούν τον αερα, τότε η γωνία διάθλασης στο γυαλί είναι θ 2 = arcsin(n 1 sin(θ 1 )/n 2 ). Για κάθε μήκος κύματος έχουμε, θ red = arcsin(1 sin(45.00 ) / 1.520) = , θ violet = arcsin(1 sin(45.00 ) / 1.538) = Η διαφορά των γωνιών Δθ = 0.35.
8 8. Μια σημειακή πηγή φωτός είναι βυθισμένη 2,2 m κάτω από την επιφάνεια μιας λίμνης και εκπέμπει ακτίνες προς όλες τις κατευθύνσεις. Στην επιφάνεια της λίμνης, ακριβώς πάνω από την πηγή, η περιοχή που φωτίζεται είναι ένας κύκλος. Ποια είναι η μέγιστη ακτίνα που θα μπορούσε να έχει αυτός ο κύκλος; Ο κύκλος ορίζεται από το φως που διαφεύγει. Το φως σε γωνίες μεγαλύτερες από την κρίσιμη γωνία ανακλάται πίσω στο νερό. Κατά την κρίσιμη γωνία, το φως που αναδύεται εντός του αέρα, διαθλάται στις 90. Χρησιμοποιώντας το νόμο της διάθλασης, nsin (θ προσ ) = n αερα sin (90 ), για να βρείτε π ρος, παίρνουμε θ προσ = arcsin(n αερα /n) = arcsin(1/1.33) = Με χρήση της γεωμετρίας, R = d tan(θ προσ ) = (2.2 m)tan( ) = 2.51 m.
9 9. Στο παρακάτω διάγραμμα, φαίνονται τα παράλληλα στρώματα του αέρα, των υδάτων (n νερού = 1.33), και του γυαλιού (n γυαλιού = 1,20). Μια ακτίνα προσπίπτει από τον αέρα υπό μία γωνία θ, διαθλάται στο νερό, και ανακλάται από το γυαλί. Το ανακλώμενο φως είναι τελείως πολωμένο. Ποια είναι η γωνία πρόσπτωσης θ; Το ανακλώμενο φως είναι εντελώς πολωμένο όταν η γωνία πρόσπτωσης είναι στη τιμή της γωνίας Brewster α = arctan(n γυαλιουs /n νερου ) = arctan(1.20/1.33) = Αυτή η γωνία σχετίζεται με τη γωνία πρόσπτωσης θ βάση του νόμου του Snell n αερα sin(θ) = n νερο sin(α). Έτσι βρίσκουμε τη γωνία πρόσπτωσης θ θ = arcsin[(n νερο /n αερα )sin(α)] = arcsin[(1.33/1)sin( )] = 63.0.
10 10. Μία δέσμη φωτός έντασης Io συναντά δύο πολωτές. Ο άξονας μετάδοσης του πρώτου πολωτή κλίνει κατά 25 ως προς την κατακόρυφο. Ο άξονας μετάδοσης του δεύτερου πολωτή κλίνει κατά 55 ως προς την κατακόρυφο. Βρείτε την ένταση του φωτός αφού περάσει μέσα από τους δύο πολωτές, αν το φως είναι αρχικά (α) μη πολωμένο, (β) πολωμένο κάθετα, (γ) πολωμένο οριζόντια. Χρηση του νομου Malus (3.2.2) I = I 0 cos 2 (θ). α) Δεδομένου ότι το φως είναι αρχικά μη πολωμένο ή τυχαίο, μόνο η μισή ενέργεια διαπερναει. Έτσι, μετά τον πρώτο πολωτή, I = ½ I ο. Αυτό το φως που εχει διαπερασει το πρωτο πολωτη, είναι τώρα πολωμένο στους 25 σε σχεση με την κατακόρυφο. Περνώντας μέσα από το δεύτερο πολωτη, η ένταση μειώνεται σε I = I 0 cos 2 (θ) = ½I ο cos 2 (55-25 ) = (3/8)I ο. (β) Το φως είναι αρχικά πολωμένο κάθετα, περνώντας μέσω του πρώτου πολωτή, μειώνεται η ένταση Ι = I 0 cos 2 (θ) = I ο cos 2 (0-25 ) = 0,8214 I ο. Αυτό το φως είναι τώρα πολωμένο κατά μήκος του άξονα 25 ως προς την κατακόρυφο. Περνώντας μέσα από το δεύτερο πολωτη, η ένταση μειώνεται περαιτέρω σε Ι = I 0 cos 2 (θ) = (0,8214 I ο ) cos 2 (55-25 ) = 0,616 I ο. (γ) Το φως αρχικά πολωμένο οριζόντια, περνώντας μέσω του πρώτου πολωτη μειώνει την ένταση Ι = I 0 cos 2 (θ) = I ο cos 2 (90-25 ) = 0,1786 I ο. Αυτό το φως είναι τώρα πολωμένο κατά μήκος του άξονα 25 ως προς την κατακόρυφο. Περνώντας μέσα από το δεύτερο πολωτη, η ένταση μειώνεται περαιτέρω Ι = I 0 cos 2 (θ) = (0,1786 I ο ) cos 2 (55-25 ) = 0,134 I ο.
11 Προβλήματα συμβολής 11. Μια επίπεδη δέσμη σύμφωνου φωτός από λασερ Ar+ με λ= 488 nm προσπίπτει σε μια επιφάνεια με δυο μικρές οπές, οι οποίες βρίσκονται σε απόσταση d=0,2mm μεταξύ τους. Οι οπές λειτουργούν ως δευτερογενή σημειακές πηγές φωτεινών κυμάτων. Σε μια οθόνη σε απόσταση r=2 μ παρατηρούμε την εικόνα της συμβολής Α. Σε πόση απόσταση από τον κεντρικό άξονα παρατηρείται ο πρώτος (m=0) σκοτεινός κροσσός? B. Σε πόση απόσταση από τον κεντρικό άξονα παρατηρείται ο πέμπτης (m=5) τάξης φωτεινός κροσσός? A.Στο υποκεφάλαιο έχουμε την συνθήκη (σχέσεις ) για ελάχιστα κατά τη συμβολή Διαφορά οπτικού δρόμου=(m+1/2)λ Διαφορά φάσης =(m+1/2)2π Ξέρουμε ότι η Διαφορά οπτικού δρόμου δίνεται από τη σχέση (5.2.9) Διαφορά οπτικού δρόμου=ad/z, όπου x απόσταση από τον κεντρικό άξονα κροσσών, d απόσταση οπών μεταξύ τους, z απόσταση από την οθόνη Οπότε έχουμε τη σχέση (5.2.14) x min =[(2m+1)λz]/[2d]. Αντικαθιστώντας σε αυτήν την σχέση, τα δεδομένα μας, θα έχουμε x min = [(2*0+1)*488*10-9 *2]/ [2*0, 2*10-3 ] =2,44mm Β. Στο υποκεφάλαιο έχουμε την συνθήκη (σχέσεις ) για μέγιστα κατά τη συμβολή Διαφορά οπτικού δρόμου=(m)λ Διαφορά φάσης =(m)2π Ξέρουμε ότι η Διαφορά οπτικού δρόμου δίνεται από τη σχέση (5.2.9) Διαφορά οπτικού δρόμου=xd/z, όπου x απόσταση από τον κεντρικό άξονα κροσσών, d απόσταση οπών μεταξύ τους, z απόσταση από την οθόνη Οπότε έχουμε τη σχέση (5.2.12) X max = [(m) λz]/ [d]. Αντικαθιστώντας σε αυτήν την σχέση, τα δεδομένα μας, θα έχουμε x min = [(5)*488*10-9 *2]/ [0, 2*10-3 ] =24,4mm δηλαδή 10 φορές μεγαλύτερη από ότι η απόσταση του πρώτου σκοτεινού κροσσού.
12 12. Μονοχρωματικό σύμφωνο φως μήκους κύματος λο=640 nm, προσπίπτει κάθετα σε μια επίπεδη επιφάνεια επίστρωσης ενός διηλεκτρικού υλικού δείκτη διάθλασης n=1,3. H επίστρωση είναι πάνω σε ένα γυάλινο επίπεδο πλακίδιο δείκτη διάθλασης n=1,6. Αν η όλη διάταξη περιβάλλεται από αέρα πόσο κάνει να είναι το ελάχιστο δυνατό πάχος της επίστρωσης έτσι ώστε να έχουμε ελάχιστο ανακλώμενο φως από τις δυο διαχωριστικές επιφάνειες αέρα επίστρωσης και επίστρωσης γυαλιού? Γυαλί n=1,6 Α. Κάνουμε χρήση τη θεωρία στο υποκεφάλαιο 5.3 Για ένα ελαχιστοποιηθεί το ανακλώμενο φως θα πρέπει οι δυο ανακλώμενες από τις δυο διαχ. επιφάνειες να συμβάλουν αποσβεστικά, δλδ να έχουν αντίθετη φάση. Η ανάκλαση από οπτικό αραιότερο σε οπτικό πυκνότερα έχει άλμα φάσης. Και στις δυο δέσμες εδώ έχουμε άλμα φάσης, οπότε δεν έχουν μεταξύ τους διαφοροποίηση φάσης κατά τις ανακλάσεις. Κάθε διαφορά φάσης θα οφείλεται λοιπόν στη διαφορά οπτικού δρόμου. Για να έχουμε αποσβεστική συμβολή στην περίπτωση εδώ κάνουμε χρήση της σχέσης[5.3.6] η της σχέσης [5.3.11] και έχουμε 4ndcosδ/λ=(2m+1)=> d=λ*(2m+1)/ [4ncosδ] => d=640*10-9 *(2*0+1)/ [4*1,3cos0] d = 123 nm (~επίστρωση του τέταρτου μήκους κύματος)
13 13. Ένα στρώμα λαδιού πάχους 200 nm επιπλέει πάνω σε ένα στρώμα νερού πάχους 400 nm το οποίο ακουμπά σε μια επίπεδη μεταλλική κατοπτρική επιφάνεια. Ο δείκτης διάθλασης του λαδιού είναι 1,24 και του νερού είναι 1,33. Μια ακτίνα του φωτός προσπίπτει κάθετα επί αυτών των στρωμάτων. Ποιο είναι το μήκος κύματος ( η ποια τα μήκη κυμάτων) ορατού φωτός της δέσμης, εάν το φως που ανακλάται από την πρώτη επιφάνεια του λαδιού (1) συμβάλει καταστροφικά με το φως που ανακλάται από την κατοπτρική επιφάνεια (2); Κάνουμε χρήση τη θεωρία στο υποκεφάλαιο 5.3 Σημειώστε ότι οι γωνίες στο σκίτσο έχουν μεγεθυνθεί για λόγους σαφήνειας. Η συμβολή διέπεται από διαφορές φάσης που προκαλούνται από την ανάκλαση και από τα διαφορετικά μήκη διαδρομής. Πρώτα να εξετάσουμε τη διαφορά φάσης που προκαλείται από την ανάκλαση. Η ακτίνα 1 ανακλάται σε μια επιφάνεια αέρα / λαδιού. Επειδή α έρα <n λαδιού, έχουμε άλμα στη φάση της ακτίνας 1 σε σχέση με την προσπίπτουσα ακτίνα. Η ακτίνα 2 ανακλάται από τη επαφή νερού / καθρέφτη. Δεν μας έχουν πει για το δείκτη διάθλασης του καθρέφτη-μέταλλο, ωστόσο, δεδομένου ότι δεν είναι επιφάνεια διαφανή, το n πρέπει να είναι άπειρο. Από ν ερού <μ έταλλου, έχουμε άλμα στη φάση της ακτίνας 2 σε σχέση με την προσπίπτουσα ακτίνα. Δεδομένου ότι και οι δύο ακτίνες έχουν άλμα στη φάση, Δ reflection /2π = 0 [1] Στη συνέχεια εξετάζουμε τη διαφορά φάσης που προκαλείται από το γεγονός ότι η ακτίνα 2 ταξιδεύει παραπάνω απόσταση σε κάθε λεπτό φιλμ, 2t λαδι και 2t νερο (t=πάχος λαδιού ή νερού, θυμηθείτε ότι υποθέτουμε ότι οι γωνίες που εμπλέκονται είναι μικρές=> cosδ~1). Αυτό αντιστοιχεί σε διαφορά φάσης του Δ travelled /2π = 2t λαδι /λ λαδι + 2t νερό /λ νερο, [2] όπου λ είναι το μήκος κύματος του φωτός στο συγκεκριμένο μέσο. Το μήκος κύματος στο φιλμ λαδιού είναι σχετικό με το μήκος κύματος στον αέρα (βλέπε ) με n λαδιου λ λαδιου = n αερα λ αερα.το μήκος κύματος στο φιλμ νερού είναι σχετικό με το μήκος κύματος στον αέρα με n νερου λ νερου = n αερα λ αερα.
14 Αφού Δ reflection /2π = 0, έχουμε αποσβεστική συμβολή, όταν Δ travelled /2π = ½m, με m = 1, 3, 5,.[3] Με χρήση της [2] θα έχουμε στη [3] 2t λαδι / (n αερα λ αερα /n λάδι ) + 2t νερό / (n αερα λ αερα /n νερό ) = ½m. λ αερα = (2/m)[ 2t λάδι / (n αερα /n λάδι ) + 2t νερό / (n αερα /n νερο )]. = 4[n λάδι t λάδι + n νερό t νερό ]/m = 4[(1.24)(200 nm) + (1.33)(400 nm)]/n = 3120 nm / m Στη συνέχεια, εξετάζουμε την περιττή τιμή του m και θα βρούμε ποια μήκη κύματος εμπίπτουν στο ορατό φάσμα. m Μόνο το ορατό φως με μήκη κύματος από 624 nm και 446 nm θα συμβάλουν καταστροφικά με αυτό το διπλό φιλμ. Όλα τα άλλα μήκη κύματος είναι εκτός του ορατού φάσματος 400 nm <ο ρατό <700 nm.
15 Προβλήματα περίθλασης 14. Αγνοώντας ατμοσφαιρικές επιδράσεις, πόσο μακριά πρέπει να είναι δύο αντικείμενα στο φεγγάρι, ώστε το μάτι να μπορεί να τα διακρίνει ως ξεχωριστά; Η απόσταση από την επιφάνεια του φεγγαριού είναι 3, m. Υποθέσουμε λ = 550 nm και n = 1,34. Υποθέτουμε ότι η διάμετρος της κόρης του ματιού είναι 2,00 mm. Κάνουμε χρήση του υποκεφαλαίου Δύο σημεία μπορούν να διακριθούν και να ειδωθούν ως δύο διακριτά σημεία, όταν η γωνία διαχωρισμού τους είναι μεγαλύτερη από ό, τι θ minimum = 1.22λ μεσου /D, (6.3.10), όπου D είναι η διάμετρος του ανοίγματος και λ μεσου είναι το μήκος κύματος του φωτός στο μέσο όπου είναι ο ανιχνευτής φωτός. Σημειώστε ότι το D είναι η διάμετρος της κόρης σε αυτή την περίπτωση και ότι ο ανιχνευτής είναι ο αμφιβληστροειδής που είναι βυθισμένος στο υαλοειδές σώμα του οφθαλμού. Καθώς n ματι λ ματι = n αερα λ αερα, έχουμε θ minimum = 1.22n αερα λ αερα /n ματι D = (1.22)(1.00)( m)/(1.34)(0.002 m) = radians Επειδή y >> Lθ, έχουμε y minimum = L minimum = ( m)( ) = 94 km. Έτσι αντικείμενα περίπου 100 χιλιόμετρα μεταξύ τους θα μπορούσε να διακριθούν ως ξεχωριστά αντικείμενα. Θα πρέπει φυσικά να είναι μεγάλα αντικείμενα, όπως βουνά ή τα παρόμοια.
16 15. Φως νατρίου με μήκη κύματος 588,99 nm και 589,59 nm προσπίπτει σε ένα φράγμα με 5500 γραμμές ανά εκατοστό. Μια οθόνη τοποθετείται 3,0 m πέρα από το φράγμα. Ποια είναι η απόσταση μεταξύ των δύο φασματικών γραμμών στο φάσμα πρώτης τάξης στην οθόνη; Στης δεύτερης τάξης φάσμα; Κάνουμε χρήση του υποκεφαλαίου 6.5 Η φασματική γραμμή που παίρνουμε είναι τα μέγιστα συμβολής και, συνεπώς, καλυπτόμαστε από την εξίσωση dsin(θ) = mλ (5.2.7, η 6.5.3) όπου λ είναι το συγκεκριμένο μήκος κύματος και d η απόσταση των σχισμών/γραμμών στο φράγμα. Η απόσταση των σχισμών/γραμμών βρίσκεται d = 1 cm / 5500 = m. Υπολογίζοντας το θ 1 μπορούμε να δούμε πόσο μεγάλες είναι οι γωνίες (6.5.24): θ 1 = arcsin(mλ/d) = arcsin( nm/ ( m)) = radians = 18 Αυτή δεν είναι μικρή γωνία, οπότε δεν μπορούμε να κάνουμε χρήση της προσεγγιστικής λύσης μικρής γωνίας, παρόλα αυτά Δy 1 >> R(θ 2 - θ 1 ) και Δy 2 >> R(θ 4 - θ 4 ). Οπότε βρίσκουμε Δy 1 >> R(θ 2 - θ 1 ) = (3.0 m)( ) = 1.05 mm, και Δy 2» R(θ 4 - θ 3 ) = (3.0 m)( ) = 2.60 mm.
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ
 ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση =0.0 mm είναι τοποθετημένο σε απόσταση =1,0 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές φωτίζεται
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση =0.0 mm είναι τοποθετημένο σε απόσταση =1,0 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές φωτίζεται
Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση Γεωµετρική θεώρηση του Φωτός Ανάκλαση ηµιουργίαειδώλουαπόκάτοπτρα. είκτης ιάθλασης Νόµος του Snell Ορατό Φάσµα και ιασπορά Εσωτερική ανάκλαση Οπτικές ίνες ιάθλαση σε
Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση Γεωµετρική θεώρηση του Φωτός Ανάκλαση ηµιουργίαειδώλουαπόκάτοπτρα. είκτης ιάθλασης Νόµος του Snell Ορατό Φάσµα και ιασπορά Εσωτερική ανάκλαση Οπτικές ίνες ιάθλαση σε
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ. Ερωτήσεις κλειστού τύπου. Ερωτήσεις ανοικτού τύπου
 ΟΠΤΙΚΗ Περιεχόμενα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ... 2 Ερωτήσεις κλειστού τύπου... 2 Ερωτήσεις ανοικτού τύπου... 2 Ασκήσεις... 3 ΚΥΜΑΤΙΚΗ ΟΠΤΙΚΗ... 4 Ερωτήσεις κλειστού τύπου... 4 Ερωτήσεις ανοικτού τύπου... 4 Ασκήσεις...
ΟΠΤΙΚΗ Περιεχόμενα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ... 2 Ερωτήσεις κλειστού τύπου... 2 Ερωτήσεις ανοικτού τύπου... 2 Ασκήσεις... 3 ΚΥΜΑΤΙΚΗ ΟΠΤΙΚΗ... 4 Ερωτήσεις κλειστού τύπου... 4 Ερωτήσεις ανοικτού τύπου... 4 Ασκήσεις...
Φύση του φωτός. Θεωρούμε ότι το φως έχει διττή φύση: διαταραχή που διαδίδεται στο χώρο. μήκος κύματος φωτός. συχνότητα φωτός
 Γεωμετρική Οπτική Φύση του φωτός Θεωρούμε ότι το φως έχει διττή φύση: ΚΥΜΑΤΙΚΗ Βασική ιδέα Το φως είναι μια Η/Μ διαταραχή που διαδίδεται στο χώρο Βασική Εξίσωση Φαινόμενα που εξηγεί καλύτερα (κύμα) μήκος
Γεωμετρική Οπτική Φύση του φωτός Θεωρούμε ότι το φως έχει διττή φύση: ΚΥΜΑΤΙΚΗ Βασική ιδέα Το φως είναι μια Η/Μ διαταραχή που διαδίδεται στο χώρο Βασική Εξίσωση Φαινόμενα που εξηγεί καλύτερα (κύμα) μήκος
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα. Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ
 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0
 Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ. G. Mitsou
 ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Διάθλαση σε σφαιρική επιφάνεια Φακοί Ορισμοί Λεπτοί φακοί Συγκλίνοντες φακοί Δημιουργία ειδώλων Αποκλίνοντες φακοί Γενικοί τύποι φακών Σύστημα λεπτών φακών σε επαφή Ασκήσεις Διάθλαση
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Διάθλαση σε σφαιρική επιφάνεια Φακοί Ορισμοί Λεπτοί φακοί Συγκλίνοντες φακοί Δημιουργία ειδώλων Αποκλίνοντες φακοί Γενικοί τύποι φακών Σύστημα λεπτών φακών σε επαφή Ασκήσεις Διάθλαση
Γεωμετρική Οπτική ΚΕΦΑΛΑΙΟ 34
 Γεωμετρική Οπτική ΚΕΦΑΛΑΙΟ 34 Γεωμετρική Οπτική Γνωρίζουμε τα βασικά Δηλαδή, πως το φως διαδίδεται και αλληλεπιδρά με σώματα διαστάσεων πολύ μεγαλύτερων από το μήκος κύματος. Ανάκλαση: Προσπίπτουσα ακτίνα
Γεωμετρική Οπτική ΚΕΦΑΛΑΙΟ 34 Γεωμετρική Οπτική Γνωρίζουμε τα βασικά Δηλαδή, πως το φως διαδίδεται και αλληλεπιδρά με σώματα διαστάσεων πολύ μεγαλύτερων από το μήκος κύματος. Ανάκλαση: Προσπίπτουσα ακτίνα
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 www.pmoira.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 www.pmoira.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
s s f 25 s ' 10 10 s ' 10 α) s ' 16.7 β) S=10 cm, άρα το αντικείμενο βρίσκεται πάνω στην εστία.
 ΑΣΚΗΣΗ 1 Δύο κάτοπτρα σχηματίζουν ορθή γωνία, όπως φαίνεται στο σχήμα. Στο σημείο Ο υπάρχει ένα αντικείμενο. Να προσδιορίσετε τη θέση των ειδώλων που σχηματίζονται ΑΣΚΗΣΗ 2 Κοίλο σφαιρικό κάτοπτρο έχει
ΑΣΚΗΣΗ 1 Δύο κάτοπτρα σχηματίζουν ορθή γωνία, όπως φαίνεται στο σχήμα. Στο σημείο Ο υπάρχει ένα αντικείμενο. Να προσδιορίσετε τη θέση των ειδώλων που σχηματίζονται ΑΣΚΗΣΗ 2 Κοίλο σφαιρικό κάτοπτρο έχει
ΠΟΥ ΔΙΑΔΙΔΕΤΑΙ ΤΟ ΦΩΣ
 1 ΦΩΣ Στο μικρόκοσμο θεωρούμε ότι το φως έχει δυο μορφές. Άλλοτε το αντιμετωπίζουμε με τη μορφή σωματιδίων που ονομάζουμε φωτόνια. Τα φωτόνια δεν έχουν μάζα αλλά μόνον ενέργεια. Άλλοτε πάλι αντιμετωπίζουμε
1 ΦΩΣ Στο μικρόκοσμο θεωρούμε ότι το φως έχει δυο μορφές. Άλλοτε το αντιμετωπίζουμε με τη μορφή σωματιδίων που ονομάζουμε φωτόνια. Τα φωτόνια δεν έχουν μάζα αλλά μόνον ενέργεια. Άλλοτε πάλι αντιμετωπίζουμε
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ
 ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση d=0.20 mm είναι τοποθετημένο σε απόσταση =1,20 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση d=0.20 mm είναι τοποθετημένο σε απόσταση =1,20 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές
EΡΩΤΗΣΕΙΣ ΑΣΚΗΣΕΙΣ ΠΡΟΒΛΗΜΑΤΑ ΣΤΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ ΟΛΙΚΗ ΑΝΑΚΛΑΣΗ
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
Όλα τα θέματα των εξετάσεων έως και το 2014 σε συμβολή, στάσιμα, ηλεκτρομαγνητικά κύματα, ανάκλαση - διάθλαση ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ
 ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ Ερωτήσεις Πολλαπλής επιλογής 1. To βάθος µιας πισίνας φαίνεται από παρατηρητή εκτός της πισίνας µικρότερο από το πραγµατικό, λόγω του φαινοµένου της: α. ανάκλασης β. διάθλασης γ. διάχυσης
ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ Ερωτήσεις Πολλαπλής επιλογής 1. To βάθος µιας πισίνας φαίνεται από παρατηρητή εκτός της πισίνας µικρότερο από το πραγµατικό, λόγω του φαινοµένου της: α. ανάκλασης β. διάθλασης γ. διάχυσης
ΑΝΑΚΛΑΣΗ. β' νόμος της ανάκλασης: Η γωνία πρόσπτωσης και η γωνία ανάκλασης είναι ίσες.
 ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
Περίθλαση και εικόνα περίθλασης
 Περίθλαση και εικόνα περίθλασης Η περίθλαση αναφέρεται στη γενική συμπεριφορά των κυμάτων, τα οποία διαδίδονται προς όλες τις κατευθύνσεις καθώς περνούν μέσα από μια σχισμή. Ο όρος εικόνα περίθλασης είναι
Περίθλαση και εικόνα περίθλασης Η περίθλαση αναφέρεται στη γενική συμπεριφορά των κυμάτων, τα οποία διαδίδονται προς όλες τις κατευθύνσεις καθώς περνούν μέσα από μια σχισμή. Ο όρος εικόνα περίθλασης είναι
ΑΝΑΚΛΑΣΗ. β' νόμος της ανάκλασης: Η γωνία πρόσπτωσης και η γωνία ανάκλασης είναι ίσες.
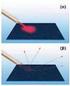 ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
Μεγεθυντικός φακός. 1. Σκοπός. 2. Θεωρία. θ 1
 Μεγεθυντικός φακός 1. Σκοπός Οι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
Μεγεθυντικός φακός 1. Σκοπός Οι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Ασκήσεις Οπτική Ι ιδάσκων: ηµήτρης Παπάζογλου Email: dpapa@iesl.forth.gr
 ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Ασκήσεις Οπτική Ι ιδάσκων: ηµήτρης Παπάζογλου Email: dpapa@iesl.forth.gr 1. Να σχεδιάσετε την διάδοση των ακτίνων στα παρακάτω οπτικά συστήµατα F F
ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Ασκήσεις Οπτική Ι ιδάσκων: ηµήτρης Παπάζογλου Email: dpapa@iesl.forth.gr 1. Να σχεδιάσετε την διάδοση των ακτίνων στα παρακάτω οπτικά συστήµατα F F
Φυσική IΙ. Ενότητα 13: Γεωμετρική οπτική. Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 Φυσική IΙ Ενότητα 13: Γεωμετρική οπτική Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Η κυματική φύση του φωτός: διάθλαση, ανάκλαση, απορρόφηση Γωνίες πρόσπτωσης, ανάκλασης
Φυσική IΙ Ενότητα 13: Γεωμετρική οπτική Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Η κυματική φύση του φωτός: διάθλαση, ανάκλαση, απορρόφηση Γωνίες πρόσπτωσης, ανάκλασης
ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ
 ΕΡΑΣΤΗΡΙ ΕΦΑΡΜΣΜΕΝΗΣ ΠΤΙΚΗΣ Άσκηση 1: Λεπτοί φακοί Εξεταζόμενες γνώσεις. Εξίσωση κατασκευαστών των φακών. Συστήματα φακών. Διαγράμματα κύριων ακτινών. Είδωλα και μεγέθυνση σε λεπτούς φακούς. Α. Λεπτοί
ΕΡΑΣΤΗΡΙ ΕΦΑΡΜΣΜΕΝΗΣ ΠΤΙΚΗΣ Άσκηση 1: Λεπτοί φακοί Εξεταζόμενες γνώσεις. Εξίσωση κατασκευαστών των φακών. Συστήματα φακών. Διαγράμματα κύριων ακτινών. Είδωλα και μεγέθυνση σε λεπτούς φακούς. Α. Λεπτοί
Εφαρμοσμένη Οπτική. Γεωμετρική Οπτική
 Εφαρμοσμένη Οπτική Γεωμετρική Οπτική Κύρια σημεία του μαθήματος Η προσέγγιση της γεωμετρικής οπτικής Νόμοι της ανάκλασης και της διάθλασης Αρχή του Huygens Αρχή του Fermat Αρχή της αντιστρεψιμότητας (principle
Εφαρμοσμένη Οπτική Γεωμετρική Οπτική Κύρια σημεία του μαθήματος Η προσέγγιση της γεωμετρικής οπτικής Νόμοι της ανάκλασης και της διάθλασης Αρχή του Huygens Αρχή του Fermat Αρχή της αντιστρεψιμότητας (principle
ΓΓ/Μ ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ. Τεύχος 6ο: Διάθλαση του φωτός Φακοί & οπτικά όργανα
 ΓΓ/Μ6 05-06 ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ Τεύχος 6ο: Διάθλαση του φωτός Φακοί & οπτικά όργανα ΕΚΔΟΤΙΚΕΣ ΤΟΜΕΣ ΟΡΟΣΗΜΟ ΠΕΡΙΟΔΙΚΗ ΕΚΔΟΣΗ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΚΑΙ ΤΟ ΛΥΚΕΙΟ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Φυσική για την Γ' Τάξη
ΓΓ/Μ6 05-06 ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ Τεύχος 6ο: Διάθλαση του φωτός Φακοί & οπτικά όργανα ΕΚΔΟΤΙΚΕΣ ΤΟΜΕΣ ΟΡΟΣΗΜΟ ΠΕΡΙΟΔΙΚΗ ΕΚΔΟΣΗ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΚΑΙ ΤΟ ΛΥΚΕΙΟ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Φυσική για την Γ' Τάξη
Να αιτιολογήσετε την απάντησή σας. Μονάδες 5
 2002 5. Να γράψετε στο τετράδιό σας τη λέξη που συµπληρώνει σωστά καθεµία από τις παρακάτω προτάσεις. γ. Η αιτία δηµιουργίας του ηλεκτροµαγνητικού κύµατος είναι η... κίνηση ηλεκτρικών φορτίων. 1. Ακτίνα
2002 5. Να γράψετε στο τετράδιό σας τη λέξη που συµπληρώνει σωστά καθεµία από τις παρακάτω προτάσεις. γ. Η αιτία δηµιουργίας του ηλεκτροµαγνητικού κύµατος είναι η... κίνηση ηλεκτρικών φορτίων. 1. Ακτίνα
Φυσική των οφθαλμών και της όρασης. Κική Θεοδώρου
 Φυσική των οφθαλμών και της όρασης Κική Θεοδώρου Περιεχόμενα Στοιχεία Γεωμετρικής Οπτικής Ανατομία του Οφθαλμού Αμφιβληστροειδής Ο ανιχνευτής φωτός του οφθαλμού Το κατώφλι της όρασης Φαινόμενα περίθλασης
Φυσική των οφθαλμών και της όρασης Κική Θεοδώρου Περιεχόμενα Στοιχεία Γεωμετρικής Οπτικής Ανατομία του Οφθαλμού Αμφιβληστροειδής Ο ανιχνευτής φωτός του οφθαλμού Το κατώφλι της όρασης Φαινόμενα περίθλασης
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0
 Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ Μάθημα προς τους ειδικευόμενους γιατρούς στην Οφθαλμολογία, Στο Κ.Οφ.Κ.Α. την 18/11/2003. Υπό: Δρος Κων. Ρούγγα, Οφθαλμιάτρου. 1. ΑΝΑΚΛΑΣΗ ΤΟΥ ΦΩΤΟΣ Όταν μια φωτεινή ακτίνα ή
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ Μάθημα προς τους ειδικευόμενους γιατρούς στην Οφθαλμολογία, Στο Κ.Οφ.Κ.Α. την 18/11/2003. Υπό: Δρος Κων. Ρούγγα, Οφθαλμιάτρου. 1. ΑΝΑΚΛΑΣΗ ΤΟΥ ΦΩΤΟΣ Όταν μια φωτεινή ακτίνα ή
Generated by Foxit PDF Creator Foxit Software http://www.foxitsoftware.com For evaluation only. ΑΣΚΗΣΗ 10 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ
 ΑΣΚΗΣΗ 0 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ . Γεωμετρική οπτική ΜΕΡΟΣ ΠΡΩΤΟ ΒΑΣΙΚΕΣ ΘΕΩΡΗΤΙΚΕΣ ΓΝΩΣΕΙΣ Η Γεωμετρική οπτική είναι ένας τρόπος μελέτης των κυμάτων και χρησιμοποιείται για την εξέταση μερικών
ΑΣΚΗΣΗ 0 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ . Γεωμετρική οπτική ΜΕΡΟΣ ΠΡΩΤΟ ΒΑΣΙΚΕΣ ΘΕΩΡΗΤΙΚΕΣ ΓΝΩΣΕΙΣ Η Γεωμετρική οπτική είναι ένας τρόπος μελέτης των κυμάτων και χρησιμοποιείται για την εξέταση μερικών
1 ο ΘΕΜΑ Α. Ερωτήσεις πολλαπλής επιλογής
 Φυσική Γ' Θετικής και Τεχνολογικής Κατ/σης ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ Θέματα Εξετάσεων 1 ο ΘΕΜΑ Α. Ερωτήσεις πολλαπλής επιλογής 1. Μια ακτίνα φωτός προσπίπτει στην επίπεδη διαχωριστική επιφάνεια δύο µέσων.
Φυσική Γ' Θετικής και Τεχνολογικής Κατ/σης ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ Θέματα Εξετάσεων 1 ο ΘΕΜΑ Α. Ερωτήσεις πολλαπλής επιλογής 1. Μια ακτίνα φωτός προσπίπτει στην επίπεδη διαχωριστική επιφάνεια δύο µέσων.
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ
 ΦΥΣΙΚΗ Γ.Π. Γ Λυκείου / Το Φως 1. Η υπεριώδης ακτινοβολία : a) δεν προκαλεί αμαύρωση της φωτογραφικής πλάκας. b) είναι ορατή. c) χρησιμοποιείται για την αποστείρωση ιατρικών εργαλείων. d) έχει μήκος κύματος
ΦΥΣΙΚΗ Γ.Π. Γ Λυκείου / Το Φως 1. Η υπεριώδης ακτινοβολία : a) δεν προκαλεί αμαύρωση της φωτογραφικής πλάκας. b) είναι ορατή. c) χρησιμοποιείται για την αποστείρωση ιατρικών εργαλείων. d) έχει μήκος κύματος
ΕΛΛΗΝΙΚΟ ΑΝΟΙKΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ η ΕΡΓΑΣΙΑ
 13/02/2005 ΕΛΛΗΝΙΚΟ ΑΝΟΙKΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 34 2004-05 4 η ΕΡΓΑΣΙΑ Προθεσμία αποστολής 8/03/2005 ΑΣΚΗΣΕΙΣ Άσκηση 1 Α) Αν φωτίσουμε τα μέταλλα λίθιο (έργο εξαγωγής 2.3eV), βηρύλλιο (έργο εξαγωγής 3.9eV),
13/02/2005 ΕΛΛΗΝΙΚΟ ΑΝΟΙKΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 34 2004-05 4 η ΕΡΓΑΣΙΑ Προθεσμία αποστολής 8/03/2005 ΑΣΚΗΣΕΙΣ Άσκηση 1 Α) Αν φωτίσουμε τα μέταλλα λίθιο (έργο εξαγωγής 2.3eV), βηρύλλιο (έργο εξαγωγής 3.9eV),
Φίλιππος Φαρμάκης Επ. Καθηγητής. Δείκτης διάθλασης. Διάδοση του Η/Μ κύματος μέσα σε μέσο
 9 η Διάλεξη Απόσβεση ακτινοβολίας, Σκέδαση φωτός, Πόλωση Φίλιππος Φαρμάκης Επ. Καθηγητής 1 Δείκτης διάθλασης Διάδοση του Η/Μ κύματος μέσα σε μέσο Η ταχύτητα διάδοσης μειώνεται κατά ένα παράγοντα n (v=c/n)
9 η Διάλεξη Απόσβεση ακτινοβολίας, Σκέδαση φωτός, Πόλωση Φίλιππος Φαρμάκης Επ. Καθηγητής 1 Δείκτης διάθλασης Διάδοση του Η/Μ κύματος μέσα σε μέσο Η ταχύτητα διάδοσης μειώνεται κατά ένα παράγοντα n (v=c/n)
Ο15. Κοίλα κάτοπτρα. 2. Θεωρία. 2.1 Γεωμετρική Οπτική
 Ο15 Κοίλα κάτοπτρα 1. Σκοπός Σκοπός της άσκησης είναι η εύρεση της εστιακής απόστασης κοίλου κατόπτρου σχετικά μεγάλου ανοίγματος και την μέτρηση του σφάλματος της σφαιρικής εκτροπής... Θεωρία.1 Γεωμετρική
Ο15 Κοίλα κάτοπτρα 1. Σκοπός Σκοπός της άσκησης είναι η εύρεση της εστιακής απόστασης κοίλου κατόπτρου σχετικά μεγάλου ανοίγματος και την μέτρηση του σφάλματος της σφαιρικής εκτροπής... Θεωρία.1 Γεωμετρική
ΠΟΛΩΣΗ ΤΟΥ ΦΩΤΟΣ. H γραφική αναπαράσταση ενός κύματος φωτός δίνεται στο Σχήμα 1(α) που ακολουθεί: ΣΧΗΜΑ 1
 ΠΟΛΩΣΗ ΤΟΥ ΦΩΤΟΣ 1. ΟΡΙΣΜΟΙ Το φως είναι ένα σύνθετο κύμα. Με εξαίρεση την ακτινοβολία LASER, τα κύματα φωτός δεν είναι επίπεδα κύματα. Κάθε κύμα φωτός είναι ένα ηλεκτρομαγνητικό κύμα στο οποίο τα διανύσματα
ΠΟΛΩΣΗ ΤΟΥ ΦΩΤΟΣ 1. ΟΡΙΣΜΟΙ Το φως είναι ένα σύνθετο κύμα. Με εξαίρεση την ακτινοβολία LASER, τα κύματα φωτός δεν είναι επίπεδα κύματα. Κάθε κύμα φωτός είναι ένα ηλεκτρομαγνητικό κύμα στο οποίο τα διανύσματα
Μελέτη συστήματος φακών με τη Μέθοδο του Newton
 Μελέτη συστήματος φακών με τη Μέθοδο του Newton.Σκοπός Σκοπός της άσκησης είναι η μελέτη της εστιακής απόστασης συστήματος φακών, η εύρεση της ισοδύναμης εστιακής απόστασης του συστήματος αυτού καθώς και
Μελέτη συστήματος φακών με τη Μέθοδο του Newton.Σκοπός Σκοπός της άσκησης είναι η μελέτη της εστιακής απόστασης συστήματος φακών, η εύρεση της ισοδύναμης εστιακής απόστασης του συστήματος αυτού καθώς και
Κυματική οπτική. Συμβολή Περίθλαση Πόλωση
 Κυματική οπτική Η κυματική οπτική ασχολείται με τη μελέτη φαινομένων τα οποία δεν μπορούμε να εξηγήσουμε επαρκώς με τις αρχές της γεωμετρικής οπτικής. Στα φαινόμενα αυτά περιλαμβάνονται τα εξής: Συμβολή
Κυματική οπτική Η κυματική οπτική ασχολείται με τη μελέτη φαινομένων τα οποία δεν μπορούμε να εξηγήσουμε επαρκώς με τις αρχές της γεωμετρικής οπτικής. Στα φαινόμενα αυτά περιλαμβάνονται τα εξής: Συμβολή
ΟΡΟΣΗΜΟ ΓΛΥΦΑΔΑΣ. 7.1 Τι είναι το ταλαντούμενο ηλεκτρικό δίπολο; Πως παράγεται ένα ηλεκτρομαγνητικό
 ΚΕΦΑΛΑΙΟ 2 Ηλεκτρομαγνητικά κύματα. Ηλεκτρομαγνητικά κύματα 7. Τι είναι το ταλαντούμενο ηλεκτρικό δίπολο; Πως παράγεται ένα ηλεκτρομαγνητικό κύμα; 7.2 Ποιες εξισώσεις περιγράφουν την ένταση του ηλεκτρικού
ΚΕΦΑΛΑΙΟ 2 Ηλεκτρομαγνητικά κύματα. Ηλεκτρομαγνητικά κύματα 7. Τι είναι το ταλαντούμενο ηλεκτρικό δίπολο; Πως παράγεται ένα ηλεκτρομαγνητικό κύμα; 7.2 Ποιες εξισώσεις περιγράφουν την ένταση του ηλεκτρικού
Οπτική και κύματα Δημήτρης Παπάζογλου dpapa@materials.uoc.gr Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης Γεωμετρική Οπτική
 Οπτική και κύματα Δημήτρης Παπάζογλου dpapa@maerals.uoc.gr Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης Γεωμετρική Οπτική Η ιδέα την απεικόνισης Σημειακή πηγή Στιγματική απεικόνιση Η ανακατεύθυνση
Οπτική και κύματα Δημήτρης Παπάζογλου dpapa@maerals.uoc.gr Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης Γεωμετρική Οπτική Η ιδέα την απεικόνισης Σημειακή πηγή Στιγματική απεικόνιση Η ανακατεύθυνση
7 σειρά ασκήσεων. Για την επίλυση των προβλημάτων να θεωρηθούν γνωστά: σταθερά του Planck 6,63 10-34 J s, ταχύτητα του φωτός στον αέρα 3 10 8 m/s
 η 7 σειρά ασκήσεων Για την επίλυση των προβλημάτων να θεωρηθούν γνωστά: σταθερά του Planck 6,63 10-34 J s, ταχύτητα του φωτός στον αέρα 3 10 8 m/s 1. Εξηγήστε γιατί, όταν φως διαπερνά μία διαχωριστική
η 7 σειρά ασκήσεων Για την επίλυση των προβλημάτων να θεωρηθούν γνωστά: σταθερά του Planck 6,63 10-34 J s, ταχύτητα του φωτός στον αέρα 3 10 8 m/s 1. Εξηγήστε γιατί, όταν φως διαπερνά μία διαχωριστική
ΚΕΦΑΛΑΙΟ 11Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση
 ΚΕΦΑΛΑΙΟ Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Ηφύσητουφωτός 643-77 Netwon Huygens 69-695 Το φως είναι δέσμη σωματιδίων Το φως
ΚΕΦΑΛΑΙΟ Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Ηφύσητουφωτός 643-77 Netwon Huygens 69-695 Το φως είναι δέσμη σωματιδίων Το φως
sin 2 n = sin A 2 sin 2 2 n = sin A = sin = cos
 1 Σκοπός Βαθμός 9.5. Ηθελε να γραψω καλύτερα το 9 ερωτημα. Σκοπός αυτής της εργαστηριακής άσκησης είναι η μελέτη της ανάκλασης, διάθλασης και πόλωσης του φωτός. Προσδιορίζουμε επίσης τον δείκτη διάθλασης
1 Σκοπός Βαθμός 9.5. Ηθελε να γραψω καλύτερα το 9 ερωτημα. Σκοπός αυτής της εργαστηριακής άσκησης είναι η μελέτη της ανάκλασης, διάθλασης και πόλωσης του φωτός. Προσδιορίζουμε επίσης τον δείκτη διάθλασης
ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ ΚΕΦΑΛΑΙΟΥ 3
 ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ ΚΕΦΑΛΑΙΟΥ 3 Η ταχύτητα του φωτός στο κενό ή στον αέρα είναι σταθερή και ίση με c o =3.10 8 m/s Η ταχύτητα του φωτός οπουδήποτε αλλού είναι c και ισχύει πάντα ότι c
ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ ΚΕΦΑΛΑΙΟΥ 3 Η ταχύτητα του φωτός στο κενό ή στον αέρα είναι σταθερή και ίση με c o =3.10 8 m/s Η ταχύτητα του φωτός οπουδήποτε αλλού είναι c και ισχύει πάντα ότι c
ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ. Διάθλαση μέσω πρίσματος - Φασματοσκοπικά χαρακτηριστικά πρίσματος.
 Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ. Διάθλαση μέσω πρίσματος - Φασματοσκοπικά χαρακτηριστικά πρίσματος. 1. Σκοπός Όταν δέσμη λευκού φωτός προσπέσει σε ένα πρίσμα τότε κάθε μήκος κύματος διαθλάται σύμφωνα με τον αντίστοιχο
Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ. Διάθλαση μέσω πρίσματος - Φασματοσκοπικά χαρακτηριστικά πρίσματος. 1. Σκοπός Όταν δέσμη λευκού φωτός προσπέσει σε ένα πρίσμα τότε κάθε μήκος κύματος διαθλάται σύμφωνα με τον αντίστοιχο
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β και Γ ΛΥΚΕΙΟΥ.
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β και Γ ΛΥΚΕΙΟΥ. ΑΝΤΙΚΕΙΜΕΝΟ : ΤΟ ΦΩΣ,( ΚΕΦ. Γ ΛΥΚΕΙΟΥ και ΚΕΦ.3 Β ΛΥΚΕΙΟΥ) ΘΕΜΑ Α Να επιλέξετε την σωστή πρόταση χωρίς να δικαιολογήσετε την απάντηση σας.. Οι Huygens
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β και Γ ΛΥΚΕΙΟΥ. ΑΝΤΙΚΕΙΜΕΝΟ : ΤΟ ΦΩΣ,( ΚΕΦ. Γ ΛΥΚΕΙΟΥ και ΚΕΦ.3 Β ΛΥΚΕΙΟΥ) ΘΕΜΑ Α Να επιλέξετε την σωστή πρόταση χωρίς να δικαιολογήσετε την απάντηση σας.. Οι Huygens
Κεφάλαιο 35 ΠερίθλασηκαιΠόλωση. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 35 ΠερίθλασηκαιΠόλωση ΠεριεχόµεναΚεφαλαίου 35 Περίθλαση απλής σχισµής ή δίσκου Intensity in Single-Slit Diffraction Pattern Περίθλαση διπλής σχισµής ιακριτική ικανότητα; Κυκλικές ίριδες ιακριτική
Κεφάλαιο 35 ΠερίθλασηκαιΠόλωση ΠεριεχόµεναΚεφαλαίου 35 Περίθλαση απλής σχισµής ή δίσκου Intensity in Single-Slit Diffraction Pattern Περίθλαση διπλής σχισµής ιακριτική ικανότητα; Κυκλικές ίριδες ιακριτική
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ
 1 ο ΘΕΜΑ Α. Ερωτήσεις πολλαπλής επιλογής ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ 1. Μια ακτίνα φωτός προσπίπτει στην επίπεδη διαχωριστική επιφάνεια δύο µέσων. Όταν η διαθλώµενη ακτίνα κινείται παράλληλα προς τη διαχωριστική
1 ο ΘΕΜΑ Α. Ερωτήσεις πολλαπλής επιλογής ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ 1. Μια ακτίνα φωτός προσπίπτει στην επίπεδη διαχωριστική επιφάνεια δύο µέσων. Όταν η διαθλώµενη ακτίνα κινείται παράλληλα προς τη διαχωριστική
Πως διαδίδονται τα Η/Μ κύματα σε διαφανή διηλεκτρικά?
 Πως διαδίδονται τα Η/Μ κύματα σε διαφανή διηλεκτρικά? (Μη-μαγνητικά, μη-αγώγιμα, διαφανή στερεά ή υγρά με πυκνή, σχετικά κανονική διάταξη δομικών λίθων). Γραμμικά πολωμένο κύμα προσπίπτει σε ηλεκτρόνιο
Πως διαδίδονται τα Η/Μ κύματα σε διαφανή διηλεκτρικά? (Μη-μαγνητικά, μη-αγώγιμα, διαφανή στερεά ή υγρά με πυκνή, σχετικά κανονική διάταξη δομικών λίθων). Γραμμικά πολωμένο κύμα προσπίπτει σε ηλεκτρόνιο
ΑΣΚΗΣΕΙΣ ΣΕ ΛΕΠΤΑ ΥΜΕΝΙΑ
 ΑΣΚΗΣΕΙΣ ΣΕ ΛΕΠΤΑ ΥΜΕΝΙΑ ΑΣΚΗΣΗ 1: Να προσδιορίσετε το ελάχιστο δυνατό πάχος ενός αντιανακλαστικού λεπτού οπτικού υμενίου από θοριούχο μαγνήσιο (M g F 2 ) το οποίο έχει τοποθετηθεί πάνω στην επιάνεια μιας
ΑΣΚΗΣΕΙΣ ΣΕ ΛΕΠΤΑ ΥΜΕΝΙΑ ΑΣΚΗΣΗ 1: Να προσδιορίσετε το ελάχιστο δυνατό πάχος ενός αντιανακλαστικού λεπτού οπτικού υμενίου από θοριούχο μαγνήσιο (M g F 2 ) το οποίο έχει τοποθετηθεί πάνω στην επιάνεια μιας
Σχηματισμός ειδώλων. Εισαγωγή
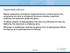 Σχηματισμός ειδώλων Είδωλα πραγματικών αντικειμένων σχηματίζονται όταν οι ακτίνες φωτός (που εκπέμπονται από αυτά τα αντικέιμενα) συναντούν επίπεδες ή καμπύλες επιφάνειες που βρίσκονται μεταξύ δύο μέσων.
Σχηματισμός ειδώλων Είδωλα πραγματικών αντικειμένων σχηματίζονται όταν οι ακτίνες φωτός (που εκπέμπονται από αυτά τα αντικέιμενα) συναντούν επίπεδες ή καμπύλες επιφάνειες που βρίσκονται μεταξύ δύο μέσων.
ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος
 Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος 1. Εισαγωγή Όταν δέσµη λευκού φωτός προσπέσει σε ένα πρίσµα τότε κάθε µήκος κύµατος διαθλάται σύµφωνα µε τον αντίστοιχο
Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος 1. Εισαγωγή Όταν δέσµη λευκού φωτός προσπέσει σε ένα πρίσµα τότε κάθε µήκος κύµατος διαθλάται σύµφωνα µε τον αντίστοιχο
ΟΠΤΙΚΗ ΦΩΤΟΜΕΤΡΙΑ. Φως... Φωτομετρικά μεγέθη - μονάδες Νόμοι Φωτισμού
 ΟΠΤΙΚΗ ΦΩΤΟΜΕΤΡΙΑ Φως... Φωτομετρικά μεγέθη - μονάδες Νόμοι Φωτισμού Ηλεκτρομαγνητικά κύματα - Φως Θα διερευνήσουμε: 1. Τί είναι το φως; 2. Πως παράγεται; 3. Χαρακτηριστικά ιδιότητες Γεωμετρική οπτική:
ΟΠΤΙΚΗ ΦΩΤΟΜΕΤΡΙΑ Φως... Φωτομετρικά μεγέθη - μονάδες Νόμοι Φωτισμού Ηλεκτρομαγνητικά κύματα - Φως Θα διερευνήσουμε: 1. Τί είναι το φως; 2. Πως παράγεται; 3. Χαρακτηριστικά ιδιότητες Γεωμετρική οπτική:
7α Γεωμετρική οπτική - οπτικά όργανα
 7α Γεωμετρική οπτική - οπτικά όργανα Εισαγωγή ορισμοί Φύση του φωτός Πηγές φωτός Δείκτης διάθλασης Ανάκλαση Δημιουργία ειδώλων από κάτοπτρα Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/katsiki Ηφύσητουφωτός
7α Γεωμετρική οπτική - οπτικά όργανα Εισαγωγή ορισμοί Φύση του φωτός Πηγές φωτός Δείκτης διάθλασης Ανάκλαση Δημιουργία ειδώλων από κάτοπτρα Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/katsiki Ηφύσητουφωτός
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ. Ανάκλαση. Κάτοπτρα. Διάθλαση. Ολική ανάκλαση. Φαινόμενη ανύψωση αντικειμένου. Μετατόπιση ακτίνας. Πρίσματα
 ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Ανάκλαση Κάτοπτρα Διάθλαση Ολική ανάκλαση Φαινόμενη ανύψωση αντικειμένου Μετατόπιση ακτίνας Πρίσματα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ - Ανάκλαση Επιστροφή σε «γεωμετρική οπτική» Ανάκλαση φωτός ονομάζεται
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Ανάκλαση Κάτοπτρα Διάθλαση Ολική ανάκλαση Φαινόμενη ανύψωση αντικειμένου Μετατόπιση ακτίνας Πρίσματα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ - Ανάκλαση Επιστροφή σε «γεωμετρική οπτική» Ανάκλαση φωτός ονομάζεται
1) Η εξάρτηση του δείκτη διάθλασης n από το μήκος κύματος για το κρύσταλλο του ιωδιούχου ρουβιδίου (RbI) παρουσιάζεται στο παρακάτω σχήμα.
 1) Η εξάρτηση του δείκτη διάθλασης n από το μήκος κύματος για το κρύσταλλο του ιωδιούχου ρουβιδίου (RbI) παρουσιάζεται στο παρακάτω σχήμα. Για τους δείκτες διάθλασης n 1 και n 2 ισχύει: n 2 = (11 / 10)
1) Η εξάρτηση του δείκτη διάθλασης n από το μήκος κύματος για το κρύσταλλο του ιωδιούχου ρουβιδίου (RbI) παρουσιάζεται στο παρακάτω σχήμα. Για τους δείκτες διάθλασης n 1 και n 2 ισχύει: n 2 = (11 / 10)
ΚΕΦΑΛΑΙΟ 2ο: ΜΗΧΑΝΙΚΑ- ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 15/9/2013 ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 15/9/2013 ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
OΠΤIKH. Επειδή είναι πάντα υ<c (
 OΠΤIKH Η ταχύτητα του φωτός δεν είναι πάντα ίδια αλλά αλλάζει όταν το φως από ένα μέσο περνά σε κάποιο άλλο. Αν c είναι η ταχύτητα του φωτός στο κενό και υ η ταχύτητά του σε ένα άλλο υλικό τότε, ορίζουμε
OΠΤIKH Η ταχύτητα του φωτός δεν είναι πάντα ίδια αλλά αλλάζει όταν το φως από ένα μέσο περνά σε κάποιο άλλο. Αν c είναι η ταχύτητα του φωτός στο κενό και υ η ταχύτητά του σε ένα άλλο υλικό τότε, ορίζουμε
6.10 Ηλεκτροµαγνητικά Κύµατα
 Πρόταση Μελέτης Λύσε απο τον Α τόµο των Γ. Μαθιουδάκη & Γ.Παναγιωτακόπουλου τις ακόλουθες ασκήσεις : 11.1-11.36, 11.46-11.50, 11.52-11.59, 11.61, 11.63, 11.64, 1.66-11.69, 11.71, 11.72, 11.75-11.79, 11.81
Πρόταση Μελέτης Λύσε απο τον Α τόµο των Γ. Μαθιουδάκη & Γ.Παναγιωτακόπουλου τις ακόλουθες ασκήσεις : 11.1-11.36, 11.46-11.50, 11.52-11.59, 11.61, 11.63, 11.64, 1.66-11.69, 11.71, 11.72, 11.75-11.79, 11.81
ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ
 ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ Όταν προσπίπτει φως σε μια διεπιφάνεια που σχηματίζεται μεταξύ δύο οπτικά διαφορετικών μέσων, ένα μέρος του υφίσταται ανάκλαση ενώ το υπόλοιπο διέρχεται από το πρώτο στο δεύτερο
ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ Όταν προσπίπτει φως σε μια διεπιφάνεια που σχηματίζεται μεταξύ δύο οπτικά διαφορετικών μέσων, ένα μέρος του υφίσταται ανάκλαση ενώ το υπόλοιπο διέρχεται από το πρώτο στο δεύτερο
Δίκτυα Τηλεπικοινωνιών. και Μετάδοσης
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Δίκτυα Τηλεπικοινωνιών και Μετάδοσης Σύστημα μετάδοσης με οπτικές ίνες Tο οπτικό φέρον κύμα μπορεί να διαμορφωθεί είτε από αναλογικό
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Δίκτυα Τηλεπικοινωνιών και Μετάδοσης Σύστημα μετάδοσης με οπτικές ίνες Tο οπτικό φέρον κύμα μπορεί να διαμορφωθεί είτε από αναλογικό
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1 η - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 14/09/2014 ΘΕΜΑ Α
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1 η - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 14/09/2014 ΘΕΜΑ Α Α1. Κατά την ανάλυση λευκού φωτός από γυάλινο πρίσμα, η γωνία εκτροπής του κίτρινου χρώματος είναι:
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1 η - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 14/09/2014 ΘΕΜΑ Α Α1. Κατά την ανάλυση λευκού φωτός από γυάλινο πρίσμα, η γωνία εκτροπής του κίτρινου χρώματος είναι:
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ
 ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Β ΘΕΜΑΤΑ ΦΩΣ» ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 04-05 ΠΟΡΕΙΑ ΑΚΤΙΝΑΣ. Β. Στο διπλανό
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Β ΘΕΜΑΤΑ ΦΩΣ» ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 04-05 ΠΟΡΕΙΑ ΑΚΤΙΝΑΣ. Β. Στο διπλανό
Η συμβολή του φωτός και η μέτρηση του μήκους κύματος μονοχρωματικής ακτινοβολίας
 Η συμβολή του φωτός και η μέτρηση του μήκους κύματος μονοχρωματικής ακτινοβολίας Α. Στόχοι Οι μαθητές: Να παρατηρήσουν το φαινόμενο της συμβολής / περίθλασης Να αξιοποιήσουν το φαινόμενο της περίθλασης
Η συμβολή του φωτός και η μέτρηση του μήκους κύματος μονοχρωματικής ακτινοβολίας Α. Στόχοι Οι μαθητές: Να παρατηρήσουν το φαινόμενο της συμβολής / περίθλασης Να αξιοποιήσουν το φαινόμενο της περίθλασης
Ασκήσεις (Ηλεκτρισμός-Οπτική) Κ.-Α. Θ. Θωμά
 Ασκήσεις (Ηλεκτρισμός-Οπτική) Ηλεκτρισμός 6 η. Ηλεκτρόνια κινούμενα με ταχύτητα 0 m / sec εισέρχονται σε χώρο μαγνητικού πεδίου όπου διαγράφουν κυκλική τροχιά ακτίνας 0.0m. Να βρεθεί η ένταση του μαγνητικού
Ασκήσεις (Ηλεκτρισμός-Οπτική) Ηλεκτρισμός 6 η. Ηλεκτρόνια κινούμενα με ταχύτητα 0 m / sec εισέρχονται σε χώρο μαγνητικού πεδίου όπου διαγράφουν κυκλική τροχιά ακτίνας 0.0m. Να βρεθεί η ένταση του μαγνητικού
Μέτρηση Γωνίας Brewster Νόμοι του Fresnel
 Μέτρηση Γωνίας Bewse Νόμοι του Fesnel [] ΕΙΣΑΓΩΓΗ Στο πείραμα, δέσμη φωτός από διοδικό lase ανακλάται στην επίπεδη επιφάνεια ενός ακρυλικού ημι-κυκλικού φακού, πολώνεται γραμμικά και ανιχνεύεται από ένα
Μέτρηση Γωνίας Bewse Νόμοι του Fesnel [] ΕΙΣΑΓΩΓΗ Στο πείραμα, δέσμη φωτός από διοδικό lase ανακλάται στην επίπεδη επιφάνεια ενός ακρυλικού ημι-κυκλικού φακού, πολώνεται γραμμικά και ανιχνεύεται από ένα
Βασικές διαδικασίες παραγωγής πολωμένου φωτός
 Πόλωση του φωτός Βασικές διαδικασίες παραγωγής πολωμένου φωτός πόλωση λόγω επιλεκτικής απορρόφησης - διχρωισμός πόλωση λόγω ανάκλασης από μια διηλεκτρική επιφάνεια πόλωση λόγω ύπαρξης δύο δεικτών διάθλασης
Πόλωση του φωτός Βασικές διαδικασίες παραγωγής πολωμένου φωτός πόλωση λόγω επιλεκτικής απορρόφησης - διχρωισμός πόλωση λόγω ανάκλασης από μια διηλεκτρική επιφάνεια πόλωση λόγω ύπαρξης δύο δεικτών διάθλασης
1. Ιδιότητες φακών. 1 Λεπτοί φακοί. 2 Απριλίου Βασικές έννοιες
 . Ιδιότητες φακών 2 Απριλίου 203 Λεπτοί φακοί. Βασικές έννοιες Φακός είναι ένα οπτικό σύστημα με δύο διαθλαστικές επιφάνειες. Ο απλούστερος φακός έχει δύο σφαιρικές επιφάνειες αρκετά κοντά η μία με την
. Ιδιότητες φακών 2 Απριλίου 203 Λεπτοί φακοί. Βασικές έννοιες Φακός είναι ένα οπτικό σύστημα με δύο διαθλαστικές επιφάνειες. Ο απλούστερος φακός έχει δύο σφαιρικές επιφάνειες αρκετά κοντά η μία με την
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΑΚΤΥΛΙΟΙ ΤΟΥ ΝΕΥΤΩΝΑ
 ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΤΙΚΗΣ - ΟΠΤΟΗΛΕΚΤΡΟΝΙΚΗΣ & LASER ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ & Τ/Υ ΑΣΚΗΣΗ ΝΟ4 ΑΚΤΥΛΙΟΙ ΤΟΥ ΝΕΥΤΩΝΑ Γ. Μήτσου εκέµβριος 007 Α. ΘΕΩΡΙΑ Εισαγωγή Στο πείραµα αυτό θα προσδιορίσουµε το µήκος
ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΤΙΚΗΣ - ΟΠΤΟΗΛΕΚΤΡΟΝΙΚΗΣ & LASER ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ & Τ/Υ ΑΣΚΗΣΗ ΝΟ4 ΑΚΤΥΛΙΟΙ ΤΟΥ ΝΕΥΤΩΝΑ Γ. Μήτσου εκέµβριος 007 Α. ΘΕΩΡΙΑ Εισαγωγή Στο πείραµα αυτό θα προσδιορίσουµε το µήκος
Πειραματικός υπολογισμός του μήκους κύματος μονοχρωματικής ακτινοβολίας
 Πειραματικός υπολογισμός του μήκους κύματος μονοχρωματικής ακτινοβολίας Τάξη : Γ Λυκείου Βασικές έννοιες και σχέσεις Μήκος κύματος - Μονοχρωματική ακτινοβολία - Συμβολή ηλεκτρομαγνητικών κυμάτων - Κροσσοί
Πειραματικός υπολογισμός του μήκους κύματος μονοχρωματικής ακτινοβολίας Τάξη : Γ Λυκείου Βασικές έννοιες και σχέσεις Μήκος κύματος - Μονοχρωματική ακτινοβολία - Συμβολή ηλεκτρομαγνητικών κυμάτων - Κροσσοί
7α Γεωµετρική οπτική - οπτικά όργανα
 7α Γεωµετρική οπτική - οπτικά όργανα Εισαγωγή ορισµοί Φύση του φωτός Πηγές φωτός είκτης διάθλασης Ανάκλαση ηµιουργία ειδώλων από κάτοπτρα Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Η φύση του
7α Γεωµετρική οπτική - οπτικά όργανα Εισαγωγή ορισµοί Φύση του φωτός Πηγές φωτός είκτης διάθλασης Ανάκλαση ηµιουργία ειδώλων από κάτοπτρα Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Η φύση του
Εισαγωγή στο φως. Εισαγωγή
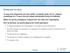 Εισαγωγή στο φως Το φως είναι απαραίτητο για όλες σχεδόν τις μορφές ζωής στη Γη. (Σήμερα γνωρίζουμε ότι) Το φως είναι μια μορφή ηλεκτρομαγνητικής ακτινοβολίας. Μέσω του φωτός μεταφέρεται ενέργεια από την
Εισαγωγή στο φως Το φως είναι απαραίτητο για όλες σχεδόν τις μορφές ζωής στη Γη. (Σήμερα γνωρίζουμε ότι) Το φως είναι μια μορφή ηλεκτρομαγνητικής ακτινοβολίας. Μέσω του φωτός μεταφέρεται ενέργεια από την
Τα πρώτα δύο ελάχιστα της έντασης βρίσκονται συμμετρικά από το μέγιστο σε απόσταση φ=±λ/α.
 Φασματόμετρα & Ιντερφερομετρα Τα φασματόμετρα και ιντερφερόμετρα (συμβολόμετρα) χρησιμοποιούνται στη φασματοσκοπία για τη μέτρηση είτε του μήκους κύματος, αλλά τα βρίσκουμε και σε συσκευές λέιζερ όπου
Φασματόμετρα & Ιντερφερομετρα Τα φασματόμετρα και ιντερφερόμετρα (συμβολόμετρα) χρησιμοποιούνται στη φασματοσκοπία για τη μέτρηση είτε του μήκους κύματος, αλλά τα βρίσκουμε και σε συσκευές λέιζερ όπου
ΔΙΑΣΚΕΔΑΣΜΟΣ & ΑΠΟΡΡΟΦΗΣΗ ΤΟΥ ΦΩΤΟΣ
 ΔΙΑΣΚΕΔΑΣΜΟΣ & ΑΠΟΡΡΟΦΗΣΗ ΤΟΥ ΦΩΤΟΣ Μάκης Αγγελακέρης 010 Εργαστήρια Οπτικής Τμήμα Φυσικής Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σκοπός της Άσκησης 1 o πείραμα: Να κατανοήσετε την έννοια του Διασκεδασμού
ΔΙΑΣΚΕΔΑΣΜΟΣ & ΑΠΟΡΡΟΦΗΣΗ ΤΟΥ ΦΩΤΟΣ Μάκης Αγγελακέρης 010 Εργαστήρια Οπτικής Τμήμα Φυσικής Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σκοπός της Άσκησης 1 o πείραμα: Να κατανοήσετε την έννοια του Διασκεδασμού
ΠΕΡΙΘΛΑΣΗ H κυματική φύση του φωτός το πρόβλημα, η λύση
 ΠΕΡΙΘΛΑΣΗ H κυματική φύση του φωτός το πρόβλημα, η λύση ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ Σύμφωνα με την καθημερινή μας εμπειρία, το φως φαίνεται σαν να ταξιδεύει ευθύγραμμα μέχρι να συναντήσει κάποιο αντικείμενο.
ΠΕΡΙΘΛΑΣΗ H κυματική φύση του φωτός το πρόβλημα, η λύση ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ Σύμφωνα με την καθημερινή μας εμπειρία, το φως φαίνεται σαν να ταξιδεύει ευθύγραμμα μέχρι να συναντήσει κάποιο αντικείμενο.
Διάθλαση φωτός και ολική ανάκλαση: Εύρεση του δείκτη διάθλασης και της γωνίας ολικής ανάκλασης
 3 Διάθλαση φωτός και ολική ανάκλαση: Εύρεση του δείκτη διάθλασης και της γωνίας ολικής ανάκλασης Μέθοδος Σε σώμα διαφανές ημικυλινδρικού σχήματος είναι εύκολο να επιβεβαιωθεί ο νόμος του Sell και να εφαρμοστεί
3 Διάθλαση φωτός και ολική ανάκλαση: Εύρεση του δείκτη διάθλασης και της γωνίας ολικής ανάκλασης Μέθοδος Σε σώμα διαφανές ημικυλινδρικού σχήματος είναι εύκολο να επιβεβαιωθεί ο νόμος του Sell και να εφαρμοστεί
Κυματική Φύση του φωτός και εφαρμογές. Περίθλαση Νέα οπτικά μικροσκόπια Κρυσταλλογραφία ακτίνων Χ
 Κυματική Φύση του φωτός και εφαρμογές Περίθλαση Νέα οπτικά μικροσκόπια Κρυσταλλογραφία ακτίνων Χ Επαλληλία κυμάτων Διαφορά φάσης Δφ=0 Ενίσχυση Δφ=180 Απόσβεση Κάθε σημείο του μετώπου ενός κύματος λειτουργεί
Κυματική Φύση του φωτός και εφαρμογές Περίθλαση Νέα οπτικά μικροσκόπια Κρυσταλλογραφία ακτίνων Χ Επαλληλία κυμάτων Διαφορά φάσης Δφ=0 Ενίσχυση Δφ=180 Απόσβεση Κάθε σημείο του μετώπου ενός κύματος λειτουργεί
Γεωμετρική Οπτική. Πρόκειται δηλαδή για μια ισοφασική επιφάνεια που ονομάζεται μέτωπο κύματος.
 Γεωμετρική Οπτική Στη Γεωμετρική Οπτική επεξεργαζόμαστε τα φαινόμενα ωσάν το φως να αποτελείται μόνο από σωματίδια, ώστε να εξασφαλίζεται την εύκολη ερμηνεία των φαινομένων της ευθύγραμμης διάδοσης του
Γεωμετρική Οπτική Στη Γεωμετρική Οπτική επεξεργαζόμαστε τα φαινόμενα ωσάν το φως να αποτελείται μόνο από σωματίδια, ώστε να εξασφαλίζεται την εύκολη ερμηνεία των φαινομένων της ευθύγραμμης διάδοσης του
Ενδεικτικές Λύσεις Θεμάτων Τελικών Εξετάσεων στη Θεματική Ενότητα ΦΥΕ34
 Κυματική ΦΥΕ34 0/07/0 Ελληνικό Ανοικτό Πανεπιστήμιο Ενδεικτικές Λύσεις Θεμάτων Τελικών Εξετάσεων στη Θεματική Ενότητα ΦΥΕ34 KYMATIKH Διάρκεια: 80 λεπτά Ονοματεπώνυμο: Τμήμα: Θέμα ο (Μονάδες:.5) Α) Θεωρούμε
Κυματική ΦΥΕ34 0/07/0 Ελληνικό Ανοικτό Πανεπιστήμιο Ενδεικτικές Λύσεις Θεμάτων Τελικών Εξετάσεων στη Θεματική Ενότητα ΦΥΕ34 KYMATIKH Διάρκεια: 80 λεπτά Ονοματεπώνυμο: Τμήμα: Θέμα ο (Μονάδες:.5) Α) Θεωρούμε
ΕΛΛΗΝΙΚΟ ΑΝΟΙKΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ η ΕΡΓΑΣΙΑ
 17/12/24 ΕΛΛΗΝΙΚΟ ΑΝΟΙKΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 34 24-5 3 η ΕΡΓΑΣΙΑ Προθεσμία παράδοσης 31/1/25 Άσκηση 1 α) Το ηλεκτρικό πεδίο ενός επιπέδου ηλεκτρομαγνητικού κύματος έχει 2 1 πλάτος 1 Vm. Βρείτε (i) το μέτρο
17/12/24 ΕΛΛΗΝΙΚΟ ΑΝΟΙKΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 34 24-5 3 η ΕΡΓΑΣΙΑ Προθεσμία παράδοσης 31/1/25 Άσκηση 1 α) Το ηλεκτρικό πεδίο ενός επιπέδου ηλεκτρομαγνητικού κύματος έχει 2 1 πλάτος 1 Vm. Βρείτε (i) το μέτρο
 1. Το σημείο Ο ομογενούς ελαστικής χορδής, τη χρονική στιγμή t= αρχίζει να εκτελεί Α.Α.Τ. με εξίσωση y=,5ημπt ( SI), κάθετα στη διεύθυνση της χορδής. Το κύμα που παράγεται διαδίδεται κατά τη θετική κατεύθυνση
1. Το σημείο Ο ομογενούς ελαστικής χορδής, τη χρονική στιγμή t= αρχίζει να εκτελεί Α.Α.Τ. με εξίσωση y=,5ημπt ( SI), κάθετα στη διεύθυνση της χορδής. Το κύμα που παράγεται διαδίδεται κατά τη θετική κατεύθυνση
ΕΡΓΑΣΤΗΡΙΟ ΑΤΟΜΙΚΗΣ ΦΥΣΙΚΗΣ
 ΕΡΓΑΣΤΗΡΙΟ ΑΤΟΜΙΚΗΣ ΦΥΣΙΚΗΣ Άσκηση 8: Μελέτη των κβαντικών μεταπτώσεων στο άτομο του Na. Επώνυμο: Όνομα: Α.Ε.Μ.: Ημ/νία παράδοσης: ΘΕΩΡΗΤΙΚΗ ΕΙΣΑΓΩΓΗ Σκοπός της άσκησης που αναλύεται παρακάτω είναι η μελέτη
ΕΡΓΑΣΤΗΡΙΟ ΑΤΟΜΙΚΗΣ ΦΥΣΙΚΗΣ Άσκηση 8: Μελέτη των κβαντικών μεταπτώσεων στο άτομο του Na. Επώνυμο: Όνομα: Α.Ε.Μ.: Ημ/νία παράδοσης: ΘΕΩΡΗΤΙΚΗ ΕΙΣΑΓΩΓΗ Σκοπός της άσκησης που αναλύεται παρακάτω είναι η μελέτη
HMY 333 Φωτονική Διάλεξη 12 Οπτικοί κυματοδηγοί
 4 Hsiu. Ha Ανάκλαση και μετάδοση του φωτός σε μια διηλεκτρική επαφή HMY 333 Φωτονική Διάλεξη Οπτικοί κυματοδηγοί i i i r i si c si v c hp://www.e.readig.ac.u/clouds/awell/ c 3 Γωνία πρόσπτωσης < κρίσιμη
4 Hsiu. Ha Ανάκλαση και μετάδοση του φωτός σε μια διηλεκτρική επαφή HMY 333 Φωτονική Διάλεξη Οπτικοί κυματοδηγοί i i i r i si c si v c hp://www.e.readig.ac.u/clouds/awell/ c 3 Γωνία πρόσπτωσης < κρίσιμη
5 Δεκεμβρίου 2015 ΛΥΚΕΙΟ:... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: ΜΟΝΑΔΕΣ:
 ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2016 ΦΥΣΙΚΗ 5 Δεκεμβρίου 2015 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2.. 3.. ΜΟΝΑΔΕΣ: Το πρόβλημα Μελέτη οπτικών ιδιοτήτων διαφανούς υλικού με τη βοήθεια πηγής φωτός laser Είστε στο δωμάτιό
ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2016 ΦΥΣΙΚΗ 5 Δεκεμβρίου 2015 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2.. 3.. ΜΟΝΑΔΕΣ: Το πρόβλημα Μελέτη οπτικών ιδιοτήτων διαφανούς υλικού με τη βοήθεια πηγής φωτός laser Είστε στο δωμάτιό
Το οπτικό μικροσκόπιο και ο τρόπος χρήσης του
 Το οπτικό μικροσκόπιο και ο τρόπος χρήσης του Το ανθρώπινο μάτι μπορεί να διακρίνει λεπτομέρειες της τάξης των 50-200 μm. Ο άνθρωπος με τις πρωτοποριακές εφευρέσεις των Malpighi, Hooke, Van Leeuwenhook
Το οπτικό μικροσκόπιο και ο τρόπος χρήσης του Το ανθρώπινο μάτι μπορεί να διακρίνει λεπτομέρειες της τάξης των 50-200 μm. Ο άνθρωπος με τις πρωτοποριακές εφευρέσεις των Malpighi, Hooke, Van Leeuwenhook
7.1 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ
 7.1 ΑΣΚΗΣΗ 7 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ ΘΕΩΡΙΑ Όταν φωτεινή παράλληλη δέσμη διαδιδόμενη από οπτικό μέσο α με δείκτη διάθλασης n 1 προσπίπτει σε άλλο οπτικό μέσο β με δείκτη διάθλασης n 2 και
7.1 ΑΣΚΗΣΗ 7 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ ΘΕΩΡΙΑ Όταν φωτεινή παράλληλη δέσμη διαδιδόμενη από οπτικό μέσο α με δείκτη διάθλασης n 1 προσπίπτει σε άλλο οπτικό μέσο β με δείκτη διάθλασης n 2 και
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΟΠΤΙΚΑ ΣΤΟΙΧΕΙΑ : ΚΑΤΟΠΤΡΑ ΔΙΟΠΤΡΑ ΦΑΚΟΙ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΟΠΤΙΚΑ ΣΤΟΙΧΕΙΑ : ΚΑΤΟΠΤΡΑ ΔΙΟΠΤΡΑ ΦΑΚΟΙ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ.
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΟΠΤΙΚΑ ΣΤΟΙΧΕΙΑ : ΚΑΤΟΠΤΡΑ ΔΙΟΠΤΡΑ ΦΑΚΟΙ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ.
papost/
 Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ
 ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ Άσκηση 4. Διαφράγματα. Θεωρία Στο σχεδιασμό οπτικών οργάνων πρέπει να λάβει κανείς υπόψη και άλλες παραμέτρους πέρα από το πού και πώς σχηματίζεται το είδωλο ενός
ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ Άσκηση 4. Διαφράγματα. Θεωρία Στο σχεδιασμό οπτικών οργάνων πρέπει να λάβει κανείς υπόψη και άλλες παραμέτρους πέρα από το πού και πώς σχηματίζεται το είδωλο ενός
ΓΓ/Μ ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ. Τεύχος 5ο: Φύση και Διάδοση φωτός Ανάκλαση του φωτός
 ΓΓ/Μ5 05-06 ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ Τεύχος 5ο: Φύση και Διάδοση φωτός Ανάκλαση του φωτός ΕΚΔΟΤΙΚΕΣ ΤΟΜΕΣ ΟΡΟΣΗΜΟ ΠΕΡΙΟΔΙΚΗ ΕΚΔΟΣΗ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΚΑΙ ΤΟ ΛΥΚΕΙΟ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Φυσική για την Γ'
ΓΓ/Μ5 05-06 ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ Τεύχος 5ο: Φύση και Διάδοση φωτός Ανάκλαση του φωτός ΕΚΔΟΤΙΚΕΣ ΤΟΜΕΣ ΟΡΟΣΗΜΟ ΠΕΡΙΟΔΙΚΗ ΕΚΔΟΣΗ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΚΑΙ ΤΟ ΛΥΚΕΙΟ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Φυσική για την Γ'
είναι τα μήκη κύματος του φωτός αυτού στα δύο υλικά αντίστοιχα, τότε: γ. 1 Β) Να δικαιολογήσετε την επιλογή σας.
 Β.1 Μονοχρωματικό φως, που διαδίδεται στον αέρα, εισέρχεται ταυτόχρονα σε δύο οπτικά υλικά του ίδιου πάχους d κάθετα στην επιφάνειά τους, όπως φαίνεται στο σχήμα. Οι χρόνοι διάδοσης του φωτός στα δύο υλικά
Β.1 Μονοχρωματικό φως, που διαδίδεται στον αέρα, εισέρχεται ταυτόχρονα σε δύο οπτικά υλικά του ίδιου πάχους d κάθετα στην επιφάνειά τους, όπως φαίνεται στο σχήμα. Οι χρόνοι διάδοσης του φωτός στα δύο υλικά
Διάθλαση φωτεινής δέσμης σε διαφανές υλικό (Επιβεβαίωση, αξιοποίηση του νόμου Snell)
 Διάθλαση φωτεινής δέσμης σε διαφανές υλικό (Επιβεβαίωση, αξιοποίηση του νόμου Snell) 1. Σκοπός Αξιοποιώντας τις μετρήσεις των γωνιών πρόσπτωσης, διάθλασης α και δ αντίστοιχα μίας πολύ στενής φωτεινής δέσμης
Διάθλαση φωτεινής δέσμης σε διαφανές υλικό (Επιβεβαίωση, αξιοποίηση του νόμου Snell) 1. Σκοπός Αξιοποιώντας τις μετρήσεις των γωνιών πρόσπτωσης, διάθλασης α και δ αντίστοιχα μίας πολύ στενής φωτεινής δέσμης
ΑΣΚΗΣΗ 8 Μελέτη φακών
 Απαραίτητα όργανα και υλικά ΑΣΚΗΣΗ 8 Μελέτη φακών 8. Απαραίτητα όργανα και υλικά. Οπτική τράπεζα.. Πέτασμα. 3. Συγκεντρωτικός φακός. 4. Φωτεινή πηγή. 5. Διάφραγμα με δακτύλιο και οπή. 6. Φίλτρο κόκκινο
Απαραίτητα όργανα και υλικά ΑΣΚΗΣΗ 8 Μελέτη φακών 8. Απαραίτητα όργανα και υλικά. Οπτική τράπεζα.. Πέτασμα. 3. Συγκεντρωτικός φακός. 4. Φωτεινή πηγή. 5. Διάφραγμα με δακτύλιο και οπή. 6. Φίλτρο κόκκινο
Φύση και διάδοση φωτός
 Σημειώσεις Γενικής Φυσικής - ΒΕΤ Μ. Μπενής / 2016 Κυματική Φύση και διάδοση φωτός Ακτινικό μοντέλο διάδοσης. Στο κεφάλαιο των κυμάτων αναπαραστήσαμε τη διάδοση των κυμάτων με τα κυματομέτωπα. Μια απλούστευση
Σημειώσεις Γενικής Φυσικής - ΒΕΤ Μ. Μπενής / 2016 Κυματική Φύση και διάδοση φωτός Ακτινικό μοντέλο διάδοσης. Στο κεφάλαιο των κυμάτων αναπαραστήσαμε τη διάδοση των κυμάτων με τα κυματομέτωπα. Μια απλούστευση
Φυσικές Επιστήμες Σχολή Θετικών Επιστημών και Τεχνολογίας
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΙΚΡΟΣΚΟΠΗΣΗ Εργαστηριακές Ασκήσεις Βιολογίας I Φυσικές Επιστήμες Σχολή Θετικών Επιστημών και Τεχνολογίας Παξινού Ευγενία Για την επιστήμη της Βιολογίας, το μικροσκόπιο αποτέλεσε τη μεγαλύτερη
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΙΚΡΟΣΚΟΠΗΣΗ Εργαστηριακές Ασκήσεις Βιολογίας I Φυσικές Επιστήμες Σχολή Θετικών Επιστημών και Τεχνολογίας Παξινού Ευγενία Για την επιστήμη της Βιολογίας, το μικροσκόπιο αποτέλεσε τη μεγαλύτερη
ΚΕΦΑΛΑΙΟ 1 - ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ
 ΚΕΦΑΛΑΙΟ 1 - ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ Σύμφωνα με την ηλεκτρομαγνητική θεωρία του Maxwell, το φως είναι εγκάρσιο ηλεκτρομαγνητικό κύμα. Η θεωρία αυτή α. δέχεται ότι κάθε φωτεινή πηγή εκπέμπει φωτόνια.
ΚΕΦΑΛΑΙΟ 1 - ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ Σύμφωνα με την ηλεκτρομαγνητική θεωρία του Maxwell, το φως είναι εγκάρσιο ηλεκτρομαγνητικό κύμα. Η θεωρία αυτή α. δέχεται ότι κάθε φωτεινή πηγή εκπέμπει φωτόνια.
