Ο15. Κοίλα κάτοπτρα. 2. Θεωρία. 2.1 Γεωμετρική Οπτική
|
|
|
- Ἁλκυόνη Ιωαννίδης
- 9 χρόνια πριν
- Προβολές:
Transcript
1 Ο15 Κοίλα κάτοπτρα 1. Σκοπός Σκοπός της άσκησης είναι η εύρεση της εστιακής απόστασης κοίλου κατόπτρου σχετικά μεγάλου ανοίγματος και την μέτρηση του σφάλματος της σφαιρικής εκτροπής... Θεωρία.1 Γεωμετρική Οπτική Το φως ως γνωστόν είναι εγκάρσιο ηλεκτρομαγνητικό κύμα. Αποτελείται δηλαδή από ένα ηλεκτρικό και ένα μαγνητικό πεδίο τα οποία παραμένουν κάθετα μεταξύ τους και κάθετα στη διεύθυνση διάδοσης. Στην προσέγγιση της γεωμετρικής οπτικής θεωρούμε ότι το φως διαδίδεται σε ευθείες γραμμές οι οποίες ονομάζονται οπτικές ακτίνες, Μπορούμε να πούμε πως οι ακτίνες φωτός συμπίπτουν με την διεύθυνση διάδοσης του ηλεκτρομαγνητικού κύματος. Αν τώρα η φωτεινή ακτίνα προσπέσει π.χ. σε ένα διάφραγμα το οποίο έχει οπή με διάμετρο πολύ μεγαλύτερη από το μήκος κύματος του φωτός τότε το φως πίσω από την οπή συνεχίζει την ευθύγραμμη πορεία του. Αν όμως η οπή έχει τις διαστάσεις του μήκους κύματος του φωτός, λόγω του φαινομένου της περίθλασης παύει να ισχύει η ευθύγραμμη διάδοση του φωτός. Το ίδιο συμβαίνει και στην περίπτωση που το φως πέσει πάνω σε αδιαφανή εμπόδια. Αν οι διαστάσεις του εμποδίου είναι πολύ μεγαλύτερες από το μήκος κύματος του φωτός, τότε η σκιά του εμποδίου είναι καθορισμένη αυστηρά. Στην περίπτωση της γεωμετρικής οπτικής θα θεωρήσουμε ότι ισχύει το μήκος κύματος του φωτός και d οι διαστάσεις της οπής ή του αντικειμένου. Αυτή η προσέγγιση περιγράφει αρκετά καλά την επίδραση των κατόπτρων και των φακών στην φωτεινή ακτίνα. Μία χρήσιμή αρχή για την κατανόηση της πορείας του φωτός είναι η αρχή του Fermat:κάθε φωτεινή ακτίνα που διέρχεται από δύο σημεία ακολουθεί τον χρονικά συντομότερο δρόμο.μία άλλη χρήσιμη αρχή είναι η αρχή αντίστροφης πορείας του φωτός: Η πορεία την οποία ακολουθεί το φως δεν αλλάζει αν αντιστρέψουμε την φορά διάδοσής του.. Ανάκλαση λ d όπου λ Όταν μία φωτεινή ακτίνα συναντήσει την διαχωριστική επιφάνεια δύο διαφορετικών οπτικών μέσων εν μέρει αλλάζει πορεία συνεχίζοντας να διαδίδεται στο ίδιο οπτικό μέσο. Το φαινόμενο αυτό ονομάζεται ανάκλαση. Νόμος της ανάκλασης Βαμβακάς Ι.,Μπάρτζης Β. 1
2 Ας θεωρήσουμε μία φωτεινή ακτίνα η οποία πέφτει σε μία λεία επιφάνεια (Σχήμα 1) και ας ονομάσουμε τις γωνίες πρόσπτωσης και ανάκλασης που σχηματίζουν π και α Σχήμα 1 η προσπίπτουσα και η ανακλώμενη ακτίνα αντίστοιχα με την κάθετο στη διαχωριστική επιφάνεια. Τότε ισχύει ότι π α (.1) και ακόμη ότι η προσπίπτουσα και η ανακλώμενη ακτίνα ορίζουν ένα επίπεδο κάθετο στη διαχωριστική επιφάνεια. Σχήμα Σχήμα 3 Φωτεινή δέσμη ονομάζουμε ένα σύνολο ακτίνων. Ας υποθέσουμε ότι ένα τέτοιο σύνολο ακτίνων παράλληλων μεταξύ τους προσπίπτει σε μία λεία και στιλπνή επιφάνεια. Μετά την ανάκλασή τους παραμένουν μεταξύ τους παράλληλες. Η ανάκλαση αυτή ονομάζεται κατοπτρική ανάκλαση (Σχήμα ). Όταν η ανάκλαση γίνεται γίνεται πάνω σε μη λεία επιφάνεια μετά την ανάκλαση οι ακτίνες κατευθύνονται ακανόνιστα προς όλες τις διευθύνσεις και το φαινόμενο αυτό ονομάζεται διάχυση (Σχήμα 3)..3 Κάτοπτρα Κάτοπτρο θεωρείται κάθε λεία και στιλπνή επιφάνεια η οποία ανακλά όλο το φως που προσπίπτει πάνω της. Επίπεδο κάτοπτρο Θα αρχίσουμε την μελέτη μας με το πιο απλό κάτοπτρο, που είναι το επίπεδο κάτοπτρο γνωστό σε μας σαν καθρέπτης Θα μελετήσουμε την ανάκλαση του φωτός πάνω επάνω σε επίπεδο κάτοπτρο ξεχωρίζοντας δύο περιπτώσεις: α) Ανάκλαση παράλληλης δέσμης: είναι ακριβώς η περίπτωση που μελετήθηκε λίγο πριν στην κατοπτρική ανάκλαση (Σχήμα ) β) Ανάκλαση αποκλίνουσας δέσμης:ας θεωρήσουμε ότι μία σημειακή φωτεινή πηγή βρίσκεται στην θέση Α (Σχήμα 4). Η πηγή αυτή εκπέμπει αποκλίνουσες Βαμβακάς Ι.,Μπάρτζης Β.
3 φωτεινές ακτίνες προς κάθε κατεύθυνση. Μερικές από αυτές προσπίπτουν στο επίπεδο κάτοπτρο και προφανώς ανακλώνται. Για κάθε μία από αυτές ισχύει ο νόμος της ανάκλασης (δηλαδή ότι η γωνία πρόσπτωσης ισούται με τη γωνία ανάκλασης). Η τομή των ανακλώμενων ακτινών ονομάζεται είδωλο. Αν η τομή προέρχεται από πραγματικές ακτίνες τότε το είδωλο ονομάζεται πραγματικό. Αν όμως προέρχεται από τομή προέκτασεων ακτίνων τότε το είδωλο ονομάζεται φαναταστικό. α = β Σχήμα 4 Σχήμα 5 Στην περίπτωσή μας το είδωλο του σημειακού φωτεινού αντικειμένου Α είναι το A' και είναι φανταστικό. Στην συνέχεια ας θεωρήσουμε ένα αντικείμενο με διαστάσεις (Σχήμα 5). Μπορούμε να θεωρήσουμε ότι αποτελούνται από ένα άπειρο πλήθος σημειακών φωτεινών πηγών κάθε μία από τις οποίες έχει το είδωλό της και όλα τα είδωλα μαζί φτιάχνουν το είδωλο του αντικειμένου (γενικότερα είδωλο ονομάζεται η απεικόνιση ενός αντικειμένου από ένα οπτικό σύστημα). Από την γεωμετρία του σχήματος προκύπτει ότι το μέγεθος του ειδώλου θα ισούται με το μέγεθος του αντικειμένου. Σφαιρικά κάτοπτρα Σφαιρικά κάτοπτρα λέγονται εκείνα που η ανακλαστική επιφάνειά τους είναι τμήμα σφαίρας (Σχήμα 6) Χωρίζονται σε δύο μεγάλες κατηγορίες : τα κοίλα και τα κυρτά σφαιρικά κάτοπτρα. Τα κύρια χαρακτηριστικά ενός σφαιρικού κατόπτρου είναι τα εξής : Σχήμα 6 καμπυλότητας του κατόπτρου. α) Το σημείο Ο το οποίο είναι το κέντρο της επιφάνειας του σφαιρικού κατόπτρου και ονομάζεται κορυφή του κατόπτρου. β) Το κέντρο C της σφαίρας στην οποία ανήκει το κάτοπτρο και ονομάζεται κέντρο καμπυλότητας του κατόπτρου. γ) Η ακτίνα CO της σφαίρας στην οποία ανήκει το κάτοπτρο και ονομάζεται ακτίνα Βαμβακάς Ι.,Μπάρτζης Β. 3
4 δ) Η ευθεία από ορίζεται από τα σημεία C και Ο που ονομάζεται κύριος άξονας του κατόπτρου. ε) Κάθε ευθεία που διέρχεται από το κέντρο καμπυλότητας C και από ένα τυχαίο σημείο Γ του κατόπτρου ονομάζεται δευτερεύον άξονας. στ) Η γωνία ACB υπο την οποία φαίνεται από το κέντρο C το κάτοπτρο ονομάζεται γωνιακό άνοιγμα του κατόπτρου. Όταν αυτή είναι μικρότερη από, το κάτοπτρο λέγεται μικρού ανοίγματος 8 Κοίλα σφαιρικά κάτοπτρα Κοίλα σφαιρικά κάτοπτρα ονομάζονται εκείνα στα οποία η ανάκλαση δημιουργείται από την εσωτερική τους επιφάνεια. Εύρεση της κύριας εστίας Ας θεωρήσουμε μία ακτίνα ΑΒ που πέφτει στο κάτοπτρο παράλληλα με τον κύριο άξονα. Μετά την ανάκλασή της, η οποία υπακούει φυσικά το νόμο της Σχήμα 7 ανάκλασης, θα περάσει από ένα σημείο του κύριου άξονα F. Η ευθεία CB είναι κάθετος στην επιφάνεια του κατόπτρου στο σημείο Β διότι είναι ακτίνα του κατόπτρου και θα ισχύει Επειδή ακόμα ισχύει έχουμε αˆ βˆ αˆ γˆ βˆ γˆ (ως εντός και εναλλάξ) Συνεπώς το τρίγωνο CFB είναι ισοσκελές και άρα θα ισχύει CF FB Στην περίπτωση που το κάτοπτρο είναι μικρού ανοίγματος τότε προσεγγιστικά μπορούμε να θεωρήσουμε ότι FB FO και συνεπώς FC FO όπου CO η ακτίνα καμπυλότητας του κατόπτρου. Σχήμα 8 Επειδή ο παραπάνω συλλογισμός ισχύει για οποιαδήποτε τυχαία ακτίνα παράλληλη με τον κύριο άξονα, εξάγουμε το συμπέρασμα ότι όλες οι ακτίνες οι παράλληλες με τον κύριο άξονα μετά την ανάκλασή τους στο κάτοπτρο θα περάσουν από το σημείο F. Βαμβακάς Ι.,Μπάρτζης Β. 4
5 Αν θεωρήσουμε λοιπόν μία παράλληλη δέσμη ακτίνων που είναι παράλληλη με τον κύριο άξονα του κατόπτρου, μετά την ανάκλασή τους στο κάτοπτρο όλες περνούν από το σημείο F του άξονα που λέγεται κύρια εστία του κατόπτρου (σχήμα 8). Η απόσταση μεταξύ της κύριας εστίας και της κορυφής O του κατόπτρου ονομάζεται εστιακή απόσταση f ( και όπως αποδείξαμε ισχύει Σχήμα 9 f (FO)) f (.) Ας θεωρήσουμε στη συνέχεια μία παράλληλη δέσμη ακτινών που πέφτει στο κάτοπτρο παράλληλα προς τη διεύθυνση ενός δευτερεύοντα άξονα CΓ (σχήμα 9). Μετά την ανάκλασή τους οι ακτίνες συγκλίνουν σε ένα σημείο, το F ', το οποίο ακολουθώντας τον ίδιο συλλογισμό με προηγουμένως μπορούμε να πούμε ότι απέχει από το κέντρο καμπυλότητας απόσταση. Λόγω του μικρού ανοίγματος του κατόπτρου μπορούμε να θεωρήσουμε ότι όλες οι δευτερεύουσες εστίες βρίσκονται πάνω σε ένα επίπεδο το οποίο ονομάζεται εστιακό επίπεδο. Θα πρέπει εδώ να τονίσουμε το γεγονός πως εξαιτίας της αρχής της αντίστροφης πορείας του φωτός κάθε ακτίνα που διέρχεται από μία κύρια ή δευτερεύουσα εστία, μετά την ανάκλασή της γίνεται παράλληλη με τον κύριο ή δευτερεύοντα άξονα Ανάκλαση αποκλίνουσας δέσμης : Ας θεωρήσουμε ένα σημειακό φωτεινό αντικείμενο A πάνω στον κύριο άξονα το οποίο βρίσκεται σε απόσταση μεγαλύτερη από την εστιακή απόσταση του κατόπτρου(σχήμα 10). Ας θεωρήσουμε μία τυχαία ακτίνα ΑΒ η οποία προσπίπτει στο κάτοπτρο. Ακολουθώντας το νόμο της ανάκλασης ( ) βρίσκουμε την ανακλώμενη ακτίνα και κατ επέκταση το σημείο A ' που αυτή τέμνει τον κύριο άξονα. Από το θεώρημα της διχοτόμου έχουμε ΑΒ Α' Β AC A'C και επειδή προσεγγιστικά για κάτοπτρα μικρού ανοίγματος ισχύει AB AOκαι έχουμε AO AC α α A'O A'C β β 1 1 α β ή α β f A'B A'O γˆ δˆ Σχήμα 10 Βαμβακάς Ι.,Μπάρτζης Β. 5
6 όπου α, β οι αποστάσεις του αντικειμένου Α και του σημείου τομής Α της ανακλώμενης ακτίνας με τον κύριο άξονα από την κορυφή Ο του κατόπτρου. Η παραπάνω ανάλυση έγινε με βάση μία τυχαία ακτίνα που ξεκινά από το σημειακό φωτεινό αντικείμενο Α. Άρα ισχύει για όλες τις ακτίνες που ξεκινούν από το Α και που μετά την ανάκλασή τους στο κάτοπτρο θα περνούν από το Α, το οποίο ονομάζεται είδωλο του Α και το οποίο είναι πραγματικό (βρίσκεται από το σημείο τομής των ανακλώμενων ακτινών)(σχήμα 11). Αν αρχίσουμε να πλησιάζουμε το αντικείμενο A, τότε το είδωλο αρχίζει να απομακρύνεται και φθάνει στο άπειρο όταν το φωτεινό αντικείμενο συμπέσει με την κύρια εστία του κατόπτρου. Αν το σημειακό φωτεινό αντικείμενο βρίσκεται μεταξύ της κύριας εστίας και της κορυφής του κατόπτρου(σχήμα 1), τότε η φωτεινή δέσμη μετά την ανάκλαση αποκλίνει και συνεπώς το είδωλο είναι φανταστικό γιατί προέρχεται από τομή προεκτάσεων ακτίνων. Σχήμα 11 Σχήμα 1 Αν α και β είναι οι αποστάσεις του αντικειμένου και του ειδώλου από την κορυφή του κατόπτρου ισχύει η σχέση (.3) α β f Μέχρι τώρα ασχοληθήκαμε με την περίπτωση που το φωτεινό αντικείμενο βρίσκεται πάνω στον κύριο άξονα. Αν όμως δεν βρίσκεται (σημείο Α στο σχήμα 13) πάνω στον κύριο άξονα, τότε οι ακτίνες μετά την ανάκλαση τέμνονται σε ένα σημείο, σχηματίζοντας έτσι το είδωλο Α του αντικειμένου Α,το οποίο δεν βρίσκεται πάνω στον κύριο άξονα και τότε η προηγούμενη σχέση (.3) ισχύει προσεγγιστικά. Γραφική εύρεση ειδώλου: Για να βρούμε γραφικά το είδωλο ενός σημειακού αντικειμένου, όπως δείχνουν τα παρακάτω Σχήμα 13 γραφικά παραδείγματα ακολουθούμε τους εξής κανόνες: α) Ακτίνα που διέρχεται από το κέντρο καμπυλότητας του κατόπτρου μετά την ανάκλαση της στο κάτοπτρο ακολουθεί την ίδια πορεία και έχει αντίθετη φορά. β)ακτίνα παράλληλη με τον κύριο άξονα μετά την ανάκλαση της στο κάτοπτρο περνά από την κύρια εστία του κατόπτρου γ) Ακτίνα που περνάει από την κύρια εστία του κατόπτρου μετά την ανάκλαση της στο κάτοπτρο γίνεται παράλληλη με τον κύριο άξονα. Βαμβακάς Ι.,Μπάρτζης Β. 6
7 δ) Ακτίνα που συναντά το κάτοπτρο στην κορυφή Ο ανακλάται με γωνία ίση με την γωνία πρόσπτωσης Για να βρούμε το είδωλο ενός σημειακού αντικειμένου μπορούμε να χρησιμοποιήσουμε δύο από τους παραπάνω κανόνες βρίσκοντας έτσι το σημείο τομής δύο χαρακτηριστικών ακτίνων και συνεπώς το είδωλό του( όλες οι ακτίνες που ξεκινούν από το σημειακό αντικείμενο αναγκαστικά θα περνούν από αυτό το σημείο μετά την ανάκλασή τους). Αν τώρα το αντικείμενό μας έχει διαστάσεις μπορούμε να βρούμε το είδωλο των άκρων του και κατ επέκταση και του ίδιου (σχήματα 14,15,16,17,18). Σχήμα 14 Σχήμα 15 Σχήμα 16 Μεγέθυνση: ονομάζεται το πηλίκο του μήκους του ειδώλου προς το μήκος του αντικειμένου (A' B') M (AB) (.4) όπου ειδώλου αντίστοιχα. Όταν το είδωλο είναι αντεστραμμένο το ( A'B' ) είναι αρνητικό. Αποδεικνύεται ότι ισχύει β M (.5) α (A,B),(A',B') τα μήκη του αντικειμένου και του Σχήμα 17 Σχήμα 18 Βαμβακάς Ι.,Μπάρτζης Β. 7
8 .4 Σφάλματα σφαιρικών κατόπτρων α)σφαιρική εκτροπή:η προηγούμενη ανάλυση των σφαιρικών κατόπτρων έγινε με βάση τις παραδοχές ότι τα κάτοπτρα είναι μικρού ανοίγματος και ότι οι ακτίνες είναι σχεδόν αξονικές (δηλαδή κοντά στον κύριο άξονα). Εάν μία από τις προηγούμενες παραδοχές δεν ισχύει,τα κάτοπτρα σχηματίζουν όταν το αντικείμενο είναι σημειακό, μη σημειακό είδωλο (κηλίδα). Κατ επέκταση, στην περίπτωση που το αντικείμενο έχει διαστάσεις τα σχηματιζόμενα είδωλά τους θα έχουν ασαφή όρια. Αυτό το σφάλμα των φακών ονομάζεται σφαιρική εκτροπή. Ένα τέτοιο κάτοπτρο με σχετικά μεγάλο άνοιγμα φαίνεται στο παραπλεύρως σχήμα 19. Όταν σε ένα τέτοιο κάτοπτρο προσπέσει δέσμη παράλληλων ακτινών δεν συγκλίνουν όλες προς το ίδιο σημείο. Αυτές που βρίσκονται κοντά στον κύριο άξονα (αξονικές) του κατόπτρου που στο σχήμα παριστάνονται ως δέσμη που δεν είναι αξονική συγκλίνει στο σημείο F. Ο γεωμετρικός τόπος των εστιών αποτελεί τμήμα περιφέρειας κύκλου. Σχήμα 19 Π 1 συγκλίνουν στην κύρια εστία F. Η δέσμη Στην συνέχεια θα ασχοληθούμε αναλυτικότερα με το σφάλμα της σφαιρικής εκτροπής. Ας θεωρήσουμε μία ακτίνα ΑΒ παράλληλη με τον κύριο άξονα και σε απόσταση d από αυτόν (σχήμα 0). Μετά την ανάκλασή της θα τέμνει τον κύριο άξονα στο σημείο πιο κοντά στην κύρια εστία F όσο η d θα γίνεται μικρότερη. Η ακριβής σχέση που δίνει την εξάρτηση της f (είναι η απόσταση της F από το οπτικό κέντρο του κατόπτρου) από την ακτίνα καμπυλότητας είναι η εξής Σχήμα 0 F' και το σημείο αυτό θα είναι τόσο f ' ( Αν στην παραπάνω σχέση θέσουμε λαμβάνει τη τιμή δηλαδή f ' 1 f ' d ) d (.7) (.6) τότε d 0 και έτσι το πηλίκο συνεπώς τότε τα σημεία F και F συμπίπτουν και το κάτοπτρο παρουσιάζει ιδανική συμπεριφορά. Αυτό όπως αντιλαμβανόμαστε συμβαίνει για τις αξονικές ακτίνες. Σχήμα 1 f ' d Η γραφική παράσταση f ( ) φαίνεται στο σχήμα 1. f ' Π Βαμβακάς Ι.,Μπάρτζης Β. 8
9 Το πρόβλημα αυτό αντιμετωπίζεται με τα παραβολικά κάτοπτρα (σχήμα )των οποίων η ανακλαστική επιφάνεια έχει σχήμα παραβολοειδούς εκ περιστροφής. Τότε αποδεικνύεται ότι οι ακτίνες θα διέλθουν όλες από ένα σημείο ανεξάρτητα από το άνοιγμα του κατόπτρου. Σχήμα β) Αστιγματική εκτροπή: Άλλος τύπος σφάλματος παρουσιάζεται όταν η προσπίπτουσα δέσμη ακτινών σχηματίζει μεγάλη γωνία με τον κύριο άξονα. Τότε οι ανακλώμενες ακτίνες δεν τέμνονται σε ένα σημείο, αλλά διέρχονται από δύο ευθείες οι οποίες είναι κάθετες μεταξύ τους και δεν βρίσκονται στο ίδιο επίπεδο. 3. Πειραματική διάταξη Η πειραματική διάταξη για τη μέτρηση της εστιακής απόστασης κοίλου κατόπτρου αποτελείται (σχήματα 3 α,β ) από μια βάση Β πάνω στην οποία βρίσκεται : α) το κοίλο κάτοπτρο του οποίου θέλουμε να μετρήσουμε την εστιακή απόσταση, β) ο κύριος άξονας του κατόπτρου ΟΟ που είναι χαραγμένος πάνω στη βάση (Β) και είναι βαθμολογημένος με κλίμακα παράλληλη σε αυτόν, το μηδέν της οποίας συμπίπτει με την κορυφή του κατόπτρου, γ) ο δείκτης (Δ) που μπορεί να μετακινείται κατά μήκος του κύριου άξονα του κατόπτρου και πάνω σε αυτόν υπάρχει η δυνατότητα να σημειωθεί το ίχνος της ανακλώμενης δέσμης (αυτό όπως θα δούμε παρακάτω χρησιμοποιείται για την ευθυγράμμιση του Laser), δ) μια πηγή Laser, της οποίας η δέσμη είναι παράλληλη με το κύριο άξονα και η οποία με τη βοήθεια κατάλληλης στροφικής διάταξης μπορεί να μετακινείται σε διεύθυνση κάθετη στον κύριο άξονα του κατόπτρου ΟΟ. Mε την βοήθεια αυτής της διάταξης μπορούμε να μετρήσουμε την απόσταση της δέσμης από τον κύριο άξονα. Στα σχήματα 3α,4 και 5 η κλίμακα ΚΚ δείχνει παραστατικά την παράλληλη μετατόπιση του laser. Σχήμα 3 α,β Σχήμα 4 Βαμβακάς Ι.,Μπάρτζης Β. 9
10 Είναι απαραίτητο να γίνει ευθυγράμμιση του συστήματος, δηλαδή η δέσμη Laser να είναι πάντα παράλληλη προς τον κύριο άξονα του κατόπτρου (ΟΟ ). Για να γίνει η ευθυγράμμιση, μετακινούμε το Laser έτσι ώστε η δέσμη του να διέρχεται ακριβώς πάνω από τον κύριο άξονα ΟΟ και κατ αυτό τον τρόπο να προσπίπτει στη κορυφή Ο του κατόπτρου (σχήμα 4), η οποία έχει σημειωθεί με μαρκαδόρο πάνω στο κάτοπτρο. Σε αυτή τη περίπτωση, η ανακλώμενη και η προσπίπτουσα δέσμη Laser θα πρέπει να αφήνουν ίχνη πάνω στο δρομέα (Δ) τα οποία να βρίσκονται στην ίδια κατακόρυφο. Σημειώνουμε πάνω στο χαρτί του δρομέα (Δ) το ίχνος της ανακλώμενης δέσμης όταν το Laser είναι ευθυγραμμισμένο. Όταν το σύστημα έχει ευθυγραμμισθεί τότε σημειώνουμε τη θέση Μ της κορυφής του κατόπτρου Ο στην κλίμακα ΚΚ (σχήμα 4).Εναλλακτικά θα μπορούσαμε να σημειώσουμε την ένδειξη του κοχλία στη στροφική διάταξη μετακίνησης του Laser. Η θέση αυτή αντιστοιχεί σε απόσταση κατόπτρου. Στρέφοντας το κοχλία μετακινούμε το Laser κατά μία απόσταση d. Θα παρατηρήσουμε αντίστοιχη μετατόπιση του σημείου πρόσπτωσης της δέσμης Laser πάνω στο κάτοπτρο. Σημειώνουμε επίσης τη θέση Μ του σημείου πρόσπτωσης της δέσμης πάνω στη κλίμακα ΚΚ (σχήμα 5). Εναλλακτικά θα μπορούσαμε να σημειώσουμε την ένδειξη του κοχλία στη στροφική διάταξη μετακίνησης του Laser. Η απόσταση MM'ισούται με το d. Σχήμα 5 MM ' d d 0 της δέσμης από τον κύριο άξονα του Κατά τον ίδιο τρόπο,η αφαίρεση των δύο ενδείξεων του κοχλία μας δίνει την απόσταση d. Αποτέλεσμα της μετακίνησης είναι ότι μετά την ανάκλασή της, η δέσμη να διέρχεται από ένα σημείο F του κύριου άξονα του κατόπτρου. Το σημείο αυτό μπορεί εύκολα να σημειωθεί με τη βοήθεια του δρομέα (Δ) (τον μετακινούμε μέχρι το ίχνος της ανακλώμενης δέσμης να συμπέσει ή να βρεθεί στην ίδια κατακόρυφο με το ίχνος της ανακλώμενης δέσμης που είχε σημειωθεί κατά την ευθυγράμμιση)και να μετρηθεί η απόσταση OF πάνω στη βαθμολογημένη κλίμακα. Η απόσταση αυτή αποτελεί την απόσταση καμπυλότητας του κατόπτρου με προσέγγιση πρώτης τάξης έχουμε f ' της σχέσης (.6). Λύνοντας τη σχέση (.6) ως προς την ακτίνα f ' f ' 0.5d (3.1) Έτσι από τον παραπάνω τύπο μπορούμε να υπολογίσουμε την ακτίνα καμπυλότητας και κατ επέκταση από τη σχέση f (3.) την εστιακή απόσταση του κατόπτρου. 4. Εργασίες 1) Θέτουμε σε λειτουργία τη συσκευή Laser και ευθυγραμμίζουμε σύμφωνα με τα προηγούμενα το σύστημα.επαληθεύουμε την ευθυγράμμιση από το γεγονός ότι η ανακλώμενη δέσμη και η προσπίπτουσα δέσμη αφήνουν πάνω στο δρομέα (Δ) ίχνη στην ίδια κατακόρυφο. ) Στη θέση αυτή σημειώνουμε την αντιστοιχία της κορυφής του κατόπτρου Ο στην κλίμακα ΚΚ (θέση Μ του σχήματος 4). Εναλλακτικά θα μπορούσαμε Βαμβακάς Ι.,Μπάρτζης Β. 10
11 να σημειώσουμε την ένδειξη του κοχλία στη στροφική διάταξη μετακίνησης του Laser. 3) Στρέφοντας το κοχλία μετακινούμε το Laser προς μία διεύθυνση, παράλληλη προς τη κλίμακα ΚΚ ανά 5mm έως τα 4cm συμπληρώνοντας τη στήλη του πίνακα 1 και για κάθε θέση σημειώνουμε με τη βοήθεια του δρομέα (Δ) το σημείο F του κύριου άξονα από το οποίο διέρχεται η δέσμη όταν ανακλάται (βλέπε πειραματική διαδικασία). 4) Υπολογίζουμε την απόσταση από την κλίμακα της βάσης για κάθε τιμή του d και συμπληρώνουμε τη στήλη 3 του πίνακα μετρήσεων 1. 5) Επαναλαμβάνουμε τη διαδικασία μετακινώντας το Laser προς την αντίθετη κατεύθυνση και καταχωρούμε τα αποτελέσματα στη στήλη 4 του πίνακα μετρήσεων 1. 6) Για κάθε απόσταση d υπολογίζουμε τη μέση τιμή των δύο μετρήσεων OF' f ' 1 f ' f ' 1 ' f και την αναγράφουμε στη στήλη 5 του πίνακα μετρήσεων 1. 7) Από τη σχέση ( 3.1 ) υπολογίζουμε την ακτίνα καμπυλότητας του κατόπτρου και αναγράφουμε τα αποτελέσματα στη στήλη 6 του πίνακα μετρήσεων 1. 8) Από τη σχέση (3. ) υπολογίζουμε την εστιακή απόσταση f του κατόπτρου και αναγράφουμε τα αποτελέσματα στη στήλη 7 του πίνακα μετρήσεων 1 9) Υπολογίζουμε τη μέση τιμή των εστιακών αποστάσεων f και αναγράφουμε τα αποτελέσματα στη στήλη 8 του πίνακα μετρήσεων 1 10) Υπολογίζουμε το τυπικό σφάλμα της μέσης τιμής καθώς και το επί τοις εκατό σχετικό σφάλμα δf % σ σχ δf f ) Γράφουμε το τελικό αποτέλεσμα στη μορφή f δf f ' f σ % 1) Από τις τιμές του πίνακα βρίσκουμε τα πηλίκα τον πίνακα μετρήσεων 13)Κατασκευάζουμε το διάγραμμα σχ f ' d f ( ) f ', d και συμπληρώνουμε Βαμβακάς Ι.,Μπάρτζης Β. 11
12 ΠΙΝΑΚΑΣ ΜΕΤΡΗΣΕΩΝ α/α d f cm cm cm cm cm cm cm f 1 ' f ' f ' f Δf (Δf ) ΠΙΝΑΚΑΣ ΜΕΤΡΗΣΕΩΝ 1 d f ' 5 Θεματολογικές ερωτήσεις κατανόησης 1)Πως τροποποιείται ο τύπος των κατόπτρων αν μετρήσουμε τις αποστάσεις αντικειμένου και ειδώλου από την κύρια εστία του κατόπτρου; ) Ισχύει ο τύπος των κατόπτρων στα επίπεδα κάτοπτρα; 3)Δίνονται δύο κοίλα κάτοπτρα της ίδιας εστιακής απόστασης αλλά διαφορετικού ανοίγματος. Σχηματίζουμε το είδωλο του ήλιου και με τα δύο σε ένα δοχείο με νερό. Σε ποιο από τα δύο θα αρχίσει να βράζει πιο γρήγορα το νερό; 4) Ένα κοίλο κάτοπτρο δίνει για ένα αντικείμενο ΑΒ το πραγματικό του είδωλο Α Β. Τι θα δούμε αν βάλουμε το μάτι μας στο Α Β. 5) Υπάρχει η δυνατότητα από ένα κοίλο κάτοπτρο να πάρουμε το είδωλο ενός αντικειμένου έτσι ώστε το ένα του μέρος να είναι πραγματικό και το άλλο φανταστικό; 6)Ένα πραγματικό αντικείμενο δίνει μέσω ενός κοίλου κατόπτρου, είδωλο πραγματικό και ίσου μεγέθους. Πόσο απέχει το αντικείμενο από το κάτοπτρο; Βαμβακάς Ι.,Μπάρτζης Β. 1
13 Βαμβακάς Ι.,Μπάρτζης Β. 13
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα. Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ
 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
Φύση του φωτός. Θεωρούμε ότι το φως έχει διττή φύση: διαταραχή που διαδίδεται στο χώρο. μήκος κύματος φωτός. συχνότητα φωτός
 Γεωμετρική Οπτική Φύση του φωτός Θεωρούμε ότι το φως έχει διττή φύση: ΚΥΜΑΤΙΚΗ Βασική ιδέα Το φως είναι μια Η/Μ διαταραχή που διαδίδεται στο χώρο Βασική Εξίσωση Φαινόμενα που εξηγεί καλύτερα (κύμα) μήκος
Γεωμετρική Οπτική Φύση του φωτός Θεωρούμε ότι το φως έχει διττή φύση: ΚΥΜΑΤΙΚΗ Βασική ιδέα Το φως είναι μια Η/Μ διαταραχή που διαδίδεται στο χώρο Βασική Εξίσωση Φαινόμενα που εξηγεί καλύτερα (κύμα) μήκος
Μελέτη συστήματος φακών με τη Μέθοδο του Newton
 Μελέτη συστήματος φακών με τη Μέθοδο του Newton.Σκοπός Σκοπός της άσκησης είναι η μελέτη της εστιακής απόστασης συστήματος φακών, η εύρεση της ισοδύναμης εστιακής απόστασης του συστήματος αυτού καθώς και
Μελέτη συστήματος φακών με τη Μέθοδο του Newton.Σκοπός Σκοπός της άσκησης είναι η μελέτη της εστιακής απόστασης συστήματος φακών, η εύρεση της ισοδύναμης εστιακής απόστασης του συστήματος αυτού καθώς και
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ. Ανάκλαση. Κάτοπτρα. Διάθλαση. Ολική ανάκλαση. Φαινόμενη ανύψωση αντικειμένου. Μετατόπιση ακτίνας. Πρίσματα
 ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Ανάκλαση Κάτοπτρα Διάθλαση Ολική ανάκλαση Φαινόμενη ανύψωση αντικειμένου Μετατόπιση ακτίνας Πρίσματα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ - Ανάκλαση Επιστροφή σε «γεωμετρική οπτική» Ανάκλαση φωτός ονομάζεται
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Ανάκλαση Κάτοπτρα Διάθλαση Ολική ανάκλαση Φαινόμενη ανύψωση αντικειμένου Μετατόπιση ακτίνας Πρίσματα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ - Ανάκλαση Επιστροφή σε «γεωμετρική οπτική» Ανάκλαση φωτός ονομάζεται
7.1 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ
 7.1 ΑΣΚΗΣΗ 7 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ ΘΕΩΡΙΑ Όταν φωτεινή παράλληλη δέσμη διαδιδόμενη από οπτικό μέσο α με δείκτη διάθλασης n 1 προσπίπτει σε άλλο οπτικό μέσο β με δείκτη διάθλασης n 2 και
7.1 ΑΣΚΗΣΗ 7 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ ΘΕΩΡΙΑ Όταν φωτεινή παράλληλη δέσμη διαδιδόμενη από οπτικό μέσο α με δείκτη διάθλασης n 1 προσπίπτει σε άλλο οπτικό μέσο β με δείκτη διάθλασης n 2 και
Generated by Foxit PDF Creator Foxit Software http://www.foxitsoftware.com For evaluation only. ΑΣΚΗΣΗ 10 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ
 ΑΣΚΗΣΗ 0 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ . Γεωμετρική οπτική ΜΕΡΟΣ ΠΡΩΤΟ ΒΑΣΙΚΕΣ ΘΕΩΡΗΤΙΚΕΣ ΓΝΩΣΕΙΣ Η Γεωμετρική οπτική είναι ένας τρόπος μελέτης των κυμάτων και χρησιμοποιείται για την εξέταση μερικών
ΑΣΚΗΣΗ 0 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ . Γεωμετρική οπτική ΜΕΡΟΣ ΠΡΩΤΟ ΒΑΣΙΚΕΣ ΘΕΩΡΗΤΙΚΕΣ ΓΝΩΣΕΙΣ Η Γεωμετρική οπτική είναι ένας τρόπος μελέτης των κυμάτων και χρησιμοποιείται για την εξέταση μερικών
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ. G. Mitsou
 ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Διάθλαση σε σφαιρική επιφάνεια Φακοί Ορισμοί Λεπτοί φακοί Συγκλίνοντες φακοί Δημιουργία ειδώλων Αποκλίνοντες φακοί Γενικοί τύποι φακών Σύστημα λεπτών φακών σε επαφή Ασκήσεις Διάθλαση
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Διάθλαση σε σφαιρική επιφάνεια Φακοί Ορισμοί Λεπτοί φακοί Συγκλίνοντες φακοί Δημιουργία ειδώλων Αποκλίνοντες φακοί Γενικοί τύποι φακών Σύστημα λεπτών φακών σε επαφή Ασκήσεις Διάθλαση
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0
 Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Γεωμετρική Οπτική ΚΕΦΑΛΑΙΟ 34
 Γεωμετρική Οπτική ΚΕΦΑΛΑΙΟ 34 Γεωμετρική Οπτική Γνωρίζουμε τα βασικά Δηλαδή, πως το φως διαδίδεται και αλληλεπιδρά με σώματα διαστάσεων πολύ μεγαλύτερων από το μήκος κύματος. Ανάκλαση: Προσπίπτουσα ακτίνα
Γεωμετρική Οπτική ΚΕΦΑΛΑΙΟ 34 Γεωμετρική Οπτική Γνωρίζουμε τα βασικά Δηλαδή, πως το φως διαδίδεται και αλληλεπιδρά με σώματα διαστάσεων πολύ μεγαλύτερων από το μήκος κύματος. Ανάκλαση: Προσπίπτουσα ακτίνα
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ Μάθημα προς τους ειδικευόμενους γιατρούς στην Οφθαλμολογία, Στο Κ.Οφ.Κ.Α. την 18/11/2003. Υπό: Δρος Κων. Ρούγγα, Οφθαλμιάτρου. 1. ΑΝΑΚΛΑΣΗ ΤΟΥ ΦΩΤΟΣ Όταν μια φωτεινή ακτίνα ή
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ Μάθημα προς τους ειδικευόμενους γιατρούς στην Οφθαλμολογία, Στο Κ.Οφ.Κ.Α. την 18/11/2003. Υπό: Δρος Κων. Ρούγγα, Οφθαλμιάτρου. 1. ΑΝΑΚΛΑΣΗ ΤΟΥ ΦΩΤΟΣ Όταν μια φωτεινή ακτίνα ή
Μεγεθυντικός φακός. 1. Σκοπός. 2. Θεωρία. θ 1
 Μεγεθυντικός φακός 1. Σκοπός Οι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
Μεγεθυντικός φακός 1. Σκοπός Οι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
ΚΕΦΑΛΑΙΟ 11Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση
 ΚΕΦΑΛΑΙΟ Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Ηφύσητουφωτός 643-77 Netwon Huygens 69-695 Το φως είναι δέσμη σωματιδίων Το φως
ΚΕΦΑΛΑΙΟ Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Ηφύσητουφωτός 643-77 Netwon Huygens 69-695 Το φως είναι δέσμη σωματιδίων Το φως
Εφαρμοσμένη Οπτική. Γεωμετρική Οπτική
 Εφαρμοσμένη Οπτική Γεωμετρική Οπτική Κύρια σημεία του μαθήματος Η προσέγγιση της γεωμετρικής οπτικής Νόμοι της ανάκλασης και της διάθλασης Αρχή του Huygens Αρχή του Fermat Αρχή της αντιστρεψιμότητας (principle
Εφαρμοσμένη Οπτική Γεωμετρική Οπτική Κύρια σημεία του μαθήματος Η προσέγγιση της γεωμετρικής οπτικής Νόμοι της ανάκλασης και της διάθλασης Αρχή του Huygens Αρχή του Fermat Αρχή της αντιστρεψιμότητας (principle
ΑΝΑΚΛΑΣΗ ΕΠΙΠΕΔΟΙ ΚΑΘΡΕΦΤΕΣ ΕΙΔΩΛΟ
 1 ο ΕΚΦΕ (Ν. ΣΜΥΡΝΗΣ) Δ Δ/ΝΣΗΣ Δ. Ε. ΑΘΗΝΑΣ 1 ΑΝΑΚΛΑΣΗ ΕΠΙΠΕΔΟΙ ΚΑΘΡΕΦΤΕΣ ΕΙΔΩΛΟ Α. ΣΤΟΧΟΙ Η ικανότητα συναρμολόγησης μιας απλής πειραματικής διάταξης. Η ικανότητα χρήσης καθρέφτη και πηγής laser. Η κατανόηση
1 ο ΕΚΦΕ (Ν. ΣΜΥΡΝΗΣ) Δ Δ/ΝΣΗΣ Δ. Ε. ΑΘΗΝΑΣ 1 ΑΝΑΚΛΑΣΗ ΕΠΙΠΕΔΟΙ ΚΑΘΡΕΦΤΕΣ ΕΙΔΩΛΟ Α. ΣΤΟΧΟΙ Η ικανότητα συναρμολόγησης μιας απλής πειραματικής διάταξης. Η ικανότητα χρήσης καθρέφτη και πηγής laser. Η κατανόηση
1. Ιδιότητες φακών. 1 Λεπτοί φακοί. 2 Απριλίου Βασικές έννοιες
 . Ιδιότητες φακών 2 Απριλίου 203 Λεπτοί φακοί. Βασικές έννοιες Φακός είναι ένα οπτικό σύστημα με δύο διαθλαστικές επιφάνειες. Ο απλούστερος φακός έχει δύο σφαιρικές επιφάνειες αρκετά κοντά η μία με την
. Ιδιότητες φακών 2 Απριλίου 203 Λεπτοί φακοί. Βασικές έννοιες Φακός είναι ένα οπτικό σύστημα με δύο διαθλαστικές επιφάνειες. Ο απλούστερος φακός έχει δύο σφαιρικές επιφάνειες αρκετά κοντά η μία με την
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 www.pmoira.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 www.pmoira.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
ΟΠΤΙΚΑ ΣΤΟΙΧΕΙΑ : ΚΑΤΟΠΤΡΑ ΔΙΟΠΤΡΑ ΦΑΚΟΙ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΟΠΤΙΚΑ ΣΤΟΙΧΕΙΑ : ΚΑΤΟΠΤΡΑ ΔΙΟΠΤΡΑ ΦΑΚΟΙ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ.
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΟΠΤΙΚΑ ΣΤΟΙΧΕΙΑ : ΚΑΤΟΠΤΡΑ ΔΙΟΠΤΡΑ ΦΑΚΟΙ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ.
7α Γεωμετρική οπτική - οπτικά όργανα
 7α Γεωμετρική οπτική - οπτικά όργανα Εισαγωγή ορισμοί Φύση του φωτός Πηγές φωτός Δείκτης διάθλασης Ανάκλαση Δημιουργία ειδώλων από κάτοπτρα Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/katsiki Ηφύσητουφωτός
7α Γεωμετρική οπτική - οπτικά όργανα Εισαγωγή ορισμοί Φύση του φωτός Πηγές φωτός Δείκτης διάθλασης Ανάκλαση Δημιουργία ειδώλων από κάτοπτρα Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/katsiki Ηφύσητουφωτός
1. Σκοπός της άσκησης... 1. 2. Στοιχεία θεωρίας... 1. 2.1 Γεωμετρική οπτική... 1. 2.2 Ο νόμος της ανάκλασης... 1. 2.3 Ο νόμος της διάθλασης...
 1. Λεπτοί Φακοί Σελίδα 1. Σκοπός της άσκησης.... 1 2. Στοιχεία θεωρίας... 1 2.1 Γεωμετρική οπτική... 1 2.2 Ο νόμος της ανάκλασης... 1 2.3 Ο νόμος της διάθλασης... 2 2.4 Είδωλα & παραξονική προσέγγιση...
1. Λεπτοί Φακοί Σελίδα 1. Σκοπός της άσκησης.... 1 2. Στοιχεία θεωρίας... 1 2.1 Γεωμετρική οπτική... 1 2.2 Ο νόμος της ανάκλασης... 1 2.3 Ο νόμος της διάθλασης... 2 2.4 Είδωλα & παραξονική προσέγγιση...
ΠΟΥ ΔΙΑΔΙΔΕΤΑΙ ΤΟ ΦΩΣ
 1 ΦΩΣ Στο μικρόκοσμο θεωρούμε ότι το φως έχει δυο μορφές. Άλλοτε το αντιμετωπίζουμε με τη μορφή σωματιδίων που ονομάζουμε φωτόνια. Τα φωτόνια δεν έχουν μάζα αλλά μόνον ενέργεια. Άλλοτε πάλι αντιμετωπίζουμε
1 ΦΩΣ Στο μικρόκοσμο θεωρούμε ότι το φως έχει δυο μορφές. Άλλοτε το αντιμετωπίζουμε με τη μορφή σωματιδίων που ονομάζουμε φωτόνια. Τα φωτόνια δεν έχουν μάζα αλλά μόνον ενέργεια. Άλλοτε πάλι αντιμετωπίζουμε
Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση Γεωµετρική θεώρηση του Φωτός Ανάκλαση ηµιουργίαειδώλουαπόκάτοπτρα. είκτης ιάθλασης Νόµος του Snell Ορατό Φάσµα και ιασπορά Εσωτερική ανάκλαση Οπτικές ίνες ιάθλαση σε
Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση Γεωµετρική θεώρηση του Φωτός Ανάκλαση ηµιουργίαειδώλουαπόκάτοπτρα. είκτης ιάθλασης Νόµος του Snell Ορατό Φάσµα και ιασπορά Εσωτερική ανάκλαση Οπτικές ίνες ιάθλαση σε
EΡΩΤΗΣΕΙΣ ΑΣΚΗΣΕΙΣ ΠΡΟΒΛΗΜΑΤΑ ΣΤΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ ΟΛΙΚΗ ΑΝΑΚΛΑΣΗ
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΑΣΚΗΣΗ 8 Μελέτη φακών
 Απαραίτητα όργανα και υλικά ΑΣΚΗΣΗ 8 Μελέτη φακών 8. Απαραίτητα όργανα και υλικά. Οπτική τράπεζα.. Πέτασμα. 3. Συγκεντρωτικός φακός. 4. Φωτεινή πηγή. 5. Διάφραγμα με δακτύλιο και οπή. 6. Φίλτρο κόκκινο
Απαραίτητα όργανα και υλικά ΑΣΚΗΣΗ 8 Μελέτη φακών 8. Απαραίτητα όργανα και υλικά. Οπτική τράπεζα.. Πέτασμα. 3. Συγκεντρωτικός φακός. 4. Φωτεινή πηγή. 5. Διάφραγμα με δακτύλιο και οπή. 6. Φίλτρο κόκκινο
ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ
 ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Άσκηση 4: Σφάλματα φακών: Ι Σφαιρική εκτροπή Εξεταζόμενες γνώσεις: σφάλματα σφαιρικής εκτροπής. Α. Γενικά περί σφαλμάτων φακών Η βασική σχέση του Gauss 1/s +1/s = 1/f που
ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Άσκηση 4: Σφάλματα φακών: Ι Σφαιρική εκτροπή Εξεταζόμενες γνώσεις: σφάλματα σφαιρικής εκτροπής. Α. Γενικά περί σφαλμάτων φακών Η βασική σχέση του Gauss 1/s +1/s = 1/f που
Διάθλαση φωτός και ολική ανάκλαση: Εύρεση του δείκτη διάθλασης και της γωνίας ολικής ανάκλασης
 3 Διάθλαση φωτός και ολική ανάκλαση: Εύρεση του δείκτη διάθλασης και της γωνίας ολικής ανάκλασης Μέθοδος Σε σώμα διαφανές ημικυλινδρικού σχήματος είναι εύκολο να επιβεβαιωθεί ο νόμος του Sell και να εφαρμοστεί
3 Διάθλαση φωτός και ολική ανάκλαση: Εύρεση του δείκτη διάθλασης και της γωνίας ολικής ανάκλασης Μέθοδος Σε σώμα διαφανές ημικυλινδρικού σχήματος είναι εύκολο να επιβεβαιωθεί ο νόμος του Sell και να εφαρμοστεί
ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ
 ΕΡΑΣΤΗΡΙ ΕΦΑΡΜΣΜΕΝΗΣ ΠΤΙΚΗΣ Άσκηση 1: Λεπτοί φακοί Εξεταζόμενες γνώσεις. Εξίσωση κατασκευαστών των φακών. Συστήματα φακών. Διαγράμματα κύριων ακτινών. Είδωλα και μεγέθυνση σε λεπτούς φακούς. Α. Λεπτοί
ΕΡΑΣΤΗΡΙ ΕΦΑΡΜΣΜΕΝΗΣ ΠΤΙΚΗΣ Άσκηση 1: Λεπτοί φακοί Εξεταζόμενες γνώσεις. Εξίσωση κατασκευαστών των φακών. Συστήματα φακών. Διαγράμματα κύριων ακτινών. Είδωλα και μεγέθυνση σε λεπτούς φακούς. Α. Λεπτοί
ΕΚΦΕ ΕΥΒΟΙΑΣ. ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΓΙΑ ΤΗΝ ΕΠΙΛΟΓΗ ΟΜΑΔΑΣ ΜΑΘΗΤΩΝ ΓΙΑ ΤΗΝ 13 η ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑΔΑ ΕΠΙΣΤΗΜΩΝ EUSO 2015 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ
 ΕΚΦΕ ΕΥΒΟΙΑΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΓΙΑ ΤΗΝ ΕΠΙΛΟΓΗ ΟΜΑΔΑΣ ΜΑΘΗΤΩΝ ΓΙΑ ΤΗΝ 13 η ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑΔΑ ΕΠΙΣΤΗΜΩΝ EUSO 2015 Διάρκεια: 60 min ΣΑΒΒΑΤΟ 06/12/2014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Μαθητές: Σχολική Μονάδα 1.
ΕΚΦΕ ΕΥΒΟΙΑΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΓΙΑ ΤΗΝ ΕΠΙΛΟΓΗ ΟΜΑΔΑΣ ΜΑΘΗΤΩΝ ΓΙΑ ΤΗΝ 13 η ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑΔΑ ΕΠΙΣΤΗΜΩΝ EUSO 2015 Διάρκεια: 60 min ΣΑΒΒΑΤΟ 06/12/2014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Μαθητές: Σχολική Μονάδα 1.
Κυματική οπτική. Συμβολή Περίθλαση Πόλωση
 Κυματική οπτική Η κυματική οπτική ασχολείται με τη μελέτη φαινομένων τα οποία δεν μπορούμε να εξηγήσουμε επαρκώς με τις αρχές της γεωμετρικής οπτικής. Στα φαινόμενα αυτά περιλαμβάνονται τα εξής: Συμβολή
Κυματική οπτική Η κυματική οπτική ασχολείται με τη μελέτη φαινομένων τα οποία δεν μπορούμε να εξηγήσουμε επαρκώς με τις αρχές της γεωμετρικής οπτικής. Στα φαινόμενα αυτά περιλαμβάνονται τα εξής: Συμβολή
7α Γεωµετρική οπτική - οπτικά όργανα
 7α Γεωµετρική οπτική - οπτικά όργανα Εισαγωγή ορισµοί Φύση του φωτός Πηγές φωτός είκτης διάθλασης Ανάκλαση ηµιουργία ειδώλων από κάτοπτρα Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Η φύση του
7α Γεωµετρική οπτική - οπτικά όργανα Εισαγωγή ορισµοί Φύση του φωτός Πηγές φωτός είκτης διάθλασης Ανάκλαση ηµιουργία ειδώλων από κάτοπτρα Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Η φύση του
Γεωμετρική Οπτική. Πρόκειται δηλαδή για μια ισοφασική επιφάνεια που ονομάζεται μέτωπο κύματος.
 Γεωμετρική Οπτική Στη Γεωμετρική Οπτική επεξεργαζόμαστε τα φαινόμενα ωσάν το φως να αποτελείται μόνο από σωματίδια, ώστε να εξασφαλίζεται την εύκολη ερμηνεία των φαινομένων της ευθύγραμμης διάδοσης του
Γεωμετρική Οπτική Στη Γεωμετρική Οπτική επεξεργαζόμαστε τα φαινόμενα ωσάν το φως να αποτελείται μόνο από σωματίδια, ώστε να εξασφαλίζεται την εύκολη ερμηνεία των φαινομένων της ευθύγραμμης διάδοσης του
Σφάλματα φακών (Σφαιρικό - Χρωματικό).
 O12 Σφάλματα φακών (Σφαιρικό - Χρωματικό). 1. Σκοπός Στην άσκηση αυτή υπολογίζονται πειραματικά δυο από τα πιο σημαντικά οπτικά σφάλματα (η αποκλίσεις) που παρουσιάζονται όταν φωτεινές ακτίνες διέλθουν
O12 Σφάλματα φακών (Σφαιρικό - Χρωματικό). 1. Σκοπός Στην άσκηση αυτή υπολογίζονται πειραματικά δυο από τα πιο σημαντικά οπτικά σφάλματα (η αποκλίσεις) που παρουσιάζονται όταν φωτεινές ακτίνες διέλθουν
ΕΡΩΤΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥ
 ΚΕΦΑΛΑΙΟ 1 ΕΡΩΤΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥ Τι είναι ένα ευθύγραμμο τμήμα ΑΒ; Πώς ονομάζονται τα σημεία Α και Β; 1 ος ορισμός : Είναι η «ίσια» γραμμή που ενώνει τα δύο σημεία Α και Β. 2 ος ορισμός : Είναι
ΚΕΦΑΛΑΙΟ 1 ΕΡΩΤΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥ Τι είναι ένα ευθύγραμμο τμήμα ΑΒ; Πώς ονομάζονται τα σημεία Α και Β; 1 ος ορισμός : Είναι η «ίσια» γραμμή που ενώνει τα δύο σημεία Α και Β. 2 ος ορισμός : Είναι
ΓΓ/Μ ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ. Τεύχος 5ο: Φύση και Διάδοση φωτός Ανάκλαση του φωτός
 ΓΓ/Μ5 05-06 ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ Τεύχος 5ο: Φύση και Διάδοση φωτός Ανάκλαση του φωτός ΕΚΔΟΤΙΚΕΣ ΤΟΜΕΣ ΟΡΟΣΗΜΟ ΠΕΡΙΟΔΙΚΗ ΕΚΔΟΣΗ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΚΑΙ ΤΟ ΛΥΚΕΙΟ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Φυσική για την Γ'
ΓΓ/Μ5 05-06 ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ Τεύχος 5ο: Φύση και Διάδοση φωτός Ανάκλαση του φωτός ΕΚΔΟΤΙΚΕΣ ΤΟΜΕΣ ΟΡΟΣΗΜΟ ΠΕΡΙΟΔΙΚΗ ΕΚΔΟΣΗ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΚΑΙ ΤΟ ΛΥΚΕΙΟ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Φυσική για την Γ'
25 Ιανουαρίου 2014 ΛΥΚΕΙΟ:... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: ΜΟΝΑΔΕΣ:
 ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗ 25 Ιανουαρίου 2014 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2..... 3..... ΜΟΝΑΔΕΣ: Το πρόβλημα Ένας φίλος σας βρήκε ένα μικρό, πολύ όμορφο τεμάχιο διαφανούς στερεού και ζητά τη γνώμη
ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗ 25 Ιανουαρίου 2014 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2..... 3..... ΜΟΝΑΔΕΣ: Το πρόβλημα Ένας φίλος σας βρήκε ένα μικρό, πολύ όμορφο τεμάχιο διαφανούς στερεού και ζητά τη γνώμη
ΑΝΑΚΛΑΣΗ. β' νόμος της ανάκλασης: Η γωνία πρόσπτωσης και η γωνία ανάκλασης είναι ίσες.
 ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
OΠΤIKH. Επειδή είναι πάντα υ<c (
 OΠΤIKH Η ταχύτητα του φωτός δεν είναι πάντα ίδια αλλά αλλάζει όταν το φως από ένα μέσο περνά σε κάποιο άλλο. Αν c είναι η ταχύτητα του φωτός στο κενό και υ η ταχύτητά του σε ένα άλλο υλικό τότε, ορίζουμε
OΠΤIKH Η ταχύτητα του φωτός δεν είναι πάντα ίδια αλλά αλλάζει όταν το φως από ένα μέσο περνά σε κάποιο άλλο. Αν c είναι η ταχύτητα του φωτός στο κενό και υ η ταχύτητά του σε ένα άλλο υλικό τότε, ορίζουμε
Φωτογραφική μηχανή - Αρχή λειτουργίας.
 Ο25 Φωτογραφική μηχανή - Αρχή λειτουργίας. 1 Σκοπός Στην άσκηση αυτή γίνεται μία παρουσίαση των βασικών στοιχείων της φωτογραφικής μηχανής (φακός φωτοφράκτης - διάφραγμα αισθητήρας) καθώς και μία σύντομη
Ο25 Φωτογραφική μηχανή - Αρχή λειτουργίας. 1 Σκοπός Στην άσκηση αυτή γίνεται μία παρουσίαση των βασικών στοιχείων της φωτογραφικής μηχανής (φακός φωτοφράκτης - διάφραγμα αισθητήρας) καθώς και μία σύντομη
sin 2 n = sin A 2 sin 2 2 n = sin A = sin = cos
 1 Σκοπός Βαθμός 9.5. Ηθελε να γραψω καλύτερα το 9 ερωτημα. Σκοπός αυτής της εργαστηριακής άσκησης είναι η μελέτη της ανάκλασης, διάθλασης και πόλωσης του φωτός. Προσδιορίζουμε επίσης τον δείκτη διάθλασης
1 Σκοπός Βαθμός 9.5. Ηθελε να γραψω καλύτερα το 9 ερωτημα. Σκοπός αυτής της εργαστηριακής άσκησης είναι η μελέτη της ανάκλασης, διάθλασης και πόλωσης του φωτός. Προσδιορίζουμε επίσης τον δείκτη διάθλασης
1 Ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ - ΕΚΦΩΝΗΣΕΙΣ
 Ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ - ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις - 4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά
Ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ - ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις - 4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά
ΑΝΑΚΛΑΣΗ. β' νόμος της ανάκλασης: Η γωνία πρόσπτωσης και η γωνία ανάκλασης είναι ίσες.
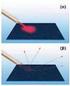 ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΚΕΦΑΛΑΙΟ 1 - ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ
 ΚΕΦΑΛΑΙΟ 1 - ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ Σύμφωνα με την ηλεκτρομαγνητική θεωρία του Maxwell, το φως είναι εγκάρσιο ηλεκτρομαγνητικό κύμα. Η θεωρία αυτή α. δέχεται ότι κάθε φωτεινή πηγή εκπέμπει φωτόνια.
ΚΕΦΑΛΑΙΟ 1 - ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ Σύμφωνα με την ηλεκτρομαγνητική θεωρία του Maxwell, το φως είναι εγκάρσιο ηλεκτρομαγνητικό κύμα. Η θεωρία αυτή α. δέχεται ότι κάθε φωτεινή πηγή εκπέμπει φωτόνια.
Q 40 th International Physics Olympiad, Merida, Mexico, July 2009
 ΠΕΙΡΑΜΑΤΙΚΟ ΠΡΟΒΛΗΜΑ No. 2 ΔΕΙΚΤΗΣ ΔΙΑΘΛΑΣΗΣ ΚΡΥΣΤΑΛΛΟΥ (MCA) Σκοπός αυτού του πειράματος είναι ο υπολογισμός του δείκτη διάθλασης ενός κρυσταλλικού υλικού (mica). ΟΡΓΑΝΑ ΚΑΙ ΥΛΙΚΑ Επιπρόσθετα από τα υλικά
ΠΕΙΡΑΜΑΤΙΚΟ ΠΡΟΒΛΗΜΑ No. 2 ΔΕΙΚΤΗΣ ΔΙΑΘΛΑΣΗΣ ΚΡΥΣΤΑΛΛΟΥ (MCA) Σκοπός αυτού του πειράματος είναι ο υπολογισμός του δείκτη διάθλασης ενός κρυσταλλικού υλικού (mica). ΟΡΓΑΝΑ ΚΑΙ ΥΛΙΚΑ Επιπρόσθετα από τα υλικά
ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ
 ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ ΑΣΚΗΣΗ 3-2017 1 Σκοπός Σε αυτή την άσκηση ο φοιτητής χειρίζεται βασικά οπτικά όργανα όπως είναι οι λεπτοί φακοί. Στο πρώτο μέρος υπολογίζεται η εστιακή απόσταση
ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ ΑΣΚΗΣΗ 3-2017 1 Σκοπός Σε αυτή την άσκηση ο φοιτητής χειρίζεται βασικά οπτικά όργανα όπως είναι οι λεπτοί φακοί. Στο πρώτο μέρος υπολογίζεται η εστιακή απόσταση
Q 40 th International Physics Olympiad, Merida, Mexico, July 2009
 ΠΕΙΡΑΜΑΤΙΚΟ ΠΡΟΒΛΗΜΑ No. 1 ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΟΥ ΜΗΚΟΥΣ ΚΥΜΑΤΟΣ ΦΩΤΟΣ ASER ΥΛΙΚΑ ΚΑΙ ΟΡΓΑΝΑ Επιπρόσθετα με τα υλικά 1), 2) και 3), αναμένεται να χρησιμοποιήσετε τα ακόλουθα: 4) Φακός ενσωματωμένος μέσα σε
ΠΕΙΡΑΜΑΤΙΚΟ ΠΡΟΒΛΗΜΑ No. 1 ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΟΥ ΜΗΚΟΥΣ ΚΥΜΑΤΟΣ ΦΩΤΟΣ ASER ΥΛΙΚΑ ΚΑΙ ΟΡΓΑΝΑ Επιπρόσθετα με τα υλικά 1), 2) και 3), αναμένεται να χρησιμοποιήσετε τα ακόλουθα: 4) Φακός ενσωματωμένος μέσα σε
ΑΣΚΗΣΗ 4 ΠΕΡΙΘΛΑΣΗ ΑΠΟ ΑΠΛΗ ΣΧΙΣΜΗ
 ΑΣΚΗΣΗ 4 ΠΕΡΙΘΛΑΣΗ ΑΠΟ ΑΠΛΗ ΣΧΙΣΜΗ 1 Σκοπός Στην άσκηση αυτή μελετάται η περίθλαση δέσμης φωτός ενός laser He-Ne από απλή σχισμή. Στο πρώτο μέρος της άσκησης προσδιορίζεται το πλάτος της σχισμής από την
ΑΣΚΗΣΗ 4 ΠΕΡΙΘΛΑΣΗ ΑΠΟ ΑΠΛΗ ΣΧΙΣΜΗ 1 Σκοπός Στην άσκηση αυτή μελετάται η περίθλαση δέσμης φωτός ενός laser He-Ne από απλή σχισμή. Στο πρώτο μέρος της άσκησης προσδιορίζεται το πλάτος της σχισμής από την
ΚΕΦΑΛΑΙΟ 2ο: ΜΗΧΑΝΙΚΑ- ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
Διάθλαση φωτεινής δέσμης σε διαφανές υλικό (Επιβεβαίωση, αξιοποίηση του νόμου Snell)
 Διάθλαση φωτεινής δέσμης σε διαφανές υλικό (Επιβεβαίωση, αξιοποίηση του νόμου Snell) 1. Σκοπός Αξιοποιώντας τις μετρήσεις των γωνιών πρόσπτωσης, διάθλασης α και δ αντίστοιχα μίας πολύ στενής φωτεινής δέσμης
Διάθλαση φωτεινής δέσμης σε διαφανές υλικό (Επιβεβαίωση, αξιοποίηση του νόμου Snell) 1. Σκοπός Αξιοποιώντας τις μετρήσεις των γωνιών πρόσπτωσης, διάθλασης α και δ αντίστοιχα μίας πολύ στενής φωτεινής δέσμης
ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Ασκήσεις Οπτική Ι ιδάσκων: ηµήτρης Παπάζογλου Email: dpapa@iesl.forth.gr
 ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Ασκήσεις Οπτική Ι ιδάσκων: ηµήτρης Παπάζογλου Email: dpapa@iesl.forth.gr 1. Να σχεδιάσετε την διάδοση των ακτίνων στα παρακάτω οπτικά συστήµατα F F
ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Ασκήσεις Οπτική Ι ιδάσκων: ηµήτρης Παπάζογλου Email: dpapa@iesl.forth.gr 1. Να σχεδιάσετε την διάδοση των ακτίνων στα παρακάτω οπτικά συστήµατα F F
ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ Επαναληπτικό στη Φυσική 1. Θέµα 1 ο
 ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ Επαναληπτικό στη Φυσική 1 Θέµα 1 ο 1. Το διάγραµµα του διπλανού σχήµατος παριστάνει τη χρονική µεταβολή της αποµάκρυνσης ενός σώµατος που εκτελεί απλή αρµονική ταλάντωση. Ποια από
ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ Επαναληπτικό στη Φυσική 1 Θέµα 1 ο 1. Το διάγραµµα του διπλανού σχήµατος παριστάνει τη χρονική µεταβολή της αποµάκρυνσης ενός σώµατος που εκτελεί απλή αρµονική ταλάντωση. Ποια από
Μεθοδολογία Έλλειψης
 Μεθοδολογία Έλλειψης Έλλειψη ονομάζεται ο γεωμετρικός τόπος των σημείων, των οποίων το άθροισμα των αποστάσεων από δύο σταθερά σημεία Ε και Ε είναι σταθερό και μεγαλύτερο από την απόσταση (ΕΕ ). Στη Φύση
Μεθοδολογία Έλλειψης Έλλειψη ονομάζεται ο γεωμετρικός τόπος των σημείων, των οποίων το άθροισμα των αποστάσεων από δύο σταθερά σημεία Ε και Ε είναι σταθερό και μεγαλύτερο από την απόσταση (ΕΕ ). Στη Φύση
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
Η συμβολή του φωτός και η μέτρηση του μήκους κύματος μονοχρωματικής ακτινοβολίας
 Η συμβολή του φωτός και η μέτρηση του μήκους κύματος μονοχρωματικής ακτινοβολίας Α. Στόχοι Οι μαθητές: Να παρατηρήσουν το φαινόμενο της συμβολής / περίθλασης Να αξιοποιήσουν το φαινόμενο της περίθλασης
Η συμβολή του φωτός και η μέτρηση του μήκους κύματος μονοχρωματικής ακτινοβολίας Α. Στόχοι Οι μαθητές: Να παρατηρήσουν το φαινόμενο της συμβολής / περίθλασης Να αξιοποιήσουν το φαινόμενο της περίθλασης
ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ
 ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ ΑΣΚΗΣΗ 3-2016 1 Σκοπός Σε αυτή την άσκηση ο φοιτητής χειρίζεται βασικά οπτικά όργανα όπως είναι οι λεπτοί φακοί. Στο πρώτο μέρος υπολογίζεται η εστιακή απόσταση
ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ ΑΣΚΗΣΗ 3-2016 1 Σκοπός Σε αυτή την άσκηση ο φοιτητής χειρίζεται βασικά οπτικά όργανα όπως είναι οι λεπτοί φακοί. Στο πρώτο μέρος υπολογίζεται η εστιακή απόσταση
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0
 Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Προγραμματισμός Ύλης Έτους Τάξη Α Κοινός Κορμός
 Προγραμματισμός Ύλης Έτους Τάξη Α Κοινός Κορμός Μάθημα: Φυσική Τμήματα:,.. Τάξη: Α Ομάδα Προσανατολισμού 1,3,4 Καθηγητές: Περ. Εβδομ: 2 ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΥΛΗ ΠΕΡΙΟΔΟΙ ΗΜΕΡΟΜΗΝΙΕΣ Φυσικά Μεγέθη Μονάδες
Προγραμματισμός Ύλης Έτους Τάξη Α Κοινός Κορμός Μάθημα: Φυσική Τμήματα:,.. Τάξη: Α Ομάδα Προσανατολισμού 1,3,4 Καθηγητές: Περ. Εβδομ: 2 ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΥΛΗ ΠΕΡΙΟΔΟΙ ΗΜΕΡΟΜΗΝΙΕΣ Φυσικά Μεγέθη Μονάδες
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
Πειραματικός υπολογισμός του μήκους κύματος μονοχρωματικής ακτινοβολίας
 Πειραματικός υπολογισμός του μήκους κύματος μονοχρωματικής ακτινοβολίας Τάξη : Γ Λυκείου Βασικές έννοιες και σχέσεις Μήκος κύματος - Μονοχρωματική ακτινοβολία - Συμβολή ηλεκτρομαγνητικών κυμάτων - Κροσσοί
Πειραματικός υπολογισμός του μήκους κύματος μονοχρωματικής ακτινοβολίας Τάξη : Γ Λυκείου Βασικές έννοιες και σχέσεις Μήκος κύματος - Μονοχρωματική ακτινοβολία - Συμβολή ηλεκτρομαγνητικών κυμάτων - Κροσσοί
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ
 ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση =0.0 mm είναι τοποθετημένο σε απόσταση =1,0 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές φωτίζεται
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση =0.0 mm είναι τοποθετημένο σε απόσταση =1,0 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές φωτίζεται
ΣΤΕΡΕΟΣΚΟΠΙΚΕΣ ΕΙΚΟΝΕΣ
 ΣΤΕΡΕΟΣΚΟΠΙΚΕΣ ΕΙΚΟΝΕΣ Η προοπτική εικόνα, είναι, όπως είναι γνωστό, η προβολή ενός χωρικού αντικειμένου, σε ένα επίπεδο, με κέντρο προβολής, το μάτι του παρατηρητή. Η εικόνα αυτή, θεωρούμε ότι αντιστοιχεί
ΣΤΕΡΕΟΣΚΟΠΙΚΕΣ ΕΙΚΟΝΕΣ Η προοπτική εικόνα, είναι, όπως είναι γνωστό, η προβολή ενός χωρικού αντικειμένου, σε ένα επίπεδο, με κέντρο προβολής, το μάτι του παρατηρητή. Η εικόνα αυτή, θεωρούμε ότι αντιστοιχεί
5 Δεκεμβρίου 2015 ΛΥΚΕΙΟ:... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: ΜΟΝΑΔΕΣ:
 ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2016 ΦΥΣΙΚΗ 5 Δεκεμβρίου 2015 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2.. 3.. ΜΟΝΑΔΕΣ: Το πρόβλημα Μελέτη οπτικών ιδιοτήτων διαφανούς υλικού με τη βοήθεια πηγής φωτός laser Είστε στο δωμάτιό
ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2016 ΦΥΣΙΚΗ 5 Δεκεμβρίου 2015 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2.. 3.. ΜΟΝΑΔΕΣ: Το πρόβλημα Μελέτη οπτικών ιδιοτήτων διαφανούς υλικού με τη βοήθεια πηγής φωτός laser Είστε στο δωμάτιό
Φυσική Εικόνας & Ήχου Ι (Ε)
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική Εικόνας & Ήχου Ι (Ε) Ενότητα 3: Γενικά περί φακών Αθανάσιος Αρααντινός Τμήμα Φωτογραφίας & Οπτικοακουστικών Τεχνών Το περιεχόμενο
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική Εικόνας & Ήχου Ι (Ε) Ενότητα 3: Γενικά περί φακών Αθανάσιος Αρααντινός Τμήμα Φωτογραφίας & Οπτικοακουστικών Τεχνών Το περιεχόμενο
Μέτρηση Γωνίας Brewster Νόμοι του Fresnel
 Μέτρηση Γωνίας Bewse Νόμοι του Fesnel [] ΕΙΣΑΓΩΓΗ Στο πείραμα, δέσμη φωτός από διοδικό lase ανακλάται στην επίπεδη επιφάνεια ενός ακρυλικού ημι-κυκλικού φακού, πολώνεται γραμμικά και ανιχνεύεται από ένα
Μέτρηση Γωνίας Bewse Νόμοι του Fesnel [] ΕΙΣΑΓΩΓΗ Στο πείραμα, δέσμη φωτός από διοδικό lase ανακλάται στην επίπεδη επιφάνεια ενός ακρυλικού ημι-κυκλικού φακού, πολώνεται γραμμικά και ανιχνεύεται από ένα
Κωνικές Τομές: Η Γεωμετρία των Σκιών. Κοινή εργασία με τους Σπύρο Στίγκα και Δημήτρη Θεοδωράκη
 Κωνικές Τομές: Η Γεωμετρία των Σκιών Κοινή εργασία με τους Σπύρο Στίγκα και Δημήτρη Θεοδωράκη Ιστορικά Η μεταφορά αντικειμένων του Χώρου των τριών διαστάσεων στο επίπεδο έχει τις ρίζες της στην προϊστορική
Κωνικές Τομές: Η Γεωμετρία των Σκιών Κοινή εργασία με τους Σπύρο Στίγκα και Δημήτρη Θεοδωράκη Ιστορικά Η μεταφορά αντικειμένων του Χώρου των τριών διαστάσεων στο επίπεδο έχει τις ρίζες της στην προϊστορική
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
γ) Να σχεδιάσετε τις γραφικές παραστάσεις απομάκρυνσης - χρόνου, για τα σημεία Α, Β και Γ, τα οποία απέχουν από το ελεύθερο άκρο αντίστοιχα,,
 1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι μετρημένα σε και
1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι μετρημένα σε και
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
Υπολογισμός της εστιακής απόστασης f λεπτού συμμετρικού συγκλίνοντος φακού απο τη γραμμική μεγέθυνση Μ
 ΟΜΑΔΑ ΟΝΟΜΑΤΕΠΩΝΥΜΑ ΜΑΘΗΤΩΝ 1)... 2)... 3)... ΗΜΕΡΟΜΗΝΙΑ : Υπολογισμός της εστιακής απόστασης f λεπτού συμμετρικού συγκλίνοντος φακού απο τη γραμμική μεγέθυνση Μ Με το πείραµα αυτό θα προσδιορίσουµε: Σκοπός
ΟΜΑΔΑ ΟΝΟΜΑΤΕΠΩΝΥΜΑ ΜΑΘΗΤΩΝ 1)... 2)... 3)... ΗΜΕΡΟΜΗΝΙΑ : Υπολογισμός της εστιακής απόστασης f λεπτού συμμετρικού συγκλίνοντος φακού απο τη γραμμική μεγέθυνση Μ Με το πείραµα αυτό θα προσδιορίσουµε: Σκοπός
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ
 ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση d=0.20 mm είναι τοποθετημένο σε απόσταση =1,20 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση d=0.20 mm είναι τοποθετημένο σε απόσταση =1,20 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές
3.2 Η ΠΑΡΑΒΟΛΗ. Ορισμός Παραβολής. Εξίσωση Παραβολής
 9 3 Η ΠΑΡΑΒΟΛΗ Ορισμός Παραβολής Έστω μια ευθεία δ και ένα σημείο Ε εκτός της δ Ονομάζεται παραβολή με εστία το σημείο Ε και διευθετούσα την ευθεία δ ο γεωμετρικός τόπος C των σημείων του επιπέδου τα οποία
9 3 Η ΠΑΡΑΒΟΛΗ Ορισμός Παραβολής Έστω μια ευθεία δ και ένα σημείο Ε εκτός της δ Ονομάζεται παραβολή με εστία το σημείο Ε και διευθετούσα την ευθεία δ ο γεωμετρικός τόπος C των σημείων του επιπέδου τα οποία
Φυσικά Μεγέθη Μονάδες Μέτρησης
 ΓΝΩΣΤΙΚΟ ΑΝΤΙΚΕΙΜΕΝΟ: ΦΥΣΙΚΗ A ΛΥΚΕΙΟΥ ΚΟΙΝΟΥ ΚΟΡΜΟΥ ΤΑΞΗ: Α Λυκείου Προσανατολισμού 1,3,4. ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΜΑΘΗΣΙΑΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ Οι μαθητές και οι μαθήτριες να είναι σε θέση να: ΑΝΤΙΣΤΟΙΧΑ
ΓΝΩΣΤΙΚΟ ΑΝΤΙΚΕΙΜΕΝΟ: ΦΥΣΙΚΗ A ΛΥΚΕΙΟΥ ΚΟΙΝΟΥ ΚΟΡΜΟΥ ΤΑΞΗ: Α Λυκείου Προσανατολισμού 1,3,4. ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΜΑΘΗΣΙΑΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ Οι μαθητές και οι μαθήτριες να είναι σε θέση να: ΑΝΤΙΣΤΟΙΧΑ
s s f 25 s ' 10 10 s ' 10 α) s ' 16.7 β) S=10 cm, άρα το αντικείμενο βρίσκεται πάνω στην εστία.
 ΑΣΚΗΣΗ 1 Δύο κάτοπτρα σχηματίζουν ορθή γωνία, όπως φαίνεται στο σχήμα. Στο σημείο Ο υπάρχει ένα αντικείμενο. Να προσδιορίσετε τη θέση των ειδώλων που σχηματίζονται ΑΣΚΗΣΗ 2 Κοίλο σφαιρικό κάτοπτρο έχει
ΑΣΚΗΣΗ 1 Δύο κάτοπτρα σχηματίζουν ορθή γωνία, όπως φαίνεται στο σχήμα. Στο σημείο Ο υπάρχει ένα αντικείμενο. Να προσδιορίσετε τη θέση των ειδώλων που σχηματίζονται ΑΣΚΗΣΗ 2 Κοίλο σφαιρικό κάτοπτρο έχει
Φυσική ΘΕΜΑ 1 ΘΕΜΑ 2 ΘΕΜΑ 3
 Φυσική ΘΕΜΑ 1 1) Υπάρχουν δύο διαφορετικά είδη φορτίου που ονομάστηκαν θετικό και αρνητικό ηλεκτρικό φορτίο αντίστοιχα. Τα σώματα που έχουν θετικό φορτίο λέμε ότι είναι θετικά φορτισμένα (π.χ. μια γυάλινη
Φυσική ΘΕΜΑ 1 1) Υπάρχουν δύο διαφορετικά είδη φορτίου που ονομάστηκαν θετικό και αρνητικό ηλεκτρικό φορτίο αντίστοιχα. Τα σώματα που έχουν θετικό φορτίο λέμε ότι είναι θετικά φορτισμένα (π.χ. μια γυάλινη
ΑΝΑΜΟΡΦΩΣΕΙΣ ΜΕΣΩ ΑΝΑΚΛΑΣΕΩΝ ΣΕ ΚΑΜΠΥΛΕΣ ΕΠΙΦΑΝΕΙΕΣ.
 ΑΝΑΜΟΡΦΩΣΕΙΣ ΜΕΣΩ ΑΝΑΚΛΑΣΕΩΝ ΣΕ ΚΑΜΠΥΛΕΣ ΕΠΙΦΑΝΕΙΕΣ. Πρόκειται για εικόνες τις οποίες μπορούμε να παρατηρήσουμε χρησιμοποιώντας κατάλληλες ανακλαστικές επιφάνειες, οι οποίες συνήθως είναι κωνικές ή κυλινδρικές
ΑΝΑΜΟΡΦΩΣΕΙΣ ΜΕΣΩ ΑΝΑΚΛΑΣΕΩΝ ΣΕ ΚΑΜΠΥΛΕΣ ΕΠΙΦΑΝΕΙΕΣ. Πρόκειται για εικόνες τις οποίες μπορούμε να παρατηρήσουμε χρησιμοποιώντας κατάλληλες ανακλαστικές επιφάνειες, οι οποίες συνήθως είναι κωνικές ή κυλινδρικές
ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ. + 1) με Ν=0,1,2,3..., όπου d το μήκος της χορδής. 4 χορδή με στερεωμένο το ένα άκρο ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ. ,στο κενό (αέρα) co
 ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ Κύματα που t x t x σχηματίζουν το y1 = A. hm2 p ( - ), y2 = A. hm2 p ( + ) T l T l στάσιμο Εξίσωση στάσιμου c κύματος y = 2 A. sun 2 p. hm2p t l T Πλάτος ταλάντωσης c A = 2A sun 2p l Κοιλίες,
ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ Κύματα που t x t x σχηματίζουν το y1 = A. hm2 p ( - ), y2 = A. hm2 p ( + ) T l T l στάσιμο Εξίσωση στάσιμου c κύματος y = 2 A. sun 2 p. hm2p t l T Πλάτος ταλάντωσης c A = 2A sun 2p l Κοιλίες,
ΠΟΛΩΣΗ ΤΟΥ ΦΩΤΟΣ. H γραφική αναπαράσταση ενός κύματος φωτός δίνεται στο Σχήμα 1(α) που ακολουθεί: ΣΧΗΜΑ 1
 ΠΟΛΩΣΗ ΤΟΥ ΦΩΤΟΣ 1. ΟΡΙΣΜΟΙ Το φως είναι ένα σύνθετο κύμα. Με εξαίρεση την ακτινοβολία LASER, τα κύματα φωτός δεν είναι επίπεδα κύματα. Κάθε κύμα φωτός είναι ένα ηλεκτρομαγνητικό κύμα στο οποίο τα διανύσματα
ΠΟΛΩΣΗ ΤΟΥ ΦΩΤΟΣ 1. ΟΡΙΣΜΟΙ Το φως είναι ένα σύνθετο κύμα. Με εξαίρεση την ακτινοβολία LASER, τα κύματα φωτός δεν είναι επίπεδα κύματα. Κάθε κύμα φωτός είναι ένα ηλεκτρομαγνητικό κύμα στο οποίο τα διανύσματα
Σχηματισμός ειδώλων. Εισαγωγή
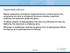 Σχηματισμός ειδώλων Είδωλα πραγματικών αντικειμένων σχηματίζονται όταν οι ακτίνες φωτός (που εκπέμπονται από αυτά τα αντικέιμενα) συναντούν επίπεδες ή καμπύλες επιφάνειες που βρίσκονται μεταξύ δύο μέσων.
Σχηματισμός ειδώλων Είδωλα πραγματικών αντικειμένων σχηματίζονται όταν οι ακτίνες φωτός (που εκπέμπονται από αυτά τα αντικέιμενα) συναντούν επίπεδες ή καμπύλες επιφάνειες που βρίσκονται μεταξύ δύο μέσων.
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ. Ερωτήσεις κλειστού τύπου. Ερωτήσεις ανοικτού τύπου
 ΟΠΤΙΚΗ Περιεχόμενα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ... 2 Ερωτήσεις κλειστού τύπου... 2 Ερωτήσεις ανοικτού τύπου... 2 Ασκήσεις... 3 ΚΥΜΑΤΙΚΗ ΟΠΤΙΚΗ... 4 Ερωτήσεις κλειστού τύπου... 4 Ερωτήσεις ανοικτού τύπου... 4 Ασκήσεις...
ΟΠΤΙΚΗ Περιεχόμενα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ... 2 Ερωτήσεις κλειστού τύπου... 2 Ερωτήσεις ανοικτού τύπου... 2 Ασκήσεις... 3 ΚΥΜΑΤΙΚΗ ΟΠΤΙΚΗ... 4 Ερωτήσεις κλειστού τύπου... 4 Ερωτήσεις ανοικτού τύπου... 4 Ασκήσεις...
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
ΓΕΩΜΕΤΡΙΑ Α ΓΥΜΝΑΣΙΟΥ
 ΚΕΦΑΛΑΙΟ 1 Ο Βασικές Γεωμετρικές Έννοιες ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Μια τεντωμένη κλωστή με άκρα δύο σημεία Α και Β μας δίνει μια εικόνα της έννοιας του.. Τα σημεία Α και Β λέγονται.. 2. Τι ονομάζεται ευθεία;..
ΚΕΦΑΛΑΙΟ 1 Ο Βασικές Γεωμετρικές Έννοιες ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Μια τεντωμένη κλωστή με άκρα δύο σημεία Α και Β μας δίνει μια εικόνα της έννοιας του.. Τα σημεία Α και Β λέγονται.. 2. Τι ονομάζεται ευθεία;..
ΦΡΟΝΤΙΣΤΗΡΙΑ ΣΥΜΒΟΛΗ ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΛΥΣΕΙΣ ΣΤΟ ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΤΙΣ
 ΕΠΙΜΕΛΕΙΑ ΛΥΣΕΩΝ : ΑΜΠΑΤΖΗΣ ΔΗΜΗΤΡΗΣ Σελίδα ΦΡΟΝΤΙΣΤΗΡΙΑ ΣΥΜΒΟΛΗ ΣΤΑΘΑΚΗΣ - ΡΟΥΣΕΛΗΣ- ΓΚΕΟΣ ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΛΥΣΕΙΣ ΣΤΟ ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΤΙΣ 6 - - 0 ΘΕΜΑ Α Α. β Α. γ Α. δ Α. β Α5.
ΕΠΙΜΕΛΕΙΑ ΛΥΣΕΩΝ : ΑΜΠΑΤΖΗΣ ΔΗΜΗΤΡΗΣ Σελίδα ΦΡΟΝΤΙΣΤΗΡΙΑ ΣΥΜΒΟΛΗ ΣΤΑΘΑΚΗΣ - ΡΟΥΣΕΛΗΣ- ΓΚΕΟΣ ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΛΥΣΕΙΣ ΣΤΟ ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΤΙΣ 6 - - 0 ΘΕΜΑ Α Α. β Α. γ Α. δ Α. β Α5.
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ» ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
Περίθλαση από µία σχισµή.
 ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 71 7. Άσκηση 7 Περίθλαση από µία σχισµή. 7.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε την συµπεριφορά των µικροκυµάτων
ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 71 7. Άσκηση 7 Περίθλαση από µία σχισµή. 7.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε την συµπεριφορά των µικροκυµάτων
Φυσική ΙΙ (Ε) Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 6: Διάθλαση μέσω οπτικού πρίσματος - Υπολογισμός δείκτη διάθλασης.
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική ΙΙ (Ε) Ενότητα 6: Διάθλαση μέσω οπτικού πρίσματος - Υπολογισμός δείκτη διάθλασης Ιωάννης Βαμβακάς Τμήμα Ναυπηγών Μηχανικών Τ.Ε.
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική ΙΙ (Ε) Ενότητα 6: Διάθλαση μέσω οπτικού πρίσματος - Υπολογισμός δείκτη διάθλασης Ιωάννης Βαμβακάς Τμήμα Ναυπηγών Μηχανικών Τ.Ε.
ΕΡΩΤΗΣΕΙΣ-ΑΣΚΗΣΕΙΣ ΣΤΗ ΦΥΣΗ ΦΩΤΟΣ
 ΕΡΩΤΗΣΕΙΣ-ΑΣΚΗΣΕΙΣ ΣΤΗ ΦΥΣΗ ΦΩΤΟΣ 1.. Ποιες από τις παρακάτω προτάσεις είναι σωστές (Σ) και ποιες λανθασμένες (Λ); α. Στη διάθλαση όταν το φως διέρχεται από ένα οπτικά πυκνότερο υλικό σε ένα οπτικά αραιότερο
ΕΡΩΤΗΣΕΙΣ-ΑΣΚΗΣΕΙΣ ΣΤΗ ΦΥΣΗ ΦΩΤΟΣ 1.. Ποιες από τις παρακάτω προτάσεις είναι σωστές (Σ) και ποιες λανθασμένες (Λ); α. Στη διάθλαση όταν το φως διέρχεται από ένα οπτικά πυκνότερο υλικό σε ένα οπτικά αραιότερο
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ
 ΦΥΣΙΚΗ Γ.Π. Γ Λυκείου / Το Φως 1. Η υπεριώδης ακτινοβολία : a) δεν προκαλεί αμαύρωση της φωτογραφικής πλάκας. b) είναι ορατή. c) χρησιμοποιείται για την αποστείρωση ιατρικών εργαλείων. d) έχει μήκος κύματος
ΦΥΣΙΚΗ Γ.Π. Γ Λυκείου / Το Φως 1. Η υπεριώδης ακτινοβολία : a) δεν προκαλεί αμαύρωση της φωτογραφικής πλάκας. b) είναι ορατή. c) χρησιμοποιείται για την αποστείρωση ιατρικών εργαλείων. d) έχει μήκος κύματος
Γ.Κονδύλη 1 & Όθωνος-Μ αρούσι Τ ηλ. Κέντρο: , /
 Γ.Κονδύλη & Όθωνος-Μ αρούσι Τ ηλ. Κέντρο:20-6.24.000, http:/ / www.akadimos.gr ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ 204 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Επιμέλεια Θεμάτων: Παπαδόπουλος Πασχάλης ΘΕΜΑ
Γ.Κονδύλη & Όθωνος-Μ αρούσι Τ ηλ. Κέντρο:20-6.24.000, http:/ / www.akadimos.gr ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ 204 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Επιμέλεια Θεμάτων: Παπαδόπουλος Πασχάλης ΘΕΜΑ
6.10 Ηλεκτροµαγνητικά Κύµατα
 Πρόταση Μελέτης Λύσε απο τον Α τόµο των Γ. Μαθιουδάκη & Γ.Παναγιωτακόπουλου τις ακόλουθες ασκήσεις : 11.1-11.36, 11.46-11.50, 11.52-11.59, 11.61, 11.63, 11.64, 1.66-11.69, 11.71, 11.72, 11.75-11.79, 11.81
Πρόταση Μελέτης Λύσε απο τον Α τόµο των Γ. Μαθιουδάκη & Γ.Παναγιωτακόπουλου τις ακόλουθες ασκήσεις : 11.1-11.36, 11.46-11.50, 11.52-11.59, 11.61, 11.63, 11.64, 1.66-11.69, 11.71, 11.72, 11.75-11.79, 11.81
Επαναληπτικό διαγώνισµα στα Κύµατα
 ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ 1 Επαναληπτικό διαγώνισµα στα Κύµατα Θέµα 1 0 Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ 1 Επαναληπτικό διαγώνισµα στα Κύµατα Θέµα 1 0 Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
papost/
 Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Αν ο κύκλος έχει κέντρο την αρχή των αξόνων Ο(0,0) τότε έχει εξίσωση της μορφής : x y και αντίστροφα. Ειδικότερα Ο κύκλος με κέντρο Ο(0,0)
 . Ο ΚΥΚΛΟΣ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Ένας κύκλος ορίζεται αν γνωρίζουμε το κέντρο του, και την ακτίνα του ρ. Αν ο κύκλος έχει κέντρο την αρχή των αξόνων Ο, τότε έχει εξίσωση της μορφής : και αντίστροφα. Ειδικότερα
. Ο ΚΥΚΛΟΣ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Ένας κύκλος ορίζεται αν γνωρίζουμε το κέντρο του, και την ακτίνα του ρ. Αν ο κύκλος έχει κέντρο την αρχή των αξόνων Ο, τότε έχει εξίσωση της μορφής : και αντίστροφα. Ειδικότερα
Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης Εφαρμογές
 Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης Εφαρμογές Να βρείτε για καθεμιά από τις παρακάτω γραμμές αν είναι γραφική παράσταση κάποιας συνάρτησης. 4-1 1 () (1) (3) (4) (5) (6) Αν υπάρχει ευθεία
Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης Εφαρμογές Να βρείτε για καθεμιά από τις παρακάτω γραμμές αν είναι γραφική παράσταση κάποιας συνάρτησης. 4-1 1 () (1) (3) (4) (5) (6) Αν υπάρχει ευθεία
Μεθοδολογία Υπερβολής
 Μεθοδολογία Υπερβολής Υπερβολή ονομάζεται ο γεωμετρικός τόπος των σημείων, των οποίων η απόλυτη τιμή της διαφοράς των αποστάσεων από δύο σταθερά σημεία Ε και Ε είναι σταθερή και μικρότερη από την απόσταση
Μεθοδολογία Υπερβολής Υπερβολή ονομάζεται ο γεωμετρικός τόπος των σημείων, των οποίων η απόλυτη τιμή της διαφοράς των αποστάσεων από δύο σταθερά σημεία Ε και Ε είναι σταθερή και μικρότερη από την απόσταση
Φ Υ ΣΙΚ Η ΚΑ ΤΕ ΥΘ ΥΝ ΣΗ Σ
 ΔΙΩΝΙΣΜ: Μ Θ Η Μ : www.paideia-agrinio.gr ΤΞΗΣ ΛΥΕΙΟΥ Φ Υ ΣΙ Η ΤΕ ΥΘ ΥΝ ΣΗ Σ Ε Π Ω Ν Τ Μ Ο :..... Ο Ν Ο Μ :...... Σ Μ Η Μ :..... Η Μ Ε Ρ Ο Μ Η Ν Ι : 23 / 0 3 / 2 0 1 4 Ε Π Ι Μ Ε Λ ΕΙ Θ ΕΜ Σ Ω Ν : ΥΡΜΗ
ΔΙΩΝΙΣΜ: Μ Θ Η Μ : www.paideia-agrinio.gr ΤΞΗΣ ΛΥΕΙΟΥ Φ Υ ΣΙ Η ΤΕ ΥΘ ΥΝ ΣΗ Σ Ε Π Ω Ν Τ Μ Ο :..... Ο Ν Ο Μ :...... Σ Μ Η Μ :..... Η Μ Ε Ρ Ο Μ Η Ν Ι : 23 / 0 3 / 2 0 1 4 Ε Π Ι Μ Ε Λ ΕΙ Θ ΕΜ Σ Ω Ν : ΥΡΜΗ
Μεθοδολογία Παραβολής
 Μεθοδολογία Παραβολής Παραβολή είναι ο γεωμετρικός τόπος των σημείων που ισαπέχουν από μια σταθερή ευθεία, την επονομαζόμενη διευθετούσα (δ), και από ένα σταθερό σημείο Ε που λέγεται εστία της παραβολής.
Μεθοδολογία Παραβολής Παραβολή είναι ο γεωμετρικός τόπος των σημείων που ισαπέχουν από μια σταθερή ευθεία, την επονομαζόμενη διευθετούσα (δ), και από ένα σταθερό σημείο Ε που λέγεται εστία της παραβολής.
Περίθλαση από ακµή και από εµπόδιο.
 ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 63 6. Άσκηση 6 Περίθλαση από ακµή και από εµπόδιο. 6.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης αυτής, καθώς και των δύο εποµένων, είναι η γνωριµία των σπουδαστών
ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 63 6. Άσκηση 6 Περίθλαση από ακµή και από εµπόδιο. 6.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης αυτής, καθώς και των δύο εποµένων, είναι η γνωριµία των σπουδαστών
Προβλήματα φακών/κατόπτρων
 Προβλήματα φακών/κατόπτρων 1. Χρησιμοποιείστε την τεχνική των ακτινών και σχηματισμών ειδώλου για να βρείτε το είδωλο, που δημιουργείται από ένα κοίλο σφαιρικό κάτοπτρο, ενός αντικειμένου που τοποθετείται
Προβλήματα φακών/κατόπτρων 1. Χρησιμοποιείστε την τεχνική των ακτινών και σχηματισμών ειδώλου για να βρείτε το είδωλο, που δημιουργείται από ένα κοίλο σφαιρικό κάτοπτρο, ενός αντικειμένου που τοποθετείται
Φυσική IΙ. Ενότητα 13: Γεωμετρική οπτική. Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 Φυσική IΙ Ενότητα 13: Γεωμετρική οπτική Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Η κυματική φύση του φωτός: διάθλαση, ανάκλαση, απορρόφηση Γωνίες πρόσπτωσης, ανάκλασης
Φυσική IΙ Ενότητα 13: Γεωμετρική οπτική Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Η κυματική φύση του φωτός: διάθλαση, ανάκλαση, απορρόφηση Γωνίες πρόσπτωσης, ανάκλασης
ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 24/04/2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΑΠΟΦΟΙΤΟΙ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΔΕΚΑΠΕΝΤΕ (15) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας
Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 24/04/2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΑΠΟΦΟΙΤΟΙ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΔΕΚΑΠΕΝΤΕ (15) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας
