Επιδόσεις κωφών & βαρήκοων μαθητών πέμπτης και έκτης τάξης Δημοτικού Σχολείου σε αριθμητικά προβλήματα

Transcript

1 Πανεπιστήμιο Πατρών Σχολή Ανθρωπιστικών & Κοινωνικών Επιστημών Παιδαγωγικό Τμήμα Δημοτικής Εκπαίδευσης Μεταπτυχιακό Πρόγραμμα Σπουδών Επιδόσεις κωφών & βαρήκοων μαθητών πέμπτης και έκτης τάξης Δημοτικού Σχολείου σε αριθμητικά προβλήματα Διπλωματική Εργασία Επιβλέπουσα: Λαμπροπούλου Βενέττα Καθηγήτρια Ειδικής Αγωγής Κωφών Ξερουδάκης Ανδρέας Α.Μ. 214 Πάτρα, 2009

2 [] 2

3 Ευχαριστίες Στους γονείς μου, Μιχάλη και Βούλα, χρωστάω ένα μεγάλο και ειλικρινές ευχαριστώ. Χωρίς την αμέριστη οικονομική αλλά κυρίως ηθική τους υποστήριξη δε θα είχα καταφέρει τίποτα από όσα μέχρι τώρα έχω επιτύχει. Στη δασκάλα μου, την Καθηγήτρια Ειδικής Αγωγής Κωφών του Παιδαγωγικού Τμήματος Δημοτικής Εκπαίδευσης του Πανεπιστημίου Πατρών, κα Λαμπροπούλου Βενέττα, της οποίας το έργο και κυρίως η επιστημονική της καθοδήγηση υπήρξε οδηγός μου. Στους μαθητές και τους δασκάλους των Ειδικών Δημοτικών Σχολείων Κωφών και Βαρηκόων Αργυρούπολης και Πάτρας καθώς και του Δημοτικού Σχολείου Γαλατά Τροιζήνας, που με μεγάλη τους χαρά συμμετείχαν και βοήθησαν σημαντικά για τη διεξαγωγή της παρούσας έρευνας. Στη Ναστάζια, για τη στήριξη και τη συμπαράσταση στη κοινή μας αυτή προσπάθεια ως φίλη, καθώς και για τη βοήθεια της ως συνάδερφο. Στον καλό μου φίλο Βαγγέλη, του οποίου το πείσμα και η έντονη πίεση λειτουργούσε καταλυτικά σε περιόδους έντονης κούρασης και απογοήτευσης, στους φίλους Ρένα, Ελισσάβετ και Μαρία για την πολύτιμη βοήθεια και αλληλοϋποστήριξη στο κοινό μας αυτό ταξίδι, και φυσικά στον Νίκο, του οποίου η παρουσία στη ζωή μου, αυτή την κρίσιμη στιγμή, μου έδωσε ενέργεια και δύναμη να ανταπεξέλθω σχεδόν σε οτιδήποτε. Σας ευχαριστώ θερμά όλους. Τέλος στη αγαπημένη παιδική μου φίλη Φρόσω, της οποίας οι δυσκολίες, λίγο πριν το τέλος της ζωή της, υπήρξαν το εφαλτήριο για έναν καινούργιο κόσμο στη δική μου ζωή. Καλό της ταξίδι. [] 3

4 Περίληψη Σκοπός της εργασίας αυτής είναι η μελέτη της επίδοσης κωφών μαθητών σε διάφορα είδη αριθμητικών προβλημάτων. Συγκεκριμένα, η μελέτη των επιδόσεων κωφών μαθητών σε αριθμητικά προβλήματα προσθετικού τύπου σε σχέση με την τάξη που παρακολουθούν, το είδος του προβλήματος, καθώς και η επίδραση της χρήσης Ελληνικής Νοηματικής Γλώσσας στη κατανόηση των προβλημάτων. Τα ερωτήματα στα οποία γίνετε μια προσπάθεια να απαντηθούν είναι: (1) σε ποιό βαθμό η χρήση Ελληνικής Νοηματικής Γλώσσας κατά την εκφώνηση του αριθμητικού προβλήματος διευκολύνει την κατανόηση του και επομένως συμβάλει θετικά στην επίλυση του, (2) σε ποιο βαθμό η επίδοση των μαθητών στα ίδια αριθμητικά προβλήματα διαφοροποιείται ανάλογα με την τάξη, την οποία παρακολουθούν, και την ηλικία τους και (3) εάν το είδος του αριθμητικού προβλήματος σχετίζεται με τη φοίτηση των μαθητών π.χ. εάν κάποια προβλήματα γίνονται κατανοητά σε παιδιά μεγαλύτερης τάξης. Στην έρευνα πήραν μέρος επτά μαθητές (Ν=7) από τα Ειδικά Δημοτικά Σχολεία Κωφών και Βαρηκόων Αργυρούπολης και Πάτρας και 30 μαθητές (Ν=30) από το Δημοτικό Σχολείο Γαλατά Τροιζήνας, οι οποίοι αποτέλεσαν την ομάδα ελέγχου. Τα αποτελέσματα έδειξαν ότι οι κωφοί και οι βαρήκοοι μαθητές παρουσιάζουν χαμηλότερες επιδόσεις στην επίλυση αριθμητικών προβλημάτων τύπου από αυτές των ακουόντων μαθητών ίδιας ηλικίας, ανεξαρτήτως τρόπου επικοινωνίας. Συγκεκριμένα, οι επιδόσεις τους στην περίπτωση που γίνετε χρήση Ε.Ν.Γ. κατά την εκφώνηση των παραπάνω προβλημάτων, παρουσιάζονται αρκετά βελτιωμένες από την περίπτωση της χρήσης γραπτού λόγου. Επιπλέον, οι επιδόσεις των κωφών και βαρήκοων μαθητών της έκτης τάξης, και με τους δύο τρόπους επικοινωνίας, είναι καλύτερες από αυτές των μαθητών της πέμπτης τάξης. Όσον αφορά τις επιδόσεις των κωφών μαθητών στα διάφορα είδη [] 4

5 αριθμητικών προβλημάτων, φαίνεται να έχουν καλύτερη επίδοση από όλους στα προβλήματα αυτά, στα οποία δίνονται όλες οι αρχικές ποσότητες και ζητείται η τελική, όπως και σε αυτά που οι λέξεις που χρησιμοποιούνται είναι συνεπείς με τις πράξεις που απαιτούνται για την επίλυση τους. Οι μαθητές της έκτης τάξης παρουσιάζουν καλύτερη επίδοση σε όλα τα υπόλοιπα προβλήματα. Τέλος, τα παραπάνω αποτελέσματα πρέπει να ληφθούν σοβαρά υπόψη από τους δασκάλους και τους μαθηματικούς, ώστε να βελτιώσουν τη διδασκαλία τους με το να χρησιμοποιούν Ελληνική Νοηματική Γλώσσα για να κατανοούν οι μαθητές πλήρως τις διάφορες έννοιες και τη μαθηματική γλώσσα. Επίσης θα πρέπει να βελτιωθεί η αναγνωστική ικανότητα των κωφών γενικότερα ώστε να μπορούν να κατανοούν τα αριθμητικά προβλήματα και να δοθεί περισσότερος χρόνος στη διδασκαλία των μαθηματικών. Λέξεις κλειδιά: Αριθμητικά προβλήματα ή προβλήματα «προσθετικού» τύπου, ερωτήσεις ή προβλήματα «Αλλαγής», ερωτήσεις ή προβλήματα «Συνδυασμού», ερωτήσεις ή προβλήματα «Σύγκρισης», κωφός Κωφός, βαρήκοος. [] 5

6 Abstract The purpose of this assignment was a first study of deaf students' performance in different types of arithmetic problems. Specifically, the study of deaf students' performance on arithmetic problems to comparison with the class monitor, the type of the problem, and the influence of Greek Sign Language use in understanding of these problems. To analyze this, there was an attempt to answer the following questions: (1) to what extent the use of Greek Sign Language in the pronunciation of arithmetic problem makes them easier for understanding and thus contribute positively to their being answered, (2) to what extent the performance of students at the same arithmetic problems varies according to the order, which follow, and their age and (3) whether the type of arithmetic problem associates with the attendance of students, e.g. if some types of problems are more understandable to older children. Seven students (N = 7) of the Special Primary Schools for Deaf and Hard of Hearing of Argyroupolis and Patras participated in this study as well as 30 students (N = 30) of the Elementary School of Galatas Trizoinias, which served as the control group. The results of the study showed that deaf and hard of hearing students are less efficient in solving arithmetic problems than their hearing piers, regardless of the method of communication. Specifically, their performance, when using G.S.L., are presented quite improved than the use of case writing. Moreover, the performance of sixth grade deaf and hard of hearing students, with both modes of communication are better than those of students of fifth grade. Regarding the performance of deaf students in different types of arithmetic problems they seem to have better performance when all the original amounts are given and the final is been asked. Also when the words used in the problems are consistent with the acts required to solve them. The students of sixth grade are better in the problems. [] 6

7 Finally, these results should be taken seriously by teachers and mathematicians to improve their teaching, by using Greek Sign Language, so as their students to understand fully the various mathematical concepts and language. Also they should try to improve the reading ability of deaf students in general so that they can understand the arithmetic problems and also give more time to the teaching of mathematics. Key words: Arithmetic problems, change questions, compare questions, combine questions, deaf-deaf, Hard of Hearing. [] 7

8 Περιεχόμενα 1.Εισαγωγή 1.1 Ερευνητικό πρόβλημα και ερωτήματα 1.2 Αναγκαιότητα της μελέτης 1.3 Διευκρίνιση όρων 1.4 Περιορισμοί 2. Ανασκόπηση βιβλιογραφίας 2.1 Ταξινόμηση προβλημάτων «προσθετικού τύπου» Ταξινόμηση με βάση σημασιολογικά κριτήρια Ταξινόμηση με βάση εννοιολογικά κριτήρια 2.2 Διαδικασίες επίλυσης προβλημάτων «προσθετικού τύπου» Διάγνωση και κατανόηση των διαδικασιών επίλυσης Κατηγοριοποίηση των διαδικασιών επίλυσης Διαδικασίες πρόσθεσης Διαδικασίες αφαίρεσης 2.3 Εργασίες και έρευνες για τα αριθμητικά προβλήματα 2.4 Εργασίες και έρευνες για τα μαθηματικά και τους κωφούς Εργασίες και έρευνες για τα αριθμητικά προβλήματα και τους κωφούς 3. Μεθοδολογία 3.1 Δείγμα 3.2 Ερευνητικό εργαλείο 3.3 Ερευνητική διαδικασία 3.4 Ανάλυση [] 8

9 4. Αποτελέσματα 4.1 Κωφοί και Ακούοντες Συνολικά αποτελέσματα 4.2 Ερωτήσεις «Συνδυασμού» 4.3 Ερωτήσεις «Αλλαγής» 4.4 Ερωτήσεις «Σύγκρισης» 5. Συμπεράσματα Βιβλιογραφία Παράρτημα Ι Παράρτημα II [] 9

10 10 [] κεφάλαιο πρώτο

11 1. Εισαγωγή 1.1 Ερευνητικό πρόβλημα και ερωτήματα Σκοπός της εργασίας αυτής είναι η μελέτη της επίδοσης κωφών και βαρήκοων μαθητών σε διάφορα είδη αριθμητικών προβλημάτων. Συγκεκριμένα σκοπός είναι η μελέτη των επιδόσεων κωφών και βαρήκοων μαθητών σε αριθμητικά προβλήματα σε σχέση με την τάξη που παρακολουθούν και το είδος του αριθμητικού προβλήματος. Επίσης η επίδραση της χρήσης Ελληνικής Νοηματικής Γλώσσας στη κατανόηση των προβλημάτων. Ερωτήματα: στην παρούσα εργασία γίνετε μια προσπάθεια να απαντηθούν τα παρακάτω ερωτήματα: (1) Σε ποιό βαθμό η χρήση Ελληνικής Νοηματικής Γλώσσας κατά την εκφώνηση του αριθμητικού προβλήματος διευκολύνει την κατανόηση του και επομένως συμβάλει θετικά στην επίλυση του. (2) Σε ποιο βαθμό η επίδοση των μαθητών στα ίδια αριθμητικά προβλήματα διαφοροποιείται ανάλογα με την τάξη, την οποία παρακολουθούν, και την ηλικία τους. (3) Εάν το είδος του αριθμητικού προβλήματος σχετίζεται με τη φοίτηση των μαθητών π.χ. εάν κάποια προβλήματα γίνονται κατανοητά σε παιδιά μεγαλύτερης τάξης. 11 []

12 1.2 Αναγκαιότητα της μελέτης Παρατηρείται τα τελευταία χρόνια το ξεκίνημα μιας περιόδου ιδιαίτερα ενδιαφέρουσας και αισιόδοξης γύρω από θέματα που έχουν να κάνουν με τους ανάπηρους. Όσον αφορά τους κωφούς μαθητές, και την εκπαίδευση τους συγκεκριμένα, όλο και περισσότεροι ειδικοί επιστήμονες και κυρίως εκπαιδευτικοί τονίζουν την ανάγκη για ορθότερη και πιο ουσιώδη εκπαίδευση των κωφών και γίνονται πιο ελαστικοί και θετικοί στη χρήση της ΕΝΓ στη διδασκαλία. Το ενδιαφέρον των ερευνητών που ασχολούνται με θέματα γύρω από την εκπαίδευση των κωφών, τις τελευταίες δεκαετίες, μονοπωλούν σχεδόν μαθήματα που έχουν να κάνουν με τη γλώσσα. Στο εξωτερικό υπάρχει ένα όλο και αυξανόμενο ερευνητικό ενδιαφέρον για την επίδοση των κωφών μαθητών στα μαθηματικά αλλά και εκεί η πλειοψηφία των ερευνών είναι γύρω από μαθήματα γλώσσας και θέματα γλωσσολογίας παρά καθαρά μαθηματικού ενδιαφέροντος. Οι έρευνες που έχουν γίνει σε χώρες όπως οι Ηνωμένες Πολιτείες Αμερικής, η Ισπανία και τη Μεγάλη Βρετανία πάνω στην επίδοση των κωφών μαθητών στα μαθηματικά, σε σχέση με τους ακούοντες, επικεντρώνουν το ενδιαφέρον τους κυρίως σε αριθμητικά προβλήματα. Δεν είναι τυχαίο αυτό. Για να μπορέσει ο οποιοσδήποτε να επιλύσει ένα μαθηματικό πρόβλημα πρέπει πρώτα απ όλα να το κατανοήσει. Στα αριθμητικά προβλήματα δεν γίνετε χρήση μαθηματικών συμβόλων και εξισώσεων αλλά κειμένου που με χρήση της ομιλούμενης γλώσσας παραθέτεται το πρόβλημα και αναζητείται η επίλυση του. Στην Ελλάδα οι έρευνες γύρω από τα μαθηματικά και την επίδοση των κωφών μαθητών είναι ανύπαρκτες. Κύριο χαρακτηριστικό της ελληνικής γλώσσας είναι το πλούσιο λεξιλόγιο της και η ύπαρξη πληθώρας συνωνύμων και αντωνύμων. Σε συνδυασμό των παραπάνω με το γεγονός ότι η μαθηματική γλώσσα γεννήθηκε σ αυτή τη χώρα είναι προφανής η αναγκαιότητα αυτής της ερευνητικής προσπάθειας. 12 []

13 1.3 Διευκρίνιση όρων Κωφός: το άτομο που είτε φοράει ακουστικά είτε όχι, δεν αντιλαμβάνεται την ομιλία με την ακοή του μόνο. Αντιλαμβάνεται τους συνομιλητές του κύρια με το οπτικό κανάλι (χειλεανάγνωση, νοηματική γλώσσα, γραπτή γλώσσα). Η ακουστική απώλεια στις περιπτώσεις αυτές είναι από 70dB και πάνω (Λαμπροπούλου, 1999). Βαρήκοος: το άτομο που είτε φοράει ακουστικά είτε όχι, δυσκολεύεται να αντιληφθεί την ομιλία με την ακοή του μόνο. Ωστόσο το μεγαλύτερο ποσοστό των πληροφοριών της ομιλίας το αντιλαμβάνεται από την ακοή του. Η ακουστική βλάβη στις περιπτώσεις αυτές είναι μεταξύ 35dB και 69dB (Λαμπροπούλου, 1999). Κωφός κωφός: σύμφωνα με τον κοινωνιολογικό-ψυχολογικό ορισμό του Woodward (Λαμπροπούλου, 1999) ο πληθυσμός των κωφών διαφοροποιείται με τα εξής κριτήρια: κωφοί (με πεζό το πρώτο γράμμα), τα άτομα με ακουστική απώλεια, τα οποία αποτελούν μια μεγάλη μερίδα του πληθυσμού και που έχουν χάσει την ακοή τους σε μεγαλύτερη κυρίως ηλικία. Επικοινωνούν με την ομιλούμενη γλώσσα, η εκπαίδευση τους έχει γίνει κυρίως σε σχολεία ακουόντων, έχουν ταυτότητα ακούοντος ατόμου και είναι ενταγμένοι στην κοινωνία των ακουόντων. Κωφοί (με κεφαλαίο το πρώτο γράμμα), ένα συγκεκριμένο σύνολο ατόμων που ανήκουν στην κοινότητα των Κωφών, ταυτίζονται με τους άλλους Κωφούς και μοιράζονται κοινή γλώσσα και κουλτούρα. Η ακουστική τους απώλεια δεν αποτελεί το κύριο κοινό χαρακτηριστικό τους αλλά οι κοινές εμπειρίες, η κοινή γλώσσα και ο κοινός τρόπος ζωής που μεταφέρεται από γενιά σε γενιά. Κοινότητα των Κωφών: στην παρούσα εργασία υιοθετείται ο ορισμός των Baker & Padden (1980) σύμφωνα με τον οποίο η κοινότητα των Κωφών περιλαμβάνει τους Κωφούς και βαρήκοους που μοιράζονται μια 13 []

14 κοινή γλώσσα, κοινές εμπειρίες, αξίες και κοινό τρόπο αλληλεπίδρασης του ενός με τον άλλον και με τους ακούοντες (Λαμπροπούλου, 1999). Ελληνική Νοηματική Γλώσσα: με τον όρο «Ελληνική Νοηματική Γλώσσα», σε συντομία ΕΝΓ, εννοούμε τη νοηματική γλώσσα που χρησιμοποιούν οι Έλληνες Κωφοί στην κοινότητα τους. Μια γλώσσα εντελώς διαφορετική από την Ελληνική ομιλούμενη γλώσσα (Λαμπροπούλου, 1999). Αριθμητικά προβλήματα ή προβλήματα «προσθετικού τύπου»: προβλήματα που για τη λύση τους απαιτείται η πράξη της πρόσθεσης ή της αφαίρεσης (Λεμονίδης, 1994). Προβλήματα «αλλαγής» ( change questions): προβλήματα τα οποία περιλαμβάνουν μια διαδικασία όπου ένα γεγονός μεταβάλλει την αξία μιας ποσότητας (Λεμονίδης, 1994; Κολέζα, 2000). Προβλήματα «συνδυασμού» ( combine questions): προβλήματα τα οποία αναφέρονται σε στατικές καταστάσεις, όπου υπάρχουν δύο ποσά, τα οποία θεωρούνται είτε ως ανεξάρτητα είτε σε σχέση το ένα με το άλλο (Λεμονίδης, 1994; Κολέζα, 2000). Προβλήματα «σύγκρισης» ( compare questions): προβλήματα τα οποία περιλαμβάνουν τη σύγκριση ανάμεσα σε δύο τιμές και τη μεταξύ τους διαφορά (Λεμονίδης, 1994; Κολέζα, 2000). 14 []

15 1.4 Περιορισμοί Η συγκεκριμένη έρευνα είναι μια πρώτη προσπάθεια παρουσίασης των επιδόσεων κωφών μαθητών πέμπτης και έκτης τάξης δημοτικού σε διαφόρων ειδών αριθμητικά προβλήματα και για αυτό το λόγο όλα τα αποτελέσματα και συμπεράσματα παρουσιάζονται με προσοχή. Τα δεδομένα αντλήθηκαν από μικρό αριθμό μαθητών σε διαφορετικά εκπαιδευτικά περιβάλλοντα λόγω της ιδιαιτερότητας της συγκεκριμένης αναπηρίας και της σχολικής κατάστασης στη χώρα μας. Τα παραπάνω δε μας επιτρέπουν γενικεύσεις και τα αποτελέσματα παρουσιάζονται με επιφύλαξη. 15 []

16 16 [] κεφάλαιο δεύτερο

17 2. Ανασκόπηση βιβλιογραφίας 2.1 Ταξινόμηση προβλημάτων «προσθετικού τύπου» Μια διαδεδομένη αντίληψη (Λεμονίδης, 1994) θεωρεί ότι τα προβλήματα αφαίρεσης είναι πιο δύσκολα από τα προβλήματα πρόσθεσης και ότι τα προβλήματα διαίρεσης πιο δύσκολα από τα προβλήματα πολλαπλασιασμού. Επομένως βάσει αυτού τα προβλήματα διαφοροποιούνται με κριτήριο τις πράξεις, δηλαδή δύο προβλήματα που για την επίλυση τους απαιτείται η ίδια πράξη είναι του ίδιου επιπέδου. Τον τελευταίο καιρό πολλές έρευνες έχουν γίνει πάνω στα προβλήματα «προσθετικού τύπου», προβλήματα τα οποία για την επίλυση τους απαιτείται η πράξη της πρόσθεσης ή της αφαίρεσης (Λεμονίδης, 1994). Η εκτίμηση της δυσκολίας των προβλημάτων αυτών δεν πρέπει να γίνετε με κριτήριο την πράξη την οποία χρησιμοποιούμε για την επίλυση τους. Η διαδικασία αυτή είναι πολύ πιο σύνθετη. Σήμερα οι ερευνητές υποστηρίζουν ότι η δυσκολία των προβλημάτων αυτών βασίζεται σε δύο κατηγορίες παραγόντων: στη σημασιολογική δομή του προβλήματος και στις συντακτικές μεταβλητές. Η σημασιολογική δομή του προβλήματος αφορά τη γνώση εννοιών που σχετίζονται με την αύξηση, τη σμίκρυνση, το συνδυασμό και τη σύγκριση στοιχείων ενός συνόλου. Οι συντακτικές μεταβλητές αφορούν την οργάνωση, τον τρόπο παρουσίασης του προβλήματος και τον τρόπο διατύπωσης των λέξεων που περιγράφουν τις πράξεις (Λεμονίδης, 1994). 17 []

18 2.1.1 Ταξινόμηση με βάση σημασιολογικά κριτήρια Βάσει της σημασιολογικής δομής τους τα προβλήματα «προσθετικού τύπου» ταξινομούνται στις ακόλουθες κατηγορίες : «Αλλαγής», «Συνδυασμού», «Σύγκρισης» και «Εξομοίωσης» (Λεμονίδης, 1994; Κολέζα, 2000). Σύμφωνα με τους Riley, Greeno και Heller (1983) και τους Lean, Clements και Del Campo (1990), ο πιο γνωστός διαχωρισμός προβλημάτων, για την επίλυση των οποίων χρησιμοποιείται η πρόσθεση και η αφαίρεση, δημιουργήθηκε από τους Heller και Green (1978). Αποτελείται από τρείς κατηγορίες προβλημάτων: «Αλλαγής», «Συνδυασμού» και «Σύγκρισης». Προβλήματα «Αλλαγής» Υπάρχουν δύο τύποι τέτοιων προβλημάτων, τα προβλήματα Αλλαγή- Ένωση και τα προβλήματα Αλλαγή-Διαχωρισμός. Στα προβλήματα Αλλαγή-Ένωση υπάρχει μια αρχική ποσότητα και ένας άμεσος ή έμμεσος μετασχηματισμός που προκαλεί μια αύξηση σε αυτή την ποσότητα ενώ στα προβλήματα Αλλαγή-Διαχωρισμός ένα υποσύνολο αποσύρεται από ένα δεδομένο σύνολο (Λεμονίδης, 1994; Κολέζα, 2000). Στον Πίνακα 2.1 μπορούμε να δούμε βλέπει μερικά σχετικά παραδείγματα τέτοιων προβλημάτων ανάλογα με την άγνωστη ποσότητα και ανάλογα με το αν θεωρείται ένωση ή διαχωρισμός. Σε αυτού του τύπου τα προβλήματα υπάρχουν τρία σχετικά μεταξύ τους κομμάτια: η «αρχή», η «αλλαγή» και το «αποτέλεσμα». Ανάλογα με το περιεχόμενο του προβλήματος προκαλείται μια αύξηση ή μείωση στην «αρχή». Υπάρχουν έξι διαφορετικές υποκατηγορίες προβλημάτων (Riley, Greeno και Heller,1983; Lean, Clements και Del Campo, 1990). Στον Πίνακα 2.1 παρουσιάζονται μερικά σχετικά παραδείγματα τέτοιων προβλημάτων. 18 []

19 Πίνακας 2.1 Προβλήματα «Αλλαγής» 1. Άγνωστος η τελική κατάσταση Ένωση Ο Χ είχε 3 μπάλες. Ο Ψ του έδωσε 5 μπάλες. Πόσες μπάλες έχει ο Ψ τώρα; Διαχωρισμός Ο Χ είχε 8 μπάλες. Έδωσε 5 μπάλες στον Ψ. Πόσες μπάλες έχει τώρα ο Χ; 2. Άγνωστος ο μετασχηματισμός Ένωση Ο Χ είχε 3 μπάλες. Ο Ψ του έδωσε μερικές. Ο Χ έχει τώρα 8 μπάλες. Πόσες μπάλες έδωσε ο Ψ στον Χ; Διαχωρισμός Ο Χ είχε 8 μπάλες. Έδωσε μερικές στον Ψ. Τώρα ο Χ έχει 3 μπάλες. Πόσες μπάλες έδωσε στον Ψ; 3. Άγνωστος η αρχική κατάσταση Ένωση Ο Χ είχε μπάλες. Ο Ψ του έδωσε άλλες 5. Τώρα ο Χ έχει 8 μπάλες. Πόσες μπάλες είχε ο Χ στην αρχή; Διαχωρισμός Ο Χ είχε μπάλες. Έδωσε 5 στον Ψ. Τώρα ο Χ έχει 3 μπάλες. Πόσες μπάλες είχε ο Χ στην αρχή; Προβλήματα «Συνδυασμού» Υπάρχουν δύο τύποι προβλημάτων «συνδυασμού», αυτά κατά τα δίνονται δύο υποσύνολα και ζητείται η ένωση τους και αυτά που δίνεται ένα από τα υποσύνολα και η ένωση τους και ζητείται το πλήθος του άλλου υποσυνόλου (Riley, Greeno και Heller, 1983; Lean, Clements και Del Campo, 1990; Λεμονίδης, 1994; Κολέζα, 2000). 19 []

20 Στον Πίνακα 2.2 παρουσιάζονται μερικά σχετικά παραδείγματα τέτοιων προβλημάτων. Πίνακας 2.2 Προβλήματα «Συνδυασμού» 4. Άγνωστη η τιμή του συνδυασμού Ο Χ έχει 3 καραμέλες. Ο Ψ έχει 5. Πόσες καραμέλες έχουν μαζί ο Χ και ο Ψ; 5. Άγνωστος ένα υποσύνολο Ο Χ και ο Ψ έχουν μαζί 8 καραμέλες. Ο Χ έχει 3 καραμέλες. Πόσες καραμέλες έχει ο Ψ; Προβλήματα «Σύγκρισης» Τα συγκεκριμένα προβλήματα περιλαμβάνουν τη σύγκριση δύο διαχωρισμένων συνόλων. Ονομάζουμε το ένα σύνολο αναφοράς και το άλλο συγκρινόμενο σύνολο. Το τρίτο σύνολο που εμφανίζεται αποτελεί τη διαφορά του μεγαλύτερου από το μικρότερο σύνολο. Κάθε ένα από τα παραπάνω σύνολα στα προβλήματα αυτά μπορεί να είναι ο άγνωστος, επομένως έχουμε έξι διαφορετικούς τύπους τέτοιων προβλημάτων (Riley, Greeno και Heller, 1983; Lean, Clements και Del Campo, 1990; Λεμονίδης, 1994; Κολέζα, 2000). Στον Πίνακα 2.3 παρουσιάζονται μερικά σχετικά παραδείγματα τέτοιων προβλημάτων ανάλογα με την άγνωστη ποσότητα. 20 []

21 Πίνακας 2.3 Προβλήματα «Σύγκρισης» 6. Άγνωστη η διαφορά Ο Χ έχει 8 αυτοκινητάκια. Ο Ψ έχει 5 αυτοκινητάκια. Πόσα περισσότερα αυτοκινητάκια έχει ο Χ από τον Ψ; Ο Χ έχει 8 αυτοκινητάκια. Ο Ψ έχει 5 αυτοκινητάκια. Πόσα λιγότερα αυτοκινητάκια έχει ο Ψ από τον Χ; 7. Άγνωστη η συγκρινόμενη ποσότητα Ο Χ έχει 3 μπάλες. Ο Ψ έχει 5 μπάλες περισσότερες από τον Χ. Πόσες μπάλες έχει ο Ψ; Ο Χ έχει 8 μπάλες. Ο Ψ έχει 5 μπάλες λιγότερες. Πόσες μπάλες έχει ο Ψ; 8. Άγνωστη η αναφερόμενη ποσότητα Ο Ψ έχει 8 μπανάνες. Έχει 5 μπανάνες περισσότερες από τον Χ. Πόσες μπανάνες έχει ο Χ; Ο Ψ έχει 3 μπανάνες. Έχει 5 μπανάνες λιγότερες από τον Χ. Πόσες μπανάνες έχει ο Χ; Προβλήματα «Εξομοίωσης» Τα προβλήματα αυτά αποτελούν μείγμα προβλημάτων «Αλλαγής» και «Σύγκρισης». Υπάρχουν οι ίδιοι μετασχηματισμοί των προβλημάτων «Αλλαγής» αλλά εδώ βασίζονται σε σύγκριση δύο διαχωρισμένων συνόλων. Αν ο μετασχηματισμός εκτελείται στο μικρότερο σύνολο έχουμε πρόβλημα «Εξομοίωσης-Ένωσης» ενώ αν εκτελείται στο μεγαλύτερο σύνολο έχουμε πρόβλημα «Εξομοίωσης-Διαχωρισμού». Ο άγνωστος μεταβάλλεται με αποτέλεσμα να υπάρχουν τρία διαφορετικά προβλήματα σε κάθε τύπο προβλήματος «Εξομοίωσης». Η συγκεκριμένη κατηγορία προβλημάτων δεν είναι διαδεδομένη για τα σχολικά δεδομένα (Λεμονίδης, 1994; Κολέζα, 2000). 21 []

22 Στον Πίνακα 2.4 παρουσιάζονται μερικά σχετικά παραδείγματα τέτοιων προβλημάτων. Πίνακας 2.4 Προβλήματα «Εξομοίωσης» 9. Ένωση Ο Χ έχει 3 μπάλες. Ο Ψ έχει 8. Πόσες μπάλες πρέπει να κερδίσει ο Χ για να έχει τόσες όσες ο Ψ; 10. Διαχωρισμός Ο Χ έχει 8 μπάλες. Ο Ψ έχει 3. Πόσες μπάλες πρέπει να χάσει ο Χ για να έχει όσες και ο Ψ; 11. Ένωση Ο Χ έχει 3 καραμέλες. Αν κερδίσει 5 καραμέλες θα έχει τις ίδιες με το Ψ. Πόσες καραμέλες έχει ο Ψ; 12. Διαχωρισμός Ο Χ έχει 3 καραμέλες. Αν ο Ψ χάσει 5 καραμέλες θα έχει τις ίδιες με τον Χ. Πόσες καραμέλες έχει ο Ψ; 13. Ένωση Ο Χ έχει 8 μπανάνες. Αν ο Ψ κερδίσει 5 μπανάνες θα έχει τις ίδιες με τον Χ. Πόσες μπανάνες έχει ο Ψ; 14. Διαχωρισμός Ο Χ έχει 8 μπανάνες. Αν χάσει 5 μπανάνες θα έχει τις ίδιες με τον Ψ. Πόσες μπανάνες έχει ο Ψ; 22 []

23 2.1.2 Ταξινόμηση με βάση εννοιολογικά κριτήρια Η ταξινόμηση με βάσει εννοιολογικών κριτηρίων δε βασίζεται ούτε στη δράση ούτε στην πράξη που πρέπει να εκτελεστεί κάθε φορά αλλά είναι καθαρά εννοιολογική. Ο Vergnaud (Λεμονίδης, 1994; Κολέζα, 2000) εισάγει και χρησιμοποιεί το «σχεσιακό λογισμό» καλύπτοντας όλες σχεδόν τις περιπτώσεις απλών προβλημάτων που για τη λύση τους χρησιμοποιείται πρόσθεση ή αφαίρεση. Υπάρχουν έξι κατηγορίες τέτοιων προβλημάτων: σύνθεση δύο καταστάσεων (ή μέτρων), μετασχηματισμός μιας κατάστασης (ή μέτρου)σε κάποια άλλη, στατική σχέση ανάμεσα σε δύο καταστάσεις(ή μέτρα), σύνθεση δύο μετασχηματισμών, μετασχηματισμός μεταξύ δύο στατικών σχέσεων και σύνθεση δύο στατικών σχέσεων. Σύνθεση δύο καταστάσεων (ή μέτρων): Δύο καταστάσεις συντίθενται για να δώσουν μια κατάσταση. (Προβλήματα όπως στον Πίνακα 2.2) Μετασχηματισμός μιας κατάστασης (ή μέτρου)σε κάποια άλλη: Ένας μετασχηματισμός δρα πάνω σε μία κατάσταση για να δώσει μία άλλη. (Προβλήματα όπως στον Πίνακα 2.1) Στατική σχέση ανάμεσα σε δύο καταστάσεις(ή μέτρα): Μία σχέση συνδέει δύο καταστάσεις. (Προβλήματα όπως στον Πίνακα 2.3) Σύνθεση δύο μετασχηματισμών: Δύο μετασχηματισμοί συντίθενται για να δώσουν ένα μετασχηματισμό. Υπάρχουν δύο κατηγορίες προβλημάτων, γνωρίζοντας τους δύο μετασχηματισμούς ζητείται η σύνθεση (Παραδείγματα στον Πίνακα 2.5) και γνωρίζοντας τη σύνθεση και ένα από τους μετασχηματισμούς και ζητείται ο άλλος (Παραδείγματα στον Πίνακα 2.6). Πρόκειται για σύνθεση μετασχηματισμών, θετικοί ή αρνητικοί μετασχηματισμοί, επομένως η κατάσταση δεν είναι η ίδια στις διάφορες περιπτώσεις. 23 []

24 Πίνακας 2.5 Σύνθεση δύο μετασχηματισμών Γνωστοί και οι δύο Ο Γιάννης έπαιξε δύο παρτίδες μπίλιες. Στην πρώτη παρτίδα κέρδισε 16 μπίλιες. Στη δεύτερη κέρδισε 9. Τι έκανε συνολικά; Ο Γιάννης έπαιξε δύο παρτίδες μπίλιες. Στην πρώτη κέρδισε 16 μπίλιες. Στη δεύτερη παρτίδα έχασε 9. Τι έκανε συνολικά; Ο Γιάννης έπαιξε δύο παρτίδες μπίλιες. Στην πρώτη κέρδισε 9 μπίλιες. Στη δεύτερη έχασε 16. Τι έκανε συνολικά; Πίνακας 2.6 Σύνθεση δύο μετασχηματισμών Γνωστός ο ένας και η σύνθεση Ο Γιάννης έπαιξε δύο παρτίδες μπίλιες. Στην πρώτη παρτίδα κέρδισε 7. Έπαιξε και μια δεύτερη παρτίδα. Συνολικά και στις δύο κέρδισε 13 μπίλιες. Τι συνέβει στη δεύτερη παρτίδα; Ο Γιάννης έπαιξε δύο παρτίδες μπίλιες. Στην πρώτη παρτίδα έχασε 9. Έπαιξε και μια δεύτερη παρτίδα. Συνολικά και στις δύο έχασε μπίλιες. Τι συνέβει στη δεύτερη παρτίδα; Ο Γιάννης έπαιξε δύο παρτίδες μπίλιες. Στην πρώτη παρτίδα κέρδισε 7. Έπαιξε και μια δεύτερη παρτίδα. Κάνοντας λογαριασμούς για τις δύο παρτίδες αντιλαμβάνεται ότι έχασε 2 μπίλιες συνολικά. Τι συνέβει στη δεύτερη παρτίδα; Μετασχηματισμός μεταξύ δύο στατικών σχέσεων: Ένας μετασχηματισμός ενεργεί πάνω σε μια σχέση για να δώσει μια σχέση. Σύνθεση δύο στατικών σχέσεων: Δύο σχέσεις συντίθενται για να δώσουν μια σχέση. 2.2 Διαδικασίες επίλυσης προβλημάτων «προσθετικού τύπου» 24 []

25 Διάφορες έρευνες έχουν γίνει με σκοπό να διαγνωστεί και να μελετηθεί η διαδικασία επίλυσης προβλημάτων «προσθετικού τύπου» από μαθητές (Λεμονίδης, 1994) Διάγνωση και κατανόηση των διαδικασιών επίλυσης Σύμφωνα με το Λεμονίδη (1994), στις έρευνες για τη διάγνωση και κατανόηση των διαδικασιών επίλυσης προβλημάτων χρησιμοποιούνται τρεις κατηγορίες μεθόδων: η μέθοδος των προσωπικών συνεντεύξεων, η μέθοδος της μέτρησης του χρόνου επίλυσης και η μέθοδος της ανάλυσης των τύπων των λαθών που κάνουν τα παιδιά. Στην πρώτη, που είναι και η πιο άμεση, παρακολουθείται ατομικά κάθε παιδί την ώρα που λύνει ένα συγκεκριμένο πρόβλημα και ο παρατηρητής του θέτει προσχεδιασμένες ερωτήσεις στην προσπάθεια του να ερμηνεύσει τον τρόπο σκέψης του. Στη δεύτερη μέθοδο υπολογίζονται και συγκρίνονται οι χρόνοι που απαιτούνται για την επίλυση προβλημάτων για τα οποία οι στρατηγικές λύσεις και τα απαιτούμενα βήματα είναι γνωστά εκ των προτέρων. Με τη τρίτη μέθοδο οι ερευνητές εξετάζοντας τους τύπους των λαθών στις διάφορες ομάδες προβλημάτων επιχειρούν να διαγνώσουν τη διαδικασία επίλυσης που χρησιμοποιεί το παιδί. Οι παραπάνω μέθοδοι έχουν περιορισμούς και ατέλειες για τη πλήρη διάγνωση και κατανόηση των διαδικασιών επίλυσης προβλημάτων «προσθετικού τύπου» από μαθητές (Λεμονίδης, 1994) Κατηγοριοποίηση των διαδικασιών επίλυσης 25 []

26 Οι διαδικασίες που χρησιμοποιούν οι μαθητές για λύσουν ένα πρόβλημα «προσθετικού τύπου» χωρίζονται σε τρεις βασικούς τύπους: τις υλικές, τις αριθμητικές και τις νοερές διαδικασίες (Λεμονίδης, 1994). Υλικές διαδικασίες ή Άμεση μοντελοποίηση Το παιδί αρχίζει κατασκευάζοντας ένα ή περισσότερα σύνολα από υλικά αντικείμενα οικεία του όπως τα δάκτυλα του ή εικονογραφημένες αναπαραστάσεις αντικειμένων. Τα αντικείμενα χρησιμοποιούνται ως άμεση αναπαράσταση των αντικειμένων του προβλήματος και οι δραστηριότητες που πραγματοποιούνται είναι αναπαραστάσεις των δραστηριοτήτων ή σχέσεων που περιέχονται στο πρόβλημα. Αριθμητικές διαδικασίες Χρησιμοποιείται η αρίθμηση και για τις διαδικασίες απαιτείται η ικανότητα ευθείας και αντίστροφης αρίθμησης. Μερικά παιδιά αριθμούν δυνατά, μερικά με τα δάκτυλα τους και μερικά από μέσα τους. Για καλύτερα αποτελέσματα χρειάζεται μια προσωπική συνέντευξη με ενδιάμεσες ερωτήσεις. Νοερές διαδικασίες Χωρίζονται σε δύο μεγάλες κατηγορίες: άμεση ανάκληση από τη μνήμη βασικών γνωστών πράξεων και παραγωγή πράξεων ή ευρετική. Μέσω της άμεσης ανάκλησης οι μαθητές ανακαλούν βασικές πράξεις τις οποίες έχουν μάθει και απομνημονεύσει και δε προσφεύγουν στην αρίθμηση. Για την παραγωγή πράξεων οι μαθητές χρησιμοποιούν τις απομνημονευμένες πράξεις για να παράγουν νέες Διαδικασίες πρόσθεσης 26 []

27 Πρόβλημα-παράδειγμα: «Η Μαρία έχει 5 μολύβια. Η Ελένη έχει 8 μολύβια περισσότερα από τη Μαρία. Πόσα μολύβια έχει η Ελένη;» Υλικές διαδικασίες Απαρίθμηση όλων: Ενώνονται δύο ή περισσότερα σύνολα φυσικών αντικειμένων που πρέπει να προστεθούν και μετριούνται όλα τα στοιχεία αρχίζοντας από το ένα, ακόμα και στην περίπτωση που ο πληθάριθμος του κάθε συνόλου είναι γνωστός. Στο παράδειγμα μας ο μαθητής με χρήση φυσικών αντικειμένων ή των δακτύλων του κατασκευάζει δύο σύνολα και απαριθμώντας την ένωση τους δίδει την απάντηση Αριθμητικές διαδικασίες Αρίθμηση όλων αρχίζοντας από τον πρώτο: Ο μαθητής αριθμεί για τον πρώτο αριθμό από το ένα μέχρι το πέντε (1,2,3,4,5) και συνεχίζει την ευθεία αυτή αρίθμηση μέχρι την αρίθμηση του δευτέρου, οκτώ, (6,7,8,9,10,11,12,13). Η απάντηση είναι ο τελευταίος αριθμός της παραπάνω αρίθμησης. Αρίθμηση όλων αρχίζοντας από το μεγαλύτερο: Ο μαθητής αριθμεί μέχρι τον μεγαλύτερο αριθμό, οκτώ, αρχίζοντας από το ένα (1,2,3,4,5,6,7,8) και συνεχίζει την ευθεία αυτή αρίθμηση μέχρι την αρίθμηση και του μικρότερου αριθμού, πέντε, (9,10,11,12,13). Η απάντηση είναι ο τελευταίος αριθμός της παραπάνω αρίθμησης. Αρίθμηση από τον πρώτο: Ο μαθητής εδώ αριθμεί αρχίζοντας από τον πληθάριθμο του πρώτου αριθμού. Στο παράδειγμα μας ο μαθητής θα ξεκινήσει από το πέντε και θα μετρήσει 6,7,8,9,10,11,12,13. Η απάντηση είναι ο τελευταίος αριθμός της παραπάνω αρίθμησης. Αρίθμηση από το μεγαλύτερο: Ο μαθητής εδώ αριθμεί αρχίζοντας από τον πληθάριθμο του μεγαλύτερου αριθμού. Στο παράδειγμα μας ο μαθητής θα ξεκινήσει από το οκτώ και θα μετρήσει 9,10,11,12,13. Η απάντηση είναι ο τελευταίος αριθμός της παραπάνω αρίθμησης. Ο μαθητής κατά τη διάρκεια της αρίθμησης και για να σταματήσει όταν φθάσει στο αποτέλεσμα θα πρέπει με κάποιο τρόπο να καταγράψει τα βήματα που έχει εκτελέσει. Πολύ συχνά αυτό γίνετε με τη χρήση των 27 []

28 δακτύλων του αλλά με διαφορετικό τρόπο από την προηγούμενη διαδικασία. Εδώ τα δάκτυλα απλά ελέγχουν την εξέλιξη της αρίθμησης και δεν αναπαριστούν τα δύο σύνολα. Νοερές διαδικασίες Άμεση ανάκληση από τη μνήμη: Ο μαθητής ανακαλεί από τη μνήμη μακράς διαρκείας του την πράξη «5 + 8 = 13» ή «8 + 5 = 13». Παραγωγή πράξης: Ο μαθητής παράγει την απάντηση του βασιζόμενος σε μία ή περισσότερες ανακαλούμενες πράξεις, «5+5=10, 10+3=13 ή , 10+3=13» Διαδικασίες αφαίρεσης Πρόβλημα-παράδειγμα: «Ο Κώστας έχει 5 αυτοκινητάκια. Ο Νίκος έχει 12 αυτοκινητάκια. Πόσα αυτοκινητάκια περισσότερα έχει ο Νίκος από τον Κώστα;» Υλικές διαδικασίες Διαχωρισμός από: Ο μαθητής κατασκευάζει το μεγαλύτερο σύνολο με χρήση φυσικών αντικειμένων ή των δακτύλων του, διαχωρίζει το μικρό σύνολο από τα παραπάνω και απαριθμεί τα υπόλοιπα ως απάντηση. Διαχωρισμός μέχρι: Παρόμοια διαδικασία με την παραπάνω με τη διαφορά ότι ο μαθητής διαχωρίζει από το μεγάλο σύνολο τόσα στοιχεία ώστε αυτά που θα μείνουν να είναι όσα στο μικρό σύνολο. Τα στοιχεία που διαχωρίστηκαν αποτελούν την απάντηση. Πρόσθεση: Ο μαθητής διαλέγει έναν αριθμό αντικειμένων (5), όσο και το μικρό σύνολο. Προσθέτει στο παραπάνω σύνολο ένα-ένα αντικείμενα μέχρι να φθάσει το σύνολο των αντικειμένων του ίσο με τον μεγαλύτερο αριθμό (12). Ο αριθμός των αντικειμένων που προστέθηκαν αποτελεί την απάντηση. 28 []

29 Αντιπαραβολή: Η διαδικασία αυτή δεν μπορεί να γίνει νοερά. Αντιπαραβάλλονται και αντιστοιχίζονται ένα προς ένα τα στοιχεία των δύο συνόλων. Η απαρίθμηση σε ότι περισσεύει δίνει την απάντηση. Αριθμητικές διαδικασίες Αντίστροφη αρίθμηση από: Ο μαθητής πραγματοποιεί μια αντίστροφη αρίθμηση από το μεγαλύτερο από τους δύο όρους, 12, τόσους όρους όσος και ο μικρότερος αριθμός, πέντε, (11,10,9,8,7). Ο τελευταίος αριθμός αποτελεί την απάντηση. Αντίστροφη αρίθμηση μέχρι: Η αντίστροφη αρίθμηση πραγματοποιείται από τον μεγαλύτερο αριθμό, 12, μέχρι να φθάσει στον μικρότερο (11,10,9,8,7,6,5). Η απάντηση είναι ο αριθμός των λέξεων-αριθμών που αριθμήθηκαν, επτά. Ευθεία αρίθμηση από δεδομένο: Ο μαθητής εκτελεί μια ευθεία αρίθμηση αρχίζοντας από το μικρότερο από τους δύο αριθμούς, πέντε, και αριθμεί μέχρι να φθάσει τον μεγαλύτερο, 12, (6,7,8,9,10,11,12). Η αρίθμηση των βημάτων αποτελεί την απάντηση. Επιλογή: Ο μαθητής επιλέγει την αρίθμηση των λιγότερων αριθμών και διαλέγει ή την αντίστροφη αρίθμηση από ή την ευθεία αρίθμηση από δεδομένο. Στο παραπάνω παράδειγμα η αντίστροφη αρίθμηση είναι πιο σύντομη από την ευθεία αρίθμηση από δεδομένο. Νοερές διαδικασίες Άμεση ανάκληση της αφαίρεσης: Ο μαθητής ανακαλεί άμεσα από τη μνήμη μακράς διαρκείας την πράξη «12-5=7». Έμμεση ανάκληση της αφαίρεσης: Ο μαθητής ανακαλεί μια έμμεση αφαιρετική πράξη άμεσα από τη μνήμη μακράς διαρκείας «12-7=5». Έμμεση ανάκληση της πρόσθεσης: Ο μαθητής ανακαλεί μια έμμεση προσθετική πράξη άμεσα από τη μνήμη «5+7=12». Παραγωγή άμεσης αφαίρεσης: Ο μαθητής βασιζόμενος σε ανακαλούμενες πράξεις, παράγει την απάντηση αφαιρώντας από τον μεγαλύτερο τον μικρότερο αριθμό («12-2=10, 10-3=7». 29 []

30 Παραγωγή έμμεσης αφαίρεσης: Ο μαθητής βασιζόμενος σε ανακαλούμενες πράξεις, παράγει την απάντηση του προσδιορίζοντας ποια ποσότητα πρέπει να αφαιρέσει από τον μεγαλύτερο αριθμό για να πάρει τον μικρότερο («12-2=10, 10-5=5 άρα η απάντηση είναι 2+5=7»). Παραγωγή έμμεσης πρόσθεσης: Ο μαθητής βασιζόμενος σε ανακαλούμενες πράξεις, παράγει την απάντηση του προσδιορίζοντας ποια ποσότητα πρέπει να προσθέσει στον μικρότερο αριθμό για να πάρει τον μεγαλύτερο («5+5=10, 10+2=12 άρα η απάντηση είναι 5+2=7»). 30 []

31 2.3 Εργασίες και έρευνες για τα αριθμητικά προβλήματα Οι Riley, Greeno και Heller (1983) μελέτησαν την ικανότητα μαθητών διαφόρων ηλικιών στην κατανόηση και την επίλυση αριθμητικών προβλημάτων, «αλλαγής», «συνδυασμού» και «σύγκρισης». Κατέλειψαν στο συμπέρασμα ότι με την ηλικία βελτιώνεται η συγκεκριμένη ικανότητα στους μαθητές. Στα ίδια συμπεράσματα κατέληξαν οι Del Campo και Clements (1987) αναλύοντας τις απαντήσεις 1195 μαθητών ηλικίας 5 12 ετών σε έξι αριθμητικά προβλήματα «αλλαγής». Οι Lean, Clements και Del Campo (1990) ανέλυσαν τις απαντήσεις σε 22 αριθμητικά προβλήματα μαθητών ηλικίας 5-15 ετών, 1195 από την Αυστραλία και 1298 από την Παπούα Νέα Γουινέα. Το τεστ δόθηκε στα αγγλικά, τη γλώσσα στην οποία εκπαιδεύονται οι μαθητές και στις δύο χώρες. Οι μαθητές από την Αυστραλία μιλούσαν τα αγγλικά ως πρώτη γλώσσα, και μόνη γλώσσα, ενώ οι υπόλοιποι μαθητές ως τρίτη ή τέταρτη. Τα αποτελέσματα έδειξαν ότι όλοι οι μαθητές ακολούθησαν παρόμοιες στρατηγικές για την επίλυση των προβλημάτων και έκαναν παρόμοια λάθη. Τα διαφορετικά είδη προβλημάτων και η ηλικία των μαθητών, που έχει να κάνει με το επίπεδο γνώσεων στην αγγλική γλώσσα, αποτέλεσαν τους παράγοντες δυσκολίας στο τεστ. Ο Adetula (1990) έδωσε σε 48 μαθητές δημόσιων και ιδιωτικών σχολείων στη Νιγηρία 10 αριθμητικά προβλήματα, στα αγγλικά και στην τοπική τους γλώσσα, κάνοντας παράλληλα συνεντεύξεις για να εξετάσει τον τρόπο που το κάθε παιδί ανέλυσε το πρόβλημα για να καταλήξει στη λύση του. Τα αποτελέσματα έδειξαν ότι όλοι οι μαθητές τόσο στην επίλυση όσο και στις στρατηγικές που ακολούθησαν είχαν καλύτερα αποτελέσματα όταν τους δόθηκαν τα προβλήματα στην τοπική τους γλώσσα. Από τις έρευνες αυτές προκύπτει ότι η ηλικία και η γλώσσα φαίνεται να αποτελούν σημαντικούς παράγοντες για την κατανόηση και επομένως την επίλυση αριθμητικών προβλημάτων. 31 []

32 2.4 Εργασίες και έρευνες για τα μαθηματικά και τους κωφούς Σύμφωνα με την Gregory (1998), οι πρώτες έρευνες σχετικά με τα μαθηματικά και τους κωφούς ασχολήθηκαν κυρίως με τις υπολογιστικές ικανότητες των μαθητών. Μια πρώτη έρευνα του Εθνικού Συμβούλιου Εκπαιδευτικών Κωφών (National Council of Teachers of the Deaf), το 1957, ανάμεσα σε 246 μαθητές από τέσσαρα σχολεία στην Αγγλία αναφέρεται σε μια μέση διαφορά κωφών και ακουόντων της τάξης των 2,5 ετών. Αργότερα, το 1965, ο Wollman κατέληξε σε παρόμοια συμπεράσματα μελετώντας το 1/3 του μαθητικού πληθυσμού από 13 σχολεία κωφών στη Μεγάλη Βρετανία με 162 μαθητές δευτεροβάθμιας γενικής εκπαίδευσης. Οι Wood, Wood και Howard (1983) μελέτησαν τις ικανότητες στα μαθηματικά 414 κωφών και 465 ακουόντων αποφοίτων σχολείου. Τα αποτελέσματα της έρευνας τους έδειξαν ότι οι κωφοί παρουσιάζουν σημαντικές ελλείψεις σε μαθηματικές ικανότητες σε σχέση με τους ακούοντες της ίδιας ηλικίας. Παρατήρησαν ότι η μαθηματική ηλικία των ακουόντων αποφοίτων ήταν 15,5 ετών ενώ των κωφών 12,3. Παρόλα αυτά, όσον αφορά τους κωφού μαθητές, το επίπεδο της ακουστικής τους απώλειας δε σχετίζεται ιδιαίτερα με την επίδοση τους στα μαθηματικά. Οι Zwiebel και Allen (1988) συνέκριναν βαθμολογίες καθηγητών σχετικά με την επίδοση στα μαθηματικά Ισραηλινών μαθητών με προβλήματα ακοής, με σοβαρές μέχρι ελαφριές βαρηκοΐες, από τρία διαφορετικά εκπαιδευτικά περιβάλλοντα: ειδικά σχολεία για μαθητές με προβλήματα ακοής, ειδικές τάξεις για μαθητές με προβλήματα ακοής σε σχολεία γενικής εκπαίδευσης, τάξεις γενικής εκπαίδευσης στις οποίες συμμετέχουν επιλεκτικά μαθητές με προβλήματα ακοής. Μια πρώτη ανάλυση έδειξε ότι οι μαθητές σε αυτά τα τρία διαφορετικά εκπαιδευτικά περιβάλλοντα διαφέρουν σε σχέση με τις επικοινωνιακές τους ικανότητες και το γνωστικό και νοητικό τους επίπεδο. Στο Ισραήλ, μετά το νηπιαγωγείο, μια επιτροπή από εκπαιδευτικούς και ψυχολόγους αποφασίζει πιο εκπαιδευτικό περιβάλλον είναι το πιο κατάλληλο για τον 32 []

33 κάθε μαθητή, με βάση το γνωστικό και νοητικό επίπεδο του μαθητή καθώς και την επικοινωνιακή του ικανότητα με τα ακούοντα παιδιά. Μια πιο πολύπλοκη ανάλυση που πραγματοποιήθηκε αργότερα έχει ως στόχο να δείξει αν η διαφορά στην επίδοση στα μαθηματικά είναι ανεξάρτητη από τις παραπάνω μεταβλητές και εξαρτάται μόνο από το εκπαιδευτικό περιβάλλον. Τα αποτελέσματα έδειξαν ότι υπάρχει σημαντική διαφορά στην επίδοση των μαθητών με προβλήματα ακοής ανάλογα με το εκπαιδευτικό περιβάλλον στο οποίο ανήκουν, χωρίς να έχει να κάνει αυτό με την επικοινωνιακή ικανότητα ή το γνωστικό και νοητικό επίπεδο του μαθητή. Οι μαθητές με προβλήματα ακοής που παρακολουθούσαν τάξεις γενικής εκπαίδευσης είχαν υψηλότερες επιδόσεις στα μαθηματικά από ότι αυτοί στα ειδικά σχολεία. Μερικά χρόνια αργότερα οι Mulhern και Budge (1993) μελέτησαν τις επιδόσεις προγλωσσικών κωφών και ακουόντων μαθητών ηλικίας ετών σε 100 απλές ασκήσεις πρόσθεσης. Από τα αποτελέσματα κατέληξαν στο συμπέρασμα ότι οι κωφοί μαθητές, σε βασικά θέματα αριθμητικής τουλάχιστον, δεν παρουσιάζουν ιδιαίτερα χαμηλότερες επιδόσεις από αυτές των ακουόντων, αν και η ταχύτητα με την οποία πραγματοποιούν απλές προσθέσεις είναι σημαντικά πιο αργή. Οι Luckner και McNeill (1994) συνέκριναν τις επιδόσεις μιας ομάδας κωφών και βαρήκοων παιδιών σχολικής ηλικίας με μια αντίστοιχη ομάδα ακουόντων σε μία σειρά εκπαιδευτικών παιχνιδιών σχετικά με την επίλυση προβλημάτων πάνω στον Πύργο του Hanoi. Συμμετείχαν 86 μαθητές, 43 κωφοί και βαρήκοοι ηλικίας 6-19 ετών και ίδιος αριθμός ακούοντες ηλικίας 6-17 ετών. Τα αποτελέσματα έδειξαν ότι η ομάδα ακουόντων γενικά είχε καλύτερες επιδόσεις. Καθώς αυξανόταν η ηλικία των παιδιών που έπαιρναν μέρος, αυξανόταν η επίδοση τους και μειωνόταν η διαφορά μεταξύ της ομάδας κωφών και βαρήκοων με αυτή των ακουόντων. Την επόμενη χρονιά ο Titus (1995), στο πλαίσιο της διδακτορικής του διατριβής, ερεύνησε την κατανόηση από κωφούς και βαρήκοους μαθητές της έννοιας των κλασμάτων μέσω της ικανότητας τους να τα συγκρίνουν ανά δύο. Επικεντρώθηκε στην επίδοση και τις στρατηγικές κωφών και βαρήκοων μαθητών ηλικίας και ετών σε σύγκριση με 33 []

34 αντίστοιχες ομάδες ακουόντων. Στην έρευνα του συμμετείχαν 21 κωφοί και βαρήκοοι και 26 ακούοντες μαθητές. Τους δόθηκαν 18 θέματα με κλάσματα σε ζεύγη και τους ζητήθηκε να βρουν ποιο είχε την μεγαλύτερη αξία. Σε τέσσερα από αυτά τα θέματα τους ζητήθηκε επιπλέον να γράψουν πως κατέληξαν σε αυτό το συμπέρασμα, ποιες στρατηγικές χρησιμοποίησαν. Τα αποτελέσματα έδειξαν ότι οι κωφοί και βαρήκοοι μαθητές, στο σύνολο τους, είχαν παρόμοιες επιδόσεις με αυτές των νεώτερων ηλικιακά ακουόντων μαθητών τόσο στο είδος των κλασμάτων τα οποία ήταν ικανοί να συγκρίνουν όσο και στις στρατηγικές που χρησιμοποιούσαν. Επίσης οι ακούοντες μαθητές, σε πλήρη αντίθεση με τους κωφούς και βαρήκοους, παρουσίαζαν μια άνοδο στην επίδοση τους, η οποία σχετίζονταν θετικά με την ηλικία τους. Ο Frostad (1996) μελέτησε τις επιδόσεις στα μαθηματικά κωφών μαθητών ηλικίας 7 με 16 ετών στην Νορβηγία. Τα αποτελέσματα της έρευνας του έδειξαν ότι καθώς οι κωφοί μαθητές μεγαλώνουν, αυξάνονται οι ελλείψεις τους σε υπολογιστικές δεξιότητες σε σχέση με ακούοντες μαθητές αντίστοιχης ηλικίας. Επιπλέον παρατήρησε ότι οι επιδόσεις στα μαθηματικά κωφών μαθητών έχουν βελτιωθεί από τι στιγμή που το εκπαιδευτικό σύστημα στη χώρα του υιοθέτησε ως τρόπο επικοινωνίας την χρήση νοηματικής γλώσσας στη διδασκαλία κωφών μαθητών σε σχέση με την χρήση της προφορικής μεθόδου. Οι Nunes και Moreno (2002) εξέτασαν με επιτυχία την αποτελεσματικότητα ενός προγράμματος παρέμβασης για την προαγωγή της αρίθμησης σε κωφά παιδιά. Το πρόγραμμα αυτό σχεδιάστηκε ώστε να αντιμετωπίσει τόσο το γεγονός ότι τα κωφά παιδιά έχουν λιγότερες ευκαιρίες για ευκαιριακή μάθηση όσο και τη δυσκολία που αντιμετωπίζουν στο να βγάζουν συμπεράσματα με χρονική αλληλουχία. Οι Zarfaty, Nunes, Bryant (2004) συνέκριναν την ικανότητα σε κωφά και ακούοντα παιδιά, ηλικίας τριών και τεσσάρων ετών, να θυμούνται και να αναπαράγουν το πλήθος διαφόρων αντικειμένων. Στο πρώτο τεστ τα αντικείμενα ήταν όλα μαζί τοποθετημένα σε σειρά ενώ στο δεύτερο τα παρουσίαζαν ένα-ένα. Τα παιδιά χωρίστηκαν σε δύο ομάδες, η κάθε μία περιελάμβανε κωφά και ακούοντα παιδιά. Στη μία ομάδα δόθηκε πρώτα το 34 []

35 πρώτο τεστ και μετά το δεύτερο ενώ στην άλλη αντίθετα. Κάθε παιδί παρατηρήθηκε ξεχωριστά. Η επίδοση των κωφών παιδιών ήταν ίδια με αυτή των ακουόντων όταν τα αντικείμενα παρουσιαζόντουσαν ένα-ένα ενώ καλύτερη όταν όλα τα αντικείμενα παρουσιάζονταν μαζί. Τα παραπάνω δείχνουν ότι η αναπαράσταση αρίθμησης στα κωφά παιδιά προσχολικής ηλικίας είναι τουλάχιστον ίδια, αν όχι καλύτερη, από αυτή των ακουόντων. Με τα παραπάνω κατέληξαν στο συμπέρασμα ότι οι δυσκολίες που αντιμετωπίζουν οι κωφοί μαθητές στα μαθηματικά δε σχετίζονται με κάποια καθυστέρηση στην αναπαράσταση αρίθμησης. Η Chen (2006) προτείνει τρόπους διδασκαλίας μαθηματικών σε κωφούς και βαρήκοους μαθητές με τη χρήση υλικών, όπως χαρτί, υποστηρίζοντας ότι οι παραπάνω τρόποι βοηθούν στην κατανόηση και αφομοίωση των μαθηματικών εννοιών (μαθηματικά origami: Ιαπωνική λέξη και σημαίνει διπλωμένο χαρτί). Στο ίδιο πνεύμα ο Masataka (2006) συνέκρινε τα αποτελέσματα απλών αφαιρέσεων ανάμεσα σε μια ομάδα ενηλίκων κωφών και μια ομάδα ενηλίκων ακουόντων. Στην πρώτη φάση της έρευνας η πράξη της αφαίρεσης γινόταν ανάμεσα σε σύνολα από τελείες και στη δεύτερη φάση σε αριθμούς. Οι κωφοί είχαν αρκετά υψηλότερη επίδοση, από αυτή των ακουόντων, στις αφαιρέσεις της πρώτης φάσης, με τα σύνολα από τελείες, και αρκετά χαμηλότερη στη δεύτερη φάση, με τους αριθμούς. Δύο άλλοι ερευνητές, οι Kelly και Gaustad (2007), μελέτησαν τη σχέση μεταξύ της επίδοσης στα μαθηματικά και την ικανότητα στην ανάγνωση, τη γλώσσα και τη μορφολογία της αγγλικής γλώσσας κωφών φοιτητών. Οι φοιτητές εξετάστηκαν σε δύο τεστ μαθηματικών, γενικά μαθηματικά άλγεβρα γεωμετρία τριγωνομετρία, και δύο γλώσσας, γραμματική λεξιλόγιο ανάγνωση ερωτήσεις σχετικές με τη μορφολογία. Η έρευνα έδειξε ότι υπάρχει θετική συσχέτιση μεταξύ της αναγνωστικής ικανότητας καθώς και των γνώσεων των κωφών στη μορφολογία της αγγλικής γλώσσας με την επίδοση τους στα μαθηματικά. Τέλος οι Lang και Pagliano (2007) στην έρευνα τους ασχολήθηκαν με την ικανότητα ανάκλησης διδαχθέντων όρων γεωμετρίας από κωφούς μαθητές λυκείου. Αρχικά παρατήρησαν ότι η ανάκληση συγκεκριμένων 35 []

36 όρων ήταν καλύτερη από αυτή των αφηρημένων όρων. Επιπροσθέτως οι όροι της γεωμετρίας οι οποίοι μπορούσαν να αναπαρασταθούν με ένα και μόνο νόημα μπορούσαν να ανακληθούν καλύτερα από αυτούς που αποδίδονταν με σύνθετα νοήματα ή με χρήση δακτυλικού αλφάβητου. 36 []

37 2.4.1 Εργασίες και έρευνες για τα αριθμητικά προβλήματα και τους κωφούς Η Suzan Gregory (1998) υποστηρίζει ότι αν οι μαθητές δεν γνωρίζουν τη γλώσσα, η οποία απαιτείται για την κατανόηση και την επίλυση μαθηματικών προβλημάτων, σίγουρα θα αντιμετωπίσουν προβλήματα στα μαθηματικά. Αναφέρει επίσης μερικούς λόγους για τους οποίους οι κωφοί μαθητές αντιμετωπίζουν ιδιαίτερα προβλήματα στην κατανόηση και επίλυση μαθηματικών, αριθμητικών, προβλημάτων. Η χρήση συγκεκριμένης ορολογίας με νέες, δύσκολες και ιδιαίτερες λέξεις (υποτείνουσα, παρονομαστής κλπ) και το διαφορετικό νόημα που έχουν στα μαθηματικά μερικές λέξεις από την καθομιλουμένη είναι μερικά από τα προβλήματα αυτά. Οι Kelly, Lang και Pagliano (2003) ερεύνησαν τις εκπαιδευτικές πρακτικές στη διδασκαλία αριθμητικών προβλημάτων 133 εκπαιδευτικών κωφών μαθητών. Τα αποτελέσματα τους έδειξαν, παρά το γεγονός ότι οι περισσότεροι δεν είχαν τα απαιτούμενα προσόντα για να διδάξουν μαθηματικά, ότι οι εκπαιδευτικοί έδιναν μεγαλύτερη έμφαση στην ικανότητα ανάγνωσης των μαθητών τους και όχι στις αναλυτικές στρατηγικές επίλυσης των προβλημάτων αυτών. Παράλληλα οι εκπαιδευτικοί ασχολήθηκαν ιδιαίτερα με ασκήσεις εξάσκησης παρά με προβλήματα μέσα από πραγματικές καταστάσεις. Οι Ansell και Pagliano (2006) μελέτησαν τις δυσκολίες, τις οποίες αντιμετωπίζουν οι κωφοί και βαρήκοοι μαθητές των πρώτων τριών τάξεων πρωτοβάθμιας εκπαίδευσης κατά την επίλυση αριθμητικών προβλημάτων «προσθετικού τύπου», όταν τα προβλήματα αυτά παρουσιαζόντουσαν στους μαθητές με χρήση Νοηματικής Γλώσσας. Κατέληξαν στο συμπέρασμα ότι οι κωφοί και βαρήκοοι μαθητές είχαν καλύτερες επιδόσεις, σε όλα τα είδη αριθμητικών προβλημάτων, όταν το ζητούμενο του προβλήματος ήταν η τελική ποσότητα και όχι όταν το ζητούμενο ήταν μία από τις αρχικές ή το μέτρο της αλλαγής σε αυτή. 37 []

38 Οι Blatto-Vallee, Kelly, Gaustad, Porter και Fonzi (2007) επίσης ερεύνησαν τη χρήση οπτικών αναπαραστάσεων στο χώρο από κωφούς και ακούοντες φοιτητές κατά τη διάρκεια της επίλυσης μαθηματικών προβλημάτων. Εξέτασαν τη διάκριση μεταξύ των οπτικών «σχηματικών» αναπαραστάσεων, οι οποίες αποκωδικοποιούν τις σχέσεις χώρου σε ένα πρόβλημα, και των οπτικών «εικονιστικών» αναπαραστάσεων στο χώρο, οι οποίες αποκωδικοποιούν μόνο την οπτική εμφάνιση των αντικειμένων σε ένα πρόβλημα. Οι επιδόσεις των 156 ακουόντων μαθητών γυμνασίου, λυκείου και φοιτητών ήταν, σε γενικές γραμμές, σημαντικά καλύτερες από αυτές των 149 κωφών μαθητών γυμνασίου, λυκείου και φοιτητών. Αν και η επίδοση των κωφών φοιτητών ήταν η καλύτερη από την ομάδα των κωφών, ήταν όμως στο ίδιο επίπεδο αυτή της ομάδας των ακουόντων μαθητών γυμνασίου. Όσον αφορά τη σχέση ανάγνωσης επίλυσης αριθμητικών προβλημάτων, ο Pau (1995), στο πλαίσιο της διδακτορικής του διατριβής, ανέλυσε την επιρροή του επιπέδου ανάγνωσης κωφών μαθητών στην επίλυση προφορικών αριθμητικών προβλημάτων. Τα αποτελέσματα έδειξαν ότι υπάρχει μια θετική συσχέτιση των παραπάνω αφού αν δεν κατανοήσουν το πρόβλημα που τους παρατίθεται προφορικά οι κωφοί μαθητές δεν μπορούν να το επιλύσουν. Οι Zevenbergen, Hyde και Power (2002) επίσης εξέτασαν τις επιδόσεις σε αριθμητικά προβλήματα κωφών και βαρήκοων μαθητών στην Νότιο-Ανατολική Αυστραλία, περιοχή Victoria. Τα αποτελέσματα τους έδειξαν ότι υπάρχει συσχέτιση της κατάκτησης της ανάγνωσης με την ικανότητα επίλυσης αριθμητικών προβλημάτων. Οι Kelly, Lang, Mousley και Davis (2003) ανέλυσαν τις επιδόσεις κωφών φοιτητών στην επίλυση αριθμητικών προβλημάτων «σύγκρισης». Τα προβλήματα που χρησιμοποιήθηκαν στην έρευνα περιείχαν αναφορικές φράσεις, οι οποίες είτε ήταν συνεπείς είτε ασυνεπείς προς την αριθμητική διαδικασία που απαιτούσε το πρόβλημα. Τα αποτελέσματα έδειξαν αφενός συσχέτιση της ικανότητας ανάγνωσης των φοιτητών με την επίδοση τους και αφετέρου ότι οι φοιτητές έκαναν πιο πολλά λάθη όταν οι αναφορικές φράσεις ήταν ασυνεπείς με τις διαδικασίες που 38 []

39 απαιτούσε η λύση του προβλήματος. Για παράδειγμα όταν το πρόβλημα ήθελε να κάνει ο φοιτητές πρόσθεση και χρησιμοποιούσε την φράση «λιγότερα από». Παράλληλα οι Hyde, Zevenbergen και Power (2003) εξέτασαν τις επιδόσεις σε αριθμητικά προβλήματα κωφών και βαρήκοων μαθητών στην Νότιο-Ανατολική Αυστραλία, περιοχή Queensland, καθώς επίσης και τις στρατηγικές που ακολούθησαν οι μαθητές για να οδηγηθούν στην λύση του κάθε προβλήματος. Τα αποτελέσματα, επιβεβαιώνοντας παλαιότερες σχετικές έρευνες, έδειξαν ότι οι κωφοί και οι βαρήκοοι μαθητές, εξαιτίας της καθυστέρηση τους στην κατάκτηση της ανάγνωσης, επηρεάζεται η ικανότητα τους στην επίλυση αριθμητικών προβλημάτων. Στηριζόμενη στην εργασία των Hyde, Zevenbergen και Power (2003), η παρούσα εργασία εξετάζει τις επιδόσεις κωφών και βαρήκοων μαθητών πέμπτης και έκτης τάξης δύο ειδικών δημοτικών σχολείων κωφών της χώρας, στην Αργυρούπολη και στην Πάτρα. Στόχος της είναι η μελέτη των επιδόσεων κωφών μαθητών σε αριθμητικά προβλήματα σε σχέση με την τάξη που παρακολουθούν και το είδος του αριθμητικού προβλήματος και η επίδραση της χρήσης Ελληνικής Νοηματικής Γλώσσας στη κατανόηση των προβλημάτων αυτών. 39 []

40 40 [] κεφάλαιο τρίτο

41 3. Μεθοδολογία 3.1 Δείγμα Η έρευνα πραγματοποιήθηκε το δεύτερο τετράμηνο του σχολικού έτους και συμμετείχαν μαθητές των Ειδικών Δημοτικών Σχολείων Κωφών και Βαρηκόων Αργυρούπολης και Πάτρας και του Δημοτικού Σχολείου Γαλατά Τροιζήνας. Την ομάδα ελέγχου αποτελούν 30 μαθητές (Ν=30) πέμπτης και έκτης τάξης του 12/θέσιου Δημοτικού Σχολείου Γαλατά Τροιζήνας, ηλικίας 9-12 ετών. Συγκεκριμένα οκτώ αγόρια και επτά κορίτσια από το πρώτο τμήμα της πέμπτης τάξης και επτά αγόρια και οκτώ κορίτσια από το πρώτο τμήμα της έκτης τάξης. Ο διαχωρισμός σε τμήματα ανά τάξη γίνεται αλφαβητικά και όχι βάση σχολικής επίδοσης. Την πειραματική ομάδα αποτελούν επτά μαθητές (Ν=7) πέμπτης και έκτης τάξης, τέσσερις από το Ειδικό Δημοτικό Σχολείο Κωφών και Βαρηκόων Αργυρούπολης και τρεις από το Ειδικό Δημοτικό Σχολείο Κωφών και Βαρηκόων Πάτρας. Συγκεκριμένα δύο κορίτσια από το πρώτο τμήμα και ένα αγόρι και ένα κορίτσι από το δεύτερο τμήμα του σχολείου της Αργυρούπολης και δύο αγόρια και ένα κορίτσι από το σχολείο της Πάτρας. Και στα δύο ειδικά δημοτικά το κάθε τμήμα περιλαμβάνει μαθητές επίπεδου πέμπτης και έκτης τάξης. Από το σύνολο των παιδιών των ειδικών σχολείων, σύμφωνα με τις αναφορές των δασκάλων τους, τέσσερις μαθητές θεωρούνται κωφοί και τρεις βαρήκοοι. Όσον αφορά την εκπαίδευση, τρείς μαθητές από αυτούς εκπαιδεύτηκαν σε ειδικό σχολείο κωφών από την αρχή της σχολικής ζωής τους, τρείς μαθητές μετά από μερικά χρόνια σε σχολείο γενικής εκπαίδευσης και ένας μετά από μερικά χρόνια σε ειδικό σχολείο για παιδιά με νοητική καθυστέρηση και αυτισμό. Δύο μόνο από τους μαθητές έχουν κωφούς γονείς. 41 []

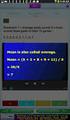
42 Πίνακας 3.1 Χαρακτηριστικά κωφών μαθητών Χαρακτηριστικά Πέμπτη τάξη Έκτη τάξη κωφός-ή 2 2 βαρήκοος-η 1 2 κωφοί γονείς 0 2 ακούοντες γονείς 3 2 φοίτηση σε ειδικό κωφών από την αρχή 1 2 φοίτηση πρώτα σε γενικής 2 1 φοίτηση πρώτα σε άλλο ειδικό []

43 3.2 Ερευνητικό εργαλείο Χρησιμοποιήθηκε το τεστ από την έρευνα των Hyde, Zevenbergen, Power (2003) με ερωτήσεις και από τις τρεις κατηγορίες αριθμητικών προβλημάτων (αλλαγής, σύγκρισης και συνδυασμού). Συνολικά χρησιμοποιήθηκαν 14 ερωτήσεις, 6 από τις πρώτες δύο κατηγορίες, αλλαγής και σύγκρισης (Πίνακες 3.2 και 3.3), και 2 από την τρίτη κατηγορία, συνδυασμού (Πίνακας 3.4). Πίνακας 3.2 Ερωτήσεις «αλλαγής» Η Βαρβάρα έχει 2 μήλα. Ο Σωτήρης έδωσε στην Βαρβάρα ένα μήλο ακόμα. Πόσα μήλα έχει τώρα η Βαρβάρα; Ο Κώστας έχει 4 μολύβια. Η Άννα πήρε από τον Κώστα τα 3 μολύβια. Πόσα μολύβια έχει τώρα ο Κώστας; Ο Πέτρος είχε 3 μπανάνες. Η Ελένη έδωσε στον Πέτρο μερικές μπανάνες ακόμα. Ο Πέτρος τώρα έχει 5 μπανάνες. Πόσες μπανάνες του έδωσε η Ελένη; Η Ειρήνη είχε 5 βιβλία. Ο Γιάννης πήρε μερικά βιβλία από την Ειρήνη. Τώρα η Ειρήνη έμεινε με 2 βιβλία μόνο. Πόσα από τα βιβλία της Ειρήνης πήρε ο Γιάννης; Ο Γιώργος είχε μερικά τετράδια. Ο πατέρας του τού έδωσε 2 τετράδια ακόμα. Τώρα αυτός έχει 5 τετράδια. Πόσα τετράδια είχε ο Γιώργος στην αρχή; Η Αλεξάνδρα έχει μερικές φωτογραφίες. Έχασε 2 από τις φωτογραφίες της. Τότε είχε 3 φωτογραφίες. Πόσες φωτογραφίες είχε στην αρχή; 43 []