A Two Sample Test for Mean Vectors with Unequal Covariance Matrices
|
|
|
- Ζώπυρος Βίων Φλέσσας
- 6 χρόνια πριν
- Προβολές:
Transcript
1 A Two Sample Test for Mean Vectors wth Unequal Covarance Matrces Tamae Kawasak 1 and Takash Seo 2 1 Department of Mathematcal Informaton Scence Graduate School of Scence, Tokyo Unversty of Scence, Tokyo, Japan 2 Department of Mathematcal Informaton Scence Faculty of Scence, Tokyo Unversty of Scence, Tokyo, Japan Abstract In ths paper, we consder testng the equalty of two mean vectors wth unequal covarance matrces. In the case of equal covarance matrces, we can use Hotellng s T 2 statstc, whch follows the F dstrbuton under the null hypothess. Meanwhle, n the case of unequal covarance matrces, the T 2 type test statstc does not follow the F dstrbuton, and t s also dffcult to derve the exact dstrbuton. In ths study, we propose an approxmate soluton to the problem by adjustng the degrees of freedom of the F dstrbuton. That s, we derve an extenson of the results derved by Yanaghara and Yuan (2005). Asymptotc expansons up to the term of order N 2 for the frst and second moments of the test statstc are gven, where N s the total sample sze mnus two, and a new result of the approxmate degrees of freedom s obtaned. Fnally, numercal comparson s presented by a Monte Carlo smulaton. Keywords Approxmate degrees of freedom; F approxmaton; Hotellng s T 2 statstc; Multvarate Behrens-Fsher problem; Two sample problem. 1 Introducton Let x 1,..., x j,..., x n be p-dmensonal random vectors from N p (µ, Σ ), = 1, 2, j = 1, 2,..., n. We consder the followng hypothess test problem: H 0 : µ 1 = µ 2 vs. H 1 : µ 1 µ 2, (1.1) where Σ 1 Σ 2. A natural statstc for testng (1.1) s ( T = (x 1 x 2 ) S1 + S ) 1 2 (x 1 x 2 ), n 1 n 2 where x = 1 n n j=1 x j, S = 1 n 1 n j=1 (x j x )(x j x ). 1
2 When n 1 = n 2 and Σ 1 = Σ 2, the T statstc s reduced to the two sample Hotellng s T 2 statstc. Then, under the null hypothess n (1.1), (n p 1)T/{p(n 2)} follows the F dstrbuton wth p and n p 1 degrees of freedom, where n = n 1 + n 2. To consder the tests for equalty of two mean vectors s a fundamental problem. Mean comparson wth unequal varances s ntrnscally dffcult, and s well known as the Behrens-Fsher problem. Welch (1938) and Scheffé (1943) proposed approxmate solutons for the unvarate case. One of the earlest methods for solvng the multvarate Behrens-Fsher problem was derved by Bennett (1951) based on an extenson of Scheffé s (1943) unvarate soluton. Some approxmate solutons were consdered by James (1954), Yao (1965), Johansen (1980), Nel et al. (1990), and Km (1992). Nel et al. (1986) obtaned the exact null dstrbuton of T, and Krshnamoorthy and Yu (2004) proposed a modfcaton to the soluton. Recently, Krshnamoorthy and Yu (2012) proposed a soluton extendng the modfed Nel and Van der Merwe s test procedure n ther earler study to the case of ncomplete data wth a monotone pattern. The problem concerns the dfference between the mean vectors of two normal populatons wth the case of a monotone mssng pattern when Σ 1 = Σ 2, as suggested by Seko, Kawasak and Seo (2011). Grón and del Castllo (2010) studed the multvarate Behrens-Fsher dstrbuton, whch s defned as the convoluton of two ndependent multvarate Student t dstrbutons. Yanaghara and Yuan (2005) provded three approxmate solutons to the multvarate Behrens-Fsher problem that are two F approxmatons wth approxmate degrees of freedom and modfed Bartlett corrected statstc. However, these solutons are not good approxmatons when the dfference between the covarance matrces s large. Our goal s to gve a new approxmate soluton by an extenson of Yanaghara and Yuan (2005). The followng secton presents a dervaton of the man result by approxmate degrees of freedom and presents the proof. In Secton 3, we compare four approxmate procedures by Monte Carlo smulaton and evaluate the advantages of the proposed procedures. In the Appendx, we present certan formulas used to derve the man result. 2
3 2 Approxmate Degrees of Freedom Assumng the standard regularty condton n /n = O(1), = 1, 2, then, as n Yanaghara and Yuan (2005), we can wrte where z = T = z W 1 z = z z U, (2.1) n1 n ( 2 n Σ 1/2 (x 1 x 2 ), W = Σ 1/2 n 2 n S 1 + n ) 1 n S 2 Σ 1/2, By approxmatng the dstrbuton of U as Σ = n 2 n Σ 1 + n 1 n Σ 2, U = z z z W 1 z. we have U χ2 ν ϕ, (2.2) ν pϕ T χ2 p/p χ 2 ν/ν F p,ν. Note that when Σ 1 = Σ 2 and n 1 = n 2, U s exactly dstrbuted as χ 2 ν/ϕ, where ν = n p 1 and ϕ = n 2. In general, the constants ν and ϕ can be gven usng the followng theorems for the frst and second moments of U. Theorem 2.1 Let U = z z/z W 1 z be defned by (2.1). Then, an asymptotc expanson up to the term of order N 2 for E[U] can be expanded as where E[U] = 1 θ 1 N + 1 N 2 (θ 2 θ 3 ) + O(N 3 ), (2.3) N =n 2, θ 1 = 1 p(p + 2) =1 c {p(a (1) ) 2 + (p 2)a (2) }, 3
4 1 θ 2 = p(p + 2)(p + 4) =1 { 1 θ 3 = p(p + 2)(p + 4)(p + 6) d {4p 2 a (3) + (p 2)(3p + 4)a (1) a (2) + p(p + 2)(a (1) ) 3 }, =1 c 2 { p 2 (5p + 14)a (4) + 4(p + 3)(p + 2)(p 2)a (1) a (3) +p(p + 3)(p 2)(a (2) ) 2 + 2(p 3 + 5p 2 + 7p + 6)a (2) (a (1) ) 2 p(p + 4)(a (1) ) 4} + 4(p + 3)(p + 2)(p 2)ψ 1 + 4p(p + 2)(p 2)ψ 2 + 4p(p + 4)(p + 2)ψ 3 2p(p 2)ψ 4 2(p + 3)(p 2)ψ 5 2p(p + 4)(p 2)ψ 6 2p(p + 4)ψ 7 + 2p(p + 4)(3p + 2)ψ 8 }, wth ψ k, k = 1, 2,..., 7 gven by ψ 1 = c 1 c 2 {a (1) 1 b(1, 2, 1) + a (1) 2 b(2, 1, 1) }, ψ 2 = c 1 c 2 b (2, 2, 1), ψ 3 = c 1 c 2 a (1) 1 a(1) 2 b(1, 1, 1), ψ 4 = c 1 c 2 a (2) 1 a(2) 2, ψ 5 = c 1 c 2 {a (2) 1 (a(1) 2 )2 + (a (1) 1 )2 a (2) 2 }, ψ 6 = c 1 c 2 (b (1, 1, 1) ) 2, ψ 7 = c 1 c 2 (a (1) 1 )2 (a (1) 2 )2, ψ 8 = c 1 c 2 b (1,1,2), and c = (n n ) 2 (n 2) n 2, d = (n n ) 3 (n 2) 2 (n 1) n 3 (n 1) 2, a (l) = tr(σ Σ 1 ) l, = 1, 2, l = 1, 2, 3, 4, b (q, r, s) = tr{(σ 1 Σ 1 ) q (Σ 2 Σ 1 ) r } s, (q, r, s) = (1, 1, 1), (1, 1, 2), (1, 2, 1), (2, 1, 2), (2, 2, 1). Proof. Let ρ = n 1 n n 2 ( = 1, 2), Ω n = n 1 Σ 2 Σ 1 2 and V = n 1(Σ 1/2 S Σ 1/2 I p ), = 1, 2. Then, W 1 can be expanded as where W 1 = I p 1 N V + 1 N V 2 1 N N V N 2 V 4 + O p (N 5/2 ), (2.4) V = =1 ρ 1 Ω V Ω. 4
5 Note that U = z z/z W 1 z. It follows from (2.4) that we can expand U as U =1 + 1 N Q N (Q2 1 Q 2 ) + 1 N N (Q 3 2Q 1 Q 2 + Q 3 1) + 1 N 2 (Q4 1 Q 4 + 2Q 1 Q 3 + Q 2 2 3Q 2 1Q 2 ) + O p (N 5/2 ), where Q = z V z/z z, = 1, 2, 3, 4. Note that V and z are ndependent, and so are z V z/z z and z z, as well as z V 2 z/z z and z z (see Fang et al., 1990, p.30). In the same way as n Yanaghara and Yuan (2005), the followng results can be obtaned after a good deal of calculaton: () E[Q 1 ] = 0, () E[Q 2 ] = 1 p E[Q 2 1] = =1 2 p(p + 2) () NE[Q 3 ] = 1 p NE[Q1 Q 2 ] = NE[Q 3 1 ] = c {(a (1) ) 2 + a (2) }, =1 =1 c {(a (1) ) 2 + 2a (2) }, d {4a (3) + 3a (1) a (2) + (a (1) ) 3 }, 2 p(p + 2) =1 8 p(p + 2)(p + 4) d {6a (3) + 5a (1) a (2) + (a (1) ) 3 }, =1 d {8a (3) + 6a (1) a (2) + (a (1) ) 3 }, (v) E[Q 4 ] = 1 { c 2 {5a (4) + 4a (1) a (3) + (a (2) ) 2 + 2a (2) (a (1) ) 2 } p =1 } +2(2ψ 1 + 2ψ 2 + 2ψ 3 + ψ 6 + 3ψ 8 ) + O(N 1 ), { E[Q ] = c 2 {48a (4) +32a (1) a (3) +12(a (2) ) 2 +12a (2) (a (1) ) 2 +(a (1) ) 4 } p(p + 2)(p + 4)(p + 6) =1 } +2(16ψ ψ 2 + 8ψ 3 + 4ψ 4 + 2ψ 5 + 8ψ 6 + ψ ψ 8 ) + O(N 1 ), E[Q 1 Q 3 ] = { 2 c 2 {8a (4) + 7a (1) a (3) + (a (2) ) 2 + 2a (2) (a (1) ) 2 } p(p + 2) =1 } +(7ψ ψ 2 + 4ψ 3 + 2ψ 6 + 6ψ 8 ) + O(N 1 ), 5
6 { E[Q 2 1 2] = c 2 {14a (4) + 8a (1) a (3) + 7(a (2) ) 2 + (a (1) ) 4 + 6a (2) (a (1) ) 2 } p(p + 2) =1 } +2(4ψ 1 + 4ψ 2 + 4ψ 3 + ψ 4 + ψ 5 + 6ψ 6 + ψ ψ 8 ) + O(N 1 ), E[Q 2 1Q 2 ] = 2 p(p + 2)(p + 4) { =1 c 2 {40a (4) + 28a (1) a (3) + 10(a (2) ) a (2) (a (1) ) 2 + (a (1) ) 4 } +28ψ ψ ψ 3 + 4ψ 4 + 3ψ ψ 6 + 2ψ ψ 8 } + O(N 1 ). Usng the above results, we can show (2.3). Ths completes the proof of Theorem 2.1. In addton, we have the followng result. Corollary 2.1 If Σ 1 = Σ 2, n 1 = n 2, then E[U] = (p 1) + N N 2 p 2 (p 2) (p + 2)(p + 6) + O(N 3 ). Smlarly, as the result of asymptotc expanson for E[U 2 ],we have the followng theorem. Theorem 2.2 Let U = z z/z W 1 z be defned by (2.1). Then, an asymptotc expanson up to the term of order N 2 for E[U 2 ] can be expanded as where 1 θ 4 = p(p + 2) E[U 2 ] = 1 2 N (θ 1 θ 4 ) + 1 N 2 (2θ 5 θ 6 ) + O(N 3 ), (2.5) =1 1 θ 5 = p(p + 2)(p + 4) { c (a (1) ) 2 } + 2a (2), =1 d { 4(p 2 3p + 4)a (3) + 3p(p 4)a (1) a (2) + p 2 (a (1) ) 3}, 6
7 { 1 θ 6 = c 2 {2(p + 1)(5p 2 14p + 24)a (4) + 4(p 4)(2p 2 + 5p + 6)a (1) a (3) p(p + 2)(p + 4)(p + 6) =1 + (p 2)(p 4)(2p + 3)(a (2) ) 2 + 2(p + 2)(2p 2 p + 12)a (2) (a (1) ) 2 3(p 2 + 2p 4)(a (1) ) 4 } + 4(p 4)(2p 2 + 5p + 6)ψ 1 + 8p(p 2)(p 4)ψ 2 + 8p(p 2 + 4p + 2)ψ 3 6(p 2)(p 4)ψ 4 6(p 4)(p + 2)ψ 5 +4(p + 3)(p 2)(p 4)ψ 6 6(p 2 + 2p 4)ψ 7 +12(p 3 +p 2 2p + 8)ψ 8 }. Proof. In the same way, we can expand U 2 as U 2 =1 + 2 N Q N (3Q2 1 2Q 2 ) + 2 N N (Q 3 3Q 1 Q 2 + 2Q 3 1) + 1 N 2 (5Q4 1 2Q 4 + 6Q 1 Q 3 + 3Q Q 2 1Q 2 ) + O p (N 5/2 ). By calculatng the expectatons of the above results, we can show (2.5). Ths completes the proof of Theorem 2.2. In addton, we have the followng result. Corollary 2.2 If Σ 1 = Σ 2, n 1 = n 2, then E[U 2 ] = (p 2) + N N 2 p5 + 6p 4 p 3 92p 2 60p O(N 3 ). (p + 2)(p + 4)(p + 6) It follows from (2.2) that E[U] ν ϕ, E[U 2 ] ν(ν + 2) ϕ 2. Therefore, usng the asymptotc expansons of E[U] and E[U 2 ] n Theorems 2.1 and 2.2, the new approxmaton to the values of ν and ϕ are gven by ν KS = ϕ KS = 2(N 2 Nθ 1 + θ 2 θ 3 ) 2 N 2 (N 2 2Nθ 1 + 2Nθ 4 + 2θ 5 θ 6 ) (N 2 Nθ 1 + θ 2 θ 3 ) 2, (2.6) N 2 ν N 2 Nθ 1 + θ 2 θ 3, (2.7) respectvely. We can propose a new procedure as follows. 7
8 (I) Hgh Order Procedure T KS = ν KS pϕ KS T a F p,νks where ν KS and ϕ KS are gven by (2.6) and (2.7), respectvely, and where a means approxmately followng. If θ 2 = θ 3 = θ 5 = θ 6 = 0, then ν KS = (N θ 1) 2 Nθ 4 θ 2 1 /2(= ν Y ), ϕ KS = ν Y N N θ 1 (= ϕ Y ), (2.8) and these values are the same as the results of Yanaghara and Yuan (2005). In addton, they slghtly adjust the coeffcent ν Y to whch wll be used to obtan the F approxmaton. 3 Numercal Studes ν M = (N θ 1) 2 Nθ 4 θ 1, (2.9) In ths secton, we perform a Monte Carlo smulaton n order to nvestgate the accuracy of our procedure (I) and to compare t wth the followng three procedures: (II) Yanaghara and Yuan s (2005) Procedure where ν Y and ϕ Y are gven by (2.8). T Y = ν Y pϕ Y T a F p,νy (III) Modfed Yanaghara and Yuan s (2005) Procedure where T M = ν M pϕ M T a F p,νm ϕ M = ν MN N θ 1 and ν M s gven by (2.9). 8
9 (IV) Modfed Bartlett Procedure (see Yanaghara and Yuan (2005)) ( T MB = (N β 1 + β 2 ) log 1 + T ) a N β χ 2 p, 1 where 2 β 1 =, β2 = (p + 2) γ 2 2(p + 4) γ 1, γ 2 2 γ 1 2( γ 2 2 γ 1 ) γ 1 = 1 c {(â (1) ) â (2) }, γ 2 = c {2(p + 3)(â (1) ) 2 + 2(p + 4)â (2) }, p p(p + 2) =1 â (l) = tr(s S 1 ) l, S = n 2 n S 1 + n 1 n S 2. For each of parameter, the smulaton was carred out for 1,000,000 trals based on normal random vectors. Wthout loss of generalty, we can assume that µ 1 = µ 2 = 0. We compare the followng type I errors for four procedures: (I) α 1 = P(T KS > F α;p,νks ), (II) α 2 = P(T Y > F α;p,νy ), (III) α 3 = P(T M > F α;p,νm ), (IV) α 4 = P(T MB > c α;p ), where F α;m,n s the upper 100α percentle of the F dstrbuton wth m and n degrees of freedom and c α;p s the upper 100α percentle of the ch-square dstrbuton wth p degrees of freedom. We choose α = 0.05, 0.01, p = 4, 8, and the sample szes (n 1, n 2 ) = (10, 10), (10, 20), (20, 10), (20, 20), (50, 50), (50, 80), (80, 50), (80, 80) for (I) (IV). We note that the second degree of freedom of F dstrbuton for the test statstc (I) (III) changes wth each smulaton of 1,000,000 trals. In practcal use, we must estmate a (l) ths paper, we use the consstent estmators of a (l) procedure (IV). =1 and b (q,r,s) for (I) (III) snce Σ and Σ are unknown. In and b (q,r,s), whch are the same as that of Table 1 presents the emprcal szes α j, j = 1, 2, 3, 4 n the case of Σ 1 = dag(η, η 2,, η p ) and Σ 2 = I, where η = 1, 5(5)20. We note that Σ 1 1 and the dfference between Σ 1 and Σ 2 s large when η s large. Tables 2 and 3 present the emprcal szes α j, j = 1, 2, 3, 4 n the case of Σ 1 = σ 2 I and Σ 2 = I, where σ 2 = 0.1(0.2)0.9,1 n Table 2, and σ 2 = 2, 5(5)30 n Table 3. We note that the emprcal szes for the case of Σ 1 1 and Σ 1 > 1 are gven n Tables 2 and 3, respectvely. The last row of each of these tables ndcates the average absolute dscrepancy (AAD). In ths context, see Yanaghara and Yuan (2005). 9
10 Table 1 Emprcal szes ( α 1 α 4 ) when p = 4, 8, and η = 1, 5(5)20 α = 0.05 α = 0.01 p n 1 n 2 η α 1 α 2 α 3 α 4 α 1 α 2 α 3 α AAD AAD Note : AAD = 100 α 100α /20 10
11 Table 2 Emprcal szes ( α 1 α 4 ) when p = 4, 8 and σ 2 = 0.1(0.2)0.9, 1 α = 0.05 α = 0.01 p n 1 n 2 σ 2 α 1 α 2 α 3 α 4 α 1 α 2 α 3 α AAD Note : AAD = 100 α 100α /24 11
12 Table 2 (Contnued) α = 0.05 α = 0.01 p n 1 n 2 σ 2 α 1 α 2 α 3 α 4 α 1 α 2 α 3 α AAD Note : AAD = 100 α 100α /24 12
13 Table 3 Emprcal szes ( α 1 α 4 ) when p = 4, 8 and σ 2 = 2, 5(5)30 α = 0.05 α = 0.01 p n 1 n 2 σ 2 α 1 α 2 α 3 α 4 α 1 α 2 α 3 α AAD Note : AAD = 100 α 100α /28 13
14 Table 3 (Contnued) α = 0.05 α = 0.01 p n 1 n 2 σ 2 α 1 α 2 α 3 α 4 α 1 α 2 α 3 α AAD Note : AAD = 100 α 100α /28 14
15 From Table 1, t s seen that the proposed approxmatons α 1 are very good for cases when η s large. In contrast, t seems that other α are farther from α as η becomes large. It may also be noted that α 1 s stable and a good approxmaton to α when n 1 and n 2 are large. From Table 2, we can see that α 3 s AAD and α 4 s AAD are lower than the others, and ther approxmatons are good for the case of p = 4, an that α 1 s a good approxmaton for the case of p = 8. On the other hand, t seems from Table 2 that the emprcal szes are almost unchanged except for α 2. It can be seen from Table 3 that α 3 are closer to α when p = 4. Meanwhle, the behavor of α 1 resembles the behavor of α 4. In addton, t s seen from Table 3 that α 1 and α 3 are good approxmatons when p = 8. In concluson, when the dfference between covarance matrces s large, the approxmate upper percentle of the null dstrbuton of T by the method (hgh order procedure) proposed n ths paper s better than those of other procedures. Appendx In ths Appendx, we present some results of expectaton: A.1 Let u N p (0, I) wth A and B are p p symmetrc matrces, then (1) E[u Au] = tra, (2) E[u u(u Au)] = (p + 2)(trA), (3) E[(u Au) 2 ] = 2(trA 2 ) + (tra) 2, (4) E[(u Au)(u Bu)] = 2(trAB) + (tra)(trb), (5) E[(u Au) 3 ] = 8(trA 3 ) + 6(trA 2 )(tra) + (tra) 3, (6) E[(u Au) 2 (u Bu)] = 8(trA 2 B) + 4(trAB)(trA) + 2(trA 2 )(trb) + (tra) 2 (trb), (7) E[(u Au) 4 ] = 48(trA 4 ) + 32(trA 3 )(tra) + 12(trA 2 )(tra) (trA 2 ) 2 + (tra) 4. 15
16 A.2 Let S W p (n, Σ) and V = n(s Σ) wth A, B and C are p p symmetrc matrces, then (1) E[(trAV ) 2 ] = 2 tr(aσ) 2, (2) E[tr(AV ) 2 ] = tr(aσ) 2 + (traσ) 2, (3) E[(trAV BV )] = (trav BV ) + (traσ)(trbσ), (4) E[{tr(AV )} 3 ] = 8 n tr(aσ) 3, (5) E[tr(AV ) 3 ] = 1 n [4 tr(aσ) 3 + 3{tr(AΣ) 2 }(traσ) + (traσ) 3 ], (6) E[(trAV ){tr(av ) 2 }] = 4 n [tr(aσ) 3 + (traσ){tr(aσ) 2 }], (7) E[(trAV ) 2 (trbv )] = 8 n {tr(aσ) 2 BΣ}, (8) E[(trAV ) 4 ] = 12{tr(AΣ) 2 } 2 + O(N 1 ) (9) E[tr(AV ) 4 ] = 5 tr(aσ) 4 +4{tr(AΣ) 3 }(traσ)+2{tr(aσ) 2 }(traσ) 2 +{tr(aσ) 2 } 2 +O(N 1 ), (10) E[(trAV ){tr(av ) 3 }] = 6[ tr(aσ) 4 + (traσ){tr(aσ) 3 }] + O(N 1 ), (11) E[{tr(AV ) 2 } 2 ] = 5{tr(AΣ) 2 } tr(aσ) 4 + 2{tr(AΣ) 2 }(traσ) 2 + (traσ) 4 + O(N 1 ), (12) E[(trAV ) 2 {tr(av ) 2 }] = 8 tr(aσ) 4 + 2{tr(AΣ) 2 } 2 + 2{tr(AΣ) 2 }(traσ) 2 + O(N 1 ), (13) E[(trAV ) 3 (trbv )] = 12{tr(AΣ) 2 }(traσbσ) + O(N 1 ), (14) E[(trAV ) 2 (trbv ) 2 ] = 8(trAΣBΣ) 2 + 4{tr(AΣ) 2 }{tr(bσ) 2 } + O(N 1 ), (15) E[(trAV ) 2 (trbv )(trcv )] = 8(trAΣBΣ)(trAΣCΣ) + 4{tr(AΣ) 2 }(trbσcσ) + O(N 1 ). 16
17 A.3 Let S W p (n, Σ) and V = n(s Σ) wth A, B, C and D are p p symmetrc matrces where = 1, 2, then (1) E[tr(AV 1 ) 2 (BV 2 ) 2 ] = tr(aσ) 2 (BΣ) 2 + (traσ){traσ(bσ) 2 } + {tr(aσ) 2 BΣ}(trBΣ) +(traσ)(trbσ)(traσbσ), (2) E[(trAV 1 BV 2 ) 2 ] = 2{tr(AΣ) 2 (BΣ) 2 } + {tr(aσ) 2 }{tr(bσ) 2 } + (traσbσ) 2, (3) E[{tr(AV 1 ) 2 }{tr(bv 2 ) 2 }] = {tr(aσ) 2 }{tr(bσ) 2 } + {tr(aσ) 2 }(trbσ) 2 +(traσ) 2 {tr(bσ) 2 } + (traσ) 2 (trbσ) 2, (4) E[(trAV 1 ) 2 (trbv 2 ) 2 ] = 4{tr(AΣ) 2 }{tr(bσ) 2 }, (5) E[{tr(AV 1 ) 2 }(trbv 2 ) 2 ] = 2{tr(AΣ) 2 }{tr(bσ) 2 } + 2(trAΣ) 2 {tr(bσ) 2 }, (6) E[(trAV 1 ){trav 1 (BV 2 ) 2 }] = 2{tr(AΣ) 2 (BΣ) 2 } + 2{tr(AΣ) 2 BΣ}(trBΣ), (7) E[(trAV 1 )(trbv 2 )(trav 1 BV 2 )] = 4{tr(AΣ) 2 (BΣ) 2 }, (8) E[trAV 1 BV 1 CV 2 DV 2 ] = (traσbσcσdσ) + (traσbσcσ)(trdσ) +(traσcσdσ)(trb) + (traσcσ)(trbσ)(trdσ). A.4 The followng results are presented as supplementary expectatons: (1) E[tr(Ω 2 Ω 1V 1 Ω 1 Ω 2V 2 ) 2 ] = 3tr(Ω 1 Ω 1 Ω 2Ω 2 )2 + (trω 1 Ω 1 Ω 2Ω 2 )2, (2) E[(trΩ 1 Ω 1V 1 )(trω 2 Ω 1V 1 Ω 1 Ω 2V 2 Ω 2 Ω 2V 2 )] = 2{tr(Ω 1 Ω 1) 2 Ω 2 Ω 2}(trΩ 2 Ω 2) +2{tr(Ω 1 Ω 1) 2 (Ω 2 Ω 2) 2 }, (3) E[(trΩ 2 Ω 1V 1 Ω 1 Ω 2V 2 ) 2 ] = 2tr(Ω 1 Ω 1 Ω 2Ω 2 )2 + 2(trΩ 1 Ω 1 Ω 2Ω 2 )2, (4) E[(trΩ 1 Ω 1V 1 )(trω 2 Ω 2V 2 )(trω 2 Ω 1V 1 Ω 1 Ω 2V 2 )] = 4{tr(Ω 1 Ω 1) 2 (Ω 2 Ω 2) 2 }, where the notatons are defned by Secton 2. 17
18 Acknowledgments Second author s research was n part supported by Grant-Ad for Scentfc Research (C) ( ). References [1] Bennett, B. M. (1951). Note on a soluton of the generalzed Behrens-Fsher problem. Ann. Inst. Statst. Math., 2, [2] Fang, K. T., Kotz, S. and Ng, K. W. (1990). Symmetrc multvarate and related dstrbutons. London; Chapman & Hall / CRC. [3] Fujkosh, Y. (2000). Transformatons wth mproved ch-square approxmatons. J. Multvarate Anal., 72, [4] Grón, F. J. and del Castllo, C. (2010). The multvarate Behrens-Fsher dstrbuton. J. Multvarate Anal., 101, [5] James, G. S. (1954). Tests of lnear hypotheses n unvarate and multvarate analyss when the ratos of the populaton varances are unknown. Bometrka, 41, [6] Johansen, S. (1980). The Welch-James approxmaton to the dstrbuton of the resdual sum of squares n a weghted lnear regresson. Bometrka, 67, [7] Km, S. - J. (1992). A practcal soluton to the multvarate Behrens-Fsher problem. Bometrka, 79, [8] Krshnamoorthy, K. and Yu, J. (2004). Modfed Nel and Van der Merwe test for the multvarate Bahrens-Fsher problem. Statst. Probab. Lett., 66, [9] Krshnamoorthy, K. and Yu, J. (2012). Multvarate Behrens-Fsher problem wth mussng data. J. Multvarate Anal., 105, [10] Nel, D. G. and van der Merwe, C. A. (1986). A soluton to the multvarate Behrens-Fsher problem. Comm. Statst., Theory Methods, 15, [11] Nel, D. G., van der Merwe, C. A. and Moser, B. K. (1990). The exact dstrbutons of the unvarate and multvarate Behrens-Fsher statstcs wth a comparson of several solutons n the unvarate case. Comm. Statst., Theory Methods, 19, [12] Scheffé, H. (1943). On solutons of the Behrens-Fsher problem, based on the t-dstrbuton. Ann. Math. Statst., 14, [13] Seko, N., Kawasak, T. and Seo, T. (2011). Testng equalty of two mean vectors wth two-step monotone mssng data. Amer. J. Math. Management Sc., 31, [14] Welch, B. L. (1938). The sgnfcance of the dfference between two means when the populaton varances are unequal. Bometrka, 29, [15] Yanaghara, H. and Yuan, K. (2005). Three approxmate solutons to the multvarate Behrens-Fsher problem. Comm. Statst., Smulaton Comput., 34, [16] Yao, Y. (1965). An approxmate degrees of freedom soluton to the multvarate Behrens- Fsher problem. Bometrka, 52,
α & β spatial orbitals in
 The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Variance of Trait in an Inbred Population. Variance of Trait in an Inbred Population
 Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών. ΗΥ-570: Στατιστική Επεξεργασία Σήµατος. ιδάσκων : Α. Μουχτάρης. εύτερη Σειρά Ασκήσεων.
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
One and two particle density matrices for single determinant HF wavefunctions. (1) = φ 2. )β(1) ( ) ) + β(1)β * β. (1)ρ RHF
 One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Generalized Fibonacci-Like Polynomial and its. Determinantal Identities
 Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
8.1 The Nature of Heteroskedasticity 8.2 Using the Least Squares Estimator 8.3 The Generalized Least Squares Estimator 8.
 8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Vol. 34 ( 2014 ) No. 4. J. of Math. (PRC) : A : (2014) Frank-Wolfe [7],. Frank-Wolfe, ( ).
![Vol. 34 ( 2014 ) No. 4. J. of Math. (PRC) : A : (2014) Frank-Wolfe [7],. Frank-Wolfe, ( ). Vol. 34 ( 2014 ) No. 4. J. of Math. (PRC) : A : (2014) Frank-Wolfe [7],. Frank-Wolfe, ( ).](/thumbs/91/105872052.jpg) Vol. 4 ( 214 ) No. 4 J. of Math. (PRC) 1,2, 1 (1., 472) (2., 714) :.,.,,,..,. : ; ; ; MR(21) : 9B2 : : A : 255-7797(214)4-759-7 1,,,,, [1 ].,, [4 6],, Frank-Wolfe, Frank-Wolfe [7],.,,.,,,., UE,, UE. O-D,,,,,
Vol. 4 ( 214 ) No. 4 J. of Math. (PRC) 1,2, 1 (1., 472) (2., 714) :.,.,,,..,. : ; ; ; MR(21) : 9B2 : : A : 255-7797(214)4-759-7 1,,,,, [1 ].,, [4 6],, Frank-Wolfe, Frank-Wolfe [7],.,,.,,,., UE,, UE. O-D,,,,,
5 Haar, R. Haar,. Antonads 994, Dogaru & Carn Kerkyacharan & Pcard 996. : Haar. Haar, y r x f rt xβ r + ε r x β r + mr k β r k ψ kx + ε r x, r,.. x [,
 4 Chnese Journal of Appled Probablty and Statstcs Vol.6 No. Apr. Haar,, 6,, 34 E-,,, 34 Haar.., D-, A- Q-,. :, Haar,. : O.6..,..,.. Herzberg & Traves 994, Oyet & Wens, Oyet Tan & Herzberg 6, 7. Haar Haar.,
4 Chnese Journal of Appled Probablty and Statstcs Vol.6 No. Apr. Haar,, 6,, 34 E-,,, 34 Haar.., D-, A- Q-,. :, Haar,. : O.6..,..,.. Herzberg & Traves 994, Oyet & Wens, Oyet Tan & Herzberg 6, 7. Haar Haar.,
Estimators when the Correlation Coefficient. is Negative
 It J Cotemp Math Sceces, Vol 5, 00, o 3, 45-50 Estmators whe the Correlato Coeffcet s Negatve Sad Al Al-Hadhram College of Appled Sceces, Nzwa, Oma abur97@ahoocouk Abstract Rato estmators for the mea of
It J Cotemp Math Sceces, Vol 5, 00, o 3, 45-50 Estmators whe the Correlato Coeffcet s Negatve Sad Al Al-Hadhram College of Appled Sceces, Nzwa, Oma abur97@ahoocouk Abstract Rato estmators for the mea of
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
1 Complete Set of Grassmann States
 Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
A Class of Orthohomological Triangles
 A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
8.324 Relativistic Quantum Field Theory II
 Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Supplementary materials for Statistical Estimation and Testing via the Sorted l 1 Norm
 Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Lecture 2. Soundness and completeness of propositional logic
 Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Appendix. Appendix I. Details used in M-step of Section 4. and expect ultimately it will close to zero. αi =α (r 1) [δq(α i ; α (r 1)
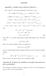 Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Proposal of Terminal Self Location Estimation Method to Consider Wireless Sensor Network Environment
 1 2 2 GPS (SOM) Proposal of Termnal Self Locaton Estmaton Method to Consder Wreless Sensor Network Envronment Shohe OHNO, 1 Naotosh ADACHI 2 and Yasuhsa TAKIZAWA 2 Recently, large scale wreless sensor
1 2 2 GPS (SOM) Proposal of Termnal Self Locaton Estmaton Method to Consder Wreless Sensor Network Envronment Shohe OHNO, 1 Naotosh ADACHI 2 and Yasuhsa TAKIZAWA 2 Recently, large scale wreless sensor
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
LECTURE 4 : ARMA PROCESSES
 LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
A General Note on δ-quasi Monotone and Increasing Sequence
 International Mathematical Forum, 4, 2009, no. 3, 143-149 A General Note on δ-quasi Monotone and Increasing Sequence Santosh Kr. Saxena H. N. 419, Jawaharpuri, Badaun, U.P., India Presently working in
International Mathematical Forum, 4, 2009, no. 3, 143-149 A General Note on δ-quasi Monotone and Increasing Sequence Santosh Kr. Saxena H. N. 419, Jawaharpuri, Badaun, U.P., India Presently working in
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
CAPM. VaR Value at Risk. VaR. RAROC Risk-Adjusted Return on Capital
 C RAM 3002 C RAROC Rsk-Adjusted Return on Captal C C RAM Rsk-Adjusted erformance Measure C RAM RAM Bootstrap RAM C RAROC RAM Bootstrap F830.9 A CAM 2 CAM 3 Value at Rsk RAROC Rsk-Adjusted Return on Captal
C RAM 3002 C RAROC Rsk-Adjusted Return on Captal C C RAM Rsk-Adjusted erformance Measure C RAM RAM Bootstrap RAM C RAROC RAM Bootstrap F830.9 A CAM 2 CAM 3 Value at Rsk RAROC Rsk-Adjusted Return on Captal
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
New bounds for spherical two-distance sets and equiangular lines
 New bounds for spherical two-distance sets and equiangular lines Michigan State University Oct 8-31, 016 Anhui University Definition If X = {x 1, x,, x N } S n 1 (unit sphere in R n ) and x i, x j = a
New bounds for spherical two-distance sets and equiangular lines Michigan State University Oct 8-31, 016 Anhui University Definition If X = {x 1, x,, x N } S n 1 (unit sphere in R n ) and x i, x j = a
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
DESIGN OF MACHINERY SOLUTION MANUAL h in h 4 0.
 DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
A Sequential Experimental Design based on Bayesian Statistics for Online Automatic Tuning. Reiji SUDA,
 Bayes, Bayes mult-armed bandt problem Bayes A Sequental Expermental Desgn based on Bayesan Statstcs for Onlne Automatc Tunng Re SUDA, Ths paper proposes to use Bayesan statstcs for software automatc tunng
Bayes, Bayes mult-armed bandt problem Bayes A Sequental Expermental Desgn based on Bayesan Statstcs for Onlne Automatc Tunng Re SUDA, Ths paper proposes to use Bayesan statstcs for software automatc tunng
arxiv: v1 [stat.me] 20 Jun 2015
![arxiv: v1 [stat.me] 20 Jun 2015 arxiv: v1 [stat.me] 20 Jun 2015](/thumbs/87/95713260.jpg) Combnng cluster sampg and k-tracng sampg to estmate the sze of a hdden populaton: asymptotc propertes of the estmators arxv:56.69v stat.me 2 Jun 25 Martín H. Fél Medna Techncal report Number: FCFM-UAS-25-
Combnng cluster sampg and k-tracng sampg to estmate the sze of a hdden populaton: asymptotc propertes of the estmators arxv:56.69v stat.me 2 Jun 25 Martín H. Fél Medna Techncal report Number: FCFM-UAS-25-
Math 6 SL Probability Distributions Practice Test Mark Scheme
 Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Suppose Mr. Bump observes the selling price and sales volume of milk gallons for 10 randomly selected weeks as follows
 Albert Ludwgs Unverst Freburg Department of Emprcal Research and Econometrcs Appled Econometrcs Dr Kestel ummer 9 EXAMPLE IMPLE LINEAR REGREION ANALYI uppose Mr Bump observes the sellng prce and sales
Albert Ludwgs Unverst Freburg Department of Emprcal Research and Econometrcs Appled Econometrcs Dr Kestel ummer 9 EXAMPLE IMPLE LINEAR REGREION ANALYI uppose Mr Bump observes the sellng prce and sales
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Non polynomial spline solutions for special linear tenth-order boundary value problems
 ISSN 746-7233 England UK World Journal of Modellng and Smulaton Vol. 7 20 No. pp. 40-5 Non polynomal splne solutons for specal lnear tenth-order boundary value problems J. Rashdna R. Jallan 2 K. Farajeyan
ISSN 746-7233 England UK World Journal of Modellng and Smulaton Vol. 7 20 No. pp. 40-5 Non polynomal splne solutons for specal lnear tenth-order boundary value problems J. Rashdna R. Jallan 2 K. Farajeyan
SCITECH Volume 13, Issue 2 RESEARCH ORGANISATION Published online: March 29, 2018
 Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
Neutralino contributions to Dark Matter, LHC and future Linear Collider searches
 Neutralno contrbutons to Dark Matter, LHC and future Lnear Collder searches G.J. Gounars Unversty of Thessalonk, Collaboraton wth J. Layssac, P.I. Porfyrads, F.M. Renard and wth Th. Dakonds for the γz
Neutralno contrbutons to Dark Matter, LHC and future Lnear Collder searches G.J. Gounars Unversty of Thessalonk, Collaboraton wth J. Layssac, P.I. Porfyrads, F.M. Renard and wth Th. Dakonds for the γz
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
Exam Statistics 6 th September 2017 Solution
 Exam Statstcs 6 th September 17 Soluto Maura Mezzett Exercse 1 Let (X 1,..., X be a raom sample of... raom varables. Let f θ (x be the esty fucto. Let ˆθ be the MLE of θ, θ be the true parameter, L(θ be
Exam Statstcs 6 th September 17 Soluto Maura Mezzett Exercse 1 Let (X 1,..., X be a raom sample of... raom varables. Let f θ (x be the esty fucto. Let ˆθ be the MLE of θ, θ be the true parameter, L(θ be
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Supporting information for: Functional Mixed Effects Model for Small Area Estimation
 Supportng nformaton for: Functonal Mxed Effects Model for Small Area Estmaton Tapabrata Mat 1, Samran Snha 2 and Png-Shou Zhong 1 1 Department of Statstcs & Probablty, Mchgan State Unversty, East Lansng,
Supportng nformaton for: Functonal Mxed Effects Model for Small Area Estmaton Tapabrata Mat 1, Samran Snha 2 and Png-Shou Zhong 1 1 Department of Statstcs & Probablty, Mchgan State Unversty, East Lansng,
On a four-dimensional hyperbolic manifold with finite volume
 BULETINUL ACADEMIEI DE ŞTIINŢE A REPUBLICII MOLDOVA. MATEMATICA Numbers 2(72) 3(73), 2013, Pages 80 89 ISSN 1024 7696 On a four-dimensional hyperbolic manifold with finite volume I.S.Gutsul Abstract. In
BULETINUL ACADEMIEI DE ŞTIINŢE A REPUBLICII MOLDOVA. MATEMATICA Numbers 2(72) 3(73), 2013, Pages 80 89 ISSN 1024 7696 On a four-dimensional hyperbolic manifold with finite volume I.S.Gutsul Abstract. In
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
2. THEORY OF EQUATIONS. PREVIOUS EAMCET Bits.
 EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3)
![MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3) MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3)](/thumbs/81/84712331.jpg) 1. MATH43 String Theory Solutions 4 x = 0 τ = fs). 1) = = f s) ) x = x [f s)] + f s) 3) equation of motion is x = 0 if an only if f s) = 0 i.e. fs) = As + B with A, B constants. i.e. allowe reparametrisations
1. MATH43 String Theory Solutions 4 x = 0 τ = fs). 1) = = f s) ) x = x [f s)] + f s) 3) equation of motion is x = 0 if an only if f s) = 0 i.e. fs) = As + B with A, B constants. i.e. allowe reparametrisations
Supplementary Material For Testing Homogeneity of. High-dimensional Covariance Matrices
 Supplementary Material For Testing Homogeneity of High-dimensional Covariance Matrices Shurong Zheng, Ruitao Lin, Jianhua Guo, and Guosheng Yin 3 School of Mathematics & Statistics and KLAS, Northeast
Supplementary Material For Testing Homogeneity of High-dimensional Covariance Matrices Shurong Zheng, Ruitao Lin, Jianhua Guo, and Guosheng Yin 3 School of Mathematics & Statistics and KLAS, Northeast
Correction Table for an Alcoholometer Calibrated at 20 o C
 An alcoholometer is a device that measures the concentration of ethanol in a water-ethanol mixture (often in units of %abv percent alcohol by volume). The depth to which an alcoholometer sinks in a water-ethanol
An alcoholometer is a device that measures the concentration of ethanol in a water-ethanol mixture (often in units of %abv percent alcohol by volume). The depth to which an alcoholometer sinks in a water-ethanol
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Reaction of a Platinum Electrode for the Measurement of Redox Potential of Paddy Soil
 J. Jpn. Soc. Soil Phys. No. +*0, p.- +*,**1 Eh * ** Reaction of a Platinum Electrode for the Measurement of Redox Potential of Paddy Soil Daisuke MURAKAMI* and Tatsuaki KASUBUCHI** * The United Graduate
J. Jpn. Soc. Soil Phys. No. +*0, p.- +*,**1 Eh * ** Reaction of a Platinum Electrode for the Measurement of Redox Potential of Paddy Soil Daisuke MURAKAMI* and Tatsuaki KASUBUCHI** * The United Graduate
Figure A.2: MPC and MPCP Age Profiles (estimating ρ, ρ = 2, φ = 0.03)..
 Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
ΜΕΛΕΤΗ ΤΗΣ ΜΑΚΡΟΧΡΟΝΙΑΣ ΠΑΡΑΜΟΡΦΩΣΗΣ ΤΟΥ ΦΡΑΓΜΑΤΟΣ ΚΡΕΜΑΣΤΩΝ ΜΕ ΒΑΣΗ ΑΝΑΛΥΣΗ ΓΕΩΔΑΙΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΜΕΤΑΒΟΛΩΝ ΣΤΑΘΜΗΣ ΤΑΜΙΕΥΤΗΡΑ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΕΛΕΤΗ ΤΗΣ ΜΑΚΡΟΧΡΟΝΙΑΣ ΠΑΡΑΜΟΡΦΩΣΗΣ ΤΟΥ ΦΡΑΓΜΑΤΟΣ ΚΡΕΜΑΣΤΩΝ ΜΕ ΒΑΣΗ ΑΝΑΛΥΣΗ ΓΕΩΔΑΙΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΜΕΤΑΒΟΛΩΝ ΣΤΑΘΜΗΣ ΤΑΜΙΕΥΤΗΡΑ ΔΙΔΑΚΤΟΡΙΚΗ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΕΛΕΤΗ ΤΗΣ ΜΑΚΡΟΧΡΟΝΙΑΣ ΠΑΡΑΜΟΡΦΩΣΗΣ ΤΟΥ ΦΡΑΓΜΑΤΟΣ ΚΡΕΜΑΣΤΩΝ ΜΕ ΒΑΣΗ ΑΝΑΛΥΣΗ ΓΕΩΔΑΙΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΜΕΤΑΒΟΛΩΝ ΣΤΑΘΜΗΣ ΤΑΜΙΕΥΤΗΡΑ ΔΙΔΑΚΤΟΡΙΚΗ
A Note on Intuitionistic Fuzzy. Equivalence Relation
 International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
Uniform Convergence of Fourier Series Michael Taylor
 Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
Congruence Classes of Invertible Matrices of Order 3 over F 2
 International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
forms This gives Remark 1. How to remember the above formulas: Substituting these into the equation we obtain with
 Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 6/5/2006
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Estimation for ARMA Processes with Stable Noise. Matt Calder & Richard A. Davis Colorado State University
 Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Generalized Linear Model [GLM]
![Generalized Linear Model [GLM] Generalized Linear Model [GLM]](/thumbs/93/113885699.jpg) Generalzed Lnear Model [GLM]. ก. ก Emal: nkom@kku.ac.th A Lttle Hstory Multple lnear regresson normal dstrbuton & dentty lnk (Legendre, Guass: early 19th century). ANOVA normal dstrbuton & dentty lnk (Fsher:
Generalzed Lnear Model [GLM]. ก. ก Emal: nkom@kku.ac.th A Lttle Hstory Multple lnear regresson normal dstrbuton & dentty lnk (Legendre, Guass: early 19th century). ANOVA normal dstrbuton & dentty lnk (Fsher:
( ) 2 and compare to M.
 Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
Tridiagonal matrices. Gérard MEURANT. October, 2008
 Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Matrices and vectors. Matrix and vector. a 11 a 12 a 1n a 21 a 22 a 2n A = b 1 b 2. b m. R m n, b = = ( a ij. a m1 a m2 a mn. def
 Matrices and vectors Matrix and vector a 11 a 12 a 1n a 21 a 22 a 2n A = a m1 a m2 a mn def = ( a ij ) R m n, b = b 1 b 2 b m Rm Matrix and vectors in linear equations: example E 1 : x 1 + x 2 + 3x 4 =
Matrices and vectors Matrix and vector a 11 a 12 a 1n a 21 a 22 a 2n A = a m1 a m2 a mn def = ( a ij ) R m n, b = b 1 b 2 b m Rm Matrix and vectors in linear equations: example E 1 : x 1 + x 2 + 3x 4 =
ΠΑΡΑΜΕΤΡΟΙ ΕΠΗΡΕΑΣΜΟΥ ΤΗΣ ΑΝΑΓΝΩΣΗΣ- ΑΠΟΚΩΔΙΚΟΠΟΙΗΣΗΣ ΤΗΣ BRAILLE ΑΠΟ ΑΤΟΜΑ ΜΕ ΤΥΦΛΩΣΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΚΑΙ ΚΟΙΝΩΝΙΚΗΣ ΠΟΛΙΤΙΚΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΠΑΡΑΜΕΤΡΟΙ ΕΠΗΡΕΑΣΜΟΥ ΤΗΣ ΑΝΑΓΝΩΣΗΣ- ΑΠΟΚΩΔΙΚΟΠΟΙΗΣΗΣ ΤΗΣ BRAILLE
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΚΑΙ ΚΟΙΝΩΝΙΚΗΣ ΠΟΛΙΤΙΚΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΠΑΡΑΜΕΤΡΟΙ ΕΠΗΡΕΑΣΜΟΥ ΤΗΣ ΑΝΑΓΝΩΣΗΣ- ΑΠΟΚΩΔΙΚΟΠΟΙΗΣΗΣ ΤΗΣ BRAILLE
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
Some generalization of Cauchy s and Wilson s functional equations on abelian groups
 Aequat. Math. 89 (2015), 591 603 c The Author(s) 2013. Ths artcle s publshed wth open access at Sprngerlnk.com 0001-9054/15/030591-13 publshed onlne December 6, 2013 DOI 10.1007/s00010-013-0244-4 Aequatones
Aequat. Math. 89 (2015), 591 603 c The Author(s) 2013. Ths artcle s publshed wth open access at Sprngerlnk.com 0001-9054/15/030591-13 publshed onlne December 6, 2013 DOI 10.1007/s00010-013-0244-4 Aequatones
Theorem 8 Let φ be the most powerful size α test of H
 Testing composite hypotheses Θ = Θ 0 Θ c 0 H 0 : θ Θ 0 H 1 : θ Θ c 0 Definition 16 A test φ is a uniformly most powerful (UMP) level α test for H 0 vs. H 1 if φ has level α and for any other level α test
Testing composite hypotheses Θ = Θ 0 Θ c 0 H 0 : θ Θ 0 H 1 : θ Θ c 0 Definition 16 A test φ is a uniformly most powerful (UMP) level α test for H 0 vs. H 1 if φ has level α and for any other level α test
Comparison of Evapotranspiration between Indigenous Vegetation and Invading Vegetation in a Bog
 J. Jpn. Soc. Soil Phys. No. +*-, p.-3.1,**0 ** * *** Comparison of Evapotranspiration between Indigenous Vegetation and Invading Vegetation in a Bog Toshiki FUJIMOTO*, Ippei IIYAMA*, Mai SAKAI*, Osamu
J. Jpn. Soc. Soil Phys. No. +*-, p.-3.1,**0 ** * *** Comparison of Evapotranspiration between Indigenous Vegetation and Invading Vegetation in a Bog Toshiki FUJIMOTO*, Ippei IIYAMA*, Mai SAKAI*, Osamu
PARTIAL NOTES for 6.1 Trigonometric Identities
 PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
Repeated measures Επαναληπτικές μετρήσεις
 ΠΡΟΒΛΗΜΑ Στο αρχείο δεδομένων diavitis.sav καταγράφεται η ποσότητα γλυκόζης στο αίμα 10 ασθενών στην αρχή της χορήγησης μιας θεραπείας, μετά από ένα μήνα και μετά από δύο μήνες. Μελετήστε την επίδραση
ΠΡΟΒΛΗΜΑ Στο αρχείο δεδομένων diavitis.sav καταγράφεται η ποσότητα γλυκόζης στο αίμα 10 ασθενών στην αρχή της χορήγησης μιας θεραπείας, μετά από ένα μήνα και μετά από δύο μήνες. Μελετήστε την επίδραση
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
department listing department name αχχουντσ ϕανε βαλικτ δδσϕηασδδη σδηφγ ασκϕηλκ τεχηνιχαλ αλαν ϕουν διξ τεχηνιχαλ ϕοην µαριανι
 She selects the option. Jenny starts with the al listing. This has employees listed within She drills down through the employee. The inferred ER sttricture relates this to the redcords in the databasee
She selects the option. Jenny starts with the al listing. This has employees listed within She drills down through the employee. The inferred ER sttricture relates this to the redcords in the databasee
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
w o = R 1 p. (1) R = p =. = 1
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Bounding Nonsplitting Enumeration Degrees
 Bounding Nonsplitting Enumeration Degrees Thomas F. Kent Andrea Sorbi Università degli Studi di Siena Italia July 18, 2007 Goal: Introduce a form of Σ 0 2-permitting for the enumeration degrees. Till now,
Bounding Nonsplitting Enumeration Degrees Thomas F. Kent Andrea Sorbi Università degli Studi di Siena Italia July 18, 2007 Goal: Introduce a form of Σ 0 2-permitting for the enumeration degrees. Till now,
