Ακολουθιακά κυκλώματα: Μανδαλωτές και Flip-Flop. Διάλεξη 6

Transcript

1 Ακολουθιακά κυκλώματα: Μανδαλωτές και Flip-Flop Διάλεξη 6

2 Δομή της διάλεξης Εισαγωγή στην ακολουθιακή λογική Ομανδαλωτής SR Latch JK Flip-Flop D Flip-Flop Timing Definitions Latch vs Flip-Flop Ασκήσεις 2

3 Ακολουθιακά κυκλώματα: Μανδαλωτές και Flip-Flop Εισαγωγή στην ακολουθιακή λογική 3

4 Εισαγωγή στην ακολουθιακή λογική Είδη λογικών κυκλωμάτων Συνδυαστικά Η έξοδός τους καθορίζεται μόνο από την παρούσα τιμή της εισόδου. Δεν έχουν μνήμη Ακολουθιακά Η έξοδός τους καθορίζεται όχι μόνο από την παρούσα τιμή της εισόδου αλλά και από προηγούμενες τιμές της. Τα κυκλώματα αυτά έχουν μνήμη. Απαιτούν ρολόι για τη λειτουργία τους 4

5 Εισαγωγή στην ακολουθιακή λογική Μοντέλο ακολουθιακού κυκλώματος (κατάσταση=μνήμη) Είσοδοι Συνδυαστική Λογική Έξοδοι Τρέχουσα κατάσταση Καταχωρητές κατάστασης Επόμενη κατάσταση 5 Ρολόι

6 Εισαγωγή στην ακολουθιακή λογική Μηχανισμοί μνήμης (αποθήκευσης) Στατική αποθήκευση Η κατάσταση διατηρείται όσο υπάρχει τροφοδοσία Έχουν θετική ανάδραση (αναγέννηση) με εσωτερική σύνδεση της εξόδου με την είσοδο Δυναμική αποθήκευση Η κατάσταση αποθηκεύεται σε παρασιτικούς πυκνωτές Η κατάσταση διατηρείται για μικρή χρονική διάρκεια (milliseconds) Απαιτείται περιοδική ανανέωση Συνήθως απλούστερη μεγαλύτερη ταχύτητα και μικρότερη κατανάλωση 6

7 Ακολουθιακά κυκλώματα: Μανδαλωτές και Flip-Flop Ομανδαλωτής 7

8 ΟΜανδαλωτής Το βασικό στοιχείο στατικής μνήμης (latch από εδώ και μπρος) Τρία πιθανά σημεία λειτουργίας Μόνο τα δύο είναι σταθερά σημεία λειτουργίας Είναι δισταθές κύκλωμα Αποθηκεύει ένα δυαδικό ψηφίο 8

9 ΟΜανδαλωτής V i1 V o1 V i2 V o2 cascaded inverters V i2 = V o1 A B ΓιαναείναιμόνοταA, C σταθερά σημεία λειτουργίας πρέπει το κέρδος στη μεταβατική περιοχή να είναι μεγαλύτερο από 1. Το B είναι ένα ασταθές σημείο λειτουργίας C V i1 = V o2 Με την παραπάνω συνθήκη, αν το κύκλωμα βρεθεί στο σημείο B, ο παραμικρός θόρυβος, ανάλογα με το πρόσημό του, ενισχύεται και αναγεννιέται γύρω από τον βρόχο του κυκλώματος αναγκάζοντας το σημείο λειτουργίας να ολισθήσει στο A ή C 9

10 Ακολουθιακά κυκλώματα: Μανδαλωτές και Flip-Flop SR Latch 10

11 SR Latch με NOR πύλες ΗχρήσηNOR δύο εισόδων παρέχει τον τρόπο σκανδαλισμού του latch Για S=R=1 Q = Q = 0, οι έξοδοι δεν είναι συμπληρωματικές για αυτό και δεν χρησιμοποιείται αυτός ο συνδυασμός των S, R Active High είσοδοι (δηλαδή χρειάζεται λογικό high στην αντίστοιχη είσοδο S,R για να γίνει η επιθυμητή ενέργεια Set, Reset) R S Q n+1! Q n Q n!q n Memory Set Reset Not allowed 11

12 SR Latch με NAND πύλες Για S=R=0 Q = Q = 1, οι έξοδοι δεν είναι συμπληρωματικές για αυτό και δεν χρησιμοποιείται αυτός ο συνδυασμός των S,R Active Low είσοδοι (στο σύμβολο υποδεικνύεται από τα κυκλάκια μπροστά από τις εισόδους S, R) S R Q n+1! Q n Q n!q n Memory Set Reset Not allowed 12

13 SR Latch Παράδειγμα λειτουργίας Reset Hold Set Reset Set Race R S Q \Q 13

14 SR Latch Θεωρητική συμπεριφορά SR=00 Πλήρες διάγραμμα SR=01 καταστάσεων Περιλαμβάνει και τις 4 πιθανές καταστάσεις (συνδυασμούς των εξόδων) Δείχνει σε ποια νέα κατάσταση πηγαίνουμε όταν έρθει ένας από τους 4 συνδυασμούς εισόδων, από οποιαδήποτε αρχική κατάσταση Να γιατί η είσοδος SR=11 είναι μη επιτρεπτή στο SR flip-flop με NOR πύλες 14 Q Q' 0 1 SR=01 Πιθανές ταλαντώσεις μεταξύ των καταστάσεων 00 και 11 SR=01 SR=11 SR=00 SR=10 SR=01 SR=11 Q Q' 0 0 Q Q' 1 1 SR=10 SR=00 SR=11 SR=11 Q Q' 1 0 SR=10 SR=00 SR=10

15 SR Latch Παρατηρούμενη συμπεριφορά Η κατάσταση QQ'=11 πολύ δύσκολα παρατηρείται Ένα από τα R, S συνήθως αλλάζει πρώτο Άρα είναι ασαφές αν θα επιστρέψει στην κατάσταση 01 ή 10 Μη ντετερμινιστική μετάβαση SR=10 SR=00 SR=01 Q Q' 0 1 SR=01 SR=01 SR=10 Q Q' 1 0 SR=00 SR=10 SR=11 SR=11 Q Q' 0 0 SR=11 15 SR=00 SR=00

16 SR Latch Υλοποιήσεις (1) 16

17 SR Latch Υλοποιήσεις (2) 17 Σε αυτή την υλοποίηση αν είναι R=S=1, και τα δύο τρανζίστορ R, S θα άγουν ρεύμα

18 SR Latch Υλοποιήσεις (3) 18

19 SR Latch Υλοποιήσεις (4) 19 CMOS υλοποίηση ενός clocked SR flip-flop Το clock signal δηλώνεται ως φ Το σχετικό τμήμα του κυκλώματος για τον καθορισμό των ελάχιστων W/L λόγων των Q5, Q6 ώστε να εξασφαλίζεται η δυνατότητα μεταγωγής

20 SR Latch Υλοποιήσεις (5) Μια απλούστερη CMOS υλοποίηση του clocked SR flip-flop. Αυτό το κύκλωμα είναι δημοφιλές ως το βασικό κελί στη σχεδίαση στατικών random-access memory (SRAM) chips 20

21 Ακολουθιακά κυκλώματα: Μανδαλωτές και Flip-Flop JK Flip-Flop 21

22 JK Latch Περιγραφή J = clocked-set είσοδος, K=clocked-reset είσοδος Active High λογική Χρήση ρολογιού, οι αλλαγές περνούν μόνο για Clock=high Για Clock=low ηέξοδοςδιατηρείται(είναι αποθηκευμένη) Λύνει το πρόβλημα της απροσδιοριστίας στην έξοδο που παρατηρείται στο SR latch για S=R=0 (NAND υλοποίηση) Για J=K=1 προκαλείται ταλάντωση στην τιμή της εξόδου Με τη χρήση της ανάδρασης και ανάλογα με την κατάσταση του latch (την έξοδό του) ενεργοποιείται, λόγω της NAND στην είσοδο, μόνο μία από τις δύο εισόδους κάθε φορά Για J, K βραχυκυκλωμένα μετατρέπεται σε T Flip-Flop (Toggle) 22

23 JK Flip-Flop Επιθυμητή λειτουργία Στο JK latch όσο χρόνο το clock είναι high, αν οι είσοδοι αλλάζουν, θα αλλάζει και η έξοδος σύμφωνα με τον πίνακα αληθείας του latch Όχι επιθυμητή λειτουργία! Σε ένα flip-flop θέλουμε η έξοδος ιδανικά να αλλάζει μόνο μετά από μία παρυφή του ρολογιού, την κατερχόμενη ή την ανερχόμενη Το θέλουμε να είναι edge-triggered στοιχείο Γι αυτό εισαγάγουμε την αρχιτεκτονική Master-Slave Παρατήρηση: Στη βιβλιογραφία μερικοί συγγραφείς ένα τέτοιο edge-triggered στοιχείο το ονομάζουν register (καταχωρητή) 23

24 Master-Slave JK Flip-Flop Λειτουργία Το master ενεργοποιείται με το ρολόι, ενώ το slave με το συμπλήρωμα του ρολογιού Μπορεί να έχει περισσότερες από μία εισόδους (εδώ φαίνονται τρεις) Στοσύμβολοφαίνονταικαιδύοασύγχρονεςείσοδοι(δεν εξαρτώνται από το ρολόι) που χρησιμοποιούνται για το ασύγχρονο preset (SD) και reset (RD) του flip-flop. Είναι active low, δηλαδή αν γίνει low η εκάστοτε ασύγχρονη είσοδος επιτελείται η λειτουργία που υπονοεί το όνομά της Λειτουργία: Clock high: το master latch είναι σε transparent mode (οι είσοδοί του επηρεάζουν την έξοδό του) ενώ το slave σε hold mode (το συμπλήρωμα του ρολογιού είναι low οπότε δεν αλλάζει η κατάστασή του Clock low: το master latch είναι σε hold mode ενώ το slave σε transparent mode 24

25 Master-Slave JK Flip-Flop Λειτουργία Με την αρχιτεκτονική Master-Slave επιτυγχάνουμε την επιθυμητή συμπεριφορά: Όταν το ρολόι είναι high, το slave latch είναι παγωμένο οπότε δεν παρατηρείται αλλαγή στις εξόδους παρόλο που οι είσοδοι μπορεί να αλλάζουν (και να επηρεάζουν τις εξόδους του master latch) Όταν το ρολόι είναι low, το master latch είναι παγωμένο οπότε οι είσοδοι J, K δεν έχουν καμία επίδραση και η έξοδος μένει πάλι σταθερή (το slave latch δυνητικά μπορεί να αλλάζει αλλά τροφοδοτείται με τις παγωμένες εξόδους του master latch, οπότε τελικά δεν παρατηρείται καμία αλλαγή) Η έξοδος αλλάζει μόνο κατά τη μετάβαση high to low του ρολογιού Άρα με την αρχιτεκτονική Master-Slave μετατρέψαμε δύο level-sensitive latches σε ένα flip-flop με συμπεριφορά edge-triggered 25

26 Ones catching πρόβλημα Έστω ότι το slave είναι σε κατάσταση reset, και το clock είναι high Λόγω της ανάδρασης και της NAND εισόδου, η J είσοδος ενεργοποιείται και η K απενεργοποιείται Οποιοδήποτε spike ή glitch (που μπορεί να προέρχεται από το κύκλωμα που οδηγεί τις εισόδους J, K) στην J είσοδο θα αναγκάσει το master latch να είναι σε κατάσταση set Πλέον είναι αδύνατο να έρθει σε κατάσταση reset το latch αυτό, διότι η K είσοδος είναι απενεργοποιημένη Η J είσοδος έπιασε ένα 1 που ακολούθως θα μεταφερθεί στο slave όταν το clock πέφτει ΗανάδρασηκαιοιNAND εισόδου που λύνουν το πρόβλημα της απροσδιοριστίας του SR latch, δημιουργούν το πρόβλημα ones catching στο master slave JK FF Λύσεις: Το ρολόι μένει στο high όσολιγότερογίνεται (μη εφαρμόσιμη λύση) Χρήση (αμιγώς) JK edge-triggered FF 26

27 JK Edge-Triggered Flip-Flop 27 Όταν το ρολόι είναι high, οι J, K είσοδοι δεν φτάνουν στο S, R latch γιατί εμποδίζονται από το δεύτερο επίπεδο πυλών NAND Όταν το ρολόι είναι low, οι J, K είσοδοι ήδη εμποδίζονται από το πρώτο επίπεδο πυλών NAND Άρα η έξοδος πλέον δεν είναι level sensitive ΗέξοδοςτουFF μεταβάλλεται καθώς το ρολόι έρχεται σε low κατάσταση, και η κατάσταση εξόδου οφείλεται στην κατάσταση των J, K εισόδων λίγο πριν (χρόνος setup) έρθει η κατερχόμενη παρυφή του ρολογιού Στην κατερχόμενη παρυφή του ρολογιού θα εμφανιστεί ένας στενός αρνητικός παλμός είτε στην S είτε στην R είσοδο, ανάλογα με τις τιμές των J, K Το κύκλωμα συγχωρεί οποιαδήποτε spikes στις εισόδους J, K πριναπότο χρόνο setup Αναλυτικά οι χρονισμοί σε επόμενη διαφάνεια Το σύμβολο > στο ρολόι υποδηλώνει edge-triggered λειτουργία, και το κυκλάκι ευαισθησία στο negative edge

28 Ακολουθιακά κυκλώματα: Μανδαλωτές και Flip-Flop D Flip-Flop 28

29 D Flip-Flop Ευρεία χρήση σε ψηφιακά κυκλώματα και συστήματα υλοποίηση καταχωρητών Ο αντιστροφέας στην είσοδο D εξασφαλίζει ότι οι S, R είσοδοι προς το latch θα είναι πάντα συμπληρωματικές Η Q έξοδος απλώς ακολουθεί την D είσοδο (προσωρινή αποθήκευση δεδομένων) Η συγκεκριμένη υλοποίηση είναι positive edge-triggered Υπάρχει και level sensitive (transparent) δηλαδή latch Άσκηση: κάνετε τις απαραίτητες τροποποιήσεις στο JK latch ώστε να το μετατρέψετε σε ένα transparent D latch 29

30 D Flip-Flop Positive edge-triggered D Flip-Flop κατάλληλο για τεχνολογία TTL (χρήση NAND πυλών) Άσκηση: Επιβεβαιώστε τη λειτουργία του 30

31 D latch Λειτουργία Για ρολόι C=1 Ηπύλημετάδοσης1 είναι on και η 2 είναι off Σπάει η ανάδραση Η κατάσταση της εισόδου D μεταφέρεται μέσω του ζεύγους αντιστροφέων στις εξόδους. Η Q ακολουθεί τη D (transparent) Για ρολόι C=0 Ηπύλημετάδοσης1 είναι off και η 2 είναι on Κλείνει ο βρόχος ανάδρασης Η είσοδος D απενεργοποιείται Η κατάσταση του ζεύγους αντιστροφέων μανδαλώνεται, παγώνει, διαμέσου της πύλης μετάδοσης 2 Λόγω της πύλης μεταφοράς είναι κατάλληλο για CMOS τεχνολογία 31

32 Master-Slave D Flip-Flop Μετατρέπεται σε edge-triggered λόγω master-slave Για ρολόι C=1 TG 1,4 είναι on και 2,3 είναι off (ισοδύναμο a) Το δεύτερο ζεύγος αντιστροφέων είναι μανδαλωτής και συγκρατεί την πληροφορία που τοποθετήθηκε προηγούμενα Για ρολόι C=0 32 TG 1,4 είναι off και 2,3 είναι on (ισοδύναμο b) Η είσοδος D απενεργοποιείται Ηπύλημετάδοσης2 μανδαλώνει την πληροφορία που υπήρχε στην είσοδο D ακριβώς πριν την αλλαγή κατάστασης του ρολογιού Κατά τη διάρκεια της μετάβασης του ρολογιού η κατάσταση της D διατηρείται προσωρινά στις κομβικές χωρητικότητες που αφορούν τους δύο πρώτους αντιστροφείς Ηπύλημετάδοσης3 μεταδίδει τα αποθηκευμένα δεδομένα στις εξόδους (ενημέρωση της εξόδου) Η Q έχει πλέον δεδομένα που ήταν αρχικά στην είσοδο D για C=1

33 Master-Slave D Flip-Flop CMOS υλοποίηση του Master-Slave D Flip-Flop που περιλαμβάνει και ασύγχρονες εισόδους θέσης και επαναφοράς (υπερισχύουν του ρολογιού) 33

34 Ακολουθιακά κυκλώματα: Μανδαλωτές και Flip-Flop Timing Definitions 34

35 Timing Definitions Χρόνοι σχετικοί με edge-triggered στοιχεία t setup : χρόνος για τον οποίο η είσοδος πρέπει να έχει σταθεροποιηθεί (να είναι έγκυρη) πριν από την παρυφή του ρολογιού t hold : χρόνος για τον οποίο η είσοδος πρέπει παραμείνει σταθερή έγκυρη μετά την παρυφή του ρολογιού t C-Q : worst case καθυστέρηση μετάδοσης (με αναφορά στην παρυφή του ρολογιού) απαραίτητος χρόνος για να αντιγραφεί η είσοδος D στην έξοδο Q CLK t su t hold t D Q D DATA STABLE t Clk t C-Q 35 Q OUTPUT STABLE t

36 Ακολουθιακά κυκλώματα: Μανδαλωτές και Flip-Flop Latch vs Flip-Flop 36

37 Latches vs Flip-Flops Μανδαλωτές (Latches) level sensitive κυκλώματα τα οποία οδηγούν τις εισόδους στην έξοδο όταν το ρολόι είναι high (ή low) - transparent mode Η είσοδος που δειγματοληπτείται στην κατερχόμενη (ανερχόμενη) παρυφή του ρολογιού διατηρείται σταθερή όσο το ρολόι είναι low (ή high) - hold mode Flip-Flops (edge-triggered) edge sensitive κυκλώματα που δειγματοληπτούν τις εισόδους σε μια μετάβαση του ρολογιού positive edge-triggered: 0 1 negative edge-triggered: 1 0 Υλοποιούνται χρησιμοποιώντας latches (π.χ., master-slave flipflops) 37

38 Latches vs Flip-Flops Ορισμοί Στη βιβλιογραφία υπάρχει σύγχυση με τους ορισμούς των στοιχείων latch, flip-flop και register Σε αυτή τη διάλεξη Ένας latch είναι level sensitive Ένας register (καταχωρητής) είναι edge-triggered Για το flip-flop διευκρινίζεται αν είναι edge-triggered ήόχι 38

39 Latches vs Flip-Flops Latch Register (positive edge-triggered) αποθηκεύει την είσοδο όταν το ρολόι είναι low αποθηκεύει την είσοδο στην ανερχόμενη παρυφή του ρολογιού D Q D Q Clk Clk Clk D Q Clk D Q 39

40 Latches vs Flip-Flops Παράδειγμα D Clk Q positive edge-triggered flip-flop D Clk D Q Qedge Clk transparent (level-sensitive) latch Qlatch Η συμπεριφορά διαφέρει όπου η είσοδος αλλάζει ενώ το ρολόι είναι high 40

41 Latches vs Flip-Flops Τύπος Πότε δειγματοληπτείται η είσοδος Πότε η έξοδος είναι έγκυρη Unclocked latch Πάντα Μετά από propagation delay από την αλλαγή της εισόδου Level-sensitive latch Clock high (T su /T h γύρω από την κατερχόμενη παρυφή του ρολογιού) Μετά από propagation delay από την αλλαγή της εισόδου ή παρυφή ρολογιού (όποιο έρθει αργότερα) Master-slave flip-flop Clock high (T su /T h γύρω από την κατερχόμενη παρυφή του ρολογιού) Μετά από propagation delay από την κατερχόμενη παρυφή του ρολογιού Negative edge-triggered flip-flop High-to-low μετάβαση του ρολογιού (T su /T h γύρω από την κατερχόμενη παρυφή του ρολογιού) Μετά από propagation delay από την κατερχόμενη παρυφή του ρολογιού 41

42 Ακολουθιακά κυκλώματα: Μανδαλωτές και Flip-Flop Ασκήσεις 42

43 Άσκηση 1 Εκφώνηση (προς λύση) Δύο αντιστροφείς CMOS που λειτουργούν με τροφοδοτικό 5V έχουν V IH και V IL 2.42 και 2.0 V αντίστοιχα και εξόδους 0.4 και 4.6 V αντίστοιχα. Οι αντιστροφείς είναι συνδεδεμένοι σε συνδεσμολογία μανδαλωτή. Προσεγγίζοντας την χαρακτηριστική μεταφοράς κάθε πύλης με μία ευθεία γραμμή μεταξύ των σημείων κατωφλίου, σχεδιάστε τη χαρακτηριστική μεταφοράς ανοιχτού βρόχου του μανδαλωτή. Ποιες είναι οι συντεταγμένες του σημείου Β; ΠοιοείναιτοκέρδοςβρόχουστοΒ; 43

44 Άσκηση 2 Εκφώνηση Για το παρακάτω κύκλωμα του SR flip-flop η V DD =5V, V T =1V και K 1 =K 2 =K 3 =K 4 =K. Βρείτε τις τιμές των K 5 =K 6 έτσι ώστε το flip-flop να αλλάζει κατάσταση όταν εφαρμοστεί σήμα θέσης ή επαναφοράς ίσο με V DD /2. 44

45 Άσκηση 2 Λύση Επειδή Κ 1 =Κ 3 =Κ 2 =Κ 4 οι δύο αντιστροφείς του latch έχουν τάση κατωφλίου V DD /2=2.5V. Ας υποθέσουμε ότι η έξοδος Q είναι high (V DD ) και συνεπώς η άλλη έξοδος θα είναι low. Το Q 3 είναι σε αγωγή με τάση V GS =-5V. Το Q 5 πρέπει να ρυθμίσει την τάση στην έξοδο Q στα 2.5V ώστε το latch να αλλάξει κατάσταση. Θεωρούμε το Q 3 και το Q 2 στην ωμική περιοχή, το Q 1, Q 4 και Q 6 στην αποκοπή και το Q 5 στην περιοχή κορεσμού: I = I DS5 DS3 ( ) ( ) ( ) 2( ) GS5 T 3 GS3 T DS3 DS3 K V V = K V V V V K K ( ) K ( ) = = 6.11K 45

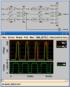
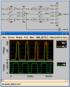
46 Άσκηση 3 Εκφώνηση και Λύση A:Οι κυματομορφές Clk, J, K που φαίνονται στο σχήμα εφαρμόζονται στο JK masterslave flip-flop της διαφάνειας 24. Με το FF αρχικά σε επαναφορά (Reset), σχεδιάστε την κυματομορφή που προκύπτει στην έξοδο Q των master και slave latches. Q: To master latch έχει την δυνατότητα να αλλάξει την κατάστασή του όσο το Clk είναι high. Έτσι, το master latch θα αλλάξει κατάσταση, αν κατά την διάρκεια του Clk=high υπάρξει είσοδος στα J και Κ τέτοια ώστε αυτό να αποκτήσει διαφορετική κατάσταση από το slave. Η αλλαγήστοmaster latch θα συμβεί όσο το Clk=high. Η κατάσταση του master latch θα περάσει στο slave στην πίπτουσα παρυφή του Clk. Οι κυματομορφές του master και του slave latch δίδονται παρακάτω: 46

47 Άσκηση 4 Εκφώνηση Επαναλάβατε την προηγούμενη άσκηση για το JK edgetriggered flip-flop του παρακάτω σχήματος. Υποθέστε ότι το flip-flop είναι αρχικά σε τοποθέτηση (Set). 47

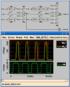
48 Άσκηση 4 Λύση Το συγκεκριμένο JK edge-triggered flip-flop δειγματοληπτεί την κατάσταση των J και K στην πίπτουσα παρυφή του Clk. Οι κυματομορφή της εξόδου δείχνεται παρακάτω: 48

49 Άσκηση 5 Εκφώνηση Για το D flip-flop της διαφάνειας 30 αριθμείστε τις πύλες 1 έως 6. (α) Με Clk=D=Low και S=R=High, προσδιορίστε την κατάσταση εξόδου της κάθε πύλης. Υποθέστε ότι αρχικά το flip-flop είναι σε τοποθέτηση. (β) Επαναλάβετε το (α) για CLK=High. 49

50 Άσκηση 5 Λύση (α) Εφόσον το Clk=D=Low οι πύλες G 2, G 3 και G 4 θα έχουν έξοδο 1. Η πύλη G 1 έχει και τις τρεις εισόδους της σε 1 και συνεπώς θα έχει έξοδο 0. To latch εξόδου έχει τις εισόδους του στο 1 και συνεπώς δεν αλλάζει κατάσταση, δηλαδή G 5 = 1 και G 6 = 0. 50

51 Άσκηση 5 Λύση (β) Εφόσον D= 0 ηέξοδοςτηςg 4 = 1. Eφ όσον το flip-flop είναι σε τοποθέτηση, οι είσοδοι της G 6 είναι όλες 1 και συνεπώς η έξοδος της G 3 = 1. ΓιανασυμβαίνειαυτόθαπρέπειηέξοδοςτηςG 2 να είναι 0 και τότε η έξοδος της G 1 θα είναι 1 και της G 5 θα είναι και αυτή 1. 51

52 Πανεπιστήμιο Πατρών, Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών & Τεχνολογίας Υπολογιστών Τομέας Ηλεκτρονικής & Υπολογιστών, Εργαστήριο Ηλεκτρονικών Εφαρμογών Η διάλεξη έγινε στο πλαίσιο του προγράμματος EΠΕΑΕΚ II από το μεταπτυχιακό φοιτητή Παπαμιχαήλ Μιχαήλ για το μάθημα ΨηφιακάΟλοκληρωμένα Κυκλώματα και Συστήματα Καθηγητής Κωνσταντίνος Ευσταθίου