ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Σημειώσεις Ανάλυσης Ι (ανανεωμένο στις 20 Νοεμβρίου 2012
|
|
|
- Ευλάλιος Τομαραίοι
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Σημειώσεις Ανάλυσης Ι ανανεωμένο στις 20 Νοεμβρίου 202 Τμήμα Θ Αποστολάτου & Π Ιωάννου Ακολουθίες - Όρια ακολουθιών Έστω η ακολουθία μια αριθμημένη σειρά δηλαδή) των αριθμών: a, a 2, a 3,, a ν, με ν-οστό στοιχείο της ακολουθίας το a ν H ακολουθία ορίζεται πλήρως με τον προσδιορισμό του τύπου που δίνει το ν-οστό στοιχείο της Πχ αν δίνεται a ν = /ν, εννοούμε την ακολουθία: a), 2, 3, Είναι προφανές ότι σε αυτή την ακολουθία για κάθε θετικό αριθμό ϵ, οσοδήποτε μικρός κι αν είναι αυτός, υπάρχει όρος της ακολουθίας τέτοιος ώστε όλοι οι επόμενοι όροι της ακολουθίας να είναι μικρότεροι του ϵ Πχ αν ϵ = 2/2357, αρκεί να λάβω από την ακολουθία a ν τον 2357ο όρο αυτής, δηλαδή τον a 2357 Αυτός και όλοι οι επόμενοί του, είναι προφανώς μικρότεροι του ϵ Αυτό συμβαίνει φυσικά για οποιαδήποτε θετική τιμή και αν δώσουμε στον ϵ Οι ακολουθίες που έχουν αυτή την ιδιότητα λέγονται μηδενικές ακολουθίες Στην πραγματικότητα, ακόμη και ακολουθίες που δεν είναι φθίνουσες, όπως η παραπάνω, αλλά καταφέρνουν να συγκεντρώνουν όλους τελικά τους όρους τους δηλαδή από κάποιον όρο και πάνω) εντός μιας οσοδήποτε λεπτής ζώνης γύρω από το μηδέν, είναι μηδενικές Ορισμός: Η a ν είναι μηδενική ακολουθία εάν για κάθε θετικό αριθμό ϵ υπάρχει ένας φυσικός αριθμός N ο οποίος εξαρτάται συνήθως από το ϵ) τέτοιος ώστε όλοι οι επόμενοι όροι της ακολουθίας, δηλ οι όροι με δείκτη ν > N, να είναι κατ απόλυτη τιμή μικρότεροι του ϵ, δηλ a ν < ϵ Για να δείξουμε ότι μία ακολουθία είναι μηδενική αρκεί λοιπόν να προσδιορίσουμε για κάθε ϵ ένα κατάλληλο Nϵ) ώστε a ν < ϵ για κάθε ν > Nϵ) Αυτό
2 á í 2 å í>íå) Íå) í Σχήμα : Γραφική αναπαράσταση μιας γενικής μηδενικής ακολουθίας και κατ επέκταση κάθε ακολουθίας με όριο) μπορεί να γίνει κατασκευάζοντας στήλες με τα ϵ και τα αντίστοιχά τους Nϵ) Για παράδειγμα θεωρήστε την ακολουθία a ν = )ν ν Μπορούμε να σχηματίσουμε την εξής λίστα τιμών ϵ Nϵ) Μάλιστα, αν για κάθε επιλογή ϵ επιλέξουμε N > /ϵ 2, τότε όλοι οι όροι μετά τον Nοστό είναι πράγματι μικρότεροι του ϵ και συνεπώς η ακολουθία είναι μηδενική Παρατηρήσεις: Μία ακολουθία μπορεί να είναι μηδενική παρότι ένας πεπερασμένος αριθμός όρων αυτής μπορεί να είναι εξαιρετικά μεγάλος, πχ η ακολουθία a ν = 0 00 /ν 0 6 ) είναι μηδενική προφανώς γι αυτή την ακολουθία δεν υπάρχει ο a 0 6 όρος) Μάλιστα, κάθε μηδενική ακολουθία είναι εξ ορισμού αναγκαστικά φραγμένη και άνω και κάτω) 2
3 Μία μηδενική ακολουθία μπορεί να περιέχει ή να μην περιέχει το μηδέν Για παράδειγμα η a ν = ν sinνπ/0) είναι μηδενική ακολουθία που παίρνει την τιμή μηδέν a ν = 0 όταν το ν είναι πολλαπλάσιο του 0 Αντιθέτως η a ν = /ν είναι μηδενική αν και κανείς όρος της δεν είναι μηδενικός Ιδιότητες των μηδενικών ακολουθιών α) Αν η a ν και η b ν είναι μηδενικές ακολουθίες, τότε και η a ν + b ν είναι μια μηδενική ακολουθία Απόδειξη: Αφού η a ν και η b ν είναι μηδενικές ακολουθίες, για κάθε ϵ/2 υπάρχει N a ϵ/2) και N b ϵ/2) ώστε a ν < ϵ/2 για κάθε ν > N a και b ν < ϵ/2 για κάθε ν > N b Συνεπώς αν λάβουμε ως N τον μεγαλύτερο από τους N a και N b, τότε όλοι οι όροι των ακολουθιών με δείκτες ν > N θα ικανοποιούν συγχρόνως τις ανισότητες: ϵ 2 < a ν < ϵ 2, ϵ 2 < b ν < ϵ 2, και προσθέτοντας ϵ < a ν + b ν < ϵ β) Αν η a ν είναι μηδενική ακολουθία και η b ν μια φραγμένη ακολουθία, τότε η a ν b ν είναι μηδενική Απόδειξη: Επειδή η b ν είναι φραγμένη υπάρχει M έτσι ώστε b ν < M για κάθε ν, και επειδή η a ν είναι μηδενική ακολουθία για κάθε θετικό αριθμό ϵ/m, υπάρχει N έτσι ώστε a ν < ϵ/m για κάθε ν > N Συνεπώς b ν a ν < M a ν < ϵ, για όλα τα ν > N, και συνεπώς η a ν b ν είναι μηδενική ακολουθία γ) Από την παραπάνω ιδιότητα προκύπτει ότι αν μια μηδενική ακολουθία a ν πολλαπλασιαστεί με μια σταθερά b θετική ή αρνητική), η ακολουθία ba ν θα είναι και αυτή μηδενική Κατανοώντας τι σημαίνει μηδενική ακολουθία μπορούμε να προχωρήσουμε και σε ακολουθίες των οποίων το όριο είναι κάποιος άλλος αριθμός, διαφορετικός από το μηδέν Όπως και με τις μηδενικές, αρκεί όλοι τελικά οι όροι της ακολουθίας από κάποιον όρο και μετά) να βρίσκονται εντός μιας οσοδήποτε λεπτής ζώνης γύρω από τον αριθμό αυτό Ορισμός: Η ακολουθία a ν έχει όριο το a εάν για κάθε θετικό αριθμό ϵ υπάρχει ένας φυσικός αριθμός N, έτσι ώστε a ν a < ϵ για κάθε ν > N, δηλ όταν η ακολουθία a ν a είναι μηδενική Κάθε ακολουθία λοιπόν με κάποιο όριο έχει παρόμοια συμπεριφορά με τις μηδενικές 3
4 Ας δούμε τώρα ένα άλλο είδος ακολουθιών, με όριο όχι κάποιο πραγματικό αριθμό αλλά το άπειρο Τα στοιχεία ακολουθιών, όπως η ακολουθία των φυσικών αριθμών, 2, 3,, ν,, έχουν την ιδιότητα να γίνονται μετά απο κάποιο δείκτη N μεγαλύτερες από οποιονδήποτε αριθμό το N εξαρτάται εν γένει από τον αριθμό που έχουμε επιλέξει) Τέτοιες ακολουθίες λέγεται ότι τείνουν στο συν άπειρο που συμβολίζεται με + Ορισμός: Η ακολουθία a ν τείνει στο άπειρο εάν για κάθε θετικό αριθμό M υπάρχει ένας φυσικός αριθμός NM), που εξαρτάται εν γένει από τον M έτσι ώστε a ν > M για κάθε ν > NM) Συμβολικά γράφουμε σε αυτή την περίπτωση: a ν + Προσέξτε ότι εδώ το είναι ένα σύμβολο και όχι κάποιος αριθμός και δεν έχουν ορισθεί πράξεις με αυτό, δηλ οι πράξεις a + κλπ δεν ορίζονται, ούτε η σχέση a = έχει νόημα Το σύμβολο αυτό δηλώνει αριθμούς που μεγαλώνουν αενάως, σύμφωνα με τον παραπάνω ορισμό Κατ αναλογία ορίζουμε ότι η ακολουθία a ν τείνει στο μείον άπειρο εάν για κάθε θετικό αριθμό M υπάρχει ένας φυσικός αριθμός NM), τέτοιος ώστε a ν < M για κάθε ν > N και γράφουμε σε αυτή την περίπτωση a ν Στο σημείο αυτό αξίζει να αναφέρουμε ότι δεν έχουν όλες οι ακολουθίες όριο, πχ η a ν = ) ν Οι ακολουθίες αυτές λέμε ότι ταλαντώνονται είτε πεπερασμένα όπως η παραπάνω, είτε απεριόριστα όπως η a ν = ) ν ν) Μερικές βασικές ιδιότητες των ορίων: α) Το όριο μίας ακολουθίας είναι μοναδικό, δηλ αν a ν a και a ν b θα είναι οπωσδήποτε a = b Απόδειξη: Ας υποθέσουμε ότι οι a, b δεν είναι ίσοι και χωρίς βλάβη της γενικότητας ας υποθέσουμε ότι ισχύει η ανισότητα a < b) Εξ ορισμού για κάθε ϵ υπάρχει δείκτης ν ϵ) ώστε για κάθε ν > ν να είναι a ν a < ϵ Ομοίως, υπάρχει ν 2 ϵ) έτσι ώστε για ν > ν 2 να είναι a ν b < ϵ Αν επιλέξουμε ϵ = b a)/2 και ως N τον μεγαλύτερο από τους ν b a 2 ) και ν 2 b a 2 ), τότε για ν > N προκύπτει από την πρώτη και δεύτερη σχέση ότι a ν a < b a 2, a ν b < b a 2 Αυτό όμως είναι άτοπο, διότι αν αφαιρέσουμε τις απόλυτες τιμές θα καταλήξουμε στο παράλογο αποτέλεσμα a ν < b + a και a ν > b + a! 2 2 Συνεπώς a = b Η πρόταση είναι προφανής εφόσον έχει κατανοήσει κανείς την έννοια του ορίου 4
5 β) Αν μία ακολουθία είναι σταθερή, δηλ a ν = a, τότε a ν a Απόδειξη: Είναι φανερό ότι όλοι οι όροι της ακολουθίας είναι οσοδήποτε κοντά στο a, για την ακρίβεια είναι σε μηδενική απόσταση από το a γ) Αν a ν a και b ν b τότε a ν + b ν a + b και a ν b ν ab Απόδειξη: Οι a ν a και b ν b είναι μηδενικές ακολουθίες, συνεπώς και το άθροισμά τους a ν +b ν ) a+b) είναι μηδενική ακολουθία Άρα a ν +b ν a + b Για το γινόμενο ακολουθιών χρησιμοποιούμε την ανισότητα: a ν b ν ab a ν b ν a ν b + a ν b ab = a ν b ν b + b a ν a H a ν είναι φραγμένη αφού έχει όριο, και η b ν b είναι μηδενική, απομένως η a ν b ν b) είναι μηδενική Ταυτόχρονα και η ba ν a) είναι μηδενική ως σταθερή επί μηδενική) Επομένως η a ν b ν ab είναι μηδενική, όέδ Στην απόδειξη αυτή φαίνεται γιατί αρχικά ορίσαμε τη μηδενική ακολουθία και της ιδιότητές της, μετατοπίζοντας το ερώτημα για το άθροισμα και το γινόμενο ακολουθιών με όρια στο όριο μηδενικών ακολουθιών δ) Αν a ν a και a 0 τότε a ν a Απόδειξη: Μπορεί κανείς να ακολουθήσει τις γραμμές της προηγούμενης απόδειξης για το γινόμενο Με την διαδοχική χρήση των παραπάνω ιδιοτήτων μπορούμε να υπολογίσουμε τα όρια σύνθετων παραστάσεων Πχ Να βρεθεί το όριο όταν ν της ακολουθίας: ) 3 ν 3 α ν = 3ν + Εργαζόμαστε ως εξης: σχηματίζουμε μηδενικές ακολουθίες γράφοντας την παράσταση στη μορφή: ) 3 3/ν 3 + /ν Επειδή η /ν είναι μηδενική θα έχουμε τα όρια 3 και και ν ν συνεπώς ) 3 ν 3 3ν
6 2 Αύξουσες και φθίνουσες ακολoυθίες Ορισμός: Η ακολουθία a ν είναι αύξουσα αν a ν+ a ν για κάθε ν Λέγεται γνησίως αύξουσα αν για κάθε ν είναι: a ν+ > a ν Ομοίως η ακολουθία a ν είναι φθίνουσα αν a ν+ α ν για κάθε ν και γνησίως φθίνουσα αν για κάθε ν είναι: a ν+ < a ν Μία ακολουθία χαρακτηρίζεται μονότονη, αν είναι είτε αύξουσα είτε φθίνουσα Θα αποδείξουμε τώρα το θεμελιώδες θεώρημα ότι οι μονότονες ακολουθίες τείνουν σε κάποιο όριο αν δεν τείνουν στο ή στο Θα θεωρήσουμε πρώτα την περίπτωση των αυξουσών ακολουθιών Θεώρημα: Έστω η αύξουσα ακολουθία a ν Η ακολουθία αυτή θα τείνει αναγκαστικά στο άπειρο ή σε κάποιο όριο Όταν η αύξουσα ακολουθία είναι επιπλέον και φραγμένη τότε τείνει αναγκαστικα σε κάποιο όριο Διακρίνουμε δύο περιπτώσεις: i) Υπάρχει κάποιος αριθμός A έτσι ώστε είναι a ν A για κάθε ν ii) Για κάθε αριθμό A υπάρχει πάντα δείκτης N τέτοιος ώστε a N > A Στην ii) περίπτωση επειδή η a ν είναι αύξουσα προκύπτει ότι για κάθε A, οσοδήποτε μεγάλο, υπάρχει δείκτης N έτσι ώστε όλοι οι επόμενοι όροι της ακολουθίας είναι a ν > A Συνεπώς η ακολουθία τείνει στο Μένει η i) περίπτωση, στην οποία η ακολουθία είναι φραγμένη Επειδή τα στοιχεία της ακολουθίας a ν είναι άνωθεν φραγμένα έχουν σύμφωνα με το θεώρημα του supremum ένα ανώτερο πέρας ξ που είναι και αυτό άνω φράγμα, δηλ όλοι οι όροι της ακολουθίας είναι a ν < ξ, και για κάθε ϵ, οσοδήποτε μικρό, υπάρχει ο όρος N της ακολουθίας που θα είναι: a N > ξ ϵ διότι αλλιώς το ανώτερο πέρας θα ήταν το ξ ϵ) Επιπλέον, επειδή η a ν είναι αύξουσα, θα είναι και a ν > ξ ϵ για κάθε ν > N Συνεπώς όλοι οι όροι μετά τον N-οστό θα βρίσκονται στο διάστημα ξ α ν < ϵ, άρα α ν ξ Το αντίστοιχο θεώρημα για τις φθίνουσες ακολουθίες αποδεικνύεται παρατηρώντας ότι αν η α ν είναι φθίνουσα τότε η α ν είναι αύξουσα 3 Σημαντικές ανισότητες Στο εδάφιο αυτό θα παραθέσουμε μια σειρά από πολύ σημαντικές ανισότητες, τις οποίες μπορούμε να χρησιμοποιήσουμε όταν διερευνούμε την ύπαρξη ή μη ορίου διαφόρων ακολουθιών 6
7 3 Ανισότητα αριθμητικού-γεωμετρικού μέσου Η πρώτη ανισότητα αφορά τους n θετκούς πραγματικούς αριθμούς α,, α n και τη σχέση του γεωμετρικού μέσου των αριθμών αυτών: και του αριθμητικού μέσου αυτών: Γ = n α α n Αποδεικνύεται ότι ισχύει η ανισότητα: A = α + + α n n Γ A Σημαντική παρατήρηση είναι ότι η ισότητα ισχύει μόνον όταν όλοι οι αριθμοί είναι ίσοι μεταξύ τους α = = α n Θα παραθέσουμε την κατασκευαστική απόδειξη που έδωσε ο Cauchy 820) Αν το n = 2 η πρόταση αληθεύει, διότι τότε είναι προφανώς: α α 2 α + α 2 2 Η πρόταση αληθεύει όταν n = 4, διότι ισχύει ανά 2 Πράγματι έχουμε: 4 α α 2 α 3 α 4 = α α 2 ) /2 α 3 α 4 ) /2) /2 ) /2 α + α 2 α 3 + α α + α 2 + α 3 + α 4 4 Με τον ίδιο τρόπο αποδεικνύεται ότι ισχύει η πρόταση όταν n = 2 k Θεωρήστε τώρα ότι ο n δεν είναι δύναμη του 2 Τότε θα υπάρχει N = 2 k > n και το θεώρημα θα ισχύει για τους N ακόλουθους αριθμούς α,, α n, A,, A, όπου ο A είναι ο αριθμητικός μέσος των πρώτων n αριθμών ενώ το πλήθος των A είναι N n Αν Γ είναι ο γεωμετρικός μέσος των πρώτων n αριθμών τότε για τους N αριθμούς θα ισχύει η ανισότητα Γ n/n A N n)/n = N Γ n A N n) na + N n)a N = A, όπου το na που εμφανίζεται στην αρχή του δεξιού σκέλους μετά την ανισότητα) είναι απλώς επαναγραφή του αθροίσματος των πρώτων n αριθμών Από την παραπάνω ανισότητα προκύπτει ότι και συνεπώς η πρόταση Γ < A Γ n/n A n/n 7
8 32 Aνισότητες Bernoulli και + α) r > + rα, αα κ r > + α) r < + rα, αα κ 0 r < Θα αποδείξουμε τις ανισότητες αυτές για ρητό r = p/q Ας υποθέσουμε κατά αρχάς ότι 0 < r = p/q < δηλαδή 0 < p < q Λαμβάνουμε q αριθμούς, από τους οποίους οι p είναι ίσοι με +α και οι υπόλοιποι q p είναι Για τους αριθμούς αυτούς o γεωμετρικός μέσος είναι και ο αριθμητικός μέσος είναι Γ = q + α) p = + α) p/q A = p + α) + q p q = + p q α Εφόσον α >, και οι δύο μέσοι A, Γ είναι θετικοί και θα ισχύει η ανισότητα Γ A, άρα: + α) p/q + p α, p/q <, α q Συνεπώς απεδείχθη η σχέση για r = p/q < Αν γράψουμε την παραπάνω ανισότητα ως + α + pq ) q/p α και θέσουμε β = pα/q τότε η ανισότητα είναι + β) q/p + q p β που αποδεικνύει την ανισότητα για r > αν β 4 Μερικές σημαντικές ακολουθίες ) Θεωρήστε πρώτα την ακολουθία a ν = a ν και την συμπεριφορά της στο όριο ν Εάν a = τότε όλοι οι όροι είναι a ν = και το όριο είναι το Ομοίως αν a = 0, το όριο είναι το μηδέν 8
9 Εάν a > τότε a = + k με k > 0 και έχουμε την ανισότητα a ν = + k) n > + nk Επειδή + nk και η ακολουθία α ν θα τείνει στο άπειρο Αν 0 < a < η ακολουθία b ν = /a ν > τείνει στο άπειρο b ν ) και επομένως είναι εύκολο να δείξει κανείς ότι η a ν = /b ν είναι μηδενική Αν < a < 0 τότε η ακολουθία b ν = a ν είναι μηδενική και συνεπώς και η a ν είναι μηδενική Αν α ν =, η ακολουθία λαμβάνει διαδοχικά τις τιμές - και, οπότε δεν έχει όριο αλλά είναι φραγμένη Αν α ν <, η υπακολουθία που αποτελείται από τους άρτιους όρους της ακολουθίας τείνει στο άπειρο, ενώ η υπακολουθία που αποτελείται από τους περιττούς όρους τείνει στο μείον άπειρο Συνεπώς η ακολουθία ταλαντώνεται απεριόριστα και δεν έχει όριο ούτε είναι και φραγμένη) 2) Θεωρήστε τώρα την ακολουθία x /n με x > 0, δηλαδή την ακολουθία όπου x, x, 3 x, 4 x, Η ανισότητα αυτή για n θετικό ακέραιο προκύπτει και από τo διωνυμικό ανάπτυγμα, δηλαδή: ) ) n n x + y) n = x n + x n y + x n l y l + y n l ) n nn )n 2) n l + ) n! = = l l! l!n l)! με 0! Το ανάπτυγμα προκύπτει από τον υπολογισμό του γινομένου x + y)x + y) x + y) που αποτελείται από το άθροισμα όρων της μορφής x n l y l όπου το l παίρνει τιμές από το 0 έως το n Ο αριθμός των όρων στους οποίους εμφανίζεται ο y l είναι ίσος με τον αριθμό των τρόπων που μπορώ να επιλέξω l ίδια αντικείμενα, τα y, από ένα διαθέσιμο σύνολο n Το πρώτο μπορώ να το επιλέξω με n τρόπους Έχοντας επιλέξει το πρώτο, το δεύτερο μπορεί να επιλεγεί με n τρόπους κοκ μέχρι το l που απομένουν n l + τρόποι Συνεπώς το y l μπορεί να επιλεγεί με nn ) n l + )/l! διαφορετικούς τρόπους διότι τα αντικείμενα είναι ίδια και ο προηγούμενος αριθμός πρέπει να διαιρεθεί διά του αριθμού των μεταθέσεων αυτών των ιδίων αντικειμένων, που είναι l! Στην περίπτωση μας έχουμε + k) n = + nk + nn ) k k n 2! Ένας άλλος τρόπος υπολογισμού του αναπτύγματος x + y) n, είναι ο απευθείας υπολογισμός του για n =, 2, 3 και στη συνέχεια η απόδειξη της γενικής μορφής με την επαγωγική μέθοδο 9
10 Αν x > θα είναι x /n > και συνεπώς το είναι κάτω φράγμα Επίσης επειδή x /n > x /n+) η ακολουθία είναι φθίνουσα Συνεπώς συγκλίνει σε κάποιο όριο α Αν όμως α > τότε επειδή x /n > α θα είναι x > α n για κάθε n, οσοδήποτε μεγάλο Αλλά αυτό είναι αδύνατο διότι σύμφωνα με το ) α n και επομένως δεν μπορεί να φραχθεί από πάνω από κανένα αριθμό Συνεπώς η ακολουθία συγκλίνει στο Με παρόμοια συλλογιστική βρίσκουμε ότι x /n όταν 0 < x < Συνεπώς για κάθε x > 0 είναι lim n x /n = 3) Οι παρακάτω ιδιότητες είναι πολύ χρήσιμες Εάν έχουμε μία θετική ακολουθία α n που ικανοποιεί την ανισότητα α n+ /α n K με K > τότε α n Διότι α n Kα n K 2 α n 2 K n α και συνεπώς η α n τείνει στο άπειρο αφού η K n τείνει στο άπειρο Παρομοίως, αν ισχύει ότι α n+ / α n < K με 0 < K < τώρα δεν είναι αναγκαίο να είναι η α n θετική) τότε η α n είναι μηδενική ακολουθία Μια ακόμη ισχυρότερη πρόταση είναι η ακόλουθη: Μια θετική ακολουθία α n τείνει στο άπειρο αν α n+ lim = K > n α n Η απόδειξη βασίζεται στην παρατήρηση ότι εφόσον α n+ /α n K > υπάρχει φυσικός N τέτοιος ώστε για n > N θα είναι α n+ /α n > M > όπου K > M > Συνεπώς για n > N + θα είναι α n > M n N α N+ και επομένως η α n τείνει στο άπειρο αφού η M n N τείνει στο άπειρο όταν n Ομοίως μία ακολουθία α n είναι μηδενική αν α n+ lim = K, < K < n α n Στη περίπτωση αυτή δεν είναι αναγκαίο η ακολουθία να είναι θετική Πρώτη σημαντική εφαρμογή των ιδιοτήτων αυτών είναι ότι x n /n αν x > και x n /n 0 αν x Επίσης αμέσως προκύπτει ότι x n /n! είναι μηδενική για κάθε τιμή του x 2 Αυτό σημαίνει ότι υπάρχει N τέτοιο ώστε για 2 Ένας πιο άμεσος τρόπος να καταλάβει κανείς γιατί η ακολουθία αυτή είναι μηδενική είναι ο ακόλουθος: Έστω N ο ακέραιος αμέσως μετά τον x Οι όροι της ακολουθίας μετά τον N-στό θα έχουν τη μορφή x x a n = a N N + N + 2 x ) n N) x n < a N N + Όμως η τελευταία αυτή ακολουθία είναι μηδενική αφού x /N + ) < Επομένως η ακολουθία a n, όντας φραγμένη από άλλη μηδενική, είναι μηδενική και επομένως και η ίδια η a n είναι μηδενική 0
11 n > N θα είναι n! > x n για κάθε δεδομένη τιμή του x, δηλαδή η n! υπερισχύει τελικά της x n Επειδή για κάθε x υπάρχει N τέτοιο ώστε για n > N να είναι n! > x n ή n!) /n > x η συμπαιρένουμε ότι n n! τείνει στο άπειρο Ο ρυθμός αύξησης της n! όταν n δίδεται απο την προσσεγγιστική έκφραση του Stirling n! n ) n 2πn e [Ερ Σκεφθείτε ποιο είναι το lim n n/n!) /n ;] 4) Τώρα μια πολύ ιδιαίτερη ακολουθία το όριο της οποίας εμφανίζεται συχνότατα στη φυσική Θα υπολογίσουμε το όριο της ακολουθίας a ν = + ) ν ν Βλέποντας αυτήν την ακολουθία δεν είναι εύκολο να αποφασίσει κανείς για τη συμπεριφορά της Καθώς το ν τείνει στό άπειρο η παρένθεση τείνει στο αλλά η δύναμη στην οποία θα πρέπει να υψωθεί αυτό το περίπου είναι απείρως μεγάλη Μένει λοιπόν κανείς με το ερώτημα τι είναι πιο δυνατό η τάση της ποσότητας μέσα στην παρένθεση στη μονάδα ώστε η ακολουθία να τείνει τελικά στο ή η δύναμη που θα εκτινάξει έναν αριθμό μεγαλύτερο της μονάδας στο όπως στην προηγούμενη ακολουθία Η απάντηση, όπως θα δούμε είναι μια περίεργη ισορροπία ανάμεσα στις δύο τάσεις Υπολογίζουμε τις πρώτες τιμές της ακολουθίας a = a 2 = + ) = 2, + 2) 2 = 225, a 3 = , a 4 = 2444, a 5 = , οι οποίες βαίνουν απ ότι φαίνεται αύξουσες, δημιουργώντας την υπόνοια ότι ίσως η ακολουθία είναι αύξουσα Αυτό πράγματι ισχύει διότι από τον τύπο του διωνύ-
12 μου έχουμε: + ) ν = + ν νν ) + ν ν 2 ν + 2 νν ) ν k + ) + k 2 ν + k νν ) ν ν + ) + ν 2 ν ν = + + ) ν + ) 2 ) k ) + 2 k ν ν ν + ) 2 ) ν ) 2 ν ν ν ν Ομοίως: + ) ν = + + ) + + ν 2 ν + ) k 2 ν ) ν ν ) k ) + ν ν ) 2 ) ν 2 ) ν ν Παρατηρούμε ότι οι όροι της a ν είναι ν + το πλήθος ενώ αυτοί της a ν είναι ν Επίσης συγκρίνοντας τον k-οστό όρο της a ν με τον k-οστό όρο της a ν εκτός από τους δύο πρώτους που είναι ίσοι) της a ν είναι μεγαλύτερος λόγω του ότι /ν < /ν )) Επομένως η a ν έχει και περισσότερους και μεγαλύτερους όρους Θα δείξουμε τώρα ότι η ακολουθία είναι φραγμένη Αρκεί να δείξουμε ότι υπάρχει κάποιος αριθμός που είναι μεγαλύτερος από όλους τους όρους της ακολουθίας Προς τούτο παρατηρούμε ότι 2 3 n < 2 n Οπότε από τον τύπο του δυωνύμου έχουμε: + ) ν < + ν ν οι όροι στις παρενθέσεις είναι όλοι μικρότεροι της μονάδας και τους θέσαμε προκειμένου να φτιάξουμε ένα άνω φράγμα Επειδή όμως το άθροισμα όρων μιας γεωμετρικής σειράς υπολογίζεται εύκολα 2
13 + x + x 2 + x n = xn+ x έχουμε ότι = 2 ν /2)ν+ ) < 2 και συνεπώς κάθε όρος της ακολουθίας ικανοποιεί την ανισότητα + ) ν < 3 ν Καταλήγουμε λοιπόν ότι αφού η ακολουθία είναι αύξουσα και φραγμένη θα έχει όριο Το όριο αυτό 3 το συμβολίζουμε με τον αριθμό e Μία δε προσεγγιστική τιμή αυτού είναι e = Παρατηρούμε άλλη μία φορά τη σημασία της κατασκευής των πραγματικών αριθμών Κάθε στοιχείο της ακολουθίας είναι ένας ρητός αριθμός Το όριο όμως της ακολουθίας δεν υπάρχει στο σύνολο των ρητών Το όριο αυτό είναι ένας άρρητος αριθμός στις ασκήσεις θα αποδείξετε ότι πράγματι ο e είναι άρρητος) Περαιτέρω μπορεί να αποδειχθεί ότι αυτός ο αριθμός είναι ακόμα πιο ιδιόρρυθμος, δεν είναι ούτε καν αλγεβρικός άρρητος αριθμός όπως ο 2, δηλαδή δεν είναι ρίζα πολυωνύμου με ακέραιους συντελεστές Ο e είναι όπως λέμε ένας υπερβατικός αριθμός Θα δείξουμε τώρα ότι το όριο e προκύπτει ακόμα και όταν ο δείκτης ν πηγαίνει στο άπειρο με οποιονδήποτε τρόπο Ας εξετάσουμε το όριο της ακολουθίας + a n ) an 3 Το e αναφέρεται ως η σταθερά του Euler προς τιμή του Ελβετού μαθηματικού και φυσικού Euler ) Ο e έχει θεμελιώδη σημασία στα μαθηματικά και στη φυσική και μαζί με τους αριθμούς 0,, π και το φαντασικό i, αποτελούν τους πιο σημαντικούς αριθμούς Ο e και ο i είναι έργο της νέας εποχής των μαθηματικών που συμβαδίζει με τις νέες θεωρίες για τη μηχανική του κόσμου Η ανακάλυψη της σταθεράς e ως το όριο που μελετήσαμε έγινε απο τον Ελβετό μαθηματικό και φυσικό Jacob Bernoulli ) Ο Bernoulli υπολόγισε αυτό το όριο επειδή ήθελε να μελετήσει την αξία μίας χρηματικής κατάθεσης η οποία τοκίζεται με συνεχή τρόπο και όρισε το αριθμό e ως την αξία μίας μονάδας χρήματος μετά την πάροδο ενός χρόνου, όταν αυτή ανατοκίζεται συνεχώς με ετήσιο τόκο 00% Διότι αν ο ανατοκισμός υπολογίζονταν ημερησίως τότε καθε μέρα η αξία θα μεγάλωνε καθημερινώς κατα + /365, και στο τέλος του χρόνου το αρχικό ποσό θα γινόταν +/365) 365 φορές μεγαλύτερο Στο όριο που ανατοκιζόταν συνεχώς η αξία μετά απο ένα χρόνο θα ήταν e Συνεπώς, αν ο ετήσιος τόκος ήταν 5% η κατάθεση ανατοκιζόμενη συνεχώς θα είχε αξία e 005 = 0527 Η πρώτη γνωστή χρήση της σταθεράς, η οποία και συμβολίζονταν με το γράμμα b, βρίσκεται σε επιστολή του Gottfried Leibniz στον Christiaan Huygens κατά τα έτη 690 και 69 Ο Euler άρχισε να χρησιμοποιεί το γράμμα e για τη σταθερά το 727 και 728, σε μία αδημοσίευτη εργασία για τις δυνάμεις που αναπτύσσονται κατά την έκρηξη κανονιών Η πρώτη φορά που εμφανίζεται το e σε δημοσίευση είναι στη Μηχανική του Euler το 736 3
14 Η a n είναι μία αύξουσα ακολουθία η οποία τείνει στο άπειρο Λαμβάνουμε τον θετικό ακέραιο ν που είναι το ακέραιο μέρος του a n και ικανοποιεί την ανισότητα ν a n ν + Συνεπώς ν + a n ν και + ) ν + ) an + ) ν+, ν + a n ν δηλ η ακολουθία γ n = + /a n ) an έχει φραχθεί απο τις ακολουθίες β n = + /ν + )) ν και δ n = + /ν) ν+ Γράφουμε την δ n ως: + ) ν+ = + ) ν + ) ν ν ν και παρατηρούμε ότι η μεν /ν είναι μηδενική επειδή το ν βαίνει αυξανόμενο προς το άπειρο, παρότι το ν δεν παίρνει διαδοχικές ακέραιες τιμές, και ομοίως η + /ν) ν e Συνεπώς Ομοίως δ n = + ) ν = ν + + ν ) ν+ e + + ν+ ν+ ) ν+ ), και η β n συγκλίνει και αυτή στον e Έχουμε δηλ δύο ακολουθίες β n και δ n που έχουν το ίδιο όριο και την ακολουθία γ n που βρίσκεται εγκιβωτισμένη μεταξύ τους δηλαδή ικανοποιεί τις ανισότητες: β n γ n δ n Είναι προφανές ότι και η γ n θα συγκλίνει τότε στο ίδιο όριο e Πράγματι, δοθέντος ϵ υπάρχει N τέτοιο ώστε όλοι οι επόμενοι όροι των ακολουθιών, δηλ όροι με δείκτες n > N, να ικανοποιούν τις ανισότητες: e ϵ < β n γ n δ n < e + ϵ Συνεπώς γ n e Η πρόταση που αποδείξαμε για τα όρια εγκιβωτισμένων ακολουθιών είναι πολύ χρήσιμη για τον προσδιορισμό ορίων Αρκεί να εγκιβωτίσουμε μία ακολουθία μεταξυ δύο άλλων περισσότερο γνώριμων ακολουθιών που έχουν το ίδιο όριο Τώρα θα δείξουμε ότι το όριο της ακολουθίας + µ) µ 4
15 όταν το λαμβάνει αρνητικές τιμές και µ είναι πάλι το e Θέτουμε, M = µ + µ) µ = = ) M M = M + M ) M M = M M + M ) M + ) M ) M = + M το οποίο έχει ως όριο όταν το M πάλι το αριθμό e Με τις παραπάνω προτάσεις μπορούμε τώρα να δείξουμε ότι το όριο της ακολουθίας lim + x n = e n n) x Αυτό προκύπτει διότι σύμφωνα με τα προηγούμενα για οποιοδήποτε x θετικό ή αρνητικό αλλά διαφορετικό από το 0) είναι + x n) n/x e ) M, και + x ) n = + x ) ) n/x x n n Βασιζόμαστε στη γενικευμένη πρόταση ότι αν a n a ας υποθέσουμε εδώ για απλότητα ότι ο a είναι θετικός) θα ισχύει ότι a x n a x, για οποιοδήποτε πραγματικό αριθμό 4 x 4 Μπορείτε να σκιαγραφήσετε πως θα ορίζατε το a x, αρχίζοντας με την πράξη του πολλαπλασιασμού; 5
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Σημειώσεις Ανάλυσης Ι (ανανεωμένο στις 5 Δεκεμβρίου 2012)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Σημειώσεις Ανάλυσης Ι (ανανεωμένο στις 5 Δεκεμβρίου 2012) Τμήμα Θ. Αποστολάτου & Π. Ιωάννου 1 Σειρές O Ζήνων ο Ελεάτης (490-430 π.χ.) στη προσπάθειά του να υποστηρίξει
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Σημειώσεις Ανάλυσης Ι (ανανεωμένο στις 5 Δεκεμβρίου 2012) Τμήμα Θ. Αποστολάτου & Π. Ιωάννου 1 Σειρές O Ζήνων ο Ελεάτης (490-430 π.χ.) στη προσπάθειά του να υποστηρίξει
ΑΝΑΛΥΣΗ 1 ΔΕΚΑΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 1 ΔΕΚΑΤΟ ΜΑΘΗΜΑ, 9-10-13 Μ. Παπαδημητράκης. 1 ΠΡΟΤΑΣΗ. Αν ισχύει y n για άπειρους n και x R και y n y R, τότε x y. Απόδειξη. Υποθέτουμε (για άτοπο) ότι y < x. Γνωρίζουμε ότι υπάρχει κάποιος αρκετά
ΑΝΑΛΥΣΗ 1 ΔΕΚΑΤΟ ΜΑΘΗΜΑ, 9-10-13 Μ. Παπαδημητράκης. 1 ΠΡΟΤΑΣΗ. Αν ισχύει y n για άπειρους n και x R και y n y R, τότε x y. Απόδειξη. Υποθέτουμε (για άτοπο) ότι y < x. Γνωρίζουμε ότι υπάρχει κάποιος αρκετά
ΑΝΑΛΥΣΗ 1 ΠΕΜΠΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 1 ΠΕΜΠΤΟ ΜΑΘΗΜΑ, 17-10-13 Μ. Παπαδημητράκης. 1 Την προηγούμενη φορά αναφέραμε (και αποδείξαμε στην περίπτωση n = 2) το θεώρημα που λέει ότι, αν n N, n 2, τότε για κάθε y 0 υπάρχει μοναδική μηαρνητική
ΑΝΑΛΥΣΗ 1 ΠΕΜΠΤΟ ΜΑΘΗΜΑ, 17-10-13 Μ. Παπαδημητράκης. 1 Την προηγούμενη φορά αναφέραμε (και αποδείξαμε στην περίπτωση n = 2) το θεώρημα που λέει ότι, αν n N, n 2, τότε για κάθε y 0 υπάρχει μοναδική μηαρνητική
Σημειώσεις Ανάλυσης Ι. Θεωρούμε γνωστούς τους φυσικούς αριθμούς
 Σημειώσεις Ανάλυσης Ι 1. Οι ρητοί αριθμοί Θεωρούμε γνωστούς τους φυσικούς αριθμούς 1, 2, 3, και τις πράξεις (πρόσθεση - πολλαπλασιασμό)μεταξύ αυτών. Οι φυσικοί αριθμοί είναι επίσης διατεταγμένοι με κάποια
Σημειώσεις Ανάλυσης Ι 1. Οι ρητοί αριθμοί Θεωρούμε γνωστούς τους φυσικούς αριθμούς 1, 2, 3, και τις πράξεις (πρόσθεση - πολλαπλασιασμό)μεταξύ αυτών. Οι φυσικοί αριθμοί είναι επίσης διατεταγμένοι με κάποια
ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ
 ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ Εισαγωγή Οι αριθμοί που εκφράζουν το πλήθος των στοιχείων ανά αποτελούν ίσως τους πιο σημαντικούς αριθμούς της Συνδυαστικής και καλούνται διωνυμικοί συντελεστές διότι εμφανίζονται
ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ Εισαγωγή Οι αριθμοί που εκφράζουν το πλήθος των στοιχείων ανά αποτελούν ίσως τους πιο σημαντικούς αριθμούς της Συνδυαστικής και καλούνται διωνυμικοί συντελεστές διότι εμφανίζονται
B = F i. (X \ F i ) = i I
 Κεφάλαιο 3 Τοπολογία μετρικών χώρων Ομάδα Α 3.1. Εστω (X, ρ) μετρικός χώρος και F, G υποσύνολα του X. Αν το F είναι κλειστό και το G είναι ανοικτό, δείξτε ότι το F \ G είναι κλειστό και το G \ F είναι
Κεφάλαιο 3 Τοπολογία μετρικών χώρων Ομάδα Α 3.1. Εστω (X, ρ) μετρικός χώρος και F, G υποσύνολα του X. Αν το F είναι κλειστό και το G είναι ανοικτό, δείξτε ότι το F \ G είναι κλειστό και το G \ F είναι
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Λυσεις Ασκησεων - Φυλλαδιο 1
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Λυσεις Ασκησεων - Φυλλαδιο ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 7 Φεβρουαρίου 03 Ασκηση. είξτε ότι
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Λυσεις Ασκησεων - Φυλλαδιο ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 7 Φεβρουαρίου 03 Ασκηση. είξτε ότι
Απειροσ τικός Λογισμός ΙΙ Πρόχειρες Σημειώσεις Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών
 Απειροστικός Λογισμός ΙΙ Πρόχειρες Σημειώσεις Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών - Περιεχόμενα Υπακολουθίες και βασικές ακολουθίες. Υπακολουθίες. Θεώρημα Bolzno Weierstrss.αʹ Απόδειξη με χρήση της
Απειροστικός Λογισμός ΙΙ Πρόχειρες Σημειώσεις Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών - Περιεχόμενα Υπακολουθίες και βασικές ακολουθίες. Υπακολουθίες. Θεώρημα Bolzno Weierstrss.αʹ Απόδειξη με χρήση της
ΑΚΟΛΟΥΘΙΕΣ ΣΕΙΡΕΣ. Ορισμός 1. Μια 1 1 (ένα προς ένα) συνάρτηση με πεδίο ορισμού το και πεδίο τιμών ένα υποσύνολο X του, δηλαδή μία 1 1 συνάρτηση
 ΑΚΟΛΟΥΘΙΕΣ ΣΕΙΡΕΣ 1. ΑΚΟΛΟΥΘΙΕΣ Ορισμός 1. Μια 1 1 (ένα προς ένα) συνάρτηση με πεδίο ορισμού το και πεδίο τιμών ένα υποσύνολο X του, δηλαδή μία 1 1 συνάρτηση : 1 λέγεται ακολουθία πραγματικών αριθμών ή
ΑΚΟΛΟΥΘΙΕΣ ΣΕΙΡΕΣ 1. ΑΚΟΛΟΥΘΙΕΣ Ορισμός 1. Μια 1 1 (ένα προς ένα) συνάρτηση με πεδίο ορισμού το και πεδίο τιμών ένα υποσύνολο X του, δηλαδή μία 1 1 συνάρτηση : 1 λέγεται ακολουθία πραγματικών αριθμών ή
> ln 1 + ln ln n = ln(1 2 3 n) = ln(n!).
 η Διάλεξη: Άρρητοι αριθμοί Το σύνολο Q των ρητών αριθμών είναι το Q = { m n : m Z, n N}. αριθμός που δεν είναι ρητός λέγεται άρρητος. Ενας πραγματικός Ασκηση: Αποδείξτε ότι το άθροισμα και το γινόμενο
η Διάλεξη: Άρρητοι αριθμοί Το σύνολο Q των ρητών αριθμών είναι το Q = { m n : m Z, n N}. αριθμός που δεν είναι ρητός λέγεται άρρητος. Ενας πραγματικός Ασκηση: Αποδείξτε ότι το άθροισμα και το γινόμενο
 Ασκήσεις Απειροστικού Λογισμού ΙΙ Πρόχειρες Σημειώσεις Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Περιεχόμενα Υπακολουθίες και ακολουθίες Cuchy Σειρές πραγματικών αριθμών 3 3 Ομοιόμορφη συνέχεια 3 4 Ολοκλήρωμα
Ασκήσεις Απειροστικού Λογισμού ΙΙ Πρόχειρες Σημειώσεις Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Περιεχόμενα Υπακολουθίες και ακολουθίες Cuchy Σειρές πραγματικών αριθμών 3 3 Ομοιόμορφη συνέχεια 3 4 Ολοκλήρωμα
Ξέρουμε ότι: Συνάρτηση-απεικόνιση με πεδίο ορισμού ένα σύνολο Α και πεδίο τιμών ένα σύνολο Β είναι κάθε μονοσήμαντη απεικόνιση f του Α στο Β.
 Η έννοια της ακολουθίας Ξέρουμε ότι: Συνάρτηση-απεικόνιση με πεδίο ορισμού ένα σύνολο Α και πεδίο τιμών ένα σύνολο Β είναι κάθε μονοσήμαντη απεικόνιση f του Α στο Β. Δηλαδή: f : A B Η ακολουθία είναι συνάρτηση.
Η έννοια της ακολουθίας Ξέρουμε ότι: Συνάρτηση-απεικόνιση με πεδίο ορισμού ένα σύνολο Α και πεδίο τιμών ένα σύνολο Β είναι κάθε μονοσήμαντη απεικόνιση f του Α στο Β. Δηλαδή: f : A B Η ακολουθία είναι συνάρτηση.
Απειροστικός Λογισμός Ι Ασκήσεις
 Απειροστικός Λογισμός Ι Ασκήσεις Μ. Παπαδημητράκης . Για καθεμία από τις ανισότητες ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΣΥΝΑΡΤΗΣΕΙΣ + >, +, + > +3 3+, ( )( 3) ( ) 0 γράψτε ως διάστημα ή ως ένωση διαστημάτων το σύνολο
Απειροστικός Λογισμός Ι Ασκήσεις Μ. Παπαδημητράκης . Για καθεμία από τις ανισότητες ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΣΥΝΑΡΤΗΣΕΙΣ + >, +, + > +3 3+, ( )( 3) ( ) 0 γράψτε ως διάστημα ή ως ένωση διαστημάτων το σύνολο
12. ΑΝΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ. είναι δύο παραστάσεις μιας μεταβλητής x πού παίρνει τιμές στο
 ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
Μερικές φορές δεν μπορούμε να αποφανθούμε για την τιμή του άπειρου αθροίσματος.
 Σειρές Σειρές και μερικά αθροίσματα: Το πρόβλημα της άθροισης μιας σειράς άπειρων όρων είναι πολύ παλιό. Μερικές φορές μια τέτοια σειρά καταλήγει σε πεπερασμένο αποτέλεσμα, μερικές φορές απειρίζεται και
Σειρές Σειρές και μερικά αθροίσματα: Το πρόβλημα της άθροισης μιας σειράς άπειρων όρων είναι πολύ παλιό. Μερικές φορές μια τέτοια σειρά καταλήγει σε πεπερασμένο αποτέλεσμα, μερικές φορές απειρίζεται και
Μαθηματικά. Ενότητα 2: Διαφορικός Λογισμός. Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη)
 Μαθηματικά Ενότητα 2: Διαφορικός Λογισμός Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Μαθηματικά Ενότητα 2: Διαφορικός Λογισμός Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου
 Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2
![0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2 0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2](/thumbs/59/43483993.jpg) ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» (ε) Κάθε συγκλίνουσα ακολουθία άρρητων αριθµών συγκλίνει σε άρρητο αριθµό.
 Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
sup(a + B) = sup A + sup B inf(a + B) = inf A + inf B.
 Ασκήσεις, Φυλλάδιο. Βρειτε το συνολο Φ A ολων των ανω ϕραγματων του A, και το συνολο φ A ολων των κατω ϕραγματων του A, οταν: a) A = m :, m N}, b) A = + m 2. Βρειτε το if και sup οποτε υπαρχουν) των συνολων
Ασκήσεις, Φυλλάδιο. Βρειτε το συνολο Φ A ολων των ανω ϕραγματων του A, και το συνολο φ A ολων των κατω ϕραγματων του A, οταν: a) A = m :, m N}, b) A = + m 2. Βρειτε το if και sup οποτε υπαρχουν) των συνολων
Επαναληπτικά θέματα στα Μαθηματικά προσανατολισμού-ψηφιακό σχολείο ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΚΕΦΑΛΑΙΟ 1 ο -ΣΥΝΑΡΤΗΣΕΙΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ Απο το Ψηφιακό Σχολείο του ΥΠΠΕΘ Επιμέλεια: Συντακτική Ομάδα mathpgr Συντονιστής:
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΚΕΦΑΛΑΙΟ 1 ο -ΣΥΝΑΡΤΗΣΕΙΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ Απο το Ψηφιακό Σχολείο του ΥΠΠΕΘ Επιμέλεια: Συντακτική Ομάδα mathpgr Συντονιστής:
ΚΕΦΑΛΑΙΟ 5 ΑΚΟΛΟΥΘΙΕΣ ΑΡΙΘΜΗΤΙΚΗ ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟΔΟΣ
 ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 5 ΑΚΟΛΟΥΘΙΕΣ ΑΡΙΘΜΗΤΙΚΗ ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟΔΟΣ ΓΙΑΝΝΗΣ ΠΑΤΕΡΑΣ ΜΑΘΗΜΑΤΙΚΟΣ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ ΑΚΟΛΟΥΘΙΕΣ ΚΕΦΑΛΑΙΟ 5 ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΟΔΟΣ ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ακολουθία ονομάζουμε
ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 5 ΑΚΟΛΟΥΘΙΕΣ ΑΡΙΘΜΗΤΙΚΗ ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟΔΟΣ ΓΙΑΝΝΗΣ ΠΑΤΕΡΑΣ ΜΑΘΗΜΑΤΙΚΟΣ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ ΑΚΟΛΟΥΘΙΕΣ ΚΕΦΑΛΑΙΟ 5 ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΟΔΟΣ ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ακολουθία ονομάζουμε
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014
 ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
ΜΕΘΟΔΟΛΟΓΙΕΣ & ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΗΝ ΑΛΓΕΒΡΑ ΤΗΣ Α ΛΥΚΕΙΟΥ
 ΜΕΘΟΔΟΛΟΓΙΕΣ & ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΗΝ ΑΛΓΕΒΡΑ ΤΗΣ Α ΛΥΚΕΙΟΥ Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός Αγαπητοί μαθητές. αυτό το βιβλίο αποτελεί ένα βοήθημα στην ύλη της Άλγεβρας Α Λυκείου, που είναι ένα από
ΜΕΘΟΔΟΛΟΓΙΕΣ & ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΗΝ ΑΛΓΕΒΡΑ ΤΗΣ Α ΛΥΚΕΙΟΥ Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός Αγαπητοί μαθητές. αυτό το βιβλίο αποτελεί ένα βοήθημα στην ύλη της Άλγεβρας Α Λυκείου, που είναι ένα από
Π Κ Τ Μ Ε Μ Λύσεις των ασκήσεων
 Π Κ Τ Μ Ε Μ Λύσεις των ασκήσεων Πρ. Η f : [0, ] R είναι συνεχής στο [0, ]. Χρησιμοποιώντας το Θεώρημα Bolzao- Weierstraß δείξτε ότι η f είναι φραγμένη στο [0, ]. Μην επικαλεστείτε κάποιο άλλο θεώρημα.
Π Κ Τ Μ Ε Μ Λύσεις των ασκήσεων Πρ. Η f : [0, ] R είναι συνεχής στο [0, ]. Χρησιμοποιώντας το Θεώρημα Bolzao- Weierstraß δείξτε ότι η f είναι φραγμένη στο [0, ]. Μην επικαλεστείτε κάποιο άλλο θεώρημα.
Άλγεβρα Α Λυκείου Κεφάλαιο 2ο. οι πράξεις και οι ιδιότητές τους
 οι πράξεις και οι ιδιότητές τους Μερικές ακόμη ταυτότητες (επιπλέον από τις αξιοσημείωτες που βρίσκονται στο σχολικό βιβλίο) ) Διαφορά δυνάμεων με ίδιο εκθέτη: ειδικά αν ο εκθέτης ν είναι άρτιος υπάρχει
οι πράξεις και οι ιδιότητές τους Μερικές ακόμη ταυτότητες (επιπλέον από τις αξιοσημείωτες που βρίσκονται στο σχολικό βιβλίο) ) Διαφορά δυνάμεων με ίδιο εκθέτη: ειδικά αν ο εκθέτης ν είναι άρτιος υπάρχει
Για να εκφράσουμε τη διαδικασία αυτή, γράφουμε: :
 Η θεωρία στα μαθηματικά προσανατολισμού Γ υκείου Τι λέμε συνάρτηση με πεδίο ορισμού το σύνολο ; Έστω ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το μία διαδικασία (κανόνα), με την
Η θεωρία στα μαθηματικά προσανατολισμού Γ υκείου Τι λέμε συνάρτηση με πεδίο ορισμού το σύνολο ; Έστω ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το μία διαδικασία (κανόνα), με την
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Εξέταση στο μάθημα Ανάλυση Ι & Εφαρμογές 26 Φεβρουαρίου 2015
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Εξέταση στο μάθημα Ανάλυση Ι & Εφαρμογές 26 Φεβρουαρίου 25 Απαντήστε και στα 4 προβλήματα με σαφήνεια και απλότητα. Όσοι έχουν πάρει προβιβάσιμο βαθμό στην Πρόοδο (πάνω
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Εξέταση στο μάθημα Ανάλυση Ι & Εφαρμογές 26 Φεβρουαρίου 25 Απαντήστε και στα 4 προβλήματα με σαφήνεια και απλότητα. Όσοι έχουν πάρει προβιβάσιμο βαθμό στην Πρόοδο (πάνω
Κεφάλαιο 12. Σειρές Ορισμός και Παραδείγματα Ορισμός
 Κεφάλαιο 2 Σειρές Στο κεφάλαιο αυτό θα εισάγουμε την έννοια της σειράς, δηλαδή του αθροίσματος ενός άπειρου πλήθους πραγματικών αριθμών. Στην Παράγραφο 2. θα ορίσουμε, καταρχάς, τις σειρές, και θα δούμε
Κεφάλαιο 2 Σειρές Στο κεφάλαιο αυτό θα εισάγουμε την έννοια της σειράς, δηλαδή του αθροίσματος ενός άπειρου πλήθους πραγματικών αριθμών. Στην Παράγραφο 2. θα ορίσουμε, καταρχάς, τις σειρές, και θα δούμε
Μεθοδική Επανα λήψή. Επιμέλεια Κων/νος Παπασταματίου. Θεωρία - Λεξιλόγιο Βασικές Μεθοδολογίες. Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.
 Μεθοδική Επανα λήψή Θεωρία - Λεξιλόγιο Βασικές Μεθοδολογίες Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 Βόλος Τηλ. 4 598 Επιμέλεια Κων/νος Παπασταματίου Περιεχόμενα Συνοπτική Θεωρία με Ερωτήσεις Απαντήσεις...
Μεθοδική Επανα λήψή Θεωρία - Λεξιλόγιο Βασικές Μεθοδολογίες Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 Βόλος Τηλ. 4 598 Επιμέλεια Κων/νος Παπασταματίου Περιεχόμενα Συνοπτική Θεωρία με Ερωτήσεις Απαντήσεις...
1 Ορισµός ακολουθίας πραγµατικών αριθµών
 ΜΑΣ 02. Απειροστικός Λογισµός Ι Ορισµός ακολουθίας πραγµατικών αριθµών Ορισµός.. Ονοµάζουµε ακολουθία πραγµατικών αριθµών κάθε απεικόνιση του συνόλου N των ϕυσικών αριθµών, στο σύνολο R των πραγµατικών
ΜΑΣ 02. Απειροστικός Λογισµός Ι Ορισµός ακολουθίας πραγµατικών αριθµών Ορισµός.. Ονοµάζουµε ακολουθία πραγµατικών αριθµών κάθε απεικόνιση του συνόλου N των ϕυσικών αριθµών, στο σύνολο R των πραγµατικών
αβ (, ) τέτοιος ώστε f(x
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΘΕΜΑ Α Άσκηση α) Έστω μια συνάρτηση f, η οποία είναι ορισμένη σε ένα κλειστό διάστημα [ αβ., ] Αν η f είναι συνεχής στο [ αβ, ]
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΘΕΜΑ Α Άσκηση α) Έστω μια συνάρτηση f, η οποία είναι ορισμένη σε ένα κλειστό διάστημα [ αβ., ] Αν η f είναι συνεχής στο [ αβ, ]
f(x) = και στην συνέχεια
 ΕΡΩΤΗΣΕΙΣ ΜΑΘΗΤΩΝ Ερώτηση. Στις συναρτήσεις μπορούμε να μετασχηματίσουμε πρώτα τον τύπο τους και μετά να βρίσκουμε το πεδίο ορισμού τους; Όχι. Το πεδίο ορισμού της συνάρτησης το βρίσκουμε πριν μετασχηματίσουμε
ΕΡΩΤΗΣΕΙΣ ΜΑΘΗΤΩΝ Ερώτηση. Στις συναρτήσεις μπορούμε να μετασχηματίσουμε πρώτα τον τύπο τους και μετά να βρίσκουμε το πεδίο ορισμού τους; Όχι. Το πεδίο ορισμού της συνάρτησης το βρίσκουμε πριν μετασχηματίσουμε
Κεφάλαιο 4: Διαφορικός Λογισμός
 ΣΥΓΧΡΟΝΗ ΠΑΙΔΕΙΑ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Κεφάλαιο 4: Διαφορικός Λογισμός Μονοτονία Συνάρτησης Tζουβάλης Αθανάσιος Κεφάλαιο 4: Διαφορικός Λογισμός Περιεχόμενα Μονοτονία συνάρτησης... Λυμένα παραδείγματα...
ΣΥΓΧΡΟΝΗ ΠΑΙΔΕΙΑ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Κεφάλαιο 4: Διαφορικός Λογισμός Μονοτονία Συνάρτησης Tζουβάλης Αθανάσιος Κεφάλαιο 4: Διαφορικός Λογισμός Περιεχόμενα Μονοτονία συνάρτησης... Λυμένα παραδείγματα...
ΑΝΑΛΥΣΗ 1 ΕΙΚΟΣΤΟ ΠΡΩΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ ΕΙΚΟΣΤΟ ΠΡΩΤΟ ΜΑΘΗΜΑ, --3 Μ. Παπαδημητράκης. Τώρα θα δούμε μια ακόμη εφαρμογή του Κριτηρίου του Ολοκληρώματος. Παράδειγμα. Γνωρίζουμε ότι η αρμονική σειρά αποκλίνει στο +, το οποίο φυσικά σημαίνει
ΑΝΑΛΥΣΗ ΕΙΚΟΣΤΟ ΠΡΩΤΟ ΜΑΘΗΜΑ, --3 Μ. Παπαδημητράκης. Τώρα θα δούμε μια ακόμη εφαρμογή του Κριτηρίου του Ολοκληρώματος. Παράδειγμα. Γνωρίζουμε ότι η αρμονική σειρά αποκλίνει στο +, το οποίο φυσικά σημαίνει
Θεώρημα Βolzano. Κατηγορία 1 η. 11.1 Δίνεται η συνάρτηση:
 Κατηγορία η Θεώρημα Βolzano Τρόπος αντιμετώπισης:. Όταν μας ζητούν να εξετάσουμε αν ισχύει το θεώρημα Bolzano για μια συνάρτηση f σε ένα διάστημα [, ] τότε: Εξετάζουμε την συνέχεια της f στο [, ] (αν η
Κατηγορία η Θεώρημα Βolzano Τρόπος αντιμετώπισης:. Όταν μας ζητούν να εξετάσουμε αν ισχύει το θεώρημα Bolzano για μια συνάρτηση f σε ένα διάστημα [, ] τότε: Εξετάζουμε την συνέχεια της f στο [, ] (αν η
1 Αριθμητική κινητής υποδιαστολής και σφάλματα στρογγύλευσης
 1 Αριθμητική κινητής υποδιαστολής και σφάλματα στρογγύλευσης Στη συγκεκριμένη ενότητα εξετάζουμε θέματα σχετικά με την αριθμητική πεπερασμένης ακρίβειας που χρησιμοποιούν οι σημερινοί υπολογιστές και τα
1 Αριθμητική κινητής υποδιαστολής και σφάλματα στρογγύλευσης Στη συγκεκριμένη ενότητα εξετάζουμε θέματα σχετικά με την αριθμητική πεπερασμένης ακρίβειας που χρησιμοποιούν οι σημερινοί υπολογιστές και τα
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ. 8. Πότε το γινόμενο δύο ή περισσοτέρων αριθμών παραγόντων είναι ίσο με το μηδέν ;
 ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ( ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ) ΠΑΡΑΤΗΡΗΣΗ : Το κεφάλαιο αυτό περιέχει πολλά θέματα που είναι επανάληψη εννοιών που διδάχθηκαν στο Γυμνάσιο γι αυτό σ αυτές δεν θα επεκταθώ αναλυτικά
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ( ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ) ΠΑΡΑΤΗΡΗΣΗ : Το κεφάλαιο αυτό περιέχει πολλά θέματα που είναι επανάληψη εννοιών που διδάχθηκαν στο Γυμνάσιο γι αυτό σ αυτές δεν θα επεκταθώ αναλυτικά
Συναρτήσεις Όρια Συνέχεια
 Κωνσταντίνος Παπασταματίου Μαθηματικά Γ Λυκείου Κατεύθυνσης Συναρτήσεις Όρια Συνέχεια Συνοπτική Θεωρία Μεθοδολογίες Λυμένα Παραδείγματα Επιμέλεια: Μαθηματικός Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 (με
Κωνσταντίνος Παπασταματίου Μαθηματικά Γ Λυκείου Κατεύθυνσης Συναρτήσεις Όρια Συνέχεια Συνοπτική Θεωρία Μεθοδολογίες Λυμένα Παραδείγματα Επιμέλεια: Μαθηματικός Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 (με
ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ Ι (2006-07)
 ΤΕΙ ΥΤΙΚΗΣ ΜΑΚΕ ΟΝΙΑΣ ΠΑΡΑΡΤΗΜΑ ΚΑΣΤΟΡΙΑΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ Ι (2006-07) Επιµέλεια Σηµειώσεων : Βασιλειάδης Γεώργιος Καστοριά, εκέµβριος 2006
ΤΕΙ ΥΤΙΚΗΣ ΜΑΚΕ ΟΝΙΑΣ ΠΑΡΑΡΤΗΜΑ ΚΑΣΤΟΡΙΑΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ Ι (2006-07) Επιµέλεια Σηµειώσεων : Βασιλειάδης Γεώργιος Καστοριά, εκέµβριος 2006
, ο αριθμός στον οποίο αντιστοιχεί ο 2 καλείται δεύτερος όρος της ακολουθίας και τον συμβολίζουμε συνήθως με
 5. ΑΚΟΛΟΥΘΙΕΣ Γενικά ακολουθία πραγματικών αριθμών είναι μια αντιστοίχιση των φυσικών αριθμών,,,...,ν,... στους πραγματικούς αριθμούς. Ο αριθμός στον οποίο αντιστοιχεί ο καλείται πρώτος όρος της ακολουθίας
5. ΑΚΟΛΟΥΘΙΕΣ Γενικά ακολουθία πραγματικών αριθμών είναι μια αντιστοίχιση των φυσικών αριθμών,,,...,ν,... στους πραγματικούς αριθμούς. Ο αριθμός στον οποίο αντιστοιχεί ο καλείται πρώτος όρος της ακολουθίας
Περιεχόμενα. Κεφάλαιο 3 Οι ιδιότητες των αριθμών... 37 3.1 Αριθμητικά σύνολα... 37 3.2 Ιδιότητες... 37 3.3 Περισσότερες ιδιότητες...
 Περιεχόμενα Πρόλογος... 5 Κεφάλαιο Βασικές αριθμητικές πράξεις... 5. Τέσσερις πράξεις... 5. Σύστημα πραγματικών αριθμών... 5. Γραφική αναπαράσταση πραγματικών αριθμών... 6.4 Οι ιδιότητες της πρόσθεσης
Περιεχόμενα Πρόλογος... 5 Κεφάλαιο Βασικές αριθμητικές πράξεις... 5. Τέσσερις πράξεις... 5. Σύστημα πραγματικών αριθμών... 5. Γραφική αναπαράσταση πραγματικών αριθμών... 6.4 Οι ιδιότητες της πρόσθεσης
1. στο σύνολο Σ έχει ορισθεί η πράξη της πρόσθεσης ως προς την οποία το Σ είναι αβελιανή οµάδα, δηλαδή
 KΕΦΑΛΑΙΟ ΤΟ ΣΥΝΟΛΟ ΤΩΝ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ιατεταγµένα σώµατα-αξίωµα πληρότητας Ένα σύνολο Σ καλείται διατεταγµένο σώµα όταν στο σύνολο Σ έχει ορισθεί η πράξη της πρόσθεσης ως προς την οποία το Σ είναι
KΕΦΑΛΑΙΟ ΤΟ ΣΥΝΟΛΟ ΤΩΝ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ιατεταγµένα σώµατα-αξίωµα πληρότητας Ένα σύνολο Σ καλείται διατεταγµένο σώµα όταν στο σύνολο Σ έχει ορισθεί η πράξη της πρόσθεσης ως προς την οποία το Σ είναι
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 3
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 3 ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 13 Μαρτίου 2013 Ασκηση 1. Αφού ϐρείτε την
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 3 ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 13 Μαρτίου 2013 Ασκηση 1. Αφού ϐρείτε την
OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 Ο ΚΕΦΑΛΑΙΟ : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β Έστω
Ο ΚΕΦΑΛΑΙΟ : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β Έστω
Μαθηματικά Γ Γυμνασίου
 Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
Ακολουθίες & Σειρές. Κώστας Γλυκός ΜΑΘΗΜΑΤΙΚΟΣ. Ασκήσεις για ΑΕΙ και ΤΕΙ. Kglykos.gr. σε Ακολουθίες, Σειρές, Δυναμοσειρές. τεχνικές.
 Ακολουθίες & Σειρές Κώστας Γλυκός Ασκήσεις για ΑΕΙ και ΤΕΙ σε Ακολουθίες Σειρές Δυναμοσειρές τεχνικές 0 ασκήσεις Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7. 0 0. 8 8. 8 8 Kglykos.gr / / 0 9 εκδόσεις Καλό
Ακολουθίες & Σειρές Κώστας Γλυκός Ασκήσεις για ΑΕΙ και ΤΕΙ σε Ακολουθίες Σειρές Δυναμοσειρές τεχνικές 0 ασκήσεις Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7. 0 0. 8 8. 8 8 Kglykos.gr / / 0 9 εκδόσεις Καλό
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ. ΜΕΡΟΣ 1ο ΑΛΓΕΒΡΑ
 1. Τι καλείται μεταβλητή; ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΑ Β ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 1ο ΑΛΓΕΒΡΑ Μεταβλητή είναι ένα γράμμα (π.χ., y, t, ) που το χρησιμοποιούμε για να παραστήσουμε ένα οποιοδήποτε στοιχείο ενός συνόλου..
1. Τι καλείται μεταβλητή; ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΑ Β ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 1ο ΑΛΓΕΒΡΑ Μεταβλητή είναι ένα γράμμα (π.χ., y, t, ) που το χρησιμοποιούμε για να παραστήσουμε ένα οποιοδήποτε στοιχείο ενός συνόλου..
Όταν η s n δεν συγκλίνει λέμε ότι η σειρά αποκλίνει.
 Όταν η s δεν συγκλίνει λέμε ότι η σειρά αποκλίνει. Παρατήρηση: Το αντίστροφο του προηγουμένου θεωρήματος δεν ισχύει. Παράδειγμα η σειρά με νιοστό όρο α = +-. Τότε lim α =0. Όμως s =α +α + +α = - + 3- +...+
Όταν η s δεν συγκλίνει λέμε ότι η σειρά αποκλίνει. Παρατήρηση: Το αντίστροφο του προηγουμένου θεωρήματος δεν ισχύει. Παράδειγμα η σειρά με νιοστό όρο α = +-. Τότε lim α =0. Όμως s =α +α + +α = - + 3- +...+
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
1. Υπολογίστε, όπου αυτές υπάρχουν, τις παραγώγους των συναρτήσεων:
 Υπολογίστε, όπου αυτές υπάρχουν, τις παραγώγους των συναρτήσεων:, g, h Απάντηση: Η με έχει παράγωγο 4 Μπορούμε όμως να εργαστούμε ως εξής: Είναι άρα 4 Η g με g έχει παράγωγο : g Η συνάρτηση h με h έχει
Υπολογίστε, όπου αυτές υπάρχουν, τις παραγώγους των συναρτήσεων:, g, h Απάντηση: Η με έχει παράγωγο 4 Μπορούμε όμως να εργαστούμε ως εξής: Είναι άρα 4 Η g με g έχει παράγωγο : g Η συνάρτηση h με h έχει
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ Επιμέλεια: Βασίλης Κράνιας wwwe-mathsgr ΑΝΑΛΥΣΗ Τι ονομάζουμε πραγματική συνάρτηση Έστω Α ένα υποσύνολο
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ Επιμέλεια: Βασίλης Κράνιας wwwe-mathsgr ΑΝΑΛΥΣΗ Τι ονομάζουμε πραγματική συνάρτηση Έστω Α ένα υποσύνολο
Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου
 Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου Αριθμοί 1. ΑΡΙΘΜΟΙ Σύνολο Φυσικών αριθμών: Σύνολο Ακέραιων αριθμών: Σύνολο Ρητών αριθμών: ακέραιοι με Άρρητοι αριθμοί: είναι οι μη ρητοί π.χ. Το σύνολο Πραγματικών
Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου Αριθμοί 1. ΑΡΙΘΜΟΙ Σύνολο Φυσικών αριθμών: Σύνολο Ακέραιων αριθμών: Σύνολο Ρητών αριθμών: ακέραιοι με Άρρητοι αριθμοί: είναι οι μη ρητοί π.χ. Το σύνολο Πραγματικών
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Λυσεις Ασκησεων - Φυλλαδιο 2
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt016/nt016.html Πέµπτη 7 Οκτωβρίου 016 Ασκηση 1. Βρείτε όλους
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt016/nt016.html Πέµπτη 7 Οκτωβρίου 016 Ασκηση 1. Βρείτε όλους
Ορισμένες σελίδες του βιβλίου
 Ορισμένες σελίδες του βιβλίου 7. Θεωρούμε το σύνολο αναφοράς 0,,. Να οριστούν τα σύνολα: Α. των τριψηφίων αριθμών που σχηματίζουν τα στοιχεία του Ω. Β. των τριψηφίων αριθμών με διαφορετικά ψηφία Γ. των
Ορισμένες σελίδες του βιβλίου 7. Θεωρούμε το σύνολο αναφοράς 0,,. Να οριστούν τα σύνολα: Α. των τριψηφίων αριθμών που σχηματίζουν τα στοιχεία του Ω. Β. των τριψηφίων αριθμών με διαφορετικά ψηφία Γ. των
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Ακολουθίες & Σειρές. Κώστας Γλυκός ΜΑΘΗΜΑΤΙΚΟΣ. Ασκήσεις για ΑΕΙ και ΤΕΙ. Kglykos.gr. σε Ακολουθίες, Σειρές, Δυναμοσειρές. τεχνικές.
 Ακολουθίες & Σειρές Κώστας Γλυκός Ασκήσεις για ΑΕΙ και ΤΕΙ σε Ακολουθίες, Σειρές, Δυναμοσειρές τεχνικές 0 ασκήσεις Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7. 0 0. 8 8. 8 8 Kglykos.gr / / 0 7 εκδόσεις Καλό
Ακολουθίες & Σειρές Κώστας Γλυκός Ασκήσεις για ΑΕΙ και ΤΕΙ σε Ακολουθίες, Σειρές, Δυναμοσειρές τεχνικές 0 ασκήσεις Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7. 0 0. 8 8. 8 8 Kglykos.gr / / 0 7 εκδόσεις Καλό
ΑΝΑΛΥΣΗ 1 ΔΕΚΑΤΟ ΠΕΜΠΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 1 ΔΕΚΑΤΟ ΠΕΜΠΤΟ ΜΑΘΗΜΑ, 8-11-13 Μ. Παπαδημητράκης. 1 Το Θεώρημα των Bolzano και Weierstrass συμπληρώνεται με την εξής Πρόταση (.16 του βιβλίου). ΠΡΟΤΑΣΗ. [α] Κάθε όχι άνω φραγμένη ακολουθία έχει
ΑΝΑΛΥΣΗ 1 ΔΕΚΑΤΟ ΠΕΜΠΤΟ ΜΑΘΗΜΑ, 8-11-13 Μ. Παπαδημητράκης. 1 Το Θεώρημα των Bolzano και Weierstrass συμπληρώνεται με την εξής Πρόταση (.16 του βιβλίου). ΠΡΟΤΑΣΗ. [α] Κάθε όχι άνω φραγμένη ακολουθία έχει
ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 10: ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ
 ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ [Ενότητα Προσδιορισμός των Τοπικών Ακροτάτων - Θεώρημα Εύρεση Τοπικών Ακροτάτων του κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ Άσκηση.
ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ [Ενότητα Προσδιορισμός των Τοπικών Ακροτάτων - Θεώρημα Εύρεση Τοπικών Ακροτάτων του κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ Άσκηση.
V. Διαφορικός Λογισμός. math-gr
 V Διαφορικός Λογισμός Παντελής Μπουμπούλης, MSc, PhD σελ blospotcom, bouboulismyschr ΜΕΡΟΣ Η έννοια της Παραγώγου Α Ορισμός Εφαπτομένη καμπύλης συνάρτησης: Έστω μια συνάρτηση και A, ένα σημείο της C Αν
V Διαφορικός Λογισμός Παντελής Μπουμπούλης, MSc, PhD σελ blospotcom, bouboulismyschr ΜΕΡΟΣ Η έννοια της Παραγώγου Α Ορισμός Εφαπτομένη καμπύλης συνάρτησης: Έστω μια συνάρτηση και A, ένα σημείο της C Αν
x είναι f 1 f 0 f κ λ
 3 Ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ [Κεφάλαια, Μέρος Β' του σχολικού βιβλίου] ΘΕΜΑ Α.Βλέπε σχολικό βιβλίο, σελίδα 4.. Βλέπε σχολικό βιβλίο, σελίδα 88, 89. 3. α) ΣΩΣΤΟ, διότι αν η f παραγωγίσιμη στο χ
3 Ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ [Κεφάλαια, Μέρος Β' του σχολικού βιβλίου] ΘΕΜΑ Α.Βλέπε σχολικό βιβλίο, σελίδα 4.. Βλέπε σχολικό βιβλίο, σελίδα 88, 89. 3. α) ΣΩΣΤΟ, διότι αν η f παραγωγίσιμη στο χ
- ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμένο Όριο στο R - Κεφ..7: Όρια Συνάρτησης
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμένο Όριο στο R - Κεφ..7: Όρια Συνάρτησης
Ο μαθητής που έχει μελετήσει τo κεφάλαιο αυτό θα πρέπει να είναι σε θέση:
 Ο μαθητής που έχει μελετήσει τo κεφάλαιο αυτό θα πρέπει να είναι σε θέση:. Να μπορεί να βρίσκει απο τη γραφική παράσταση μιας συνάρτησης το πεδίο ορισμού της το σύνολο τιμών της την τιμή της σε ένα σημείο..
Ο μαθητής που έχει μελετήσει τo κεφάλαιο αυτό θα πρέπει να είναι σε θέση:. Να μπορεί να βρίσκει απο τη γραφική παράσταση μιας συνάρτησης το πεδίο ορισμού της το σύνολο τιμών της την τιμή της σε ένα σημείο..
με Τέλος πάντων, έστω ότι ξεκινάει ένα άλλο υποθετικό σενάριο που απλά δεν διευκρινίζεται. Για το i) θα έχουμε , 2
 Άσκηση 75 Σε έναν οργανισμό, αρχικά υπάρχουν 04800 βακτήρια. Μετά από 1 ώρα υπάρχουν 10400 βακτήρια, μετά από ώρες 5100 βακτήρια, και γενικά ο αριθμός των βακτηρίων υποδιπλασιάζεται κάθε μια ώρα. α) Πόσα
Άσκηση 75 Σε έναν οργανισμό, αρχικά υπάρχουν 04800 βακτήρια. Μετά από 1 ώρα υπάρχουν 10400 βακτήρια, μετά από ώρες 5100 βακτήρια, και γενικά ο αριθμός των βακτηρίων υποδιπλασιάζεται κάθε μια ώρα. α) Πόσα
Να υπολογίζουμε τη λύση ή ρίζα ενός πολυωνύμου της μορφής. Να υπολογίζουμε τη ν-οστή ρίζα ενός μη αρνητικού αριθμού.
 Ενότητα 3 Ρίζες Πραγματικών Αριθμών Στην ενότητα αυτή θα μάθουμε: Να υπολογίζουμε τη λύση ή ρίζα ενός πολυωνύμου της μορφής Ρ x x ν α. Να υπολογίζουμε τη ν-οστή ρίζα ενός μη αρνητικού αριθμού. Τις ιδιότητες
Ενότητα 3 Ρίζες Πραγματικών Αριθμών Στην ενότητα αυτή θα μάθουμε: Να υπολογίζουμε τη λύση ή ρίζα ενός πολυωνύμου της μορφής Ρ x x ν α. Να υπολογίζουμε τη ν-οστή ρίζα ενός μη αρνητικού αριθμού. Τις ιδιότητες
Περιεχόμενα. Κεφάλαιο 3 Οι ιδιότητες των αριθμών Αριθμητικά σύνολα Ιδιότητες Περισσότερες ιδιότητες...
 Περιεχόμενα Πρόλογος 5 Κεφάλαιο Βασικές αριθμητικές πράξεις 5 Τέσσερις πράξεις 5 Σύστημα πραγματικών αριθμών 5 Γραφική αναπαράσταση πραγματικών αριθμών 6 Οι ιδιότητες της πρόσθεσης και του πολλαπλασιασμού
Περιεχόμενα Πρόλογος 5 Κεφάλαιο Βασικές αριθμητικές πράξεις 5 Τέσσερις πράξεις 5 Σύστημα πραγματικών αριθμών 5 Γραφική αναπαράσταση πραγματικών αριθμών 6 Οι ιδιότητες της πρόσθεσης και του πολλαπλασιασμού
Συνέχεια συνάρτησης σε κλειστό διάστημα
 8 Συνέχεια συνάρτησης σε κλειστό διάστημα Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ 1 Μια συνάρτηση f θα λέμε ότι είναι: i Συνεχής σε ένα ανοιχτό διάστημα (α,β) όταν είναι συνεχής σε κάθε σημείο του διαστήματος (α,β)
8 Συνέχεια συνάρτησης σε κλειστό διάστημα Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ 1 Μια συνάρτηση f θα λέμε ότι είναι: i Συνεχής σε ένα ανοιχτό διάστημα (α,β) όταν είναι συνεχής σε κάθε σημείο του διαστήματος (α,β)
2ογελ ΣΥΚΕΩΝ 2ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ο ΓΕΛ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β ΛΥΚΕΙΟΥ ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΣΧΟΛΙΚΟ ΕΤΟΣ -4 ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Επιμέλεια: ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ
ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ο ΓΕΛ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β ΛΥΚΕΙΟΥ ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΣΧΟΛΙΚΟ ΕΤΟΣ -4 ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Επιμέλεια: ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ
ΑΝΑΛΥΣΗ 1 ΔΩΔΕΚΑΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 1 ΔΩΔΕΚΑΤΟ ΜΑΘΗΜΑ, 1-11-13 Μ. Παπαδημητράκης. 1 Άσκηση 2.2.7. Έστω ϵ 0 > 0. Αποδείξτε ότι x n x αν και μόνο αν για κάθε ϵ με 0 < ϵ ϵ 0 ισχύει τελικά x n N x ϵ). Λύση: Έχουμε να αποδείξουμε την
ΑΝΑΛΥΣΗ 1 ΔΩΔΕΚΑΤΟ ΜΑΘΗΜΑ, 1-11-13 Μ. Παπαδημητράκης. 1 Άσκηση 2.2.7. Έστω ϵ 0 > 0. Αποδείξτε ότι x n x αν και μόνο αν για κάθε ϵ με 0 < ϵ ϵ 0 ισχύει τελικά x n N x ϵ). Λύση: Έχουμε να αποδείξουμε την
Συνεχή Κλάσματα. Εμμανουήλ Καπνόπουλος Α.Μ 282
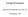 Συνεχή Κλάσματα Εμμανουήλ Καπνόπουλος Α.Μ 282 5 Νοεμβρίου 204 Ορισμός και ιδιότητες: Ορισμός: Έστω a 0, a, a 2,...a n ανεξάρτητες μεταβλητές, n N σχηματίζουν την ακολουθία {[a 0, a,..., a n ] : n N} όπου
Συνεχή Κλάσματα Εμμανουήλ Καπνόπουλος Α.Μ 282 5 Νοεμβρίου 204 Ορισμός και ιδιότητες: Ορισμός: Έστω a 0, a, a 2,...a n ανεξάρτητες μεταβλητές, n N σχηματίζουν την ακολουθία {[a 0, a,..., a n ] : n N} όπου
2.1 ΠΡΑΞΕΙΣ ΚΑΙ ΟΙ ΙΔΙΟΤΗΤΕΣ ΤΟΥΣ
 ΚΕΦΑΛΑΙΟ : ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ. ΠΡΑΞΕΙΣ ΚΑΙ ΟΙ ΙΔΙΟΤΗΤΕΣ ΤΟΥΣ Ρητός ονομάζεται κάθε αριθμός που έχει ή μπορεί να πάρει τη μορφή κλάσματος, όπου, είναι ακέραιοι με 0. Ρητοί αριθμοί : Q /, 0. Έτσι π.χ.
ΚΕΦΑΛΑΙΟ : ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ. ΠΡΑΞΕΙΣ ΚΑΙ ΟΙ ΙΔΙΟΤΗΤΕΣ ΤΟΥΣ Ρητός ονομάζεται κάθε αριθμός που έχει ή μπορεί να πάρει τη μορφή κλάσματος, όπου, είναι ακέραιοι με 0. Ρητοί αριθμοί : Q /, 0. Έτσι π.χ.
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 2
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt014/nt014.html https://sites.google.com/site/maths4edu/home/14
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt014/nt014.html https://sites.google.com/site/maths4edu/home/14
Ανάλυση Ι και Εφαρμογές Σημειώσεις από τις παραδόσεις Α. Γιαννόπουλος Τμήμα Φυσικής Πανεπιστήμιο Αθηνών Αθήνα 2018
 Ανάλυση Ι και Εφαρμογές Σημειώσεις από τις παραδόσεις Α. Γιαννόπουλος Τμήμα Φυσικής Πανεπιστήμιο Αθηνών Αθήνα 08 Περιεχόμενα Το σύνολο των πραγματικών αριθμών. Φυσικοί, ακέραιοι και ρητοί αριθμοί............................
Ανάλυση Ι και Εφαρμογές Σημειώσεις από τις παραδόσεις Α. Γιαννόπουλος Τμήμα Φυσικής Πανεπιστήμιο Αθηνών Αθήνα 08 Περιεχόμενα Το σύνολο των πραγματικών αριθμών. Φυσικοί, ακέραιοι και ρητοί αριθμοί............................
ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΟΔΟΣ. Σύμφωνα με τα παραπάνω, για μια αριθμητική πρόοδο που έχει πρώτο όρο τον ...
 ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΟΔΟΣ Ορισμός : Μία ακολουθία ονομάζεται αριθμητική πρόοδος, όταν ο κάθε όρος της, δημιουργείται από τον προηγούμενο με πρόσθεση του ίδιου πάντοτε αριθμού. Ο σταθερός αριθμός που προστίθεται
ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΟΔΟΣ Ορισμός : Μία ακολουθία ονομάζεται αριθμητική πρόοδος, όταν ο κάθε όρος της, δημιουργείται από τον προηγούμενο με πρόσθεση του ίδιου πάντοτε αριθμού. Ο σταθερός αριθμός που προστίθεται
Περιεχόμενα μεθόδευση του μαθήματος
 Περιεχόμενα μεθόδευση του μαθήματος. Πως ορίζεται η έννοια. Το όριο. To f() f() ; f() εφόσον υπάρχει είναι μονοσήμαντα ορισμένο; εξαρτιέται από τα άκρα α, β των ( α, ) και (, β ) ;. Πως ορίζονται τα πλευρικά
Περιεχόμενα μεθόδευση του μαθήματος. Πως ορίζεται η έννοια. Το όριο. To f() f() ; f() εφόσον υπάρχει είναι μονοσήμαντα ορισμένο; εξαρτιέται από τα άκρα α, β των ( α, ) και (, β ) ;. Πως ορίζονται τα πλευρικά
Ακουλουθίες ρ. Κωνσταντίνα Παναγιωτίδου
 Ακουλουθίες ρ. Κωνσταντίνα Παναγιωτίδου Σχολή Ναυτικών οκίµων Ακ. Ετος 2018-2019 Εισαγωγικά Βασικοί Ορισµοί Μονοτονία Ακολουθίας Φραγµένη Ακολουθία Υπακολουθίες Σύγκλιση - Απόκλιση Ακολουθιών N = {1, 2,
Ακουλουθίες ρ. Κωνσταντίνα Παναγιωτίδου Σχολή Ναυτικών οκίµων Ακ. Ετος 2018-2019 Εισαγωγικά Βασικοί Ορισµοί Μονοτονία Ακολουθίας Φραγµένη Ακολουθία Υπακολουθίες Σύγκλιση - Απόκλιση Ακολουθιών N = {1, 2,
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Λυσεις Ασκησεων - Φυλλαδιο 1
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 1 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt01b/nt01b.html Πέµπτη 1 Οκτωβρίου 01 Ασκηση 1. είξτε ότι
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 1 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt01b/nt01b.html Πέµπτη 1 Οκτωβρίου 01 Ασκηση 1. είξτε ότι
Συνέχεια συνάρτησης σε διάστημα. Η θεωρία και τι προσέχουμε. x, ισχύει: lim f (x) f ( ).
 Κεφάλαιο 4 Συνέχεια συνάρτησης σε διάστημα 411 Ερώτηση θεωρίας 1 Η θεωρία και τι προσέχουμε Πότε μια συνάρτηση f θα λέμε ότι είναι συνεχής σε ένα ανοικτό διάστημα (, ) αβ; Απάντηση Μια συνάρτηση f θα λέμε
Κεφάλαιο 4 Συνέχεια συνάρτησης σε διάστημα 411 Ερώτηση θεωρίας 1 Η θεωρία και τι προσέχουμε Πότε μια συνάρτηση f θα λέμε ότι είναι συνεχής σε ένα ανοικτό διάστημα (, ) αβ; Απάντηση Μια συνάρτηση f θα λέμε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΕ ΕΦΑΡΜΟΓΕΣ ΣΤΗ ΒΙΟΪΑΤΡΙΚΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΕ ΕΦΑΡΜΟΓΕΣ ΣΤΗ ΒΙΟΪΑΤΡΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΑΝΑΛΥΣΗ Ι ΣΕΙΡΕΣ Διδάσκουσα : Δρ Μαρία Αδάμ Λυμένες ασκήσεις ) Να μελετηθούν ως προς τη σύγκλισή
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΕ ΕΦΑΡΜΟΓΕΣ ΣΤΗ ΒΙΟΪΑΤΡΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΑΝΑΛΥΣΗ Ι ΣΕΙΡΕΣ Διδάσκουσα : Δρ Μαρία Αδάμ Λυμένες ασκήσεις ) Να μελετηθούν ως προς τη σύγκλισή
ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ 1 ο : Όριο Συνέχεια Συνάρτησης
 ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ ο : Όριο Συνέχεια Συνάρτησης Φυλλάδιο Φυλλάδι555 4 ο ο.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ ο : Όριο Συνέχεια Συνάρτησης Φυλλάδιο Φυλλάδι555 4 ο ο.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
h(x, y) = card ({ 1 i n : x i y i
 Κεφάλαιο 1 Μετρικοί χώροι 1.1 Ορισμός και παραδείγματα Ορισμός 1.1.1 μετρική). Εστω X ένα μη κενό σύνολο. Μετρική στο X λέγεται κάθε συνάρτηση ρ : X X R με τις παρακάτω ιδιότητες: i) ρx, y) για κάθε x,
Κεφάλαιο 1 Μετρικοί χώροι 1.1 Ορισμός και παραδείγματα Ορισμός 1.1.1 μετρική). Εστω X ένα μη κενό σύνολο. Μετρική στο X λέγεται κάθε συνάρτηση ρ : X X R με τις παρακάτω ιδιότητες: i) ρx, y) για κάθε x,
Ιγνάτιος Ιωαννίδης Χρήσιμες Γνώσεις 5
 Ιγνάτιος Ιωαννίδης Χρήσιμες Γνώσεις 5 Α Σύνολα αριθμών Για τα σύνολα των αριθμών γνωρίζουμε ότι N Z Q R. ) Το N= { 0,,,,... } είναι το σύνολο των φυσικών αριθμών. ) Το Z = { 0, ±, ±, ±,... } είναι το σύνολο
Ιγνάτιος Ιωαννίδης Χρήσιμες Γνώσεις 5 Α Σύνολα αριθμών Για τα σύνολα των αριθμών γνωρίζουμε ότι N Z Q R. ) Το N= { 0,,,,... } είναι το σύνολο των φυσικών αριθμών. ) Το Z = { 0, ±, ±, ±,... } είναι το σύνολο
35 Χρήσιμες Προτάσεις με αποδείξεις Γ Λυκείου Μαθηματικά Κατεύθυνσης
 4 5 35 Χρήσιμες Προτάσεις με αποδείξεις Γ Λυκείου Μαθηματικά Κατεύθυνσης Περίληψη: Στο ένθετο αυτό περιλαμβάνονται 35 βασικές προτάσεις, μικρά λήμματα χρήσιμα για τις εξετάσεις. Μας βοηθούν να «ξεκλειδώνουμε»
4 5 35 Χρήσιμες Προτάσεις με αποδείξεις Γ Λυκείου Μαθηματικά Κατεύθυνσης Περίληψη: Στο ένθετο αυτό περιλαμβάνονται 35 βασικές προτάσεις, μικρά λήμματα χρήσιμα για τις εξετάσεις. Μας βοηθούν να «ξεκλειδώνουμε»
ΑΝΑΛΥΣΗ 1 ΤΕΤΑΡΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 1 ΤΕΤΑΡΤΟ ΜΑΘΗΜΑ, 15-10-13 Μ. Παπαδημητράκης. 1 Παράδειγμα. Ως εφαρμογή της Αρχιμήδειας Ιδιότητας θα μελετήσουμε το σύνολο { 1 } A = n N = {1, 1 n 2, 1 } 3,.... Κατ αρχάς το σύνολο A έχει προφανώς
ΑΝΑΛΥΣΗ 1 ΤΕΤΑΡΤΟ ΜΑΘΗΜΑ, 15-10-13 Μ. Παπαδημητράκης. 1 Παράδειγμα. Ως εφαρμογή της Αρχιμήδειας Ιδιότητας θα μελετήσουμε το σύνολο { 1 } A = n N = {1, 1 n 2, 1 } 3,.... Κατ αρχάς το σύνολο A έχει προφανώς
Σήματα και Συστήματα. Διάλεξη 1: Σήματα Συνεχούς Χρόνου. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ. Να εξετάσετε αν είναι ίσες οι συναρτήσεις f, g όταν: x x 2 x x. x x g x. ln x ln x 1 και
 Α ΟΜΑΔΑ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Να εξετάσετε αν είναι ίσες οι συναρτήσεις, όταν: () με R και (). Σ Υ Ν Α Ρ Τ Η Σ Ε Ι Σ Το πεδίο ορισμού της είναι A R. Επομένως A A R Α Θα εξετάσουμε αν για κάθε R ισχύει.
Α ΟΜΑΔΑ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Να εξετάσετε αν είναι ίσες οι συναρτήσεις, όταν: () με R και (). Σ Υ Ν Α Ρ Τ Η Σ Ε Ι Σ Το πεδίο ορισμού της είναι A R. Επομένως A A R Α Θα εξετάσουμε αν για κάθε R ισχύει.
Ακολουθίες πραγματικών αριθμών
 ΚΕΦΑΛΑΙΟ Ακολουθίες πραγματικών αριθμών Όταν διαδοχικές τιµές που παίρνει µία μεταβλητή προσεγγίζουν απεριόριστα µία συγκεκριµένη τιµή έτσι ώστε τελικά να διαφέρουν από αυτήν λιγότερο από όσο επιθυµεί
ΚΕΦΑΛΑΙΟ Ακολουθίες πραγματικών αριθμών Όταν διαδοχικές τιµές που παίρνει µία μεταβλητή προσεγγίζουν απεριόριστα µία συγκεκριµένη τιµή έτσι ώστε τελικά να διαφέρουν από αυτήν λιγότερο από όσο επιθυµεί
Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ
 Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ (Α ΜΕΡΟΣ: ΣΥΝΑΡΤΗΣΕΙΣ) Επιμέλεια: Καραγιάννης Ιωάννης, Σχολικός Σύμβουλος Μαθηματικών
Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ (Α ΜΕΡΟΣ: ΣΥΝΑΡΤΗΣΕΙΣ) Επιμέλεια: Καραγιάννης Ιωάννης, Σχολικός Σύμβουλος Μαθηματικών
APEIROSTIKOS LOGISMOS I
 APEIROSTIKOS LOGISOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου. Άσκηση : Αποδείξτε με τον ορισμό ότι:. lim ( ) = +,. lim =,. lim ln( + ) = ln, + 4. lim + =. Λύση:. Θεωρούμε αυθαίρετο
APEIROSTIKOS LOGISOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου. Άσκηση : Αποδείξτε με τον ορισμό ότι:. lim ( ) = +,. lim =,. lim ln( + ) = ln, + 4. lim + =. Λύση:. Θεωρούμε αυθαίρετο
f x x, ν Ν-{0,1} είναι παραγωγίσιμη στο R
 ΟΕΦΕ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Θέμα Α Α Να αποδείξετε ότι η συνάρτηση ν ν και ισχύει f ν f, νν-{,} είναι παραγωγίσιμη στο R
ΟΕΦΕ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Θέμα Α Α Να αποδείξετε ότι η συνάρτηση ν ν και ισχύει f ν f, νν-{,} είναι παραγωγίσιμη στο R
7. ΑΝΩΜΑΛΑ ΣΗΜΕΙΑ, ΠΟΛΟΙ ΚΑΙ ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΟΛΟΚΛΗΡΩΤΙΚΩΝ ΥΠΟΛΟΙΠΩΝ. και σε κάθε γειτονιά του z
 7. ΑΝΩΜΑΛΑ ΣΗΜΕΙΑ, ΠΟΛΟΙ ΚΑΙ ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΟΛΟΚΛΗΡΩΤΙΚΩΝ ΥΠΟΛΟΙΠΩΝ Ένα σημείο λέγεται ανώμαλο σημείο της συνάρτησης f( ) αν η f( ) δεν είναι αναλυτική στο και σε κάθε γειτονιά του υπάρχει ένα τουλάχιστον
7. ΑΝΩΜΑΛΑ ΣΗΜΕΙΑ, ΠΟΛΟΙ ΚΑΙ ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΟΛΟΚΛΗΡΩΤΙΚΩΝ ΥΠΟΛΟΙΠΩΝ Ένα σημείο λέγεται ανώμαλο σημείο της συνάρτησης f( ) αν η f( ) δεν είναι αναλυτική στο και σε κάθε γειτονιά του υπάρχει ένα τουλάχιστον
ΑΝΑΛΥΣΗ 1 ΕΙΚΟΣΤΟ ΕΒΔΟΜΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 1 ΕΙΚΟΣΤΟ ΕΒΔΟΜΟ ΜΑΘΗΜΑ, 6-12-13 Μ. Παπαδημητράκης. 1 Τώρα θα δούμε την απόδειξη του Θεωρήματος που διατυπώσαμε στο τέλος του προηγούμενου μαθήματος. Απόδειξη. [α] Θεωρούμε συνάρτηση f : A R και
ΑΝΑΛΥΣΗ 1 ΕΙΚΟΣΤΟ ΕΒΔΟΜΟ ΜΑΘΗΜΑ, 6-12-13 Μ. Παπαδημητράκης. 1 Τώρα θα δούμε την απόδειξη του Θεωρήματος που διατυπώσαμε στο τέλος του προηγούμενου μαθήματος. Απόδειξη. [α] Θεωρούμε συνάρτηση f : A R και
Διακριτά Μαθηματικά. Απαρίθμηση: Διωνυμικοί συντελεστές
 Διακριτά Μαθηματικά Απαρίθμηση: Διωνυμικοί συντελεστές Συνδυασμοί Το πλήθος των συνδυασμών r από n στοιχεία, C(n,r) συμβολίζεται και ως Ο αριθμός αυτός λέγεται και διωνυμικός συντελεστής Οι αριθμοί αυτοί
Διακριτά Μαθηματικά Απαρίθμηση: Διωνυμικοί συντελεστές Συνδυασμοί Το πλήθος των συνδυασμών r από n στοιχεία, C(n,r) συμβολίζεται και ως Ο αριθμός αυτός λέγεται και διωνυμικός συντελεστής Οι αριθμοί αυτοί
Αριθμητική εύρεση ριζών μη γραμμικών εξισώσεων
 Αριθμητική εύρεση ριζών μη γραμμικών εξισώσεων Με τον όρο μη γραμμικές εξισώσεις εννοούμε εξισώσεις της μορφής: f( ) 0 που προέρχονται από συναρτήσεις f () που είναι μη γραμμικές ως προς. Περιέχουν δηλαδή
Αριθμητική εύρεση ριζών μη γραμμικών εξισώσεων Με τον όρο μη γραμμικές εξισώσεις εννοούμε εξισώσεις της μορφής: f( ) 0 που προέρχονται από συναρτήσεις f () που είναι μη γραμμικές ως προς. Περιέχουν δηλαδή
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. 2x 1. είναι Τότε έχουμε: » τον χρησιμοποιούμε κυρίως σε θεωρητικές ασκήσεις.
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ : ΣΥΝΑΡΤΗΣΗ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ [Υποκεφάλαιο. Μονότονες συναρτήσεις Αντίστροφη συνάρτηση του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ : ΣΥΝΑΡΤΗΣΗ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ [Υποκεφάλαιο. Μονότονες συναρτήσεις Αντίστροφη συνάρτηση του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.
Να γράψετε 5 φυσικούς αριθμούς ξεκινώντας από τον μικρότερο. Ποιοι αριθμοί λέγονται ρητοί και ποιοι άρρητοι;
 Φυσικοί, Ακέραιοι, Ρητοί, Άρρητοι, Πραγματικοί, Απόλυτη Τιμή, Ομόσημοι, Ετερόσημοι, Αντίθετοι, Αντίστροφοι. Να γράψετε 5 φυσικούς αριθμούς ξεκινώντας από τον μικρότερο. Ποιοι αριθμοί λέγονται ακέραιοι;
Φυσικοί, Ακέραιοι, Ρητοί, Άρρητοι, Πραγματικοί, Απόλυτη Τιμή, Ομόσημοι, Ετερόσημοι, Αντίθετοι, Αντίστροφοι. Να γράψετε 5 φυσικούς αριθμούς ξεκινώντας από τον μικρότερο. Ποιοι αριθμοί λέγονται ακέραιοι;
Μηχανική ΙI. Μετασχηματισμοί Legendre. διπλανό σχήμα ότι η αντίστροφη συνάρτηση dg. λέγεται μετασχηματισμός Legendre της f (x)
 Τμήμα Π Ιωάννου & Θ Αποστολάτου 7/5/000 Μηχανική ΙI Μετασχηματισμοί Legendre Έστω μια πραγματική συνάρτηση f (x) Ορίζουμε την παράγωγο συνάρτηση df (x) της f (x) : ( x) (η γραφική της παράσταση δίνεται
Τμήμα Π Ιωάννου & Θ Αποστολάτου 7/5/000 Μηχανική ΙI Μετασχηματισμοί Legendre Έστω μια πραγματική συνάρτηση f (x) Ορίζουμε την παράγωγο συνάρτηση df (x) της f (x) : ( x) (η γραφική της παράσταση δίνεται
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ.2.6 Μέρος Β του σχολικού βιβλίου].
![ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ.2.6 Μέρος Β του σχολικού βιβλίου]. ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ.2.6 Μέρος Β του σχολικού βιβλίου].](/thumbs/52/29746903.jpg) ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ..6 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα 1. ΘΕΜΑ Β Να μελετηθούν ως προς την μονοτονία
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ..6 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα 1. ΘΕΜΑ Β Να μελετηθούν ως προς την μονοτονία
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Λυσεις Ασκησεων - Φυλλαδιο 3
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 3 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2016/nt2016.html Πέµπτη 3 Νοεµβρίου 2016 Ασκηση 1. Αφού ϐρείτε
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 3 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2016/nt2016.html Πέµπτη 3 Νοεµβρίου 2016 Ασκηση 1. Αφού ϐρείτε
