Οπτικι και κφματα. Δθμιτρθσ Παπάηογλου Τμιμα Επιςτιμθσ και Τεχνολογίασ Υλικών Πανεπιςτιμιο Κριτθσ
|
|
|
- Τωβίτ Κοντολέων
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Οπτικι και κφματα Δθμιτρθσ Παπάηογλου Τμιμα Επιςτιμθσ και Τεχνολογίασ Υλικών Πανεπιςτιμιο Κριτθσ
2 Δθμιτρθσ Παπάηογλου 2013 Άδειεσ Χριςθσ -Το παρόν εκπαιδευτικό υλικό υπόκειται ςτθν άδεια χριςθσ Creative Commons και ειδικότερα Αναφορά - Μη εμπορική Χρήςη - Όχι Παράγωγο Έργο v. 3.0 (Attribution Non Commercial Non-derivatives) - Για εκπαιδευτικό υλικό, όπωσ εικόνεσ, που υπόκειται ςε άλλου τφπου άδειασ χριςθσ, θ άδεια χριςθσ αναφζρεται ρθτϊσ.
3 Γεωμετρικι Οπτικι
4 Δθμιτρθσ Παπάηογλου 2013 Η ιδζα τθν απεικόνιςθσ Σημειακή πηγή Στιγματική απεικόνιση Η ανακατεφκυνςθ όλων των ακτίνων που ξεκινοφν από ζνα ςθμείο του αντικειμζνου ςε ζνα ςθμείο του ειδώλου Εκτεταμένη πηγή αντικείμενο είδωλο Απεικονιστικό σύστημα
5 Δθμιτρθσ Παπάηογλου 2013 Κατοπτρικι ανάκλαςθ Στθν κατοπτρικι ανάκλαςθ θ ανακλώμενθ βρίςκεται ςτο επίπεδο πρόςπτωςθσ r i επίπεδο ππόζπηυζηρ Κατοπτρικό είδωλο
6 Δθμιτρθσ Παπάηογλου 2013 Διάχυτθ ανάκλαςθ Στθν διάχυτθ ανάκλαςθ θ ανακλώμενθ δζςμθ, λόγω τθσ μικροδομισ τθσ επιφάνειασ, δεν βρίςκεται ςε ζνα επίπεδο. r i επίπεδο ππόζπηυζηρ ηςπική μικποδομή ηηρ ανακλαζηικήρ επιθάνειαρ ζηην διάσςηη ανάκλαζη
7 Δθμιτρθσ Παπάηογλου 2013 Διάκλαςθ Νόμορ ηος Snell n sin n sin i i t t Η διακλώμενθ βρίςκεται ςτο επίπεδο πρόπτωςθσ ni nt i n t i nt i t επίπεδο ππόζπηυζηρ
8 Δθμιτρθσ Παπάηογλου 2013 Ειδικι περίπτωςθ: ολικι ανάκλαςθ Διάθλαζη από οπηικά πςκνό ζε οπηικά απαιό μέζο ni nt i t t o 90 sin c i οπιακή γυνία n n t i Τςπική ηιμή n n i t c 1.5 ( glass) 1 ( air) 41.8 o evanescent waves Για γωνίεσ πρόπτωςθσ θ i >θ c θ ανακλαςτικότθτα είναι 100%
9 Απεικόνιςθ
10 Δθμιτρθσ Παπάηογλου 2013 Ανάκλαςθ από επίπεδθ επιφάνεια i r s s Η απεικόνιζη είναι ζηιγμαηική! Εθαπμογή: ποιο ππέπει να είναι ηο ύτορ ηος καθπέπηη για να βλέπει ο παπαηηπηηήρ όλο ηος ηο ζώμα;
11 Διάκλαςθ από επίπεδθ επιφάνεια ni sini nt sint h h sin i, sin 2 2 t 2 2 s h s h n n 2 t 2 i 2 s s (1 ) h 2 ni nt Η απεικόνιζη δεν είναι ζηιγμαηική αθού κάθε ακηίνα ανηιζηοισεί ζε διαθοπεηικό είδυλο! n h s s n Για ζσεδόν t κάθεηερ ακηίνερ: 0 Δθμιτρθσ Παπάηογλου 2013 dpapa@materials.uoc.gr i θαινομένη ανύτυζη
12 Δθμιτρθσ Παπάηογλου 2013 Διάκλαςθ από ςφαιρικι επιφάνεια ζθαιπικό δίοπηπο Για να υπολογίςουμε τθν ςχζςθ τθσ κζςθσ του ειδώλου (Β) με τθν κζςθ του αντικειμζνου (Α) για κάκε ακτίνα που διακλάται από το ςφαιρικό δίοπτρο κα αξιοποιιςουμε τθν αρχι του Fermat ( OPL) L n l n l i i t t
13 Δθμιτρθσ Παπάηογλου 2013 ανάλςζη για ηην είζοδο li ( s Ro) R li li R ( s R) 2 R( s R)cos lt ( s Ro) R lt lt R ( s R) 2 R( s R)cos απσή Fermat dl 2 R( s R)sin 2 R( s R)sin L nili ntlt ni nt 0 d l l i ανάλςζη για ηην έξοδο ni ( s R) nt ( s R) ni lt 0 s ( s R) R l l n l i t t i Η απεικόνιςθ δεν είναι ςτιγματικι αφοφ κάκε ακτίνα αντιςτοιχεί ςε διαφορετικό είδωλο! t
14 Δθμιτρθσ Παπάηογλου 2013 Παραξονικι προςζγγιςθ ( 0) 0 cos 1 l s, l s i t ni ( s R) nt ( s R) ni ( s R) nt ( s R) 0 0 l l s s i t n n n n i t t i s s R Η απεικόνιζη είναι ζηιγμαηική!
15 Δθμιτρθσ Παπάηογλου 2013 Συμβάςεισ για ςφαιρικά δίοπτρα n i n t Πρόςθμο + - s αριςτερά του φακοφ (πραγματικό αντικείμενο) δεξιά του φακοφ (φανταςτικό αντικείμενο) s' δεξιά του φακοφ (πραγματικό είδωλο) αριςτερά του φακοφ (φανταςτικό είδωλο) R κυρτό ( κοίλο )
16 Δθμιτρθσ Παπάηογλου 2013 Θζςθ εςτιών κσρηό δίοπηρο n n n n s s R i t t i n i n t nr i s s f n t n i 0 εζηία R 0 Τςπική ηιμή n 1 ( air), n 1.5 ( glass) f 2R 0 t t n i n t s s f nr t n t n i 0 Τςπική ηιμή n 1 ( air), n 1.5 ( glass) f 3R 0 t t f f
17 Δθμιτρθσ Παπάηογλου 2013 κοίλο δίοπηρο n i n t nr i s s f n t n i 0 R 0 Τςπική ηιμή n 1 ( air), n 1.5 ( glass) f 2R 0 t t n i n t s s f nr t n t n i 0 Τςπική ηιμή n 1 ( air), n 1.5 ( glass) f 3R 0 t t f f
18 Δθμιτρθσ Παπάηογλου 2013 Φακοί Ζνασ φακόσ είναι ουςιαςτικά μια αλλθλουχία ςφαιρικών διόπτρων n n n n s s R m L L m o 1 n n n n L m m L ( so d) s R 2 μηδενίζεηαι όηαν d0 1 1 nl nm 1 1 nl d ( ) s s n R R n ( s d) s m 1 2 m o o
19 Δθμιτρθσ Παπάηογλου 2013 Λεπτοί φακοί d s s f ( s f )( s f ) f ζσέζη Gauss ζσέζη Newton 2 1 nl 1 1 ( 1)( ) f n R R m 1 2 ζσέζη καηαζκεςαζηή θακών
20 Δθμιτρθσ Παπάηογλου 2013 Ιςοδυναμία ςχζςεων Gauss-Newton ζσέζη Newton ( s f ) ( s f ) f s s ( s s) f f f f s s ( s s) f s s ζσέζη Gauss
21 Δθμιτρθσ Παπάηογλου 2013 Κανονικοποίθςθ των μεταβλθτών Newton Μεηπάμε ζε εζηιακέρ αποζηάζειρ 2 x x f x x 1, f f Gauss Μεηπάμε ζε εζηιακέρ αποζηάζειρ s s f s s, f f
22 Δθμιτρθσ Παπάηογλου 2013 Τφποι λεπτών φακών Συγκλίνοντεσ f 0 Αποκλίνοντεσ f 0
23 Δθμιτρθσ Παπάηογλου 2013 Κφρια ςθμεία λεπτών φακών Συγκλίνοντες Αποκλίνοντες Οπηικό κένηπο Οπηικό κένηπο εμππόρ εζηία πίζω εζηία πίζω εζηία εμππόρ εζηία οπηικόρ άξοναρ οπηικόρ άξοναρ εμππόρ εζηιακό επίπεδο πίζω εζηιακό επίπεδο πίζω εζηιακό επίπεδο εμππόρ εζηιακό επίπεδο
24 Δθμιτρθσ Παπάηογλου 2013 Απεικόνιςθ με λεπτό φακό Συγκλίνων υακός Αποκλίνων υακός
25 Δθμιτρθσ Παπάηογλου 2013 Μεγζκυνςθ Εγκάρσια μεγέθσνση: λόγορ ηων εγκάπζιων διαζηάζεων ειδώλος -ανηικειμένος M T h s f x h s x f >0 ορκό είδωλο <0 αντεςτραμμζνο είδωλο Διαμήκης μεγέθσνση λόγορ μεηαηόπιζηρ ηος ειδώλος για μια απειποζηή μεηαηόπιζη ηος ανηικειμένος M L 2 dx f M 2 dx x 2 T
26 Δθμιτρθσ Παπάηογλου 2013 Μεγζκυνςθ με κανονικοποιθμζνεσ ςυντεταγμζνεσ Newton h f x MT h x f M 2 T dx f M L 2 dx x 2 M L x x, f f απλοποίηζη ηυν ςπολογιζμών 1 1 2
27 Δθμιτρθσ Παπάηογλου 2013 Gauss h s MT h s M dx 2 ML MT dx M s s, f f δεν έσοςμε οςζιαζηική απλοποίηζη ηυν ςπολογιζμών T L 2 2
28 Δθμιτρθσ Παπάηογλου 2013 Μεγζκυνςθ και κζςθ ειδώλου για απεικόνιςθ με λεπτοφσ φακοφσ Σςγκλίνονηερ θακοί θανηαζηικό, οπθό ππαγμαηικό ανηεζηπαμμένο Αποκλίνονηερ θακοί
29 Δθμιτρθσ Παπάηογλου 2013 Πωσ απεικονίηονται τριςδιάςτατα αντικείμενα; Σςγκλίνονηερ θακοί Αποκλίνονηερ θακοί
30 Δθμιτρθσ Παπάηογλου 2013 Κάτοπτρα Η λειτουργία τουσ ςτθρίηεται ςτθν ανάκλαςθ του φωτόσ! κυρτά κοίλα επίπεδα ςφαιρικά αςφαιρικά Λειτουργία ςε ευρεία περιοχι του φάςματοσ Ευκολότερθ καταςκευι (μόνο μια χριςιμθ επιφάνεια). Μποροφμε να καταςκευάςουμε ευκολότερα μεγάλων διαςτάςεων κάτοπτρα όχι όμωσ και φακοφσ Αντιςτροφι τθσ πορείασ τθσ δζςμθσ
31 Δθμιτρθσ Παπάηογλου 2013 Τφποι κατόπτρων 1 ης επιυάνειας 2 ης επιυάνειας Διηλεκτρικά
32 Δθμιτρθσ Παπάηογλου 2013 Ανάκλαςθ από ςφαιρικι επιφάνεια ζθαιπικό κάηοπηπο concave R 0 convex R 0 Για να υπολογίςουμε τθν ςχζςθ τθσ κζςθσ του ειδώλου (Β) με τθν κζςθ του αντικειμζνου (Α) για κάκε ακτίνα που ανακλάται από το ςφαιρικό κάτοπτρο κα αξιοποιιςουμε και πάλι τθν αρχι του Fermat ( OPL) L n l n l i i i r
33 Δθμιτρθσ Παπάηογλου 2013 ανάλςζη για ηην είζοδο ανάλςζη για ηην έξοδο li ( s Ro) R li li R [ s ( R)] 2 R[ s ( R)]cos lr ( s Ro) R lr lr R [ s ( R)] 2 R[ s ( R)]cos απσή Fermat dl 2 R( s R)sin 2 R( s R)sin L nili nilr ni ni 0 d l l i ( s R) ( s R) lr 0 s ( s R) R l l l i r i r Η απεικόνιςθ δεν είναι ςτιγματικι αφοφ κάκε ακτίνα αντιςτοιχεί ςε διαφορετικό είδωλο!
34 Δθμιτρθσ Παπάηογλου 2013 Παραξονικι προςζγγιςθ ( 0) 0 cos 1 s l, s l i r s R R s ( s R) R 1 1 s s s s s R f Η απεικόνιζη είναι ζηιγμαηική!
35 Δθμιτρθσ Παπάηογλου 2013 Συμβάςεισ για ςφαιρικά κάτοπτρα s Πρόςθμο + - αριςτερά του κατόπτρου (πραγματικό αντικείμενο) δεξιά του κατόπτρου (φανταςτικό αντικείμενο) s' αριςτερά του κατόπτρου (πραγματικό είδωλο) δεξιά του κατόπτρου (φανταςτικό είδωλο) R κυρτό ( κοίλο ) f κοίλο ) κυρτό (
36 Παραδείγματα απεικόνιςθσ με κάτοπτρα Δθμιτρθσ Παπάηογλου 2013
37 Δθμιτρθσ Παπάηογλου 2013 Πρίςματα Ανάκλασης Διασποράς Αντικακιςτοφν τα κάτοπτρα εξαςφαλίηουν ςτακερότθτα ςυνικωσ αξιοποιοφν τθν ολικι ανάκλαςθ Χρθςιμοποιοφνται ςτθν φαςματικι ανάλυςθ αξιοποιοφν το φαινόμενο τθσ διαςποράσ (dispersion)
38 Δθμιτρθσ Παπάηογλου 2013 Πρίςματα ανάκλαςθσ ορθής εκτροπής σταθερής εκτροπής Porro ζύζηημα Porro Dove Πεντάπρισμα
39 Δθμιτρθσ Παπάηογλου 2013 Πρίςματα Διαςποράσ ( i1 t1) ( t 2 i2) a t1i2 i1 t2 a i 1 sin sin n sin i 1 sini 1 cos a ελάσιζηη εκηποπή a 60 o a 45 o n 1.5
40 Δθμιτρθσ Παπάηογλου 2013 Σηην ελάσιζηη εκηποπή ιζσύει όηι: t i i t a min min 2 i 1 i 1 2 a a 2 t sin sin 1 t 1 i n Σςνθήκερ ελάσιζηηρ εκηποπήρ a 2 2 min nsin sin( ) n 2 a sin 2 min sin( )
41 Δθμιτρθσ Παπάηογλου 2013 Ειδικι περίπτωςθ: οπτικζσ ςφινεσ Σε μια οπτικι ςφινα θ γωνία α του πρίςματοσ είναι πολφ μικρι α δ nsin sint n t ( n 1) a t εκηποπή Τςπικέρ ηιμέρ: n a 1.5 o 4 2 o
42 Σφάλματα απεικόνιςθσ Δθμιτρθσ Παπάηογλου 2013
43 Δθμιτρθσ Παπάηογλου 2013 Η αςτοχία ενόσ οπτικοφ ςυςτιματοσ να κατευκφνει όλεσ τισ ακτίνεσ από ζνα ςθμείο του αντικειμζνου ςε ζνα ςθμείο του ειδϊλου ονομάηεται ςφάλμα απεικόνιςθσ ( QQ) OPL Σφάλμα μετϊπου κφματοσ Κφρια ςφάλματα Seidel (περιγράφονται αναλυτικά) Σφάλματα υψθλότερθσ τάξθσ (αναλφονται με αρικμθτικζσ μεκόδουσ)
44 Δθμιτρθσ Παπάηογλου 2013 Σφαιρικοί φακοί κφρια ςφάλματα 3 θσ τάξθσ (Seidel) ςφαιρικισ εκτροπισ καμπφλωςθσ πεδίου κόμθσ (4) (2 cos 2 ) cos 3 B C D ro E ro Fro cos 4 2 Αςτιγματιςμόσ παραμόρφωςθ
45 Δθμιτρθσ Παπάηογλου 2013 Σφάλμα ςφαιρικισ εκτροπισ (spherical aberration) 3 x S1 sin 3 y S1 cos 1 4 B (4) 4 Εμφανίηεται ακόμθ και ςε αξονικά αντικείμενα
46 Δθμιτρθσ Παπάηογλου 2013 Σφάλμα κόμθσ (coma aberration) x 2 2S2 yo cos sin 2 2 y S2 yo (1 cos ) παπαξονική εζηία (4) 3 cos Fr o καταςτρζφει τθν ςυμμετρία τθσ δζςμθσ γφρω από τθν κφρια ακτίνα
47 Δθμιτρθσ Παπάηογλου 2013 Αςτιγματιςμόσ (astigmatism) x 0 y 2 2S3yo cos Ccos r (4) o οφείλεται ςτθν αςυμμετρία μεταξφ του μεςθμβρινοφ και του εγκάρςιου επιπζδου.
48 Δθμιτρθσ Παπάηογλου 2013 Καμπφλωςθ πεδίου (field curvature) x S y sin o y S y cos o Dr o (4) 2 2 Καμπύλυζη πεδίος και αζηιγμαηιζμόρ
49 Δθμιτρθσ Παπάηογλου 2013 Παραμόρφωςθ (distortion) x y 0 S y 5 3 o (4) 3 cos Er o οφείλεται ςτο ότι θ εγκάρςια μεγζκυνςθ είναι ςυνάρτθςθ τθσ απόςταςθσ του αντικειμζνου από τον οπτικό άξονα.
50 Δθμιτρθσ Παπάηογλου 2013 Χρωματικά ςφάλματα Τα χρωματικά ςφάλματα οφείλονται ςτο φαινόμενο τθσ διαςποράσ του φωτόσ.
51 Δθμιτρθσ Παπάηογλου 2013 Διαμικεσ χρωματικό ςφάλμα Χρωματικά ςφάλματα ςυναντάμε ακόμθ και ςτθν παραξονικι περιοχι! 1 1 n ( ) ( 1) s s n ( ) R R f ( ) Εξαπηάηαι από L m 1 2 ηο μήκορ κύμαηορ
52 Δθμιτρθσ Παπάηογλου 2013 Αχρωματικοί φακοί Eνασ αχρωματικόσ φακόσ ςχεδιάηεται ζτςι ώςτε να ταυτίηονται θ εςτία ςτο κόκκινο και το μπλε. Σσνθήκη ατρωμαηικόηηηας για λεπηούς θακούς ζε επαθή V f Y Y 1 1 V2 f2 0 V n( Y ) 1 n ( ) n ( ) B R Απιθμόρ Abbe 589 nm, 656 nm, 486nm Y R B
53 οπτικά ςυςτιματα Δθμιτρθσ Παπάηογλου 2013
54 Δθμιτρθσ Παπάηογλου 2013 Οφκαλμόσ διακριτικι ικανότθτα : ~ 1 (arcmin) ςθμείο ευκρινοφσ όραςθσ: ~250 mm
55 Δθμιτρθσ Παπάηογλου 2013 Στερεοςκοπικι όραςθ d 2 R Rmin d ηςπικέρ ηιμέρ min min min 65 mm, 10 R 8 R 100m ηπιζδιάζηαηη ανηίλητη
56 Δθμιτρθσ Παπάηογλου 2013 Διακλαςτικά προβλιματα τθσ όραςθσ Μυωπία Διακλαςτικι διόρκωςθ Υπερμετρωπία /πρεςβυωπία Αςτιγματιςμόσ: Αναμορφικόσ κερατοειδισ φακόσ. Διορκϊνεται με αναμορφικό φακό Καταράκτθσ: Μείωςθ τθσ διαφγειασ του κερατοειδι φακοφ. Αφαίρεςθ του φακοφ
57 Δθμιτρθσ Παπάηογλου 2013 Μεγεκυντικόσ φακόσ Η τυπικι μεγζκυνςθ ενόσ μεγεκυντικοφ φακοφ ορίηεται για είδωλο ςτο άπειρο M tan 250mm z 1 tan f x z 250mm M typ ( x z 0) f
58 Μικροςκόπιο Τυπικό μικοσ ςωλινα L 160 mm Η μεγζκυνςθ δίνεται από το γινόμενο τθσ γραμμικήσ μεγέθυνςησ του αντικειμενικοφ με τθν γωνιακή μεγέθυνςη του προςοφθαλμίου (τελικό είδωλο ςτο άπειρο). M L f o 250mm f e Διακπιηική ικανόηηηα Ωθέλιμη μεγέθςνζη 2NA, NA nsin αρικμθτικό άνοιγμα A Δθμιτρθσ Παπάηογλου 2013 dpapa@materials.uoc.gr 500 NA M 1000 NA opt
59 Δθμιτρθσ Παπάηογλου 2013 Τθλεςκόπιο M tan tan f f o e Διακπιηική ικανόηηηα min 1.22 D διάμετροσ αντικειμενικοφ Ωθέλιμη μεγέθςνζη opt 0.2 D M 0.75 D D 6m 0.02, D 90mm 550nm min min
60 Δθμιτρθσ Παπάηογλου 2013 Φωτογραφικοί φακοί Ο φωτιςμόσ του ειδώλου είναι αντιςτρόφωσ ανάλογοσ του αρικμοφ #F I 1 (#F) 2 (#F) f D Γυνιακό πεδίο 1 2 tan 2 f ανιχνευτισ 40 o o o o τθλεφακόσ (telephoto) κανονικόσ (normal) ευρυγώνιοσ (wide angle)
Οπτική και κύματα Δημήτρης Παπάζογλου dpapa@materials.uoc.gr Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης Γεωμετρική Οπτική
 Οπτική και κύματα Δημήτρης Παπάζογλου dpapa@maerals.uoc.gr Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης Γεωμετρική Οπτική Η ιδέα την απεικόνισης Σημειακή πηγή Στιγματική απεικόνιση Η ανακατεύθυνση
Οπτική και κύματα Δημήτρης Παπάζογλου dpapa@maerals.uoc.gr Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης Γεωμετρική Οπτική Η ιδέα την απεικόνισης Σημειακή πηγή Στιγματική απεικόνιση Η ανακατεύθυνση
Εφαρμοσμένη Οπτική. Κεφάλαιο 2. Χρήσιμα διαγράμματα-σχήματα (συμπληρωματικά. των σημειώσεων)
 Εφαρμοσμένη Οπτική Κεφάλαιο 2 Χρήση πινάκων στην παραξονική οπτική Χρήσιμα διαγράμματα-σχήματα (συμπληρωματικά των σημειώσεων) Κύρια σημεία του μαθήματος Παχύς φακός Χαρακτηριστικά σημεία χαρακτηριστικά
Εφαρμοσμένη Οπτική Κεφάλαιο 2 Χρήση πινάκων στην παραξονική οπτική Χρήσιμα διαγράμματα-σχήματα (συμπληρωματικά των σημειώσεων) Κύρια σημεία του μαθήματος Παχύς φακός Χαρακτηριστικά σημεία χαρακτηριστικά
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0
 Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0
 Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ Μάθημα προς τους ειδικευόμενους γιατρούς στην Οφθαλμολογία, Στο Κ.Οφ.Κ.Α. την 18/11/2003. Υπό: Δρος Κων. Ρούγγα, Οφθαλμιάτρου. 1. ΑΝΑΚΛΑΣΗ ΤΟΥ ΦΩΤΟΣ Όταν μια φωτεινή ακτίνα ή
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ Μάθημα προς τους ειδικευόμενους γιατρούς στην Οφθαλμολογία, Στο Κ.Οφ.Κ.Α. την 18/11/2003. Υπό: Δρος Κων. Ρούγγα, Οφθαλμιάτρου. 1. ΑΝΑΚΛΑΣΗ ΤΟΥ ΦΩΤΟΣ Όταν μια φωτεινή ακτίνα ή
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα. Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ
 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
Εστιομετρία φακών και κατόπτρων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ, ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Εστιομετρία
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ, ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Εστιομετρία
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ. G. Mitsou
 ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Διάθλαση σε σφαιρική επιφάνεια Φακοί Ορισμοί Λεπτοί φακοί Συγκλίνοντες φακοί Δημιουργία ειδώλων Αποκλίνοντες φακοί Γενικοί τύποι φακών Σύστημα λεπτών φακών σε επαφή Ασκήσεις Διάθλαση
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Διάθλαση σε σφαιρική επιφάνεια Φακοί Ορισμοί Λεπτοί φακοί Συγκλίνοντες φακοί Δημιουργία ειδώλων Αποκλίνοντες φακοί Γενικοί τύποι φακών Σύστημα λεπτών φακών σε επαφή Ασκήσεις Διάθλαση
Γεωμετρική Οπτική ΚΕΦΑΛΑΙΟ 34
 Γεωμετρική Οπτική ΚΕΦΑΛΑΙΟ 34 Γεωμετρική Οπτική Γνωρίζουμε τα βασικά Δηλαδή, πως το φως διαδίδεται και αλληλεπιδρά με σώματα διαστάσεων πολύ μεγαλύτερων από το μήκος κύματος. Ανάκλαση: Προσπίπτουσα ακτίνα
Γεωμετρική Οπτική ΚΕΦΑΛΑΙΟ 34 Γεωμετρική Οπτική Γνωρίζουμε τα βασικά Δηλαδή, πως το φως διαδίδεται και αλληλεπιδρά με σώματα διαστάσεων πολύ μεγαλύτερων από το μήκος κύματος. Ανάκλαση: Προσπίπτουσα ακτίνα
Εφαρμοσμένη Οπτική. Γεωμετρική Οπτική
 Εφαρμοσμένη Οπτική Γεωμετρική Οπτική Κύρια σημεία του μαθήματος Η προσέγγιση της γεωμετρικής οπτικής Νόμοι της ανάκλασης και της διάθλασης Αρχή του Huygens Αρχή του Fermat Αρχή της αντιστρεψιμότητας (principle
Εφαρμοσμένη Οπτική Γεωμετρική Οπτική Κύρια σημεία του μαθήματος Η προσέγγιση της γεωμετρικής οπτικής Νόμοι της ανάκλασης και της διάθλασης Αρχή του Huygens Αρχή του Fermat Αρχή της αντιστρεψιμότητας (principle
7.1 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ
 7.1 ΑΣΚΗΣΗ 7 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ ΘΕΩΡΙΑ Όταν φωτεινή παράλληλη δέσμη διαδιδόμενη από οπτικό μέσο α με δείκτη διάθλασης n 1 προσπίπτει σε άλλο οπτικό μέσο β με δείκτη διάθλασης n 2 και
7.1 ΑΣΚΗΣΗ 7 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ ΘΕΩΡΙΑ Όταν φωτεινή παράλληλη δέσμη διαδιδόμενη από οπτικό μέσο α με δείκτη διάθλασης n 1 προσπίπτει σε άλλο οπτικό μέσο β με δείκτη διάθλασης n 2 και
Σθλεςκόπιο. Ιςτορία. Σο τθλεςκόπιο εφευρζκθκε το 1608 ςτθν Ολλανδία και θ αρχικι
 Σθλεςκόπιο Σο τθλεςκόπιο είναι ζνα όργανο ςχεδιαςμζνο για τθν παρατιρθςθ μακρινϊν αντικειμζνων μζςω τθσ ςυλλογισ θλεκτρομαγνθτικισ ακτινοβολίασ. Σα πρϊτα γνωςτά ςχεδόν λειτουργικά τθλεςκόπια ανακαλφφκθκαν
Σθλεςκόπιο Σο τθλεςκόπιο είναι ζνα όργανο ςχεδιαςμζνο για τθν παρατιρθςθ μακρινϊν αντικειμζνων μζςω τθσ ςυλλογισ θλεκτρομαγνθτικισ ακτινοβολίασ. Σα πρϊτα γνωςτά ςχεδόν λειτουργικά τθλεςκόπια ανακαλφφκθκαν
ΑΝΑΚΛΑΣΗ. β' νόμος της ανάκλασης: Η γωνία πρόσπτωσης και η γωνία ανάκλασης είναι ίσες.
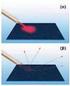 ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΑΝΑΚΛΑΣΗ. β' νόμος της ανάκλασης: Η γωνία πρόσπτωσης και η γωνία ανάκλασης είναι ίσες.
 ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 www.pmoira.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 www.pmoira.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
Σχηματισμός ειδώλων. Εισαγωγή
 Σχηματισμός ειδώλων Είδωλα πραγματικών αντικειμένων σχηματίζονται όταν οι ακτίνες φωτός (που εκπέμπονται από αυτά τα αντικέιμενα) συναντούν επίπεδες ή καμπύλες επιφάνειες που βρίσκονται μεταξύ δύο μέσων.
Σχηματισμός ειδώλων Είδωλα πραγματικών αντικειμένων σχηματίζονται όταν οι ακτίνες φωτός (που εκπέμπονται από αυτά τα αντικέιμενα) συναντούν επίπεδες ή καμπύλες επιφάνειες που βρίσκονται μεταξύ δύο μέσων.
Generated by Foxit PDF Creator Foxit Software http://www.foxitsoftware.com For evaluation only. ΑΣΚΗΣΗ 10 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ
 ΑΣΚΗΣΗ 0 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ . Γεωμετρική οπτική ΜΕΡΟΣ ΠΡΩΤΟ ΒΑΣΙΚΕΣ ΘΕΩΡΗΤΙΚΕΣ ΓΝΩΣΕΙΣ Η Γεωμετρική οπτική είναι ένας τρόπος μελέτης των κυμάτων και χρησιμοποιείται για την εξέταση μερικών
ΑΣΚΗΣΗ 0 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ . Γεωμετρική οπτική ΜΕΡΟΣ ΠΡΩΤΟ ΒΑΣΙΚΕΣ ΘΕΩΡΗΤΙΚΕΣ ΓΝΩΣΕΙΣ Η Γεωμετρική οπτική είναι ένας τρόπος μελέτης των κυμάτων και χρησιμοποιείται για την εξέταση μερικών
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ. Ερωτήσεις κλειστού τύπου. Ερωτήσεις ανοικτού τύπου
 ΟΠΤΙΚΗ Περιεχόμενα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ... 2 Ερωτήσεις κλειστού τύπου... 2 Ερωτήσεις ανοικτού τύπου... 2 Ασκήσεις... 3 ΚΥΜΑΤΙΚΗ ΟΠΤΙΚΗ... 4 Ερωτήσεις κλειστού τύπου... 4 Ερωτήσεις ανοικτού τύπου... 4 Ασκήσεις...
ΟΠΤΙΚΗ Περιεχόμενα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ... 2 Ερωτήσεις κλειστού τύπου... 2 Ερωτήσεις ανοικτού τύπου... 2 Ασκήσεις... 3 ΚΥΜΑΤΙΚΗ ΟΠΤΙΚΗ... 4 Ερωτήσεις κλειστού τύπου... 4 Ερωτήσεις ανοικτού τύπου... 4 Ασκήσεις...
ΟΠΤΙΚΑ ΣΤΟΙΧΕΙΑ : ΚΑΤΟΠΤΡΑ ΔΙΟΠΤΡΑ ΦΑΚΟΙ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΟΠΤΙΚΑ ΣΤΟΙΧΕΙΑ : ΚΑΤΟΠΤΡΑ ΔΙΟΠΤΡΑ ΦΑΚΟΙ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ.
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΟΠΤΙΚΑ ΣΤΟΙΧΕΙΑ : ΚΑΤΟΠΤΡΑ ΔΙΟΠΤΡΑ ΦΑΚΟΙ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ.
Σφάλματα φακών (Σφαιρικό - Χρωματικό).
 O12 Σφάλματα φακών (Σφαιρικό - Χρωματικό). 1. Σκοπός Στην άσκηση αυτή υπολογίζονται πειραματικά δυο από τα πιο σημαντικά οπτικά σφάλματα (η αποκλίσεις) που παρουσιάζονται όταν φωτεινές ακτίνες διέλθουν
O12 Σφάλματα φακών (Σφαιρικό - Χρωματικό). 1. Σκοπός Στην άσκηση αυτή υπολογίζονται πειραματικά δυο από τα πιο σημαντικά οπτικά σφάλματα (η αποκλίσεις) που παρουσιάζονται όταν φωτεινές ακτίνες διέλθουν
ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Ασκήσεις Οπτική Ι ιδάσκων: ηµήτρης Παπάζογλου Email: dpapa@iesl.forth.gr
 ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Ασκήσεις Οπτική Ι ιδάσκων: ηµήτρης Παπάζογλου Email: dpapa@iesl.forth.gr 1. Να σχεδιάσετε την διάδοση των ακτίνων στα παρακάτω οπτικά συστήµατα F F
ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Ασκήσεις Οπτική Ι ιδάσκων: ηµήτρης Παπάζογλου Email: dpapa@iesl.forth.gr 1. Να σχεδιάσετε την διάδοση των ακτίνων στα παρακάτω οπτικά συστήµατα F F
Φύση του φωτός. Θεωρούμε ότι το φως έχει διττή φύση: διαταραχή που διαδίδεται στο χώρο. μήκος κύματος φωτός. συχνότητα φωτός
 Γεωμετρική Οπτική Φύση του φωτός Θεωρούμε ότι το φως έχει διττή φύση: ΚΥΜΑΤΙΚΗ Βασική ιδέα Το φως είναι μια Η/Μ διαταραχή που διαδίδεται στο χώρο Βασική Εξίσωση Φαινόμενα που εξηγεί καλύτερα (κύμα) μήκος
Γεωμετρική Οπτική Φύση του φωτός Θεωρούμε ότι το φως έχει διττή φύση: ΚΥΜΑΤΙΚΗ Βασική ιδέα Το φως είναι μια Η/Μ διαταραχή που διαδίδεται στο χώρο Βασική Εξίσωση Φαινόμενα που εξηγεί καλύτερα (κύμα) μήκος
Γεωμετρική Οπτική. Πρόκειται δηλαδή για μια ισοφασική επιφάνεια που ονομάζεται μέτωπο κύματος.
 Γεωμετρική Οπτική Στη Γεωμετρική Οπτική επεξεργαζόμαστε τα φαινόμενα ωσάν το φως να αποτελείται μόνο από σωματίδια, ώστε να εξασφαλίζεται την εύκολη ερμηνεία των φαινομένων της ευθύγραμμης διάδοσης του
Γεωμετρική Οπτική Στη Γεωμετρική Οπτική επεξεργαζόμαστε τα φαινόμενα ωσάν το φως να αποτελείται μόνο από σωματίδια, ώστε να εξασφαλίζεται την εύκολη ερμηνεία των φαινομένων της ευθύγραμμης διάδοσης του
ΑΣΚΗΣΗ 8 Μελέτη φακών
 Απαραίτητα όργανα και υλικά ΑΣΚΗΣΗ 8 Μελέτη φακών 8. Απαραίτητα όργανα και υλικά. Οπτική τράπεζα.. Πέτασμα. 3. Συγκεντρωτικός φακός. 4. Φωτεινή πηγή. 5. Διάφραγμα με δακτύλιο και οπή. 6. Φίλτρο κόκκινο
Απαραίτητα όργανα και υλικά ΑΣΚΗΣΗ 8 Μελέτη φακών 8. Απαραίτητα όργανα και υλικά. Οπτική τράπεζα.. Πέτασμα. 3. Συγκεντρωτικός φακός. 4. Φωτεινή πηγή. 5. Διάφραγμα με δακτύλιο και οπή. 6. Φίλτρο κόκκινο
ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ
 ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ Όταν προσπίπτει φως σε μια διεπιφάνεια που σχηματίζεται μεταξύ δύο οπτικά διαφορετικών μέσων, ένα μέρος του υφίσταται ανάκλαση ενώ το υπόλοιπο διέρχεται από το πρώτο στο δεύτερο
ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ Όταν προσπίπτει φως σε μια διεπιφάνεια που σχηματίζεται μεταξύ δύο οπτικά διαφορετικών μέσων, ένα μέρος του υφίσταται ανάκλαση ενώ το υπόλοιπο διέρχεται από το πρώτο στο δεύτερο
Παρατηρησιακή Αστροφυσική. Κεφάλαιο 2 : Βασικά όργανα μέτρησης ακτινοβολίας : Οπτικά τηλεσκόπια
 Παρατηρησιακή Αστροφυσική Κεφάλαιο 2 : Βασικά όργανα μέτρησης ακτινοβολίας : Οπτικά τηλεσκόπια Κύρια σημεία του μαθήματος Βασικές αρχές γεωμετρικής οπτικής Αρχές του Fermat και του Huygens Νόμοι ανάκλασης
Παρατηρησιακή Αστροφυσική Κεφάλαιο 2 : Βασικά όργανα μέτρησης ακτινοβολίας : Οπτικά τηλεσκόπια Κύρια σημεία του μαθήματος Βασικές αρχές γεωμετρικής οπτικής Αρχές του Fermat και του Huygens Νόμοι ανάκλασης
ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ
 ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Άσκηση 4: Σφάλματα φακών: Ι Σφαιρική εκτροπή Εξεταζόμενες γνώσεις: σφάλματα σφαιρικής εκτροπής. Α. Γενικά περί σφαλμάτων φακών Η βασική σχέση του Gauss 1/s +1/s = 1/f που
ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Άσκηση 4: Σφάλματα φακών: Ι Σφαιρική εκτροπή Εξεταζόμενες γνώσεις: σφάλματα σφαιρικής εκτροπής. Α. Γενικά περί σφαλμάτων φακών Η βασική σχέση του Gauss 1/s +1/s = 1/f που
Προβλήματα φακών/κατόπτρων
 Προβλήματα φακών/κατόπτρων 1. Χρησιμοποιείστε την τεχνική των ακτινών και σχηματισμών ειδώλου για να βρείτε το είδωλο, που δημιουργείται από ένα κοίλο σφαιρικό κάτοπτρο, ενός αντικειμένου που τοποθετείται
Προβλήματα φακών/κατόπτρων 1. Χρησιμοποιείστε την τεχνική των ακτινών και σχηματισμών ειδώλου για να βρείτε το είδωλο, που δημιουργείται από ένα κοίλο σφαιρικό κάτοπτρο, ενός αντικειμένου που τοποθετείται
ΟΠΤΙΚΗ Ι ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ. ηµήτρης Παπάζογλου. ιατµηµατικό Μεταπτυχιακό Πρόγραµµα Σπουδών «Οπτική και Όραση»
 ΟΠΤΙΚΗ Ι ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ηµήτρης Παπάζογλου ιατµηµατικό Μεταπτυχιακό Πρόγραµµα Σπουδών «Οπτική και Όραση» Πανεπιστήµιο Κρήτης 2005 Διατμηματικό Μεταπτυχιακό πρόγραμμα
ΟΠΤΙΚΗ Ι ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ηµήτρης Παπάζογλου ιατµηµατικό Μεταπτυχιακό Πρόγραµµα Σπουδών «Οπτική και Όραση» Πανεπιστήµιο Κρήτης 2005 Διατμηματικό Μεταπτυχιακό πρόγραμμα
Φυσική Εικόνας & Ήχου ΙΙ (Ε)
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική Εικόνας & Ήχου ΙΙ (Ε) Ενότητα 3: Σφάλματα φακών (Σφαιρικό - Χρωματικό) Αθανάσιος Αραβαντινός Τμήμα Φωτογραφίας & Οπτικοακουστικών
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική Εικόνας & Ήχου ΙΙ (Ε) Ενότητα 3: Σφάλματα φακών (Σφαιρικό - Χρωματικό) Αθανάσιος Αραβαντινός Τμήμα Φωτογραφίας & Οπτικοακουστικών
Ο15. Κοίλα κάτοπτρα. 2. Θεωρία. 2.1 Γεωμετρική Οπτική
 Ο15 Κοίλα κάτοπτρα 1. Σκοπός Σκοπός της άσκησης είναι η εύρεση της εστιακής απόστασης κοίλου κατόπτρου σχετικά μεγάλου ανοίγματος και την μέτρηση του σφάλματος της σφαιρικής εκτροπής... Θεωρία.1 Γεωμετρική
Ο15 Κοίλα κάτοπτρα 1. Σκοπός Σκοπός της άσκησης είναι η εύρεση της εστιακής απόστασης κοίλου κατόπτρου σχετικά μεγάλου ανοίγματος και την μέτρηση του σφάλματος της σφαιρικής εκτροπής... Θεωρία.1 Γεωμετρική
Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση Γεωµετρική θεώρηση του Φωτός Ανάκλαση ηµιουργίαειδώλουαπόκάτοπτρα. είκτης ιάθλασης Νόµος του Snell Ορατό Φάσµα και ιασπορά Εσωτερική ανάκλαση Οπτικές ίνες ιάθλαση σε
Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση Γεωµετρική θεώρηση του Φωτός Ανάκλαση ηµιουργίαειδώλουαπόκάτοπτρα. είκτης ιάθλασης Νόµος του Snell Ορατό Φάσµα και ιασπορά Εσωτερική ανάκλαση Οπτικές ίνες ιάθλαση σε
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 210-7722479 - e-mail:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 210-7722479 - e-mail:
1. Ιδιότητες φακών. 1 Λεπτοί φακοί. 2 Απριλίου Βασικές έννοιες
 . Ιδιότητες φακών 2 Απριλίου 203 Λεπτοί φακοί. Βασικές έννοιες Φακός είναι ένα οπτικό σύστημα με δύο διαθλαστικές επιφάνειες. Ο απλούστερος φακός έχει δύο σφαιρικές επιφάνειες αρκετά κοντά η μία με την
. Ιδιότητες φακών 2 Απριλίου 203 Λεπτοί φακοί. Βασικές έννοιες Φακός είναι ένα οπτικό σύστημα με δύο διαθλαστικές επιφάνειες. Ο απλούστερος φακός έχει δύο σφαιρικές επιφάνειες αρκετά κοντά η μία με την
ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ
 ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ Άσκηση 4. Διαφράγματα. Θεωρία Στο σχεδιασμό οπτικών οργάνων πρέπει να λάβει κανείς υπόψη και άλλες παραμέτρους πέρα από το πού και πώς σχηματίζεται το είδωλο ενός
ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ Άσκηση 4. Διαφράγματα. Θεωρία Στο σχεδιασμό οπτικών οργάνων πρέπει να λάβει κανείς υπόψη και άλλες παραμέτρους πέρα από το πού και πώς σχηματίζεται το είδωλο ενός
ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ
 ΕΡΑΣΤΗΡΙ ΕΦΑΡΜΣΜΕΝΗΣ ΠΤΙΚΗΣ Άσκηση 1: Λεπτοί φακοί Εξεταζόμενες γνώσεις. Εξίσωση κατασκευαστών των φακών. Συστήματα φακών. Διαγράμματα κύριων ακτινών. Είδωλα και μεγέθυνση σε λεπτούς φακούς. Α. Λεπτοί
ΕΡΑΣΤΗΡΙ ΕΦΑΡΜΣΜΕΝΗΣ ΠΤΙΚΗΣ Άσκηση 1: Λεπτοί φακοί Εξεταζόμενες γνώσεις. Εξίσωση κατασκευαστών των φακών. Συστήματα φακών. Διαγράμματα κύριων ακτινών. Είδωλα και μεγέθυνση σε λεπτούς φακούς. Α. Λεπτοί
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
MEΡΙΚΑ ΣΤΟΙΧΕΙΑ ΓΕΩΜΕΤΡΙΚΗΣ ΟΠΤΙΚΗΣ
 MEΡΙΚΑ ΣΤΟΙΧΕΙΑ ΓΕΩΜΕΤΡΙΚΗΣ ΟΠΤΙΚΗΣ Δ. Χατζηδημητρίου Βιβλιογραφία: Introduction to Optics, Pedrotti et al., 006, 3 rd edition, εκδ. Benjamin Cummings Optics and Photonics, An Introduction F. G. Smith
MEΡΙΚΑ ΣΤΟΙΧΕΙΑ ΓΕΩΜΕΤΡΙΚΗΣ ΟΠΤΙΚΗΣ Δ. Χατζηδημητρίου Βιβλιογραφία: Introduction to Optics, Pedrotti et al., 006, 3 rd edition, εκδ. Benjamin Cummings Optics and Photonics, An Introduction F. G. Smith
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
Γενικά Μαθηματικά ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 5 η : Μερικι Παράγωγοσ Ι Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 5 η : Μερικι Παράγωγοσ Ι Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
Κ.- Α. Θ. Θωμά. Οπτική
 Κ.- Α. Θ. Θωμά Οπτική Θεωρίες για τη φύση του φωτός Η ανάγκη διατύπωσης διαφορετικών θεωριών προέρχεται από την παρατήρηση ότι το φώς άλλες φορές συμπεριφέρεται σαν σωματίδιο και άλλοτε σαν κύμα, που είναι
Κ.- Α. Θ. Θωμά Οπτική Θεωρίες για τη φύση του φωτός Η ανάγκη διατύπωσης διαφορετικών θεωριών προέρχεται από την παρατήρηση ότι το φώς άλλες φορές συμπεριφέρεται σαν σωματίδιο και άλλοτε σαν κύμα, που είναι
Φύση και διάδοση φωτός
 Σημειώσεις Γενικής Φυσικής - ΒΕΤ Μ. Μπενής / 2016 Κυματική Φύση και διάδοση φωτός Ακτινικό μοντέλο διάδοσης. Στο κεφάλαιο των κυμάτων αναπαραστήσαμε τη διάδοση των κυμάτων με τα κυματομέτωπα. Μια απλούστευση
Σημειώσεις Γενικής Φυσικής - ΒΕΤ Μ. Μπενής / 2016 Κυματική Φύση και διάδοση φωτός Ακτινικό μοντέλο διάδοσης. Στο κεφάλαιο των κυμάτων αναπαραστήσαμε τη διάδοση των κυμάτων με τα κυματομέτωπα. Μια απλούστευση
Μέτρηση καμπυλότητας σφαιρικών και τοροειδών επιφανειών με οπτικές και μηχανικές μεθόδους
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ, ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Μέτρηση
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ, ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Μέτρηση
Γενικά Μαθηματικά ΙΙ Αςκήςεισ 11 ησ Ενότητασ
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Γενικά Μαθηματικά ΙΙ Αςκήςεισ 11 ησ Ενότητασ Λουκάσ Βλάχοσ Τμιμα Φυςικισ Α.Π.Θ. Θεςςαλονίκθ, 2014 Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ χριςθσ
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Γενικά Μαθηματικά ΙΙ Αςκήςεισ 11 ησ Ενότητασ Λουκάσ Βλάχοσ Τμιμα Φυςικισ Α.Π.Θ. Θεςςαλονίκθ, 2014 Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ χριςθσ
Μεγεθυντικός φακός. 1. Σκοπός. 2. Θεωρία. θ 1
 Μεγεθυντικός φακός 1. Σκοπός Οι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
Μεγεθυντικός φακός 1. Σκοπός Οι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Εργαστήριο Φυσικής ΙΙΙ - Οπτική. Πέτρος Ρακιτζής. Τμήμα Φυσικής
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Εργαστήριο Φυσικής ΙΙΙ - Οπτική Πέτρος Ρακιτζής Φ-08: Εργαστήριο Φυσικής ΙΙΙ Οπτική. Σκοπός. ΜΕΛΕΤΗ ΛΕΠΤΩΝ ΦΑΚΩΝ Εξοικείωση με βασικές αρχές γεωμετρικής οπτικής
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Εργαστήριο Φυσικής ΙΙΙ - Οπτική Πέτρος Ρακιτζής Φ-08: Εργαστήριο Φυσικής ΙΙΙ Οπτική. Σκοπός. ΜΕΛΕΤΗ ΛΕΠΤΩΝ ΦΑΚΩΝ Εξοικείωση με βασικές αρχές γεωμετρικής οπτικής
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
Προγραμματισμός Ύλης Έτους Τάξη Α Κοινός Κορμός
 Προγραμματισμός Ύλης Έτους Τάξη Α Κοινός Κορμός Μάθημα: Φυσική Τμήματα:,.. Τάξη: Α Ομάδα Προσανατολισμού 1,3,4 Καθηγητές: Περ. Εβδομ: 2 ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΥΛΗ ΠΕΡΙΟΔΟΙ ΗΜΕΡΟΜΗΝΙΕΣ Φυσικά Μεγέθη Μονάδες
Προγραμματισμός Ύλης Έτους Τάξη Α Κοινός Κορμός Μάθημα: Φυσική Τμήματα:,.. Τάξη: Α Ομάδα Προσανατολισμού 1,3,4 Καθηγητές: Περ. Εβδομ: 2 ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΥΛΗ ΠΕΡΙΟΔΟΙ ΗΜΕΡΟΜΗΝΙΕΣ Φυσικά Μεγέθη Μονάδες
ΚΕΦΑΛΑΙΟ 11Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση
 ΚΕΦΑΛΑΙΟ Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Ηφύσητουφωτός 643-77 Netwon Huygens 69-695 Το φως είναι δέσμη σωματιδίων Το φως
ΚΕΦΑΛΑΙΟ Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Ηφύσητουφωτός 643-77 Netwon Huygens 69-695 Το φως είναι δέσμη σωματιδίων Το φως
ΘΥ101: Ειςαγωγι ςτθν Πλθροφορικι
 Παράςταςη κινητήσ υποδιαςτολήσ ςφμφωνα με το πρότυπο ΙΕΕΕ Δρ. Χρήστος Ηλιούδης το πρότυπο ΙΕΕΕ 754 ζχει χρθςιμοποιθκεί ευρζωσ ςε πραγματικοφσ υπολογιςτζσ. Το πρότυπο αυτό κακορίηει δφο βαςικζσ μορφζσ κινθτισ
Παράςταςη κινητήσ υποδιαςτολήσ ςφμφωνα με το πρότυπο ΙΕΕΕ Δρ. Χρήστος Ηλιούδης το πρότυπο ΙΕΕΕ 754 ζχει χρθςιμοποιθκεί ευρζωσ ςε πραγματικοφσ υπολογιςτζσ. Το πρότυπο αυτό κακορίηει δφο βαςικζσ μορφζσ κινθτισ
ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ. Διάθλαση μέσω πρίσματος - Φασματοσκοπικά χαρακτηριστικά πρίσματος.
 Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ. Διάθλαση μέσω πρίσματος - Φασματοσκοπικά χαρακτηριστικά πρίσματος. 1. Σκοπός Όταν δέσμη λευκού φωτός προσπέσει σε ένα πρίσμα τότε κάθε μήκος κύματος διαθλάται σύμφωνα με τον αντίστοιχο
Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ. Διάθλαση μέσω πρίσματος - Φασματοσκοπικά χαρακτηριστικά πρίσματος. 1. Σκοπός Όταν δέσμη λευκού φωτός προσπέσει σε ένα πρίσμα τότε κάθε μήκος κύματος διαθλάται σύμφωνα με τον αντίστοιχο
Φυσική IΙ. Ενότητα 13: Γεωμετρική οπτική. Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 Φυσική IΙ Ενότητα 13: Γεωμετρική οπτική Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Η κυματική φύση του φωτός: διάθλαση, ανάκλαση, απορρόφηση Γωνίες πρόσπτωσης, ανάκλασης
Φυσική IΙ Ενότητα 13: Γεωμετρική οπτική Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Η κυματική φύση του φωτός: διάθλαση, ανάκλαση, απορρόφηση Γωνίες πρόσπτωσης, ανάκλασης
ΓΕΩΔΑΙΣΙΑ Ι Μάθημα 3 0. Ι.Μ. Δόκας Επικ. Καθηγητής
 ΓΕΩΔΑΙΣΙΑ Ι Μάθημα 3 0 Ι.Μ. Δόκας Επικ. Καθηγητής Επίγειες Γεωδαιτικές Μετρήσεις Μήκη Γωνίες Υψομετρικές διαφορές Παράμετροι οργάνων μέτρησης Ανάγνωση/Μέτρηση Σφάλμα/Αβεβαιότητα Μήκη Μέτρηση Μήκους Άμεση
ΓΕΩΔΑΙΣΙΑ Ι Μάθημα 3 0 Ι.Μ. Δόκας Επικ. Καθηγητής Επίγειες Γεωδαιτικές Μετρήσεις Μήκη Γωνίες Υψομετρικές διαφορές Παράμετροι οργάνων μέτρησης Ανάγνωση/Μέτρηση Σφάλμα/Αβεβαιότητα Μήκη Μέτρηση Μήκους Άμεση
Κεφάλαιο 33 ΦακοίκαιΟπτικάΣτοιχεία. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 33 ΦακοίκαιΟπτικάΣτοιχεία ΠεριεχόµεναΚεφαλαίου 33 Λεπτοί Φακοί- ιάδοση Ακτίνας Εξίσωση Λεπτού Φακού-Μεγέθυνση Συνδυασµός Φακών ΟιεξίσωσητουΟπτικού Φωτογραφικές Μηχανές : Ψηφιακές και Φιλµ ΤοΑνθρώπινοΜάτι;
Κεφάλαιο 33 ΦακοίκαιΟπτικάΣτοιχεία ΠεριεχόµεναΚεφαλαίου 33 Λεπτοί Φακοί- ιάδοση Ακτίνας Εξίσωση Λεπτού Φακού-Μεγέθυνση Συνδυασµός Φακών ΟιεξίσωσητουΟπτικού Φωτογραφικές Μηχανές : Ψηφιακές και Φιλµ ΤοΑνθρώπινοΜάτι;
Φυσική Εικόνας & Ήχου Ι (Ε)
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική Εικόνας & Ήχου Ι (Ε) Ενότητα 3: Γενικά περί φακών Αθανάσιος Αρααντινός Τμήμα Φωτογραφίας & Οπτικοακουστικών Τεχνών Το περιεχόμενο
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική Εικόνας & Ήχου Ι (Ε) Ενότητα 3: Γενικά περί φακών Αθανάσιος Αρααντινός Τμήμα Φωτογραφίας & Οπτικοακουστικών Τεχνών Το περιεχόμενο
Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη
 Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη MSc Τραπεζική & Χρηματοοικονομική Τεχνολογικό Εκπαιδευτικό Ίδρυμα Δυτικής Μακεδονίας Western Macedonia University of Applied Sciences Κοίλα Κοζάνης 50100 Kozani GR
Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη MSc Τραπεζική & Χρηματοοικονομική Τεχνολογικό Εκπαιδευτικό Ίδρυμα Δυτικής Μακεδονίας Western Macedonia University of Applied Sciences Κοίλα Κοζάνης 50100 Kozani GR
Μελέτη συστήματος φακών με τη Μέθοδο του Newton
 Μελέτη συστήματος φακών με τη Μέθοδο του Newton.Σκοπός Σκοπός της άσκησης είναι η μελέτη της εστιακής απόστασης συστήματος φακών, η εύρεση της ισοδύναμης εστιακής απόστασης του συστήματος αυτού καθώς και
Μελέτη συστήματος φακών με τη Μέθοδο του Newton.Σκοπός Σκοπός της άσκησης είναι η μελέτη της εστιακής απόστασης συστήματος φακών, η εύρεση της ισοδύναμης εστιακής απόστασης του συστήματος αυτού καθώς και
Οπτικι και κφματα. Δθμιτρθσ Παπάηογλου Τμιμα Επιςτιμθσ και Τεχνολογίασ Υλικών Πανεπιςτιμιο Κριτθσ
 Οπτικι και κφματα Δθμιτρθσ Παπάηογλου daa@materials.uc.gr Τμιμα Επιςτιμθσ και Τεχνολογίασ Υλικών Πανεπιςτιμιο Κριτθσ Άδειεσ Χριςθσ -Το παρόν εκπαιδευτικό υλικό υπόκειται ςτθν άδεια χριςθσ Creative Cmmns
Οπτικι και κφματα Δθμιτρθσ Παπάηογλου daa@materials.uc.gr Τμιμα Επιςτιμθσ και Τεχνολογίασ Υλικών Πανεπιςτιμιο Κριτθσ Άδειεσ Χριςθσ -Το παρόν εκπαιδευτικό υλικό υπόκειται ςτθν άδεια χριςθσ Creative Cmmns
Αρχζσ ηλεκτρονικήσ. Μικροςκοπίασ
 Αρχζσ ηλεκτρονικήσ Μικροςκοπίασ Ειςαγωγικά Louis de Broglie 1924 : διατφπωςθ τθσ υπόκεςθσ περί διπλισ φφςθσ του φωτόσ και κάκε ςωματιδίου. Ειςιγαγε τον όρο «υλοκφμα» για κάκε ςτοιχειϊδεσ ςωματίδιο αντιςτοιχϊντασ
Αρχζσ ηλεκτρονικήσ Μικροςκοπίασ Ειςαγωγικά Louis de Broglie 1924 : διατφπωςθ τθσ υπόκεςθσ περί διπλισ φφςθσ του φωτόσ και κάκε ςωματιδίου. Ειςιγαγε τον όρο «υλοκφμα» για κάκε ςτοιχειϊδεσ ςωματίδιο αντιςτοιχϊντασ
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών. Κοσμάς Γαζέας
 Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Κοσμάς Γαζέας Κεφάλαιο 1 Εισαγωγή Οι φακοί ήταν γνωστοί από την αρχαιότητα Οι πρώτες χρήσεις των φακών ήταν για την ανάφλεξη υλικών Χρησιμοποιήθηκαν για να
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Κοσμάς Γαζέας Κεφάλαιο 1 Εισαγωγή Οι φακοί ήταν γνωστοί από την αρχαιότητα Οι πρώτες χρήσεις των φακών ήταν για την ανάφλεξη υλικών Χρησιμοποιήθηκαν για να
Μθχανολογικό Σχζδιο, από τθ κεωρία ςτο πρακτζο Χριςτοσ Καμποφρθσ, Κων/νοσ Βαταβάλθσ
 Λεπτζσ Αξονικζσ γραμμζσ χρθςιμοποιοφνται για να δθλϊςουν τθν φπαρξθ ςυμμετρίασ του αντικειμζνου. Υπενκυμίηουμε ότι οι άξονεσ ςυμμετρίασ χρθςιμοποιοφνται μόνον όταν το ίδιο το εξάρτθμα είναι πραγματικά
Λεπτζσ Αξονικζσ γραμμζσ χρθςιμοποιοφνται για να δθλϊςουν τθν φπαρξθ ςυμμετρίασ του αντικειμζνου. Υπενκυμίηουμε ότι οι άξονεσ ςυμμετρίασ χρθςιμοποιοφνται μόνον όταν το ίδιο το εξάρτθμα είναι πραγματικά
OΠΤIKH. Επειδή είναι πάντα υ<c (
 OΠΤIKH Η ταχύτητα του φωτός δεν είναι πάντα ίδια αλλά αλλάζει όταν το φως από ένα μέσο περνά σε κάποιο άλλο. Αν c είναι η ταχύτητα του φωτός στο κενό και υ η ταχύτητά του σε ένα άλλο υλικό τότε, ορίζουμε
OΠΤIKH Η ταχύτητα του φωτός δεν είναι πάντα ίδια αλλά αλλάζει όταν το φως από ένα μέσο περνά σε κάποιο άλλο. Αν c είναι η ταχύτητα του φωτός στο κενό και υ η ταχύτητά του σε ένα άλλο υλικό τότε, ορίζουμε
7α Γεωμετρική οπτική - οπτικά όργανα
 7α Γεωμετρική οπτική - οπτικά όργανα Εισαγωγή ορισμοί Φύση του φωτός Πηγές φωτός Δείκτης διάθλασης Ανάκλαση Δημιουργία ειδώλων από κάτοπτρα Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/katsiki Ηφύσητουφωτός
7α Γεωμετρική οπτική - οπτικά όργανα Εισαγωγή ορισμοί Φύση του φωτός Πηγές φωτός Δείκτης διάθλασης Ανάκλαση Δημιουργία ειδώλων από κάτοπτρα Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/katsiki Ηφύσητουφωτός
Εισαγωγή στην οπτική μικροσκοπία
 Εισαγωγή στην οπτική μικροσκοπία Ιστορική αναδρομή οπτικής μικροσκοπίας Η χρήση μεγεθυντικών φακών αναφέρεται σε κείμενα Ρωμαίων φιλοσόφων του 1 ου αιώνα μ.χ. Ο Γαλιλαίος διατυπώνει τις αρχές που διέπουν
Εισαγωγή στην οπτική μικροσκοπία Ιστορική αναδρομή οπτικής μικροσκοπίας Η χρήση μεγεθυντικών φακών αναφέρεται σε κείμενα Ρωμαίων φιλοσόφων του 1 ου αιώνα μ.χ. Ο Γαλιλαίος διατυπώνει τις αρχές που διέπουν
ΠΟΥ ΔΙΑΔΙΔΕΤΑΙ ΤΟ ΦΩΣ
 1 ΦΩΣ Στο μικρόκοσμο θεωρούμε ότι το φως έχει δυο μορφές. Άλλοτε το αντιμετωπίζουμε με τη μορφή σωματιδίων που ονομάζουμε φωτόνια. Τα φωτόνια δεν έχουν μάζα αλλά μόνον ενέργεια. Άλλοτε πάλι αντιμετωπίζουμε
1 ΦΩΣ Στο μικρόκοσμο θεωρούμε ότι το φως έχει δυο μορφές. Άλλοτε το αντιμετωπίζουμε με τη μορφή σωματιδίων που ονομάζουμε φωτόνια. Τα φωτόνια δεν έχουν μάζα αλλά μόνον ενέργεια. Άλλοτε πάλι αντιμετωπίζουμε
ΦΥΕ 14 ΑΚΑΔ. ΕΤΟΣ Η ΕΡΓΑΣΙΑ. Ημερομηνία παράδοςησ: 12 Νοεμβρίου (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 10 μονάδεσ θ κάκε μία)
 ΦΥΕ ΑΚΑΔ. ΕΤΟΣ 007-008 Η ΕΡΓΑΣΙΑ Ημερομηνία παράδοςησ: Νοεμβρίου 007 (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 0 μονάδεσ θ κάκε μία) Άςκηςη α) Να υπολογιςκεί θ προβολι του πάνω ςτο διάνυςμα όταν: (.
ΦΥΕ ΑΚΑΔ. ΕΤΟΣ 007-008 Η ΕΡΓΑΣΙΑ Ημερομηνία παράδοςησ: Νοεμβρίου 007 (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 0 μονάδεσ θ κάκε μία) Άςκηςη α) Να υπολογιςκεί θ προβολι του πάνω ςτο διάνυςμα όταν: (.
Διαγώνιςμα Γ Λυκείου Ιανουάριοσ2018
 Διαγώνιςμα Γ Λυκείου Ιανουάριοσ08 Διάρκεια Εξζταςησ 3ώρεσ Ονοματεπώνυμο. ΘΕΜΑ Α: Στισ ερωτήςεισ Α ωσ και Α4 επιλζξτε την ςωςτή απάντηςη: Α.Αν το πλάτοσ Α μιασ φκίνουςασ ταλάντωςθσ μεταβάλλεται με το χρόνο
Διαγώνιςμα Γ Λυκείου Ιανουάριοσ08 Διάρκεια Εξζταςησ 3ώρεσ Ονοματεπώνυμο. ΘΕΜΑ Α: Στισ ερωτήςεισ Α ωσ και Α4 επιλζξτε την ςωςτή απάντηςη: Α.Αν το πλάτοσ Α μιασ φκίνουςασ ταλάντωςθσ μεταβάλλεται με το χρόνο
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών. Κοσμάς Γαζέας
 Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Κοσμάς Γαζέας Κεφάλαιο 1 Εισαγωγή Οι φακοί ήταν γνωστοί από την αρχαιότητα Οι πρώτες χρήσεις των φακών ήταν για την ανάφλεξη υλικών Χρησιμοποιήθηκαν για να
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Κοσμάς Γαζέας Κεφάλαιο 1 Εισαγωγή Οι φακοί ήταν γνωστοί από την αρχαιότητα Οι πρώτες χρήσεις των φακών ήταν για την ανάφλεξη υλικών Χρησιμοποιήθηκαν για να
Κλαςικι Ηλεκτροδυναμικι
 Κλαςικι Ηλεκτροδυναμικι Ενότθτα 21: Διάδοςθ θλεκτρομαγνθτικών κυμάτων Ανδρζασ Τερηισ Σχολι Θετικών Επιςτθμών Τμιμα Φυςικισ Σκοποί ενότθτασ Σκοπόσ τθσ ενότθτασ είναι να ςυνεχίςει τθν μελζτθ που αφορά τθν
Κλαςικι Ηλεκτροδυναμικι Ενότθτα 21: Διάδοςθ θλεκτρομαγνθτικών κυμάτων Ανδρζασ Τερηισ Σχολι Θετικών Επιςτθμών Τμιμα Φυςικισ Σκοποί ενότθτασ Σκοπόσ τθσ ενότθτασ είναι να ςυνεχίςει τθν μελζτθ που αφορά τθν
Οπτική και κύματα. Δημήτρης Παπάζογλου Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης
 Οπτική και κύματα Δημήτρης Παπάζογλου dpapa@materal.uoc.gr Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης Θεωρία πινάκων Διάνυσμα ακτίνας Παραξονική προσέγγιση ta διάνυσμα ακτίνας y αριθμητικό
Οπτική και κύματα Δημήτρης Παπάζογλου dpapa@materal.uoc.gr Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης Θεωρία πινάκων Διάνυσμα ακτίνας Παραξονική προσέγγιση ta διάνυσμα ακτίνας y αριθμητικό
Γενικά Μαθηματικά ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 7 η : Σφνκετεσ Συναρτιςεισ Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 7 η : Σφνκετεσ Συναρτιςεισ Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
Γενικά Μαθηματικά ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 10 η : Εφαρμογζσ Διανυςματικών Συναρτιςεων Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 10 η : Εφαρμογζσ Διανυςματικών Συναρτιςεων Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό
Βάςεισ Δεδομζνων Ι. Ενότητα 12: Κανονικοποίηςη. Δρ. Τςιμπίρθσ Αλκιβιάδθσ Τμιμα Μθχανικών Πλθροφορικισ ΤΕ
 Βάςεισ Δεδομζνων Ι Ενότητα 12: Κανονικοποίηςη Δρ. Τςιμπίρθσ Αλκιβιάδθσ Τμιμα Μθχανικών Πλθροφορικισ ΤΕ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ χριςθσ Creative Commons. Για εκπαιδευτικό
Βάςεισ Δεδομζνων Ι Ενότητα 12: Κανονικοποίηςη Δρ. Τςιμπίρθσ Αλκιβιάδθσ Τμιμα Μθχανικών Πλθροφορικισ ΤΕ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ χριςθσ Creative Commons. Για εκπαιδευτικό
Φυσικά Μεγέθη Μονάδες Μέτρησης
 ΓΝΩΣΤΙΚΟ ΑΝΤΙΚΕΙΜΕΝΟ: ΦΥΣΙΚΗ A ΛΥΚΕΙΟΥ ΚΟΙΝΟΥ ΚΟΡΜΟΥ ΤΑΞΗ: Α Λυκείου Προσανατολισμού 1,3,4. ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΜΑΘΗΣΙΑΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ Οι μαθητές και οι μαθήτριες να είναι σε θέση να: ΑΝΤΙΣΤΟΙΧΑ
ΓΝΩΣΤΙΚΟ ΑΝΤΙΚΕΙΜΕΝΟ: ΦΥΣΙΚΗ A ΛΥΚΕΙΟΥ ΚΟΙΝΟΥ ΚΟΡΜΟΥ ΤΑΞΗ: Α Λυκείου Προσανατολισμού 1,3,4. ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΜΑΘΗΣΙΑΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ Οι μαθητές και οι μαθήτριες να είναι σε θέση να: ΑΝΤΙΣΤΟΙΧΑ
Το οπτικό μικροσκόπιο και ο τρόπος χρήσης του
 Το οπτικό μικροσκόπιο και ο τρόπος χρήσης του Το ανθρώπινο μάτι μπορεί να διακρίνει λεπτομέρειες της τάξης των 50-200 μm. Ο άνθρωπος με τις πρωτοποριακές εφευρέσεις των Malpighi, Hooke, Van Leeuwenhook
Το οπτικό μικροσκόπιο και ο τρόπος χρήσης του Το ανθρώπινο μάτι μπορεί να διακρίνει λεπτομέρειες της τάξης των 50-200 μm. Ο άνθρωπος με τις πρωτοποριακές εφευρέσεις των Malpighi, Hooke, Van Leeuwenhook
Βάςεισ Δεδομζνων Ι. Ενότητα 4: Μετατροπή ςχήματοσ Ο/Σ ςε ςχεςιακό. Δρ. Τςιμπίρθσ Αλκιβιάδθσ Τμιμα Μθχανικϊν Ρλθροφορικισ ΤΕ
 Βάςεισ Δεδομζνων Ι Ενότητα 4: Μετατροπή ςχήματοσ Ο/Σ ςε ςχεςιακό Δρ. Τςιμπίρθσ Αλκιβιάδθσ Τμιμα Μθχανικϊν Ρλθροφορικισ ΤΕ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ χριςθσ Creative Commons.
Βάςεισ Δεδομζνων Ι Ενότητα 4: Μετατροπή ςχήματοσ Ο/Σ ςε ςχεςιακό Δρ. Τςιμπίρθσ Αλκιβιάδθσ Τμιμα Μθχανικϊν Ρλθροφορικισ ΤΕ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ χριςθσ Creative Commons.
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
s s f 25 s ' 10 10 s ' 10 α) s ' 16.7 β) S=10 cm, άρα το αντικείμενο βρίσκεται πάνω στην εστία.
 ΑΣΚΗΣΗ 1 Δύο κάτοπτρα σχηματίζουν ορθή γωνία, όπως φαίνεται στο σχήμα. Στο σημείο Ο υπάρχει ένα αντικείμενο. Να προσδιορίσετε τη θέση των ειδώλων που σχηματίζονται ΑΣΚΗΣΗ 2 Κοίλο σφαιρικό κάτοπτρο έχει
ΑΣΚΗΣΗ 1 Δύο κάτοπτρα σχηματίζουν ορθή γωνία, όπως φαίνεται στο σχήμα. Στο σημείο Ο υπάρχει ένα αντικείμενο. Να προσδιορίσετε τη θέση των ειδώλων που σχηματίζονται ΑΣΚΗΣΗ 2 Κοίλο σφαιρικό κάτοπτρο έχει
ΗΥ101: Ειςαγωγι ςτθν Πλθροφορικι
 Παράςταςη κινητήσ υποδιαςτολήσ Δρ. Χρήστος Ηλιούδης Θζματα διάλεξησ Παράςταςη ςταθεροφ ςημείου Παράςταςη αριθμών κινητοφ ςημείου 2 Παράςταςη ςταθεροφ ςημείου Στθν παράςταςθ αρικμϊν ςτακεροφ ςθμείου (Fixed
Παράςταςη κινητήσ υποδιαςτολήσ Δρ. Χρήστος Ηλιούδης Θζματα διάλεξησ Παράςταςη ςταθεροφ ςημείου Παράςταςη αριθμών κινητοφ ςημείου 2 Παράςταςη ςταθεροφ ςημείου Στθν παράςταςθ αρικμϊν ςτακεροφ ςθμείου (Fixed
1. Σκοπός της άσκησης... 1. 2. Στοιχεία θεωρίας... 1. 2.1 Γεωμετρική οπτική... 1. 2.2 Ο νόμος της ανάκλασης... 1. 2.3 Ο νόμος της διάθλασης...
 1. Λεπτοί Φακοί Σελίδα 1. Σκοπός της άσκησης.... 1 2. Στοιχεία θεωρίας... 1 2.1 Γεωμετρική οπτική... 1 2.2 Ο νόμος της ανάκλασης... 1 2.3 Ο νόμος της διάθλασης... 2 2.4 Είδωλα & παραξονική προσέγγιση...
1. Λεπτοί Φακοί Σελίδα 1. Σκοπός της άσκησης.... 1 2. Στοιχεία θεωρίας... 1 2.1 Γεωμετρική οπτική... 1 2.2 Ο νόμος της ανάκλασης... 1 2.3 Ο νόμος της διάθλασης... 2 2.4 Είδωλα & παραξονική προσέγγιση...
Φυσική των οφθαλμών και της όρασης. Κική Θεοδώρου
 Φυσική των οφθαλμών και της όρασης Κική Θεοδώρου Περιεχόμενα Στοιχεία Γεωμετρικής Οπτικής Ανατομία του Οφθαλμού Αμφιβληστροειδής Ο ανιχνευτής φωτός του οφθαλμού Το κατώφλι της όρασης Φαινόμενα περίθλασης
Φυσική των οφθαλμών και της όρασης Κική Θεοδώρου Περιεχόμενα Στοιχεία Γεωμετρικής Οπτικής Ανατομία του Οφθαλμού Αμφιβληστροειδής Ο ανιχνευτής φωτός του οφθαλμού Το κατώφλι της όρασης Φαινόμενα περίθλασης
3. Απλά οπτικά όργανα
 3. Απλά οπτικά όργανα 20 Απριλίου 2013 1 Διαφράγματα Στο σχεδιασμό οπτικών οργάνων πρέπει να λάβει κανείς υπόψη και άλλες παραμέτρους πέρα από το πού και πώς σχηματίζεται το είδωλο ενός αντικειμένου. Μας
3. Απλά οπτικά όργανα 20 Απριλίου 2013 1 Διαφράγματα Στο σχεδιασμό οπτικών οργάνων πρέπει να λάβει κανείς υπόψη και άλλες παραμέτρους πέρα από το πού και πώς σχηματίζεται το είδωλο ενός αντικειμένου. Μας
E mm E, mm Ρ Ρ mm mm
 Οπτική της Όρασης E E ΡΡΝ Ν Ρ Ρ Ν Ν Σχήμα 3-1: Τα έξι θεμελιώδη σημεία του οφθαλμού EmmE, mm ΡΡ mmmm ΝΝ mmmm 3. Οπτική του Ανθρώπινου Οφθαλμού PEmm P E mm n n mρdpt P 1 n' PE P ' E ' 1 1.333 17.1 mm 22.79
Οπτική της Όρασης E E ΡΡΝ Ν Ρ Ρ Ν Ν Σχήμα 3-1: Τα έξι θεμελιώδη σημεία του οφθαλμού EmmE, mm ΡΡ mmmm ΝΝ mmmm 3. Οπτική του Ανθρώπινου Οφθαλμού PEmm P E mm n n mρdpt P 1 n' PE P ' E ' 1 1.333 17.1 mm 22.79
Γενικά Μαθηματικά ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 13 η : Επαναλθπτικι Ενότθτα Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 13 η : Επαναλθπτικι Ενότθτα Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΙΔΙΟΤΗΤΕΣ ΜΑΓΝΗΤΙΚΩΝ ΦΑΚΩΝ. Ηλεκτροστατικοί και Μαγνητικοί Φακοί Βασική Δομή Μαγνητικών Φακών Υστέρηση Λεπτοί Μαγνητικοί Φακοί Εκτροπές Φακών
 ΙΔΙΟΤΗΤΕΣ ΜΑΓΝΗΤΙΚΩΝ ΦΑΚΩΝ Βασική Δομή Μαγνητικών Φακών Υστέρηση Λεπτοί Μαγνητικοί Φακοί Εκτροπές Φακών ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ ΓΥΑΛΙΝΟΙ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΟΙ ΦΑΚΟΙ Οι φακοί χρησιμοποιούνται για να εκτρέψουν μία
ΙΔΙΟΤΗΤΕΣ ΜΑΓΝΗΤΙΚΩΝ ΦΑΚΩΝ Βασική Δομή Μαγνητικών Φακών Υστέρηση Λεπτοί Μαγνητικοί Φακοί Εκτροπές Φακών ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ ΓΥΑΛΙΝΟΙ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΟΙ ΦΑΚΟΙ Οι φακοί χρησιμοποιούνται για να εκτρέψουν μία
ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος
 Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος 1. Εισαγωγή Όταν δέσµη λευκού φωτός προσπέσει σε ένα πρίσµα τότε κάθε µήκος κύµατος διαθλάται σύµφωνα µε τον αντίστοιχο
Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος 1. Εισαγωγή Όταν δέσµη λευκού φωτός προσπέσει σε ένα πρίσµα τότε κάθε µήκος κύµατος διαθλάται σύµφωνα µε τον αντίστοιχο
Φύση του φωτός (κύμα ή σωμάτιο)
 Φύση του φωτός (κύμα ή σωμάτιο) Για τη μελέτη της συμπεριφοράς του φωτός απαιτείται η εισαγωγή κριτηρίων ως προς τα μεγέθη που περιγράφουν την διάδοση και την αλληλεπίδραση του φωτός με την ύλη. Κριτήρια
Φύση του φωτός (κύμα ή σωμάτιο) Για τη μελέτη της συμπεριφοράς του φωτός απαιτείται η εισαγωγή κριτηρίων ως προς τα μεγέθη που περιγράφουν την διάδοση και την αλληλεπίδραση του φωτός με την ύλη. Κριτήρια
ΚΕΦΑΛΑΙΟ 3. Οπτικά όργανα. Α. Οι βασικοί νόµοι της Οπτικής
 ΚΕΦΑΛΑΙΟ 3 Οπτικά όργανα 3.1 Η φύση του φωτός Α. Οι βασικοί νόµοι της Οπτικής Το φως είναι ηλεκτροµαγνητικά κύµατα που διαδίδονται στο χώρο. ηλαδή, µεταβολές ηλεκτρικού και µαγνητικού πεδίου που διαδίδονται
ΚΕΦΑΛΑΙΟ 3 Οπτικά όργανα 3.1 Η φύση του φωτός Α. Οι βασικοί νόµοι της Οπτικής Το φως είναι ηλεκτροµαγνητικά κύµατα που διαδίδονται στο χώρο. ηλαδή, µεταβολές ηλεκτρικού και µαγνητικού πεδίου που διαδίδονται
7α Γεωµετρική οπτική - οπτικά όργανα
 7α Γεωµετρική οπτική - οπτικά όργανα Εισαγωγή ορισµοί Φύση του φωτός Πηγές φωτός είκτης διάθλασης Ανάκλαση ηµιουργία ειδώλων από κάτοπτρα Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Η φύση του
7α Γεωµετρική οπτική - οπτικά όργανα Εισαγωγή ορισµοί Φύση του φωτός Πηγές φωτός είκτης διάθλασης Ανάκλαση ηµιουργία ειδώλων από κάτοπτρα Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Η φύση του
HMY 333 Φωτονική. Διάλεξη 04 Απεικόνιση. Οι λόγοι για τους οποίους χρησιμοποιούμε τους φακούς:
 1 2 HMY 333 Φωτονική Διάλεξη 04 Απεικόνιση Το ηλεκτρομαγνητικό φάσμα μπορεί να χρησιμοποιηθεί για τις επικοινωνίες (π.χ. ραδιοκύματα ή οπτικές ίνες). Ένας άλλος τομέας χρήσης της ηλεκτρομαγνητικής ακτινοβολίας
1 2 HMY 333 Φωτονική Διάλεξη 04 Απεικόνιση Το ηλεκτρομαγνητικό φάσμα μπορεί να χρησιμοποιηθεί για τις επικοινωνίες (π.χ. ραδιοκύματα ή οπτικές ίνες). Ένας άλλος τομέας χρήσης της ηλεκτρομαγνητικής ακτινοβολίας
Φωτογραφική μηχανή - Αρχή λειτουργίας.
 Ο25 Φωτογραφική μηχανή - Αρχή λειτουργίας. 1 Σκοπός Στην άσκηση αυτή γίνεται μία παρουσίαση των βασικών στοιχείων της φωτογραφικής μηχανής (φακός φωτοφράκτης - διάφραγμα αισθητήρας) καθώς και μία σύντομη
Ο25 Φωτογραφική μηχανή - Αρχή λειτουργίας. 1 Σκοπός Στην άσκηση αυτή γίνεται μία παρουσίαση των βασικών στοιχείων της φωτογραφικής μηχανής (φακός φωτοφράκτης - διάφραγμα αισθητήρας) καθώς και μία σύντομη
Ψθφιακι Επεξεργαςία ιματοσ
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακι Επεξεργαςία ιματοσ Ενότθτα 8 : Διακριτόσ Μεταςχθματιςμόσ Fourier Κωνςταντίνοσ Αγγζλθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου Σμιμα
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακι Επεξεργαςία ιματοσ Ενότθτα 8 : Διακριτόσ Μεταςχθματιςμόσ Fourier Κωνςταντίνοσ Αγγζλθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου Σμιμα
Θεςιακά ςυςτιματα αρίκμθςθσ
 Θεςιακά ςυςτιματα αρίκμθςθσ Δρ. Χρήστος Ηλιούδης αρικμθτικό ςφςτθμα αρίκμθςθσ (Number System) Αξία (value) παράςταςθ Οι αξίεσ (π.χ. το βάροσ μιασ ποςότθτασ μιλων) μποροφν να παραςτακοφν με πολλοφσ τρόπουσ
Θεςιακά ςυςτιματα αρίκμθςθσ Δρ. Χρήστος Ηλιούδης αρικμθτικό ςφςτθμα αρίκμθςθσ (Number System) Αξία (value) παράςταςθ Οι αξίεσ (π.χ. το βάροσ μιασ ποςότθτασ μιλων) μποροφν να παραςτακοφν με πολλοφσ τρόπουσ
Τα πρώτα δύο ελάχιστα της έντασης βρίσκονται συμμετρικά από το μέγιστο σε απόσταση φ=±λ/α.
 Φασματόμετρα & Ιντερφερομετρα Τα φασματόμετρα και ιντερφερόμετρα (συμβολόμετρα) χρησιμοποιούνται στη φασματοσκοπία για τη μέτρηση είτε του μήκους κύματος, αλλά τα βρίσκουμε και σε συσκευές λέιζερ όπου
Φασματόμετρα & Ιντερφερομετρα Τα φασματόμετρα και ιντερφερόμετρα (συμβολόμετρα) χρησιμοποιούνται στη φασματοσκοπία για τη μέτρηση είτε του μήκους κύματος, αλλά τα βρίσκουμε και σε συσκευές λέιζερ όπου
ΓΓ/Μ ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ. Τεύχος 6ο: Διάθλαση του φωτός Φακοί & οπτικά όργανα
 ΓΓ/Μ6 05-06 ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ Τεύχος 6ο: Διάθλαση του φωτός Φακοί & οπτικά όργανα ΕΚΔΟΤΙΚΕΣ ΤΟΜΕΣ ΟΡΟΣΗΜΟ ΠΕΡΙΟΔΙΚΗ ΕΚΔΟΣΗ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΚΑΙ ΤΟ ΛΥΚΕΙΟ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Φυσική για την Γ' Τάξη
ΓΓ/Μ6 05-06 ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ Τεύχος 6ο: Διάθλαση του φωτός Φακοί & οπτικά όργανα ΕΚΔΟΤΙΚΕΣ ΤΟΜΕΣ ΟΡΟΣΗΜΟ ΠΕΡΙΟΔΙΚΗ ΕΚΔΟΣΗ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΚΑΙ ΤΟ ΛΥΚΕΙΟ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Φυσική για την Γ' Τάξη
Δείκτεσ Διαχείριςθ Μνιμθσ. Βαγγζλθσ Οικονόμου Διάλεξθ 8
 Δείκτεσ Διαχείριςθ Μνιμθσ Βαγγζλθσ Οικονόμου Διάλεξθ 8 Δείκτεσ Κάκε μεταβλθτι ςχετίηεται με μία κζςθ ςτθν κφρια μνιμθ του υπολογιςτι. Κάκε κζςθ ςτθ μνιμθ ζχει τθ δικι τθσ ξεχωριςτι διεφκυνςθ. Με άμεςθ
Δείκτεσ Διαχείριςθ Μνιμθσ Βαγγζλθσ Οικονόμου Διάλεξθ 8 Δείκτεσ Κάκε μεταβλθτι ςχετίηεται με μία κζςθ ςτθν κφρια μνιμθ του υπολογιςτι. Κάκε κζςθ ςτθ μνιμθ ζχει τθ δικι τθσ ξεχωριςτι διεφκυνςθ. Με άμεςθ
Modellus 4.01 Συ ντομοσ Οδηγο σ
 Νίκοσ Αναςταςάκθσ 4.01 Συ ντομοσ Οδηγο σ Περιγραφή Σο είναι λογιςμικό προςομοιϊςεων που ςτθρίηει τθν λειτουργία του ςε μακθματικά μοντζλα. ε αντίκεςθ με άλλα λογιςμικά (π.χ. Interactive Physics, Crocodile
Νίκοσ Αναςταςάκθσ 4.01 Συ ντομοσ Οδηγο σ Περιγραφή Σο είναι λογιςμικό προςομοιϊςεων που ςτθρίηει τθν λειτουργία του ςε μακθματικά μοντζλα. ε αντίκεςθ με άλλα λογιςμικά (π.χ. Interactive Physics, Crocodile
ΠΕΡΙΘΛΑΣΗ H κυματική φύση του φωτός το πρόβλημα, η λύση
 ΠΕΡΙΘΛΑΣΗ H κυματική φύση του φωτός το πρόβλημα, η λύση ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ Σύμφωνα με την καθημερινή μας εμπειρία, το φως φαίνεται σαν να ταξιδεύει ευθύγραμμα μέχρι να συναντήσει κάποιο αντικείμενο.
ΠΕΡΙΘΛΑΣΗ H κυματική φύση του φωτός το πρόβλημα, η λύση ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ Σύμφωνα με την καθημερινή μας εμπειρία, το φως φαίνεται σαν να ταξιδεύει ευθύγραμμα μέχρι να συναντήσει κάποιο αντικείμενο.
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
