USHTRIMET PËR LËNDËN E DINAMIKËS MUND TË SHKARKOHET NGA VEGËZA: Ose
|
|
|
- Βίων Γούναρης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 USHTIMT Ë LËNDËN DINMIKËS MUND TË SHKKOHT N VËZ: wwwshalaahe Ose LII I USHTIM TË OF SO HMT SHL I SHKKU N VZ TIJ ËSHTË DHËNË NË VIJIM
2 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab I II M III IV ishinë
3 D sc he Shala T H Ë N I K libë pëban ushie na Meania III Dinaia e piës Meania IV Dinaia e sisei aeial si edhe na Dinaia në ëësi ë cila i a baju që na ii shll 99/95 në Faulein e Maineisë në ishinë ëbajja dhe ëndija e ëij libi ëshë pëafësish e njëjë e planpain e lëndës Dinaia e cila ndëjhe në seesin e III -ë në ë jiha dejie e Faulei ë Maineisë pë sudie achel sipas Delaaës së lnjës Qëllii i haii ë ëij libi ëshë që ë lehëshe pëehësii i ësaj lënde dhe ë nie cilësia dhe nieli i sudiee due aë paassh se pë lëndën e Dinaiës në ëësi aq sa a infaa unë j ëshë pëbledhja e paë në juhën shqipe Me ëë libë a bëë një nibu pë plësiin e zbazësiës dhe unesës së adhe që ndihe pë ese në juhën shqipe jihashu në ëë libë a bëë pëpjeje që ë paqes undësinë e shfëzii ë pjuei në sudiin e siseee aeiale Një undësi ë illë e a paaqiu e shfëziin e sfei Malab i cili llaie si juhë pauese jaf e pëpaua dhe jaf e pëfesinua pë analiza dhe sineza siulie ë siseee aeiale pëaësish edelee dinaie ë e K libë und iu shëbejë sudenëe ë aineisë ndëiaisë ehaisë si dhe inhinieëe e punëëe shencë pa ë jihë ae që ien e sudiin e siseee në pëjihësi Në ëë libë janë dhënë dhe zjidhu dea aaeisie pë neiziin e pjesës eie Me ëë as pëzeësish e falëndej pfesin D sc he eca pfes dina në Faulein e Maineisë pë ëejje sjeie dhe ndihesën që ë a dhënë jaë pëaijes së ëij libi K libë und ë ëë lëshie dhe ë ea unë ja i hapu ndaj ë jihë ae që pë ëë d ë a eheqin ëejjen e sujeie e e qëlli ia e ëshu në as ibii ë pëeëshen ishinë Jana ui
4 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab ebajja Dinaia e piës aeiale5 blei i paë dhe i dë i Dinaiës5 Dea : blei i paë i Dinaiës5 Dea : Fca funsin i hës F f 7 Dea : ënia e lië fca funsin i dinaës F fz 9 Dea : Saelië aificial ë Tës Dea 5 Hedhja e pjeë: Dea 6: Lëizja e piës nën epiin e fcae ëheqëse6 Lije e pëjihshe ë dinaiës 8 Dea Sasia e lëizjes8 Dea Sasia e lëizjes9 Dea : Meni inei 9 Dea Lëizja e piës nën epiin e fcës qende euacini i ineu Dea 5: nejia ineie puna e fcae Dea 6:nejia ineie sasia e lëizjes puna e fcae 5 Dea 7: Lajeësi aeai9 Dea 8: aii Dalabei pë pië aeiale Lëundje dejize ë piës aeiale5 Dea : Lëundje e lia që nu shuhen5 Dea : Lëundje e lia që shuhen7 Dea : Lëundje e deuaa që nu shuhen8 Dea : Lëundje e deuaa në abien e ezisencë 9 Lëizja e pëbëë e piës Dea : asi u lëizja zhendsësh dhe aj elaie janë anslaie T-T Dea : lëizja zhendsëse ulluese use aj elaie anslaie -T Dea : lëizja zhendsëse anslaie use aj elaie ulluese T- 7 Dea : lëizja zhendsëse dhe aj elaie janë ulluese -5 Dinaia e sisei aeial 5 Lëizja e qendës së asës së inecisë ë sisei aeial5 Dea :5 Dea :5 Dea :57 Dea :6 Dea 5:6
5 D sc he Shala Lëizja e upi e asë ë ndshueshe aiabël 65 Dea :65 Dea :67 Sasia e lëizjes Meni i sasisë së lëizjes eni inei i sisei aeial69 Tabela e enee ë inecisë ë disa upae hjen 69 zia e asee dhe fa e upi 69 Dea :7 Dea :7 Dea :76 DTY : 78 Dea 5:8 Lëizja plane e upi ë nuë 8 Dea :8 Dea :8 Dea :87 DTY : 89 nejia ineie e sisei aeial una e fcae ë jashe9 Dea :9 Dea :9 Dea :97 Dea : uacini i pëjihshë i dinaiës aii i Dalabe-laanzhi pë sise aeial Dea : Dea :6 uacine e Laanzhi ë llji ë dë pë sise aeial8 Dea :8 Dea : Dea : Dea :7 Dea 5:9 Mdelii dinai i siseee aeiale Vaiabla e jendjes naliza e deli dinai due shfëzua sfein MTL5 Lieaua:
6 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab DINMIK IKËS MTIL OLMI I Ë DH I DYTË I DINMIKËS DTY : blei i paë i Dinaiës ia aeiale M e asë lëiz nëpë ajeen në fë spiale e cila ëshë dhënë e euacinin e u ρ paaqesin dinaa plae ë piës M Due e diu që pia aeiale jaë ëë hës lëiz nëpë ajee e shpejësi nsane ë cahe fca që e shan ëë lëizje Zjidhje: F M n F Fc c Sipas liji ë dë ë Dinaiës ei: F a Dië se niii në dinaa plae ëshë: a a a c a d a c d ajë dinaa dhe d s d M d M M ds Na ai i jaësisë eleenae ë hau shih eëndëshin e pëafë MM M në fiuën paapae ei: ds d d use na e jedhë që: d e d d Zëendësjë në euacinin : ds d d d pej na: ds d ds Na: ds d d d Na d shpehje e fundi ai: 5
7 d d / d d D sc he Shala ë ei pej na e e aëheë: Na d d d ei: d e inei ei: d d d pëaësish: d dhe ai: ln ln ln ln d Na jedhë që: d d Na jedhë që: ln d ëheë pnenë e niii d ë jenë: a d d ac d d Na shpehja jedhë që: F a a a c Meqë F a ëshë nal e Fc ac aëheë inensiei i fcës F ëshë: F a ac Meqë shpejësia ëshë nsane pa ns aëheë: d a d T a an që d ë hë se fca a dejiin e niii nal pëaësish dejiin e nales në ajee 6
8 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab DTY : Fca funsin i hës F f ia aeiale e asë lëiz në afshin hiznal nën epiin e fcës F F sin i F cs j u F janë nsane Të cahen lije e lëizjes së ësaj pie aeiale nëse në çasin fillesa pa: ei: dhe Zjidhje: F Y j i X Sipas liji ë dë ë Dinaiës ei; a F F pjejë në dhe ei: : X F sin i F sin d F sin d / d F d sin d / F d sin d F F cs cs F cs d F cs / d d F d d cs d / F d d cs d d F sin as zëendësii ë ushee fillesae ei: 7
9 D sc he Shala F F sin sin : Y F cs F cs d F cs d / d F d cs d / F d cs d F F sin sin F sin d F sin / d d F d d sin d / d d F sin d F F cs cs as zëendësii ë ushee fillesae ei: F F cs cs 8
10 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab DTY : ënia e lië fca funsin i dinaës F fz Një up e asë i cili und ë nsidehe si pië aeiale bie liish në sipëfaqe ë Tës na laësia H Të cahe shpejësia e ënies së ëij upi në sipëfaqen e Tës due aë që fca ëheqëse e Tës në up ëshë e shpehu nëpëes liji ë dë ë Dinaiës bi M aiacinin e pëjihshë pa: F u: M asa e Tës disanca e upi na qenda e Tës nsane e pëjihshe e aiacini që duhe caua Zjidhje: H F Ku upi nddhe në sipëfaqe ë Tës pzicini ei: F pa pej na jedhë se: M pëaësish: M Due e diu se: H aëheë fca e aiacini ë pëjihshë d ë jeë: M F f H Këshu pa fca e cila epn në upin piën aeiale ëshë funsin i dinaës Sipas liji ë dë ë Dinaiës pë pzicinin e çfaëdshë ei: a F pjejë në deji ë asi ë lëizjes dhe fijë: F /: H 9
11 D sc he Shala d d d / d d d d H d d / H d d H H H H H H ë H upi bie bi sipëfaqe ë Tës aëheë: H H H H H H H H Shpehja e fundi paaqe shpejësinë e ënies së lië ë upi bi sipëfaqe ë Tës ap ndshe quhe edhe shpejësia e ënies së lië e llaiu sipas Njuni Nëse laësia H na e cila bie upi nu ëshë aq e adhe në ap e ezen e Tës aëheë: H << d ë ei: H H H Shpehja e fundi quhe shpejësia e ënies së lië e llaiu sipas alileu Këshu pë 67 98/s dhe H ei: H Sipas Njuni: 59 H 67 s Sipas alileu: H s Kuse pë H d ë ei: Sipas Njuni: Sipas alileu: H H 67 s H s Na analiza e fundi und ë nludhe se shpehje ë e saë ëshë shpehja e dhënë sipas Njuni p pë laësi ë la ë ënies H ë d shpehje janë ë pëafëa DTY : Saelië aificial ë Tës Due e diu se ezja e Tës ëshë 67 dhe shpejësia ënde e ullii ë saj eh 5 ad bshi ë e qendës ëshë 7 ë cahe laësia bi sipëfaqe ë Tës në ë s
12 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab cilën duhe ë endse një up pië aeiale e asë ashu që ai ë jeë saeli aificial i Tës psh panuesi-dhënësi ë sinjali eleizië saeli Zjidhje: s S a s F h Një pië në sipëfaqen e Tës e a shpejësinë: Një up pië aeiale nëse ëshë saeli aificial i Tës aëheë d ë eë shpejësinë ndaj qendës së Tës: s h Sipas deës paapae në ëë up saeli aificial ë Tës epn fca e aiacini ë pëjihshë e cila ëshë: F h h u ëshë caua na F dhe h pej ë cilës jedhë: Meqë Ta dihe se ullhe e shpejësi ënde nsane aëheë niii i upi - saelii ëshë i baabaë e niiin nal pa: a s a N s L as h Sipas liji ë Njuni pë ëë saeli ei: a s F pjejë në deji ë nales asi dhe fijë: a N F s h h h h h h
13 D sc he Shala h h h h
14 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab DTY 5 Hedhja e pjeë: Na një aë ushaae TO aileie i endsu në laësinë bideae h ëshë bëë një juajje e një pedhe në deji ë një cau në sipëfaqen e dei edha në enin e daljes na pi i Tpi a shpejësinë fillesae dejii i ë cilës e hiznalen fn ëndin α Të cahen euacine e lëizjes euacini i ajees laësia H dhe laësia L e ënies së pedhës M M O α H h L Sipas lijin ë dë ë dinaiës ei: a F e pjejë në dhe fijë: d d a X a Y d d Ndajë ndshe: d ns d d / dhe ejë ineiin e paë: d d / d d d / d Ndajë ndshe: d / d d dhe ejë ineiin e dë: ë ei: h csα sinα Na ë ushe fillesae cajë nsane e ineii: csα h sinα
15 D sc he Shala Këshu pjesine e shpejësisë d ë jenë: sin cs α α Lije e lëizjes së piës d ë jenë: csα h α sin Tajeja e piës Tajeja cahe due eliinua hën na shpehje e euacinee ë lëizjes ashu që fijë euacinin f pa: α α cs cs h α sin h α α α sin cs cs cs h α α Shpehja e fundi paaqe euacinin e ajees së pedhës Laësia e ënies së pedhës Laësia e ënies së pedhës L cahe pë dhe L pa: cs cs α α L h h α α sin sin pej na ha e nejshe pë ë aiu në laësinë L pia ëshë: sin sin h ± α α h sin sin α α Mee sepse > Kuse laësia asiale ëshë: α α α cs sin sin h L Laësia ë e adhe Laësia ë e adhe H dinaa M e piës M cahe na shpejësia në deji eial në piën ë ë laë ëshë ze pa: sin sin α α
16 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab u ëshë: sinα ha e nejshe pë ë aiu laësinë ë ë adhe as zëendësii ë hës në euacinin e lëizjes pë : sinα h fijë laësinë H ë ë adhe: H sinα h sinα H sinα sinα h H h sin α H h sin α 5
17 D sc he Shala DTY 6: Lëizja e piës nën epiin e fcae ëheqëse ia aeiale M e asë lëiz nën epiin e d fcae ëheqëse F dhe F qenda e ëheqjes së ë cilae janë pia a dhe b Inensiei i fcae ëshë ppcinal e disancën e piës M na qenda e ëheqjes e eficien ppcinaliei Të cahen euacine e lëizjes së piës Në çasin fillesa pia aeiale nddhej në pzicinin dhe a shpejësinë fillesae e cila ëshë paalel e asin hiznal Zjidhje: M b F F O a Sipas liji ë Njuni ei: a F F Fca ëheqëse ah si e ëshë: F M use F M u: M a i j use M i b j aëheë F M a i j use F M i b j uacinin e pjejë në deji ë asee dhe : : a : b a b h h h cs sin h cs sin K ns K ns a a b b K K K K cs a b sin cs sin Knsane dhe cahen na ushe fillesae: a dhe dhe ajë deiae: 6
18 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab cs sin cs sin Zëendësjë ushe fillesae në euacine dhe : a a b pej na ai: a b Këshu pëfundiish fijë euacine e lëizjes: sin cs a a dhe cs b b 7
19 D sc he Shala LIJT ËJITHSHM TË DINMIKËS DTY Sasia e lëizjes eplani e peshë 985 N filln lëizjen në pisë e ç as ndshii ndëje fcës ëheqëse dhe fcës së ezisencës ëshë nsan dhe aë F N Të cahe: a sa hë i nejie aeplani që ë shëpue na sipëfaqja e Tës nëse shpejësia në ë cilën ai e ain ëë ëshë 6/s dhe b sa hë i nejie aeplani që ë shëpue na sipëfaqja e Tës nëse senda e paë aiizhen ë ndihës ë cilën anë fcë shëse nsane dhe aë 5N O F pisa Zjidhje: Lëizjen e aeplani nëpë pisë d a nsidejë si lëizje anslaie dejize pëaësish si lëizje dejize ë piës aeiale a ë ë caua hën e shëpujes nisei na liji bi ndshiin e sasisë së lëizjes: T sh F d pjejë në deji ë lëizjes : F d u: aëheë: T sh 6 / s F N ns Tsh F d F T sh pej na: Tsh s F 985 b Kha e shëpujes edhe në ëë as cahe na liji bi ndshiin e sasisë së lëizjes: T sh Fpd F d pjejë në deji ë lëizjes : Fpd F d u: F p 5N ns e cila epn seunda e paë aëheë: pej na: T 6 / s F N ns Tsh p d F d Fp F sh F T Fp s F F 985 sh T sh 8
20 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab DYT Sasia e lëizjes Një pedhë e asë ëshë lansua e shpejësi fillesae dejii i ë cilës e hiznalen fn ëndin α ani hën e nejshe që pedha ë aijë laësinë ë ë adhe dhe shpejësinë pë ëë pzicin Zjidhje: M M H O α Zbaj lijin bi ndshiin e sasisë së lëizjes pej pzicini O në M: M T d pjejë në deji ë asi : sinα T pej na ha e aijes së laësisë ë ë adhe d ë jeë: sinα T Nëse pjejë në deji ë asi ei: M cs α pej na shpejësia në pzicinin u pedha ain laësinë asiale ëshë: M csα DTY : Meni inei Nëpë pllaën e lëua hiznale ëshqe sfea M e asë e cila ëshë e lidhu e një lia Liai aln nëpë një ië ë hapu në pllaë dhe ëhiqe e shpejësi nsane Në çasin fillesa sfea jende në disancën na ia O dhe a një shpejësi fillesae e cila a deji nal në disancën Të cahe liji i lëizjes së sfeës dhe fca në lia z M O M Zjidhje: ë pzicinin e çfaëdshë ë sfeës M bëjë liiin na lidhje dhe zbajë lijin bi ndshiin e eni inei pë piën O 9
21 dl d n i M j Fi O D sc he Shala n j F Na fiua e ëpshe shihe se M i ëshë e baabaë e ze pasi që asnjë fcë nu jep en pë piën O i O z N S O M M Na shpehja paapae jedhë që: L ns pëaësish eni inei në çfaëd çasi ë hës ëshë i baabaë e enin inei në çasin fillesa pa: L L L L ëshu: Me deë ëshë dhënë se shpejësia e ë cilën ëhiqe liai ëshë nsane dhe aë e inensie aëheë: ëshu: d d d d pëaësish: d d Zëendësjë në shpehjen pë shpejësi ënde dhe fijë:
22 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab d d d d d d Nëse zbajë lijin e Njuni ë pjeua në deji ë ei pëaësish disancës OM d ë ei: a S a u: d d eqë ns d d aëheë: S S DTY Lëizja e piës nën epiin e fcës qende euacini i ineu Të cahe fca qende F nën epiin e ë cilës lëiz pia aeiale e asë nëse p ajeja e saj ëshë dhënë në dinaa plae e shpehjen u p dhe e janë ecs nsane Zjidhje Na eia dië se euacini i ineu pë lëizje ë piës nën epiin e fcës qende a fën: d F d c u: F fca qende - dinaa plae ë piës aeiale e asë c - shpejësia seiale e piës Na shpehja e ajees ai që: ecs p pëaësish:
23 D sc he Shala d d e e cs cs d d p p as zëendësii në euacin ë ineu fijë: e F cs e cs p p c pej na: c e e e F cs cs p p p pëaësish fca qende d ë jeë: e c F p DTY 5: nejia ineie puna e fcae Sa duhe ë jeë h pë ë cilën duhe shpu shuua susën e nuësi c 5N/ dhe jaësi fillesae e cila ëshë e endsu në pin e pjeë ashu që sfea e asë që und ë nsidehe si pië aeiale ë alj penesën e cila e a laësinë asiale 5 në piën 9; Keficieni i fëii ndëje pi dhe sfeës ëshë µ jihashu cani laësinë D u bie sfea ezisenca jea ë nelizhhen 8 c h M 9; 5 D 6 Zjidhje:
24 8 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab c α h 6 α M F c F µ 9; 5 D Së pai analizjë pin Me qëlli ë caii ë shpejësisë në pzicinin zbajë lijin bi ndshiin e enejisë ineie pej pzicini M ai që susa ëshë shpu pë adhësinë h ë cilën duhe caua pasaj dei në pzicinin që ëshë i baabaë e punën e fcae që epjnë në aë pjesë e që janë puna e peshës puna e fcës së susës F c dhe puna e fcës së fëii F µ pa: M µ M F F c eqë sfea lëshhe liish pa shpejësi fillesae H H h sinα h h h h h 5 F F F µ N µ µ h µ na N csα csα N cs α 5 Fµ Fµ h µ h 5 F c ch as zëendësii në shpehjen fijë: h µ h ch 5 5 pej na: 8 6 c µ h h 5 5
25 D sc he Shala ë lëizjen e sfeës pas daljes na pi zbajë lijin e dë ë Dinaiës hedhja e pjeë dhe ei: a pëaësish ë pjeua në deji ë asee dhe : dhe pas zjidhjes së ëe euacinee difeenciale dhe zëendësii ë ushee fillesae: csα dhe sinα euacine e lëizjes së sfeës d ë jenë: csα sinα Laësia ë e adhe H 5 cahe e shpehjen: H sinα u: ha pë ë cilën sfea ain laësinë ë ë adhe H dhe aë H 5 aëheë: 5 5 Na ushi që laësia ë e adhe ëshë në piën 9; pa pë 9 ei: csα 5 9 pej na: 5 Zëendësjë në euacinin dhe fijë: due e ahasua e shpehjen ei: 8 6 c 5 µ h h 5 5 c h µ h 5 5 as zëendësii ë ë dhënae fijë ëë euacin uadai sipas h pa: 5h 6865 h pej na ei d zjidhje: h pëeëshe shuii i susës ë i adh se ze si 758 undësi eale pa h 7 58 jihashu dihe se pë hedhje ë pjeë laësia ë e adhe cahe na: sinα csα L pas zëendësiee fijë laësinë u bie sfea: sinα csα L
26 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab DTY 6:nejia ineie sasia e lëizjes puna e fcae Sfea e asë lëizë nëpë një p asi i ë cili shihe në afshin eial Në çasin fillesa aj nddhej në pzicinin e cila nddhe në laësinë H Nëse sfea lëshhe pa shpejësi fillesae ë cahe shpejësia e sfeës u aj ain në pzicine D dhe adhësia e shuii asial h ë susës e nuësi c në ahasi e jaësinë e saj fillesae ë padefua l ë pzicinin ë cahe shpja e sfeës në p jesën D ë anali sfea e aln pë hen τ Fëii ë nelizhhe në pjesën ehe use në aë ijëdejë ë ee µ H h F Zjidhje: α α β β D H F µ α N α α β β D h h N jesa Në ëë pjesë e qëlli ë caii ë shpejësisë së sfeës në pzicinin eqë dihe ua jaësia zbajë lijin bi ndshiin e enejisë ineie pej pzicini në që ëshë i baabaë e shuën e punëe ë ë jiha fcae që epjnë në aë pjesë pa: Fµ N n h F h N F µ F c β 5
27 D sc he Shala pasi që sfea lëshhe ë lëiz pa shpejësi fillesae H H Fµ Fµ µ N sinα Na: N csα N csα eqë sfea nu und ë lëizë në deji nal e asin e pi aëheë: H Fµ Fµ µ csα µ H cα sinα N eqë pjesini i fcës së easini N në deji ë lëizjes ëshë ze as zëendësii ei: H µ H cα pej na: H µ H cα pëaësish H µ cα jesa Së pai cajë shpejësinë e sfeës në pzicinin pëes liji bi ndshiin e enejisë ineie pej pzicini në pa: h csα as zëendësii ei: csα pej na: csα pëaësish csα Sipas liji ë dë ë Njuni pë pzicinin ë pjeua në deji ë nales n ei: a N N u: an aëheë shpja easini e pi në sfeë në pzicinin d ë jeë: N jesa D Me qëlli ë caii ë shpejësisë së sfeës u aj ain në pzicinin D zbajë lijin bi ndshiin e enejisë ineie pej pzicini në D pa: 6 D
28 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab D D h cs β as zëendësii ei: D csβ pej na: D csβ pëaësish D csβ jesa D Meqë pë pjesën D dihe se aë sfea e aln pë hën τ zbajë lijin bi ndshiin e sasisë së lëizjes pej pzicini D në që ëshë i baabaë e ipulsin e fcae pë ë njëjën hë pëaësish ë pjeua në deji ë lëizjes asi pa: I I F D µ D D F µ µ N µ cs β Na: N cs β N cs β eqë sfea nu und ë lëizë në deji nal e asin e pi I sin β τ I F F τ µ cs β τ µ µ as zëendësii fijë shpehjen pë shpejësinë e sfeës në pzicinin e ë cilën aj e de susën pa: D sin β τ µ cs β τ pëaësish: D sin β µ cs β τ jesa F Shënjë e F pzicinin në ë cilën supzjë se d ë aijë sfea pas dijes së susës në pzicinin e shpejësi Kuphe që pzicinin F e ei aë ashu që në aë pzicin sfea ndale pa shpejësinë e a ze dhe susën e shp shun pë adhësinë h ë cilën duhe caua Kushiish und ë ai që në ëë as dihe ua h ë cilën e aln sfea aëheë zbajë lijin bi ndshiin e enejisë ineie pej pzicini në F pa: F µ F F F F F c pasi që sfea ndale h h sin β F F F µ N h µ µ Na: N cs β N cs β eqë sfea nu und ë lëizë në deji nal e asin e pi 7
29 D sc he Shala aëheë: Fµ Fµ F µ cs β h µ h csβ F c h h Fc d c d c c h shenja - eqë fca në susë në ëë as e penn lëizjen as zëendësii ei: h h sin β µ h csβ c pej na ei fiua një euacin uadai sipas h pa: c h sin β µ csβ h pej na ei zjidhje: h / pëaësish: h / sin β µ csβ ± sin β µ csβ ± h sin β µ csβ c sin β µ csβ c Meqë eale ëshë që adhësia h ëshë ë e adhe se e baabaë e ze aëheë adhësia asiale pë ë cilën ëshë shpu shuua susa ëshë: sin β µ csβ h sin β µ csβ c pëaësish: c h sin β µ csβ sin β µ csβ c dhe uphe se duhe ë plëshe ushi: c sin β µ csβ sin β µ csβ c c c 8
30 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab DTY 7: Lajeësi aeai ia aeiale M e asë ëshë e lidhu pëes liai ë pazjashë pë piën O dhe lëshhe na pzicini M e shpejësi fillesae u M O L e eialen fn ëndin α jaë lëizjes në afshin eial liai e de një penesë që jende në piën O u O O l dhe e eialen fn ëndin β Të cahe sa duhe ë jeë jaësia l ashu që jaë dijes së liai në penesën O fca në lia ë ie pë d heë dhe pë ëë l ë caua sa duhe ë jeë shpejësia fillesae e piës aeiale M ashu që liai pas dijes në penesën O ë bëshille pëeh ësaj pie O M O ψ β α M Zjidhje: M O M βψ S O ψ n β α n S a T a N M M Lëizja e piës pë α β ëshë lëizje ulluese nëpë ehin e eze L aëheë shpejësia e piës M ëshë: d L u d Niii i piës eqë aj bën lëizje ehe ëshë: a a T a N u: a T L dhe a L N 9
31 D sc he Shala uacini heel i Dinaiës së piës j ë lië ë lidhu ëshë: a S ap ë pjeua në deji ë anjenes dhe nales n fijë: a a T L sin α b a N L cs α S Na shpehja b S L cs α pa cahe fca në lia në funsin ë ëndi dhe shpejësisë ënde ë cila cahen na shpehja a: d d d d L L L sin α / d d d d d d sin α d / L d sin α d L cs α L L cs α csα L L as zëendësii fca në lia d ë jeë: S L cs α cs α cs α csα cs α L cs α csα S cs α csα Këshu në çasin u liai e de penesën O ëndi α β aëheë fca në lia d ë jeë: S α β cs α α β csα S α β cs β csα as dijes në penesën O pia aeiale M d ë azhdjë lëizjen p si lajeës aeai e jaësi L l Lëizjen e lajeësi në ëë as e pëcan ndshii i ëndi ψ dhe pë ψ π β liji i pëjihshë i Dinaiës d ë jeë: a S ap i pjeua në deji ë nales n a N cs β ψ S L l pej na: S cs β ψ L l Shpejësinë und ë cajë due pjeua në deji ë anjenes se ndsha ë lehë ëshë due zbaua lijin bi ndshiin e enejisë ineie pej pzicini dei në pzicinin M ë pëcaua e ëndin ψ pa: [ L cs β l cs β L lcs β ψ ]
32 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab [cs β cs β ψ ] L l L l aëheë e baaziin e e ai: S cs β ψ [cs β cs β ψ ] L l S cs β ψ cs β L l Me deë ëshë dhënë se j fcë duhe ë ie pë d heë aëheë na ush jejë se sa duhe ë jeë jaësia l pa: S ψ S α β β S ψ cs β cs β cs L l L l S α β [ cs β csα] aëheë: cs β [ cs β csα] L l L l 8 cs β 6 csα L l 8 cs β 6 csα l L 8 cs β 6 csα Në enin e dijes ëndi ψ aëheë: [ L cs β l cs β L lcs β ] Na: L cs α csα L L pë α β ei: L aëheë: cs β csα L L L Lcsβ csα as zëendësii në fijë jaësinë e nejshe l: L Lcs β csα l L 8 cs β 6 csα l L cs β csα L L 8 cs β 6 csα cs β csα 8 cs β 6 csα
33 D sc he Shala 6 cs β csα l L 8 cs β 6 csα Në ënë që liai ë bëshille pëeh penesës O ush i nejshë ëshë që pë ψ π β pzicini ë i laë i piës aeiale fca në lia ë jeë ë e adhe se baas e ze pa: S ψ π β pëaësish: cs β π β cs β L l csπ cs L l β L l cs β Liji bi ndshiin e enejisë ineie pej pzicini fillesa M dei në pzicinin ëshë: Lcs β csα Lcs β csα pëaësish: L l cs β Lcs β csα DTY 8: aii Dalabei pë pië aeiale zia fillesae e eanizi aëhallësh O O ë endsu në afshin eial si në fiuën e ëpshe ëshë e pëcaua e ëndin Shufa e ëij eanizi anë asa ë la që nelizhhen use O O l Në fundin e shufës ëshë e endsu naesa e peshë e cila und ë nsidehe si pië aeiale Nëse eanizi na pzicini fillesa filln lëizjen na qeësia ë cahen fca në shufa O dhe O në funsin ë ndshii ë O O Zjidhje: N a S O O in F T N a T a T S a n in F N Meqë O O l shufa bën lëizje anslae aëheë shpejësië e piae dhe janë ë baabaa pa:
34 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab O l jihashu edhe niie: N T a a a aëheë: N N N a a a O l T T T a a O l a Sipas paii ë Dalabei pë shufën pëaësish piën aeiale ei: in S S F in in in in N u: F FN FT F a l in T N dhe FT a l se ë pjeua në deji ë asee n dhe : in N n: cs S S F F in T : sin Meqë shufa bën lëizje anslae aëheë shua e enee ë ëe fcae duhe ë jeë ze në cilënd pië le ë ai pë piën pa: S cs S cs Na shpehja cajë niiin ënd dhe shpejësinë ënde ë shufës funsin ë ëndi pa: sin l pej na: sin l d d d sin / d d d d l sin d d / l sin d d l cs cs cs l l l pëaësish: cs cs l l Na shpehja jedhë që: S cs l S cs l pëaësish: S S Zëendësjë në shpehjen dhe ei: S cs S l S cs l O në
35 D sc he Shala S cs l l cs cs use: S S cs Këshu psh pë 6 fijë: S cs 6 use: S
36 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab LËKUNDJT DJTVIZO TË IKËS MTIL DTY : Lëundje e lia që nu shuhen ë naesën e asë që ëshë e au në një susë e nuësi c dhe jaësi fillesae l ë cahe zjaja saie e susës pzicini i euilibi sai liji i lëundjee ndaj ëij pzicini feuenca ehe dhe peida e lëundjee ë lia due aë që lëundje lëizja e naesës pshë-laë janë dejize dhe pëeç fcës në susë dhe peshës së naesës jeë ezisencë nu a Në çasin fillesa naesa ëhiqe pshë pë adhësinë dhe a shpejësinë Zjidhje: Nëse zbajë lijin heel ë dinaiës në piën e au në susën eiale si në fiuën e ëpshe d ë ei: F e u: dhe Fe c fs asa e naesës së au në susë pesha e naesës aiei ës c nuësia e susës f s zjaja saie e susës zjaja pë sha ë peshës së naesës quhe saie sepse nu ei lëizje l jaësia e susës në jendje ë panaua paaqe zjajen enale ë susës pej pzicini euilibues l c l l f s f s F e ëheë e zëendësiin e shpehjee paapae në euacinin ei: c cf s Zjaja saie f s cahe na ushe e euilibi sai pa: dhe u e zëendësi ë ëe ushee në euacinin fijë: f s c c 5
37 D sc he Shala dhe ëë adhësi ë f s e zëendësjë në fijë: c pëaësish: u: c Këshu pa nëse fillii i dinaës ee në pzicinin e euilibi sai pesha e naesës nu ee në euacinin difeencial e zjaja e susës llaie pej ëij pzicini Në ëë as feuencën und a shpehi pëes zjajes saie pa: f s c f s c c f s c f s eida e ëe lëundjee d ë jeë: π f s T π π c Me qëlli ë caii ë liji ë lëundjee duhe ë zjidhi euacinin difeencial Supzhe zjidhja: λ λ λ e pej na: λe dhe λ e ë cila i zëendësjë në dhe fijë euacinin aaeisi: λ λ λ e / : e pëaësish: λ zjidhje e ë cili janë: λ / ± i Këshu zjidhja e pëjihshe e euacini difeencial d ë jeë: i i e e cs isin ai nsane e eja: dhe i aëheë zjidhja e pëjihshe eë fën: cs sin pej na: sin cs 5 Knsane dhe cahen na ushe fillesae ë cila i zëendësjë në shpehje dhe 5 pa: aëheë: aëheë liji i lëundjee ë naesës d ë jeë: cs sin 6
38 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab DTY : Lëundje e lia që shuhen Një pië aeiale e asë und ë lëunde nëpë afshin e lëua hiznal Kë lëundje shahe na susa e nuësi c dhe aizhen zëlhen na shuaësi aizei i cili a eficien ë shuajes b u fca e ezisencës isze ë shuaësi ëshë ppcinale e shallën e paë ë shpejësisë së piës aeiale e eficien ppcinaliei b Të cahe ushi që duhe ë plësjë eficieni i shuajes b ashu që ë ei lëundje peidie benda apliudae Zjidhje: Fcën elasie në susë ëshë: F e c Fca e ezisencës në shuaës: b e cila siç p shihe a ahen e undë e shpejësinë c l b Na fiua paapae shihe se nëse zbajë lijin heel ë dinaiës: a FN F e dhe e pjejë në deji ë lëizjes fijë: F e u: b b F e c dhe pas zëendësii dhe eullii ë euacini fijë: n u: b c n dhe uacini paaqe euacin difeencial hjen ë plë ë endi ë dë linea e eficien nsan jejësish paaqe lëundje e lia në abien e ezisencë se lëundje e lia që shuhen aizhen Zjidhjen e ëij euacini difeencial e supzjë në fën: λ e pej na: λ λ e λ λ e as zëendësii në euacinin ei: λ λ e λ n λ / e pëaësish euacinin aaaeisi ë euacini difeencial : λ n λ na i cili ei d ënjë ë ij: λ ± n n Në ashëi na api i n dhe i ënjë e euacini aaeisi ndshjnë dhe pë asin në duhe që lëundje ë jenë peidie aëheë duhe ë plëshe ushi ezisenca e la n < pej na ai që: O F e M F N 7
39 D sc he Shala b c n < pëaësish ushi që duhe ë plësjë eficieni i shuajes b ashu që ë ei lëundje peidie benda apliudae ëshë: b < c Ëshë e ëndësi ë cee se pë b c paaqie asi i ezisencae ufiae use pë b > c ei asin e ezisencae ë ëdha aëheë në ë d ase ei lëizje apeidie jlëundëse DTY : Lëundje e deuaa që nu shuhen Nëse në një pië aeiale e asë pëeç fcës elasie ë susës F e c epn edhe fca e cila ëshë funsin peidi i hës pa FΩ F sinω u F dhe Ω janë nsane ë shuhe liji i lëundjee dhe ë cahe apliuda e lëundjee ë deuaa O Zjidhje: Zbajë lijin e dë ë Njuni dhe e pjejë në deji ë lëizjes aëheë fijë euacinin difeencial: Fe FΩ c F sin Ω jedhiish c F sin Ω dhe së fundi h sin Ω u: asa e piës niii c eficieni i nuësisë së susës disanca e piës na pzicini i euilibi F c h c F e F N F Ω - quhe feuenca ehe e lëundjee ë lia Ω - feuenca ehe e lëundjee ë deuaa e njejë e feuencën e fcës nacuese Zjidhja e euacini pëbëhe na pjesa hjene dhe pjesa e eçanë j hjene pa: h Zjidhja e pjesës hjene nënupn zjidhjen e euacini difeencial në fën: h h që në analji e ase e ëpae ë lëundjee ë lia që nu shuhen dihe që zjidhja e pëjihshe e ij d ë jeë: h cs sin Zjidhjen e eçanë e supzjë në fën: 8
40 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab sin Ω Ω csω dhe Ω sin Ω as zëendësii në euacinin ei: Ω sin Ω h sin Ω na u jedhë se apliuda e lëundjee ë deuaa që nu shuhen ëshë: h F Ω c Ω na ai që zjidhja e eçanë që paaqe lëundje e deuaa që nu shuhen ëshë: h d sinω sinω Ω Këshu zjidhja e pëjihshe e euacini ëshë: h cs sin sin Ω Ω dhe deiai i ij: h sin cs ΩcsΩ Ω u dhe janë nsane ë ineii që cahen na ushe fillesae: pas zëendësii ë ëe ushee fillesae ei: h h Ω Ω dhe h Ω h Ω Ω Ω Ku i zëendësjë shpehje e fiuaa pë ë nsane ë ineii fijë lijin e lëundjee ë deuaa që nu shuhën pa: h h Ω c F cs sin sin Ω u: h Ω Ω DTY : Lëundje e deuaa në abien e ezisencë Nëse në një pië aeiale e asë e cila bën lëizje dejize në afshin e lëua hiznal epjnë fca elasie F e c fca nacuese FΩ F cs Ω dhe shuaësi e fcë ë ezisencës e cila ëshë ppcinale e shallën e paë ë shpejësisë e eficien ppcinaliei b b ë cahe liji i lëundjee dejize ë ësaj pie aeiale due aë që ezisenca janë ë la n < e cila në çasin fillesa nddhe në qeësi Zjidhje: Mdeli eani ëshë paaqiu në fiuën e ëpshe 9
41 D sc he Shala b F e F N F Ω uacini difeencial që i pëshuan ë lëundje d ë jeë: Fe FΩ b c F csω b c F csω n h csω u: b c F n dhe h Shpehja paaqe euacinin difeencial ë lëundjee ë deuaa në abien e ezisencë që ëshë euacin difeencial jhjen i endi ë dë linea e eficien nsanë Zjidhja e euacini pëbëhe na pjesa hjene dhe e eçanë pa: h Zjidhja e pjesës hjene në aësi ë api n e und ë jeë si ë lëundje e lia që shuhen: n a e cs p sin p nëse n < h p n n b e nëse n dhe h c h λ e e λ nëse n > Zjidhjen e eçanë e supzjë në fën: cs Ω β Ωsin Ω β dhe Ω cs Ω β u: d - paaqe zjidhjen e eçanë pëaësish lëundje e deuaa që shuhen paaqe apliudën e lëundjee ë deuaa që shuhen β - quhe ëndi i ndshii faz as zëendësii në euacinin ei: Ω cs Ω β n Ωsin Ω β cs Ω β h csω dhe due diu se: Ω β ψ u ψ paaqe fazën e lëundjee ë deuaa aëheë ei: Ω csψ n Ωsinψ hcs ψ β pëaësish: Ω na u jedhë se: csψ n Ωsinψ h csβ csψ h sin β sinψ
42 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab Ω h csβ n Ω h sin β aëheë ei: [ Ω n Ω ] h na u jedhë se: Ω h n Ω / / që paaqe apliudën e lëundjee ë deuaa që shuhen Këndi i ndshii faz β cahe due i pjesëua shpehje pa: n Ω n Ω an β Ω Ω Këshu zjidhja e pëjihshe nëse n < ëshë: n e cs p sin p cs Ω dhe deiai i ij: n β n ne cs p sin p e psin p p cs p Ωsin Ω β u dhe cahen na ushe fillesae: pas zëendësii ë ëe ushee fillesae në shpehje 5a dhe 5b ei: cs β cs β dhe n p Ω sin β pëaësish: n Ωsin β n cs β Ω sin β p p as zëendësii ë nsanee ë ineii dhe në zjidhjen e pëjihshe fijë lëundje e deuaa që shuhen në ezisenca ë la n < : n ncs β Ωsin β e csβ cs p sin p cs Ω β p
43 D sc he Shala LËVIZJ ËËË IKËS DTY : asi u lëizja zhendsësh dhe aj elaie janë anslaie T-T llaa dejëndëshe lëiz nëpë afshin hiznal pëes d shufae ë lidhua e nje O dhe O u O O l Në pllaë ëshë i hapu anali paalel e nëpë ë cilën lëiz sfea M e asë due fillua na pia O Nëse shufa O ullhe e shpejësi ënde nsane cani lijin e lëizjes së sfeës nëpë anal dhe shpjen easinin e pllaës në sfeë Fëii ë nelizhhe O M O O Zjidhje: O a a e n N M e in F e a O O uacini eial i lëizjes elaie në asin e pëjihshë a fën: in in a Fi Fe Fc ë asin në deën në ei: a a F i N N easini shpja e pllaës në sfeë in N in Fe ae ae a a l Fe ae l in Fc e e sepse pllaa nu ullhe Këshu euacini eial i lëizjes elaie pë asin në d ë jeë:
44 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab in a N F e jejë në deji ë asi dhe : in : a F sin l sin e in e : N F cs N l cs d Na ns ai që aëheë euacine paapae ain fën: d : l sin d l sin d d l sin d d l sin d l cs l cs l cs d l cs d d l cs d d l d cs d as zjidhjes së inealee fijë lijin e lëizjes së sfeës nëpë anal: l sin Shpja e pllaës në sfeë cahe na: : N l cs N l cs
45 D sc he Shala DTY : lëizja zhendsëse ulluese use aj elaie anslaie -T pi i dejë e jaësi l që shihe në afshin hiznal ëshë i lidhu nuësish pë shufën O e jaësi l e cila ullhe eh çënieës O e shpejësi ënde nsane Sfea M e asë e cila jende në p në çasin fillesa nddhej në pzicin dhe a shpejësinë fillesae l ndaj pi Të cahe liji i lëizjes së sfeës nëpë p dhe pë pzicinin : ha e aijes së sfeës shpejësia abslue dhe shpja easini e pi në sfeë M l l O Zjidhje: O l z F N a e a c F N in F c M e in F e a uacini eial i lëizjes elaie në asin e pëjihshë a fën: in in a Fi Fe Fc ë asin në deën në ei: a a Fi F N FN FN FN easini shpja e pi në sfeë in N in Fe ae ae ae OM l F ae l in Fc e e 9 aëheë: in Fc e sin sin 9 Këshu euacini eial i lëizjes elaie pë asin në d ë jeë: e
46 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab in c in e N F F F a jejë në deji ë asi dhe z: : sin in e l l F a : l l l F F F F N in c in e N cs l F N pej na: l F N z: N F pej na: F N Na shpehja pë fijë: supzjë: aëheë dhe fijë euacinin aaeisi: e λ e λ λ λ pej na: λ ± / aëheë zjidhja e pëjihshe d ë jeë: e e e e λ λ pëaësish deiai i saj: e e nsane dhe cahen na ushe fillesae: Këshu liji i lëizjes së sfeës nëpë p d ë jeë: e e l e e e e e e se due diu se sinus hipebli sinh ëshë: sinh α α α e e aëheë: sinh l e e l e e l Shpejësia elaie e sfeës shpejësia e sfeës ndaj pi d ë jeë: e e e e se due diu se sinus hipebli csh ëshë: csh α α α e e aëheë: 5
47 D sc he Shala e e csh Shpejësinë elaie ë sfeës në çasin u aj ain në pzicin e cajë na: - pë pzicinin dinaa ëshë: l pej na: l l sinh pej na cahe ha pë ë cilën sfea ain në pzicinin : asinh sinh e e e e e e zëendësjë s s s e s s s s aëheë: ± ± s / ± eqë ha duhe ë jeë ë e adhe se ze aëheë: s e s pej na: ln Shpehjen e fiua pë e zëendësjë në shpehjen pë dhe fijë: csh csh ln csh ln ln ln e e ë l pzicini ëndi 5 dhe: e l l l use dihe se: u: 6 e cs 5 e sin 5
48 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab aëheë shpejësia abslue në pzicinin ëshë: Shpja e pi në sfeë d ë jeë: FN l l l l l F N aëheë: N N F N F F l DTY : lëizja zhendsëse anslaie use aj elaie ulluese T- ia e ajes së lajeësi aeai O M l lëiz nëpë analin hiznal sipas liji a sin p u a dhe p janë adhësi nsane Të cahe liji i lëundjee ë lajeësi aeai due aë që ai bën lëundje ë la pa due apsiua që sin dhe cs sipas neje dhe ë cahe fca në lia Lajeësi në çasin fillesa jendej në qeësi O O l M Zjidhje: O O n e l in F e ae S a N M a T e a e uacini eial i lëizjes elaie në asin e pëjihshë a fën: 7
49 a F F F i in e in c D sc he Shala ë asin në deën në ei: a an at u: a l N a T l F i S S fca në lia in d Fe ae a e in asin p ap sin p F a ap p e e sin d in Fc e e eqë lëizja zhendsëse ëshë anslaie Këshu euacini eial i lëizjes elaie pë asin në d ë jeë: in a S F e jejë euacinin në deji ë nales n: n: a l cs S in sin T F e l cs S ap sin p sin S l cs ap sin p sin ëshu pë ë pëcaua plësish fcën në lia S duhe ë cajë lijin e lëundjee ë lajeësi dhe shpejësinë ënde ë lajeësi pëaësish ain e saj ë ëë azhdjë e pjei ë euacini eial në deji ë anjenes : in : a l sin cs T F e l sin ap sin p cs ap sin sin p cs l l ap sin sin p cs l l Due apsiua pë lëundje ë la < ± 6 sin dhe cs shpehje e fundi ain fën: S ap sin p l l l ap sin p l l ap zëendësjë: h aëheë: l l hsin p ë euacinin difeencial ë fundi dihe se zjidhja e pjesës hjene ëshë: h cs sin use aj e eçanë cahe aësish na fa e pjesës jhjene në asin në supzhe: sin p pej na: p sin p dhe zëendësjë në euacinin : p sin p sin p hsin p pej na: h p ëshu zjidhja e eçanë ëshë: 8
50 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab h sin p sin p p Zjidhja e pëjihshe e euacini eë fën: h h cs sin sin p p pëaësish deiai i saj: h sin cs p cs p p Knsane e ineii dhe cahen na ushe fillesae: h p h ph p p p Këshu liji i lëundjee ë lajeësi d ë jeë: ph h sin sin p p p h p sin p sin p ap se u zëendësjë: h fijë lijin e lëundjee ë la ë lajeësi: l ap p sin p sin l p pëaësish deiai i saj: ap cs p cs u: l p l 9
51 D sc he Shala DTY : lëizja zhendsëse dhe aj elaie janë ulluese - pi në fë ë jsëehi e eze ullhe eh asi eial e shpejësi ënde nsane Në çasin fillesa në p jende një sfeë e asë në pzicinin ë ë ulë ë pi e ças i jepe një shpejësi fillesae Të cahe liji i ndshii ë shpejësisë së sfeës nëpë p shpejësia e ë cilën aj del na pi dhe shpja easini i pi në sfeë pë ëë pzicin Fëii ndëje sfeës dhe pi ë nelizhhe O M M Zjidhje: M O n M F N a N a e b M c a T in F e F N a c in F c uacini eial i lëizjes elaie në asin e pëjihshë a fën: in in a Fi Fe Fc ë asin në deën në ei: a an at u: a N a T Fi F N FN FN FN easini shpja e pi në sfeë in N T F a a a MM ' sin a MM ' ε e e e e e e b 5
52 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab d in ε e ns Fe ae sin d in Fc e e 9 aëheë: in Fc sin sin9 cs Këshu euacini eial i lëizjes elaie pë asin në d ë jeë: in in a FN FN Fe Fc jejë në deji ë asi n dhe b: in n: an cs FN Fe sin N in T F e cs F N sin sin F cs sin : a sin cs sin sin cs sin d d d d d d d d sin sin d sin sin d sin sin d sin d cs cs cs cs ë pzicinin ëndi 9 shpehja d ë jeë: 9 cs9 cs 9 9 Shpejësia e sfeës nëpë p në funsin ë ëndi ëshë: cs cs cs cs Ku sfea ain në pzicinin ëndi ëshë 9 aëheë shpejësia elaie e sfeës në dalje ë pi pzicini ëshë: 5
53 c c c 9 D sc he Shala cs9 Shpejësia zhendsëse e sfeës në pzicinin d ë jeë: c e cs 9 Na fiua paapae shihe se ë d pnene janë nale në njëa jeën aëheë: c c c e pëaësish inensiei i shpejësisë së sfeës në pzicinin d ë jeë: c c c ce > Shpja easini i pi në sfeë pë pzicinin na shpehja dhe due zëendësua shpehjen d ë jeë: F cs sin N cs9 sin FN 9 F N N F Kpnenen F N ë shpjes easini së pi në sfeë e cajë due e pjeua euacinin eial ë lëizjes elaie në deji ë binal b pa: a FN F in c a sepse sfea nu und ë lëizë në ëë deji in FN Fc 9 cs9 Këshu pëfundiish shpja easini i pi në sfeë u aj ain në pzicinin d ë jeë: F N N F 5
54 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab DINMIK SISTMIT MTIL LËVIZJ QNDËS SË MSËS SË INISË TË SISTMIT MTIL DTY : ë eanizin e eua në fiuë ë shuhen euacine e lëizjes së qendës ë asës së inecisë dhe euacini i ajees së saj nëse: Shufa O ëshë e jaësi a dhe asë shufa D e jaësi a dhe asë use ëshqiësi dhe D që und ë een si pia aeiale anë asa ë njëja ia paaqe esin e shufës D D Zjidhje: Qenda e asës së inecisë pë shufën O ëshë pia e dinaa: a a cs dhe sin Qenda e asës së inecisë pë shufën D ëshë pia e dinaa: a cs dhe a sin Qenda e asës së inecisë pë ëshqiësin ëshë eë pia e dinaa: a cs dhe eqë O aëheë edhe O Qenda e asës së inecisë pë ëshqiësin D ëshë eë pia D e dinaa: D dhe D a sin Qenda e asës së inecisë në deji ë asi cahe e shpehjen: i i D D c i a 9 cs a cs a cs a cs 9 c a cs 5 Qenda e asës së inecisë në deji ë asi cahe e shpehjen: i i D D c i D D a 9 sin asin asin asin 9 c a sin 5 uacinin e ajees e cajë due eleinua ëndin na shpehje pë c dhe c pa due i niu në aë dhe bledhu anë pë anë euacine dhe : 5
55 D sc he Shala c c a cs a sin a pa ajeja e qendës së asës së ëij eanizi paaqe ehin e qendë në filli ë sisei 9 dinai dhe eze a ajeja c f c 9 a O DTY : ë eanizin e eua në fiuën e ëpshe ë shuhen euacine e lëizjes së qendës ë asës së inecisë nëse: Shufa O ëshë e jaësi l dhe asë shufa O e jësi l dhe asë shufa e jaësi l dhe asë shufa D e jaësi l dhe asë use ëshqiësi D që und ë ee si pië aeiale a asë 5 Shufa D ëshë e lidhu pë esin e shufës dhe ëshqiësin D e çëniea O O l ca euacinin e ajees së qendës së asës së inecisë l Zjidhje: 5
56 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab θ ψ l Sisei i dhënë aeial pëbëhe na pesë upa Shufa O e qendë ë asë në ë cila cahen na: l O cs cs dhe sin sin l O Shufa O e qendë ë asë në ë cila cahen na: eqë O O l aëheë ëndi që fn shufa O e asin ëshë ψ pa: l l OO O cs l cs dhe O sin sin Shufa e qendë ë asë në ë cila cahen na: O cs l l cs dhe O sin l sin Shufa D e qendë ë asës në ë cila cahen na: eqë: O cs D csθ l l cs l l csθ l csθ cs θ aëheë ëndi që fn shufa D e asin ëshë θ pa: l l l l D cs l cs dhe O sin sin l sin sin sin ëshqiësi D e qendë ë asës në D 5 5 ë cila cahen na: 5 l i dhënë e deë dhe O sin D sin l sin l sin l sin Qenda e asës së inecisë në deji ë asi cahe e shpehjen: i i 55 c i l l l cs l cs l l cs l cs l c 5 55
57 D sc he Shala l l cs c 6 7 6l l cs c 6 ëshu liji i lëizjes së qendës së asës së ëij sisei në deji ë asi d ë jeë: 7 c l l cs Qenda e asës së inecisë në deji ë asi cahe e shpehjen: i i 5 5 c i l l l sin sin l sin sin l sin c l sin l sin c c 6 6 ëshu liji i lëizjes së qendës së asës së ëij sisei në deji ë asi d ë jeë: c l sin uacinin e ajees e cajë due eliinua ëndin na shpehje pë c dhe c pa due i niu në aë dhe bledhu anë pë anë euacine dhe : c l c cs sin 7 l l pa ajeja e qendës së asës së ëij eanizi paaqe elipsën e qendë në piën Ql dhe e jsëbshe: 7 - në deji ë asi : a l në deji ë asi : b l 5 l ajeja c f c O l Q 7 l 56
58 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab DTY : lei e peshë ëshë i endsu në bazaenin e lëua hiznal ë bsh ë elei nën ënd ë dejë ëshë i lidhu njëi saj i shufës O e jaësi l dhe peshë Q use në sajin jeë ë shufës jende naesa e peshë e cila und ë nsidehe si pië aeiale Nëse bshi i elei në filli ishe në qeësi pasaj filln ë ullhe e shpejësi ënde nsane ë cahe: a Liji sipas ë cili elei lëiz në deji ë hiznales nëse ai nu ëshë i lidhu pë bazaen e bulna b Fcën asiale në deji hiznal e cila epn në bulna pëes ë cilëe lidhe elei e bazaen c ani shpejësinë ënde ë ë ël ë elei e ë cilën ai d ë fillj ë ëcej shëpue bi bazaen nëse nu ëshë i lidhu e bulna l O Zjidhje: O Q F a Sisei i dhënë pëbëhe na e upa le ë i cajë dinaa e qendae ë asae: lei qendën e asës e a në piën O u: dhe Shufa O qendën e asës e a në esin e jaësisë së saj pa pia u: l l sin dhe cs Naesa si pië aeiale qendën e asës e a në piën u: l sin dhe l cs F N 57
59 D sc he Shala Sisei në ëësi qendën e asës e a në piën c c ë cila cahen na: i i el sh n i el sh n l Q sin l sin c Q due e diu se: d aëheë: pa: d l Q sin l sin c Q Q Q l sin c Q Nëse shpehjen e deijë d heë aëheë fijë: Q Q l sin c Q Në bazë ë liji ë dë ë Njuni ei se: M a c F i i pë deën në nëse ëë euacin e pjejë në deji ë asi X sepse ë jiha fca pesha janë eiale elei ende nu ëshë i lidhu e bulna pë bazaen F nu ezisn u nu a bulna aëheë: M c X i i pej na: c Këshu pa shpehja duhe ë baazhe e ze pa: Q Q l sin c Q pej na: Q Q l sin Q l sin Q pas ineii fijë: Q l cs Q pas edhe një ineii: Q l sin Q Knsane e ineii dhe cahen na ushe fillesae u eqë sisei në çasin fillesa ishe në qeësi aëheë: 58 i i
60 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab Q Q l l Q Q Këshu liji i lëizjes së elei nëpë afshin e lëua hiznal d ë jeë: Q Q l l sin Q Q b Ku janë ë endsu bulna pë pëfci ë elei e bazaen aëheë shpehja e pjeua në deji ë asi d ë jeë: M X F c i i Në ëë as niii i qendës së elei ëshë ze pa: aëheë në bazë ë shpehjes ei: Q l sin Q pëaësish e zëendësi në fijë: Q l sin Q F M c Q Q F l sin shenja - en se fca eale në bulna a ahen e undë e aë ë supzua pa inensiei eal i fcës F ëshë: Q F l sin lea ë e adhe e ë cilës aihe pë sin 9 pa: Q F a l c Në enin u elei d ë fillj ë shëpue na bazaeni nëse nu a bulna lidhës aëheë easini inial i bazaeni në ele d ë jeë ë i ël se baas e ze pej na d ë pjë ë cajë ushin e shpejësisë ënde ë elei pa: F 5 N in Sipas shpehjes ë pjeua në deji ë asi ei: M Y F Q c i i N F N Q M c 6 Kdinaën c e qendës së asës së ëij sisei e cajë e shpehjen: i i el sh n c i el sh n l Q cs l cs c Q d due e diu se aëheë: pa: d 59
61 D sc he Shala l Q cs l cs c Q Q Q l cs c 7 Q Nëse shpehjen 7 e deijë d heë aëheë fijë: Q Q l cs c Q dhe eqë elei nu bën ë lëiz në deji ë asi aëheë pa: Q l cs Q c l cs 8 Q Q Nëse e zëendësjë shpehjen 8 në 6 dhe due aë në nsidei ushin 5 fijë: F Q M N in c Q Q Q l cs cs ee pë F Nin Q Q Q l pej na shpejësia ënde iie e elei nëse e plësn ushin: Q Q l elei d ë fillj ë ëcej shëpue na bazaeni në ëë as nejie endsja e bulnae pë lidhje e bazaen DTY : Meanizi anielë-bielë pëbëhe na shufa O e asë dhe jaësi l në ë cilën epn eni ai M ashu që shufa ullhe e shpejësi ënde nsane shufa e asë dhe jaësi l ëshqiësi e asë eanizë ëshë i endsu bi pllaën e peshë Nëse pllaa ëshë e endsu bi bazaen e ças eficieni i fëii ndëje pllaës dhe bazaeni ëshë µ ë cahe: a Fca e fëii dhe fca e shpjes easini nale ë bazaeni në pllaë në funsin ë ëndi ë ullii ë anielës O dhe b ani peshën iniale ë pllaës ashu që ë s ije dei e ëshqija e pllaës ndaj bazaeni O M Zjidhje: 6
62 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab O M F µ a Nisei na ushi që pllaa nu lëiz pa liji i dë i Dinaiës d ë jeë: j a c F i i Në asin në sisei pëbëhe na aë upa pa: a a a a F F N p N F µ se ë pjeua në deji ë asee dhe : : : p p F µ F Kdinaa e qendae ë asae pë secilin up eç e eç janë: Maniela O a qendën e asës ë cila në funsin ë ëndi janë: O cs l cs eqë ns aëheë pa: l cs pëaësish pas deiii d heë: l cs N l sin pëaësish pas deiii d heë: l sin iela a qendën e asës ë cila në funsin ë ëndi janë: eqë O aëheë ëndi O Ocs cs l cs l cs l cs l cs pëaësish pas deiii d heë: l cs l sin pëaësish pas deiii d heë: l sin ëshqiësi si pië aeiale a qendën e asës ë cila në funsin ë ëndi janë: Ocs cs l cs l cs l cs l cs pëaësish pas deiii d heë: l cs pëaësish pas deiii d heë: ëshqiësi nu und ë lëiz në deji ë asi llaa si up nu duhe ë lëiz aëheë dinaa e qendës së saj janë adhësi nsane pa: p ns pëaësish pas deiii d heë: p p ns pëaësish pas deiii d heë: p 6
63 D sc he Shala Me zëendësi në shpehje dhe fijë: pej na: l cs l cs l cs F l sin l sin Fµ 8l cs F N F N l sin u: b Që ë s ie dei e ëshqija e pllaës nëpë bazaen duhe që ë plëshe jbaazii: F µ F µ < N u: µ - paaqe eficienin e fëii ndëje pllaës dhe bazaeni Nëse zëendësjë shpehje e fiuaa ë paë jbaazii eë fën: 8l cs < µ l sin 8l cs > l sin µ 8l > cs l sin µ p ej na le ë jejë deiain sipas hës ë dhe i cili duhe ë baazhe e ze ashu që ë cahe pesha iniale dhe në end ë > ai pa: d 8l sin l cs d µ pëaësish: sin cs µ µ an an aëheë pesha iniale e pllaës pë ë cilën d ë fillj ëshqija d ë jeë: l 8 cs l sin µ dhe pë çd > nu d ë ei ëshqije ë pllaës nëpë bazaen µ 6
64 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab DTY 5: iza në fë ë paalelai ënddejë e peshë ëshë i bësheu në afshin e lëua hiznal dhe a një sipëfaqe ë bendshe në fë jsësfeës e eze nëpë ë cilën lëiz sfea e peshë dhe eze due fillua na pzicini pa shpejësi fillesae Të cahe pë sa d ë zhendse piza u sfea ain në pzicinin Zjidhje: c c Siç shihe na fiua lëizja he nën epiin e peshae ë cila anë deji eialish pshë Le ë zbajë lijin bi ndshiin e sasisë së lëizjes së ëij sisei: dk j Fi d i jejë në deji hiznal : dk X i d i pej na jedhë se: K ns pëaësish K K eqë lëizja filln na qeësia pa sasia e lëizjes në deji ë asi uhe dhe aj ëshë e njëjë si në çasin u sfea ëshë në pzicinin ashu edhe u aj ain në pzicinin Sasia e lëizjes u sfea ëshë në pzicinin : K M c Le ë llaisi sasinë e lëizjes së ëij sisei pë çasin u sfea ain në pzicinin si në fiuën paapae pa: 6
65 K M c Këshu pa: M M c c c c c d c c c c inejë: D sc he Shala shuëzjë e asën e ëë sisei M: M c M c ë pzicinin fillesa ei: M c ë pzicinin ei: Mc c c Due zëendësua në shpehjen fijë: Na fiua shihe se > aëheë shenja - en se pllaa d ë lëizë në ahe ë undë e aë ë supzua 6
66 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab LËVIZJ TUIT M MSË TË NDYSHUSHM VIËL DTY : aea e asë në çasin fillesa lëiz në fushën hjene ë aiei ë Tës eialish la ë e nii nsan a Shpejësia e jedhjes së azae hahii ë abuani ëshë nsan e ns Të cahe liji i ndshii ë asës së aeës ha pë ë cilën asa e aeës zëlhe pëjsë jihashu pë ëë hë ë cahe se sa ëshë adhësia e shpejësisë së aeës d he laësia në ë cilën ain ezisenca e abieni ë nelizhhe Zjidhje: a Φ uacini i Meshqesi pë lëizje ë upi e asë ë ndshueshe ëshë: d j d F Φ d d F j u: - paaqe peshën e aeës d Φ - paaqe fcën eaie d asa e aeës në një ças ë hës Nëse euacinin e pjejë në deji ë lëizjes fijë: d d d d d a d O 65
67 d a d inejë d a a ln d a D sc he Shala e Le ë ai se asa fillesae e aeës pas një he T d ë zëlhe pëjsë pa: pej na: a T e a T e a T ln ln ln ëshu ha pë ë cilën pëjshe asa e aeës ëshë: T ln a uphe nu ëshë eale që në ëë as asa e abuani në çasin fillesa ë eë qenë ë e ël se jsa e asës së pëjihshe ë aeës Meqë aea lëiz e nii nsan a aëheë: a ns pej na: d a ns a d d a d ëshu nëse e zëendësjë hën T pë ë cilën asa e aeës ëshë pëjsua fijë shpejësinë e aeës në aë ças: T a T a ln azhdjë a d ad d a d T H T H a pëaësish e zëendësi ë hës T pë ë cilën asa e aeës ëshë pëjsua fijë laësinë në ë cilën a aiu aea: ln H a T a a 66
68 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab DTY : aea lëizë në fushën e fcës së aiei sipas ijës hiznale Shpejësia e elaie e jedhjes së azae abuani ëshë e inensie nsan dhe dejii i saj e hiznalen fn ëndin α Nëse ëshë nui i ialsi api ndëje asës fillesae ë abuani dhe asës së aeës pa lëndë djeëse abuan jeni adhësinë e shpejësisë së aeës në çasin u ëshë hahua lënda djeëse abuani dhe uën ë cilën aj e a alua dei në aë ças Në çasin fillesa aea a qenë në qeësi ezisenca e aji ë nelizhhe Zjidhje: s O α uacini i Meshqesi pë lëizje ë upi e asë ë ndshueshe ëshë: d d d d Nëse ëë euacin e pjejë në deji ë asee dhe fijë: : d d cs α d d : d sinα d N a jedhë: d d sinα aa se ë inejë le ë ai ë shënie: - asa e aeës e lëndë djeëse në çasin fillesa ns l d ns l d - asa e aeës e lëndë djeëse në çasin ë hës ns - asa nsane e aeës asa e nsusini ë aeës - asa e lëndës djeëse abuani në çasin fillesa ld ld - asa e lëndës djeëse abuani në çasin ë hës Nëse inejë anë pë anë euacinin ei: d d sinα ln pej na: sinα 67
69 sinα sinα ln ln sinα ln ns ns l d l d D sc he Shala l d Madhësia quhe nui i ialsi aëheë ha pë ë cilën hahhe e ëë lënda ns djeëse abuani ëshë: l d ns l d ns l d l d l d sinα T ln Na jedhë se: d d csα d d d d csα due zëendësua na fijë: d d csα d cα d sinα anα inejë d cα d c α Këshu pë T në enin e hahii ë lëndës djeëse abuani shpejësia e aeës d ë jeë: sinα csα T cα T cα ln sinα ln csα ln sinα Due e diu se: ds c α d aëheë ds c α d inejë s T ds cα d aëheë ua e alua dei në çasin e hahii ë lëndës djeëse abuani ëshë: T sin α csα sin α s T cα cα ln ln sinα sinα csα sin α s T ln ln 68
70 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab SSI LËVIZJS MOMNTI I SSISË SË LËVIZJS MOMNTI KINTIK I SISTMIT MTIL Tabela e enee ë inecisë ë disa upae hjen Fa upi e OZIT KSV DH FOM TUIT Meni i inecisë Shufa e hllë Unaza ehe eli në fë ë ehi z O z l/ l/ J l J z J l J z J J J J z llaa në fë ë unazës ehe llaa ënddej b a J J J z llaa ehe J J J z b J a J J z a b 69
71 D sc he Shala llaa në fë ë elipsës b a b J a J J z a b llaa në fë ë eëndshi llaa e hllë ënddejë h b z a a b h/ h/ J h 8 J h 6 J h b J J a b a J z z z aalelpipedi ënddej c a b ubi e binjë a: J J J z 6 a J J J z a J b c J c a J z a b J b c J c a J z a b 7
72 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab ull iaida e bazë ë e h/ z h/ b a z J a h 8 J b h 8 J z a b iaida e eull aëfaqëse ab: h J J a J a z h ilind i i d ejë e H J J H J J H J z J H z pi cilindi H J z ilindi e ue ë hlla: J J 6 H J z 7
73 D sc he Shala Kni i dejë eh h/ h/ z H J J h 8 J z Kni i dejë i cunua e laësi H: 5 5 J z z Sfea J J J z 5 J 5 z jsë sfea /8 O J J J J z 5 8 J z lipsidi eas z c b a J b c 5 J c a 5 J z a b 5 J b 6c 5 7
74 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab DTY : ë eh cilindi e peshë dhe eze i cili und ë ullhe eh asi hiznal Oz ëshë i pëshjellu një lia Në d saje dhe ë liai bahen e dua d njeëz e pesha ë njëja çd ë bëhe e njeiun sa d ë jeë shpejësia e ij nëse njeiu filln ë nië la nëpë lia e shpejësi Masa e liai dhe fëii ë nelizhhen Zjidhje: O z Siç shihe na fiua ei ë bëjë e ulliin e sisei ë upae eh asi ë palëizshë në asin në asi hiznal O z Liji bi ndshiin e eni inei pë asin Oz a fën: dl j z F i M d i në deën në ei: dl j z F M i d i pej na: Lz ns pa ei ë bëjë e uajjen e eni inei ëshu: L z L z L sepse lëizja a fillua na qeësia aëheë: z z L z L Llaisi enin inei pë një ças ë hës u ei i pjesë ë ij dhe aë pë cilindë pë njeiun dhe njeiun : Lz J z J z - eni i inecisë së cilindi pë asin z - shpejësia ënde e ullii ë cilindi eh asi z 7
75 D sc he Shala - asa e njeiu - asa e njeiu na fiua shihe se: as zëendësii në shpehjen dhe due aë paassh shpehjen ei: pej na: ëshu shpejësia e njeiu nëse njeiu nië laë liai e shpejësi d ë jeë: DTY : Unaza pe ehe e peshë dhe eze e cila shihe në afshin eial i ëshë dhënë një shpejësi ënde fillesae Nëpë unazë lëizë sfea M e asë due fillua na pzicini ë i laë Të cahe api ndëje shpejësisë ënde asiale dhe asaj iniale ë unazës Zjidhje: z X Y M e Z O X O O Y O Liji bi ndshiin e eni inei pë asin Oz a fën: dl j z F i M d në deën në ei: i 7
76 dl d ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab z j M F i i sepse ë jiha pesha janë paalele e asin z use dejie e easinee aljnë nëpë asin z K ëshu: L z ns pa e i ë bëjë e uajjen e eni inei: L z Lz Meni inei në çasin fillesa ëshë: Lz J z Sipas abelës së enee ë inecisë ai unazën pe si një el i hllë eh dhe a pëjije eni i inecisë pë asin use në deën në ëshë i eëua z pa: J z - eni i inecisë së unazës pe pë asin z - shpejësia ënde e ullii ë pllaës në çasin fillesa Zëendësjë në : Lz Meni inei i ëij sisei në çasin u pzicini i sfeës pëcahe e ëndin d ë jeë: Lz J z e sin e sin aëheë: L z sin sin L z sin Zëendësjë në shpehjen dhe fijë: L z L z sin aëheë shpejësia ënde e unazës në funsin ë ëndi d ë jeë: sin Na shpehja shihe se shpejësia ënde e unazës d ë eë leë asiale pë ëndin pa: a sin 5 a use leën iniale d a eë pë ëndin 9 pa: in sin 9 in 6 Due i pjesëua ndëje ei shpehje 5 dhe 6 cajë apin ndëje shpejësisë ënde asiale dhe iniale ë unazës pa: a in 75
77 D sc he Shala DTY : lafa ehe e peshë dhe eze hiznale ullhe eh asi eial ë aiei e shpejësi ënde nsane jaë ësaj në plafë jenden aë njeëz e pesha ë njëja D në pia dhe në saje ë plafës e d jeë në pia dhe D në laësi / na bshi ë ullii Të cahe ndshii i shpejësisë ënde ë plafës nëse njeëzi dhe filljnë ë lëizin nëpë peifei ë plafës e shpejësi use njeëzi në pia dhe D filljnë ë lëizin e shpejësi nëpë ajeen e eze / Të jihë njeëzi lëizin në ahe ë njëjë e ulliin e plafës jihashu ë cahe adhësia e shpejësisë elaie pë ë cilën plafa d ë ndale lafa ë nsidehe pllaë ehe hjene use njeëzi si pia aeiale Zjidhje: z O z D Liji bi ndshiin e eni inei pë asin Oz a fën: dl j z F i M d i në deën në ei: F dl j z M i sepse ë jiha pesha janë paalele e asin z d i pej na: L z ns pa ei ë bëjë e uajjen e eni inei ëshu: L L 76 z z
78 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab Meni inei në çasin fillesa ëshë: J L D z z J - eni i inecisë së pllaës pë asin z z - shpejësia ënde e ullii ë pllaës në çasin fillesa shpejësia fillesae e njeiu shpejësia fillesae e njeiu shpejësia fillesae e njeiu D shpejësia fillesae e njeiu D Zëendësjë në : L z z L Meni inei L z ëshë: D z z J L - shpejësia ënde e ullii ë pllaës në çfaëd çasi shpejësia abslue e njeiu shpejësia abslue e njeiu shpejësia abslue e njeiu D shpejësia abslue e njeiu D Zëendësjë në : L z z L 5 Sipas shpehjes shpehje 5 dhe janë ë baabaa pa: ëshu shpejësia ënde e plafës në funsin ë shpejësisë elaie d ë jeë: ë u ndalu plafa duhe që pej na caj : ë ' pëaësish: ' 77
79 D sc he Shala DTY : Shufa D e jaësi l dhe asë M ullhe eh asi eial Oz nën epiin e eni ë qifi ë fcae M F u l -ha Nëpë shufë und ë lëizin unaza dhe e asa Nëse shufa D ullhe eh esi ë saj asi Oz use unaza nu zhendsen na laësia l/ na asi Oz pasaj epii i eni M F ndëpie pas sendës së dë ë cahe shpejësia ënde e shufës në enin u unaza ain në pia saje pëaësish D due e diu se a lëizin e shpejësi ë njëja ns nëpë shufë M F D l/ l/ Zjidhje: M F D e e l/ l/ M nalizjë lëizjen e ëij sisei pë hën dei në s: 78
80 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab Liji bi ndshiin e eni inei pë asin Oz a fën: dl j z F M i d i në deën në ei: dl j z F M i M F l d i Meni inei pë asin z d ë jeë: l l Lz J z J Ml z - eni i inecisë së shufës pë asin Oz l shpejësia e unazës në pzicinin pëaësish Zëendësjë në : l l l L l z Ml L z M l pëaësish deiai i ij: dl z d M l d d zëendësjë në shpehjen dhe fijë: d M l l d d d M inejë anë pë anë d d M M pë hën s cajë shpejësinë ënde ë shufës në çasin u ndale epii i eni pa: M 8 M ë inealin e hës pas d sendae epii i eni ndale aëheë liji bi ndshiin e eni inei pë asin Oz a fën: dl j z F M i d i pej na ai: L z ns pëaësish eni inei u unaza nddhen në pzicine pëaësish ëshë i njëjë e aë u unaza aijnë në pzicine pëaësish D pa: L L z z D 79
81 D sc he Shala Meni inei u unaza janë në pzicine pëaësish llaie sipas shpehjes pë pa: 8 Lz Lz M l M l M Lz l 5 Meni inei u unaza aijnë në pzicine pëaësish D llaie e shpehjes: l l Lz D J z e e l e aëheë: l l l L l z D Ml Lz D M 6 l 6 Sipas shpehjes shpehje 5 dhe 6 janë ë baabaa pa: l M 6 l ëshu shpejësia ënde u unaza aijnë në pzicine pëaësish D d ë jeë: M 6 DTY 5: llaa ehe hjene e eze dhe peshë und ë ullhe eh asi eial Oz i cili ëshë nal në afshin e pllaës Në pllaë jende anali O në fë ë jsëehi nëpë ë cilin und ë lëiz pia aeiale M e peshë Në çasin fillesa në pllaë filln ë epi eni i çifi ë fcae M F u / dhe në fund ë sendës së eë epii i eni ndale use pia filln lëizjen nëpë anal pej pzicini ah sipas liji s /π Në çasin fillesa sisei nddhej në qeësi Të cahe shpejësia ënde e pllaës në çasin u pia aeiale ain në pzicinin 8
82 Zjidhje: ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab e Lëizjen e ëij sisei e analizjë në d pjesë ë hën s ei: dl j z F M i M F d Llaisi enin inei pë asin z pëaësish pë piën O: Lz J z O J z O O L z J z O deijë sipas hës: dl z d d d pej n a due zëendësua në shpehjen fijë: d d d 6 d inejë: 6 d d 8
83 D sc he Shala pëaësish shpejësia ënde e pllaës pas e sendae d ë jeë: 6 7 ë inealin pas e sendae eni pushn së epuai pia aeiale filln lëizjen ëshu ei: dlz F M i j d pej na: L z ns pa: L L z z Meni inei u sfea jende në pzicin use pllaa ullhe e shpejësi d ë jeë: 7 7 Lz 7 L z Meni inei u sfea ain në pzicinin use pllaa ullhe e shpejësi d ë jeë: e L z J z O ds d d d π π p ë ei: π hën e cajë na baazii i jaësisë së hau pa: π π na ëu ei: π π [ s] Lz π L z Na L z Lz ei: 7 pëaësish shpejësia ënde e pllaës u pia aeiale ain në pzicinin : 58 8
84 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab LËVIZJ LN TUIT TË NUTË DTY : Nën epiin e eni M cilindi e peshë dhe eze ullise pa ëshqije nëpë afshin hiznal Të cahe liji i lëizjes së qendës së asës së cilindi dhe fca e fëii ndëje cilindi dhe afshi ë pjeë Keficieni i fëii në ullisje ëshë Lëizja a fillua na qeësia M Zjidhje: M c F µ F N Shjë euacine e lëizjes plane pë ëë cilindë: F µ c c F N c sepse qenda e asës së cilindi nu lëiz në deji ë asi aëheë na euacini ai që: F F J N N c M Fµ F N 8
85 D sc he Shala u eni i inecisë së cilindi pë qendën e asës c ëshë: J c use na lidhje ineaie: c c c pëaësish e deii: c Zëendësjë në euacinin : c M Fµ M c Fµ N a euacini fijë: c F µ 5 zëendësjë në euacinin dhe cajë fcën e fëii: M F F µ µ M Fµ M Fµ Zëendësjë në euacinin 5 dhe fijë niiin e qendës së asës ë cilindi : M c pas d heë ineii fijë lijin e lëizjes së qendës së asës ë cilindi : M c DTY : ilindi e ue ë hlla e peshë dhe eze nië e ndihën e liai i cili aln nëpë aaaë dhe siç ëshë paaqiu në fiuë Në saje e liai epjnë fca pëaëse F dhe F Due e nelizhua asën e liai ë cahe niii i qendës ë asës së inecisë së cilindi shpejësia ënde dhe ha pë ë cilën qenda e ij nië pë laësinë h F F 8
86 Zjidhje: ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab F F F F c Shjë euacine e lëizjes plane pë unazën e hllë : c pej na: c sepse qenda e unazës nu lëiz në deji ë asi c F F J c F F u eni i inecisë së unazës pë qendën e asës ëshë: J c Na euacini ai: F F F F pej na: d F F d d F F d inejë: d F F d aëheë shpejësia ënde e unaz ës së hllë d ë jeë: F F 85
87 Na euaci ni ai: F c F pej na: d c F F d F F d c d inejë: c F F d c d pej na: F F c d c F F d F F d c d inejë: c d c F F d D sc he Shala pej na liji i lëizjes së qendës së asës së unazës ëshë: F F c K hën pë ë cilën qenda e unazës a alua uën h e cajë na: c h h pa: F F h c h h pej na ha pë ë cilën qenda e unazës nië pë laësinë h ëshë: h h F F 86
88 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab DTY : Sisei i eua në fiuë pëbëhe na ëndi e asë dhe disu hjen eh e asë dhe eze Këndi jende bi afshin hiznal ndësa disu b bi ënd Në dis ëshë bëshjell liai i cili në njëin saj ëshë i lidhu pë piën ë ëndi liai pej disu dei ëndi ëshë hiznal Të cahe fca në lia nëse në dis epn eni ai M Keficieni i fëii në ëshqije ndëje disu dhe ëndi ëshë µ Masa e liai ë nelizhhe M Zjidhje: S F µ M S N N F µ N uacine e lëizjes plane pë disun hjen : c S F µ c N c sepse qenda e disu nu lëiz në deji ë asi aëheë pej euacini cajë easinin e ëndi në disun : N J c M S Fµ u eni i inecisë pë qendë ë disu ëshë: 87
89 D sc he Shala J c uacine e lëizjes plane pë ëndin janë eë d pasi që ai bënë lëizje anslaie: S F µ N N 5 sepse ëndi bënë lëizje dejize eë në deji ë asi aëheë pej euacini 5 cajë easinin e afshi hiznal në ëndin : N N N N Na lidhje ineaie ei: K K K K Nëse pjesëjë ë d shpehje fijë: c K K pej na: K c K c pëaësish shpejësia ënde e disu : c K K c pej na pas deiii: c Due e diu se eficieni i fëii ëshë µ aëheë sipas liji ë Kulni ei: Fµ µ N aëheë: F µ µ as zëendësii fijë: S : µ c : M S µ : S µ 88
90 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab Nëse zëendësjë në fijë: µ c µ aëheë fca në lia na ëshë: M M S µ c µ Due e diu se e ei ë dhënë M aëheë: S µ due e baazua ëë dhe shpehjen fijë niiin e ëndi : µ 7 use niii i qendës së disu d ë jeë: µ 7 dhe pëfundiish fca në lia d ë jeë: S µ µ S 7 DTY : S isei aeial i eua në fi pëbëhe na: Disu e eze dhe peshë pë ë cilin ëshë i bëshjellu njëi saj i liai use saji jeë që aln nëpë aaanë dhe bëshille pë disun e dfishë e eze pëaësish dhe peshë Due s e pëfillu asën e liai fëiin në lia diensine e aaasë ë cahe easini i afshee ë pjeëa në cilinda dhe fca në lia dhe niii i qendës së disu α α 89
91 Zjidhje: D sc he Shala S S F α F µ N F µ N α F α α Sisei a një shallë liie uacine e lëizjes plane pë disun janë: S Fµ sinα N csα sepse qenda e disu nu lëiz në deji ë asi aëheë pej euacini caj ë easinin e afshi ë pjeë në disun : N csα J S F µ u eni i inecisë pë qendën e disu ëshë: J uacine e lëizjes plane pë disun janë: S Fµ sinα N csα 5 sepse qenda e disu nu lëiz në deji ë asi aëheë pej euacini 5 cajë easinin e afshi ë pjeë në disun : N csα J S F 6 µ u eni i inecisë ë disun ëshë: J Na lidhje ineaie ei: F 9
92 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab na ëu ei: pëaësish: pëaësish: 8 8 pëaësish: as zëendësii në euacine dhe 6 ei: : S Fµ sinα : 8 S Fµ : S Fµ sinα 6: S Fµ Këshu ei fiua sise pej aë euacinesh e aë ë panjhua S F F µ µ e zjidhje ë ë cili fijë: ej ei: S Fµ 8 zëendësjë në fijë: Fµ sinα a 6 aëheë fca në lia d ë jeë: 9 S sinα sinα b Na euacini 6 fijë: 9 F µ S sinα 6 Fµ sinα c zëendësjë në dhe fijë: 9 : sinα sinα sinα 6 9 sinα 6 5 sinα pëfundiish niii i qendës së disu d ë jeë: sinα Zëendësjë në shpehjen a dhe cajë fcën e fëii ndëje disu dhe afshi ë pjeë: 9
93 D sc he Shala sinα F µ sinα α 6 6 sin F µ sinα Na shpehja b fca në lia d ë jeë: 9 sinα 9 α S sin sin α S sinα Na shpehja c fcën e fëii ndëje disu dhe afshi ë pjeë d ë jeë: sinα µ sinα F sinα sinα F µ sinα NJI KINTIK SISTMIT MTIL UN FOV TË JSHTM DTY : Qendës së cilindi eh e eze dhe peshë i cili und ë ullise sipas sipëfaqes ehe e eze i jepe një shpejësi fillesae Nëse në çasin fillesa cilindi jendej në pzicinin ë ë ulë ë sipëfaqes ehe ë cahe liji i ndshii ë shpejësisë ënde ë ij O θ Zjidhje: 9
94 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab O θ h M M F µ F N Meqë duhe ë cahe liji i ndshii ë shpejësisë ënde due diu shpejësinë fillesae ë qendës së cilindi aëheë zbajë lijin bi ndshiin e enejisë ineie pej pzicini filles a dei në pzicinin e caua e ëndin θ pa: j F nejia ineie në çasin fillesa i ëshë: J c eni i inecisë së cilindi pë qendën e asës së ij: J c use shpejësia ënde fillesae e cilindi ëshë: aëheë: nejia ineie në çasin e pëcaua e ëndinθ ëshë: c J c shpejësinë e qendës së cilindi e cajë na: c aëheë: c 9
95 D sc he Shala j una e fcae ë jashe paaqe punën e peshës së eë cilindi use fca jea F dhe F µ nu ejnë punë pasi që epjnë në qendë ë çasi ë shpejësie e cila e a inensiein ze ëshu puna e peshës së cilindi ëshë: j F h csθ i F i csθ Zëendësjë shpehje dhe në euacinin dhe d ë ei: csθ cs θ csθ 5 Nëse dua që shpejësinë ënde ë shpehi pëes ëndi eja ë ullii ë cilindi aëheë nisei na ushi që nu a ëshqije aëheë hau M duhe ë jeë i baabaë e haun M pa: θ θ zëendësjë në 5: cs DTY : Naesa dhe e asa ihen në lëizje nëpëje d aaae u qenda e aaasë O ëshë e palëizshe use e asaj e lëizshe Naesa në një ças ë hës a shpejësinë Sa uë duhe ë alj naesa që shpejësia e saj ë ie d heë nëse aaaë anë asa pëaëse / dhe eze Fëii në liaë ë s pëfille use eficieni i fëii ndëje naesës dhe afshi hiznal ë ee µ N 9
96 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab Zjidhje: K sise i upae a një shallë liie ëeësjë pë dinaë ë pëjihësua zhendsjen e naesës pëaësish shpejë sinë e saj eialish pshë si në fiuën ijuese D F µ D N D Liji bi ndshiin e enejisë ineie pej një pzicini në një pzicin jeë ëshë: j F i pzicini nënupn çasin u naesa a shpejësinë use pzicini nënupn çasin u shpejësia e naesës ie d heë në ahasi e aë paapae Supzjë se ua e alua ëshë s e cila duhe ë cahe Le ë llaisi enejinë ineie pë ëë sise në funsin ë shpejësisë së naesës : O u: nejia ineie e naesës : nejia ineie e aaasë : J J u enin e inecisë pë qendë ë aaasë p e ai si pë dis: J na fiua shihe se: në anën jeë: aëheë enejia ineie e aaasë d ë jeë: 8 95
97 D sc he Shala nejia ineie e aaasë O: O J u enin e inecisë pë qendë ë aaasë O papë e ai si pë dis: J O na fiua shihe se: D në anën jeë: D D aëheë enejia ineie e aaasë O d ë jeë: O nejia ineie e naesës : u na fiua shihe se: D aëheë ei: Këshu pas zëendësii në shpehja pë eneji ineie ë ëij sisei në funsin ë e fën: ë pzicinin ei ë dhënë se shpejësia e naesës ëshë aëheë na : ëshu enejia ineie pë pzicinin d ë jeë: use pë pzicinin duhe që shpejësia e naesës ë ie pë d heë aëheë d ë jeë: ëshu enejia ineie pë pzicinin d ë jeë: Në deën në punë ejnë pesha e naesës pesha e aaasë dhe fca e fëii ndëje naesës dhe afshi hiznal pa due e diu se ua e alua e naesës d ë jeë njëfaë s fijë: j Fi s s Fµ s u fca e fëii cahe na liji i dë i Njuni i pjeua në deji eial pë naesën pa: N N sepse naesa nu lëiz në deji eial use due e diu se sipas liji ë Kulni ei apin: 96
98 F ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab µ µ N u µ ëshë eficieni i dhënë i fëii ndëje naesës dhe afshi hiznal aëheë fca e fëii ëshë: F µ µ Na shpehja pë shpejësinë e naesës : pas ineii ai se: s s s s ëshu pas zëendësii puna e fcae d ë eë fën: j Fi s s µ s µ s Nëse ë jiha ë llaije i zëendësjë në shpehjen : j F i 7 7 µ s 8 pej na ua ë cilën e aln naesa d ë jeë: 8 s 6 µ DTY : Sisei aeial pëbëhe na cilindi hjen e peshë dhe eze cilindi jihashu e peshë dhe eze si dhe aaaja Njëi saj i liai ëshë i bëshjellu pëeh cilindi dhe pasaj aln nëpë aaanë e peshë / dhe eze dhe saji jeë bëshille pë cilindin ilindi und ë ullise pa ëshqije nëpë afshin e pjeësi α në ë cilin epn eni ai ullues M b pa i cili ëshë ppcinal e ëndin e ullii cilindi b - nsane use cilindi und ë ullise pa ëshqije nëpë afshin e pjeësi β6 e ças eficieni i fëii në ullisje pë ë d cilinda ëshë ε Due e nelizhua fëiin në lia ë cahe shpejësia e qendës së cilindi në çasin u aj a alua uën s Sisei në çasin fillesa nddhej në qeësi M α β 97
99 Zjidhje: D sc he Shala M N ε α F µ α N ε F µ β β K sise i upae a një shallë liie ëeësjë pë dinaë ë pëjihësua zhendsjen e naesës pëaësish shpejësinë e saj si në fiuën paapae Liji bi ndshiin e enejisë ineie pej një pzicini fillesa në një pzicin jeë ë çfaëdshë ëshë: j Fi nejia ineie në çasin fillesa ëshë ze sepse sisei nddhej në qeësi pa: neji në ineie pë ëë sise në një ças ë hës ëshë: u: nejia ineie e cilindi : J u enin e inecisë pë qendë ë cilindi ëshë: J na fiua shihe se: aëheë enejia ineie e cilindi d ë jeë: nejia ineie e cilindi : J u enin e inecisë pë qendë ë cilindi ëshë: J na fiu a shihe se: 98
100 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab aëheë enejia ineie e cilindi d ë jeë: nejia ineie e aaasë : J u enin e inecisë pë qendë ë aaasë : J na fiua shihe se: aëheë enejia ineie e aaasë d ë jeë: Këshu pas zëendësii në shpehja pë eneji ineie ë ëij sisei në funsin ë e fën: 7 Në sisein e dhënë punë ejnë pesha e cilindi dhe fca e easini eqë a shajnë en në ullisje pë qenda e asae ë cilindae dhe eni ai M pa: j N F M M i M 5 una e peshës së cilindi : sinα s una e eni ë fcës së easini N : N M N ε na liji i Njuni i pjeua në deji nal e lëizjen e qendës së cilindi cajë fcën e easini N pa: N csα N csα sepse qenda e cilindi nu lëiz në deji ë asi aëheë: N M ε csα una e peshës së cilindi : sin β s u zhendsjen e qendës ë cilindi e cajë e inei ë: pej na: s s pa puna e pe shës së cilindi d ë jeë: sin β s una e eni ë fcës së easini N : N M N ε N 99
101 D sc he Shala na liji i Njuni i pjeua në deji nal e lëizjen e qendës së cilindi cajë fcën e easini N pa: N cs β N N cs β sepse qenda e cilindi nu lëiz në deji ë asi aëheë: N M ε cs β una e eni ai M ëshë: M M b u ëndi ullii ë cilindi cahe e inei ë shpehjes: s pej na: s s ëshu puna e eni ai M d ë jeë: b M b s Me zëendësi në shpehjen 5 fijë: j s s b Fi sinα s ε csα sin β s ε cs β s j ε b Fi [ sinα sin β csα cs β s ] s 6 Me zëendësi ë shpehjee dhe 6 në shpehjen fijë: 7 ε b [ sinα sin β csα cs β s ] s ε b [ sinα sin β csα cs β s ] s 7 pë ëndin α β6 dhe pë uën e alua s ë qendës së cilindi d ë fijë ëë shpejësi ë qendës : b [ ε s] s 7 ε b [ s] s 7
102 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab DTY : S isei aeial pëbëhe na piza e peshë e cila und ë lëiz nëpë afshin e lëua hiznal naesa e peshë / e cila und ë lëiz nëpë afshin e pjeë ë pizës c ilindi e peshë / dhe eze i cili nën epiin e eni M ullhe eh qendës së ij ë lidhu pë pizën dhe cilindi D e peshë dhe eze i cili und ë ullise pa ëshqije nëpë afshin e pjeë ë pizës e pjeësi α Due e diu se sisein në çasin fillesa nddhej në qeësi ë cahe niii i naesës ndaj pizës M D z α α Zjidhje: z M z z D α α / z α α α / α F N Meqë sisei jende nën epiin e fcae ë peshae dhe eni ai i cili si e ëshë nal në afsh ë lëizjes ë cila në deji ë asi pjesinin e anë ze aëheë sasia e lëizjes në deji ë ëij asi uhe pa: K K Le ë cajë sasinë e lëizjes së ëij sisei ë pjeua në deji ë asi : K z csα z csα K z csα z csα D
103 D sc he Shala z csα z csα z csα 8 z csα pej na pas deiii: z csα 8 Nii e naesës d a cajë na liji bi ndshi e enejisë ineie në fën: d δ d d Llaisi enejinë ineie ë sisei nejia ineie e pizës eqë aj bën lëizje anslaie ëshë: nejia ineie e naesës eqë aj bën lëizje ë pëbëë d anslaie ëshë: [ ] [ z csα z sinα ] z cs z α nejia ineie e cilindi eqë ai bën lëizje ë pëbëë qenda lëizje anslaie dhe ulli ndaj qendës ëshë: J z z u: z z - nejia ineie e cilindi D eqë ai bën lëizje ë pëbëë qenda lëizje anslaie dhe ulli ndaj qendës ëshë: D DD J D D [ csα sinα ] D z z D D [ z csα z ] z
104 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab Këshu enejia ineie e ëij sisei d ë jeë: D [ z csα z ] z [ z csα z ] z 9 z csα z 8 pas deiii sipas hës ei: d 9 [ z z csα z z ] d una eleenae e fcae që epjnë në ëë sise ëshë puna eleenae e fcae ë peshae dhe aë ë peshës së naesës cilindi D dhe puna eleenae e eni M pa: δ δ δ D δ M δ δz sin α D δz sin α M δ δz δ δz sinα δz sinα M M δ sinα δz pëaësish: δ M δz sinα d d δ M sinα z d as baazii ë shpehjee dhe sipas ei: 9 M [ z z csα zz ] sinα z 9 M z z csα zz sinα z Zëendësjë shpehjen pëaësish edhe z csα dhe fijë: 8 9 M z csα z csα z csα z z csα z csα zz sinα z M z cs α cs α z sinα z / : z / M 6M 8sinα 8sinα z 6 9 cs α 7 9sin α
105 D sc he Shala KUIONI I ËJITHSHËM I DINMIKËS IMI I DLMT-LNZHIT Ë SISTM MTIL DTY : ilindi hjen e peshë Q dhe eze due u ullisu pa ëshqije nëpë afshin e pjeësi α nië laë nëpëje liai ë pazjashë naesën e peshë Liai aln nëpë aaanë e peshë Q dhe eze Due s e pëfillu asën e liai dhe fëiin në lia jeni niiin e cilindi e qendës së cilindi Maaaja ë nsidehe si dis hjen Zjidhje: α δ in M M in δ Q α in F α δ aii i Dalabe-Laanzhi pë sise aeial e lidhje ideale a fën: n n i i n i i i i n in F in F F i δ δ δ iδi i i i i pa pë çfaëd llj ë lëizjes së sisei e lidhje ideale shua e punëe eleenae ë ë jiha fcae dhe enee aie që epjnë bi sise dhe fcae dhe enee ë inecisë jaë zhendsjes eleenae ë undshe ë çfaëdshe pë çd ças ëshë ze Shpehja duhe ë pjehe në deji ë lëizjes së qendës së upi pëaës ëshu pë deën në d ë jeë: in in in in Q sinα δ δ F δ F δ M δ M δ Meqë sisei a një shallë liie aëheë ë jiha zhendsje e undshe duhe i shpehi në funsin ë zhendsjes së undshe δ na lidhje ineaie fijë: Q δ in F
106 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab na j ai: δ δ δ δ δ δ δ δ a n j ai: na j ai: δ δ Fca e inecisë janë: in Q F in F u e deii ë ei fiua Mene e inecisë janë: in J M u e deii ë Q Q ei Q Q M in J ii ë ei u e de Zëendësjë në shpehjen : sin Q Q Q Q δ δ δ δ δ δ α Q Q α sin Q Q δ : δ / sin Q Q Q Q α sin Q Q α pëfundiish niii i qendës së cilindi d ë jeë: Q Q sinα 5
107 D sc he Shala DTY : Shufa D e peshë Q shihe bi e cilinda dhe e pesha ë njëja dhe eze Në s hufë epn fca F e deji hiznal që ënë në lëizje shufën dhe cilinda Due e nelizhua fëiin ndëje shufës dhe cilindae dhe cilindae dhe afshi hiznal ë cahe niii shufës u shufa dhe cilinda nsidehen upa hjen D F Zjidhje: in F D Q D δ D in in in F F F in M δ in M δ in M δ F δ δ δ aii i Dalabe-Laanzhi pë sise aeial e lidhje ideale a fën: n n n n in F in Fi i Fi i i δ δ i δi iδi i i i i Nëse shpehja zbahe pë deën në dhe aë ë pjeua në deji ë lëizjes së qendës së upi pëaës d ë ei: in in in in in in in FδD F δ F δ F δ FD δd M δ M δ M δ Meqë sisei a një shallë liie aëheë ë jiha zhendsje e undshe duhe i shpehi në funsin ë zhendsjes së undshe δ D na lidhje ineaie fijë: D D jihashu pë niie e qendae len: D 6
108 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab ë shpejësië ënde ei: D na j D δ δ δ δ ai: D δ δ δ na j ai: na j ai: D δ δ δ na j ai: D δ δ δ Fca e inecisë janë: F D in D in F D F in D D D in D Q F Mene e inecisë janë: D D in J M D D in J M D D in Z J M ëendësjë në shpehjen : Q F D D D D D D D D D D D D D D D δ δ δ δ δ δ δ δ D D D Q F [ δ δ : / ] D Q F 8 pëfundiish niii i shufës D d ë jeë: Q F D
109 D sc he Shala KUIONT LNZHIT TË LLOJIT TË DYTË Ë SISTM MTIL DTY : ilindi I e peshë dhe eze und ë ullhe eh çënieës O ëes liai lëizja pëcille në cilindin e dfishë II e peshë dhe eze pëaësish i cili und ë ullhe eh qendës së ij O ë cilindin II bëshille liai njëin saj i ë cili ëshë i lidhu pë qendën O ë aaasë III e peshë dhe eze Nëpë aaanë III bëshille një lia në sajin e ë cili ëshë e au naesa IV e peshë Nëse në cilindin I epn eni ai MHsinΩ u -ha dhe due s e pëfillu fëiin në lia ë shuhen euacine difeenciale ë lëizjes së ëij sisei I II M II III IV Zjidhje: I II M II III IV Sisei a d shallë liie le ë ai pë dinaa ë pëjihësuaa ulliin e cilindi I dhe zhendsjen eiale ë naesës IV pa: q dhe q pëaësish shpejësië e pëjihësuaa: q dhe q 8
110 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab uacine e Laanzhi ë llji ë dë anë fën: d δ d δ d δ d δ Lidhje ineaie: Na fiua paapae shihe se shpejësia e piës dhe ëshë e baabaë pa: pej na: use shpejësia e piës që ëshë e baabaë edhe e shpejësinë e qendës së aaasë III d ë jeë: O Meqë zhendsjen e naesës IV e ei aë dinaë ë pëjihësua aëheë shpejësia e naesës IV dhe shpejësia e piës së shënua e ëshë e njëjë dhe aë: Këshu pë aaanë III ei fiua se dihen shpejësië e d piae ë saja aëheë siç ëshë paaqiu në fiuën ijuese und ë cajë shpejësinë ënde ë saj pa: O Na fijë: nejia ineie e ëij sisei d ë jeë: I II III IV nejia ineie e cilindi I eqë ai bën lëizje ulluese ëshë: I 9 J O nejia ineie e cilindi II eqë ai bën lëizje ulluese ëshë: II 9 J O nejia ineie e aaasë III eqë aj bën lëizje plane ëshë: 9
111 D sc he Shala J O O III III nejia ineie e naesës IV eqë ai bën lëizje anslaie ëshë: Zëendësjë në shpehjen dhe fijë: IV Deiae e nejshe pë zëendësi në euacine ë Laanzhi ë llji ë dë janë: d d d d una eleenae e eni M dhe peshae dhe d ë jeë: M δ δ δ δ na ai δ δ aëheë: M δ δ δ δ M δ δ δ pej na: M δ δ δ δ as zëendësii në shpehje - euacine e Laanzhi ë llji ë dë fijë ë euacine ifeenciale ë lëizjes së ëij sisei: d H M Ω sin 8 9
112 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab DTY : Tupi e asë und ë lëizë në afshin eial sipas udhëzueses eiale eh piës ë ëij upi und ë ullhe cilindi e eze dhe asë në peifeinë e ë cili ëshë i bëshjellu saji i një liai i cili aln nëpë aaanë dhe saji jeë bëshille në cilindin O e asë dhe eze i cili und ë ullhe eh piës O Në qfë se lëizja e ëij sisei në afshin eial shahe na epii i peshae ë ëe upae si dhe eni ullues M në cilindin O due spëfillu fëiin në lia dhe diensine e aaasë ë shuhen euacine difeenciale ë lëizjes së ëij sisei dhe pë asin u ee që upi bënë lëizje ë njëajshe cns ë cahe eni M Zjidhje: Sisei a d shallë liie le ë ai pë dinaa ë pëjihësuaa ulliin e cilindi O dhe zhendsjen eiale ë upi pa: q dhe q pëaësish shpejësië e pëjihësuaa: q dhe q uacine e Laanzhi ë llji ë dë anë fën: d δ d δ d δ d δ
113 D sc he Shala Lidhje ineaie: Na fiua paapae shihe se shpejësië e piae dhe janë ë baabaa pa: në anën jeë shpejësia e eëua si ëshë njëheësh edhe shpejësia e piës së eëua D pa: D Këshu pë disun ei fiua se dihen shpejësië e d piae ë ij aëheë siç ëshë paaqiu në fiuën ijuese und ë cajë shpejësinë ënde ë ij pa: D Na dhe D fijë: i d ë jeë: O nejia ineie e ëij sise nejia ineie e upi eqë ai bënë lëizje anslaie sipas udhëzueses eiale ëshë: nejia ineie e disu eqë ai bën lëizje plane ëshë: J nejia ineie e cilindi O eqë ai bën lëizje ulluese ëshë: J O Zëendësjë në shpehjen dhe fijë: Deiae e nejshe pë zëendësi në euacine ë Laanzhi ë llji ë dë janë: d d
114 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab d d una eleenae e eni M dhe peshae dhe d ë jeë: M δ δ δ δ M δ δ δ pej na: M δ δ δ δ as zëendësii në shpehje - euacine e Laanzhi ë llji ë dë fijë ë euacine di enciale ë lëizjes së ëij sisei: fe M ns Na ushi që upi bën lëizje ë njëajshe aëheë: a zëendësjë në euacine difeenciale ë lëizjes dhe fijë: M M aëheë eni M duhe ë jeë: M M
115 D sc he Shala DTY : Kaca e peshë lëiz bi aë a që und ë nsidehen si disqe hjene e pesha Q dhe eze nëpë afshin hiznal u eficieni i fëii në ullisje ndëje ae ë acës dhe afshi hiznal ëshë ε Mbi acë jende cilindi e peshë dhe eze i cili und ë ullise pa ëshqije nëpë sipëfaqen hiznale ë acës Nëse aca ihe në lëizje nëpëje fcës hiznale F ë cahe niii i qendës së cilindi ndaj acës dhe shpejësia ënde e ullii ë ae ë acës F Zjidhje: F µii F µi F Q N II ε Q N I Sisei a d shallë liie le ë ai pë dinaa ë pëjihësuaa ëndin ullii ë ae dhe lëizjen dejize ë qendës së cilindi lëizjen elaie pa: q dhe q pëaësish shpejësië e pëjihësuaa: q dhe q uacine e Laanzhi ë llji ë dë anë fën:
116 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab d d δ δ δ d d δ ë ë Lidhje ineaie: Na fiua paapae shihe se shpejësië e qendae ë ae dhe shpejësia e acës jan baabaa pa: Këshu pë cilindin ei fiua se dihe shpejësia abslue e piës së nai e acë që ëshë e njëjë e aë ë acës sepse aca bën lëizje anslaie dhe jihashu dihe shpejësia elaie e qend ës së cilindi aëheë sipas fiuës paapae und ë cajë shpejësinë ënde ë cilindi pa: use shpejësia abslue e qendës së cilindi ëshë: nejia ineie e ëij sisei d ë jeë: nejia ineie e ae eqë a bëjnë lëizje plane ëshë: Q Q Q J Q nejia ineie e acës eqë aj bën lëizje anslaie ëshë: nejia ineie e cilindi eqë ai bën lëizje plane ëshë: J Zëendësjë në shpehjen dhe fijë: Q Q Deiae e nejshe pë zëendësi në euacine ë Laanzhi ë llji ë dë janë: Q Q Q d d d d 5
117 D sc he Shala una eleenae e eni M dhe peshae dhe d ë jeë: δ Fδ N I N II εδ Shuën e easinee N I N II e cajë na shua e pjesinee ë ë jiha fcae që epjnë në ëë sise ë pjeua në deji ë asi eial që duhe ë jeë ze pasi që qenda e asae ë ëij sisei nu lëizin në ëë deji pa: N I N II Q dhe na pej na ai: δ δ aëheë puna eleenae d ë eë fën: δ Fδ Q εδ [ F Q ε ] δ pej na: δ F Q ε δ δ δ as zëendësii në shpehje - euacine e Laanzhi ë llji ë dë fijë ë euacine difeenciale ë lëizjes së ëij sisei: Q F Q ε 6
118 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab DTY : ilindi hjen e peshë dhe eze due u ullisu pa ëshqije nëpë pizën e peshë Q e cila undë ë ëshqasë nëpë afshin e pjeësi α nië laë nëpëje liai ë pazjashë naesën D e peshë Liai aln nëpë cilindin e peshë dhe eze Due s e pëfillu asën e liai dhe fëiin në lia ë shuhen euacine difeenciale ë lëizjes së ëij sisei D α Zjidhje: D D α D D α α Q Sisei a d shallë liie le ë ai pë dinaa ë pëjihësuaa lëizjen dejize ë pizës nëpë afshin e pjeë dhe nijen eialish laë ë naesës D: q dhe q pëaësish shpejësië e pëjihësuaa: q dhe q uacine e Laanzhi ë llji ë dë anë fën: d δ d δ d δ d δ Lidhje ineaie: Na fiua paapae shihe se shpejësia e naesës D dhe shpejësia e qendës së disu janë ë baabaa pa: D si dhe: 7
119 D sc he Shala 8 D iza bën lëizje anslaie dejize aëheë shpejësia e saj ëshë: Këshu pë cilindin ei fiua se dihen shpejësia abslue ë d piae ë ij aëheë sipas fiuës ijuese und ë cahe shpejësia ënde e ij pa: Na ë d euacine ai që: nejia ineie e ëij sisei d ë jeë: D nejia ineie e cilindi eqë ai bën lëizje plane ëshë: J nejia ineie e pizës eqë aj bën lëizje anslaie ëshë: Q Q nejia ineie e cilindi eqë ai bën lëizje ulluese ëshë: J nejia ineie e naesës eqë aj bën lëizje anslaie ëshë: D D Zëendësjë në shpehjen dhe fijë: Q Q Deiae e nejshe pë zëendësi në euacine ë Laanzhi ë llji ë dë janë: Q Q Q d d
120 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab d d una eleenae e peshae Q dhe d ë jeë: δ sin α δ Qsinα δ δd na ai: δ δ na ai: δ δ na D D ai: δ D δ aëheë puna eleenae d ë eë fën: δ sin α δ Q sinα δ δ Q sinα δ sinα δ pej na: δ δ Q sinα sin α δ δ as zëendësii në shpehje - euacine e Laanzhi ë llji ë dë fijë ë euacine difeenciale ë lëizjes së ëij sisei: Q Qsinα sinα DTY 5: ilindi e asë dhe eze ullise pa ëshqije nëpë sipëfaqen e bendshe ë një pi cilindi e asë M dhe eze ë bendshe i cili und ë ullhe eh asi hiznal O Due e aë që eni i inecisë së pi cilindi ëshë M ë shuhen euacine difeenciale ë lëizjes së ëij sisei O 9
121 Zjidhje: D sc he Shala O M θ ψ Sisei a d shallë liie le ë ai ënde θ ë paaqiua në fiuën paapae pë dinaa ë pëjihësuaa pa: q dhe q θ pëaësish shpejësië e pëjihësuaa: q dhe q θ uacine e Laanzhi ë llji ë dë anë fën: d δ d δ d δ d θ θ δθ Lidhje ineaie: Na fiua paapae shihe se shpejësia e piës qendës së cilindi ëshë: Due e diu se hau dhe hau janë ë baabaë eqë nu a ëshqije pa: θ ψ pej na ai se: ψ θ u e deii ë ësaj shpehje fijë: ψ θ nejia ineie e ëij sisei d ë jeë: O nejia ineie e cilindi eqë ai bën lëizje plane ëshë: ψ J θ
122 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab θ nejia ineie e pi cilindi O eqë ai bën lëizje ulluese ëshë: θ θ M J O O Zëendësjë në shpehjen dhe fijë: θ θ M Deiae e nejshe pë zëendësi në euacine ë Laanzhi ë llji ë dë janë: θ θ θ θ d d θ θ M θ θ M d d una eleenae e peshës d ë jeë: ] cs [ p δ δ sin p use θ δθ δ p as zëendësii në shpehje - euacine e Laanzhi ë llji ë dë fijë ë euacine difeenciale ë lëizjes së ëij sisei: θ sin θ M
123 D sc he Shala MODLIMI DINMIK I SISTMV MTIL Mdelii dinai i një sisei aeial nënupn pëshiin e aij sisei pëes shpehjee aeaie Një epi i illë ëshë i nejshë e qëlli ë analizës dhe sinezës së siseee në pëjihësi ëes deli dinai ë sisei aeial ijhe undësia e sudii ë jihanshë ei dhe pai ë sisei eal due e shfëzua ainën ë ë fashe që a ijua njeiu jeë ë s pjuein Shqie që i ei bëë jeë ë ani në lëin e Dinaiës anë ealizua një qëlli ë illë pa e ë shqie ei aie ë fijë delin dinai ë sisei aeial Këshu due shfëzua paie e pëjihshe dhe ë eçana ë Dinaiës si lijin e pëjihshë ë Dinaiës ë njhu si Liji i dë i Njuni lije e jea ë pëjihshe ë Dinaiës si aii i Dalabei ej që në fa janë jedhie na ai i pai pasaj në fund due shfëzua euacine e Laanzhi ë llji ë dë që në ealie paaqesin euacine ë së shui ë pëdua në paia e huluuese shencë fihe deli dinai i sisei aeial Në asin e pëjihshë një del dinai i illë paaqie pëes sisei ë euacinee difeenciale Nui i euacinee ae na nui i shallëe ë liisë ë sisei aeial Me qëlli ë sudii ë siseee aeiale si hap i paë ëshë definii i ë ashuquajuae aiablae ë jendjes
124 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab VILT JNDJS Me qëlli ë upii sa ë ë lehë ë ncini aiabla ë jendjes shpjeiin e e d a bëjë due aë shebuj ne dhe aë delin dinai ë siseee aeiale ë fiuaa pëes euacinee ë Laanzhi ë llji ë dë Le ë ai Deën Në ëë as pëes euacinee ë Laanzhi ë llji ë dë ei fiua delin dinai ë sisei aeial i cili paaqe euacine difeenciale ë lëizjes në iji: 9 8 H sin Ω Shpehja paaqe sise ë euacinee difeenciale lineae jhjene ë endi ë dë e eficien nsan Në shpehjen adhësi ë dhëna ë njhua janë: - pesha e upae H Ω adhësi jeeie ap dinaie ha në senda dhe nsana e aiacini eqë shqhen sisee që jenden nën epiin e aiacini ës aëheë ai ee nsan dhe aë 985 /s Me qëlli ë uljes së endi ë euacinee difeenciale bëhe ansfii i shpehjes na aiabla ineai-dinaie në aiabla ë jendjes Madhësië: dhe dhe dhe paaqesin aiabla ineai-dinaie pëaësish: dinaa shpejësië niie e pëjihësuaa pej ë cilae jedhin aiabla e jendjes ëes aiablae ë jendjes duhe ë bëhe ansfii i deli dinai ë dhënë e shpehjen na aiabla adhësië ineai-dinaie dhe dhe dhe në aiabla e eja ë ashuquajua aiabla ë jendjes që due i u pëshau sfei Malab i shënjë e i i ëshu pëden zëendësie:
125 D sc he Shala ëshu pa dinaa dhe shpejësië e pëjihësuaa janë zëendësua e aë aiabla ë jendjes i i Niie e pëjihësuaa që paaqesin deiae difeenciale e aiablae ë jendjes dhe aëheë janë: d d Me ali na aiabla ineai-dinaie në aiabla ë jendjes bëhe ulja e endi ë euacinee difeenciale ëshu na d euacine ë endi ë dë fijë aë euacine ë endi ë paë Nëse aiabla neai-dinaie i zëendësjë e aiabla e jendjes aëheë shpehja eë fën: d d 9 8 d ap në fë aice: 9 8 d se shuë: dx U pej na: dx U ap në Malab shuhe: d H sin Ω d d d sin d H Ω d dx in * U Shpehja paaqe fën e pëshashe pë ealizi ë zjidhjes së euacinee difeenciale ë sisei aeial due shfëzua sfein Malab
126 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab NLIZ MODLIT DINMIK DUK SHFYTËZU SOFTVIN MTL Në iji ëshë paaqiu hap pas hapi ijii i File-i esë ë ealizua në Malab- Siulin pë zjidhjen e ëij sisei ë euacinee difeenciale Sajë sfein Malab na file ezeui i ij Malabee dhe hape diaja e quaju and windw : në ëë diae shuajë udhin siulin dhe ezeujë e shpje ë asi ne dhe hape diaja: Na enja ese në File hapi një file ë i: që d ë hape një diae si në iji: 5
127 D sc he Shala Këë file e uajë psh e ein zjidhja : aja e diaee ë hapua dei ani due si në iji: lijë në dulin Nnlinea dhe ei ëë diae: 6
128 ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab në ëë diae ai dulin S-Funcin dhe ëheqi e anë ë iu se e di-cp dhe e ali në diaen e file-i zjidhja e di-pase e pjjë aë dhe diaja e file-i esë zjidhja a ëë paje: Mduli S-Funcin e ealizn hijen e nënpai pë zjidhje ë sisei ë euacinee difeenciale sipas shpehjes Nënpai und ia endsi çfaëd ei psh deli aëheë e lii në dulin S-Funcin na hape j diae: dh në end ë sse e shuajë deli dhe shpi OK aëheë diaja e file-i zjidhja d ë due: 7
129 D sc he Shala Këshu duli S-Funcin a pë deë ë hëe nënpain deli i cili duhe ë ijhe dhe ë uhe e ein deli Vendi u duhe ë uhe file ëshë :\Malab\in\ pëndshe nu d ë funsinjë Në file-n zjidhja si hje endsi naciin në sise pa në asin në enin ai M H sin Ω Këë e ealizjë pëes duli F Wspace që jende në siulin- Suces dhe ëheqi në file-n zjidhja pa: Këë dul F Wspace e lidhi si sinjal hës në dulin S-Funcin Lidhja bëhe pëes iu Në ëë as [T U] und iu ndshhe eëii pë asin në 8
130 ai ëbledhje deash ë zjidhua na DINMIK dhe apliii i sfei Malab T që paaqe hën në senda dhe aë zanish pë siuli ap ezeui ë zjidhjes së deli dinai ee 7 senda pa pa ë shuë se π use U M pa e enin e dhënë ai - nacues Ëshë e ëndësi ë cee se dhe M duhe ë shuhen në and Windw paa siulii ë deli dhe aë në fën: >> H ; O ; ::7 ; M H*sinO*; Në dalje na duli S-Funcin d ë ei zjidhjen e euacinee difeenciale dhe aë dhe pëaësish afe e e due e ndaë sinjalin në aë deë e një dul Deu që ee në Siulin-nnecins dhe due i aë aë dule pë paaqije afie që een na Siulin-Sins ëshu pëfundiish diaja e file-i esë zjidhja d ë due: aa se ë filljë siuliin duhe ë shuajë nënpain deli pë zjidhje ë euacinee difeenciale Në iji ëshë dhënë ai nenpa i cili shuhe e Nepad se Wdpad që e psedn çd Windws dhe uhe e esenzin pa si M-file 9
131 D sc he Shala Me shpjen në File-n esë zjidhja në Siulain-Sa fihen ë diaae:
USHTRIMET PËR LËNDËN MEKANIKA TEKNIKE II MUND TË SHKARKOHET NGA VEGËZA: Ose
 USHTIET PË LËNËN EKNIK TEKNIKE II UN TË SHKKOHET NG VEGËZ: wwwshlhmek Ose LII I USHTIE TË POF SO HET SHL I SHKKU NG VEGZ E TIJ ËSHTË HËNË NË VIJI sc hme Shl z () O ρ ρ z Kpësj O O e l S N mg i F e e T
USHTIET PË LËNËN EKNIK TEKNIKE II UN TË SHKKOHET NG VEGËZ: wwwshlhmek Ose LII I USHTIE TË POF SO HET SHL I SHKKU NG VEGZ E TIJ ËSHTË HËNË NË VIJI sc hme Shl z () O ρ ρ z Kpësj O O e l S N mg i F e e T
Levizja ne dy dhe tre dimensione
 Kpiulli, Leizj e d dhe re dimesioe Leizj e d dhe re dimesioe. Nje mkie udheo km e peredim dhe km e ju-peredim. S eshe zhedosj rezule e mkies e lidhje me pike e isjes (drejimi dhe ler e sj )? S S S S cos
Kpiulli, Leizj e d dhe re dimesioe Leizj e d dhe re dimesioe. Nje mkie udheo km e peredim dhe km e ju-peredim. S eshe zhedosj rezule e mkies e lidhje me pike e isjes (drejimi dhe ler e sj )? S S S S cos
Parts Manual. Trio Mobile Surgery Platform. Model 1033
 Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
!"!# ""$ %%"" %$" &" %" "!'! " #$!
 " "" %%"" %" &" %" " " " % ((((( ((( ((((( " %%%% & ) * ((( "* ( + ) (((( (, (() (((((* ( - )((((( )((((((& + )(((((((((( +. ) ) /(((( +( ),(, ((((((( +, 0 )/ (((((+ ++, ((((() & "( %%%%%%%%%%%%%%%%%%%(
" "" %%"" %" &" %" " " " % ((((( ((( ((((( " %%%% & ) * ((( "* ( + ) (((( (, (() (((((* ( - )((((( )((((((& + )(((((((((( +. ) ) /(((( +( ),(, ((((((( +, 0 )/ (((((+ ++, ((((() & "( %%%%%%%%%%%%%%%%%%%(
HONDA. Έτος κατασκευής
 Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V
Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V
Q π (/) ^ ^ ^ Η φ. <f) c>o. ^ ο. ö ê ω Q. Ο. o 'c. _o _) o U 03. ,,, ω ^ ^ -g'^ ο 0) f ο. Ε. ιη ο Φ. ο 0) κ. ο 03.,Ο. g 2< οο"" ο φ.
 II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
Το άτομο του Υδρογόνου
 Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
Detyra për ushtrime PJESA 4
 0 Detyr për ushtrime të pvrur g lëd ANALIZA MATEMATIKE I VARGJET NUMERIKE Detyr për ushtrime PJESA 4 3 Të jehsohet lim 4 3 ( ) Të tregohet se vrgu + + uk kovergjo 3 Le të jeë,,, k umr relë joegtivë Të
0 Detyr për ushtrime të pvrur g lëd ANALIZA MATEMATIKE I VARGJET NUMERIKE Detyr për ushtrime PJESA 4 3 Të jehsohet lim 4 3 ( ) Të tregohet se vrgu + + uk kovergjo 3 Le të jeë,,, k umr relë joegtivë Të
(... )..!, ".. (! ) # - $ % % $ & % 2007
 (! ), "! ( ) # $ % & % $ % 007 500 ' 67905:5394!33 : (! ) $, -, * +,'; ), -, *! ' - " #!, $ & % $ ( % %): /!, " ; - : - +', 007 5 ISBN 978-5-7596-0766-3 % % - $, $ &- % $ % %, * $ % - % % # $ $,, % % #-
(! ), "! ( ) # $ % & % $ % 007 500 ' 67905:5394!33 : (! ) $, -, * +,'; ), -, *! ' - " #!, $ & % $ ( % %): /!, " ; - : - +', 007 5 ISBN 978-5-7596-0766-3 % % - $, $ &- % $ % %, * $ % - % % # $ $,, % % #-
KAPITULLI4. Puna dhe energjia, ligji i ruajtjes se energjise
 Kapitui 4 Pua de eerjia KPIULLI4 Pua de eerjia, iji i ruajtjes se eerjise.ratori tereq e je rrue e au je tru e spejtesi 8/. Me care spejtesie do te tereqi tratori truu e je rrue te pastruar ur uqia e otorit
Kapitui 4 Pua de eerjia KPIULLI4 Pua de eerjia, iji i ruajtjes se eerjise.ratori tereq e je rrue e au je tru e spejtesi 8/. Me care spejtesie do te tereqi tratori truu e je rrue te pastruar ur uqia e otorit
!"#$ "%&$ ##%&%'()) *..$ /. 0-1$ )$.'-
 !!" !"# "%& ##%&%',-... /. -1.'- -13-',,'- '-...4 %. -5"'-1.... /..'-1.....-"..'-1.. 78::8
!!" !"# "%& ##%&%',-... /. -1.'- -13-',,'- '-...4 %. -5"'-1.... /..'-1.....-"..'-1.. 78::8
BAZAT E INFRASTRUKTURES NË KOMUNIKACION
 MANUALI NË LËNDEN: BAZAT E INFRASTRUKTURES NË KOMUNIKACION Prishtinë,0 DETYRA : Shtrirja e trasesë së rrugës. Llogaritja e shkallës, tangjentës, dhe sekondit: 6 0 0 0.67 6 6. 0 0 0. 067 60 600 60 600 60
MANUALI NË LËNDEN: BAZAT E INFRASTRUKTURES NË KOMUNIKACION Prishtinë,0 DETYRA : Shtrirja e trasesë së rrugës. Llogaritja e shkallës, tangjentës, dhe sekondit: 6 0 0 0.67 6 6. 0 0 0. 067 60 600 60 600 60
ITU-R P (2012/02) &' (
 ITU-R P.530-4 (0/0) $ % " "#! &' ( P ITU-R P. 530-4 ii.. (IPR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.itu.int/itu-r/go/patents/en. ITU-T/ITU-R/ISO/IEC (http://www.itu.int/publ/r-rec/en ) () ( ) BO BR BS
ITU-R P.530-4 (0/0) $ % " "#! &' ( P ITU-R P. 530-4 ii.. (IPR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.itu.int/itu-r/go/patents/en. ITU-T/ITU-R/ISO/IEC (http://www.itu.int/publ/r-rec/en ) () ( ) BO BR BS
rs r r â t át r st tíst Ó P ã t r r r â
 rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
ΓΗ ΚΑΙ ΣΥΜΠΑΝ. Εικόνα 1. Φωτογραφία του γαλαξία μας (από αρχείο της NASA)
 ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
 !"#!"!"# $ "# '()!* '+!*, -"*!" $ "#. /01 023 43 56789:3 4 ;8< = 7 >/? 44= 7 @ 90A 98BB8: ;4B0C BD :0 E D:84F3 B8: ;4BG H ;8
!"#!"!"# $ "# '()!* '+!*, -"*!" $ "#. /01 023 43 56789:3 4 ;8< = 7 >/? 44= 7 @ 90A 98BB8: ;4B0C BD :0 E D:84F3 B8: ;4BG H ;8
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.
 Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα
... 5 A.. RS-232C ( ) RS-232C ( ) RS-232C-LK & RS-232C-MK RS-232C-JK & RS-232C-KK
 RS-3C WIWM050 014.1.9 P1 :8... 1... 014.0.1 1 A... 014.0. 1... RS-3C()...01.08.03 A.. RS-3C()...01.08.03 3... RS-3C()... 003.11.5 4... RS-3C ()... 00.10.01 5... RS-3C().008.07.16 5 A.. RS-3C().0 1.08.
RS-3C WIWM050 014.1.9 P1 :8... 1... 014.0.1 1 A... 014.0. 1... RS-3C()...01.08.03 A.. RS-3C()...01.08.03 3... RS-3C()... 003.11.5 4... RS-3C ()... 00.10.01 5... RS-3C().008.07.16 5 A.. RS-3C().0 1.08.
5 Ι ^ο 3 X X X. go > 'α. ο. o f Ο > = S 3. > 3 w»a. *= < ^> ^ o,2 l g f ^ 2-3 ο. χ χ. > ω. m > ο ο ο - * * ^r 2 =>^ 3^ =5 b Ο? UJ. > ο ο.
 728!. -θ-cr " -;. '. UW -,2 =*- Os Os rsi Tf co co Os r4 Ι. C Ι m. Ι? U Ι. Ι os ν ) ϋ. Q- o,2 l g f 2-2 CT= ν**? 1? «δ - * * 5 Ι -ΐ j s a* " 'g cn" w *" " 1 cog 'S=o " 1= 2 5 ν s/ O / 0Q Ε!θ Ρ h o."o.
728!. -θ-cr " -;. '. UW -,2 =*- Os Os rsi Tf co co Os r4 Ι. C Ι m. Ι? U Ι. Ι os ν ) ϋ. Q- o,2 l g f 2-2 CT= ν**? 1? «δ - * * 5 Ι -ΐ j s a* " 'g cn" w *" " 1 cog 'S=o " 1= 2 5 ν s/ O / 0Q Ε!θ Ρ h o."o.
!!" #7 $39 %" (07) ..,..,.. $ 39. ) :. :, «(», «%», «%», «%» «%». & ,. ). & :..,. '.. ( () #*. );..,..'. + (# ).
 1 00 3 !!" 344#7 $39 %" 6181001 63(07) & : ' ( () #* ); ' + (# ) $ 39 ) : : 00 %" 6181001 63(07)!!" 344#7 «(» «%» «%» «%» «%» & ) 4 )&-%/0 +- «)» * «1» «1» «)» ) «(» «%» «%» + ) 30 «%» «%» )1+ / + : +3
1 00 3 !!" 344#7 $39 %" 6181001 63(07) & : ' ( () #* ); ' + (# ) $ 39 ) : : 00 %" 6181001 63(07)!!" 344#7 «(» «%» «%» «%» «%» & ) 4 )&-%/0 +- «)» * «1» «1» «)» ) «(» «%» «%» + ) 30 «%» «%» )1+ / + : +3
-! " #!$ %& ' %( #! )! ' 2003
 -! "#!$ %&' %(#!)!' ! 7 #!$# 9 " # 6 $!% 6!!! 6! 6! 6 7 7 &! % 7 ' (&$ 8 9! 9!- "!!- ) % -! " 6 %!( 6 6 / 6 6 7 6!! 7 6! # 8 6!! 66! #! $ - (( 6 6 $ % 7 7 $ 9!" $& & " $! / % " 6!$ 6!!$#/ 6 #!!$! 9 /!
-! "#!$ %&' %(#!)!' ! 7 #!$# 9 " # 6 $!% 6!!! 6! 6! 6 7 7 &! % 7 ' (&$ 8 9! 9!- "!!- ) % -! " 6 %!( 6 6 / 6 6 7 6!! 7 6! # 8 6!! 66! #! $ - (( 6 6 $ % 7 7 $ 9!" $& & " $! / % " 6!$ 6!!$#/ 6 #!!$! 9 /!
Note: Please use the actual date you accessed this material in your citation.
 MIT OpeCueWae hp://cw.m.eu 6.13/ESD.13J Elecmagec a pplca, Fall 5 Pleae ue he llwg ca ma: Maku Zah, Ech Ippe, a Dav Sael, 6.13/ESD.13J Elecmagec a pplca, Fall 5. (Maachue Iue Techlgy: MIT OpeCueWae). hp://cw.m.eu
MIT OpeCueWae hp://cw.m.eu 6.13/ESD.13J Elecmagec a pplca, Fall 5 Pleae ue he llwg ca ma: Maku Zah, Ech Ippe, a Dav Sael, 6.13/ESD.13J Elecmagec a pplca, Fall 5. (Maachue Iue Techlgy: MIT OpeCueWae). hp://cw.m.eu
Αλληλεπίδραση ακτίνων-χ με την ύλη
 Άσκηση 8 Αλληλεπίδραση ακτίνων-χ με την ύλη Δ. Φ. Αναγνωστόπουλος Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2013 Άσκηση 8 ii Αλληλεπίδραση ακτίνων-χ με την ύλη Πίνακας περιεχομένων
Άσκηση 8 Αλληλεπίδραση ακτίνων-χ με την ύλη Δ. Φ. Αναγνωστόπουλος Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2013 Άσκηση 8 ii Αλληλεπίδραση ακτίνων-χ με την ύλη Πίνακας περιεχομένων
Solutions - Chapter 4
 Solutions - Chapter Kevin S. Huang Problem.1 Unitary: Ût = 1 ī hĥt Û tût = 1 Neglect t term: 1 + hĥ ī t 1 īhĥt = 1 + hĥ ī t ī hĥt = 1 Ĥ = Ĥ Problem. Ût = lim 1 ī ] n hĥ1t 1 ī ] hĥt... 1 ī ] hĥnt 1 ī ]
Solutions - Chapter Kevin S. Huang Problem.1 Unitary: Ût = 1 ī hĥt Û tût = 1 Neglect t term: 1 + hĥ ī t 1 īhĥt = 1 + hĥ ī t ī hĥt = 1 Ĥ = Ĥ Problem. Ût = lim 1 ī ] n hĥ1t 1 ī ] hĥt... 1 ī ] hĥnt 1 ī ]
Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α
 Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
T : g r i l l b a r t a s o s Α Γ Ί Α Σ Σ Ο Φ Ί Α Σ 3, Δ Ρ Α Μ Α. Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 0 1 : 0 0 π μ
 Α Γ Ί Α Σ Σ Ο Φ Ί Α Σ 3, Δ Ρ Α Μ Α g r i l l b a r t a s o s Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 1 : 0 π μ Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 0 1 : 0 0 π μ T ortiyas Σ ο υ
Α Γ Ί Α Σ Σ Ο Φ Ί Α Σ 3, Δ Ρ Α Μ Α g r i l l b a r t a s o s Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 1 : 0 π μ Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 0 1 : 0 0 π μ T ortiyas Σ ο υ
Sarò signor io sol. α α. œ œ. œ œ œ œ µ œ œ. > Bass 2. Domenico Micheli. Canzon, ottava stanza. Soprano 1. Soprano 2. Alto 1
 Sarò signor io sol Canzon, ottava stanza Domenico Micheli Soprano Soprano 2 Alto Alto 2 Α Α Sa rò si gnor io sol del mio pen sie io sol Sa rò si gnor io sol del mio pen sie io µ Tenor Α Tenor 2 Α Sa rò
Sarò signor io sol Canzon, ottava stanza Domenico Micheli Soprano Soprano 2 Alto Alto 2 Α Α Sa rò si gnor io sol del mio pen sie io sol Sa rò si gnor io sol del mio pen sie io µ Tenor Α Tenor 2 Α Sa rò
ΝΟΜΟΣ ΤΗΣ ΠΕΡΙΟ ΙΚΟΤΗΤΑΣ : Οι ιδιότητες των χηµικών στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.
 1. Ο ΠΕΡΙΟ ΙΚΟΣ ΠΙΝΑΚΑΣ Οι άνθρωποι από την φύση τους θέλουν να πετυχαίνουν σπουδαία αποτελέσµατα καταναλώνοντας το λιγότερο δυνατό κόπο και χρόνο. Για το σκοπό αυτό προσπαθούν να οµαδοποιούν τα πράγµατα
1. Ο ΠΕΡΙΟ ΙΚΟΣ ΠΙΝΑΚΑΣ Οι άνθρωποι από την φύση τους θέλουν να πετυχαίνουν σπουδαία αποτελέσµατα καταναλώνοντας το λιγότερο δυνατό κόπο και χρόνο. Για το σκοπό αυτό προσπαθούν να οµαδοποιούν τα πράγµατα
( [T]. , s 1 a as 1 [T] (derived category) Gelfand Manin [GM1] Chapter III, [GM2] Chapter 4. [I] XI ). Gelfand Manin [GM1]
![( [T]. , s 1 a as 1 [T] (derived category) Gelfand Manin [GM1] Chapter III, [GM2] Chapter 4. [I] XI ). Gelfand Manin [GM1] ( [T]. , s 1 a as 1 [T] (derived category) Gelfand Manin [GM1] Chapter III, [GM2] Chapter 4. [I] XI ). Gelfand Manin [GM1]](/thumbs/49/25424945.jpg) 1 ( ) 2007 02 16 (2006 5 19 ) 1 1 11 1 12 2 13 Ore 8 14 9 2 (2007 2 16 ) 10 1 11 ( ) ( [T] 131),, s 1 a as 1 [T] 15 (, D ), Lie, (derived category), ( ) [T] Gelfand Manin [GM1] Chapter III, [GM2] Chapter
1 ( ) 2007 02 16 (2006 5 19 ) 1 1 11 1 12 2 13 Ore 8 14 9 2 (2007 2 16 ) 10 1 11 ( ) ( [T] 131),, s 1 a as 1 [T] 15 (, D ), Lie, (derived category), ( ) [T] Gelfand Manin [GM1] Chapter III, [GM2] Chapter
d 2 y dt 2 xdy dt + d2 x
 y t t ysin y d y + d y y t z + y ty yz yz t z y + t + y + y + t y + t + y + + 4 y 4 + t t + 5 t Ae cos + Be sin 5t + 7 5 y + t / m_nadjafikhah@iustacir http://webpagesiustacir/m_nadjafikhah/courses/ode/fa5pdf
y t t ysin y d y + d y y t z + y ty yz yz t z y + t + y + y + t y + t + y + + 4 y 4 + t t + 5 t Ae cos + Be sin 5t + 7 5 y + t / m_nadjafikhah@iustacir http://webpagesiustacir/m_nadjafikhah/courses/ode/fa5pdf
ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ
 ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ Περίοδοι περιοδικού πίνακα Ο περιοδικός πίνακας αποτελείται από 7 περιόδους. Ο αριθμός των στοιχείων που περιλαμβάνει κάθε περίοδος δεν είναι σταθερός, δηλ. η περιοδικότητα
ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ Περίοδοι περιοδικού πίνακα Ο περιοδικός πίνακας αποτελείται από 7 περιόδους. Ο αριθμός των στοιχείων που περιλαμβάνει κάθε περίοδος δεν είναι σταθερός, δηλ. η περιοδικότητα
Errata (Includes critical corrections only for the 1 st & 2 nd reprint)
 Wedesday, May 5, 3 Erraa (Icludes criical correcios oly for he s & d repri) Advaced Egieerig Mahemaics, 7e Peer V O eil ISB: 978474 Page # Descripio 38 ie 4: chage "w v a v " "w v a v " 46 ie : chage "y
Wedesday, May 5, 3 Erraa (Icludes criical correcios oly for he s & d repri) Advaced Egieerig Mahemaics, 7e Peer V O eil ISB: 978474 Page # Descripio 38 ie 4: chage "w v a v " "w v a v " 46 ie : chage "y
Déformation et quantification par groupoïde des variétés toriques
 Défomation et uantification pa goupoïde de vaiété toiue Fédéic Cadet To cite thi veion: Fédéic Cadet. Défomation et uantification pa goupoïde de vaiété toiue. Mathématiue [math]. Univeité d Oléan, 200.
Défomation et uantification pa goupoïde de vaiété toiue Fédéic Cadet To cite thi veion: Fédéic Cadet. Défomation et uantification pa goupoïde de vaiété toiue. Mathématiue [math]. Univeité d Oléan, 200.
SIEMENS Squirrel Cage Induction Standard Three-phase Motors
 - SIEMENS Squirrel Cage Induction Standard Three-phase Motors 2 pole 3000 rpm 50Hz Rated current Power Efficiency Rated Ratio Noise Output Frame Speed Weight 3V 400V 415V factor Class 0%Load 75%Load torque
- SIEMENS Squirrel Cage Induction Standard Three-phase Motors 2 pole 3000 rpm 50Hz Rated current Power Efficiency Rated Ratio Noise Output Frame Speed Weight 3V 400V 415V factor Class 0%Load 75%Load torque
Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ. Παππάς Χρήστος Επίκουρος Καθηγητής
 ΗΛΕΚΤΡΟΝΙΚΗ ΟΜΗ ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ Παππάς Χρήστος Επίκουρος Καθηγητής ΤΟ ΜΕΓΕΘΟΣ ΤΩΝ ΑΤΟΜΩΝ Ατομική ακτίνα (r) : ½ της απόστασης μεταξύ δύο ομοιοπυρηνικών ατόμων, ενωμένων με απλό ομοιοπολικό δεσμό.
ΗΛΕΚΤΡΟΝΙΚΗ ΟΜΗ ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ Παππάς Χρήστος Επίκουρος Καθηγητής ΤΟ ΜΕΓΕΘΟΣ ΤΩΝ ΑΤΟΜΩΝ Ατομική ακτίνα (r) : ½ της απόστασης μεταξύ δύο ομοιοπυρηνικών ατόμων, ενωμένων με απλό ομοιοπολικό δεσμό.
( ) ( ) ( ) ( ) ( ) λ = 1 + t t. θ = t ε t. Continuum Mechanics. Chapter 1. Description of Motion dt t. Chapter 2. Deformation and Strain
 Continm Mechanics. Official Fom Chapte. Desciption of Motion χ (,) t χ (,) t (,) t χ (,) t t Chapte. Defomation an Stain s S X E X e i ij j i ij j F X X U F J T T T U U i j Uk U k E ( F F ) ( J J J J)
Continm Mechanics. Official Fom Chapte. Desciption of Motion χ (,) t χ (,) t (,) t χ (,) t t Chapte. Defomation an Stain s S X E X e i ij j i ij j F X X U F J T T T U U i j Uk U k E ( F F ) ( J J J J)
MÉTHODES ET EXERCICES
 J.-M. MONIER I G. HABERER I C. LARDON MATHS PCSI PTSI MÉTHODES ET EXERCICES 4 e édition Création graphique de la couverture : Hokus Pokus Créations Dunod, 2018 11 rue Paul Bert, 92240 Malakoff www.dunod.com
J.-M. MONIER I G. HABERER I C. LARDON MATHS PCSI PTSI MÉTHODES ET EXERCICES 4 e édition Création graphique de la couverture : Hokus Pokus Créations Dunod, 2018 11 rue Paul Bert, 92240 Malakoff www.dunod.com
Ó³ Ÿ , º 1(130).. 7Ä ±μ. Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê
 Ó³ Ÿ. 006.. 3, º 1(130).. 7Ä16 Š 530.145 ˆ ƒ ˆ ˆŒ ˆŸ Š ƒ.. ±μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê É μ ² Ö Ó μ μ Ö μ μ²õ μ É μ ÌÉ ±ÊÎ É ² ³ É μ - Î ±μ μ ÊÌ ±μ Ëμ ³ μ- ±² μ ÒÌ ³μ ²ÖÌ Ê ±. ³ É ÔÉμ μ μ μ Ö, Ö ²ÖÖ Ó ±μ³
Ó³ Ÿ. 006.. 3, º 1(130).. 7Ä16 Š 530.145 ˆ ƒ ˆ ˆŒ ˆŸ Š ƒ.. ±μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê É μ ² Ö Ó μ μ Ö μ μ²õ μ É μ ÌÉ ±ÊÎ É ² ³ É μ - Î ±μ μ ÊÌ ±μ Ëμ ³ μ- ±² μ ÒÌ ³μ ²ÖÌ Ê ±. ³ É ÔÉμ μ μ μ Ö, Ö ²ÖÖ Ó ±μ³
M p f(p, q) = (p + q) O(1)
 l k M = E, I S = {S,..., S t } E S i = p i {,..., t} S S q S Y E q X S X Y = X Y I X S X Y = X Y I S q S q q p+q p q S q p i O q S pq p i O S 2 p q q p+q p q p+q p fp, q AM S O fp, q p + q p p+q p AM
l k M = E, I S = {S,..., S t } E S i = p i {,..., t} S S q S Y E q X S X Y = X Y I X S X Y = X Y I S q S q q p+q p q S q p i O q S pq p i O S 2 p q q p+q p q p+q p fp, q AM S O fp, q p + q p p+q p AM
MICROMASTER Vector MIDIMASTER Vector
 s MICROMASTER Vector MIDIMASTER Vector... 2 1.... 4 2. -MICROMASTER VECTOR... 5 3. -MIDIMASTER VECTOR... 16 4.... 24 5.... 28 6.... 32 7.... 54 8.... 56 9.... 61 Siemens plc 1998 G85139-H1751-U553B 1.
s MICROMASTER Vector MIDIMASTER Vector... 2 1.... 4 2. -MICROMASTER VECTOR... 5 3. -MIDIMASTER VECTOR... 16 4.... 24 5.... 28 6.... 32 7.... 54 8.... 56 9.... 61 Siemens plc 1998 G85139-H1751-U553B 1.
Ligji I Ohmit Gjatë rrjedhës së rrymës nëpër përcjellës paraqitet. rezistenca. Georg Simon Ohm ka konstatuar
 Rezistenca elektrike Ligji I Ohmit Gjatë rrjedhës së rrymës nëpër përcjellës paraqitet rezistenca. Georg Simon Ohm ka konstatuar varësinë e ndryshimit të potencialit U në skajët e përcjellësit metalik
Rezistenca elektrike Ligji I Ohmit Gjatë rrjedhës së rrymës nëpër përcjellës paraqitet rezistenca. Georg Simon Ohm ka konstatuar varësinë e ndryshimit të potencialit U në skajët e përcjellësit metalik
..,..,.. ! " # $ % #! & %
 ..,..,.. - -, - 2008 378.146(075.8) -481.28 73 69 69.. - : /..,..,... : - -, 2008. 204. ISBN 5-98298-269-5. - -,, -.,,, -., -. - «- -»,. 378.146(075.8) -481.28 73 -,..,.. ISBN 5-98298-269-5..,..,.., 2008,
..,..,.. - -, - 2008 378.146(075.8) -481.28 73 69 69.. - : /..,..,... : - -, 2008. 204. ISBN 5-98298-269-5. - -,, -.,,, -., -. - «- -»,. 378.146(075.8) -481.28 73 -,..,.. ISBN 5-98298-269-5..,..,.., 2008,
a,b a f a = , , r = = r = T
 !" #$%" &' &$%( % ) *+, -./01/ 234 5 0462. 4-7 8 74-9:;:; < =>?@ABC>D E E F GF F H I E JKI L H F I F HMN E O HPQH I RE F S TH FH I U Q E VF E WXY=Z M [ PQ \ TE K JMEPQ EEH I VF F E F GF ]EEI FHPQ HI E
!" #$%" &' &$%( % ) *+, -./01/ 234 5 0462. 4-7 8 74-9:;:; < =>?@ABC>D E E F GF F H I E JKI L H F I F HMN E O HPQH I RE F S TH FH I U Q E VF E WXY=Z M [ PQ \ TE K JMEPQ EEH I VF F E F GF ]EEI FHPQ HI E
Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design
 Supplemental Material for Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design By H. A. Murdoch and C.A. Schuh Miedema model RKM model ΔH mix ΔH seg ΔH
Supplemental Material for Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design By H. A. Murdoch and C.A. Schuh Miedema model RKM model ΔH mix ΔH seg ΔH
ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s
 P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
ΠΛΗΡΟΦΟΡΙΑΚΟ ΔΕΛΤΙΟ ΑΣΦΑΛΕΙΑΣ. Methanol
 ΠΛΗΡΟΦΟΡΙΑΚΟ ΔΕΛΤΙΟ ΣΕΛΙΔΑ : 1/ 11 Αριθμός αναθεώρησης Ημερομηνία έκδοσης : ΕΝΟΤΗΤΑ 1: Στοιχεία ουσίας/παρασκευάσματος και εταιρείας/επιχείρησης 1.1. Αναγνωριστικός κωδικός προϊόντος Εμπορική Ονομασία
ΠΛΗΡΟΦΟΡΙΑΚΟ ΔΕΛΤΙΟ ΣΕΛΙΔΑ : 1/ 11 Αριθμός αναθεώρησης Ημερομηνία έκδοσης : ΕΝΟΤΗΤΑ 1: Στοιχεία ουσίας/παρασκευάσματος και εταιρείας/επιχείρησης 1.1. Αναγνωριστικός κωδικός προϊόντος Εμπορική Ονομασία
Vn 1: NHC LI MT S KIN TH C LP 10
 Vn : NHC LI MT S KIN TH C LP 0 Mc ích ca vn này là nhc li mt s kin thc ã hc lp 0, nhng có liên quan trc tip n vn s hc trng lp. Vì thi gian không nhiu (khng tit) nên chúng ta s không nhc li lý thuyt mà
Vn : NHC LI MT S KIN TH C LP 0 Mc ích ca vn này là nhc li mt s kin thc ã hc lp 0, nhng có liên quan trc tip n vn s hc trng lp. Vì thi gian không nhiu (khng tit) nên chúng ta s không nhc li lý thuyt mà
Αναπληρωτής Καθηγητής Τμήμα Συντήρησης Αρχαιοτήτων και Έργων Τέχνης Πανεπιστήμιο Δυτικής Αττικής - ΣΑΕΤ
 Γενική και Ανόργανη Χημεία Περιοδικές ιδιότητες των στοιχείων. Σχηματισμός ιόντων. Στ. Μπογιατζής 1 Αναπληρωτής Καθηγητής Τμήμα Συντήρησης Αρχαιοτήτων και Έργων Τέχνης Π Δ Χειμερινό εξάμηνο 2018-2019 Π
Γενική και Ανόργανη Χημεία Περιοδικές ιδιότητες των στοιχείων. Σχηματισμός ιόντων. Στ. Μπογιατζής 1 Αναπληρωτής Καθηγητής Τμήμα Συντήρησης Αρχαιοτήτων και Έργων Τέχνης Π Δ Χειμερινό εξάμηνο 2018-2019 Π
( ) ρ ρ + + = + d dt. ME 309 Formula Sheet. dp g dz = ρ. = f +ΣΚ and HS. +α + z = +α + z. δ =δ = δ =θ= τ =ρ =ρ. Page 1 of 7. Basic Equations.
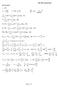 Basic Eqaions ME 9 Fomla Shee R µ F F A A ηv V el η η A Vssem ( ) V el A F F V A ( ) S B XYZ XYZ el g F F a V V A S B / XYZ el M M A V ( ) S B el ( ) Q W ev e A hee V e g ino on el V consan (o invisci
Basic Eqaions ME 9 Fomla Shee R µ F F A A ηv V el η η A Vssem ( ) V el A F F V A ( ) S B XYZ XYZ el g F F a V V A S B / XYZ el M M A V ( ) S B el ( ) Q W ev e A hee V e g ino on el V consan (o invisci
(2), ,. 1).
 178/1 L I ( ) ( ) 2019/1111 25 2019,, ( ), 81 3,,, ( 1 ), ( 2 ),, : (1) 15 2014 ( ). 2201/2003. ( 3 ) ( ). 2201/2003,..,,. (2),..,,, 25 1980, («1980»),.,,. ( 1 ) 18 2018 ( C 458 19.12.2018,. 499) 14 2019
178/1 L I ( ) ( ) 2019/1111 25 2019,, ( ), 81 3,,, ( 1 ), ( 2 ),, : (1) 15 2014 ( ). 2201/2003. ( 3 ) ( ). 2201/2003,..,,. (2),..,,, 25 1980, («1980»),.,,. ( 1 ) 18 2018 ( C 458 19.12.2018,. 499) 14 2019
DC BOOKS. a-pl½-z-v iao-w Da-c-n
 a-pl½-z-v iao-w Da-c-n 1945 P-q-s-s-e 24þ\-v I-mkÀ-t-I-m-U-v aq-s-w-_-b-e-nâ P-\-n -p. {-K-Ù-I-À- -mh-v-, h-n-hà- I³-, d-n-«. A-²-y-m-]-I³. C-c-p-]- -n-\-m-e-p hàj-s- A-²-y-m-]-IP-o-h-n-X- -n-\-pt-i-j-w
a-pl½-z-v iao-w Da-c-n 1945 P-q-s-s-e 24þ\-v I-mkÀ-t-I-m-U-v aq-s-w-_-b-e-nâ P-\-n -p. {-K-Ù-I-À- -mh-v-, h-n-hà- I³-, d-n-«. A-²-y-m-]-I³. C-c-p-]- -n-\-m-e-p hàj-s- A-²-y-m-]-IP-o-h-n-X- -n-\-pt-i-j-w
Γενικό ποσοστό συμμετοχής στην αγορά εργασίας πληθυσμού χρονών - σύνολο
 πληθυσμού 15-64 χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το γενικό ποσοστό συμμετοχής στην αγορά εργασίας πληθυσμού 15-64 χρονών υπολογίζεται με τη διαίρεση του αριθμού του οικονομικά ενεργού
πληθυσμού 15-64 χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το γενικό ποσοστό συμμετοχής στην αγορά εργασίας πληθυσμού 15-64 χρονών υπολογίζεται με τη διαίρεση του αριθμού του οικονομικά ενεργού
KALKULIMI TERMIK I MOTORIT DIESEL. 1. Sasia teorike e nevojshme për djegien e 1 kg lëndës djegëse: kmol ajër / kg LD.
 A KALKULII TERIK I OTORIT DIESEL. Sasa terke e nevjshme ër djegen e kg lëndës djegëse: 8 L C 8H O 0.3 3 C H O 0. 4 3 kml ajër / kg LD kg ajër / kg LD. Sasja e vërtetë e ajrt ër djegen e kg lëndë djegëse:
A KALKULII TERIK I OTORIT DIESEL. Sasa terke e nevjshme ër djegen e kg lëndës djegëse: 8 L C 8H O 0.3 3 C H O 0. 4 3 kml ajër / kg LD kg ajër / kg LD. Sasja e vërtetë e ajrt ër djegen e kg lëndë djegëse:
Γενικό ποσοστό απασχόλησης ισοδύναμου πλήρως απασχολούμενου πληθυσμού - σύνολο
 απασχολούμενου πληθυσμού - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το γενικό ποσοστό απασχόλησης ισοδύναμου πλήρως απασχολούμενου πληθυσμού υπολογίζεται με τη διαίρεση του αριθμού του ισοδύναμου πλήρως
απασχολούμενου πληθυσμού - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το γενικό ποσοστό απασχόλησης ισοδύναμου πλήρως απασχολούμενου πληθυσμού υπολογίζεται με τη διαίρεση του αριθμού του ισοδύναμου πλήρως
www.absolualarme.com met la disposition du public, via www.docalarme.com, de la documentation technique dont les rιfιrences, marques et logos, sont
 w. ww lua so ab me lar m.co t me la sit po dis ion du c, bli pu via lar ca do w. ww me.co m, de la ion nta t do cu me on t ed hn iqu tec les en ce s, rι fιr ma rq ue se t lo go s, so nt la pr op riι tι
w. ww lua so ab me lar m.co t me la sit po dis ion du c, bli pu via lar ca do w. ww me.co m, de la ion nta t do cu me on t ed hn iqu tec les en ce s, rι fιr ma rq ue se t lo go s, so nt la pr op riι tι
Appendix B Table of Radionuclides Γ Container 1 Posting Level cm per (mci) mci
 3 H 12.35 Y β Low 80 1 - - Betas: 19 (100%) 11 C 20.38 M β+, EC Low 400 1 5.97 13.7 13 N 9.97 M β+ Low 1 5.97 13.7 Positrons: 960 (99.7%) Gaas: 511 (199.5%) Positrons: 1,199 (99.8%) Gaas: 511 (199.6%)
3 H 12.35 Y β Low 80 1 - - Betas: 19 (100%) 11 C 20.38 M β+, EC Low 400 1 5.97 13.7 13 N 9.97 M β+ Low 1 5.97 13.7 Positrons: 960 (99.7%) Gaas: 511 (199.5%) Positrons: 1,199 (99.8%) Gaas: 511 (199.6%)
())*+,-./0-1+*)*2, *67()(,01-+4(-8 9 0:,*2./0 30 ;+-7 3* *),+*< 7+)0 3* (=24(-) 04(-() 18(4-3-) 3-2(>*+)(3-3*
 ! " # $ $ %&&' % $ $! " # ())*+,-./0-1+*)*2,-3-4050+*67()(,01-+4(-8 9 0:,*2./0 30 ;+-7 3* *),+*< 7+)0 3* *),+-30 *5 35(2(),+-./0 30 *,0+ 3* (=24(-) 04(-() 18(4-3-) 3-2(>*+)(3-3* *3*+-830-+-2?< +(*2,-30+
! " # $ $ %&&' % $ $! " # ())*+,-./0-1+*)*2,-3-4050+*67()(,01-+4(-8 9 0:,*2./0 30 ;+-7 3* *),+*< 7+)0 3* *),+-30 *5 35(2(),+-./0 30 *,0+ 3* (=24(-) 04(-() 18(4-3-) 3-2(>*+)(3-3* *3*+-830-+-2?< +(*2,-30+
Η γεωργία στην ΕΕ απαντώντας στην πρόκληση των κλιματικών αλλαγών
 Ευρωπαϊκή Επιτροπή Γε ν ι κ ή Δ ι ε ύ θ υ ν σ η Γε ω ρ γ ί α ς κ α ι Αγ ρ ο τ ι κ ή ς Α ν ά π τ υ ξ η ς Ευρωπαϊκή Επιτροπή Γεωργία και αγροτική ανάπτυξη Για περισσότερες πληροφορίες 200 Rue de la Loi,
Ευρωπαϊκή Επιτροπή Γε ν ι κ ή Δ ι ε ύ θ υ ν σ η Γε ω ρ γ ί α ς κ α ι Αγ ρ ο τ ι κ ή ς Α ν ά π τ υ ξ η ς Ευρωπαϊκή Επιτροπή Γεωργία και αγροτική ανάπτυξη Για περισσότερες πληροφορίες 200 Rue de la Loi,
SUPPLEMENTAL INFORMATION. Fully Automated Total Metals and Chromium Speciation Single Platform Introduction System for ICP-MS
 Electronic Supplementary Material (ESI) for Journal of Analytical Atomic Spectrometry. This journal is The Royal Society of Chemistry 2018 SUPPLEMENTAL INFORMATION Fully Automated Total Metals and Chromium
Electronic Supplementary Material (ESI) for Journal of Analytical Atomic Spectrometry. This journal is The Royal Society of Chemistry 2018 SUPPLEMENTAL INFORMATION Fully Automated Total Metals and Chromium
Γενικός ρυθμός μεταβολής οικονομικά ενεργού πληθυσμού χρονών - σύνολο
 15-64 χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Ο γενικός ρυθμός μεταβολής οικονομικά ενεργού πληθυσμού 15-64 χρονών υπολογίζεται με τη διαίρεση της ετήσιας αύξησης του οικονομικά ενεργού πληθυσμού
15-64 χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Ο γενικός ρυθμός μεταβολής οικονομικά ενεργού πληθυσμού 15-64 χρονών υπολογίζεται με τη διαίρεση της ετήσιας αύξησης του οικονομικά ενεργού πληθυσμού
Marin Chirciu INEGALITĂŢI TRIGONOMETRICE DE LA INIŢIERE LA PERFORMANŢĂ EDITURA PARALELA 45
 Main Chiiu INEGLITĂŢI TIGONOMETICE DE L INIŢIEE L PEFOMNŢĂ Cuins Consideații eliminae... 7 Soluţii Caitolul Inegalități u unghiui. Inegalitatea lui Jensen... 4 4 Caitolul Funții tigonometie ale jumătății
Main Chiiu INEGLITĂŢI TIGONOMETICE DE L INIŢIEE L PEFOMNŢĂ Cuins Consideații eliminae... 7 Soluţii Caitolul Inegalități u unghiui. Inegalitatea lui Jensen... 4 4 Caitolul Funții tigonometie ale jumătății
! "# $ % $&'& () *+ (,-. / 0 1(,21(,*) (3 4 5 "$ 6, ::: ;"<$& = = 7 + > + 5 $?"# 46(A *( / A 6 ( 1,*1 B"',CD77E *+ *),*,*) F? $G'& 0/ (,.
 ! " #$%&'()' *('+$,&'-. /0 1$23(/%/4. 1$)('%%'($( )/,)$5)/6%6 7$85,-9$(- /0 :/986-$, ;2'$(2$ 1'$-/-$)('')5( /&5&-/ 5(< =(4'($$,'(4 1$%$2/996('25-'/(& ;/0->5,$ 1'$-/%'')$(($/3?$%9'&-/?$( 5(< @6%-'9$
! " #$%&'()' *('+$,&'-. /0 1$23(/%/4. 1$)('%%'($( )/,)$5)/6%6 7$85,-9$(- /0 :/986-$, ;2'$(2$ 1'$-/-$)('')5( /&5&-/ 5(< =(4'($$,'(4 1$%$2/996('25-'/(& ;/0->5,$ 1'$-/%'')$(($/3?$%9'&-/?$( 5(< @6%-'9$
# " $! % $ " & "! # '' '!" ' ' ( &! )!! ' ( *+ & '
 " # " $ % $ " & " # '' '" ' ' ( & ) ' ( *+ & ' "#$% &% '($&)$'%$ *($+,& #,-%($%./*, -./ "' ' + -0,$1./ 2 34 2 51 2 6.77.8. 9:7 ; 9:.? 9 9@7 9:> 9@>.77 9 9=< 9@>./= 9:=.7: 9=@.7@ 9::.87./>./7
" # " $ % $ " & " # '' '" ' ' ( & ) ' ( *+ & ' "#$% &% '($&)$'%$ *($+,& #,-%($%./*, -./ "' ' + -0,$1./ 2 34 2 51 2 6.77.8. 9:7 ; 9:.? 9 9@7 9:> 9@>.77 9 9=< 9@>./= 9:=.7: 9=@.7@ 9::.87./>./7
Ποσοστό απασχόλησης στον τριτογενή τομέα του πληθυσμού χρονών - σύνολο
 Ποσοστό απασχόλησης στον τριτογενή τομέα του πληθυσμού 15-64 χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το ποσοστό απασχόλησης στον τριτογενή τομέα του πληθυσμού 15-64 χρονών υπολογίζεται με
Ποσοστό απασχόλησης στον τριτογενή τομέα του πληθυσμού 15-64 χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το ποσοστό απασχόλησης στον τριτογενή τομέα του πληθυσμού 15-64 χρονών υπολογίζεται με
!"! # $ %"" & ' ( ! " # '' # $ # # " %( *++*
 !"! # $ %"" & ' (! " # $% & %) '' # $ # # '# " %( *++* #'' # $,-"*++* )' )'' # $ (./ 0 ( 1'(+* *++* * ) *+',-.- * / 0 1 - *+- '!*/ 2 0 -+3!'-!*&-'-4' "/ 5 2, %0334)%3/533%43.15.%4 %%3 6!" #" $" % & &'"
!"! # $ %"" & ' (! " # $% & %) '' # $ # # '# " %( *++* #'' # $,-"*++* )' )'' # $ (./ 0 ( 1'(+* *++* * ) *+',-.- * / 0 1 - *+- '!*/ 2 0 -+3!'-!*&-'-4' "/ 5 2, %0334)%3/533%43.15.%4 %%3 6!" #" $" % & &'"
Ποσοστό μακροχρόνιας ανεργίας (διάρκεια 12+ μήνες) οικονομικά ενεργού πληθυσμού 15+ χρονών - σύνολο
 οικονομικά ενεργού πληθυσμού 15+ χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το ποσοστό μακροχρόνιας ανεργίας (διάρκεια 12+ μήνες) οικονομικά ενεργού πληθυσμού 15+ χρονών υπολογίζεται με τη διαίρεση
οικονομικά ενεργού πληθυσμού 15+ χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το ποσοστό μακροχρόνιας ανεργίας (διάρκεια 12+ μήνες) οικονομικά ενεργού πληθυσμού 15+ χρονών υπολογίζεται με τη διαίρεση
!" #$! '() -*,*( *(*)* *. 1#,2 (($3-*-/*/330%#& !" #$ -4*30*/335*
 !" #$ %#&! '( (* + #*,*(**!',(+ *,*( *(** *. * #*,*(**( 0* #*,*(**(***&, 1#,2 (($3**330%#&!" #$ 4*30*335* ( 6777330"$% 8.9% '.* &(",*( *(** *. " ( : %$ *.#*,*(**." %#& 6 &;" * (.#*,*(**( #*,*(**(***&,
!" #$ %#&! '( (* + #*,*(**!',(+ *,*( *(** *. * #*,*(**( 0* #*,*(**(***&, 1#,2 (($3**330%#&!" #$ 4*30*335* ( 6777330"$% 8.9% '.* &(",*( *(** *. " ( : %$ *.#*,*(**." %#& 6 &;" * (.#*,*(**( #*,*(**(***&,
! "#" "" $ "%& ' %$(%& % &'(!!")!*!&+ ,! %$( - .$'!"
 ! "#" "" $ "%& ' %$(%&!"#$ % &'(!!")!*!&+,! %$( -.$'!" /01&$23& &4+ $$ /$ & & / ( #(&4&4!"#$ %40 &'(!"!!&+ 5,! %$( - &$ $$$".$'!" 4(02&$ 4 067 4 $$*&(089 - (0:;
! "#" "" $ "%& ' %$(%&!"#$ % &'(!!")!*!&+,! %$( -.$'!" /01&$23& &4+ $$ /$ & & / ( #(&4&4!"#$ %40 &'(!"!!&+ 5,! %$( - &$ $$$".$'!" 4(02&$ 4 067 4 $$*&(089 - (0:;
τροχιακά Η στιβάδα καθορίζεται από τον κύριο κβαντικό αριθµό (n) Η υποστιβάδα καθορίζεται από τους δύο πρώτους κβαντικούς αριθµούς (n, l)
 ΑΤΟΜΙΚΑ ΤΡΟΧΙΑΚΑ Σχέση κβαντικών αριθµών µε στιβάδες υποστιβάδες - τροχιακά Η στιβάδα καθορίζεται από τον κύριο κβαντικό αριθµό (n) Η υποστιβάδα καθορίζεται από τους δύο πρώτους κβαντικούς αριθµούς (n,
ΑΤΟΜΙΚΑ ΤΡΟΧΙΑΚΑ Σχέση κβαντικών αριθµών µε στιβάδες υποστιβάδες - τροχιακά Η στιβάδα καθορίζεται από τον κύριο κβαντικό αριθµό (n) Η υποστιβάδα καθορίζεται από τους δύο πρώτους κβαντικούς αριθµούς (n,
Byeong-Joo Lee
 yeg-j ee OTECH - ME alphad@psteh.a.k yeg-j ee www.psteh.a.k/~alphad ufae Tast ad Allyg Effet N.M. Hwag et al., 000. ue W W 0.4wt% N Vau Aealg yeg-j ee www.psteh.a.k/~alphad Abal a wth f N.M. Hwag yeg-j
yeg-j ee OTECH - ME alphad@psteh.a.k yeg-j ee www.psteh.a.k/~alphad ufae Tast ad Allyg Effet N.M. Hwag et al., 000. ue W W 0.4wt% N Vau Aealg yeg-j ee www.psteh.a.k/~alphad Abal a wth f N.M. Hwag yeg-j
10.0 C N = = = electrons C/electron C/electron. ( N m 2 /C 2 )( C) 2 (0.050 m) 2.
 Electric Forces and Fields Section Review, p. 633 Givens Chapter 17 3. q 10.0 C q 10.0 C N 6.5 10 19 electrons 1.60 10 19 C/electron 1.60 10 19 C/electron Practice 17A, p. 636 1. q 1 8.0 C q 8.0 C r 5.0
Electric Forces and Fields Section Review, p. 633 Givens Chapter 17 3. q 10.0 C q 10.0 C N 6.5 10 19 electrons 1.60 10 19 C/electron 1.60 10 19 C/electron Practice 17A, p. 636 1. q 1 8.0 C q 8.0 C r 5.0
Š Šˆ ATLAS: ˆ ˆŸ ˆ Šˆ, Œ ˆ Œ ˆ.. ƒê ±μ,. ƒ ² Ï ², ƒ.. Š ± ²,. Œ. Ò,.. ŒÖ²±μ ±,.. Ï Ìμ μ,.. Ê ±μ Î,.. ±μ,. Œ. μ
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2010.. 41.. 1 Š ƒ ˆ ˆŸ Å Š Šˆ ATLAS: ˆ ˆŸ ˆ Šˆ, Œ ˆ Œ ˆ.. ƒê ±μ,. ƒ ² Ï ², ƒ.. Š ± ²,. Œ. Ò,.. ŒÖ²±μ ±,.. Ï Ìμ μ,.. Ê ±μ Î,.. ±μ,. Œ. μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê. ÉÉÊ,. Ê μ μ ± Ö μ Í Ö Ö ÒÌ
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2010.. 41.. 1 Š ƒ ˆ ˆŸ Å Š Šˆ ATLAS: ˆ ˆŸ ˆ Šˆ, Œ ˆ Œ ˆ.. ƒê ±μ,. ƒ ² Ï ², ƒ.. Š ± ²,. Œ. Ò,.. ŒÖ²±μ ±,.. Ï Ìμ μ,.. Ê ±μ Î,.. ±μ,. Œ. μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê. ÉÉÊ,. Ê μ μ ± Ö μ Í Ö Ö ÒÌ
5.1 CIKLI IDEAL TE MOTORI OTO KATËRKOHESH
 5 CIKLE E PUNËS Dlloen ilet iele e rele të unës. e morët termie zilloen ilet e unës të ilt rqesin semën e nërrimee susesie të gjenjes të mteries unuese. Cili iel i morit rse uste iele më të ilët zilloet
5 CIKLE E PUNËS Dlloen ilet iele e rele të unës. e morët termie zilloen ilet e unës të ilt rqesin semën e nërrimee susesie të gjenjes të mteries unuese. Cili iel i morit rse uste iele më të ilët zilloet
ΠΕΡΙΟΔΙΚΟ ΣΥΣΤΗΜΑ ΤΩΝ ΣΤΟΙΧΕΙΩΝ (1) Ηλία Σκαλτσά ΠΕ ο Γυμνάσιο Αγ. Παρασκευής
 ΠΕΡΙΟΔΙΚΟ ΣΥΣΤΗΜΑ ΤΩΝ ΣΤΟΙΧΕΙΩΝ (1) Ηλία Σκαλτσά ΠΕ04.01 5 ο Γυμνάσιο Αγ. Παρασκευής Όπως συμβαίνει στη φύση έτσι και ο άνθρωπος θέλει να πετυχαίνει σπουδαία αποτελέσματα καταναλώνοντας το λιγότερο δυνατό
ΠΕΡΙΟΔΙΚΟ ΣΥΣΤΗΜΑ ΤΩΝ ΣΤΟΙΧΕΙΩΝ (1) Ηλία Σκαλτσά ΠΕ04.01 5 ο Γυμνάσιο Αγ. Παρασκευής Όπως συμβαίνει στη φύση έτσι και ο άνθρωπος θέλει να πετυχαίνει σπουδαία αποτελέσματα καταναλώνοντας το λιγότερο δυνατό
Μερίδιο εργοδοτουμένων με μερική ή / και προσωρινή απασχόληση στον εργοδοτούμενο πληθυσμό 15+ χρονών - σύνολο
 Μερίδιο εργοδοτουμένων με μερική ή / και προσωρινή απασχόληση στον εργοδοτούμενο πληθυσμό 15+ χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το μερίδιο εργοδοτουμένων με μερική ή/και προσωρινή απασχόληση
Μερίδιο εργοδοτουμένων με μερική ή / και προσωρινή απασχόληση στον εργοδοτούμενο πληθυσμό 15+ χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το μερίδιο εργοδοτουμένων με μερική ή/και προσωρινή απασχόληση
SOLUTIONS & ANSWERS FOR KERALA ENGINEERING ENTRANCE EXAMINATION-2018 PAPER II VERSION B1
 SOLUTIONS & ANSWERS FOR KERALA ENGINEERING ENTRANCE EXAMINATION-8 PAPER II VERSION B [MATHEMATICS]. Ans: ( i) It is (cs5 isin5 ) ( i). Ans: i z. Ans: i i i The epressin ( i) ( ). Ans: cs i sin cs i sin
SOLUTIONS & ANSWERS FOR KERALA ENGINEERING ENTRANCE EXAMINATION-8 PAPER II VERSION B [MATHEMATICS]. Ans: ( i) It is (cs5 isin5 ) ( i). Ans: i z. Ans: i i i The epressin ( i) ( ). Ans: cs i sin cs i sin
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ
 3/5/016 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΣΥΡΜΑΤΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Παραδείγματα Κεραιών Αθανάσιος Κανάτας Καθηγητής Παν/μίου Πειραιώς Δίπολο Hetz L d
3/5/016 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΣΥΡΜΑΤΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Παραδείγματα Κεραιών Αθανάσιος Κανάτας Καθηγητής Παν/μίου Πειραιώς Δίπολο Hetz L d
Edexcel FP3. Hyperbolic Functions. PhysicsAndMathsTutor.com
 Eeel FP Hpeoli Futios PhsisAMthsTuto.om . Solve the equtio Leve lk 7seh th 5 Give ou swes i the fom l whee is tiol ume. 5 7 Sih 5 Cosh osh 7 Sih 5osh's 7 Ee e I E e e 4 e te 5e 55 O 5e 55 te e 4 O Ge 45
Eeel FP Hpeoli Futios PhsisAMthsTuto.om . Solve the equtio Leve lk 7seh th 5 Give ou swes i the fom l whee is tiol ume. 5 7 Sih 5 Cosh osh 7 Sih 5osh's 7 Ee e I E e e 4 e te 5e 55 O 5e 55 te e 4 O Ge 45
Indukcioni elektromagnetik
 Shufra pingul mbi ijat e fushës magnetike Indukcioni elektromagnetik Indukcioni elektromagnetik në shufrën përçuese e cila lëizë në fushën magnetike ijat e fushës magnetike homogjene Bazat e elektroteknikës
Shufra pingul mbi ijat e fushës magnetike Indukcioni elektromagnetik Indukcioni elektromagnetik në shufrën përçuese e cila lëizë në fushën magnetike ijat e fushës magnetike homogjene Bazat e elektroteknikës
' ( )* * +,,, ) - ". &!: &/#&$&0& &!& $#/&! 1 2!#&, #/&2!#&3 &"&!3, #&- &2!#&, "#4 $!&$3% 2!% #!.1 & &!" //! &-!!
 ..!! "#$% #&" 535.34 ' ( )* *,,, ) - ". &!: 1.4.7 &/#&$&& &!&11 5.7.1 $#/&! 1!#&, #/&!#&3 &"&!3, #&- &!#&, "#4 $!&$3%!% #!.1 & &!" //! &-!!% 3 #&$&/!: /&!&# &-!!%, "#&&# 56$.., //! &-!!% ).. &$ 13 .
..!! "#$% #&" 535.34 ' ( )* *,,, ) - ". &!: 1.4.7 &/#&$&& &!&11 5.7.1 $#/&! 1!#&, #/&!#&3 &"&!3, #&- &!#&, "#4 $!&$3%!% #!.1 & &!" //! &-!!% 3 #&$&/!: /&!&# &-!!%, "#&&# 56$.., //! &-!!% ).. &$ 13 .
Παρουσιαστές: ??ast?s??? Τσάκας. ?/?t?? t???/?s????p???af???? t??????? ?a??a Se???t?
 Παρουσιαστές:??ast?s??? Τσάκας?/?t?? t???/?s????p???af???? t????????a??a Se???t???p????f?????a???????? Master of Applied Science (M.App.Sci)? a?ep?s t?µ?? G?a s?? ί???/?s????p???af???? t??????? Τα κυριότερα
Παρουσιαστές:??ast?s??? Τσάκας?/?t?? t???/?s????p???af???? t????????a??a Se???t???p????f?????a???????? Master of Applied Science (M.App.Sci)? a?ep?s t?µ?? G?a s?? ί???/?s????p???af???? t??????? Τα κυριότερα
!"! #!"!!$ #$! %!"&' & (%!' #!% #" *! *$' *.!! )#/'.0! )#/.*!$,)# * % $ %!!#!!%#'!)$! #,# #!%# ##& )$&# 11!!#2!
 # $ #$ % (% # )*%%# )# )$ % # * *$ * #,##%#)#% *-. )#/###%. )#/.0 )#/.* $,)# )#/ * % $ % # %# )$ #,# # %# ## )$# 11 #2 #**##%% $#%34 5 # %## * 6 7(%#)%%%, #, # ## # *% #$# 8# )####, 7 9%%# 0 * #,, :;
# $ #$ % (% # )*%%# )# )$ % # * *$ * #,##%#)#% *-. )#/###%. )#/.0 )#/.* $,)# )#/ * % $ % # %# )$ #,# # %# ## )$# 11 #2 #**##%% $#%34 5 # %## * 6 7(%#)%%%, #, # ## # *% #$# 8# )####, 7 9%%# 0 * #,, :;
Συμβούλιο της Ευρωπαϊκής Ένωσης Βρυξέλλες, 7 Μαρτίου 2017 (OR. en)
 Συμβούλιο της Ευρωπαϊκής Ένωσης Βρυξέλλες, 7 Μαρτίου 2017 (OR. en) 7057/17 ADD 1 TRANS 97 ΔΙΑΒΙΒΑΣΤΙΚΟ ΣΗΜΕΙΩΜΑ Αποστολέας: Ημερομηνία Παραλαβής: Αποδέκτης: Για τον Γενικό Γραμματέα της Ευρωπαϊκής Επιτροπής,
Συμβούλιο της Ευρωπαϊκής Ένωσης Βρυξέλλες, 7 Μαρτίου 2017 (OR. en) 7057/17 ADD 1 TRANS 97 ΔΙΑΒΙΒΑΣΤΙΚΟ ΣΗΜΕΙΩΜΑ Αποστολέας: Ημερομηνία Παραλαβής: Αποδέκτης: Για τον Γενικό Γραμματέα της Ευρωπαϊκής Επιτροπής,
ο ο 3 α. 3"* > ω > d καΐ 'Ενορία όλις ή Χώρί ^ 3 < KN < ^ < 13 > ο_ Μ ^~~ > > > > > Ο to X Η > ο_ ο Ο,2 Σχέδι Γλεγμα Ο Σ Ο Ζ < o w *< Χ χ Χ Χ < < < Ο
 18 ρ * -sf. NO 1 D... 1: - ( ΰ ΐ - ι- *- 2 - UN _ ί=. r t ' \0 y «. _,2. "* co Ι». =; F S " 5 D 0 g H ', ( co* 5. «ΰ ' δ". o θ * * "ΰ 2 Ι o * "- 1 W co o -o1= to»g ι. *ΰ * Ε fc ΰ Ι.. L j to. Ι Q_ " 'T
18 ρ * -sf. NO 1 D... 1: - ( ΰ ΐ - ι- *- 2 - UN _ ί=. r t ' \0 y «. _,2. "* co Ι». =; F S " 5 D 0 g H ', ( co* 5. «ΰ ' δ". o θ * * "ΰ 2 Ι o * "- 1 W co o -o1= to»g ι. *ΰ * Ε fc ΰ Ι.. L j to. Ι Q_ " 'T
Formulario Básico ( ) ( ) ( ) ( ) ( 1) ( 1) ( 2) ( 2) λ = 1 + t t. θ = t ε t. Mecánica de Medios Continuos. Grado en Ingeniería Civil.
 Mecánica e Meios Continos. Gao en Ingenieía Ciil. Fomlaio Básico Tema. Descipción el moimiento χ (,) t χ (,) t (,) t χ (,) t t t Tema. Defomación s S X E X e i ij j i ij j F X X U F J T T T U U i j Uk
Mecánica e Meios Continos. Gao en Ingenieía Ciil. Fomlaio Básico Tema. Descipción el moimiento χ (,) t χ (,) t (,) t χ (,) t t t Tema. Defomación s S X E X e i ij j i ij j F X X U F J T T T U U i j Uk
]Zp _[ I 8G4G /<4 6EE =A>/8E>4 06? E6/<; 6008:6> /8= 4; /823 ;1A :40 >176/812; 98/< ;76//40823 E182/;G g= = 4/<1
![]Zp _[ I 8G4G /<4 6EE =A>/8E>4 06? E6/<; 6008:6> /8= 4; /823 ;1A :40 >176/812; 98/< ;76//40823 E182/;G g= = 4/<1 ]Zp _[ I 8G4G /<4 6EE =A>/8E>4 06? E6/<; 6008:6> /8= 4; /823 ;1A :40 >176/812; 98/< ;76//40823 E182/;G g= = 4/<1](/thumbs/84/90712514.jpg) ! " #$ # %$ & ' ( ) *+, ( -+./0123 045067/812 15 96:4; 82 /178/? = 1@4> 82/01@A74; B824= 6/87 60/8567/; C 71 04D47/10; C 82/1 /
! " #$ # %$ & ' ( ) *+, ( -+./0123 045067/812 15 96:4; 82 /178/? = 1@4> 82/01@A74; B824= 6/87 60/8567/; C 71 04D47/10; C 82/1 /
Meren virsi Eino Leino
 œ_ œ _ q = 72 Meren virsi Eino Leino Toivo Kuua o. 11/2 (1909) c c F c Kun ne F iu L? c œ J J J J œ_ œ_ nœ_ Min ne rien nät, vie ri vä vir ta? Kun ne c c F c Kun ne F iu L? c œ J J J J œ_ œ_ nœ_ Min ne
œ_ œ _ q = 72 Meren virsi Eino Leino Toivo Kuua o. 11/2 (1909) c c F c Kun ne F iu L? c œ J J J J œ_ œ_ nœ_ Min ne rien nät, vie ri vä vir ta? Kun ne c c F c Kun ne F iu L? c œ J J J J œ_ œ_ nœ_ Min ne
Veliine u mehanici. Rad, snaga i energija. Dinamika. Meunarodni sustav mjere (SI) 1. Skalari. 2. Vektori - poetak. 12. dio. 1. Skalari. 2.
 Vele u ehc Rd, g eegj D. do. Sl. Veo 3. Tezo II. ed 4. Tezo IV. ed. Sl: 3 0 pod je jedc (ezo ulog ed). Veo: 3 3 pod je jedc (ezo pog ed) 3. Tezo dugog ed 3 9 pod je jedc 4. Tezoeog ed 3 4 8 pod je jedc
Vele u ehc Rd, g eegj D. do. Sl. Veo 3. Tezo II. ed 4. Tezo IV. ed. Sl: 3 0 pod je jedc (ezo ulog ed). Veo: 3 3 pod je jedc (ezo pog ed) 3. Tezo dugog ed 3 9 pod je jedc 4. Tezoeog ed 3 4 8 pod je jedc
Đường tròn : cung dây tiếp tuyến (V1) Đường tròn cung dây tiếp tuyến. Giải.
 Đường tròn cung dây tiếp tuyến BÀI 1 : Cho tam giác ABC. Đường tròn có đường kính BC cắt cạnh AB, AC lần lượt tại E, D. BD và CE cắt nhau tại H. chứng minh : 1. AH vuông góc BC (tại F thuộc BC). 2. FA.FH
Đường tròn cung dây tiếp tuyến BÀI 1 : Cho tam giác ABC. Đường tròn có đường kính BC cắt cạnh AB, AC lần lượt tại E, D. BD và CE cắt nhau tại H. chứng minh : 1. AH vuông góc BC (tại F thuộc BC). 2. FA.FH
Problemas resueltos del teorema de Bolzano
 Problemas resueltos del teorema de Bolzano 1 S e a la fun ción: S e puede af irm a r que f (x) está acotada en el interva lo [1, 4 ]? P or no se r c ont i nua f (x ) e n x = 1, la f unció n no e s c ont
Problemas resueltos del teorema de Bolzano 1 S e a la fun ción: S e puede af irm a r que f (x) está acotada en el interva lo [1, 4 ]? P or no se r c ont i nua f (x ) e n x = 1, la f unció n no e s c ont
Erkki Mäkinen ja Timo Poranen Algoritmit
 rkki Mäkinen ja Timo Poranen Algoritmit TITOJNKÄSITTLYTITIDN LAITOS TAMPRN YLIOPISTO D 2008 6 TAMPR 2009 TAMPRN YLIOPISTO TITOJNKÄSITTLYTITIDN LAITOS JULKAISUSARJA D VRKKOJULKAISUT D 2008 6, TOUKOKUU 2009
rkki Mäkinen ja Timo Poranen Algoritmit TITOJNKÄSITTLYTITIDN LAITOS TAMPRN YLIOPISTO D 2008 6 TAMPR 2009 TAMPRN YLIOPISTO TITOJNKÄSITTLYTITIDN LAITOS JULKAISUSARJA D VRKKOJULKAISUT D 2008 6, TOUKOKUU 2009
Λύση: Ισολογισµός ισχύος στο Λέβητα Καυσαερίων: (1)
 6 η Οµάδα Ασκήσεων Άσκηση 6.1 Η πρόωση πλοίου επιτυγχάνεται µε Βραδύστροφο, -Χ κινητήρα Dieel µέγιστης συνεχούς ισχύος στον άξονα 6100 PS. Η ειδική κατανάλωση του κινητήρα είναι 15 gr/psh σε φορτίο 100
6 η Οµάδα Ασκήσεων Άσκηση 6.1 Η πρόωση πλοίου επιτυγχάνεται µε Βραδύστροφο, -Χ κινητήρα Dieel µέγιστης συνεχούς ισχύος στον άξονα 6100 PS. Η ειδική κατανάλωση του κινητήρα είναι 15 gr/psh σε φορτίο 100
! " #$ (!$ )* ' & )* # & # & ' +, #
 ! " #$ %%%$&$' %$($% (!$ )* ' & )* # & # & ' +, # $ $!,$$ ' " (!!-!.$-/001 # #2 )!$!$34!$ )$5%$)3' ) 3/001 6$ 3&$ '(5.07808.98: 23*+$3;'$3;',;.8/ *' * $
! " #$ %%%$&$' %$($% (!$ )* ' & )* # & # & ' +, # $ $!,$$ ' " (!!-!.$-/001 # #2 )!$!$34!$ )$5%$)3' ) 3/001 6$ 3&$ '(5.07808.98: 23*+$3;'$3;',;.8/ *' * $
ΤΡΙΠΥΡΗΝΙΚΕΣ ΠΛΕΙΑΔΕΣ ΜΕ ΔΕΣΜΟΥΣ Μ-Μ
 ΤΡΙΠΥΡΗΝΙΚΕΣ ΠΛΕΙΑΔΕΣ ΜΕ ΔΕΣΜΟΥΣ Μ-Μ Re 5 Δ Design? Re Re Re Re Re Re H 6-12 M Re Re Re 3- [Re 3 9 ] n [Re 3 12 ] 3- ΤΡΙΠΥΡΗΝΙΚΕΣ ΠΛΕΙΑΔΕΣ ΜΕ ΔΕΣΜΟΥΣ Μ-Μ Παραδείγματα περιλαμβάνουν το [Re 3 9 (Η 2 Ο) 3
ΤΡΙΠΥΡΗΝΙΚΕΣ ΠΛΕΙΑΔΕΣ ΜΕ ΔΕΣΜΟΥΣ Μ-Μ Re 5 Δ Design? Re Re Re Re Re Re H 6-12 M Re Re Re 3- [Re 3 9 ] n [Re 3 12 ] 3- ΤΡΙΠΥΡΗΝΙΚΕΣ ΠΛΕΙΑΔΕΣ ΜΕ ΔΕΣΜΟΥΣ Μ-Μ Παραδείγματα περιλαμβάνουν το [Re 3 9 (Η 2 Ο) 3
ŒˆŠ Š ˆ Š ˆ ˆ ˆ œ ƒ ƒˆƒ Š ƒ.. ˆÏÌ μ,.. ²
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2007.. 38.. 2 ŒˆŠ Š ˆ Š ˆ ˆ ˆ œ ƒ ƒˆƒ Š ƒ.. ˆÏÌ μ,.. ² ÊÎ μ- ² μ É ²Ó ± É ÉÊÉ Ö μ Ë ± ³... ±μ ²ÓÍÒ, Œƒ, Œμ ± μ ³Ê² Ê É Ö μ É Ö μ²ê³ ± μ ±μ Î ± Ö ³μ ²Ó, μ μ²öõð Ö ÊÎ ÉÓ ² Ö Ëμ - ³ Í μ ÒÌ,
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2007.. 38.. 2 ŒˆŠ Š ˆ Š ˆ ˆ ˆ œ ƒ ƒˆƒ Š ƒ.. ˆÏÌ μ,.. ² ÊÎ μ- ² μ É ²Ó ± É ÉÊÉ Ö μ Ë ± ³... ±μ ²ÓÍÒ, Œƒ, Œμ ± μ ³Ê² Ê É Ö μ É Ö μ²ê³ ± μ ±μ Î ± Ö ³μ ²Ó, μ μ²öõð Ö ÊÎ ÉÓ ² Ö Ëμ - ³ Í μ ÒÌ,
 Molekulare Ebene (biochemische Messungen) Zelluläre Ebene (Elektrophysiologie, Imaging-Verfahren) Netzwerk Ebene (Multielektrodensysteme) Areale (MRT, EEG...) Gene Neuronen Synaptische Kopplung kleine
Molekulare Ebene (biochemische Messungen) Zelluläre Ebene (Elektrophysiologie, Imaging-Verfahren) Netzwerk Ebene (Multielektrodensysteme) Areale (MRT, EEG...) Gene Neuronen Synaptische Kopplung kleine
ot ll1) r/l1i~u (X) f (Gf) Fev) f:-;~ (v:v) 1 lý) æ (v / find bt(xi (t-i; i/r-(~ v) ta.jpj -- (J ~ Cf, = 0 1l 3 ( J) : o-'t5 : - q 1- eft-1
 - la /:_ )( -( = Y () :: ÚlJl:: ot ll) r/li~u (X) f (Gf) Fev) f:-;~ (v:v) lý) æ (v / find bt(i (t-i; i/r-(~ v) bj Ll, :: Qy -+ 4",)( + 3' r.) '.J ta.jpj -- (J ~ Cf, = l 3 ( J) : o-'t5 : - q - eft- F ~)ç2..'
- la /:_ )( -( = Y () :: ÚlJl:: ot ll) r/li~u (X) f (Gf) Fev) f:-;~ (v:v) lý) æ (v / find bt(i (t-i; i/r-(~ v) bj Ll, :: Qy -+ 4",)( + 3' r.) '.J ta.jpj -- (J ~ Cf, = l 3 ( J) : o-'t5 : - q - eft- F ~)ç2..'
Αναλογικά Συστήματα Ενδοεπικοινωνίας. Τιμή σε ΕΥΡΩ τύπος περιγραφή χωρίς ΦΠΑ με ΦΠΑ 23% Μεγαφωνικά συστήματα μικρής ισχύος Σειρές LEM & LEF
 Μεγαφωνικά συστήματα μικρής ισχύος Σειρές LEM & LEF Συσκευές επιτραπέζιες ή επίτοιχες LEM-1 Κέντρο 1 γραμμής. 73,00 89,79 LEM-1DL Το ίδιο αλλά με button για αυτόματο άνοιγμα πόρτας. 100,00 123,00 LEM-3
Μεγαφωνικά συστήματα μικρής ισχύος Σειρές LEM & LEF Συσκευές επιτραπέζιες ή επίτοιχες LEM-1 Κέντρο 1 γραμμής. 73,00 89,79 LEM-1DL Το ίδιο αλλά με button για αυτόματο άνοιγμα πόρτας. 100,00 123,00 LEM-3
Α Ρ Ι Θ Μ Ο Σ : 6.913
 Α Ρ Ι Θ Μ Ο Σ : 6.913 ΠΡΑΞΗ ΚΑΤΑΘΕΣΗΣ ΟΡΩΝ ΔΙΑΓΩΝΙΣΜΟΥ Σ τ η ν Π ά τ ρ α σ ή μ ε ρ α σ τ ι ς δ ε κ α τ έ σ σ ε ρ ι ς ( 1 4 ) τ ο υ μ ή ν α Ο κ τ ω β ρ ί ο υ, η μ έ ρ α Τ ε τ ά ρ τ η, τ ο υ έ τ ο υ ς δ
Α Ρ Ι Θ Μ Ο Σ : 6.913 ΠΡΑΞΗ ΚΑΤΑΘΕΣΗΣ ΟΡΩΝ ΔΙΑΓΩΝΙΣΜΟΥ Σ τ η ν Π ά τ ρ α σ ή μ ε ρ α σ τ ι ς δ ε κ α τ έ σ σ ε ρ ι ς ( 1 4 ) τ ο υ μ ή ν α Ο κ τ ω β ρ ί ο υ, η μ έ ρ α Τ ε τ ά ρ τ η, τ ο υ έ τ ο υ ς δ
K Î Ì ÓÙ Ù applefi Ú ÛÈ
 K ÏÔÎ ÈÚ applefi M. ÌappleÙË 12 A PI IOY 2009 ñ ºY O 1.627 ñ appleâú Ô Ô B B EK O H TIMH: E ÚÒ 2 (EÎ ÔÛË ÌÂ appleúôûêôú Â ÚÒ 4) E. 62 8 MAPTIOY 2009 ñ ºY O 1.622 ñ appleâú Ô Ô YNENTEY H KPI TIN A KAPNT.
K ÏÔÎ ÈÚ applefi M. ÌappleÙË 12 A PI IOY 2009 ñ ºY O 1.627 ñ appleâú Ô Ô B B EK O H TIMH: E ÚÒ 2 (EÎ ÔÛË ÌÂ appleúôûêôú Â ÚÒ 4) E. 62 8 MAPTIOY 2009 ñ ºY O 1.622 ñ appleâú Ô Ô YNENTEY H KPI TIN A KAPNT.
