2
|
|
|
- Χριστός Πολίτης
- 6 χρόνια πριν
- Προβολές:
Transcript
1 6 /9 / Downloaded fom enegy.kahanu.ac. at :7 + on Tueday Octobe th 8 * y.hok6@aut.ac. afzalan@bu.ac. : لا.. T-S. T-S «(PDC)». لا Lyapunov. (PID) لا.. : *
2 7... Downloaded fom enegy.kahanu.ac. at :7 + on Tueday Octobe th 8... (PDC). 5.[5].... (PDC) ). [6].( () : Rule : f z( t) M and... and zn( t) M n then () xt &() = Axt () + But () =,..., xt () = [ x(),..., t x ()] t T z () ut () = [ u (),..., t u()] T j t l t M j () t.. () m..[ ] PID ptch. [].. [] ptch ptch. PID.. [6 5] PID. [8 7] [ 9]. [١٢ ١١] [8]... [] [].. - [].. Paallel dtbuted compenaton 5. Gan chedulng.. popotonal-ntegal-devatve.
3 8 Downloaded fom enegy.kahanu.ac. at :7 + on Tueday Octobe th 8. LPV.. LPV. [8] LTI B A.(5 ) xt &() Apt ( ()) B( pt ()) xt () = (5) yt () C( pt ()) D( pt ()) ut () (LPV).. : T (, ) (6) = ρπ R V Cp λ β T = av + bω + cβ λ Rω R ρ λ = V ω C p V. ptch β : R T T B = v g g g ωg ω ω ( R ) + ( ωl) = π f f ω = p f ω g ω ωg = ω ( ) (7) p f v. ω. ω g = ( ±.) ω B g (7). ω = ω g ω. ω = ω g. xt &() = = M ( z)[ Ax( t) + Bu( t)] = M ( z) PDC () : Rule : f z( t) M and... and zn( t) M n then () xt &() = Axt () + But () =,...,. K ١ : () p T [ A BK j] p p[ A BK j] < () fo, j,,.., & M M j. (). [7] ).( [8] ()... (). V β T ω ω g T g [8] :() v f. Lnea Paamete Vayng. Lnea Tme Invaant. Lyapunov. Lnea Matx Inequalty
4 9... Downloaded fom enegy.kahanu.ac. at :7 + on Tueday Octobe th 8 () ω ω b(θ ) b(θ )... [,]m. - Rule: f V bg then b( θ) = ρπr C pmax, λopt Rule: f V mall then b( ) = R C pmax, λopt Ampltude θ ρπ wnd peed(m/) b(θ ) :() bg mall (). ptch. ().[8].( I ) :().( ω < ω g ) LPV : x& = A( θ ) x+ B( θ ) u G : (8) y = Cx+ Du T T T x & = [ θ ω ωg β ], u = [ V βd ωz ], y = [ ωg Tg ] b( θ ) B K J B J c( θ ) J J θ = A( ) B + Bg K J g B J g J g τ a( θ ) J B( θ ) =, C =, Bg J g B g τ D = Bg ω z ptch β d J g J K ptch τ B. θ = [ V ω β ] c(θ ) b( θ ), a( θ ) ) T-S (.. ) ( (6). (6) (9) T (, ) ( ) (9) = ρπ R V Cp λ β T = b θ ω λ : C 5 pω T = ρπ R V Cp( λ, β ) b( θ ) = ρπ R λ λ (). Takag - Sugeno
5 Downloaded fom enegy.kahanu.ac. at :7 + on Tueday Octobe th 8 (8) (5). m. - (5). m. -. (5). PI (6). (6) (5) (7).. (7).. (8) PDC (5). () (9) ) 7 m. - m. -. ( () (8) (5) (9). () ().. PID PDC (). PID ( C p ). Betz /59 [9] = 8 β = / λ opt. (8) ptch λ (). ω = _ ef ω z optv R. (θ ) :() [8] PID. PID. () () (). 5 C() = + K = 56, K = 76 () (). SUT- MW.[] SUT- MW..[6]
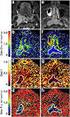
6 ... Downloaded fom enegy.kahanu.ac. at :7 + on Tueday Octobe th 8 Roto Speed Eo (ad/ec) :() Outpt Powe (W) c p Ampltude - - ω z :() :().. (). p : A =.88.., A = K [ 56] K [ 76] = = Output Powee (W) 5 x 5.5 x Roto Speed Eo (ad/ec) m. - m :(5) :(6) Omega (ad/ec) PDC PID ω z Ampltude.... c p change : (7).5.5 PDC PID :(8) p (). Outpt Powe (W) 6 x p = :(9)
7 Downloaded fom enegy.kahanu.ac. at :7 + on Tueday Octobe th 8.. [] Mohammad, K., et al. "Pedctng the wnd powe denty baed upon exteme leanng machne" Eleve, Enegy, Vol. 86, pp. 9, 5. [] Yang, Wenxan, et al. "Wnd tubne condton montong: techncal and commecal challenge." Wly, Wnd Enegy, Vol. 7, No. 5, pp , May. [] Hand, M. M, Vaable-peed wnd tubne contolle ytematc degn methodology: a compaon of nonlnea and lnea model-baed degn, Natonal Renewable Enegy Lab., Golden, CO, NREL/TP-5-55, July 999. [] ÇOKÜNLÜ Güol, Wnd Tubne Modelng and Contolle Degn, M.Sc. The. Itanbul Techncal Unvety. Date of ubmon: May 7. [5] Hanen, M. H, Hanen, A, Laen, T. J, Oye. S, Soenen, P, Fuglang, P, "Contol Degn fo a Ptch-egulated Vaable-peed Wnd Tubne" Repot #R-5(EN) Ro Natonal Laboatoy, Roklde, Denmak, 5. [6] Leth, D. J. and Lethead, W. E, "Appopate ealzaton of gan-cheduled contolle wth applcaton to wnd tubne" Taylo & Fanc, Intenatonal Jounal of Contol 65(), pp. 8, 996. [7] Rocha, R, Squea, L, Flho, M, A Multvaable H Contol fo Wnd Enegy Conveon Sytem Poceedng of IEEE confeence on contol applcaton, Vol., pp.6-,. [8] Takaa, H, Chda, Y, Sakua, K, Iobe, T, Ptch angle contol of wnd tubne geneato ung le conevatve obut contol 8th IEEE Intenatonal Confeence on Contol Applcaton, 9. [9] Rezae,V., and Salma. F., "Robut Adaptve Fault Toleant Ptch Contol of Wnd Tubne" Wnd Engneeng, Vol.8, No.6, pp.6-6,. [] Banch, F.D, Mantz, R.J, Chtanen. C.F, Contol of.5 PDC. vaable-peed wnd tubne by LPV gan chedulng Wly, Wnd Enegy, Vol. 7, pp. 8,. [] Johnon, K. E, Adaptve toque contol of vaable peed wnd tubne, Natonal Renewable Enegy Lab, Golden CO, NREL/TP-5-665, Aug. [] Johnon, Kathyn. E, et al, "Contol of vaable-peed wnd tubne: tandad and adaptve technque fo maxmzng enegy captue" Contol Sytem, IEEE Vol.6, No., pp.7-8, 6. [] Johnon. K. E, Fngeh. L. J, "Adaptve ptch contol of vaable peed wnd tubne" Amecan Socety of Mechancal Engnee, Jounal of Sola Enegy Eng., Vol., No., Augut 8. [] RAJENDRAN. Saavanakuma, and J. E. N. A. Debahha. "Backteppng ldng mode contol of a vaable peed wnd tubne fo powe optmzaton" Spnge, Jounal of Moden Powe Sytem and Clean Enegy, pp.-9, 5. [5] Rechet. R.T, Rugh. W.J, Nchol. R. A, "Gan chedulng fo H-nfnty contolle: a flght contol example," IEEE Tan. Contol Sytem Technology, Vol., No., pp , Jun. 99. [6] H.Yng, "The Takag Sugeno fuzzy contolle ung the mplfed lnea contol ule ae nonlnea vaable gan contolle" Eleve, Automatca, Vol., No., 998. [7] Boyd Stephen, et al, Lnea Matx Inequalte n Sytem and Contol Theoy, Phladelpha: Socety fo Indutal and Appled Mathematc SIAM, 99. [8] Banch. F.D, H. D. Battta, Mantz. R.J, Wnd Tubne Contol Sytem: Pncple, modelng and ganchedulng degn, Spnge-Velag London, 7. [9] Yao, Xng-ja, Guo Chang-Chun, and L Yan. "LPV H- nfnty contolle degn fo vaable-ptch vaablepeed wnd tubne" IEEE 6th Intenatonal Powe
8 ... Electonc and Moton Contol Confeence, IPEMC'9, 9. [] Petkovć. Dalbo, et al. "Adaptve neuo-fuzzy maxmal powe extacton of wnd tubne wth contnuouly vaable tanmon" Eleve, Enegy, pp ,. Downloaded fom enegy.kahanu.ac. at :7 + on Tueday Octobe th 8
Συμπεριφορά Ασύγχρονου Κινητήρα τροφοδοτούμενος από 3φασικό Αντιστροφέα οδηγούμενος με οδήγηση διανυσματικής διαμόρφωσης μαγνητικής ροής
 Συμπεριφορά Ασύγχρονου Κινητήρα τροφοδοτούμενος από 3φασικό Αντιστροφέα οδηγούμενος με οδήγηση διανυσματικής διαμόρφωσης μαγνητικής ροής Βαγδάτης Παρασκευάς, Μεταπτυχιακός φοιτητής Δ.Π.Θ. Τμήμα Η.Μ&Μ.Υ.
Συμπεριφορά Ασύγχρονου Κινητήρα τροφοδοτούμενος από 3φασικό Αντιστροφέα οδηγούμενος με οδήγηση διανυσματικής διαμόρφωσης μαγνητικής ροής Βαγδάτης Παρασκευάς, Μεταπτυχιακός φοιτητής Δ.Π.Θ. Τμήμα Η.Μ&Μ.Υ.
ΤΟ ΟΜΟΓΕΝΕΣ MΑΡΚΟΒΙΑΝΟ ΣΥΣΤΗΜΑ ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ ΜΕ ΠΕΠΕΡΑΣΜΕΝΗ ΧΩΡΗΤΙΚΟΤΗΤΑ ΣΕ ΜΙΑ ΚΑΤΑΣΤΑΣΗ
 Ελληνικό Στατιστικό Ινστιτούτο Πρακτικά 2 ου Πανελληνίου Συνεδρίου Στατιστικής (27) σελ 3- ΤΟ ΟΜΟΓΕΝΕΣ MΑΡΚΟΒΙΑΝΟ ΣΥΣΤΗΜΑ ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ ΜΕ ΠΕΠΕΡΑΣΜΕΝΗ ΧΩΡΗΤΙΚΟΤΗΤΑ ΣΕ ΜΙΑ ΚΑΤΑΣΤΑΣΗ Γ Βασιλειάδης Γ Τσακλίδης
Ελληνικό Στατιστικό Ινστιτούτο Πρακτικά 2 ου Πανελληνίου Συνεδρίου Στατιστικής (27) σελ 3- ΤΟ ΟΜΟΓΕΝΕΣ MΑΡΚΟΒΙΑΝΟ ΣΥΣΤΗΜΑ ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ ΜΕ ΠΕΠΕΡΑΣΜΕΝΗ ΧΩΡΗΤΙΚΟΤΗΤΑ ΣΕ ΜΙΑ ΚΑΤΑΣΤΑΣΗ Γ Βασιλειάδης Γ Τσακλίδης
 9 /393 / Downloaded from energy.kashanu.ac.r at 5:3 0330 on Saturday October 0th 08 * hajakbar@grad.kashanu.ac.r mohammad@kashanu.ac.r. (shunt-apf) :... PSIM. : * 3... Downloaded from energy.kashanu.ac.r
9 /393 / Downloaded from energy.kashanu.ac.r at 5:3 0330 on Saturday October 0th 08 * hajakbar@grad.kashanu.ac.r mohammad@kashanu.ac.r. (shunt-apf) :... PSIM. : * 3... Downloaded from energy.kashanu.ac.r
Aerodynamics & Aeroelasticity: Eigenvalue analysis
 Εθνικό Μετσόβιο Πολυτεχνείο Natonal Techncal Unversty of Athens Aerodynamcs & Aeroelastcty: Egenvalue analyss Σπύρος Βουτσινάς / Spyros Voutsnas Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Εθνικό Μετσόβιο Πολυτεχνείο Natonal Techncal Unversty of Athens Aerodynamcs & Aeroelastcty: Egenvalue analyss Σπύρος Βουτσινάς / Spyros Voutsnas Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
EQUIVALENT MODEL OF HVDC-VSC AND ITS HYBRID SIMULATION TECHNIQUE
 7 Vol. 7 No. 003 Power Sytem Technology Fe. 003 000-36730030-0004-05 T7. A 3007 EQIVALENT ODEL OF HVDC-VSC AND ITS HYBRID SILATION TECHNIQE WANG Guan, CAI Ye, ZHANG Gu-n, X Zheng Department of Electrcal
7 Vol. 7 No. 003 Power Sytem Technology Fe. 003 000-36730030-0004-05 T7. A 3007 EQIVALENT ODEL OF HVDC-VSC AND ITS HYBRID SILATION TECHNIQE WANG Guan, CAI Ye, ZHANG Gu-n, X Zheng Department of Electrcal
The following are appendices A, B1 and B2 of our paper, Integrated Process Modeling
 he followng ae appendes A, B1 and B2 of ou pape, Integated Poess Modelng and Podut Desgn of Bodesel Manufatung, that appeas n the Industal and Engneeng Chemsty Reseah, Deembe (2009). Appendx A. An Illustaton
he followng ae appendes A, B1 and B2 of ou pape, Integated Poess Modelng and Podut Desgn of Bodesel Manufatung, that appeas n the Industal and Engneeng Chemsty Reseah, Deembe (2009). Appendx A. An Illustaton
تحلیل پایداری سیستمهای سوئیچشوندۀ خطی گسستهزمان با در نظر گرفتن تاخیر زمانی و عدم قطعیت پارامتری
 I S I C E مجله کنترل ISSN 28-8345 جلد 9 شماره 4 زمستان 1394 صفحه 77-85 تحلیل پایداری سیستمهای سوئیچشوندۀ خطی گسستهزمان با در نظر گرفتن تاخیر زمانی و عدم قطعیت پارامتری Downloaded fom joc.kntu.ac. at 14:46
I S I C E مجله کنترل ISSN 28-8345 جلد 9 شماره 4 زمستان 1394 صفحه 77-85 تحلیل پایداری سیستمهای سوئیچشوندۀ خطی گسستهزمان با در نظر گرفتن تاخیر زمانی و عدم قطعیت پارامتری Downloaded fom joc.kntu.ac. at 14:46
 f RF f LO f RF ±f LO Ιδανικός μείκτης RF Είσοδος f RF f RF ± f LO IF Έξοδος f LO LO Είσοδος f RF f LO (ω RF t) (ω LO t) = 1 2 [(ω RF + ω LO )t + (ω RF ω LO )t] RF LO IF f RF ± f LO 0 180 +1 RF IF 1 LO
f RF f LO f RF ±f LO Ιδανικός μείκτης RF Είσοδος f RF f RF ± f LO IF Έξοδος f LO LO Είσοδος f RF f LO (ω RF t) (ω LO t) = 1 2 [(ω RF + ω LO )t + (ω RF ω LO )t] RF LO IF f RF ± f LO 0 180 +1 RF IF 1 LO
Κεφάλαιο 7. Σύνοψη Στο κεφάλαιο αυτό παρουσιάζονται βασικά μοντέλα πνευματικών ενεργοποιητών καθώς επίσης και βασικοί αλγόριθμοι ελέγχου τους.
 Κεφάλαιο 7 Σύνοψη Στο κεφάλαιο αυτό παρουσιάζονται βασικά μοντέλα πνευματικών ενεργοποιητών καθώς επίσης και βασικοί αλγόριθμοι ελέγχου τους. Προαπαιτούμενη γνώση Η προαπαιτούμενη γνώση για την κατανόηση
Κεφάλαιο 7 Σύνοψη Στο κεφάλαιο αυτό παρουσιάζονται βασικά μοντέλα πνευματικών ενεργοποιητών καθώς επίσης και βασικοί αλγόριθμοι ελέγχου τους. Προαπαιτούμενη γνώση Η προαπαιτούμενη γνώση για την κατανόηση
() min. xt δεν έχει μετασχηματισμό LAPLACE () () () Αν Λ= το σήμα ( ) Αν Λ, έστω σ. Το σύνολο μιγαδικών αριθμών. s Q το ολοκλήρωμα (1) υπάρχει.
 Έστω xt : Ο (αμφίπλευρος) μετασχηματισμός LAPLACE ορίζεται : X: L { xt} : X xt e dt = = μιγαδική συνάρτηση της μιγαδικής μεταβλητής = σ+ j Ο (μονόπλευρος) μετασχηματισμός LAPLACE ορίζεται : L { xt } :
Έστω xt : Ο (αμφίπλευρος) μετασχηματισμός LAPLACE ορίζεται : X: L { xt} : X xt e dt = = μιγαδική συνάρτηση της μιγαδικής μεταβλητής = σ+ j Ο (μονόπλευρος) μετασχηματισμός LAPLACE ορίζεται : L { xt } :
Approximate System Reliability Evaluation
 Appoximate Sytem Reliability Evaluation Up MTTF Down 0 MTBF MTTR () Time Fo many engineeing ytem component, MTTF MTBF i.e. failue ate, failue fequency, f Fequency, Duation and Pobability Indice: failue
Appoximate Sytem Reliability Evaluation Up MTTF Down 0 MTBF MTTR () Time Fo many engineeing ytem component, MTTF MTBF i.e. failue ate, failue fequency, f Fequency, Duation and Pobability Indice: failue
Parts Manual. Trio Mobile Surgery Platform. Model 1033
 Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
RMTP Journal of Software. Vol.13, No /2002/13(08) , )
 000-985/00/3(08)70-08 00 Joun of oftwe Vo3, No8 T,,, (, 00876) E-m: {b0073056,wdwng,chd}@bupteducn http://wwwbupteducn : T(ebe mutct tnpot potoco) (ep eve) T,T ;,T,,T : ; ; ; : T393 : A Intenet,, T ],
000-985/00/3(08)70-08 00 Joun of oftwe Vo3, No8 T,,, (, 00876) E-m: {b0073056,wdwng,chd}@bupteducn http://wwwbupteducn : T(ebe mutct tnpot potoco) (ep eve) T,T ;,T,,T : ; ; ; : T393 : A Intenet,, T ],
CS348B Lecture 10 Pat Hanrahan, Spring 2002
 Page 1 Reflecton Models I Today Types of eflecton models The BRDF and eflectance The eflecton equaton Ideal eflecton and efacton Fesnel effect Ideal dffuse Next lectue Glossy and specula eflecton models
Page 1 Reflecton Models I Today Types of eflecton models The BRDF and eflectance The eflecton equaton Ideal eflecton and efacton Fesnel effect Ideal dffuse Next lectue Glossy and specula eflecton models
IF(Ingerchange Format) [7] IF C-STAR(Consortium for speech translation advanced research ) [8] IF 2 IF
![IF(Ingerchange Format) [7] IF C-STAR(Consortium for speech translation advanced research ) [8] IF 2 IF IF(Ingerchange Format) [7] IF C-STAR(Consortium for speech translation advanced research ) [8] IF 2 IF](/thumbs/91/106522878.jpg) 100080 e-mal:{gdxe, cqzong, xubo}@nlpr.a.ac.cn tel:(010)82614468 IF 1 1 1 IF(Ingerchange Format) [7] IF C-STAR(Consortum for speech translaton advanced research ) [8] IF 2 IF 2 IF 69835003 60175012 [6][12]
100080 e-mal:{gdxe, cqzong, xubo}@nlpr.a.ac.cn tel:(010)82614468 IF 1 1 1 IF(Ingerchange Format) [7] IF C-STAR(Consortum for speech translaton advanced research ) [8] IF 2 IF 2 IF 69835003 60175012 [6][12]
ΜΕΘΟΔΟΙ ΟΙΚΟΝΟΜΙΚΗΣ ΑΠΟΤΙΜΗΣΗΣ ΣΧΕΔΙΩΝ ΣΥΝΕΧΟΥΣ ΔΕΙΓΜΑΤΟΛΗΨΙΑΣ
 Ελληνικό Στατιστικό Ινστιτούτο Πρακτικά 21 ου Πανελληνίου Συνεδρίου Στατιστικής (2008), σελ 307-314 ΜΕΘΟΔΟΙ ΟΙΚΟΝΟΜΙΚΗΣ ΑΠΟΤΙΜΗΣΗΣ ΣΧΕΔΙΩΝ ΣΥΝΕΧΟΥΣ ΔΕΙΓΜΑΤΟΛΗΨΙΑΣ Νίκος Φαρμάκης, Μαυρουδής Ελευθερίου Αριστοτέλειο
Ελληνικό Στατιστικό Ινστιτούτο Πρακτικά 21 ου Πανελληνίου Συνεδρίου Στατιστικής (2008), σελ 307-314 ΜΕΘΟΔΟΙ ΟΙΚΟΝΟΜΙΚΗΣ ΑΠΟΤΙΜΗΣΗΣ ΣΧΕΔΙΩΝ ΣΥΝΕΧΟΥΣ ΔΕΙΓΜΑΤΟΛΗΨΙΑΣ Νίκος Φαρμάκης, Μαυρουδής Ελευθερίου Αριστοτέλειο
ΔΗΜΟΤΙΚΕΣ ΕΚΛΟΓΕΣ 18/5/2014 ΑΚΥΡΑ
 ΔΗΜΟΤΙΚΕΣ ΕΚΛΟΓΕΣ 18/5/2014 ΑΚΥΡΑ ΑΔΑΜΗΣ Δ.Κ. / Τ.Κ. E.T. ΕΓΓ/ΝΟΙ ΨΗΦΙΣΑΝ ΕΓΚΥΡΑ ΓΙΟΒΑΣ ΙΩΑΝΝΗΣ ΛΕΥΚΑ ΠΑΝΑΓΙΩΤΗΣ ΜΑΝΤΑΣ ΠΑΝΑΓΙΩΤΗΣ ΔΑΛΙΑΝΗΣ ΓΕΩΡΓΙΟΣ ΑΣΤΡΟΣ 5 2.728 1.860 36 1.825 69 3,8% 152 8,3% 739 40,5%
ΔΗΜΟΤΙΚΕΣ ΕΚΛΟΓΕΣ 18/5/2014 ΑΚΥΡΑ ΑΔΑΜΗΣ Δ.Κ. / Τ.Κ. E.T. ΕΓΓ/ΝΟΙ ΨΗΦΙΣΑΝ ΕΓΚΥΡΑ ΓΙΟΒΑΣ ΙΩΑΝΝΗΣ ΛΕΥΚΑ ΠΑΝΑΓΙΩΤΗΣ ΜΑΝΤΑΣ ΠΑΝΑΓΙΩΤΗΣ ΔΑΛΙΑΝΗΣ ΓΕΩΡΓΙΟΣ ΑΣΤΡΟΣ 5 2.728 1.860 36 1.825 69 3,8% 152 8,3% 739 40,5%
Optimized Design of Fully Integrated VCO on Si Based Process
 LSI VCO Optimized Desin of Fully Interated VCO on Si Based Proess Nobuyuki Itoh Semiondutor Company, Toshiba Corporation 47-8585 -5-1 -5-1, Kasama, Sakae-ku, Yokohama, 47-8585, Japan Tel: +81-45-890-41,
LSI VCO Optimized Desin of Fully Interated VCO on Si Based Proess Nobuyuki Itoh Semiondutor Company, Toshiba Corporation 47-8585 -5-1 -5-1, Kasama, Sakae-ku, Yokohama, 47-8585, Japan Tel: +81-45-890-41,
Theoretical Competition: 12 July 2011 Question 1 Page 1 of 2
 Theoetical Competition: July Question Page of. Ένα πρόβλημα τριών σωμάτων και το LISA μ M O m EIKONA Ομοεπίπεδες τροχιές των τριών σωμάτων. Δύο μάζες Μ και m κινούνται σε κυκλικές τροχιές με ακτίνες και,
Theoetical Competition: July Question Page of. Ένα πρόβλημα τριών σωμάτων και το LISA μ M O m EIKONA Ομοεπίπεδες τροχιές των τριών σωμάτων. Δύο μάζες Μ και m κινούνται σε κυκλικές τροχιές με ακτίνες και,
e.mail:
 ΙΑΝΥΣΜΑΤΙΚΟΣ ΕΛΕΓΧΟΣ ΤΡΙΦΑΣΙΚΩΝ ΑΣΥΓΧΡΟΝΩΝ ΚΙΝΗΤΗΡΩΝ Ε. Μητρονίκας, Λέκτορας Πανεπιστήµιο Πατρών Τµήµα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Εργαστήριο Ηλεκτροµηχανικής Μετατροπής Ενέργειας
ΙΑΝΥΣΜΑΤΙΚΟΣ ΕΛΕΓΧΟΣ ΤΡΙΦΑΣΙΚΩΝ ΑΣΥΓΧΡΟΝΩΝ ΚΙΝΗΤΗΡΩΝ Ε. Μητρονίκας, Λέκτορας Πανεπιστήµιο Πατρών Τµήµα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Εργαστήριο Ηλεκτροµηχανικής Μετατροπής Ενέργειας
(2), ,. 1).
 178/1 L I ( ) ( ) 2019/1111 25 2019,, ( ), 81 3,,, ( 1 ), ( 2 ),, : (1) 15 2014 ( ). 2201/2003. ( 3 ) ( ). 2201/2003,..,,. (2),..,,, 25 1980, («1980»),.,,. ( 1 ) 18 2018 ( C 458 19.12.2018,. 499) 14 2019
178/1 L I ( ) ( ) 2019/1111 25 2019,, ( ), 81 3,,, ( 1 ), ( 2 ),, : (1) 15 2014 ( ). 2201/2003. ( 3 ) ( ). 2201/2003,..,,. (2),..,,, 25 1980, («1980»),.,,. ( 1 ) 18 2018 ( C 458 19.12.2018,. 499) 14 2019
ΜΟΝΤΕΡΝΑ ΘΕΩΡΙΑ ΕΛΕΓΧΟΥ ΜΑΘΗΜΑΤΙΚΗ ΘΕΩΡΙΑΣ ΣΥΣΤΗΜΑΤΩΝ ΙΙ Τμήμα Μαθηματικών - Τομέας Υπολογιστών & Αριθμητικής Ανάλυσης Εξετάσεις Σεπτεμβρίου 2016
 ΜΟΝΤΕΡΝΑ ΘΕΩΡΙΑ ΕΛΕΓΧΟΥ ΜΑΘΗΜΑΤΙΚΗ ΘΕΩΡΙΑΣ ΣΥΣΤΗΜΑΤΩΝ ΙΙ Τμήμα Μαθηματικών - Τομέας Υπολογιστών & Αριθμητικής Ανάλυσης Εξετάσεις Σεπτεμβρίου 016 Θέμα 1. α) (Μον.1.5) Αποδείξτε ότι αν το σύστημα στο χώρο
ΜΟΝΤΕΡΝΑ ΘΕΩΡΙΑ ΕΛΕΓΧΟΥ ΜΑΘΗΜΑΤΙΚΗ ΘΕΩΡΙΑΣ ΣΥΣΤΗΜΑΤΩΝ ΙΙ Τμήμα Μαθηματικών - Τομέας Υπολογιστών & Αριθμητικής Ανάλυσης Εξετάσεις Σεπτεμβρίου 016 Θέμα 1. α) (Μον.1.5) Αποδείξτε ότι αν το σύστημα στο χώρο
Novel Ensemble Analytic Discrete Framelet Expansion for Machinery Fault Diagnosis 1
 50 17 2014 9 OURNAL OF MECHANICAL ENGINEERING Vol.50 No.17 Sep. 2014 DOI10.3901/ME.2014.17.077 * 1 2 2 2, 3 (1. 361005 2. 710049 3. 710049) -- () - TH17 Novel Ensemble Analytc Dscrete Framelet Expanson
50 17 2014 9 OURNAL OF MECHANICAL ENGINEERING Vol.50 No.17 Sep. 2014 DOI10.3901/ME.2014.17.077 * 1 2 2 2, 3 (1. 361005 2. 710049 3. 710049) -- () - TH17 Novel Ensemble Analytc Dscrete Framelet Expanson
r r t r r t t r t P s r t r P s r s r r rs tr t r r t s ss r P s s t r t t tr r r t t r t r r t t s r t rr t Ü rs t 3 r r r 3 rträ 3 röÿ r t
 r t t r t ts r3 s r r t r r t t r t P s r t r P s r s r P s r 1 s r rs tr t r r t s ss r P s s t r t t tr r 2s s r t t r t r r t t s r t rr t Ü rs t 3 r t r 3 s3 Ü rs t 3 r r r 3 rträ 3 röÿ r t r r r rs
r t t r t ts r3 s r r t r r t t r t P s r t r P s r s r P s r 1 s r rs tr t r r t s ss r P s s t r t t tr r 2s s r t t r t r r t t s r t rr t Ü rs t 3 r t r 3 s3 Ü rs t 3 r r r 3 rträ 3 röÿ r t r r r rs
Reflection Models. Reflection Models
 Reflecon Models Today Types of eflecon models The BRDF and eflecance The eflecon equaon Ideal eflecon and efacon Fesnel effec Ideal dffuse Thusday Glossy and specula eflecon models Rough sufaces and mcofaces
Reflecon Models Today Types of eflecon models The BRDF and eflecance The eflecon equaon Ideal eflecon and efacon Fesnel effec Ideal dffuse Thusday Glossy and specula eflecon models Rough sufaces and mcofaces
5 Haar, R. Haar,. Antonads 994, Dogaru & Carn Kerkyacharan & Pcard 996. : Haar. Haar, y r x f rt xβ r + ε r x β r + mr k β r k ψ kx + ε r x, r,.. x [,
 4 Chnese Journal of Appled Probablty and Statstcs Vol.6 No. Apr. Haar,, 6,, 34 E-,,, 34 Haar.., D-, A- Q-,. :, Haar,. : O.6..,..,.. Herzberg & Traves 994, Oyet & Wens, Oyet Tan & Herzberg 6, 7. Haar Haar.,
4 Chnese Journal of Appled Probablty and Statstcs Vol.6 No. Apr. Haar,, 6,, 34 E-,,, 34 Haar.., D-, A- Q-,. :, Haar,. : O.6..,..,.. Herzberg & Traves 994, Oyet & Wens, Oyet Tan & Herzberg 6, 7. Haar Haar.,
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n 1
 d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n1 x dx = 1 2 b2 1 2 a2 a b b x 2 dx = 1 a 3 b3 1 3 a3 b x n dx = 1 a n +1 bn +1 1 n +1 an +1 d dx d dx f (x) = 0 f (ax) = a f (ax) lim d dx f (ax) = lim 0 =
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n1 x dx = 1 2 b2 1 2 a2 a b b x 2 dx = 1 a 3 b3 1 3 a3 b x n dx = 1 a n +1 bn +1 1 n +1 an +1 d dx d dx f (x) = 0 f (ax) = a f (ax) lim d dx f (ax) = lim 0 =
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών. HY-215: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 2013 ιδάσκων : Π.
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-25: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 203 ιδάσκων : Π. Τσακαλίδης Λύσεις Πέµπτης Σειράς Ασκήσεων Ηµεροµηνία Ανάθεσης : 23/05/203 Ηµεροµηνία
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-25: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 203 ιδάσκων : Π. Τσακαλίδης Λύσεις Πέµπτης Σειράς Ασκήσεων Ηµεροµηνία Ανάθεσης : 23/05/203 Ηµεροµηνία
ΚΑΘΟΔΗΓΗΣΗ ΚΙΝΟΥΜΕΝΟΥ ΡΟΜΠΟΤ ΜΕ ΤΗΝ ΧΡΗΣΗ ΑΣΥΡΜΑΤΟΥ ΔΙΚΤΥΟΥ ΑΙΣΘΗΤΗΡΩΝ
 ΚΑΘΟΔΗΓΗΣΗ ΚΙΝΟΥΜΕΝΟΥ ΡΟΜΠΟΤ ΜΕ ΤΗΝ ΧΡΗΣΗ ΑΣΥΡΜΑΤΟΥ ΔΙΚΤΥΟΥ ΑΙΣΘΗΤΗΡΩΝ ΠΑΝΟΣ ΜΑΡΑΝΤΟΣ, ΙΩΑΝΝΗΣ ΚΩΒΑΙΟΣ, ΙΩΑΝΝΗΣ ΣΤΕΡΓΙΟΠΟΥΛΟΣ, ΑΘΑΝΑΣΙΑ ΠΑΝΟΥΣΟΠΟΥΛΟΥ και ΑΝΤΩΝΙΟΣ ΤΖΕΣ 1 Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων
ΚΑΘΟΔΗΓΗΣΗ ΚΙΝΟΥΜΕΝΟΥ ΡΟΜΠΟΤ ΜΕ ΤΗΝ ΧΡΗΣΗ ΑΣΥΡΜΑΤΟΥ ΔΙΚΤΥΟΥ ΑΙΣΘΗΤΗΡΩΝ ΠΑΝΟΣ ΜΑΡΑΝΤΟΣ, ΙΩΑΝΝΗΣ ΚΩΒΑΙΟΣ, ΙΩΑΝΝΗΣ ΣΤΕΡΓΙΟΠΟΥΛΟΣ, ΑΘΑΝΑΣΙΑ ΠΑΝΟΥΣΟΠΟΥΛΟΥ και ΑΝΤΩΝΙΟΣ ΤΖΕΣ 1 Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων
Η Πολυεδρική Προσέγγιση στην Ανάλυση και Σύνθεση Συστηµάτων Ελέγχου. Εργαστήριο Συστηµάτων Αυτοµάτου Ελέγχου
 Η Πολυεδρική Προσέγγιση στην Ανάλυση και Σύνθεση Συστηµάτων Ελέγχου Εργαστήριο Συστηµάτων Αυτοµάτου Ελέγχου Η Τετραγωνική Προσέγγιση Ευκλείδια Απόσταση (Eucldean dstance) Ευκλείδια νορµ (Eucldean norm)
Η Πολυεδρική Προσέγγιση στην Ανάλυση και Σύνθεση Συστηµάτων Ελέγχου Εργαστήριο Συστηµάτων Αυτοµάτου Ελέγχου Η Τετραγωνική Προσέγγιση Ευκλείδια Απόσταση (Eucldean dstance) Ευκλείδια νορµ (Eucldean norm)
Supplementary material for: Efficient moment calculations for variance components in large unbalanced crossed random effects models
 Supplementay mateal fo: Effcent moment calculaton fo vaance component n lage unbalanced coed andom effect model Katelyn Gao Stanfod Unvety At B Owen Stanfod Unvety Augut 015 Abtact Th a upplementay document
Supplementay mateal fo: Effcent moment calculaton fo vaance component n lage unbalanced coed andom effect model Katelyn Gao Stanfod Unvety At B Owen Stanfod Unvety Augut 015 Abtact Th a upplementay document
AD8114/AD8115* AD8114/AD8115 SER/PAR D0 D1 D2 D3 D4 A0 A1 A2 A3 CLK DATA OUT DATA IN UPDATE RESET 16 OUTPUT G = +1, G = +2
 AD4/AD5* DATA IN UPDATE CE RESET SER/PAR AD4/AD5 D D D2 D3 D4 256 OUTPUT G = +, G = +2 A A A2 A3 DATA OUT AD4/AD5 AD4/AD5 t t 3 t 2 t 4 DATA IN OUT7 (D4) OUT7 (D3) OUT (D) t 5 t 6 = UPDATE = t 7 DATA OUT
AD4/AD5* DATA IN UPDATE CE RESET SER/PAR AD4/AD5 D D D2 D3 D4 256 OUTPUT G = +, G = +2 A A A2 A3 DATA OUT AD4/AD5 AD4/AD5 t t 3 t 2 t 4 DATA IN OUT7 (D4) OUT7 (D3) OUT (D) t 5 t 6 = UPDATE = t 7 DATA OUT
ΚΕΦΑΛΑΙΟ 2. Περιγραφή της Κίνησης. 2.1 Κίνηση στο Επίπεδο
 ΚΕΦΑΛΑΙΟ 2 Περιγραφή της Κίνησης Στο κεφάλαιο αυτό θα δείξουμε πώς να προγραμματίσουμε απλές εξισώσεις τροχιάς ενός σωματιδίου και πώς να κάνουμε βασική ανάλυση των αριθμητικών αποτελεσμάτων. Χρησιμοποιούμε
ΚΕΦΑΛΑΙΟ 2 Περιγραφή της Κίνησης Στο κεφάλαιο αυτό θα δείξουμε πώς να προγραμματίσουμε απλές εξισώσεις τροχιάς ενός σωματιδίου και πώς να κάνουμε βασική ανάλυση των αριθμητικών αποτελεσμάτων. Χρησιμοποιούμε
Design and Simulation of a Wilkinson Power Divider with High Isolation for Tri-Band Operation Using PSO Algorithm
 394 - - - PSO () () () - () 394/4/ : 394//7 : :.. PSO. WiMAX WLAN UMTS GSM 900 GSM 800 GPS GSM 900 GSM 850. CST-MW 03...PSO : Design and Simulation of a Wilkinson Power Divider with High Isolation for
394 - - - PSO () () () - () 394/4/ : 394//7 : :.. PSO. WiMAX WLAN UMTS GSM 900 GSM 800 GPS GSM 900 GSM 850. CST-MW 03...PSO : Design and Simulation of a Wilkinson Power Divider with High Isolation for
A Method of Trajectory Tracking Control for Nonminimum Phase Continuous Time Systems
 IIC-11-8 A Method of Trajectory Tracking Control for Nonminimum Phase Continuous Time Systems Takayuki Shiraishi, iroshi Fujimoto (The University of Tokyo) Abstract The purpose of this paper is achievement
IIC-11-8 A Method of Trajectory Tracking Control for Nonminimum Phase Continuous Time Systems Takayuki Shiraishi, iroshi Fujimoto (The University of Tokyo) Abstract The purpose of this paper is achievement
Η γεωργία στην ΕΕ απαντώντας στην πρόκληση των κλιματικών αλλαγών
 Ευρωπαϊκή Επιτροπή Γε ν ι κ ή Δ ι ε ύ θ υ ν σ η Γε ω ρ γ ί α ς κ α ι Αγ ρ ο τ ι κ ή ς Α ν ά π τ υ ξ η ς Ευρωπαϊκή Επιτροπή Γεωργία και αγροτική ανάπτυξη Για περισσότερες πληροφορίες 200 Rue de la Loi,
Ευρωπαϊκή Επιτροπή Γε ν ι κ ή Δ ι ε ύ θ υ ν σ η Γε ω ρ γ ί α ς κ α ι Αγ ρ ο τ ι κ ή ς Α ν ά π τ υ ξ η ς Ευρωπαϊκή Επιτροπή Γεωργία και αγροτική ανάπτυξη Για περισσότερες πληροφορίες 200 Rue de la Loi,
J. of Math. (PRC) Banach, , X = N(T ) R(T + ), Y = R(T ) N(T + ). Vol. 37 ( 2017 ) No. 5
 Vol. 37 ( 2017 ) No. 5 J. of Math. (PRC) 1,2, 1, 1 (1., 225002) (2., 225009) :. I +AT +, T + = T + (I +AT + ) 1, T +. Banach Hilbert Moore-Penrose.. : ; ; Moore-Penrose ; ; MR(2010) : 47L05; 46A32 : O177.2
Vol. 37 ( 2017 ) No. 5 J. of Math. (PRC) 1,2, 1, 1 (1., 225002) (2., 225009) :. I +AT +, T + = T + (I +AT + ) 1, T +. Banach Hilbert Moore-Penrose.. : ; ; Moore-Penrose ; ; MR(2010) : 47L05; 46A32 : O177.2
Θεωρία Βέλτιστου Ελέγχου Ασκήσεις
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Θεωρία Βέλτιστου Ελέγχου Νικόλαος Καραμπετάκης Τμήμα Α.Π.Θ. Θεσσαλονίκη, Οκτώβριος 3 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Cretive
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Θεωρία Βέλτιστου Ελέγχου Νικόλαος Καραμπετάκης Τμήμα Α.Π.Θ. Θεσσαλονίκη, Οκτώβριος 3 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Cretive
Μοντέρνα Θεωρία Ελέγχου
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Μαθηματικά Μοντέλα Συστημάτων Νίκος Καραμπετάκης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Μαθηματικά Μοντέλα Συστημάτων Νίκος Καραμπετάκης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ωλi τ~γ ο (ανεξάρτητα από το πόσο μεγάλο είναι το γ ο ) [Μη ρεαλιστικό; ισχύει μόνο για μικρά γ ο ]
![ωλi τ~γ ο (ανεξάρτητα από το πόσο μεγάλο είναι το γ ο ) [Μη ρεαλιστικό; ισχύει μόνο για μικρά γ ο ] ωλi τ~γ ο (ανεξάρτητα από το πόσο μεγάλο είναι το γ ο ) [Μη ρεαλιστικό; ισχύει μόνο για μικρά γ ο ]](/thumbs/53/31123289.jpg) ΓΡΑΜΜΙΚΗ ΙΞΩΔΟΕΛΑΣΤΙΚΟΤΗΤΑ 1. Κατανομή χρόνων χαλάρωσης Το φάσμα Rouse : To μοντέλο δίνει φάσμα χρόνων λ, και μέτρων G =G=vkT για όλα τα. Φάσμα χρόνων χαλάρωσης (ελέγξιμο πειραματικά). Πείραμα: Small amptude
ΓΡΑΜΜΙΚΗ ΙΞΩΔΟΕΛΑΣΤΙΚΟΤΗΤΑ 1. Κατανομή χρόνων χαλάρωσης Το φάσμα Rouse : To μοντέλο δίνει φάσμα χρόνων λ, και μέτρων G =G=vkT για όλα τα. Φάσμα χρόνων χαλάρωσης (ελέγξιμο πειραματικά). Πείραμα: Small amptude
Design and Fabrication of Water Heater with Electromagnetic Induction Heating
 U Kamphaengsean Acad. J. Vol. 7, No. 2, 2009, Pages 48-60 ก 7 2 2552 ก ก กก ก Design and Fabrication of Water Heater with Electromagnetic Induction Heating 1* Geerapong Srivichai 1* ABSTRACT The purpose
U Kamphaengsean Acad. J. Vol. 7, No. 2, 2009, Pages 48-60 ก 7 2 2552 ก ก กก ก Design and Fabrication of Water Heater with Electromagnetic Induction Heating 1* Geerapong Srivichai 1* ABSTRACT The purpose
apj1 SSGA* hapla P6 _1G hao1 1Lh_PSu AL..AhAo1 *PJ"AL hp_a*a
 n n 1/2 n (n 1) 0/1 l 2 E x X X x X E x X g(x) := 1 g(x). X f : X C L p f p := (E x X f(x) p ) 1/p f,g := E x X f(x)g(x) x X X X X := {f : X [0, ) : f 1 =1}. X µ A A X x X µ A (x) :=α 1 1 A (x) 1 A A α
n n 1/2 n (n 1) 0/1 l 2 E x X X x X E x X g(x) := 1 g(x). X f : X C L p f p := (E x X f(x) p ) 1/p f,g := E x X f(x)g(x) x X X X X := {f : X [0, ) : f 1 =1}. X µ A A X x X µ A (x) :=α 1 1 A (x) 1 A A α
Assessment of otoacoustic emission probe fit at the workfloor
 Assessment of otoacoustic emission probe fit at the workfloor t s st tt r st s s r r t rs t2 t P t rs str t t r 1 t s ér r tr st tr r2 t r r t s t t t r t s r ss r rr t 2 s r r 1 s r r t s s s r t s t
Assessment of otoacoustic emission probe fit at the workfloor t s st tt r st s s r r t rs t2 t P t rs str t t r 1 t s ér r tr st tr r2 t r r t s t t t r t s r ss r rr t 2 s r r 1 s r r t s s s r t s t
Physics 401 Final Exam Cheat Sheet, 17 April t = 0 = 1 c 2 ε 0. = 4π 10 7 c = SI (mks) units. = SI (mks) units H + M
 Maxwell' s Equations in vauum E ρ ε Physis 4 Final Exam Cheat Sheet, 7 Apil E B t B Loent Foe Law: F q E + v B B µ J + µ ε E t Consevation of hage: J + ρ t µ ε ε 8.85 µ 4π 7 3. 8 SI ms) units q eleton.6
Maxwell' s Equations in vauum E ρ ε Physis 4 Final Exam Cheat Sheet, 7 Apil E B t B Loent Foe Law: F q E + v B B µ J + µ ε E t Consevation of hage: J + ρ t µ ε ε 8.85 µ 4π 7 3. 8 SI ms) units q eleton.6
A Determination Method of Diffusion-Parameter Values in the Ion-Exchange Optical Waveguides in Soda-Lime glass Made by Diluted AgNO 3 with NaNO 3
 大阪電気通信大学研究論集 ( 自然科学編 ) 第 51 号 A Determination Method of Diffusion-Parameter Values in the Ion-Exchange Optical Waveguides in Soda-Lime glass Made by Diluted AgNO 3 with NaNO 3 Takuya IWATA and Kiyoshi
大阪電気通信大学研究論集 ( 自然科学編 ) 第 51 号 A Determination Method of Diffusion-Parameter Values in the Ion-Exchange Optical Waveguides in Soda-Lime glass Made by Diluted AgNO 3 with NaNO 3 Takuya IWATA and Kiyoshi
12/3/2008. Χρωµατογραφία µοριακής διήθησης
 Χρωµατογραφία µοριακής διήθησης Χρωµατογραφία µοριακής διήθησης To υλικό χρωµατογραφίας που χρησιµοποιείται αποτελείται από πορώδη σφαιρίδια ενός πολυµερούς υλικού όπως cross-linked πολυδεξτράνες και crosslinked
Χρωµατογραφία µοριακής διήθησης Χρωµατογραφία µοριακής διήθησης To υλικό χρωµατογραφίας που χρησιµοποιείται αποτελείται από πορώδη σφαιρίδια ενός πολυµερούς υλικού όπως cross-linked πολυδεξτράνες και crosslinked
( ) ( ) ( ) ( ) ( ) λ = 1 + t t. θ = t ε t. Continuum Mechanics. Chapter 1. Description of Motion dt t. Chapter 2. Deformation and Strain
 Continm Mechanics. Official Fom Chapte. Desciption of Motion χ (,) t χ (,) t (,) t χ (,) t t Chapte. Defomation an Stain s S X E X e i ij j i ij j F X X U F J T T T U U i j Uk U k E ( F F ) ( J J J J)
Continm Mechanics. Official Fom Chapte. Desciption of Motion χ (,) t χ (,) t (,) t χ (,) t t Chapte. Defomation an Stain s S X E X e i ij j i ij j F X X U F J T T T U U i j Uk U k E ( F F ) ( J J J J)
( )( ) ( ) ( )( ) ( )( ) β = Chapter 5 Exercise Problems EX α So 49 β 199 EX EX EX5.4 EX5.5. (a)
 hapter 5 xercise Problems X5. α β α 0.980 For α 0.980, β 49 0.980 0.995 For α 0.995, β 99 0.995 So 49 β 99 X5. O 00 O or n 3 O 40.5 β 0 X5.3 6.5 μ A 00 β ( 0)( 6.5 μa) 8 ma 5 ( 8)( 4 ) or.88 P on + 0.0065
hapter 5 xercise Problems X5. α β α 0.980 For α 0.980, β 49 0.980 0.995 For α 0.995, β 99 0.995 So 49 β 99 X5. O 00 O or n 3 O 40.5 β 0 X5.3 6.5 μ A 00 β ( 0)( 6.5 μa) 8 ma 5 ( 8)( 4 ) or.88 P on + 0.0065
 y(t) S x(t) S dy dx E, E E T1 T2 T1 T2 1 T 1 T 2 2 T 2 1 T 2 2 3 T 3 1 T 3 2... V o R R R T V CC P F A P g h V ext V sin 2 S f S t V 1 V 2 V out sin 2 f S t x 1 F k q K x q K k F d F x d V
y(t) S x(t) S dy dx E, E E T1 T2 T1 T2 1 T 1 T 2 2 T 2 1 T 2 2 3 T 3 1 T 3 2... V o R R R T V CC P F A P g h V ext V sin 2 S f S t V 1 V 2 V out sin 2 f S t x 1 F k q K x q K k F d F x d V
Ο Γραμμικός Τετραγωνικός Ρυθμιστής: Ευρεση Νόμου Ελέγχου
 Ο Γραμμικός Τετραγωνικός Ρυθμιστής: Ευρεση Νόμου Ελέγχου Για την ανεύρεση της µορφής των λύσεων στρεφόµαστε προς τις αναγκαίες συνθήκες, αρχικά στις Εξισώσεις Euler-Lagrange: Τ Τ Τ! f d! f = 0 t t0, t
Ο Γραμμικός Τετραγωνικός Ρυθμιστής: Ευρεση Νόμου Ελέγχου Για την ανεύρεση της µορφής των λύσεων στρεφόµαστε προς τις αναγκαίες συνθήκες, αρχικά στις Εξισώσεις Euler-Lagrange: Τ Τ Τ! f d! f = 0 t t0, t
Vol. 37 No. 6 JOURNAL OF BEIJING UNIVERSITY OF TECHNOLOGY. Jun. 2011 70% . 2009-10-25.
 37 6 2011 6 Vol 37 No 6 JOURNAL OF BEIJING UNIVERSITY OF TECHNOLOGY Jun 2011 100124 2 BP BP BP U 491 A 0254-0037 2011 06-0882 - 06 1 70% BP 1 2 2 2 2009-10-25 50578003 2006BAG01A01 1984 6 883 2 1 3 3 5
37 6 2011 6 Vol 37 No 6 JOURNAL OF BEIJING UNIVERSITY OF TECHNOLOGY Jun 2011 100124 2 BP BP BP U 491 A 0254-0037 2011 06-0882 - 06 1 70% BP 1 2 2 2 2009-10-25 50578003 2006BAG01A01 1984 6 883 2 1 3 3 5
Some Theorems on Multiple. A-Function Transform
 Int. J. Contemp. Math. Scences, Vol. 7, 202, no. 20, 995-004 Some Theoems on Multple A-Functon Tansfom Pathma J SCSVMV Deemed Unvesty,Kanchpuam, Tamlnadu, Inda & Dept.of Mathematcs, Manpal Insttute of
Int. J. Contemp. Math. Scences, Vol. 7, 202, no. 20, 995-004 Some Theoems on Multple A-Functon Tansfom Pathma J SCSVMV Deemed Unvesty,Kanchpuam, Tamlnadu, Inda & Dept.of Mathematcs, Manpal Insttute of
Sampling Basics (1B) Young Won Lim 9/21/13
 Sampling Basics (1B) Copyright (c) 2009-2013 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any
Sampling Basics (1B) Copyright (c) 2009-2013 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any
= f(0) + f dt. = f. O 2 (x, u) x=(x 1,x 2,,x n ) T, f(x) =(f 1 (x), f 2 (x),, f n (x)) T. f x = A = f
 2 n dx (x)+g(x)u () x n u (x), g(x) x n () +2 -a -b -b -a 3 () x,u dx x () dx () + x x + g()u + O 2 (x, u) x x x + g()u + O 2 (x, u) (2) x O 2 (x, u) x u 2 x(x,x 2,,x n ) T, (x) ( (x), 2 (x),, n (x)) T
2 n dx (x)+g(x)u () x n u (x), g(x) x n () +2 -a -b -b -a 3 () x,u dx x () dx () + x x + g()u + O 2 (x, u) x x x + g()u + O 2 (x, u) (2) x O 2 (x, u) x u 2 x(x,x 2,,x n ) T, (x) ( (x), 2 (x),, n (x)) T
«Η ΑΤΜΟΣΦΑΙΡΑ ΚΑΤΑΣΤΗΜΑΤΟΣ ΚΑΙ Η ΕΠΙΔΡΑΣΗ ΤΗΣ ΣΤΟΝ ΕΛΛΗΝΑ ΚΑΤΑΝΑΛΩΤΗ»
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗ ΔΙΟΙΚΗΣΗ ΕΠΙΧΕΙΡΗΣΕΩΝ (M.B.A) ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «Η ΑΤΜΟΣΦΑΙΡΑ ΚΑΤΑΣΤΗΜΑΤΟΣ ΚΑΙ Η ΕΠΙΔΡΑΣΗ ΤΗΣ ΣΤΟΝ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗ ΔΙΟΙΚΗΣΗ ΕΠΙΧΕΙΡΗΣΕΩΝ (M.B.A) ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «Η ΑΤΜΟΣΦΑΙΡΑ ΚΑΤΑΣΤΗΜΑΤΟΣ ΚΑΙ Η ΕΠΙΔΡΑΣΗ ΤΗΣ ΣΤΟΝ
ELE 3310 Tutorial 11. Reflection of plane waves Wave impedance of the total field
 L 0 Tuto Rfcton of pn wvs Wv mpdnc of th tot fd Rfcton of M wvs Rfcton tks pc whn n M wv hts on bound. Pt of th wv gts fctd, nd pt of t gts tnsmttd. Popgton dctons nd mptuds of th fctd nd tnsmttd wvs dpnd
L 0 Tuto Rfcton of pn wvs Wv mpdnc of th tot fd Rfcton of M wvs Rfcton tks pc whn n M wv hts on bound. Pt of th wv gts fctd, nd pt of t gts tnsmttd. Popgton dctons nd mptuds of th fctd nd tnsmttd wvs dpnd
ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΣΥΣΤΗΜΑΤΩΝ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ Ι
 ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΣΥΣΤΗΜΑΤΩΝ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ Ι ΕΛΕΓΧΟΣ ΘΕΣΗΣ/ΤΑΧΥΤΗΤΑΣ ΣΕΡΒΟΚΙΝΗΤΗΡΑ DC 1. ΠΕΡΙΓΡΑΦΗ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΙΑΤΑΞΗΣ Τα βασικά µέρη της εργαστηριακής διάταξης (υλικό και λογισµικό) είναι κατασκευασµένα
ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΣΥΣΤΗΜΑΤΩΝ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ Ι ΕΛΕΓΧΟΣ ΘΕΣΗΣ/ΤΑΧΥΤΗΤΑΣ ΣΕΡΒΟΚΙΝΗΤΗΡΑ DC 1. ΠΕΡΙΓΡΑΦΗ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΙΑΤΑΞΗΣ Τα βασικά µέρη της εργαστηριακής διάταξης (υλικό και λογισµικό) είναι κατασκευασµένα
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών. ΗΥ-570: Στατιστική Επεξεργασία Σήµατος. ιδάσκων : Α. Μουχτάρης. εύτερη Σειρά Ασκήσεων.
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Αυτόματος Έλεγχος. Ενότητα 4 η : Πρότυπα μεταβλητών κατάστασης. Παναγιώτης Σεφερλής. Εργαστήριο Δυναμικής Μηχανών Τμήμα Μηχανολόγων Μηχανικών
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 4 η : Πρότυπα μεταβλητών κατάστασης Παναγιώτης Σεφερλής Εργαστήριο Δυναμικής Μηχανών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 4 η : Πρότυπα μεταβλητών κατάστασης Παναγιώτης Σεφερλής Εργαστήριο Δυναμικής Μηχανών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Laplace s Equation in Spherical Polar Coördinates
 Laplace s Equation in Spheical Pola Coödinates C. W. David Dated: Januay 3, 001 We stat with the pimitive definitions I. x = sin θ cos φ y = sin θ sin φ z = cos θ thei inveses = x y z θ = cos 1 z = z cos1
Laplace s Equation in Spheical Pola Coödinates C. W. David Dated: Januay 3, 001 We stat with the pimitive definitions I. x = sin θ cos φ y = sin θ sin φ z = cos θ thei inveses = x y z θ = cos 1 z = z cos1
STEADY, INVISCID ( potential flow, irrotational) INCOMPRESSIBLE + V Φ + i x. Ψ y = Φ. and. Ψ x
 STEADY, INVISCID ( potential flow, iotational) INCOMPRESSIBLE constant Benolli's eqation along a steamline, EQATION MOMENTM constant is a steamline the Steam Fnction is sbsititing into the continit eqation,
STEADY, INVISCID ( potential flow, iotational) INCOMPRESSIBLE constant Benolli's eqation along a steamline, EQATION MOMENTM constant is a steamline the Steam Fnction is sbsititing into the continit eqation,
Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών. Διάλεξη 9
 Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Τομέας Συστημάτων και Αυτομάτου Ελέγχου ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΕΛΕΓΧΟΣ Διάλεξη 9 Πάτρα 2008 Ρύθμιση ελαχίστης διασποράς Η στρατηγική
Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Τομέας Συστημάτων και Αυτομάτου Ελέγχου ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΕΛΕΓΧΟΣ Διάλεξη 9 Πάτρα 2008 Ρύθμιση ελαχίστης διασποράς Η στρατηγική
Power allocation under per-antenna power constraints in multiuser MIMO systems
 33 0 Vol.33 No. 0 0 0 Journal on Councatons October 0 do:0.3969/.ssn.000-436x.0.0.009 IO 009 IO IO N94 A 000-436X(0)0-007-06 Power allocaton under er-antenna ower constrants n ultuser IO systes HAN Sheng-qan,
33 0 Vol.33 No. 0 0 0 Journal on Councatons October 0 do:0.3969/.ssn.000-436x.0.0.009 IO 009 IO IO N94 A 000-436X(0)0-007-06 Power allocaton under er-antenna ower constrants n ultuser IO systes HAN Sheng-qan,
Lecture 21: Scattering and FGR
 ECE-656: Fall 009 Lecture : Scattering and FGR Professor Mark Lundstrom Electrical and Computer Engineering Purdue University, West Lafayette, IN USA Review: characteristic times τ ( p), (, ) == S p p
ECE-656: Fall 009 Lecture : Scattering and FGR Professor Mark Lundstrom Electrical and Computer Engineering Purdue University, West Lafayette, IN USA Review: characteristic times τ ( p), (, ) == S p p
ME 365: SYSTEMS, MEASUREMENTS, AND CONTROL (SMAC) I
 ME 365: SYSTEMS, MEASUREMENTS, AND CONTROL SMAC) I Dynamicresponseof 2 nd ordersystem Prof.SongZhangMEG088) Solutions to ODEs Forann@thorderLTIsystem a n yn) + a n 1 y n 1) ++ a 1 "y + a 0 y = b m u m)
ME 365: SYSTEMS, MEASUREMENTS, AND CONTROL SMAC) I Dynamicresponseof 2 nd ordersystem Prof.SongZhangMEG088) Solutions to ODEs Forann@thorderLTIsystem a n yn) + a n 1 y n 1) ++ a 1 "y + a 0 y = b m u m)
ΜΕΛΕΤΗ ΤΗΣ ΥΝΑΤΟΤΗΤΑΣ ΑΞΙΟΠΟΙΗΣΗΣ ΤΟΥ ΓΕΩΘΕΡΜΙΚΟΥ ΠΕ ΙΟΥ ΘΕΡΜΩΝ ΝΙΓΡΙΤΑΣ (Ν. ΣΕΡΡΩΝ)
 ελτίο της Ελληνικής Γεωλογικής Εταιρίας τοµ. XXXVI, 2004 Πρακτικά 10 ου ιεθνούς Συνεδρίου, Θεσ/νίκη Απρίλιος 2004 Bulletin of the Geological Society of Greece vol. XXXVI, 2004 Proceedings of the 10 th
ελτίο της Ελληνικής Γεωλογικής Εταιρίας τοµ. XXXVI, 2004 Πρακτικά 10 ου ιεθνούς Συνεδρίου, Θεσ/νίκη Απρίλιος 2004 Bulletin of the Geological Society of Greece vol. XXXVI, 2004 Proceedings of the 10 th
ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΑΛΑΜΑΤΑΣ ΣΧΟΛΗ: Σ.Δ.Ο ΤΜΗΜΑ:Δ.Μ.Υ.Π ΣΠΟΥΔΑΣΤΡΙΕΣ: ΧΑΝΤΖΙΑΡΑ ΒΑΙΑ- ΠΕΤΡΑΚΗ ΙΩΑΝΝΑ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΑΛΑΜΑΤΑΣ ΣΧΟΛΗ: Σ.Δ.Ο ΤΜΗΜΑ:Δ.Μ.Υ.Π ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ : Η ΚΑΤΑΘΛΙΨΗ ΣΠΟΥΔΑΣΤΡΙΕΣ: ΧΑΝΤΖΙΑΡΑ ΒΑΙΑ- ΠΕΤΡΑΚΗ ΙΩΑΝΝΑ ΥΠΕΥΘΥΝΗ ΚΑΘΗΓΗΤΡΙΑ: ΣΑΚΕΛΛΑΡΙΟΥ ΜΑΡΙΑ ΚΑΛΑΜΑΤΑ 2004
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΑΛΑΜΑΤΑΣ ΣΧΟΛΗ: Σ.Δ.Ο ΤΜΗΜΑ:Δ.Μ.Υ.Π ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ : Η ΚΑΤΑΘΛΙΨΗ ΣΠΟΥΔΑΣΤΡΙΕΣ: ΧΑΝΤΖΙΑΡΑ ΒΑΙΑ- ΠΕΤΡΑΚΗ ΙΩΑΝΝΑ ΥΠΕΥΘΥΝΗ ΚΑΘΗΓΗΤΡΙΑ: ΣΑΚΕΛΛΑΡΙΟΥ ΜΑΡΙΑ ΚΑΛΑΜΑΤΑ 2004
Research Article Dirac Equation under Scalar, Vector, and Tensor Cornell Interactions
 Hndaw Publhng Copoaton Advance n Hgh Enegy Phyc Volume 0, Atcle ID 70704, 7 page do:0.55/0/70704 Reeach Atcle Dac Equaton unde Scala, Vecto, and Teno Conell Inteacton H. Haanabad, E. Maghood, S. Zankama,
Hndaw Publhng Copoaton Advance n Hgh Enegy Phyc Volume 0, Atcle ID 70704, 7 page do:0.55/0/70704 Reeach Atcle Dac Equaton unde Scala, Vecto, and Teno Conell Inteacton H. Haanabad, E. Maghood, S. Zankama,
! "#$#% & '( K, X3/H }" I q +W R%2. >2" *+ + 1 LN6 H+ +ˆ,
 K+3 }K3" K+5 K, X3/H }" G +9), ;3 K, D 3 A +9),- ;3-SK, E E! +/ >HO A+< \ -S;? P A" ( 6M [ X& 5 +; \ ; D7 ] +; I$ X & >?# ; U (6 3 I q +W R% RBH % a >M 5 د! "#$#% & '( a.khan9@ms.tabrzu.a.r >" *+ + LN6
K+3 }K3" K+5 K, X3/H }" G +9), ;3 K, D 3 A +9),- ;3-SK, E E! +/ >HO A+< \ -S;? P A" ( 6M [ X& 5 +; \ ; D7 ] +; I$ X & >?# ; U (6 3 I q +W R% RBH % a >M 5 د! "#$#% & '( a.khan9@ms.tabrzu.a.r >" *+ + LN6
A Method for Determining Service Level of Road Network Based on Improved Capacity Model
 30 4 2013 4 Journal of Hghway and Transportaton Research and Development Vol. 30 No. 4 Apr. 2013 do10. 3969 /j. ssn. 1002-0268. 2013. 04. 018 1 1 2 1. 4000742. 201804 2 U491. 1 + 3 A 1002-0268 201304-0101
30 4 2013 4 Journal of Hghway and Transportaton Research and Development Vol. 30 No. 4 Apr. 2013 do10. 3969 /j. ssn. 1002-0268. 2013. 04. 018 1 1 2 1. 4000742. 201804 2 U491. 1 + 3 A 1002-0268 201304-0101
Q π (/) ^ ^ ^ Η φ. <f) c>o. ^ ο. ö ê ω Q. Ο. o 'c. _o _) o U 03. ,,, ω ^ ^ -g'^ ο 0) f ο. Ε. ιη ο Φ. ο 0) κ. ο 03.,Ο. g 2< οο"" ο φ.
 II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
Λ. Ζαχείλας. Επίκουρος Καθηγητής Εφαρμοσμένων Μαθηματικών Τμήμα Οικονομικών Επιστημών Πανεπιστήμιο Θεσσαλίας. Οικονομική Δυναμική 29/6/14
 1 Λ. Ζαχείλας Επίκουρος Καθηγητής Εφαρμοσμένων Μαθηματικών Τμήμα Οικονομικών Επιστημών Πανεπιστήμιο Θεσσαλίας Οικονομική Δυναμική 9 Συνεχή δυναμικά συστήματα Μέρος 1 ο Λουκάς Ζαχείλας Ορισμός Διαφορικής
1 Λ. Ζαχείλας Επίκουρος Καθηγητής Εφαρμοσμένων Μαθηματικών Τμήμα Οικονομικών Επιστημών Πανεπιστήμιο Θεσσαλίας Οικονομική Δυναμική 9 Συνεχή δυναμικά συστήματα Μέρος 1 ο Λουκάς Ζαχείλας Ορισμός Διαφορικής
Formulas of Agrawal s Fiber-Optic Communication Systems NA n 2 ; n n. NA( )=n1 a
 Formula o grawal Fiber-Oti Communiation Sytem Chater (ntroution) 8 / max m M / E nh N h M m 4 6.66. J e 9.6 / m log /mw SN / / /, NZ SN log / Z max N E Chater (Otial Fiber) Setion - (Geometrial Oti erition)
Formula o grawal Fiber-Oti Communiation Sytem Chater (ntroution) 8 / max m M / E nh N h M m 4 6.66. J e 9.6 / m log /mw SN / / /, NZ SN log / Z max N E Chater (Otial Fiber) Setion - (Geometrial Oti erition)
x(t) ax 1 (t) y(t) = 1 ax 1 (t) = (1/a)y 1(t) x(t t 0 ) y(t t 0 ) =
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-25: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 26-7 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λύσεις Τρίτης Σειράς Ασκήσεων Ηµεροµηνία Ανάθεσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-25: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 26-7 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λύσεις Τρίτης Σειράς Ασκήσεων Ηµεροµηνία Ανάθεσης
Vol. 31,No JOURNAL OF CHINA UNIVERSITY OF SCIENCE AND TECHNOLOGY Feb
 Ξ 31 Vol 31,No 1 2 0 0 1 2 JOURNAL OF CHINA UNIVERSITY OF SCIENCE AND TECHNOLOGY Feb 2 0 0 1 :025322778 (2001) 0120016205 (, 230026) : Q ( m 1, m 2,, m n ) k = m 1 + m 2 + + m n - n : Q ( m 1, m 2,, m
Ξ 31 Vol 31,No 1 2 0 0 1 2 JOURNAL OF CHINA UNIVERSITY OF SCIENCE AND TECHNOLOGY Feb 2 0 0 1 :025322778 (2001) 0120016205 (, 230026) : Q ( m 1, m 2,, m n ) k = m 1 + m 2 + + m n - n : Q ( m 1, m 2,, m
VBA Microsoft Excel. J. Comput. Chem. Jpn., Vol. 5, No. 1, pp (2006)
 J. Comput. Chem. Jpn., Vol. 5, No. 1, pp. 29 38 (2006) Microsoft Excel, 184-8588 2-24-16 e-mail: yosimura@cc.tuat.ac.jp (Received: July 28, 2005; Accepted for publication: October 24, 2005; Published on
J. Comput. Chem. Jpn., Vol. 5, No. 1, pp. 29 38 (2006) Microsoft Excel, 184-8588 2-24-16 e-mail: yosimura@cc.tuat.ac.jp (Received: July 28, 2005; Accepted for publication: October 24, 2005; Published on
Στοιχεία εισηγητή Ημερομηνία: 10/10/2017
 Θέμα μεταπτυχιακής διατριβής: Λογισμικά μελέτης και σχεδίασης ρομποτικών συστημάτων - συγκρτική μελέτη και εφαρμογές. 1) Μελέτη των δημοφιλών λογισμικών σχεδίασης ρομποτικών συστημάτων VREP και ROS. 2)
Θέμα μεταπτυχιακής διατριβής: Λογισμικά μελέτης και σχεδίασης ρομποτικών συστημάτων - συγκρτική μελέτη και εφαρμογές. 1) Μελέτη των δημοφιλών λογισμικών σχεδίασης ρομποτικών συστημάτων VREP και ROS. 2)
Exact linearization control scheme of DFIG
 3 29 EL ECR ICMACH IN ESANDCON ROL Vol3 No Jan. 29, 2,, (., 224; 2., 232) :,,,,,,,, :; ; ; ; : M35 : A : 7-449X (29) - 57-6 Exact linearization control cheme of DFIG GUO J ia2hu, 2, ZHANG Lu2hua, CA I
3 29 EL ECR ICMACH IN ESANDCON ROL Vol3 No Jan. 29, 2,, (., 224; 2., 232) :,,,,,,,, :; ; ; ; : M35 : A : 7-449X (29) - 57-6 Exact linearization control cheme of DFIG GUO J ia2hu, 2, ZHANG Lu2hua, CA I
Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté
 Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté Alexis Nuttin To cite this version: Alexis Nuttin. Physique des réacteurs
Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté Alexis Nuttin To cite this version: Alexis Nuttin. Physique des réacteurs
Noriyasu MASUMOTO, Waseda University, Okubo, Shinjuku, Tokyo , Japan Hiroshi YAMAKAWA, Waseda University
 A Study on Predctve Control Usng a Short-Term Predcton Method Based on Chaos Theory (Predctve Control of Nonlnear Systems Usng Plural Predcted Dsturbance Values) Noryasu MASUMOTO, Waseda Unversty, 3-4-1
A Study on Predctve Control Usng a Short-Term Predcton Method Based on Chaos Theory (Predctve Control of Nonlnear Systems Usng Plural Predcted Dsturbance Values) Noryasu MASUMOTO, Waseda Unversty, 3-4-1
Ταλαντώσεις 6.1 Απλή Αρµονική Ταλάντωση σε µία ιάσταση Ελατήριο σε οριζόντιο επίπεδο Σχήµα 6.1
 6 Ταλαντώσεις 6.1 Απλή Αρµονική Ταλάντωση σε µία ιάσταση 6.1.1 Ελατήριο σε οριζόντιο επίπεδο Υποθέτουµε ότι το ελατήριο έχει αρχικό µήκος µηδέν, ιδανικό ελατήριο. F=-kx x K M x Σχήµα 6.1 ιαστάσεις µεγεθών
6 Ταλαντώσεις 6.1 Απλή Αρµονική Ταλάντωση σε µία ιάσταση 6.1.1 Ελατήριο σε οριζόντιο επίπεδο Υποθέτουµε ότι το ελατήριο έχει αρχικό µήκος µηδέν, ιδανικό ελατήριο. F=-kx x K M x Σχήµα 6.1 ιαστάσεις µεγεθών
1, +,*+* + +-,, -*, * : Key words: global warming, snowfall, snowmelt, snow water equivalent. Ohmura,,**0,**
 1, +,*+* + +-,, + : /+* m,1+ m, -*, * +3132* : Key words: global warming, snowfall, snowmelt, snow water equivalent + IPCC,,**+ Inoue and,**2 Yokoyama,**- Ohmura,,**0,**0 +331 +332 + +2- **+, ++,* 14 1,
1, +,*+* + +-,, + : /+* m,1+ m, -*, * +3132* : Key words: global warming, snowfall, snowmelt, snow water equivalent + IPCC,,**+ Inoue and,**2 Yokoyama,**- Ohmura,,**0,**0 +331 +332 + +2- **+, ++,* 14 1,
PID.
 - :... PID. PID...PID :. [ ].[].. []. [] []......... // //. hrf.mehd@gml.com rfee@du.c.r ... [].... PID. ().... () u v (,, u (, (,, v (, (,, w (, w Z Z Z w w Z eor ctutor : ().. -.. [].. [] -. []. [] [].
- :... PID. PID...PID :. [ ].[].. []. [] []......... // //. hrf.mehd@gml.com rfee@du.c.r ... [].... PID. ().... () u v (,, u (, (,, v (, (,, w (, w Z Z Z w w Z eor ctutor : ().. -.. [].. [] -. []. [] [].
EL 625 Lecture 2. State equations of finite dimensional linear systems
 EL 625 Lecture 2 EL 625 Lecture 2 State equations of finite dimensional linear systems Continuous-time: ẋ(t) = A(t)x(t) + B(t)u(t) y(t) = C(t)x(t) + D(t)u(t) Discrete-time: x(t k+ ) = A(t k )x(t k ) +
EL 625 Lecture 2 EL 625 Lecture 2 State equations of finite dimensional linear systems Continuous-time: ẋ(t) = A(t)x(t) + B(t)u(t) y(t) = C(t)x(t) + D(t)u(t) Discrete-time: x(t k+ ) = A(t k )x(t k ) +
Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design
 Supplemental Material for Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design By H. A. Murdoch and C.A. Schuh Miedema model RKM model ΔH mix ΔH seg ΔH
Supplemental Material for Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design By H. A. Murdoch and C.A. Schuh Miedema model RKM model ΔH mix ΔH seg ΔH
Phasor Diagram of an RC Circuit V R
 ESE Lecture 3 Phasor Dagram of an rcut VtV m snt V t V o t urrent s a reference n seres crcut KVL: V m V + V V ϕ I m V V m ESE Lecture 3 Phasor Dagram of an L rcut VtV m snt V t V t L V o t KVL: V m V
ESE Lecture 3 Phasor Dagram of an rcut VtV m snt V t V o t urrent s a reference n seres crcut KVL: V m V + V V ϕ I m V V m ESE Lecture 3 Phasor Dagram of an L rcut VtV m snt V t V t L V o t KVL: V m V
Self and Mutual Inductances for Fundamental Harmonic in Synchronous Machine with Round Rotor (Cont.) Double Layer Lap Winding on Stator
 Sel nd Mutul Inductnces or Fundmentl Hrmonc n Synchronous Mchne wth Round Rotor (Cont.) Double yer p Wndng on Sttor Round Rotor Feld Wndng (1) d xs s r n even r Dene S r s the number o rotor slots. Dene
Sel nd Mutul Inductnces or Fundmentl Hrmonc n Synchronous Mchne wth Round Rotor (Cont.) Double yer p Wndng on Sttor Round Rotor Feld Wndng (1) d xs s r n even r Dene S r s the number o rotor slots. Dene
ECE 308 SIGNALS AND SYSTEMS FALL 2017 Answers to selected problems on prior years examinations
 ECE 308 SIGNALS AND SYSTEMS FALL 07 Answers to selected problems on prior years examinations Answers to problems on Midterm Examination #, Spring 009. x(t) = r(t + ) r(t ) u(t ) r(t ) + r(t 3) + u(t +
ECE 308 SIGNALS AND SYSTEMS FALL 07 Answers to selected problems on prior years examinations Answers to problems on Midterm Examination #, Spring 009. x(t) = r(t + ) r(t ) u(t ) r(t ) + r(t 3) + u(t +
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ (Τ.Ε.Ι.) ΚΡΗΤΗΣ Τµήµα Εφαρµοσµένης Πληροφορικής & Πολυµέσων. Ψηφιακή Σχεδίαση. Κεφάλαιο 5: Σύγχρονη Ακολουθιακή
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ (Τ.Ε.Ι.) ΚΡΗΤΗΣ Τµήµα Εφαρµοσµένης Πληροφορικής & Πολυµέσων Ψηφιακή Σχεδίαση Κεφάλαιο 5: Σύγχρονη Ακολουθιακή Λογική Σύγχρονα Ακολουθιακά Κυκλώµατα Είσοδοι Συνδυαστικό κύκλωµα
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ (Τ.Ε.Ι.) ΚΡΗΤΗΣ Τµήµα Εφαρµοσµένης Πληροφορικής & Πολυµέσων Ψηφιακή Σχεδίαση Κεφάλαιο 5: Σύγχρονη Ακολουθιακή Λογική Σύγχρονα Ακολουθιακά Κυκλώµατα Είσοδοι Συνδυαστικό κύκλωµα
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΗΣ ΙΣΧΥΟΣ Λειτουργία Α/Γ υπό Αυξηµένη Γωνιακή Ταχύτητα ροµέα προς Συµµετοχή της σε Ρύθµιση Φορτίου- Συχνότητας
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΗΣ ΙΣΧΥΟΣ Λειτουργία Α/Γ υπό Αυξηµένη Γωνιακή Ταχύτητα ροµέα προς Συµµετοχή της σε Ρύθµιση Φορτίου- Συχνότητας
ΑΝΑΛΥΣΗ ΚΑΙ ΕΛΕΓΧΟΣ ΟΛΟΚΛΗΡΩΜΕΝΩΝ ΣΥΣΤΗΜΑΤΩΝ ΜΕΤΑΤΡΟΠΕΩΝ ΙΣΧΥΟΣ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΜΕ ΕΦΑΡΜΟΓΕΣ ΣΤΗΝ ΗΛΕΚΤΡΟΚΙΝΗΣΗ ΚΑΙ ΤΙΣ ΑΝΑΝΕΩΣΙΜΕΣ ΠΗΓΕΣ ΕΝΕΡΓΕΙΑΣ
 ΑΝΑΛΥΣΗ ΚΑΙ ΕΛΕΓΧΟΣ ΟΛΟΚΛΗΡΩΜΕΝΩΝ ΣΥΣΤΗΜΑΤΩΝ ΜΕΤΑΤΡΟΠΕΩΝ ΙΣΧΥΟΣ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΜΕ ΕΦΑΡΜΟΓΕΣ ΣΤΗΝ ΗΛΕΚΤΡΟΚΙΝΗΣΗ ΚΑΙ ΤΙΣ ΑΝΑΝΕΩΣΙΜΕΣ ΠΗΓΕΣ ΕΝΕΡΓΕΙΑΣ ΔΙΔΑΚΤΟΡΙΚΗ ΔΙΑΤΡΙΒΗ ΓΕΩΡΓΙΟΥ Κ. ΚΩΝΣΤΑΝΤΟΠΟΥΛΟΥ ΔΙΠΛΩΜΑΤΟΥΧΟΥ
ΑΝΑΛΥΣΗ ΚΑΙ ΕΛΕΓΧΟΣ ΟΛΟΚΛΗΡΩΜΕΝΩΝ ΣΥΣΤΗΜΑΤΩΝ ΜΕΤΑΤΡΟΠΕΩΝ ΙΣΧΥΟΣ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΜΕ ΕΦΑΡΜΟΓΕΣ ΣΤΗΝ ΗΛΕΚΤΡΟΚΙΝΗΣΗ ΚΑΙ ΤΙΣ ΑΝΑΝΕΩΣΙΜΕΣ ΠΗΓΕΣ ΕΝΕΡΓΕΙΑΣ ΔΙΔΑΚΤΟΡΙΚΗ ΔΙΑΤΡΙΒΗ ΓΕΩΡΓΙΟΥ Κ. ΚΩΝΣΤΑΝΤΟΠΟΥΛΟΥ ΔΙΠΛΩΜΑΤΟΥΧΟΥ
d 2 y dt 2 xdy dt + d2 x
 y t t ysin y d y + d y y t z + y ty yz yz t z y + t + y + y + t y + t + y + + 4 y 4 + t t + 5 t Ae cos + Be sin 5t + 7 5 y + t / m_nadjafikhah@iustacir http://webpagesiustacir/m_nadjafikhah/courses/ode/fa5pdf
y t t ysin y d y + d y y t z + y ty yz yz t z y + t + y + y + t y + t + y + + 4 y 4 + t t + 5 t Ae cos + Be sin 5t + 7 5 y + t / m_nadjafikhah@iustacir http://webpagesiustacir/m_nadjafikhah/courses/ode/fa5pdf
Χρονική απόκριση συστημάτων, Τύποι συστημάτων και Σφάλματα
 Χρονική απόκριση συστημάτων, Τύποι συστημάτων και Σφάλματα 1. Χρονική απόκριση συστημάτων αυτομάτου ελέγχου Στα περισσότερα συστήματα αυτομάτου ελέγχου χρησιμοποιείται ως ανεξάρτητη μεταβλητή ο χρόνος,
Χρονική απόκριση συστημάτων, Τύποι συστημάτων και Σφάλματα 1. Χρονική απόκριση συστημάτων αυτομάτου ελέγχου Στα περισσότερα συστήματα αυτομάτου ελέγχου χρησιμοποιείται ως ανεξάρτητη μεταβλητή ο χρόνος,
Το άτομο του Υδρογόνου
 Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
L A TEX 2ε. mathematica 5.2
 Διδασκων: Τσαπογας Γεωργιος Διαφορικη Γεωμετρια Προχειρες Σημειωσεις Πανεπιστήμιο Αιγαίου, Τμήμα Μαθηματικών Σάμος Εαρινό Εξάμηνο 2005 στοιχεοθεσια : Ξενιτιδης Κλεανθης L A TEX 2ε σχεδια : Dia mathematica
Διδασκων: Τσαπογας Γεωργιος Διαφορικη Γεωμετρια Προχειρες Σημειωσεις Πανεπιστήμιο Αιγαίου, Τμήμα Μαθηματικών Σάμος Εαρινό Εξάμηνο 2005 στοιχεοθεσια : Ξενιτιδης Κλεανθης L A TEX 2ε σχεδια : Dia mathematica
Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α
 Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
ο ο 3 α. 3"* > ω > d καΐ 'Ενορία όλις ή Χώρί ^ 3 < KN < ^ < 13 > ο_ Μ ^~~ > > > > > Ο to X Η > ο_ ο Ο,2 Σχέδι Γλεγμα Ο Σ Ο Ζ < o w *< Χ χ Χ Χ < < < Ο
 18 ρ * -sf. NO 1 D... 1: - ( ΰ ΐ - ι- *- 2 - UN _ ί=. r t ' \0 y «. _,2. "* co Ι». =; F S " 5 D 0 g H ', ( co* 5. «ΰ ' δ". o θ * * "ΰ 2 Ι o * "- 1 W co o -o1= to»g ι. *ΰ * Ε fc ΰ Ι.. L j to. Ι Q_ " 'T
18 ρ * -sf. NO 1 D... 1: - ( ΰ ΐ - ι- *- 2 - UN _ ί=. r t ' \0 y «. _,2. "* co Ι». =; F S " 5 D 0 g H ', ( co* 5. «ΰ ' δ". o θ * * "ΰ 2 Ι o * "- 1 W co o -o1= to»g ι. *ΰ * Ε fc ΰ Ι.. L j to. Ι Q_ " 'T
Mean-Variance Analysis
 Mean-Variance Analysis Jan Schneider McCombs School of Business University of Texas at Austin Jan Schneider Mean-Variance Analysis Beta Representation of the Risk Premium risk premium E t [Rt t+τ ] R1
Mean-Variance Analysis Jan Schneider McCombs School of Business University of Texas at Austin Jan Schneider Mean-Variance Analysis Beta Representation of the Risk Premium risk premium E t [Rt t+τ ] R1
physicsandmathstutor.com
 physicsadmathstuto.com physicsadmathstuto.com Jauay 009 blak 3. The ectagula hypebola, H, has paametic equatios x = 5t, y = 5 t, t 0. (a) Wite the catesia equatio of H i the fom xy = c. Poits A ad B o
physicsadmathstuto.com physicsadmathstuto.com Jauay 009 blak 3. The ectagula hypebola, H, has paametic equatios x = 5t, y = 5 t, t 0. (a) Wite the catesia equatio of H i the fom xy = c. Poits A ad B o
Design Method of Driving Force and Electric Power Steering Control to Improve Vehicle Lateral Motion Characteristics
 Deign Metod o Diving Foce and Electic Poe Steeing Contol to Ipove Veicle Lateal Motion Caacteitic Tutou TASHIRO Sigeyuki HOSOE In ti pape, e popoe ne contol and appopiate deign etod o diving oce and Electic
Deign Metod o Diving Foce and Electic Poe Steeing Contol to Ipove Veicle Lateal Motion Caacteitic Tutou TASHIRO Sigeyuki HOSOE In ti pape, e popoe ne contol and appopiate deign etod o diving oce and Electic
