Πλειάδες φαντάσματα (phantoms)
|
|
|
- Ἑρμογένης Δημητρακόπουλος
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Πλειάδες φαντάσματα (phantoms) Τα phantoms είναι πλειάδες που θα έπρεπε να έχουν φραγή αλλά δεν έχουν, γιατί δεν υπήρχαν όταν αποκτήθηκε το lock Παράδειγμα: σχέση R (E#, name, ) constraint: E# is key χρήση κλειδώματος στις πλειάδες R E# Name. o1 55 Smith o2 75 Jones 132
2 Πλειάδες φαντάσματα (phantoms) T1: Insert <95,White, > into R T2: Insert <95,Black, > into R Για την εισαγωγή κάθε μιας από τις παραπάνω δεν υπάρχει lock στις πλειάδες και ο περιορισμός στο κλειδί δεν παραβιάζεται αν οι Τ1 και Τ2 γίνονται παράλληλα. Λύση: Για να αποφύγουμε την εμφάνιση πλειάδωνφαντασμάτων, πρέπει να θεωρήσουμε την εισαγωγή/διαγραφή μιας πλειάδας σαν πράξη εγγραφής επί της σχέσης (δηλαδή να λάβουμε αποκλειστικό φραγμό στην σχέση συνολικά και όχι μεμονωμένα στις πλειάδες). 133
3 Δενδρικό Πρωτόκολλο (Tree Protocol) Δενδρικά δεδομένα που όμως οι κόμβοι δεν έχουν ιεραρχική δομή βασισμένη στον αποκλεισμό. Ξένα μεταξύ τους κομμάτια που συνδέονται μέσω του μητρικού κόμβου π.χ. B-tree Διαφορετικές δυνατότητες για πολιτικές φραγμών 2PL δεν είναι καθόλου ευέλικτο σε αυτές τις περιπτώσεις: θέτει φραγμούς στο ριζικό κόμβο. Αν χρησιμοποιήσουμε ένα συνηθισμένο σύνολο φραγμών (S, X, U κλπ) σε επίπεδο κόμβου, η σύγχρονη χρήση του B- tree είναι σχεδόν αδύνατη: κάθε δοσοληψία ξεκινά από την ρίζα του δέντρου και κλειδώνονται όλοι οι κόμβοι στην διαδρομή (μαζί με την ρίζα). 134
4 Δενδρικό Πρωτόκολλο (Tree Protocol) Επιπλέον προβλήματα με το 2PL εισαγωγές/διαγραφές μπορεί να δημιουργήσουν επανεγγραφές στον ριζικό κόμβο. Exclusive ή update locks πρέπει να χρησιμοποιηθούν στην ρίζα οι πράξεις μόνο ανάγνωσης μπορούν να εκτελεστούν παράλληλα Αν άρουμε τον φραγμό στην ρίζα νωρίτερα, τότε θα είχαμε περισσότερες δυνατότητες αλλά θα παραβίαζε το 2PL και την σειριομορφία Χρειαζόμαστε εξειδικευμένα πρωτόκολλα που μπορεί να παραβιάζουν το 2PL. Πρέπει να εκμεταλλευτούμε την σειρά προσπέλασης στους κόμβους για να διασφαλίσουμε σειριομορφία. 135
5 Κανόνες προσπέλασης δενδροειδώς δομημένων δεδομένων Το Δενδρικό πρωτόκολλο (Tree Protocol) Υποθέσεις: έχουμε μόνο ένα είδους φραγμού, οι δοσοληψίες είναι συνεπείς, τα χρονοπρογράμματα είναι legal Κανόνες: 1. Ο πρώτος φραγμός κάθε δοσοληψίας μπορεί να αφορά οποιοδήποτε κόμβο του δέντρου. 2. Επόμενοι φραγμοί μπορούν να αποκτηθούν μόνο αν η δοσοληψία κατέχει εκείνη την στιγμή έναν φραγμό επί του μητρικού κόμβου. 3. Φραγμοί επί των κόμβων μπορούν να αρθούν οποιαδήποτε στιγμή. 4. Αν μια δοσοληψία άρει έναν φραγμό επί ενός κόμβου, δεν μπορεί να θέσει εκ νέου φραγμό σε αυτόν, ακόμα και αν εξακολουθεί να κατέχει φραγμό επί του μητρικού κόμβου. 136
6 Δενδρικό Πρωτόκολλο (Tree Protocol) Παράδειγμα 137
7 Λειτουργεί σωστά το δενδρικό πρωτόκολλο? Ορίζει εμμέσως μια σειριακή διάταξη εκτέλεσης των δοσοληψιών: αν στο χρονοδιάγραμμα S, οι Ti και Tj φράζουν ένα κόμβο από κοινού και η Ti τον φράζει πρώτη, τότε η Ti προηγείται της Tj Μπορούμε να φτιάξουμε ένα γράφο προήγησης για την αναπαράσταση αυτών σχέσεων προήγησης στο χρονοπρόγραμμα Αν δεν έχει κύκλους ο γράφος, τότε κάθε τοπολογική διάταξη δοσοληψιών αποτελεί ισοδύναμο σειριακό χρονοδιάγραμμα Ισχυρισμός: χρονοδιαγράμματα που ακολουθούν το δενδρικό πρωτόκολλο πάντα παράγουν γράφους χωρίς κύκλους αν δύο δοσοληψίες φράσσουν πολλά στοιχεία από κοινού, τότε όλα φράσσονται με την ίδια σειρά αν η Ti φράσσει την ρίζα πριν την Tj, τότε η Ti φράσσει κάθε κόμβο που είναι κοινός μεταξύ των Ti και Tj πριν την Tj. 138
8 Εξασφάλιση σειριομορφίας (Ensuring Serializability) Μπορούμε να αποδείξουμε ότι, για κάθε χρονοδιάγραμμα S που ακολουθεί το δενδρικό πρωτόκολλο, υπάρχει κάποια σειριακή διάταξη ισοδύναμη με το S Σχεδιάγραμμα της απόδειξης: (με επαγωγή στον αριθμό των κόμβων) Base case: 1 node (root); follows by the previous observations Induction hypothesis: there is a serial order for all the transactions that lock nodes in any subtree containing more than one node Induction: Must merge the serial orders of the subtrees. Consider for each subtree the set of transactions that lock one or more nodes in the subtree. These sets have as common elements the transactions that lock the root. These transactions lock every common node in the same order they lock the root. Build a serial order for the entire set by starting with the transactions that lock the root in the appropriate order. The rest only need to be placed consistently with the serial order of their subtrees. 139
9 Εξασφάλιση σειριομορφίας (Ensuring Serializability) Παράδειγμα: Έστω ότι έχουμε 10 δοσοληψίες, T 1, T 2,, T 10 από τις οποίες οι T 1, T 3, T 4, T 6 κλειδώνουν την ρίζα, με αυτή την σειρά. Υποθέτουμε επίσης ότι ο ριζικός κόμβος έχει δύο θυγατρικούς κόμβους: ο πρώτος κόμβος έχει κλειδωθεί από τις δοσοληψίες με περιττό αριθμό και την T 4, ενώ ο δεύτερος από τις δοσοληψίες με άρτιο αριθμό και την T 3. Σειριακή διάταξη στο 1 ο υποδέντρο: T 9, T 1, T 5, T 7, T 3,T 4 Σειριακή διάταξη στο 2 ο υποδέντρο : T 8, T 3, T 10, T 4, T 2, T 6 T 5 T 2 T 9 T 1 T 7 T 4 T 6 T 8 T 10 T 3 Μια από την πολλές τοπολογικές ταξινομήσεις είναι: T 9, T 8, T 1, T 5, T 7, T 3,T 10,T 4, T 2, T 6 140
10 Δενδρικό Πρωτόκολλο (Tree Protocol) Άσκηση: Θεωρείστε τις ακόλουθες δοσοληψίες που ενεργούν στο διπλανό δέντρο T1: r1(a); r1(b); r1(e) T2: r2(a); r2(c); r2(b) T3: r3(b); r3(e); r3(f) Αν τα χρονοδιαγράμματα ακολουθούν το δενδρικό πρωτόκολλο, πόσα προγράμματα σύγχρονης εκτέλεσης (συμπλεγμένα) υπάρχουν : a) T1 και T2 b) T1 και T3 c) T1, T2 και T3 141
11 Έλεγχος συγχρονικότητας με χρονοσήμανση (Timestamp-based Concurrency Control) Βασικές ιδέες: Σε κάθε δοσοληψία βάζουμε μια «χρονοσήμανση» (timestamp) Καταγράφονται τα χρονόσημα των δοσοληψιών που έγραψαν ή διάβασαν τελευταίες ένα στοιχείο της ΒΔ Συγκρίνουμε αυτές τις τιμές με τα χρονόσημα των δοσοληψιών για να διασφαλίσουμε ότι το σειριακό χρονοδιάγραμμα με βάση τα χρονόσημα είναι ισοδύναμο με το πραγματικό χρονοδιάγραμμα των δοσοληψιών Αισιόδοξη (optimistic) προσέγγιση: υποθέτει ότι δεν θα προκύψει μησειριόμορφη συμπεριφορά και τα προβλήματα επιδιορθώνονται αν υπάρξει κάποια παραβίαση η μόνη θεραπεία είναι η ακύρωση και επανεκκίνηση Οι μέθοδοι κλειδώματος είναι απαισιόδοξες (pessimistic) και αποτρεπτικές (preventive). Οι διεργασίες καθυστερούν αλλά δεν ακυρώνονται. Γενικά, ο αισιόδοξος χρονοπρογραμματισμός είναι καλύτερος από τις φραγές όταν υπάρχουν πολλές δοσοληψίες που κάνουν μόνο ανάγνωση. 142
12 Χρονόσημα (Timestamps) Σε κάθε δοσοληψία T αποδίδεται ένα μοναδικό χρονόσημο (unique timestamp) TS(T) Τα χρονόσημα αποδίδονται με αύξουσα σειρά όταν οι δοσοληψίες αρχίζουν Τα χρονόσημα μπορούν να παράγονται με δύο διαφορετικούς τρόπους: χρησιμοποιώντας το ρολόι του συστήματος χρησιμοποιώντας έναν μετρητή που τηρεί ο χρονοδιαγραμματιστής (scheduler), ο οποίος αυξάνεται κατά 1 κάθε φορά που ξεκινά μια δοσοληψία O scheduler πρέπει να τηρεί έναν πίνακα με τις ενεργές δοσοληψίες την τρέχουσα χρονική στιγμή και τα αντίστοιχα χρονόσημά τους. 143
13 Χρονόσημα (Timestamps) Για να χρησιμοποιήσουμε χρονόσημα ως μέθοδο έλεγχου συγχρονικότητας, πρέπει να συσχετίσουμε κάθε στοιχείο της ΒΔ με δύο χρονόσημα και ένα επιπλέον bit: RT(X): χρόνος ανάγνωσης του X, το μεγαλύτερο από τα χρονόσημα των δοσοληψιών που έχουν διαβάσει το Χ WT(X): χρόνος εγγραφής του X, το μεγαλύτερο από τα χρονόσημα των δοσοληψιών που έχουν γράψει το Χ C(X): bit οριστικοποίησης για το X, είναι 1 αν και μόνο αν η πιο πρόσφατη δοσοληψία που έγραψε το Χ έχει ήδη οριστικοποιηθεί Το bit αυτό χρησιμοποιείται για την αποφυγή της κατάστασης όπου μια δοσοληψία Τ διαβάζει δεδομένα τα οποία γράφει μια άλλη δοσοληψία U και αργότερα η U ακυρώνεται (dirty read on uncommitted data) 144
14 Προβλήματα με τα χρονόσημα Ο scheduler υποθέτει ότι η σειρά χρονοσήμανσης των δοσοληψιών είναι επίσης η σειριακή διάταξη με την οποία πρέπει να φαίνεται πως εκτελούνται Ο scheduler πρέπει να ελέγχει ότι κάθε φορά που γίνεται μια ανάγνωση ή εγγραφή, αυτό που συμβαίνει στον πραγματικό χρόνο θα μπορούσε να είχε συμβεί αν κάθε δοσοληψία είχε εκτελεστεί στιγμιαία την χρονική στιγμή του χρονόσημού της. Σε αντίθετη περίπτωση μπορεί να προκύψουν δύο ειδών προβλήματα: Καθυστερημένη ανάγνωση: Η T προσπαθεί να διαβάσει το X, αλλά ο χρόνος εγγραφής WT(X) φανερώνει ότι η τρέχουσα τιμή του Χ εγγράφηκε μετά την θεωρητική εκτέλεση της T, δηλαδή TS(T) < WT(X). Η T δεν πρέπει να διαβάσει το X και ο scheduler πρέπει να ακυρώσει την T. Καθυστερημένη εγγραφή: Η T προσπαθεί να γράψει το X, αλλά ο χρόνος διαβάσματος RT(X) φανερώνει ότι κάποια άλλη δοσοληψία έπρεπε να είχε διαβάσει την τιμή που γράφτηκε από την T αλλά αντί αυτής διάβασε κάποια άλλη τιμή, δηλαδή WT(X) < TS(T) < RT(X) 145
15 Προβλήματα με τα χρονόσημα Καθυστερημένη ανάγνωση T2 γράφει το Χ Τ1 διαβάζει το Χ έναρξη της Τ1 έναρξη της T2 Καθυστερημένη εγγραφή T2 διαβάζει το Χ Τ1 γράφει το Χ έναρξη της Τ1 έναρξη της T2 146
16 Περισσότερα προβλήματα Η T1 διαβάζει το X το οποίο γράφτηκε τελευταία από την T2 και TS(T2) < TS(T1). Τι θα γίνει αν μετά την ανάγνωση του Χ από την Τ1, η T2 ακυρωθεί; είναι καλύτερο να καθυστερήσουμε την ανάγνωση από την Τ1 μέχρι η T2 να οριστικοποιηθεί ή να ακυρωθεί μπορούμε να ελέγξουμε το C(X) για να δούμε αν η T2 έχει οριστικοποιηθεί TS(T1) < TS(T2) και η T2 γράφει πρώτη το X. Όταν η T1 προσπαθήσει να γράψει, δεν κάνουμε τίποτα Κανόνας εγγραφής του Thomas: οι εγγραφές μπορούν να παραλειφθούν όταν έχει πραγματοποιηθεί ήδη μια εγγραφή με μεταγενέστερο χρόνο εγγραφής Πολιτική: όταν η T εγγράφει ένα στοιχείο X, η εγγραφή είναι δοκιμαστική (tentative write) και μπορεί να αναιρεθεί αν η Τ ματαιωθεί. Το C(X) γίνεται 0 και ο scheduler δημιουργεί ένα αντίγραφο της παλιάς τιμής του X και του προηγούμενου χρόνου εγγραφής WT(X) 147
17 Περισσότερα προβλήματα Dirty read T2 γράφει το Χ Τ1 διαβάζει το Χ έναρξη της T2 έναρξη της Τ1 η T2 ακυρώνεται T2 γράφει το Χ Τ1 γράφει το Χ έναρξη της Τ1 έναρξη της T2 T1 commits T2 aborts 148
18 Κανόνες χρονοπρογραμματισμού με χρονόσημα 1. Αν ο scheduler λάβει ένα αίτημα από την δοσοληψία T για να διαβάσει το X τότε: a. If TS(T) >= WT(X) then i. If C(X)=1, grant the request. If TS(T) > RT(X), set RT(X):=TS(T); otherwise do not change RT(X) ii. If C(X)=0, delay T until C(X) becomes 1 or the transaction that wrote X aborts b. If TS(T) < WT(X) then abort T and restart it with a new, higher timestamp 149
19 Κανόνες χρονοπρογραμματισμού με χρονόσημα 2. Αν ο scheduler λάβει ένα αίτημα από την δοσοληψία T για να γράψει το X τότε: a. If TS(T) >= RT(X) and TS(T) >= WT(X) then i. Write the new value for X ii. Set WT(X):=TS(T) iii. Set C(X):=0 b. If TS(T) >= RT(X) but TS(T) < WT(X) then there is already a later value for X. i. If C(X)=1, ignore the write by T ii. If C(X)=0, delay T 150
20 Κανόνες χρονοπρογραμματισμού με χρονόσημα 3. Αν ο scheduler λάβει ένα αίτημα οριστικοποίησης της Τ, τότε πρέπει να βρεθούν όλα τα στοιχεία της ΒΔ που γράφτηκαν από την T και το commit bit C(X) να τεθεί σε 1 4. Αν ο scheduler λάβει ένα αίτημα ματαίωσης της Τ ή αποφασίζει να ανακαλέσει (roll back) την Τ, τότε κάθε δοσοληψία που περίμενε κάποιο στοιχείο X που ενέγραψε η T πρέπει να επαναλάβει την απόπειρά της να διαβάσει ή να γράψει. 151
21 Πολυεκδοχικά χρονόσημα Υπάρχουν παραλλαγές της χρονοσήμανσης που χρησιμοποιούν παλιές εκδοχές των στοιχείων της ΒΔ εκτός από την τρέχουσα έκδοση. Η μέθοδος είναι χρήσιμη αν τα στοιχεία της ΒΔ είναι disk blocks ή pages. χρονόσημα έναρξης των δοσοληψιών TS(T x ) Αν ήταν διαθέσιμη η παλιά τιμή του Α, θα μπορούσε να επιτραπεί στην Τ3 να τη διαβάσει και να μην ματαιωθεί. T 1 T 2 T 3 T 4 A r 1 (A) RT(A)=150 w 1 (A) WT(A)=150 r 2 (A) RT(A)=200 w 2 (A) WT(A)=200 r 3 (A) abort r 4 (A) RT(A)=
22 Χρονόσημα έναντι Φραγής (Timestamp-based Scheduling vs Locking) Η χρονοσήμανση υπερέχει της φραγής όταν οι περισσότερες δοσοληψίες κάνουν μόνο ανάγνωση ή σπάνια υπάρχουν συγχρονικές δοσοληψίες που προσπαθούν να διαβάσουν και να γράψουν το ίδιο στοιχείο. Σε καταστάσεις που συμβαίνουν πολλές συγκρούσεις, η φραγή έχει καλύτερες επιδόσεις: Η φραγή συχνά καθυστερεί τις δοσοληψίες καθώς περιμένουν για κάποιο lock. Ακόμα και αν έχουμε deadlock, κάποια από τις δοσοληψίες θα ανακληθεί (rolled back). Αλλά αν τα rollbacks είναι συχνά, εισάγεται ακόμα μεγαλύτερη καθυστέρηση. Πολλά εμπορικά συστήματα ακολουθούν συμβιβαστικές λύσεις: Οι δοσοληψίες χωρίζονται σε read-only και read/write Οι read/write εκτελούνται με 2PL ενώ οι read-only εκτελούνται με χρονοσήμανση (με πολυεκδοχικά χρονόσημα). 153
23 Έλεγχος συγχρονικότητας με επικύρωση (Validation-based Concurrency Control ) Μια άλλη αισιόδοξη στρατηγική ελέγχου συγχρονικότητας: Οι δοσοληψίες επιτρέπεται να έχουν πρόσβαση στα δεδομένα χωρίς κλειδώματα Ελέγχουμε αν οι δοσοληψίες συμπεριφέρθηκαν σειριόμορφα Ακριβώς πριν ξεκινήσει η δοσοληψία να εγγράφει τιμές σε στοιχεία της ΒΔ, περνά από μια φάση επικύρωσης όπου τα σύνολα των στοιχείων που διάβασε και πρόκειται να εγγράψει συγκρίνονται με τα σύνολα εγγραφής των άλλων ενεργών δοσοληψιών. Αν υπάρχει κίνδυνος φυσικώς μη πραγματοποιήσιμης συμπεριφοράς, η δοσοληψία ανακαλείται (roll back). Οι δοσοληψίες εκτελούνται σε 3 φάσεις Read Validate Write 154
24 Έλεγχος συγχρονικότητας με επικύρωση (Validation-based Concurrency Control ) Κάθε δοσοληψία που επικυρώνεται επιτυχώς είναι σαν να εκτελείται την στιγμή της επικύρωσής της. Ένας scheduler επικυρωτικού τύπου διαθέτει μια υποθετική σειριακή διάταξη των δοσοληψιών με βάση τους χρόνους επικύρωσης, για να αποφασίσει αν η συμπεριφορά των δοσοληψιών είναι συνεπείς με αυτή την διάταξη. Ο scheduler τηρεί τρία σύνολα: START: το σύνολο των δοσοληψιών που έχουν ξεκινήσει αλλά δεν έχουν ακόμα ολοκληρώσει την επικύρωση. START(T): ο χρόνος που ξεκίνησε η T VAL: το σύνολο των δοσοληψιών που έχουν επικυρωθεί αλλά δεν έχουν τελειώσει ακόμα την φάση εγγραφής. VAL(T): ο χρόνος που η T επικυρώθηκε FIN: το σύνολο των δοσοληψιών που έχουν ολοκληρώσει την φάση 3. FIN(T): ο χρόνος που τελείωσε η T 155
25 Κανόνες της Επικύρωσης RS(T): το σύνολο των στοιχείων της ΒΔ που διαβάζει η T WS(T): το σύνολο των στοιχείων της ΒΔ που γράφει η T Όταν η Τ επιχειρεί να επικυρώσει: 1. Σύγκρινε το RS(T) με WS(U) για κάθε U έτσι ώστε FIN(U) > START(T) και έλεγξε αν RS(T) WS(U) = 2. Σύγκρινε το WS(T) με WS(U) για κάθε U έτσι ώστε FIN(U) > VAL(T) και έλεγξε αν WS(T) WS(U) = 156
26 Προβλήματα με την επικύρωση Πρόβλημα όταν RS(T) WS(U) T διαβάζει το Χ U γράφει το Χ Ενδέχεται η Τ και U να μην είναι συνεπείς με την υποθετική διάταξη (διακεκομμένες γραμμές) Η Τ πρέπει να ανακληθεί και στις δύο περιπτώσεις Πρόβλημα όταν WS(T) WS(U) έναρξη της U έναρξη της T επικύρωση της U T γράφει το Χ επικύρωση της T U γράφει το Χ επικύρωση της U επικύρωση της T λήξη της U 157
27 Σύγκριση των μηχανισμών ελέγχου συγχρονικότητας Χρησιμοποίηση αποθηκευτικού χώρου: Φραγή: ο χώρος στον πίνακα φραγμών είναι ανάλογος του πλήθους των φραγμένων στοιχείων της ΒΔ Χρονόσημα: Σε μια απλοϊκή υλοποίηση: απαιτείται χώρος για τους χρόνους ανάγνωσης και εγγραφής κάθε στοιχείου της ΒΔ Όλα τα χρονόσημα που είναι προγενέστερα της παλαιότερης ενεργής δοσοληψίας δεν χρειάζονται. Αποθηκεύουμε μόνο τους χρόνους των στοιχείων που προσπελάστηκαν «πρόσφατα». Επικύρωση: χώρος για τα χρονόσημα και για τα σύνολα ανάγνωσης/εγγραφής κάθε ενεργής δοσοληψίας Τα Timestamping και Validation μπορεί να χρησιμοποιούν ελαφρώς περισσότερο χώρο από το Locking. 158
28 Σύγκριση των μηχανισμών ελέγχου συγχρονικότητας Χρόνοι καθυστέρησης: εξαρτάται από το βαθμό αλληλεπίδρασης δηλαδή την πιθανότητα μια δοσοληψία να προσπελάσει ένα στοιχείο που προσπελάζεται συγχρόνως από μια άλλη Η φραγή καθυστερεί τις δοσοληψίες αλλά αποφεύγει τις ανακλήσεις (rollbacks) εκτός από περιπτώσεις deadlock - ακόμα και όταν η αλληλεπίδραση είναι υψηλή. Τα χρονόσημα και η επικύρωση δεν καθυστερούν τις δοσοληψίες αλλά μπορούν να προκαλέσουν την ανάκλησή τους, η οποία περιλαμβάνει περισσότερες καθυστερήσεις και σπατάλη πόρων. Αν η αλληλεπίδραση είναι χαμηλή, τότε τα χρονόσημα και η επικύρωση δεν θα προκαλέσουν πολλές ανακλήσεις και μπορεί να είναι προτιμότερα από την φραγή. Όταν είναι απαραίτητη μια ανάκληση, τα χρονόσημα εντοπίζουν νωρίτερα τα προβλήματα από την επικύρωση (η οποία αφήνει πάντοτε μια δοσοληψία να κάνει όλη την δουλεία πριν εξετάσει αν θα πρέπει να ανακληθεί). 159
29 View Serializability Conflict serializability guarantees serializability independently of what transactions actually do But. it is a quite strong condition on schedules of concurrent execution A weaker notion that still guarantees serializability is view serializability The main difference between conflict and view serializability appears in situations where a transaction writes a value that no other transaction reads (but possibly writes later) under view serializability such a write action can be repositioned in the schedule (might be prohibited under conflict serializability) 160
30 Definitions Let S 1 and S 2 be two schedules involving the same set of transactions; let T I be a hypothetical transaction that writes initial values for each DB element read by any transaction in the schedule; let T F be a hypothetical transaction that reads every element written by the transactions after the schedule ends for every R i (A), we can find the W j (A) that most closely precedes it; transaction T j is called the source of the read action S 1 and S 2 are called view equivalent if for every read action in S 1 its source is the same in S 2, and vice versa. A schedule that is view equivalent to a serial schedule is called view serializable 161
31 Example Consider the following schedule S: T 1 : R 1 (A) W 1 (B) T 2 : R 2 (B) W 2 (A) W 2 (B) T 3 : R 3 (A) W 3 (B) only the value of B written by T 3 is read by T F S is not conflict serializable sources for read actions: o source of R 2 (B) is T I o source of R 1 (A) and R 3 (A) is T 2 o source of R F (A) is T 2 o source of R F (B) is T 3 S is view serializable; equivalent serial schedule: (T 2, T 1, T 3 ) 162
32 Testing View Serializability Polygraphs: a generalization of precedence graphs a node for each transaction and additional nodes for the two hypothetical transactions an arc from Tj to T i for each action R i (X) with source Tj if Tj is the source of R i (X) and T k is another transaction that writes X, T k must appear either before Tj or after T i. This is denoted by two arcs in the graph (can choose one of the two). Special cases: if Tj is TI, then the arc from T i to T k is introduced if T i is TF, then the arc from T k to Tj is introduced 163
Φραγή σε πολλαπλά επίπεδα λεπτομέρειας Τι αντικείμενα κλειδώνουμε?
 Φραγή σε πολλαπλά επίπεδα λεπτομέρειας Τι αντικείμενα κλειδώνουμε? Το κλείδωμα δουλεύει σε κάθε περίπτωση, αλλά πρέπει να διαλέξουμε μικρά ή μεγάλα αντικείμενα? Αν κλειδώνουμε μεγάλα αντικείμενα (π.χ.,
Φραγή σε πολλαπλά επίπεδα λεπτομέρειας Τι αντικείμενα κλειδώνουμε? Το κλείδωμα δουλεύει σε κάθε περίπτωση, αλλά πρέπει να διαλέξουμε μικρά ή μεγάλα αντικείμενα? Αν κλειδώνουμε μεγάλα αντικείμενα (π.χ.,
Επαναληπτικές ασκήσεις
 Επαναληπτικές ασκήσεις Ασκ 1: Θεωρείστε τα παρακάτω χρονοδιαγράμματα σύγχρονης εκτέλεσης : S 1 = r 1 (A); w 4 (B); w 1 (C); w 3 (D); r 2 (C); w 3 (A); w 1 (A); r 3 (B); w 3 (B); r 2 (D); w 2 (A) S 2 =
Επαναληπτικές ασκήσεις Ασκ 1: Θεωρείστε τα παρακάτω χρονοδιαγράμματα σύγχρονης εκτέλεσης : S 1 = r 1 (A); w 4 (B); w 1 (C); w 3 (D); r 2 (C); w 3 (A); w 1 (A); r 3 (B); w 3 (B); r 2 (D); w 2 (A) S 2 =
Χρονοδιάγραμμα/Χρονοπρόγραμμα
 Χρονοδιάγραμμα/Χρονοπρόγραμμα Χρονοδιάγραμμα ή Χρονοπρόγραμμα (Schedule) είναι μια σειρά/ακολουθία ενεργειών που πραγματοποιούνται από μια ή περισσότερες δοσοληψίες. Σημαντικές ενέργειες: ανάγνωση, εγγραφή
Χρονοδιάγραμμα/Χρονοπρόγραμμα Χρονοδιάγραμμα ή Χρονοπρόγραμμα (Schedule) είναι μια σειρά/ακολουθία ενεργειών που πραγματοποιούνται από μια ή περισσότερες δοσοληψίες. Σημαντικές ενέργειες: ανάγνωση, εγγραφή
Locking to ensure serializability
 Locking to ensure serializability Concurrent access to database items is controlled by strategies based on locking, timestamping or certification A lock is an access privilege to a single database item
Locking to ensure serializability Concurrent access to database items is controlled by strategies based on locking, timestamping or certification A lock is an access privilege to a single database item
Συστήματα Διαχείρισης Βάσεων Δεδομένων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Συστήματα Διαχείρισης Βάσεων Δεδομένων Φροντιστήριο 9: Transactions - part 1 Δημήτρης Πλεξουσάκης Τμήμα Επιστήμης Υπολογιστών Tutorial on Undo, Redo and Undo/Redo
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Συστήματα Διαχείρισης Βάσεων Δεδομένων Φροντιστήριο 9: Transactions - part 1 Δημήτρης Πλεξουσάκης Τμήμα Επιστήμης Υπολογιστών Tutorial on Undo, Redo and Undo/Redo
Έλεγχος συγχρονικότητας Μέρος 2 Βάσεις Δεδομένων Διδάσκων: Μαρία Χαλκίδη
 Έλεγχος συγχρονικότητας Μέρος 2 Βάσεις Δεδομένων Διδάσκων: Μαρία Χαλκίδη με βάση slides από A. Silberschatz, H. Korth, S. Sudarshan, Database System Concepts, 5 th edition Πρωτόκολλα βασισμένα σε γράφο
Έλεγχος συγχρονικότητας Μέρος 2 Βάσεις Δεδομένων Διδάσκων: Μαρία Χαλκίδη με βάση slides από A. Silberschatz, H. Korth, S. Sudarshan, Database System Concepts, 5 th edition Πρωτόκολλα βασισμένα σε γράφο
Επεξεργασία οσοληψιών (συνέχεια)
 Επανάληψη: οσοληψίες Επεξεργασία οσοληψιών (συνέχεια) Πρόβληµα «Σωστή» εκτέλεση προγραµµάτων όταν επιτρέπουµε ταυτοχρονισµό και ακόµα και αν υπάρχουν αποτυχίες 1 2 οσοληψία (transaction) Επανάληψη: οσοληψίες
Επανάληψη: οσοληψίες Επεξεργασία οσοληψιών (συνέχεια) Πρόβληµα «Σωστή» εκτέλεση προγραµµάτων όταν επιτρέπουµε ταυτοχρονισµό και ακόµα και αν υπάρχουν αποτυχίες 1 2 οσοληψία (transaction) Επανάληψη: οσοληψίες
Αρχεία και Βάσεις Δεδομένων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αρχεία και Βάσεις Δεδομένων Διάλεξη 16η: Διαχείριση Δοσοληψιών Μέρος 2ο - 2PL Δημήτρης Πλεξουσάκης Τμήμα Επιστήμης Υπολογιστών Locking to ensure serializability
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αρχεία και Βάσεις Δεδομένων Διάλεξη 16η: Διαχείριση Δοσοληψιών Μέρος 2ο - 2PL Δημήτρης Πλεξουσάκης Τμήμα Επιστήμης Υπολογιστών Locking to ensure serializability
Έλεγχος Ταυτοχρονισμού
 Έλεγχος Ταυτοχρονισμού Κεφάλαιο 17 Database Management Systems 3ed, R. Ramakrishnan and J. Gehrke Ελληνική Μετάφραση: Γεώργιος Ευαγγελίδης 1 Συγκρουσιακώς Σειριοποιήσιμα Χρονοπρογράμματα Δυο χρονοπρογράμματα
Έλεγχος Ταυτοχρονισμού Κεφάλαιο 17 Database Management Systems 3ed, R. Ramakrishnan and J. Gehrke Ελληνική Μετάφραση: Γεώργιος Ευαγγελίδης 1 Συγκρουσιακώς Σειριοποιήσιμα Χρονοπρογράμματα Δυο χρονοπρογράμματα
ΗΥ360 Αρχεία και Βάσεις εδοµένων ιδάσκων: ημήτρης Πλεξουσάκης
 ΗΥ360 Αρχεία και Βάσεις εδοµένων ιδάσκων: ημήτρης Πλεξουσάκης Συναλλαγές ιαχείριση Συναλλαγών Αυγουστάκη Αργυρώ Συναλλαγές Κράτησε για τον κ. Χ την θέση 13Α για LA! Κράτησε για τον κ. Y την θέση 13Α για
ΗΥ360 Αρχεία και Βάσεις εδοµένων ιδάσκων: ημήτρης Πλεξουσάκης Συναλλαγές ιαχείριση Συναλλαγών Αυγουστάκη Αργυρώ Συναλλαγές Κράτησε για τον κ. Χ την θέση 13Α για LA! Κράτησε για τον κ. Y την θέση 13Α για
ΗΥ360 Αρχεία και Βάσεις εδοµένων ιδάσκων:. Πλεξουσάκης
 ΗΥ360 Αρχεία και Βάσεις εδοµένων ιδάσκων:. Πλεξουσάκης Συναλλαγές ιαχείριση Συναλλαγών Τζικούλης Βασίλειος Credits:Γιάννης Μακρυδάκης Συναλλαγές Η ταυτόχρονες συναλλαγές (δοσοληψίες, transactions) µε µια
ΗΥ360 Αρχεία και Βάσεις εδοµένων ιδάσκων:. Πλεξουσάκης Συναλλαγές ιαχείριση Συναλλαγών Τζικούλης Βασίλειος Credits:Γιάννης Μακρυδάκης Συναλλαγές Η ταυτόχρονες συναλλαγές (δοσοληψίες, transactions) µε µια
ΗΥ360 Αρχεία και Βάσεις εδοµένων ιδάσκων: ημήτρης Πλεξουσάκης
 ΗΥ360 Αρχεία και Βάσεις εδοµένων ιδάσκων: ημήτρης Πλεξουσάκης Συναλλαγές ιαχείριση Συναλλαγών Αυγουστάκη Αργυρώ Συναλλαγές Κράτησε για τον κ. Χ την θέση 13Α για LA! Κράτησε για τον κ. Y την θέση 13Α για
ΗΥ360 Αρχεία και Βάσεις εδοµένων ιδάσκων: ημήτρης Πλεξουσάκης Συναλλαγές ιαχείριση Συναλλαγών Αυγουστάκη Αργυρώ Συναλλαγές Κράτησε για τον κ. Χ την θέση 13Α για LA! Κράτησε για τον κ. Y την θέση 13Α για
Δοσοληψίες. Κατανεμημένα Συστήματα
 Δοσοληψίες Κατανεμημένα Συστήματα 2016-2017 http://www.cslab.ece.ntua.gr/courses/distrib Στο προηγούμενο μάθημα Group communication Multicast για FIFO διάταξη Multicast για ολική διάταξη Sequencer ISIS
Δοσοληψίες Κατανεμημένα Συστήματα 2016-2017 http://www.cslab.ece.ntua.gr/courses/distrib Στο προηγούμενο μάθημα Group communication Multicast για FIFO διάταξη Multicast για ολική διάταξη Sequencer ISIS
Δοσοληψίες. Κατανεμημένα Συστήματα
 Δοσοληψίες Κατανεμημένα Συστήματα 2018-2019 http://www.cslab.ece.ntua.gr/courses/distrib Στο προηγούμενο μάθημα Group communication Multicast για FIFO διάταξη Multicast για ολική διάταξη Sequencer ISIS
Δοσοληψίες Κατανεμημένα Συστήματα 2018-2019 http://www.cslab.ece.ntua.gr/courses/distrib Στο προηγούμενο μάθημα Group communication Multicast για FIFO διάταξη Multicast για ολική διάταξη Sequencer ISIS
Επεξεργασία οσοληψιών
 οσοληψίες Επεξεργασία οσοληψιών Ηταυτόχρονη εκτέλεση προγραµµάτων χρηστών είναι απαραίτητη για την καλή απόδοση ενός Σ Β Επειδή οι προσπελάσεις στο δίσκο είναι συχνές και σχετικά αργές, είναι σηµαντικό
οσοληψίες Επεξεργασία οσοληψιών Ηταυτόχρονη εκτέλεση προγραµµάτων χρηστών είναι απαραίτητη για την καλή απόδοση ενός Σ Β Επειδή οι προσπελάσεις στο δίσκο είναι συχνές και σχετικά αργές, είναι σηµαντικό
Επεξεργασία οσοληψιών
 Επανάληψη: οσοληψίες Επεξεργασία οσοληψιών Ανακεφαλαίωση Πρόβληµα «Σωστή» εκτέλεση προγραµµάτων όταν επιτρέπουµε ταυτοχρονισµό και ακόµα και αν υπάρχουν αποτυχίες Βάσεις εδοµένων II 2003-2004 Ευαγγελία
Επανάληψη: οσοληψίες Επεξεργασία οσοληψιών Ανακεφαλαίωση Πρόβληµα «Σωστή» εκτέλεση προγραµµάτων όταν επιτρέπουµε ταυτοχρονισµό και ακόµα και αν υπάρχουν αποτυχίες Βάσεις εδοµένων II 2003-2004 Ευαγγελία
Προχωρημένα Θέματα Βάσεων Δεδομένων
 Προχωρημένα Θέματα Βάσεων Δεδομένων 1ο Σετ Ασκήσεων ΕΡΩΤΗΜΑ 1 Ατομικότητα : Η ατομικότητα πρακτικά εξασφαλίζει ότι είτε όλες οι πράξεις μιας δοσοληψίας θα εκτελεστούν ή καμμιά από αυτές δεν θα εκτελεστεί.
Προχωρημένα Θέματα Βάσεων Δεδομένων 1ο Σετ Ασκήσεων ΕΡΩΤΗΜΑ 1 Ατομικότητα : Η ατομικότητα πρακτικά εξασφαλίζει ότι είτε όλες οι πράξεις μιας δοσοληψίας θα εκτελεστούν ή καμμιά από αυτές δεν θα εκτελεστεί.
ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ. Πανεπιστήμιο Πειραιώς Τμήμα Ψηφιακών Συστημάτων Μανουσόπουλος Χρήστος
 ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ Πανεπιστήμιο Πειραιώς Τμήμα Ψηφιακών Συστημάτων Μανουσόπουλος Χρήστος cman@unipi.gr Δοσοληψίες Concurrent Data Access (Ταυτόχρονη Πρόσβαση σε Δεδομένα) Συνήθως πολλοί χρήστες έχουν ταυτόχρονη
ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ Πανεπιστήμιο Πειραιώς Τμήμα Ψηφιακών Συστημάτων Μανουσόπουλος Χρήστος cman@unipi.gr Δοσοληψίες Concurrent Data Access (Ταυτόχρονη Πρόσβαση σε Δεδομένα) Συνήθως πολλοί χρήστες έχουν ταυτόχρονη
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Έλεγχος συγχρονικότητας Μέρος 1 Βάσεις Δεδομένων Διδάσκων: Μαρία Χαλκίδη
 Έλεγχος συγχρονικότητας Μέρος 1 Βάσεις Δεδομένων Διδάσκων: Μαρία Χαλκίδη με βάση slides από A. Silberschatz, H. Korth, S. Sudarshan, Database System Concepts, 5 th edition Έλεγχος συγχρονικότητας Διάφορες
Έλεγχος συγχρονικότητας Μέρος 1 Βάσεις Δεδομένων Διδάσκων: Μαρία Χαλκίδη με βάση slides από A. Silberschatz, H. Korth, S. Sudarshan, Database System Concepts, 5 th edition Έλεγχος συγχρονικότητας Διάφορες
ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ ΙΙ. Επεξεργασία οσοληψιών. το πώς βλέπει το Σ Β τα προγράµµατα των χρηστών. οσοληψία (transaction)
 Ύλη Ύλη Έννοιες Επεξεργασίας οσοληψιών Τεχνικές Ελέγχου Συνδροµικότητας ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ ΙΙ Τεχνικές Ανάκαµψεις από Σφάλµατα Κατανεµηµένες και Παράλληλες Βάσεις εδοµένων Βάσεις εδοµένων και ιαδίκτυο Βάσεις
Ύλη Ύλη Έννοιες Επεξεργασίας οσοληψιών Τεχνικές Ελέγχου Συνδροµικότητας ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ ΙΙ Τεχνικές Ανάκαµψεις από Σφάλµατα Κατανεµηµένες και Παράλληλες Βάσεις εδοµένων Βάσεις εδοµένων και ιαδίκτυο Βάσεις
ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ. Πανεπιστήμιο Πειραιώς Τμήμα Ψηφιακών Συστημάτων Μανουσόπουλος Χρήστος
 ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ Πανεπιστήμιο Πειραιώς Τμήμα Ψηφιακών Συστημάτων Μανουσόπουλος Χρήστος cman@unipi.gr Δοσοληψίες (Transactions) Μέχρι στιγμής θεωρούσαμε πως υπάρχει μόνο ένας DB χρήστης που εκτελεί μία
ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ Πανεπιστήμιο Πειραιώς Τμήμα Ψηφιακών Συστημάτων Μανουσόπουλος Χρήστος cman@unipi.gr Δοσοληψίες (Transactions) Μέχρι στιγμής θεωρούσαμε πως υπάρχει μόνο ένας DB χρήστης που εκτελεί μία
Δοσοληψίες Βάσεις Δεδομένων Διδάσκων: Μαρία Χαλκίδη
 Δοσοληψίες Βάσεις Δεδομένων Διδάσκων: Μαρία Χαλκίδη με βάση slides από A. Silberschatz, H. Korth, S. Sudarshan, Database System Concepts, 5 th edition Βασικές έννοιες της δοσοληψίας Δοσοληψία είναι μία
Δοσοληψίες Βάσεις Δεδομένων Διδάσκων: Μαρία Χαλκίδη με βάση slides από A. Silberschatz, H. Korth, S. Sudarshan, Database System Concepts, 5 th edition Βασικές έννοιες της δοσοληψίας Δοσοληψία είναι μία
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Συστήματα Διαχείρισης Βάσεων Δεδομένων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Συστήματα Διαχείρισης Βάσεων Δεδομένων Φροντιστήριο 10: Transactions - part 2 Δημήτρης Πλεξουσάκης Τμήμα Επιστήμης Υπολογιστών Tutorial on 2-Phase Locking and Other
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Συστήματα Διαχείρισης Βάσεων Δεδομένων Φροντιστήριο 10: Transactions - part 2 Δημήτρης Πλεξουσάκης Τμήμα Επιστήμης Υπολογιστών Tutorial on 2-Phase Locking and Other
Έλεγχος Συγχρονικότητας. (Concurrency Control)
 Έλεγχος Συγχρονικότητας (Concurrency Control) Συγχρονικότητα δοσοληψιών Οι αλληλεπιδράσεις ανάμεσα σε πολλαπλές δοσοληψίες που εκτελούνται ταυτόχρονα (multiple transactions execute concurrently) μπορεί
Έλεγχος Συγχρονικότητας (Concurrency Control) Συγχρονικότητα δοσοληψιών Οι αλληλεπιδράσεις ανάμεσα σε πολλαπλές δοσοληψίες που εκτελούνται ταυτόχρονα (multiple transactions execute concurrently) μπορεί
Επεξεργασία οσοληψιών
 οσοληψίες Επεξεργασία οσοληψιών Ηταυτόχρονη εκτέλεση προγραµµάτων χρηστών είναι απαραίτητη για την καλή απόδοση ενός Σ Β Επειδή οι προσπελάσεις στο δίσκο είναι συχνές και σχετικά αργές, είναι σηµαντικό
οσοληψίες Επεξεργασία οσοληψιών Ηταυτόχρονη εκτέλεση προγραµµάτων χρηστών είναι απαραίτητη για την καλή απόδοση ενός Σ Β Επειδή οι προσπελάσεις στο δίσκο είναι συχνές και σχετικά αργές, είναι σηµαντικό
Άσκηση 1 (15 μονάδες) (Επεκτατός Κατακερματισμός)
 ΗΥ460 Τελική Εξέηαζη 29 Ιανουαπίου 2013 Σελίδα 1 από 8 Πανεπιστήμιο Κρήτης Τμήμα Επιστήμης Υπολογιστών ΗΥ-460 Συστήματα Διαχείρισης Βάσεων Δεδομένων Δημήτρης Πλεξουσάκης Βασίλης Χριστοφίδης Επαναληπτική
ΗΥ460 Τελική Εξέηαζη 29 Ιανουαπίου 2013 Σελίδα 1 από 8 Πανεπιστήμιο Κρήτης Τμήμα Επιστήμης Υπολογιστών ΗΥ-460 Συστήματα Διαχείρισης Βάσεων Δεδομένων Δημήτρης Πλεξουσάκης Βασίλης Χριστοφίδης Επαναληπτική
Βάσεις Δεδομένων. Τ.Ε.Ι. Ιονίων Νήσων Σχολή Διοίκησης και Οικονομίας - Λευκάδα
 Βάσεις Δεδομένων Τ.Ε.Ι. Ιονίων Νήσων Σχολή Διοίκησης και Οικονομίας - Λευκάδα Στέργιος Παλαμάς, Υλικό Μαθήματος «Βάσεις Δεδομένων», 2015-2016 Κεφάλαιο 7: Transactions (Συναλλαγές) Ο λόγος που αναπτύχθηκαν
Βάσεις Δεδομένων Τ.Ε.Ι. Ιονίων Νήσων Σχολή Διοίκησης και Οικονομίας - Λευκάδα Στέργιος Παλαμάς, Υλικό Μαθήματος «Βάσεις Δεδομένων», 2015-2016 Κεφάλαιο 7: Transactions (Συναλλαγές) Ο λόγος που αναπτύχθηκαν
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Βάσεις Δεδομένων και Ευφυή Πληροφοριακά Συστήματα Επιχειρηματικότητας. Πληροφοριακά Συστήματα και Βάσεις Δεδομένων. Δρ. Κωνσταντίνος Χ.
 Βάσεις Δεδομένων και Ευφυή Πληροφοριακά Συστήματα Επιχειρηματικότητας Πληροφοριακά Συστήματα και Βάσεις Δεδομένων Δρ. Κωνσταντίνος Χ. Γιωτόπουλος ΧΡΟΝΟΠΡΟΓΡΑΜΜΑΤΑ και ΔΥΝΑΤΟΤΗΤΑ ΑΝΑΚΑΜΨΗΣ Όταν οι δοσοληψίες
Βάσεις Δεδομένων και Ευφυή Πληροφοριακά Συστήματα Επιχειρηματικότητας Πληροφοριακά Συστήματα και Βάσεις Δεδομένων Δρ. Κωνσταντίνος Χ. Γιωτόπουλος ΧΡΟΝΟΠΡΟΓΡΑΜΜΑΤΑ και ΔΥΝΑΤΟΤΗΤΑ ΑΝΑΚΑΜΨΗΣ Όταν οι δοσοληψίες
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Transaction Processing (Διαχείριση Δοσοληψιών)
 Transaction Processing (Διαχείριση Δοσοληψιών) In modern applications databases are shared by more than one users at the same time who can query and update them It is not possible to provide each user
Transaction Processing (Διαχείριση Δοσοληψιών) In modern applications databases are shared by more than one users at the same time who can query and update them It is not possible to provide each user
Επεξεργασία οσοληψιών
 Επανάληψη: οσοληψίες Επεξεργασία οσοληψιών Ανακεφαλαίωση Πρόβληµα «Σωστή» εκτέλεση προγραµµάτων προσπέλασης µίας βδ, στην περίπτωση: ταυτοχρονισµού αποτυχιών 1 2 Επανάληψη: οσοληψίες Επανάληψη: οσοληψίες
Επανάληψη: οσοληψίες Επεξεργασία οσοληψιών Ανακεφαλαίωση Πρόβληµα «Σωστή» εκτέλεση προγραµµάτων προσπέλασης µίας βδ, στην περίπτωση: ταυτοχρονισµού αποτυχιών 1 2 Επανάληψη: οσοληψίες Επανάληψη: οσοληψίες
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 24/3/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
Αποκατάσταση συστήματος Βάσεις Δεδομένων
 Αποκατάσταση συστήματος Βάσεις Δεδομένων με βάση slides από A. Silberschatz, H. Korth, S. Sudarshan, Database System Concepts, 5 th edition Κατηγοριοποίηση αποτυχιών Αποτυχία συναλλαγής (Transaction failure):
Αποκατάσταση συστήματος Βάσεις Δεδομένων με βάση slides από A. Silberschatz, H. Korth, S. Sudarshan, Database System Concepts, 5 th edition Κατηγοριοποίηση αποτυχιών Αποτυχία συναλλαγής (Transaction failure):
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ ΙΙ. Σχετικά µε το µάθηµα: Αξιολόγηση. Σχετικά µε το µάθηµα:faq ΟΧΙ ΝΑΙ. Λιγότερος! (ας πούµε το 1/3-1/4)
 ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ ΙΙ Κάποιες γενικές πληροφορίες συνοπτικά... Βάσεις εδοµένων II 2004-2005 Ευαγγελία Πιτουρά 1 Βάσεις εδοµένων II 2004-2005 Ευαγγελία Πιτουρά 2 Σχετικά µε το µάθηµα: Ύλη Σχετικά µε το µάθηµα:
ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ ΙΙ Κάποιες γενικές πληροφορίες συνοπτικά... Βάσεις εδοµένων II 2004-2005 Ευαγγελία Πιτουρά 1 Βάσεις εδοµένων II 2004-2005 Ευαγγελία Πιτουρά 2 Σχετικά µε το µάθηµα: Ύλη Σχετικά µε το µάθηµα:
Βάσεις Δεδομένων ΙΙ. Διάλεξη 1 η Επεξεργασία Δοσοληψιών. Σύστημα Επεξεργασίας Δοσοληψιών
 Βάσεις Δεδομένων ΙΙ Διάλεξη 1 η Επεξεργασία Δοσοληψιών Δ. Χριστοδουλάκης - Α. Φωκά Τμήμα Μηχανικών Η/Υ & Πληροφορικής - Εαρινό Εξάμηνο 2007 Ορισμός Προβλήματος Σύστημα Επεξεργασίας Δοσοληψιών Συστήματα
Βάσεις Δεδομένων ΙΙ Διάλεξη 1 η Επεξεργασία Δοσοληψιών Δ. Χριστοδουλάκης - Α. Φωκά Τμήμα Μηχανικών Η/Υ & Πληροφορικής - Εαρινό Εξάμηνο 2007 Ορισμός Προβλήματος Σύστημα Επεξεργασίας Δοσοληψιών Συστήματα
Θεµατολόγιο. Α) Πρακτικά Θέµατα στον Έλεγχο Ταυτοχρονισµού
 Θεµατολόγιο Α) Πρακτικά Θέµατα στον Έλεγχο Ταυτοχρονισµού Φαντάσµατα Κλείδωµα δέντρων Κλείδωµα σε διαφορετικά επίπεδα διακριτότητας Πώς τα βάζω όλα µαζί Β) Εναλλακτικές Τεχνικές Αισιόδοξος έλεγχος ταυτοχρονισµού
Θεµατολόγιο Α) Πρακτικά Θέµατα στον Έλεγχο Ταυτοχρονισµού Φαντάσµατα Κλείδωµα δέντρων Κλείδωµα σε διαφορετικά επίπεδα διακριτότητας Πώς τα βάζω όλα µαζί Β) Εναλλακτικές Τεχνικές Αισιόδοξος έλεγχος ταυτοχρονισµού
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
The challenges of non-stable predicates
 The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
Αρχεία και Βάσεις Δεδομένων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αρχεία και Βάσεις Δεδομένων Διάλεξη 15η: Διαχείριση Δοσοληψιών Δημήτρης Πλεξουσάκης Τμήμα Επιστήμης Υπολογιστών Transaction Processing (Διαχείριση Δοσοληψιών) In
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αρχεία και Βάσεις Δεδομένων Διάλεξη 15η: Διαχείριση Δοσοληψιών Δημήτρης Πλεξουσάκης Τμήμα Επιστήμης Υπολογιστών Transaction Processing (Διαχείριση Δοσοληψιών) In
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Βάσεις Δεδομένων ΙΙ. Διάλεξη 2 η Tεχνικές Ελέγχου Συνδρομικότητας
 Βάσεις Δεδομένων ΙΙ Διάλεξη 2 η Tεχνικές Ελέγχου Συνδρομικότητας Δ. Χριστοδουλάκης - Α. Φωκά Τμήμα Μηχανικών Η/Υ & Πληροφορικής - Εαρινό Εξάμηνο 2007 Τεχνικές Ελέγχου Συνδρομικότητας Ο χρήστης δεν ασχολείται
Βάσεις Δεδομένων ΙΙ Διάλεξη 2 η Tεχνικές Ελέγχου Συνδρομικότητας Δ. Χριστοδουλάκης - Α. Φωκά Τμήμα Μηχανικών Η/Υ & Πληροφορικής - Εαρινό Εξάμηνο 2007 Τεχνικές Ελέγχου Συνδρομικότητας Ο χρήστης δεν ασχολείται
Έλεγχος Ταυτοχρονισμού
 Έλεγχος Ταυτοχρονισμού (εμπλουτισμένο λ έ υλικό) http://delab.csd.auth.gr/courses/c_dbimpl/ Ευχαριστίες Μέρος του υλικού είναι βασισμένο στο βιβλίο Database Systems: The Complete Book Κεφάλαια 18.1 18.3
Έλεγχος Ταυτοχρονισμού (εμπλουτισμένο λ έ υλικό) http://delab.csd.auth.gr/courses/c_dbimpl/ Ευχαριστίες Μέρος του υλικού είναι βασισμένο στο βιβλίο Database Systems: The Complete Book Κεφάλαια 18.1 18.3
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Σημεία ελέγχου (Checkpoints)
 Σημεία ελέγχου (Checkpoints) Από την στιγμή που γίνεται ένα σε ένα Undo Recovery θα μπορούσε κανείς να υποθέσει ότι τα πρακτικά της δοσοληψίας μέχρι το δεν είναι πλέον απαραίτητα για
Σημεία ελέγχου (Checkpoints) Από την στιγμή που γίνεται ένα σε ένα Undo Recovery θα μπορούσε κανείς να υποθέσει ότι τα πρακτικά της δοσοληψίας μέχρι το δεν είναι πλέον απαραίτητα για
Κεφάλαιο 13 Δοσοληψίες
 Κεφάλαιο 13 Δοσοληψίες Σύνοψη Στο παρόν κεφάλαιο θα παρουσιασθούν βασικά στοιχεία όσον αφορά τις δοσοληψίες, την έννοια της σειριοποιησιμότητας και των διαφόρων επιπέδων απομόνωσης. Προαπαιτούμενη γνώση
Κεφάλαιο 13 Δοσοληψίες Σύνοψη Στο παρόν κεφάλαιο θα παρουσιασθούν βασικά στοιχεία όσον αφορά τις δοσοληψίες, την έννοια της σειριοποιησιμότητας και των διαφόρων επιπέδων απομόνωσης. Προαπαιτούμενη γνώση
Physical DB Design. B-Trees Index files can become quite large for large main files Indices on index files are possible.
 B-Trees Index files can become quite large for large main files Indices on index files are possible 3 rd -level index 2 nd -level index 1 st -level index Main file 1 The 1 st -level index consists of pairs
B-Trees Index files can become quite large for large main files Indices on index files are possible 3 rd -level index 2 nd -level index 1 st -level index Main file 1 The 1 st -level index consists of pairs
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 6/5/2006
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Ευρετήρια. Βάσεις Δεδομένων. Διδάσκων: Μαρία Χαλκίδη
 Ευρετήρια Βάσεις Δεδομένων Διδάσκων: Μαρία Χαλκίδη Βασικές έννοιες Οι μηχανισμοί δεικτοδότησης χρησιμοποιούνται για να επιταχύνουν την προσπέλαση σε επιθυμητά δεδομένα. π.χ., author catalog in library
Ευρετήρια Βάσεις Δεδομένων Διδάσκων: Μαρία Χαλκίδη Βασικές έννοιες Οι μηχανισμοί δεικτοδότησης χρησιμοποιούνται για να επιταχύνουν την προσπέλαση σε επιθυμητά δεδομένα. π.χ., author catalog in library
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
ω ω ω ω ω ω+2 ω ω+2 + ω ω ω ω+2 + ω ω+1 ω ω+2 2 ω ω ω ω ω ω ω ω+1 ω ω2 ω ω2 + ω ω ω2 + ω ω ω ω2 + ω ω+1 ω ω2 + ω ω+1 + ω ω ω ω2 + ω
 0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
Συστήματα Διαχείρισης Βάσεων Δεδομένων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Συστήματα Διαχείρισης Βάσεων Δεδομένων Διάλεξη 9η: Transactions - part 2 Δημήτρης Πλεξουσάκης Τμήμα Επιστήμης Υπολογιστών Transaction Management Comparison of Undo
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Συστήματα Διαχείρισης Βάσεων Δεδομένων Διάλεξη 9η: Transactions - part 2 Δημήτρης Πλεξουσάκης Τμήμα Επιστήμης Υπολογιστών Transaction Management Comparison of Undo
ΙΑΧΕΙΡΙΣΗ ΟΣΟΛΗΨΙΩΝ Να θυµηθούµε:
 ΙΑΧΕΙΡΙΣΗ ΟΣΟΛΗΨΙΩΝ Να θυµηθούµε: Μια βάση δεδοµένων είναι σε συνεπή κατάσταση (consistent state) εάν όλοι οι περιορισµοί ακεραιότητας που έχουν δηλωθεί για αυτήν πληρούνται. Οι αλλαγές στην κατάσταση
ΙΑΧΕΙΡΙΣΗ ΟΣΟΛΗΨΙΩΝ Να θυµηθούµε: Μια βάση δεδοµένων είναι σε συνεπή κατάσταση (consistent state) εάν όλοι οι περιορισµοί ακεραιότητας που έχουν δηλωθεί για αυτήν πληρούνται. Οι αλλαγές στην κατάσταση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ - ΤΜΗΥΠ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ ΙI
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ - ΤΜΗΥΠ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ ΙI Β. Μεγαλοοικονόμου Επεξεργασία Δοσοληψιών (Transaction Processing) (παρουσίαση βασισμένη εν μέρη σε σημειώσεις των Silberchatz, Korth και Sudarshan και του
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ - ΤΜΗΥΠ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ ΙI Β. Μεγαλοοικονόμου Επεξεργασία Δοσοληψιών (Transaction Processing) (παρουσίαση βασισμένη εν μέρη σε σημειώσεις των Silberchatz, Korth και Sudarshan και του
Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων. Εξάμηνο 7 ο
 Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων Εξάμηνο 7 ο Oracle SQL Developer An Oracle Database stores and organizes information. Oracle SQL Developer is a tool for accessing and maintaining the data
Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων Εξάμηνο 7 ο Oracle SQL Developer An Oracle Database stores and organizes information. Oracle SQL Developer is a tool for accessing and maintaining the data
Ακεραιότητα και Ασφάλεια Μέρος 1 Σχεδιασμός Βάσεων Δεδομένων
 Ακεραιότητα και Ασφάλεια Μέρος 1 Σχεδιασμός Βάσεων Δεδομένων με βάση slides από A. Silberschatz, H. Korth, S. Sudarshan, Database System Concepts, 5 th edition Περιορισμοί πεδίου τιμών Περιορισμοί ακεραιότητας
Ακεραιότητα και Ασφάλεια Μέρος 1 Σχεδιασμός Βάσεων Δεδομένων με βάση slides από A. Silberschatz, H. Korth, S. Sudarshan, Database System Concepts, 5 th edition Περιορισμοί πεδίου τιμών Περιορισμοί ακεραιότητας
Βάσεις Δεδομένων ΙΙ Ενότητα 1
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Βάσεις Δεδομένων ΙΙ Ενότητα 1: Επεξεργασία Δοσοληψιών Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Βάσεις Δεδομένων ΙΙ Ενότητα 1: Επεξεργασία Δοσοληψιών Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Βάσεις Δεδομένων 2. Φροντιστήριο Δοσοληψίες Τεχνικές ελέγχου συνδρομικότητας. Ημερ: 05/5/2009 Ακ.Έτος 2008-09
 Βάσεις Δεδομένων 2 Φροντιστήριο Δοσοληψίες Τεχνικές ελέγχου συνδρομικότητας Ημερ: 05/5/2009 Ακ.Έτος 2008-09 Θεωρία-Επανάληψη Δοσοληψία-ορισμός Το πρόβλημα της απώλειας των ενημερώσεων Το πρόβλημα της προσωρινής
Βάσεις Δεδομένων 2 Φροντιστήριο Δοσοληψίες Τεχνικές ελέγχου συνδρομικότητας Ημερ: 05/5/2009 Ακ.Έτος 2008-09 Θεωρία-Επανάληψη Δοσοληψία-ορισμός Το πρόβλημα της απώλειας των ενημερώσεων Το πρόβλημα της προσωρινής
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Lecture 2. Soundness and completeness of propositional logic
 Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Τεχνικές Ελέγχου Συνδροµικότητας
 Τεχνικές Ελέγχου Συνδροµικότητας Τεχνικές Ελέγχου Συνδροµικότητας Ο χρήστης δεν ασχολείται µε τη συνδροµικότητα Το Σ Β εξασφαλίζει «σωστή συνδροµικότητα», γενικά δροµολογεί τις πράξεις των δοσοληψιών ώστε
Τεχνικές Ελέγχου Συνδροµικότητας Τεχνικές Ελέγχου Συνδροµικότητας Ο χρήστης δεν ασχολείται µε τη συνδροµικότητα Το Σ Β εξασφαλίζει «σωστή συνδροµικότητα», γενικά δροµολογεί τις πράξεις των δοσοληψιών ώστε
Υ- 07 Παράλληλα Συστήματα Transac9onal memory
 Υ- 07 Παράλληλα Συστήματα Transac9onal memory Αρης Ευθυμίου Παρ. προγρ/μός με κλειδιά Χαμηλού επιπέδου πολύ κοντά στα μέσα και τις δομές του υλικού πολλές λεπτομέρειες, εύκολα γίνεται λάθος χαμηλή παραγωγικότητα
Υ- 07 Παράλληλα Συστήματα Transac9onal memory Αρης Ευθυμίου Παρ. προγρ/μός με κλειδιά Χαμηλού επιπέδου πολύ κοντά στα μέσα και τις δομές του υλικού πολλές λεπτομέρειες, εύκολα γίνεται λάθος χαμηλή παραγωγικότητα
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in
 Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Reminders: linear functions
 Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Διαχείριση Δοσοληψιών
 Διαχείριση Δοσοληψιών Ορισμός της δοσοληψίας Συνδρομικές εκτελέσεις (concurrency) Έλεγχος σειριοποιησιμότητας Ανάκαμψη δοσοληψιών (recovery) Υλοποίηση της Απομόνωσης Βασική πηγή διαφανειών: Silberschatz
Διαχείριση Δοσοληψιών Ορισμός της δοσοληψίας Συνδρομικές εκτελέσεις (concurrency) Έλεγχος σειριοποιησιμότητας Ανάκαμψη δοσοληψιών (recovery) Υλοποίηση της Απομόνωσης Βασική πηγή διαφανειών: Silberschatz
Στο εστιατόριο «ToDokimasesPrinToBgaleisStonKosmo?» έξω από τους δακτυλίους του Κρόνου, οι παραγγελίες γίνονται ηλεκτρονικά.
 Διαστημικό εστιατόριο του (Μ)ΑστροΈκτορα Στο εστιατόριο «ToDokimasesPrinToBgaleisStonKosmo?» έξω από τους δακτυλίους του Κρόνου, οι παραγγελίες γίνονται ηλεκτρονικά. Μόλις μια παρέα πελατών κάτσει σε ένα
Διαστημικό εστιατόριο του (Μ)ΑστροΈκτορα Στο εστιατόριο «ToDokimasesPrinToBgaleisStonKosmo?» έξω από τους δακτυλίους του Κρόνου, οι παραγγελίες γίνονται ηλεκτρονικά. Μόλις μια παρέα πελατών κάτσει σε ένα
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
TMA4115 Matematikk 3
 TMA4115 Matematikk 3 Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet Trondheim Spring 2010 Lecture 12: Mathematics Marvellous Matrices Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet
TMA4115 Matematikk 3 Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet Trondheim Spring 2010 Lecture 12: Mathematics Marvellous Matrices Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Overview. Transition Semantics. Configurations and the transition relation. Executions and computation
 Overview Transition Semantics Configurations and the transition relation Executions and computation Inference rules for small-step structural operational semantics for the simple imperative language Transition
Overview Transition Semantics Configurations and the transition relation Executions and computation Inference rules for small-step structural operational semantics for the simple imperative language Transition
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
2. THEORY OF EQUATIONS. PREVIOUS EAMCET Bits.
 EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
Βάσεις Δεδομένων ΙΙ. Διάλεξη 3 η Tεχνικές Aνάκαμψης. Ιδιότητες Δοσοληψιών
 Βάσεις Δεδομένων ΙΙ Διάλεξη 3 η Tεχνικές Aνάκαμψης Δ. Χριστοδουλάκης - Α. Φωκά Τμήμα Μηχανικών Η/Υ & Πληροφορικής - Εαρινό Εξάμηνο 2007 Επιθυμητές Ιδιότητες μιας Δοσοληψίας Ιδιότητες Δοσοληψιών Αtomicity
Βάσεις Δεδομένων ΙΙ Διάλεξη 3 η Tεχνικές Aνάκαμψης Δ. Χριστοδουλάκης - Α. Φωκά Τμήμα Μηχανικών Η/Υ & Πληροφορικής - Εαρινό Εξάμηνο 2007 Επιθυμητές Ιδιότητες μιας Δοσοληψίας Ιδιότητες Δοσοληψιών Αtomicity
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Επεξεργασία οσοληψιών (συνέχεια)
 Επανάληψη: οσοληψίες Επεξεργασία οσοληψιών (συνέχεια) Πρόβληµα «Σωστή» εκτέλεση προγραµµάτων όταν επιτρέπουµε ταυτοχρονισµό και ακόµα και αν υπάρχουν αποτυχίες 1 2 οσοληψία (transaction) Επανάληψη: οσοληψίες
Επανάληψη: οσοληψίες Επεξεργασία οσοληψιών (συνέχεια) Πρόβληµα «Σωστή» εκτέλεση προγραµµάτων όταν επιτρέπουµε ταυτοχρονισµό και ακόµα και αν υπάρχουν αποτυχίες 1 2 οσοληψία (transaction) Επανάληψη: οσοληψίες
Math 6 SL Probability Distributions Practice Test Mark Scheme
 Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Έλεγχος Ταυτοχρονισμού
 Έλεγχος Ταυτοχρονισμού (εμπλουτισμένο λ έ υλικό) http://delab.csd.auth.gr/courses/c_dbimpl/ Ευχαριστίες Μέρος του υλικού είναι βασισμένο στο βιβλίο Database Systems: The Complete Book 2 Εισαγωγικά γ Ένα
Έλεγχος Ταυτοχρονισμού (εμπλουτισμένο λ έ υλικό) http://delab.csd.auth.gr/courses/c_dbimpl/ Ευχαριστίες Μέρος του υλικού είναι βασισμένο στο βιβλίο Database Systems: The Complete Book 2 Εισαγωγικά γ Ένα
PARTIAL NOTES for 6.1 Trigonometric Identities
 PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
Transactions Management. (Διαχείριση Δοσοληψιών)
 Transactions Management (Διαχείριση Δοσοληψιών) Επισκόπηση διαλέξεων Αντιμετώπιση αστοχιών συστήματος (failure recovery) Χρήση ιστορικού/πρακτικού - Logging (Undo, Redo, Undo/Redo) Χρονοπρογράμματα Δοσοληψιών
Transactions Management (Διαχείριση Δοσοληψιών) Επισκόπηση διαλέξεων Αντιμετώπιση αστοχιών συστήματος (failure recovery) Χρήση ιστορικού/πρακτικού - Logging (Undo, Redo, Undo/Redo) Χρονοπρογράμματα Δοσοληψιών
( y) Partial Differential Equations
 Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Advanced Subsidiary Unit 1: Understanding and Written Response
 Write your name here Surname Other names Edexcel GE entre Number andidate Number Greek dvanced Subsidiary Unit 1: Understanding and Written Response Thursday 16 May 2013 Morning Time: 2 hours 45 minutes
Write your name here Surname Other names Edexcel GE entre Number andidate Number Greek dvanced Subsidiary Unit 1: Understanding and Written Response Thursday 16 May 2013 Morning Time: 2 hours 45 minutes
Section 9.2 Polar Equations and Graphs
 180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
ΗΥ360 Αρχεία και Βάσεις εδοµένων
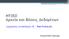 1 ΗΥ360 Αρχεία και Βάσεις εδοµένων ιαχείριση Συναλλαγών II - Tree Protocols Αυγουστάκη Αργυρώ 2 Διαχείριση Συναλλαγών - Επανάληψη Συναλλαγή (Τ) είναι ένα σύνολο από ενέργειες σε κάποιο αντικείμενο της
1 ΗΥ360 Αρχεία και Βάσεις εδοµένων ιαχείριση Συναλλαγών II - Tree Protocols Αυγουστάκη Αργυρώ 2 Διαχείριση Συναλλαγών - Επανάληψη Συναλλαγή (Τ) είναι ένα σύνολο από ενέργειες σε κάποιο αντικείμενο της
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ - ΤΜΗΥΠ ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ ΙI
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ - ΤΜΗΥΠ ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ ΙI Β. Μεγαλοοικονόµου Έλεγχος συνδροµικότητας (παρουσίαση βασισµένη εν µέρη σε σηµειώσεις των Silberchatz, Korth και Sudarshan και του C. Faloutsos) Γενική Επισκόπηση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ - ΤΜΗΥΠ ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ ΙI Β. Μεγαλοοικονόµου Έλεγχος συνδροµικότητας (παρουσίαση βασισµένη εν µέρη σε σηµειώσεις των Silberchatz, Korth και Sudarshan και του C. Faloutsos) Γενική Επισκόπηση
