ΣΥΜΠΕΡΙΦΟΡΕΣ ΜΑΘΗΤΩΝ ΣΤ ΤΑΞΗΣ ΔΗΜΟΤΙΚΟΥ ΣΤΟ ΘΕΜΑ ΤΗΣ ΜΕΤΑΦΟΡΑΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ
|
|
|
- Νίκων Παπαγεωργίου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Καβούζη, Ι., Μεσαρίτης, Γ., & Λεμονίδης, Χ., (2008). Συμπεριφορές μαθητών ΣΤ τάξης δημοτικού στο θέμα της μεταφοράς στα μαθηματικά. Πρακτικά 10 ου Παγκύπριου Συνεδρίου Μαθηματικής Παιδείας και Επιστήμης, Πάφος 1-3 Φεβρουαρίου, σελ ΣΥΜΠΕΡΙΦΟΡΕΣ ΜΑΘΗΤΩΝ ΣΤ ΤΑΞΗΣ ΔΗΜΟΤΙΚΟΥ ΣΤΟ ΘΕΜΑ ΤΗΣ ΜΕΤΑΦΟΡΑΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Ισαβέλλα Καβούζη*, Γιώργος Μεσαρίτης* & Χαράλαμπος Λεμονίδης** *Τμήμα Επιστημών της Αγωγής, Πανεπιστήμιο Κύπρου **Καθηγητής Διδακτικής των Μαθηματικών, Πανεπιστήμιο Δυτικής Μακεδονίας ΠΕΡΙΛΗΨΗ Σύμφωνα με τα αποτελέσματα σύγχρονων ερευνών οι μαθητές δυσκολεύονται να μεταφέρουν και να εφαρμόσουν μαθηματικές έννοιες που διδάσκονται στο σχολείο σε προβλήματα των οποίων το πλαίσιο αναφέρεται σε καταστάσεις από την καθημερινή ζωή. Η παρούσα εργασία επιδιώκει να εξετάσει κατά πόσο παιδιά της Στ τάξης του Δημοτικού Σχολείου είναι σε θέση να μεταφέρουν τη μαθηματική τους γνώση σε προβληματικές καταστάσεις που παρουσιάζουν τα ίδια δομικά χαρακτηριστικά. Τα προβλήματα σε πλαίσιο που προτείνονται στους μαθητές διαφοροποιούνται σε τρία είδη: άγνωστο πλαίσιο, γνωστό πλαίσιο σχολικού τύπου και πλαίσιο παρόμοιο με δεδομένη άσκηση. Τα αποτελέσματα της έρευνας δείχνουν ότι η πλειοψηφία των μαθητών αποτυγχάνει κατά τη μεταφορά στο πρόβλημα με άγνωστο πλαίσιο. Φαίνεται επίσης ότι η επίδοση των μαθητών στα μαθηματικά δεν είναι ανάλογη με την επιτυχία τους στη μεταφορά. Εισαγωγή Αρκετές έρευνες έχουν δείξει ότι οι μαθητές δυσκολεύονται να μεταφέρουν τις μαθηματικές έννοιες που μαθαίνουν σε καταστάσεις λύσης προβλήματος με πλαίσιο από την καθημερινή ζωή το οποίο δεν έχουν συναντήσει προηγουμένως (Van Eck και Dempsey, 2002; VanderStoep & Seifert, 1993). Κατά την επίλυση προβληματικών καταστάσεων μέσα σε πλαίσιο, οι οποίες απαιτούν τη μεταφορά της μαθηματικής γνώσης, οι μαθητές βασίζονται σε μεγάλο βαθμό στα επιφανειακά χαρακτηριστικά του προβλήματος. Αυτά φαίνεται να τους παραπέμπουν σε προηγούμενα προβλήματα, τα οποία παρουσιάζουν επιφανειακή ομοιότητα με τα υπό επίλυση προβλήματα, και ως εκ τούτου, υπάρχει ο κίνδυνος να ανακαλέσουν λανθασμένες διαδικασίες επίλυσης. Αντίθετα, η κατηγοριοποίηση προβλημάτων με βάση κοινά δομικά χαρακτηριστικά οδηγεί τους μαθητές σε επιτυχία στη μεταφορά.
2 Στην παρούσα έρευνα εξετάζεται η ικανότητα μεταφοράς που επιδεικνύουν οι μαθητές της Στ τάξης του Δημοτικού Σχολείου σε τρεις τύπους προβλημάτων με πλαίσιο: α) πρόβλημα του οποίο τα επιφανειακά χαρακτηριστικά του πλαισίου είναι παρόμοια με δεδομένη αποπλαισιωμένη άσκηση (πρόβλημα με τις σανίδες), β) πρόβλημα του οποίου το πλαίσιο είναι σύνηθες για τα σχολικά δεδομένα (πρόβλημα με τις ανθοδέσμες) και γ) πρόβλημα με πλαίσιο άγνωστο στους μαθητές (πρόβλημα με τα φυτά). Οι μαθητές αρχικά καλούνται να απαντήσουν σε ασκήσεις αποπλαισιωμένες που αναφέρονται στις ίδιες μαθηματικές έννοιες με αυτές των προβλημάτων με πλαίσιο. Οι αποπλαισιωμένες ασκήσεις και τα προβλήματα σε πλαίσιο που προτείνονται στους μαθητές έχουν τα ίδια δομικά χαρακτηριστικά, δηλαδή είναι όμοια ως προς τη διαδικασία επίλυσης. Στην εργασία αυτή θα αναλύσουμε τις συμπεριφορές των μαθητών σχετικά με το θέμα της μεταφοράς μαθηματικών εννοιών που είναι γνωστές στα τρία είδη των αποπλαισιωμένων προβλημάτων. Θα καταγράψουμε τις διαφορές που παρουσιάζονται στις συμπεριφορές των μαθητών ανάλογα με το είδος του κάθε προβλήματος. 1. ΘΕΩΡΗΤΙΚΟ ΠΛΑΙΣΙΟ 1.1. Ο όρος μεταφορά και η σημασία της Ο Royer (1979), όρισε τη «μεταφορά» ως το βαθμό στον οποίο η εκμάθηση μιας εκπαιδευτικής έννοιας συμβάλλει ή μειώνει την επόμενη επίλυση προβλήματος ή την εκμάθηση των επόμενων εκπαιδευτικών εννοιών. Ο ίδιος αναφέρει ότι η μεταφορά στη μάθηση φαίνεται από την ικανότητα του μαθητή να εφαρμόζει μια ικανότητα ή γνώση σε καταστάσεις που διαφέρουν από εκείνες που συνάντησε κατά τη διδασκαλία (αναφορά στους Van Eck και Dempsey, 2002). Σύμφωνα με τους Van Eck και Dempsey (2002) η μεταφορά είναι μια υψηλή νοητική ικανότητα που περιλαμβάνει ακριβή ερμηνεία και αναπαράσταση του προβλήματος, ανάκληση προηγούμενης γνώσης και διατύπωση κανόνων για το πότε και που θα εφαρμοστεί η γνώση. Ο Haskell (2001) αναφέρει ότι η μεταφορά αποτελεί τη βάση της νοητικής αφαίρεσης, των αναλογικών σχέσεων, της ταξινόμησης, της γενίκευσης και της επαγωγής, του λογικού συμπεράσματος και του σχηματισμού νοητικών μοντέλων (αναφορά στον Evans, 1999). Σύμφωνα με τους VanderStoep και Seifert (1993) η επίλυση προβλημάτων με μεταφορά απαιτεί την αναγνώριση σχέσεων μεταξύ δύο προβλημάτων, έστω και αν αυτά φαίνονται να μοιράζονται ελάχιστα χαρακτηριστικά. Η μεταφορά μπορεί να λάβει διαφορετικές μορφές, όπως: χρήση ενός σχολικού θέματος (π.χ μαθηματικά) σε ένα διαφορετικό πλαίσιο (π.χ στη φυσική ή στα οικονομικά), εφαρμογή της γνώσης από ένα παιδαγωγικό πλαίσιο (π.χ σχολείο) στην εργασία ή καθημερινή ζωή και τέλος, αξιοποίηση ( harnessing ) εξωσχολικών δραστηριοτήτων προς όφελος της μάθησης στο σχολείο (αναφορά στον Evans, 1999).
3 Οι ερευνητές που υποστηρίζουν τη διδασκαλία των μαθηματικών που σχετίζονται με την καθημερινή ζωή πιστεύουν ότι μια τέτοια προσέγγιση όχι μόνο προετοιμάζει τα παιδιά για το συγκεκριμένο περιεχόμενο, αλλά και οι ερωτήσεις που αναφέρονται στον «πραγματικό κόσμο», δημιουργούν μια γέφυρα ανάμεσα στον αφηρημένο ρόλο των μαθηματικών και το ρόλο τους ως μέλη της κοινωνίας (Broomes,1989, αναφορά στον Boaler, 1993). Παράλληλα, οι Masingila et al. (1996) υποστηρίζουν ότι τα άτομα χρειάζονται τις εμπειρίες μέσα στο σχολείο, αλλά ακόμη περισσότερο τις εμπειρίες μέσα από την καθημερινή ζωή, για να μπορεί η μάθηση να έχει πραγματικό νόημα (αναφορά στον Evans, 1999). Σύμφωνα με τους Fuchs et al. (2002) τα παιδιά μαθαίνουν καλύτερα όταν κατανοούν και αντιλαμβάνονται τι και γιατί μαθαίνουν μέσα από καταστάσεις της πραγματικής ζωής (αναφορά στον Evans, 1999) Το πρόβλημα της μεταφοράς Οι Gick και Holyoak (1980, 1983) έδειξαν ότι τα άτομα συνήθως αποτυγχάνουν να αναγνωρίσουν πότε η προηγούμενη τους γνώση μπορεί να χρησιμοποιηθεί για την επίλυση προβλημάτων που αντιμετωπίζουν (αναφορά στους VanderStoep και Seifert, 1993). Σύμφωνα με τους Van Eck και Dempsey (2002) oι μαθητές σπάνια δείχνουν να κάνουν επιτυχή μεταφορά και αυτό διότι η λύση προβλήματος και η μεταφορά εξαρτώνται από το πλαίσιο και συνεπώς, απαιτούν πολλαπλές ευκαιρίες πρακτικής σε μια ποικιλία πλαισίων. Δυστυχώς οι ευκαιρίες αυτές συνήθως είναι περιορισμένες στο σχολείο και στην εκπαίδευση γενικότερα. Έρευνες που ενασχολήθηκαν σχετικά με ομοιότητες μεταξύ προβλημάτων σε συγκεκριμένη μαθηματική έννοια, έδειξαν ότι οι μαθητές, ειδικά οι αρχάριοι, συχνά στηρίζονται σε επιφανειακά και άσχετα χαρακτηριστικά του προβλήματος κατά τη διαδικασία επίλυσης, και ως εκ τούτου ανακαλούν παλαιότερα προβλήματα από τη μνήμη τους βασισμένοι στην επιφανειακή ομοιότητα που έχουν με τα υπό εξέταση προβλήματα (αναφορά στους VanderStoep και Seifert, 1993). Με τον όρο επιφανειακά χαρακτηριστικά εννοούμε ομοιότητες σε στοιχεία των προβλημάτων, όπως πλοκή, αντικείμενα και άλλες μη σχετικές πληροφορίες, ενώ ο όρος όμοια δομικά χαρακτηριστικά απευθύνεται στην ομοιότητα ως προς τη διαδικασία επίλυσης. Οι Rattermann και Gentner (1987) υποστηρίζουν ότι η πρόσβαση σε παλαιότερα προβλήματα ή παραδείγματα που βρίσκονται αποθηκευμένα στη μνήμη των παιδιών είναι συχνότερη όταν οι μαθητές βασίζονται σε όμοια επιφανειακά παρά σε δομικά χαρακτηριστικά. Όμοια, o Ross (1984, 1987, 1989a), ο οποίος εξέτασε αρχάριους μαθητές, έδειξε ότι σε αρκετές περιπτώσεις τα παιδιά στηρίζονται στα επιφανειακά χαρακτηριστικά των προβλημάτων για να τα λύσουν (αναφορά στους VanderStoep και Seifert, 1993). Ακόμη, σύμφωνα με τους VanderStoep και Seifert (1993) οι αρχάριοι μαθητές φαίνεται να βασίζονται στα πιο προσβάσιμα και εμφανή χαρακτηριστικά του προβλήματος κατά τη μεταφορά και επίλυση του, καθώς δεν αντιλαμβάνονται ποια από τα χαρακτηριστικά του προβλήματος είναι σημαντικά και χρήσιμα για τη διαδικασία επίλυσης. To πρόβλημα της μεταφοράς στα μαθηματικά ίσως να οφείλεται μεταξύ άλλων και στην
4 αδυναμία των μαθητών να κατανοήσουν τη δομή των μαθηματικών προβλημάτων (Ross,1987; Νovick,1988; Bassok & Holyoak, 1993, αναφορά στον Benardo, 2001 και Evans, 1999). Οι Stanic και Lester (1989) αναφέρονται στα ευρήματα των ερευνητών Carraher και των συνεργατών τους, οι οποίοι μελέτησαν τις μη τυπικές διαδικασίες που τα παιδιά χρησιμοποιούν για να λύσουν προβλήματα σε φυσικά, εξωσχολικά πλαίσια. Συγκεκριμένα, μελετώντας παιδιά ηλικίας 9-15 ετών που εργάζονταν στην αγορά, παρατήρησαν ότι εκείνα που ήταν σε θέση να λύσουν ένα αριθμητικό πρόβλημα μέσα σε φυσικό καθημερινό πλαίσιο, συχνά αποτύγχαναν να το επιλύσουν όταν αυτό παρουσιαζόταν εκτός του φυσικού του πλαισίου. Οι ίδιοι αναφέρουν τους πιθανούς λόγους αυτής της διαφοράς στην απόδοση των παιδιών σε μαθηματικά προβλήματα στο σχολείο και στην καθημερινή ζωή, τα οποία διαφέρουν ουσιαστικά ως προς το πλαίσιο. Πρώτο, τα πλαίσια μέσα στα οποία παρουσιάζονται τα μαθηματικά προβλήματα της καθημερινής ζωής έχουν νόημα για τους λύτες. Ως εκ τούτου, το παιδί είναι ικανό να εφαρμόζει τη μη τυπική γνώση του σε προβλήματα που, ουσιαστικά, έχουν διαμορφωθεί μέσα από τις εμπειρίες του ίδιου. Ο δεύτερος λόγος έγκειται στο ότι στην καθημερινή ζωή τα άτομα συχνά χρησιμοποιούν μαθηματικές διαδικασίες και σκέψεις, αρκετά διαφορετικές από τα όσα έχουν μάθει στο σχολείο. 2. ΕΡΕΥΝΑ Σκοπός και ερευνητικά ερωτήματα Σκοπός της παρούσας έρευνας είναι να διερευνήσει κατά πόσο παιδιά της Στ τάξης δημοτικού είναι σε θέση να μεταφέρουν τη μαθηματική τους γνώση σε προβληματικές καταστάσεις που έχουν τα ίδια δομικά χαρακτηριστικά. Ακόμη, διερευνάται, με ποιοτικό τρόπο, κατά πόσο η σχολική επίδοση των μαθητών στα μαθηματικά επηρεάζει το βαθμό επιτυχίας στη μεταφορά. Επιπλέον, θα γίνει προσπάθεια όπως δοθούν κάποιες εξηγήσεις για την αποτυχία ή επιτυχία των παιδιών κατά τη μεταφορά. Ειδικότερα, επιχειρήθηκε να δοθούν απαντήσεις, στα παρακάτω ερωτήματα: Είναι σε θέση οι μαθητές να αναγνωρίζουν όμοια δομικά χαρακτηριστικά μεταξύ των μαθηματικών εννοιών που παρουσιάζονται υπό μορφή ασκήσεων και προβλημάτων με πλαίσιο; Με ποιον τρόπο επιτυγχάνεται η μεταφορά στα παρακάτω τρία είδη προβλημάτων: α) άγνωστο πλαίσιο (πρόβλημα με τα φυτά), β) σύνηθες σχολικό πλαίσιο (πρόβλημα με τις ανθοδέσμες) και γ) πλαίσιο παρόμοιο με δεδομένη άσκηση (πρόβλημα με τις σανίδες). Τα παιδιά με ψηλότερη επίδοση στα μαθηματικά παρουσιάζουν καλύτερες συμπεριφορές στη μεταφορά; Μεθοδολογία
5 Δείγμα Το δείγμα αποτέλεσαν τέσσερα παιδιά Στ τάξης δημοτικού σχολείου της επαρχίας Λευκωσίας. Στάλθηκαν επιστολές προς όλους τους γονείς της Στ τάξης του δημοτικού σχολείου με σκοπό να εξασφαλιστεί έγκριση από μέρους τους για συμμετοχή των παιδιών τους στην έρευνα. Έπειτα, από τα παιδιά που συμφώνησαν να συμμετάσχουν επιλέχθηκαν τέσσερα από τη δασκάλα της τάξης τους, ώστε το δείγμα να αποτελείται από παιδιά διαφορετικών επιδόσεων στα μαθηματικά. Τα δύο πρώτα παιδιά, η Γεωργία και ο Άγγελος, είχαν άριστες επιδόσεις στα μαθηματικά, το δεύτερο παιδί, ο Άρης, παρουσίαζε χαμηλή επίδοση, ενώ το τελευταίο, ο Χριστόδουλος, παρουσίαζε μέτρια επίδοση στα μαθηματικά. Τα ονόματα των παιδιών είναι συμβολικά ώστε να τηρηθεί η ανωνυμία. Μέσα συλλογής δεδομένων και ανάλυση Για την επίτευξη των στόχων της έρευνας θεωρήθηκε απαραίτητος ο καταρτισμός ενός δοκιμίου ως μέσου συλλογής δεδομένων. Κάθε μαθητής συμπλήρωσε ένα δοκίμιο με έξι έργα. Ανά δύο τα έργα είχαν την ίδια δομή, αλλά διέφεραν στο πλαίσιο μέσα στο οποίο δινόταν το πρόβλημα. Συγκεκριμένα, το ένα από τα δύο ήταν απλά εφαρμογή της μαθηματικής γνώσης ενώ το άλλο εντασσόταν μέσα σε ένα πλαίσιο. Για την κατασκευή του δοκιμίου βασιστήκαμε στην έρευνα του Boaler (1993). Η συλλογή των δεδομένων έγινε μέσα από παρατήρηση της πορείας εργασίας του κάθε παιδιού με ταυτόχρονη κλινική συνέντευξη. Οι συζητήσεις με τα παιδιά που είχαν χαρακτήρα ημι-δομημένης συνέντευξης, μαγνητοφωνήθηκαν και στη συνέχεια καταγράφηκαν. Η κάθε συνέντευξη διήρκησε περίπου μιάμιση ώρα. Για την ανάλυση των δεδομένων χρησιμοποιήθηκαν ποιοτικές μέθοδοι. Ασκήσεις και προβλήματα που δόθηκαν στους μαθητές 1. Βρες τον Μ.Κ.Δ. των αριθμών 72, 60, Κοίταξε τους αριθμούς : 9, 9, 9, 8, 7, 7, 7, 5, 5, 5, 4, 4, 4, 4, 3, 3, 3. Τοποθετήστε όλους αυτούς τους αριθμούς σε διαφορετικές ομάδες. Προσπάθησε η κάθε ομάδα να έχει άθροισμα όσο το δυνατό πιο κοντά στο 24. Καμιά ομάδα δεν πρέπει να έχει άθροισμα μεγαλύτερο από 24. Γράψε τον τρόπο που σκέφτηκες για να δημιουργήσεις τις ομάδες. 3. Σημειώστε ποιο είναι το μεγαλύτερο κλάσμα από κάθε ζεύγος και γράψτε γιατί. α) 3/10 ή 6/15, β) 2/5 ή 7/15, γ) 8/20 ή 14/ Ο Αντρέας φύτεψε μερικούς σπόρους σε δύο διαφορετικές γλάστρες. Η κάθε γλάστρα περιείχε διαφορετικό λίπασμα και ο Αντρέας ήθελε να εξετάσει ποιο λίπασμα από τα δύο είναι το καλύτερο. Έτσι ο Αντρέας έκανε ένα πείραμα κατά τη διάρκεια του καλοκαιριού, φυτεύοντας σπόρους στις γλάστρες και παρατηρώντας κάθε φορά πόσοι σπόροι βλάστησαν. Κάθε φορά φύτευε 15 σπόρους στη γλάστρα Α και 10 σπόρους στη γλάστρα Β. Παρακάτω φαίνονται τα αποτελέσματα:
6 Γλάστρα Α Γλάστρα Β Ιούνιος 5 φυτά 3 φυτά Ιούλιος 6 φυτά 4 φυτά Αύγουστος 3 φυτά 2 φυτά Ποιο από τα δυο λιπάσματα είναι το καλύτερο; Πως αποφάσισες ότι αυτό είναι το καλύτερο; 5. Ένας ανθοπώλης αγόρασε 66 άσπρα τριαντάφυλλα, 90 κόκκινα τριαντάφυλλα και 96 ροζ τριαντάφυλλα. Θέλει να φτιάξει όσες περισσότερες όμοιες ανθοδέσμες. Μπορείς να βρεις πόσες ανθοδέσμες μπορεί να φτιάξει; Πόσα τριαντάφυλλα από το κάθε χρώμα θα χρησιμοποιήσει σε κάθε ανθοδέσμη; Γράψε τον τρόπο που σκέφτηκες. 6. Ένα μικρό ξυλουργείο έχει πολλές σανίδες στην αποθήκη του που έχουν όλες μήκος 20 m. Ένας πελάτης θα κατασκευάσει ένα ερμάρι και χρειάζεται τα ακόλουθα μεγέθη σανίδων: 9m, 8m, 7m, 7m, 5m, 5m, 4m, 4m, 4m, 4m, 4m, 4m, 3m, 3m, 3m, 3m, 3m. Δείξε πως το ξυλουργείο θα πρέπει να κόψει τις σανίδες των 20 m στα μεγέθη που θέλει ο πελάτης. Προσπάθησε να μην σπαταλήσεις ξύλο από τις σανίδες των 20 m. Γράψε τον τρόπο σκέψης σου. 3. ΑΠΟΤΕΛΕΣΜΑΤΑ Στη συνέχεια παρουσιάζονται τα αποτελέσματα από τις παρατηρήσεις και τις κλινικές συνεντεύξεις των τεσσάρων μαθητών, κατά την επίλυση των έξι έργων του δοκιμίου. Επειδή η μελέτη διερευνά τη μεταφορά και τους λόγους αποτυχίας ή επιτυχίας σε αυτήν, δίνεται έμφαση στην παρουσίαση των αποτελεσμάτων των προβλημάτων 4, 5 και 6, καθώς αυτά είναι προβλήματα που αφορούν τη μεταφορά. Στις ασκήσεις 1, 2 και 3 όπου τα παιδιά αντιμετώπιζαν δυσκολία, οι ερευνητές με διευκρινήσεις και επισημάνσεις καθοδηγούσαν τον τρόπο σκέψης τους, ώστε να τις επιλύσουν. Όλοι οι μαθητές κατάφεραν χωρίς ιδιαίτερη δυσκολία να επιλύσουν την άσκηση 2, ενώ για την άσκηση 1 χρειάστηκε οι ερευνητές να υπενθυμίσουν τη διαδικασία εύρεσης του Μ.Κ.Δ. Επίσης, τόσο οι άριστοι όσο και ο μέτριος μαθητής έλυσαν την άσκηση 3 χωρίς να δυσκολευτούν ιδιαίτερα, σε αντίθεση με τον αδύνατο μαθητή που χρειάστηκε ιδιαίτερη καθοδήγηση. Φάνηκε ότι οι άριστοι και ο μέτριος μαθητής γνώριζαν καλύτερα τις συγκεκριμένες μαθηματικές έννοιες στις ασκήσεις 1, 2 και 3, σε σχέση με τον αδύνατο μαθητή. Πρόβλημα 4 (Τα φυτά) Όσον αφορά το πρόβλημα 4, η Γεωργία (άριστη επίδοση) αρχικά δεν είχε αντιληφθεί ότι έπρεπε να εμπλέξει την έννοια του κλάσματος για να συγκρίνει τις ποσότητες. Αντίθετα, προσπαθεί να βρει μέτρο σύγκρισης προσθέτοντας πέντε σπόρους στο συνολικό αριθμό των σπόρων που φυτεύτηκαν στη γλάστρα Β και ως εκ τούτου, προσθέτει πέντε στα φυτά που δε βλάστησαν.
7 «Νομίζω ότι είναι η γλάστρα Β γιατί μετέτρεψα το 10 για να το συγκρίνω. Έκανα το 10 ως 15. Προσθέτω 5, άρα αφού αρχικά βλάστησαν 3 φυτά στη γλάστρα Β και δεν έχουν βλαστήσει τα 7, προσθέτοντας ακόμη 5 σπόρους τα φυτά που δε βλάστησαν γίνονται 12.» Στη συνέχεια, η Γεωργία προσπάθησε να συγκρίνει τους σπόρους που δε βλάστησαν στην κάθε γλάστρα σε κάθε μήνα για να αποφασίσει ποιο λίπασμα είναι το καλύτερο. Έπειτα καταλήγει στο συμπέρασμα ότι το καλύτερο λίπασμα είναι αυτό στη γλάστρα Β, στην οποία οι σπόροι που δε βλάστησαν είναι λιγότεροι σε σχέση με τη γλάστρα Α. «Το λίπασμα Β είναι η απάντηση γιατί από τους 10 σπόρους δε βλάστησαν οι 7, ενώ στο λίπασμα Α δε βλάστησαν οι 10. Τον Ιούλη στη γλάστρα Β δε βλάστησαν οι 6 σπόροι, ενώ στη γλάστρα Α δε βλάστησαν οι 9. Τον Αύγουστο στη γλάστρα Β δε βλάστησαν οι 8 σπόροι από τους 10, ενώ στη γλάστρα Α δε βλάστησαν οι 12 από τους σπόρους. Άρα είχε περισσότερους σπόρους που δε βλάστησαν στη γλάστρα Α. Άρα το καλύτερο λίπασμα είναι το Β.» Παρόμοια, ο Άρης (χαμηλή επίδοση) προσπαθεί να συγκρίνει τα δύο λιπάσματα βρίσκοντας τα φυτά που δε βλάστησαν στην κάθε γλάστρα, στον κάθε μήνα. Έτσι, καταλήγει στην απάντηση ότι καλύτερο λίπασμα είναι αυτό της γλάστρας Β. «Η απάντηση είναι η γλάστρα Β γιατί η γλάστρα Α θέλει ακόμη 10 σπόρους για να έχουν βλαστήσει όλοι, ενώ η γλάστρα Β θέλει μόνο 7. Μετά πάλι τον Ιούλιο η γλάστρα Α θέλει 9 ενώ η Β θέλει 6. Τον Αύγουστο η γλάστρα Α θέλει ακόμη 12 σπόρους που δε βλάστησαν, ενώ η Β γλάστρα 8. [ ] Η γλάστρα Β συμφέρει, το λίπασμα Β, γιατί απομένουν 8 σπόροι στη γλάστρα Β, ενώ στη γλάστρα Α απομένουν 12 σπόροι που δε βλάστησαν.» Η Γεωργία και ο Άρης φαίνεται να αποτυγχάνουν στη μεταφορά, καθώς δεν αντιλαμβάνονται τη δομή του προβλήματος και έτσι δεν εφαρμόζουν την έννοια του κλάσματος για να φτάσουν στη λύση. Ο Άγγελος (άριστη επίδοση), αρχικά, δεν μπόρεσε να αντιληφθεί ότι έπρεπε να εμπλέξει την έννοια του κλάσματος για να λύσει το πρόβλημα 4 και προσπαθούσε με άτυπες στρατηγικές να φτάσει στην απάντηση. Συγκεκριμένα, αρχικά, αφαιρούσε 5 σπόρους από τη γλάστρα Α σε κάθε μήνα, ώστε κατά την άποψη του να δημιουργήσει ισοδύναμες ομάδες. Ακολούθως, λόγω του ότι με τη στρατηγική αυτή κατέληγε σε μη λογικά αποτελέσματα, πρόσθετε 5 σπόρους στη γλάστρα Β για κάθε μήνα. «(Αφαιρεί 5 για να ισοζυγίσει τις ομάδες) Άγγελος: Όμως 3-5 δε γίνεται. (Προσθέτει 5 στη γλάστρα Β) Άγγελος: Άρα η γλάστρα Β είναι καλύτερη αφού βλάστησαν περισσότεροι σπόροι. Ερευνητής: Δηλαδή εκεί που γράφεις 8 εννοείς ότι θα βλαστήσουν 8 σπόροι; Άγγελος: Ναι.
8 Ερευνητής: Ναι, αλλά αν βάλεις 5 σπόρους στη γλάστρα Β θα είναι σίγουρο ότι βλάστησαν και οι 5; Άγγελος: Όχι» Τα παραπάνω έκαναν τον Άγγελο να αναθεωρήσει τη σκέψη του και να ανατρέξει σε διαφορετική στρατηγική (διαίρεση). Ακολούθως, μετά από συζήτηση και διευκρινιστικές ερωτήσεις από μέρους του ερευνητή ο μαθητής σκέφτηκε ότι στη γλάστρα Α φυτρώνουν 14 σπόροι από τους 45, ενώ στη γλάστρα Β φυτρώνουν 9 σπόροι από τους 30. Αυτό όμως δεν ήταν αρκετό για να παραπέμψει το μαθητή στην έννοια του κλάσματος. «Ερευνητής: [ ] Από τους 45 σπόρους στη γλάστρα Α πόσοι βλάστησαν; Άγγελος: Οι 14 σπόροι. Ερευνητής: Και από τους 30 στη γλάστρα Β, βλάστησαν οι Άγγελος: 9 Ερευνητής: Αυτό δε σου θυμίζει μια έννοια που κάνατε στο σχολείο; Σκέφτεται λίγο. Άγγελος: Όχι» Ακόμη, σε ερώτηση του ερευνητή εάν το συγκεκριμένο πρόβλημα του θυμίζει κάποιο από τα προηγούμενα που έλυσε, απάντησε λανθασμένα. Συγκεκριμένα, αρχικά απάντησε ότι το παρόν πρόβλημα μοιάζει με την άσκηση 1 του Μ.Κ.Δ. και στη συνέχεια, αναθεώρησε αναφέροντας ότι μοιάζει με την άσκηση 3. Αμέσως, αλλάζει και πάλι γνώμη, αναφέροντας ότι δε μοιάζουν τελικά επειδή η άσκηση 3 περιέχει κλάσματα. Τέλος, μετά από επιπρόσθετη επισήμανση του ερευνητή, ο Άγγελος αντιλαμβάνεται ότι η άσκηση 3 και το πρόβλημα 4 μοιάζουν και μπορεί να μετατρέψει τα δεδομένα σε κλάσματα και να τα συγκρίνει. «Άγγελος: Α, στο πρόβλημα 3 συγκρίνουμε 2 κλάσματα Μοιάζει επειδή συγκρίνουμε δύο πράγματα Ε, στο πρόβλημα 4 είναι διαφορετικός ο παρονομαστής. Ερευνητής: Αφού μου είπες ότι στο πρόβλημα 4 δεν έχει κλάσματα Άγγελος: Ναι, αλλά σκέφτηκα ότι δε μοιάζει με τα άλλα προβλήματα. Μόνο στο πρόβλημα 3 μου ζητά να συγκρίνω. Ερευνητής: Μπορείς τώρα να λύσεις το 4; Άγγελος: Ναι, αν πω 14/45 και 9/30. Αν τα κάνω ομώνυμα, 9/30=27/90 και 14/45=28/90.» Από τα παραπάνω δεδομένα φαίνεται ότι ουσιαστικά η μεταφορά δεν έχει γίνει, καθώς το παιδί δεν αντιλήφθηκε από μόνο του τη δομή του προβλήματος και το ότι έπρεπε να εφαρμόσει τις γνώσεις του για το κλάσμα στο συγκεκριμένο πρόβλημα. Αυτό, εν τέλει, επιτεύχθηκε μέσα από τις πολλές διευκρινίσεις και παρεμβάσεις του ερευνητή. Το τέταρτο παιδί, ο Χριστόδουλος (μέτρια επίδοση), αρχικά προσθέτει τους σπόρους που βλάστησαν όλους τους μήνες στην κάθε γλάστρα και βρίσκει ότι στη γλάστρα Α φύτρωσαν 14 και στη γλάστρα Β βλάστησαν 9, αναφέροντας ότι καλύτερο λίπασμα
9 είναι το Α. Δε λαμβάνει υπόψη του τον αριθμό των σπόρων που φυτεύει κάθε μήνα, ο οποίος διαφέρει σε κάθε γλάστρα. Στη συνέχεια, μετά από παρέμβαση του ερευνητή, ο μαθητής προσπαθεί να εξισορροπήσει τις δύο ποσότητες, προσθέτοντας 5 σπόρους στη γλάστρα Β, στρατηγική που στη συνέχεια αναιρείται. «Ερευνητής: Ναι, αλλά φυτεύει 15 σπόρους κάθε μήνα στη γλάστρα Α, ενώ στη Β φυτεύει 10. Χριστόδουλος: Άρα αν προσθέσω ακόμα 5 σπόρους στη Β βγαίνουν 14. Ερευνητής: Όμως είσαι σίγουρος ότι οι 5 σπόροι που προσθέτεις θα βλαστήσουν όλοι; Χριστόδουλος: Όχι Ερευνητής: Είναι 15 ή 10 σπόρους που φύτεψε; Χριστόδουλος: Χμ, όχι 45 στη γλάστρα Α και 30 στη γλάστρα Β.» Έπειτα από την πιο πάνω συζήτηση ο Χριστόδουλος, προσπαθώντας να βρει ένα κοινό μέτρο σύγκρισης, σκέφτεται να αναγάγει τους αριθμούς στο 30. Έτσι, πολλαπλασιάζει τους σπόρους που βλάστησαν κάθε μήνα στη γλάστρα Α με το 2 και τους σπόρους στη γλάστρα Β με το 3. Φαίνεται δηλαδή, ότι αντιλαμβάνεται τη δομή του προβλήματος και ότι πρέπει να εμπλέξει την έννοια του κλάσματος, εφαρμόζοντας αναλογική σκέψη, επιτυγχάνοντας έτσι τη μεταφορά. Κατόπιν ερώτησης του ερευνητή κατά πόσο το πρόβλημα αυτό μοιάζει με κάποιο άλλο στο δοκίμιο, ο Χριστόδουλος απάντησε ότι μοιάζει με την άσκηση 3, αιτιολογώντας το με το ότι ακολούθησε την ίδια διαδικασία, δηλαδή έκανε ομώνυμα. Όμως, παρόλο που χρησιμοποίησε την έννοια του κλάσματος, εν τούτοις δεν το συνειδητοποιεί. Τα παραπάνω αποτελέσματα δείχνουν ότι οι μαθητές δυσκολεύονται πολύ να μεταφέρουν την έννοια του κλάσματος και της αναλογίας σε πρόβλημα του οποίου τα επιφανειακά χαρακτηριστικά τους είναι άγνωστα. Σχεδόν όλοι οι μαθητές σκέφτονται προσθετικά και δεν αναγνωρίζουν την κατάσταση της αναλογίας για να χρησιμοποιήσουν κλάσματα. Οι συμπεριφορές των μαθητών στη μεταφορά δε φαίνεται να επηρεάζονται από τις επιδόσεις τους στα μαθηματικά του σχολείου. Τόσο οι μαθητές με υψηλή επίδοση στα μαθηματικά του σχολείου όσο και οι υπόλοιποι αντιμετωπίζουν τις ίδιες δυσκολίες. Πρόβλημα 5 (Οι ανθοδέσμες) Όσον αφορά το πρόβλημα 5, η Γεωργία κατανοεί ότι πρέπει να βρει έναν αριθμό που να διαιρεί και τις τρεις ποσότητες του προβλήματος, δηλαδή το Μ.Κ.Δ. «Ερευνητής: Τι δοκιμάζεις; Γεωργία: Θέλω να βρω έναν αριθμό όσον πιο μεγάλο που να τα διαιρεί Ερευνητής: Χμ, πώς μπορείς να βρεις τον πιο μεγάλο αριθμό που διαιρεί και τους 3, ξέρεις; Γεωργία: Α, μπορώ να βρω το Μ.Κ.Δ!»
10 Ακολούθως, η Γεωργία βρίσκει το Μ.Κ.Δ και φαίνεται να αντιλαμβάνεται ότι ο αριθμός αυτός αντιπροσωπεύει τις ανθοδέσμες. Ως εκ τούτου, φαίνεται ότι η μαθήτρια επιτυγχάνει τη μεταφορά. Ο Άγγελος στο πρόβλημα 5, αρχικά, δοκιμάζει να αφαιρεί κάθε φορά ένα σταθερό αριθμό από τις ποσότητες των τριών λουλουδιών και ταυτόχρονα, σημειώνει κάθε φορά τον αριθμό των ανθοδεσμών που δημιουργεί. Συγκεκριμένα, δοκιμάζει να αφαιρεί κάθε φορά 3 τριαντάφυλλα αλλά αντιλαμβάνεται ότι αφαιρώντας τον ίδιο αριθμό κάθε φορά από άνισες ποσότητες, σε κάποια στιγμή τα άσπρα τριαντάφυλλα θα τέλειωναν πριν από τα κόκκινα. Στη συνέχεια, δοκιμάζει να αφαιρεί 6 ροζ, 3 κόκκινα και 1 άσπρο τριαντάφυλλα κάθε φορά, χωρίς θετικό αποτέλεσμα. Εν τέλει, ο μαθητής παρατηρώντας τις ασκήσεις του δοκιμίου που έλυσε προηγουμένως, αντιλαμβάνεται ότι το πρόβλημα 5 μοιάζει με την πρώτη άσκηση και επομένως, εφαρμόζει τη διαδικασία υπολογισμού του Μ.Κ.Δ. «Ερευνητής: Έχει κάποιο άλλο τρόπο; Άγγελος: (Κοιτάζει τις ασκήσεις). Α! Μοιάζει με το Μ.Κ.Δ. Ερευνητής: Γιατί μοιάζει με το Μ.Κ.Δ.; Άγγελος: Επειδή Όμως θέλουμε τον πιο μικρό αριθμό στο πρόβλημα 5, ενώ στο πρόβλημα 1 τον πιο μεγάλο. Ερευνητής: Γιατί τον πιο μικρό; Άγγελος: Επειδή θέλω τις περισσότερες ανθοδέσμες, άρα θέλω τον πιο μικρό (εννοεί τα τριαντάφυλλα).» Ο Άγγελος φαίνεται να εντοπίζει την ομοιότητα του προβλήματος 5 με την άσκηση 1 ως προς τα επιφανειακά χαρακτηριστικά, αφού αντιλαμβάνεται ότι πρέπει να υπολογίσει το Μ.Κ.Δ., αλλά δεν κατανοεί ότι στο πρόβλημα 5 αναζητούμε επίσης το μεγαλύτερο αριθμό. Ο μαθητής φαίνεται να στηρίχθηκε σε επιφανειακά χαρακτηριστικά για να συνδέσει την άσκηση 1 και το πρόβλημα 5 μεταξύ τους, αφού δεν κατανοεί πώς εφαρμόζεται ο Μ.Κ.Δ. στο πρόβλημα 5, αναφέροντας ότι το «6» δεν είναι οι ανθοδέσμες, αλλά τα τριαντάφυλλα που χρησιμοποιούνται κάθε φορά. Ο Χριστόδουλος (μέτρια επίδοση) επιτυγχάνει τη μεταφορά στο πρόβλημα 5, καθώς εντοπίζει την ομοιότητα με την άσκηση 1. Εφαρμόζει σωστά τη διαδικασία εύρεσης του Μ.Κ.Δ. και αντιλαμβάνεται ότι η απάντηση «6» του Μ.Κ.Δ. αντιστοιχεί στις όμοιες ανθοδέσμες που μπορεί να φτιάξει. Παράλληλα, χρησιμοποιεί το Μ.Κ.Δ. για να βρει με επιτυχία τις ποσότητες άσπρων, κόκκινων και ροζ τριαντάφυλλων της κάθε ανθοδέσμης. Αντίθετα, ο Άρης (χαμηλή επίδοση) φαίνεται να αποτυγχάνει στη μεταφορά στο πρόβλημα 5. Συγκεκριμένα, προσπάθησε να εφαρμόσει άτυπες στρατηγικές, όπως να υπολογίσει το μέσο όρο τριών αριθμών. Ειδικότερα, πρόσθεσε τις ποσότητες των τριαντάφυλλων και στη συνέχεια διαίρεσε διά 3 ( = 252, 252/3=84). Αναφέρει ότι θα φτιαχτούν 3 ανθοδέσμες από 84 τριαντάφυλλα η καθεμιά.
11 «Ερευνητής: Γιατί διαιρείς με το 3; Άρης: Γιατί είναι αυτό που σκέφτηκα. [ ] Ερευνητής: Εντάξει. Είναι το 3 ο μεγαλύτερος αριθμός που μπορείς να το κάνεις αυτό; Το 3 είναι ο μεγαλύτερος δυνατός αριθμός όμοιων ανθοδεσμών που μπορούμε να φτιάξουμε με αυτά τα λουλούδια που έχουμε; Άρης: Δε βρίσκω άλλο αριθμό. Ερευνητής: Σου θυμίζει κάτι το ότι ψάχνουμε τον πιο μεγάλο αριθμό που διαιρεί και τους 3 αριθμούς λουλουδιών; Άρης: Όχι, δεν μπορώ να σκεφτώ κάτι άλλο Παρατηρούμε ότι ο Άρης δεν αντιλαμβάνεται τη δομή του προβλήματος και ότι αυτό μοιάζει με την άσκηση 1 που περιλαμβάνει χρήση του Μ.Κ.Δ. Επίσης, πιθανόν να βασίζεται στα επιφανειακά χαρακτηριστικά του προβλήματος, τα οποία τον παραπέμπουν σε προηγούμενα προβλήματα που αντιμετώπισε και στα οποία εφάρμοσε τη διαδικασία εύρεσης του μέσου όρου. Επιφανειακά χαρακτηριστικά, όπως τα τρία είδη λουλουδιών που δίνονται σε σειρά, καθώς και η φράση: «περισσότερες όμοιες ανθοδέσμες», παραπέμπουν στην έννοια του μέσου όρου. Ακόμη, παρόλο που διευκρινίζεται ρητώς από τον ερευνητή ότι πρέπει να βρεθεί ο πιο μεγάλος αριθμός που διαιρεί και τις 3 ποσότητες λουλουδιών, ο μαθητής δεν αντιλαμβάνεται ότι πρέπει να βρει το Μ.Κ.Δ. Η επιτυχία στη μεταφορά φαίνεται να είναι ψηλότερη στο πρόβλημα με τις ανθοδέσμες σε σχέση με το πρόβλημα με τα φυτά. Το πρόβλημα με τις ανθοδέσμες είναι ένα από τα συνηθισμένα είδη προβλημάτων που διδάσκονται στο σχολείο για την έννοια του Μ.Κ.Δ. Εδώ επειδή ο τρόπος παρουσίασης του προβλήματος είναι συνήθης στο σχολείο, δηλαδή τα επιφανειακά χαρακτηριστικά του προβλήματος είναι σχολικού τύπου, η επίδοση των μαθητών στα μαθηματικά του σχολείου φαίνεται να επηρεάζει την ικανότητά τους στη μεταφορά. Οι μαθητές υψηλής και μεσαίας επίδοσης επιτυγχάνουν στη μεταφορά ενώ ο μαθητής χαμηλής επίδοσης αποτυγχάνει. Πρόβλημα 6 (Οι σανίδες) Όσον αφορά το πρόβλημα 6, ο Άρης αντιλαμβάνεται ότι θα πρέπει να προσθέσει με διάφορους τρόπους τους αριθμούς που του δίνονται, ώστε να φτιάξει τον αριθμό 20. «Ερευνητής: Πώς κατάλαβες ότι πρέπει να λύσεις το πρόβλημα με αυτό τον τρόπο; Άρης: Με το που κοίταξα το πρόβλημα κατάλαβα τον τρόπο! Ερευνητής: Έχει κάποιο πρόβλημα που του μοιάζει; Άρης: Το πρόβλημα 2. Ερευνητής: Σε τι μοιάζει δηλαδή;
12 Άρης: Το πρόβλημα λέει: τοποθέτησε για να βγαίνουν 25 και στο άλλο για 20 μέτρα. Όταν το είδα μου έφερε στο μυαλό μου το πρόβλημα 2. Μοιάζουν στην πράξη.» Αντιλαμβάνεται ότι και τα δύο προβλήματα μοιάζουν τόσο στη δομή («μοιάζουν στην πράξη») όσο και σε επιφανειακά χαρακτηριστικά («όταν το είδα μου έφερε στο μυαλό μου το πρόβλημα 2») και ως τούτου, εφαρμόζει την ίδια στρατηγική όπως και προηγουμένως για να βρει την απάντηση. Όμοια, η Γεωργία, ο Άγγελος, και ο Χριστόδουλος επιτυγχάνουν τη μεταφορά στο πρόβλημα 6. Συγκεκριμένα, αντιλαμβάνονται ότι το πρόβλημα 6 μοιάζει με την άσκηση 2, τόσο σε επιφανειακά χαρακτηριστικά, όπως το ότι δίνονται πολλοί αριθμοί σε σειρά, όσο και σε δομικά χαρακτηριστικά, όπως το ότι θα πρέπει να ομαδοποιήσουν τους αριθμούς για να δώσουν απάντηση. Εδώ παρατηρούμε ότι οι μαθητές αναγνωρίζουν την ομοιότητα ανάμεσα στο πρόβλημα με τις σανίδες και τη δεδομένη άσκηση 2, αφού και οι δύο καταστάσεις παρουσιάζουν παρόμοια επιφανειακά χαρακτηριστικά και κοινά δομικά χαρακτηριστικά. Επιτυγχάνουν όλοι οι μαθητές ανεξάρτητα με την επίδοσή τους στο μάθημα των μαθηματικών. 4. ΣΥΜΠΕΡΑΣΜΑΤΑ Από την παρουσίαση των αποτελεσμάτων προκύπτουν ορισμένα συμπεράσματα, τα οποία σε αρκετές περιπτώσεις συμφωνούν με τη βιβλιογραφία. Αξίζει να σημειωθεί ότι τα παιδιά πέτυχαν σε μεγαλύτερο βαθμό στα τρία πρώτα έργα του δοκιμίου σε σχέση με τα τρία τελευταία, τα οποία ενέπλεκαν τη μαθηματική γνώση σε προβληματικές καταστάσεις. Οι δυσκολίες που τα παιδιά αντιμετώπισαν στα τρία τελευταία έργα παραπέμπει στο γεγονός ότι οι περισσότεροι μαθητές δεν είναι ικανοί να μεταφέρουν τη μαθηματική γνώση σε νέες καταστάσεις, διαφορετικές από εκείνες που συνάντησαν κατά τη διδασκαλία. Ως εκ τούτου, όταν τα μαθηματικά έργα είναι ενταγμένα μέσα σε πλαίσιο φαίνεται να δυσκολεύουν τους μαθητές. Από τα αποτελέσματα προκύπτει ότι οι μαθητές επιτυγχάνουν σε μεγαλύτερο βαθμό σε έργα, όπου τα επιφανειακά τους χαρακτηριστικά μοιάζουν με τα εξωτερικά χαρακτηριστικά της αποπλαισιωμένης άσκησης (π.χ. προβλήματα «τύπου σανίδας»). Σε τέτοιου τύπου προβλήματα οι μαθητές επιτυγχάνουν ανεξάρτητα με την επίδοσή τους στα μαθηματικά. Οι Ratternann και Gentner (1987) όμοια υποστηρίζουν ότι η πρόσβαση σε παλαιότερα προβλήματα ή παραδείγματα που βρίσκονται αποθηκευμένα στη μνήμη των παιδιών είναι συχνότερη όταν οι μαθητές βασίζονται σε όμοια επιφανειακά χαρακτηριστικά παρά σε δομικά χαρακτηριστικά. Ακόμη, ο Ross (1984, 1987, 1989a) συμφωνεί ότι τα παιδιά στηρίζονται στα επιφανειακά χαρακτηριστικά των προβλημάτων για να τα λύσουν.
13 Κατά την επίλυση προβληματικών καταστάσεων μέσα σε πλαίσιο, οι οποίες απαιτούν τη μεταφορά της μαθηματικής γνώσης, τα παιδιά βασίζονται σε μεγάλο βαθμό στα επιφανειακά χαρακτηριστικά του προβλήματος. Αυτά πιθανόν να τους παραπέμπουν σε προηγούμενα προβλήματα, τα οποία παρουσιάζουν επιφανειακή ομοιότητα με τα υπό επίλυση προβλήματα, και ως εκ τούτου, ανακαλούν λανθασμένες διαδικασίες επίλυσης. Τέτοιο παράδειγμα αποτελεί η ανάκληση και χρήση της διαδικασίας εύρεσης του μέσου όρου από το μαθητή χαμηλής επίδοσης στην έρευνα, ο οποίος φαίνεται να βασίστηκε σε επιφανειακά χαρακτηριστικά, όπως η διατύπωση του προβλήματος και η παρουσίαση των δεδομένων. Ακόμη, σε αρκετές περιπτώσεις φαίνεται οι μαθητές να χρησιμοποιούν κάποιες άτυπες και μη ορθολογιστικές στρατηγικές, οι οποίες πιθανόν να ανακαλούνται από παλαιότερες εμπειρίες που μοιράζονται όμοια επιφανειακά χαρακτηριστικά με το παρόν πρόβλημα. Με τα παραπάνω συμφωνούν και οι VanderStoep και Seifert (1993), οι οποίοι αναφέρουν ότι οι αρχάριοι μαθητές στηρίζονται σε επιφανειακά και άσχετα χαρακτηριστικά του προβλήματος κατά τη διαδικασία επίλυσης και ως εκ τούτου, ανακαλούν παλαιότερα προβλήματα από τη μνήμη τους βασισμένοι στην επιφανειακή ομοιότητα που έχουν με τα υπό εξέταση προβλήματα. Όσον αφορά τα προβλήματα, των οποίων το πλαίσιο είναι σύνηθες για τα σχολικά δεδομένα (π.χ. πρόβλημα «τύπου ανθοδέσμης»), οι μαθητές συνήθως πετυχαίνουν στη μεταφορά. Οι μαθητές δηλαδή πετυχαίνουν στη μεταφορά σε γνωστές καταστάσεις στις οποίες ήδη έχουν πραγματοποιήσει και ασκηθεί στο σχολείο. Σε αυτή την περίπτωση φαίνεται ότι η επίδοση των μαθητών στα μαθηματικά επηρεάζει την ικανότητα τους στη μεταφορά. Επιπρόσθετα, όσον αφορά την κατηγορία των προβλημάτων με άγνωστο, για τα παιδιά, πλαίσιο, δηλαδή προβλήματα που περιλαμβάνουν πλαίσια στα οποία τα επιφανειακά τους χαρακτηριστικά είναι άγνωστα, οι συμπεριφορές των μαθητών δε φαίνεται να επηρεάζονται από τις επιδόσεις τους στα μαθηματικά του σχολείου. Τόσο οι μαθητές με υψηλή επίδοση στα μαθηματικά όσο και οι υπόλοιποι αντιμετωπίζουν τις ίδιες δυσκολίες. Σύμφωνα και με τον Royer (1979) μεταφορά στη μάθηση συμβαίνει εάν ο μαθητής είναι ικανός να εφαρμόζει μια ικανότητα ή γνώση σε καταστάσεις που διαφέρουν από εκείνες που συνάντησε κατά τη διδασκαλία. Ως εκ τούτου, οι μαθητές δυσκολεύονται πολύ να μεταφέρουν τη μαθηματική έννοια σε τέτοια προβλήματα, καθώς δύσκολα αντιλαμβάνονται τις δομικές ομοιότητες. Οι μαθητές δυσκολεύονται να αναγνωρίσουν σχέσεις μεταξύ δύο προβλημάτων τα οποία μοιράζονται τα ίδια δομικά χαρακτηριστικά, αλλά διαφέρουν στα επιφανειακά χαρακτηριστικά. Αντίθετα, όταν τα παιδιά αντιλαμβάνονται την ομοιότητα ανάμεσα σε δύο μαθηματικά έργα λόγω κοινών δομικών χαρακτηριστικών τείνουν να εφαρμόζουν με επιτυχία τη μαθηματική γνώση και να πετυχαίνουν τη μεταφορά (Ross,1987; Νovick,1988; Bassok & Holyoak, 1993, αναφορά στον Benardo, 2001 και Evans, 1999). Κάτι τέτοιο μπορεί να επιτευχθεί εάν οι εκπαιδευτικοί διδάσκουν στα παιδιά πώς να αναλύουν τα κοινά ή παρόμοια και διαφορετικά χαρακτηριστικά ανάμεσα στα
14 αρχικά και στα έργα-στόχους, δηλαδή στα διαφορετικά πλαίσια. Ως εκ τούτου, ο αρχικός στόχος πρέπει να διδάσκεται σε περισσότερα από ένα πλαίσιο αναφοράς και να συσχετίζεται με την καθημερινή ζωή. Όμοια, ο Evans (1999) υποστηρίζει ότι με αυτό τον τρόπο ο μαθητής θα μπορέσει να εκτιμήσει το εύρος μιας γενίκευσης καθώς και τους περιορισμούς της. Η ικανότητα των μαθητών να αναγνωρίζουν τα όμοια δομικά χαρακτηριστικά μεταξύ των μαθηματικών εννοιών που παρουσιάζονται υπό μορφή ασκήσεων και προβλημάτων με πλαίσιο, εξαρτάται από τον τύπο προβλήματος. Συγκεκριμένα, σε προβλήματα όπου το πλαίσιο είναι άγνωστο για τα παιδιά, αυτά αδυνατούν να εντοπίσουν ομοιότητες στα δομικά χαρακτηριστικά, ενώ είναι σε θέση να το πράξουν στα προβλήματα με σύνηθες σχολικό πλαίσιο και σε προβλήματα με χαρακτηριστικά πλαισίου παρόμοια με την αποπλαισιωμένη άσκηση. ΒΙΒΛΙΟΓΡΑΦΙΑ Bernardo, A. B. I. (2001). Analogical Problem Construction and Transfer in Mathematical Problem Solving. Educational Psychology, 21(2), Boaler, J. (1993). Encouraging the transfer of school mathematics to the real world through the integration of process and content, context and culture. Educational Studies in Mathematics, 25, Evans, J. (1999). Building bridges: Reflections on the problem of transfer of learning in mathematics. Educational Studies in Mathematics, 39, Stanic, G.M.A, & Lester, F.K. (1989). Mathematical problem solving in and out of school. Arithmetic Teacher, 37 (3), Van Eck, R., & Dempsey, J. (2002). The effect of competition and contextualized advisement on the transfer of mathematics skills in a computer-based instructional simulation game. Educational Technology Research and Development, 50(3), VanderStoep, S. W., & Seifert, C. M. (1993). Learning How versus learning When : Improving transfer of problem-solving Principles. The Journal of the learning sciences, 3(1),
5.4. ΑΠΟΤΕΛΕΣΜΑΤΑ ΕΡΕΥΝΩΝ ΜΕ ΡΗΤΟΥΣ ΑΡΙΘΜΟΥΣ ΤΗΣ ΣΧΟΛΗΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΤΗΣ ΦΥΣΗΣ ΚΑΙ ΤΗΣ ΖΩΗΣ
 5.4. ΑΠΟΤΕΛΕΣΜΑΤΑ ΕΡΕΥΝΩΝ ΜΕ ΡΗΤΟΥΣ ΑΡΙΘΜΟΥΣ ΤΗΣ ΣΧΟΛΗΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΤΗΣ ΦΥΣΗΣ ΚΑΙ ΤΗΣ ΖΩΗΣ 5.4.1. Αποτελέσματα από το πρόγραμμα εξ αποστάσεως επιμόρφωσης δασκάλων και πειραματικής εφαρμογής των νοερών
5.4. ΑΠΟΤΕΛΕΣΜΑΤΑ ΕΡΕΥΝΩΝ ΜΕ ΡΗΤΟΥΣ ΑΡΙΘΜΟΥΣ ΤΗΣ ΣΧΟΛΗΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΤΗΣ ΦΥΣΗΣ ΚΑΙ ΤΗΣ ΖΩΗΣ 5.4.1. Αποτελέσματα από το πρόγραμμα εξ αποστάσεως επιμόρφωσης δασκάλων και πειραματικής εφαρμογής των νοερών
ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ
 ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Y404. ΔΙΜΕΠΑ: ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗ ΕΡΓΑΣΙΑ ΠΕΙΡΑΜΑΤΙΣΜΟΥ ΜΕ ΜΑΘΗΤΗ ΔΙΔΑΣΚΩΝ: ΧΑΡΑΛΑΜΠΟΣ ΛΕΜΟΝΙΔΗΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΔΗΜΗΤΡΙΑΔΗΣ ΗΡΑΚΛΗΣ ΑΕΜ: 3734 Περιεχόμενα
ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Y404. ΔΙΜΕΠΑ: ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗ ΕΡΓΑΣΙΑ ΠΕΙΡΑΜΑΤΙΣΜΟΥ ΜΕ ΜΑΘΗΤΗ ΔΙΔΑΣΚΩΝ: ΧΑΡΑΛΑΜΠΟΣ ΛΕΜΟΝΙΔΗΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΔΗΜΗΤΡΙΑΔΗΣ ΗΡΑΚΛΗΣ ΑΕΜ: 3734 Περιεχόμενα
ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ: ΜΑΘΗΜΑΤΙΚΑ ΣΤ ΔΗΜΟΤΙΚΟΥ «ΤΑ ΚΛΑΣΜΑΤΑ»
 ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ: ΜΑΘΗΜΑΤΙΚΑ ΣΤ ΔΗΜΟΤΙΚΟΥ «ΤΑ ΚΛΑΣΜΑΤΑ» Νικόλαος Μπαλκίζας 1. ΕΙΣΑΓΩΓΗ Σκοπός του σχεδίου μαθήματος είναι να μάθουν όλοι οι μαθητές της τάξης τις έννοιες της ισοδυναμίας των κλασμάτων,
ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ: ΜΑΘΗΜΑΤΙΚΑ ΣΤ ΔΗΜΟΤΙΚΟΥ «ΤΑ ΚΛΑΣΜΑΤΑ» Νικόλαος Μπαλκίζας 1. ΕΙΣΑΓΩΓΗ Σκοπός του σχεδίου μαθήματος είναι να μάθουν όλοι οι μαθητές της τάξης τις έννοιες της ισοδυναμίας των κλασμάτων,
6.5. ΑΠΟΤΕΛΕΣΜΑΤΑ ΕΡΕΥΝΩΝ ΣΤΟΥΣ ΚΑΤ ΕΚΤΙΜΗΣΗ ΥΠΟΛΟΓΙΣΜΟΥΣ ΤΗΣ ΣΧΟΛΗΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΤΗΣ ΦΥΣΗΣ ΚΑΙ ΤΗΣ ΖΩΗΣ
 6.5. ΑΠΟΤΕΛΕΣΜΑΤΑ ΕΡΕΥΝΩΝ ΣΤΟΥΣ ΚΑΤ ΕΚΤΙΜΗΣΗ ΥΠΟΛΟΓΙΣΜΟΥΣ ΤΗΣ ΣΧΟΛΗΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΤΗΣ ΦΥΣΗΣ ΚΑΙ ΤΗΣ ΖΩΗΣ 6.5.1. Οι γνώσεις υποψηφίων δασκάλων για την υπολογιστική εκτίμηση Σε μια έρευνα των Lemonidis
6.5. ΑΠΟΤΕΛΕΣΜΑΤΑ ΕΡΕΥΝΩΝ ΣΤΟΥΣ ΚΑΤ ΕΚΤΙΜΗΣΗ ΥΠΟΛΟΓΙΣΜΟΥΣ ΤΗΣ ΣΧΟΛΗΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΤΗΣ ΦΥΣΗΣ ΚΑΙ ΤΗΣ ΖΩΗΣ 6.5.1. Οι γνώσεις υποψηφίων δασκάλων για την υπολογιστική εκτίμηση Σε μια έρευνα των Lemonidis
ΘΕΜΑ ΕΡΓΑΣΙΑΣ: ΠΕΙΡΑΜΑΤΙΣΜΟΣ ΜΕ ΜΑΘΗΤΗ ΔΗΜΟΤΙΚΟΥ ΚΑΙ ΕΞΑΓΩΓΗ ΣΥΜΠΕΡΑΣΜΑΤΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΦΛΩΡΙΝΑΣ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΜΑΘΗΜΑ: Υ404 ΔΙΔΑΚΤΙΚΗ ΜΑΘΗΜΑΤΙΚΩΝ ( Β ΦΑΣΗ ΔΙ.ΜΕ.Π.Α.) ΔΙΔΑΣΚΩΝ: ΛΕΜΟΝΙΔΗΣ ΧΑΡΑΛΑΜΠΟΣ ΕΠΙΜΕΛΕΙΑ ΕΡΓΑΣΙΑΣ: ΜΑΛΕΓΑΝΕΑ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΦΛΩΡΙΝΑΣ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΜΑΘΗΜΑ: Υ404 ΔΙΔΑΚΤΙΚΗ ΜΑΘΗΜΑΤΙΚΩΝ ( Β ΦΑΣΗ ΔΙ.ΜΕ.Π.Α.) ΔΙΔΑΣΚΩΝ: ΛΕΜΟΝΙΔΗΣ ΧΑΡΑΛΑΜΠΟΣ ΕΠΙΜΕΛΕΙΑ ΕΡΓΑΣΙΑΣ: ΜΑΛΕΓΑΝΕΑ
Η προβληματική κατάσταση Χρήστος Πανούτσος
 Η προβληματική κατάσταση Χρήστος Πανούτσος Η Τζούλι και η μαμά της έχουν βγει για να αγοράσουν ένα τζιν για το σχολείο. Παρατηρούν έναν πάγκο με την εξής ταμπέλα πάνω: 40% έκπτωση των τιμών στις ετικέτες
Η προβληματική κατάσταση Χρήστος Πανούτσος Η Τζούλι και η μαμά της έχουν βγει για να αγοράσουν ένα τζιν για το σχολείο. Παρατηρούν έναν πάγκο με την εξής ταμπέλα πάνω: 40% έκπτωση των τιμών στις ετικέτες
ΝΟΕΡΟΙ ΥΠΟΛΟΓΙΣΜΟΙ- ΣΤΡΑΤΗΓΙΚΕΣ Ε.Κολέζα
 ΝΟΕΡΟΙ ΥΠΟΛΟΓΙΣΜΟΙ- ΣΤΡΑΤΗΓΙΚΕΣ Ε.Κολέζα Οι νοεροί υπολογισμοί απαιτούν ικανότητα οπτικοποίησης: να μπορείς να φανταστείς κάτι και να δουλέψεις με το νου.. Είναι ένα είδος νοητικού πειράματος, η νοερή
ΝΟΕΡΟΙ ΥΠΟΛΟΓΙΣΜΟΙ- ΣΤΡΑΤΗΓΙΚΕΣ Ε.Κολέζα Οι νοεροί υπολογισμοί απαιτούν ικανότητα οπτικοποίησης: να μπορείς να φανταστείς κάτι και να δουλέψεις με το νου.. Είναι ένα είδος νοητικού πειράματος, η νοερή
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ-Β ΦΑΣΗ ΘΕΜΑ ΔΙΔΑΣΚΑΛΙΑΣ: ΣΤΡΑΤΗΓΙΚΕΣ ΔΙΑΧΕΙΡΙΣΗΣ ΑΡΙΘΜΩΝ-19 ο ΚΕΦΑΛΑΙΟ ΣΧΟΛΕΙΟ: 2 ο ΠΕΙΡΑΜΑΤΙΚΟ ΦΛΩΡΙΝΑΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ-Β ΦΑΣΗ ΘΕΜΑ ΔΙΔΑΣΚΑΛΙΑΣ: ΣΤΡΑΤΗΓΙΚΕΣ ΔΙΑΧΕΙΡΙΣΗΣ ΑΡΙΘΜΩΝ-19 ο ΚΕΦΑΛΑΙΟ ΣΧΟΛΕΙΟ: 2 ο ΠΕΙΡΑΜΑΤΙΚΟ ΦΛΩΡΙΝΑΣ
ΣΥΓΚΡΙΤΙΚΗ ΜΕΛΕΤΗ ΜΑΘΗΣΙΑΚΩΝ ΑΠΟΤΕΛΕΣΜΑΤΩΝ ΜΕ ΤΗ ΧΡΗΣΗ Η ΧΩΡΙΣ ΤΗ ΧΡΗΣΗ Η/Υ ΓΙΑ ΤΗ ΔΙΔΑΣΚΑΛΙΑ ΚΛΑΣΜΑΤΩΝ
 3 Ο ΣΥΝΕΔΡΙΟ ΣΤΗ ΣΥΡΟ-ΤΠΕ ΣΤΗΝ ΕΚΠΑΙΔΕΥΣΗ 415 ΣΥΓΚΡΙΤΙΚΗ ΜΕΛΕΤΗ ΜΑΘΗΣΙΑΚΩΝ ΑΠΟΤΕΛΕΣΜΑΤΩΝ ΜΕ ΤΗ ΧΡΗΣΗ Η ΧΩΡΙΣ ΤΗ ΧΡΗΣΗ Η/Υ ΓΙΑ ΤΗ ΔΙΔΑΣΚΑΛΙΑ ΚΛΑΣΜΑΤΩΝ Μεταφετζής Γιώργος Δάσκαλος, 1ο ΔΣ Βόλου gmetafetz@in.gr
3 Ο ΣΥΝΕΔΡΙΟ ΣΤΗ ΣΥΡΟ-ΤΠΕ ΣΤΗΝ ΕΚΠΑΙΔΕΥΣΗ 415 ΣΥΓΚΡΙΤΙΚΗ ΜΕΛΕΤΗ ΜΑΘΗΣΙΑΚΩΝ ΑΠΟΤΕΛΕΣΜΑΤΩΝ ΜΕ ΤΗ ΧΡΗΣΗ Η ΧΩΡΙΣ ΤΗ ΧΡΗΣΗ Η/Υ ΓΙΑ ΤΗ ΔΙΔΑΣΚΑΛΙΑ ΚΛΑΣΜΑΤΩΝ Μεταφετζής Γιώργος Δάσκαλος, 1ο ΔΣ Βόλου gmetafetz@in.gr
Παράδειγμα 1 Γράψε ένα δεκαδικό αριθμό μεταξύ του 2 και του 3 που δεν περιέχει το 5 που περιέχει το 7 και που βρίσκεται όσο πιο κοντά γίνεται με το
 Παράδειγμα 1 Γράψε ένα δεκαδικό αριθμό μεταξύ του 2 και του 3 που δεν περιέχει το 5 που περιέχει το 7 και που βρίσκεται όσο πιο κοντά γίνεται με το 5/2 1 Παράδειγμα 2: Γράψε ένα κλάσμα που χρησιμοποιεί
Παράδειγμα 1 Γράψε ένα δεκαδικό αριθμό μεταξύ του 2 και του 3 που δεν περιέχει το 5 που περιέχει το 7 και που βρίσκεται όσο πιο κοντά γίνεται με το 5/2 1 Παράδειγμα 2: Γράψε ένα κλάσμα που χρησιμοποιεί
ΔΙΜΕΠΑ Πρακτική Άσκηση Μαθηματικών Β' Φάση. Εργασία πειραματισμού με μαθητή
 ΔΙΜΕΠΑ Πρακτική Άσκηση Μαθηματικών Β' Φάση Εργασία πειραματισμού με μαθητή Διδάσκων: Χαράλαμπος Λεμονίδης Φοιτήτρια: Χατζή Κυριακή- Ιωάννα ΑΕΜ: 3659 Εξάμηνο: ΣΤ Περιεχόμενα 1. Εισαγωγή... 2. Περιγραφή
ΔΙΜΕΠΑ Πρακτική Άσκηση Μαθηματικών Β' Φάση Εργασία πειραματισμού με μαθητή Διδάσκων: Χαράλαμπος Λεμονίδης Φοιτήτρια: Χατζή Κυριακή- Ιωάννα ΑΕΜ: 3659 Εξάμηνο: ΣΤ Περιεχόμενα 1. Εισαγωγή... 2. Περιγραφή
Τι είναι τα πολλαπλάσια ;
 Μαθηματικά Κεφάλαιο 10 Πολλαπλάσια και διαιρέτες Όνομα: Ημερομηνία: / / Θεωρία Πώς τα βρίσκουμε; Τι είναι τα πολλαπλάσια ; Πολλαπλάσια ενός φυσικού αριθμού ονομάζονται οι αριθμοί που προκύπτουν όταν τον
Μαθηματικά Κεφάλαιο 10 Πολλαπλάσια και διαιρέτες Όνομα: Ημερομηνία: / / Θεωρία Πώς τα βρίσκουμε; Τι είναι τα πολλαπλάσια ; Πολλαπλάσια ενός φυσικού αριθμού ονομάζονται οι αριθμοί που προκύπτουν όταν τον
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΦΛΩΡΙΝΑΣ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΔΙ.ΜΕ.Π.Α Β ΦΑΣΗ: ΔΙΔΑΚΤΙΚΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΦΛΩΡΙΝΑΣ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΔΙ.ΜΕ.Π.Α Β ΦΑΣΗ: ΔΙΔΑΚΤΙΚΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ Φοιτητής: Παύλου Νικόλαος, Α.Ε.Μ: 2245, Ε Εξάμηνο Σχολείο: 1 ο Πειραματικό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΦΛΩΡΙΝΑΣ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΔΙ.ΜΕ.Π.Α Β ΦΑΣΗ: ΔΙΔΑΚΤΙΚΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ Φοιτητής: Παύλου Νικόλαος, Α.Ε.Μ: 2245, Ε Εξάμηνο Σχολείο: 1 ο Πειραματικό
ΜΑΘΗΜΑΤΙΚΑ A ΓΥΜΝΑΣΙΟΥ
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΦΥΛΛΑΔΙΟ ΧΡΙΣΤΟΥΓΕΝΝΩΝ 2016 14 ΙΑΝΟΥΑΡΙΟΥ 2017 Δ.Ε. ΚΟΝΤΟΚΩΣΤΑΣ 1 η ΑΣΚΗΣΗ Τρεις φίλοι, ο Γιώργος, ο Κώστας και ο Δημήτρης συνεννοήθηκαν να πηγαίνουν στο Δημοτικό στάδιο, για τρέξιμο. Λόγω
ΕΠΑΝΑΛΗΠΤΙΚΟ ΦΥΛΛΑΔΙΟ ΧΡΙΣΤΟΥΓΕΝΝΩΝ 2016 14 ΙΑΝΟΥΑΡΙΟΥ 2017 Δ.Ε. ΚΟΝΤΟΚΩΣΤΑΣ 1 η ΑΣΚΗΣΗ Τρεις φίλοι, ο Γιώργος, ο Κώστας και ο Δημήτρης συνεννοήθηκαν να πηγαίνουν στο Δημοτικό στάδιο, για τρέξιμο. Λόγω
ΔΙΔΑΣΚΑΛΙΑ ΓΝΩΣΤΙΚΗΣ ΣΤΡΑΤΗΓΙΚΗΣ ΓΙΑ ΤΗΝ ΚΑΤΑΝΟΗΣΗ Δρ. Ζαφειριάδης Κυριάκος Οι ικανοί αναγνώστες χρησιμοποιούν πολλές στρατηγικές (συνδυάζουν την
 1 ΔΙΔΑΣΚΑΛΙΑ ΓΝΩΣΤΙΚΗΣ ΣΤΡΑΤΗΓΙΚΗΣ ΓΙΑ ΤΗΝ ΚΑΤΑΝΟΗΣΗ Δρ. Ζαφειριάδης Κυριάκος Οι ικανοί αναγνώστες χρησιμοποιούν πολλές στρατηγικές (συνδυάζουν την παλαιότερη γνώση τους, σημειώνουν λεπτομέρειες, παρακολουθούν
1 ΔΙΔΑΣΚΑΛΙΑ ΓΝΩΣΤΙΚΗΣ ΣΤΡΑΤΗΓΙΚΗΣ ΓΙΑ ΤΗΝ ΚΑΤΑΝΟΗΣΗ Δρ. Ζαφειριάδης Κυριάκος Οι ικανοί αναγνώστες χρησιμοποιούν πολλές στρατηγικές (συνδυάζουν την παλαιότερη γνώση τους, σημειώνουν λεπτομέρειες, παρακολουθούν
ΒΛΑΣΤΗΣΗ (ΜΑΤΘΑΙΟΥ) !"Τίτλος διερεύνησης: Ποιοι παράγοντες επηρεάζουν το πόσο γρήγορα θα βλαστήσουν τα σπέρματα των οσπρίων.
 ΒΛΑΣΤΗΣΗ (ΜΑΤΘΑΙΟΥ)!"Τίτλος διερεύνησης: Ποιοι παράγοντες επηρεάζουν το πόσο γρήγορα θα βλαστήσουν τα σπέρματα των οσπρίων.!"σύντομη περιγραφή διερεύνησης: Στη διερεύνησή μας μετρήθηκε ο χρόνος που χρειάστηκαν
ΒΛΑΣΤΗΣΗ (ΜΑΤΘΑΙΟΥ)!"Τίτλος διερεύνησης: Ποιοι παράγοντες επηρεάζουν το πόσο γρήγορα θα βλαστήσουν τα σπέρματα των οσπρίων.!"σύντομη περιγραφή διερεύνησης: Στη διερεύνησή μας μετρήθηκε ο χρόνος που χρειάστηκαν
ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΦΥΛΛΑΔΙΟ ΧΡΙΣΤΟΥΓΕΝΝΩΝ 20 ΔΕΚΕΜΒΡΙΟΣ 20 Δ.Ε. ΚΟΝΤΟΚΩΣΤΑΣ Οι ασκήσεις να λυθούν σε χαρτί Α4 η ΑΣΚΗΣΗ Τρεις φίλοι, ο Γιώργος, ο Κώστας και ο Δημήτρης συνεννοήθηκαν να πηγαίνουν στο Δημοτικό
ΕΠΑΝΑΛΗΠΤΙΚΟ ΦΥΛΛΑΔΙΟ ΧΡΙΣΤΟΥΓΕΝΝΩΝ 20 ΔΕΚΕΜΒΡΙΟΣ 20 Δ.Ε. ΚΟΝΤΟΚΩΣΤΑΣ Οι ασκήσεις να λυθούν σε χαρτί Α4 η ΑΣΚΗΣΗ Τρεις φίλοι, ο Γιώργος, ο Κώστας και ο Δημήτρης συνεννοήθηκαν να πηγαίνουν στο Δημοτικό
ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ : ΛΕΜΟΝΙΔΗΣ ΧΑΡΑΛΑΜΠΟΣ ΑΠΟΣΠΑΣΜΕΝΗ ΕΚΠΑΙΔΕΥΤΙΚΟΣ : ΚΑΠΠΑΤΟΥ ΝΑΤΑΣΣΑ ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗ ΘΕΜΑ ΔΙΔΑΣΚΑΛΙΑΣ:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ : ΛΕΜΟΝΙΔΗΣ ΧΑΡΑΛΑΜΠΟΣ ΑΠΟΣΠΑΣΜΕΝΗ ΕΚΠΑΙΔΕΥΤΙΚΟΣ : ΚΑΠΠΑΤΟΥ ΝΑΤΑΣΣΑ ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗ ΘΕΜΑ ΔΙΔΑΣΚΑΛΙΑΣ:
ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ 2013/14. Μιχαηλίδου Αγγελική Λάλας Γεώργιος
 ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ 2013/14 Μιχαηλίδου Αγγελική Λάλας Γεώργιος Περιγραφή Πλαισίου Σχολείο: 2 ο Πρότυπο Πειραματικό Γυμνάσιο Αθηνών Τμήμα: Β 3 Υπεύθυνος καθηγητής: Δημήτριος Διαμαντίδης Συνοδός: Δημήτριος Πρωτοπαπάς
ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ 2013/14 Μιχαηλίδου Αγγελική Λάλας Γεώργιος Περιγραφή Πλαισίου Σχολείο: 2 ο Πρότυπο Πειραματικό Γυμνάσιο Αθηνών Τμήμα: Β 3 Υπεύθυνος καθηγητής: Δημήτριος Διαμαντίδης Συνοδός: Δημήτριος Πρωτοπαπάς
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗΣ Θέμα Διδασκαλίας Προβλήματα με πρόσθεση και αφαίρεση κλασμάτων (Κεφάλαιο 23 ο ) Σχολείο: 2 ο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗΣ Θέμα Διδασκαλίας Προβλήματα με πρόσθεση και αφαίρεση κλασμάτων (Κεφάλαιο 23 ο ) Σχολείο: 2 ο
Εκπαίδευση Ενηλίκων: Εμπειρίες και Δράσεις ΑΘΗΝΑ, Δευτέρα 12 Οκτωβρίου 2015
 Εκπαίδευση Ενηλίκων: Εμπειρίες και Δράσεις ΑΘΗΝΑ, Δευτέρα 12 Οκτωβρίου 2015 Μάθηση και γνώση: μια συνεχής και καθοριστική αλληλοεπίδραση Αντώνης Λιοναράκης Στην παρουσίαση που θα ακολουθήσει θα μιλήσουμε
Εκπαίδευση Ενηλίκων: Εμπειρίες και Δράσεις ΑΘΗΝΑ, Δευτέρα 12 Οκτωβρίου 2015 Μάθηση και γνώση: μια συνεχής και καθοριστική αλληλοεπίδραση Αντώνης Λιοναράκης Στην παρουσίαση που θα ακολουθήσει θα μιλήσουμε
Πανεπιστήμιο Δυτικής Μακεδονίας Παιδαγωγική Σχολή Τμήμα Δημοτικής Εκπαίδευσης
 Πανεπιστήμιο Δυτικής Μακεδονίας Παιδαγωγική Σχολή Τμήμα Δημοτικής Εκπαίδευσης Εργασία: Επίλυση προβλήματος Καθηγητής : Χαράλαμπος Λεμονίδης Όνομα φοιτήτριας: Μπεσικιώτη Ζωή, Α.Ε.Μ. 4385 από το σχολικό
Πανεπιστήμιο Δυτικής Μακεδονίας Παιδαγωγική Σχολή Τμήμα Δημοτικής Εκπαίδευσης Εργασία: Επίλυση προβλήματος Καθηγητής : Χαράλαμπος Λεμονίδης Όνομα φοιτήτριας: Μπεσικιώτη Ζωή, Α.Ε.Μ. 4385 από το σχολικό
Πορεία παρουσίασης 1. Θεωρητικό πλαίσιο - Άξονες περιεχοµένων 2. Επιλογή κεφαλαίου 3. Προσδιορισµός κυρίαρχου στόχου 4. Υλοποίηση δραστηριότητας ανακά
 Θεωρητικό πλαίσιο Μαθηµατικά Β Γιώργος Αλβανόπουλος Σχολικός 1 Πορεία παρουσίασης 1. Θεωρητικό πλαίσιο - Άξονες περιεχοµένων 2. Επιλογή κεφαλαίου 3. Προσδιορισµός κυρίαρχου στόχου 4. Υλοποίηση δραστηριότητας
Θεωρητικό πλαίσιο Μαθηµατικά Β Γιώργος Αλβανόπουλος Σχολικός 1 Πορεία παρουσίασης 1. Θεωρητικό πλαίσιο - Άξονες περιεχοµένων 2. Επιλογή κεφαλαίου 3. Προσδιορισµός κυρίαρχου στόχου 4. Υλοποίηση δραστηριότητας
Δημοτικό Σχολείο Σωτήρας Β Η δική μας πρόταση- εμπειρία
 Δημοτικό Σχολείο Σωτήρας Β Η δική μας πρόταση- εμπειρία Συμμετοχή στο Πρόγραμμα του Παιδαγωγικού Ινστιτούτου ΥΠΟΣΤΗΡΙΞΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΜΑΘΗΣΗΣ ΜΕΣΩ ΕΡΕΥΝΑΣ-ΔΡΑΣΗΣ Σχολική χρονιά: 2015-2016 ΤΟ ΠΡΟΦΙΛ ΤΗΣ
Δημοτικό Σχολείο Σωτήρας Β Η δική μας πρόταση- εμπειρία Συμμετοχή στο Πρόγραμμα του Παιδαγωγικού Ινστιτούτου ΥΠΟΣΤΗΡΙΞΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΜΑΘΗΣΗΣ ΜΕΣΩ ΕΡΕΥΝΑΣ-ΔΡΑΣΗΣ Σχολική χρονιά: 2015-2016 ΤΟ ΠΡΟΦΙΛ ΤΗΣ
Διαμορφωτική Αξιολόγηση του Μαθητή: Από τη Θεωρία στη Χάραξη Πολιτικής. Λεωνίδας Κυριακίδης, Τμήμα Επιστημών της Αγωγής, Πανεπιστήμιο Κύπρου
 Διαμορφωτική Αξιολόγηση του Μαθητή: Από τη Θεωρία στη Χάραξη Πολιτικής Λεωνίδας Κυριακίδης, Τμήμα Επιστημών της Αγωγής, Πανεπιστήμιο Κύπρου 1 Δομή παρουσίασης Αξιολόγηση: Έννοια & Σημασία Σκοποί Αξιολόγησης
Διαμορφωτική Αξιολόγηση του Μαθητή: Από τη Θεωρία στη Χάραξη Πολιτικής Λεωνίδας Κυριακίδης, Τμήμα Επιστημών της Αγωγής, Πανεπιστήμιο Κύπρου 1 Δομή παρουσίασης Αξιολόγηση: Έννοια & Σημασία Σκοποί Αξιολόγησης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Υπεύθυνος καθηγητής Χαράλαμπος Λεμονίδης Μέντορας Γεώργιος Γεωργιόπουλος ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗΣ Θέμα Διδασκαλίας Πρόσθεση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Υπεύθυνος καθηγητής Χαράλαμπος Λεμονίδης Μέντορας Γεώργιος Γεωργιόπουλος ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Β ΦΑΣΗΣ Θέμα Διδασκαλίας Πρόσθεση
Γράφοντας ένα σχολικό βιβλίο για τα Μαθηματικά. Μαριάννα Τζεκάκη Αν. Καθηγήτρια Α.Π.Θ. Μ. Καλδρυμίδου Αν. Καθηγήτρια Πανεπιστημίου Ιωαννίνων
 Γράφοντας ένα σχολικό βιβλίο για τα Μαθηματικά Μαριάννα Τζεκάκη Αν. Καθηγήτρια Α.Π.Θ. Μ. Καλδρυμίδου Αν. Καθηγήτρια Πανεπιστημίου Ιωαννίνων Εισαγωγή Η χώρα μας απέκτησε Νέα Προγράμματα Σπουδών και Νέα
Γράφοντας ένα σχολικό βιβλίο για τα Μαθηματικά Μαριάννα Τζεκάκη Αν. Καθηγήτρια Α.Π.Θ. Μ. Καλδρυμίδου Αν. Καθηγήτρια Πανεπιστημίου Ιωαννίνων Εισαγωγή Η χώρα μας απέκτησε Νέα Προγράμματα Σπουδών και Νέα
Μαθηματικά: Αριθμητική και Άλγεβρα. Μάθημα 3 ο, Τμήμα Α. Τρόποι απόδειξης
 Μαθηματικά: Αριθμητική και Άλγεβρα Μάθημα 3 ο, Τμήμα Α Ο πυρήνας των μαθηματικών είναι οι τρόποι με τους οποίους μπορούμε να συλλογιζόμαστε στα μαθηματικά. Τρόποι απόδειξης Επαγωγικός συλλογισμός (inductive)
Μαθηματικά: Αριθμητική και Άλγεβρα Μάθημα 3 ο, Τμήμα Α Ο πυρήνας των μαθηματικών είναι οι τρόποι με τους οποίους μπορούμε να συλλογιζόμαστε στα μαθηματικά. Τρόποι απόδειξης Επαγωγικός συλλογισμός (inductive)
παραδειγματα επεισοδίων
 παραδειγματα επεισοδίων ΜΑΘΗΜΑΤΙΚΟ ΝΟΗΜΑ Οι μαθητές ερμηνεύουν τα δρώμενα στην τάξη: ως προς το νόημα εννοιών και διαδικασιών ως προς τη φύση και την αξία αυτών στο μάθημα των μαθηματικών Καλδρυμίδου,
παραδειγματα επεισοδίων ΜΑΘΗΜΑΤΙΚΟ ΝΟΗΜΑ Οι μαθητές ερμηνεύουν τα δρώμενα στην τάξη: ως προς το νόημα εννοιών και διαδικασιών ως προς τη φύση και την αξία αυτών στο μάθημα των μαθηματικών Καλδρυμίδου,
Μαθηματικά A Δημοτικού. Πέτρος Κλιάπης Σεπτέμβρης 2007
 Μαθηματικά A Δημοτικού Πέτρος Κλιάπης Σεπτέμβρης 2007 Το σύγχρονο μαθησιακό περιβάλλον των Μαθηματικών Ενεργή συμμετοχή των παιδιών Μάθηση μέσα από δραστηριότητες Κατανόηση ΌΧΙ απομνημόνευση Αξιοποίηση
Μαθηματικά A Δημοτικού Πέτρος Κλιάπης Σεπτέμβρης 2007 Το σύγχρονο μαθησιακό περιβάλλον των Μαθηματικών Ενεργή συμμετοχή των παιδιών Μάθηση μέσα από δραστηριότητες Κατανόηση ΌΧΙ απομνημόνευση Αξιοποίηση
ΟΙ ΣΤΡΑΤΗΓΙΚΕΣ ΠΡΟΣΘΕΣΗΣ ΚΑΙ ΑΦΑΙΡΕΣΗΣ ΜΕ ΑΡΙΘΜΟΥΣ ΜΕΧΡΙ ΤΟ 20
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΚΑΘΗΓΗΤΗΣ Χ. ΛΕΜΟΝΙΔΗΣ ΟΙ ΣΤΡΑΤΗΓΙΚΕΣ ΠΡΟΣΘΕΣΗΣ ΚΑΙ ΑΦΑΙΡΕΣΗΣ ΜΕ ΑΡΙΘΜΟΥΣ ΜΕΧΡΙ ΤΟ 20 Στη διδασκαλία συνήθως τα παιδιά αρχικά διδάσκονται τις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΚΑΘΗΓΗΤΗΣ Χ. ΛΕΜΟΝΙΔΗΣ ΟΙ ΣΤΡΑΤΗΓΙΚΕΣ ΠΡΟΣΘΕΣΗΣ ΚΑΙ ΑΦΑΙΡΕΣΗΣ ΜΕ ΑΡΙΘΜΟΥΣ ΜΕΧΡΙ ΤΟ 20 Στη διδασκαλία συνήθως τα παιδιά αρχικά διδάσκονται τις
ΛΟΓΟΤΕΧΝΙΑ - ΚΡΙΤΙΚΗ ΣΚΕΨΗ
 ΛΟΓΟΤΕΧΝΙΑ - ΚΡΙΤΙΚΗ ΣΚΕΨΗ Το μάθημα συνδυάζει τη διδασκαλία δύο κειμένων διαφορετικής εποχής που διδάσκονται στη Γ Γυμνασίου. (Αυτοβιογραφία, Ελισάβετ Μουτζάν- Μαρτινέγκου, Η μεταμφίεση, Ρέα Γαλανάκη)
ΛΟΓΟΤΕΧΝΙΑ - ΚΡΙΤΙΚΗ ΣΚΕΨΗ Το μάθημα συνδυάζει τη διδασκαλία δύο κειμένων διαφορετικής εποχής που διδάσκονται στη Γ Γυμνασίου. (Αυτοβιογραφία, Ελισάβετ Μουτζάν- Μαρτινέγκου, Η μεταμφίεση, Ρέα Γαλανάκη)
Πανεπιστήμιο Δυτικής Μακεδονίας Παιδαγωγική Σχολή Τμήμα Δημοτικής Εκπαίδευσης
 Πανεπιστήμιο Δυτικής Μακεδονίας Παιδαγωγική Σχολή Τμήμα Δημοτικής Εκπαίδευσης Εργασία: Επίλυση προβλήματος Καθηγητής : Χαράλαμπος Λεμονίδης Όνομα φοιτήτριας: Μπεσικιώτη Ζωή, Α.Ε.Μ. 4385 από το σχολικό
Πανεπιστήμιο Δυτικής Μακεδονίας Παιδαγωγική Σχολή Τμήμα Δημοτικής Εκπαίδευσης Εργασία: Επίλυση προβλήματος Καθηγητής : Χαράλαμπος Λεμονίδης Όνομα φοιτήτριας: Μπεσικιώτη Ζωή, Α.Ε.Μ. 4385 από το σχολικό
Τι μαθησιακός τύπος είναι το παιδί σας;
 Για τους γονείς και όχι μόνο από το Τι μαθησιακός τύπος είναι το παιδί σας; Ακουστικός, οπτικός ή μήπως σφαιρικός; Ανακαλύψτε ποιος είναι ο μαθησιακός τύπος του παιδιού σας, δηλαδή με ποιο τρόπο μαθαίνει
Για τους γονείς και όχι μόνο από το Τι μαθησιακός τύπος είναι το παιδί σας; Ακουστικός, οπτικός ή μήπως σφαιρικός; Ανακαλύψτε ποιος είναι ο μαθησιακός τύπος του παιδιού σας, δηλαδή με ποιο τρόπο μαθαίνει
Αξιολόγηση. Χαρίκλεια Τσαλαπάτα 3/10/2016
 Αξιολόγηση Χαρίκλεια Τσαλαπάτα 3/10/2016 Εκπαιδευτική Αξιολόγηση Τι γνωρίζουν οι μαθητές; (Pellegrino, Chudowsky) Σε ποιο βαθμό; Τι δεν μάθανε; Βάσει ενδείξεων Τι λένε Τι κάνουν Βοηθά να δούμε αν πετύχαμε
Αξιολόγηση Χαρίκλεια Τσαλαπάτα 3/10/2016 Εκπαιδευτική Αξιολόγηση Τι γνωρίζουν οι μαθητές; (Pellegrino, Chudowsky) Σε ποιο βαθμό; Τι δεν μάθανε; Βάσει ενδείξεων Τι λένε Τι κάνουν Βοηθά να δούμε αν πετύχαμε
Ο ρόλος των αναπαραστάσεων στην επίλυση προβλήματος
 Ο ρόλος των αναπαραστάσεων στην επίλυση προβλήματος Μητροσούδης Απόστολος ΑΜ 945 Παπαϊωάννου Ιωάννα ΑΜ 927 Παπλωματά Χρυσούλα ΑΜ 930 Τσάκου Ελένη ΑΜ 942 Χατζησάββα Ελένη ΑΜ 938 Οπτικοποίηση (Visualization)
Ο ρόλος των αναπαραστάσεων στην επίλυση προβλήματος Μητροσούδης Απόστολος ΑΜ 945 Παπαϊωάννου Ιωάννα ΑΜ 927 Παπλωματά Χρυσούλα ΑΜ 930 Τσάκου Ελένη ΑΜ 942 Χατζησάββα Ελένη ΑΜ 938 Οπτικοποίηση (Visualization)
ΥΔΡΟΠΕΡΑΤΟΤΗΤΑ (ΧΡΙΣΤΟΦΟΡΟΥ) Τίτλος διερεύνησης: Ποιοί παράγοντες επηρεάζουν το πόσο νερό συγκρατεί το χώμα;
 ΥΔΡΟΠΕΡΑΤΟΤΗΤΑ (ΧΡΙΣΤΟΦΟΡΟΥ) Τίτλος διερεύνησης: Ποιοί παράγοντες επηρεάζουν το πόσο νερό συγκρατεί το χώμα; Σύντομη περιγραφή διερεύνησης: Σκοπός αυτής της διερεύνησης ήταν να κάνουν κάποιες υποθέσεις
ΥΔΡΟΠΕΡΑΤΟΤΗΤΑ (ΧΡΙΣΤΟΦΟΡΟΥ) Τίτλος διερεύνησης: Ποιοί παράγοντες επηρεάζουν το πόσο νερό συγκρατεί το χώμα; Σύντομη περιγραφή διερεύνησης: Σκοπός αυτής της διερεύνησης ήταν να κάνουν κάποιες υποθέσεις
Οδηγός διαφοροποίησης για την πρωτοβάθµια
 Οδηγός διαφοροποίησης για την πρωτοβάθµια Γιατί χρειάζεται να κάνουµε τόσο ειδική διαφοροποίηση; Τα παιδιά που βρίσκονται στο φάσµα του αυτισµού έχουν διαφορετικό τρόπο σκέψης και αντίληψης για τον κόσµο,
Οδηγός διαφοροποίησης για την πρωτοβάθµια Γιατί χρειάζεται να κάνουµε τόσο ειδική διαφοροποίηση; Τα παιδιά που βρίσκονται στο φάσµα του αυτισµού έχουν διαφορετικό τρόπο σκέψης και αντίληψης για τον κόσµο,
Μεθοδολογία Έρευνας Κοινωνικών Επιστημών
 Μεθοδολογία Έρευνας Κοινωνικών Επιστημών Dr. Anthony Montgomery Επίκουρος Καθηγητής Εκπαιδευτικής & Κοινωνικής Πολιτικής antmont@uom.gr Ποιός είναι ο σκοπός του μαθήματος μας? Στο τέλος του σημερινού μαθήματος,
Μεθοδολογία Έρευνας Κοινωνικών Επιστημών Dr. Anthony Montgomery Επίκουρος Καθηγητής Εκπαιδευτικής & Κοινωνικής Πολιτικής antmont@uom.gr Ποιός είναι ο σκοπός του μαθήματος μας? Στο τέλος του σημερινού μαθήματος,
ΤΟ ΔΗΜΟΚΡΑΤΙΚΟ ΣΧΟΛΕΙΟ ΣΤΗΝ ΠΡΑΞΗ ΜΕΣΑ ΑΠο ΤΗΝ ΕΜΠΕΔΩΣΗ Ο ΡΟΛΟΣ ΤΟΥ ΔΙΕΥΘΥΝΤΗ Δρ Μάριος Στυλιανίδης, ΕΔΕ ΚB Παγκύπριο Συνέδριο Διευθυντών
 ΤΟ ΔΗΜΟΚΡΑΤΙΚΟ ΣΧΟΛΕΙΟ ΣΤΗΝ ΠΡΑΞΗ ΜΕΣΑ ΑΠο ΤΗΝ ΕΜΠΕΔΩΣΗ Ο ΡΟΛΟΣ ΤΟΥ ΔΙΕΥΘΥΝΤΗ Δρ Μάριος Στυλιανίδης, ΕΔΕ ΚB Παγκύπριο Συνέδριο Διευθυντών 15 Μαΐου 2012 Τι είναι Εμπέδωση; ΠΡΙΝ Εξατομίκευση Θεραπευτική
ΤΟ ΔΗΜΟΚΡΑΤΙΚΟ ΣΧΟΛΕΙΟ ΣΤΗΝ ΠΡΑΞΗ ΜΕΣΑ ΑΠο ΤΗΝ ΕΜΠΕΔΩΣΗ Ο ΡΟΛΟΣ ΤΟΥ ΔΙΕΥΘΥΝΤΗ Δρ Μάριος Στυλιανίδης, ΕΔΕ ΚB Παγκύπριο Συνέδριο Διευθυντών 15 Μαΐου 2012 Τι είναι Εμπέδωση; ΠΡΙΝ Εξατομίκευση Θεραπευτική
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΑΓΩΓΗΣ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΑΓΩΓΗΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΑΓΩΓΗΣ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΑΓΩΓΗΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Ονοματεπώνυμα Σπουδαστριών: Μποτονάκη Ειρήνη (5422), Καραλή Μαρία (5601) Μάθημα: Β06Σ03 Στατιστική
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΑΓΩΓΗΣ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΑΓΩΓΗΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Ονοματεπώνυμα Σπουδαστριών: Μποτονάκη Ειρήνη (5422), Καραλή Μαρία (5601) Μάθημα: Β06Σ03 Στατιστική
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΦΛΩΡΙΝΑ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΦΛΩΡΙΝΑ ΕΡΓΑΣΙΑ ΓΙΑ ΤΟ ΜΑΘΗΜΑ: ΚΑΤΑΣΚΕΥΗ ΕΚΠΑΙΔΕΥΤΙΚΟΥ ΥΛΙΚΟΥ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΜΕ ΧΡΗΣΗ ΤΠΕ ΘΕΜΑ ΕΡΓΑΣΙΑΣ: ΜΕΤΑΤΡΟΠΗ ΤΟΥ ΣΕΝΑΡΙΟΥ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΦΛΩΡΙΝΑ ΕΡΓΑΣΙΑ ΓΙΑ ΤΟ ΜΑΘΗΜΑ: ΚΑΤΑΣΚΕΥΗ ΕΚΠΑΙΔΕΥΤΙΚΟΥ ΥΛΙΚΟΥ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΜΕ ΧΡΗΣΗ ΤΠΕ ΘΕΜΑ ΕΡΓΑΣΙΑΣ: ΜΕΤΑΤΡΟΠΗ ΤΟΥ ΣΕΝΑΡΙΟΥ
"Οι ερωτήσεις που ακολουθούν αφορούν την πρόσθετη διδασκαλία που παρακολουθείς αυτό το σχολικό έτος, στα σχολικά μαθήματα ή σε άλλα μαθήματα.
 "Οι ερωτήσεις που ακολουθούν αφορούν την πρόσθετη διδασκαλία που παρακολουθείς αυτό το σχολικό έτος, στα σχολικά μαθήματα ή σε άλλα μαθήματα. Η διδασκαλία αυτή μπορεί να γίνεται στο σχολείο ή κάπου αλλού,
"Οι ερωτήσεις που ακολουθούν αφορούν την πρόσθετη διδασκαλία που παρακολουθείς αυτό το σχολικό έτος, στα σχολικά μαθήματα ή σε άλλα μαθήματα. Η διδασκαλία αυτή μπορεί να γίνεται στο σχολείο ή κάπου αλλού,
Αξιολόγηση Προγράμματος Αλφαβητισμού στο Γυμνάσιο Πρώτο Έτος Αξιολόγησης (Ιούλιος 2009)
 Αξιολόγηση Προγράμματος Αλφαβητισμού στο Γυμνάσιο Πρώτο Έτος Αξιολόγησης (Ιούλιος 2009) 1. Ταυτότητα της Έρευνας Το πρόβλημα του λειτουργικού αναλφαβητισμού στην Κύπρο στις ηλικίες των 12 με 15 χρόνων
Αξιολόγηση Προγράμματος Αλφαβητισμού στο Γυμνάσιο Πρώτο Έτος Αξιολόγησης (Ιούλιος 2009) 1. Ταυτότητα της Έρευνας Το πρόβλημα του λειτουργικού αναλφαβητισμού στην Κύπρο στις ηλικίες των 12 με 15 χρόνων
Μαθηματικά: Αριθμητική και Άλγεβρα. Μάθημα 7 ο, Τμήμα Α
 Μαθηματικά: Αριθμητική και Άλγεβρα Μάθημα 7 ο, Τμήμα Α Δεδομένα Συχνότητα Μέτρα θέσης Μέτρα διασποράς Στοχαστικά μαθηματικά διαφέρουν από τα κλασσικά μαθηματικά διότι τα φαινόμενα δεν είναι αιτιοκρατικά,
Μαθηματικά: Αριθμητική και Άλγεβρα Μάθημα 7 ο, Τμήμα Α Δεδομένα Συχνότητα Μέτρα θέσης Μέτρα διασποράς Στοχαστικά μαθηματικά διαφέρουν από τα κλασσικά μαθηματικά διότι τα φαινόμενα δεν είναι αιτιοκρατικά,
Ανάλυση των δραστηριοτήτων κατά γνωστική απαίτηση
 Ανάλυση των δραστηριοτήτων κατά γνωστική απαίτηση Πέρα όµως από την Γνωσιακή/Εννοιολογική ανάλυση της δοµής και του περιεχοµένου των σχολικών εγχειριδίων των Μαθηµατικών του Δηµοτικού ως προς τις έννοιες
Ανάλυση των δραστηριοτήτων κατά γνωστική απαίτηση Πέρα όµως από την Γνωσιακή/Εννοιολογική ανάλυση της δοµής και του περιεχοµένου των σχολικών εγχειριδίων των Μαθηµατικών του Δηµοτικού ως προς τις έννοιες
«ΕΦΑΡΜΟΣΜΕΝΗ ΔΙΔΑΚΤΙΚΗ ΜΑΘΗΜΑΤΙΚΩΝ» ΠΡΑΚΤΙΚΕΣ Β ΦΑΣΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΠΡΟΣΧΟΛΙΚΗΣ ΑΓΩΓΗΣ ΚΑΙ ΤΟΥ ΕΚΠΑΙΔΕΥΤΙΚΟΥ ΣΧΕΔΙΑΣΜΟΥ «ΕΦΑΡΜΟΣΜΕΝΗ ΔΙΔΑΚΤΙΚΗ ΜΑΘΗΜΑΤΙΚΩΝ» ΠΡΑΚΤΙΚΕΣ Β ΦΑΣΗΣ ΣΥΝΟΠΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ Διδάσκουσες:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΠΡΟΣΧΟΛΙΚΗΣ ΑΓΩΓΗΣ ΚΑΙ ΤΟΥ ΕΚΠΑΙΔΕΥΤΙΚΟΥ ΣΧΕΔΙΑΣΜΟΥ «ΕΦΑΡΜΟΣΜΕΝΗ ΔΙΔΑΚΤΙΚΗ ΜΑΘΗΜΑΤΙΚΩΝ» ΠΡΑΚΤΙΚΕΣ Β ΦΑΣΗΣ ΣΥΝΟΠΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ Διδάσκουσες:
Σχολείο Δεύτερης Ευκαιρίας. Ιωαννίνων. Αριθμητικός Γραμματισμός. Εισηγήτρια : Σεντελέ Καίτη
 Σχολείο Δεύτερης Ευκαιρίας Ιωαννίνων Αριθμητικός Γραμματισμός Εισηγήτρια : Σεντελέ Καίτη ΘΕΜΑ ΕΙΣΗΓΗΣΗΣ «Προγραμματισμός-Οργάνωση και υλοποίηση μιας διδακτικής ενότητας στον Αριθμητικό Γραμματισμό» ΠΡΟΣΘΕΣΗ
Σχολείο Δεύτερης Ευκαιρίας Ιωαννίνων Αριθμητικός Γραμματισμός Εισηγήτρια : Σεντελέ Καίτη ΘΕΜΑ ΕΙΣΗΓΗΣΗΣ «Προγραμματισμός-Οργάνωση και υλοποίηση μιας διδακτικής ενότητας στον Αριθμητικό Γραμματισμό» ΠΡΟΣΘΕΣΗ
ΦΟΙΤΗΤΡΙΑ: ΠΑΤΣΑΤΖΑΚΗ ΕΛΕΝΗ, ΑΕΜ:3196 ΕΡΓΑΣΙΑ ΣΤΟ ΜΑΘΗΜΑ : ΥΕ258 ΕΝΑΛΛΑΚΤΙΚΕΣ ΜΟΡΦΕΣ ΑΞΙΟΛΟΓΗΣΗΣ ΤΩΝ ΓΛΩΣΣΙΚΩΝ ΔΕΞΙΟΤΗΤΩΝ
 2015 ΕΡΓΑΣΙΑ ΣΤΟ ΜΑΘΗΜΑ : ΥΕ258 ΕΝΑΛΛΑΚΤΙΚΕΣ ΜΟΡΦΕΣ ΑΞΙΟΛΟΓΗΣΗΣ ΤΩΝ ΓΛΩΣΣΙΚΩΝ ΔΕΞΙΟΤΗΤΩΝ ΦΟΙΤΗΤΡΙΑ: ΠΑΤΣΑΤΖΑΚΗ ΕΛΕΝΗ, ΑΕΜ:3196 ΕΠΙΒΛΕΠΟΥΣΑ ΚΑΘΗΓΗΤΡΙΑ: ΓΡΙΒΑ ΕΛΕΝΗ 5/2/2015 ΕΙΣΑΓΩΓΗ Αυτό το portfolio φτιάχτηκε
2015 ΕΡΓΑΣΙΑ ΣΤΟ ΜΑΘΗΜΑ : ΥΕ258 ΕΝΑΛΛΑΚΤΙΚΕΣ ΜΟΡΦΕΣ ΑΞΙΟΛΟΓΗΣΗΣ ΤΩΝ ΓΛΩΣΣΙΚΩΝ ΔΕΞΙΟΤΗΤΩΝ ΦΟΙΤΗΤΡΙΑ: ΠΑΤΣΑΤΖΑΚΗ ΕΛΕΝΗ, ΑΕΜ:3196 ΕΠΙΒΛΕΠΟΥΣΑ ΚΑΘΗΓΗΤΡΙΑ: ΓΡΙΒΑ ΕΛΕΝΗ 5/2/2015 ΕΙΣΑΓΩΓΗ Αυτό το portfolio φτιάχτηκε
ΕΝΤΑΣΗ ΗΛΕΚΤΡΙΚΟΥ ΡΕΥΜΑΤΟΣ (Ε.Χαραλάμπους)
 ΕΝΤΑΣΗ ΗΛΕΚΤΡΙΚΟΥ ΡΕΥΜΑΤΟΣ (Ε.Χαραλάμπους) Όνομα Παιδιού: Ναταλία Ασιήκαλη ΤΙΤΛΟΣ ΔΙΕΡΕΥΝΗΣΗΣ: Πως οι παράγοντες υλικό, μήκος και πάχος υλικού επηρεάζουν την αντίσταση και κατ επέκταση την ένταση του ρεύματος
ΕΝΤΑΣΗ ΗΛΕΚΤΡΙΚΟΥ ΡΕΥΜΑΤΟΣ (Ε.Χαραλάμπους) Όνομα Παιδιού: Ναταλία Ασιήκαλη ΤΙΤΛΟΣ ΔΙΕΡΕΥΝΗΣΗΣ: Πως οι παράγοντες υλικό, μήκος και πάχος υλικού επηρεάζουν την αντίσταση και κατ επέκταση την ένταση του ρεύματος
ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ ΓΙΑ ΔΙΔΑΣΚΑΛΙΑ ΚΟΙΝΩΝΙΚΩΝ ΔΕΞΙΟΤΗΤΩΝ 1
 ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ ΓΙΑ ΔΙΔΑΣΚΑΛΙΑ ΚΟΙΝΩΝΙΚΩΝ ΔΕΞΙΟΤΗΤΩΝ 1 ΠΡΟΣΔΟΚΙΑ: Σεβασμός Κοινωνική δεξιότητα: Ακούω τον ομιλητή στο μάθημα Στόχοι μαθήματος: Ο μαθητής να: 1. Ονομάζει τα βασικά βήματα της κοινωνικής
ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ ΓΙΑ ΔΙΔΑΣΚΑΛΙΑ ΚΟΙΝΩΝΙΚΩΝ ΔΕΞΙΟΤΗΤΩΝ 1 ΠΡΟΣΔΟΚΙΑ: Σεβασμός Κοινωνική δεξιότητα: Ακούω τον ομιλητή στο μάθημα Στόχοι μαθήματος: Ο μαθητής να: 1. Ονομάζει τα βασικά βήματα της κοινωνικής
Αντιλήψεις-Στάσεις των μαθητών του γυμνασίου και των Λ.Τ. τάξεων σχετικά με την σχολική ζωή
 Αντιλήψεις-Στάσεις των μαθητών του γυμνασίου και των Λ.Τ. τάξεων σχετικά με την σχολική ζωή 2016-2017 Βαβαρούτα Κατερίνα Σπυρόπουλος Βασίλης Ψηλοπαναγιώτη Άννα Ψυχομάνη Γεωργία Ριόλος 2016-17 1 ΠΕΡΙΕΧΟΜΕΝΑ
Αντιλήψεις-Στάσεις των μαθητών του γυμνασίου και των Λ.Τ. τάξεων σχετικά με την σχολική ζωή 2016-2017 Βαβαρούτα Κατερίνα Σπυρόπουλος Βασίλης Ψηλοπαναγιώτη Άννα Ψυχομάνη Γεωργία Ριόλος 2016-17 1 ΠΕΡΙΕΧΟΜΕΝΑ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΑΓΩΓΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΑΓΩΓΗΣ Αγαπητέ μαθητή/ αγαπητή μαθήτρια, Διεξάγουμε μια έρευνα και θα θέλαμε να μάθουμε την άποψή σου για τo περιβάλλον μάθησης που επικρατεί στην τάξη σου. Σε παρακαλούμε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΑΓΩΓΗΣ Αγαπητέ μαθητή/ αγαπητή μαθήτρια, Διεξάγουμε μια έρευνα και θα θέλαμε να μάθουμε την άποψή σου για τo περιβάλλον μάθησης που επικρατεί στην τάξη σου. Σε παρακαλούμε
Μαθηματικά για Διδασκαλία III
 Μαθηματικά για Διδασκαλία III Μαριάννα Τζεκάκη Απαραίτητα στον εκπαιδευτικό Μαθηματικό περιεχόμενο γνώση Ζητήματα των στόχων της διδασκαλίας των μαθηματικών μάθησης και του σχετικού μαθηματικού περιεχομένου
Μαθηματικά για Διδασκαλία III Μαριάννα Τζεκάκη Απαραίτητα στον εκπαιδευτικό Μαθηματικό περιεχόμενο γνώση Ζητήματα των στόχων της διδασκαλίας των μαθηματικών μάθησης και του σχετικού μαθηματικού περιεχομένου
Ενότητα εκπαίδευσης και κατάρτισης για τις δεξιότητες ηγεσίας
 3 Ενότητα εκπαίδευσης και κατάρτισης για τις δεξιότητες ηγεσίας Παρακινώντας τους άλλους Οι ενότητες κατάρτισης για τις δεξιότητες ηγεσίας έχουν αναπτυχθεί για να σας βοηθήσουν να προετοιμαστείτε για το
3 Ενότητα εκπαίδευσης και κατάρτισης για τις δεξιότητες ηγεσίας Παρακινώντας τους άλλους Οι ενότητες κατάρτισης για τις δεξιότητες ηγεσίας έχουν αναπτυχθεί για να σας βοηθήσουν να προετοιμαστείτε για το
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΔΙΔΑΚΤΙΚΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ»
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΔΙΔΑΚΤΙΚΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ» ΕΙΔΙΚΑ ΘΕΜΑΤΑ ΔΙΔΑΚΤΙΚΗΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ Μαριάννα Τζεκάκη Παρουσίαση των άρθρων:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΔΙΔΑΚΤΙΚΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ» ΕΙΔΙΚΑ ΘΕΜΑΤΑ ΔΙΔΑΚΤΙΚΗΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ Μαριάννα Τζεκάκη Παρουσίαση των άρθρων:
Δραστηριότητες & Υλικό για τα Μαθηματικά του Δημοτικού
 Δραστηριότητες & Υλικό για τα Μαθηματικά του Δημοτικού Πέτρος Κλιάπης kliapis@sch.gr 1 Ο Ρόλος του εκπαιδευτικού Αξιολογεί την αρχική μαθηματική κατάσταση κάθε παιδιού, ομαδοποιεί τα παιδιά σύμφωνα με
Δραστηριότητες & Υλικό για τα Μαθηματικά του Δημοτικού Πέτρος Κλιάπης kliapis@sch.gr 1 Ο Ρόλος του εκπαιδευτικού Αξιολογεί την αρχική μαθηματική κατάσταση κάθε παιδιού, ομαδοποιεί τα παιδιά σύμφωνα με
Για τα παιδιά (αλλά και για τους γονείς)...
 Eισαγωγικό σημείωμα: «Οι κατ οίκον εργασίες στη διδασκαλία των μαθηματικών» Οι εργασίες «για το σπίτι» ή όπως λέγονται στις παιδαγωγικές επιστήμες οι κατ οίκον εργασίες αποτελούν αναπόσπαστο κομμάτι της
Eισαγωγικό σημείωμα: «Οι κατ οίκον εργασίες στη διδασκαλία των μαθηματικών» Οι εργασίες «για το σπίτι» ή όπως λέγονται στις παιδαγωγικές επιστήμες οι κατ οίκον εργασίες αποτελούν αναπόσπαστο κομμάτι της
Αξιολόγηση του μαθητή για βελτίωση των μαθησιακών αποτελεσμάτων
 Αξιολόγηση του μαθητή για βελτίωση των μαθησιακών αποτελεσμάτων Λεωνίδας Κυριακίδης Τμήμα Επιστημών της Αγωγής, Πανεπιστήμιο Κύπρου kyriakid@ucy.ac.cy Διήμερο Εκπαιδευτικού Μέσης Γενικής και Μέσης Τεχνικής
Αξιολόγηση του μαθητή για βελτίωση των μαθησιακών αποτελεσμάτων Λεωνίδας Κυριακίδης Τμήμα Επιστημών της Αγωγής, Πανεπιστήμιο Κύπρου kyriakid@ucy.ac.cy Διήμερο Εκπαιδευτικού Μέσης Γενικής και Μέσης Τεχνικής
Η διάρκεια πραγματοποίησης της ανοιχτής εκπαιδευτικής πρακτικής ήταν 2 διδακτικές ώρες
 ΣΧΟΛΕΙΟ Η εκπαιδευτική πρακτική αφορούσε τη διδασκαλία των μεταβλητών στον προγραμματισμό και εφαρμόστηκε σε μαθητές της τελευταίας τάξης ΕΠΑΛ του τομέα Πληροφορικής στα πλαίσια του μαθήματος του Δομημένου
ΣΧΟΛΕΙΟ Η εκπαιδευτική πρακτική αφορούσε τη διδασκαλία των μεταβλητών στον προγραμματισμό και εφαρμόστηκε σε μαθητές της τελευταίας τάξης ΕΠΑΛ του τομέα Πληροφορικής στα πλαίσια του μαθήματος του Δομημένου
Έρευνες με χρήση φορητής μάθησης στα Μαθηματικά
 Έρευνες με χρήση φορητής μάθησης στα Μαθηματικά Οι Drigas & Pappas (2015) κάνουν μια ανασκόπιση των ερευνών της φορητής μάθησης στα Μαθηματικά. Με βάση την ιδέα της ενσωμάτωσης της κινητής μάθησης στην
Έρευνες με χρήση φορητής μάθησης στα Μαθηματικά Οι Drigas & Pappas (2015) κάνουν μια ανασκόπιση των ερευνών της φορητής μάθησης στα Μαθηματικά. Με βάση την ιδέα της ενσωμάτωσης της κινητής μάθησης στην
Μαθηματικά Ε Δημοτικού
 Μαθηματικά Ε Δημοτικού Πέτρος Κλιάπης 2014 Πέτρος Κλιάπης 12η Περιφέρεια Θεσσαλονίκης Το σύγχρονο μαθησιακό περιβάλλον των Μαθηματικών Ενεργή συμμετοχή των παιδιών Μάθηση μέσα από δραστηριότητες Κατανόηση
Μαθηματικά Ε Δημοτικού Πέτρος Κλιάπης 2014 Πέτρος Κλιάπης 12η Περιφέρεια Θεσσαλονίκης Το σύγχρονο μαθησιακό περιβάλλον των Μαθηματικών Ενεργή συμμετοχή των παιδιών Μάθηση μέσα από δραστηριότητες Κατανόηση
ΑΛΛΑΓΗ ΣΤΗ ΔΙΔΑΣΚΑΛΙΑ ΤΩΝ ΜΑΘΗΜΑΤΙΚΏΝ:
 ΑΛΛΑΓΗ ΣΤΗ ΔΙΔΑΣΚΑΛΙΑ ΤΩΝ ΜΑΘΗΜΑΤΙΚΏΝ: σύγχρονες αναγνώσεις Καβάλα 14/11/2015 ΜΑΡΙΑΝΝΑ ΤΖΕΚΑΚΗ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ 2 Γιατί αλλαγές; 1 3 Για ουσιαστική μαθηματική ανάπτυξη, Σύγχρονο πρόγραμμα
ΑΛΛΑΓΗ ΣΤΗ ΔΙΔΑΣΚΑΛΙΑ ΤΩΝ ΜΑΘΗΜΑΤΙΚΏΝ: σύγχρονες αναγνώσεις Καβάλα 14/11/2015 ΜΑΡΙΑΝΝΑ ΤΖΕΚΑΚΗ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ 2 Γιατί αλλαγές; 1 3 Για ουσιαστική μαθηματική ανάπτυξη, Σύγχρονο πρόγραμμα
ΕΠΙΜΟΡΦΩΤΙΚΕΣ ΑΝΑΓΚΕΣ ΠΑΙΔΑΓΩΓΩΝ ΠΡΟΣΧΟΛΙΚΗΣ ΗΛΙΚΙΑΣ: ΜΙΑ ΠΙΛΟΤΙΚΗ ΕΡΕΥΝΑ ΣΤΟΥΣ ΠΑΙΔΙΚΟΥΣ ΣΤΑΘΜΟΥΣ ΤΟΥ ΔΗΜΟΥ ΗΡΑΚΛΕΙΟΥ
 ΕΠΙΜΟΡΦΩΤΙΚΕΣ ΑΝΑΓΚΕΣ ΠΑΙΔΑΓΩΓΩΝ ΠΡΟΣΧΟΛΙΚΗΣ ΗΛΙΚΙΑΣ: ΜΙΑ ΠΙΛΟΤΙΚΗ ΕΡΕΥΝΑ ΣΤΟΥΣ ΠΑΙΔΙΚΟΥΣ ΣΤΑΘΜΟΥΣ ΤΟΥ ΔΗΜΟΥ ΗΡΑΚΛΕΙΟΥ ΠΕΡΔΙΚΑΚΗ ΕΛΕΝΗ ΒΡΕΦΟΝΗΠΙΟΚΟΜΟΣ Med candidate Επιμορφωτικές & διοικητικές λειτουργίες
ΕΠΙΜΟΡΦΩΤΙΚΕΣ ΑΝΑΓΚΕΣ ΠΑΙΔΑΓΩΓΩΝ ΠΡΟΣΧΟΛΙΚΗΣ ΗΛΙΚΙΑΣ: ΜΙΑ ΠΙΛΟΤΙΚΗ ΕΡΕΥΝΑ ΣΤΟΥΣ ΠΑΙΔΙΚΟΥΣ ΣΤΑΘΜΟΥΣ ΤΟΥ ΔΗΜΟΥ ΗΡΑΚΛΕΙΟΥ ΠΕΡΔΙΚΑΚΗ ΕΛΕΝΗ ΒΡΕΦΟΝΗΠΙΟΚΟΜΟΣ Med candidate Επιμορφωτικές & διοικητικές λειτουργίες
ΕΝΟΤΗΤΑ 10 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΚΑΙ ΔΙΑΙΡΕΣΗ
 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΚΑΙ ΔΙΑΙΡΕΣΗ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΑΡΙΘΜΟΙ Υπολογισμοί και εκτίμηση Αρ1.15 Αναπτύσσουν την έννοια του πολλαπλασιασμού ως αθροιστικής επανάληψης ίσων προσθετέων και διαισθητικά την έννοια της
ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΚΑΙ ΔΙΑΙΡΕΣΗ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΑΡΙΘΜΟΙ Υπολογισμοί και εκτίμηση Αρ1.15 Αναπτύσσουν την έννοια του πολλαπλασιασμού ως αθροιστικής επανάληψης ίσων προσθετέων και διαισθητικά την έννοια της
Μάθηση & Εξερεύνηση στο περιβάλλον του Μουσείου
 Βασίλειος Κωτούλας vaskotoulas@sch.gr h=p://dipe.kar.sch.gr/grss Αρχαιολογικό Μουσείο Καρδίτσας Μάθηση & Εξερεύνηση στο περιβάλλον του Μουσείου Η Δομή της εισήγησης 1 2 3 Δυο λόγια για Στόχοι των Ερευνητική
Βασίλειος Κωτούλας vaskotoulas@sch.gr h=p://dipe.kar.sch.gr/grss Αρχαιολογικό Μουσείο Καρδίτσας Μάθηση & Εξερεύνηση στο περιβάλλον του Μουσείου Η Δομή της εισήγησης 1 2 3 Δυο λόγια για Στόχοι των Ερευνητική
ΠΡΟΔΙΑΓΡΑΦΕΣ - ΟΔΗΓΙΕΣ ΔΙΑΜΟΡΦΩΣΗΣ ΘΕΜΑΤΩΝ ΓΙΑ ΤΟ ΜΑΘΗΜΑ
 ΠΡΟΔΙΑΓΡΑΦΕΣ - ΟΔΗΓΙΕΣ ΔΙΑΜΟΡΦΩΣΗΣ ΘΕΜΑΤΩΝ ΓΙΑ ΤΟ ΜΑΘΗΜΑ Μαθηματικά (Άλγεβρα - Γεωμετρία) Α ΤΑΞΗ ΗΜΕΡΗΣΙΟΥ και Α, Β ΤΑΞΕΙΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Α ΤΑΞΗ ΗΜΕΡΗΣΙΟΥ και Α ΤΑΞΗ ΕΣΠΕΡΙΝΟΥ ΕΠΑΛ ΚΕΝΤΡΙΚΗ
ΠΡΟΔΙΑΓΡΑΦΕΣ - ΟΔΗΓΙΕΣ ΔΙΑΜΟΡΦΩΣΗΣ ΘΕΜΑΤΩΝ ΓΙΑ ΤΟ ΜΑΘΗΜΑ Μαθηματικά (Άλγεβρα - Γεωμετρία) Α ΤΑΞΗ ΗΜΕΡΗΣΙΟΥ και Α, Β ΤΑΞΕΙΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Α ΤΑΞΗ ΗΜΕΡΗΣΙΟΥ και Α ΤΑΞΗ ΕΣΠΕΡΙΝΟΥ ΕΠΑΛ ΚΕΝΤΡΙΚΗ
ΕΝΟΤΗΤΑ 10 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΚΑΙ ΔΙΑΙΡΕΣΗ
 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΚΑΙ ΔΙΑΙΡΕΣΗ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΑΡΙΘΜΟΙ Υπολογισμοί και εκτίμηση Αρ1.15 Αναπτύσσουν την έννοια του πολλαπλασιασμού ως αθροιστικής επανάληψης ίσων προσθετέων και διαισθητικά την έννοια της
ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΚΑΙ ΔΙΑΙΡΕΣΗ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΑΡΙΘΜΟΙ Υπολογισμοί και εκτίμηση Αρ1.15 Αναπτύσσουν την έννοια του πολλαπλασιασμού ως αθροιστικής επανάληψης ίσων προσθετέων και διαισθητικά την έννοια της
3. Πώς θα ήθελα να είναι / συμπεριφέρονται τα παιδιά για να είμαι ευχαριστημένος/η; Παράρτημα ΙΙ
 Παράρτημα Ι Εργαλείο 1: Γνωριμία - Διερεύνηση προσωπικών θεωριών 1. Τα πιο σημαντικά πράγματα που θέλω να πετύχω στην τάξη μου είναι: Α. Β. Γ. Δ. 2. Είμαι ευχαριστημένος/η από τη δουλειά μου όταν: Α. Β.
Παράρτημα Ι Εργαλείο 1: Γνωριμία - Διερεύνηση προσωπικών θεωριών 1. Τα πιο σημαντικά πράγματα που θέλω να πετύχω στην τάξη μου είναι: Α. Β. Γ. Δ. 2. Είμαι ευχαριστημένος/η από τη δουλειά μου όταν: Α. Β.
Διδακτική Μεθοδολογία
 Διδακτική Μεθοδολογία Εαρινό εξάμηνο 2018-19 Διδασκαλία και Κριτική Σκέψη Βασικοί παιδαγωγικοί όροι Κοινωνικοποίηση Διδασκαλία Μόρφωση Εκπαίδευση Διαδικασία ένταξης και δραστηριοποίησης με την εκμάθηση
Διδακτική Μεθοδολογία Εαρινό εξάμηνο 2018-19 Διδασκαλία και Κριτική Σκέψη Βασικοί παιδαγωγικοί όροι Κοινωνικοποίηση Διδασκαλία Μόρφωση Εκπαίδευση Διαδικασία ένταξης και δραστηριοποίησης με την εκμάθηση
Μαθηματικά της Φύσης και της Ζωής
 Μαθηματικά της Φύσης και της Ζωής Τάξη: Ε Η ομάδα χορού 1. Σε μια ομάδα παραδοσιακών χορών συμμετέχουν 39 αγόρια και 23 κορίτσια. Κάθε εβδομάδα προστίθενται στην ομάδα 6 νέα αγόρια και 8 νέα κορίτσια.
Μαθηματικά της Φύσης και της Ζωής Τάξη: Ε Η ομάδα χορού 1. Σε μια ομάδα παραδοσιακών χορών συμμετέχουν 39 αγόρια και 23 κορίτσια. Κάθε εβδομάδα προστίθενται στην ομάδα 6 νέα αγόρια και 8 νέα κορίτσια.
Πειραματιζόμενοι με αριθμούς στο περιβάλλον του Microworlds Pro: διαθεματική προσέγγιση περί «πολλαπλασίων και διαιρετών»
 Πειραματιζόμενοι με αριθμούς στο περιβάλλον του Microworlds Pro: διαθεματική προσέγγιση περί «πολλαπλασίων και διαιρετών» μια Νίκος Δαπόντες Φυσικός Δευτεροβάθμιας Εκπαίδευσης Το περιβάλλον Microworlds
Πειραματιζόμενοι με αριθμούς στο περιβάλλον του Microworlds Pro: διαθεματική προσέγγιση περί «πολλαπλασίων και διαιρετών» μια Νίκος Δαπόντες Φυσικός Δευτεροβάθμιας Εκπαίδευσης Το περιβάλλον Microworlds
Α.2.1 Η ΕΝΝΟΙΑ ΤΟΥ ΚΛΑΣΜΑΤΟΣ
 ΚΕΦΑΛΑΙΟ Ο ΚΛΑΣΜΑΤΑ Α.. Η ΕΝΝΟΙΑ ΤΟΥ ΚΛΑΣΜΑΤΟΣ ΜΕΘΟΔΟΛΟΓΙΑ ΣΥΓΚΡΙΣΗ ΚΛΑΣΜΑΤΟΣ ΜΕ ΤΟ Αν ο αριθμητής ενός κλάσματος είναι μεγαλύτερος από τον παρανομαστή, τότε το κλάσμα είναι μεγαλύτερο από το. Αν ο αριθμητής
ΚΕΦΑΛΑΙΟ Ο ΚΛΑΣΜΑΤΑ Α.. Η ΕΝΝΟΙΑ ΤΟΥ ΚΛΑΣΜΑΤΟΣ ΜΕΘΟΔΟΛΟΓΙΑ ΣΥΓΚΡΙΣΗ ΚΛΑΣΜΑΤΟΣ ΜΕ ΤΟ Αν ο αριθμητής ενός κλάσματος είναι μεγαλύτερος από τον παρανομαστή, τότε το κλάσμα είναι μεγαλύτερο από το. Αν ο αριθμητής
Σύγχρονες απόψεις για τη μάθηση και θέματα αξιολόγησης. Άννα Κουκά
 Σύγχρονες απόψεις για τη μάθηση και θέματα αξιολόγησης Άννα Κουκά 1. Εισαγωγή Εξελίξεις στις προσεγγίσεις για τη μάθηση Τα πορίσματα της εκπαιδευτικής έρευνας δημιουργούν αλλαγές στο σημερινό σχολείο Η
Σύγχρονες απόψεις για τη μάθηση και θέματα αξιολόγησης Άννα Κουκά 1. Εισαγωγή Εξελίξεις στις προσεγγίσεις για τη μάθηση Τα πορίσματα της εκπαιδευτικής έρευνας δημιουργούν αλλαγές στο σημερινό σχολείο Η
Διερευνητική μάθηση We are researchers, let us do research! (Elbers and Streefland, 2000)
 Διερευνητική μάθηση We are researchers, let us do research! (Elbers and Streefland, 2000) Πρόκειται για την έρευνα που διεξάγουν οι επιστήμονες. Είναι μια πολύπλοκη δραστηριότητα που απαιτεί ειδικό ακριβό
Διερευνητική μάθηση We are researchers, let us do research! (Elbers and Streefland, 2000) Πρόκειται για την έρευνα που διεξάγουν οι επιστήμονες. Είναι μια πολύπλοκη δραστηριότητα που απαιτεί ειδικό ακριβό
Διδακτική οργάνωση και διαχείριση του μαθηματικού περιεχομένου και της διαπραγμάτευσης των δραστηριοτήτων στην τάξη
 Διδακτική οργάνωση και διαχείριση του μαθηματικού περιεχομένου και της διαπραγμάτευσης των δραστηριοτήτων στην τάξη Φαινόμενα Εμπειρίες φαινομένων Οργάνωση φαινομένων Νοούμενα (πρώτες μαθηματικές έννοιες
Διδακτική οργάνωση και διαχείριση του μαθηματικού περιεχομένου και της διαπραγμάτευσης των δραστηριοτήτων στην τάξη Φαινόμενα Εμπειρίες φαινομένων Οργάνωση φαινομένων Νοούμενα (πρώτες μαθηματικές έννοιες
Εφαρµοσµένη ιδακτική των Φυσικών Επιστηµών (Πρακτικές Ασκήσεις Β Φάσης)
 Πανεπιστήµιο Αιγαίου Παιδαγωγικό Τµήµα ηµοτικής Εκπαίδευσης Μιχάλης Σκουµιός Εφαρµοσµένη ιδακτική των Φυσικών Επιστηµών (Πρακτικές Ασκήσεις Β Φάσης) Παρατήρηση ιδασκαλίας και Μοντέλο Συγγραφής Έκθεσης
Πανεπιστήµιο Αιγαίου Παιδαγωγικό Τµήµα ηµοτικής Εκπαίδευσης Μιχάλης Σκουµιός Εφαρµοσµένη ιδακτική των Φυσικών Επιστηµών (Πρακτικές Ασκήσεις Β Φάσης) Παρατήρηση ιδασκαλίας και Μοντέλο Συγγραφής Έκθεσης
ΟΙ ΔΙΔΑΚΤΙΚΕΣ ΠΡΑΚΤΙΚΕΣ ΠΟΥ ΕΦΑΡΜΟΖΟΥΝ ΟΙ ΕΚΠΑΙΔΕΥΤΙΚΟΙ ΠΡΩΤΟΒΑΘΜΙΑΣ ΕΚΠΑΙΔΕΥΣΗΣ ΚΑΤΑ ΤΗ ΔΙΔΑΣΚΑΛΙΑ ΤΩΝ ΦΑΙΝΟΜΕΝΩΝ ΕΞΑΤΜΙΣΗΣ ΚΑΙ ΥΓΡΟΠΟΙΗΣΗΣ
 Δημοκρίτειο Πανεπιστήμιο Θράκης Τμήμα Επιστημών Αγωγής Παιδαγωγικό Τμήμα Δημοτικής Εκπαίδευσης Τομέας Θετικών Επιστημών ΟΙ ΔΙΔΑΚΤΙΚΕΣ ΠΡΑΚΤΙΚΕΣ ΠΟΥ ΕΦΑΡΜΟΖΟΥΝ ΟΙ ΕΚΠΑΙΔΕΥΤΙΚΟΙ ΠΡΩΤΟΒΑΘΜΙΑΣ ΕΚΠΑΙΔΕΥΣΗΣ
Δημοκρίτειο Πανεπιστήμιο Θράκης Τμήμα Επιστημών Αγωγής Παιδαγωγικό Τμήμα Δημοτικής Εκπαίδευσης Τομέας Θετικών Επιστημών ΟΙ ΔΙΔΑΚΤΙΚΕΣ ΠΡΑΚΤΙΚΕΣ ΠΟΥ ΕΦΑΡΜΟΖΟΥΝ ΟΙ ΕΚΠΑΙΔΕΥΤΙΚΟΙ ΠΡΩΤΟΒΑΘΜΙΑΣ ΕΚΠΑΙΔΕΥΣΗΣ
Σύστημα Προώθησης Θετική Συμπεριφοράς: Η Στρατηγική «Ελέγχω και Αποχωρώ» στη δευτερογενή πρόληψη
 Σύστημα Προώθησης Θετική Συμπεριφοράς: Η Στρατηγική «Ελέγχω και Αποχωρώ» στη δευτερογενή πρόληψη Η στρατηγική Ελέγχω και Αποχωρώ επικεντρώνεται στην ανάπτυξη αυτοελέγχου σε μαθητές με δυσκολίες συμπεριφοράς.
Σύστημα Προώθησης Θετική Συμπεριφοράς: Η Στρατηγική «Ελέγχω και Αποχωρώ» στη δευτερογενή πρόληψη Η στρατηγική Ελέγχω και Αποχωρώ επικεντρώνεται στην ανάπτυξη αυτοελέγχου σε μαθητές με δυσκολίες συμπεριφοράς.
Νέες τάσεις στη διδακτική των Μαθηματικών
 Νέες τάσεις στη διδακτική των Μαθηματικών Μέχρι πριν λίγα χρόνια ηαντίληψη που επικρατούσε ήταν ότι ημαθηματική γνώση είναι ένα αγαθό που έχει παραχθεί και καλούνται οι μαθητές να το καταναλώσουν αποστηθίζοντάς
Νέες τάσεις στη διδακτική των Μαθηματικών Μέχρι πριν λίγα χρόνια ηαντίληψη που επικρατούσε ήταν ότι ημαθηματική γνώση είναι ένα αγαθό που έχει παραχθεί και καλούνται οι μαθητές να το καταναλώσουν αποστηθίζοντάς
Βάσεις και Βασικές Έννοιες των Φυσικών Επιστηµών. Εισαγωγή
 Βάσεις και Βασικές Έννοιες των Φυσικών Επιστηµών Εισαγωγή Δοµή Μαθήµατος Εισαγωγή Τι είναι Φ.Ε. ερωτήµατα για τον κόσµο (ιδεοθύελλα) Εµπειρίες µε Φ.Ε. Ζωγράφισε ένα επιστήµονα Γιατί είναι σηµαντική η διδασκαλία
Βάσεις και Βασικές Έννοιες των Φυσικών Επιστηµών Εισαγωγή Δοµή Μαθήµατος Εισαγωγή Τι είναι Φ.Ε. ερωτήµατα για τον κόσµο (ιδεοθύελλα) Εµπειρίες µε Φ.Ε. Ζωγράφισε ένα επιστήµονα Γιατί είναι σηµαντική η διδασκαλία
1. Η σκοπιμότητα της ένταξης εργαλείων ψηφιακής τεχνολογίας στη Μαθηματική Εκπαίδευση
 1. Η σκοπιμότητα της ένταξης εργαλείων ψηφιακής τεχνολογίας στη Μαθηματική Εκπαίδευση Στη βασική παιδεία, τα μαθηματικά διδάσκονται με στατικά μέσα α) πίνακα/χαρτιού β) κιμωλίας/στυλού γ) χάρτινου βιβλίου.
1. Η σκοπιμότητα της ένταξης εργαλείων ψηφιακής τεχνολογίας στη Μαθηματική Εκπαίδευση Στη βασική παιδεία, τα μαθηματικά διδάσκονται με στατικά μέσα α) πίνακα/χαρτιού β) κιμωλίας/στυλού γ) χάρτινου βιβλίου.
Κεφάλαιο 9. Έλεγχοι υποθέσεων
 Κεφάλαιο 9 Έλεγχοι υποθέσεων 9.1 Εισαγωγή Όταν παίρνουμε ένα ή περισσότερα τυχαία δείγμα από κανονικούς πληθυσμούς έχουμε τη δυνατότητα να υπολογίζουμε στατιστικά, όπως μέσους όρους, δειγματικές διασπορές
Κεφάλαιο 9 Έλεγχοι υποθέσεων 9.1 Εισαγωγή Όταν παίρνουμε ένα ή περισσότερα τυχαία δείγμα από κανονικούς πληθυσμούς έχουμε τη δυνατότητα να υπολογίζουμε στατιστικά, όπως μέσους όρους, δειγματικές διασπορές
«Άρτος και Ευρωπαϊκή Ένωση»
 «Άρτος και Ευρωπαϊκή Ένωση» Εκπαιδευτικός: Βαμβουνάκη Άρτεμις (ΠΕ 70) Επιβλέπων επιμορφωτής: Μανωλάκης Κωνσταντίνος Σχολείο Διεξαγωγής: Εκπαιδευτήρια Μαυροματάκη-Μητέρα Χανιά, Μάιος 2017 Εισαγωγή Η παρούσα
«Άρτος και Ευρωπαϊκή Ένωση» Εκπαιδευτικός: Βαμβουνάκη Άρτεμις (ΠΕ 70) Επιβλέπων επιμορφωτής: Μανωλάκης Κωνσταντίνος Σχολείο Διεξαγωγής: Εκπαιδευτήρια Μαυροματάκη-Μητέρα Χανιά, Μάιος 2017 Εισαγωγή Η παρούσα
Αξιολόγηση και Αυτοαξιολόγηση Εκπαιδευομένων- Αξιολόγηση Εκπαιδευτικού
 Αξιολόγηση και Αυτοαξιολόγηση Εκπαιδευομένων- Αξιολόγηση Εκπαιδευτικού Σεντελέ Αικατερίνη, Εκπαιδευτικός Β/θμιας Εκπαίδευσης ΠΡΟΛΟΓΟΣ Αξιολόγησα τους μαθητές μου θεωρώντας την αξιολόγηση σαν μια διαδικασία
Αξιολόγηση και Αυτοαξιολόγηση Εκπαιδευομένων- Αξιολόγηση Εκπαιδευτικού Σεντελέ Αικατερίνη, Εκπαιδευτικός Β/θμιας Εκπαίδευσης ΠΡΟΛΟΓΟΣ Αξιολόγησα τους μαθητές μου θεωρώντας την αξιολόγηση σαν μια διαδικασία
Αξιολόγηση του Προγράμματος Ταχύρρυθμης Εκμάθησης της Ελληνικής στη Μέση Εκπαίδευση (Ιούνιος 2010)
 Αξιολόγηση του Προγράμματος Ταχύρρυθμης Εκμάθησης της Ελληνικής στη Μέση Εκπαίδευση (Ιούνιος 2010) 1. Ταυτότητα της Έρευνας Με απόφαση του Υπουργικού Συμβουλίου της 29 ης Ιουλίου, 2008, τέθηκε σε εφαρμογή
Αξιολόγηση του Προγράμματος Ταχύρρυθμης Εκμάθησης της Ελληνικής στη Μέση Εκπαίδευση (Ιούνιος 2010) 1. Ταυτότητα της Έρευνας Με απόφαση του Υπουργικού Συμβουλίου της 29 ης Ιουλίου, 2008, τέθηκε σε εφαρμογή
Αγαπητοί γονείς, Αντιγόνη Λυκοτραφίτη
 Αγαπητοί γονείς, Το βιβλίο αυτό είναι γραμμένο σύμφωνα με την ύλη του σχολικού βιβλίου «Μαθηματικά Γ Δημοτικού». Είναι δομημένο σε αντίστοιχα κεφάλαια και λειτουργεί παράλληλα αλλά και συμπληρωματικά με
Αγαπητοί γονείς, Το βιβλίο αυτό είναι γραμμένο σύμφωνα με την ύλη του σχολικού βιβλίου «Μαθηματικά Γ Δημοτικού». Είναι δομημένο σε αντίστοιχα κεφάλαια και λειτουργεί παράλληλα αλλά και συμπληρωματικά με
Τρίτη 24 και Τετάρτη 25 Οκτωβρίου 2017
 Τρίτη 24 και Τετάρτη 25 Οκτωβρίου 2017 Παιδαγωγικές προσεγγίσεις και διδακτικές πρακτικές - η σχέση τους με τις θεωρίες μάθησης Παρατηρώντας τη μαθησιακή διαδικασία Τι είδους δραστηριότητες παρατηρήσατε
Τρίτη 24 και Τετάρτη 25 Οκτωβρίου 2017 Παιδαγωγικές προσεγγίσεις και διδακτικές πρακτικές - η σχέση τους με τις θεωρίες μάθησης Παρατηρώντας τη μαθησιακή διαδικασία Τι είδους δραστηριότητες παρατηρήσατε
THE ROLE OF IMPLICIT MODELS IN SOLVING VERBAL PROBLEMS IN MULTIPLICATION AND DIVISION
 THE ROLE OF IMPLICIT MODELS IN SOLVING VERBAL PROBLEMS IN MULTIPLICATION AND DIVISION E F R A I M F I S C H B E I N, T E L - A V I V U N I V E R S I T Y M A R I A D E R I, U N I V E R S I T Y O F P I S
THE ROLE OF IMPLICIT MODELS IN SOLVING VERBAL PROBLEMS IN MULTIPLICATION AND DIVISION E F R A I M F I S C H B E I N, T E L - A V I V U N I V E R S I T Y M A R I A D E R I, U N I V E R S I T Y O F P I S
ΠΡΟΓΡΑΜΜΑ ΠΡΟΫΠΗΡΕΣΙΑΚΗΣ ΚΑΤΑΡΤΙΣΗΣ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ (Απογευματινή φοίτηση ) ΕΚΠΑΙ ΕΥΤΙΚΗ ΑΞΙΟΛΟΓΗΣΗ
 ΠΡΟΡΑΜΜΑ ΠΡΟΫΠΗΡΕΣΙΑΚΗΣ ΚΑΤΑΡΤΙΣΗΣ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ (Απογευματινή φοίτηση ) ΕΚΠΑΙ ΕΥΤΙΚΗ ΑΞΙΟΛΟΗΣΗ Όνομα : εωργίου Ιακώβου Ελένη Ομάδα :ΛΕΥΑ1 Ειδικότητα :Μαθηματικός Αρ. Ταυτότητας :77876
ΠΡΟΡΑΜΜΑ ΠΡΟΫΠΗΡΕΣΙΑΚΗΣ ΚΑΤΑΡΤΙΣΗΣ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ (Απογευματινή φοίτηση ) ΕΚΠΑΙ ΕΥΤΙΚΗ ΑΞΙΟΛΟΗΣΗ Όνομα : εωργίου Ιακώβου Ελένη Ομάδα :ΛΕΥΑ1 Ειδικότητα :Μαθηματικός Αρ. Ταυτότητας :77876
Η ΔΙΑΦΟΡΟΠΟΙΗΣΗ ΤΗΣ ΔΙΔΑΣΚΑΛΙΑΣ ΣΤΗΝ ΤΑΞΗ.
 Η ΔΙΑΦΟΡΟΠΟΙΗΣΗ ΤΗΣ ΔΙΔΑΣΚΑΛΙΑΣ ΣΤΗΝ ΤΑΞΗ. Σκοταράς Νικόλαος Επ. Σχ. Σύμβουλος ΠΕ12, Δρ Ε.Μ.Π. skotaras@sch.gr Web: http://users.att.sch.gr/skotaras 1 1. Η σύγχρονη σχολική τάξη.(1 ) 2. Η γνώση που έχουμε
Η ΔΙΑΦΟΡΟΠΟΙΗΣΗ ΤΗΣ ΔΙΔΑΣΚΑΛΙΑΣ ΣΤΗΝ ΤΑΞΗ. Σκοταράς Νικόλαος Επ. Σχ. Σύμβουλος ΠΕ12, Δρ Ε.Μ.Π. skotaras@sch.gr Web: http://users.att.sch.gr/skotaras 1 1. Η σύγχρονη σχολική τάξη.(1 ) 2. Η γνώση που έχουμε
Μαθηματικά της Φύσης και της Ζωής
 Μαθηματικά της Φύσης και της Ζωής Τάξη: ΣΤ Η γάτα και το ποντίκι 1. Ένα ποντίκι βρίσκεται πάνω σε έναν τοίχο ύψους 2 μέτρων και κάτω στο έδαφος, περιμένοντας το, βρίσκεται μια γάτα. Κατά τη διάρκεια της
Μαθηματικά της Φύσης και της Ζωής Τάξη: ΣΤ Η γάτα και το ποντίκι 1. Ένα ποντίκι βρίσκεται πάνω σε έναν τοίχο ύψους 2 μέτρων και κάτω στο έδαφος, περιμένοντας το, βρίσκεται μια γάτα. Κατά τη διάρκεια της
Καρτσιώτου Θωμαϊς M.Sc. Δασκάλα Δ.Σ. Παληού Καβάλας tzoymasn@hol.gr. Περίληψη
 33 Πρόταση διδασκαλίας με τη χρήση των ΤΠΕ στο μάθημα της Μελέτης Περιβάλλοντος της Δ τάξης Δημοτικού: Μαθαίνω για τα σημαντικά έργα που υπάρχουν στην Ελλάδα μέσα από το google earth Καρτσιώτου Θωμαϊς
33 Πρόταση διδασκαλίας με τη χρήση των ΤΠΕ στο μάθημα της Μελέτης Περιβάλλοντος της Δ τάξης Δημοτικού: Μαθαίνω για τα σημαντικά έργα που υπάρχουν στην Ελλάδα μέσα από το google earth Καρτσιώτου Θωμαϊς
ΕΝΟΤΗΤΑ 9 ΠΡΟΣΘΕΣΗ ΜΕΧΡΙ ΤΟ 100 ΜΟΤΙΒΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΥ 3 ΚΑΙ 4
 ΠΡΟΣΘΕΣΗ ΜΕΧΡΙ ΤΟ 100 ΜΟΤΙΒΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΥ 3 ΚΑΙ 4 ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΑΡΙΘΜΟΙ Διερεύνηση αριθμών Αρ1.7 Αναπαριστούν εναδικά κλάσματα ( ) ενός συνόλου ή μιας επιφάνειας, χρησιμοποιώντας αντικείμενα, εικόνες
ΠΡΟΣΘΕΣΗ ΜΕΧΡΙ ΤΟ 100 ΜΟΤΙΒΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΥ 3 ΚΑΙ 4 ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΑΡΙΘΜΟΙ Διερεύνηση αριθμών Αρ1.7 Αναπαριστούν εναδικά κλάσματα ( ) ενός συνόλου ή μιας επιφάνειας, χρησιμοποιώντας αντικείμενα, εικόνες
Άδειες Χρήσης. Διδακτική Μαθηματικών I. Κατηγορίες προβλημάτων - Ρεαλιστικά Μαθηματικά. Διδάσκων: Επίκουρος Καθ. Κ. Τάτσης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης Διδακτική Μαθηματικών I Κατηγορίες προβλημάτων - Ρεαλιστικά Μαθηματικά Διδάσκων: Επίκουρος Καθ. Κ. Τάτσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης Διδακτική Μαθηματικών I Κατηγορίες προβλημάτων - Ρεαλιστικά Μαθηματικά Διδάσκων: Επίκουρος Καθ. Κ. Τάτσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Αναλυτικό Πρόγραμμα Μαθηματικών
 Αναλυτικό Πρόγραμμα Μαθηματικών Σχεδιασμός... αντιμετωπίζει ενιαία το πλαίσιο σπουδών (Προδημοτική, Δημοτικό, Γυμνάσιο και Λύκειο), είναι συνέχεια υπό διαμόρφωση και αλλαγή, για να αντιμετωπίζει την εξέλιξη,
Αναλυτικό Πρόγραμμα Μαθηματικών Σχεδιασμός... αντιμετωπίζει ενιαία το πλαίσιο σπουδών (Προδημοτική, Δημοτικό, Γυμνάσιο και Λύκειο), είναι συνέχεια υπό διαμόρφωση και αλλαγή, για να αντιμετωπίζει την εξέλιξη,
Θεμελιώδεις Αρχές Επιστήμης και Μέθοδοι Έρευνας
 Θεμελιώδεις Αρχές Επιστήμης και Μέθοδοι Έρευνας Dr. Anthony Montgomery Επίκουρος Καθηγητής Εκπαιδευτικής & Κοινωνικής Πολιτικής antmont@uom.gr Θεμελιώδεις Αρχές Επιστήμης και Μέθοδοι Έρευνας Αυτό το μάθημα
Θεμελιώδεις Αρχές Επιστήμης και Μέθοδοι Έρευνας Dr. Anthony Montgomery Επίκουρος Καθηγητής Εκπαιδευτικής & Κοινωνικής Πολιτικής antmont@uom.gr Θεμελιώδεις Αρχές Επιστήμης και Μέθοδοι Έρευνας Αυτό το μάθημα
Μαθηματικά Δ Δημοτικού. Πέτρος Κλιάπης 12η περιφέρεια Θεσ/νικης
 Μαθηματικά Δ Δημοτικού Πέτρος Κλιάπης 12η περιφέρεια Θεσ/νικης Το σύγχρονο μαθησιακό περιβάλλον των Μαθηματικών Ενεργή συμμετοχή των παιδιών Μάθηση μέσα από δραστηριότητες Κατανόηση ΌΧΙ απομνημόνευση Αξιοποίηση
Μαθηματικά Δ Δημοτικού Πέτρος Κλιάπης 12η περιφέρεια Θεσ/νικης Το σύγχρονο μαθησιακό περιβάλλον των Μαθηματικών Ενεργή συμμετοχή των παιδιών Μάθηση μέσα από δραστηριότητες Κατανόηση ΌΧΙ απομνημόνευση Αξιοποίηση
ΣΤΑΘΕΡΟΤΗΤΑ ΧΕΡΙΟΥ (Π. ΚΟΥΠΑΝΟΣ)
 "Πανηγύρι της Επιστήμης" ΣΤΑΘΕΡΟΤΗΤΑ ΧΕΡΙΟΥ (Π. ΚΟΥΠΑΝΟΣ) Το Πανηγύρι της Επιστήμης είναι μια από τις δραστηριότητες που διοργανώνεται στα πλαίσια του μαθήματος ΕΠΑ 336 Διδακτική των Φυσικών Επιστημών.
"Πανηγύρι της Επιστήμης" ΣΤΑΘΕΡΟΤΗΤΑ ΧΕΡΙΟΥ (Π. ΚΟΥΠΑΝΟΣ) Το Πανηγύρι της Επιστήμης είναι μια από τις δραστηριότητες που διοργανώνεται στα πλαίσια του μαθήματος ΕΠΑ 336 Διδακτική των Φυσικών Επιστημών.
Εφαρμογές (apps) για εξάσκηση με τα κλάσματα σε επίπεδο Γ Δημοτικού
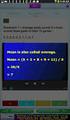 Εφαρμογές (apps) για εξάσκηση με τα κλάσματα σε επίπεδο Γ Δημοτικού Fractions & Smart Pirates (δωρεάν) Ένα διαδραστικό παιχνίδι όπου οι μαθητές πρέπει να φέρουν εις πέρας δοκιμασίες που τους ανατίθενται.
Εφαρμογές (apps) για εξάσκηση με τα κλάσματα σε επίπεδο Γ Δημοτικού Fractions & Smart Pirates (δωρεάν) Ένα διαδραστικό παιχνίδι όπου οι μαθητές πρέπει να φέρουν εις πέρας δοκιμασίες που τους ανατίθενται.
