Bayesian Biostatistics Using BUGS 1
|
|
|
- Τρυφωσα Αυγερινός
- 9 χρόνια πριν
- Προβολές:
Transcript
1 Bayesian BioStatistics Using BUGS Βιοστατιστική κατά Bayes με τη χρήση του Λογισμικού BUGS Ioannis Ntzoufras Department of Business Administration, University of the Aegean ΠΕΡΙΕΧΟΜΕΝΑ ΜΑΘΗΜΑ 1: ΕΙΣΑΓΩΓΗ ΣΤΟ BUGS ΜΑΘΗΜΑ 2: ΕΙΣΑΓΩΓΗ ΣΤΟ WINBUGS ΜΑΘΗΜΑ 3: ΣΥΝΘΕΤΑ ΠΑΡΑΔΕΙΓΜΑΤΑ ΜΑΘΗΜΑ 4: ΣΥΓΚΡΙΣΗ ΜΟΝΤΕΛΩΝ Bayesian BioStatistics Using BUGS ΜΑΘΗΜΑ 1: ΕΙΣΑΓΩΓΗ ΣΤΟ BUGS Ioannis Ntzoufras Department of Business Administration, University of the Aegean ΠΕΡΙΕΧΟΜΕΝΑ 1ου ΜΑΘΗΜΑΤΟΣ 1 ΕΙΣΑΓΩΓΗ ΣΤΑ ΓΕΝΙΚΕΥΜΕΝΑ ΓΡΑΜΜΙΚΑ ΜΟΝΤΕΛΑ 2 ΕΙΣΑΓΩΓΗ ΣΤΟΥΣ ΑΛΓΟΡΙΘΜΟΥΣ MCMC 3 ΜΠΕΥΖΙΑΝΗ ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ ΜΕ ΤΗ ΧΡΗΣΗ ΤΟΥ BUGS 1 ΕΙΣΑΓΩΓΗ ΣΤΑ ΓΕΝΙΚΕΥΜΕΝΑ ΓΡΑΜΜΙΚΑ ΜΟΝΤΕΛΑ ΓΕΝΙΚΕΥΣΗ ΤΩΝ ΠΑΛΙΝΔΡΟΜΙΚΩΝ ΜΟΝΤΕΛΩΝ ΞΕΚΙΝΗΣΑΝ ΑΠΟ ΤΟΝ LEGENDRE (1805) KAI TON GAUSS (1809) 1.1. ΔΕΔΟΜΕΝΑ RESPONSE VARIABLE (Υ): εξαρτημένη ή ενδογενής μεταβλητή ή μεταβλητή απόκρισης/αντίδρασης Y είναι τυχαία μεταβλητή EXPLANATORY VARIABLES (Χ j ): Ανεξάρτητες ή εξογενείς ή επεξηγηματικές μεταβλητές Χ j θεωρούνται συνήθως σταθερές από το σχεδιασμό του πειράματος Bayesian Biostatistics Using BUGS 1
2 ΚΥΡΙΕΣ ΣΥΝΙΣΤΩΣΕΣ ΤΥΧΑΙΑ ΣΥΝΙΣΤΩΣΑ (random component) Υ i ~ ΚΑΤΑΝΟΜΗ( θ ) θ : διάνυσμα παραμέτρων ΣΥΣΤΗΜΑΤΙΚΗ ΣΥΝΙΣΤΩΣΑ (systematic component) η i = β 0 +β 1 Χ 1i + + β p Χ pi η i λέγεται γραμμικός προσδιορισμός του μοντέλου (linear predictor) ΣΥΝΔΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ (link function) Ο τρόπος συνδεσης των παραμέτρων της τυχαίας συνιστώσας με το γραμμικό προσδιορισμό g(θ) = η i = β 0 +β 1 Χ 1i + + β p Χ pi συνήθως θ είναι ο μέσος της Υ 1.3. ΚΑΝΟΝΙΚΟ ΜΟΝΤΕΛΟ ΤΥΧΑΙΑ ΣΥΝΙΣΤΩΣΑ: Υ ποσοτική μεταβλητή Υ i ~ NORMAL( μ i, σ 2 ) ΣΥΣΤΗΜΑΤΙΚΗ ΣΥΝΙΣΤΩΣΑ: Χ j ποσοτικές ή κατηγορικές ΣΥΝΔΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ μ i = η i = β 0 +β 1 Χ 1i + + β p Χ pi αρα συνδετική συνάρτηση: g(μ)=μ 1.4. ΜΟΝΤΕΛΑ BERNOULLI ΤΥΧΑΙΑ ΣΥΝΙΣΤΩΣΑ: Υ δίτιμη μεταβλητή (0/1) Υ i ~ Bernoulli ( p i ) ΣΥΣΤΗΜΑΤΙΚΗ ΣΥΝΙΣΤΩΣΑ: Χ j ποσοτικές ή κατηγορικές ΣΥΝΔΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ log ( p i /(1- p i ) ) = η i = β 0 +β 1 Χ 1i + + β p Χ pi αρα συνδετική συνάρτηση: g(p)=logit(p) 1.5. ΔΙΩΝΥΜΙΚΑ ΜΟΝΤΕΛΑ ΤΥΧΑΙΑ ΣΥΝΙΣΤΩΣΑ: Υ: # επιτυχιών σε σύνολο n επαναλήψεων Υ i ~ Binomial ( p i, n i ) ΣΥΣΤΗΜΑΤΙΚΗ ΣΥΝΙΣΤΩΣΑ: Χ j ποσοτικές ή κατηγορικές ΣΥΝΔΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ log ( p i /(1- p i ) ) = η i = β 0 +β 1 Χ 1i + + β p Χ pi αρα συνδετική συνάρτηση: g(p)=logit(p) 1.6. ΜΟΝΤΕΛΑ POISSON ΤΥΧΑΙΑ ΣΥΝΙΣΤΩΣΑ: Υ: # επιτυχιών σε ένα χρονικό διάστημα Υ i ~ Poisson ( λ i ) ΣΥΣΤΗΜΑΤΙΚΗ ΣΥΝΙΣΤΩΣΑ: Χ j ποσοτικές ή κατηγορικές ΣΥΝΔΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ log (λ i ) = η i = β 0 +β 1 Χ 1i + + β p Χ pi αρα συνδετική συνάρτηση: g(λ)=log(λ) Bayesian Biostatistics Using BUGS 2
3 1.7. ΓΕΝΙΚΕΣ ΑΡΧΕΣ ΜΟΝΤΕΛΟΠΟΙΗΣΗΣ 1.8. ΜΕΡΙΚΑ ΙΣΤΟΡΙΚΑ ΣΤΟΙΧΕΙΑ ΕΙΝΑΙ ΤΕΧΝΗ ΟΛΑ ΤΑ ΜΟΝΤΕΛΑ ΕΙΝΑΙ ΛΑΘΟΣ ΜΕΡΙΚΑ ΠΙΟ ΧΡΗΣΙΜΑ ΨΑΧΝΟΥΜΕ ΕΝΑ ΜΟΝΤΕΛΟ ΠΟΥ ΠΕΡΙΓΡΑΦΕΙ ΠΕΡΙΛΗΠΤΙΚΑ ΤΗΝ ΠΡΑΓΜΑΤΙΚΟΤΗΤΑ ΕΛΕΓΧΟΥΜΕ ΠΟΛΛΑ ΔΙΑΦΟΡΕΤΙΚΑ ΜΟΝΤΕΛΑ ΠΡΕΠΕΙ ΝΑ ΓΙΝΕΤΑΙ ΕΛΕΓΧΟΣ ΚΑΛΗΣ ΠΡΟΣΑΡΜΟΓΗΣ 1805: LEGENDRE: ορίζει τα κατάλοιπα Εκτιμάει τις παραμέτρους παλινδρόμησης μέσω των ελαχίστων τετραγώνων 1809: GAUSS: Εισάγει την Κανονική κατανομή 1.8. ΜΕΡΙΚΑ ΙΣΤΟΡΙΚΑ ΣΤΟΙΧΕΙΑ 1.8. ΜΕΡΙΚΑ ΙΣΤΟΡΙΚΑ ΣΤΟΙΧΕΙΑ 1805: LEGENDRE: ορίζει τα κατάλοιπα Εκτιμάει τις παραμέτρους παλινδρόμησης μέσω των ελαχίστων τετραγώνων 1823: GAUSS (Theoria Combinationis) Εγκαταλείπει την κανονικότητα Η ομοσκεδαστικοτητα διατηρεί κάποιες καλές ιδιότητες Wedderburn (1974, biometrika) απέδειξε το ίδιο για τα GLM : Fisher διατυπώνει τη θεωρία Πειραματικού σχεδιασμού (Experimental Design). 1922: Ο Έλεγχος Περιεκτικότητας του Fisher και τo 1o γενικευμένο γραμμικό μοντέλο (RSS) 1935: Η Μελέτη βιολογική περιεκτικότητας του Bliss. Τα μοντέλα Probit (Ann.Appl.Biol.) & 1951: O Berkston εισάγει τα μοντέλα logit (JASA & Biometrics) 1952 (biometrics) Dyke & Patterson εφαρμογή λογιστικής παλινδρόμησης σε κατηγορικά δεδομένα με 4 μεταβλητές Bayesian Biostatistics Using BUGS 2 ΕΙΣΑΓΩΓΗ ΣΤΟΥΣ ΑΛΓΟΡΙΘΜΟΥΣ MCMC 2 ΕΙΣΑΓΩΓΗ ΣΤΟΥΣ ΑΛΓΟΡΙΘΜΟΥΣ MCMC Department of Business Administration, University of the Aegean Η ΜΠΕΥΖΙΑΝΗ ΠΡΟΣΕΓΓΙΣΗ ΠΡΟΣΟΜΟΙΩΣΗ ΑΠΟ ΤΗΝ ΕΚ-ΤΩΝ-ΥΣΤΕΡΩΝ (posterior) ΚΑΤΑΝΟΜΗ O Αλγόριθμος Metropolis-Hastings Ο Δειγματολήπτης Gibbs ΠΑΡΑΔΕΙΓΜΑ ΑΠΛΗΣ ΠΑΛΙΝΔΡΟΜΙΣΗΣ Bayesian Biostatistics Using BUGS 3
4 2.1. Η Μπευζιανή προσέγγιση Κλασσική στατιστική: βασίζεται στην πιθανοφάνεια f (y θ) θ διάνυσμα παραμέτρων=> άγνωστες προς εκτίμηση ποσότητες Εκτίμηση γίνεται μέσω εκτιμητριών συναρτήσεων με κάποιες καλές ιδιότητες (π.χ. μεροληψία) Εκτιμήτριες βρίσκονται μεγιστοποιώντας την πιθανοφάνεια ΠΑΡΑΔΕΙΓΜΑ: για Υ i ~Ν(μ,σ 2 ) n 1 μ εκτιμάται από το δειγματικό μέσο y = y i n i= 1 Στατιστική κατά Μπέυες: Θεωρεί τις παραμέτρους τυχαίες μεταβλητές Ορίζει εκ-των-προτέρων (prior) κατανομών f(θ) βασίζεται στην εκ-των-υστερων (posterior) κατανομή f (θ y) Πλεονεκτήματα Πιο καθάρη και πιθανοθεωρητική προσέγγιση Μπορεί να συμπεριλάβει πληροφορία ειδικών ή αποτελέσματα άλλων μελετών (metaanalysis) Μειονεκτήματα Υποκειμενικότητα αποτελεσμάτων λόγω της prior Δυσκολίες υπολογισμου των posterior Κατανομών Η Εκ-των-υστέρων κατανομή υπολογίζεται από το Θεώρημα του Bayes f (θ y) = f (θ,y) / f (y) = f (y θ)f (θ) / f (y) f (y θ)f (θ) Posterior = Likelihood x Prior ΠΑΡΑΔΕΙΓΜΑ: ΕΚΤΙΜΗΣΗ ΜΕΣΟΥ ΠΙΘΑΝΟΦΑΝΕΙΑ: Υ i ~ N( μ, σ 2 ) σ 2 γνωστή σταθερή ποσότητα PRIOR: μ ~ N( μ 0, τ 2 ) POSTERIOR: f (μ y) = N( w y + (1-w) μ 0, w σ 2 /n) w= τ 2 /(τ 2 + σ 2 /n) Υπολογισμός της posterior Κατανομής είναι δύσκολος. Συζυγείς εκ-των-προτέρων κατανομές (conjugate priors, 70s) Ασυμπτωτικές Προσεγγίσεις (80ς) Προσομοίωση μέσω MCMC (90ς) Bayesian Biostatistics Using BUGS 4
5 MCMC Προϋπήρχαν σε άλλες επιστήμες 1954 Metropolis etal. (Metropolis Algorithm) 1970 Hastings (Metropolis-Hastings Algorithm) 1984 Geman and Geman (Gibbs Sampling) 1990 Smith etal (Εφαρμογή των MCMC σε Μπευζιανά Προβλήματα) 1995 Green (Reversible Jump MCMC) Η ΙΔΕΑ: ΑΦΟΥ ΔΕΝ ΜΠΟΡΟΥΜΕ ΝΑ ΥΠΟΛΟΓΙΣΟΥΜΕ ΤΗΝ ΤΟΤΕ ΝΑ ΒΡΟΥΜΕ ΕΝΑ ΕΝΑΝ ΑΛΓΟΡΙΘΜΟ ΚΑΙ ΝΑ ΠΡΟΣΟΜΟΙΩΣΟΥΜΕ ΤΥΧΑΙΕΣ ΤΙΜΕΣ ΑΠΟ ΑΥΤΗ Η ΛΟΓΙΚΗ: ΦΤΙΑΧΝΟΥΜΕ ΜΙΑ ΜΑΡΚΟΒΙΑΝΗ ΑΛΥΣΙΔΑ ΤΗΣ ΟΠΟΙΑΣ Η ΣΤΑΣΙΜΗ ΚΑΤΑΝΟΜΗ ΕΙΝΑΙ ΙΣΗ ΜΕ ΤΗ ΖΗΤΟΥΜΕΝΗ (ΕΚ-ΤΩΝ-ΥΣΤΕΡΩΝ) ΚΑΤΑΝΟΜΗ. ΚΑΘΕ ΒΗΜΑ ΕΞΑΡΤΑΤΑΙ ΜΟΝΟ ΑΠΟ ΤΟ ΠΡΟΗΓΟΥΜΕΝΟ ΧΡΗΣΙΜΟΠΟΙΟΥΜΕ ΑΥΤΗ ΤΗΝ ΑΛΥΣΙΔΑ ΓΙΑ ΝΑ ΚΑΤΑΣΚΕΥΑΣΟΥΜΕ ΕΝΑ ΔΕΙΓΜΑ ΑΠΟ ΤΗ ΣΤΑΣΙΜΗ ΚΑΤΑΝΟΜΗ Η ΔΙΑΔΙΚΑΣΙΑ ΟΡΙΖΟΥΜΕ ΑΥΘΑΙΡΕΤΑ ΚΑΠΟΙΕΣ ΑΡΧΙΚΕΣ ΤΙΜΕΣ ΓΙΑ ΤΙΣ ΠΑΡΑΜΕΤΡΟΥΣ ΜΑΣ θ (0) ΓΙΑ t=1,..., T ΓΕΝΝΑΜΕ ΤΙΜΕΣ ΣΥΜΦΩΝΑ ΜΕ ΤΟΝ ΑΛΓΟΡΙΘΜΟ ΜΑΣ ΟΤΑΝ ΒΕΒΑΙΩΘΟΥΜΕ ΟΤΙ Η ΑΛΥΣΙΔΑ ΓΕΝΝΑΕΙ ΤΙΜΕΣ ΑΠΟ ΤΗ ΣΤΑΣΙΜΗ ΔΙΑΔΙΚΑΣΙΑ (ΔΗΛΑΔΗ ΕΧΕΙ ΣΥΓΚΛΙΝΕΙ) ΣΤΑΜΑΤΑΜΕ ΠΕΤΑΜΕ ΤΙΣ ΠΡΩΤΕΣ Κ ΤΙΜΕΣ ΓΙΑ ΝΑ ΑΠΟΦΥΓΟΥΜΕ ΤΥΧΟΝ ΕΠΙΡΡΟΗ ΤΟΥ ΑΡΧΙΚΟΥ ΣΗΜΕΙΟΥ. ΟΡΟΛΟΓΙΑ INITIAL VALUES (ΑΡΧΙΚΕΣ ΤΙΜΕΣ) ΤΗΣ ΑΛΥΣΙΔΑΣ ΛΕΓΟΝΤΑΙ ΟΙ ΤΙΜΕΣ θ (0) ΑΠΟ ΟΠΟΥ ΞΕΚΙΝΑΜΕ ΤΟΝ ΑΛΓΟΡΙΘΜΟ ΜΑΣ ITERATION (ΕΠΑΝΑΛΗΨΗ): ΚΑΘΕ ΠΡΟΣΟΜΟΙΩΜΕΝΗ ΠΑΡΑΤΗΡΗΣΗ ΑΝΤΙΣΤΟΙΧΕΙ ΣΕ ΜΙΑ ΕΠΑΝΑΛΗΨΗ ΤΟΥ ΑΛΓΟΡΙΘΜΟΥ BURN-IN PERIOD: ΟΙ ΠΕΡΙΟΔΟΣ ΜΕΧΡΙ ΝΑ ΑΡΧΙΣΟΥΜΕ ΝΑ ΠΕΡΝΟΥΜΕ ΤΙΜΕΣ ΑΠΟ ΤΗ ΣΤΑΣΙΜΗ ΚΑΤΑΝΟΜΗ ΟΡΟΛΟΓΙΑ CONVERGENCE (ΣΥΓΚΛΙΣΗ): ΟΤΑΝ Η ΔΙΑΔΙΚΑΣΙΑ ΜΑΣ ΕΧΕΙ ΔΩΣΕΙ ΤΙΜΕΣ ΑΠΟ ΤΗ ΣΤΑΣΙΜΗ ΚΑΤΑΝΟΜΗ CONVERGENCE DIAGNOSTICS: ΔΙΑΓΝΩΣΤΙΚΟΙ ΕΛΕΓΧΟΙ ΣΥΓΛΙΣΗΣ EQUILIBRIUM: ΣΤΑΣΙΜΗ ΚΑΤΑΝΟΜΗ MCMC OUTPUT: ΤΟ ΠΡΟΣΟΜΟΙΩΜΕΝΟ ΔΕΙΓΜΑ Bayesian Biostatistics Using BUGS 5
6 ΟΡΟΛΟΓΙΑ ΕΠΕΙΔΗ ΟΙ ΑΛΓΟΡΙΘΜΟΙ MCMC ΒΑΣΙΖΟΝΤΑΙ ΣΕ ΜΑΡΚΟΒΙΑΝΕΣ ΑΛΥΣΙΔΕΣ, ΤΟ ΠΡΟΣΟΜΟΙΩΜΕΝΟ ΔΕΙΓΜΑ ΔΕΝ ΕΙΝΑΙ I.I.D. ΕΞΑΛΕΙΨΗ ΑΥΤΟΣΥΣΧΕΤΙΣΗΣ ΒΛΕΠΟΥΜΕ ΤΙΣ ΑΥΤΟΣΥΣΧΕΤΙΣΕΙΣ (AUTOCORRELATIONS) ΚΡΑΤΑΜΕ 1 ΠΑΡΑΤΗΡΗΣΗ ΑΝΑ L ΕΠΑΝΑΛΗΨΕΙΣ. Η ΠΟΣΟΤΗΤΑ L ΛΕΓΕΤΑΙ THIN (ΛΕΠΤΥΝΣΗ) ΤΗΣ ΑΛΥΣΙΔΑΣ ΛΕΠΤΥΝΣΗ ΕΝΟΣ ΠΡΟΣΟΜΟΙΩΜΕΝΟΥ ΔΕΙΓΜΑΤΟΣ ΜΠΟΡΕΙ ΝΑ ΓΙΝΕΙ ΚΑΙ ΛΟΓΩ ΑΝΑΛΥΣΗΣ Η ΑΠΟΘΗΚΕΥΤΙΚΟΥ ΧΩΡΟΥ ΑΛΓΟΡΙΘΜΟΙ ΑΛΓΟΡΙΘΜΟΣ METROPOLIS-HASTINGS ΔΕΙΓΜΑΤΟΛΗΠΤΗΣ GIBBS ΑΛΓΟΡΙΘΜΟΣ METROPOLIS- HASTINGS Έστω θ η τρέχουσα τιμή των παραμέτρων Δειγματοληπτούμε θ can από μία κατανομή εισήγησης (proposal distribution) q(θ can θ ). can can f ( θ y) q( θ θ ) Υπολογίζουμε a = min 1, can f ( θ y) q( θ θ ) Θέτουμε θ = θ can με πιθανότητα α και θ = θ με πιθανότητα (1-α) ΑΛΓΟΡΙΘΜΟΣ METROPOLIS- HASTINGS Συνήθως q(θ can θ ) = Ν(θ, c 2 ). c 2 λέγεται και tuning parameter και επηρεάζει τη σύγκλιση. Επιλέγεται έτσι ωστε να δεχόμαστε 30-40% Η πιθανότητα αποδοχής α απλοποιείται can f ( θ y) a = min 1, f ( θ y) ΔΕΙΓΜΑΤΟΛΗΠΤΗΣ GIBBS Έστω θ η τρέχουσα τιμή των παραμέτρων και θ =(θ 1,, θ p ) Τ θ 1 ~f (θ 1 θ 2,, θ p,y) θ j ~f (θ j θ 1,,θ j-1,θ j+1,, θ p,y) θ p ~f (θ j θ 1,,θ p-1,y) ΔΕΙΓΜΑΤΟΛΗΠΤΗΣ GIBBS f (θ j θ 1,,θ j-1,θ j+1,, θ p,y) ονομαζέται full conditional posterior distribution και συμβολίζεταιf (θ j ) Bayesian Biostatistics Using BUGS 6
7 ΔΕΙΓΜΑΤΟΛΗΠΤΗΣ GIBBS Διαφορές με Μ-Η θ θ σε κάθε επανάληψη Gibbs υποπεριπτωση Μ-Η για q()=f (θ j ) Κάθε φορά ανανεώνουμε μία-μία τις τιμές f (θ j ) μπορεί να είναι άγνωστη => Χρήση adaptive rejection sampling για logconvave κατανομές (Gilks & Wild, 1992) Στα GLM οι posterior είναι log-concave (Dellaportas & Smith, 1993) Χρησιμοποιείται στο BUGS 2.3 ΠΑΡΑΔΕΙΓΜΑ: GIBBS SAMPLING ΣΤΗΝ ΑΠΛΗ ΠΑΛΙΝΔΡΟΜΗΣΗ Y i ~ N( μ i, σ 2 ) για i=1,2,...,n μ i = α + β Χ i θ=(α,β,σ 2 ) Τ PRIORS: f (θ)=f (α,β,σ 2 )= f (α)f (β)f (σ 2 ) f (α) = Normal(μ α, τ α2 ) f (β) = Normal(μ β, τ β2 ) f (σ 2 )=Inverse Gamma(γ, δ) αν τ= σ -2 τότε f(τ)=gamma(γ, δ) 2.3 ΠΑΡΑΔΕΙΓΜΑ: GIBBS SAMPLING ΣΤΗΝ ΑΠΛΗ ΠΑΛΙΝΔΡΟΜΗΣΗ 2.3 ΠΑΡΑΔΕΙΓΜΑ: GIBBS SAMPLING ΣΤΗΝ ΑΠΛΗ ΠΑΛΙΝΔΡΟΜΗΣΗ Full Conditional Posteriors f(α β, σ 2,y)= N w ( y bx) + (1 w1 )μ w 1 = τ 2 /(τ 2 +σ 2 /n) 1 α, 1 2 σ w n Full Conditional Posteriors f(σ 2 α, β,y)=ig( γ+n/2, δ+ Σ(y i -α-βx i ) 2 /2) n xi yi anx f(β α, σ 2,y)= i= 1 N w2 + (1 w n 2 )μβ, w 2 xi i= 1 w 2 = τ 2 /(τ 2 +σ 2 / Σx i2 ) 2 σ 2 n 2 xi i= 1 Bayesian Biostatistics Using BUGS 3.1. Εισαγωγή: Τι είναι το BUGS 3... Μπεϋζιανή Συμπερασματολογία με τη Xρήση του BUGS Department of Business Administration, University of the Aegean BUGS: Bayesian inference Using Gibbs Sampling Γλώσσα προγραμματισμού που ορίζουμε μοντέλο (πιθανοφάνεια, prior) Υπολογίζει τις full conditional και προσομοιώνει από log-convave posterior κατανομές Bayesian Biostatistics Using BUGS 7
8 3.1. Εισαγωγή: Τι είναι το BUGS Ξεκίνησε γύρω στο 1995 Γύρω στο 1998 βγήκε η έκδοση για Windows (Winbugs) Οφείλεται σε μια ομάδα του MRC στο Cambridge (Spiegelhalter, Gilks, Best, Thomas) 3.1. Εισαγωγή: Τι είναι το BUGS ΠΡΟΣΟΧΗ: Ο ΔΕΙΓΜΑΤΟΛΗΠΤΗΣ GIBBS ΜΠΟΡΕΙ ΝΑ ΕΙΝΑΙ ΕΠΙΚΙΝΔΥΝΟΣ ΓΙΑΤΙ; 3.1. Εισαγωγή: Τι είναι το BUGS ΓΙΑΤΙ; ΛΑΘΟΣ ΑΠΟΤΕΛΕΣΜΑΤΑ ΛΟΓΩ ΜΗ ΣΥΓΚΛΙΣΗΣ ΠΟΛΥ ΑΡΓΗ ΣΥΓΚΛΙΣΗ ΚΑΚΕΣ ΑΡΧΙΚΕΣ ΤΙΜΕΣ ΚΑΚΗ ΕΠΙΛΟΓΗ ΜΟΝΤΕΛΟΥ ΥΠΕΡ-ΠΑΡΑΜΕΤΡΟΠΟΙΗΣΗ (overparametrazation) ΣΠΑΣΙΜΟ ΝΕΥΡΩΝ 3.1. Εισαγωγή: Τι είναι το BUGS ΓΙΑΤΙ; ΛΑΘΟΣ ΑΠΟΤΕΛΕΣΜΑΤΑ ΛΟΓΩ ΜΗ ΣΥΓΚΛΙΣΗΣ ΠΟΛΥ ΑΡΓΗ ΣΥΓΚΛΙΣΗ ΚΑΚΕΣ ΑΡΧΙΚΕΣ ΤΙΜΕΣ ΚΑΚΗ ΕΠΙΛΟΓΗ ΜΟΝΤΕΛΟΥ ΥΠΕΡ-ΠΑΡΑΜΕΤΡΟΠΟΙΗΣΗ (overparametrazation) ΣΠΑΣΙΜΟ ΝΕΥΡΩΝ 3.1. Εισαγωγή: Τι είναι το BUGS 3.1. Εισαγωγή: Τι είναι το BUGS ΑΡΧΕΙΑ BUGS *.DAT:Αρχείο Δεδομένων *.INI: Αρχείο Αρχικών τιμών *.BUG: Αρχείο Moντέλου *.CMD: Αρχείο Εντολών προσομοίωσης *.LOG: Αρχείο Αποτελεσμάτων προσομοίωσης *.OUT: Αρχείο Προσομοιωμένων τιμών *.IND: Αρχείο με Περιεχόμενα του *.OUT Προετοιμασία των των Δεδομένων Δεδομένων Συντάκτης Κειμένων Στατιστικά Πακέτα Spread sheet Μπευζιανή Ανάλυση WinBUGS BUGS Ανάλυση Προσομοιωμένων Τιμών Τιμών R/Splus STATA Bayesian Biostatistics Using BUGS 8
9 3.2. Ένα Απλό Παράδειγμα στο BUGS 3.2. Ένα Απλό Παράδειγμα στο BUGS Green & Touchston (1963, Am.Jour. Of Obsterics & Gynecology) Μελέτη σχέσης Y : Βάρος γέννησης (birthweight) ενός παιδιού X : Επίπεδο οιστριόλης (estriol) των εγκύων γυναικών n=31 Το γράφημα που ακολουθεί δείχνει ότι υπάρχει συσχέτιση BIRTHWEIGHT g/ ESTRIOL mg/24hr Χτίζοντας το Μοντέλο Δημιουργία Μοντέλων στο BUGS ΤΥΧΑΙΑ ΣΥΝΙΣΤΩΣΑ: Birth i ~ Normal(μ i, σ 2 ) ΣΥΣΤΗΜΑΤΙΚΗ ΣΥΝΙΣΤΩΣΑ: η i = α+β Estriol i ΣΥΝΔΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ: μ i =η i =α+β Estriol i για i=1,...,31 PRIORS (Non-informative) f (α)=normal ( 0, 10 4 ) f (β)=normal ( 0, 10 4 ) f (σ 2 )=Inverse Gamma (10-4, 10-4 ) ή f (τ=σ -2 )=Gamma (10-4, 10-4 ) ΣΕ *.BUG Ορίζουμε το μοντέλο μας Εντολές => BUGS MANUAL σελ ΔΟΜΗ: Προκαταρκτικό κομμάτι: δηλώνουμε μεταβλητές, σταθερές, δεδομένα και αρχικές τιμές Κυρίως μοντέλο: εδώ ορίζουμε πιθανοφάνεια και priors Δημιουργία Μοντέλων στο BUGS Δημιουργία Μοντέλων στο BUGS ΠΡΟΚΑΤΑΡΚΤΙΚΟ ΚΟΜΜΑΤΙ <;>: τελειώνει κάθε εντολή του BUG file model <όνομα μοντέλου>; const <σταθερά 1=#>,..., <σταθερά κ=#>; Ορισμός σταθερών παραμέτρων var <μεταβλητή 1>,..., <μεταβλητή κ>; Ορισμός τυχαίων μεταβλητών data <μεταβλητή 1>,..., <μεταβλητή κ> in <ονομα αρχείου>, <μεταβλητή κ+1>,..., <μεταβλητή κ+λ> in <ονομα αρχείου2> : ορισμός αρχείων δεδομένων inits in <ονομα αρχείου> : ορισμός αρχείων με αρχικές τιμές ΚΥΡΙΩΣ ΜΟΝΤΕΛΟ Το κυρίως μοντέλο αρχίζει και τελειώνει με {} ~ : ορίζουμε τις τυχαίες μεταβλητές <- : ισότητα/ ανάθεση Οι κατανομές ορίζονται στις σελίδες Αν θέλουμε να περιορίσουμε μία κατανομή σε ένα διάστημα (α,β) τότε η κατανομή ακολουθείται από Ι(α,β) Bayesian Biostatistics Using BUGS 9
10 Δημιουργία Μοντέλων στο BUGS ΚΥΡΙΩΣ ΜΟΝΤΕΛΟ Κανονικη Κατανομη: y~dnorm( mu, tau ) mu= μέσος tau= ακρίβεια (precision) =1/σ 2 Γάμμα Κατανομη: y~dgamma( a, b ) μέσος = a/b x[i] : i στοιχείο του διανύσματος x d[i,j] : στοιχείο της i γραμμής και j στήλης του πίνακα d Εισαγωγή του Μοντέλου του Παραδείγματος στο BUGS (1) Birth i ~ Normal(μ i, σ 2 ) (2) η i = α+β Estriol i (3) μ i =η i =α+β Estriol i για i=1,...,31 PRIORS f (α)=normal ( 0, 10 4 ) f (β)=normal ( 0, 10 4 ) f (τ=σ -2 )=Gamma(10-4, 10-4 ) σ 2 =1/ τ for (i in 1:n) { Birth[i]~dnorm(mu[i],tau) mu[i] <-a+b*estriol[i] } a~dnorm(0.0,1.0e-04) b~dnorm(0.0,1.0e-04) tau~dgamma(1.0e-04,1.0e-04) s2<-1/tau Εισαγωγή του Μοντέλου του Παραδείγματος στο BUGS Προσομοιώνοντας από την posterior ΠΡΟΚΑΤΑΡΚΤΙΚΟ ΚΟΜΜΑΤΙ model example1; const n=31; # n=sample size var estriol[n], # estriol level of pregnant woman birth[n], # birthweight mu[n], # regression expected value a,b,tau,s2; # model parameters, # tau = precision, s2=1/tau varianc data estriol,birth in 'estriol.dat'; inits in 'estriol.in'; ΕΝΤΟΛΕΣ ΠΡΟΣΟΜΟΙΩΣΗΣ (σελ 31, BUGS MANUAL) bugs [enter] ΞΕΚΙΝΗΜΑ ΤΟΥ BUGS compile( estriol.bug ) ΤΣΕΚΑΡΕΙ ΤΗ ΣΥΝΤΑΞΗ ΤΟΥ ΜΟΝΤΕΛΟΥ, ΒΡΙΣΚΕΙ ΤΙΣ CONDITIONALS ΚΑΙ ΤΙΣ ΑΡΧΙΚΕΣ ΤΙΜΕΣ update(1000) ΠΡΟΣΟΜΟΙΩΝΕΙ 1000 ΤΙΜΕΣ monitor(a) monitor(b) ΑΠΟ ΤΗ ΣΤΙΓΜΗ ΑΥΤΗ ΑΠΟΘΗΚΕΥΕΙ monitor(s2) ΤΙΣ ΠΡΟΣΟΜΟΙΩΜΕΝΕΣ ΤΙΜΕΣ monitor(s2,10) ΑΠΟΘΗΚΕΥΣΗ ΑΝΑ 10 (ΤΗΙΝ=10) Προσομοιώνοντας από την posterior Προσομοιώνοντας από την posterior ΕΝΤΟΛΕΣ ΠΡΟΣΟΜΟΙΩΣΗΣ (σελ 31, BUGS MANUAL) update(1000) ΠΡΟΣOΜΟΙΩΝΟΥΜΕ 1000 ΤΙΜΕΣ stats(a) ΣΤΑΤΙΣΤΙΚΟΙ ΔΕΙΚΤΕΣ stats(b) ΤΩΝ ΠΡΟΣΟΜΟΙΩΜΕΝΩΝ ΤΙΜΩΝ stats(s2) (ΤΗΣ posterior ΚΑΤΑΝΟΜΗΣ) diag(a) diag(b) ΔΙΑΓΝΩΣΤΙΚΟ ΤΕΣΤ ΣΥΓΚΛΙΣΗΣ diag(s2) q() ΕΞΟΔΟΣ ΑΠΟ ΤΟ BUGS EDIT BUGS.LOG ΒΛΕΠΟΥΜΕ ΟΛΑ ΤΑ ΑΠΟΤΕΛΕΣΜΑΤΑ EDIT BUGS.IND ΠΕΡΙΕΧΟΜΕΝΑ BUGS.OUT ΕΙΣΑΓΟΥΜΕ ΤΟ BUGS.OUT ΣΕ ΣΤΑΤΙΣΤΙΚΟ ΠΑΚΕΤΟ ΓΙΑ ΑΝΑΛΥΣΗ ΠΡΟΣΟΜΟΙΩΣΗ ΣΤΟ ΠΑΡΑΣΚΗΝΙΟ Γράφουμε τις εντολές ένα αρχείο με κατάληξη CMD πχ. Example1.cmd Τρέχουμε το μοντέλο στο παρασκήνιο με την εντολη backbugs <όνομα αρχείου CMD> π.χ. backbugs example.cmd Τα αποτελέσματα τα βλέπουμε με τον ίδιο τρόπο όπως παραπάνω δηλ. EDIT BUGS.LOG ΒΛΕΠΟΥΜΕ ΟΛΑ ΤΑ ΑΠΟΤΕΛΕΣΜΑΤΑ EDIT BUGS.IND ΠΕΡΙΕΧΟΜΕΝΑ BUGS.OUT ΕΙΣΑΓΟΥΜΕ ΤΟ BUGS.OUT ΣΕ ΣΤΑΤΙΣΤΙΚΟ ΠΑΚΕΤΟ ΓΙΑ ΑΝΑΛΥΣΗ Bayesian Biostatistics Using BUGS 10
11 ΔΙΑΓΡΑΜΜΑ 1: Trace of Posterior Values Simulated Values ΔΙΑΓΡΑΜΜΑ 2: ΕΡΓΟΔΙΚΟΙ ΜΕΣΟΙ ERGODIC MEAN alpha ΕΝΔΕΙΞΗ ΜΗ ΣΥΓΚΛΙΣΗΣ ΚΑΙ ΥΨΗΛΩΝ ΑΥΤΟΣΥΣΧΕΤΙΣΕΩΝ Iterations Simulated Values Iterations beta Iterations Simulated Values Sigma^ alpha ERGODIC MEAN beta Iterations ERGODIC MEAN sigma^ Iterations Iterations ΔΙΑΓΡΑΜΜΑ 3: ΑΥΤΟΣΥΣΧΕΤΙΣΕΙΣ ΓΙΑ ΤΗΝ ΠΑΡΑΜΕΤΡΟ α Series : a ΔΙΑΓΡΑΜΜΑ 4: ΑΥΤΟΣΥΣΧΕΤΙΣΕΙΣ ΓΙΑ ΤΗΝ ΠΑΡΑΜΕΤΡΟ β Series : b ACF ACF ΔΙΑΓΡΑΜΜΑ 5: ΑΥΤΟΣΥΣΧΕΤΙΣΕΙΣ ΓΙΑ ΤΗΝ ΠΑΡΑΜΕΤΡΟ σ Προσομοιώνοντας από την posterior ACF Series : s2 ΔΙΟΡΘΩΣΗ ΤΗΣ ΑΥΤΟΣΥΣΧΕΤΙΣΗΣ (1) ΑΥΞΑΝΟΥΜΕ ΤΟ ΔΙΑΣΤΗΜΑ ΛΕΠΤΥΝΣΗΣ (Thin=25) ΣΤΟ CMD ΑΡΧΕΙΟ ΤΟΥ BUGS monitor(a,25) monitor(b,25) Bayesian Biostatistics Using BUGS 11
12 ΔΙΑΓΡΑΜΜΑ 6: Trace of Posterior Values (5000 Iterations, Thin=25) ΔΙΑΓΡΑΜΜΑ 7: ΑΥΤΟΣΥΣΧΕΤΙΣΕΙΣ (5000 Iterations, Thin=25) Series : a1 a : b :200 s Series : b Series : s : Προσομοιώνοντας από την posterior Προσομοιώνοντας από την posterior ΔΙΟΡΘΩΣΗ ΤΗΣ ΑΥΤΟΣΥΣΧΕΤΙΣΗΣ (2) ΑΛΛΑΖΟΥΜΕ ΤΗΝ ΠΑΡΑΜΕΤΡΟΠΟΙΗΣΗ ΤΟΥ ΜΟΝΤΕΛΟΥ ΑΦΑΙΡΕΣΗ ΤΟΥ ΜΕΣΟΥ ΑΠΟ ΚΑΘΕ ΕΠΕΞΗΓΗΜΑΤΙΚΗ ΜΕΤΑΒΛΗΤΗ ΒΟΗΘΑΕΙ ΣΤΗ ΣΥΓΚΛΙΣΗ ΑΡΑ η i = α*+β(x i - x) α= α*-β x ΔΙΟΡΘΩΣΗ ΤΗΣ ΑΥΤΟΣΥΣΧΕΤΙΣΗΣ (2) ΑΛΛΑΖΟΥΜΕ ΤΗΝ ΠΑΡΑΜΕΤΡΟΠΟΙΗΣΗ ΤΟΥ ΜΟΝΤΕΛΟΥ ΑΦΑΙΡΕΣΗ ΤΟΥ ΜΕΣΟΥ ΑΠΟ ΚΑΘΕ ΕΠΕΞΗΓΗΜΑΤΙΚΗ ΜΕΤΑΒΛΗΤΗ ΒΟΗΘΑΕΙ ΣΤΗ ΣΥΓΚΛΙΣΗ ΑΡΑ ΣΤΟ BUGS mu[i]) <- a.star+b*(estriol[i]-mean(estriol[])); a<-a.star-b*mean(estriol[]); a.star~dnorm(0.0, 1.0E-04); ΔΙΑΓΡΑΜΜΑ 8: Trace of Posterior Values ΔΙΑΓΡΑΜΜΑ 9: ΑΥΤΟΣΥΣΧΕΤΙΣΕΙΣ Series : a2 a :1000 b :1000 s Series : b Series : s : Bayesian Biostatistics Using BUGS 12
13 ΔΙΑΓΡΑΜΜΑ 10: ΙΣΤΟΓΡΑΜΜΑΤΑ POSTERIOR ΤΙΜΩΝ ΔΙΑΓΡΑΜΜΑ 11: ΕΚΤΙΜΩΜΕΝΕΣ POSTERIOR ΚΑΤΑΝΟΜΕΣ Histogram of Posterior Values for alpha ksmooth(a2, bandwidth = 5)$y Posterior Density of alpha a2 ksmooth(a2, bandwidth = 5)$x Histogram of Posterior Values for beta b2 ksmooth(b2, bandwidth = 0.3)$y Posterior Density of beta ksmooth(b2, bandwidth = 0.3)$x Histogram of Posterior Values for sigma^ s22 ksmooth(s22, bandwidth = 5.3)$y Posterior Density of sigma^ ksmooth(s22, bandwidth = 5.3)$x Προσομοίωση στο Παρασκήνιο 3.3. Παράδειγμα 2: Μοντέλα για Διωνυμικά Δεδομένα ΔΗΜΙΟΥΡΓΟΥΜΕ ΕΝΑ ΑΡΧΕΙΟ ΜΕ ΤΙΣ ΠΡΟΗΓΟΥΜΕΝΕΣ ΕΝΤΟΛΕΣ (ESTRIOL.CMD) ΠΡΟΣΟΜΟΙΩΝΟΥΜΕ ΤΙΜΕΣ ΜΕ BACKBUGS ESTRIOL.CMD ΣΤΟΝ ΚΑΤΑΛΟΓΟ ΤΟΥ BUGS ΒΛΕΠΟΥΜΕ ΤΑ ΑΠΟΤΕΛΕΣΜΑΤΑ ΣΤΟ ΑΡΧΕΙΟ BUGS.LOG ΠΑΡΑΔΕΙΓΜΑ 12, BUGS EXAMPLES vol 2 σελ. 43 Bliss (1935) Εκθέτουμε 8 ομάδες εντόμων σε διαφορετικά επίπεδα Carbon dislphide και καταγράφουμε Συγκέντρωση (Χ i ) Συνολικός Αριθμός εντόμων στην ομάδα (n i ) Αριθμός εντόμων που απεβίωσαν (r i ) 3.3. Παράδειγμα 2: Μοντέλα για Διωνυμικά Δεδομένα (1) r i ~ Binomial(p i, n i ) (2) η i = α*+β(x i - x) (3) logit(p i ) =η i για i=1,...,8 PRIORS f (α)=normal ( 0, 10 4 ) f (β)=normal ( 0, 10 4 ) α=α*-β x LINK FUNCTIONS logit(p)=log{p/(1-p)} probit(p)=φ -1 (p) cloglog(p)=log(-log(1-p)) for (i in 1:n) { r[i]~dbinom(p[i],n[i]) logit(p[i])<-a.star+b*x[i] } a~dnorm(0.0,1.0e-04) b~dnorm(0.0,1.0e-04) a<-a.star-b*mean(x[]) 3.3. Παράδειγμα 2: Μοντέλα για Διωνυμικά Δεδομένα ΜΕΡΙΚΑ ΣΧΟΛΙΑ ΑΝΑΜΕΝΟΜΕΝΕΣ ΤΙΜΕΣ ΥΠΟΛΟΓΙΖΟΝΤΑΙ ΩΣ r.hat[i]<-n[i]*p[i]; ODDS RATIO ΓΙΑ LOGIT MODELS odds.ratio<-exp(b); Bayesian Biostatistics Using BUGS 13
14 3.4. Παράδειγμα 3: Μοντέλα για Δίτιμες Μεταβλητές 3.4. Παράδειγμα 3: Μοντέλα για Δίτιμες Μεταβλητές Ένα δείγμα ηλικιωμένων ατόμων εξετάστηκαν ψυχιατρικά αν έχουν κάποια συμπτώματα γηρατειών (senility symptoms). Μια επεξηγηματική μεταβλητή είναι είναι το σκορ σε ένα υπο-τεστ της κλίμακας ενήλικης ευφυΐας Wechsler (Wecshler Adult Intelligence Scale - WAIS). Να βρεθεί ποιο x αντιστοιχεί σε p=1/2 και να βρεθεί και η posterior κατανομή της πιθανότητας για κάποιον με WAIS ίσο με το μέσο όρο ΜΕΡΙΚΑ ΣΧΟΛΙΑ Το μοντέλο for (i in 1:n) { symptom[i]~dbern( p[i] ); logit( p[i] ) <- a+b*wais[i]; } Το x για p=1/2 βρίσκεται ως x.half<- -a/b; To ποσοστό για κάποιον με μέσο σκορ WAIS p.mean<exp(a+b*mean(x[]))/(1+exp(a+b*mean(x[]))); 3.5. Παράδειγμα 4: Μοντέλα Poisson για 2x2 & Η Posterior Κατανομή του Odds Ratio 3.5. Παράδειγμα 4: Μοντέλα Poisson για 2x2 & Η Posterior Κατανομή του Odds Ratio Mahon et.al. (1970) bulletin of the world health organazation Μελέτη για την πιθανή θετική σχέση μεταξύ ηλικίας στην 1η γέννα και καρκίνου του μαστο. Οι περιπτώσεις (cases) προέρχονται από επιλεγμένα νοσοκομεία στις ΗΠΑ, Ελλάδα, Γιουγκοσλαβία, Βραζιλία, Ταϊβάν & Ιαπωνία Οι Μάρτυρες (controls) επιλέχθηκαν απο γυναίκες με συγκρίσιμη ηλικία από τα ίδια νοσοκομεία AGE AT FIRST BIRTH STATUS Age>29 (1) Age<30 (0) Case (1) Control (0) Παράδειγμα 4: Μοντέλα Poisson για 2x2 & Η Posterior Κατανομή του Odds Ratio 3.5. Παράδειγμα 4: Μοντέλα Poisson για 2x2 & Η Posterior Κατανομή του Odds Ratio Status Age Counts ΤΟ ΜΟΝΤΕΛΟ for (i in 1:4) { counts[i]~dpois(lambda[i]); log (lambda[i])<-mu+ a*status[i]+b*age[i]+ab*status[i]*age[i]; } ODDS RATIO odds.ratio<-exp(ab); Bayesian Biostatistics Using BUGS 14
15 Σε πίνακες 2x2xJ η εκτίμηση ενός κοινού OR γίνεται από το Maentel-Haenzel OR MH =(Σα i d i /n i )/(Σb i c i /n i ) Sandler, Everson & Wilcox (1985) Amer.Journal of Epidemiology Μελέτη με 518 καρκινοπαθείς με ηλικίες και 518 μάρτυρες (ομάδα ελέγχου) ταιριασμένοι (matched) ως προς φύλο και ηλικία Σκοπός: εκτίμηση της επίδρασης του παθητικού καπνίσματος στον κίνδυνο εμφάνισης καρκίνου. Το παθητικό κάπνισμα ορίστικε θετικά αν η σύζυγος κάπνιζε τουλάχιστον 1 τσιγάρο ημερησίως τους τελευταίους 6 μήνες. Συγχυτικός παράγοντας (confounder) αν το ίδιο άτομο καπνίζει Non Smokers (0) Smokers (1) Passive Smoker (1) Non Passive Smoker(0) Passive Smoker (1) Non Passive Smoker (0) Case(1) Control (0) ΚΑΝΟΥΜΕ ΔΥΟ ΑΝΑΛΥΣΕΙΣ ΑΝΑΛΥΣΗ 1: ΧΕΙΡΙΖΟΜΑΣΤΕ ΞΕΧΩΡΙΣΤΑ ΤΟΝ ΚΑΘΕ ΠΙΝΑΚΑ ΚΑΙ ΕΚΤΙΜΟΥΜΕ ΕΝΑ ODDS RATIO ΓΙΑ ΚΑΘΕ ΠΙΝΑΚΑ (ΟΠΩΣ ΠΑΡΑΔΕΙΓΜΑ 4) ΣΥΓΚΡΙΝΟΥΜΕ ΤΙΣ POSTERIOR ΚΑΤΑΝΟΜΕΣ ΤΟΥΣ ΑΝΑΛΥΣΗ 2: ΧΕΙΡΙΖΟΜΑΣΤΕ ΞΕΧΩΡΙΣΤΑ ΤΟΝ ΚΑΘΕ ΠΙΝΑΚΑ ΕΚΤΙΜΟΥΜΕ ΕΝΑ ΚΟΙΝΟ ODDS RATIO ΓΙΑ ΚΑΘΕ ΠΙΝΑΚΑ ΑΝΑΛΥΣΗ 1: ΠΡΟΚΑΤΑΡΤΙΚΟ ΚΟΜΜΑΤΙ var, b[2,4], or[2]; ΜΟΝΤΕΛΟ #model for 1st table (nonsmokers) for (i in 1:4) { counts[i]~dpois( lambda[i] ); log(lambda[i])<-b[1,1]+b[1,2]*status[i] +b[1,3]*passive[i] +b[1,4]*status[i]*passive[i]; } ΑΝΑΛΥΣΗ 1: ΠΡΟΚΑΤΑΡΤΙΚΟ ΚΟΜΜΑΤΙ var, b[2,4], or[2]; ΜΟΝΤΕΛΟ #model for 2nd table (smokers) for (i in 5:8) { counts[i]~dpois( lambda[i] ); log(lambda[i])<-b[2,1]+b[2,2]*status[i] +b[2,3]*passive[i] +b[2,4]*status[i]*passive[i]; } ΑΝΑΛΥΣΗ 1: ΠΡΟΚΑΤΑΡΤΙΚΟ ΚΟΜΜΑΤΙ var, b[2,4], or[2]; ΜΟΝΤΕΛΟ #priors for (i in 1:2){ for (j in 1:p){ b[i,j]~dnorm(0.0, 1.0E-04) } } Bayesian Biostatistics Using BUGS 15
16 ΑΝΑΛΥΣΗ 2: ΜΟΝΤΕΛΟ #model for 1st table (nonsmokers) for (i in 1:4) { counts[i]~dpois( lambda[i] ); log(lambda[i])<-b[1,1]+b[1,2]*status[i] +b[1,3]*passive[i] +b[1,4]*status[i]*passive[i];} #model for 2nd table (smokers) for (i in 5:8) { counts[i]~dpois( lambda[i] ); log(lambda[i])<-b[2,1]+b[2,2]*status[i] +b[2,3]*passive[i] +b[2,4]*status[i]*passive[i]; } ΑΝΑΛΥΣΗ 2: ΜΟΝΤΕΛΟ #model for 1st table (nonsmokers) for (i in 1:4) { counts[i]~dpois( lambda[i] ); log(lambda[i])<-b[1,1]+b[1,2]*status[i] +b[1,3]*passive[i] + ab *status[i]*passive[i];} #model for 2nd table (smokers) for (i in 5:8) { counts[i]~dpois( lambda[i] ); log(lambda[i])<-b[2,1]+b[2,2]*status[i] +b[2,3]*passive[i] + ab *status[i]*passive[i]; } ΔΙΑΓΡΑΜΜΑ 12: ΕΚΤΙΜΩΜΕΝΕΣ POSTERIOR ΚΑΤΑΝΟΜΕΣ ΤΩΝ ODDS RATIOS ΑΠΟΤΕΛΕΣΜΑΤΑ ΑΝΑΛΥΣΗ 1 95% posterior MLE Posterior Mean credible interval OR ± OR ± ΑΝΑΛΥΣΗ 2 Common OR MH ± Density OR 1 ( Καπνιστές) OR 0 (Μη Καπνιστές) Odds Ratio Values ΔΙΑΓΡΑΜΜΑ 13: ΕΚΤΙΜΩΜΕΝΕΣ POSTERIOR ΚΑΤΑΝΟΜΕΣ ΤΩΝ ODDS RATIOS Bayesian Biostatistics Using BUGS OR 1 ( Καπνιστές) Κοινό OR Density OR 0 (Μη Καπνιστές) ΤΕΛΟΣ ΕΙΣΑΓΩΓΙΚΟΥ ΜΑΘΗΜΑΤΟΣ ΕΠΟΜΕΝΟ: WINBUGS ntzoufras@aegean.gr Department of Business Administration, University of the Aegean Odds Ratio Values Bayesian Biostatistics Using BUGS 16
Μπεϋζιανή Στατιστική και MCMC Μέρος 2 ο : MCMC
 Μπεϋζιανή Στατιστική και MCMC Μέρος 2 ο : MCMC Περιεχόμενα Μαθήματος Εισαγωγή στο Πρόβλημα. Monte Carlo Εκτιμητές. Προσομοίωση. Αλυσίδες Markov. Αλγόριθμοι MCMC (Metropolis Hastings & Gibbs Sampling).
Μπεϋζιανή Στατιστική και MCMC Μέρος 2 ο : MCMC Περιεχόμενα Μαθήματος Εισαγωγή στο Πρόβλημα. Monte Carlo Εκτιμητές. Προσομοίωση. Αλυσίδες Markov. Αλγόριθμοι MCMC (Metropolis Hastings & Gibbs Sampling).
Μπεϋζιανή Στατιστική και MCMC Μέρος 2 ο : MCMC
 Μπεϋζιανή Στατιστική και MCMC Μέρος 2 ο : MCMC Δημήτρης Φουσκάκης, Επίκουρος Καθηγητής, Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών, Τομέας Μαθηματικών, Τηλέφωνο: (210) 772-1702, Φαξ: (210) 772-1775.
Μπεϋζιανή Στατιστική και MCMC Μέρος 2 ο : MCMC Δημήτρης Φουσκάκης, Επίκουρος Καθηγητής, Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών, Τομέας Μαθηματικών, Τηλέφωνο: (210) 772-1702, Φαξ: (210) 772-1775.
WinBUGS. Το BUGS (Bayesian inference Using Gibbs Sampling) είναι ένα ελεύθερο λογισµικό στο διαδίκτυο (http://www.mrcbsu.cam.ac.uk/bugs/welcome.
 WinBUGS Το BUGS (Bayesian inference Using Gibbs Sampling) είναι ένα ελεύθερο λογισµικό στο διαδίκτυο (http://www.mrcbsu.cam.ac.uk/bugs/welcome.shtml) το οποίο χρησιµοποιεί MCMC µεθόδους για την επίλυση
WinBUGS Το BUGS (Bayesian inference Using Gibbs Sampling) είναι ένα ελεύθερο λογισµικό στο διαδίκτυο (http://www.mrcbsu.cam.ac.uk/bugs/welcome.shtml) το οποίο χρησιµοποιεί MCMC µεθόδους για την επίλυση
Bayesian Biostatistics Using BUGS
 Bayesian Biostatistics Using BUGS Βιο-Στατιστική κατά Bayes µε τη χρήση του Λογισµικού BUGS ΜΑΘΗΜΑ 2: ΕΙΣΑΓΩΓΗ ΣΤΟ WINBUGS I. Ntzoufras E-mail: ntzoufras@aueb.gr Department of Statistics, Athens University
Bayesian Biostatistics Using BUGS Βιο-Στατιστική κατά Bayes µε τη χρήση του Λογισµικού BUGS ΜΑΘΗΜΑ 2: ΕΙΣΑΓΩΓΗ ΣΤΟ WINBUGS I. Ntzoufras E-mail: ntzoufras@aueb.gr Department of Statistics, Athens University
Παράδειγμα. Στις χρονοσειρές σημαντικό ρόλο παίζει η αυτοσυσχέτιση: η αυτοσυσχέτιση. (lag k) ισούται με όπου γ
 MCMC Η Monte Carlo μεθοδολογία για την δημιουργία αριθμητικών προσεγγίσεων διαφόρων τιμών της εκ των υστέρων κατανομής, όπως του μέσου και της τυπικής απόκλισης, στηρίζεται στους Ασθενείς Νόμους των Μεγάλων
MCMC Η Monte Carlo μεθοδολογία για την δημιουργία αριθμητικών προσεγγίσεων διαφόρων τιμών της εκ των υστέρων κατανομής, όπως του μέσου και της τυπικής απόκλισης, στηρίζεται στους Ασθενείς Νόμους των Μεγάλων
HMY 795: Αναγνώριση Προτύπων
 HMY 795: Αναγνώριση Προτύπων Διάλεξη 5 Κατανομές πιθανότητας και εκτίμηση παραμέτρων Κατανομές πιθανότητας και εκτίμηση παραμέτρων δυαδικές τυχαίες μεταβλητές Διαχωριστικές συναρτήσεις Ταξινόμηση κανονικών
HMY 795: Αναγνώριση Προτύπων Διάλεξη 5 Κατανομές πιθανότητας και εκτίμηση παραμέτρων Κατανομές πιθανότητας και εκτίμηση παραμέτρων δυαδικές τυχαίες μεταβλητές Διαχωριστικές συναρτήσεις Ταξινόμηση κανονικών
HMY 795: Αναγνώριση Προτύπων
 HMY 795: Αναγνώριση Προτύπων Διάλεξη 5 Κατανομές πιθανότητας και εκτίμηση παραμέτρων δυαδικές τυχαίες μεταβλητές Bayesian decision Minimum misclassificaxon rate decision: διαλέγουμε την κατηγορία Ck για
HMY 795: Αναγνώριση Προτύπων Διάλεξη 5 Κατανομές πιθανότητας και εκτίμηση παραμέτρων δυαδικές τυχαίες μεταβλητές Bayesian decision Minimum misclassificaxon rate decision: διαλέγουμε την κατηγορία Ck για
HMY 795: Αναγνώριση Προτύπων
 HMY 795: Αναγνώριση Προτύπων Διάλεξη 6 Κατανομές πιθανότητας και εκτίμηση παραμέτρων Κατανομές πιθανότητας και εκτίμηση παραμέτρων κανονικές τυχαίες μεταβλητές Εκτίμηση παραμέτρων δυαδικές τυχαίες μεταβλητές
HMY 795: Αναγνώριση Προτύπων Διάλεξη 6 Κατανομές πιθανότητας και εκτίμηση παραμέτρων Κατανομές πιθανότητας και εκτίμηση παραμέτρων κανονικές τυχαίες μεταβλητές Εκτίμηση παραμέτρων δυαδικές τυχαίες μεταβλητές
MCMC στα Γενικευμένα Γραμμικά Μοντέλα
 MCMC στα Γενικευμένα Γραμμικά Μοντέλα Response Variable (Y): Εξαρτημένη Μεταβλητή. Explanatory Variables (X j ): Επεξηγηματικές Μεταβλητές. Random Component (Τυχαία Συνιστώσα). Y (X 1,,X p )~ ΚΑΤΑΝΟΜΗ
MCMC στα Γενικευμένα Γραμμικά Μοντέλα Response Variable (Y): Εξαρτημένη Μεταβλητή. Explanatory Variables (X j ): Επεξηγηματικές Μεταβλητές. Random Component (Τυχαία Συνιστώσα). Y (X 1,,X p )~ ΚΑΤΑΝΟΜΗ
Βιοστατιστική κατά Bayes µε τη χρήση του Λογισµικού BUGS
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΙΠΛΩΜΑ ΒΙΟΣΤΑΤΙΣΤΙΚΗΣ ΜΑΘΗΜΑ: ΜΠΕΫΖΙΑΝΗ ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ Ι ΑΣΚΟΝΤΕΣ: Ι. Ντζούφρας, Π. Τσιαµυρτζής Ι ΑΚΤΙΚΟ ΥΛΙΚΟ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΜΠΕΫΖΙΑΝΗ ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ: Βιοστατιστική
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΙΠΛΩΜΑ ΒΙΟΣΤΑΤΙΣΤΙΚΗΣ ΜΑΘΗΜΑ: ΜΠΕΫΖΙΑΝΗ ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ Ι ΑΣΚΟΝΤΕΣ: Ι. Ντζούφρας, Π. Τσιαµυρτζής Ι ΑΚΤΙΚΟ ΥΛΙΚΟ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΜΠΕΫΖΙΑΝΗ ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ: Βιοστατιστική
Bayesian Biostatistics Using BUGS
 Bayesian Biostatistics Using BUGS Βιο-Στατιστική κατά Bayes µε τη χρήση του Λογισµικού BUGS ΜΑΘΗΜΑ 4: ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΕΛΕΓΧΟ ΥΠΟΘΕΣΕΩΝ, ΕΠΙΛΟΓΗ ΜΟΝΤΕΛΩΝ ΚΑΙ ΜΕΤΑΒΛΗΤΩΝ ΚΑΤΑ BAYES ΜΕ ΤΟ WINBUGS I. Ntzoufras
Bayesian Biostatistics Using BUGS Βιο-Στατιστική κατά Bayes µε τη χρήση του Λογισµικού BUGS ΜΑΘΗΜΑ 4: ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΕΛΕΓΧΟ ΥΠΟΘΕΣΕΩΝ, ΕΠΙΛΟΓΗ ΜΟΝΤΕΛΩΝ ΚΑΙ ΜΕΤΑΒΛΗΤΩΝ ΚΑΤΑ BAYES ΜΕ ΤΟ WINBUGS I. Ntzoufras
Υ: Νόσος. Χ: Παράγοντας Κινδύνου 1 (Ασθενής) 2 (Υγιής) Σύνολο. 1 (Παρόν) n 11 n 12 n 1. 2 (Απών) n 21 n 22 n 2. Σύνολο n.1 n.2 n..
 Μέτρα Κινδύνου για Δίτιμα Κατηγορικά Δεδομένα Σε αυτή την ενότητα θα ορίσουμε δείκτες μέτρησης του κινδύνου εμφάνισης μίας νόσου όταν έχουμε δίτιμες κατηγορικές μεταβλητές. Στην πιο απλή περίπτωση μας
Μέτρα Κινδύνου για Δίτιμα Κατηγορικά Δεδομένα Σε αυτή την ενότητα θα ορίσουμε δείκτες μέτρησης του κινδύνου εμφάνισης μίας νόσου όταν έχουμε δίτιμες κατηγορικές μεταβλητές. Στην πιο απλή περίπτωση μας
Στόχος µαθήµατος: Παράδειγµα 1: µελέτη ασθενών-µαρτύρων ΒΙΟΣΤΑΤΙΣΤΙΚΗ ΙΙ
 ΠΜΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΥΓΕΙΑ, ΙΑΧΕΙΡΙΣΗ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΙΜΗΣΗ ΑΚ. ΕΤΟΣ 2006-2007, 3ο εξάµηνο ΒΙΟΣΤΑΤΙΣΤΙΚΗ ΙΙ ΜΑΘΗΜΑ 5 ΕΡΓΑΣΤΗΡΙΟ 1 ΜΕΤΡΑ ΚΙΝ ΥΝΟΥ & ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ ΜΕ ΤΗΝ ΧΡΗΣΗ SPSS
ΠΜΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΥΓΕΙΑ, ΙΑΧΕΙΡΙΣΗ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΙΜΗΣΗ ΑΚ. ΕΤΟΣ 2006-2007, 3ο εξάµηνο ΒΙΟΣΤΑΤΙΣΤΙΚΗ ΙΙ ΜΑΘΗΜΑ 5 ΕΡΓΑΣΤΗΡΙΟ 1 ΜΕΤΡΑ ΚΙΝ ΥΝΟΥ & ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ ΜΕ ΤΗΝ ΧΡΗΣΗ SPSS
Λογαριθμικά Γραμμικά Μοντέλα Poisson Παλινδρόμηση Παράδειγμα στο SPSS
 Λογαριθμικά Γραμμικά Μοντέλα Poisson Παλινδρόμηση Παράδειγμα στο SPSS Ο παρακάτω πίνακας παρουσιάζει θανάτους από καρδιακή ανεπάρκεια ανάμεσα σε άνδρες γιατρούς οι οποίοι έχουν κατηγοριοποιηθεί κατά ηλικία
Λογαριθμικά Γραμμικά Μοντέλα Poisson Παλινδρόμηση Παράδειγμα στο SPSS Ο παρακάτω πίνακας παρουσιάζει θανάτους από καρδιακή ανεπάρκεια ανάμεσα σε άνδρες γιατρούς οι οποίοι έχουν κατηγοριοποιηθεί κατά ηλικία
Γενικευμένα Γραμμικά Μοντέλα (GLM) Επισκόπηση
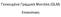 Γενικευμένα Γραμμικά Μοντέλα (GLM) Επισκόπηση Γενική μορφή g( E[ Y X ]) Xb Κατανομή της Υ στην εκθετική οικογένεια Ανεξάρτητες παρατηρήσεις Ενας όρος για το σφάλμα g(.) Συνδετική συνάρτηση (link function)
Γενικευμένα Γραμμικά Μοντέλα (GLM) Επισκόπηση Γενική μορφή g( E[ Y X ]) Xb Κατανομή της Υ στην εκθετική οικογένεια Ανεξάρτητες παρατηρήσεις Ενας όρος για το σφάλμα g(.) Συνδετική συνάρτηση (link function)
ΠΑΡΑΡΤΗΜΑ 1 (4 ου ΜΑΘΗΜΑΤΟΣ): ΠΑΡΑ ΕΙΓΜΑΤΑ ΕΛΕΓΧΩΝ ΥΠΟΘΕΣΕΩΝ, ΕΠΙΛΟΓΗΣ ΜΟΝΤΕΛΩΝ ΚΑΙ ΜΕΤΑΒΛΗΤΩΝ
 ΠΑΡΑΡΤΗΜΑ 1 (4 ου ΜΑΘΗΜΑΤΟΣ): ΠΑΡΑ ΕΙΓΜΑΤΑ ΕΛΕΓΧΩΝ ΥΠΟΘΕΣΕΩΝ, ΕΠΙΛΟΓΗΣ ΜΟΝΤΕΛΩΝ ΚΑΙ ΜΕΤΑΒΛΗΤΩΝ 1 ΠΑΡΑ ΕΙΓΜΑ WINBUGS 1: Ένας Απλός Έλεγχος Υπόθεσης (ESTRIOL DATASET) model estriol; { definition of likelihood
ΠΑΡΑΡΤΗΜΑ 1 (4 ου ΜΑΘΗΜΑΤΟΣ): ΠΑΡΑ ΕΙΓΜΑΤΑ ΕΛΕΓΧΩΝ ΥΠΟΘΕΣΕΩΝ, ΕΠΙΛΟΓΗΣ ΜΟΝΤΕΛΩΝ ΚΑΙ ΜΕΤΑΒΛΗΤΩΝ 1 ΠΑΡΑ ΕΙΓΜΑ WINBUGS 1: Ένας Απλός Έλεγχος Υπόθεσης (ESTRIOL DATASET) model estriol; { definition of likelihood
HMY 795: Αναγνώριση Προτύπων. Διάλεξη 2
 HMY 795: Αναγνώριση Προτύπων Διάλεξη 2 Επισκόπηση θεωρίας πιθανοτήτων Θεωρία πιθανοτήτων Τυχαία μεταβλητή: Μεταβλητή της οποίας δε γνωρίζουμε με βεβαιότητα την τιμή (αντίθετα με τις ντετερμινιστικές μεταβλητές)
HMY 795: Αναγνώριση Προτύπων Διάλεξη 2 Επισκόπηση θεωρίας πιθανοτήτων Θεωρία πιθανοτήτων Τυχαία μεταβλητή: Μεταβλητή της οποίας δε γνωρίζουμε με βεβαιότητα την τιμή (αντίθετα με τις ντετερμινιστικές μεταβλητές)
ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ 3 ΔΕΣΜΕΥΜΕΝΗ ΠΙΘΑΝΟΤΗΤΑ, ΟΛΙΚΗ ΠΙΘΑΝΟΤΗΤΑ ΘΕΩΡΗΜΑ BAYES, ΑΝΕΞΑΡΤΗΣΙΑ ΚΑΙ ΣΥΝΑΦΕΙΣ ΕΝΝΟΙΕΣ 71
 ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ ΠΙΘΑΝΟΤΗΤΕΣ 11 ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΗ 13 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 19 2.1 Αβεβαιότητα, Τυχαία Διαδικασία, και Συναφείς Έννοιες 21 2.1.1 Αβεβαιότητα και Τυχαίο Πείραμα
ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ ΠΙΘΑΝΟΤΗΤΕΣ 11 ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΗ 13 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 19 2.1 Αβεβαιότητα, Τυχαία Διαδικασία, και Συναφείς Έννοιες 21 2.1.1 Αβεβαιότητα και Τυχαίο Πείραμα
HMY 795: Αναγνώριση Προτύπων
 HMY 795: Αναγνώριση Προτύπων Διαλέξεις 7 8 Μπεϋζιανή εκτίμηση συνέχεια Μη παραμετρικές μέθοδοι εκτίμησης πυκνότητας Εκτίμηση ML για την κανονική κατανομή Μπεϋζιανή εκτίμηση για την κανονική κατανομή Γνωστή
HMY 795: Αναγνώριση Προτύπων Διαλέξεις 7 8 Μπεϋζιανή εκτίμηση συνέχεια Μη παραμετρικές μέθοδοι εκτίμησης πυκνότητας Εκτίμηση ML για την κανονική κατανομή Μπεϋζιανή εκτίμηση για την κανονική κατανομή Γνωστή
ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ: ΠΙΘΑΝΟΤΗΤΕΣ 11 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 13
 ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ: ΠΙΘΑΝΟΤΗΤΕΣ 11 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 13 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 20 2.1 Αβεβαιότητα, Τυχαία Διαδικασία, και Συναφείς Έννοιες 20 2.1.1 Αβεβαιότητα
ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ: ΠΙΘΑΝΟΤΗΤΕΣ 11 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 13 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 20 2.1 Αβεβαιότητα, Τυχαία Διαδικασία, και Συναφείς Έννοιες 20 2.1.1 Αβεβαιότητα
Υ: Νόσος. Χ: Παράγοντας Κινδύνου 1 (Ασθενής) 2 (Υγιής) Σύνολο. 1 (Παρόν) n 11 n 12 n 1. 2 (Απών) n 21 n 22 n 2. Σύνολο n.1 n.2 n..
 Μέτρα Κινδύνου για Δίτιμα Κατηγορικά Δεδομένα Σε αυτή την ενότητα θα ορίσουμε δείκτες μέτρησης του κινδύνου εμφάνισης μίας νόσου όταν έχουμε δίτιμες κατηγορικές μεταβλητές. Στην πιο απλή περίπτωση μας
Μέτρα Κινδύνου για Δίτιμα Κατηγορικά Δεδομένα Σε αυτή την ενότητα θα ορίσουμε δείκτες μέτρησης του κινδύνου εμφάνισης μίας νόσου όταν έχουμε δίτιμες κατηγορικές μεταβλητές. Στην πιο απλή περίπτωση μας
Λογιστική Παλινδρόµηση
 Κεφάλαιο 10 Λογιστική Παλινδρόµηση Στο κεφάλαιο αυτό ϑα δούµε την µέθοδο της λογιστικής παλινδρόµησης η οποία χρησιµεύει στο να αναπτύξουµε σχέση µίας δίτιµης ανεξάρτητης τυχαίας µετα- ϐλητής και συνεχών
Κεφάλαιο 10 Λογιστική Παλινδρόµηση Στο κεφάλαιο αυτό ϑα δούµε την µέθοδο της λογιστικής παλινδρόµησης η οποία χρησιµεύει στο να αναπτύξουµε σχέση µίας δίτιµης ανεξάρτητης τυχαίας µετα- ϐλητής και συνεχών
Διάλεξη 1: Στατιστική Συμπερασματολογία - Εκτίμηση Σημείου
 Διάλεξη 1: Στατιστική Συμπερασματολογία - Εκτίμηση Σημείου Στατιστική Συμπερασματολογία Εκτιμητική Έλεγχος Στατιστικών Υποθέσεων εκτιμήτρια συνάρτηση, ˆ θ σημειακή εκτίμηση εκτίμηση με διάστημα εμπιστοσύνης
Διάλεξη 1: Στατιστική Συμπερασματολογία - Εκτίμηση Σημείου Στατιστική Συμπερασματολογία Εκτιμητική Έλεγχος Στατιστικών Υποθέσεων εκτιμήτρια συνάρτηση, ˆ θ σημειακή εκτίμηση εκτίμηση με διάστημα εμπιστοσύνης
Μαρκοβιανές Αλυσίδες
 Μαρκοβιανές Αλυσίδες { θ * } Στοχαστική Ανέλιξη είναι μια συλλογή τ.μ. Ο χώρος Τ (συνήθως είναι χρόνος) μπορεί να είναι είτε διακριτός είτε συνεχής και καλείται παραμετρικός χώρος. Το σύνολο των δυνατών
Μαρκοβιανές Αλυσίδες { θ * } Στοχαστική Ανέλιξη είναι μια συλλογή τ.μ. Ο χώρος Τ (συνήθως είναι χρόνος) μπορεί να είναι είτε διακριτός είτε συνεχής και καλείται παραμετρικός χώρος. Το σύνολο των δυνατών
HMY 795: Αναγνώριση Προτύπων
 HMY 795: Αναγνώριση Προτύπων Διάλεξη 2 Επισκόπηση θεωρίας πιθανοτήτων Τυχαίες μεταβλητές: Βασικές έννοιες Τυχαία μεταβλητή: Μεταβλητή της οποίας δε γνωρίζουμε με βεβαιότητα την τιμή (σε αντίθεση με τις
HMY 795: Αναγνώριση Προτύπων Διάλεξη 2 Επισκόπηση θεωρίας πιθανοτήτων Τυχαίες μεταβλητές: Βασικές έννοιες Τυχαία μεταβλητή: Μεταβλητή της οποίας δε γνωρίζουμε με βεβαιότητα την τιμή (σε αντίθεση με τις
HMY 795: Αναγνώριση Προτύπων
 HMY 795: Αναγνώριση Προτύπων Διαλέξεις 7-8 Μπεϋζιανή εκτίμηση - συνέχεια Μη παραμετρικές μέθοδοι εκτίμησης πυκνότητας Δυαδικές τ.μ. κατανομή Bernoulli : Εκτίμηση ML: Εκτίμηση Bayes για εκ των προτέρων
HMY 795: Αναγνώριση Προτύπων Διαλέξεις 7-8 Μπεϋζιανή εκτίμηση - συνέχεια Μη παραμετρικές μέθοδοι εκτίμησης πυκνότητας Δυαδικές τ.μ. κατανομή Bernoulli : Εκτίμηση ML: Εκτίμηση Bayes για εκ των προτέρων
ΤΕΙ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Μεταπτυχιακό Τραπεζικής & Χρηματοοικονομικής
 ΤΕΙ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Μεταπτυχιακό Τραπεζικής & Χρηματοοικονομικής Υποθέσεις του Απλού γραμμικού υποδείγματος της Παλινδρόμησης Η μεταβλητή ε t (διαταρακτικός όρος) είναι τυχαία μεταβλητή με μέσο όρο
ΤΕΙ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Μεταπτυχιακό Τραπεζικής & Χρηματοοικονομικής Υποθέσεις του Απλού γραμμικού υποδείγματος της Παλινδρόμησης Η μεταβλητή ε t (διαταρακτικός όρος) είναι τυχαία μεταβλητή με μέσο όρο
ΜΗ ΓΡΑΜΜΙΚΗ ΠΑΛΙΝΔΡΟΜΙΣΗ
 ΜΗ ΓΡΑΜΜΙΚΗ ΠΑΛΙΝΔΡΟΜΙΣΗ Τα μη γραμμικά μοντέλα έχουν την πιο κάτω μορφή: η μορφή αυτή μοιάζει με τη μορφή που έχουμε για τα γραμμικά μοντέλα ( δηλαδή η παρατήρηση Y i είναι το άθροισμα της αναμενόμενης
ΜΗ ΓΡΑΜΜΙΚΗ ΠΑΛΙΝΔΡΟΜΙΣΗ Τα μη γραμμικά μοντέλα έχουν την πιο κάτω μορφή: η μορφή αυτή μοιάζει με τη μορφή που έχουμε για τα γραμμικά μοντέλα ( δηλαδή η παρατήρηση Y i είναι το άθροισμα της αναμενόμενης
Στατιστική Συμπερασματολογία
 Στατιστική Συμπερασματολογία Διαφάνειες 1 ου κεφαλαίου Βιβλίο: Κολυβά Μαχαίρα, Φ. & Χατζόπουλος Στ. Α. (2016). Μαθηματική Στατιστική, Έλεγχοι Υποθέσεων. [ηλεκτρ. βιβλ.] Αθήνα: Σύνδεσμος Ελληνικών Ακαδημαϊκών
Στατιστική Συμπερασματολογία Διαφάνειες 1 ου κεφαλαίου Βιβλίο: Κολυβά Μαχαίρα, Φ. & Χατζόπουλος Στ. Α. (2016). Μαθηματική Στατιστική, Έλεγχοι Υποθέσεων. [ηλεκτρ. βιβλ.] Αθήνα: Σύνδεσμος Ελληνικών Ακαδημαϊκών
Ανάλυση Δεδομένων με χρήση του Στατιστικού Πακέτου R
 Ανάλυση Δεδομένων με χρήση του Στατιστικού Πακέτου R Δημήτρης Φουσκάκης, Επίκουρος Καθηγητής, Τομέας Μαθηματικών, Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών, Εθνικό Μετσόβιο Πολυτεχνείο. Περιεχόμενα
Ανάλυση Δεδομένων με χρήση του Στατιστικού Πακέτου R Δημήτρης Φουσκάκης, Επίκουρος Καθηγητής, Τομέας Μαθηματικών, Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών, Εθνικό Μετσόβιο Πολυτεχνείο. Περιεχόμενα
Σημειακή εκτίμηση και εκτίμηση με διάστημα. 11 η Διάλεξη
 Σημειακή εκτίμηση και εκτίμηση με διάστημα 11 η Διάλεξη Εκτιμήτρια Κάθε στατιστική συνάρτηση που χρησιμοποιείται για την εκτίμηση μιας παραμέτρου ενός πληθυσμού (π.χ. ο δειγματικός μέσος) Σημειακή εκτίμηση
Σημειακή εκτίμηση και εκτίμηση με διάστημα 11 η Διάλεξη Εκτιμήτρια Κάθε στατιστική συνάρτηση που χρησιμοποιείται για την εκτίμηση μιας παραμέτρου ενός πληθυσμού (π.χ. ο δειγματικός μέσος) Σημειακή εκτίμηση
διαγνωστικούς ελέγχους MCMC diagnostics CODA
 MCMC DIAGNOSTICS Πόσο πρέπει να περιμένουμε για να επιτευχθεί η στασιμότητα; Πόσο μεγάλο πρέπει να είναι το m (μετά την στασιμότητα για πόσο πρέπει να τρέξεις την αλυσίδα σου); Από που να ξεκινήσεις; Για
MCMC DIAGNOSTICS Πόσο πρέπει να περιμένουμε για να επιτευχθεί η στασιμότητα; Πόσο μεγάλο πρέπει να είναι το m (μετά την στασιμότητα για πόσο πρέπει να τρέξεις την αλυσίδα σου); Από που να ξεκινήσεις; Για
σ = και σ = 4 αντιστοίχως. Τότε θα ισχύει
 Θέματα ομάδας A 1. Σε κάποιο πείραμα τύχης μία τυχαία μεταβλητή λαμβάνει τις τιμές = 10 και = 10. Τότε η μέση τιμή x της θα είναι α. 10 β. 10 γ.,5 10 δ. 19,5 10 1= 10, = 10,. Δυο τυχαίες μεταβλητές, ακολουθούν
Θέματα ομάδας A 1. Σε κάποιο πείραμα τύχης μία τυχαία μεταβλητή λαμβάνει τις τιμές = 10 και = 10. Τότε η μέση τιμή x της θα είναι α. 10 β. 10 γ.,5 10 δ. 19,5 10 1= 10, = 10,. Δυο τυχαίες μεταβλητές, ακολουθούν
Ανάλυση Δεδοµένων µε χρήση του Στατιστικού Πακέτου R
 Ανάλυση Δεδοµένων µε χρήση του Στατιστικού Πακέτου R, Επίκουρος Καθηγητής, Τοµέας Μαθηµατικών, Σχολή Εφαρµοσµένων Μαθηµατικών και Φυσικών Επιστηµών, Εθνικό Μετσόβιο Πολυτεχνείο. Περιεχόµενα Εισαγωγή στη
Ανάλυση Δεδοµένων µε χρήση του Στατιστικού Πακέτου R, Επίκουρος Καθηγητής, Τοµέας Μαθηµατικών, Σχολή Εφαρµοσµένων Μαθηµατικών και Φυσικών Επιστηµών, Εθνικό Μετσόβιο Πολυτεχνείο. Περιεχόµενα Εισαγωγή στη
Στατιστική. Εκτιμητική
 Στατιστική Εκτιμητική Χατζόπουλος Σταύρος 28/2/2018 και 01 /03/2018 Εισαγωγή Το αντικείμενο της Στατιστικής είναι η εξαγωγή συμπερασμάτων που αφορούν τον πληθυσμό ή το φαινόμενο που μελετάμε, με τη βοήθεια
Στατιστική Εκτιμητική Χατζόπουλος Σταύρος 28/2/2018 και 01 /03/2018 Εισαγωγή Το αντικείμενο της Στατιστικής είναι η εξαγωγή συμπερασμάτων που αφορούν τον πληθυσμό ή το φαινόμενο που μελετάμε, με τη βοήθεια
Στατιστική Συμπερασματολογία
 4. Εκτιμητική Στατιστική Συμπερασματολογία εκτιμήσεις των αγνώστων παραμέτρων μιας γνωστής από άποψη είδους κατανομής έλεγχο των υποθέσεων που γίνονται σε σχέση με τις παραμέτρους μιας κατανομής και σε
4. Εκτιμητική Στατιστική Συμπερασματολογία εκτιμήσεις των αγνώστων παραμέτρων μιας γνωστής από άποψη είδους κατανομής έλεγχο των υποθέσεων που γίνονται σε σχέση με τις παραμέτρους μιας κατανομής και σε
ΣΤΟΧΑΣΤΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ & ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ Αίθουσα Νέα Κτίρια ΣΗΜΜΥ Ε.Μ.Π.
 ΣΤΟΧΑΣΤΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ & ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ Αίθουσα 005 - Νέα Κτίρια ΣΗΜΜΥ Ε.Μ.Π. Προσομοίωση Monte Carlo Αλυσίδων Markov: Αλγόριθμοι Metropolis & Metropolis-Hastings Προσομοιωμένη Ανόπτηση Simulated Annealing
ΣΤΟΧΑΣΤΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ & ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ Αίθουσα 005 - Νέα Κτίρια ΣΗΜΜΥ Ε.Μ.Π. Προσομοίωση Monte Carlo Αλυσίδων Markov: Αλγόριθμοι Metropolis & Metropolis-Hastings Προσομοιωμένη Ανόπτηση Simulated Annealing
Εισόδημα Κατανάλωση 1500 500 1600 600 1300 450 1100 400 600 250 700 275 900 300 800 352 850 400 1100 500
 Εισόδημα Κατανάλωση 1500 500 1600 600 1300 450 1100 400 600 250 700 275 900 300 800 352 850 400 1100 500 Πληθυσμός Δείγμα Δείγμα Δείγμα Ο ρόλος της Οικονομετρίας Οικονομική Θεωρία Διατύπωση της
Εισόδημα Κατανάλωση 1500 500 1600 600 1300 450 1100 400 600 250 700 275 900 300 800 352 850 400 1100 500 Πληθυσμός Δείγμα Δείγμα Δείγμα Ο ρόλος της Οικονομετρίας Οικονομική Θεωρία Διατύπωση της
ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΙΔΙΚΑ ΘΕΜΑΤΑ. Κεφάλαιο 10. Εισαγωγή στην εκτιμητική
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΙΔΙΚΑ ΘΕΜΑΤΑ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΙΔΙΚΑ ΘΕΜΑΤΑ
ΧΡΟΝΙΚΕΣ ΣΕΙΡΕΣ. Παπάνα Αγγελική
 ΧΡΟΝΙΚΕΣ ΣΕΙΡΕΣ 7ο μάθημα: Πολυμεταβλητή παλινδρόμηση (ΕΠΑΝΑΛΗΨΗ) Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & ΠΑΜΑΚ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr Webpage: http://users.auth.gr/agpapana
ΧΡΟΝΙΚΕΣ ΣΕΙΡΕΣ 7ο μάθημα: Πολυμεταβλητή παλινδρόμηση (ΕΠΑΝΑΛΗΨΗ) Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & ΠΑΜΑΚ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr Webpage: http://users.auth.gr/agpapana
Σκοπός του μαθήματος
 Σκοπός του μαθήματος Στο μάθημα αυτό γίνεται εφαρμογή, με τη βοήθεια του υπολογιστή και τη χρήση του στατιστικού προγράμματος S.P.S.S., της στατιστικής θεωρίας που αναπτύχθηκε στα μαθήματα «Εισαγωγή στη
Σκοπός του μαθήματος Στο μάθημα αυτό γίνεται εφαρμογή, με τη βοήθεια του υπολογιστή και τη χρήση του στατιστικού προγράμματος S.P.S.S., της στατιστικής θεωρίας που αναπτύχθηκε στα μαθήματα «Εισαγωγή στη
HMY 795: Αναγνώριση Προτύπων
 HMY 795: Αναγνώριση Προτύπων Διάλεξη 3 Επιλογή μοντέλου Επιλογή μοντέλου Θεωρία αποφάσεων Επιλογή μοντέλου δεδομένα επικύρωσης Η επιλογή του είδους του μοντέλου που θα χρησιμοποιηθεί σε ένα πρόβλημα (π.χ.
HMY 795: Αναγνώριση Προτύπων Διάλεξη 3 Επιλογή μοντέλου Επιλογή μοντέλου Θεωρία αποφάσεων Επιλογή μοντέλου δεδομένα επικύρωσης Η επιλογή του είδους του μοντέλου που θα χρησιμοποιηθεί σε ένα πρόβλημα (π.χ.
Σημερινό μάθημα: Εκτιμήτριες συναρτήσεις, σημειακή εκτίμηση παραμέτρων και γραμμική παλινδρόμηση Στατιστική συμπερασματολογία (ή εκτιμητική ): εξαγωγή
 Πιθανότητες και Αρχές Στατιστικής (10η Διάλεξη) Σωτήρης Νικολετσέας, καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής, Πανεπιστήμιο Πατρών Ακαδημαϊκό Ετος 2017-2018 Σωτήρης Νικολετσέας, καθηγητής 1 / 48 Σημερινό
Πιθανότητες και Αρχές Στατιστικής (10η Διάλεξη) Σωτήρης Νικολετσέας, καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής, Πανεπιστήμιο Πατρών Ακαδημαϊκό Ετος 2017-2018 Σωτήρης Νικολετσέας, καθηγητής 1 / 48 Σημερινό
ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ ΠΙΘΑΝΟΤΗΤΕΣ 13 ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΗ 15 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 19
 ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ ΠΙΘΑΝΟΤΗΤΕΣ 13 ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΗ 15 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 19 2.1 Αβεβαιότητα, Τυχαία Διαδικασία, και Συναφείς Έννοιες 21 2.1.1 Αβεβαιότητα και Τυχαίο Πείραμα
ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ ΠΙΘΑΝΟΤΗΤΕΣ 13 ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΗ 15 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 19 2.1 Αβεβαιότητα, Τυχαία Διαδικασία, και Συναφείς Έννοιες 21 2.1.1 Αβεβαιότητα και Τυχαίο Πείραμα
Μάστερ στην Εφαρµοσµένη Στατιστική
 Μάστερ στην Εφαρµοσµένη Στατιστική Πρότυπο Πρόγραµµα Master Εξάµηνο Σπουδών Κωδικός Τίτλος Μαθήµατος ιδακτικές Μονάδες 1 ο Εξάµηνο ΜΑΣ650 Μαθηµατική Στατιστική 10 ΜΑΣ655 ειγµατοληψία 10 ΜΑΣ658 Στατιστικά
Μάστερ στην Εφαρµοσµένη Στατιστική Πρότυπο Πρόγραµµα Master Εξάµηνο Σπουδών Κωδικός Τίτλος Μαθήµατος ιδακτικές Μονάδες 1 ο Εξάµηνο ΜΑΣ650 Μαθηµατική Στατιστική 10 ΜΑΣ655 ειγµατοληψία 10 ΜΑΣ658 Στατιστικά
Πρόλογος... xv. Κεφάλαιο 1. Εισαγωγικές Έννοιες... 1
 Πρόλογος... xv Κεφάλαιο 1. Εισαγωγικές Έννοιες... 1 1.1.Ιστορική Αναδρομή... 1 1.2.Βασικές Έννοιες... 5 1.3.Πλαίσιο ειγματοληψίας (Sampling Frame)... 9 1.4.Κατηγορίες Ιατρικών Μελετών.... 11 1.4.1.Πειραµατικές
Πρόλογος... xv Κεφάλαιο 1. Εισαγωγικές Έννοιες... 1 1.1.Ιστορική Αναδρομή... 1 1.2.Βασικές Έννοιες... 5 1.3.Πλαίσιο ειγματοληψίας (Sampling Frame)... 9 1.4.Κατηγορίες Ιατρικών Μελετών.... 11 1.4.1.Πειραµατικές
Κλινική Επιδηµιολογία
 Κλινική Επιδηµιολογία Ρυθµιστικοί παράγοντες Συγχυτικοί παράγοντες Ενδιάµεσοι παράγοντες Πρέπει να πιστέψουµε τις µετρήσεις µας; Κάπνισµα Καρκίνος Πνεύµονα OR = 9.1 Πραγµατική σχέση αιτιολογική µη-αιτιολογική
Κλινική Επιδηµιολογία Ρυθµιστικοί παράγοντες Συγχυτικοί παράγοντες Ενδιάµεσοι παράγοντες Πρέπει να πιστέψουµε τις µετρήσεις µας; Κάπνισµα Καρκίνος Πνεύµονα OR = 9.1 Πραγµατική σχέση αιτιολογική µη-αιτιολογική
HMY 795: Αναγνώριση Προτύπων
 HMY 795: Αναγνώριση Προτύπων Διαλέξεις 9 10 Γραμμική παλινδρόμηση (Linear regression) Μπεϋζιανή εκτίμηση για την κανονική κατανομή Γνωστή μέση τιμή μ, άγνωστη διασπορά σ 2. Ακρίβεια λ=1/σ 2 : conjugate
HMY 795: Αναγνώριση Προτύπων Διαλέξεις 9 10 Γραμμική παλινδρόμηση (Linear regression) Μπεϋζιανή εκτίμηση για την κανονική κατανομή Γνωστή μέση τιμή μ, άγνωστη διασπορά σ 2. Ακρίβεια λ=1/σ 2 : conjugate
Ενότητα 1: Εισαγωγή. ΤΕΙ Στερεάς Ελλάδας. Τμήμα Φυσικοθεραπείας. Προπτυχιακό Πρόγραμμα. Μάθημα: Βιοστατιστική-Οικονομία της υγείας Εξάμηνο: Ε (5 ο )
 ΤΕΙ Στερεάς Ελλάδας Τμήμα Φυσικοθεραπείας Προπτυχιακό Πρόγραμμα Μάθημα: Βιοστατιστική-Οικονομία της υγείας Εξάμηνο: Ε (5 ο ) Ενότητα 1: Εισαγωγή Δρ. Χρήστος Γενιτσαρόπουλος Λαμία, 2017 1.1. Σκοπός και
ΤΕΙ Στερεάς Ελλάδας Τμήμα Φυσικοθεραπείας Προπτυχιακό Πρόγραμμα Μάθημα: Βιοστατιστική-Οικονομία της υγείας Εξάμηνο: Ε (5 ο ) Ενότητα 1: Εισαγωγή Δρ. Χρήστος Γενιτσαρόπουλος Λαμία, 2017 1.1. Σκοπός και
ΚΕΦΑΛΑΙΟ 0. Απλή Γραμμική Παλινδρόμηση. Ένα Πρόβλημα. Η επιδιωκόμενη ιδιότητα. Ένα χρήσιμο γράφημα. Οι υπολογισμοί. Η μέθοδος ελαχίστων τετραγώνων ...
 ΚΕΦΑΛΑΙΟ 0 Ένα Πρόβλημα Δεδομένα.6 3. 3.8 4. 4.4 5.8 6.0 6.7 7. 7.8 5.6 7.9 8.0 8. 8. 9. 9.5 9.4 9.6 9.9 Απλή Γραμμική Παλινδρόμηση Μωυσιάδης Χρόνης 6 o Εξάμηνο Μαθηματικών Έχει σχέση το με το ; Ειδικότερα
ΚΕΦΑΛΑΙΟ 0 Ένα Πρόβλημα Δεδομένα.6 3. 3.8 4. 4.4 5.8 6.0 6.7 7. 7.8 5.6 7.9 8.0 8. 8. 9. 9.5 9.4 9.6 9.9 Απλή Γραμμική Παλινδρόμηση Μωυσιάδης Χρόνης 6 o Εξάμηνο Μαθηματικών Έχει σχέση το με το ; Ειδικότερα
ΠΕΡΙΕΧΟΜΕΝΑ. Πιθανότητες. Τυχαίες μεταβλητές - Κατανομές ΙΑΤΡΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΚΕΦΑΛΑΙΟ 1 ΚΕΦΑΛΑΙΟ 2
 ΠΕΡΙΕΧΟΜΕΝΑ ΙΑΤΡΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΚΕΦΑΛΑΙΟ 1 Πιθανότητες 1.1 Πιθανότητες και Στατιστική... 5 1.2 ειγματικός χώρος Ενδεχόμενα... 7 1.3 Ορισμοί και νόμοι των πιθανοτήτων... 10 1.4 εσμευμένη πιθανότητα Ολική
ΠΕΡΙΕΧΟΜΕΝΑ ΙΑΤΡΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΚΕΦΑΛΑΙΟ 1 Πιθανότητες 1.1 Πιθανότητες και Στατιστική... 5 1.2 ειγματικός χώρος Ενδεχόμενα... 7 1.3 Ορισμοί και νόμοι των πιθανοτήτων... 10 1.4 εσμευμένη πιθανότητα Ολική
Αναλυτική Στατιστική
 Αναλυτική Στατιστική Συμπερασματολογία Στόχος: εξαγωγή συμπερασμάτων για το σύνολο ενός πληθυσμού, αντλώντας πληροφορίες από ένα μικρό υποσύνολο αυτού Ορισμοί Πληθυσμός: σύνολο όλων των υπό εξέταση μονάδων
Αναλυτική Στατιστική Συμπερασματολογία Στόχος: εξαγωγή συμπερασμάτων για το σύνολο ενός πληθυσμού, αντλώντας πληροφορίες από ένα μικρό υποσύνολο αυτού Ορισμοί Πληθυσμός: σύνολο όλων των υπό εξέταση μονάδων
Εισαγωγή στη Στατιστική
 Εισαγωγή στη Στατιστική Μετεκπαιδευτικό Σεμινάριο στην ΨΥΧΟΚΟΙΝΩΝΙΚΗ ΑΠΟΚΑΤΑΣΤΑΣΗ ΨΥΧΟΚΟΙΝΩΝΙΚΕΣ ΘΕΡΑΠΕΥΤΙΚΕΣ ΠΡΟΣΕΓΓΙΣΕΙΣ Δημήτρης Φουσκάκης, Επίκουρος Καθηγητής, Τομέας Μαθηματικών, Σχολή Εφαρμοσμένων
Εισαγωγή στη Στατιστική Μετεκπαιδευτικό Σεμινάριο στην ΨΥΧΟΚΟΙΝΩΝΙΚΗ ΑΠΟΚΑΤΑΣΤΑΣΗ ΨΥΧΟΚΟΙΝΩΝΙΚΕΣ ΘΕΡΑΠΕΥΤΙΚΕΣ ΠΡΟΣΕΓΓΙΣΕΙΣ Δημήτρης Φουσκάκης, Επίκουρος Καθηγητής, Τομέας Μαθηματικών, Σχολή Εφαρμοσμένων
Σ ΤΑΤ Ι Σ Τ Ι Κ Η ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ
 Σ ΤΑΤ Ι Σ Τ Ι Κ Η i ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ Κατανομή Δειγματοληψίας του Δειγματικού Μέσου Ο Δειγματικός Μέσος X είναι μια Τυχαία Μεταβλητή. Καθώς η επιλογή και χρήση διαφορετικών δειγμάτων από έναν
Σ ΤΑΤ Ι Σ Τ Ι Κ Η i ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ Κατανομή Δειγματοληψίας του Δειγματικού Μέσου Ο Δειγματικός Μέσος X είναι μια Τυχαία Μεταβλητή. Καθώς η επιλογή και χρήση διαφορετικών δειγμάτων από έναν
Μαθηματικά Και Στατιστική Στη Βιολογία
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μαθηματικά Και Στατιστική Στη Βιολογία Ενότητα 5 : Εκτιμήσεις Ι. Αντωνίου, Χ. Μπράτσας Τμήμα Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μαθηματικά Και Στατιστική Στη Βιολογία Ενότητα 5 : Εκτιμήσεις Ι. Αντωνίου, Χ. Μπράτσας Τμήμα Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό
Μοντέλα Παλινδρόμησης. Άγγελος Μάρκος, Λέκτορας ΠΤ Ε, ΠΘ
 Μοντέλα Παλινδρόμησης Άγγελος Μάρκος, Λέκτορας ΠΤ Ε, ΠΘ Εισαγωγή (1) Σε αρκετές περιπτώσεις επίλυσης προβλημάτων ενδιαφέρει η ταυτόχρονη μελέτη δύο ή περισσότερων μεταβλητών, για να προσδιορίσουμε με ποιο
Μοντέλα Παλινδρόμησης Άγγελος Μάρκος, Λέκτορας ΠΤ Ε, ΠΘ Εισαγωγή (1) Σε αρκετές περιπτώσεις επίλυσης προβλημάτων ενδιαφέρει η ταυτόχρονη μελέτη δύο ή περισσότερων μεταβλητών, για να προσδιορίσουμε με ποιο
ΚΕΦΑΛΑΙΟ ΙΙΙ ΠΟΛΛΑΠΛΗ ΠΑΛΙΝΔΡΟΜΗΣΗ
 ΚΕΦΑΛΑΙΟ ΙΙΙ ΠΟΛΛΑΠΛΗ ΠΑΛΙΝΔΡΟΜΗΣΗ ΕΝΟΤΗΤΕΣ 1. ΓΕΝΙΚΗ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΟΛΛΑΠΛΗ ΠΑΛΙΝΔΡΟΜΗΣΗ 2. ΕΠΙΛΟΓΗ ΜΟΝΤΕΛΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ ΤΟΥ ΑΠΟΚΛΕΙΣΜΟΥ ΜΕΤΑΒΛΗΤΩΝ 3. ΕΠΙΛΟΓΗ ΜΟΝΤΕΛΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ ΤΗΣ ΠΡΟΟΔΕΥΤΙΚΗΣ ΠΡΟΣΘΗΚΗΣ
ΚΕΦΑΛΑΙΟ ΙΙΙ ΠΟΛΛΑΠΛΗ ΠΑΛΙΝΔΡΟΜΗΣΗ ΕΝΟΤΗΤΕΣ 1. ΓΕΝΙΚΗ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΟΛΛΑΠΛΗ ΠΑΛΙΝΔΡΟΜΗΣΗ 2. ΕΠΙΛΟΓΗ ΜΟΝΤΕΛΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ ΤΟΥ ΑΠΟΚΛΕΙΣΜΟΥ ΜΕΤΑΒΛΗΤΩΝ 3. ΕΠΙΛΟΓΗ ΜΟΝΤΕΛΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ ΤΗΣ ΠΡΟΟΔΕΥΤΙΚΗΣ ΠΡΟΣΘΗΚΗΣ
ΣΤΑΤΙΣΤΙΚΕΣ ΕΝΝΟΙΕΣ. Στατιστική????? Κάθε μέρα ερχόμαστε σε επαφή 24/02/2018
 ΣΤΑΤΙΣΤΙΚΕΣ ΕΝΝΟΙΕΣ Αντώνης Κ. Τραυλός (B.A., M.A., Ph.D.) Καθηγητής ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ Σχολή Επιστημών Ανθρώπινης Κίνησης και Ποιότητας Ζωής Τμήμα Οργάνωσης και Διαχείρισης Αθλητισμού Στατιστική?????
ΣΤΑΤΙΣΤΙΚΕΣ ΕΝΝΟΙΕΣ Αντώνης Κ. Τραυλός (B.A., M.A., Ph.D.) Καθηγητής ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ Σχολή Επιστημών Ανθρώπινης Κίνησης και Ποιότητας Ζωής Τμήμα Οργάνωσης και Διαχείρισης Αθλητισμού Στατιστική?????
ΚΑΤΑΝΟΜΈΣ. 8.1 Εισαγωγή. 8.2 Κατανομές Συχνοτήτων (Frequency Distributions) ΚΕΦΑΛΑΙΟ
 ΚΑΤΑΝΟΜΈΣ ΚΕΦΑΛΑΙΟ 8 81 Εισαγωγή Οι κατανομές διακρίνονται σε κατανομές συχνοτήτων, κατανομές πιθανοτήτων και σε δειγματοληπτικές κατανομές Στη συνέχεια θα γίνει αναλυτική περιγραφή αυτών 82 Κατανομές
ΚΑΤΑΝΟΜΈΣ ΚΕΦΑΛΑΙΟ 8 81 Εισαγωγή Οι κατανομές διακρίνονται σε κατανομές συχνοτήτων, κατανομές πιθανοτήτων και σε δειγματοληπτικές κατανομές Στη συνέχεια θα γίνει αναλυτική περιγραφή αυτών 82 Κατανομές
Μέθοδος μέγιστης πιθανοφάνειας
 Μέθοδος μέγιστης πιθανοφάνειας Αν x =,,, παρατηρήσεις των Χ =,,,, τότε έχουμε διαθέσιμο ένα δείγμα Χ={Χ, =,,,} της κατανομής F μεγέθους με από κοινού σ.κ. της Χ f x f x Ορισμός : Θεωρούμε ένα τυχαίο δείγμα
Μέθοδος μέγιστης πιθανοφάνειας Αν x =,,, παρατηρήσεις των Χ =,,,, τότε έχουμε διαθέσιμο ένα δείγμα Χ={Χ, =,,,} της κατανομής F μεγέθους με από κοινού σ.κ. της Χ f x f x Ορισμός : Θεωρούμε ένα τυχαίο δείγμα
Λήψη αποφάσεων κατά Bayes
 Λήψη αποφάσεων κατά Bayes Σημειώσεις μαθήματος Thomas Bayes (1701 1761) Στυλιανός Χατζηδάκης ECE 662 Άνοιξη 2014 1. Εισαγωγή Οι σημειώσεις αυτές βασίζονται στο μάθημα ECE662 του Πανεπιστημίου Purdue και
Λήψη αποφάσεων κατά Bayes Σημειώσεις μαθήματος Thomas Bayes (1701 1761) Στυλιανός Χατζηδάκης ECE 662 Άνοιξη 2014 1. Εισαγωγή Οι σημειώσεις αυτές βασίζονται στο μάθημα ECE662 του Πανεπιστημίου Purdue και
StatXact ΒΙΟΣΤΑΤΙΣΤΙΚΗ ΙΙ. StatXact. ΜΑΘΗΜΑ 5 ΕΡΓΑΣΤΗΡΙΟ 1 - συνέχεια ΜΕΤΡΑ ΚΙΝ ΥΝΟΥ & ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ ΜΕ ΤΗΝ ΧΡΗΣΗ StatXact
 ΠΜΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΥΓΕΙΑ, ΙΑΧΕΙΡΙΣΗ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΙΜΗΣΗ ΑΚ. ΕΤΟΣ 2006-2007, 3ο εξάµηνο StatXact ΒΙΟΣΤΑΤΙΣΤΙΚΗ ΙΙ ΜΑΘΗΜΑ 5 ΕΡΓΑΣΤΗΡΙΟ 1 - συνέχεια ΜΕΤΡΑ ΚΙΝ ΥΝΟΥ & ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ
ΠΜΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΥΓΕΙΑ, ΙΑΧΕΙΡΙΣΗ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΙΜΗΣΗ ΑΚ. ΕΤΟΣ 2006-2007, 3ο εξάµηνο StatXact ΒΙΟΣΤΑΤΙΣΤΙΚΗ ΙΙ ΜΑΘΗΜΑ 5 ΕΡΓΑΣΤΗΡΙΟ 1 - συνέχεια ΜΕΤΡΑ ΚΙΝ ΥΝΟΥ & ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ
Διάλεξη 1 Βασικές έννοιες
 Εργαστήριο SPSS Ψ-4201 (ΕΡΓ) Λεωνίδας Α. Ζαμπετάκης Β.Sc., M.Env.Eng., M.Ind.Eng., D.Eng. Εmail: statisticsuoc@gmail.com Διαλέξεις αναρτημένες στο: Διαλέξεις: ftp://ftp.soc.uoc.gr/psycho/zampetakis/ Διάλεξη
Εργαστήριο SPSS Ψ-4201 (ΕΡΓ) Λεωνίδας Α. Ζαμπετάκης Β.Sc., M.Env.Eng., M.Ind.Eng., D.Eng. Εmail: statisticsuoc@gmail.com Διαλέξεις αναρτημένες στο: Διαλέξεις: ftp://ftp.soc.uoc.gr/psycho/zampetakis/ Διάλεξη
Σ ΤΑΤ Ι Σ Τ Ι Κ Η. Statisticum collegium iv
 Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium iv Στατιστική Συμπερασματολογία Ι Σημειακές Εκτιμήσεις Διαστήματα Εμπιστοσύνης Στατιστική Συμπερασματολογία (Statistical Inference) Το πεδίο της Στατιστικής Συμπερασματολογία,
Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium iv Στατιστική Συμπερασματολογία Ι Σημειακές Εκτιμήσεις Διαστήματα Εμπιστοσύνης Στατιστική Συμπερασματολογία (Statistical Inference) Το πεδίο της Στατιστικής Συμπερασματολογία,
ΠΕΡΙΕΧΟΜΕΝΑ. Πρόλογος... 13
 ΠΕΡΙΕΧΟΜΕΝΑ / 7 ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος... 13 Κεφάλαιο 1: Περιγραφική Στατιστική... 15 1.1 Περιγραφική και Συμπερασματική Στατιστική... 15 1.2 Μεταβλητές - Τιμές - Παρατηρήσεις... 19 1.3 Είδη μεταβλητών...
ΠΕΡΙΕΧΟΜΕΝΑ / 7 ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος... 13 Κεφάλαιο 1: Περιγραφική Στατιστική... 15 1.1 Περιγραφική και Συμπερασματική Στατιστική... 15 1.2 Μεταβλητές - Τιμές - Παρατηρήσεις... 19 1.3 Είδη μεταβλητών...
X = = 81 9 = 9
 Πιθανότητες και Αρχές Στατιστικής (11η Διάλεξη) Σωτήρης Νικολετσέας, καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής, Πανεπιστήμιο Πατρών Ακαδημαϊκό Ετος 2018-2019 Σωτήρης Νικολετσέας, καθηγητής 1 / 35 Σύνοψη
Πιθανότητες και Αρχές Στατιστικής (11η Διάλεξη) Σωτήρης Νικολετσέας, καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής, Πανεπιστήμιο Πατρών Ακαδημαϊκό Ετος 2018-2019 Σωτήρης Νικολετσέας, καθηγητής 1 / 35 Σύνοψη
ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 7. ΚΕΦΑΛΑΙΟ 1: Εισαγωγικές Έννοιες 13
 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 7 ΚΕΦΑΛΑΙΟ 1: Εισαγωγικές Έννοιες 13 1.1. Εισαγωγή 13 1.2. Μοντέλο ή Υπόδειγμα 13 1.3. Η Ανάλυση Παλινδρόμησης 16 1.4. Το γραμμικό μοντέλο Παλινδρόμησης 17 1.5. Πρακτική χρησιμότητα
ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 7 ΚΕΦΑΛΑΙΟ 1: Εισαγωγικές Έννοιες 13 1.1. Εισαγωγή 13 1.2. Μοντέλο ή Υπόδειγμα 13 1.3. Η Ανάλυση Παλινδρόμησης 16 1.4. Το γραμμικό μοντέλο Παλινδρόμησης 17 1.5. Πρακτική χρησιμότητα
ΑΝΑΛΥΣΗ ΔΙΑΚΥΜΑΝΣΗΣ. Επικ. Καθ. Στέλιος Ζήμερας. Τμήμα Μαθηματικών Κατεύθυνση Στατιστικής και Αναλογιστικά Χρηματοοικονομικά Μαθηματικά
 ΑΝΑΛΥΣΗ ΔΙΑΚΥΜΑΝΣΗΣ Επικ Καθ Στέλιος Ζήμερας Τμήμα Μαθηματικών Κατεύθυνση Στατιστικής και Αναλογιστικά Χρηματοοικονομικά Μαθηματικά 5 Έστω για την σύγκριση δειγμάτων συλλέγουμε παρατηρήσεις Υ =,,, από
ΑΝΑΛΥΣΗ ΔΙΑΚΥΜΑΝΣΗΣ Επικ Καθ Στέλιος Ζήμερας Τμήμα Μαθηματικών Κατεύθυνση Στατιστικής και Αναλογιστικά Χρηματοοικονομικά Μαθηματικά 5 Έστω για την σύγκριση δειγμάτων συλλέγουμε παρατηρήσεις Υ =,,, από
Συγγραφή και κριτική ανάλυση επιδημιολογικής εργασίας
 Εργαστήριο Υγιεινής Επιδημιολογίας και Ιατρικής Στατιστικής Ιατρική Σχολή, Πανεπιστήμιο Αθηνών Συγγραφή και κριτική ανάλυση επιδημιολογικής εργασίας Δ. Παρασκευής Εργαστήριο Υγιεινής Επιδημιολογίας και
Εργαστήριο Υγιεινής Επιδημιολογίας και Ιατρικής Στατιστικής Ιατρική Σχολή, Πανεπιστήμιο Αθηνών Συγγραφή και κριτική ανάλυση επιδημιολογικής εργασίας Δ. Παρασκευής Εργαστήριο Υγιεινής Επιδημιολογίας και
ΠΕΡΙΓΡΑΦΗ ΚΑΙ ΑΝΑΛΥΣΗ ΔΕΔΟΜΕΝΩΝ
 ΠΕΡΙΓΡΑΦΗ ΚΑΙ ΑΝΑΛΥΣΗ ΔΕΔΟΜΕΝΩΝ Είδη μεταβλητών Ποσοτικά δεδομένα (π.χ. ηλικία, ύψος, αιμοσφαιρίνη) Ποιοτικά δεδομένα (π.χ. άνδρας/γυναίκα, ναι/όχι) Διατεταγμένα (π.χ. καλό/μέτριο/κακό) 2 Περιγραφή ποσοτικών
ΠΕΡΙΓΡΑΦΗ ΚΑΙ ΑΝΑΛΥΣΗ ΔΕΔΟΜΕΝΩΝ Είδη μεταβλητών Ποσοτικά δεδομένα (π.χ. ηλικία, ύψος, αιμοσφαιρίνη) Ποιοτικά δεδομένα (π.χ. άνδρας/γυναίκα, ναι/όχι) Διατεταγμένα (π.χ. καλό/μέτριο/κακό) 2 Περιγραφή ποσοτικών
Τμήμα Διοίκησης Επιχειρήσεων (Γρεβενά) Μάθημα: Στατιστική II Διάλεξη 1 η : Εισαγωγή-Επανάληψη βασικών εννοιών Εβδομάδα 1 η : ,
 Τμήμα Διοίκησης Επιχειρήσεων (Γρεβενά) Μάθημα: Στατιστική II Διάλεξη 1 η : Εισαγωγή-Επανάληψη βασικών εννοιών Εβδομάδα 1 η :1-0-017, 3-0-017 Διδάσκουσα: Κοντογιάννη Αριστούλα Σκοπός του μαθήματος Η παρουσίαση
Τμήμα Διοίκησης Επιχειρήσεων (Γρεβενά) Μάθημα: Στατιστική II Διάλεξη 1 η : Εισαγωγή-Επανάληψη βασικών εννοιών Εβδομάδα 1 η :1-0-017, 3-0-017 Διδάσκουσα: Κοντογιάννη Αριστούλα Σκοπός του μαθήματος Η παρουσίαση
Ανάλυση Δεδομένων με χρήση του Στατιστικού Πακέτου R
 Ανάλυση Δεδομένων με χρήση του Στατιστικού Πακέτου R, Επίκουρος Καθηγητής, Τομέας Μαθηματικών, Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών, Εθνικό Μετσόβιο Πολυτεχνείο. Περιεχόμενα Εισαγωγή στο
Ανάλυση Δεδομένων με χρήση του Στατιστικού Πακέτου R, Επίκουρος Καθηγητής, Τομέας Μαθηματικών, Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών, Εθνικό Μετσόβιο Πολυτεχνείο. Περιεχόμενα Εισαγωγή στο
Βιοστατιστική ΒΙΟ-309
 Βιοστατιστική ΒΙΟ-309 Χειμερινό Εξάμηνο Ακαδ. Έτος 2015-2016 Ντίνα Λύκα lika@biology.uoc.gr 1. Εισαγωγή Εισαγωγικές έννοιες Μεταβλητότητα : ύπαρξη διαφορών μεταξύ ομοειδών μετρήσεων Μεταβλητή: ένα χαρακτηριστικό
Βιοστατιστική ΒΙΟ-309 Χειμερινό Εξάμηνο Ακαδ. Έτος 2015-2016 Ντίνα Λύκα lika@biology.uoc.gr 1. Εισαγωγή Εισαγωγικές έννοιες Μεταβλητότητα : ύπαρξη διαφορών μεταξύ ομοειδών μετρήσεων Μεταβλητή: ένα χαρακτηριστικό
HMY 795: Αναγνώριση Προτύπων
 HMY 795: Αναγνώριση Προτύπων Διαλέξεις 11-12 Γραμμική παλινδρόμηση συνέχεια Γραμμική παλινδρόμηση συνέχεια Γραμμικές διαχωριστικές συναρτήσεις Γραμμική παλινδρόμηση (Linear regression) y = w + wx + + w
HMY 795: Αναγνώριση Προτύπων Διαλέξεις 11-12 Γραμμική παλινδρόμηση συνέχεια Γραμμική παλινδρόμηση συνέχεια Γραμμικές διαχωριστικές συναρτήσεις Γραμμική παλινδρόμηση (Linear regression) y = w + wx + + w
ΜΑΘΗΜΑ 3ο. Υποδείγματα μιας εξίσωσης
 ΜΑΘΗΜΑ 3ο Υποδείγματα μιας εξίσωσης Οι βασικές υποθέσεις 1. Ο διαταρακτικός όρος u t είναι μια τυχαία μεταβλητή με μέσο το μηδέν. Eu t = 0 για t = 1,2,3..n 2. Η διακύμανση της τυχαίας μεταβλητής u t είναι
ΜΑΘΗΜΑ 3ο Υποδείγματα μιας εξίσωσης Οι βασικές υποθέσεις 1. Ο διαταρακτικός όρος u t είναι μια τυχαία μεταβλητή με μέσο το μηδέν. Eu t = 0 για t = 1,2,3..n 2. Η διακύμανση της τυχαίας μεταβλητής u t είναι
Bayesian statistics. DS GA 1002 Probability and Statistics for Data Science.
 Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών. Χρόνου (Ι)
 HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 5: Στοχαστικά/Τυχαία Σήματα Διακριτού Διάλεξη 5: Στοχαστικά/Τυχαία Σήματα Διακριτού Χρόνου (Ι) Στοχαστικά σήματα Στα προηγούμενα: Ντετερμινιστικά
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 5: Στοχαστικά/Τυχαία Σήματα Διακριτού Διάλεξη 5: Στοχαστικά/Τυχαία Σήματα Διακριτού Χρόνου (Ι) Στοχαστικά σήματα Στα προηγούμενα: Ντετερμινιστικά
Μέρος II. Στατιστική Συμπερασματολογία (Inferential Statistics)
 Μέρος II. Στατιστική Συμπερασματολογία (Inferential Statistics) Τυχαίο δείγμα και στατιστική συνάρτηση Χ={x 1, x,, x n } τυχαίο δείγμα μεγέθους n προερχόμενο από μια (παραμετρική) κατανομή με σ.π.π. f(x;θ).
Μέρος II. Στατιστική Συμπερασματολογία (Inferential Statistics) Τυχαίο δείγμα και στατιστική συνάρτηση Χ={x 1, x,, x n } τυχαίο δείγμα μεγέθους n προερχόμενο από μια (παραμετρική) κατανομή με σ.π.π. f(x;θ).
ΕΦΑΡΜΟΣΜΕΝΗ ΣΤΑΤΙΣΤΙΚΗ Ι Συμπληρωματικές Σημειώσεις Δημήτριος Παντελής
 ΕΦΑΡΜΟΣΜΕΝΗ ΣΤΑΤΙΣΤΙΚΗ Ι Συμπληρωματικές Σημειώσεις Δημήτριος Παντελής ΣΤΑΤΙΣΤΙΚΕΣ ΕΚΤΙΜΗΣΕΙΣ Οι συναρτήσεις πιθανότητας ή πυκνότητας πιθανότητας των διαφόρων τυχαίων μεταβλητών χαρακτηρίζονται από κάποιες
ΕΦΑΡΜΟΣΜΕΝΗ ΣΤΑΤΙΣΤΙΚΗ Ι Συμπληρωματικές Σημειώσεις Δημήτριος Παντελής ΣΤΑΤΙΣΤΙΚΕΣ ΕΚΤΙΜΗΣΕΙΣ Οι συναρτήσεις πιθανότητας ή πυκνότητας πιθανότητας των διαφόρων τυχαίων μεταβλητών χαρακτηρίζονται από κάποιες
ΑΣΚΗΣΕΙΣ ΔΙΑΣΤΗΜΑΤΩΝ ΕΜΠΙΣΤΟΣΥΝΗΣ. Άσκηση 1. Βρείτε δ/μα εμπιστοσύνης για τη μέση τιμή μ κανονικού πληθυσμού όταν n=20,
 ΜΕΜ64: Εφαρμοσμένη Στατιστική 1 ΑΣΚΗΣΕΙΣ ΔΙΑΣΤΗΜΑΤΩΝ ΕΜΠΙΣΤΟΣΥΝΗΣ Άσκηση 1. Βρείτε δ/μα εμπιστοσύνης για τη μέση τιμή μ κανονικού πληθυσμού όταν n=0, X = 7.5, σ = 16, α = 5%. Πως αλλάζει το διάστημα αν
ΜΕΜ64: Εφαρμοσμένη Στατιστική 1 ΑΣΚΗΣΕΙΣ ΔΙΑΣΤΗΜΑΤΩΝ ΕΜΠΙΣΤΟΣΥΝΗΣ Άσκηση 1. Βρείτε δ/μα εμπιστοσύνης για τη μέση τιμή μ κανονικού πληθυσμού όταν n=0, X = 7.5, σ = 16, α = 5%. Πως αλλάζει το διάστημα αν
3. ΣΕΙΡΙΑΚΟΣ ΣΥΝΤΕΛΕΣΤΗΣ ΣΥΣΧΕΤΙΣΗΣ
 3. ΣΕΙΡΙΑΚΟΣ ΣΥΝΤΕΛΕΣΤΗΣ ΣΥΣΧΕΤΙΣΗΣ Πρόβλημα: Ένας ραδιοφωνικός σταθμός ενδιαφέρεται να κάνει μια ανάλυση για τους πελάτες του που διαφημίζονται σ αυτόν για να εξετάσει την ποσοστιαία μεταβολή των πωλήσεων
3. ΣΕΙΡΙΑΚΟΣ ΣΥΝΤΕΛΕΣΤΗΣ ΣΥΣΧΕΤΙΣΗΣ Πρόβλημα: Ένας ραδιοφωνικός σταθμός ενδιαφέρεται να κάνει μια ανάλυση για τους πελάτες του που διαφημίζονται σ αυτόν για να εξετάσει την ποσοστιαία μεταβολή των πωλήσεων
Μάθηση Λανθανόντων Μοντέλων με Μερικώς Επισημειωμένα Δεδομένα (Learning Aspect Models with Partially Labeled Data) Αναστασία Κριθαρά.
 Μάθηση Λανθανόντων Μοντέλων με Μερικώς Επισημειωμένα Δεδομένα (Learning Aspect Models with Partially Labeled Data) Αναστασία Κριθαρά Xerox Research Centre Europe LIP6 - Université Pierre et Marie Curie
Μάθηση Λανθανόντων Μοντέλων με Μερικώς Επισημειωμένα Δεδομένα (Learning Aspect Models with Partially Labeled Data) Αναστασία Κριθαρά Xerox Research Centre Europe LIP6 - Université Pierre et Marie Curie
ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ 1
 ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ 1 ΣΥΝΔΥΑΣΤΙΚΗ 1.1 ΒΑΣΙΚΗ ΑΡΧΗ ΑΠΑΡΙΘΜΗΣΗΣ... 13 1.2 ΠΡΟΣΘΕΤΙΚΗ ΑΡΧΗ ΑΠΑΡΙΘΜΗΣΗΣ... 15 1.3 ΔΙΑΤΑΞΕΙΣ..... 16 1.4 ΜΕΤΑΘΕΣΕΙΣ... 18 1.5 ΣΥΝΔΥΑΣΜΟΙ... 20 1.6 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΜΕΤΑΘΕΣΕΙΣ......
ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ 1 ΣΥΝΔΥΑΣΤΙΚΗ 1.1 ΒΑΣΙΚΗ ΑΡΧΗ ΑΠΑΡΙΘΜΗΣΗΣ... 13 1.2 ΠΡΟΣΘΕΤΙΚΗ ΑΡΧΗ ΑΠΑΡΙΘΜΗΣΗΣ... 15 1.3 ΔΙΑΤΑΞΕΙΣ..... 16 1.4 ΜΕΤΑΘΕΣΕΙΣ... 18 1.5 ΣΥΝΔΥΑΣΜΟΙ... 20 1.6 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΜΕΤΑΘΕΣΕΙΣ......
Δειγματοληψία στην εκπαιδευτική έρευνα. Είδη δειγματοληψίας
 Δειγματοληψία στην εκπαιδευτική έρευνα Είδη δειγματοληψίας Γνωρίζουμε ότι: Με τη στατιστική τα δεδομένα γίνονται πληροφορίες Στατιστική Δεδομένα Πληροφορία Αλλά από πού προέρχονται τα δεδομένα; Πώς τα
Δειγματοληψία στην εκπαιδευτική έρευνα Είδη δειγματοληψίας Γνωρίζουμε ότι: Με τη στατιστική τα δεδομένα γίνονται πληροφορίες Στατιστική Δεδομένα Πληροφορία Αλλά από πού προέρχονται τα δεδομένα; Πώς τα
27-Ιαν-2009 ΗΜΥ 429. 2. (ι) Βασική στατιστική (ιι) Μετατροπές: αναλογικό-σεψηφιακό και ψηφιακό-σε-αναλογικό
 ΗΜΥ 429 2. (ι) Βασική στατιστική (ιι) Μετατροπές: αναλογικό-σεψηφιακό και ψηφιακό-σε-αναλογικό 1 (i) Βασική στατιστική 2 Στατιστική Vs Πιθανότητες Στατιστική: επιτρέπει μέτρηση και αναγνώριση θορύβου και
ΗΜΥ 429 2. (ι) Βασική στατιστική (ιι) Μετατροπές: αναλογικό-σεψηφιακό και ψηφιακό-σε-αναλογικό 1 (i) Βασική στατιστική 2 Στατιστική Vs Πιθανότητες Στατιστική: επιτρέπει μέτρηση και αναγνώριση θορύβου και
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 6-7 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Λέκτορας v.koutras@fme.aegea.gr Τηλ: 735468 Σε αρκετές εφαρμογές
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 6-7 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Λέκτορας v.koutras@fme.aegea.gr Τηλ: 735468 Σε αρκετές εφαρμογές
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΣΚΕΨΗ ΤΟΜΟΣ ΙΙ
 Ι. ΠΑΝΑΡΕΤΟΥ & Ε. ΞΕΚΑΛΑΚΗ Καθηγητών του Τμήματος Στατιστικής του Οικονομικού Πανεπιστημίου Αθηνών ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΣΚΕΨΗ ΤΟΜΟΣ ΙΙ (Εισαγωγή στις Πιθανότητες και την Στατιστική Συμπερασματολογία)
Ι. ΠΑΝΑΡΕΤΟΥ & Ε. ΞΕΚΑΛΑΚΗ Καθηγητών του Τμήματος Στατιστικής του Οικονομικού Πανεπιστημίου Αθηνών ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΣΚΕΨΗ ΤΟΜΟΣ ΙΙ (Εισαγωγή στις Πιθανότητες και την Στατιστική Συμπερασματολογία)
iii ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος
 iii ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος xi 1 Αντικείμενα των Πιθανοτήτων και της Στατιστικής 1 1.1 Πιθανοτικά Πρότυπα και Αντικείμενο των Πιθανοτήτων, 1 1.2 Αντικείμενο της Στατιστικής, 3 1.3 Ο Ρόλος των Πιθανοτήτων
iii ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος xi 1 Αντικείμενα των Πιθανοτήτων και της Στατιστικής 1 1.1 Πιθανοτικά Πρότυπα και Αντικείμενο των Πιθανοτήτων, 1 1.2 Αντικείμενο της Στατιστικής, 3 1.3 Ο Ρόλος των Πιθανοτήτων
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 7-8 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutras@fme.aegea.gr Τηλ: 735468 Σε αρκετές εφαρμογές
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 7-8 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutras@fme.aegea.gr Τηλ: 735468 Σε αρκετές εφαρμογές
Εκτιμητές Μεγίστης Πιθανοφάνειας (Maximum Likelihood Estimators MLE)
 Εκτιμητές Μεγίστης Πιθανοφάνειας (Maximum Likelihood Estimators MLE) Εστω τ.δ. X={x, x,, x } με κατανομή με σ.π.π. f(x;θ). Η από-κοινού σ.π.π. των δειγμάτων είναι η συνάρτηση L f x, x,, x; f x i ; και
Εκτιμητές Μεγίστης Πιθανοφάνειας (Maximum Likelihood Estimators MLE) Εστω τ.δ. X={x, x,, x } με κατανομή με σ.π.π. f(x;θ). Η από-κοινού σ.π.π. των δειγμάτων είναι η συνάρτηση L f x, x,, x; f x i ; και
Είδη Μεταβλητών. κλίµακα µέτρησης
 ΠΕΡΙΕΧΟΜΕΝΑ Κεφάλαιο 1 Εισαγωγικές Έννοιες 19 1.1 1.2 1.3 1.4 1.5 1.6 1.7 Η Μεταβλητότητα Η Στατιστική Ανάλυση Η Στατιστική και οι Εφαρµοσµένες Επιστήµες Στατιστικός Πληθυσµός και Δείγµα Το στατιστικό
ΠΕΡΙΕΧΟΜΕΝΑ Κεφάλαιο 1 Εισαγωγικές Έννοιες 19 1.1 1.2 1.3 1.4 1.5 1.6 1.7 Η Μεταβλητότητα Η Στατιστική Ανάλυση Η Στατιστική και οι Εφαρµοσµένες Επιστήµες Στατιστικός Πληθυσµός και Δείγµα Το στατιστικό
Βιοστατιστική ΒΙΟ-309
 Βιοστατιστική ΒΙΟ-309 Χειμερινό Εξάμηνο Ακαδ. Έτος 2017-2018 Ντίνα Λύκα lika@biology.uoc.gr 1. Εισαγωγή Εισαγωγικές έννοιες Μεταβλητότητα : ύπαρξη διαφορών μεταξύ ομοειδών μετρήσεων Μεταβλητή: ένα χαρακτηριστικό
Βιοστατιστική ΒΙΟ-309 Χειμερινό Εξάμηνο Ακαδ. Έτος 2017-2018 Ντίνα Λύκα lika@biology.uoc.gr 1. Εισαγωγή Εισαγωγικές έννοιες Μεταβλητότητα : ύπαρξη διαφορών μεταξύ ομοειδών μετρήσεων Μεταβλητή: ένα χαρακτηριστικό
Εισαγωγή στη θεωρία ακραίων τιμών
 Εισαγωγή στη θεωρία ακραίων τιμών Αντικείμενο της θεωρίας ακραίων τιμών αποτελεί: Η ανάπτυξη και μελέτη στοχαστικών μοντέλων με σκοπό την επίλυση προβλημάτων που σχετίζονται με την εμφάνιση «πολύ μεγάλων»
Εισαγωγή στη θεωρία ακραίων τιμών Αντικείμενο της θεωρίας ακραίων τιμών αποτελεί: Η ανάπτυξη και μελέτη στοχαστικών μοντέλων με σκοπό την επίλυση προβλημάτων που σχετίζονται με την εμφάνιση «πολύ μεγάλων»
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 06-07 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Λέκτορας v.koutras@fme.aegea.gr Τηλ: 7035468 Τυχαίο Δείγμα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 06-07 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Λέκτορας v.koutras@fme.aegea.gr Τηλ: 7035468 Τυχαίο Δείγμα
Για να ελέγξουµε αν η κατανοµή µιας µεταβλητής είναι συµβατή µε την κανονική εφαρµόζουµε το test Kolmogorov-Smirnov.
 A. ΈΛΕΓΧΟΣ ΚΑΝΟΝΙΚΟΤΗΤΑΣ A 1. Έλεγχος κανονικότητας Kolmogorov-Smirnov. Για να ελέγξουµε αν η κατανοµή µιας µεταβλητής είναι συµβατή µε την κανονική εφαρµόζουµε το test Kolmogorov-Smirnov. Μηδενική υπόθεση:
A. ΈΛΕΓΧΟΣ ΚΑΝΟΝΙΚΟΤΗΤΑΣ A 1. Έλεγχος κανονικότητας Kolmogorov-Smirnov. Για να ελέγξουµε αν η κατανοµή µιας µεταβλητής είναι συµβατή µε την κανονική εφαρµόζουµε το test Kolmogorov-Smirnov. Μηδενική υπόθεση:
ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ ΠΡΩΤΟ
 ΠΕΡΙΕΧΟΜΕΝΑ Εισαγωγή 1. Γενικά... 25 2. Έννοια και Είδη Μεταβλητών... 26 3. Κλίμακες Μέτρησης Μεταβλητών... 29 3.1 Ονομαστική κλίμακα... 30 3.2. Τακτική κλίμακα... 31 3.3 Κλίμακα ισοδιαστημάτων... 34 3.4
ΠΕΡΙΕΧΟΜΕΝΑ Εισαγωγή 1. Γενικά... 25 2. Έννοια και Είδη Μεταβλητών... 26 3. Κλίμακες Μέτρησης Μεταβλητών... 29 3.1 Ονομαστική κλίμακα... 30 3.2. Τακτική κλίμακα... 31 3.3 Κλίμακα ισοδιαστημάτων... 34 3.4
Στατιστική Συμπερασματολογία
 Στατιστική Συμπερασματολογία Διαφάνειες 2 ου κεφαλαίου Σταύρος Χατζόπουλος 20/02/2017, 06/03/2017, 13/03/2017 1 Κεφάλαιο 2. Έλεγχος Απλών Υποθέσεων Τα προβλήματα ελέγχου υποθέσεων απορρέουν από παρατηρήσεις
Στατιστική Συμπερασματολογία Διαφάνειες 2 ου κεφαλαίου Σταύρος Χατζόπουλος 20/02/2017, 06/03/2017, 13/03/2017 1 Κεφάλαιο 2. Έλεγχος Απλών Υποθέσεων Τα προβλήματα ελέγχου υποθέσεων απορρέουν από παρατηρήσεις
ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΔΙΔΑΣΚΩΝ: ΘΑΝΑΣΗΣ ΚΑΖΑΝΑΣ. Οικονομετρία
 ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΔΙΔΑΣΚΩΝ: ΘΑΝΑΣΗΣ ΚΑΖΑΝΑΣ Οικονομετρία 4.1 Πολλαπλό Γραμμικό Υπόδειγμα Παλινδρόμησης Γενικεύοντας τη διμεταβλητή (Y, X) συνάρτηση
ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΔΙΔΑΣΚΩΝ: ΘΑΝΑΣΗΣ ΚΑΖΑΝΑΣ Οικονομετρία 4.1 Πολλαπλό Γραμμικό Υπόδειγμα Παλινδρόμησης Γενικεύοντας τη διμεταβλητή (Y, X) συνάρτηση
ΧΡΟΝΙΚΕΣ ΣΕΙΡΕΣ. Παπάνα Αγγελική
 ΧΡΟΝΙΚΕΣ ΣΕΙΡΕΣ 7o Μάθημα: Απλή παλινδρόμηση (ΕΠΑΝΑΛΗΨΗ) Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & ΠΑΜΑΚ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr Webpage: http://users.auth.gr/agpapana
ΧΡΟΝΙΚΕΣ ΣΕΙΡΕΣ 7o Μάθημα: Απλή παλινδρόμηση (ΕΠΑΝΑΛΗΨΗ) Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & ΠΑΜΑΚ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr Webpage: http://users.auth.gr/agpapana
Είδη Μεταβλητών Κλίμακα Μέτρησης Οι τεχνικές της Περιγραφικής στατιστικής ανάλογα με την κλίμακα μέτρησης Οι τελεστές Π και Σ
 ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ 1 Εισαγωγικές Έννοιες 19 1.1 1.2 1.3 1.4 1.5 1.6 1.7 Η Μεταβλητότητα Η Στατιστική Ανάλυση Η Στατιστική και οι Εφαρμοσμένες Επιστήμες Στατιστικός Πληθυσμός και Δείγμα Το στατιστικό
ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ 1 Εισαγωγικές Έννοιες 19 1.1 1.2 1.3 1.4 1.5 1.6 1.7 Η Μεταβλητότητα Η Στατιστική Ανάλυση Η Στατιστική και οι Εφαρμοσμένες Επιστήμες Στατιστικός Πληθυσμός και Δείγμα Το στατιστικό
