Geophysical fluids in Motion
|
|
|
- Ζωτικός Ανδρέου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Τµήµα Φυσικής, Πανεπιστήµιο Αθηνών Τοµέας Φυσικής Περιβάλλοντος Μετεωρολογίας Μάθηµα: Δυναµική των Ρευστών Geophysical fluids in Motion Η επίδραση της περιστροφής Γεωστροφική ισορροπία Στρώµατα Ekman Βαρυντικά κύµατα παρουσία περιστροφής Η επίδραση της στρωµάτωσης Μοντέλα στρωµάτων Γεωστροφική προσαρµογή Εσωτερικά κύµατα Σαράντης Σοφιανός
2 Γεωστροφική/υδροστατική προσέγγιση (µεγάλες κλίµακες) Για σύστηµα που χαρακτηρίζεται από: Ro = U fl 1 Ek = A H fl 2 1! H L Geoffrey Ingram + + = = = + A H fu+ A u 2 + A 2 + A 2 + A 2 w g + A w 2 + A f = (1) fu = 1 0 (2) = g (3) The geostrophic hydrostatic limit
3 Weather systems L H (Schematic)
4 The + = @y =0 Non-divergent horizontal flow (2D) Boussinesq + + or w =0
5 Τα στρώµατα Ekman (ροή παρουσία τριβής) Οι τυπικές γεωστροφικές ροές (πραγµατικές ή σε δεξαµενές) έχουν πολύ µικρό αριθµό Ekman. Ατµόσφαιρα: Η ~ 10 4 m, Α V ~ 1 m 2 s -1 E k = A V / fh 2 ~10-4 Ωκεανός: Η ~ 10 3 m, Α V ~ 10-2 m 2 s -1 E k = A V / fh 2 ~10-4 άρα η τριβή σε µεγάλης κλίµακας φαινόµενα είναι αµελητέα. Όµως κοντά σε όρια (π.χ. επιφάνεια της γης, βυθός, επιφάνεια θάλασσας κλπ.), σε περιοχές οριακών στρωµάτων, η κλίµακα του βάθους H είναι πολύ µικρότερη και η τριβή αρχίζει να παίζει σηµαντικό ρόλο. Στα στρώµατα αυτά ο E k είναι Ο(1), οπότε Ek 1 ) A V fh 2 1 ) d = H = s A V f Vagn Walfrid Ekman Ατµόσφαιρα: d ~ 100 m Ωκεανός: d ~ 10 m Άρα, µερικές εκατοντάδες µέτρα κοντά στην επιφάνεια της γης και µερικές δεκάδες µέτρα κοντά στο βυθό της θάλασσας, η τριβή είναι σηµαντική και η δυναµική ισορροπία είναι διαφορετική. Τα στρώµατα αυτά λέγονται στρώµατα Ekman. Τα στρώµατα αυτά νοιώθουν την ύπαρξη του και τις διεργασίες που συµβαίνουν δίπλα στο όριο (δες και διάλεξη για Τύρβη). Στη µελέτη αυτή θα ασχοληθούµε µε το κατώτερο στρώµα Ekman (το στρώµα που έχει στο κάτω µέρος σταθερό όριο).
6 a. Scaling H L 1 z Ro = U fl 1 Ek(vertical) = A V fh 2 1 αλλά A H r 2 Hu A 2 2 Και οι εξισώσεις κίνησης γίνονται: (µεγάλη οριζόντια κλίµακα) interior u g f + A V fu + A 2 2 (4) z = 0 Ekman layer u(z) d
7 b. Οριακές συνθήκες Bottom (z = 0) : u =0 Interior (z!1): u = u g z Στην περιοχή αυτή (interior) υπάρχει µόνο γεωστροφική ροή (και για απλούστευση θεωρούµε ότι η γεωστροφική ροή είναι µόνο στη διεύθυνση x, υ g = 0). Στο όριο αυτό ισχύει η γεωοστροφική ισορροπία: fu g = Οι οριζόντιες βαθµίδες πίεσης παραµένουν σταθερές σε όλη τη στήλη και αντικαθιστώντας τους όρους της βαθµίδας πίεσης (5) στην (4) = A 2 2 (6) f(u u g )=A 2 2 (7) z = 0 Εξισώσεις Ekman interior Ekman layer u(z) u g d
8 Πολλαπλασιάζοντας την (7) µε i = p 1 και προσθέτοντας την (6): d 2 V dz 2 = if A V (V u g ) (8) where V u + i remember (u g, g) / z (purely barotropic) z Οι οριακές συνθήκες είναι τώρα: V = u g at z!1 V = 0 at z =0 Μια ειδική λύση της (8) είναι V = u g και η γενική λύση είναι interior u g όπου V = Ae (1 i)z/ + Be (1+i)z/ + u g s 2A V f Για να ισχύει η πρώτη οριακή συνθήκη πρέπει Β = 0. Για να ισχύει και η δεύτερη οριακή συνθήκη πρέπει A = -u g. z = 0 Ekman layer u(z) d
9 Άρα η λύση είναι: u = u g "1 e z/ cos = u g e z/ sin z! (10) z!# (9) Henry M. Stommel Ekman Spiral u g Η επίδραση της τριβής περιορίζεται, βασικά, σε ένα στρώµα p 2A V /f που το πάχος του αυξάνει µε το A V και µειώνεται µε το f. Η u g δεν παίζει ρόλο (σε αντίθεση µε τα µη περιστρεφόµενα συστήµατα. Στην ατµόσφαιρα, όπου παρατηρείται οριακό στρώµα της τάξης του 1 km (για f ~ 10-4 s -1 ) το A V ~ 50 m 2 s -1 (αντίστοιχα στον ωκεανό A V ~ 0.5 m 2 s -1 ).
10 Η µεταφορά κατά Ekman κάθετα στην κύρια ροή υπολογίζεται από την ολοκλήρωση της (10): Z 1 και είναι στα αριστερά της γεωστροφικής ροής. 0 dz = u g s A V 2f = 1 2 u g Στο παράδειγµα αυτό όπου η ροή είναι κυκλωνική γεωστροφική στο εσωτερικό του ρευστού (Taylor columns) δηµιουργείται ένα στρώµα Ekman κοντά στον πυθµένα µε τη ροή κατά Ekman προς το κέντρο της δεξαµενής. Ekman layer L
11 Βαροτροπικά κύµατα παρουσία περιστροφής η λ Μήκος κύµατος (λ): Η απόσταση ανάµεσα σε δύο διαδοχικές κορυφές και Κυµαταριθµός (K) K 2 Περίοδος (Τ): Ο χρόνος που απαιτείται για δύο συνεχόµενες κορυφές να περάσουν από το ίδιο σηµείο και Συχνότητα (ω)! 2 T y Φασική ταχύτητα (C): C! K = T 2! K l Οµαδική ταχύτητα (C g ) - κυµατοπακέτο: = 2 K 2 k x
12 Εξισώσεις εργασίας (Single-shallow layer dynamics) (free surface) z z =0 H h = 0 H(flat bottom) z = H dw 0 dt W 0 T WU U H 0 L L U 0 L UH 2 H 0 L 2 H U 2 H 2 0 HL 2 ) 0 dw dt g 0 U 2 H 2 ghl 2 = 0F 2 R 2 a 1 hydrostatic approximation = 0g ) dp = 0 g dz ) Z z dp = Z z 0 g dz ) p( ) p(z) = 0 g( z) a = H L 1 F R = U p gh 1 ) p = 0 g ( (x, y) z)+p atm )r H p = 0 g r H
13 Ξεκινώντας + + = = + A H fu+ A u 2 + A 2 + A 2 + A @y @t A H fu+ A u 2 + A 2 + A 2 + A 2 2 Εξισώσεις διατήρησης της ορµής Τώρα = f(x, y) ανεξάρτητο από το z και άρα οι ταχύτητες u και υ είναι ανεξάρτητες από το z, δηλ. (u,υ) = f (x,y,t).
14 Εξίσωση διατήρησης της + + Z Z H / x, y Z H [u ( + H)] [ ( + H)] + w( ) w (H) but: w (H) =0, w( + @t H Shallow-water equations (single layer model) + A H fu+ A @y! u 2 + A 2
15 Θα µελετήσουµε βαροτροπικά (οµογενές µέσο) κύµατα, µεγάλης κλίµακας, όπου Ro = U fl 1 (γραµµικά κύµατα) αλλά τώρα Ro T = Temporal changes Rotation = U T τώρα Τ είναι της τάξης της περιόδου και όχι U/L. Επιπλέον, για απλούστευση θα χρησιµοποιήσουµε 1 fu = 1 ft 1 Ek = A H fl 2 or A V fh 2! = = + + f fu (12)! = 0 (13) Εξισώσεις εργασίας
16 Επιφανειακά κύµατα παρουσία περιστροφής (Poincare waves) Θεωρώντας µεγάλη κλίµακα (αλλά όχι πλανητική) η f µπορεί να θεωρηθεί σταθερή, οι κυµατικές λύσεις για τα u, υ και η µπορούν να γραφούν ως u = u 0 e i(kx+ly!t) Henri Poincaré i(kx+ly!t) = 0 e = 0 e i(kx+ly!t) όπου k και l είναι οι x- και y-συνιστώσες του κυµαταριθµού και ω η συχνότητα του κύµατος. Αντικαθιστώντας στις εξισώσεις (11) έως (13): i!u f = igk i! + fu = igl i! + H (iku + il )=0 για µη τετριµµένη λύση, η ορίζουσα των συντελεστών πρέπει να είναι ίση µε µηδέν, άρα!! 2 f 2 gh k 2 + l 2 = 0 (14) Μία λύση είναι ω = 0 (steady state - γεωστροφία). Η άλλες λύσεις είναι:! = p f 2 + ghk 2 (15) όπου K = (k 2 +l 2 ) 1/2. Τα κύµατα που περιγράφονται από τη σχέση αυτή διασποράς ονοµάζονται κύµατα Poincare.
17 Στο όριο f = 0 (ή αντίστοιχα Κ 2 >> f 2 /gh ή Κ 2 >> 1/R 2 ) η σχέση διασποράς γίνεται! = p ghk που είναι η σχέση διασποράς για τα απλά επιφανειακά µακρά κύµατα βαρύτητας και William Thomson, Lord Kelvin R = p gh f η Ακτίνα Αποδιαµόρφωσης Rossby (Rossby Radius of Deformation) που δείχνει τη σηµαντικότητα της περιστροφής σε σχέση µε την κλίµακα L. Σε αντίθετη περίπτωση (λ >> R) ω = f αδρανειακές κινήσεις (inertial oscillations).
18 Πλανητικά κύµατα (Rossby waves) Η επόµενη κατηγορία κυµάτων που θα µελετήσουµε έχει κλίµακες τόσο µεγάλες και τα κύµατα είναι τόσο αργά, που δέχονται όχι µόνο την επίδραση της περιστροφής αλλά και της µεταβολές της σε σχέση µε το γεωγραφικό πλάτος (planetary effect - f = 2Ω sin φ - τα κύµατα αυτά είναι οι µηχανισµοί εξέλιξης των µεγάλων γεωστροφικών πλανητικών συστηµάτων που µελετήσαµε σε προηγούµενες διαφάνειες) Carl-Gustaf Arvid Rossby Αν θεωρήσουµε ότι φ 0 είναι το γεωγραφικό πλάτος στο µέσο της περιοχής που εξελίσσεται ένα τέτοιο κύµα, µπορούµε να προσεγγίσουµε το γεωγραφικό πλάτος ως φ = φ 0 + y/a (* για µικρές γωνίες sin φ φ), όπου a είναι η ακτίνα του πλανήτη (a Γη = 6371 km). Θεωρώντας το y/a µικρή µεταβολή µπορούµε να αναπτύξουµε τη συχνότητα Coriolis σε σειρά Taylor f =2 sin ' 0 +2 y a cos ' κρατώντας µόνο τους δύο πρώτους όρους, µπορούµε να γράψουµε f = f y (16) όπου β0 = 2 (Ω/a) cos φ 0 ονοµάζεται παράµετρος β (β parameter). Τυπικές τιµές για µεσαία γεωγραφικά πλάτη είναι f 0 = 10-4 s -1 και β 0 = s -1 m -1. Η προσέγγιση κατά την οποία κρατάµε µόνο τον πρώτο όρο της σειράς Taylor ονοµάζεται f-plane approximation και η προσέγγιση (16) β-plane approximation.
19 Αντικαθιστώντας την (16) στις εξισώσεις εργασίας (11-13) (f y) +(f y) u @t + + = 0 (19) Λόγω της πολύ αργής εξέλιξης των διαδικασιών αυτών, µια πρώτη προσέγγιση είναι ότι οι ταχύτητες καθορίζονται από τη γεωστροφική ισορροπία (quasi-geostrophic approximation) και οι µεγάλοι όροι (που περιέχουν τα f 0, g και Η) ορίζουν τη γεωστροφική δυναµική του συστήµατος (ενώ οι µικρότεροι όροι ορίζουν τις διαταραχές γύρω από τη δυναµική αυτή). Με τη προσέγγιση αυτή ' f (20) u ' g (21) Quasi-geostrophic approximation
20 Αντικαθιστώντας τις (20-21) στους µικρούς όρους των εξισώσεων εργασίας (17-18) 2 f f 0 2 f + f 0u 0g f = 0g f @y και λύνοντας ως προς u, υ u = g g f g f 2 (22) = g g f g f 2 (23) geostrophic a-geostrophic Αντικαθιστώντας τις (22-23) r2 H = 0 (24) όπου R = p gh/f είναι η ακτίνα αποδιαµόρφωσης Rossby.
21 Αναζητούµε και πάλι κυµατική λύση της µορφής i(kx+ly!t) = 0 e! = 0R 2 k 1+R 2 (k 2 + l 2 ) (25) Σχέση διασποράς κυµάτων Rossby (ή πλανητικών κυµάτων) Στο όριο β 0 = 0 και ω = 0 και η λύση αντιστοιχεί στη γεωστροφική ισορροπία σε f-plane. Διερεύνηση µε βάση το µήκος κύµατος λ (= 2π/K)των κυµάτων Rossby: Βραχέα κύµατα Rossby: <R! K 2 1 R 2!! ' 0k K 2 for l =0!! ' 0 k! Μακρά κύµατα Rossby: >R! K 2 1 R 2!! ' 0KR 2 for l =0!! ' 0kR 2 Φασική ταχύτητα (στη x-διεύθυνση) c x = ω/k c x! k = 0R 2 1+R 2 (k 2 + l 2 ) πάντα αρνητική ενώ η φασική ταχύτητα (στη y-διεύθυνση) c y = ω/l µπορεί να έχει οποιοδήποτε πρόσηµο (η φασική ταχύτητα έχει γενική δυτική διεύθυνση W NW - SW).
22 Για τη µελέτη της οµαδικής ταχύτητας θα περιοριστούµε στη x-διεύθυνση (l = 0) και 0k! = 1 R 2 + k2 Βραχέα κύµατα Rossby: Μακρά κύµατα Rossby: Από την (25) και <R!! ' >R!! ' c g (long) >c g (short) 0 k! = 0 k 2 0kR 2! = 0R 2 ω β 0 R lr! 2 k l 2 = 2!! ! R 2 που περιγράφει κύκλο στο χώρο των κυµαταριθµών (k,l) kr
23 Πλανητικά κύµατα (παραδείγµατα) Atmospheric Oceanic (Homvoller diagram)
24 Ο µηχανισµός των πλανητικών κυµάτων Θεωρώντας ασήµαντες απώλειες από τις µη συντηρητικές δυνάµεις (τριβή) και για τη διατήρηση του δυναµικού στροβιλισµού d (f + ) =0 dt
25 Μπορούµε να προσοµοιάσουµε το β-effect µε τις αντίστοιχες µεταβολές στην τοπογραφία (θ, σε πλανητική κλίµακα). Η σχέση διασποράς είναι αντίστοιχη των κυµάτων Rossby. Αξιοποιούµε αυτό το γεγονός για τη µελέτη στο εργαστήριο των ιδιοτήτων των κυµάτων Rossby.! = g f k 1+R 2 (k 2 + l 2 ) N S
26 Η επίδραση της στρωµάτωσης και ο Froude number z ρ(z) U N = s L (z) H Για να ορίσουµε ένα αριθµό που εκτιµάει την επίδραση της στρωµάτωσης χρησιµοποιούµε το διπλανό παράδειγµα, π.χ. άνεµος πάνω από εµπόδιο. Η στρωµάτωση προσπαθεί να περιορίσει την κατακόρυφη µετατόπιση για την υπερπήδηση του εµποδίου. Ο χρόνος που απαιτείται για την υπερπήδηση του εµποδίου είναι T = L/U και η αντίστοιχη κατακόρυφη µετατόπιση Δz = WT = WL/U. Οι κατακόρυφες µετατοπίσεις θα προκαλέσουν µεταβολή στη στρωµάτωση z = 0N 2 g U William Froude Οι µεταβολές πυκνότητας δηµιουργούν µεταβολές στην πίεση (µέσω υδροστατικής ισορροπίας) P = gh = 0N 2 HLW U Αντίστοιχα, οι µεταβολές στην πίεση θα επιφέρουν µεταβολές στην ταχύτητα /@t (1/ 0 )@p/@x u T U L/U P 0 L ) U 2 N 2 HLW ) W/H U U/L U 2 N 2 H 2 Αν U < NH η κατακόρυφη απόκλιση είναι πολύ µικρότερη από την οριζόντια και το ρευστό µετατοπίζεται οριζόντια και όχι κατακόρυφα (το /@x εξισορροπείται από /@y και όχι από Ορίζουµε ως αριθµό Froude Fr = U NH Froude number
27 Αν στο προηγούµενο παράδειγµα θεωρήσουµε γεωστροφική ισορροπία Αυτό σηµαίνει ότι σε µεγάλες χωρικές κλίµακες (R o 1) αυξάνει η κλίµακα της κατακόρυφης ταχύτητας (να βοηθάει τις κατακόρυφες µετατοπίσεις). Όµως W/H U/L (δεν µπορούµε να έχουµε κατακόρυφη απόκλιση χωρίς οριζόντια), οπότε Fr 2 apple Ro άρα fu Στα γεωφυσικά ρευστά, συνήθως, H < L αλλά και f < N, ώστε ο αριθµός να µπορεί να είναι κοντά στη µονάδα. Αν B u <1 (F r2 /R o < R o ) η στρωµάτωση κυριαρχεί και περιορίζει τις διαταραχές. Αν B u > 1 ισχύει το αντίθετο. Τέλος, αν B u = 1 οι δύο µηχανισµοί είναι ισοδύναµοι και Ατµόσφαιρα: ~500 km Ωκεανός: ~50 km) P 0 L ) W/H U/L U 2 fl N 2 H 2 U = Fr2 Ro U apple N 2 H 2 fl που ορίζει ένα ανώτατο όριο για την κλίµακα ταχύτητας. Αν αυτή είναι ορισµένη από εξωτερικούς παράγοντες (π.χ. γενική κυκλοφορία) η σχέση αυτή καθορίζει τις επιτρεπτές χωρικές κλίµακες των κατακόρυφων διαταραχών. Αν όλες οι συνθήκες είναι εξωτερικά καθορισµένες ώστε να µην ισχύει η ανισότητα αναπτύσσονται ειδικοί τύποι κυκλοφορίας (π.χ. Taylor columns). Ορίζουµε ως αριθµό Burger L = NH f Bu = = R i NH! 2 = Ro fl Fr! 2 Εσωτερική Ακτίνα Αποδιαµόρφωσης Rossby Internal Rossby Radius of Deformation
28 Μοντέλα στρωµάτων (Reduced gravity models) z P Η h 1, ρ 1 P 2, ρ 2 Η T & 1 # & 1 # Homogeneous $ 1! layers $ 2! layers % 2 " % 2 " P 1 = P a 1 gz and P 2 = Pa+ 1 gh 2 g (z + h) r H P 2 =0 )r H P a + 1 gr H h 2 gr H h =0 )r H P a =( 2 1 ) gr H h ) 1 r H P 1 = ( 2 1 ) gr H h = g 0 r H h f = + fu
29 @x Z 0 @t + Z 0 h / x, y Z ( h)+w(0) w ( h) but: w (0) = 0, w( (h g 0 = g (h h wdz=0 z Η P 2, ρ 2 f = + fu h P 1, ρ 1 Η T Reduced gravity equations Τώρα µπορούµε να γράψουµε τη συχνότητα Brunt Vaissala: N 2 = g 0 H = g0 H Και η Internal Rossby Radius of deformation: R = NH f = g' H f
30 Εσωτερικά κύµατα βαρύτητας: απλή στρωµάτωση (Internal gravity waves (layers) Δύο άπειρα στρώµατα (ένα µε πυκνότητα ρ 1, πάνω σε ένα άπειρο στρώµα µε πυκνότητα ρ 2 ) ασυµπίεστου ρευστού. Για ευκολία θα αγνοήσουµε την περιστροφή και θα µελετήσουµε το σύστηµά σε δύο διαστάσεις (x,z). Ορίζουµε ένα δυναµικό ταχύτητας ϕ, τέτοιο ώστε z x ρ 1 ρ 2 >ρ 1 ζ z=0 (27) (26) Λόγω της εξίσωσης συνέχειας (σε δύο διαστάσεις) καταλήγουµε στην εξίσωση =0 Στο παράδειγµα µας έχουµε δύο στρώµατα, οπότε ορίζουµε δύο δυναµικά ϕ 1 και ϕ 2 και θα επιλύσουµε το παρακάτω σύστηµα εξισώσεων (µε τις κατάλληλες οριακές =0 1 = Ae kz + Ce kz i(kx!t) e µε γενικές λύσεις και 2 = Be kz + De kz i(kx!t) e = ae i(kx = be i(kx!t)!t)
31 Οι οριακές συνθήκες σχετίζονται µε µηδενική ταχύτητα στο άπειρο (όχι άπειρη κινητική ενέργεια) και συνεχείς λύσεις στην διεπιφάνεια: at z!1 1! 0 at z! 1 2! 0 at z @t Οι δύο πρώτες οριακές συνθήκες οδηγούν στο C = 0 και D = 0 στις παραπάνω λύσεις και άρα Χρησιµοποιώντας την τρίτη οριακή συνθήκη (continuity of velocity solution) at z =0 + 1g = + 2g (continuity of pressure - from Bernoulli equ.) 1 = Ae kz i(kx!t) e 2 = Be kz i(kx!t) e Ake 0 e i(kx!t) = Bke 0 i(kx!t) e A = B and A = Αντικαθιστώντας στην τέταρτη οριακή συνθήκη v! u! = t 2 1 gk ia! k (28) Σχέση διασποράς βαρυντικών κυµάτων σε διεπιφάνεια
32 Αν αντικαταστήσουµε τις λύσεις για ϕ1 και ϕ2 στις (34) c u 1 =!ae kz i(kx!t) e u 2 =!aekz e i(kx!t) z ρ 1 ρ 2 x z=0 Για ρ 0 = (ρ 1 +ρ 2 )/2 µπορούµε να γράψουµε τη σχέση διασποράς ως όπου και! = v u t 2 1 g 2 0 g 0 = g s 0 g 0! c! k = 2k s = 1 g 0 2 2k k = s g 0 k 2 Reduced Gravity (29) φασική ταχύτητα οµαδική ταχύτητα
33 Εσωτερικά κύµατα βαρύτητας (η έκφραση τους στην επιφάνεια της θάλασσας και στην κορυφή της ατµόσφαιρας) 33
34 Γεωστροφική προσαρµογή (Geostrophic adjustment) Θεωρώντας ότι δεν υπάρχουν βαθµίδες στην y-διεύθυνση (άπειρες + u f = + u@ + fu = @t (hu) = 0 Αρχικός δυναµικός στροβιλισµός: q i = f H Τελικός δυναµικός στροβιλισµός: Αρχικές συνθήκες: u = =0 h = H for x<0 h = 0 for x>0 Οριακές συνθήκες: u,! 0, h! H at x! 1 u = da dt, q f = f /@x h h = 0 at x = a(t) f H = f /@x h (33)
35 Μόλις ολοκληρωθεί η προσαρµογή, οι παράγωγοι του χρόνου µηδενίζονται: f = (34) 6= 0 (το h µηδενίζεται σε κάποιο σηµείο ενώ παίρνει τιµές σε άλλα σηµεία του x): + fu = (hu) = 0 Η λύσεις για (33) και (37): " H = H 1 exp x a!# R = p g 0 H exp x a! R p! g0 H where R = f από την (36) το u είναι µηδέν παντού µετά την ολοκλήρωση της προσαρµογής. Αντικαθιστώντας στην (34): Για να βρούµε το a, χρησιµοποιούµε τη διατήρηση του όγκου: που δίνει: f = (37) Z 0 1 (H h) dx = a = R = p g0 H f Z a 0 hdx
γ. Στην εξίσωση διατήρησης της τυρβώδους κινητικής ενέργειας (ΤΚΕ) εξηγείστε ποιοι όροι δηµιουργούν ΤΚΕ και ποιοι καταναλώνουν ΤΚΕ.
 ΔΥΝΑΜΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ ΙΟΥΝΙΟΣ 2014 ΘΕΜΑ 1 α. Στο παρακάτω σχήµα, δίδονται δύο στρώµατα ρευστού (30 o N), που βρίσκονται σε γεωστροφική ισορροπία. Στο κατώτερο στρώµα καταγράφεται ταχύτητα 10 cm/s, ενώ η
ΔΥΝΑΜΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ ΙΟΥΝΙΟΣ 2014 ΘΕΜΑ 1 α. Στο παρακάτω σχήµα, δίδονται δύο στρώµατα ρευστού (30 o N), που βρίσκονται σε γεωστροφική ισορροπία. Στο κατώτερο στρώµα καταγράφεται ταχύτητα 10 cm/s, ενώ η
Εξισώσεις Κίνησης (Equations of Motion)
 Εξισώσεις Κίνησης (Equations of Motion) Αναλύουμε την απόκριση ενός ρευστού υπό την επίδραση εσωτερικών και εξωτερικών δυνάμεων. Η εφαρμογή της ρευστομηχανικής στην ωκεανογραφία βασίζεται στη Νευτώνεια
Εξισώσεις Κίνησης (Equations of Motion) Αναλύουμε την απόκριση ενός ρευστού υπό την επίδραση εσωτερικών και εξωτερικών δυνάμεων. Η εφαρμογή της ρευστομηχανικής στην ωκεανογραφία βασίζεται στη Νευτώνεια
ΕΞΙΣΩΣΕΙΣ ΚΙΝΗΣΗΣ (Equations of Motion)
 ΚΕΦΑΛΑΙΟ 4 ΕΞΙΣΩΣΕΙΣ ΚΙΝΗΣΗΣ (Equations of Motion) Με τις Εξισώσεις Κίνησης αναλύουμε την απόκριση ενός ρευστού υπό την επίδραση εσωτερικών και εξωτερικών δυνάμεων. Οι εξισώσεις αυτές προκύπτουν από τη
ΚΕΦΑΛΑΙΟ 4 ΕΞΙΣΩΣΕΙΣ ΚΙΝΗΣΗΣ (Equations of Motion) Με τις Εξισώσεις Κίνησης αναλύουμε την απόκριση ενός ρευστού υπό την επίδραση εσωτερικών και εξωτερικών δυνάμεων. Οι εξισώσεις αυτές προκύπτουν από τη
Μετεωρολογία. Ενότητα 7. Δρ. Πρόδρομος Ζάνης Αναπληρωτής Καθηγητής, Τομέας Μετεωρολογίας-Κλιματολογίας, Α.Π.Θ.
 Μετεωρολογία Ενότητα 7 Δρ. Πρόδρομος Ζάνης Αναπληρωτής Καθηγητής, Τομέας Μετεωρολογίας-Κλιματολογίας, Α.Π.Θ. Ενότητα 7: Η κίνηση των αέριων μαζών Οι δυνάμεις που ρυθμίζουν την κίνηση των αέριων μαζών (δύναμη
Μετεωρολογία Ενότητα 7 Δρ. Πρόδρομος Ζάνης Αναπληρωτής Καθηγητής, Τομέας Μετεωρολογίας-Κλιματολογίας, Α.Π.Θ. Ενότητα 7: Η κίνηση των αέριων μαζών Οι δυνάμεις που ρυθμίζουν την κίνηση των αέριων μαζών (δύναμη
Μετεωρολογία. Ενότητα 7. Δρ. Πρόδρομος Ζάνης Αναπληρωτής Καθηγητής, Τομέας Μετεωρολογίας-Κλιματολογίας, Α.Π.Θ.
 Μετεωρολογία Ενότητα 7 Δρ. Πρόδρομος Ζάνης Αναπληρωτής Καθηγητής, Τομέας Μετεωρολογίας-Κλιματολογίας, Α.Π.Θ. Ενότητα 7: Η κίνηση των αέριων μαζών Οι δυνάμεις που ρυθμίζουν την κίνηση των αέριων μαζών (δύναμη
Μετεωρολογία Ενότητα 7 Δρ. Πρόδρομος Ζάνης Αναπληρωτής Καθηγητής, Τομέας Μετεωρολογίας-Κλιματολογίας, Α.Π.Θ. Ενότητα 7: Η κίνηση των αέριων μαζών Οι δυνάμεις που ρυθμίζουν την κίνηση των αέριων μαζών (δύναμη
ΓΕΩΣΤΡΟΦΙΚΗ ΚΥΚΛΟΦΟΡΙΑ (GEOSTROPHIC CIRCULATION)
 ΚΕΦΑΛΑΙΟ 5 ΓΕΩΣΤΡΟΦΙΚΗ ΚΥΚΛΟΦΟΡΙΑ (GEOSTROPHIC CIRCULATION) Αδρανειακή Κίνηση Αν θεωρήσουμε τις εξής παραδοχές : 1) δεν υπάρχει οριζόντια πιεσοβαθμίδα, ) οι δυνάμεις F είναι μηδενικές, και 3) η κατακόρυφη
ΚΕΦΑΛΑΙΟ 5 ΓΕΩΣΤΡΟΦΙΚΗ ΚΥΚΛΟΦΟΡΙΑ (GEOSTROPHIC CIRCULATION) Αδρανειακή Κίνηση Αν θεωρήσουμε τις εξής παραδοχές : 1) δεν υπάρχει οριζόντια πιεσοβαθμίδα, ) οι δυνάμεις F είναι μηδενικές, και 3) η κατακόρυφη
Γεωστροφική Εξίσωση. Στην εξίσωση κίνησης θεωρούμε την απλούστερη λύση της. Έστω ότι το ρευστό βρίσκεται σε ακινησία. Και παραμένει σε ακινησία
 Γεωστροφική Εξίσωση Στο εσωτερικό του ωκεανού, η οριζόντια πιεσοβαθμίδα προκαλεί την εμφάνιση οριζόντιων ρευμάτων αλλά στη συνέχεια αντισταθμίζεται από τη δύναμη Coriolis, η οποία προκύπτει από τα οριζόντια
Γεωστροφική Εξίσωση Στο εσωτερικό του ωκεανού, η οριζόντια πιεσοβαθμίδα προκαλεί την εμφάνιση οριζόντιων ρευμάτων αλλά στη συνέχεια αντισταθμίζεται από τη δύναμη Coriolis, η οποία προκύπτει από τα οριζόντια
Αρχές Μετεωρολογίας και Κλιματολογίας (Διαλέξεις 7&8)
 ΧΑΡΟΚΟΠΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΓΕΩΓΡΑΦΙΑΣ ΕΛ. ΒΕΝΙΖΕΛΟΥ 70, 76 7 ΑΘΗΝΑ Αρχές Μετεωρολογίας και Κλιματολογίας (Διαλέξεις 7&8) Πέτρος Κατσαφάδος pkatsaf@hua.gr Τμήμα Γεωγραφίας Χαροκόπειο Πανεπιστήμιο Αθηνών
ΧΑΡΟΚΟΠΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΓΕΩΓΡΑΦΙΑΣ ΕΛ. ΒΕΝΙΖΕΛΟΥ 70, 76 7 ΑΘΗΝΑ Αρχές Μετεωρολογίας και Κλιματολογίας (Διαλέξεις 7&8) Πέτρος Κατσαφάδος pkatsaf@hua.gr Τμήμα Γεωγραφίας Χαροκόπειο Πανεπιστήμιο Αθηνών
Δυνάμεις που καθορίζουν την κίνηση των αέριων μαζών
 Κίνηση αερίων μαζών Πηγές: Fleae and Businer, An introduction to Atmosheric Physics Πρ. Ζάνης, Σημειώσεις, ΑΠΘ Π. Κατσαφάδος και Ηλ. Μαυροματίδης, Αρχές Μετεωρολογίας και Κλιματολογίας, Χαροκόπειο Παν/μιο.
Κίνηση αερίων μαζών Πηγές: Fleae and Businer, An introduction to Atmosheric Physics Πρ. Ζάνης, Σημειώσεις, ΑΠΘ Π. Κατσαφάδος και Ηλ. Μαυροματίδης, Αρχές Μετεωρολογίας και Κλιματολογίας, Χαροκόπειο Παν/μιο.
ΑΝΕΜΟΓΕNΗΣ ΚΥΚΛΟΦΟΡΙΑ (Wind-induced circulation)
 ΚΕΦΑΛΑΙΟ 6 ΑΝΕΜΟΓΕNΗΣ ΚΥΚΛΟΦΟΡΙΑ (Wind-induced circulation) Η γενική κυκλοφορία του επιφανειακού στρώματος του ωκεανού είναι ωρολογιακή στο Β. ημισφαίριο και αντι-ωρολογιακή στο Ν. ημισφαίριο. Τόσο η ανεμογενής
ΚΕΦΑΛΑΙΟ 6 ΑΝΕΜΟΓΕNΗΣ ΚΥΚΛΟΦΟΡΙΑ (Wind-induced circulation) Η γενική κυκλοφορία του επιφανειακού στρώματος του ωκεανού είναι ωρολογιακή στο Β. ημισφαίριο και αντι-ωρολογιακή στο Ν. ημισφαίριο. Τόσο η ανεμογενής
Introduction to Geophysical Fluid Dynamics
 Τµήµα Φυσικής, Πανεπιστήµιο Αθηνών Τοµέας Φυσικής Περιβάλλοντος Μετεωρολογίας Μάθηµα: Δυναµική των Ρευστών Introduction to Geophysical Fluid Dynamics Εισαγωγικές έννοιες Η επίδραση της περιστροφής Η επίδραση
Τµήµα Φυσικής, Πανεπιστήµιο Αθηνών Τοµέας Φυσικής Περιβάλλοντος Μετεωρολογίας Μάθηµα: Δυναµική των Ρευστών Introduction to Geophysical Fluid Dynamics Εισαγωγικές έννοιες Η επίδραση της περιστροφής Η επίδραση
ΩΚΕΑΝΟΓΡΑΦΙΑ E ΕΞΑΜΗΝΟ
 ΩΚΕΑΝΟΓΡΑΦΙΑ E ΕΞΑΜΗΝΟ Θαλάσσια ρεύματα και Ωκεάνια κυκλοφορία Οι θαλάσσιες μάζες δεν είναι σταθερές ΑΙΤΙΑ: Υπάρχει (αλληλ)επίδραση με την ατμόσφαιρα (π.χ., ο άνεμος ασκεί τριβή στην επιφάνεια της θάλασσας,
ΩΚΕΑΝΟΓΡΑΦΙΑ E ΕΞΑΜΗΝΟ Θαλάσσια ρεύματα και Ωκεάνια κυκλοφορία Οι θαλάσσιες μάζες δεν είναι σταθερές ΑΙΤΙΑ: Υπάρχει (αλληλ)επίδραση με την ατμόσφαιρα (π.χ., ο άνεμος ασκεί τριβή στην επιφάνεια της θάλασσας,
Ακουστικό Ανάλογο Μελανών Οπών
 Ακουστικό Ανάλογο Μελανών Οπών ιάδοση ηχητικών κυµάτων σε ρευστά. Ηχητικά κύµατα σε ακίνητο ρευστό. Εξίσωση συνέχειας: ρ t + ~ (ρ~v) =0 Εξίσωση Euler: ~v t +(~v ~ )~v = 1 ρ ~ p ( ~ Φ +...) Μικρές διαταραχές:
Ακουστικό Ανάλογο Μελανών Οπών ιάδοση ηχητικών κυµάτων σε ρευστά. Ηχητικά κύµατα σε ακίνητο ρευστό. Εξίσωση συνέχειας: ρ t + ~ (ρ~v) =0 Εξίσωση Euler: ~v t +(~v ~ )~v = 1 ρ ~ p ( ~ Φ +...) Μικρές διαταραχές:
1. Για το σύστηµα που παριστάνεται στο σχήµα θεωρώντας ότι τα νήµατα είναι αβαρή και µη εκτατά, τις τροχαλίες αµελητέας µάζας και. = (x σε μέτρα).
 Θέμα ο. ια το σύστηµα που παριστάνεται στο σχήµα θεωρώντας ότι τα νήµατα είναι αβαρή και µη εκτατά, τις τροχαλίες αµελητέας µάζας και M= M = M, υπολογίστε την επιτάχυνση της µάζας. ίνεται το g. (0) Λύση.
Θέμα ο. ια το σύστηµα που παριστάνεται στο σχήµα θεωρώντας ότι τα νήµατα είναι αβαρή και µη εκτατά, τις τροχαλίες αµελητέας µάζας και M= M = M, υπολογίστε την επιτάχυνση της µάζας. ίνεται το g. (0) Λύση.
Παραδείγματα Λυμένες ασκήσεις Κεφαλαίου 5
 Παραδείγματα Λυμένες ασκήσεις Κεφαλαίου 5 Παράδειγμα : Υπενθυμίζεται η γενική μορφή της σχέσεως διασποράς για την περίπτωση αλληλεπίδρασης κύματος-ρεύματος, παρουσία και των επιδράσεων της επιφανειακής
Παραδείγματα Λυμένες ασκήσεις Κεφαλαίου 5 Παράδειγμα : Υπενθυμίζεται η γενική μορφή της σχέσεως διασποράς για την περίπτωση αλληλεπίδρασης κύματος-ρεύματος, παρουσία και των επιδράσεων της επιφανειακής
p = p n, (2) website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Ιδανικά ρευστά Μαάιτα Τζαμάλ-Οδυσσέας 7 Απριλίου 2019 1 Καταστατικές εξισώσεις ιδανικού ρευστού Ιδανικό ρευστό είναι ένα υποθετικό
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Ιδανικά ρευστά Μαάιτα Τζαμάλ-Οδυσσέας 7 Απριλίου 2019 1 Καταστατικές εξισώσεις ιδανικού ρευστού Ιδανικό ρευστό είναι ένα υποθετικό
( ) ( ) ( )! r a. Στροφορμή στερεού. ω i. ω j. ω l. ε ijk. ω! e i. ω j ek = I il. ! ω. l = m a. = m a. r i a r j. ra 2 δ ij. I ij. ! l. l i.
 Στροφορμή στερεού q Η στροφορµή του στερεού γράφεται σαν: q Αλλά ο τανυστής αδράνειας έχει οριστεί σαν: q H γωνιακή ταχύτητα δίνεται από: ω = 2 l = m a ra ω ω ra ω e a ΦΥΣ 211 - Διαλ.31 1 r a I j = m a
Στροφορμή στερεού q Η στροφορµή του στερεού γράφεται σαν: q Αλλά ο τανυστής αδράνειας έχει οριστεί σαν: q H γωνιακή ταχύτητα δίνεται από: ω = 2 l = m a ra ω ω ra ω e a ΦΥΣ 211 - Διαλ.31 1 r a I j = m a
AΝΕΜΟΓΕΝΕΙΣ ΚΥΜΑΤΙΣΜΟΙ
 ΝΕΜΟΓΕΝΕΙΣ ΚΥΜΑΤΙΣΜΟΙ ΓΕΝΕΣΗ ΑΝΕΜΟΓΕΝΩΝ ΚΥΜΑΤΙΣΜΩΝ: Μεταφορά ενέργειας από τα κινούμενα κατώτερα ατμοσφαιρικά στρώματα στις επιφανειακές θαλάσσιες μάζες. η ενέργεια αρχικά περνά από την ατμόσφαιρα στην
ΝΕΜΟΓΕΝΕΙΣ ΚΥΜΑΤΙΣΜΟΙ ΓΕΝΕΣΗ ΑΝΕΜΟΓΕΝΩΝ ΚΥΜΑΤΙΣΜΩΝ: Μεταφορά ενέργειας από τα κινούμενα κατώτερα ατμοσφαιρικά στρώματα στις επιφανειακές θαλάσσιες μάζες. η ενέργεια αρχικά περνά από την ατμόσφαιρα στην
ΚΕΦΑΛΑΙΑ 3,4. Συστήµατα ενός Βαθµού ελευθερίας. k Για E 0, η (1) ισχύει για κάθε x. Άρα επιτρεπτή περιοχή είναι όλος ο άξονας
 ΚΕΦΑΛΑΙΑ,4. Συστήµατα ενός Βαθµού ελευθερίας. Να βρεθούν οι επιτρεπτές περιοχές της κίνησης στον άξονα ' O για την απωστική δύναµη F, > και για ενέργεια Ε. (α) Είναι V και οι επιτρεπτές περιοχές της κίνησης
ΚΕΦΑΛΑΙΑ,4. Συστήµατα ενός Βαθµού ελευθερίας. Να βρεθούν οι επιτρεπτές περιοχές της κίνησης στον άξονα ' O για την απωστική δύναµη F, > και για ενέργεια Ε. (α) Είναι V και οι επιτρεπτές περιοχές της κίνησης
ΑΚΤΟΜΗΧΑΝΙΚΗ ΚΑΙ ΠΑΡΑΚΤΙΑ ΕΡΓΑ
 ΑΚΤΟΜΗΧΑΝΙΚΗ ΚΑΙ ΠΑΡΑΚΤΙΑ ΕΡΓΑ ΔΟΜΗ ΜΑΘΗΜΑΤΟΣ i. ΣΤΟΙΧΕΙΑ ΚΥΜΑΤΟΜΗΧΑΝΙΚΗΣ ii. ΚΥΚΛΟΦΟΡΙΑ ΑΝΑΜΙΞΗ ΚΑΙ ΜΕΤΑΦΟΡΑ ΙΖΗΜΑΤΩΝ iii.παρακτια ΤΕΧΝΙΚΑ ΕΡΓΑ ΚΑΙ ΜΟΡΦΟΛΟΓΙΑ ΑΚΤΩΝ ΣΤΟΙΧΕΙΑ ΚΥΜΑΤΟΜΗΧΑΝΙΚΗΣ 1. Εισαγωγικά
ΑΚΤΟΜΗΧΑΝΙΚΗ ΚΑΙ ΠΑΡΑΚΤΙΑ ΕΡΓΑ ΔΟΜΗ ΜΑΘΗΜΑΤΟΣ i. ΣΤΟΙΧΕΙΑ ΚΥΜΑΤΟΜΗΧΑΝΙΚΗΣ ii. ΚΥΚΛΟΦΟΡΙΑ ΑΝΑΜΙΞΗ ΚΑΙ ΜΕΤΑΦΟΡΑ ΙΖΗΜΑΤΩΝ iii.παρακτια ΤΕΧΝΙΚΑ ΕΡΓΑ ΚΑΙ ΜΟΡΦΟΛΟΓΙΑ ΑΚΤΩΝ ΣΤΟΙΧΕΙΑ ΚΥΜΑΤΟΜΗΧΑΝΙΚΗΣ 1. Εισαγωγικά
Ρεύµατα παρουσία τριβής ανεµογενής κυκλοφορία
 Ρεύµατα παρουσία τριής ανεµογενής κυκλοφορία 6. Wind drien circulation Sarantis Sofianos Dept. of Physics, niersity of thens Ekman Theory Serdrup theory for the wind-drien circulation Stommel and Munk
Ρεύµατα παρουσία τριής ανεµογενής κυκλοφορία 6. Wind drien circulation Sarantis Sofianos Dept. of Physics, niersity of thens Ekman Theory Serdrup theory for the wind-drien circulation Stommel and Munk
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ. ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Σεπτέµβριος 2004
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Σεπτέµβριος 2004 Τµήµα Π. Ιωάννου & Θ. Αποστολάτου Θέµα 1 (25 µονάδες) Ένα εκκρεµές µήκους l κρέµεται έτσι ώστε η σηµειακή µάζα να βρίσκεται ακριβώς
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Σεπτέµβριος 2004 Τµήµα Π. Ιωάννου & Θ. Αποστολάτου Θέµα 1 (25 µονάδες) Ένα εκκρεµές µήκους l κρέµεται έτσι ώστε η σηµειακή µάζα να βρίσκεται ακριβώς
Αρµονικοί ταλαντωτές
 Αρµονικοί ταλαντωτές ΦΥΣ 131 - Διαλ. 31 Εκκρεµή - Απλό εκκρεµές θ l T mg r F Αυτή η εξίσωση είναι δύσκολο να λυθεί. Δεν µοιάζει µε τη γνωστή εξίσωση Για µικρές γωνίες θ µπορούµε όµως να γράψουµε Εποµένως
Αρµονικοί ταλαντωτές ΦΥΣ 131 - Διαλ. 31 Εκκρεµή - Απλό εκκρεµές θ l T mg r F Αυτή η εξίσωση είναι δύσκολο να λυθεί. Δεν µοιάζει µε τη γνωστή εξίσωση Για µικρές γωνίες θ µπορούµε όµως να γράψουµε Εποµένως
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 3//7/2013 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ
 ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 3//7/013 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα μάζας m=0.1 Kg κινείται σε οριζόντιο δάπεδο ευθύγραμμα με την
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 3//7/013 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα μάζας m=0.1 Kg κινείται σε οριζόντιο δάπεδο ευθύγραμμα με την
( ) Απειροστές περιστροφές και γωνιακή ταχύτητα ( ) = d! r dt = d! u P. = ω! r
 ΦΥΣ 211 - Διαλ.28 1 Απειροστές περιστροφές και γωνιακή ταχύτητα q Θεωρήστε ότι έχετε ένα σώµα το οποίο περιστρέφεται ως προς άξονα: q Θεωρήστε ότι ένα σηµείο P πάνω στο σώµα µε διάνυσµα θέσης r t O r t
ΦΥΣ 211 - Διαλ.28 1 Απειροστές περιστροφές και γωνιακή ταχύτητα q Θεωρήστε ότι έχετε ένα σώµα το οποίο περιστρέφεται ως προς άξονα: q Θεωρήστε ότι ένα σηµείο P πάνω στο σώµα µε διάνυσµα θέσης r t O r t
Κεφάλαιο M4. Κίνηση σε δύο διαστάσεις
 Κεφάλαιο M4 Κίνηση σε δύο διαστάσεις Κινηµατική σε δύο διαστάσεις Θα περιγράψουµε τη διανυσµατική φύση της θέσης, της ταχύτητας, και της επιτάχυνσης µε περισσότερες λεπτοµέρειες. Θα µελετήσουµε την κίνηση
Κεφάλαιο M4 Κίνηση σε δύο διαστάσεις Κινηµατική σε δύο διαστάσεις Θα περιγράψουµε τη διανυσµατική φύση της θέσης, της ταχύτητας, και της επιτάχυνσης µε περισσότερες λεπτοµέρειες. Θα µελετήσουµε την κίνηση
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Παράκτια Ωκεανογραφία
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διάλεξη 3η: Παράκτια Υδροδυναμική Κυκλοφορία Γιάννης Ν. Κρεστενίτης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διάλεξη 3η: Παράκτια Υδροδυναμική Κυκλοφορία Γιάννης Ν. Κρεστενίτης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
L = T V = 1 2 (ṙ2 + r 2 φ2 + ż 2 ) U (3)
 ΥΠΟΛΟΓΙΣΤΙΚΗ ΑΣΤΡΟΔΥΝΑΜΙΚΗ 3): Κινήσεις αστέρων σε αστρικά συστήματα Βασικές έννοιες Θεωρούμε αστρικό σύστημα π.χ. γαλαξία ή αστρικό σμήνος) αποτελούμενο από μεγάλο αριθμό αστέρων της τάξης των 10 8 10
ΥΠΟΛΟΓΙΣΤΙΚΗ ΑΣΤΡΟΔΥΝΑΜΙΚΗ 3): Κινήσεις αστέρων σε αστρικά συστήματα Βασικές έννοιες Θεωρούμε αστρικό σύστημα π.χ. γαλαξία ή αστρικό σμήνος) αποτελούμενο από μεγάλο αριθμό αστέρων της τάξης των 10 8 10
ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΕΝΟΤΗΤΑ 3: Η ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΕΝΕΡΓΕΙΑΣ ΚΑΙ Η ΕΞΙΣΩΣΗ BERNOULLI ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ 3 Ο : ΡΕΥΣΤΑ ΣΕ ΚΙΝΗΣΗ ΕΝΟΤΗΤΑ 3: Η ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΕΝΕΡΓΕΙΑΣ ΚΑΙ Η ΕΞΙΣΩΣΗ BERNOULLI ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση 1. ΘΕΜΑ Β Στο οριζόντιο σωλήνα του διπλανού σχήματος ρέει ιδανικό υγρό. Με τον οριζόντιο
ΚΕΦΑΛΑΙΟ 3 Ο : ΡΕΥΣΤΑ ΣΕ ΚΙΝΗΣΗ ΕΝΟΤΗΤΑ 3: Η ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΕΝΕΡΓΕΙΑΣ ΚΑΙ Η ΕΞΙΣΩΣΗ BERNOULLI ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση 1. ΘΕΜΑ Β Στο οριζόντιο σωλήνα του διπλανού σχήματος ρέει ιδανικό υγρό. Με τον οριζόντιο
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ Ι Φεβρουάριος 2013
 ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ Ι Φεβρουάριος 0 ΘΕΜΑ α) Να βρεθούν οι επιτρεπτές περιοχές της κίνησης στον άξονα x Ox για την απωστική δύναµη F x, > 0 και για ενέργεια Ε. β) Υλικό σηµείο µάζας m µπορεί να κινείται
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ Ι Φεβρουάριος 0 ΘΕΜΑ α) Να βρεθούν οι επιτρεπτές περιοχές της κίνησης στον άξονα x Ox για την απωστική δύναµη F x, > 0 και για ενέργεια Ε. β) Υλικό σηµείο µάζας m µπορεί να κινείται
Ανεμογενείς Κυματισμοί
 Ανεμογενείς Κυματισμοί Γένεση Ανεμογενών Κυματισμών: Μεταφορά ενέργειας από τα κινούμενα κατώτερα ατμοσφαιρικά στρώματα στις επιφανειακές θαλάσσιες μάζες. Η ενέργεια αρχικά περνά από την ατμόσφαιρα στην
Ανεμογενείς Κυματισμοί Γένεση Ανεμογενών Κυματισμών: Μεταφορά ενέργειας από τα κινούμενα κατώτερα ατμοσφαιρικά στρώματα στις επιφανειακές θαλάσσιες μάζες. Η ενέργεια αρχικά περνά από την ατμόσφαιρα στην
ΑΕΡΟ ΥΝΑΜΙΚΗ ΕΡΓ Νο2 ΡΟΗ ΑΕΡΑ ΓΥΡΩ ΑΠΟ ΚΥΛΙΝ ΡΟ
 ΑΕΡΟ ΥΝΑΜΙΚΗ ΕΡΓ Νο2 ΡΟΗ ΑΕΡΑ ΓΥΡΩ ΑΠΟ ΚΥΛΙΝ ΡΟ Η µελέτη της ροής µη συνεκτικού ρευστού γύρω από κύλινδρο γίνεται µε την µέθοδο της επαλληλίας (στην προκειµένη περίπτωση: παράλληλη ροή + ροή διπόλου).
ΑΕΡΟ ΥΝΑΜΙΚΗ ΕΡΓ Νο2 ΡΟΗ ΑΕΡΑ ΓΥΡΩ ΑΠΟ ΚΥΛΙΝ ΡΟ Η µελέτη της ροής µη συνεκτικού ρευστού γύρω από κύλινδρο γίνεται µε την µέθοδο της επαλληλίας (στην προκειµένη περίπτωση: παράλληλη ροή + ροή διπόλου).
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών. HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2016 ιδάσκων : Γ. Καφεντζής. εύτερη Σειρά Ασκήσεων - Λύσεις.
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2016 ιδάσκων : Γ. Καφεντζής εύτερη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. Από το ύψος και τη γωνία που µας δίνεται, έχουµε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2016 ιδάσκων : Γ. Καφεντζής εύτερη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. Από το ύψος και τη γωνία που µας δίνεται, έχουµε
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ η ΕΡΓΑΣΙΑ. Προθεσµία παράδοσης 16/11/10
 9// ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 3 - η ΕΡΓΑΣΙΑ Προθεσµία παράδοσης 6// Άσκηση A) Θεωρούµε x την απόσταση της µάζας m από το σηµείο ισορροπίας της και x, x3 τις αποστάσεις των µαζών m και m3 από το
9// ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 3 - η ΕΡΓΑΣΙΑ Προθεσµία παράδοσης 6// Άσκηση A) Θεωρούµε x την απόσταση της µάζας m από το σηµείο ισορροπίας της και x, x3 τις αποστάσεις των µαζών m και m3 από το
Ενότητα 9: Ασκήσεις. Άδειες Χρήσης
 Μηχανική των Ρευστών Ενότητα 9: Ασκήσεις Βασίλειος Λουκόπουλος, Επίκουρος Καθηγητής Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Μηχανική των Ρευστών Ενότητα 9: Ασκήσεις Βασίλειος Λουκόπουλος, Επίκουρος Καθηγητής Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
V. ΜΙΞΗ ΣΕ ΛΙΜΝΕΣ ΤΑΜΙΕΥΤΗΡΕΣ. 1. Εποχιακός Κύκλος
 V. ΜΙΞΗ ΣΕ ΛΙΜΝΕΣ ΤΑΜΙΕΥΤΗΡΕΣ 1. Εποχιακός Κύκλος Οι διαδικασίες µίξης σε λίµνες και ταµιευτήρες διέπονται κυρίως απο τη δράση του ανέµου, απο τις θερµικές ανταλλαγές στην επιφάνεια λόγω ηλιακής ακτινοβολίας
V. ΜΙΞΗ ΣΕ ΛΙΜΝΕΣ ΤΑΜΙΕΥΤΗΡΕΣ 1. Εποχιακός Κύκλος Οι διαδικασίες µίξης σε λίµνες και ταµιευτήρες διέπονται κυρίως απο τη δράση του ανέµου, απο τις θερµικές ανταλλαγές στην επιφάνεια λόγω ηλιακής ακτινοβολίας
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 12 ΙΟΥΝΙΟΥ 2017 ΕΚΦΩΝΗΣΕΙΣ
 ΘΕΜΑ Α ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 1 ΙΟΥΝΙΟΥ 017 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει σωστά την
ΘΕΜΑ Α ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 1 ΙΟΥΝΙΟΥ 017 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει σωστά την
ΦΥΕ14-5 η Εργασία Παράδοση
 ΦΥΕ4-5 η Εργασία Παράδοση.5.9 Πρόβληµα. Συµπαγής οµογενής κύλινδρος µάζας τυλιγµένος µε λεπτό νήµα αφήνεται να κυλίσει από την κορυφή κεκλιµένου επιπέδου µήκους l και γωνίας φ (ϐλέπε σχήµα). Το ένα άκρο
ΦΥΕ4-5 η Εργασία Παράδοση.5.9 Πρόβληµα. Συµπαγής οµογενής κύλινδρος µάζας τυλιγµένος µε λεπτό νήµα αφήνεται να κυλίσει από την κορυφή κεκλιµένου επιπέδου µήκους l και γωνίας φ (ϐλέπε σχήµα). Το ένα άκρο
Κεφάλαιο 14 Ταλαντώσεις. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 14 Ταλαντώσεις Ταλαντώσεις Ελατηρίου Απλή αρµονική κίνηση Ενέργεια απλού αρµονικού ταλαντωτή Σχέση απλού αρµονικού ταλαντωτή και κυκλικής κίνησης Το απλό εκκρεµές Περιεχόµενα 14 Το φυσικό εκκρεµές
Κεφάλαιο 14 Ταλαντώσεις Ταλαντώσεις Ελατηρίου Απλή αρµονική κίνηση Ενέργεια απλού αρµονικού ταλαντωτή Σχέση απλού αρµονικού ταλαντωτή και κυκλικής κίνησης Το απλό εκκρεµές Περιεχόµενα 14 Το φυσικό εκκρεµές
Διαταραχές Τροχιάς (2)
 Διαταραχές Τροχιάς (2) Μάθημα 6 ο Βαρυτικές διαταραχές δυναμικό πεπλατυσμένου σώματος Επίδραση τρίτου σώματος (α) γραμμική αέναη κίνηση (β) κίνηση σε συντονισμό Μη βαρυτικές διαταραχές Μεταβολές του μεγάλου
Διαταραχές Τροχιάς (2) Μάθημα 6 ο Βαρυτικές διαταραχές δυναμικό πεπλατυσμένου σώματος Επίδραση τρίτου σώματος (α) γραμμική αέναη κίνηση (β) κίνηση σε συντονισμό Μη βαρυτικές διαταραχές Μεταβολές του μεγάλου
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου 1ο Επαναληπτικό Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου 1ο Επαναληπτικό Ενδεικτικές Λύσεις Θέµα Α Α.1. Καθώς µια στοιχειώδης επιφάνεια αλλάζει προσανατολισµό χωρίς όµως το κέντρο της να αλλάξει ϐάθος εντός του υγρού, τότε αλλάζει
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου 1ο Επαναληπτικό Ενδεικτικές Λύσεις Θέµα Α Α.1. Καθώς µια στοιχειώδης επιφάνεια αλλάζει προσανατολισµό χωρίς όµως το κέντρο της να αλλάξει ϐάθος εντός του υγρού, τότε αλλάζει
ΔΟΜΗ ΚΑΙ ΣΥΣΤΑΣΗ. Εισαγωγή στη Φυσική της Ατμόσφαιρας: Ασκήσεις Α. Μπάης
 ΔΟΜΗ ΚΑΙ ΣΥΣΤΑΣΗ 1. Να υπολογιστούν η ειδική σταθερά R d για τον ξηρό αέρα και R v για τους υδρατμούς. 2. Να υπολογιστεί η μάζα του ξηρού αέρα που καταλαμβάνει ένα δωμάτιο διαστάσεων 3x5x4 m αν η πίεση
ΔΟΜΗ ΚΑΙ ΣΥΣΤΑΣΗ 1. Να υπολογιστούν η ειδική σταθερά R d για τον ξηρό αέρα και R v για τους υδρατμούς. 2. Να υπολογιστεί η μάζα του ξηρού αέρα που καταλαμβάνει ένα δωμάτιο διαστάσεων 3x5x4 m αν η πίεση
1. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου.
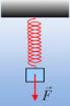 ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΚΡΟΥΣΗ.. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Σώμα μάζας = g κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα υ μέτρου υ = 5 /s συγκρούεται
ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΚΡΟΥΣΗ.. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Σώμα μάζας = g κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα υ μέτρου υ = 5 /s συγκρούεται
Ελληνικό Ανοικτό Πανεπιστήµιο Ενδεικτικές Λύσεις Θεµάτων Τελικών εξετάσεων στη Θεµατική Ενότητα ΦΥΕ34. Ιούλιος 2008 KYMATIKH. ιάρκεια: 210 λεπτά
 Κυµατική ΦΥΕ4 5/7/8 Ελληνικό Ανοικτό Πανεπιστήµιο Ενδεικτικές Λύσεις Θεµάτων Τελικών εξετάσεων στη Θεµατική Ενότητα ΦΥΕ4 Ιούλιος 8 KYMATIKH ιάρκεια: λεπτά Θέµα ο (Μονάδες:.5) A) Θεωρούµε τις αποστάσεις
Κυµατική ΦΥΕ4 5/7/8 Ελληνικό Ανοικτό Πανεπιστήµιο Ενδεικτικές Λύσεις Θεµάτων Τελικών εξετάσεων στη Θεµατική Ενότητα ΦΥΕ4 Ιούλιος 8 KYMATIKH ιάρκεια: λεπτά Θέµα ο (Μονάδες:.5) A) Θεωρούµε τις αποστάσεις
Το ελαστικο κωνικο εκκρεμε ς
 Το ελαστικο κωνικο εκκρεμε ς 1. Εξισώσεις Euler -Lagrange x 0 φ θ z F l 0 y r m B Το ελαστικό κωνικό εκκρεμές αποτελείται από ένα ελατήριο με σταθερά επαναφοράς k, το οποίο αναρτάται από ένα σταθερό σημείο,
Το ελαστικο κωνικο εκκρεμε ς 1. Εξισώσεις Euler -Lagrange x 0 φ θ z F l 0 y r m B Το ελαστικό κωνικό εκκρεμές αποτελείται από ένα ελατήριο με σταθερά επαναφοράς k, το οποίο αναρτάται από ένα σταθερό σημείο,
ΕΞΕΤΑΣΕΙΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ, 8 Μαρτίου 2019 Διδάσκοντες: Βαρσάμης Χρήστος, Φωτόπουλος Παναγιώτης
 ΕΞΕΤΑΣΕΙΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 218-219 ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ, 8 Μαρτίου 219 Διδάσκοντες: Βαρσάμης Χρήστος, Φωτόπουλος Παναγιώτης ΘΕΜΑ 1 Διάρκεια εξέτασης 2 ώρες Υλικό σημείο κινείται ευθύγραμμα πάνω στον άξονα
ΕΞΕΤΑΣΕΙΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 218-219 ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ, 8 Μαρτίου 219 Διδάσκοντες: Βαρσάμης Χρήστος, Φωτόπουλος Παναγιώτης ΘΕΜΑ 1 Διάρκεια εξέτασης 2 ώρες Υλικό σημείο κινείται ευθύγραμμα πάνω στον άξονα
Ορμή και Δυνάμεις. Θεώρημα Ώθησης Ορμής
 501 Ορμή και Δυνάμεις Θεώρημα Ώθησης Ορμής «Η μεταβολή της ορμής ενός σώματος είναι ίση με την ώθηση της δύναμης που ασκήθηκε στο σώμα» = ή Το θεώρημα αυτό εφαρμόζεται διανυσματικά. 502 Θεώρημα Ώθησης
501 Ορμή και Δυνάμεις Θεώρημα Ώθησης Ορμής «Η μεταβολή της ορμής ενός σώματος είναι ίση με την ώθηση της δύναμης που ασκήθηκε στο σώμα» = ή Το θεώρημα αυτό εφαρμόζεται διανυσματικά. 502 Θεώρημα Ώθησης
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΝΑΥΤΙΚΗΣ ΚΑΙ ΘΑΛΑΣΣΙΑΣ ΥΔΡΟΔΥΝΑΜΙΚΗΣ ΘΕΩΡΙΑ ΚΥΜΑΤΙΣΜΩΝ
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΝΑΥΤΙΚΗΣ ΚΑΙ ΘΑΛΑΣΣΙΑΣ ΥΔΡΟΔΥΝΑΜΙΚΗΣ ΘΕΩΡΙΑ ΚΥΜΑΤΙΣΜΩΝ . Εισαγωγή Ενα από τα βασικά θέματα της ναυτικής υδροδυναμικής είναι τα θαλάσσια κύματα. Τα θαλάσσια κύματα που ενδιαφέρουν την ναυτική
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΝΑΥΤΙΚΗΣ ΚΑΙ ΘΑΛΑΣΣΙΑΣ ΥΔΡΟΔΥΝΑΜΙΚΗΣ ΘΕΩΡΙΑ ΚΥΜΑΤΙΣΜΩΝ . Εισαγωγή Ενα από τα βασικά θέματα της ναυτικής υδροδυναμικής είναι τα θαλάσσια κύματα. Τα θαλάσσια κύματα που ενδιαφέρουν την ναυτική
( ) ( ) ( ) Μη αδρανειακά συστήματα αναφοράς. ( x, y,z) καρτεσιανό. !!z = h x, y,z. !! y = q. x = f. !! z = h
 Μη αδρανειακά συστήματα αναφοράς ΦΥΣ 211 - Διαλ.27 1 q Μέχρι τώρα έχουµε χρησιµοποιήσει συστήµατα αναφοράς όπως ( x, y,z) καρτεσιανό q όπου ο 2 ος νόµος του Newton F = m a x = f x, y,z έχει την µορφή:
Μη αδρανειακά συστήματα αναφοράς ΦΥΣ 211 - Διαλ.27 1 q Μέχρι τώρα έχουµε χρησιµοποιήσει συστήµατα αναφοράς όπως ( x, y,z) καρτεσιανό q όπου ο 2 ος νόµος του Newton F = m a x = f x, y,z έχει την µορφή:
ΑΤΜΟΣΦΑΙΡΙΚΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ. Η ατμόσφαιρα συμπεριφέρεται σαν ιδανικό αέριο (ειδικά για z>10 km)
 ΑΤΜΟΣΦΑΙΡΙΚΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ Η ατμόσφαιρα συμπεριφέρεται σαν ιδανικό αέριο (ειδικά για z>1 km) Οι αποστάσεις μεταξύ των μορίων είναι πολύ μεγάλες σχετικά με τον όγκο που κατέχουν Οι συγκρούσεις μεταξύ τους
ΑΤΜΟΣΦΑΙΡΙΚΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ Η ατμόσφαιρα συμπεριφέρεται σαν ιδανικό αέριο (ειδικά για z>1 km) Οι αποστάσεις μεταξύ των μορίων είναι πολύ μεγάλες σχετικά με τον όγκο που κατέχουν Οι συγκρούσεις μεταξύ τους
Ανασκόπηση εννοιών ρευστομηχανικής
 Υδραυλική &Υδραυλικά Έργα Ανασκόπηση εννοιών ρευστομηχανικής Δημήτρης Κουτσογιάννης Τομέας Υδατικών Πόρων Εθνικό Μετσόβιο Πολυτεχνείο Φωτογραφίες σχηματισμού σταγόνων νερού Φωτογραφίες schlieren θερμικά
Υδραυλική &Υδραυλικά Έργα Ανασκόπηση εννοιών ρευστομηχανικής Δημήτρης Κουτσογιάννης Τομέας Υδατικών Πόρων Εθνικό Μετσόβιο Πολυτεχνείο Φωτογραφίες σχηματισμού σταγόνων νερού Φωτογραφίες schlieren θερμικά
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Εξέταση στη Μηχανική I 2 Σεπτεμβρίου 2010
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Εξέταση στη Μηχανική I Σεπτεμβρίου 00 Απαντήστε και στα 0 ερωτήματα με σαφήνεια και απλότητα. Οι ολοκληρωμένες απαντήσεις εκτιμώνται ιδιαιτέρως. Καλή σας επιτυχία.. Ένας
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Εξέταση στη Μηχανική I Σεπτεμβρίου 00 Απαντήστε και στα 0 ερωτήματα με σαφήνεια και απλότητα. Οι ολοκληρωμένες απαντήσεις εκτιμώνται ιδιαιτέρως. Καλή σας επιτυχία.. Ένας
ΕΞΕΤΑΣΕΙΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ Διδάσκοντες: Βαρσάμης Χρήστος, Φωτόπουλος Παναγιώτης
 ΕΞΕΤΑΣΕΙΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 218-219 ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ Διδάσκοντες: Βαρσάμης Χρήστος, Φωτόπουλος Παναγιώτης ΘΕΜΑ 1 Διάρκεια εξέτασης 2 ώρες Υλικό σημείο κινείται ευθύγραμμα πάνω στον άξονα x με ταχύτητα,
ΕΞΕΤΑΣΕΙΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 218-219 ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ Διδάσκοντες: Βαρσάμης Χρήστος, Φωτόπουλος Παναγιώτης ΘΕΜΑ 1 Διάρκεια εξέτασης 2 ώρες Υλικό σημείο κινείται ευθύγραμμα πάνω στον άξονα x με ταχύτητα,
Αρµονικοί ταλαντωτές
 Αρµονικοί ταλαντωτές ΦΥΣ 111 - Διαλ. 38 Εκκρεµή - Απλό εκκρεµές θ T mg r F τ = r F = mgsinθ τ = I M d θ α, Ι = M dt = Mgsinθ d θ dt = g sinθ θ = g sinθ Διαφορική εξίσωση Αυτή η εξίσωση είναι δύσκολο να
Αρµονικοί ταλαντωτές ΦΥΣ 111 - Διαλ. 38 Εκκρεµή - Απλό εκκρεµές θ T mg r F τ = r F = mgsinθ τ = I M d θ α, Ι = M dt = Mgsinθ d θ dt = g sinθ θ = g sinθ Διαφορική εξίσωση Αυτή η εξίσωση είναι δύσκολο να
1 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΕΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ
 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΕΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού Οριακού
η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΕΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού Οριακού
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2017 Β ΦΑΣΗ ÅÐÉËÏÃÇ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 017 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ηµεροµηνία: Μ Τετάρτη 1 Απριλίου 017 ιάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 017 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ηµεροµηνία: Μ Τετάρτη 1 Απριλίου 017 ιάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις
ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης 02/06/2017 1
 ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης /6/7 Διάρκεια ώρες. Θέμα. Θεωρηστε ενα συστημα δυο σωματων ισων μαζων (μαζας Μ το καθενα) και δυο ελατηριων (χωρις μαζα) με σταθερες ελατηριων
ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης /6/7 Διάρκεια ώρες. Θέμα. Θεωρηστε ενα συστημα δυο σωματων ισων μαζων (μαζας Μ το καθενα) και δυο ελατηριων (χωρις μαζα) με σταθερες ελατηριων
Ακτομηχανική και λιμενικά έργα
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διάλεξη 12 η. Θαλάσσια ρεύματα, κυκλοφορία, μετεωρολογική παλίρροια Θεοφάνης Καραμπάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διάλεξη 12 η. Θαλάσσια ρεύματα, κυκλοφορία, μετεωρολογική παλίρροια Θεοφάνης Καραμπάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ. ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 07 ΑΠΡΙΛΙΟΥ 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΠΤΑ (7) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 07 ΑΠΡΙΛΙΟΥ 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΠΤΑ (7) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε
7. Ταλαντώσεις σε συστήµατα µε πολλούς βαθµούς ελευθερίας
 7 Ταλαντώσεις σε συστήµατα µε πολλούς βαθµούς ελευθερίας Συζευγµένες ταλαντώσεις Βιβλιογραφία F S Crawford Jr Κυµατική (Σειρά Μαθηµάτων Φυσικής Berkeley, Τόµος 3 Αθήνα 979) Κεφ H J Pai Φυσική των ταλαντώσεων
7 Ταλαντώσεις σε συστήµατα µε πολλούς βαθµούς ελευθερίας Συζευγµένες ταλαντώσεις Βιβλιογραφία F S Crawford Jr Κυµατική (Σειρά Μαθηµάτων Φυσικής Berkeley, Τόµος 3 Αθήνα 979) Κεφ H J Pai Φυσική των ταλαντώσεων
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα. ΔΙΑΛΕΞΗ 09 Ροπή Αδρανείας Στροφορμή
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 09 Ροπή Αδρανείας Στροφορμή ΦΥΣ102 1 Υπολογισμός Ροπών Αδράνειας Η Ροπή αδράνειας
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 09 Ροπή Αδρανείας Στροφορμή ΦΥΣ102 1 Υπολογισμός Ροπών Αδράνειας Η Ροπή αδράνειας
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 19 Ταλαντώσεις Απλή αρμονική κίνηση ΦΥΣ102 1 Ταλαντώσεις Ελατηρίου Όταν ένα αντικείμενο
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 19 Ταλαντώσεις Απλή αρμονική κίνηση ΦΥΣ102 1 Ταλαντώσεις Ελατηρίου Όταν ένα αντικείμενο
Κίνηση στερεών σωμάτων - περιστροφική
 Κίνηση στερεών σωμάτων - περιστροφική ΦΥΣ 211 - Διαλ.29 1 q Ενδιαφέρουσα κίνηση: Ø Αρκετά περίπλοκη Ø Δεν καταλήγει σε κίνηση ενός βαθµού ελευθερίας q Τι είναι το στερεό σώµα: Ø Συλλογή υλικών σηµείων
Κίνηση στερεών σωμάτων - περιστροφική ΦΥΣ 211 - Διαλ.29 1 q Ενδιαφέρουσα κίνηση: Ø Αρκετά περίπλοκη Ø Δεν καταλήγει σε κίνηση ενός βαθµού ελευθερίας q Τι είναι το στερεό σώµα: Ø Συλλογή υλικών σηµείων
ΦΥΣ Διαλ Δυναµική
 ΦΥΣ 131 - Διαλ.08 1 Δυναµική Ø F(δύναµη), m(µάζα), E(ενέργεια), p(ορµή), Ø Πως ένα σώµα αλληλεπιδρά µε το περιβάλλον του Ø Γιατί σώµατα κινούνται µε το τρόπο που κινούνται q Θεµελιώδεις νόµοι της µηχανικής:
ΦΥΣ 131 - Διαλ.08 1 Δυναµική Ø F(δύναµη), m(µάζα), E(ενέργεια), p(ορµή), Ø Πως ένα σώµα αλληλεπιδρά µε το περιβάλλον του Ø Γιατί σώµατα κινούνται µε το τρόπο που κινούνται q Θεµελιώδεις νόµοι της µηχανικής:
E = 1 2 k. V (x) = Kx e αx, dv dx = K (1 αx) e αx, dv dx = 0 (1 αx) = 0 x = 1 α,
 Μαθηματική Μοντελοποίηση Ι 1. Φυλλάδιο ασκήσεων Ι - Λύσεις ορισμένων ασκήσεων 1.1. Άσκηση. Ενα σωμάτιο μάζας m βρίσκεται σε παραβολικό δυναμικό V (x) = 1/2x 2. Γράψτε την θέση του σαν συνάρτηση του χρόνου,
Μαθηματική Μοντελοποίηση Ι 1. Φυλλάδιο ασκήσεων Ι - Λύσεις ορισμένων ασκήσεων 1.1. Άσκηση. Ενα σωμάτιο μάζας m βρίσκεται σε παραβολικό δυναμικό V (x) = 1/2x 2. Γράψτε την θέση του σαν συνάρτηση του χρόνου,
ΑΠΑΝΤΗΣΕΙΣ ΣΤΟ ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ Θέμα Α. 1. β 2. α 3. γ 4. β 5. Λ,Λ,Λ,Λ,Λ.
 ΑΠΑΝΤΗΣΕΙΣ ΣΤΟ ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ- 07 Θέμα Α.. β. α 3. γ 4. β 5. Λ,Λ,Λ,Λ,Λ. Β Στην επιφάνεια ελαστικού μέσου υπάρχουν δύο πανομοιότυπες πηγές κυμάτων που ξεκινούν ταυτόχρονα την ταλάντωση τους. Σε
ΑΠΑΝΤΗΣΕΙΣ ΣΤΟ ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ- 07 Θέμα Α.. β. α 3. γ 4. β 5. Λ,Λ,Λ,Λ,Λ. Β Στην επιφάνεια ελαστικού μέσου υπάρχουν δύο πανομοιότυπες πηγές κυμάτων που ξεκινούν ταυτόχρονα την ταλάντωση τους. Σε
Σχολή E.Μ.Φ.Ε ΦΥΣΙΚΗ ΙΙΙ (ΚΥΜΑΤΙΚΗ) Κανονικές Εξετάσεις Χειµερινού εξαµήνου t (α) Αν το παραπάνω σύστηµα, ( m, s,
 Σχολή E.Μ.Φ.Ε ΦΥΣΙΚΗ ΙΙΙ (ΚΥΜΑΤΙΚΗ) Κανονικές Εξετάσεις Χειµερινού εξαµήνου 9-1 ιάρκεια εξέτασης :3 5//1 Ι. Σ. Ράπτης Ε. Φωκίτης Θέµα 1. Ένας αρµονικός ταλαντωτής µε ασθενή απόσβεση (µάζα m σταθερά ελατηρίου
Σχολή E.Μ.Φ.Ε ΦΥΣΙΚΗ ΙΙΙ (ΚΥΜΑΤΙΚΗ) Κανονικές Εξετάσεις Χειµερινού εξαµήνου 9-1 ιάρκεια εξέτασης :3 5//1 Ι. Σ. Ράπτης Ε. Φωκίτης Θέµα 1. Ένας αρµονικός ταλαντωτής µε ασθενή απόσβεση (µάζα m σταθερά ελατηρίου
v = r r + r θ θ = ur + ωutθ r = r cos θi + r sin θj v = u 1 + ω 2 t 2
 ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΉΣ Ι ΤΜΗΜΑ ΧΗΜΕΙΑΣ, 9 ΙΑΝΟΥΑΡΙΟΥ 019 ΚΏΣΤΑΣ ΒΕΛΛΙΔΗΣ, cvellid@phys.uoa.r, 10 77 6895 ΘΕΜΑ 1: Σώµα κινείται µε σταθερή ταχύτητα u κατά µήκος οριζόντιας ράβδου που περιστρέφεται
ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΉΣ Ι ΤΜΗΜΑ ΧΗΜΕΙΑΣ, 9 ΙΑΝΟΥΑΡΙΟΥ 019 ΚΏΣΤΑΣ ΒΕΛΛΙΔΗΣ, cvellid@phys.uoa.r, 10 77 6895 ΘΕΜΑ 1: Σώµα κινείται µε σταθερή ταχύτητα u κατά µήκος οριζόντιας ράβδου που περιστρέφεται
website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 31 Μαρτίου 2019 1 Δυνάμεις μάζας και επαφής Δυνάμεις μάζας ή δυνάμεις όγκου ονομάζονται οι δυνάμεις που είναι
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 31 Μαρτίου 2019 1 Δυνάμεις μάζας και επαφής Δυνάμεις μάζας ή δυνάμεις όγκου ονομάζονται οι δυνάμεις που είναι
ΦΥΕ 14 5η ΕΡΓΑΣΙΑ Παράδοση ( Οι ασκήσεις είναι βαθμολογικά ισοδύναμες) Άσκηση 1 : Aσκηση 2 :
 ΦΥΕ 14 5 η ΕΡΓΑΣΙΑ Παράδοση 19-5-8 ( Οι ασκήσεις είναι βαθμολογικά ισοδύναμες) Άσκηση 1 : Συμπαγής κύλινδρος μάζας Μ συνδεδεμένος σε ελατήριο σταθεράς k = 3. N / και αμελητέας μάζας, κυλίεται, χωρίς να
ΦΥΕ 14 5 η ΕΡΓΑΣΙΑ Παράδοση 19-5-8 ( Οι ασκήσεις είναι βαθμολογικά ισοδύναμες) Άσκηση 1 : Συμπαγής κύλινδρος μάζας Μ συνδεδεμένος σε ελατήριο σταθεράς k = 3. N / και αμελητέας μάζας, κυλίεται, χωρίς να
Κεφάλαιο 3 TΑΣΗ ΚΑΙ ΠΑΡΑΜΟΡΦΩΣΗ
 Κεφάλαιο 3 TΑΣΗ ΚΑΙ ΠΑΡΑΜΟΡΦΩΣΗ ΚΑΤΑ ΤΗΝ ΔΙΑΔΟΣΗ ΤΩΝ ΣΕΙΣΜΙΚΩΝ ΚΥΜΑΤΩΝ ΜΕΣΑ ΣΤΗ ΓΗ ΔΕΧΟΜΑΣΤΕ: ΟΤΙ ΤΟ ΥΛΙΚΟ ΔΙΑΔΟΣΗΣ ΕΧΕΙ ΑΠΟΛΥΤΑ ΕΛΑΣΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΔΕΧΟΜΑΣΤΕ ΜΕ ΑΛΛΑ ΛΟΓΙΑ ΟΤΙ ΤΑ ΣΕΙΣΜΙΚΑ ΚΥΜΑΤΑ ΕΙΝΑΙ
Κεφάλαιο 3 TΑΣΗ ΚΑΙ ΠΑΡΑΜΟΡΦΩΣΗ ΚΑΤΑ ΤΗΝ ΔΙΑΔΟΣΗ ΤΩΝ ΣΕΙΣΜΙΚΩΝ ΚΥΜΑΤΩΝ ΜΕΣΑ ΣΤΗ ΓΗ ΔΕΧΟΜΑΣΤΕ: ΟΤΙ ΤΟ ΥΛΙΚΟ ΔΙΑΔΟΣΗΣ ΕΧΕΙ ΑΠΟΛΥΤΑ ΕΛΑΣΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΔΕΧΟΜΑΣΤΕ ΜΕ ΑΛΛΑ ΛΟΓΙΑ ΟΤΙ ΤΑ ΣΕΙΣΜΙΚΑ ΚΥΜΑΤΑ ΕΙΝΑΙ
400 = t2 (2) t = 15.1 s (3) 400 = (t + 1)2 (5) t = 15.3 s (6)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2016 ιδάσκων : Γ. Καφεντζής Πρώτη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. Θεωρούµε ως χρονικό σηµείο αναφοράς τη στιγµή που
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2016 ιδάσκων : Γ. Καφεντζής Πρώτη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. Θεωρούµε ως χρονικό σηµείο αναφοράς τη στιγµή που
Ανεμογενής Κυκλοφορία
 Ρεύματα με Τριβή Ανεμογενής Κυκλοφορία - Έστω αναπτύσσεται μια επιφανειακή τάση F T - Η δύναμη αυτή προκαλεί τη κίνηση της μάζας νερού προς μία κατεύθυνση, οπότε ξεκινά να ενεργεί και η δύναμη Coriolis
Ρεύματα με Τριβή Ανεμογενής Κυκλοφορία - Έστω αναπτύσσεται μια επιφανειακή τάση F T - Η δύναμη αυτή προκαλεί τη κίνηση της μάζας νερού προς μία κατεύθυνση, οπότε ξεκινά να ενεργεί και η δύναμη Coriolis
dv 2 dx v2 m z Β Ο Γ
 Μηχανική Ι Εργασία #2 Χειμερινό εξάμηνο 218-219 Ν Βλαχάκης 1 Στην άσκηση 4 της εργασίας #1 αρχικά για t = είναι φ = και η ταχύτητα του σώματος είναι v με φορά κάθετη στο νήμα ώστε αυτό να τυλίγεται στον
Μηχανική Ι Εργασία #2 Χειμερινό εξάμηνο 218-219 Ν Βλαχάκης 1 Στην άσκηση 4 της εργασίας #1 αρχικά για t = είναι φ = και η ταχύτητα του σώματος είναι v με φορά κάθετη στο νήμα ώστε αυτό να τυλίγεται στον
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 03/05/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΠΑΝΤΗΣΕΙΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 03/05/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Τζαγκαράκης Γιάννης, Δημοπούλου Ηρώ, Αδάμη Μαρία, Αγγελίδης Άγγελος, Παπαθανασίου Θάνος, Παπασταμάτης Στέφανος
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 03/05/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Τζαγκαράκης Γιάννης, Δημοπούλου Ηρώ, Αδάμη Μαρία, Αγγελίδης Άγγελος, Παπαθανασίου Θάνος, Παπασταμάτης Στέφανος
Ονοματεπώνυμο: Μάθημα: Ύλη: Επιμέλεια διαγωνίσματος: Αξιολόγηση: Φυσική Προσανατολισμού Ρευστά Ιωάννης Κουσανάκης
 Ονοματεπώνυμο: Μάθημα: Ύλη: Επιμέλεια διαγωνίσματος: Αξιολόγηση: Φυσική Προσανατολισμού Ρευστά Ιωάννης Κουσανάκης ΘΕΜΑ Α Α1. Το ανοιχτό κυλινδρικό δοχείο του σχήματος βρίσκεται εντός πεδίο βαρύτητας με
Ονοματεπώνυμο: Μάθημα: Ύλη: Επιμέλεια διαγωνίσματος: Αξιολόγηση: Φυσική Προσανατολισμού Ρευστά Ιωάννης Κουσανάκης ΘΕΜΑ Α Α1. Το ανοιχτό κυλινδρικό δοχείο του σχήματος βρίσκεται εντός πεδίο βαρύτητας με
ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ
 ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 10//10/01 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα μάζας 1 Kg βρίσκεται πάνω σε κεκλιμένο επίπεδο γωνίας κλίσης 45º. Μεταξύ
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 10//10/01 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα μάζας 1 Kg βρίσκεται πάνω σε κεκλιμένο επίπεδο γωνίας κλίσης 45º. Μεταξύ
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2017 Β ΦΑΣΗ. Ηµεροµηνία: Μ. Τετάρτη 12 Απριλίου 2017 ιάρκεια Εξέτασης: 2 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 07 Ε_3.Φλ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ Ηµεροµηνία: Μ. Τετάρτη Απριλίου 07 ιάρκεια Εξέτασης: ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις Α - Α4 να γράψετε να γράψετε
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 07 Ε_3.Φλ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ Ηµεροµηνία: Μ. Τετάρτη Απριλίου 07 ιάρκεια Εξέτασης: ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις Α - Α4 να γράψετε να γράψετε
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Γ έκδοση
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Γ έκδοση Α.1. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων παραµένει
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Γ έκδοση Α.1. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων παραµένει
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) 23 ΜΑΪOY 2016 ΕΚΦΩΝΗΣΕΙΣ
 ΘΕΜΑ Α ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) 3 ΜΑΪOY 016 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει
ΘΕΜΑ Α ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) 3 ΜΑΪOY 016 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει
Ακτομηχανική και λιμενικά έργα
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διάλεξη 2 η. Επιφανειακοί κυματισμοί- κύματα Γιάννης Ν. Κρεστενίτης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διάλεξη 2 η. Επιφανειακοί κυματισμοί- κύματα Γιάννης Ν. Κρεστενίτης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Διατήρηση της Ενέργειας Εικόνα: Η μετατροπή της δυναμικής ενέργειας σε κινητική κατά την ολίσθηση ενός παιχνιδιού σε μια πλατφόρμα. Μπορούμε να αναλύσουμε τέτοιες καταστάσεις με τις
Φυσική για Μηχανικούς Διατήρηση της Ενέργειας Εικόνα: Η μετατροπή της δυναμικής ενέργειας σε κινητική κατά την ολίσθηση ενός παιχνιδιού σε μια πλατφόρμα. Μπορούμε να αναλύσουμε τέτοιες καταστάσεις με τις
ΘΕΜΑΤΑ ΓΡΑΠΤΩΝ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΠΕΡΙΟΔΟΥ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2016
 9o ΓΕΝ. ΛΥΚΕΙΟ ΠΕΙΡΑΙΑ ΣΧΟΛ. ΕΤΟΣ 06-7 ΘΕΜΑΤΑ ΓΡΑΠΤΩΝ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΠΕΡΙΟΔΟΥ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 06 Τάξη: Γ Λυκείου Ημερομηνία: 5-5-07 Μάθημα: Φυσική Θετικού Προσανατολισμού ΘΕΜΑ Α Στις ερωτήσεις A-A5
9o ΓΕΝ. ΛΥΚΕΙΟ ΠΕΙΡΑΙΑ ΣΧΟΛ. ΕΤΟΣ 06-7 ΘΕΜΑΤΑ ΓΡΑΠΤΩΝ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΠΕΡΙΟΔΟΥ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 06 Τάξη: Γ Λυκείου Ημερομηνία: 5-5-07 Μάθημα: Φυσική Θετικού Προσανατολισμού ΘΕΜΑ Α Στις ερωτήσεις A-A5
Ροπή αδράνειας. q Ας δούµε την ροπή αδράνειας ενός στερεού περιστροφέα: I = m(2r) 2 = 4mr 2
 ΦΥΣ 131 - Διαλ.22 1 Ροπή αδράνειας q Ας δούµε την ροπή αδράνειας ενός στερεού περιστροφέα: m (α) m (β) m r r 2r 2 2 I =! m i r i = 2mr 2 1 I = m(2r) 2 = 4mr 2 Ø Είναι δυσκολότερο να προκαλέσεις περιστροφή
ΦΥΣ 131 - Διαλ.22 1 Ροπή αδράνειας q Ας δούµε την ροπή αδράνειας ενός στερεού περιστροφέα: m (α) m (β) m r r 2r 2 2 I =! m i r i = 2mr 2 1 I = m(2r) 2 = 4mr 2 Ø Είναι δυσκολότερο να προκαλέσεις περιστροφή
ΦΥΕ34 Λύσεις 5 ης Εργασίας
 ΦΥΕ3 Λύσεις 5 ης Εργασίας ) Έστω αρµονικό κύµα της (εκθετικής) µορφής: F( x, t) i( kx ωt+ ϕ ) = Ae. Παραγωγίζοντας βρίσκουµε: = iωf( x, t) t = ikf( x, t) x Παραγωγίζοντας αυτές τις δύο σχέσεις µία ακόµη
ΦΥΕ3 Λύσεις 5 ης Εργασίας ) Έστω αρµονικό κύµα της (εκθετικής) µορφής: F( x, t) i( kx ωt+ ϕ ) = Ae. Παραγωγίζοντας βρίσκουµε: = iωf( x, t) t = ikf( x, t) x Παραγωγίζοντας αυτές τις δύο σχέσεις µία ακόµη
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ η ΕΡΓΑΣΙΑ. Προθεσµία παράδοσης 11/11/08
 //8 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 4 8-9 η ΕΡΓΑΣΙΑ Προθεσµία παράδοσης //8 Άσκηση Α) Έστω, οι µετατοπίσεις των µαζών από τη θέση ισορροπίας όπως στο Σχήµα. Στη µάζα ενεργούν µόνο οι δυνάµεις από τα
//8 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 4 8-9 η ΕΡΓΑΣΙΑ Προθεσµία παράδοσης //8 Άσκηση Α) Έστω, οι µετατοπίσεις των µαζών από τη θέση ισορροπίας όπως στο Σχήµα. Στη µάζα ενεργούν µόνο οι δυνάµεις από τα
ΥΔΡΑΥΛΙΚΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ
 ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΞΑΝΘΗ ΥΔΡΑΥΛΙΚΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Αγγελίδης Π., Αναπλ. καθηγητής ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ ΚΑΙ ΑΡΧΕΣ ΣΥΓΚΕΝΤΡΩΣΗ ΡΥΠΟΥ Έστω η συγκέντρωση
ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΞΑΝΘΗ ΥΔΡΑΥΛΙΚΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Αγγελίδης Π., Αναπλ. καθηγητής ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ ΚΑΙ ΑΡΧΕΣ ΣΥΓΚΕΝΤΡΩΣΗ ΡΥΠΟΥ Έστω η συγκέντρωση
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 17/4/2016 ΘΕΜΑ Α
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 7/4/06 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις - 7 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα σε κάθε αριθμό το γράµμα που αντιστοιχεί στη σωστή απάντηση:
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 7/4/06 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις - 7 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα σε κάθε αριθμό το γράµμα που αντιστοιχεί στη σωστή απάντηση:
Theory Greek (Greece) Παρακαλώ διαβάστε τις Γενικές Οδηγίες που θα βρείτε σε ξεχωριστό φάκελο πριν ξεκινήσετε να εργάζεστε στο πρόβλημα αυτό.
 Q1-1 Δύο προβλήματα Μηχανικής (10 Μονάδες) Παρακαλώ διαβάστε τις Γενικές Οδηγίες που θα βρείτε σε ξεχωριστό φάκελο πριν ξεκινήσετε να εργάζεστε στο πρόβλημα αυτό. Μέρος A. Ο Κρυμμένος Δίσκος (3.5 Μονάδες)
Q1-1 Δύο προβλήματα Μηχανικής (10 Μονάδες) Παρακαλώ διαβάστε τις Γενικές Οδηγίες που θα βρείτε σε ξεχωριστό φάκελο πριν ξεκινήσετε να εργάζεστε στο πρόβλημα αυτό. Μέρος A. Ο Κρυμμένος Δίσκος (3.5 Μονάδες)
Παραµόρφωση σε Σηµείο Σώµατος. Μεταβολή του σχήµατος του στοιχείου (διατµητική παραµόρφωση)
 Παραµόρφωση σε Σηµείο Σώµατος Η ολική παραµόρφωση στερεού σώµατος στη γειτονιά ενός σηµείου, Ο, δηλαδή η συνολική παραµόρφωση ενός µικρού τµήµατος (στοιχείου) του σώµατος γύρω από το σηµείο µπορεί να αναλυθεί
Παραµόρφωση σε Σηµείο Σώµατος Η ολική παραµόρφωση στερεού σώµατος στη γειτονιά ενός σηµείου, Ο, δηλαδή η συνολική παραµόρφωση ενός µικρού τµήµατος (στοιχείου) του σώµατος γύρω από το σηµείο µπορεί να αναλυθεί
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Δυναμική ενέργεια στο βαρυτικό πεδίο. Θετική ή αρνητική;
 ράφει το σχολικό βιβλίο: Δυναμική ενέργεια στο βαρυτικό πεδίο. Θετική ή αρνητική; Μια πρώτη ένσταση θα µπορούσε να διατυπωθεί, για την απουσία της δυναµικής ενέργειας από τον παραπάνω ορισµό. ιατί να µην
ράφει το σχολικό βιβλίο: Δυναμική ενέργεια στο βαρυτικό πεδίο. Θετική ή αρνητική; Μια πρώτη ένσταση θα µπορούσε να διατυπωθεί, για την απουσία της δυναµικής ενέργειας από τον παραπάνω ορισµό. ιατί να µην
Δυναµική. ! F(δύναµη), m(µάζα), E(ενέργεια), p(ορµή),! Πως ένα σώµα αλληλεπιδρά µε το περιβάλλον του! Γιατί σώµατα κινούνται µε το τρόπο που κινούνται
 1 Δυναµική F(δύναµη), m(µάζα), E(ενέργεια), p(ορµή), Πως ένα σώµα αλληλεπιδρά µε το περιβάλλον του Γιατί σώµατα κινούνται µε το τρόπο που κινούνται " Θεµελιώδεις νόµοι της µηχανικής: Οι τρεις νόµοι του
1 Δυναµική F(δύναµη), m(µάζα), E(ενέργεια), p(ορµή), Πως ένα σώµα αλληλεπιδρά µε το περιβάλλον του Γιατί σώµατα κινούνται µε το τρόπο που κινούνται " Θεµελιώδεις νόµοι της µηχανικής: Οι τρεις νόµοι του
Ακτομηχανική και λιμενικά έργα
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διάλεξη 10 η. Γεωστροφικός άνεμος, κυματισμοί, στατιστική ανάλυση και ενεργειακά φάσματα Θεοφάνης Καραμπάς Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διάλεξη 10 η. Γεωστροφικός άνεμος, κυματισμοί, στατιστική ανάλυση και ενεργειακά φάσματα Θεοφάνης Καραμπάς Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 3) ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 3) ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΣΗΜΕΙΩΣΕΙΣ ΡΕΥΣΤΟΜΗΧΑΝΙΚΗΣ - ΜΕΡΟΣ Α
 ΣΗΜΕΙΩΣΕΙΣ ΡΕΥΣΤΟΜΗΧΑΝΙΚΗΣ - ΜΕΡΟΣ Α ΣΤΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ ΕΙΣΑΓΩΓΙΚΑ Ως ρευστά θεωρούµε τα σώµατα εκείνα, τα οποία δεν έχουν δικό τους σχήµα, αλλά παίρνουν το σχήµα του δοχείου που τα περιέχει, τέτοια είναι
ΣΗΜΕΙΩΣΕΙΣ ΡΕΥΣΤΟΜΗΧΑΝΙΚΗΣ - ΜΕΡΟΣ Α ΣΤΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ ΕΙΣΑΓΩΓΙΚΑ Ως ρευστά θεωρούµε τα σώµατα εκείνα, τα οποία δεν έχουν δικό τους σχήµα, αλλά παίρνουν το σχήµα του δοχείου που τα περιέχει, τέτοια είναι
ΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ / ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΞΑΝΘΗ ΡΕΥΣΤΟΜΗΧΑΝΙΚΗ. Αγγελίδης Π., Επίκ. καθηγητής
 ΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ / ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΞΑΝΘΗ ΡΕΥΣΤΟΜΗΧΑΝΙΚΗ Αγγελίδης Π., Επίκ. καθηγητής ΘΕΩΡΙΑ ΟΜΟΙΩΜΑΤΩΝ ΘΕΩΡΙΑ ΟΜΟΙΩΜΑΤΩΝ Πριν την κατασκευή μεγάλων Υδραυλικών
ΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ / ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΞΑΝΘΗ ΡΕΥΣΤΟΜΗΧΑΝΙΚΗ Αγγελίδης Π., Επίκ. καθηγητής ΘΕΩΡΙΑ ΟΜΟΙΩΜΑΤΩΝ ΘΕΩΡΙΑ ΟΜΟΙΩΜΑΤΩΝ Πριν την κατασκευή μεγάλων Υδραυλικών
α. µόνο µεταφορική. β. µόνο στροφική. γ. σύνθετη. δ. ακινησία.
 ΠΡΟΣΟΜΟΙΩΣΗ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 24 ΑΠΡΙΛΙΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΟΜΑ Α ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΘΕΜΑ Α (Μονάδες 25) A1. Σε
ΠΡΟΣΟΜΟΙΩΣΗ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 24 ΑΠΡΙΛΙΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΟΜΑ Α ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΘΕΜΑ Α (Μονάδες 25) A1. Σε
