ΝΑΥΤΙΛΙΑ. Όταν για µεγάλα χρονικά διαστήµατα, δεν έχουµε οπτική επαφή µε την στεριά
|
|
|
- Παρασκευή Αλεξίου
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ΝΑΥΤΙΛΙΑ ΕΙΣΑΓΩΓΗ Ναυτιλία ονοµάζεται το σύνολο των µεθόδων, διαδικασιών και ενεργειών που εφαρµόζονται έτσι ώστε, ένα σκάφος, να ταξιδέψει από ένα µέρος της γης σ ένα άλλο, αφ ενός µε ασφάλεια αφ ετέρου το ταχύτερο δυνατόν. Η ναυτιλία είναι ταυτόχρονα επιστήµη και τέχνη. Με την γνώση της, υπολογίζουµε την πορεία µας και βρίσκουµε το στίγµα (θέση) µας στην θάλασσα. Από την αρχαιότητα µέχρι σήµερα, η θάλασσα αποτέλεσε το φορέα επαφής µεταξύ των λαών και συνέβαλε στη βελτίωση του πολιτισµού, στην ανταλλαγή των αγαθών, στην κυκλοφορία των πνευµατικών ιδεών και στην κατανόηση µεταξύ των διαφόρων πολιτισµών. Οι πρώτοι καπετάνιοι, διαπίστωσαν γρήγορα τις τεράστιες δυνατότητες επικοινωνίας που προσφέρουν οι θαλασσινοί δρόµοι. Η γνώση της ναυτιλίας ήταν απαραίτητη για την ασφάλεια αλλά και την συντόµευση των πλόων. Η ναυτιλία χωρίζεται σε δύο βασικές κατηγορίες: 1. Ακτοπλοΐα: Όταν για µεγάλα χρονικά διαστήµατα, έχουµε οπτική επαφή µε την στεριά. Στην ακτοπλοΐα, για να βρούµε την θέση µας (στίγµα), βασιζόµαστε σε παρατηρήσεις φυσικών ή τεχνητών καταφανών σηµείων της στεριάς. Σαν φυσικά βοηθήµατα µπορούµε να θεωρήσουµε κάβους, οικισµούς, χαρακτηριστικά κτίρια ή διαµορφώσεις της ακτής, ψηλές κορυφές βουνών κ.ά. Τεχνητά βοηθήµατα είναι οι φάροι και διάφορα ειδικά σηµάδια ή σχήµατα που θα αναφερθούµε αργότερα. 2. Ωκεανοπλοΐα: Όταν για µεγάλα χρονικά διαστήµατα, δεν έχουµε οπτική επαφή µε την στεριά οπότε για τον υπολογισµό του στίγµατος χρησιµοποιούµε είτε τον ήλιο και τα άστρα (αστροναυτιλία), είτε ραδιοβοηθήµατα ή δορυφορικά ηλεκτρονικά βοηθήµατα (ηλεκτρονική ναυτιλία). Όλοι οι πλόες στις Ελληνικές θάλασσες, θεωρούνται ακτοπλοϊκοί. Αυτό σηµαίνει, ότι πρέπει να εξασκήσουµε: A. Την παρατηρητικότητά µας, ώστε να είµαστε σε θέση να αναγνωρίζουµε πάνω στο ν. χάρτη καταφανή σηµεία που συναντούµε κατά το ταξίδι µας (κάβους, βραχονησίδες, νησιά, διαµόρφωση της ακτής κλπ.) B. Την φαντασία µας, ώστε να είµαστε σε θέση - από την µελέτη του ν. χάρτη να γνωρίζουµε τι ακριβώς περιµένουµε να δούµε στην συνέχεια του ταξιδιού. Η ραγδαία εξέλιξη και η απλοποίηση των ηλεκτρονικών βοηθηµάτων (διότι µόνον σαν βοηθήµατα πρέπει να χρησιµεύουν) (GPS) της ναυτιλίας τα τελευταία χρόνια, οδήγησε πολλούς κυβερνήτες σκαφών αναψυχής στο λανθασµένο συµπέρασµα ότι οι βασικές γνώσεις ναυτιλίας είναι πλέον περιττές. Το συµπέρασµα αυτό οδηγεί στην - επικίνδυνη για την ασφάλεια του ταξιδιού - εξάρτηση αποκλειστικά και µόνο από τα ηλεκτρονικά βοηθήµατα για τον υπολογισµό της πορείας και του στίγµατος.
2 Η ΓΗ Όπως γνωρίζουµε, η γη είναι µία σφαίρα που περιστρέφεται γύρω από έναν νοητό άξονα ο οποίος περνά από τους πόλους της (Βόρειο και Νότιο). Θεωρούµε ένα επίπεδο που τέµνει την γη κάθετα στον άξονά της και περνά από το κέντρο της. Η περιφέρεια που ορίζεται από την τοµή του επιπέδου αυτού µε την γη ονοµάζεται Ισηµερινός. Ο Ισηµερινός χωρίζει την γη σε δύο ηµισφαίρια: το Βόρειο και το Νότιο. ΠΑΡΑΛΛΗΛΟΙ-ΜΕΣΗΜΒΡΙΝΟΙ Κάθε κύκλος στην επιφάνεια της γης παράλληλος στον Ισηµερινό, ονοµάζεται Παράλληλος. Θα πρέπει να παρατηρήσουµε ότι: Η απόσταση µεταξύ δύο παράλληλων κύκλων, παραµένει (εξ` ορισµού) σε όλο το µήκος της περιφέρειάς τους ίδια. Η περίµετρος των παραλλήλων µειώνεται καθώς πηγαίνουµε από τον Ισηµερινό προς στους πόλους, όπου και µηδενίζεται. Παράλληλος Ισηµερινός Γεωγραφικό πλάτος παραλλήλου Σχήµα 1 Οι µέγιστοι κύκλοι στην επιφάνεια της γης που περνούν από τους πόλους, ονοµάζονται Μεσηµβρινοί. Συγκρίνοντας τις ιδιότητες των παραλλήλων µε αυτές των µεσηµβρινών, παρατηρούµε ότι: Η απόσταση µεταξύ δύο µεσηµβρινών, δεν είναι ίδια σε όλο τους το µήκος. Είναι µέγιστη στον Ισηµερινό, µειώνεται προς τους πόλους, όπου και µηδενίζεται (εφ` όσον τέµνονται). Η περίµετροι των µεσηµβρινών είναι ίσες.
3 Ορίζουµε σαν πρώτο µεσηµβρινό, αυτόν που περνά από το αστεροσκοπείο του Greenwich του Λονδίνου. Ο πρώτος µεσηµβρινός, χωρίζει την γη σε δύο ηµισφαίρια: ανατολικό και δυτικό. Μεσηµβρινός Πρώτος µεσηµβρινός Γεωγραφικό µήκος Σχήµα 2 ΓΕΩΓΡΑΦΙΚΟ ΠΛΑΤΟΣ- ΓΕΩΓΡΑΦΙΚΟ ΜΗΚΟΣ Κάθε παράλληλος ορίζεται από το τόξο, επί του µεσηµβρινού, µεταξύ αυτού (του παράλληλου) και του ισηµερινού. Το τόξο αυτό µετράται σε µοίρες και ονοµάζεται γεωγραφικό πλάτος «φ» (σχήµα 1) του συγκεκριµένου παραλλήλου. Μία τιµή γεωγραφικού πλάτους, ορίζει ένα και µόνο παράλληλο. Τα γεωγραφικά πλάτη, κυµαίνονται από ο Βόρειο στο βόρειο ηµισφαίριο και Ο Νότιο στο νότιο ηµισφαίριο, όπου, Ο 0 είναι ο Ισηµερινός και 90 0 οι πόλοι. Κάθε µεσηµβρινός ορίζεται από το τόξο, επί του ισηµερινού, µεταξύ αυτού (του µεσηµβρινού) και του πρώτου µεσηµβρινού. Το τόξο αυτό µετράται σε µοίρες και ονοµάζεται γεωγραφικό µήκος «λ» (σχήµα 2) του συγκεκριµένου µεσηµβρινού. Μία τιµή γεωγραφικού µήκους, ορίζει ένα και µόνο µεσηµβρινό. Τα γεωγραφικά µήκη, κυµαίνονται από Ανατολικά στο ανατολικό ηµισφαίριο και υτικά στο δυτικό ηµισφαίριο, όπου, 0 0 και βρίσκονται σε αντιδιαµετρικά σηµεία του πρώτου µεσηµβρινού. ΓΕΩΓΡΑΦΙΚΕΣ ΣΥΝΤΕΤΑΓΜΕΝΕΣ Κάθε σηµείο επάνω στην επιφάνεια της γης, ορίζεται σαν η τοµή ενός παραλλήλου µε ένα µεσηµβρινό. Το γεωγραφικό πλάτος του παράλληλου και το γεωγραφικό µήκος του µεσηµβρινού, που περνούν από το συγκεκριµένο σηµείο, ονοµάζονται γεωγραφικές συντεταγµένες του και ορίζουν το στίγµα του σηµείου.
4 ΝΑΥΤΙΚΟ ΜΙΛΙ Ένα ναυτικό µίλι ορίζεται σαν το γραµµικό ανάπτυγµα (µήκος) τόξου µεσηµβρινού ενός πρώτου (1 ) της µοίρας. Λόγω του σχήµατος της γης, το µήκος 1 διαφέρει ελαφρά σε διαφορετικά γεωγραφικά πλάτη. Κοντά στον Ισηµερινό είναι 1842,8 µέτρα ενώ στους πόλους είναι 1864 µέτρα. Σαν τιµή του λαµβάνεται διεθνώς η µέση ίση µε 1852 µ. ΚΟΜΒΟΣ Ο κόµβος είναι µονάδα µέτρησης της ταχύτητας στην θάλασσα και ισούται µε ένα ναυτικό µίλι την ώρα. ΒΟΡΡΑΣ - ΚΑΤΕΥΘΥΝΣΕΙΣ ΤΟΥ ΒΟΡΡΑ Τα σηµεία του Β και Ν πόλου απ` όπου περνά ο νοητός άξονας της γης, αποτελούν τον γεωγραφικό Βορρά και γεωγραφικό Νότο αντίστοιχα. Η γη αποτελεί ένα τεράστιο φυσικό µαγνήτη µε µαγνητικό βόρειο και µαγνητικό νότιο πόλο. Οι µαγνητικοί πόλοι της γης βρίσκονται κοντά στους γεωγραφικούς αλλά δεν συµπίπτουν µε αυτούς. Οι γεωγραφικοί πόλοι είναι σταθερά σηµεία στην επιφάνεια της γης. Αντίθετα οι µαγνητικοί δεν είναι σταθεροί αλλά περιστρέφονται γύρω από τους γεωγραφικούς µε περίοδο εκατοντάδων ετών. Από τα προηγούµενα συµπεραίνουµε ότι, από κάθε σηµείο της επιφάνειας της γης, έχουµε τρεις κατευθύνσεις του βορρά: κατεύθυνση του γεωγραφικού Β κατεύθυνση του µαγνητικού Β, όπου θα είναι αυτή που δείχνει η µαγνητική βελόνα (ή η πυξίδα µας), όταν δεν επηρεάζεται από άλλα µαγνητικά πεδία. κατεύθυνση του Β της πυξίδας µας, εάν, (λόγω κακής ρύθµισης, ή λόγω επηρεασµού της από µεταλλικά αντικείµενα ή όργανα τοποθετηµένα πλησίον της) δεν συµπίπτει µε τον µαγνητικό Β. ΚΑΤΕΥΘΥΝΣΕΙΣ ΣΤΗΝ ΝΑΥΤΙΛΙΑ: 1. Πορεία ενός σκάφους ορίζεται η γωνία που σχηµατίζει η κατεύθυνση της προχώρησης του σκάφους µε την κατεύθυνση του Βορρά (σχ. 3). 2. Απόλυτη διόπτευση ενός σηµείου ορίζεται η γωνία που σχηµατίζει από το σκάφος η κατεύθυνση του σηµείου µε την κατεύθυνση του Βορρά (σχ. 3). Σηµείωση ονοµάζουµε γεωγραφική την πορεία και την απόλυτη διόπτευση ενός σηµείου εφ όσον αναφέρονται στην κατεύθυνση του γεωγραφικού Βορρά και µαγνητική εφ όσον αναφέρονται σε αυτήν του µαγνητικού Βορρά.
5 3. Σχετική διόπτευση ενός σηµείου ορίζεται η γωνία που σχηµατίζει από το σκάφος η κατεύθυνση του σηµείου µε την κατεύθυνση του σκάφους. Βορράς Πορεία σκάφους Φάρος απόλυτη διόπτευση κατεύθυνση σκάφους Σχήµα 3: Πορεία σκάφους απόλυτη διόπτευση από φάρο ΑΠΟΚΛΙΣΗ ΠΑΡΕΚΤΡΟΠΗ - ΠΑΡΑΛΛΑΓΗ Η γωνία που σχηµατίζει - σ ένα συγκεκριµένο τόπο- η κατεύθυνση του γεωγραφικού Β µε αυτήν του µαγνητικού Β ονοµάζεται απόκλιση. Η απόκλιση χαρακτηρίζεται ανατολική (Α) και θεωρείται θετική (+), όταν ο µαγνητικός Β βρίσκεται ανατολικά από τον γεωγραφικό. Όταν βρίσκεται ο µαγνητικός Β δυτικά του γεωγραφικού, χαρακτηρίζεται δυτική ( ) και θεωρείται αρνητική (-). Γεωγραφικός Β Μαγνητικός Β Μαγνητικός Β Γεωγραφικός Β Ανατολική απόκλιση Α(+) υτική Απόκλιση (-) Σχήµα 4: Ανατολική (+) και υτική (-) απόκλιση Η µεταβολή της απόκλισης επηρεάζεται από τρεις παραµέτρους: Τον τόπο: την ίδια χρονική στιγµή, η απόκλιση διαφέρει από τόπο σε τόπο. Τον χρόνο: σε συγκεκριµένο τόπο, η απόκλιση µεταβάλλεται συναρτήσει του χρόνου. Από τοπικές µαγνητικές διαταραχές. Θα πρέπει να είµαστε σε θέση να γνωρίζουµε ποία είναι η απόκλιση την χρονική περίοδο που ταξιδεύουµε στην συγκεκριµένη περιοχή.
6 Στον ναυτικό χάρτη υπάρχει αποτυπωµένος ένας κύκλος, που είναι αναπαράσταση του κύκλου του ορίζοντα και διαιρείται σε µε το 0 0 να δείχνει την κατεύθυνση του γεωγραφικού βορρά. Ο κύκλος αυτός ονοµάζεται ανεµολόγιο (σχ. 5) Σχήµα 5: ανεµολόγιο Η απόκλιση για την περιοχή που βρίσκεται το ανεµολόγιο (για συγκεκριµένη χρονολογία) βρίσκεται σηµειωµένη στην διάµετρο του ανεµολογίου, µε την ακόλουθη σύντµηση: Α 1986, (4 Α). Η σύντµηση µας βοηθάει να υπολογίσουµε την απόκλιση σήµερα και διαβάζεται ως εξής: ανατολικά το 1986 και αλλάζει Ανατολικά (Α) 4 ετησίως. Άρα σε 15 έτη (το 2001) η τιµή της απόκλισης θα είναι 15Χ4=60, =
7 Η γωνία που σχηµατίζει η κατεύθυνση του µαγνητικού Β µε τον Β πυξίδας ονοµάζεται παρεκτροπή. Η µαγνητική πυξίδα κάθε σκάφους, πρέπει να διαθέτει πίνακα παρεκτροπών, όπου αναγράφεται η παρεκτροπή για κάποιες αντιπροσωπευτικές πορείες (π.χ.ανά 30 0 ή 45 0 ). Η γωνία που σχηµατίζει η κατεύθυνση του Β πυξίδας µε αυτή του γεωγραφικού Β ονοµάζεται παραλλαγή. Όταν βρίσκουµε µία πορεία στον ν. χάρτη, η τιµή της είναι µε βάση τον γεωγραφικό Β (εφ' όσον το ανεµολόγιο αναγράφει γεωγραφικό Β). Θα πρέπει να την µετατρέψουµε σε πορεία πυξίδας. Η µετατροπή της γεωγρ. πορείας σε πορεία πυξίδας γίνεται ως εξής: 1. Βρίσκουµε την γεωγρ. πορεία (όπως θα περιγράψουµε παρακάτω) 2. Υπολογίζουµε την σηµερινή τιµή της απόκλισης (όπως ήδη περιγράψαµε) 3. Υπολογίζουµε την µαγνητική πορεία σύµφωνα µε τον τύπο: µαγνητική πορ.= γεωγραφική πορ. - (απόκλιση) Θυµίζουµε ότι όταν η απόκλιση είναι ανατολική θεωρείται θετική. 4. Βρίσκουµε την παρεκτροπή της πυξίδας µας στην πορεία από τον αντίστοιχο πίνακα και την προσθέτουµε αλγεβρικά στην µαγνητική πορεία για να βρούµε την πορεία πυξίδας την οποία τελικά θα ακολουθήσουµε. Πορ. Πυξίδας = µαγνητική πορ. - (παρεκτροπή) (Όταν ο Β πυξίδας βρίσκεται ανατολικά από τον µαγνητικό Β η παρεκτροπή θεωρείται θετική). ΠΥΡΣΟΙ Κατηγορίες πυρσών: Φάροι είναι µεγάλης φωτιστικής εµβέλειας (10-25 νµ), χρησιµεύουν σαν ναυτιλιακό βοήθηµα (εντοπισµό στίγµατος) και είναι λευκοί Φανάρια ή φανοί είναι µικρότερης φωτιστικής εµβέλειας (5-10 νµ) και χρησιµεύουν για επισήµανση ναυτιλιακών κινδύνων ή για ένδειξη εισόδου λιµανιών ή διαύλων. Είναι λευκοί, ερυθροί ή πράσινοι. Φωτοσηµαντήρες είναι µικρής εµβέλειας (< 5 νµ) και βρίσκονται αγκυροβοληµένοι.
8 Το µεγαλύτερο µέρος του δικτύου των φάρων στην Ελλάδα χτίσθηκε την περίοδο µεταξύ και είναι από τα τελειότερα παγκοσµίως. Οι φάροι αυτοί αποτελούν, από αρχιτεκτονικής άποψης, πραγµατικά έργα τέχνης αλλά και τεχνολογικά επιτεύγµατα. Οι µηχανισµοί τους, κατασκευασµένοι οι περισσότεροι από Γάλλους µηχανικούς, ήταν πρωτοποριακοί για εκείνη την εποχή. Οι περισσότεροι από αυτούς αποτελούν µνηµεία της πολιτιστικής µας κληρονοµιάς και είναι απαραίτητη η συντήρησή τους, ακόµη και εάν σήµερα έχουν αντικατασταθεί από νεότερους. Όλοι οι φάροι της Ελλάδας µε τα πλήρη χαρακτηριστικά τους, βρίσκονται καταγραµµένοι στον "Φαροδείκτη των Ελληνικών ακτών" που εκδίδεται από την Υδρογραφική Υπηρεσία. ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΤΩΝ ΠΥΡΣΩΝ: Χρώµα, µπορεί να είναι λευκό, ερυθρό ή πράσινο (όταν επισηµαίνουν εισόδους λιµανιών ή διαύλων, αφήνουµε αριστερά τους ερυθρούς δεξιά τους πράσινους) Χαρακτήρας φωτός, η σχέση φωτεινής σκοτεινής φάσης [µπορεί να είναι αναλάµπων (Αν), διαλείπων ( λ), ισοφασικός (Ισ), σταθερός (Στ)] και πόσες φορές επαναλαµβάνεται Περίοδος, ο χρόνος (σε δευτερόλεπτα) κατά τον οποίο επιτυγχάνεται µία πλήρης εναλλαγή των χαρακτηριστικών του Εστιακό ύψος, σε µέτρα από την επιφάνεια της θάλασσας Ονοµαστική φωτοβολία, η απόσταση σε ν. µίλια από την οποία είναι ορατός Παράδειγµα: η σύντµηση Αν(2)11δ7µ10Μ σηµαίνει ότι ο φάρος είναι λευκός (εφ' όσον δεν υπάρχει σύντµηση που να αναφέρει άλλο χρώµα), αναλάµπων, κάνει δύο αναλαµπές, η περίοδός του είναι 11 δευτερόλεπτα, το ύψος του από την επιφάνεια της θάλασσας είναι 7 µ και είναι ορατός από απόσταση 10 µιλίων. ΠΡΟΣΟΧΗ!! Για να βρούµε την περίοδο του πυρσού, µετράµε τον χρόνο για µία πλήρη εναλλαγή των χαρακτηριστικών του δηλ. από την πρώτη αναλαµπή µέχρι την επόµενη πρώτη. ΝΑΥΤΙΚΟΙ ΧΑΡΤΕΣ Ο ναυτικός χάρτης είναι η αποτύπωση, σε επίπεδο, ενός τµήµατος της σφαίρας της γης (είναι προφανές ότι η αποτύπωση αυτή είναι αδύνατη χωρίς να προκύψουν παραµορφώσεις). Υπάρχουν προβολές διαφόρων ειδών (κωνική προβολή, πολυκωνική προβολή, γνωµονική προβολή, κυλινδρική προβολή κ.ά.). Για την κατασκευή των ναυτικών χαρτών χρησιµοποιούνται διαφορετικές προβολές, ανάλογα µε το γεωγραφικό πλάτος στο οποίο βρίσκεται η περιοχή που αποτυπώνεται. Για γεωγραφικά πλάτη µέχρι 60 0 χρησιµοποιείται ένα είδος κυλινδρικής προβολής που ονοµάζεται Μερκατορική προβολή (από τον Φλαµανδό χαρτογράφο Gerardus Mercator, που τo 1556 µ.χ. κατασκεύασε χάρτη χρησιµοποιώντας αυτή την προβολή) (σχ 4).
9 Σχήµα 6: Μερκατορική προβολή Στην Μερκατορική προβολή, προκύπτουν οι εξής παραµορφώσεις: Η απόσταση µεταξύ δύο µεσηµβρινών παραµένει ίδια σε όλο τους το µήκος (φαίνονται σαν παράλληλοι),ενώ, όπως προαναφέραµε, στην πραγµατικότητα είναι µέγιστη στον Ισηµερινό και µηδενίζεται στους πόλους. Η γραµµικές αποστάσεις µεταξύ παραλλήλων µε την ίδια διαφορά γεωγραφικού πλάτους είναι διαφορετικές, ανάλογα µε το πλάτος που βρισκόµαστε (µεγαλώνει σε µεγαλύτερα γεωγραφικά πλάτη), ενώ, στην πραγµατικότητα, είναι ίσες. Με δεδοµένο ότι οι ναυτικοί χάρτες είναι πολύ µικρά κοµµάτια του πλήρους αναπτύγµατος της γης, οι παραµορφώσεις αυτές είναι µηδαµινές και µπορούµε να τις θεωρήσουµε µηδενικές. Στο κατακόρυφο περιθώριο του ναυτικού χάρτη, υπάρχουν υποδιαιρέσεις µε τα γεωγραφικά πλάτη και ονοµάζεται κλίµακα πλάτους. Στο οριζόντιο περιθώριο, υπάρχουν υποδιαιρέσεις µε τα γεωγραφικά µήκη και ονοµάζεται κλίµακα µήκους. Στην κλίµακα πλάτους, 1 ισούται µε ένα ναυτικό µίλι Για να υπολογίσουµε µία απόσταση στον ν. χάρτη, την µεταφέρουµε στην κλίµακα πλάτους όπου µετράµε µε πόσα πρώτα λεπτά ισούται, τα οποία αντιστοιχούν σε ν. µίλια (σχ. 7). Προσοχή! η προς µέτρηση απόσταση πρέπει να µεταφέρεται στο πλησιέστερο δυνατό σε αυτήν γεωγραφικό πλάτος, διότι, διαφορετικά, θα υπάρχει σφάλµα οφειλόµενο στην παραµόρφωση που προαναφέραµε.
10 Σχήµα 7: Μέτρηση απόστασης σε Μερκατορικό χάρτη Στους ναυτικούς χάρτες, βρίσκονται αποτυπωµένα όλα τα χαρακτηριστικά και καταφανή σηµεία της στεριάς που µας χρησιµεύουν στην αναγνώριση των ακτών: τα βάθη, οι ισοβαθείς καµπύλες, οι ναυτιλιακοί κίνδυνοι (ύφαλοι, σκόπελοι, ναυάγια κ.α.). Όλα αυτά τα στοιχεία σηµειώνονται µε σύµβολα ή επιτµήσεις που τις επεξηγήσεις τους βρίσκουµε σε ειδική έκδοση της Υδρογραφικής Υπηρεσίας του Πολεµικού Ναυτικού. Όπως γίνεται κατανοητό, οι ν. χάρτες, µας παρέχουν όλες τις απαραίτητες πληροφορίες. Για τον λόγο αυτό είναι σηµαντικό να γίνεται προσεκτική µελέτη του χάρτη της περιοχής που πρόκειται να ταξιδεύσουµε πριν αλλά και κατά την διάρκεια του πλου. Έτσι, έχοντας πλήρη γνώση της περιοχής της ναυτιλίας µας και των κινδύνων που υπάρχουν σε αυτή, αποφεύγουµε δυσάρεστες καταστάσεις όπως πρόσκρουση σε ύφαλο ή απώλεια του στίγµατός µας κ.ά. ΚΛΙΜΑΚΑ ΤΩΝ ΝΑΥΤΙΚΩΝ ΧΑΡΤΩΝ Η κλίµακα του ν. χάρτη δηλώνει πόσες φορές έχει σµικρυνθεί η περιοχή που απεικονίζει. Οι ναυτικοί χάρτες ανάλογα µε την κλίµακά τους διακρίνονται σε: I. Γενικοί χάρτες κλίµακας 1: έως 1: , απεικονίζουν µεγάλες II. θαλάσσιες επιφάνειες και χρησιµεύουν στην σχεδίαση του πλου Ακτοπλοϊκοί χάρτες κλίµακας 1: έως 1: , απεικονίζουν µικρότερες θαλάσσιες επιφάνειες και χρησιµεύουν κατά την ακτοπλοΐα καθώς δείχνουν µε περισσότερες λεπτοµέρειες τις ακτές, ναυτιλιακούς κινδύνους, πυρσούς κ.α.
11 III. Λιµενοδείκτες ή πορτολάνες κλίµακας 1:2.000 έως 1: απεικονίζουν µε µεγάλη λεπτοµέρεια περιορισµένες θαλάσσιες περιοχές, όπως λιµάνια, όρµους αγκυροβολίας, διαύλους κ.α. ΝΑΥΤΙΛΙΑΚΕΣ ΕΚ ΟΣΕΙΣ Η Υδρογραφική υπηρεσία, εκτός από τους ναυτικούς χάρτες, εκδίδει και τα ακόλουθα: Ναυτιλιακές οδηγίες ή πλοηγοί, περιέχουν πληροφορίες για λιµάνια, ναυτιλιακούς κινδύνους, ναυτιλιακά βοηθήµατα, επικρατούντες ανέµους κ.α. Φαροδείκτης, περιέχουν όλα τα στοιχεία των πυρσών Ευρετήρια χαρτών, περιέχουν καταλόγους των χαρτών που εκδίδει η υδρογραφική υπηρεσία Σύµβολα και επιτµήσεις που χρησιµοποιούνται στους ναυτικούς χάρτες ΟΡΓΑΝΑ ΝΑΥΤΙΛΙΑΣ Τα ελάχιστα απαιτούµενα όργανα ναυτιλίας που πρέπει, µαζί µε τους χάρτες και την πυξίδα, να βρίσκονται στο σκάφος είναι τα εξής (σχ.8): ιπαράλληλος: διπλός κανόνας, ο οποίος µας επιτρέπει να µεταφέρουµε ευθείες παράλληλα επάνω στον ν. χάρτη. Ναυτικός διαβήτης ή κουµπάσο: είδος διαβήτη-διαστηµόµετρου, µε δύο όµοια σκέλη, χωρίς γραφίδα, µε το οποίο µετρούµε αποστάσεις στον ν. χάρτη. Πυξίδα διόπτευσης: πυξίδα χειρός µε σκόπευτρο µε την οποία παίρνουµε διόπτευση κάποιου σηµείου (η γωνία, µε κορυφή το σκάφος, που σχηµατίζει αυτό το σηµείο µε τον µαγνητικό Β). Μοιρογνωµόνιο Μολύβι και γοµολάστιχα
12 Σχήµα 8: Κουµπάσο και διπαράλληλος ΥΠΟΛΟΓΙΣΜΟΣ ΤΗΣ ΠΟΡΕΙΑΣ ΤΟΥ ΣΚΑΦΟΥΣ Πορεία ενός σκάφους, ονοµάζεται η γωνία που σχηµατίζει η κατεύθυνσή του µε αυτήν του Β. Εάν η γωνία είναι υπολογισµένη µε βάση την κατεύθυνση του γεωγραφικού Β ονοµάζεται γεωγραφική, ενώ, εάν είναι υπολογισµένη µε βάση αυτή του µαγνητικού, ονοµάζεται µαγνητική. Για να υπολογίσουµε την µαγνητική πορεία ακολουθούµε τα εξής: Χαράσσουµε την ευθεία της πορείας του σκάφους στον ν. χάρτη, ενώνοντας µε µία ευθεία τα σηµεία απόπλου και κατάπλου. Ελέγχουµε εάν κατά µήκος της ευθείας αυτής υπάρχουν εµπόδια ή ναυτιλιακοί κίνδυνοι (αν υπάρχει κάποιο εµπόδιο (ύφαλος, κάβος, νησί κτλ), θα πρέπει να το παρακάµψουµε, χαράσσοντας µια τεθλασµένη γραµµή και υπολογίζοντας να περάσουµε µε την µικρότερη απόσταση ασφαλείας από το εµπόδιο). Μεταφέρουµε - µε την βοήθεια του διπαράλληλου - την ευθεία της πορείας µας, παράλληλα, µέχρι να γίνει διάµετρος στο πλησιέστερο ανεµολόγιο. ιαβάζουµε στο ανεµολόγιο τις µοίρες που µας δείχνει ο διπαράλληλος (στην κατεύθυνση της πορείας µας). Αυτή είναι η πραγµατική (ή γεωγραφική) πορεία του σκάφους. Υπολογίζουµε την απόκλιση σήµερα (είναι σηµειωµένη στο ανεµολόγιο). Βρίσκουµε την µαγνητική πορεία, αφαιρώντας (αλγεβρικά) την απόκλιση από την πραγµατική πορεία. Σηµειώνουµε την τιµή της µαγν. πορείας κοντά στην ευθεία που έχουµε χαράξει (ή στο σηµειωµατάριό µας), µαζί µε ένα βέλος που θα µας δείχνει την κατεύθυνση στην οποία αντιστοιχεί η πορεία αυτή. Υπολογίζουµε την απόσταση που θα διανύσουµε, τοποθετώντας τα σκέλη του κουµπάσου στα σηµεία απόπλου και κατάπλου και µεταφέροντας αυτό το
13 διάστηµα στην κλίµακα πλάτους (όπου, 1 της µοίρας αντιστοιχεί σε 1 ναυτ. µίλι), προσέχοντας να είµαστε σε κοντινό στην πορεία µας γεωγρ. πλάτος. Σηµειώνουµε την τιµή της απόστασης δίπλα σε αυτή της µαγν. πορείας. Εάν η πορεία µας είναι τεθλασµένη γραµµή, έχει δηλαδή περισσότερα από ένα σκέλη, υπολογίζουµε την µαγν. πορεία και την απόσταση για κάθε σκέλος χωριστά και το σηµειώνουµε. ΠΡΟΣΟΧΗ! Ο υπολογισµός της πορείας είναι ένα µέρος µόνο (και ίσως το απλούστερο) της όλης διαδικασίας που πρέπει να ακολουθήσει ο ναυτιλλόµενος προκειµένου να κάνει σωστή ακτοπλοΐα. Το δυσκολότερο και περισσότερο πολύπλοκο κοµµάτι της ναυτιλίας, αποτελεί η παρατήρηση και µελέτη του χάρτη που πρέπει να γίνει πολύ προσεκτικά. Εκεί θα εντοπιστούν οι κίνδυνοι και τα χαρακτηριστικά καταφανή σηµεία που θα συναντήσουµε καθώς και τα ασφαλή αγκυροβόλια και θα κρατηθούν οι σχετικές σηµειώσεις και παρατηρήσεις. Έτσι, θα πρέπει να είναι σε θέση, σε οποιοδήποτε σηµείο του ταξιδιού να αναγνωρίσει στον χάρτη ό,τι βλέπει γύρω του, αλλά και να γνωρίζει τι πρόκειται να δει. Αυτή είναι απαραίτητη προϋπόθεση για να κάνει κανείς σωστή και ασφαλή ακτοπλοΐα. Εκτός αυτών, θα πρέπει, τουλάχιστον κάθε µία ώρα (µε άσχηµες καιρικές συνθήκες κάθε µισή ώρα) να βρίσκει το στίγµα, µε τους τρόπους που θα περιγράψουµε παρακάτω. ΥΠΟΛΟΓΙΣΜΟΣ ΤΗΣ ΑΠΟΣΤΑΣΗΣ Για τον υπολογισµό της απόστασης, χρησιµοποιούµε το κουµπάσο ως εξής: Τοποθετούµε τα δύο σκέλη του κουµπάσου στα σηµεία απόπλου και κατάπλου της πορείας µας και το µεταφέρουµε στην κατακόρυφη κλίµακα πλάτους όπου κάθε 1 της µοίρας αντιστοιχεί σε 1 νµ. Εάν η πορεία µας δεν είναι ευθεία, αλλά αποτελεί τεθλασµένη γραµµή, µετράµε την απόσταση του κάθε σκέλους χωριστά. ΓΡΑΜΜΕΣ ΘΕΣΕΩΣ Γραµµή θέσεως είναι µια γραµµή που προκύπτει µε κατάλληλες µετρήσεις και κάθε σηµείο της αποτελεί πιθανή θέση του σκάφους. Οι κυριότερες γραµµές θέσεως είναι: I. Απόλυτη διόπτευση ενός αντικειµένου, που µετριέται µε την πυξίδα διοπτεύσεως (σχ 9α) II. Ευθυγράµµιση δύο αντικειµένων (σχ. 9β) III. Ισοβαθής καµπύλη που προσδιορίζεται µε µέτρηση του βάθους µε την βοήθεια του βυθοµέτρου του σκάφους IV. Απόσταση ενός αντικειµένου, που µετριέται µε συσκευή RADAR
14 Σχήµα 9: (α) απόλυτη διόπτευση (β) ευθυγράµµιση ΥΠΟΛΟΓΙΣΜΟΣ ΤΟΥ ΣΤΙΓΜΑΤΟΣ ΤΟΥ ΣΚΑΦΟΥΣ Στίγµα, όπως προαναφέραµε, ονοµάζεται το σηµείο που βρίσκεται το σκάφος και η τιµή του δίνεται από το γεωγραφικό πλάτος και το γεωγραφικό µήκος του σηµείου αυτού. Η τοµή δύο ή περισσότερων γραµµών θέσεως, µας δίνει το στίγµα του σκάφους. Για να υπολογίσουµε το στίγµα µε δύο απόλυτες διοπτεύσεις καταφανών σηµείων, προϋποθέτει: - Να βλέπουµε δύο σηµεία (π.χ. ένα φάρο και ένα κάβο) τα οποία µπορούµε να αναγνωρίσουµε στον χάρτη. - Για να έχουµε µεγαλύτερη ακρίβεια στην µέτρησή µας, θα πρέπει αυτά τα δύο σηµεία να σχηµατίζουν µε εµάς την πλησιέστερη δυνατή στις 90 0 γωνία (>30 0, <120 0 ). - Θα πρέπει να είναι "σηµεία" δηλ. να µην έχουν µεγάλη έκταση (π.χ. το αεροδρόµιο). Η διαδικασία που ακολουθούµε για τον υπολογισµό του στίγµατος µε δύο απόλυτες διοπτεύσεις, είναι η εξής (σχ. 10): 1. Παίρνουµε - µε την βοήθεια της πυξίδας διοπτεύσεως - διόπτευση από το κάθε σηµείο και την σηµειώνουµε. 2. Πηγαίνουµε στο ανεµολόγιο του ν. χάρτη και τοποθετούµε σ αυτό τον διπαράλληλο, διαµετρικά, στις µοίρες της πρώτης µέτρησης (αφού προηγουµένως έχουµε υπολογίσει την απόκλιση και την έχουµε προσθέσει στην τιµή της µαγν. διόπτευσης).
15 3. Μεταφέρουµε την ευθεία αυτή παράλληλα, µέχρι να περάσει από το σηµείο το οποίο διοπτεύσαµε. Το σκάφος µας θα βρίσκεται κάπου επάνω σ αυτή την ευθεία. 4. Εφαρµόζουµε την ίδια διαδικασία για την δεύτερη διόπτευση και µεταφέρουµε την ευθεία µέχρι να περάσει από το δεύτερο σηµείο που διοπτεύσαµε. Το σκάφος θα βρίσκεται κάπου επάνω και σ αυτή την ευθεία. 5. Το σηµείο τοµής των δύο ευθειών είναι το στίγµα µας. 6. Για µεγαλύτερη ακρίβεια αλλά και για επιβεβαίωση των µετρήσεών µας, µπορούµε να πάρουµε διόπτευση και από τρίτο σηµείο. Η τοµή των τριών ευθειών θα σχηµατίζει ένα τρίγωνο. Το στίγµα µας θα βρίσκεται στο κέντρο του τριγώνου. Το µήκος των πλευρών του τριγώνου είναι ενδεικτικό της ακρίβειας των µετρήσεών µας (σχ. 11). Παρατήρηση: Κατά τον υπολογισµό του στίγµατος µε διόπτευση, πρέπει να είµαστε σίγουροι ότι τα σηµεία που διοπτεύουµε είναι αυτά που αναγνωρίζουµε στον χάρτη. Κάθε νησί που βλέπουµε, έχει δύο χαρακτηριστικά σηµεία από τα οποία µπορούµε να πάρουµε διόπτευση: τους δύο ακραίους κάβους του που εφάπτονται στην θάλασσα (δεξιά και αριστερά). εν είµαστε ποτέ σε θέση να γνωρίζουµε ποιοι είναι αυτοί οι κάβοι στον χάρτη. Θα το µάθουµε, µόνο, αφού πάρουµε διόπτευση από τον κάθε ένα και προσπαθήσουµε να την αποτυπώσουµε στον χάρτη. Τότε, ο πρώτος κάβος που θα συναντάµε όταν κινούµε τον διπαράλληλο από την θάλασσα προς την στεριά, στην τιµή της διόπτευσης, θα είναι αυτός που διοπτεύσαµε. Σχήµα 10: απόλυτη διόπτευση (α) δύο σηµείων (β) τριών σηµείων
16 Σχήµα 11: Ακρίβεια υπολογισµού στίγµατος µε τρεις διοπτεύσεις Η αναµέτρηση, είναι απλούστερος αλλά λιγότερο αξιόπιστος τρόπος υπολογισµού του στίγµατος. Γνωρίζοντας το σηµείο από το οποίο έχουµε αποπλεύσει (ή έχουµε πάρει το τελευταίο στίγµα) και για κάποιο συγκεκριµένο χρονικό διάστηµα (π.χ. 1 ώρα) πλέουµε µε σταθερή πορεία (π.χ ) και ταχύτητα (π.χ. 6 κόµβους). Υπολογίζουµε πόση απόσταση έχουµε διανύσει (6 µίλια). Ακολούθως πηγαίνουµε στον χάρτη και αποτυπώνουµε το διάστηµα που έχουµε διανύσει επάνω στην ευθεία της πορείας µας. Στο τέλος του διαστήµατος αυτού θα είναι το στίγµα µας. Όπως γίνεται φανερό, για να έχουµε ακρίβεια στον υπολογισµό του στίγµατος µε αναµέτρηση, πρέπει καθ όλη την διάρκεια της µέτρησης να είµαστε βέβαιοι ότι κρατάµε σταθερή πορεία και ταχύτητα. Εάν υπάρχουν ρεύµατα ή εκπεσµός και δεν τα υπολογίσουµε, θα οδηγηθούµε σε σηµαντικό σφάλµα. Η αναµέτρηση είναι ο µοναδικός τρόπος υπολογισµού του στίγµατος όταν δεν έχουµε οπτική επαφή µε την στεριά ή όταν υπάρχει περιορισµένη ορατότητα. Στην περίπτωση αυτή, ο ναυτίλος πρέπει να ενηµερώνεται από τον τιµονιέρη σχετικά µε κάθε αλλαγή στην πορεία ή την ταχύτητα του σκάφους. Ακολούθως να πηγαίνει στον χάρτη και να αποτυπώνει την αλλαγή αυτή, ώστε, µε αυτό τον τρόπο, να παρακολουθεί συνεχώς την πορεία του σκάφους στον χάρτη και να είναι ανά πάσα στιγµή σε θέση να δώσει το στίγµα.
Επειδή ο μεσημβρινός τέμνει ξανά τον παράλληλο σε αντιδιαμετρικό του σημείο θα θεωρούμε μεσημβρινό το ημικύκλιο και όχι ολόκληρο τον κύκλο.
 ΝΑΥΣΙΠΛΟΪΑ Η ιστιοπλοΐα ανοιχτής θαλάσσης δεν διαφέρει στα βασικά από την ιστιοπλοΐα τριγώνου η οποία γίνεται με μικρά σκάφη καi σε προκαθορισμένο στίβο. Όταν όμως αφήνουμε την ακτή και ανοιγόμαστε στο
ΝΑΥΣΙΠΛΟΪΑ Η ιστιοπλοΐα ανοιχτής θαλάσσης δεν διαφέρει στα βασικά από την ιστιοπλοΐα τριγώνου η οποία γίνεται με μικρά σκάφη καi σε προκαθορισμένο στίβο. Όταν όμως αφήνουμε την ακτή και ανοιγόμαστε στο
1o ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑΤΟΣ «ΜΗΧΑΝΙΚΗ ΤΩΝ ΩΚΕΑΝΩΝ» Χάρτες: Προσδιορισμός θέσης
 1o ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑΤΟΣ «ΜΗΧΑΝΙΚΗ ΤΩΝ ΩΚΕΑΝΩΝ» Χάρτες: Προσδιορισμός θέσης Απαραίτητο όλων των ωκεανογραφικών ερευνών και μελετών Προσδιορισμός θέσης & πλοήγηση σκάφους Σε αυτό το εργαστήριο.. Τι περιλαμβάνει
1o ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑΤΟΣ «ΜΗΧΑΝΙΚΗ ΤΩΝ ΩΚΕΑΝΩΝ» Χάρτες: Προσδιορισμός θέσης Απαραίτητο όλων των ωκεανογραφικών ερευνών και μελετών Προσδιορισμός θέσης & πλοήγηση σκάφους Σε αυτό το εργαστήριο.. Τι περιλαμβάνει
Δρ. Απόστολος Ντάνης. Σχολικός Σύμβουλος Φυσικής Αγωγής
 Δρ. Απόστολος Ντάνης Σχολικός Σύμβουλος Φυσικής Αγωγής *Βασικές μορφές προσανατολισμού *Προσανατολισμός με τα ορατά σημεία προορισμού στη φύση *Προσανατολισμός με τον ήλιο *Προσανατολισμός από τη σελήνη
Δρ. Απόστολος Ντάνης Σχολικός Σύμβουλος Φυσικής Αγωγής *Βασικές μορφές προσανατολισμού *Προσανατολισμός με τα ορατά σημεία προορισμού στη φύση *Προσανατολισμός με τον ήλιο *Προσανατολισμός από τη σελήνη
2
 ΝΑΥΤΙΛΙΑ Ναυτιλία είναι η τέχνη του να γνωρίζεις, µέσα στο απέραντο γαλάζιο της θάλασσας, που βρίσκεσαι και τι πορεία πρέπει να ακολουθήσεις για να φτάσεις στον προορισµό σου. Επιµέλεια : Ηλίας. Γεωργίου
ΝΑΥΤΙΛΙΑ Ναυτιλία είναι η τέχνη του να γνωρίζεις, µέσα στο απέραντο γαλάζιο της θάλασσας, που βρίσκεσαι και τι πορεία πρέπει να ακολουθήσεις για να φτάσεις στον προορισµό σου. Επιµέλεια : Ηλίας. Γεωργίου
ΓΕΩΛΟΓΙΑ - ΓΕΩΓΡΑΦΙΑ Α ΓΥΜΝΑΣΙΟΥ
 ΓΕΩΛΟΓΙΑ - ΓΕΩΓΡΑΦΙΑ Α ΓΥΜΝΑΣΙΟΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 2018 2019 ΤΟ ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ ΜΕ ΕΡΩΤΗΣΕΙΣ- ΑΠΑΝΤΗΣΕΙΣ 1 Περιεχόμενα ΕΝΟΤΗΤΑ Α : ΧΑΡΤΕΣ Α1.4 Ποιον χάρτη να διαλέξω;. 3 Α1.3 Η χρήση των χαρτών στην καθημερινή
ΓΕΩΛΟΓΙΑ - ΓΕΩΓΡΑΦΙΑ Α ΓΥΜΝΑΣΙΟΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 2018 2019 ΤΟ ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ ΜΕ ΕΡΩΤΗΣΕΙΣ- ΑΠΑΝΤΗΣΕΙΣ 1 Περιεχόμενα ΕΝΟΤΗΤΑ Α : ΧΑΡΤΕΣ Α1.4 Ποιον χάρτη να διαλέξω;. 3 Α1.3 Η χρήση των χαρτών στην καθημερινή
Εισηγητής: Καραγιώργος Θωμάς, MSc, PhD candidate in Sport Management & Recreation ΤΜΗΜΑ ΕΠΙΣΤΙΜΗΣ ΦΥΣΙΚΗΣ ΑΓΩΓΗΣ & ΑΘΛΗΤΙΣΜΟΥ ΑΡΙΣΤOΤΕΛΕΙΟ
 Εισηγητής: Καραγιώργος Θωμάς, MSc, PhD candidate in Sport Management & Recreation ΤΜΗΜΑ ΕΠΙΣΤΙΜΗΣ ΦΥΣΙΚΗΣ ΑΓΩΓΗΣ & ΑΘΛΗΤΙΣΜΟΥ ΑΡΙΣΤOΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Γεωδαιτικό σύστημα Χάρτης Πυξίδα Χάραξη
Εισηγητής: Καραγιώργος Θωμάς, MSc, PhD candidate in Sport Management & Recreation ΤΜΗΜΑ ΕΠΙΣΤΙΜΗΣ ΦΥΣΙΚΗΣ ΑΓΩΓΗΣ & ΑΘΛΗΤΙΣΜΟΥ ΑΡΙΣΤOΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Γεωδαιτικό σύστημα Χάρτης Πυξίδα Χάραξη
Άλλοι χάρτες λαμβάνουν υπόψη και το υψόμετρο του αντικειμένου σε σχέση με ένα επίπεδο αναφοράς
 ΤΟΠΟΓΡΑΦΙΚΟΙ ΧΑΡΤΕΣ Ένας χάρτης είναι ένας τρόπος αναπαράστασης της πραγματικής θέσης ενός αντικειμένου ή αντικειμένων σε μια τεχνητά δημιουργουμένη επιφάνεια δύο διαστάσεων Πολλοί χάρτες (π.χ. χάρτες
ΤΟΠΟΓΡΑΦΙΚΟΙ ΧΑΡΤΕΣ Ένας χάρτης είναι ένας τρόπος αναπαράστασης της πραγματικής θέσης ενός αντικειμένου ή αντικειμένων σε μια τεχνητά δημιουργουμένη επιφάνεια δύο διαστάσεων Πολλοί χάρτες (π.χ. χάρτες
ΤΟΠΟΓΡΑΦΙΚΟΣ ΧΑΡΤΗΣ. Στοιχεία τοπογραφικών χαρτών
 ΤΟΠΟΓΡΑΦΙΚΟΣ ΧΑΡΤΗΣ Στοιχεία τοπογραφικών χαρτών ρ. Ε. Λυκούδη Αθήνα 2005 Τοπογραφικοί χάρτες Βασικό στοιχείο του χάρτη αποτελεί : το τοπογραφικό υπόβαθρο, που αναπαριστά µε τη βοήθεια γραµµών (ισοϋψών)
ΤΟΠΟΓΡΑΦΙΚΟΣ ΧΑΡΤΗΣ Στοιχεία τοπογραφικών χαρτών ρ. Ε. Λυκούδη Αθήνα 2005 Τοπογραφικοί χάρτες Βασικό στοιχείο του χάρτη αποτελεί : το τοπογραφικό υπόβαθρο, που αναπαριστά µε τη βοήθεια γραµµών (ισοϋψών)
Απαντήσεις πανελληνίων θεμάτων στην. Ναυσιπλοΐα ΙΙ 12/06/2018
 Απαντήσεις πανελληνίων θεμάτων στην Ναυσιπλοΐα ΙΙ 12/06/2018 ΘΕΜΑ Α Α1. α. Λ β. Σ γ. Λ δ. Λ ε. Σ Α2. 1 ε 2 στ 3 - β 4 α 5 - γ ΘΕΜΑ Β Β1. α)(σελ 13) Το επίπεδο κάθετο προς τη κατακόρυφο που διέρχεται από
Απαντήσεις πανελληνίων θεμάτων στην Ναυσιπλοΐα ΙΙ 12/06/2018 ΘΕΜΑ Α Α1. α. Λ β. Σ γ. Λ δ. Λ ε. Σ Α2. 1 ε 2 στ 3 - β 4 α 5 - γ ΘΕΜΑ Β Β1. α)(σελ 13) Το επίπεδο κάθετο προς τη κατακόρυφο που διέρχεται από
Κεφάλαιο 5. 5 Συστήματα συντεταγμένων
 Κεφάλαιο 5 5 Συστήματα συντεταγμένων Στις Γεωεπιστήμες η μορφή της γήινης επιφάνειας προσομοιώνεται από μια επιφάνεια, που ονομάζεται γεωειδές. Το γεωειδές είναι μια ισοδυναμική επιφάνεια του βαρυτικού
Κεφάλαιο 5 5 Συστήματα συντεταγμένων Στις Γεωεπιστήμες η μορφή της γήινης επιφάνειας προσομοιώνεται από μια επιφάνεια, που ονομάζεται γεωειδές. Το γεωειδές είναι μια ισοδυναμική επιφάνεια του βαρυτικού
β. Το τρίγωνο που σχηματίζεται στην επιφάνεια της σφαίρας, του οποίου οι πλευρές αποτελούν τόξα μεγίστων κύκλων, ονομάζεται σφαιρικό τρίγωνο.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑΔΑ Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΘΕΜΑ 1 ο ΤΕΤΑΡΤΗ 16/04/2014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΝΑΥΣΙΠΛΟΪΑ II ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΑΠΑΝΤΗΣΕΙΣ 1) Να χαρακτηρίσετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑΔΑ Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΘΕΜΑ 1 ο ΤΕΤΑΡΤΗ 16/04/2014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΝΑΥΣΙΠΛΟΪΑ II ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΑΠΑΝΤΗΣΕΙΣ 1) Να χαρακτηρίσετε
Tοπογραφικά Σύμβολα. Περιγραφή Χάρτη. Συνήθως στους χάρτες υπάρχει υπόμνημα με τα σύμβολα που χρησιμοποιούνται. Τα πιο συνηθισμένα είναι τα εξής:
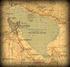 Tοπογραφικά Σύμβολα Συνήθως στους χάρτες υπάρχει υπόμνημα με τα σύμβολα που χρησιμοποιούνται. Τα πιο συνηθισμένα είναι τα εξής: Κεντρική Αρτηρία Ρέμα Δευτερεύουσα Αρτηρία Πηγάδι Χωματόδρομος Πηγή Μονοπάτι
Tοπογραφικά Σύμβολα Συνήθως στους χάρτες υπάρχει υπόμνημα με τα σύμβολα που χρησιμοποιούνται. Τα πιο συνηθισμένα είναι τα εξής: Κεντρική Αρτηρία Ρέμα Δευτερεύουσα Αρτηρία Πηγάδι Χωματόδρομος Πηγή Μονοπάτι
Φύλλο Εργασίας. Θέμα : Περπατώντας στο Πήλιο Θέλετε να οργανώσετε έναν ορειβατικό περίπατο από την Αγριά στην Δράκεια Πηλίου.
 Ενότητα Χάρτες Φύλλο Εργασίας Μελέτη χαρτών Τάξη Α Γυμνασίου Ονοματεπώνυμο.Τμήμα..Ημερομηνία. Σκοποί του φύλλου εργασίας Η εξοικείωση 1. Με την χρήση των χαρτών 2. Με την χρήση της πυξίδας 3. Με την εργασία
Ενότητα Χάρτες Φύλλο Εργασίας Μελέτη χαρτών Τάξη Α Γυμνασίου Ονοματεπώνυμο.Τμήμα..Ημερομηνία. Σκοποί του φύλλου εργασίας Η εξοικείωση 1. Με την χρήση των χαρτών 2. Με την χρήση της πυξίδας 3. Με την εργασία
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΓΕΩΓΡΑΦΙΚΕΣ ΣΥΝΤΕΤΑΓΜΕΝΕΣ (ΤΑΞΗ Α ΓΥΜΝΑΣΙΟΥ).
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΓΕΩΓΡΑΦΙΚΕΣ ΣΥΝΤΕΤΑΓΜΕΝΕΣ (ΤΑΞΗ Α ΓΥΜΝΑΣΙΟΥ). Ονοματεπώνυμο: Ημερομηνία... Ατομική εργασία: Παρατήρησε την υδρόγειο σφαίρα καθώς και τον παγκόσμιο χάρτη που βρίσκεται κρεμασμένος στον τοίχο
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΓΕΩΓΡΑΦΙΚΕΣ ΣΥΝΤΕΤΑΓΜΕΝΕΣ (ΤΑΞΗ Α ΓΥΜΝΑΣΙΟΥ). Ονοματεπώνυμο: Ημερομηνία... Ατομική εργασία: Παρατήρησε την υδρόγειο σφαίρα καθώς και τον παγκόσμιο χάρτη που βρίσκεται κρεμασμένος στον τοίχο
Προσανατολισμός. Γιώργος Τσεβεκίδης. Υπεύθυνοι Καθηγητές: Σμυρλή Ιωάννα. Πιτένη Αναστασία. Καραγιάννης Στέργιος
 Προσανατολισμός Γιώργος Τσεβεκίδης Υπεύθυνοι Καθηγητές: Σμυρλή Ιωάννα Πιτένη Αναστασία Καραγιάννης Στέργιος ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ Προσανατολισμός είναι η διαδικασία με την οποία καθορίζουμε τη θέση του Βορρά
Προσανατολισμός Γιώργος Τσεβεκίδης Υπεύθυνοι Καθηγητές: Σμυρλή Ιωάννα Πιτένη Αναστασία Καραγιάννης Στέργιος ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ Προσανατολισμός είναι η διαδικασία με την οποία καθορίζουμε τη θέση του Βορρά
15 ος Πανελλήνιος Μαθητικός Διαγωνισµός Αστρονοµίας και Διαστηµικής 2010 Θέµατα για το Γυµνάσιο
 15 ος Πανελλήνιος Μαθητικός Διαγωνισµός Αστρονοµίας και Διαστηµικής 2010 Θέµατα για το Γυµνάσιο 1.- Από τα πρώτα σχολικά µας χρόνια µαθαίνουµε για το πλανητικό µας σύστηµα. Α) Ποιος είναι ο πρώτος και
15 ος Πανελλήνιος Μαθητικός Διαγωνισµός Αστρονοµίας και Διαστηµικής 2010 Θέµατα για το Γυµνάσιο 1.- Από τα πρώτα σχολικά µας χρόνια µαθαίνουµε για το πλανητικό µας σύστηµα. Α) Ποιος είναι ο πρώτος και
β. Το τρίγωνο που σχηματίζεται στην επιφάνεια της σφαίρας, του οποίου οι πλευρές αποτελούν τόξα μεγίστων κύκλων, ονομάζεται σφαιρικό τρίγωνο.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑΔΑ Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 19/04/2017 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΝΑΥΣΙΠΛΟΪΑ ΙΙ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ 1 ο 1) Να χαρακτηρίσετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑΔΑ Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 19/04/2017 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΝΑΥΣΙΠΛΟΪΑ ΙΙ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ 1 ο 1) Να χαρακτηρίσετε
ΓΕΩΓΡΑΦΙΚΑ ΣΥΣΤΗΜΑΤΑ ΠΛΗΡΟΦΟΡΙΩΝ ΚΑΙ ΤΗΛΕΠΙΣΚΟΠΗΣΗ ΣΤΗΝ ΕΦΑΡΜΟΣΜΕΝΗ ΓΕΩΛΟΓΙΑ
 ΓΕΩΓΡΑΦΙΚΑ ΣΥΣΤΗΜΑΤΑ ΠΛΗΡΟΦΟΡΙΩΝ ΚΑΙ ΤΗΛΕΠΙΣΚΟΠΗΣΗ ΣΤΗΝ ΕΦΑΡΜΟΣΜΕΝΗ ΓΕΩΛΟΓΙΑ Ενότητα 9: Προβολικά Συστήματα (Μέρος 1 ο ) Νικολακόπουλος Κωνσταντίνος, Επίκουρος Καθηγητής Σχολή Θετικών Επιστημών Τμήμα Γεωλογίας
ΓΕΩΓΡΑΦΙΚΑ ΣΥΣΤΗΜΑΤΑ ΠΛΗΡΟΦΟΡΙΩΝ ΚΑΙ ΤΗΛΕΠΙΣΚΟΠΗΣΗ ΣΤΗΝ ΕΦΑΡΜΟΣΜΕΝΗ ΓΕΩΛΟΓΙΑ Ενότητα 9: Προβολικά Συστήματα (Μέρος 1 ο ) Νικολακόπουλος Κωνσταντίνος, Επίκουρος Καθηγητής Σχολή Θετικών Επιστημών Τμήμα Γεωλογίας
39 40'13.8"N 20 51'27.4"E ή , καταχωρουνται στο gps ως
 ΣΥΝΤΕΤΑΓΜΕΝΕΣ,ΑΝΑΛΥΣΗ ΕΝΝΟΙΩΝ &ΤΡΟΠΟΙ ΚΑΤΑΓΡΑΦΗΣ ΣΕ GPS Το γεωγραφικό πλάτος (latitude) είναι ένα από τα δύο μεγέθη των γεωγραφικών συντεταγμένων με τα οποία προσδιορίζεται η θέση των διαφόρων τόπων και
ΣΥΝΤΕΤΑΓΜΕΝΕΣ,ΑΝΑΛΥΣΗ ΕΝΝΟΙΩΝ &ΤΡΟΠΟΙ ΚΑΤΑΓΡΑΦΗΣ ΣΕ GPS Το γεωγραφικό πλάτος (latitude) είναι ένα από τα δύο μεγέθη των γεωγραφικών συντεταγμένων με τα οποία προσδιορίζεται η θέση των διαφόρων τόπων και
ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ
 B ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ ΔΙΑΓΩΝΙΣΜΟΣ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΕΤΟΥΣ 2005 ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΟΥ Κλάδος-Ειδικότητα: ΠΕ 1861 ΝΑΥΤΙΚΩΝ ΜΑΘΗΜΑΤΩΝ (ΠΛΟΙΑΡΧΟΙ) ΕΞΕΤΑΣΗ ΣΤΗΝ ΠΡΩΤΗ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ
B ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ ΔΙΑΓΩΝΙΣΜΟΣ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΕΤΟΥΣ 2005 ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΟΥ Κλάδος-Ειδικότητα: ΠΕ 1861 ΝΑΥΤΙΚΩΝ ΜΑΘΗΜΑΤΩΝ (ΠΛΟΙΑΡΧΟΙ) ΕΞΕΤΑΣΗ ΣΤΗΝ ΠΡΩΤΗ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ
ΤΟ ΣΧΗΜΑ ΚΑΙ ΤΟ ΜΕΓΕΘΟΣ ΤΗΣ ΓΗΣ
 ΤΟ ΣΧΗΜΑ ΚΑΙ ΤΟ ΜΕΓΕΘΟΣ ΤΗΣ ΓΗΣ Χαρτογραφία Ι 1 Το σχήμα και το μέγεθος της Γης [Ι] Σφαιρική Γη Πυθαγόρεια & Αριστοτέλεια αντίληψη παρατηρήσεις φυσικών φαινομένων Ομαλότητα γεωμετρικού σχήματος (Διάμετρος
ΤΟ ΣΧΗΜΑ ΚΑΙ ΤΟ ΜΕΓΕΘΟΣ ΤΗΣ ΓΗΣ Χαρτογραφία Ι 1 Το σχήμα και το μέγεθος της Γης [Ι] Σφαιρική Γη Πυθαγόρεια & Αριστοτέλεια αντίληψη παρατηρήσεις φυσικών φαινομένων Ομαλότητα γεωμετρικού σχήματος (Διάμετρος
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΚΑΙ ΦΥΣΙΚΩΝ ΠΟΡΩΝ ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗΣ ΓΕΩΛΟΓΙΑΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΚΑΙ ΦΥΣΙΚΩΝ ΠΟΡΩΝ ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗΣ ΓΕΩΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ 1: ΤΟΠΟΓΡΑΦΙΚΟΙ ΧΑΡΤΕΣ ΔΙΔΑΣΚΩΝ : Ι. ΖΑΧΑΡΙΑΣ ΑΓΡΙΝΙΟ, 2015 ΕΡΓΑΣΤΗΡΙΟ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΚΑΙ ΦΥΣΙΚΩΝ ΠΟΡΩΝ ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗΣ ΓΕΩΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ 1: ΤΟΠΟΓΡΑΦΙΚΟΙ ΧΑΡΤΕΣ ΔΙΔΑΣΚΩΝ : Ι. ΖΑΧΑΡΙΑΣ ΑΓΡΙΝΙΟ, 2015 ΕΡΓΑΣΤΗΡΙΟ
ΤΟ ΒΙΒΛΙΟ ΕΙΝΑΙ ΕΓΧΡΩΜΟ
 ΨΗΦΙΑΚΗ ΕΚΔΟΣΗ Διατίθεται σε δύο αντίτυπα: ένα για χρήση σε P.C. και ένα για χρήση σε Tablet ή Smartphone 200 σελίδες μεγέθους Β5 (182 257) Κόστος 15,00 Ευρώ για χρήση ενός έτους (*) Κόστος 25,00 Ευρώ
ΨΗΦΙΑΚΗ ΕΚΔΟΣΗ Διατίθεται σε δύο αντίτυπα: ένα για χρήση σε P.C. και ένα για χρήση σε Tablet ή Smartphone 200 σελίδες μεγέθους Β5 (182 257) Κόστος 15,00 Ευρώ για χρήση ενός έτους (*) Κόστος 25,00 Ευρώ
Α Γ Γ Ε Λ Ι Ε Σ Γ Ι Α
 ΚΕΝΤΡΙΚΗ ΥΠΗΡΕΣΙΑ ΥΠΟΚΑΤΑΣΤΗΜΑΤΑ (Γραφεία Πώλησης Εκδόσεων) Ταχυδρομική Διεύθυνση: ΠΟΛΕΜΙΚΟ ΝΑΥΤΙΚΟ, ΥΔΡΟΓΡΑΦΙΚΗ ΥΠΗΡΕΣΙΑ, Διεύθυνση Ασφάλειας Ναυσιπλοΐας ΤΓΝ 1040, ΑΘΗΝΑ Τηλ: (+30) 210 655 1772 (+30)
ΚΕΝΤΡΙΚΗ ΥΠΗΡΕΣΙΑ ΥΠΟΚΑΤΑΣΤΗΜΑΤΑ (Γραφεία Πώλησης Εκδόσεων) Ταχυδρομική Διεύθυνση: ΠΟΛΕΜΙΚΟ ΝΑΥΤΙΚΟ, ΥΔΡΟΓΡΑΦΙΚΗ ΥΠΗΡΕΣΙΑ, Διεύθυνση Ασφάλειας Ναυσιπλοΐας ΤΓΝ 1040, ΑΘΗΝΑ Τηλ: (+30) 210 655 1772 (+30)
ΝΑΥΣΙΠΛΟΪΑ. 1 o ΔΙΑΓΩΝΙΣΜΑ
 ΝΑΥΣΙΠΛΟΪΑ 1 o ΔΙΑΓΩΝΙΣΜΑ α. Τι είναι έξαρμα του πόλου υπέρ τον ορίζοντα και γιατί ενδιαφέρει τον ναυτιλλόμενο. β. Να ορίσετε τα είδη των αστέρων (αειφανείς, αφανείς και Αμφιφανείς)και να γράψετε τις συνθήκες
ΝΑΥΣΙΠΛΟΪΑ 1 o ΔΙΑΓΩΝΙΣΜΑ α. Τι είναι έξαρμα του πόλου υπέρ τον ορίζοντα και γιατί ενδιαφέρει τον ναυτιλλόμενο. β. Να ορίσετε τα είδη των αστέρων (αειφανείς, αφανείς και Αμφιφανείς)και να γράψετε τις συνθήκες
Επίδραση μαγνητικού πεδίου της Γης. (συνοδεύει τις διαφάνειες)
 Επίδραση μαγνητικού πεδίου της Γης (συνοδεύει τις διαφάνειες) Επίδραση μαγνητικού πεδίου της Γης. Ένα σωματίδιο με ατομικό αριθμό Ζ, που κινείται σε μαγνητικά πεδίο Β με ταχύτητα υ. Η κεντρομόλος δύναμη
Επίδραση μαγνητικού πεδίου της Γης (συνοδεύει τις διαφάνειες) Επίδραση μαγνητικού πεδίου της Γης. Ένα σωματίδιο με ατομικό αριθμό Ζ, που κινείται σε μαγνητικά πεδίο Β με ταχύτητα υ. Η κεντρομόλος δύναμη
Β.Π. Ουράνιος Ισηµερινός Ν.Π.
 Β.Π. Ουράνιος Ισηµερινός Ν.Π. Ανάδροµη Φορά Ορθή Φορά Η ορθή και ανάδροµη φορά περιστροφής της Ουράνιας Σφαίρας, όπως φαίνονται από το Βόρειο και το Νότιο ηµισφαίριο, αντίστοιχα Κύκλος Απόκλισης Μεσηµβρινός
Β.Π. Ουράνιος Ισηµερινός Ν.Π. Ανάδροµη Φορά Ορθή Φορά Η ορθή και ανάδροµη φορά περιστροφής της Ουράνιας Σφαίρας, όπως φαίνονται από το Βόρειο και το Νότιο ηµισφαίριο, αντίστοιχα Κύκλος Απόκλισης Μεσηµβρινός
ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ
 ΔΙΑΓΩΝΙΣΜΟΣ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΕΤΟΥΣ 2008 ( ΠΡΟΚΗΡΥΞΗ 4Π /2008) ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΟΥ Κλάδος-Ειδικότητα: ΠΕ 18.23 ΝΑΥΤΙΚΩΝ ΜΑΘΗΜΑΤΩΝ (ΠΛΟΙΑΡΧΟΙ) ΕΞΕΤΑΣΗ ΣΤΗΝ ΠΡΩΤΗ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ Γνωστικό αντικείμενο:
ΔΙΑΓΩΝΙΣΜΟΣ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΕΤΟΥΣ 2008 ( ΠΡΟΚΗΡΥΞΗ 4Π /2008) ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΟΥ Κλάδος-Ειδικότητα: ΠΕ 18.23 ΝΑΥΤΙΚΩΝ ΜΑΘΗΜΑΤΩΝ (ΠΛΟΙΑΡΧΟΙ) ΕΞΕΤΑΣΗ ΣΤΗΝ ΠΡΩΤΗ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ Γνωστικό αντικείμενο:
2ο ΕΡΕΥΝΗΤΙΚΟ ΠΕΔΙΟ: Πρακτικοί τρόποι και μέσα προσανατολισμού από την αρχαιότητα μέχρι και την πυξίδα.
 2ο ΕΡΕΥΝΗΤΙΚΟ ΠΕΔΙΟ: Πρακτικοί τρόποι και μέσα προσανατολισμού από την αρχαιότητα μέχρι και την πυξίδα. Ομάδα εργασίας : Παπαγεωργίου Κριστίνα, Σπύρου Μάρθα, Χαρδαλούπα Ελένη, Χαρδαλούπα Μαριάννα. Αρχαίοι
2ο ΕΡΕΥΝΗΤΙΚΟ ΠΕΔΙΟ: Πρακτικοί τρόποι και μέσα προσανατολισμού από την αρχαιότητα μέχρι και την πυξίδα. Ομάδα εργασίας : Παπαγεωργίου Κριστίνα, Σπύρου Μάρθα, Χαρδαλούπα Ελένη, Χαρδαλούπα Μαριάννα. Αρχαίοι
Η κατακόρυφη ενός τόπου συναντά την ουράνια σφαίρα σε δύο υποθετικά σηµεία, που ονοµάζονται. Ο κατακόρυφος κύκλος που περνά. αστέρα Α ονοµάζεται
 Sfaelos Ioannis Τα ουράνια σώµατα φαίνονται από τη Γη σαν να βρίσκονται στην εσωτερική επιφάνεια µιας γιγαντιαίας σφαίρας, απροσδιόριστης ακτίνας, µε κέντρο τη Γη. Τη φανταστική αυτή σφαίρα τη λέµε "ουράνια
Sfaelos Ioannis Τα ουράνια σώµατα φαίνονται από τη Γη σαν να βρίσκονται στην εσωτερική επιφάνεια µιας γιγαντιαίας σφαίρας, απροσδιόριστης ακτίνας, µε κέντρο τη Γη. Τη φανταστική αυτή σφαίρα τη λέµε "ουράνια
ΝΑΥΣΙΠΛΟΙΑ ΙΙ ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ
 ΝΑΥΣΙΠΛΟΙΑ ΙΙ 3/02/2019 ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ ΘΕΜΑ 1 ο 1) Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι σωστή
ΝΑΥΣΙΠΛΟΙΑ ΙΙ 3/02/2019 ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ ΘΕΜΑ 1 ο 1) Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι σωστή
ΓΕΩΓΡΑΦΙΚΑ ΣΥΣΤΗΜΑΤΑ ΠΛΗΡΟΦΟΡΙΩΝ-2 (ο χάρτης)
 ΓΕΩΓΡΑΦΙΚΑ ΣΥΣΤΗΜΑΤΑ ΠΛΗΡΟΦΟΡΙΩΝ-2 (ο χάρτης) Ο χάρτης ως υπόβαθρο των ΓΣΠ Tα ΓΣΠ βασίζονται στη διαχείριση πληροφοριών που έχουν άμεση σχέση με το γεωγραφικό χώρο, περιέχουν δηλαδή δεδομένα με γεωγραφική
ΓΕΩΓΡΑΦΙΚΑ ΣΥΣΤΗΜΑΤΑ ΠΛΗΡΟΦΟΡΙΩΝ-2 (ο χάρτης) Ο χάρτης ως υπόβαθρο των ΓΣΠ Tα ΓΣΠ βασίζονται στη διαχείριση πληροφοριών που έχουν άμεση σχέση με το γεωγραφικό χώρο, περιέχουν δηλαδή δεδομένα με γεωγραφική
ΜΕΤΡΩΝΤΑΣ ΤΟΝ ΠΛΑΝΗΤΗ ΓΗ
 του Υποπυραγού Αλέξανδρου Μαλούνη* Μέρος 2 ο - Χαρτογραφικοί μετασχηματισμοί Εισαγωγή Είδαμε λοιπόν ως τώρα, ότι η γη θα μπορούσε να χαρακτηρισθεί και σφαιρική και αυτό μπορεί να γίνει εμφανές όταν την
του Υποπυραγού Αλέξανδρου Μαλούνη* Μέρος 2 ο - Χαρτογραφικοί μετασχηματισμοί Εισαγωγή Είδαμε λοιπόν ως τώρα, ότι η γη θα μπορούσε να χαρακτηρισθεί και σφαιρική και αυτό μπορεί να γίνει εμφανές όταν την
Α Γ Γ Ε Λ Ι Ε Σ Γ Ι Α
 ΚΕΝΤΡΙΚΗ ΥΠΗΡΕΣΙΑ ΥΠΟΚΑΤΑΣΤΗΜΑΤΑ (Γραφεία Πώλησης Εκδόσεων) Ταχυδρομική Διεύθυνση: ΠΟΛΕΜΙΚΟ ΝΑΥΤΙΚΟ, ΥΔΡΟΓΡΑΦΙΚΗ ΥΠΗΡΕΣΙΑ, Διεύθυνση Ασφάλειας Ναυσιπλοΐας ΤΓΝ 1040, ΑΘΗΝΑ Τηλ: (+30) 210 655 1772 (+30)
ΚΕΝΤΡΙΚΗ ΥΠΗΡΕΣΙΑ ΥΠΟΚΑΤΑΣΤΗΜΑΤΑ (Γραφεία Πώλησης Εκδόσεων) Ταχυδρομική Διεύθυνση: ΠΟΛΕΜΙΚΟ ΝΑΥΤΙΚΟ, ΥΔΡΟΓΡΑΦΙΚΗ ΥΠΗΡΕΣΙΑ, Διεύθυνση Ασφάλειας Ναυσιπλοΐας ΤΓΝ 1040, ΑΘΗΝΑ Τηλ: (+30) 210 655 1772 (+30)
Ευρωπαϊκή Ολυµπιάδα Φυσικών Επιστηµών 2010 Προκαταρκτικός διαγωνισµός στη Φυσική. Σχολείο:
 ΕΚΦΕ ΑΝΑΤΟΛΙΚΗΣ ΑΤΤΙΚΗΣ Ευρωπαϊκή Ολυµπιάδα Φυσικών Επιστηµών 010 Προκαταρκτικός διαγωνισµός στη Φυσική Σχολείο: Ονόµατα των µαθητών της οµάδας 1) ) 3) Οι στόχοι του πειράµατος 1. Η µέτρηση της επιτάχυνσης
ΕΚΦΕ ΑΝΑΤΟΛΙΚΗΣ ΑΤΤΙΚΗΣ Ευρωπαϊκή Ολυµπιάδα Φυσικών Επιστηµών 010 Προκαταρκτικός διαγωνισµός στη Φυσική Σχολείο: Ονόµατα των µαθητών της οµάδας 1) ) 3) Οι στόχοι του πειράµατος 1. Η µέτρηση της επιτάχυνσης
ΓΕΩΔΑΙΣΙΑ Ι Μάθημα 1 0. Ι.Μ. Δόκας Επικ. Καθηγητής
 ΓΕΩΔΑΙΣΙΑ Ι Μάθημα 1 0 Ι.Μ. Δόκας Επικ. Καθηγητής Γεωδαισία Μοιράζω τη γη (Γη + δαίομαι) Ακριβής Έννοια: Διαίρεση, διανομή /μέτρηση της Γής. Αντικείμενο της γεωδαισίας: Ο προσδιορισμός της μορφής, του
ΓΕΩΔΑΙΣΙΑ Ι Μάθημα 1 0 Ι.Μ. Δόκας Επικ. Καθηγητής Γεωδαισία Μοιράζω τη γη (Γη + δαίομαι) Ακριβής Έννοια: Διαίρεση, διανομή /μέτρηση της Γής. Αντικείμενο της γεωδαισίας: Ο προσδιορισμός της μορφής, του
4/11/2018 ΝΑΥΣΙΠΛΟΙΑ ΙΙ ΓΈΠΑΛ ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ. ΘΕΜΑ 1 ο
 ΝΑΥΣΙΠΛΟΙΑ ΙΙ ΓΈΠΑΛ 4/11/2018 ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ ΘΕΜΑ 1 ο 1) Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι
ΝΑΥΣΙΠΛΟΙΑ ΙΙ ΓΈΠΑΛ 4/11/2018 ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ ΘΕΜΑ 1 ο 1) Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι
Η εργασία που επέλεξες θα σου δώσει τη δυνατότητα να συνεργαστείς με συμμαθητές σου και να σχεδιάσετε μια εικονική εκδρομή με το Google Earth.
 Μια εικονική εκδρομή με το Google Earth Αγαπητέ μαθητή, Η εργασία που επέλεξες θα σου δώσει τη δυνατότητα να συνεργαστείς με συμμαθητές σου και να σχεδιάσετε μια εικονική εκδρομή με το Google Earth. Εσύ
Μια εικονική εκδρομή με το Google Earth Αγαπητέ μαθητή, Η εργασία που επέλεξες θα σου δώσει τη δυνατότητα να συνεργαστείς με συμμαθητές σου και να σχεδιάσετε μια εικονική εκδρομή με το Google Earth. Εσύ
Point to Point Navigation Using RMI only
 Point to Point Navigation Using RMI only Γειά χαρά, κατόπιν συζητήσεων που εχουν γίνει σε συναντήσεις Ελλήνων FlightSimmers έκρινα σκόπιµο να γίνει µια παρουσίαση του πως γινεται η point-to-point αεροναυτιλία
Point to Point Navigation Using RMI only Γειά χαρά, κατόπιν συζητήσεων που εχουν γίνει σε συναντήσεις Ελλήνων FlightSimmers έκρινα σκόπιµο να γίνει µια παρουσίαση του πως γινεται η point-to-point αεροναυτιλία
11 Το ολοκλήρωµα Riemann
 Το ολοκλήρωµα Riem Το πρόβληµα υπολογισµού του εµβαδού οποιασδήποτε επιφάνειας ( όπως κυκλικοί τοµείς, δακτύλιοι και δίσκοι, ελλειπτικοί δίσκοι, παραβολικά και υπερβολικά χωρία κτλ) είναι γνωστό από την
Το ολοκλήρωµα Riem Το πρόβληµα υπολογισµού του εµβαδού οποιασδήποτε επιφάνειας ( όπως κυκλικοί τοµείς, δακτύλιοι και δίσκοι, ελλειπτικοί δίσκοι, παραβολικά και υπερβολικά χωρία κτλ) είναι γνωστό από την
Να το πάρει το ποτάµι;
 Να το πάρει το ποτάµι; Είναι η σκιά ενός σώµατος που το φωτίζει ο Ήλιος. Όπως η σκιά του γνώµονα ενός ηλιακού ρολογιού που µε το αργό πέρασµά της πάνω απ τα σηµάδια των ωρών και µε το ύφος µιας άλλης εποχής
Να το πάρει το ποτάµι; Είναι η σκιά ενός σώµατος που το φωτίζει ο Ήλιος. Όπως η σκιά του γνώµονα ενός ηλιακού ρολογιού που µε το αργό πέρασµά της πάνω απ τα σηµάδια των ωρών και µε το ύφος µιας άλλης εποχής
Η ΓΗ ΣΑΝ ΠΛΑΝΗΤΗΣ. Γεωγραφικά στοιχεία της Γης Σχήµα και µέγεθος της Γης - Κινήσεις της Γης Βαρύτητα - Μαγνητισµός
 Η ΓΗ ΣΑΝ ΠΛΑΝΗΤΗΣ Γεωγραφικά στοιχεία της Γης Σχήµα και µέγεθος της Γης - Κινήσεις της Γης Βαρύτητα - Μαγνητισµός ρ. Ε. Λυκούδη Αθήνα 2005 Γεωγραφικά στοιχεία της Γης Η Φυσική Γεωγραφία εξετάζει: τον γήινο
Η ΓΗ ΣΑΝ ΠΛΑΝΗΤΗΣ Γεωγραφικά στοιχεία της Γης Σχήµα και µέγεθος της Γης - Κινήσεις της Γης Βαρύτητα - Μαγνητισµός ρ. Ε. Λυκούδη Αθήνα 2005 Γεωγραφικά στοιχεία της Γης Η Φυσική Γεωγραφία εξετάζει: τον γήινο
Προβολές Συστήματα Συντεταγμένων
 Πανεπιστήμιο Θεσσαλίας Πολυτεχνική Σχολή Τμήμα Μηχανικών Χωροταξίας Πολεοδομίας και Περιφερειακής Ανάπτυξης Προβολές Συστήματα Συντεταγμένων Ιωάννης Φαρασλής Τηλ : 24210-74466, Πεδίον Άρεως, Βόλος http://www.prd.uth.gr/el/staff/i_faraslis
Πανεπιστήμιο Θεσσαλίας Πολυτεχνική Σχολή Τμήμα Μηχανικών Χωροταξίας Πολεοδομίας και Περιφερειακής Ανάπτυξης Προβολές Συστήματα Συντεταγμένων Ιωάννης Φαρασλής Τηλ : 24210-74466, Πεδίον Άρεως, Βόλος http://www.prd.uth.gr/el/staff/i_faraslis
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ ΕΡΓΑΣΤΗΡΙΟ 1 Ο ΤΟΠΟΓΡΑΦΙΚΟΙ ΧΑΡΤΕΣ Δρ. ΜΑΡΙΑ ΦΕΡΕΝΤΙΝΟΥ 2008-2009
 ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ ΕΡΓΑΣΤΗΡΙΟ 1 Ο ΤΟΠΟΓΡΑΦΙΚΟΙ ΧΑΡΤΕΣ Δρ. ΜΑΡΙΑ ΦΕΡΕΝΤΙΝΟΥ 2008-2009 Τοπογραφικοί Χάρτες Περίγραμμα - Ορισμοί - Χαρακτηριστικά Στοιχεία - Ισοϋψείς Καμπύλες - Κατασκευή τοπογραφικής τομής
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ ΕΡΓΑΣΤΗΡΙΟ 1 Ο ΤΟΠΟΓΡΑΦΙΚΟΙ ΧΑΡΤΕΣ Δρ. ΜΑΡΙΑ ΦΕΡΕΝΤΙΝΟΥ 2008-2009 Τοπογραφικοί Χάρτες Περίγραμμα - Ορισμοί - Χαρακτηριστικά Στοιχεία - Ισοϋψείς Καμπύλες - Κατασκευή τοπογραφικής τομής
ΕΡΓΑΣΤΗΡΙΟ ΩΚΕΑΝΟΓΡΑΦΙΑΣ
 ΧΑΡΟΚΟΠΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Τ Μ Η Μ Α Γ Ε Ω Γ Ρ Α Φ Ι Α Σ ΕΛ. ΒΕΝΙΖΕΛΟΥ, 70 17671 ΚΑΛΛΙΘΕΑ-ΤΗΛ: 210-9549151 FAX: 210-9514759 ΕΡΓΑΣΤΗΡΙΟ ΩΚΕΑΝΟΓΡΑΦΙΑΣ Δ ΕΞΑΜΗΝΟ ΒΥΘΟΜΕΤΡΙΚΟΙ ΧΑΡΤΕΣ Από Καψιμάλη Βασίλη Κύριο
ΧΑΡΟΚΟΠΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Τ Μ Η Μ Α Γ Ε Ω Γ Ρ Α Φ Ι Α Σ ΕΛ. ΒΕΝΙΖΕΛΟΥ, 70 17671 ΚΑΛΛΙΘΕΑ-ΤΗΛ: 210-9549151 FAX: 210-9514759 ΕΡΓΑΣΤΗΡΙΟ ΩΚΕΑΝΟΓΡΑΦΙΑΣ Δ ΕΞΑΜΗΝΟ ΒΥΘΟΜΕΤΡΙΚΟΙ ΧΑΡΤΕΣ Από Καψιμάλη Βασίλη Κύριο
ΗΈνταξητουλογισµικού SalsaJσε. σεµιαδιαθεµατική προσέγγισητης Αστρονοµίας. Γρηγόρης Ζυγούρας Φυσικός Τεχνολόγος 2 ο Γυµνάσιο Χαλανδρίου
 ΗΈνταξητουλογισµικού SalsaJσε σεµιαδιαθεµατική προσέγγισητης Αστρονοµίας Γρηγόρης Ζυγούρας Φυσικός Τεχνολόγος 2 ο Γυµνάσιο Χαλανδρίου ΧΡΗΣΗΤΟΥ ΤΟΥΛΟΓΙΣΜΙΚΟΥ SALSAJ ΓΙΑΤΟΝ ΤΟΝΥΠΟΛΟΓΙΣΜΟ ΤΗΣΜΑΖΑΣ ΜΑΖΑΣΤΟΥ
ΗΈνταξητουλογισµικού SalsaJσε σεµιαδιαθεµατική προσέγγισητης Αστρονοµίας Γρηγόρης Ζυγούρας Φυσικός Τεχνολόγος 2 ο Γυµνάσιο Χαλανδρίου ΧΡΗΣΗΤΟΥ ΤΟΥΛΟΓΙΣΜΙΚΟΥ SALSAJ ΓΙΑΤΟΝ ΤΟΝΥΠΟΛΟΓΙΣΜΟ ΤΗΣΜΑΖΑΣ ΜΑΖΑΣΤΟΥ
Περίθλαση από µία σχισµή.
 ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 71 7. Άσκηση 7 Περίθλαση από µία σχισµή. 7.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε την συµπεριφορά των µικροκυµάτων
ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 71 7. Άσκηση 7 Περίθλαση από µία σχισµή. 7.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε την συµπεριφορά των µικροκυµάτων
Φυσική Γ Λυκείου. Ορμή. Ορμή συστήματος σωμάτων Τ Υ Π Ο Λ Ο Γ Ι Ο Κ Ρ Ο Υ Σ Ε Ω Ν. Θετικού προσανατολισμού
 Τ Υ Π Ο Λ Ο Γ Ι Ο Κ Ρ Ο Υ Σ Ε Ω Ν Φυσική Γ Λυκείου Θετικού προσανατολισμού Ορμή Ορμή Ρ ενός σώματος ονομάζουμε το διανυσματικό μέγεθος που έχει μέτρο το γινόμενο της μάζας m του σώματος επί την ταχύτητά
Τ Υ Π Ο Λ Ο Γ Ι Ο Κ Ρ Ο Υ Σ Ε Ω Ν Φυσική Γ Λυκείου Θετικού προσανατολισμού Ορμή Ορμή Ρ ενός σώματος ονομάζουμε το διανυσματικό μέγεθος που έχει μέτρο το γινόμενο της μάζας m του σώματος επί την ταχύτητά
sin ϕ = cos ϕ = tan ϕ =
 Τ.Ε.Ι. ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΟΜΙΚΩΝ ΕΡΓΩΝ ΜΗΧΑΝΙΚΗ 1 ΠΑΡΑ ΕΙΓΜΑ 1 ΚΑΤΑΣΚΕΥΗ ΙΑΓΡΑΜΜΑΤΩΝ MQN ΣΕ ΟΚΟ ιδάσκων: Αριστοτέλης Ε. Χαραλαµπάκης Εισαγωγή Με το παράδειγµα αυτό αναλύεται
Τ.Ε.Ι. ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΟΜΙΚΩΝ ΕΡΓΩΝ ΜΗΧΑΝΙΚΗ 1 ΠΑΡΑ ΕΙΓΜΑ 1 ΚΑΤΑΣΚΕΥΗ ΙΑΓΡΑΜΜΑΤΩΝ MQN ΣΕ ΟΚΟ ιδάσκων: Αριστοτέλης Ε. Χαραλαµπάκης Εισαγωγή Με το παράδειγµα αυτό αναλύεται
ΧΑΡΤΟΓΡΑΦΙΑ. Στοιχεία χαρτογραφίας Σύστηµα γεωγραφικών συντεταγµένων
 ΧΑΡΤΟΓΡΑΦΙΑ Στοιχεία χαρτογραφίας Σύστηµα γεωγραφικών συντεταγµένων ρ. Ε. Λυκούδη Αθήνα 2005 Χώρος Η ανάπτυξη της ικανότητας της αντίληψης του χώρου, ως προς τις διαστάσεις του και το περιεχόµενό του είναι
ΧΑΡΤΟΓΡΑΦΙΑ Στοιχεία χαρτογραφίας Σύστηµα γεωγραφικών συντεταγµένων ρ. Ε. Λυκούδη Αθήνα 2005 Χώρος Η ανάπτυξη της ικανότητας της αντίληψης του χώρου, ως προς τις διαστάσεις του και το περιεχόµενό του είναι
Συστήματα Συντεταγμένων
 Σφαιρικό Σύστημα Συντεταγμένων DD = Degrees + ( Minutes / 60 ) + ( Seconds / 3600 ) Greenwich meridian =0 Z N Meridian of longitude Parallel of latitude P X W O Equator =0 R E - Geographic longitude -
Σφαιρικό Σύστημα Συντεταγμένων DD = Degrees + ( Minutes / 60 ) + ( Seconds / 3600 ) Greenwich meridian =0 Z N Meridian of longitude Parallel of latitude P X W O Equator =0 R E - Geographic longitude -
Ποια μπορεί να είναι η κίνηση μετά την κρούση;
 Ποια μπορεί να είναι η κίνηση μετά την κρούση; ή Η επιτάχυνση και ο ρυθµός µεταβολής του µέτρου της ταχύτητας. Ένα σώµα Σ ηρεµεί, δεµένο στο άκρο ενός ελατηρίου. Σε µια στιγµή συγκρούεται µε ένα άλλο κινούµενο
Ποια μπορεί να είναι η κίνηση μετά την κρούση; ή Η επιτάχυνση και ο ρυθµός µεταβολής του µέτρου της ταχύτητας. Ένα σώµα Σ ηρεµεί, δεµένο στο άκρο ενός ελατηρίου. Σε µια στιγµή συγκρούεται µε ένα άλλο κινούµενο
Νίκος Μαζαράκης Αθήνα 2010
 Νίκος Μαζαράκης Αθήνα 2010 Οι χάρτες των 850 Hpa είναι ένα από τα βασικά προγνωστικά επίπεδα για τη παράµετρο της θερµοκρασίας. Την πίεση των 850 Hpa τη συναντάµε στην ατµόσφαιρα σε ένα µέσο ύψος περί
Νίκος Μαζαράκης Αθήνα 2010 Οι χάρτες των 850 Hpa είναι ένα από τα βασικά προγνωστικά επίπεδα για τη παράµετρο της θερµοκρασίας. Την πίεση των 850 Hpa τη συναντάµε στην ατµόσφαιρα σε ένα µέσο ύψος περί
Τηλεπισκόπηση - Φωτοερμηνεία
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Τηλεπισκόπηση - Φωτοερμηνεία Ενότητα 9: Συστήματα Συντεταγμένων. Κωνσταντίνος Περάκης Ιωάννης Φαρασλής Τμήμα Μηχανικών Χωροταξίας, Πολεοδομίας και Περιφερειακής Ανάπτυξης Άδειες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Τηλεπισκόπηση - Φωτοερμηνεία Ενότητα 9: Συστήματα Συντεταγμένων. Κωνσταντίνος Περάκης Ιωάννης Φαρασλής Τμήμα Μηχανικών Χωροταξίας, Πολεοδομίας και Περιφερειακής Ανάπτυξης Άδειες
ΥΠΟΛΟΓΙΣΜΟΣ ΑΝΑΠΤΥΓΜΑΤΟΣ FOURIER ΜΕ ΑΡΙΘΜΗΤΙΚΟ ΤΡΟΠΟ
 ΣΧΟΛΗ Ν. ΟΚΙΜΩΝ ΘΕΩΡΙΑ ΚΥΚΛΩΜΑΤΩΝ ΙΙ Σ.Α.Ε. ΥΠΟΛΟΓΙΣΜΟΣ ΑΝΑΠΤΥΓΜΑΤΟΣ FOURIER ΜΕ ΑΡΙΘΜΗΤΙΚΟ ΤΡΟΠΟ ΕΚΕΜΒΡΙΟΣ 3 ) Αρχικό σήµα ( ) Στο παρακάτω σχήµα φαίνεται ένα περιοδικό σήµα ( ), το οποίο έχει ληφθεί από
ΣΧΟΛΗ Ν. ΟΚΙΜΩΝ ΘΕΩΡΙΑ ΚΥΚΛΩΜΑΤΩΝ ΙΙ Σ.Α.Ε. ΥΠΟΛΟΓΙΣΜΟΣ ΑΝΑΠΤΥΓΜΑΤΟΣ FOURIER ΜΕ ΑΡΙΘΜΗΤΙΚΟ ΤΡΟΠΟ ΕΚΕΜΒΡΙΟΣ 3 ) Αρχικό σήµα ( ) Στο παρακάτω σχήµα φαίνεται ένα περιοδικό σήµα ( ), το οποίο έχει ληφθεί από
ΗλιακήΓεωµετρία. Γιάννης Κατσίγιαννης
 ΗλιακήΓεωµετρία Γιάννης Κατσίγιαννης ΗηλιακήενέργειαστηΓη Φασµατικήκατανοµήτηςηλιακής ακτινοβολίας ΗκίνησητηςΓηςγύρωαπότονήλιο ΗκίνησητηςΓηςγύρωαπότονήλιοµπορεί να αναλυθεί σε δύο κύριες συνιστώσες: Περιφορά
ΗλιακήΓεωµετρία Γιάννης Κατσίγιαννης ΗηλιακήενέργειαστηΓη Φασµατικήκατανοµήτηςηλιακής ακτινοβολίας ΗκίνησητηςΓηςγύρωαπότονήλιο ΗκίνησητηςΓηςγύρωαπότονήλιοµπορεί να αναλυθεί σε δύο κύριες συνιστώσες: Περιφορά
lim είναι πραγµατικοί αριθµοί, τότε η f είναι συνεχής στο x 0. β) Να εξετάσετε τη συνέχεια της συνάρτησης f (x) =
 Ερωτήσεις ανάπτυξης. ** α) Να αποδείξετε ότι αν τα όρια lim - f () - f - είναι πραγµατικοί αριθµοί, τότε η f είναι συνεχής στο. ( ) και β) Να εξετάσετε τη συνέχεια της συνάρτησης f () = lim + στο σηµείο
Ερωτήσεις ανάπτυξης. ** α) Να αποδείξετε ότι αν τα όρια lim - f () - f - είναι πραγµατικοί αριθµοί, τότε η f είναι συνεχής στο. ( ) και β) Να εξετάσετε τη συνέχεια της συνάρτησης f () = lim + στο σηµείο
Άσκηση Η15. Μέτρηση της έντασης του μαγνητικού πεδίου της γής. Γήινο μαγνητικό πεδίο (Γεωμαγνητικό πεδίο)
 Άσκηση Η15 Μέτρηση της έντασης του μαγνητικού πεδίου της γής Γήινο μαγνητικό πεδίο (Γεωμαγνητικό πεδίο) Το γήινο μαγνητικό πεδίο αποτελείται, ως προς την προέλευσή του, από δύο συνιστώσες, το μόνιμο μαγνητικό
Άσκηση Η15 Μέτρηση της έντασης του μαγνητικού πεδίου της γής Γήινο μαγνητικό πεδίο (Γεωμαγνητικό πεδίο) Το γήινο μαγνητικό πεδίο αποτελείται, ως προς την προέλευσή του, από δύο συνιστώσες, το μόνιμο μαγνητικό
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΣΤΡΟΝΟΜΙΑ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΣΤΡΟΝΟΜΙΑ 1 η ΟΜΑΔΑ ΑΣΚΗΣΕΩΝ Κεφάλαιο 2 ο Συστήματα αστρονομικών συντεταγμένων και χρόνος ΑΣΚΗΣΗ 1 η (α) Να εξηγηθεί γιατί το αζιμούθιο της ανατολής και της δύσεως του Ηλίου σε ένα τόπο,
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΣΤΡΟΝΟΜΙΑ 1 η ΟΜΑΔΑ ΑΣΚΗΣΕΩΝ Κεφάλαιο 2 ο Συστήματα αστρονομικών συντεταγμένων και χρόνος ΑΣΚΗΣΗ 1 η (α) Να εξηγηθεί γιατί το αζιμούθιο της ανατολής και της δύσεως του Ηλίου σε ένα τόπο,
ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΗΣ ΜΙΚΡΟΣΚΟΠΙΑΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ «ΒΙΟΛΟΓΙΑΣ ΚΥΤΤΑΡΟΥ» Ονοµατεπώνυµο...ΑΜ...
 ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΗΣ ΜΙΚΡΟΣΚΟΠΙΑΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ «ΒΙΟΛΟΓΙΑΣ ΚΥΤΤΑΡΟΥ» ΑΣΚΗΣΗ 2 η Μετρήσεις µε το µικροσκόπιο Κ. Φασσέας. Ονοµατεπώνυµο...ΑΜ... Σκοπός της άσκησης είναι: Να µάθουµε πώς γίνεται η
ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΗΣ ΜΙΚΡΟΣΚΟΠΙΑΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ «ΒΙΟΛΟΓΙΑΣ ΚΥΤΤΑΡΟΥ» ΑΣΚΗΣΗ 2 η Μετρήσεις µε το µικροσκόπιο Κ. Φασσέας. Ονοµατεπώνυµο...ΑΜ... Σκοπός της άσκησης είναι: Να µάθουµε πώς γίνεται η
ΗΛΙΑΚΗ ΓΕΩΜΕΤΡΙΑ Δ. Κουζούδης Πανεπιστήμιο Πατρών
 ΗΛΙΑΚΗ ΓΕΩΜΕΤΡΙΑ Δ. Κουζούδης Πανεπιστήμιο Πατρών Συντεταγμένες του τόπου (γεωγραφικό μήκος και πλάτος) Π.χ. το Google Maps δίνει για το Παν. Πατρών 38.3, 21.8. Προσοχή, το πρώτο είναι το γεωγραφικό πλάτος
ΗΛΙΑΚΗ ΓΕΩΜΕΤΡΙΑ Δ. Κουζούδης Πανεπιστήμιο Πατρών Συντεταγμένες του τόπου (γεωγραφικό μήκος και πλάτος) Π.χ. το Google Maps δίνει για το Παν. Πατρών 38.3, 21.8. Προσοχή, το πρώτο είναι το γεωγραφικό πλάτος
ΤΑΧΥ Ο ΟΙΠΟΡΙΚΟ. 3. Αζιµούθιο: Είναι η δεξιόστροφη γωνία που σχηµατίζεται µεταξύ του µαγνητικού βορρά, του σηµείου στάσεως και του σηµείου σκοπεύσεως.
 ΤΑΧΥ Ο ΟΙΠΟΡΙΚΟ Α. Όροι και Ορισµοί 1. Θ7: Είναι συνώνυµο µε το ταχύ οδοιπορικό. 2. Κλίµακα: Είναι η µαθηµατική αναλογία του γραφικού µήκους που απεικονίζεται στο χάρτη µε το φυσικό µήκος στο οποίο αναφέρεται.
ΤΑΧΥ Ο ΟΙΠΟΡΙΚΟ Α. Όροι και Ορισµοί 1. Θ7: Είναι συνώνυµο µε το ταχύ οδοιπορικό. 2. Κλίµακα: Είναι η µαθηµατική αναλογία του γραφικού µήκους που απεικονίζεται στο χάρτη µε το φυσικό µήκος στο οποίο αναφέρεται.
Περίθλαση από ακµή και από εµπόδιο.
 ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 63 6. Άσκηση 6 Περίθλαση από ακµή και από εµπόδιο. 6.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης αυτής, καθώς και των δύο εποµένων, είναι η γνωριµία των σπουδαστών
ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 63 6. Άσκηση 6 Περίθλαση από ακµή και από εµπόδιο. 6.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης αυτής, καθώς και των δύο εποµένων, είναι η γνωριµία των σπουδαστών
ΙΑΝΥΣΜΑΤΑ ΘΕΩΡΙΑ ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ. Τι ονοµάζουµε διάνυσµα; αλφάβητου επιγραµµισµένα µε βέλος. για παράδειγµα, Τι ονοµάζουµε µέτρο διανύσµατος;
 ΙΝΥΣΜΤ ΘΕΩΡΙ ΘΕΜΤ ΘΕΩΡΙΣ Τι ονοµάζουµε διάνυσµα; AB A (αρχή) B (πέρας) Στη Γεωµετρία το διάνυσµα ορίζεται ως ένα προσανατολισµένο ευθύγραµµο τµήµα, δηλαδή ως ένα ευθύγραµµο τµήµα του οποίου τα άκρα θεωρούνται
ΙΝΥΣΜΤ ΘΕΩΡΙ ΘΕΜΤ ΘΕΩΡΙΣ Τι ονοµάζουµε διάνυσµα; AB A (αρχή) B (πέρας) Στη Γεωµετρία το διάνυσµα ορίζεται ως ένα προσανατολισµένο ευθύγραµµο τµήµα, δηλαδή ως ένα ευθύγραµµο τµήµα του οποίου τα άκρα θεωρούνται
ΠΕΡΙΕΧΟΜΕΝΑ. 2. Προσανατολισμός με πυξίδα
 ΠΕΡΙΕΧΟΜΕΝΑ 1. Προσανατολισμός Αρχαίων α. Προσανατολισμός β. Τρόποι προσανατολισμού Αρχαίων γ. Όργανα προσανατολισμού δ. Προσανατολισμός στην αρχιτεκτονική των Αρχαίων 2. Προσανατολισμός με πυξίδα α. Γεωγραφικό
ΠΕΡΙΕΧΟΜΕΝΑ 1. Προσανατολισμός Αρχαίων α. Προσανατολισμός β. Τρόποι προσανατολισμού Αρχαίων γ. Όργανα προσανατολισμού δ. Προσανατολισμός στην αρχιτεκτονική των Αρχαίων 2. Προσανατολισμός με πυξίδα α. Γεωγραφικό
ΠΡΟΣΑΝΑΤΟΛΙ ΣΜΟΣ ΚΑΙ ΧΑΡΤΕΣ
 ΠΡΟΣΑΝΑΤΟΛΙ ΣΜΟΣ ΚΑΙ ΧΑΡΤΕΣ Η ΠΥΞΙΔΑ Η πυξίδα είναι ένα όργανο προσανατολισμού που δείχνει τα σημεία του ορίζοντα και άλλες πληροφορίες προσανατολισμού ως προς τα σημεία του ορίζοντα, όπως το αζιμούθιο
ΠΡΟΣΑΝΑΤΟΛΙ ΣΜΟΣ ΚΑΙ ΧΑΡΤΕΣ Η ΠΥΞΙΔΑ Η πυξίδα είναι ένα όργανο προσανατολισμού που δείχνει τα σημεία του ορίζοντα και άλλες πληροφορίες προσανατολισμού ως προς τα σημεία του ορίζοντα, όπως το αζιμούθιο
20 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ
 ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 0 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ Κυριακή, 19 Μαρτίου, 006 Ώρα: 10:30-13:30 Θέµα 1 0 (µονάδες 10) α ) Το βέλος δέχεται σταθερή επιτάχυνση για όλη τη διάρκεια της κίνησης (
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 0 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ Κυριακή, 19 Μαρτίου, 006 Ώρα: 10:30-13:30 Θέµα 1 0 (µονάδες 10) α ) Το βέλος δέχεται σταθερή επιτάχυνση για όλη τη διάρκεια της κίνησης (
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών. Κοσμάς Γαζέας
 Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Κοσμάς Γαζέας Σφαιρικό Τρίγωνο Σφαιρικό τρίγωνο λέγεται το μέρος της σφαίρας, το οποίο περικλείεται μεταξύ των τόξων τριών μέγιστων κύκλων, με την προϋπόθεση
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Κοσμάς Γαζέας Σφαιρικό Τρίγωνο Σφαιρικό τρίγωνο λέγεται το μέρος της σφαίρας, το οποίο περικλείεται μεταξύ των τόξων τριών μέγιστων κύκλων, με την προϋπόθεση
ηλιακού μας συστήματος και ο πέμπτος σε μέγεθος. Ηρακλή, καθώς και στην κίνηση του γαλαξία
 Sfaelos Ioannis 1. ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΣΤΟΙΧΕΙΑ ΤΗΣ ΓΗΣ Η Γη είναι ο τρίτος στη σειρά πλανήτης του ηλιακού μας συστήματος και ο πέμπτος σε μέγεθος. έ θ Η μέση απόστασή της από τον Ήλιο είναι 149.600.000 km.
Sfaelos Ioannis 1. ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΣΤΟΙΧΕΙΑ ΤΗΣ ΓΗΣ Η Γη είναι ο τρίτος στη σειρά πλανήτης του ηλιακού μας συστήματος και ο πέμπτος σε μέγεθος. έ θ Η μέση απόστασή της από τον Ήλιο είναι 149.600.000 km.
Υπάρχουν πολλά είδη Ηλιακών Ρολογιών. Τα σημαντικότερα και συχνότερα απαντόμενα είναι:
 ΗΛΙΑΚΑ ΩΡΟΛΟΓΙΑ Υπάρχουν πολλά είδη Ηλιακών Ρολογιών. Τα σημαντικότερα και συχνότερα απαντόμενα είναι: Οριζόντια Κατακόρυφα Ισημερινά Το παρακάτω άρθρο αναφέρεται στον τρόπο λειτουργίας αλλά και κατασκευής
ΗΛΙΑΚΑ ΩΡΟΛΟΓΙΑ Υπάρχουν πολλά είδη Ηλιακών Ρολογιών. Τα σημαντικότερα και συχνότερα απαντόμενα είναι: Οριζόντια Κατακόρυφα Ισημερινά Το παρακάτω άρθρο αναφέρεται στον τρόπο λειτουργίας αλλά και κατασκευής
14 Εφαρµογές των ολοκληρωµάτων
 14 Εφαρµογές των ολοκληρωµάτων 14.1 Υπολογισµός εµβαδών µε την µέθοδο των παράλληλων διατοµών Θεωρούµε µια ϕραγµένη επίπεδη επιφάνεια A µε οµαλό σύνορο, δηλαδή που περιγράφεται από µια συνεχή συνάρτηση.
14 Εφαρµογές των ολοκληρωµάτων 14.1 Υπολογισµός εµβαδών µε την µέθοδο των παράλληλων διατοµών Θεωρούµε µια ϕραγµένη επίπεδη επιφάνεια A µε οµαλό σύνορο, δηλαδή που περιγράφεται από µια συνεχή συνάρτηση.
6 Γεωμετρικές κατασκευές
 6 Γεωμετρικές κατασκευές 6.1 Γενικά Στα σχέδια εφαρμόζουμε γεωμετρικές κατασκευές, προκειμένου να επιλύσουμε προβλήματα που απαιτούν μεγάλη σχεδιαστική και κατασκευαστική ακρίβεια. Τα γεωμετρικά - σχεδιαστικά
6 Γεωμετρικές κατασκευές 6.1 Γενικά Στα σχέδια εφαρμόζουμε γεωμετρικές κατασκευές, προκειμένου να επιλύσουμε προβλήματα που απαιτούν μεγάλη σχεδιαστική και κατασκευαστική ακρίβεια. Τα γεωμετρικά - σχεδιαστικά
Σχολή Ναυτικών Δοκίμων
 Σχολή Ναυτικών Δοκίμων Μάθημα: ΣΤΟΙΧΕΙΑ ΜΑΥΤΙΛΙΑΣ Α ΜΗΧ Θεματική Ενότητα: ΕΙΔΗ ΠΛΟΥ. ΟΡΘΟΔΡΟΜΙΑ, ΛΟΞΟΔΡΟΜΙΑ Καθηγητής Δρ. Α. Παλληκάρης Απρίλιος 2016 ΠΑΡΑΔΟΣΙΑΚΗ ΝΑΥΣΙΠΛΟΪΑ ΜΕ ΧΡΗΣΗ ΕΝΤΥΠΩΝ ΝΑΥΤΙΚΩΝ ΧΑΡΤΩΝ
Σχολή Ναυτικών Δοκίμων Μάθημα: ΣΤΟΙΧΕΙΑ ΜΑΥΤΙΛΙΑΣ Α ΜΗΧ Θεματική Ενότητα: ΕΙΔΗ ΠΛΟΥ. ΟΡΘΟΔΡΟΜΙΑ, ΛΟΞΟΔΡΟΜΙΑ Καθηγητής Δρ. Α. Παλληκάρης Απρίλιος 2016 ΠΑΡΑΔΟΣΙΑΚΗ ΝΑΥΣΙΠΛΟΪΑ ΜΕ ΧΡΗΣΗ ΕΝΤΥΠΩΝ ΝΑΥΤΙΚΩΝ ΧΑΡΤΩΝ
1.3 Σχεδίαση µε ελεύθερο χέρι (Σκαρίφηµα)
 20 1.3 Σχεδίαση µε ελεύθερο χέρι (Σκαρίφηµα) 1.3.1 Ορισµός- Είδη - Χρήση Σκαρίφηµα καλείται η εικόνα ενός αντικειµένου ή εξαρτήµατος που µεταφέρεται σε χαρτί µε ελεύθερο χέρι (χωρίς όργανα σχεδίασης ή
20 1.3 Σχεδίαση µε ελεύθερο χέρι (Σκαρίφηµα) 1.3.1 Ορισµός- Είδη - Χρήση Σκαρίφηµα καλείται η εικόνα ενός αντικειµένου ή εξαρτήµατος που µεταφέρεται σε χαρτί µε ελεύθερο χέρι (χωρίς όργανα σχεδίασης ή
Κεφάλαιο 10 Περιστροφική Κίνηση. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 10 Περιστροφική Κίνηση Περιεχόµενα Κεφαλαίου 10 Γωνιακές Ποσότητες Διανυσµατικός Χαρακτήρας των Γωνιακών Ποσοτήτων Σταθερή γωνιακή Επιτάχυνση Ροπή Δυναµική της Περιστροφικής Κίνησης, Ροπή και
Κεφάλαιο 10 Περιστροφική Κίνηση Περιεχόµενα Κεφαλαίου 10 Γωνιακές Ποσότητες Διανυσµατικός Χαρακτήρας των Γωνιακών Ποσοτήτων Σταθερή γωνιακή Επιτάχυνση Ροπή Δυναµική της Περιστροφικής Κίνησης, Ροπή και
Ιστιοφόρο σκάφος και ταξίδεμα στα όρτσα
 Ιστιοφόρο σκάφος και ταξίδεμα στα όρτσα Πόσες αλλαγές μπράτσου χρειάζονται για να φτάσουμε στον προορισμό μας Του Μάκη Ματιάτου Δεν είναι λίγες οι φορές που το λιμάνι του προορισμού μας βρίσκεται σε τέτοιο
Ιστιοφόρο σκάφος και ταξίδεμα στα όρτσα Πόσες αλλαγές μπράτσου χρειάζονται για να φτάσουμε στον προορισμό μας Του Μάκη Ματιάτου Δεν είναι λίγες οι φορές που το λιμάνι του προορισμού μας βρίσκεται σε τέτοιο
9. Τοπογραφική σχεδίαση
 9. Τοπογραφική σχεδίαση 9.1 Εισαγωγή Το κεφάλαιο αυτό εξετάζει τις παραμέτρους, μεθόδους και τεχνικές της τοπογραφικής σχεδίασης. Η προσέγγιση του κεφαλαίου γίνεται τόσο για την περίπτωση της συμβατικής
9. Τοπογραφική σχεδίαση 9.1 Εισαγωγή Το κεφάλαιο αυτό εξετάζει τις παραμέτρους, μεθόδους και τεχνικές της τοπογραφικής σχεδίασης. Η προσέγγιση του κεφαλαίου γίνεται τόσο για την περίπτωση της συμβατικής
ΧΑΡΤΟΓΡΑΦΙΚΕΣ ΠΡΟΒΟΛΕΣ
 ΣΧΟΛΗ ΝΑΥΤΙΚΩΝ ΔΟΚΙΜΩΝ ΜΑΘΗΜΑ: ΘΕΩΡΗΤΙΚΗ ΝΑΥΤΙΛΙΑ Καθηγητής Δρ. Α. Παλληκάρης ΧΑΡΤΟΓΡΑΦΙΚΕΣ ΠΡΟΒΟΛΕΣ Νοέμβριος 2016 ΕΝΔΕΙΚΤΙΚΗ ΔΙΑΔΙΚΑΣΙΑ ΑΠΕΙΚΟΝΙΣΗΣ ΤΗΣ ΕΠΙΦΑΝΕΙΑΣ ΤΗΣ ΓΗΣ ΣΕ ΕΠΙΠΕΔΟ (ΚΑΤΑΣΚΕΥΗ ΧΑΡΤΩΝ)
ΣΧΟΛΗ ΝΑΥΤΙΚΩΝ ΔΟΚΙΜΩΝ ΜΑΘΗΜΑ: ΘΕΩΡΗΤΙΚΗ ΝΑΥΤΙΛΙΑ Καθηγητής Δρ. Α. Παλληκάρης ΧΑΡΤΟΓΡΑΦΙΚΕΣ ΠΡΟΒΟΛΕΣ Νοέμβριος 2016 ΕΝΔΕΙΚΤΙΚΗ ΔΙΑΔΙΚΑΣΙΑ ΑΠΕΙΚΟΝΙΣΗΣ ΤΗΣ ΕΠΙΦΑΝΕΙΑΣ ΤΗΣ ΓΗΣ ΣΕ ΕΠΙΠΕΔΟ (ΚΑΤΑΣΚΕΥΗ ΧΑΡΤΩΝ)
ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ ΓΕΩΜΕΤΡΙΑ ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΕΝΟΤΗΤΑ.1.1. Σημείο - Ευθύγραμμο τμήμα - Ευθεία - Ημιευθεία - Επίπεδο - Ημιεπίπεδο. ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΗΜΕΡΟΜΗΝΙΑ / / 1. Σχεδιάστε το ευθύγραμμο τμήμα Α και το ευθύγραμμο τμήμα ΓΔ A B Γ Δ 2.
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΕΝΟΤΗΤΑ.1.1. Σημείο - Ευθύγραμμο τμήμα - Ευθεία - Ημιευθεία - Επίπεδο - Ημιεπίπεδο. ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΗΜΕΡΟΜΗΝΙΑ / / 1. Σχεδιάστε το ευθύγραμμο τμήμα Α και το ευθύγραμμο τμήμα ΓΔ A B Γ Δ 2.
ΙΣΟΥΨΕΙΣ ΚΑΜΠΥΛΕΣ- ΣΗΜΕΙΩΣΕΙΣ
 ΜΑΘΗΜΑ 16_10_2012 ΙΣΟΥΨΕΙΣ ΚΑΜΠΥΛΕΣ- ΣΗΜΕΙΩΣΕΙΣ 2.1 Απεικόνιση του ανάγλυφου Μια εδαφική περιοχή αποτελείται από εξέχουσες και εισέχουσες εδαφικές μορφές. Τα εξέχοντα εδαφικά τμήματα βρίσκονται μεταξύ
ΜΑΘΗΜΑ 16_10_2012 ΙΣΟΥΨΕΙΣ ΚΑΜΠΥΛΕΣ- ΣΗΜΕΙΩΣΕΙΣ 2.1 Απεικόνιση του ανάγλυφου Μια εδαφική περιοχή αποτελείται από εξέχουσες και εισέχουσες εδαφικές μορφές. Τα εξέχοντα εδαφικά τμήματα βρίσκονται μεταξύ
Ä ÑÁÓÔÇÑÉÏÔÇÔÁ 1ç. Απάντηση Οι γωνίες που σχηµατίζονται είναι: Α. αµβλεία Β. ευθεία Γ. πλήρης. οξεία Ε. ορθή Ζ. αµβλεία Η. οξεία.
 Ä ÑÁÓÔÇÑÉÏÔÇÔÁ 1ç Σε όλα τα παρακάτω αντικείµενα σχηµατίζονται διάφορες γωνίες ανάλογα µε τη σχετική θέση, κάθε φορά, δύο ηµιευθειών που έχουν ένα κοινό ση- µείο, όπως π.χ. είναι οι δείκτες του ρολογιού,
Ä ÑÁÓÔÇÑÉÏÔÇÔÁ 1ç Σε όλα τα παρακάτω αντικείµενα σχηµατίζονται διάφορες γωνίες ανάλογα µε τη σχετική θέση, κάθε φορά, δύο ηµιευθειών που έχουν ένα κοινό ση- µείο, όπως π.χ. είναι οι δείκτες του ρολογιού,
10. ΓΕΩΔΑΙΤΙΚΕΣ ΕΦΑΡΜΟΓΕΣ
 77 10. ΓΕΩΔΑΙΤΙΚΕΣ ΕΦΑΡΜΟΓΕΣ Ολοκληρώνοντας την συνοπτική παρουσίαση των εννοιών και μεθόδων της Γεωδαιτικής Αστρονομίας θα κάνουμε μια σύντομη αναφορά στην αξιοποίηση των μεγεθών που προσδιορίστηκαν,
77 10. ΓΕΩΔΑΙΤΙΚΕΣ ΕΦΑΡΜΟΓΕΣ Ολοκληρώνοντας την συνοπτική παρουσίαση των εννοιών και μεθόδων της Γεωδαιτικής Αστρονομίας θα κάνουμε μια σύντομη αναφορά στην αξιοποίηση των μεγεθών που προσδιορίστηκαν,
2 Η ΠΡΟΟΔΟΣ. Ενδεικτικές λύσεις κάποιων προβλημάτων. Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση
 2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
2 Β Βάσεις παραλληλογράµµου Βαρύκεντρο Γ Γεωµετρική κατασκευή Γεωµετρικός τόπος (ς) Γωνία Οι απέναντι πλευρές του. Κέντρο βάρους τριγώνου, δηλ. το σηµ
 1 ΛΕΞΙΚΟ ΓΕΩΜΕΤΡΙΚΩΝ ΟΡΩΝ Α Ακτίνιο Ακτίνα κύκλου Ακτίνα σφαίρας Άκρα ευθύγραµµου τµήµατος Αµβλεία γωνία Αµβλυγώνιο Ανάλογα ευθύγραµµα τµήµατα Αντιδιαµετρικό σηµείο Αντικείµενες ηµιευθείες Άξονας συµµετρίας
1 ΛΕΞΙΚΟ ΓΕΩΜΕΤΡΙΚΩΝ ΟΡΩΝ Α Ακτίνιο Ακτίνα κύκλου Ακτίνα σφαίρας Άκρα ευθύγραµµου τµήµατος Αµβλεία γωνία Αµβλυγώνιο Ανάλογα ευθύγραµµα τµήµατα Αντιδιαµετρικό σηµείο Αντικείµενες ηµιευθείες Άξονας συµµετρίας
ΣΧΟΛΗ ΝΑΥΤΙΚΩΝ ΔΟΚΙΜΩΝ ΧΑΡΤΟΓΡΑΦΙΚΕΣ ΠΡΟΒΟΛΕΣ ΕΦΑΡΜΟΓΕΣ ΣΤΗ ΝΑΥΤΙΛΙΑ ΚΑΙ ΤΙΣ ΝΑΥΤΙΚΕΣ ΕΠΙΧΕΙΡΗΣΕΙΣ. Δρ. ΑΘΑΝΑΣΙΟΣ Η. ΠΑΛΛΗΚΑΡΗΣ Αν.
 ΣΧΟΛΗ ΝΑΥΤΙΚΩΝ ΔΟΚΙΜΩΝ ΧΑΡΤΟΓΡΑΦΙΚΕΣ ΠΡΟΒΟΛΕΣ ΕΦΑΡΜΟΓΕΣ ΣΤΗ ΝΑΥΤΙΛΙΑ ΚΑΙ ΤΙΣ ΝΑΥΤΙΚΕΣ ΕΠΙΧΕΙΡΗΣΕΙΣ Δρ. ΑΘΑΝΑΣΙΟΣ Η. ΠΑΛΛΗΚΑΡΗΣ Αν. καθηγητής ΣΝΔ ΠΕΙΡΑΙΑΣ 2011 Απαγορεύεται η αντιγραφή, αποθήκευση και διανομή
ΣΧΟΛΗ ΝΑΥΤΙΚΩΝ ΔΟΚΙΜΩΝ ΧΑΡΤΟΓΡΑΦΙΚΕΣ ΠΡΟΒΟΛΕΣ ΕΦΑΡΜΟΓΕΣ ΣΤΗ ΝΑΥΤΙΛΙΑ ΚΑΙ ΤΙΣ ΝΑΥΤΙΚΕΣ ΕΠΙΧΕΙΡΗΣΕΙΣ Δρ. ΑΘΑΝΑΣΙΟΣ Η. ΠΑΛΛΗΚΑΡΗΣ Αν. καθηγητής ΣΝΔ ΠΕΙΡΑΙΑΣ 2011 Απαγορεύεται η αντιγραφή, αποθήκευση και διανομή
3. ΤΟ ΤΡΙΓΩΝΟ ΘΕΣΗΣ τρίγωνο θέσης position triangle astronomical triangle
 21 3. ΤΟ ΤΡΙΓΩΝΟ ΘΕΣΗΣ Ως τώρα είδαμε πως ορίζονται διάφορα συστήματα αναφοράς και πως οι συντεταγμένες, σε κάθε σύστημα, αλλάζουν ανάλογα με την διεύθυνση παρατήρησης, τον τόπο και τον χρόνο. Για να γίνουν
21 3. ΤΟ ΤΡΙΓΩΝΟ ΘΕΣΗΣ Ως τώρα είδαμε πως ορίζονται διάφορα συστήματα αναφοράς και πως οι συντεταγμένες, σε κάθε σύστημα, αλλάζουν ανάλογα με την διεύθυνση παρατήρησης, τον τόπο και τον χρόνο. Για να γίνουν
Physics by Chris Simopoulos
 Στο παρακάτω σχήµα: ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ Β ΓΥΜΝΑΣΙΟΥ ΠΑΡΑ ΕΙΓΜΑ ο α) Να ορίσετε τις θέσεις των σηµείων (Α), (Β) και (Γ). β) Να υπολογίσετε τη µετατόπιση (ΑΓ). γ) Να υπολογίσετε το διάστηµα (ΑΒΓ).
Στο παρακάτω σχήµα: ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ Β ΓΥΜΝΑΣΙΟΥ ΠΑΡΑ ΕΙΓΜΑ ο α) Να ορίσετε τις θέσεις των σηµείων (Α), (Β) και (Γ). β) Να υπολογίσετε τη µετατόπιση (ΑΓ). γ) Να υπολογίσετε το διάστηµα (ΑΒΓ).
 ΣΧΕ ΙΑΣΜΟΣ ΕΠΙΦΑΝΕΙΑΣ Με το σχεδιασµό επιφάνειας (Custom επιφάνεια) µπορούµε να σχεδιάσουµε επιφάνειες και αντικείµενα που δεν υπάρχουν στους καταλόγους του 1992. Τι µπορούµε να κάνουµε µε το σχεδιασµό
ΣΧΕ ΙΑΣΜΟΣ ΕΠΙΦΑΝΕΙΑΣ Με το σχεδιασµό επιφάνειας (Custom επιφάνεια) µπορούµε να σχεδιάσουµε επιφάνειες και αντικείµενα που δεν υπάρχουν στους καταλόγους του 1992. Τι µπορούµε να κάνουµε µε το σχεδιασµό
Ο χώρος. 1.Μονοδιάστατη κίνηση
 Ο χώρος Τα χελιδόνια έρχονται και ξανάρχονται. Κάθε χρόνο βρίσκουν μια γωνιά για να χτίσουν τη φωλιά, που θα γίνει το επίκεντρο του χώρου τους. Ο χώρος είναι ένας οργανικός χώρος, όπως εκείνος που αφορά
Ο χώρος Τα χελιδόνια έρχονται και ξανάρχονται. Κάθε χρόνο βρίσκουν μια γωνιά για να χτίσουν τη φωλιά, που θα γίνει το επίκεντρο του χώρου τους. Ο χώρος είναι ένας οργανικός χώρος, όπως εκείνος που αφορά
Γυµ.Ν.Λαµψάκου Α Γυµνασίου Γεωµ.Β2.6 γωνίες από 2 παράλληλες + τέµνουσα 19/3/10 Φύλλο εργασίας
 Φύλλο εργασίας Mπορείτε να βρείτε τη γωνία κάβων; ραστηριότητα Ένα δεξαµενόπλοιο που στο σχήµα είναι στο σηµείο Β, πλέει προς την είσοδο µιας διώρυγας µε την βοήθεια δύο ρυµουλκών που απεικονίζονται µε
Φύλλο εργασίας Mπορείτε να βρείτε τη γωνία κάβων; ραστηριότητα Ένα δεξαµενόπλοιο που στο σχήµα είναι στο σηµείο Β, πλέει προς την είσοδο µιας διώρυγας µε την βοήθεια δύο ρυµουλκών που απεικονίζονται µε
ΔΕΙΓΜΑ ΠΡΙΝ ΤΙΣ ΔΙΟΡΘΩΣΕΙΣ - ΕΚΔΟΣΕΙΣ ΚΡΙΤΙΚΗ
 Συναρτήσεις Προεπισκόπηση Κεφαλαίου Τα μαθηματικά είναι μια γλώσσα με ένα συγκεκριμένο λεξιλόγιο και πολλούς κανόνες. Πριν ξεκινήσετε το ταξίδι σας στον Απειροστικό Λογισμό, θα πρέπει να έχετε εξοικειωθεί
Συναρτήσεις Προεπισκόπηση Κεφαλαίου Τα μαθηματικά είναι μια γλώσσα με ένα συγκεκριμένο λεξιλόγιο και πολλούς κανόνες. Πριν ξεκινήσετε το ταξίδι σας στον Απειροστικό Λογισμό, θα πρέπει να έχετε εξοικειωθεί
ΕΡΓΑΣΙΕΣ 4 ου ΚΕΦΑΛΑΙΟΥ. 1 η Ομάδα: Ερωτήσεις πολλαπλής επιλογής
 ΕΡΓΑΣΙΕΣ 4 ου ΚΕΦΑΛΑΙΟΥ 1 η Ομάδα: Ερωτήσεις πολλαπλής επιλογής 1. Σύμφωνα με το νόμο της προσφοράς: α) Η προσφερόμενη ποσότητα ενός αγαθού αυξάνεται όταν μειώνεται η τιμή του στην αγορά β) Η προσφερόμενη
ΕΡΓΑΣΙΕΣ 4 ου ΚΕΦΑΛΑΙΟΥ 1 η Ομάδα: Ερωτήσεις πολλαπλής επιλογής 1. Σύμφωνα με το νόμο της προσφοράς: α) Η προσφερόμενη ποσότητα ενός αγαθού αυξάνεται όταν μειώνεται η τιμή του στην αγορά β) Η προσφερόμενη
Inbound-Outbound Tutorial
 Inbound-Outbound Tutorial Διαδικασίες, για χρήση με το Flight Simulator. Μανώλης Στεφανάκης pneumakithiki@yahoo.gr Στις παρακάτω γραμμές θα προσπαθήσουμε να εξηγήσουμε απλά και περιληπτικά τις δύο πολύ
Inbound-Outbound Tutorial Διαδικασίες, για χρήση με το Flight Simulator. Μανώλης Στεφανάκης pneumakithiki@yahoo.gr Στις παρακάτω γραμμές θα προσπαθήσουμε να εξηγήσουμε απλά και περιληπτικά τις δύο πολύ
Μέτρηση της επιτάχυνσης της βαρύτητας με τη βοήθεια του απλού εκκρεμούς.
 Μ2 Μέτρηση της επιτάχυνσης της βαρύτητας με τη βοήθεια του απλού εκκρεμούς. 1 Σκοπός Η εργαστηριακή αυτή άσκηση αποσκοπεί στη μέτρηση της επιτάχυνσης της βαρύτητας σε ένα τόπο. Αυτή η μέτρηση επιτυγχάνεται
Μ2 Μέτρηση της επιτάχυνσης της βαρύτητας με τη βοήθεια του απλού εκκρεμούς. 1 Σκοπός Η εργαστηριακή αυτή άσκηση αποσκοπεί στη μέτρηση της επιτάχυνσης της βαρύτητας σε ένα τόπο. Αυτή η μέτρηση επιτυγχάνεται
ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟ ΕΙΞΕΙΣ ΣΥΝΤΟΜΕΣ ΛΥΣΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ
 ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟ ΕΙΞΕΙΣ ΣΥΝΤΟΜΕΣ ΛΥΣΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ 4 o Κεφάλαιο ΑΝΑΛΥΣΗ Απαντήσεις στις ερωτήσεις του τύπου Σωστό-Λάθος. Σ 0. Σ 9. Λ. Λ. Σ 40. Σ. Σ. Σ 4. Λ 4. Λ. Σ 4. Σ 5. Σ 4. Σ 4. Λ 6. Σ 5. Λ 44.
ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟ ΕΙΞΕΙΣ ΣΥΝΤΟΜΕΣ ΛΥΣΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ 4 o Κεφάλαιο ΑΝΑΛΥΣΗ Απαντήσεις στις ερωτήσεις του τύπου Σωστό-Λάθος. Σ 0. Σ 9. Λ. Λ. Σ 40. Σ. Σ. Σ 4. Λ 4. Λ. Σ 4. Σ 5. Σ 4. Σ 4. Λ 6. Σ 5. Λ 44.
Ηλιακήενέργεια. Ηλιακή γεωµετρία. Εργαστήριο Αιολικής Ενέργειας Τ.Ε.Ι. Κρήτης. ηµήτρης Αλ. Κατσαπρακάκης
 Ηλιακήενέργεια Ηλιακή γεωµετρία Εργαστήριο Αιολικής Ενέργειας Τ.Ε.Ι. Κρήτης ηµήτρης Αλ. Κατσαπρακάκης Ηλιακήγεωµετρία Ηλιακήγεωµετρία Η Ηλιακή Γεωµετρία αναφέρεται στη µελέτη της θέσης του ήλιου σε σχέση
Ηλιακήενέργεια Ηλιακή γεωµετρία Εργαστήριο Αιολικής Ενέργειας Τ.Ε.Ι. Κρήτης ηµήτρης Αλ. Κατσαπρακάκης Ηλιακήγεωµετρία Ηλιακήγεωµετρία Η Ηλιακή Γεωµετρία αναφέρεται στη µελέτη της θέσης του ήλιου σε σχέση
Μαγνητικά φαινόµενα: Σύντοµη ιστορική αναδροµή
 Μαγνητικά φαινόµενα: Σύντοµη ιστορική αναδροµή 13ος αιώνας π.χ.: Οι Κινέζοι χρησιµοποιούσαν την πυξίδα. Η πυξίδα διαθέτει µαγνητική βελόνα (πιθανότατα επινόηση των Αράβων ή των Ινδών). 800 π.χ.: Έλληνες
Μαγνητικά φαινόµενα: Σύντοµη ιστορική αναδροµή 13ος αιώνας π.χ.: Οι Κινέζοι χρησιµοποιούσαν την πυξίδα. Η πυξίδα διαθέτει µαγνητική βελόνα (πιθανότατα επινόηση των Αράβων ή των Ινδών). 800 π.χ.: Έλληνες
ΣΥΝΑΡΤΗΣΕΩΝ. f3 x = και
 7 ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Στο κεφάλαιο αυτό θα δούμε πώς, με τη βοήθεια των πληροφοριών που α- ποκτήσαμε μέχρι τώρα, μπορούμε να χαράξουμε με όσο το δυνατόν μεγαλύτερη ακρίβεια τη γραφική παράσταση
7 ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Στο κεφάλαιο αυτό θα δούμε πώς, με τη βοήθεια των πληροφοριών που α- ποκτήσαμε μέχρι τώρα, μπορούμε να χαράξουμε με όσο το δυνατόν μεγαλύτερη ακρίβεια τη γραφική παράσταση
