Πτυχιακή Εργαςία. Θζμα: Καταςκευή διδακτικοφ πακζτου προςομοίωςησ τησ ευθφγραμμησ ομαλά μεταβαλλόμενησ κίνηςησ ςτο MaTLaB.
|
|
|
- Ολυμπία Σπηλιωτόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΣΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΤΣΙΚΟ ΙΔΡΤΜΑ ΕΡΡΩΝ ΧΟΛΗ ΣΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΣΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗ Πτυχιακή Εργαςία Θζμα: Καταςκευή διδακτικοφ πακζτου προςομοίωςησ τησ ευθφγραμμησ ομαλά μεταβαλλόμενησ κίνηςησ ςτο MaTLaB. Φοιτήτρια: Ράλλη Γεωργία 3346 Επιβλέπων: κ. Κοσϊροσκίδης Απόζηολος 2016 ~ 1 ~
2 Ευχαριςτίεσ Κατά κφριο λόγο, οφείλω να εκφράςω τισ κερμζσ μου ευχαριςτίεσ ςτον επιβλζποντα Κακθγθτι κ Κοσϊροσκίδη Απόζηολο, ο οποίοσ προςζφερε το ενδιαφζρον κζμα και μου ζδειξε εμπιςτοςφνθ δίνοντάσ μου τθ δυνατότθτα να εκπονιςω τθν πτυχιακι μου εργαςία. Τον ευχαριςτϊ επίςθσ για τισ πολφτιμεσ γνϊςεισ και ςυμβουλζσ που μου παρείχε κακ όλθ τθ διάρκεια τθσ εργαςίασ, κακϊσ και για τθν απρόςκοπτθ υποςτιριξθ και κακοδιγθςθ που μου παρείχε κακ όλθ τθ διάρκεια των ςπουδϊν μου. Τζλοσ, κα ικελα επίςθσ να απευκφνω τισ ευχαριςτίεσ μου ςτουσ γονείσ μου, οι οποίοι ςτιριξαν τισ ςπουδζσ μου με διάφορουσ τρόπουσ, φροντίηοντασ για τθν καλφτερθ δυνατι μόρφωςθ μου και τουσ φίλουσ μου για τθν κατανόθςθ και τθ ςυμπαράςταςι τουσ. Με εκτίμθςθ, άλλθ Γεωργία ~ 2 ~
3 ΠΡΟΛΟΓΟ ΚΑΙ ΠΕΡΙΛΗΨΗ ΠΣΤΧΙΑΚΉ ΕΡΓΑΙΑ Στθν πτυχιακι αυτι εργαςία καταςκευάςτθκε ζνα ολοκλθρωμζνο πρόγραμμα προςομοίωςθσ τθσ Φυςικισ για τθν Ευκφγραμμθ Ομαλά Μεταβαλλόμενθ Κίνθςθ, με ςκοπό τθ διευκόλυνςθ τθσ διδαςκαλίασ με ςφγχρονα οπτικά μζςα και μεκόδουσ αυτενζργειασ και πειραματιςμοφ, που κα δθμιουργιςουν και κα ενιςχφςουν το ενδιαφζρον των μακθτϊν προσ το μάκθμα. Το πακζτο αυτό ζχει διαδραςτικό χαρακτιρα με αναλυτικι ανάπτυξθ τθσ κεωρίασ και προςομοιωμζνο εργαςτιριο για πειράματα πάνω ςτθν Φυςικι, ςε όλο το δυνατό εφροσ τιμϊν των παραμζτρων του προβλιματοσ. ~ 3 ~
4 ΠΕΡΙΕΧΟΜΕΝΑ: Ειςαγωγι Ρερίλθψθ.3 Κεφάλαιο 1 ο : Κινιςεισ Ευκφγραμμθ Ομαλι Κίνθςθ 5 Ευκφγραμμθ Ομαλά Επιταχυνόμενθ Κίνθςθ 6 Ευκφγραμμθ Ομαλά Επιβραδυνόμενθ Κίνθςθ...7 Κεφάλαιο 2 ο :Ρεριγραφι και βαςικζσ λειτουργίεσ του Matlab Διανφςματα.8 Συςτιματα με χρϊμα 8 Κίνθςθ ςχθμάτων 10 Καμπφλεσ και ςχιματα 11 Άλλεσ Εντολζσ.13 Ραράρτθμα: Κϊδικασ Ο κϊδικασ που χρθςιμοποιικθκε για τθν Ευκφγραμμθ Ομαλά Μεταβαλλόμενθ Κίνθςθ.14 Βιβλιογραφία.67 ~ 4 ~
5 Κεφάλαιο:1 ο Κινήςεισ ΕΤΘΤΓΡΑΜΜΗ ΟΜΑΛΗ ΚΙΝΗΗ Ευθφγραμμη ομαλή κίνηςη: λζγεται θ κίνθςθ που κάνει ζνα ςϊμα κινοφμενο πάνω ςε μια ευκεία με ςτακερι ταχφτθτα. Εναλλακτικά, ορίηεται θ κίνθςθ ενόσ ςϊματοσ που κινείται ςε ευκεία γραμμι και ςε ίςoυσ χρόνουσ, διανφει ίςα διαςτιματα. Η ευκφγραμμθ ομαλι κίνθςθ είναι ζνα είδοσ κίνθςθσ και επομζνωσ χαρακτθρίηεται από τα τρία φυςικά μεγζκθ τθσ κίνθςθσ. Ειδικότερα: Θζςη (χ) Η κζςθ ενόσ ςϊματοσ χαρακτθρίηεται ςυνικωσ από ζνα διάνυςμα. Δθλϊνει το που βρίςκεται αυτό ςε ςχζςθ με κάποια αρχι μζτρθςθσ των ςυντεταγμζνων. Στθν ευκφγραμμθ ομαλι κίνθςθ, θ κζςθ μεταβάλλεται ανάλογα με τον χρόνο. Σαχφτητα (u) Η ταχφτθτα είναι το φυςικό μζγεκοσ που εκφράηει το ρυκμό μεταβολισ τθσ κζςθσ του ςϊματοσ ςτθ μονάδα του χρόνου. Εκφράηεται και αυτι από ζνα διάνυςμα για να δθλϊνεται θ κατεφκυνςθ τθσ κίνθςθσ. Στθν ευκφγραμμθ ομαλι κίνθςθ θ ταχφτητα (v) είναι ςτακερι και θ διεφκυνςθ τθσ είναι παράλλθλθ με τθν ευκφγραμμθ τροχιά τθσ κίνθςθσ. Επιτάχυνςη (α) Η επιτάχυνςθ είναι το φυςικό μζγεκοσ που εκφράηει το ρυκμό μεταβολισ τθσ ταχφτθτασ του ςϊματοσ ςτθ μονάδα του χρόνου. Στθν ευκφγραμμθ ομαλι κίνθςθ θ επιτάχυνση (a) είναι μθδενικι. Συπολόγιο: Ταχφτθτα: Μετατόπιςθ: Θζςθ (τελικι): Χρονικι διάρκεια: u=x/t x=u*t x=x o + u*t t=x/u ~ 5 ~
6 ΕΤΘΤΓΡΑΜΜΗ ΟΜΑΛΑ ΕΠΙΣΑΧΤΝΟΜΕΝΗ ΚΙΝΗΗ Ευθφγραμμη ομαλά επιταχυνόμενη κίνηςη: είναι θ κίνθςθ που κάνει κάποιο ςϊμα ςτθν οποία θ τροχιά τθσ είναι ευκφγραμμθ και θ επιτάχυνςθ τθσ μζνει ςτακερι και διαφορετικι από τθ μθδενικι. Κατά αυτόν τον τρόπο το ςϊμα επιταχφνεται με ςτακερι επιτάχυνςθ, επομζνωσ θ ταχφτθτα του αυξάνεται με ςτακερό ρυκμό, αφοφ θ επιτάχυνςθ είναι ουςιαςτικά ο ρυκμόσ μεταβολισ τθσ ταχφτθτα ωσ προσ το χρόνο. Η ευκφγραμμθ ομαλά επιταχυνόμενθ κίνθςθ χαρακτθρίηεται από τα τζςςερα φυςικά μεγζκθ τθσ κίνθςθσ. Ειδικότερα: Σαχφτητα (u) Η ταχφτθτα, είναι διανυςματικό μζγεκοσ με διεφκυνςι τθν τροχιά και φορά τθν φορά τθσ κίνθςθσ. Επιτάχυνςη (α) Η επιτάχυνςθ, είναι επίςθσ διανυςματικό μζγεκοσ με διεφκυνςι τθν τροχιά τθσ κίνθςθσ. Μετατόπιςη (χ) Η μετατόπιςθ, είναι το διανυςματικό μζγεκοσ που δθλϊνει τθ διαφορά τθσ αρχικισ κζςθσ του ςϊματοσ με τθν τρζχουςα ι τελικι του κζςθ. Χρόνοσ (t) Ο χρόνοσ, είναι το μονόμετρο μζγεκοσ που δθλϊνει τθ διάρκεια για τθν οποία εξελίςςεται το φαινόμενο προσ παρατιρθςθ. Συνικωσ θ αρχι τθσ κίνθςθσ επιλζγεται ωσ θ χρονικι ςτιγμι ςτθν οποία ξεκινά να μετριζται ο χρόνοσ ( ). Επιτάχυνςθ: Ταχφτθτα: a=ςτακερι (επιτάχυνςθ) u=u o +a*t Μετατόπιςθ: x=u o *t+(1/2)*a*t 2 όπου u o θ αρχικι ταχφτθτα ~ 6 ~
7 ΕΤΘΤΓΡΑΜΜΗ ΟΜΑΛΑ ΕΠΙΒΡΑΔΤΝΟΜΕΝΗ ΚΙΝΗΗ Ευθφγραμμη ομαλά επιβραδυνόμενη κίνηςη: είναι θ κίνθςθ που κάνει κάποιο ςϊμα όταν θ επιτάχυνςθ είναι αρνθτικι και θ ταχφτθτα μειϊνεται με ςτακερό ρυκμό. Η ευκφγραμμθ ομαλά επιβραδυνόμενθ κίνθςθ χαρακτθρίηεται από τα τζςςερα φυςικά μεγζκθ τθσ κίνθςθσ. Ειδικότερα: Σαχφτητα (u) Η ταχφτθτα, είναι διανυςματικό μζγεκοσ με διεφκυνςι τθν τροχιά και φορά τθν φορά τθσ κίνθςθσ. Επιτάχυνςη (α) Η επιτάχυνςθ, είναι επίςθσ διανυςματικό μζγεκοσ με διεφκυνςι τθν τροχιά τθσ κίνθςθσ. Μετατόπιςη (χ) Η μετατόπιςθ, είναι το διανυςματικό μζγεκοσ που δθλϊνει τθ διαφορά τθσ αρχικισ κζςθσ του ςϊματοσ με τθν τρζχουςα ι τελικι του κζςθ. Χρόνοσ (t) Ο χρόνοσ, είναι το μονόμετρο μζγεκοσ που δθλϊνει τθ διάρκεια για τθν οποία εξελίςςεται το φαινόμενο προσ παρατιρθςθ. Συνικωσ θ αρχι τθσ κίνθςθσ επιλζγεται ωσ θ χρονικι ςτιγμι ςτθν οποία ξεκινά να μετριζται ο χρόνοσ ( ). Επιτάχυνςθ: Ταχφτθτα: a=ςτακερι (επιβράδυνςθ) u=u o -a*t Μετατόπιςθ: x=u o -(1/2)a*t 2 Χρόνοσ: t=u o /a *ολικόσ χρόνοσ κίνθςθσ+ x o =u o 2 /(2*a) *ολικό διάςτθμα που διανφεται+ όπου u o θ αρχικι ταχφτθτα ~ 7 ~
8 Κεφάλαιο:2 ο ΠΕΡΙΓΡΑΦΗ ΚΑΙ ΒΑΙΚΕ ΛΕΙΣΟΤΡΓΙΕ ΣΟΤ MATLAB Γενικά θ γλϊςςα προγραµµατιςµοφ MATLAB (το όνοµα προιλκε από τισ λζξεισ Matrix Laboratory) λειτουργεί ωσ διερµθνζασ εντολϊν (command interpreter), οι οποίεσ δίνονται µζςω του παρακφρου εντολϊν τθσ (MATLAB command window). Οι εντολζσ αυτζσ µπορεί να είναι: 1. οριςµοί µεταβλθτϊν και πράξεισ 2. κλιςθ ενςωµατωµζνων ςυναρτιςεων τθσ MATLAB και των εγκατεςτθµζνων εργαλειοκθκϊν τθσ (toolboxes) 3. κλιςθ ςυναρτιςεων (functions) ι αρχείων εντολϊν MATLAB (scripts) που καταςκευάηονται από τουσ χριςτεσ µε τθ µορφι m-file. Οι πιο κφριεσ εντολζσ και μία χοντρικι περιγραφι του κϊδικα του Matlab που χρειάηονται και χρθςιμοποιικθκαν κυρίωσ ςτουσ κϊδικεσ τθσ εφαρμογισ είναι οι παρακάτω: 1) ΔΙΑΝΤΜΑΣΑ: >> x=[1,2,3,4,5,6] 2) ΧΗΜΑΣΑ ΜΕ ΧΡΩΜΑ: (x1,y1) (x2,y2) xsquare=[x1,x2,x3,x4] ysquare=[y1,y2,y3,y4] (x4,y4) (x3,y3) fill(xsquare,ysquare, [c1,c2,c3]) όπου color=[c1,c2,c3] και 0<=c1,c2,c3<=1 c1=κόκκινο, c2=πράςινο, c3=μπλε ~ 8 ~
9 Ραράδειγμα ςε mfile: >>xs=[1,2,2,1] >>ys=[2,2,1,1] >>fill(xs,ys,[0.7,0.3,0.2],... 'Linestyle','None') >> axis([0,3,0,3]) axis([xmin,xmax,ymin,ymax]) >> axis off >> text(1,2.2,'a','color',[0.8,0.2,0.2],'fontsize',12) Στθν αρχι μποροφμε να βάλουμε το BACKGROUND: xback=[x1,x2,x3,x4] yback=[y1,y2,y3,y4] ςε ότι χρϊμα κζλουμε >> xback=[0,0,3,3] >> yback=[0,3,3,0] >> fill(xback,yback,[0.2,0.3,0.7],... xs,ys,[0.7,0.3,0.2],... 'Linestyle', 'None') Και οι άξoνεσ να είναι ςτο μζγεκοσ του background: >> axis([0,3,0,3]) >>axis off ~ 9 ~
10 3) ΚΙΝΗΗ ΧΗΜΑΣΩΝ: Ξανά παίρνουμε το τετράγωνο με πλευρά 1 και γράφουμε τα διανφςματα: xsq=[x1,x1+1,x1+1,x1] (x1,2) (x1+1,2) ysq=[1,1,2,2] (x1,1) (x1+1,1) και κάνουμε το x1 να μεταβάλλεται μζςα ςε μια εντολι FOR >> for t=0:0.1:1 όπου step=0.1 >>x1=t*t; >>xsq=[x1,x1+1,x1+1,x1] >>ysq=[1,1,2,2] >>fill(xsq,ysq,[0.7,0.3,0.2],...'linestyle', 'None') >>axis([0,3,0,3]) >> axis off >> pause (ryt) ρυκμόσ παφςθσ (μικρόσ αρικμόσ) π.χ 0.01 >> Πςο μικρότερο είναι το ryt τόςο πιο γριγορα κινείται θ προςομοίωςθ. Πςο μεγαλφτερο είναι το ryt τόςο πιο αργά κινείται θ προςομοίωςθ. Πςο μεγαλφτερο το step τόςο πιο ομαλι θ κίνθςθ (π.χ. 0.01). Πταν το step είναι μεγάλο, τότε φαίνεται θ κίνθςθ να κάνει αλματάκια κάτι το οποίο δεν κζλουμε διότι είναι άςχθμο. Μποροφμε να δϊςουμε και κίνθςθ ςτο text π.χ >> text(x1,2.2,'a','color',[0.8,0.2,0.2],'fontsize',12) ~ 10 ~
11 4) ΚΑΜΠΤΛΕ ΚΑΙ ΧΗΜΑΣΑ: Κάκε καμπφλθ μποροφμε να τθ ηωγραφίςουμε ςαν ζνα πολφγωνο με πολφ μικρό μικοσ πλευράσ. >> xp[1,1.5,2,1.8,1.3] >> yp=[1,1.2,1.5,2,1.7] >> fill(xp,yp,[0.7,0.3,0.2],...,'linestyle','none'] >> axis([0,3,0,3]) Για το ςχιμα ΑΒΓΔ με τθν καμπφλθ γράφουμε, επειδι είναι θμικφκλιο, μια παράμετρο γωνίασ κ, από κ=π ξεκινϊντασ από το Α, μζχρι κ=0 ςτο Β, με πολφ μικρό step (π.χ 0.01) για να είναι ζνα πολφγωνο με πολφ μικρζσ πλευρζσ (δθλ. μια ομαλι καμπφλθ). Άρα xs=[xa, xp, xb, xγ, xδ] ys=[ya, yp,yb, yγ, yδ] οπότε: >> th=pi:-0.01:0; >> xs=[1, *cos(th),2,2,1]; >> ys=[2,2+0.5*sin(th),2,1,1]; >> fill(xs,ys,[0.7,0.3,0.2],...,'linestyle','none') >> axis([0,3,0,3]) (Βλ.ςχήμα παρακάτω) ~ 11 ~
12 χήμα: P(xP,yP) xp=1,5+0.5cosκ (1,2)Α Β(2,2) yp=2+0.5sinκ (1,1)Δ Γ(2,1) Το κζντρο O(1.5,2) βρίςκεται ανάμεςα ςτο Α(1,2) και Β(2,2), ΟΡ=ρ=0.5 είναι θ ακτίνα του θμικυκλίου και θ θ γωνία τθσ ακτίνασ με τον οριηόντιο άξονα ΟΒ. ~ 12 ~
13 5) ΑΛΛΕ ΕΝΣΟΛΕ: Μζςα ςτο κϊδικα τθσ ςελ:10, αν βάλουμε τθν εντολι: >>nx1=num2str(0.01*round(100*x1)); >>text(2.5,2.5,nx1) Βγάηει τθν αρικμθτικι τιμι τθσ μεταβλθτισ x1 όπου κζλουμε π.χ ςτο ςθμείο (2.5,2.5) Στθν αρχι κάκε προγράμματοσ πολλζσ φορζσ είναι καλό να βάηουμε τισ εντολζσ: >>clear all; >>clc; (κακαρίηει τισ μεταβλθτζσ) (κακαρίηει τθν οκόνθ) 6) Γραφική Διεπιφάνεια Χρήςτη Graphical User Interface (GUI) Η εφαρμογι GUI είναι ζνασ φιλικόσ τρόποσ να καταςκευάηουμε Γραφικζσ Διεπιφάνειεσ Χριςτθ. Εκκινεί με τθν παρακάτω εντολι: >>guide Ρεριςςότερα ςτθν Αναφορά 1. ~ 13 ~
14 Παράρτημα: Κώδικασ Ο κϊδικασ που αναπτφχκθκε για τθν εφαρμογι τθσ Ευκφγραμμθσ Ομαλά Μεταβαλλόμενθσ Κίνθςθσ είναι ο εξισ: function varargout = g_central(varargin) % G_CENTRAL M-file for g_central.fig % G_CENTRAL, by itself, creates a new G_CENTRAL or raises the existing % singleton*. % % H = G_CENTRAL returns the handle to a new G_CENTRAL or the handle to % the existing singleton*. % % G_CENTRAL('CALLBACK',hObject,eventData,handles,...) calls the local % function named CALLBACK in G_CENTRAL.M with the given input arguments. % % G_CENTRAL('Property','Value',...) creates a new G_CENTRAL or raises the % existing singleton*. Starting from the left, property value pairs are % applied to the GUI before g_central_openingfcn gets called. An % unrecognized property name or invalid value makes property application % stop. All inputs are passed to g_central_openingfcn via varargin. % % *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one % instance to run (singleton)". % % See also: GUIDE, GUIDATA, GUIHANDLES % Edit the above text to modify the response to help g_central % Last Modified by GUIDE v Feb :50:20 % Begin initialization code - DO NOT EDIT gui_singleton = 1; gui_state = struct('gui_name', mfilename,... 'gui_singleton', gui_singleton,... 'gui_layoutfcn', [],... 'gui_callback', []); if nargin && ischar(varargin{1}) gui_state.gui_callback = str2func(varargin{1}); ~ 14 ~
15 if nargout [varargout{1:nargout}] = gui_mainfcn(gui_state, varargin{:}); else gui_mainfcn(gui_state, varargin{:}); % End initialization code - DO NOT EDIT % --- Executes just before g_central is made visible. function g_central_openingfcn(hobject, eventdata, handles, varargin) % This function has no output args, see OutputFcn. % hobject handle to figure % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % varargin command line arguments to g_central (see VARARGIN) %% % x=imread('moderncar','jpg'); axes(handles.axes1) image(x); %% % % Choose default command line output for g_central handles.output = hobject; % Update handles structure guidata(hobject, handles); % UIWAIT makes g_central wait for user response (see UIRESUME) % uiwait(handles.figure1); % --- Outputs from this function are returned to the command line. function varargout = g_central_outputfcn(hobject, eventdata, handles) % varargout cell array for returning output args (see VARARGOUT); % hobject handle to figure % eventdata reserved - to be defined in a future version of MATLAB ~ 15 ~
16 % handles structure with handles and user data (see GUIDATA) % Get default command line output from handles structure varargout{1} = handles.output; % --- Executes on button press in pushbutton1. function pushbutton1_callback(hobject, eventdata, handles) % hobject handle to pushbutton1 (see GCBO) % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) g_omaln; % --- Executes on button press in pushbutton2. function pushbutton2_callback(hobject, eventdata, handles) % hobject handle to pushbutton2 (see GCBO) % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) g_epitaxuvomevn; % --- Executes on button press in pushbutton3. function pushbutton3_callback(hobject, eventdata, handles) % hobject handle to pushbutton3 (see GCBO) % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) g_epibraduvomevn; % --- Executes on button press in pushbutton4. function pushbutton4_callback(hobject, eventdata, handles) % hobject handle to pushbutton4 (see GCBO) % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) hfin=questdlg('έξοδορ από ηο ππόγπαμμα;'); switch hfin case 'Yes' closereq; ~ 16 ~
17 Η απεικόνιςθ ςε Matlab τθσ εφαρμογισ τθσ Ευκφγραμμθσ Ομαλισ Κίνθςθσ: Η απεικόνιςθ ςε Matlab τθσ εφαρμογισ τθσ Ευκφγραμμθσ Ομαλισ ΕπιταχυνόμενθσΚίνθςθσ: ~ 17 ~
18 Η απεικόνιςθ ςε Matlab τθσ εφαρμογισ τθσ Ευκφγραμμθσ Ομαλισ Επιβραδυνόμενθσ Κίνθςθσ: ~ 18 ~
19 function varargout = g_omaln(varargin) % G_OMALN M-file for g_omaln.fig % G_OMALN, by itself, creates a new G_OMALN or raises the existing % singleton*. % % H = G_OMALN returns the handle to a new G_OMALN or the handle to % the existing singleton*. % % G_OMALN('CALLBACK',hObject,eventData,handles,...) calls the local % function named CALLBACK in G_OMALN.M with the given input arguments. % % G_OMALN('Property','Value',...) creates a new G_OMALN or raises the % existing singleton*. Starting from the left, property value pairs are % applied to the GUI before g_omaln_openingfcn gets called. An % unrecognized property name or invalid value makes property application % stop. All inputs are passed to g_omaln_openingfcn via varargin. % % *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one % instance to run (singleton)". % % See also: GUIDE, GUIDATA, GUIHANDLES % Edit the above text to modify the response to help g_omaln % Last Modified by GUIDE v Feb :45:05 % Begin initialization code - DO NOT EDIT gui_singleton = 1; gui_state = struct('gui_name', mfilename,... 'gui_singleton', gui_singleton,... 'gui_layoutfcn', [],... 'gui_callback', []); if nargin && ischar(varargin{1}) gui_state.gui_callback = str2func(varargin{1}); if nargout [varargout{1:nargout}] = gui_mainfcn(gui_state, varargin{:}); else gui_mainfcn(gui_state, varargin{:}); % End initialization code - DO NOT EDIT % --- Executes just before g_omaln is made visible. function g_omaln_openingfcn(hobject, eventdata, handles, varargin) % This function has no output args, see OutputFcn. % hobject handle to figure ~ 19 ~
20 % handles structure with handles and user data (see GUIDATA) % varargin command line arguments to g_omaln (see VARARGIN) % Choose default command line output for g_omaln handles.output = hobject; % Update handles structure guidata(hobject, handles); % UIWAIT makes g_omaln wait for user response (see UIRESUME) % uiwait(handles.figure1); % --- Outputs from this function are returned to the command line. function varargout = g_omaln_outputfcn(hobject, eventdata, handles) % varargout cell array for returning output args (see VARARGOUT); % hobject handle to figure % handles structure with handles and user data (see GUIDATA) % Get default command line output from handles structure varargout{1} = handles.output; function edit1_callback(hobject, eventdata, handles) % hobject handle to edit1 (see GCBO) % handles structure with handles and user data (see GUIDATA) % Hints: get(hobject,'string') returns contents of edit1 as text % str2double(get(hobject,'string')) returns contents of edit1 as a double % --- Executes during object creation, after setting all properties. function edit1_createfcn(hobject, eventdata, handles) % hobject handle to edit1 (see GCBO) % handles empty - handles not created until after all CreateFcns called % Hint: edit controls usually have a white background on Windows. % See ISPC and COMPUTER. if ispc && isequal(get(hobject,'backgroundcolor'), get(0,'defaultuicontrolbackgroundcolor')) set(hobject,'backgroundcolor','white'); function edit2_callback(hobject, eventdata, handles) % hobject handle to edit2 (see GCBO) % handles structure with handles and user data (see GUIDATA) % Hints: get(hobject,'string') returns contents of edit2 as text ~ 20 ~
21 % str2double(get(hobject,'string')) returns contents of edit2 as a double % --- Executes during object creation, after setting all properties. function edit2_createfcn(hobject, eventdata, handles) % hobject handle to edit2 (see GCBO) % handles empty - handles not created until after all CreateFcns called % Hint: edit controls usually have a white background on Windows. % See ISPC and COMPUTER. if ispc && isequal(get(hobject,'backgroundcolor'), get(0,'defaultuicontrolbackgroundcolor')) set(hobject,'backgroundcolor','white'); function edit3_callback(hobject, eventdata, handles) % hobject handle to edit3 (see GCBO) % handles structure with handles and user data (see GUIDATA) % Hints: get(hobject,'string') returns contents of edit3 as text % str2double(get(hobject,'string')) returns contents of edit3 as a double % --- Executes during object creation, after setting all properties. function edit3_createfcn(hobject, eventdata, handles) % hobject handle to edit3 (see GCBO) % handles empty - handles not created until after all CreateFcns called % Hint: edit controls usually have a white background on Windows. % See ISPC and COMPUTER. if ispc && isequal(get(hobject,'backgroundcolor'), get(0,'defaultuicontrolbackgroundcolor')) set(hobject,'backgroundcolor','white'); % --- Executes on button press in pushbutton1. function pushbutton1_callback(hobject, eventdata, handles) % hobject handle to pushbutton1 (see GCBO) % handles structure with handles and user data (see GUIDATA) %%% global ryt; global tmax; global v; tmax=str2double(get(handles.edit1,'string')); ~ 21 ~
22 v=str2double(get(handles.edit2,'string')); ryt=str2double(get(handles.edit3,'string')); global stam; stam=0; set(handles.pushbutton2,'string','διακοπή'); global status; status=0; global status1; status1=0; rryt=1.005-ryt; if (ryt>1 ryt<0.001) h=warndlg('βάληε ζηo πςθμό πποζομοίωζηρ ηιμή μεηαξύ και 1.0'); return if (tmax>20 tmax<10) h=warndlg('βάληε ζηo σπόνο κίνηζηρ ηιμή μεηαξύ 10 και 20'); return if (v>10 v<5) h=warndlg('βάληε ζηη ηασύηηηα ηιμή μεηαξύ 10 και 20'); return set(handles.edit1,'enable','off'); set(handles.edit2,'enable','off'); set(handles.edit3,'enable','off'); set(handles.pushbutton1,'enable','off'); %%% scale_x=0.35; scale_y=0.7; scale_cx=0.07; scale_cy=0.17; %%% %5<=v<=10; %10<=t<=20; % v=10; % tmax=20; xmax=v*tmax; %xmegisto=200 %xelaxisto=50 %%% % x=imread('moderncar','jpg'); % image(x); ~ 22 ~
23 xupoba8ro=[0.0,4.0,4.0,0.0]; yupoba8ro=[0.0,0.0,3.0,3.0]; x0=1.8; y0=1.0; th0=0:0.01:2*pi; th1=0:0.01:pi/2; xb1= *cos(th1); yb1= *sin(th1); th1_1=pi/2:-0.01:0; xb1_1= *cos(th1_1); yb1_1= *sin(th1_1); xb2=-0.4:-0.01:-3.6; yb2=( *exp(-1.1*1.8^2))+0.45*exp(-1.1*(xb2+2.2).^2); yb2_edge=( *exp(-1.1*1.8^2))+0.5*exp(-1.1*( ).^2); th3=pi/2:0.01:pi; xb3= *cos(th3); yb3=yb2_edge *sin(th3); th3_1=0:0.01:pi/2; xb3_1= *cos(th3_1); yb3_1=yb2_edge *sin(th3_1); th4=pi:0.01:3*pi/2; xb4= *cos(th4); yb4=yb2_edge *sin(th4); xb5=-2.9; yb5=yb2_edge-0.4; th6=pi:-0.01:0.0; xb6= *cos(th6); yb6=yb5+0.25*sin(th6); xb7=-1.1; yb7=yb5; th8=pi:-0.01:0.0; xb8= *cos(th8); yb8=yb5+0.25*sin(th8); th9=3*pi/2:0.01:2*pi; xb9= *cos(th9); yb9=0.0-yb5*sin(th9); xb10=-1.1:-0.01:-3.0; yb10=( *exp(-1.1*1.8^2))+0.40*exp(-1.1*(xb10+2.2).^2); yb10_edge=( *exp(-1.1*1.8^2))+0.40*exp(-1.1*( ).^2); th11=0.0:0.01:2*pi; xb11= *cos(th11); yb11=yb5+0.23*sin(th11); ~ 23 ~
24 th12=0.0:0.01:2*pi; xb12= *cos(th12); yb12=yb5+0.17*sin(th12); th13=0.0:0.01:2*pi; xb13= *cos(th13); yb13=yb5+0.23*sin(th13); th14=0.0:0.01:2*pi; xb14= *cos(th14); yb14=yb5+0.17*sin(th14); %%% % ryt=0.9; % rryt=1.005-ryt; %%% xcfield1=[0.0,4.0,4.0,0.0]; ycfield1=[0.0,0.0,0.8,0.8]; xcroad=[0.0,4.0,4.0,0.0]; ycroad=[0.8,0.8,1.2,1.2]; xcfield2=[0.0,4.0,4.0,0.0]; ycfield2=[1.2,1.2,2.2,2.2]; xcsky=[0.0,4.0,4.0,0.0]; ycsky=[2.2,2.2,3.0,3.0]; xb1=0.1:0.01:1.5; xcbouvo1=[0.1,xb1,1.5]; ycbouvo1=[1.9, *exp(-6.1*(xb1-0.8).^2),1.9]; xb2=1.4:0.01:3.6; xcbouvo2=[1.4,xb2,3.6]; ycbouvo2=[2.0, *exp(-2.1*(xb2-2.5).^2),2.0]; xb3=3.1:0.01:4.0; xcbouvo3=[3.1,xb3,4.0]; ycbouvo3=[1.8, *exp(-7.1*(xb3-4.0).^2),1.8]; xcline1=[0.0,0.2,0.2,0.0]; ycline1=[0.99,0.99,1.01,1.01]; xcline2=[0.0,0.2,0.2,0.0]+0.4; ycline2=[0.99,0.99,1.01,1.01]; xcline3=[0.0,0.2,0.2,0.0]+2*0.4; ycline3=[0.99,0.99,1.01,1.01]; xcline4=[0.0,0.2,0.2,0.0]+3*0.4; ycline4=[0.99,0.99,1.01,1.01]; xcline5=[0.0,0.2,0.2,0.0]+4*0.4; ycline5=[0.99,0.99,1.01,1.01]; ~ 24 ~
25 xcline6=[0.0,0.2,0.2,0.0]+5*0.4; ycline6=[0.99,0.99,1.01,1.01]; xcline7=[0.0,0.2,0.2,0.0]+6*0.4; ycline7=[0.99,0.99,1.01,1.01]; xcline8=[0.0,0.2,0.2,0.0]+7*0.4; ycline8=[0.99,0.99,1.01,1.01]; xcline9=[0.0,0.2,0.2,0.0]+8*0.4; ycline9=[0.99,0.99,1.01,1.01]; xcline10=[0.0,0.2,0.2,0.0]+9*0.4; ycline10=[0.99,0.99,1.01,1.01]; xcline_begin=[0.3,0.35,0.36,0.31]; ycline_begin=[0.8,0.8,1.2,1.2]; xcline_=[0.3,0.35,0.36,0.31]+3.6*(xmax/200); ycline_=[0.8,0.8,1.2,1.2]; xfield1=[0.0,4.0,4.0,0.0]; yfield1=[0.0,0.0,0.6,0.6]; xroad=[0.0,4.0,4.0,0.0]; yroad=[0.6,0.6,1.6,1.6]; xfield2=[0.0,4.0,4.0,0.0]; yfield2=[1.6,1.6,3.0,3.0]; x0v=1.0; y0v=1.8; lv=v*1.5/10; xvectorv=x0v+scale_x*[0.0,0.0,lv,lv,lv+0.2,lv,lv]; yvectorv=y0v+scale_y*[0.075,-0.075,-0.075,-0.15,0.0,0.20,0.075]; xgv=x0v+scale_x*lv/2; ygv=y0v+0.5; %%% %%%%xmin=0.3 %%%%xmax=3.9 iimax=(11*(tmax/20)-1); %%% for ii=1:0.1:11*(tmax/20) if (status1==1) return if (status==1) closereq; return ~ 25 ~
26 if (stam==1) cc1=stam; while (cc1==1) cc1=stam; pause(0.01); if (status1==1) return if (status==1) return tt=(ii-1)*tmax/(11*(tmax/20)-1); xx=v*tt; ntt=num2str(0.01*round(100*tt)); nxx=num2str(0.01*round(100*xx)); tgr=tt+(tmax/133)*cos(th0); xgr=xx+(xmax/54)*sin(th0); vgr=v+(v/29)*sin(th0); cx0=0.3+(xx/xmax)*(3.6*xmax/200); cy0=1.0; th15=0.0:0.01:2*pi; xb15= *cos(th15); yb15=yb5+0.08*sin(th15); phi= *(xx/200)/0.17; xb15_1=-2.9+[0.08*cos(phi-pi/12),0.17*cos(phi),0.08*cos(phi+pi/12)]; yb15_1=yb5+[0.08*sin(phi-pi/12),0.17*sin(phi),0.08*sin(phi+pi/12)]; th16=0.0:0.01:2*pi; xb16= *cos(th16); yb16=yb5+0.08*sin(th16); xb16_1=-0.85+[0.08*cos(phi-pi/12),0.17*cos(phi),0.08*cos(phi+pi/12)]; yb16_1=yb5+[0.08*sin(phi-pi/12),0.17*sin(phi),0.08*sin(phi+pi/12)]; xb15_2=-2.9+[0.08*cos(phipi/12+2*pi/3),0.17*cos(phi+2*pi/3),0.08*cos(phi+pi/12+2*pi/3)]; yb15_2=yb5+[0.08*sin(phipi/12+2*pi/3),0.17*sin(phi+2*pi/3),0.08*sin(phi+pi/12+2*pi/3)]; xb15_3=-2.9+[0.08*cos(phipi/12+4*pi/3),0.17*cos(phi+4*pi/3),0.08*cos(phi+pi/12+4*pi/3)]; yb15_3=yb5+[0.08*sin(phipi/12+4*pi/3),0.17*sin(phi+4*pi/3),0.08*sin(phi+pi/12+4*pi/3)]; xb16_2=-0.85+[0.08*cos(phipi/12+2*pi/3),0.17*cos(phi+2*pi/3),0.08*cos(phi+pi/12+2*pi/3)]; ~ 26 ~
27 yb16_2=yb5+[0.08*sin(phipi/12+2*pi/3),0.17*sin(phi+2*pi/3),0.08*sin(phi+pi/12+2*pi/3)]; xb16_3=-0.85+[0.08*cos(phipi/12+4*pi/3),0.17*cos(phi+4*pi/3),0.08*cos(phi+pi/12+4*pi/3)]; yb16_3=yb5+[0.08*sin(phipi/12+4*pi/3),0.17*sin(phi+4*pi/3),0.08*sin(phi+pi/12+4*pi/3)]; xb17=[xb3,xb3_1]; yb17=[yb3,yb3_1]; xb18=[xb1,xb1_1]; yb18=[yb1,yb1_1]; %%% %%% xcar1=x0+scale_x*[xb1,xb2,xb3,xb4,xb5,xb6,xb7,xb8,xb9]; ycar1=y0+scale_y*[yb1,yb2,yb3,yb4,yb5,yb6,yb7,yb8,yb9]; xcar2=x0+scale_x*[xb10]; ycar2=y0+scale_y*[yb10]; xcar3=x0+scale_x*[-2.5,-2.55,-2.55,-2.5]; ycar3=y0+scale_y*(yb10_edge+[0.0,0.0,0.3,0.3]); xcar4=x0+scale_x*[-2.5,-2.5,-1.20,-1.19]; ycar4=y0+scale_y*(yb10_edge+[0.04,-0.38,-0.38,0.007]); xcar5=x0+scale_x*[-2.475,-2.475,-1.21,-1.20]; ycar5=y0+scale_y*(yb10_edge+[0.035,-0.37,-0.37,0.002]); xcar6=x0+scale_x*[xb11]; ycar6=y0+scale_y*[yb11]; xcar7=x0+scale_x*[xb12]; ycar7=y0+scale_y*[yb12]; xcar8=x0+scale_x*[xb13]; ycar8=y0+scale_y*[yb13]; xcar9=x0+scale_x*[xb14]; ycar9=y0+scale_y*[yb14]; xcar10=x0+scale_x*[xb15]; ycar10=y0+scale_y*[yb15]; xcar10_1=x0+scale_x*xb15_1; ycar10_1=y0+scale_y*yb15_1; xcar10_2=x0+scale_x*xb15_2; ycar10_2=y0+scale_y*yb15_2; xcar10_3=x0+scale_x*xb15_3; ycar10_3=y0+scale_y*yb15_3; ~ 27 ~
28 xcar11=x0+scale_x*[xb16]; ycar11=y0+scale_y*[yb16]; xcar11_1=x0+scale_x*xb16_1; ycar11_1=y0+scale_y*yb16_1; xcar11_2=x0+scale_x*xb16_2; ycar11_2=y0+scale_y*yb16_2; xcar11_3=x0+scale_x*xb16_3; ycar11_3=y0+scale_y*yb16_3; xcar12=x0+scale_x*xb17; ycar12=y0+scale_y*yb17; xcar13=x0+scale_x*xb18; ycar13=y0+scale_y*yb18; %%% xccar1=cx0+scale_cx*[xb1,xb2,xb3,xb4,xb5,xb6,xb7,xb8,xb9]; yccar1=cy0+scale_cy*[yb1,yb2,yb3,yb4,yb5,yb6,yb7,yb8,yb9]; xccar2=cx0+scale_cx*[xb10]; yccar2=cy0+scale_cy*[yb10]; xccar3=cx0+scale_cx*[-2.5,-2.55,-2.55,-2.5]; yccar3=cy0+scale_cy*(yb10_edge+[0.0,0.0,0.3,0.3]); xccar4=cx0+scale_cx*[-2.5,-2.5,-1.20,-1.19]; yccar4=cy0+scale_cy*(yb10_edge+[0.04,-0.38,-0.38,0.007]); xccar5=cx0+scale_cx*[-2.49,-2.49,-1.21,-1.20]; yccar5=cy0+scale_cy*(yb10_edge+[0.035,-0.37,-0.37,0.002]); xccar6=cx0+scale_cx*[xb11]; yccar6=cy0+scale_cy*[yb11]; xccar7=cx0+scale_cx*[xb12]; yccar7=cy0+scale_cy*[yb12]; xccar8=cx0+scale_cx*[xb13]; yccar8=cy0+scale_cy*[yb13]; xccar9=cx0+scale_cx*[xb14]; yccar9=cy0+scale_cy*[yb14]; xccar10=cx0+scale_cx*[xb15]; yccar10=cy0+scale_cy*[yb15]; xccar10_1=cx0+scale_cx*xb15_1; yccar10_1=cy0+scale_cy*yb15_1; xccar10_2=cx0+scale_cx*xb15_2; yccar10_2=cy0+scale_cy*yb15_2; xccar10_3=cx0+scale_cx*xb15_3; yccar10_3=cy0+scale_cy*yb15_3; ~ 28 ~
29 xccar11=cx0+scale_cx*[xb16]; yccar11=cy0+scale_cy*[yb16]; xccar11_1=x0+scale_cx*xb16_1; yccar11_1=y0+scale_cy*yb16_1; xccar11_2=cx0+scale_cx*xb16_2; yccar11_2=cy0+scale_cy*yb16_2; xccar11_3=cx0+scale_cx*xb16_3; yccar11_3=cy0+scale_cy*yb16_3; xccar12=cx0+scale_cx*xb17; yccar12=cy0+scale_cy*yb17; xccar13=cx0+scale_cx*xb18; yccar13=cy0+scale_cy*yb18; %%% xline0=[2.2, , ,2.2]-1*2.0-(ii-1)*18.0*(xmax/200)/iimax; yline0=[1.05,1.05,1.15,1.15]; xline1=[2.2, , ,2.2]-(ii-1)*18.0*(xmax/200)/iimax; yline1=[1.05,1.05,1.15,1.15]; xline2=[2.2, , ,2.2]+1*2.0-(ii-1)*18.0*(xmax/200)/iimax; yline2=[1.05,1.05,1.15,1.15]; xline3=[2.2, , ,2.2]+2*2.0-(ii-1)*18.0*(xmax/200)/iimax; yline3=[1.05,1.05,1.15,1.15]; xline4=[2.2, , ,2.2]+3*2.0-(ii-1)*18.0*(xmax/200)/iimax; yline4=[1.05,1.05,1.15,1.15]; xline5=[2.2, , ,2.2]+4*2.0-(ii-1)*18.0*(xmax/200)/iimax; yline5=[1.05,1.05,1.15,1.15]; xline6=[2.2, , ,2.2]+5*2.0-(ii-1)*18.0*(xmax/200)/iimax; yline6=[1.05,1.05,1.15,1.15]; xline7=[2.2, , ,2.2]+6*2.0-(ii-1)*18.0*(xmax/200)/iimax; yline7=[1.05,1.05,1.15,1.15]; xline8=[2.2, , ,2.2]+7*2.0-(ii-1)*18.0*(xmax/200)/iimax; yline8=[1.05,1.05,1.15,1.15]; xline9=[2.2, , ,2.2]+8*2.0-(ii-1)*18.0*(xmax/200)/iimax; yline9=[1.05,1.05,1.15,1.15]; xline10=[2.2, , ,2.2]+9*2.0-(ii-1)*18.0*(xmax/200)/iimax; yline10=[1.05,1.05,1.15,1.15]; xline11=[2.2, , ,2.2]+10*2.0-(ii- 1)*18.0*(xmax/200)/iimax; yline11=[1.05,1.05,1.15,1.15]; ~ 29 ~
30 ~ 30 ~ xline_begin=[1.75,1.95,2.05,1.90]-(ii-1)*18.0*(xmax/200)/iimax; yline_begin=[0.6,0.6,1.6,1.6]; xline_=[1.75,1.95,2.05,1.90]+9*2.0*(xmax/200)-(ii- 1)*18.0*(xmax/200)/iimax; yline_=[0.6,0.6,1.6,1.6]; %%% %subplot(2,1,1) axes(handles.axes3) fill(xupoba8ro,yupoba8ro,[1.0,1.0,1.0],... xfield1,yfield1,[0.2,0.8,0.2],... xroad,yroad,[0.4,0.4,0.4],... xfield2,yfield2,[0.2,0.8,0.2],... xline0,yline0,[0.9,0.9,0.9],... xline1,yline1,[0.9,0.9,0.9],... xline2,yline2,[0.9,0.9,0.9],... xline3,yline3,[0.9,0.9,0.9],... xline4,yline4,[0.9,0.9,0.9],... xline5,yline5,[0.9,0.9,0.9],... xline6,yline6,[0.9,0.9,0.9],... xline7,yline7,[0.9,0.9,0.9],... xline8,yline8,[0.9,0.9,0.9],... xline9,yline9,[0.9,0.9,0.9],... xline10,yline10,[0.9,0.9,0.9],... xline11,yline11,[0.9,0.9,0.9],... xline_begin,yline_begin,[0.9,0.3,0.3],... xline_,yline_,[0.9,0.9,0.3],... xcar1,ycar1,[0.3,0.5,0.8],... xcar2,ycar2,[0.9,0.9,0.9],... xcar3,ycar3,[0.3,0.5,0.8],... xcar4,ycar4,[0.4,0.4,0.4],... xcar5,ycar5,[0.3,0.5,0.8],... xcar6,ycar6,[0.4,0.4,0.4],... xcar7,ycar7,[0.8,0.8,0.8],... xcar8,ycar8,[0.4,0.4,0.4],... xcar9,ycar9,[0.8,0.8,0.8],... xcar10,ycar10,[0.6,0.6,0.6],... xcar10_1,ycar10_1,[0.6,0.6,0.6],... xcar10_2,ycar10_2,[0.6,0.6,0.6],... xcar10_3,ycar10_3,[0.6,0.6,0.6],... xcar11,ycar11,[0.6,0.6,0.6],... xcar11_1,ycar11_1,[0.6,0.6,0.6],... xcar11_2,ycar11_2,[0.6,0.6,0.6],... xcar11_3,ycar11_3,[0.6,0.6,0.6],... xcar12,ycar12,[0.8,0.6,0.6],... xcar13,ycar13,[0.8,0.6,0.6],... xvectorv,yvectorv,[0.8,0.2,0.8],... 'Linestyle','None') text(xgv,ygv,'v','color',[0.8,0.2,0.8],'fontsize',11)
31 ~ 31 ~ text(3.4,2.8,'t=','fontsize',11) text(3.525,2.8,ntt,'fontsize',11) text(3.78,2.8,'sec','fontsize',11) text(3.4,2.5,'x=','fontsize',11) text(3.55,2.5,nxx,'fontsize',11) text(3.78,2.5,'m','fontsize',11) axis([0.0,4.0,0.0,3.0]) axis off %subplot(2,1,2) axes(handles.axes4) fill(xupoba8ro,yupoba8ro,[1.0,1.0,1.0],... xcfield1,ycfield1,[0.2,0.8,0.2],... xcroad,ycroad,[0.4,0.4,0.4],... xcfield2,ycfield2,[0.2,0.8,0.2],... xcsky,ycsky,[0.7,0.7,0.9],... xcbouvo1,ycbouvo1,[0.2,0.6,0.2],... xcbouvo2,ycbouvo2,[0.3,0.5,0.3],... xcbouvo3,ycbouvo3,[0.25,0.45,0.25],... xcline1,ycline1,[0.9,0.9,0.9],... xcline2,ycline2,[0.9,0.9,0.9],... xcline3,ycline3,[0.9,0.9,0.9],... xcline4,ycline4,[0.9,0.9,0.9],... xcline5,ycline5,[0.9,0.9,0.9],... xcline6,ycline6,[0.9,0.9,0.9],... xcline7,ycline7,[0.9,0.9,0.9],... xcline8,ycline8,[0.9,0.9,0.9],... xcline9,ycline9,[0.9,0.9,0.9],... xcline10,ycline10,[0.9,0.9,0.9],... xcline_begin,ycline_begin,[0.9,0.3,0.3],... xcline_,ycline_,[0.9,0.9,0.3],... xccar1,yccar1,[0.3,0.5,0.8],... xccar2,yccar2,[0.9,0.9,0.9],... xccar3,yccar3,[0.3,0.5,0.8],... xccar4,yccar4,[0.4,0.4,0.4],... xccar5,yccar5,[0.3,0.5,0.8],... xccar6,yccar6,[0.4,0.4,0.4],... xccar7,yccar7,[0.8,0.8,0.8],... xccar8,yccar8,[0.4,0.4,0.4],... xccar9,yccar9,[0.8,0.8,0.8],... xccar10,yccar10,[0.6,0.6,0.6],... xccar10_1,yccar10_1,[0.6,0.6,0.6],... xccar10_2,yccar10_2,[0.6,0.6,0.6],... xccar10_3,yccar10_3,[0.6,0.6,0.6],... xccar11,yccar11,[0.6,0.6,0.6],... xccar11_1,yccar11_1,[0.6,0.6,0.6],... xccar11_2,yccar11_2,[0.6,0.6,0.6],... xccar11_3,yccar11_3,[0.6,0.6,0.6],... xccar12,yccar12,[0.8,0.6,0.6],... xccar13,yccar13,[0.8,0.6,0.6],... 'Linestyle','None') axis([0.0,4.0,0.0,3.0]) axis off
32 axes(handles.axes1) fill(tgr,vgr,[0.8,0.2,0.2],... 'Linestyle','None') axis([0,tmax,0,2*v]) xlabel('t') ylabel('v') %subplot(1,2,2) axes(handles.axes2) fill(tgr,xgr,[0.8,0.2,0.2],... 'Linestyle','None') axis([0,tmax,0,v*tmax]) xlabel('t') ylabel('x') if (ii==1) pause(5.0) pause(rryt) tgr=0:0.01:tmax; vgr=v; xgr=v*tgr; %subplot(1,2,1) axes(handles.axes1) plot(tgr,v) axis([0,tmax,0,2*v]) xlabel('t') ylabel('v') %subplot(1,2,2) axes(handles.axes2) plot(tgr,xgr) axis([0,tmax,0,v*tmax]) xlabel('t') ylabel('x') %%% %%% % --- Executes on button press in pushbutton2. function pushbutton2_callback(hobject, eventdata, handles) ~ 32 ~
33 % hobject handle to pushbutton2 (see GCBO) % handles structure with handles and user data (see GUIDATA) global stam; if (stam==0) set(handles.pushbutton2,'string','σςνέσεια') stam=1; elseif (stam==1) set(handles.pushbutton2,'string','διακοπή') stam=0; else guidata(hobject, handles); % --- Executes on button press in pushbutton3. function pushbutton3_callback(hobject, eventdata, handles) % hobject handle to pushbutton3 (see GCBO) % handles structure with handles and user data (see GUIDATA) global ryt; global tmax; global v; axes(handles.axes1) cla axes(handles.axes2) cla axes(handles.axes3) cla axes(handles.axes4) cla global status1; status1=1; clear ryt; clear tmax; clear v; set(handles.edit1,'enable','on','string','20'); set(handles.edit2,'enable','on','string','10'); set(handles.edit3,'enable','on','string','0.9'); set(handles.pushbutton1,'enable','on'); guidata(hobject, handles); % --- Executes on button press in pushbutton4. function pushbutton4_callback(hobject, eventdata, handles) % hobject handle to pushbutton4 (see GCBO) % handles structure with handles and user data (see GUIDATA) global status; ~ 33 ~
34 hfin=questdlg('έξοδορ από ηο ππόγπαμμα;'); switch hfin case 'Yes' status=1; closereq; function varargout = g_epitaxuvomevn(varargin) % G_EPITAXUVOMEVN M-file for g_epitaxuvomevn.fig % G_EPITAXUVOMEVN, by itself, creates a new G_EPITAXUVOMEVN or raises the existing % singleton*. % % H = G_EPITAXUVOMEVN returns the handle to a new G_EPITAXUVOMEVN or the handle to % the existing singleton*. % % G_EPITAXUVOMEVN('CALLBACK',hObject,eventData,handles,...) calls the local % function named CALLBACK in G_EPITAXUVOMEVN.M with the given input arguments. % % G_EPITAXUVOMEVN('Property','Value',...) creates a new G_EPITAXUVOMEVN or raises the % existing singleton*. Starting from the left, property value pairs are % applied to the GUI before g_epitaxuvomevn_openingfcn gets called. An % unrecognized property name or invalid value makes property application % stop. All inputs are passed to g_epitaxuvomevn_openingfcn via varargin. % % *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one % instance to run (singleton)". % % See also: GUIDE, GUIDATA, GUIHANDLES % Edit the above text to modify the response to help g_epitaxuvomevn % Last Modified by GUIDE v Feb :52:04 % Begin initialization code - DO NOT EDIT gui_singleton = 1; gui_state = struct('gui_name', mfilename,... 'gui_singleton', gui_singleton,... 'gui_layoutfcn', [],... 'gui_callback', []); if nargin && ischar(varargin{1}) gui_state.gui_callback = str2func(varargin{1}); if nargout [varargout{1:nargout}] = gui_mainfcn(gui_state, varargin{:}); else ~ 34 ~
35 gui_mainfcn(gui_state, varargin{:}); % End initialization code - DO NOT EDIT % --- Executes just before g_epitaxuvomevn is made visible. function g_epitaxuvomevn_openingfcn(hobject, eventdata, handles, varargin) % This function has no output args, see OutputFcn. % hobject handle to figure % handles structure with handles and user data (see GUIDATA) % varargin command line arguments to g_epitaxuvomevn (see VARARGIN) % Choose default command line output for g_epitaxuvomevn handles.output = hobject; % Update handles structure guidata(hobject, handles); % UIWAIT makes g_epitaxuvomevn wait for user response (see UIRESUME) % uiwait(handles.figure1); % --- Outputs from this function are returned to the command line. function varargout = g_epitaxuvomevn_outputfcn(hobject, eventdata, handles) % varargout cell array for returning output args (see VARARGOUT); % hobject handle to figure % handles structure with handles and user data (see GUIDATA) % Get default command line output from handles structure varargout{1} = handles.output; function edit1_callback(hobject, eventdata, handles) % hobject handle to edit1 (see GCBO) % handles structure with handles and user data (see GUIDATA) % Hints: get(hobject,'string') returns contents of edit1 as text % str2double(get(hobject,'string')) returns contents of edit1 as a double % --- Executes during object creation, after setting all properties. function edit1_createfcn(hobject, eventdata, handles) % hobject handle to edit1 (see GCBO) % handles empty - handles not created until after all CreateFcns called % Hint: edit controls usually have a white background on Windows. % See ISPC and COMPUTER. if ispc && isequal(get(hobject,'backgroundcolor'), get(0,'defaultuicontrolbackgroundcolor')) ~ 35 ~
36 set(hobject,'backgroundcolor','white'); function edit2_callback(hobject, eventdata, handles) % hobject handle to edit2 (see GCBO) % handles structure with handles and user data (see GUIDATA) % Hints: get(hobject,'string') returns contents of edit2 as text % str2double(get(hobject,'string')) returns contents of edit2 as a double % --- Executes during object creation, after setting all properties. function edit2_createfcn(hobject, eventdata, handles) % hobject handle to edit2 (see GCBO) % handles empty - handles not created until after all CreateFcns called % Hint: edit controls usually have a white background on Windows. % See ISPC and COMPUTER. if ispc && isequal(get(hobject,'backgroundcolor'), get(0,'defaultuicontrolbackgroundcolor')) set(hobject,'backgroundcolor','white'); function edit3_callback(hobject, eventdata, handles) % hobject handle to edit3 (see GCBO) % handles structure with handles and user data (see GUIDATA) % Hints: get(hobject,'string') returns contents of edit3 as text % str2double(get(hobject,'string')) returns contents of edit3 as a double % --- Executes during object creation, after setting all properties. function edit3_createfcn(hobject, eventdata, handles) % hobject handle to edit3 (see GCBO) % handles empty - handles not created until after all CreateFcns called % Hint: edit controls usually have a white background on Windows. % See ISPC and COMPUTER. if ispc && isequal(get(hobject,'backgroundcolor'), get(0,'defaultuicontrolbackgroundcolor')) set(hobject,'backgroundcolor','white'); function edit4_callback(hobject, eventdata, handles) ~ 36 ~
37 % hobject handle to edit4 (see GCBO) % handles structure with handles and user data (see GUIDATA) % Hints: get(hobject,'string') returns contents of edit4 as text % str2double(get(hobject,'string')) returns contents of edit4 as a double % --- Executes during object creation, after setting all properties. function edit4_createfcn(hobject, eventdata, handles) % hobject handle to edit4 (see GCBO) % handles empty - handles not created until after all CreateFcns called % Hint: edit controls usually have a white background on Windows. % See ISPC and COMPUTER. if ispc && isequal(get(hobject,'backgroundcolor'), get(0,'defaultuicontrolbackgroundcolor')) set(hobject,'backgroundcolor','white'); % --- Executes on button press in pushbutton1. function pushbutton1_callback(hobject, eventdata, handles) % hobject handle to pushbutton1 (see GCBO) % handles structure with handles and user data (see GUIDATA) %%% global ryt; global tmax; global v; global a; tmax=str2double(get(handles.edit1,'string')); v=str2double(get(handles.edit2,'string')); a=str2double(get(handles.edit3,'string')); ryt=str2double(get(handles.edit4,'string')); global stam; stam=0; set(handles.pushbutton2,'string','διακοπή'); global status; status=0; global status1; status1=0; rryt=1.005-ryt; if (ryt>1 ryt<0.001) h=warndlg('βάληε ζηo πςθμό πποζομοίωζηρ ηιμή μεηαξύ και 1.0'); ~ 37 ~
38 return if (tmax>20 tmax<10) h=warndlg('βάληε ζηo σπόνο κίνηζηρ ηιμή μεηαξύ 10 και 20'); return if (v>10 v<5) h=warndlg('βάληε ζηη ηασύηηηα ηιμή μεηαξύ 10 και 20'); return if (a>5 a<1) h=warndlg('βάληε ζηη επιηάσςνζη ηιμή μεηαξύ 1 και 5'); return set(handles.edit1,'enable','off'); set(handles.edit2,'enable','off'); set(handles.edit3,'enable','off'); set(handles.edit4,'enable','off'); set(handles.pushbutton1,'enable','off'); %%% scale_x=0.35; scale_y=0.7; scale_cx=0.07; scale_cy=0.17; %%% %5<=v<=10; %10<=t<=20; %1<=a<=5; % v=10; % tmax=20; % a=5; vmax=v+a*tmax; xmax=v*tmax+0.5*a*tmax*tmax; %xmegisto=1200 %xelaxisto=100 %%% % x=imread('moderncar','jpg'); % image(x); xupoba8ro=[0.0,4.0,4.0,0.0]; yupoba8ro=[0.0,0.0,3.0,3.0]; x0=1.8; y0=1.0; th0=0:0.01:2*pi; ~ 38 ~
39 th1=0:0.01:pi/2; xb1= *cos(th1); yb1= *sin(th1); th1_1=pi/2:-0.01:0; xb1_1= *cos(th1_1); yb1_1= *sin(th1_1); xb2=-0.4:-0.01:-3.6; yb2=( *exp(-1.1*1.8^2))+0.45*exp(-1.1*(xb2+2.2).^2); yb2_edge=( *exp(-1.1*1.8^2))+0.5*exp(-1.1*( ).^2); th3=pi/2:0.01:pi; xb3= *cos(th3); yb3=yb2_edge *sin(th3); th3_1=0:0.01:pi/2; xb3_1= *cos(th3_1); yb3_1=yb2_edge *sin(th3_1); th4=pi:0.01:3*pi/2; xb4= *cos(th4); yb4=yb2_edge *sin(th4); xb5=-2.9; yb5=yb2_edge-0.4; th6=pi:-0.01:0.0; xb6= *cos(th6); yb6=yb5+0.25*sin(th6); xb7=-1.1; yb7=yb5; th8=pi:-0.01:0.0; xb8= *cos(th8); yb8=yb5+0.25*sin(th8); th9=3*pi/2:0.01:2*pi; xb9= *cos(th9); yb9=0.0-yb5*sin(th9); xb10=-1.1:-0.01:-3.0; yb10=( *exp(-1.1*1.8^2))+0.40*exp(-1.1*(xb10+2.2).^2); yb10_edge=( *exp(-1.1*1.8^2))+0.40*exp(-1.1*( ).^2); th11=0.0:0.01:2*pi; xb11= *cos(th11); yb11=yb5+0.23*sin(th11); th12=0.0:0.01:2*pi; xb12= *cos(th12); yb12=yb5+0.17*sin(th12); th13=0.0:0.01:2*pi; xb13= *cos(th13); yb13=yb5+0.23*sin(th13); ~ 39 ~
40 th14=0.0:0.01:2*pi; xb14= *cos(th14); yb14=yb5+0.17*sin(th14); %%% ryt=0.9; rryt=1.005-ryt; %%% xcfield1=[0.0,4.0,4.0,0.0]; ycfield1=[0.0,0.0,0.8,0.8]; xcroad=[0.0,4.0,4.0,0.0]; ycroad=[0.8,0.8,1.2,1.2]; xcfield2=[0.0,4.0,4.0,0.0]; ycfield2=[1.2,1.2,2.2,2.2]; xcsky=[0.0,4.0,4.0,0.0]; ycsky=[2.2,2.2,3.0,3.0]; xb1=0.1:0.01:1.5; xcbouvo1=[0.1,xb1,1.5]; ycbouvo1=[1.9, *exp(-6.1*(xb1-0.8).^2),1.9]; xb2=1.4:0.01:3.6; xcbouvo2=[1.4,xb2,3.6]; ycbouvo2=[2.0, *exp(-2.1*(xb2-2.5).^2),2.0]; xb3=3.1:0.01:4.0; xcbouvo3=[3.1,xb3,4.0]; ycbouvo3=[1.8, *exp(-7.1*(xb3-4.0).^2),1.8]; xcline1=[0.0,0.2,0.2,0.0]; ycline1=[0.99,0.99,1.01,1.01]; xcline2=[0.0,0.2,0.2,0.0]+0.4; ycline2=[0.99,0.99,1.01,1.01]; xcline3=[0.0,0.2,0.2,0.0]+2*0.4; ycline3=[0.99,0.99,1.01,1.01]; xcline4=[0.0,0.2,0.2,0.0]+3*0.4; ycline4=[0.99,0.99,1.01,1.01]; xcline5=[0.0,0.2,0.2,0.0]+4*0.4; ycline5=[0.99,0.99,1.01,1.01]; xcline6=[0.0,0.2,0.2,0.0]+5*0.4; ycline6=[0.99,0.99,1.01,1.01]; xcline7=[0.0,0.2,0.2,0.0]+6*0.4; ycline7=[0.99,0.99,1.01,1.01]; xcline8=[0.0,0.2,0.2,0.0]+7*0.4; ycline8=[0.99,0.99,1.01,1.01]; ~ 40 ~
41 xcline9=[0.0,0.2,0.2,0.0]+8*0.4; ycline9=[0.99,0.99,1.01,1.01]; xcline10=[0.0,0.2,0.2,0.0]+9*0.4; ycline10=[0.99,0.99,1.01,1.01]; xcline_begin=[0.3,0.35,0.36,0.31]; ycline_begin=[0.8,0.8,1.2,1.2]; xcline_=[0.3,0.35,0.36,0.31]+3.6*(xmax/1200); ycline_=[0.8,0.8,1.2,1.2]; xfield1=[0.0,4.0,4.0,0.0]; yfield1=[0.0,0.0,0.6,0.6]; xroad=[0.0,4.0,4.0,0.0]; yroad=[0.6,0.6,1.6,1.6]; xfield2=[0.0,4.0,4.0,0.0]; yfield2=[1.6,1.6,3.0,3.0]; x0v=1.0; y0v=1.8; la=a*2.5/10; lv=v*1.5/10; xvectora=x0v+scale_x*[0.0,0.0,la,la,la+0.2,la,la]; yvectora=y0v+scale_y*[0.075,-0.075,-0.075,-0.15,0.0,0.20,0.075]+0.6; xgv=x0v+scale_x*lv/2; ygv=y0v+0.5; %%% %%%%xmin=0.3 %%%%xmax=3.9 iimax=(11*(tmax/20)-1); jjmax=v*tmax+0.5*a*tmax*tmax; %%% for ii=1:0.1:11*(tmax/20) if (status1==1) return if (status==1) closereq; return if (stam==1) cc1=stam; while (cc1==1) cc1=stam; pause(0.01); if (status1==1) ~ 41 ~
42 return if (status==1) return tt=(ii-1)*tmax/(11*(tmax/20)-1); xx=v*tt+0.5*a*tt*tt; UU=v+a*tt; lu=(v+0.13*a*tt)*1.5/10; xvectorv=x0v+scale_x*[0.0,0.0,lu,lu,lu+0.2,lu,lu]; yvectorv=y0v+scale_y*[0.075,-0.075,-0.075,-0.15,0.0,0.20,0.075]; agr=a+(a/39)*sin(th0); tgr=tt+(tmax/63)*cos(th0); xgr=xx+(xmax/54)*sin(th0); vgr=uu+(vmax/49)*sin(th0); ntt=num2str(0.01*round(100*tt)); nxx=num2str(0.01*round(100*xx)); nuu=num2str(0.01*round(100*uu)); cx0=0.3+(xx/xmax)*(3.6*xmax/1200); cy0=1.0; th15=0.0:0.01:2*pi; xb15= *cos(th15); yb15=yb5+0.08*sin(th15); phi=0.0-(ii-1)*14*pi/iimax; xb15_1=-2.9+[0.08*cos(phi-pi/12),0.17*cos(phi),0.08*cos(phi+pi/12)]; yb15_1=yb5+[0.08*sin(phi-pi/12),0.17*sin(phi),0.08*sin(phi+pi/12)]; xb15_2=-2.9+[0.08*cos(phipi/12+2*pi/3),0.17*cos(phi+2*pi/3),0.08*cos(phi+pi/12+2*pi/3)]; yb15_2=yb5+[0.08*sin(phipi/12+2*pi/3),0.17*sin(phi+2*pi/3),0.08*sin(phi+pi/12+2*pi/3)]; xb15_3=-2.9+[0.08*cos(phipi/12+4*pi/3),0.17*cos(phi+4*pi/3),0.08*cos(phi+pi/12+4*pi/3)]; yb15_3=yb5+[0.08*sin(phipi/12+4*pi/3),0.17*sin(phi+4*pi/3),0.08*sin(phi+pi/12+4*pi/3)]; th16=0.0:0.01:2*pi; xb16= *cos(th16); yb16=yb5+0.08*sin(th16); xb16_1=-0.85+[0.08*cos(phi-pi/12),0.17*cos(phi),0.08*cos(phi+pi/12)]; yb16_1=yb5+[0.08*sin(phi-pi/12),0.17*sin(phi),0.08*sin(phi+pi/12)]; ~ 42 ~
43 xb16_2=-0.85+[0.08*cos(phipi/12+2*pi/3),0.17*cos(phi+2*pi/3),0.08*cos(phi+pi/12+2*pi/3)]; yb16_2=yb5+[0.08*sin(phipi/12+2*pi/3),0.17*sin(phi+2*pi/3),0.08*sin(phi+pi/12+2*pi/3)]; xb16_3=-0.85+[0.08*cos(phipi/12+4*pi/3),0.17*cos(phi+4*pi/3),0.08*cos(phi+pi/12+4*pi/3)]; yb16_3=yb5+[0.08*sin(phipi/12+4*pi/3),0.17*sin(phi+4*pi/3),0.08*sin(phi+pi/12+4*pi/3)]; xb17=[xb3,xb3_1]; yb17=[yb3,yb3_1]; xb18=[xb1,xb1_1]; yb18=[yb1,yb1_1]; %%% %%% xcar1=x0+scale_x*[xb1,xb2,xb3,xb4,xb5,xb6,xb7,xb8,xb9]; ycar1=y0+scale_y*[yb1,yb2,yb3,yb4,yb5,yb6,yb7,yb8,yb9]; xcar2=x0+scale_x*[xb10]; ycar2=y0+scale_y*[yb10]; xcar3=x0+scale_x*[-2.5,-2.55,-2.55,-2.5]; ycar3=y0+scale_y*(yb10_edge+[0.0,0.0,0.3,0.3]); xcar4=x0+scale_x*[-2.5,-2.5,-1.20,-1.19]; ycar4=y0+scale_y*(yb10_edge+[0.04,-0.38,-0.38,0.007]); xcar5=x0+scale_x*[-2.475,-2.475,-1.21,-1.20]; ycar5=y0+scale_y*(yb10_edge+[0.035,-0.37,-0.37,0.002]); xcar6=x0+scale_x*[xb11]; ycar6=y0+scale_y*[yb11]; xcar7=x0+scale_x*[xb12]; ycar7=y0+scale_y*[yb12]; xcar8=x0+scale_x*[xb13]; ycar8=y0+scale_y*[yb13]; xcar9=x0+scale_x*[xb14]; ycar9=y0+scale_y*[yb14]; xcar10=x0+scale_x*[xb15]; ycar10=y0+scale_y*[yb15]; xcar10_1=x0+scale_x*xb15_1; ycar10_1=y0+scale_y*yb15_1; xcar10_2=x0+scale_x*xb15_2; ycar10_2=y0+scale_y*yb15_2; xcar10_3=x0+scale_x*xb15_3; ~ 43 ~
44 ycar10_3=y0+scale_y*yb15_3; xcar11=x0+scale_x*[xb16]; ycar11=y0+scale_y*[yb16]; xcar11_1=x0+scale_x*xb16_1; ycar11_1=y0+scale_y*yb16_1; xcar11_2=x0+scale_x*xb16_2; ycar11_2=y0+scale_y*yb16_2; xcar11_3=x0+scale_x*xb16_3; ycar11_3=y0+scale_y*yb16_3; xcar12=x0+scale_x*xb17; ycar12=y0+scale_y*yb17; xcar13=x0+scale_x*xb18; ycar13=y0+scale_y*yb18; %%% xccar1=cx0+scale_cx*[xb1,xb2,xb3,xb4,xb5,xb6,xb7,xb8,xb9]; yccar1=cy0+scale_cy*[yb1,yb2,yb3,yb4,yb5,yb6,yb7,yb8,yb9]; xccar2=cx0+scale_cx*[xb10]; yccar2=cy0+scale_cy*[yb10]; xccar3=cx0+scale_cx*[-2.5,-2.55,-2.55,-2.5]; yccar3=cy0+scale_cy*(yb10_edge+[0.0,0.0,0.3,0.3]); xccar4=cx0+scale_cx*[-2.5,-2.5,-1.20,-1.19]; yccar4=cy0+scale_cy*(yb10_edge+[0.04,-0.38,-0.38,0.007]); xccar5=cx0+scale_cx*[-2.49,-2.49,-1.21,-1.20]; yccar5=cy0+scale_cy*(yb10_edge+[0.035,-0.37,-0.37,0.002]); xccar6=cx0+scale_cx*[xb11]; yccar6=cy0+scale_cy*[yb11]; xccar7=cx0+scale_cx*[xb12]; yccar7=cy0+scale_cy*[yb12]; xccar8=cx0+scale_cx*[xb13]; yccar8=cy0+scale_cy*[yb13]; xccar9=cx0+scale_cx*[xb14]; yccar9=cy0+scale_cy*[yb14]; xccar10=cx0+scale_cx*[xb15]; yccar10=cy0+scale_cy*[yb15]; xccar10_1=cx0+scale_cx*xb15_1; yccar10_1=cy0+scale_cy*yb15_1; xccar10_2=cx0+scale_cx*xb15_2; yccar10_2=cy0+scale_cy*yb15_2; ~ 44 ~
45 xccar10_3=cx0+scale_cx*xb15_3; yccar10_3=cy0+scale_cy*yb15_3; xccar11=cx0+scale_cx*[xb16]; yccar11=cy0+scale_cy*[yb16]; xccar11_1=x0+scale_cx*xb16_1; yccar11_1=y0+scale_cy*yb16_1; xccar11_2=cx0+scale_cx*xb16_2; yccar11_2=cy0+scale_cy*yb16_2; xccar11_3=cx0+scale_cx*xb16_3; yccar11_3=cy0+scale_cy*yb16_3; xccar12=cx0+scale_cx*xb17; yccar12=cy0+scale_cy*yb17; xccar13=cx0+scale_cx*xb18; yccar13=cy0+scale_cy*yb18; %%% xline0=[2.2, , ,2.2]-1*2.0-(xx)*18.0*(xmax/1200)/jjmax; yline0=[1.05,1.05,1.15,1.15]; xline1=[2.2, , ,2.2]-(xx)*18.0*(xmax/1200)/jjmax; yline1=[1.05,1.05,1.15,1.15]; xline2=[2.2, , ,2.2]+1*2.0-(xx)*18.0*(xmax/1200)/jjmax; yline2=[1.05,1.05,1.15,1.15]; xline3=[2.2, , ,2.2]+2*2.0-(xx)*18.0*(xmax/1200)/jjmax; yline3=[1.05,1.05,1.15,1.15]; xline4=[2.2, , ,2.2]+3*2.0-(xx)*18.0*(xmax/1200)/jjmax; yline4=[1.05,1.05,1.15,1.15]; xline5=[2.2, , ,2.2]+4*2.0-(xx)*18.0*(xmax/1200)/jjmax; yline5=[1.05,1.05,1.15,1.15]; xline6=[2.2, , ,2.2]+5*2.0-(xx)*18.0*(xmax/1200)/jjmax; yline6=[1.05,1.05,1.15,1.15]; xline7=[2.2, , ,2.2]+6*2.0-(xx)*18.0*(xmax/1200)/jjmax; yline7=[1.05,1.05,1.15,1.15]; xline8=[2.2, , ,2.2]+7*2.0-(xx)*18.0*(xmax/1200)/jjmax; yline8=[1.05,1.05,1.15,1.15]; xline9=[2.2, , ,2.2]+8*2.0-(xx)*18.0*(xmax/1200)/jjmax; yline9=[1.05,1.05,1.15,1.15]; xline10=[2.2, , ,2.2]+9*2.0-(xx)*18.0*(xmax/1200)/jjmax; yline10=[1.05,1.05,1.15,1.15]; ~ 45 ~
46 ~ 46 ~ xline11=[2.2, , ,2.2]+10*2.0-(xx)*18.0*(xmax/1200)/jjmax; yline11=[1.05,1.05,1.15,1.15]; xline_begin=[1.75,1.95,2.05,1.90]-(xx)*18.0*(xmax/1200)/jjmax; yline_begin=[0.6,0.6,1.6,1.6]; xline_=[1.75,1.95,2.05,1.90]+9*2.0*(xmax/1200)- (xx)*18.0*(xmax/1200)/jjmax; yline_=[0.6,0.6,1.6,1.6]; %%% %subplot(2,1,1) axes(handles.axes4) fill(xupoba8ro,yupoba8ro,[1.0,1.0,1.0],... xfield1,yfield1,[0.2,0.8,0.2],... xroad,yroad,[0.4,0.4,0.4],... xfield2,yfield2,[0.2,0.8,0.2],... xline0,yline0,[0.9,0.9,0.9],... xline1,yline1,[0.9,0.9,0.9],... xline2,yline2,[0.9,0.9,0.9],... xline3,yline3,[0.9,0.9,0.9],... xline4,yline4,[0.9,0.9,0.9],... xline5,yline5,[0.9,0.9,0.9],... xline6,yline6,[0.9,0.9,0.9],... xline7,yline7,[0.9,0.9,0.9],... xline8,yline8,[0.9,0.9,0.9],... xline9,yline9,[0.9,0.9,0.9],... xline10,yline10,[0.9,0.9,0.9],... xline11,yline11,[0.9,0.9,0.9],... xline_begin,yline_begin,[0.9,0.3,0.3],... xline_,yline_,[0.9,0.9,0.3],... xcar1,ycar1,[0.3,0.5,0.8],... xcar2,ycar2,[0.9,0.9,0.9],... xcar3,ycar3,[0.3,0.5,0.8],... xcar4,ycar4,[0.4,0.4,0.4],... xcar5,ycar5,[0.3,0.5,0.8],... xcar6,ycar6,[0.4,0.4,0.4],... xcar7,ycar7,[0.8,0.8,0.8],... xcar8,ycar8,[0.4,0.4,0.4],... xcar9,ycar9,[0.8,0.8,0.8],... xcar10,ycar10,[0.6,0.6,0.6],... xcar10_1,ycar10_1,[0.6,0.6,0.6],... xcar10_2,ycar10_2,[0.6,0.6,0.6],... xcar10_3,ycar10_3,[0.6,0.6,0.6],... xcar11,ycar11,[0.6,0.6,0.6],... xcar11_1,ycar11_1,[0.6,0.6,0.6],... xcar11_2,ycar11_2,[0.6,0.6,0.6],... xcar11_3,ycar11_3,[0.6,0.6,0.6],... xcar12,ycar12,[0.8,0.6,0.6],... xcar13,ycar13,[0.8,0.6,0.6],... xvectorv,yvectorv,[0.8,0.2,0.8],... xvectora,yvectora,[0.8,0.8,0.2],... 'Linestyle','None') text(xgv,ygv-0.2,'v','color',[0.8,0.2,0.8],'fontsize',11)
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕ ΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕ ΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ ΤΙΤΛΟΣ ΠΤΥΧΙΑΚΗΣ ΕΡΓΑΣΙΑΣ ΑΝΑΠΤΥΞΗ ΕΚΠΑΙΔΕΥΤΙΚΟΥ ΠΑΚΕΤΟΥ ΑΣΚΗΣΕΩΝ ΣΤΟ MATLAB ΓΙΑ ΤΟΝ ΠΡΟΣΔΙΟΡΙΣΜΟ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕ ΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ ΤΙΤΛΟΣ ΠΤΥΧΙΑΚΗΣ ΕΡΓΑΣΙΑΣ ΑΝΑΠΤΥΞΗ ΕΚΠΑΙΔΕΥΤΙΚΟΥ ΠΑΚΕΤΟΥ ΑΣΚΗΣΕΩΝ ΣΤΟ MATLAB ΓΙΑ ΤΟΝ ΠΡΟΣΔΙΟΡΙΣΜΟ
Κατασκευή πακέτου προσομοίωσης σε Matlab εργαστηριακών ασκήσεων του εργαστηρίου Ηλεκτρικών Κυκλωμάτων σε σχέση με το ισοδύναμο κύκλωμα Thevenin
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ Κατασκευή πακέτου προσομοίωσης σε Matlab εργαστηριακών ασκήσεων του εργαστηρίου Ηλεκτρικών Κυκλωμάτων
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ Κατασκευή πακέτου προσομοίωσης σε Matlab εργαστηριακών ασκήσεων του εργαστηρίου Ηλεκτρικών Κυκλωμάτων
ΚΑΤΑΣΚΕΥΗ ΕΚΠΑΙΔΕΥΤΙΚΟΥ ΠΑΚΕΤΟΥ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΕΙΡΑΜΑΤΩΝ ΥΔΡΟΣΤΑΤΙΚΗΣ ΓΥΜΝΑΣΙΟΥ ΣΕ ΠΕΡΙΒΑΛΛΟΝ MATLAB
 Τ Ε Χ Ν Ο Λ Ο Γ Ι Κ Ο Ε Κ Π Α Ι Δ Ε Υ Τ Ι Κ Ο Ι Δ Ρ Υ Μ Α Σ Ε Ρ Ρ Ω Ν Σ Χ Ο Λ Η Τ Ε Χ Ν Ο Λ Ο Γ Ι Κ Ω Ν Ε Φ Α Ρ Μ Ο Γ Ω Ν Τ Μ Η Μ Α Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ & Ε Π Ι Κ Ο Ι Ν Ω Ν Ι Ω Ν ΚΑΤΑΣΚΕΥΗ ΕΚΠΑΙΔΕΥΤΙΚΟΥ
Τ Ε Χ Ν Ο Λ Ο Γ Ι Κ Ο Ε Κ Π Α Ι Δ Ε Υ Τ Ι Κ Ο Ι Δ Ρ Υ Μ Α Σ Ε Ρ Ρ Ω Ν Σ Χ Ο Λ Η Τ Ε Χ Ν Ο Λ Ο Γ Ι Κ Ω Ν Ε Φ Α Ρ Μ Ο Γ Ω Ν Τ Μ Η Μ Α Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ & Ε Π Ι Κ Ο Ι Ν Ω Ν Ι Ω Ν ΚΑΤΑΣΚΕΥΗ ΕΚΠΑΙΔΕΥΤΙΚΟΥ
Θέμα: ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ. Πτυχιακή Εργασία
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Πτυχιακή Εργασία Θέμα: Ανάπτυξη εκπαιδευτικού πακέτου ασκήσεων στο MatlaB για τα φαινόμενα των χημικών και
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Πτυχιακή Εργασία Θέμα: Ανάπτυξη εκπαιδευτικού πακέτου ασκήσεων στο MatlaB για τα φαινόμενα των χημικών και
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ Πτυχιακή εργασία Κατασκευή πακέτου προσομοίωσης σε Matlab της κυκλικής κίνησης στην Φυσική Επιβλέπων
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ Πτυχιακή εργασία Κατασκευή πακέτου προσομοίωσης σε Matlab της κυκλικής κίνησης στην Φυσική Επιβλέπων
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ. Πτυχιακή Εργασία
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Πτυχιακή Εργασία Κατασκευή διδακτικού πακέτου προσομοίωσης των φαινομένων της τάσης και έντασης
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Πτυχιακή Εργασία Κατασκευή διδακτικού πακέτου προσομοίωσης των φαινομένων της τάσης και έντασης
Πτυχιακή Εργασία. Θέμα: Ανάπτυξη εκπαιδευτικού πακέτου ασκήσεων στο MatlaB για τα «Μαγνητικά αποτελέσματα του Ηλεκτρικού Ρεύματος».
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Πτυχιακή Εργασία Θέμα: Ανάπτυξη εκπαιδευτικού πακέτου ασκήσεων στο MatlaB για τα «Μαγνητικά αποτελέσματα
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Πτυχιακή Εργασία Θέμα: Ανάπτυξη εκπαιδευτικού πακέτου ασκήσεων στο MatlaB για τα «Μαγνητικά αποτελέσματα
ΚΑΤΑΣΚΕΥΗ ΕΚΠΑΙ ΕΥΤΙΚΟΥ ΠΑΚΕΤΟΥ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΕΙΡΑΜΑΤΩΝ ΚΙΝΗΤΙΚΗΣ ΘΕΩΡΙΑΣ ΑΕΡΙΩΝ ΣΕ ΠΕΡΙΒΑΛΛΟΝ MATLAB
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕ ΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΕ ΚΑΤΑΣΚΕΥΗ ΕΚΠΑΙ ΕΥΤΙΚΟΥ ΠΑΚΕΤΟΥ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΕΙΡΑΜΑΤΩΝ ΚΙΝΗΤΙΚΗΣ ΘΕΩΡΙΑΣ ΑΕΡΙΩΝ ΣΕ ΠΕΡΙΒΑΛΛΟΝ MATLAB Πτυχιακή εργασία
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕ ΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΕ ΚΑΤΑΣΚΕΥΗ ΕΚΠΑΙ ΕΥΤΙΚΟΥ ΠΑΚΕΤΟΥ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΕΙΡΑΜΑΤΩΝ ΚΙΝΗΤΙΚΗΣ ΘΕΩΡΙΑΣ ΑΕΡΙΩΝ ΣΕ ΠΕΡΙΒΑΛΛΟΝ MATLAB Πτυχιακή εργασία
Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Ε.Ο.Κ. και Ε.Ο.Μ.Κ.
 Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Ε.Ο.Κ. και Ε.Ο.Μ.Κ. Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα
Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Ε.Ο.Κ. και Ε.Ο.Μ.Κ. Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα
Modellus 4.01 Συ ντομοσ Οδηγο σ
 Νίκοσ Αναςταςάκθσ 4.01 Συ ντομοσ Οδηγο σ Περιγραφή Σο είναι λογιςμικό προςομοιϊςεων που ςτθρίηει τθν λειτουργία του ςε μακθματικά μοντζλα. ε αντίκεςθ με άλλα λογιςμικά (π.χ. Interactive Physics, Crocodile
Νίκοσ Αναςταςάκθσ 4.01 Συ ντομοσ Οδηγο σ Περιγραφή Σο είναι λογιςμικό προςομοιϊςεων που ςτθρίηει τθν λειτουργία του ςε μακθματικά μοντζλα. ε αντίκεςθ με άλλα λογιςμικά (π.χ. Interactive Physics, Crocodile
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΑΠΟ ΘΕΜΑΤΑ ΤΕΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ
 Λφκειο Ακρόπολθσ 2015 Επιμζλεια Μάριοσ Πουργουρίδθσ ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΑΠΟ ΘΕΜΑΤΑ ΤΕΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 1. Η πιο κάτω μπάλα αφινεται να πζςει από το ςθμείο Α,κτυπά ςτο ζδαφοσ ςτο ςθμείο Ε και αναπθδά ςε μικρότερο
Λφκειο Ακρόπολθσ 2015 Επιμζλεια Μάριοσ Πουργουρίδθσ ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΑΠΟ ΘΕΜΑΤΑ ΤΕΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 1. Η πιο κάτω μπάλα αφινεται να πζςει από το ςθμείο Α,κτυπά ςτο ζδαφοσ ςτο ςθμείο Ε και αναπθδά ςε μικρότερο
Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ
 Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί ςτθ
Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί ςτθ
Άπειρεσ κροφςεισ. Τθ χρονικι ςτιγμι. t, ο δακτφλιοσ ςυγκροφεται με τον τοίχο με ταχφτθτα (κζντρου μάηασ) μζτρου
 Άπειρεσ κροφςεισ Δακτφλιοσ ακτίνασ κυλάει ςε οριηόντιο δάπεδο προσ ζνα κατακόρυφο τοίχο όπωσ φαίνεται ςτο ςχιμα. Ο ςυντελεςτισ τριβισ ίςκθςθσ του δακτυλίου με το δάπεδο είναι, ενϊ ο τοίχοσ είναι λείοσ.
Άπειρεσ κροφςεισ Δακτφλιοσ ακτίνασ κυλάει ςε οριηόντιο δάπεδο προσ ζνα κατακόρυφο τοίχο όπωσ φαίνεται ςτο ςχιμα. Ο ςυντελεςτισ τριβισ ίςκθςθσ του δακτυλίου με το δάπεδο είναι, ενϊ ο τοίχοσ είναι λείοσ.
ΧΕΔΙΑΜΟ ΠΡΟΪΟΝΣΩΝ ΜΕ Η/Τ
 ΧΕΔΙΑΜΟ ΠΡΟΪΟΝΣΩΝ ΜΕ Η/Τ ΚΑΜΠΤΛΕ ΕΛΕΤΘΕΡΗ ΜΟΡΦΗ Χριςιμεσ για τθν περιγραφι ομαλών και ελεφκερων ςχθμάτων Αμάξωμα αυτοκινιτου, πτερφγια αεροςκαφών, ςκελετόσ πλοίου χιματα χαρακτιρων κινουμζνων ςχεδίων Περιγραφι
ΧΕΔΙΑΜΟ ΠΡΟΪΟΝΣΩΝ ΜΕ Η/Τ ΚΑΜΠΤΛΕ ΕΛΕΤΘΕΡΗ ΜΟΡΦΗ Χριςιμεσ για τθν περιγραφι ομαλών και ελεφκερων ςχθμάτων Αμάξωμα αυτοκινιτου, πτερφγια αεροςκαφών, ςκελετόσ πλοίου χιματα χαρακτιρων κινουμζνων ςχεδίων Περιγραφι
Διαγώνισμα Φυσική ς Α Λυκει ου Δυναμική σε μι α δια στασή και στο επι πεδο
 Διαγώνισμα Φυσική ς Α Λυκει ου Δυναμική σε μι α δια στασή και στο επι πεδο Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα
Διαγώνισμα Φυσική ς Α Λυκει ου Δυναμική σε μι α δια στασή και στο επι πεδο Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα
ΛΕΙΤΟΥΓΙΚΆ ΣΥΣΤΉΜΑΤΑ. 5 ο Εργαςτιριο Ειςαγωγι ςτθ Γραμμι Εντολϊν
 ΛΕΙΤΟΥΓΙΚΆ ΣΥΣΤΉΜΑΤΑ 5 ο Εργαςτιριο Ειςαγωγι ςτθ Γραμμι Εντολϊν Τι είναι θ Γραμμι Εντολϊν (1/6) Στουσ πρϊτουσ υπολογιςτζσ, και κυρίωσ από τθ δεκαετία του 60 και μετά, θ αλλθλεπίδραςθ του χριςτθ με τουσ
ΛΕΙΤΟΥΓΙΚΆ ΣΥΣΤΉΜΑΤΑ 5 ο Εργαςτιριο Ειςαγωγι ςτθ Γραμμι Εντολϊν Τι είναι θ Γραμμι Εντολϊν (1/6) Στουσ πρϊτουσ υπολογιςτζσ, και κυρίωσ από τθ δεκαετία του 60 και μετά, θ αλλθλεπίδραςθ του χριςτθ με τουσ
ΤΕΧΝΙΚΕΣ ΕΠΕΞΕΡΓΑΣΙΑΣ ΕΙΚΟΝΑΣ ΜΕ ΤΗ ΧΡΗΣΗ MATLAB
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΗΠΕΙΡΟΥ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Τ.Ε. TECHNOLOGICAL EDUCATIONAL INSTITUTE OF EPIRUS SCHOOL OF APPLIED TECHNOLOGY DEPARTMENT OF COMPUTER
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΗΠΕΙΡΟΥ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Τ.Ε. TECHNOLOGICAL EDUCATIONAL INSTITUTE OF EPIRUS SCHOOL OF APPLIED TECHNOLOGY DEPARTMENT OF COMPUTER
ΡΟΓΑΜΜΑΤΙΣΤΙΚΟ ΡΕΙΒΑΛΛΟΝ MICRO WORLDS PRO
 ΡΟΓΑΜΜΑΤΙΣΤΙΚΟ ΡΕΙΒΑΛΛΟΝ MICRO WORLDS PRO Το Micro Worlds Pro είναι ζνα ολοκλθρωμζνο περιβάλλον προγραμματιςμοφ. Χρθςιμοποιεί τθ γλϊςςα προγραμματιςμοφ Logo (εξελλθνιςμζνθ) Το Micro Worlds Pro περιλαμβάνει
ΡΟΓΑΜΜΑΤΙΣΤΙΚΟ ΡΕΙΒΑΛΛΟΝ MICRO WORLDS PRO Το Micro Worlds Pro είναι ζνα ολοκλθρωμζνο περιβάλλον προγραμματιςμοφ. Χρθςιμοποιεί τθ γλϊςςα προγραμματιςμοφ Logo (εξελλθνιςμζνθ) Το Micro Worlds Pro περιλαμβάνει
Γραφικά περιβάλλοντα από τον χρήστη Graphical User Interfaces (GUI)
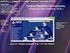 Γραφικά περιβάλλοντα από τον χρήστη Graphical User Interfaces (GUI) Θα γράψουμε το πρώτο μας GUI το οποίο : 1. Θα σχεδιάζει μια συνάρτηση 2. Θα παρέχει κουμπιά για να αλλάζουμε το χρώμα του γραφήματος
Γραφικά περιβάλλοντα από τον χρήστη Graphical User Interfaces (GUI) Θα γράψουμε το πρώτο μας GUI το οποίο : 1. Θα σχεδιάζει μια συνάρτηση 2. Θα παρέχει κουμπιά για να αλλάζουμε το χρώμα του γραφήματος
Α1. Ροιεσ από τισ δυνάμεισ του ςχιματοσ ζχουν μθδενικι ροπι ωσ προσ τον άξονα (ε) περιςτροφισ του δίςκου;
 ΜΑΘΗΜΑ /ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΡΩΝΥMΟ: ΗΜΕΟΜΗΝΙΑ: 1/3/2015 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: ΚΥΜΑΤΑ ΚΑΙ ΣΤΕΕΟ ΣΩΜΑ ΘΕΜΑ Α Α1. Ροιεσ από τισ δυνάμεισ του ςχιματοσ ζχουν μθδενικι ροπι ωσ προσ τον άξονα (ε)
ΜΑΘΗΜΑ /ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΡΩΝΥMΟ: ΗΜΕΟΜΗΝΙΑ: 1/3/2015 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: ΚΥΜΑΤΑ ΚΑΙ ΣΤΕΕΟ ΣΩΜΑ ΘΕΜΑ Α Α1. Ροιεσ από τισ δυνάμεισ του ςχιματοσ ζχουν μθδενικι ροπι ωσ προσ τον άξονα (ε)
Interactive Physics Σύ ντομος Οδηγο ς
 Νίκοσ Αναςταςάκθσ Σύ ντομος Οδηγο ς Εγκατάσταση Από τον φάκελο του προγράμματοσ IP2005, τρζχουμε το αρχείο «IPInstaller.exe», επιλζγουμε τθν εγκατάςταςθ που κζλουμε (1 θ 2 θ επιλογι) και ακολουκοφμε τισ
Νίκοσ Αναςταςάκθσ Σύ ντομος Οδηγο ς Εγκατάσταση Από τον φάκελο του προγράμματοσ IP2005, τρζχουμε το αρχείο «IPInstaller.exe», επιλζγουμε τθν εγκατάςταςθ που κζλουμε (1 θ 2 θ επιλογι) και ακολουκοφμε τισ
ΓΡΑΜΜΙΚΟΣ & ΔΙΚΤΥΑΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 ΓΡΑΜΜΙΚΟΣ & ΔΙΚΤΥΑΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ενότητα 12: Συνοπτική Παρουσίαση Ανάπτυξης Κώδικα με το Matlab Σαμαράς Νικόλαος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΓΡΑΜΜΙΚΟΣ & ΔΙΚΤΥΑΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ενότητα 12: Συνοπτική Παρουσίαση Ανάπτυξης Κώδικα με το Matlab Σαμαράς Νικόλαος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Διαδικασία με βήματα. 1. Αλλάηω το χρϊμα ςκθνικοφ ςε γκρι(#3333).
 Διαδικασία με βήματα 1. Αλλάηω το χρϊμα ςκθνικοφ ςε γκρι(#3333). 2. Διαλζγω το Polystar Tool. Από τα Options κάνω το Polygon ςε Star και τα υπόλοιπα όπωσ είναι. Ζωγραφίηω ζνα αςτζρι πάνω αριςτερά. Fill
Διαδικασία με βήματα 1. Αλλάηω το χρϊμα ςκθνικοφ ςε γκρι(#3333). 2. Διαλζγω το Polystar Tool. Από τα Options κάνω το Polygon ςε Star και τα υπόλοιπα όπωσ είναι. Ζωγραφίηω ζνα αςτζρι πάνω αριςτερά. Fill
ΑΛΕΞΑΝΔΡΕΙΟ ΣΕΙ ΘΕΑΛΟΝΙΚΗ ΣΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗ Σ.Ε. ΜΑΘΗΜΑ : ΑΛΓΟΡΙΘΜΙΚΗ ΚΑΙ ΠΡΟΓΡΑΜΜΑΣΙΜΟ ΔΙΔΑΚΩΝ : ΓΟΤΛΙΑΝΑ ΚΩΣΑ
 ΑΛΕΞΑΝΔΡΕΙΟ ΣΕΙ ΘΕΑΛΟΝΙΚΗ ΣΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗ Σ.Ε. ΜΑΘΗΜΑ : ΑΛΓΟΡΙΘΜΙΚΗ ΚΑΙ ΠΡΟΓΡΑΜΜΑΣΙΜΟ ΔΙΔΑΚΩΝ : ΓΟΤΛΙΑΝΑ ΚΩΣΑ υνοπτικόσ Οδθγόσ για Γράψιμο Εκτζλεςθ Προγραμμάτων Java ςε Περιβάλλον DOS και NetBeans
ΑΛΕΞΑΝΔΡΕΙΟ ΣΕΙ ΘΕΑΛΟΝΙΚΗ ΣΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗ Σ.Ε. ΜΑΘΗΜΑ : ΑΛΓΟΡΙΘΜΙΚΗ ΚΑΙ ΠΡΟΓΡΑΜΜΑΣΙΜΟ ΔΙΔΑΚΩΝ : ΓΟΤΛΙΑΝΑ ΚΩΣΑ υνοπτικόσ Οδθγόσ για Γράψιμο Εκτζλεςθ Προγραμμάτων Java ςε Περιβάλλον DOS και NetBeans
Το καλωςόριςμα των μαθητών ςτο Εργαςτήριο Φυςικών Επιςτημών
 Το καλωςόριςμα των μαθητών ςτο Εργαςτήριο Φυςικών Επιςτημών Η ΟΡΙΖΟΝΣΙΑ ΒΟΛΗ ΜΕΑ ΑΠΟ ΣΙ ΝΕΕ ΣΕΧΝΟΛΟΓΙΕ Εισαγωγή Ο καταλλθλότεροσ χϊροσ για ζνα επιτυχθμζνο μάκθμα φυςικισ είναι το εργαςτιριο φυςικϊν επιςτθμϊν.
Το καλωςόριςμα των μαθητών ςτο Εργαςτήριο Φυςικών Επιςτημών Η ΟΡΙΖΟΝΣΙΑ ΒΟΛΗ ΜΕΑ ΑΠΟ ΣΙ ΝΕΕ ΣΕΧΝΟΛΟΓΙΕ Εισαγωγή Ο καταλλθλότεροσ χϊροσ για ζνα επιτυχθμζνο μάκθμα φυςικισ είναι το εργαςτιριο φυςικϊν επιςτθμϊν.
ΕΡΓΑΣΗΡΙΟ ΕΦΑΡΜΟΜΕΝΗ ΠΛΗΡΟΦΟΡΙΚΗ
 Στο εργαςτιριο αυτό κα δοφμε πωσ μποροφμε να προςομοιϊςουμε μια κίνθςθ χωρίσ τθ χριςθ εξειδικευμζνων εργαλείων, παρά μόνο μζςω ενόσ προγράμματοσ λογιςτικϊν φφλλων, όπωσ είναι το Calc και το Excel. Τα δφο
Στο εργαςτιριο αυτό κα δοφμε πωσ μποροφμε να προςομοιϊςουμε μια κίνθςθ χωρίσ τθ χριςθ εξειδικευμζνων εργαλείων, παρά μόνο μζςω ενόσ προγράμματοσ λογιςτικϊν φφλλων, όπωσ είναι το Calc και το Excel. Τα δφο
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΡΗΤΗΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΡΗΤΗΣ ΠΑΡΑΡΤΗΜΑ ΧΑΝΙΩΝ-ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΗΣ ΒΟΗΘΗΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΑΞΙΟΠΟΙΗΣΗΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΜΕΤΡΗΣΕΩΝ ΣΕ ΠΕΡΙΒΑΛΛΟΝ GUI (GRAPHICAL USER INTERFACE) MATLAB ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΠΑΦΗΣ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΡΗΤΗΣ ΠΑΡΑΡΤΗΜΑ ΧΑΝΙΩΝ-ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΗΣ ΒΟΗΘΗΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΑΞΙΟΠΟΙΗΣΗΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΜΕΤΡΗΣΕΩΝ ΣΕ ΠΕΡΙΒΑΛΛΟΝ GUI (GRAPHICAL USER INTERFACE) MATLAB ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΠΑΦΗΣ
16. Πίνακεσ και Συναρτήςεισ
 Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 16. Πίνακεσ και Συναρτήςεισ Ιωάννθσ Κατάκθσ Σιμερα o Κλιςθ με τιμι o Κλιςθ με αναφορά o Πίνακεσ και ςυναρτιςεισ o Παραδείγματα Ειςαγωγι o Στισ προθγοφμενεσ
Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 16. Πίνακεσ και Συναρτήςεισ Ιωάννθσ Κατάκθσ Σιμερα o Κλιςθ με τιμι o Κλιςθ με αναφορά o Πίνακεσ και ςυναρτιςεισ o Παραδείγματα Ειςαγωγι o Στισ προθγοφμενεσ
Multi Logo. Προγραμματιςμόσ Η/Υ με Multi Logo. Σχεδίαςη και ανάπτυξη εφαρμογήσ κίνηςησ αντικειμζνου
 Multi Logo Βαθμίδα Μάθημα Αντικείμενο Τίτλοσ Διάρκεια Μορφή Διδακτικοί ςτόχοι: Επιδιωκόμενο αποτζλεςμα: Προαπαιτούμενεσ γνώςεισ: Εργαλεία Μζςα: Γυμνάςιο Πληροφορική Προγραμματιςμόσ Η/Υ με Multi Logo Σχεδίαςη
Multi Logo Βαθμίδα Μάθημα Αντικείμενο Τίτλοσ Διάρκεια Μορφή Διδακτικοί ςτόχοι: Επιδιωκόμενο αποτζλεςμα: Προαπαιτούμενεσ γνώςεισ: Εργαλεία Μζςα: Γυμνάςιο Πληροφορική Προγραμματιςμόσ Η/Υ με Multi Logo Σχεδίαςη
ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ ΜΕΛΕΣΗ ΣΗ ΚΙΝΗΗ ΩΜΑΣΟ Ε ΠΛΑΓΙΟ ΕΠΙΠΕΔΟ - ΜΕΣΡΗΗ ΣΟΤ ΤΝΣΕΛΕΣΗ ΣΡΙΒΗ ΟΛΙΘΗΗ
 ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ ΜΕΛΕΣΗ ΣΗ ΚΙΝΗΗ ΩΜΑΣΟ Ε ΠΛΑΓΙΟ ΕΠΙΠΕΔΟ - ΜΕΣΡΗΗ ΣΟΤ ΤΝΣΕΛΕΣΗ ΣΡΙΒΗ ΟΛΙΘΗΗ ΕΚΦΕ Α & Β ΑΝΑΣΟΛΙΚΗ ΑΣΣΙΚΗ τόχοι Μετά το πζρασ τθσ εργαςτθριακισ άςκθςθσ, οι μακθτζσ κα πρζπει να είναι ςε κζςθ:
ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ ΜΕΛΕΣΗ ΣΗ ΚΙΝΗΗ ΩΜΑΣΟ Ε ΠΛΑΓΙΟ ΕΠΙΠΕΔΟ - ΜΕΣΡΗΗ ΣΟΤ ΤΝΣΕΛΕΣΗ ΣΡΙΒΗ ΟΛΙΘΗΗ ΕΚΦΕ Α & Β ΑΝΑΣΟΛΙΚΗ ΑΣΣΙΚΗ τόχοι Μετά το πζρασ τθσ εργαςτθριακισ άςκθςθσ, οι μακθτζσ κα πρζπει να είναι ςε κζςθ:
ΣΔΥΝΟΛΟΓΙΚΟ ΔΚΠΑΙΓΔΤΣΙΚΟ ΙΓΡΤΜΑ ΔΡΡΩΝ ΥΟΛΗ ΣΔΝΟΛΟΓΙΚΩΝ ΔΦΑΡΜΟΓΩΝ ΣΜΗΜΑ ΜΗΥΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗ. Πηςσιακή Δπγαζία
 ΣΔΥΝΟΛΟΓΙΚΟ ΔΚΠΑΙΓΔΤΣΙΚΟ ΙΓΡΤΜΑ ΔΡΡΩΝ ΥΟΛΗ ΣΔΝΟΛΟΓΙΚΩΝ ΔΦΑΡΜΟΓΩΝ ΣΜΗΜΑ ΜΗΥΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗ Πηςσιακή Δπγαζία «ΑΝΑΠΣΤΞΗ ΔΚΠΑΙΓΔΤΣΙΚΟΤ ΠΑΚΔΣΟΤ ΑΚΗΔΩΝ ΣΟ MATLAB ΓΙΑ ΣΑ ΦΑΙΝΟΜΔΝΑ ΣΩΝ ΥΗΜΙΚΩΝ ΑΠΟΣΔΛΔΜΑΣΩΝ
ΣΔΥΝΟΛΟΓΙΚΟ ΔΚΠΑΙΓΔΤΣΙΚΟ ΙΓΡΤΜΑ ΔΡΡΩΝ ΥΟΛΗ ΣΔΝΟΛΟΓΙΚΩΝ ΔΦΑΡΜΟΓΩΝ ΣΜΗΜΑ ΜΗΥΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗ Πηςσιακή Δπγαζία «ΑΝΑΠΣΤΞΗ ΔΚΠΑΙΓΔΤΣΙΚΟΤ ΠΑΚΔΣΟΤ ΑΚΗΔΩΝ ΣΟ MATLAB ΓΙΑ ΣΑ ΦΑΙΝΟΜΔΝΑ ΣΩΝ ΥΗΜΙΚΩΝ ΑΠΟΣΔΛΔΜΑΣΩΝ
x n D 2 ENCODER m - σε n (m 2 n ) x 1 Παραδείγματα κωδικοποιθτϊν είναι ο κωδικοποιθτισ οκταδικοφ ςε δυαδικό και ο κωδικοποιθτισ BCD ςε δυαδικό.
 Κωδικοποιητές Ο κωδικοποιθτισ (nor) είναι ζνα κφκλωμα το οποίο διακζτει n γραμμζσ εξόδου και το πολφ μζχρι m = 2 n γραμμζσ ειςόδου και (m 2 n ). Οι ζξοδοι παράγουν τθν κατάλλθλθ λζξθ ενόσ δυαδικοφ κϊδικα
Κωδικοποιητές Ο κωδικοποιθτισ (nor) είναι ζνα κφκλωμα το οποίο διακζτει n γραμμζσ εξόδου και το πολφ μζχρι m = 2 n γραμμζσ ειςόδου και (m 2 n ). Οι ζξοδοι παράγουν τθν κατάλλθλθ λζξθ ενόσ δυαδικοφ κϊδικα
Διαγώνισμα Φυσική ς Α Λυκει ου Έργο και Ενε ργεια
 Διαγώνισμα Φυσική ς Α Λυκει ου Έργο και Ενε ργεια Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί
Διαγώνισμα Φυσική ς Α Λυκει ου Έργο και Ενε ργεια Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί
Εγκατάσταση λογισμικού και αναβάθμιση συσκευής Device software installation and software upgrade
 Για να ελέγξετε το λογισμικό που έχει τώρα η συσκευή κάντε κλικ Menu > Options > Device > About Device Versions. Στο πιο κάτω παράδειγμα η συσκευή έχει έκδοση λογισμικού 6.0.0.546 με πλατφόρμα 6.6.0.207.
Για να ελέγξετε το λογισμικό που έχει τώρα η συσκευή κάντε κλικ Menu > Options > Device > About Device Versions. Στο πιο κάτω παράδειγμα η συσκευή έχει έκδοση λογισμικού 6.0.0.546 με πλατφόρμα 6.6.0.207.
Αν η ςυνάρτηςη ƒ είναι ςυνεχήσ ςτο να προςδιορίςετε το α.
 1 AΣΚΗΣΕΙΣ 1. Να υπολογιςθοφν τα παρακάτω όρια Ι. ΙΙ. ΙΙΙ. Ιν. ν. νι. νιι. νιιι. 2. Να βρεθοφν τα όρια Ι. ΙΙ. 3. Αν ƒ(χ)= α. Να βρείτε το πεδίο οριςμοφ Β. Να βρείτε τα όρια Ι. ΙΙ. 4. Δίνεται η ςυνάρτηςη
1 AΣΚΗΣΕΙΣ 1. Να υπολογιςθοφν τα παρακάτω όρια Ι. ΙΙ. ΙΙΙ. Ιν. ν. νι. νιι. νιιι. 2. Να βρεθοφν τα όρια Ι. ΙΙ. 3. Αν ƒ(χ)= α. Να βρείτε το πεδίο οριςμοφ Β. Να βρείτε τα όρια Ι. ΙΙ. 4. Δίνεται η ςυνάρτηςη
Φυσική Α Λυκείου Νίκοσ Αναςταςάκθσ Γενικό Λφκειο Βάμου 2008-2010
 Φυσική Α Λυκείου Νίκοσ Αναςταςάκθσ Γενικό Λφκειο Βάμου 2008-2010 Περιεχόμενα Μεγζκθ Κίνθςθσ: ελίδεσ 1-4 Μετατόπιςθ, Σαχφτθτα, Μζςθ Σαχφτθτα Ευκφγραμμεσ Κινιςεισ: ελίδεσ 5-20 Ευκφγραμμθ Ομαλι Ευκ. Ομαλά
Φυσική Α Λυκείου Νίκοσ Αναςταςάκθσ Γενικό Λφκειο Βάμου 2008-2010 Περιεχόμενα Μεγζκθ Κίνθςθσ: ελίδεσ 1-4 Μετατόπιςθ, Σαχφτθτα, Μζςθ Σαχφτθτα Ευκφγραμμεσ Κινιςεισ: ελίδεσ 5-20 Ευκφγραμμθ Ομαλι Ευκ. Ομαλά
MATLAB - Graphical User Interfaces. Σημειώσεις GUI για το εργαστήριο του μαθήματος Ασαφή Συστήματα. Δημήτριος Βαρσάμης Εργαστηριακός συνεργάτης
 Tεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Σχολή Τεχνολογικών Εφαρμογών Τμήμα Πληροφορικής & Επικοινωνιών MATLAB - Graphical User Interfaces Σημειώσεις GUI για το εργαστήριο του μαθήματος Ασαφή Συστήματα Δημήτριος
Tεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Σχολή Τεχνολογικών Εφαρμογών Τμήμα Πληροφορικής & Επικοινωνιών MATLAB - Graphical User Interfaces Σημειώσεις GUI για το εργαστήριο του μαθήματος Ασαφή Συστήματα Δημήτριος
Τιτλος πτυχιακής εργασίας:
 Τιτλος πτυχιακής εργασίας: "Κατηγοριοποίηση βίντεο ως προς το είδος τους με τη χρήση της λογιστικής παλινδρόμησης " Τμήμα Μηχανικών Πληροφορικής Τ.Ε. Φοιτητής: Βρέττος Γιώργος Α.Ε.Μ.:2482 Επιβλέπων καθηγητής:
Τιτλος πτυχιακής εργασίας: "Κατηγοριοποίηση βίντεο ως προς το είδος τους με τη χρήση της λογιστικής παλινδρόμησης " Τμήμα Μηχανικών Πληροφορικής Τ.Ε. Φοιτητής: Βρέττος Γιώργος Α.Ε.Μ.:2482 Επιβλέπων καθηγητής:
Γενικά Μαθηματικά ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 13 η : Επαναλθπτικι Ενότθτα Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 13 η : Επαναλθπτικι Ενότθτα Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΜΑΘΗΜΑΣΙΚΑ Γ ΓΕΝΙΚΗ ( ΑΠΟ ΘΕΜΑΣΑ ΛΤΚΕΙΩΝ ) ΕΡΩΣΗΕΙ ΩΣΟΤ ΛΑΘΟΤ ΑΝΑΛΤΗ
 ΜΑΘΗΜΑΣΙΚΑ Γ ΓΕΝΙΚΗ ( ΑΠΟ ΘΕΜΑΣΑ ΛΤΚΕΙΩΝ ) ΕΡΩΣΗΕΙ ΩΣΟΤ ΛΑΘΟΤ ΑΝΑΛΤΗ 1. Αν οι ςυναρτιςεισ f και g ζχουν όρια ςτο x πραγματικοφσ αρικμοφσ, δθλαδι lim f( x) l 1 και lim g( x) l 2 με l 1, l 2 IR, τότε lim
ΜΑΘΗΜΑΣΙΚΑ Γ ΓΕΝΙΚΗ ( ΑΠΟ ΘΕΜΑΣΑ ΛΤΚΕΙΩΝ ) ΕΡΩΣΗΕΙ ΩΣΟΤ ΛΑΘΟΤ ΑΝΑΛΤΗ 1. Αν οι ςυναρτιςεισ f και g ζχουν όρια ςτο x πραγματικοφσ αρικμοφσ, δθλαδι lim f( x) l 1 και lim g( x) l 2 με l 1, l 2 IR, τότε lim
Μάκθςθ Κατανομϊν Πικανότθτασ και Ομαδοποίθςθ
 Μάκθςθ Κατανομϊν Πικανότθτασ και Ομαδοποίθςθ Κϊςτασ Διαμαντάρασ Τμιμα Πλθροφορικισ ΤΕΙ Θεςςαλονίκθσ 1 Μάκθςθ κατανομισ πικανότθτασ Σε όλθ τθν ανάλυςθ μζχρι τϊρα ζγινε ςιωπθρά θ παραδοχι ότι γνωρίηουμε
Μάκθςθ Κατανομϊν Πικανότθτασ και Ομαδοποίθςθ Κϊςτασ Διαμαντάρασ Τμιμα Πλθροφορικισ ΤΕΙ Θεςςαλονίκθσ 1 Μάκθςθ κατανομισ πικανότθτασ Σε όλθ τθν ανάλυςθ μζχρι τϊρα ζγινε ςιωπθρά θ παραδοχι ότι γνωρίηουμε
Απάντηση ΘΕΜΑ1 ΘΕΜΑ2. t=t 1 +T/2. t=t 1 +3T/4. t=t 1 +T ΔΙΑΓΩΝΙΣΜΑ ΣΕ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΥΜΑΤΑ 1) (Β), 2. (Γ), 3. (Γ), 4. (Γ), 5. (Δ).
 Απάντηση ΘΕΜΑ1 1) (Β), 2. (Γ), 3. (Γ), 4. (Γ), 5. (Δ). ΘΕΜΑ2 Α)Ανάκλαςθ ςε ακίνθτο άκρο. Το προςπίπτον κφμα ςε χρόνο Τ/2 κα ζχει μετακινθκεί προσ τα δεξιά κατά 2 τετράγωνα όπωσ φαίνεται ςτο ςχιμα. Για
Απάντηση ΘΕΜΑ1 1) (Β), 2. (Γ), 3. (Γ), 4. (Γ), 5. (Δ). ΘΕΜΑ2 Α)Ανάκλαςθ ςε ακίνθτο άκρο. Το προςπίπτον κφμα ςε χρόνο Τ/2 κα ζχει μετακινθκεί προσ τα δεξιά κατά 2 τετράγωνα όπωσ φαίνεται ςτο ςχιμα. Για
Δείκτεσ Διαχείριςθ Μνιμθσ. Βαγγζλθσ Οικονόμου Διάλεξθ 8
 Δείκτεσ Διαχείριςθ Μνιμθσ Βαγγζλθσ Οικονόμου Διάλεξθ 8 Δείκτεσ Κάκε μεταβλθτι ςχετίηεται με μία κζςθ ςτθν κφρια μνιμθ του υπολογιςτι. Κάκε κζςθ ςτθ μνιμθ ζχει τθ δικι τθσ ξεχωριςτι διεφκυνςθ. Με άμεςθ
Δείκτεσ Διαχείριςθ Μνιμθσ Βαγγζλθσ Οικονόμου Διάλεξθ 8 Δείκτεσ Κάκε μεταβλθτι ςχετίηεται με μία κζςθ ςτθν κφρια μνιμθ του υπολογιςτι. Κάκε κζςθ ςτθ μνιμθ ζχει τθ δικι τθσ ξεχωριςτι διεφκυνςθ. Με άμεςθ
Πνομα Ομάδασ: Προγραμματιςμόσ ενόσ κινοφμενου ρομπότ
 Φφλλο Εργαςίασ : Ακολοφθηςε τισ εντολζσ μου! Τάξθ: Β Γυμναςίου Ενότθτα: Λφνω προβλιματα με υπολογιςτικά φφλλα Εμπλεκόμενεσ ζννοιεσ: ρομποτικι, Lego Mindstorms, υπολογιςτικά φφλλα, ςυναρτιςεισ, γραφιματα
Φφλλο Εργαςίασ : Ακολοφθηςε τισ εντολζσ μου! Τάξθ: Β Γυμναςίου Ενότθτα: Λφνω προβλιματα με υπολογιςτικά φφλλα Εμπλεκόμενεσ ζννοιεσ: ρομποτικι, Lego Mindstorms, υπολογιςτικά φφλλα, ςυναρτιςεισ, γραφιματα
Σράπεζα θεμάτων Θετικού Προςανατολιςμού Κεφ. 1 Θέμα Δ
 Σράπεζα θεμάτων Θετικού Προςανατολιςμού Κεφ. 1 Θέμα Δ ΚΑΜΠΤΛΟΓΡΑΜΜΕ ΚΙΝΗΕΙ 1.1 ΟΡΙΖΟΝΣΙΑ ΒΟΛΗ 1. Τα ςκαλοπάτια μιασ ςκάλασ είναι όλα όμοια μεταξφ τουσ και ζχουν φψοσ h = 20 cm και πλάτοσ d = 40 cm. Από
Σράπεζα θεμάτων Θετικού Προςανατολιςμού Κεφ. 1 Θέμα Δ ΚΑΜΠΤΛΟΓΡΑΜΜΕ ΚΙΝΗΕΙ 1.1 ΟΡΙΖΟΝΣΙΑ ΒΟΛΗ 1. Τα ςκαλοπάτια μιασ ςκάλασ είναι όλα όμοια μεταξφ τουσ και ζχουν φψοσ h = 20 cm και πλάτοσ d = 40 cm. Από
GNSS Solutions guide. 1. Create new Project
 GNSS Solutions guide 1. Create new Project 2. Import Raw Data Αναλόγωσ τον τφπο των δεδομζνων επιλζγουμε αντίςτοιχα το Files of type. παράδειγμα ζχουν επιλεγεί για ειςαγωγι αρχεία τφπου RINEX. το Με τθν
GNSS Solutions guide 1. Create new Project 2. Import Raw Data Αναλόγωσ τον τφπο των δεδομζνων επιλζγουμε αντίςτοιχα το Files of type. παράδειγμα ζχουν επιλεγεί για ειςαγωγι αρχεία τφπου RINEX. το Με τθν
Συστήματα Αναμονής (Queuing Systems)
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ - ΕΜΠ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧ. ΥΠΟΛΟΓΙΣΤΩΝ Τομέας Επικοινωνιών, Ηλεκτρονικής & Συστημάτων Πληροφορικής Εργαστήριο Διαχείρισης & Βέλτιστου Σχεδιασμού Δικτύων Τηλεματικής
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ - ΕΜΠ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧ. ΥΠΟΛΟΓΙΣΤΩΝ Τομέας Επικοινωνιών, Ηλεκτρονικής & Συστημάτων Πληροφορικής Εργαστήριο Διαχείρισης & Βέλτιστου Σχεδιασμού Δικτύων Τηλεματικής
ΘΥ101: Ειςαγωγι ςτθν Πλθροφορικι
 Παράςταςη κινητήσ υποδιαςτολήσ ςφμφωνα με το πρότυπο ΙΕΕΕ Δρ. Χρήστος Ηλιούδης το πρότυπο ΙΕΕΕ 754 ζχει χρθςιμοποιθκεί ευρζωσ ςε πραγματικοφσ υπολογιςτζσ. Το πρότυπο αυτό κακορίηει δφο βαςικζσ μορφζσ κινθτισ
Παράςταςη κινητήσ υποδιαςτολήσ ςφμφωνα με το πρότυπο ΙΕΕΕ Δρ. Χρήστος Ηλιούδης το πρότυπο ΙΕΕΕ 754 ζχει χρθςιμοποιθκεί ευρζωσ ςε πραγματικοφσ υπολογιςτζσ. Το πρότυπο αυτό κακορίηει δφο βαςικζσ μορφζσ κινθτισ
SingularLogic Galaxy. Οδηγίες εγκαηάζηαζης Galaxy
 Οδηγίες εγκαηάζηαζης Galaxy 1 Προαπαιτούμενα Windows Installer 3.1.Net 4 Full Τα προαπαιτοφμενα αυτά δεν ςυμπεριλαμβάνονται ςτο Galaxy.exe Εγκατάςταςη Galaxy Για να εγκαταςτακεί θ εφαρμογι πρζπει να εκτελεςτεί
Οδηγίες εγκαηάζηαζης Galaxy 1 Προαπαιτούμενα Windows Installer 3.1.Net 4 Full Τα προαπαιτοφμενα αυτά δεν ςυμπεριλαμβάνονται ςτο Galaxy.exe Εγκατάςταςη Galaxy Για να εγκαταςτακεί θ εφαρμογι πρζπει να εκτελεςτεί
Προγραμματισμός στο Matlab
 Κλάδοι με την εντολή if Προγραμματισμός στο Matlab Σαν ένα απλό παράδειγμα κλάδου με την εντολή if ας θεωρήσουμε το παρακάτω παράδειγμα που υπολογίζει την απόλυτη τιμή ενός πραγματικού αριθμού. function
Κλάδοι με την εντολή if Προγραμματισμός στο Matlab Σαν ένα απλό παράδειγμα κλάδου με την εντολή if ας θεωρήσουμε το παρακάτω παράδειγμα που υπολογίζει την απόλυτη τιμή ενός πραγματικού αριθμού. function
Η ίδια κατά μζτρο δφναμθ όταν εφαρμοςκεί ςε διαφορετικά ςθμεία τθσ πόρτασ προκαλεί διαφορετικά αποτελζςματα Ροιά;
 ; Η ίδια κατά μζτρο δφναμθ όταν εφαρμοςκεί ςε διαφορετικά ςθμεία τθσ πόρτασ προκαλεί διαφορετικά αποτελζςματα Ροιά; 30/1/ 2 Η φυςικι τθσ ςθμαςία είναι ότι προςδιορίηει τθ ςτροφικι κίνθςθ ενόσ ςτερεοφ ωσ
; Η ίδια κατά μζτρο δφναμθ όταν εφαρμοςκεί ςε διαφορετικά ςθμεία τθσ πόρτασ προκαλεί διαφορετικά αποτελζςματα Ροιά; 30/1/ 2 Η φυςικι τθσ ςθμαςία είναι ότι προςδιορίηει τθ ςτροφικι κίνθςθ ενόσ ςτερεοφ ωσ
ΜΑΘΗΜΑΤΙΚΑ ΕΠΙΠΕΔΟ 11 12 (Β - Γ Λυκείου)
 ΕΠΙΠΕΔΟ 11 12 (Β - Γ Λυκείου) 19 Μαρτίου 2011 10:00-11:15 3 point/μονάδες 1) Στθν πιο κάτω εικόνα πρζπει να υπάρχει αρικμόσ ςε κάκε κουκκίδα ϊςτε το άκροιςμα των αρικμϊν ςτα άκρα κάκε ευκφγραμμου τμιματοσ
ΕΠΙΠΕΔΟ 11 12 (Β - Γ Λυκείου) 19 Μαρτίου 2011 10:00-11:15 3 point/μονάδες 1) Στθν πιο κάτω εικόνα πρζπει να υπάρχει αρικμόσ ςε κάκε κουκκίδα ϊςτε το άκροιςμα των αρικμϊν ςτα άκρα κάκε ευκφγραμμου τμιματοσ
ΧΗΥΙΑΚΟ ΔΚΠΑΙΔΔΤΣΙΚΟ ΒΟΗΘΗΜΑ «ΥΤΙΚΗ ΘΔΣΙΚΗ ΚΑΙ ΣΔΦΝΟΛΟΓΙΚΗ ΚΑΣΔΤΘΤΝΗ» ΦΥΣΙΚΗ ΘΔΤΙΚΗΣ ΚΑΙ ΤΔΧΝΟΛΟΓΙΚΗΣ ΚΑΤΔΥΘΥΝΣΗΣ ΘΔΜΑ Α ΘΔΜΑ Β
 4 o ΔΙΓΩΝΙΜ ΠΡΙΛΙΟ 04: ΔΝΔΔΙΚΣΙΚΔ ΠΝΣΗΔΙ ΦΥΣΙΚΗ ΘΔΤΙΚΗΣ ΚΙ ΤΔΧΝΟΛΟΓΙΚΗΣ ΚΤΔΥΘΥΝΣΗΣ 4 ο ΔΙΓΩΝΙΣΜ ΔΝΔΔΙΚΤΙΚΔΣ ΠΝΤΗΣΔΙΣ ΘΔΜ. β. β 3. α 4. γ 5. α.σ β.σ γ.λ δ.σ ε.λ. ΘΔΜ Β Σωςτι είναι θ απάντθςθ γ. Έχουμε ελαςτικι
4 o ΔΙΓΩΝΙΜ ΠΡΙΛΙΟ 04: ΔΝΔΔΙΚΣΙΚΔ ΠΝΣΗΔΙ ΦΥΣΙΚΗ ΘΔΤΙΚΗΣ ΚΙ ΤΔΧΝΟΛΟΓΙΚΗΣ ΚΤΔΥΘΥΝΣΗΣ 4 ο ΔΙΓΩΝΙΣΜ ΔΝΔΔΙΚΤΙΚΔΣ ΠΝΤΗΣΔΙΣ ΘΔΜ. β. β 3. α 4. γ 5. α.σ β.σ γ.λ δ.σ ε.λ. ΘΔΜ Β Σωςτι είναι θ απάντθςθ γ. Έχουμε ελαςτικι
ΕΝΟΤΗΤΑ 2: ΤΟ ΛΟΓΙΣΜΙΚΟ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ. ΚΕΦΑΛΑΙΟ 6: Το γραφικό περιβάλλον Επικοινωνίασ (Γ.Π.Ε)
 ΕΝΟΤΗΤΑ 2: ΤΟ ΛΟΓΙΣΜΙΚΟ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ ΚΕΦΑΛΑΙΟ 6: Το γραφικό περιβάλλον Επικοινωνίασ (Γ.Π.Ε) Γραφικό Περιβάλλον Επικοινωνίασ Περιβάλλον Εντολϊν Γραμμισ (Graphical User Interface/GUI), (Command Line Interface),
ΕΝΟΤΗΤΑ 2: ΤΟ ΛΟΓΙΣΜΙΚΟ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ ΚΕΦΑΛΑΙΟ 6: Το γραφικό περιβάλλον Επικοινωνίασ (Γ.Π.Ε) Γραφικό Περιβάλλον Επικοινωνίασ Περιβάλλον Εντολϊν Γραμμισ (Graphical User Interface/GUI), (Command Line Interface),
Τυπικζσ Γλϊςςεσ Περιγραφισ Υλικοφ Διάλεξθ 4
 Τμήμα Μησανικών Πληποφοπικήρ, Τ.Ε.Ι. Ηπείπος Ακαδημαϊκό Έτορ 2016-2017, 6 ο Εξάμηνο Τυπικζσ Γλϊςςεσ Περιγραφισ Υλικοφ Διάλεξθ 4 Διδάςκων Τςιακμάκθσ Κυριάκοσ, Phd MSc in Electronic Physics (Radioelectrology)
Τμήμα Μησανικών Πληποφοπικήρ, Τ.Ε.Ι. Ηπείπος Ακαδημαϊκό Έτορ 2016-2017, 6 ο Εξάμηνο Τυπικζσ Γλϊςςεσ Περιγραφισ Υλικοφ Διάλεξθ 4 Διδάςκων Τςιακμάκθσ Κυριάκοσ, Phd MSc in Electronic Physics (Radioelectrology)
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 24/3/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
ΕΝΟΣΗΣΑ 1: ΓΝΩΡIΖΩ ΣΟΝ ΤΠΟΛΟΓΙΣΗ. ΚΕΦΑΛΑΙΟ 3: Εργονομία
 ΕΝΟΣΗΣΑ 1: ΓΝΩΡIΖΩ ΣΟΝ ΤΠΟΛΟΓΙΣΗ Εργονομία, ωςτι ςτάςθ εργαςίασ, Εικονοςτοιχείο (pixel), Ανάλυςθ οκόνθσ (resolution), Μζγεκοσ οκόνθσ Ποιεσ επιπτϊςεισ μπορεί να ζχει θ πολφωρθ χριςθ του υπολογιςτι ςτθν
ΕΝΟΣΗΣΑ 1: ΓΝΩΡIΖΩ ΣΟΝ ΤΠΟΛΟΓΙΣΗ Εργονομία, ωςτι ςτάςθ εργαςίασ, Εικονοςτοιχείο (pixel), Ανάλυςθ οκόνθσ (resolution), Μζγεκοσ οκόνθσ Ποιεσ επιπτϊςεισ μπορεί να ζχει θ πολφωρθ χριςθ του υπολογιςτι ςτθν
ΑΝΑΠΤΥΞΗ ΛΟΓΙΣΜΙΚΟΥ ΓΙΑ ΤΗ ΔΙΕΝΕΡΓΕΙΑ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΜΕΛΕΤΩΝ
 ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΑΝΑΠΤΥΞΗ ΛΟΓΙΣΜΙΚΟΥ ΓΙΑ ΤΗ ΔΙΕΝΕΡΓΕΙΑ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΜΕΛΕΤΩΝ ΠΛΟΣΚΑΣ ΝΙΚΟΛΑΟΣ Α.Μ. 123/04 ΕΠΙΒΛΕΠΩΝ: ΣΑΜΑΡΑΣ ΝΙΚΟΛΑΟΣ ΘΕΣΣΑΛΟΝΙΚΗ, ΙΟΥΝΙΟΣ 2007 Περιεχόμενα
ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΑΝΑΠΤΥΞΗ ΛΟΓΙΣΜΙΚΟΥ ΓΙΑ ΤΗ ΔΙΕΝΕΡΓΕΙΑ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΜΕΛΕΤΩΝ ΠΛΟΣΚΑΣ ΝΙΚΟΛΑΟΣ Α.Μ. 123/04 ΕΠΙΒΛΕΠΩΝ: ΣΑΜΑΡΑΣ ΝΙΚΟΛΑΟΣ ΘΕΣΣΑΛΟΝΙΚΗ, ΙΟΥΝΙΟΣ 2007 Περιεχόμενα
Αυτόνομοι Πράκτορες. Αναφορά Εργασίας Εξαμήνου. Το αστέρι του Aibo και τα κόκαλα του
 Αυτόνομοι Πράκτορες Αναφορά Εργασίας Εξαμήνου Το αστέρι του Aibo και τα κόκαλα του Jaohar Osman Η πρόταςθ εργαςίασ που ζκανα είναι το παρακάτω κείμενο : - ξ Aibo αγαπάει πάρα πξλύ ρα κόκαλα και πάμρα ρα
Αυτόνομοι Πράκτορες Αναφορά Εργασίας Εξαμήνου Το αστέρι του Aibo και τα κόκαλα του Jaohar Osman Η πρόταςθ εργαςίασ που ζκανα είναι το παρακάτω κείμενο : - ξ Aibo αγαπάει πάρα πξλύ ρα κόκαλα και πάμρα ρα
lim x και lim f(β) f(β). (β > 0)
 . Δίνεται θ παραγωγίςιμθ ςτο * α, β + ( 0 < α < β ) ςυνάρτθςθ f για τθν οποία ιςχφουν: f(α) lim (-) a και lim ( f(β)) = Να δείξετε ότι: α. f(α) < α και f(β) > β β. Αν g() = τότε θ C f και C g ζχουν ζνα
. Δίνεται θ παραγωγίςιμθ ςτο * α, β + ( 0 < α < β ) ςυνάρτθςθ f για τθν οποία ιςχφουν: f(α) lim (-) a και lim ( f(β)) = Να δείξετε ότι: α. f(α) < α και f(β) > β β. Αν g() = τότε θ C f και C g ζχουν ζνα
SOAP API. https://bulksmsn.gr. Table of Contents
 SOAP API https://bulksmsn.gr Table of Contents Send SMS...2 Query SMS...3 Multiple Query SMS...4 Credits...5 Save Contact...5 Delete Contact...7 Delete Message...8 Email: sales@bulksmsn.gr, Τηλ: 211 850
SOAP API https://bulksmsn.gr Table of Contents Send SMS...2 Query SMS...3 Multiple Query SMS...4 Credits...5 Save Contact...5 Delete Contact...7 Delete Message...8 Email: sales@bulksmsn.gr, Τηλ: 211 850
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 17
 ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 17 10 Νοεµβρίου, 2006 Γεώργιος Έλληνας Επίκουρος Καθηγητής ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 17 10 Νοεµβρίου, 2006 Γεώργιος Έλληνας Επίκουρος Καθηγητής ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ
Διαγώνισμα Φυσική ς Κατευ θυνσής Γ Λυκει ου - Ταλαντώσεις
 Διαγώνισμα Φυσική ς Κατευ θυνσής Γ Λυκει ου - Ταλαντώσεις Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί
Διαγώνισμα Φυσική ς Κατευ θυνσής Γ Λυκει ου - Ταλαντώσεις Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί
ΠΡΟΓΡΑΜΜΑΣΙΜΌ ΤΠΟΛΟΓΙΣΏΝ. Κεφάλαιο 8 Η γλϊςςα Pascal
 ΠΡΟΓΡΑΜΜΑΣΙΜΌ ΤΠΟΛΟΓΙΣΏΝ Κεφάλαιο 8 Η γλϊςςα Pascal Παράγραφοσ 8.2 Βαςικοί τφποι δεδομζνων Σα δεδομζνα ενόσ προγράμματοσ μπορεί να: είναι αποκθκευμζνα εςωτερικά ςτθν μνιμθ είναι αποκθκευμζνα εξωτερικά
ΠΡΟΓΡΑΜΜΑΣΙΜΌ ΤΠΟΛΟΓΙΣΏΝ Κεφάλαιο 8 Η γλϊςςα Pascal Παράγραφοσ 8.2 Βαςικοί τφποι δεδομζνων Σα δεδομζνα ενόσ προγράμματοσ μπορεί να: είναι αποκθκευμζνα εςωτερικά ςτθν μνιμθ είναι αποκθκευμζνα εξωτερικά
ΠΡΟΦΟΡΑ ΖΗΣΗΗ ΚΡΑΣΘΚΗ ΠΑΡΕΜΒΑΗ
 ΠΡΟΦΟΡΑ ΖΗΣΗΗ ΚΡΑΣΘΚΗ ΠΑΡΕΜΒΑΗ 1 Ειςαγωγι: Οι αγοραίεσ δυνάµεισ τθσ προςφοράσ και ηιτθςθσ Προσφορά και Ζήτηση είναι οι πιο γνωςτοί οικονοµικοί όροι. Η λειτουργία των αγορϊν προςδιορίηεται από δφο βαςικζσ
ΠΡΟΦΟΡΑ ΖΗΣΗΗ ΚΡΑΣΘΚΗ ΠΑΡΕΜΒΑΗ 1 Ειςαγωγι: Οι αγοραίεσ δυνάµεισ τθσ προςφοράσ και ηιτθςθσ Προσφορά και Ζήτηση είναι οι πιο γνωςτοί οικονοµικοί όροι. Η λειτουργία των αγορϊν προςδιορίηεται από δφο βαςικζσ
ΦΥΕ 14 ΑΚΑΔ. ΕΤΟΣ Η ΕΡΓΑΣΙΑ. Ημερομηνία παράδοςησ: 12 Νοεμβρίου (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 10 μονάδεσ θ κάκε μία)
 ΦΥΕ ΑΚΑΔ. ΕΤΟΣ 007-008 Η ΕΡΓΑΣΙΑ Ημερομηνία παράδοςησ: Νοεμβρίου 007 (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 0 μονάδεσ θ κάκε μία) Άςκηςη α) Να υπολογιςκεί θ προβολι του πάνω ςτο διάνυςμα όταν: (.
ΦΥΕ ΑΚΑΔ. ΕΤΟΣ 007-008 Η ΕΡΓΑΣΙΑ Ημερομηνία παράδοςησ: Νοεμβρίου 007 (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 0 μονάδεσ θ κάκε μία) Άςκηςη α) Να υπολογιςκεί θ προβολι του πάνω ςτο διάνυςμα όταν: (.
1. Εγκατάςταςη κειμενογράφου JCE
 1. Εγκατάςταςη κειμενογράφου JCE 1.1. Πθγαίνουμε ςτθν ακόλουκθ διεφκυνςθ https://www.joomlacontenteditor.net/downloads/editor/joomla-3 και κατεβάηουμε τον JCE Editor 2.5.8. Εναλλακτικά βρίςκουμε το αρχείο
1. Εγκατάςταςη κειμενογράφου JCE 1.1. Πθγαίνουμε ςτθν ακόλουκθ διεφκυνςθ https://www.joomlacontenteditor.net/downloads/editor/joomla-3 και κατεβάηουμε τον JCE Editor 2.5.8. Εναλλακτικά βρίςκουμε το αρχείο
Σ ΤΑΤ Ι Σ Τ Ι Κ Η. Statisticum collegium V
 Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium V Στατιςτική Συμπεραςματολογία Ι Σημειακζσ Εκτιμήςεισ Διαςτήματα Εμπιςτοςφνησ Στατιςτική Συμπεραςματολογία (Statistical Inference) Το πεδίο τθσ Στατιςτικισ Συμπεραςματολογία,
Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium V Στατιςτική Συμπεραςματολογία Ι Σημειακζσ Εκτιμήςεισ Διαςτήματα Εμπιςτοςφνησ Στατιςτική Συμπεραςματολογία (Statistical Inference) Το πεδίο τθσ Στατιςτικισ Συμπεραςματολογία,
1. Αν θ ςυνάρτθςθ είναι ΠΟΛΤΩΝΤΜΙΚΗ τότε το πεδίο οριςμοφ είναι το διότι για κάκε x θ f(x) δίνει πραγματικό αρικμό.
 ΜΕΘΟΔΟΛΟΓΙΑ ΓΙΑ ΝΑ ΒΡΙΚΟΤΜΕ ΣΟ ΠΕΔΙΟ ΟΡΙΜΟΤ ΤΝΑΡΣΗΗ Για να οριςκεί μια ςυνάρτθςθ πρζπει να δοκοφν δφο ςτοιχεία : Σο πεδίο οριςμοφ τθσ Α και Η τιμι τθσ f() για κάκε Α. Οριςμζνεσ φορζσ μασ δίνουν μόνο τον
ΜΕΘΟΔΟΛΟΓΙΑ ΓΙΑ ΝΑ ΒΡΙΚΟΤΜΕ ΣΟ ΠΕΔΙΟ ΟΡΙΜΟΤ ΤΝΑΡΣΗΗ Για να οριςκεί μια ςυνάρτθςθ πρζπει να δοκοφν δφο ςτοιχεία : Σο πεδίο οριςμοφ τθσ Α και Η τιμι τθσ f() για κάκε Α. Οριςμζνεσ φορζσ μασ δίνουν μόνο τον
Στο εστιατόριο «ToDokimasesPrinToBgaleisStonKosmo?» έξω από τους δακτυλίους του Κρόνου, οι παραγγελίες γίνονται ηλεκτρονικά.
 Διαστημικό εστιατόριο του (Μ)ΑστροΈκτορα Στο εστιατόριο «ToDokimasesPrinToBgaleisStonKosmo?» έξω από τους δακτυλίους του Κρόνου, οι παραγγελίες γίνονται ηλεκτρονικά. Μόλις μια παρέα πελατών κάτσει σε ένα
Διαστημικό εστιατόριο του (Μ)ΑστροΈκτορα Στο εστιατόριο «ToDokimasesPrinToBgaleisStonKosmo?» έξω από τους δακτυλίους του Κρόνου, οι παραγγελίες γίνονται ηλεκτρονικά. Μόλις μια παρέα πελατών κάτσει σε ένα
ΑΔΡΑΝΕΙΑ ΜΑΘΗΣΕ: ΜΑΡΙΑΝΝΑ ΠΑΡΑΘΤΡΑ ΑΝΑΣΑΗ ΠΟΤΛΙΟ ΠΑΝΑΓΙΩΣΗ ΠΡΟΔΡΟΜΟΤ ΑΝΑΣΑΙΑ ΠΟΛΤΧΡΟΝΙΑΔΟΤ ΙΩΑΝΝΑ ΠΕΝΓΚΟΤ
 ΑΔΡΑΝΕΙΑ ΜΑΘΗΣΕ: ΜΑΡΙΑΝΝΑ ΠΑΡΑΘΤΡΑ ΑΝΑΣΑΗ ΠΟΤΛΙΟ ΠΑΝΑΓΙΩΣΗ ΠΡΟΔΡΟΜΟΤ ΑΝΑΣΑΙΑ ΠΟΛΤΧΡΟΝΙΑΔΟΤ ΙΩΑΝΝΑ ΠΕΝΓΚΟΤ Οριςμόσ: Με τον όρο αδράνεια ςτθ Φυςικι ονομάηεται θ χαρακτθριςτικι ιδιότθτα των ςωμάτων να αντιςτζκονται
ΑΔΡΑΝΕΙΑ ΜΑΘΗΣΕ: ΜΑΡΙΑΝΝΑ ΠΑΡΑΘΤΡΑ ΑΝΑΣΑΗ ΠΟΤΛΙΟ ΠΑΝΑΓΙΩΣΗ ΠΡΟΔΡΟΜΟΤ ΑΝΑΣΑΙΑ ΠΟΛΤΧΡΟΝΙΑΔΟΤ ΙΩΑΝΝΑ ΠΕΝΓΚΟΤ Οριςμόσ: Με τον όρο αδράνεια ςτθ Φυςικι ονομάηεται θ χαρακτθριςτικι ιδιότθτα των ςωμάτων να αντιςτζκονται
Automating Complex Workflows using Processing Modeler
 Automating Complex Workflows using Processing Modeler QGIS Tutorials and Tips Author Ujaval Gandhi http://google.com/+ujavalgandhi Translations by Christina Dimitriadou Paliogiannis Konstantinos Tom Karagkounis
Automating Complex Workflows using Processing Modeler QGIS Tutorials and Tips Author Ujaval Gandhi http://google.com/+ujavalgandhi Translations by Christina Dimitriadou Paliogiannis Konstantinos Tom Karagkounis
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 14
 ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 14 20 Οκτωβρίου, 2005 Ηλίας Κυριακίδης Λέκτορας ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ 2005Ηλίας Κυριακίδης,
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 14 20 Οκτωβρίου, 2005 Ηλίας Κυριακίδης Λέκτορας ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ 2005Ηλίας Κυριακίδης,
Joomla! - User Guide
 Joomla! - User Guide τελευταία ανανέωση: 10/10/2013 από την ICAP WEB Solutions 1 Η καταςκευι τθσ δυναμικισ ςασ ιςτοςελίδασ ζχει ολοκλθρωκεί και μπορείτε πλζον να προχωριςετε ςε αλλαγζσ ι προςκικεσ όςον
Joomla! - User Guide τελευταία ανανέωση: 10/10/2013 από την ICAP WEB Solutions 1 Η καταςκευι τθσ δυναμικισ ςασ ιςτοςελίδασ ζχει ολοκλθρωκεί και μπορείτε πλζον να προχωριςετε ςε αλλαγζσ ι προςκικεσ όςον
Δομζσ Αφαιρετικότθτα ςτα Δεδομζνα
 Δομζσ Αφαιρετικότθτα ςτα Δεδομζνα Περιεχόμενα Ζννοια δομισ Οριςμόσ δομισ Διλωςθ μεταβλθτϊν Απόδοςθ Αρχικϊν τιμϊν Αναφορά ςτα μζλθ μιασ δομισ Ζνκεςθ Δομισ Πίνακεσ Δομϊν Η ζννοια τθσ δομισ Χρθςιμοποιιςαμε
Δομζσ Αφαιρετικότθτα ςτα Δεδομζνα Περιεχόμενα Ζννοια δομισ Οριςμόσ δομισ Διλωςθ μεταβλθτϊν Απόδοςθ Αρχικϊν τιμϊν Αναφορά ςτα μζλθ μιασ δομισ Ζνκεςθ Δομισ Πίνακεσ Δομϊν Η ζννοια τθσ δομισ Χρθςιμοποιιςαμε
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ
 ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Α ΔΙΑΓΩΝΙΣΜΟΣ ΕΠΙΛΟΓΗΣ IMC (Key Stage II) 9 Μαρτίου 2016 ΧΡΟΝΟΣ: 2 ΩΡΕΣ Λύςεισ : Πρόβλημα 1 (α) Να βρείτε τθν τιμι του για να ιςχφει θ πιο κάτω ςχζςθ: (β) Ο Ανδρζασ τελειϊνει
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Α ΔΙΑΓΩΝΙΣΜΟΣ ΕΠΙΛΟΓΗΣ IMC (Key Stage II) 9 Μαρτίου 2016 ΧΡΟΝΟΣ: 2 ΩΡΕΣ Λύςεισ : Πρόβλημα 1 (α) Να βρείτε τθν τιμι του για να ιςχφει θ πιο κάτω ςχζςθ: (β) Ο Ανδρζασ τελειϊνει
5 ΜΕΘΟΔΟΙ - ΠΑΡΑΜΕΤΡΟΙ
 5 ΜΕΘΟΔΟΙ - ΠΑΡΑΜΕΤΡΟΙ Να γραφεί πρόγραμμα, το οποίο κα δίνει τισ τιμζσ 5 και 6 ςε δφο μεταβλθτζσ a και b και κα υπολογίηει και κα εμφανίηει το άκροιςμά τουσ sum. ΛΟΓΙΚΟ ΔΙΑΓΡΑΜΜΑ a 5 b 6 sum a+b sum ΑΛΓΟΡΙΘΜΟ
5 ΜΕΘΟΔΟΙ - ΠΑΡΑΜΕΤΡΟΙ Να γραφεί πρόγραμμα, το οποίο κα δίνει τισ τιμζσ 5 και 6 ςε δφο μεταβλθτζσ a και b και κα υπολογίηει και κα εμφανίηει το άκροιςμά τουσ sum. ΛΟΓΙΚΟ ΔΙΑΓΡΑΜΜΑ a 5 b 6 sum a+b sum ΑΛΓΟΡΙΘΜΟ
Σύ ντομος Οδηγο ς χρη σης wikidot για τα projects
 Σύ ντομος Οδηγο ς χρη σης wikidot για τα projects Ειςαγωγή κοπόσ αυτοφ του κειμζνου είναι να δϊςει ςφντομεσ οδθγίεσ για τθν επεξεργαςία των ςελίδων του wiki τθσ ερευνθτικισ εργαςίασ. Πλιρθσ οδθγόσ για
Σύ ντομος Οδηγο ς χρη σης wikidot για τα projects Ειςαγωγή κοπόσ αυτοφ του κειμζνου είναι να δϊςει ςφντομεσ οδθγίεσ για τθν επεξεργαςία των ςελίδων του wiki τθσ ερευνθτικισ εργαςίασ. Πλιρθσ οδθγόσ για
ΘΕΜΑΣΑ ΕΡΓΑΙΩΝ ΓΙΑ ΣΟ ΜΑΘΗΜΑ ΠΡΟΟΜΟΙΩΗ
 ΘΕΜΑΣΑ ΕΡΓΑΙΩΝ ΓΙΑ ΣΟ ΜΑΘΗΜΑ ΠΡΟΟΜΟΙΩΗ Οι εργαςίεσ αναλαμβάνονται από ομάδεσ φοιτθτών όπου θ κάκε ομάδα αποτελείται από ζωσ και 4 άτομα. Περιςςότερεσ από μία ομάδεσ μποροφν να αναλάβουν το ίδιο κζμα. Στη
ΘΕΜΑΣΑ ΕΡΓΑΙΩΝ ΓΙΑ ΣΟ ΜΑΘΗΜΑ ΠΡΟΟΜΟΙΩΗ Οι εργαςίεσ αναλαμβάνονται από ομάδεσ φοιτθτών όπου θ κάκε ομάδα αποτελείται από ζωσ και 4 άτομα. Περιςςότερεσ από μία ομάδεσ μποροφν να αναλάβουν το ίδιο κζμα. Στη
ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Δίκτυα Επικοινωνιών ΙΙ Διδάςκων: Απόςτολοσ Γκάμασ (Διδάςκων ΠΔ 407/80) Βοθκόσ Εργαςτθρίου: Δθμιτριοσ Μακρισ Ενδεικτική Λύση 1
ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Δίκτυα Επικοινωνιών ΙΙ Διδάςκων: Απόςτολοσ Γκάμασ (Διδάςκων ΠΔ 407/80) Βοθκόσ Εργαςτθρίου: Δθμιτριοσ Μακρισ Ενδεικτική Λύση 1
ΕΝΟΤΗΤΑ 2: ΕΠΙΚΟΙΝΩΝΩ ΜΕ ΤΟΝ ΥΠΟΛΟΓΙΣΤΗ. ΚΕΦΑΛΑΙΟ 5: Αρχεία - Φάκελοι
 ΕΝΟΤΗΤΑ 2: ΕΠΙΚΟΙΝΩΝΩ ΜΕ ΤΟΝ ΥΠΟΛΟΓΙΣΤΗ Αρχείο (File) Φάκελοσ (Folder) Διαχειριςτισ Αρχείων (File Manager) Τφποι Αρχείων Σε τι εξυπθρετεί θ οργάνωςθ των εργαςιϊν μασ ςτουσ υπολογιςτζσ; Πϊσ κα οργανϊςουμε
ΕΝΟΤΗΤΑ 2: ΕΠΙΚΟΙΝΩΝΩ ΜΕ ΤΟΝ ΥΠΟΛΟΓΙΣΤΗ Αρχείο (File) Φάκελοσ (Folder) Διαχειριςτισ Αρχείων (File Manager) Τφποι Αρχείων Σε τι εξυπθρετεί θ οργάνωςθ των εργαςιϊν μασ ςτουσ υπολογιςτζσ; Πϊσ κα οργανϊςουμε
Εργαςτιριο Βάςεων Δεδομζνων
 Εργαςτιριο Βάςεων Δεδομζνων 2010-2011 Μάθημα 1 ο 1 Ε. Σςαμούρα Σμήμα Πληροφορικήσ ΑΠΘ Σκοπόσ του 1 ου εργαςτθριακοφ μακιματοσ Σκοπόσ του πρϊτου εργαςτθριακοφ μακιματοσ είναι να μελετιςουμε ερωτιματα επιλογισ
Εργαςτιριο Βάςεων Δεδομζνων 2010-2011 Μάθημα 1 ο 1 Ε. Σςαμούρα Σμήμα Πληροφορικήσ ΑΠΘ Σκοπόσ του 1 ου εργαςτθριακοφ μακιματοσ Σκοπόσ του πρϊτου εργαςτθριακοφ μακιματοσ είναι να μελετιςουμε ερωτιματα επιλογισ
Πανελλαδικε σ Εξετα ςεισ Γ Τα ξησ Ημερη ςιου και Δ Τα ξησ Εςπερινου Γενικου Λυκει ου
 Ζνωςθ Ελλινων Χθμικϊν Πανελλαδικε σ Εξετα ςεισ Γ Τα ξησ Ημερη ςιου και Δ Τα ξησ Εςπερινου Γενικου Λυκει ου Χημεία 03/07/2017 Τμιμα Παιδείασ και Χθμικισ Εκπαίδευςθσ 0 Πανελλαδικε σ Εξετα ςεισ Γ Τα ξησ Ημερη
Ζνωςθ Ελλινων Χθμικϊν Πανελλαδικε σ Εξετα ςεισ Γ Τα ξησ Ημερη ςιου και Δ Τα ξησ Εςπερινου Γενικου Λυκει ου Χημεία 03/07/2017 Τμιμα Παιδείασ και Χθμικισ Εκπαίδευςθσ 0 Πανελλαδικε σ Εξετα ςεισ Γ Τα ξησ Ημερη
Ηλεκτρονικι Επιχειρθςιακι Δράςθ Εργαςτιριο 1
 1. Εγκατάςταςη Xampp Προκειμζνου να γίνει θ εγκατάςταςθ κα πρζπει πρϊτα να κατεβάςετε και εγκαταςτιςετε το XAMPP ωσ ακολοφκωσ. 1.1. Πάμε ςτθν ακόλουκθ διεφκυνςθ https://www.apachefriends.org/download.html
1. Εγκατάςταςη Xampp Προκειμζνου να γίνει θ εγκατάςταςθ κα πρζπει πρϊτα να κατεβάςετε και εγκαταςτιςετε το XAMPP ωσ ακολοφκωσ. 1.1. Πάμε ςτθν ακόλουκθ διεφκυνςθ https://www.apachefriends.org/download.html
ΝΟΜΟΙ ΚΙΝΗΗ ΠΛΑΝΗΣΩΝ ΣΟΤ ΚΕΠΛΕΡ
 ΝΟΜΟΙ ΚΙΝΗΗ ΠΛΑΝΗΣΩΝ ΣΟΤ ΚΕΠΛΕΡ 1. Νόμοσ των ελλειπτικών τροχιών Η τροχιζσ των πλανθτϊν είναι ελλείψεισ, των οποίων τθ μία εςτία κατζχει ο Ήλιοσ. Προφανϊσ όλοι οι πλανιτεσ του ίδιου πλανθτικοφ ςυςτιματοσ
ΝΟΜΟΙ ΚΙΝΗΗ ΠΛΑΝΗΣΩΝ ΣΟΤ ΚΕΠΛΕΡ 1. Νόμοσ των ελλειπτικών τροχιών Η τροχιζσ των πλανθτϊν είναι ελλείψεισ, των οποίων τθ μία εςτία κατζχει ο Ήλιοσ. Προφανϊσ όλοι οι πλανιτεσ του ίδιου πλανθτικοφ ςυςτιματοσ
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
ΔΙΑΔΙΚΑΙΑ ΚΑΙ ΡΤΘΜΙΕΙ ΓΙΑ ΤΝΔΕΗ ΣΟ INTRANET ΣΟΤ ΕΚΕΣΑ-ΙΣΧΗΔ
 ΔΙΑΔΙΚΑΙΑ ΚΑΙ ΡΤΘΜΙΕΙ ΓΙΑ ΤΝΔΕΗ ΣΟ INTRANET ΣΟΤ ΕΚΕΣΑ-ΙΣΧΗΔ Πρόλογος Τα ςθμεία αςφρματθσ δικτυακισ ςφνδεςθσ του ΕΚΕΤΑ (WiFi access points) και κατά ςυνζπεια και του ΙΤΧΗΔ, δθμοςιεφουν δφο δίκτυα. 1. Το
ΔΙΑΔΙΚΑΙΑ ΚΑΙ ΡΤΘΜΙΕΙ ΓΙΑ ΤΝΔΕΗ ΣΟ INTRANET ΣΟΤ ΕΚΕΣΑ-ΙΣΧΗΔ Πρόλογος Τα ςθμεία αςφρματθσ δικτυακισ ςφνδεςθσ του ΕΚΕΤΑ (WiFi access points) και κατά ςυνζπεια και του ΙΤΧΗΔ, δθμοςιεφουν δφο δίκτυα. 1. Το
Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων. 19. Αλφαριθμητικά II. Ιωάννθσ Κατάκθσ. ΕΠΛ 032: Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων
 Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 19. Αλφαριθμητικά II Ιωάννθσ Κατάκθσ Αλφαρικμθτικά ςτθ C Ζνα string είναι μία ακολουκία αλφαρικμθτικϊν χαρακτήρων, ςθμείων ςτίξθσ κτλ. Π.χ. Hello How are you?
Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 19. Αλφαριθμητικά II Ιωάννθσ Κατάκθσ Αλφαρικμθτικά ςτθ C Ζνα string είναι μία ακολουκία αλφαρικμθτικϊν χαρακτήρων, ςθμείων ςτίξθσ κτλ. Π.χ. Hello How are you?
Visual C Express - Οδηγός Χρήσης
 Visual C++ 2008 Express - Οδηγός Χρήσης Ζερβός Μιχάλης, Πρίντεζης Νίκος Σκοπόσ του οδθγοφ αυτοφ είναι να παρουςιάςει τισ βαςικζσ δυνατότθτεσ του Visual C++ 2008 Express Edition και πωσ μπορεί να χρθςιμοποιθκεί
Visual C++ 2008 Express - Οδηγός Χρήσης Ζερβός Μιχάλης, Πρίντεζης Νίκος Σκοπόσ του οδθγοφ αυτοφ είναι να παρουςιάςει τισ βαςικζσ δυνατότθτεσ του Visual C++ 2008 Express Edition και πωσ μπορεί να χρθςιμοποιθκεί
Ιδιότθτεσ πεδίων Γενικζσ.
 Οι ιδιότθτεσ των πεδίων διαφζρουν ανάλογα με τον τφπο δεδομζνων που επιλζγουμε. Ορίηονται ςτο κάτω μζροσ του παρακφρου ςχεδίαςθσ του πίνακα, ςτθν καρτζλα Γενικζσ. Ιδιότθτα: Μζγεκοσ πεδίου (Field size)
Οι ιδιότθτεσ των πεδίων διαφζρουν ανάλογα με τον τφπο δεδομζνων που επιλζγουμε. Ορίηονται ςτο κάτω μζροσ του παρακφρου ςχεδίαςθσ του πίνακα, ςτθν καρτζλα Γενικζσ. Ιδιότθτα: Μζγεκοσ πεδίου (Field size)
ΟΔΗΓΙΕ ΓΙΑ ΣΗΝ ΕΙΑΓΩΓΗ ΕΚΔΡΟΜΩΝ & ΝΕΩΝ - ΑΝΑΚΟΙΝΩΕΩΝ ΣΗΝ ΙΣΟΕΛΙΔΑ ΣΗ Δ.Δ.Ε. ΘΕΠΡΩΣΙΑ
 ΟΔΗΓΙΕ ΓΙΑ ΣΗΝ ΕΙΑΓΩΓΗ ΕΚΔΡΟΜΩΝ & ΝΕΩΝ - ΑΝΑΚΟΙΝΩΕΩΝ ΣΗΝ ΙΣΟΕΛΙΔΑ ΣΗ Δ.Δ.Ε. ΘΕΠΡΩΣΙΑ ΕΙΑΓΩΓΗ Ο νζοσ δικτυακόσ τόποσ τθσ Δ.Δ.Ε. Θεςπρωτίασ παρζχει πλζον τθ δυνατότθτα τθσ καταχϊρθςθσ νζων, ειδιςεων και
ΟΔΗΓΙΕ ΓΙΑ ΣΗΝ ΕΙΑΓΩΓΗ ΕΚΔΡΟΜΩΝ & ΝΕΩΝ - ΑΝΑΚΟΙΝΩΕΩΝ ΣΗΝ ΙΣΟΕΛΙΔΑ ΣΗ Δ.Δ.Ε. ΘΕΠΡΩΣΙΑ ΕΙΑΓΩΓΗ Ο νζοσ δικτυακόσ τόποσ τθσ Δ.Δ.Ε. Θεςπρωτίασ παρζχει πλζον τθ δυνατότθτα τθσ καταχϊρθςθσ νζων, ειδιςεων και
Ένα πρόβλθμα γραμμικοφ προγραμματιςμοφ βρίςκεται ςτθν κανονικι μορφι όταν:
 Μζθοδος Simplex Η πλζον γνωςτι και περιςςότερο χρθςιμοποιουμζνθ μζκοδοσ για τθν επίλυςθ ενόσ γενικοφ προβλιματοσ γραμμικοφ προγραμματιςμοφ, είναι θ μζκοδοσ Simplex θ οποία αναπτφχκθκε από τον George Dantzig.
Μζθοδος Simplex Η πλζον γνωςτι και περιςςότερο χρθςιμοποιουμζνθ μζκοδοσ για τθν επίλυςθ ενόσ γενικοφ προβλιματοσ γραμμικοφ προγραμματιςμοφ, είναι θ μζκοδοσ Simplex θ οποία αναπτφχκθκε από τον George Dantzig.
Τεχνικι Παρουςιάςεων με PowerPoint
 Τεχνικι Παρουςιάςεων με PowerPoint Δρ. Παφλοσ Θεοδϊρου Ανϊτατθ Εκκλθςιαςτικι Ακαδθμία Ηρακλείου Κριτθσ Περιεχόμενα Ειςαγωγι Γιατί πρζπει να γίνει παρουςίαςθ τθσ εργαςίασ μου Βαςικι προετοιμαςία Δομι παρουςίαςθσ
Τεχνικι Παρουςιάςεων με PowerPoint Δρ. Παφλοσ Θεοδϊρου Ανϊτατθ Εκκλθςιαςτικι Ακαδθμία Ηρακλείου Κριτθσ Περιεχόμενα Ειςαγωγι Γιατί πρζπει να γίνει παρουςίαςθ τθσ εργαςίασ μου Βαςικι προετοιμαςία Δομι παρουςίαςθσ
Ειςαγωγή ςτο Matlab Μζροσ Β. Κυριακίδης Ιωάννης 2011
 Ειςαγωγή ςτο Matlab Μζροσ Β Κυριακίδης Ιωάννης 2011 Ειςαγωγι ςτα Μ-Files Τα m-files τθσ Matlab είναι τα αντίςτοιχα των ςυναρτιςεων (functions) και των υπορουτινϊν (subroutines) που ςυναντάμε ςε άλλεσ γλϊςςεσ
Ειςαγωγή ςτο Matlab Μζροσ Β Κυριακίδης Ιωάννης 2011 Ειςαγωγι ςτα Μ-Files Τα m-files τθσ Matlab είναι τα αντίςτοιχα των ςυναρτιςεων (functions) και των υπορουτινϊν (subroutines) που ςυναντάμε ςε άλλεσ γλϊςςεσ
Δϋ Δθμοτικοφ 12 θ Κυπριακι Μακθματικι Ολυμπιάδα Απρίλιοσ 2011
 1. Αν τϊρα είναι Απρίλθσ, ποιοσ μινασ κα είναι μετά από 100 μινεσ; Α. Απρίλθσ Β. Αφγουςτοσ. Σεπτζμβρθσ Δ. Μάρτθσ Ε. Ιοφλθσ 2. Ποιο είναι το αποτζλεςμα των πιο κάτω πράξεων; ; Α. 135 Β. 27. 63 Δ. 21 Ε.
1. Αν τϊρα είναι Απρίλθσ, ποιοσ μινασ κα είναι μετά από 100 μινεσ; Α. Απρίλθσ Β. Αφγουςτοσ. Σεπτζμβρθσ Δ. Μάρτθσ Ε. Ιοφλθσ 2. Ποιο είναι το αποτζλεςμα των πιο κάτω πράξεων; ; Α. 135 Β. 27. 63 Δ. 21 Ε.
Φυςικό Α Λυκεύου-Χ.Κ.Φιρφιρόσ. Ειςαγωγό. Α. Μονόμετρα ό διανυςματικϊ μεγϋθη. Β. ύςτημα μονϊδων S.I. 2.Σασ δίνεται θ παρακάτω εικόνα:
 1 Φυςικό Α Λυκεύου-Χ.Κ.Φιρφιρόσ.Σασ δίνεται θ παρακάτω εικόνα: Ειςαγωγό Α. Μονόμετρα ό διανυςματικϊ μεγϋθη ΜΕ ΙΚΕΣ Χ ΘΣΙΜΕΣ ΕΝΝΟΙΕΣ Μονόμετρα μεγζκθ Ζνα μζγεκοσ λζγεται μονόμετρο όταν για να οριςτεί πλιρωσ
1 Φυςικό Α Λυκεύου-Χ.Κ.Φιρφιρόσ.Σασ δίνεται θ παρακάτω εικόνα: Ειςαγωγό Α. Μονόμετρα ό διανυςματικϊ μεγϋθη ΜΕ ΙΚΕΣ Χ ΘΣΙΜΕΣ ΕΝΝΟΙΕΣ Μονόμετρα μεγζκθ Ζνα μζγεκοσ λζγεται μονόμετρο όταν για να οριςτεί πλιρωσ
Πωσ δημιουργώ μάθημα ςτο e-class του ΠΣΔ [επίπεδο 1]
![Πωσ δημιουργώ μάθημα ςτο e-class του ΠΣΔ [επίπεδο 1] Πωσ δημιουργώ μάθημα ςτο e-class του ΠΣΔ [επίπεδο 1]](/thumbs/26/9402061.jpg) Το e-class του Πανελλινιου Σχολικοφ Δίκτυου [ΠΣΔ/sch.gr] είναι μια πολφ αξιόλογθ και δοκιμαςμζνθ πλατφόρμα για αςφγχρονο e-learning. Ανικει ςτθν κατθγορία του ελεφκερου λογιςμικοφ. Αρχίηουμε από τθ διεφκυνςθ
Το e-class του Πανελλινιου Σχολικοφ Δίκτυου [ΠΣΔ/sch.gr] είναι μια πολφ αξιόλογθ και δοκιμαςμζνθ πλατφόρμα για αςφγχρονο e-learning. Ανικει ςτθν κατθγορία του ελεφκερου λογιςμικοφ. Αρχίηουμε από τθ διεφκυνςθ
Προχωρθμζνα Θζματα Συςτθμάτων Ελζγχου
 ΠΑΝΕΠΙΣΗΜΙΟ ΑΙΓΑIΟΤ & ΑΕΙ ΠΕΙΡΑΙΑ Σ.Σ. Σμήματα Ναυτιλίας και Επιχειρηματικών Τπηρεσιών & Μηχ. Αυτοματισμού ΣΕ Π.Μ.. «Νέες Σεχνολογίες στη Ναυτιλία και τις Μεταφορές» Προχωρθμζνα Θζματα Συςτθμάτων Ελζγχου
ΠΑΝΕΠΙΣΗΜΙΟ ΑΙΓΑIΟΤ & ΑΕΙ ΠΕΙΡΑΙΑ Σ.Σ. Σμήματα Ναυτιλίας και Επιχειρηματικών Τπηρεσιών & Μηχ. Αυτοματισμού ΣΕ Π.Μ.. «Νέες Σεχνολογίες στη Ναυτιλία και τις Μεταφορές» Προχωρθμζνα Θζματα Συςτθμάτων Ελζγχου
Γενικά Μαθηματικά ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 10 η : Εφαρμογζσ Διανυςματικών Συναρτιςεων Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 10 η : Εφαρμογζσ Διανυςματικών Συναρτιςεων Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα
 Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα Αυτζσ οι οδθγίεσ ζχουν ςτόχο λοιπόν να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο του Άβακα. Παρουςίαςη
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα Αυτζσ οι οδθγίεσ ζχουν ςτόχο λοιπόν να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο του Άβακα. Παρουςίαςη
